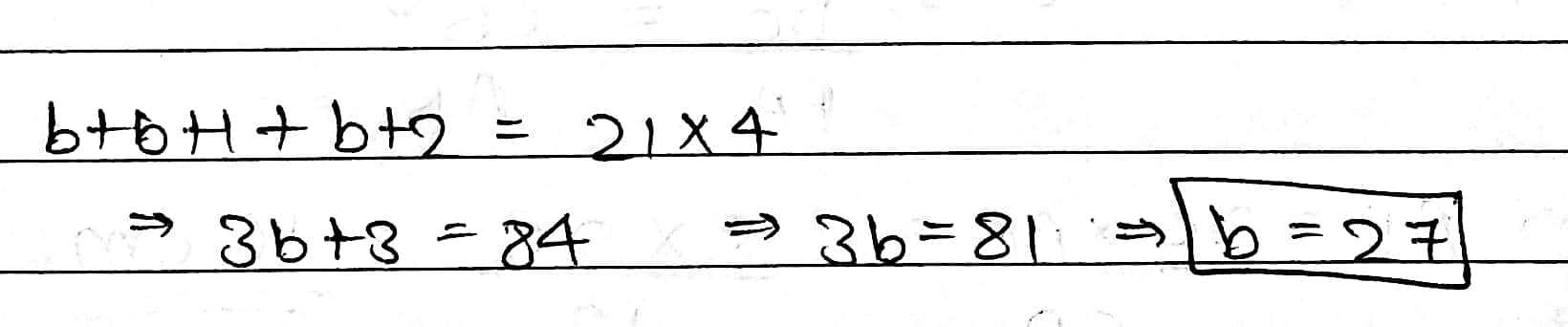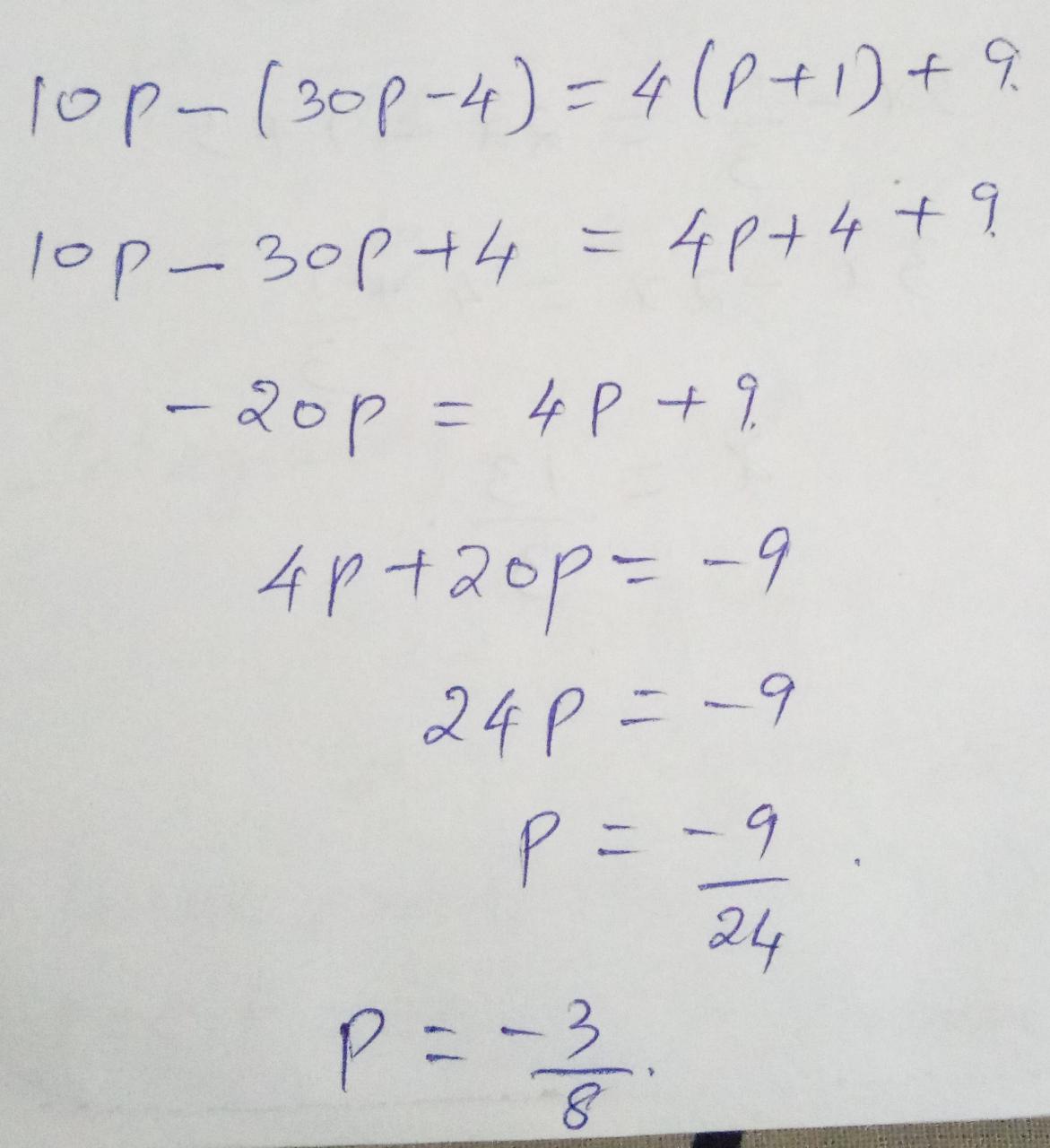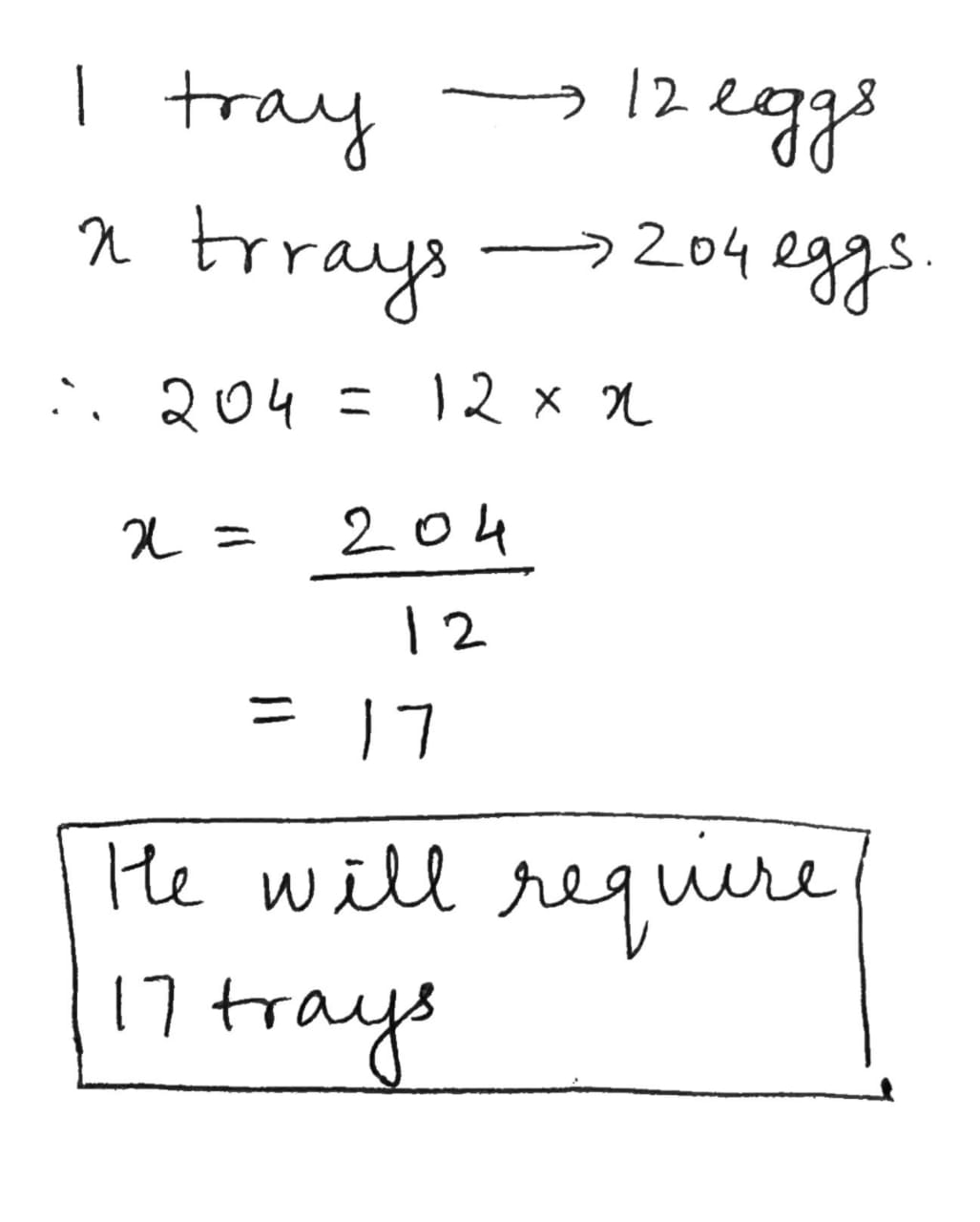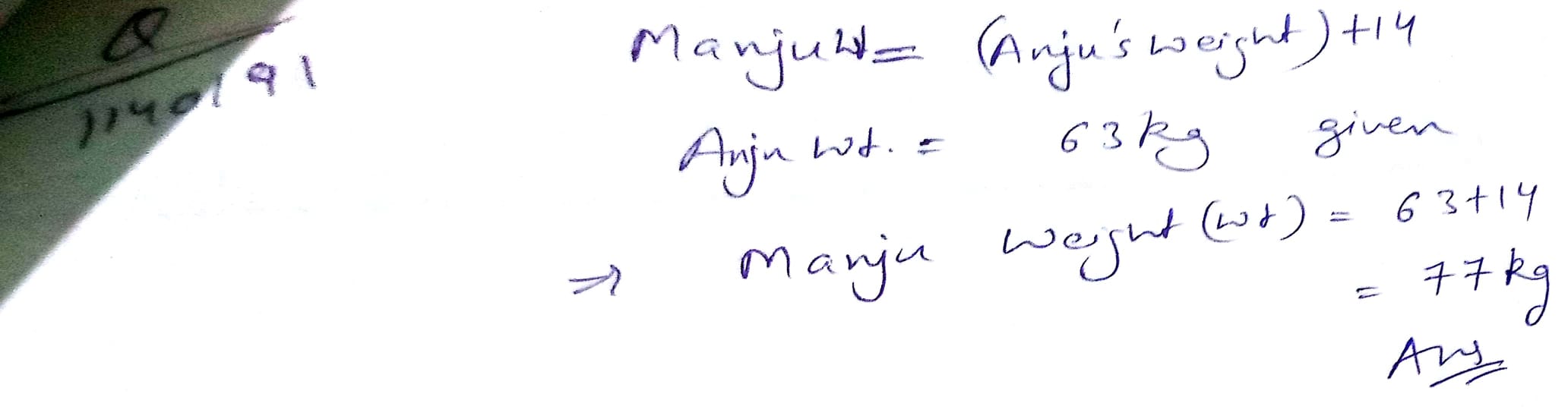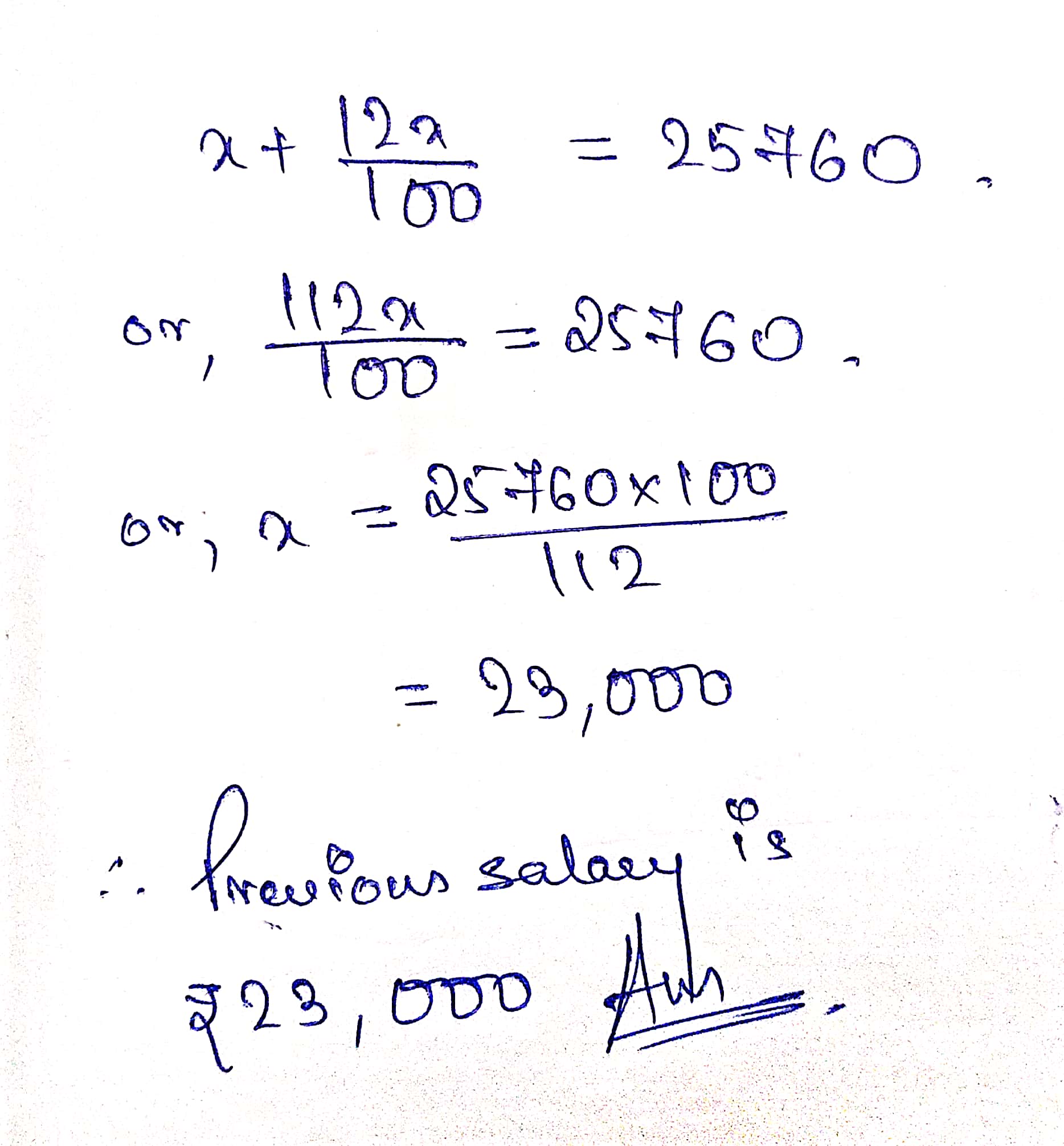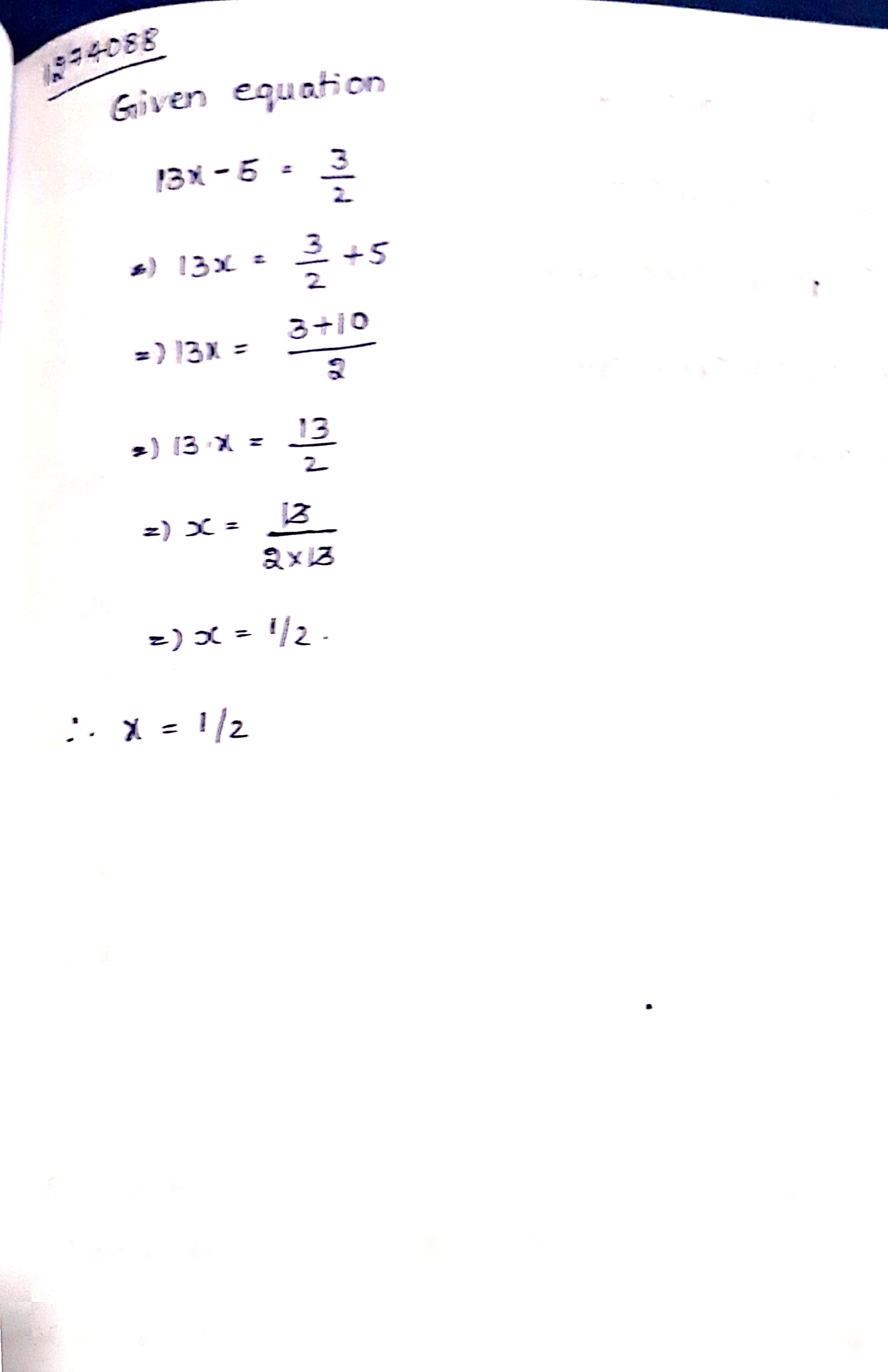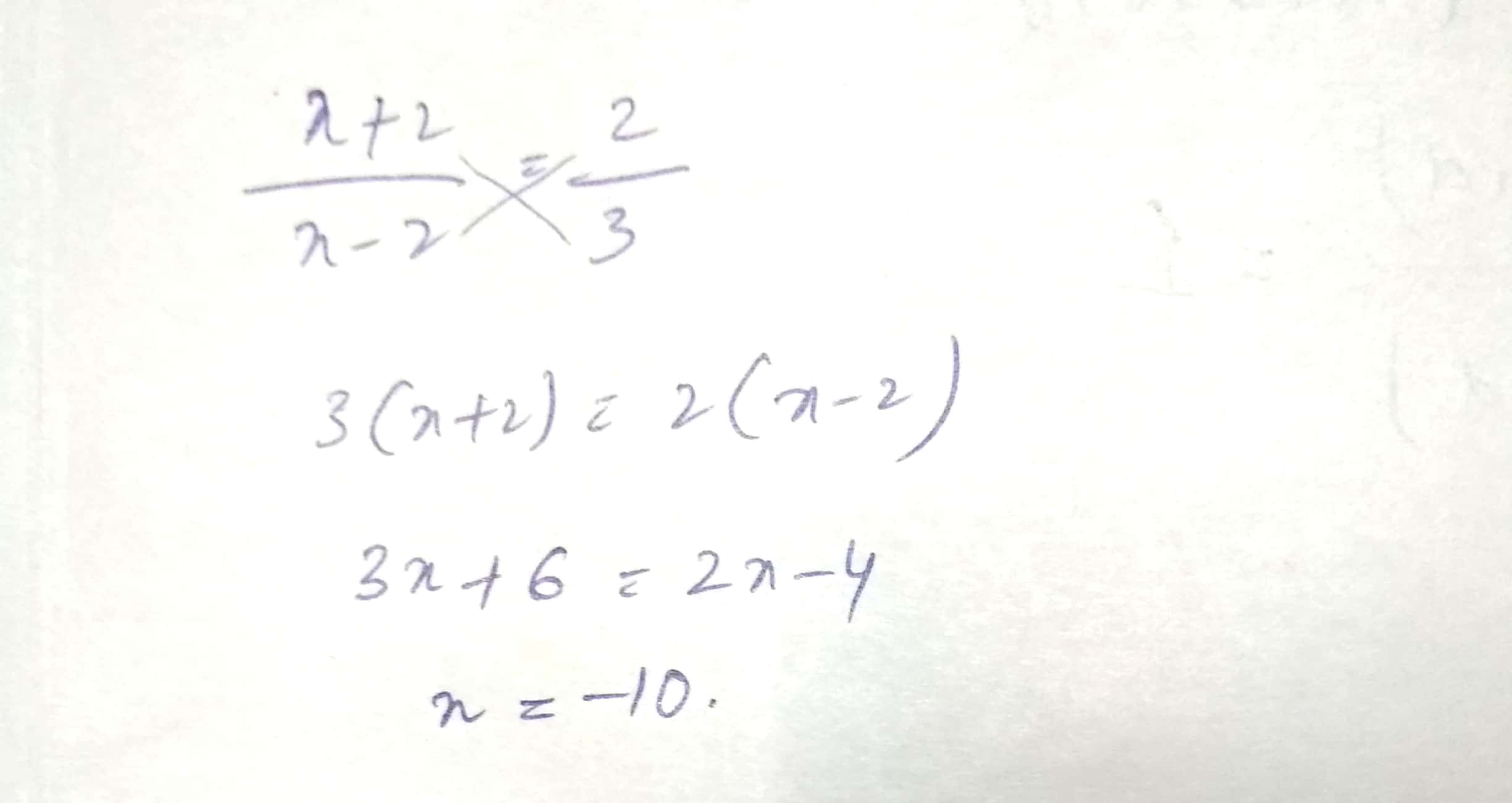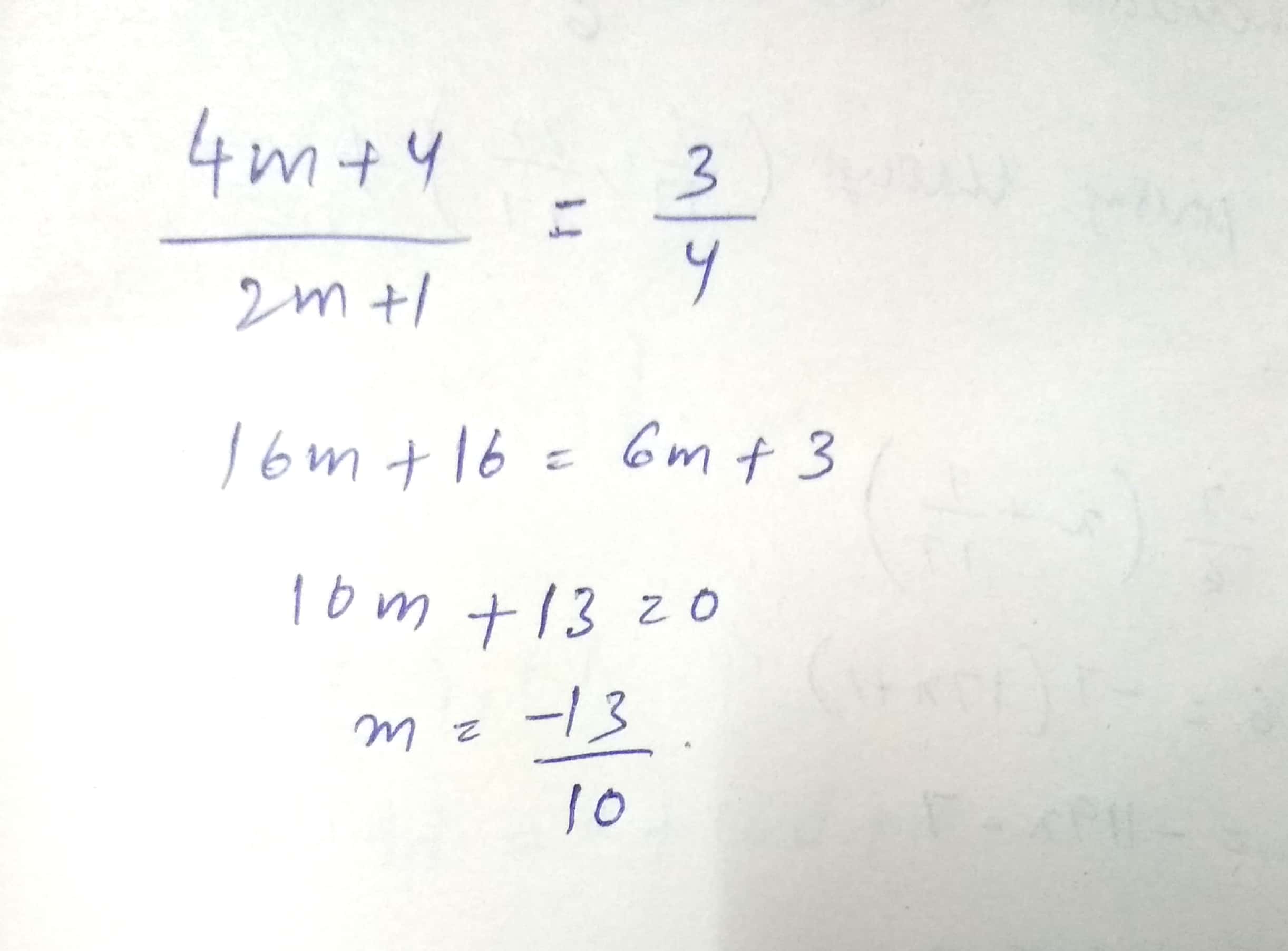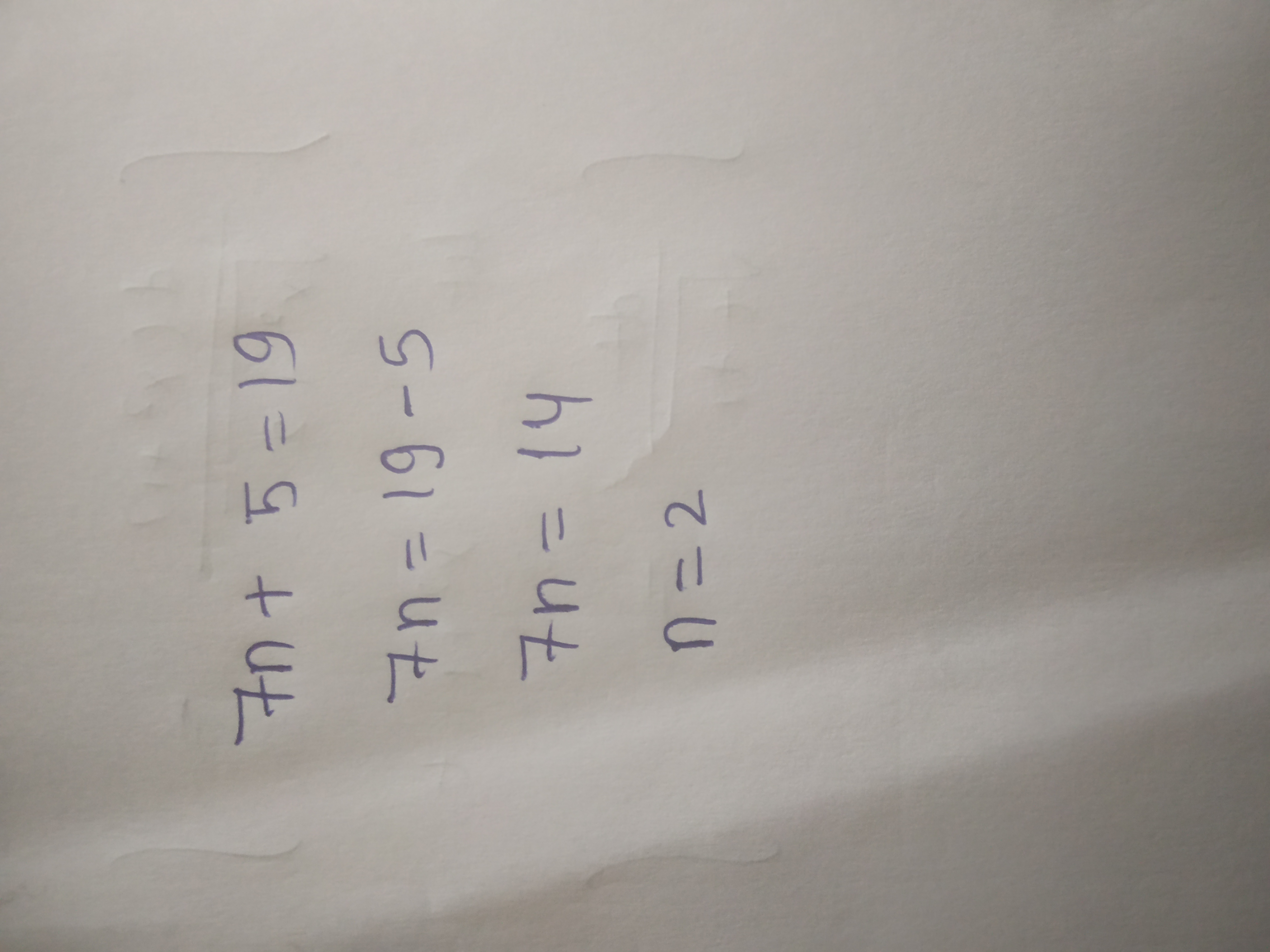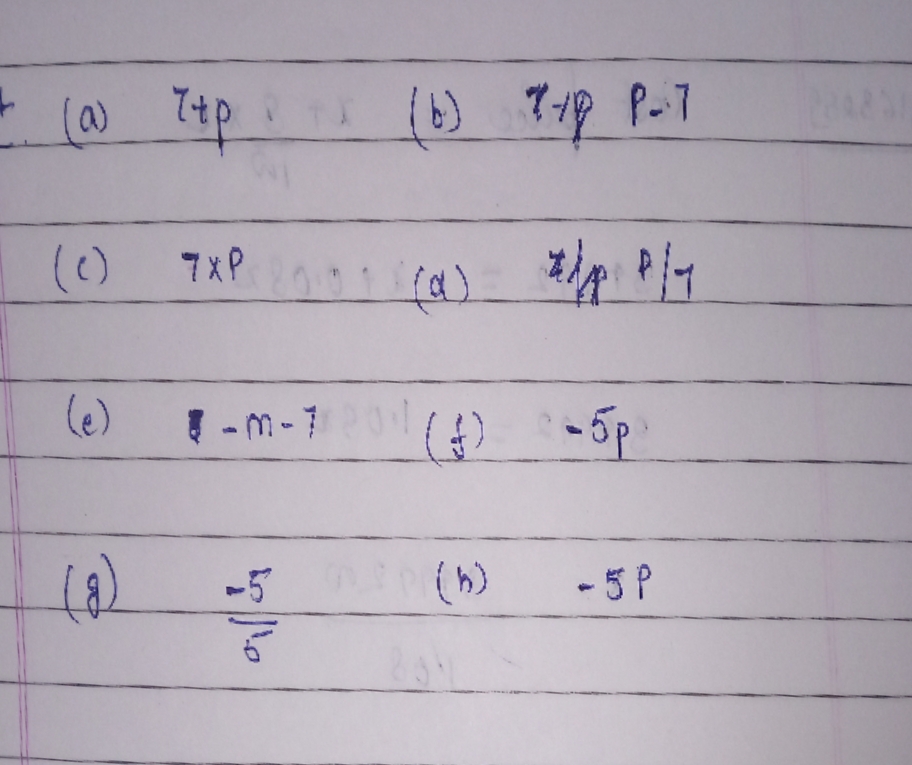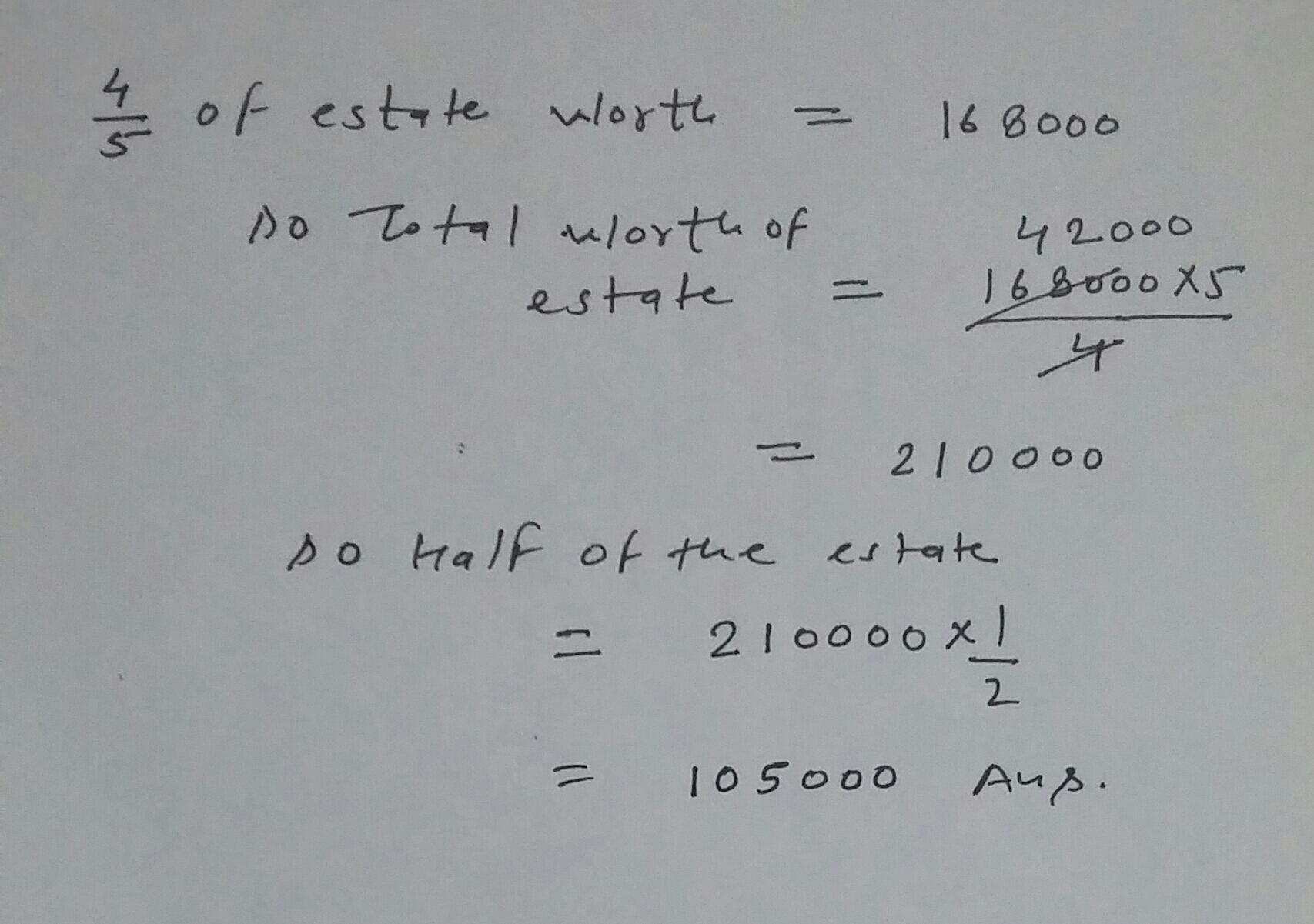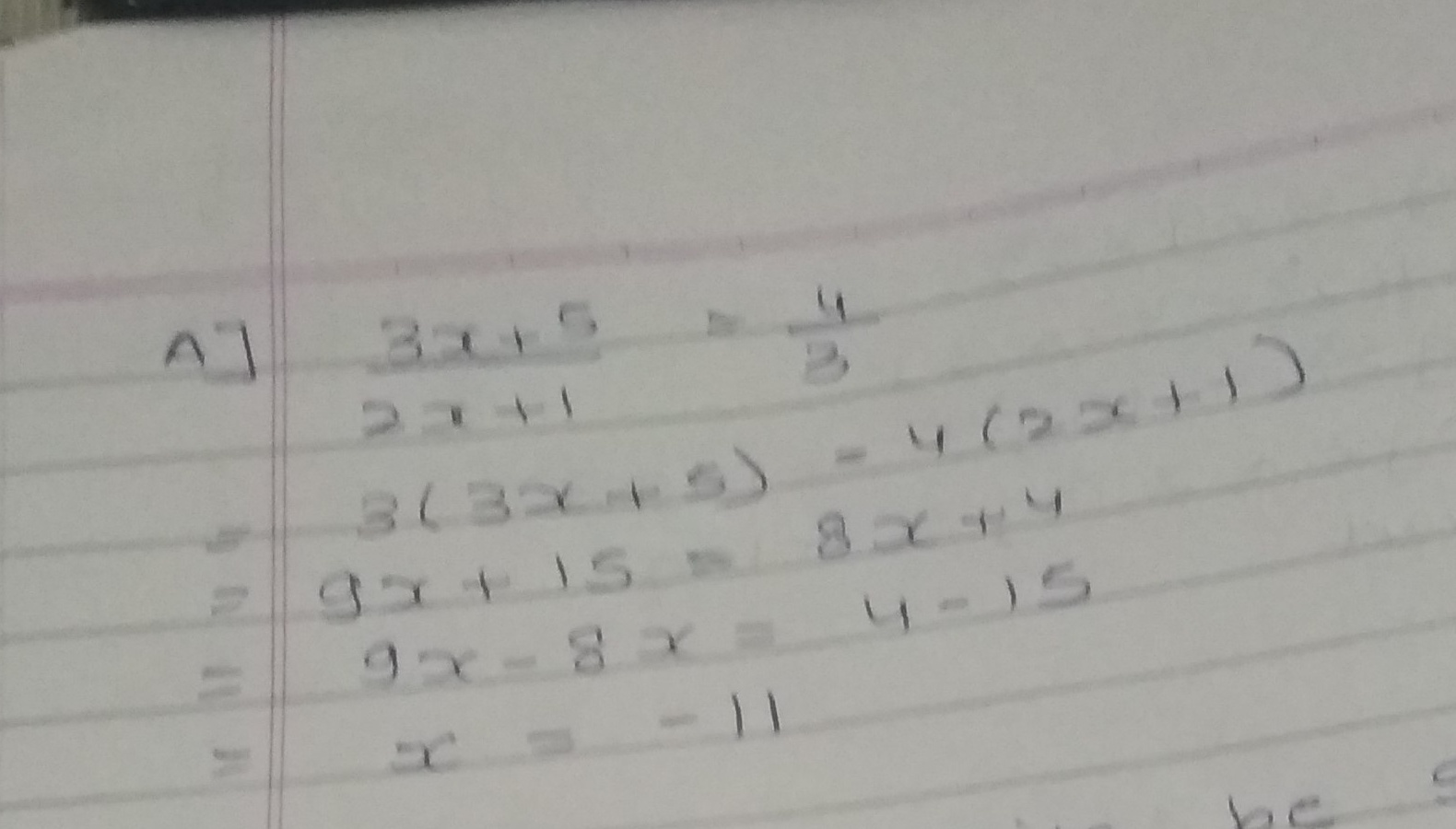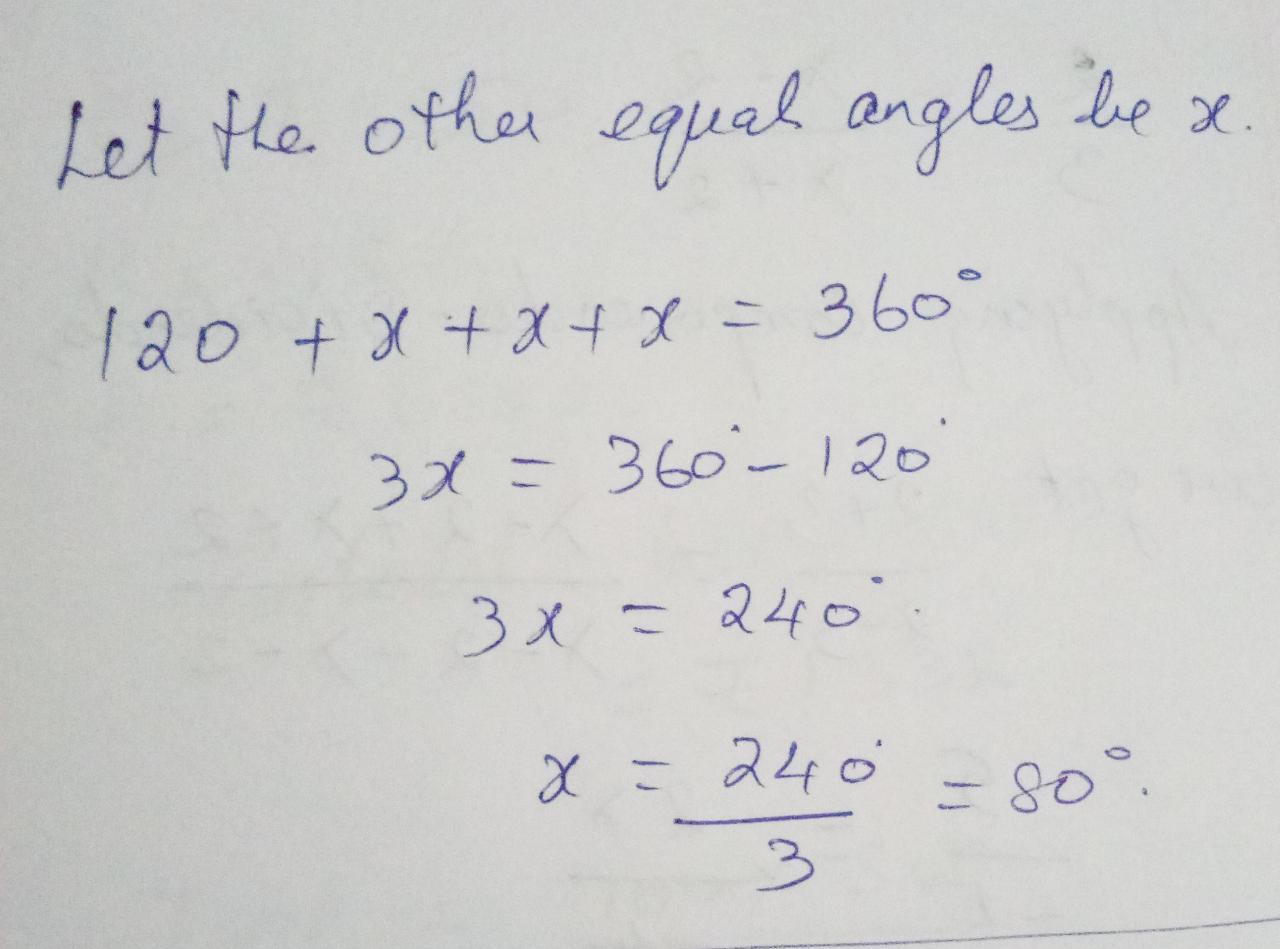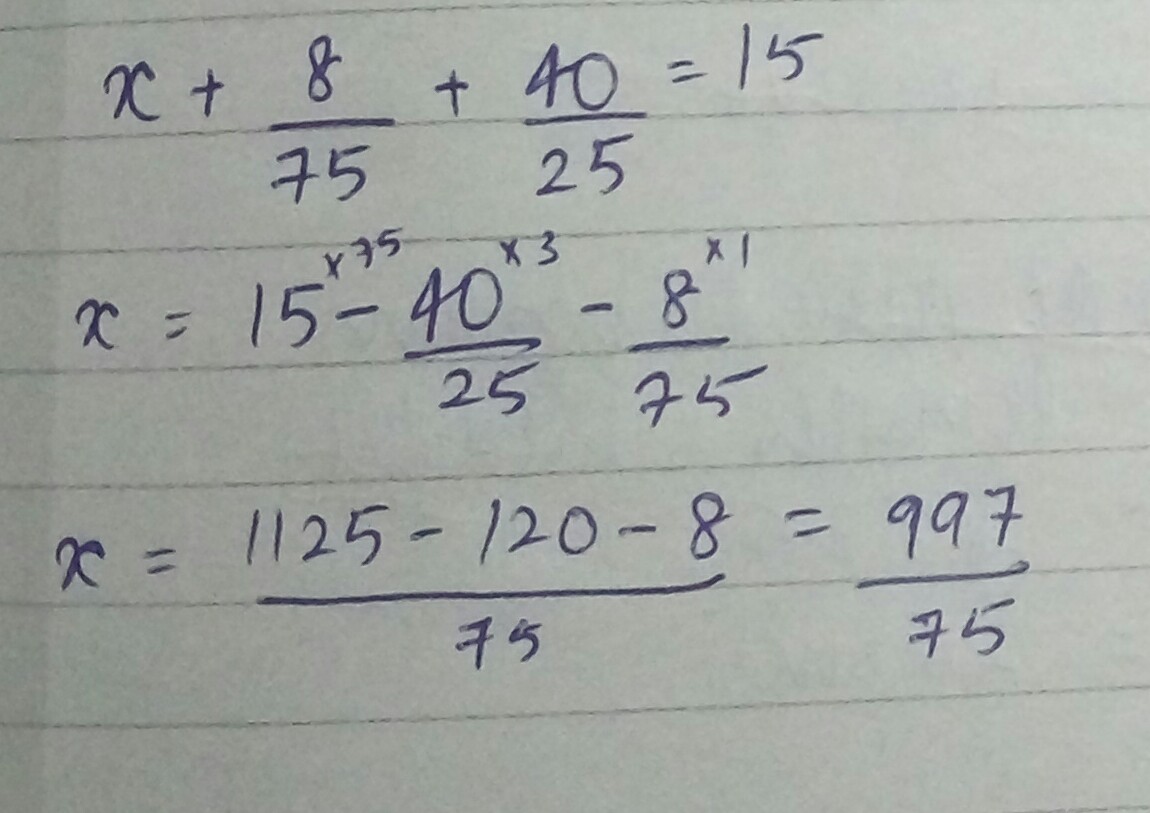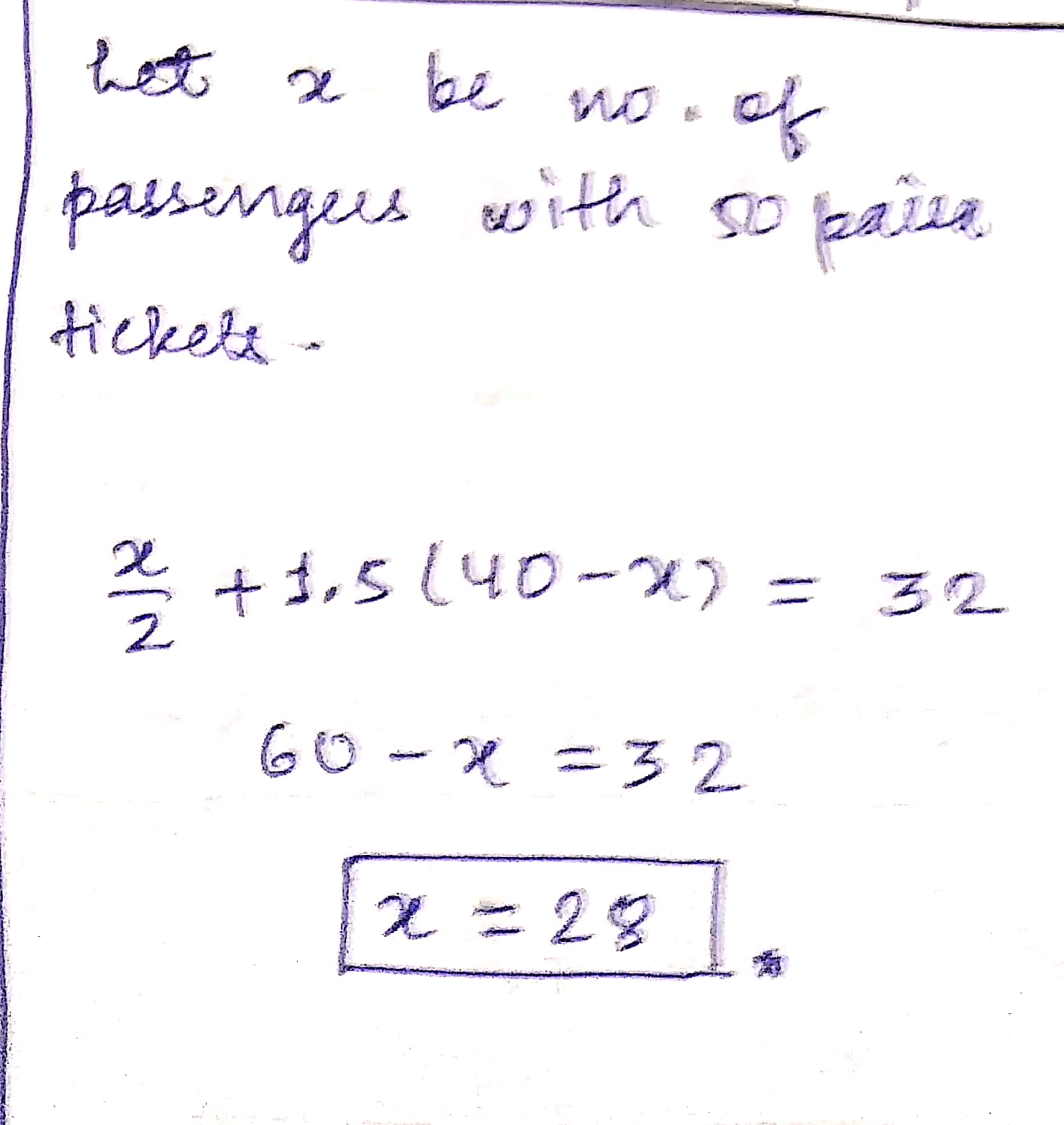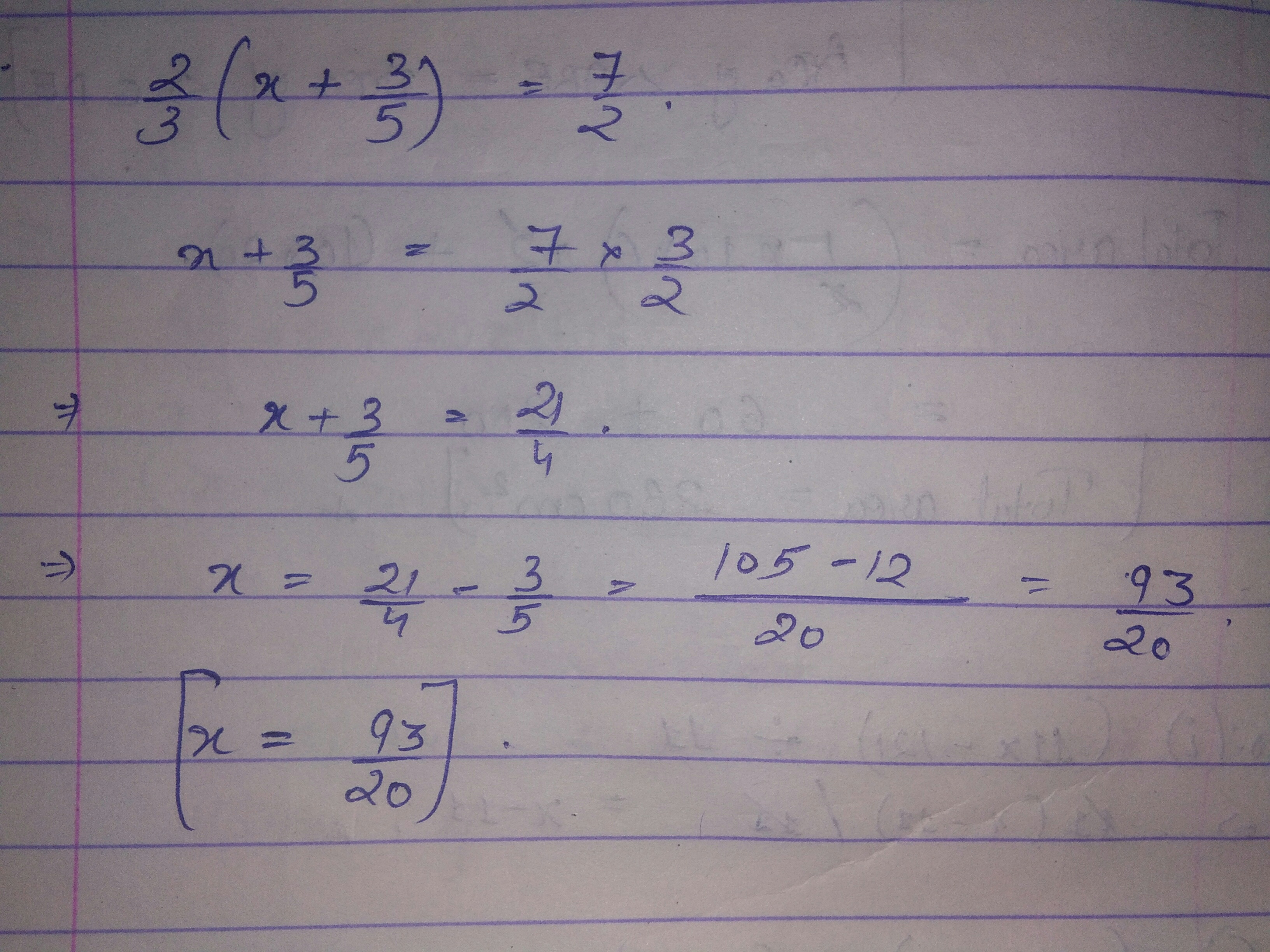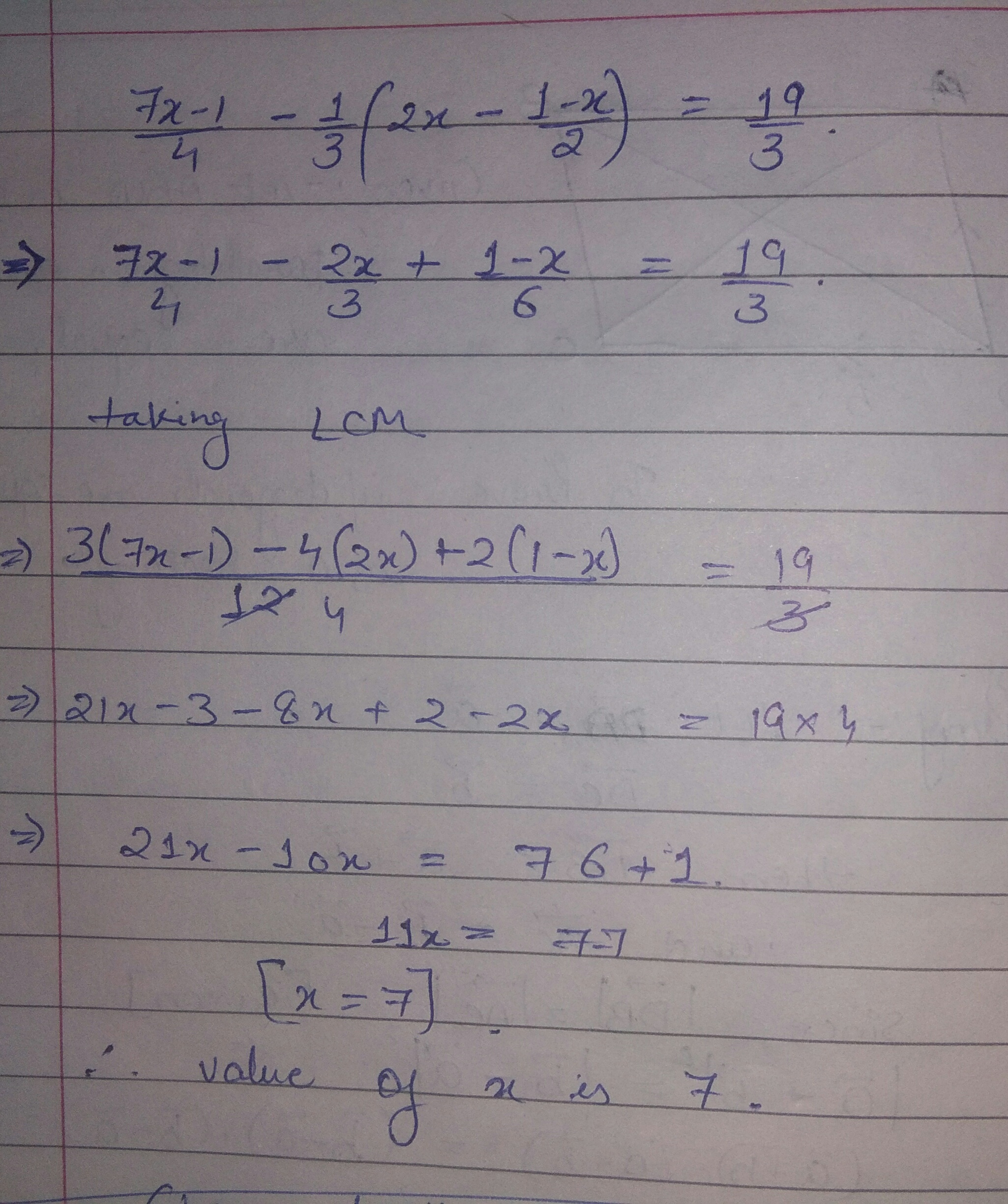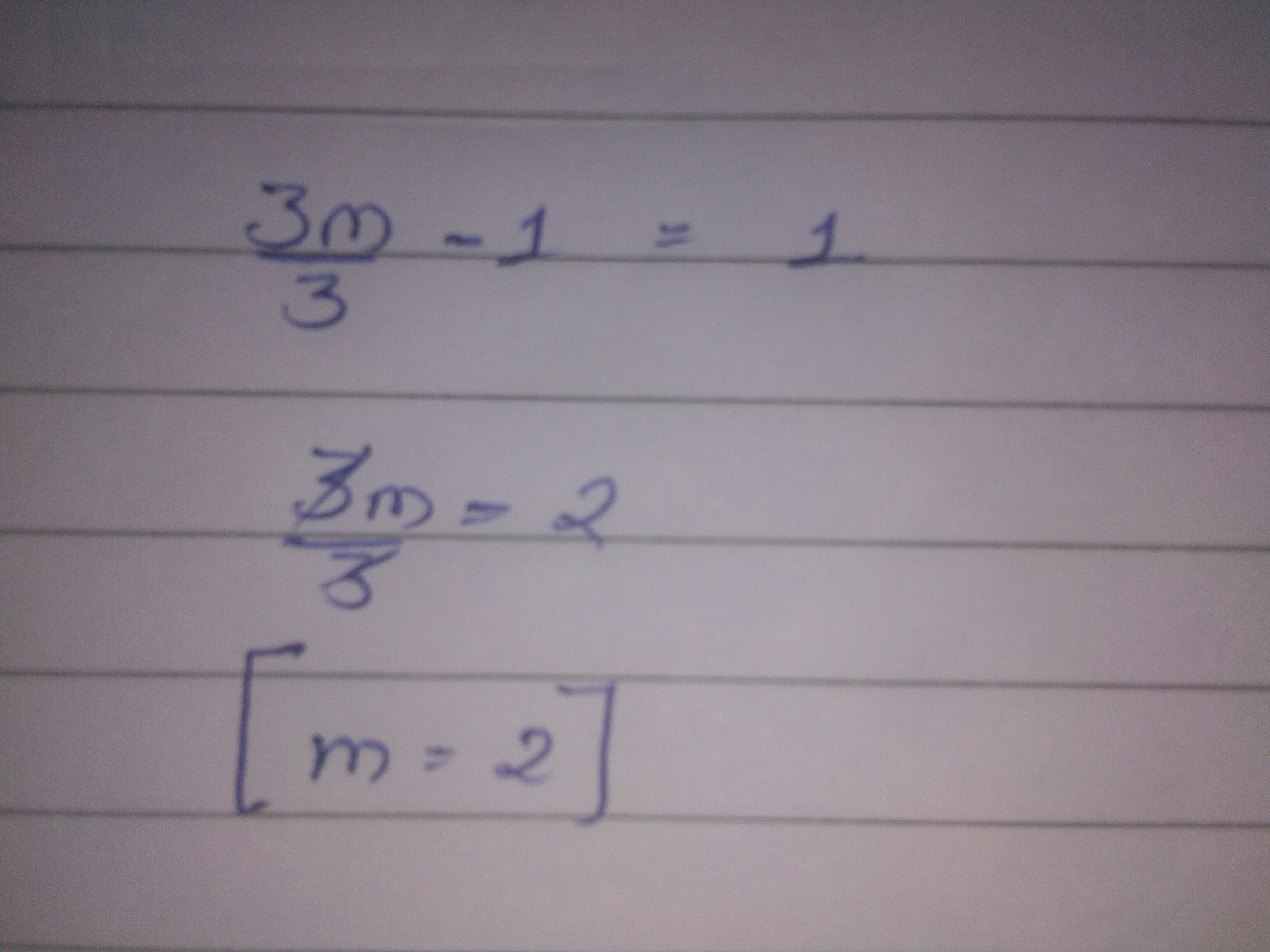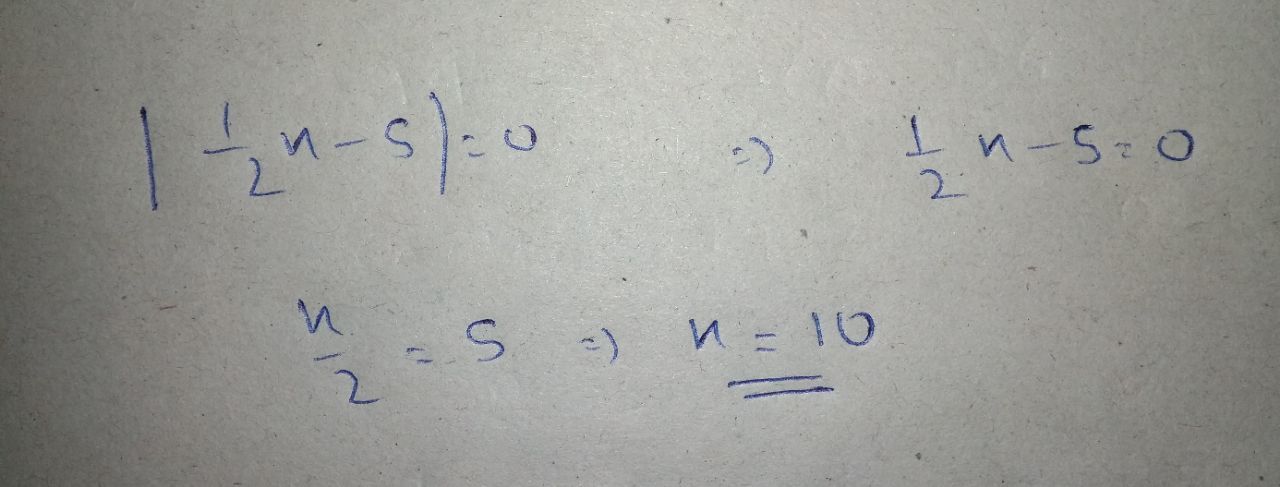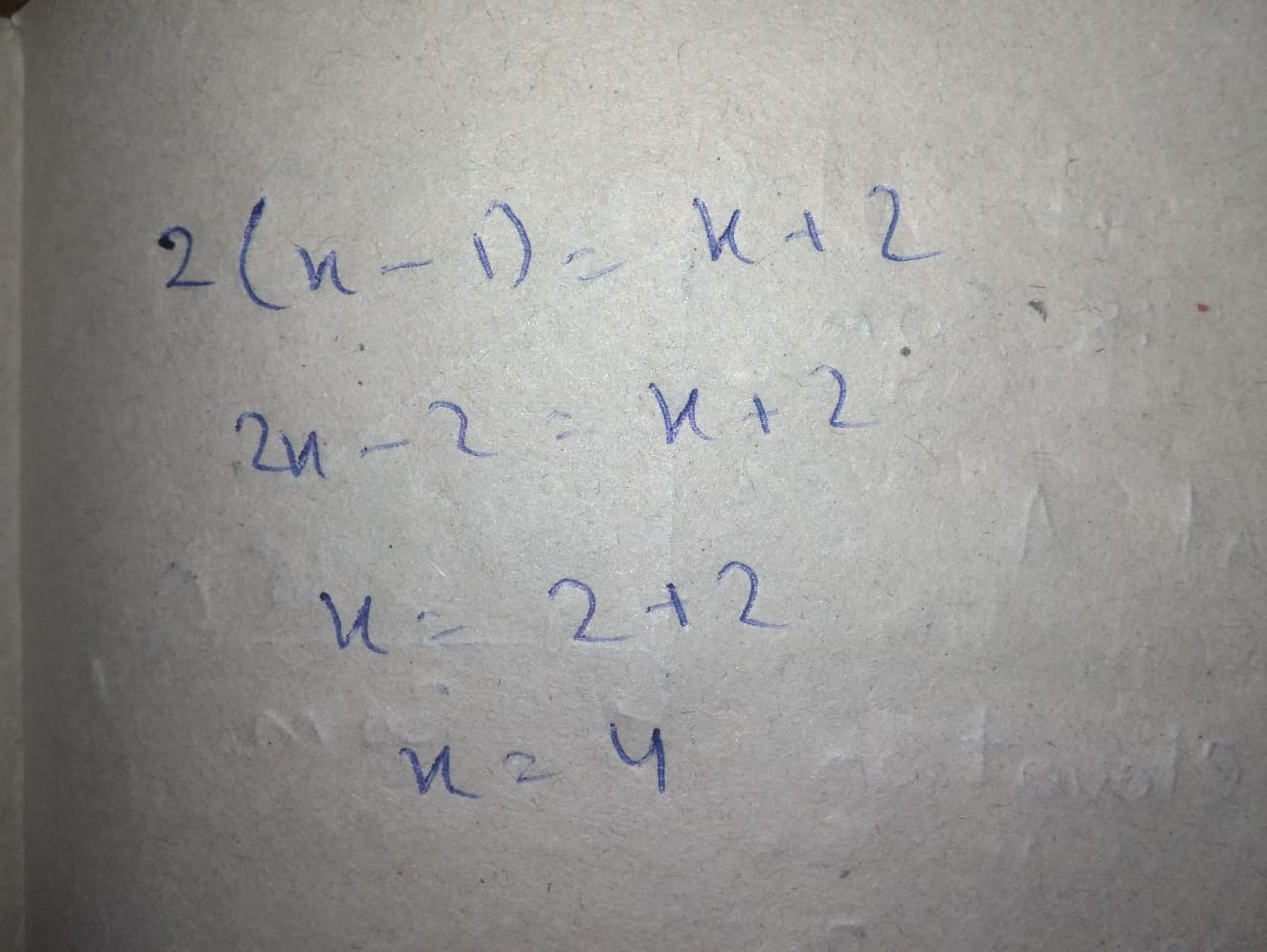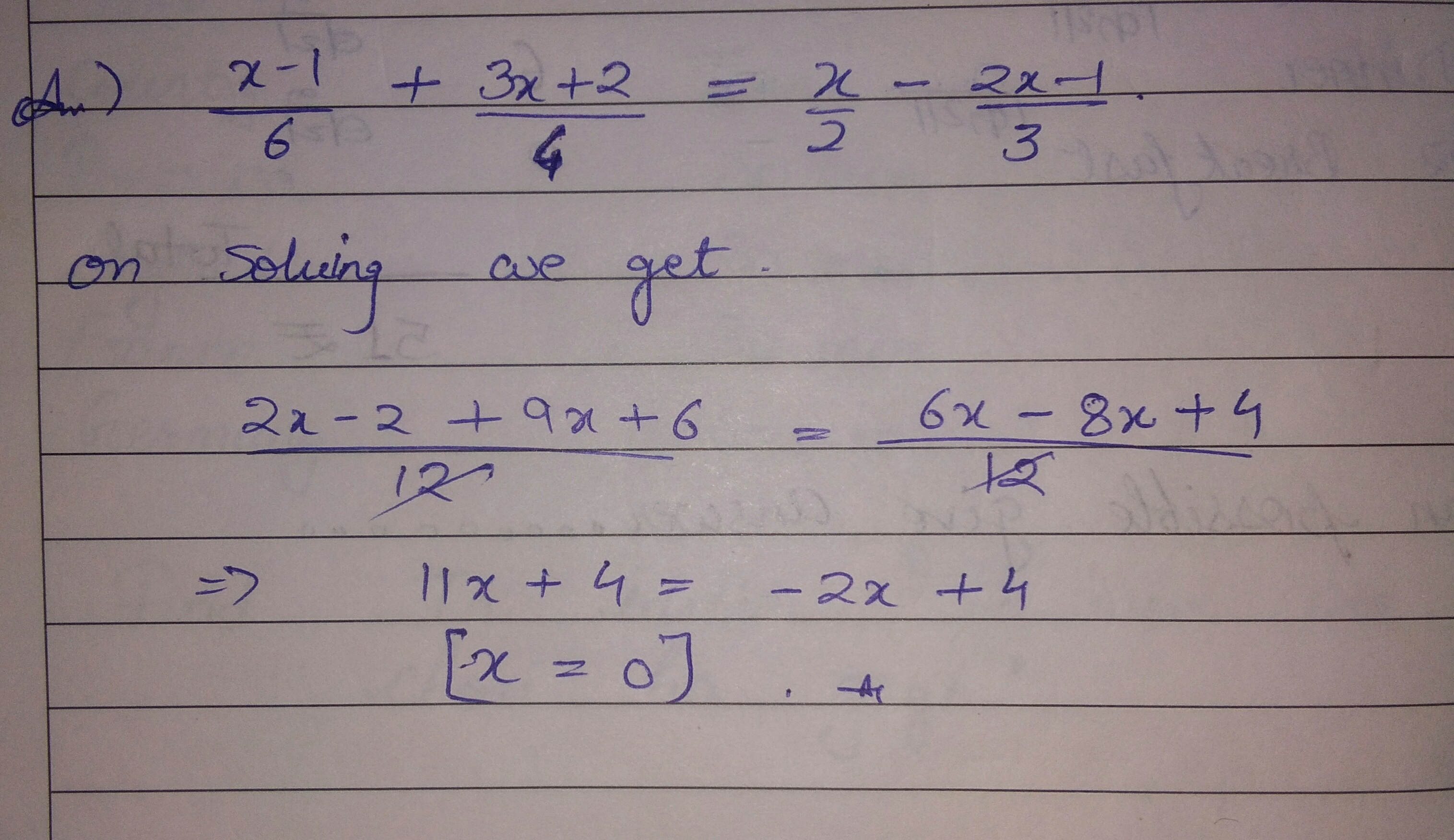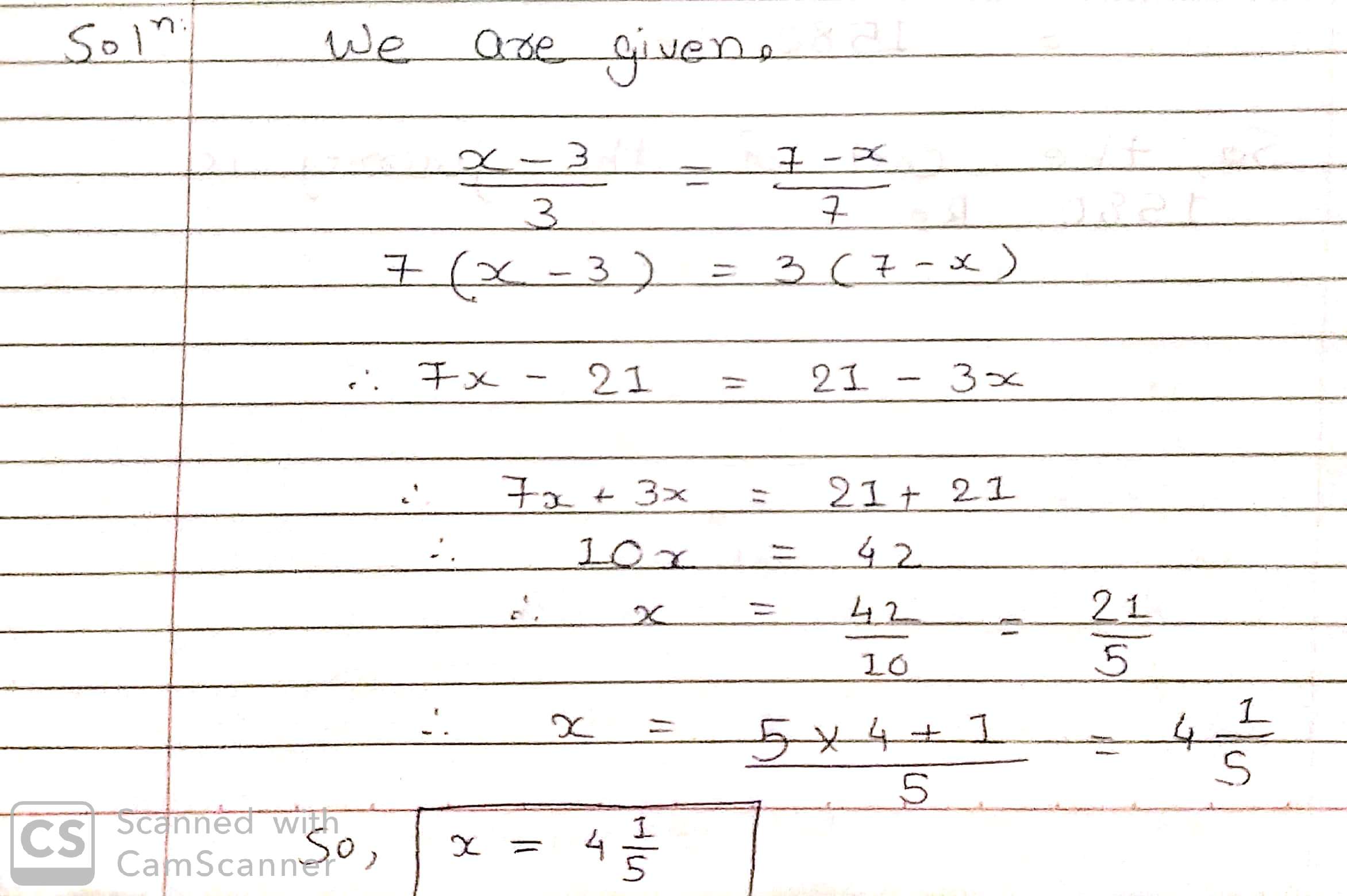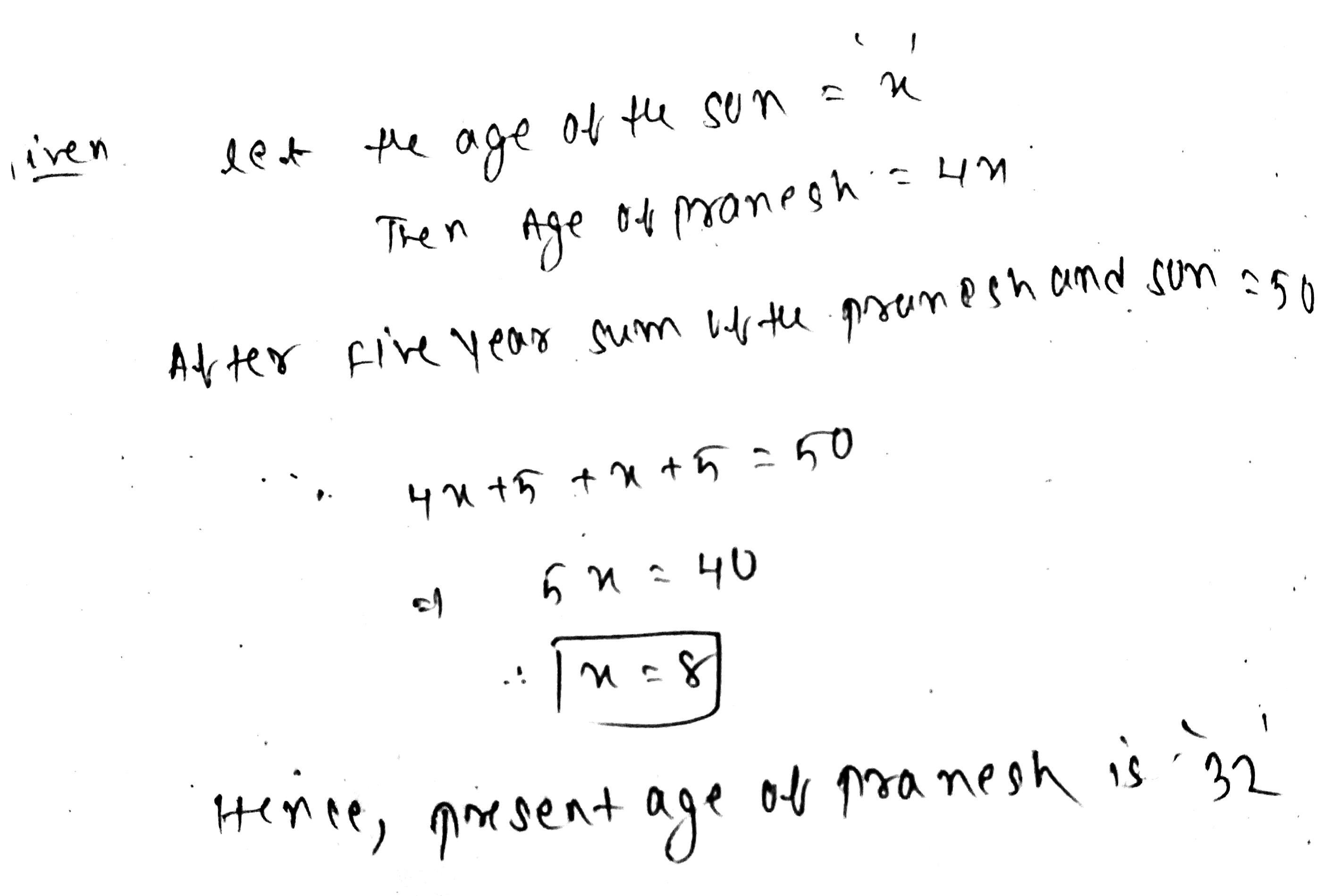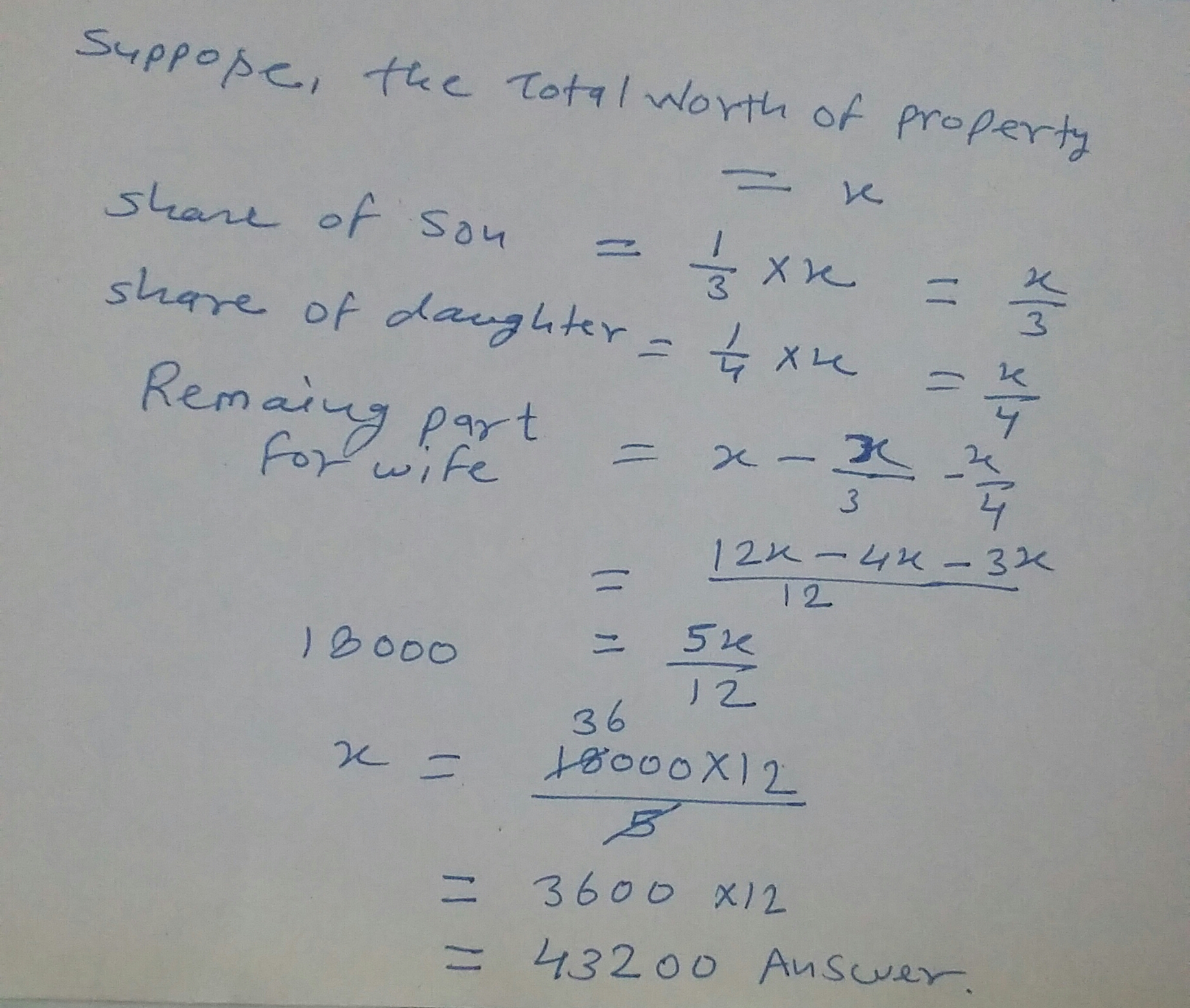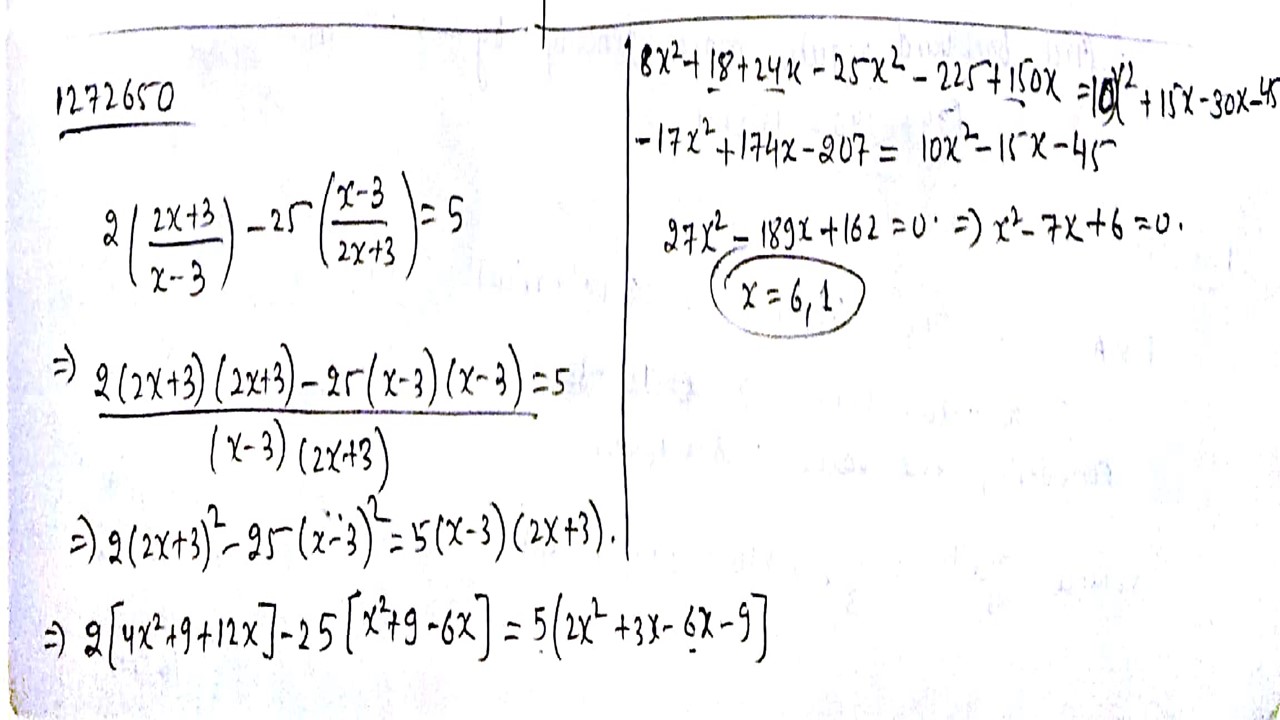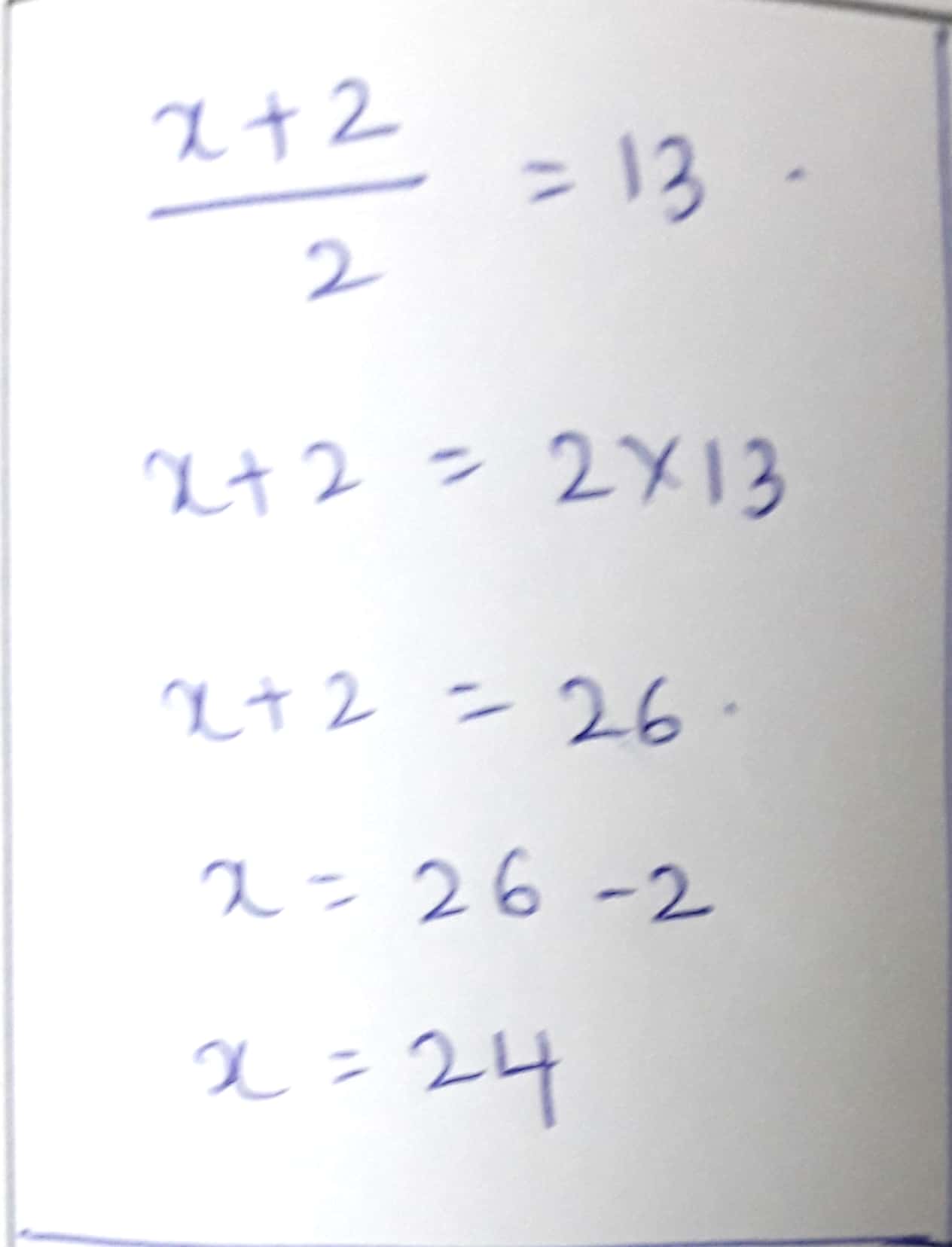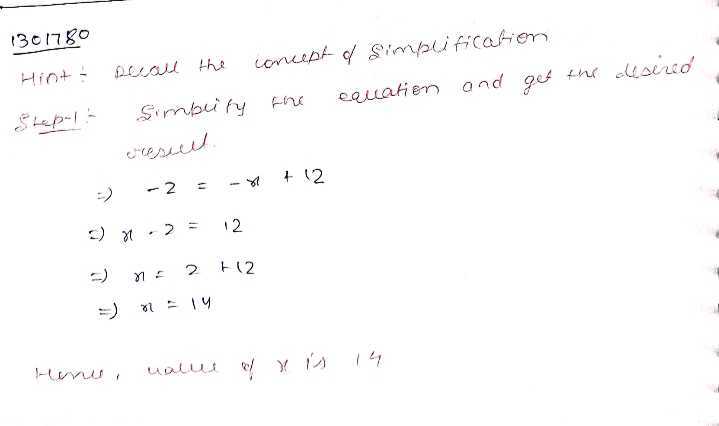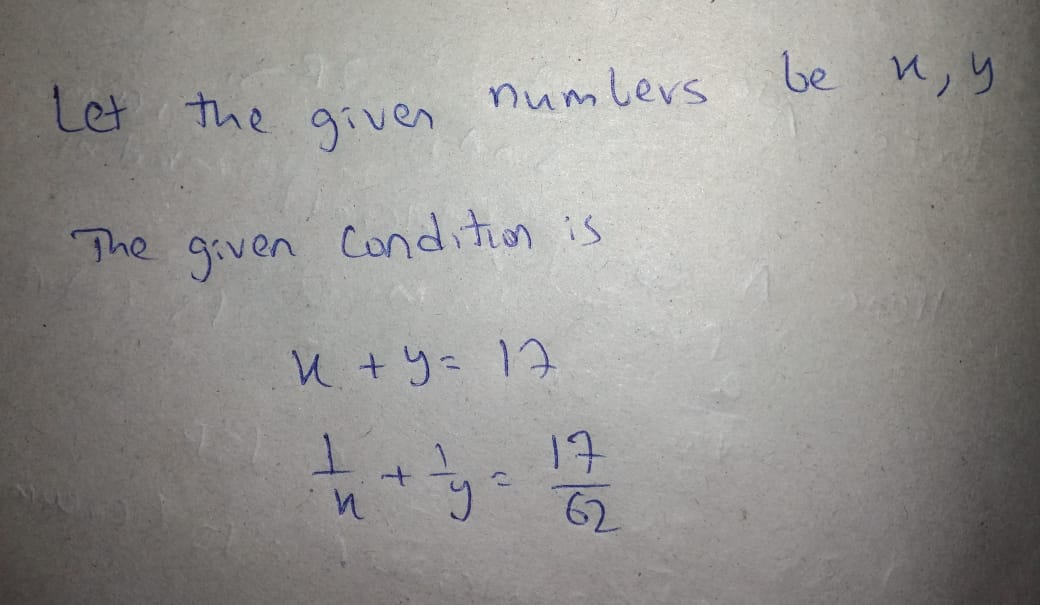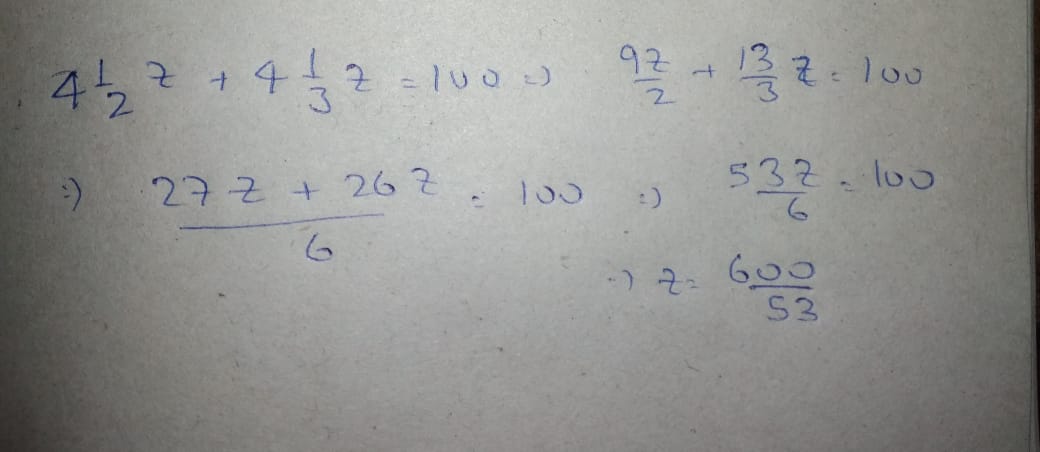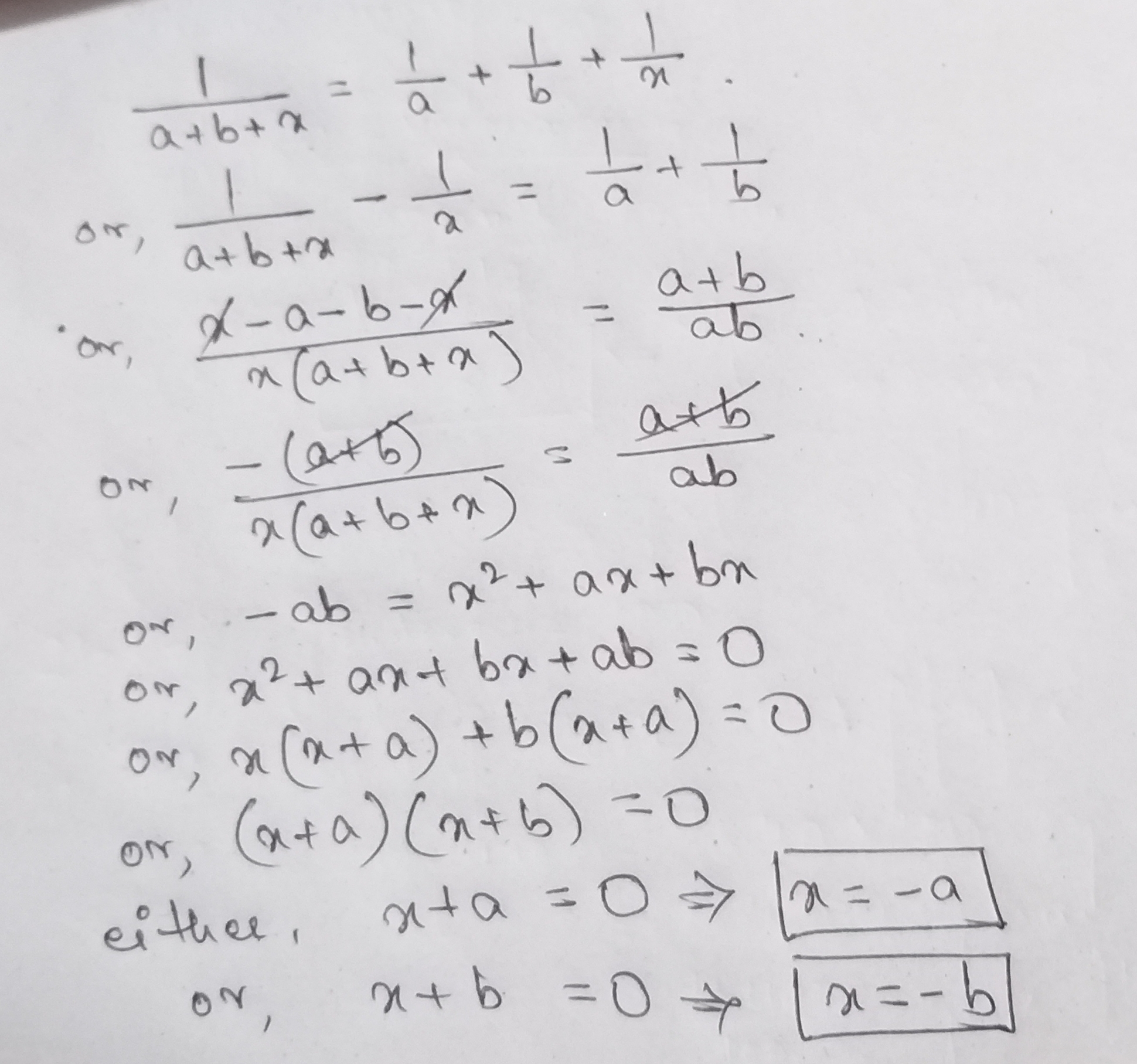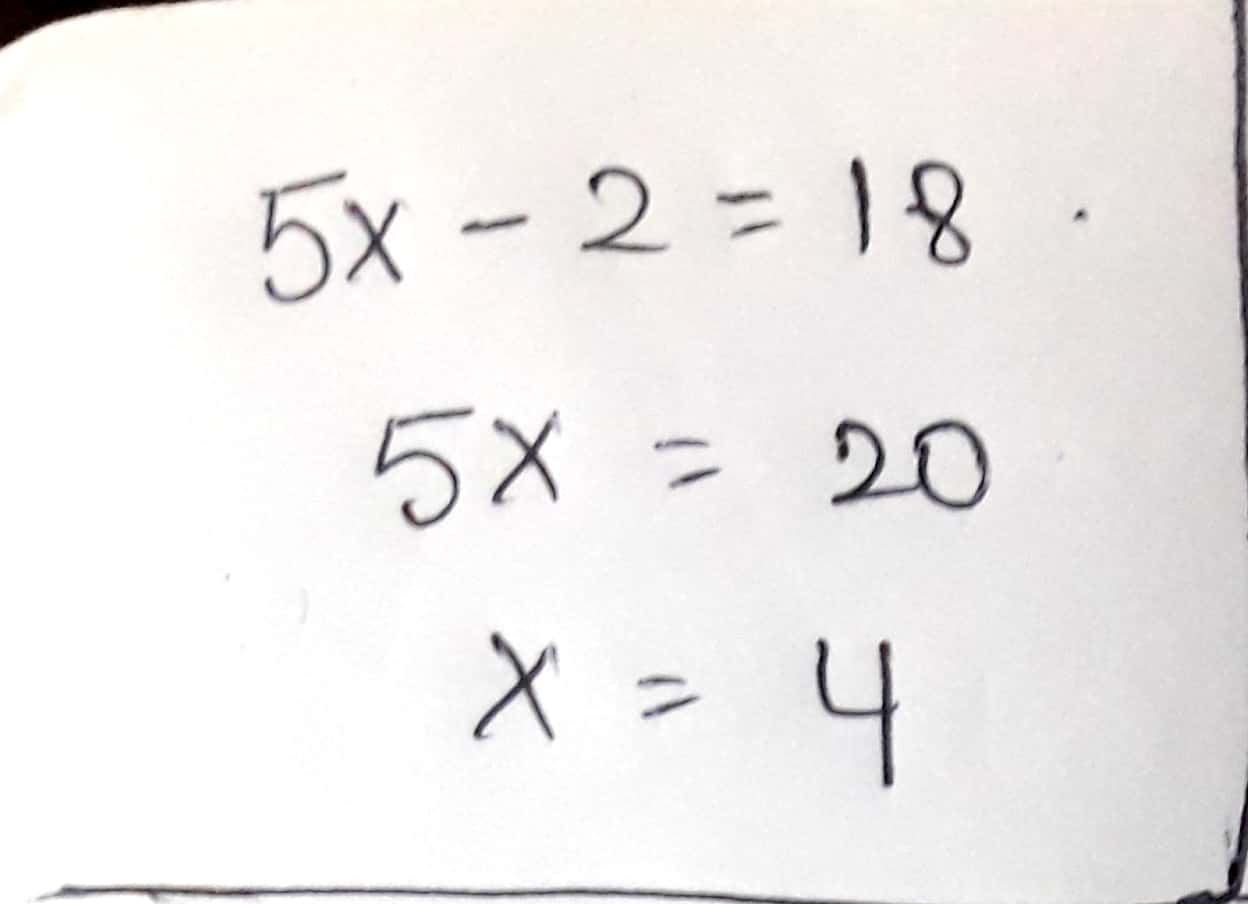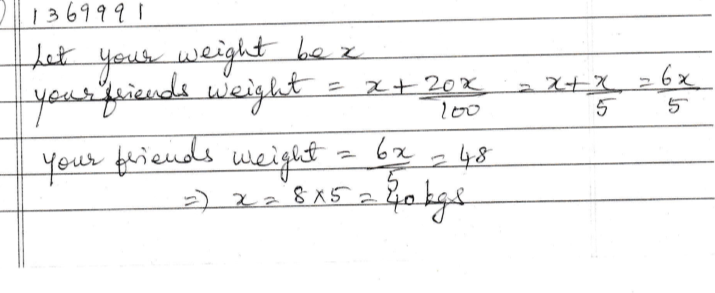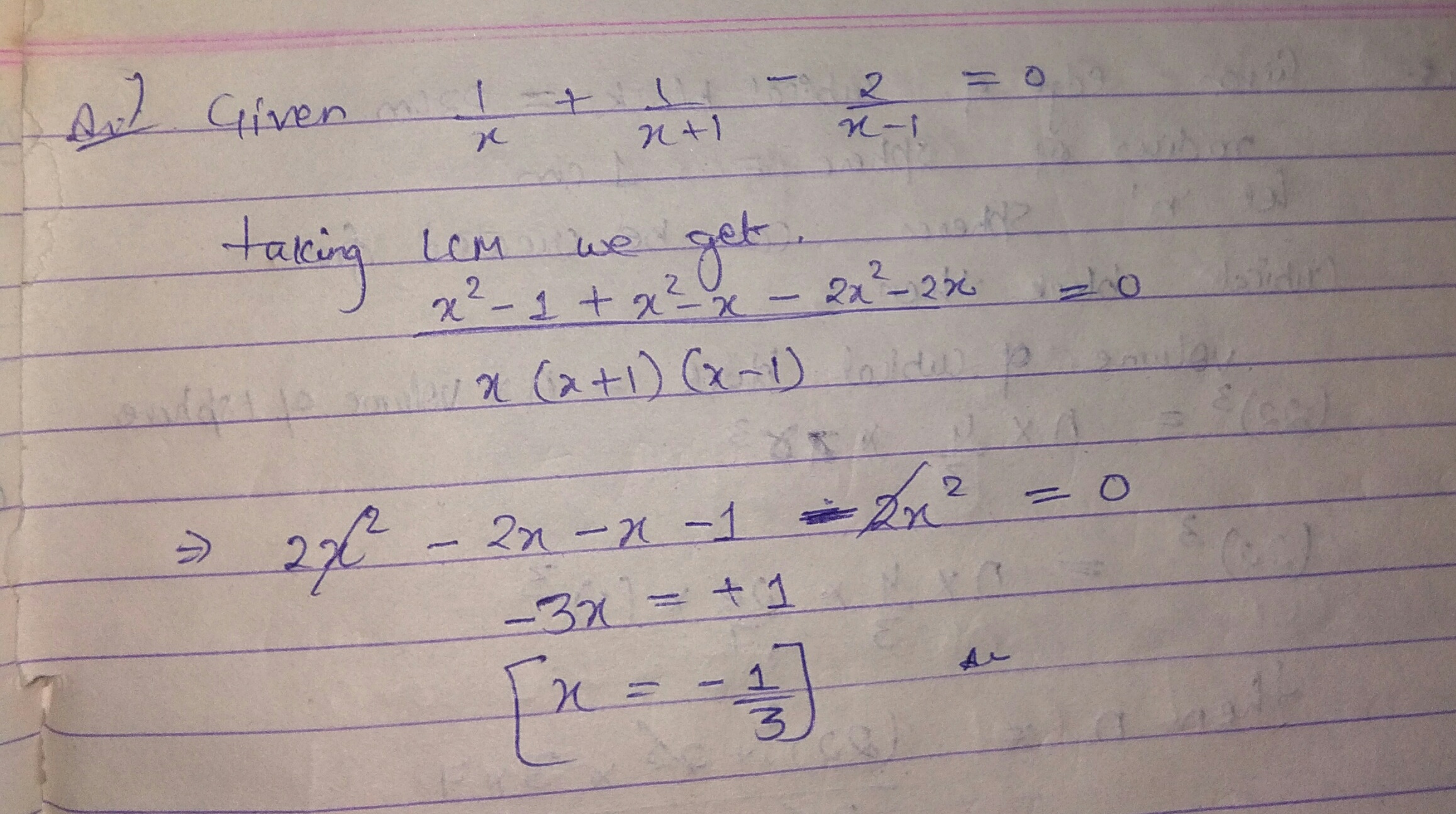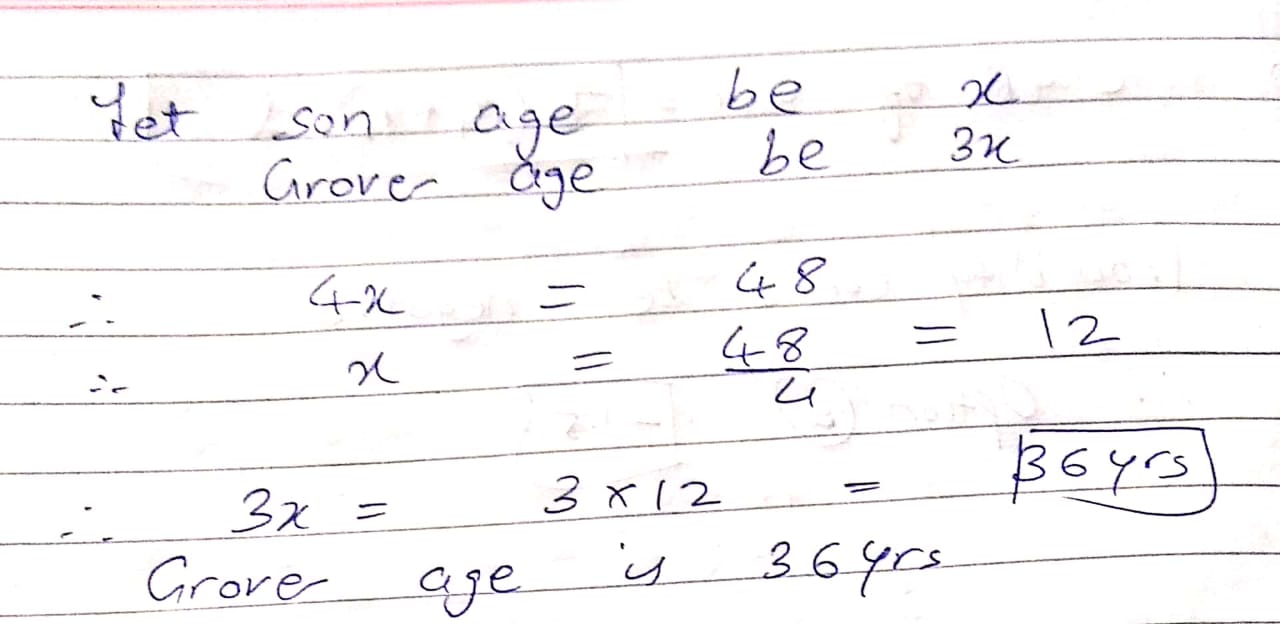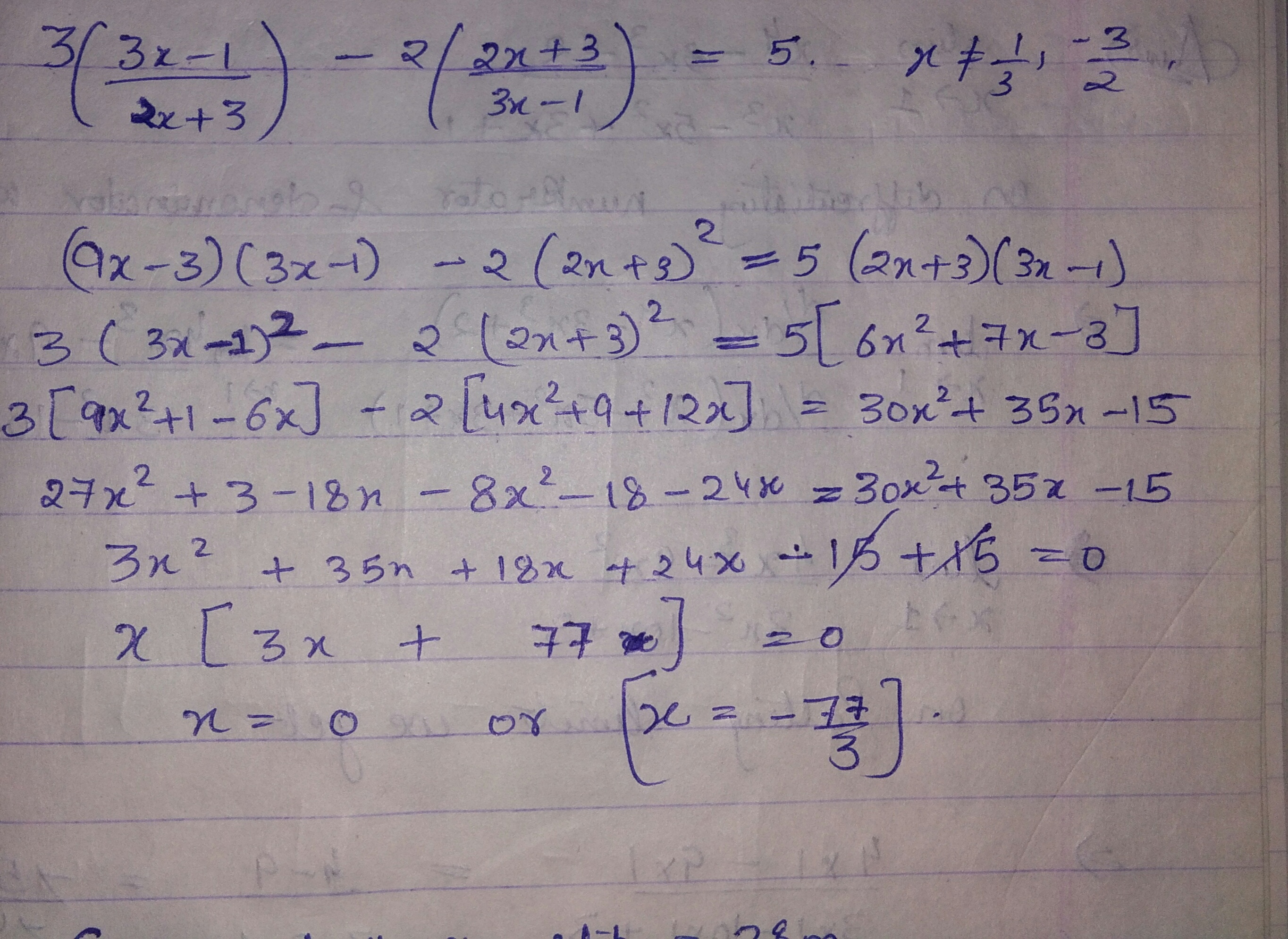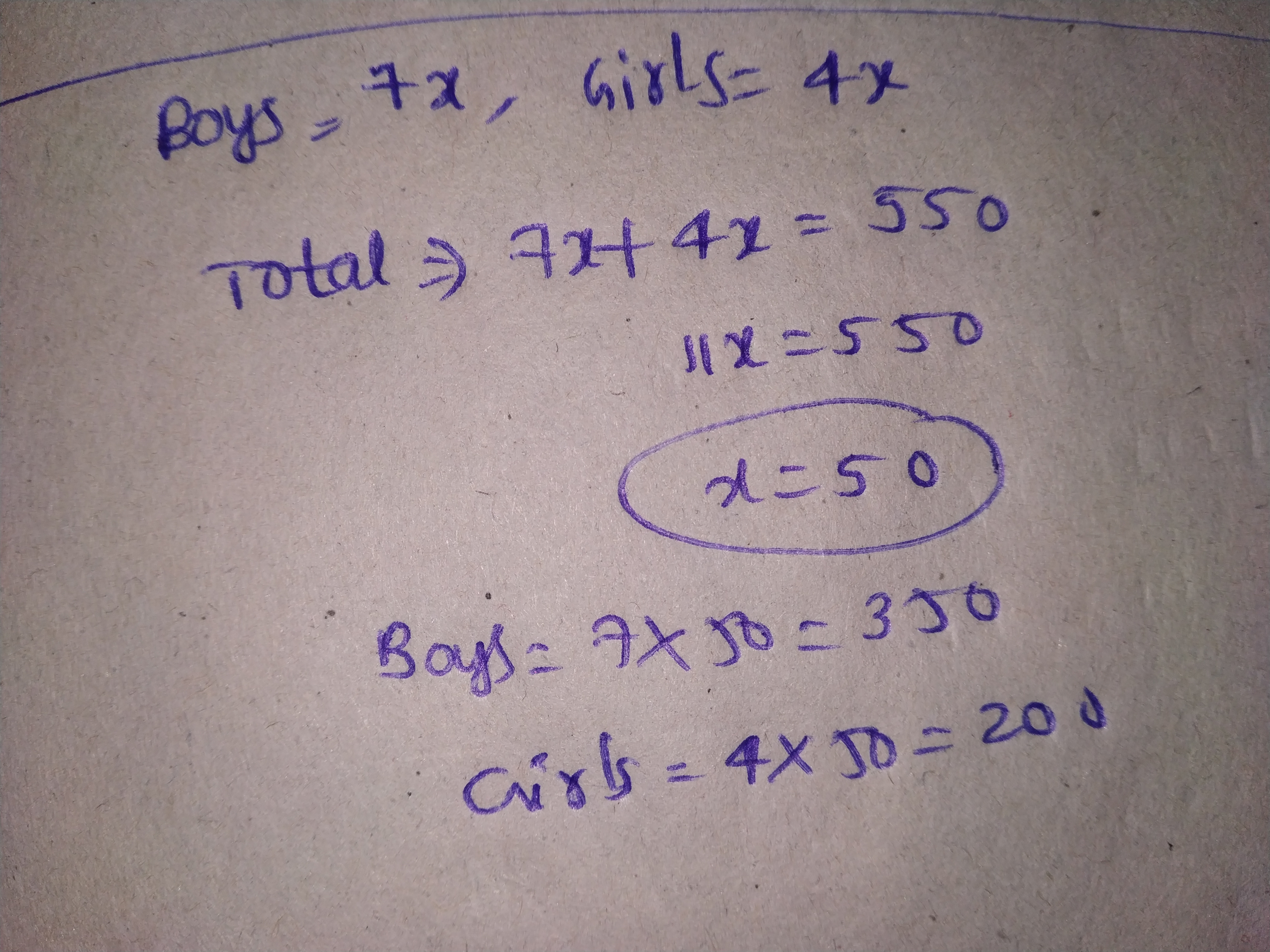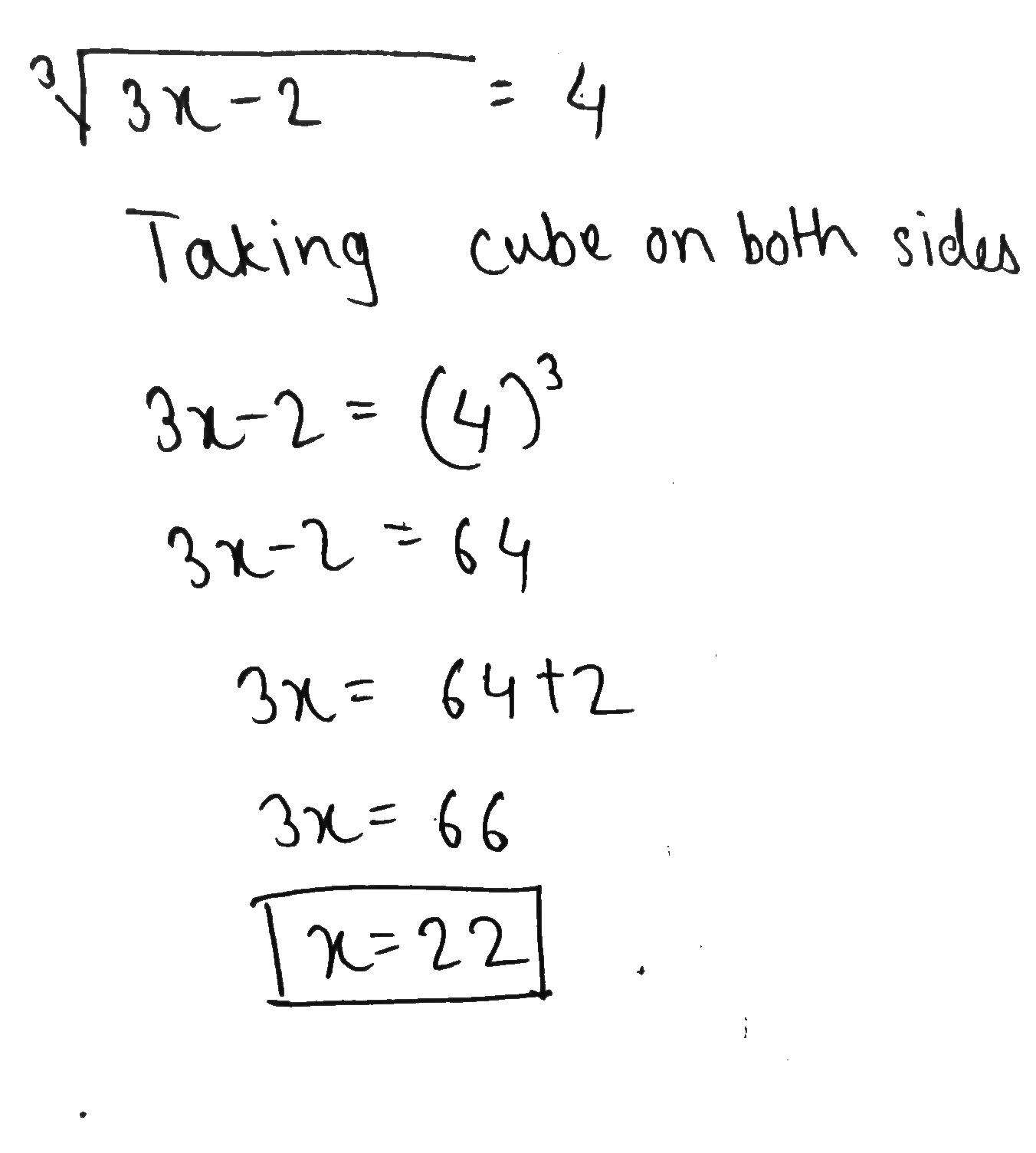Linear Equations In One Variable - Class 8 Maths - Extra Questions
The sum of an integer and twice the next integer is $$41$$. Find the two integers.
Solve the following equations:
(a) $$7x-4=10$$ (b) $$96+x=300$$ (c) $$4x+3=2x+11$$
Solve: $$\dfrac{7}{y} + 1 = 29$$
Solve: $$7n + 49 = 497$$
Solve:
$$\dfrac{1}{3}{x^2} - \dfrac{8}{x}=0$$
Solve the following equation
$$\dfrac{b+\left(b+1\right)+\left(b+2\right)}{4}=21$$
Three consecutive numbers add up to $$48 .$$ What are the numbers ?
Dakarai thinks of a number. He divides it by $$3$$ then subtracts $$7$$. The answer is $$4$$. What number did Dakarai think of.
Find the value of $$p$$
$$10 p - ( 30 p - 4 ) = 4 ( p + 1 ) + 9$$
Find the value of $$\lambda$$ $$\frac { 2 } { 3 } = \frac { \lambda - 2 } { \lambda + 2 }$$
I have a total of Rs $$300$$ in coins of denomination $$Rs. 1, Rs. 2$$ and $$Rs. 5$$. The number of $$Rs .2$$ coins is $$3$$ times the number of $$Rs .5$$ coins. The total number of coins is $$160$$. How many coins of each denomination are with me
A man walks $$20km$$, then travels a certain distance by train and then by bus as far as twice by the train. If the whole journey is of $$70km$$, how far did he travel by train?
The cost of $$5\dfrac{3}{5}\;kg$$ of salt is $$Rs.\,50\dfrac{3}{10}.$$ What is the cost of $$1\;kg$$ salt?
A labourer is engaged for $$20$$ days on the condition that he will revive $$Rs.\ 280$$ for each day he works and will be fined Rs. 60 for each day he is absent. If he receives $$Rs.\ 2540$$ in all, for how many days did he remain absent?
The product of two numbers is $$9$$. If one of them is $$3\dfrac {3}{7}$$, then find the other number .
Solve the following equations by systematic method.
$$\dfrac{a}{4}-3=8$$
Solve the following equations by systematic method.
$$5x-6=9$$
A shopkeeper has 204 eggs. He puts them in egg trays. Each tray has the capacity of 12 eggs.a) How many trays will he need?
$$9$$ years later, a girl will be $$3$$ times an old as she was $$9$$ years ago. How old is she now?
Fourteen added to thrice a whole number gives $$56$$. Find the number
The teacher tells the class that the highest marks obtained by a student in her class is twice the lowest marks plus $$7$$. The highest mark is $$87$$. What is the lowest mark?
In a school, the monthly fee collection of $$350$$ students in INR $$3,85,000$$. What will be the collection fee of $$58$$ students for a month?
How many pieces of tape $$3\dfrac {4}{7}cm$$ long can be cut from a tape, which is $$1$$ metre $$75\ cm$$?
Find $$x$$, if:
$$\dfrac{1}{4!} + \dfrac{3}{6!} = \dfrac{x}{8}$$
Solve $$7 + 2(a + 1) - 3a = 5a$$
Solve: $$\dfrac{x}{3} - \dfrac{x}{4} = \dfrac{1}{12}$$.
Solve $$\dfrac {x+3}{3}-\dfrac {x-2}{2}=1$$. Hence find $$p$$ if $$\dfrac {1}{x}+p=1$$
Manju's weight is $$14%$$ more than Anju's weight. If Anju's weight is $$63\ kg$$, find Manju's weight.
Fifteen years from now Ravi's age will be four times his present age. What is Ravi's present age?
Due to increase in salary of Ajit singh by 12 % new salary becomes Rs. 25760 . Find his previous salary .
Solve the following equations:
$$\cfrac{2x-3}{3x+2}=\cfrac{-2}{3}$$
In an election there was only two candidates. The winner polled $$53\%$$ votes and won by $$9600$$ votes. Find the total number of votes polled.
If $$x + 20 = 80;$$ find $$x$$
Solve the following equation
$$13x-5=\dfrac{3}{2}$$
What number is that of which the third part exceeds the fifth part by $$4$$?
A teacher shares sweets among $$8$$ students so that they get $$6$$ each. How many sweets would they each have got, had there been $$12$$ students?
The $$2$$ consecutive integers has their sum as $$67$$ find the numbers
The sum of $$3$$ consecutive terms is $$69$$ find the numbers
Set up equations and solve them to find the unknown numbers in the following cases:
When $$I$$ subtracted 11 from twice a number, the result was 15.
Express the given linear equations in the form $$ax + by + c = 0$$ and indicate the values of $$a, b$$ and $$c$$ in given case:
$$4 = 3x$$.
The product of two rational numbers is $$15$$. If one of the numbers is $$-10$$, find the other.
Set up equations and solve them to find the unknown numbers in the following case:
Add $$4$$ to eight times a number you get $$60.$$
The sum of three prime numbers is $$100$$. If one of them exceeds another by $$36$$, then find larger number.
If the sum of two consecutive odd integers is $$20$$, find the numbers
Frame and solve the equations for the following statements:
Sum of three consecutive numbers is $$90$$. Find the numbers
Frame and solve the equations for the following statements:
Half of a certain number added to its one third gives $$15$$. Find the number
solve:
$$\dfrac{4}{3}$$ $$+ 8x = 14$$
A packet of soup makes 9 bowls of servings. How many $${3 \over 4}$$ bowls of servings are possible ?
If four fifths of a number is greater than three fourths of the number by $$4$$. Find the number.
Find a number which when multiplied by $$7$$ and then reduced by $$3$$ is equal to $$53$$.
The measures of the angle of a triangle are in the ratio $$2:3:4$$. Find the smallest angle.
The perimeter of an equilateral triangle is $$16.5\ cm$$. Find the length of its side. $$(in\ cm)$$
The difference between two numbers isIf one-third of the smaller number is greater than one-seventh of the larger number by 4 then what is the value of greater number?
Sum of two numbers is $$95$$. If one exceeds the other number by $$15$$, find the numbers.
Solve: $$\dfrac { x }{ 4 } -\dfrac { x+10 }{ 5 } +4\dfrac { 3 }{ 4 } =x-1-\dfrac { x-2 }{ 3 } $$
Solve $$10 = z + 3$$ for the value of $$z$$.
The sum of two numbers is $$45$$ and their ratio is $$7:8$$. Find the numbers.
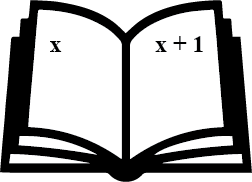
The sum of the page numbers on the facing pages of a book is $$373$$. What are the page numbers?
(Hint: Let the page numbers of open pages are $$x$$ and $$x+1$$)
If $$4$$ is added to a number and the sum is multiplied by $$3$$, the result is $$30$$. Find the number.
The product of two numbers is $$2\dfrac{2}{3}$$. One of the numbers is $$8$$. Find the other.
Solve $$2\sqrt {\dfrac {x}{a}} + 3 \sqrt {\dfrac {a}{x}} = \dfrac {b}{a} + \dfrac {6a}{b}$$.
Solve the following equations by transposing the terms $$2a-3=5$$
Solve the following equations by transposing the terms
$$5(x+4)=35$$
Solve the following equations by transposing the terms
$$2t-5=3$$
Solve the following equations by transposing the terms
$$-3x=15$$
Solve the following equations by transposing the terms
$$14 = 27 - x$$.
Solve the following equations by transposing the terms
$$2+y=7$$
Solve the following equations by transposing the terms $$10-q=6$$
Solve the following equations.
$$\displaystyle\, 3^{2x + 1} = 3^{x + 2} + \sqrt{1 - 6.3^x + 3^{2(x + 1)}}$$
Solve the following equations.
$$\displaystyle (a \, - \, 2) \ \sqrt{x \, + \, 4} \, = \, 1.$$
Solve the following equation:
$$\displaystyle\, \left ( \frac{4}{9} \right )^{\sqrt{x}} = (2.25)^{\sqrt{x} - 4}$$
If $$\dfrac {x+2}{x-2}=\dfrac {2}{3}$$. Find $$x$$ ?
The perimeter of a rectangular field is $$\dfrac{3}{5}$$ km. If the length of the field is twice its width then find the area of the rectangle in $$m^2$$
By What number $$\dfrac{3}{5}$$ be multiplied to get $$\dfrac{5}{6}$$?
Solve for 't'.$$16=4+3(t+2)$$
Find the net weight in grams of the contents of a breakfast cereal package if the gross weight is 1kg 200g and the packaging weighs 15 g.
Solve the equation: $$\dfrac { 4m+4 }{ 2m+1 } -\dfrac { 3 }{ 4 } $$
During the launch of a new book, the publisher gave away $$30$$ copies of the book as complimentary copies of the $$VIPs$$ who were present at the launch and sold the remaining at a cost of $$Rs 500$$ each. If the total collection on that day was $$Rs 7,35,000$$, how many books were given out on that day as complimentary copies?
$$1200$$ soldiers in a fort had enough food for $$28\ days$$. After $$4\ days$$, some soldiers were sent to another fort and thus the food lasted for $$32$$ more days. How many soldiers left the fort?
If the cost of $$14\ m$$ of cloth is$$Rs.18990$$, find the cost of $$6\ m$$ of cloth.
Solve: $$3n+7=25$$
Solve the following
$$\dfrac{x - 1}{4} + \dfrac{x - 2}{3} = 4\dfrac{1}{6}$$
(i) $$\dfrac {2}{3}x=4$$ then $$x=$$.............. (ii) $$\dfrac {5}{7}x=15$$ then $$x=$$................
verify using transposition method: $$3\left( {n - 4} \right) = 30$$
Find the value of $$m$$: $$8m - \dfrac{{19}}{2} = 12$$
The ratio of boys and girls in a school is $$8:3$$. If the total number of girls be $$375$$, find the number of boys in the school.
$$x-\dfrac {20}{100}x= 13500$$
The teacher said, I have through of a number. If you add $$7$$ to $$3$$ times the number, you get $$31$$. What number have I through of ? can your answer the teachers questions?
Solve the following equation:
i) $$4 = 5(p -2)$$
ii) $$4 + 5(p -1) = 34$$
Solve:
(i) $$3x + 2 = 0$$
(ii) $$y - 2 = 0$$
$$\dfrac { x-3 }{ 5 } -2=\dfrac { 2x }{ 5 }$$ find he value of $$x$$.
Solve :
$$\dfrac{9x + 7}{2} - \left(x - \dfrac{x - 2}{7} \right) = -36$$
Solve: $$x - 5\dfrac{1}{3} = 3\dfrac{1}{3}$$.
$$20$$ labour can dig a pond in $$12$$ days. How many days will it take $$16$$ laborers to dig the same pond?
The sides of a triangle are in the ratio $$3 : 2 : 4$$. If the perimeter of the triangle is $$27\ cm$$, find the length of each sides.
Solve: $$\dfrac{x}{3} - \dfrac{x}{4} = 2$$
Solve: $$\dfrac{1}{5x} + \dfrac{1}{6x} = 12$$
Find n if $$7n + 5 = 19$$
Solve: $$p - 8 = 23$$
Find the value of $$x$$

Solve: $$\dfrac{1}{3x} - \dfrac{3}{7x} = 8$$
The product of two numbers is $$900$$. If one of the number is $$90$$. Find the other?
If $$8$$ tins holds $$42 \dfrac{2}{3} \ l$$ of oil. How many liters can $$1$$ such tin hold?
A cart is running at an average speed of $$3.6 km/hr$$. How much time will it take to go $$380$$ metres?
$$\dfrac{2x-3}{3x-5}=-1\dfrac{1}{5}$$.
Find $$2y+\cfrac { 5 }{ 2 } =\cfrac { 37 }{ 2 } $$
Which number should be multiplied by $$\frac{{ - 3}}{5}$$ to get $$\frac{{ - 1}}{5}$$?
One-third of a number is eight less than the number. What is the number?
$$\dfrac{x-5}{2}-\dfrac{x-3}{5}=\dfrac{1}{2}$$
If $$\cfrac{2}{3}$$ is added to a number and the sum is multiplied by $$2$$, the answer is $$\cfrac{16}{3}$$. What is the number?
Sum of three consecutive integers is $$'18'$$. Find the numbers.
Solve:
$$ - x+3 + \left( { - 19} \right) + 15 + \left( { - 10} \right)$$
Irfan says that he has $$7$$ marbles more then five times the marbles Parmit has, Irfan has $$37$$ marbles. How many marbles does Parmit have?
A piece of wire $$12\ \text{m}$$ long is cut into two pieces, one piece is $$4.29\ \text{m}$$ long. What is the length of the other piece?
Find x :
$$\dfrac{1}{2}(x+5)-\dfrac{1}{3}(x-2)=4$$
The sum of three consecutive number is $$39$$. Find the number.
A number consists of two digits whose sum is $$13$$. If $$27$$ is subtracted from the number , the digits are reversed. Find the number.
Solve:$$(x-2)(x+1)=(x-1)(x+3)$$
Find four consecutive numbers whose sum is $$74$$
Solve:-
$$(4 - x)(\sqrt x + 3)$$
A number plus itself, plus twice itself, added to $$4$$ times itself equals $$-104$$. What is the number?
Solve the following equations:
(a) $$x-5=7$$ (b) $$3x+18=48$$ (c) $$2x=48$$ (d) $$5(x-1)+3=23$$
Solve the following equations:
$$\text {} \dfrac { 8 x - 3 } { 3 x } = 2\\$$
$$\text {} \dfrac { 9 x } { 7 - 6 x } = 15\\$$
$$\text {} \dfrac { 3 y + 4 } { 2 - 6 y } = \dfrac { - 2 } { 5 }\\$$
$$\text {} \dfrac { 7 y + 4 } { y + 2 } = \dfrac { - 4 } { 3 }\\$$
Give expressions for the following cases.
(a) $$7$$ added to $$p$$
(b) $$7$$ subtracted from$$p$$
(c) $$p$$ multiply by $$7$$
(d) $$p$$ divide by $$7$$
(e) $$7$$ subtracted from $$-m$$
(f) $$-p$$ multiply by $$5$$
(g) $$-5$$ divided by $$5$$
(h) $$p$$ multiply by $$-5$$
Solve the following:
(a) $$5x+8=23$$ (b) $$2y-4=-8$$ (c) $$2(t+1)+!5=3$$ (d) $$-y+46=32$$ (e) $$2x+3=3$$
The weight of $$72$$ books is $$9$$kg. What is the weight of $$40$$ such books?
$$x=2+\dfrac{1}{2+\dfrac{1}{2+....\infty }}$$, then $$x$$ is equals
If $$5$$ is substracted $$8$$ times from a number the remainder is $$4$$ . What is the number ?
The product of $$\dfrac {-7}{12}, \dfrac {-4}{9}$$ & $$\dfrac {6}{14}$$ is equal to the sum of $$\dfrac {8}{10}$$ and a number. Find the number.
Solve the following equations:
(1) $$x-4=3 $$,
(2) $$2a + 4= 0, $$
(3) $$17 p-2=49$$ (4) $$2m +7 =9$$
(5) $$5(x-3)=3(x+2)$$ (6) $$13x-5=\dfrac{3}{2}$$
(5) $$5(x-3)=3(x+2)$$
Solve the following equations :
$$3x + 2(x+2) = 20(2x-5)$$
Find the value of $$p$$ :-
$$3p - 7 = 0$$
Set up equations and solve them to find the unknown numbers in the following cases :
(a) Add 4 to eight times a number ; you get 60 .
(b) One - fifth of a number minus 4 gives 3 .
(c) If I take three -fourths of a number and add 3 to it . I get 21 .
(d) When I substracted 11 from twice a number , the result was 15 .
(e) Munna substracts thrice the number of notebooks he has from 50 , he finds the result to be 8 .
(f) Ibenhal thinks of a number . If she adds 19 to it and divides the sum by 5 , she will get 8 .
If the sum of four consecutive integers is 266, find the integers.
If $$\dfrac{4}{5}$$ of estate be worth $$Rs.168000,$$ find the value of half of the estate.
Solve:
$$\dfrac{x+3}{7}-\dfrac{2(x-4)}{3}=1$$
If $$\dfrac{3x+5}{2x+1}=\dfrac{4}{3}$$, find the value of $$x$$
10 boys can dig a pitch in 12 hours. How long will 8 boys take to do it?
A quadrilateral has one angle equal to $$120 ^ { \circ }$$ and its other three angles are equal. The measure of each of the equal angles is .....................
Solve: $$3n + 7 = 1$$
solve
$$(7\times 20)-8z = 0$$
solve
$$2x+1=5$$
Product of a number with $$5$$ subtracted from $$70$$ is $$30$$. Find the number .
$$12$$ times a number divided by $$10$$ is $$6$$. Find the number.
solve
$$x\ (21-7)+7\times 2 = 70$$
Solve for $$x$$ : $$\cfrac{{\sqrt {4x + 1} + \sqrt {x + 3} }}{{\sqrt {4x + 1} - \sqrt {x + 3} }} = \cfrac{4}{1}$$
Rohan thought of a number, doubled it and subtract $$25$$ from it. The result was $$49$$. Find the number.
Solve:
$$x+\dfrac{8}{75}+\dfrac{40}{25}=15$$
sum of $$x + 2y\,\,{\rm{and}}\,\,3x - y$$ is
A local bus is carrying $$40$$ passengers, some with $$50$$ paisa tickets and the remaining with $$Rs\ 1.50$$ tickets. If the total money collected from the passengers is $$Rs\ 32$$, then find the number of passengers with $$50$$ paisa tickets.
Solve the following equations.
(a) $$\dfrac{2x}{3}+\dfrac{5}{2}=4$$
The sum of two consecutive multiplies of $$3$$ is $$69$$. Find them.
Solve for $$x$$:
$$\frac { 8 x } { 10 } =15$$
Find the value of $$x$$ for the following
(1)$$\dfrac { 2 }{ 5 } =\dfrac { 8 }{ x } $$
(2)$$\dfrac { 12 }{ x } =\dfrac { 11 }{ 8 } $$
(3)$$\dfrac { x }{ 40 } =\dfrac { 11 }{ 8 } $$
(1)$$\dfrac { 2 }{ 5 } =\dfrac { 8 }{ x } $$
(2)$$\dfrac { 12 }{ x } =\dfrac { 11 }{ 8 } $$
(3)$$\dfrac { x }{ 40 } =\dfrac { 11 }{ 8 } $$
$$\dfrac{2}{3}\left ( x+\dfrac{3}{5} \right )=\dfrac{7}{2}$$
Solve for $$x$$:$$2x-\dfrac{1}{2}=3$$
Solve for $$x$$:$$\dfrac{7x-1}{4}-\dfrac{1}{3}\left ( 2x-\dfrac{1-x}{2} \right )=\dfrac{19}{3}$$
Find the number when tripled and added to $$2$$ gives $$8$$
Solved:
$$x+8=11$$
Solve:
$$n+5=19$$
A swarm of $$62$$ bees flies in a garden. If $$3$$ bees land on each flower, $$8$$ bees are left with no flowers. Find the number of flowers in the garden.
Solve the following equation :
$$\displaystyle \dfrac{x + 4}{2} + \dfrac{4x}{3} = 9$$
Solve for $$m$$: $$\dfrac{3m}{3}-1=1$$
Solve:
$$\dfrac{x-1}{3}-1=\dfrac{x-2}{4}$$
Prove that:
$$2x-3=7$$
Solve:
$$\dfrac{1}{10}-\dfrac{7}{x}=35$$
Find the value of x, if $$\left|\dfrac{1}{2}x-5\right|=0$$
The sum of two consecutive numbers is $$35$$ find their product.
Solve: $$x+2\dfrac{1}{3}=5$$
Find the value of $$x$$, if $$\dfrac 8x=4$$.
A number is subtracted from $$72$$. The new number is divided by $$6$$ to give $$10$$. Find the number.
Nine added to thrice a whole number gives $$45$$. Find the number.
Simplify : $$3x=$$ $$24$$
Solve:
$$2x-5\left[7-(x-6)+3x\right]-28=39$$
Sum of three consecutive number is $$39$$. Find the numbers.
Solve:
$$\dfrac {x+2}{x-2}=\dfrac {7}{3}$$
If $$\left(\dfrac{8}{15}\right)^{3}-\left(\dfrac{1}{3}\right)^{3}-\left(\dfrac{1}{5}\right)^{3}=\dfrac{x}{75}$$, Find $$x$$.
$$2(x -1) = x + 2$$
Factorize : $$x^{2}-17x+72$$
Solve: $$\dfrac 1x+4=7$$
Solve: $$ \frac { x - 1 } { 6 } + \frac { 3 x + 2 } { 4 } = \frac { x } { 2 } - \frac { 2 x - 1 } { 3 } $$
Solve for x ;5x - 2 = 8
The solution of $$\frac{2x+3}{2x-1}=\frac{3x-1}{3x+1}$$ is
Solve $$\frac{x-3}{3}=\frac{7-x}{7}$$
Solve $$\dfrac{45-x}{6}=7$$
Solve : $$14-y-8=13$$
Sum of $$3$$ consecutive numbers is $$33$$. Find those numbers.
Complete the last column of the table:
| Sr. No. | Equation | Value | Say, whether the Equation is satisfied. (Yes / No) |
| (i) | $$x + 3 = 0$$ | $$x = 2$$ | |
| (ii) | $$x + 3 = 0$$ | $$x = 0$$ | |
| (iii) | $$x + 3 = 0$$ | $$x = -3$$ | |
| (iv) | $$x -7 = 1$$ | $$x = 7$$ | |
| (v) | $$x -7 = 1$$ | $$x=8$$ | |
| (vi) | $$5x=25$$ | $$x=0$$ | |
| (vii) | $$5x=25$$ | $$x=5$$ | |
| (viii) | $$5x=25$$ | $$x=-5$$ | |
| (ix) | $$\dfrac{m}{3} = 2$$ | $$m=-6$$ | |
| (x) | $$\dfrac{m}{3}=2$$ | $$m=0$$ | |
| (xi) | $$\dfrac{m}{3}=2$$ | $$m=6$$ |
Verify that $$x=6$$ is a root of the equation $$2x-4=8$$
The sum of two numbers is $$184$$. If one-third of the one exceeds one-seventh of the other by $$8$$, find the smaller number.
The sum of $$2$$ consecutive numbers are $$35$$ find those numbers
The sum of $$3$$ consecutive numbers is $$36$$ find those numbers
Solve$$4a-3=-27$$
$$\sqrt{2}x+\sqrt{3}x=0$$
Solve : $$3-5(y-2)=-18$$
Solve:$$7A-16=9A$$
Solve the following equation: $$7m+\dfrac{19}{2} =13$$
Solve the following equation $$3(n-5)=21$$
Solve the following equation $$34-5(p-1)=4$$
Write equations for the following statements:
If you take away 6 from 6 times $$y$$, you get $$60$$.
Write equations for the following statements:
$$2$$ subtract from $$y$$ is $$8$$
Write the following equations in statement form:
$$\dfrac{3m}{5} =6$$
In an examination, a candidate had to answer $$25$$ questions each requiring a single answer 'True' or 'False'. It was marked by giving $$2$$ marks for each correct answer and $$-1$$ for each incorrect answer.
Use your formula to find out how many of his answer were correct, if he answered all the questions and scored a total of $$2$$ marks.
A vessel is filled with liquid $$3$$ parts of which are water and $$5$$ parts syrup How much of the mixture must be drown off and replaced with water so that the mixture may be half water and half syrup?
A bag contains $$50 p$$, $$25 p$$ and $$10 p$$ coins in the ratio $$5 : 9 : 4$$ amounting to $$Rs.206$$. Find the number of $$50p$$ coins.
In a bundle of $$154$$ shirts, the number of white shirts is $$3$$ less than the number of red shirts, but $$5$$ more than the green shirts. Then how many red shirts are there?
A rabbit hutch consists of some hares and some doves. The hutch contains $$35$$ heads and $$98$$ feet. Find the number of doves in the hutch
Two numbers are in the ratio $$5:3$$. If they differ by $$18$$, what are the numbers?
The perimeter of a rectangular swimming pool is $$154\ m$$. Its length is $$2\ m$$ more than twice its breadth. What are the length and the breadth of the pool?
Three consecutive integers add up to $$51$$. What are these integers
Three consecutive integers are such that when they are taken in increasing order and multiplied by $$2,\ 3$$ and $$4$$ respectively, they add upto $$74$$. Find these numbers.
If you subtract $$\dfrac {1}{2}$$ from a number and multiply the result by $$\dfrac {1}{2},$$ you get $$\dfrac {1}{8}$$. What is the number?
A rational number is such that when you multiply it by $$\dfrac {5}{2}$$ and add $$\dfrac {2}{3}$$ to the product, you get $$\dfrac {-7}{12}$$. What is the number?
Solve the following equation and check your results:
$$3x = 2x + 18$$
The organisers of an essay competition decide that winner of the competition gets a prize of $$Rs\ 100$$ and a participant who does not win gets $$Rs\ 25$$ for his participation. The total prize money distributed is $$Rs\ 3000$$. Find number of winners, if total number of participants is $$63$$.
The number of boys and girls in a class are in ratio $$7:5$$. The number of boys is $$8$$ more than the number of girls. What is the total class strength?
Baichung's father is $$26$$ years younger than Baichung's grandfather and $$29$$ years older than Baichung. The sum of the ages of all the three is $$135$$ years. What is the age of each of each one of them?
Lakshmi is a cashier in a bank. She has currency notes of denominations $$Rs. 100, Rs. 50$$ and $$Rs. 10$$ respectively. The ratio of number of these notes is $$2 : 3 : 5$$. The total cash with lakshmi is $$Rs. 4,00,000$$. How many notes of each denomination does she have?
Solve the following equation and check your results:
$$5t - 3 = 3t - 5$$
Solve the equation: $$5x + 9 = 5 + 3x$$
Solve the following equation and check your result:
$$8x + 4 = 3 (x - 1) + 7$$
Solve the following linear equation:
$$3(t - 3) = 5(2t + 1)$$
Solve the following equation and check your results:
$$3m = 5m - \dfrac {8}{5}$$
Solve the following equation and check your result:
$$x = \dfrac {4}{5} (x + 10)$$
Solve the following equation and check your results:
$$2y + \dfrac {5}{3} = \dfrac {26}{3} - y$$
Solve the equation $$4z + 3 = 6 + 2z$$ and check your results.
Solve linear equation:
$$x + 7 - \dfrac {8x}{3} = \dfrac {17}{6} - \dfrac {5x}{2}$$
Solve linear equation: $$\dfrac {3t - 2}{4} - \dfrac {2t + 3}{3} = \dfrac {2}{3} - t$$
Solve the following equation:
$$\dfrac {3y + 4}{2 - 6y} = \dfrac {-2}{5}$$
Solve the following equation:
$$\dfrac {9x}{7 - 6x} = 15$$
Simplify and solve the following linear equation:
$$3(5z - 7) - 2 (9z - 11) = 4(8z - 13) - 17$$
Solve the following equation:
$$\dfrac {8x - 3}{3x} = 2$$
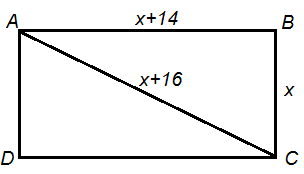
The diagonal of a rectangular field is 16 metres more than the shorter side. If the longer side is 14 metres more than the shorter side, then find the lengths of the sides of the field.
The ages of Hari and Harry are in ratio $$5:7$$. Four years from now the ratio of their ages will be $$3:4$$. Find their present ages.
The denominator of a rational number is greater than its numerator by $$8$$. If numerator is increased by $$17$$ and denominator is decreased by $$1$$, the number obtained is $$\dfrac {3}{2}$$. Find rational number.
Simplify and solve the linear equation: $$0.25 (4f - 3) = 0.05 (10f - 9)$$
Solve the following equation: $$\dfrac {z}{z + 15} = \dfrac {4}{9}$$
The value of $$x$$ that satisfies the equation $$\dfrac{2}{3}(5x+7)=8x$$ is
Solve the equation $$5(-3x-2)-(x+1)=-4(3x+5)+13$$
Find four consecutive even integers so that the sum of the first two added to twice the sum of the last two is equal to $$742$$.
The sum of three consecutive even integers is equal to $$84$$. Find the least number.
The sum of two numbers is $$20$$. The larger number is four less than twice the smaller number. What are the two numbers?
Find three consecutive integers whose sum is equal to $$366$$.
Find two consecutive integers whose sum is equal $$129$$.
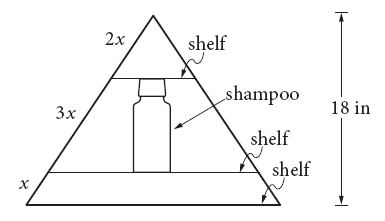
Jim has a triangular shelf system that attaches to his showerhead. The total height of the system is 18 inches, and there are three parallel shelves as shown above. What is the maximum height, in inches, of a shampoo bottle that can stand upright on the middle shelf?
If $$h$$ hours and $$30$$ minutes is equal to $$450$$ minutes, what is the value of $$h$$?
At least how much money should a man have so that he may be left with not less than Rs.$$600$$ after giving half of his money to his wife and one-eight to each of his two sons?
The length of a rectangle is $$5\ cm$$ less than twice its breadth. If the length is decreased by $$5\ cm$$ and breadth is increased by $$2 \ cm$$, the perimeter of the resulting rectangle will be $$74\ cm$$. Find the length and breadth of the original rectangle.
Sristi's salary is $$4$$ times Azar's salary. If together they earn Rs. $$3,750$$ a month, find their individual salaries.
A saleman's commission is $$5\%$$ on all sales upto Rs. $$10,000$$ and $$4\%$$ on all sales exceeding this. He remits Rs. $$31,100$$ to his parent company after deducting his commission. Find the total sales.
The length of a rectangular field is twice its breadth. If the perimeter of the field is $$288 \ \mathrm{m}$$. Find the dimensions of the field.
The sum of three consecutive even numbers is $$336$$. Find them.
If $$5$$ is subtracted from three times a number, the result is $$16$$. Find the number.
Two friends $$A$$ and $$B$$ start a joint business with a capital $$60,000$$. If $$A$$'s share is twice that of $$B$$, how much have each invested?
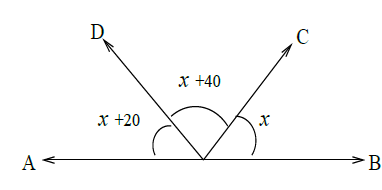
In the figure, $$AB$$ is a straight line. Find $$x$$.
Find two numbers such that one of them exceeds the other by $$9$$ and their sum is $$81$$
Find the number whose sixth part exceeds its eighth part by $$3$$.
The sum of three consecutive multiples of $$7$$ is $$777$$. Find these multiples.
(Hint: Three consecutive multiples of $$7$$ are '$$x$$','$$x+7$$', '$$x+14$$')
The cost of $$7\dfrac{2}{3}$$ meters of cloth is Rs. $$12 \dfrac{3}{4}$$. Find the cost per metre.
What number should $$-\dfrac{33}{16}$$ be divided by to get $$-\dfrac{11}{4}$$?
The distance around a rectangular field is $$400$$ metres. The length of the field is $$26$$ meters more than the breadth. Calculate the length and breadth of the field?
Which is the number when $$40$$ is subtracted gives one-third of the original number?
If $$\dfrac{2}{5}$$ of a number exceeds $$\dfrac{1}{7}$$ of the same number by $$36$$. Find the number.
Venay bought a prizza and cut it into three pieces. When he weighed the first piece he found that it was $$7g$$ lighter than the second piece and $$4g$$ heavier than the third piece. If the whole pizza weighed $$300g$$. How much did each of the three pieces weigh?
Two equal sides of a triangle are each $$5$$ meters less than twice the third side. If the perimeter of the triangle is $$55$$ meters, find the length of its sides?
Solve the following equations:
$$9\cfrac{1}{4}=y-1\cfrac{1}{3}$$
Solve the following equations:
$$\cfrac{z}{2}+\cfrac{z}{3}-\cfrac{z}{6}=8$$
Solve the following equations:
$$\cfrac{2p}{3}-\cfrac{p}{5}=11\cfrac{2}{3}$$
Find three consecutive numbers such that if they are divided by $$10,17,26$$ respectively, the sum of their quotients will be $$10$$.
Solve the following equations:
$$\cfrac{8p-5}{7p+1}=\cfrac{-2}{4}$$
A sum Rs.$$500$$ is in the form of denominations of Rs.$$5$$ and Rs.$$10$$. If the total number of notes is $$90$$ find the number of notes of each denomination.
(Hint: let the number of $$5$$ rupee notes be '$$x$$', then number of $$10$$ rupee notes $$=90-x$$)
Solve the following equations:
$$\cfrac{x}{2}-\cfrac{4}{5}+\cfrac{x}{5}+\cfrac{3x}{10}=\cfrac{1}{5}$$
The difference between two positive integers is $$36$$. The quotient when one integer is divided by other is $$4$$. Find the integers.
In class of $$40$$ pupils the number of girls is three-fifths of the number of boys. Find the number of boys in the class.
Ration is available for $$100$$ students in a hostel for $$40$$ days. How long will it be last, if $$20$$ more students join in the hostel after $$4$$ days?
The present age of Vijaya's mother is four times the present age of Vijaya. After $$6$$ years the sum of their ages will be $$62$$ years. Find their present ages.
Find the two consecutive positive odd integers whose sum is $$32.$$
Solve $$\cfrac{7}{4}-p=11$$
The product of two numbers is $$1296$$. If one number is $$16$$ times the other, find the two numbers?
The largest of $$50$$ measurements is $$3.84$$ kg. If the range is $$0.46$$ kg, find the smallest measurement.
Four times a number reduced by $$5$$ equals $$19$$. Find the number.
Sum of two numbers is $$29$$ and one number exceeds another by $$5$$. Find the numbers.
A rational number is such that when we multiply it by $$\dfrac {5}{2}$$ and add $$\dfrac {2}{3}$$ to the product we get $$\dfrac {-7}{12}$$. What is the number?
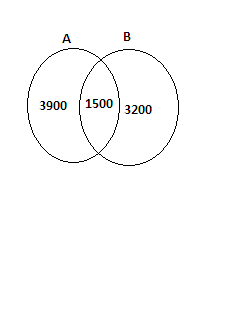
The population of town isOut of these 5400 persons read newspaper A and 4700 read newspaper B. 1500 persons read both the newspapers. Find the number of persons who do not read either of the two papers.
Two trains leave a railway station at the same time. The first train travels due west and the second train due north. The first train travels $$5 km/hr$$ faster than the second train. If after two hours, they are $$50 km$$ apart, find the average speed of each train.
Solve the following equations.
$$\displaystyle \frac{\sqrt{x}}{\sqrt{1 \, + \, x}} \, + \, \sqrt{\frac{1 \, + \, x}{x}} \, = \, \frac{5}{2}.$$
Arun is now half as old as his father. Twelve years ago the fathers age was three times as old as Arun. Find their present ages
One third of one half of one fifth of a number is $$15$$. Find the number
What is the simplest way for a person who has only guineas to pay $$10s. 6d.$$ to another who has only half-crowns?
What is the smallest number of florins that must be given to discharge a debt of pounds $$6s. 6d$$., if the change is to be paid in half-crowns only?
Laxmi's father is $$49$$ years old. He is $$4$$ years older than three time Laxmi's age. What is Laxmi's age?
Separate 178 into two parts, so that the first part is 8 less than twice the second part. Find out the two parts.
To a certain number $$6$$ is added. The sum is multiplied by $$6$$ and the product is divided by $$13$$, then $$7$$ is subtracted from the quotient. If the number obtained after these operations is $$5$$, then the original number is
Solve the following equations, $$\displaystyle \sqrt{x \, + \, 8 \, + \, 2 \sqrt{x \, + \, 7}} \, + \, \sqrt{x \, + \, 1 \, - \, \sqrt{x \, + \, 7}} \, = \, 4.$$
Sharma family went out for a picnic and took three different types of sandwiches with them. Vegetable, grilled and cheese sandwiches were made in a ratio of $$5$$ to $$7$$ to $$8$$. If a total of $$120$$ sandwiches were made, how many grilled sandwiches were made?
The lengths of the sides of a triangle are proportional to the numbers 5, 12, and The largest side of the triangle exceeds the smallest side by 1.6 m. Find the perimeter and the area of the triangle.
If x satisfies $$ | x \, - \, 1 | \, + \,|x \, - \, 2| \, + \,|x \, - \, 3|\,\geq \,6$$ then prove that all numbers x which satisfy the above relation are given by $$x \,\leq \,0$$ or $$x \,\geq \,4$$
Sachin scored twice as many runs as Rahul. Together, their runs fell two short of a double century. How many runs did each one score ?
Solve the following equations and check the solution $$\dfrac{30}{x-5}=5$$
Write down the information in the form of algebraic expression and simplify. there is a rectangular farm with length $$2{ a }^{ 2 }+3{ b }^{ 2 }$$ metre and breadth $${ a }^{ 2 }+{ b }^{ 2 }$$ metre. The farmer used a square shaped plot of the farm to build a house. The side of the plot was $${ a }^{ 2 }-{ b }^{ 2 }$$ metre. What is the area of the remaining part of the farm
Solve $$2x+2=10$$
The sum of three consecutive odd numbers is $$111$$. Find the middle number .
If (-2, 3) and (2, -2) are two solutions of a equation, find equation.
If $$\dfrac{3}{5}$$ is added to twice the reciprocal of a number, the result is $$1$$. Find the number.
Half of a herd of deer are grazing in the filed and three fourth of the remaining are playing nearby, The rest $$9$$ are drinking water from the pond. Find the number of deer in the herd.
A shopkeeper sells mangoes in two types of boxes, one small and one large. A large box contains as many mangoes as $$8$$ small boxes plus $$4$$ loose mangoes If a large box has $$100$$ mangoes, find the number of mangoes, a small box has
Five times a number when added with $$14$$ gives $$49$$. Find the number.
Ankitesh and his friend Jimmy together sold tickets for a charity show for $$Rs\ 3800$$. If Ankitesh sold $$1\dfrac{3}{8}$$ times as much as Jimmy sold, how much did each of them sell the tickets for?
If a labourer earn $$Rs. 672$$ per week, how much will he earn in $$18$$ days?
The sum of three coseccutive multiples of $$7$$ is $$777$$. Find these multiples
Find $$x $$ $$296+x=-148$$
Solve the equation:
$$\dfrac{z}{3}=\dfrac{8}{6}$$
Find $$'x'$$. $$3x+8=5x+2$$.
Solve the following:
The teacher tells the class that the highest marks obtained by a student in her class is twice the lowest marks plus $$7$$. The highest score is $$87$$. What is the lowest score?
If $$8$$ meters cloth cost $$Rs.250$$, find the cost of $$5.8$$ meters of the same cloth.
Population of Sundarnagar was $$234339$$ in the year $$1991$$. In the year $$2001$$ it was found to be increased by $$52303$$. What was the population of the city in $$2001$$
Kanchan spends $$\dfrac{1}{2}$$ of her money in one shop. she spends $$\dfrac{1}{3}$$ of what was left with her on rickshaw fair. At the end she has $$Rs.20$$ with her. How much did she have in the beginning
In an exam, A got $$10\%$$ marks less than B. B got $$25\%$$ more than C, C got $$20\%$$ less than D. If A got $$360$$ marks of $$500$$, what percent did D get
Neha went to a 'sale' to purchase some pants and skirts. When her friend asked her how many of each she had bought, she answered: "The number of skirts is two less than twice the number of pants purchased". Find the number of skirts is four less than four times the number of pants purchased. Help her friend to find how many pants and skirts Neha bought.
Find the value of k, if $$x = -1$$ and $$y = 2$$ is a solution of the equation $$4x - ky = 10.$$
Solve the following linear equations.1) $$2(3 - 2x) = 13$$
2) $$\dfrac{x}{2} = 5 + \dfrac{x}{3}$$
3) $$7(x - 2) =2( 2x - 4)$$
4) $$3x - \dfrac{1}{3} = 2\left( {x - \dfrac{1}{2}} \right) + 5$$
If the wheel of a carriage $$500$$ cm in circumference takes $$\frac{1}{2}$$ second more to complete one revolution, the rate of the carriage per hour will be reduced by $$3$$ km/h. How fast is the carriage travelling ?
$$14\dfrac { 2 }{ 3 } %$$ of a number is 176, find the number.
A fraction becomes $$\dfrac{4}{5}$$ if 1 is added to both numerator and denominator of how ever s is subtracted from both numerator and denominator , the fraction becomes $$\dfrac{1}{2}$$. what is the fraction?
The perimeter of an isosceles triangle is 90m. if the length of the two equal sides is $$\dfrac { 3 }{ 4 }$$ of the length of unequal side, find the dimensions of the triangle?
Find the value of $$p$$ from $$\dfrac{2}{x} +\dfrac{3p}{45}=1$$, when $$\dfrac{x-5}{5} +\dfrac{x-3}{2}=1$$
The sum of two consecutive numbers is $$53$$. Find the numbers
Ibenhal thinks of a number. If she adds 19 to it and divides the sum by 5, she will get 8.
Ram purchased a pen for $$Rs18.50$$, a book for $$Rs70.25$$ and geometry box for $$Rs55.95$$ How much money did Ram spend in all
The sum of a natural number and its reciprocal is $$\dfrac{5}{2}$$ , then the number is __
Set up equations and solve them to find the unknown numbers in the following cases:
Munna subtracts thrice the number of notebooks he has from $$50$$, he finds the result to be $$8$$.
The organisers of an essay competition decide that a winner in the competition gets a prize of Rs $$100$$ and a participant who does not win gets a prize of Rs $$25$$. The total prize money distributed is Rs $$3,000$$. Find the number of winners, if the total number of participants is $$63$$.
Solve $$\dfrac {2x - (7 - 5x)}{9x - (3 + 4x)} = \dfrac {7}{6}$$
The length and width of a rectangle are consecutive odd integers and the perimeter is $$168\ cm$$. Find the length and width of the rectangular.
Evaluate $$x = a + 4\sqrt 5 $$ then, $$\sqrt x - \dfrac{1}{{\sqrt x }} = $$ ?
A car travels $$195\ km$$ in $$3$$ hours.
How long will take to travel $$520\ km$$?
The cost of $$4m$$ of a particular quality of cloth is $$Rs 240$$. Tabulate the cost of $$2m,7m$$ and $$9m$$ cloth of the same type.
If $$8$$ pens cost $$Rs.\ 356$$, what is the cost of $$14$$ pens?
The three sides of a triangle are consecutive integers and their perimeter is $$72\ cm$$. Find the measure of each side of the triangle.
Twice the number is $$24$$ greater than its half. Find the number.
Solve for x in terms of a and f:$$\dfrac{a}{x - f} + \dfrac{f}{x - a} = 2 , \, x \neq o$$.
Solve the equation $$(y-1)=-y+5$$ and represent the solution on:
The cartesian plane
Solve it
$$3x+3y=1 \ \ (i)$$
$$3x+5y=2 \ \ (ii)$$
$$x=?\ y=?$$
Solve the equation $$(y-1)=-y+5$$ and represent the solution on:
the number line
The numerator of a fraction is $$6$$ less then the denomiator. If $$3$$ is added to the numerator, the fraction becomes equal to $$\dfrac {2}{3}$$. Find the original fraction.
Three bags contain $$64.2\ kg$$ of sugar. The second bag contain $$\dfrac {4}{5}$$ of the contents of the first and third contains $$45 \dfrac {1}{2}%$$ of what there is in the second bag. How much sugar is there in each bag?
A workforce of $$420$$ men with a contractor can finish a certain piece of work in $$9$$ months. How many extra men mist be employ to complete the job in $$7$$ months?
$$\begin{array} { l } { \dfrac { 1 } { 3 }^{rd} \text { share of Anwar's property is equal to Rs. } 15000 \text { , find the value of } \dfrac { 2 } { 5 } th\text { part of } } \\ { \text { property? } } \end{array}$$
Present age of Pranesh is four times the age of his son. Five years ago, the sum of their ages was 50 years. What is the present age of Pranesh?
If the weight of $$12$$ sheets of thick paper is $$40$$ grams, how many sheets of the same paper would weigh $$16\dfrac{2}{3}$$ kilogram?
The sum of $$2$$ consecutive numbers is $$45$$ find those numbers.
Alka spends $$90\%$$ of the money that she receives every month, and save $$Rs. 120$$. How much money does she receives monthly?
If $$y=7,$$ find the value of $$y^3-3(y-2)$$.
If $$19=353\times 32.63\left[ \dfrac { 1 }{ 302.5 } -\dfrac { \left( m+1 \right) }{ m } \dfrac { 1 }{ 643 } \right] $$ then find the value of $$m$$.
Deeepak is twice as old as his brother Vikas. If the difference of their ages be $$11$$ years, find their present ages.
find the value of:-
$$200y - 51 = 49$$
In the year 2010 in the village there were 4000 people who were literate. Every year the number of literate people increases byHow many people will be literate in the year 2020?
Hari Babu left one third of his property to his son,one -fourth to his daughter and the remainder to his wife. If his wife share is $$Rs.18000$$,what was the worth of his total property?
A man spent $$72\%$$ of his salary and remaining were his savings. If he saved $$Rs\ 7,200$$ per month, find his month income.
By what number should $$\left[\left(\dfrac{-5}{2}\right)\right]^{3}$$ be multiplied to get $$\left(\dfrac{-2}{5}\right)^{5}$$?
$$20\%$$ of dolls produced in a factory were defecting , $$25\%$$ of the remaining were damaged, if $$4800$$ dolls were left over , what was the original number of dolls?
In a $$3-digit$$ number, the hundreds digit is twice the tens digit while the units digit is thrice the tens digits. Also , the sum of its digits is $$18$$. Find the number.
Archana bought some kilograms of wheat. She requires $$12\ kg$$ per month and she got enough wheat milled for $$3$$ months. After that , she had $$14\ kg$$ left. How much wheat had Archana bought altogether ?
Mrs. Ghosh bought 1 kg of grapes and served each member of her family an equal amount. How many people did she serve it to if each person got $$\dfrac 14$$ of a kg?
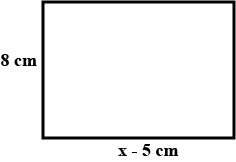
If the perimeter is $$40\ \text{cm}$$, make an equation, and find $$x$$.
Oranges are to be transferred from larger boxes to smaller boxes. When a larger box is emptied, the oranges from it fill $$3$$ smaller boxes and still $$7$$ oranges are left. If the number of oranges in a small box are taken to be $$x$$, then what is the number of oranges in the larger box
Solve the following equations by systematic method.
$$n-\dfrac{3}{5}=8$$
Solve for x$$\dfrac { \sqrt { 4x+1 } +\sqrt { x+3 } }{ \sqrt { 4x+1 } -\sqrt { x+3 } } =\dfrac { 4 }{ 1 } $$
Solve the following equations by systematic method.
$$-7a=84$$
The sum of five consecutive odd numbers is 85 . Find the numbers.
Add $$7$$ to $$3$$ times of a number, you get $$34$$. Find the number.
Solve for $$x:2 \left(\dfrac{2x + 3}{x - 3}\right) - 25 \left(\dfrac{x - 3}{2x + 3}\right) = 5$$.
2 \left(\dfrac{2x + 3}{x - 3}\right) - 25 \left(\dfrac{x - 3}{2x + 3}\right) = 5$$.
The difference between the square of two consecutive numbers is $$31$$. Find the numbers.
Solve:
$$\dfrac {x+2}{2}=13$$
A bird flies $$1$$ kilometer in one minute. Can you express the distance covered by the bird in terms of its flying time in minutes? [use $$t$$ for flying time in minutes]
Radha takes some flowers in a basket and visit three temples one by one. At each temple, she offers one half of the flowers from the basket. If she is left with $$3$$ flowers at the end, find the number of flowers she had in the beginning.
Purse contains $$Rs. 250$$ in the domination of $$Rs. 10$$ and $$Rs. 50$$. If the no. of $$Rs. 10$$ notes is one more than that of $$50$$ notes.
The sum of two consecutive odd integers is $$44$$. Find the two integers.
The sum of two consecutive integers is $$39$$. Find the two integers.
Find the value of $$x$$ : $$- 2 = - x + 12$$
Find three consecutive even numbers whose sum is $$66$$.
Find the distance covered by the wheel of a car in 500 revolutions if the diameter of the wheel is 77 cm.
If sum of two number is 17 and sum of their reciprocal is $$\dfrac{17}{62}$$ write the representation of given situation
If $$11$$ is subtracted from $$4$$ times a number, the result is $$89$$. Find the number.
Solve the following riddle:
I am a number, Tell my identity!
Take me seven times over, And add a fifty!
To reach a triple century, You still need forty!
The difference between 2 no. is6 times the smaller number plus the smaller number is 77.
Solve:
$$\dfrac { 2 } { 3 } \left( x + \dfrac { 3 } { 5 } \right) = \dfrac { 7 } { 2 }$$
A chemist needs to strengten as $$15$$% alcoholic solution of one of $$32$$% alcoholic. How much pure alcohol should be added to $$800\ mL$$ of $$15$$% solution?
The sum of ages of Priyanka and Deepika is $$34$$ years. Priyanka is elder to Deepika by $$6$$ years. Then find Priyanka's present age.
A train $$320\ m$$ long is travelling at a uniform speed of $$66\ km/hr.$$ If it passes a platform is $$42$$ seconds, find the length of the platform .
$$4\dfrac{1}{2} z + 4\dfrac{1}{3}$$ $$z = 100$$ find $$z$$.
Find the value of $$x$$ is $$\dfrac{1-x}{6}+\dfrac{2x}{3}-\dfrac{1-\dfrac{3}{7x}}{4}=2\dfrac{1}{6}$$
In a garage, there are a total of $$40$$ cars and motorbikes. The total number of tyres of these $$40$$ vehicles is $$140$$ , Find the number of cars.
solve x: $$\dfrac { 1 }{ a+b+x } =$$$$\dfrac { 1 }{ a } +\dfrac { 1 }{ b } +\dfrac { 1 }{ x } $$
Six years ago a father was seven times as old as his son.After six years he will be three times as old as his son.Determine their present ages.
The average of $$3$$ angles of a quadrilateral which are in the ratio of $$2:4:5$$ is $$77^{o}$$. Find all the angles of the quadrilateral.
A photograph of a bacteria enlarged 50,000 times attains a length of 5 cm as shown in the diagram. What is the actual length of the bacteria? If the photograph is enlarged 20,000 times only, what would be its enlarged length in cm?
A natural number, when increased by 12, becomes equal to 160 times its reciprocal. Find the number.
Solve the following equations
$$5x-2=18$$
Sameer changed $$\text{Rs.}\ 200$$ into $$\text{Rs.}\ 5, \text{Rs.}\ 20$$ and $$\text{Rs.}\ 50$$ notes. If the number of $$\text{Rs.}\ 5$$ notes was double the number of $$\text{Rs.}\ 20$$ notes, and the $$\text{Rs.}\ 50$$ notes were one-fifth the $$\text{Rs.}\ 20$$ notes, how many notes of each denomination did he get?
Some tickets of $$Rs.200$$ and some of $$Rs.100$$, of a drama in a theater were sold. The number of tickets of $$Rs.200$$ sold was $$20$$ more than the number of tickets of $$Rs.100$$. The total amount received by the theatre by sale of tickets was $$Rs.37000$$. Find the number of $$Rs.100$$ tickets sold.
A man buys 12.60 kg of one type of rice for Rs 30 per kg and 15 kg of another type of rice for Rs 67.90 per kg. If he mixes them and makes packets, each containing 3,450 g of rice, how many such packets of rice are there and what is the cost of each packet ?
If $$\dfrac {1}{2}$$ is subtracted from a number, and the difference is multiplied by $$4$$, the result obtained is $$5$$. Find the number.
When Raju multiplies a certain number by $$17$$ and adds $$40$$ to the product, he gets $$225$$.Find the number?
Solve:$$\dfrac { x+2 }{ 6 } -\left( \dfrac { 11-x }{ 3 } -\dfrac { 1 }{ 2 } \right) =\dfrac { 3x-4 }{ 12 } $$
The price of $$2$$ tables and $$3$$ chairs is $$Rs.340$$. A table costs $$Rs.20$$ more than a chair. What is the price of a table ?
Find your weight if your friend's weight is $$20$$% more than you and your friend's weight is $$48\ kg$$.
By what number should $${ (15) }^{ -1 }$$ be multiplied so that the product may be equal to $${ (-5) }^{ -1 }$$?
Solve:$$\dfrac{2x-3}{2}-\dfrac{x+1}{3}=\dfrac{3x-8}{4}$$
Solve:$$5x-3=3x+5$$
Solve:$$3x+\dfrac{1}{2}=\dfrac{3}{8}+\dfrac{x}{4}$$
A father is now three times as old as his son. Five years back, he was four times as old as his son. The present age of the son(in years) is
Two numbers are in the ratio $$5:3$$. If their difference is $$18$$ then find the numbers.
Solve :- $$8x+3 = 27 +2x$$
Sum of two integers is $$36$$. If one of the number be the half of the other then find the numbers.
Solve:
$$\dfrac{3a-2}{7}-\dfrac{a-2}{4}=2$$
Solve and check the solution in the following equation.
1. $$x+7=9$$
2.$$\dfrac{x}{4}=25$$
3.$$9y=-135$$
4.$$15-x=4$$
5.$$3(x-3)=15$$
6.$$7y+3=9$$
The digit of tens place of a 2 digit is 3 times the digit at a unit place of the digit are reversed, the new number will be 36 less the original number. Find the original number.
$$2x-3=55$$
The sum of $$3$$ consecutive numbers is $$36$$ find the numbers.
If the speed of a car is increased by 10 km per hr, it takes 18 minutes less to cover a distance of 36 km. find the speed of the car.
Solve each of the following system of equations in R.
$$x+\dfrac { 1 }{ 3 } >\dfrac { 8 }{ 3 } $$
How are the points $$(-1,-2), (-2, 3)$$ and $$(1, 4)$$ situated with respect to the circle $${x}^{2}+{y}^{2}-2x–5y+3=0$$
Solve each of the following of equations in R.
$$ \dfrac { 3x-4 }{ 2 } \le \dfrac { 5 }{ 12 } $$
The sum of two angles is $$90$$ degrees. The angles are in the ratio $$2:3.$$ Find the measure of each angle.
In a circket match,Sachin makes his score thrice the Sehwags's score. Both of them together make a total score of $$200$$ runs.
A number is $$25$$ more than its $$\left(\dfrac{5}{6}\right)^{th}$$ part. Find the number.
If the weight of the boy holding flower pot is $$47.5$$kgs Find the weight of the cat

Solve:
$$\dfrac { 1 }{ x } +\dfrac { 1 }{ x+1 } -\dfrac { 2 }{ x-1 } =0$$
In $$\triangle$$ $$ PQR$$ if $$\angle$$ $$P = 45^{\circ }$$ , and $$\angle Q = 75^{\circ}$$ , then the measure of $$\angle R = $$ is ..............
2 . The exponential form of $$225$$ is ...........
3 . The algebraic expression whit three terms is called .......
4 . $$65$$ % in the simple interest from is ......
5 . the area of parallelogram is $$320 sq. c m$$ and base is $$4 0 c m$$ , its height is ..........
Mr. Grover is three times as old as his son and the sum of their ages is $$48$$. How old is each?
Andy has twice as many marbles as pandy, and sandy has half as many has Andy and pandy put together. If Andy has $$75$$ marbles more than Sandy. How many does each of them have
solve for x :$$ 3\left( \dfrac { 3x-1 }{ 2x+3 } \right) -2\left( \dfrac { 2x+3 }{ 3x-1 } \right) =5;x\neq \dfrac { 1 }{ 3 } ,-\dfrac { 3 }{ 2 } $$
It the cinema hall, 500 tickets was sold. The total sale was Rs. 12,The tickets were of denomination of Rs. 15 and Rs.How many of each denomination were sold
An odd number of stones are placed at equal intervals of $$10$$ meters in a row on the field.All stones are be gathered at the place of the stone are be gathered at the place of the stone in the middle.If a man can carry only one stone at a time and starts from one of the end stones,he has to cover $$3km$$ for the work.How many stones were there?
The sum of three consecutive natural numbers isFind the numbers.
Six more than four times a number is four less than five times the number. Find the number.
The sum of the squares of two consecutive odd numbers is 394. Find the numbers.
Solve $$3x-14=4$$
Ranjana's mother gave her Rs. 245 for buying New Year cards. If she got some 10 -rupee cards, $$ \dfrac { 2 } { 3 } $$ as many 5 rupee cards, and $$ \dfrac { 1 } { 5 } $$ as many 15 -rupee cards, how many of each kind did she buy?
Shalini's weight is 3500 g greater than her younger brother. The weight of her brother is 35 kg. Find shalin's weight.
Solve $$12q-5=25$$
$$\frac{x}{2.8}=\frac{1}{1.4}$$
$$\displaystyle \frac{x+6}{4}-\frac{5x-4}{8}+\frac{x-3}{5}=0$$
$$4w=30$$
$$c-2=-5$$
The temperature at $$07:00$$ is $$-3^{\circ}C$$. This temperature is $$11^{\circ}C$$ higher than the temperature at $$01:00$$. Find the temperature at $$01: 00$$.
Teacher tells the class that the highest score obtained by a student are 9 more than thrice the lowest score. If the highest score isWhat is the lowest score?
Express the given linear equation in the form $$ax + by + c = 0$$ and indicate the values of $$a, b$$ and $$c$$ in given case:
$$y - 5 = 0$$.
The boys and the girls in a school are in the ratio of $$7:4$$. If the total strength of the school is $$550$$, then find the number of boys and girls.
Sum of two numbers is $$81$$. One is twice the other.
If smaller number is $$x$$, the other number is _______.
The sum of two numbers is $$60$$ and their difference is $$30$$.
The difference of numbers in term of $$x$$ is ______.
Find the value of x in the following.
$$\sqrt[3]{3x-2}=4$$.
Solve for $$x$$: $$\sqrt{x + 1} - \sqrt{x - 1}$$ = 1
Sum of two numbers is $$81$$. One is twice the other.
The solution of the equation is _______.
On simplification $$\dfrac{3x+3}{3}$$ = __________ .
In a test Abha gets twice the marks as that of Palak. Two times Abha's marks and three times Palak's marks make $$280$$.
Marks obtained by Abha are ______.
Sum of the digits of a two-digit number is $$11$$. The given number is less than the number obtained by interchanging the digits by $$9$$. Find the number.
What number divided by 520 gives the same quotient as 85 divided by 0.625?
Solve: $$\dfrac{3x-8}{2x}=1$$
In a bag, there are $$5$$ and $$2$$ rupee coins. If they are equal in number and their worth is $$Rs 70$$, then
There are _______ $$5$$ rupee coins and _______ $$2$$ rupee coins.
Solve: $$\frac{5(1-x)+3(1+x)}{1-2x}=8$$.
Sum of two numbers is $$81$$. One is twice the other.
The numbers are ______ and ______.
For what value of $$c,$$ the linear equation $$2x+ cy = 8$$ has equal values of $$x$$ and $$y$$ for its solution.
The sum of two consecutive multiples of $$10$$ is $$210$$. Find the smaller multiple..
Two numbers are in the ratio $$ 5 : 6 . $$ If $$ 8 $$ is subtracted from each of the numbers , the ratio becomes $$ 4 : 5 $$ find the numbers.
Fill the blanks to make the statement true:
After $$18$$ years, Swarnim will be $$4$$ times as old as he is now. His present age is ________.
Fill the blanks to make the statement true:
The share of $$A$$ when Rs. $$25$$ are divided between $$A$$ and $$B$$ so that $$A$$ get Rs $$8$$ more than $$B$$ is ________.
Fill the blanks to make the statement true:
When a number is divided by $$8$$, the result is $$-3$$. The number is _______.
Orange are to be transferred from larger boxes into smaller boxes. When a large box is emptied, the oranges from it fill two smaller boxes and still, $$10$$ oranges remain outside, if the number of oranges in a small box are taken to be x, what is the number of oranges in the larger box?
If the length of the sides of a triangle is in the ratio $$3:4:5$$ and its perimeter is $$48$$ cm, find its sides.
The length of a rectangle is $$ 5 \,cm $$ less than twice its breadth . If the length is decreased by $$ 3 \,cm $$ and breadth increased by $$ 2 \,cm $$ , the perimeter of the resulting rectangle is $$ 72 \,cm $$ . Find the area of the original rectangle.
The differences between an integer $$x$$ and $$(-9)$$ is $$6$$. Find all possible values of $$x$$.
A rectangle is $$ 10 \,cm $$ long and $$ 8 \,cm $$ wide . When each side of the rectangle is increased by $$ x \,cm $$ , its perimeter is doubled . Find the equation in $$ x $$ and hence find the area of the new rectangle.
Solve the following equation:
$$ \dfrac{(2x - 3)}{(2x - 1)} = \dfrac{(3x - 1)}{(3x + 1)} $$
What is the condition for an equation of the form $$ax^2 + bx + c = 0$$ to become a linear equation.
In a competitive examination , 1 mark is awarded for each correct answer while $$ 1/2 $$ marks is deducted for every wrong answer . jayanti answered $$ 120 $$ question and got $$ 90 $$marks . How many question did she answer correctly $$ Rs $$.
A box contains $$x\ 50$$ paise coins, $$2x\ $$one-rupee coins and $$5x$$ two-rupee coins. If the total value of these coins is Rs. $$25$$ what is the value of $$x$$?
A family is using Liquefied petroleum gas (LPG) of weight 14.2 kg for consumption. (full weight 29.5 kg includes the empty cylinders tare weight of 15.3 kg.). If it is use with constant rate then it last for 24 days. Then the new cylinder is replaced
Find the equation relating the quantity of gas in the cylinder to the days
In a study of bat migration habits, $$240$$ male bats and $$160$$ female bats have been tagged. If $$100$$ more female bats are tagged, how many more male bats must be tagged so that $$\displaystyle \frac{3}{5}$$ of the total number of bats in the study are male?
The sum of $$3$$ consecutive multiples of $$8$$ is $$888$$. Find the multiples
If $$f(x)=4x^3-6x^2\cos 2a+3x\cdot \sin 2a\cdot \sin 6a+\sqrt {\log(2a-a^2)}$$, then show that $$f'\left (\dfrac {1}{2}\right ) > 0$$
According to a plan, a team of woodcutters had to cut $$216 m^3$$ of wood in several days. The. first three days, the team fulfilled the daily assignment, and then it cut 8 $$m^3$$ of wood over and above the plan every day. Therefore, a day before the planned date they cut $$232 m^3$$ of wood. How many cubic metres of wood a day did the team have to cut according to the plan?
Some ticket of 200 and some of 100, of a drama in theatre were sold. The number of tickets of 200 sold was 20 more than the number of tickets of The total amount received by the theatre by sale of tickets was Find the number of 100 tickets sold.
In a scout camp, there is a food provision for 300 cadets for 42 days. If 50 more persons join the camp for have days will the provision last?
The teacher tells the class that the highest marks obtained by a student in her class is twice the lowest marks plus $$7$$. The highest score is $$87$$. What is the lowest score?
$$Rs\ 6400$$ were divided equally among $$x$$ persons. Had this money been divided equally among $$(x+14)$$ persons, each would have got $$Rs\ 28$$ less. Find the value of $$x$$
Class 8 Maths Extra Questions
- Algebraic Expressions And Identities Extra Questions
- Comparing Quantities Extra Questions
- Cubes And Cube Roots Extra Questions
- Data Handling Extra Questions
- Direct And Inverse Proportions Extra Questions
- Exponents And Powers Extra Questions
- Factorisation Extra Questions
- Introduction To Graphs Extra Questions
- Linear Equations In One Variable Extra Questions
- Mensuration Extra Questions
- Playing With Numbers Extra Questions
- Practical Geometry Extra Questions
- Rational Numbers Extra Questions
- Squares And Square Roots Extra Questions
- Understanding Quadrilaterals Extra Questions
- Visualising Solid Shapes Extra Questions