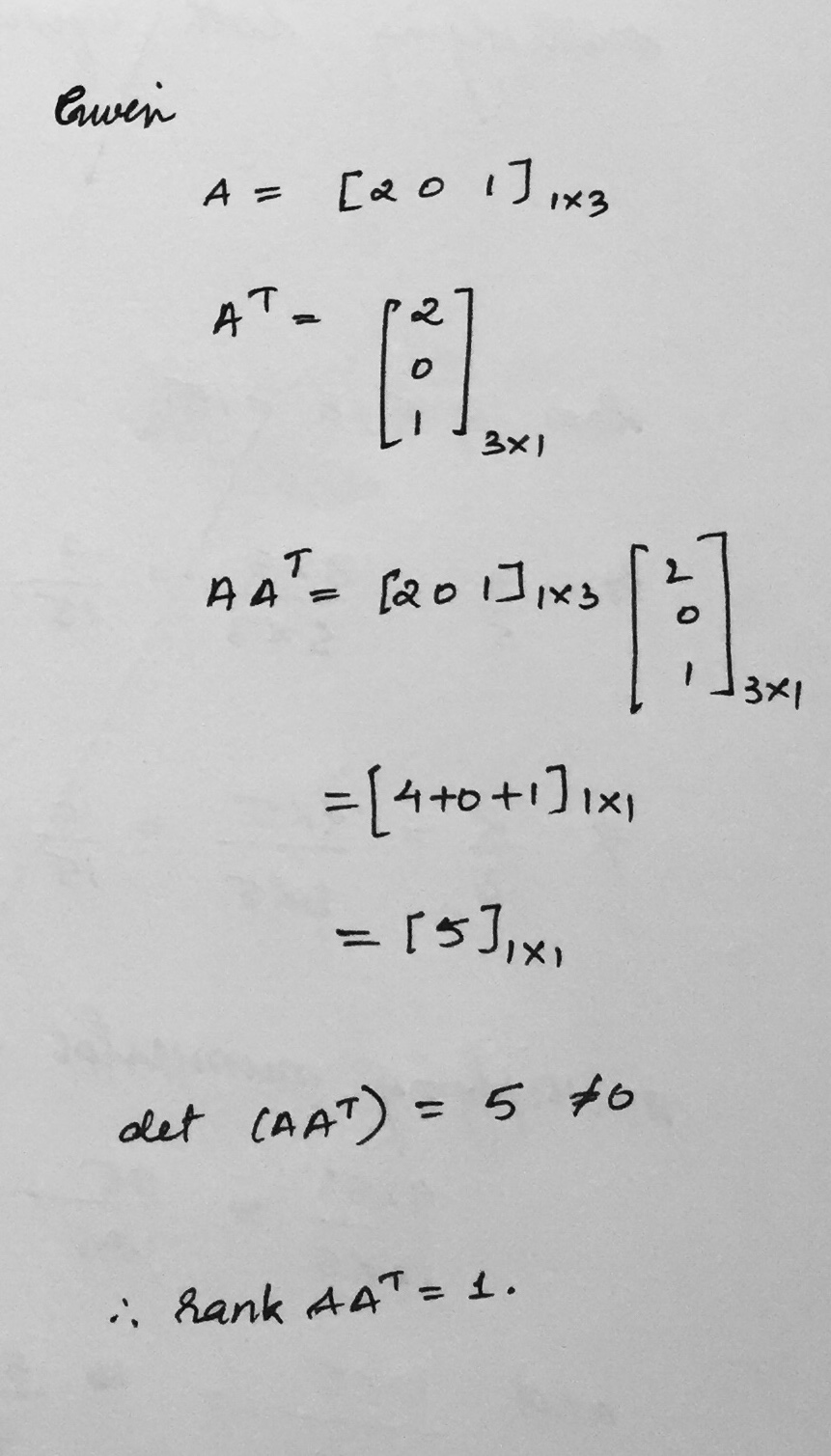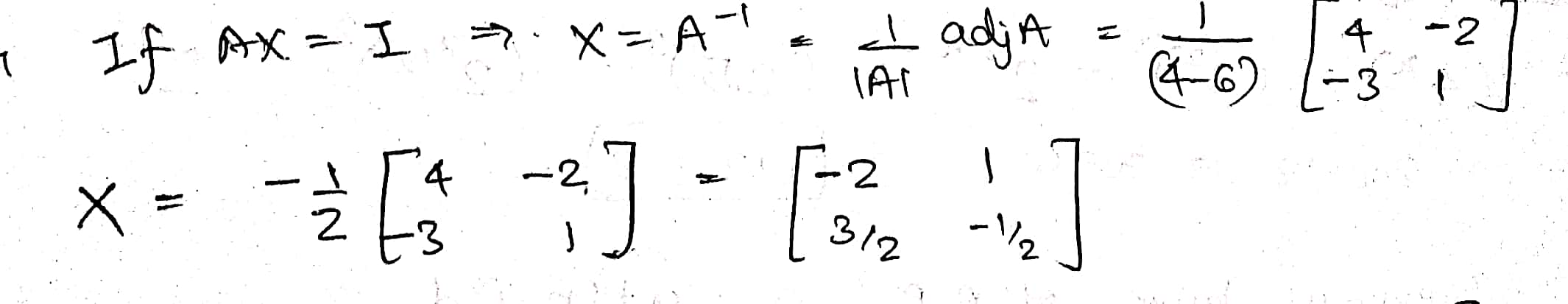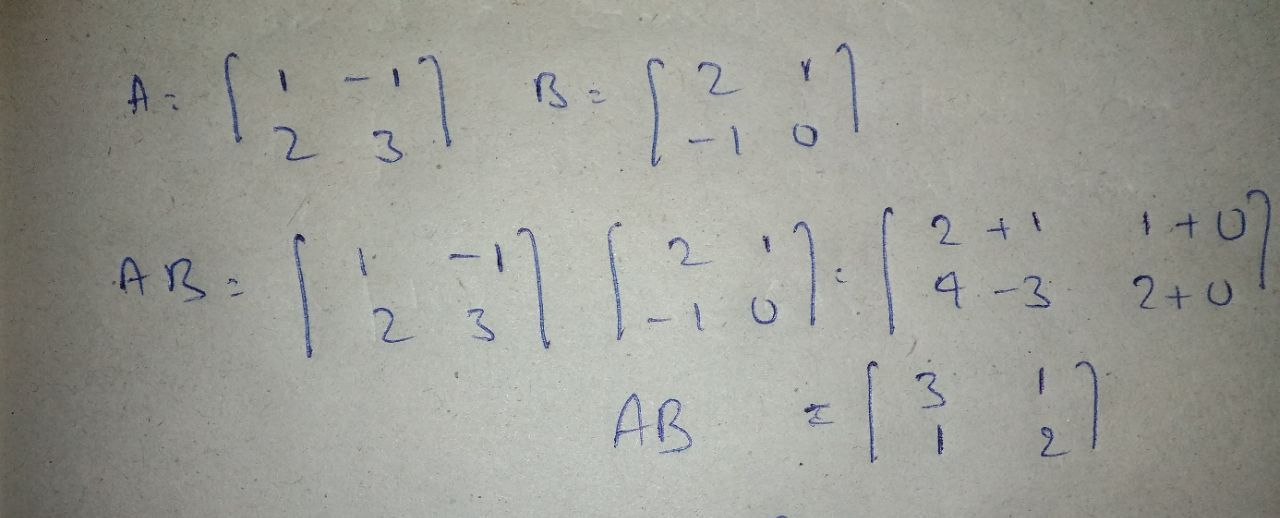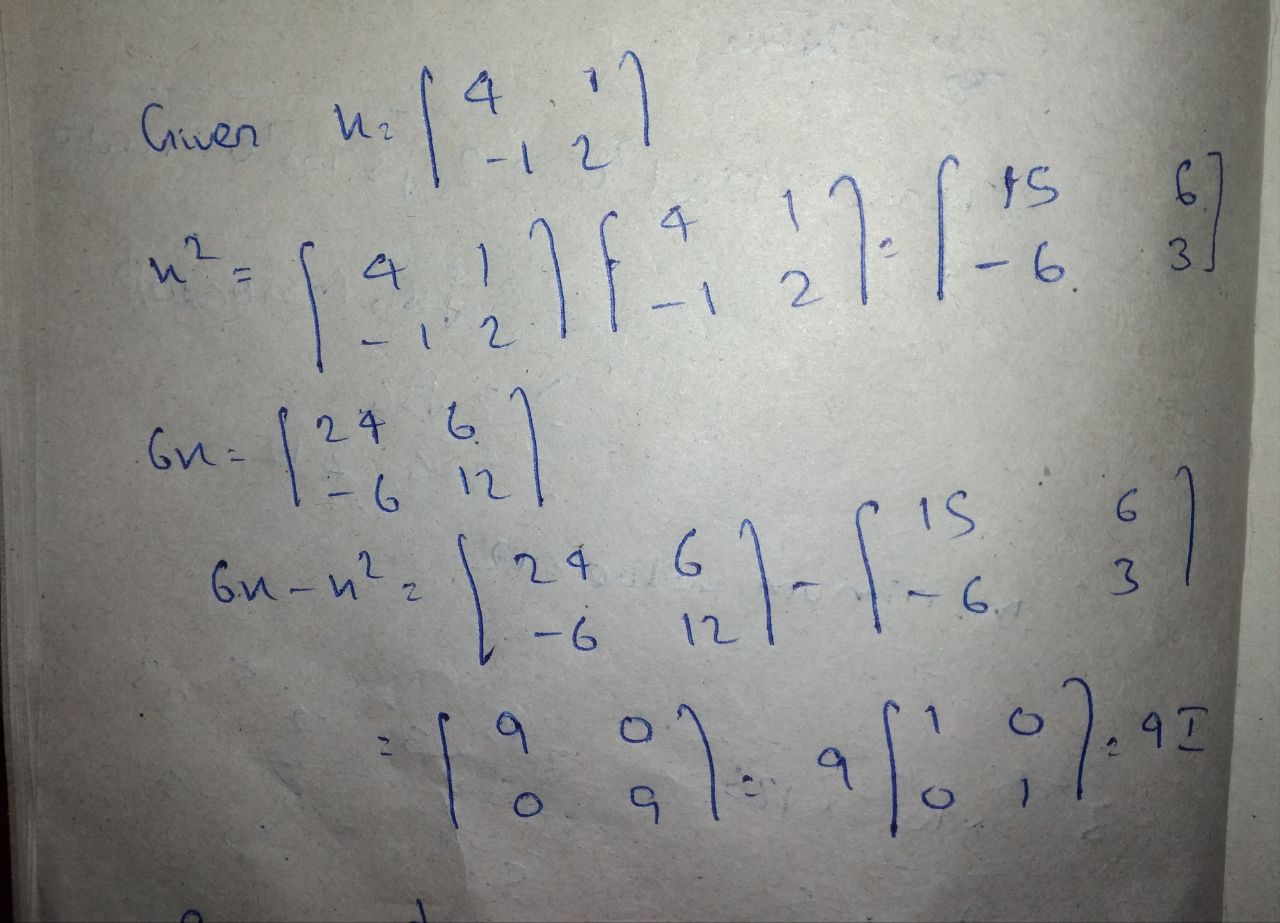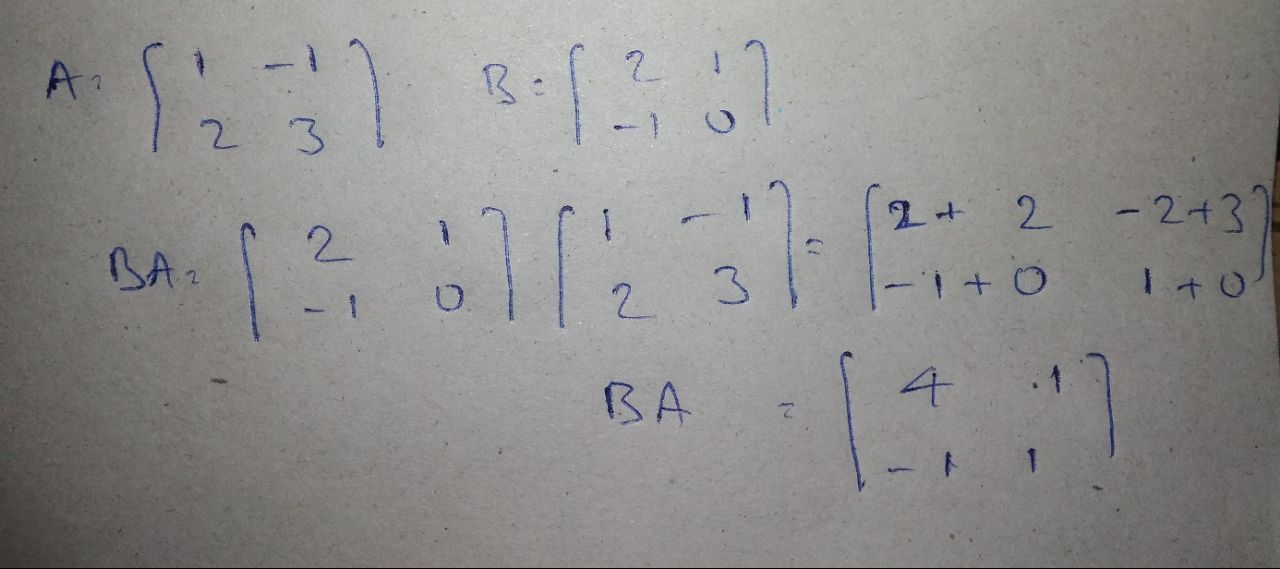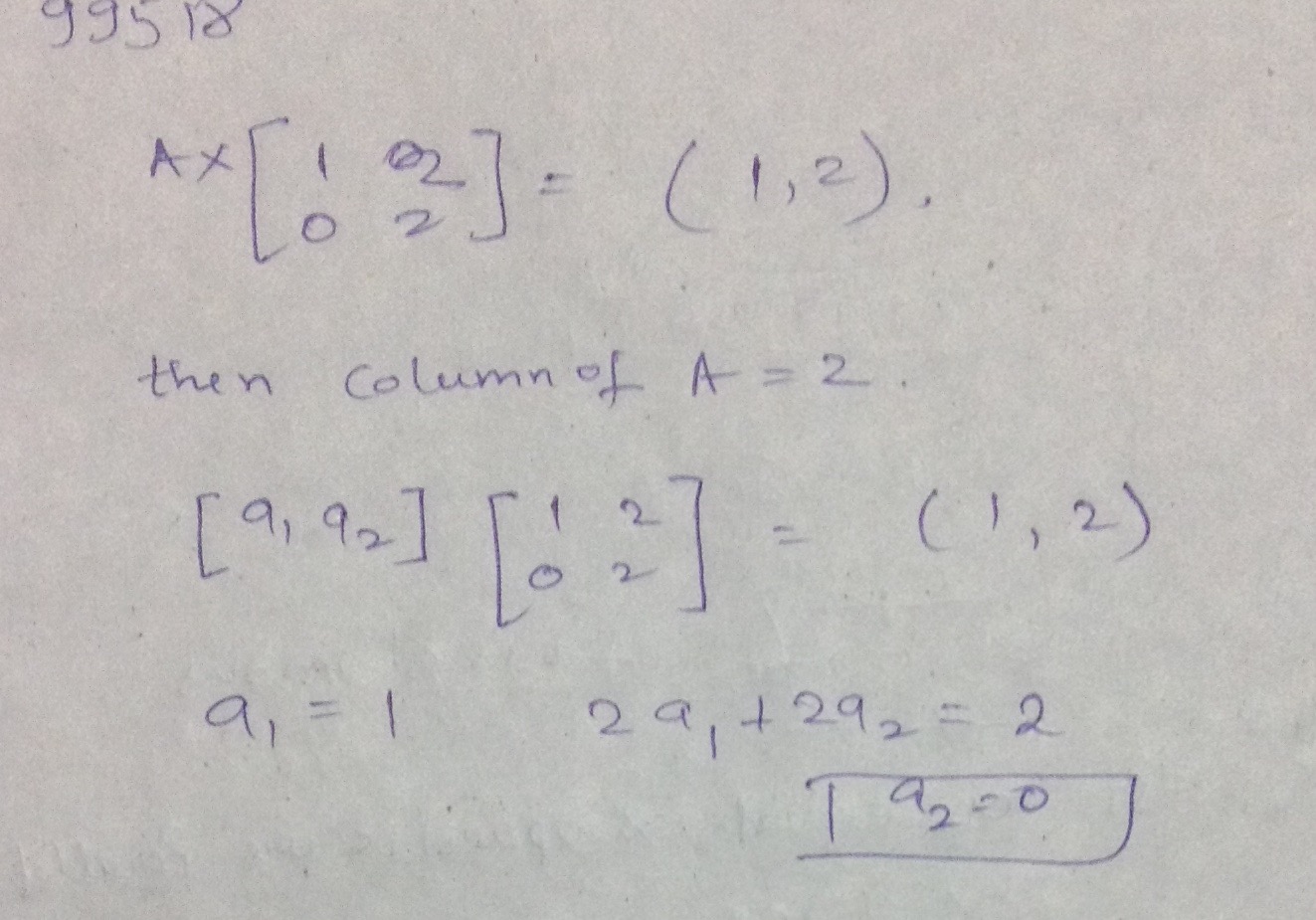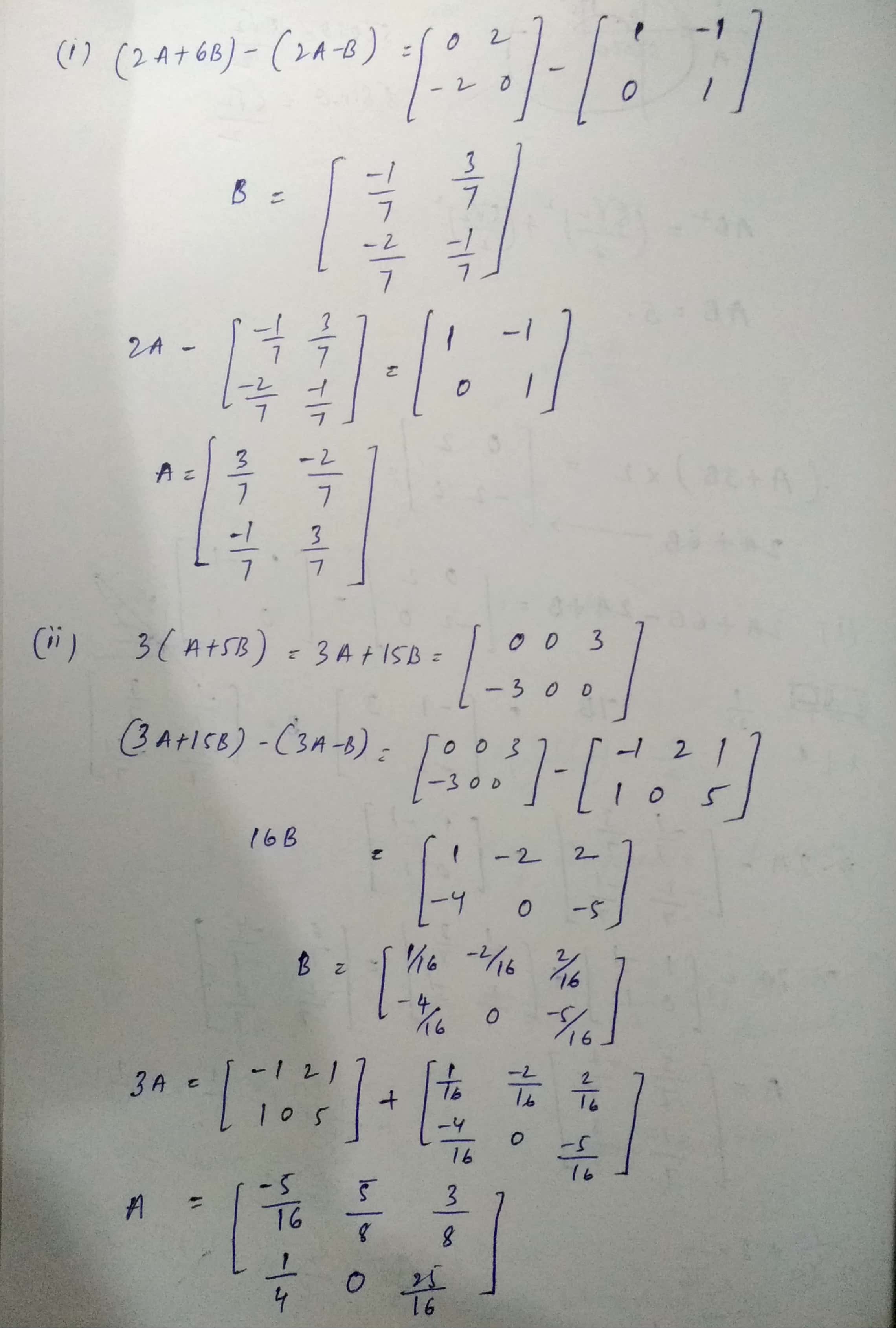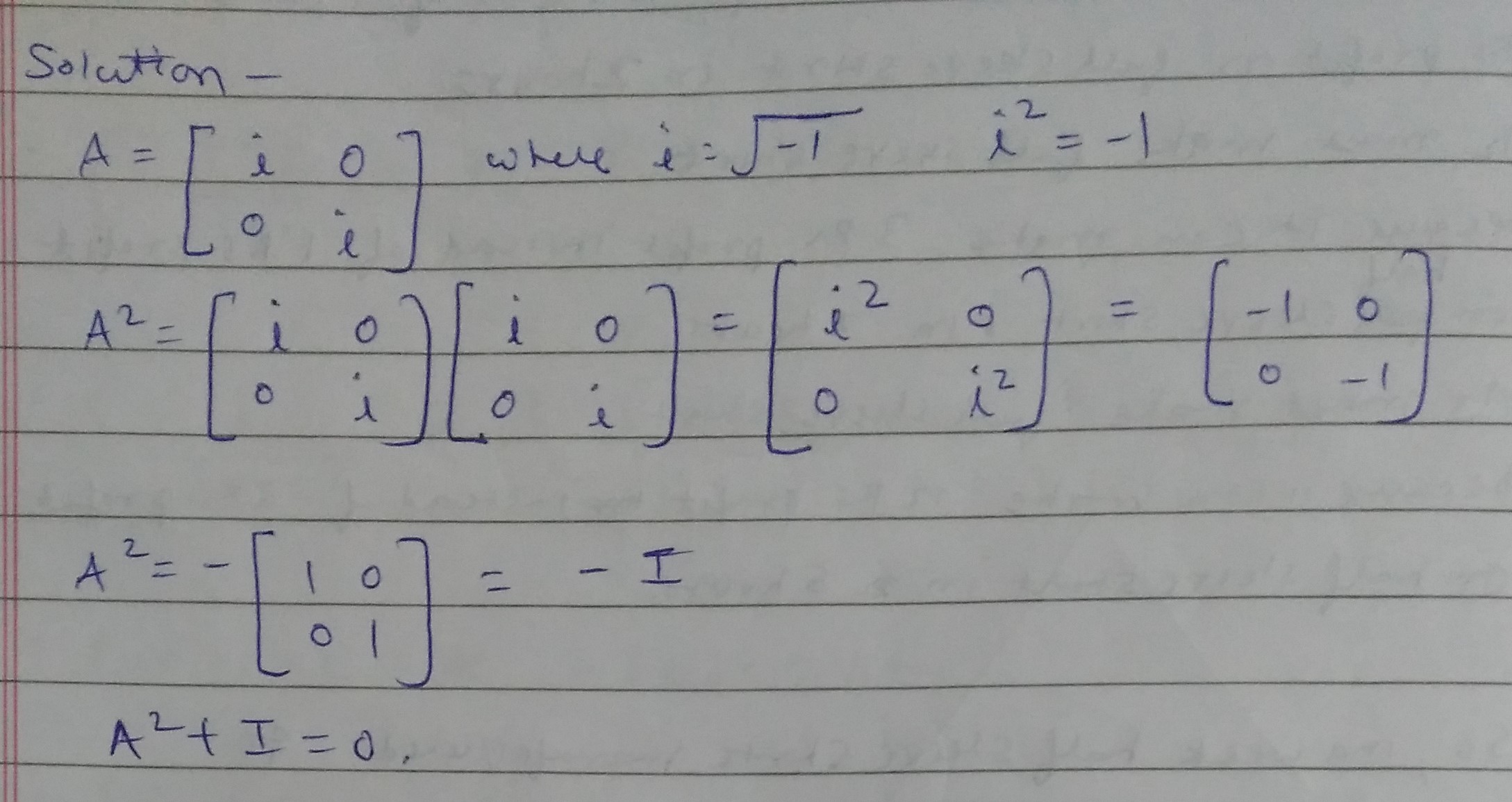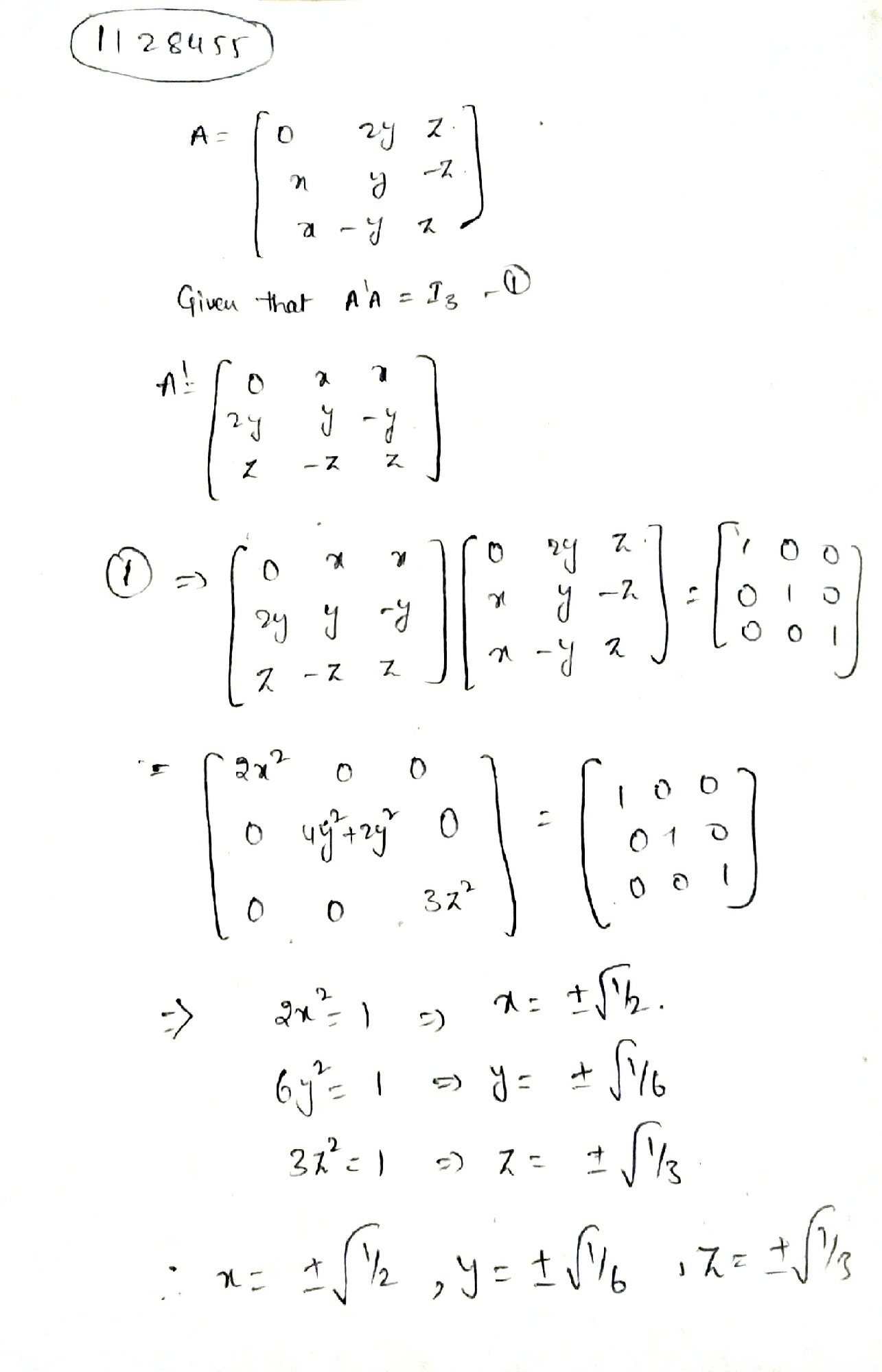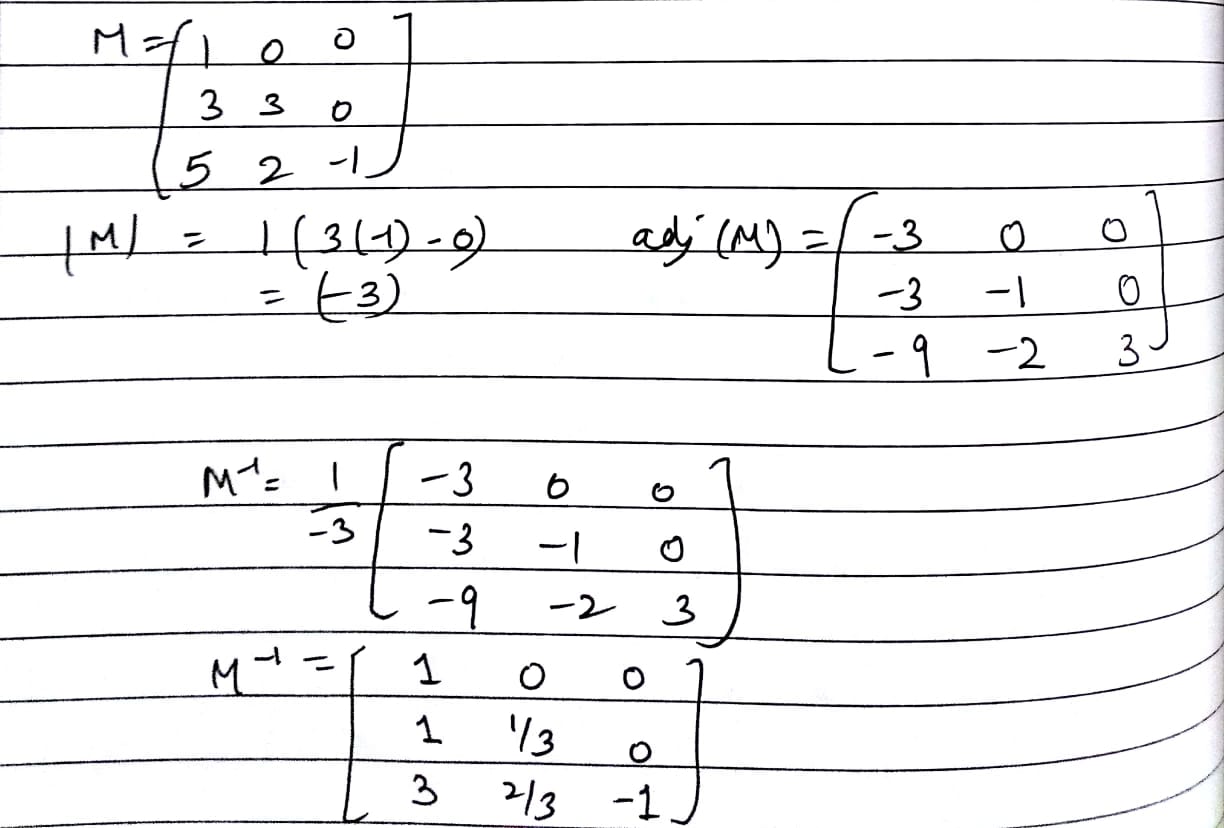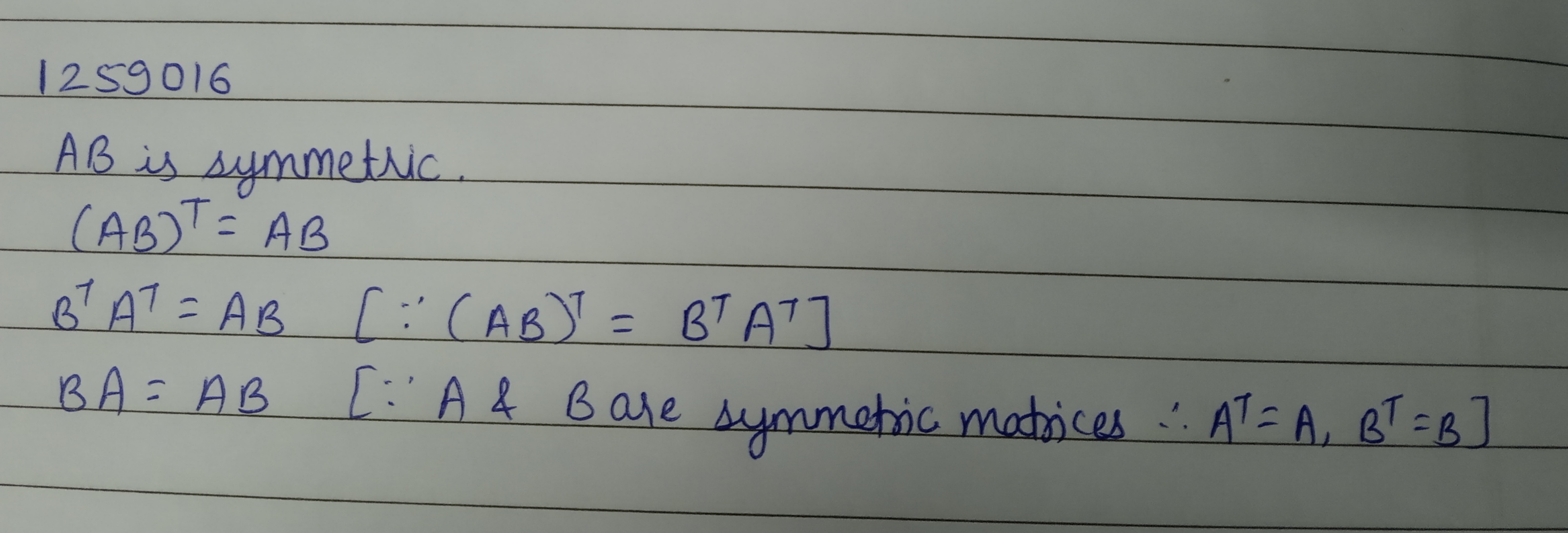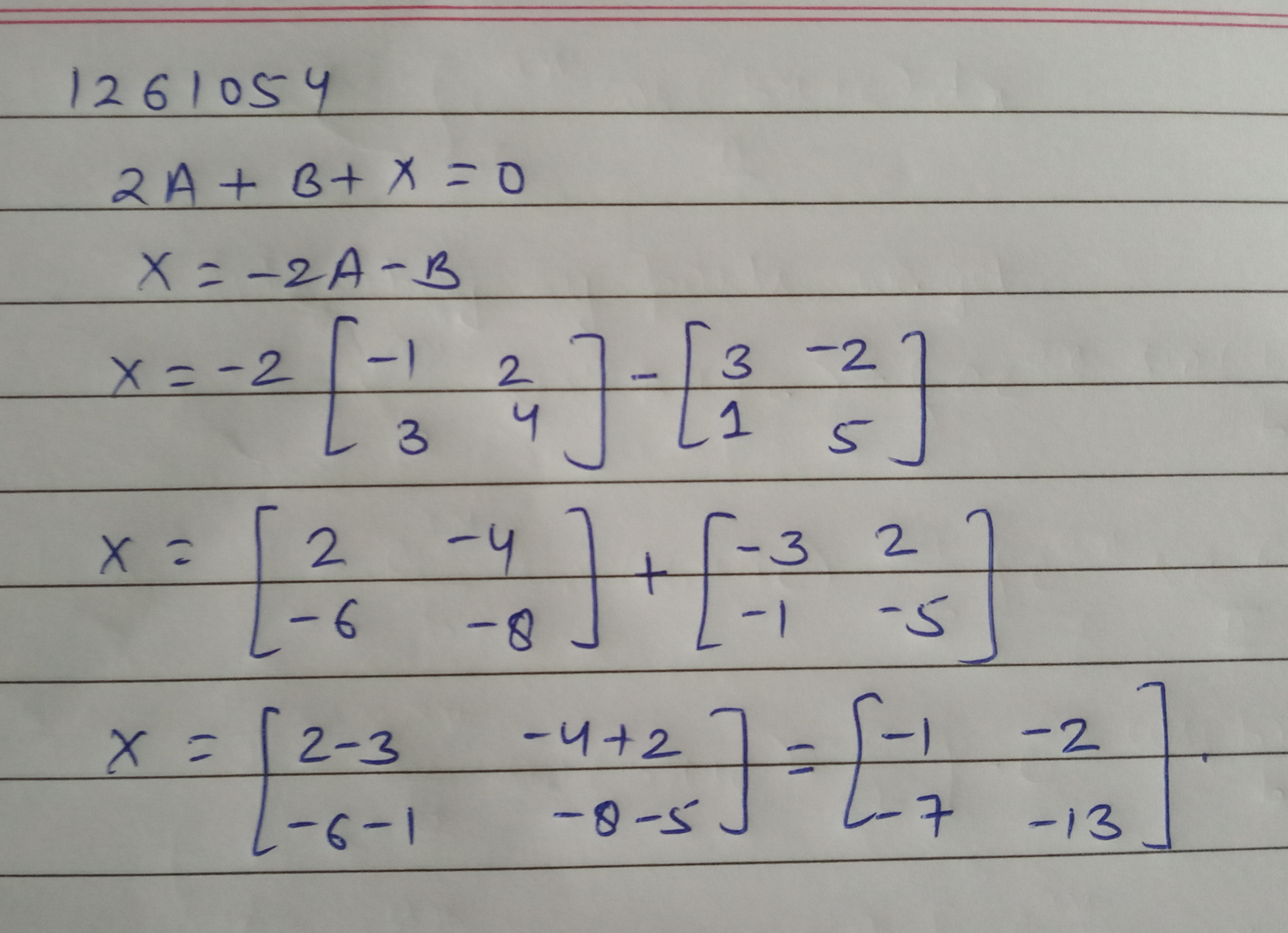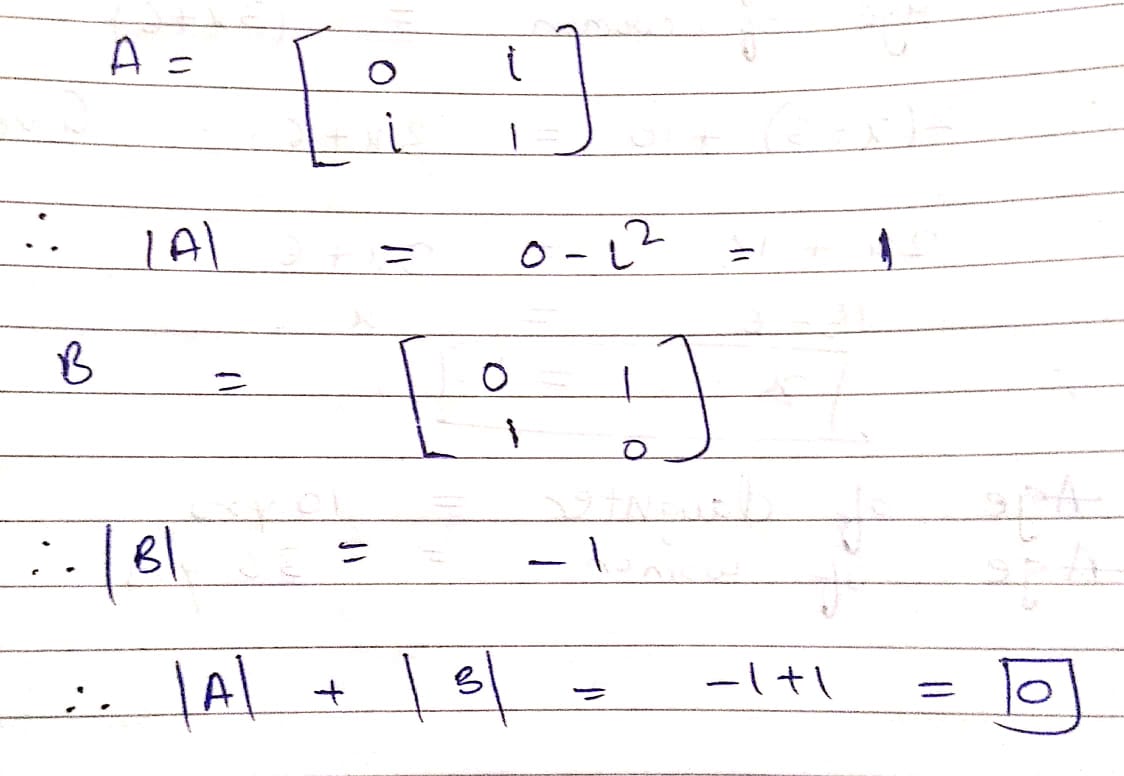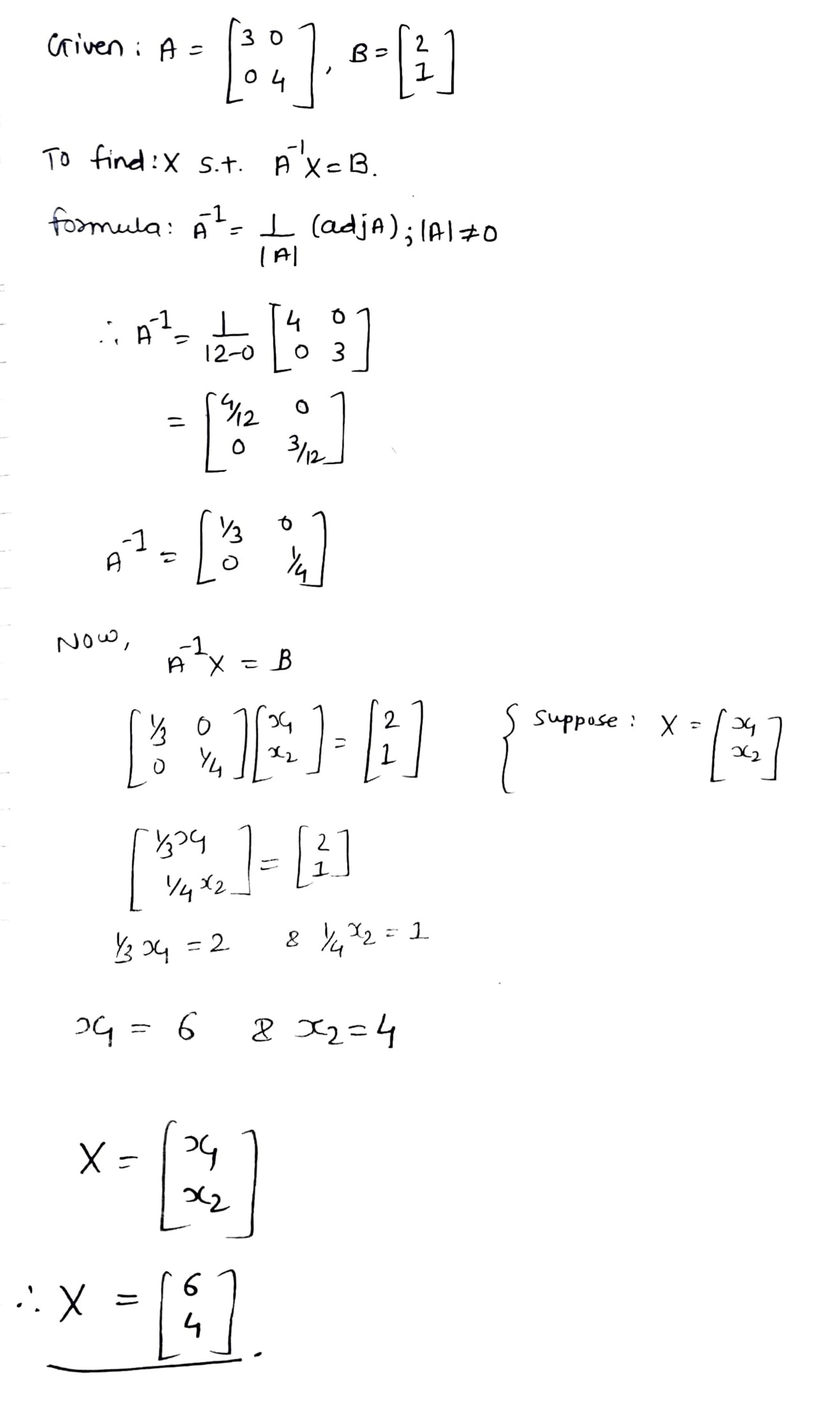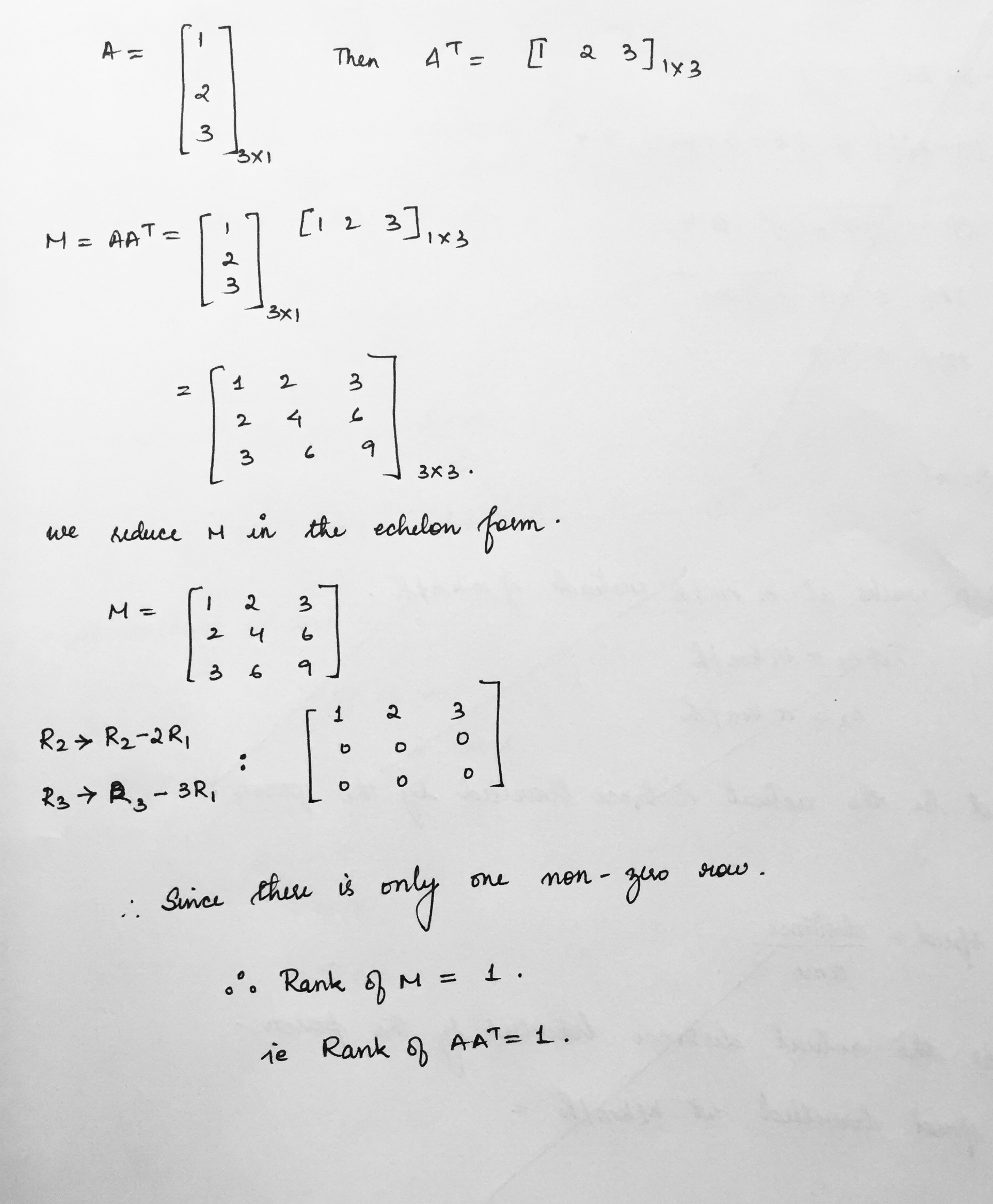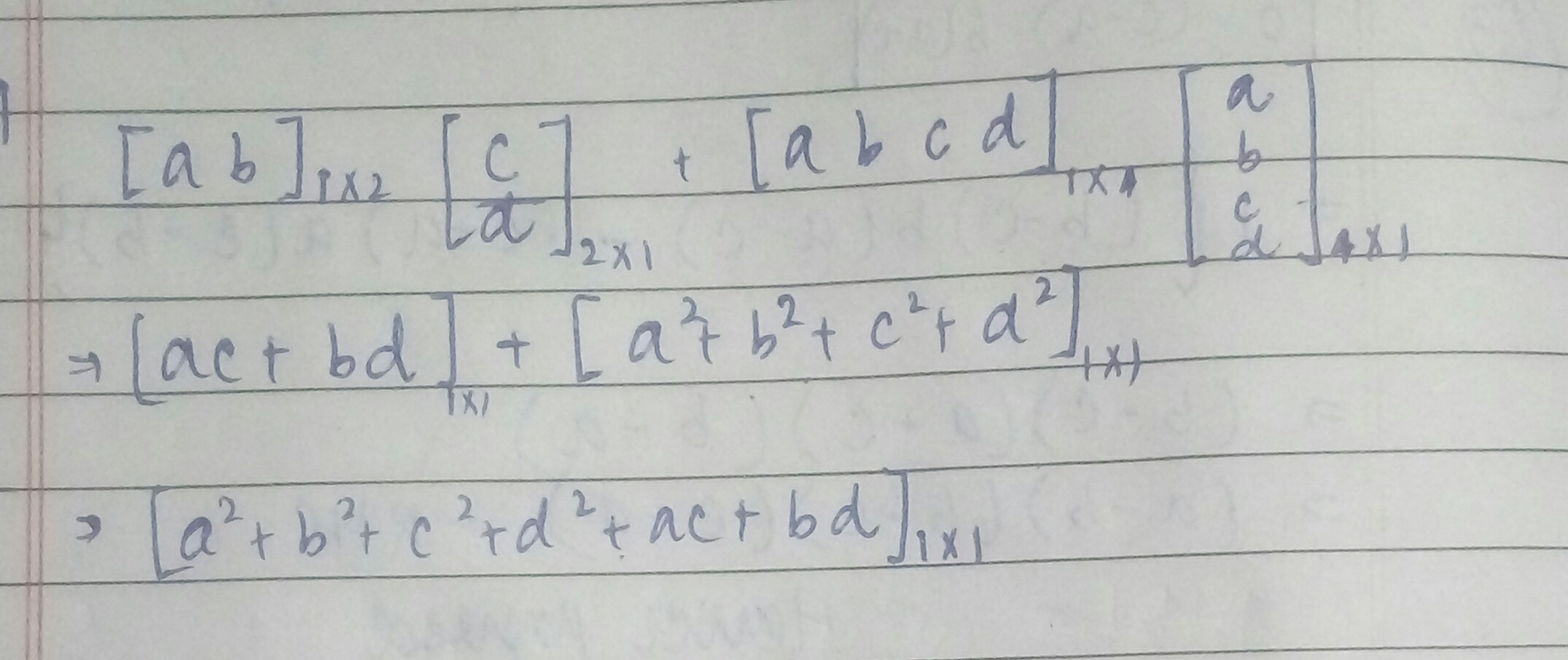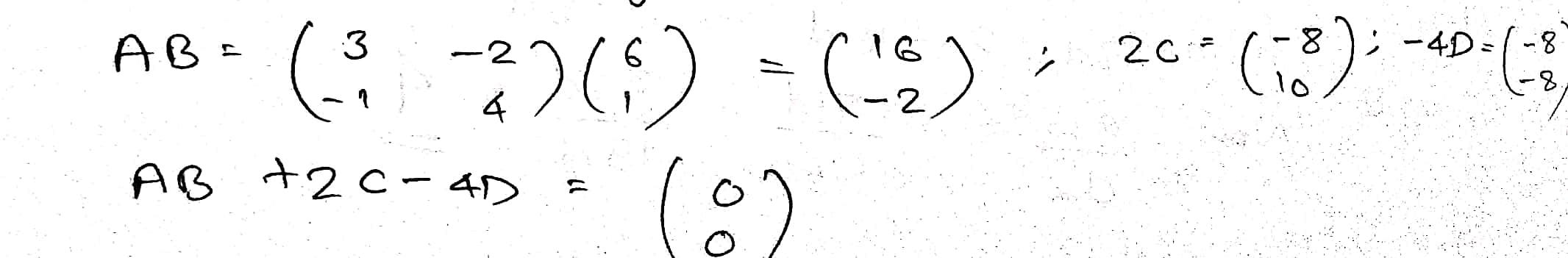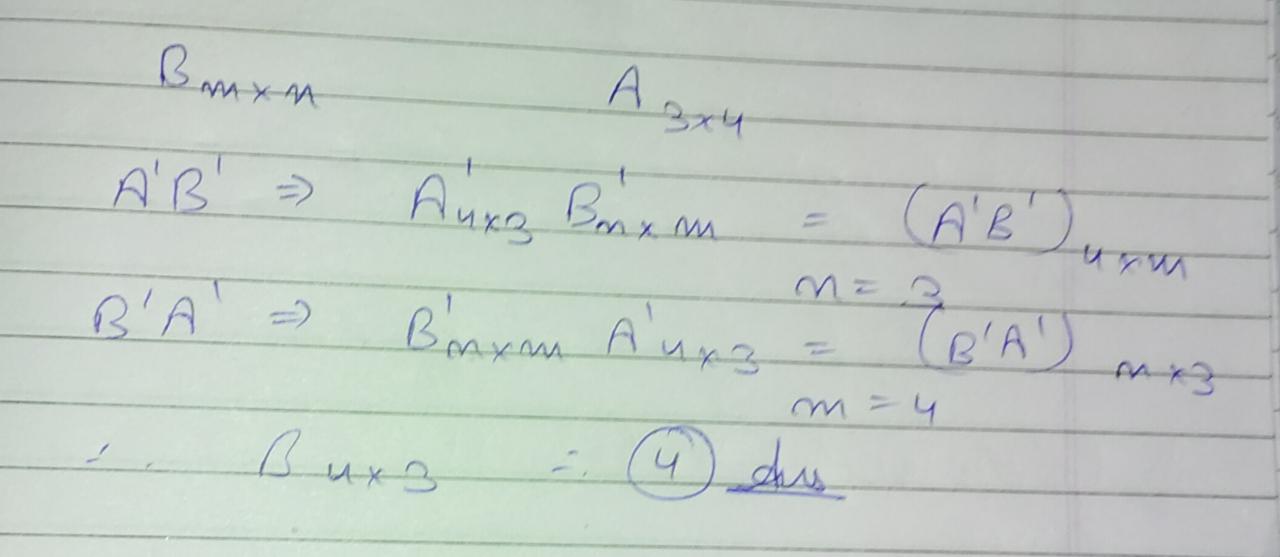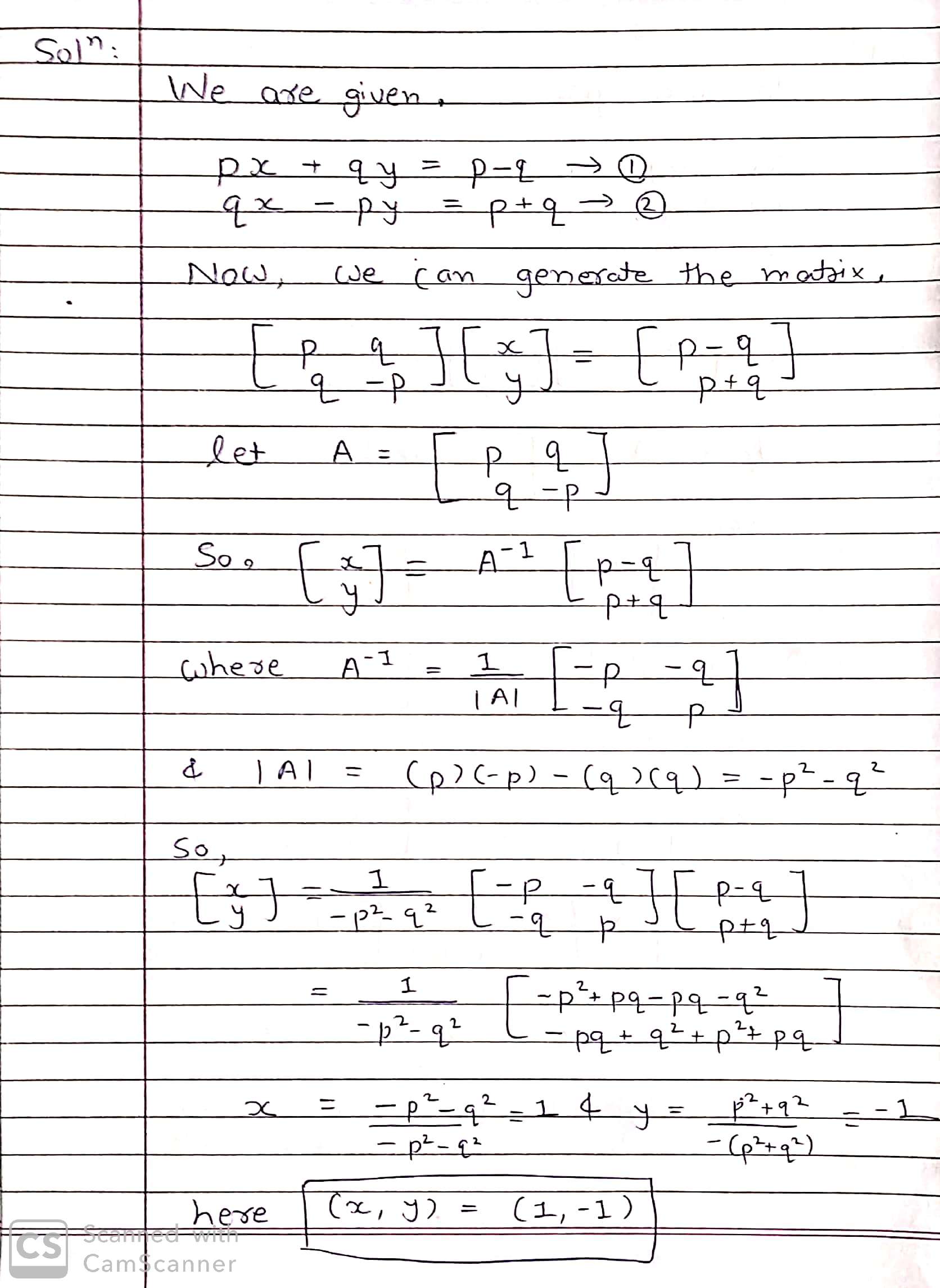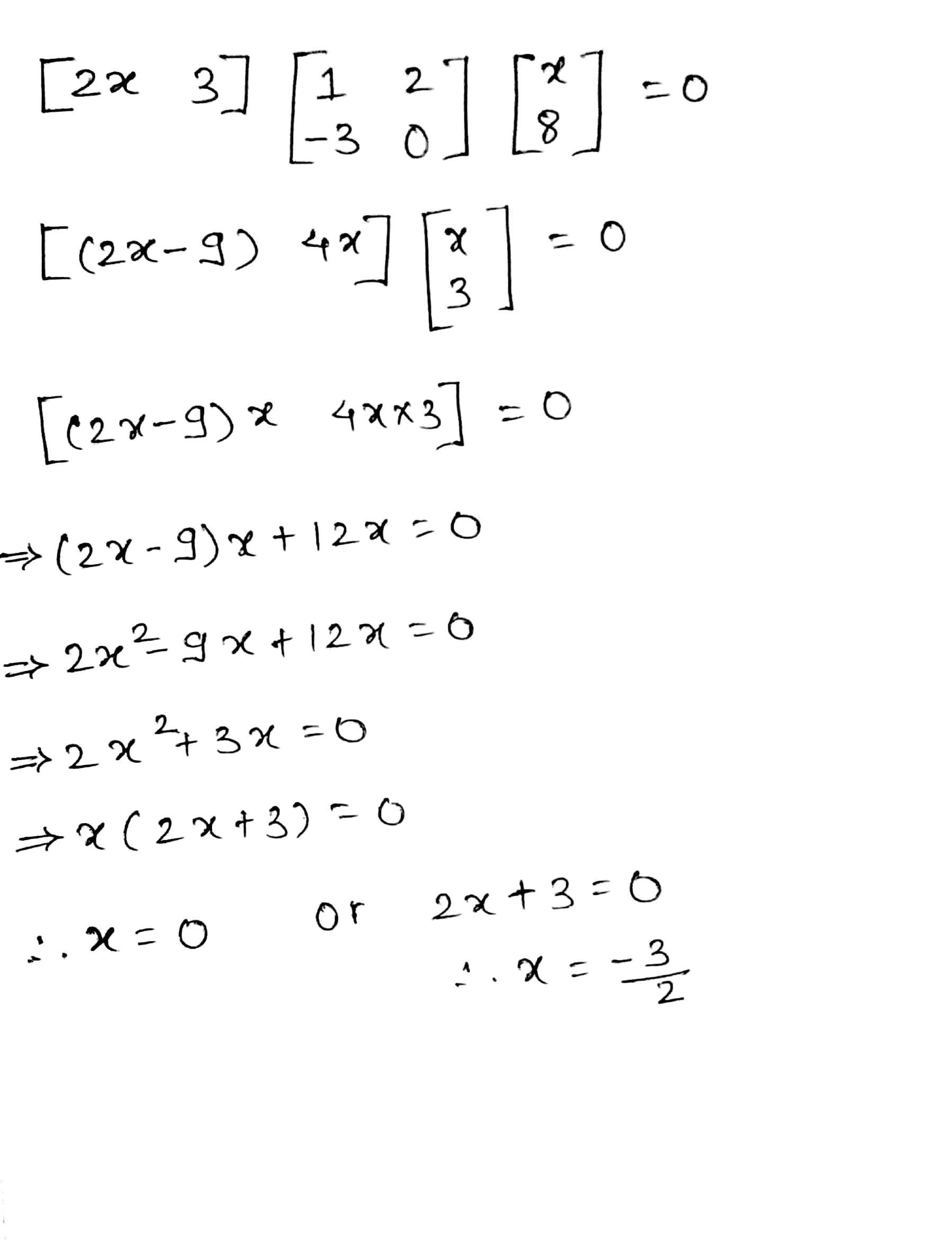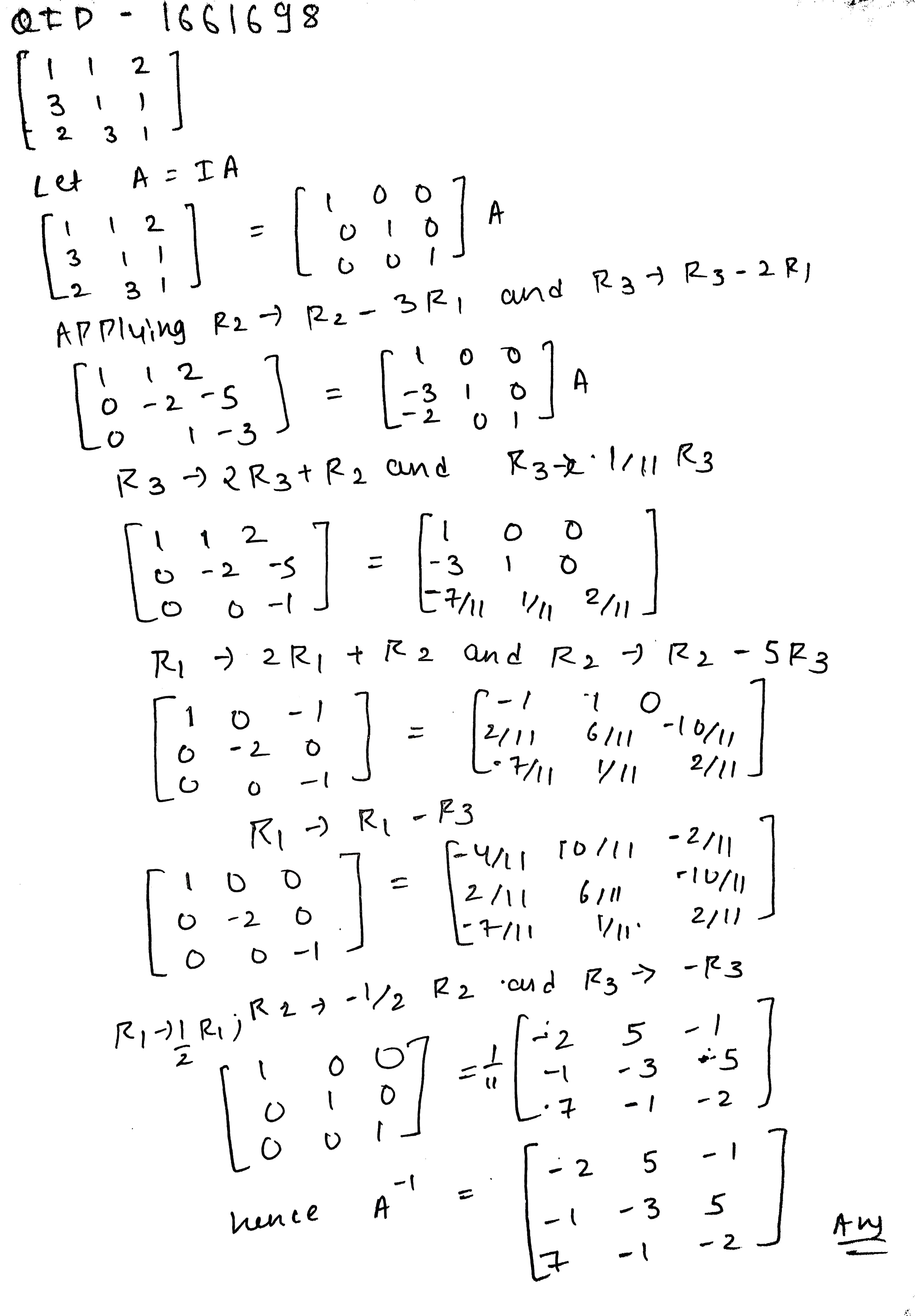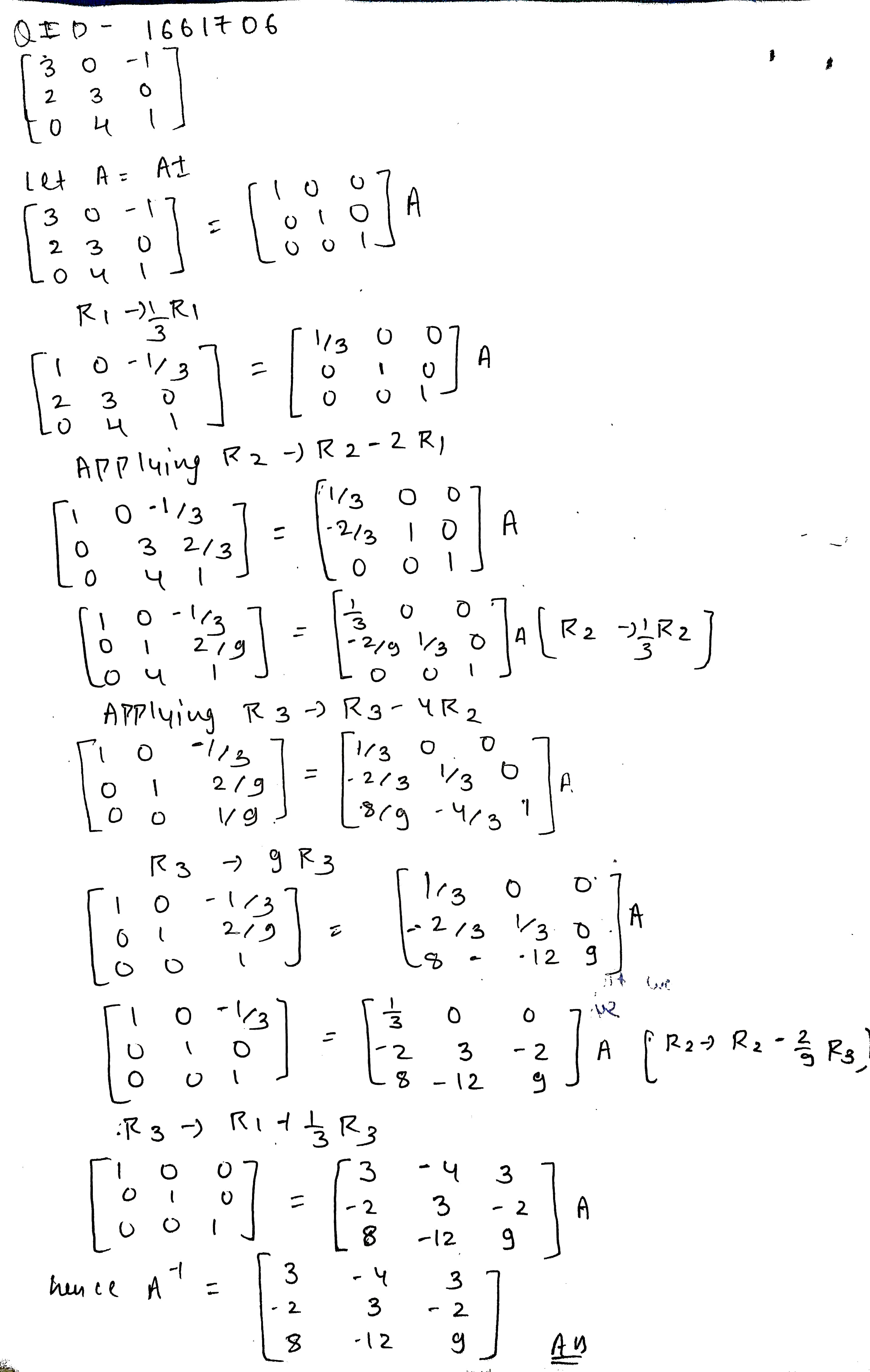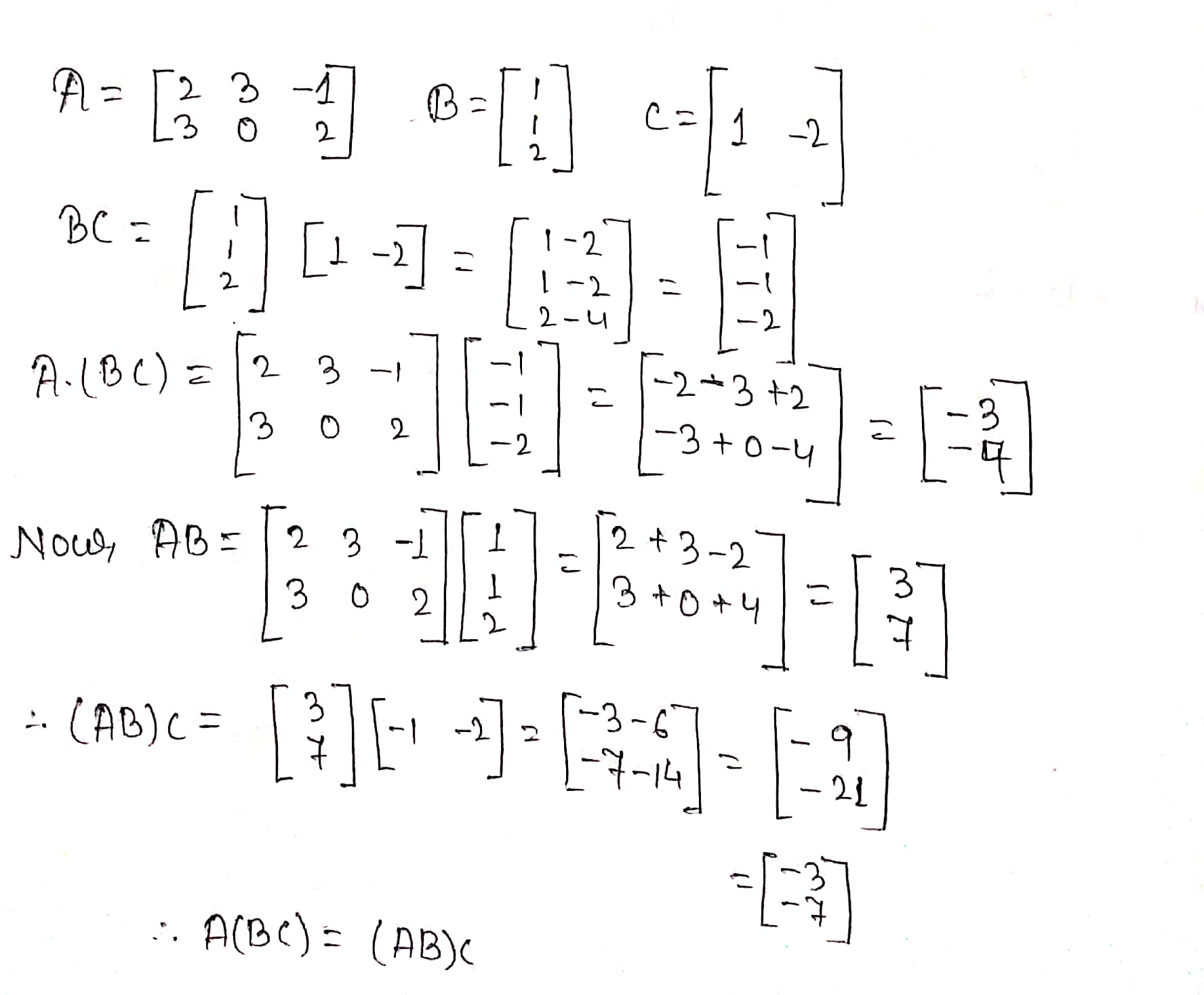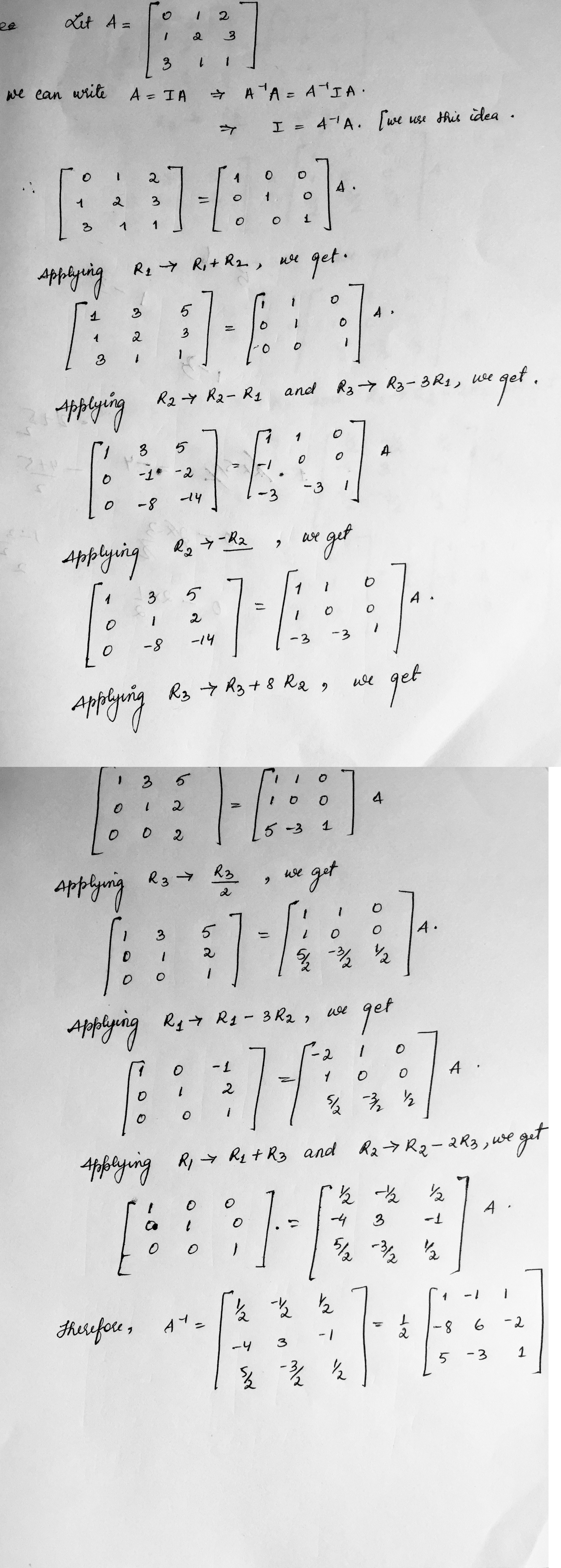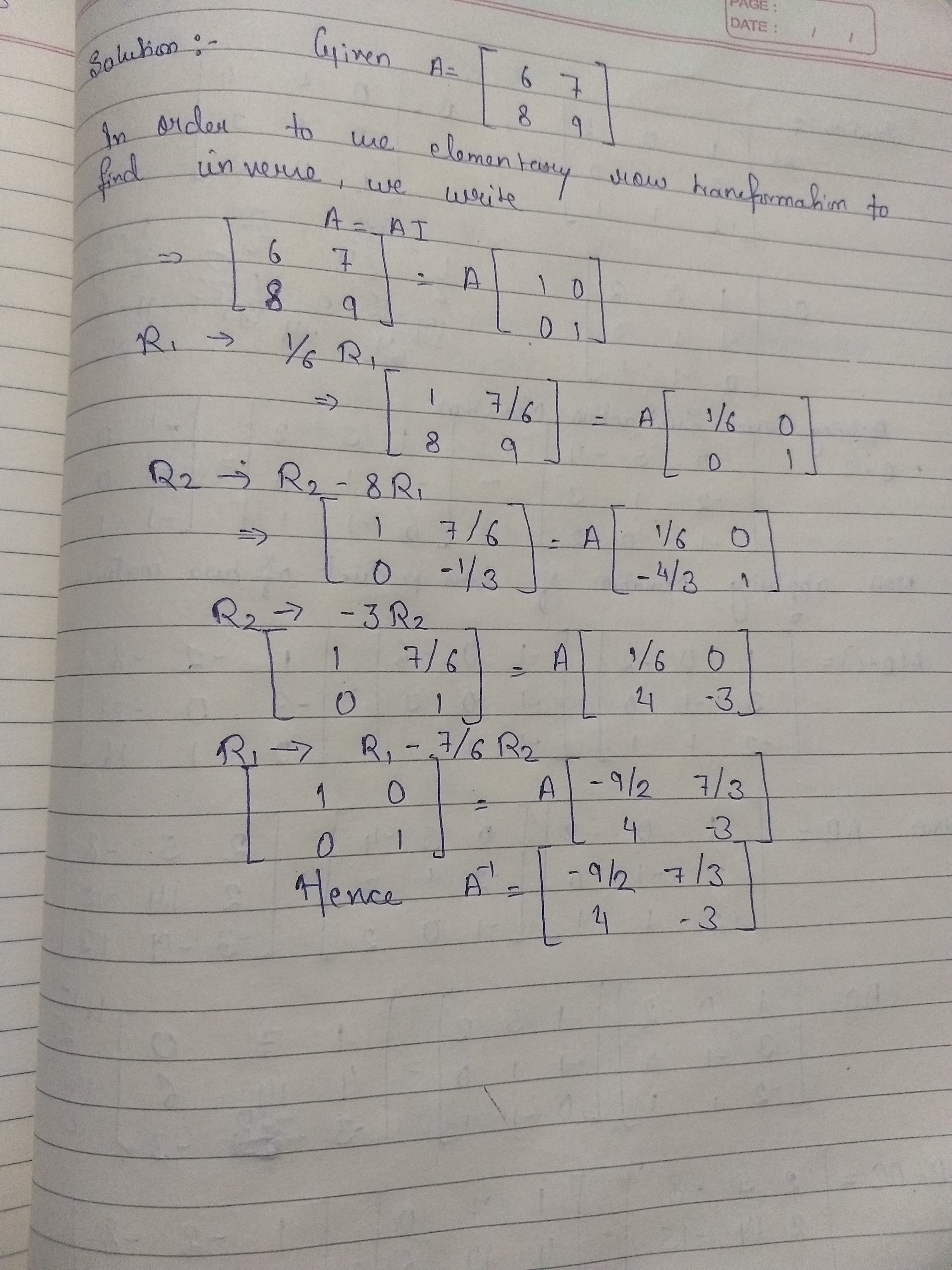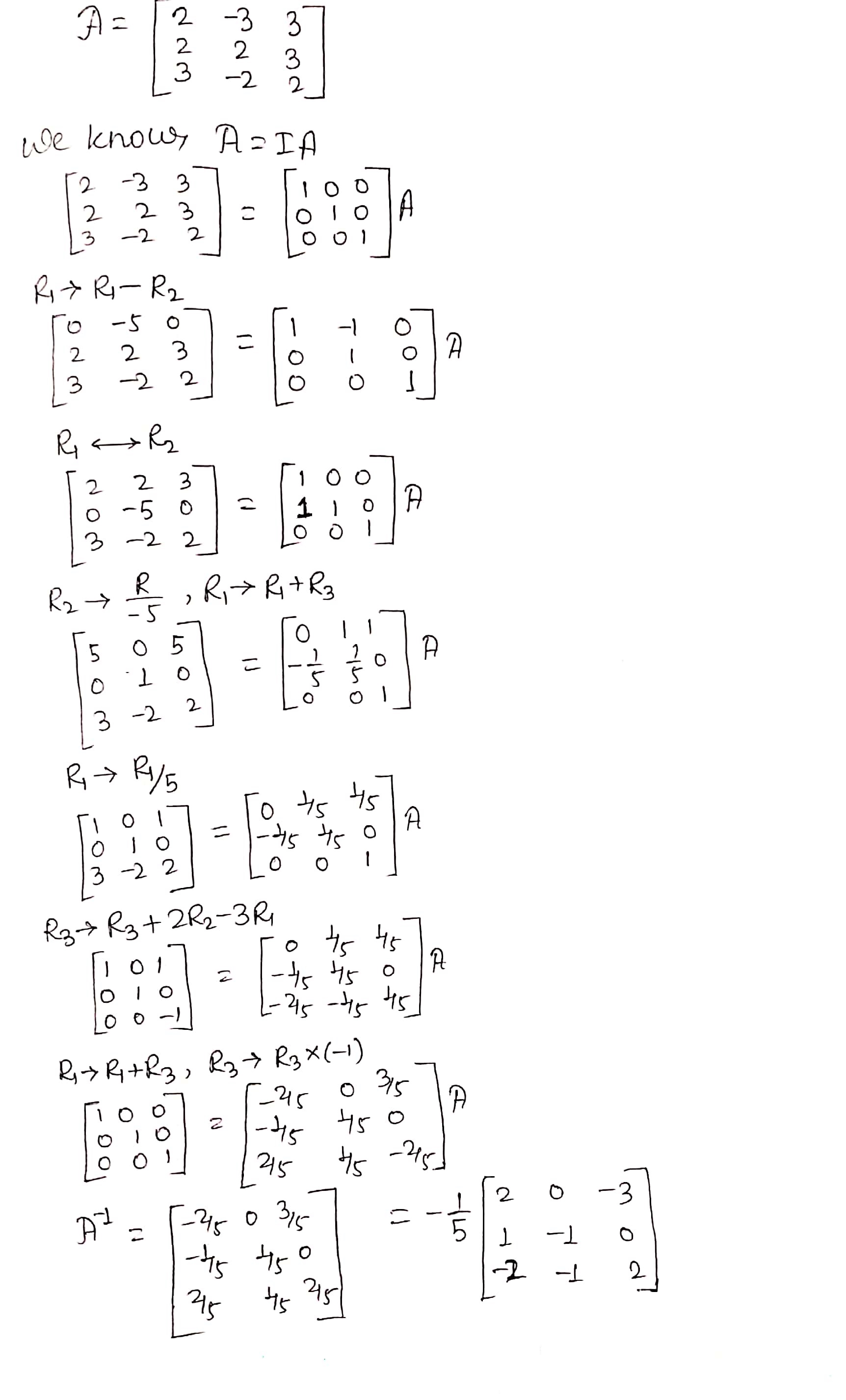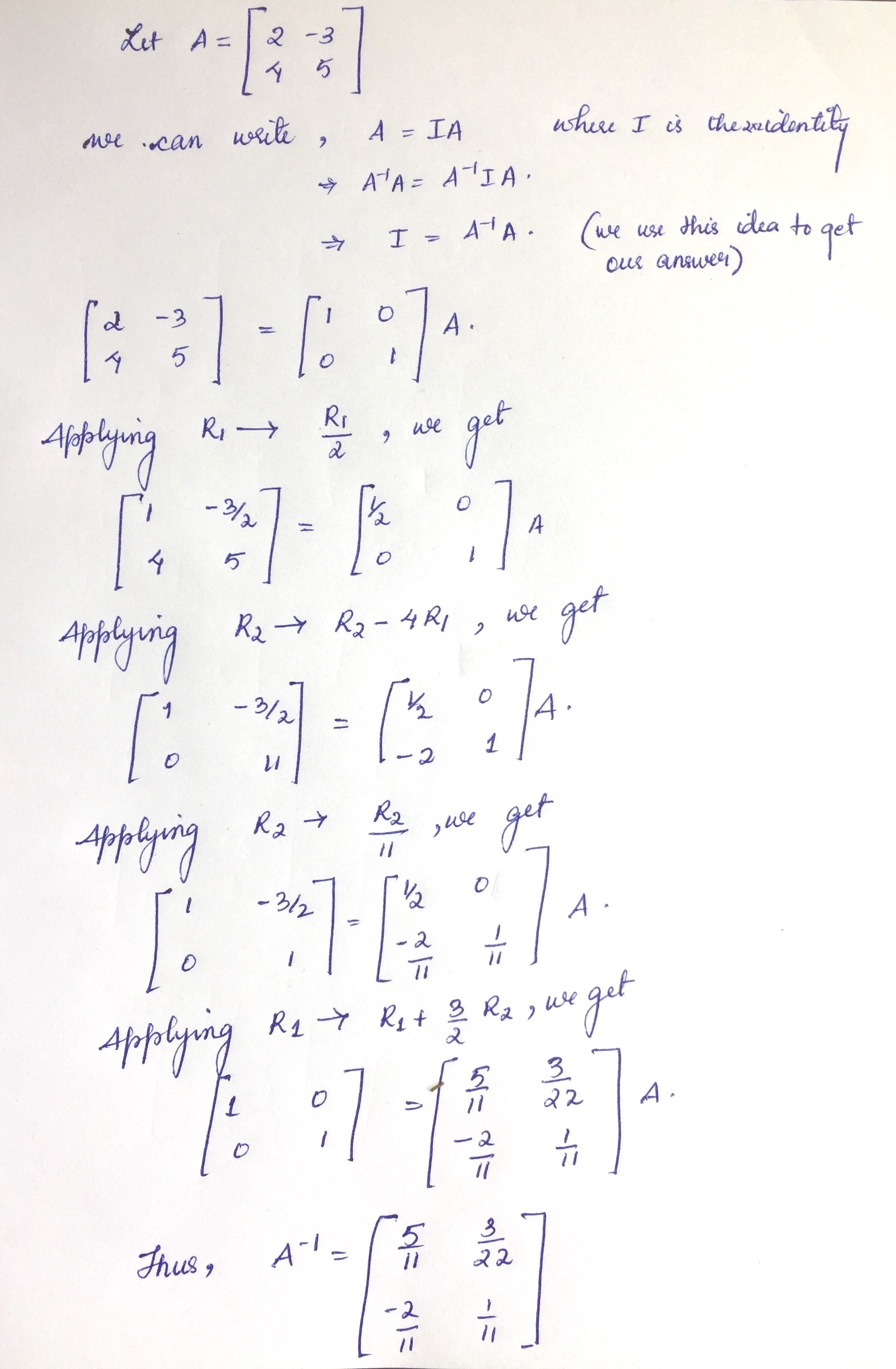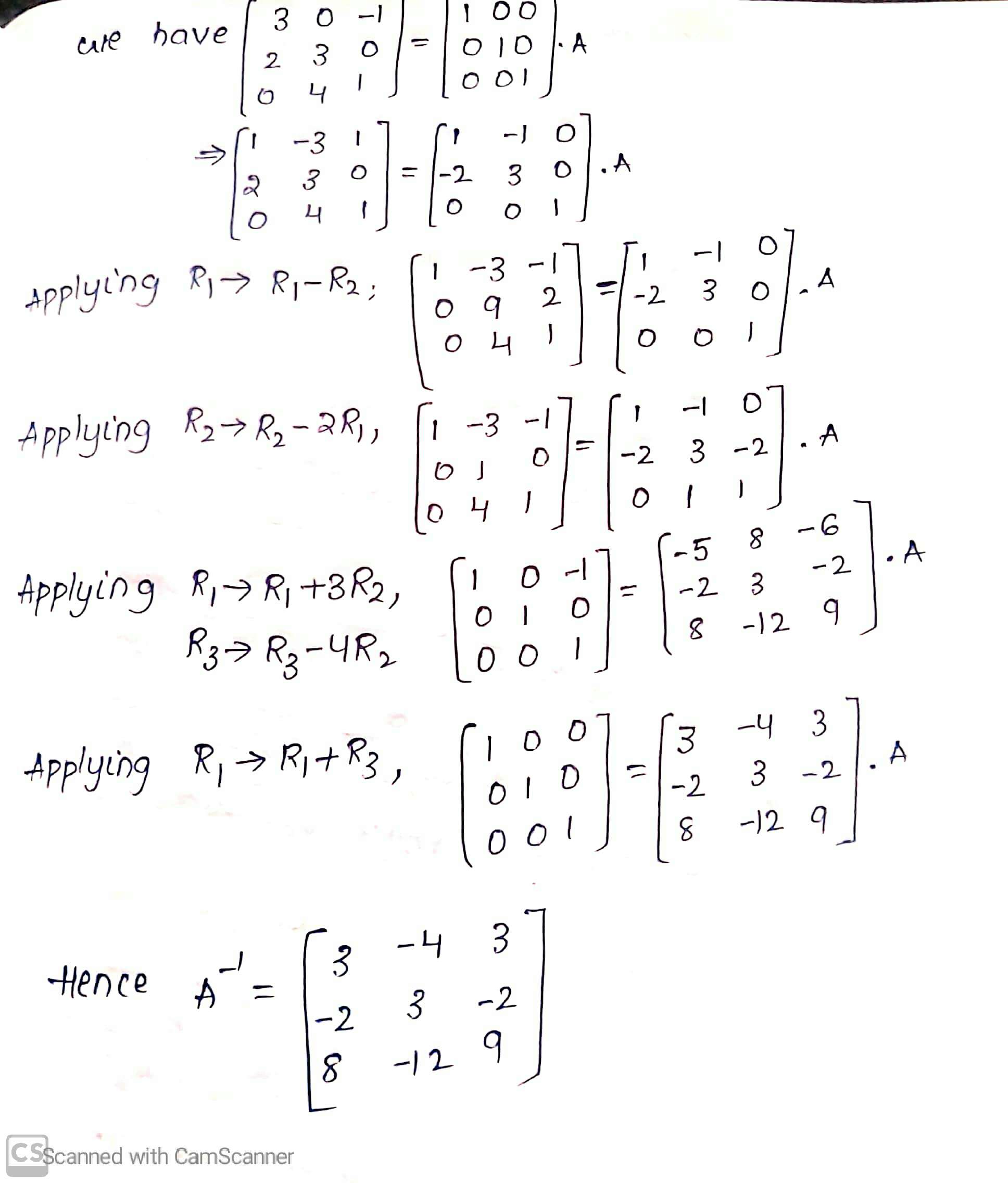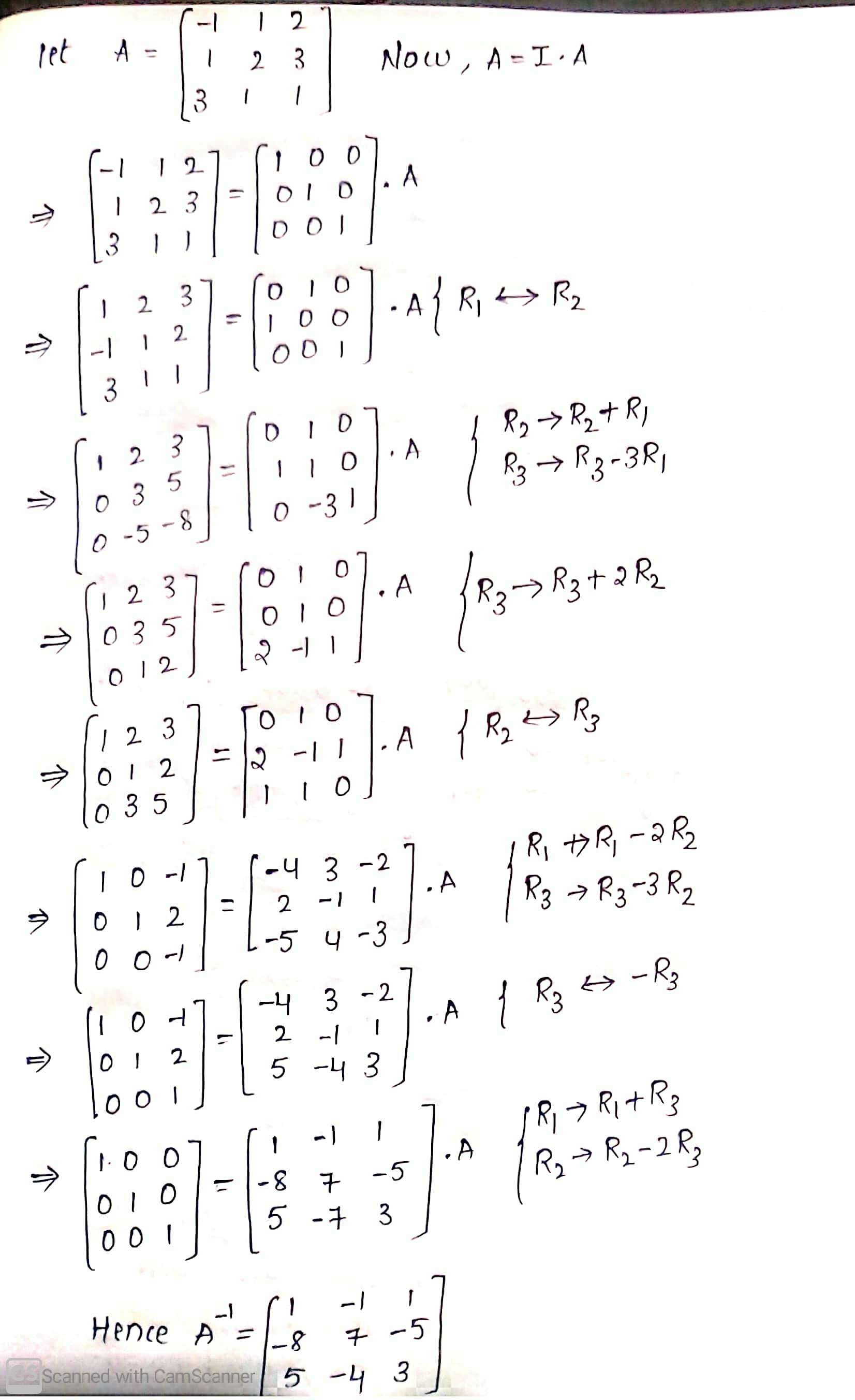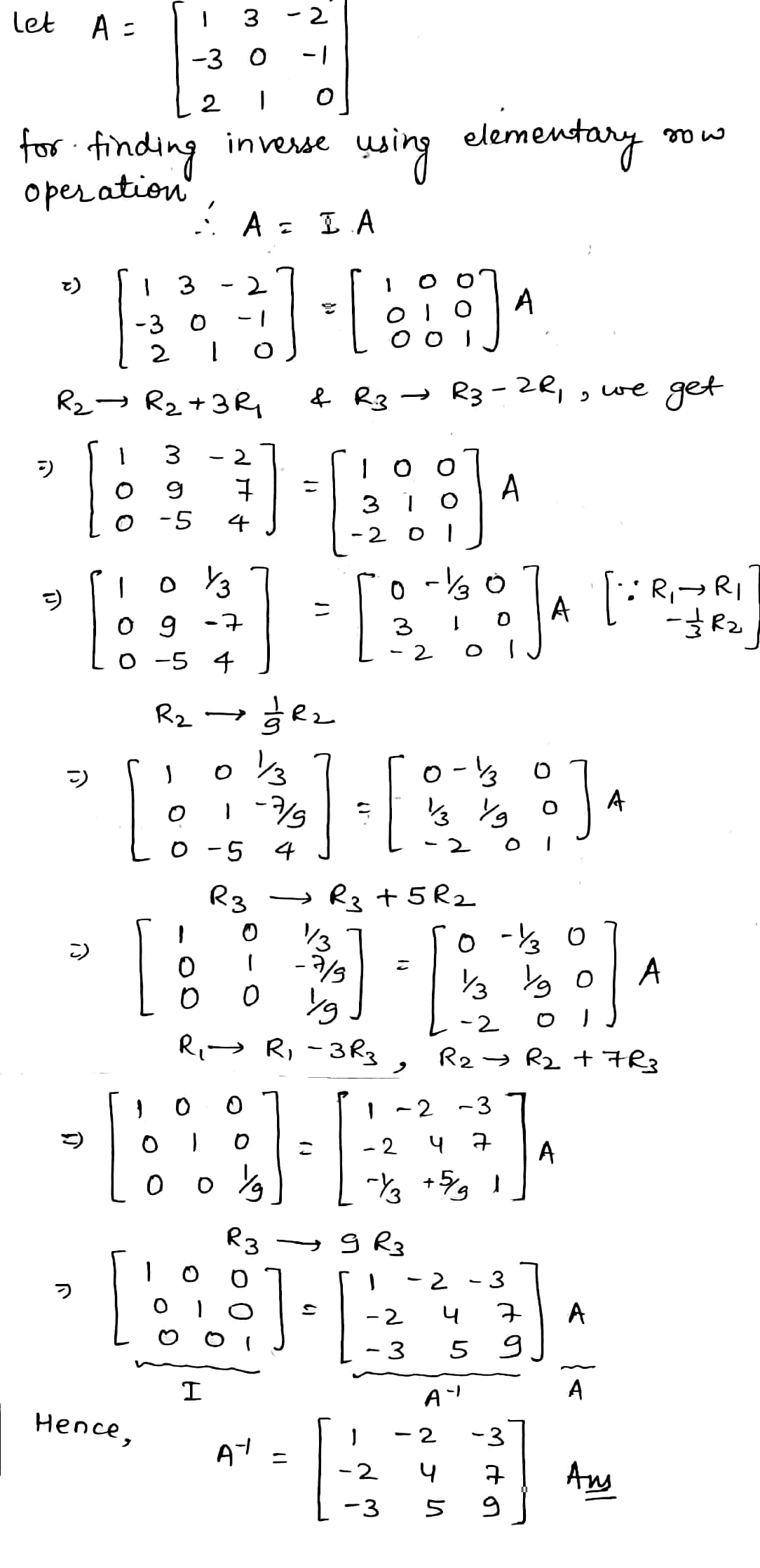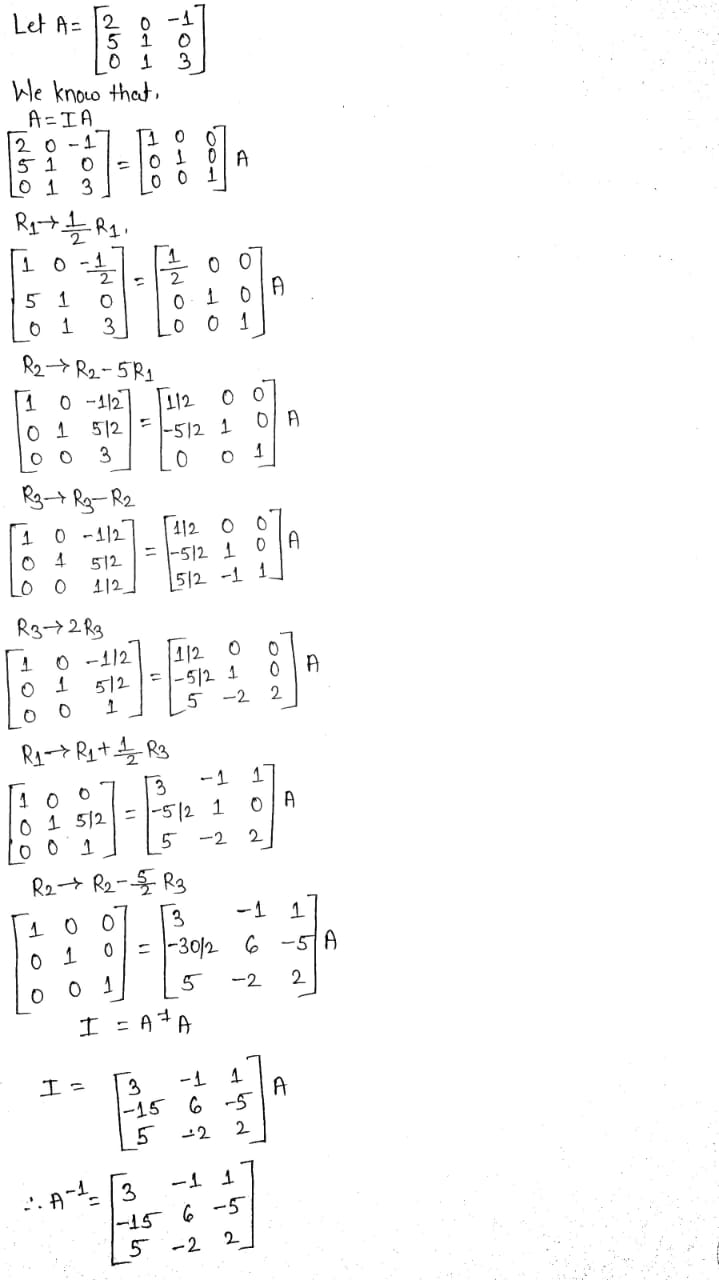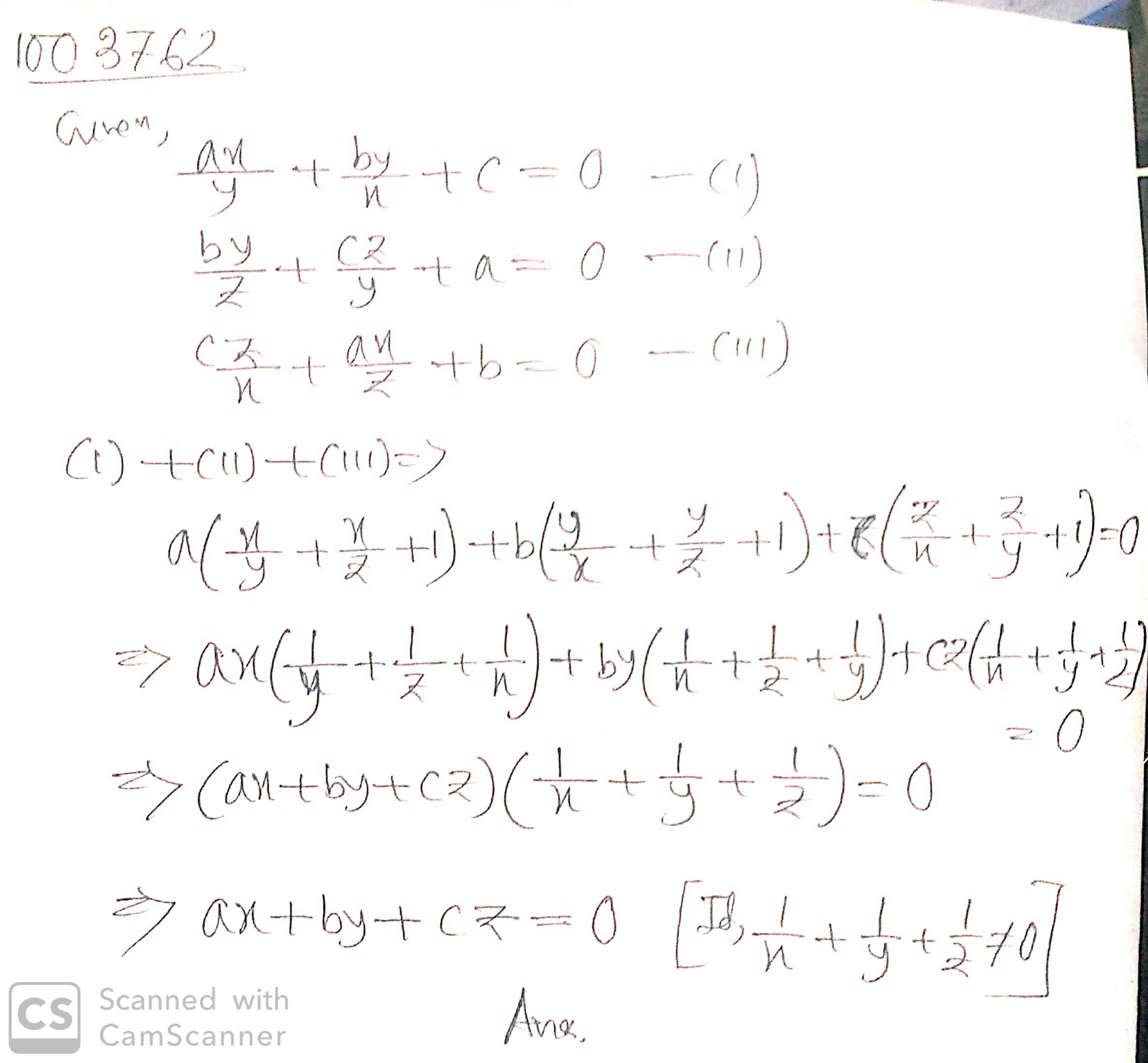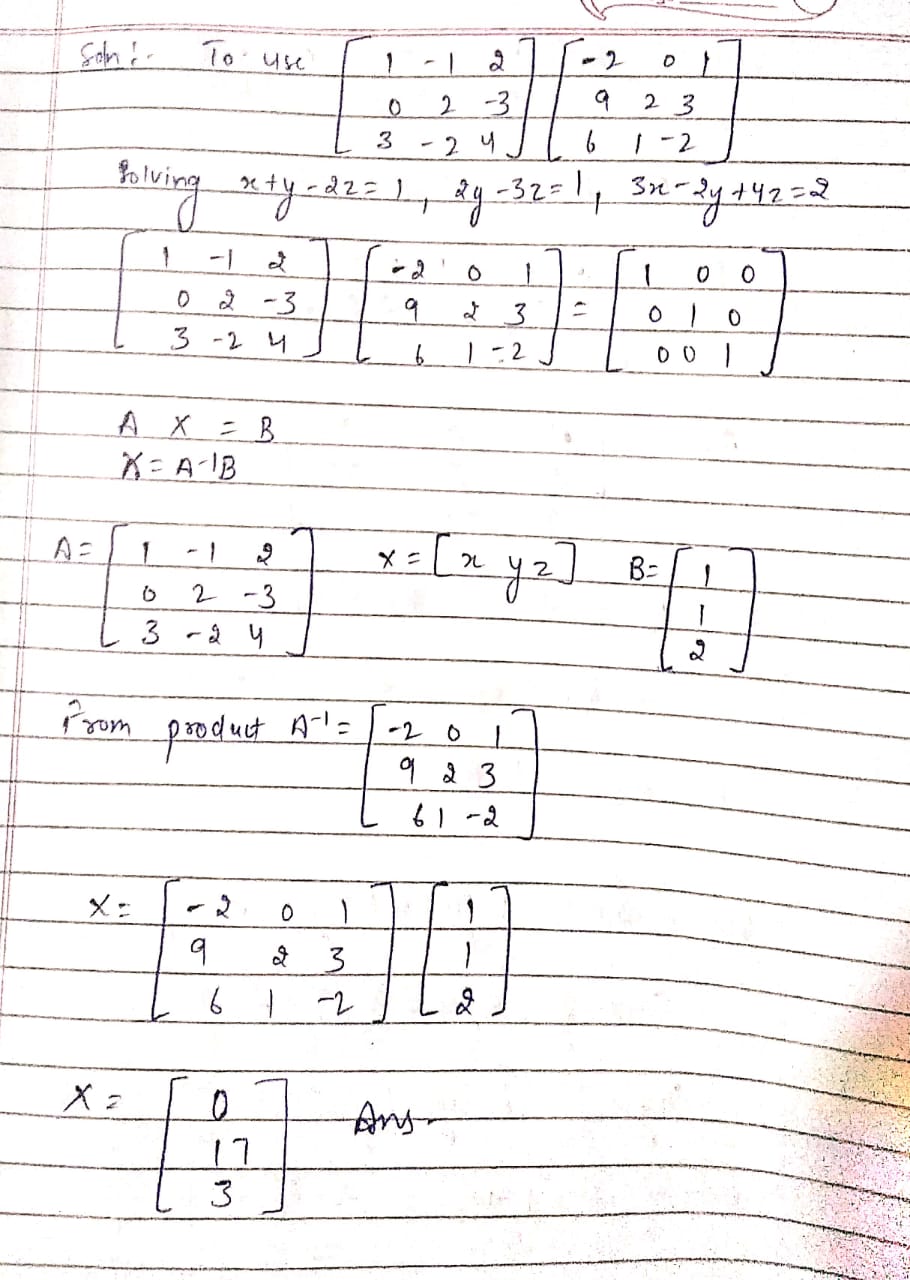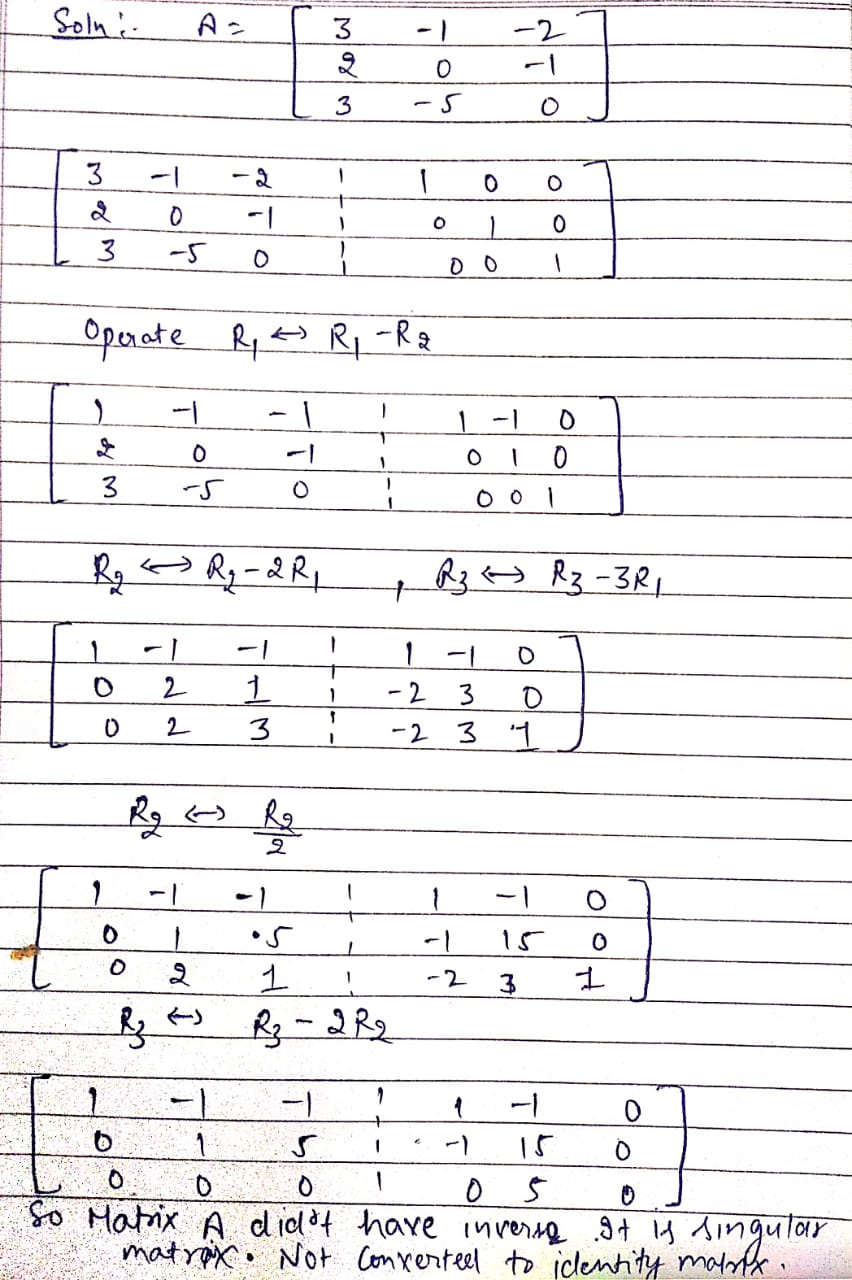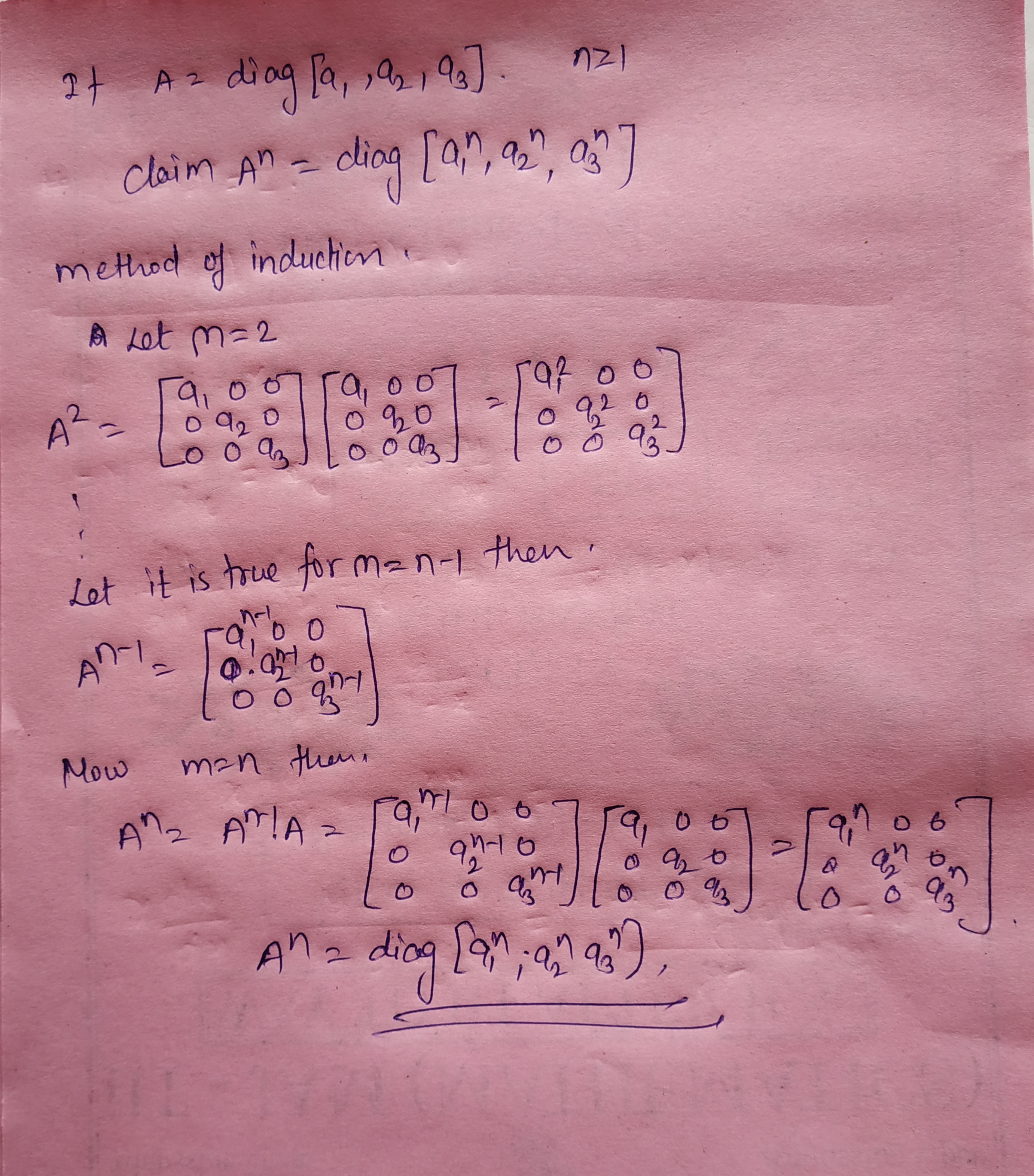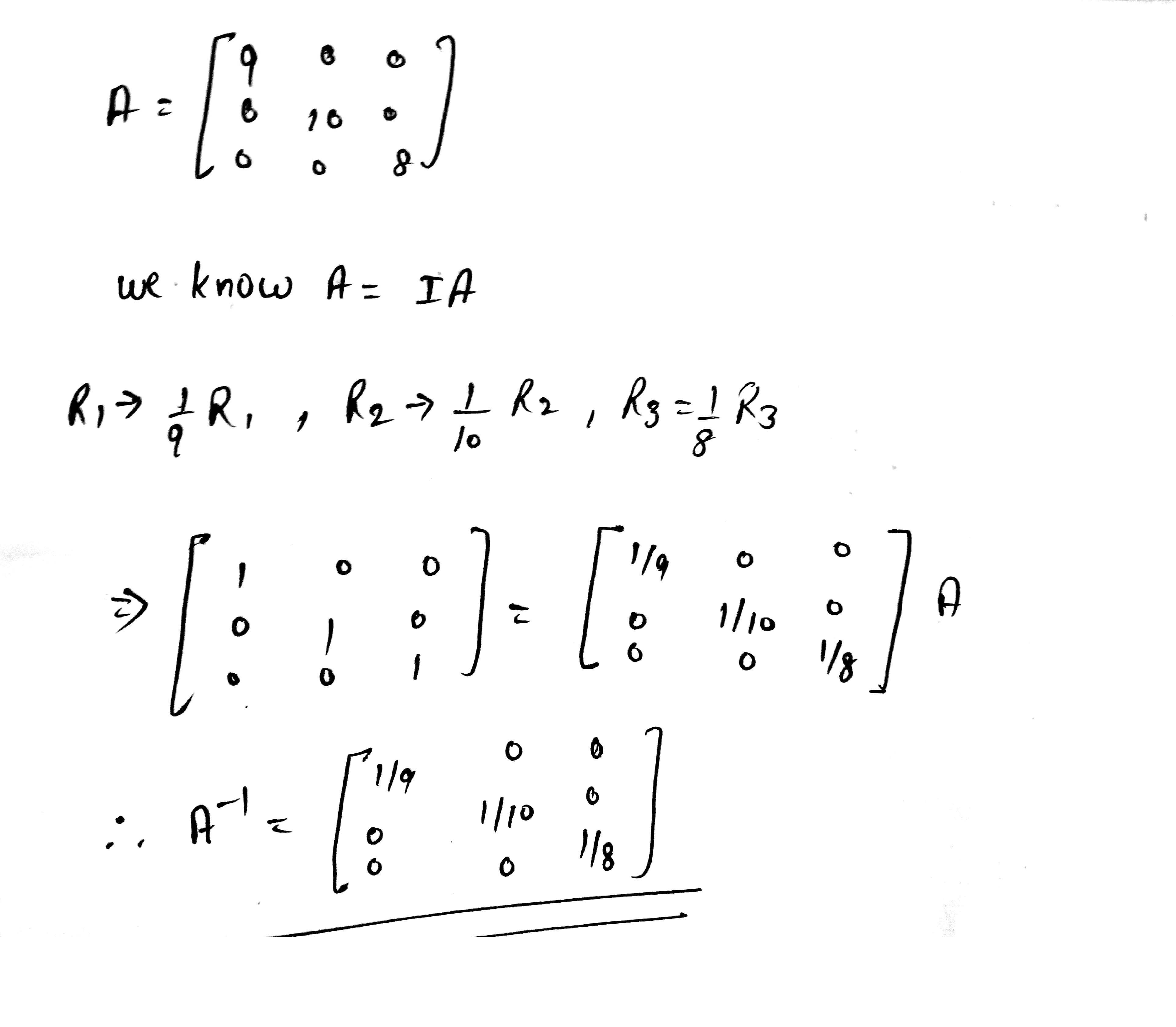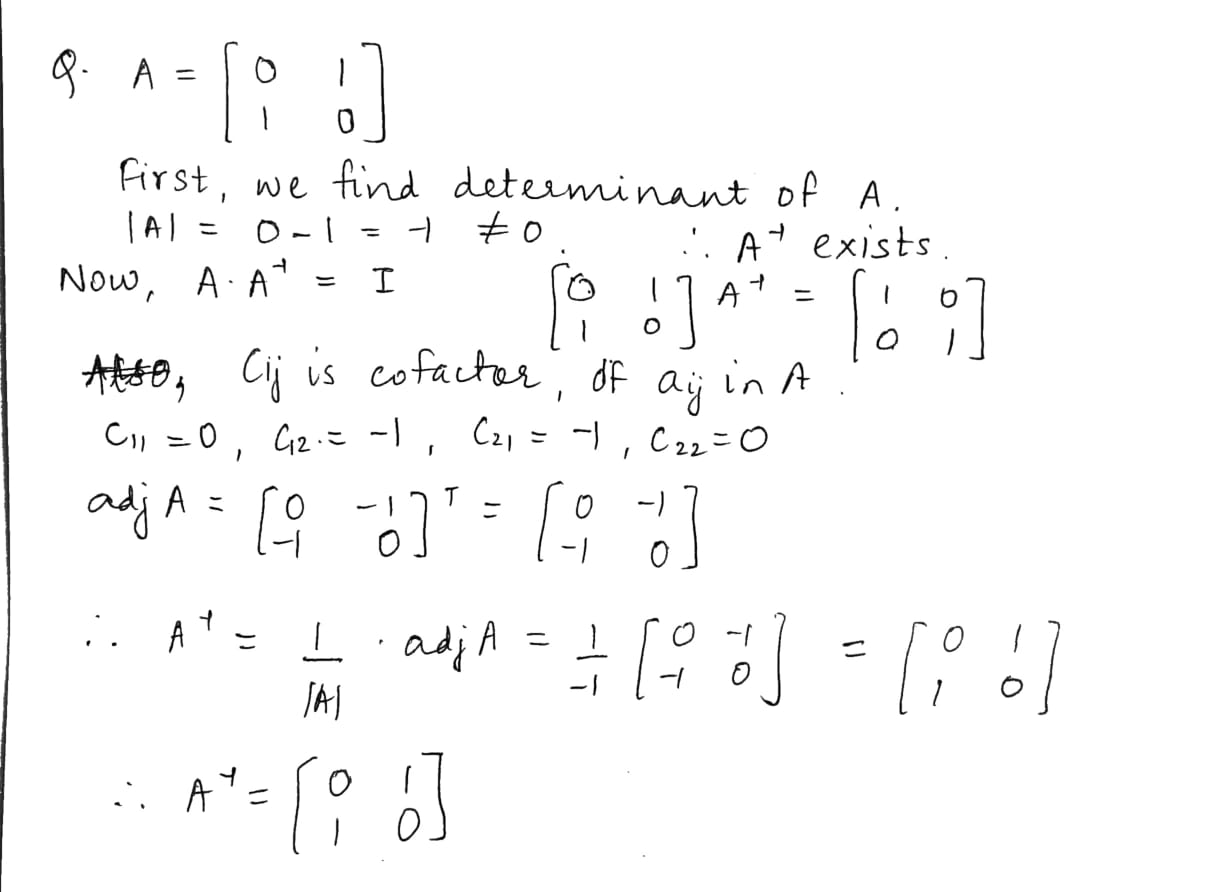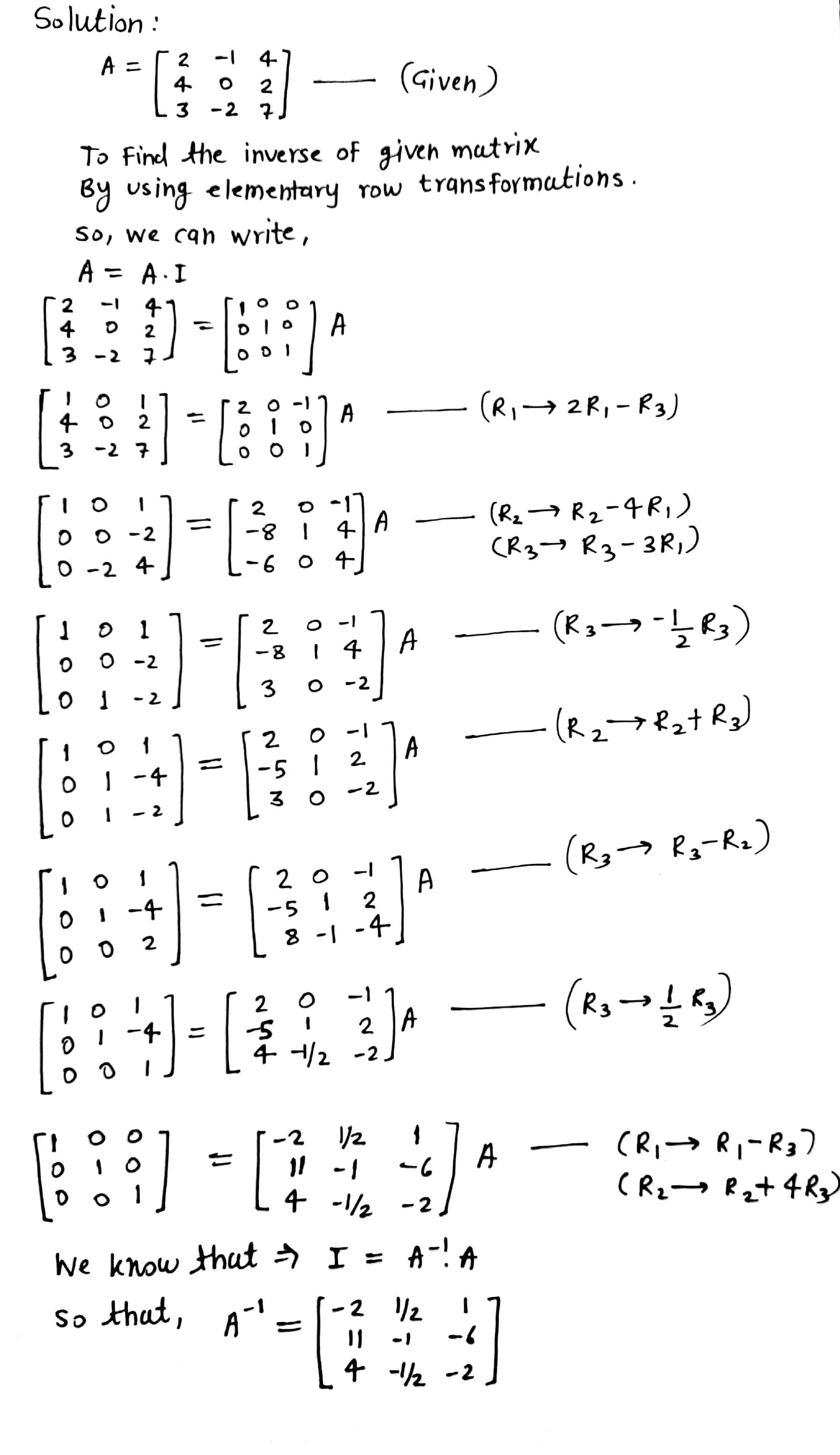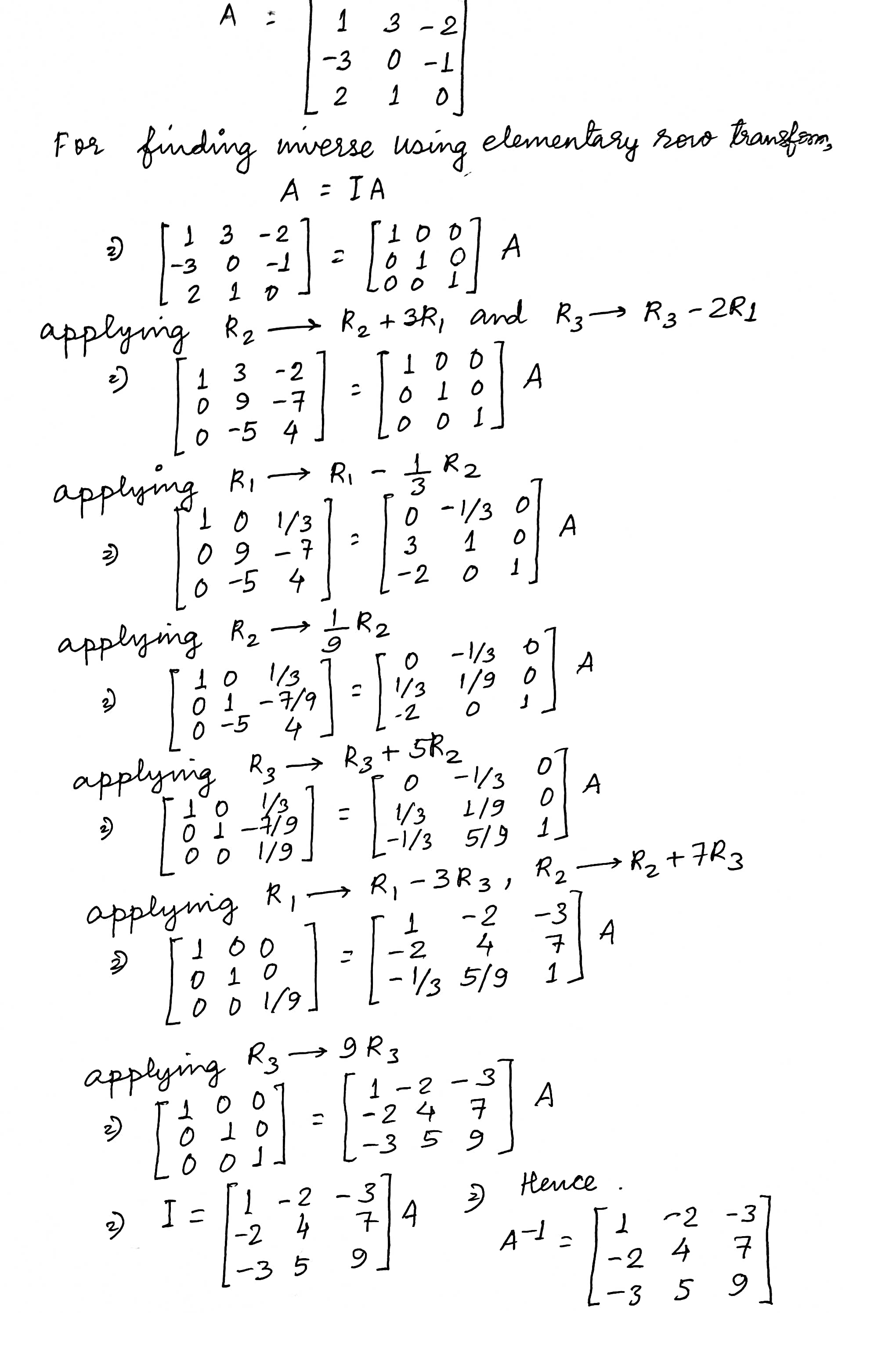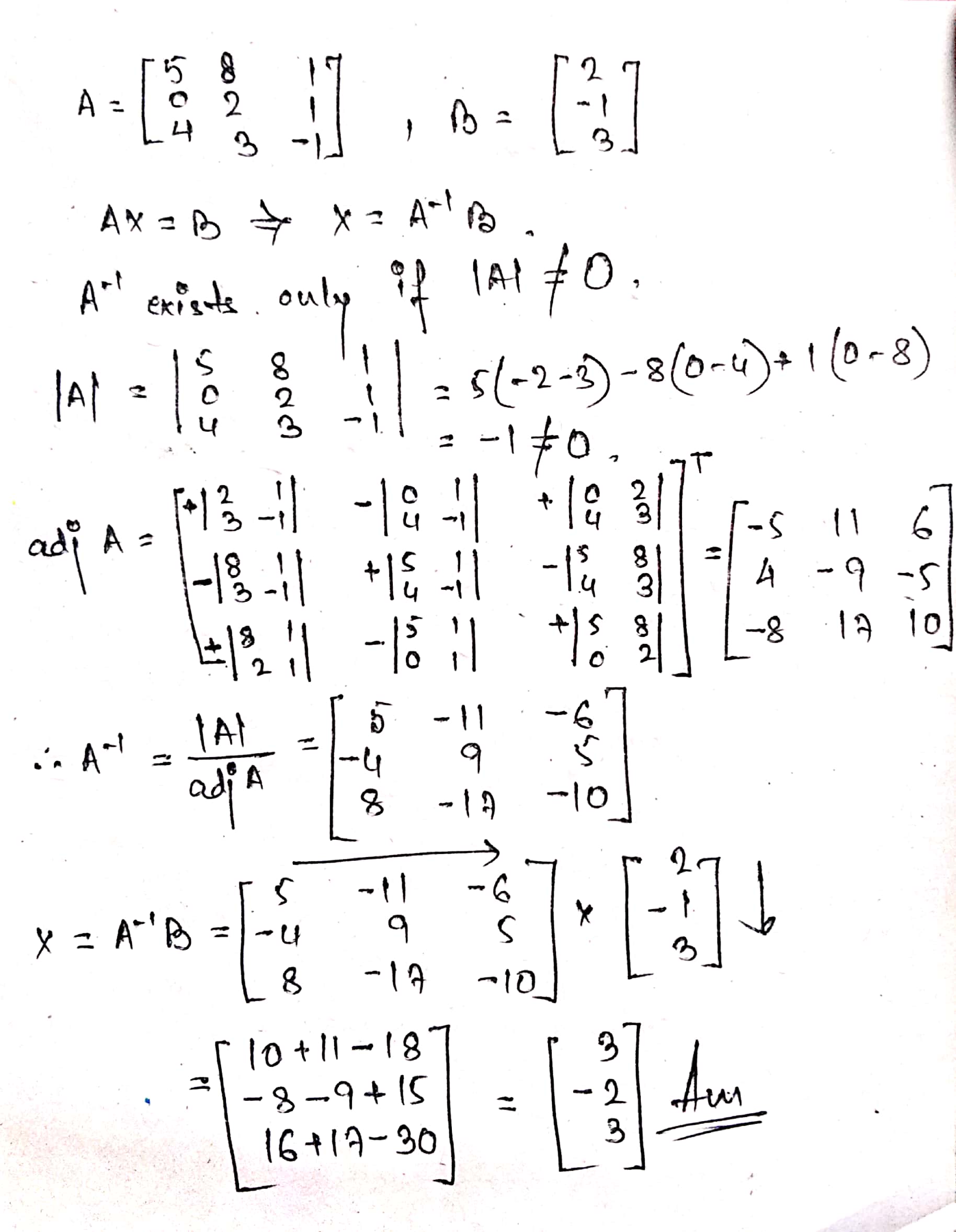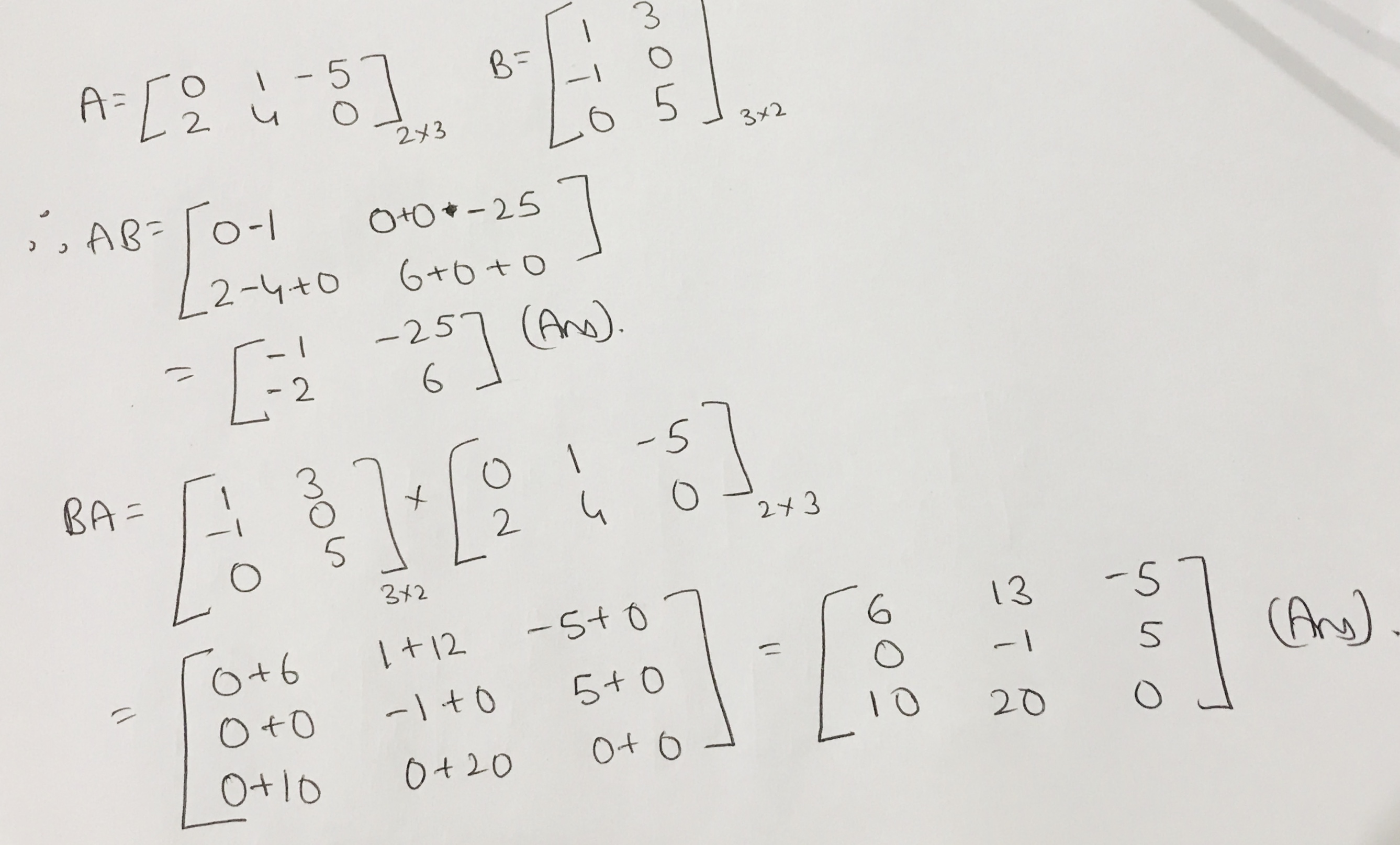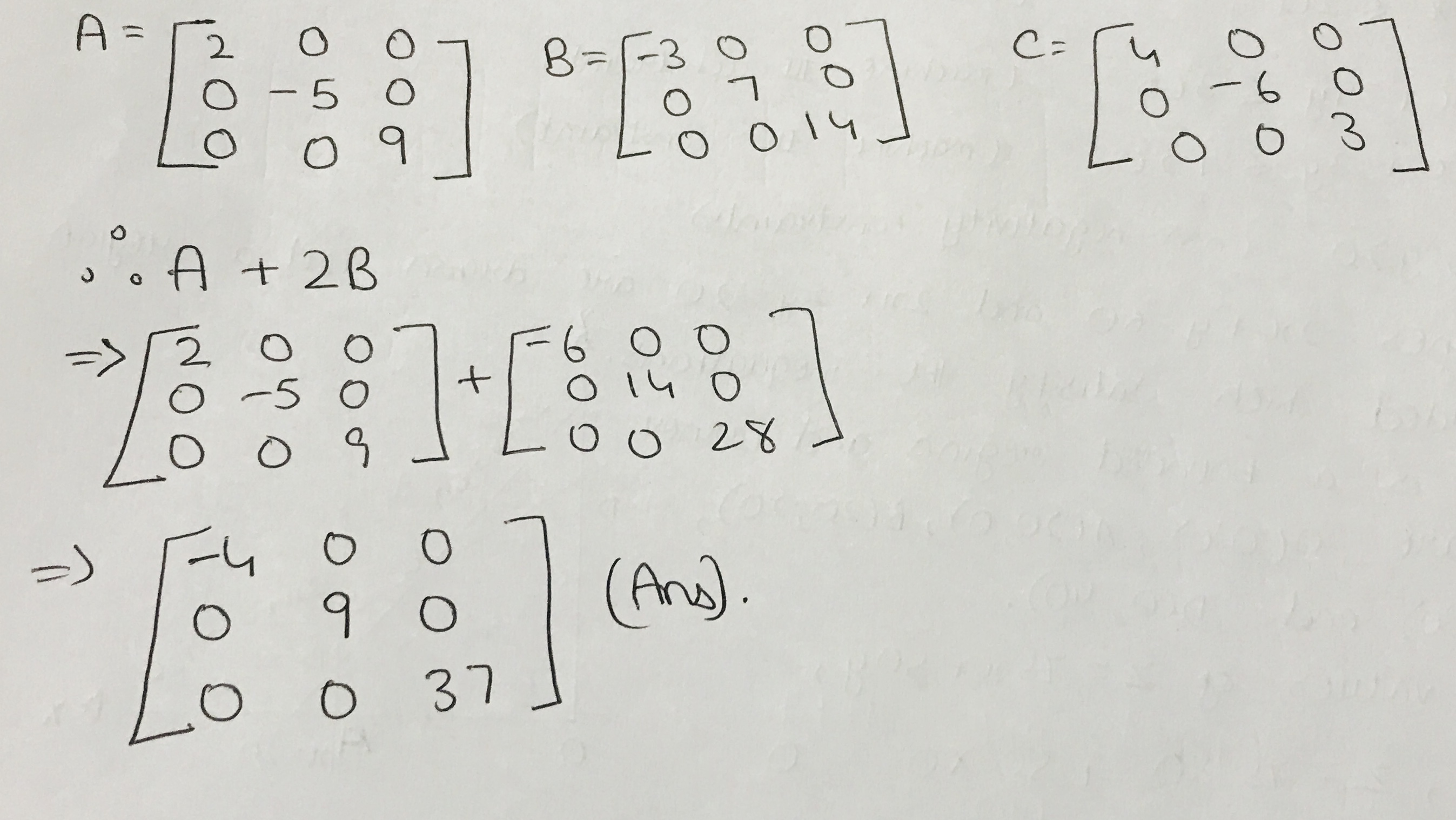Matrices - Class 12 Commerce Maths - Extra Questions
Find a matrix $$X$$ such that $$2A+B+X=O,$$ where $$A=\begin{bmatrix} -1 & 2 \\ 3 & 4 \end{bmatrix}$$ $$B=\begin{bmatrix} 3 & -2 \\ 1 & 5 \end{bmatrix}$$
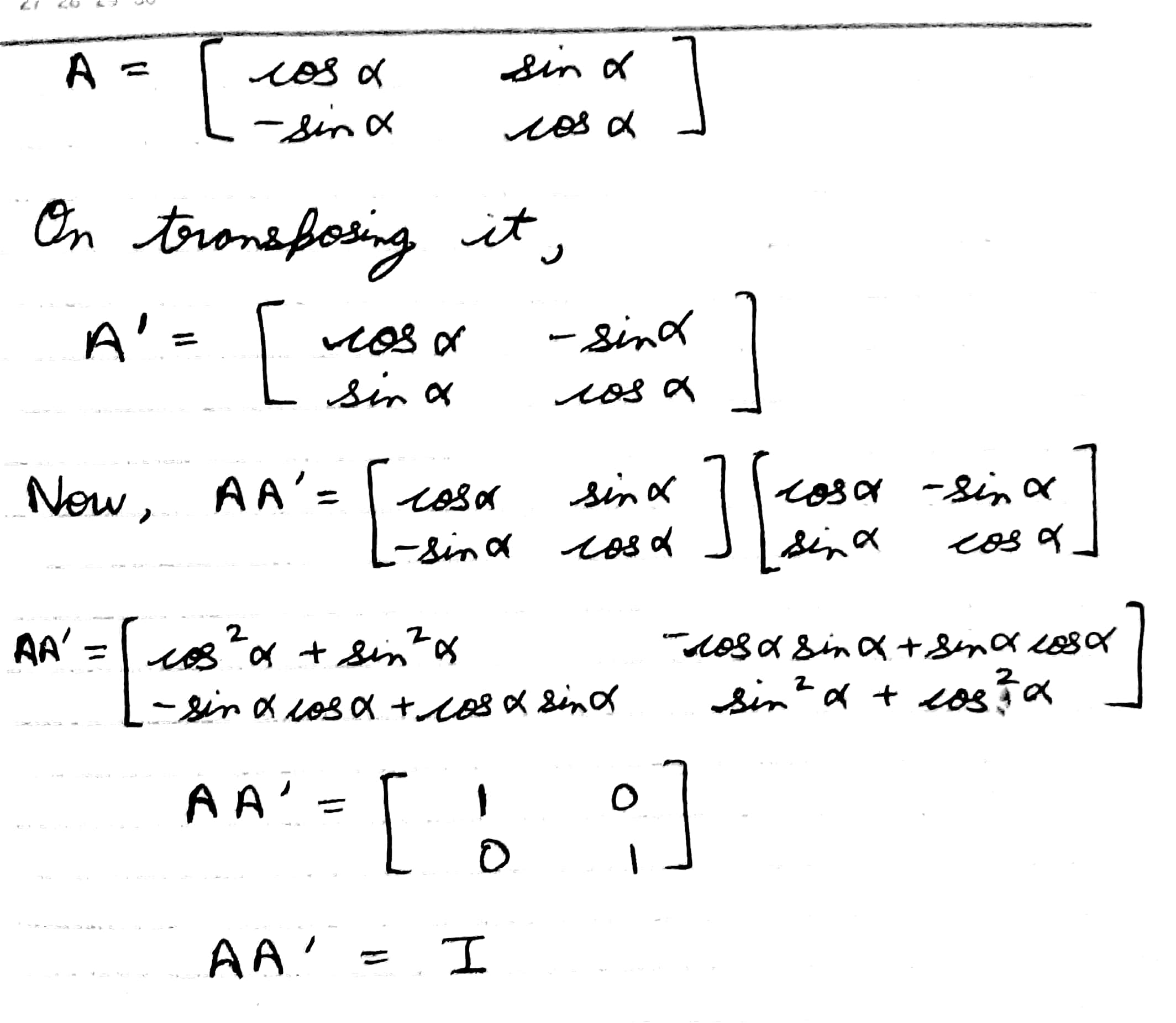
Write the inverse of the matrix $$\begin{bmatrix} \cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{bmatrix}$$
A is $$2\times 2$$ matrix such that $$AB=BA$$ when ever B is $$2\times 2$$ matrix. Prove that A must be of the form kI, where 'k' is real number and I is the identify matrix.
Let $$A=\begin{bmatrix} 1 & -2 & 3 \\ 3 & 2 & -1 \end{bmatrix}$$ and $$B=\begin{bmatrix} 2 & 3 \\ -1 & 2 \\ 4 & -5 \end{bmatrix}$$. Find AB and BA and show that $$AB\neq BA.$$
Given that $$\begin{bmatrix} 4 \\ 1 \\ 3 \end{bmatrix} A = \begin{bmatrix} -4 & 8 & 4 \\ -1 & 2 & 1 \\ -3 & 6 & 3 \end{bmatrix},$$ if $$A = \begin{bmatrix} a & b & c \end{bmatrix}.$$ Find $$a+b+c.$$
Compute the following:
(i) $$\displaystyle \begin{bmatrix} a & b \\ -b & a \end{bmatrix}+\begin{bmatrix} a & b \\ b & a \end{bmatrix}$$
(ii) $$\displaystyle \begin{bmatrix} { a }^{ 2 }+{ b }^{ 2 } & { b }^{ 2 }+{ c }^{ 2 } \\ { a }^{ 2 }+{ c }^{ 2 } & { a }^{ 2 }+{ b }^{ 2 } \end{bmatrix}+\begin{bmatrix} 2ab & 2bc \\ -2ac & -2ab \end{bmatrix}$$
(iii) $$\displaystyle \left[ \begin{matrix} -1 \\ 8 \\ 2 \end{matrix}\begin{matrix} 4 \\ 5 \\ 8 \end{matrix}\begin{matrix} -6 \\ 16 \\ 5 \end{matrix} \right] +\left[ \begin{matrix} 12 \\ 8 \\ 3 \end{matrix}\begin{matrix} 7 \\ 0 \\ 2 \end{matrix}\begin{matrix} 6 \\ 5 \\ 4 \end{matrix} \right] $$
(iv) $$\displaystyle \begin{bmatrix} { \cos }^{ 2 }x & { \sin }^{ 2 }x \\ { \sin }^{ 2 }x & { \cos }^{ 2 }x \end{bmatrix}+\begin{bmatrix} { \sin }^{ 2 }x & { \cos }^{ 2 }x \\ { \cos }^{ 2 }x & { \sin }^{ 2 }x \end{bmatrix}$$
Solve the equation for $$x,y,z$$ and $$t$$ if $$\displaystyle 2\left[ \begin{matrix} x & z \\ y & t \end{matrix} \right] +3\begin{bmatrix} 1 & -1 \\ 0 & 2 \end{bmatrix}=3\begin{bmatrix} 3 & 5 \\ 4 & 6 \end{bmatrix}$$
If $$\displaystyle x\left[ \begin{matrix} 2 \\ 3 \end{matrix} \right] +y\left[ \begin{matrix} -1 \\ 1 \end{matrix} \right] =\left[ \begin{matrix} 10 \\ 5 \end{matrix} \right] $$
Find values of $$x$$ and $$y$$.
Find $$X$$, if $$\displaystyle Y=\begin{bmatrix} 3 & 2 \\ 1 & 4 \end{bmatrix}$$ and $$\displaystyle 2X+Y=\begin{bmatrix} 1 & 0 \\ -3 & 2 \end{bmatrix}$$
Find $$X$$ and $$Y$$ , if $$\displaystyle 2\begin{bmatrix} 1 & 3 \\ 0 & x \end{bmatrix}+\begin{bmatrix} y & 0 \\ 1 & 2 \end{bmatrix}=\begin{bmatrix} 5 & 6 \\ 1 & 8 \end{bmatrix}$$
Simplify: $$\displaystyle \cos { \theta } \begin{bmatrix} \cos { \theta } & \sin { \theta } \\ -\sin { \theta } & \cos { \theta } \end{bmatrix}+\sin { \theta } \begin{bmatrix} \sin { \theta } & -\cos { \theta } \\ \cos { \theta } & \sin { \theta } \end{bmatrix}$$
Given matrix $$A = \begin{bmatrix}4\sin 30^{\circ} & \cos 0^{\circ} \\ \cos 0^{\circ} & 4\sin 30^{\circ} \end{bmatrix}$$ and $$B = \begin{bmatrix}4\\5
\end{bmatrix}$$ If $$AX = B$$
Write the order the matrix $$X$$
Determine whether given matrices product is defined or not. If the product is defined, state the dimension of the product matrix.$$A_{2 \times 5}$$ and $$B_{5 \times 4}$$
If $$A$$ is a matrix of order $$(m\times n)$$ and $$B$$ is a matrix of order $$(n\times p)$$ then order of $$AB$$ is ................
For the matrices $$A$$ and $$B$$, the product $$AB$$ exists but $$BA$$ does not exist. What can you say about the order of $$A$$ and $$B$$?
If $$A$$ is any square matrix then $$(A-A')$$ is always ______
If $$A=\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}$$, find $$A\cdot { A }^{ \prime }$$.
If $$A=\begin{bmatrix}1&2&3\\3&2&1\end{bmatrix}$$ and $$B=\begin{bmatrix}3&2&1\\1&2&3\end{bmatrix}$$, find $$3B-2A$$.
If $$A=\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}$$, then find $$A'A$$.
If $$[x - 3] \begin{bmatrix}2x\\ 6\end{bmatrix}= 0$$, then find the value of x.
Solve $$\bigl[\begin{matrix} x& 1\end{matrix}\bigr] \bigl[\begin{matrix} 1& 0 \\ -2 & -3\end{matrix}\bigr] \bigl[\begin{matrix}x \\ y \end{matrix}\bigr] = (0).$$
If $$A=\begin{bmatrix} 1 & 3\\ 3 & 4\end{bmatrix}$$ and $$B=\begin{bmatrix} -2 & 1\\ -3 & 2\end{bmatrix}$$ and $$5A^2-B^2=5C$$. Find matrix C where C is a $$2$$ by $$2$$ matrix.
By row transformation find $$A^{-1}$$ if:
$$A = \begin{bmatrix} 2 &1 \\ 4 & 2 \end{bmatrix}$$
If $$A=\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix};B=\begin{bmatrix} a & c \\ b & d \end{bmatrix}$$, then show that $${ \left( A.B \right) }^{ -1 }={ B }^{ -1 }.{ A }^{ -1 }$$
If 2X - Y = $$\begin{bmatrix}3 & -3 & 0\\ 3 & 3 & 2 \end{bmatrix}$$ and 2Y + X = $$\begin{bmatrix}4 & 1 & 5\\ -1 & 4 & -4 \end{bmatrix}$$
then find X and Y
If $$A=\begin{bmatrix}2&-1\\ 3&2\end{bmatrix}$$, $$B=\begin{bmatrix}0&4\\ -1&7\end{bmatrix}$$. Find $$3A^2 - 2B + 1$$.
If A = $$\begin{bmatrix}1 & 3\\ 3 & 2\\ 2 &5 \end{bmatrix}$$, B = $$\begin{bmatrix}-1 & -2\\ 0 & 5\\ 3 & 1 \end{bmatrix}$$.Find the matrices D such that $$A + B - D = O$$ i. e. zero matrices
Solve for $$x$$ and $$y$$:$$2\begin{bmatrix} x & 7 \\ 9 & y-5 \end{bmatrix}+\begin{bmatrix} 6 & -7 \\ 4 & 5 \end{bmatrix}=\begin{bmatrix} 10 & 7 \\ 22 & 15 \end{bmatrix}$$
If $$\begin{bmatrix} x-y & z \\ 2x-y & w \end{bmatrix} =\begin{bmatrix} -1 & 4 \\ 0 & 5 \end{bmatrix}$$, then find the value of $$x+y$$.
If A = $$\begin{bmatrix}0 & 1 & 2\\ 2 & 3 & 4\\ 4 & 5 & 6 \end{bmatrix}$$, B = $$ \begin{bmatrix}1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{bmatrix}$$
Find 3A - 4B
Can the following two matrices be added
$$\begin{bmatrix}1 & 2 & 3\\ 3 & 4 & 5\\ 5& 6 &7 \end{bmatrix}$$ and $$\begin{bmatrix}4 & 3 \\ 5 & 6 \\ 9 & 8 \end{bmatrix}$$
If $$A$$ is $$n$$ squared matrix then $$AA'$$ and $$A'A$$ are symmetric.
If $$A= \left [ \begin{array}{c}4\hspace{0.5cm}3\\2\hspace{0.5cm}5\end{array}\right ],$$ find $$x + y$$ such that $$A^2-xA+yI=O.$$
By using elementary transformation find the inverce of $$A=\left[ \begin{matrix} 1 \\ 2\end{matrix}\begin{matrix} 2 \\ -1 \end{matrix} \right]$$.
Solution:- Given $$A=\left[ \begin{matrix} 1 \\ 2\end{matrix}\begin{matrix} 2 \\ -1 \end{matrix} \right]$$
Now we find $$ A^{-1} $$ by elementary row transformation
so, we can write
$$ A = A.I $$
$$\left[ \begin{matrix} 1 \\ 2\end{matrix}\begin{matrix} 2 \\ -1 \end{matrix} \right] = \left[ \begin{matrix} 1 \\ 0\end{matrix}\begin{matrix} 0 \\ 1 \end{matrix} \right]. A $$
$$ R_{2}\rightarrow R_{2}-2R_{1} $$
$$\left[ \begin{matrix} 1 \\ 0\end{matrix}\begin{matrix} 2 \\ -5 \end{matrix} \right] = \left[ \begin{matrix} 1 \\ -2\end{matrix}\begin{matrix} 0 \\ 1 \end{matrix} \right].A $$
$$ R_{1}\rightarrow R_{1}+\dfrac{2}{5}\times R_{2} $$
$$\left[ \begin{matrix} 1 \\ 0\end{matrix}\begin{matrix} 0 \\ -5 \end{matrix} \right] = \left[ \begin{matrix} 1/5 \\ -2\end{matrix}\begin{matrix} \dfrac{2}{5} \\ 1 \end{matrix} \right].A $$
$$ R_{2}\rightarrow R_{2}/-5 $$
$$\left[ \begin{matrix} 1 \\ 0\end{matrix}\begin{matrix} 0 \\ 1 \end{matrix} \right] = \left[ \begin{matrix} 1/5 \\ \dfrac{2}{5}\end{matrix}\begin{matrix} 2/5 \\ -1/5 \end{matrix} \right].A $$
this from is $$ I = A^{-1}.A $$ So, $$ A^{-1} = \left[ \begin{matrix} 1/5 \\ 2/5 \end{matrix}\begin{matrix} 2/5 \\ -1/5 \end{matrix} \right] $$
If $$A=\left[ \begin{matrix} 1 \\ 2 \\ 3 \end{matrix} \right]$$, then $$AA=$$
Find the value of $$a$$ and $$b$$ if $$\begin{bmatrix} a+3 & b^{ 2 }+2 \\ 0 & -6 \end{bmatrix}=\begin{bmatrix} 2a+1 & 3b \\ 0 & b^ 2-5b \end{bmatrix}$$.
By using elementary transformation find the inverse of $$A=\left[ \begin{matrix} 1 \\ 2\end{matrix}\begin{matrix} 2 \\ -1 \end{matrix} \right]$$.
Write the following as a single matrix $$ \begin{bmatrix} -1 & 2 \\ 1 & -2 \\ 3 & -1 \end{bmatrix}+\begin{bmatrix} 0 & 1 \\ -1 & 0 \\ -2 & 1 \end{bmatrix}$$
$$A$$ and $$B$$ are two matrices of same order $$3 \times3$$, where $$A=\begin{bmatrix} 1 & 2 & 3 \\ 2 & 3 & 4 \\ 5 & 6 & 8 \end{bmatrix}$$ and $$B=\begin{bmatrix} 3 & 2 & 5 \\ 2 & 3 & 8 \\ 7 & 2 & 9 \end{bmatrix}4$$. Find AB
If $${A_x} = \left[ {\begin{array}{*{20}{c}}{\cos x}&{\sin x}\\{ - \sin x}&{\cos x}\end{array}} \right]$$ and $${A_y} = \left[ {\begin{array}{*{20}{c}}{{\mathop{\rm cosy}\nolimits} }&{\sin y}\\{ - \sin y}&{\cos y}\end{array}} \right]$$ Show that $${A_x}{A_y} = {A_{x + y}}$$.
$$
\left[
\begin {array}{11}
2 & 1\\
1 & 0 \\
-3 & 4\\
\end{array}
\right]
$$ +$$
\left[
\begin{array}{111}
-1 & -8 \\
1 & -2 \\
9 & 22 \\
\end{array}
\right ]
$$
Determine the product $$\begin{bmatrix}-4 & 4 & 4\\ -7 & 1 & 3\\ 5 & -3 & -1\end{bmatrix} \begin{bmatrix}1 & -1 & 1\\ 1 & -2 & -2\\ 2 & 1 & 3\end{bmatrix}$$.
If $$x+y=\begin{bmatrix} 5 & 2 \\ 0 & 9 \end{bmatrix}$$ and $$x-y=\begin{bmatrix} 3 & 6 \\ 0 & -1 \end{bmatrix}$$Find the value of $$x$$ and $$y$$
Find the matrix $$A$$ such that $$\left[ {\begin{array}{*{20}{c}}2&{ - 1}\\1&0\\{ - 3}&4\end{array}} \right]A = \left[ {\begin{array}{*{20}{c}}{ - 1}&{ - 8}\\1&{ - 2}\\9&{22}\end{array}} \right]$$.
If $$A=\begin{bmatrix}3&4\\7&2\end {bmatrix}B=\begin{bmatrix}7&4\\0&9\end {bmatrix}$$ Then $$AB$$
Determine the product $$\begin{bmatrix} -4 & 4 & 4 \\ -7 & 1 & 3 \\ 5 & -3 & -1 \end{bmatrix}\begin{bmatrix} 1 & -1 & 1 \\ 1 & -2 & -2 \\ 2 & 1 & 3 \end{bmatrix}$$
$$\left[ {\begin{array}{*{20}{c}}1&3\\0&0\end{array}} \right]\,\left[ {\begin{array}{*{20}{c}}2\\{ - 1}\end{array}} \right]\, = \left[ {\begin{array}{*{20}{c}}x\\0\end{array}} \right]$$, find the value of $$ x $$
Compute $$\begin{bmatrix} \cos ^{ 2 }{ x } & \sin ^{ 2 }{ x } \\ \sin ^{ 2 }{ x } & \cos ^{ 2 }{ x } \end{bmatrix}+\begin{bmatrix} \sin ^{ 2 }{ x } & \cos ^{ 2 }{ x } \\ \cos ^{ 2 }{ x } & \sin ^{ 2 }{ x } \end{bmatrix}$$
Let $$A=\begin{bmatrix} i\ 0\\0\ i\end{bmatrix}$$, then find $$A^4$$. Where $$i=\sqrt{-1}$$.
If A = -1, 1
A = {-1, 1}
A = {-1, 1}
A - {-1, 1}
Find $$A \times A \times A$$
If $$\left[ { \begin{array} { *{ 20 }{ c } }{ a+4 } & { 3b } \\ 8 & { -6 } \end{array} } \right] =\left[ { \begin{array} { *{ 20 }{ c } }{ 2a+2 } & { b+2 } \\ 8 & { a-8b } \end{array} } \right] $$ then find the value of $$(a-2b)$$.
If $$A=\begin{pmatrix} a & 1 \\ 0 & a \end{pmatrix}$$, then $$A^2$$ equals to-
Solve: $$f(x) = \begin{bmatrix}\cos x & -\sin x & 0\\ \sin x & \cos x & 0\\ 0 & 0 & 1\end{bmatrix}$$ show that $$f(x) f(y) = f(x + y)$$.
If $$x+y=\begin{bmatrix} 5 & 2 \\ 0 & 9 \end{bmatrix}$$ and $$x-y=\begin{bmatrix} 3 & 6 \\ 0 & -1 \end{bmatrix}$$
find the value of $$x$$ and $$y$$.
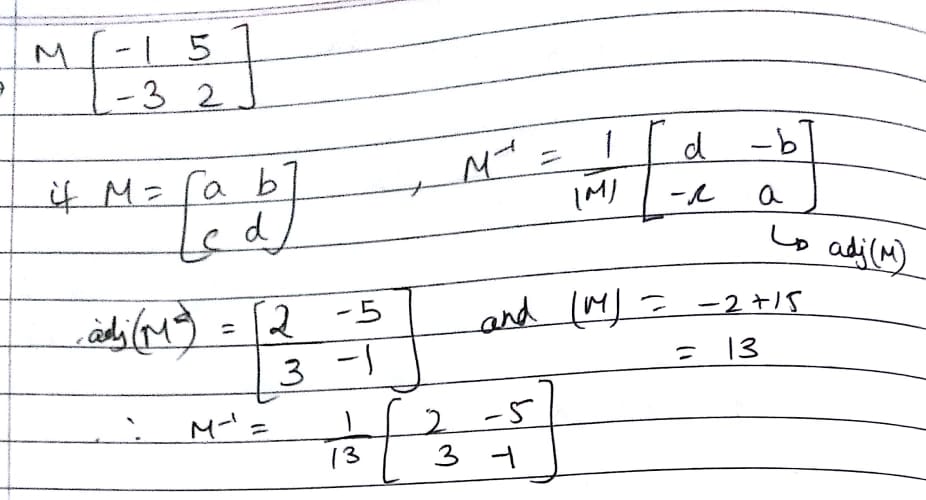
Find the inverse of the following matrices by the adjoint method $$\begin{bmatrix} -1 & 5 \\ -3 & 2 \end{bmatrix} \\ $$
$$ \begin{bmatrix} 2 & -2 \\ 4 & 3 \end{bmatrix}$$
$$\begin{bmatrix} 1 & 0 & 0 \\ 3 & 3 & 0 \\ 5 & 2 & -1 \end{bmatrix}$$
$$\begin{bmatrix} 1 & 2 & 3 \\ 0 & 2 & 4 \\ 0 & 0 & 5 \end{bmatrix}$$
$$ \begin{bmatrix} 2 & -2 \\ 4 & 3 \end{bmatrix}$$
If $$A = \left[ {\begin{array}{*{20}{c}}i & 0\\0 & i\end{array}} \right]$$, find $$A^2$$.
If $$A = \left[ {\begin{array}{*{20}{c}}4&3\\1&2\end{array}} \right]\,\,\,\,\,\,\,\,\,B = \left[ {\begin{array}{*{20}{c}}2&1\\1&2\end{array}} \right]$$ Verify $${\left( {AB} \right)^\prime } = {B^\prime }A'$$
If $$A=\left[ \begin{matrix} -2 & 3 \\ 4 & 5 \end{matrix} \right] $$ and $$B=\left[ \begin{matrix} 5 & 2 \\ -7 & 3 \end{matrix} \right] $$ , find the matrix $$C$$ such that $$A+B-C=0$$
Determine the product $$\begin{bmatrix} -4 & 4 & 4 \\ -7 & 1 & 3 \\ 5 & -3 & -1 \end{bmatrix} \, \begin{bmatrix} 1 & -1 & 1 \\ 1 & -2 & -2 \\ 2 & 1 & 3 \end{bmatrix}$$.
Find the value of $$y-x$$ from the following equation.
$$2\begin{bmatrix} x & 5 \\ 7 & y-3 \end{bmatrix}+\begin{bmatrix} 3 & -4 \\ 1 & 2 \end{bmatrix}=\begin{bmatrix} 7 & 6 \\ 15 & 14 \end{bmatrix}$$
By using the elementary transformation, find the inverse of the matrix $$A=\left[ \begin{matrix} 1 & -2 \\ 2 & 1 \end{matrix} \right] $$.
Given: $$3\begin{bmatrix} x & y \\ z & w \end{bmatrix}=\begin{bmatrix} x & 6 \\ -1 & 2w \end{bmatrix}+\begin{bmatrix} 4 & x+y \\ z+w & 3 \end{bmatrix}$$, find the values of $$x,y,z$$ and $$w$$.
If $$A=\left[ \begin{matrix} 1 & -2 & 3 \\ 0 & -1 & 4 \\ -2 & 2 & 1 \end{matrix} \right] $$ find $$(A')^{-1}$$
$$A=\begin{bmatrix} 1 & -2 & 3\\ 0 & -1 & 4\\ -2 & 2 & 1\end{bmatrix}$$ $$\rightarrow$$ $$\begin{bmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 1 & 0\end{bmatrix}$$
$$\Rightarrow \begin{bmatrix} 1 & -2 & 3\\ -1 & 1 & 1\\ -2 & 2 & 1\end{bmatrix}=\begin{bmatrix} 1 & 0 & 0\\ -1 & 1 & 0\\ 0 & 1 & 0\end{bmatrix}$$
$$\begin{bmatrix} -1 & -2 & 3\\ 0 & 1 & 1\\ 0 & 2 & 1\end{bmatrix}=\begin{bmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 1 & 1\end{bmatrix}$$
$$\begin{bmatrix} -1 & -2 & 3\\ 0 & 1 & 1\\ -1 & 0 & 4\end{bmatrix} =\begin{bmatrix} 1 & 0 & 0\\ 1 & 1 & 0\\ 0 & 2 & 1\end{bmatrix} \Rightarrow \begin{bmatrix} -1 & 0 & 5\\ 0 & 1 & 1\\ -1 & 0 & 4\end{bmatrix} =\begin{bmatrix} 3 & 2 & 0\\ 1 & 1 & 0\\ 0 & 2 & 1\end{bmatrix}$$
$$\begin{bmatrix} -1 & 0 & 5\\ 0 & 1 & 1\\ 0 & 0 & 1\end{bmatrix}=\begin{bmatrix} 3 & 2 & 0\\ 1 & 1 & 0\\ 3 & 0 & -1\end{bmatrix}\Rightarrow \begin{bmatrix} +1 & 0 & 0\\ 0 & 1 & 1\\ 0 & 0 & 1\end{bmatrix}=\begin{bmatrix} -3 & 0 & 1\\ 1 & 1 & 0\\ 0 & 2 & 1\end{bmatrix}$$
$$\Rightarrow \begin{bmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1\end{bmatrix}=\begin{bmatrix} -3 & 0 & 1\\ 1 & -1 & -1\\ 0 & 2 & 1\end{bmatrix}=A^{-1}$$.
Simplify:
$$\cos\theta.\left[ \begin{matrix} \cos { \theta } & \sin { \theta } \\ -\sin { \theta } & \cos { \theta } \end{matrix} \right] +\sin\theta.\left[ \begin{matrix} \sin { \theta } & -\cos { \theta } \\ \cos { \theta } & \sin { \theta } \end{matrix} \right]$$
Find the matrix $$A$$ such that $$\begin{bmatrix} 2 & -1 \\ 1 & 0 \\ -3 & 4 \end{bmatrix}A=\begin{bmatrix} -1 & -8 & -10 \\ 1 & -2 & -5 \\ 9 & 22 & 15 \end{bmatrix}$$
Find $$AB$$, if $$A=\begin{bmatrix} 1 & 2 & 3 \\ 1 & -2 & 3 \end{bmatrix}$$ and $$B=\begin{bmatrix} 1 & -1 \\ 1 & 2 \\ 1 & -2 \end{bmatrix}$$
Examine whether $$AB$$ has inverse or not.
Prove that adjoint of a symmetric matrix is also a symmetric matrix.
If $$A = \left[ \begin{array} { c c c } { 1 } & { - 2 } & { 0 } \\ { 2 } & { 1 } & { 3 } \\ { 0 } & { - 2 } & { 1 } \end{array} \right]$$,then $$A ^ { - 1 } =$$
If $$A=[2\ 0\ 1],$$ then rank of $$AA^T$$ is
Given $$A=\begin{bmatrix}2 & 0 & 1\end{bmatrix}_{1\times 3}$$
$$A^T=\begin{bmatrix} 2 \\ 0 \\ 1\end{bmatrix}_{3\times 1}$$
$$AA^{T}=\begin{bmatrix} 2 & 0 & 1\end{bmatrix}_{1\times 3}\begin{bmatrix} 2 \\ 0\\ 1\end{bmatrix}_{3\times 1}$$
$$=[4 + 0 +1]_{1\times 1}$$
$$=[5]_{1\times 1}$$
$$det(AA^T)=5\neq 0$$
$$\therefore$$ Rank $$AA^T=1$$.
Find the inverse of matrix by elementary row transformations.
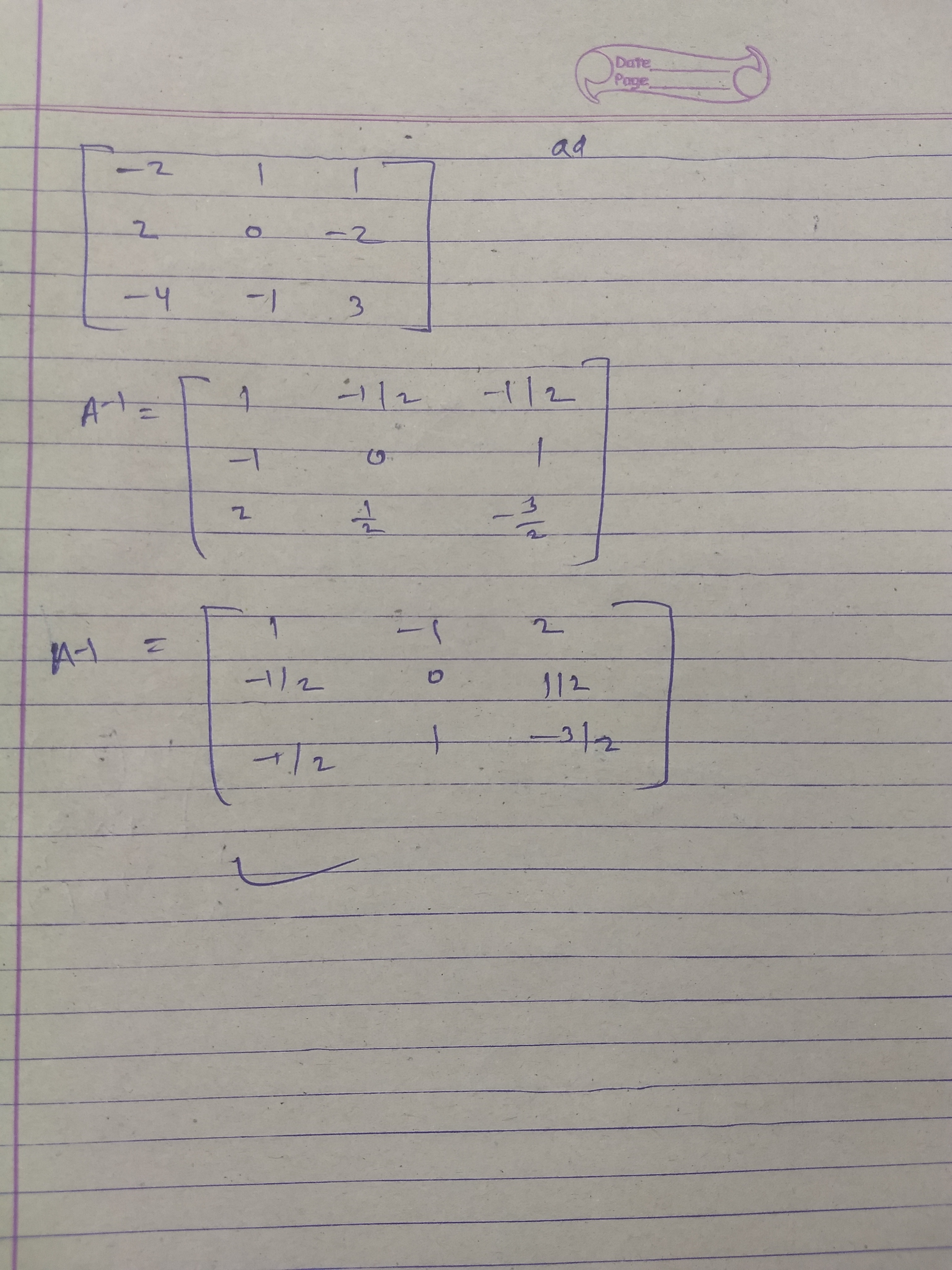
$$A = \left[ \begin{array} { r r r } { 1 } & { 2 } & { 1 } \\ { - 1 } & { 0 } & { 2 } \\ { 2 } & { 1 } & { - 3 } \end{array} \right]$$
If $$2\left[ \begin{matrix} x & 5 \\ 7 & y-3 \end{matrix} \right] +\left[ \begin{matrix} 3 & 4 \\ 1 & 2 \end{matrix} \right] =\left[ \begin{matrix} 7 & 14 \\ 15 & 14 \end{matrix} \right] $$, find the value of $$x$$ and $$y$$.
Given,$$A=\begin{bmatrix} 1 & 3 & 5 \\ -1 & 0 & 2\\0 & 4 & -3 \end{bmatrix}$$ and $$B=\begin{bmatrix} 0 & 3 \\ -2 & 0 \\0 & -4 \end{bmatrix}$$ Find $$A+B$$
If $$A=\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix},$$ such that $$AX=I$$, then find $$X$$.
If $$AX=I$$
$$\Rightarrow X=A^{-1}$$
$$=\dfrac{1}{|A|} adj A=\dfrac{1}{(4-6)}\begin{bmatrix} 4 & -2\\ -3 & 1\end{bmatrix}$$
$$x=-\dfrac{1}{2}\begin{bmatrix} 4 & -2\\ -3 & 1\end{bmatrix}$$
$$=\begin{bmatrix} -2 & 1\\ 3/2 & -1/2\end{bmatrix}$$.
Let E =$$\left[ \begin{matrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \end{matrix} \right] .\quad F=\left[ \begin{matrix} 0 & 0 & 0 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{matrix} \right] \quad and\quad x \in R,$$ then find $$E+F$$.
$$A=\begin{bmatrix} 1 & -1 \\ 2 & 3 \end{bmatrix}, B=\begin{bmatrix} 2 & 1 \\ -1 & 0 \end{bmatrix}$$
Find $$AB$$
If $$x = $$$$\begin{bmatrix}4&1\\-1&2\end{bmatrix}$$, show that $$6x - x^2 = 9I$$, where $$I$$ is the units matrix.
$$A=|_{ 1 }^{ 1 }\quad _{ 3 }^{ 3 }|\quad $$ and $$B=|_{ 1 }^{ -1 }\quad _{ -1 }^{ 1 }|\quad $$. Find AB.
If A = $$\begin{bmatrix} 4 & 8 \\ -2 & -4 \end{bmatrix}$$ find $${ A }^{ 2 }$$
$$A=\begin{bmatrix} 1 & 8 \\ 9 & 4 \end{bmatrix}B=\begin{bmatrix} 6 & 7 \\ 3 & 5 \end{bmatrix}$$ Find $$A+B$$
Find the value of 'x' and 'y' if :
$$2\begin{bmatrix} x & 7 \\ 9y & 5 \end{bmatrix}+\begin{bmatrix} 6 & -7 \\ 4 & 5 \end{bmatrix}=\begin{bmatrix} 10 & 7 \\ 22 & 15 \end{bmatrix}$$
If $$A=\begin{bmatrix} 2 & 4 \\ k & -2 \end{bmatrix}$$ and $$A^2=O$$, then find the value of k.
If $$A=\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}B=\begin{bmatrix} 1 & 2 \\ 3 & 5 \end{bmatrix}$$ then $$A+B$$
If $$A = \begin{bmatrix}4 & 3\\ 1 & 2\end{bmatrix}$$ and $$B = \begin{bmatrix}-4\\ 3
\end{bmatrix}$$, then find $$AB$$.
$$A=\begin{bmatrix} 1 & -1 \\ 2 & 3 \end{bmatrix}, B=\begin{bmatrix} 2 & 1 \\ -1 & 0 \end{bmatrix}$$
Find $$BA$$
If $$A=\begin{pmatrix} 3 & 2 \\ 4 & 0 \end{pmatrix}$$ and $$B=\begin{pmatrix} 3 & 0 \\ 3 & 2 \end{pmatrix}$$ then, find $$AB\, and\, BA$$.
If matrix $$A = \begin{bmatrix}2 & -2\\ -2 & 2\end{bmatrix}$$ and $$A^{2} = pA$$, then write the value of $$p$$.
Find $${A}^{2}$$ if $$A= \begin{bmatrix} 1 & 2 & 5 \\ 3 & 4 & 1 \\ 1 & -1 & 2 \end{bmatrix}$$
If $$A$$ is symmetric matrix and $$n\in N$$, write whether $$A^{n}$$ is symmetric or skew-symmetric or neither of these two.
Evaluate the following :
$$\begin{bmatrix} 1 & 2 & 3 \\ -1 & 4 & 5 \\ 0 & 3 & 6 \end{bmatrix}\begin{bmatrix} -4 & -3 & -2 \\ -6 & -1 & 0 \\ -5 & -2 & 1 \end{bmatrix}$$
$$\begin{bmatrix} 1 & 2 & 3 \\ -1 & 4 & 5 \\ 0 & 3 & 6 \end{bmatrix}\begin{bmatrix} -4 & -3 & -2 \\ -6 & -1 & 0 \\ -5 & -2 & 1 \end{bmatrix}$$
Find $$A+B$$$$A=\begin{bmatrix} 1 & 3 & -1 \\ 2 & -5 & 4 \\ 3 & 2 & -6 \end{bmatrix}$$ and $$B=\begin{bmatrix} 2 & 4 & 0 \\ 3 & -4 & 5 \\ 2 & 3 & -5 \end{bmatrix}$$
$$A=\begin{bmatrix}3&5\\2&2\end{bmatrix}$$
$$A^2=?$$
Show by an example that for $$2\times 2$$ matrices $$A \neq O$$ and $$B \neq O, AB=O$$.
If $$A = \begin{bmatrix}ab & b^{2}\\ -a^{2} & -ab\end{bmatrix}$$, then show that $$A^{2} = 0$$.
Using elementary transformations, find the inverse of matrix, $$A=\begin{bmatrix} 1 & 3 \\ 2 & 7 \end{bmatrix}$$.
Multiply the given matrix:$$\begin{bmatrix}a & b\\ -b & a\end{bmatrix}\begin{bmatrix}a & -b\\ b & a\end{bmatrix}$$
If matrix $$A=\begin{bmatrix} 1 & 2 & 3 \end{bmatrix}$$, write $$AA'$$.
If $$A=\begin{bmatrix} ab & b^2 \\ -a^2 & -ab \end{bmatrix}$$, show that $$A^{2}=O$$.
Perform the given operation: $$\begin{bmatrix} a& b\end{bmatrix} \begin{bmatrix}c\\ d
\end{bmatrix} + \begin{bmatrix}a & b & c & d\end{bmatrix} \begin{bmatrix}a\\ b\\ c\\ d
\end{bmatrix}$$
Find the inverse of the following matrix by using elementary row transformation :
$$\begin{bmatrix} 2 & 5 \\ 1 & 3 \end{bmatrix}$$
Addition of matrices defined if order of the matrices is _______ .
If $$ A\quad =\quad \left[ \begin{matrix} 2 \\ 5 \end{matrix} \right] ,\quad B\quad =\quad \left[ \begin{matrix} 1 \\ 4 \end{matrix} \right] \quad and\quad C\quad =\quad \left[ \begin{matrix} 6 \\ -2 \end{matrix} \right] $$
$$ A-B+C $$
Given $$ A\quad =\begin{bmatrix} 4 & 1 \\ 2 & 3 \end{bmatrix}\quad and\quad B\quad =\begin{bmatrix} 1 & 0 \\ -2 & 1 \end{bmatrix} $$ Find
$$ AB $$
Let $$ A=\begin{bmatrix} 2 & 4 \\ 3 & 2 \end{bmatrix},B=\begin{bmatrix} 1 & 3 \\ -2 & 5 \end{bmatrix},C=\begin{bmatrix} -2 & 5 \\ 3 & 4 \end{bmatrix} $$
Find the following:
$$ A+B $$
If $$ A\quad =\quad \left[ \begin{matrix} 2 \\ 5 \end{matrix} \right] ,\quad B\quad =\quad \left[ \begin{matrix} 1 \\ 4 \end{matrix} \right] \quad and\quad C\quad =\quad \left[ \begin{matrix} 6 \\ -2 \end{matrix} \right] $$
$$ B+C $$
if $$ A = [ 8\ \ -3] $$ and $$ B = [ 4\ \ -5] $$ find
$$ (i) A +B $$
Compute the following
$$ \begin{bmatrix} a & b \\ -b & a \end{bmatrix}+\begin{bmatrix} a & b \\ b & a \end{bmatrix} $$
Evaluate :
$$ 7\begin{bmatrix} -1 & 2 \\ 0 & 1 \end{bmatrix} $$
Evaluate :
$$ 3 [ 5-2 ] $$
Given $$ A\quad =\begin{bmatrix} 4 & 1 \\ 2 & 3 \end{bmatrix}\quad and\quad B\quad =\begin{bmatrix} 1 & 0 \\ -2 & 1 \end{bmatrix} $$Find
$$ A^2 $$
Compute the indicated products
$$ \begin{bmatrix} a & b \\ -b & a \end{bmatrix}\begin{bmatrix} a & -b \\ b & a \end{bmatrix} $$
Compute the indicated products
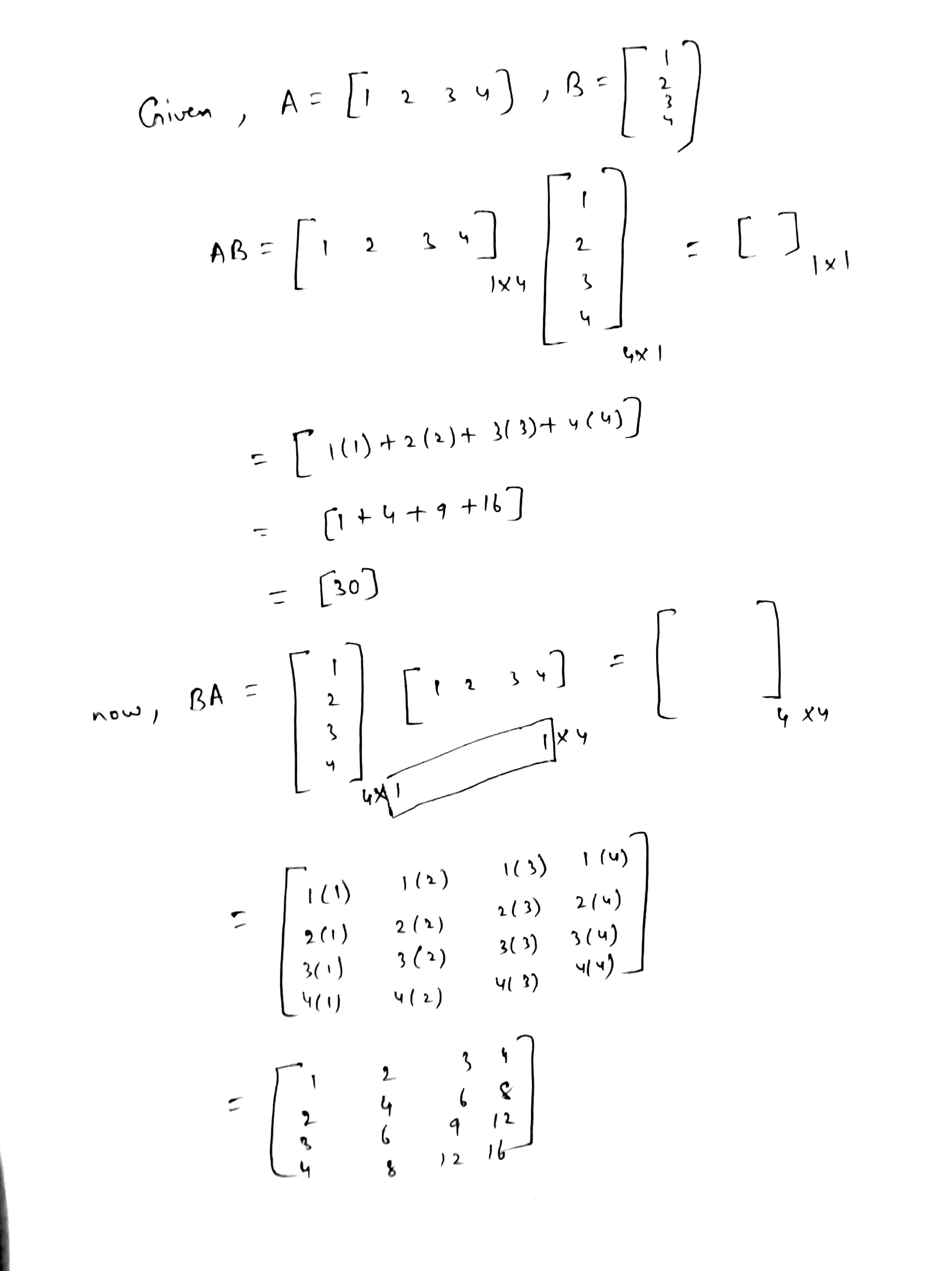
$$ \left[ \begin{matrix} 1 \\ 2 \\ 3 \end{matrix} \right] \left[ \begin{matrix} 2 & 3 & 4 \end{matrix} \right] $$
If $$A = \begin{bmatrix} 1 & 0\\ 2 & -7 \end{bmatrix}; B = \begin{bmatrix} 3 & 8\\ 7 & 5 \end{bmatrix}; C = \begin{bmatrix} -8 & -3\\ 0 & 9 \end{bmatrix},$$ then A (B + C) =
If $$\begin{bmatrix} 1 & -1 \\ 2 & -1 \end{bmatrix}, B=\begin{bmatrix} a & 1 \\ b & -1 \end{bmatrix}$$ and $$ (A+B)^2=A^2+B^2 $$, find $$a$$ and $$b$$.
If $$A=\begin{bmatrix} 1 & 0 \\ -1 & 7 \end{bmatrix} $$ and $$\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix},$$ then find the $$k$$ so that $$A^{2}=8A+kI.$$
If $$A\times \begin{bmatrix} 1 & 2 \\ 0 & 2 \end{bmatrix}=(1, 2)$$, then $$A=$$
If $$A=\begin{bmatrix} 3 & 2 \\ 7 & 5 \end{bmatrix}$$ and $$B=\begin{bmatrix} 6 & 7 \\ 8 & 9 \end{bmatrix}$$, verify that $$(AB)^{-1}=B^{-1}A^{-1}$$
Determine all $$2\times 2$$ matrices A such that $$A^{2}=I.$$
If $$A=\begin{bmatrix} x & 1 \\ 1 & 0 \end{bmatrix}$$ and $$ A^{2}=I,$$ then find $$x.$$
Find the value of $$(x \times y)$$ if $$\begin{bmatrix}3 & -2\\ 3 & 0\\ 2 & 4\end{bmatrix} \begin{bmatrix}y & y\\ x & x\end{bmatrix} = \begin{bmatrix}3 & 3\\ 3y & 3y\\ 10 & 10\end{bmatrix}.$$
The elements on the main diagonal of a skew-symmetric matrix are all ...........
If $$A = \begin{bmatrix} 1 & 4 & 0 \\ 2 & 5 & 0 \\ 3 & 6 & 0 \end{bmatrix}$$ and $$B = \begin{bmatrix} 3 & 2 & 1 \\ 1 & 2 & 3 \\ 4 & 5 & 6 \end{bmatrix}$$ and $$C = \begin{bmatrix} 3 & 2 & 1 \\ 1 & 2 & 3 \\ 7 & 8 & 9 \end{bmatrix}$$, Then evaluate matrix $$AB - BC$$
If $$A = \begin{bmatrix} 1 & 4 & 0 \\ 2 & 5 & 0 \\ 3 & 6 & 0 \end{bmatrix}$$ and $$B = \begin{bmatrix} 3 & 2 & 1 \\ 1 & 2 & 3 \\ 4 & 5 & 6 \end{bmatrix}$$ and $$C = \begin{bmatrix} 3 & 2 & 1 \\ 1 & 2 & 3 \\ 7 & 8 & 9 \end{bmatrix}$$, Then evaluate $$AB - BC$$
If $$A = \begin{bmatrix}0 & 1 & 2 \\ 1 & 2 & 3 \\ 2 & 3 & 4 \end{bmatrix}$$ and $$B = \begin{bmatrix}1 & -2 \\ -1 & 0 \\ 2 & -1\end{bmatrix}$$, Check $$AB=BA$$?
By the method of matrix inversion, solve the system
$$\begin{bmatrix}1&1&1 \\ 2&5&7 \\ 2&1&-1\end{bmatrix}\begin{bmatrix}x&u \\ y&v \\ z&w\end{bmatrix} = \begin{bmatrix}9&2 \\ 52&15 \\ 0&-1\end{bmatrix}$$
and find the value of $$ xyz-uvw$$
Find the inverse of $$A = \begin{bmatrix}0& 1 & 2 \\ 1 & 2 & 3 \\ 3 & 1 & 1\end{bmatrix}$$ if
$$ A^{-1} = \quad \begin{bmatrix}1/2 & -1/2 & 1/2 \\ a & 3 & b \\ c & -3/2 & 1/2\end{bmatrix}$$
Find $$|abc|?$$
Let $$A =\begin{bmatrix}1 &1 &3 \\5 &2 &6 \\-2 &-1 &-3 \end{bmatrix}.$$ Find the smallest $$n\in N,$$ such that $$A^n=O$$.
Show that, $$\displaystyle \begin{bmatrix}1 &-\tan \frac{\theta }{2} \\ \tan \frac{\theta }{2}&1 \end{bmatrix} \begin{bmatrix}1 &\tan \frac{\theta }{2} \\ -\tan \frac{\theta }{2}&1 \end{bmatrix}^{-1}=\begin{bmatrix}\cos \theta & -\sin \theta \\ \sin \theta& \cos \theta \end{bmatrix}.$$
If $$A =\begin{bmatrix} 1&0 &2 \\0 &2 &1 \\2 &0 &3 \end{bmatrix}$$, then show that the matrix A is a root of the polynomial $$f(x) = x^3 - 6x^2 + 7x + 2$$.
If $$A =$$ $$\begin{bmatrix}2 &-3 \\ 4 & 1\end{bmatrix},\, B\, =\, \begin{bmatrix}2 & 3 \\ 5 & 0\end{bmatrix}\, $$ and $$\, C\, =\, \begin{bmatrix}-1 & 2 \\ 0 & 5\end{bmatrix}$$, then find $$A (B + C)$$.
Find $$X$$ and $$Y$$, if
(i) $$\displaystyle X+Y=\begin{bmatrix} 7 & 0 \\ 2 & 5 \end{bmatrix}$$ and $$\displaystyle X-Y=\begin{bmatrix} 3 & 0 \\ 0 & 3 \end{bmatrix}$$
(ii) $$\displaystyle 2X+3Y=\begin{bmatrix} 2 & 3 \\ 4 & 0 \end{bmatrix}$$ and $$\displaystyle 3X+2Y=\begin{bmatrix} 2 & -2 \\ -1 & 5 \end{bmatrix}$$
Let $$\displaystyle A=\begin{bmatrix} 2 & 4 \\ 3 & 2 \end{bmatrix},B=\begin{bmatrix} 1 & 3 \\ -2 & 5 \end{bmatrix},C=\begin{bmatrix} -2 & 5 \\ 3 & 4 \end{bmatrix}$$
Find each of the following
(i) $$A+B$$
(ii) $$A-B$$
(iii) $$3A-C$$
(iv) $$AB$$
(v) $$BA$$
Compute the indicated products
(i) $$\displaystyle \begin{bmatrix} a & b \\ -b & a \end{bmatrix}\begin{bmatrix} a & -b \\ b & a \end{bmatrix}$$
(ii) $$\displaystyle \left[ \begin{matrix} 1 \\ 2 \\ 3 \end{matrix} \right] \left[ \begin{matrix} 2 & 3 & 4 \end{matrix} \right] $$
(iii) $$\displaystyle \begin{bmatrix} 1 & -2 \\ 2 & 3 \end{bmatrix}\left[ \begin{matrix} 1 & 2 & 3 \\ 2 & 3 & 1 \end{matrix} \right] $$
(iv) $$\displaystyle \left[ \begin{matrix} 2 \\ 3 \\ 4 \end{matrix}\begin{matrix} 3 \\ 4 \\ 5 \end{matrix}\begin{matrix} 4 \\ 5 \\ 6 \end{matrix} \right] \left[ \begin{matrix} 1 \\ 0 \\ 3 \end{matrix}\begin{matrix} -3 \\ 2 \\ 0 \end{matrix}\begin{matrix} 5 \\ 4 \\ 5 \end{matrix} \right] $$
(v) $$\displaystyle \left[ \begin{matrix} 2 \\ 3 \\ -1 \end{matrix}\begin{matrix} 1 \\ 2 \\ 1 \end{matrix} \right] \left[ \begin{matrix} 1 & 0 & 1 \\ -1 & 2 & 1 \end{matrix} \right] $$
(vi) $$\displaystyle \left[ \begin{matrix} 3 & -1 & 3 \\ -1 & 0 & 2 \end{matrix} \right] \left[ \begin{matrix} 2 \\ 1 \\ 3 \end{matrix}\begin{matrix} -3 \\ 0 \\ 1 \end{matrix} \right] $$
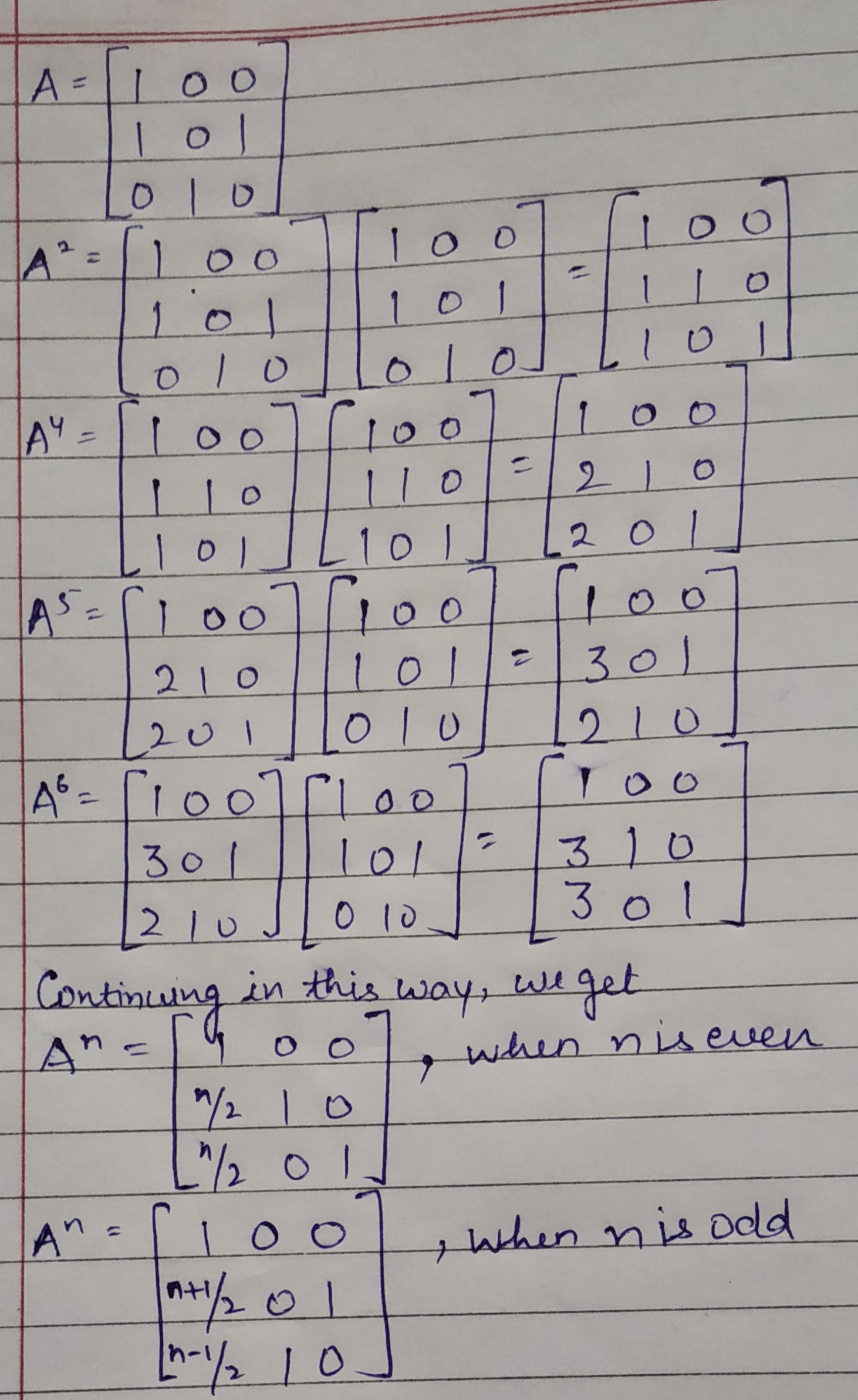
If $$\displaystyle A=\begin{bmatrix} 3 & -4 \\ 1 & -1 \end{bmatrix}$$, then prove $$\displaystyle { A }^{ n }=\begin{bmatrix} 1+2n & -4n \\ n & 1-2n \end{bmatrix}$$ where n is any positive integer
Given : $$\displaystyle 3\begin{bmatrix} x & y \\ z & w \end{bmatrix}=\begin{bmatrix} x & 6 \\ -1 & 2w \end{bmatrix}+\begin{bmatrix} 4 & x+y \\ z+w & 3 \end{bmatrix}$$
Find the values of $$x,y,z$$ and $$w$$.
If $$\displaystyle A=\left[ \begin{matrix} 1 \\ 5 \\ 1 \end{matrix}\begin{matrix} 2 \\ 0 \\ -1 \end{matrix}\begin{matrix} -3 \\ 2 \\ 1 \end{matrix} \right] ,B=\left[ \begin{matrix} 3 \\ 4 \\ 2 \end{matrix}\begin{matrix} -1 \\ 2 \\ 0 \end{matrix}\begin{matrix} 2 \\ 5 \\ 3 \end{matrix} \right] $$ and $$\displaystyle C=\left[ \begin{matrix} 4 \\ 0 \\ 1 \end{matrix}\begin{matrix} 1 \\ 3 \\ -2 \end{matrix}\begin{matrix} 2 \\ 2 \\ 3 \end{matrix} \right] $$, then compute $$(A+B)$$ and $$(B-C)$$.
Also, verify that $$\displaystyle A+\left( B-C \right) =\left( A+B \right) -C$$
For what values of $$x$$.$$\begin{bmatrix} 1 &2&1\end{bmatrix}\begin{bmatrix} 1&2&0\\2&0&1\\1&0&2\end{bmatrix}\begin{bmatrix}0\\2\\x \end{bmatrix} = 0$$?
If A=$$\displaystyle \begin{bmatrix} 2 & -3 \\ 4 & 1 \end{bmatrix}$$ B=$$\displaystyle \begin{bmatrix} 2 & 3 \\ 5 & 0 \end{bmatrix}$$ and C=$$\displaystyle \begin{bmatrix} -1 & 2 \\ 0 & 5 \end{bmatrix}$$, then find $$A(B+C)$$.
Show that
$$(i)$$ $$\begin{bmatrix} 5 & -1 \\ 6 & 7 \end{bmatrix}\begin{bmatrix} 2 & 1 \\ 3 & \ 4 \end{bmatrix} \neq \begin{bmatrix} 2 & 1 \\ 3 & 4 \end{bmatrix}\begin{bmatrix} 5 & -1 \\ 6 & 7 \end{bmatrix}$$
$$(ii)$$ $$\left[ \begin{matrix} 1 \\ 0 \\ 0 \end{matrix}\quad \begin{matrix} 2 \\ 1 \\ 1 \end{matrix}\quad \begin{matrix} 3 \\ 0 \\ 0 \end{matrix} \right] \left[ \begin{matrix} -1 \\ 0 \\ 2 \end{matrix} \begin{matrix} 1 \\ -1 \\ 3 \end{matrix}\quad \begin{matrix} 0 \\ 1 \\ 4 \end{matrix} \right] \neq \left[ \begin{matrix} -1 \\ 0 \\ 2 \end{matrix}\quad \begin{matrix} 1 \\ -1 \\ 3 \end{matrix}\quad \begin{matrix} 0 \\ 1 \\ 4 \end{matrix} \right] \left[ \begin{matrix} 1 \\ 0 \\ 0 \end{matrix}\quad \begin{matrix} 2 \\ 1 \\ 1 \end{matrix}\quad \begin{matrix} 3 \\ 0 \\ 0 \end{matrix} \right] $$
$$(ii)$$ $$\left[ \begin{matrix} 1 \\ 0 \\ 0 \end{matrix}\quad \begin{matrix} 2 \\ 1 \\ 1 \end{matrix}\quad \begin{matrix} 3 \\ 0 \\ 0 \end{matrix} \right] \left[ \begin{matrix} -1 \\ 0 \\ 2 \end{matrix} \begin{matrix} 1 \\ -1 \\ 3 \end{matrix}\quad \begin{matrix} 0 \\ 1 \\ 4 \end{matrix} \right] \neq \left[ \begin{matrix} -1 \\ 0 \\ 2 \end{matrix}\quad \begin{matrix} 1 \\ -1 \\ 3 \end{matrix}\quad \begin{matrix} 0 \\ 1 \\ 4 \end{matrix} \right] \left[ \begin{matrix} 1 \\ 0 \\ 0 \end{matrix}\quad \begin{matrix} 2 \\ 1 \\ 1 \end{matrix}\quad \begin{matrix} 3 \\ 0 \\ 0 \end{matrix} \right] $$
If $$\displaystyle A=\left[ \begin{matrix} 1 \\ 1 \\ 1 \end{matrix}\begin{matrix} 1 \\ 1 \\ 1 \end{matrix}\begin{matrix} 1 \\ 1 \\ 1 \end{matrix} \right] $$, prove that $$\displaystyle { A }^{ n }=\left[ \begin{matrix} { 3 }^{ n-1 } \\ { 3 }^{ n-1 } \\ { 3 }^{ n-1 } \end{matrix}\begin{matrix} { 3 }^{ n-1 } \\ { 3 }^{ n-1 } \\ { 3 }^{ n-1 } \end{matrix}\begin{matrix} { 3 }^{ n-1 } \\ { 3 }^{ n-1 } \\ { 3 }^{ n-1 } \end{matrix} \right] ,n\in N$$
Find the matrix $$X$$ so that $$\displaystyle X\left[ \begin{matrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{matrix} \right] =\left[ \begin{matrix} -7 & -8 & -9 \\ 2 & 4 & 6 \end{matrix} \right] $$
Find $$x$$, if $$\displaystyle \begin{bmatrix} x&-5&-1 \end{bmatrix}\begin{bmatrix}1&0&2\\0&2&1\\2&0&3 \end{bmatrix}\begin{bmatrix}x\\4\\1\end{bmatrix}=0$$
If $$\begin{bmatrix}9 &-1 &4 \\ -2&1 &3 \\ \end{bmatrix}= A+\begin{bmatrix}1 &2 &-1 \\ 0&4 &9 \\ \end{bmatrix}$$, then find the matrix $$A$$
$$\left[ \begin{matrix} 9 & -1 & 4 \\ -2 & 1 & 3 \end{matrix} \right] =A+\left[ \begin{matrix} 1 & 2 & -1 \\ 0 & 4 & 9 \end{matrix} \right] $$
Let, $$A=\left[ \begin{matrix} a & b & c \\ d & e & f \end{matrix} \right] $$
$$\Rightarrow \left[ \begin{matrix} 9 & -1 & 4 \\ -2 & 1 & 3 \end{matrix} \right] =\left[ \begin{matrix} a & b & c \\ d & e & f \end{matrix} \right] +\left[ \begin{matrix} 1 & 2 & -1 \\ 0 & 4 & 9 \end{matrix} \right] $$
$$\Rightarrow \left[ \begin{matrix} 9 & -1 & 4 \\ -2 & 1 & 3 \end{matrix} \right] =\left[ \begin{matrix} a+1 & b+2 & c-1 \\ d+0 & e+4 & f+9 \end{matrix} \right] $$
$$\therefore A=\left[ \begin{matrix} 8 & -3 & 5 \\ -2 & -3 & -6 \end{matrix} \right] $$
Hence, the answer s $$\left[ \begin{matrix} 8 & -3 & 5 \\ -2 & -3 & -6 \end{matrix} \right].$$
If matrix $$A = \begin{bmatrix} 1 & -1 \\ -1 & 1 \end{bmatrix}$$ and $$A^2 = KA$$, then write the value of $$K.$$
Simplify:
$$\cos \theta \begin{bmatrix} \cos \theta & \sin \theta\\ -\sin \theta & \cos \theta \end{bmatrix} + \sin \theta \begin{bmatrix}\sin \theta & -\cos \theta\\ \cos \theta & \sin \theta\end{bmatrix}.$$
The monthly incomes of Aryan and Babban are in the ratio $$3 : 4$$ and their monthly expenditures are in the ratio $$5 : 7$$. If each saves Rs. $$15000$$ per month, find their monthly incomes using matrix method. This problem reflects which value?
If $$\begin{bmatrix} 2 & 3 \\ 5 & 7 \end{bmatrix} \begin{bmatrix} 1 & -3 \\ -2 & 4 \end{bmatrix} = \begin{bmatrix} -4 & 6 \\ -9 & x \end{bmatrix}$$, write the value of $$x$$.
Matrix $$A = \begin{bmatrix} 0& 2b & -2\\ 3 & 1 & 3\\ 3a & 3 & -1\end{bmatrix}$$ is given to be symmetric, find values of $$a$$ and $$b$$
If $$\begin{bmatrix} x - y& z\\ 2x - y & w\end{bmatrix} = \begin{bmatrix} -1& 4\\ 0 & 5\end{bmatrix}$$, find the value of $$x + y.$$
If $$A$$ is a square matrix such that $$A^{2} = A$$, then write the value of $$7A - (I + A)^{3}$$, where $$I$$ is an identity matrix.
If $$A=\begin{bmatrix}2&0&1\\2&1&3\\1&-1&0\end{bmatrix}$$, find $$A^2-5A+4I$$ and hence find a matrix $$X$$ such that $$A^2-5A+4I+X=0$$.
Solve the following matrix equation for $$x : [x \space 1] \begin{bmatrix} 1& 0\\ -2 & 0\end{bmatrix} = 0.$$
Three school A, B and C organized a mela for collecting funds for helping the rehabilitation of flood victims. They sold hand made fans, mats and plates from recycled material at a cost of Rs $$25$$, Rs $$100$$ and Rs $$50$$ each. The number of articles sold are given below:
| Articles | School A | School B | School C |
| Hand-fans | $$40$$ | $$25$$ | $$35$$ |
| Mats | $$50$$ | $$40$$ | $$50$$ |
| Plates | $$20$$ | $$30$$ | $$40$$ |
To promote the making of toilets for women, an organization tried to generate awarencess through:(i) house calls(ii) letters(iii) announcements.
The cost for each mode per attempt is given below:
(i) Rs $$50$$
(i) Rs $$20$$
(i) Rs $$40$$
The number of attempts made in three villages X, Y and Z are given below:
(i) (ii) (iii) X $$400$$ $$300$$ $$100$$ Y $$300$$ $$250$$ $$75$$ Z $$500$$ $$400$$ $$150$$
Find the total cost incurred by the organization for the three villages separately, using matrices.
Write one value generated by the organization in the society.
(ii) letters
(iii) announcements.
The cost for each mode per attempt is given below:
(i) Rs $$50$$
(i) Rs $$20$$
(i) Rs $$40$$
The number of attempts made in three villages X, Y and Z are given below:
Find the total cost incurred by the organization for the three villages separately, using matrices.
Write one value generated by the organization in the society.
The cost for each mode per attempt is given below:
(i) Rs $$50$$
(i) Rs $$20$$
(i) Rs $$40$$
The number of attempts made in three villages X, Y and Z are given below:
| (i) | (ii) | (iii) | |
| X | $$400$$ | $$300$$ | $$100$$ |
| Y | $$300$$ | $$250$$ | $$75$$ |
| Z | $$500$$ | $$400$$ | $$150$$ |
Write one value generated by the organization in the society.
Given $$\begin{bmatrix}2&1\\-3&4\end{bmatrix}X=\begin{bmatrix}7\\6\end{bmatrix}$$. Write:
(i) the order of the matrix $$X$$
(ii) the matrix $$X$$.
Find $$x+y$$ if $$\begin{bmatrix} x & 3x\\y & 4y\end{bmatrix}$$ $$\begin{bmatrix}2 \\ 1 \end{bmatrix}$$ $$=\begin{bmatrix}5 \\1 2\end{bmatrix}$$.
If $$A=\begin{bmatrix} 3 & 7 \\ 2 & 4 \end{bmatrix}$$, $$B=\begin{bmatrix} 0 & 2 \\ 5 & 3 \end{bmatrix}$$ and $$C=\begin{bmatrix} 1 & -5 \\ -4 & 6 \end{bmatrix}$$. Find $$AB-5C$$.
Find $$x+ y$$ if $$\begin{bmatrix}-2 & 0\\ 3 & 1\end{bmatrix} \begin{bmatrix} -1\\ 2x \end{bmatrix} + 3 \begin{bmatrix} -2\\ 1\end{bmatrix} = 2 \begin{bmatrix}y \\ 3\end{bmatrix}.$$
Given A$$=\begin{bmatrix} 2 & -6\\2 & 0\end{bmatrix}, B=\begin{bmatrix} -3 & 2\\ 4 & 0\end{bmatrix}, C=\begin{bmatrix} 4 & 0\\0 & 2\end{bmatrix}$$. Find the matrix X such that $$A+2X=2B+C$$.
If $$A=\begin{bmatrix}3&1\\-1&2\end{bmatrix}$$ and $$I=\begin{bmatrix} 1& 0 \\ 0& 1 \end{bmatrix}$$, find $$A^2-5A+7I$$
Given $$A = \begin{bmatrix}2 & 0\\ -1 & 7\end{bmatrix}$$ and $$I = \begin{bmatrix}1 & 0\\ 0 & 1\end{bmatrix}$$ and $$A^{2} = 9A + mI$$. Find $$m.$$
Given matrix $$A = \begin{bmatrix}4\sin 30^{\circ} & \cos 0^{\circ} \\ \cos 0^{\circ} & 4\sin 30^{\circ} \end{bmatrix}$$ and $$B = \begin{bmatrix}4\\5
\end{bmatrix}$$. If $$AX = B$$.
Find the matrix $$X$$.
Find $$A$$, if $$A + B = \begin{bmatrix}5 & 2\\ 0 & 9\end{bmatrix}$$ and $$A - B = \begin{bmatrix}-3 & -6\\ 4 & -1\end{bmatrix}$$
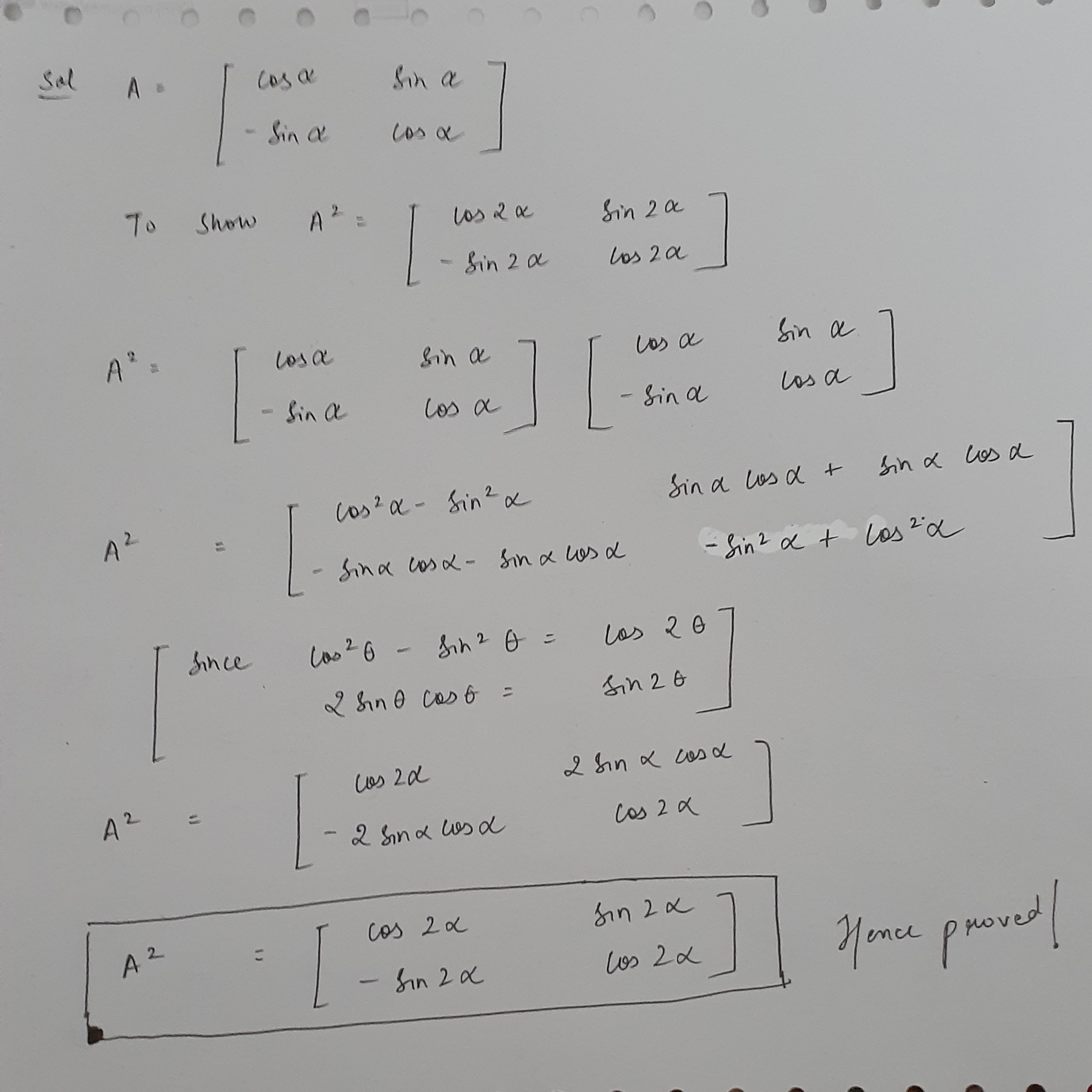
If $$A=\begin{bmatrix} \cos { \alpha } & \sin { \alpha } \\ -\sin { \alpha } & \cos { \alpha } \end{bmatrix}$$, then find $${A}^{2}$$.
Let $$A = \begin{bmatrix} 2& 1\\ 0 & -2\end{bmatrix}, B = \begin{bmatrix}4 & 1\\ -3 & -2\end{bmatrix}$$ and $$C = \begin{bmatrix}-3 & 2\\ -1 & 4\end{bmatrix}$$. Find $$A^{2} + AC - 5B$$
If $$A = \begin{bmatrix}-2\\ 4\\ 6
\end{bmatrix}$$ and $$B = [1\ 4\ -6]$$ then find $$AB$$
Find the matrix $$B$$, such that
$$\begin{bmatrix} 4 & 3 \\ 3 & 2 \end{bmatrix}B=\begin{bmatrix} 2 & 5 \\ 1 & 3 \end{bmatrix}$$
Find the matrix for which:
$$\begin{bmatrix} 5 & 4 \\ 1 & 1 \end{bmatrix}X=\begin{bmatrix} 1 & -2 \\ 1 & 3 \end{bmatrix}$$
Solve for x and y if $$\left(\begin{matrix} {y^2}\\ {x^2} \end{matrix}\right) + 2 \left( \begin{matrix}{3y}\\{2x}\end{matrix} \right ) = 3 \left (\begin{matrix}{-3}\\{7} \end{matrix}\right )$$
If $$2A + B = \begin{bmatrix} 3& -1\\ 2 & 4\end{bmatrix}$$ and $$B = \begin{bmatrix}-1 & -5\\ 0 & 2\end{bmatrix}$$ , then find $$A$$.
If $$(A - 2I)(A - 3I) = 0$$, where $$A =\begin{bmatrix}4 & 2\\ -1 & x\end{bmatrix}$$ and $$I =\begin{bmatrix}1& 0\\ 0& 1 \end{bmatrix}$$ , find the value of $$x$$.
If $$A = \begin{bmatrix}2 & 0 & 1\\ 2& 1 & 3\\ 1 & -1 & 0\end{bmatrix}$$, then find the value of $$A^{2} - 5A + 6I$$
Find the matrix $$X$$, given that $$X + 2I = \begin{bmatrix}3 & -1\\ 1 & 2\end{bmatrix}$$
If $$A=\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}$$; $$B=\begin{bmatrix} 3 & 8 \\ 7 & 2 \end{bmatrix}$$ and $$2X + A = B$$, then find $$X$$.
If $$A=\begin{bmatrix} 2 & 5 \\ -1 & 0 \end{bmatrix}$$ and $$B=\begin{bmatrix} 2 & 3 \\ -2 & 4 \end{bmatrix}$$, find the matrix $$P$$ when $$2A + P = B$$.
If $$A = \begin{bmatrix}a &b \\ c & d\end{bmatrix}$$ and $$I = \begin{bmatrix}1 & 0\\ 0 & 1\end{bmatrix}$$, then show that $$A^{2} - (a + d) A = (bc - ad)I$$
Find the product of the matrices $$\begin{pmatrix} 3& -2\\ 5 & 1\end{pmatrix} \begin{pmatrix}4 & 1\\ 2 & 7\end{pmatrix}$$
If $$A=\begin{bmatrix} 2 & 4 \\ -1 & k \end{bmatrix}$$ and $${ A }^{ 2 }=O$$ (null matrix), then find the value of $$k$$.
If $$A = \begin{bmatrix}1 &4 \\ 2 &1 \end{bmatrix}, B = \begin{bmatrix}-3 & 2\\ 4 & 0\end{bmatrix}, C = \begin{bmatrix}1 & 0\\ 0 & 2\end{bmatrix}$$; find $$A^{2} + BC$$
Let $$A = \bigl(\begin{smallmatrix}3 & 2\\ 5 & 1\end{smallmatrix}\bigr) $$ and $$B = \bigl(\begin{smallmatrix}8 & -1\\ 4 & 3\end{smallmatrix}\bigr)$$. Find the matrix C if $$C = 2A + B$$.
Matrix A shows the weight of four boys and four girls in kg at the beginning of a diet programme to lose weight. Matrix B shows the corresponding weights after the diet programme.
$$A = \begin{bmatrix}35 & 40 & 28 & 45\\ 42 & 38 & 41 & 30\end{bmatrix}\underset{Girls}{Boys}, B = \begin{bmatrix}32 & 35 & 27 & 41\\ 40 & 30 & 34 & 27\end{bmatrix} \underset{Girls}{Boys}$$
Find the weight loss of the Boys and Girls.
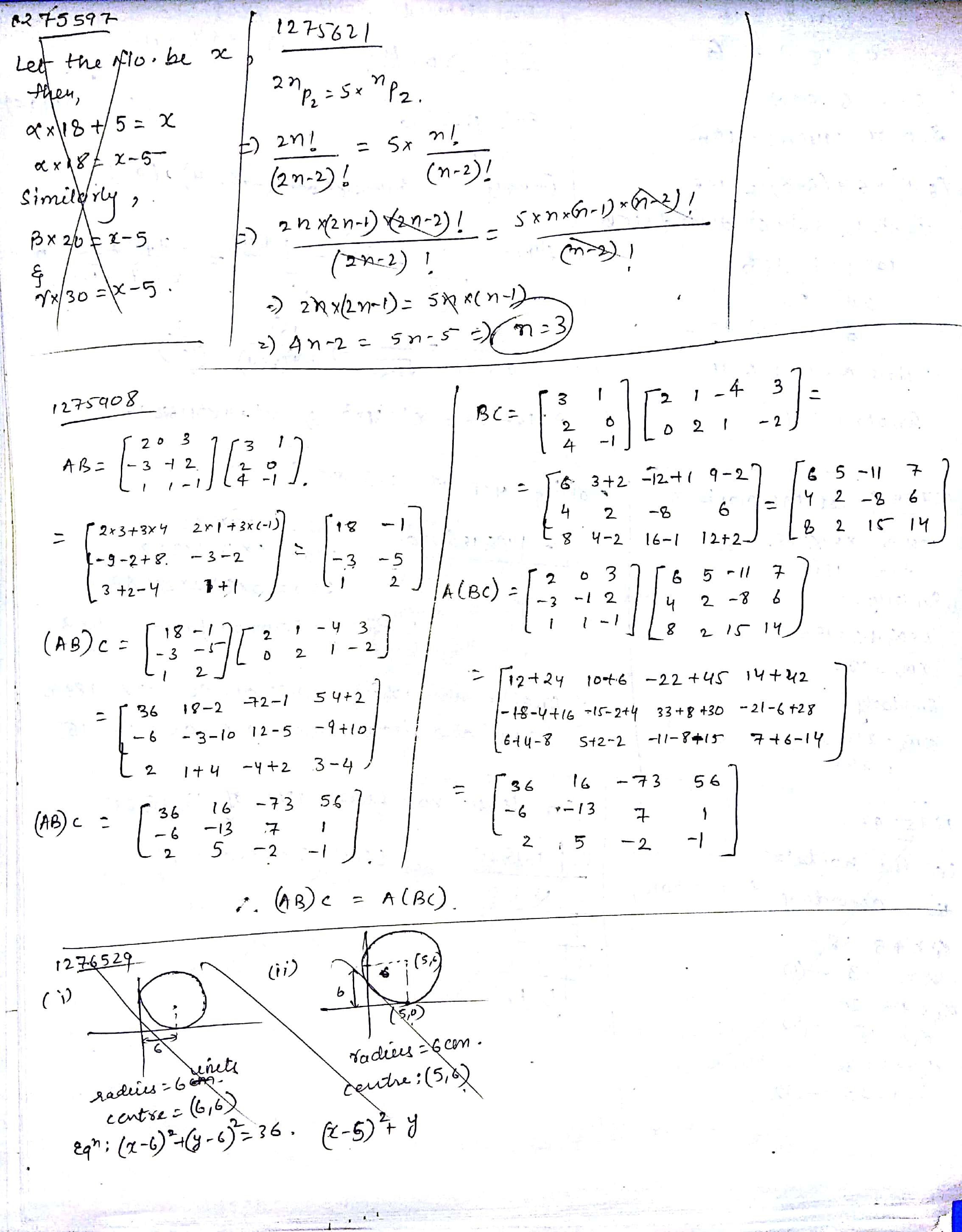
If $$A = \bigl(\begin{smallmatrix}-1 & 2 & 1 \\ 1 & 2 & 3\end{smallmatrix}\bigr), B = \bigl(\begin{smallmatrix} 0 \\ 1 \\ 2 \end{smallmatrix}\bigr)$$ and $$C = \bigl(\begin{smallmatrix} 2 & 1\end{smallmatrix}\bigr)$$ verify (AB)C = A(BC).
Find the product of the matrices, if exists.$$\bigl(\begin{smallmatrix} 3& -2 \\ 5 & 1\end{smallmatrix}\bigr) \bigl(\begin{smallmatrix}4 & 1\\ 2 & 7 \end{smallmatrix}\bigr)$$
Find the product of the matrices, if exists.
$$\left(\begin{matrix} 6\\ -3\end{matrix}\right) \left(\begin{matrix} 2 & 7\end{matrix}\right)$$
The amount of fat, carbohydrate and protein in grams present in each food item respectively are as follows
| Item 1 | Item 2 | Item 3 | Item 4 | |
| Fat | 5 | 0 | 1 | 10 |
| Carbohydrate | 0 | 15 | 6 | 9 |
| Protein | 7 | 1 | 2 | 8 |
$$\left[ \begin{matrix} 5 & 0 & 1 \\ 0 & 15 & 6 \\ 7 & 1 & 2 \end{matrix}\begin{matrix} 10 \\ 9 \\ 8 \end{matrix} \right] _{ 3\times 4 }$$
$$\left[ \begin{matrix} 5 & 0 & 7 \\ 0 & 15 & 1 \\ 1 & 6 & 2 \\ 10 & 9 & 8 \end{matrix} \right] _{ 4\times 3 }$$
Hence, solved.
Find the product of the matrices, if exists.$$\bigl(\begin{smallmatrix}2 & 9 & -3\\ 4 & -1 & 0\end{smallmatrix}\bigr) \bigl(\begin{smallmatrix} 4& 2 \\ -6 & 7 \\ -2 & 1\end{smallmatrix}\bigr)$$
If $$A = \begin{bmatrix}5 & 6 & -2 & 3\\ 1 & 0 & 4 & 2\end{bmatrix}$$ and $$B = \begin{bmatrix}3 & -1 & 4 & 7\\ 2 & 8 & 2 & 3\end{bmatrix}$$, then find A + B.
If $$A = \bigl(\begin{smallmatrix} 8& -7 \\ -2 &4 \\ 0 & 3 \end{smallmatrix}\bigr)$$ and $$B = \bigl(\begin{smallmatrix} 9& -3 & 2\\ 6 & -1 & -5\end{smallmatrix}\bigr)$$, then find AB and BA if they exists.
If $$A=\begin{bmatrix}1&2\\2&1\end{bmatrix}.B = \begin{bmatrix}2&0\\1&3\end{bmatrix}$$ and $$C=\begin{bmatrix}1&1\\2&3\end{bmatrix}$$ calculate $$AC, BC$$ and $$(A+B)C$$. Also verify that $$(A+B)C=AC+BC.$$
If $$M=\begin{bmatrix}7 & 5\\2 & 3\end{bmatrix}$$, then verify the equation $$M^2-10M+11 I_2=0$$.
For matrices $$A=\begin{bmatrix} 2 & 1 \\ 3 & 2 \end{bmatrix}$$ and $$B=\begin{bmatrix} 2 & 3 \\ 1 & 2 \end{bmatrix}$$, write $$A+B$$ and $$A-B$$.
(i) $$2i-j$$ is the $$(i,j)$$th element of a $$2\times 2$$ matrix $$A$$.
(ii) Find the matrix $$B$$ such that $$3A-2B=\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}$$
(iii) Prove that $${ A }^{ 2 }+2I=3A$$
Given matrix $$B=\begin{bmatrix} 1 & 1\\ 8 & 3\end{bmatrix}$$. Find the matrix X if, $$X=B^2-4B$$. Hence solve for a and b given $$X\begin{bmatrix} a \\ b\end{bmatrix}=\begin{bmatrix} 5 \\ 50\end{bmatrix}$$.
If the matrix $$\begin{pmatrix}6 & -x^2\\ 2x-15 & 10\end{pmatrix}$$ is symmetric, find the value of $$x$$.
If $$A=\begin{bmatrix} \cos 2\theta & \sin 2\theta \\ -\sin 2\theta & \cos 2\theta\end{bmatrix}$$. Find the value $$A^2$$.
Find the inverse of $$A = \begin{bmatrix} \cos \alpha& -\sin \alpha & 0\\ \sin \alpha & \cos \alpha & 0\\ 0 & 0 & 1\end{bmatrix}$$ using elementary transformation.
If $$A =\begin{bmatrix} 1 & 3 & 3 \\ 1 & 4 & 3 \\ 1 & 3 & 4 \end{bmatrix}$$ then find $$A^{-1}$$
If $$A = \begin{bmatrix} 0& 6 & 7\\ -6 & 0 &8 \\ 7 & -8 & 0\end{bmatrix}, B = \begin{bmatrix}0 & 1 & 1\\ 1 & 0 & 2\\ 1 & 2 & 0\end{bmatrix}, C = \begin{bmatrix}2 \\ -2 \\ 3\end{bmatrix}$$, calculate $$AC, BC$$ and $$(A + B)C$$.
Also, verify that $$(A + B)C = AC + BC$$.
If $$A=\begin{bmatrix}
\cos \alpha & -\sin \alpha\\
\sin \alpha & \cos \alpha
\end{bmatrix}$$, $$B=\begin{bmatrix}
\cos 2\beta & \sin 2\beta\\
\sin 2\beta & -\cos 2\beta
\end{bmatrix}$$, where $$0<\beta<\large{\frac{\pi}{2}}$$, then prove that $$BAB=A^{-1}$$. .
Is it possible to define the matrix A + B when
A has 3 rows and B has 2 rows
If $$A=\begin{bmatrix}x&y&z\end{bmatrix},$$ $$ B=\begin{bmatrix}a&h&g\\h&b&f\\g&f&c\end{bmatrix}, C=\begin{bmatrix}\alpha & \beta & \gamma \end{bmatrix}^{T}$$ then $$ABC$$ is
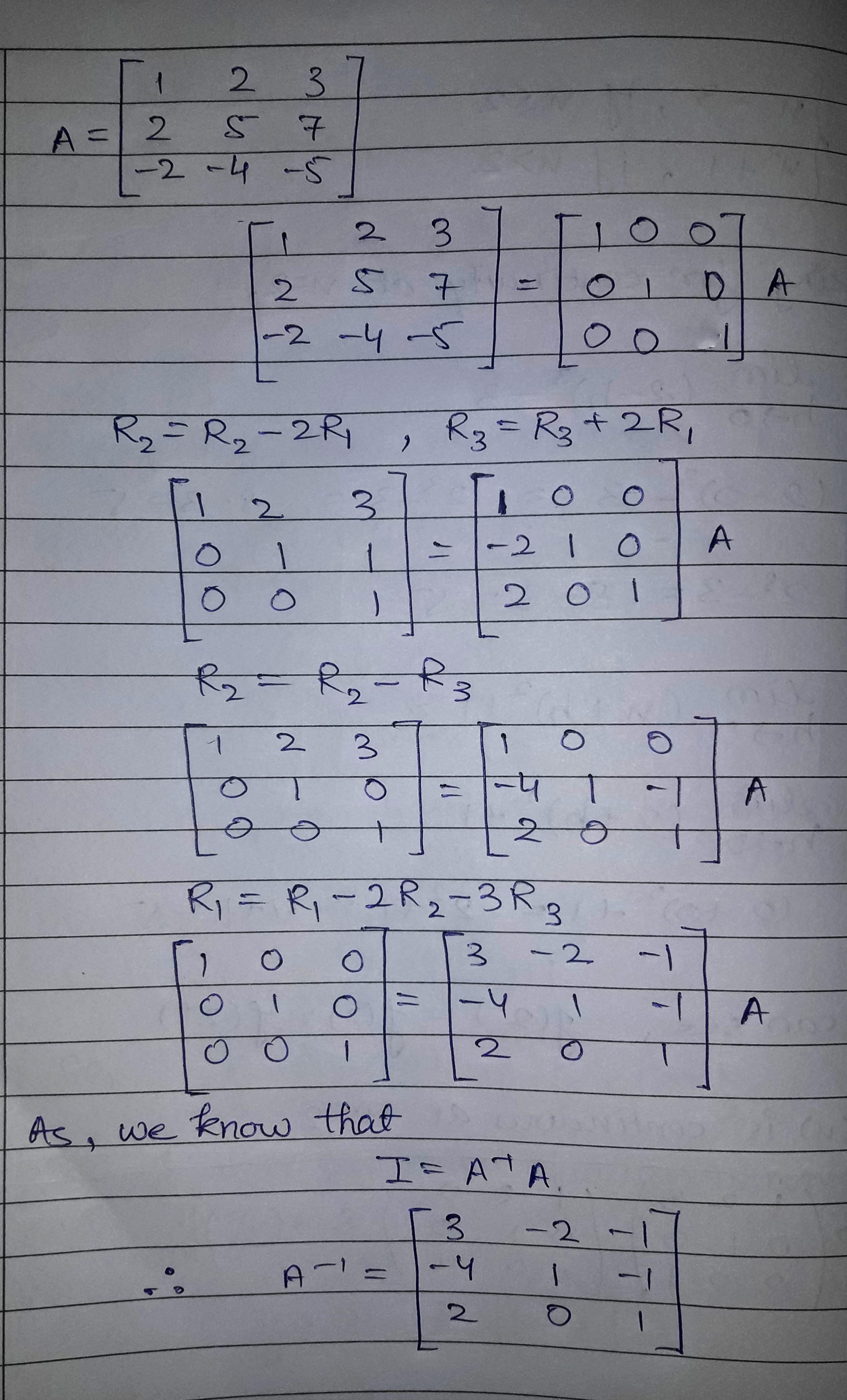
Using elementary row transformation, find the inverse of the matrix $$A=\begin{bmatrix}1&2&3\\2&5&7\\-2&-4&-5\end{bmatrix}$$.
Is it possible to define the matrix A + B when
A has 3 rows and B has 2 columns
If $$A = \begin{vmatrix} 1 & 2 & 2 \\ 2 & 1 & 2 \\ 2 & 2 & 1 \end{vmatrix}$$, then prove that $$A^2 - 4A - 5 I_3 = 0$$ and hence obtain $$A^{-1}$$.
If $$A=\begin{bmatrix}1&1&1\\0&1&1\\ 0&0&1\end{bmatrix},$$ show that $$ A^n=\begin{bmatrix}1&n&\dfrac{n(n+1)}{2}\\0&1&n\\0&0&1\end{bmatrix}\forall n \in \mathbb{N}$$.
Is it possible to define the matrix A + B when
A has 2 columns and B has 4 columns
If $$\omega = e^{2i\pi /3}$$. Find the inverse of the matrix.
A = $$\begin{bmatrix}
1 & 1 & 1 \\[0.3em]
1 & \omega & \omega^2 \\[0.3em]
1 & \omega^2 & \omega
\end{bmatrix}$$
Compute $$A^2 \, - \, 4A \, - \, 5 $$ Where A = $$\begin{bmatrix}1 & 2 & 2 \\ 2 & 1 & 1 \\ 2 & 2 & 1\end{bmatrix}$$
and I is a unit matrix
If A + B =$$\begin{bmatrix}1 & 0 & 2\\ 2 & 2 & 2\\ 1 & 1 & 1 \end{bmatrix}$$ and A - B = $$\begin{bmatrix}1 & 4 & 4\\ 4 & 2 & 0\\ -1 & -1 & 2 \end{bmatrix}$$
then prove that
A = $$\begin{bmatrix}1 & 2 & 3\\ 3 & 2 & 1\\ 0 & 0 & 2 \end{bmatrix}$$ and B = $$\begin{bmatrix}0 & -2 & -1\\ -1 & 0 & 1\\ 1 & 1 & 0 \end{bmatrix}$$
If $$A_\alpha \, = \, \begin{bmatrix}cos \, \, n\alpha & sin \, n\alpha \\ -sin \, n\alpha & cos \, \, n\alpha \end{bmatrix}$$, then prove the following
$$(A_\alpha)^n \, = \, \begin{bmatrix}cos \, \, n\alpha & sin \, n\alpha \\ -sin \, n\alpha & cos \, \, n\alpha \end{bmatrix}$$
Find the inverse of the following matrices:
(a) $$\begin{bmatrix}
1 & 4 & 0 \\[0.3em]
-1 & 2 & 2 \\[0.3em]
0 & 0 & 2
\end{bmatrix}$$
(b)$$\begin{bmatrix}
cos\theta & -sin\theta & 0 \\[0.3em]
sin\theta & cos\theta & 0 \\[0.3em]
0 & 0 & 1
\end{bmatrix}$$
(c) $$\begin{bmatrix}
2 & 2 & 2 \\[0.3em]
2 & 5 & 5 \\[0.3em]
2 & 5 & 11
\end{bmatrix}$$
(d) $$\begin{bmatrix}
1 & 2 & 3 \\[0.3em]
2 & 4 & 5 \\[0.3em]
3 & 5 & 6
\end{bmatrix}$$
(e) $$\begin{bmatrix}
1 & 4 & 0 \\[0.3em]
-1 & 2 & 2 \\[0.3em]
0 & 0 & 2
\end{bmatrix}$$
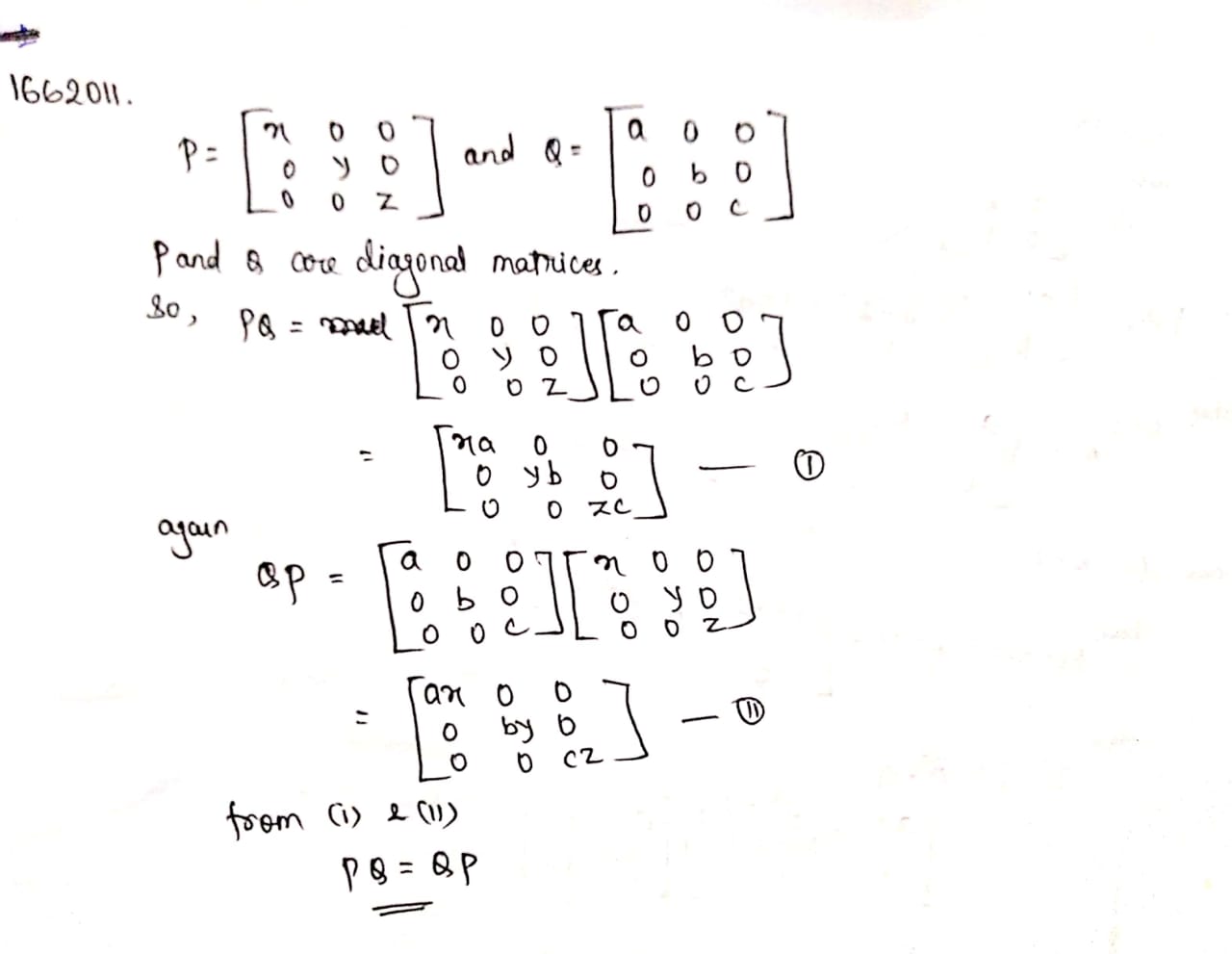
If A is a diagonal matrix diag $$(d_1 , d_2 \, , ...... d_n )$$ then $$A^n , n \epsilon R\ is\ diag (d^n_1 \, , d^n_2 \, .....d^n_n )$$
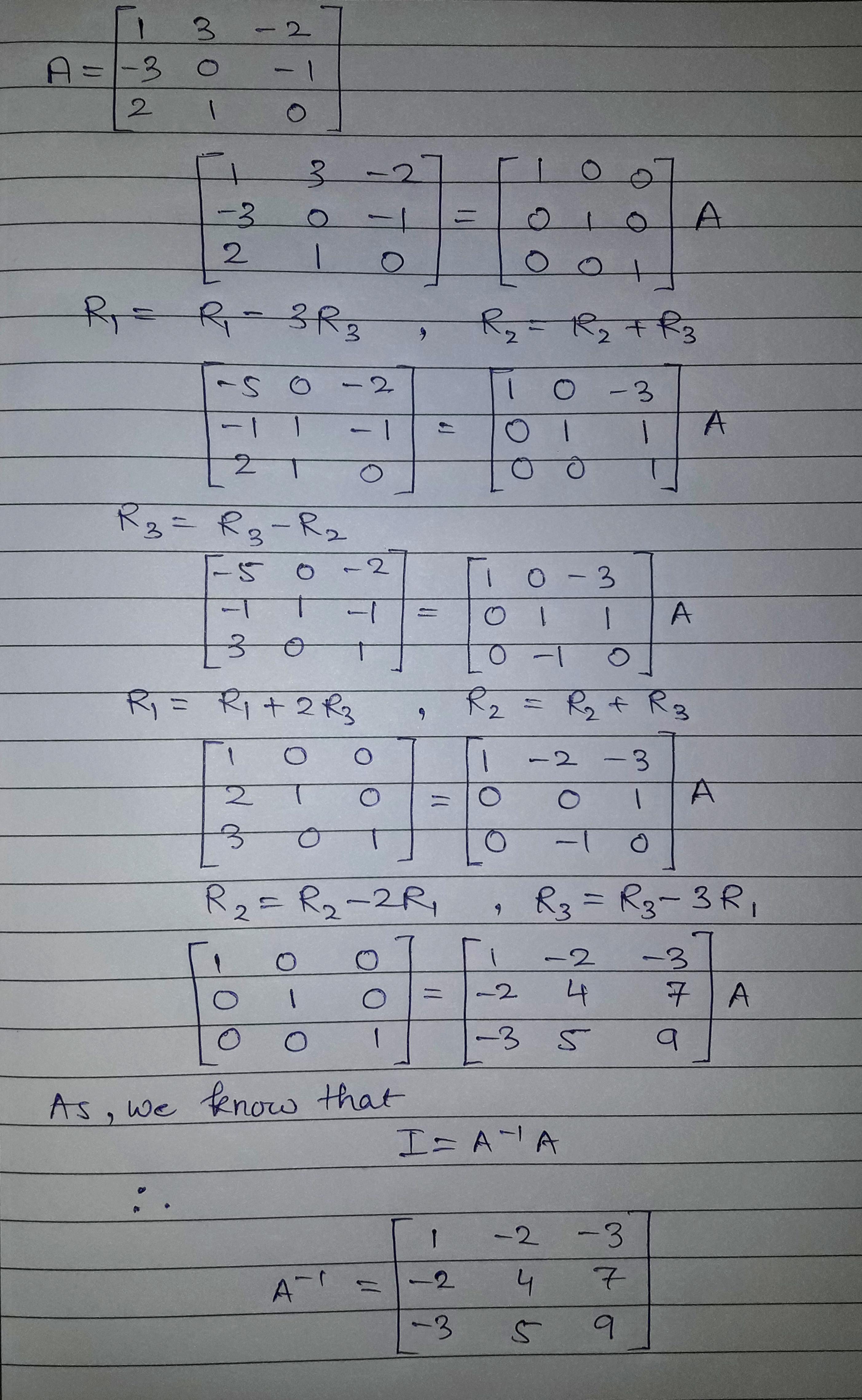
$$\left( {\matrix{
1 & 3 & { - 2} \cr
{ - 3} & 0 & 1 \cr
2 & 1 & 0 \cr
} } \right)$$
Find Inverse Elementary transformation
Find the inverse of matrix
$$\begin{bmatrix}
14 & 3 & -2 \\[0.3em]
6 & 8 & -1 \\[0.3em]
0 & 2 & -7
\end{bmatrix}.$$
If $$A=\begin{bmatrix} 1 & 2 & -3 \\ 5 & 0 & 2 \\ 1 & -1 & 1 \end{bmatrix},B=\begin{bmatrix} 3 & -1 & 2 \\ 4 & 2 & 5 \\ 2 & 0 & 3 \end{bmatrix},C=\begin{bmatrix} 4 & 1 & 2 \\ 0 & 3 & 2 \\ 1 & -2 & 3 \end{bmatrix}$$, Then Compute $$(A+B)$$ and $$(B-C)$$. Also, verify that $$A+(B-C)=(A+B)-C$$
Find matrix $$X$$ so that $$X \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{bmatrix} = \begin{bmatrix} -7 & -8 & -9 \\ 2 & 4 & 6\end {bmatrix}$$ .
If $$A=\left[ \begin{matrix} -1 & 2 & 0 \\ -1 & 1 & 1 \\ 0 & 1 & 0 \end{matrix} \right] $$ , Show that $$\\ { A }^{ 2 }={ A }^{ -1 }$$
Using elementary row transformations, find the inverse of the matrix$$\begin{bmatrix}1 & 2 & 3\\ 2& 5 &7 \\ -2 &-4 & 5\end{bmatrix}$$
Given $$F(x) = \begin{bmatrix} \cos x & -\sin x & 0 \\ \sin x & \cos x & 0 \\ 0 & 0 & 1 \end{bmatrix}$$ If $$x \in R$$ Then prove $$y$$, $$F(x + y) = F(x) F(y)$$
If $$f\left( \alpha \right) =\begin{bmatrix} \cos { \alpha } & -\sin { \alpha } & 0 \\ \sin { \alpha } & \cos { \alpha } & 0 \\ 0 & 0 & 1 \end{bmatrix}$$,
Find
(i) $$f\left( -\alpha \right)$$
(ii) $$f\left( -\alpha \right) +f\left( \alpha \right)$$.
If $$A=\begin{bmatrix} 1 & -2 & 3 \\ -4 & 2 & 5 \end{bmatrix} $$ and $$ \begin{bmatrix} 2 & 3 \\ 4 & 5 \\ 5 & 1 \end{bmatrix}$$ and $$BA=(b_0)$$, then find $$b_{21}+b_{32} $$
Let $$A=\begin{bmatrix}0&1\\1&0\end{bmatrix}$$ then $$A^4=$$.
If $$\omega$$ is complex (non real) cube root of $$1$$ then show that $$ \begin{vmatrix} 1 & \omega & { \omega }^{ 2 } \\ \omega & { \omega }^{ 2 } & 1 \\ { \omega }^{ 2 } & 1 & \omega \end{vmatrix}=0$$.
If $$A=\begin{bmatrix} 0 & -\tan { \dfrac { \alpha }{ 2 } } \\ \tan { \dfrac { \alpha }{ 2 } } & 0 \end{bmatrix}$$ and $$I$$ is the identity matrix of order $$2$$, show that $$I+A=\left( I-A \right) \begin{bmatrix} \cos { \alpha } & -\sin { \alpha } \\ \sin { \alpha } & \cos { \alpha } \end{bmatrix}$$
$$AB=0$$ where
$$A=\begin{bmatrix} \cos ^{ 2 }{ \theta } & \cos { \theta } \sin { \theta } \\ \cos { \theta } \sin { \theta } & \sin ^{ 2 }{ \theta } \end{bmatrix}$$
$$B=\begin{bmatrix} \cos ^{ 2 }{ \phi } & \cos { \phi } \sin { \phi } \\ \cos { \phi } \sin { \phi } & \sin ^{ 2 }{ \phi } \end{bmatrix}$$
then find $$\left| \theta -\phi \right| =?$$
$$AB=\begin{bmatrix} \cos ^{ 2 }{ \theta } & \cos { \theta } \sin { \theta } \\ \cos { \theta } \sin { \theta } & \sin ^{ 2 }{ \theta } \end{bmatrix}$$
$$\begin{bmatrix} \cos ^{ 2 }{ \phi } & \cos { \phi } \sin { \phi } \\ \cos { \phi } \sin { \phi } & \sin ^{ 2 }{ \phi } \end{bmatrix}$$
$$ = cos^{2}\theta cos^{2} \phi + cos \theta sin \theta cos\phi sin \phi = 0$$
$$ \left [ cos \theta \, cos \phi \right ] \left [ cos \theta \, cos \phi + sin\theta \, sin \phi \right ] =0$$
$$ cos \theta \,cos \phi = -sin \theta \, sin\phi $$
$$ tan \phi = - cot \theta $$
$$ \phi = - tan^{-1} \left [ \dfrac{1}{tan \theta} \right ]$$
$$ \phi = - \left [ \dfrac{\pi}{2}- \theta \right ]$$
$$ \left | \theta - \phi \right | = \left | \theta + \dfrac{\pi}{2}- \theta \right | = \dfrac{\pi}{2}.$$
Given $$A=\left[ \begin{matrix} 1 & 1 & 1 \\ 2 & 4 & 1 \\ 2 & 3 & 1 \end{matrix} \right] ,B=\begin{bmatrix} 2 & 3 \\ 3 & 4 \end{bmatrix}$$. Find $$P$$ such that $$BPA=\left[ \begin{matrix} 1 & 0 & 1 \\ 0 & 1 & 0 \end{matrix} \right]$$.
Find matrices $$A$$ and $$B$$, where
(i) $$2A-B=\begin{bmatrix} 1 & -1 \\ 0 & 1 \end{bmatrix}$$ and $$A+3B=\begin{bmatrix} 0 & 1 \\ -1 & 0 \end{bmatrix}$$
(ii)$$3A-B=\left[ \begin{matrix} -1 & 2 & 1 \\ 1 & 0 & 5 \end{matrix} \right]$$ an $$A+5B=\left[ \begin{matrix} 0 & 0 & 1 \\ -1 & 0 & 0 \end{matrix} \right]$$
$$ \displaystyle (1)\quad (2A+6B)-(2A-B)= \begin{bmatrix} 0 & 2 \\ -2 & 0 \end{bmatrix} -\begin{bmatrix} 1 & -1 \\ 0 & 1 \end{bmatrix} $$
$$ \displaystyle \quad B = \begin{bmatrix} \dfrac{-1}{7} & \dfrac{3}{7} \\ \dfrac{-2}{7} & \dfrac{-1}{7} \end{bmatrix} $$
$$ \displaystyle \quad 2A- \begin{bmatrix} \dfrac{-1}{7} & \dfrac{3}{7} \\ \dfrac{-2}{7} & \dfrac{-1}{7} \end{bmatrix} = \begin{bmatrix} 1 & -1\\ 0 & 1 \end{bmatrix} $$
$$ \displaystyle \quad A = \begin{bmatrix} \dfrac{3}{7} & \dfrac{-2}{7} \\ \dfrac{-1}{7} & \dfrac{3}{7} \end{bmatrix} $$
$$ \displaystyle (2)\quad 3(A+5B) = 3A+15B = \left[ \begin{matrix} 0 & 0 &3 \\ -3 & 0 & 0 \end{matrix}\right] $$
$$ \displaystyle \quad (3A+15B) - (3A-B) =\left[ \begin{matrix} 0 & 0 &3 \\ -3 & 0 & 0 \end{matrix}\right] - \left[ \begin{matrix} -1 & 2 & 1 \\ 1 & 0 & 5 \end{matrix}\right]$$
$$ \displaystyle \quad 16B = \left[ \begin{matrix} 1 & -2 & 2 \\ -4 & 0 & -5 \end{matrix}\right] $$
$$ \displaystyle \quad B=\left[ \begin{matrix} \dfrac { 1 }{ 16 } & \dfrac { -2 }{ 16 } & \dfrac { 2 }{ 16 } \\ \dfrac { -4 }{ 16 } & 0 & \dfrac { -5 }{ 16 } \end{matrix} \right] $$
$$ \displaystyle \quad 3A =\left[ \begin{matrix} -1 & 2 &1 \\ 1 & 0&0 \end{matrix}\right] + \left[ \begin{matrix} \dfrac{1}{16} & \dfrac{-2}{16} & \dfrac{2}{16} \\ \dfrac{-4}{16} & 0 & \dfrac{-5}{16} \end{matrix}\right]$$
$$ \displaystyle \quad A = \left[ \begin{matrix} \dfrac{-5}{16} & \dfrac{5}{8} & \dfrac{3}{8} \\ \dfrac{1}{4} & 0 & \dfrac{25}{16} \end{matrix}\right] $$
Given $$ M\times \begin{bmatrix} 1 & 1 \\ 0 & 2 \end{bmatrix}=\left[ \begin{matrix} 1 & 2 \end{matrix} \right]$$
Find:
(i)The order of matrix $$M$$ ?
(ii)The matrix $$M$$. ?
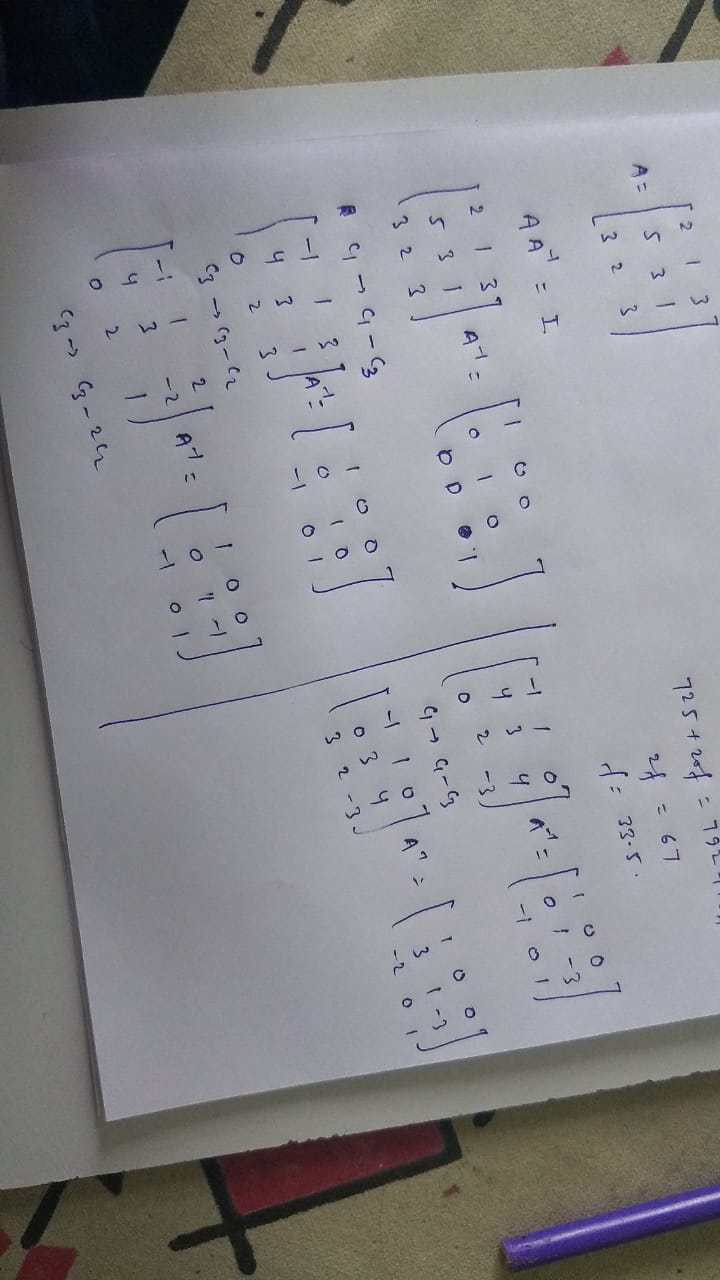
Using elementary tranormtion, find the inverse of $$\begin{bmatrix} 1 & 3 & -2 \\ -3 & 0 & -5 \\ 2 & 5 & 0 \end{bmatrix}$$
If $$3\begin{bmatrix} x & y \\ z & w \end{bmatrix}=\begin{bmatrix} x & 6 \\ -1 & 2w \end{bmatrix}+\begin{bmatrix} 4 & x+y \\ z+w & 3 \end{bmatrix}$$, find the values of $$x,y,z$$ & $$w$$.
If $$M = \begin{bmatrix} 1 & 2 \\ 2 & 3 \end{bmatrix} $$ and $$ M^2 - \lambda M - I = O,$$ then $$ \lambda =$$ ____.
If $$ {A=[\begin{matrix} 2 & 4 \\ -1 & k \end{matrix}]}$$ and $${A}^{2}=0$$, find $$k$$
Given that $$\begin{bmatrix}1&x\end{bmatrix} \begin{bmatrix}2& -1\\1&2\end{bmatrix} \begin{bmatrix}1\\3\end{bmatrix} =O.$$ Find $$7x.$$
Find a $$2 \times 2$$ matrix A such that $$A \begin{bmatrix} 1 & -2 \\ 1 & 4 \end{bmatrix} = 6I_2$$
If $$\theta-\phi=\pi/2$$, then show that $$\begin{bmatrix} \cos ^{ 2 }{ \theta } & \cos { \theta } \sin { \theta } \\ \cos { \theta } \sin { \theta } & \sin ^{ 2 }{ \theta } \end{bmatrix}\begin{bmatrix} \cos ^{ 2 }{ \varphi } & \cos { \varphi } \sin { \varphi } \\ \cos { \varphi } \sin { \varphi } & \sin ^{ 2 }{ \varphi } \end{bmatrix}=0 $$
If $$\theta - \phi = \pi/2$$ then show that $$\begin{bmatrix} \cos^{2} \theta& \cos \theta \sin \theta \\ \cos \theta \sin \theta & \sin^{2} \theta \end{bmatrix}\begin{bmatrix} \cos^{2}\phi& \cos \phi \sin \phi \\ \cos \phi \sin \phi & \sin \phi\end{bmatrix} = 0$$
If $$P=\begin{bmatrix} 1 & 2 & -3 \\ 3 & -1 & 2\\ -2 & 1 & 3\end{bmatrix}$$, $$Q=\begin{bmatrix} 2 & 3 & 1\\ 3 & 1 & 2\\ 1 & 2 & 3\end{bmatrix}$$, then find matrix R such that $$P+Q+R$$ is a zero matrix.
If $$A=\begin{bmatrix} 2 & 0 & 1\\ 2 & 1 & 3\\ 1 & -1 & 0\end{bmatrix}$$ find $$A^2-5A+4I$$ and hence find a matrix X such that $$A^2-5A+4I+X=0$$.
If the system of equations $$3x-2y+z=0,\lambda x-14y+15z=0,x+2y-3z=0$$ have non zero solution, then find $$\lambda $$
If $$A=$$ diagonal $$[1,-2,5],B=$$ diagonal $$[3,0,-4]$$ and $$C=$$ diagonal $$[-2,7,0]$$, then find $$A+2B-3C$$.
If $$A = \left[ {\begin{array}{*{20}{c}}1&2\\{ - 1}&{ - 2}\end{array}} \right],B = \left[ {\begin{array}{*{20}{c}}2&a\\{ - 1}&b\end{array}} \right]$$ and if $${\left( {A + B} \right)^2} = {A^2} + {B^2}$$, find the values of $$a$$ and $$b$$.
Show that the matrix $$A=\begin{bmatrix} 5 & 3 \\ 12 & 7 \end{bmatrix}$$ satisfies the equation $$A^{2}-12A-I=0$$
Find the inverse of $$\begin{bmatrix} 3 & -1 & -2 \\ 2 & 0 & -1 \\ 3 & -5 & 0 \end{bmatrix}$$ by using elementary row transformations.
[2x 3]$$ \begin{bmatrix} 1 & 2\\ -3 & 0\end{bmatrix}\begin{bmatrix} x\\ 3\end{bmatrix}=0$$ then find x.
If A and B are two matrices of same order $$3 \times 3$$ where A= $$ \begin{bmatrix}1 & 2 &3 \\ 2 & 3 &4 \\ 5 & 6 &7 \end{bmatrix} $$ and B= $$ \begin{bmatrix}3 & 2 &5 \\ 2 & 3 &8 \\ 7 & 2 &9 \end{bmatrix} $$ AB=?
Find $$x$$ and $$y$$ , when $$x + y = \left[ {\begin{array}{*{20}{c}}7&0\\2&5\end{array}} \right]$$ and $$x - y = \left[ {\begin{array}{*{20}{c}}3&0\\0&3\end{array}} \right]$$.
Let $$A+B =I$$, where A=$$
\left[
\begin{array}{cc}
0 & 1 & -1\\
4 & -3 & 4\\
3 & -3 & 4\\
\end {array}
\right]
$$ Find $$B$$
Find the vector equation of the plane passing through points $$4i-3j-k,3i+7j-10k$$ and $$2i+5j-7k$$ and show that the point $$i+2j-3k$$ lies in the plane.
Let $$A$$ be a $$3\times3$$ matrix given by $$A=[a_{ij}]$$.
If for every column vector $$X$$, $$X^T AX=0$$ and $$a_{23}=-1008$$,then the sum of the digits of $$a_{32}$$ is
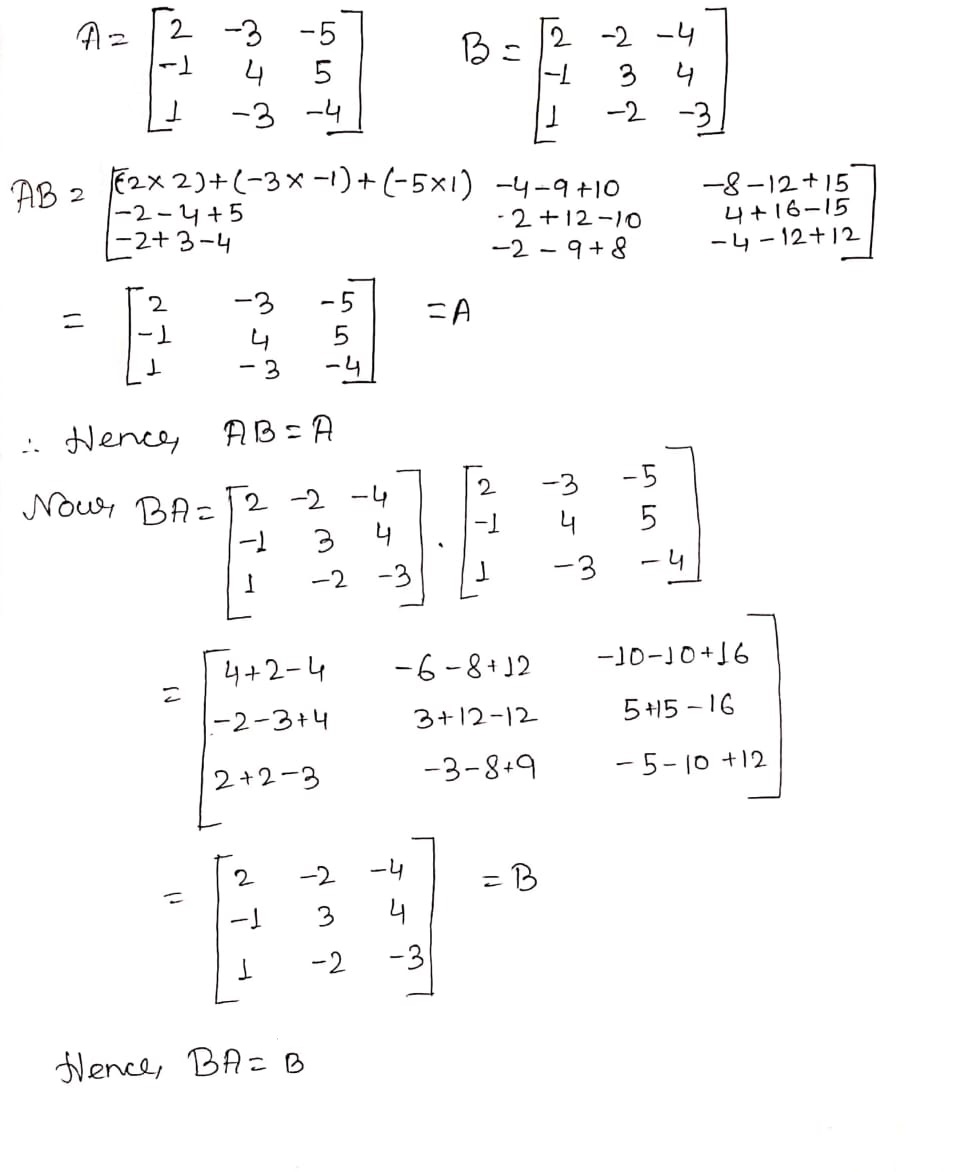
Let $$A=\begin{bmatrix}3 & 7\\ 2 & 5\end{bmatrix}$$ & $$B = \begin{bmatrix}6 & 8\\ 7 & 9\end{bmatrix}$$ check whether $$AB=BA$$ or not.
If $$A = \begin{bmatrix}1 & -1 & 0\\ 2 & 3 & 4\\ 0 & 1 & 2\end{bmatrix}$$ and $$B = \begin{bmatrix}2 & 2 & -4\\ -4 & 2 & -4\\ 2 & -1 & 5\end{bmatrix}$$ are two square matrices, find $$AB$$.
If $$A=\begin{bmatrix} 1 & 2\\ 3 & -4 \\ 5 & 6\end{bmatrix}$$ and $$B=\begin{bmatrix} 4 & 5 & 6\\ 7 & -8 & 2\end{bmatrix}$$ will $$AB$$ be equal to $$BA$$. Also find $$AB$$ & $$BA$$.
If $$A=\begin{bmatrix} 3 & -4\\ 1 & -1\end{bmatrix}$$, then show that $$A^3=\begin{bmatrix} 7 & -12 \\ 3 & -5\end{bmatrix}$$.
Find the matrix $$A$$ for which $$\begin{bmatrix} 2 & 1\\ 3 & 2\end{bmatrix} A\begin{bmatrix} -3 & 2\\ 5 & -3\end{bmatrix}=\begin{bmatrix} 1 & 0\\ 0 & 1\end{bmatrix}$$.
If A = $$\left[ \begin{matrix} 1 & 2 \\ 2 & 3 \end{matrix} \right]$$ then find $${A}^{2}$$
If $$ A=\begin{bmatrix} 1 & -1 & 1 \\ 2 & 1 & 3 \\ 1 & 1 & 1 \end{bmatrix}$$ , Find $$ A^-1$$. Using $$ A^-1$$, solve the following system or liner equation.
$$x+2y+z=4 ;\, -z+y+z=0;\, x-3y+z=2.$$
$$ \begin{bmatrix} -2 & 1 & 1 \\ 2 & 0 & -2 \\ -4 & -1 & 3 \end{bmatrix}$$
$$ A^{-1} = \begin{bmatrix} 1 & -1/2 & -1/2 \\ -1 & 0 & 1 \\ 2 & \dfrac{1}{2} & \dfrac{-3}{2} \end{bmatrix}$$
$$ A^{-1} = \begin{bmatrix} 1 & -1 & 2 \\ -1/2 & 0 & 1/2 \\ -1/2 & 1 & -3/2 \end{bmatrix}$$
Find the inverse of $$\begin{bmatrix} 1 & 2 & 3 \\ 1 & 1 & 5 \\ 2 & 4 & 7 \end{bmatrix}$$ by adjoint method.
If $$ A=\begin{bmatrix} 1 & -2 & 3 \\ 0 & -1 & 4 \\ -2 & 2 & 1 \end{bmatrix}$$ then find $$(A^{T})^{-1}$$
If $$A = \left[ {\begin{array}{*{20}{c}}i&0\\0&i\end{array}} \right]$$ , find $${A^2}$$.
Find $$x$$ and $$y$$ if $$\left[ \begin{array}{l}\,\,\,3\,\,\,\,\,\,\,2\\ - 1\,\,\,\,\,\,\,4\end{array} \right]\left[ \begin{array}{l}2x\\\,\,1\end{array} \right] + 2\left[ \begin{array}{l} - 4\\\,\,\,5\end{array} \right] = 4\left[ \begin{array}{l}2\\y\end{array} \right]$$
For a real number $$\alpha$$, if the system $$\begin{bmatrix} 1 & \alpha & \alpha^2\\ \alpha & 1 & \alpha\\ \alpha^2 & \alpha & 1\end{bmatrix}\begin{bmatrix} x \\ y \\ z\end{bmatrix}=\begin{bmatrix} 1 \\ -1 \\ 1\end{bmatrix}$$ of linear equations, has infinitely many solutions, then $$1+\alpha +\alpha^2=?$$
Find inverse of the matrix $$\begin{bmatrix} 1 & -1 & 1 \\ 0 & 1 & 1 \\ 3 & 2 & -4 \end{bmatrix}$$ by elementary transformation.
If $$A = \begin{bmatrix} 1& -2 & 3\\ -4 & 2 & 5\end{bmatrix}$$ and $$B = \begin{bmatrix} 2& 3\\ 4 & 5\\2 & 1 \end{bmatrix}$$, then find $$AB$$
To find the inverse of the matrix $$A=[1 2 1; 0 1 1; 3 1 1]$$ by elementary transformation method.
If $$A = \begin{bmatrix}0 & -\tan \dfrac {\alpha}{2}\\ \tan \dfrac {\alpha}{2} & 0\end{bmatrix}$$ and $$I$$ the identity matrix of order $$2$$, show that $$I + A = (I - A) \begin{bmatrix}\cos \alpha & -\sin \alpha\\ \sin \alpha & \cos \alpha\end{bmatrix}$$.
If $$x \begin{bmatrix} 2 \\ 3 \end{bmatrix}+y\begin{bmatrix} -1 \\ 1 \end{bmatrix}=\begin{bmatrix} 10 \\ 5 \end{bmatrix}$$, find the value of $$x$$ and $$y$$.
If $$A=\left| \begin{matrix} 0 & -\tan { \frac { \alpha }{ 2 } } \\ \tan { \frac { \alpha }{ 2 } } & 0 \end{matrix} \right| $$ and $$I$$ is the identity matrix of order $$2$$, show that $$I+A=(I-A)\left[ \begin{matrix} \cos { \alpha } & -\sin { \alpha } \\ \sin { \alpha } & \cos { \alpha } \end{matrix} \right] $$.
If $$2A + B = \left[ {\begin{array}{*{20}{c}}1&{ - 1}\\\begin{array}{l}0\\1\end{array}&\begin{array}{l}1\\ - 2\end{array}\end{array}} \right]A - 2B = \left[ {\begin{array}{*{20}{c}}0&1\\\begin{array}{l} - 2\\1\end{array}&\begin{array}{l}0\\ - 1\end{array}\end{array}} \right]$$ find $$A$$ and $$B$$
Find the values of $$x,\ y,\ z$$ if the matrix $$A= \left[ \begin{matrix} 0 \\ x \\ x \end{matrix}\begin{matrix} 2y \\ y \\ -y \end{matrix}\begin{matrix} z \\ -z \\ z \end{matrix} \right]$$ satisfy the equation $$A'A=I_{3}.$$
If $$A=\left[ \begin{matrix} 1 & 2 \\ 3 & 4 \end{matrix} \right] $$, find $$A^{-1}$$ by elementary transformation.
Using elementary tansormations, find the inverse of each of the matrices, if it exists in
$$\begin{bmatrix}2&3\\5&7\end{bmatrix}$$
Find the inverse of matrices by elementary raw transformations
$$\left| \begin{matrix} \cos { \theta } & -\sin { \theta } & 0 \\ \sin { \theta } & \cos { \theta } & 0 \\ 0 & 0 & 1 \end{matrix} \right| $$
Using elementary tansormations, find the inverse of each of the matrices, if it exists in
$$\begin{bmatrix}1&3\\2&7 \end{bmatrix}$$
Using elementary tansormations, find the inverse of each of the matrices, if it exists in
$$\begin{bmatrix}2&5\\1&3 \end{bmatrix}$$
Using elementary tansormations, find the inverse of each of the matrices, if it exists in
$$\begin{bmatrix}2&1\\1&1 \end{bmatrix}$$
Using elementary tansormations, find the inverse of each of the matrices, if it exists in
$$\begin{bmatrix}2&1\\7&4 \end{bmatrix}$$
Using elementary tansormations, find the inverse of each of the matrices, if it exists in
$$\begin{bmatrix}1&-1\\2&3\end{bmatrix}$$
If $$A = \begin{pmatrix} 1 & 0 & 2 \\ 0 & 2 & 1 \\ 2 & 0 & 3 \end{pmatrix}$$ and $$A^3 - 6A^2 + 7 A + kI^3 = 0$$, find k.
Find the inverse of the following martrices by using transformation method.
$$\left[ \begin{matrix} 2 & -3 \\ -1 & 2 \end{matrix} \right]$$
Find the inverse of the following matrices by the adjoining method
\begin{bmatrix} 1 & 2 & 3 \\ 0 & 2 & 4 \\ 0 & 0 & 5 \end{bmatrix}
$$ M = \begin{bmatrix} 1 & 2 & 3 \\ 0 & 2 & 4 \\ 0 & 0 & 5 \end{bmatrix}$$
$$ (M) = 1(2(5)) $$
$$ = 10 $$
adj (m ) $$ = \begin{bmatrix} 10 & -10 & 2 \\ 0 & 5 & -4 \\ 0 & 0 & 2 \end{bmatrix}$$
$$ m^{-1} = \dfrac{1}{10}$$ $$ \begin{bmatrix} 10 & -10 & 2 \\ 0 & 5 & -4 \\ 0 & 0 & 2 \end{bmatrix}$$
$$ M^{-1} = $$ $$\begin{bmatrix} 1 & -1 & 1/5 \\ 0 & 1/2 & -2/5 \\ 0 & 0 & 1/5 \end{bmatrix}$$
If $$A=\left| \begin{matrix} 1! & 2! & 3! \\ 2! & 3! & 4! \\ 3! & 4! & 5! \end{matrix} \right| $$ then find $$A^{-1}$$ and hence prove that $$A^{2}-4A-5I=0$$
Find the inverse of the following matrices by the adjoining method
$$\begin{bmatrix} -1 & 5 \\ -3 & 2 \end{bmatrix}$$
$$M\begin{bmatrix} -1 & 5 \\ -3 & 2 \end{bmatrix}$$
if m = $$\begin{bmatrix} a & b \\ c & d \end{bmatrix}$$ , $$ M^{-1} = \dfrac{1}{\left | M \right |}$$ $$\begin{bmatrix} d & -b \\ -c & a \end{bmatrix}$$ adj (M)
adj(M) = $$\begin{bmatrix} 2 & -5 \\ 3 & -1 \end{bmatrix}$$ and $$ \left | M \right | = -2+15$$
$$ = 13 $$
$$ \therefore M^{-1} = \dfrac{1}{13} $$ $$\begin{bmatrix} 2 & -5 \\ 3 &-1 \end{bmatrix}$$
Find the inverse of the following martrices by using transformation method.
$$\left[ \begin{matrix} 0 & 1 & 2 \\ 1 & 2 & 3 \\ 3 & 1 & 1 \end{matrix} \right]$$
Find the inverse of the following martrices by using transformation method.
$$\left[ \begin{matrix} 1 & 2 \\ 2 & -1 \end{matrix} \right]$$
Find the inverse of the following martrices by using transformation method.
$$\begin{matrix} 2 & 0 & -1 \\ 5 & 1 & 0 \\ 0 & 1 & 3 \end{matrix}$$
If $$A=diag[2,-3,-5],\ B=diag[4,-6,-3]$$ and $$C=diag[-3,4,1]$$ then find
$$2A+B-5C$$
A and B are matricesShow by an example that for $$A \neq O$$ and $$B\neq O, AB =O$$.
Find the inverse of the following matrices by the adjoining method
$$\begin{bmatrix} 1 & 0 & 0 \\ 3 & 3 & 0 \\ 5 & 2 & -1 \end{bmatrix}$$
$$ M = \begin{bmatrix} 1 & 0 & 0 \\ 3 & 3 & 0 \\ 5 & 2 & -1 \end{bmatrix}$$
$$ (M) = 1(3(-1)-0) $$
$$ = (-3) $$
adj (m ) $$ = \begin{bmatrix} -3 & 0 & 0 \\ -3 & -1 & 0 \\ -9 & -2 & 3 \end{bmatrix}$$
$$ m^{-1} = \dfrac{1}{-3}$$ $$ \begin{bmatrix} -3 & 0 & 0 \\ -3 & -1 & 0 \\ -9 & -2 & 3 \end{bmatrix}$$
$$ M^{-1} = $$ $$\begin{bmatrix} 1 & 0 & 0 \\ 1 & 1/3 & 0 \\ 3 & 2/3 & -1 \end{bmatrix} $$
Find the matrices $$A$$ and $$B$$ such that $$A+B=\left[ \begin{matrix} 5 & 4 \\ 7 & 3 \end{matrix} \right] $$ and $$A-B=\left[ \begin{matrix} 11 & 2 \\ -1 & 7 \end{matrix} \right] $$
If $$A=\left[ \begin{matrix} 6 & 2 \\ 5 & -4 \end{matrix} \right] $$ and $$B=\left[ \begin{matrix} 1 & 2 \\ -5 & 1 \end{matrix} \right] $$, find a matrix $$X$$ such that $$2A+3B-5X=0$$
If $$A=\left[ \begin{matrix} 3 & 1 \\ -1 & 2 \end{matrix} \right] $$ and $$I=\left[ \begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix} \right] $$,then show that $$A^{2}-5A+7I_{2}=0$$
In a city there are two factories A and B. Each factory produces sports clothes for boys and girls. There are three types of clothes produced in both the factories ,type I,II and III are70 and 65 in factory A and 85,65 and 72 in factory B. For girls the number of units of I,II and III are 80,75.90 in factory A and 50,55,80 in factory B. Express this information in terms of matrices and using matrix algebra answer the following questions.1.Total units of type $$I$$ produced for boys?
2.Total production of each type for boys?
3.Total production of each type for girls?
Find the inverse of matrices by
elementary row transformation.
$$A=\left| \begin{matrix} 1 & 2 & 1 \\ -1 & 0 & 2 \\ 2 & 1 & -3 \end{matrix} \right| $$
$$B=\left| \begin{matrix} cos\theta & -sin\theta & 0 \\ sin\theta & cos\theta & 0 \\ 0 & 0 & 1 \end{matrix} \right|$$
$$A^{-1}=\left( \begin{matrix} cos\theta & sin\theta & 0 \\ -sin\theta & cos\theta & 0 \\ 0 & 0 & 1 \end{matrix} \right) $$
If $$A=\begin{bmatrix} 1 & -1 \\ 2 & -1 \end{bmatrix}$$ , $$B=\begin{bmatrix} 2 & 1 \\ 1 & -1 \end{bmatrix}$$, find $$AB$$.
The cost of 4 kg onion, 3 kg wheat and 2 kg rice is Rs.The cost of 2 kg onion, 4 kg wheat and 6 kg rice is Rs.70.Find the cost of each item per kg by matrix method.
Evaluate:
$$\left[ \begin{matrix} 3 & 4 & 1 \end{matrix} \right] \left[ \begin{matrix} 3 \\ -1 \\ 3 \end{matrix} \right] = [?]$$
If $$A=\left[ \begin{matrix} 2 & 2 \\ -3 & 1 \\ 4 & 0 \end{matrix} \right] ,B=\left[ \begin{matrix} 6 & 2 \\ 1 & 3 \\ 0 & 4 \end{matrix} \right] $$, find matrix $$C$$ such that $$A+B+C=0$$, where $$O$$ is the zero matrix.
Given $$A=\left[ \begin{matrix} p & 0 \\ 0 & 2 \end{matrix} \right] $$ and $$B=\left[ \begin{matrix} 0 & -q \\ 1 & 0 \end{matrix} \right] $$, and $$C=\left[ \begin{matrix} 2 & -2 \\ 2 & 2 \end{matrix} \right] $$ and $$BA=C^{2}$$, find the values of $$p$$ and $$q$$
If $$A=\begin{bmatrix} 0 & -\tan { \dfrac { \alpha }{ 2 } } \\ \tan { \dfrac { \alpha }{ 2 } } & 0 \end{bmatrix}$$ and $$I$$ is the unit matrix, show that $$I+A=(I-A)\begin{bmatrix} \cos { \alpha } & \sin { \alpha } \\ \sin { \alpha } & \cos { \alpha } \end{bmatrix}$$.
If A $$\left[ \begin{matrix} 3 & 2 & -1 \\ 2 & -2 & 0 \\ 1 & 3 & 1 \end{matrix} \right] $$, B $$\left[ \begin{matrix} -3 & -1 & 0 \\ 2 & 1 & 3 \\ 4 & -1 & 2 \end{matrix} \right] $$ and $$X = A+B$$ then find $$X$$
$$A = \left| {\begin{array}{*{20}{c}}1&1\\2&2\\3&{ - 1}\end{array}} \right|$$ and $$B = \left| {\begin{array}{*{20}{c}}2&1\\1&2\\{ - 1}&0\end{array}} \right|$$, then find matrix $$C$$ if $$A+2B+C=0$$.
If $$A = \left[ \begin{gathered} 4\,\,5 \hfill \\ 2\,\,1 \hfill \\ \end{gathered} \right]$$, then show that $${A^{ - 1}} = \frac{1}{6}\left( {A - 5I} \right)$$.
If A=$$\left[ \begin{matrix} 3 & 4 & -2 \\ 2 & 1 & 0 \end{matrix} \right] $$ B =$$\left[ \begin{matrix} 2 & -1 \\ 3 & 4 \\ 0 & 2 \end{matrix} \right] $$ find AB
If A=$$\left[ \begin{matrix} 2 \\ -5 \end{matrix}\begin{matrix} -4 \\ 3 \end{matrix} \right] $$ then find $${\text{ - A + }}{{\text{A}}^{{\text{1}}\;}}\;{\text{and}}\;{\text{ - A}}{{\text{A}}^{\text{1}}}$$
If $$A= \left[ \begin{matrix} \alpha & \beta \\ \gamma & -\alpha \end{matrix} \right] $$ and $$A^{2}=I$$. Find the relation given by $$a^{2}=I$$.
If $$A=\begin{bmatrix} 1 & -2 & 3 \\ 0 & -1 & 4 \\ -2 & 2 & 1 \end{bmatrix}$$, find $$(A')^{-1}$$.
If $$A=\left[ \begin{matrix} 4 & 1 \\ -1 & 2 \end{matrix} \right] $$ show that $$6A-A^{2}=9I$$
If $$A=\begin{pmatrix} p & q \\ 0 & 1 \end{pmatrix}$$, then show that
$$\displaystyle{ A }^{ 8 }=\begin{pmatrix} { p }^{ 8 } & \quad q\left( \dfrac { { p }^{ 8 }-1 }{ p-1 } \right) \\ 0 & 1 \end{pmatrix}$$
Find the inverse of the following matrix using transformation method.
$$\begin{bmatrix} 2 & -3 \\ -1 & 2 \end{bmatrix}$$
Solve the following system of equations by matrix methods: $$x + y + z = 6; y + 3z = 11$$ and $$x - 2y + z = 0.$$
If $$A = \left[ \begin{array} { l l } { 1 } & { - 1 } \\ { 2 } & { - 1 } \end{array} \right] , B = \left[ \begin{array} { c c } { a } & { 1 } \\ { b } & { - 1 } \end{array} \right]$$ and $$( A + B ) ^ { 2 } = A ^ { 2 } + B ^ { 2 }$$ ,find $$a$$ and $$b$$.
Find the inverse of the following matrix using transformation method.
$$\begin{bmatrix} 1 & 2 \\ 2 & -1 \end{bmatrix}$$
Find $$x,y$$ if $$\begin{bmatrix} -2 & 0 \\ 3 & 1 \end{bmatrix}\begin{bmatrix} -1 \\ 2x \end{bmatrix}+3\begin{bmatrix} -2 \\ 1 \end{bmatrix}=2\begin{bmatrix} y \\ 3 \end{bmatrix}$$
Find the inverse of $$A=\begin{bmatrix} 1 & 3 & 3 \\ 1 & 4 & 3 \\ 1 & 3 & 4 \end{bmatrix}$$ by column transformation.
Find the $${{\text{A}}^{{\text{ - 1}}}}$$ of following matrix of by elementary transformation.
(a) $$\left[ \begin{matrix} 1 \\ 0 \\ 1 \end{matrix}\begin{matrix} 0 \\ 2 \\ 2 \end{matrix}\begin{matrix} 1 \\ 3 \\ 1 \end{matrix} \right] $$ (b) $$\left[ \begin{matrix} 1 \\ 0 \\ -1 \end{matrix}\begin{matrix} 2 \\ -2 \\ 3 \end{matrix}\begin{matrix} -2 \\ 1 \\ 0 \end{matrix} \right] $$
Given $$3\begin{bmatrix} x & y \\ z & w \end{bmatrix}=\begin{bmatrix} x & 6 \\ -1 & 2w \end{bmatrix}+\begin{bmatrix} 4 & x+y \\ z+w & 3 \end{bmatrix}$$, find the values of $$x,y,z$$ and $$w$$.
If $$A = \begin{bmatrix}1 & 0 & 0\\ 1 & 0 & 1\\ 0 & 1 &0\end{bmatrix}$$ then for $$n \ge 4, A^n =$$
Find inverse ?
$$\left[ \begin{array} { c c c } { 2 } & { - 1 } & { 4 } \\ { 4 } & { 0 } & { 2 } \\ { 3 } & { - 2 } & { 7 } \end{array} \right]$$
Find multiplication of following matrix:
$$\begin{bmatrix} 6 & 4 \\ 3 & -1 \end{bmatrix}\begin{bmatrix} -1 \\ 3 \end{bmatrix}$$
If $$ A=\begin{bmatrix} 2 & 5 \\ 4 & 4 \end{bmatrix},\quad B=\begin{bmatrix} 0 & 5 \\ 1 & 6 \end{bmatrix}$$, find $$5A'+3B'$$
Let $$A = \left[ \begin{array} { l l l } { 1 } & { 0 } & { 0 } \\ { 1 } & { 1 } & { 0 } \\ { 1 } & { 1 } & { 1 } \end{array} \right]$$ and $$B = A ^ { 10 }$$
Then the sum of elements of the first column of $$B$$ is
Find the matrix $$A$$ satisfying the matrix equation $$\begin{bmatrix} 2 & 1 \\ 3 & 2 \end{bmatrix}A\begin{bmatrix} -3 & 2 \\ 5 & -3 \end{bmatrix}=\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}$$
show that $$\left| {\matrix{ { - bc} & {ca + ab} & {ca + ab} \cr {ab + bc} & { - ca} & {ab + bc} \cr {bc + ca} & {bc + ca} & { - ab} \cr
} } \right| = {(\sum {ab} )^3}$$
If $$A=\begin{pmatrix} p & q \\ 0 & 1 \end{pmatrix}$$, then show that $$A^{8}=\begin{pmatrix} { p }^{ 8 } & q\left( \dfrac { { p }^{ 8 }-1 }{ p-1 } \right) \\ 0 & 1 \end{pmatrix}$$
If $$f(x) = \left| {\matrix{ 0 & {{x^2} - \sin x} & {\cos x - 2} \cr {\sin x - {x^2}} & 0 & {1 - 2x} \cr {2 - \cos x} & {2x - 1} & 0 \cr
} } \right|,$$ then $$\int {f(x)dx} $$ is equal to
Given,$$A=\begin{bmatrix} 1 & 3 & 5 \\ -1 & 0 & 2\\0 & 4 & -3 \end{bmatrix}$$ and $$C=\begin{bmatrix} 4 & 1 & -2 \\ 3 & 2 & 1 \\2 & -1 & 7 \end{bmatrix}$$ Find $$A+C$$
Given,$$A=\begin{bmatrix} 1 & 3 & 5 \\ -1 & 0 & 2\\0 & 4 & -3 \end{bmatrix}$$ and $$C=\begin{bmatrix} 4 & 1 & -2 \\ 3 & 2 & 1 \\2 & -1 & 7 \end{bmatrix}$$ Find $$A+C$$
Using elementary transformation, find the inverse of the matrix $$\left[ \begin{matrix} 2 & -3 & 3 \\ 2 & 2 & 3 \\ 3 & -2 & 2 \end{matrix} \right] $$.
To raise money for an orphanage, students of three schools A, B and C organized an exhibition in their locality, where they sold paper bags, scrap books and pastel sheets made by them using recycled paper at the rate of $$\square 20$$, $$\square 15$$, and $$\square 10$$ per unit respectively. School A sold $$25$$ paper bags, $$10$$ scrap books and $$30$$ pastel-sheets. School B sold $$20$$ paper bags, $$15$$ scrap books and $$30$$ pastel-sheets while School C sold $$25$$ paper bags, $$18$$ scrap books and $$35$$ pastel-sheets. Using matrices, find the total amount raised by each school.
Find the values of $$x, y$$ and $$z$$ if $$\begin{bmatrix} x+2 & 6 \\ 3 & 5z \end{bmatrix}=\begin{bmatrix} -5 & { y }^{ 2 }+y \\ 3 & -20 \end{bmatrix}$$
If $$\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}\begin{bmatrix} 3 & 1 \\ 2 & 5 \end{bmatrix}=\begin{bmatrix} 7 & 11 \\ K & 23 \end{bmatrix}$$ find the value of $$k$$.
Find the inverse of the following matrix using elementary row transformation.
$$\begin{bmatrix} 1 & 2 \\ 2 & -1 \end{bmatrix}$$
If $$A = \left[ \begin{array} { l l l } { a ^ { 2 } } & { a b } & { a c } \\ { a b } & { b ^ { 2 } } & { b c } \\ { a c } & { b c } & { c ^ { 2 } } \end{array} \right]$$ and $$a ^ { 2 } + b ^ { 2 } + c ^ { 2 } = 1$$ then $$A ^ { 2 } =$$
If A and B are symmetric matrices, then show that AB is symmetric iff AB = BA i.e. A and B commute.
Find a matrix X such that $$2A+B+X=O$$, where $$A=\begin{bmatrix} -1 & 2 \\ 3 & 4 \end{bmatrix}$$ and, $$B=\begin{bmatrix} 3 & -2 \\ 1 & 5 \end{bmatrix}$$.
Find the value of $$X$$ and $$Y$$ if
$$2X+3Y=\begin{bmatrix} 2 & 3 \\ 4 & 0 \end{bmatrix}$$ and $$3X+2Y=\begin{bmatrix} 2 & -2 \\ -1 & 5 \end{bmatrix}$$
Find the value of $$X$$ and $$Y$$ if
$$2X+3Y=\begin{bmatrix} 2 & 3 \\ 4 & 0 \end{bmatrix}$$ $$3X+2Y=\begin{bmatrix} 2 & -2 \\ -1 & 5 \end{bmatrix}$$
$$ \rightarrow $$ let Assume $$ \begin{bmatrix} 2 & 3 \\ 4 & 0 \end{bmatrix}$$ = A
$$ \begin{bmatrix} 2 & -2 \\ -1 & 5 \end{bmatrix}$$ = B
$$ \rightarrow 2x +3y = A $$ __ (i)
$$ 3x + 2y = B $$ __ (ii)
$$ \rightarrow $$ multiple equation (i) with 2 & equation (ii) with (3)
$$ 4x + 6y = 2A$$
$$ 9x + 6y = 3B $$
________________
$$ -5x = 2A - 3B $$
$$ \therefore x = \frac{-1}{5}\left [ 2A - 3B \right ]$$
$$ \therefore x = \frac{3B}{5}-\frac{2A}{5}$$
$$ = \frac{3}{5} \begin{bmatrix} 2 & -2 \\ -1 & 5 \end{bmatrix} - \frac{2}{5} \begin{bmatrix} 2 & 3 \\ 4 & 0 \end{bmatrix}$$
$$ = \begin{bmatrix} 6/5 & -6/5 \\ -3/5 & 3 \end{bmatrix}-\begin{bmatrix} 4/5 & 6/5 \\ 8/5 & 0 \end{bmatrix}$$
$$=\begin{bmatrix} 6/5 & -4/5 & -4/5 &-6/5 \\ -3/5 & -8/5 & 3 & -0 \end{bmatrix}$$
$$ \therefore x = \begin{bmatrix} 1/5 & -12/5 \\ -11/5 & 3 \end{bmatrix}$$
$$ \rightarrow $$ value of x put in equation (i)
$$ \therefore \begin{bmatrix} 2/5 & -24/5 \\ -22/5 & 6 \end{bmatrix} + 3y = \begin{bmatrix} 2 & 3 \\ 4 & 0 \end{bmatrix}$$
$$ \therefore 3y = \begin{bmatrix} 2-2/5 & 3+24/5 \\ 4+22/5 & 0-6 \end{bmatrix} = \begin{bmatrix} 8/5 & 39/5 \\ 42/5 & -6 \end{bmatrix}$$
$$ \therefore y = \begin{bmatrix} 8/15 & 39/15 \\ 42/15 & -2 \end{bmatrix}$$
Find $$x$$ and $$y$$, if
$$\left( \begin{matrix} |x| & 2 \\ 5 & |y-2| \end{matrix} \right) = \left( \begin{matrix} <3 & 2 \\ 5 & <4 \end{matrix} \right) $$
If $$A= \begin{bmatrix} 0 & i \\ i & 1 \end{bmatrix}$$ and $$B=\begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix}$$, find the value of $$|A|+|B|$$.
If $$A=\begin{bmatrix} 3 & 0 \\ 0 & 4 \end{bmatrix}, B=\begin{bmatrix} 2 \\ 1 \end{bmatrix}$$, then find the matrix $$X$$ such that $$A^{-1}X=B$$
$$A=\begin{bmatrix} 2 & 3 \\ 5 & 7 \end{bmatrix}B=\begin{bmatrix} 0 & 4 \\ -1 & 7 \end{bmatrix}C=\begin{bmatrix} 1 & 0 \\ -1 & 4 \end{bmatrix}$$
find $$AC+B^{2}-10C$$.
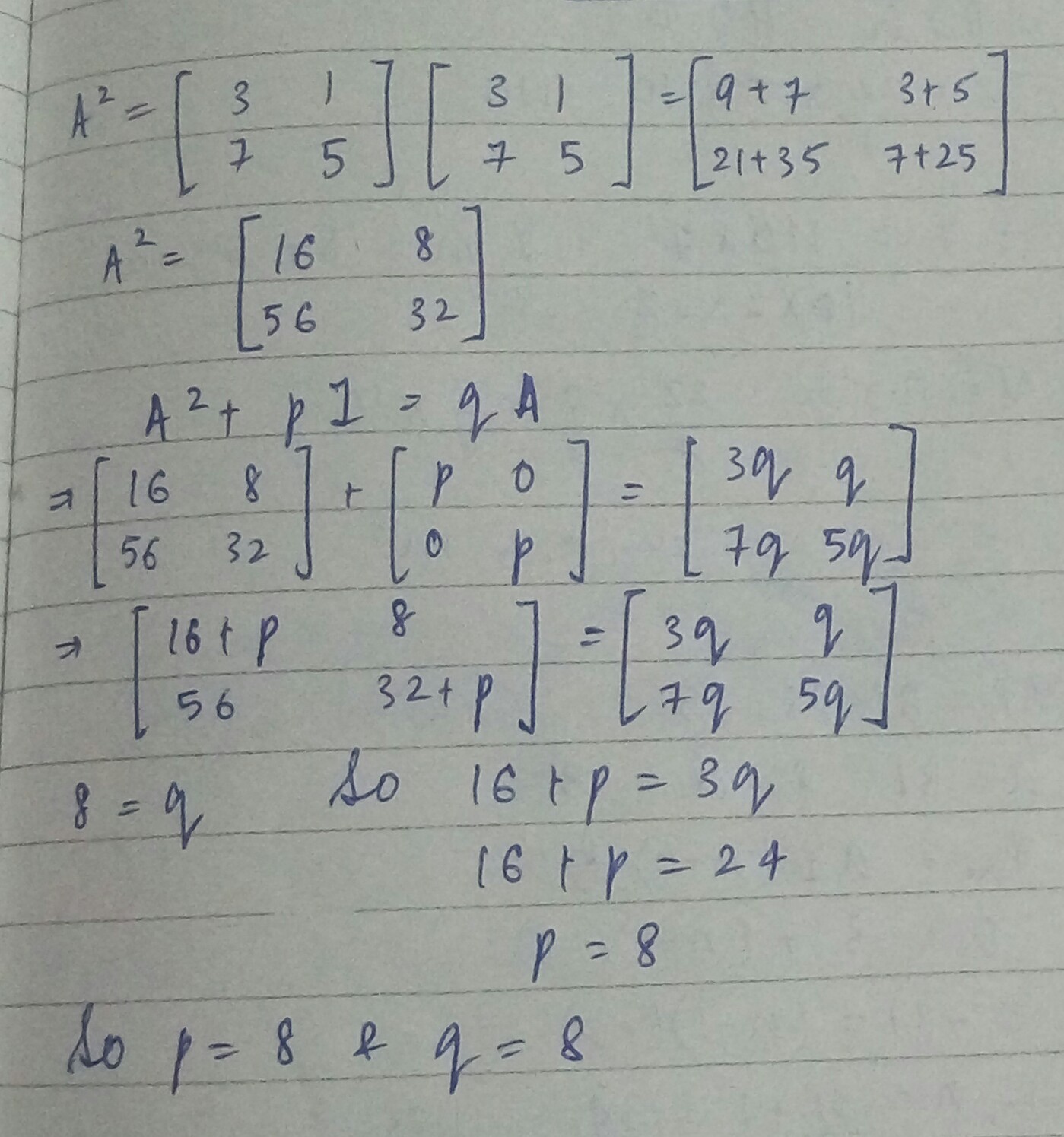
Find the value of $$p$$ and $$q$$ such that $$A^2 + pI = qA$$, where $$A = \begin{bmatrix} 3 & 1 \\ 7 & 5 \end{bmatrix}$$.
find the inverse of the matrix using row column transformations
$$\left | \begin{matrix} 2 & 1 & 3 \\ 1 & 0 & 1 \\ 2 & 1 & 1 \end{matrix}\right |$$
$$A=\left[ \begin{matrix} 1 \\ 2 \\ 3 \end{matrix} \right] ,$$ then the rank of $$AA^T$$ is
P- symmetric matrix, Q- skew symmetric matrix, P and Q are square matrice of same order, then what type of a matrix is PQ-QP
Solve the following by Matrix method
(i) 2x + 3y = 0
2x + y - 2z = 2
2x - z = 5
$$2x+3y=0$$
$$2x+y-2z=2$$
$$2x-z=5$$
$$\Rightarrow A=\begin{bmatrix} 2 & 3 & 0\\ 2 & 1 & -2\\ 2 & 0 & -1\end{bmatrix}$$ $$B=\begin{bmatrix} 0\\ 2 \\ 5\end{bmatrix}$$, $$x=\begin{bmatrix} x & y & z\end{bmatrix}$$
For $$A^{-1}\Rightarrow \begin{bmatrix} 2 & 3 & 0\\ 2 & 1 & -2\\ 2 & 0 & -1\end{bmatrix}=\begin{bmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1\end{bmatrix}$$
$$\Rightarrow \begin{bmatrix} 2 & 3 & 0\\ 0 & -4 & -4\\ 0 & -6 & -2\end{bmatrix}=\begin{bmatrix} 1 & 0 & 0\\ -2 & 2 & 0\\ -2 & 0 & 2\end{bmatrix}$$
$$\Rightarrow \begin{bmatrix} -4 & 0 & 6\\ 0 & -4 & -4\\ 0 & 0 & -8\end{bmatrix}=\begin{bmatrix} 1 & -3 & 0\\ -2 & 2 & 0\\ -2 & 6 & 4\end{bmatrix}$$
$$\Rightarrow \begin{bmatrix} -8 & 0 & 0\\ 0 & -8 & 0\\ 0 & 0 & -8\end{bmatrix}=\begin{bmatrix} -1 & 3 & -6\\ -2 & -2 & 4\\ -2 & 6 & -4\end{bmatrix}$$
$$\Rightarrow \begin{bmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1\end{bmatrix}\times -8=\begin{bmatrix} -1 & +3 & -6\\ -2 & -2 & +4\\ -2 & +6 & -4\end{bmatrix}$$
$$\therefore A^{-1}=\begin{bmatrix} +1/8 & -3/8 & 3/4\\ 1/4 & 1/4 & -1/2\\ 1/4 & -3/4 & 1/2\end{bmatrix}$$
$$x=A^{-1}B$$
$$\begin{bmatrix} x\\ y \\ z\end{bmatrix}=\begin{bmatrix} 1/8 & -3/8 & 3/4\\ 1/4 & 1/4 & -1/2\\ 1/4 & -3/4 & 1/2\end{bmatrix}\times \begin{bmatrix} 0\\ 2 \\ 5\end{bmatrix}=\begin{bmatrix} 3\\ -2 \\ 1\end{bmatrix}$$
$$\therefore x=3$$
$$y=-2$$
$$z=1$$.
If $$A = \left[ \begin{array} { c c } { i } & { 0 } \\ { 0 } & { - i } \end{array} \right]$$ then show that $$A ^ { 2 } = - I$$
Evaluate : $$\left[ a\quad b \right] \left[ _{ d }^{ c } \right] +\left[ a\quad b\quad c\quad d \right] \left[ \underset { \underset { d }{ c } }{ \overset { a }{ b } } \right] $$
$$[ab]_{1\times 2} \begin{bmatrix}c\\ d\end{bmatrix}_{2\times 1}+[ a\, b\, c\, d]_{1\times 4} \begin{bmatrix}a\\ b\\ c\\ d\end{bmatrix}_{4\times 1}$$
$$\Rightarrow [ac+bd]_{1\times 1} +[a^2+b^2+c^2+d^2]_{1\times 1}$$
$$\Rightarrow [a^2+b^2+c^2+d^2 + ac + bd]_{1\times 1}$$
If $$A=\begin{bmatrix} 3 & 0 & 0 \\ 0 & 3 & 0 \\ 0 & 0 & 3 \end{bmatrix}$$ then find $$A^{4}$$.
Using elementary transformation find the inverse of $$A=\begin{pmatrix} 1 & 3 \\ 2 & 7 \end{pmatrix}$$
$$A=\begin{bmatrix} 1 & 3\\ 2 & 7\end{bmatrix}$$
$$[A/I]=\left[\begin{matrix} 1 & 3\\ 2 & 7\end{matrix}\right|\left.\begin{matrix} 1 & 0\\ 0 & 1\end{matrix}\right]\overset{R_2-2R}{\rightarrow}$$,
$$=\left[\begin{matrix} 1 & 3\\ 0 & 1\end{matrix}\right|\left.\begin{matrix} 1 & 0\\ -2 & 1\end{matrix}\right]\overset{R_1-3R_2}{\rightarrow} \left[\begin{matrix} 1 & 0\\ 0 & 1\end{matrix}\right|\left.\begin{matrix} 1 & -3\\ 0 & 1\end{matrix}\right]$$
$$\therefore A^{-1}=\begin{bmatrix} 1 & -3\\ 0 & 1\end{bmatrix}$$.
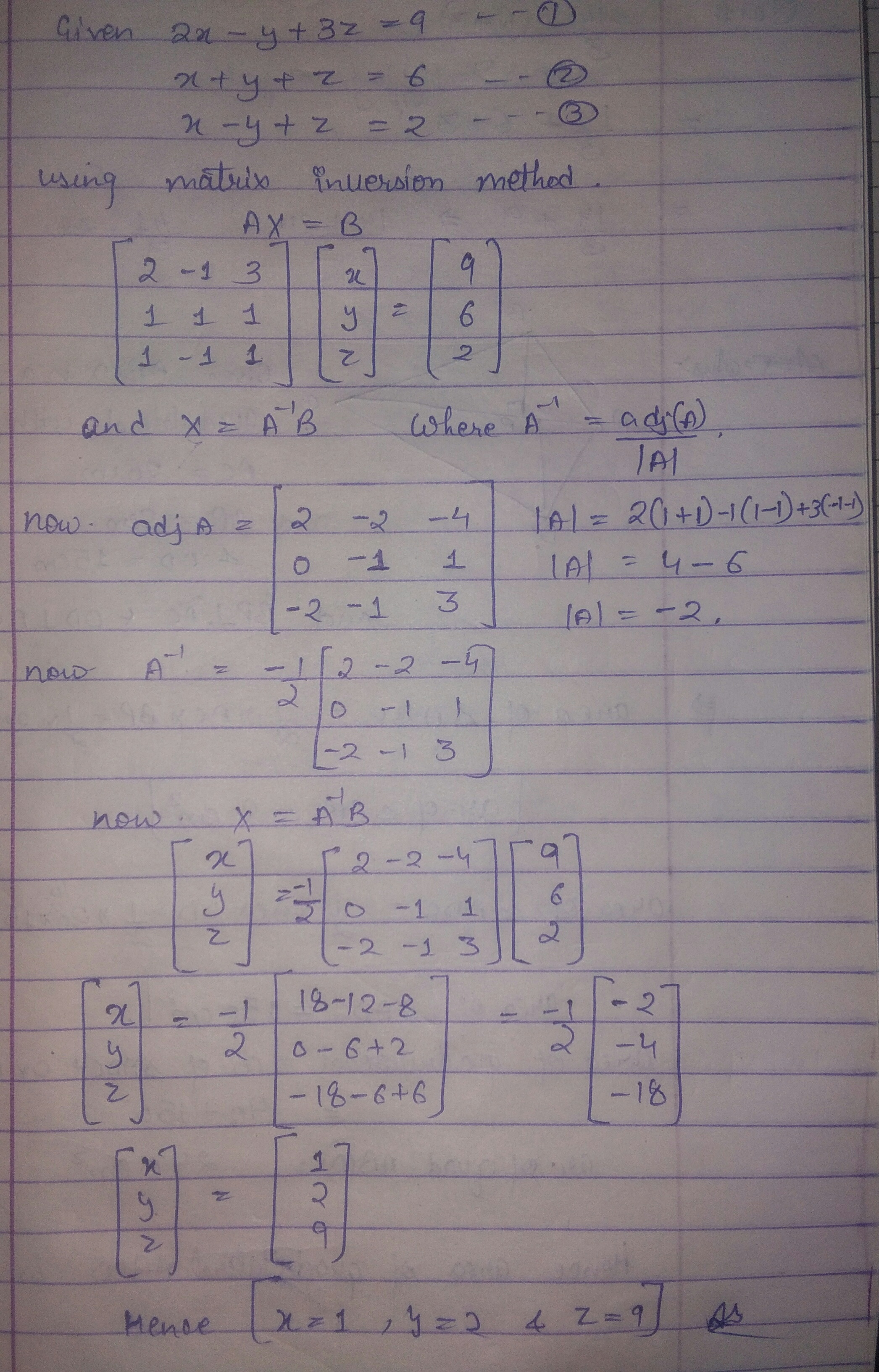
Solve the following system of equations by using Matrix inversion method.
$$2x-y+3z=9,x+y+z=6,x-y+z=2$$
Given
$$2x-y+3z=9$$ ………..$$(1)$$
$$x+y+z=6$$ …………..$$(2)$$
$$x-y+z=2$$ …………….$$(3)$$
using matrix inversion method
$$AX=B$$
$$\begin{bmatrix} 2 & -1 & 3\\ 1 & 1 & 1\\ 1 & -1 & 1\end{bmatrix}$$ $$\begin{bmatrix} x \\ y \\ z\end{bmatrix} =\begin{bmatrix} 9\\ 6 \\ 2\end{bmatrix}$$
and $$X=A^{-1}B$$ where $$A^{-1}=\dfrac{adj(A)}{|A|}$$
Now $$adj A=\begin{bmatrix} 2 & -2 & -4\\ 0 & -1 & 1\\ -2 & -1 & 3\end{bmatrix}$$
$$|A|=2(1+1)-1(1-1)+3(-1-1)$$
$$|A|=4-6$$
$$|A|=-2$$.
Now $$A^{-1}=\dfrac{-1}{2}\begin{bmatrix} 2 & -2 & -4\\ 0 & -1 & 1\\ -2 & -1 & 3\end{bmatrix}$$
Now $$X=A^{-1}B$$
$$\begin{bmatrix} x \\ y \\ z\end{bmatrix} =\dfrac{-1}{2}\begin{bmatrix} 2 & -2 & -4\\ 0 & -1 & 1\\ -2 & -1 & 3\end{bmatrix} \begin{bmatrix} 9 \\ 6 \\ 2\end{bmatrix}$$
$$\begin{bmatrix} x \\ y\\ z\end{bmatrix}=\dfrac{-1}{2}\begin{bmatrix} 18-12-8\\ 0-6+2\\ -18-6+6\end{bmatrix} =\dfrac{-1}{2}\begin{bmatrix} -2\\ -4\\ -18\end{bmatrix}$$
$$\begin{bmatrix} x \\ y \\ z\end{bmatrix} =\begin{bmatrix} 1 \\ 2\\ 9\end{bmatrix}$$
Hence $$[x=1, y=2$$ & $$z=9]$$.
Show that the matrix $$A=\begin{bmatrix} 2 & 3 \\ 1 & 2 \end{bmatrix}$$ satisfies the equation $$A^ {2}-4A+I=0$$, where $$I$$ is $$2\times 2$$ identity matrix and $$0$$ is $$2\times 2$$ zero matrix. Using this equation,find $$A^ {-1}$$.
Find $$x$$ if $$[1\ x\ 1] \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 3 & 2 & 5 \end{bmatrix} \begin{bmatrix} 1 \\ -2 \\ 3 \end{bmatrix}=0$$
If $$A=\begin{bmatrix} 2 & 3 \\ -1 & 4 \end{bmatrix}$$ and $$B=\begin{bmatrix} -3 & 1 \\ 4 & -2 \end{bmatrix}$$ then find $$A-B$$.
If A = $$\left[ \begin{matrix} 1 & 2 & x \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{matrix} \right] and\quad B=\left[ \begin{matrix} 1 & -2 & y \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{matrix} \right] \quad and$$ $${ AB=I}_{ 3 },\quad then\quad x+y\quad is\quad equal\quad to$$
Find the inverse of the following matrice by elementary transformation :
$$\begin {bmatrix} 1 & 2 & 3 \\ 2 & 3 & 4 \\ 3 & 4 & 5 \end {bmatrix}$$
Find the adjoint of the matrix A = $$\begin {bmatrix} 1 & 4 & 3 \\ 4 & 2 & 1 \\ 3 & 2 & 2 \end {bmatrix}$$ .
Find the cofactor matrix of $$\begin{bmatrix} 2 & -3 & 3 \\ 2 & 2 & 3 \\ 3 & -2 & 2 \end{bmatrix}$$
If $$A=\left[ \begin{matrix} 3 & 7 \\ 2 & 5 \end{matrix} \right]$$ and $$B=\left[ \begin{matrix} -3 & 2 \\ 4 & -1 \end{matrix} \right]$$ find the $$A+B$$
Determine the value of $$(x+y)$$ if $$\left[ \begin{matrix} 2x+y & 4x \\ 5x-7 & 4x \end{matrix} \right] =\left[ \begin{matrix} 7 & 7y-12 \\ y & x+6 \end{matrix} \right] $$
Find the value of x,y, z $$\left[ \begin{matrix} x+2 & 6 \\ 3 & { 5 }{ z } \end{matrix} \right] =\left[ \begin{matrix} 3 & { y }^{ 2 }+4 \\ 3 & 20 \end{matrix} \right] $$
If $$A = \left[ \begin{array} { c c c } { - 1 } & { 0 } & 2\\ { 2 } & { 3 } & { 4 } \\ { 0 } & { 1 } & { 2 } \end{array} \right] \quad B = \left[ \begin{array} { c c c } { 2 } & { 2 } & { - 4 } \\ { - 4 } & { 2 } & { - 4 } \\ { 2 } & { - 1 } & { 5 } \end{array} \right] ,$$ Find $$B+A$$
The Cartesian product of $$\{2,4\} \{3,3\} \{0, 1\}$$ is ?
Given $$A=\begin{pmatrix} 3 & -2 \\ -1 & 4 \end{pmatrix}\ B=\begin{pmatrix} 6 \\ 1 \end{pmatrix}\ C=\begin{pmatrix} -4 \\ 5 \end{pmatrix}$$ and $$D=\begin{pmatrix} 2 \\ 2 \end{pmatrix}$$.
Find $$AB+2C-4D$$
$$AB=\left(\begin{matrix} 3 & -2\\ -1 & 4\end{matrix}\right)\left(\begin{matrix} 6 \\ 1\end{matrix}\right)=\left(\begin{matrix} 16\\ -2\end{matrix}\right)$$; $$2c=\left(\begin{matrix} -8\\ 10\end{matrix}\right)$$; $$-4D=\left(\begin{matrix} -8\\ -8\end{matrix}\right)$$
$$AB+2C-4D=\left(\begin{matrix} 0\\ 0\end{matrix}\right)$$.
If $$A=\left[ \begin{matrix} 3 & 7 \\ 2 & 5 \end{matrix} \right]$$ and $$B=\left[ \begin{matrix} -3 & 2 \\ 4 & -1 \end{matrix} \right]$$ find the matrix $$C$$ if $$2C=A+B$$
If $$A=\left[ \begin{matrix} a & b \\ c & d \end{matrix} \right]$$ and $$B=\left[ \begin{matrix} p & q \\ r & s \end{matrix} \right]$$ then find $$AB$$
If $$A=\left[ \begin{matrix} a & b \\ c & d \end{matrix} \right]$$ and $$B=\left[ \begin{matrix} k & l \\ m & n \end{matrix} \right]$$ then find $$AB$$
If $$A=\left[ \begin{matrix} a & b \\ c & d \end{matrix} \right],\,\,\,B=\left[ \begin{matrix} p & q \\ r & s \end{matrix} \right]$$ and $$C=\left[ \begin{matrix} k & l \\ m & n \end{matrix} \right]$$ then find $$AB+AC$$
If $$3A - 2B =\begin{pmatrix} 1 & -2 \\ 3 & 0 \end{pmatrix}$$ and $$2A - 3B =\begin{pmatrix} -3 & 3 \\ 1 & -1 \end{pmatrix}$$ then find $$B$$
Let M = [1 -2] and N = $$\left[ \begin{matrix} 2 & 1 \\ -1 & 2 \end{matrix} \right] .$$
show that MN exists and write its order.
Let M = [1 -2] and N = $$\left[ \begin{matrix} 2 & 1 \\ -1 & 2 \end{matrix} \right] .$$
Dotes NM exist ? Give reasons.
Let M = [1 -2] and N = $$\left[ \begin{matrix} 2 & 1 \\ -1 & 2 \end{matrix} \right] .$$
Find MN.
If $$A=\left[ \begin{matrix} 3 & 2 & 0 \\ 1 & 4 & 0 \\ 0 & 0 & 5 \end{matrix} \right]$$.Find $${A}^{2}$$
Find the inverse of $$\left[\begin{matrix} 1 & 3 & 3 \\ 1 & 4 & 3 \\ 1 & 3 & 4 \end{matrix}\right]$$ by column transformation
If $$A=\left[ \begin{matrix} 2 & -1 \\ 3 & 4 \end{matrix} \right]\,\, B=\left[ \begin{matrix} 5 & -2 \\ 7 & 4 \end{matrix} \right]$$ and $$C=\left[ \begin{matrix} 2 & 5 \\ -3 & -8 \end{matrix} \right] ,$$ find the value of $$A+B+C$$
If $$A = \left[ \begin{array} { l l l } { 2 } & { 0 } & { 0 } \\ { 0 } & { 2 } & { 0 } \\ { 0 } & { 0 } & { 2 } \end{array} \right] ,$$ then find $$A ^ { 5 }$$.
Let $$A = \begin{pmatrix}3 & 2\\ 5 & 1\end{pmatrix}$$ and $$B = \begin{pmatrix}8 & -1 \\ 4 & 3\end{pmatrix}$$. Find the matrix $$C$$, if $$C = 2A + B$$.
If $$A = \left[ \begin{matrix} 1 & 2 \\ 2 & 1 \end{matrix} \right] $$ and $$B \left[ \begin{matrix} 2 & 1 \\ 1 & 2 \end{matrix} \right] $$ find $$A(BA)$$.
If $$A =$$ $$\left[ \begin{matrix} 1 & 3 \\ -3 & 2 \end{matrix} \right]$$ and $$B = \left[ \begin{matrix} -2 & 1 \\ -3 & 2 \end{matrix} \right]$$. Then find $$A^2 - 5B^2 $$.
$$A=\begin{bmatrix} 1 & 3\\ -3 & 2\end{bmatrix}$$ $$B=\begin{bmatrix} -2 & 1\\ -3 & 2\end{bmatrix}$$
$$A^2=\begin{bmatrix} 1 & 3\\ -3 & 2\end{bmatrix}\begin{bmatrix} 1 & 3\\ -3 & 2\end{bmatrix} .\begin{bmatrix} 1-9 & 3+6\\ -3-6 & -9+4\end{bmatrix}$$ $$=\begin{bmatrix} -8 & 9\\ -9 & -5\end{bmatrix}$$
$$B^2=\begin{bmatrix} -2 & 1\\ -3 & 2\end{bmatrix}$$ $$\begin{bmatrix} -2 & 1\\ -3 & 2\end{bmatrix}$$. $$\begin{bmatrix} 4-3 & -2+2\\ 6-6 & -3+4\end{bmatrix}$$
$$=\begin{bmatrix} 1 & 0\\ 0 & 1\end{bmatrix}$$
$$A^2-5B^2=\begin{bmatrix} -8 & 9\\ -9 & -5\end{bmatrix} -5\begin{bmatrix} 1 & 0\\ 0 & 1\end{bmatrix}$$
$$=\begin{bmatrix} -8 & 9\\ -9 & -5\end{bmatrix}-\begin{bmatrix} 5 & 0\\ 0 & 5\end{bmatrix}$$
$$=\begin{bmatrix} -13 & 9\\ -9 & -10\end{bmatrix}$$.
If $$2\begin{bmatrix} 3 & 4 \\ 5 & x \end{bmatrix}+\begin{bmatrix} 1 & y \\ 0 & 1 \end{bmatrix}=\begin{bmatrix} 7 & 0 \\ 10 & 5 \end{bmatrix}$$ on matrices. Find the value of $$x$$ & $$y$$.
Using elementary row transformation, find the inverse of $$\left[ \begin{matrix} 2 & 0 & -1 \\ 5 & 1 & 0 \\ 0 & 1 & 3 \end{matrix} \right] $$
$$A=\begin{bmatrix}1&2\\2&3\end{bmatrix}$$
$$A^2=?$$
Using elementary transformations find the inverse of
$$\begin{bmatrix} 3 & 2 & 1 \\ 2 & 4 & 3 \\ 2 & -1 & 2 \end{bmatrix}$$
If A is $$3 \times 4$$ matrix and B is a matrix such that $$A'B'$$ and $$B'A'$$ are both defined. Then the order of B is
1. $$3 \times 4$$
2. $$4 \times 4$$
3. $$3 \times 3$$
4. $$4 \times 3$$
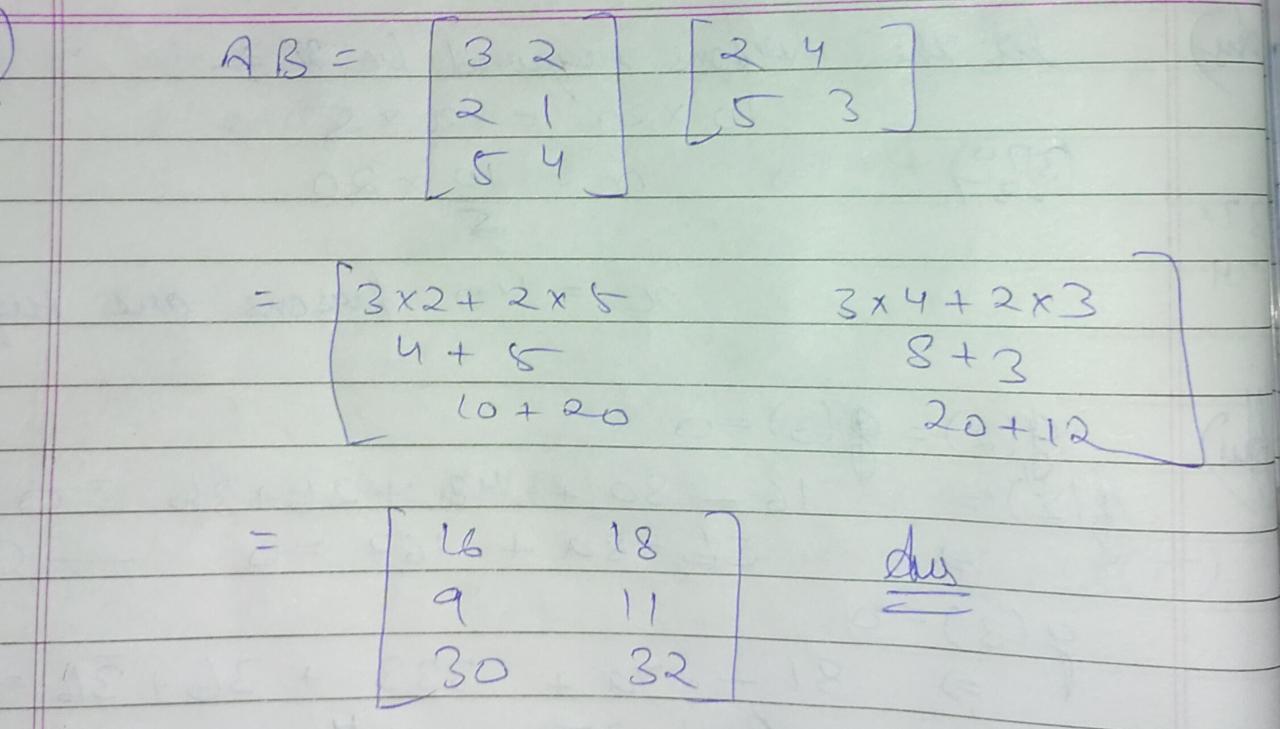
Perform the multiplication of the matrices $$A=\left[\begin{matrix} 3 & 2 \\ 2 & 1 \\ 5 & 4 \end{matrix}\right]$$, $$B=\begin{bmatrix} 2 & 4 \\ 5 & 3 \end{bmatrix}$$
Find the inverse of the following matrix, using elementary transformations :
$$A = \begin{bmatrix} 2 & 3 & 1 \\ 2 & 4 & 1 \\ 3 & 7 & 2 \end{bmatrix}$$
Find the inverse of A=$$\left[ \begin{matrix} cos\theta & -sin\theta & 0 \\ sin\theta & cos\theta & 0 \\ 0 & 0 & 1 \end{matrix} \right] $$ by
elementary row transformations.
For the matrix $$A=\begin{bmatrix} 3 & 2 \\ 1 & 1 \end{bmatrix}$$. Find the values of a and b
Such that A$$^{2}$$+aA+bI$$\neq $$0
Find the inverse of A=$$\left[ \begin{matrix} cos\theta & -sin\theta & 0 \\ sin\theta & cos\theta & 0 \\ 0 & 0 & 1 \end{matrix} \right] $$ by
elementary column transformations.
Show that $$\mathrm { A } ^ { \prime } \mathrm { A }$$ and $$\mathrm { AA } ^ { \prime }$$ are both symmetric matrices for any matrix $$A.$$
Find $$X$$, if $$Y = \begin{bmatrix}3 & 2\\ 1 & 4\end{bmatrix}$$ and $$2X + Y = \begin{bmatrix} 1& 0\\ -3 & 2\end{bmatrix}$$.
Solve the following pairs of linear equations :
$$Px+qy=p-q$$
$$qx-py=p+q$$
Solve the following pair of linear equations :
$$ax+by=c$$
$$bx+ay=1+c$$
Compute the following sum:
$$A=\begin{bmatrix} 3& -2\\ 1 & 4\end{bmatrix} $$and $$B= \begin{bmatrix} -2& 4\\ 1 & 3\end{bmatrix}$$
If $$A = \begin{bmatrix} 2& 3\\ 5 & 7\end{bmatrix}, B = \begin{bmatrix} -1& 0 & 2\\ 3 & 4 & 1\end{bmatrix}, C = \begin{bmatrix}-1 & 2 & 3\\ 2 & 1& 0\end{bmatrix}$$, then find $$A + B$$ and $$B + C$$.
If the matrix $$A = \begin{bmatrix}5 & 2 & x\\ y & z & -3\\ 4 & t & -7\end{bmatrix}$$ is a symmetric matrix, find the values of $$x, y, z$$ and $$t$$.
If $$A = \begin{bmatrix}3 & 2 & 7\\ 1 & 4 & 3\\ -2 & 5 & 8\end{bmatrix}$$, then find matrices $$X$$ and $$Y$$, such that $$X + Y = A$$, where $$X$$ is a symmetric.
If $$A = \begin{bmatrix}-3 & 0\\ 0 & -3\end{bmatrix}$$, then find $$A^{4}$$.
If $$A = \begin{bmatrix} -1& 0 & 0\\ 0 &-1 & 0\\ 0 & 0 & -1\end{bmatrix}$$, then find $$A^{2}$$.
Define a symmetric matrix. Prove that $$A+ A^{T}$$ is a symmetric matrix where $$A^{T}$$ is the transpose of $$A$$.
If $$A = \begin{bmatrix} -1& 0 & 0\\ 0 &-1 & 0\\ 0 & 0 & -1\end{bmatrix}$$, then find $$A^{3}$$.
If $$A = \begin{bmatrix}1& -1\\ -1 & 1\end{bmatrix}$$, satisfies the matrix equation $$A^{2} = kA$$, write the value of $$k$$.
Matrix $$A = \begin{bmatrix}0 & 2b & -2\\ 3 & 1 & 3\\ 3a & 3 &-1 \end{bmatrix}$$ is given to be symmetric, find the values of $$a$$ and $$b$$.
If $$A$$ and $$B$$ are symmetric matrices, then write the condition for which $$AB$$ is also symmetric.
If $$X$$ and $$Y$$ are $$2\times 2$$ matrices, then solve the following matrix equations for $$X$$ and $$Y$$.
$$2X + 3Y = \begin{bmatrix}2 & 3\\ 4 & 0\end{bmatrix}, 3X + 2Y = \begin{bmatrix} -2& 2\\ 1 & -5\end{bmatrix}$$
Show that $$AB \neq BA$$ in the following matrices:
$$A = \begin{bmatrix} 1& 3 & 0\\ 1 & 1 & 0\\ 4 & 1 & 0\end{bmatrix}$$ and $$B = \begin{bmatrix}0 & 1 & 0\\ 1 & 0 & 0\\ 0 & 5 & 1\end{bmatrix}$$
Show that $$AB \neq BA$$ in the following matrices:
$$A = \begin{bmatrix}5 & -1\\ 6 & 7\end{bmatrix}$$ and $$B = \begin{bmatrix} 2& 1\\ 3 & 4\end{bmatrix}$$
Multiply the given matrices:$$\begin{bmatrix}1 & -2\\ 2 & 3\end{bmatrix} \begin{bmatrix} 1& 2 & 3\\ -3 & 2 & -1\end{bmatrix}$$
Multiply the given matrix:$$\begin{bmatrix}2 & 3 & 4\\ 3 & 4 & 5\\ 4 & 5 & 6\end{bmatrix} \begin{bmatrix}1 &-3 & 5\\ 0 & 2 & 4\\ 3 & 0 & 5\end{bmatrix}$$
Show that $$AB \neq BA$$ in the following matrices:
$$A = \begin{bmatrix} -1& 1 & 0\\ 0 & -1 & 1\\ 2 & 3 & 4\end{bmatrix}$$ and $$B = \begin{bmatrix}1 & 2 & 3\\ 0 & 1 & 0\\ 1 & 1 & 0\end{bmatrix}$$
Compute the products $$AB$$ and $$BA$$ whichever exists in the following case:
$$A = \begin{bmatrix} 1& -2\\ 2 & 3\end{bmatrix}$$ and $$B = \begin{bmatrix}1 & 2 & 3\\ 2 & 3 & 1\end{bmatrix}$$
Compute the products $$AB$$ and $$BA$$ whichever exists in the following case:
$$A = \begin{bmatrix} 3& 2\\ -1 & 0\\ -1 & 1\end{bmatrix}$$ and $$B = \begin{bmatrix}4 & 5 & 6\\ 0 & 1 & 2\end{bmatrix}$$
Find :$${A}^{2}$$ if
$$A =\begin{bmatrix} 1 & 3 & 2 \\ -5 & 1 & 0 \\ 1 & 2 & 5 \end{bmatrix}$$
Compute the product $$AB$$ and $$BA$$ whichever exists in the following case:
$$A = \begin{bmatrix}1 & -1 & 2 & 3\end{bmatrix}$$ and $$B = \begin{bmatrix}0\\1 \\3 \\2
\end{bmatrix}$$
Show that $$AB \neq BA$$ in the following matrices:
$$A = \begin{bmatrix} 1& 3 & -1\\ 2 & -1 & -1\\ 3 & 0 & -1\end{bmatrix}$$ and $$B = \begin{bmatrix}-2 & 3 & -1\\ -1 & 2 & -1\\ -6 & 9 & -4\end{bmatrix}$$.
If $$A = \begin{bmatrix} 2& -3 & -5\\ -1 & 4 & 5\\ 1 & -3 & -4\end{bmatrix}$$ and $$B = \begin{bmatrix}-1 & 3 & 5\\ 1 & -3 & -5\\ -1 & 3 & 5\end{bmatrix}$$, show that $$AB = BA = 0_{3\times 3}$$.
If $$A = \begin{bmatrix} 0& c & -b\\ -c & 0 & a\\ b & -a & 0\end{bmatrix}$$ and $$B = \begin{bmatrix}a^{2} & ab & ac\\ ab & b^{2} & bc\\ ac & bc & c^{2}\end{bmatrix}$$, show that $$AB = BA = 0_{3\times 3}$$.
If $$A = \begin{bmatrix} \cos 2\theta& \sin 2 \theta\\ -\sin 2\theta & \cos 2\theta\end{bmatrix}$$, find $$A^{2}$$.
Evaluate the following:
$$\begin{bmatrix} 1& 2 & 3\end{bmatrix}\begin{bmatrix}1 & 0 & 2\\ 2 & 0 & 1\\ 0 & 1 & 2\end{bmatrix}\begin{bmatrix}2\\ 4\\ 6
\end{bmatrix}$$
If $$A = \begin{bmatrix}1 &1 \\ 0 & 1\end{bmatrix}$$, show that $$A^{2} = \begin{bmatrix}1 & 2\\ 0 & 1\end{bmatrix}$$ and $$A^{3} = \begin{bmatrix}1 & 3\\ 0 & 1\end{bmatrix}$$.
Show that $$AB \neq BA$$ in the following matrices:
$$A = \begin{bmatrix} 10& -4 & -1\\ -11 & 5 & 0\\ 9 & -5 & 0\end{bmatrix}$$ and $$B = \begin{bmatrix}1 & 2 & 1\\ 3 & 4 & 2\\ 1 & 3 & 2\end{bmatrix}$$.
If $$A = \begin{bmatrix}1 & 0\\ 0 & 1\end{bmatrix}, B = \begin{bmatrix} 1& 0\\ 0 & -1\end{bmatrix}$$ and $$C = \begin{bmatrix}0 & 1\\ 1 & 0\end{bmatrix}$$, then show that $$A^{2} =B^{2} = C^{2} = I_{2}$$.
If $$A = \begin{bmatrix}2 &-3 & -5\\ -1 & 4 & 5\\ 1 & -3 & -4\end{bmatrix}$$ and $$B = \begin{bmatrix}2 & -2 & -4\\ -1 & 3 & 4\\ 1 & -2 & -3\end{bmatrix}$$, show that $$AB = A$$ and $$BA = B$$.
Evaluate the following:
$$\begin{bmatrix} 1& -1\\ 0 & 2\\ 2 & 3\end{bmatrix}\left (\begin{bmatrix} 1& 0 & 2\\ 2 & 0 & 1\end{bmatrix} - \begin{bmatrix}0 & 1 & 2\\ 1 & 0 & 2\end{bmatrix}\right )$$
Find the inverse of the following matrix by using elementary row transformation:
$$\begin{bmatrix} 5 & 2 \\ 2 & 1 \end{bmatrix}$$
Find the inverse of the following matrix by using elementary row transformation :
$$\begin{bmatrix} 3 & 10 \\ 2 & 7 \end{bmatrix}$$
Solve the following matrix and find value of $$x$$:
$$\begin{bmatrix}2x & 3\end{bmatrix}\begin{bmatrix}1 & 2\\ -3 & 0\end{bmatrix} \begin{bmatrix}x\\ 8
\end{bmatrix} = 0$$.
Find the inverse of the following matrix by using elementary row transformations :
$$\begin{bmatrix} 1 & 1 & 2 \\ 3 & 1 & 1 \\ 2 & 3 & 1 \end{bmatrix}$$
Find the inverse of the following matrix by using elementary row transformation:
$$\begin{bmatrix} 2 & 0 & -1 \\ 5 & 1 & 0 \\ 0 & 1 & 3 \end{bmatrix}$$
Find the inverse of the following matrix by using elementary row transformation:
$$\begin{bmatrix} 1 & 2 \\ 2 & -1 \end{bmatrix}$$
Solve the following matrix:
$$\begin{bmatrix} x& 1\end{bmatrix} \begin{bmatrix}1 & 0\\ -2 & -3\end{bmatrix}\begin{bmatrix}x\\ 5
\end{bmatrix} = 0$$
Find the inverse of the following matrix by using elementary row transformation:
$$\begin{bmatrix} 3 & -3 & 4 \\ 2 & -3 & 4 \\ 0 & -1 & 1 \end{bmatrix}$$
Find the inverse of the following matrix by using elementary row transformations :
$$\begin{bmatrix} 1 & 2 & 0 \\ 2 & 3 & -1 \\ 1 & -1 & 3 \end{bmatrix}$$
Find the inverse of the following matrices by using elementary row transformations :
$$\begin{bmatrix} 2 & -1 & 3 \\ 1 & 2 & 4 \\ 3 & 1 & 1 \end{bmatrix}$$
Find the inverse of the following matrix by using elementary row transformation :
$$\begin{bmatrix} 0 & 1 & 2 \\ 1 & 2 & 3 \\ 3 & 1 & 1 \end{bmatrix}$$
Find the inverse of the following matrix by using elementary row transformations :
$$\begin{bmatrix} -1 & 1 & 2 \\ 1 & 2 & 3 \\ 3 & 1 & 1 \end{bmatrix}$$
If $$P = \begin{bmatrix} x& 0 & 0\\ 0 & y & 0\\ 0 & 0 & z\end{bmatrix}$$ and $$Q = \begin{bmatrix}a & 0 & 0\\ 0 & b & 0\\ 0 & 0 & c\end{bmatrix}$$, then prove that $$PQ = \begin{bmatrix}xa & 0 & 0\\ 0 & yb & 0\\ 0 & 0 & zc\end{bmatrix} = QP$$.
Find the inverse of the following matrix by using elementary row transformations :
$$\begin{bmatrix} 3 & 0 & -1 \\ 2 & 3 & 0 \\ 0 & 4 & 1 \end{bmatrix}$$
Find the inverse of each of the matrices given below:
$$\begin{bmatrix}4 & 1\\2 & 3\end{bmatrix}$$
Compute the indicated products
(i) $$\displaystyle \begin{bmatrix} a & b \\ -b & a \end{bmatrix}\begin{bmatrix} a & -b \\ b & a \end{bmatrix}$$
(ii) $$\displaystyle \left[ \begin{matrix} 1 \\ 2 \\ 3 \end{matrix} \right] \left[ \begin{matrix} 2 & 3 & 4 \end{matrix} \right] $$
(iii) $$\displaystyle \begin{bmatrix} 1 & -2 \\ 2 & 3 \end{bmatrix}\left[ \begin{matrix} 1 & 2 & 3 \\ 2 & 3 & 1 \end{matrix} \right] $$
(iv) $$\displaystyle \left[ \begin{matrix} 2 \\ 3 \\ 4 \end{matrix}\begin{matrix} 3 \\ 4 \\ 5 \end{matrix}\begin{matrix} 4 \\ 5 \\ 6 \end{matrix} \right] \left[ \begin{matrix} 1 \\ 0 \\ 3 \end{matrix}\begin{matrix} -3 \\ 2 \\ 0 \end{matrix}\begin{matrix} 5 \\ 4 \\ 5 \end{matrix} \right] $$
(v) $$\displaystyle \left[ \begin{matrix} 2 \\ 3 \\ -1 \end{matrix}\begin{matrix} 1 \\ 2 \\ 1 \end{matrix} \right] \left[ \begin{matrix} 1 & 0 & 1 \\ -1 & 2 & 1 \end{matrix} \right] $$
(vi) $$\displaystyle \left[ \begin{matrix} 3 & -1 & 3 \\ -1 & 0 & 2 \end{matrix} \right] \left[ \begin{matrix} 2 \\ 1 \\ 3 \end{matrix}\begin{matrix} -3 \\ 0 \\ 1 \end{matrix} \right] $$
Given that $$A = \begin{bmatrix}1 & 1 & 1\\ 3 & 3 & 3\end{bmatrix}, B = \begin{bmatrix}3 & 1\\ 5 & 2\\ -2 & 4\end{bmatrix}$$ and $$C = \begin{bmatrix}4 & 2\\ -3& 5\\ 5 & 0\end{bmatrix}$$.
Verify that $$AB= AC$$ though $$B\neq C, A\neq 0$$.
Find the inverse of each of the matrices given below:
$$\begin{bmatrix}3 & -5\\ -1 & 2\end{bmatrix}$$
Let $$A=\begin{bmatrix} 2 & 4 \\ 3 & 2 \end{bmatrix}, B=\begin{bmatrix} 1 & 3 \\ -2 & 5 \end{bmatrix}$$ and $$C=\begin{bmatrix} -2 & 5 \\ 3 & 4 \end{bmatrix}$$. Find:
$$A+2B$$
Find the inverse of each of the matrices given below:
$$\begin{bmatrix}2 & -3\\4 & 6\end{bmatrix}$$
Find the inverse of each of the matrices given below:
$$\begin{bmatrix}0 & 0 & -1\\ 3& 4 & 5 \\ -2 & -4 & -7\end{bmatrix}$$
Find the inverse of each of the matrices given below:
$$\begin{bmatrix}8 & -4 & 1\\ 10& 0 & 6 \\ 8 & 1 & 6\end{bmatrix}$$
Find the inverse of each of the matrices given below:
$$\begin{bmatrix}2 & -3 & 3\\ 2& 2 & 3 \\ 3 & -2 & 2\end{bmatrix}$$
Find the inverse of each of the matrices given below:
$$\begin{bmatrix}1 & 2 & 5\\ 1& -1 & -1 \\ 2 & 3 & -1\end{bmatrix}$$
Find the inverse of each of the matrices given below:
$$\begin{bmatrix}2 & -1 & 1\\ 3& 0 & -1 \\ 2 & 6 & 0\end{bmatrix}$$
If $$A=\begin{bmatrix} 2 & -3 & 5 \\ -1 & 0 & 3 \end{bmatrix}$$ and $$B=\begin{bmatrix} 3 & 2 & -2 \\ 4 & -3 & 1 \end{bmatrix}$$, verify that $$(A+B)=(B+A)$$.
Find the inverse of each of the matrices given below:
$$\begin{bmatrix}2 & -1 & 4\\ -3& 0 & 1 \\ -1 & 1 & 2\end{bmatrix}$$
Find the inverse of each of the matrices given below:
$$\begin{bmatrix}a & b\\ c& d\end{bmatrix}$$, when $$(ad - bc) \neq 0$$.
If $$A=\begin{bmatrix} 0 & c & -b \\ -c & 0 & a \\ b & -a & 0 \end{bmatrix}$$ and $$B=\begin{bmatrix} { a }^{ 2 } & ab & ac \\ ab & { b }^{ 2 } & bc \\ ac & bc & { c }^{ 2 } \end{bmatrix}$$, show that $$AB$$ is z zero matrix.
Using elementary row transformations, find the inverse of the following matrix:
$$\begin{bmatrix} 1 & 2 \\ 2 & -1 \end{bmatrix}$$
Find matrix $$X$$, if $$\begin{bmatrix} 3 & 5 & -9 \\ -1 & 4 & -7 \end{bmatrix}+X=\begin{bmatrix} 6 & 2 & 3 \\ 4 & 8 & 6 \end{bmatrix}$$.
Compute $$AB$$ and $$BA$$, whichever exists when
$$A=\begin{bmatrix} -1 & 1 \\ -2 & 2 \\ -3 & 3 \end{bmatrix}$$ and $$B=\begin{bmatrix} 3 & -2 & 1 \\ 0 & 1 & 2 \\ -3 & 4 & -5 \end{bmatrix}$$
Using elementary row transformations, find the inverse of the following matrix:
$$\begin{bmatrix} 1 & 2 \\ 3 & 7 \end{bmatrix}$$
Compute $$AB$$ and $$BA$$, whichever exists when
$$A=\begin{bmatrix} 2 & -1 \\ 3 & 0 \\ -1 & 4 \end{bmatrix}$$ and $$B=\begin{bmatrix} -2 & 3 \\ 0 & 4 \end{bmatrix}$$
For the following matrices, verify that $$A(BC)=(AB)C$$:
$$A=\begin{bmatrix} 2 & 3 & -1 \\ 3 & 0 & 2 \end{bmatrix},\quad B=\begin{bmatrix} 1 \\ 1 \\ 2 \end{bmatrix}$$ and $$C=\begin{bmatrix} 1 & -2 \end{bmatrix}$$
If $$A=\begin{bmatrix} 2 & -3 & -5 \\ -1 & 4 & 5 \\ 1 & -3 & -4 \end{bmatrix}$$ and $$B=\begin{bmatrix} 2 & -2 & -4 \\ -1 & 3 & 4 \\ 1 & -2 & -3 \end{bmatrix}$$, show that $$AB=A$$ and $$BA=B$$
If $$A=\begin{bmatrix} \cos \alpha & \sin \alpha \\ -\sin \alpha & \cos \alpha \end{bmatrix}$$, show that $$A'A=I$$.
For the following matrices, verify that $$A(BC)=(AB)C:$$
$$A=\begin{bmatrix} 1 & 2 & 5 \\ 0 & 1 & 3 \end{bmatrix},\quad B=\begin{bmatrix} 2 & 3 & 0 \\ 1 & 0 & 4 \\ 1 & -1 & 2 \end{bmatrix}$$ and $$C=\begin{bmatrix} 1 \\ 4 \\ 5 \end{bmatrix}$$
Using elementary row transformations, find the inverse of the following matrix:
$$\begin{bmatrix} 0 & 1 & 2 \\ 1 & 2 & 3 \\ 3 & 1 & 1 \end{bmatrix}$$
Using elementary row transformations, find the inverse of the following matrix:
$$\begin{bmatrix} 6 & 7 \\ 8 & 9 \end{bmatrix}$$
Using elementary row transformations, find the inverse of the following matrix:
$$\begin{bmatrix} 1 & 3 & -2 \\ -3 & 0 & -1 \\ 2 & 1 & 0 \end{bmatrix}$$
Using elementary row transformations, find the inverse of the following matrix:
$$\begin{bmatrix} 4 & 0 \\ 2 & 5 \end{bmatrix}$$
Using elementary row transformations, find the inverse of the following matrix:
$$\begin{bmatrix} 2 & 5 \\ -3 & 1 \end{bmatrix}$$
Using elementary row transformations, find the inverse of the following matrix:
$$\begin{bmatrix} 3 & -1 & -2 \\ 2 & 0 & -1 \\ 3 & -5 & 0 \end{bmatrix}$$
Using elementary row transformations, find the inverse of the following matrix:
$$\begin{bmatrix} 1 & 2 & -3 \\ 2 & 3 & 2 \\ 3 & -3 & -4 \end{bmatrix}$$
Using elementary row transformations, find the inverse of the following matrix:
$$\begin{bmatrix} 3 & 0 & 2 \\ 1 & 5 & 9 \\ 6 & 4 & 7 \end{bmatrix}$$
Using elementary row transformations, find the inverse of the following matrix:
$$\begin{bmatrix} 2 & -3 & 3 \\ 2 & 2 & 3 \\ 3 & -2 & 2 \end{bmatrix}$$
Using elementary row transformations, find the inverse of the following matrix:
$$\begin{bmatrix} 2 & -3 \\ 4 & 5 \end{bmatrix}$$
Find the matrix $$A$$ such that $$A.\begin{bmatrix} 2 & 3 \\ 4 & 5 \end{bmatrix}=\begin{bmatrix} 0 & -4 \\ 10 & 3 \end{bmatrix}$$
If $$A=\begin{bmatrix} \cos { \alpha } & \sin { \alpha } \\ -\sin { \alpha } & \cos { \alpha } \end{bmatrix}$$, show that $$A^{2}=\begin{bmatrix} \cos { 2\alpha } & \sin { 2\alpha } \\ -\sin { 2\alpha } & \cos { 2\alpha } \end{bmatrix}$$
Using elementary row transformations, find the inverse of the following matrix:
$$\begin{bmatrix} 3 & 0 & -1 \\ 2 & 3 & 0 \\ 0 & 4 & 1 \end{bmatrix}$$
Find the matrix $$A$$ such that $$\begin{bmatrix} 5 & -7 \\ -2 & 3 \end{bmatrix}.A=\begin{bmatrix} -16 & -6 \\ 7 & 2 \end{bmatrix}$$
Using elementary row transformations, find the inverse of the following matrix:
$$\begin{bmatrix} 1 & 2 & 3 \\ 2 & 5 & 7 \\ -2 & -4 & -5 \end{bmatrix}$$
If $$A=\begin{bmatrix} 3 & -2 \\ 4 & -2 \end{bmatrix}$$, find $$k$$ so that $$A^{2}=kA-2I$$
Using elementary row transformations, find the inverse of the following matrix:
$$\begin{bmatrix} -1 & 1 & 2 \\ 1 & 2 & 3 \\ 3 & 1 & 1 \end{bmatrix}$$
If $$A=\begin{bmatrix} 4 & -1 & -4 \\ 3 & 0 & -4 \\ 3 & -1 & -3 \end{bmatrix}$$, show that $$A^{2}=I$$
If $$A=\begin{bmatrix} 2 & -2 & -4 \\ -1 & 3 & 4 \\ 1 & -2 & -3 \end{bmatrix}$$, show that $$A^{2}=A$$.
Show that $$\cos\theta.\begin{bmatrix} \cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{bmatrix}+\sin { \theta } \begin{bmatrix} \sin \theta & -\cos \theta \\ \cos \theta & \sin \theta \end{bmatrix}=I$$.
If $$A=\begin{bmatrix} \cos \alpha & \sin \alpha \\ -\sin \alpha & \cos \alpha \end{bmatrix}$$, show that $$A'A=I$$.
If A is a matrix of order $$3 \times 3$$, then find $$(A^2)^{-1}$$.
Using elementary transformations, find the inverse of the matrix $$A = \begin{bmatrix}
1 & 3 & -2 \\
-3 & 0 & -1 \\
2 & 1 & 0
\end{bmatrix}
$$
If A is non-singular square matrix such that $$A^{-1}$$ = $$\begin{bmatrix} 5 & 3 \\ -2 & -1
\end{bmatrix}$$ then find $$(A^T)^{-1}$$.
Find the inverse of $$A = \Bigg( \begin{matrix}
3 & -1 \\
-4 & 1
\end{matrix}
\Bigg)$$ using elementary transformations.
Find the inverse of the following matrix using elementary operations:
$$A = \Bigg(\begin{matrix}
1 & 2 & -2 \\
-1 & 3 & 0 \\
0 & -2 & 1
\end{matrix}
\Bigg)$$
If $$\begin{bmatrix}
1 & -1 & 0 \\
2 & 3 & 4 \\
0 & 1 & 2
\end{bmatrix}
\begin{bmatrix}
2 & 2 & -4 \\
-4 & 2 & -4 \\
2 & -1 & 5
\end{bmatrix}
$$ are two square matrices, find $$AB$$ and hence solve the following system of linear equations:
$$x - y = 3, 2x + 3y + 4z = 17$$ and $$y + 2z = 7$$
If $$A^{-1} = \begin{bmatrix}
3 & -1 & 1 \\
-15 & 6 & -5 \\
5 & -2 & 2
\end{bmatrix}
$$ and $$B = \begin{bmatrix}
1 & 2 & -2 \\
-1 & 3 & 0 \\
0 & -2 & 1
\end{bmatrix}
$$, find $$(AB){-1}$$.
$$\text { If } P=\left[\begin{array}{cc}4 & 6 \\2 & -8\end{array}\right], Q=\left[\begin{array}{cc}2 & -3 \\-1 & 1\end{array}\right]$$
Find $$2PQ.$$
If possible, find the sum of the matrices $$A$$ and $$B$$, where $$A=\begin{bmatrix} \sqrt { 3 } & 1 \\ 2 & 3 \end{bmatrix}$$ and $$B=\begin{bmatrix} x & y & z \\ a & b & c \end{bmatrix}$$
Determine the product $$\begin{bmatrix}
-4 & 4 & 4 \\
-7 & 1 & 3 \\
5 & -3 & -1
\end{bmatrix}
\begin{bmatrix}
1 & -1 & 1 \\
1 & -2 & -2 \\
2 & 1 & 3
\end{bmatrix}
$$ and use it to solve the system of equations:
$$x - y + z = 4, x - 2y - 2z = 9, 2x + y + 3z = 1$$.
If $$A=\left[\begin{array}{cc}3 & 5 \\ 4 & -2\end{array}\right]$$ and $$B=\left[\begin{array}{l}2 \\ 4\end{array}\right],$$ is the product $$A B$$ possible $$?$$ Give a reason. If yes find AB.
If $$X=\begin{bmatrix} 3 & 1 & -1 \\ 5 & -2 & -3 \end{bmatrix}$$ and $$Y=\begin{bmatrix} 2 & 1 & -1 \\ 7 & 2 & 4 \end{bmatrix}$$, then find $$X+Y$$.
If $$A=\begin{bmatrix} \cos { \quad q } & \sin { \quad q } \\ -\sin { \quad q } & \cos { \quad q } \end{bmatrix}$$ then show that $${ A }^{ 2 }=\begin{bmatrix} \cos { \quad 2q } & \sin { \quad 2q } \\ -\sin { \quad 2q } & \cos { \quad 2q } \end{bmatrix}$$
If $$X=\begin{bmatrix} 3 & 1 & -1 \\ 5 & -2 & -3 \end{bmatrix}$$ and $$Y=\begin{bmatrix} 2 & 1 & -1 \\ 7 & 2 & 4 \end{bmatrix}$$, then find $$2x-3Y$$.
Find the values of $$a,\ b,\ c$$ and $$d,$$ if $$3\begin{bmatrix} a & b \\ c & d \end{bmatrix}=\begin{bmatrix} a & 6 \\ -1 & 2d \end{bmatrix}+\begin{bmatrix} 4 & a+b \\ c+d & 3 \end{bmatrix}.$$
If $$X=\begin{bmatrix} 3 & 1 & -1 \\ 5 & -2 & -3 \end{bmatrix}$$ and $$Y=\begin{bmatrix} 2 & 1 & -1 \\ 7 & 2 & 4 \end{bmatrix}$$, then a matrix $$Z$$ such that $$X+Y+Z$$ is a zero matrix.
Find the value of $$x$$, if $$\begin{bmatrix} 1 & x & 1 \end{bmatrix}\begin{bmatrix} 1 & 3 & 2 \\ 2 & 5 & 1 \\ 15 & 3 & 2 \end{bmatrix}\begin{bmatrix} 1 \\ 2 \\ x \end{bmatrix}=0$$
If $$A= \begin{bmatrix} 1 & 5 \\ 7 & 12 \end{bmatrix} $$ and $$B=\begin{bmatrix} 9 & 1 \\ 7 & 8 \end{bmatrix}$$, find a matrix $$C$$ such that $$3A+5B+2C$$ is a null matrix.
Find the matrix $$A$$ such that $$\begin{bmatrix} 2 & -1 \\ 1 & 0 \\ -3 & 4 \end{bmatrix}A=\begin{bmatrix} -1 & -8 & -10 \\ 1 & -2 & -5 \\ 9 & 22 & 15 \end{bmatrix}.$$
If $$A=\begin{bmatrix} 2 & 3 \\ 1 & 2 \end{bmatrix}, B=\begin{bmatrix} 1 & 3 & 2 \\ 4 & 3 & 1 \end{bmatrix}, C=\begin{bmatrix} 1\\2 \end{bmatrix}, D=\begin{bmatrix} 4 & 6 & 8 \\ 5 & 7 & 9 \end{bmatrix}$$Then which of the sums $$A+B, B+C, C+D$$ and $$B+D$$ is defined?
If $$A= \begin{bmatrix} 3 & -5 \\ -4 & 2 \end{bmatrix} $$, then find $$A^2-5A-14I$$. Hence, obtain $$A^3$$.
The negative of a matrix is obtained by multiplying it by _______ .
If $$A$$ is a skew symmetric matrix then $$A^{2}$$ is a ______.
If $$A$$ and $$B$$ are symmetric matrices then
$$BA-2AB$$ is a _______.
If $$A$$ and $$B$$ are symmetric matrices then
$$AB-BA$$ is a _______.
If $$A$$ is symmetric matrix, then $$A^{3}$$ is a _______ matrix.
If $$\begin{bmatrix} 2x & 3 \end{bmatrix}\begin{bmatrix} 1 & 2 \\ -3 & 0 \end{bmatrix}\begin{bmatrix} x \\ 8 \end{bmatrix}=0$$, Find the value of $$x$$.
If $$A$$ and $$B$$ are symmetric matrices of same order, then $$AB$$ is symmetric if and only if _______.
In applying one or more row operations while finding $$A^{-1}$$ by elementary row operations, we obtain all zeroes in one or more, then $$A^{-1}$$ ______.
Given $$ \left[ \begin{matrix} x & y+2 \\ 3 & z-1 \end{matrix} \right] =\begin{bmatrix} 3 & 1 \\ 3 & 2 \end{bmatrix} $$ find $$ x, y $$ and $$ z $$.
Solve for $$ a, b $$ and $$ c $$ if
$$ \left[ \begin{matrix} a & a-b \\ b+c & 0 \end{matrix} \right] =\begin{bmatrix} 3 & -1 \\ 2 & 0 \end{bmatrix} $$
If possible, using elementary row transformations, find the inverse of the following matrix.
$$\begin{bmatrix} 2 & 3 & -3 \\ -1 & -2 & 2 \\ 1 & 1 & -1 \end{bmatrix}$$
Evaluate :
$$ 2\begin{bmatrix} -1 & 0 \\ 2 & -3 \end{bmatrix}+\begin{bmatrix} 3 & 3 \\ 5 & 0 \end{bmatrix} $$
Given $$ A = \begin{bmatrix} 1 & 4 \\ 2 & 3 \end{bmatrix}\quad and\quad B\quad =\quad \begin{bmatrix} -4 & -1 \\ -3 & -2 \end{bmatrix}\quad $$
Find the matrix $$ 2A +B $$
If possible, using elementary row transformations, find the inverse of the following matrix.
$$\begin{bmatrix} 2 & -1 & 3 \\ -5 & 3 & 1 \\ -3 & 2 & 3 \end{bmatrix}$$
Solve for $$ a, b $$ and $$ c $$ if
$$ \left[ \begin{matrix} -4 & a+5 \\ 3 & 2 \end{matrix} \right] =\begin{bmatrix} b+4 & 2 \\ 3 & c-1 \end{bmatrix} $$
If $$ A\quad =\quad \begin{bmatrix} 0 & 2 \\ 5 & -2 \end{bmatrix},\quad B\quad =\quad \begin{bmatrix} 1 & -1 \\ 3 & 2 \end{bmatrix}\quad $$ and $$ I $$ is unit matrix of order $$ 2 \times 2 $$ Find :
$$ AB $$
If possible, using elementary row transformations, find the inverse of the following matrix.
$$\begin{bmatrix} 2 & 0 & -1 \\ 5 & 1 & 0 \\ 0 & 1 & 3 \end{bmatrix}$$
If $$ A = \begin{bmatrix} x & 0 & 0 \\ 0 & y & 0 \\ 0 & 0 & z \end{bmatrix} $$ is a non singular matrix, then find $$A^{-1} $$ by using elementary row tranformation. Hence, find the inverse of $$ \begin{bmatrix} 2 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & -1 \end{bmatrix} $$
If $$ A\quad =\quad \begin{bmatrix} 0 & 2 \\ 5 & -2 \end{bmatrix},\quad B\quad =\quad \begin{bmatrix} 1 & -1 \\ 3 & 2 \end{bmatrix}\quad $$ and $$ I $$ is unit matrix of order $$ 2 \times 2 $$ Find :
$$ IB $$
Given $$ A\quad =\quad \left[ \begin{matrix} 0 & 4 & 6 \\ 3 & 0 & -1 \end{matrix} \right] \quad and\quad B\quad \quad =\quad \left[ \begin{matrix} 0 & 1 \\ -1 & 2 \\ -5 & -6 \end{matrix} \right] $$ is the following possible :
$$ A^2 $$
If $$ A\quad =\quad \begin{bmatrix} 0 & 2 \\ 5 & -2 \end{bmatrix},\quad B\quad =\quad \begin{bmatrix} 1 & -1 \\ 3 & 2 \end{bmatrix}\quad $$ and $$ I $$ is unit matrix of order $$ 2 \times 2 $$ Find :
$$ AI $$
If $$ A\quad =\quad \begin{bmatrix} 0 & 2 \\ 5 & -2 \end{bmatrix},\quad B\quad =\quad \begin{bmatrix} 1 & -1 \\ 3 & 2 \end{bmatrix}\quad $$ and $$ I $$ is unit matrix of order $$ 2 \times 2 $$ Find :
$$ BA $$
Find the inverse of the following matrix by elementary row of transformations if they exist.
$$ A = \begin{bmatrix} 1 & 2 & -2 \\ 0 & -2 & 1 \\ -1 & 3 & 0 \end{bmatrix} $$
If $$ A\quad =\quad \begin{bmatrix} 0 & 2 \\ 5 & -2 \end{bmatrix},\quad B\quad =\quad \begin{bmatrix} 1 & -1 \\ 3 & 2 \end{bmatrix}\quad $$ and $$ I $$ is unit matrix of order $$ 2 \times 2 $$ Find :
$$ A^2 $$
If $$ A\quad =\quad \begin{bmatrix} 0 & 2 \\ 5 & -2 \end{bmatrix},\quad B\quad =\quad \begin{bmatrix} 1 & -1 \\ 3 & 2 \end{bmatrix}\quad $$ and $$ I $$ is unit matrix of order $$ 2 \times 2 $$ Find :
$$ B^2 $$
Given $$ A\quad =\quad \left[ \begin{matrix} 0 & 4 & 6 \\ 3 & 0 & -1 \end{matrix} \right] \quad and\quad B\quad \quad =\quad \left[ \begin{matrix} 0 & 1 \\ -1 & 2 \\ -5 & -6 \end{matrix} \right] $$ is the following possible :
$$ BA $$
Given $$ A\quad =\quad \left[ \begin{matrix} 0 & 4 & 6 \\ 3 & 0 & -1 \end{matrix} \right] \quad and\quad B\quad \quad =\quad \left[ \begin{matrix} 0 & 1 \\ -1 & 2 \\ -5 & -6 \end{matrix} \right] $$ is the following possible :
$$ AB $$
Find the inverse of $$ A = \begin{bmatrix} 1 & 0 & 1 \\ 0 & 2 & 3 \\ 1 & 2 & 1 \end{bmatrix} $$ by using elementary column transformations.
Let $$ A=\begin{bmatrix} 2 & 4 \\ 3 & 2 \end{bmatrix},B=\begin{bmatrix} 1 & 3 \\ -2 & 5 \end{bmatrix},C=\begin{bmatrix} -2 & 5 \\ 3 & 4 \end{bmatrix} $$
Find the following:
$$ BA $$
Compute the indicated products
$$ \left[ \begin{matrix} 1 & -2 \\ 2 & 3 \end{matrix} \right] \left[ \begin{matrix} 1 & 2 & 3 \\ 2 & 3 & 1 \end{matrix} \right] $$
Compute the indicated products
$$ \left[ \begin{matrix} 2 & 1 \\ 3 & 2 \\ -1 & 1 \end{matrix} \right] \left[ \begin{matrix} 1 & 0 & 1 \\ -1 & 2 & 1 \end{matrix} \right] $$
Compute the following
$$ \begin{bmatrix} { a }^{ 2 }+{ b }^{ 2 } & { b }^{ 2 }+{ c }^{ 2 } \\ { a }^{ 2 }+{ c }^{ 2 } & { a }^{ 2 }+{ b }^{ 2 } \end{bmatrix}+\begin{bmatrix} 2ab & 2bc \\ -2ac & -2ab \end{bmatrix} $$
Let $$ A=\begin{bmatrix} 2 & 4 \\ 3 & 2 \end{bmatrix},B=\begin{bmatrix} 1 & 3 \\ -2 & 5 \end{bmatrix},C=\begin{bmatrix} -2 & 5 \\ 3 & 4 \end{bmatrix} $$
Find the following:
$$ AB $$
Compute the indicated products
$$ \left[ \begin{matrix} 2 & 3 & 4 \\ 3 & 4 & 5 \\ 4 & 5 & 6 \end{matrix} \right] \left[ \begin{matrix} 1 & -3 & 5 \\ 0 & 2 & 4 \\ 3 & 0 & 5 \end{matrix} \right] $$
Find the inverse of $$ \begin{bmatrix} 1 & 2 & 3 \\ 1 & 1 & 5 \\ 2 & 4 & 7 \end{bmatrix} $$ by using elementary row transformations.
Compute the following
$$ \left[ \begin{matrix} -1 & 4 & -6 \\ 8 & 5 & 16 \\ 2 & 8 & 5 \end{matrix} \right] +\left[ \begin{matrix} 12 & 7 & 6 \\ 8 & 0 & 5 \\ 3 & 2 & 4 \end{matrix} \right] $$
Compute the following
$$ \begin{bmatrix} { cos }^{ 2 }x & { sin }^{ 2 }x \\ { sin }^{ 2 }x & { cos }^{ 2 }x \end{bmatrix}+\begin{bmatrix} { sin }^{ 2 }x & { cos }^{ 2 }x \\ { cos }^{ 2 }x & { sin }^{ 2 }x \end{bmatrix} $$
If $$ x\left[ \begin{matrix} 2 \\ 3 \end{matrix} \right] +y\left[ \begin{matrix} -1 \\ 1 \end{matrix} \right] =\left[ \begin{matrix} 10 \\ 5 \end{matrix} \right] $$
Using elementary transformations , find the inverse of each of the matrices,
$$ \begin{bmatrix} 1 & 3 \\ 2 & 7 \end{bmatrix} $$
Simplify
$$ cos \theta \begin{bmatrix} cos\theta & sin\theta \\ -sin\theta & cos \end{bmatrix}+sin\theta \begin{bmatrix} sin\theta & -cos\theta \\ cos\theta & sin\theta \end{bmatrix} $$
Solve the equation for $$ x,y,z $$ and $$ t $$, if
$$ 2\begin{bmatrix} x & z \\ y & t \end{bmatrix}+3\begin{bmatrix} 1 & -1 \\ 0 & 2 \end{bmatrix}=3\begin{bmatrix} 3 & 5 \\ 4 & 6 \end{bmatrix}$$
Compute the indicated products
$$ \left[ \begin{matrix} 3 & -1 & 3 \\ -1 & 0 & 2 \end{matrix} \right] \left[ \begin{matrix} 2 & -3 \\ 1 & 0 \\ 3 & 1 \end{matrix} \right] $$
Find $$ X $$ and $$ Y $$, if
$$ 2X+3Y=\begin{bmatrix} 2 & 3 \\ 4 & 0 \end{bmatrix}and\quad 3X+2Y\\ =\begin{bmatrix} 2 & -2 \\ -1 & 5 \end{bmatrix} $$
Given
$$ 3\begin{bmatrix} x & y \\ z & w \end{bmatrix}=\begin{bmatrix} x & 6 \\ -1 & 2w \end{bmatrix}+\begin{bmatrix} 4 & x+y \\ z+w & 3 \end{bmatrix} $$
Find the value of $$ x,y,z $$ and $$ w $$
Using elementary transformations, find the inverse of each of the matrices, if it exists.$$ \begin{bmatrix} 1 & -1 \\ 2 & 3 \end{bmatrix}$$
Find $$ X $$ and $$ Y $$, if $$ 2 \begin{bmatrix} 1 & 3 \\ 0 & x \end{bmatrix}+\begin{bmatrix} y & 0 \\ 1 & 2 \end{bmatrix}=\begin{bmatrix} 5 & 6 \\ 1 & 8 \end{bmatrix} $$
Find $$ X $$, if $$ Y=\begin{bmatrix} 3 & 2 \\ 1 & 4 \end{bmatrix}and\quad 2X+Y=\begin{bmatrix} 1 & 0 \\ -3 & 2 \end{bmatrix} $$
Using elementary transformations, find the inverse of the matrix,
$$ \left[ \begin{matrix} 2 & -3 & 3 \\ 2 & 2 & 3 \\ 3 & -2 & 2 \end{matrix} \right] $$
Using elementary transformations , find the inverse of each of the matrices,
$$ \begin{bmatrix} 6 & -3 \\ -2 & 1 \end{bmatrix} $$
If $$A=\begin{bmatrix} 1 & 2 \\ -3 & 4 \end{bmatrix}$$ and $$B=\begin{bmatrix} 5 \\ -1 \end{bmatrix}$$, then find $$AB$$
Using elementary transformations , find the inverse of each of the matrices,
$$ \begin{bmatrix} 2 & -6 \\ 1 & -2 \end{bmatrix} $$
If $$A=\begin{bmatrix} 2 & 3 & -4 \\ -1 & 2 & 3 \end{bmatrix}$$ and $$B=\begin{bmatrix} -1 & 2 \\ 3 & 4 \\ -5 & -6 \end{bmatrix}$$ then find $$A+B^T$$.
Using elementary transformations, find the inverse of the matrix
$$ \left[ \begin{matrix} 2 & 0 & -1 \\ 5 & 1 & 0 \\ 0 & 1 & 3 \end{matrix} \right] $$
Using elementary transformations , find the inverse of each of the matrices,
$$ \begin{bmatrix} 3 & -1 \\ -4 & 2 \end{bmatrix} $$
Using elementary transformations , find the inverse of each of the matrices,
$$ \begin{bmatrix} 4 & 5 \\ 3 & 4 \end{bmatrix} $$
$$A=\begin{bmatrix} 2 & -3 & 5 \\ 3 & 2 & -4 \\ 1 & 1 & -2 \end{bmatrix}$$ find $${A}^{-1}$$ using $${A}^{-1}$$ solve
$$2x-3y+5z=11$$
$$3x+2y-4z=-5$$
$$x+y-2z=-3$$
Using elementary transformations , find the inverse of each of the matrices,
$$ \left[ \begin{matrix} 1 & 3 & -2 \\ -3 & 0 & -5 \\ 2 & 5 & 0 \end{matrix} \right] $$
If $$\begin{bmatrix} 1 & x & 1 \end{bmatrix}\begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 3 & 2 & 5 \end{bmatrix}\begin{bmatrix} 1 \\ 2 \\ 3 \end{bmatrix}=0$$, then find $$x$$.
Find the inverse of the following matrix using elementary operations.
$$A = \begin{bmatrix} 1 & 2 & -2 \\ -1 & 3 & 0 \\ 0 & -2 & 1 \end{bmatrix}$$
If $$A$$ is a square matrix such that $$A^{2} = A$$, then write the value of $$7A (I + A)^{3}$$, where $$I$$ is an identity matrix
If $$A= \begin{bmatrix} 2 & 0 & -1\\ 5 & 1 & 0\\ 0 & 1 & 3 \end{bmatrix}$$, then find $$A^{-1}$$ using elementary row operations.
In a development plan of a city, a contractor has taken a contract to construct certain houses for which he needs building materials like stones, sand, etc. There are three firms $$A, B, C$$ that can supply him these materials. At one time these firms $$A, B, C$$ supplied him $$40, 35,$$ and $$35$$ truckloads of stones and $$10,5$$ and $$8$$ truckloads of sand and sand respectively. If the cost of one truckload of stone and sand are $$Rs.\space 1,200$$ and $$500$$ respectively, then find the total amount paid by the contractor to each of these firms $$A, B, C$$ separately be a, b, c respectively, find a+b-2c in Rs
If $$A=\begin{bmatrix} 1 & 2 & 2\\ 2 & 1 & 2\\ 2 & 2 & 1 \end{bmatrix}$$, then show that $$A^2- 4A - 5I = 0$$, and hence find $$A^{-1}$$.
If $$\begin{bmatrix}9&-1&4\\-2&1&3\end{bmatrix}=A+\begin{bmatrix}1&2&-1\\0&4&9\end{bmatrix}$$, then find the matrix A.
If matrix $$A = \begin{bmatrix}2&-2\\-2&2\end{bmatrix}$$ and $$A^2 = pA$$, then write the value of $$p$$.
If $$A = \begin{bmatrix} 3& 2\\ -1 & 4\end{bmatrix}; B = \begin{bmatrix} -2& 5\\ 6 & 7\end{bmatrix}$$ and $$C = \begin{bmatrix} 1& 1\\ -5 & 3\end{bmatrix}$$ verify that $$A(B + C) = AB + AC.$$
If matrix $$A = \begin{bmatrix}3&-3 \\-3&3\end{bmatrix}$$ and $$A^2 = \lambda A$$, then write the value of $$\lambda$$.
If $$\displaystyle A=\left( \begin{matrix} 1 \\ 0 \\ 2 \end{matrix}\begin{matrix} 0 \\ 2 \\ 0 \end{matrix}\begin{matrix} 2 \\ 1 \\ 3 \end{matrix} \right) $$ and $$\displaystyle { A }^{ 3 }-6{ A }^{ 2 }+7A+k{ I }_{ 3 }=O$$ find $$k.$$
If $$A = \begin{bmatrix}3 &1 \\ 7 & 5\end{bmatrix}$$, find the values of $$x$$ and $$y$$ such that $$A^{2} + x I_{2} = yA$$
Find the value of $$x + y$$ from the following equation:
$$2 \bigl(\begin{smallmatrix} 1& 3\\ 0 & x\end{smallmatrix}\bigr) + \bigl(\begin{smallmatrix}y & 0\\ 1 & 2\end{smallmatrix}\bigr) = \bigl(\begin{smallmatrix}5 & 6\\ 1 & 8\end{smallmatrix}\bigr)$$
If $$A=\begin{bmatrix} 3 & x \\ 0 & 1 \end{bmatrix}$$ and $$B=\begin{bmatrix} 9 & 16 \\ 0 & -y \end{bmatrix}$$, find $$x$$ and $$y$$ when $${ A }^{ 2 }=B$$.
Solve for $$x$$ and $$y$$, if $$ \begin{pmatrix} { x }^{ 2 } \\ { y }^{ 2 } \end{pmatrix}+3\begin{pmatrix} 2x \\ -y \end{pmatrix}=\begin{pmatrix} -9 \\ 4 \end{pmatrix}$$
An electronic company records each type of entertainment device sold at three of their branch stores so that they can monitor their purchases of supplies. The sales in two weeks are shown in the following spreadsheets.
| T.V. | DVD | Videogames | CD Players | ||
| Week I | Store I | 30 | 15 | 12 | 10 |
| Store II | 40 | 20 | 15 | 15 | |
| Store III | 25 | 18 | 10 | 12 | |
| Week II | Store I | 25 | 12 | 8 | 6 |
| Store II | 32 | 10 | 10 | 12 | |
| Store III | 22 | 15 | 8 | 10 |
Find a and b if $$a \bigl(\begin{smallmatrix}2 \\ 3 \end{smallmatrix}\bigr)+ b \bigl(\begin{smallmatrix} -1 \\ 1 \end{smallmatrix}\bigr) = \bigl(\begin{smallmatrix}10 \\ 5 \end{smallmatrix}\bigr)$$.
$$A=\left( \begin{matrix} 3 & 2 \\ -1 & 4 \end{matrix} \right) ,B=\left( \begin{matrix} -2 & 5 \\ 6 & 7 \end{matrix} \right) $$ and $$C=\left( \begin{matrix} 1 & 1 \\ -5 & 3 \end{matrix} \right) $$, then verify that $$A\left( B+C \right) =AB+AC$$
Solve for x and y if $$\bigl(\begin{smallmatrix} x^2 \\ y^2 \end{smallmatrix}\bigr) + 3 \bigl(\begin{smallmatrix}2x \\ -y \end{smallmatrix}\bigr) = \bigl(\begin{smallmatrix} -9\\ 4 \end{smallmatrix}\bigr)$$.
If $$A = \bigl(\begin{smallmatrix}8 & 3 & 2\\ 5 & 9 & 1\end{smallmatrix}\bigr)$$ and $$B = \bigl(\begin{smallmatrix}1 & -1\\ 3 & 0 \end{smallmatrix}\bigr)$$. Find A + B if it exists.
The table shows a five-day forecast indicating high (H) and Low(L) temperatures in Fahrenheit. Organise the temperatures in a matrix where the first and second rows represent the High and Low temperatures respectively and identify which day will be the warmest?
$$=\left[ \begin{matrix} 88 & 90 & \begin{matrix} 86 & 84 \end{matrix} \\ 54 & 56 & \begin{matrix} 53 & 52 \end{matrix} \end{matrix}\begin{matrix} 85 \\ 52 \end{matrix} \right] $$Thursday is the warmest day.
Hence, the answer is Thursday.
Find X and Y if $$2X + 3Y = \bigl(\begin{smallmatrix}2 & 3\\4 & 0\end{smallmatrix}\bigr)$$ and $$3X + 2Y = \bigl(\begin{smallmatrix} 2& -2\\ -1 & 5\end{smallmatrix}\bigr)$$.
If $$A = \bigl(\begin{smallmatrix} 4 &-2 \\ 5 & -9\end{smallmatrix}\bigr)$$ and $$B = \bigl(\begin{smallmatrix} 8& 2\\ -1 & -3\end{smallmatrix}\bigr)$$ find 6A - 3B.
If $$A = \begin{pmatrix} 1& -1\\ 2 & 3\end{pmatrix}$$, then show that $$A^{2} - 4A + 5I_{2} = 0$$
If $$A = \bigl(\begin{smallmatrix} 5& 3 \\ 7 & 5\end{smallmatrix}\bigr), X = \bigl(\begin{smallmatrix} x \\ y\end{smallmatrix}\bigr)$$ and $$C = \bigl(\begin{smallmatrix} -5 \\ -11\end{smallmatrix}\bigr)$$ and if $$AX = C$$, then find the values of x and y.
Find the product of the matrices, if exists. $$\bigl(\begin{smallmatrix} 2& -1\end{smallmatrix}\bigr) \bigl(\begin{smallmatrix} 5 \\ 4 \end{smallmatrix}\bigr)$$
Solve $$\bigl(\begin{smallmatrix}3 & 2\\ 4 & 5\end{smallmatrix}\bigr) \bigl(\begin{smallmatrix}x \\ y \end{smallmatrix}\bigr) = \bigl(\begin{smallmatrix} 8 \\ 13 \end{smallmatrix}\bigr)$$
By using elementary transformation find the inverse of the matrix $$A=\begin{bmatrix}1&2\\2&1\end{bmatrix}$$.
A fruit vendor sells fruits from his shop. Selling prices of Apple, Mango and Orange are Rs. 20, Rs. 10 and Rs. 5 each respectively. The sales in three days are given below
| Day | Apples | Mangoes | Oranges |
| 1 | 50 | 60 | 30 |
| 2 | 40 | 70 | 20 |
| 3 | 60 | 40 | 10 |
Find the values of x and y if $$ \bigl(\begin{smallmatrix} 1& 2 \\ 3 & 3\end{smallmatrix}\bigr) \bigl(\begin{smallmatrix} x & 0\\ 0 & y\end{smallmatrix}\bigr) = \bigl(\begin{smallmatrix}x & 0\\ 9 & 0\end{smallmatrix}\bigr)$$
Given that: $$A=\begin{pmatrix}1 & -1 & 0\\ 2 & 3 & 4\\ 0 & 1 & 2\end{pmatrix}$$ and $$B=\begin{pmatrix}2 & 2 & -4\\ -4 & 2 & -4\\ 2 & -1 & 5\end{pmatrix}$$, find AB.
Using this result, solve the following system of equation:
$$x-y=3, 2x+3y+4z=17$$ and $$y+2x=7$$
Let $$A=\begin{bmatrix} \alpha & \beta \\ \gamma & \delta \end{bmatrix}$$ such that $$A^3=0$$ , then sum of all the elements of $$A^2$$ is........
If $$A=\begin{bmatrix}1&2&3\\3&-2&1\\ 4&2&1\end{bmatrix},$$ show that $$ A^3-23A-40I=0.$$
If $$A=\begin{bmatrix}2&-3&5\\3&2&-4\\1&1&-2\end{bmatrix}$$, find $$A^{-1}$$. Use it to solve the system of equations
$$2x-3y+5z=11$$
$$3x+2y-4z=-5$$
$$x+y-2z=-3$$
If $$A=\begin{bmatrix}3&1\\-1&2\end{bmatrix},$$ show that $$ A^2-5A+7I=0.$$ Use the result to find $$A^4$$.
Solve the following matrix equation for $$x$$ :$$[x-5-1] \begin{bmatrix} 1&0&2 \\0&2&1\\ 2&0&3 \end{bmatrix}\begin{bmatrix} x \\4\\1 \end{bmatrix}=0$$
Find the inverse of the matrix, $$A = \begin{bmatrix}1 & 2 & -2\\ -1 & 3 & 0\\ 0 & -2 & 1\end{bmatrix}$$ using elementary row transformations.
Find the inverse of the matrix $$A = \begin{bmatrix} 1 & 2 \\ 1 & 3 \end{bmatrix}$$ using elementry transformations.
If $$A$$ = $$ \begin{bmatrix}1 & 2 & 2 \\ 2 & 1 & 2 \\ 2 & 2 & 1 \end{bmatrix} $$ , then prove that $$ A^2 - 4A - 5I = 0 $$
Find the inverse of the matrix
$$\left[ {\begin{array}{*{20}{c}}1&0&0\\3&3&0\\5&2&1\end{array}} \right]$$
If $$\frac{ax}{y} + \frac{by}{x} +c = 0, \frac{by}{z} + \frac{cz}{y}+a =0, \frac{cz}{x} + \frac{ax}{z} +b =0, $$ then find the value of $$ax + by + cz$$.
If $$A = \left[ {\matrix{ 4 & 3 \cr 2 & 5 \cr
} } \right]$$, find $$x$$ and $$y$$ such that $${A^2} - xA + yI = 0$$
If $$F (x) = \left [\begin {array} \ \cos x & -\sin x & 0 \\ \sin x &\cos x & 0 \\ 0 & 0 & 1 \end {array}\right]$$, show that $$F(x) \ F(y) = F(x + y)$$
Let $$A = \left[ {\matrix{ 1 & 0 \cr 1 & 1 \cr
} } \right],$$ and $$I = \left[ {\matrix{ 1 & 0 \cr 0 & 1 \cr
} } \right]$$ then prove that $${A^n} = nA - (n - 1)I,n \ge 1.$$
Find $$x$$ if $$\begin{bmatrix}x&-5&-1\end{bmatrix}\begin{bmatrix}1&0&2\\0&2&1\\2&0&3\end{bmatrix}\begin{bmatrix}x\\4\\1\end{bmatrix} =0$$
To promote making of toilets for women, an organisation tried to generate awarness through (i) house calls (ii) letters, and (iii) announcements. The cost for each mode per attempt is given below:
(i) Rs. 50 (ii) Rs. 20 (iii) Rs. 40
The number of attempts made in three village X, Y and Z are given below:
(i) (ii) (iii)
X 400 300 100
Y 300 250 75
Z 500 400 150
Find the total cost incurred by the organisation for three villages separately, using matrics.
Prove the following $$\begin{bmatrix}1 &3 &2 & 0\\ 4 & 1 & 5 & 9\\ 3 &2 & 1 & 3\end{bmatrix}$$ $$\pm$$ $$\begin{bmatrix}1 &0 &5 & 8\\ 2 & 3& 5 & 8\\ 1 &-5 & 2 & 3\end{bmatrix}$$
= $$\begin{bmatrix}2 &3 &7 & 8\\ 6 & 4& 9& 14\\ 4 &-3 & 3 & 6\end{bmatrix}$$ for plus
=$$\begin{bmatrix}0 &3 & -3 & -8 \\ 4 & 2 & 1 & 4 \\ 0 & 7 & -1 & 0\end{bmatrix}$$ for minus
Find the inverse of the following matrices
$$A = \left( {\matrix{
2 & 3 & 3 \cr
1 & 2 & 2 \cr
1 & 1 & 1 \cr
} } \right)$$
For the matrix $$A=\left[ \begin{matrix} 4 & -4 & 5 \\ -2 & 3 & -3 \\ 3 & -3 & 4 \end{matrix} \right] $$ find $$A^{-2}$$.
Use product $$\begin{vmatrix} 1 & -1 & 2 \\ 0 & 2 & -3 \\ 3 & -2 & 4 \end{vmatrix} $$ $$\begin{bmatrix} -2 & 0 & 1 \\ 9 & 2 & -3 \\ 6 & 1 & -2 \end{bmatrix}$$ to solve the system of equation $$x-y+2z=1;2y-3z=1;3x-2y+4z=2.$$
Find the inverse of the matrix $$\left[\begin {array} \ 5 & 11 \\ 4 & 9 \end {array}\right]$$ by elementary transformations.
Find the inverse of the following matrices$$A = \left[ {\matrix{
3 & { - 1} & { - 2} \cr
2 & 0 & { - 1} \cr
3 & { - 5} & 0 \cr
} } \right]$$
Find the inverse of the following matrices $$A = \left( {\matrix{
2 & 1 & 3 \cr
5 & 3 & 1 \cr
3 & 2 & 3 \cr
} } \right)$$
Find the inverse of the following matrices$$A = \left( {\matrix{
2 & 0 & 1 \cr
1 & 2 & 3 \cr
3 & 1 & 1 \cr
} } \right)$$
$$\begin{bmatrix}1&-1&2\\ 0&2&-3\\ 3&-2&4\end{bmatrix}\begin{bmatrix}-2&0&1\\ 9&2&-3\\ 6&1&-2\end{bmatrix}$$
If \begin{bmatrix} 2 & 3 \\ 5 & 7 \end {bmatrix}\begin{bmatrix} 1 & -3 \\ -2 & 4 \end {bmatrix}=\begin{bmatrix} -4 & 6 \\ -9 & x \end{bmatrix} Write the value of x.
If $$A = \operatorname { diag } \left[ a _ { 1 } , a _ { 2 } , a _ { 3 } \right]$$ , then for any integer $$n \geq 1$$ show that $$A ^ { n } = \operatorname { diag } \left[ a _ { 1 } ^ { n } , a _ { 2 } ^ { n } , a _ { 3 } ^ { n } \right]$$ .
If for $$A X = B , B = \left[ \begin{array} { c } { 9 } \\ { 52 } \\ { 0 } \end{array} \right]$$ and $$A ^ { - 1 } = \left[ \begin{array} { c c c } { 3 } & { - 1 / 2 } & { - 1 / 2 } \\ { - 4 } & { 3 / 4 } & { 5 / 4 } \\ { 2 } & { - 1 / 4 } & { - 3 / 4 } \end{array} \right]$$ then $$x$$ is equal to
$$If\left[ \begin{matrix} 2 \\ 5 \end{matrix}\begin{matrix} 3 \\ 7 \end{matrix} \right] \left[ \begin{matrix} 1 \\ -2 \end{matrix}\begin{matrix} -3 \\ 4 \end{matrix} \right] =\left[ \begin{matrix} -4 \\ -9 \end{matrix}\begin{matrix} 6 \\ x \end{matrix} \right]$$, write the value of $$x$$.
If $$A=\begin{bmatrix} 1 & 1 \\ 2 & 2 \end{bmatrix}, B=\begin{bmatrix} 1 & 1 \\ 3 & 4 \end{bmatrix}$$ then find $$|AB|$$
$$If\left[ \begin{matrix} 1 \\ 3 \end{matrix}\begin{matrix} 2 \\ 4 \end{matrix} \right] \left[ \begin{matrix} 3 \\ 2 \end{matrix}\begin{matrix} 1 \\ 5 \end{matrix} \right] =\left[ \begin{matrix} 7 \\ k \end{matrix}\begin{matrix} 11 \\ 23 \end{matrix} \right]$$ then writ the value of $$k$$
If $$A = \left[ \begin{array} { c c c } { 1 } & { 2 } & { 1 } \\ { 3 } & { 0 } & { - 1 } \\ { 3 } & { 2 } & { 1 } \end{array} \right]$$ and $$A ^ { 3 } + x A ^ { 2 } + y { A } + z I = 0$$ then $$x+y+z=$$
If $$A=\begin{bmatrix} 2 & -1\\ -1 & 2\end{bmatrix}$$ and $$I$$ is the unit matrix of order $$2$$, then $$A^2$$ equals
$$A = \begin{bmatrix}2 & 0 & 3\\ -3 ^ -1 & 2\\ 1 & 1 & -1\end{bmatrix}, B = \begin{bmatrix}3 & 1\\ 2 & 0\\ 4 & -1\end{bmatrix}, C = \begin{bmatrix}2 & 1 & -4 & 3\\ 0 & 2 & 1 & -2\end{bmatrix}$$
Prove that $$(AB)C = A(BC)$$
$$(AB)C = A(BC)$$
For what values of $$x:[1\ \ 2\ \ 1]\left[ \begin{matrix} 1 & 2 & 0 \\ 2 & 0 & 1 \\ 1 & 0 & 2 \end{matrix} \right] \left[ \begin{matrix} 0 \\ 2 \\ x \end{matrix} \right] =0$$
If $$I\equiv \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}$$ and $$E\equiv \begin{bmatrix} 0 & 1 \\ 0 & 0 \end{bmatrix}$$ then show that $$\left( al+bE \right) ^{ 3 }={ a }^{ 3 }l+3{ a }^{ 2 }bE$$, where I is unit matrix of order $$2$$.
if$$ A=\left[ \begin{matrix} 9 & 0 & 0 \\ 0 & 10 & 0 \\ 0 & 0 & 8 \end{matrix} \right] $$, then $${ A }^{ -1 } =$$
$$if\quad A=\left[ \begin{matrix} 0 \\ 1 \end{matrix}\begin{matrix} 1 \\ 0 \end{matrix} \right] then\quad { A }^{ 1 }$$
$$\begin{vmatrix}{x}^{2}+1 & x+2 & 2 \\ 2{x}^{2}+1 & x-1 & 1 \\3{x}^{2}+1 & 4x-1 & 1 \end{vmatrix}=A{x}^{3}+B{x}^{2}+Cx+D$$ then the value of $$C$$ is
Let $$A = \begin{bmatrix} x + y & y \\ 2x & x - y \end{bmatrix}, B = \begin{bmatrix} 2 \\ -1 \end{bmatrix}$$ and $$C = \begin{bmatrix} 3 \\ 2 \end{bmatrix}.$$ If $$AB = C$$, then find $$x$$ and $$y$$
Find the inverse of the following matrix by using elementary row transformations :
$$\begin{bmatrix} 2 & -1 & 4 \\ 4 & 0 & 2 \\ 3 & -2 & 7 \end{bmatrix}$$
Find the inverse of the following matrix by using elementary row transformation:
$$\begin{bmatrix} 2 & 3 & 1 \\ 2 & 4 & 1 \\ 3 & 7 & 2 \end{bmatrix}$$
Find the inverse of $$\left[ \begin{matrix} 2 & 1 & 3 \\ 5 & 3 & 1 \\ 3 & 2 & 3 \end{matrix} \right] $$ using elementary column transformation.
Find the inverse of the following matrix by using elementary row transformations :
$$\begin{bmatrix} 1 & 2 & 3 \\ 2 & 5 & 7 \\ -2 & -4 & -5 \end{bmatrix}$$
Find the inverse of the following matrix by using elementary row transformations :
$$\begin{bmatrix} 1 & 3 & -2 \\ -3 & 0 & 1 \\ 2 & 1 & 0 \end{bmatrix}$$
Find the inverse of the matrix $$\begin{pmatrix} 1 & 0 & 1 \\ 0 & 2 & 3 \\ 1 & 2 & 1 \end{pmatrix}$$ by using elementary column transformation.
If for $$A=\begin{bmatrix} 5 & 8 & 1\\ 0 & 2 & 1\\ 4 & 3 & -1\end{bmatrix}, B=\begin{bmatrix} 2 \\ -1 \\ 3\end{bmatrix}; AX=B$$ then find out X.
If possible, find the value of $$BA$$ and $$AB$$, where $$A=\begin{bmatrix} 2 & 1 & 2 \\ 1 & 2 & 4 \end{bmatrix}\quad B=\begin{bmatrix} 4 & 1 \\ 2 & 3 \\ 1 & 2 \end{bmatrix}\quad $$
Find $$A$$, if $$\begin{bmatrix} 4 \\ 1 \\ 3 \end{bmatrix}A=\begin{bmatrix} -4 & 8 & 4 \\ -1 & 2 & 1 \\ -3 & 6 & 3 \end{bmatrix}$$
Compute $$AB$$ and $$BA$$, whichever exists when
$$A=\begin{bmatrix} 1 & 2 & 3 & 4 \end{bmatrix}$$ and $$B=\begin{bmatrix} 1 \\ 2 \\ 3 \\ 4 \end{bmatrix}$$
Compute $$AB$$ and $$BA$$, whichever exists when
$$A=\begin{bmatrix} 2 & 1 \\ 3 & 2 \\ -1 & 1 \end{bmatrix}$$ and $$B=\begin{bmatrix} 1 & 0 & 1 \\ -1 & 2 & 1 \end{bmatrix}$$
Compute $$AB$$ and $$BA$$, whichever exists when
$$A=\begin{bmatrix} 0 & 1 & -5 \\ 2 & 4 & 0 \end{bmatrix}$$ and $$B=\begin{bmatrix} 1 & 3 \\ -1 & 0 \\ 0 & 5 \end{bmatrix}$$
Find matrices $$A$$ and $$B$$, if
$$A+B=\begin{bmatrix} 1 & 0 & 2 \\ 5 & 4 & -6 \\ 7 & 3 & 8 \end{bmatrix}$$ and $$A-B=\begin{bmatrix} -5 & -4 & 8 \\ 11 & 2 & 0 \\ -1 & 7 & 4 \end{bmatrix}$$.
Show by an example that for $$A \ne 0,\ B \ne 0,\ AB=0$$
If $$A=\begin{bmatrix} 3 & 5 \\ -2 & 0 \\ 6 & -1 \end{bmatrix}, B=\begin{bmatrix} -1 & -3 \\ 4 & 2 \\ -2 & 3 \end{bmatrix}$$ and $$C=\begin{bmatrix} 0 & 2 \\ 3 & -4 \\ 1 & 6 \end{bmatrix}$$,
verify that $$(A+B)+C=A+(B+C)$$.
If $$A=diag\ \begin{bmatrix} 2 & -5 & 9 \end{bmatrix}, B=diag\ \begin{bmatrix} -3 & 7 & 14 \end{bmatrix}$$ and $$C=diag\ \begin{bmatrix} 4 & -6 & 3 \end{bmatrix}$$, find:
$$A+2B$$
Calculate :
$$ \begin{pmatrix} 3 & 7 \\ -1 & 4 \end{pmatrix} \begin{pmatrix} -2 & 1 \\ 4 & 2 \end{pmatrix} $$
If $$\begin{bmatrix} 2 & 1 & 3 \end{bmatrix}\begin{bmatrix} -1 & 0 & -1 \\ -1 & 1 & 0 \\ 0 & 1 & 1 \end{bmatrix}\begin{bmatrix} 1 \\ 0 \\ -1 \end{bmatrix}=A$$, then find the value of $$A$$
Show that if $$A$$ and $$B$$ are square matrices such that $$AB=BA$$.then $$(A+B)^2=A^2+2AB+B^2$$
Class 12 Commerce Maths Extra Questions
- Application Of Derivatives Extra Questions
- Application Of Integrals Extra Questions
- Continuity And Differentiability Extra Questions
- Determinants Extra Questions
- Differential Equations Extra Questions
- Integrals Extra Questions
- Inverse Trigonometric Functions Extra Questions
- Linear Programming Extra Questions
- Matrices Extra Questions
- Probability Extra Questions
- Relations And Functions Extra Questions
- Three Dimensional Geometry Extra Questions
- Vector Algebra Extra Questions