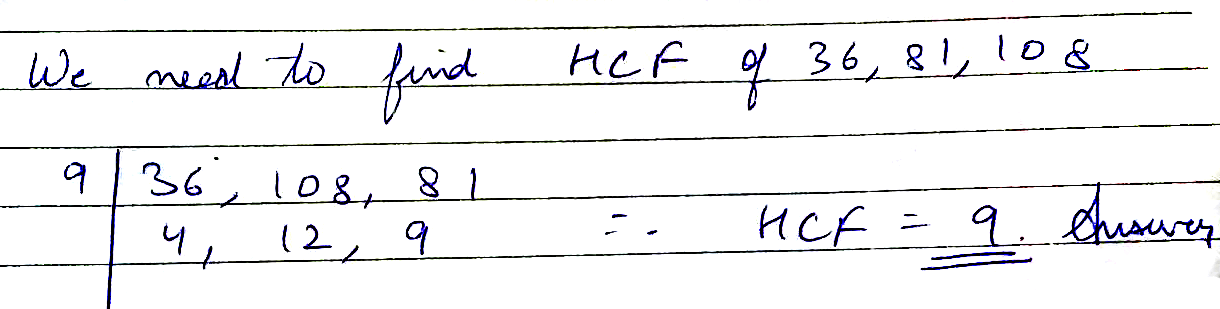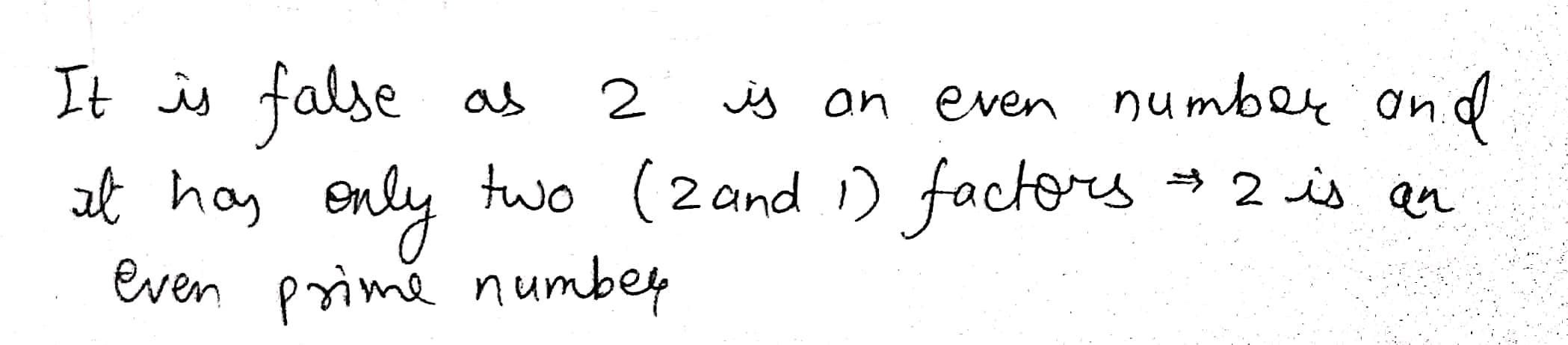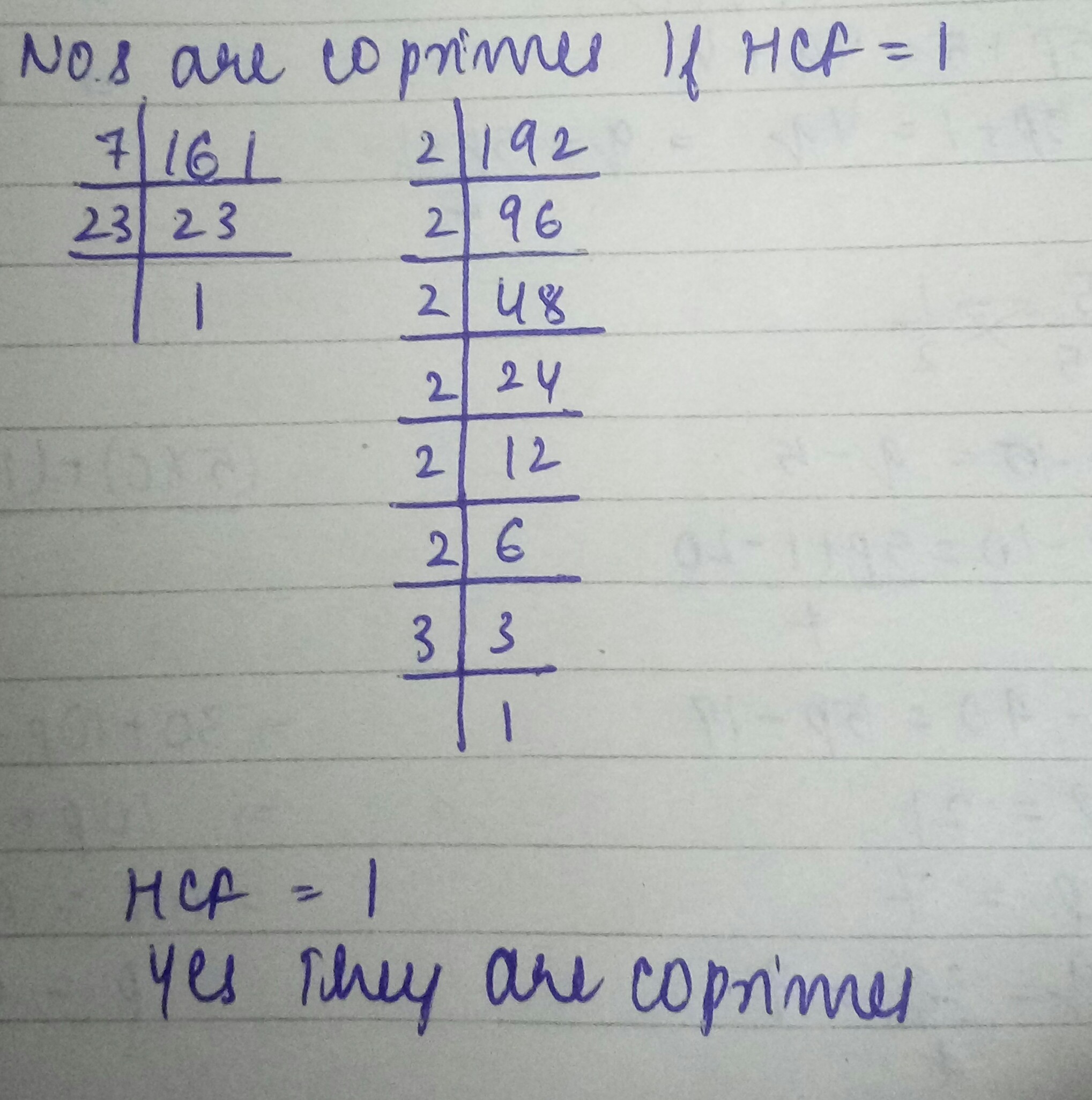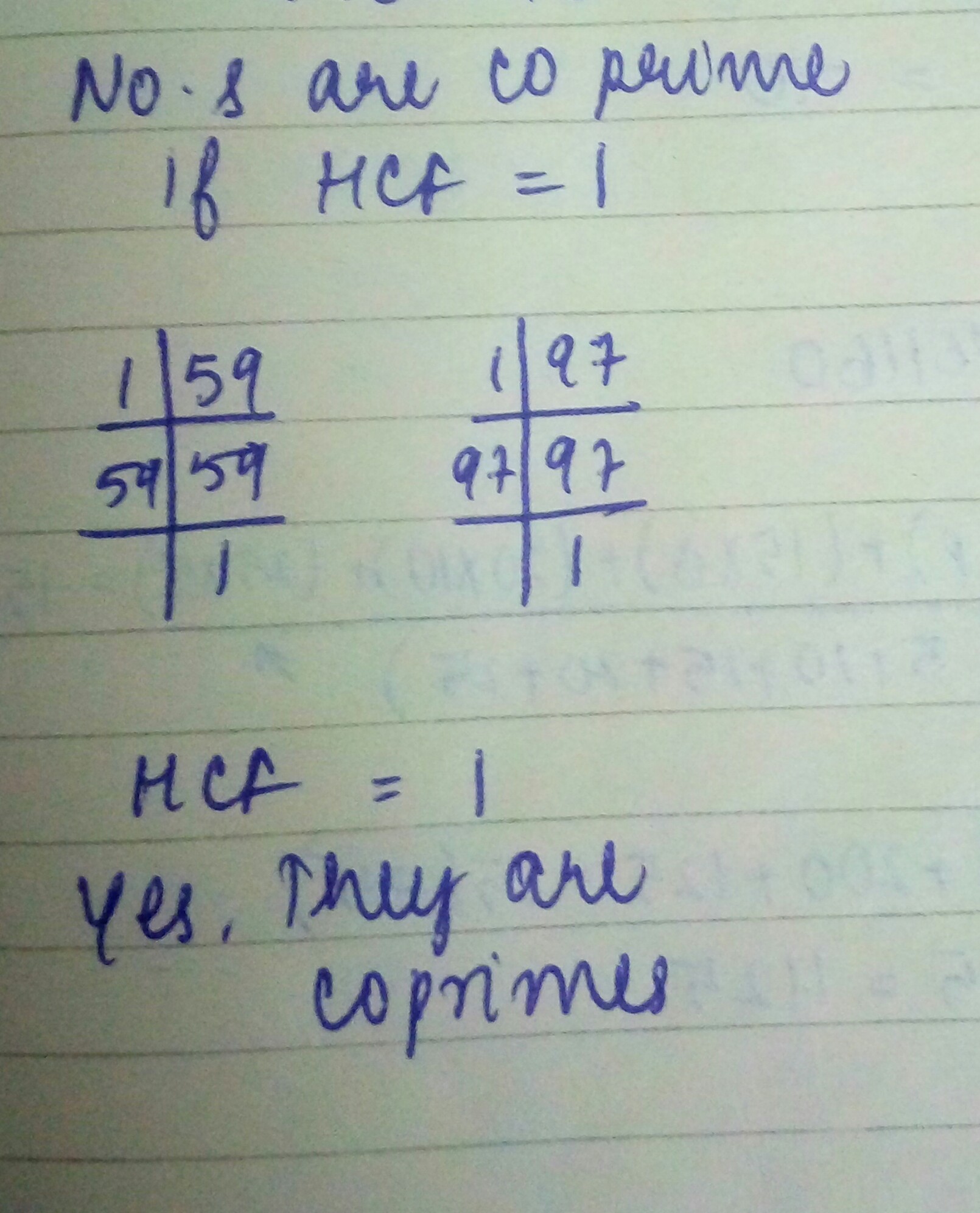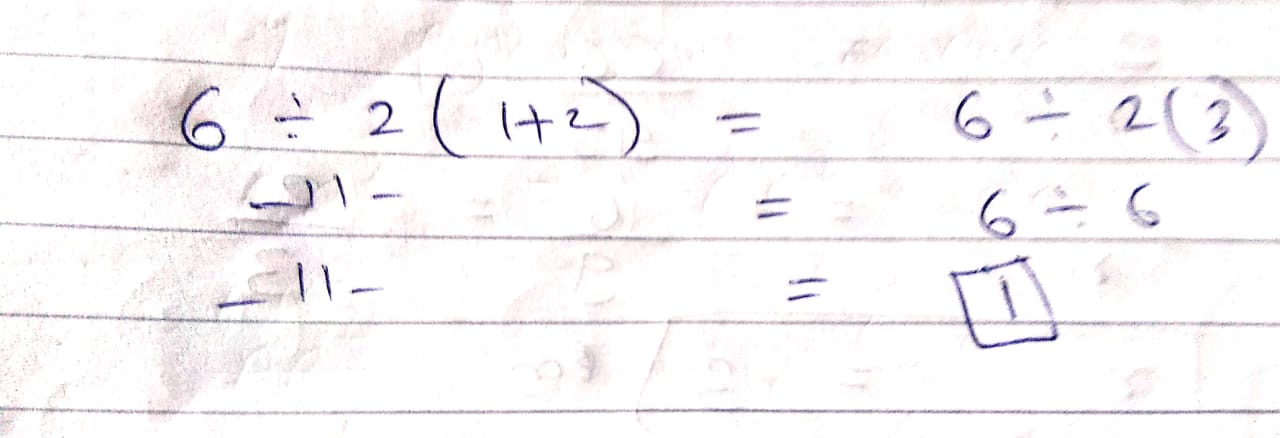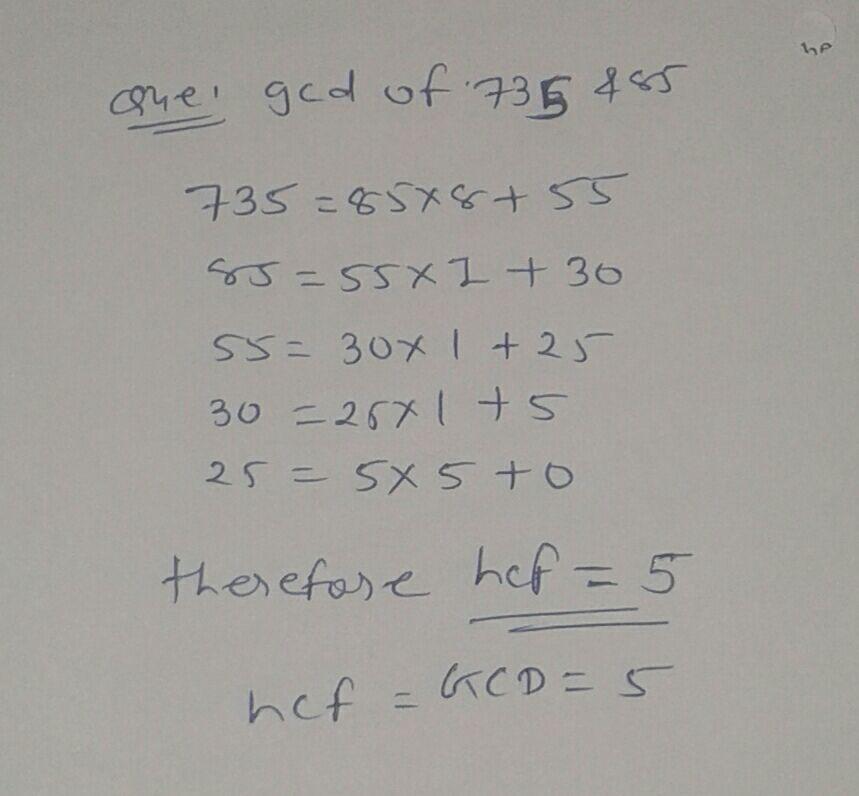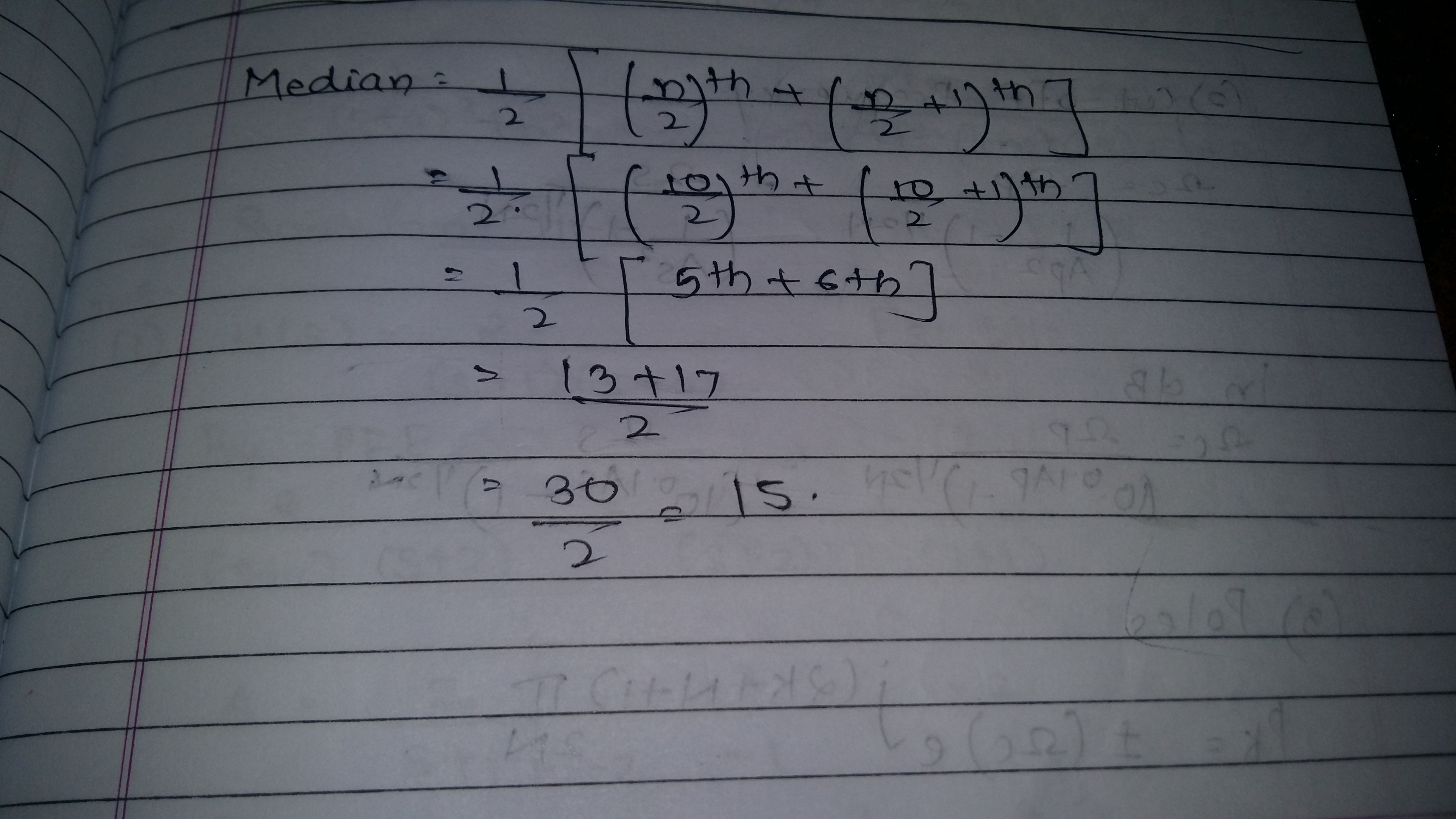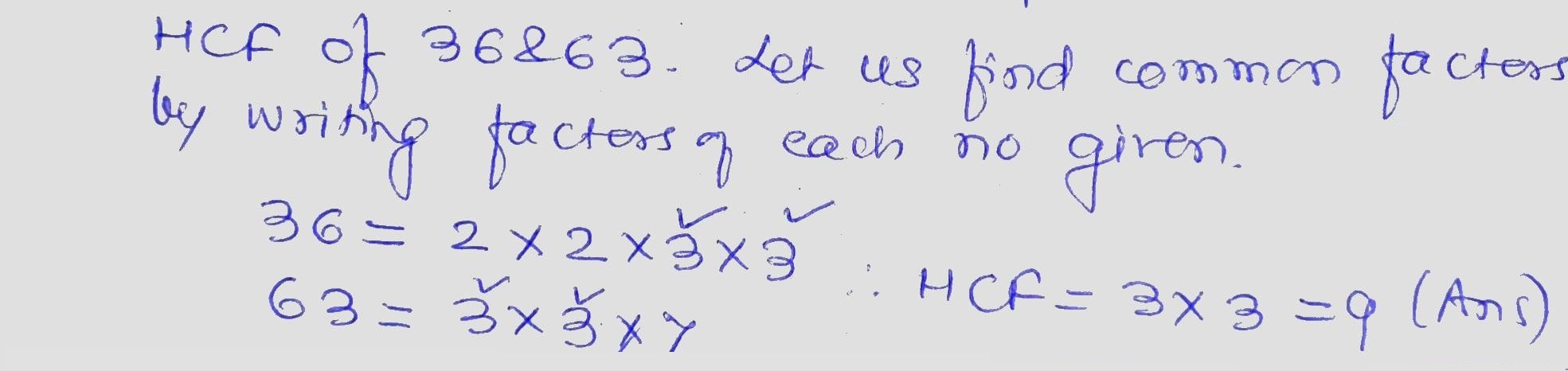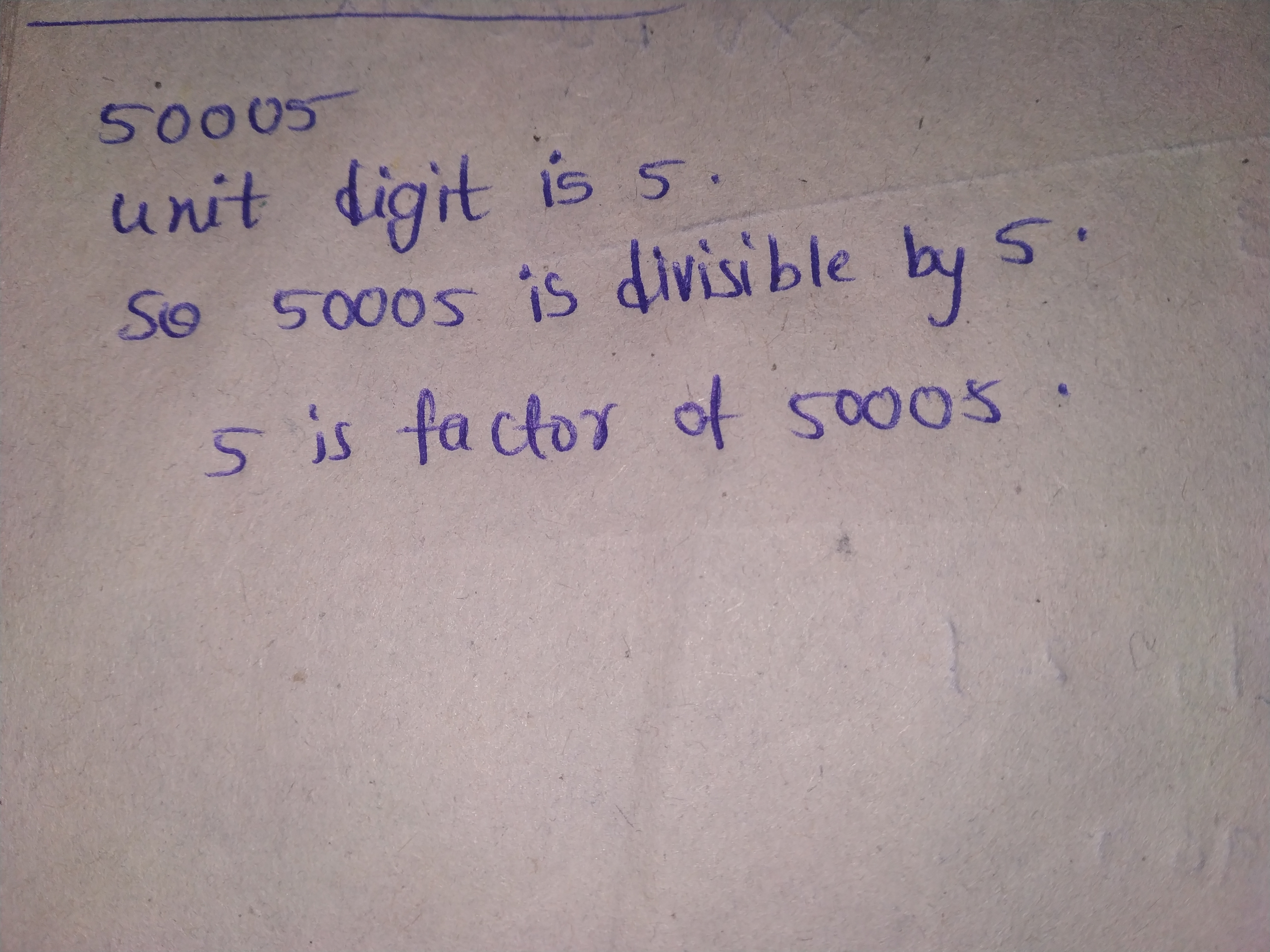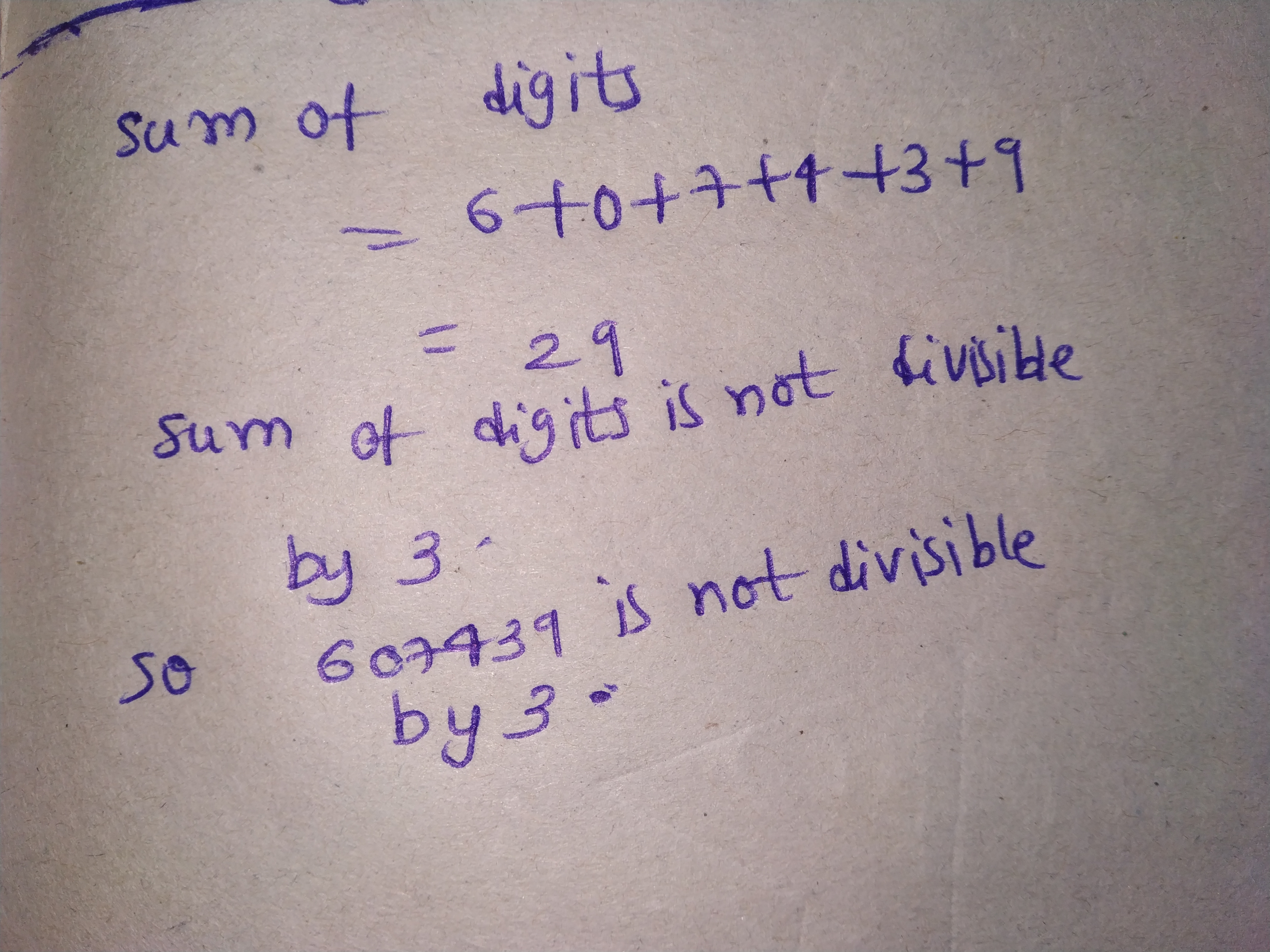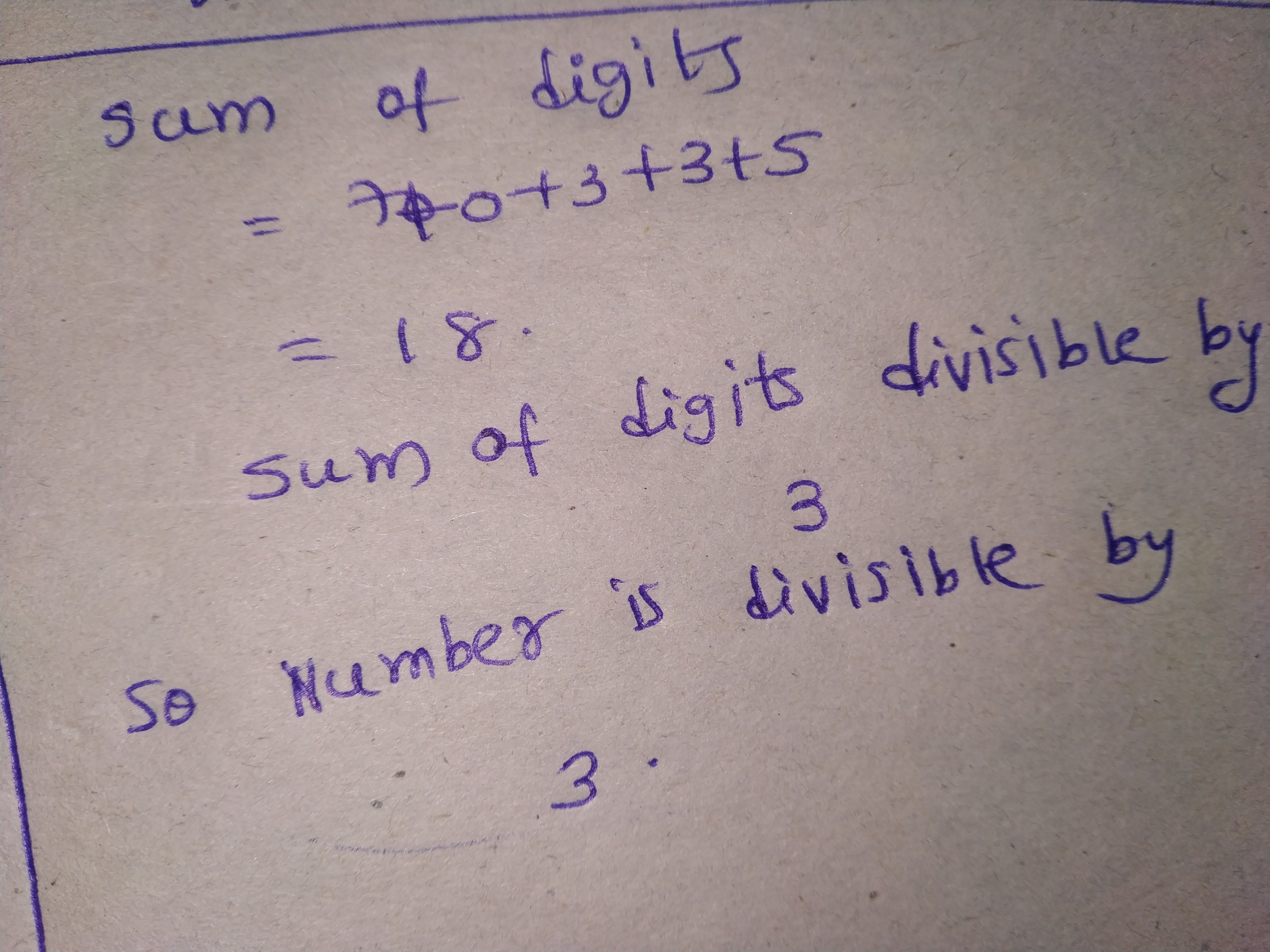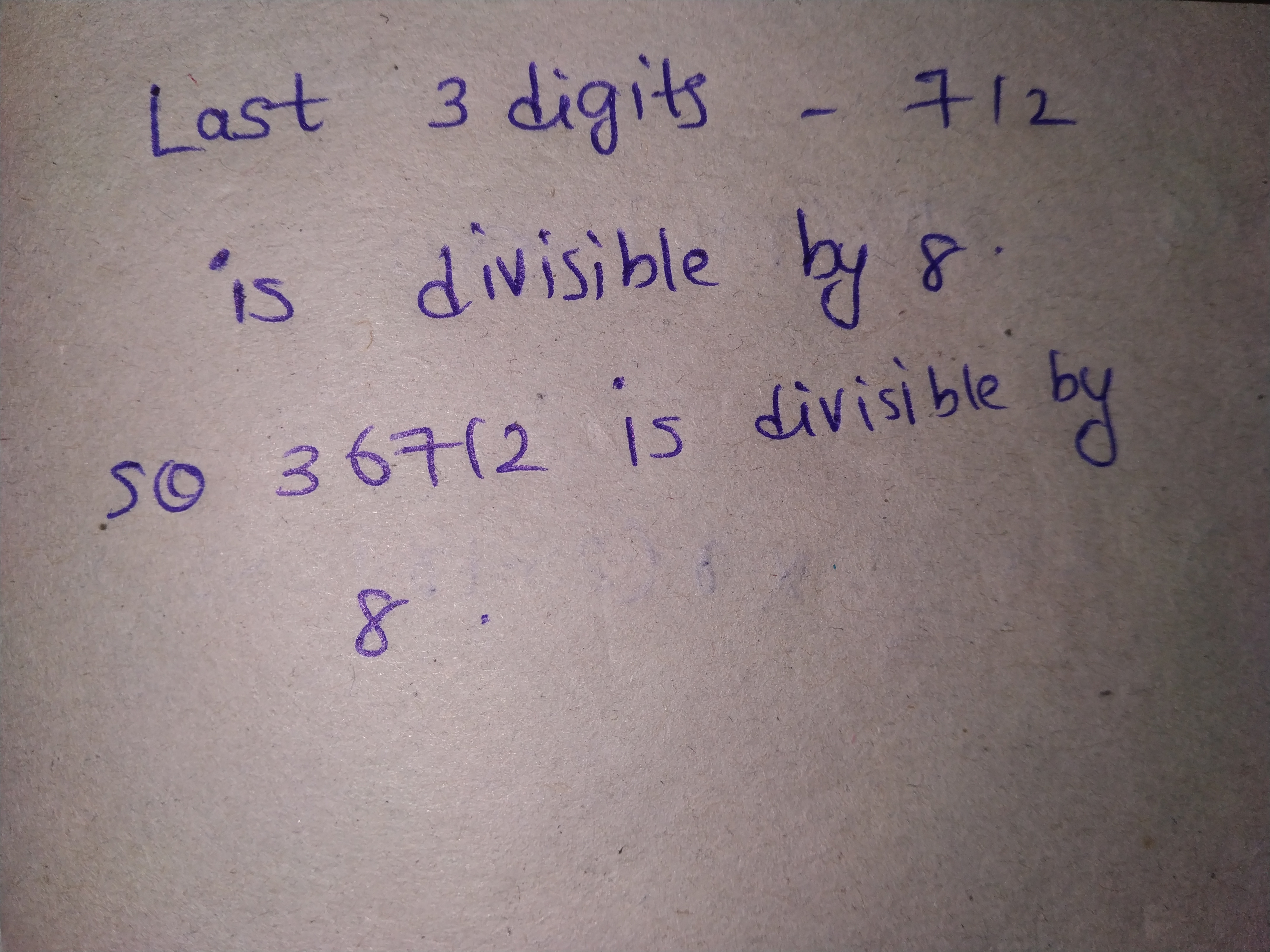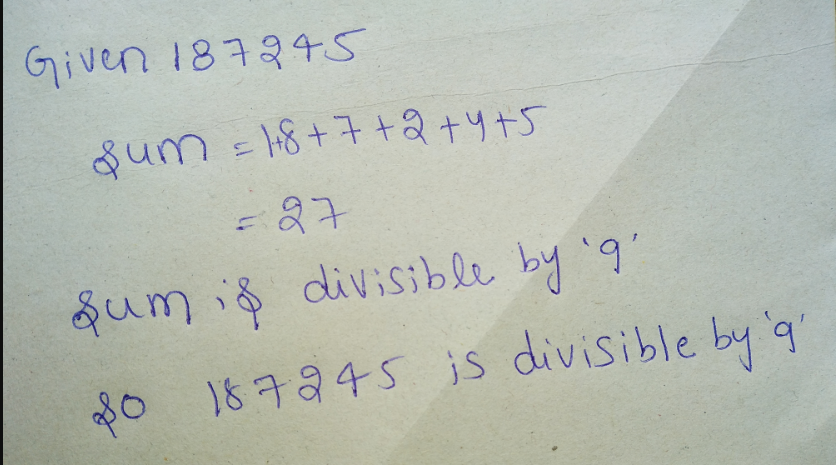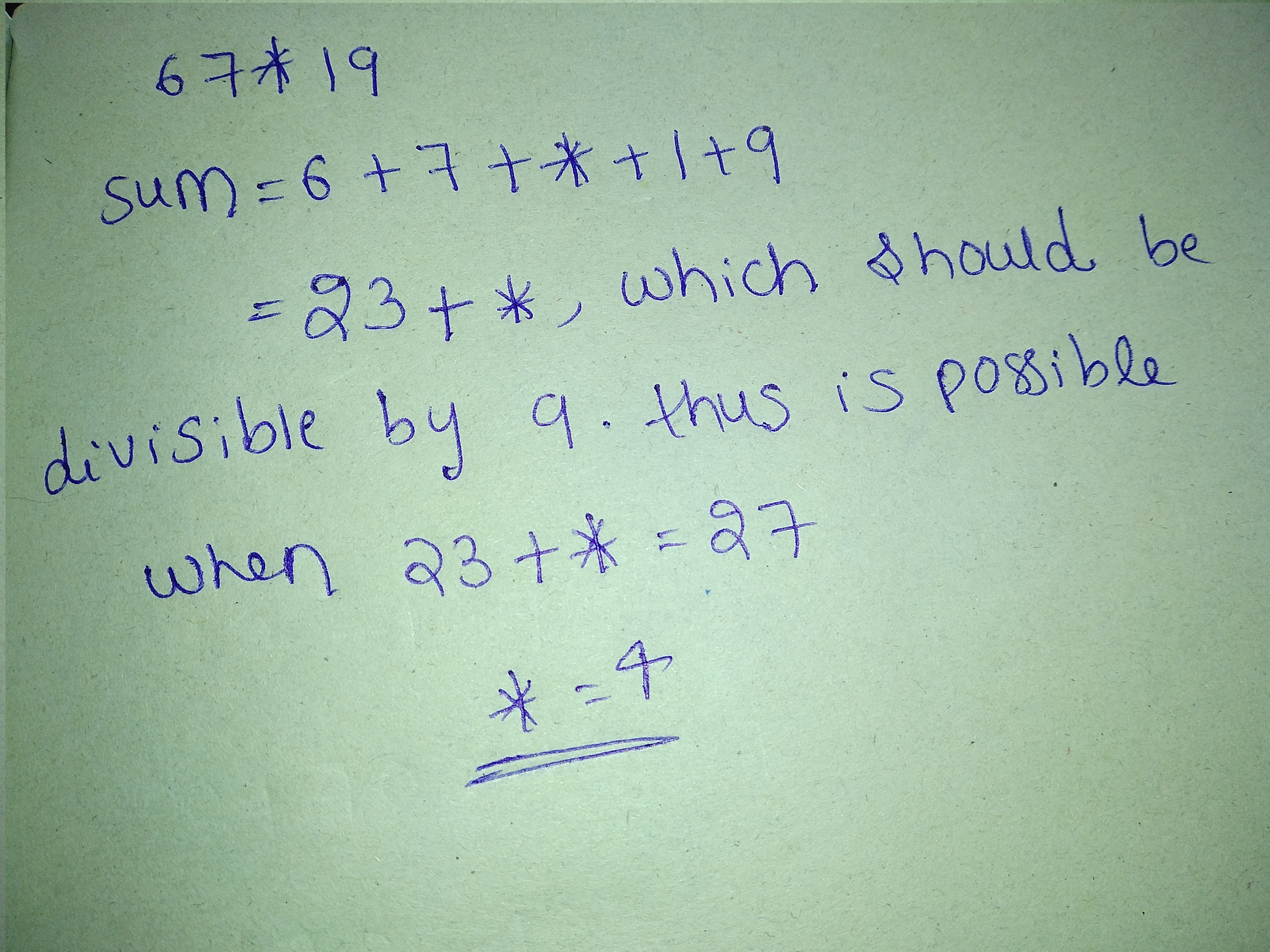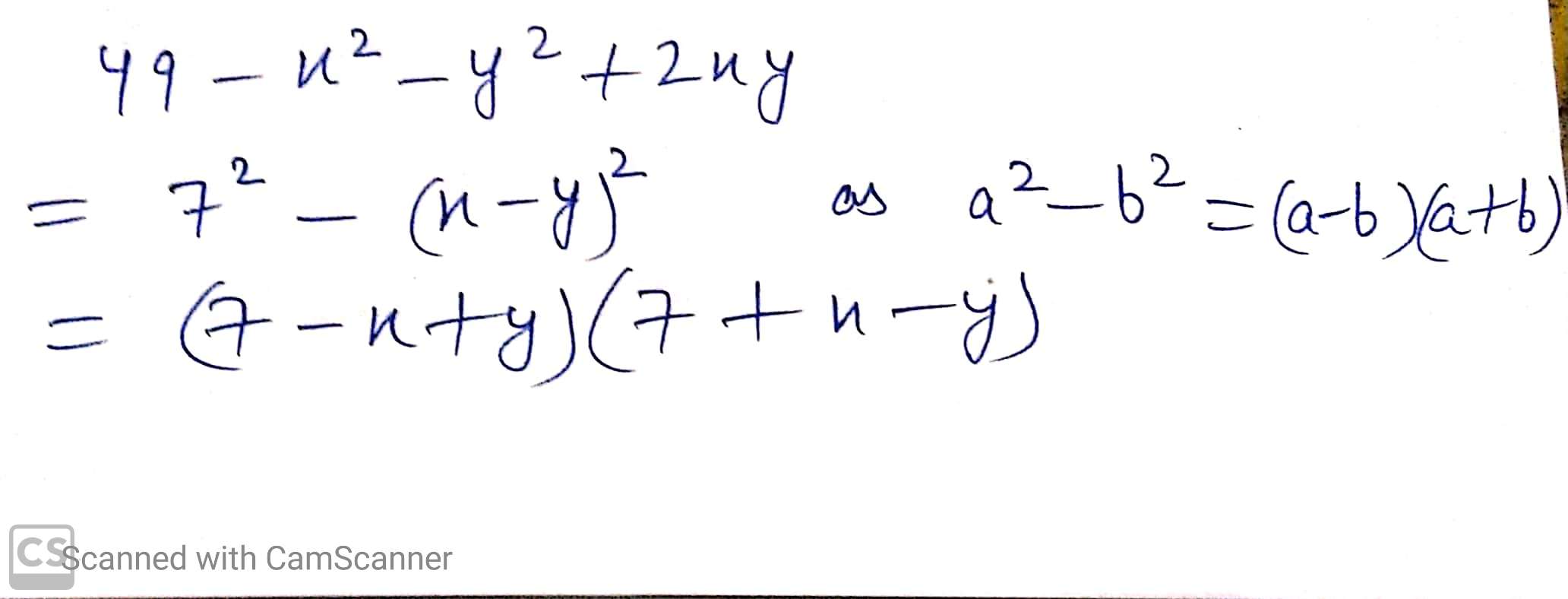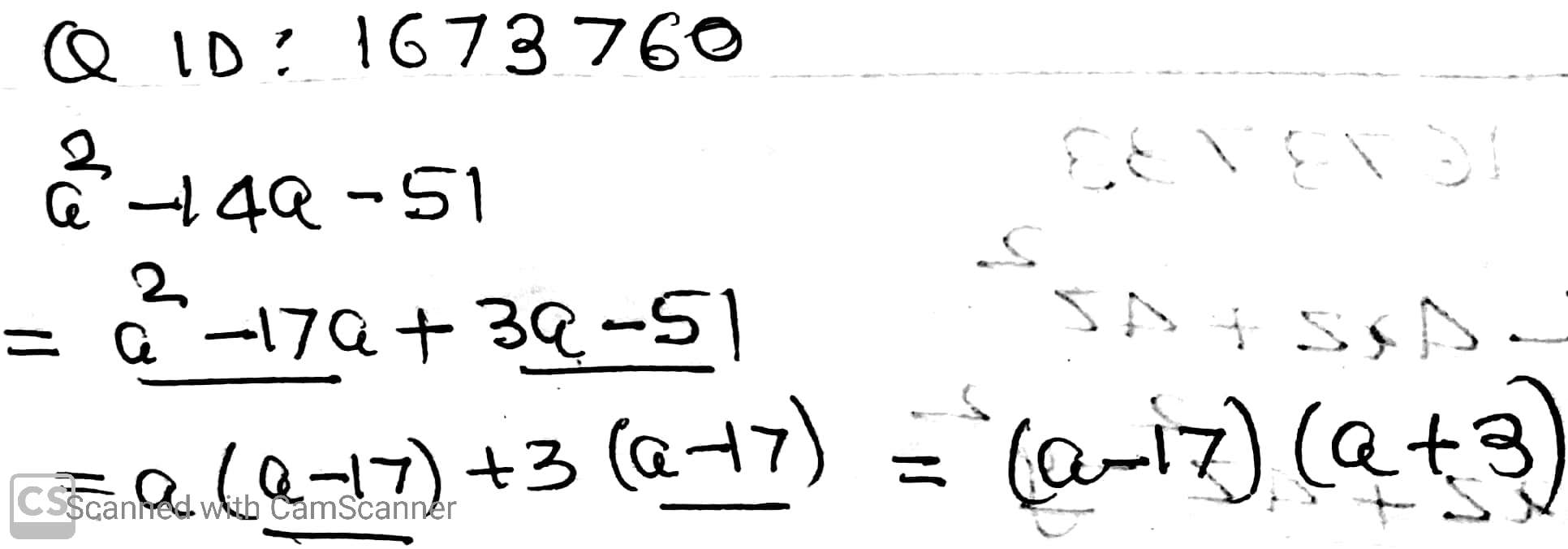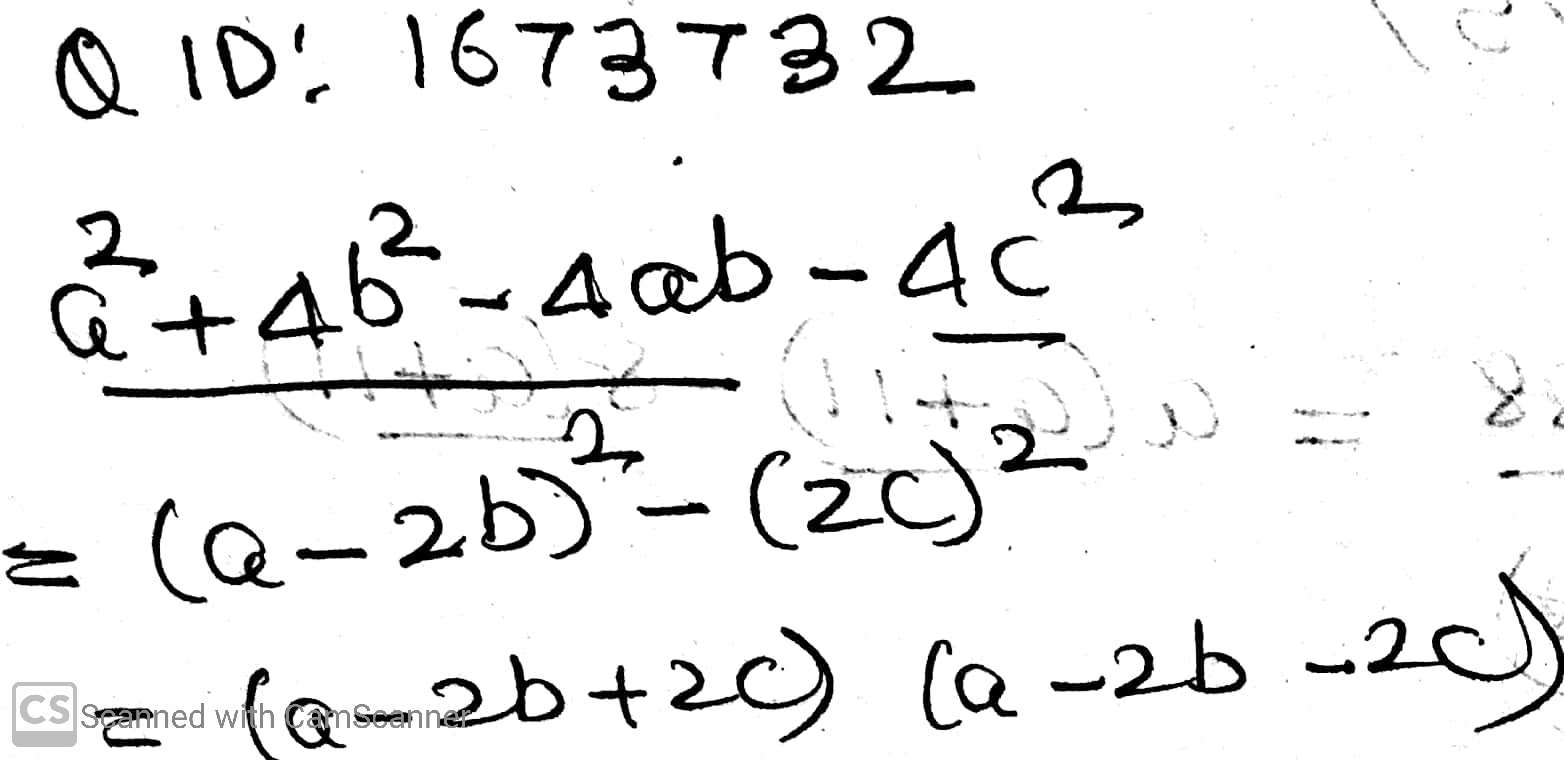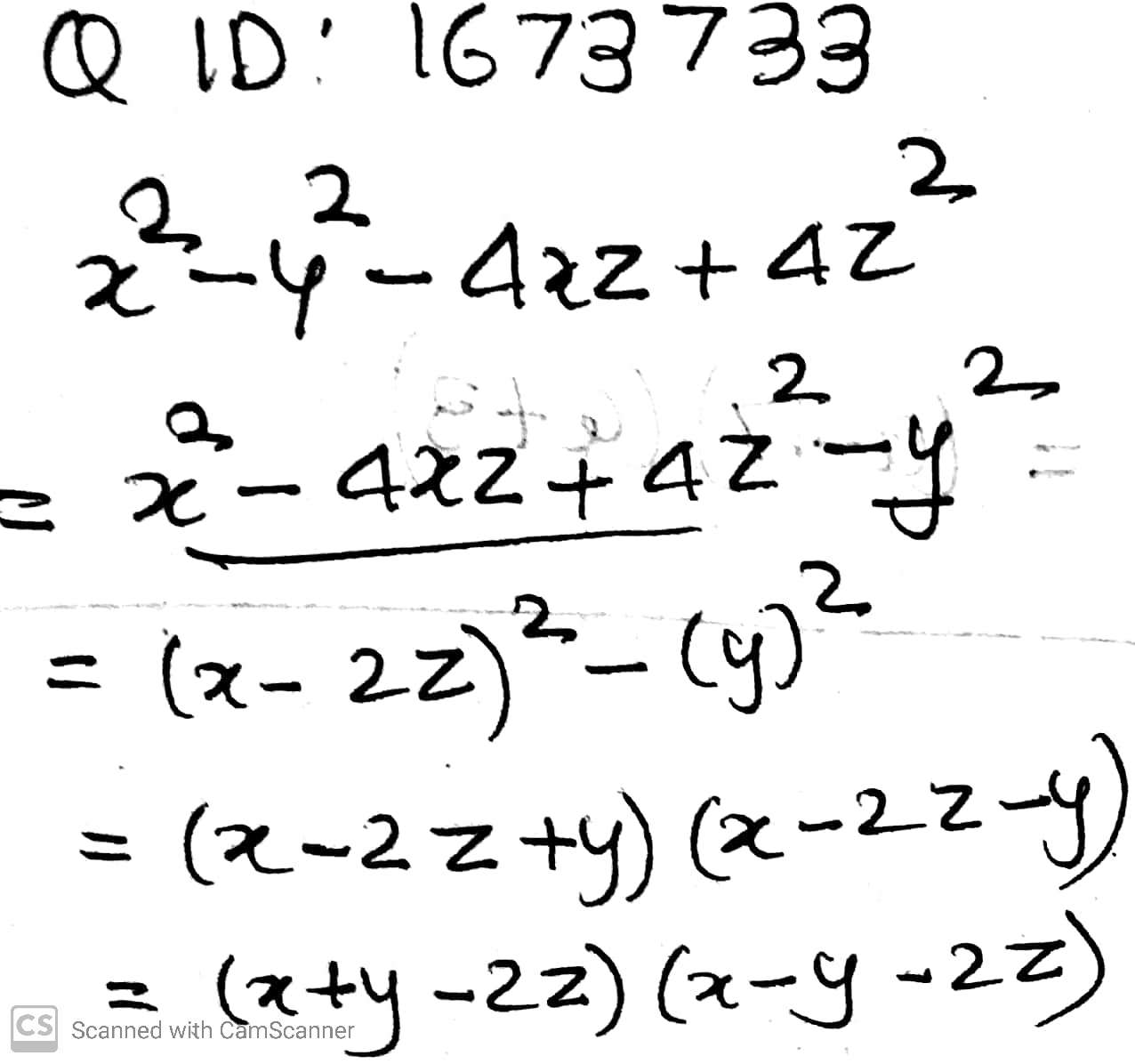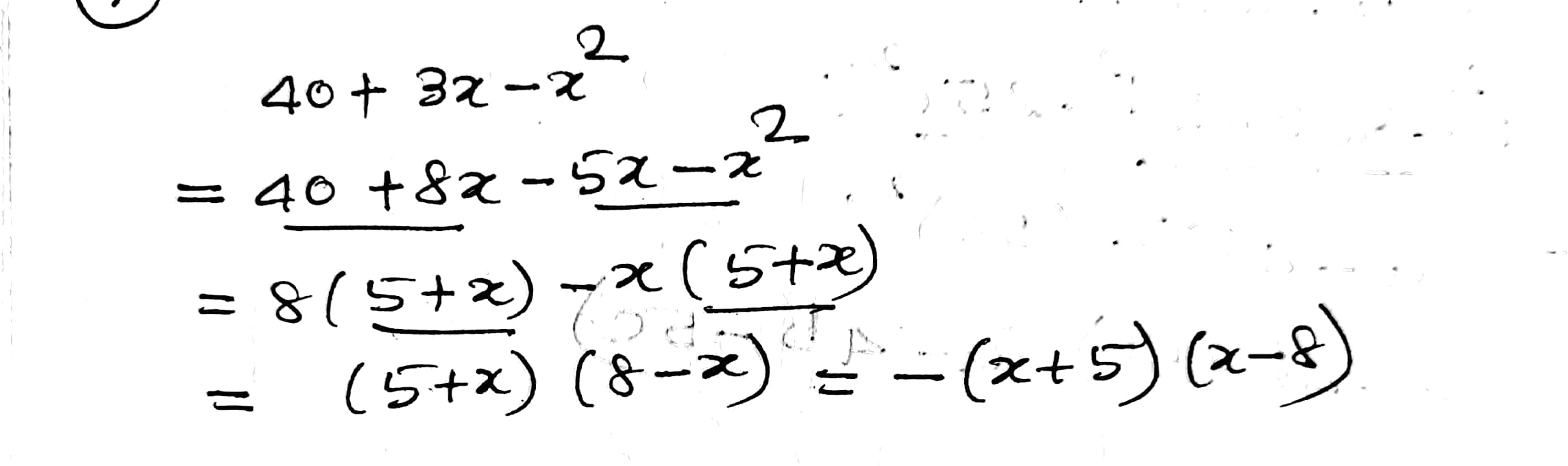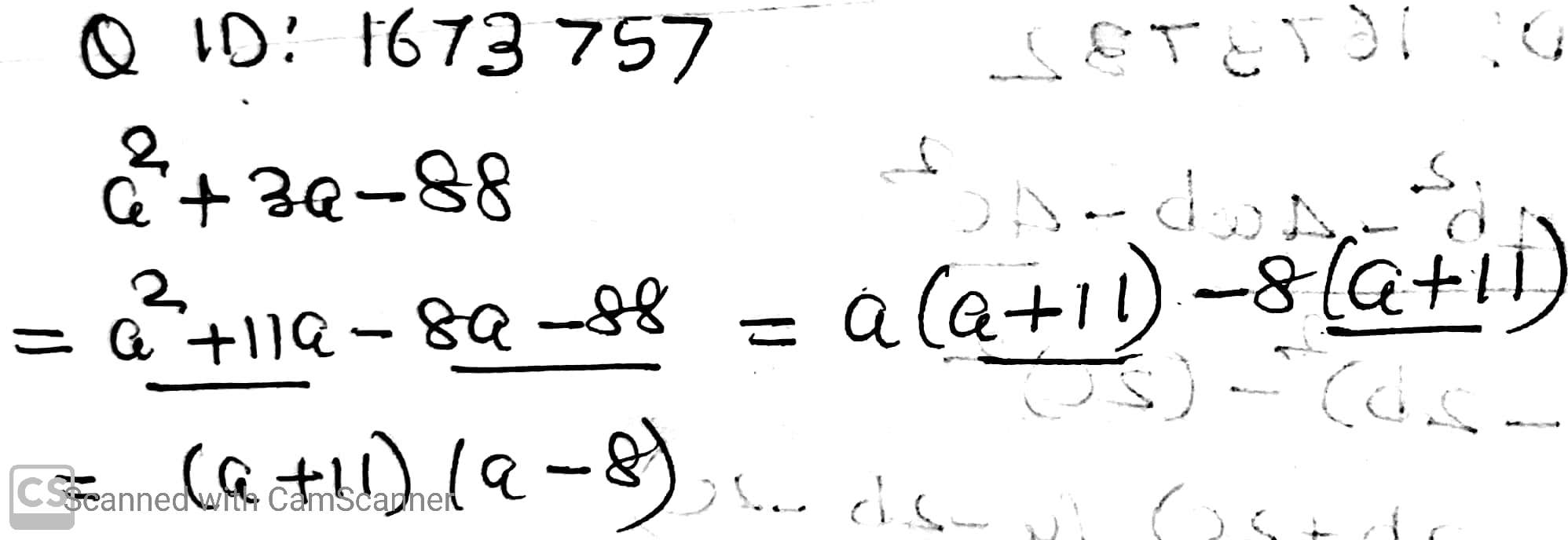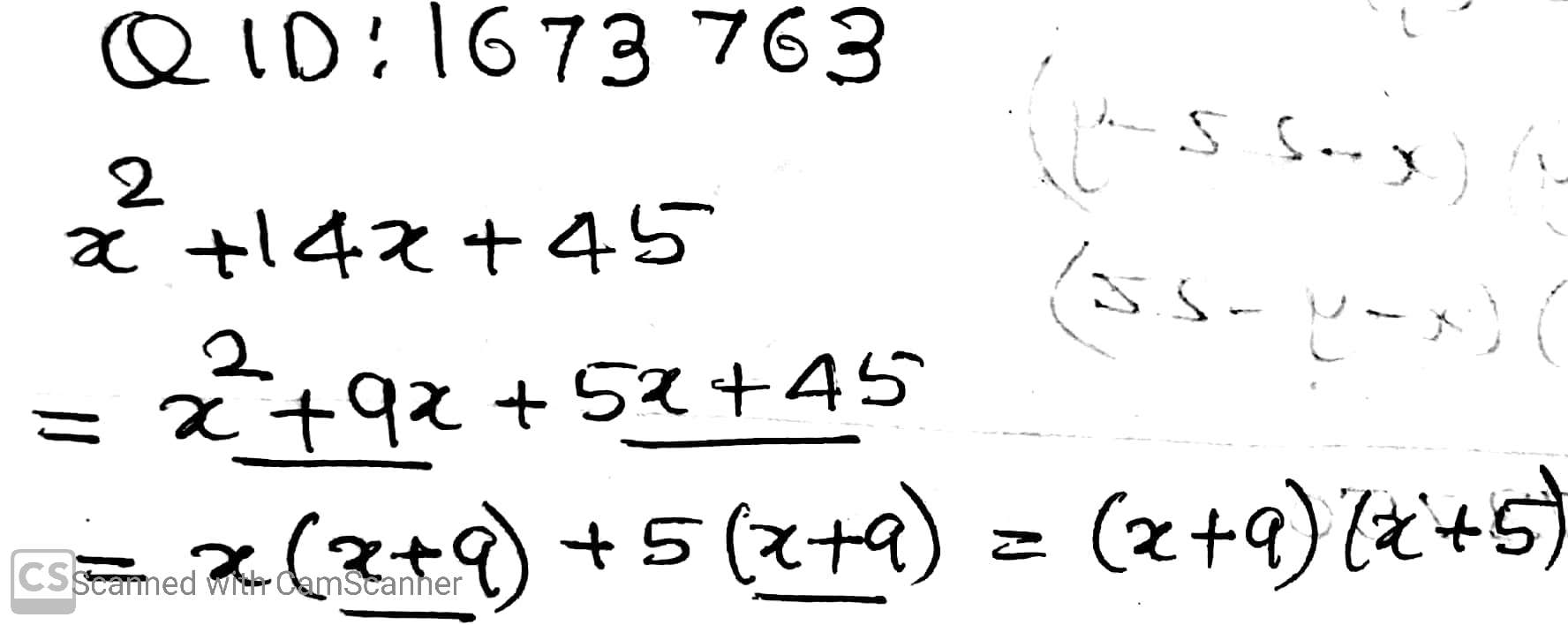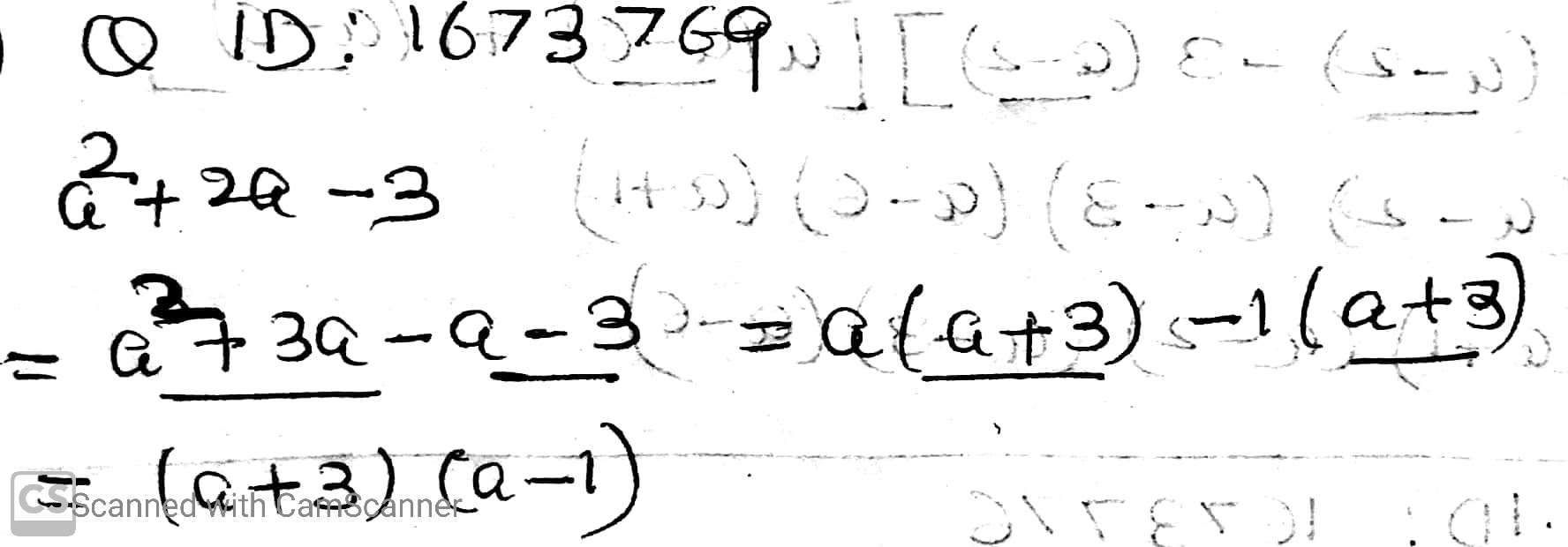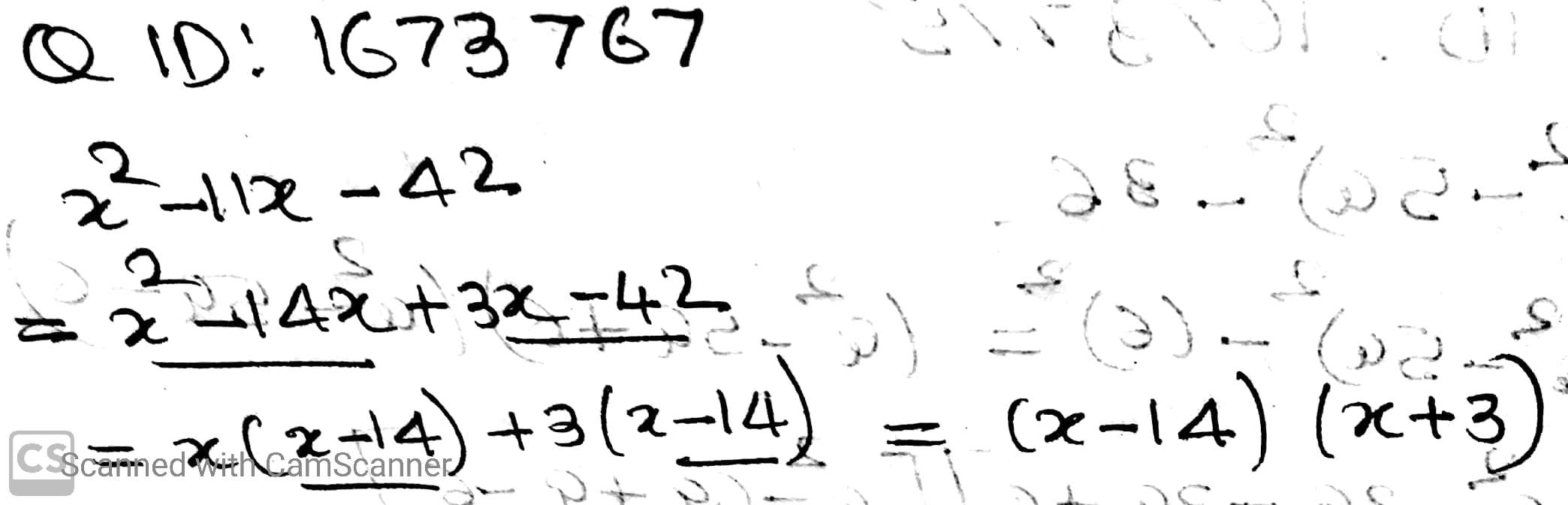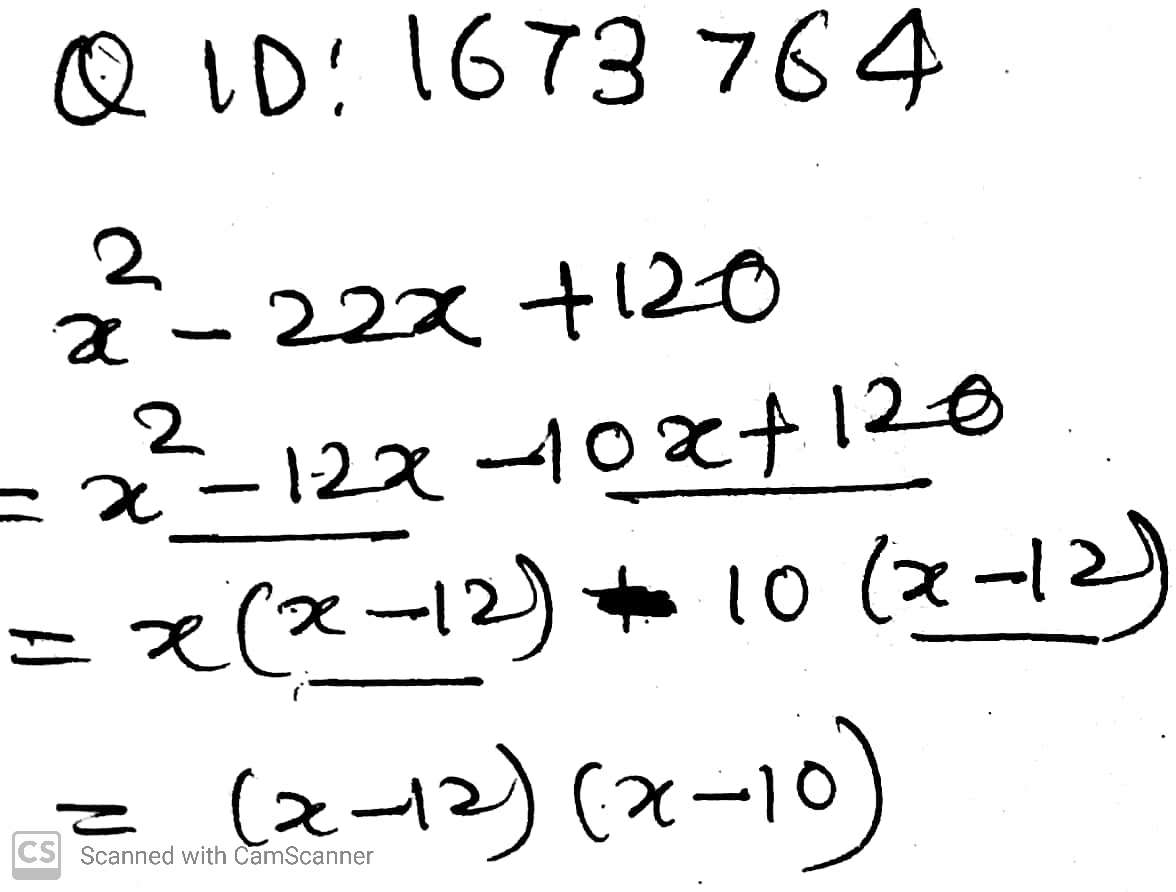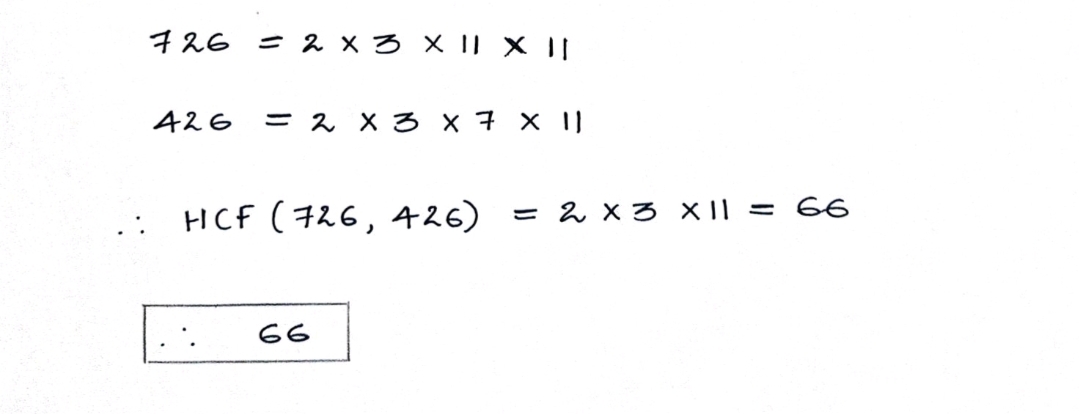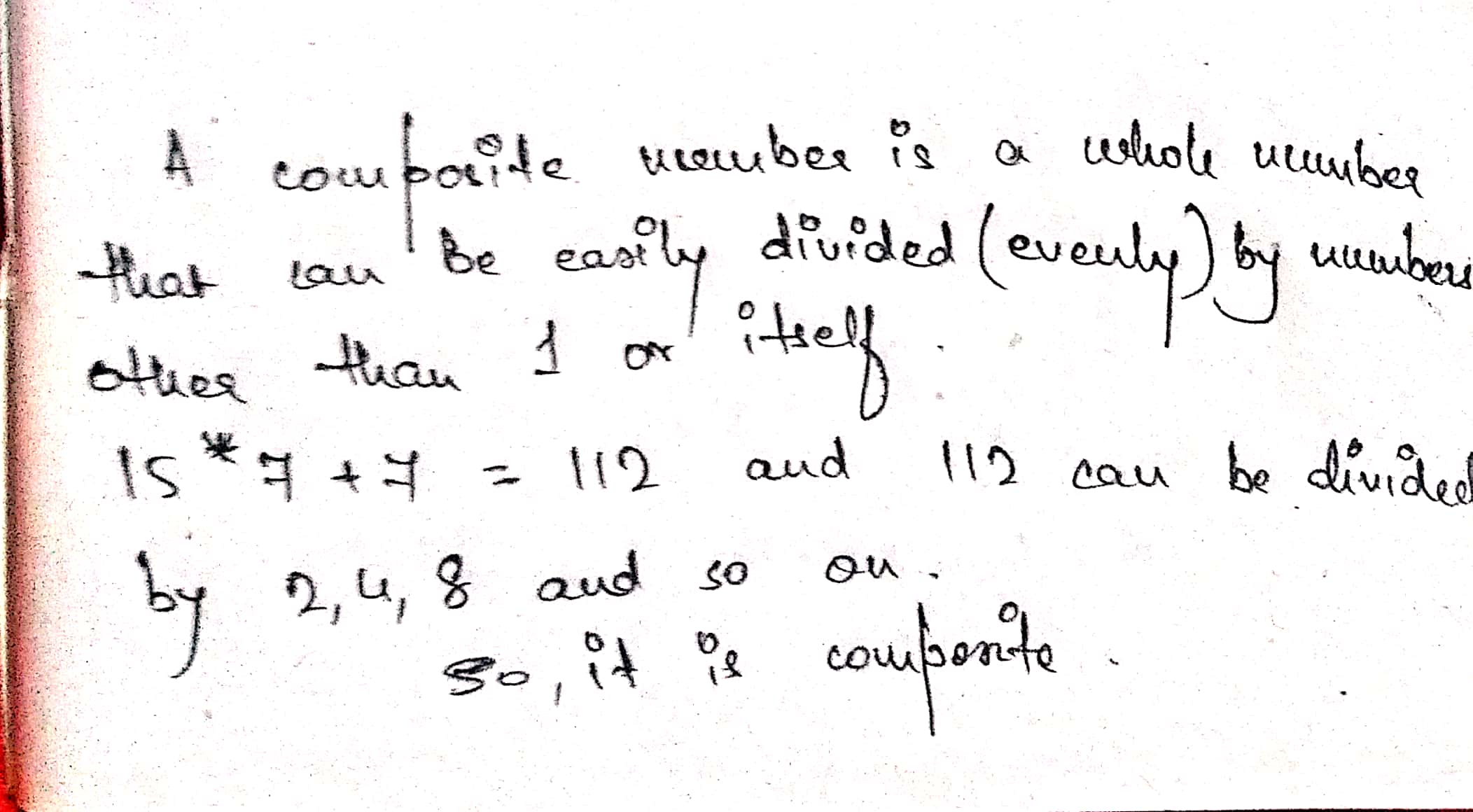Class 6 Maths - Playing With Numbers

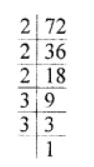
Find the HCF of $$6, 72$$ and $$120$$

$$6$$, $$72$$ and $$120$$

Factors of $$6=2\times 3$$
Factors of $$72=2\times 2\times 2\times 3\times 3$$

Factors of $$120=2\times 2\times 2\times 3\times 5$$

Thus, H.C.F of $$6$$, $$72$$ and $$120$$ $$= 2\times 3=6$$

If a and b are two odd prime numbers, show that $$a^2 -b^2$$ is composite.

$$a^2-b^2$$ $$=(a+b)(a-b)$$ {standard Identity}
Since $$(a+b)$$ and $$(a-b)$$ are factors, therefore, the number is a composite number.

Find the HCF of $$56$$ and $$814$$?

$$56=2\times2\times2\times7$$

$$814=2\times11\times37$$
Hence, the $$HCF$$ of $$56$$ and $$814 = 2$$

A man can row $$\displaystyle 9\frac{1}{3}$$ kmph in still water and finds that it takes him thrice as much time to row up than as to row down the same distance in the river Find the speed of the current

Let speed upstream be x kmph Then speed downstream = 3x kmph
Speed in still water = $$ \frac{1}{2}(3x+x) kmph = 2x kmph $$
$$\therefore 2x=\frac{28}{3}$$
$$\Rightarrow x=\frac{14}{3}$$
So Speed upstream = $$ \frac{14}{3} km/hr$$
Speed downstream = 14 km/hr
Hence speed of the current = $$ \frac{1}{2}\left ( 14-\frac{14}{3} \right )km/hr=\frac{14}{3}km/hr=4\frac{2}{3}km/hr$$

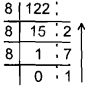
Convert $$\displaystyle (122)_{10}$$ to base 8 system

The number in decimal is consecutively divided by the number of the base

to which we are converting the decimal number Then list down all the

remainders in the reverse sequence to get the number in that base
So here $$\displaystyle (122)_{10}=(172)_{8}$$

Least prime number is

Prime number:

A number that is divisible only by itself and $$1$$ $$($$e.g. $$2, 3, 5, 7, 11$$ etc.$$)$$

So, least prime number is $$2$$

The sum of the prime numbers between $$90$$ and $$100$$ is

Prime numbers are those numbers which are only divisible by itself and one.
So $$97$$ is the only prime number between $$90$$ and $$100$$

hence, the sum$$=97$$

What is the greatest common factor of 420 and 660?

$$420 = 2 \times 2 \times 3 \times 5 \times 7$$

$$660 = 2 \times 2 \times 3 \times 5 \times 11$$

The greatest common factor is the product of the primes in the shared factors only $$2 \times 2 \times 3 \times 5 = 60$$

Find the HCF and LCM of 18 and 45 by prime factorisation method.

Express 18 and 45 as product of primes.
$$18=2 \times 3\times 3\times=2\times 3^2$$
$$45 = 3 \times 3 \times 5= 3^2\times 5$$
$$\therefore$$ HCF of $$18$$ and $$45= 3 \times 3 =9$$
LCM of $$18$$ and $$45 = 3\times 3\times 2\times 5=90$$
Recall : HCF of any 2 positive integers is the product of the smallest power of each common prime factor of the numbers.
LCM of any 2 positive integers is the product of the greatest power of each factor of the numbers.

Find the HCF of 344 and 60 by prime factorisation method. Hence find their LCM.

The prime factorsation $$344 = 2 \times 2 \times 2 \times 43 = 2^3 \times 43$$
$$60 = 2 \times 2 \times 3 \times 5 = 2^2 \times 3 \times 5$$
$$\therefore HCF (344, 60) = 2^2$$
We know that, $$LCM (a, b) \times HCF (a, b)=a\times b$$
$$\therefore \displaystyle LCM (a, b) =\frac{a\times b}{HCF(a,b)}$$
$$\displaystyle LCM (344, 60) =\frac{344 \times 60}{2 \times 2}= 5160$$

Using divisibility tests , determine which of the following numbers are divisible by $$5$$
(a) $$438750$$ (b) $$179015$$ (c) $$125$$ (d) $$639210$$ (e) $$17852$$

A number is $$divisible$$ by $$5$$ if the last digit is either $$0$$ or $$5.$$

So, $$438750,179015,125,639210$$ are divisible by $$5$$ and $$17852$$ is not divisible by $$5$$.

Find the HCF of 96 and 404

By Prime factorisation method, prime factors of $$96$$ and $$404$$ are:

$$96 =\boldsymbol{2}\times \boldsymbol{2}\times 2\times 2\times 2\times 3$$

$$404 = \boldsymbol{2}\times \boldsymbol{2}\times 101$$

HCF = Product of common primes factors in given numbers.

$$\therefore$$ HCF of $$96$$ & $$404$$ = $$2\times 2 = 4$$

Using divisibility tests, determine which of following numbers are divisible by $$2$$
$$(a) 2144 \ (b) 1258 \ (c) 4336 \ (d) 633 \ (e) 1352$$

A number is $$divisible$$ by $$2$$ if the last digit is $$0, 2, 4, 6 $$ or $$ 8.$$

So, $$2144,1258,4336,1352$$ are divisible by $$2$$ and $$633$$ is not divisible by $$2$$.

How many numbers from $$201$$ to $$250$$ are divisible by $$5$$, but not by $$3$$?

Here again, the numbers divisible by $$5$$ are $$205, 210, 215, 220, 225, 230, 235, 240, 245, 250$$. Now you compute the digital sum of these numbers: you get $$7, 3, 8, 4, 9, 5, 10, 5, 11, 7$$. Among these, the only numbers divisible by $$3$$ are $$3, 6, 9$$. Thus among the $$10$$ numbers divisible by $$5$$, only three numbers are also divisible by $$3$$. The remaining $$7$$ numbers are not divisible by $$3$$.

Is the number $$12345678$$ divisible by $$4$$?

The number formed by the last $$2$$ digits is $$78$$, which is not divisible by $$4$$. Hence the given number is not divisible by $$4$$.

Restate the following statements with appropriate conditions, so that they become true statements.
All numbers can be represented in prime factorization.

A prime number can only be divided by 1 or itself, so it cannot be factored any further.

Every other natural number can be broken down into prime number factors.

Then statement is true in case of natural numbers

Check whether the number $$12345321$$ is divisible by $$3$$. Is it divisible by $$9$$?

If the sum of the digits of a number are divisible by $$3$$, then the number itself is also divisible by $$3$$.

The sum of the digits $$=1 + 2 + 3 + 4 + 5 + 3 + 2 + 1 = 21$$

Since, $$21$$ is divisible by $$3$$, so the number is also divisible by $$3$$.

Similarly, if the sum of the digits of a number are divisible by $$9$$, then the number itself is also divisible by $$9$$.

The sum of the digits $$=1 + 2 + 3 + 4 + 5 + 3 + 2 + 1 = 21$$

Since, $$21$$ is not divisible by $$9$$, so the number is also not divisible by $$9$$.

Hence, the given number is divisible by $$3$$ but not by $$9$$.

Is $$444445$$ divisible by $$3$$?

The sum of the digits is $$25$$, which is not divisible by $$3$$. Hence $$444445$$ is not divisible by $$3$$. Here the remainder is $$1$$.

Find L.C.M. and H.C.F. of $$72$$ and $$108$$ by the prime factorization method.

Applying prime factorisation method, we get

$$72=2\times 2\times 2\times 3\times 3$$

$$108=2\times 2\times 3\times 3\times 3$$

L.C.M is $$216$$ $$(72\times 3) (108\times 2)$$

H.C.F is $$2\times 2\times 3\times 3=36$$

Write seven consecutive composite numbers less than 100.

1348828_700622_ans_053c5512afb94a478f01aec919bc6d9b.jpg

Write the prime numbers between 50 to 100.

Prime numbers are the numbers whose factors are only $$1$$ and the number itself. So, prime numbers between $$50$$ and $$100$$ are:

$$53,59,61,67,71,73,79,83,89$$ and $$97$$

Find HCF of $$45, 65$$ and $$80$$.

Factorization of the following.

$$45 = 1 \times 3 \times 3 \times 5$$

$$65 = 1 \times 5 \times 13$$

$$80 = 1 \times 2 \times 2 \times 2 \times 2 \times 5$$

Since, The common factor is $$1,5$$. This implies that

$$HCF = 5$$

Write the greatest 4 digit number and express it in the form of it's prime factors?

Greatest $$4$$ digit number is $$\rightarrow 9999$$

$$9999$$ can be expressed as $$9999=3\times 3\times 11\times 101$$

LCM of two or more prime numbers is equals to its ___________.

LCM of two or more prime numbers is equals to its $$product$$

The greatest common factor of given numbers is called ____________.

The greatest common factor of given numbers is called $$H.C.F$$

Find HCF: $$15, 24$$.

Factorization of the following.

$$15 = 3 \times 5$$

$$24 = 2 \times 2 \times2\times 3$$

Since, the common factor is $$3$$.

$$ H.C.F.=3$$

Find HCF:
$$12, 18$$ and $$24$$.

Factorization of the following.

$$12 = 1 \times 2 \times 2 \times 3$$

$$18 = 1 \times 2 \times 3 \times 3$$

$$24 = 1 \times 2 \times 3 \times 4$$

Hence,The common factor is $$1,2,3$$. This implies that

$$HCF=(1\times 2\times 3)=6$$

Find HCF: $$5, 13$$.

Factorization of the following.

$$5 = 1 \times 5$$

$$13 = 1 \times 13$$

Hence, The common factor is $$1$$

$$ HCF=1$$

Find the HCF of 12 , 24 and 48 by listing factors

$$12=2\times2\times3\\24=2\times2\times2\times3\\48=2\times2\times2\times2\times3$$

So, H.C.F$$=2\times2\times3=12$$

Solve $$\dfrac{1}{16}-\dfrac{3}{4}$$

$$\dfrac{1}{16} - \dfrac{3}{4} = \dfrac{1 - 3\times 4}{16} = \dfrac{1 - 12}{16} = \dfrac{-11}{16}$$

How to identify Prime Number?

A number is greater than 1 is called a prime number, if it has only two factors, namely 1 and the number itself.

Prime numbers up to 100 are:

$$ 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97 $$

Procedure to find out the prime number

Suppose A is given number.

Step 1: Find a whole number nearly greater than the square root of A. $$ K >\sqrt(A) $$

Step 2: Test whether A is divisible by any prime number less than K.

If yes, A is not a prime number.

If not, A is prime number.

For example:

Find out whether $$ 337 $$ is a prime number or not?

Step 1: $$ 19 > \sqrt 337 $$

Prime numbers less than $$19$$ are $$2, 3, 5, 7, 11, 13, 17$$

Step 2: $$337$$ is not divisible by any of them

Therefore $$337$$ is a prime number

Fnd the HCF of the following pair of numbers:
$$32$$ and $$54$$

$$32 = 2\times 2\times 2 \times 2 \times 2$$

$$54= 2\times 3\times 3\times 3\times 3 $$

common factors in both number is $$2$$

so the HCF of 32 and 54 is 2.

Express each number as a product of its prime factors:
(i) $$140$$ (ii) $$156$$ (iii) $$3825$$

We have

(i) $$140=7\times 5\times 2^2$$

(ii) $$156=13\times 3\times 2^2$$

(iii) $$3825=17\times 3^2\times 5^2$$.

These are the required prime factorization.

Solve $$2\dfrac {4}{8}\div 2\dfrac {1}{2}$$

$$2\dfrac{4}{8} \div 2\dfrac{1}{2}$$

$$= \dfrac{20}{8} \div \dfrac{5}{2}$$

$$= \dfrac{20}{8} \times \dfrac{2}{5}$$

$$ = \dfrac{40}{40} = 1$$ (Ans)

Explain why $$11 \times 13 \times 15 \times 17 \div 17$$ is a composite number.

Given number is $$11\times 13\times 15\times 17\div17$$

On simplifying the number, we get:

$$11\times 13\times 15$$

We know that, $$prime\times composite=composite$$

Here, out of $$11,13\text{ and }15,\ 15$$ is a composite number.

So, the overall product will also be composite.

Hence, the given number is composite because it contains a composite number, $$15$$.

Fill in the blanks
A number is divisible by _____ if it divisible by $$4$$ and $$9$$.

$$6$$ Ans

Is $$4$$ a factor of $$28$$?

Yes , because

$$7 \times 2 \times 2 = 28$$

The ____________ of two or more numbers is the smallest number which is divisible by each of the given numbers.

The $$\underline {\;HCF\;} $$ of two or more number is the smallest number which is divisible by each of the given number

What least number should be replaced for $$$$ so that the number $$67301 2$$ is exactly divisible by $$9$$?

A number is divisible by $$9$$ if the sum of its digits is divisible by $$9$$.

Now, Sum of the digits in given number $$=6+7+3+0+1+2=19$$, which is not divisible by $$9$$.

But, if we add $$8$$ to this sum, it becomes $$19+8=27$$, which is divisible by $$9$$

So, $$6730182$$ is divisible by $$9$$

So, the least number is $$8$$ which should replace for $$\ast $$ in the given number.

State fundamental theorem of Arithmetic.If $$17 \times 11 \times 13+13$$ a composite number ? Justify.

$$17\times11\times13+13$$

$$(17\times11\times13)+13$$

$$2431+13$$

$$2444$$

which is a composite number

As $$=2444=2\times1222$$

Look at the following pairs of numbers and determine whether they are co-prime or prime :
(i) $$8,9$$ (ii) $$11,13$$ (iii) $$15,16$$ (iv) $$64,65$$ (v) $$71,73$$

(A) co-prime (since their H.C.F is 1)

(B) Both are prime numbers with difference of 2, So,they are twin prime

(D) co-prime (since their H.C.F is 1)

(E) Both are prime numbers with difference of 2, So,they are twin prime

Fill in the blanks
The smallest digit by which $$$$ should be replaced in $$50956$$, so that it is divisible by $$4$$ is _____.

For a number to be divisible by $$4$$ last two digits of that number number should be divisible by $$4$$.

Since $$16$$ is divisible by $$4$$, smallest number by which $$*$$ can be replaced is $$1$$.

Write the smallest digit and greater digit in the blank space of each of the following numbers so that the number formed is divisible to by $$3$$

Sum of digits $$=6+7+2+4=19$$

Smallest digit that we can add to the sum to make it multiple of $$3$$ is $$2$$.

Doing so,we get sum of digits $$=19+2=21$$ which is the multiple of $$3$$.

Greatest digit that we can add to the sum to make it multiple of $$3$$ is $$8$$.

Doing so, the sum of digits $$=19+8=27$$ which is the multiple of $$3$$.

Find the greatest number which can divide $$36,81$$ and $$108$$.

We need to find HCF of $$36,81,108$$

$$36,108,81$$

$$4,12,9$$

$$\therefore HCF =9$$

1065130_1094711_ans_835fadde181143488eef37b65f603144.png

Find the $$H.C.F$$ of $$16$$ and $$40$$

Factors of $$16=2\times 2\times 2\times 2$$

Factors of $$40=2\times 2\times 2\times 5$$

Hence, the $$H.C.F$$ of $$16$$ and $$40$$ is $$2\times 2\times 2=8.$$

Show that $${3}^{2n+2}-8n-9$$ is divisible by $$8$$, where $$n$$ is any natural number.

We have,

$$ {3}^{(2n+2)}-8n-9$$

If the number is divisible by 8, then

$$8 \times 1=8$$

$$8 \times 2=16$$

$$8 \times 3 = 24$$

$$8 \times 4 = 32$$ and so on.

where n is a natural number.

Let $$P(n) = {3}^{(2n+2)} -8n -9 = 8m$$,

Where $$ a \in N$$, i.e. a is a natural number.

For n = 1

LHS $$ = {3}^{(2\times1+2)}-8\times1-9$$

$$ ={3}^{4}-17$$

$$ =81 -17$$

$$ = 64= 8\times 8$$

Therefore, $$P(n) $$ is true for $$n = 1$$.

Suppose, $$P(k)$$ is true.

$${3}^{(2k+2)} -8k-9=8a $$ ........... (1)

where $$a\in N$$.

Now, we will prove that $$P(k+1)$$ is true.

LHS $$={3}^{2(k+1)+2}-8(k+1) -9$$

$$= 9[{3}^{(2k+2)}] -8k -17$$

From equation (1), we get

$$=9[8a+9+8k]-8k-17$$

$$=72a+64k+64$$

$$=8(9a+8k+8)$$

$$ = 8b$$

where $$b = 9a+8k+8$$ and $$b$$ is natural number.

Therefore, $$P(k+1)$$ is true whenever $$P(k)$$ is true.

Therefore, $$ P(n)$$ is true for $$n$$, where $$n $$ is a natural number.

Hence, the given equation is divisible by $$8$$.

What is the greatest number that divides $$720$$ and $$810$$ without leaving any remainder?

Suppose we have two numbers A and B and the greatest number which divides both A and B is the greatest common factor of A and B.

Now we have to find $$g.c.d$$ of $$720$$ and $$810$$.

Since for any number we can factories in its prime factors then,

$$720=2\times2\times2\times2\times3\times3\times5$$;

$$810=2\times3\times3\times3\times3\times5$$

Then greatest common factor is $$2\times3\times3\times5 =90 $$, then $$90$$ is the greatest number that divides $$720$$ and $$810$$.

Show that "the range of the first seven multiples of the smallest odd prime number is also a multiple of that prime number . "

$$\Rightarrow$$ The smallest odd prime is $$3$$.

$$\Rightarrow$$ The first seven multiple of $$3=3,\,6,\,9,\,12,\,15,\,18,\,21$$.

$$\Rightarrow$$ Here, the highest number is $$21$$ and lowest number is $$3$$.

$$\Rightarrow$$ The range of this multiples = Highest number - lowest number

$$\Rightarrow$$ The range of this multiples $$=21-3=18$$

$$\Rightarrow$$ We know that $$18$$ is divisible by $$3$$.

Hence, we proved that, "the range of the first seven multiples of the smallest odd prime number is also a multiple of that prime number . "

State Euclid's division lemma and Fundamental theorem of Arithmetic statement.

Euclid Division lemma statement:- For any two positive integer a and b, there exist a unique whole no. q and r.

Such that a=bq + r where $$(0\leq r<b)$$

Fundamental theorem of Arithmetic statement:-Every integer greater than one either is prime number or unique.

Find the number of divisions of $$1980$$.
i) How many of them are multiple of $$11$$?

According to the question,
$$1980 = {2^2} \times {3^2} \times 5 \times 11$$
No. of division,
$$=(2+1) (2+1) (1+1) (1+1)$$
$$ = 3 \times 3 \times 2 \times 2$$
$$=36$$
No. of division of 1980 which are multiple of 11.
$$ = 3 \times 3 \times 2 $$
$$=18$$

Define even numbers. How can we identify them?

The numbers which are divisible by $$2$$ are even numbers.Since the divisibility rule of $$2$$ states that the number ending with $$2,4,6,8,0$$ are divisible by $$2$$. Therefore,it can also be said that, even numbers are the numbers which have $$2,4,6,8,0$$ at their ones place

Which of the following numbers are divisible by $$9$$?
$$369, 1008, 753321$$

According to the divisibility test a number is divisible by $$9$$ if the sum of all its digits is divisible by $$9$$.

Given the numbers are $$369, 1008, 753321$$.

For $$369$$, the sum of digits is $$=3+6+9=18$$, divisible by $$9$$ so the number is also divisible by $$9$$.

For $$1008$$, the sum of digits is $$=1+0+0+8=9$$, divisible by $$9$$ so the number is also divisible by $$9$$

For $$753321$$, the sum of digits is $$=7+5+3+3+2+1=21$$, not divisible by $$9$$ so the number is not divisible by $$9$$

Express each of the following numbers as the sum of three odd primes:
a)$$21$$
b)$$31$$
c)$$53$$
d)$$61$$

a) $$ 21=3+7+11 $$

b) $$ 31=5+7+19 $$

c) $$ 53=3+19+31 $$

d) $$61=11+19+31 $$

Test whether the following numbers are divisible by $$6$$
$$75642$$

$$75642$$ is divisible by $$6$$ if it is divisible by both $$2$$ and $$3$$

(1) digit is even $$\therefore$$ it is divisible by $$2$$

(2) $$7+5+6+4+2=24$$

and $$24$$ is divisible by $$3$$ $$\therefore 75642$$ is divisible by$$3$$

$$\therefore 75642$$ is divisible by $$6$$.

Why $$5\times 6\times 7\times 11-2\times 3\times 7\times 11$$ is composite number.

Multiplication of those number is equal to 1848. Where 1848 comes on the table of 2,3,4...therefore $$5×6×7×11-2×3×7×11$$ is composite number

Find the smallest three- digit number divisible by $$2$$ as well as $$3$$.

If a number is divisible by $$2$$ as well as $$3$$, then it will be divisible by $$6$$

Now, the smallest $$3$$ digit number is $$100$$

If we divide $$100$$ by $$6$$ , the remainder is $$4$$

So, to make the number divisible, we have to add $$(6-4)=2$$ to the number $$100$$

So, the smallest $$3$$-digit number divisible by $$2$$ and $$3$$ is $$=100+2=102$$

Test whether the following numbers are divisible by $$6$$.
$$30654$$

$$30654\Rightarrow $$ last digit is even $$\because$$ it is divisible by $$2$$.

$$\Rightarrow 3+6+5+4+0=18$$

$$18$$ is divisible by $$3 \therefore$$

$$30654$$ is divisible by $$3$$.

Since it is divisible by both $$2$$ and $$3$$.

$$\therefore 30654$$ is divisible by $$6$$.

_________ is a factor of every number.

$$1$$ is a factor of every number

Which of the following numbers are prime?
i) $$101$$
ii) $$251$$

A prime number is a whole number greater than $$1$$, whose only factors are $$1$$ and itself.

$$101$$ can be divided, without a remainder, only by $$1$$ and $$101$$

So, $$101$$ is a prime number.

$$251$$ can be divided, without a remainder, only by $$1$$ and $$251$$

So, $$251$$ is a prime number.

The greatest factor of $$364$$ is_________?

The greatest factor of 364 is 364 itself.

Test whether the following numbers are divisible by $$6$$
$$56523$$

$$56523$$ is divisible by $$6$$ if it is divisible by both (2) and (3)

now,

since last digit of $$56523$$ is $$3$$ which is odd.

$$\therefore $$ it is not divisible by $$2$$ .

$$\therefore 56523$$ is not divisible by $$ 6$$.

Test whether the following numbers are divisible by $$6$$.
$$324368$$

$$\rightarrow $$ Last digit $$8=even$$

$$\therefore$$ divisible by $$2$$.

$$\rightarrow$$ sum of digits $$=3+2+4+3+6+8=26$$

=not divisible by $$3$$

$$\therefore 324368$$ is not divisible by $$3$$

$$\therefore$$ it is not divisible by $$6$$ also.

Find G.C.D of $$78$$ and $$455$$

Prime factor of $$78= 2\times 3\times 13$$

Prime factor of $$455= 5\times 7\times 13$$

so G.C.D (Greatest common divisor) is $$= 13$$

HCF and LCM
18,20,24

We have,

$$ 18=2\times 3\times 3 $$

$$ 12=2\times 2\times 3 $$

$$ 24=2\times 2\times 2\times 3 $$

Then,

H.C.F.

$$2\times 3=6$$

L.C.M.

$$2\times 3\times 3\times 2\times 2=72$$

Hence, this is the answer.

Find g.c.d of (i) $$135$$ and $$225$$ (ii) $$38220$$ and $$196$$ by Euclid's algorithm.

By division algorithm

$$225=135(1)+90\\ 135=90(1)+45\\ 90=45(2)+0$$

$$ gcd(135,225)=45$$

As we know $$38220>196$$

We know $$a=bq+r 0\le r\le b$$

$$38220=196\times 195+0$$

So, $$196$$ is gcd.

Hence, this is the answer.

$$42\times 8$$ divisible by $$4$$?

Yes.
As $$8$$ is divisible by $$4$$, its multiples are also divisible.

Find the factors of the following:
(i) $$7$$ (ii) $$9$$ (iii) $$16$$
(iv) $$25$$ (v) $$48$$ (vi) $$63$$

1114340_1206016_ans_d97850fb23484229aa0288183231c59b.jpg

Given that $$L C M ( 91,26 ) = 182 ,$$ find $$H C F ( 91,26 ).$$

As $$LCM\times HCF=$$Produnct of two numbers

Two numbers are 91 and 26.

Produnct of two numbers $$=91\times 26=2366$$

$$LCM(91,26)=182$$

Now $$182\times HCF=2366$$

$$HCF=13$$

Hence the HCF is 13.

Which number is neither a prime number nor a composite number?

$$1$$ is neither prime nor composite number

HCF of $$960 \text { and } 432$$ is ........

Let $$a$$ and $$b$$ are two positive

integers . Then there exists two

unique whole numbers $$q$$ and $$r$$

such that

$$a = bq + r ,$$

$$0 ≤ r < 0$$

Now ,

Start with the larger integer , that

is $$960$$ , Apply the division lemma

to $$960$$ and $$432 ,$$ to get

$$960 = 432 × 2 + 96 $$

$$432 = 96 × 4 + 48$$

$$96 = 48 × 2 + 0$$

The remainder has now become

zero , so our procedure stops.

Since , the divisor at this stage is

$$48 , $$

Therefore ,

$$HCF ( 960 , 432 ) = 48$$

The $$H.C.F$$. of $$30$$ and $$210$$ in Prime Factors is

$$\begin{array}{l} 210=2\times 3\times 5\times 7 \\ 30=2\times 3\times 5 \\ HCD=HCF=2\times 3\times 5=30 \end{array}$$

Express $$30$$ as sum of two prime numbers.

$$30$$ as two prime number are:-

$$1+29$$

$$7+23$$

$$11+19$$

$$13+17$$

Find the $$HCF$$ of the following
$$18,48$$

$$18 = 2 \times 3 \times 3 = 2 \times {3}^{2}$$

$$48 = 2 \times 2 \times 2 \times 2 \times 3 = {2}^{4} \times 3$$

Highest common factor-

$$HCF \left( 18, 48 \right) = 2 \times 3 = 6$$

If $$HCF$$ of $$210$$ and $$55$$ is expressible in the form $$2105+55A$$, then find the value of $$(2-A)$$.

$$210 > 55$$

$$210 = 55 \times 3 + 45$$

$$55 = 45 \times 1 + 10$$

$$45 = 10 \times 4 + 5$$

$$10 = 5 \times 2 + 0$$

$$\therefore HCF = 5$$

$$5 = 45 - \left( {10 \times 4} \right)$$

$$ = 45 - \left( {55 - 45 \times 1} \right) \times 4$$

$$ = 45 - \left( {55 \times 4} \right) + \left( {45 \times 4} \right)$$

$$ = \left( {45 \times 4} \right) - \left( {55 \times 4} \right)$$

$$ = \left\{ {\left( {210 - 55 \times 3} \right) \times 5} \right\} - \left( {55 \times 4} \right)$$

$$ = \left( {210 \times 5} \right) - \left( {55 \times 15} \right) - \left( {55 \times 4} \right)$$

$$ = \left( {210 \times 5} \right) - \left( {55 \times 19} \right)$$

$$ = \left( {210 \times 5} \right) + \left( {55 \times - 19} \right)$$

$$\therefore A = - 19$$

value of $$\left( {2 - A} \right)$$ $$=2+19=21$$.

Every even number greater than $$2$$ can be expressed as the sum of two prime numbers.Verify this statement for every even number up to, $$16$$ .

Solution:

$$4=2+2$$

$$6=3+3$$

$$8=3+5$$

$$10=3+7$$

$$12=5+7$$

$$14=3+11$$

$$16=5+11$$.

Find the HCF of 16, 28.

HCF is the product of the common factors of the given numbers.

First, we need to find the prime factors of the given numbers:

$$16=2\times 2 \times 2\times 2=2^4$$

$$28=2\times 2\times 7=2^2\times 7$$

So, $$\mathrm{H.C.F.}=2^2 =4$$

Hence, HCF if the given numbers is $$4.$$

Find the $$ g.c.d$$ of
$$144,\ 233$$

144 = 2⁴ × 3²;
233 is a prime number, it cannot be prime factorized into other prime factors;

Take all the common prime factors, by the lowest exponents.
But the two numbers have no common prime factors.

Greatest common divisor:
gcd (144; 233) = 1;

Find the $$ g.c.d $$ of
$$765,\ 65$$

765 = 3² × 5 × 17;
65 = 5 × 13;

common prime factor is 5

Greatest (highest) common factor (divisor):

gcd of (765; 65) = 5;

Write the factors of $$120$$ as pairs.

The factor pairs of $$120$$ are

$$(1, 120) (2, 60) (3, 40) (4, 30) (5, 24) (6, 20) (8, 15) (10, 12)$$.

Express the following in standard form:
$$(i)28\,\,\,\,(ii)100\,\,\,\,(iii)144\,\,\,\,(iv)1296\,\,\,\,(v)2100$$

$$(i) \ 28=2\times 2\times 7={2}^{2}\times {7}^{1}$$

$$(ii) \ 100=5\times 5\times 2\times 2={5}^{2}\times{2}^{2}$$

$$(iii) \ 144=2\times 2\times 2\times 2\times 3\times 3={2}^{4}\times{3}^{2}$$

$$(iv) \ 1296=2\times 2\times 2\times 2\times 3\times 3\times 3\times 3$$ $$={2}^{4}\times{3}^{4}$$

$$(v) \ 2100=2\times 2\times 5\times 5\times 3\times 7$$ $$={2}^{2}\times{5}^{2}\times{3}^{1}\times{7}^{1}$$

Show that $$496$$ is a perfect number.

A number in which the sum of all its factors is equal to twice the number is called a perfect number.

Factors of $$496=1,2,4,8,16,31,62,124,248,496$$

Sum of all factors$$=1+2+4+8+16+31+62+124+248+496=992=496\times 2‬$$

Hence $$496$$ is a perfect number.

What are Composite Number ?

$$\textbf{Step -1: Defining composite numbers.}$$

$$\text{Composite numbers are numbers that have more than 2 factors}$$

$$\text{That is, they have factors other than 1 and the number itself.}$$

$$\textbf{Hence , composite numbers are numbers that have more than 2 factors.}$$

What is a prime number ?

A prime number is a whole number greater the 1 whose only factors are 1 and itself.

Write all prime numbers between 1 and 10.

Prime numbers between 1 and 10 are 2, 3, 5, 7.

Fill in the blanks:
The only even prime number is ______

Prime numbers are 2, 3, 5, 7, 11, etc.

Even numbers are 0, 2, 4, 6, 8, 10, etc.

The only even prime number is 2.

Write the prime factors of $$24$$

Factors of $$24=2\times 3\times 2\times 2$$

Prime factors $$=\left\{2,\,3\right\}$$

Write the prime factors of $$360$$

Factors of $$360=2\times 2\times 2\times 3\times 3\times 5$$

Prime factors $$=\left\{2,\,3,\,5\right\}$$

Find the number of odd and even divisors of $$600$$

$$600=2\times 3\times 2\times 2\times 5\times 5={2}^{3}\times{3}^{1}\times{5}^{2}$$

Number of divisors$$=\left(3+1\right)\left(1+1\right)\left(2+1\right)=4\times 2\times 3=24$$

Number of odd divisors$$=\left(1+1\right)\left(2+1\right)=2\times 3=6$$

Number of even divisors$$=24-6=18$$

Explain why $$3\times 5 \times 7+7$$ is a composite number.

$$3 \times 5 \times 7 + 7 = 105 + 7 = 112$$. $$112$$ is an even number and is therefore a composite number. Also, $$112$$ is divisible by other numbers such as $$2, 4, 7, 8, 14, 16, 28$$ and $$56$$ apart from itself $$112$$ and $$1$$

Hence $$3\times5\times 7+7$$ is a composite number

Find the HCF of $$21,28$$.

$$21 = 3 \times 7$$

$$28 = 4\times 7$$

$$\Rightarrow$$ HCF is $$7$$

Express the given numbers in the form of product of primes
(i) 78 (ii) 75 (iii) 96

$$78=2\times3\times13\\75=3\times5\times5\\96=2\times2\times2\times2\times2\times3$$

Find the H.C.F of $$52,\,48$$

Factors of $$52=2\times 2\times 13$$

Factors of $$48=2\times 2\times 2\times 2\times 3$$

Common factor$$=2\times 2=4$$

$$\therefore$$ H.C.F$$=4$$

Is the statement true or not:
All prime number are odd.

It is false as $$2$$ is an even number and it has only two ($$2$$ and $$1$$) factors $$\Rightarrow 2$$ is an even prime number.
1214878_1396648_ans_2a3afb856728482bb6d215c6b625fc03.jpg

1214878_1396648_ans_2a3afb856728482bb6d215c6b625fc03.jpg

Write first 5 prime numbers .

First 5 prime numbers are 2, 3, 5, 7, 11.

Write all prime numbers between 1 to 50.

We know that a prime number is a number having exactly two factors, $$1$$ and the number itself.

Hence, the prime numbers between $$1$$ to $$50$$ are:

$$2,\,3,\,5,\,7,\,11,\,13,\,17,\,19,\,23,\,29,\,31,\,37,\,41,\,43,\,47$$.

What is a Prime number? Given an example.

Numbers that are divisible only by itself and $$1$$.

Example: $$2, 3, 5, 7, 11, ......$$

Find G.C.D. of $$(120,504,882)$$.

To find = GCD of $$120, 504, 882$$

Factors of:

(1) $$120 = 2\times 2\times 3\times 2\times 5$$

(2) $$504 = 2\times 252 = 8\times 63 = 2^3\times 3^2\times 7$$

(3) $$882 = 2\times 441 = 2\times 3^2\times 7^2$$

$$\therefore GCD = 2\times3\times1=6$$

Find HCF of 72 and 120

$$72=8\times 9=2^{3}\times 3^{2}=2^3\times 3^2\times 5^{0}$$

$$120=12\times 10 =4\times 3\times 2\times 5=2^3\times 3\times 5=2^3\times 3^{1}\times 5^{1}$$
Taking highest powers of each prime factor, we write

$$HCF=2^{3}\times 3^{1}\times 5^{0}=24$$

Which of the following numbers are prime?
(a) $$23$$
(b) $$51$$
(c) $$37$$
(d) $$26$$.

(a)
$$23$$,
$$23=1\times 23$$,
$$23=23\times 1$$
$$23$$ has only two factors, $$1$$ and $$23$$. Therefore, it is a prime number.
(b) $$51$$,
$$51=1\times 51$$,
$$51=3\times 17$$
$$51$$ has four factors, $$1, 3, 17, 51$$. Therefore, it is not a prime number. It is a composite number.
(c) $$37$$
It has only two factors, $$1$$ and $$37$$. Therefore, it is a prime number.
(d) $$26$$
$$26$$ has four factors $$(1, 2, 13, 26)$$. Therefore, it is not a prime number. It is a composite number.

Show that the following numbers are co-primes:
161,192

Numbers are co-primes if their HCF$$=1$$

$$7|161$$ $$2|192$$

__________ _____________

$$23|23$$ $$2|96$$

__________ _____________

$$1$$ $$2|48$$

______________

$$2|24$$

______________

$$2|12$$

_____________

$$2|6$$

_____________

$$3|3$$

_____________

$$1$$

HCF$$=1$$

Yes, they are co-primes.

1209740_1461293_ans_0685e3eac310483ead9421f1985c8f74.jpg

What is the greatest prime number between $$1$$ and $$10$$?

Prime numbers between $$1$$ and $$10$$ are $$2, 3, 5$$ and $$7$$. Among these numbers, $$7$$ is the greatest number.

Express $$31$$ as the sum of three odd primes.

the three odd prime numbers here are $$5$$,$$7$$ and $$19$$

$$31=5+7+19$$.

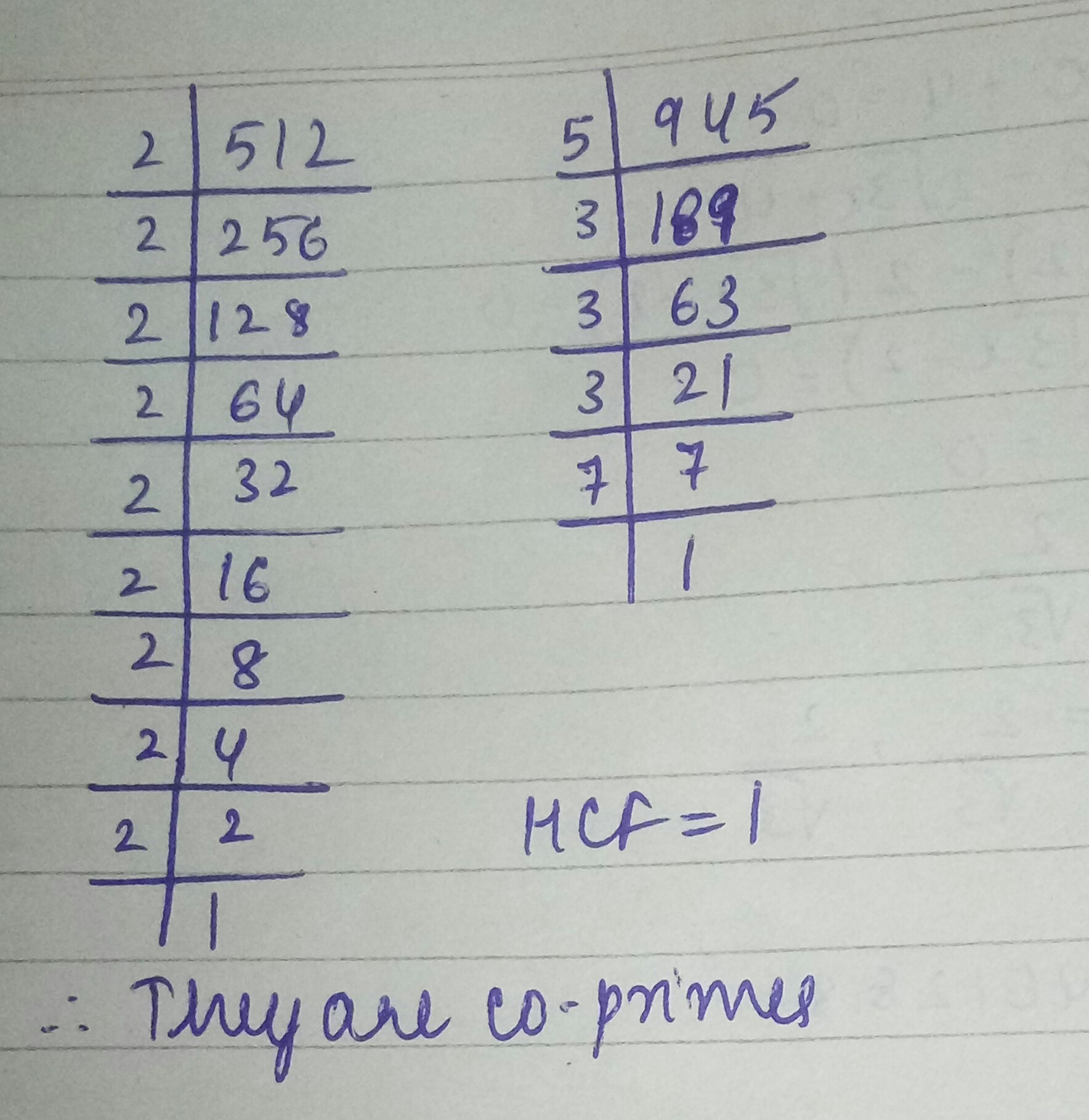
Show that the following pairs are co-primes
512,945

$$2| 512$$ $$5|945$$

__________ ___________

$$2|256$$ $$3|189$$

__________ ___________

$$2| 128$$ $$3|63$$

__________ ____________

$$2|64$$ $$3|21$$

__________ ____________

$$2|32$$ $$7|7$$

__________ ____________

$$2|16$$ $$1$$

__________

$$2|8$$

__________

$$2|4$$

__________

$$2|2$$

__________

$$1$$

HCF$$=1$$

$$\therefore$$ They are co-primes.

1209742_1461297_ans_34c544d06f3b4271a57844f9d0beedb5.jpg

Prime factorization of $$417496$$.

1326941_1494337_ans_063195f4f15e49bbb7d9ee14674e0d5c.JPG

Show that the following pairs are co-primes
59,97

No.s are co-prime if HCF$$=1$$

$$1|59$$ $$1|97$$

___________ ___________

$$59|59$$ $$97|97$$

___________ ___________

$$1$$ $$1$$

HCF$$=1$$

Yes, they are co-primes.

1209737_1461290_ans_1593c3cfac8f4dcb8738048f33bcece6.jpg

Find LCM of $$26,65$$

$$26=2\times 13\\65=13\times 5\\LCM=2\times 5\times 13=130$$

Express the following as the sum of two odd primes.
$$44$$.

the two odd primes are $$37$$ and $$7$$

So, $$37+7$$=$$44$$

What is a composite number?

$$\textbf{Step -1: Defining composite numbers.}$$

$$\text{Composite numbers are numbers that have more than 2 factors}$$

$$\text{That is, they have factors other than 1 and the number itself.}$$

$$\textbf{Hence , composite numbers are numbers that have more than 2 factors.}$$

Fill in the blank.
A number which has only two factors is called a _______.

A number which has only two factors is called a $$Prime$$ $$Number$$

Using divisibility tests, determine if the following number is divisible by $$6$$ or not.
$$4335$$.

The last digit of the number is $$5$$, which is not divisible by $$2$$. Therefore, the given number is also not divisible by $$2$$.

On adding all the digits of the number, the sum obtained is $$15(i.e,4+3+3+5)$$. Since $$15$$ is divisible by $$3$$, the given number is also divisible by $$3$$.
As the number is not divisible by both $$2$$ and $$3$$, therefore it is not divisible by $$6$$.

Find the common factors of $$15$$ and $$25$$.

Factors of $$15=1, 3, 5, 15$$
Factors of $$25=1, 5, 25$$
Common factors$$=1, 5$$.

Express the following number as the sum of three odd primes.
$$53$$.

The three odd prime numbers here are $$31$$, $$19$$ and $$5$$ to make their sum equal to $$53$$.

So,

$$53=3+19+31$$.

Write five pairs of prime numbers less than $$20$$ whose sum is divisibly by $$5$$.

$$3+7=10$$
$$2+3=5$$
$$2+13=15$$
$$3+17=20$$
$$7+13=20$$
$$19+11=30$$.

Fill in the blank.
The smallest composite number is _______.

The smallest composite number in number system is

$$4$$.

Fill in the blank.
The smallest prime number is _______.

The smallest prime number in number system is $$2$$.

Find the common factors of $$20$$ and $$28$$.

Factors of $$20=1, 2, 4, 5, 10, 20$$
Factors of $$28=1, 2, 4, 7, 14, 28$$
Common factors $$=1, 2, 4$$.

Express the following number as the sum of three odd prime.
$$61$$.

The three odd prime numbers here are $$31$$,$$19$$ and $$11$$

$$61=11+19+31$$.

Fill in the blanks.
A number which has more than two factors is called a _______.

A number which has more than two factors is called a

$$Composite$$ $$Number$$

Find the common factors of $$56$$ and $$120$$.

Factors of $$56=1, 2, 4, 7, 8, 14, 28, 56$$
Factors of $$120=1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60, 120$$
Common factors $$=1, 2, 4, 8$$.

Find the common factors of $$35$$ and $$50$$.

Factors of $$35=1, 5, 7, 35$$
Factors of $$50=1, 2, 5, 10, 25, 50$$
Common factors$$=1, 5$$.

Find the HCF of $$91, 112,$$ and $$49$$

The given numbers are $$91,112$$ and $$49$$

$$91=7\times 13$$
$$112=2\times 2\times 2\times 2\times 7$$
$$49=7\times 7$$

Thus, HCF$$=7$$.

Find the common factors of $$5, 15$$ and $$25$$.

$$5, 15$$ and $$25$$
Factors of $$5=1, 5$$
Factors of $$15=1, 3, 5, 15$$
Factors of $$25=1, 5, 25$$
Common factors $$=1, 5$$.

Find the HCF of the following numbers.
$$36, 84$$.

$$36=2\times 3\times 3\times 3$$
$$84=2\times 2\times 3\times 7$$
HCF$$=2\times 2\times 3=12$$.

Find the HCF of $$30$$, $$42$$

$$30=2\times 3\times 5$$
$$42=2\times 3\times 7$$
HCF$$=2\times 3=6$$.

Find the HCF of $$70, 105, 175$$

$$ 70, 105, 175 $$

Factors of $$ 70 = \underline{1}, 2, \underline {5}, 7, 10,14 \underline {35} , 70 $$
Factors of $$ 105 = \underline {1}, 3 , \underline {5} , \underline {7} , 10, 14, \underline {35} , 105 $$
Factors of $$ 175 = \underline {1} , \underline {5} , \underline {7} , 25, \underline {35}, 175 $$
$$ \therefore $$ Common factors $$ 1, 5, 7 ,35 $$
$$ \therefore $$ H.C.F. of $$ 70, 105, 175 $$ is $$ 35 $$

Determine the following numbers are co-prime.
$$81$$ and $$16$$.

Factors of $$81=1, 3, 9, 27, 81$$
Factors of $$16=1, 2, 4, 8, 16$$
Common factors $$=1$$

Therefore, the given two numbers are co-prime.

Determine the following numbers are co-prime.
$$17$$ and $$68$$.

Factors of $$17=1, 17$$
Factors of $$68=1, 2, 4, 17, 34, 68$$
Common factors $$=1, 17$$
As these numbers have a common factor other than $$1$$, the given two numbers are non co-prime.

Find the HCF of the following numbers.
$$18, 48$$.

$$18=2\times 3\times 3$$
$$48=2\times 2\times 2\times 2\times 3$$
HCF$$=2\times 3=6$$.

Test the divisibility of the following number by $$2$$:
$$2398$$

we know that if the unit place digit is divisible by $$2$$ then our given number is divisible by $$2$$.

Here, the unit place the given number is $$8$$ which is divisible by $$2$$

$$\therefore$$ the given number $$2398$$ is divisible by $$2$$.

Test the divisibility of the following number by $$2$$:
$$46821$$

we know that if the unit place digit is divisible by $$2$$ then our given number is divisible by $$2$$.

Here, the unit place the given number is $$1$$ which is not divisible by $$2$$

$$\therefore$$ the given number $$46821$$ is not divisible by $$2$$.

If $$x$$ and $$y$$ are positive integers,and if $$x-y$$ is even, show that $$x^2-y^2$$ is divisible by 4.

1574088_1745433_ans_c5c70427c847444695e623a8c630108a.png

Test the divisibility of the following number by $$2$$:
$$84463$$

we know that if the unit place digit is divisible by $$2$$ then our given number is divisible by $$2$$.

Here, the unit place the given number is $$3$$ which is not divisible by $$2$$

$$\therefore$$ the given number $$84663$$ is not divisible by $$2$$.

Test the divisibility of the following number by $$2$$:
$$79532$$

we know that if the unit place digit is divisible by $$2$$ then our given number is divisible by $$2$$.

Here, the unit place the given number is $$2$$ which is divisible by $$2$$

$$\therefore$$ the given number $$79532$$ is divisible by $$2$$.

Find the HCF of the following numbers.
$$12, 45, 75$$.

$$12=2\times 2\times 3$$
$$45=3\times 3\times 5$$
$$75=3\times 5\times 5$$
HCF$$=2$$.

Test the divisibility of the following number by $$2$$:
$$570$$

we know that if the unit place digit is divisible by $$2$$ then our given number is divisible by $$2$$.

Here, the unit place the given number is $$0$$ which is divisible by $$2$$

$$\therefore$$ the given number $$570$$ is divisible by $$2$$.

Test the divisibility of the following number by $$2$$:
$$94$$

we know that if the unit place digit is divisible by $$2$$ then our given number is divisible by $$2$$.

Here, the unit place the given number is $$4$$ which is divisible by $$2$$

$$\therefore$$ the given number $$94$$ is divisible by $$2$$.

Test the divisibility of the following number by $$2$$:
$$285$$

we know that if the unit place digit is divisible by $$2$$ then our given number is divisible by $$2$$.

Here, the unit place the given number is $$5$$ which is not divisible by $$2$$

$$\therefore$$ the given number $$285$$ is not divisible by $$2$$.

Test the divisibility of the following number by $$2$$:
$$13576$$

we know that if the unit place digit is divisible by $$2$$ then given number is also divisible by $$2$$.

Here, the unit place the given number is $$6$$ which is divisible by $$2$$

$$\therefore$$ The given number $$13576$$ is divisible by $$2$$.

Test the divisibility of the following number by $$5$$:
$$1056$$

we know that if the unit place digit is divisible by $$5$$ then our given number is divisible by $$5$$.

Here, the unit place the given number is $$6$$ which is not divisible by $$5$$

$$\therefore$$ the given number $$1056$$ is not divisible by $$5$$.

Test the divisibility of the following number by $$5$$:
$$95$$

we know that if the unit place digit is divisible by $$5$$ then our given number is divisible by $$5$$.

Here, the unit place the given number is $$5$$ which is divisible by $$5$$

$$\therefore$$ the given number $$95$$ is divisible by $$5$$.

Test the divisibility of the following number by $$3$$:
$$83$$

we know that if the sum of digit of the number is divisible by $$3$$ then the number is divisible by $$3$$.

Sum of the digit of $$83$$ is $$11$$, which is not divisible by $$3$$

$$\therefore$$ the given number $$83$$ is not divisible by $$3$$.

Test the divisibility of the following number by $$5$$:
$$55053$$

we know that if the unit place digit is divisible by $$5$$ then our given number is divisible by $$5$$.

Here, the unit place the given number is $$3$$ which is not divisible by $$5$$

$$\therefore$$ the given number $$55053$$ is not divisible by $$5$$.

Test the divisibility of the following number by $$5$$:
$$35790$$

we know that if the unit place digit is divisible by $$5$$ then our given number is divisible by $$5$$.

Here, the unit place the given number is $$0$$ which is divisible by $$5$$

$$\therefore$$ the given number $$35790$$ is divisible by $$5$$.

Test the divisibility of the following number by $$5$$:
$$470$$

we know that if the unit place digit is divisible by $$5$$ then our given number is divisible by $$5$$.

Here, the unit place the given number is $$0$$ which is divisible by $$5$$

$$\therefore$$ the given number $$470$$ is divisible by $$5$$.

Test the divisibility of the following number by $$3$$:
$$378$$

we know that if the sum of digit of the number is divisible by $$3$$ then the number is divisible by $$3$$.

Sum of the digit of $$378$$ is $$18$$, which is divisible by $$3$$

$$\therefore$$ the given number $$378$$ is divisible by $$3$$.

Test the divisibility of the following number by $$5$$:
$$42658$$

we know that if the unit place digit is divisible by $$5$$ then our given number is divisible by $$5$$.

Here, the unit place the given number is $$8$$ which is not divisible by $$5$$

$$\therefore$$ the given number $$42658$$ is not divisible by $$5$$.

Test the divisibility of the following number by $$5$$:
$$77990$$

we know that if the unit place digit is divisible by $$5$$ then our given number is divisible by $$5$$.

Here, the unit place the given number is $$0$$ which is divisible by $$5$$

$$\therefore$$ the given number $$77990$$ is divisible by $$5$$.

Test the divisibility of the following number by $$5$$:
$$2735$$

we know that if the unit place digit is divisible by $$5$$ then our given number is divisible by $$5$$.

Here, the unit place the given number is $$5$$ which is divisible by $$5$$

$$\therefore$$ the given number $$2735$$ is divisible by $$5$$.

What are prime numbers? Give ten examples

A number which has only two factors namely $$1$$ and itself is called as prime numbers
Examples: $$2, 3, 5, 7, 11, 13, 17, 19, 23$$ and $$29$$ are prime numbers

Test the divisibility of the following number by $$9$$:
$$7524$$

we know that if the sum of digit of the number is divisible by $$9$$ then the number is divisible by $$9$$.

Sum of the digit of $$7524$$ is $$18$$, which is divisible by $$9$$

$$\therefore$$ the given number $$7524$$ is divisible by $$9$$.

Test the divisibility of the following number by $$3$$
$$20701$$

A number is divisible by $$3$$ when sum of its digits is divisible by $$3$$
Sum of its digits $$= 2 + 0 + 7 + 0 + 1 = 10$$
Since $$10$$ is not divisible by $$3$$
$$\therefore 20701$$ is not divisible by $$3$$

Test the divisibility of the following number by $$3$$:
$$474$$

we know that if the sum of digit of the number is divisible by $$3$$ then the number is divisible by $$3$$.

Sum of the digits of $$474$$ is $$15$$, which is divisible by $$3$$

$$\therefore$$ the given number $$474$$ is divisible by $$3$$.

Test the divisibility of the following number by $$3$$:
$$67035$$

we know that if the sum of digit of the number is divisible by $$3$$ then the number is divisible by $$3$$.

Sum of the digit of $$67035$$ is $$21$$, which is divisible by $$3$$

$$\therefore$$ the given number $$67035$$ is divisible by $$3$$.

Test the divisibility of the following number by $$3$$:
$$1693$$

we know that if the sum of digit of the number is divisible by $$3$$ then the number is divisible by $$3$$.

Sum of the digit of $$1693$$ is $$19$$, which is not divisible by $$3$$

$$\therefore$$ the given number $$1693$$ is not divisible by $$3$$.

Test the divisibility of the following number by $$3$$:
$$20345$$

we know that if the sum of digit of the number is divisible by $$3$$ then the number is divisible by $$3$$.

Sum of the digit of $$20345$$ is $$14$$, which is not divisible by $$3$$

$$\therefore$$ the given number $$20345$$ is not divisible by $$3$$.

Test the divisibility of the following number by $$3$$
$$733$$

A number is divisible by $$3$$ when sum of its digits is divisible by $$3$$
Sum of its digits $$= 7 + 3 + 3 = 13$$
Since $$13$$ is not divisible by $$3$$
$$\therefore 733$$ is not divisible by $$3$$

Test the divisibility of the following number by $$9$$:
$$327$$

we know that if the sum of digit of the number is divisible by $$9$$ then the number is divisible by $$9$$.

Sum of the digit of $$327$$ is $$12$$, which is not divisible by $$9$$

$$\therefore$$ the given number $$327$$ is not divisible by $$9$$.

Test the divisibility of the following number by 2:
$$2650$$

A number is divisible by $$2$$ only if its ones digit is $$0, 2, 4, 6$$ and $$8$$
Since $$0$$ is in one's digits place in $$2650$$
$$\therefore$$ It is divisible by $$2$$

What is greatest prime number between $$ 1 $$ and $$ 15 $$ ?

Greatest prime number between $$ 1 $$ and $$ 15 $$ is $$ 13 $$

Test the divisibility of the following number by $$9:$$
$$647514$$

If the sum of its digits is divisible by $$9$$ then the given number is divisible by $$9$$
$$647514$$
Sum of its digits $$= 6 + 4 + 7 + 5 + 1 + 4 = 27$$
$$27$$ is divisible by $$9$$
Hence $$647514$$ is divisible by $$9$$

Test the divisibility of the following number by $$9:$$
$$3333$$

If the sum of its digits is divisible by $$9$$ then the given number is divisible by $$9$$
$$3333$$
Sum of its digits $$= 3 + 3 + 3 + 3 = 12$$
$$12$$ is not divisible by $$9$$
Hence $$3333$$ is not divisible by $$9$$

Test the divisibility of the following number by $$5$$:
$$4965$$

If the ones digit of a number is $$0$$ or $$5$$ then the number is divisible by $$5$$
Since $$5$$ is in ones place
$$\therefore 4965$$ is divisible by $$5$$

Which of the following numbers are prime?
$$ 29 $$

We have , $$ 29 = 1 \times 29 $$
$$ \Rightarrow \, 29 $$ has exactly two factors $$ 1 $$ and $$ 29 $$ itself.
$$ \therefore \, 29 $$ is a prime number.

Test the divisibility of the following number by $$9:$$
$$2358$$

If the sum of its digits is divisible by $$9$$ then the given number is divisible by $$9$$
$$2358$$
Sum of its digits $$= 2 + 3 + 5 + 8 = 18$$
$$18$$ is divisible by $$9$$
Hence $$2358$$ is divisible by $$9$$

Test the divisibility of the following number by $$9:$$
$$257106$$

If the sum of its digits is divisible by $$9$$ then the given number is divisible by $$9$$
$$257106$$
Sum of its digits $$= 2 + 5 + 7 + 1 + 6 = 21$$
$$21$$ is not divisible by $$9$$
Hence $$257106$$ is not divisible by $$9$$

Express each of the following numbers as the sum of twin primes :
$$ 24 $$

$$ 11$$ and $$13$$ area twin prime numbers
$$ \Rightarrow \, 24 = 11 + 13 $$

Which of the following pairs of numbers are co-prime ?
$$ 12 $$ and $$ 35 $$

$$ 12 $$ and $$ 35 $$
The factors of $$ 12 $$ are $$ 1 , 2 , 3 , 4, 6, 12 $$
The factor of $$ 35 $$ are $$ 1 , 5 , 7 , 35 $$
Since , the common factor of $$ 12 $$ and $$ 35 $$ is $$ 1 $$
$$ \therefore \, $$ They are co-prime.

Which of the following numbers are prime?
$$ 61 $$

We have , $$ 61 = 1 \times 61 $$
$$ \Rightarrow \, 61 $$ has exactly two factors $$ 1 $$ and $$ 61 $$ itself.
$$ \therefore \, 61 $$ is a prime number.

Which of the following pairs of numbers are co-prime ?
$$ 515 $$ and $$ 516 $$

$$ 515 $$ and $$ 516 $$
The factors of $$ 515 $$ are $$ 1 , 5 , 103 , 515 $$
The factors of $$ 516 $$ are $$ 1 , 2 , 3 , 4 , 6 , 12 , 43 , 86 , 129 , 172 , 258 , 516 $$
Since , the common factor of $$ 515 $$ and $$ 516 $$ are only $$ 1 $$
$$ \therefore \, $$ So , they are co-prime.

Which of the following pairs of numbers are co-prime ?
$$ 17 $$ and $$ 85 $$

$$ 17 $$ and $$ 85 $$
The factors of $$ 17 $$ are $$ 1 , 17 $$
The factors of $$ 85 $$ are $$ 1 , 5 , 17 , 85 $$
The common factors of $$ 17 $$ and $$ 85 $$ are $$ 1 $$ and $$ 17 $$
$$ \therefore \, $$ They are not co-prime because they have more than $$ 1$$ common factor.

Which of the following pairs of numbers are co-prime ?
$$ 15 $$ and $$ 37 $$

$$ 15 $$ and $$ 37 $$
The factor of $$ 15 $$ are $$ 1 , 3 , 5 , 15 $$
The factor of $$ 37 $$ are $$ 1 , 37 $$
The common factor of $$ 15 $$ and $$ 37 $$ is $$ 1 $$
$$ \therefore \, $$ They are co-prime.

Which of the following numbers are prime?
$$ 57 $$

We have , $$ 57 = 1 \times 57 = 3 \times 19 = 57 $$
$$ \therefore \, $$ Factors of $$ 57 $$ are $$ 1 , 3 , 19 $$ and $$ 57 $$
$$ \Rightarrow \, 57 $$ has more than two factors
$$ \therefore \, 57 $$ is not a prime.

Which of the following numbers are prime?
$$ 43 $$

We have , $$ 43 = 1 \times 43 $$
$$ \Rightarrow \, 43 $$ has exactly two factors $$ 1 $$ and $$ 43 $$ itself.
$$ \therefore \,43 $$ is a prime number.

Which of the following pairs of numbers are co-prime ?
$$ 215 $$ and $$ 415 $$

$$ 215 $$ and $$ 415 $$
The factors of $$215 $$ are $$ 1 , 5 , 43 , 215 $$
The factors of $$ 415 $$ are $$ 1 , 5 , 83 , 415 $$
Since , the common factor of $$ 215 $$ and $$ 415 $$ are $$ 1 $$ and $$ 5 $$
$$ \therefore \, $$ So , they are not co-prime.

Which of the following pairs of numbers are co-prime ?
$$ 27 $$ and $$ 32 $$

$$ 27 $$ and $$ 32 $$
The factor of $$ 27 $$ are $$ 1 , 3 , 9 , 27 $$
The factors of $$ 32 $$ are $$ 1 , 2 , 4 , 8 , 16 , 32 $$
Since , the common factor of $$ 27 $$ and $$ 32 $$ is only $$ 1$$.
They are co-prime

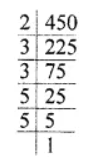
Find the prime factorization of the number :
$$ 450 $$

$$ \therefore \, 450 = 2 \times 3 \times 3 \times 5 \times 5 $$
1751995_1789104_ans_16033c2487a9454eb2410077cbd1c507.png

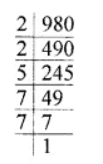
Find the prime factorization of the number :
$$ 980 $$

$$ \therefore \, 980 = 2 \times 2 \times 5 \times 7 \times 7 $$
1751990_1789107_ans_49d4d65df3cf48bc9159ea6ea7eeb4b8.png

Number of prime between $$1$$ to $$100$$ is ____.

Prime number between $$1$$ to $$100$$ are $$2,\ 3,\ 5,\ 7,\ 11,\ 13,\ 17,\ 19,\ 23, \ 29,\ 31,\ 37,\ 41,\ 43,\ 47,\ 53,\ 59,\ 61,\ 67,\ 71,\ 73,\ 79,\ 83,\ 89,\ and\\ 97.$$
so, total $$25$$ prime number between $$1$$ to $$100$$

A number for which the sum of all its factors is equal to twice the number is called a _______ number.

A number for which the sum of all its factors is equal to twice the number is called a Perfect number.

Find the prime factorization of the number :
$$ 72 $$

$$ \therefore \, 72 = 2 \times 2 \times 2 \times 3 \times 3 $$
1752005_1789097_ans_9b8235204ae7458bae47a7ab1fce05cd.png

Two numbers having only $$1$$ as a common factor are called ______ numbers.

Two numbers having only $$1$$ as a common factor are called co-prime numbers.

Find the prime factorization of the number :
$$ 13500 $$

$$ \therefore \, 13500 = 2 \times 2 \times 3 \times 3 \times 3 \times 5 \times 5 \times 5 $$
1751980_1789116_ans_c242b2163d9f4603abe09db0382a1885.png

$$2$$ is the only _____ number which is even.

$$2$$ is the only Prime number which is even.

Find the prime factorization of the number :
$$ 8712 $$

From the above prime factorization we can summarize that,

$$ 8712 = 2 \times 2 \times 2 \times 3 \times 3 \times 11 \times 11 $$
1751985_1789109_ans_14a2c02a86c94e2b84212243ea8d26ea.png

A number is divisible by $$5$$ if it has or _ in its one's place.

A number is divisible by $$5$$ if it has Zero or five in its one's place.

Using the divisibility tests, determine if the following number is divisible by $$4$$?
$$21084$$

According to divisible property, only those numbers are divisible by $$4$$ if there last two digits divisible by $$4$$ or zero.
$$21084$$ is divisible by $$$$ because last two $$84$$ digits divisible by $$4$$.

Using the divisibility tests. Determine if the following number is divisible by $$9$$?
$$672$$

According to divisible property, only those numbers are divisible by $$9$$ if there last two digits divisible by $$9$$.
$$672$$
Since, $$(6+7+2=15), 15$$ are divisible by $$9$$, therefore $$672$$ is also not divisible by $$9$$.

Is the number given below divisible by $$ 3 $$ and $$ 9 $$:
$$ 59031 $$

A number is divisible by $$ 3 $$ and $$9$$ if the sum of its digit is divisible by both $$ 3 $$ and $$ 9 $$.

$$ 59031 = 5 + 9 + 0 + 3 + 1 = 18 $$ which is divisible by both $$3$$ and $$9$$

Therefore the number $$59021$$ is divisible by $$ 3 , 9 $$.

Write all factors of :
$$ 88 $$

88={1,2,4,8,11,22,44,88}88={1,2,4,8,11,22,44,88}

Using the divisibility tests. Determine if the following number is divisible by $$9$$?
$$5652$$

According to divisible property, only those numbers are divisible by $$9$$ if there last two digits divisible by $$9$$.
$$5652$$
$$5652\ (5+6+5+2=18), 18$$ are divisible by $$9$$, therefore $$5652$$ is also divisible by $$9$$.

Examine the following numbers for divisibility by $$ 6 $$ :
$$ 5034126 $$

A number is divided by $$ 6 $$ if it is divisible by $$ 2 $$ as well as by $$ 3 $$.
$$ 5034126 $$ : divisible by $$ 6 $$ , as it is divisible by both $$ 2 $$ and $$ 3 $$.
The last digit of $$ 5034126 $$ is $$ 6 $$, which is divisible by $$ 2 $$.
Now , sum of $$ 5034126 = 5 + 0 + 3 + 4 + 1 + 2 + 6 = 21 $$
$$ 21 $$ is divisible by $$ 3$$.
Hence , given number $$ 5034126 $$ is divisible by $$ 6 $$.

Using the divisibility tests, determine if the following number is divisible by $$4$$?
$$31795012$$

According to divisible property, only those numbers are divisible by $$4$$ if there last two digits divisible by $$4$$ or zero.
$$31795012$$ is divisible by $$4$$ because last two $$12$$ digits divisible by $$4$$.

Using the divisibility tests, determine if the following number is divisible by $$4$$?
$$4096$$

According to divisible property, only those numbers are divisible by $$4$$ if there last two digits divisible by $$4$$ or zero.
$$4096$$ is divisible by $$$$ because last two $$96$$ digits divisible by $$4$$.

Which of the following numbers are prime :
$$ 101 $$

We have , $$ 101 = 1 \times 101 $$
$$ \Rightarrow \, 101 $$ has exactly two factors $$ 1 $$ and $$ 101 $$ itself.
$$ \therefore \,101 $$ is a prime number

Which of the following numbers are prime?
$$ 323 $$

We have , $$ 323 = 1 \times 323 = 17 \times 19 $$
$$ \therefore \, $$ Factors of $$ 323 $$ are $$ 1 , 17 , 19 , 323 $$
$$ \Rightarrow \, 323 $$ has more than two factors .
$$ \therefore \, 323 $$ is not a prime number.

Using the common factor method, find the H.C.F. of:
$$16$$ and $$35$$

Common factors of $$16$$ and $$35$$ are as follows:
$$F (16) = 1, 2, 4, 8, 16$$
$$F (35) = 1, 5, 7, 35$$
The common factors between $$16$$ and $$35 = 1$$
$$∴$$ The $$H.C.F.$$ of $$16$$ and $$35 = 1$$

Which of the following numbers are prime?
$$ 397 $$

We have , $$ 397 = 1 \times 397 $$
$$ \Rightarrow \, 397 $$ has exactly two factors $$ 1 $$ and $$ 397 $$ itself.
$$ \therefore \, 397 $$ is a prime number

$$20x3$$ is a multiple of $$3$$ if the digit $$x $$ is _ or or ___ .

A number is divisible by $$3$$ if the sum of its digits is also divisible by $$3$$

Therefore, $$2+0+x+3=$$ is multiple of $$3$$

$$x+5=6,9,12$$, for other multiples of $$3$$, $$x$$ becomes negative or double digit.

Hence $$x=1, 4$$ or $$7$$

Which of the following numbers are prime?
$$ 251 $$

We have , $$ 251 = 1 \times 251 $$
$$ \Rightarrow \, 251 $$ has exactly two factors $$ 1 $$ and $$ 251 $$ itself.
$$ \therefore \,251 $$ is a prime number

$$1x35$$ is divisible by $$9$$, if $$x= $$ ______ .

A number is divisible by $$9$$ if the sum of its digits is also divisible by $$9$$

Therefore, $$1+x+3+5=$$ A number multiple of $$9$$

$$\implies x+9=9$$, as for other multiples of $$9$$, $$x$$ will become double digit number or negative number.

According the question, it is a single digit number.

Hence, $$x=0$$.

In each of the following replace $$ \ast $$ by (i) the smallest digit (ii) the greatest digit so that the number formed is divisible by $$ 3 $$ :
$$ 4 \ast 672 $$

(i) Smallest digit
Sum of the given digits $$ = 4 + 6 + 7 + 2 = 19 $$
$$ \because \, 19 $$ is not divisible by $$ 3 $$
$$ \therefore \, $$ Smallest digit (non-zero) is $$ = 2 $$

(ii) Greatest digit
The greatest digit is $$ 8 $$
i.e., $$ 19 + 8 = 27 $$ which is divisible by $$ 3 $$

Fill in the blanks :
............... is factor of every number.

One is factor of every number.

Fill in the blanks :
Every number is a factor of ..................

Every number is a factor of itself

Using the common factor method, find the H.C.F. of:
$$25$$ and $$20$$

Common factors of $$25$$ and $$20$$ are as follows:
Factors of $$ (25) = 1, 5, 25$$
Factors of $$ (20) = 1, 2, 4, 5, 10, 20$$
The common factors between $$25$$ and $$20 = 1, 5$$
$$∴$$ The $$H.C.F.$$ of $$25$$ and $$20 = 5$$

Show that $$45$$ and $$56$$ are $$co-prime$$ numbers.

The $$H.C.F.$$ of two $$co-prime$$ numbers is always $$1$$

The prime factors $$45$$ and $$56$$ are as follows:
$$45=3\times 3\times 5$$

$$56=2\times 2\times 2\times 7$$

There is no common factor in $$45$$ and $$56$$

Hence,$$H.C.F.$$ of $$45$$ and $$56 = 1$$
$$∴ 45$$ and $$56$$ are $$co-prime$$ numbers

Using the common factor method, find the H.C.F. of:
$$8, 12$$ and $$18$$

Common factors between $$8, 12$$ and $$18$$ are as follows:
$$F (8) = 1, 2, 4, 8$$
$$F (12) = 1, 2, 3, 4, 6, 12$$
$$F (18) = 1, 2, 3, 6, 9, 18$$
Common factors between $$8, 12$$ and $$18 = 1, 2$$
$$∴$$ The $$H.C.F.$$ of $$8, 12$$ and $$18 = 2$$

Fill in the blanks :
Factor of a number is ............... of ...............

Factor of a number is an exact division of the number

Write all prime numbers:
(i) less than $$25$$
(ii) between $$15$$ and $$35$$
(iii) between $$8$$ and $$76$$

(i) $$2, 3, 5, 7, 11, 13, 17, 19$$ and $$23$$ are the prime numbers less than $$25$$
(ii) $$17, 19, 23, 29$$ and $$31$$ are the prime numbers between $$15$$ and $$35$$
(iii) $$11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71$$ and $$73$$ are the prime numbers between $$8$$ and $$76$$

Write the prime numbers from:
(i) $$5$$ to $$45$$
(ii) $$2$$ to $$32$$
(iii) $$8$$ to $$48$$
(iv) $$9$$ to $$59$$

(i) The prime numbers from $$5$$ to $$45$$ are $$5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41$$ and $$43$$
(ii) The prime numbers from $$2$$ to $$32$$ are $$2, 3, 5, 7, 11, 13, 17, 19, 23, 29$$ and $$31$$
(iii) The prime numbers from $$8$$ to $$48$$ are $$11, 13, 17, 19, 23, 29, 31, 37, 41, 43$$ and $$47$$
(iv) The prime numbers from $$9$$ to $$59$$ are $$11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53$$ and $$59$$

Using the common factor method, find the H.C.F. of:
$$24, 36, 45$$ and $$60$$

Common factors between $$24, 36, 45$$ and $$60$$ are as follows:
$$F (24) = 1, 2, 3, 4, 6, 8, 12, 24$$
$$F (36) = 1, 2, 3, 4, 6, 12, 18, 36$$
$$F (45) = 1, 3, 5, 9, 15, 45$$
$$F (60) = 1, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60$$
Common factors between $$24, 36, 45,$$ and $$60 = 1, 3$$
$$∴$$ The $$H.C.F.$$ of $$24, 36, 45$$ and $$60 = 3$$

Using the common factor method, find the H.C.F. of:
$$27$$ and $$75$$

Common factors between $$27$$ and $$75$$ are as follows:
$$F (27) = 1, 3, 9, 27$$
$$F (75) = 1, 3, 5, 15, 25, 75$$
The common factors between $$27$$ and $$75 = 1, 3$$
$$∴$$ The $$H.C.F.$$ of $$27$$ and $$75 = 3$$

Write all the factors of :
$$ 16 $$

$$1\times16=16$$
$$2\times8=16$$
$$4\times4=16$$
$$\therefore 1 , 2 , 4 , 8 $$ and $$ 16 $$ is a factor of $$16$$

Write all the factors of :
$$39$$

$$1\times39=39$$
$$3\times13=39$$
$$ 1 , 3 , 13 , 39 $$ is a factor of $$39$$

Write all the factors of :
$$ 48$$

$$1\times48=48$$
$$2\times24=48$$
$$3\times16=48$$
$$4\times12=48$$
$$6\times8=48$$
$$ 1 , 2 , 3 , 4 , 6 , 8 , 12 , 16 , 24 $$ and $$48 $$ are factors of $$48$$

Find which of the following numbers are divisible by $$2$$ :
$$ 352 $$

The given number $$ = 352 $$
Digit at unit’s place $$ = 2 $$ (even)
Hence, the number is divisible by $$ 2 $$

Without actual division, show that each of the following numbers is divisible by $$8$$
$$ 240008 $$

$$ 240008 $$
This can written as
$$ = 240000 + 8 $$
$$ = 8 \times (30000 + 1) $$
$$ = 8 \times 30001 $$
Clearly , $$ 240008 $$ is divisible by $$ 8 $$

Without actual division, show that each of the following numbers is divisible by $$8$$
$$ 56008 $$

$$ 56008 $$
This can be written as
$$ = 56000 + 8 $$
$$ = 8 \times (7000 + 1) $$
$$ = 8 \times 7001 $$
Clearly , $$ 56008 $$ is divisible by $$ 8 $$

Write all the factors of :
$$98 $$

$$1\times98=98$$
$$2\times49=98$$
$$7\times14=98$$
$$\therefore 1 , 2 , 7 , 14 , 49 ,$$ and $$ 98 $$ is a factor of $$98$$

Without actual division, show that each of the following numbers is divisible by $$8$$
$$ 1608 $$

$$ 1608 $$
This can be written as
$$ = 1600 + 8 $$
$$ = 8 \times (200 + 1) $$
$$ = 8 \times 201 $$
Clearly , $$ 1608 $$ is divisible by $$ 8 $$

Fill in the blanks :
For every number , its factor are .............. and its multiples are .................

For every number , its factor are finite and its multiple are infinite

Write all the factors of :
$$ 64 $$

$$1\times64=64$$
$$2\times32=64$$
$$4\times16=64$$
$$8\times8=64$$
$$\therefore 1 , 2 , 4 , 8 , 16 , 32 ,$$ and $$ 64 $$ is a factor of $$64$$

Find which of the following number are divisible by $$ 8 $$ :
$$ 92760 $$

The given number $$ = 92760 $$

The number formed by hundred’s, ten’s and unit digit is $$ 760 $$, which is divisible by $$8$$

Hence, $$ 92760 $$ is divisible by $$8$$

Find which of the following number are divisible by $$ 4 $$ :
$$ 9232 $$

The given number $$ = 9232 $$

The number formed by ten’s and unit digit is $$32$$, which is divisible by $$4$$

Hence, the number is divisible by $$4$$

Find which of the following number are divisible by $$ 4 $$ :
$$ 222 $$

The given number $$ = 222 $$
The number formed by ten’s and unit digit is $$ 22 $$, which is not divisible by $$4$$.
Hence, the number is not divisible by $$4$$

Find which of the following number are divisible by $$ 8 $$ :
$$ 2536 $$

The given number $$ = 2536 $$

The number formed by hundred’s, ten’s and unit digit is $$536$$, which is divisible by $$8$$

Hence, $$2536$$ is divisible by $$8$$

Find which of the following numbers are divisible by $$2$$ :
$$ 523 $$

The given number $$ = 523 $$
Digit at unit’s place $$ = 3 $$ (odd)
Hence, the number is not divisible by $$2$$

Find which of the following numbers are divisible by $$2$$ :
$$ 649$$

The given number $$ = 649 $$
Digit at unit’s place $$ = 9 $$ (odd)
Hence, the number is not divisible by $$2$$

Find which of the following numbers are divisible by $$2$$ :
$$496 $$

The given number $$ = 496 $$
Digit at unit’s place $$ = 6 $$ (even)
Hence, the number is divisible by $$2$$

Find which of the following number are divisible by $$ 8 $$ :
$$ 324 $$

The given number $$ = 324 $$

The number formed by hundred’s, ten’s and unit digit is $$ 324 $$, which is not divisible by $$8$$

Hence, $$324$$ is not divisible by $$8$$

Find which of the following number are divisible by $$ 4 $$ :
$$ 678 $$

The given number $$ = 678 $$

The number formed by ten’s and unit digit is $$78$$, which is not divisible by $$4$$

Hence, the number is not divisible by $$4$$

Find which of the following number are divisible by $$ 4 $$ :
$$532 $$

The given number $$ = 532 $$

The number formed by ten’s and unit digit is $$32$$, which is divisible by $$4$$.

Hence, the number is divisible by $$4$$

Find which of the following number are divisible by $$ 9 $$ :
$$ 53247 $$

The given number $$ = 53247 $$

For a number to be divisible by $$9$$, sum of digits must be divisible by $$9$$

Sum of digits $$ = 5 + 3 + 2 + 4 + 7 = 21 $$

Since $$21$$ is not divisible by $$ 9 $$

Hence, $$53247$$ is not divisible by $$9$$

Find which of the following number are divisible by $$ 9 $$ :
$$ 4968 $$

The given number $$ = 4968 $$

For a number to be divisible by $$9$$, sum of digits must be divisible by $$9$$

Sum of digits $$ = 4 + 9 + 6 + 8 = 27 $$

Since $$27$$ is divisible by $$9$$

Hence, $$ 4968 $$ is divisible by $$9$$

Find which of the following number are divisible by $$ 3 $$ :
$$ 221 $$

The given number $$ = 221 $$

For a number to be divisible by $$3$$, sum of digits must be divisible by $$3$$

Sum of digits $$ = 2 + 2 + 1 = 5 $$

Since $$5$$ is not divisible by $$3$$

Hence, $$ 221 $$ is not divisible by $$3$$

Find which of the following number are divisible by $$ 6 $$ :
$$ 2010 $$

A number which is divisible by both $$2$$ and $$3$$ or both then the given number is divisible by $$6$$

Last digit is 0, hence divisible by 2.

The given number $$ = 2010 $$

Sum of digits $$= 2 + 0 + 1 + 0 = 3 $$

which is divisible by $$3$$

Therefore, $$ 2010 $$ is divisible by $$6$$

Find which of the following number are divisible by $$ 3 $$ :
$$ 543 $$

The given number $$ = 543 $$

For a number to be divisible by $$3$$, sum of digits must be divisible by $$3$$

Sum of digits $$ = 5 + 4 + 3 = 12 $$

Since $$12$$ is divisible by $$3$$

Hence, $$543$$ is divisible by $$3$$

Find which of the following number are divisible by $$ 6 $$ :
$$ 324 $$

A number which is divisible by both $$2$$ and $$3$$ or then the given number is divisible by $$6$$

Last digit is 4, hence divisible by 2.

The given number $$ = 324 $$

Sum of digits $$ = 3 + 2 + 4 = 9 $$

which is divisible by $$3$$

Therefore, $$324$$ is divisible by $$6$$

Find which of the following number are divisible by $$ 9 $$ :
$$ 200314 $$

The given number $$ = 200314 $$

For a number to be divisible by $$9$$, sum of digits must be divisible by $$9$$

Sum of digits $$ = 2 + 0 + 0 + 3 + 1 + 4 = 10 $$

Since $$10$$ is not divisible by $$9$$

Hence, $$ 200314 $$ is not divisible by $$9$$

Find which of the following number are divisible by $$ 3 $$ :
$$ 92349 $$

The given number $$ 92349 $$

For a number to be divisible by $$3$$, sum of digits must be divisible by $$3$$

Sum of digits $$ = 9 + 2 + 3 + 4 + 9 = 27 $$

Since $$27$$ is divisible by $$3$$

Hence, $$92349$$ is divisible by $$3$$

Find which of the following number are divisible by $$ 9 $$ :
$$ 1332 $$

The given number $$ = 1332 $$

For a number to be divisible by $$9$$, sum of digits must be divisible by $$9$$

Sum of digits $$ = 1 + 3 + 3 + 2 = 9 $$

Since $$9$$ is divisible by $$9$$

Hence, $$1332$$ is divisible by $$9$$

Find which of the following number are divisible by $$ 8 $$ :
$$ 444320 $$

The given number $$ = 444320 $$

The number formed by hundred’s, ten’s and unit digit is $$320$$, which is divisible by $$8$$

Hence, $$ 444320 $$ is divisible by $$8$$

Find which of the following number are divisible by $$ 5 $$ :
$$ 66666 $$

The given number $$ = 66666 $$

For a number to be divisible by $$5$$, unit digit must be $$0$$ or $$5$$

Here, unit digit is $$6$$

Therefore, $$ 66666 $$ is not divisible by $$5$$

Write the following terminating decimal in the form of $$\frac{p}{q},q\neq 0$$ and $$p,q$$ are co primes.
$$0.4$$

$$0.4=\dfrac4{10}=\dfrac4{2*5}=\dfrac25$$

The smallest prime number is __

Prime number is a number which has only two divisor, 1 and the number itself.

The smallest prime number is $$ 2 $$

Find which of the following number are divisible by $$ 5 $$ :
$$ 9207 $$

The given number $$ = 9207 $$

For a number to be divisible by $$5$$, unit digit must be $$0$$ or $$5$$

Here, unit digit is $$7$$

Therefore, $$9207$$ is not divisible by $$5$$

Find which of the following number are divisible by $$ 6 $$ :
$$ 15505 $$

A number which is divisible by both $$2$$ and $$3$$ or both then the given number is divisible by $$6$$

The given number $$ = 15505 $$

Sum of digits $$ = 1 + 5 + 5 + 0 + 5 = 16 $$

which is not divisible by $$3$$

Therefore, $$15505$$ is not divisible by $$6$$

Find which of the following number are divisible by $$ 5 $$ :
$$ 755 $$

The given number $$ = 755 $$

For a number to be divisible by $$5$$, unit digit must be $$0$$ or $$5$$

Here, unit digit is $$5$$

Therefore, $$755$$ is divisible by $$5$$

Write the set of odd factors of 72.

$$1 \times 72 = 72$$
$$2 \times 36 = 72$$
$$3 \times 24 = 72$$
$$4 \times 18 = 72$$
$$6 \times 12 = 72$$
$$8 \times 9 = 72$$
Factors of $$72 $$ are $$ 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 38, 72$$
Set of odd factors of $$72 = \left \{ 1, 3, 9 \right \}$$

Find which of the following number are divisible by $$ 5 $$ :
$$5080$$

The given number $$ = 5080 $$

For a number to be divisible by $$5$$, unit digit must be $$0$$ or $$5$$

Here, unit digit is $$0$$

Therefore, $$ 5080 $$ is divisible by $$5$$

Write the set of even factors of 124.

$$1 \times 124 = 124$$
$$2 \times 62 = 124$$
$$4 \times 31 = 124$$
Factors of $$124 = 1, 2, 4, 31, 62, 124$$
Set of even factors of $$124 = \left \{ 2, 4, 62, 124 \right \}$$

Find which of the following number are divisible by $$ 6 $$ :
$$ 33278 $$

A number which is divisible by both $$2$$ and $$3$$ or both then the given number is divisible by $$6$$

The given number $$ = 33278 $$

Sum of digits $$ = 3 + 3 + 2 + 7 + 8 = 23 $$

Unit digit is $$3$$ , which is odd

Therefore, $$ 33278 $$ is not divisible by $$6$$

Write down the next prime number after $$19$$.

Ans :- 23

Next prime number after 19 is 23.

Prove that an integer is divisible by 9 if and only if the sum of its digits is divisible by 9.

Let $$a=a_{n} ........ a_{3}a_{2}a_{1}$$ be an integer
[Note a is not the product of $$a_{1}, a_{2}, a_{3}, ........a_{n} but a_{1}, a_{2}, a_{3}, ........a_{n} $$ are digits in the value of a. For example 368 is not the product of 3, 6 and 8 rather 3, 6, 8 are digits in value of 368
$$=8+6\times 10+3\times (10)^{2}$$ ]
$$a=a_{n}....a_{3}a_{2}a_{1}$$
$$=a_{1}+(10)^{1}a_{2}+(10)^{2}a_{3}+(10)^{3}a_{4}+.....+(10)^{n-1}a_{n}$$
$$=a_{1}+10a_{2}+100a_{3}+1000a_{4}+.........$$
$$=a_{1}+(a_{2}+9a_{2})+(a_{3}+99a_{3})+(a_{4}+999a_{4})+..........$$
$$=(a_{1}+a_{2}+a_{3}+a_{4}+.........)+(9a_{2}+99a_{3}+999a_{4}+........)$$ .....(1)
or $$a=S+(a_{2}+11a_{3}+111a_{4}+.....)$$
$$\therefore 9 |(a-S)$$ .......(2)
Part 1:
a is divisible by 9
i.e., $$9 | a$$ .........(3)
$$\therefore 9| \left [ a-(a-S) \right ]$$ [From (2) and (3)]
i.e., $$9 | S$$ i.e., sum of digits is divisible by 9

Part 2:
S (sum of digits) is divisible by 9
i.e., $$9 | S$$ .... (4)
From (2) and (4), $$9 | \left [ (a-S)+S \right ]$$
i.e., $$9 | a$$
i.e., the integer a is divisible by 9.

The numbers $$525$$ and $$3000$$ are both divisible only by $$3, 5, 15, 25$$ and $$75$$ . What is $$HCF$$ $$(525, 3000).$$

The Highest common factor of 525 and 3000 is 75.

Hence, the HCF is 75

If m $$=$$ 18027, $$n = 2002 \times 2003 \times 2004$$ then find the G.C.D of 'm' and 'n' ?

Factors of 18027 $$=$$ 9 $$\times$$ 2003.

and $$n=2002\times2003\times2004=2002\times2003\times3\times167$$

G.C.D of m and n is $$3\times2003$$ = $$ 6009$$

Two positive integers $$'m'$$ and $$'n'$$ follow the conditions:
(i) $$m < n$$
(ii) They are not relatively prime
(iii) Their product is $$13013$$
Find their gcd and hence determine all such ordered pairs $$(m, n).$$

Two numbers are "relatively prime" when they have no common factors other than $$1$$

In other words you cannot evenly divide both by some common value.
$$13013=7\times 11\times 13\times 13$$
$$(m,n)$$ are not relatively prime. Thus, $$(m,n)$$ can be $$(91, 143)$$ or $$(13, 1001)$$
GCD of $$(91, 143)$$ is $$13$$
GCD of $$(13, 1001)$$ is $$13$$

Prove that every two consecutive integers are co-prime.

Let $$n$$ and $$n+1$$ be two consecutive integers.
Let $$(n, n+1)=d$$ $$[~$$H.C.F. of $$n$$ and $$n+1$$ is $$d~]$$
$$\therefore d | n ~~\text{and} ~~ d | n+1$$
$$\implies d | (n+1)-n $$

$$\implies d | 1$$
$$\therefore d=1$$
$$\therefore (n, n+1)=1$$
i.e., $$n$$ and $$(n+1)$$ are relatively prime

Prove that 4 does not divide $$(m^{2}+2)$$ for any integer m.

Since, m is an integer
$$\therefore $$ Either m is even or m is odd
Case-I: m is even
So let $$m=2k$$
$$\therefore m^{2}+2=(2k)^{2}+2$$
$$=4k^{2}+2$$
$$=2(2k^{2}+1)$$
$$=(2\times an odd integer)$$
Which is not divisible by 4.
Case-II: m is odd
Let $$m=2k+1$$
$$\therefore m^{2}+2=(2k+1)^{2}+2$$
$$=4k^{2}+1+4k+2$$
$$=(2+4k+4k^{2})+1$$
Which being an odd integer is not divisible by 4.

Determine all positive integer n for which $$2^{n}+1$$ is divisible by 3.

$$2^{n}+1$$ is divisible by 3.
$$\Rightarrow (3-1)^{n}+1$$ is divisible by 3
$$\Rightarrow (-1)^{n}+1$$ is divisible by 3
$$\Rightarrow n\ is\ odd$$
Set of all odd natural numbers in the set of all those positive integer for which $$2^{n}+1$$ is divisible by 3.

If a and b are relatively prime, then any common divisor of ac and b is a divisor of c.

a and b are relatively prime
$$\therefore \exists $$ integers x and y such that
$$ax+by=1$$ ..........(1)
Let d be any common divisor of ac and b.
since, $$d   |   ac,   \exists $$ an integer m such that
$$ac=dm$$ ....(2)
since, $$d   |   b,   \exists $$ an integer n such that
$$b=dn$$ ....(3)
Multiplying both sides of (1) by c
$$acx+bcy=c$$ ............(4)
Putting the values of ac and b from (2) and (3) in (4).
$$dmx+dncy=c$$
or $$d(mx+ncy)=c$$
$$\therefore d   |   c$$

Find H.C.F. $$1836, 810, 1296$$ and $$702$$.

By applying prime factorisation we get,

$$1836=2\times 2\times 3\times 3\times 3\times 17\\ 810=2\times 3\times 3\times 3\times 3\times 5\\ 1296=2\times 2\times 2\times 2\times 3\times 3\times 3\times 3\\ 702=2\times 3\times 3\times 3\times 13$$

The HCF will be

$$=2\times 3\times 3\times 3\\ =54$$

Determine whether the number 1111...1 of 91 digits is prime or composite ?

Let $$N = 111111....... =1+10+10^2+10^3+10^4+..............10^{90} = \cfrac{10^{91}-1}{9}$$
Now $$10^{91} =(9+1)^{91} = ^{91}C_09^{91}+^{91}C_19^{90}+.............+^{91}C_19+1 $$
Thus $$N = ^{91}C_09^{90}+^{91}C_19^{89}+..................+^{91}C_29+^{91}C_1$$
Hence given number is composite.

The number of common factors of $$20, 36$$ and $$48$$ is

Factors of $$ 20 = 1, 2, 4, 5, 10, $$ and $$ 20 $$

Factors of $$ 36 = 1, 2, 3, 4, 6, 9, 12, 18 $$ and $$ 36 $$

Factors of $$ 48 = 1, 2, 3, 4, 6, 8, 12, 16, 24 $$ and $$ 48 $$

Hence, common factors of $$20,36,48$$ are $$ 1, 2, 4.$$ So, total numbers of common factors is equal to $$3.$$

Show that $$5309$$ and $$3072$$ are prime to each other

Factor of $$3072 =1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, 64, 96, 128, 192, 256, 384, 512, 768, 1024, 1536, 3072$$
Factor of $$ 5309= 1, 5309$$
Since H.C.F of both the number is $$1 $$
So the two numbers are co-prime.

Find H.C.F.of $$805, 1127\ and \ 1449$$.

Factors of $$ 805 = 1, 5, 7, 23, 35, 115, 161, 805 $$

Factors of $$ 1127 = 1,7,23,49,161,1127 $$

Factors of $$ 1449 =1,3,7,9,21,23,63,69,161,207,483,1449 $$

Common factors are $$ = 1,7, 23,161 $$
=> HCF $$ = 161 $$

Find the HCF of 12576 and 4052

$$4052 = 2 \times 2 \times 1013$$
$$12576 = 2 \times 2 \times 2 \times 2 \times 2 \times 3 \times 131$$
The HCF of 4052,12576 is: $$2 \times 2 = 4$$

Find the $$HCF$$ of $$8ab^3, 4a^2b^2$$, and $$6a^3b.$$

$$8a{b^3} = 2 \times 2 \times 2 \times {a^1} \times {b^3}$$

$$ = {2^3} \times {a^1} \times {b^3}$$

$$4{a^2}{b^2} = 2 \times 2 \times {a^2} \times {b^2}$$

$$ = {2^2} \times {a^2} \times {b^2}$$

$$6{a^3}b = 2 \times 3 \times {a^3} \times b$$

$$ = {2^1} \times {3^1} \times {a^3} \times {b^1}$$

To find the $$HCF$$ of the three terms we will multiply each factor with the lowest power which is present in all three terms. So,

$$HCF = {2^1} \times {a^1} \times {b^1}$$

$$ = 2ab$$

Find the HCF of $$6(a^2-b^2), 21(a^3-3a^2b + 3ab^2-b^3)$$, and $$15(a^2+ 2ab + b^2)$$

The $$HCF$$ of $$6, 21,$$ and $$15$$ is $$3$$.
$$a^2-b^2=(a +b)(a -b)$$
$$a^3-3a^2b +3ab^2-b^3= (a -b)^3$$
$$a^2+ 2ab + b^2=(a + b)^2$$
Lowest power of $$(a +b)=(a +b)$$
Lowest power of $$(a -b)=(a -b)$$
$$\therefore HCF=3(a +b) (a -b)$$

Convert $$\displaystyle (1987.725)_{10}\rightarrow (.....)_{8}$$

First convert non-decimal part into base 8
8 | 1987 |
8 | 248 | 3
8 | 31 | 0
8 | 3 | 7
| 0 | 3
$$\displaystyle \therefore (1987)_{10}=(3703)_{8}$$
Now we have to convert $$\displaystyle (0.725)_{10}\rightarrow(........)_{8}$$
Multiply
0.725 x 8 = [5.8] .....5
0.8 x 8 = [6.4] .....6
0.4 x 8 = [3.2] .....3
0.2 x 8 = [1.6] .....1
0.6 x 8 = [4.8] .....4
Keep on accomplishing integral parts after multiplication with decimal part till decimal part is zero
$$\displaystyle \therefore (0.725)_{10}=(0.56314...)_{8}$$
$$\displaystyle \therefore (1987.725)_{10}=(3703.56314)_{8}$$

Express each number as a product of its prime factors:
(i) $$140$$ (ii) $$156$$ (iii) $$3825$$ (iv) $$5005 $$ (v) $$7429$$

(i) $$140$$

$$140 = 2 \times 70$$

$$= 2 \times 2 \times 35$$

$$= 2 \times 2 \times 5 \times 7$$

$$= 2 \times 2 \times 5 \times 7 \times 1$$

(ii) $$156$$

$$156 = 2 \times 78$$

$$= 2 \times 2 \times 39$$

$$= 2 \times 2 \times 3 \times 13$$

$$= 2 \times 2 \times 3 \times 13 \times 1$$

(iii) $$3825$$

$$3825 = 3 \times 1275$$

$$= 3 \times 3 \times 425$$

$$= 3 \times 3 \times 5 \times 85$$

$$= 3 \times 3 \times 5 \times 5 \times 17$$

$$= 3 \times 3 \times 5 \times 5 \times 17 \times 1$$

(iv) $$5005$$

$$5005 = 5 \times 1001$$

$$= 5 \times 7 \times 143$$

$$= 5 \times 7 \times 11 \times 13$$

$$= 5 \times 7 \times 11 \times 13 \times 1$$

(v) $$7429$$

$$7429 = 17 \times 437$$

$$= 17 \times 19 \times 23$$

$$= 17 \times 19 \times 23 \times 1$$

Check whether $$6^n$$ can end with the digit $$0$$ for any natural number $$n$$.

If any digit has the last digit $$10$$ that means it divisible by $$10.$$

The factor of $$10 = 2 \times 5,$$

So value of $$6^n$$ should be divisible by $$2$$ and $$5.$$

Both $$6^n$$ is divisible by $$2$$ but not divisible by $$5.$$

So, it can not end with $$0.$$

If $$31z5$$ is a multiple of $$3$$, where $$z$$ is a digit, what might be the values of $$z$$?

For $$31z5$$ to be a multiple of $$3$$,

$$3+1+z+5$$ should be a multiple of $$3$$.

So, the values of $$z$$ can be $$0, 3, 6$$ or $$9$$.

If $$z = 0$$, then the sum is $$9$$.

If $$z = 3$$, sum is $$12$$

If $$z = 6$$, sum is $$15$$

If $$z = 9$$, then the sum is $$18$$

In the above cases, we see that the sums are all multiples of $$3$$.

Hence, $$z$$ can be $$0,3,6$$ or $$9$$.

Check whether $$28765432$$ is divisible by $$8$$?

If the last three digits of a whole number are divisible by $$8$$, then the entire number is divisible by $$8$$.

Since, $$432$$ is divisible by $$8$$

Hence, the Number is divided by $$8$$

How many numbers from $$1001$$ to $$2000$$ are divisible by $$4$$?

The number of numbers from $$1$$ to $$1000$$, which are divisible by $$4$$ is:

$$\cfrac { 1000 }{ 4 } =250$$

The number of numbers from $$1$$ to $$2000$$, which are divisible by $$4$$ is:

$$\cfrac { 2000 }{ 4 } =500$$

Therefore, the number of numbers from $$1001$$ to $$2000$$, which are divisible by $$4$$ is:

$$500-250=250$$

Hence, there are $$250$$ numbers from $$1001$$ to $$2000$$, which are divisible by $$4$$.

Find the HCF and LCM of $$42$$ and $$72$$ by prime factorisation method i.e, by fundamental theorem of arithmetic.

Prime factorisation of $$42 = 2 \times 3 \times 7$$
Prime factorisation of $$72=2\times 2\times 2\times 3\times 3=2^3\times 3^2$$

$$\therefore HCF (42, 72) = 2 \times 3 = 6$$

And, $$LCM (42, 72) = 2^3 \times 3^2 \times 7^1 = 504$$

Check whether the given numbers are divisible by $$6$$ or not ?
(a) $$273432$$ (b) $$100533$$ (c) $$784076$$ (d) $$24684$$

for a number to be divisible by $$6$$ it has to be even(divisible by $$2$$) and sum of its digits must be divisible by $$3$$

So, According to above rules
$$273432,24684$$ are divisible by $$6$$
and
$$100533,784076 $$ are not divisible by $$6$$

List all of the prime numbers between $$50$$ and $$90$$.

Prime number means it should have only two factors which are $$1$$ and itself.
The prime numbers between $$50$$ and $$90$$ are $$53,59,61,71,73,79,83,89$$.

Show that one and only one out of n, n + 1 or n + 2 is divisible by 3, where n is any positive integer.

Since $$n$$, $$n+1$$, $$n+2$$ are three consecutive integers then there must be one number divisible by $$3$$ at least.

If the remainder at dividing $$n$$ by $$3$$ is $$ 1$$, then $$n+2$$ must be divisible by $$3$$ and if the remainder at dividing $$n$$ by $$3$$ is $$2$$, then $$n+1$$ must be divisible by $$3$$. Similarly for $$n+1$$ and $$n+2$$.

Let $$n$$ be divisible by $$3$$.

$$\dfrac{n+1}{3} = \dfrac{n}{3}+\dfrac{1}{3}$$

Now, n is divisible by 3 but 1 is not. So we get $$n+1$$ not divisible by $$3$$. Similarly,$$ n+2$$ will not be divisible by $$3$$ as well if $$n$$ is divisible by $$3$$.

$$\dfrac{n+2}{3} =\dfrac{n}{3}+\dfrac{2}{3}$$

In the same way, if $$ n+1$$ is divisible by $$3$$ then $$n$$ and $$n+2$$ can't be divisible by $$3$$. If $$n+2$$ is divisible by $$3$$ then $$n$$ and $$n+1$$ cannot be divisible by $$3$$.

Check whether $$6582$$ is divisible by $$4$$?

A whole number is divisible by $$4$$ only if the last two digits of the whole number are divisible by $$4.$$

Now, $$82$$ is not divisible by $$4$$

Hence, $$6582$$ is not divisible by $$4$$

Check whether $$32^{2}$$ is divisible by $$4$$ or $$8$$ or by both $$4$$ and $$8$$?

$$32^2=(4\times 4\times 2)^2=4^2\times 4^2\times 2^2=16\times 16\times 4=8\times 2\times 8\times 2\times 4$$

As we can see above, The Given number can be divisible by both $$4$$ and $$8$$

Check whether $$876$$ and $$345$$ are divisible by $$3$$? Also check whether $$3$$ divides the difference of $$876$$ and $$345$$?

For Divisible by 3, we need to check if the sum of the digits is divisible by 3.

Now, Let us use the above rule as follows $$:-$$

For $$876$$, $$8+7+6=21$$ which is divisible by $$3$$.
Similarly, For $$345$$, $$3+4+5=12$$ which is divisible by $$3$$.
Therefore, Both numbers are divisible by $$3$$

Now, Difference $$\rightarrow 876-345=531$$

Applying the same Rule as above,For $$531$$, $$5+3+1=9$$ which is divisible by $$3$$.
Therefore it is divisible by $$3$$

Find the H.C.F. of numbers $$44$$ and $$99$$.

$$44 = 2 \times 2 \times 11 $$
and $$99 = 3 \times 3 \times 11$$
(H.C.F.) $$ = 11 $$

Divide $$15et20$$ by $$9$$ in the scale of twelve.

$$\Rightarrow 15=1\times T+5=$$seventeen ($$\because $$ in scale of twelve i.e., 'T')

Seventeen$$=1\times 9+8$$, We put $$'1'$$ down and take carry $$8$$

Now,

$$8\times T+e=$$One hundred and seven

($$\because $$ 'T' is twelve and 'e' is 'eleven' )

$$\therefore 9\times e+8$$ We put 'e' down and tale carry $$8$$

Now,

$$8\times T+t=$$One hundred and six

$$9\times e+7$$ and so on

Find the GCD of the following :
(i) 90, 150, 225
(ii) $$15x^4y^3z^2, 12x^2y^7z^2$$
(iii) $$6(2x^2-3x-2), 8(4x^2+4x+1), 12(2x^2+7x+3)$$

(i) Let us write the numbers 90, 150 and 225 in the product of their prime factors as
$$90 \times= 2\times 3 \times 3 \times 5, 150= 2\times 3\times 5\times 5$$ and $$ 225= 3\times 3 \times 5\times 5$$
From the above 3 and 5 are common prime factors of all the given numbers.
Hence the GCD = $$ 3\times 5=15$$
(ii) We shall use similar technique to find the GCD of algebraic expressions. Now let us take the given expressions $$15x^4y^3z^2$$ and $$12x^2y^7z^2$$.
Here the common divisors of the given expressions are $$3, x^2, y^3$$ and $$z^2$$.
Therefore, GCD $$= 3 \times x^2 \times y^3 \times z^2=3x^2y^3z^2$$.
(iii) Given expressions are $$6(2x^2-3x-2), 8(4x^2+4x+1), 12(2x^2+7x+3)$$
Now, GCD of 6, 8, 12 is 2.
Next let us find the factors of quadratic expressions.
$$2x^2-3x-2=(2x+1)(x-2)$$
$$4x^2+4x+1=(2x+1)(2x+1)$$
$$2x^2+7x+3=(2x+1)(x+3)$$
Common factor of the above quadratic expressions is (2x+1).
Therefore, GCD = 2(2x+1).

Number of $$9$$ digits numbers divisible by nine using the digits from $$0$$ to $$9$$ if each digit is used at most once is $$K\cdot 8!$$, then K has the value equal to _________.

$$9$$ digit no$$:$$ divisible by $$9,$$ means the sum of digits is equal to that number which is divisible by $$9.$$

Check whether the given numbers are divisible by $$4$$ or not ?
(a) $$3024$$ (b) $$1000$$ (c) $$412$$ (d) $$56240$$

If the last two digits of a whole number are divisible by $$4$$, then the entire number is divisible by $$4$$

Above Rule can be applied as

$$(a)3024\Rightarrow$$ Last Digits are $$24$$ and $$24$$ is divisible by $$4(24=6\times 4)$$
therefore, the Number is divisible by $$4$$.

$$(b)1000\Rightarrow$$ Last Digits are $$00$$ or $$0$$ and $$0$$ is divisible by $$4$$ as $$0$$ is divisible by every integer or $$(0=4\times 0)$$.
therefore, the Number is divisible by $$4$$.

$$(c)412\Rightarrow$$ Last Digits are $$12$$ and $$12$$ is divisible by $$4(12=4\times 3)$$
therefore, the Number is divisible by $$4$$.

$$(d)56240\Rightarrow$$ Last Digits are $$40$$ and $$40$$ is divisible by $$4(40=4\times 10)$$
therefore, the Number is divisible by $$4$$.

Check whether the given numbers are divisible by $$8$$ or not ?
(a) $$4808$$ (b) $$1324$$ (c) $$1000$$ (d) $$76728$$

If the last three digits of a whole number are divisible by $$8$$, then the entire number is divisible by $$8$$.
Above Rule can be applied as:

(a) $$4808\Rightarrow$$ Last $$3$$ digits are $$808$$ and $$808$$ is divisible by $$8$$ $$(\because 808=8\times 101)$$
Therefore, the number is divisible by $$8$$.

(b) $$1324\Rightarrow$$ Last $$3$$ digits are $$324$$ and $$324$$ is not divisible by $$8\left (\because \dfrac{324}{8}=40.5\right)$$
Therefore, the number is $$ NOT$$ divisible by $$8$$.

(c) $$1000\Rightarrow$$ Last $$3$$ digits are $$000$$ or $$0$$ and $$0$$ is divisible by $$8$$ $$ (\because 0=8\times 0)$$
Therefore, the number is divisible by $$8$$.

(d) $$76728\Rightarrow$$ Last $$3$$ digits are $$728$$ and $$728$$ is divisible by $$8$$ $$(\because 728=8\times 91)$$
Therefore, the number is divisible by $$8$$.

Check whether $$2^{2} + 2^{3} + 2^{4}$$ is divisible by $$2$$ or $$4$$ or by both $$2$$ and $$4$$?

We can write given Equation as
$$2^2+2^3+2^4=2^2(1+2+2^2)=4(1+2+4)=4\times 7=28$$

Therefore it is divisible by both $$4$$ and $$2$$ as $$4=2\times 2$$

Find the HCF of integers 375 and 675

$$375 = 5\times5\times5 \times 3$$

$$675 = 5\times5 \times 3\times3\times3$$

Hence HCF $$= 5\times5 \times 3$$

$$= 75$$

Find HCF of following numbers:
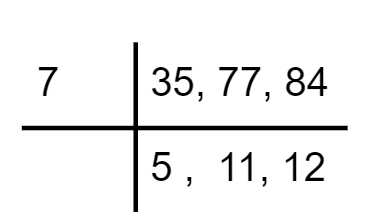
$$35, 77$$ and $$84$$.

So, HCF of $$35, 77, 84 = 7$$
1496886_711035_ans_4ae8af2e975744a6ae26f05066514b30.PNG

Which of the following pairs are co-prime?
17 and 68

Factors of $$ 17=1,17$$

Factors of $$ 68=1,2,4,17,34,68 $$

Common factors= $$ 1,17$$

As these numbers have a common factors other than $$ 1 $$, the given two numbers are not co-prime

Find $$HCF$$ by finding factors:
$$24, 60$$ and $$84$$.

After prime factorization of the given numbers.

$$24 = 2 \times 2 \times 2 \times 3$$

$$60 = 2 \times 2 \times 3 \times 5$$

$$84 = 2 \times 2 \times 3 \times 7$$

Since, the common factor is $$1,2,2,3.$$

$$HCF = 2 \times 2 \times 3$$

$$=12$$

Write the smallest digit and the greatest possible digit in the blank space of each of the following numbers so that the number formed is divisible by
= __ 6724

$$6 + 7 + 2 + 4 = 19$$

If we add 2 then the digit is divisible by $$3 (19 + 2 = 21).$$

$$2$$ is the smallest digit

$$26724 = 2 + 6 + 7 + 2 + 4 = 21.$$

If we add 8 then the digit is divisible by $$3(19 + 8 = 27)$$

$$8$$ is the largest digit

$$86724 = 8 + 6 + 7 + 2 + 4 = 27.$$

Which of the following pairs are co-prime?
18 and 35

Factors of $$ 18=1,2,3,6,9,18 $$

Factors of $$ 35=1,5,7,35 $$

Common factors= $$ 1$$

Therefore, the given two numbers are co-prime

Write the smallest digit and the greatest possible digit in the blank space of each of the following numbers so that the number formed is divisible by $$3$$$$= 4765\__\ 2$$

The given number is $$ 4765 $$ __ $$ 2 $$ is divisible by 3.

By the divisibility rule of 3, any number is divisible by 3 if the sum of its digit is divisible by 3.

Let the digit on the blank space be $$ a $$.

$$ 4+7+6+5+a+2 $$

$$ \Rightarrow a+24 $$

In order to make required number divisible by 3 , the least value of $$ a $$ is 0 and the maximum value of $$ a $$ is 9.

If $$ a=0 $$, then $$ 0+24=24 $$. This is divisible by 3.

If $$ a=9 $$, then $$ 9+24=33 $$. This is divisible by 3.

Are the numbers $$30$$ and $$415$$ coprimes?

Prime Factors of $$ 30=1\times 2\times 3\times 5$$
Prime Factors of $$ 415=1\times 5\times 83 $$
Common factors = $$ 1,5$$
As these numbers have a common factor other than $$ 1 $$, therefore the given two numbers are not co-prime

Find HCF of following numbers:
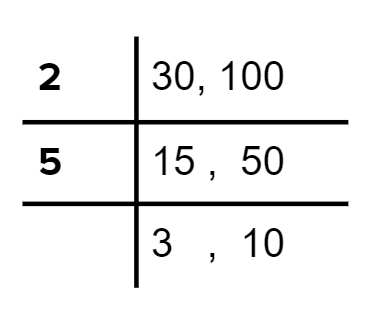
$$30$$ and $$110$$.

So, HCF of 30 and 100 = 10
1496887_711036_ans_5b5ea187e1984d8fbd84de5109ceffd2.PNG

Can the number $$\displaystyle n^4 + n$$ be prime for $$n\in N$$? If it can, find the prime number.

yes, we can say that $$n^4+n$$ can be prime when $$n=1$$

For, $$n=1, n^4+n=1+1=2$$

Which is prime.

Show that exactly one of the numbers $$n, n+2, n+4$$ is divisible by $$3$$.

Case I:
If $$n=3q$$
$$n+4=3q+4\\
n+2=3q+2$$
here $$n$$ is only divisible by $$3$$

Case II:
If $$n = 3q+1$$
$$n+4=3q+5\\
n+2=3q+3=3(q+1)$$
Here only $$n+2$$ is divisible by $$3$$

Case III:
If $$n=3q+2$$
$$n+2=3q+4$$

$$n+4=3q+2+4$$ $$=3q+6$$
Here only $$n+4$$ is divisible by $$3$$

Hence, only one of the numbers $$n,n+2,n+4$$ is divisible by $$3$$.

Prove that for any integer of the form $$n^3-n$$ is divisible by $$3$$.

$$N^3-n=n(n^2-1)=n(n-1)(n+1)$$ is divided by $$3$$ then possible remainder $$0, 1$$ and $$2[\because$$i $$P=ab+r$$, then $$0\le r<a$$ by Euclid lemma]

$$\therefore $$ Let $$n=3r, 3r+1, 3r+2$$, where $$r$$ is an integer

Case 1 :- when $$n=3r$$

Then, $$n^3-n$$ is divisible by $$3[\because n^3-n=n(n-1)(n+1)=3r(3r-1)(3r+1)$$ , clearly shown it is divisible by $$3]$$

Case 2:- when $$n=3r+1$$

e.g., $$n-1=3r+1-1=3r$$

Then, $$n^3-n=(3r+1)(3r)(3r+2)$$, it is divisible by $$3$$

Case 3:- when $$n=3r-1$$

e.g., $$n+1=3r-1+1=3r$$

Then, $$n^3-n=(3r-1)(3r-2)(3r)$$, it is divisible by $$3$$

Find $$HCF$$ and $$LCM$$ of $$404$$ and $$96$$ and verify that $$HCF \times LCM =$$ Product of the two given numbers.

Let $$a = 404$$ and $$ b = 96$$

Expressing the number as a product of prime number

$$404=2\times 2\times 101$$

$$96=2\times 2\times 2\times 2\times 2\times 3$$

$$\therefore$$ LCM of $$404$$ and $$96$$ is $$2\times 2\times 2\times 2\times 2\times 101\times 3=9696$$

$$\therefore$$ HCF of $$404$$ and $$96$$ is $$2\times 2=4$$

Now $$HCF \times LCM=4\times 9696=38784$$

Product of two given numbers $$404 \times 96=38784$$

Hence $$HCM \times LCM=$$ product of two given numbers.

Problems Set at an Oral Examination.
Assume that p and q are two successive prime numbers, Can their sum be a prime number?

Yes,

It can be possible when $$p=2$$ and $$q=3$$ then $$p+q=5$$ which is prime.

But this is the only example.

After this , any two prime numbers $$p$$ and $$q$$ will be odd and their sum $$p+q$$ will be even and hence will never be odd.

Show that there are infinitely many positive primes.

Let us assume that there are a finite number of positive primes $${p}_{1},\ {p}_{2},\ ,\ .\ .\ .\ ,{p}_{n}$$ such that $$ { p }_{ 1 }<{ p }_{ 2 }<{ p }_{ 3 }<...<{ p }_{ n }$$

Let $$x=1+{ p }_{ 1 }\ { p }_{ 2 }\ { p }_{ 3 }\ .\ .\ .\ { p }_{ n }$$

We know that $${p}_{1}\ {p}_{2}\ {p}_{3}\ .\ .\ .\ {p}_{n}$$ is divisible by each of $$ { p }_{ 1 },{ p }_{ 2 },{ p }_{ 3 }<...<{ p }_{ n }$$

But $$x=1+{ p }_{ 1 }\ { p }_{ 2 }\ { p }_{ 3 }\ .\ .\ .\ { p }_{ n }$$ is not divisible by any one of $$ { p }_{ 1 },{ p }_{ 2 },...,{ p }_{ n }$$

$$\therefore \ x$$ is a prime number or we can say that it has prime divisors other then $$ { p }_{ 1 },{ p }_{ 2 },...,{ p }_{ n }$$

There exists a positive prime divisor other than $$ { p }_{ 1 },{ p }_{ 2 },...,{ p }_{ n }$$

This contradicts our assumption that there are a finite number of positive primes.

Hence, the number of positive primes is infinite.

Prove that the product of three consecutive positive integer is divisible by $$6$$.

Let $$n$$ be any positive integer is of the form $$6q$$ or, $$6q+1$$ or, $$6q+2$$ or, $$6q+3$$ or, $$6q+4$$ or, $$6q+5.$$

If $$n=6q$$, then

$$n\left( n+1 \right) (n+2)=6q(6q+1)(6q+2),$$ which is divisible by $$6$$

If $$n=6q+1,$$ then

$$n(n+1)(n+2)=(6q+1)(6q+2)(6q+3)=6(6q+1)(3q+1)(2q+1),$$

which is divisible by $$6$$.

If $$n=6q+2,$$ then

$$n(n+1)(n+2)=(6q+2)(6q+3)(6q+4)=12(3q+1)(2q+1)(2q+3),$$

which is divisible by $$6$$.

Similarly , $$n(n+1)(n+2)$$ is divisible by $$6$$ if $$n=6q+3$$ or, $$6q+4$$ or, $$6q+5.$$

How many different numbers of six digits (without repetition of digit) can be formed from the digits 3, 1, 7, 0, 9, 5?
(i) How many of them will have 0 in the unit place?
(ii) How many of them are divisible by 5?
(iii) How many of them are not divisible by 5?

3, 1, 7, 0, 9, 5, i.e. 6 digits.
The total numbers of 6 digit numbers
6! - 5! = 720-120 = 600.
(i) 5! = 120 having 0 at the end.
(ii) Divisible by 5.
They will have zero in the last place and hence the remaining 5 can be arranged in 5! = 120 ways.
They may have 5 in the last place and as above we will have 5! = 120 ways. These' will also include numbers which will have zero in the first place. Therefore the numbers having zero in 1st and 5 in last place will be 4!
Therefore 6 digit numbers having 5 in the end will be
5! -4! = 120 - 2.4 = 96.
Therefore the total number of 6 digit numbers divisible by 5 is
120 + 96 = 216.
(iii) Not divisible by 5.
= Total - (divisible by 5)
=600 - 216 = 384.

For any Positive integer $$n$$, prove that $${n}^{3}-n$$ divisible by $$6$$.

The condition for any number to be divisible by $$6$$ is that the number must be individually divisible by $$3$$ and $$2.$$

Check whether $$ n^{3}-n $$ is divisible by $$3.$$

$$ n^{3}-n=n\left ( n+1 \right )\left ( n-1 \right ) $$

When a number is divided by $$3$$ then by the remainder theorem, the remainder obtained is either $$0$$ or $$1$$ or $$2.$$

$$ n=3p $$ or $$ n=3p+1 $$ or $$ n=3p+2 $$, where $$ p $$ is some integer.

If $$ n=3p $$, then the number is divisible by $$3.$$

If $$ n=3p+1 $$, then $$ n-1=3p+1-1=3p $$. The number is divisible by $$3.$$

If $$ n=3p+2 $$, then $$ n+1=3p+2+1=3\left ( p+1 \right ) $$. The number is divisible by $$3.$$

So, any number in the form of $$ n^{3}-n=n\left ( n+1 \right )\left ( n-1 \right ) $$ is divisible by $$3.$$

Check whether $$ n^{3}-n $$ is divisible by $$2.$$

When a number is divided by $$2$$, the remainder obtained is either $$0$$ or $$1$$ by the remainder theorem.

$$ n=2p $$ or $$ n=2p+1 $$, where $$ p $$ is some integer.

If $$ n=2p $$, then the number is divisible by $$2.$$

If $$ n=2p+1 $$ then $$ n-1=2p+1-1=2p $$. The number is divisible by $$2.$$

So, any number in the form of $$ n^{3}-n=n\left ( n+1 \right )\left ( n-1 \right ) $$ is divisible by $$2.$$

Since, the given number $$ n^{3}-n=n\left ( n+1 \right )\left ( n-1 \right ) $$ is divisible by both $$3$$ and $$2.$$ Therefore, according to the divisibility rule of 6, the given number is divisible by $$6$$.

Hence, $$ n^{3}-n=n\left ( n+1 \right )\left ( n-1 \right ) $$ is divisible by $$6.$$

$${2^{x - 7}} \times {5^{x - 4}} = 1250$$ find $$x$$

$${ 2 }^{ x-7 }\times{ 5 }^{ x-4 }=1250\\ { 2 }^{ x-7 }\times{ 5 }^{ x-4 }=2\times625\\ { 2 }^{ x-7 }\times{ 5 }^{ x-4 }={ 2 }^{ 1 }\times{ 5 }^{ 4 }\\ x-7=1\\ x=8\\ x-4=4\\ x=8$$

Explain why $$7 \times 11 \times 13 + 13$$ and $$7 \times 6 \times 5\times 4 \times 3 \times 2 \times 1 + 5$$ are composite numbers

Since,

$$ 7\times 11\times 13+13 $$

$$ =13\left( 7\times 11+1 \right) $$

$$ =13\times \left( 77+1 \right) $$

$$ =13\times 78 $$

$$ =13\times 13\times 6 $$

$$ =13\times 13\times 3\times 2 $$

Hence, it has more then two factors $$\left( 13\times 78 \right)$$ and $$\left( 1,2,3,13, \right)$$

It is a composite number.

$$ 7\times 6\times 5\times 4\times 3\times 2\times 1+5 $$

$$ =5\left( 7\times 6\times 4\times 3\times 2\times 1 \right) $$

$$ =5\left( 1008+1 \right) $$

$$ =5\left( 1009 \right) $$

Now,

Hence, it has more then two factors $$\left( 5\times 1009 \right)$$ and $$\left( 1,5,1009 \right)$$

It is a composite number.

If two positive integers $$a$$ and $$b$$ are written as $$a=x^2y^2$$ and $$b=xy^2$$; $$x$$, $$y$$ are prime numbers then the $$HCF(a,\,b)$$ is

HCF by using the prime factorization method.

Step1:

$$\text{Find the prime factorization of each of the number}$$

Step2:

$$\text{The product of all common prime factor is the HCF}$$

Here,

$$\Rightarrow a=x\times x\times y\times y$$

$$\Rightarrow b=x\times y\times y$$

common Factors are $$x\times y\times y$$

Thus ,

$$HCF(a,b)= xy^2$$

Explain why $$(3 \times 5 \times 13 \times 46)+23$$ is a composite number.

$$(3\times5\times13\times46)+23$$

$$(3\times5\times13\times2\times23)+23$$

$$23(3\times5\times13\times2)+1)$$

Since the number is divisble by $$23$$ and $$(3\times5\times13\times2)+1)$$

therefore $$(3\times5\times13\times46)+23$$ is a composite number

The LCM of any two consecutive numbers is their _____________

The LCM of any two consecutive numbers is their product

What will be the $$HCF$$ of $$(2\times 3\times 7\times 9)$$ $$,(2\times 3\times 9\times 11)$$ and $$(2\times 3\times 4\times 5)?$$

Given factors,

$$(2\times 3\times 7\times 9)$$ $$,(2\times 3\times 9\times 11)$$ $$,(2\times 3\times 4\times 5)$$

Therefore,

Required $$HCF=$$ Product of common prime factors having least powers

$$=2\times 3=6$$

Hence, this is the answer.

Show that only one of the number $$n, n+2$$ and $$n+4$$ is divisible by $$3$$.

We know that any positive integer of the form $$3q$$ or, $$3q+1$$ or $$3q+2$$ for some integer $$q$$ and one and only one of these possibilities can occur.

So, we have following cases:

Case-I: When $$n = 3q$$

In this case, we have

$$n= 3q$$, which is divisible by $$3$$

Now, $$n = 3q$$

$$n+2 = 3q+2$$

$$n+2$$ leaves remainder $$2$$ when divided by $$3$$

Again, $$n = 3q$$

$$n+4 = 3q+4=3(q+1)+1$$

$$n+4$$ leaves remainder $$1$$ when divided by $$3$$

$$n+4$$ is not divisible by $$3$$.

Thus, $$n$$ is divisible by $$3$$ but $$n+2$$ and $$n+4$$ are not divisible by $$3$$.

Case-II: when $$n = 3q+1$$

In this case, we have

$$n= 3q+1,$$

$$n$$ leaves remainder $$1$$ when divided by $$3$$.

$$n$$ is divisible by $$3$$

Now, $$n = 3q+1$$

$$n+2 = (3q+1)+2=3(q+1)$$

$$n+2$$ is divisible by $$3$$.

Again, $$n = 3q+1$$

$$n+4 = 3q+1+4=3q+5=3(q+1)+2$$

$$n+4$$ leaves remainder $$2$$ when divided by $$3$$

$$n+4$$ is not divisible by $$3$$.

Thus, $$n+2$$ is divisible by $$3$$ but $$n$$ and $$n+4$$ are not divisible by $$3$$.

Case-III: When $$n= 3q+2$$

In this case, we have

$$n= 3q+2$$

$$n$$ leaves remainder $$2$$ when divided by $$3$$.

$$n$$ is not divisible by $$3$$.

Now, $$n = 3q+2$$

$$n+2 = 3q+2+2=3(q+1)+1$$

$$n+2$$ leaves remainder $$1$$ when divided by $$3$$

$$n+2$$ is not divisible by $$3$$.

Again, $$n = 3q+2$$

$$n+4 = 3q+2+4=3(q+2)$$

$$n+4$$ is divisible by $$3$$.

Hence, $$n+4$$ is divisible by $$3$$ but $$n$$ and $$n+2$$ are not divisible by $$3$$.

How many numbers of two digits are divisible by $$9$$?

$$\textbf{Step 1: Find the first term and common difference of A.P.}$$

$$\text{We observe that 18 is the first two-digit number divisible by 9 and 99 is the last two-digit }$$

$$\text{number divisible by 9}$$.

$$\text{Thus, we have to determine the number of terms in the sequence.}$$
$$18, 27, 36,..., 99$$

$$\text{Clearly, it is an A.P. with first term }=18$$ $$\text{and common difference }= 9$$ $$\text{i.e. }a = 18$$ $$\text{and }d = 9$$.

$$\textbf{Step 2: Find number of terms using general term formula.}$$

$$\text{Let 99 be the }n^{th}$$ $$\text{term in this A.P.}$$

$$\text{Then, }n^{th}$$ $$\text{term }= 99$$

$$\Rightarrow 18 + (n - 1) \times 9= 99$$ $$[\because \boldsymbol{a_n=a+(n-1)d}]$$
$$\Rightarrow 18 + 9n - 9 = 99$$
$$\Rightarrow 9n = 90$$

$$\Rightarrow n = 10$$

$$\textbf{Hence, there are 10 numbers of two digits which are divisible by 9}$$.

Fill in the blanks
Fill in the missing digit in units place so that the number is divisible by $$2$$ and $$3$$. $$15383$$

$$15383x$$

four number should are divisible by 3

$$\begin{array}{l} 1+5+3+8+3+x \\ 20+x=21 \\ x=1,\, 4,7 \end{array}$$

for number should also divisible by 2

$$x=4$$

Find the common factors of :
a) $$4, 8$$ and $$12$$
b) $$5, 15$$ and $$25$$

A) The factors of $$4$$ are $$1,2,4$$

The factors of $$8$$ are $$1,2,4,8$$

The factors of $$12$$ are $$1,2,3,4,6,12$$

Therefore, the common factors are $$1,2,4$$

B) The factors of $$5$$ are $$1,5$$

The factors of $$15$$ are $$1,3,5,15$$

The factors of $$25$$ are $$1,5,25$$

Therefore, the common factors are $$1,5$$

Find the value of p and q, so that the prime factorisation of 2520 can be expressed as $${2^3} \times {3^p} \times q \times 7$$.

$$2520=2^3\times3^p\times q\times 7$$

Since

$$2520=2^3\times3^2\times5\times7$$

On comparing $$p=2, q=5$$

Explain why 7 x 11 x 13 + 13 and 7 x 6 x 5 x 4 x 3 x 2 x 1 + 5 are composite numbers.

Given $$ 7 \times 11\times 13 +13$$

$$=13 \times (7 \times 11 +1)=3 \times 78$$

This number is multiple of two integers.Hence it has more than two factors.Hence it is a composite number.

similarly in

$$7 \times 6 $$$$ \times 5 $$$$ \times 4 $$$$ \times 3 $$ $$ \times 2 $$$$ \times 1 +5$$

$$= 5$$($$7 \times 6 $$$$ \times 4 $$$$ \times 3 $$ $$ \times 2 $$$$ \times 1 +1 )=5 \times 1009$$

This number is multiple of two integers.Hence it has more than two factors.Hence it is a composite number.

Write all the factors of $$68.$$

The factors of $$68$$ are $$1,2,4,17,34,68$$

Test the divisibility of $$387144$$ by $$6$$.

Place commas correctly and write the numerical-Four crore fifty thousand sixteen.

How many right angles are there in $$\dfrac{3}{4}$$ of a revolution?

1. $$387144$$ is divisible by $$2$$ because last digit is even

Now it is divisible by $$3$$ also because digit sum $$=27$$

which is divisible by $$3$$

so it is also divisible by $$6$$

2. Four crore fifty the used sixteen

$$40,050,016$$

After every $$3$$ digits from right, are comma is placed

3. Total right angles in $$\dfrac {3}{4}$$ of a revolution $$=\dfrac {3}{4}\times \dfrac {360^o}{90^o}$$

$$=\dfrac {3}{4}\times 4$$ $$=3$$

Fill in the blanks
$$45 = 3 \times 3 \times 5$$, so _, _, _ and _ are the factors of 45.

$$45=3\times 3\times 5$$

so, $$3,5,9,15$$ are factors of $$45$$

What is the greatest number that divides $$720$$ and $$810$$ without leaving any remainder?

We have to find $$H.c.f $$ of $$720 and 810$$.

factors of 720$$=$$ $$2\times2 \times2 \times2 \times 3\times 3\times 5$$

and factors of 810$$=$$ $$2\times3 \times3 \times3 \times 3\times 5$$

So, $$H. C. F$$ of 810 and 720 $$=$$$$2 \times 3\times 3\times 5$$$$=$$90

So , the required no. is 90.

Find the number of factors of $$4800$$ that are of form $$4k+2$$

$$4800=2^{6}.5^{2}.3^{1}$$

$$4K+2=(2)(2k+1)$$

$$=(2)(add)$$

$$\therefore $$ No. of factors of $$4k+2$$ form

$$=(1)(2+1)(1+1)$$

$$= 3\times 2$$

$$=6$$

Write the smallest digit and the greatest digit in the blank space of each of the following number so that the number formed is divisible by $$3$$ ?
_$$6724$$

$$6+7+2+4= 19$$
if we add 2 then the digit is divisible by 3 $$ ( 19+2=21)$$

2 is the smallest digit

$$26724 = 2 + 6 + 7 + 2 + 4 = 21$$

if we add 8 then the digit is divisible by 3 $$( 19+8=27)$$

8 is the largest digit
$$86724 = 8+ 6 + 7 + 2 + 4 = 36$$

HCF of co-prime numbers 4 and 15 was found as follows by fatorisation:
$$4 = 2 \times 2\,\,and\,\,15 = 3 \times 5$$ since there is no common prime factor, so HCF of 4 and 15 isIs the answer correct? If not, what is the correct HCF?

H.C.F of $$4\,,15\neq 0$$

Factors of $$4=2\times 2\times 1$$

Factors of $$15=3\times 5\times 1$$

$$\therefore$$ H.C.F$$=1$$ is the correct H.C.F

Find the HCF of $$40,50$$ and $$60$$

$$\left.\begin{matrix}2\\ 5\\\\\end{matrix}\right|\begin{matrix}40 & 50 &60 \\ 20 & 25 & 30\\ 4& 5&6 \end{matrix}$$

$$\therefore$$ HCF =$$2\times 5=10$$

Find the Highest Common Factor of $$12$$ and $$18$$.

The $$HCF$$ of $$12$$ and $$18$$ is,

$$12=2×2×3$$

$$18=2×3×3$$

$$Considering $$ $$the $$ $$common$$ $$ factors$$

$$Therefore$$ $$HCF$$ = $$2×3$$ = $$6$$

Find the truth values of the following statements:
$$14$$ is a composite number or $$15$$ is a prime number.
It is not true that $$4+3i$$ is a real number.

1) It comprises of two statements connected by 'OR'.

The first statement is correct while the second is false.

Overall truth vaule is TRUE.

2)$$ 4+3i$$ is not real.

therefore given statement is TRUE.

If $$31 m4 $$ is divisible by $$3$$, then what is the value of $$m $$?

Given, 31m431m4 is divisible by

$$\Rightarrow 3+1+m+4$$ is a multiple of 3

$$\Rightarrow 8+m$$ is a multiple of 3

this can happen, when $$m=1,4,7$$

$$7\times 11\times13\times15+15$$ is a prime number. Is it true? justify

Given number $$7\times 11\times 13\times 15+15$$ can also be written as $$15(7\times 11\times 13+1).$$

As it is a product of two composite numbers, hence it is not a prime number.

$$n^2 - 1$$ is divisible by $$8$$, if $$n$$ is ___ number.

Any odd positive integer is in the form of 4p + 1 or 4p+ 3 for some integer p.

Let $$n = 4p+ 1$$,

$$(n^2 – 1) = (4p + 1)^2 – 1 = 16p^2 + 8p + 1 = 16p^2 + 8p = 8p (2p + 1)$$

$$\Rightarrow (n^2 – 1)$$ is divisible by 8.

$$(n^2 – 1) = (4p + 3)^2 – 1 = 16p^2 + 24p + 9 – 1 = 16p^2 + 24p + 8 = 8(2p^2 + 3p + 1)$$

$$\Rightarrow n^2– 1$$ is divisible by 8.

Therefore, $$n^2– 1$$ is divisible by 8 if n is an odd positive integer.

Find the smallest number which is divisible by $$85$$ and $$119$$.

To find the smallest number which is divisible by 85 and 119, we have to take L. C. M. of $$85$$ and$$ 119.$$

Prime Factors of $$85 = 5 × 17$$

Prime Factors of $$119 = 7 × 17$$

So,

L. C. M. of$$ 85$$ and $$119 = 5 × 7 × 17 $$

L. C. M. of $$85$$ and $$119 = 595$$

So,$$ 595$$ is the smallest number which is divisible by$$ 85$$ and$$ 119.$$

Prove that the square of an odd integer decreased by $$1$$ is a multiple of $$8$$.

1180788_1151874_ans_3bd0be9801ee4a04b561727a8e7d3c0d.jpg

Express $$1947$$ into product of prime factors.

We can write

$$1947=3*11*59$$

How many even integers between $$81$$ to $$1000$$ divisible by $$3$$?

1351876_1130437_ans_9d67a307cb9b47f88d12e95d8ffeb074.jpg

If 21y5 is a multiple of 9 , what is the value of y?

$$A$$ $$number$$ $$divisible$$ $$by$$ $$9$$ $$should$$ $$have$$ $$the$$ $$sum$$ $$of$$ $$its$$ $$digits$$ $$equal$$ $$to$$ $$a$$ $$multiple$$ $$of$$ $$9.$$

$$Here,$$

$$2 + 1 + y + 5 = 9x$$

$$8 + y = 9x$$

$$\frac {8+y} {9}$$ $$=$$ $$x$$

$$If$$ $$y = 0,$$ $$\frac {8} {9}$$ $$is$$ $$not$$ $$divisible$$ $$by$$ $$9$$

$$If$$ $$y = 1,$$ $$\frac {9} {9}$$ $$is$$ $$divisible$$ $$by$$ $$9$$

$$So$$ $$the$$ $$least$$ $$possible$$ $$value$$ $$of$$ $$y$$ $$is$$ $$1.$$

$$\{ {(3(230 + x))^2}\} \, = \,492a04$$ then find the value of $$a$$.

$$\left\{ { \left( 3\left( 230+x \right) \right) }^{ 2 } \right\} =492a04$$

$$\Rightarrow 9{ \left( 230+x \right) }^{ 2 }=492a04$$

$$\Rightarrow 492a04$$ is divisible by $$9$$

$$\Rightarrow 4+9+2+a+0+4=9k$$

$$\Rightarrow 19+a=9k$$

$$\Rightarrow a=8\quad \left[ k=3 \right] $$

In how many ways the number $$10800$$ can be resolved as a product of two factors.

Step 1: Prime factorization of $$10800$$ i.e. we write $$10800={2}^{4}\times{3}^{2}\times{5}^{3}$$

Step 2: Number of factors of $$10800$$ will be $$\left(4+1\right)\left(2+1\right)\left(3+1\right)=5\times 3\times 4=60$$

Step 3: Hence number of ways to express $$10800$$ as a product of two numbers is exactly half its number of factors i.e.$$\dfrac{1}{2}\times 60=30$$

If $$GCD\;(24,20)=3x+1$$, then $$x=$$_______

$$G.C.D$$ of $$20$$ and $$24$$

$$20=2\times 2\times 5$$ [prime factorisation]

$$24=2\times 2\times 2\times 3$$

$$G.C.D=$$ multiplying all prime factors common to each other [only multiply then common number, not whole number]

$$=2\times 2$$ [no other numbers are common]

$$G.C.D=4$$

$$4=3x+1$$

$$3x=4-1$$

$$3x=3$$

$$x=1$$

How many even prime numbers are there ?

There is only one even prime number i.e., 2.

Solve:
$$6\div 2(1+2)$$

1305972_1204726_ans_ef0768f4d6a747e0b188b479ca802c87.jpeg

Suppose $$P$$ and $$Q$$ both represent prime numbers such that $$5\bullet P+7\bullet Q=109$$. Find the value of the prime $$P$$

On observation, we get

$$5\times 19+7\times 2=109$$

Where $$19$$ and $$2$$ are primes.

On comparing with,

$$5P+7Q=109\\P=19$$

If a number $$43y$$ is a multiple of $$9$$, where $$y$$ is a digit, then find the value of $$y$$.

A number is a multiple of 9, if sum of its digits is equal to $$9.$$

Sum of digits of $$43y$$ =$$9$$
$$4+3+y=9$$
$$y=9-7=2$$
$$y=2 $$

If 24a is divisible by 9, find the value of a.

$$A$$ $$number$$ $$divisible$$ $$by$$ $$9$$ $$should$$ $$have$$ $$the$$ $$sum$$ $$of$$ $$its$$ $$digits$$ $$equal$$ $$to$$ $$a$$ $$multiple$$ $$of$$ $$9.$$

$$Here,$$

$$2 + 4 + a = 9x$$

$$6 + a = 9x$$

$$\frac {6+a} {9}$$ $$=$$ $$x$$

$$x$$ $$is$$ $$a$$ $$multiple$$ $$of$$ $$9$$

$$If$$ $$a = 0,$$ $$\frac {6} {9}$$ $$is$$ $$not$$ $$divisible$$ $$by$$ $$9$$

$$If$$ $$a = 1,$$ $$\frac {7} {9}$$ $$is$$ $$not$$ $$divisible$$ $$by$$ $$9$$

$$If$$ $$a = 2,$$ $$\frac {8} {9}$$ $$is$$ $$not$$ $$divisible$$ $$by$$ $$9$$

$$If$$ $$a = 3,$$ $$\frac {9} {9}$$ $$is$$ $$divisible$$ $$by$$ $$9$$

$$So,$$ $$3$$ $$is$$ $$the$$ $$least$$ $$possible$$ $$value$$ $$of$$ $$a.$$

The product of three consecutive positive integers is divisible by $$6$$. Is this statement true or false? Justify your answer .

let the integer be=$$x,x+1,x+2$$

$$x(x+1)(x+2)$$=6

$$x(x+1)(x+2)=1\times2\times3$$

compare $$x=1,x+1=2$$

so numbers are 1,2,3

hence given statement is true

How many positive integers $$\leq 462$$ are relatively prime to $$462$$?

$$462=2\times 3\times 7\times 11$$

Total positive numbers relatively prime to $$462=462-$$numbers which are not relatively prime to 462

$$=$$$$462-\left( _{ }^{ 4 }{ { C }_{ 1 }^{ }+{ _{ }^{ 4 }{ C } }_{ 2 }^{ } }+{ _{ }^{ 4 }{ C } }_{ 3 }^{ }+{ _{ }^{ 4 }{ C } }_{ 4 }^{ } \right) $$

$$=$$$$462-(4+6+6+4)$$

$$=$$$$462-20$$

$$=$$$$442$$

Find the common factors of :
$$15$$ and $$25$$
$$56$$ and $$120$$
$$8,12$$ and $$48$$

$$(1)$$ $$HCF$$ of $$15$$ and $$25$$

$$15=3\times 5$$

$$25=5\times 5$$

So, $$HCF=5$$

$$(2)$$ $$HCF$$ of $$56$$ and $$120$$

$$56=2\times 2\times 2\times 7$$

$$120=2\times2\times 2\times \times 3\times 5$$

So, $$HCF=2\times 2\times 2=8$$

$$(3)$$ $$HCF$$ of $$8$$,$$12$$ and $$48$$

$$8=2\times 2\times 2$$

$$20=2\times2\times 3$$

$$48=2\times 2\times 2\times 2\times 3$$

So, $$HCF=2\times 2=4$$

Find the $$GCD$$ of $$735$$ and $$85$$ by using Eulidls algorithm.

gcd of 735 & 85

$$ 735 = 85\times 8+55$$

$$ 85 = 55\times 1+30$$

$$ 55 = 30\times 1+25$$

$$ 30 = 25\times 1+5$$

$$ 25 = 5\times 5+0$$

therefore hcf = 5

hcf = GCD = 5

1167743_1248143_ans_9d2aacffa9fd4928947abd47b8a8cabe.jpg

Explain why 13233343563715 is a composite number?

$$\textbf{Step 1 : Find the factor of the given number}$$

$$\text{Since it's last term is 5}$$,

$$\therefore \text{ it is divisible by 5}$$

$$\Rightarrow \text{It is a composite number.}$$

$$\textbf{Hence , 13233343563715 is a composite number}$$

Which of these is the odd one out?
$$2012, 2010, 2008, 2004$$.

Out of $$2012,2010,2008,2004$$.

$$2010$$ is odd one out since rest all are divisible by $$4$$ but $$2010$$ is not divisible by $$4$$.

also it is not a leap year

Write the number from $$1$$ to $$100$$ highlight the number with colour pencil which are divisible by $$2$$ and $$5$$

We have,

Write the number from $$1$$ to $$100$$.

So,

Divisible by $$2$$ and $$5$$

$$10,20,30,40,50,60,70,80,90,100$$

Total ways $$=10$$

Which are divisible by $$2$$ and $$5$$ both.

Hence, this is the answer.

Find the sum of all natural numbers from $$100$$ to $$300$$.
Which are divisible by $$5$$.
Which are divisible by $$6$$.
Which are divisible by $$5$$ and $$6$$.

Numbers divisible by $$5$$ between $$100$$ and $$300$$ are

$$105,110,----295$$

$$a=100,d=5$$ last term $$l=295$$

$$t_n=a+(n-1)d\Rightarrow 295=100+(n-1)\times 5$$
$$\Rightarrow \cfrac{195}{5}=n-1$$
$$\Rightarrow 39=n-1$$
$$\Rightarrow n=39+1=40$$
$$ \therefore Sum =\cfrac{n}{2}(a+l)=\cfrac{40}{2}(105+295)$$
$$=20\times 400=8000$$

Numbers divisible by $$6$$ are

$$102,108,114...294$$

$$a=102,l=294$$

and $$294=102+(n+1)\times6\\ \Rightarrow 294-102=(n-1)\times 6$$
$$\Rightarrow(n-1)\times 6=192$$
$$ \Rightarrow n-1=32$$
$$\Rightarrow n=32+1=33$$
$$ \therefore sum=\cfrac{33}{2}(102+294)=\cfrac{33}{2}\times396\\=6534$$

Numbers divisible by both $$5$$ and $$6$$ are

$$120,150,180,210,240,270\\a=120,d=30$$
$$l=270$$

Also $$n=6$$

$$\therefore sum=\cfrac{6}{2}(120+270)=3\times 390=1170$$

In the natural numbers from $$10$$ to $$250$$, how many are divisible by $$4$$?

$$\textbf{Step-1: Forming the Arithmetic Progression}$$

$$\text{Now, here the smallest number divisible by}$$ $$4$$ $$\text{is}$$ $$12.$$

$$a=12,d=4$$

$$\textbf{Step-2: Finding the value of n}$$

$$\text{The}$$ $$n^{th}$$ $$\text{term in an A.P. is given by}$$

$$t_n=a+(n-1)d$$

$$248=12+(n-1)4$$

$$248=12+4n-4$$

$$4n=248-8$$

$$4n=240$$

$$n=60$$

$$\textbf{Hence, between 10 to 250, 60 numbers are divisible by 4.}$$

Show that the product of three positive integers is divisible by $$6$$.

Let three consecutive positive integers be, $$a, a + 1 , a + 2$$.

when a number is divided 2, the remainder obtained is 0 or 1.

$$\therefore a = 2c $$ or $$ 2c + 1$$, where c is some integer.

If $$a = 2c \Rightarrow a $$ and $$a + 2 = 2c + 2 = 2(c + 1)$$ are divisible by 2.

If $$a = 2c + 1 ⇒ a + 1 = 2c + 1 + 1 = 2c + 2 = 2 (c + 1)$$ is divisible by 2.

So, we can say that one of the numbers among a, a + 1 and a + 2 is always

divisible by 2.

$$\Rightarrow a (a + 1) (a + 2)$$ is divisible by 2.

Similarly,

When a number is divided by 3, the remainder obtained is either 0 or 1 or 2.

$$\therefore a = 3b$$ or $$3b + 1$$ or $$ 3b + 2$$, where p is some integer.

If $$a = 3b$$, then a is divisible by 3.

If $$a = 3b + 1, \Rightarrow⇒ a + 2 = 3b + 1 + 2 = 3b + 3 = 3(b + 1)$$ is divisible by 3.

If $$a = 3b + 2, \Rightarrow a + 1 = 3b + 2 + 1 = 3b + 3 = 3(b + 1)$$ is divisible by 3.

So, we can say that one of the numbers among n, n + 1 and n + 2 is always

divisible by 3.

$$\Rightarrow a (a + 1) (a + 2)$$ is divisible by 3.

Hence a (a + 1) (a + 2) is divisible by 2 and 3.

$$\therefore a (a + 1) (a + 2)$$ is divisible by 6.

Write the natural numbers from $$102$$ to $$113$$.What fraction of them are prime numbers?

Natural numbers from $$102$$ to $$113$$

$$=102,\,103,\,104,\,105,\,106,\,107,\,108,\,109,\,110,\,111,\,112,\,113$$

Numbers divisible by $$2$$

Number ending with $$2,\,4,\,6,\,8,\,0$$ are divisible by $$2$$

So,$$102,\,104,\,106,\,108,\,110,\,112$$ are not prime.

Numbers divisible by $$3$$

If sum of digits is divisible by $$3,$$ it is divisible by $$3$$

So,$$105,\,111$$ are not prime.

Rest all numbers are not divisible by $$5,\,7,\,11$$

$$\therefore \,103,\,107,\,109,\,113$$ are prime

$$\therefore$$ total numbers$$=12$$

Number of prime numbers$$=4$$

$$\therefore$$ Fraction$$=\dfrac{4}{12}=\dfrac{1}{3}$$

$$24x$$ is a three-digit number. Find all the possible values of $$x$$ so that it is divisible by $$3$$.

The divisibility test for $$3$$ is that if the sum of the digits of a number is divisible by $$3$$ then the number itself will be divisible by $$3$$.

For $$24x$$ to be divisible by $$3$$,

$$2+4+x=6+x$$ must be divisible by $$3$$.

Hence, for this the values of $$x$$ are $$0,3,6,9$$.

For what possible values of $$x$$, the number $$36x$$ i.e. $$3\times 100+6\times 10\ +x$$ is divisible by $$3$$ ?

The number is $$36x$$.

For the number to be divisible by $$3$$, the sum of digits i.e. $$(3+6+x)$$ must be divisible by $$3.$$

Hence, $$x=0,3,6,9$$

Write the odd factors of 240.

All factors of $$240$$ are:

$$1,\,2,\,3,\,4,\,5,\,6,\,8,\,10,\,12,\,15,\,16,\,20,\,24,\,30,\,40,\,48,\,60,\,80,\,120,\,240$$

Amongst them, the odd factors of are $$1,\,3,\,5,\,15.$$

Find the number of odd and even divisors of $$18$$

$$18=2\times 3\times 3={2}^{1}\times{3}^{2}$$

Number of divisors$$=\left(1+1\right)\left(2+1\right)=2\times 3=6$$

Number of odd divisors$$=2+1=3$$

Number of even divisors$$=6-3=3$$

Find the truth value
Neither $$21$$ is a prime number nor it is divisible by $$3$$

From the statement given,

$$21$$ is divisible by $$3$$

$$\because$$ $$21=3\times7$$

$$\Rightarrow $$ $$21$$ is also not prime

So, $$\neg \left( 21\epsilon P \right) \Lambda \neg \left( 3/21 \right) $$

$$=\neg false\Lambda \neg T$$

$$=T\Lambda F$$

$$=F$$

$$\therefore$$ the truth value of the statement is false.

Find the median of first ten odd prime numbers.

Median $$ = \frac{1}{2}[(\frac{n}{2})^{th}+(\frac{n}{2}+1)^{th}]$$

$$ =\frac{1}{2}[(\frac{10}{2})^{th}+(\frac{10}{2}+1)^{th}]$$

$$ =\frac{1}{2} [5th + 5th]$$

$$ = \frac{13+17}{2}$$

$$ =\frac{30}{2} = 15.$$

1210484_1348180_ans_0611c5e3272b42f7938aa0714a93b4a1.jpg

What are coprime ?

Two numbers are called coprime or relative primes, if they have only one common factor which is 1 e.g., (7,9) is coprime but 15 and 21 is not coprime.

Find the digits $$p$$ and $$q$$ if $$p76q$$ is divisible by $$30$$.

If a number, be divisible by $$30$$ it should be divisible by $$3$$ and as well as $$10$$

For $$p76q $$ to be divisible by $$10$$ $$q$$ must be $$0$$

so now for $$p760$$ to be divisible by $$3$$

$$p+7+6+0=13+p$$ must be divisible by $$3$$

$$\implies p=2,5,8$$

The HCF and LCM of two numbers are 8 and 48 respectively. if one of the numbers is 24, then the other number is

We know that H.C.F$$\times$$L.C.M$$=$$product of the numbers.

Let $$x$$ be the other number

$$\Rightarrow 8\times 48=24\times x$$

$$\Rightarrow 24x=8\times 48$$

$$\Rightarrow x=\dfrac{8\times 48}{24}=8\times 2=16$$

$$\therefore$$ the other number is $$16$$

Without performing actual division find the remainders left when $$192837465$$ is divided by $$9$$.

A number is said to be divisible by $$9$$ if the sum of its digits are divisible by $$9$$

$$192837465=1+9+2+8+3+7+4+6+5=45=5\times 9$$

$$\therefore 192837465$$ is divisible by $$9$$

$$\therefore$$ Remainder$$=0$$

Without actual division, find whether $$342218064$$ is divisible by $$3$$ or not.

According to the divisibility test for $$3$$, if the sum of digits of a number is divisible by $$3$$ then the number itself is divisible by $$3$$.

So, applying the divisibility test for $$3$$,

$$3+4+2+2+1+8+6+4=30$$

$$3+0=3$$, which is divisible by $$3$$.

Hence, the given number is divisible by $$3$$.

Determine if 25110 is divisible by 45.

Given number $$25110$$

It need to be divisile by both $$5,9$$ to make sure that it is divisible by $$45$$

Since the unit digit is $$0$$ it is divisible by $$5$$

The sum of digits is $$2+5+1+1+0=9$$ so it is divisible by $$9$$

Hence it is divisibel by $$45$$

Check the divisibility conditions of $$2,\,3$$ for the following numbers:
$$(i)\,872645$$
$$(ii)\,46523$$
$$(iii)\,71232$$
$$(iv)\,89632$$
$$(v)\,251730$$

A natural number is divisible by $$2$$ if and only if, the digit in its units's place is either $$2$$ or $$4$$ or $$6$$ or $$8$$ or $$0$$

A natural number is divisible by $$3$$ if and only if, the sum of the digits is divisible by $$3$$

Numbers	Divisibility by $$2$$	Divisibility by $$3$$
$$(i)\,872645$$	The last digit is $$5$$.So it is not divisible by $$2$$	$$8+7+2+6+4+5=32$$ is not divisible by $$3$$. Hence $$872645$$ is not divisible by $$3$$
$$(ii)\,46523$$	The last digit is $$3$$.So it is not divisible by $$2$$	$$4+6+5+2+3=20$$ is not divisible by $$3$$.Hence $$46523$$ is not divisible by $$3$$
$$(iii)\,71232$$	The last digit is $$2$$.So it is divisible by $$2$$	$$7+1+2+3+2=15$$ is divisible by $$3$$. Hence 71232 is divisible by 3.
$$(iv)\,89632$$	The last digit is $$2$$.So it is divisible by $$2$$	$$8+9+6+3+2=28$$ is not divisible by $$3$$. Hence 89632 is not divisible by 3.
$$(v)\,251730$$	The last digit is $$0$$.So it is divisible by $$2$$	$$2+5+1+7+3+0=18$$ is divisible by $$3$$. Hence $$251730$$ is divisible by $$3$$

What least number of five digits is exactly divisible by 7?

The least $$5$$ digit number is $$10000$$

The remainder when $$10000$$ id divided by $$7$$ is $$4$$

So $$3$$ must be added to it to make it divisible by $$7$$

So the least $$5$$ digit number divisible by $$7$$ is $$10003$$

HCF of co-prime numbers $$4$$ and $$15$$ was found as follows by factorization:$$4=2\times 2$$ and $$15=3\times 5$$ since there is no common prime factor, so HCF of $$4$$ and $$15$$ is $$0$$.Is the answer correct?If not, what is the correct HCF?

Factors of $$4=2\times 2\times 1$$

Factors of $$15=3\times 5\times 1$$

Since the only common factor is $$1$$

H.C.F$$=1$$

$$\therefore$$ H.C.F will not be $$0$$, but $$1$$

Express $$140$$ as a product of its prime factors.

$${\textbf{Step-1: Writing prime factors.}}$$

$${\text{In other words, prime numbers that can be multiplied to obtain the original}}$$

$${\text{number are called prime factors of a number.}}$$

$${\text{So, to express}}$$ $$ 140$$

$$140=2\times70 $$

$$140=2\times2\times35$$

$$140=2\times2\times5\times7$$

$${\text{So, the prime factors of}}$$ $$ 140 $$ $${\text{are}}$$ $$(2,5,7).$$

$${\text{And the product can be expressed as}}$$ $$ 140=2\times2\times5\times7.$$

$${\textbf{Hence, the prime factors of}}$$ $${\mathbf{140}}$$ $${\textbf{ are}}$$ $${\mathbf{2,5,7.}}$$

Explain why $$1323343563715$$ is a composite no.?

The number 1323343563715 is divisible by 5. Since the number is divisible by a number other than 1 and itself, it is not a prime number. Therefore, the number 1323343563715 is a composite number because it is divisible by 5.

Prove that one and only one out of $$n,n+2$$ and $$n+4$$ is divisible by 3, where $$n$$ is any positive integer.

By Euclid's division algorithm , $$ a = bq + r $$ where $$ a , b , q , r $$ are non-negative integers and $$ 0 \leq r < b$$.

On putting $$ b = $$ we get

$$ a = 3q + r $$, where $$r = 0, 1, 2$$

Thus any number is in the form of $$3q ,\ 3q+1$$ or $$3q+2$$.

Case I : if $$n =3q$$

$$⇒n = 3q = 3(q)$$ is divisible by $$3.$$

$$⇒ n + 2 = 3q + 2$$ is not divisible by $$3.$$

$$⇒ n + 4 = 3q + 4 = 3(q + 1) + 1$$ is not divisible by $$3.$$

Case II : if $$n =3q + 1$$

$$⇒ n = 3q + 1$$ is not divisible by $$3.$$

$$⇒ n + 2 = 3q + 1 + 2 = 3q + 3 = 3(q + 1)$$ is divisible by $$3.$$

$$⇒ n + 4 = 3q + 1 + 4 = 3q + 5 = 3(q + 1) + 2$$ is not divisible by $$3.$$

Case III : if $$n = 3q + 2$$

$$⇒ n =3q + 2$$ is not divisible by $$3.$$

$$⇒ n + 2 = 3q + 2 + 2 = 3q + 4 = 3(q + 1) + 1$$ is not divisible by $$3.$$

$$⇒ n + 4 = 3q + 2 + 4 = 3q + 6 = 3(q + 2)$$ is divisible by $$3.$$

Thus one and only one out of $$n , n+2, n+4$$ is divisible by $$3.$$

If a three digit number 24x is divisible by 9, then find out the value of x, where x is a digit.

A number is divisible by $$9$$, if sum of the digits of the number are divisible by $$9$$.

Sum of digits of given number $$=2+4+x=6+x$$

Let us say that $$(x+6)$$ is a multiple of $$9$$,

$$\implies x+6=9$$

$$x=3$$

Find the common factors of $$8, 20$$.

$$8=2\times2\times2$$

$$20=2\times2\times5$$

common factor $$=2\times2=4$$

Write all factors of the following number.
$$60$$.

$$60$$ can be written as

$$1×60=60$$

$$2×30=60$$

$$3×20=60$$

$$4×15=60$$

$$5×12=60$$

$$6×10=60$$

Thus, factors of $$60$$ are $$1,\ 2,\ 3,\ 4,\ 5,\ 6,\ 10,\ 12,\ 15,\ 20,\ 30$$ and $$60$$

Find the highest common factor (HCF) of $$36$$ and $$63$$.

1695348_1647174_ans_2e6905a1cde246808dfa693c0e7ca075.jpg

Write the smallest digit and the greatest digit in the blank space of the following number so that the number formed is divisible by $$3$$.
$$4765$$_$$2$$.

Sum of the remaining digits$$=24$$
To make the number divisible by $$3$$, the sum of its digits should be divisible by $$3$$. As $$24$$ is already divisible by $$3$$, the smallest number that can be placed here is $$0$$.
Now, $$0+3=3$$
$$3+3=6$$
$$3+3+3=9$$
How ever, $$3+3+3+3=12$$
If we put $$9$$, then the sum of the digits will be $$33$$ and as $$33$$ is divisible by $$3$$, the number will also be divisible by $$3$$.
Therefore, the largest number is $$9$$.

The numbers 13 and 31 are prime numbers. Both these numbers have same digits, 1 andFind such pairs of prime numbers up to 100.

Given that, $$13$$ and $$31$$ are prime numbers comprising of same digits, $$1$$ and $$3$$.

To fin out: Prime numbers up to $$100$$ which comprises of the same digits.

All prime numbers up to $$100$$ are:

$$2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97$$

In the above list, we can see that there are $$3$$ pairs of prime numbers that comprise of same digits. They are:

$$17, 71$$
$$37, 73$$
$$79, 97$$

Hence, there are $$3$$ more pairs similar to $$13, 31$$. They are $$17, 71,\ \ 37, 73\ and\ 79, 97$$.

Write all the factors of the following number.
$$24$$.

$$24$$

$$24=1\times24$$

$$24=2\times12$$

$$24=3\times8$$

$$24=4\times6=6\times4$$

$$\therefore$$ factors of $$24$$ are $$1,2,3,4,6,8,12$$ and $$24$$

Using divisibility tests, determine the following number is divisible by $$6$$.
$$1790184$$.

Since the last digit of the number is $$4$$, it is divisible by $$2$$. On adding all the digits of the number, the sum obtained is $$30$$. Since $$30$$ is divisible by $$3$$, the given number is also divisible by $$3$$.
As the number is divisible by both $$2$$ and $$3$$, it is divisible by $$6$$.

Using divisibility tests, determine whether $$297144$$ is divisible by $$6.$$

Divisibility by $$2$$

Since $$297144$$ ends with $$4$$

It is divisible by $$2$$

Divisibility by $$3$$ sum of the digits

$$=2+9+7+1+4+4$$

$$=27$$

since $$27$$ is divisible by $$3$$

so $$297144$$ is divisible by $$3$$

since $$297144$$ is divisible by both $$2 \ and \ 3$$

It is divisible by $$6$$

Write all the factors of the following numbers.
$$15$$.

$$15$$
$$15=1\times 15$$,
$$15=3\times 5$$,
$$15=5\times 3$$
$$\therefore$$ Factors of $$15$$ are $$1, 3, 5$$ and $$15$$.

Find numbers between $$1$$ and $$100$$ having exactly three factors.

All the prime numbers, for example 2,3,5,7... have only 2 factors, that is, 1 and the number itself.

All composite numbers, for example 4,6,8,9...have more than 3 factors.

So, only the squares of the prime numbers are the only numbers which have exactly three factors.

Such numbers between 1 and 100 are 4,9,25 and 49.

Without actual division show that the following number is divisible by $$5$$.
$$5555$$.

1504641_1658817_ans_edf23f966ffe43ecb86dcf3f9a7d8315.jpg

Which of the following numbers have $$15$$ as their factor?
(i) $$15625$$
(ii) $$123015$$.

1) 15625

Since 15625 is not divisible by 15

.So, 15625 is not a factor of 15.

2) 123015

Since 123015 is divisible by 15,

So, 123015 is a factor of 15.

Write all factors of the following number.
$$729$$.

1×729=729

3×243=729

9×81=729

27×27=729

So, the factors of 729 are 1,3,9,27,81,243 and 729

Without actual division show that the following number is divisible by $$5$$.
$$55$$.

Given no.:$$55$$

unit digit is $$5$$

So, $$55$$ is divisible by $$5$$.

So $$5$$ is a factor of $$55$$

Write all factors of the following number.
$$125$$.

1×125=125

5×25=125

Thus, factors of 125 are 1,5,25 and 125

Without actual division show that the following number is divisible by $$5$$.
$$555$$.

The number will one's digit 0 or 5 is divisible by 5.

Since 555 has one's digit as 5, so it is divisible by 5.

Without actual division show that the following number is divisible by $$5$$.
$$50005$$.

1504645_1658818_ans_43bf6251ff314803b95838e42a43f0c9.jpg

Write all factors of the following number.
$$76$$.

To find the factors of 76,

1×76=76

2×38=76

4×19=76

Thus, the factors of 76 are 1,2,4,19,38 and 76

Is there any natural number having no factor at all?

1504649_1658819_ans_9787bf6439474c8bb1c2622cea3b7042.jpg

What is the smallest prime number? Is it an even number?

The least prime number is $$2$$
yes it's an even number

Write all prime numbers between $$60$$ and $$100$$.

Prime numbers are the numbers which have only 2 factors, that is,1 and the number itself.

So, the prime numbers between $$60$$ and $$100$$ are $$61,67,71,73,79,83,89$$ and $$97.$$

Write all prime numbers between $$10$$ and $$50$$.

1504688_1658832_ans_abd303f89a8140748f18d28139adf6e9.jpg

Write all prime numbers between $$70$$ and $$90$$.

The prime numbers between $$70$$ and $$90$$ are

$$71,73,79,83$$ and $$89$$

What are prime numbers? List all primes between $$1$$ and $$30$$.

A prime number is a number which has only two factors i.e. $$1$$ and the number itself. Prime numbers between $$1$$ and $$30$$ are:

$$2,3,5,7,11,13,17,19,23,29$$

Find the common factors of $$2, 6$$ and $$8$$.

1504671_1658826_ans_8ee41042bfd04a31905d401d0fbd7d51.jpg

What are co-primes? Give examples of five pairs of co-primes. Are co-primes always prime? If no, illustrate your answer by an example.

$$ \Rightarrow$$ Two integers a and b are said to be relatively prime, mutually prime, or coprime (also written co-prime) if the only positive integer (factor) that divides both of them is 1. ... A set of integers can also be called coprime

$$\Rightarrow$$ Pairs of co-prime are: $$2, 3; 3, 4; 4, 5; 5, 6; 6, 7$$.

$$\Rightarrow$$ No, $$15, 16$$ are co-prime but none of them is prime.

A list consists of the following pairs of numbers:
$$51, 53; 55, 57; 59, 61; 63, 65; 67, 69; 71, 73$$.
Categorize them as pairs of co-primes.

Co-prime number is a set of numbers or integers which have only 1 as their common factor i.e. their highest common factor (HCF) will be 1.

$$51, 53- $$ is pair of co-primes

$$55, 57-$$ is pair of co-primes

$$59, 61-$$ is pair of co-primes

$$63, 65-$$ is pair of co-primes

$$67, 69-$$ is pair of co-primes

$$71, 73-$$ is pair of co-primes

Fill in the blank in the following.
$$1$$ is neither _ nor __.

1 is neither prime nor composite.

What are composite numbers? Can a composite number be odd? If yes, write the smallest odd composite number.

Composite number is a number which have three or more factors, that is 1 , the number itself and at least one more number.

Example- 4, factors of 4 are 1,2 and 4

Yes, a composite number can be odd

The smallest odd composite number is 9 as factors of 9 are 1,3 and 9.

Test the divisibility of the following number by $$3$$.
$$9082746$$.

The divisibility test of 3 states that - A number is divisible by 3 if sum of its digits is divisible by 3

So , for 9082746 -

9+0+8+2+7+4+6= 36

And 36 is divisible by 3

So, 9082746 is divisible by 3

Test the divisibility of the following number by $$6$$.
$$56423$$.

1502949_1659092_ans_fabddb9b73634778bb32a14c5116caad.jpg

Test the divisibility of the following number by $$3$$.
$$607439$$.

1504913_1659085_ans_49418f71e61c47b89824bf5c929615c4.jpg

Test the divisibility of the following number by $$2$$.
$$984325$$.

1504910_1659079_ans_f4e625711d964a96bfa1a8b1579aa32b.jpg

Test the divisibility of the following number by $$2$$.
$$367314$$.

1504911_1659081_ans_1341c377bb4b488f9874c091f7ce976f.jpg

Test the divisibility of the following number by $$6$$.
$$7020$$.

1502945_1659088_ans_9a25366d7be44d2995ca093f0f2d3cc5.PNG

Test the divisibility of the following number by $$3$$.
$$70335$$.

1504912_1659083_ans_1557964dd32d4306a4d1132b97d1fd0c.jpg

Fill in the blank in the following.
The smallest prime number is _______.

We know that, a prime number is a number having exactly two factors, $$1$$ and the number itself.

Hence, the smallest prime number is $$2$$.

Fill in the blank in the following.
The smallest composite number is _______.

Composite numbers starts from 4. So 4 is the smallest composite number.

Test the divisibility of the following number by $$2$$.
$$6520$$.

A number is said to be divisible by $$2$$ if its units digit is divisible by $$2$$. In the given number units place digit is $$0$$ which is divisible by every number. Hence given number is divisible by $$2$$

Test the divisibility of the following by $$6$$.
$$8364$$.

1504934_1659109_ans_0fc7eafe277347cca8286e8789c18bec.jpg

Test the divisibility of the following number by $$4$$.
$$1020531$$.

Given no. is 1020531.

Last 2 digit 31 are not divisible by 4.

1020531 is not divisible by 4. ..... (by divisibility rule for 4.)

Test the divisibility of the following number by $$4$$.
$$9801523$$.

Last 2 digits of $$9801523$$ is $$23$$ which is not divisible by $$4$$.

So $$9801523$$ is not divisible by $$4$$.

Check whether $$732510$$ is divisible by $$6$$

1502952_1659094_ans_a4dc3132429341fda8769518479d2789.jpg

Test the divisibility of the following number by $$8$$.
$$36712$$.

1505080_1659112_ans_fa93b9418eb64d6dad2e02e7722e6341.jpg

Test the divisibility of the following number by $$4$$.
$$786532$$.

Last $$2$$ digits of $$786532$$ is $$32$$ is divisible by $$4$$. So, $$786532$$ is divisible by $$4$$

Test the divisibility of the following number by $$8$$.
$$7314$$.

Divisibility test of 8 states that a number is divisible by 8 is its last three digits are divisible by 8

In 7314, last 3 digits are 314 and since 314 is not divisible by 8

So, 7314 is not divisible by 8

Test the divisibility of the following number by $$9$$.
$$187245$$.

1502704_1659113_ans_74c4a6c148864637a39f34e5635ccf0e.PNG

Test the divisibility of the following number by $$9$$.
$$547218$$.

1502708_1659115_ans_1211b71b6c1d4a55a8aecaaf3bc7194d.PNG

Test the divisibility of the following number by $$9$$.
$$3478$$.

1502706_1659114_ans_39ab796a898a4dba8509c2ba749cdac9.jpg

Show that the following pair is co-prime.
$$875, 1859$$.

Factors of $$1859=13\times 13\times 11\times 1$$

Factors of $$875=5\times 5\times 5\times 7\times 1$$

Since the only common factor is $$1$$.

Therefore, the given pair $$(875,1859)$$ is coprime.

In the following number, replace $$\ast$$ by the smallest number to make it divisible by $$9$$.
$$67\ast 19$$.

1503484_1659131_ans_2f19e60c634c472b938576ba4bd89a59.PNG

In the following number, replace $$\ast$$ by the smallest number to make it divisible by $$3$$.
$$18\ast 71$$.

1503468_1659129_ans_4a113034e4b34d8fa9ceddc49f2244df.jpg

Given an example of a number which is divisible by $$2$$ but not by $$4$$.

Twice of Any odd no. is divisible by 2 but not by 4.
1505105_1659139_ans_8bc53d80a6fb4ea39b3bae375310a04b.jpg

In the following number, replace $$\ast$$ by the smallest number to make it divisible by $$9$$.
$$538\ast 8$$.

1503497_1659134_ans_463215da60d74ff89f27d5de1a5d27dc.jpg

In the following number, replace $$x$$ by the smallest number to make it divisible by $$3$$.
$$75x 5$$.

Given that, the number $$75x5$$ is divisible by $$3$$.

To find out: The smallest value of $$x$$.

The divisibility rule for $$3$$ states that a number is completely divisible by $$3$$ if the sum of its digits is divisible by $$3$$.

Sum of digits $$= 7 + 5 + x + 5$$

$$= 17 + x$$

If we take $$x = 1, 4, 7$$, the no. will be divisible by 3.

Hence, the smallest value of $$x$$ for which $$75x5$$ is divisible by $$3$$ is $$1$$.

Show that the following pairs are co-prime.
$$59, 97$$.

1505790_1659176_ans_5dc9b2728b11461c9aeb82d89788681c.jpg

In the following number, replace $$x$$ by the smallest number to make it divisible by $$3$$.
$$35x 64$$.

Divisibility rule for 3 states that a number is completely divisible by 3 if the sum of its digits is divisible by 3 i.e., it is a multiple of 3.

Sum of digits $$= 3 + 5 + x + 6 + 4$$

$$= 18 + x$$

If we take $$x = 0, 3, 6,9$$,number is divisible by 3.

Taking Smallest value $$x= 0$$.

In the following number, replace $$\ast$$ by the smallest number to make it divisible by $$9$$.
$$66784\ast$$.

Given that, the number $$66784*$$ is divisible by $$9$$.

To find out: The smallest value of $$*$$.

We know that, a number is divisible by $$9$$, if the sum of its digits is divisible by $$9$$.

The sum of digits of the give number $$=6+6+7+8+4+*$$

$$\Rightarrow 31+*$$

The smallest number after $$31$$ which is divisible by $$9$$ is $$36$$.

Hence, for the smallest value of $$*$$, the sum of digits should be $$36$$.

$$\therefore \ 31+*=36$$

$$\Rightarrow *=36-31=5$$

Hence, the smallest value of $$*$$ for which the number $$66784*$$ is divisible by $$9$$, is $$5$$.

Show that the following pairs are co-prime.
$$288, 1375$$.

Since $$1375>288$$, we apply the division lemma to $$1375$$ and $$288$$ to obtain:

$$1375=288\times 4+223$$

Since remainder $$223\neq 0$$, we apply the division lemma to $$288$$ and $$223$$ to obtain:

$$288=223\times 1+65$$

We consider the new divisor $$223$$ and new remainder $$65$$, and apply the division lemma to obtain

$$223=65\times 3+28$$

We consider the new divisor $$65$$ and new remainder $$28$$, and apply the division lemma to obtain

$$65=28\times 2+9$$

We consider the new divisor $$28$$ and new remainder $$9$$, and apply the division lemma to obtain

$$28=9\times 3+1$$

We consider the new divisor $$9$$ and new remainder $$1$$, and apply the division lemma to obtain

$$9=1\times 9+0$$

Since the remainder is zero, the process stops.

Also, the divisor at this stage is $$1$$,

Hence, the

H C F

of $$1375$$ and $$288$$ is $$1$$.

Co-prime number is a set of numbers or integers which have only 1 as their common factor i.e. their HCF will be 1.

Hence, $$1375\ and\ 288$$ are co-prime numbers.

Fill in the blank.
A number which has only two factors is called a ________.

A number which has only two factors is called a prime number.
like $$3$$ & $$5$$, which only has $$1$$ and the number itself as the factors

Fill in the blank.
The HCF of two consecutive odd numbers is ________.

Two consecutive odd numbers always have common factor as 1. So HCF of two consecutive odd numbers is 1.
e.g. $$3$$ & $$5$$

Define a perfect number. Write two perfect numbers.

A Perfect Number “n”, is a positive integer which is equal to the sum of its factors, excluding “n” itself.

e.g.-$$6 \rightarrow 1+2+3=6$$

$$28 \rightarrow 1+2+4+7+14=28$$

What is a perfect number?Give example.

A perfect number is a positive integer that is equal to the sum of its positive divisors, excluding the number itself.

Example .,

$$6$$ has divisors $$1, 2$$ and $$3$$ (excluding itself),

and $$1 + 2 + 3 = 6$$,

So $$6$$ is a perfect number.

Similarly,

$$28$$ has divisors $$1,2,4,7$$ and $$14$$(excluding itself).

and $$1+2+4+7+14=28$$

So, $$28$$ is a perfect number.

Write all prime numbers between $$50$$ and $$100$$.

Prime numbers:

The natural number greater than 1 is said to be a prime number, if it has only two factors 1 and itself.

53,59,61,67,71,73,79,83,89,97 are the prime numbers between 50 to 100.

Factorize the following algebraic expression.
$$49-x^2-y^2+2xy$$.

1539529_1673730_ans_6be3796500034e5a99bdddf1e3b208d5.jpg

Factorize the following algebraic expression.
$$a^2-14a-51$$.

1588666_1673760_ans_05006ef829a743dabeb5d8e109f277ff.jpg

Factorize the following algebraic expression.
$$a^2+4b^2-4ab-4c^2$$.

1588654_1673732_ans_1e39a1f7080d4c0dac9501066b0ed2fb.jpg

Factorize the following algebraic expression.
$$x^2-y^2-4xz+4z^2$$.

1588656_1673733_ans_29e7ef64bef64c08bdacbbed4f3a3f20.jpg

Factorize the following algebraic expression.
$$40+3x-x^2$$.

1590439_1673755_ans_086137765abc4e91ba64f004f86c1d95.jpg

Fill in the blank.
Two perfect numbers are _ and _.

A perfect number is a positive integer that is equal to the sum of its positive divisors, excluding the number itself.

Example .,

$$6$$ has divisors $$1, 2$$ and $$3$$ (excluding itself),

and $$1 + 2 + 3 = 6$$,

So $$6$$ is a perfect number.

Similarly,

$$28$$ has divisors $$1,2,4,7$$ and $$14$$(excluding itself).

and $$1+2+4+7+14=28$$

So, $$28$$ is a perfect number.

So, two perfect numbers are $$\underline{6}$$ and $$\underline{28}.$$

Factorize the following algebraic expression.
$$a^2+3a-88$$.

1588664_1673757_ans_a1085fc6965d4810993b9749f8599335.jpg

Factorize the following algebraic expression.
$$x^2+14x+45$$.

1588696_1673763_ans_4079c6b4853c47e3abc19f94a5d86b0c.jpg

Test the divisibility of the following number by $$2$$:
$$66669$$

we know that if the unit place digit is divisible by $$2$$ then our given number is divisible by $$2$$.

Here, the unit place the given number is $$9$$ which is not divisible by $$2$$

$$\therefore$$ the given number $$66669$$ is not divisible by $$2$$.

Factorize the following algebraic expression.
$$a^2+2a-3$$.

1588703_1673769_ans_c42353d4476545bea9af8a5e2f016faf.jpg

Test the divisibility of the following number by $$5$$:
$$98765$$

we know that if the unit place digit is divisible by $$5$$ then our given number is divisible by $$5$$.

Here, the unit place the given number is $$5$$ which is divisible by $$5$$

$$\therefore$$ the given number $$98765$$ is divisible by $$5$$.

Test the divisibility of the following number by $$3$$:
$$100002$$

we know that if the sum of digit of the number is divisible by $$3$$ then the number is divisible by $$3$$.

Sum of the digit of $$100002$$ is $$3$$, which is divisible by $$3$$

$$\therefore$$ the given number $$100002$$ is divisible by $$3$$.

Test the divisibility of the following number by $$3$$:
$$591282$$

we know that if the sum of digit of the number is divisible by $$3$$ then the number is divisible by $$3$$.

Sum of the digit of $$591282$$ is $$27$$, which is divisible by $$3$$

$$\therefore$$ the given number $$591282$$ is divisible by $$3$$.

Factorize the following algebraic expression.
$$x^2-11x-42$$.

1588700_1673767_ans_6a2b5342449c4737b356fc12e4f53918.jpg

Factorize the following algebraic expression.
$$x^2-22x+120$$.

1588697_1673764_ans_b6e56acc72e745d1832179c7dd25e6be.jpg

Show that $$10^n+3.4^{n+2} +5$$ is divisible by 9.

1574070_1745508_ans_62ce765f5e1d4e33b0a24469e94b0398.jpg

Test the divisibility of the following number by $$4$$:
$$134$$

we know that if the number formed by last two digits of a given number is divisible by $$4$$ then the whole number is divisible by $$4$$.

The number formed by the last two digits is $$34$$, which is not divisible by $$4$$

$$\therefore$$ the given number $$134$$ is not divisible by $$4$$.

Test the divisibility of the following number by $$9$$:
$$14799$$

we know that if the sum of digit of the number is divisible by $$9$$ then the number is divisible by $$9$$.

Sum of the digit of $$14799$$ is $$30$$, which is not divisible by $$9$$

$$\therefore$$ the given number $$14799$$ is not divisible by $$9$$.

Test the divisibility of the following number by $$9$$:
$$64302$$

we know that if the sum of digit of the number is divisible by $$9$$ then the number is divisible by $$9$$.

Sum of the digit of $$64302$$ is $$15$$, which is not divisible by $$9$$

$$\therefore$$ the given number $$64302$$ is not divisible by $$9$$.

Test the divisibility of the following number by $$4$$:
$$3928$$

we know that if the number formed by last two digits of a given number is divisible by $$4$$ then the whole number is divisible by $$4$$.

The number formed by the last two digits is $$28$$, which is divisible by $$4$$

$$\therefore$$ the given number $$3928$$ is divisible by $$4$$.

Test the divisibility of the following number by $$4$$:
$$618$$

we know that if the number formed by last two digits of a given number is divisible by $$4$$ then the whole number is divisible by $$4$$.

The number formed by the last two digits is $$18$$, which is not divisible by $$4$$

$$\therefore$$ the given number $$618$$ is not divisible by $$4$$.

Test the divisibility of the following number by $$9$$:
$$66888$$

we know that if the sum of digit of the number is divisible by $$9$$ then the number is divisible by $$9$$.

Sum of the digit of $$66888$$ is $$36$$, which is divisible by $$9$$

$$\therefore$$ the given number $$66888$$ is divisible by $$9$$.

Test the divisibility of the following number by $$9$$:
$$30006$$

we know that if the sum of digit of the number is divisible by $$9$$ then the number is divisible by $$9$$.

Sum of the digit of $$30006$$ is $$9$$, which is divisible by $$9$$

$$\therefore$$ the given number $$30006$$ is divisible by $$9$$.

Test the divisibility of the following number by $$9$$:
$$32022$$

we know that if the sum of digit of the number is divisible by $$9$$ then the number is divisible by $$9$$.

Sum of the digit of $$32022$$ is $$9$$, which is divisible by $$9$$

$$\therefore$$ the given number $$32022$$ is divisible by $$9$$.

Test the divisibility of the following number by $$9$$:
$$33333$$

we know that if the sum of digit of the number is divisible by $$9$$ then the number is divisible by $$9$$.

Sum of the digit of $$33333$$ is $$15$$, which is not divisible by $$9$$

$$\therefore$$ the given number $$33333$$ is not divisible by $$9$$.

Test the divisibility of the following number by $$9$$:
$$89361$$

we know that if the sum of digit of the number is divisible by $$9$$ then the number is divisible by $$9$$.

Sum of the digit of $$89361$$ is $$27$$, which is divisible by $$9$$

$$\therefore$$ the given number $$89361$$ is divisible by $$9$$.

Test the divisibility of the following number by $$8$$:
$$59312$$

we know that if the number formed by last three digits of a given number is divisible by $$8$$ then the whole number is divisible by $$8$$.

The number formed by the last three digits is $$312$$, which is divisible by $$8$$

$$\because 312\div8=39$$

$$\therefore$$ the given number $$59312$$ is divisible by $$8$$.

Test the divisibility of the following number by $$4$$:
$$66666$$

we know that if the number formed by last two digits of a given number is divisible by $$4$$ then the whole number is divisible by $$4$$.

The number formed by the last two digits is $$66$$, which is not divisible by $$4$$

$$\therefore$$ the given number $$66666$$ is not divisible by $$4$$.

Test the divisibility of the following number by $$8$$:
$$7304$$

we know that if the number formed by last three digits of a given number is divisible by $$8$$ then the whole number is divisible by $$8$$.

The number formed by the last three digits is $$304$$, which is divisible by $$8$$

$$\because 304\div8=38$$

$$\therefore$$ the given number $$7304$$ is divisible by $$8$$.

Test the divisibility of the following number by $$4$$:
$$99918$$

we know that if the number formed by last two digits of a given number is divisible by $$4$$ then the whole number is divisible by $$4$$.

The number formed by the last two digits is $$18$$, which is not divisible by $$4$$

$$\therefore$$ the given number $$99918$$ is not divisible by $$4$$.

Test the divisibility of the following number by $$4$$:
$$56794$$

we know that if the number formed by last two digits of a given number is divisible by $$4$$ then the whole number is divisible by $$4$$.

The number formed by the last two digits is $$94$$, which is not divisible by $$4$$

$$\therefore$$ the given number $$56794$$ is not divisible by $$4$$.

Test the divisibility of the following number by $$4$$:
$$50176$$

we know that if the number formed by last two digits of a given number is divisible by $$4$$ then the whole number is divisible by $$4$$.

The number formed by the last two digits is $$76$$, which is divisible by $$4$$

$$\therefore$$ the given number $$50176$$ is divisible by $$4$$.

Test the divisibility of the following number by $$8$$:
$$6132$$

we know that if the number formed by last three digits of a given number is divisible by $$8$$ then the whole number is divisible by $$8$$.

The number formed by the last three digits is $$132$$, which is not divisible by $$8$$

$$\because 132\div8=16.5$$

$$\therefore$$ the given number $$6132$$ is not divisible by $$8$$.

Test the divisibility of the following number by $$4$$:
$$86102$$

we know that if the number formed by last two digits of a given number is divisible by $$4$$ then the whole number is divisible by $$4$$.

The number formed by the last two digits is $$02$$, which is not divisible by $$4$$

$$\therefore$$ the given number $$86102$$ is not divisible by $$4$$.

Test the divisibility of the following number by $$4$$:
$$39392$$

we know that if the number formed by last two digits of a given number is divisible by $$4$$ then the whole number is divisible by $$4$$.

The number formed by the last two digits is $$92$$, which is divisible by $$4$$

$$\therefore$$ the given number $$39392$$ is divisible by $$4$$.

Test the divisibility of the following number by $$4$$:
$$77736$$

we know that if the number formed by last two digits of a given number is divisible by $$4$$ then the whole number is divisible by $$4$$.

The number formed by the last two digits is $$36$$, which is divisible by $$4$$

$$\therefore$$ the given number $$77736$$ is divisible by $$4$$.

Write all prime numbers between:
$$80$$ and $$100$$

$$83, 89$$ and $$97$$ are all prime numbers between $$80$$ and $$100$$

Test the divisibility of the following number by $$8$$:
$$44444$$

we know that if the number formed by last three digits of a given number is divisible by $$8$$ then the whole number is divisible by $$8$$.

The number formed by the last three digits is $$444$$, which is not divisible by $$8$$

$$\because 444\div8=55.5$$

$$\therefore$$ the given number $$44444$$ is not divisible by $$8$$.

Test the divisibility of the following number by $$8$$:
$$66664$$

we know that if the number formed by last three digits of a given number is divisible by $$8$$ then the whole number is divisible by $$8$$.

The number formed by the last three digits is $$664$$, which is divisible by $$8$$

$$\because 664\div8=83$$

$$\therefore$$ the given number $$66664$$ is divisible by $$8$$.

Write all the prime numbers between:
$$40$$ and $$80$$

$$41, 43, 47, 53, 59, 61, 67, 71, 73$$ and $$79$$ are all prime numbers between $$40$$ and $$80$$

Write all the prime numbers between $$10$$ and $$40.$$

$$11,13, 17, 19, 23, 29, 31$$ and $$37$$ are all prime numbers between $$10$$ and $$40$$.

Test the divisibility of the following number by $$8$$:
$$998818$$

we know that if the number formed by last three digits of a given number is divisible by $$8$$ then the whole number is divisible by $$8$$.

The number formed by the last three digits is $$818$$, which is not divisible by $$8$$

$$\because 818\div8=102.25$$

$$\therefore$$ the given number $$998818$$ is not divisible by $$8$$.

Test the divisibility of the following number by $$8$$:
$$265472$$

we know that if the number formed by last three gidits of a given number is divisible by $$8$$ then the whole number is divisible by $$8$$.

The number formed by the last three digits is $$472$$, which is divisible by $$8$$

$$\because 472\div8=59$$

$$\therefore$$ the given number $$265472$$ is divisible by $$8$$.

Test the divisibility of the following number by $$3$$:
$$903164$$

we know that if the sum of digit of the number is divisible by $$3$$ then the number is divisible by $$3$$.

Sum of the digital is $$23$$, which is not divisible by $$3$$

$$\therefore$$ the given number $$903164$$ is not divisible by $$3$$.

Test the divisibility of the following number by $$8$$:
$$7350162$$

we know that if the number formed by last three gidits of a given number is divisible by $$8$$ then the whole number is divisible by $$8$$.

The number formed by the last three digits is $$162$$, which is not divisible by $$8$$

$$\because 162\div8=20.25$$

$$\therefore$$ the given number $$7350162$$ is not divisible by $$8$$.

Test the divisibility of the following number by $$8$$:
$$154360$$

we know that if the number formed by last three digits of a given number is divisible by $$8$$ then the whole number is divisible by $$8$$.

The number formed by the last three digits is $$360$$, which is divisible by $$8$$

$$\because 360\div8=45$$

$$\therefore$$ the given number $$154360$$ is divisible by $$8$$.

Find out the following number is prime or not ?
$$63$$

$$1, 3, 7, 9, 21$$ and $$63$$ are the divisors of $$63$$
Hence, $$63$$ has more than $$2$$ factors
$$\therefore 63$$ is not a prime number

Find out the following number is prime or not ?
$$87$$

$$1,3,29$$ and $$87$$ are the divisors of $$87$$
Hence $$87$$ has more than $$2$$ factors
$$\therefore 87$$ is not a prime number

List all even prime numbers

$$2$$ is only the even prime number.
All even numbers other than 2 have $$2$$ as a factor, they can't be prime.

Test the divisibility of the following number by 2:
$$69435$$

A number is divisible by $$2$$ only if its ones digit is $$0, 2, 4, 6$$ and $$8$$
Since $$0,2,4,6$$ or $$8$$ is not in ones digits place in $$69435$$
$$\therefore$$ It is not divisible by $$2$$

Find out the following number is prime or not ?
$$89$$

$$1$$ and $$89$$ are the divisors of $$89$$
$$\therefore 89$$ is a prime number

Write the smallest prime number.

$$2$$ is the smallest prime number

Test the divisibility of the following numbers by $$2$$:
$$59628$$

A number is divisible by $$2$$ only if its ones digit is $$0, 2, 4, 6$$ and $$8$$
Since $$8$$ is in ones digits place in $$59628$$
$$\therefore$$ It is divisible by $$2$$

Write the smallest odd prime number

$$3$$ is the smallest odd prime number

Find out the following number is prime or not ?
$$91$$

$$1, 7, 13$$ and $$91$$ are the divisors of $$91$$
Hence $$91$$ has more than two factors
$$\therefore 91$$ is not a prime number

Write all the prime numbers between
$$30$$ and $$40$$

$$31$$ and $$37$$ are prime numbers between $$30$$ and $$40$$

Test the divisibility of the following number by $$4$$
$$2314$$

A number is divisible by $$4$$ if the digits in its ones and tens place are divisible by $$4$$
$$2314$$ is not divisible by $$4$$ since last two digits is $$14$$ is not divisible by $$4$$

Test the divisibility of the following numbers by $$2$$:
$$789403$$

A number is divisible by $$2$$ only if its ones digit is $$0, 2, 4, 6$$ and $$8$$
Since $$0, 2, 4, 6,$$ or $$8$$ is not in ones digits place in $$789403$$
$$\therefore$$ It is not divisible by $$2$$

Test the divisibility of the following numbers by $$2$$:
$$357986$$

A number is divisible by $$2$$ only if its ones digit is $$0, 2, 4, 6$$ and $$8$$
Since $$6$$ is in ones digits place in $$357986$$
$$\therefore$$ It is divisible by $$2$$

Test the divisibility of the following number by $$3$$
$$872645$$

A number is divisible by $$3$$ when sum of its digits is divisible by $$3$$
Sum of its digits $$8 + 7 + 2 + 6 + 4 + 5 = 32$$
Since $$32$$ is not divisible by $$3$$
$$\therefore 872645$$ is not divisible by $$3$$

Test the divisibility of the following number by $$3$$
$$10038$$

A number is divisible by $$3$$ when sum of its digits is divisible by $$3$$
Sum of its digits $$= 1 + 0 + 0+ 3 +8 = 12$$
Since $$12$$ is divisible by $$3$$
$$\therefore 10038$$ is divisible by $$3$$

Test the divisibility of the following number by $$4$$
$$63712$$

A number is divisible by $$4$$ if the digits in its ones and tens place are divisible by $$4$$
$$63712$$ is divisible by $$4$$ since last two digits $$12$$ is divisible by $$4$$

Test the divisibility of the following number by $$4$$
$$618$$

A number is divisible by $$4$$ if the digits in its ones and tens place are divisible by $$4$$
$$618$$ is not divisible by $$4$$ since the last two digits $$18$$ is not divisible by $$4$$

Test the divisibility of the following numbers by $$2$$:
$$367314$$

A number is divisible by $$2$$ only if its ones digit is $$0, 2, 4, 6$$ and $$8$$
Since $$4$$ is in ones digits place in $$367314$$
$$\therefore$$ It is divisible by $$2$$

Test the divisibility of the following number by $$3$$
$$79124$$

A number is divisible by $$3$$ when sum of its digits is divisible by $$3$$
Sum of its digits $$= 7+ 9 + 1 + 2 + 4 = 23$$
Since $$23$$ is not divisible by $$3$$
$$\therefore 79124$$ is not divisible by $$3$$

Test the divisibility of the following number by $$3$$
$$524781$$

A number is divisible by

Test the divisibility of the following number by $$4$$
$$35056$$

A number is divisible by $$4$$ if the digits in its ones and tens place are divisible by $$4$$
$$35056$$ is divisible by $$4$$ since last two digits $$56$$ is divisible by $$4$$

Test the divisibility of the following number by $$6:$$
$$46523$$

If the number is divisible by both $$2$$ and $$3$$ then the number is divisible by $$6$$
Divisibility by $$2 =$$ Since $$3$$ is in ones place it is not divisible by $$2$$
$$\therefore 46523$$ is not divisible neither by $$2$$ or $$6$$

Test the divisibility of the following number by $$4$$
$$946126$$

A number is divisible by $$4$$ if the digits in its ones and tens place are divisible by $$4$$
$$946126$$ is not divisible by $$4$$ since last two digits $$26$$ is not divisible by $$4$$

Test the divisibility of the following number by $$4$$
$$810524$$

A number is divisible by $$4$$ if the digits in its ones and tens place are divisible by $$4$$
$$810524$$ is divisible by $$4$$ since last two digits $$24$$ is divisible by $$4$$

Test the divisibility of the following number by $$6:$$
$$2070$$

If the number is divisible by both $$2$$ and $$3$$ then the number is divisible by $$6$$
Divisibility by $$2$$ = Since $$0$$ is in ones place. It is divisible by $$2$$
Divisibility by $$3$$ = Since the sum of digits $$= 2 + 0 + 7 + 0 = 9$$
$$9$$ is divisible by $$3$$
$$\therefore 2070$$ is divisible by $$6$$

Test the divisibility of the following numbers by $$5$$:
$$124684$$

If the ones digit of a number is $$0$$ or $$5$$ then the number is divisible by $$5$$
Since $$4$$ is in ones place
$$\therefore 124684$$ is not divisible by $$5$$

Test the divisibility of the following number by $$5$$:
$$23590$$

If the ones digit of a number is $$0$$ or $$5$$ then the number is divisible by $$5$$
Since $$0$$ is in ones place
$$\therefore 23590$$ is divisible by $$5$$

Test the divisibility of the following numbers by $$5$$:
$$438750$$

If the ones digit of a number is $$0$$ or $$5$$ then the number is divisible by $$5$$
Since $$0$$ is in ones place
$$\therefore 438750$$ is divisible by $$5$$

Test the divisibility of the following numbers by $$5$$:
$$723405$$

If the ones digit of a number is $$0$$ or $$5$$ then the number is divisible by $$5$$
Since $$5$$ is in ones place
$$\therefore 723405$$ is divisible by $$5$$

Test the divisibility of the following numbers by $$5$$:
$$35208$$

If the ones digit of a number is $$0$$ or $$5$$ then the number is divisible by $$5$$
Since $$8$$ is in ones place
$$\therefore 35208$$ is not divisible by $$5$$

Test the divisibility of $$71232$$ by $$6$$

A number is divisible by $$6$$ only if the number is divisible by both $$2$$ and $$3.$$

The one's place in $$71232$$ is $$2,$$ hence it is divisible by $$2$$

And the sum of the digits of $$71232$$ is $$7 + 1 + 2 + 3 + 2 = 15$$

We know that $$15$$ is divisible by $$3$$

Hence $$71232$$ is also divisible by $$3$$

$$\therefore 71232$$ is divisible by $$6,$$ as it is divisible by $$2$$ and $$3$$

Test the divisibility of the following number by $$6:$$
$$251780$$

If the number is divisible by both $$2$$ and $$3$$ then the number is divisible by $$6$$
Divisibility by $$3 =$$ since sum of digits $$= 2 + 5 + 1 + 7 + 8 + 0 = 23$$
$$23$$ is not divisible by $$3$$
$$\therefore 251780$$ is not divisible by $$6$$

Test the divisibility of the following number by $$6:$$
$$872536$$

If the number is divisible by both $$2$$ and $$3$$ then the number is divisible by $$6$$
Divisibility by $$3 =$$ since sum of digits $$= 8 + 7 + 2 + 5 + 3 +6 = 31$$
$$31$$ is not divisible by $$3$$
$$\therefore 872536$$ is not divisible by $$6$$

Test the divisibility of the following number by $$6:$$
$$934706$$

If the number is divisible by both 22 and 33 then the number is divisible by 66

Divisibility by 3=3= since sum of digits

$$=9+3+4+7+0+6=29 $$

$$29$$ is not divisible by $$3$$

$$\therefore 934706$$ is not divisible by 6

Test the divisibility of the following number by $$9:$$
$$326999$$

If the sum of its digits is divisible by $$9$$ then the given number is divisible by $$9$$
$$326999$$
Sum of its digits $$= 3 + 2 + 6 + 9 + 9 + 9 = 38$$
$$38$$ is not divisible by $$9$$
Hence $$326999$$ is not divisible by $$9$$

Test the divisibility of the following number by $$9:$$
$$98712$$

If the sum of its digits is divisible by $$9$$ then the given number is divisible by $$9$$
$$98712$$
Sum of its digits $$= 9 + 8 + 7 + 1 + 2 = 27$$
$$27$$ is divisible by $$9$$
Hence $$98712$$ is divisible by $$9$$

How many three-digit numbers are divisible by 9?

$${\textbf{Step -1: Find the terms to be placed in the formula of general term of A.P}}{\textbf{.}}$$

$${\text{The three digits numbers which are divisible by}}$$ $$9$$ $${\text{are}}$$

$$108,117,126.........,999$$

$${\text{Let first term }}a =108 {\text{ and common difference = d = }}9.$$

$${\text{Last term = 999 }}$$$$ = $$ $${ a_n}$$

$${\textbf{Step -2: Find number of terms using general term of A.P}}{\textbf{.}}$$

$$999 = 108 + \left( {n - 1} \right)9$$ $$[\because\boldsymbol{{a_n} = a + \left( {n - 1} \right)d}]$$

$$999 - 108 = 9n - 9$$

$$891 + 9 = 9n$$

$$900 = 9n$$

$$n = \dfrac{{900}}{9}$$

$$n = 100$$

$${\textbf{Hence, there are 100 three digits numbers divisible by 9}}{\textbf{.}}$$

Fill in the blanks :
The smallest odd composite number is ______

The smallest odd composite number is $$ 9 $$.

Fill in the blanks :
All prime numbers (except $$ 2$$) are _____

All prime numbers (except $$ 2$$) are odd numbers.

If the sum of the digits in a number is a _____ of $$3$$, then the number is divisible by $$3$$.

We use a rule to check whether the number is divisible by 3 or not.

A number is divisible by 3 if the sum of the digits is evenly divisible by 3 or the sum of digits is a multiple of 3.

If the number $$725498$$ is divisible by $$22$$, the digit at is

Option C is right
If $$7254*98$$ is divisible by $$22$$, then it is also divisible by $$2$$ And $$11$$.
The number is divisible by $$11$$, therefore, $$(7+5+*+8)-(2+4+9)$$ or $$(20+*)-15$$ or $$5+*$$ is also divisible by $$11$$.
Hence, the digit at $$*$$ is $$6$$.

Using each of the digit $$1,2,3$$ and $$4$$ only once, determine the smallest $$4$$ digit number divisible by $$4$$.

$$\textbf{We know that if the last two digits of a number are divisible by 4 then the number is also divisible}$$

$$\textbf{by 4}$$.

$$\textbf{Finding the smallest number:}$$

For the smallest number, we will arrange the given digits in ascending order.

The ascending order of the digits are: $$1, 2, 3, 4$$

Therefore the smallest $$4$$-digit number formed $$= 1234$$, but here, the last two digits of the numbers are not divisible by $$4$$.

Therefore the number $$1234$$ is not correct.

So let interchange the digit of $$2$$ and $$3$$ the number formed is $$1324$$, here last two digits are divisible by $$4$$.

$$\textbf{Hence, the smallest 4- digit number which is divisible by 4 from the given digits is 1324}$$.

Write all factors of :
$$ 105 $$

$$ 105 = \left \{ 1 , 3 , 5 , 7 , 15 , 21 , 35 , 105 \right \} $$

Which of the following pairs of numbers are co prime ?
$$ 59 $$ and $$ 97 $$

$$ 59 $$ and $$ 97 $$
The factors of $$ 59 $$ are $$ 1 , 59 $$
The factors of $$ 97 $$ are $$ 1 , 97 $$
The common factors of $$ 59 $$ and $$ 97 $$ is $$ 1 $$
$$ \therefore \, $$ They are co-prime.

Write all factors of :
$$ 96 $$

$$ 96 = \left \{ 1 , 2 , 3 , 4 , 6 , 8 , 12 , 16 , 24 , 32 , 48 , 96 \right \} $$

Which of the following numbers are divisible by $$ 3 $$ or $$ 9 $$ :
$$ 7341 $$

A number is divisible by $$ 3 $$ if the sum of its digit is divisible by $$ 3 $$ or $$ 9 $$.
$$ 7341 = 7 + 3 + 4 + 1 = 15 $$ ; divisible by $$ 3 $$ but not by $$9$$.

Which of the following pairs of numbers are co prime ?
$$ 25 $$ and $$ 105 $$

$$ 25 $$ and $$ 105 $$

The factors of $$ 25 $$ are $$ 1 , 5 , 25 $$

The factors of $$ 105 $$ are $$ 1 , 3 , 5 , 7 , 15 , 21 , 35 , 105 $$

The common factors of $$ 25 $$ and $$ 105 $$ are $$ 1 , 5 $$

$$ \therefore \, $$ They are not co-prime.

Which of the following pairs of numbers are co prime ?
$$ 161 $$ and $$ 192 $$

$$ 161 $$ and $$ 192 $$

The factors of $$ 161 $$ are $$ 1 , 161 $$

The factors of $$ 192 $$ are $$ 1 , 2, 3 , 4 , 6 , 8 , 12 , 16 , 24 , 32 , 48 , 64 , 96 , 192 $$

The common factors of $$ 161 , 192 $$ is $$ 1 $$

$$ \therefore \, $$ They are co-prime.

In each of the following replace $$ \ast $$ by (i) the smallest digit $$ 0 $$ the greatest digit so that the number formed is divisible by $$ 6 $$ :
$$ 5825 \ast 34 $$

If the number is divisible by $$ 6 $$ , then it should get divisible by $$2 $$ and $$ 3 $$.
$$ \Rightarrow \, $$The last number is $$ 4 $$, so it is divisible by $$ 2 $$
$$ \Rightarrow\,$$ The sum of $$ 5825 \ast 34 $$
$$ = 5 + 8 + 2 + 5 + 3 + 4 = 27 $$

(i) The smallest number to be added in $$ 27 $$ is $$ 0 27 + 0 = 27 $$ ( $$ 27 $$ is divided by $$ 3 $$)
(ii) Greatest number to be added in $$ 27 $$ is $$ 9 $$
i.e., $$ 27 + 9 = 36 $$
$$ 36 $$ is divided by $$ 3 $$

Which of the following numbers are divisible by $$ 3 $$ or $$ 9 $$ :
$$ 560319 $$

A number is divisible by $$ 3 $$ if the sum of its digit is divisible by $$ 3 $$ or $$ 9 $$.

$$ 560319 = 5 + 6 + 0 + 3 + 1 + 9 = 24 $$; divisible by $$ 3 $$, but not by $$9$$

Which of the following numbers are divisible by $$ 3 $$ or $$ 9 $$ :
$$ 3721509 $$

number is divisible by $$ 3 $$ if the sum of its digit is divisible by $$ 3 $$ or $$ 9 $$.
$$ 3721509 = 3 + 7 + 2 + 1 + 5 + 0 + 9 = 27 $$ : divisible by $$ 3 , 9 $$.

In each of the following replace $$ \ast $$ by a digit so that the number formed is divisible by $$ 9 $$ :
$$ 70 \ast 356722 $$

$$ 70 \ast 356722 $$
The given number $$ = 70 \ast 356722 $$ Sum of its given digits
$$ = 7 + 0 + 3 + 5 + 6 + 7 + 2 + 2 = 32 $$
The number next to $$ 32 $$ which is divisible by $$ 9 $$ is $$ 36 $$.
$$ \therefore \, $$ required smallest number $$ = 36 - 32 = 4 $$

Examine the following numbers for divisibility by $$ 6 $$ :
$$ 93573 $$

A number is divided by $$ 6 $$ if it is divisible by $$ 2 $$ as well as by $$ 3 $$.

$$ 93573 $$ : not divisible by $$ 6 $$ because , it is not divisible by $$ 2 $$.

In each of the following replace $$ \ast $$ by (i) the smallest digit $$ 0 $$ the greatest digit so that the number formed is divisible by $$ 6 $$ :
$$ 2 \ast 4706 $$

If the number is divisible by $$ 6 $$ then the number should also get divisible by $$ 2 $$ and $$ 3 $$
$$ \Rightarrow \, $$ The last digit of $$ 2 \ast 4706 $$ is $$ 6 $$ , so it is divisible by $$ 2 $$
$$ \Rightarrow \, $$ The sum of $$ 2 \ast 4706 $$
$$ = 2 + 4 + 7 + 0 + 6 = 19 $$

(i) Smallest required number to be added in $$ 19 $$ is $$ 2 $$.
As $$ 19 + 2 = 21 $$ (i.e., $$ 21 $$ is divisible by $$ 3 $$)
(ii) Greatest required number to be added in $$ 19 $$ is $$ 8 $$
As $$ 19 + 8 = 27 $$ (i.e., $$ 27 $$ is divisible by $$ 3 $$)

Which of the following numbers are divisible by $$ 3 $$ or $$ 9 $$ :
$$ 12345678 $$

A number is divisible by $$ 3 $$ if the sum of its digit is divisible by $$ 3 $$ or $$ 9 $$.

$$ 12345678 = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 = 36 $$ ; divisible by both $$ 3 \ and \ 9 $$

Which of the following numbers are divisible by $$ 3 $$ or $$ 9 $$ :
$$ 720634 $$

A number is divisible by $$ 3 $$ if the sum of its digit is divisible by $$ 3 $$ or $$ 9 $$.

$$ 720634 = 7 + 2 + 0 + 6 + 3 + 4 = 22 $$; not divisible by $$ 3 , 9 $$.

In each of the following replace $$ \ast $$ by (i) the smallest digit (ii) the greatest digit so that the number formed is divisible by $$ 3 $$ :
$$ 4756 \ast 2 $$

(i) Smallest digit
Sum of the given digits $$ = 4 + 7 + 5 + 6 = 24 $$
$$ \because \, 24 $$ is divisible by $$ 3 $$
$$ \therefore \, $$ Smallest digit is $$ 0 $$.

(ii) Greatest digit
The greatest digit is $$ 9 $$
i.e., $$ 24 + 9 = 33 $$ which is divisible by $$ 3 $$.

Write the greatest common factor of the following terms: $$l^{2}m^{2}n$$, $$lm^{2}n^{2}$$, $$l^{2}mn^{2}$$

$$lmn(lm, mn, ln)$$

Greatest common factor is $$lmn$$

Find the value of $$k$$ where $$31k\ 2$$ is divisible by $$6$$.

As $$31k2$$ is divisible by $$6$$

For divisible by $$6$$ it must be divisible by both $$2$$ and $$3$$

So, $$31k2$$ will also be divisible by $$2$$ and $$3$$

It is divisible by $$2$$ as there is even digit at unit place

If $$31k2$$ is divisible by $$3$$, sum of digits will be multiple of $$3$$.

i.e., $$3+1+k+2$$ should be one among $$0,3,6,9,12,15.....\ etc$$

$$\Rightarrow \ k+6$$ should be one among $$0,3,6,9,12,15.....\ etc$$

It is possible for $$ \ k=0,3,6,9$$

Hence possible value of $$k$$ are $$0,3,6,9$$

A three digit number $$2$$a$$3$$ is added to the number $$326$$ to give a three digit number $$5b9$$ which is divisible by $$9$$. Find the value of $$b,a$$.

$$\dfrac { \begin{matrix} 2 & a & 3 \\ +3 & 2 & 6 \end{matrix} }{ \begin{matrix} 5 & b & 9 \end{matrix} } $$

It is given that $$5b9$$ is divisible by $$9$$

For, divisibility by $$9$$ sum of digits ,st be divisible by $$9$$

So, $$5+b+9=14+b$$ is divisible by $$9$$

So, $$14+b=18$$, because for $$27$$ $$b$$ has to be double digit which is not possible

Hence $$14+b=18$$

$$\Rightarrow b=4$$

From $$ones$$ column.

$$3+6=9$$

So, no carry over

From $$10's$$ Column.

$$a+2=b$$

$$\Rightarrow a+2=4$$

$$\Rightarrow a=2$$

So, $$a=2,b=4$$

Find the least value that must be given to number a so that the number $$91876a2$$ is divisible by $$8$$.

A number is divisible by $$8$$ if the number formed by last $$3$$ digits is a loso divisible by $$8$$
Therefore, $$6a2$$ divisible by $$8$$
$$a=0$$ to $$9$$
For $$a=0, 6a2=602$$ (not divisible by $$8$$)
For $$a=1, 6a2=612$$ (not divisible by $$8$$)
For $$a=2, 6a2=622$$ (not divisible by $$8$$)
For $$a=3, 6a2=632$$ (divisible by $$8$$)
Hence, $$a=3$$

which of the following is a pair of co-primes: $$(32,62)$$

1789090_1814376_ans_366fc4245c344101827c724f65618ec4.PNG

Which of the following is a pair of co-prime: $$(31,93)$$.

1789098_1814383_ans_aa7a9034e2d1470db7115824498e7750.PNG

Which of the following numbers are divisible by $$ 3 $$ or $$ 9:$$
$$ (i) 45639 $$
$$ (ii) 301248 $$
$$ (iii) 567081 $$
$$ (iv) 345903 $$
$$ (v) 345046 $$

A number is divisible by $$ 3 $$ if the sum of its digits is divisible by $$ 3.$$
A number is divisible by $$ 9 $$ if the sum of its digits is divisible by $$ 9. $$
So the numbers $$ 45639, 301248, 567081, 345903 $$ are divisible by $$ 3. $$
And $$ 49639, 301248, 467081 $$ are divisible by $

In each of the following replace * by a digit so that the number formed is divisible by $$ 6 $$:$$ (i) 97 * 542 $$$$ (ii) 709 * 94 $$

(i) $$ 97 * 542 $$
it is divisible by $$ 6 $$
It is divisible by $$ 2 $$ and $$ 3 $$
Since it unit digit is $$ 2 $$
$$ \therefore $$ it is divisible by $$2 $$

It is divisible by $$ 3 $$
Since , its um of its digits $$ 9 + 7 + 5+ 4 = 27 $$ [ which is divisible by $$3 $$ ]
$$ 27 +'*'= 27 $$ or $$ 30 , 33, 36 $$
$$ \therefore $$ the $$ '*'$$ place can be replaced by $$ 0 $$ or $$ 3 $$ or $$ 6 $$ or $$ 9 $$.

(ii) $$ 709 * 94 $$
i is divisible by $$ 6 $$
It is divisible by $$ 2 $$ and $$ 3 $$
we know that its unit digit is $$ 4 $$
$$ \therefore $$ it is divisible by $$ 2 $$
It is divisible by $$ 3 $$
Since its sum of its digits = $$ 7 + 0 + 9 + 9 + 4 + * = 29 + * $$ [ which is divisible by $$ 3 $$]
$$ 29 + * = 30 $$ or $$ 33 , $$ or $$ 36 $$
$$ \therefore $$ the $$ '*' $$place can be replaced by $$ 1 $$ or $$ 4 $$ or $$ 7 $$.

Which of the following pair of co-prime: $$(18,25)$$

1789093_1814381_ans_5b70e84ba3d643e3900d7cd1cc9b0cb2.PNG

$$3x5$$ is divisible by $$9$$ if the digit $$x$$ is _______ .

We know that, a number is divisible by $$9$$ if the sum of its digits is also divisible by $$9$$.

Therefore, $$3+x+5=x+8$$ must be a multiple of $$9$$

The multiple can't be $$18$$ or any other higher multiple of $$9$$, because then $$x$$ will be double digit number.

$$\therefore \ x+8=9$$

$$\Rightarrow x=1$$

Hence, $$3x5$$ is divisible by $$9$$ if the digit $$x$$ is $$1$$.

$$3134673$$ is divisible by $$3$$ and _______ .

Sum of digits of $$3134673$$ is $$3+1+3+4+6+7+3=27$$

Which is divisible by $$9$$

And we know that if sum of digits is divisible by $$9$$ then number is divisible by both $$3$$ and $$9$$

Hence, $$3134673$$ is divisible by $$3$$ and $$9$$.

Find the HCF of $$14$$ and $$21.$$

By prime factorization of $$14$$ and $$21$$ we get
$$14=1 \times 2 \times 7$$
$$21=1 \times 3 \times 7$$

As we can see the highest common factor between $$14$$ and $$21$$ is $$7$$

So, $$H.C.F. (14 \ and \ 21)=7$$

Which of the following numbers are divisible by $$ 6 $$:
$$ (i)15414 $$
$$ (ii) 213888 $$
$$(iii) 469876$$

A number is divisible by $$ 6 $$ if it is divisible by $$ 2 $$ as well as by $$ 3. $$

So the numbers $$ 15414 $$ and $$ 213888 $$ are divisible by $$ 6 $$.

In each of the following replace $$ $$ by a digit so that the number formed is divisible by $$ 9: $$
$$ (i) 49 \times 2207 $$
$$(ii) 5938 \times 623$$

(i) $$ 49 \times 2207 $$ is divisible by $$ 9 $$
Then $$ 4+ 9 + z+2 +2 + 0 +7 $$ is divisible by $$ 9 $$
$$ 24 + x $$ is divisible by $$ 9 $$
$$ 24 + x = 27 $$
$$ x = 27 -24 $$
$$ = 3 $$ , which is divisible by $$ 9 $$
$$ \therefore x = 3 $$

(ii) $$ 5938 \times 623 $$ is divisible by $$ 9 $$
Then , $$ 5 + 9 + + 8 + x +6 +2+ 3 $$ is divisible by $$ 9 $$
$$ 36 +x $$ is divisible by $$ 9 $$
So $$ 36 +x = 36 \quad or \quad 45 $$
$$ x = 36 -36 = 0 \quad or \quad x = 45 -36 = 9 $$
$$ \therefore x = 0 , 9 $$

Write all the factors of:
(i) $$15$$
(ii) $$55$$
(iii) $$48$$
(iv) $$36$$
(v) $$84$$

(i) The factors of $$15$$ are $$1, 3, 5$$ and $$15$$
$$∴ F(15) = 1, 3, 5$$ and $$15$$
(ii) The factors of $$55$$ are $$1, 5, 11$$ and $$55$$
$$∴F(55) = 1, 5, 11$$ and $$55$$
(iii) The factors of $$48$$ are $$1, 2, 3, 4, 6, 8, 12, 16, 24$$ and $$48$$
$$∴F (48) = 1, 2, 3, 4, 6, 8, 12, 16, 24$$ and $$48$$
(iv) The factors of $$36$$ are $$1, 2, 3, 4, 6, 9, 12, 18$$ and $$36$$
$$∴F (36) = 1, 2, 3, 4, 6, 9, 12, 18$$ and $$36$$
(v) The factors of $$84$$ are $$1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42$$ and $$84$$
$$∴ F (84) = 1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42$$ and $$84$$

In each of the following numbers, replace M by the smallest number to make resulting number divisible by $$3$$ :
$$ 64 \,{\text{M}}\,3 $$

The given number = $$ 64 \,{\text{M}}\,3 $$
For a number to be divisible by $$3$$ sum of digits must be divisible by $$3$$
Sum of digits $$ = 6 + 4 + 3 = 13 $$
The number which is divisible by $$3$$ next to $$13$$ is $$15$$
Required smallest number $$ = 15 – 13 = 2 $$
Hence, value of $$M$$ is $$2$$

Write the following terminating decimal in the form of $$\frac{p}{q},q\neq 0$$ and $$p,q$$ are co primes.
$$15.265$$.

$$15.265=\dfrac{15265}{1000}=\dfrac{15265}{2^3*5^3}=\dfrac{3053}{2^3*5^2}$$

In each of the following numbers, replace M by the smallest number to make resulting number divisible by $$3$$ :
$$ 46 \,{\text{M}}\,46 $$

The given number = $$ 46 \,{\text{M}}\,46 $$
For a number to be divisible by $$3$$ sum of digits must be divisible by $$3$$
Sum of digits $$ = 4 + 6 + 4 + 6 = 20 $$
The number which is divisible by $$3$$ next to $$20$$ is $$21$$
Required smallest number $$ = 21 – 20 = 1 $$
Hence, the value of $$M$$ is $$ 1 $$

Find which of the following number are divisible by $$ 3 $$ :
$$ 28492 $$

The given number $$ = 28492 $$

For a number to be divisible by $$3$$, sum of digits must be divisible by $$3$$

Sum of digits $$ = 2 + 8 + 4 + 9 + 2 = 25 $$

Since $$25$$ is not divisible by $$3$$

Hence, $$ 28492 $$ is not divisible by $$3$$

In each of the following numbers replace M by the smallest number to make resulting number divisible by $$9$$ :
$$ 627 \,{\text{M}} \,9 $$

The given number = $$ 627 \,{\text{M}} \,9 $$
For a number to be divisible by $$9$$ sum of digits must be divisible by $$9$$
Sum of digits $$ = 6 + 2 + 7 + 9 = 24 $$
The number which is divisible by $$9$$ next to $$24$$ is $$27$$
Required smallest number $$ = 27 – 24 = 3 $$
Hence, the value of $$M$$ is $$3$$

In each of the following numbers replace M by the smallest number to make resulting number divisible by $$9$$ :
$$ 76\,{\text{M}} \,91 $$

The given number is = $$ 76\,{\text{M}} \,91 $$
For a number to be divisible by $$9$$ sum of digits must be divisible by $$9$$
Sum of digits $$ = 7 + 6 + 9 + 1 = 23 $$
The number which is divisible by $$9$$ next to $$23$$ is $$27 $$
Required smallest number $$ = 27 – 23 = 4 $$
Hence, the value of $$M$$ is $$4$$

In each of the following numbers, replace M by the smallest number to make resulting number divisible by $$3$$ :
$$ 27 \,{\text{M}}\,53 $$

The given number = $$ 27 \,{\text{M}}\,53 $$
For a number to be divisible by $$3$$ sum of digits must be divisible by $$3$$
Sum of digits $$ = 2 + 7 + 5 + 3 = 17 $$
The number which is divisible by $$3$$ next to $$17$$ is $$18$$
Required smallest number $$ = 18 - 17 = 1 $$
Hence, the value of $$M$$ is $$1$$

In each of the following numbers replace M by the smallest number to make resulting number divisible by $$9$$ :
$$ 77548\,{\text{M}} $$

The given number = $$ 77548\,{\text{M}} $$
For a number to be divisible by $$9$$ sum of digits must be divisible by $$9$$
Sum of digits $$ = 7 + 7 + 5 + 4 + 8 = 31 $$
The number which is divisible by $$9$$ next to $$31$$ is $$36$$
Required smallest number $$ = 36 – 31 = 5 $$
Hence, the value of $$M$$ is $$5$$

Write the following terminating decimal in the form of $$\frac{p}{q},q\neq 0$$ and $$p,q$$ are co primes.
$$24.34$$.

$$24.34=\dfrac{2434}{100}=\dfrac{2434}{2^2*5^2}=\dfrac{1217}{2*5^2}$$

Which of the following numbers are co-prime ?
$$ 216 $$ and $$ 215 $$

Factors of $$ 216=1,2,3,4,6,8,9,12,18,24,17,36,54,72,108,216$$
Factors of $$ 215=1,5,43,215$$
Common factors= $$ 1$$
The given two numbers are prime.

Which of the following numbers are co-prime ?
$$ 81 $$ and $$ 16 $$

Factors of $$ 81=1,3,9,27,81$$
Factors of $$16=1,2,4,8,16$$
Common factors= $$ 1$$
The given two numbers are co-prime.

If the H.C.F of two numbers are ______ , then they are said to be co-prime.

If HCF of two numbers is 1, then the numbers are called as co-prime numbers

Write the following terminating decimal in the form of $$\frac{p}{q},q\neq 0$$ and $$p,q$$ are co primes.
$$1215.8$$.

$$1215.8=\dfrac{12158}{10}=\dfrac{12158}{2*5}=\dfrac{6079}{5}$$

Write the following terminating decimal in the form of $$\frac{p}{q},q\neq 0$$ and $$p,q$$ are co primes.
$$0.1255$.

$$0.1255=\dfrac{1255}{10000}$$

$$=\dfrac{1255}{2^4\times5^4}$$

$$=\dfrac{251}{2^4\times5^3}$$

$$=\dfrac{251}{2000}$$

Which of the following numbers are co-prime ?
$$ 15 $$ and $$ 37 $$

Factors of $$ 15=1,3,5,15$$
Factors of $$ 37=1,37$$
Common factors= $$ 1$$
Therefore, the given two numbers are co-prime

Write the even prime number.

The only even number that is prime is 2 as it has only two factors viz. 1 and 2.

Without actual division using divisibility rules, classify the following numbers as divisible by $$3,\ 4,\ 5,\ 11$$
$$803,875,474,583,1067,350,657,684,2187,4334,1905,2548$$

1) Divisibility test of $$3$$-

If sum of all digits of number is a multiple of $$3$$, then a number is divisible by $$3$$

Thus, numbers divisible by $$3$$ are $$474,\ 657,\ 684,\ 2187,\ 1905$$

2) Divisibility test of $$4$$-

If a number formed by last two digits of a number is multiple of $$4$$, then whole number is divisible by $$4$$

Thus, numbers divisible by $$4$$ are $$684,\ 2548$$

3) Divisibility test of $$5$$-

If units place of a number contains $$0$$ or $$5$$, then entire number is divisible by $$5$$
Thus, numbers divisible by $$5$$ are $$875,\ 350,\ 1905$$

4) Divisibility test of $$11$$-

Take the sum of alternate digits of given number to get two numbers. If difference between these two numbers is either $$0$$ or multiple of $$11$$, then the entire number is divisible by $$11$$

Thus, numbers divisible by $$11$$ are $$803,\ 583,\ 1067,\ 4334$$

Prove that the sum of the cubes of three consecutive natural numbers is always divisible by $$$$

Let the 3 consecutive natural num-bers be $$ x, x+1 $$ and $$ x+2 $$
Sum of their cubes $$ =x+(x+1) ^3+(x+2)^{3}=x^{3}+x^{3}+1^{3}+3 x(x+1)+x^{3}+2^{3}+6 x(x+2)=x^{3}+x^{3}+1+3 x^{2}+3 x+x^{3}+8 +6 x^{2}+12 x=3 x^{3}+9 x^{2}+15 x+9 .=3\left(x^{3}+3 x^{2}+5 x+3\right) $$
Sum of their cubes is a multiple of 3 which means that it is always divisible by $$ 3. $$

How many two digit natural number which are divisible by 3?

$$a=12,d=3,l=99$$

$$l= a+(n-1)d$$

$$99=12+(n-1)3$$
$$\implies \ n-1 = \dfrac{87}{3} = 29$$

$$\implies \ n= 29 + 1 = 30$$
Hence, two digit natural number which are divisible by 3 are 30.

How many numbers from 1001 to 2000 are divisible by $$ 4? $$

A number is divisible by 4 if the last two-digit number is divisible by $$ 4. $$
The numbers between 1001 and 1100 which are divisible by 4 are $$ 1004,1008,1012 \ldots .1100 $$ we get 25 numbers.
Similarly from 1101 to 2000, we get numbers from 1201 to 1300 we get 25 numbers and so on.
Hence from 1001 to 2000, we get $$ 25 \times 10=250 $$ numbers which are divisible by 4

Find the sum of odd integers from $$1$$ to $$101$$, which is divisible by $$3$$.

$$a=3,d=6,l=99$$

$$l= a+ (n+1)d$$

$$99=3+(n-1)6$$

$$6n-6=96$$

$$6n=102$$
$$n=17$$

$$S_n=\dfrac{n(a+l)}{2}$$

$$=\dfrac{17(3+99)}{2}$$
$$S_{17} = \dfrac{17}{2} \times 102$$

$$=17 \times 51 = 867$$

Suppose a 3 digit number abc is divisible by $$ 3 . $$ Prove that $$ \overline{a b c}+\overline{b c a}+\overline{c a b} $$ is divisible by $$ 9 . $$

A number is divisible by 3 Sum of the digits is divisible by 3.
$$ a+b+c $$ is a multiple of 3
Hence $$ \mathrm{b}+\mathrm{c}+\mathrm{a} $$ and $$ \mathrm{c}+\mathrm{a}+\mathrm{b} $$ are multiples of $$ 3 . $$
$$ \overline{a b c}+\overline{b c a}+\overline{c a b} $$
$$ =a+b+c+b+c+a+c+a+b $$
$$ =3 a+3 b+3 c=3(a+b+c) a+b+c $$ is divisible by 3
Hence it is a multiple of 3 .
$$ \therefore 3(a+b+c) $$ is a multiple of 9
$$ \therefore \overline{a b c}+\overline{b c a}+\overline{c a b} $$ is divisible by 9.

Suppose a 3 digit number abc is divisible byProve that abc + bca + cab is divisible by 9.

We have a $$3$$ digit number $$abc$$ that is divisible by $$3$$.

We know by divisibility rule of $$3$$, if we take sum of the digits and the result is divisible by $$3$$, then the original number is divisible by $$3$$.

Therefore, we can say that:

$$(a+b+c)$$ is also divisible by $$3$$ ......... (1)

As given $$abc+bca+cab$$, so we can write it as:

$$100a+10b+c+100b+10c+a+100c+10a+b\\ \Rightarrow 111a+111b+111c\\ \Rightarrow 111(a+b+c)$$

Now we conclude that, $$111$$ is divisible by $$3$$ and

$$(a+b+c)$$ is also divisible by $$3$$ [ From (1) ]

Therefore, $$111(a+b+c)$$ is divisible by $$9$$.

Hence, $$abc+bca+cab$$ is divisible by $$9$$.

Find the LCM and HCF of the following integers by expressing them as product of primes $$18, 81$$ and $$108$$.

The given integers $$18$$, $$81$$ and $$108$$ can be factorised as follows:

$$18=2×3×3\\ 81=3×3×3×3\\ 108=2×2×3×3×3$$

$$2$$ and $$3$$ are prime numbers as these are the numbers that are only divisible by themselves.

We know that $$HCF$$ is the highest common factor, therefore, the $$HCF$$ of $$18$$, $$81$$ and $$108$$ is:

$$HCF=3\times 3=9$$

Also, the $$LCM$$ is the least common multiple, therefore, the $$LCM$$ of $$18$$, $$81$$ and $$108$$ is:

$$LCM=2×2×3×3×3×3=324$$

Hence, the $$HCF$$ is $$9$$ and $$LCM$$ is $$324$$.

Find the HCF and LCM of the pairs of integers and verify that $$LCM (a, b) \times HCF (a, b)= a\times b$$ for $$16$$ and $$80$$

The given integers $$16$$ and $$80$$ can be factorised as follows:

$$16=2×2×2×2\\ 80=2×2×2×2×5$$

$$2$$ and $$5$$ are prime numbers as these are the numbers that are only divisible by themselves.

We know that $$HCF$$ is the highest common factor, therefore, the $$HCF$$ of $$16$$ and $$80$$ is:

$$HCF=2×2×2×2=16$$

Also, the $$LCM$$ is the least common multiple, therefore, the $$LCM$$ of $$16$$ and $$80$$ is:

$$LCM=2×2×2×2×5=80$$

Therefore, the $$HCF$$ is $$16$$ and $$LCM$$ is $$80$$.

Now, let $$a=16$$ and $$b=80$$, then the product of $$a$$ and $$b$$ is:

$$a\times b=16\times 80=1280.......(1)$$

Also, the product of the $$LCM$$ and $$HCF$$ of $$a$$ and $$b$$ is:

$$LCM(a,b)\times HCF(a,b)=80\times 16=1280.......(2)$$

Hence, from equations 1 and 2, we get $$LCM(a,b)\times HCF(a,b)=a\times b$$.

Given $$f(x)=\displaystyle \frac{1}{(1-x)},g(x)=f\{f(x)\}$$ and $$h(x)=f\{f\{f(x)\}\}$$, then find the value of $$f(x) g(x) h(x)$$.

$$f(x)=\displaystyle \frac{1}{(1-x)},g(x)=f\{f(x)\}$$ and $$h(x)=f\{f\{f(x)\}\}$$

Now, $$g(x)=f\{ f(x)\} $$
$$\displaystyle =f(\frac { 1 }{ (1-x) } )$$

$$\displaystyle =\frac { 1 }{ 1-\cfrac { 1 }{ (1-x) } } $$

$$\Rightarrow \displaystyle g(x) =\frac { x-1 }{ x } $$

Now, $$h(x)=f\{ f\{ f(x)\} \} $$

$$\Rightarrow h(x)= f\{g(x)\}$$

$$\displaystyle =f(\frac { x-1 }{ x } )$$

$$\displaystyle =\frac { 1 }{ 1-\cfrac { x-1 }{ x } } $$

$$\Rightarrow h(x)=x$$

Consider, $$f(x)g(x)h(x)=\cfrac { 1 }{ (1-x) } \cfrac { (x-1) }{ x } x$$
$$\Rightarrow f(x)g(x)h(x)=-1$$

Find the HCF and LCM of the pairs of integers and verify that $$LCM (a, b) \times HCF (a, b)= a\times b$$ for $$125$$ and $$55$$

The given integers $$125$$ and $$55$$ can be factorised as follows:

$$125=5×5×5\\ 55=5×11$$

$$5$$ and $$11$$ are prime numbers as these are the numbers that are only divisible by themselves.

We know that $$HCF$$ is the highest common factor, therefore, the $$HCF$$ of $$125$$ and $$55$$ is:

$$HCF=5$$

Also, the $$LCM$$ is the least common multiple, therefore, the $$LCM$$ of $$125$$ and $$55$$ is:

$$LCM=5\times 5\times 5\times 11\\=1375$$

Therefore, the $$HCF$$ is $$5$$ and $$LCM$$ is $$1375$$.

Now, let $$a=125$$ and $$b=55$$, then the product of $$a$$ and $$b$$ is:

$$a\times b=125\times 55\\=6875.......(1)$$

Also, the product of the $$LCM$$ and $$HCF$$ of $$a$$ and $$b$$ is:

$$LCM(a,b)\times HCF(a,b)=1375\times 5\\=6875.......(2)$$

Hence, from equations 1 and 2, we get $$LCM(a,b)\times HCF(a,b)=a\times b$$.

Find the LCM and HCF of the following integers by expressing them as product of primes
$$12, 15$$ and $$30$$.

The given integers $$12$$, $$15$$ and $$30$$ can be factorised as follows:

$$12=2×2×3\\ 15=3×5\\ 30=2×3×5$$

$$2,3$$ and $$5$$ are prime numbers as these are the numbers that are only divisible by themselves.

We know that $$HCF$$ is the highest common factor, therefore, the $$HCF$$ of $$12$$, $$15$$ and $$30$$ is:

$$HCF=3$$

Also, the $$LCM$$ is the least common multiple, therefore, the $$LCM$$ of $$12$$, $$15$$ and $$30$$ is:

$$LCM=2×2×3×5=60$$

Hence, the $$HCF$$ is $$3$$ and $$LCM$$ is $$60$$.

Find the sum of all natural numbers lying between 153 and 436 divisible by 8.

Between $$153$$ and $$436$$

number divisible by $$8$$ are $$160, 168, 176, .....,432$$

Let Total number are $$n$$

$$\Rightarrow T_{n}=432, nth$$ term of $$A.P.$$

(number are forming an $$A.P.$$)

$$\Rightarrow T_{n} = a+(n-1)d$$

$$a=160, d=8$$

$$\Rightarrow 432 =160+ (n-1)8$$

dividing by $$8$$

$$54=20+(n-1)$$

$$\Rightarrow n-1=34$$

$$\Rightarrow n=35$$

Name sum of these $$35$$ numbers.

$$=S=\dfrac{35}{2} [160+432]$$

using $$S= \dfrac{n}{2} [a+l]$$

$$l=$$ last term

$$=\dfrac{35}{2} (592)$$

$$=10360$$

$$\Rightarrow Sum= 10360$$

Fill in the blanks
The smallest digit that can be put in the units place of $$37842$$, so that it is divisible by $$6$$ is _____.

$$\begin{array}{l} 37842x \\ since =3+7+8+4+2+x=30 \\ 24+x \\ x\, should\, \, be\, \, 6 \end{array}$$

to be divisible by 6 it should be divisible by 2 and 3

Given a three digit number $$x+5+y$$ where $$x$$ is the digit at hundreds place and $$y$$ is the digit at ones. If the number $$x+5+y$$ is divisible by $$9$$, find least positive value $$x+y$$ ?

By divisibility test of 9 sum of digits must be divisible by 9
hence x+y+5=y
where y is a real number
minimum value of y possible is 9
hence
x+y+5=9
x+y=4

Show that exactly one of the numbers $$n,n + 2\,or\,n + 4$$ is divisible by $$3$$.

1309984_1197186_ans_a0030eb8d4404da5a792acf76b8ba54b.jpg

$$n(n+1)(n+5)$$ is a multiple of $$3$$.

We will prove it by using the formula of mathematical induction for all $$n\ \epsilon\ N$$

Let $$P(n)=n(n+1)(n+5)=3d$$ where $$d\ \epsilon\ N$$

For $$n=1$$

$$P(1)=1(2)(6)=12$$ which is divisible by $$3$$

Let $$P(k) $$ is true

$$P(k)=k(k+1)(k+5)=3m$$ where $$m\ \epsilon\ N$$

$$\implies k^3+6k^2+5k=3m$$

$$\implies k^3=-6k^2-5k+3m$$

Now we will prove that $$P(k+1) $$ is true

$$P(k+1)=(k+1)(k+2)(k+6)=k^3+9k^2+20k+12$$

Putting the value of $$k^3$$ in above equation we get,

$$(3m-6k^2-5k)+9k^2+20k+12$$

$$=3m+3k^2+15k+12$$

$$=3(m+k^2+5k+4)$$

$$3r$$ where $$r=m+k^2+5k+4$$

Since $$P(k+1)$$ is true whenever $$P(k) $$ is true.

So, by the principle of induction, $$P(n)$$ is divisible by $$3$$ for all $$n\ \epsilon\ N$$

find $$HCF$$ of $$726$$ and $$462$$

1970406_1315322_ans_b66facdc0e484046bec336160252003e.jpg

Express why $$15\times 7+7$$ is a composite number.

1298380_1508107_ans_f07432c1f3944707a27c9afe474360c7.jpg

Playing With Numbers - Class 6 Maths - Extra Questions

Find the HCF of $$6, 72$$ and $$120$$

If a and b are two odd prime numbers, show that $$a^2 -b^2$$ is composite.

Find the HCF of $$56$$ and $$814$$?

A man can row $$\displaystyle 9\frac{1}{3}$$ kmph in still water and finds that it takes him thrice as much time to row up than as to row down the same distance in the river Find the speed of the current

Convert $$\displaystyle (122)_{10}$$ to base 8 system

Least prime number is

The sum of the prime numbers between $$90$$ and $$100$$ is

What is the greatest common factor of 420 and 660?

Find the HCF and LCM of 18 and 45 by prime factorisation method.

Find the HCF of 344 and 60 by prime factorisation method. Hence find their LCM.

Using divisibility tests , determine which of the following numbers are divisible by $$5$$(a) $$438750$$ (b) $$179015$$ (c) $$125$$ (d) $$639210$$ (e) $$17852$$

Find the HCF of 96 and 404

Using divisibility tests, determine which of following numbers are divisible by $$2$$$$(a) 2144 \ (b) 1258 \ (c) 4336 \ (d) 633 \ (e) 1352$$

How many numbers from $$201$$ to $$250$$ are divisible by $$5$$, but not by $$3$$?

Is the number $$12345678$$ divisible by $$4$$?

Restate the following statements with appropriate conditions, so that they become true statements.All numbers can be represented in prime factorization.

Check whether the number $$12345321$$ is divisible by $$3$$. Is it divisible by $$9$$?

Is $$444445$$ divisible by $$3$$?

Find L.C.M. and H.C.F. of $$72$$ and $$108$$ by the prime factorization method.

Write seven consecutive composite numbers less than 100.

Write the prime numbers between 50 to 100.

Find HCF of $$45, 65$$ and $$80$$.

Write the greatest 4 digit number and express it in the form of it's prime factors?

LCM of two or more prime numbers is equals to its ___________.

The greatest common factor of given numbers is called ____________.

Find HCF: $$15, 24$$.

Find HCF:$$12, 18$$ and $$24$$.

Find HCF: $$5, 13$$.

Find the HCF of 12 , 24 and 48 by listing factors

Solve $$\dfrac{1}{16}-\dfrac{3}{4}$$

How to identify Prime Number?

Fnd the HCF of the following pair of numbers:$$32$$ and $$54$$

Express each number as a product of its prime factors:(i) $$140$$ (ii) $$156$$ (iii) $$3825$$

Solve $$2\dfrac {4}{8}\div 2\dfrac {1}{2}$$

Explain why $$11 \times 13 \times 15 \times 17 \div 17$$ is a composite number.

Fill in the blanks A number is divisible by _____ if it divisible by $$4$$ and $$9$$.

Is $$4$$ a factor of $$28$$?

The ____________ of two or more numbers is the smallest number which is divisible by each of the given numbers.

What least number should be replaced for $$*$$ so that the number $$67301 * 2$$ is exactly divisible by $$9$$?

State fundamental theorem of Arithmetic.If $$17 \times 11 \times 13+13$$ a composite number ? Justify.

Look at the following pairs of numbers and determine whether they are co-prime or prime :(i) $$8,9$$ (ii) $$11,13$$ (iii) $$15,16$$ (iv) $$64,65$$ (v) $$71,73$$

Fill in the blanksThe smallest digit by which $$*$$ should be replaced in $$5095*6$$, so that it is divisible by $$4$$ is _____.

Write the smallest digit and greater digit in the blank space of each of the following numbers so that the number formed is divisible to by $$3$$

Find the greatest number which can divide $$36,81$$ and $$108$$.

Find the $$H.C.F$$ of $$16$$ and $$40$$

Show that $${3}^{2n+2}-8n-9$$ is divisible by $$8$$, where $$n$$ is any natural number.

What is the greatest number that divides $$720$$ and $$810$$ without leaving any remainder?

Show that "the range of the first seven multiples of the smallest odd prime number is also a multiple of that prime number . "

State Euclid's division lemma and Fundamental theorem of Arithmetic statement.

Find the number of divisions of $$1980$$.i) How many of them are multiple of $$11$$?

Define even numbers. How can we identify them?

Which of the following numbers are divisible by $$9$$?$$369, 1008, 753321$$

Express each of the following numbers as the sum of three odd primes:a)$$21$$b)$$31$$c)$$53$$d)$$61$$

Test whether the following numbers are divisible by $$6$$$$75642$$

Why $$5\times 6\times 7\times 11-2\times 3\times 7\times 11$$ is composite number.

Find the smallest three- digit number divisible by $$2$$ as well as $$3$$.

Test whether the following numbers are divisible by $$6$$.$$30654$$

_________ is a factor of every number.

Which of the following numbers are prime? i) $$101$$ii) $$251$$

The greatest factor of $$364$$ is_________?

Test whether the following numbers are divisible by $$6$$$$56523$$

Test whether the following numbers are divisible by $$6$$.$$324368$$

Find G.C.D of $$78$$ and $$455$$

HCF and LCM18,20,24

Find g.c.d of (i) $$135$$ and $$225$$ (ii) $$38220$$ and $$196$$ by Euclid's algorithm.

$$42\times 8$$ divisible by $$4$$?

Find the factors of the following:(i) $$7$$ (ii) $$9$$ (iii) $$16$$(iv) $$25$$ (v) $$48$$ (vi) $$63$$

Given that $$L C M ( 91,26 ) = 182 ,$$ find $$H C F ( 91,26 ).$$

Which number is neither a prime number nor a composite number?

HCF of $$960 \text { and } 432$$ is ........

The $$H.C.F$$. of $$30$$ and $$210$$ in Prime Factors is

Express $$30$$ as sum of two prime numbers.

Find the $$HCF$$ of the following $$18,48$$

If $$HCF$$ of $$210$$ and $$55$$ is expressible in the form $$210*5+55*A$$, then find the value of $$(2-A)$$.

Every even number greater than $$2$$ can be expressed as the sum of two prime numbers.Verify this statement for every even number up to, $$16$$ .

Find the HCF of 16, 28.

Find the $$ g.c.d$$ of$$144,\ 233$$

144 = 24 × 32; 233 is a prime number, it cannot be prime factorized into other prime factors;

Take all the common prime factors, by the lowest exponents. But the two numbers have no common prime factors.

Using divisibility tests , determine which of the following numbers are divisible by $$5$$
(a) $$438750$$ (b) $$179015$$ (c) $$125$$ (d) $$639210$$ (e) $$17852$$

Using divisibility tests, determine which of following numbers are divisible by $$2$$
$$(a) 2144 \ (b) 1258 \ (c) 4336 \ (d) 633 \ (e) 1352$$

Restate the following statements with appropriate conditions, so that they become true statements.
All numbers can be represented in prime factorization.

Find HCF:
$$12, 18$$ and $$24$$.

Fnd the HCF of the following pair of numbers:
$$32$$ and $$54$$

Express each number as a product of its prime factors:
(i) $$140$$ (ii) $$156$$ (iii) $$3825$$

Fill in the blanks
A number is divisible by _____ if it divisible by $$4$$ and $$9$$.

What least number should be replaced for $$$$ so that the number $$67301 2$$ is exactly divisible by $$9$$?

Look at the following pairs of numbers and determine whether they are co-prime or prime :
(i) $$8,9$$ (ii) $$11,13$$ (iii) $$15,16$$ (iv) $$64,65$$ (v) $$71,73$$

Fill in the blanks
The smallest digit by which $$$$ should be replaced in $$50956$$, so that it is divisible by $$4$$ is _____.

Find the number of divisions of $$1980$$.
i) How many of them are multiple of $$11$$?

Which of the following numbers are divisible by $$9$$?
$$369, 1008, 753321$$

Express each of the following numbers as the sum of three odd primes:
a)$$21$$
b)$$31$$
c)$$53$$
d)$$61$$

Test whether the following numbers are divisible by $$6$$
$$75642$$

Test whether the following numbers are divisible by $$6$$.
$$30654$$

Which of the following numbers are prime?
i) $$101$$
ii) $$251$$

Test whether the following numbers are divisible by $$6$$
$$56523$$

Test whether the following numbers are divisible by $$6$$.
$$324368$$

HCF and LCM
18,20,24

Find the factors of the following:
(i) $$7$$ (ii) $$9$$ (iii) $$16$$
(iv) $$25$$ (v) $$48$$ (vi) $$63$$

Find the $$HCF$$ of the following
$$18,48$$

If $$HCF$$ of $$210$$ and $$55$$ is expressible in the form $$2105+55A$$, then find the value of $$(2-A)$$.

Find the $$ g.c.d$$ of
$$144,\ 233$$

144 = 2⁴ × 3²;
233 is a prime number, it cannot be prime factorized into other prime factors;

Take all the common prime factors, by the lowest exponents.
But the two numbers have no common prime factors.

Greatest common divisor:
gcd (144; 233) = 1;

Find the $$ g.c.d $$ of
$$765,\ 65$$

765 = 3² × 5 × 17;
65 = 5 × 13;

Express the following in standard form:
$$(i)28\,\,\,\,(ii)100\,\,\,\,(iii)144\,\,\,\,(iv)1296\,\,\,\,(v)2100$$

Fill in the blanks:
The only even prime number is ______

Express the given numbers in the form of product of primes
(i) 78 (ii) 75 (iii) 96

Is the statement true or not:
All prime number are odd.

Which of the following numbers are prime?
(a) $$23$$
(b) $$51$$
(c) $$37$$
(d) $$26$$.

Show that the following numbers are co-primes:
161,192

Show that the following pairs are co-primes
512,945

Show that the following pairs are co-primes
59,97

Express the following as the sum of two odd primes.
$$44$$.

Fill in the blank.
A number which has only two factors is called a _______.

Using divisibility tests, determine if the following number is divisible by $$6$$ or not.
$$4335$$.

Express the following number as the sum of three odd primes.
$$53$$.

Fill in the blank.
The smallest composite number is _______.

Fill in the blank.
The smallest prime number is _______.

Express the following number as the sum of three odd prime.
$$61$$.

Fill in the blanks.
A number which has more than two factors is called a _______.

Find the HCF of the following numbers.
$$36, 84$$.

Determine the following numbers are co-prime.
$$81$$ and $$16$$.

Determine the following numbers are co-prime.
$$17$$ and $$68$$.

Find the HCF of the following numbers.
$$18, 48$$.

Test the divisibility of the following number by $$2$$:
$$2398$$

Test the divisibility of the following number by $$2$$:
$$46821$$

Test the divisibility of the following number by $$2$$:
$$84463$$

Test the divisibility of the following number by $$2$$:
$$79532$$

Find the HCF of the following numbers.
$$12, 45, 75$$.

Test the divisibility of the following number by $$2$$:
$$570$$

Test the divisibility of the following number by $$2$$:
$$94$$

Test the divisibility of the following number by $$2$$:
$$285$$

Test the divisibility of the following number by $$2$$:
$$13576$$

Test the divisibility of the following number by $$5$$:
$$1056$$

Test the divisibility of the following number by $$5$$:
$$95$$

Test the divisibility of the following number by $$3$$:
$$83$$

Test the divisibility of the following number by $$5$$:
$$55053$$