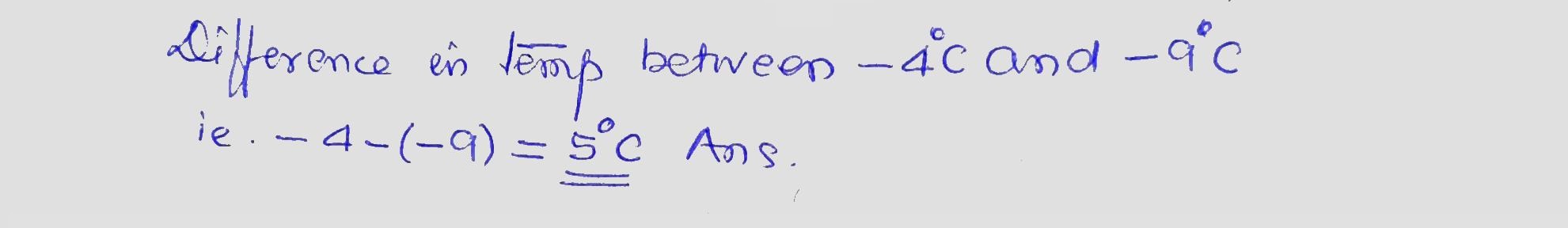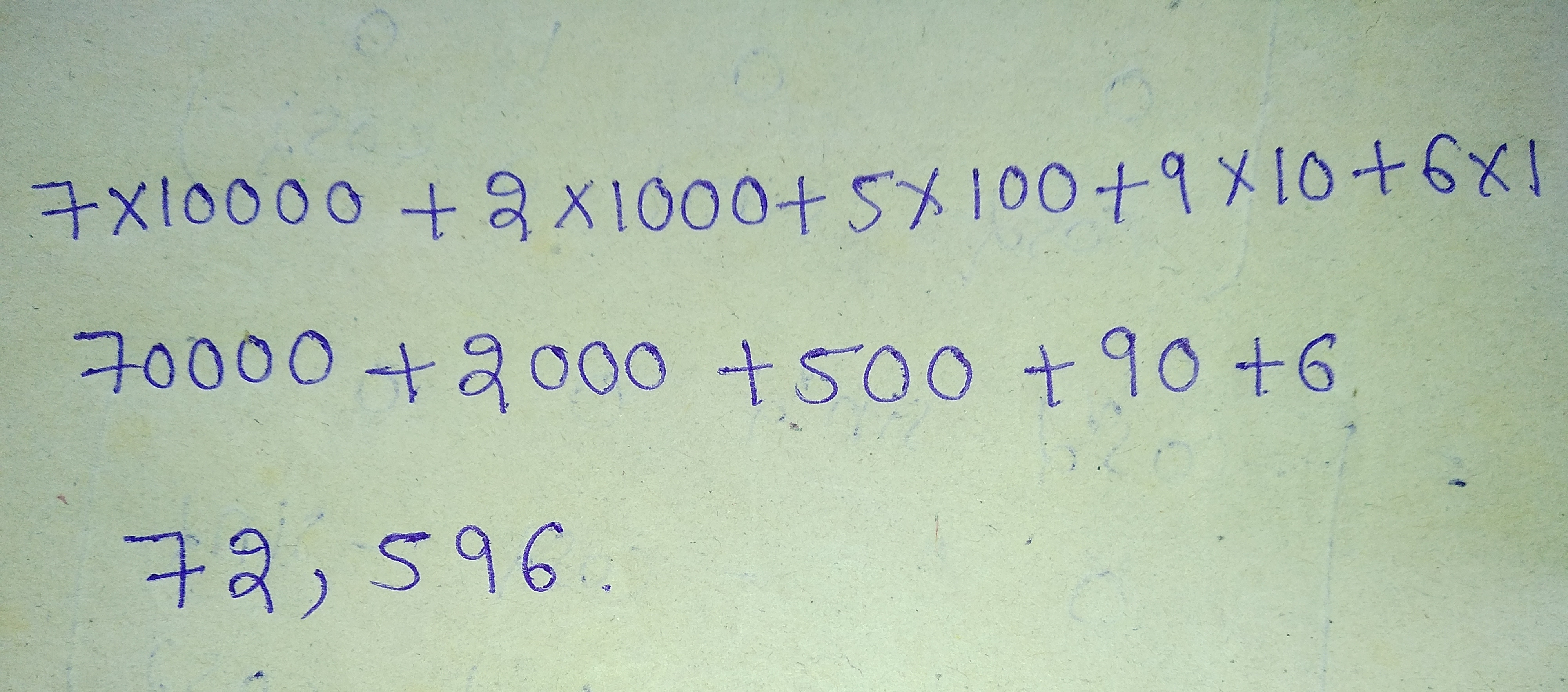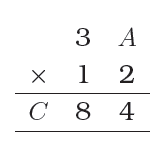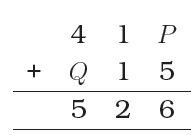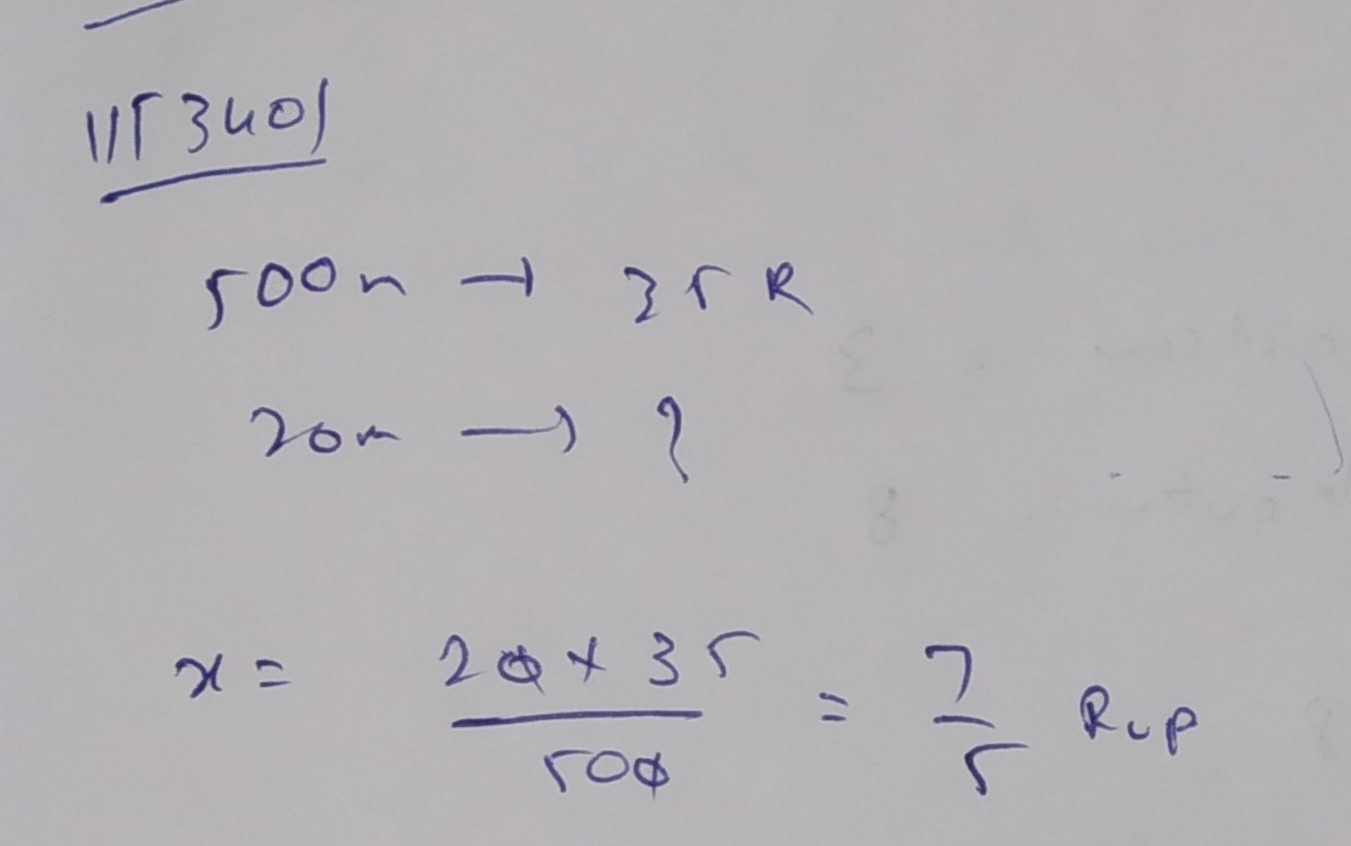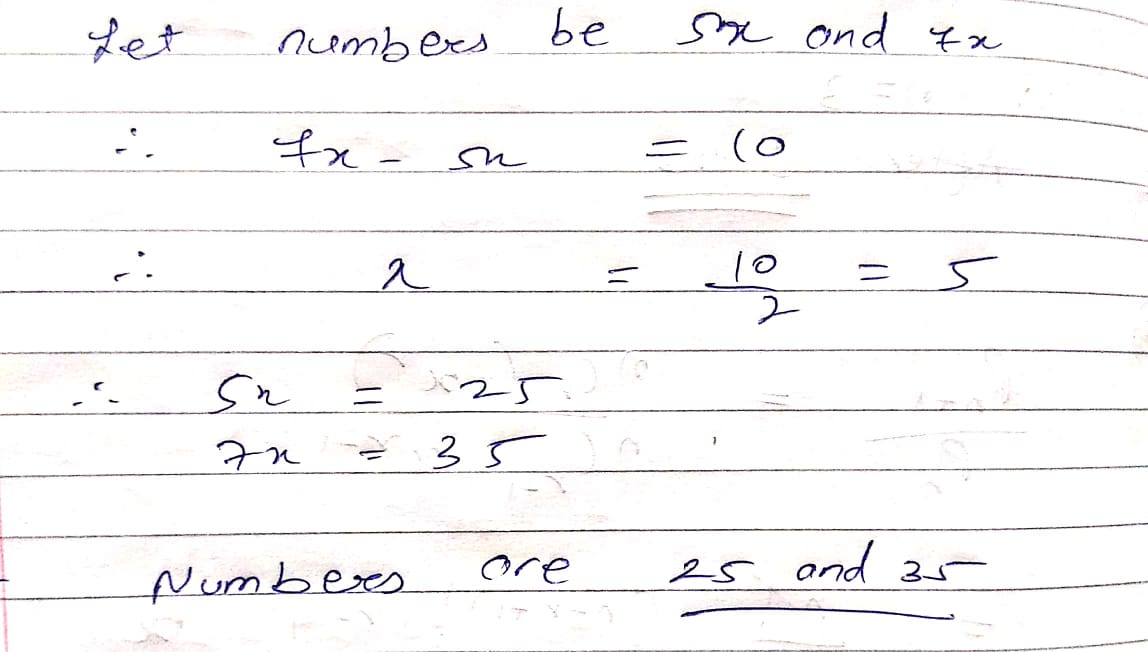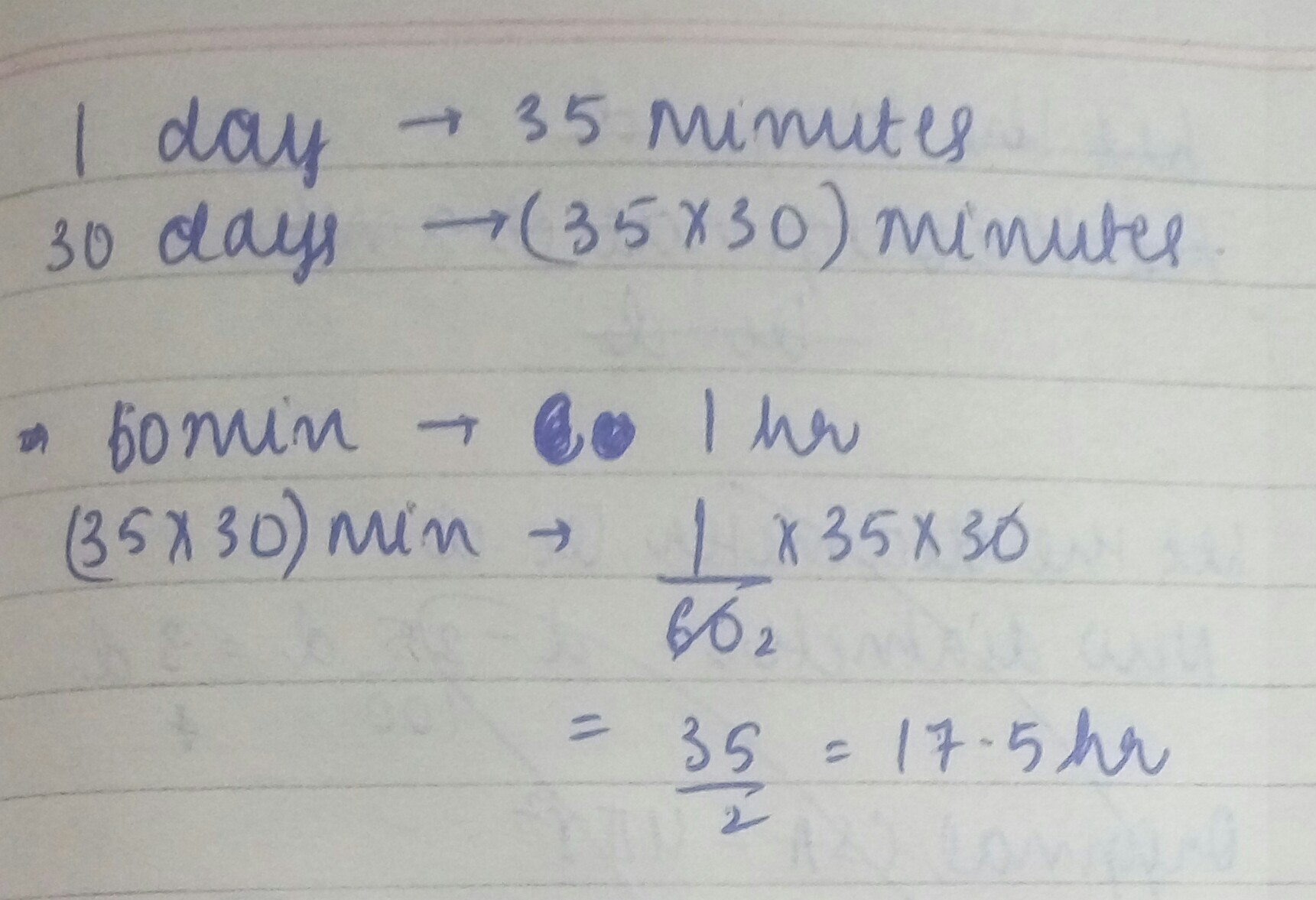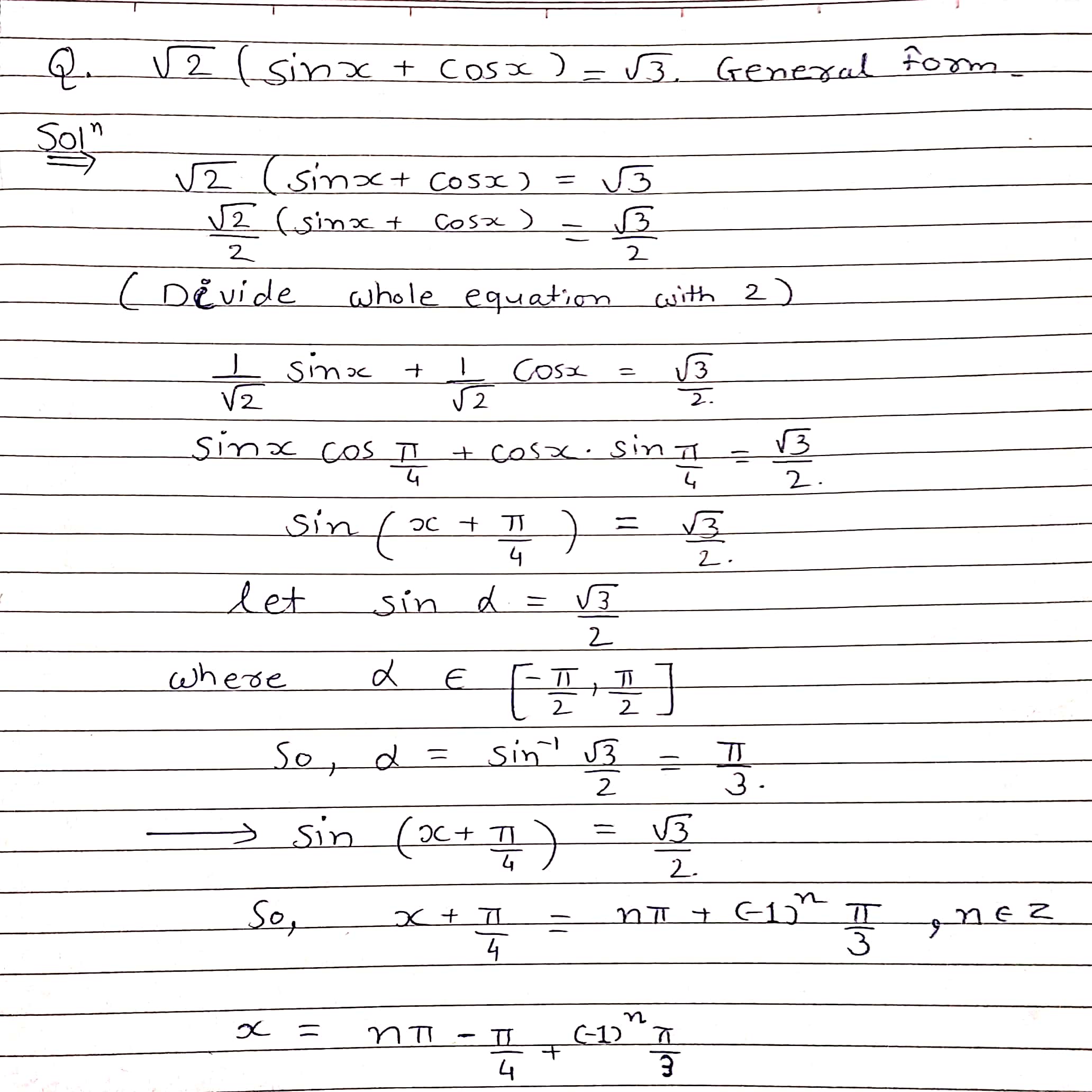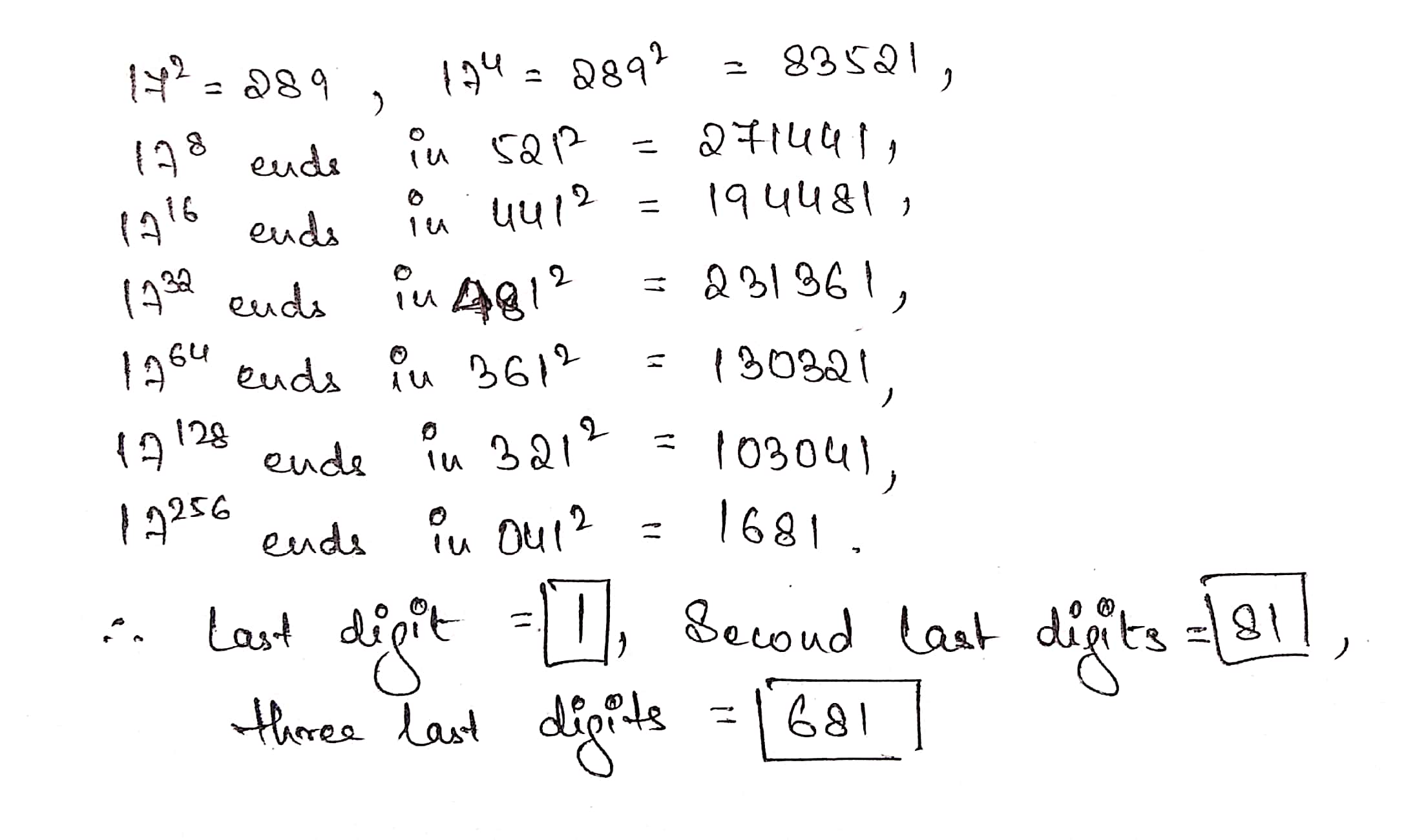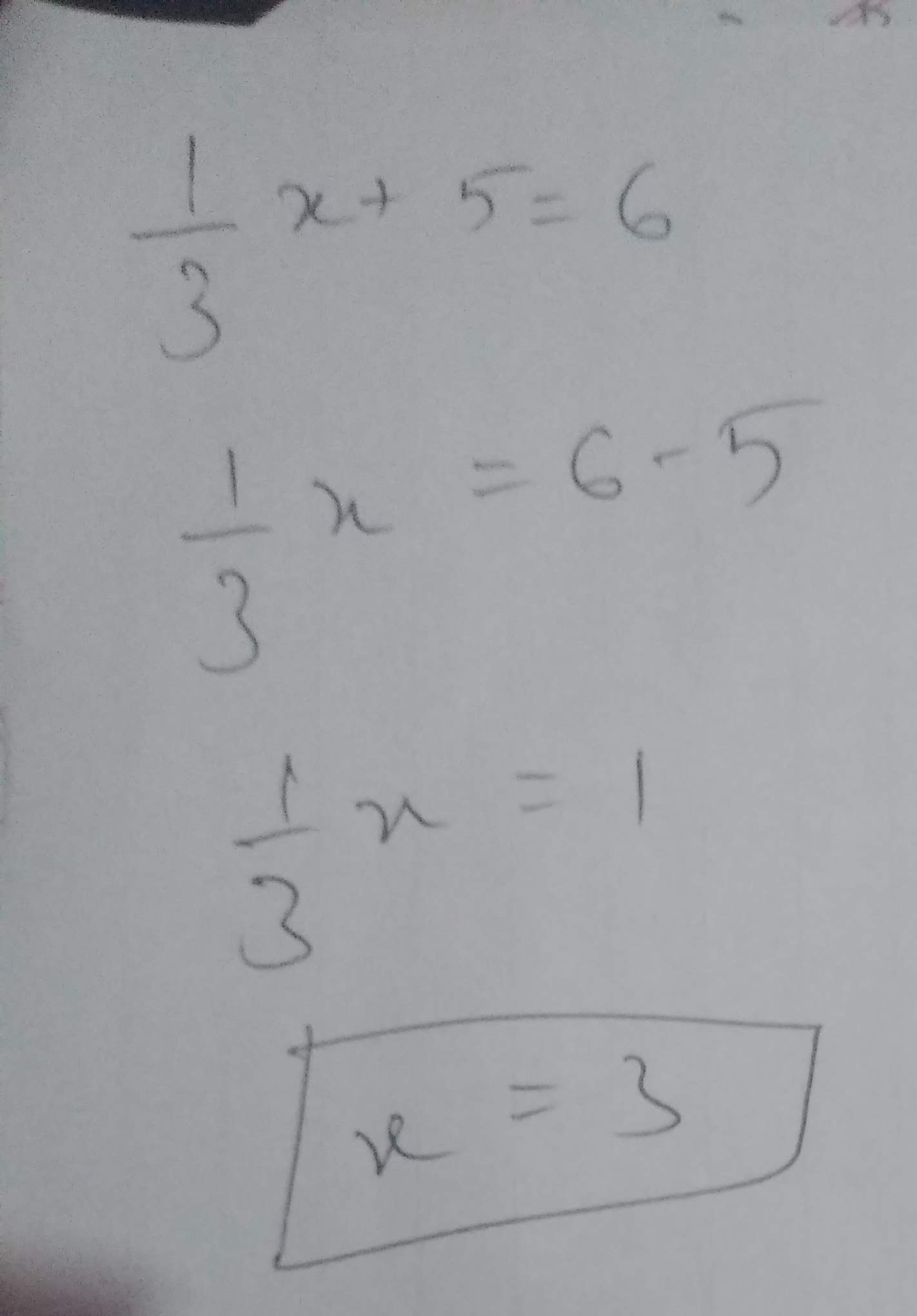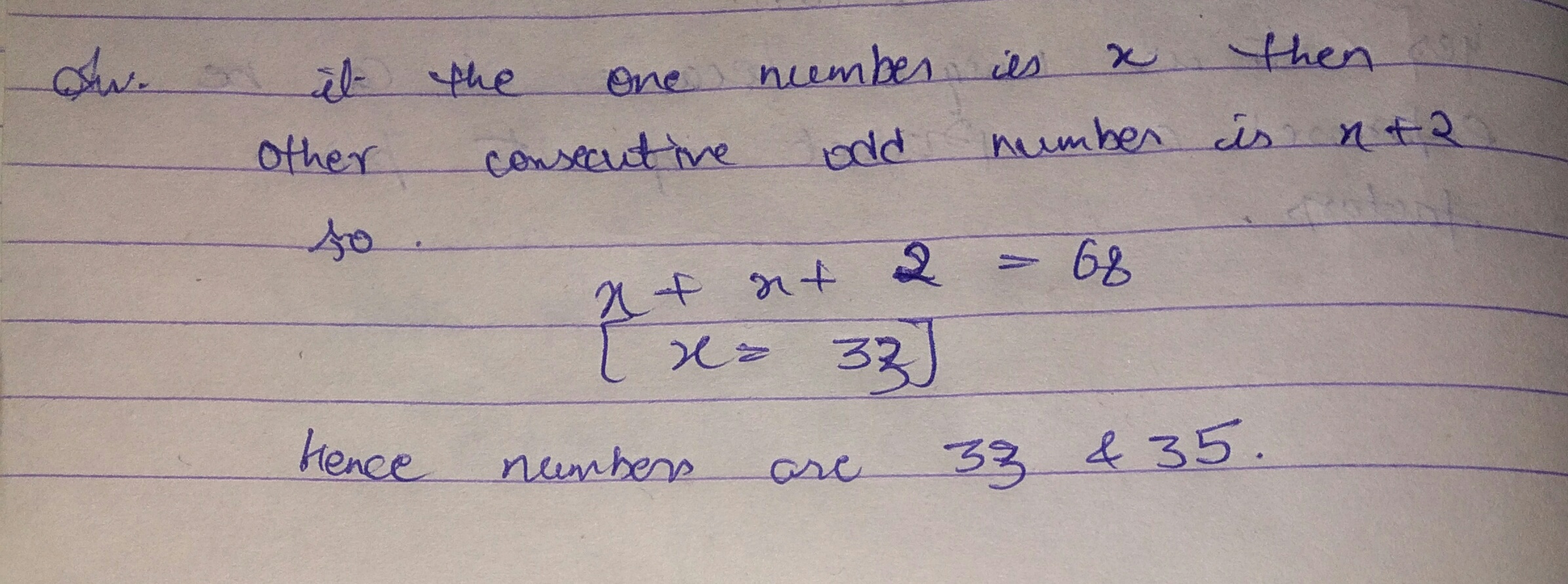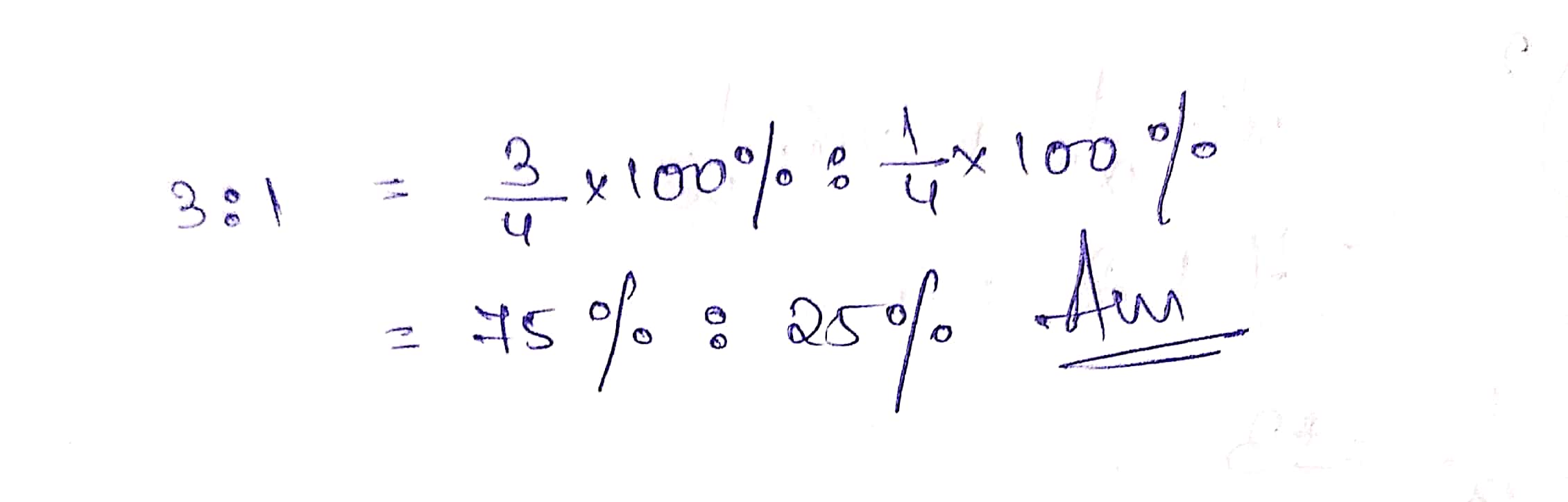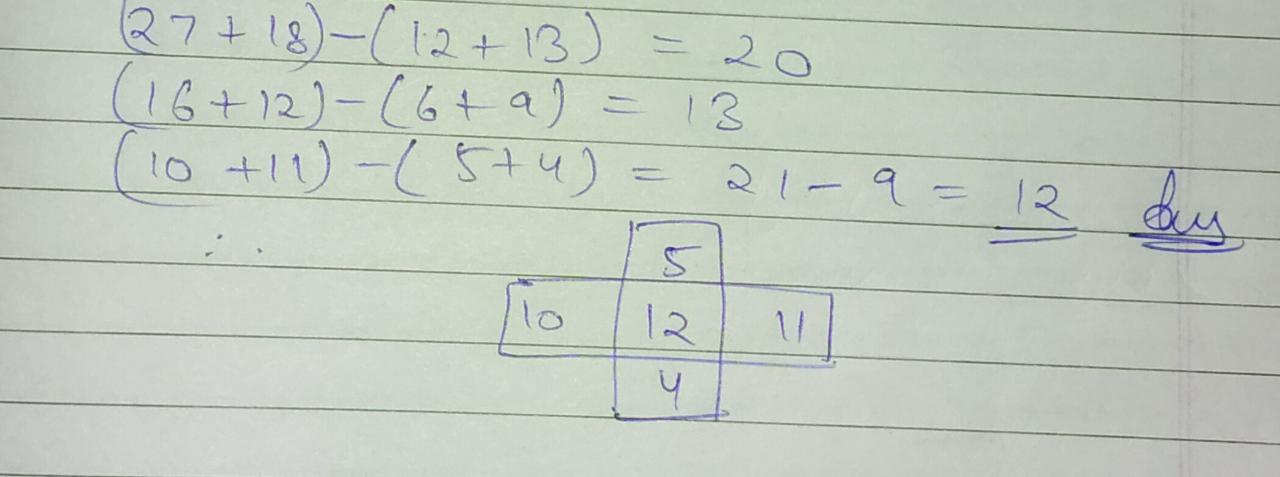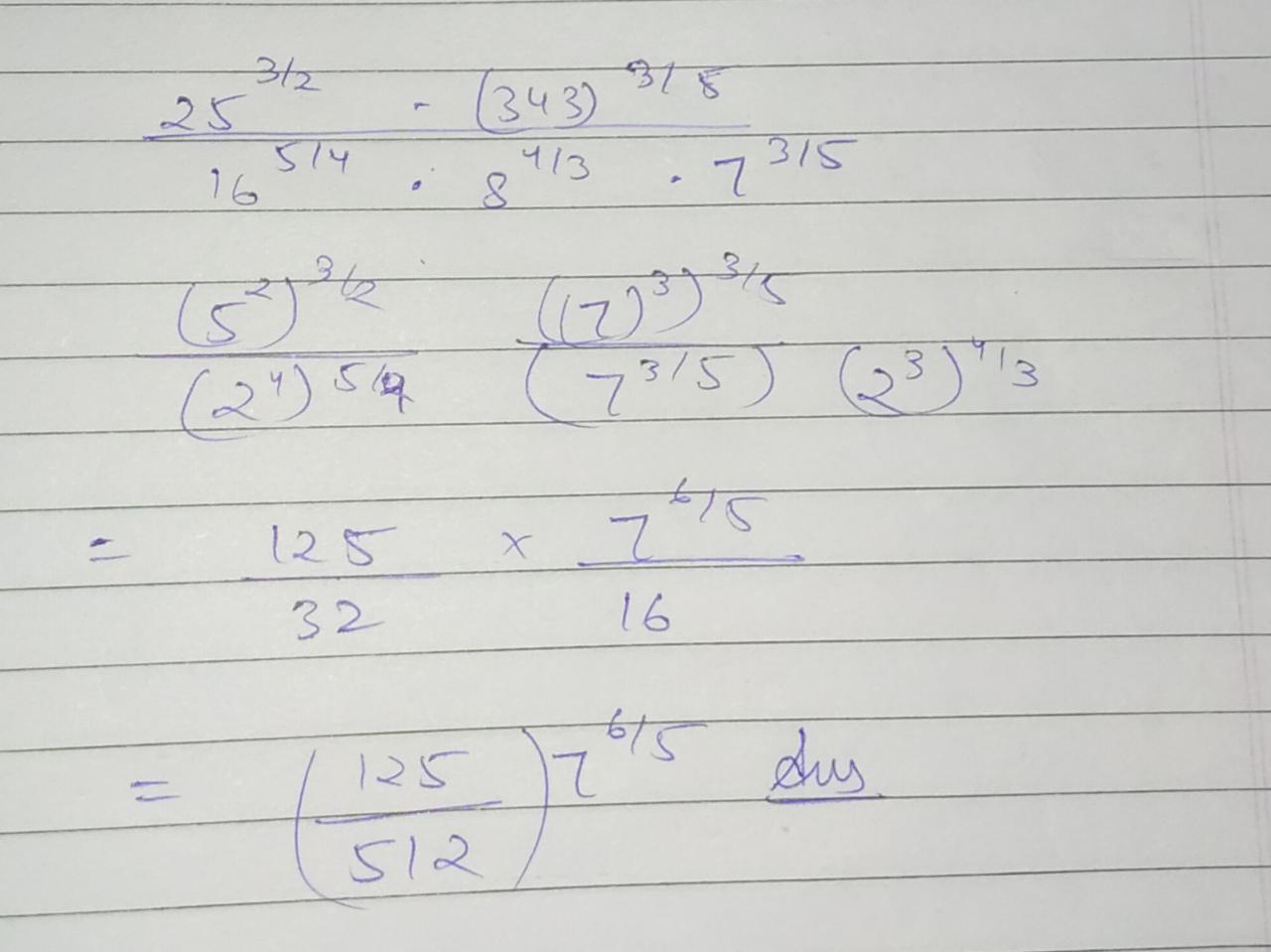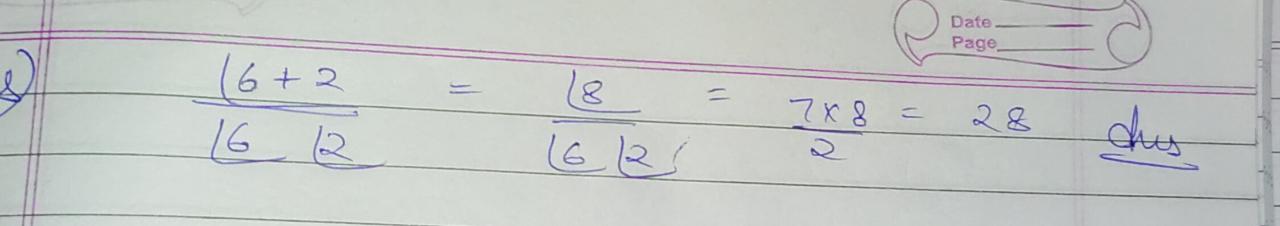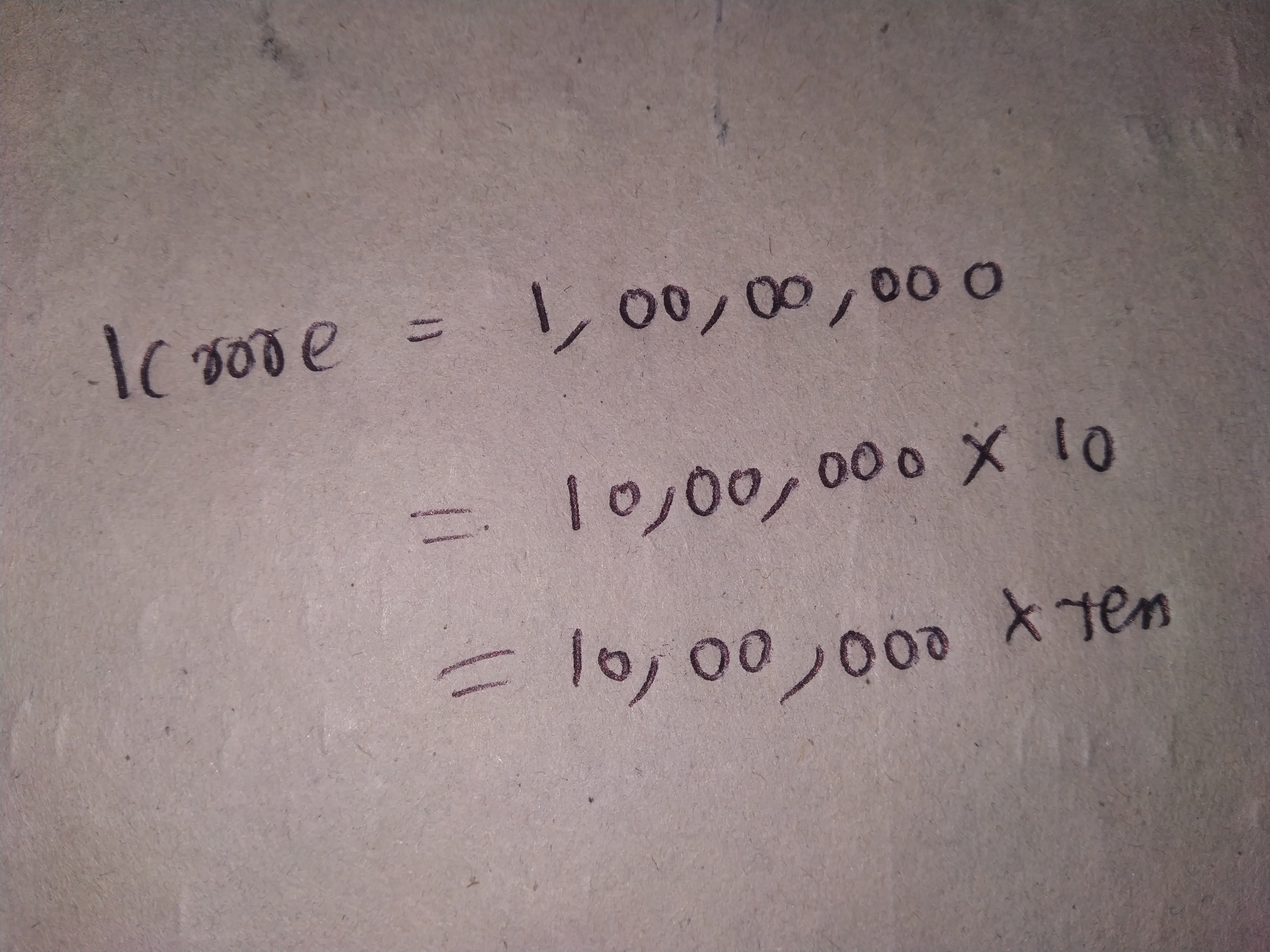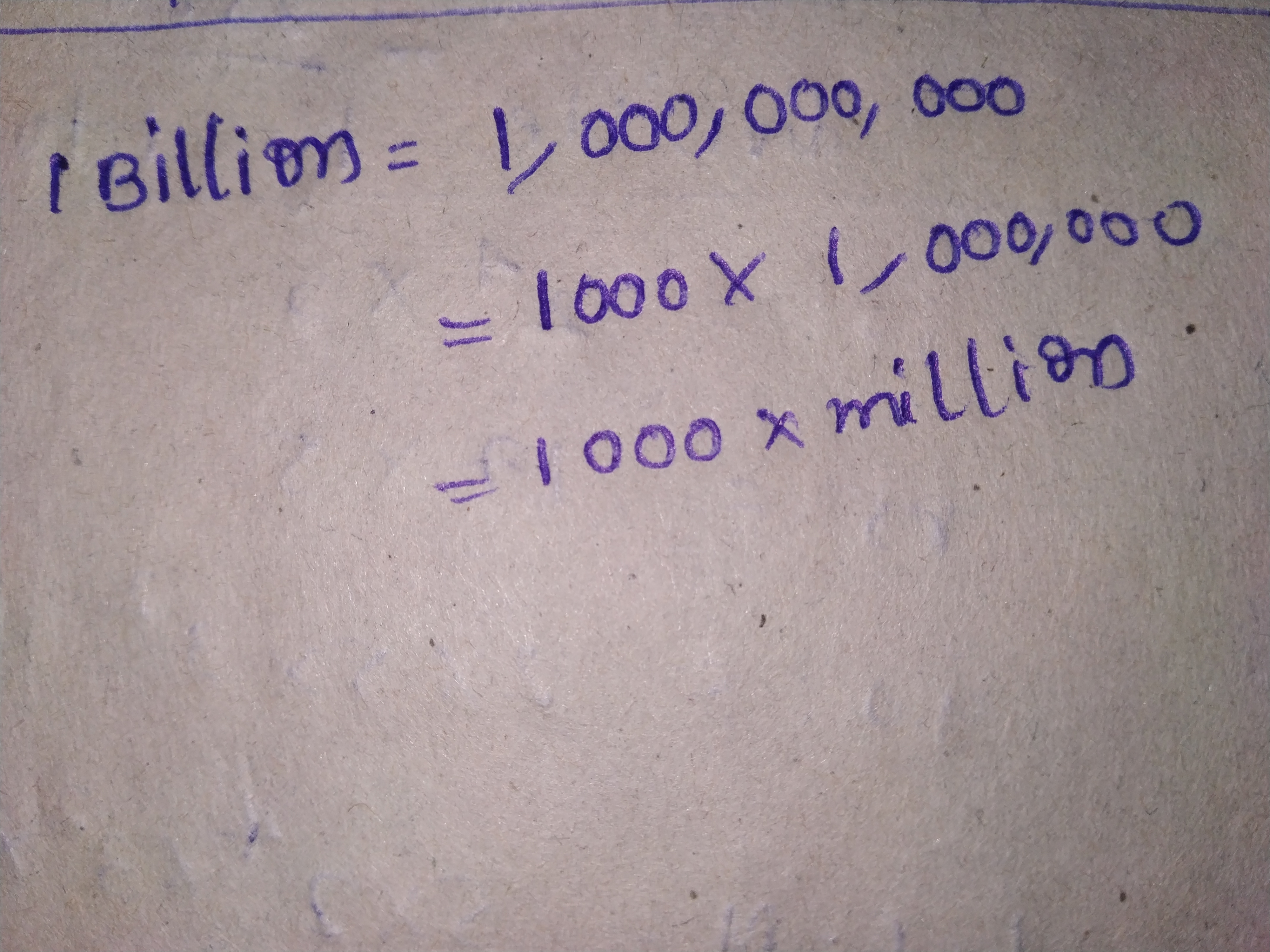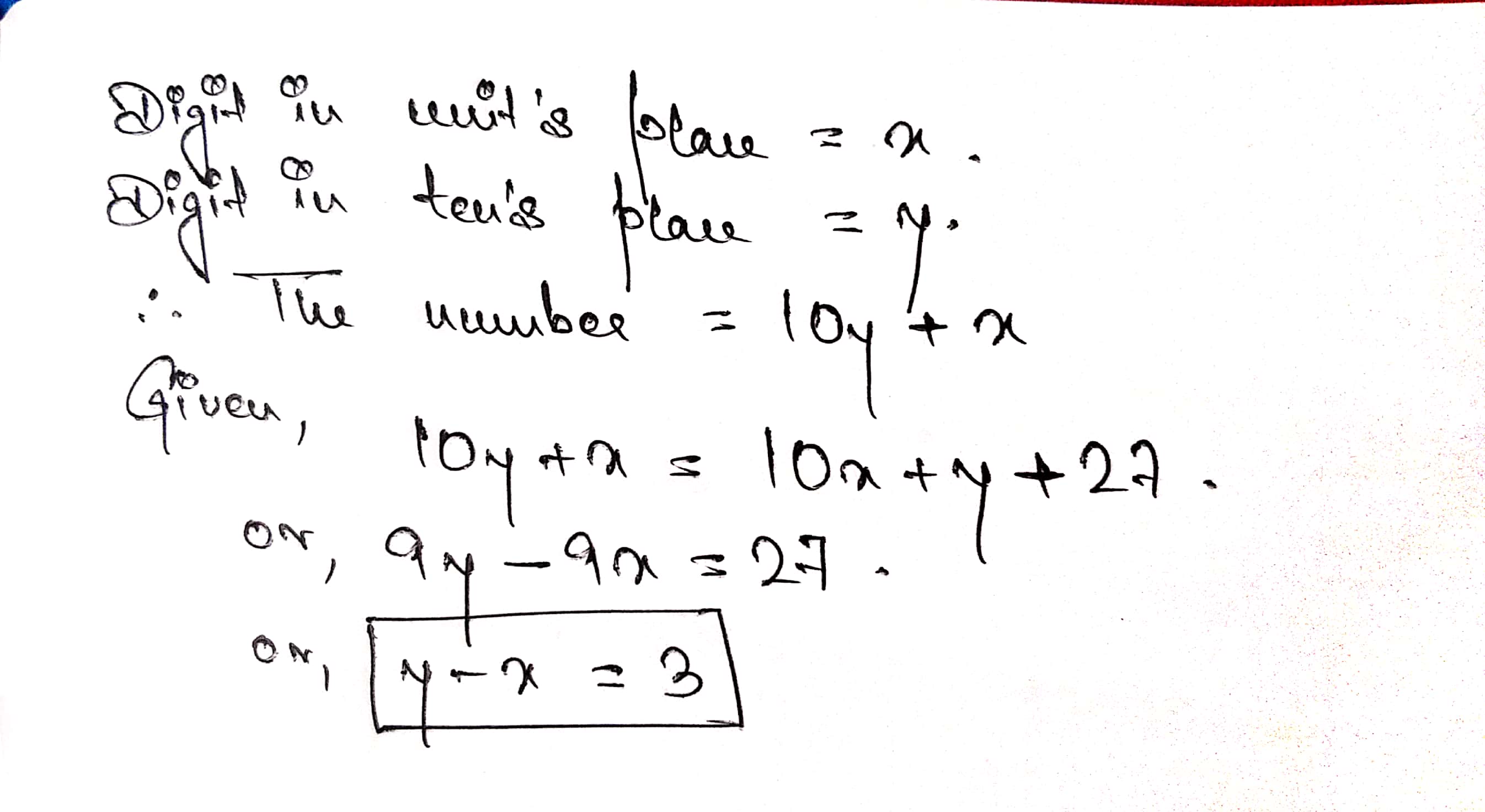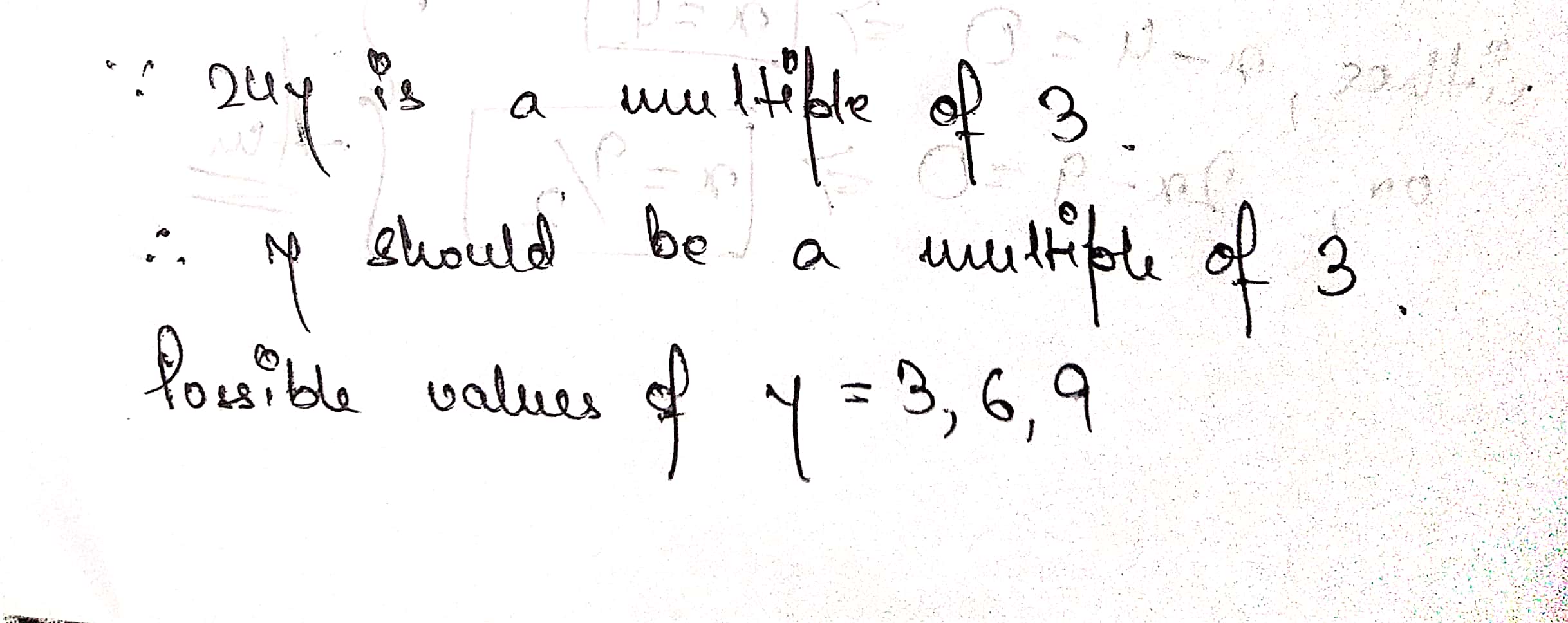Class 8 Maths - Playing With Numbers

Test the divisibility of the following number by $10$ :
$60005$

we know that if the unit place digit is divisible by

$10$ i.e. the unit place is having the value

$0$ then given number is divisible by

$10$ .

Here, the unit place the given number is

$5$ which is not divisible by

$10$

$\therefore$ the given number

$60005$ is not divisible by

$10$ .

Test the divisibility of the following number by $10$ :
$205$

we know that if the unit place digit is divisible by

$10$ i.e. the unit place is having the value

$0$ then given number is divisible by

$10$ .

Here, the unit place the given number is

$5$ which is not divisible by

$10$

$\therefore$ the given number

$205$ is not divisible by

$10$ .

Find:
$\cfrac{5}{63}-\left( \cfrac { -6 }{ 21 } \right)$

$\cfrac { 5 }{ 63 } -\left( \cfrac { -6 }{ 21 } \right) =\cfrac { 5\times 1 }{ 63\times 1 } -\left( \cfrac { -6 }{ 21 } \right) =\cfrac { 5\times 1 }{ 63\times 1 } -\left( \cfrac { -6\times 3 }{ 21\times 3 } \right) =\cfrac { 5 }{ 63 } -\cfrac { -18 }{ 63 } =\cfrac { 5-(-18) }{ 63 } =\cfrac { 5+18 }{ 63 } =\cfrac { 23 }{ 63 }$
L.C.M of

$63$ and

$21$ is

$63$

Find the sum:
$\cfrac{5}{3}+\cfrac{3}{5}$

$\cfrac { 5 }{ 3 } +\cfrac { 3 }{ 5 } =\cfrac { 5\times 5 }{ 3\times 5 } +\cfrac { 3\times 3 }{ 5\times 3 } =\cfrac { 25 }{ 15 } +\cfrac { 9 }{ 15 } =\cfrac { 25+9 }{ 15 } =\cfrac { 34 }{ 15 } =2\cfrac { 4 }{ 15 }$

L.C.M of

$3$ and

$5$ is

$15$ .

Find:
$-2\cfrac{1}{9}-6$

$-2\cfrac { 1 }{ 9 } -6=\cfrac { -19 }{ 9 } -\cfrac { 6 }{ 1 } =\cfrac { -19\times 1 }{ 9\times 1 } -\cfrac { 6\times 9 }{ 1\times 9 } =\cfrac { -19 }{ 9 } -\cfrac { 54 }{ 9 } =\cfrac { -19-54 }{ 9 } =\cfrac { -73 }{ 9 } =-8\cfrac { 1 }{ 9 }$
L.C.M of

$9$ and

$1$ is

$9$

Find the sum:
$\cfrac{-3}{-11}+\cfrac{5}{9}$

$\cfrac { -3 }{ -11 } +\cfrac { 5 }{ 9 } =\cfrac { -3\times 9 }{ -11\times 9 } +\cfrac { 5\times 11 }{ 9\times 11 } =\cfrac { 27 }{ 99 } +\cfrac { 55 }{ 99 } =\cfrac { 27+55 }{ 99 } =\cfrac { 82 }{ 99 }$
L.C.M of

$11$ and

$9$ is

$99$

Find:
$\cfrac{7}{24}-\cfrac{17}{36}$

$\cfrac { 7 }{ 24 } -\cfrac { 17 }{ 36 } =\cfrac { 7\times 3 }{ 24\times 3 } -\cfrac { 17\times 2 }{ 36\times 2 } =\cfrac { 21 }{ 72 } -\cfrac { 34 }{ 72 } =\cfrac { 21-34 }{ 72 } =\cfrac { -13 }{ 72 } L.C.M of$ 24

$and$ 36

$is$ 72$$

Find the sum:
$\cfrac{-9}{10}+\cfrac{22}{15}$

$\cfrac { -9 }{ 10 } +\cfrac { 22 }{ 15 } =\cfrac { -9\times 3 }{ 10\times 3 } +\cfrac { 22\times 2 }{ 15\times 2 } =\cfrac { -27 }{ 30 } +\cfrac { 44 }{ 30 } =\cfrac { -27+44 }{ 30 } =\cfrac { 17 }{ 30 }$
L.C.M of

$10$ and

$15$ is

$30$

Find the sum:
$\cfrac{-8}{19}+\cfrac{(-2)}{57}$

$\cfrac { -8 }{ 19 } +\cfrac { (-2) }{ 57 } =\cfrac { -8\times 3 }{ 19\times 3 } +\cfrac { (-2)\times 1 }{ 57\times 1 } =\cfrac { -24 }{ 57 } +\cfrac { (-2) }{ 57 } =\cfrac { -24-2 }{ 57 } =\cfrac { -26 }{ 57 }$
L.C.M of

$19$ and

$57$ is

$57$

Find the sum:
$-2\cfrac{1}{3}+4\cfrac{3}{5}$

$-2\cfrac { 1 }{ 3 } +4\cfrac { 3 }{ 5 } =\cfrac { -7 }{ 3 } +\cfrac { 23 }{ 5 } =\cfrac { -7\times 5 }{ 3\times 5 } +\cfrac { 23\times 3 }{ 5\times 3 } =\cfrac { -35 }{ 15 } +\cfrac { 69 }{ 15 } =\cfrac { -35+69 }{ 15 } =\cfrac { 34 }{ 15 } =2\cfrac { 4 }{ 15 }$
L.C.M of

$3$ and

$5$ is

$15$

Find the product:
$\cfrac{3}{7}\times \left( \cfrac { -2 }{ 5 } \right)$

$\cfrac { 3 }{ 7 } \times \left( \cfrac { -2 }{ 5 } \right) =\cfrac { 3\times (-2) }{ 7\times 5 } =\cfrac { -6 }{ 35 }$

Find the product:
$\cfrac{3}{10}\times (-9)$

$\cfrac { 3 }{ 10 } \times (-9)=\cfrac { 3\times (-9) }{ 10 } =\cfrac { -27 }{ 10 } =-2\cfrac { 7 }{ 10 }$

Find the product:
$\cfrac{9}{2}\times \left( \cfrac { -7 }{ 4 } \right)$

$\cfrac { 9 }{ 2 } \times \left( \cfrac { -7 }{ 4 } \right) =\cfrac { 9\times (-7) }{ 2\times 4 } =\cfrac { -63 }{ 8 } =-7\cfrac { 7 }{ 8 }$

Find the product:
$\cfrac{-6}{5}\times \cfrac{9}{11}$

$\cfrac { -6 }{ 5 } \times \cfrac { 9 }{ 11 } =\cfrac { (-6)\times 9 }{ 5\times 11 } =\cfrac { -54 }{ 55 }$

Find the value of:
$(-4)\div \cfrac{2}{3}$

$\quad (-4)\div \cfrac { 2 }{ 3 } =(-4)\times \cfrac { 3 }{ 2 } =(-2)\times 3=-6$

Find the product:
$\cfrac{3}{11}\times \cfrac{2}{5}$

$\cfrac { 3 }{ 11 } \times \cfrac { 2 }{ 5 } =\cfrac { 3\times 2 }{ 11\times 5 } =\cfrac { 6 }{ 55 }$

Find the product:
$\cfrac{3}{-5}\times \cfrac{5}{3}$

$\cfrac { 3 }{ -5 } \times \left( \cfrac { -5 }{ 3 } \right) =\cfrac { 3\times (-5) }{ -5\times 3 } =1$

Find the value of :
$\cfrac{-3}{5}\div 2$

$\cfrac { -3 }{ 5 } \div 2=\cfrac { -3 }{ 5 } \times \cfrac { 1 }{ 2 } =\cfrac { (-3)\times 1 }{ 5\times 2 } =\cfrac { -3 }{ 10 }$

Find the value of:
$\cfrac{-1}{8}\div \cfrac{3}{4}$

$\cfrac { -1 }{ 8 } \div \cfrac { 3 }{ 4 } =\cfrac { -1 }{ 8 } \times \cfrac { 4 }{ 3 } =\cfrac { (-1)\times 1 }{ 2\times 3 } =\cfrac { -1 }{ 6 }$

Find the value of:
$\cfrac{-4}{5}\div (-3)$

$\cfrac { -4 }{ 5 } \div (-3)=\cfrac { (-4) }{ 5 } \times \cfrac { 1 }{ (-3) } =\cfrac { (-4)\times 1 }{ 5\times (-3) } =\cfrac { 4 }{ 15 }$

Write the following in expanded notation.
$3057$

$3057$

$\Rightarrow 3000+50+7$

$\Rightarrow 3\times 1000+0\times 100+5\times 10+7\times 1$

Write the following in expanded notation.
$235060$ .

$2,35,060$

$=200000+30000+5000+60$

$= 2\times 100000+3\times 10000+5\times 1000+0\times 100+6\times 10+0\times 1$

Write the following in expanded notation.
$12345$ .

$12345= 10000+2000+300+40+5$ .

$12345=1\times 10000+2\times 1000+3\times 100+4\times 10+5\times 1$ .

Write the corresponding numeral for the following.
$4\times 100000+5\times 1000+1\times 100+7\times 1$ .

$4\times 100000+5\times 1000+1\times 100+7\times 1$ .

$=400000+5000+100+7$ .

$=4,05,107$ .

Find the value of:
$\cfrac{-7}{12}\div \left( \cfrac { 2 }{ 13 } \right)$

$\cfrac { -7 }{ 12 } \div \left( \cfrac { -2 }{ 13 } \right) =\cfrac { -7 }{ 12 } \times \cfrac { 13 }{ (-2) } =\cfrac { (-7)\times 13 }{ 12\times (-2) } =\cfrac { -91 }{ 24 } =3\cfrac { 19 }{ 24 } \quad$

Write down the difference in temperature between $-4^oC$ and $-9^oC$ .
_______ $^oC$ .

1695341_1647163_ans_b979816b397a485ea26a33619a437c82.jpg

Write the corresponding numeral for the following.
$7\times 10000+2\times 1000+5\times 100+9\times 10+6\times 1$ .

1501853_1658370_ans_631963cea44e4256b3483b2e0d4cec9d.jpg

Write the following is expanded notation.
$10205$ .

$10205$

$=10000+200+5$

$=1\times 10000+0\times 1000+2\times 100+0\times 10+5\times 1$

Find the value of:
$\cfrac{3}{13}\div \left( \cfrac { -4 }{ 65 } \right)$

$\cfrac { 3 }{ 13 } \div \left( \cfrac { -4 }{ 65 } \right) =\cfrac { 3 }{ 13 } \times \cfrac { 65 }{ (-4) } =\cfrac { 3\times (-5) }{ 1\times 4 } =\cfrac { -15 }{ 4 } =-3\cfrac { 3 }{ 4 }$

Find the value of:
$\cfrac{-2}{13}\div \cfrac{1}{7}$

$\cfrac { -2 }{ 13 } \div \cfrac { 1 }{ 7 } =\cfrac { -2 }{ 13 } \times \cfrac { 7 }{ 1 } =\cfrac { (-2)\times 7 }{ 13\times 1 } =\cfrac { -14 }{ 13 } =-1\cfrac { 1 }{ 13 }$

Fill in the blank.
$1$ lakh $=$ _______ ten.

$1$ lakh

$=1,00,000$

$=10\times 10,000$

$=10,000$ Tens.

Fill in the blank.
$1$ lakh $=$ ______ hundred.

1 lakh = 1,00,000

After removing commas, we get

1 lakh = 100000

1 lakh = 1000×(100)

So, 1 lakh = 1000 hundred

Fill in the blank.
$1$ crore $=$ ______ hundred.

1 crore = 1,00,00,000

On removing commas,

1 crore = 10000000

So, 1 crore = 1,00,000×(100)

1 crore = (1,00,000) hundred

Which digits have the same face value and place value in $92078634$ ?

92078634

Face value is the actual value of the digit.

Place value is the value of digit based on its position in the given number.

Here, the face value of

$4=4$

Place value of

$4=4$

So,

$4$ has the same place value and the face value

Write the corresponding numeral for the following.
$5\times 10000000+7\times 1000000+8\times 1000+9\times 10+4$ .

= (5×10000000) + (7×1000000) + (8×1000) + (9×10) + 4

= (50000000) + (7000000) + (8000) + (90) +4

= 57008094

How many millions make a billion?

We know that

$1 \text{ million} =1,000,000$

$1 \text{ billion} =1,000,000,000$

So,

$1 \text{ billion} =1,000 \times (1,000,000)$

Hence,

$1 \text{ billion} =1,000 \text{ million}$

Fill in the blank.
$1$ crore $=$ ______ ten lakh.

1 crore = 1,00,00,000

After removing commas, we get

1 crore = 10000000

So, 1 crore = 10 × (10,00,000)

1 crore = 10 ten lakhs

$\dfrac { \begin{matrix} 8 & 5 \\ +4 & A \end{matrix} }{ B\ C\ 3 }$

From the

$1' s$ column
The value of

$5+A$ is a two-digit number whose last digit is

$3$ .
Therefore,

$5+A=13\Rightarrow A=8$
From the column

$10's$

$10B+C=8+4+1$

$10B+C=13=10\times 1+3$
Hence

$A=8, B=1$ and

$C=3$

$\dfrac { \begin{matrix} A & 01 & B \\ +1 & 0A & B \end{matrix} }{ \begin{matrix} B & 10 & 8 \end{matrix} }$

From the

$1' s$ column

$B+B=8$

$B=9$ (

$B+B$ not satisfy the

$1000's$ column)
From the

$10's$ column

$A+1+1=0$

$A=8$
Hence,

$A=8$ and

$B=9$

Find the values of the letters in each of the following and give reasons for the steps involved
$1 \quad 8 \quad A$
$+ B \quad A \quad 7$
__________
$C \quad B \quad 2$

Since we know that,

$5+7 =12$

$\therefore A=5$

$B=4,C=6$

$1 \quad 8 \quad5$

$+ 4 \quad 5 \quad 7$
____________

$6 \quad 4 \quad 2$
Hence,

$A = 5, B = 4, C = 6$

Write the following numbers in generalized form:
$(i) 89$
$(ii)207$
$(iii)369$

The generalized form is as follows:

$(i) 89=8 \times 10 + 9$

$(ii) 207=2 \times 100+0\times 10+7\times 1$

$(iii) 369=3\times 100+6\times 10+9\times 1$

If $A \times 3=1A$ , then $A=$ ______ .

From the question,

$3\times A=$ a two digit number with unit digit

$A$

$A=0$ to

$9$

Only

$5$ is a number whose product with

$3$ is a two digit number with unit digit itself

$(5)$

Hence,

$A=5$

Fill in the blanks :
In $24,673$ , the place value of $6$ is .........

$24,673$ , the place value of

$6$ is

$6 \times 100$

$= 600$

Write $25$ in generalised from:

We have,

$25=2\times 10+5$

$[\because xy=10\times x+y$ where x, y are ten's and one's place digit]

Find the digits $A$ and $C$ in the following multiplication

Here the last digit of

$2\times A$ is

$4$ . Hence either

$A = 2$ or

$A = 7$ .
Suppose

$A = 2$ . Then you get the product as

$32\times 12 = 384$ . This shows that

$C = 3$ . On the other hand, if

$A = 7$ , then the product is

$37\times 12 = 444$ . However, the digit in the ten's place of the result must be

$8$ and not

$4$ . We may therefore reject

$A = 7$ . We conclude

$A = 2$ and

$C = 3$ .

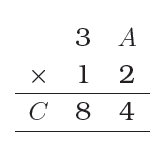
If $21y5$ is multiple of $9$ , where $y$ is a digit, what is the value of $y$ ?

Since the number

$21y5$ is a multiple of

$9$ .

So, the sum of its digits

$2 + 1 + y + 5 = 8 + y$ is a multiple of

$9$ .

$\therefore (8 + y)$ is either

$0$ or

$9$ or

$18$ or ...

Since

$y$ is a digit, so

$(8 + y)$ must be equal to

$9$ .

i.e.,

$8 + y = 9$

$\Rightarrow y = 9 -8 = 1$

Find the digit represented by P in the following addition

We see that P, being a digit, cannot exceed

$9$ . The only way you can arrive to

$6$ from

$5$ is adding

$1$ . Hence

$P = 1$ . Similarly, you get

$Q = 1$ . We may check that

$411 + 1215 = 526$ .

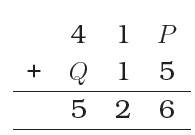
Frame and solve the equations for the following statements:
The sum of the two numbers is $21$ and their difference is $3$ . Find the numbers

Let the numbers be

$x$ and

$y$

Now, Sum is

$21$

$\Rightarrow x+y=21$ ......................................(1)

and assuming that

$x$ is the Larger Number

Putting

$x-y=3\Rightarrow x=y+3$ in eq(1) we get

$\Rightarrow 2y+3=21\rightarrow y=9$

So,

$x+9=21\rightarrow x=12$

Hence, the numbers are

$9$ and

$12$ .

Express the following in the standard form:
$3.02\times {10}^{-6}$

$3.02\times {10}^{-6}=\dfrac{3.02}{10}^{6}=\dfrac{3.02}{1000000}=0.00000302$

Express the following in the standard form:
$1.0001\times {10}^{9}$

$1.0001\times {10}^{9}=1.0001\times 1000000000=1000100000$

Test the divisibility of the following number by $10$ :
$90$

we know that if the unit place digit is divisible by

$10$ i.e. the unit place is having the value

$0$ then given number is divisible by

$10$ .

Here, the unit place the given number is

$0$ which is divisible by

$10$

$\therefore$ the given number

$90$ is divisible by

$10$ .

Frame and solve the equations for the following statements:
Sum of two numbers is $60$ . The bigger number is $4$ times the smaller one. Find the numbers

Let the numbers be

$x$ and

$y$

Now, Sum is

$60$

$\Rightarrow x+y=60$ ......................................(1)

and assuming that

$x$ is the smaller number

$4x=y$

Putting

$4x=y$ in eq(1) we get

$\Rightarrow 5x=60\rightarrow x=12$

So,

$12+y=60\rightarrow y=48$

Hence, the numbers are

$12$ and

$48$ .

Frame and solve the equations for the following statements:
Two numbers are in the ratio $5 : 3$ . If they differ by $18$ , what are the numbers?

Let the numbers be

$x$ and

$y$

Now, Difference is

$18$

$\Rightarrow x-y=18$ ......................................(1)

and assuming that

$x$ is the Larger number

and

$\dfrac{5}{3}=\dfrac{x}{y}\rightarrow y=\dfrac{3x}{5}$

Putting

$y=\dfrac{3x}{5}$ in eq(1) we get

$\Rightarrow x-\dfrac{3x}{5}=18\rightarrow \dfrac{2x}{5}=18\rightarrow x=45$

So,

$45-y=18\rightarrow y=63$

Hence, the numbers are

$45$ and

$63$ .

Mala has a collection of bangles. She have 20 gold bangles and 10 silver bangles. What is the percentage of bangles of each type? Can you put it in a tabular form as done in the above example?

Siver bangles

$=10$

gold bangles

$=20$

total bangles

$=10+20=30$

percentage of silver bangles

$=\dfrac{10}{30}\times 100=33.3$

percentage of gold bangles

$=\dfrac{20}{30}\times 100=66.6$

Solve the alphanumeric puzzle: $\begin{matrix} 2 & P & Q \\ +3 & P & Q \\ Q & 1 & 2 \end{matrix}$

Take

$\displaystyle \,Q =6 \quad \quad \,{2\quad 5\quad 6}$

$\displaystyle P=5 \quad +\, \underline{ 3\quad 5\quad 6}$

$\quad \quad \quad \quad \quad \, \quad \, \, \,6\quad 1\quad 2\quad$

1048231_1038024_ans_dc557e1dbf3f4038b5d156045abc0fb6.jpg

Replace the letters by the numerals to make it correct.
A 6 B 4 C

+1 7 2 5 5

9 D 0 E 8

$\quad \quad \quad \quad \quad \, \quad \quad \quad \, A\, \, \, 6\, \, \, B\, \, \, 4\, \, \, C\\ \quad \quad \quad \quad \quad \quad \quad \quad +\, 1\, \, \, 7\, \, \, 2\, \, \, \, 5\, \, \, \, 5\\ \overline { A\to 7,B\to 8,C\to 3,D\to 4,E\to 9 }$

$7\, \, \, 6\, \, \, 8\, \, \, 4\, \, \, 3\\ 1\, \, \, 7\, \, \, 2\, \, \, 5\, \, \, 5\\ \overline { 9\, \, \, 4\, \, \, 0\, \, \, 9\, \, \, 8 }$

Write expanded form:
a) $67586412$
b) $1234800007$

(a)

$67586412$

$= 6 \times 10000000 + 7 \times 1000000 + 5 \times 100000 + 8 \times 10000 + 6 \times 1000 + 4 \times 100 + 1 \times 10 + 2 \times 1$

$= 60000000 + 7000000 + 500000 + 80000 + 6000 + 400 + 10 + 2$

(b)

$1234800007$

$= 1 \times 1000000000 + 2 \times 100000000 + 3 \times 10000000 + 4 \times 1000000 + 8 \times 100000 + 0 \times 10000$

$+ 0 \times 1000 + 0 \times 100 + 0 \times 10 + 7 \times 1$

$= 1000000000 + 200000000 + 30000000 + 4000000 + 800000 + 7$

Write each of the following in expanded from using exponents:
(i) $2357.328$
(ii) $432.476$
(iii) $38.0325$

(i)

$2357.328 = 2 \times {10^3} + 3 \times {10^2} + 5 \times 10 + 7 \times 1 + 3 \times {10^{ - 1}} + 2 \times {10^{ - 2}} + 8 \times {10^{ - 3}}$

(ii)

$432.476 = 4 \times {10^2} + 3 \times 10 + 2 \times 1 + 4 \times {10^{ - 1}} + 7 \times {10^{ - 2}} + 6 \times {10^{ - 3}}$

(iii)

$38.0325 = 3 \times 10 + 8 \times 1 + 0 \times {10^{ - 1}} + 3 \times {10^{ - 2}} + 2 \times {10^{ - 3}} + 5 \times {10^{ - 4}}$

Make the greatest and the smallest 4 digit numbers by using any one digit twice:
(i) 6, 3, 2
(ii) 1, 0, 6

i) The greatest and smallest

$4-$ digit number by using any one digit twice from

$6,3,2$ are

$6632$ and

$2236$ .

ii) The greatest and smallest

$4-$ digit number by using any one digit twice from

$1,0,6$ are

$6610$ and

$1006$ .

Fill in the blank
$1\ g=..................mg$

$1 g=1000 mg$ .

Write the number :
$4 \times 10^6 + 8 \times 10^5 + 6 \times 10^4 + 4 \times 10^3 + 4 \times 10^2 + 6 \times 10 + 9 \times 10^0$

$4\times 10^6+8\times 10^5+6\times 10^4+4\times 10^3+4\times 10^2+6\times 10+9\times 10^0$

$=4\times1000000+8\times100000+6\times10000+4\times1000+4\times100+6\times10+9\times0$

$=4000000+800000+60000+4000+400+60+0$

$=4864460$

$4\times 10^6+8\times 10^5+6\times 10^4+4\times 10^3+4\times 10^2+6\times 10+9\times 10^0=4864460$

Express the number :
$8 \times 10^5 + 7 \times 10^4 + 5 \times 10^3 + 4 \times 10^2 + 6 \times 10^1 + 9 \times 10^0$

$8\times 10^{5}+7\times 10^{4}+5\times 10^{3}+4\times 10^{2}+6\times 10^{1}+9\times 10^{0}$

$=8\times 100000+7\times 10000+5\times 1000+4\times 100+6\times 10+9\times 1$

$=800000+70000+5000+400+60+9$

$=875469$

Write the value of $|15 \times 3-(7\times 2)\times 4|$

$|15\times 3-(7\times 2)\times 4|$

First we are going to solve brackets.

$\Rightarrow$

$|15\times 3-14\times 4|$

$\Rightarrow$

$|45-56|$

$\Rightarrow$

$|-11|$

$\Rightarrow$

$11$

Express the number in expanded form:
$9 \times 10^4 + 6 \times 10^3 + 4 \times 10^2 + 5 \times 10 + 7 \times 10^o$

$9\times 10^{4}+6\times 10^{3}+4\times 10^{2}+5\times 10^{1}+7\times 10^{0}$

$=9\times 10000+6\times 1000+4\times 100+5\times 10+7\times 1$

$=90000+6000+400+50+7$

$=96457$

Write each of the following as power of $10$ .
$1000000$

We have,

$1000000 = {\left( {10} \right)^6}$

Simplify
$\dfrac{25 \times 5^{2}\times t^{8}}{10^{3} \times t^{4}}$

$\dfrac{25\times 5^2\times t^8}{10^3\times t^4}$

$\Rightarrow$

$\dfrac{5^2\times 5^2\times t^8}{10^3\times t^4}$

$\Rightarrow$

$\dfrac{5^{(2+2)}\times t^8}{10^3\times t^4}$ [

$a^m\times a^n=a^{(m+n)}$ ]

$\Rightarrow$

$\dfrac{5^4\times t^8}{10^3\times t^4}$

$\Rightarrow$

$\dfrac{5^4\times t^{(8-4)}}{10^3}$ [

$\dfrac{a^m}{a^n}=a^{m-n}$ ]

$\Rightarrow$

$\dfrac{625\times t^4}{1000}$

$\Rightarrow$

$0.625\,t^4$

Solve $2+4+3$

$2+4+3$

$\Rightarrow 2+4+3=9$

Name the property involved in the following example.
$\dfrac{3}{7}\times 1=\dfrac{3}{7}=1\times \dfrac{3}{7}$ .

$\cfrac {3}{7}\times1=\cfrac {3}{7}=1\times\cfrac {3}{7}.$

$\because a\times b=b\times a.$

$\therefore$ Hence it is an commutative property

$.$

Using appropriate properties find. $-\dfrac {2}{3}\times \dfrac {3}{5}+ \dfrac {5}{2}-\dfrac {3}{5}\times \dfrac {1}{6}$

$-\dfrac{2}{3}\times \dfrac{3}{5}+\dfrac{5}{2}-\dfrac{3}{5}\times \dfrac{1}{6}$

$\Rightarrow$

$-\dfrac{2}{3}\times \dfrac{3}{5}-\dfrac{3}{5}\times \dfrac{1}{6}+\dfrac{5}{2}$ [ Using commutativity of rational numbers ]

$\Rightarrow$

$-\dfrac{3}{5}\times \left(\dfrac{2}{3}+\dfrac{1}{6}\right)+\dfrac{5}{2}$ [ By distributions ]

$\Rightarrow$

$-\dfrac{3}{5}\times \left(\dfrac{2\times 2+1}{6}\right)+\dfrac{5}{2}$

$\Rightarrow$

$-\dfrac{3}{5}\times \dfrac{5}{6}+\dfrac{5}{2}$

$\Rightarrow$

$\dfrac{-1}{2}+\dfrac{5}{2}$

$\Rightarrow$

$\dfrac{-1+5}{2}=\dfrac{4}{2}=2$

Find the number of the following expanded forms :
$6 \times 10^3 + 5 \times 10^2 + 0 \times 10 + 6 \times 10^0$

Place value chart of the given expanded form is:

Thousands	Hundreds	Tens	Ones
6	5	0	6

So the number is

$6506$

Solve $3\times 2(4+6)$

$3\times 2(4+6)$

$\Rightarrow 3\times2(10)$

$\Rightarrow 3\times 20$

$\Rightarrow 60$

Therefore,

$\Rightarrow 3\times 2(4+6)=60$

Simplify: $3$ $^{3}_{}\sqrt{40}$ - $4$ $^{3}_{}\sqrt{320}$

For this we must know how to find out the cube root of a number.

We need to simply

$[3\times ({40})^{\dfrac {1}{3}}]-[4\times ({320})^{\dfrac{1}{3}}]$

$({40})^\dfrac {1}{3}=[2\times ({5})^\dfrac {1}{3}]$

$({320})^\dfrac {1}{3}=[4\times ({5})^\dfrac {1}{3}]$

Therefore the equation becomes

$[3\times 2\times ({5})^\dfrac {1}{3}]-[4\times 4\times ({5})^\dfrac {1}{3}]=[-10\times ({5})^\dfrac {1}{3}]$

Write an equivalent fraction of $\dfrac{8}{9}$ with numerator $32$

Consider the given fraction.

$\dfrac{8}{9}$

According to the question

$=\dfrac{8}{9}\times \dfrac{4}{4}$

$=\dfrac{32}{36}$

Hence, this is the answer.

Solve $2\sqrt { 54 } -6\sqrt { \dfrac { 2 }{ 3 } } -\sqrt { 96 } =?$

$2\sqrt{54}-6\sqrt{\dfrac{2}{3}}-\sqrt{96}$

This can be written as

$\Rightarrow 2\times 3\sqrt{6}-6\sqrt{\dfrac{2}{3}}-4\sqrt {6}$

$\Rightarrow 6\sqrt {6}-6\sqrt{\dfrac{2}{3}}-4\sqrt {6}$

$\Rightarrow 2\sqrt 6-6\dfrac{\sqrt 2}{\sqrt 3}$

$\Rightarrow 2\sqrt 2\sqrt 3-6\dfrac{\sqrt 2}{\sqrt 3}$

$\Rightarrow \dfrac{2\sqrt 2\times 3-6\sqrt 2}{\sqrt 3}$

$\Rightarrow \dfrac{6\sqrt 2-6\sqrt 2}{\sqrt 3}=0$

Simlify: ${\left( {\dfrac{{625}}{{81}}} \right)^{ - 3/4}}\times\left[ {{{\left( {\dfrac{4}{{25}}} \right)}^{ - 3/2}} \div {{\left( {\dfrac{2}{3}} \right)}^{ - 3}}} \right]$

We have,

${{\left( \dfrac{625}{81} \right)}^{-\frac{3}{4}}}\times \left[ {{\left( \dfrac{4}{25} \right)}^{\frac{-3}{2}}}\div {{\left( \dfrac{2}{3} \right)}^{-3}} \right]$

$={{\left( \dfrac{81}{625} \right)}^{\frac{3}{4}}}\times \left[ {{\left( \dfrac{25}{4} \right)}^{\frac{3}{2}}}\div {{\left( \dfrac{3}{2} \right)}^{3}} \right]$

$={{\left( \dfrac{{{3}^{4}}}{{{5}^{4}}} \right)}^{\frac{3}{4}}}\times \left[ \left( \dfrac{25}{4} \right)\times \left( \dfrac{5}{2} \right)\times {{\left( \dfrac{2}{3} \right)}^{3}} \right]$

$={{\left( \dfrac{3}{5} \right)}^{3}}\times \left[ \left( \dfrac{125}{8} \right)\times {{\left( \dfrac{2}{3} \right)}^{3}} \right]$

$=\left( \dfrac{27}{125} \right)\times \left( \dfrac{125}{27} \right)$

$=1$

Hence, this is the answer.

Write the number names for the following numbers.
i) $26,04,783$
ii) $5,901,080$
iii) $70,051,900$
iv} $17,25,09,250$

$i) 26,04,783$

two million six hundred four thousand seven hundred eighty-three

$ii) 5,901,080$

five million nine hundred one thousand eighty

$iii) 70,051,900$

seventy million fifty-one thousand nine hundred

$iv} 17,25,09,250$

one hundred seventy-two million five hundred nine thousand two hundred fifty

Find: $375(a-b)^3+3$

$375(a-b)^3+3$

$=375(a^3-b^3-3ab(a-b))+3$

$=375a^3-375b^3-1125a^2b+1125ab^2+3$

Write each of the following as power of $10$ .
$\dfrac{1}{100}$

$\begin{array}{l} Now\, \, given\, \, numbers=\dfrac { 1 }{ { 100 } } =\dfrac { 1 }{ { 10 } } \times \dfrac { 1 }{ { 10 } } =0.01 \\ now\, \, solution\, \, of\, \, the\, \, number=\dfrac { 1 }{ { 100 } } { { in } }\, \, terms\, \, of\, \, power\, \, of\, \, 10 \\ ={ 10^{ -2 } } \end{array}$

Solve $\dfrac{3}{2}+\dfrac{2}{3}$

$\dfrac{3}{2}+\dfrac{2}{3}$

$L.C.M$ of

$2,3$ is

$6$

$\Rightarrow \dfrac{3}{2}+\dfrac{2}{3}=\dfrac{(3\times 3)+(2\times 2)}{3\times 2}$

$\Rightarrow \dfrac{3}{2}+\dfrac{2}{3}=\dfrac{9+4}{6}=\dfrac{13}{6}$

Therefore,

$\Rightarrow \dfrac{3}{2}+\dfrac{2}{3}=\dfrac{13}{6}$

Simplify $\cfrac { { 9 }^{ \dfrac { 1 }{ 3 } }{ 27 }^{ \dfrac { -1 }{ 2 } } }{ 3^{ \dfrac { 1 }{ 6 } }{ 3 }^{ \dfrac { -2 }{ 3 } } }$

$\displaystyle \frac{3^{\displaystyle \frac{2}{3}}*3^{\displaystyle \frac{-3}{2}}}{3^{\displaystyle \frac{1}{6}}*3^{\displaystyle \frac{-2}{3}}}=\frac{3^{\displaystyle \frac{-5}{6}}}{3^{\displaystyle \frac{-3}{6}}}=3^{\displaystyle \frac{-1}{3}}$

Find the ratio number in which in its standard form is equal to $\dfrac{4}{5}$ and the sum of its numbers and denometor is 27

Given:-

Standard form of the rational number

$= \dfrac{4}{5}$

Let the required rational number be

$\dfrac{4x}{5x}$ .

Also given that the sum of numerator and denominator is

$27$ .

Therefore,

$4x + 5x = 27$

$\Rightarrow 9x = 27$

$\Rightarrow x = \dfrac{27}{9} = 3$

$\therefore$ Required rational number

$= \dfrac{4 \times 3}{5 \times 3} = \dfrac{12}{15}$

Hence the required rational no. is

$\dfrac{12}{15}$ .

A gardener wishes to plant 8281 plants in the form of a square ad found that there were 8 plants left. How many plants ere planted in each row?

Total number of planted which are already planted is

${ 8289 }-{ 8 }={ 8281 }$

$\\ { 8281 }={ 13 }\times { 13 }\times { 7 }\times { 7 }$

Total number of plant planted in each row is

$\\ \sqrt { 8281 } =\sqrt { { 13 }^{ 2 }\times { 7 }^{ 2 } } ={ 91 }$

Write the ususal form of $100a+b+10c$ .

usual of of

$100a+10C+b=abc$

A cloth of 500 meters is sold at 35 rupees. What will be the cost of 20 meters of cloth of the same types?

$500 \rightarrow 35$

$20 \rightarrow x$

By doing cross multiplication

$x = \dfrac {20 \times 35}{500}= \dfrac {7}{5}Rs$

1241157_1153401_ans_a0fceeb456314ff498a8a7f21fd507f4.jpg

Evaluate :
$34+(5 \times 0)-34 \times 0$

Given:

$34+(5\times 0)-34\times 0$

$=34+0-0$

$=34$

Write the following number in the form $10a+b$ :
$56$

$56=50+6$

$=10(5)+6$

$=10a+b$

$a=5 , b=6$

Write opposites of the following :
$100\ \text{m}$ above sea level

The opposite to

$100\ \text{m}$ above sea level is

$100\ \text{m}$ below the sea level.

$a+6=10$ , $b+a=15$
Then find $b= ?$

$a+6=10$

$a=4$

Now,

$b+a=15$

$b+4=15$

$b=11$

Find :
$0.46 \div 10$

We have,

$0.46\div 10$

$=\dfrac{0.46}{10}$

$=0.046$

Hence, this is the answer.

$\dfrac{8m-1}{2m+3}=2$

We have,

$\dfrac{8m-1}{2m+3}=2$

$8m-1=4m+6$

$4m=7$

$m=\dfrac{7}{4}$

Hence, this is the answer.

The sum of squares of two consecutive odd whole numbers is $34$ . Find the numbers.

Let the numbers be

$a-1,a+1$

${ (a-1) }^{ 2 }+{ (a+1) }^{ 2 }=34\\ { a }^{ 2 }+1-2a+{ a }^{ 2 }+1+2a=34\\ 2{ a }^{ 2 }+2=34\\ 2{ a }^{ 2 }=32\\ { a }^{ 2 }=16\\ a=\pm 4$

$\therefore$ numbers are

$4-1,4+1$ or

$-4-1,-4+1$

$3,5$ or

$-5,-3$

What is $\dfrac{1}{9}$ of $9$ ?

$\dfrac{1}{9}$

$\times9$ =

$1$

A chair costs $Rs\ 250$ and a table costs $Rs\ 400$ . If a housewife purchased a certain number of chair and two tables of $Rs\ 2800$ , find the number of chairs she purchased.

Let the number of chairs she purchased be

$n$ .

Cost of

$1$ chair

$= Rs. 250$

Cost of

$1$ teble

$= Rs. 400$

Now according to the question-

$250 \times x + 400 \times 2 = 2800$

$250 x + 800 = 2800$

$\Rightarrow 250 x = 2800 - 800$

$\Rightarrow x = \cfrac{2000}{250} = 8$

Hence the no. of chairs she purchased is

$8$ .

Time taken to complete 500 vibration = 1 second
Find time taken to complete 1 vibration ?

Time taken to complete 1 vibration =

$\frac{1}{500}$ =0.002 second

value it:
${170^2} + 0 - 1272x = 0$

$170^2+0-1272x=0$

$1272x=28900$

$x=\dfrac{28900}{1272}=22.72$

If product of $695$ and $52AA72A$ is $3645083180$ , then find the value of $(20236565 \times A)$ .

Given

$695\times 52AA72A=3645083180$

$\implies 52AA71A=\cfrac{3645083180}{695}$

$\implies 52AA72A=5244724$

by comparing we get

$\implies A=4$

So,

$20236565\times A =20236565\times 4=80946260$

$40$ benches are required to seat $$160$$ students. How many benches will be required to seat $$240$$ students at the same rate ?

$160$ students are required to seat $=40$ benches

$1$ students are required to seat $=\dfrac{40}{160}$

Therefore,

$240$ students are required to seat

$=\dfrac{40}{160}\times 240$ benches

$=60$ benches.

Hence, this is the answer.

Make up as many expressions with numbers (no variables) as you from three numbers 5, 7 andEvery number should be used not more than once. Use only addition, subtraction and multiplication.

Solution :

using 5,8,7 we need to make expressions

Expressions can be

$5+(8+7)$

$5-(8+7)$

$5\times (8-7)$

$5+(8-7)$

$5-(8-7)$

$5\times (7-8)$

$5+(7-8)$

$5-(7-8)$

$5\times (8\times 7)$

$5+(8\times 7)$

$5-(8\times 7)$

$5\times (8+7)$

$8+(5-7)$

$8-(5+7)$

$8\times (5+7)$

$8+(7-5)$

$8-(5-7)$

$8\times (5-7)$

$8+(5\times 7)$

$8-(7-5)$

$8\times (7-5)$

$8-(5\times 7)$

$7+(8-5)$

$7-(5+8)$

$7\times (5+8)$

$7+(5-8)$

$7-(8-5)$

$7\times (8-5)$

$7+(5\times 8)$

$7-(5-8)$

$7\times (5-8)$

$7-(5\times 8)$

If the 1st January of a certain year, which was not a leap year, was a Thursday, then what day of the week was the 31st December of that year ?

The given year is a non-leap year and contains

$365$ days.

(The number of days from

$1st$ January to

$31st$ December is

$365$ )

$365 \equiv 1$

$(mod 7)$

The

$365th$ day is equivalent to the first day of the year.

But the first day of the week is Thursday.

Hence,

$31st$ December is Thursday.

How many 3-digit even numbers can be made using the digits 1, 2, 3, 4, 5, 6, 7, if no digits is repeated?

From the digits,

$1, 2, 3, 4, 5, 6, 7,$ only

$3$ digits

$(2, 4, 6)$ are possible at the unit's place.

Therefore, the unit's place can be filled in

$3$ different ways.

Ten's place can be filled in

$5$ ways.

Hundred's places can be filled in

$4$ ways.

Therefore, number of

$3$ digit even numbers =

$3\times 5\times 4 = 60$

Write whether the rational number $\frac{64}{455}$ will have a terminating decimal expansion or a non-terminating repeating decimal expansion

$\dfrac{64}{455}$ can be written as below

$\dfrac{64}{455}=\dfrac{64}{5\times{7}\times{13}}$

Clearly the denominator, 455 is not in the form of

$2^m\times5^n$ .

So the decimal expansion of

$\dfrac{64}{455}$ is non terminating repeating.

Find the unit's digit in the product $(256\ \times 27\ \times 159 \times 182)$ .

unit digit of product

$(256\times 27\times159\times182 )$

is =

$(6\times7\times9\times 2)$

$18\times42$

=756

$\therefore$ unit digit of given product is 6.

1215407_1368985_ans_826f64d38cf04e44ba820d736da67615.JPG

If $$ and $\sim$ are two operations such that $ab=a\times b+2\quad and\quad a\sim b=a+b-1$ , find $\{ (33)3\} \sim 3$ .

$\{ (3*3)*3\} \sim 3$ =

$[{11 *3}] \sim 3$ =

$35 \sim 3$ =

$35+3-1$ =

$37$

A husband and wife have five married sons and each of them have four children. How many members are there in the family ?

Total family members

$=$ Husband + Wife + Their five married sons + Each son have four children$$

$= 1+1+10+20$

$= 32$

For what possible values of x, the number 36x, i.e., $3\times 100+6\times 10+x$ is divisible by 3?

The number is

$36x$ .

For the number to be divisible by

$3, (9+x)$ must be divisible by

$3.$

Hence,

$x=0,3,6,9$

Solve $3 ^ { 0 } \times 4 ^ { 0 } \times 5 ^ { 2 }$

We have,

$3^0\times 4^0\times 5^2$

$=1\times 1\times 25$

$=25$

Hence, this is the answer.

The difference between the smallest six-digit number and the largest four digit number is

smallest number of six digits=

$100000$

Largest number of four digits=

$9999$

Difference=

$90001$

What is the difference between the place value of the
two eights in $878513$ ?

$800000-8000=792000$

Write each of the following numerals in expanded form.
$8629$

$8629=8000+600+20+9$

$=8\times{10}^{3}+6\times {10}^{2}+2\times{10}^{1}+9\times{10}^{0}$

Write each of the following numerals in expanded form.
$9470$

$9470=9000+400+70$

$=9\times{10}^{3}+4\times {10}^{2}+7\times{10}^{1}+0\times{10}^{0}$

Write each of the following numerals in expanded form.
$6054$

$6054=6000+50+4$

$=6\times{10}^{3}+0\times {10}^{2}+5\times{10}^{1}+4\times{10}^{0}$

Find the value of :
$11.6-9.847$

$11.6 - 9.847$

$=> 11.600 - 9.847$

$=> 1.753$

Simplify $\left( 5 ^ { 0 } \times 3 ^ { 0 } + 7 ^ { 0 } \times 8 ^ { 0 } \right) \times 4 ^ { 0 }$

$(5^{0}\times 3^0+7^0\times 8^0)\times 4^0\\\\(1\times 1+1\times 1)\times 1=1+1=2$

Find the value of :
$21.05-15.27$

$=21.05-15.27$

$=5.78$

Solve: $\dfrac { 9 ^ { 3 } \times a ^ { 5 } \times b ^ { 2 } } { 3 ^ { 6 } \times a ^ { 3 } \times b }$

We have,

$\dfrac{9^3\times a^5\times b^2}{3^6\times a^3\times b}$

$=\dfrac{9^3\times a^2\times b}{3^6}$

$=\dfrac{(3\times3)^3\times a^2\times b}{3^6}$

$=\dfrac{(3^2)^3\times a^2\times b}{3^6}$

$=\dfrac{3^3\times a^2\times b}{3^6}$

$=a^2b$

Hence, this is the answer.

Find the value of :
$18.5-6.79$

$=18.5-6.79$

$=11.71$

A number is divided by $8$ . The new number obtained is divided by $9$ to give $1$ . Find the number.

Let the number be

$x$

If the number is divided by

$8$ to give new number

Then the new number be

$\dfrac{x}{8}$

If the new number is divided by

$9$ to give

$1$

$\implies \dfrac{\frac{x}{8}}{9}=1$

$\implies \dfrac{x}{8}=9$

$\implies x=72$

The number is

$72$

Find HCF of $650$ and $1170$ .

Factorizing the given numbers:

$650= 2\times 5\times 5\times 13$

$1170=2\times 3\times 3\times 5\times 13$

$\mathrm{HCF}$ is the product of common numbers:

$\mathrm{HCF}=2\times 5\times 13=130$

Simplify: $\dfrac 45\times 65\div \dfrac 23$

given,

$\dfrac 45\times 65\div \dfrac 23$

$= 4\times 13\times \dfrac 32$

$=2\times 13\times 3=78$

The sum of $2$ consecutive numbers is $33$ find those numbers.

Let the numbers be

$x,x-1$

Their sum is

$x+x-1=33$

$2x-1=33$

$2x=34$

$x=17$

The numbers are

$17,16$

Find the sum:
$\dfrac{-3}{11}+\dfrac{5}{9}$

The sum of

$-\dfrac{3}{11}$ and

$\dfrac{5}{9}$ is

$-\dfrac{3}{11}+\dfrac{5}{9}$

$=-\dfrac{3\times 9}{11\times 9}+\dfrac{5\times 11}{9\times 11}$

$=-\dfrac{27}{99}+\dfrac{55}{99}$

$=\dfrac{-27+55}{99}$

$=\dfrac{28}{99}$

Solve: $56\times 4$

$56\times 4=14 \times 16=224$

Two numbers are in the ratio 5:7.Their difference isfind the numbers.

1312676_1419337_ans_82af9a6cefe64da5b75041d60b2a6c01.jpeg

If the sum of two continuous odd number is 32, Find the numbers.

1314643_1488615_ans_36f75693691646b68fbe3c5b36920eb7.JPG

Simplify: $\dfrac 12 (27)^{1/3}$

given,

$\dfrac 12 (27)^{1/3}$

$=\dfrac 12(3^3)^{1/3}$

$=\dfrac 12(3)=\dfrac 32$

Simplify :
$0.089\times 0.76\div 0.19$

$0.089\times 0.76\div 0.19=0.089\times \dfrac{0.76}{0.19}$

$=0.089\times \dfrac{0.19\times 4}{0.19}$

$=0.089\times 4$

$=0.356$

Daniel goes for painting class everyday for 35 minutes. How many hours does he learn painting in a month?

$1$ day

$\rightarrow 35$ minutes

$30$ days

$\rightarrow (35\times 30)$ minutes

$\Rightarrow 60$ min

$\rightarrow 1$ hr

$(35\times 30)$ min

$\rightarrow \dfrac{1}{60}\times 35\times 30$

$=\dfrac{35}{2}=17.5$ hr.

1205602_1448822_ans_664296aa544a4074959aa75f7e527c25.jpg

Find the whole quantity if $5$ % of it is $600$

Let the whole quantity be

$x$ in given question:

$5$ % of

$x=600$

$\Rightarrow$

$\cfrac{5}{100}\times x =600$

$\Rightarrow$

$x=\cfrac{600\times 100}{5}=12,000$

Find: $15$ % of $250$

$15$ % of

$250=\cfrac{15}{100}\times 250=15\times 2.5=37.5$

Give five examples where the number of things counted would be more than $6$ -digit number.

$1$ . The population of Chandigarh.

$2$ . Numbers of stars in the sky.

$3$ . Numbers of cars in India.

$4$ . Numbers of trees in India.

$5$ . Numbers of mobiles in India.

Find: $75$ % of $1\ \text{kg}$

$75\ \%$ of

$1\ \text{kg}=75\ \%$ of

$1000\ \text{g}=\cfrac{75}{100}\times 1000\ \text{g}=750\ \text{g}=0.750\ \text{kg}$

$10 - 5 \times 10 - 8 \times 10 6 \times ( - 1 ) 3 10 - 4 \times ( - 1 ) 8$

$\textbf{Step 1: Solving Multiplications first.}$

$10-5\times10-8\times106\times(-1)310-4\times(-1)8$

$=10-{5×10}-{8×106×(-1)×310}-{4×(-1)×8}$

$=10-50-(-262880)-(-32)$

$\textbf{Step 2: Resolving signs.}$

$10 - 5 \times 10 - 8 \times 10 6 \times ( - 1 ) 3 10 - 4 \times ( - 1 ) 8$

$= 10-50-(-262880)-(-32)$

$=10-50+262880+32$

$\mathbf{[\because (-)×(-)=(+)]}$

$\textbf{Step 3: Solving the expression from left to right.}$

$10 - 5 \times 10 - 8 \times 10 6 \times ( - 1 ) 3 10 - 4 \times ( - 1 ) 8$

$=-40+262880+32$

$=262840+32$

$=262872$

$\textbf{Hence, }\mathbf{10-5×10-8×106×\left(-1\right)310-4×\left(-1\right)8 = 262872}$

Find: $20$ % of Rs. $2500$

$20$ % percent of Rs.

$2500=\cfrac{20}{100}\times 2500=20\times 25=Rs. 500$

Find the sum:
$\cfrac{-2}{3}+0$

$\cfrac { -2 }{ 3 } +0=\cfrac { -2 }{ 3 }$

Test the divisibility of the following number by $10$ :
$57930$

we know that if the unit place digit is divisible by

$10$ i.e. the unit place is having the value

$0$ then given number is divisible by

$10$ .

Here, the unit place the given number is

$0$ which is divisible by

$10$

$\therefore$ the given number

$57930$ is divisible by

$10$ .

Test the divisibility of the following number by $10:$
$5790$

If the ones digit of a number is 0
then the given number is divisible by 10
5790
Here the ones digit is 0

505

∴ 5790∴63215 is divisible by

Write in expanded form: $574021$

$574021=5\times 100000+7\times 10000+4\times 1000+0\times 100+2\times 10+1$

Test the divisibility of the following number by $10:$
$55555$

If the ones digit of a number is

$0$ then the given number is divisible by

$10$

$55555$
Here the ones digit is

$5$

$\therefore 55555$ is not divisible by

$10$

Write in expanded form: $74836$

$74836=7\times 10000+4\times 1000+8\times 100+3\times 10+6\times 1$

Write in expanded form: $8907010$

The expanded form is

$8907010=8\times 1000000+9\times 100000+0\times 10000+7\times 1000+0\times 100+1\times 10+0\times 1$

Read and write the following number in words and also in expanded form :
$40,075$

$40,075$ in words is "Forty thousand seventy five"
Expanded form is

$4 \times 10000 + 7 \times 10 + 5 \times 1$

Read and write the following numbers in words and also in expanded form :
$35,000$ = ......

$35,000$ = Thirty five thousands

$3 \times 10000 + 5 \times 1000$

Read and write the following numbers in words and also in expanded form :
$6,23,000$ = .........

$6,23,000$ = Six lakhs twenty three thousands

$6 \times 100000 + 2 \times 10000 + 3 \times 1000$

Read and write the following numbers in words and also in expanded form :
$76,000$ = ............

$76,000$ = Seventy six thousands

$7 \times 10000 + 6 \times 1000$

Read and write the following numbers in words and also in expanded form :
$50,004$ = .............

$50,004$ = Fifty thousand four

$5 \times 10000 + 4 \times 1$

Find which of the following number are divisible by $10$ :
$8976$

The given number

$= 8976$

For a number to be divisible by

$10$ , unit’s digit must be

$0$

Here, unit digit is

$6$

Therefore,

$8976$ is not divisible by

$10$

Write the following in the decimal form.
$(6 \times 1000)+(5 \times 10)+(8 \times 1)$

$(6 \times 1000)+(5 \times 10)+(8 \times 1)$

$6000+50+8=6058$

Find which of the following number are divisible by $10$ :
$9990$

The given number

$= 9990$

For a number to be divisible by

$10$ , unit’s digit must be

$0$

Here, unit digit is

$0$

Therefore,

$9990$ is divisible by

$10$

Write the following in the decimal form.
$(1 \times 1000)+(1 \times 10)$

$(1 \times 1000)+(1 \times 10)$

$1000+10=1010$

Write the following in the decimal form.
$(7 \times 1000)+(6 \times 1)$

$(7 \times 1000)+(6 \times 1)$

$7000+6=7006$

Find which of the following number are divisible by $10$ :
$0$

The given number

$= 0$

For a number to be divisible by

$10$ , unit’s digit must be

$0$

Here, unit digit is

$0$

Therefore,

$0$ is divisible by

$10$

Write the following in the decimal form.
$(7 \times 100)+(5 \times 10)+(8 \times 1)$

$(7 \times 100)+(5 \times 10)+(8 \times 1)$

$700+50+8=758$

Write the following in the decimal form.
$(5 \times 10)+(6 \times 1)$

$(5 \times 10)+(6 \times 1)$

$50+6=56$

Find which of the following number are divisible by $10$ :
$847$

The given number

$= 847$

For a number to be divisible by

$10$ , unit’s digit must be

$0$

Here, unit digit is

$7$

Therefore,

$847$ is not divisible by

$10$

Show that every odd prime can be put either in the form $4k+1$ or $4k+3 (i.e., 4k-1),$ where k is a positive integer.

Let n be any odd prime. If we divide any n by 4, we get

$n=4k+r$
where

$0\leq r\leq 4$ i.e.,

$r=0, 1, 2, 3$

$\therefore either n=4k or n=4k+1$
or

$n=4k+2 or n=4k+3$
Clearly, 4n is never prime and

$4n+2=2(2n+1)$ cannot be prime unless

$n=0$
(since, 4 and 2 cannot be factors of an odd prime).

$\therefore$ An odd prime n is either of the form

$4k+1 or 4k+3$
But

$4k+3=4(k+1)-4+3=4{k}'-1$
(where

${k}'=k+1$ )

$\therefore$ An odd prime n is either of the form

$4k+1 or (4k+3) i.e., 4{k}'-1$

Prove that for every positive integer n, $1^{n}+8^{n}-3^{n}-6^{n}$ is divisible by 10.

Since 10 is the product of two primes 2 and 5, it will suffice to show that the given expression is divisible both by 2 and 5. To do so, we shall use the simple fact that if a and b be any positive integers, then

$a^{n}-b^{n}$ is always divisible by

$a-b$ .
Writting

$A \equiv 1^{n}+8^{n}-3^{n}-6^{n}$

$=(8^{n}-3^{n})-(6^{n}-1^{n})$
we find that

$8^{n}-3^{n}$ and

$6^{n}-1^{n}$ are both divisible by 5, and consequently A is by

$5(=8-3=6-1)$ . Again, writing

$(8^{n}-6^{n})-(3^{n}-1^{n})$ , we find that A is divisible by 2(

$=8-6=3-1$ ). Hence A is divisible by 10.

If n is an integer. Prove that $n(n+1)(n+5)$ is a multiple of 6.

$n(n+1)(n+5)=n(n+1)\left [ (n+2)+3 \right ]$

$=n(n+1)(n+2)+3n(n+1)$
Now,

$n(n+1)(n+2)$ being the product of three consecutive integers is divisible by

$3!=6$ .

$n(n+1)$ being the product of two consecutive integers is divisible by

$2!=2$

$\therefore 3n(n+1)$ is divisible by 6

$\therefore n(n+1)(n+5)$

$=n(n+1)(n+2)+3n(n+1)$ is divisible by 6
i.e.,

$n(n+1)(n+5)=M(6)$

Solve the following cryptarithm:

$3{\;}7$
$\underline {+A{\;}B}$
$\underline {9{\;}A}$

$37+AB=9A$

$numbers\quad in\quad the\quad tens\quad position\quad are\quad multiplied\quad by\quad 10\quad when\quad we\quad break\quad the\quad number$

$(30+7)+(10A+B)=90+A$

$7+B=A$

$3+A=9$

$If\quad A=6,\quad B=-1,\quad not\quad possible$

$7+B=10+A$

$3+A=8$

$i.e,\quad A=5,\quad B=8$

Find the values of the letters in the following, and give reasons for the steps involved.
${\;} A{\;}1$
$\underline {+1{\;}B}$
$\underline { B{\;}0}$

$A1+1B=B0,\quad$

$numbers\quad in\quad the\quad tens\quad position\quad are\quad multiplied\quad by\quad 10\quad when\quad we\quad break\quad the\quad number$

$(10A+1)+(10+B)=10B+0$

$1+B=0,\quad B=-1,\quad not\quad possible$

$1+B=10$

$B=9$

$(10A+1)+(10+9)=(90+0)$

$10A=70$

$A=7$

$\ \ \ \ \ \ 1\ \ A\\\underline{\ \ \ \ \times\ \ A\ \ }\\\underline{\ \ \ \ \ \ 9\ \ A\ \ }$

According to the question that when a digit

$A$ multiplies with itself then the unit digit of the answer should be

$A$ .

$1, 5$ and

$6$ are those numbers which satisfy the above condition

so put

$1, 5$ and

$6$ in place of

$A$ and check

$11 \times 1= 11$

$15\times 5= 75$

$16 \times 6 = 96$

So, the value of

$A$ is

$6$ .

Find the values of the letters in the following and give reasons for the steps involved.
$\ \ \ \ \ \ A\ \ B\\\underline{\ +\ 3\ \ 7\ \ }\\\underline{\ \ \ \ \ \ 6\ \ A\ \ }$

From the ten's place, we can say that either A has to be 2 or 3.

$A = 3$ , then the sum is not satisfied. So,

$A= 2$ .

Then,

$B = 5.$

$A = 2$ and

$B = 5$

Find the values of the letters in the following and give reasons for the steps involved.
$\ \ \ \ \ \ 4\ \ A\\\underline{\ +\ 9\ \ 8\ \ }\\\underline{\ \ C \ \ B\ \ 3\ \ }$

$A + 8 = 3$ , then A has to be 5 because unit digit of the sum has to be 3.

There is a carry-over of

$1$ .

So,

$4 + 9 + 1 = 14$

$A = 5, B = 4$ and

$C = 1$

Find the values of the letters in the following and give reasons for the steps involved.
$\ \ \ \ \ \ 3\ \ A\\\underline{\ +\ 2\ \ 5\ \ }\\ \underline{\ \ \ \ \ \ B\ \ 2\ \ }$

$A + 5$ must give

$2$ as the unit digit of the sum , then

$A$ has to be

$7$ .

$B = 3 +2+1$ (carry over)

$= 6$

$A = 7$ and

$B = 6$

Find the values of the letters in the following and give reasons for the steps involved.
$\ \ \ \ \ \ A\ \ B\\\underline{\ \ \ \ \times\ \ 3\ \ }\\\underline{\ \ C \ \ A\ \ B\ \ }$

In the given problem, if

$B \times 3$ has to end with

$B$ , then

$B$ has to be either

$0$ or

$5$ , because only

$0$ or

$5$ , when multiplied by

$3$ , will give the same number.

$B = 5$ , then there will be a carry-over, which will not give the next product as

$C\ A$ .

Thus,

$B = 0.$

Also,

$A \times 3$ ends with

$A$ , so

$A=5$ .

And

$3\times 5=15$

$\therefore \ C=1$

Hence,

$A = 5, B = 0\ and \ C = 1.$

Find the values of the letters in the following and give reasons for the steps involved.
$\ \ \ \ \ \ \ A\ \ 1\\\underline{\ +\ 1\ \ B\ \ }\\\underline{\ \ \ \ \ \ B\ \ 0\ \ }$

$1 + B = 0$ , then

$B$ has to be

$9$ .

With

$B = 9$ ,

Now, we have condition

$A + 1 + 1($ carry over

$) = B$ .

i.e.

$A+2=9$

So,

$A = 7, B = 9$

If $24x$ is a multiple of $3$ , where $x$ is a digit, what is the value of $x$ ?

Since

$24x$ is a multiple of

$3$ , its sum of digits

$6+x$ is a multiple of

$3$ ;

So,

$6+x$ is one of these numbers:

$0,\,3,\,6,\,9,\,13,\,15,\,18,\,\dots$ .

Since

$x$ is a digit, it can only be that

$6+x=6$ or

$9$ or

$12$ or

$15$ .

Therefore,

$x=0$ or

$3$ or

$6$ or

$9$ .

Thus,

$x$ can have any of four different values.

Find the values of the letters in the following and give reasons for the steps involved.
$\ \ \ \ \ \ A\ \ B\\\underline{\ \ \ \ \times\ \ 6\ \ }\\\underline{\ \ B \ \ B\ \ B\ \ }$

$B\times6$ has to end with

$B$ , then

$B$ can be

$2, 4 , 8$ or

$6$ .

But with

$B$ as

$2$ and

$6$ , the above condition is not satisfied to arrive at a value for

$A$ .

$B = 4$ , then

$A$ has to be

$7$ to give the product as

$444$ .

If we consider

$B$ to be

$8$ , then

$A$ has to be a two digit number to give the product as

$888$ .

Hence,

$B = 4$ and

$A = 7$ .

In the following, find the digits represented by the letters:
$1\ A$
$\underline {\times \ 1\ A}$
$\underline {1\ B\ A}$

In the given problem, the multiplication of

$A$ with

$A$ itself gives a number whose ones digit is

$A$ again. This happens only when

$A=1,5,6$ .

$A=1$ then the multiplication will be

$11\times 11=121$ . However, here the tens digit is given as

$B$ , therefore,

$A=1$ and

$B=2$ are possible.

Hence, the letter

$A=1$ and

$B=2$ .

No of $6$ digits no whose sum of digit is $49$

If we take

$9$ six times then its sum is

$54$ , To make it

$49$ ,

we have to subtract

$1$ from

$5$ digit.

$\therefore \,\,Number\,\,is\,\,\underline {988888}$

Find the values of the letters in the following and give reasons for the steps involved.
$\ \ \ \ \ \ 2\ \ A\ \ B\\\underline{\ +\ A\ \ B\ \ 1\ \ }\\\underline{\ \ \ \ \ \ \ B\ \ 1\ \ 8 \ \ }$

$B + 1 = 8$ , then

$B$ has to be

$7$ .

Now we have

$A + 7$ has to end with

$1$ , so it has to be

$11$ ,

$\therefore A$ has to be

$4$ .

Then,

$2 + A + 1($ carry over

$) = B$

Thus,

$A = 4, B = 7$

Find the values of the letters in the following and give reasons for the steps involved.
$\ \ \ \ \ \ 1\ \ 2\ \ A\\\underline{\ +\ 6\ \ A\ \ B\ \ }\\\underline{\ \ \ \ \ \ \ A\ \ 0\ \ 9 \ \ }$

Lets assume,

$A+B >9$

We know that

$A$ and

$B$ both can attain maximum value of

$9$ ,

If both

$A=B=9$ then we get

$18$ where unit digit is

$8$ , so its not possible to achieve unit digit as

$9$

This implies that sum must be

$= 9$

Now focusing on ten's digit,

$2+A = 0$

Here,

$A$ has to be

$8$ as there is no carry over from unit digit addition.

Now, we know that

$A=8$

$\therefore B =9 - A=9-8= 1$

Hence,

$A = 8$ and

$B = 1$ .

Find the values of the letters in the following and give reasons for the steps involved.
$\ \ \ \ \ \ A\ \ B\\\underline{\ \ \ \ \times\ \ 5\ \ }\\\underline{\ \ C \ \ A\ \ B\ \ }$

$B \times 5 = B$ , B has to be either

$5$ or

$0$ .

$B = 0$ , then A has to be 5 as

$A \times 5=A$ .

So,

$A = 5, B = 0$ and

$C = 2.$

$B = 5$ , then

$A = 2$ so that

$A \times 5$ with carry over ends with

$A$ .

Hence,

$A = 2, B = 5, C = 1.$

Write the following in the normal form:
(i) $(5\times 10) + (6\times 1)$ ;
(ii) $(7\times 100) + (5\times 100) + (8\times 1)$ ;
(iii) $(6\times 1000) + (5\times 10) + (8\times 1)$ ;
(iv) $(7\times 1000) + (6\times 1)$ ;
(v) $(1\times 1000) + (1\times 100)$

The given numbers can be written in normal form as follows:

(a)

$(5×10)+(6×1)=(50)+(6)=56$

(b)

$(7×100)+(5×10)+(8×1)=(700)+(50)+(8)=758$

(c)

$(6×1000)+(5×10)+(8×1)=(6000)+(50)+(8)=6058$

(d)

$(7×1000)+(6×1)=(7000)+(6)=7006$

(e)

$(1×1000)+(1×100)=(1000)+(100)=1100$

Write the expanded form of the number:
$- 4348$

We have,

$-4348$

$\Rightarrow -(4000+300+40+8)$ is the expanded form of

$-4348$ .

Hence, this is the answer.

Examine would this work?
Choose a number. Double it. Add nine. Add your original number. Divide by three. Add four. Subtract your original number. Your result is seven.

Let our original number be n. Then we are doing the following operations.

$n\rightarrow2n\rightarrow2n+9\rightarrow2n+9=3n+9\rightarrow\dfrac{3n+9}{3}=n+3\rightarrow n+3+4=n+7\rightarrow n+7-n=7$

Therefore whatever we take the Value of

$n$ the Result Would be

$7$

Frame and solve the equations for the following statements:
The denominator of a fraction is $2$ more than its numerator. If one is added to both the numerator and their denominator the fraction becomes $\dfrac {2}{3}$ . Find the fraction

Let the fraction be

$=\dfrac{x}{y}$

Therefore Numerator is

$x$ and Denominator is

$y$

according to the question

$y=x+2$

Now, adding

$1$ to

$x$ and

$y$

$\Rightarrow \dfrac{x+1}{y+1}=\dfrac{2}{3}$

Now, Putting

$y=x+2$

$\Rightarrow \dfrac{x+1}{x+2+1}=\dfrac{2}{3}\Rightarrow 3x+3=2x+6\Rightarrow x=3$

Since,

$y=x+2\Rightarrow y=5$

Hence, the numbers are

$3$ and

$5$ .

Explain how they work?
Write down any three-digit number(for example, $425$ ). Make a six-digit number by repeating these digits in the same order $(425425)$ . Your new number is divisible by $7, 11$ , and $13$ .

Note that

$7\times 11\times 13=1001$
Take any three digit number say,

$abc$ .

Then

$abc\times 1001=abcabc$

Therefore, the six digit number

$abcabc$ is divisible by

$7,11$ and

$13$

According to the Question

$\Rightarrow$ Let a 3 digit number be

$abc$

Now repeating it we get

$abcabc$

On Dividing

$abcabc$ by

$abc$ we get

$1001$

$\Rightarrow abc\times 1001=abcabc$

Therefore

$1001$ is factor of

$abcabc$ and

$1001=13\times 7\times 11$

Therefore

$abcabc$ is divisible by

$7,11$ and

$13$

In the following addition, A, B, C represent different digits. Find them and the sum

Here we observe that the last digit of

$A + B + C$ is C, so that

$A + B = 10$ . Since C is a digit,

$C\leq 9$ . Hence the carry from unit's place to ten's place is

$1$ .
Since we are adding only

$3$ digits, the carry in ten's place of the sum cannot exceed

$2$ . Hence

$B$ cannot be more than

$2$ . Thus we observe that

$B = 1$ or

$2$ . The addition of digits in ten's place gives (along with carry

$1$ from unit's place)

$A + B + C + 1 = 10 + C + 1$ and this must leave remainder

$A$ when divided by

$10$ .
If

$B = 1$ , then

$A = 9$ and hence

$C + 1 = 9$ giving

$C = 8$ . We get

$99 + 11 + 88 = 198$ , which is a correct answer. If

$B = 2$ , you get

$A = 8$ and

$C + 1 = 8$ giving

$C = 7$ . But then

$88 + 22 + 77 = 187$ . This does not fit in as hundred's place in the sum is

$1$ but not

$2$ .
The correct answer is

$99 + 11 + 88 = 198$ .

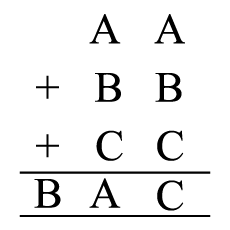
Using divisibility tests, determine which of the following numbers are divisible by $10$ :
(a) $54450$ (b) $10800$ (c) $7138965$ (d) $7016930$ (e) $10101010$

A number is

$divisible$ by

$10$ if the last digit is

$0$

So,

$54450,10800,7016930,10101010$ are divisible by

$10$ and

$7138965$ is not divisible by

$10$ .

Find the sum of all two-digit numbers which give a remainder of 3 when they are divided by 7.

The two digit number which gives a remainder of

$3$ when divided by

$7$ are:

$10, 17, 24 ..... 94$

Now, these number are in AP series with
1st Term,

$a = 10$
Number of Terms,

$n = 13$
Last term, L = 94 and
Common Difference

$d = 7$
Sum

$= {n\times \dfrac{(a+L)}{2}}$

$= 13\times 52 = 676$ .

Write the following numbers in the standard form :
$4,18,25,00,000$

given number is

$4,18,25,00,000$

there are

$9$ digits after

$4$ therefore

in standard form it is written as

$4.1825 \times 10^9$

In a four-digit number, the sum of the digits of the thousands and tens is equal to $4$ . The sum of the digits of the hundreds and the units is $15$ , and the digit of the units exceeds by $7$ the digit of the thousands. Among all the numbers satisfying these conditions, find the number the sum of the product of whose digit of the thousands by the digit of the units and the product of the digit of the hundreds by that of the tens assumes the least value.

let the number be

$abcd$ .

According to the statement:

$a+c=4$

$b+d=15$

$d-a=7$

From the equations, following conclusions can be drawn:

$a$ can be

$1,2,3,4$ from

$a+c=4$ , but a cannot be

$3$ and

$4$ from

$d-a=7$ as

$d$ exceeds

$9$ , which is not possible.

For

$a=1$ , the number is

$1738$ and for

$a=2$ the number is

$2629$

Hence, the required number is

$1738$ as we were supposed to find the least value.

Write the following numbers in the standard form :
$80,00,000$

given number is

$80,00,000$

there are 6 zeros in total therefore the standard form is

$80,00,000=8\times 10^6$

Solve: $2+2$

$\textbf{Step -1: Draw the lines for the given numbers.}$

$\text{For adding }2+2,$

$\text{Draw two lines}+\text{Draw two lines}$

$(||)+(||)$

$\textbf{Step -2: Count all the drawn lines.}$

$\text{Number of drawn lines}=4$

$\textbf{Therefore, }\mathbf{2+2=4.}$

Write the following numbers in the standard form :
$5682.026$

given number is

$5682.026$

there are

$3$ digits after

$5$ excluding the digits after decimal

in standard form it is written as

$5.682026 \times 10^3$

Write the following numbers in the standard form :
$93045.08$

given number is

$93045.08$

there are

$4$ digits after

$9$ excluding the points after decimal

in standard form it is written as

$9.304508 \times 10^4$

Write the following numbers in the standard form :
$480767$

given number is

$480767$

there are

$5$ digits after

$4$ therefore

in standard form it is written as

$4.80767 \times 10^5$

$\sqrt{2}(\sin x+\cos x)=\sqrt{3}$ . General form.

1169752_1059355_ans_15b59839c3774a18a0f828f827a2e32c.jpg

Evaluate: $\dfrac{4^2-(0.41)^2}{2.41}$

Now,

$\dfrac{4-(0.41)^2}{2.41}$

$=\dfrac{2^2-(0.41)^2}{2.41}$

$=\dfrac{(2+0.41)(2-0.41)}{2.41}$

$=\dfrac{(2.41)(1.59)}{2.41}$

$=1.59$ .

Write the following numbers in the standard form :
$855970$

given number is

$855970$

there are

$5$ digits after

$8$

in standard form it is written as

$8.55970 \times 10^5$

Solve $\dfrac { 1 }{ \sqrt { 19-\sqrt { 360 } } } -\dfrac { 1 }{ \sqrt { 21-\sqrt { 440 } } } +\dfrac { 2 }{ \sqrt { 20+\sqrt { 396 } } } =?$

Consider the first term

$\Rightarrow \dfrac{1}{\sqrt {19-\sqrt {360}}}$

On rationalizing, we get

$\Rightarrow \dfrac{\sqrt {19+\sqrt {360}}}{\sqrt {19^2-360}}=\sqrt {19+\sqrt {360}}$

$\Rightarrow \sqrt{19+\sqrt{360}}=\sqrt{19+2\sqrt{90}}=\sqrt{9+10+2\sqrt{9}\sqrt {10}}=\sqrt{(\sqrt 9+\sqrt 10)^2}=\sqrt 9+\sqrt {10}$

Now consider the second term

$\Rightarrow \dfrac{1}{\sqrt {21-\sqrt {440}}}$

On rationalizing, we get

$\Rightarrow \dfrac{\sqrt {21+\sqrt {440}}}{\sqrt {21^2-440}}=\sqrt {21+\sqrt {440}}$

$\Rightarrow \sqrt{21+\sqrt{440}}=\sqrt{21+2\sqrt{110}}=\sqrt{10+11+2\sqrt{10}\sqrt {11}}=\sqrt{(\sqrt {10}+\sqrt {11})^2}=\sqrt {10}+\sqrt {11}$

Now consider the third term

$\Rightarrow \dfrac{2}{\sqrt {20-\sqrt {396}}}$

On rationalizing, we get

$\Rightarrow \dfrac{2\sqrt {20-\sqrt {396}}}{\sqrt {20^2-396}}=\sqrt {20-\sqrt {396}}$

$\Rightarrow \sqrt{20-\sqrt{396}}=\sqrt{20-2\sqrt{99}}=\sqrt{9+11-2\sqrt{9}\sqrt {11}}=\sqrt{(\sqrt {11}-\sqrt {9})^2}=\sqrt {11}-\sqrt {9}$

Substituting these values in the given expression we get,

$\Rightarrow (\sqrt 9+\sqrt {10})-(\sqrt {10}+\sqrt {11})+(\sqrt {11}-\sqrt {9})$

$\Rightarrow 0$

Write each of the following as power of $10$ .
$100000000$

$\begin{array}{l} Now\, \, given\, \, numbers=100000000 \\ =10\times { 10^{ 3 } }\times { 10^{ 2 } }\times { 10^{ 2 } } \\ =1\times 10\times 10\times 10\times 10\times 10\times 10\times 10\times 10 \\ =1\times { 10^{ 8 } } \end{array}$

The denominator of a fraction is $3$ more than its numerator. The sum of the fraction and its reciprocal is $2 \frac{9}{10}$ . Find the fraction

Let the dfraction is $\dfrac{x}{y}$

Then, according to given question

$y=x+3\,\,\,\,.......\,\,\,\,\left( 1 \right)$

Again,

$\dfrac{x}{y}+\dfrac{y}{x}=2\dfrac{9}{10}$

$\dfrac{{{x}^{2}}+{{y}^{2}}}{xy}=\dfrac{29}{10}$

$10{{x}^{2}}+10{{y}^{2}}=29xy\,\,\,\,\,.......\,\,\,\,\left( 2 \right)$

Put the value of y in equation (2).

$10{{x}^{2}}+10{{\left( x+3 \right)}^{2}}=29x\left( x+3 \right)$

$\Rightarrow 10{{x}^{2}}+10\left( {{x}^{2}}+9+6x \right)\,=29{{x}^{2}}+87x$

$\Rightarrow 10{{x}^{2}}+10{{x}^{2}}+90+60x=29{{x}^{2}}+87x$

$\Rightarrow 20{{x}^{2}}-29{{x}^{2}}+60x-87x+90=0$

$\Rightarrow -9{{x}^{2}}-27x+90=0$

$\Rightarrow -9\left( {{x}^{2}}+3x-10 \right)=0$

$\Rightarrow {{x}^{2}}+3x-10=0$

$\Rightarrow \left( x+5 \right)\left( x-2 \right)=0\,\,\,\,\,\,\,\,\,\,\,\,by\,\,\,\,factorize$

$\Rightarrow x+5=0\,\,\,\,\,\,\,\,\,\,\,\,\,\,x-2=0$

$\Rightarrow x=-5\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x=2\,\,\,\,\,\,\,\,\,\,$

Put $x=2$ In equation (1)

$y=2+3=5$

fraction $\dfrac{x}{y}=\dfrac{2}{5}$ $ans.$

The sum of a two digit number and the number obtained by interchanging the digits of the number is $121$ . If digits of the number differ by $3$ , find the number.

$\textbf{Step-1: Assume the digits to be equal to some variables & then apply all given information's }$

$\text{Let the digit in the unit place be y and digit in the ten's place be x.}$

$\therefore$ $\text{Two digit number = 10x+y}$

$\text{According to the given question,}$

$\text{The sum of a two digit number and the number obtained by interchanging}$

$\text{the digits of the number is 121}$

$\left( 10x+y \right)+\left( 10y+x \right)=121$

$\Rightarrow 11x+11y=121$

$\Rightarrow x+y=11\,\,\,\,\,........\,\,\,\left( 1 \right)$

$\text{Again, we know that, digits of the number differ by 3}$

$x-y=3\,\,\,........\,\,\,\,\left( 2 \right)$

$\textbf{Step-2: Simplify unknown.}$

$\text{By equation (1) and (2) , we get}$

$x=7$

$\text{Put in the equation (1) and we get,}$

$7+y=11$

$y=4$

$\text{So, the number is}$

$=10\times 7+4$

$=74$

$\textbf{Hence, the number is 74.}$

Find the value of ${ x }^{ 3 }+{ y }^{ 3 }-12xy+64$ , when $x+y=-4$ .

$x^{3}+y^{3}+3xy(x+y)+64=(-4)^{3}+64=0$

Bear a two-digit number in mind.Without disclosing it, cunstruct a puzzle create two algebraic relations between the two digits of the number and solve the puzzle.

I am a number, tell my identity, three times of me, add fifty. You still need forty to have a triple century.

Let the number be

$x.$

$\begin{aligned}{}(3x + 50) + 40 &= 300\\3x &= 300 - 90\\3x &= 210\\x &= 70\end{aligned}$

Hence, this is the answer.

Find a two digit number such that product of the digits is 14 and four times the unit's digit is six less than twice the ten's digit.

Let the two digit number is $10x+y$ whose digits is $x\,\And \,y$ .

Then, According to given question,

$x\times y=14$

$y=\dfrac{14}{x}\,\,\,\,.........\,\,\,\left( 1 \right)$

Now again, according to given question,

$4\times x=2y-6$

$\Rightarrow 4x-2y+6=0\,\,\,\,........\,\,\,\left( 2 \right)$

Put the value of $y$ by equation (1) in to (2), we get,

$4x-2\times \dfrac{14}{x}+6=0$

$\Rightarrow 4{{x}^{2}}-28+6x=0$

$\Rightarrow 4{{x}^{2}}+6x-28=0$

$\Rightarrow 2{{x}^{2}}+3x-14=0$

$\Rightarrow 2{{x}^{2}}+\left( 7-4 \right)x-14=0$

$\Rightarrow 2{{x}^{2}}+7x-4x-14=0$

$\Rightarrow 2{{x}^{2}}-4x+7x-14=0$

$\Rightarrow 2x\left( x-2 \right)+7\left( x-2 \right)=0$

$\Rightarrow \left( x-2 \right)\left( 2x+7 \right)=0$

$\Rightarrow x-2=0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,2x+7=0$

$\Rightarrow x=2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x=-\dfrac{7}{2}$

Put the value of x in equation (1) and we get,

$y=\dfrac{14}{x}$

$y=\dfrac{14}{2}=7$

Then the number is

$=10x+y$

$=10\times 2+7$

$=27$

Hence, this is the answer.

Simplify: $\left\{ { \left( \cfrac { 1 }{ 5 } \right) }^{ -2 }-{ \left( \cfrac { 1 }{ 6 } \right) }^{ -2 }{ \left( \cfrac { 1 }{ 3 } \right) }^{ -2 } \right\}$

$\{(\dfrac{1}{5})^{-2}-(\dfrac{1}{6})^{-2}(\dfrac{1}{3})^{-2}\}$

$\Rightarrow \{ (5^{-1})^{-2}-(6^{-1})^{-2}(3^{-1})^{-2}\}$

$\Rightarrow \{5^2-6^23^2 \}$

$\Rightarrow \{25-36\times 9 \}$

$\Rightarrow 25-324=-299$

$\left| 200-303 \right| =?$

$\left| 200-303 \right| =\left| -103 \right| = 103$

Simplify: ${2}^{o}+{3}^{-1}+\cfrac{1}{{5}^{-1}}+{2}^{-1}$

We need to simplify

$2^0+3^{-1}+\dfrac{1}{5^{-1}}+2^{-1}$

$2^0+3^{-1}+\dfrac{1}{5^{-1}}+2^{-1}=1+\dfrac{1}{3}+\dfrac{1}{\dfrac{1}{5}}+\dfrac{1}{2}$

$=1+\dfrac{1}{3}+5+\dfrac{1}{2}$

$=6+\dfrac{1}{3}+\dfrac{1}{2}$

$=\dfrac{36+2+3}{6}$

$=\dfrac{41}{6}$

$\therefore 2^0+3^{-1}+\dfrac{1}{5^{-1}}+2^{-1}=\dfrac{41}{6}$

If $a^{3}+b^{3}=(8-3a-3b)ab$ and show that $\log{\dfrac{a+b}{2}}=\dfrac{1}{3}(\log{a}+\log{b})$

$a^{3}+b^{3}=(8-3a-3b)ab$

$a^{3}+b^{3}=8ab-3a^{2}b-3ab^{2}$

$a^{3}+b^{3}+3a^{2}b+3ab^{2}=8ab$

$\dfrac{(a+b)^{3}}{2}=\log ab$

$\log \left(\dfrac{a+b}{2}\right)=\dfrac{1}{3}\log (a+b)$

The tens digits of a two-digit number exceeds the units digit byIf the digits are reversed, the new number is less byIf the sum of their digits is 9, find the numbers.

Let the digit in the units place be

$x$

Hence the digit in the tens place is

$\left( x + 5 \right)$

The original number

$= 10 \left( x + 5 \right) + x = 11x + 50$

Number formed by reversing the digits

$= 10x + \left( x + 5 \right) = 11x + 5$

Given that:-

$\left( 11x + 50 \right) + \left( 11x + 5 \right) = 99$

$\Rightarrow 22x + 55 = 99$

$\Rightarrow 22x = 99 - 55 = 44$

$\Rightarrow x = 2$

$\therefore$ Original number

$= 11x + 50 = 11 \left( 2 \right) + 50 = 72$

Hence the original number is

$72$ .

Hence the correct answer is

$72$ .

$6$ . The number itself is equal to ten times the sum of digits. Find the number.

Let the number is

$10y+x$ where x is the unit digit and y is the ten's digit. Then by the given question,

$y=x+6$

$10y+x=10(x+y)$

$10y+x=10x+10y$

$x-10x=0\Rightarrow x=0$

$y=0+6\Rightarrow y=6$

the given number is

$10\times 6+0=60$

One fourth of a number exceeds one-sixth of its succeeding number by $5$ . Find the number.

Let the number be

$a.$

Then,

$\begin{aligned}{}\frac{a}{4} - \frac{{a + 1}}{6} &= 5\\\frac{{6a - 4\left( {a + 1} \right)}}{{24}} &= 5\\6a - 4a - 4 &= 5 \times 24\\2a& = 120 + 4\\2a& = 124\\a& = 62\end{aligned}$

Thus the required number is

$62.$

The sum of digits of a two digit number is '9' . If 45 is added to the number than the digits in the resulted number are reversed . Find the number ?

Hint ; Assume that the given two digit number be 10x+y where x is in tens digit and y is in units digits.

Step 1: Write the sum of digits of number as the first equation

$x+y = 9$

Step 2: Write second equation of addng 45 to the number

$10x+y+45 = 10y+x$

$9x - 9y = -45$

$x - y = -5$ ……(1)

$x + y = 9$ ……(2)

(1) + (2) : 2x = 4

x = 2 & y = 7

Hence the given Number is 27

$4.32$ chairs can be purchased for $Rs 4,480$ .
i) How much cost is of $45$ chairs?
ii) How many chairs can be bought with $Rs 8,400$ at the same rate?

$32$ chairs

$=4480\ Rs$

$1$ chairs

$=4480/32$

$(1)$

$45=\dfrac{4480}{32}\times 45=6300$

$(2)$ No of chairs

$=\dfrac{8400}{4480}\times 32$

$=60$

The sum of the digits of a two-digit number isThe number obtained by interchanging its digits exceeds the given number byFind the number.

$\textbf{Step - 1: Creating equations}$

$\text{Let the unit digit of the required number be b and tens digit be a}$

$\text{Hence the required number is }10a+b$

$\text{On interchanging we get }10b+a$

$\textbf{Step - 2: Solving}$

$\implies 10b+a=10a+b+18$

$\implies 9b=9a+18$

$\implies b=a+2$

$a+b=12 .....\text{(Given)}$

$a=5,b=7$

$\textbf{Thus, the required number is 57}$

Find the biggest four-digit number divisible by $5$ as well as $10$ .

The biggest

$4$ digit number to be divisible by

$5$ and

$10$ has to be divisible by

$10$

$\therefore 9990$ is the biggest

$4$ digit number divisible by both

$5$ and

$10$ .

The number of numbers between $2,000$ and $5,000$ that can be formed with the digits $0, 1, 2, 3, 4$ (repetition of digits is not allowed) and are multiple of 3 is:

1158670_1217136_ans_d369449a0caa461cb2e166b034c9f600.pdf

Simplify:
$\dfrac{m^2-n^2}{(m+n)^2}\times \dfrac{m^2+mn+n^2}{m^3-n^3}$ .

$\cfrac { m^{ 2 }-n^{ 2 } }{ (m+n)^{ 2 } } \times \cfrac { m^{ 2 }+mn+n^{ 2 } }{ (m^{ 3 }-n^{ 3 }) } =\cfrac { (m+n)(m-n) }{ (m+n)^{ 2 } } \times \cfrac { (m^{ 2 }+mn+n^{ 2 }) }{ (m-n)\times (m^{ 2 }+mn+n^{ 2 }) } \\ =\cfrac { 1 }{ m+n }$

The sum of a two digit number and the number obtained by interchanging its digits isFind the number.

Let the two digit number be 10x + y.

Number obtained on interchanging the digits = 10y + x.

The sum of a two digit number and the number obtained by interchanging its digits is 99.

10x + y + 10y + x = 99

⇒ 11x + 11y = 99

⇒ x + y = 9

With the given information, only one equation can be formed. So, the number can be 18, 81, 54, 45, 27, 72, 36, 63.

Find the value of x ; if $x = (2\times3) + 11$

$x = (2\times3) + 11$

$x = 6 + 11$

$x = 17$

Show that $3 ^ { n } \times 4 ^ { m }$ cannot end with the digit 0 or 5 for any natural numbers $'n'$ and $'m'$

S.T

$3^n\times 4^m$ cant end with

$0$ or

$5$ .

For a number to end with

$0$ , the number

must have

$2$ &

$5$ as factors.

$10=2\times 5$

$100=2^2\times 5^2$

For a number to end with

$5$ , the number must have

$5$ as a factor.

$30=5\times 6$

$3^n\times (2^2)^m=3^n\times 2^2m$

This number dosent have

$5$ or

$5$ and

$2$ as its factors. Therefore the number cant end with

$0$ o

$5$ .

The sum of a two-digit number and the number obtained by reversing its digits is $99$ and if digits differ by 3.Find the number.

We have,

Case (I)-

$\Rightarrow$

$1$ unit place

$=x$

$\Rightarrow$

$10$ unit place

$=y$

$\therefore 10y+x$

Case (II)

$10$ units place

$=x$

$1$ unit place

$=y$

$\therefore y+10x$

$10y+x+y+10x=99$

$11y+11x=99$

$11(y+x)=99\quad ---(I)$

$x+y=9$

$\therefore x-y=3\quad----(II)$

put the value

$(i)-(ii)$

$2x=12$

$\Rightarrow$

$x=6$

$\therefore$ sum of two-digit number

$36$ or

$63$

Hence this is the answer.

Find (i) the last digit ,( ii) the last two digits , and (iii) the last three digits of ${17^{256}}$ .

1293003_1269451_ans_c686448f2fea4e4dbbc1caeb82048f54.jpg

Solve:
$B + B = 2$
$B + C = 5$
$B + C \times 2 =$ ?

$B + B = 2$

$\Rightarrow 2B = 2$

$\Rightarrow B = 1$

$B + C = 5$

$\Rightarrow 1 + C = 5$

$\Rightarrow C=4$

Now,

$B + C\times 2$

$= 1+4\times 2$

$=1+8$

$=9$

Find:
$\cfrac{-6}{13}-\left( \cfrac { -7 }{ 15 } \right)$

$\cfrac { -6 }{ 13 } -\left( \cfrac { -7 }{ 15 } \right) =\cfrac { -6\times 15 }{ 13\times 15 } -\left( \cfrac { -7\times 13 }{ 15\times 13 } \right) =\cfrac { -90 }{ 195 } -\left( \cfrac { -91 }{ 195 } \right) =\cfrac { -90-(91) }{ 195 } =\cfrac { -90+91 }{ 195 } =\cfrac { 1 }{ 195 }$
L.C.M of

$13$ and

$15$ is

$195$

The digit in the tens place of a two-digit number is four times the digit in the units place. When the digits are reversed, the number obtained is $27$ less than the original numbers. Find the original number.

Let the digit's in tens place be

$x$

and digit in units place be

$y$

Hence the original number will be

$xy=10\times x+y$

Given that

$x=4y$

Then the reversed number will be

$yx=10\times y+x$

Given:

$yx=xy-27$

$10y+x=10x+y-27$

$9x=9y+27$

$x=y+3$

$4y=y+3$

$[\ \because \ x=4y\ ]$

$3y=3$

$y=1$

and

$x=4(1)=4$

$\therefore$ The original number

$=41$

The average of two numbers $'a'$ and $'b'$ is $68$ and the average of $'b'$ and $'c'$ is $70$ and that of $'a'$ and $'c'$ is $71$ . Find the values of $a,b,c$ .

Given:

$\dfrac{a+b}{2}=68$

$\Rightarrow a+b=136$ ......

$(1)$

$\dfrac{b+c}{2}=70$

$\Rightarrow b+c=140$ ......

$(2)$

$\dfrac{c+a}{2}=71$

$\Rightarrow c+a=142$ ......

$(3)$

$\Rightarrow \dfrac{a+b+b+c+c+a}{2}=68+70+71$

$\Rightarrow a+b+c=209$

$\Rightarrow a+\left(b+c\right)=209$ from

$(1)$

$\Rightarrow a+140=209$

$\therefore a=209-140=69$

$\Rightarrow a+b+c=209$

$\Rightarrow \left(a+b\right)+c=209$

$\Rightarrow 136+c=209$

$\therefore c=209-136=73$

$\Rightarrow a+c+b=209$

$\Rightarrow \left(a+c\right)+b=209$

$\Rightarrow 142+b=209$

$\therefore b=209-142=67$

$\therefore a=69,b=67,c=73$

Simplify; $\frac{{\left( { - 18\frac{1}{3} \times 2\frac{8}{{11}}} \right) - \left( {4\frac{5}{7} \times 2\frac{1}{3}} \right)}}{{\left| {\frac{3}{5} + \left( {\frac{{ - 9}}{{10}}} \right)} \right| + \left| { - \frac{{\left( { - 3} \right)}}{5}} \right|}}$

$=\frac{{\left( { - 18\frac{1}{3} \times 2\frac{8}{{11}}} \right) - \left( {4\frac{5}{7} \times 2\frac{1}{3}} \right)}}{{\left| {\frac{3}{5} + \left( {\frac{{ - 9}}{{10}}} \right)} \right| + \left| { - \frac{{\left( { - 3} \right)}}{5}} \right|}}$

$=\frac{{\left( { - \frac{55}{3} \times \frac{30}{{11}}} \right) - \left( {\frac{33}{7} \times \frac{7}{3}} \right)}}{{\left| {\frac{3}{5} + {\frac{{ - 9}}{{10}}} } \right| + \left| { \frac{{{ 3} }}{5}} \right|}}$

$=\dfrac{(-50) - (11)}{\dfrac{3}{10} + \dfrac{3}{5}}$

$=\dfrac{-61}{\dfrac{3+6}{10}}$

$=\dfrac{-61}{\dfrac{9}{10}}$

$=\dfrac{-610}{9}$

How many numbers can be formed using digits $0,1,2..........9$ which is more than or equal to $6000$ and less than $7000$ and is divisible by $5$ whereas any number can be repeated as many times?

Thousand Place must be filled with 6. $=1$

Unit place filled with either 0 or 5 because its divided by 5. $=2$

Hundredth place filled with remaining 8 digits. $=8$

Similarly, tenth place filled with 7 digits. $=7$

So, total positive integer $= 1 \times 2 \times 8 \times 7 = 112$

Solve : $\dfrac{1}{3}x+5=6$

$\frac{1}{3}x+5 = 6$

$\frac{1}{3}x = 6-5$

$\frac{1}{3}x = 1$

$x = 3$

1177622_1274966_ans_c2d388c64c7d449aa459fd859a00a6c2.jpg

The total number of numbers that can be formed with the help of digits 1, 2, 3, 4, 3, 2, 10 digit always occupy odd places is

1239339_1227429_ans_acabbb857ed942389702a38323df15c1.jpg

The sum of two consecutive multiples of $6$ is $66$ . Find these multiples.

Let the two consecutive multiples of

$6$ be

$6x$ and

$6x+6$

According to the given condition,

$6x+6x+6=66$

$12x+6=66$

$12x=60$

$x=5$

Thus required multiples are

$30$ and

$36$ .

Seven times a two number is equal to four times the number obtained by reversing the order of its digits. If the difference of the digits is $3$ , determine the number.

Let;-

$y=$ once place

$x=$ thence place

digit

$=10x+y$

$\begin{array}{l} 7\left( { 10x+y } \right) =4\left( { 10y+x } \right) \\ 70x+7y=40y+4x \\ 70x-4x=40y-7y \\ 66x=33y \\ 2x=y..............equation1 \\ x-y=3 \\ x-2x=3 \\ -x=3 \\ x=-3 \end{array}$

putting the value of

$x$ in equation

$1$

we have,

$\begin{array}{l} x-y=3 \\ -3-y=3 \\ y=-6 \end{array}$

hence

there are

$36$ digits

Write each of the following as power of $10$ .
$0.0001$

Now given numbers

$=0.0001$

$=\dfrac { { 0.0001 } }{ 1 }$

$\Rightarrow$ Now in above terms of numerator as decimal points there

are four terms and three zero.

$\Rightarrow$ Now remove decimal points and put four terms as four

zeroes after 1

$\Rightarrow \dfrac { { 0.0001 } }{ { 10000 } } =\dfrac { 1 }{ { 10,000 } } ={ 10^{ -4 } }$

Find the least number which must be added to each of the following numbers to make them a perfect square. Also find the square root's of the perfect square number so obtained.
$5678$

$\begin{array}{l} { 75^{ 2 } }<5678 \\ \Rightarrow { 76^{ 2 } }=5776 \\ \Rightarrow number\, \, to\, \, be\, \, added \\ \, \, \, \, \, \, { 76^{ 2 } }-{ 75^{ 2 } }=5776-5678\, \, \, =98 \\ \Rightarrow Therefore,\, \, the\, \, perfect\, \, square\, \, so\, \, obtained\, \, is \\ \, \, \, \, \, \, \, \, 5678+98=5776 \\ \Rightarrow Its\, \, square\, \, root\, \, =\sqrt { 5776 } =78\, \, Ans. \end{array}$

The sum of the digits of a $2-digit$ number is $9$ . The number is $6$ times the unit digit. Find the number.

Let the digit in the tens place be

$x$ and the digit in the

$y$

The number is

$10x+y$

The sum of the digits is

$9$

$x+y=9$

$\Rightarrow y=9-x$

The number is

$6$ times the units place

$10x+y=6y$

Put the two equations together

$x=9-y$ .....

$(1)$

$10x+y=6y$ .....

$(2)$

Eqn

$(2)-$ Eqn

$(1)$ we get

$10\left(9-y\right)+y=6y$

$\Rightarrow 90-10y+y=6y$

$\Rightarrow 90-9y=6y$

$\Rightarrow 15y=90$

$\Rightarrow y=\dfrac{90}{15}=6$

When

$y=6$ then

$x=9-6=3$

$\therefore$ the number

$=10x+y=10\times 3+6=30+6=36$

Write each of the following as power of $10$ .
$200000$

$\begin{array}{l} Write\, \, power\, \, od\, \, 10\, \, in\, \, terms=200000 \\ now\, \, solution\, \, are=2\times 100\times 100\times 10 \\ =2\times 10\times 10\times 10\times 10\times 10 \\ =2\times { 10^{ 5 } } \end{array}$

Raju bought a book for $Rs\ 35.65$ . He gave $Rs\ 50$ to the shopkeeper.How much money did he get from the shopkeeper?

Cost of books=

$Rs.\, 35.65$

Money given to shopkeeper=

$Rs.\, 50$

Shopkeeper gave tack money=

$\begin{array}{l} Rs.50-Rs.35.65 \\ Rs.14.35 \end{array}$

Verify that the difference of $746$ and the number obtained by reversing the order of digits is divisible by $99.$

$746-647$

$99/99=1$

Hence, it is divisible by

$99.$

The sum of a two digit number and the number by interchanging the no is $132$ if $12$ is added to number the new becomes $5$ times the sum of digit. Find the number?

Let the number be

$xy = 10x + y$

Number obtained by interchanging the digits

$= yx = 10y + x$

From the given information, we have:

$10x + y + 10y + x = 132$

$\Rightarrow 11x + 11y = 132$

$\Rightarrow x + y = 12$ ...

$(1)$

Also, we have:

$\Rightarrow 10x + y + 12 = 5\left(x + y\right)$

$\Rightarrow 10x + y + 12 - 5x - 5y = 0$

$\Rightarrow 5x - 4y + 12 = 0$ ...

$(2)$

Multiplying

$(1)$ by

$4$ , we get

$\Rightarrow 4x + 4y - 48 = 0$ ...

$(3)$

Adding

$(2)$ and

$(3)$ , we get,

$\Rightarrow 9x - 36 = 0$

$\therefore x = 4$

So,

$y = 12 - 4 = 8$

Thus, the number is

$48$ .

Show that every positive even integer is of the form $2n$ and every positive odd integer is of the form $2n+1$ .

By the definition of even number, every even number is divisble by

$2$ .

$E=2n$ where

$n \in N$ .

By the definition of odd number, every odd number is not divisble by

$2$ . The only possible remainder when divided with

$2$ is

$1$ .

Hence odd numbers can be of the form

$2n+1$ where

$n$ is the quotient when divided with

$2$ .

$O=2n+1$ where

$n \in W$

Find the sum of $1^{2}+(1^{2}+2^{2})+(1^{2}+2^{2}+3^{2})+.......$

First term

$={1}^{2}$

Second term

$={1}^{2}+{2}^{2}$

Third term

$={1}^{2}+{2}^{2}+{3}^{2}$ ...

${n}^{th}$ term

$={1}^{2}+{2}^{2}+{3}^{2}+...+{n}^{2}$

Here

${a}_{n}={1}^{2}+{2}^{2}+{3}^{2}+...+{n}^{2}$

$=\dfrac{n\left(n+1\right)\left(2n+1\right)}{6}$

$=\dfrac{2{n}^{3}+{n}^{2}+2{n}^{2}+n}{6}$

$=\dfrac{2{n}^{3}+3{n}^{2}+n}{6}$

Now, the sum of

$n$ terms is

${S}_{n}=\sum_{n=1}^{n}{{a}_{n}}$

$=\sum_{n=1}^{n}{\dfrac{2{n}^{3}+3{n}^{2}+n}{6}}$

$=\dfrac{1}{6}\left(2\sum_{n=1}^{n}{{n}^{3}}+3\sum_{n=1}^{n}{{n}^{2}}+\sum_{n=1}^{n}{n}\right)$

$=\dfrac{1}{6}\left(\dfrac{2{n}^{2}{\left(n+1\right)}^{2}}{2}+\dfrac{3n\left(n+1\right)\left(2n+1\right)}{6}+\dfrac{n\left(n+1\right)}{2}\right)$

$=\dfrac{n\left(n+1\right)}{12}\left[n\left(n+1\right)+\left(2n+1\right)+1\right]$

$=\dfrac{n\left(n+1\right)}{12}\left[{n}^{2}+n+2n+1+1\right]$

$=\dfrac{n\left(n+1\right)}{12}\left[{n}^{2}+3n+2\right]$

$=\dfrac{n\left(n+1\right)}{12}\left[{n}^{2}+2n+n+2\right]$

$=\dfrac{n\left(n+1\right)}{12}\left[\left(n+1\right)\left(n+2\right)\right]$

$=\dfrac{n{\left(n+1\right)}^{2}\left(n+2\right)}{12}$

Thus, the required sum is

$\dfrac{n{\left(n+1\right)}^{2}\left(n+2\right)}{12}$

$N=(3+1)\left( {3}^{2}+1 \right )\left( {3}^{4}+1 \right )\left( {3}^{8}+1 \right ).\left( {3}^{64}+1 \right )$ . If $N$ can be simplified as $\dfrac{\left( {3}^{n}-1 \right )}{2}$ then find the value of $n$ :

$\begin{array}{l} N=\left( { 3+1 } \right) \left( { { 3^{ 2 } }+1 } \right) \left( { { 3^{ 4 } }+1 } \right) ......\left( { { 3^{ 64 } }+1 } \right) \\ N=\frac { 1 }{ { \left( { 3-1 } \right) } } \left[ {(3^2-1) \left( { { 3^{ 2 } }+1 } \right) \left( { { 3^{ 4 } }+1 } \right) ......\left( { { 3^{ 64 } }+1 } \right) } \right] \\ =\dfrac {(3^2-1) { \left[ { \left( { { 3^{ 2 } }+1 } \right) \left( { { 3^{ 4 } }+1 } \right) ......\left( { { 3^{ 64 } }+1 } \right) } \right] } }{ 2 } \\ =\dfrac { { \left( { { 3^{ 128 } }-1 } \right) } }{ 2 } \\ Hence,\, n=128. \end{array}$

Find two numbers such that one of them exceeds the other by $18$ and their sum is $92$

1312697_1339664_ans_534511726b76420fbbcf91f5fd7b2670.jpeg

A two-digit number has tens digit greater than the unit's digit. If the sum of its digits is equal to twice the difference, how many such numbers are possible?

Let the two numbers be

$a,b$

Given,

$a>b$

$(a+b)=2(a-b)$

$\implies a=3b$

Put values of

$b$ such that

$a<10$ (otherwise it would be a 3 digit number)

$b=1,2,3$

$a=3,6,9$

So, the possible numbers are

$31,62,93$ .

Hence,

$3$ such numbers are possible.

What would be the digit in Ten-thousand's place in the sum of 96,573 and 8,379?

Sum

$=96,573+8379=1,04,952‬$

The digit in ten-thousand's place is

$0$

A two digit number is such that the product of the digits isWhen 45 is added to the number, then the digits are reversed. Find the number.

Let the tens digit be x.

Then, unit's digit =

$\dfrac{14}{x}$

Therefore, Number =

$10x+\dfrac{14}{x}$

Number formed by reversing the digits =

$10\times \dfrac{14}{x}+x$

Therefore,

$10x+\dfrac{14}{x}+45=10\times \dfrac{14}{x}+x$

$9x-\dfrac{126}{x}+45=0$

$9x^{2}+45x-126=0$

$x^{2}+5x-14=0$

$x^{2}+7x-2x-14=0$

$(x+7)(x-2)=0$

$x=2$

Therefore, Number =

$20+7=27$

Write in expanded form.
$4810$

$4810=4000+800+10+0$

$=4\times{1000}+8\times {100}+1\times{10}+0\times{1}$

Show that any positive integer is of the form 3q or, 3q+1 or,3q+2 for some integer q.

Let a be any positive integer and b=3. Applying division lemma with a and b=3, we have

a=3q+r ,where,0 is less than or equal to r and r is less than 3 and q is some integer.

a=3q+0 or,3q+1 or, 3q+2

a=3q or,a=3q+1 or, a=3q+2 for some integer q.

Write each of the following numerals in expanded form.
$5309$

$5309=5000+300+9$

$=5\times{10}^{3}+3\times {10}^{2}+0\times{10}^{1}+9\times{10}^{0}$

The least $3$ digit number divisible by $7$ is

The least

$3$ digit number is

$100$

The remainder when

$100$ id divided by

$7$ is

$2$

$5$ must be added to it to make it divisible by

$7$

So the least

$3$ digit number divisible by

$7$ is

$105$

Show that one and only out of n, n + 4, n + 8, n + 12 and n + 16 is divided by 5, where n is any positive integer.

n,n+4,n+8,n+12,n+16 be integers.
where n can take the form 5q, 5q+1 ,5q+2 , 5q + 3 , 5q + 4.
Case I when n=5q
Then n is divisible by 5.
but neither of 5q+1 ,5q+2 , 5q + 3 , 5q + 4 is divisible by 5.
Case II when n=5q+1
Then n is not divisible by 5.
n+4 = 5q+1+4 = 5q+5=5(q +1),
which is divisible by 5.(else not)
Case III when n=5q+2
Then n is not divisible by 5.
n+8 = 5q+2+8 =5q+10=5(q+2),
which is divisible by 5.(else not)
Case IV when n=5q+3
Then n is not divisible by 5.
n+12 = 5q+3+12 =5q+15=5(q+3),
which is divisible by 5.(else not)
Case V when n=5q+4
Then n is not divisible by 5.
n+16 = 5q+4+16 =5q+20=5(q+4),
which is divisible by 5.(else not)
Hence, one of n, n+4,n+8,n +12 and n+16 is divisible by 5.

The sum of two consecutive odd numbers is $68$ . Find the numbers.

1323468_1491988_ans_45906c44c00b48c4a924da1b8ad7f413.JPG

The sum of $3$ consecutive numbers is $51$ find the numbers.

Let the numbers be

$x-1,x,x+1$

The sum of numbers is

$51$

$3x=51\\$

$\implies x=17\\$

$\implies x-1=16\\$

$\implies x+1=18\\$

The numbers are

$16,17,18$

The sum of $2$ consecutive numbers is $89$ find the product of the numbers

Let the numbers be

$x,x-1$

The sum is

$89$

$x+x-1=89$

$2x-1=89$

$2x=90$

$x=45$

So the numbers are

$45,44$

The product is

$44 \times 45=1980$

If 2791A is divisible by 9, supply the missing digit in place of 'A'.

Given: $2791A$ is divisible by $9$

$⇒$ Sum of the digits of a number $2791A$ must be divisible by $9$

$$⇒ 2 + 7 + 9 + 1 + A = 19 + A $must be divisible by$ 9$$

Substitute $A$ value from $0$ to $9$ by trial-error method

We get

$A = 8$ as $27918$ is divisible by $9.$

$\Rightarrow 19 + 8 = 27$ is divisible by $9.$

Hence, $A$ is $8.$

Simplify: $(3+\sqrt{23})-\sqrt{23}$

${\textbf{Step -1: Open the bracket and simplify it.}}$

$\left( {3 + \sqrt {23} } \right) - \sqrt {23}$ $= 3 + \sqrt {23} - \sqrt {23}$

$= 3$

${\textbf{Hence, the result is 3}}{\text{.}}$

The sum of the digits of a two - digit number is $9$ . The number is $6$ times the units digit. Find the numbers.

1311377_1585985_ans_bc58350e69c04a979a995b04d91414f1.jpg

Convert part of the ratio to percentage.
$3 : 1$ .

1326798_1585312_ans_bf03434dc7064a3482dbc6a4ea78a1f0.jpg

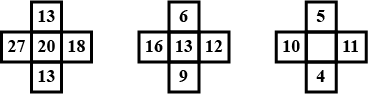
Find the missing number.

1315137_1535930_ans_2b46a26d4b4e4cf28f8c8570753ca0c8.jpeg

Simplify : $\dfrac{(25)^{3/2} \times (343)^{3/5}}{16^{5/4} \times 8^{4/3} \times 7^{3/5}}$

1327929_1566484_ans_41f9bf9537ad4d258ae196e08e7e8e20.jpeg

Find:
$\cfrac{-3}{8}-\cfrac{7}{11}$

$\cfrac { -3 }{ 8 } -\cfrac { 7 }{ 11 } =\cfrac { -3\times 11 }{ 8\times 11 } -\cfrac { 7\times 8 }{ 11\times 8 } =\cfrac { -33 }{ 88 } -\cfrac { 56 }{ 88 } =\cfrac { -33-56 }{ 88 } =\cfrac { -89 }{ 88 } =-1\cfrac { 1 }{ 88 }$
L.C.M of

$8$ and

$11$ is

$88$

The sum of the digits of a two-digit number isIf the new number formed by reversing the digits is greater than the original number by 54, find the original number.

$\textbf{Step - 1:Forming equations using the given informations.}$

$\text{Let ten's digit be }a \text{ and the one's digit be }b$

$\text{So, the number can be expressed as }10a+b$

$\text{The sum of the digits is 12}$

$\Rightarrow a+b=12$

$\Rightarrow b=12-a......(1)$

$\textbf{Step - 2:Reversing the number}$

$\text{The number that we get after reversing the digits is : }$

$10b+a$

$\text{ATQ, }$

$\Rightarrow (10b+a)=(10a+b)+54$

$\Rightarrow 9b-9a=54$

$\Rightarrow b-a=6$

$\Rightarrow 12-a-a=6$

$\textbf{[From (1)]}$

$\Rightarrow -2a=-6$

$\Rightarrow a=3$

$\text{Putting the value of a in eq(1)}$

$\Rightarrow b=12-3$

$\Rightarrow b=9$

$\text{So, required number = }10a+b=39$

$\textbf{Hence, the required number is 39.}$

How many different eight digit binary sequences are there with six 1's and two 0's.

1314174_1535649_ans_b9477e13058d418a9fbceed9c70ee61d.jpeg

Find: $1$ % of $1$ hour.

$1$ % of

$1$ hours

$=1$ % of

$60$ minutes

$=1$ % of

$(60\times 60)$ seconds

$=\cfrac{1}{100}\times 60\times 60=6\times 6=36$ seconds.

Read and expand the numbers wherever there are blanks.
Number Number Name Expansion
20000 twenty thousand $2 \times 10000$
26000 twenty six thousand $2 \times 10000 + 6 \times 1000$
38400 thirty eight thousand four hundred $3\times 10000 + 8 \times 1000 + 4 \times 100$
65740 sixty five thousand seven hundred forty $6\times 10000+5 \times 1000 + 7\times 100 + 4\times 10$
89324 eighty nine thousand three hundred twenty four $8\times 10000 + 9 \times 1000 + 3 \times 100+ 2 \times 10 + 4 \times 1$
50000 ----- ----
41000 ---- ----
47300 ---- ----
57630 ---- ----
29485 ---- ----
29085 ---- ----
20085 ---- ----
Write five more 5-digit numbers, read them and expand them.

$50000$ --- fifty thousand ---

$5\times 10000$

$41000$ --- forty one thousand ---

$4\times 10000+1\times 1000$

$47300$ --- forty seven thousand three hundred ----

$4\times 10000+7\times 1000+3\times 100$

$57630$ --- fifty seven thousand six hundred thirty ----

$5\times 10000+7\times 1000+6\times 100+3\times 10$

$29485$ --- twenty nine thousand four hundred eighty five ----

$2\times 10000+9\times 1000+4\times 100+8\times 10+5\times 1$

$29085$ --- twenty nine thousand eighty five ---

$2\times 10000+9\times 1000+8\times 10+5\times 1$

$20085$ - twenty thousand eighty five ----

$2\times 10000+8\times 10+5\times 1$

Rs. 9,000 were divided equally among a certain number of persons . Had there been 20 more persons each would have got Rs.160 less. Find the original number of persons.

Let the original no. of persons be x, then

9000 divided equally between x persons, each one get

$\dfrac {9000} {x}$

9000 divided equally between

$(x + 20)$ persons, each one get

$\dfrac {9000} {(x + 20)}$

According to the que,

$\dfrac {9000} {(x + 20)} = \dfrac {9000} {x} - 160\\ \implies 9000x = (x+20)(9000 - 160x) \\ \implies 9000x = 9000x - 160x^2 + 180000 - 3200x\\ \implies160x^2 + 3200x - 180000 = 0\\ \implies x^2 + 20x - 1125 = 0\\ \implies x^2 + 45x - 25x - 1125 = 0\\ \implies x(x + 45) - 25(x + 45) = 0\\ \implies (x + 45)(x - 25) = 0$

Either

$(x + 45) = 0$ or

$( x - 25) = 0$

$(x + 45) = 0 = x = - 45$ (not possible)

Therefore,

$(x - 25) = 0 => x = 25.$ ans

If $\sqrt {2} = 1.414, \sqrt {3} = 1.732$ , then find the value of $\dfrac {4}{3\sqrt {3} - 2\sqrt {2}} + \dfrac {3}{3\sqrt {3} + 2\sqrt {2}}$ .

We have

$\dfrac {4}{3\sqrt {3} - 2\sqrt {2}} + \dfrac {3}{3\sqrt {3} + 2\sqrt {2}}$ .

$= \dfrac {4(\sqrt {3} + 2\sqrt {2}) + 3(3\sqrt {3} - 2\sqrt {2})}{(3\sqrt {3} - 2\sqrt {2})(3\sqrt {3} + 2\sqrt {2})}\\$

$= \dfrac {12\sqrt {3} + 8\sqrt {2} + 9\sqrt {3} - 6\sqrt {2}}{(3\sqrt {3})^{2} - (2\sqrt {2})^{2}} = \dfrac {21\sqrt {3} + 2\sqrt {2}}{27 - 8}\\$

$= \dfrac {21\sqrt {3} + 2\sqrt {2}}{19} = \dfrac {21(1.732) +2(1.414)}{19}\\$

$= \dfrac {36.372 + 2.828}{19} = 2.063$ .

Find the sum:
$\cfrac { 5 }{ 4 } +\left( \cfrac { -11 }{ 4 } \right)$

$\cfrac { 5 }{ 4 } +\left( \cfrac { -11 }{ 4 } \right) \quad =\cfrac { 5-11 }{ 4 } =\cfrac { -6 }{ 4 } =\cfrac { -3 }{ 2 }$

Find the sum : $\displaystyle \frac{-9}{10}+\frac{22}{15}$

Given,

$-\dfrac{9}{10}+\dfrac{22}{15}$

$=-\dfrac{9\times 3}{10\times 3}+\dfrac{22\times 2}{15\times 2}$

$=-\dfrac{27}{30}+\dfrac{44}{30}$

$=\dfrac{-27+44}{30}$

$=\dfrac{17}{30}$

Simplify $8\sqrt[3]{216}-7\sqrt[5]{243}\sqrt[4]{4096}-6\sqrt[6]{64}$

Given,

$8\sqrt[3]{216}-7\sqrt[5]{243}\sqrt[4]{4096}-6\sqrt[6]{64}=8\sqrt[3]{6^3}-7\sqrt[5]{3^5}\sqrt[4]{8^4}-6\sqrt[6]{2^6}$

$=8(6^3)^{1/3}-7\times (3^5)^{1/5}\times (8^4)^{1/4}-6\times (2^6)^{1/6}$

$=8\times 6^{3\times \frac{1}{3}}-7\times 3^{5\times \frac{1}{5}}\times 8^{4\times \frac{1}{4}}-6\times 2^{6\times \frac{1}{6}}$

$=8\times 6-7\times 3\times 8-6\times 2$

$=48-168-12$

$=-132$

Write each of the following as an equation in two variables x and y :
(i) x=-3
(ii) y=4
(iii) 3x=2
(iv) 7y=3

1308209_1609014_ans_93a9435b4ddb4f998538ac19c452f708.jpg

Determine the difference between the place value and the face value of $5$ in $78654321$ .

$78654321$

$\Rightarrow$ Place value

$\rightarrow '5'$ is place at

$10,000$ place

$5\times 10,000=50,000$

$\Rightarrow$ Face value

$\rightarrow$ The face value of

$5$ is same.

$'5'$

Difference

$\Rightarrow$

$50,000$

$5$

$\overline{49,995}$

$\Rightarrow 49,995$

Fill in the blank:
$1$ crore $=$ _________ ten.

1502530_1658395_ans_5ddabad0e3244d9fb9895f5e23615c2f.jpg

Write the corresponding numeral for the following.
$8\times 1000000+3\times 1000+6\times 1$ .

$8 \times 1000000 + 3 \times 1000 + 6 \times 1$

$8000000 + 3000 + 6$

$\Rightarrow 8000000$

$3000$

$\underline{\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,6\,\,\,\,\,}$

$80,03,006$

$\Rightarrow 80,03,006$

How many $8$ -digit numbers are there in all?

Greatest 8- digit number =9,99,99,999

Smallest 8- digit number =1,00,00,000

Total 8-digit numbers = (Greatest 8-digit)-(Smallest 8-digit)+1

Total 8-digit numbers =(9,99,99,999)-(1,00,00,000)+1

Total 8-digit numbers =9,00,00,000

How many four-digit numbers are there in all?

Four digit numbers range from

$1000$ to

$9999$

So, total number of

$4$ digit numbers

$=(9999-1000)+1$

$=9000$

Simplify the following.
$(13+7)\times (9-4)-18$ .

$(13+7)×(9−4)−18\\=20\times5-18\\=100-18\\=82$

Write the given statement using numbers, literals and signs of basic operations.
$7$ taken away from x.

We know that the word 'taken away' means 'subtraction'

so,

$7$ taken away from

$x$ =

$x$ -

$7$ .

Write the given statement using number, literals and signs of basic operations.
Number y less than a number $7$ .

We know that the word 'less than' represents 'subtraction'

so,

Number

$y$ less than a number

$7$ = subtracting

$y$ from

$7$

$7$ -

$y$

Fill in the blank.
$1$ billion $=$ _____ million.

1507679_1660210_ans_73245ce9c12c45a9ae23cb115c63405c.jpg

Write the given statement using numbers, literals and signs of basic operations.
$2$ less than the quotient of $x$ and $y$ .

We know that the word 'quotient' means 'division'. the word 'less than' a certain quantity means 'subtracting' from the quantity.

so,

The quotient of

$x$ and

$y$ =

$\dfrac{x}{y}$

Thus,

2 less than the quotient of

$x$ and

$y$ =

$\dfrac{x}{y}-2$

Write the given statement using numbers, literals and signs of basic operations.
$4$ times $x$ taken away from one-third of $y$ .

We know that, the word 'taken away' means subtraction.

one third of

$y = \dfrac{1}{3}\times y$

$= \dfrac{y}{3}$

4 times

$x = 4\times x$

$= 4x$

So,

$4$ times

$x$ taken away from one-third of

$y = \dfrac{y}{3} - 4x$

Write the following numbers in expanded form:
$6,06,06,006$

The expanded form of the given number,

$6,06,06,006 = (6 \times 10000000) + (6 \times 100000) + (6 \times 1000) + (6 \times 1)$

Test the divisibility of the following number by $10:$
$63215$

If the ones digit of a number is

$0$ then the given number is divisible by

$10$

$63215$
Here the ones digit is

$5$

$\therefore 63215$ is not divisible by

$10$

Find the number which when divided by $38$ gives the quotient $23$ and remainder $17.$

smallest 5 digit number

$= 10000$
On dividing

$10000$ by

$254,$ we get
Remainder = 94
So

$254 - 94 = 160$ should be added to

$10000$ to get the smallest 5 digit number divisible by

$254.$

$\therefore 10000 + 160 = 10160$

Write the following number in expanded form:
$5032109$

Expanded form:

$5032109 = 5000000 + 30000 + 2000 + 100 + 9$

Find the difference between the number $895$ and that obtained on reversing its digits.

First number

$= 895$
Reversed number

$= 598$
difference

$=895-598=297$

Write the following number in expanded form:
$750687$

Expanded form:

$750687 = 700000 + 50000 + 600 + 80 + 7$

$= 7\times 100000 + 5\times10000 +0\times1000+ 6\times100 + 8\times10 + 7\times1$

$\dfrac { \begin{matrix} A & B \\ \times & 6 \end{matrix} }{ \begin{matrix} C & 6 & 8 \end{matrix} }$

$6\times B$ is a number with unit digit

$8$
Therefore,

$B=3$ or

$8$
For

$B=3$ equation

$A\times 6+1=C6$ is not satisfied.
For

$B=8$ equation

$A\times 6+4=C6$ is satisfied.
Hence,

$A=7$ and

$B=8$

$C=4$ .

Fill in the blanks to make the statements true.
By reversing the order of digits of the greatest number made by five different non-zero digits, the new number is the ______ number of five digits.

Let us consider the digits

$1, 3, 5, 7$ and

$9$ .

As,

$9 > 7 > 5 > 3 > 1$ , greatest number which can be formed using these digits is

$97531$ .

L	TH	H	T	O
$9$	$7$	$5$	$3$	$1$

On reversing the digits in the number

$97531$ , we get

$13579$ .

L	TH	H	T	O
$1$	$3$	$5$	$7$	$9$

Clearly the digits are in ascending order now

So the number formed is the smallest

$5$ digit number that can be formed by using these digits.

$\textbf{Hence, the resulting number will be the smallest}$ .

If a number has ____ in one's place, then it is divisible by $10$ .

If a number has zero in one's place, then it is divisible by

$10$ .

Observe the following patterns and fill in the blanks to make the statements true:
7 4 = 28
7 3 = ___ = 28 7
7 2 = = _ 7
7 1 = 7 = _ 7
7 0 = _ = _
7 1 = 7 = _ _
7 2 = _ = _ _
7 3 = _ = _ ______

7 4 = 28
7 3 = _21_ = 28 7
7 2 = __14 __ = _21_ 7
7 1 = 7 = _14_ 7
7 0 = _0_ = _7_ _7_
7 1 = 7 = _0_ _7_
7 2 = _14_ = _7_ _7_
7 3 = _ 21_ = _14_ _7_

If $\frac { \begin{matrix} 1 & P \\ \times & P \end{matrix} }{ Q\ \ \ \ 6 }$ where $Q-P=3$ , find the values of $P$ and $Q$ .

Gives,

$Q-P=3$
From the question,
Therefore,

$P=4$ or

$6$
If,

$P=4, Q=5$ not suitable for the question
Hence,

$P=6$ and

$Q=9$ .

If $AB+7C=102$ , where $B\neq 0, C\neq 0$ and $A+B+C=14$ , then find $A,B\ and\ C$

True
From the equation,

$B+C=2$ or a two-digit number with unit digit

$2$ and less than

$14$ .
Therefore,

$B=1, 5, 7$ and

$C=1, 5, 7$

$B=1$ and

$C=1$ is not suitable for equation.
Hence, For

$B=5, C=7$ and

$A=2$
For

$B=7, C=5$ and

$A=2$

$\dfrac { \begin{matrix} B & 6 \\ +8 & A \end{matrix} }{ C\ A\ 2}$

From the

$1' s$ column

$6+A=12\Rightarrow A+6$
From the

$10's$ column

$CA=B+8+1$

$C6=B+9$
From the above equation,

$B+9$ is a number with unit digit

$6$

$B=7$

$C=1$
Hence

$A=6, B=7$ and

$C=1$

$\dfrac { \begin{matrix} C & BA \\ +C & BA \end{matrix} }{ 1A\ 30}$

From the

$1' s$ column

$A+A=0\Rightarrow A=0$ or

$5$
From the

$10's$ column

$B+B+1=3$

$B=1,6$
From the

$100's$ column.

$C+C+1=1A$

$A=0$ is not satisfy the condition of

$10's$ column.
Therefore

$A=5$

$C+C=15-1\Rightarrow C=7$

$B=1$ is not satisfy the condition of

$10's$ column.
Therefore,

$B=6$
Hence,

$A=5, B=6$ and

$C=7$

If $1AB+CCA=697$ and there is no carry-over in addition, find the value of $A+B+C$ .

$1+C=6$

$C=5$

$A+C=9\Rightarrow A=4$
Now,

$B+A=7$
Hence

$A+B+C=12$

$\dfrac { \begin{matrix} 1 & B\ \ A \\ +A & B \ \ A \end{matrix} }{8\ \ \ \ B\ \ \ 2 }$

From the

$1' s$ column

$A+A=12\Rightarrow A=6$
From the

$10's$ column

$B+B+1=B$
The above condition is fulfil when

$B=9$
From the

$100's$ column.

$A+1+1=8$

$A=6=$ Satisfy

$1's$ column value.
Hence

$A=6, B=9$ .

$\dfrac { \begin{matrix} B & AA \\ +B & AA \end{matrix} }{ 3\ A\ 8 }$

From the

$1' s$ column

$A+A=8\Rightarrow A=4,9$ (because

$A+A$ is not a single digit number, otherwise B+B can not be 3)

From the

$100's$ column

$B+B+1=3$

$B=1$
Hence,

$A=9$ and

$B=1$

$\dfrac { \begin{matrix} A & B \\ \times & B \end{matrix} }{ C\ A\ B }$

$AB\times B=$ three digit number, that has unit digit

$B$

Therefore

$A$ can be

$2-9$ , As

$10\times 9=90$ which is two digit

$B$ is a unit place digit such that its square has same unit place

So, possibilities of

$B$ are

$0,1,5,6$

But

$0$ and

$1$ are neglected because they cannot give three digit number when multiplied by

$2$ digit number.

So,

$B=5\ or\ 6$

$B=5$ then

$2$ will be added in

$A\times B$ to get

$CA$ and If

$B=6$ then

$3$ will be added in

$A\times B$ to get

$CA$

So, for

$B=5$ , product

$A\times B$ will produce unit place

$0$ and

$5$ and adding

$2$ to it will give unit place

$2$ and

$7$ that means

$A=2\ or\ 7$

So, for

$25\times5=125$ which follows and for

$75\times5=375$ which also follows this condition.

Now, when

$B=6$ product

$A\times B$ will produce unit place

$6,2,8,4$ and

$0$ and adding

$3$ to it will give unit place

$9,5,1,7$ and

$3$ that means

$A=9,5,1,7\ or\ 3$

So, for

$96\times6=576$ which does not follows

For

$56\times6=336$ which also does not follows this condition.

For

$16\times6=96$ which also does not follows this condition.

For

$76\times6=456$ which also does not follows this condition.

For

$36\times6=216$ which also does not follows this condition.

So,

$A=2,B=5$ and

$A=7,B=5$ follows given product.

hence,

$A=25,B=5,C=1$ or

$A=7,B=5,C=3$

Find the value of the letters in each of the following questions.
$\dfrac { \begin{matrix} A & A \\ +A & A \end{matrix} }{ XA\ Z }$

From the

$1' s$ column

$A=0$ to

$9$
From the

$10's$ column

$A=5$ to

$9$ (The

$A+A$ is two digit number)

$A=5$ to

$8$ is not satisfy the

$10's$ column
Hence

$A=9$ and then

$Z=8$ and

$X=1$ .

Let $D=3, L=7$ and $A=8$ . Find the other digits in the sum
$\dfrac { \begin{matrix} M & A & D \\ + & A & S \\ + & & A \end{matrix} }{ \begin{matrix} B & U & L & L \end{matrix} }$

From

$1's$ column

$3+S+8=11+S$ is a two digit number with unit digit is

$7$

Therefore,

$S=6$

And

$1$ is carry over.

So, from

$10's$ column

$2A+1=16+1=17$ which confirms

$L=7$

and carry over

$1$

From

$100's$ column,

$M+1$ is a

$2$ digit number and

$M$ is single digit number.

So, only possible value of

$M=9$

Now,

$M+1=9+1=10\\\Rightarrow B=1, U=0$

Hence

$S=6, M=9, B=1$ and

$U=0$

$\dfrac { \begin{matrix} PQ \\ \times \ 6 \end{matrix} }{ QQQ }$

Find $P,Q$

$\dfrac { \begin{matrix} PQ \\ \times \ 6 \end{matrix} }{ QQQ }$

From the first column

$Q$ is a unit place digit such that product

$Q\times 6$ also has unit place digit

$Q$

For

$Q=2$ carry over is

$1$

$P\times6+1=22\\\Rightarrow P\times6=21$

So, not possible.

For

$Q=4$ carry over is

$2$

$P\times6+2=44\\\Rightarrow P\times6=42\\\Rightarrow P=7$

For

$Q=6$ carry over is

$3$

$P\times6+3=66\\\Rightarrow P\times6=63$

So, not possible.

For

$Q=8$ carry over is

$4$

$P\times6+4=48\\\Rightarrow P\times6=44$

So, not possible.

So, only one pair of

$P$ and

$Q$ is possible that is

$P=7,Q=4$

Work out following multiplication,
$\dfrac { \begin{matrix} 123456789 \\ \times \ 9 \end{matrix} }{ }$
Use the result to answer the following questions.
What will be $123456789 \times 63$ ?

$\dfrac { \begin{matrix} 123456789 \\ \times \ 9 \end{matrix} }{ 1111111101 }$

So,

$123456789\times63=123456789\times9\times7$

$=1111111101\times7=7777777707$

So,

$\dfrac { \begin{matrix} 123456789 \\ \times \ 63\end{matrix} }{ 7777777707 }$

$\dfrac { \begin{matrix} 8 & A & B & C \\ -A & B & C & 5 \end{matrix} }{ \begin{matrix} D & 4 & 8 & 8 \end{matrix} }$

The ones column

$=C-5=8$

We know,

$13-5=8$ therefore

$C=3$

And also

$1$ is carried from

$B$ in tens column.

So, In the ten's column

$(B-1)-C=8$

$\Rightarrow \ B=8+C+1$

$\Rightarrow \ B=8+3+1$

$\Rightarrow \ B=12$

Therefore

$B=2$

That means

$1$ was carried from

$A$ in hundred's column.

In the hundred's column

$(A-1)-B=4$

$\Rightarrow \ A=4+B+1$

$\Rightarrow \ A=4+2+1=7$

In the thousand's column

$8-A=D$

$\Rightarrow \ 8-7=D$

$\Rightarrow \ D=1$

Thus,

$A=7, B=2, C=3$ and

$D=1$

A three digit number $3$ a $7$ is added to the number $212$ to give a three digit number $5b9$ which is divisible by $9$ . Find the value of $a,b$ .

$\dfrac { \begin{matrix} 3 & a & 7 \\ +2 & 1 & 2 \end{matrix} }{ \begin{matrix} 5 & b & 9 \end{matrix} }$

It is given that

$5b9$ is divisible by

$9$

For, divisibility by

$9$ sum of digits ,st be divisible by

$9$

So,

$5+b+9=14+b$ is divisible by

$9$

So,

$14+b=18$ , because for

$27$

$b$ has to be double digit which is not possible

Hence

$14+b=18$

$\Rightarrow b=4$

From

$ones$ column.

$7+2=9$

So, no carry over

From

$10's$ Column.

$a+1=b$

$\Rightarrow a+1=4$

$\Rightarrow a=3$

So,

$a=3,b=4$

If $2A7\div A=33$ , then findthe value of $A$ .

$\text{Number = unit place +10 x tens place + 100 x hundred'd place+ and so on}$

WRiting given number in this form,

$\cfrac {200+10A+7}{A}=33$

$200+10A+7=33A$

$207=23A$

$\Rightarrow A=\cfrac {207}{23}=9$

If from a two digits number, we subtract the number formed reversing its digits then the result so obtained is a perfect cube. How many such numbers are possible?
Write all of them.

let

$ab$ is a two digit number.

Then reversing number is

$ba$

$ab-ba=(10a+b)-(10b+a)$

$ab-ba=9(a-b)$

$ab-ba$ is perfect cube number and multiple of

$9$

So, perfect cube can be

$27$ , therefore,

$a-b=3$

For, bigger perfect cubes

$a-b$ is two or three digit numbers which is not possible.

In above equation,

$b=0$ to

$6$ , for

$b>6$ ,

$a$ becomes double digit number.

For

$b=0, a=3$ and number is

$30$

For

$b=1, a=4$ and number is

$41$

For

$b=2, a=5$ and number is

$52$

For

$b=3, a=6$ and number is

$63$

For

$b=4, a=7$ and number is

$74$

For

$b=5, a=8$ and number is

$85$

For

$b=6, a=9$ and number is

$96$

So, these are possible numbers.

Let $E=3, B=7$ and $A=4$ . Find the other digits in the sum
$\dfrac { \begin{matrix} B & A & S & E \\ +B & A & L & L \end{matrix} }{ \begin{matrix} G & A&M & E & S \end{matrix} }$

From

$1's$ column

$3+L=S$

$\Rightarrow S-L=3 ....(1)$

From

$10's$ column

$S+L=3 ....(2)$

Solving equation

$(1)$ and

$(2)$

$S=3$ and

$L=0$

From

$100's$ column

$4+4=M$

$\Rightarrow M=8$

From

$1000's$ column

$7+7=G4$

$\Rightarrow 14=G4$

$\Rightarrow G=1$

Hence,

$S=3,L=0, M=8$ and

$G=1$

$\dfrac { \begin{matrix} A & B \\ -B & 7 \end{matrix} }{ 4\ 5 }$

In the ones column

$=B-7=5$

As,

$12-7=5$ So,

$B=2$

and

$1$ is carried over from

$A$ ,

So, now

$(A-1)-B=4$

$\Rightarrow A-1-2=4$

$\Rightarrow A=7$

Hence,

$A=7,B=2$ and

$72-27=45$

$\dfrac { \begin{matrix} 2 & L & M \\ +L & M & 1 \end{matrix} }{ \begin{matrix} M & 1 & 8 \end{matrix} }$

From ones column

$M+1=8$

Therefore,

$M=7$

and no carry over

So, from tens column

$L+M=1$ number with unit digit

$1$

Therefore,

$L+7=1$

Hence

$L=4$ and carry over is

$1$

So, in third column it confirms that

$(2+1)+4=7$

Hence,

$M=7,L=4$

If $\begin{matrix} A & B \\ \times & B \\ 9 & 6 \end{matrix}$ then then $A=$ and $B=$

From the question,

$B\times B=6$

Therefore, the value of

$B$ is

$4$ or

$6$

For

$B=4$

$B\times B=16$

Carry over is

$1$

$\Rightarrow A\times B+1=9$

$\Rightarrow 4A=8$

$\Rightarrow A=2$

Hence,

$A=2$ and

$B=4$

And For

$B=6$

$B\times B=36$

Carry over is

$3$

$\Rightarrow A\times B+3=9$

$\Rightarrow 6A=6$

$\Rightarrow A=1$

Hence,

$A=1$ and

$B=6$

So, possible values are

$A=1,B=6$ and

$A=2,B=4$

Write the quotient, when the sum of a $2-$ digit number $34$ and number obtained by reversing the digits is divided by
$(i) 11$
$(ii)$ sum of digits

Sum of two-digit number

$34$ and the number
obtained by reversing the digit

$43 = 34 + 43$

$=77$

$(i) 77 \div 11=7$

$(ii) 77 \div$ (Sum of digit)=

$77 \div (4+3)$

$= 77 \div 7$

$=11$

The difference of a two- digit number and the number obtained by reversing is digit is always divisible by ________ .

Lets

$xy$ is a two digit number.

From the question, we have to check for

$xy-yx$

$xy-yx=(10x+y)-(10y+x)=9x-9y=9(x+y)$

Which is always divisible by

$9$ .

Hence the difference of a two digit number and the number obtained by reversing the digit is always divisible by

$9$ .

The sum of a two digit number and the number obtained by reversing the digits is always divisible by _________ .

Lets

$xy$ is a two digit number.

From the question, we have to check for

$xy+yx$

$xy+yx=10x+y+10y+x=11x+11y=11(x+y)$

So, this number is always divisible by

$11$

Hence the sum of a two digit number and the number obtained by reversing the digit is always divisible by

$11$ .

If a $3-$ digit number $abc$ is divisible by $11$ , then _____ is either $0$ or multiple of $11$ .

A number is divisible by

$11$ if the difference between the sum of its digit at even place and sum of its digit at odd place is

$0$ or multiple of

$11$ .

So,

$a+c-b=0,11,22,..$

Hence, if a

$3-$ digit number

$abc$ is divisible by

$11$ , then

$(a+c)-b$ is either

$0$ or multiple of

$11$ .

Write the quotient when the difference of a 2-digit number 73 and number obtained by reversing the digits is divided by
$(i) 9$
$(ii)$ a difference of digits.

Given:
Difference of two digit number

$73$ and the number
obtained by reversing the digits is

$= 73 – 37 = 36$
(i) divide by

$9$
So,

$36 \div 9 = 4$
(ii) a difference of digits.

$36 \div (7 – 3) = 36 + 4$

$= 9$

If $\begin{matrix} 2 & B \\ +A & B \\ 8 & A \end{matrix}$ then then $A=$ and $B=$ .

From the question

$2B=A$ ,

So, there are two cases

Case

$1:$

$B<5$

In this case

$2B$ will be less than

$10$ ,

and there will be no carry over.

So, simply

$2+A=8$

$\Rightarrow A=6$

$\Rightarrow B=\cfrac{A}2=\cfrac62=3$

So,

$A=6,B=3$ is one result.

Now,

Case

$2:$

$10>B\geq5$

In this case

$2B$ will be greater than or equal than

$10$ and less than

$20$

So, there will be

$1$ carry over.

So, simply

$1+2+A=8$

$\Rightarrow A=5$

But

$A=2B$ , so

$A$ must be even.

So, case

$2$ is not possible

Hence, we have only one result that is

$A=6,B=3$

If $\begin{matrix} B & 1 \\ \times & B \\ 4 & 9B \end{matrix}$ then $B=$ ______

From the question,

$B\times 1=B$

So, no carry over as it was multiplies by

$1$ so

$B$ is single digit number.

Now,

$B\times B=49$

Hence

$B=7$

In a $3-$ digit number, units digit, tens digit and hundreds digit are in the ratio $1 : 2 : 3.$ If the difference of original number and the number obtained by reversing the digits is $594,$ find the number.

Given:
Ratio in the digits of a three digit number =

$1 : 2 : 3$
Let us consider unit digit be

$‘x’$
Tens digit be

$‘2x’$
and hundreds digit be

$‘3x’$
So the number is

$x + 10 \times 2x + 100 × 3x$

$= x + 20x + 300x$

$= 321x$
By reversing the digits,
Unit digit be

$‘3x’$
Ten’s digit be

$‘2x’$
Hundreds digit be

$‘x’$
So the number is

$3x + 10 \times 2x + 100 × x$

$= 3x + 20x + 100x$

$= 123x$
According to the condition,

$321x – 123x = 594$

$198x = 594$

$x = 594/198$

$= 3$

$\therefore$ The number is =

$321x$

$= 321 \times 3 = 963$

Write the quotient when the difference of a 3-digit number 843 and number obtained by reversing the digits is divided by
$(i) 99$
$(ii) 5$

Given:
Difference of

$3-$ digit number

$843$ and the number
obtained by reversing the digit is

$348$

$= 843-348$

$= 495$
(i) Dividing by

$99,$ we get

$\dfrac{495}{99} =5$
(ii) Dividing by

$5,$ we get

$\dfrac{495}{ 5}=99$

Find the values of the letters in each of the following and give reasons for the steps involved
$A \quad B$
$\times A \quad B$
____________
$6 \quad A \quad B$

Since we know that ,

$B \times B = B$

$B = 1, 6, 5$
IF

$B = 5$ and

$A= 2$ then

$25 \times 25 = 625$

$25$

$\times 25$
_____________

$625$
hence

$A = 2$ and

$B = 5$

The sum of digits of a 2-digit number is $11$ . If the number obtained by reversing the digits is $9$ less than the original number, find the number.

Given:
Sum of two digit number =

$11$
Let unit’s digit be

$‘x’$
and tens digit be

$‘y’,$
then

$x + y = 11 … (i)$
and number =

$x + 10y$
By reversing the digits,
Unit digit be

$‘y’$
and tens digit be

$‘x’$
and number

$= y + 10x + 9$
Now by equating both numbers,

$y + 10x + 9 = x + 10y$

$10x + y – 10y – x = -9$

$9x – 9y = -9$

$x – y = -1 … (ii)$
Adding (i) and (ii), we get

$2x = 10$

$x = 10/2$

$= 5$

$\therefore y = 1 + 5 = 6$
By substituting the vales of x and y, we get
Number =

$x + 10y$

$= 5 + 10 × 6$

$= 5 + 60$

$= 65$

$\therefore$ The number is

$65$ .

Find the values of the letters in each of the following and give reasons for the steps involved
$A \quad A$
$+ A \quad A$
__________
$B \quad A \quad 8$

Since we know that,

$A = 4 \quad or \quad 9$

$A \neq 4$ as

$A+A=A,4+4 \neq 4$

$A=9$

$B=1$

$9\quad 9$

$+ 9\quad 9$
_______

$1 \quad 9 \quad 8$
Hence

$A = 9, B = 1$

Find the values of the letters in each of the following and give reasons for the steps involved
$5 \quad A$
$+ 7 \quad 9$
__________
$C \quad B \quad 3$

Since we know that,

$9 + 4 = 13, \therefore A = 4$

$B$ =

$1 + 5 + 7$ =

$3$
C = 1

$5 \quad 4$

$+ 7 \quad 9$
________

$1 \quad 3 \quad 3$
Hence,

$A = 4, B = 3, C = 1$

Find the values of the letters in each of the following and give reasons for the steps involved
$4 \quad A$
$+ 3 \quad 5$
__________
$B \quad 2$

Since we know that,
12 – 5 = 7 = A
So, B = 8

$4 \quad 7$

$+ 3 \quad 5$
__________

$8 \quad 2$
Hence, A = 7 and B = 8

Find the values of the letters in each of the following and give reasons for the steps involved
$4 \quad 2 \quad A$
$+ 2 \quad A \quad 5$
__________
$A \quad 0 \quad 2$

Since we know that,

$5 + 7 = 12, \therefore A = 7$

$1 + 2 + 7$ =

$10$

$1 + 4 + 2$ =

$7$ =

$A$

$4 \quad 2 \quad 7$

$+ 2 \quad 7 \quad 5$
______

$7 \quad 0 \quad 2$
Hence,

$A = 7$

If the sum of two-digit number and number obtained by reversing the digits is $55$ , find the sum of the digits of the $2-$ digit number.

Let us consider unit digit be

$‘x’$
and tens digit be

$‘y’$
So the number is

$x + 10y$
By reversing the digits
Unit digit be

$‘y’$
and tens digit be

$‘x’$
The number is

$y + 10x = 55$
Now by adding both numbers,

$x + 10y + y + 10x = 55$

$11x + 11y = 55$

$11(x + y) = 55$

$x + y = 55/11$

$x + y = 5$

$\therefore$ sum of the digits of the number is

$5.$

If the difference of two-digit number and the number obtained by reversing the digits is $36$ , find the difference between the digits of the $2-$ digit number.

Let us consider the unit digit be

$‘x’$
and tens digit be

$‘y’$
So, the number is

$= x + 10y$
By reversing the digits
Unit digit be

$‘y’$
and tens digit be

$‘x’$
The number is

$y + 10x = 36$
Now by equating both numbers,

$x + 10y – y – 10x = 36$

$-9x + 9y = 36$

$(y – x) = 36/9$

$y – x = 4$

$\therefore$ The difference between digits of the

$2-$ digit number is

$y – x = 4.$

Without actual calculation, write the quotient when the sum of a 3-digit number abc and the number obtained by changing the order of digits cyclically i.e. bca and cab is divided by
(i) $111$
(ii) $(a+b+c)$
(iii) $37$
(iv) $3$

Given:
Sum of

$3$ -digit number abc and the number
obtained by changing the order of digits i.e. bca and cab.

$\therefore abc + bca + cab$

$= 100a + 10b + c + 100b + 10c + a + 100c + 10a + b$

$= 111a + 111b + 111c = 111 (a + b + c)$
(i) When divided by

$111$ , we get

$111 (a + b + c) ÷ 111 = a + b + c$
(ii) When divided by

$(a + b + c),$ we get

$111 (a + b + c) ÷ (a + b + c) = 111$
(iii) When divided by

$37$ , we get

$111 (a + b + c) ÷ 37 = 3(a + b + c)$
(iv) When divided by

$3,$ we get

$111 (a + b + c) ÷ 3 = 37(a + b + c)$

Find the values of the letters in each of the following and give reasons for the steps involved
$A \quad A$
$\times 4 \quad A$
____________
$9 \quad A \quad 4$

Since we know that ,

$A= 2$ or

$8$
Let

$A = 2$

$22$

$\times 42$
________________

$924$
Hence

$A = 2$

Find the values of the letters in each of the following and give reasons for the steps involved
$A \quad B$
$-B \quad 6$
____________
$4 \quad 7$

Since we know that ,

$B- 6 = 7$

$B = 3$

$A-1-B = 4$

$A -1 - 3 = 4 , A = 4+4 = 8$

$83$

$- 36$
__________

$47$
Hence

$A = 8 , B= 3$

Find the values of the letters in each of the following and give reasons for the steps involved
$B \quad 3 \quad 4 \quad 5$
$+C \quad 9 \quad B \quad A$
____________
$8 \quad B \quad A \quad 2$

Since we know that ,

$A = 7 ( \because 5 +7 = 12 )$

$1 + 4 + 2 = 7(A)$

$\therefore B = 2$

$1 +2 +5 = 8, C= 5$

$2345$

$+ 5927$
_____________

$8272$
hence

$A= 7 ,B= 2 , C = 5$

Find the values of the letters in each of the following and give reasons for the steps involved
$A \quad 2 \quad 1 \quad B$
$+1 \quad C \quad A \quad B$
____________
$B \quad 4 \quad 9 \quad 6$

Since we know that,

$B = 3 \quad or \quad 8$
If

$B = 8$

$1+1+7 = 9$ then

$A = 7$

$C = 4-2 = 2$

$7 + 1 = 8 = B$

$7128$

$+ 1278$
_____________

$8496$
Hence

$A = 7, B = 8, C= 2$

Find the values of the letters in each of the following and give reasons for the steps involved
$2 \quad A$
$\times 3 \quad A$
____________
$B \quad 7 \quad A$

Since we know that ,

$A = 1$ or

$6$ or

$5$ as

$1 \times 1 = 1$
or

$6 \times 6 = 6$
or

$5 \times 5 = 5$
Taking

$A= 5$

$B = 8$

$\quad 25$

$\times 35$
_____________

$\quad 125$

$75 \times$
______________

$\quad 875$
Hence

$A = 5, B= 8$

Fill in the blanks :
In $8,039$ , the place value of $8$ is ......

$8,039$ , the place value of

$8$ is

$8 \times 1000$

$= 8000$

The product of two numbers is $528$ . If the product of their units digits is $8$ and the product of their tens digits is $4$ ; find the numbers.

Given the product of unit’s digits

$= 8$ i.e.,

$2 * 4$ ,

Hence, unit’s digits are

$2$ and

$4$ ,

So, the numbers are either

$24$ or

$22$ ,

$24 * 22 = 528$ ,

The required numbers are

$528$ .

Find the difference in the place values of two sevens in the number $8, 72, 574$ .

In the number

$8 , 72 , 574$ the first

$7$ occur at thousand place

Its place value is

$70000$

The second

$7$ occurs at tens place

Its place value is

$70$

The difference of the two place value of

$7 = 70000 - 70$

$= 69930$

Hence , the difference in the place value of two

$7$ in number

$872574$ is

$69930 .$

Write the following numbers in a generalized form
52

$52=50+2$

$=(10 \times 5)+(2 \times 1)$

$=10\times5+2$

Write the following numbers in a generalized form
628

$628=600+20+8=(6 \times 100)+(2 \times 10)+(8 \times 1)$

Write the following numbers in a generalized form
359

$359=300+50+9=(3 \times 100)+(5 \times 10)+(9 \times 1)$

Write the following numbers in a generalized form
3458

$3458=3000+400+50+8\\\ \ \ \ \ \ \ =(3 \times 1000)+(4 \times 100)+(5 \times 10)+(8 \times 1)$

Write the following numbers in a generalized form
9502

$9502=9000+500+2=(9 \times 1000)+(5 \times 100)+(0 \times 10)+(2 \times 1)$

Write the following numbers in a generalized form
7000

$7000=7000+0+0+0=(7 \times 1000)+(0 \times 100)+(0 \times 10)+(0 \times 1)$

Write the following numbers in a generalized form
106

$106=100+6=(1 \times 100)+(0 \times 10)+(6 \times 1)$

Write the following numbers in a generalized form
39

$39=30+9$

$=(10 \times 3)+(9 \times 1)$

$=10\times3+9$

In a two digit number, the unit digit is three times of tens digit. If $10$ is added to two times the number, the digits are reserved. Find the number.

Let a two digit number be

$10x + y,$ where

$x$ is tens place digit and

$y$ is unit place digit.
According to question

$y = 3x$ .......(i)
and

$2(10x + y) + 10 = 10y + x$

$\Rightarrow 20x + 2y + 10 = 10y + x$

$\Rightarrow 19x - 8y = -10$ .....(ii)
Putting

$y = 3x$ in (ii), we get

$19x - 8 \times 3x = -10$

$\Rightarrow19x - 24x = -10$

$\Rightarrow -5x = -10$

$\Rightarrow x = 2$

$y = 3 \times 2 = 6$
Hence, the required number is

$10x + y = 10 \times 2 + 6 = 26.$

In the following, find the digits represented by the letters:
$\ \ \ \ \ 3$
$\underline {+\ \ B}$
$\underline {\ \ \ \ \ 7}$

The given problem can be rewritten as

$3+B=7$ , now, subtract

$3$ from both sides as follows:

$(3+B)-3=7-3\\ \Rightarrow 3+B-3=4\\ \Rightarrow B=4$

Hence, the letter

$B=4$ .

In the following, find the digits represented by the letters:
$\ \ \ 2\ \ \ A$
$\underline {\ \times \ \ A}$
$\underline {1\ 2\ \ A}$

In the given problem, the multiplication of

$A$ with

$A$ itself gives a number whose ones digit is

$A$ again. This happens only when

$A=1,5,6$ .

$A=1$ then the multiplication will be

$21\times 1=21$ . However, here the tens digit is given as

$12$ , therefore,

$A=1$ is not possible.

Similarly if

$A=5$ then the multiplication will be

$25\times 5=125$ , therefore,

$A=5$ is possible.

Hence, the letter

$A=5$ .

In the following, find the digits represented by the letters:
$1\ A\ A$
$\underline {+\ 1\ A\ A}$
$\underline {2\ A\ A}$

In the given problem, the addition of

$A$ with

$A$ itself gives a number whose ones digit is

$A$ again. This happens only when

$A=0$ . In the next step, the same will be done that is:

$A+A=A\\ \Rightarrow 0+0=0$

In the last step, it is given that

$1+1=2$ and therefore, the required sum with

$A=0$ is

$100+100=200$

Hence, the letter

$A=0$ .

In the following, find the digits represented by the letters:
$3\ A$
$\underline {\times\ A}$
$\underline {2\ B\ A}$

In the given problem, the multiplication of

$A$ with

$A$ itself gives a number whose ones digit is

$A$ again. This happens only when

$A=1,5,6$ .

$A=1$ then the multiplication will be

$31\times 1=31$ . However, here the tens digit is given as

$B$ and hundred digit is

$2$ , therefore,

$A=1$ is not possible.

Similarly, if

$A=5$ then the multiplication will be

$35\times 5=175$ . However, here the tens digit is given as

$B$ and hundred digit is

$2$ , therefore,

$A=5$ is not possible.

Now, if

$A=6$ then the multiplication will be

$36\times 6=216$ . However, here the tens digit is given as

$B$ and hundred digit is

$2$ , therefore,

$A=6$ and

$B=1$ are possible.

Hence, the letter

$A=6$ and

$B=1$ .

Write the following numbers in generalised form:
$39, 52, 106,359, 628, 3458, 9502, 7000$

The given numbers can be written in generalised form as follows:

(a)

$39=(3\times 10)+(9\times 1)=(3\times 10^{ 1 })+(9\times 10^{ 0 })$

(b)

$52=(5\times 10)+(2\times 1)=(5\times 10^{ 1 })+(2\times 10^{ 0 })$

(c)

$106=(1\times 100)+(0\times 10)+(6\times 1)=(1\times 10^{ 2 })+(0\times 10^{ 1 })+(6\times 10^{ 0 })$

(d)

$359=(3\times 100)+(5\times 10)+(9\times 1)=(3\times 10^{ 2 })+(5\times 10^{ 1 })+(9\times 10^{ 0 })$

(e)

$628=(6\times 100)+(2\times 10)+(8\times 1)=(6\times 10^{ 2 })+(2\times 10^{ 1 })+(8\times 10^{ 0 })$

(f)

$3458=(3\times 1000)+(4\times 100)+(5\times 10)+(8\times 1)=(3\times 10^{ 3 })+(4\times 10^{ 2 })+(5\times 10^{ 1 })+(8\times 10^{ 0 })$

(g)

$9502=(9\times 1000)+(5\times 100)+(0\times 10)+(2\times 1)=(9\times 10^{ 3 })+(5\times 10^{ 2 })+(0\times 10^{ 1 })+(2\times 10^{ 0 })$

(h)

$7000=(7\times 1000)+(0\times 100)+(0\times 10)+(0\times 1)=(7\times 10^{ 3 })+(0\times 10^{ 2 })+(0\times 10^{ 1 })+(0\times 10^{ 0 })$

Call a natural number $n$ faithful, if there exist numbers $a\,<\,b\,<\,c$ such that $a$ divides $b,\;b$ divides $c\;$ and $\;n\;=\;a+b+c$ . Show that all but a finite number of natural numbers are faithful. Find the sum of all natural numbers which are not faithful.

Suppose

$n\;\in\;\mathbb{N}$ is faithful.
Let

$k\;\in\;\mathbb{N}$ and consider

$kn$ . Since

$n\;=\;a+b+c$ , with

$a\,>\,b\,>\,c,\;c|b\;and\;b|a$ , we see that

$kn=ka+kb+kc$ which shows that

$kn$ is faithful.
Let

$p\,>\,5$ be a prime.
Then

$p$ is odd and

$p=(p-3)+2+1$ shows that

$p$ is faithful.
If

$n\;\in\;\mathbb{N}$ contains a prime factor

$p\,>\,5$ , then the above observation shows that

$n$ is faithful.
This shows that a number which is not faithful must be of the form

$2^{\alpha}3^{\beta}5^{\gamma}$ .
We also observe that

$2^4=16=12+3+1,\;3^2=9=6+2+1\;and\;5^2=25=22+2+1$ , so that

$2^4,\,3^2\;and\;5^2$ are faithful.

$\therefore n\;in\;\mathbb{N}$ is also faithful if it contains a factor of the form

$2^{\alpha}$ where

$\alpha\;\ge\;4$ ; a factor of the form

$3^{\beta}$ where

$\beta\;\ge\;2$ ; or a factor of the form

$5^{\gamma}$ where

$\gamma\;\ge\;2$ .
Thus the numbers which are not faithful are of the form

$2^{\alpha}3^{\beta}5^{\gamma}$ , where

$\alpha\;\le\;3,\;\beta\;\le\;1\;and\;\gamma\;\le\;1$ . We may enumerate all such numbers :

$1,\,2,\,3,\,4,\,5,\,6,\,8,\,10,\,12,\,15,\,20,\,24,\,30,\,40,\,60,\,120$ .
Among these

$120=112+7+1,\\\;60=48+8+4,\\\;40=36+3+1,\\\;30=18+9+3,\\\;20=12+6+2,\\\;15=12+2+1,\;and\;10=6+3+1$ .
It is easy to check that the other numbers cannot be written in the required form. Hence the only numbers which are not faithful are

$1,\,2,\,3,\,4,\,5,\,6,\,8,\,12,\,24$ .
Their sum is

$65$ .

In the following, find the digits represented by the letters:
$\ \ \ \ 1\ 6$
$\underline {+\ 2\ A}$
$\underline {\ \ \ B\ 1}$

In the given problem, the addition of

$6$ and

$A$ is giving

$1$ that is a number whose one's digit is

$1$ . In that case addition of

$6$ and

$A=5$ will give

$11$ and thus

$1$ will be carried for the next step.

In the next step,

$1+1+2=B\\ \Rightarrow B=4$

Hence, the letters

$A=5$ and

$B=4$ .

The product of a two-digit number by a number consisting of the same digits written in the reverse order is equal to $2430$ . Find the number.

The last digit of $2340$ is $0$

This indicates that one of the numbers must end in with $5$ and the other number must be even.

Let the missing digit be $x$

The number $x5$ has a value $10x+5$

The number $5x$ has a value $50+x$

The product is $2340$

$(10x+5)(50+x)=2430$

$500x+10x^2+250+5x=2430$

$10x^2+505x-2180=0$ ...... (divide both side by $5$ )

$2x^2+101x-436=0$

Using ac method:

$2\times 436=872$

Find the factor of $872$ which differ by $101$

$1,2,4,8........109,218,432,872$

$\Rightarrow (2x+109)(x-4)=0$

By solving equation we have

$x=-54.5$ ..... (ignore as $x$ is an integer)

$\Rightarrow x=4$

If $x=4,$ then the numbers are $45$ and $54$ .

The sum of the squares of the digits of a two-digit number is $13$ . If we subtract $9$ from that number, we get a number consisting of the same digits written in the reverse order. Find the number.

Let the digits be

$x$ and

$y$

The sum of square of the number is

$13$

$\Rightarrow x^2+y^2=13$

Given that if

$9$ is subtracted from the number, it get reversed

$\Rightarrow (10x+y)-9=10y+x$

$9x-9y=9$

$x-y=1$

Now,

$(x-y)^2 =x^2+y^2-2x y$

$\Rightarrow 1 =13-2x y$

$\Rightarrow 2x y = 12$

$\Rightarrow xy = 6 \Rightarrow y=\dfrac{6}{x}$

$\Rightarrow x-y=1$

$\Rightarrow x-\dfrac{6}{x}=1$

$\Rightarrow x^2-6=x$

$\Rightarrow x^2-x-6=0$

$\Rightarrow x^2+2x-3x-6=0$

$\Rightarrow x(x+2)-3(x+2)=0$

$\Rightarrow (x+2)(x-3)=0$

$\Rightarrow (x+2)=0$ and

$(x-3)=0$

$\Rightarrow x=2,3$

Hence, the number is

$32$ .

The sum of the digits of a three-digit number is $17$ and the sum of the squares of its digits is $109$ . If we subtract $495$ from that number, we shall get a number consisting of the same digits written in the reverse order. Find the number.

Let three digit number is

$100x+10y+z$

According to question,

CONDITION 1: a sum of the digits of a three-digit number is 17

i.e

$x+y+z=17.................(i)$

CONDITION 2: the sum of the squares of its digits is 109

i.e

$x^2 +y^2+z^2=109............(ii)$

CONDITION 3: if we subtract 495 from that number, we shall get a number consisting of the same digits written in the reverse order

i.e

$100x+10y+z-495=100z+10y+x$

$\Rightarrow 99x-99z=495$

$\Rightarrow x-z=5$

$\Rightarrow x=z+5..............(iii)$

From

$(i)\ and\ (iii)$

$(z+5)+y+z=17$

$\Rightarrow y = 12-2z...........(iv)$

From

$(i),(iii),\ and\ (iv)$

$(z+5)^2 +(12-2z)^2+z^2=109$

$z^2 + 25 +10z +144 +4z^2-48z+z^2=109$

$\Rightarrow3z^2-19z +30= 0$ which is a quadratic equation

on solving we get

$z=\dfrac{10}{3} \ and\ z= 3$

$z=\dfrac{10}{3}$ is not possible as digit of any number can't be a fraction

hence,

$z=3$

now,

from

$(iii)\ and\ (iv)$

$y=6 \ and \ x=8$

thus,

the required number is

$863$

How many four-digit numbers are there whose decimal notation contains not more than two different digits?

If three digits are different then three digits can be arranged in six different ways

Number of four digit numbers are

$9.10.10.10-9.9.8.7-9.9.8(6)=9000-4536-3888=576$

If we multiply a certain two-digit number by the sum of its digits, we get $405$ . If we multiply the number consisting of the same digits written in the reverse order by the sum of the digits, we get $486$ . Find the number.

Given condition:
Number

$\times$ Sum of the Digits

$= 405$
Now, factors of

$405$ will give the required number.
Factors of

$405 = 5\times 3\times 3\times 3\times 3 = 15 \times 27 = 45 \times 9$

$45 \times 9 = 405$

Also,

$54\times 9=486$
So, Required number

$= 45$

There is a natural number which becomes equal to the square of a natural number when $100$ is added to it, and to the square of another natural number when $168$ is added to it. Find the number.

From the question, we can write that

$a$ +

$100$ =

$b^2$

$a$ +

$168$ =

$c^2$

=>

$c^2-b^2$ = 68
=>

$(c - b)(c + b) = 1\times68$

Now solve the equation for

$(c-b)=1$ and

$(c+b)=68$

We get

$c=35$ and

$b=34$ . (here

$c=34.5$ which is

$35$ and

$b=33.5$ which can be written as

$34$ by ignoring the point )

$a+100=b^2$

$a=34^2-100$

$a=1156-100=1056$ hence this the required number.

Find the two-digit number if the number of its units exceeds by $2$ the number of its tens and the product of the required number, by the sum of its digits is equal to $144$ .

Let the tenth digit be $10x$

Then, unit's unit $=x+2$

Number $=10x+(x+2)=11x+2$

Sum of digits $=x+x+2= 2x+2$

$(11x+2)(2x+2)=144$

$\Rightarrow 11x^2 +26x-140=0$

$\Rightarrow 11x^2 +13x-70=0$

$\Rightarrow (x-2)(11x+35)=0$

$\Rightarrow x=2$

Hence the required number is $(11\times2)+2=24$ .

In a $3$ -digit number, unit's digit is one more than the hundred's digit and ten's digit is one less than that hundred's digit. If the sum of the original $3$ -digit number and numbers obtained by changing the order of digits cyclically is $2664$ , find the number.

Let hundred digit

$= x$

ten digit

$= x-1$

unit digit

$= x-1$

First form of Number

$=100\times x +100(x-1)+x+1$

$=111 x-9$

Second form of Number

$=(x+1)100+x\times 10+x-1$

$=111 x+99$

third form of number

$=(x-1)100+(x+1)10+x$

$=111 x-90$

$111 x-9+111 x+99+111 x-90=2664$

$111 x=2664$

$x=8$

So the number

$8\times 100+7\times 10+9$

$=879$

Product of two numbers is $18.75$ . If one number is three times the other, then find larger number.

$\begin{array}{l} 1st\, \, number=x \\ 2nd\, \, number=3x \\ x\times 3x=18.75 \\ \Rightarrow 3{ x^{ 2 } }=18.75 \\ \Rightarrow { x^{ 2 } }=\dfrac { { 18.75 } }{ 3 } =6.25 \\ \Rightarrow x=\pm 2.5 \\ ler\, \, no. \\ \Rightarrow 3\times \pm 2.5 \\ \Rightarrow \pm 7.5 \\ -7.5\, \, or\, \, 7.5 \end{array}$

The sum of the squares of the digits constituting a certain positive three-digit number is $74$ . The hundreds digit of the number is equal to the doubled sum of the digits in the tens and units places. Find the number if it is known that the difference between that number and the number written by the same digits in the reverse order is $495$ .

Let three digit number is

$100x+10y+z$

According to question,

CONDITION 1: The sum of the squares of the digits constituting a certain positive three-digit number is 74

74.

i.e

$x^2+y^2+z^2=74.................(i)$

CONDITION 2: The hundreds digit of the number is equal to the doubled sum of the digits in the tens and units places

i.e

$x= 2(y+z)............(ii)$

CONDITION 3: the difference between that number and the number written by the same digits in the reverse order is 495.

i.e

$100x+10y+z-(100z+10y+x)=495$

$\Rightarrow 99x-99z=495$

$\Rightarrow x-z=5$

$\Rightarrow x=z+5..............(iii)$

From

$(ii)\ and\ (iii)$

$z+5=2y+2z$

$\Rightarrow y = \dfrac{5-z}{2}...........(iv)$

From

$(i),(iii),\ and\ (iv)$

$(z+5)^2 +(\dfrac{5-z}{2})^2+z^2=74$

$9z^2+30z-171=0$

$\Rightarrow3z^2+10-57= 0$ which is a quadratic equation

on solving we get

$z=\dfrac{-19}{3} \ and\ z= 3$

$z=\dfrac{-19}{3}$ is not possible as digit of any number can't be a fraction

hence,

$z=3$

now,

from

$(iii)\ and\ (iv)$

$y=\ 1 \ and \ x=8$

thus,

the required number is

$813$

The sum of the digits of a three-digit number is $11$ . If we subtract $594$ from the number consisting of the same digits written in the reverse order, we shall get a required number. Find that three-digit number, if the sum of all pairwise products of the digits constituting that number is $31$ .

Let three digit number be

$100x+10y+z$

According to question:

CONDITION 1:

The sum of the digits of a three-digit number is 11

$x+y+z=11\dots (1)$

CONDITION 2 : the sum of all pairwise products of the digits constituting that number is 31

$xy+yz+zx=31\dots (2)$

CONDITION 3 : if we subtract

$594$ from that number, we shall get a number consisting of the same digits written in the reverse order

$100x+10y+z-594=100z+10y+x$

$99x-99z=594$

$x-z=6$

$x=z+6\dots (3)$

From

$(1)\ and\ (3)$

$(z+6)+y+z=11$

$\Rightarrow y = 5-2z\dots (4)$

From

$(2),(3),$ and

$(4)$ :

$(z+6)\times(5-2z)+(5-2z)\times(z)+(z)\times(z+6)=31$

$5z+30-2z^2-12z+5z-2z^2+z^2+6z=31$

$3z^2-4z+1=0$ , which is a quadratic equation

Splitting the middle term:

$3z^2-3z-z+1=0$

$3z(z-1)-1(z-1)=0$

$(3z-1)(z-1)=0$

$z=\dfrac{1}{3}$ or

$z= 1$

$z=\dfrac{1}{3}$ is not possible as digit of any number can't be a fraction

Hence,

$z=1$ .

From

$(3)$ and

$(4)$ :

$y=3$ and

$x=7$

Required number

$=100(7)+10(3)+1=731$

Thus, the required number is

$731$ .

Pradeep gave away $8$ sweets to his friends. This number was one-fifth of the number of sweets that he had with him at first. How many sweets did Pradeep have with him at first?

Let Pradeep had

$x$ sweets at first.

Then according to the problem,

$\begin{array}{l} 1/5\, \, of\, \, x=8 \\ x=8\times 5 \\ x=40 \end{array}$

Some students planned a picnic. The budget for food was $Rs.\ 480$ . But eight of these failed to go and thus the cost of food for each member increased by $Rs.\ 10$ . How many students attended the picnic?

$\textbf{Step -1: Calculating}$

$\text{Let the total number of students be }x$

$\text{Budget for food was Rs. 480}$

$\text{Total price of food}=480x$

$\text{Since 8 children failed to come the total must be paid by x-8 students}$

$\implies 480x=490(x-8)$

$\implies 10x=490\times8$

$\implies x=392$

$\implies \text{Number of students who attended the picnic}=x-8= 392 - 8 = 384$

$\textbf{Hence, the number of students who attended the picnic was 384 .}$

Find the last two digit of ${3^{400}}?$

We have,

${3}^{400}={\left({3}^{2}\right)}^{200}={9}^{200}={\left(10-1\right)}^{200}$

$={\left(10\right)}^{200}-^{200}{{C}_{1}}{\left(10\right)}^{199}+^{200}{{C}_{2}}{\left(10\right)}^{198}-^{200}{{C}_{3}}{\left(10\right)}^{197}+...+^{200}{{C}_{198}}{\left(10\right)}^{2}-^{200}{{C}_{199}}\left(10\right)+1$

$=100\mu-^{200}{{C}_{199}}\left(10\right)+1$ where

$\mu\in I$

$=100\mu-^{200}{{C}_{1}}\left(10\right)+1$

$=100\mu-2000+1$

$=100\left(\mu-20\right)+1$

$=100p+1$ where

$p$ is an integer.

Hence, last two digits of

${3}^{400}$ is

$00+1=01$

A number is 27 more than the number obtained by reversing its digits. If its unit's and ten's digit are x and y respectively. write the linear equation representing the above statement.

1311933_1589423_ans_b39492de26d746238b59ba69ac516094.jpg

A three digit number 24 y is a multiple of 3, what might be the values of y?

1311873_1588769_ans_156f7615d01f40a2aa1446906a485d46.jpg

Find the least number which must be added to $6203$ to obtain a perfect square. Also, find the square root of the number so obtained.

1315513_1584617_ans_469eb3a5f1d44913bbb8e71ecffbf864.jpg

Find the number nearest to 110000 but greater than 100000 which is exactly divisible by each of 8,15 and 21.

1309740_1328546_ans_cd0047e2b15840b5aefb30f546211c22.jpg

How many numbers greater than $40000$ can be formed using the digits $1,2,3,4$ and $5$ if each is used only once in a number?

The given digits are

$1,\,2,\,3,\,4$ and

$5$ which are

$5$ in number.

As the number

$40000$ has five digits and the numbers greater than

$40000$ are to be formed by using each of the given digit only once, the numbers of only five digits are to be formed.

Ten thousands place can be filled up by any of the digits

$4$ or

$5$ in

$2$ different ways.

Remaining

$4$ places can be filled up by the remaining

$4$ digits in

$^{4}{{P}_{4}}$ ways.

$\Rightarrow$ The required number of numbers

$=2\times ^{4}{{P}_{4}}=2\times 4!=2\times 4\times 3\times 2\times 1=48$

Number	Number Name	Expansion
20000	twenty thousand	$2 \times 10000$
26000	twenty six thousand	$2 \times 10000 + 6 \times 1000$
38400	thirty eight thousand four hundred	$3\times 10000 + 8 \times 1000 + 4 \times 100$
65740	sixty five thousand seven hundred forty	$6\times 10000+5 \times 1000 + 7\times 100 + 4\times 10$
89324	eighty nine thousand three hundred twenty four	$8\times 10000 + 9 \times 1000 + 3 \times 100+ 2 \times 10 + 4 \times 1$
50000	-----	----
41000	----	----
47300	----	----
57630	----	----
29485	----	----
29085	----	----
20085	----	----

Playing With Numbers - Class 8 Maths - Extra Questions

Test the divisibility of the following number by 1010:6000560005

Test the divisibility of the following number by 1010:205205

Find:563−(−621)\cfrac{5}{63}-\left( \cfrac { -6 }{ 21 } \right)

Find the sum:53+35\cfrac{5}{3}+\cfrac{3}{5}

Find:−219−6-2\cfrac{1}{9}-6

Find the sum:−3−11+59\cfrac{-3}{-11}+\cfrac{5}{9}

Find:724−1736\cfrac{7}{24}-\cfrac{17}{36}

Find the sum:−910+2215\cfrac{-9}{10}+\cfrac{22}{15}

Find the sum:−819+(−2)57\cfrac{-8}{19}+\cfrac{(-2)}{57}

Find the sum:−213+435-2\cfrac{1}{3}+4\cfrac{3}{5}

Find the product:37×(−25)\cfrac{3}{7}\times \left( \cfrac { -2 }{ 5 } \right)

Find the product:310×(−9)\cfrac{3}{10}\times (-9)

Find the product:92×(−74)\cfrac{9}{2}\times \left( \cfrac { -7 }{ 4 } \right)

Find the product:−65×911\cfrac{-6}{5}\times \cfrac{9}{11}

Find the value of:(−4)÷23(-4)\div \cfrac{2}{3}

Find the product:311×25\cfrac{3}{11}\times \cfrac{2}{5}

Find the product:3−5×53\cfrac{3}{-5}\times \cfrac{5}{3}

Find the value of :−35÷2\cfrac{-3}{5}\div 2

Find the value of:−18÷34\cfrac{-1}{8}\div \cfrac{3}{4}

Find the value of:−45÷(−3)\cfrac{-4}{5}\div (-3)

Write the following in expanded notation.30573057

Write the following in expanded notation.235060235060.

Write the following in expanded notation.1234512345.

Write the corresponding numeral for the following.4×100000+5×1000+1×100+7×14\times 100000+5\times 1000+1\times 100+7\times 1.

Find the value of:−712÷(213)\cfrac{-7}{12}\div \left( \cfrac { 2 }{ 13 } \right)

Write down the difference in temperature between −4oC-4^oC and −9oC-9^oC._______oC^oC.

Write the corresponding numeral for the following.7×10000+2×1000+5×100+9×10+6×17\times 10000+2\times 1000+5\times 100+9\times 10+6\times 1.

Write the following is expanded notation.1020510205.

Find the value of:313÷(−465)\cfrac{3}{13}\div \left( \cfrac { -4 }{ 65 } \right)

Find the value of:−213÷17\cfrac{-2}{13}\div \cfrac{1}{7}

Fill in the blank.11 lakh== _______ ten.

Fill in the blank.11 lakh==______ hundred.

Fill in the blank.11 crore==______ hundred.

Which digits have the same face value and place value in 9207863492078634?

Write the corresponding numeral for the following.5×10000000+7×1000000+8×1000+9×10+45\times 10000000+7\times 1000000+8\times 1000+9\times 10+4.

How many millions make a billion?

Fill in the blank.11 crore ==______ ten lakh.

85+4AB C 3\dfrac { \begin{matrix} 8 & 5 \\ +4 & A \end{matrix} }{ B\ C\ 3 }

A01B+10ABB108\dfrac { \begin{matrix} A & 01 & B \\ +1 & 0A & B \end{matrix} }{ \begin{matrix} B & 10 & 8 \end{matrix} }

Find the values of the letters in each of the following and give reasons for the steps involved 18A 1 \quad 8 \quad A +BA7 + B \quad A \quad 7 __________CB2 C \quad B \quad 2

Write the following numbers in generalized form:(i)89 (i) 89 (ii)207 (ii)207 (iii)369 (iii)369

If A×3=1AA \times 3=1A, then A=A= ______ .

Fill in the blanks : In 24,673 24,673 , the place value of 6 6 is .........

Write 2525 in generalised from:

Find the digits AA and CC in the following multiplication

If 21y521y5 is multiple of 99, where yy is a digit, what is the value of yy?

Find the digit represented by P in the following addition

Frame and solve the equations for the following statements:The sum of the two numbers is 2121 and their difference is 33. Find the numbers

Express the following in the standard form:3.02×10−63.02\times {10}^{-6}

Express the following in the standard form:1.0001×1091.0001\times {10}^{9}

Test the divisibility of the following number by 1010:9090

Frame and solve the equations for the following statements:Sum of two numbers is 6060. The bigger number is 44 times the smaller one. Find the numbers

Frame and solve the equations for the following statements:Two numbers are in the ratio 5:35 : 3. If they differ by 1818, what are the numbers?

Mala has a collection of bangles. She have 20 gold bangles and 10 silver bangles. What is the percentage of bangles of each type? Can you put it in a tabular form as done in the above example?

Solve the alphanumeric puzzle:2PQ+3PQQ12\begin{matrix} 2 & P & Q \\ +3 & P & Q \\ Q & 1 & 2 \end{matrix}

Replace the letters by the numerals to make it correct. A 6 B 4 C+1 7 2 5 5____________ 9 D 0 E 8____________

Write expanded form:a) 6758641267586412b) 12348000071234800007

Write each of the following in expanded from using exponents:(i) 2357.3282357.328(ii) 432.476432.476(iii) 38.032538.0325

Make the greatest and the smallest 4 digit numbers by using any one digit twice:(i) 6, 3, 2(ii) 1, 0, 6

Fill in the blank1 g=..................mg1\ g=..................mg

Write the number :4×106+8×105+6×104+4×103+4×102+6×10+9×1004 \times 10^6 + 8 \times 10^5 + 6 \times 10^4 + 4 \times 10^3 + 4 \times 10^2 + 6 \times 10 + 9 \times 10^0

Express the number :8×105+7×104+5×103+4×102+6×101+9×1008 \times 10^5 + 7 \times 10^4 + 5 \times 10^3 + 4 \times 10^2 + 6 \times 10^1 + 9 \times 10^0

Write the value of |15×3−(7×2)×4||15 \times 3-(7\times 2)\times 4|

Express the number in expanded form:9×104+6×103+4×102+5×10+7×10o9 \times 10^4 + 6 \times 10^3 + 4 \times 10^2 + 5 \times 10 + 7 \times 10^o

Write each of the following as power of 1010.10000001000000

Simplify 25×52×t8103×t4\dfrac{25 \times 5^{2}\times t^{8}}{10^{3} \times t^{4}}

Solve 2+4+32+4+3

Name the property involved in the following example.37×1=37=1×37\dfrac{3}{7}\times 1=\dfrac{3}{7}=1\times \dfrac{3}{7}.

Using appropriate properties find.−23×35+52−35×16-\dfrac {2}{3}\times \dfrac {3}{5}+ \dfrac {5}{2}-\dfrac {3}{5}\times \dfrac {1}{6}

Find the number of the following expanded forms :6×103+5×102+0×10+6×1006 \times 10^3 + 5 \times 10^2 + 0 \times 10 + 6 \times 10^0

Solve 3×2(4+6)3\times 2(4+6)

Simplify: 33 3√40^{3}_{}\sqrt{40} - 44 3√320^{3}_{}\sqrt{320}

Write an equivalent fraction of 89\dfrac{8}{9} with numerator 3232

Solve 2√54−6√23−√96=?2\sqrt { 54 } -6\sqrt { \dfrac { 2 }{ 3 } } -\sqrt { 96 } =?

Simlify: (62581)−3/4×[(425)−3/2÷(23)−3]{\left( {\dfrac{{625}}{{81}}} \right)^{ - 3/4}}\times\left[ {{{\left( {\dfrac{4}{{25}}} \right)}^{ - 3/2}} \div {{\left( {\dfrac{2}{3}} \right)}^{ - 3}}} \right]

Write the number names for the following numbers.i) 26,04,78326,04,783ii) 5,901,0805,901,080iii) 70,051,90070,051,900iv} 17,25,09,25017,25,09,250

Find: 375(a−b)3+3375(a-b)^3+3

Write each of the following as power of 1010.1100\dfrac{1}{100}

Solve 32+23\dfrac{3}{2}+\dfrac{2}{3}

Test the divisibility of the following number by $10$ :
$60005$

Test the divisibility of the following number by $10$ :
$205$

Find:
$\cfrac{5}{63}-\left( \cfrac { -6 }{ 21 } \right)$

Find the sum:
$\cfrac{5}{3}+\cfrac{3}{5}$

Find:
$-2\cfrac{1}{9}-6$

Find the sum:
$\cfrac{-3}{-11}+\cfrac{5}{9}$

Find:
$\cfrac{7}{24}-\cfrac{17}{36}$

Find the sum:
$\cfrac{-9}{10}+\cfrac{22}{15}$

Find the sum:
$\cfrac{-8}{19}+\cfrac{(-2)}{57}$

Find the sum:
$-2\cfrac{1}{3}+4\cfrac{3}{5}$

Find the product:
$\cfrac{3}{7}\times \left( \cfrac { -2 }{ 5 } \right)$

Find the product:
$\cfrac{3}{10}\times (-9)$

Find the product:
$\cfrac{9}{2}\times \left( \cfrac { -7 }{ 4 } \right)$

Find the product:
$\cfrac{-6}{5}\times \cfrac{9}{11}$

Find the value of:
$(-4)\div \cfrac{2}{3}$

Find the product:
$\cfrac{3}{11}\times \cfrac{2}{5}$

Find the product:
$\cfrac{3}{-5}\times \cfrac{5}{3}$

Find the value of :
$\cfrac{-3}{5}\div 2$

Find the value of:
$\cfrac{-1}{8}\div \cfrac{3}{4}$

Find the value of:
$\cfrac{-4}{5}\div (-3)$

Write the following in expanded notation.
$3057$

Write the following in expanded notation.
$235060$ .

Write the following in expanded notation.
$12345$ .

Write the corresponding numeral for the following.
$4\times 100000+5\times 1000+1\times 100+7\times 1$ .

Find the value of:
$\cfrac{-7}{12}\div \left( \cfrac { 2 }{ 13 } \right)$

Write down the difference in temperature between $-4^oC$ and $-9^oC$ .
_______ $^oC$ .

Write the corresponding numeral for the following.
$7\times 10000+2\times 1000+5\times 100+9\times 10+6\times 1$ .

Write the following is expanded notation.
$10205$ .

Find the value of:
$\cfrac{3}{13}\div \left( \cfrac { -4 }{ 65 } \right)$

Find the value of:
$\cfrac{-2}{13}\div \cfrac{1}{7}$

Fill in the blank.
$1$ lakh $=$ _______ ten.

Fill in the blank.
$1$ lakh $=$ ______ hundred.

Fill in the blank.
$1$ crore $=$ ______ hundred.

Which digits have the same face value and place value in $92078634$ ?

Write the corresponding numeral for the following.
$5\times 10000000+7\times 1000000+8\times 1000+9\times 10+4$ .

Fill in the blank.
$1$ crore $=$ ______ ten lakh.

$\dfrac { \begin{matrix} 8 & 5 \\ +4 & A \end{matrix} }{ B\ C\ 3 }$

$\dfrac { \begin{matrix} A & 01 & B \\ +1 & 0A & B \end{matrix} }{ \begin{matrix} B & 10 & 8 \end{matrix} }$

Find the values of the letters in each of the following and give reasons for the steps involved
$1 \quad 8 \quad A$
$+ B \quad A \quad 7$
__________
$C \quad B \quad 2$

Write the following numbers in generalized form:
$(i) 89$
$(ii)207$
$(iii)369$

If $A \times 3=1A$ , then $A=$ ______ .

Fill in the blanks :
In $24,673$ , the place value of $6$ is .........

Write $25$ in generalised from:

Find the digits $A$ and $C$ in the following multiplication

If $21y5$ is multiple of $9$ , where $y$ is a digit, what is the value of $y$ ?

Frame and solve the equations for the following statements:
The sum of the two numbers is $21$ and their difference is $3$ . Find the numbers

Express the following in the standard form:
$3.02\times {10}^{-6}$

Express the following in the standard form:
$1.0001\times {10}^{9}$

Test the divisibility of the following number by $10$ :
$90$

Frame and solve the equations for the following statements:
Sum of two numbers is $60$ . The bigger number is $4$ times the smaller one. Find the numbers

Frame and solve the equations for the following statements:
Two numbers are in the ratio $5 : 3$ . If they differ by $18$ , what are the numbers?

Solve the alphanumeric puzzle: $\begin{matrix} 2 & P & Q \\ +3 & P & Q \\ Q & 1 & 2 \end{matrix}$

Replace the letters by the numerals to make it correct.
A 6 B 4 C

+1 7 2 5 5

9 D 0 E 8

Write expanded form:
a) $67586412$
b) $1234800007$

Write each of the following in expanded from using exponents:
(i) $2357.328$
(ii) $432.476$
(iii) $38.0325$

Make the greatest and the smallest 4 digit numbers by using any one digit twice:
(i) 6, 3, 2
(ii) 1, 0, 6

Fill in the blank
$1\ g=..................mg$

Write the number :
$4 \times 10^6 + 8 \times 10^5 + 6 \times 10^4 + 4 \times 10^3 + 4 \times 10^2 + 6 \times 10 + 9 \times 10^0$

Express the number :
$8 \times 10^5 + 7 \times 10^4 + 5 \times 10^3 + 4 \times 10^2 + 6 \times 10^1 + 9 \times 10^0$

Write the value of $|15 \times 3-(7\times 2)\times 4|$

Express the number in expanded form:
$9 \times 10^4 + 6 \times 10^3 + 4 \times 10^2 + 5 \times 10 + 7 \times 10^o$

Write each of the following as power of $10$ .
$1000000$

Simplify
$\dfrac{25 \times 5^{2}\times t^{8}}{10^{3} \times t^{4}}$

Solve $2+4+3$

Name the property involved in the following example.
$\dfrac{3}{7}\times 1=\dfrac{3}{7}=1\times \dfrac{3}{7}$ .

Using appropriate properties find. $-\dfrac {2}{3}\times \dfrac {3}{5}+ \dfrac {5}{2}-\dfrac {3}{5}\times \dfrac {1}{6}$

Find the number of the following expanded forms :
$6 \times 10^3 + 5 \times 10^2 + 0 \times 10 + 6 \times 10^0$

Solve $3\times 2(4+6)$

Simplify: $3$ $^{3}_{}\sqrt{40}$ - $4$ $^{3}_{}\sqrt{320}$

Write an equivalent fraction of $\dfrac{8}{9}$ with numerator $32$

Solve $2\sqrt { 54 } -6\sqrt { \dfrac { 2 }{ 3 } } -\sqrt { 96 } =?$

Simlify: ${\left( {\dfrac{{625}}{{81}}} \right)^{ - 3/4}}\times\left[ {{{\left( {\dfrac{4}{{25}}} \right)}^{ - 3/2}} \div {{\left( {\dfrac{2}{3}} \right)}^{ - 3}}} \right]$

Write the number names for the following numbers.
i) $26,04,783$
ii) $5,901,080$
iii) $70,051,900$
iv} $17,25,09,250$

Find: $375(a-b)^3+3$

Write each of the following as power of $10$ .
$\dfrac{1}{100}$

Solve $\dfrac{3}{2}+\dfrac{2}{3}$

Simplify $\cfrac { { 9 }^{ \dfrac { 1 }{ 3 } }{ 27 }^{ \dfrac { -1 }{ 2 } } }{ 3^{ \dfrac { 1 }{ 6 } }{ 3 }^{ \dfrac { -2 }{ 3 } } }$

Find the ratio number in which in its standard form is equal to $\dfrac{4}{5}$ and the sum of its numbers and denometor is 27

Write the ususal form of $100a+b+10c$ .

Evaluate :
$34+(5 \times 0)-34 \times 0$