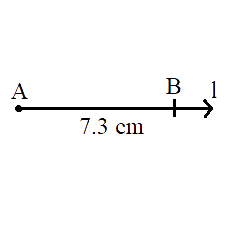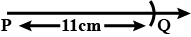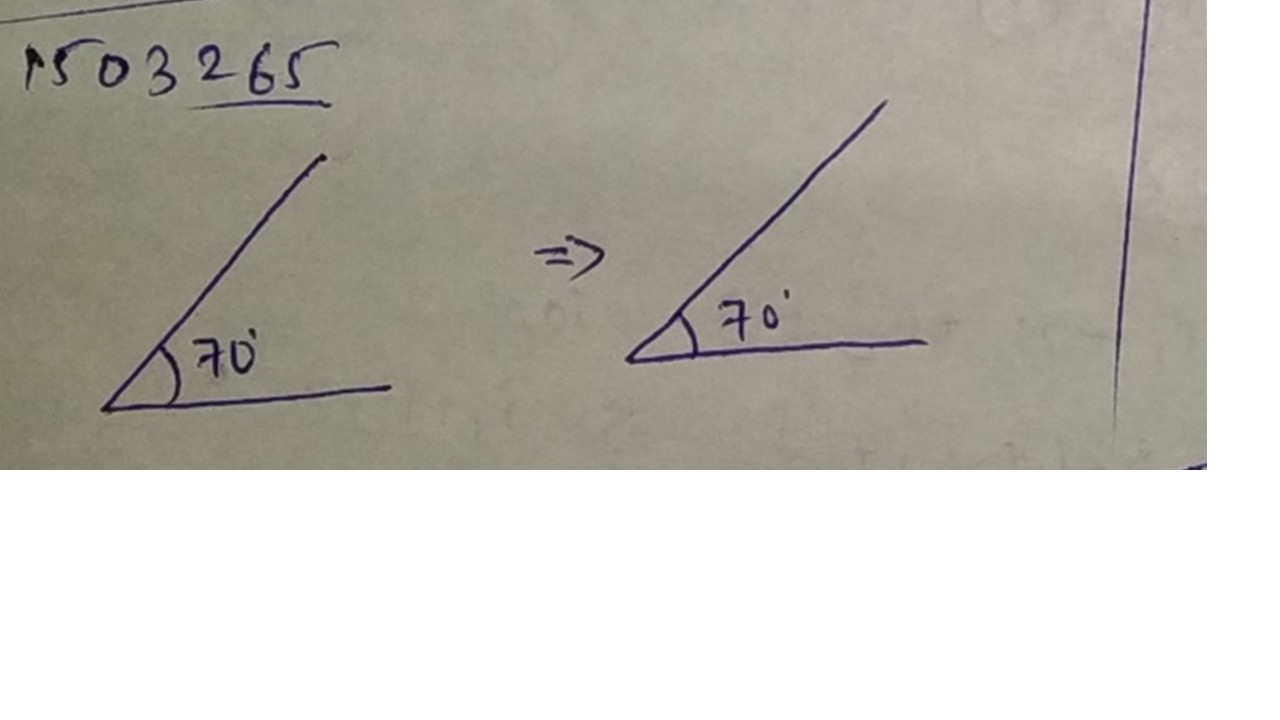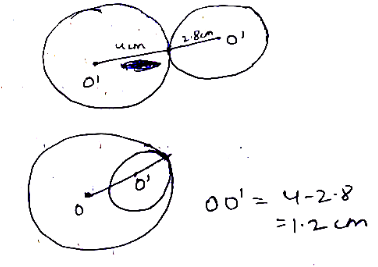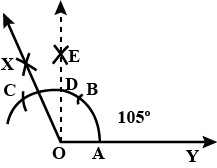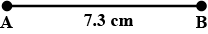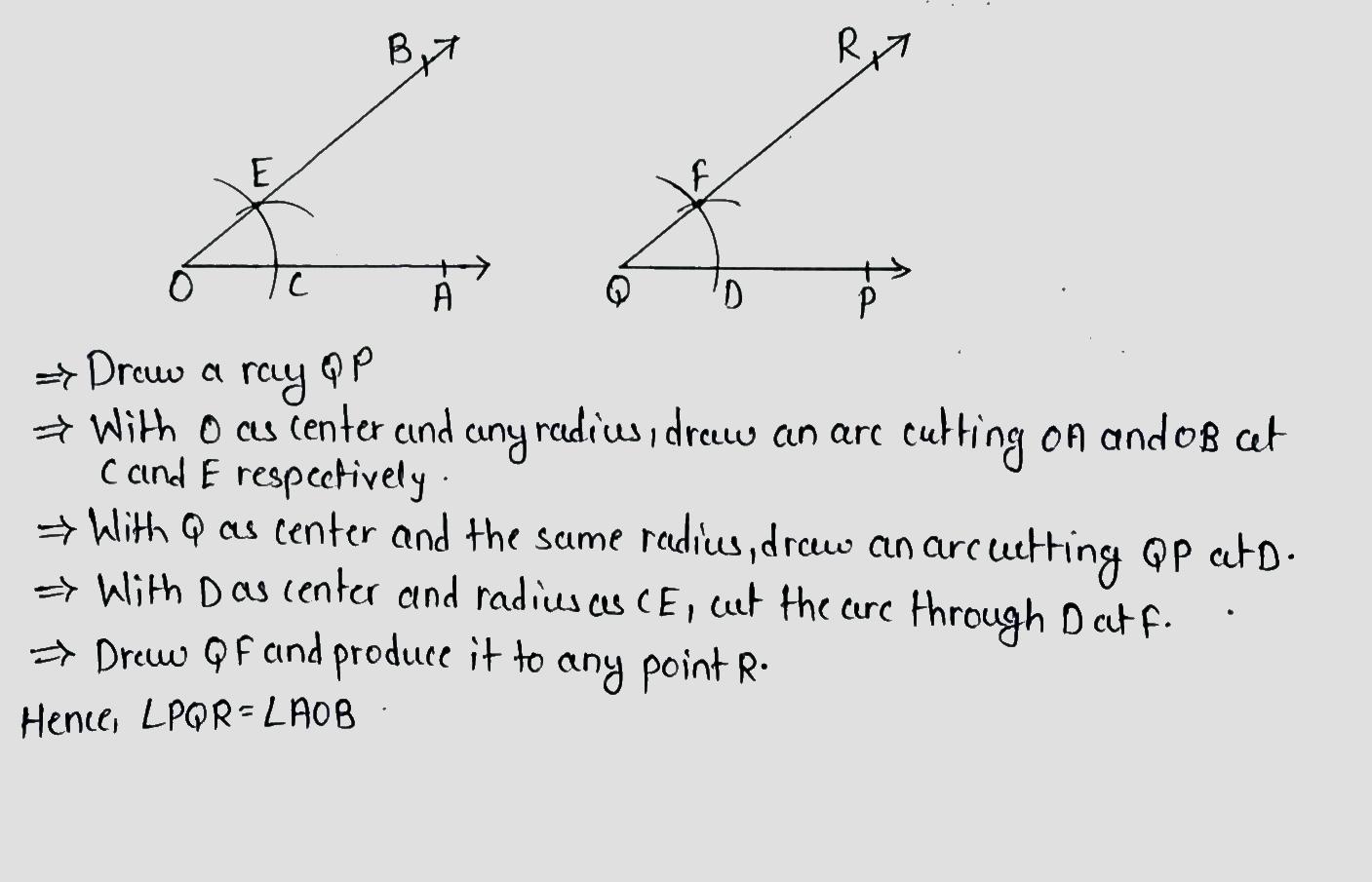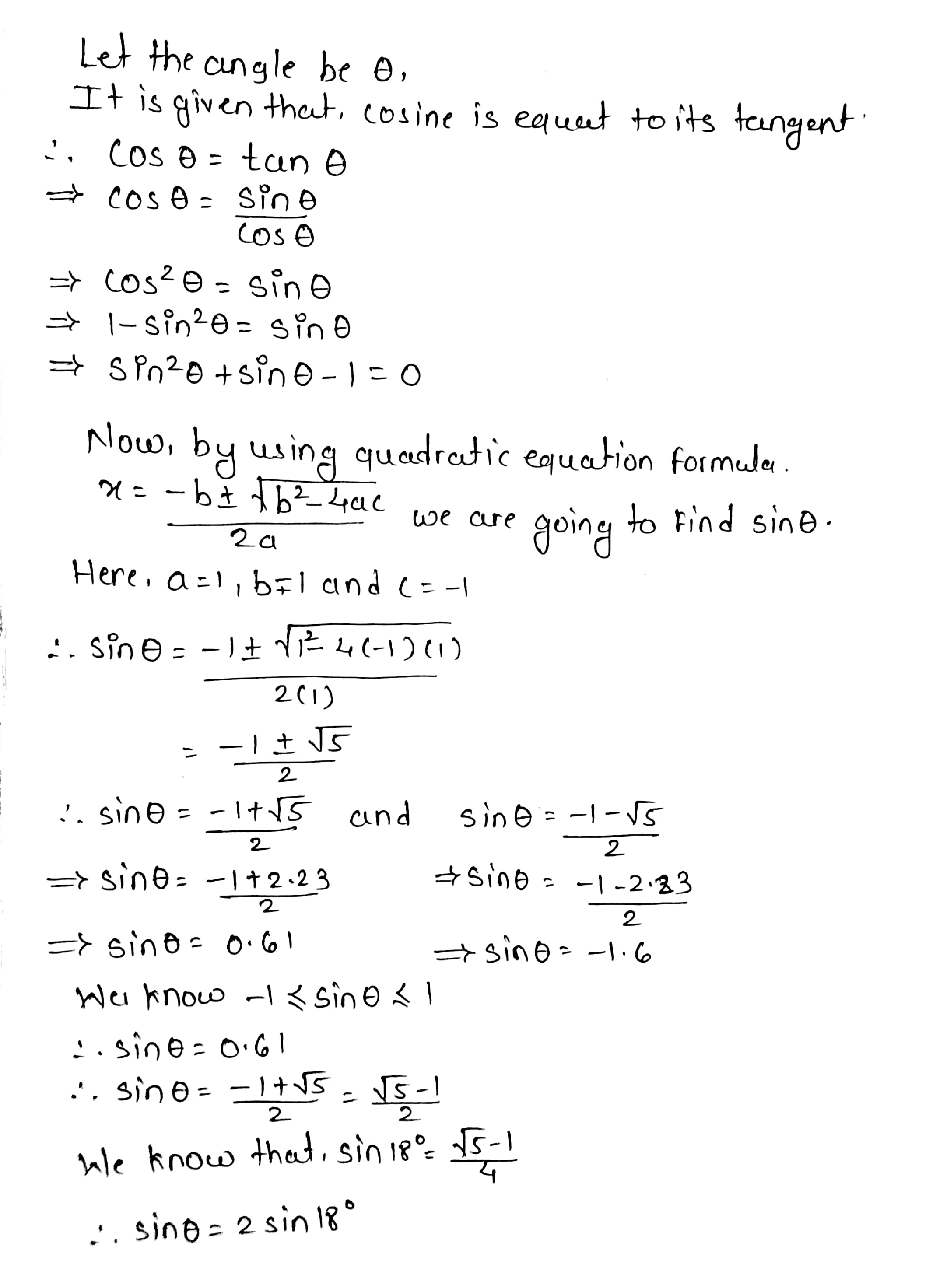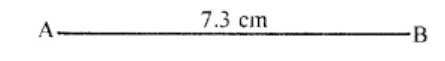Practical Geometry - Class 6 Maths - Extra Questions
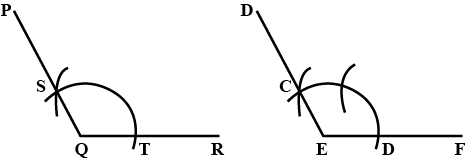
Given a line segment SR of 2.5 cm. Construct a line segment PT perpendicular to SR.
In the figure $$A=S,B=R,C=P,D=R$$
Draw a line segment $$SR=2.5 cm$$
Open compass and draw curve upper and down side of line $$SR$$ at point $$S$$ and $$R$$
These curves cut each other at $$P$$ and $$T$$ as shown in the figure
Join $$P$$ to $$T$$ line
$$PT$$ is the line perpendicular to $$SR$$
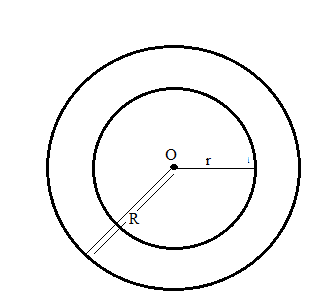
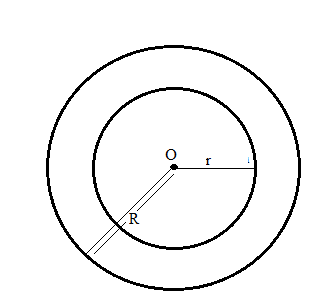
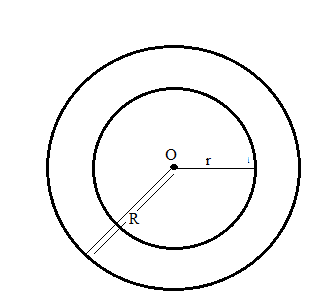
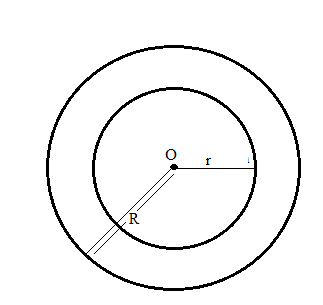
Draw concentric circles having radii 3.5 cm and 5.5 cm . Find out the width of circular ring.
Step 1 - Draw a circle with radius $$r=3.5$$ cm and name the centre as $$O$$.
Step 2- Taking $$O$$ as the centre, draw another circle of radius $$R=5.5$$ cm.
Then, the figure results into concentric circles with radius $$5.5$$ and $$3.5$$ cm.
Then width of circular ring $$=R-r=5.5-3.5=2$$ cm
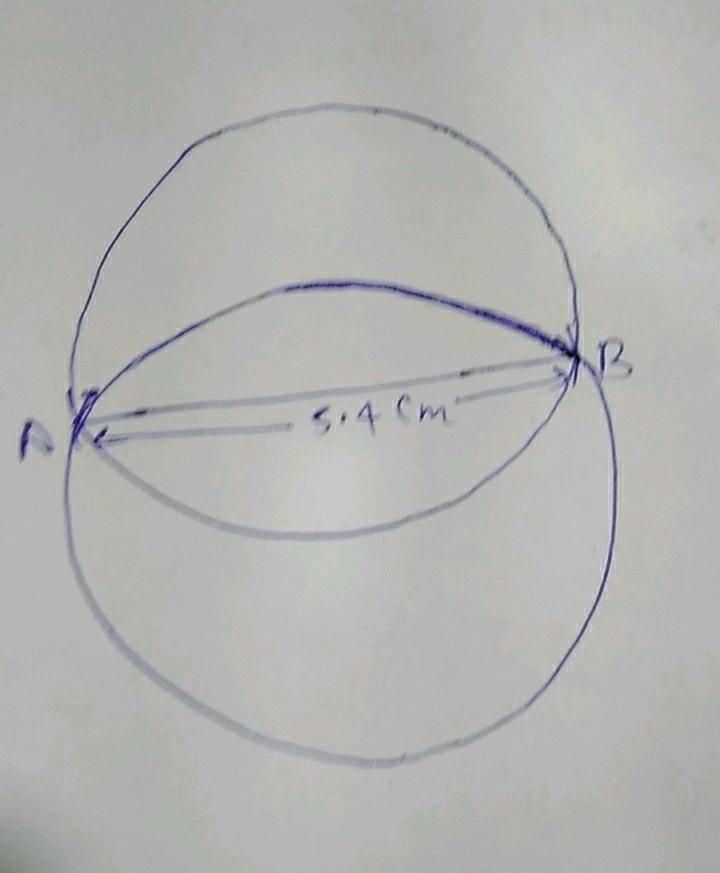
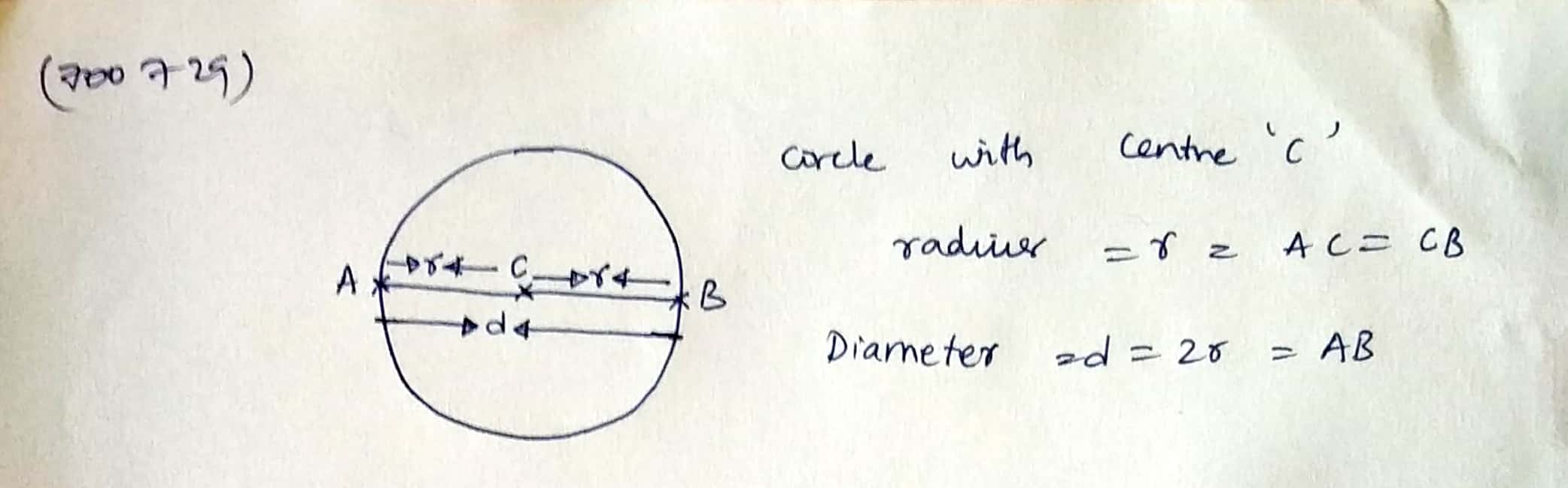
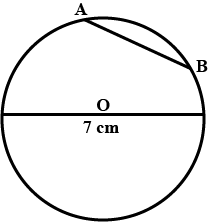
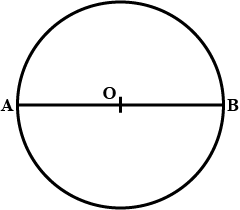
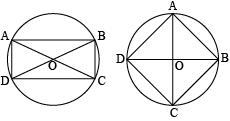
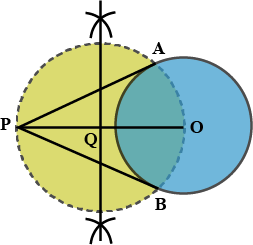
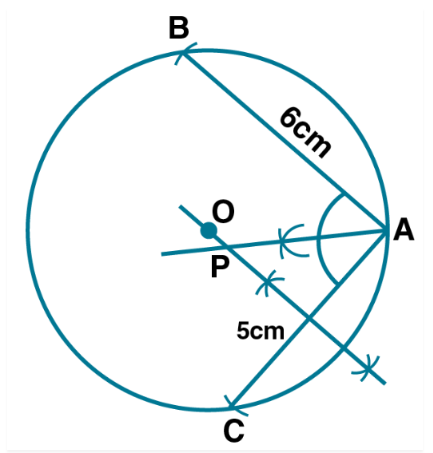
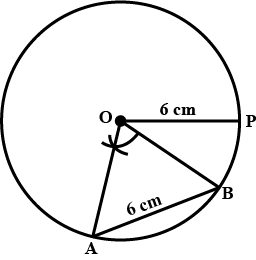
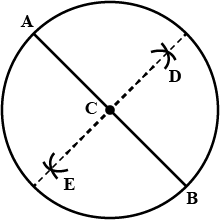
Draw two circles passing through A, B where AB = 5.4 cm
Draw concentric circle for the radii measuring 5.3 cm and 7 cm. Find out the width of circular ring.
Step 1 - Draw a circle with radius $$r=5.3$$ cm and name the centre as $$O$$.
Step 2- Taking $$O$$ as the centre, draw another circle of radius $$R=7$$ cm.
Then, the figure results into concentric circles with radius $$7$$ and $$5.3$$ cm.
So, width of circular ring $$=R-r$$
$$=7-5.3$$
$$=1.7$$ cm
Draw concentric circle for the radii measuring $$5\ cm$$ and $$6.5\ cm$$. Find out the width of circular ring.
Step 1 - Draw a circle with radius $$r=5\ cm$$ and name the centre as $$O$$.
Step 2- Taking $$O$$ as the centre, draw another circle of radius $$R=6.5\ cm$$.
Then, the figure results into concentric circles with radius $$6.5$$ and $$5\ cm$$ .
Then width of circular ring $$=R-r=6.5-5=1.5\ cm$$
Draw a circle and name its centre, a radius, a diameter and arc.
Circle with centre 'C'
radius$$=r=AC=CB$$
Diameter$$=d=2r=AB$$.
Draw a circle $$4.5\ cm$$ radius & divide the circle in $$8$$ equal parts.
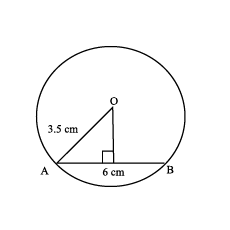
Draw a circle of radius 3.5 cm and construct a chord of length 6 cm in it. Measure and write the distance between the centre and the chord.
$$\text{OA is the radius of circle & AB is the chord}$$
$$\text{Now draw a perpendicular line from the chord to the centre of circle}$$$$\text{Let us say the point on the chord 'D' }$$
$$\text{Now we can see two triangles }\Delta OAD \text{ &} \Delta OBD$$
$$\text{In these two triangles we see that OA = OB & OD is common, So by the properties of triangles AD = DB = 3 cm}$$
$$\text{Now applying pythagoras theorem in triangle OAD (because it is a right angle triangle)}$$
$$AO^2=AD^2+OD^2$$
$$(3.5)^2=3^2+OD^2$$
$$OD^2=12.25-9=3.25\text{ cm}$$
$$OD=1.80\text{ cm}$$
Draw a line segment of length $$7.2\ cm$$ and divide it in the ratio $$5:3$$. Measure the two parts.
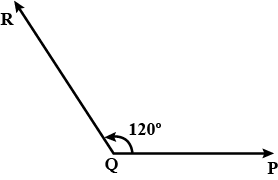
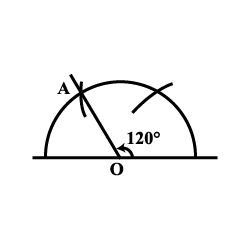
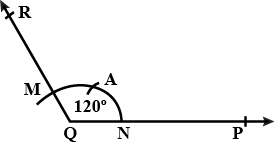
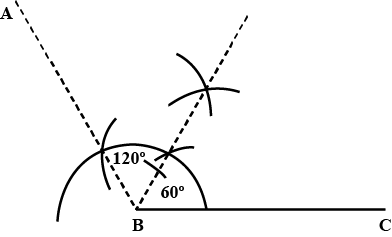
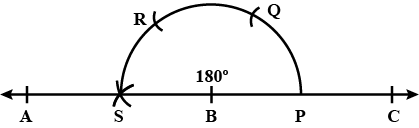
Draw an $$\angle PQR$$ of $$120^o$$.
draw a straight line parallel to the plane
Using compass measure 120 and mark a point
Draw a line joining the point to the straight line.
Mark the points as P,Q and R respectively.
Marking $$\angle Q=120^{\circ}$$
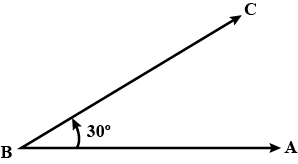
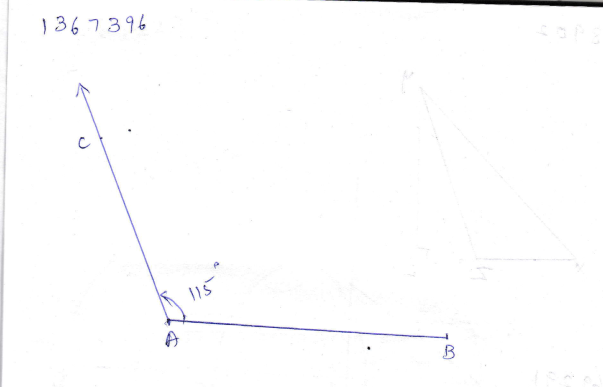
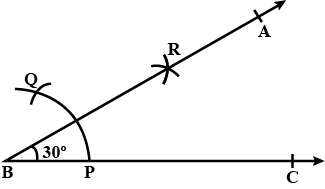
Draw an $$\angle ABC$$ of $$30^0$$.
draw a straight line parallel to the plane
Using compass measure 30 and mark a point
Draw a line joining the point to the straight line.
Mark the points as A,B and C respectively.
Marking ∠B=30∘
Draw a line segment of length $$7.3$$ cm using a ruler.
Draw a line $$l$$
Mark a point $$A$$ on the line.
From point $$A$$ using compass draw an arc of length of $$7.3$$cm
Mark that point as $$B$$
Hence, $$AB$$ is a line segment of length $$7.3$$cm
Sketch proper figure and answer the questions :
If A-B-C and $$\ell (AC) = 11 , \, \ell (BC) = 6.5 \,\, then \,\, \ell (AB)$$ = ?
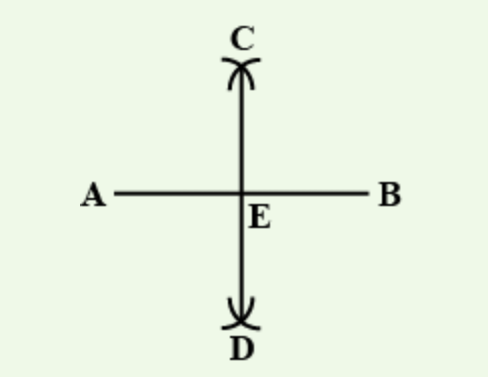
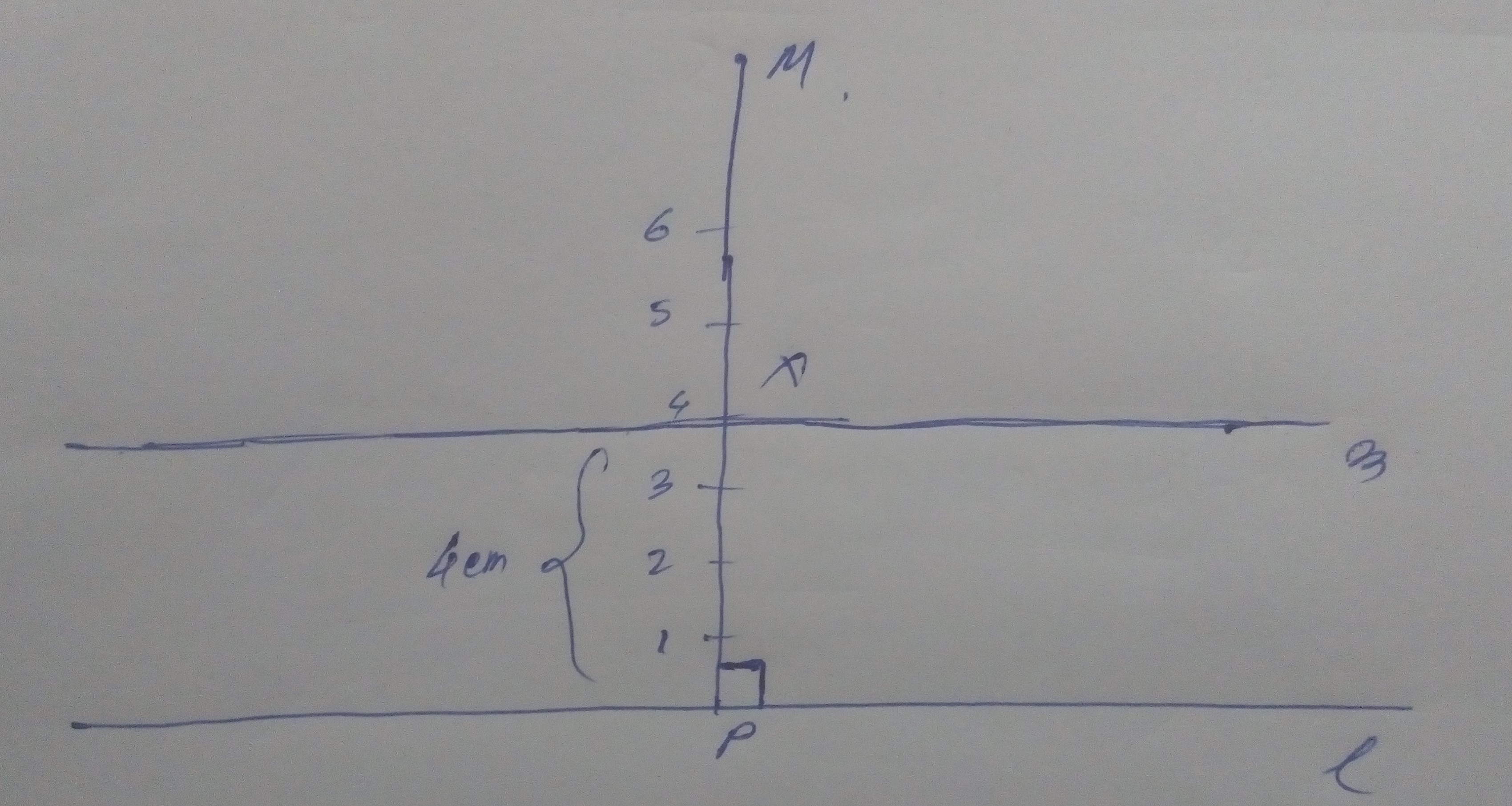
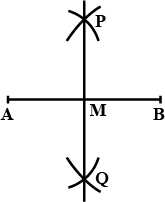
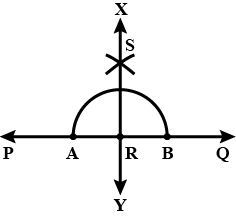
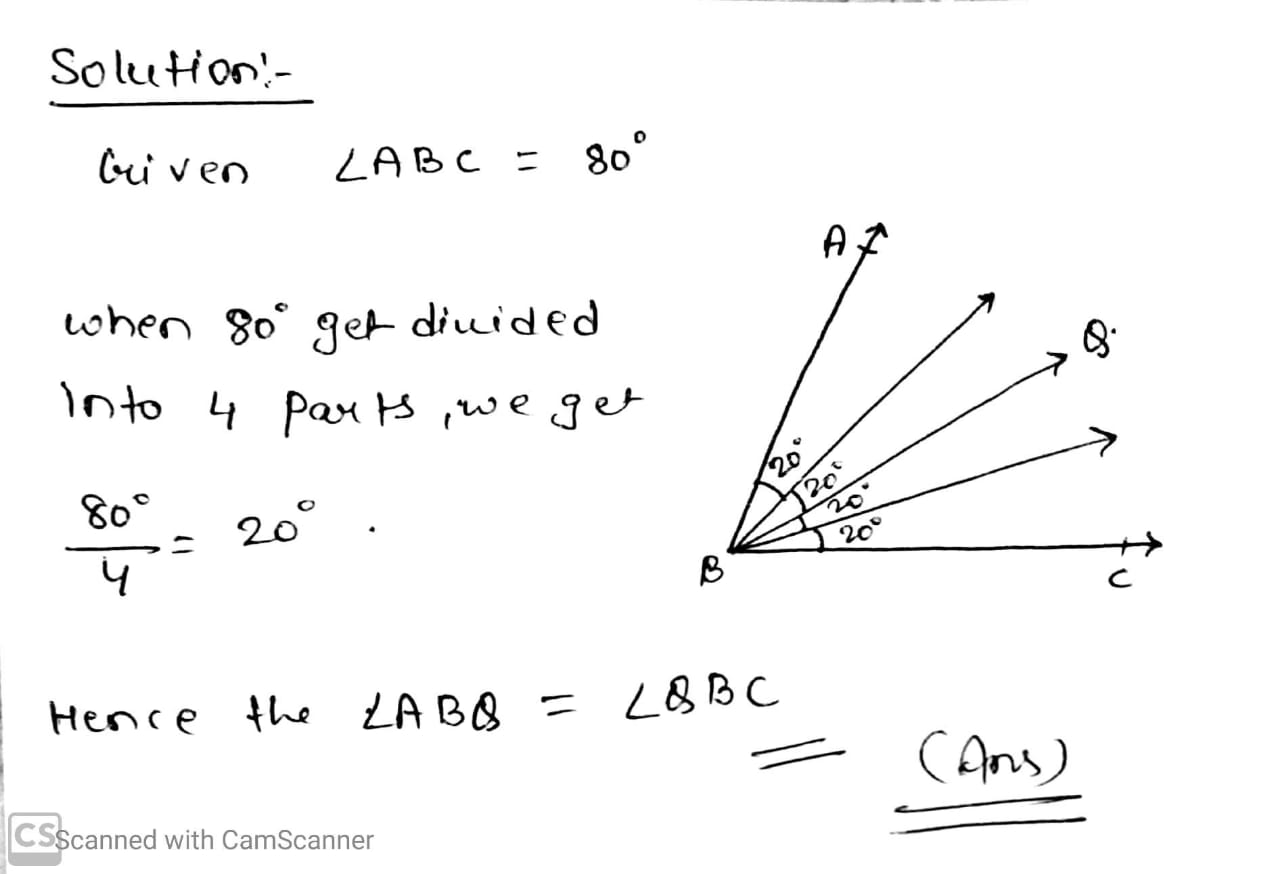
Draw any line segments $$\overline{AB}$$. Mark any point $$M$$ on it. Through $$M$$, draw a perpendicular to $$\overline{AB}$$.
(use ruler and compasses)
R.E.F image
Follow these steps :-
1 Given a line segment AB
mark point M on it
2. Now length A as center and caduis same then AM
draw an arc. Also
with B as center and same cadiun as before draw
an arc.
3. Mark the point of intersection of arc at point
o. Join O and M
Now, MN is $$ \perp$$ (perpendicular) to AB
Draw a line segment $$PQ = 11$$ cm.
Mark a point P
From point P using compass draw arc at a length of 11cm
Mark that point Q
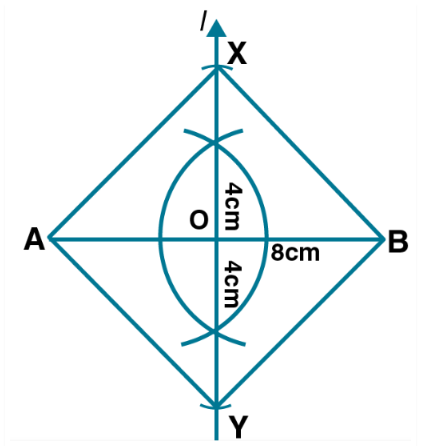
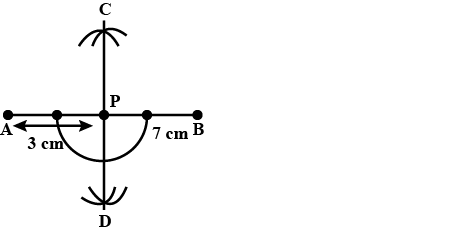
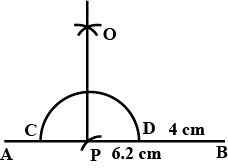
Draw a line AB=6 cm. Draw the locus of all the points which are equidistant from A and B.
Steps of construction:
(i) Draw a line segment $$AB $$ of $$6$$ cm.
(ii) Draw perpendicular bisector $$LM$$ of $$ AB.$$ $$LM$$ is the required locus.
(iii) Take any point on $$LM$$ say $$P$$. i.e. $$PA = PB$$ Hence, Perpendicular bisector of $$AB$$ is the locus of all points which are equidistant from $$A$$ and $$B.$$
(iv) Join $$PA$$ and $$PB.$$ Since, $$P$$ lies on the right bisector of line $$AB.$$ Therefore, $$P$$ is equidistant from $$A$$ and $$B.$$
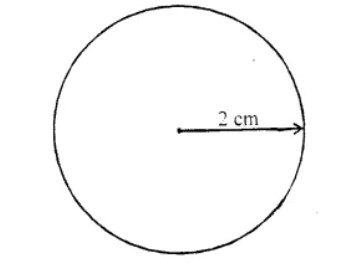
Draw a circle using a compass with the radius $$5$$ cm.
Draw a circle and mark-
(a) its centre (b) a radius (c) a segment (d) its largest chord (e) a sector (f) an arc
In figure,
$$O$$ is center.
$$RO$$ is the radius.
$$AB$$ is the largest chord.
$$AOR$$ is a sector.
$$RB$$ is an arc.
$$PS$$ is a segment.
Hence, this is the answer.
Draw a line segment PQ=$$8$$cm. Take a point R on it such that $$l\left( {PR} \right):l\left( {RQ} \right) = 3:2$$ find PR and RQ.
Given that:
$$l(PR):l(QR)=3:2$$, $$PQ=8cm$$
To find: $$PR$$ and $$RQ$$
Solution:
$$PR=3x$$ and $$QR=2x$$
Point $$R$$ is on $$PQ$$ then,
$$PR+RQ=PQ$$
$$3x+2x=8$$
$$x=1.6cm$$
Hence, $$l(PR)=4.8cm$$ and $$l(RQ)=3.2cm$$
Three equal circles of radius 1 cm touches each other. What is smallest radius of circle touching all three.
Use protector to draw the angle of the following measure and bisect the angle $$90^o$$.
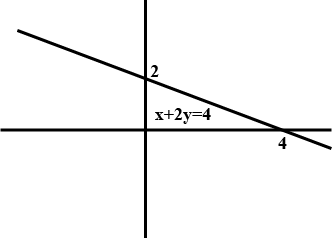
Draw the graph of $$x+2y=4$$
To make the graph, we have to write the Equation in intercept form
Dividing both sides by 4
$$\dfrac x4+\dfrac y2=1$$
Hence, x-intercept will be 4
and y-intercept will be 2
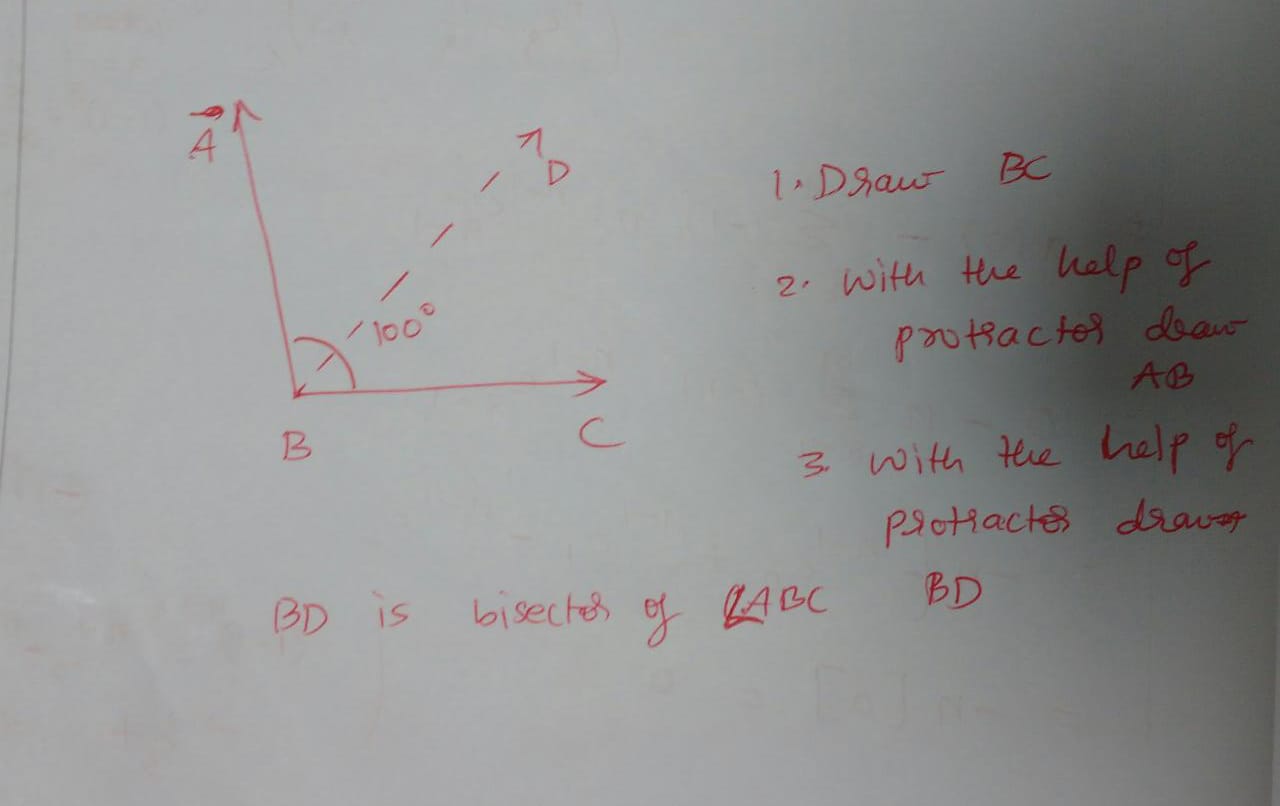
Draw a $$\angle ABC $$ of measure 100$$^{0}$$ . Bisect it.
$$1$$. Draw BC.
$$2$$. With the help of protractor draw AB.
$$3$$. With the help of protractor drawn BD.
BD is bisector of $$\angle$$ABC
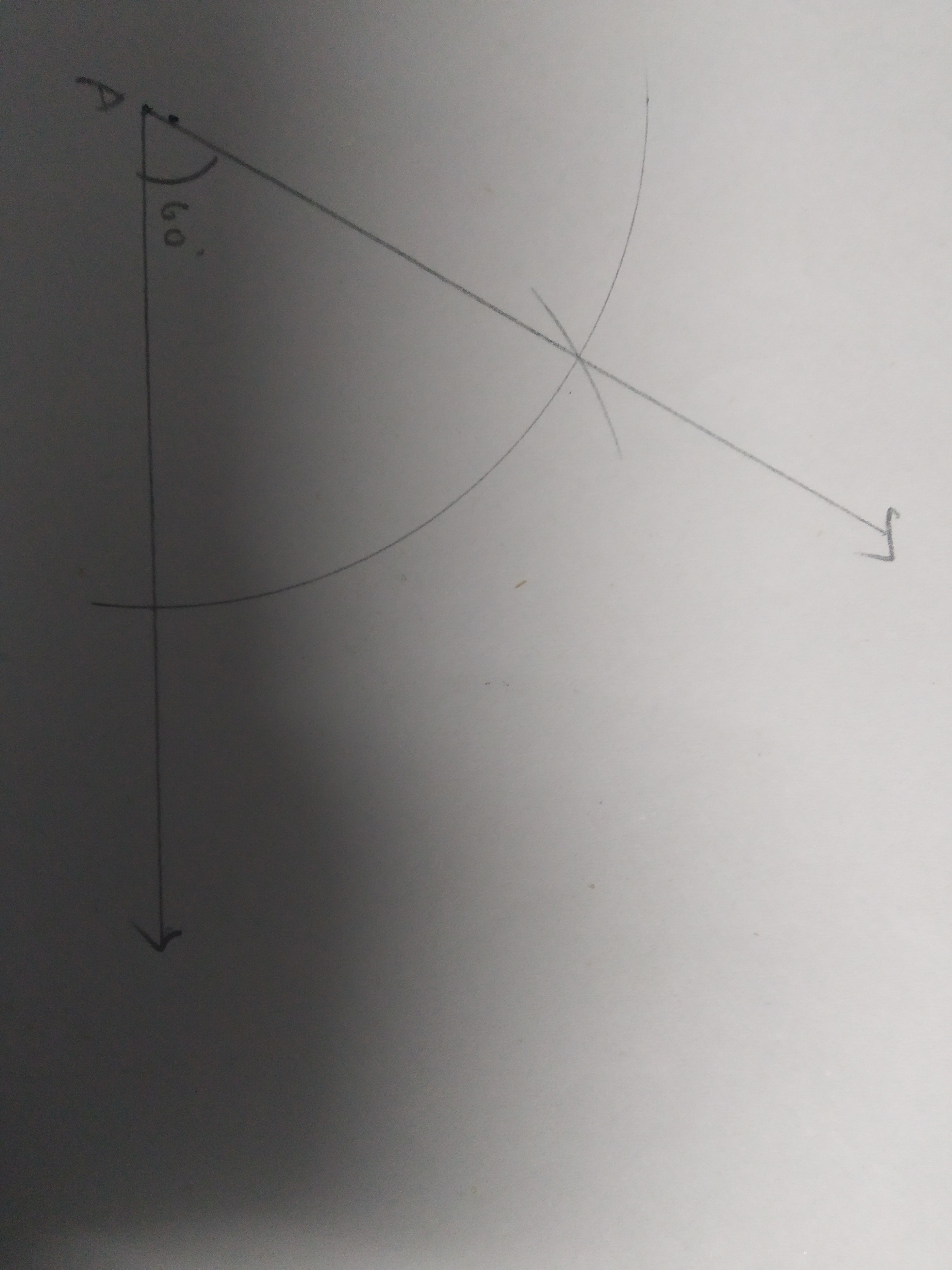
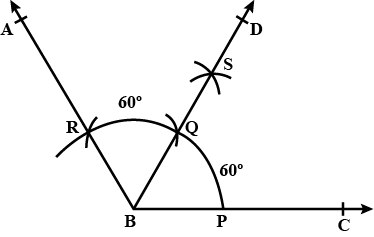
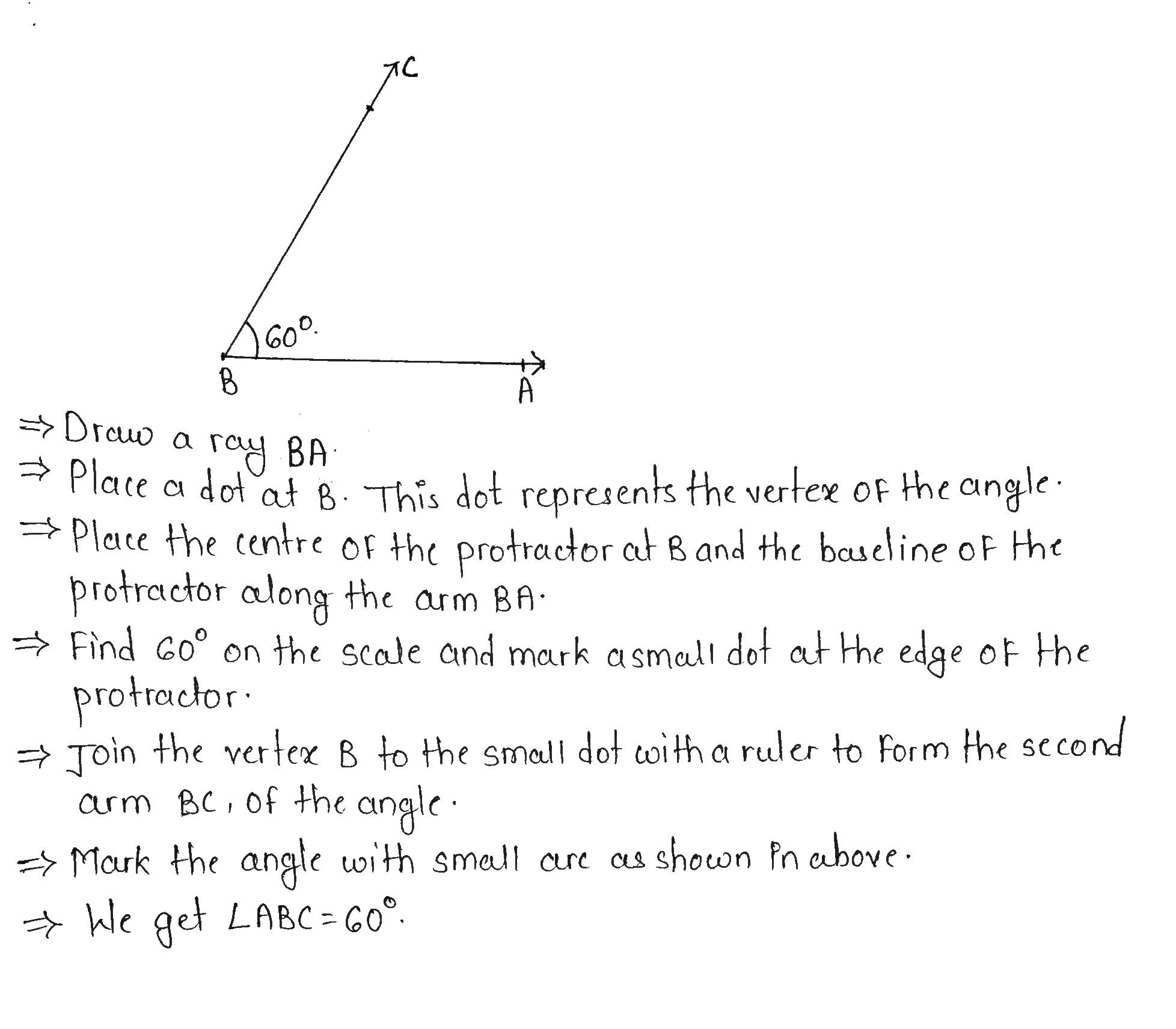
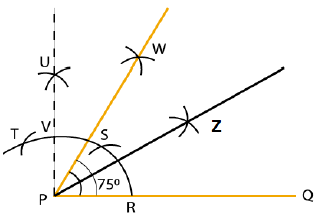
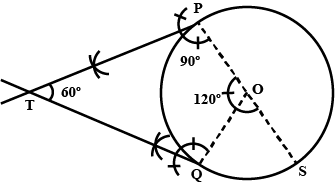
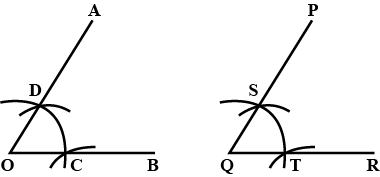
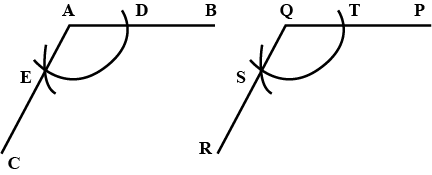
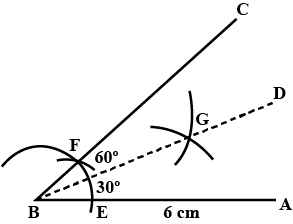
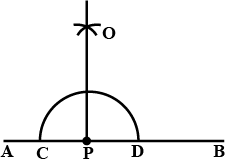
Draw an angle of $$60^{\circ}$$ and name it $$\angle A$$. Using compasses and ruler.
Draw an angle of $$70^{o}$$. Make a copy of it using only a straight edge and compasses.
Ref.Image
steps of construction:
(a) Draw an angle 70 degree with protractor i.e $$\angle $$ POQ = 70 degree
(b) Draw a ray AB
(c) Place the compasses at O and draw an arc to cut rays of $$\angle $$ POQ at L and M.
(d) Use the same compasses, setting to draw an arc A as center, cutting AB, at x.
(e) Set your compasses setting to the length LM with same radius.
(f) Place the compasses pointer at x and draw the arc to cut the arc drawn earlier at y.
(g) Join AY .Thus $$\angle $$ YAX = 70 degree.
Draw $$\overline {AB}$$ of length $$7.3\ cm$$ and find its axis of symmetry.
Let's first draw a line segment of length 7.3 cm .
1) Draw a line l, mark point A on it.
2) Since length is 7.3 cm, we measure 7.3 cm using ruler and compass.
3) Now keeping compass opened the same length, we keep pointed end at point A and draw an arc on line l.
So, the required line segment is AB = 7.3 cm .
Now, we need to find its axis of symmetry.
1) Given a line segment AB.
2) Now with A as centre, and radius more than half AB, draw an arc on top and bottom of AB.
3) Now with B as centre, and same radius, draw an arc on top and bottom of AB.
4) Where the two arcs intersect above AB is point C and where the two arcs intersect below AB is point D.
Join CD.
CD is the line of symmetry of line segment AB.
Draw a line segment of length $$4.9$$ cm and divide it in the ratio $$3:4$$ , measure the two parts.
Steps of construction:
1)Draw a line segment AB=4.9 cm.
2)Draw any ray making an acute angleangleBAXangleBAX at A3 intersecting AB at C.
The point C so obtained is the required point, which divides AB internally in the ratio 3:4.
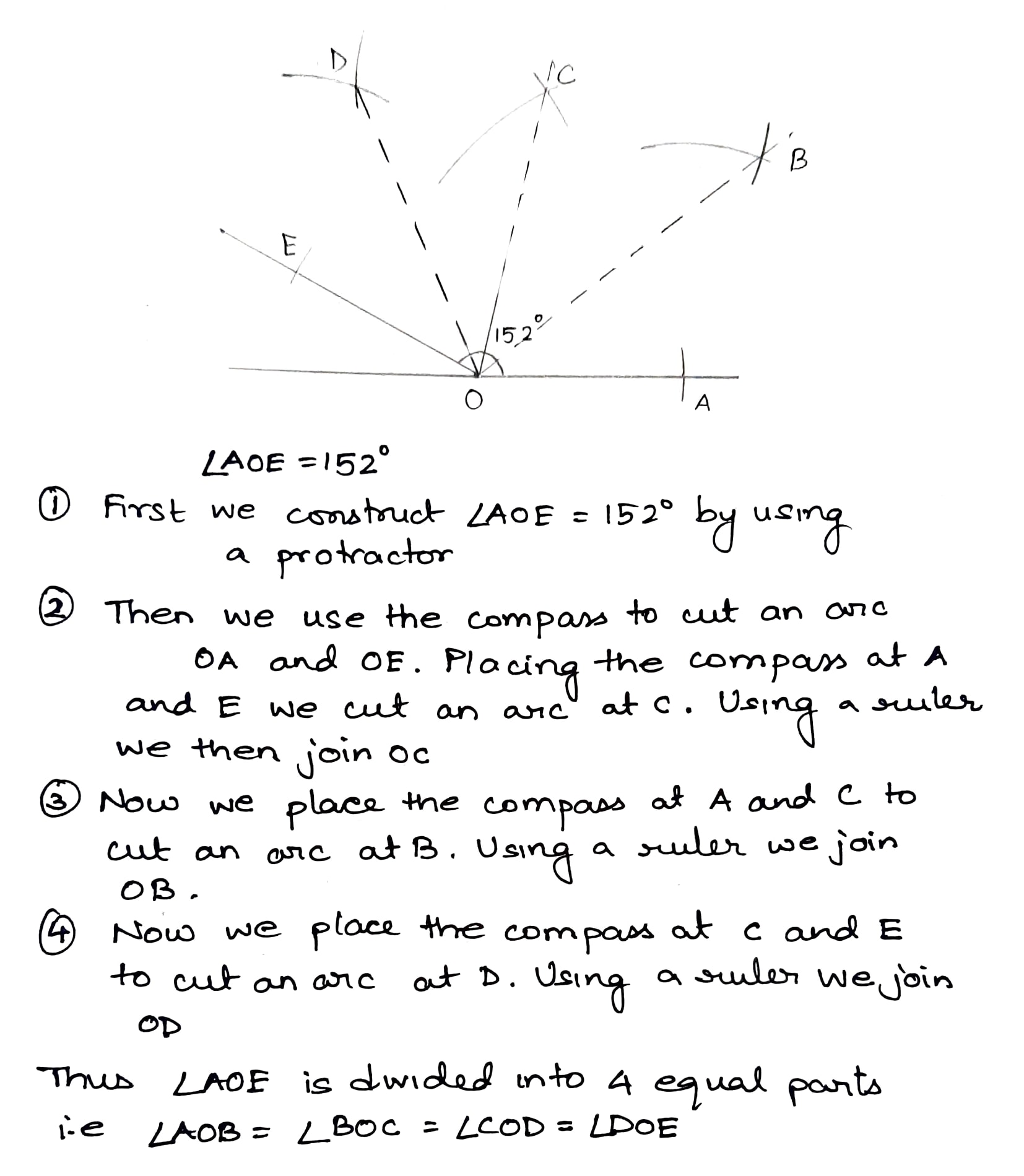
Draw an angle of measure $${153}^{\circ}$$ using protractor.
$$1.$$Draw a ray $$BC$$
$$2.$$Place center of protractor on point $$B,$$ and coincide line $$BC$$ and protractor line.
$$3.$$Mark point $$A$$ on $${153}^{\circ}$$
$$4.$$Join $$AB$$
$$\therefore \angle{ABC}={153}^{\circ}$$
Construct with ruler and compasses, angle of the following measure:
$$120^{o}$$
Step 1: $$A$$ ray from $$O$$ is drawn.
Step 2: Construct an arc from $$O$$ and with the same measurement construct $$2$$ arcs from the previous arcs.
Step 3: Join $$OA$$
$$\therefore \angle{AOX}={120}^{\circ}$$
Thus,$$\angle{AOX}$$ is the required angle making $${120}^{\circ}$$
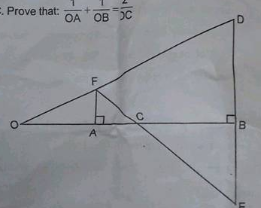
In the figure,OB is the perpndicular bisector of the line segment DE, $$FA\perp OB $$ and E intersects OB at the point C. Prove that $$\dfrac{1}{OA}+\dfrac{1}{OB}=\dfrac{2}{OC}$$
Draw a line segment $$PQ=4\ cm$$. Draw a perpendicular bisector to $$PQ$$
$$1.$$Draw a straight line $$PQ=4$$cm
$$2.$$Using compass bisect the line $$PQ$$
Result:$$PA=AQ=2$$cm is the required perpendicular bisector.
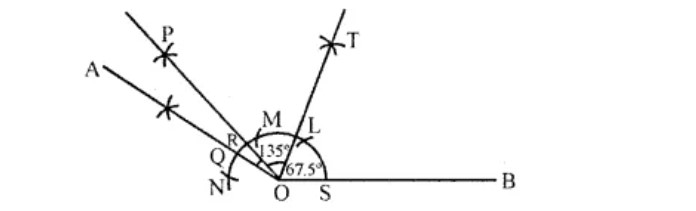
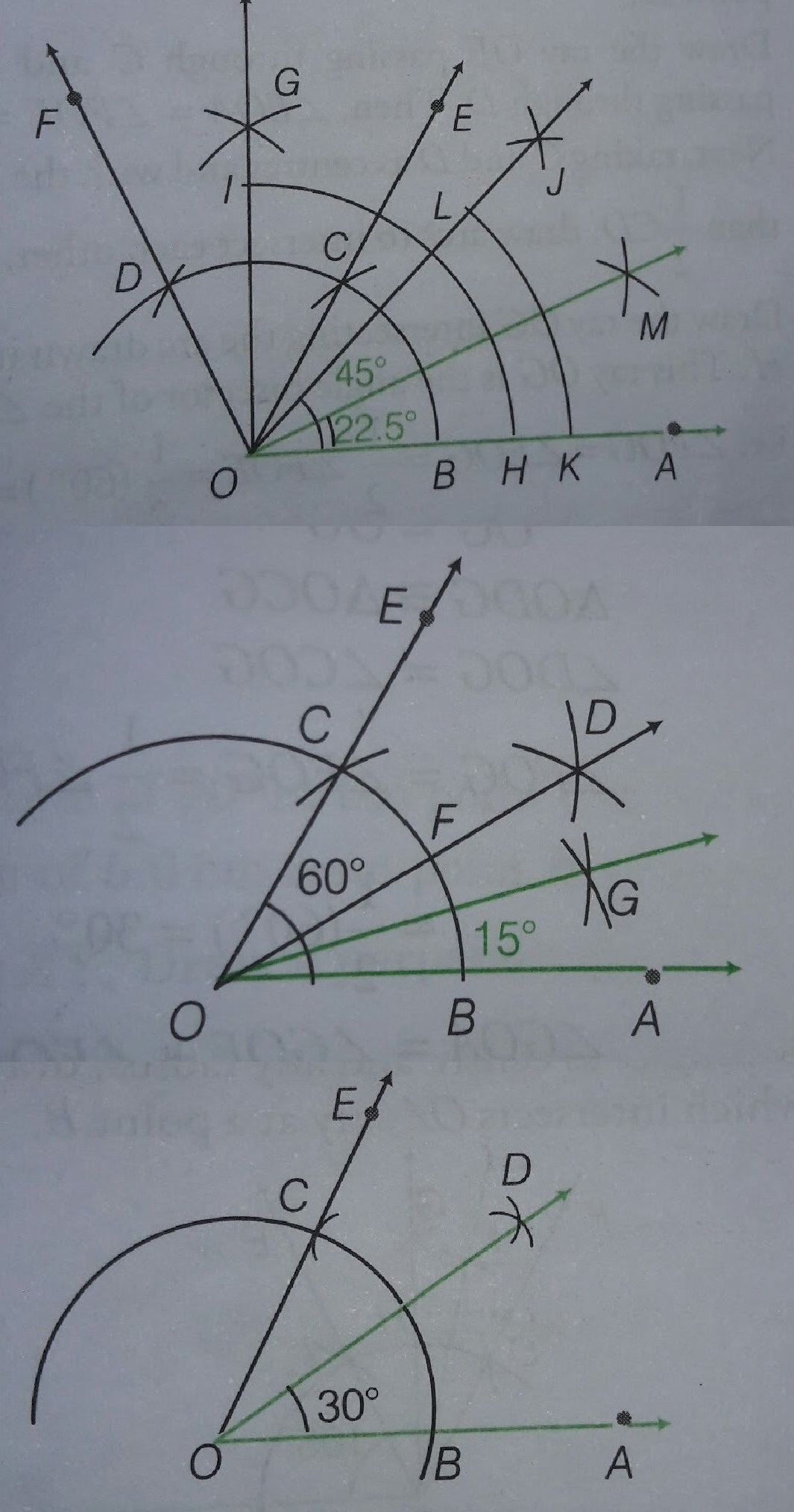
Explain how to use a pair of compasses to construct $$67\dfrac{1}{2}^{o}$$.
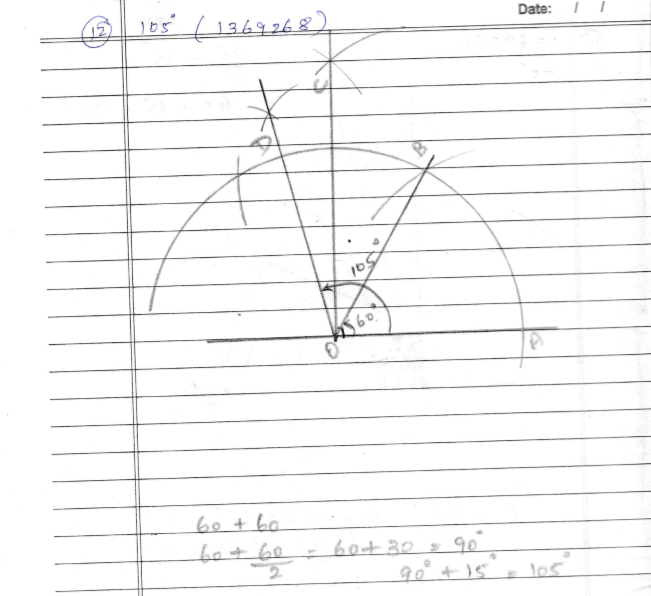
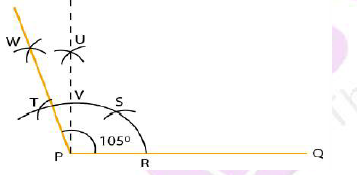
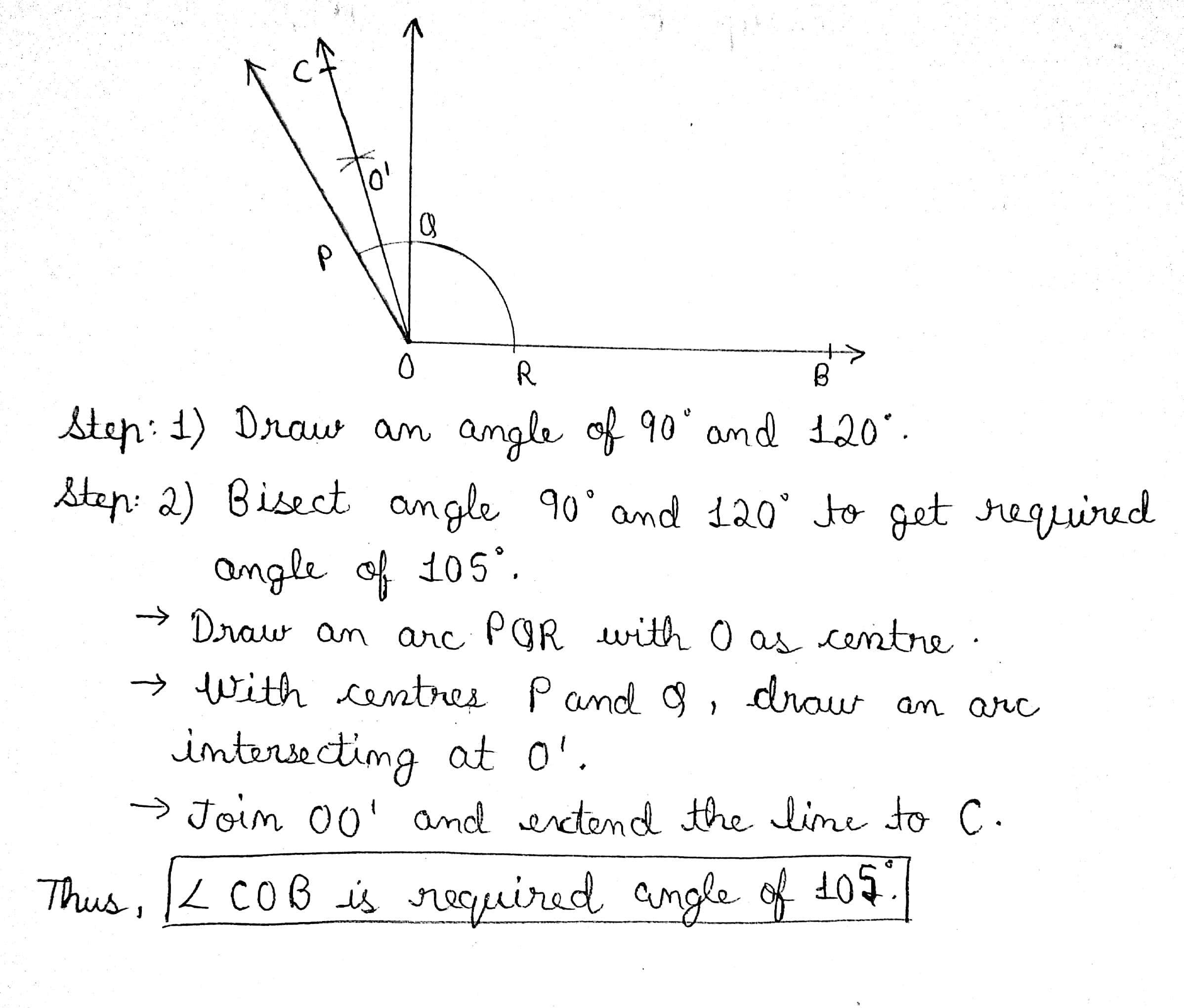
Explain how to construct $$105^{o}$$ using a pair of compasses.
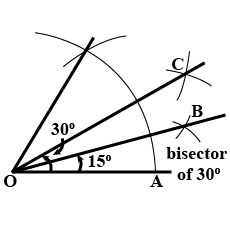
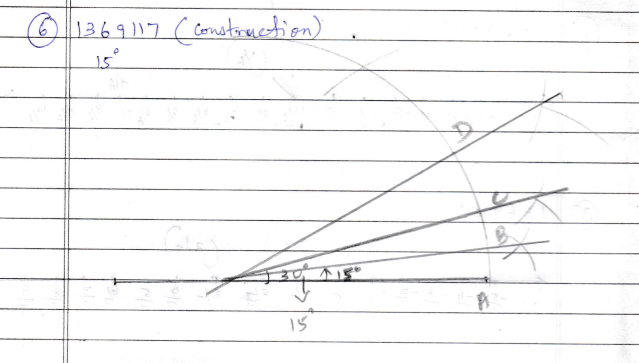
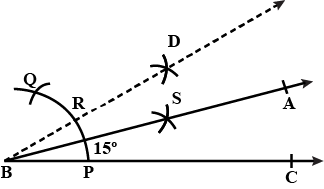
Explain how to construct $$15^{o}$$ using a pair of compasses.
If AB = 3 cm then draw 3 AB
We know if AB $$=3 cm $$
Then 3 AB $$=(3\times{3})cm=9cm$$
Step of construction -
Draw a line segment of measure 9 cm using a ruler
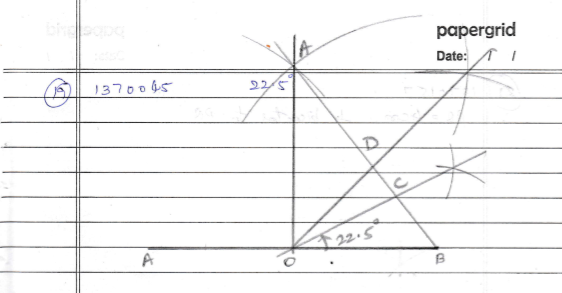
Explain how to construct $$22\dfrac{1}{2}^{o}$$ using a pair of compasses.
Explain how to draw an obtuse angle using protractor.
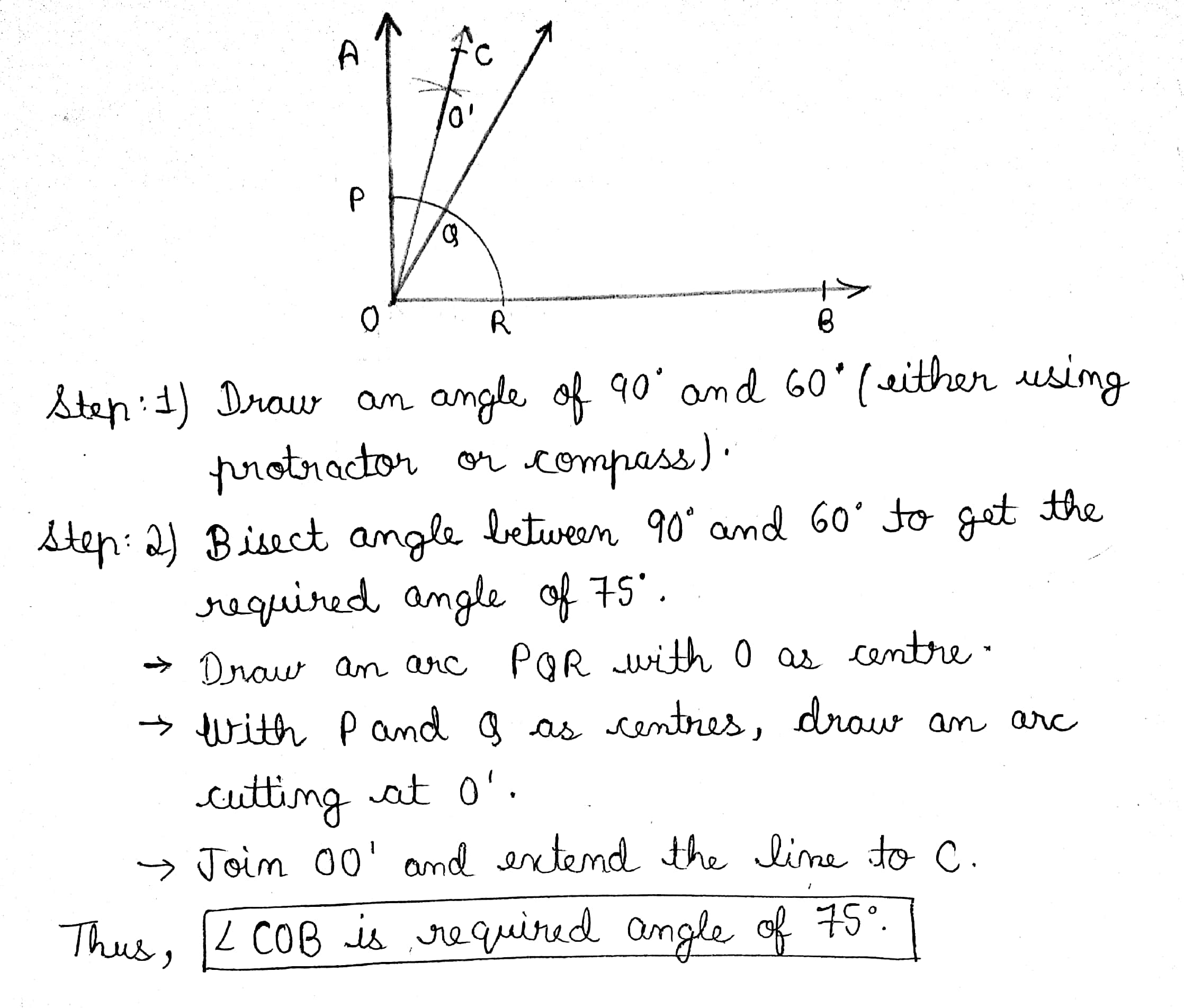
Explain how to construct $$75^{o}$$ using a pair of compasses.
Explain how to draw an acute angle using protractor.
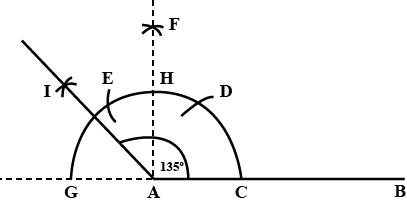
Explain how to construct $$135^{o}$$ using a pair of compasses.
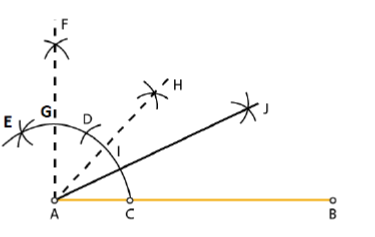
Explain how to use a pair of compasses to construct $$45^{o}$$.
Draw the following angles using compasses.
$${ 165 }^{ \circ }$$
$$1.$$Draw a line segment $$AB=6$$cm.Mark a point $$O$$ where $$AO=OB=3$$cm
$$2.$$From $$B$$ draw an arc.Name it as $$C$$
$$3.$$From $$C$$ draw another arc of same length as $$BC$$
$$4.$$Bisect the arc $$DA$$.Join $$EO$$
$$\therefore\,\,\angle{EOB}={120}^{\circ}$$
$$5$$Bisect $$\angle{EOA}=\dfrac{{30}^{\circ}}{2}={15}^{\circ}$$.Join $$OF$$
$$\therefore \angle{BOF}={60}^{\circ}+{60}^{\circ}+{30}^{\circ}+{15}^{\circ}={165}^{\circ}$$
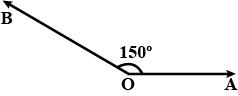
Construct an angle $${ 150 }^{ \circ}$$ using protractor and scale.
Step-$$1:$$ Draw a line segment $$OA$$
Step-$$2:$$ Place the midpoint of the protractor at point $$O$$.
Step-$$3:$$ On $$OA$$, from the right, start counting from $${0}^{\circ}$$ in the ascending order and mark a point $$B$$ using a sharp pencil at the point showing $${150}^{\circ}$$ on the semi-circular edge of the protractor.
Step-$$4:$$ Remove the protractor and join $$OB$$ using the scale.
Hence, $$\angle{AOB}={150}^{\circ}$$ is the required angle.
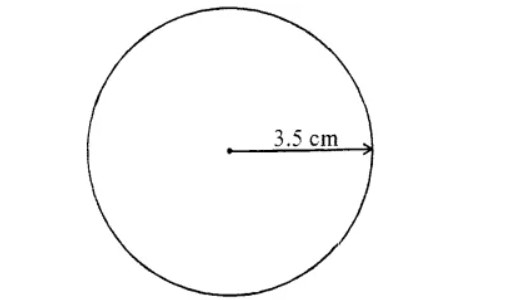
Draw a circle of radius $$3.2$$cm.
The required circle can be drawn as follows.
Step $$1$$
First, open the compasses for the required radius $$3.2$$cm.
Step $$2$$
Make a point 'O' where we want the centre of the circle to be.
Step $$3$$
Picture the pointer of compasses on O.
Step $$4$$
Turn the compasses slowly to draw the circle.
Step $$1$$
First, open the compasses for the required radius $$3.2$$cm.
Step $$2$$
Make a point 'O' where we want the centre of the circle to be.
Step $$3$$
Picture the pointer of compasses on O.
Step $$4$$
Turn the compasses slowly to draw the circle.
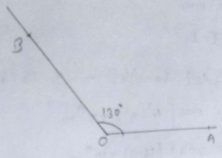
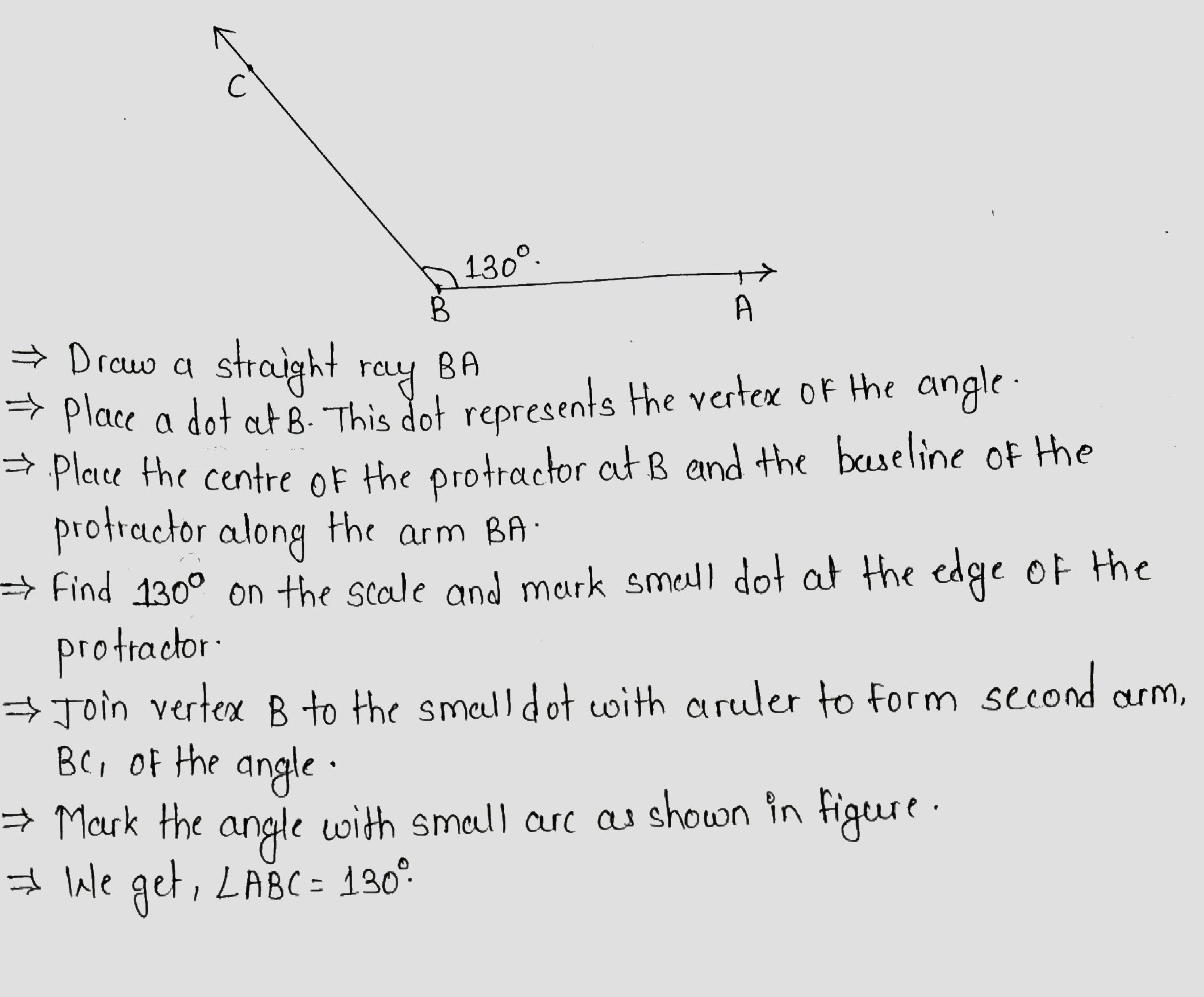
Construct an angle of $${ 130 }^{ 0 }$$ using protractor.
Step-$$1$$Draw a line segment $$OA$$
Step$$2$$Place the mid-point of the protractor at point $$O$$.
Step-$$3$$On $$OA$$ from the right start counting from $${0}^{\circ}$$ in the ascending order mark a point $$B$$ using a sharp pencil at the point showing $${130}^{\circ}$$ on the semi-circular edge of the protractor.
Step-$$4$$Remove the protractor and join $$OB$$.
Result: $$\angle{AOB}={130}^{\circ}$$ is the required angle.
Draw an angle of $$ 70 ^ { \circ } $$. Make a copy of it using only a straight edge and compasses.
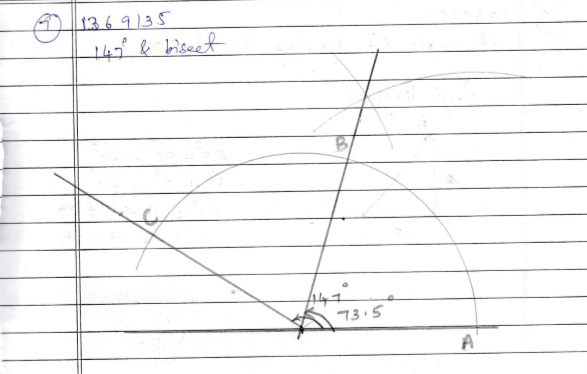
Draw an angle of measure $$147^o$$ and construct its bisector.
The below-given steps will be followed to construct an angle of $$147^o$$ measure and its bisector.
$$(1)$$ Draw a line $$l$$ and mark a point O on it. Place the center of the protractor at point O and the zero edge along line $$l.$$
$$(2)$$ Mark a point A at $$147^o$$. Join OA. OA is the required ray making $$147^o$$ with line $$l$$.
$$(3)$$ Draw an arc of convenient radius, while taking point O as center. Let it intersects both rays of angle $$147^o$$ at point A and the line $$l$$ at B.
$$(4)$$ Taking A and B as centers, draw arc of radius more than half of the length of AB in the interior of angle of $$147^o$$. Let those intersect each other at C. Join OC.
OC is the required bisector of $$147^o$$ angle.
$$(1)$$ Draw a line $$l$$ and mark a point O on it. Place the center of the protractor at point O and the zero edge along line $$l.$$
$$(2)$$ Mark a point A at $$147^o$$. Join OA. OA is the required ray making $$147^o$$ with line $$l$$.
$$(3)$$ Draw an arc of convenient radius, while taking point O as center. Let it intersects both rays of angle $$147^o$$ at point A and the line $$l$$ at B.
$$(4)$$ Taking A and B as centers, draw arc of radius more than half of the length of AB in the interior of angle of $$147^o$$. Let those intersect each other at C. Join OC.
OC is the required bisector of $$147^o$$ angle.
With the same centre O, draw two circles of radii $$4$$cm and $$2.5$$cm.
The required circle can be drawn as follows.
Step $$1$$
First, open the compasses for the required radius $$4$$cm.
Step $$2$$
Make a point 'O' where we want the centre of the circle to be.
Step $$3$$
Place the pointer of compasses on O.
Step $$4$$
Turn the compasses slowly to draw the circle.
Step $$5$$
Now, open the compasses for $$2.5$$cm.
Step $$6$$
Again put the pointer of the compasses on point 'O' and turn the compasses slowly to draw the circle.
Step $$1$$
First, open the compasses for the required radius $$4$$cm.
Step $$2$$
Make a point 'O' where we want the centre of the circle to be.
Step $$3$$
Place the pointer of compasses on O.
Step $$4$$
Turn the compasses slowly to draw the circle.
Step $$5$$
Now, open the compasses for $$2.5$$cm.
Step $$6$$
Again put the pointer of the compasses on point 'O' and turn the compasses slowly to draw the circle.
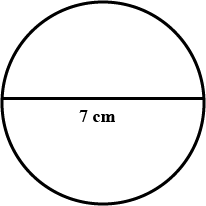
In the space, draw a circle with diameter $$7$$cm. On your diagram, draw a chord.
Why it better to use a divider and a ruler than a ruler only, while measuring the length of a line segment?
In the space, draw a circle with diameter $$7$$cm.
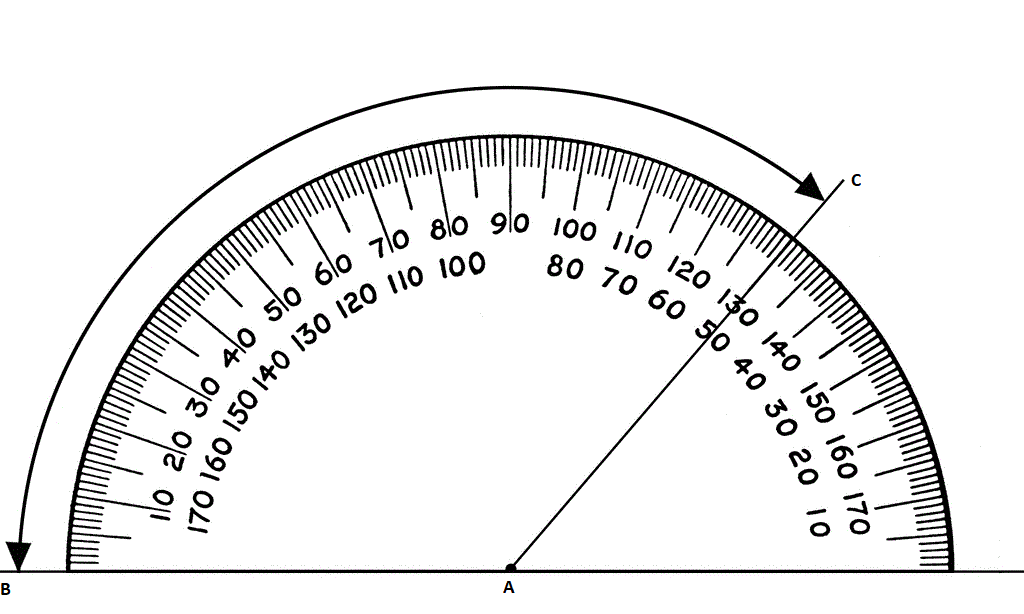
Use your protector to measure each of the angles marked in the following figures:
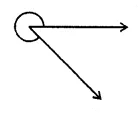
Use your protector to measure the reflex angles marked in the following figures:
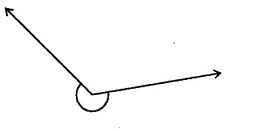
Use your protector to measure the reflex angles marked in the following figures:
The common properties in the two set-squares of a geometry box are that they have a ________ angle and they are of the shape of a ______ .
Draw rough diagrams of two angles such that they have
Two point in common.
$$\angle AOB$$ and $$\angle OBC$$ have two points $$O$$ and $$B$$ in common.
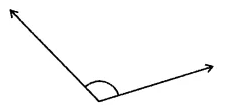
Use your protector to measure each of the angles marked in the following figures:
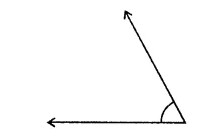
Use your protector to measure each of the angles marked in the following figures:
Draw an angle of $$ 80^{\circ} $$ using a protractor and divide it into four equal parts, using ruler and compasses. Check your construction by measurement.
The diagram will be as shown above.
Step I- With the help of protractor, draw an angle of $$ 80^{\circ}$$. Name the rays $$OA$$ and $$OB$$.
Step II - Cut $$OA$$ and $$OB$$ at $$Q$$ and $$P$$, taking $$O$$ as the center and any convenient radius, with the help of the compass.
Step III - With vertex $$P$$, by using compass take more than half of arc $$PQ$$ and draw arc.
Step IV - With vertex $$Q$$, by using compass with same length, cut the previous arc at $$R$$.
Step V- With help of ruler, join the point $$O$$ and $$R$$.
$$ \therefore $$ $$ \angle AOR = \angle ROB $$
Step VI - Similarly, bisect the arcs $$QS$$ and $$SP$$
$$ \therefore $$ $$ \angle AOV = \angle VOR $$ and $$ \angle ROU = \angle UOB $$
Thus, $$ \angle AOV $$, $$ \angle VOR $$, $$ \angle ROU $$ and $$ \angle UOB $$ divide $$ \angle BOA $$ in four equal parts
You can verify this by using a protractor.
$$ \therefore \ \angle AOV = \angle VOR = \angle ROU = \angle UOB = 20^{\circ} $$
Hence, this is the required construction.
Draw an angle of $$ 80^{\circ} $$ using a protractor and divide it into four equal parts, using ruler and compasses. Check your construction by measurement
Steps of construction:
Step I- With the help of protractor, draw $$ \angle 80^{\circ} $$.
Step II - cut OA and OB at Q and P, taking P as the center and any convenient radius.
Step II - With vertex P, by using compass take more than half of arc PQ and draw arc.
Step III - With vertex Q , by using compass with same length, cut the previous arc at R.
Step IV- With help of ruler join the point O and R.
$$ \therefore $$ $$ \angle AOR $$ = $$ \angle ROB $$
Step V - similarly, bisect the arcs QS and SP
$$ \therefore $$ $$ \angle AOV $$ = $$ \angle VOR $$ And $$ \angle ROU $$ = $$ \angle UOB $$
Thus, $$ \angle AOV $$, $$ \angle VOR $$, $$ \angle ROU $$ and $$ \angle UOB $$ divide $$ \angle BOA $$
in four equal parts
$$ \therefore $$ $$ \angle AOV $$ = $$ \angle VOR $$ = $$ \angle ROU $$ = $$ \angle UOB $$ = $$ 20^{\circ} $$
Step I- With the help of protractor, draw $$ \angle 80^{\circ} $$.
Step II - cut OA and OB at Q and P, taking P as the center and any convenient radius.
Step II - With vertex P, by using compass take more than half of arc PQ and draw arc.
Step III - With vertex Q , by using compass with same length, cut the previous arc at R.
Step IV- With help of ruler join the point O and R.
$$ \therefore $$ $$ \angle AOR $$ = $$ \angle ROB $$
Step V - similarly, bisect the arcs QS and SP
$$ \therefore $$ $$ \angle AOV $$ = $$ \angle VOR $$ And $$ \angle ROU $$ = $$ \angle UOB $$
Thus, $$ \angle AOV $$, $$ \angle VOR $$, $$ \angle ROU $$ and $$ \angle UOB $$ divide $$ \angle BOA $$
in four equal parts
$$ \therefore $$ $$ \angle AOV $$ = $$ \angle VOR $$ = $$ \angle ROU $$ = $$ \angle UOB $$ = $$ 20^{\circ} $$
Draw a line segment of length $$6.5$$ cm and divide it into four equal parts, using ruler and compasses..
Steps of construction :
Step I - Draw a line segment AB = $$6.5$$ cm with the help of ruler.
Step II - with vertex A, by using compass take more than half of AB and draw arcs, one each side of side of AB.
Step III - with vertex B, by using compass with same length, cut the previous arcs at E and F respectively.
Step IV - with help of ruler join the point E and F.
Thus, Q is midpoint of Ab ($$\therefore $$ AQ = BQ)
Step V - similarly, bisect the lines AQ and BQ
Thus, P, is midpoint of AQ and R, is midpoint of BQ Now, points P, Q and R divided the line segment AB in four equal parts
$$\therefore $$ AP = PQ = QR = RB
Step I - Draw a line segment AB = $$6.5$$ cm with the help of ruler.
Step II - with vertex A, by using compass take more than half of AB and draw arcs, one each side of side of AB.
Step III - with vertex B, by using compass with same length, cut the previous arcs at E and F respectively.
Step IV - with help of ruler join the point E and F.
Thus, Q is midpoint of Ab ($$\therefore $$ AQ = BQ)
Step V - similarly, bisect the lines AQ and BQ
Thus, P, is midpoint of AQ and R, is midpoint of BQ Now, points P, Q and R divided the line segment AB in four equal parts
$$\therefore $$ AP = PQ = QR = RB
Draw a circle of radius 6cm using ruler and compasses. Draw on of its diameters. Draw the perpendicular bisector of this diameter. Does this perpendicular bisector contain another diameter of the circle
Steps of construction:
Step I- Draw a circle of radius 6 cm with center O.
Step II - drae a diameter AB= 12 cm with the help of ruler.
Step II - With vertex A, by using compass take more than half of diameter AB and draw arcs, one each side of side of AB.
Step III - With vertex B, by using compass with same length cut the previous arcs at X and Y respectively.
Step IV - with help of ruler join the point X and Y
Thus, XY is the perpendicular bisector of diameter AB and perpendicular bisector contain another diameter of the circle.
Draw a line segment of length $$7$$cm. Draw its perpendicular bisector, using ruler and compasses.
Steps of construction:
Step I - Draw a line segment AB = $$7$$ cm with the help ruler.
Step II - with vertex A, by using compass take more than half of AB and draw arcs, one each side of AB.
Step III - with vertex B, by using compass with same length, cut the previous arcs at X and Y respectively.
Step IV - with help of ruler join the point X and Y Thus XY is the perpendicular bisector of line AB.
Step I - Draw a line segment AB = $$7$$ cm with the help ruler.
Step II - with vertex A, by using compass take more than half of AB and draw arcs, one each side of AB.
Step III - with vertex B, by using compass with same length, cut the previous arcs at X and Y respectively.
Step IV - with help of ruler join the point X and Y Thus XY is the perpendicular bisector of line AB.
Enter 1 if it's true else enter 0.A divider is used to compare lengths of the line segment.
Enter 1 if it's true else enter 0.A ruler is used to draw the line and to measure their length.
Enter 1 if its true else enter 0A protractor is used to draw and measure angles.
Enter 1 if its true else enter 0The set squares are two triangular pieces having angles of $$30°, 60°, 90°$$ and $$45°, 45°, 90°$$.
Enter 1 if it's true else enter 0.A compass is used to draw circles or arcs of circles.
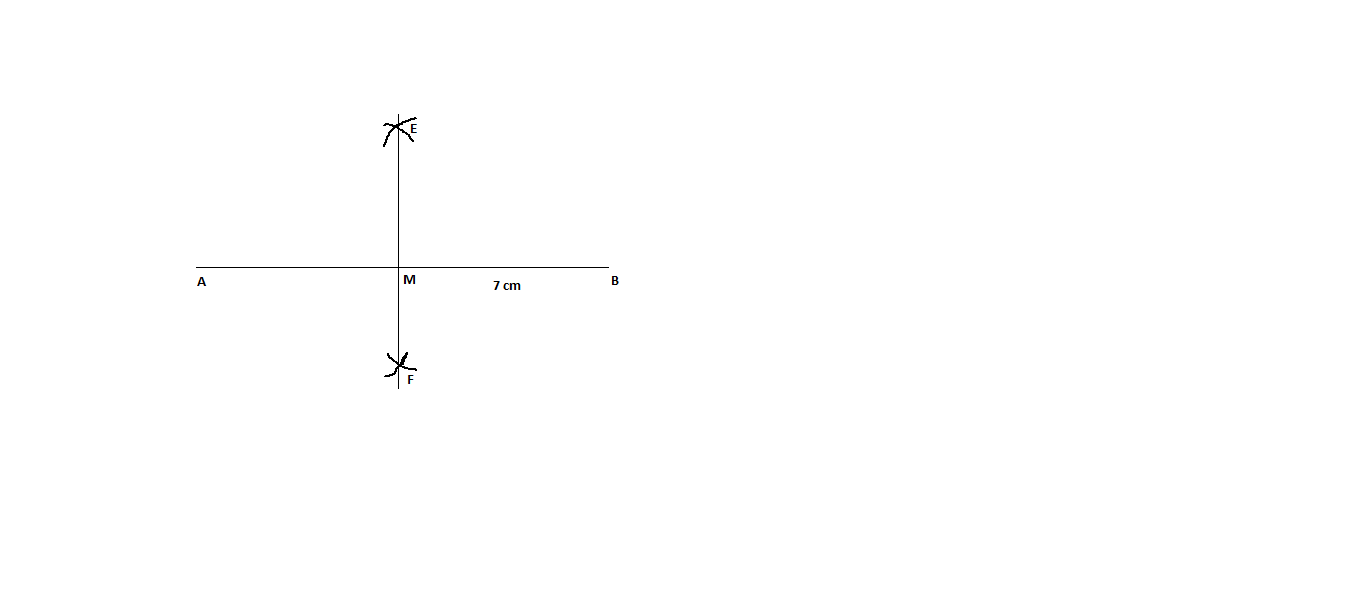
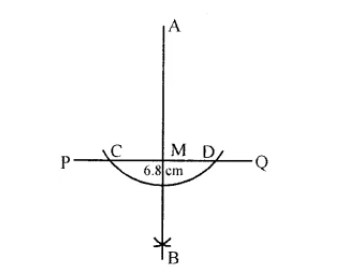
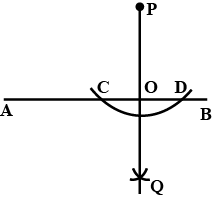
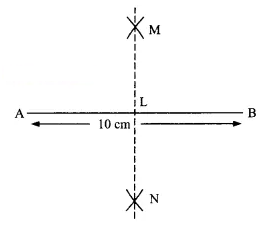
Draw a line segment of length 6 cm. Construct its perpendicular bisector. Measure the two parts of the line segment.
Steps of construction:
Step I - draw a line segment AB= 6 cm with the help of ruler.
Step II - With vertex A, by using compass take more than half of AB and draw arcs, one each side of side of AB.
Step I - draw a line segment AB= 6 cm with the help of ruler.
Step II - With vertex A, by using compass take more than half of AB and draw arcs, one each side of side of AB.
Step III- With vertex B, by using compass with same length, cut the previous arcs at X and Y respectively.
Each part measures $$=3\ cm$$
Enter 1 if its true else enter 0To bisect a line segment of length $$7$$ cm, the opening of the compass should be more than $$3.5$$ cm.
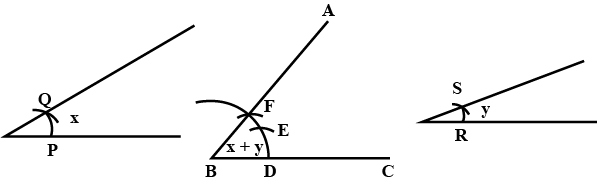
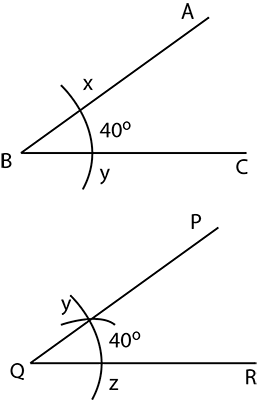
Given below are the angles $$x$$ and $$y$$.
Without measuring these angles, construct:
$$\angle ABC=x+y$$
Steps of construction:
1. Construct a line segment $$BC$$ of any suitable length.
2. Taking $$B$$ as center, construct an arc of any suitable radius. With the same radius, construct arcs with the vertices of given angles as centers. Consider these arcs to cut arc $$x$$ at points $$P$$ and $$Q$$ and arms of angle $$y$$ at points $$R$$ and $$S$$.
3.From the arc, with $$B$$ as center, cut $$DE=PQ$$ arc of $$x$$ and $$EF=RS$$ arc of $$y$$.
4. Now join $$BF$$ and produce up to point $$A$$.
Therefore, $$\angle ABC=x+y$$
1. Construct a line segment $$BC$$ of any suitable length.
2. Taking $$B$$ as center, construct an arc of any suitable radius. With the same radius, construct arcs with the vertices of given angles as centers. Consider these arcs to cut arc $$x$$ at points $$P$$ and $$Q$$ and arms of angle $$y$$ at points $$R$$ and $$S$$.
3.From the arc, with $$B$$ as center, cut $$DE=PQ$$ arc of $$x$$ and $$EF=RS$$ arc of $$y$$.
4. Now join $$BF$$ and produce up to point $$A$$.
Therefore, $$\angle ABC=x+y$$
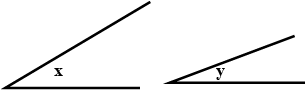
Draw a line segment $$BC=4cm.$$ construct angle $$ABC=60^o.$$
Steps of construction:
1. Construct a line segment $$BC=4cm$$
2. Taking $$B$$ as center, construct an arc of any suitable radius which cuts $$BC$$ at the point $$D$$.
3. Taking $$D$$ as center, and the same radius as in step $$2$$, construct one more arc which cuts the previous arc at point $$E$$.
4. Now join $$BE$$ and produce it to the point $$A$$.
Therefore, $$\angle ABC=60^o$$
1. Construct a line segment $$BC=4cm$$
2. Taking $$B$$ as center, construct an arc of any suitable radius which cuts $$BC$$ at the point $$D$$.
3. Taking $$D$$ as center, and the same radius as in step $$2$$, construct one more arc which cuts the previous arc at point $$E$$.
4. Now join $$BE$$ and produce it to the point $$A$$.
Therefore, $$\angle ABC=60^o$$
Draw a circle with diameter : $$6\ \text{cm}$$
Measure the length of the radius of the circle drawn.
$$AB$$ is the diameter of circle $$AB=6\ \text{cm}$$ and $$OA$$ is the radius of the circle.
The radius of the circle is,
$$r=\dfrac{1}{2} \times 6\ \text{cm}=3\ \text{cm}$$
Therefore, $$OA=OB=3\ \text{cm}$$
The radius of the circle is,
$$r=\dfrac{1}{2} \times 6\ \text{cm}=3\ \text{cm}$$
Therefore, $$OA=OB=3\ \text{cm}$$
What is the locus of a points at a distance of $$2cm$$ from a fixed line.
The locus of points which are at a distance of $$2cm$$ from a fixed line
$$AB$$ are a pair of straight lines $$l$$ and $$m$$ which are parallel
to the given line which a distance of $$2cm$$
Draw rough diagrams of two angles such that they have Three points in common
$$\angle{AOB}$$ and $$\angle{BOC}$$ have points $$O, E, B$$ in common
What is the locus of a point at a distance of $$3cm$$ from a fixed point.
The locus of a point which is at a distance of $$3cm$$ away from a fixed
point is circumference of a circle whose radius is $$3cm$$ and the
fixed point as the centre of the circle.
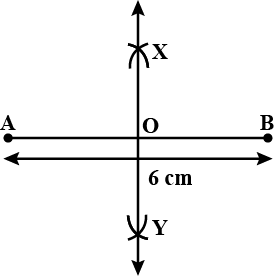
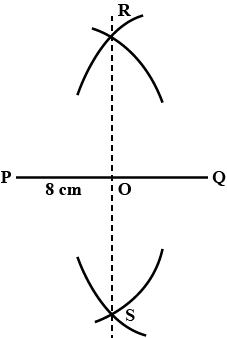
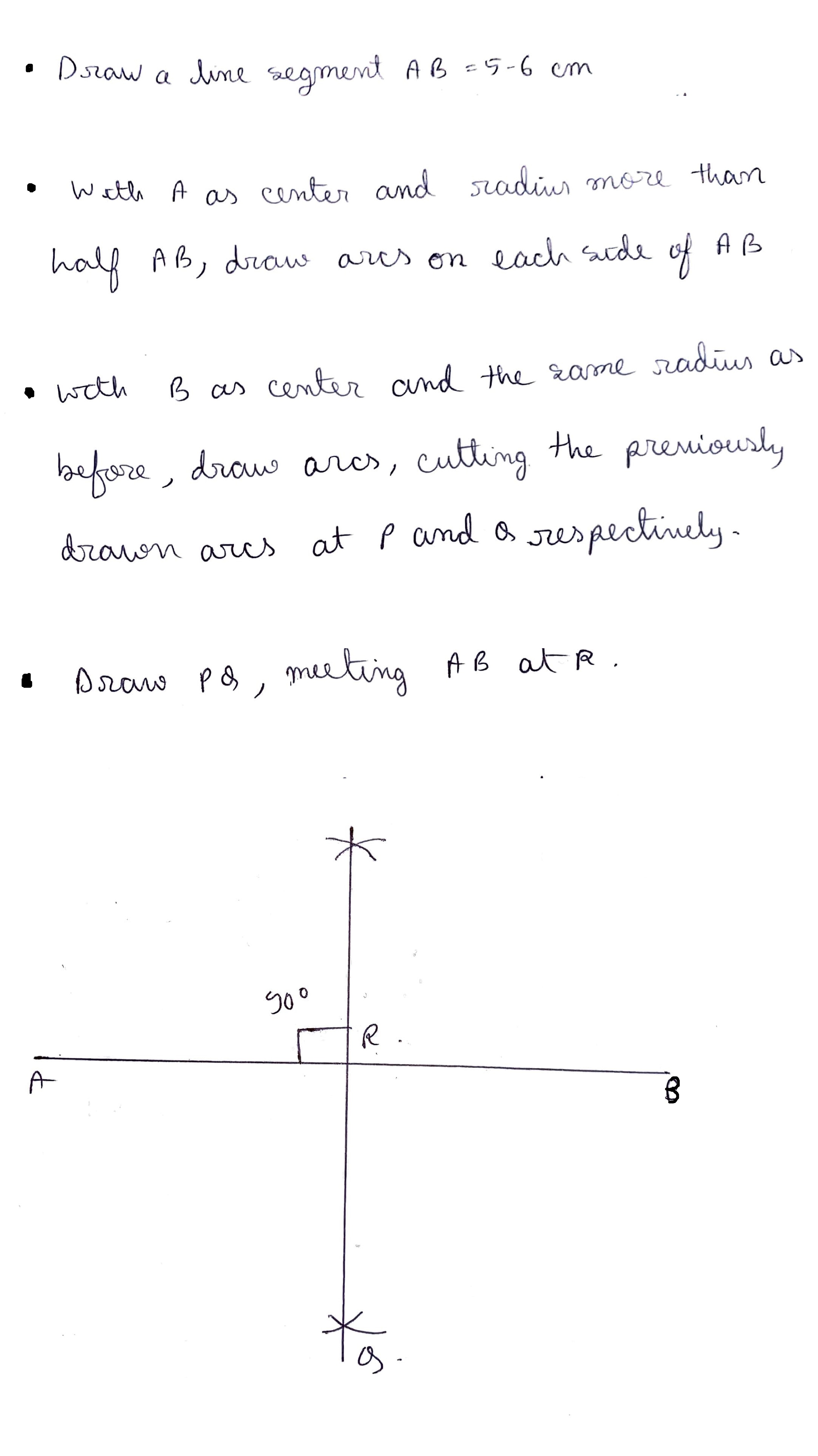
Draw a line segment OP of 5.2 cm. Construct a line perpendicular to OP.
In the figure $$A=O,B=P$$
Draw a line segment $$OP=5.2 cm$$Open compass and draw curve upper and down side of line $$OP$$ at point $$O$$ and $$P$$
These curves cut each other at $$C$$ and $$D$$ as shown in the figure
Join $$C$$ to $$D$$ line
$$CD$$ is the line perpendicular to $$OP$$
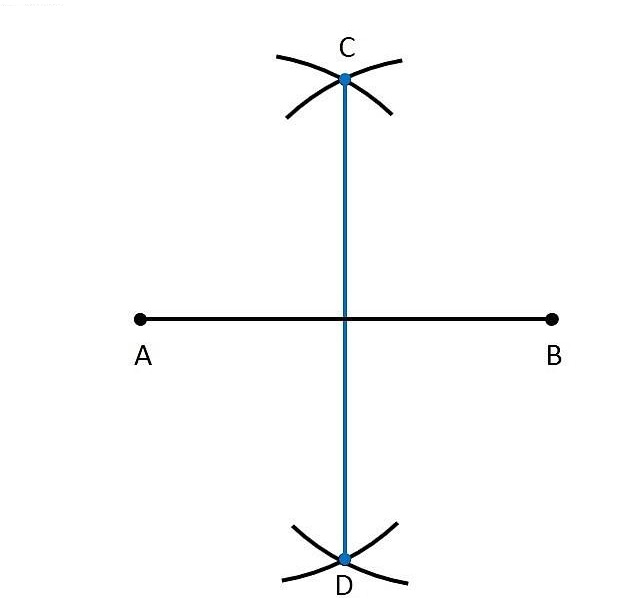
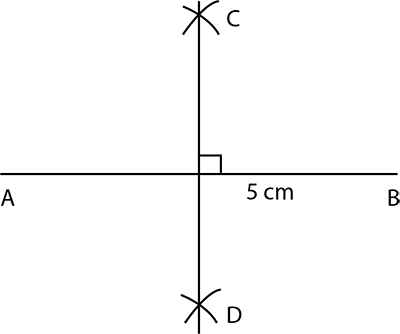
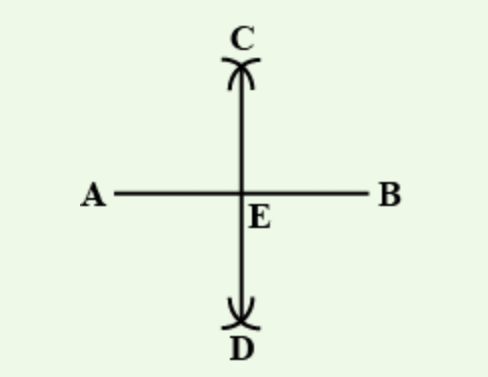
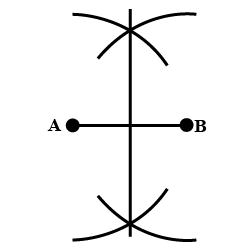
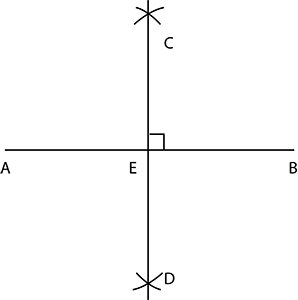
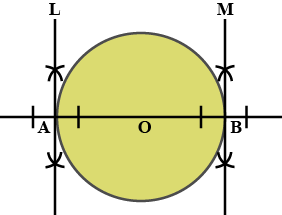
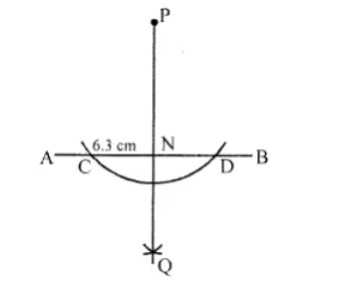
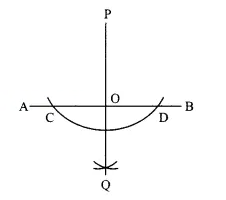
Given a line AB of 5 cm. Draw the perpendicular bisector of AB.
1. Draw a line segment AB = 5 cm.
2. With any radius greater than 2.5 cm, and compass fixed at A, draw 2 arcs, one above and one below AB.
3. With the same radius, compass at B, cut the 2 arcs drawn in step 2.
4. The line joining these two arcs is the perpendicular bisector of AB.
i.e. CD is the perpendicular bisector of AB.
Given a line segment AB =10 cm. Draw a line perpendicular to it.
Draw a line segment $$AB=10 cm$$
Open compass and draw curve upper and down side of line $$AB$$ at point $$A$$ and $$B$$
These curves cut each other at $$C$$ and $$D$$ as shown in the figure
Join $$C$$ to $$D$$ line
$$CD$$ is the line perpendicular to $$AB$$
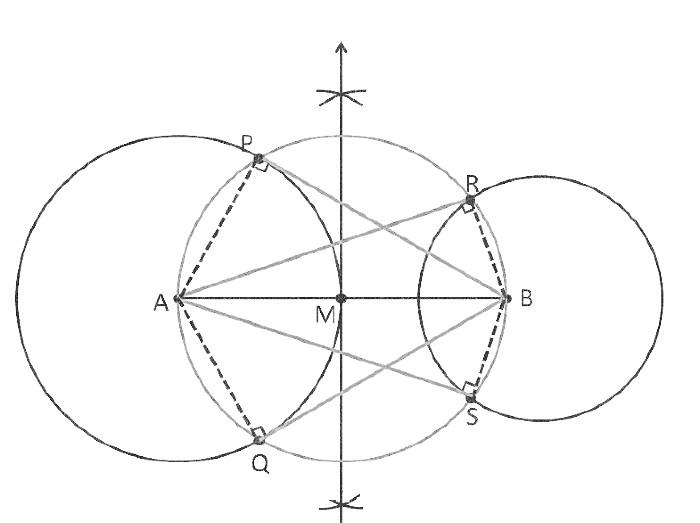
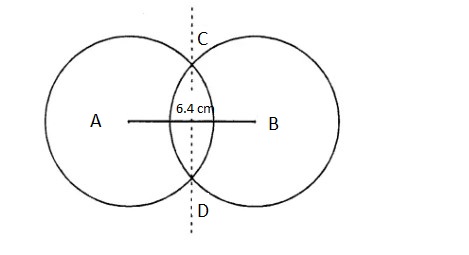
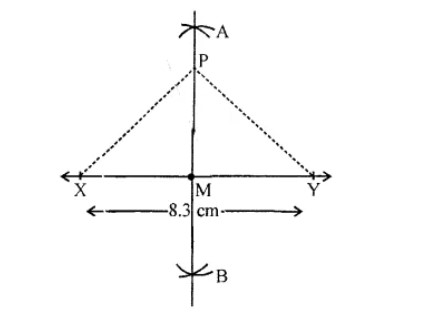
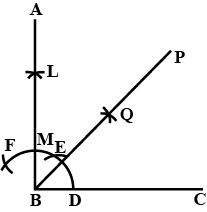
Mark two points A and B, 6.4 cm apart. Construct the line of symmetry so that the points A and B are symmetric with respect to this line.
1. Draw a line AB of length $$ 6.4 cm $$
2. From A, using a compass of some length, draw an arc on both sides of the line AB
3. Using the same length of compass, draw arcs from B on both sides of the line AB
4. Draw a vertical line connecting the points of intersection of the arcs.
2. From A, using a compass of some length, draw an arc on both sides of the line AB
3. Using the same length of compass, draw arcs from B on both sides of the line AB
4. Draw a vertical line connecting the points of intersection of the arcs.
The line obtained is the required line of symmetry.
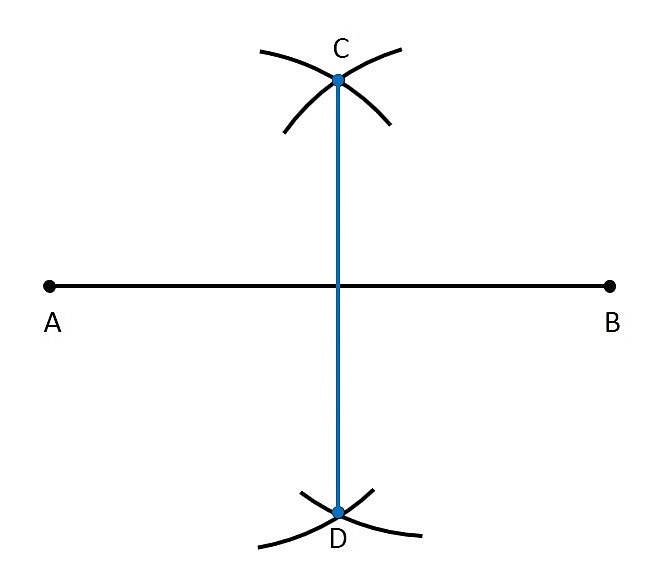
Construct perpendicular bisector of a line segment.
Step 1: Draw the line segment AB with given measure
Step 2: With a radius, more than half of the length of AB cut arcs above and below the line segment AB, taking A and B as centers respectively
Step 3: Call the points where the arcs cut as C and D.
Step 4: CD is the required perpendicular bisector.
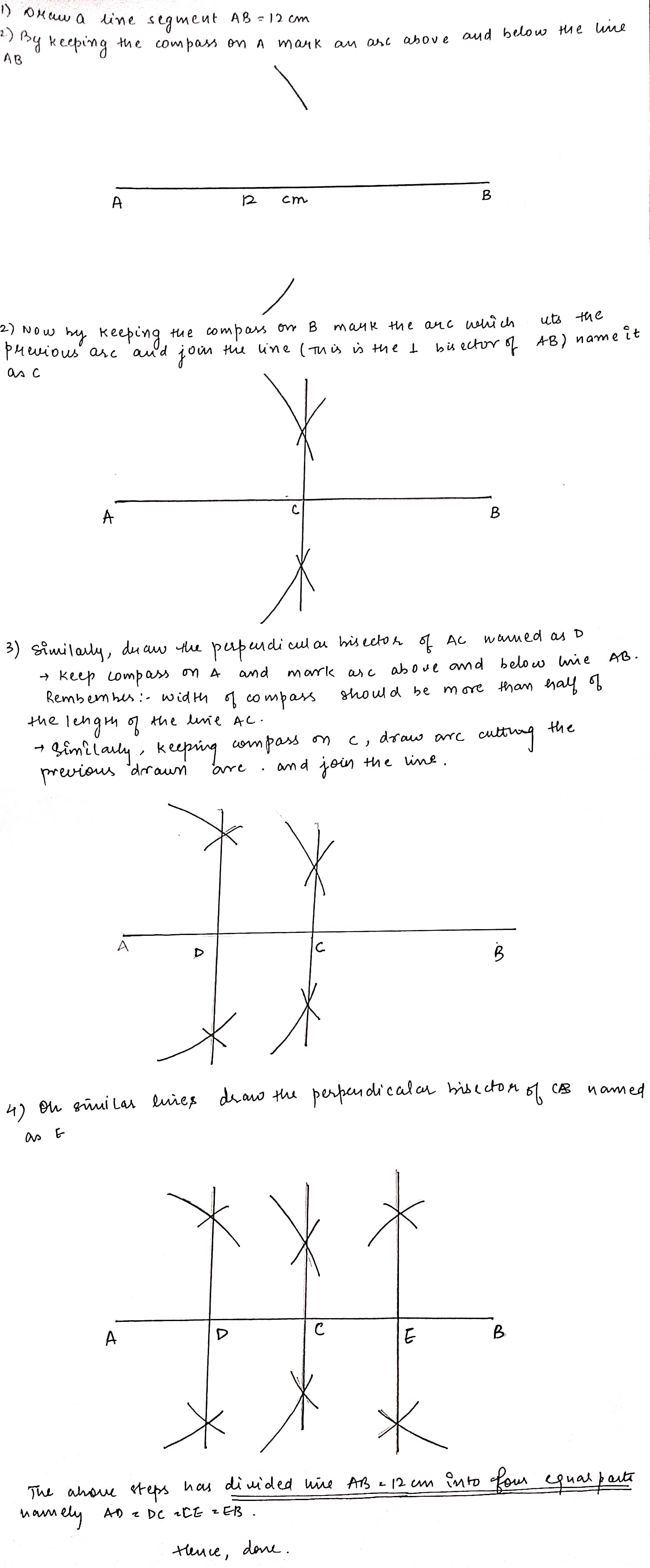
Construct a line segment perpendicular to line segment $$AB = 12$$ $$cm.$$
Steps of Construction
1. Draw a line segment AB =12 cm 2. With A as centre and a radius more than half, draw an arcs at C and D
3. With B as centre and with same radius, draw arcs to cut the previous arcs at C and D
4. Join C to D line cut AB at point E .
5. CD is the required perpendicular to the line segment AB
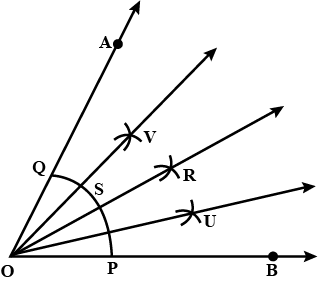
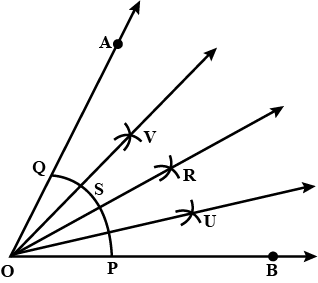
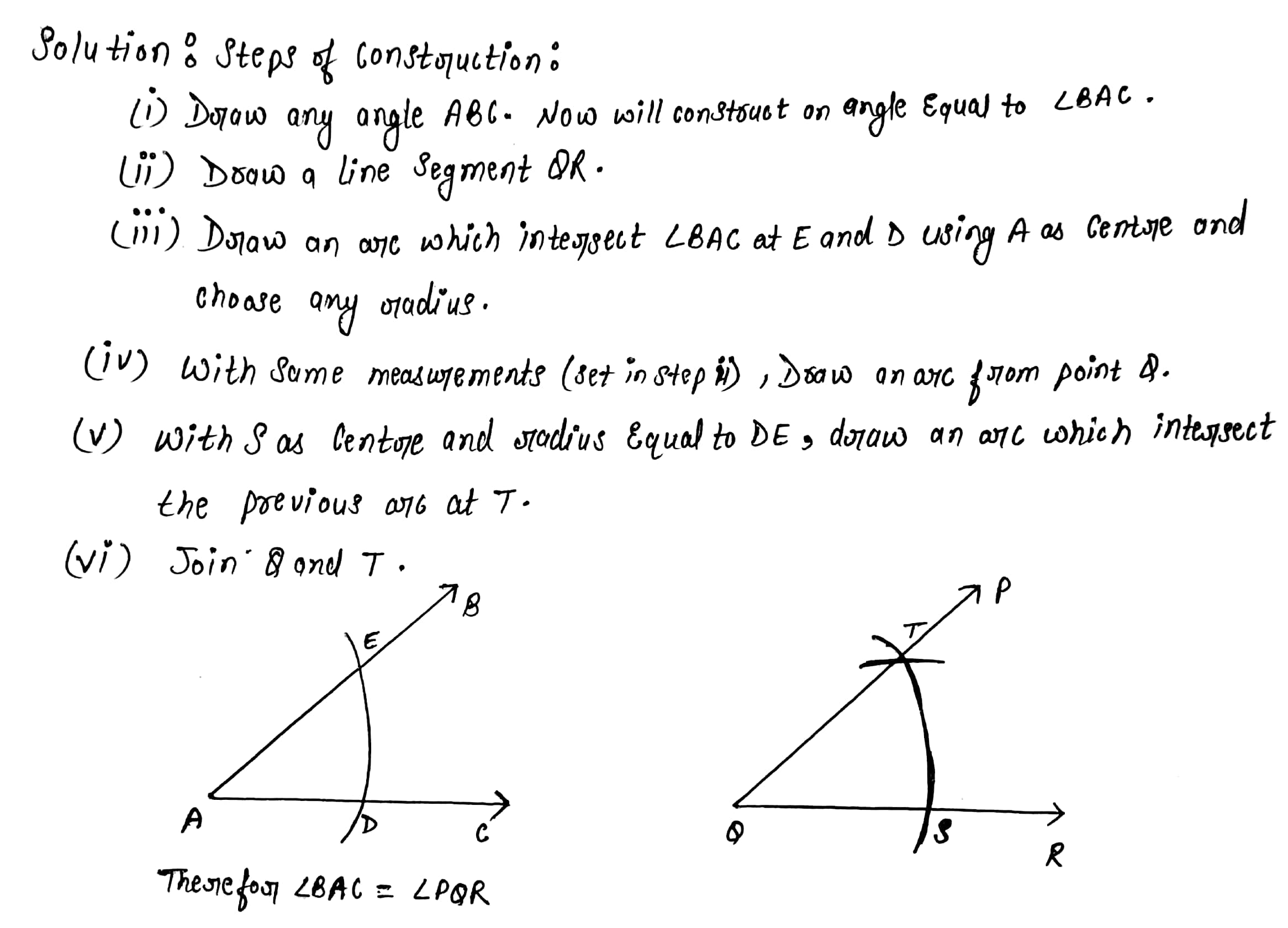
Construct an $$\angle ABC = 40^o$$. Draw another $$\angle PQR$$ congruent to the given angle without using a protractor.
1) Construct angle ABC of $$40^o$$ and draw a curve XY on point B.
2) Draw a line segment QR and draw a curve equivalent to curve XY at point Q.
3) This curve cut line QR at point Z.
4) Now measure length of arc XY and cut on the second figure and mark the point of intersection as Y.
5) Join YQ and extend it to P.
6) Then angle PQR is the required angle similar to angle ABC
Show that of all line segments drawn from a given point, not on it, the perpendicular line segment is the shortest.
Consider a line $$l$$ on which $$Y$$ and $$Z$$ lies.
Now, a point $$X$$ away from $$YZ$$ such that $$XY \perp l$$ and $$Z$$ is a point on line $$l$$ other than $$Y.$$
In $$\triangle XYZ$$,
$$\angle Y=90^{\circ}$$
So, in $$\Delta XYZ,$$
$$\Rightarrow \angle YXZ+\angle XZY+\angle XYZ=180^{\circ}$$
Putting $$\angle XYZ=90^{\circ}$$
$$\Rightarrow \angle YXZ+\angle XZY=90^{\circ}$$
$$\Rightarrow \angle X+\angle Z=90^{\circ}$$
$$\Rightarrow \angle Z<90^{\circ}$$
$$\Rightarrow \angle Z<\angle Y $$
$$\Rightarrow XY < XZ $$
(Side opposite to greater angle is greater)
$$XY$$ is the shortest of all line segments from $$X$$ to $$YZ.$$
Perimeter of a circle is $$10\pi$$. Find the radius of the circle and then draw the circle.
Perimeter of a circle = $$2\pi r$$ [where r is the radius of a circle]
Given
perimeter=$$10\pi$$
therefore
$$2\pi r=10\pi$$
$$r=5$$
Radius of a circle is 5
In figure OA is the radius.
Draw a circle of radius $$4.8$$cm. Take a point on the circle. Draw the tangent at that point using the tangent-chord theorem.
$$Step\ 1:$$ With $$O$$ as the center, draw a circle of radius $$4.8\ cm$$.
$$Step\ 2:$$: Take a point $$P$$ on the circle.
$$Step\ 3:$$ Through $$P$$, draw any chord $$PQ$$.
$$Step\ 4:$$ Mark a point $$R$$ distinct from $$P$$ and $$Q$$ on the circle so that $$P, Q$$ and $$R$$ are in counter clockwise direction.
$$Step\ 5:$$ Join $$PR$$ and $$QR$$.
$$Step\ 6:$$ At $$P$$, construct $$\angle QPX = \angle PRQ$$
$$Step\ 7:$$ Produce $$XP$$ to $$Y$$ get the required tangent line $$XY$$.
Thus, this is the resulting figure.
Draw concentric circle for the radii measuring 4 cm and 6 cm. Find out the width of circular ring.
Step 1 - Draw a circle with radius $$r=4$$ cm and name the centre as $$O$$.
Step 2- Taking $$O$$ as the centre, draw another circle of radius $$R=6$$ cm.
Then, the figure results into concentric circles with radius $$6$$ and $$4$$ cm.
Then width of circular ring $$=R-r=6-4=2$$ cm
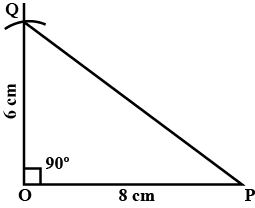
The diameter of the circle is $$8$$cm. Calculate the radius and draw a circle using this radius with the help of a compass. The radius of this circle is
therefore
$$Diameter=2r$$
$$2r=8cm$$ [Given diameter=8cm]
$$r=\dfrac{8}{2}$$
so, $$r=4cm$$
Radius of a circle is 4cm
Draw a circle of radius $$4\ cm$$ with centre $$O.$$ Draw a diameter $$POQ.$$ Through $$P$$ or $$Q$$ draw tangent to the circle.
We follow the following steps.
Steps of construction :$$STEP\ I$$
Taking $$O$$ as centre and radius equal to $$4\ cm$$ draw a circle.
$$STEP\ II$$
Draw diameter of $$POQ$$.
Draw diameter of $$POQ$$.
$$STEP\ III$$
Construct $$\angle PQT=90^{o}$$
Construct $$\angle PQT=90^{o}$$
$$STEP\ IV$$
Produce $$TQ$$ to $$T'$$ to obtain the required tangent $$TQT'$$.
Produce $$TQ$$ to $$T'$$ to obtain the required tangent $$TQT'$$.
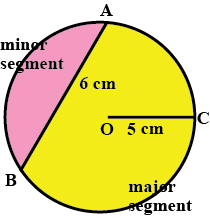
Draw a circle of radius $$5$$ cm. In the circle, draw a chord $$AB = 6$$ cm, then shade the minor and major segments.
In the above figure, $$AB$$ is the chord of length $$6cm$$ and $$OC=5cm$$ is the radius of the circle.
The pink shaded region is the minor segment with less area and the yellow shaded region is the major segment with more area.
Using a set square and a ruler construct a line perpendicular to given line at a point on it.
Step 1 :
(i) Draw a line $$AB$$ with the help of a ruler.
(ii) Mark a point $$P$$ on it.
Step 2 :
(i) Place a ruler on the line $$AB$$
(ii) Place one edge of a set square containing the right angle along the given line $$AB$$.
Step 3 :
(i) Pressing the ruler tightly with the left hand, slide the set square along the ruler till the edge of the set square touches the point P.
(ii) Through $$P$$, draw a line $$PQ$$ along the edge
Step 4 :
$$PQ$$ is the required line perpendicular to $$AB$$. Measure and check if m$$\angle APQ = m\angle BPQ = 90°$$
Draw an angle of $$40^o$$. Find its supplementary angle.
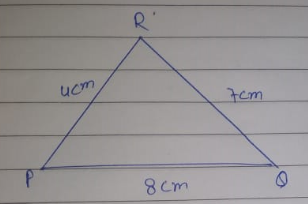
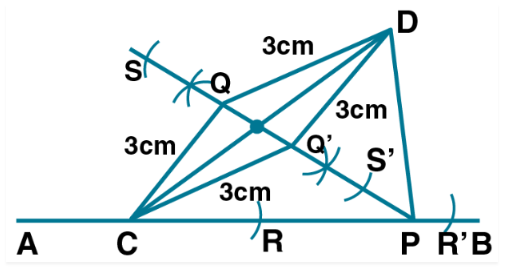
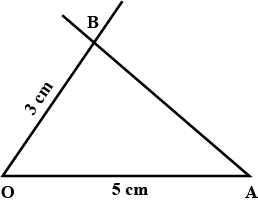
Construct $$\triangle PQR$$ with $$PQ=4cm, \,QR =7cm$$ and $$PR=8cm$$
Given that
$$PQ=4cm$$
$$QR=7cm$$
$$PR=8cm$$
step of construction
(i) Draw a line segment $$PR=8cm$$
(ii) With $$R$$ as center and radius $$7cm$$ draw an arc.
(iii) With $$P$$ as center and radius $$4cm$$ draw an arc cutting the previous arc at $$Q$$
(iv) join $$RQ$$ and $$PQ$$ then $$\Delta PQR$$ is the required triangle.
If radii of two circles are $$4$$cm and $$2.8$$ cm. Draw figure of these circles touching each other (i) externally (ii) internally.
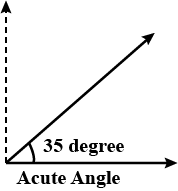
Construct an angle measuring $$35^{o}$$ using protractor.
STEPS OF CONSTRUCTION:
1. Draw a circle. Place the hole in the protractor over the center of the circle.
2. Use the inner scale on the protractor and mark at $$0^\circ$$ and $$35^\circ$$.
3. Use a scale to draw two rays originating from the center of the circle to each mark.
4. The angle between the two rays is $$35^\circ$$.
Using a set square and a ruler draw a line parallel to the given line through a point $$5$$ $$\text cm$$ above it.
Step 1 :
(i) Draw a line $$XY$$ using a ruler and mark a point $$A$$ on it.
(ii) Draw $$AM = 5cm$$ with the help of a set square
Step 2 :
(i) Place the set square on the line segment $$XY$$
Step 3 :
(i) Pressing tightly the ruler along the line segment AM, slide the set square along the ruler till the edge of the set square touches the point $$M$$.
(ii) Through $$M$$, draw a line $$MN$$ along the edge.
(iii) $$MN$$ is the required line parallel to $$XY$$ through $$M$$.
Draw a line segment of length 7.6 cm and divide it in the ratio 5 :Measure the two parts.
Steps of construction:
1. Draw a line segment $$AB=7.6$$ cm.
2. Draw a ray $$AX$$ making an acute angle at $$A$$ with $$AB$$.
3. Draw another ray $$BY$$ parallel to $$AX$$ making an acute angle.
Make sure angle must be same as considered in step 2.
4. Taking $$A$$ as centre draw an arc cutting at $$A_1$$ on the line.
Taking same radius consider $$A_1$$ as a centre and draw another arc cutting line at $$A_2$$.
Repeat the same procedure and divide the line $$AX$$ into $$5$$ points $$A_1,A_2,A_3,A_4$$.and $$A_5$$
In such a way, $$AA_1=A_1A_2=A_2A_3=A_3A_4$$
5. Similar to step $$4$$,
Taking $$B$$ as centre draw an arc cutting at $$B_1$$ on the line.
Taking same radius (set in step 4) consider $$B_1$$ as a centre and draw another arc cutting arc cutting line at $$B_2$$.
Repeat the same procedure and divide the line $$BY$$ into $$8$$ points in such a way that $$BB_1=B_1B_2=B_2B_3=B_3B_4=B_4B_5=B_5B_6=B_6B_7=B_7B_8$$
6. Join $$A_5B_8$$
7. Line $$A_5B_8$$ intersect $$AB$$ at a point $$P$$ in the ratio $$5:8$$
8. Measurement : $$PB=4.7$$ cm and $$AP=2.9$$ cm
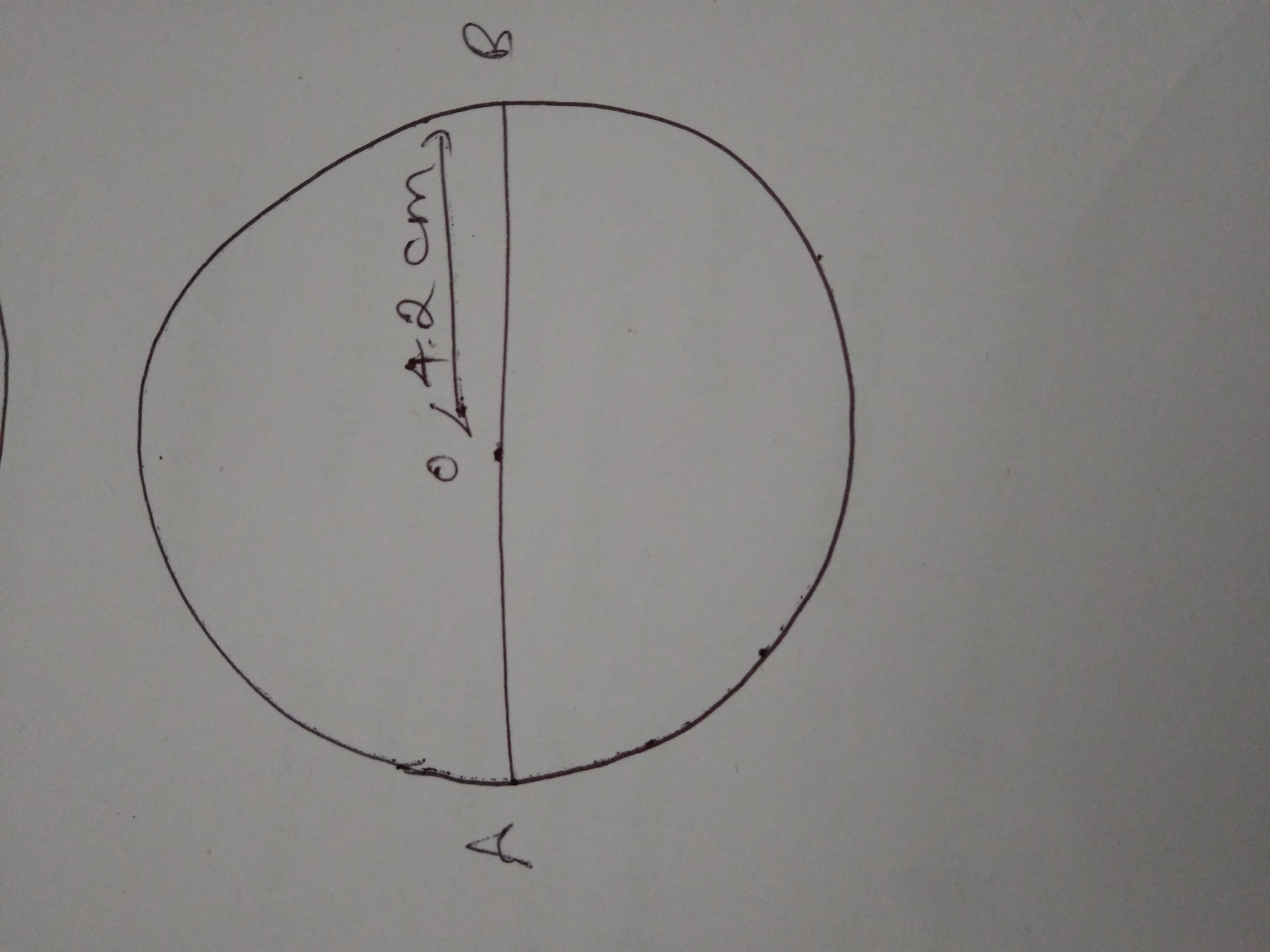
Draw a circle of radius $$4.2\ cm$$.
$$Find\quad the\quad foot\quad of\quad the\quad perpendicular\quad from\quad (7,14,5)\quad to\quad 2x+4y-z=2.$$
Construct a line segment of length $$5.6\ cm$$ using ruler and compasses.
Draw a line 'l ' Mark a point A on this line.
Place the compasses pointer on zero mark of the ruler. Open it to place the pencil point up to 5.6 cm mark.
Without changing the opening of the compasses. Place the pointer on A and cut an arc 'l ' at B.
AB is the required line segment of length 5.6 cm.
Draw a line segment $$AB$$ using a ruler and compass, obtain a line segment of length $$\dfrac {3}{4}(AB)$$.
1. Draw a line segment AB
2. With center A and radius more than 1/2 AB draw arcs one on each side of AB.
3. With center B and same radius draw arcs cutting previous arcs at P and Q respectively.
4. Join PQ and which intersect AB at C
5. With center C and radius more than 1/2 CB draw arcs, one on each side of CB.
6. With center B and same radius, draw arcs cutting previous arcs at R and s respectively
7. Join RS and which intersect CB at D
AD = 3/4 AB.
Construct $$\overline{AB}$$ of length $$7.8\ cm$$. Find this, cut off $$AC$$ of length $$4.7\ cm$$ . Measure $$\overline {BC}$$
Step$$1$$ Draw a line $$l$$.Mark a point $$A$$ on it.
Step$$2$$ Since length of $$AB$$ is $$7.8$$cm, we measure $$7.8$$cm using ruler and compass.
Step$$3$$Now keeping compass opened the same length.We keep pointed end at point $$A$$, and draw an arc on line $$l$$.So the required line segment is $$\bar{AB}=7.8$$cm
Step$$4$$Now, we need to cut of $$AC$$ of length $$4.7$$cm.We measure $$4.7$$cm using ruler and compass.
Step$$5$$Now keeping compass opened the same length.We keep pointed end at point $$A$$, and draw an arc on line $$l$$.
Result:The required line segment $$\bar{AC}=4.7$$cm
Draw a line $$l$$. Draw a perpendicular to $$l$$ at any point on $$l$$.On this perpendicular choose a point $$X,4\ cm $$ away from $$l$$. Through $$X$$,draw a line $$m$$ parallel to $$l$$ .
$$First\quad we\quad draw\quad a\quad line\quad l\quad \left( as\quad shown\quad in\quad the\quad figure \right) \\ Let\quad "p"\quad be\quad any\quad oint\quad on\quad l\quad \\ Next\quad we\quad draw\quad a\quad line\quad Mp\quad perpendicular\quad to\quad l\quad \quad \left( Mp\bot l \right) \\ we\quad plot\quad the\quad point\quad "X"\quad on\quad Mp\quad which\quad is\quad 4cm\quad away\quad from\quad l.\\ Now\quad we\quad draw\quad a\quad line\quad m\quad passing\quad through\quad the\quad point\quad "X"\quad which\quad is\quad perpendicular\quad to\quad Mp\\ The\quad line\quad m\quad is\quad parallel\quad to\quad l\quad \left( m\parallel l \right) $$
Find the measure of the complement of $$(i){115}^{\circ}\,\,(ii){25}^{\circ}\,\,(iii){15}^{\circ}\,\,(iv){35}^{\circ}$$.
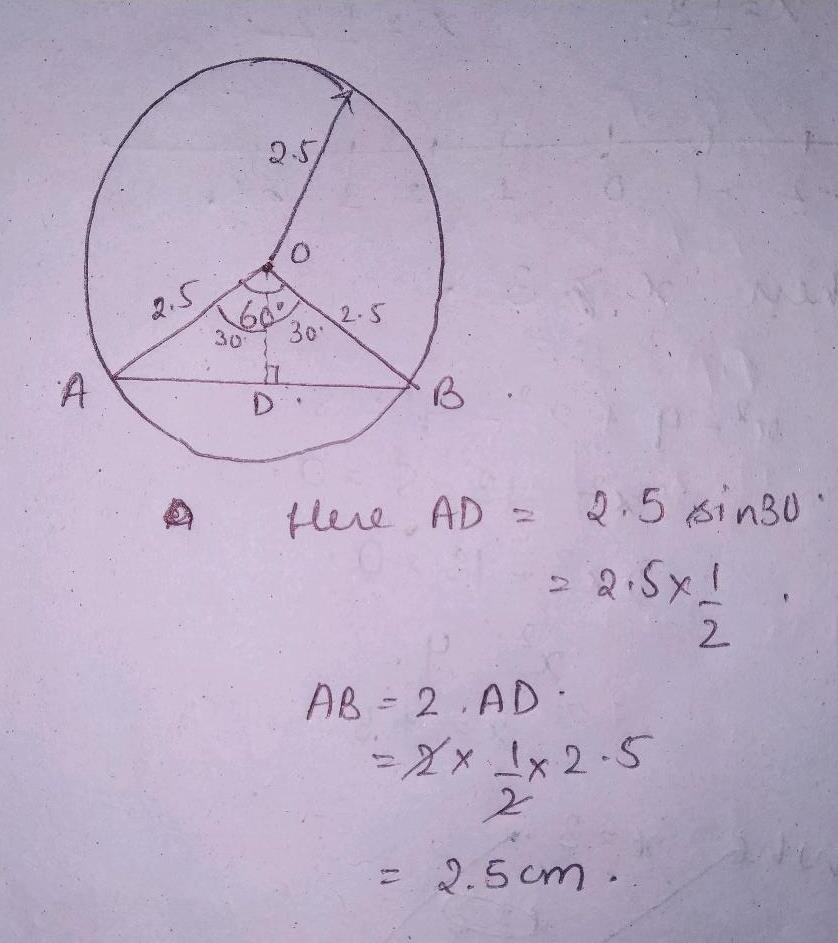
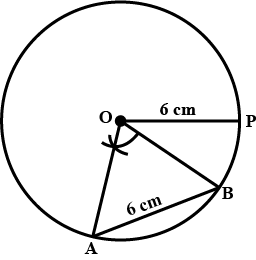
Draw a circle with centre $$O$$ and radius $$2.5\ cm$$. Draw two radii $$OA$$ and $$OB$$ such that $$\angle A O B = 60 ^ { \circ }$$. Measure the length of chord $$AB$$.
1. Draw a circle, taking centre as $$O$$ and radius equal to $$2.5\ cm$$.
2. Join $$OA$$, where $$A$$ is any point on the circle
3. Draw $$\angle AOB$$ equal to $$60^o$$
4. Now, join $$AB$$.
As shown in the figure, it can be seen that by pointing out the point $$D$$
and as we can see that the central angle gets bisected thus making $$\angle AOD=30^0$$
and on measuring as shown in image we get, AB $$= 2.5 cm$$
2. Join $$OA$$, where $$A$$ is any point on the circle
3. Draw $$\angle AOB$$ equal to $$60^o$$
4. Now, join $$AB$$.
As shown in the figure, it can be seen that by pointing out the point $$D$$
and as we can see that the central angle gets bisected thus making $$\angle AOD=30^0$$
and on measuring as shown in image we get, AB $$= 2.5 cm$$
$$ABC$$ and $$DBC$$ are two isosceles triangles on the same side of $$BC.$$ Prove that :
$$(i) DA (or AD)$$ produced bisects $$BC$$ at right angle.
$$(ii) \angle BDA = \angle CDA$$
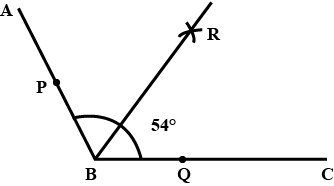
Using your protractor, draw an angle of measure $$108 ^ { \circ }$$.With this angle as given, draw an angle of $$54 ^ { \circ }$$.
Steps of construction:
1. Draw an angle ABC of 108°
2. With center B and any radius, draw an arc which intersects AB at P and BC at Q
3. With center P and Q and radius more than half of PQ draw two arcs,which intersect at R.
4. Join BR mRBC = 54°
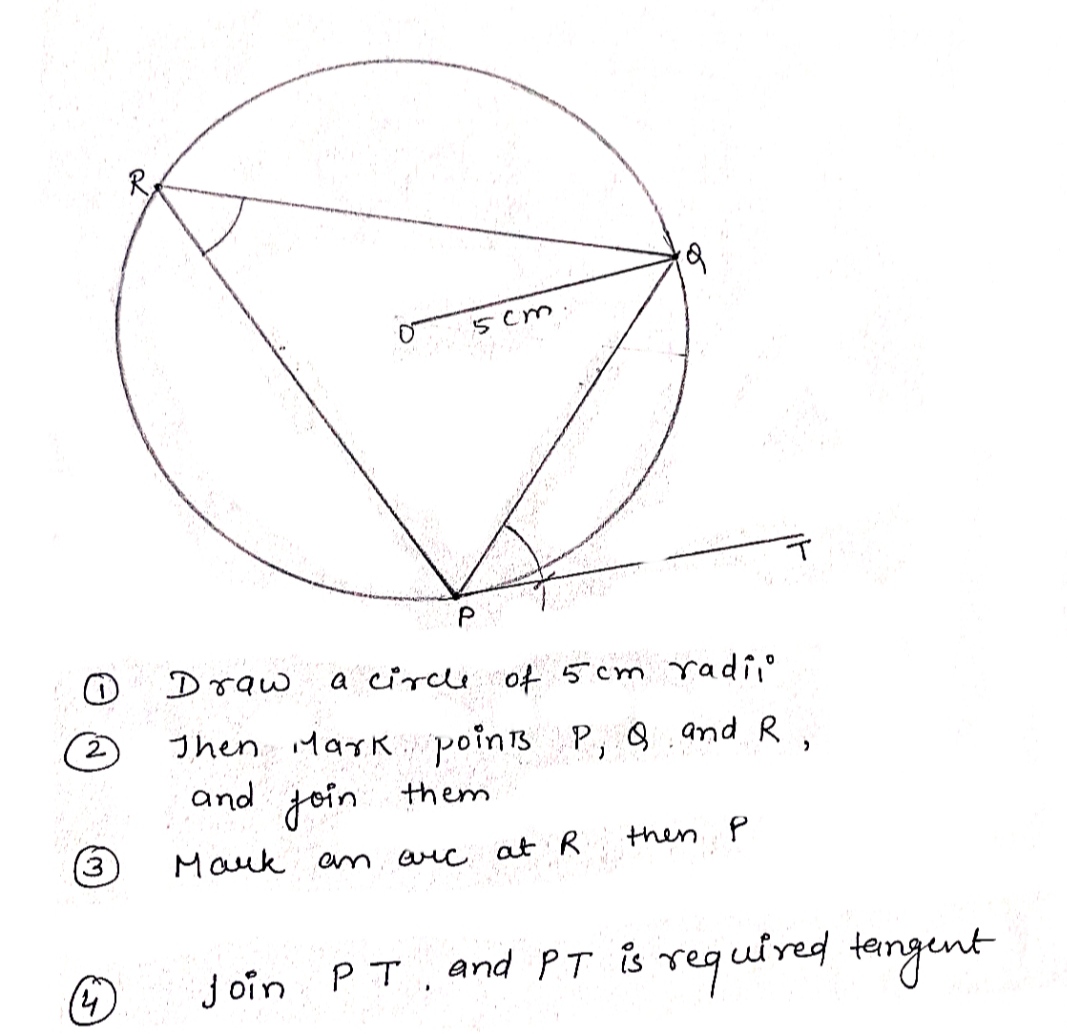
Draw a pair of tangents to a circle of radius 2 cm which are inclined at an angle of 90$$^o$$.
Steps of construction are as follows:
(1) Draw a circle of radius $$2\ cm$$ and draw a horizontal radius PO where O is the centre and P is point on the circle.
(2) Draw $$90^0$$ from point O such that the ray of angle intersect the circle at R.
(3) Now at P, draw $$90^0$$
(4) Now, at R, draw $$90^0$$
(5) Where the two arcs intersect, mark it as point Q. And thus PQ and PR are two tangents at an angle $$90^0$$
Now to prove angle between PQ and QR is $$90^0$$, then in quadrilateral OPQR, sum of angles $$=360^0$$
$$\therefore \ \angle P+\angle Q+\angle R+\angle O=360^0$$
$$90^0+90^0+90^0+\angle Q=360^0$$
$$270^0+\angle Q=360^0$$
$$\angle Q=360^0-270^0=90^0$$
$$\angle Q=90^0$$
Hence the angle between PQ and PR is $$90^0$$.
Construct the following angles and verify by measuring them by a protractor:
$$135^{o}$$
Step 1: A ray OY is drawn.
Step 2: An arc ABC is drawn with O as a centre.
Step 3: With A as a centre, two arcs are B and C are made on the arc ABC.
Step 4: With B and C as centres, arcs are made to intersect at E and ∠EOY = 90° is made.
Step 5: With B and C as centres, arcs are made to intersect at X
Step 6: OX is joined and and ∠XOY = 105° is constructed.
Thus, ∠XOY is the required angle making 105° with OY.
Step 2: An arc ABC is drawn with O as a centre.
Step 3: With A as a centre, two arcs are B and C are made on the arc ABC.
Step 4: With B and C as centres, arcs are made to intersect at E and ∠EOY = 90° is made.
Step 5: With B and C as centres, arcs are made to intersect at X
Step 6: OX is joined and and ∠XOY = 105° is constructed.
Thus, ∠XOY is the required angle making 105° with OY.
In a $$\Delta A B C ,$$ the sides $$B C = 5 , C A = 4 , A B = 3.$$ If $$A ( 0,0 )$$ and the internal bisector of angle $$A$$ meet $$B C$$ in $$D \left( \dfrac { 12 } { 7 } , \dfrac { 12 } { 7 } \right)$$ then in-centre of $$\Delta \mathrm { ABC }$$
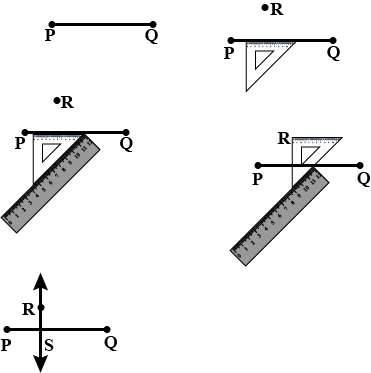
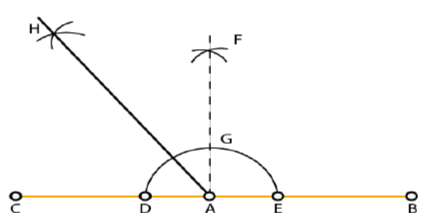
Draw any line segment $$AB$$ and mark any point $$P$$ on it. Using a ruler and a compass draw a perpendicular on $$AB$$ through point $$P$$.
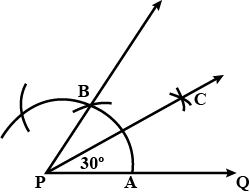
Drawn an angle of measure $$30^{o}$$ and construct its bisector.
Step $$1:$$ Draw a line segment. Mark the left end as point $$O$$ and the right end as point $$A$$.
Step $$2:$$ Take the compass and open it up to a convenient radius. Place its pointer at $$O$$ and with the pencil-head make an arc which meets the line $$OA$$
Step $$3:$$ Place the compass pointer at $$A$$ and mark an arc with the same radius as $$OA$$ we get $$D$$
Step $$4:$$ Draw a line from $$O$$ through $$D$$.
We get the angle i.e. $$\angle{AOD}= 60$$-degree angle.
A $$30$$-degree angle is the half of $$60$$-degree angle. For its construction, you first construct a $$60$$-degree angle as discussed above. Then, you bisect this angle. You get two $$30$$ degree angles.
Again $$15$$-degree angle is the half of $$30$$-degree angle. You get two $$15$$ degree angles.
Draw any line segment $$AB$$. Mark any point $$M$$ on it. Through $$M$$, draw a perpendicular using ruler and compass.
Steps of construction:
$$(i)$$ With $$M$$ as centre and a convenient radius, draw an arc intersecting the line $$AB$$ at two points $$C$$ and $$B$$.
$$(ii)$$ With $$C$$ and $$D$$ as centres and a radius greater than $$MC$$, draw two arcs, which cut each other at $$P$$.
$$(iii)$$ Join $$PM$$. Then $$PM$$ is perpendicular to $$AB$$ through the point $$M$$.
Bisect a line of length 7 cm. Write down the steps of construction.
Steps of construction :
1) Draw a line segment AB = 7 cm by using a graduated ruler.
2) With A as centre and radius more than half of AB, draw arcs, one on each side of AB.
3) With B as centre and the same radius as in step 2, draw arcs cutting the arcs drawn in step 2 at E and F respectively.
4) Draw the line segment with E and F as end-points. Suppose it meets AB at M. Then, M bisects the line segment AB.
By measuring, AM=MB = 3.5 cm
Draw a line, say, $$MN$$. From a point $$P$$ outside it, draw a line parallel to $$MN$$ using ruler and and compasses only.
Draw a circle and any two of its (non- perpendicular) diameter. If you join the ends of these diameters, what is the figure obtained? What figure is obtained if the diameters are perpendicular to each other? How do you check the answer?
We know that angle in a semicircle is $$90^o$$
Consider the case of two non perpendicular diameters
$$\therefore \angle ABC=\angle ADC =90^o$$
Similarly, $$\angle DAB=\angle DCB=90^o$$
So, in $$ABCD$$ all angles of vertices are $$90^o$$
Thus, $$ABCD$$ is a rectangle.
Now consider the case of perpendicular diameters
If $$\angle AOB=\angle BOC=90^o$$
$$AO=CO,\ OB=OC$$..... (radius of circle)
then $$\Delta AOB\cong \Delta COB$$
Thus $$AB=CB$$ (by cpet),
Hence $$ABCD$$ becomes square.
Thus,
$$(i)$$ On joining the ends of any two diameters of the circle, the figure obtained is a rectangle.
$$(ii)$$ On joining the ends of any two diameters of the circle, perpendicular to each other, the figure obtained is a square.
$$(ii)$$ On joining the ends of any two diameters of the circle, perpendicular to each other, the figure obtained is a square.
Draw a line segment PQ= 8 cm. Construct the perpendicular bisector of the line segment PQ. Let the perpendicular bisector drawn meets PQ at point R. Measure the length of PR and QR. Is PR=QR?
Steps of Construction :
$$1.$$ With $$P$$ and $$Q$$ as centers, draw arcs on both sides of $$PQ$$ with equal radii. The radius should be more than half the length of $$PQ$$.
$$2.$$ Let these arcs cut each other at points $$R$$ and $$RS$$
$$3.$$ Join $$RS$$ which cuts $$PQ$$ at $$D$$. Then $$RS = PQ$$. Also $$\angle{POR} = {90}^{\circ}$$.
Hence, the line segment $$RS$$ is the perpendicular bisector of $$PQ$$ as it bisects $$PQ$$ at $$P$$ and is also perpendicular to $$PQ$$. On measuring the lengths of $$PR = 4$$cm, $$QR = 4$$ cm Since $$PR = QR$$, both are $$4$$cm each
$$\therefore PR = QR$$.
Draw a triangle $$ABC$$ in which $$\angle A=120^{o}$$ and $$AB=AC=3\ cm$$. Draw the bisectors angle $$A$$.
$$!(BAD)=!(DAC)=60^0$$
$$=60^0$$
$$1.$$Draw a line segment $$AB=3$$cm
$$2.$$ Using protractor from $$B$$ measure from $${0}^{\circ}$$ and mark a point at $${120}^{\circ}$$
$$3.$$From the point $$A$$ using compass draw an arc of length $$3$$cm
$$\therefore AB=AC=3$$cm
$$4.$$Join $$BC$$
$$5.$$Draw an arc at $$\angle{A}$$
$$6.$$Bisect the arc at $$\angle{A}$$ and name the point of intersection of the arc as $$D$$
$$7.$$Join $$AD$$
$$\\therefore AD$$ is the angle bisector.
Hence $$\angle{BAD}=\angle{DAC}={60}^{\circ}$$
'
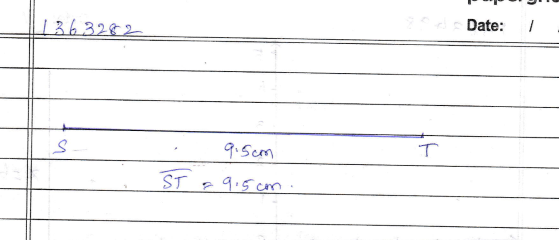
Draw a line segment $$ST$$, measuring $$9.5\ cm$$.
Using ruler mark a point at $$0$$ and name it as $$S$$ and from $$S$$ measure $$9.5$$cm and mark that point as $$T$$.Join $$ST$$.Check :$$ST=9.5$$cm
Result:$$ST=9.5$$cm
Draw a line $$l .$$ Draw a perpendicular to $$l$$ at any point on $$l.$$ On this perpendicular choose a point $$X , 4 \mathrm { cm }$$ away from $$l$$. Through $$\mathrm { X } ,$$ draw a line $$m$$ parallel to $$l$$.
Given:
A line l.
Required:
A line parallel to l which is $$4$$cm away from l.
Steps of construction:
$$1$$. Draw a line l.
$$2$$. Take any point A on it.
$$3$$. Draw a perpendicular AY to l.
$$4$$. Take a point x on AY such that AX$$=4$$cm
$$5$$. Draw a perpendicular to AY through X.
$$6$$. $$\therefore m || l$$.
Draw an angle of measure $$147^{o}$$ using protractor and construct its bisector.
$$1$$Draw a line $$OA$$.
$$2$$using protractor and center $$O$$ draw an $$\angle{AOB} ={147}^{\circ}$$
$$3$$ Now taking $$O$$ as center and any radius draw an arc that intersects $$OA$$ and $$OB$$ at $$p$$ and $$q$$.
$$4$$ Now take $$p$$ and $$q$$ as centers and radius more than half of $$PQ$$, draw arcs
$$5$$ Both the arcs intersect at $$R$$
$$6$$ join $$OR$$ and produce it.
$$7$$.$$OB$$ is the required bisector of $$\angle{AOB}$$
Construct an angle of measure $${22.5}^{o}$$ using compass and ruler.
Step 1: A ray from $$OB$$ is drawn.
Step 2: Draw a perpendicular bisector to the line $${A}^{\prime}B$$.Join $$AO$$ and $$AB$$
Step 3: Draw a perpendicular bisector to the line $$AB$$ then $$\angle{BOD}={45}^{\circ}$$
$$\therefore \angle{BOD}={45}^{\circ}$$
Step 4: Draw a perpendicular bisector to the line $$BD$$
$$\therefore \angle{BOC}={22.5}^{\circ}$$
Thus,$$\angle{BOC}$$ is the required angle making $${22.5}^{\circ}$$
Construct the following angles and verify by measuring them by a protractor.
$$75^{o}$$
Step 1: A ray $$OA$$ is drawn.
Step 2: An arc is drawn with $$O$$ as a centre.
Step 3: With the same length $$OA$$ construct an arc from $$A$$ to $$B$$ and join $$OB\therefore \angle{AOB}=60^{\circ}$$
Step 4: With the same length $$AB$$ construct another arc from $$B$$
Step 5: Construct a perpendicular bisector to another arc which is $$D$$.Join $$OD$$
$$\therefore \angle{AOD}={90}^{\circ}$$
Step 6: Construct a perpendicular bisector to $$BD=\dfrac{30}{2}={15}^{\circ}$$ .Join $$OC$$
$$\therefore \angle{AOC}={70}^{\circ}$$
Thus,$$\angle{AOC}$$ is the required angle making $${75}^{\circ}$$
Construct with ruler and compasses, angle of the following measure:
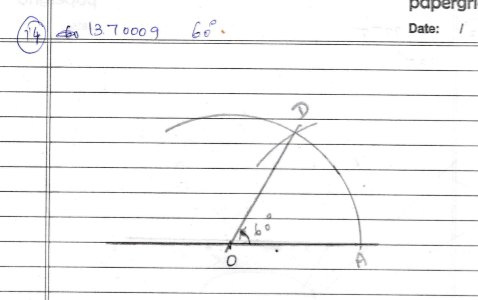
$$60^{o}$$
Step 1: A ray $$OA$$ is drawn.
Step 2: An arc $$OD$$ is drawn from $$O$$ as a centre with the same length as $$OA$$
Step 3:Join OD
$$\therefore \angle{AOD}={60}^{\circ}$$
Thus,$$\angle{AOD}$$ is the required angle making $${60}^{\circ}$$
Construct the following angles and verify by measuring them by a protractor:
$$105^{o}$$
Step 1: A ray $$OA$$ is drawn.
Step 2: An arc is drawn with $$O$$ as a centre.
Step 3:With the same length $$AB$$ construct another arc from $$B$$
Step 4: Construct a perpendicular bisector to another arc which is $$D$$.Join $$OD$$
$$\therefore \angle{AOC}={90}^{\circ}$$
Step 5: Construct a perpendicular bisector from $$C$$ to another point of the arc .Join $$OD$$
$$\therefore \angle{AOD}={105}^{\circ}$$
Thus,$$\angle{AOD}$$ is the required angle making $${105}^{\circ}$$
Construct the angle $$130^{\circ}$$ using protractor.
$$1.$$Draw a line $$AB$$
$$2.$$ Using protractor from the point $$A$$ measure $${130}^{\circ}$$ and mark it as $$C$$
$$3.$$Join $$AC$$
Result:
$$\therefore \angle{BAC}={130}^{\circ}$$
Construct the following angles and verify by measuring them by a protractor:
$$135^{o}$$
$$60^{\circ}+60^{\circ}=120^{\circ}$$
$$120^{\circ}+\dfrac{60^{\circ}}{2}=120^{\circ}+30^{\circ}$$
$$=120^{\circ}+\dfrac{30^{\circ}}{2}$$
$$=120^{\circ}+15^{\circ}$$
$$=135^{\circ}$$
Step 1: A ray $$OA$$ is drawn.
Step 2: An arc $$OB$$ is drawn with $$O$$ as a centre.
Step 3:With the same length $$BC$$ and from $$C$$ which touches the base line.
Step 4: Construct a perpendicular bisector to another arc which is $$C$$ to the base line.Join $$OE$$
Step 4: Construct a perpendicular bisector to another arc which is $$CE$$ .Join $$OD$$
$$\therefore \angle{AOC}={90}^{\circ}$$
Step 5: Construct a perpendicular bisector from $$C$$ to another point of the arc .Join $$OD$$
$$\therefore \angle{AOD}={135}^{\circ}$$
Thus,$$\angle{AOD}$$ is the required angle making $${135}^{\circ}$$
Construct the angle $$115^{o}$$ using protractor.
$$1.$$Draw a line $$AB$$
$$2.$$ Using protractor from the point $$A$$ measure $${130}^{\circ}$$ and mark it as $$C$$
$$3.$$Join $$AC$$
Result:$$\therefore \angle{BAC}={130}^{\circ}$$
Construct an angle of $$15^{o}$$.
First construct $${60}^{\circ}$$ angle
Bisect $${60}^{\circ}$$ angle to get $${30}^{\circ}$$
Lastly again bisect $${30}^{\circ}$$ angle to get $${15}^{\circ}$$
Draw any line segment PQ. take any point R not on it .through R, draw perpendicular to PQ. (use ruler and set - square)
(i) Place a set-square on PQ such that one arm of its right angle aligns along PQ.
(ii) Place a ruler along the edge opposite to the right angle of the set-square.
(iii) Hold the ruler fixed. Slide the
set-square along the ruler till the point R touches the other arm of the set-square.
(iv) Join RM along the edge through R meeting PQ at M. Then RM ┴ PQ
Draw an angle of measure $$70^{\circ}$$ with protractor. Bisect this angle using compasses and rules.
Steps of construction
Step I - Draw a ray OA as shown in figure
Step II - With the help of a protractor construct an angle AOB measure $$70^o$$
Step III - With a centre O and a convenient radius draw an arc cutting sides OA and OB at P and Q respectively.
Step IV - With centre P and radius more than half PQ , draw an arc.
Step V - With centre Q and the same radius, as in the previous step ,draw another arc intersecting the arc drawn in the previous step at R .
Step VI - Join OR and produce it to form ray OX .
The angle AOX and angle BOX so formed are equal
Draw an angle of measure $${153}^{\circ}$$ and divide it into four equal parts.
$$1.$$ Draw a ray $$BC$$
$$2.$$ Place the center of the protractor on point $$B,$$ and coincide line $$BC$$ with the protractor line.
$$3.$$ Mark point $$A$$ on $${153}^{\circ}$$
$$4.$$ Join $$AB$$
$$\therefore \angle{ABC}={153}^{\circ}$$
$$5.$$ With $$B$$ as centre and any suitable radius draw an arc cutting $$BC$$ at $$D$$ and $$AB$$ at $$E.$$
$$6.$$ Now, taking $$D$$ and $$E$$ as centers and with the radius more than $$\dfrac{1}{2}DE,$$ draw arcs to intersect each other.
$$7.$$ Let the point of intersection be $$X.$$
$$8.$$ Join $$B$$ and $$X$$
$$\therefore\,\,BX$$ is bisector of $$\angle{ABC}={153}^{\circ}$$
$$9.$$ Mark point $$F$$ where $$BX$$ intersects the arc.
$$10.$$ Now, taking $$E$$ and $$F$$ as centers and with a radius more than $$\dfrac{1}{2}$$ of $$EF,$$ draw arcs to intersect each other.
$$11.$$ Let the arcs intersect each other at point $$Y$$
$$12.$$ Join $$B$$ and $$Y$$
$$\therefore\,\,BY$$ is bisector of $$\angle{ABX}$$
Now we draw bisector of $$\angle{CBX}$$
$$13.$$ Taking $$D$$ and $$F$$ as centers and with the radius more than $$\dfrac{1}{2}$$ of $$DF,$$ draw arcs to intersect each other.
$$14.$$ Let them intersect at point $$Z$$
$$15.$$ Join $$B$$ and $$Z$$
$$\therefore\,\,BZ$$ is bisector of $$\angle{CBX}$$
Thus, we have divided $${153}^{\circ}$$ into $$4$$ equal parts.
Draw $$\angle ABC = 120^\circ .$$ Bisect the angle using the ruler and compasses only. Measure each angle so obtained and check whether the angles obtained on bisecting $$\angle ABC$$ are equal or not.
Steps of Construction:
1.Construct a line segment $$ BC $$.
2.Taking $$ B $$ as centre and some suitable radius construct an arc which meets $$ BC $$ at the point $$ P $$.
3. Taking $$ P $$ as centre and with same radius cut off the arcs $$ PQ $$ and $$ QR $$.
4.Now join $$ BR $$ and produce it to point $$ A $$
$$ \angle ABC=120^o $$
5.Taking $$ P $$ and $$ R $$ as centres construct two arcs which intersect each other at the points $$ S$$.
6.Now join $$ BS $$ and produce it to point $$ D $$.
Here $$ BD $$ is the bisector of $$ \angle ABC $$
By measuring each angle we get to know that is it $$ 60^o $$ yes,both the angles are of equal measure.
1.Construct a line segment $$ BC $$.
2.Taking $$ B $$ as centre and some suitable radius construct an arc which meets $$ BC $$ at the point $$ P $$.
3. Taking $$ P $$ as centre and with same radius cut off the arcs $$ PQ $$ and $$ QR $$.
4.Now join $$ BR $$ and produce it to point $$ A $$
$$ \angle ABC=120^o $$
5.Taking $$ P $$ and $$ R $$ as centres construct two arcs which intersect each other at the points $$ S$$.
6.Now join $$ BS $$ and produce it to point $$ D $$.
Here $$ BD $$ is the bisector of $$ \angle ABC $$
By measuring each angle we get to know that is it $$ 60^o $$ yes,both the angles are of equal measure.
Draw a line segment of length $$7.3\ cm$$ using a ruler.
Place the zero mark of the ruler at a point A.
Mark a point B at a distance of 7.3 cm from A.
Join AB.
AB is the required line segment of length 7.3 cm.
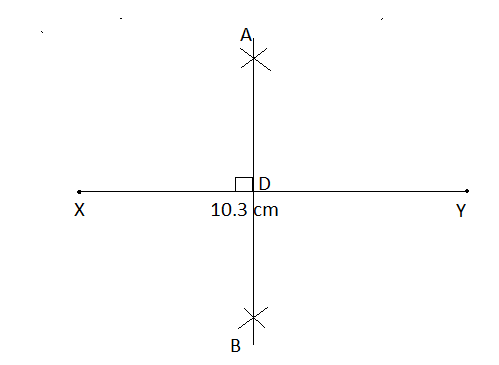
Draw the perpendicular bisector of $$ { XY } $$, whose length is $$10.3$$ cm
Steps of construction -
Step I - Draw a line segment, $$XY =10.3\text{ cm}$$ by using a graduated ruler.
Step II - With X as center and radius more than half of XY, draw arcs on each side of XY.
Step III - With Y as a center and the same radius as in step II, draw arcs cutting the arcs drawn in step II at A and B respectively.
Step IV - Draw the line segment with A and B as endpoints. Suppose it meets XY at D. Then, D bisects the line segment XY.
draw a line segment of length 7.6 cm and construct its perpendicular bisector
1) Draw a line l . Mark point A on it.
2) Since length is 7.6 cm, we measure 7.6 cm using ruler and compass.
3) Now keeping compass opened the same length, we keep pointed end at point A, and draw an arc on line l.
4) So, the required line segment is AB=7.6 cm
5) Now with A as centre and radius more than half AB, draw an arc on top and bottom of AB.
6) Now with B as centre and same radius, draw an arc on top and bottom of AB.
7) Where the two arcs intersect above AB is point C and where the two arcs intersect below AB is point D.
8) Join CD.
CD is the perpendicular bisector of AB.
Construct a perpendicular bisector of a given line segment.
Let, $$AB$$ be the given line.
$$1.$$Taking $$A$$ as center, and radius more than half of $$AB$$, draw arcs on above and below $$AB$$ .
$$2.$$Again, taking $$B$$ as center, and radius as before, draw arcs on above and below $$AB$$
$$3.$$Let the point where arcs intersect on above $$AB$$ be $$P$$ and the point where arcs intersect at below be $$Q$$. Join $$PQ$$
$$4.$$Let $$PQ$$ intersects $$AB$$ at the point $$M$$.
Thus, line $$PMQ$$ is the required perpendicular bisector of $$AB$$.
Draw an angle of $${ 152 }^{ o }$$ and divide the into four equal parts.
Draw a circle of radius $$3$$cm.At a point $$P$$ on it, draw a tangent to the circle without using centre.
$$1.$$Draw a circle with radius $$3$$cm
$$2.$$Take a point $$P$$ on the circle.
$$3.$$Through $$P,$$ draw any chord $$PQ$$
$$4.$$Mark a point $$R$$ either in major arc or in minor arc.
$$5.$$Join $$PR$$ and $$QR$$
$$6.$$At $$P,\,\,$$construct $$\angle{QPT}$$ equal to $$\angle{PRQ}$$ on the opposite side of the chord $$PQ$$
$$7.$$Produce $$TP$$ to $${T}^{\prime}$$ to get a straight line $${T}^{\prime}PT$$.
Construct a $$\Delta ABC$$ in which $$CA = 6 \,cm, AB = 5 \,cm$$ and $$\angle BAC = 45^o$$. Then construct a triangle whose sides are $$\dfrac{3}{5}$$ of the corresponding sides of $$\Delta ABC$$.
Steps Of construction
Step $$1:$$ Draw a line $$AB=5\text{cm}$$
Step $$2:$$ With $$A$$ as center Measure $$45^{\circ}$$ using Protractor and draw a ray $$\overrightarrow {AX}$$
Step $$3:$$ With $$B$$ as center Cut an arc of Radius $$6\text{cm}$$ on the $$\overrightarrow {AX}$$
Step $$4:$$ Mark the intersection as $$C$$ Join $$B,C$$
Step $$5:$$ Now divide the line $$AB$$ in the ratio $$\dfrac{3}{5}$$
Step $$6:$$ Mark a point $$B'$$ $$3\text{cm}$$ apart from $$A$$ on the line $$AB$$
Step $$7:$$ Draw a line parallel to $$BC$$ passing through $$B'$$
Step $$8:$$ Mark the intersection as $$C'$$
Draw an angle of $$40^\circ.$$ Copy its supplementary angle.
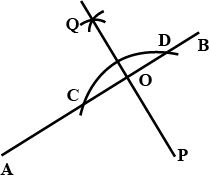
Draw an angle and label it as $$\angle BAC$$. Construct another angle equal to $$\angle BAC$$.
Draw $$105 ^\circ$$ using rounder.
$$105^o=90^o+15^o$$
$$105^o=90^o+30^o/2$$
So, to make $$105^o$$, we make $$90^o$$ and then bisector of $$30^o$$.
$$1$$. Draw a line OA.
$$2$$. Taking O as centre and any radius, draw an arc cutting OA at B.
$$3$$. Now, with B as centre and same radius as before, draw an arc intersecting the previously drawn arc at point c.
$$4$$. Now, with c as centre, and same radius, draw another arc intersecting previously drawn arc at point D.
$$5$$. Draw ray OE passing through C and ray of passing through D.
$$6$$. Taking C and D as centre, with radius more than $$\dfrac{1}{2}CD$$, draw arcs intersecting at P.
$$7$$. Join OP.
$$8$$. Taking Q as centre, with radius more than $$\dfrac{1}{2}QC$$, draw arc intersecting at R.
$$9$$. Join OR.
Thus, $$\angle AOR=105^o$$.
Draw any line segment $$\overline{PQ}$$. Take any point R, not on it, through R, draw a perpendicular to $$\overline{PQ}$$. (use ruler and set-square).
$$(1)$$ Take the given line segment $$\overline{PQ}$$ and mark any point R outside $$\overline{PQ}$$.
$$(2)$$ Place a set square on $$\overline{PQ}$$ such that one arm of its right angle aligns along $$\overline{PQ}$$.
$$(3)$$ Place the ruler along the edge opposite to the right angle of the set square.
$$(4)$$ Hold the ruler fixed. Slide the set square along the ruler till the point R touches the other arm of the set square.
$$(5)$$ Draw a line along the edge of the set square which will be passing through R. It is the required line, which is perpendicular to $$\overline{PQ}$$.
$$(2)$$ Place a set square on $$\overline{PQ}$$ such that one arm of its right angle aligns along $$\overline{PQ}$$.
$$(3)$$ Place the ruler along the edge opposite to the right angle of the set square.
$$(4)$$ Hold the ruler fixed. Slide the set square along the ruler till the point R touches the other arm of the set square.
$$(5)$$ Draw a line along the edge of the set square which will be passing through R. It is the required line, which is perpendicular to $$\overline{PQ}$$.
Draw rough sketches for the following.
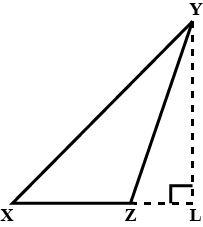
In $$\Delta$$XYZ, YL is an altitude in the exterior of the triangle.
YL is an altitude in the exterior of $$\Delta$$XYZ.
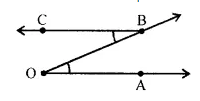
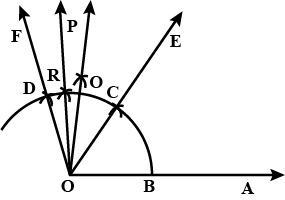
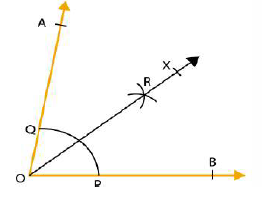
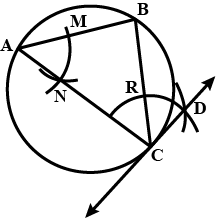
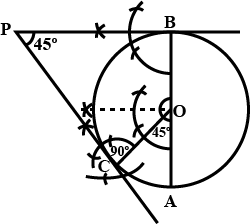
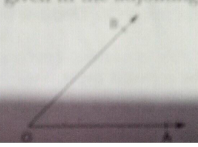
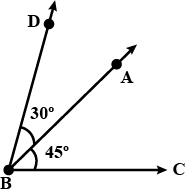
Draw an angle equal to $$\angle AOB$$ given in the adjoining figure.
Draw a line segment AB of length 8 cm . Taking A as centre, draw a circle of radius 4 cm and taking B as centre draw another circle of radius 3 cm Construct tangents to each circle from the centre of the other circle .
$${\textbf{Step 1: Draw line segment AB of length 8 cm.}}$$
$${\textbf{Step 2: Taking A as center, draw a circle of radius 4 cm.}}$$
$${\textbf{Step 3: Taking B as center, draw a circle of radius 3 cm.}}$$
$${\textbf{Step 4: Make perpendicular bisector of AB. Let M be the mid - point of AB.}}$$
$${\textbf{Step 5: Taking M as center and MA as radius, draw a circle.}}$$
$${\textbf{Step 6: Let the circle intersect left circle at P,Q and right circle at R,S.}}$$
$${\textbf{Step 7: Join BP, BQ, AR and AS.}}$$
$${\textbf{Hence, AR, AS and BP, BQ are the required tangents.}}$$
Draw a line segment $$\bar {AB} $$ of length $$6.4$$ cm and construct its axis of symmetry (use ruler and compass).
Steps of construction :
(i) Draw a line segment $$\bar { AB } $$ of length $$6.4$$ cm.
(ii) With A as the center, using a compass, draw a circle. The radius of this circle should be more than half of the length of $$\bar { AB } $$.
(iii) With the same radius and with B as center, draw another circle using a compass. Let it cut the previous circle at C and D.
(iv) Join $$\bar { CD } $$. Then, $$\bar { CD } $$ is the axis of symmetry of line segment $$\bar { AB } $$.
The diameter of a circle is $$14\ cm$$, find the radius.
Fill in the blanks:
A radius of a circle is a line segment with one end at ______ and the other end at _______
Radius of a circle is a line segment with one end at centre of the circle and other end at a point which lies on the circle.
Draw a line segment $$AB$$ and bisect it. Bisect one of the equal parts to obtain a line segment of length $$\dfrac{1}{2}(AB)$$.
ABCD is a square E,F,G and H are points on AB, BC, CD and DA respectively, such that $$ AE = BF = CG = DH. $$ Prove that EFGH is a square.
Draw an angle and label it as $$ \angle BAC.$$ Construct another angle, equal to $$ \angle BAC.$$
Steps of construction:
Step 1: Draw any angle $$BAC$$.
Now will construct an angle equal to $$∠BAC$$.
Step 2: Draw a line segment $$QR$$.
Step 3: Draw an arc that intersects $$∠BAC$$ at $$E$$ and $$D$$ using $$A$$ as a center and choose any radius.
Step 4: With the same measurements (as in step 3), Draw an arc from point $$Q$$.
Step 5: With $$S$$ as center and radius equal to $$DE$$, draw an arc which intersects the previous arc at $$T$$.
Step 6: Join $$Q$$ and $$T$$.
$$\angle PQR$$ is our new angle equal to $$\angle BAC$$
Using a protractor, draw the following angles.
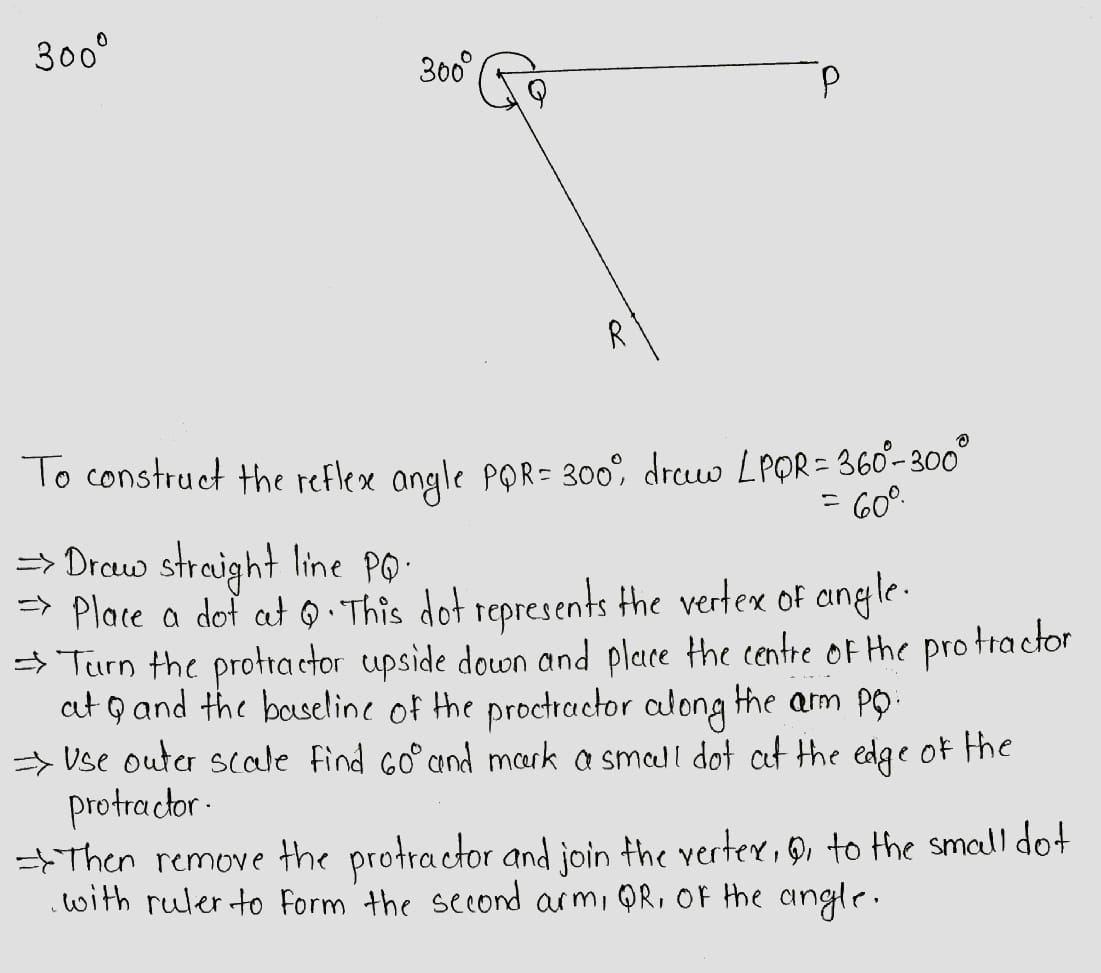
$${ 300 }^{ o }$$
Using a protractor, draw the following angles.
$${ 130 }^{ o }\quad $$
Using a protractor, draw the following angles.
$${ 430 }^{ o }$$
Using a protractor, draw the following angles.
$${ 60 }^{ o }$$
Draw a line PQ. Take a point R on it. Draw a line perpendicular to PQ and passing through R.(Using ruler and compasses)
Step I: Draw a line $$PQ$$ and take a point $$R$$ on it.
Step II: With $$R$$ as centre and a convenient radius construct an arc touching the line $$PQ$$ at two points $$A$$ and $$B$$.
Step III: With $$A$$ and $$B$$ as centres and a radius greater than $$RA$$ construct two arcs cutting each other at $$S$$.
Step IV: Join $$RS$$ and extend it in both directions to get a line perpendicular to $$PQ$$.
Thus, $$XY$$ is the line required which is perpendicular to $$PQ$$ and passes through $$R$$ as shown in the above image.
Using a protractor, draw the following angles.
$$-{ 40 }^{ o }$$
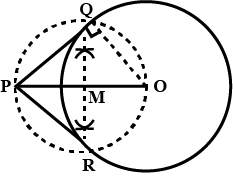
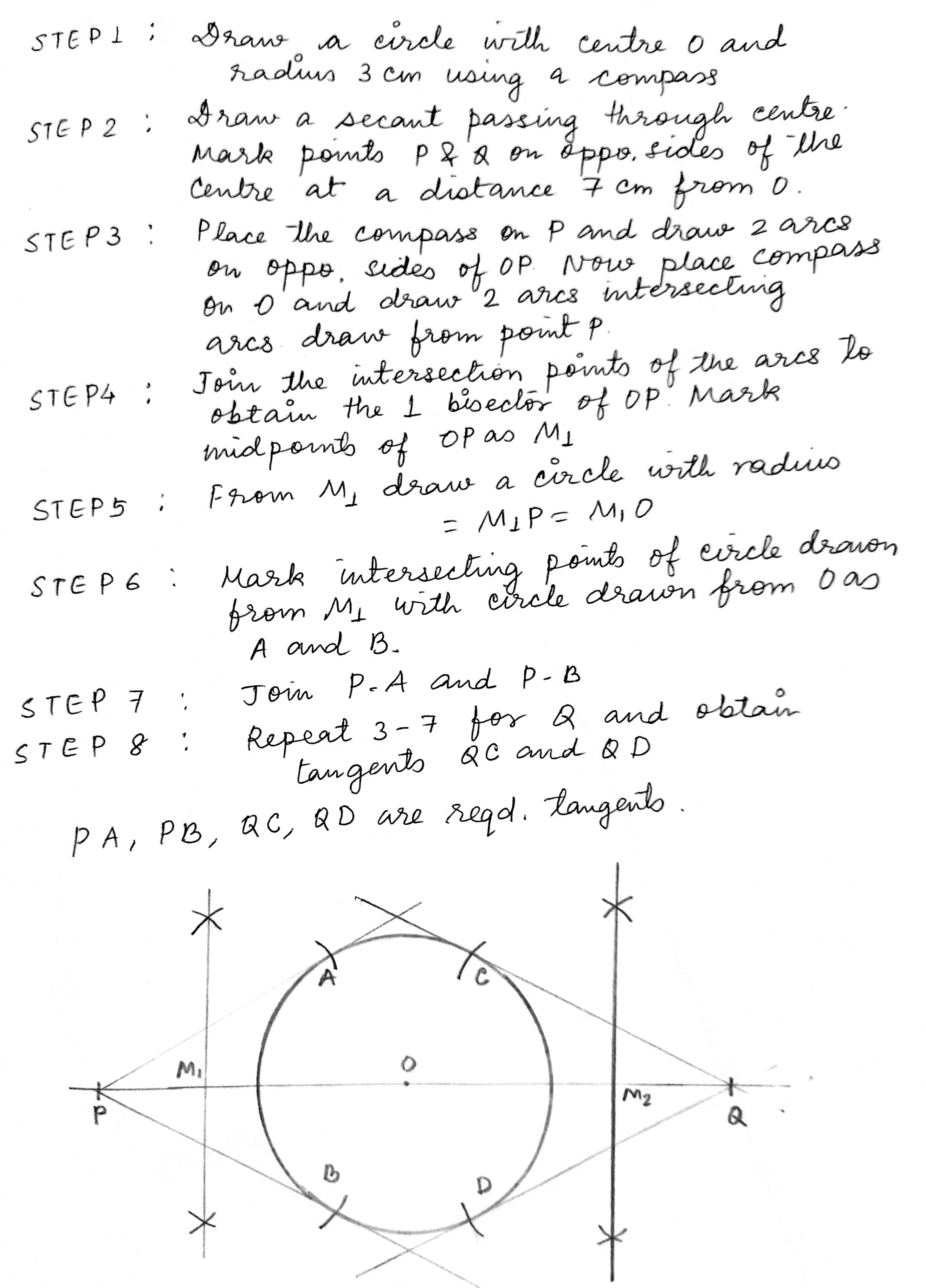
Draw a circle of radius $$3$$ cm. From a point $$P$$, $$7$$ cm away from the centre of the circle, draw two tangents to the circle. Also, measures the triangle of the tangents.
Steps of Construction :
1. Draw a circle of radius $$3$$ cm from centre $$O$$
2. Set a point $$P$$ which is $$7$$ cm far from point $$O$$. Join $$OP$$.
3. Draw a perpendicular bisector of $$OP$$ which cuts $$OP$$ at point $$Q$$.
4. Now, considering $$Q$$ as a centre and equal radius $$(OQ=PQ)$$.Draw a circle.
5. Both circles intersect at points $$A$$ and $$B$$.
Join $$PA$$ and $$PB$$.
Therefore, $$AP$$ and $$BP$$ are the required tangents.
Measurements : $$AP=BP=6.1$$ cm
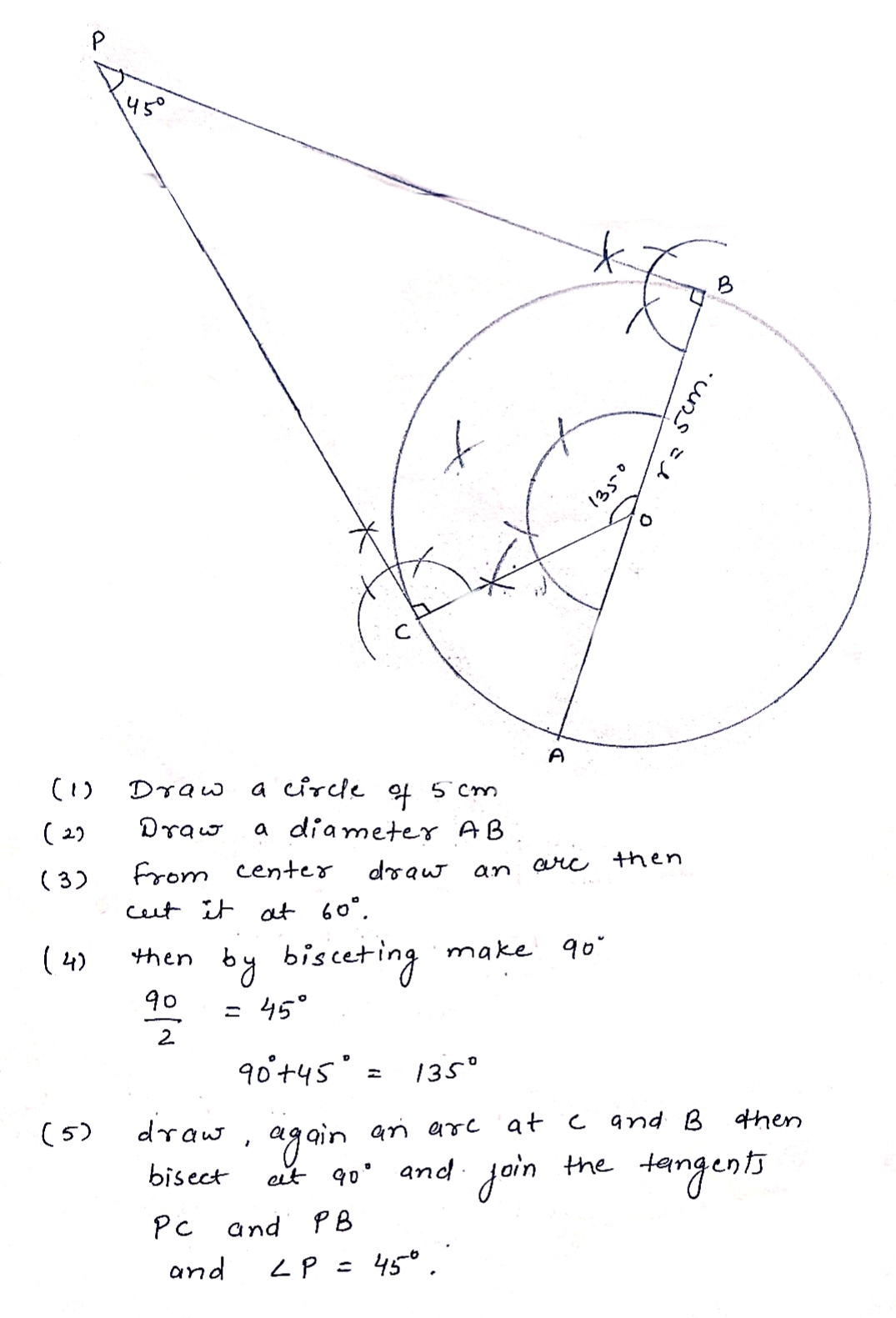
Draw a circle of radius $$4.2$$ cm. Draw a pair of tangents to this circle inclined to each other at an angle of $$45^0$$.;
Steps of construction :
1) Draw a circle with radius $$4.2$$ cm and centre $$O$$.
2) Draw diameter $$AB$$
3) With $$OB$$ as base, draw $$\angle BOC=45^0$$
4) At $$C$$, draw a line perpendicular to $$OC$$
5) At $$A$$, draw a line perpendicular to $$OA$$
Both the lines intersect each other at point $$P$$. So $$PC$$ and $$PA$$ tangents.
Construct each of the following angles, using ruler and compasses:
$$75^o$$
Step of construction
Construct a line segment
Considering $$P$$ as centre and any radius construct and arc which intersects the line $$PQ$$ at the point $$R$$
Considering $$R$$ as centre and same radius construct an arc which intersects the previous arc at the point $$S$$
Considering $$S$$ as centre and same radius construct an arc which intersect the previous arc in step $$2$$ at the point $$T$$
Considering $$T$$ and $$S$$ as centre and radius more than half of $$TS$$, construct arcs which intersects each other at the point $$U$$
Join the line $$PU$$ which intersects the arc in step $$2$$ at the point $$V$$
Considering $$V$$ and $$S$$ as centers and radius more than half of $$VS$$, construct arcs which intersects each others at the point $$W$$
Join the line $$PW$$
Therefore, we know that $$\angle WPQ=75^o$$
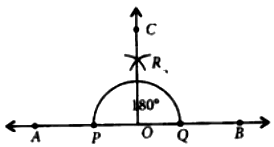
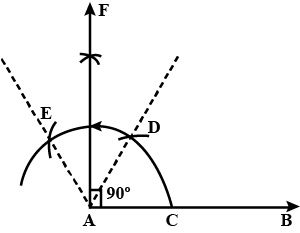
Construct an angle of $$90^o$$ using ruler and compasses and bisect it.
Step of Construction:
Construct a line segment $$OA$$
Considering $$O$$ as centre and suitable radius construct an arc cutting the line $$OA$$ at the point $$B$$
Considering $$B$$ as a centre and suitable radius as before constructing an arc to cut the previous arc at the point $$C$$
Considering $$C$$ as centre and same radius cut the arc at the point $$D$$
Considering $$C$$ as a centre and the radius more than half of $$CD$$ construct an arc
Considering $$D$$ as a centre and same radius construct another arc to cut the previous arc at the point $$E$$
Join $$E$$ so we get $$\angle AOE=90^o$$
Considering $$B$$ as centre and radius more than half of $$CB$$construct and arc
Considering $$C$$ as the centre and same radius construct an arc with cuts the previous arc at the point $$F$$
Join $$OF$$
Therefore, $$F$$ is the bisector of the right $$\angle AOE$$.
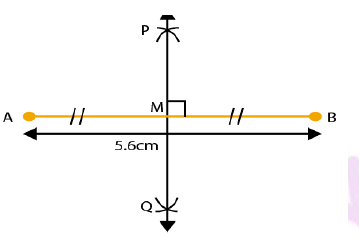
Draw a line segment $$AB=5.6\ cm$$ and draw its perpendicular bisector. Measure the length of each part.
Steps of construction:
Construct a line segment $$AB=5.6\ cm$$
Considering $$A$$ as centre and radius more than half of line segment $$AB$$, draw two arcs on the each side of the line segment $$AB$$
Considering $$B$$ as centre and radius more than half of line segment $$AB$$, draw arcs which cuts the previous arcs at the point $$P$$ and $$Q$$
Join the points $$PQ$$ such that it intersects the line segment $$AB$$ at the point $$M$$
Therefore, $$PQ$$ is the perpendicular bisector of the line segment $$AB$$.
So the length of each part is $$AM=BM=2.8\ cm$$
Construct each of the following angles, using ruler and compasses:
$$37.5^o$$
Step of construction
Construct a line segment $$PQ$$
Considering $$P$$ as centre and any radius, construct and arc which intersects the line $$PQ$$ at the point $$R$$
Considering $$R$$ as centre and same radius construct an arc which intersects the previous arc at the point $$S$$
Considering $$S$$ as centre and same radius construct an arc which intersect the previous arc in step $$2$$ at the point $$T$$
Considering $$T$$ and $$S$$ as centre and radius more than half of $$TS$$, construct arcs which intersects each other at the point $$U$$
Join the line $$PU$$ which intersects the arc in step $$2$$ at the point $$V$$
Considering $$V$$ and $$S$$ as centers and radius more than half of $$VS$$, construct arcs which intersects each others at the point $$W$$
Join the line $$PW$$ and $$\angle WPQ=75^o$$
Bisects the $$\angle WPQ$$
Therefore, we know that $$\angle ZPQ=37.5^o$$
Draw a circle with centre $$O$$ and radius $$4$$ cm. Draw any diameter $$AB$$ of this circle. Construct tangents to the circle at each of the two end pointsd of the diameter $$AB$$.
Steps of construction:
1) Draw a circle with centre $$O$$ and radius $$4$$ cm.
2) Draw any diameter $$AB$$.
3) Draw line $$L\bot OA$$ such that $$\angle OAL=90^0$$
4) Draw line $$M\bot OB$$ such that $$\angle OBM=90^0$$
Thus, $$LA$$ and $$LB$$ are the required tangents.
Draw an angle of $$80^o$$ with the help of a protractor and bisect it. Measure each part of the bisected angle.
Steps of construction:
Construct a ray $$OB$$
Using the protractor construct $$\angle AOB$$ of $$80^o$$
Considering $$O$$ as centre and convenient radius construct an arc cutting the sides $$OA$$ and $$OB$$ at the points $$Q$$ and $$P$$
Considering $$Q$$ as centre and radius more than half of the angle $$PQ$$, construct an arc
Considering $$P$$ as the centre and radius more than half of the angle $$PQ$$, construct another arc which intersects the previous arc at the point $$R$$
Join the points $$OR$$ and produce it in order to from a ray $$OX$$
Therefore, $$OX$$ is the bisects of the $$\angle AOB$$
So the measure of each parts of the bisected angle is $$\angle AOX =\angle BOX=40^o$$
Construct each of the following angles, using ruler and compasses:
$$135^o$$
Step of construction
Construct a line segment $$AB$$ and produce $$MA$$ to $$C$$
Considering $$A$$ as centre and any radius, construct and arc which intersecting $$AC$$ at the point $$D$$ and $$AB$$ at point $$E$$
Considering $$D$$ and $$E$$ as centre and same radius more than half $$DE$$, construct Two arch intersecting each other at the point $$F$$
Join the points $$FA$$ which intersects the arc in step $$2$$ at point $$G$$
Considering $$G$$ and $$D$$ as centre and radius more than half of $$GD$$ construct two arcs intersecting each other at the point $$H$$
Join $$HA$$
Therefore, we know that $$\angle HAB=135^o$$
Construct the angle whose cosine is equal to its tangent.
Construct each of the following angles with the help of a protractor:
$$72^{o}$$
Step 1-Draw a line segment PQ, which is one of the arms of the angle that is to be constructed.
Step 2-Place the protractor with its point O on the point Q of the line segment PQ.
Step 2-Align OA along the edge PQ.
Step 4-The protractor has two-way markings. We consider the scale which has 0 degrees near point P for construction. Mark point R next to the 72 degrees mark on the scale.
Step 5-Join points Q and R. ∠PQR = 72 degrees is the required angle.
Construct each of the following angles with the help of a protractor:
$$25^{o}$$
Steps of Construction :
1)Draw a line segment $$PQ$$ which is one of the arms of the angle that is to be constructed.
2)Place the protractor with its point $$O$$ on the point $$Q$$ of the line segment PQ.
3)Align $$OA$$ along the edge $$PQ$$
4)The protractor has two-way markings. We consider the scale which has $$0^o$$ near point $$P$$ for construction. Mark point $$R$$ next to the $$25^o$$ mark on the scale.
5)Jointhe points $$Q$$ and $$R$$.
$$\angle PQR = 25^o$$ is the required angle.
Draw a line segment $$AB=5.6 \ cm$$. Draw the perpendicular bisector of $$AB$$.
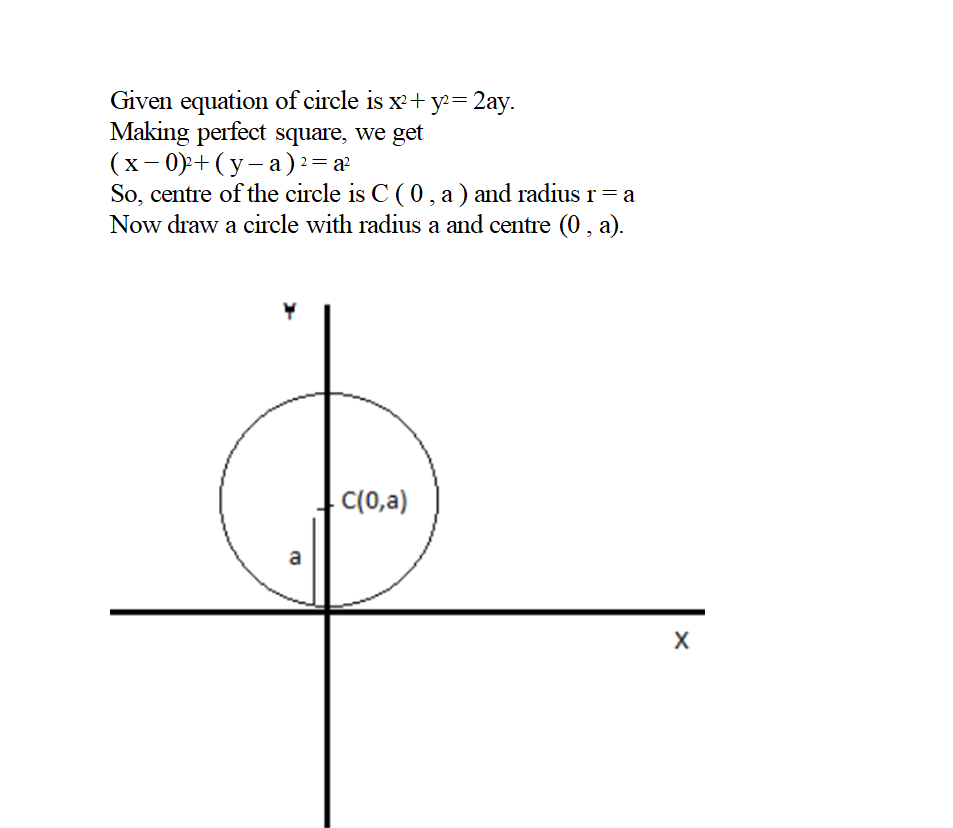
Draw the circles whose equations are $$x^{2} + y^{2} = 2ay$$.
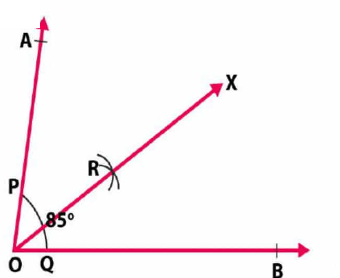
Construct $$\angle AOB=85^o$$ with the hepl of a protector. Draw a ray OX bisecting $$\angle AOB$$.
Draw an angle of $$50^o$$ with the help of a protractor. Draw a ray bisecting this angle.
Draw a line AB. Take a point P on it. Draw a line passing through P and perpendicular to AB
Construct each of the following angles, using ruler and compasses:
$$105^o$$
Step of construction
Construct a line segment $$PQ$$
Considering $$P$$ as centre and any radius, construct an arc which intersects $$PQ$$ at the point $$R$$
Considering $$R$$ as centre and same radius, construct and arc which intersects the previous arc at the point $$S$$
Considering $$S$$ as centre and same radius, construct and arc which intersects the arc in step $$2$$ at the point $$T$$
Considering $$T$$ and $$S$$ as centre and radius more than half of $$TS$$, construct arcs which intersects each other at point $$U$$
Join $$PU$$ which intersects the arc in step $$2$$ at point $$V$$
Considering $$T$$ and $$V$$ as centres and radius more than half of $$TV$$, construct arc intersecting in each other the point $$W$$
Join $$PW$$ which is makes $$105^o$$ with the ray $$PQ$$
Therefore, we know that $$\angle WPQ=105^o$$.
Construct each of the following angles, using ruler and compasses:
$$22.5^o$$
Step of construction
Construct a line segment $$AB$$
Considering $$A$$ as a centre and any radius, construct an arc which intersects $$AB$$ at the point $$C$$
Considering $$C$$ as a centre and the same radius, construct an arc which intersects the previous arc at the point $$D$$
Considering $$D$$ as a centre and same radius, construct an arc which intersects the arc in step $$2$$ at the point $$E$$
Considering $$E$$ and $$D$$ as centre and radius more than half of $$ED$$, construct arcs which intersect each other at point $$F$$
Join the points $$AF$$ which intersects the arc in step $$2$$ at point $$G$$
Considering $$G$$ and $$C$$ as centres and radius more than half of $$GC$$, construct arc intersecting in each other at the point $$H$$
Join $$AH$$ which is intersects the arc in step $$2$$ at the point $$I$$
Considering $$I$$ and $$C$$ as centres and radius more than half of $$IC$$, construct arcs which intersect each other at the point $$J$$
Join $$AJ$$
Therefore, we know that $$\angle JAB=22.5^o$$.
Construct each of the following angles with the help of a protractor:
$$180^{o}$$
Step 1-Draw a line segment QR, which is one of the arms of the angle that is to be constructed.
Step 2-Place the protractor with its point O on the point Q of the line segment QR.
Step 2-Align OA along the edge QR.
Step 4-The protractor has two-way markings. We consider the scale which has 0 degrees near point R for construction. Mark point P next to the 180 degrees mark on the scale.
Step 5-Join points P and Q. ∠PQR = 180 degrees is the required angle.
Construct each of the following angles with the help of a protractor:
$$48^{o}$$
Step 1-Draw a line segment QR, which is one of the arms of the angle that is to be constructed.
Step 2-Place the protractor with its point O on the point Q of the line segment QR.
Step 2-Align OA along the edge QR.
Step 4-The protractor has two-way markings. We consider the scale which has 0 degrees near point R for construction. Mark point P next to the 48 degrees mark on the scale.
Step 5-Join points P and Q. ∠PQR = 48 degrees is the required angle.
Using a pair of compasses construct the following angles:
$$90^o$$
Draw a line PX
Let Q be a point on AC. With Centre Q and any radius, draw an arc cutting AX at M and N
respectively
With centre N and radius more than half MN, draw an arc.
With centre M and the same radius as before, draw another arc to cut the previous arc at W
Join Qm and produced it to R
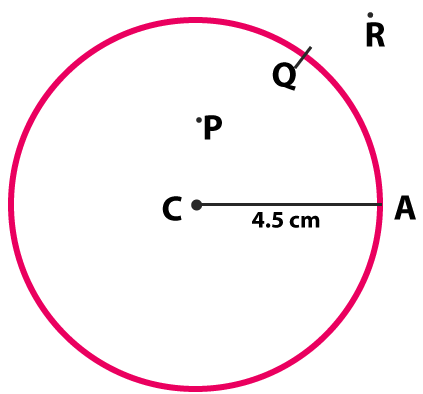
Draw a circle with centre C and radius $$4.5\, cm.$$ Mark points P, Q, R such that P lies in the interior of the circle, Q lies on the circle, and R lies in the exterior of the circle.
Construct the following angle with the help of a protractor:
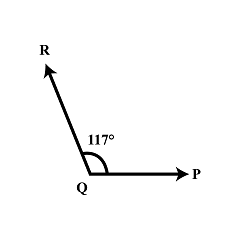
$$117^{o}$$
Step 1-Draw a line segment PQ, which is one of the arms of the angle that is to be constructed.
Step 2-Place the protractor with its point O on the point Q of the line segment PQ.
Step 2-Align the horizontal line passing through O (on protractor) along the edge PQ.
Step 4-The protractor has two-way markings. We consider the scale which has 0 degrees near point P for construction. Mark point R next to the 117 degrees mark on the scale.
Step 5-Join points Q and R.
$$\angle PQR = 117^o$$ is the required angle.
Using a pair of compasses construct the following angles:
$$60^o$$
Draw a ray QP
With Q as centre and any suitable radius, draw an arc cutting QP at a point N.
With N as centre and the same radius as before, draw another arc to cut the previous arc at M.
Draw QM and produce it to R
Hence $$\angle PQR=60^o$$
Construct each of the following angles with the help of a protractor:
$$23^{o}$$
Step 1-Draw a line segment $$PQ$$, which is one of the arms of the angle that is to be constructed.
Step 2-Place the protractor with its point $$O$$ on the point $$Q$$ of the line segment $$PQ$$.
Step 2-Align $$OA$$ along the edge $$PQ$$.
Step 4-The protractor has two-way markings. We consider the scale which has $$0$$ degrees near point P for construction. Mark point $$R$$ next to the $$23$$ degrees mark on the scale.
Step 5-Join points $$Q$$ and $$R$$. $$\angle PQR = 23^o$$ degrees is the required angle.
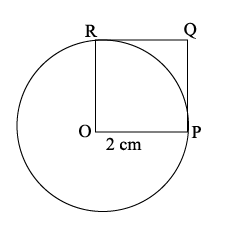
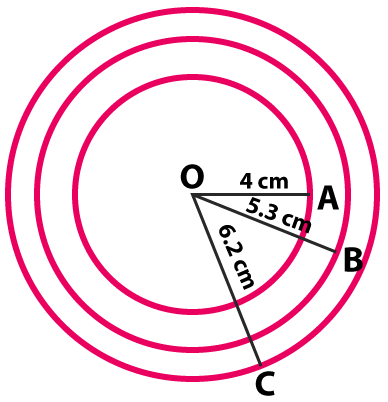
Take a point O on your notebook and draw circles of radii $$4\, cm, 5.3\, cm$$ and $$6.2\, cm$$, each having the same centre O.
Using a pair of compasses construct the following angles:
$$120^o$$
Draw a ray $$QP$$
With $$Q$$ as centre and any suitable radius, draw an arc cutting $$QP$$ at a point $$N$$.
With $$N$$ as centre and the same radius, cut the arc at $$A$$. Again with $$A$$ as centre and the same radius
cut the arc at $$M$$
Join $$QM$$ and produce it to $$R$$
Hence $$\angle PQR=120^{\circ}$$
Construct each of the following angles with the help of a protractor:
$$90^{o}$$
Step 1-Draw a line segment PQ, which is one of the arms of the angle that is to be constructed.
Step 2-Place the protractor with its point O on the point Q of the line segment PQ.
Step 2-Align OA along the edge PQ.
Step 4-The protractor has two-way markings. We consider the scale which has 0 degrees near point P for construction. Mark point R next to the 90 degrees mark on the scale.
Step 5-Join points Q and R. ∠PQR = 90 degrees is the required angle.
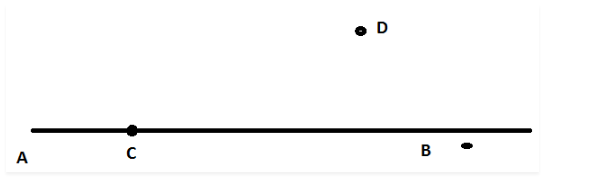
In the diagram, $$A, B$$ and $$C$$ are fixed collinear points; $$D$$ is a fixed point outside the line. Locate:
Are the points $$P, Q, R$$ collinear?
No, the points $$P, Q, R$$ are not collinear.
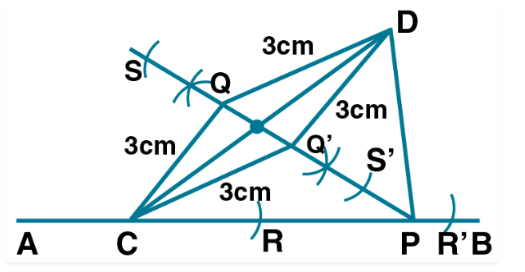
Without using set-squares or protractor construct:
Draw the locus of a point which moves so that it is always $$2.5$$ cm from $$B$$.
Taking $$B$$ as centre and $$2.5$$ cm radius draw a circle
circumference of this circle is the required locus which is always $$2.5cm$$ away from $$B$$
circumference of this circle is the required locus which is always $$2.5cm$$ away from $$B$$
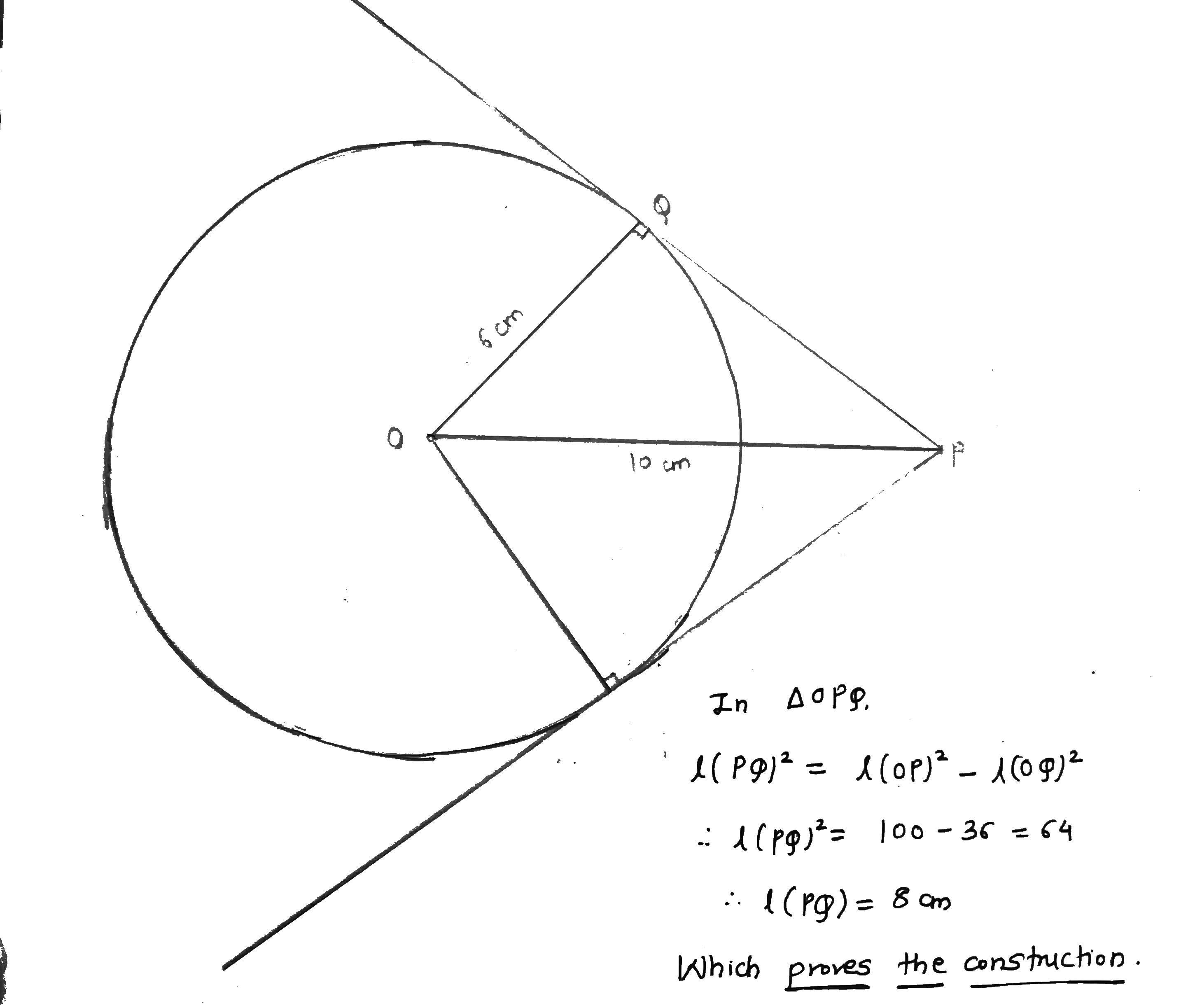
Draw a circle of radius 6 cm. From a point 10 cm away from its centre, construct a pair of tangents to the circle and measure their lengths.
Steps of Construction:
1. A circle with radius $$6\ cm$$ is drawn taking $$O$$ as centre
2. Point $$P$$ is marked at $$10\ cm$$ away from centre of circle.
3. With the half of compass mark $$M$$ which is the midpoint of $$OP$$.
4. Draw a circle with centre $$M$$, taking radius $$MO$$ or $$MP$$ which intersects the given circle at $$Q$$ and $$R$$.
5. Now join $$PQ$$ and $$PR$$. These are the tangents of the circle.
1. A circle with radius $$6\ cm$$ is drawn taking $$O$$ as centre
2. Point $$P$$ is marked at $$10\ cm$$ away from centre of circle.
3. With the half of compass mark $$M$$ which is the midpoint of $$OP$$.
4. Draw a circle with centre $$M$$, taking radius $$MO$$ or $$MP$$ which intersects the given circle at $$Q$$ and $$R$$.
5. Now join $$PQ$$ and $$PR$$. These are the tangents of the circle.
We know that, the tangent to a circle is perpendicular to the radius through the point of contact.
$$\therefore \ $$In $$\triangle OPQ, \ OQ\perp QP$$
and in $$\triangle OPR, \ OR\perp PR$$
Hence, both $$\triangle OPQ$$ and $$\triangle OPR$$ are right angle triangles.
Applying Pythagoras theorem to both $$\triangle s$$, we get:
$$OP^2=OQ^2+PQ^2$$
and $$OP^2=OR^2+PR^2$$
$$OQ=OR=radius=6\ cm$$ and $$OP=10\ cm$$
$$\therefore \ 10^2=6^2+PQ^2$$
and $$10^2=6^2+PR^2$$
$$\Rightarrow PQ^2=100-36=64$$
and $$PR^2=100-36=64$$
$$\therefore \ PQ=PR=8\ cm$$
Hence, the length of the tangents to a circle of radius $$6\ cm$$, from a point $$10\ cm$$ away from the centre of the circle, is $$8\ cm$$.
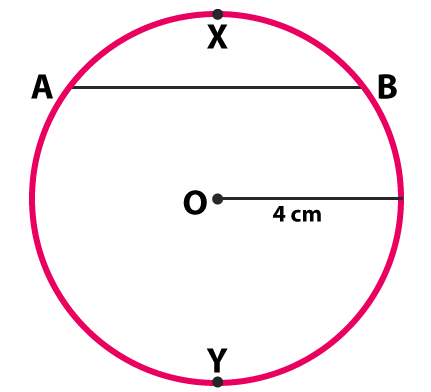
Draw a circle with centre O and radius $$4\, cm.$$ Draw a chord AB of the circle. Indicate by marking points X and Y, the minor arc AXB and the major arc AYB of the circle.
In the diagram, $$A, B$$ and $$C$$ are fixed collinear points; $$D$$ is a fixed point outside the line. Locate:
the points $$S$$ such that $$CS = DS$$ and $$S$$ is $$4$$ cm away from the line $$CD$$. How many such points are possible?
Steps of construction:-
(i) Join $$C\,\&\,D$$ and draw perpendicular bisector of $$CD$$ which intersect $$AB$$ at $$P$$ and bisect $$CD$$ at $$M$$
(ii) Extend the line $$PM$$
(iii) Taking $$M$$ as centre and $$radius=4cm$$ cut the extended line $$PM$$ at $$S\,\&\,S'$$ above and below $$CD$$
(iv) thus $$CS=DS$$ and $$CS'=DS'$$ and $$S\,\&\,S'$$ are $$4cm$$ away from $$CD$$
Two such Points are possible $$S\,\&\,S'$$
(i) Join $$C\,\&\,D$$ and draw perpendicular bisector of $$CD$$ which intersect $$AB$$ at $$P$$ and bisect $$CD$$ at $$M$$
(ii) Extend the line $$PM$$
(iii) Taking $$M$$ as centre and $$radius=4cm$$ cut the extended line $$PM$$ at $$S\,\&\,S'$$ above and below $$CD$$
(iv) thus $$CS=DS$$ and $$CS'=DS'$$ and $$S\,\&\,S'$$ are $$4cm$$ away from $$CD$$
Two such Points are possible $$S\,\&\,S'$$
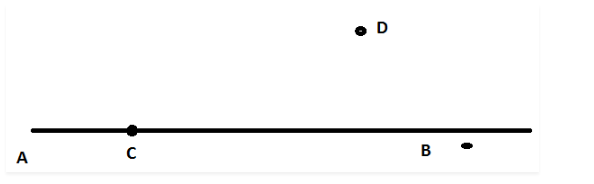
In the diagram, $$A$$, $$B$$ and $$C$$ are fixed collinear points; $$D$$ is a fixed point outside the line. Locate:
the points $$R$$ on $$AB$$ such that $$DR = 4$$ cm. How many such points are possible?
Here the points $$A, B$$ and $$C$$ are collinear and $$D$$ is any point which is outside $$AB$$
Taking $$D$$ as centre and $$4$$ cm radius construct an arc which intersects $$AB$$ at $$R$$ and $$R’$$
Here $$R$$ and $$R’$$ are the two points on $$AB.$$
Taking $$D$$ as centre and $$4$$ cm radius construct an arc which intersects $$AB$$ at $$R$$ and $$R’$$
Here $$R$$ and $$R’$$ are the two points on $$AB.$$
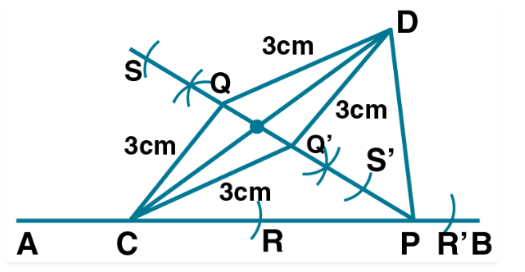
Use ruler and compasses only for this question. Draw a circle of radius $$4$$ cm and mark two chords $$AB$$ and $$AC$$ of the circle of length $$6$$ cm and $$5$$ cm respectively.
Construct the locus of points, inside the circle, that are equidistant from $$AB$$ and $$AC$$.
Mark a point $$A$$ on this circle
Taking $$A$$ and centre and $$6$$ cm radius construct an arc which cuts the circle at $$B$$.
Again with $$5$$ cm radius, construct another arc which cuts the circle at $$C$$.
Construct the perpendicular bisector of $$AC$$.
Here any point on it will be equidistant from $$A$$ and $$C$$.
Construct the angle bisector of$$\angle A$$ which intersects the perpendicular bisector of $$AC$$ at the point $$P$$.
Hence, $$P$$ is the required locus
Taking $$A$$ and centre and $$6$$ cm radius construct an arc which cuts the circle at $$B$$.
Again with $$5$$ cm radius, construct another arc which cuts the circle at $$C$$.
Construct the perpendicular bisector of $$AC$$.
Here any point on it will be equidistant from $$A$$ and $$C$$.
Construct the angle bisector of$$\angle A$$ which intersects the perpendicular bisector of $$AC$$ at the point $$P$$.
Hence, $$P$$ is the required locus
There are two set-squares in your geometry box. What are measures of the angles formed at their corners? Do they have any measure that is common?
A straight line $$AB$$ is $$8$$ cm long. Locate by construction the locus of a point which is:
Mark two points $$X$$ and $$Y$$, which are $$4$$ cm from $$AB$$ and equidistant from $$A$$ and $$B$$.
(iii) Here any point on $$l$$ is equidistant from $$A$$ and $$B$$.
(iv) Now cut off $$OX = OY = 4$$ cm. $$X$$ and $$Y$$ are the required loci which is equidistant from $$AB$$ and also from point $$A$$ and $$B$$.
(v) Join$$ AX, XB, BY$$ and $$YA$$.
The figures $$AXBY$$ is square shaped as its diagonals are equal and bisect each other at right angles.
(iv) Now cut off $$OX = OY = 4$$ cm. $$X$$ and $$Y$$ are the required loci which is equidistant from $$AB$$ and also from point $$A$$ and $$B$$.
(v) Join$$ AX, XB, BY$$ and $$YA$$.
The figures $$AXBY$$ is square shaped as its diagonals are equal and bisect each other at right angles.
In the diagram, $$A, B$$ and $$C$$ are fixed collinear points; $$D$$ is a fixed point outside the line. Locate:
Are the points $$P, Q, S$$ collinear?
Yes, the points $$P, Q, S$$ are collinear.
Draw an angle of $$ 60^{\circ} $$ using ruler and compasses and divide it into four equal parts. Measure each part.
Steps of constructions
Step I - With the help of protractor, draw $$\angle AOB= \angle 60^{\circ} $$
Step II - Cut $$OA$$ and $$OB$$ at $$U$$ and $$X$$, taking $$O$$ as the center and any convenient radius.
Step II - With vertex $$X$$ as centre, by using compass take more than half of arc $$UX$$ and draw an arc.
Step V- With vertex $$W$$ as centre, by using a compass with same length cut the previous arc at $$Z$$ and extend it to point $$D$$
Step VII- With vertex $$U$$ as centre, by using a compass with same length cut the previous arc at $$P$$ and extend it to point $$E$$
Each part measures $$=\dfrac{60^o}{4}=15^0$$
Step I - With the help of protractor, draw $$\angle AOB= \angle 60^{\circ} $$
Step II - Cut $$OA$$ and $$OB$$ at $$U$$ and $$X$$, taking $$O$$ as the center and any convenient radius.
Step II - With vertex $$X$$ as centre, by using compass take more than half of arc $$UX$$ and draw an arc.
Step III- With vertex $$U$$ as centre , by using a compass with the same length cut the previous arc at $$V$$ and extend it to point $$C$$.
Step IV - With point $$X$$ as centre, by using a compass take more than half of arc $$WX$$ and draw an arc.
Step V- With vertex $$W$$ as centre, by using a compass with same length cut the previous arc at $$Z$$ and extend it to point $$D$$
Step VI - With point $$W$$ as centre, by using a compass take more than half of arc $$UW$$ and draw an arc.
Step VII- With vertex $$U$$ as centre, by using a compass with same length cut the previous arc at $$P$$ and extend it to point $$E$$
Draw two acute angles and one obtuse angle without using a protractor. Estimate the measures of the angles. Measure them with the help of a protractor and see how much accurate is your estimate
Two acute angles made without using protractor are as shown above.
Measure of ∠ABC will be less than 45° and that of ∠PQR seems to be more than 45°.
On measuring the two angles with the help of protractor we get,
∠ABC=35°
PQR=60°
So, our estimation for both angles are pretty much accurate.
Above figure shows an obtuse angle ∠XYZ which has been drawn without using a protractor.
Estimate measure of this angle seems to be close to 120°.
Let us find the measure of above angle using protractor.
XYZ=120°
So, our estimation for both angles are pretty much accurate.
Bisect a straight angle , Using ruler and compasses. Measure each part.
Steps of construction:
Step I - draw a line segment AB with the help of ruler.
Step II - Draw an arc of $$ 180^{\circ} $$ which meets the ray $$ \underset{OA} {\rightarrow } $$ at $$P$$ and $$ \underset{OB} {\rightarrow } $$ at $$Q.$$
Step III - Taking P and Q as the centers and radius more than $$\dfrac{1}{2} $$ PQ, draw two arc which intersect each other a R.
Step VI- Joint OR and Produce it to any point C.
Step II - $$\underset{OC}{\rightarrow } $$ bisect the straight angle.
$$ \therefore $$ $$ \angle BOC $$ = $$ \angle AOC $$ = $$ 90^{\circ} $$
Draw an angle of $$140^{o}$$ with help of a protractor and bisect it using ruler and compasses.
Steps of construction:
Step I - With the help of protractor, draw $$\angle BAC= 140^{o}$$
Step II - With $$A$$ as center and any convenient radius, draw an arc, cutting $$AC$$ and $$AB$$ at $$Q$$ and $$P$$ respectively.
Step III - With center $$P$$ and radius more than half of arc $$PQ$$, draw an arc.
Step IV - With center $$Q$$ and the same radius as before, draw another arc, cutting the previously drawn arc at point $$S$$.
Step V - Join $$AS$$ and produce it to any point $$X$$.
Thus, ray $$AX$$ bisects $$\angle CAB$$
Step I - With the help of protractor, draw $$\angle BAC= 140^{o}$$
Step II - With $$A$$ as center and any convenient radius, draw an arc, cutting $$AC$$ and $$AB$$ at $$Q$$ and $$P$$ respectively.
Step III - With center $$P$$ and radius more than half of arc $$PQ$$, draw an arc.
Step IV - With center $$Q$$ and the same radius as before, draw another arc, cutting the previously drawn arc at point $$S$$.
Step V - Join $$AS$$ and produce it to any point $$X$$.
Thus, ray $$AX$$ bisects $$\angle CAB$$
Bisect a right angle, using ruler and compasses. Measure each part. Bisect each of these parts. What will be the measure of each of these parts What will be the measure of each of these parts
Steps of construction:
Step I - with the help of protractor, draw $$ 90^{\circ} $$
Step II - Cut OA and OB at Y and U, taking U as the center and any convenient radius.
Step II - With vertex U, by using compass take more than half of arc YU and draw arc.
Step III - With vertex Y, by using compass with same length, cut the previous arc at Q and extant to point D.
Step I - with the help of protractor, draw $$ 90^{\circ} $$
Step II - Cut OA and OB at Y and U, taking U as the center and any convenient radius.
Step II - With vertex U, by using compass take more than half of arc YU and draw arc.
Step III - With vertex Y, by using compass with same length, cut the previous arc at Q and extant to point D.
Draw an angle ABC of measure $$ 45^{\circ} $$, using ruler and compasses. Now draw an angle DBA of measure 30 o, using ruler and compasses as shown in Fig, 9.14, What is the measure of $$ \angle DBC $$
Step I- Draw a ray BC→
Step II - With B as center and any radius draw an arc which cuts BC at P.
Step III- With center P and Same radius, draw an arc which cuts the previously drawn arc at Q.
Step IV - Similarly, with Q as center and same radius draw another arc which cuts the previously drawn arc at R.
Draw an angle of $$ 80^{\circ} $$ with the help of a protractor . Then construct angles of (i) $$ 40^{\circ} $$ (ii) $$ 160^{\circ} $$ and (iii) $$ 120^{\circ} $$ .
Steps of construction :
$$1$$. Draw a ray OA.
$$2$$. With the help of a protractor , construction $$ \angle $$ BOA = $$ 80^{\circ} $$
$$3$$. Taking O as center and any suitable radius , draw an arc to intersect rays OA and OB at points P and Q respectively .
$$4$$. Take radius more than half the radius $$OP$$.With this radius make an arc from point $$P$$ and $$Q$$ which will intersect at $$X$$ . By joining $$O$$ and $$X$$ we get bisector of $$\angle AOB$$ .
Let ray OC be the bisector of $$ \angle $$ BOA , then $$ \angle $$ COA = $$ \dfrac{1}{2} \, \angle $$ BOA = $$ \dfrac{1}{2} \times 80^{\circ} = 40^{\circ} $$ .
$$5$$. With Q as center and radius equal to PQ , draw an arc to cut the extended arc PQ at R . Join OR and produce it to form ray OD , then $$ \angle $$ DOA = $$ 2\, \angle $$ BOA = $$ 2 \times 80^{\circ} = 160^{\circ} $$.
$$6$$. Bisect $$ \angle $$ DOB as done in step $$4$$. Let OE be the bisector of $$ \angle $$ DOB is then
$$ \angle $$ EOA = $$ \angle $$ EOB + $$ \angle $$ BOA = $$ \dfrac{1}{2} \, \angle $$ DOB + $$ \angle $$ BOA = $$ \dfrac{1}{2} (80)^{\circ} + 80^{\circ} = 40^{\circ} + 80^{\circ} = 120^{\circ} $$
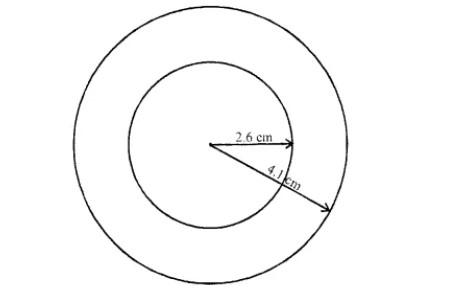
With the same centre O, draw two circles of radii $$2.6$$ cm and $$4.1$$ cm.
Steps of construction :
(a) For a circle of radius $$4.1$$ cm
(i) Pen the cor.npasses for the required radius $$4.1$$ cm,
by putting the pointer on $$0$$ and opening the pencil up to $$4.1$$ cm.
(ii) Place the pointer of the compasses at $$0$$.
(iii) Turn the compasses slowly to draw the circle.
(b) For a circle of radius of $$2.6$$ crm
(i) Open the compasses for the required radius $$2.6$$ cm,
by putting the pointer on $$0$$ and opening the pencil up to $$2.6$$ cm.
(ii) Place the pointer of the compasses at O.
(iii) Turn the compasses slowly to draw the circle.
(a) For a circle of radius $$4.1$$ cm
(i) Pen the cor.npasses for the required radius $$4.1$$ cm,
by putting the pointer on $$0$$ and opening the pencil up to $$4.1$$ cm.
(ii) Place the pointer of the compasses at $$0$$.
(iii) Turn the compasses slowly to draw the circle.
(b) For a circle of radius of $$2.6$$ crm
(i) Open the compasses for the required radius $$2.6$$ cm,
by putting the pointer on $$0$$ and opening the pencil up to $$2.6$$ cm.
(ii) Place the pointer of the compasses at O.
(iii) Turn the compasses slowly to draw the circle.
Prove that through a given point , we can draw one perpendicular to a given line.
[Hint : Use proof by contradiction].
From the point P , a perpendicular PM is drawn to the given line AB.
$$ \therefore $$ $$ \angle $$ PMB = $$ 90^{\circ} $$
Let if possible , we can draw another perpendicular PN to the line AB. Then ,
$$ \angle $$ PMB = $$ 90^{\circ} $$
$$ \therefore $$ $$ \angle $$ PMB = $$ \angle $$ PNB , which is possible only when PM and PN coincide with each other.
Hence , through a given point , we can draw only one perpendicular to a given line.
Construct a circle of radius:
$$3.5$$ cm
Steps of construction:
(i) Open the compasses for the required radius $$3.5$$ cm, by putting the pointer on $$0$$ and opening the pencil up to $$3.5$$ cm
(ii) Draw a point with a sharp pencil and marks it as Q in the centre.
(iii) Place the pointer of the compasses where the centre has been marked.
(iv) Turn the compasses slowly to draw the circle.
(i) Open the compasses for the required radius $$3.5$$ cm, by putting the pointer on $$0$$ and opening the pencil up to $$3.5$$ cm
(ii) Draw a point with a sharp pencil and marks it as Q in the centre.
(iii) Place the pointer of the compasses where the centre has been marked.
(iv) Turn the compasses slowly to draw the circle.
Draw an angle of $$ 110^{\circ} $$ with the help of a protractor and bisect it.
Given : An angle ABC = $$ 110^{\circ} $$ .
To construct : The bisector of $$ \angle $$ ABC
Steps of construction :
$$1$$. With B as center and a convenient radius draw an arc to intersect the ray's BA and BC at P and Q respectively.
$$2$$. With center P and a radius greater than half of PQ , draw an arc.
$$3$$. With center Q and the same radius (as in step $$2$$), draw another arc to cut the previous arc at R .
$$4$$. Draw ray BR. This ray is the required bisector of $$ \angle $$ ABC.
Construct a circle of radius:
$$2$$ cm
Steps of construction:
(i) Open the compasses for the required radius $$2$$ cm, by putting the pointer on $$0$$ and opening the pencil up to $$2$$ cm
(ii) Draw a point with a sharp pencil and marks it as Q in the centre.
(iii) Place the pointer of the compasses where the centre has been marked.
(iv) Turn the compasses slowly to draw the circle.
(i) Open the compasses for the required radius $$2$$ cm, by putting the pointer on $$0$$ and opening the pencil up to $$2$$ cm
(ii) Draw a point with a sharp pencil and marks it as Q in the centre.
(iii) Place the pointer of the compasses where the centre has been marked.
(iv) Turn the compasses slowly to draw the circle.
Draw a circle of radius $$ 3 \,cm $$ and draw its diameter and label it as AC. Construct its perpendicular bisector and let it intersect the circle at B and D. What type of quadrilateral is ABCD?
Steps for comstruction :
Step 1. Taking center $$O$$ and radius $$OC = 3\,cm $$ , draw a circle.
Step 2. Join $$A$$ and $$C$$ and draw a perpendicular bisector of $$AC$$ that intersects the circumference of circle at $$B$$ and $$D$$.
Step 3. Join $$B$$ and $$D$$
The required quadrilateral ABCD is a cyclic quadrilateral.
Draw a circle of radius $$4 \,cm.$$ Construct a pair of tangents to it, the angle between which is $$60^\circ.$$ Also, justify the construction. Measure the distance between the centre of the circle and the point of intersection of tangents.
Angle between tangents is $$60^\circ.$$ So angles between their radii is $$180^\circ - 60^\circ = 120^\circ.$$
As the angles between tangents and their corresponding radii are supplementary.
Steps of construction:
(i) Draw a circle of radius $$4 \,cm.$$
(ii) Draw any diameter POS.
(iii) Draw OQ making $$\angle AOC = 120^\circ.$$
(iv) Draw tangent at P by drawing $$\angle OPT = 90^\circ.$$
(v) Similarly, draw $$\angle OQT$$ equal to $$90^\circ$$ to draw tangent.
(vi) Both PT, QT tangents intersect at T and make angle of $$60^\circ.$$
Hence, the two tangents on circle are TP and TQ inclined at $$60^\circ.$$
Justification: Because the radius OP and tangent PT at contact point makes angle $$\angle TPO = 90^\circ$$
Similarly, $$\angle TQO = 90^\circ$$
In quadrilateral $$TPOQ,$$
$$\angle T + \angle P + \angle O + \angle Q = 360^\circ$$
$$\Rightarrow \angle T + 90^\circ + 120^\circ + 90^\circ = 360^\circ$$ [$$\because \angle O = 120^\circ$$ by construction]
$$\Rightarrow \angle T = 360^\circ - 300^\circ$$
$$\Rightarrow T = 60^\circ.$$
Hence, verified.
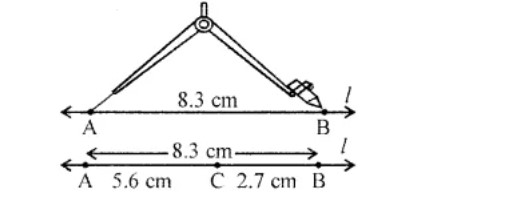
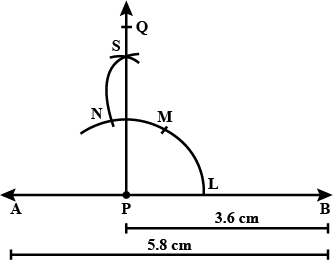
Construct $$\overset{\_}{AB}$$ of length $$8.3$$ cm. From this cut off $$\overset{\_}{AC}$$ of length $$5.6$$ cm. Measure the length of BC...
Steps of construction :
(i) Draw a line |. Mark a point A on line L.
(ii) Place the compass pointer on the zero marks of the ruler. Open it to place the pencil point up to the $$8.3$$ cm mark.
(iii) Without changing the opening of the compass, place the pointer on A and swing an arc to cut | at B.
(iv) $$\overset{\_}{AB}$$ is a line segment of the required length of $$8.3$$ cm.
(v) Place the compass pointer on the zero marks of the ruler. Open it to place the pencil point up to $$5.6$$ cm mark.
(vi) Without changing the opening of the compass, place the pointer on A and swing ana rc to cut | at C.
(vii) $$\overset{\_}{AC}$$ is a line segment of length $$5.6$$ cm.On measurement, $$\overset{\_}{BC} = 2.7$$ cm.
(i) Draw a line |. Mark a point A on line L.
(ii) Place the compass pointer on the zero marks of the ruler. Open it to place the pencil point up to the $$8.3$$ cm mark.
(iii) Without changing the opening of the compass, place the pointer on A and swing an arc to cut | at B.
(iv) $$\overset{\_}{AB}$$ is a line segment of the required length of $$8.3$$ cm.
(v) Place the compass pointer on the zero marks of the ruler. Open it to place the pencil point up to $$5.6$$ cm mark.
(vi) Without changing the opening of the compass, place the pointer on A and swing ana rc to cut | at C.
(vii) $$\overset{\_}{AC}$$ is a line segment of length $$5.6$$ cm.On measurement, $$\overset{\_}{BC} = 2.7$$ cm.
Construct a line segment of the length of $$7.3$$ cm using ruler and compass.
Using ruler, we mark two points A and B which are $$7.3$$ cm apart.
Join A and B and get AB.
AB is a line segment of length $$7.3$$ cm
Join A and B and get AB.
AB is a line segment of length $$7.3$$ cm
Draw $$\angle{AOB} = 76^\circ$$ with the help of a protractor. Bisect this angle by using a ruler and compass. Measure the two parts by your protractor and see how accurate you are.
Steps of construction:
1. Draw a line segment OB.
2. Construct $$\angle{AOB}$$ with the help of protector $$= 76°$$.
3. With the help of compass and O as centre draw an arc meeting OB and OA at P and Q respectively.
4. With P and Q as centre and radius more than $$\frac{1}{2}$$PQ draw two arcs meeting each other at R.
5. OD is the bisector of $$\angle{AOB}$$.
6. On measuring $$\angle{AOD}= \angle{DOB}= 38^\circ$$.
1. Draw a line segment OB.
2. Construct $$\angle{AOB}$$ with the help of protector $$= 76°$$.
3. With the help of compass and O as centre draw an arc meeting OB and OA at P and Q respectively.
4. With P and Q as centre and radius more than $$\frac{1}{2}$$PQ draw two arcs meeting each other at R.
5. OD is the bisector of $$\angle{AOB}$$.
6. On measuring $$\angle{AOD}= \angle{DOB}= 38^\circ$$.
Draw a circle with centre C and radius $$4.2$$ cm. Draw any chord AB. Construct the perpendicular bisector of AB and examine if it passes through C.
Steps of construction :
(i) Draw a point with a sharp pencil aid mark it as C.
(ii) Open the compass for the required radius of $$4.2$$ cm,
by putting the pointer on 0 and opening the pencil up to $$4.2$$ cm.
(iii) Place the pointer of the compass at C.
(iv) Turn the compass slowly to draw the circle.
(v) Draw any chord $$\overline{AB}$$ of this circle.
(vi) With A as the centre, using a compass, draw a arc.
The radius of this circle should be more than half of the length of $$\overline{AB}$$.
(vii) With the same radius and with B as centre,
draw another arc using a compass.
Let it cut the previous arc at D and E.
(viii) Join $$\overline{DE}$$.
Then $$\overline{DE}$$ is the perpendicular bisector of the line segment ‘AB.
On examination, we find that it passes through C.
(i) Draw a point with a sharp pencil aid mark it as C.
(ii) Open the compass for the required radius of $$4.2$$ cm,
by putting the pointer on 0 and opening the pencil up to $$4.2$$ cm.
(iii) Place the pointer of the compass at C.
(iv) Turn the compass slowly to draw the circle.
(v) Draw any chord $$\overline{AB}$$ of this circle.
(vi) With A as the centre, using a compass, draw a arc.
The radius of this circle should be more than half of the length of $$\overline{AB}$$.
(vii) With the same radius and with B as centre,
draw another arc using a compass.
Let it cut the previous arc at D and E.
(viii) Join $$\overline{DE}$$.
Then $$\overline{DE}$$ is the perpendicular bisector of the line segment ‘AB.
On examination, we find that it passes through C.
Draw a line segment $$\overline{PQ} =5.6$$ cm. Draw a perpendicular to it from a point outside $$\overline{PQ}$$ by using ruler and compass.
Given: A-Line segment $$\overline{PQ}= 5.6$$ cm and a point A outside the line. Required: To draw a 1 ar to $$\overline{PQ}$$ from point A.
Steps of construction :
(i) With A as the centre and any suitable radius,
drawn an arc to cut the line $$\overline{PQ}$$ at points C and D.
(ii) With C and D as centres, drawn two arcs of the equal radius ($$\overline{CD}$$) cutting each other at B on the other side of $$\overline{PQ}$$.
(iii) Join A and B to meet the line $$\overline{PQ}$$ at N,
then $$\overline{AN}$$ is the required perpendicular from the point A to the line $$\overline{PQ}$$.
Steps of construction :
(i) With A as the centre and any suitable radius,
drawn an arc to cut the line $$\overline{PQ}$$ at points C and D.
(ii) With C and D as centres, drawn two arcs of the equal radius ($$\overline{CD}$$) cutting each other at B on the other side of $$\overline{PQ}$$.
(iii) Join A and B to meet the line $$\overline{PQ}$$ at N,
then $$\overline{AN}$$ is the required perpendicular from the point A to the line $$\overline{PQ}$$.
Draw a line segment $$AB = 5.4\ \text{cm}$$. Construct perpendicular at A by using a ruler and compass.
Steps of construction:
1. Draw $$AB = 5.4\ \text{cm}$$.
2. With any radius draw an arc which cuts $$AB$$ at $$M$$.
3. With $$M$$ as a centre and the same radius, cut the previous arc at $$N$$ and $$P$$.
4. With $$N$$ and $$P$$ as centres draw arcs which intersect at $$L$$.
5. $$AL$$ is the required perpendicular.
1. Draw $$AB = 5.4\ \text{cm}$$.
2. With any radius draw an arc which cuts $$AB$$ at $$M$$.
3. With $$M$$ as a centre and the same radius, cut the previous arc at $$N$$ and $$P$$.
4. With $$N$$ and $$P$$ as centres draw arcs which intersect at $$L$$.
5. $$AL$$ is the required perpendicular.
Draw a line segment $$\overline{AB} = 6.2$$ cm. Draw a perpendicular to it at a point M on $$\overline{AB}$$ by using ruler and compass.
Given: A-line $$AB = 6.2$$ cm and a point P on it.
Required: To draw a perpendicular arc to AB at point P.
Step of Construction :
(i) With P as a centre and any suitable radius, draw an arc to cut the line AB at points C and D.
(ii) With C and D as centres, draw two arcs of the equal radius (>$$\frac{1}{2}$$CD) cutting each other at Q.
(iii) Join P and Q.then QP is the required perpendicular to the line AB at the point P
Required: To draw a perpendicular arc to AB at point P.
Step of Construction :
(i) With P as a centre and any suitable radius, draw an arc to cut the line AB at points C and D.
(ii) With C and D as centres, draw two arcs of the equal radius (>$$\frac{1}{2}$$CD) cutting each other at Q.
(iii) Join P and Q.then QP is the required perpendicular to the line AB at the point P
By using and compass, construct an angle of $$135^\circ$$ and bisect it. Measure any one part by protractor and see how accurate you are.
Steps of construction:
1. Draw a line OB with the help of a ruler.
2. With O as a centre and any suitable radius draw an arc to meet OB at S.
3. With S as a centre and same radius draw an arc to meet the previous arc at L.With L as the centre and the same radius draws another arc M.Again M as centre draws another arc to meet the first arc at N.
4. With Mand N as centres draw two arcs of the equal radius (>$$\frac{1}{2}$$SL) cutting each other at A.
5. Join OA intersecting the radius at point Q.
6. Now taking Q and M as a centre draw two arcs cf equal radius cutting each other at P.
7. Join PO.
8. Measuring the $$\angle{POB}$$ with protractor we get $$\angle{POB}$$ equal to $$135^\circ$$.
9. Taking S and R as a centres draw two arcs cutting each other at T.
Join TO.
10. $$\angle{TOB}$$ is the bisector of $$\angle{POB}. \angle{TOB} = \angle{TOP} = 67.5^\circ$$.
1. Draw a line OB with the help of a ruler.
2. With O as a centre and any suitable radius draw an arc to meet OB at S.
3. With S as a centre and same radius draw an arc to meet the previous arc at L.With L as the centre and the same radius draws another arc M.Again M as centre draws another arc to meet the first arc at N.
4. With Mand N as centres draw two arcs of the equal radius (>$$\frac{1}{2}$$SL) cutting each other at A.
5. Join OA intersecting the radius at point Q.
6. Now taking Q and M as a centre draw two arcs cf equal radius cutting each other at P.
7. Join PO.
8. Measuring the $$\angle{POB}$$ with protractor we get $$\angle{POB}$$ equal to $$135^\circ$$.
9. Taking S and R as a centres draw two arcs cutting each other at T.
Join TO.
10. $$\angle{TOB}$$ is the bisector of $$\angle{POB}. \angle{TOB} = \angle{TOP} = 67.5^\circ$$.
Draw the perpendicular bisector of $$\overline{XY}$$ whose length is $$8.3$$ cm.
{i} Take any point P on the bisector drawn. Examine whether PX = PY.
(ii) If M is the mid-point of XY, what can you say about the lengths MX and MY?
Steps of construction :
(i} Draw a line segment $$\overline{XY}$$ of length $$8.3$$ cm.
(ii) With X as the centre, using a compass, draw a circle. The radius of this circle should be more than half of the length of $$\overline{XY}$$.
(iii) With the same radius and with Y as the centre, draw another circle using a compass. Let it cut the previous circle at A and B.
(iv) Join $$\overline{AB}$$.
Then, $$\overline{AB}$$ is the perpendicular bisector of the line segment $$\overline{XY}$$.
(a) On examination, we find the PX = PY.
(b) We can say that the length of MX is Equal to the length of MY.
(i} Draw a line segment $$\overline{XY}$$ of length $$8.3$$ cm.
(ii) With X as the centre, using a compass, draw a circle. The radius of this circle should be more than half of the length of $$\overline{XY}$$.
(iii) With the same radius and with Y as the centre, draw another circle using a compass. Let it cut the previous circle at A and B.
(iv) Join $$\overline{AB}$$.
Then, $$\overline{AB}$$ is the perpendicular bisector of the line segment $$\overline{XY}$$.
(a) On examination, we find the PX = PY.
(b) We can say that the length of MX is Equal to the length of MY.
Draw a line segment $$PQ = 6.8$$ cm. Draw a perpendicular to it from a point A outside PQ by using ruler and Compass.
Steps of construction:
1. Draw a line segment $$PQ = 6.8$$ cm and take a point A outside PQ.
2. With A as the centre and any suitable radius, draw an arc to cut line PQ at point C and D.
3. With C and D as centres, draw two arcs of equal radius cutting each other at B on the other side of line PQ.
4. Join AB to meet the line PQ at M.
1. Draw a line segment $$PQ = 6.8$$ cm and take a point A outside PQ.
2. With A as the centre and any suitable radius, draw an arc to cut line PQ at point C and D.
3. With C and D as centres, draw two arcs of equal radius cutting each other at B on the other side of line PQ.
4. Join AB to meet the line PQ at M.
Draw the plan for the information given below:
Scale 20 m=1cm
| Metre To C | ||
To D 50 To E 30 | 140 100 60 40 | 40 to B |
| From A |
Scale $$20m=1 cm$$
$$\therefore \boxed {1m= \dfrac {1}{20}cm}$$
now for every $$1m$$ data in given table we will use the above conversion to represent the construction in $$cm$$
As per the given table and scale reference the steps of construction are as follows:
$$1.$$ Draw $$AC=140m=\dfrac {140}{20}cm=7cm (as \ per \ scale)$$
$$2.$$ Now, at a distance of $$40m=\dfrac {40}{20}cm=2cm (as \ per \ scale)$$ draw a perpendicular at the left side of $$AC$$ $$30m=1.5cm$$ and then join the the top of the drawn perp. with $$A$$ to get $$AE$$
$$3.$$ Similarly at a distance of $$100m=5 cm (as \ per scale)$$ on left side of $$AC$$ draw a perpendicular of $$50m=2.5cm (as \ per \ scale)$$ and join the top of the perp. with A to get $$AD.$$
$$4. $$Similarly at a distance of $$60m=3 cm (as \ per scale)$$ on right side of $$AC$$ draw a perpendicular of $$40m=2cm (as \ per \ scale)$$ and join the top of the perp. with A to get $$AB.$$
Thus, the above drawn plan is obtained.
$$\therefore \boxed {1m= \dfrac {1}{20}cm}$$
now for every $$1m$$ data in given table we will use the above conversion to represent the construction in $$cm$$
As per the given table and scale reference the steps of construction are as follows:
$$1.$$ Draw $$AC=140m=\dfrac {140}{20}cm=7cm (as \ per \ scale)$$
$$2.$$ Now, at a distance of $$40m=\dfrac {40}{20}cm=2cm (as \ per \ scale)$$ draw a perpendicular at the left side of $$AC$$ $$30m=1.5cm$$ and then join the the top of the drawn perp. with $$A$$ to get $$AE$$
$$3.$$ Similarly at a distance of $$100m=5 cm (as \ per scale)$$ on left side of $$AC$$ draw a perpendicular of $$50m=2.5cm (as \ per \ scale)$$ and join the top of the perp. with A to get $$AD.$$
$$4. $$Similarly at a distance of $$60m=3 cm (as \ per scale)$$ on right side of $$AC$$ draw a perpendicular of $$40m=2cm (as \ per \ scale)$$ and join the top of the perp. with A to get $$AB.$$
Thus, the above drawn plan is obtained.
Draw a circle of radius $$6\ cm$$. In case circle, draw a chord $$AB=6\ cm$$. Assign a special name to $$\triangle AOB$$
$$\triangle AOB$$ is an equilateral triangle.
In your note-book copy the following angles using ruler and a pair compass only.
Steps of construction:
1. Draw a line EF, at a point E
2. Taking E as centre, draw an arc of any suitable radius, to cut the arms of the angle at points C and D
3. Taking Q as centre, draw an arc of the same size as drawn for points C and D. Let this arc cuts line QR at point T
4. With the help of compasses, take the distance equal to the distance between C and D; and then taking T as centre, draw an arc which cuts the earlier arc at point S
5. Join QS and produce up to a suitable point S. Now, the obtained $$\angle PQR$$ is the angle equal to the given $$\angle DEF$$
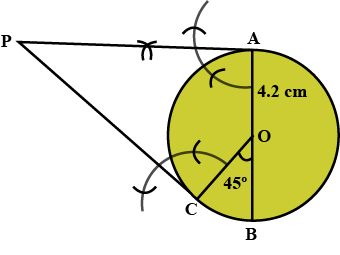
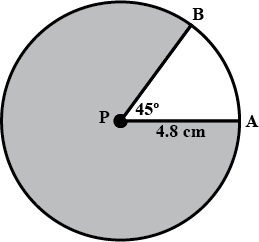
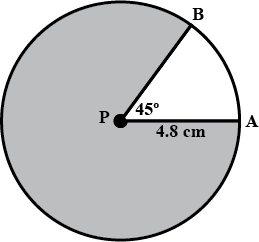
Draw a circle of radius $$4.8\ cm$$ and mark its centre as $$P$$
Draw radii $$PA$$ and $$PB$$ such that $$\angle APM=45^o$$
$$PA$$ is the radius of circle
$$PA=4.8\ cm$$
$$\angle =45^o.\ P$$ is the centre of the circle and $$PA$$ and $$PB$$ are radii of circle
$$PA=4.8\ cm$$
$$\angle =45^o.\ P$$ is the centre of the circle and $$PA$$ and $$PB$$ are radii of circle
In your note-book copy the following angles using ruler and a pair compass only.
Steps of Construction:
1. Draw line $$QR = OB$$ at point Q
2. Keeping O as centre, draw an arc of any suitable radius, to cut the arms of the angle at points C and D
3. Keeping Q as centre, draw the arc of the same size as drawn for C and D. Let this arc line cuts line QR at point T
4. With the help of compasses, take the distance equal to distance between C and D; and then taking T as centre, draw an arc which cuts the earlier arc at point S.
5. Join QS and produce up to a suitable point P. Now, the obtained $$\angle PQR$$ , is the angle equal to the given $$\angle AOB$$
Draw a circle of radius $$3.6\ cm$$. In the circle, draw a chord $$AB=5\ cm$$. Now shade the minor segment of the circle.
$$(i)\ OP$$ is the radius of the circle i.e. $$OP=3.6\ cm$$
$$AB$$ is the chord of the circle i.e $$AB=5\ cm$$
$$(ii)$$ Major segment of the circle is shaded in the given circle.
$$AB$$ is the chord of the circle i.e $$AB=5\ cm$$
$$(ii)$$ Major segment of the circle is shaded in the given circle.
Draw a circle of radius $$4.8\ cm$$ and mark its center as $$P$$Draw radii $$PA$$ and $$PB$$ such that $$\angle APM=45^o$$
Shade the major sector of the circle.
Shade the major sector of the circle.
Major sector of circle is shaded in the given figure.
Draw a circle of radius $$ 3 \,cm $$. Draw any diameter of the circle. AT the end points of the diameter of the circle , draw tangents to the circle. Any they parallel ?
Draw a circle of radius $$4.2\ cm$$. Mark its centre as $$O$$. Take a point $$A$$ on the circumference of the circle. Join $$AO$$ and extend it till it meets point $$B$$ on the circumference of the circle,
Assign a special name to $$AB$$
$$AB$$ is diameter of the circle.
Draw a circle of radius $$6\ cm$$. In case circle, draw a chord $$AB=6\ cm$$. Write the measure of angle $$AOB$$
Since, $$\triangle AOB$$ is equivalent triangle
Hence, $$\angle AOB=60^o$$
Hence, $$\angle AOB=60^o$$
Using ruler and compasses, construct the following angles:
$$ 30^o $$
Steps of Construction:
1. Construct a line segment $$ BC. $$
2. Taking $$ B $$ as centre and a suitable radius construct an arc which meets $$BC $$ at the point $$ P. $$
3. Taking $$ P $$ as centre and same redius cut off the arc at the point $$ Q $$.
4. Consider $$ P $$ and $$ Q $$ as centre construct two arcs which intersect each other at the point $$ R $$.
5. Now join $$ BR $$ and product it to point $$ A $$ forming $$ ZABC=30^0 $$
1. Construct a line segment $$ BC. $$
2. Taking $$ B $$ as centre and a suitable radius construct an arc which meets $$BC $$ at the point $$ P. $$
3. Taking $$ P $$ as centre and same redius cut off the arc at the point $$ Q $$.
4. Consider $$ P $$ and $$ Q $$ as centre construct two arcs which intersect each other at the point $$ R $$.
5. Now join $$ BR $$ and product it to point $$ A $$ forming $$ ZABC=30^0 $$
In your note-book copy the following angles using ruler and a pair compass only.
Steps of Construction:
1. Draw a line AB = QP at a point A
2. Taking Q as centre, draw an arc of any suitable radius, to cut the arms of the angle T and S
3. Taking A as centre, draw an arc of the same size as drawn for points T and S. Let this arc cuts the line AB at point D
4. With the help of compasses, take the distance equal to the distance between T and S; and then taking D as centre, draw an arc which cuts the earlier arc at point E
5. Join AE produced up to a suitable point C. The obtained $$\angle BAC$$ is the angle equal to the given $$\angle PQR$$
Draw a line segment $$OP = 8 \,cm.$$ Use set-square to construct $$\angle POQ = 90^\circ;$$ such that $$OQ = 6 \,cm.$$ Join P and Q; then measure the length of PQ.
The required diagram is drawn in given figure.
Measuring the length of $$PQ = 10 \,cm$$
Draw a line segment $$OA = 5 \,cm.$$ Use set-square to construct angle $$AOB = 60^\circ,$$ such that $$OB = 3 \,cm.$$ Join A and B; then measure the length of AB.
The required diagram is drawn in given figure.
The length of $$AB = 4.4 \,cm$$ (approximately)
Using ruler and compasses, construct the following angles:
$$ 75^o $$
Steps to Construction:
1. Construct a line segment $$ BC $$.
2. Taking $$ B $$ as centre and suitable radius construct an arc and cut off $$ PQ $$ then $$ QR $$ of the same radius.
3. Taking $$ Q $$ and $$ R $$ as centre, construct two arcs which intersect each other at the point $$ S $$.
4. Now join $$ SB $$.
5. Taking $$ Q $$ and $$ D $$ as centre construct two arcs which interects each other at the point $$ T $$.
6.Now join $$ BT $$ and produce it to point $$ A $$.
$$ \angle ABC=75^o $$.
1. Construct a line segment $$ BC $$.
2. Taking $$ B $$ as centre and suitable radius construct an arc and cut off $$ PQ $$ then $$ QR $$ of the same radius.
3. Taking $$ Q $$ and $$ R $$ as centre, construct two arcs which intersect each other at the point $$ S $$.
4. Now join $$ SB $$.
5. Taking $$ Q $$ and $$ D $$ as centre construct two arcs which interects each other at the point $$ T $$.
6.Now join $$ BT $$ and produce it to point $$ A $$.
$$ \angle ABC=75^o $$.
Using ruler and compasses, construct the following angles:
$$ 15^o $$
Step to construction.
1. Construct a line segment $$ BC $$.
2. Taking $$ B $$ as centre and a suitable radius construct an arc which meets $$ BC $$ at the point $$ P $$.
3. Taking $$ P $$ as centre and same radius cut off the arc at the point $$ Q > $$
4. Consider $$ P $$ and $$ Q $$ as crves, construct two acrs which intersect each other at the point $$ D $$ and join $$ BD$$.
5. Taking $$ P $$ and $$ R $$ as centre construct two more arcs which intersect each other at the point $$ S $$.
6. Now join $$ BS $$ and produce it to point $$ A $$.
$$ \angle ABC=15^0 $$
1. Construct a line segment $$ BC $$.
2. Taking $$ B $$ as centre and a suitable radius construct an arc which meets $$ BC $$ at the point $$ P $$.
3. Taking $$ P $$ as centre and same radius cut off the arc at the point $$ Q > $$
4. Consider $$ P $$ and $$ Q $$ as crves, construct two acrs which intersect each other at the point $$ D $$ and join $$ BD$$.
5. Taking $$ P $$ and $$ R $$ as centre construct two more arcs which intersect each other at the point $$ S $$.
6. Now join $$ BS $$ and produce it to point $$ A $$.
$$ \angle ABC=15^0 $$
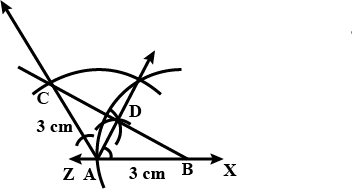
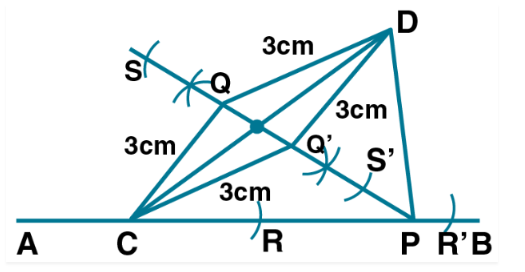
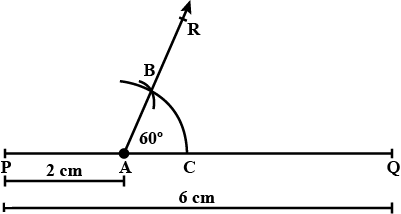
Draw a line $$AB = 6 \,cm.$$ Construct angle $$ABC = 60^\circ.$$ Then draw the bisector of angle ABC.
Steps of Construction:
1. Draw a line segment $$AB$$ of length $$6\ cm$$
2. Using compass construct $$\angle CBA = 60^\circ$$
3. Bisect $$\angle CBA,$$ using compass, take any radius which meet line $$AB$$ and $$BC$$ at points $$E$$ and $$F$$
4. Now, with the help of compass take radius more than $$\dfrac{1}{2}$$ of $$EF$$ and draw two arcs from point $$E$$ and $$F$$, where both the arcs intersects at point $$G$$, proceed $$BG$$ towards $$D$$. Now the $$\angle DBA$$ is bisector of $$\angle CBA$$
Draw $$\angle ABC = 120^\circ.$$ Bisect the angle using ruler and compasses. Measure each angle so obtained and check whether or not the new angles obtained on bisecting $$\angle ABC$$ are equal.
The required diagram is drawn in given figure.
Each angle measure $$= 60^\circ$$
Yea, the angles obtained on bisecting $$\angle ABC$$ are equal.
Draw $$\angle PQR = 75^\circ$$ by using set-squares. On PQ mark a point M such that $$MQ = 3 \,cm.$$ On QR mark a point N such that $$QN = 4 \,cm.$$ Join M and N. Measure the length of MN.
The required diagram is drawn in given figure.
The length of $$MN = 4.3 \,cm$$
Draw a line segment $$AB = 7 \text{ cm}.$$ Mark a point $$AB$$ such that $$AP = 3 \text{ cm}.$$ Draw perpendicular on to $$AB$$ at point $$P$$.
- Draw a line segment $$AB$$ of length $$7 \text{ cm}.$$
- Mark a point $$P$$ on $$AB$$ such that, $$AB - AP = 4 \text{ cm}.$$
- From point $$P$$, cut an arc on the outside of $$AB$$, and mark them as point $$E$$ and $$F$$.
- Now, from points $$E$$ and $$F$$ cut arcs on both sides intersecting each other at points $$C$$ and $$D$$.
- Join points $$P, C,$$ and $$D$$.
- Which is the required perpendicular.
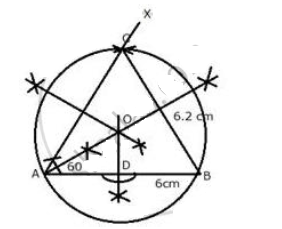
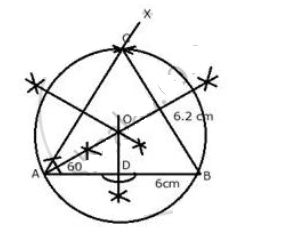
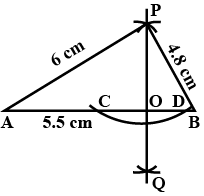
Using ruler and compasses only,Construct a triangle ABC with a following data:$$Base\ AB=6\ cm,\ BC=6.2\ cm$$ and $$\angle CAB=60^o$$Prove that AD = BD
Construct a triangle ABC with a following data:
$$Base\ AB=6\ cm,\ BC=6.2\ cm$$ and $$\angle CAB=60^o$$
Prove that AD = BD
Steps of construction:
i) Draw a line segment $$AB = 6 cm$$
ii)Draw ray at A , Making an angle of $$ 60^{0} $$ with BC .
iii) With B as center and Radius $$= 6.2$$ cm draw an arc which intersecting $$AX$$ ray at $$C .$$
iv)join BC
v)Draw the perpendicular bisector of AB and AC intersecting each other at O
vi) With center O, and radius as OA or OB or OC, draw a circle which will pass through A,B and C .,
vii) From O draw $$ OD \perp AB ,$$
Proof ; In right $$ \Delta OAD $$ and $$ \Delta OBD $$
$$OA = OB$$ [Raddi of same circle ]
$$OD = OD$$ [Common]
$$ \Delta OAD \cong \Delta OBD $$ by RHS congruence criterion
Hence , by $$CPTC$$
$$AD = BD$$
i) Draw a line segment $$AB = 6 cm$$
ii)Draw ray at A , Making an angle of $$ 60^{0} $$ with BC .
iii) With B as center and Radius $$= 6.2$$ cm draw an arc which intersecting $$AX$$ ray at $$C .$$
iv)join BC
v)Draw the perpendicular bisector of AB and AC intersecting each other at O
vi) With center O, and radius as OA or OB or OC, draw a circle which will pass through A,B and C .,
vii) From O draw $$ OD \perp AB ,$$
Proof ; In right $$ \Delta OAD $$ and $$ \Delta OBD $$
$$OA = OB$$ [Raddi of same circle ]
$$OD = OD$$ [Common]
$$ \Delta OAD \cong \Delta OBD $$ by RHS congruence criterion
Hence , by $$CPTC$$
$$AD = BD$$
Using ruler and compasses only,
Construct a triangle ABC with a following data:$$Base\ AB=6\ cm,\ BC=6.2\ cm$$ and $$\angle CAB=60^o$$Draw a perpendicular from O to AB which meets AB in D .
Steps of construction:
i) Draw a line segment AB = 6 cm
ii)Draw ray at A , Making an angle of $$ 60^{0} $$ with BC .
iii) With B as center and Radius = 6.2 cm draw an arc which intersecting AX ray at C .
iv)join BC
v)Draw the perpendicular bisector of AB and AC intersecting each other at O
vi) With center O, and radius as OA or OB or OC, draw a circle which will pass through A,B and C .,
vii) From O draw $$ OD \perp AB ,$$
i) Draw a line segment AB = 6 cm
ii)Draw ray at A , Making an angle of $$ 60^{0} $$ with BC .
iii) With B as center and Radius = 6.2 cm draw an arc which intersecting AX ray at C .
iv)join BC
v)Draw the perpendicular bisector of AB and AC intersecting each other at O
vi) With center O, and radius as OA or OB or OC, draw a circle which will pass through A,B and C .,
vii) From O draw $$ OD \perp AB ,$$
Construct an angle of $$ 75^o $$ and then bisect it.
Steps of Construction:
1.Construct a line segment $$ BC $$.
2.At the point $$ B $$ construct an angle $$ ABC $$ which is qual to $$ 75^o $$
3.Taking $$ P $$ and $$ T $$ as centres construct arcs which intersect each other at the point $$ L. $$
4. Now join $$ BL $$ and produce it to point $$ D$$.
Here $$ BD $$ bisects $$ \angle ABC$$.
1.Construct a line segment $$ BC $$.
2.At the point $$ B $$ construct an angle $$ ABC $$ which is qual to $$ 75^o $$
3.Taking $$ P $$ and $$ T $$ as centres construct arcs which intersect each other at the point $$ L. $$
4. Now join $$ BL $$ and produce it to point $$ D$$.
Here $$ BD $$ bisects $$ \angle ABC$$.
Using ruler and compasses, construct the following angles:
$$ 165^o $$
Steps of Construction:
1.Construct a line segment $$ BC $$.
2.Taking $$ B $$ as centre and some suitable radius construct an arc which meets $$ BC $$ at the point $$ P $$.
3.Taking $$ P $$ as centre and same radius cut off arcs at $$ PQ, QR $$ and then $$ RS.$$
4.Now join $$ SB $$.
5.Taking $$ R $$ and $$ S $$ as centres construct two arcs which intersect each other at the point $$ M $$.
6. Taking $$ T $$ and $$ S $$ as centres construct two arcs which intersect each other at the point $$ L. $$
7.Now join $$ BL $$ and produce it to point $$ A$$.
$$ \angle ABC=165^o $$
1.Construct a line segment $$ BC $$.
2.Taking $$ B $$ as centre and some suitable radius construct an arc which meets $$ BC $$ at the point $$ P $$.
3.Taking $$ P $$ as centre and same radius cut off arcs at $$ PQ, QR $$ and then $$ RS.$$
4.Now join $$ SB $$.
5.Taking $$ R $$ and $$ S $$ as centres construct two arcs which intersect each other at the point $$ M $$.
6. Taking $$ T $$ and $$ S $$ as centres construct two arcs which intersect each other at the point $$ L. $$
7.Now join $$ BL $$ and produce it to point $$ A$$.
$$ \angle ABC=165^o $$
Draw a line segment $$ PQ=6 cm $$. Mark a point $$ A $$ in $$ PQ $$ so that $$ AP=2 cm $$. At point $$ A $$, construct angle $$ QAR=60^o $$.
Steps of Construction:
1.Construct a line segment $$ PQ=6cm $$.
2.Now mark point $$ A $$ on $$ PQ $$ so that $$ AP=2 cm. $$
3. Taking $$ A $$ as centre and some suitable radius construct an arc which meets $$ AQ $$ at the point $$ C $$.
4.Taking $$ C $$ as centre and with same radius cut the arc $$ CB $$.
5.Now join $$ AB $$ and produce it to point $$ R $$.
$$ \angle QAR=60^o $$.
1.Construct a line segment $$ PQ=6cm $$.
2.Now mark point $$ A $$ on $$ PQ $$ so that $$ AP=2 cm. $$
3. Taking $$ A $$ as centre and some suitable radius construct an arc which meets $$ AQ $$ at the point $$ C $$.
4.Taking $$ C $$ as centre and with same radius cut the arc $$ CB $$.
5.Now join $$ AB $$ and produce it to point $$ R $$.
$$ \angle QAR=60^o $$.
Using ruler and compasses, construct the following angles:
$$ 180^o $$
Steps of Construction:
1. Construct a line segment $$ BC $$.
2. Taking $$ B $$ as centre and some suitable radius construct an arc which meets $$ BC $$ at the point $$ P $$.
3.Taking $$ P $$ as centre and with same sadius cut off the arcs $$ PQ,QR $$ and $$ RS. $$
4. Now join $$ BS $$ and produce it to point $$ A $$.
$$ \angle ABC=180^o $$
1. Construct a line segment $$ BC $$.
2. Taking $$ B $$ as centre and some suitable radius construct an arc which meets $$ BC $$ at the point $$ P $$.
3.Taking $$ P $$ as centre and with same sadius cut off the arcs $$ PQ,QR $$ and $$ RS. $$
4. Now join $$ BS $$ and produce it to point $$ A $$.
$$ \angle ABC=180^o $$
Draw a line segment of length $$ 6.4\;cm. $$ Draw its perpendicular bisector.
Steps of Construction :
1. Construct a line segment $$ AB=6.4 cm. $$
2. Taking $$ A $$ and $$ B $$ as centre and with some suitable radius, construct arcs which intersect each other at the points $$ S $$ and $$ R $$.
3. Now join $$ SR $$ which intersect $$ AB $$ at the point $$ Q $$.
Here $$ PQR $$ is the perpendicular bisector of the line segment $$ AB$$.
1. Construct a line segment $$ AB=6.4 cm. $$
2. Taking $$ A $$ and $$ B $$ as centre and with some suitable radius, construct arcs which intersect each other at the points $$ S $$ and $$ R $$.
3. Now join $$ SR $$ which intersect $$ AB $$ at the point $$ Q $$.
Here $$ PQR $$ is the perpendicular bisector of the line segment $$ AB$$.
Draw a line segment $$ AM=5.8 cm. $$ Mark a point $$ P $$ in $$ AB $$ such that $$ PB=3.6 cm $$ At $$ P $$, draw perpendicular to $$ AB $$.
Steps of Construction:
1.Construct a line segment $$ AB=5.8 cm. $$
2.Now mark a point $$ P $$ on the line segment $$ AB $$ such that $$ PB=3.6 cm. $$
3.Taking $$ P $$ as centre and some suitable radius construct and arc which meets $$ AB $$ at the point $$ L.$$
4.Taking $$ L $$ as centre and same radius cut off the arcs $$ LM $$ and then as $$ N. $$
5.Now bisect the arc $$ MN $$ at the point $$ S. $$
6. Join $$ PS $$ and produce it to point $$ Q. $$
Here $$ PQ $$ is perpendicular to the line segment $$ AB $$ at point $$ P. $$
1.Construct a line segment $$ AB=5.8 cm. $$
2.Now mark a point $$ P $$ on the line segment $$ AB $$ such that $$ PB=3.6 cm. $$
3.Taking $$ P $$ as centre and some suitable radius construct and arc which meets $$ AB $$ at the point $$ L.$$
4.Taking $$ L $$ as centre and same radius cut off the arcs $$ LM $$ and then as $$ N. $$
5.Now bisect the arc $$ MN $$ at the point $$ S. $$
6. Join $$ PS $$ and produce it to point $$ Q. $$
Here $$ PQ $$ is perpendicular to the line segment $$ AB $$ at point $$ P. $$
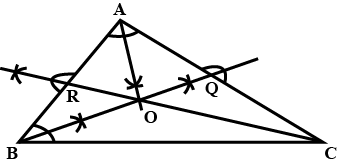
The bisector of angle A and B a scalene triangle ABC meet at O
OR and OQ are draw perpendicular to AB and CA respectively . What is the relation between OR and OQ ?
OR and OQ are the radii of the incircle and OR = OQ.
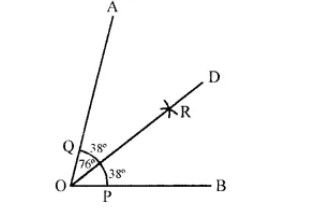
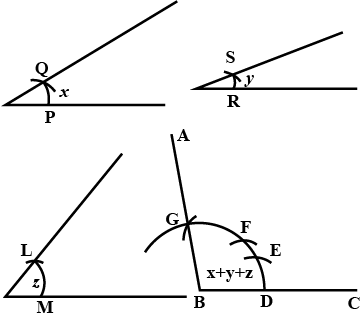
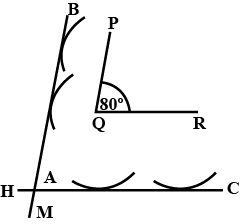
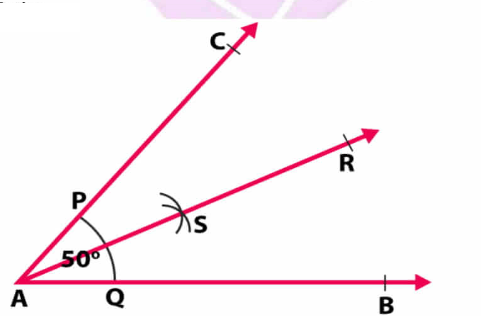
Given below are the angles $$x,y$$ and $$z$$.
Without measuring these angles construct:
$$\angle ABC=x+y+z$$
Steps of construction:
1. Construct line segment $$BC$$ of any suitable length.
2. Taking $$B$$ center, construct an arc of any suitable radius. With the same radius, construct arcs with the vertices of given angles as centers.
Let these arcs cut arms of the angle $$x$$ at the points $$P$$ and $$Q$$ and arms of the angle $$y$$ at points $$R$$ and $$S$$ and arms of the angle $$z$$ at the points $$L$$ and $$M$$.
3. From the arc, with $$B$$ as center, cut $$DE=PQ=arc$$ of $$x$$, $$EF=RS=arc$$ of $$y$$ and $$FG=LM=arc$$ of $$z$$
4. Now join $$BG$$ and produce it up to $$A$$.
Therefore, $$\angle ABC=x+y+z$$
1. Construct line segment $$BC$$ of any suitable length.
2. Taking $$B$$ center, construct an arc of any suitable radius. With the same radius, construct arcs with the vertices of given angles as centers.
Let these arcs cut arms of the angle $$x$$ at the points $$P$$ and $$Q$$ and arms of the angle $$y$$ at points $$R$$ and $$S$$ and arms of the angle $$z$$ at the points $$L$$ and $$M$$.
3. From the arc, with $$B$$ as center, cut $$DE=PQ=arc$$ of $$x$$, $$EF=RS=arc$$ of $$y$$ and $$FG=LM=arc$$ of $$z$$
4. Now join $$BG$$ and produce it up to $$A$$.
Therefore, $$\angle ABC=x+y+z$$
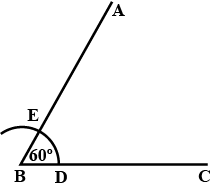
Draw angle $$ABC$$ of any suitable measure.
Are the angles $$ABQ$$ and $$QBC$$ equal?
In each of the following, draw perpendicular through point $$P$$ to the line segment $$AB$$.
Steps of construction:
1. Taking $$P$$ as center, construct an arc of any suitable radius which cuts $$AB$$ at points $$C$$ and $$D$$.
2. Taking $$C$$ and $$D$$ as centers, construct arcs of equal radii which intersect each other at point $$O$$.
[This radius must be more than half of $$CD$$ and let these arc intersect each other at the point $$O$$]
3. Now join $$P$$ and $$O$$. Then $$OP$$ is the required perpendicular.
$$\angle OPA=\angle OPB=90^o$$
1. Taking $$P$$ as center, construct an arc of any suitable radius which cuts $$AB$$ at points $$C$$ and $$D$$.
2. Taking $$C$$ and $$D$$ as centers, construct arcs of equal radii which intersect each other at point $$O$$.
[This radius must be more than half of $$CD$$ and let these arc intersect each other at the point $$O$$]
3. Now join $$P$$ and $$O$$. Then $$OP$$ is the required perpendicular.
$$\angle OPA=\angle OPB=90^o$$
Construct angle $$ABC=90^{\circ}$$. Draw $$BP$$, the bisector of angle $$ABC$$. State the measure of angle $$PBC$$.
Steps constructions:
1. Construct a line segment $$BC$$
2. With center $$B$$, construct an arc of any suitable radius, which cuts $$BC$$ at the point $$D$$.
3. Taking $$D$$ as a center and the radius, as taken in step $$2$$, construct an arc that cuts the previous arc at point $$E$$.
4. Taking $$E$$ as a center and the same radius, construct one more arc which cuts the first arc at point $$F$$.
5. Taking $$E$$ and $$F$$ as center and radii equal to more than half the distance between $$E$$ at $$F$$, construct arc which cut each other at point $$L$$.
6. Now join $$BL$$ to meet $$EF$$ at $$M$$ and produce to point $$A$$. Then $$\angle ABC=90^{\circ}$$
7. Construct $$BP$$, the bisector of angle $$ABC$$. [with $$D,M$$ as centers and suitable radius construct two arc meeting each other at $$Q$$ produced it to $$P$$]
$$\implies \angle PBC=45^{\circ} ~~~[\therefore BP$$ is bisector of $$\angle ABC]$$
1. Construct a line segment $$BC$$
2. With center $$B$$, construct an arc of any suitable radius, which cuts $$BC$$ at the point $$D$$.
3. Taking $$D$$ as a center and the radius, as taken in step $$2$$, construct an arc that cuts the previous arc at point $$E$$.
4. Taking $$E$$ as a center and the same radius, construct one more arc which cuts the first arc at point $$F$$.
5. Taking $$E$$ and $$F$$ as center and radii equal to more than half the distance between $$E$$ at $$F$$, construct arc which cut each other at point $$L$$.
6. Now join $$BL$$ to meet $$EF$$ at $$M$$ and produce to point $$A$$. Then $$\angle ABC=90^{\circ}$$
7. Construct $$BP$$, the bisector of angle $$ABC$$. [with $$D,M$$ as centers and suitable radius construct two arc meeting each other at $$Q$$ produced it to $$P$$]
$$\implies \angle PBC=45^{\circ} ~~~[\therefore BP$$ is bisector of $$\angle ABC]$$
Draw a line segment $$PQ=4.8cm.$$ Construct the perpendicular bisector of $$PQ$$.
Steps of Construction:
1. Construct a line segment $$PQ=4.8cm$$.
2. Taking $$P$$ as center and radius equal than half of $$PQ$$, construct arc on both the $$PQ$$.
3. TAking $$Q$$ as center and the same radius as taken in step $$2$$, construct arcs on both sides of $$PQ$$.
4. Let the arcs intersect each other at point $$A$$ and $$B$$
5. Now join $$A$$ and $$B$$.
6. The line $$AB$$ cuts the line segment $$PQ$$ at the point $$O$$. Here $$OP=OQ$$ and $$\angle AOQ=90^o$$ Then the line $$AB$$ is perpendicular bisector of $$PQ$$.
1. Construct a line segment $$PQ=4.8cm$$.
2. Taking $$P$$ as center and radius equal than half of $$PQ$$, construct arc on both the $$PQ$$.
3. TAking $$Q$$ as center and the same radius as taken in step $$2$$, construct arcs on both sides of $$PQ$$.
4. Let the arcs intersect each other at point $$A$$ and $$B$$
5. Now join $$A$$ and $$B$$.
6. The line $$AB$$ cuts the line segment $$PQ$$ at the point $$O$$. Here $$OP=OQ$$ and $$\angle AOQ=90^o$$ Then the line $$AB$$ is perpendicular bisector of $$PQ$$.
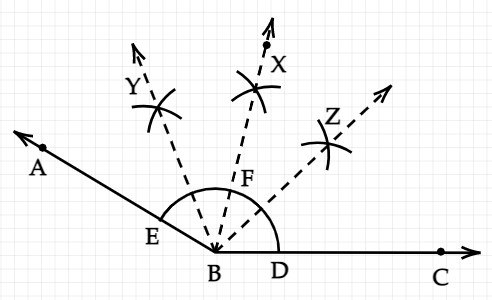
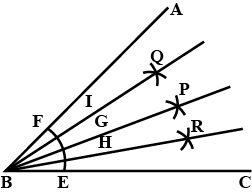
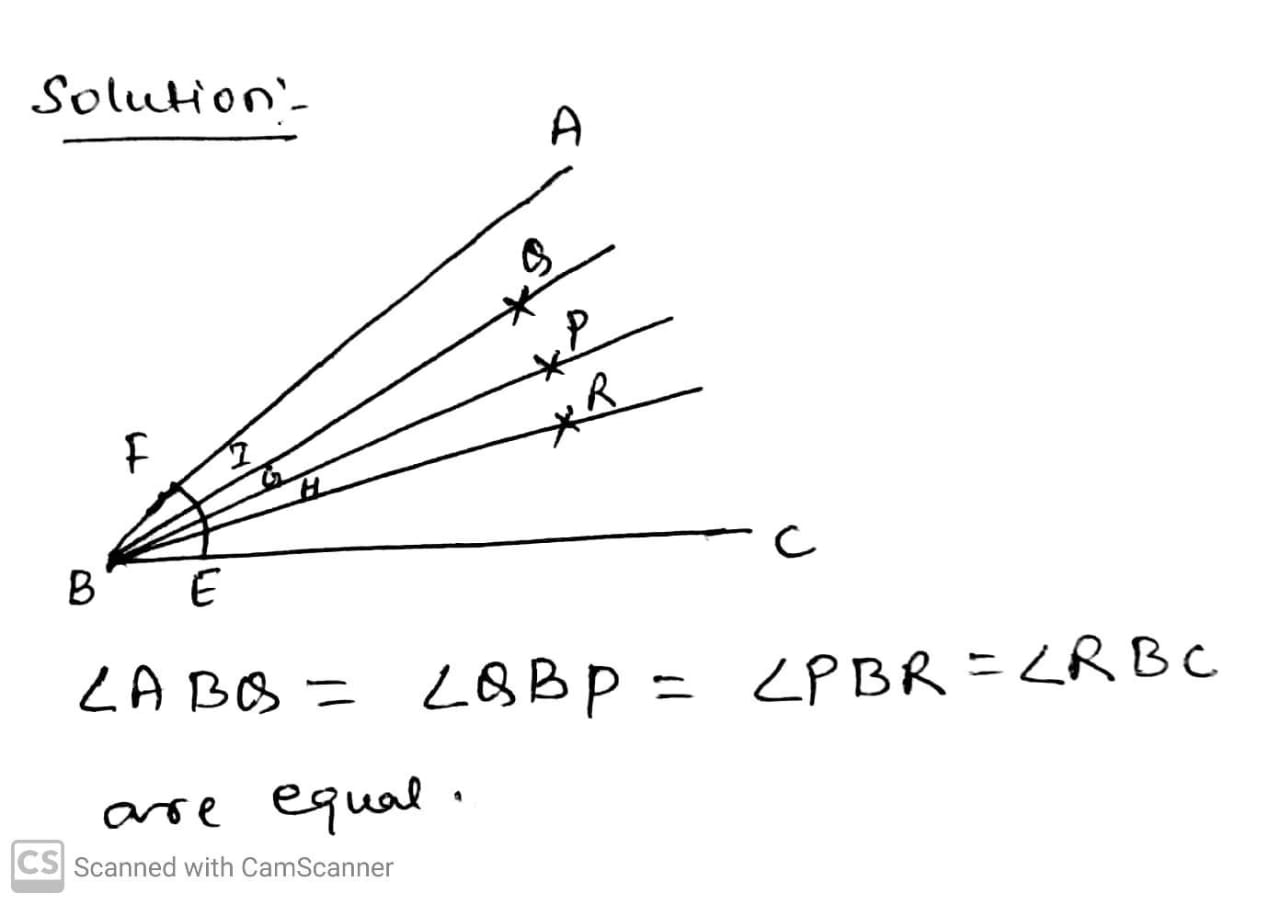
Draw angle $$ABC$$ of any suitable measure.
(i) Draw $$BP$$, the bisector of angle $$ABC$$.
(ii) Draw $$BR$$, the bisector of angle $$PBC$$ and draw $$BQ$$, the bisector of angle $$ABP$$
(iii) Are the angles $$ABQ,QBP,PBR$$ and $$RBC$$ equal?
(iv) Are the angles $$ABQ$$ and $$QBC$$ equal?
1. Draw any angle $$ABC$$
2. Taking $$B$$ as center, construct an arc $$EF$$ meeting $$BC$$ at $$E$$ and $$AB$$ at $$F$$.
3. Taking $$E,F$$ as centers construct two arc of equal radii meeting each other a the point $$P$$
4. Now join $$BP$$. is the bisector of
$$\angle ABC=\angle ABP=\angle PBC=\dfrac{1}{2}\angle ABC$$
5. In the same way draw $$BR$$, the bisector of $$\angle PBC$$ and draw $$BQ$$ as the bisector of $$\angle ABP$$ [with the same method as in step $$2,3$$]
6. Then $$\angle ABQ=\angle QBP=\angle PBR=\angle RBO$$
7. $$\angle ABR=\dfrac{3}{4}\angle ABC$$ and $$\angle QBC=\dfrac{3}{4}\angle ABC=\angle ABR=\angle QBC$$
2. Taking $$B$$ as center, construct an arc $$EF$$ meeting $$BC$$ at $$E$$ and $$AB$$ at $$F$$.
3. Taking $$E,F$$ as centers construct two arc of equal radii meeting each other a the point $$P$$
4. Now join $$BP$$. is the bisector of
$$\angle ABC=\angle ABP=\angle PBC=\dfrac{1}{2}\angle ABC$$
5. In the same way draw $$BR$$, the bisector of $$\angle PBC$$ and draw $$BQ$$ as the bisector of $$\angle ABP$$ [with the same method as in step $$2,3$$]
6. Then $$\angle ABQ=\angle QBP=\angle PBR=\angle RBO$$
7. $$\angle ABR=\dfrac{3}{4}\angle ABC$$ and $$\angle QBC=\dfrac{3}{4}\angle ABC=\angle ABR=\angle QBC$$
In each of the following, draw perpendicular through point $$P$$ to the line segment $$AB$$.
Steps of construction:
1. Taking $$P$$ as center, construct an arc of a suitable radius which cuts $$AB$$ at point $$C$$ and $$D$$
2. Taking $$C$$ and $$D$$ as center, construct arcs of equal radii and let these arcs intersect each other at the point $$Q$$[ The radius of these arcs must be more than half of $$CD$$ and both the arcs must be drawn on the other side]
3. Now join $$P$$ and $$Q$$
4. Let $$PQ$$ cut $$AB$$ at the point $$O$$.
Therefore, $$OP$$ is the required perpendicular clearly, $$\angle AOP=\angle BOP=90^o$$
1. Taking $$P$$ as center, construct an arc of a suitable radius which cuts $$AB$$ at point $$C$$ and $$D$$
2. Taking $$C$$ and $$D$$ as center, construct arcs of equal radii and let these arcs intersect each other at the point $$Q$$[ The radius of these arcs must be more than half of $$CD$$ and both the arcs must be drawn on the other side]
3. Now join $$P$$ and $$Q$$
4. Let $$PQ$$ cut $$AB$$ at the point $$O$$.
Therefore, $$OP$$ is the required perpendicular clearly, $$\angle AOP=\angle BOP=90^o$$
In each of the following, draw perpendicular through point $$P$$ to the line segment $$AB$$.
Steps of construction:
1. Taking PP
1. Taking PP
Draw angle $$ABC$$ of any suitable measure.
Are the angles $$ABQ,QBP,PBR$$ and $$RBC$$ equal?
Draw a line segment $$AB=6.2\ cm$$ Mark a point $$P$$, in $$AB$$ such that $$BP=4\ cm$$ through point $$P$$ draw perpendicular to $$AB$$.
Steps of construction:
1. Construct a line segment $$AB=6.2\ cm$$
2. Taking $$B$$ as center and radius $$=4\ cm$$ construct arc $$BP=4\ cm$$
3. Take $$P$$ as center and some radius construct arc meeting $$AB$$ at the points $$C,D$$.
4. Take $$C,D$$ as centers and equal radii [each is more than half of $$CD$$] construct two arcs, meeting each other at the point $$O$$.
5. Now join $$OP$$. Then $$OP$$ is perpendicular for $$AB$$.
1. Construct a line segment $$AB=6.2\ cm$$
2. Taking $$B$$ as center and radius $$=4\ cm$$ construct arc $$BP=4\ cm$$
3. Take $$P$$ as center and some radius construct arc meeting $$AB$$ at the points $$C,D$$.
4. Take $$C,D$$ as centers and equal radii [each is more than half of $$CD$$] construct two arcs, meeting each other at the point $$O$$.
5. Now join $$OP$$. Then $$OP$$ is perpendicular for $$AB$$.
Construct an angle $$PQR=80^o$$. Draw a line parallel to $$PQ$$ at a distance of $$3cm$$ from it and another line parallel to $$QR$$ at a distance of $$3.5cm$$ from it. Mark the point of intersection of these parallel lines as $$A$$.
Steps of construction:
1. Construct $$\angle PQR=80^o$$
2. Taking $$P$$ as center construct an arc of radius $$2cm$$.
3. Again with $$Q$$ as center, Construct another arc of radius $$2cm$$. Then $$BM$$ is a line which touches the two arcs. Then $$BM$$ is a line parallel to $$PQ$$.
4. Taking $$Q$$ as center, construct an arc of radius $$3.5cm.$$ Taking $$R$$ as center construct another arc of radius $$3.5$$. Construct a line $$HC$$ which touches these two arcs. Let these two parallel lines intersect at $$A$$.
1. Construct $$\angle PQR=80^o$$
2. Taking $$P$$ as center construct an arc of radius $$2cm$$.
3. Again with $$Q$$ as center, Construct another arc of radius $$2cm$$. Then $$BM$$ is a line which touches the two arcs. Then $$BM$$ is a line parallel to $$PQ$$.
4. Taking $$Q$$ as center, construct an arc of radius $$3.5cm.$$ Taking $$R$$ as center construct another arc of radius $$3.5$$. Construct a line $$HC$$ which touches these two arcs. Let these two parallel lines intersect at $$A$$.
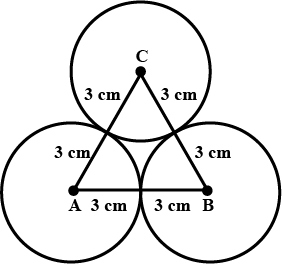
Draw circles with centers $$A, B$$ and $$C$$ each of radius $$3$$ cm, such that each circle touches the other two circles.
Let circles have centers as A, B, C.
Radius of each circle $$= 3 cm$$
If two circles touch each other externally, then the distance between their centres is equal to the sum of their radii.
$$\therefore AB = 3 cm + 3 cm = 6 cm$$
$$BC = 3 cm + 3 cm = 6 cm$$
$$CA = 3 cm + 3 cm = 6 cm$$
Construction:
(1) Draw a line seg $$AB = 6 cm$$.
(2) With $$A$$ as centre and radius $$= 6 cm$$, mark an arc.
(3) With $$B$$ as center and radius $$= 6 cm$$, mark an arc intersecting the previously drawn arc at $$C$$.
(4) Join $$AC$$ and $$BC$$.
(5) Now, with $$A, B$$ and $$C$$ as centers and radius $$= 3 cm$$, draw three circles.
It can be seen that each circle touches the other two circles.
Draw a circle of radius $$ 3.6 cm$$. Draw a tangent to the circle at any point on it without using the centre.
Steps of Construction:
Step 1: Draw a circle with centre $$ 3.6 cm $$. Make any point $$ C $$ on it.
Step 2: Draw chord $$ CB $$ and an inscribed $$ \angle CAB $$.
Step 3:With the centre $$ A $$ and any convenient radius draw an arc intersecting the sides of $$ \angle BAC $$ in points $$ M $$ and $$ N $$.
Step 4: Using the same radius and centre $$ C$$, draw an arc intersecting the cord $$ CB $$ at point $$ R$$.
Step 5: Taking the radius equal to $$ d(MN)$$ and centre $$ R$$, draw an arc intersecting the arc draw in step $$ 4 $$. Suppose $$ D $$ be the point of intersection of these arcs. Draw line $$ CD$$.
Here, line $$ CD $$ is the required tangent to the circle.
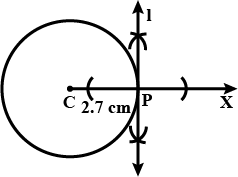
Draw a circle of radius $$ 2.7 cm$$. Draw a tangent to the circle at any point on it.
Steps of Construction:
Step 1: Draw a circle with centre $$ C $$ and radius $$ 2.7 cm$$.
Step 2: Take any point $$ P $$ on the circle.
Step 3: Draw ray $$ CX $$.
Step 4: Draw line $$ l $$ perpendicular to ray $$ CX $$ through point $$ P $$.
Here, line $$ l $$ is the required tangent to the circle at the point $$ P $$.
Draw rough diagrams of two angles such that they have Four points in common.
$$\angle{BOA}$$ and $$\angle{COA}$$ have points $$O, E, D, A$$ in common
Draw rough diagrams of two angles such that they have One point in common.
$$\angle{COP}$$ and $$\angle{AOD}$$ have point O in common
Draw a line segment $$A\ B=5.5cm$$ Mark a point $$P$$, such that $$P\ A=6cm$$ and $$P\ B=4.8cm$$. From the point $$P$$ draw perpendicular to $$AB$$.
Steps of construction:
1. Construct a line segment $$AB=5.5cm$$
2. Taking $$A$$ as center and radius $$=6cm$$ construct an arc.
3. Taking $$B$$ as center and radius $$=4.8cm$$ construct another arc.
4. Let these arcs meet each other at the point $$P$$. $$PA=6cm,PB=4.8$$
5. Take $$P$$ as center and some suitable radius construct and arc meeting $$AB$$ at the point $$C$$ and $$D$$.
6. Take $$C$$ as center and same radius more than half of $$CD$$ construct an arc.
7. Take $$D$$ as center and same radius as in step $$6$$, construct an arc.
8. Let these arcs meet each other at the point $$Q$$.
9. Now join $$PQ$$.
10, The $$PQ$$ meet $$AB$$ at point $$O$$.
Then $$POAB$$ i.e; $$\angle AOP=90^o=\angle POB$$
1. Construct a line segment $$AB=5.5cm$$
2. Taking $$A$$ as center and radius $$=6cm$$ construct an arc.
3. Taking $$B$$ as center and radius $$=4.8cm$$ construct another arc.
4. Let these arcs meet each other at the point $$P$$. $$PA=6cm,PB=4.8$$
5. Take $$P$$ as center and some suitable radius construct and arc meeting $$AB$$ at the point $$C$$ and $$D$$.
6. Take $$C$$ as center and same radius more than half of $$CD$$ construct an arc.
7. Take $$D$$ as center and same radius as in step $$6$$, construct an arc.
8. Let these arcs meet each other at the point $$Q$$.
9. Now join $$PQ$$.
10, The $$PQ$$ meet $$AB$$ at point $$O$$.
Then $$POAB$$ i.e; $$\angle AOP=90^o=\angle POB$$
Draw a circle of diameter $$ 6.4 cm$$. Take a point $$ R $$ at a distance equal to its diameter from the centre. Draw tangents from point $$ R $$.
Step 1 : Construct a circle of radius $$ = \dfrac { 6.4}{2} = 3.2 cm $$ with centre O.
Step 2 : Take a point R in the exterior of the circle such that $$ OR = 6.4 cm $$
Step 3 : Draw segment OR .draw perpendicular bisector of segment OR to get its midpoint M.
Step 4 : Draw a circle with radius OM and centre M
Step 5 : Name the point of intersection of the two circle as A and B
Step 6 : draw the RA and line RB.
Here , line RA and line RB are tangents to the circle from point R
Draw rough diagrams of two angles such that they have Two points in common.
$$\angle{AOB}$$ and $$\angle{BOC}$$ have point O and B in common
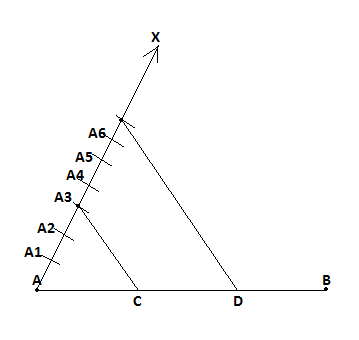
Construct an angle of $$45^0$$ at the initial point of a given ray and justify the construction.
Data: To construct an angle of 45° at the initial point of a given ray. I. G
A Steps of Construction
1. Draw straight line with any measurement.
2. Taking A as centre with any radius draw an arc, which meet AB at C.
3. With C centre, with the same radius draw an arc which meet at D.
4. With D centre, with the same radius, draw an arc which meet at D.
5. With centres E and D, with previous radius draw two arcs which rrieet at F.
6. Now AF is joined. Now AP1AF at A. Hence $$\angle BAF = 90^0$$.
7. Now, AG which is angular bisector of $$\angle BAF$$ is drawn.
8. $$\angle BAG = 45^0$$ is constructed.
$$\angle FAB = 90^0$$
AG is the angular bisector of $$\angle FAB$$
$$\therefore \angle FAG = \angle GAB = 45^0$$
$$\therefore \angle GAB = 45^0$$.
A Steps of Construction
1. Draw straight line with any measurement.
2. Taking A as centre with any radius draw an arc, which meet AB at C.
3. With C centre, with the same radius draw an arc which meet at D.
4. With D centre, with the same radius, draw an arc which meet at D.
5. With centres E and D, with previous radius draw two arcs which rrieet at F.
6. Now AF is joined. Now AP1AF at A. Hence $$\angle BAF = 90^0$$.
7. Now, AG which is angular bisector of $$\angle BAF$$ is drawn.
8. $$\angle BAG = 45^0$$ is constructed.
$$\angle FAB = 90^0$$
AG is the angular bisector of $$\angle FAB$$
$$\therefore \angle FAG = \angle GAB = 45^0$$
$$\therefore \angle GAB = 45^0$$.
Construct the following angles and verify by measuring them by a protractor :
(i) $$75^0$$
(i) To construct angle $$75^0$$ :
Steps of Construction :
1. Draw AB with any measurement.
2. With A as centre, with convenient scale draw an arc AB which intersect at C.
3. With C as centre with same radius draw an arc which intersect at D. $$\angle DAB= 60^0$$.
4. With D as centre with same radius draw an arc which intersect at E.
5. With Centres E and D, by taking more than half of ED draw two arcs which meet at E. AF is joined.
Now, $$\angle FAB = 90^0$$.
6. Draw AG bisector of $$\angle EAD$$, AG joined. $$\angle GAD = 15^0$$.
7. $$\angle GAD + \angle DAB = 15 + 60 = 75^0$$
$$\therefore \angle GAB = 75^0$$
Steps of Construction :
1. Draw AB with any measurement.
2. With A as centre, with convenient scale draw an arc AB which intersect at C.
3. With C as centre with same radius draw an arc which intersect at D. $$\angle DAB= 60^0$$.
4. With D as centre with same radius draw an arc which intersect at E.
5. With Centres E and D, by taking more than half of ED draw two arcs which meet at E. AF is joined.
Now, $$\angle FAB = 90^0$$.
6. Draw AG bisector of $$\angle EAD$$, AG joined. $$\angle GAD = 15^0$$.
7. $$\angle GAD + \angle DAB = 15 + 60 = 75^0$$
$$\therefore \angle GAB = 75^0$$
Draw a line segment of length $$9.5\,cm$$ and construct its perpendicular bisector.
The below given steps will be followed to construct a line segment of length $$9.5\,cm$$ and its perpendicular bisector.
(1) Draw a line segment $$\overline {PQ}$$ of $$9.5\,cm.$$
(2) Taking P as centre, draw a circle by using compasses. The radius of circle should be more than half the length of $$\overline {PQ}.$$
(3) With the same radius as before, draw another circle using compasses while taking point Q as centre. Let it cut the previous circle at R and S.
(4) Join RS. $$\overline {RS}$$ is the axis of symmetry i.e., the perpendicular bisector of line PQ.
(1) Draw a line segment $$\overline {PQ}$$ of $$9.5\,cm.$$
(2) Taking P as centre, draw a circle by using compasses. The radius of circle should be more than half the length of $$\overline {PQ}.$$
(3) With the same radius as before, draw another circle using compasses while taking point Q as centre. Let it cut the previous circle at R and S.
(4) Join RS. $$\overline {RS}$$ is the axis of symmetry i.e., the perpendicular bisector of line PQ.
Construct the following angles and verify by measuring them by a protractor :
(i) $$135^0$$
To construct an angle $$135^0$$
Steps of Construction :
1. Draw a straight line AB.
2. With A as centre, semicircle is drawn which meets AB at C and it intersects produced BA line at G.
3. With C as centre with same radius and centre CD, draw radius of arc DE.
4. With centres E and D by taking radius more than half draw two arcs which meet at F. Join AF. $$\angle FAB = 90^0$$. AF intersects ED at H.
5. With G and H centres by taking radius more than $$\frac{1}{2}$$ of the radius GH draw arts which meet at l. Al is joined. Now, $$\angle IAF = 45^0$$.
6. $$\angle IAF + \angle FAB =45^0 + 90^0 = 135^0$$ ,
$$\therefore \angle IAB= 135^0$$ is constructed.
Steps of Construction :
1. Draw a straight line AB.
2. With A as centre, semicircle is drawn which meets AB at C and it intersects produced BA line at G.
3. With C as centre with same radius and centre CD, draw radius of arc DE.
4. With centres E and D by taking radius more than half draw two arcs which meet at F. Join AF. $$\angle FAB = 90^0$$. AF intersects ED at H.
5. With G and H centres by taking radius more than $$\frac{1}{2}$$ of the radius GH draw arts which meet at l. Al is joined. Now, $$\angle IAF = 45^0$$.
6. $$\angle IAF + \angle FAB =45^0 + 90^0 = 135^0$$ ,
$$\therefore \angle IAB= 135^0$$ is constructed.
Construct an angle of $$90^0$$ at the initial point of a given ray and justify the construction.
Data: Constructing an angle of $$90^0$$ at the initial point of a given ray.
Steps of Construction:
1. Draw AB straight line.
2. Taking A as centre and any radius draw an arc and intersect AB at C.
3. Taking C as centre with same radius draw an arc which intersect at D.
4. With same radius taking D as centre, it intersects at E.
5. With centres E and D with same radius draw two arcs which meet both at F.
6. If AF is joined, AB straight line is the line in the point A with $$90^0$$, i.e., AF.
In the above construction $$\angle DAB = 60^0$$ and $$\angle DAE = 60^0$$.
Angular bisector of $$\angle DAE$$ is AF.
$$\therefore \ \angle DAF = \angle EAF = 30^0$$
$$\therefore \angle BAF = \angle DAB + \angle DAE = 60^0 + 30^0$$
$$\therefore \angle BAF= 90^0$$.
Steps of Construction:
1. Draw AB straight line.
2. Taking A as centre and any radius draw an arc and intersect AB at C.
3. Taking C as centre with same radius draw an arc which intersect at D.
4. With same radius taking D as centre, it intersects at E.
5. With centres E and D with same radius draw two arcs which meet both at F.
6. If AF is joined, AB straight line is the line in the point A with $$90^0$$, i.e., AF.
In the above construction $$\angle DAB = 60^0$$ and $$\angle DAE = 60^0$$.
Angular bisector of $$\angle DAE$$ is AF.
$$\therefore \ \angle DAF = \angle EAF = 30^0$$
$$\therefore \angle BAF = \angle DAB + \angle DAE = 60^0 + 30^0$$
$$\therefore \angle BAF= 90^0$$.
Construct the angles of the following measurements:
(i) $$22 \frac{1}{2}^0$$
To draw an angle of $$22 \frac{1}{2}^0$$
Steps of Construction:
1. Draw a straight line AB.
2. With center 'A', taking a convenient radius draw an arc that intersects AB at P.
3. With P as a center with the same radius draw an arc at Q, with Q as center with same radius draw an arc that intersects at R.
4. With R and Q as centers with the same radius draw two arcs that intersect at S. Join AS, $$\angle BAS = 90^0$$.
5. Now construct AT which is the angular bisector of $$\angle BAS$$, and join AT, $$\angle TAB= 45^0$$.
6. Now construct AU which is the angular bisector of $$\angle TAB$$, and Join AU. Now, $$\angle UAB =$$ $$ 22\frac{1}{2}^0$$
Steps of Construction:
1. Draw a straight line AB.
2. With center 'A', taking a convenient radius draw an arc that intersects AB at P.
3. With P as a center with the same radius draw an arc at Q, with Q as center with same radius draw an arc that intersects at R.
4. With R and Q as centers with the same radius draw two arcs that intersect at S. Join AS, $$\angle BAS = 90^0$$.
5. Now construct AT which is the angular bisector of $$\angle BAS$$, and join AT, $$\angle TAB= 45^0$$.
6. Now construct AU which is the angular bisector of $$\angle TAB$$, and Join AU. Now, $$\angle UAB =$$ $$ 22\frac{1}{2}^0$$
Hence the required angle $$ 22\frac{1}{2}^0$$ has been constructed
Construct an angle of the $$30^0$$ measurement.
(i) To construct $$30^0$$ angle :
Steps of Construction :
1. Draw PQ straight line.
2. With P as a centre with any radius draw an arc that intersects PQ at A.
3. With A as a centre with the same radius draw an arc that intersects at B. Join PB and produce it.
4. With A and B centres, with a radius more than half of AB, draw two arcs that intersect at C. Join PC.
5. $$\angle BPC = \angle CPQ = 30^0$$.
Steps of Construction :
1. Draw PQ straight line.
2. With P as a centre with any radius draw an arc that intersects PQ at A.
3. With A as a centre with the same radius draw an arc that intersects at B. Join PB and produce it.
4. With A and B centres, with a radius more than half of AB, draw two arcs that intersect at C. Join PC.
5. $$\angle BPC = \angle CPQ = 30^0$$.
Draw rough diagrams of two angles such that they have One ray in common.
Ray $$\overrightarrow{OC}$$ is common between $$\angle{BOC}$$ and $$\angle{AOC}.$$
Construct the following angles and verify by measuring them by a protractor :
(i) $$105^0$$
(i) To construct angle $$105^0$$ :
Steps of Construction :
1. Draw PQ with any measurement.
2. With P as centre and with any radius, draw an arc which intersects PQ at A.
3. With A as centre, with same radius draw an arc which intersect at B.
4. With B as centre with same radius draw another arc, it intersects at C.
5. With centres C and 6 if two arcs are drawn these two meet at D. Join PD. $$\angle DPQ = 90^0$$. Straight line PD intersects the arc CB at E.
6. Now taking radius half of CE, if line is drawn from C to E it intersects at F. FP is joined. Now $$\angle FPD =15^0$$.
7.$$\angle FPD + \angle DPQ = 15 + 90 =105^0$$.
$$\therefore \angle FPQ =105^0$$ is constructed.
Steps of Construction :
1. Draw PQ with any measurement.
2. With P as centre and with any radius, draw an arc which intersects PQ at A.
3. With A as centre, with same radius draw an arc which intersect at B.
4. With B as centre with same radius draw another arc, it intersects at C.
5. With centres C and 6 if two arcs are drawn these two meet at D. Join PD. $$\angle DPQ = 90^0$$. Straight line PD intersects the arc CB at E.
6. Now taking radius half of CE, if line is drawn from C to E it intersects at F. FP is joined. Now $$\angle FPD =15^0$$.
7.$$\angle FPD + \angle DPQ = 15 + 90 =105^0$$.
$$\therefore \angle FPQ =105^0$$ is constructed.
Construct the angles of the following measurements
(i) $$15^0$$
(i) To construct an angle $$15^0$$ :
Steps of Construction :
1. Draw a straight line AB.
2. With A as centre with convenient radius draw an arc which intersect AB at C.
3. With C as centre, with same radius, draw an arc which intersect at D.
Now. $$\angle DAB = 60^0$$
4. Construct AE, the bisector of $$\angle DAB$$. Join then, $$\angle EAB = 30^0$$.
5. Construct AF, the bisector of $$\angle EAB$$. Join then, $$\angle FAB = 15^0$$.
Steps of Construction :
1. Draw a straight line AB.
2. With A as centre with convenient radius draw an arc which intersect AB at C.
3. With C as centre, with same radius, draw an arc which intersect at D.
Now. $$\angle DAB = 60^0$$
4. Construct AE, the bisector of $$\angle DAB$$. Join then, $$\angle EAB = 30^0$$.
5. Construct AF, the bisector of $$\angle EAB$$. Join then, $$\angle FAB = 15^0$$.
Draw a circle with centre C and radius $$3.4\,cm.$$ Draw any chord $$\overline {AB}.$$ Construct the perpendicular bisector of $$\overline {AB}$$ and examine if it passes through C, if $$\overline {AB}$$ happens to be a diameter.
(1) Mark any point C on the sheet.
(2) By adjusting the compasses up to $$3.4\,cm$$ and by putting the pointer of the compasses at point C, turn the compasses slowly to draw the circle. It is the required circle of $$3.4\,cm$$ radius.
(3) Mark any diameter $$\overline{AB}$$ in the circle.
(4) Now, taking A and B as centres, draw arcs on both sides $$\overline{AB}$$ taking radius more than $$\overline{AB}.$$ Let these intersect each other at D and E.
(5) Join DE, which is the perpendicular bisector of AB. It can be observed that $$\overline{DE}$$ is passing through the centre C of the circle.
(2) By adjusting the compasses up to $$3.4\,cm$$ and by putting the pointer of the compasses at point C, turn the compasses slowly to draw the circle. It is the required circle of $$3.4\,cm$$ radius.
(3) Mark any diameter $$\overline{AB}$$ in the circle.
(4) Now, taking A and B as centres, draw arcs on both sides $$\overline{AB}$$ taking radius more than $$\overline{AB}.$$ Let these intersect each other at D and E.
(5) Join DE, which is the perpendicular bisector of AB. It can be observed that $$\overline{DE}$$ is passing through the centre C of the circle.
Draw a line segment of length 6 cm. From a point P outside the line, draw a perpendicular on this line.
Steps of construction:
1. First of all draw a line segment $$AB = 6 cm$$
2. Take a point P (outside the line) and draw an arc in such a way that it cuts $$AB$$ into two points $$C$$ and $$D.$$ Again by taking $$C$$ & $$D$$ as centre take suitable arc and draw two arc which intersect at $$Q$$. Join $$PQ.$$
Hence, $$PQ$$ is the required perpendicular on $$AB$$ from $$P.$$
1. First of all draw a line segment $$AB = 6 cm$$
2. Take a point P (outside the line) and draw an arc in such a way that it cuts $$AB$$ into two points $$C$$ and $$D.$$ Again by taking $$C$$ & $$D$$ as centre take suitable arc and draw two arc which intersect at $$Q$$. Join $$PQ.$$
Hence, $$PQ$$ is the required perpendicular on $$AB$$ from $$P.$$
Construct $$\angle ABC = 120^o$$. Through A draw a line parallel to BC.
Steps of construction:
1. Draw a line segment BC of any measure.
2. By taking B as centre, draw an angle of $$120^o$$ with the help of compass and ruler.
3. Now at A, we will draw a line parallel to BC by making $$60^o$$ at A.
1. Draw a line segment BC of any measure.
2. By taking B as centre, draw an angle of $$120^o$$ with the help of compass and ruler.
3. Now at A, we will draw a line parallel to BC by making $$60^o$$ at A.
To a circle of radius 4.5, draw two tangents such that the angle between them is $$45^\circ$$, also verify it.
Draw a line segment AB $$= 10$$ cm. Bisect this line segment and verify by measuring the lengths of the two segments.
- Taking A as center, radius more than half of the length of line segment AB, draw arcs on both sides of AB
- Taking B as center, radius more than half of the length of line segment AB, draw arcs on both sides of AB
- Name M and N as the points where the arcs intersect each other
- Join M and N, which bisects AB at points L
- Measure AL and BL , AL $$+$$ BL $$=$$ AB
Construct an angle $$120^o$$. Bisect angle and verify by measuring the two angles.
Steps of Construction:
1. Draw a line segment of any measure named as $$PQ$$.
2. With $$P$$ as centre draw an angle of $$120^o$$ with the help of protractor.
3. With $$P$$ as centre again draw an arc which cuts line segments $$PQ$$ and $$PS$$ at $$M$$ and $$N$$.
4. With $$M$$ and $$N$$ as centres and with radius little more than half the arc, draw arcs cutting each other at $$T$$. Join $$PT$$ which is the required bisector of $$\angle SPQ = 120^o$$
$$\therefore \angle TPQ =\angle TPS = 60^o$$ (each)
1. Draw a line segment of any measure named as $$PQ$$.
2. With $$P$$ as centre draw an angle of $$120^o$$ with the help of protractor.
3. With $$P$$ as centre again draw an arc which cuts line segments $$PQ$$ and $$PS$$ at $$M$$ and $$N$$.
4. With $$M$$ and $$N$$ as centres and with radius little more than half the arc, draw arcs cutting each other at $$T$$. Join $$PT$$ which is the required bisector of $$\angle SPQ = 120^o$$
$$\therefore \angle TPQ =\angle TPS = 60^o$$ (each)
Draw an angle of $$40^o$$ using protractor. Now with the help of ruler and compass, construct an angle to this angle.
Steps of Construction:
1. Draw $$\angle BAC = 40^o$$ using protractor. By taking $$A$$ as centre draw an arc which cuts $$AB$$ and $$AC$$ at $$P$$ and $$Q.$$
2. Now take $$O$$ as centre on another line segment $$EF$$ and taking the same radius $$PQ$$ draw an arc which cuts $$OF$$ at $$R.$$ Now again take $$R$$ as centre and draw the arc which cut at $$S.$$
3. Join O to S which is the required $$\angle ROS = 40^o$$
1. Draw $$\angle BAC = 40^o$$ using protractor. By taking $$A$$ as centre draw an arc which cuts $$AB$$ and $$AC$$ at $$P$$ and $$Q.$$
2. Now take $$O$$ as centre on another line segment $$EF$$ and taking the same radius $$PQ$$ draw an arc which cuts $$OF$$ at $$R.$$ Now again take $$R$$ as centre and draw the arc which cut at $$S.$$
3. Join O to S which is the required $$\angle ROS = 40^o$$
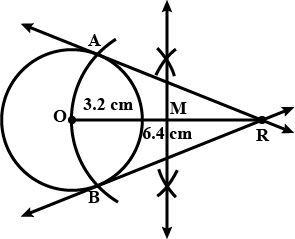
Draw a circle of radius 2.5 cm. Take a point a part 6.5 cm from its center and from this point draw the tangents to the circle. Measure the length of tangent also find the length of tangents by calculation.
Draw a line segment AB of length 85 cm. Taking A and B as centers and radii respectively 5 cm and 3 cm draw two circle. From the center of each circle draw the tangents to the other circle.
With the same center O, draw two circles of radii 4 cm and 2.5 cm.
draw BN=12 CM . divide the line segment BN in four equal parts with the help of compasses a ruler
Construct the angles of the following measurements:
$$30 ^ { \circ }$$
$$15 ^ { \circ }$$
$$22.5 ^ { \circ }$$
(i) 30°
- Steps of Construction:
1.Taking O as centre and
some radius , draw an arc of a circle, which intersects OA, say at a point B.
2.Taking B as centre and
with the same radius as before, draw an arc intersecting the previously drawn
arc, say at a point C.
3.Draw the ray OE
passing through C. Then ∠EOA = 60°.
4. Taking B and C as
centres and with the radius more than 1/2 BC, draw arcs to intersect each other, at D.
5. Draw the ray OD. This
ray OD is the bisector of the ∠ EOA, i.e.,
∠EOD = ∠AOD =1/2 ∠EOA = 1/2(60°) = 30∘.
∠AOD =30∘.
(ii) 22½°
- Steps of Construction:
1. Taking O as centre and
some radius, draw an arc of a circle, which intersects OA, at a point B.
2.Taking B as centre and
with the same radius as before, draw an arc intersecting the previously drawn
arc,at a point C .
3.Taking C as centre and
with the same radius as before, draw an arc intersecting the arc drawn in step
1, at D.
4. Draw the ray OE
passing through C. Then ∠EOA = 60∘.
5. Draw the ray OF
passing through D. Then ∠ FOE = 60∘.
6. Next, taking C and D
as centres and with radius more than 1/2 CD, draw arcs to intersect each other, say at G.
7. Draw the ray OG. This
ray OG is the bisector of the ∠ FOE, i.e.,
∠FOG = ∠EOG = 1/2 ∠FOE = 1/2 (60∘) = 30∘.
Thus, ∠GOA = ∠GOE + ∠EOA = 30∘ + 60∘ = 90∘.
8. Now, taking O as
centre and any radius, draw an arc to intersect the rays OA and OG, say at H
and I.
9. Next, taking H and I
as centres and with the radius more than 1/2HI, draw arcs to intersect each other, at J.
10. Draw the ray OJ. This ray OJ is the bisector of the∠ GOA.
i.e.,
∠GOJ = ∠AOJ = 1/2 ∠GOA = 1/2( 90∘) = 45∘.
11. Now, taking O as centre and any radius, draw an arc to intersect
the rays OA and OJ, say at K and L.
12. Next, taking K and L as centres and with the radius more
than 1/2KL, draw arcs to
intersect each other, at M.
13. Draw the ray OM. This ray OM is the bisector of the angle AOJ,
i.e., ∠JOM = ∠AOM = 1/2 ∠AOJ = 1/2( 45∘ ) = 22½∘
∠AOM = 22½∘
(iii) 15∘
- Steps of construction:
1. Taking O as centre and
some radius, draw an arc of a circle, which intersects OA, at a point B.
2. Taking B as centre and
with the same radius as before, draw an arc intersecting the previously drawn
arc,at a point C.
3. Draw the ray OE
passing through C. Then ∠EOA =60∘.
4.Now, taking B and C as
centres and with the radius more than 1/2BC, draw arcs to intersect each other, at D.
5. Draw the ray OD
intersecting the arc drawn in step 1 at F. This ray OD is the bisector of the
angle EOA,
i.e., ∠EOD = ∠AOD = 1/2 ∠EOA = 1/2 (60∘) = 30∘.
6. Now, taking B and F as
centres and with the radius more than 1/2 BF, draw arcs to intersect each other, at G.
7. Draw the ray OG. This
ray OG is the bisector of the∠AOD, i.e.,
∠DOG = ∠AOG = 1/2 ∠AOD = 1/2 (30∘) = 15∘.
∠AOG = 15∘.
Show that of all line segments drawn from a given point not on it. the perpendicular line segment is the shortest.
Hint; If one angle in the triangle is 90 degrees, then the other angles must be acute.
Step 1: Take a line l and from point P, that is, not lying on thd line l, draw two line segments PN and PM.
Step 2: Assume PN be perpendicular to line l and PM is drawn at some other angle to line l
Step 1: Take a line l and from point P, that is, not lying on thd line l, draw two line segments PN and PM.
Step 2: Assume PN be perpendicular to line l and PM is drawn at some other angle to line l
From fig, In ΔPNM, ∠N = 90o
∠P + ∠N + ∠M = 180o (Angle sum property of a triangle)
∠P + ∠M = 90o
Clearly, ∠M is an acute angle.
∠M < ∠N
PN < PM (Side opposite to the smaller angle is smaller)
Similarly, by drawing different line segments from P to l, it is evident that PN is smaller in comparison to all other drawn lines from P to line l.
Conclusion : Therefore,of all line segments drawn from a given point not on it. the perpendicular line segment is the shortest.
If the sum of the distance of point from two perpendicular lines in a plane is $$1$$, then prove that its locus is a square.
Draw a circle of radius $$4\ cm$$. Draw two tangents to the circle such that they include an angle of $$135^{o}$$.
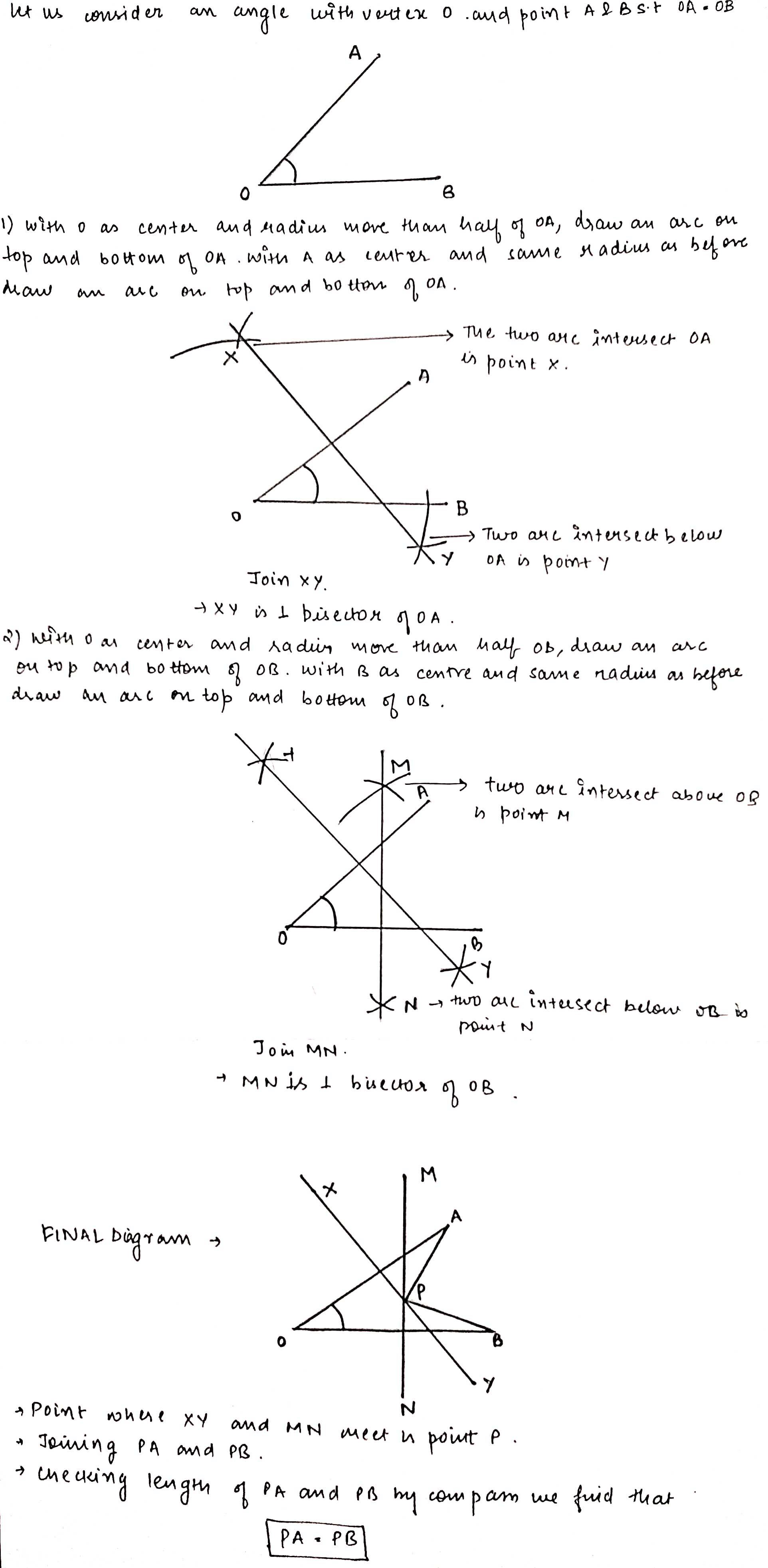
draw any angle with vertex o.take a point A on one of its arms and B on another such that OA=OB. draw the perpendiculr bisectors of $$\bar { OA } and\bar { OB } $$ let them meet at P.Is PA=PB
Draw a circle of radius 6 cm. From a point 10 cm away from, its centre , construct the pair of tangents to the circle and measure their length
Draw circles for the following radius.
i) 3.5 cm ii) 4.3 cm iii) 4.5 cm
Using a protractor, draw an angle of measure $$72^{o}$$. With this angle as given, draw angles of measure $$36^{o}$$ and $$54^{o}$$.
Take a point on your notebook and draw circle of radii $$4\ cm,\ 3\ cm$$ and $$6.5\ cm$$, each having the same centre $$O$$.
The given figure shows circles of radii $$4$$ cm, $$3$$ cm and $$6.5$$ cm, respectively.
Draw a line segment AB = 5.6 cm. Draw the right bisector of AB.
Draw a circle with centre $$O$$ and any radius. Draw $$AC$$ and $$BD$$ two perpendicular diameter on the circle. Join $$AB, BC, CD$$ and $$DA$$.
The figure is shown below:
Construct the angles of the following measurements:
$$15^{o}$$
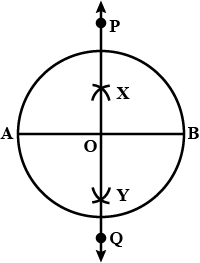
Using ruler and compass, construct a right angle.
Construct the angles of the following measurements:
$$75^{o}$$
Construct the angles of the following measurements:
$$105^{o}$$
Draw a circle of radius 3 cm. Take two points P and Q on one of its extended diameter each at a distance of 7 cm from its centre. Draw tangents to the circle from these two points P and Q. Give the justification of the construction.
Using a protractor, draw the following angles.
$${ -400 }^{ o }$$
Draw a circle radius $$ 5\,cm $$ . Take a point P on the circle. Draw the tangent of the circle at point P without using the center of the circle.
Draw a circle radius $$ 5 \,cm $$ . Draw any line through the center of the circle. Draw a tangent to the circle making an angle of $$ 45^{\circ} $$ with the line . What is the length of the tangent ?
Using a protractor, draw the following angles.
$${ -310 }^{ o }$$
Using a protractor, draw the following angles.
$${ -220 }^{ o }$$
Class 6 Maths Extra Questions
- Algebra Extra Questions
- Basic Geometrical Ideas Extra Questions
- Data Handling Extra Questions
- Decimals Extra Questions
- Fractions Extra Questions
- Integers Extra Questions
- Knowing Our Numbers Extra Questions
- Mensuration Extra Questions
- Playing With Numbers Extra Questions
- Practical Geometry Extra Questions
- Ratio And Proportion Extra Questions
- Symmetry Extra Questions
- Understanding Elementary Shapes Extra Questions
- Whole Numbers Extra Questions