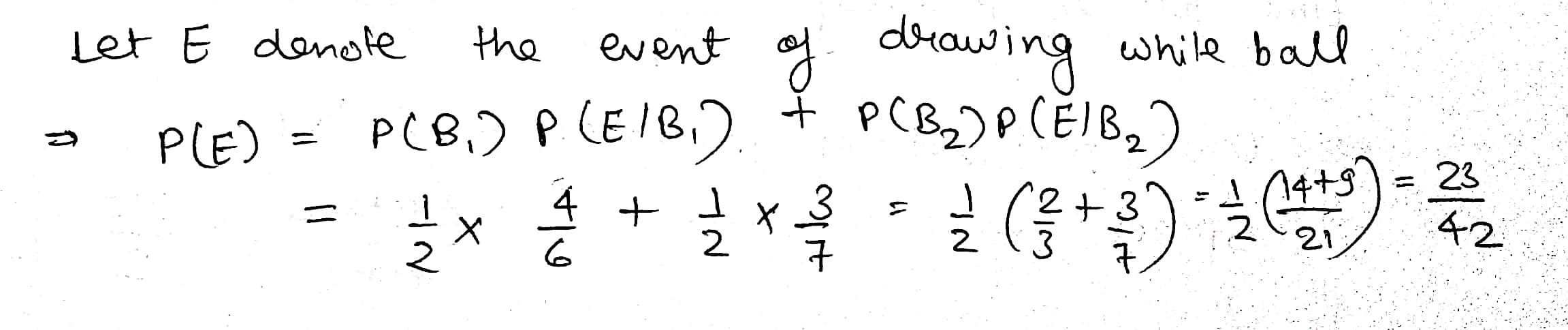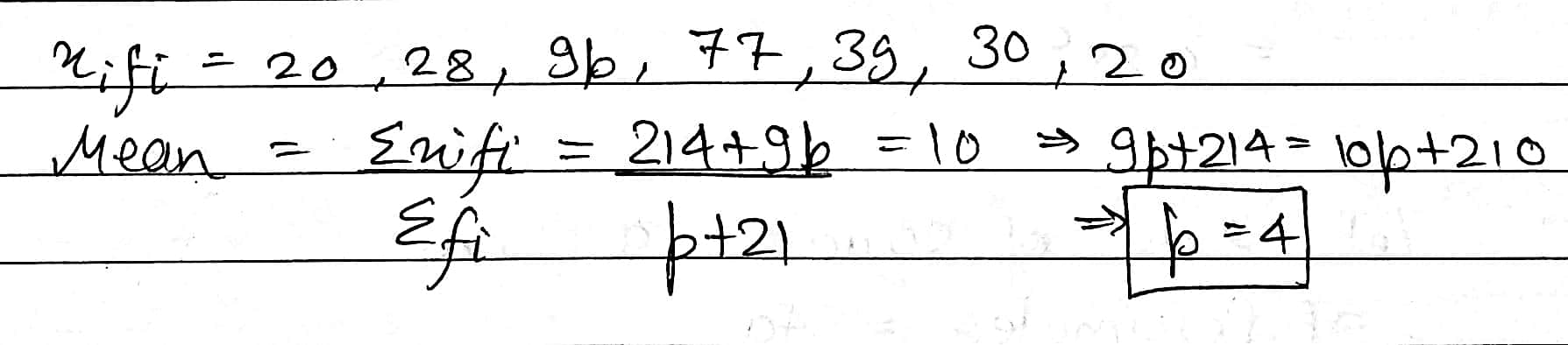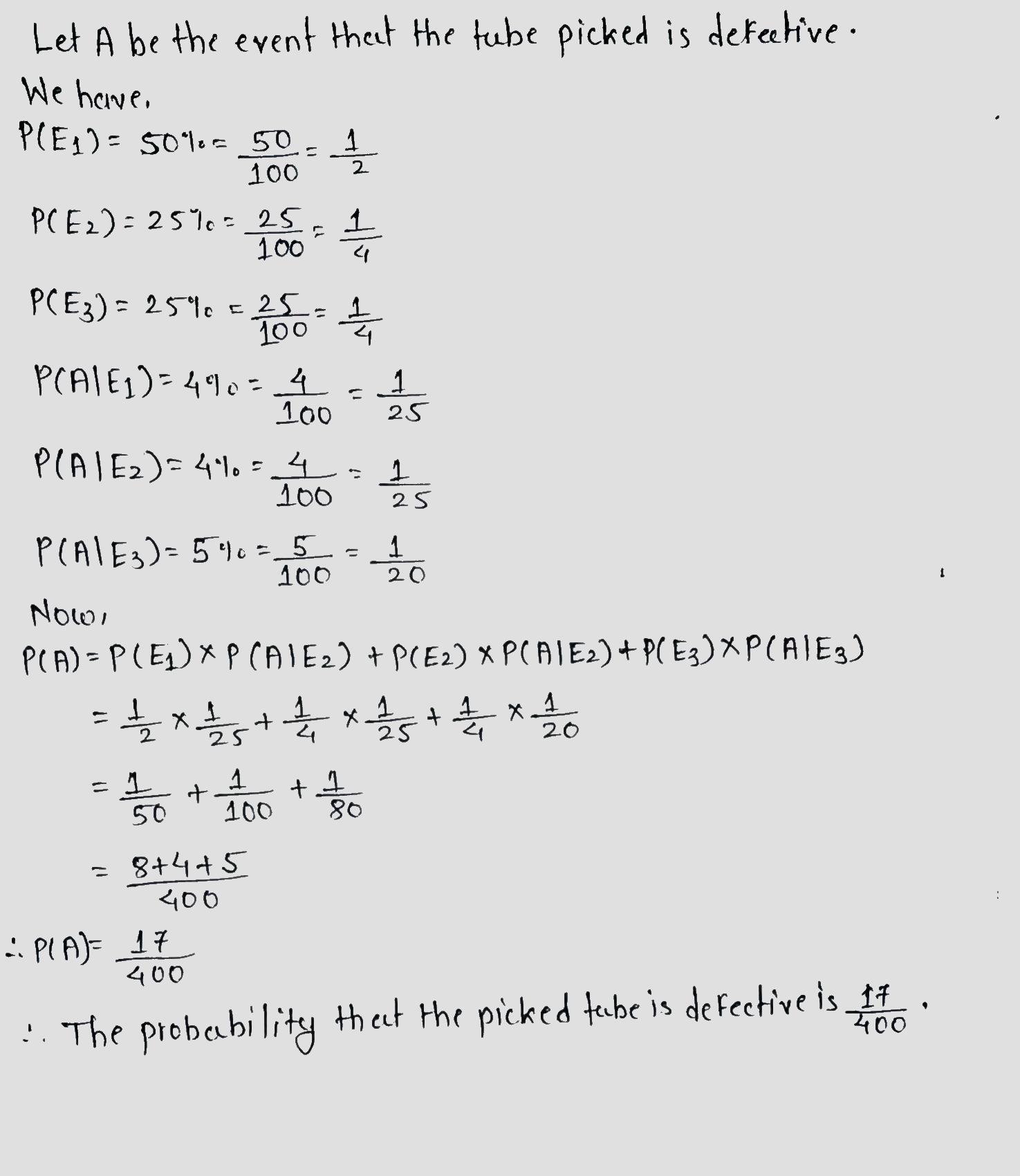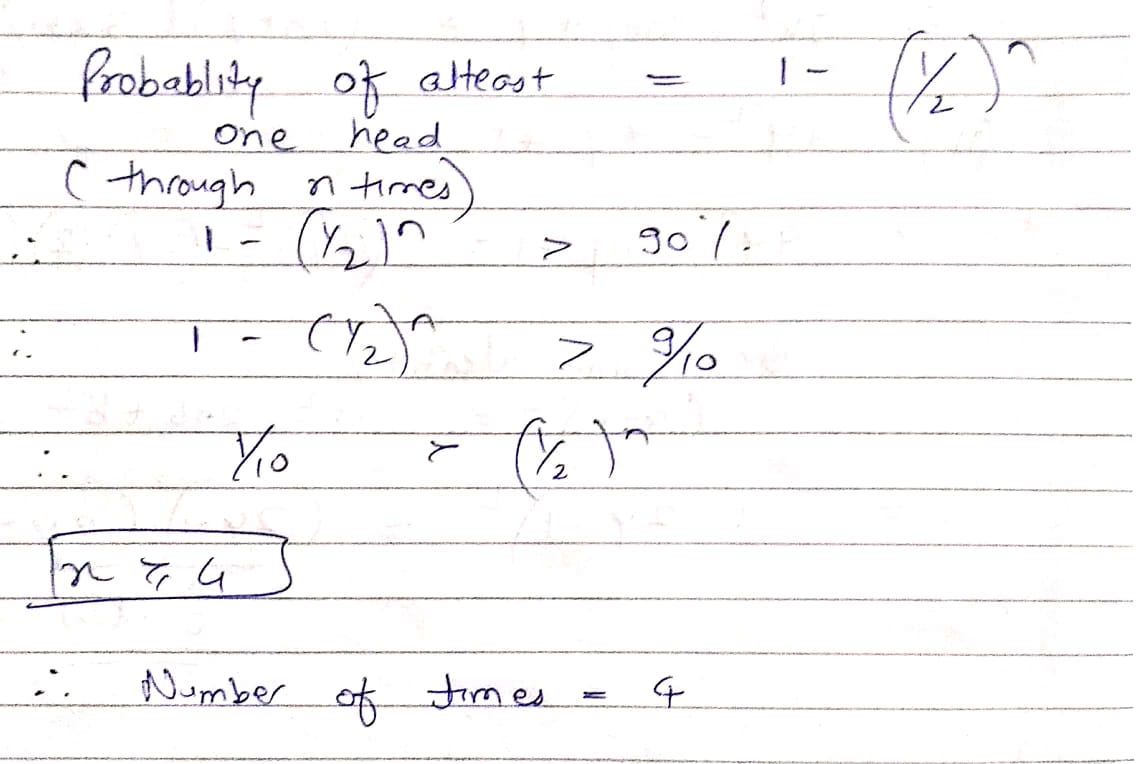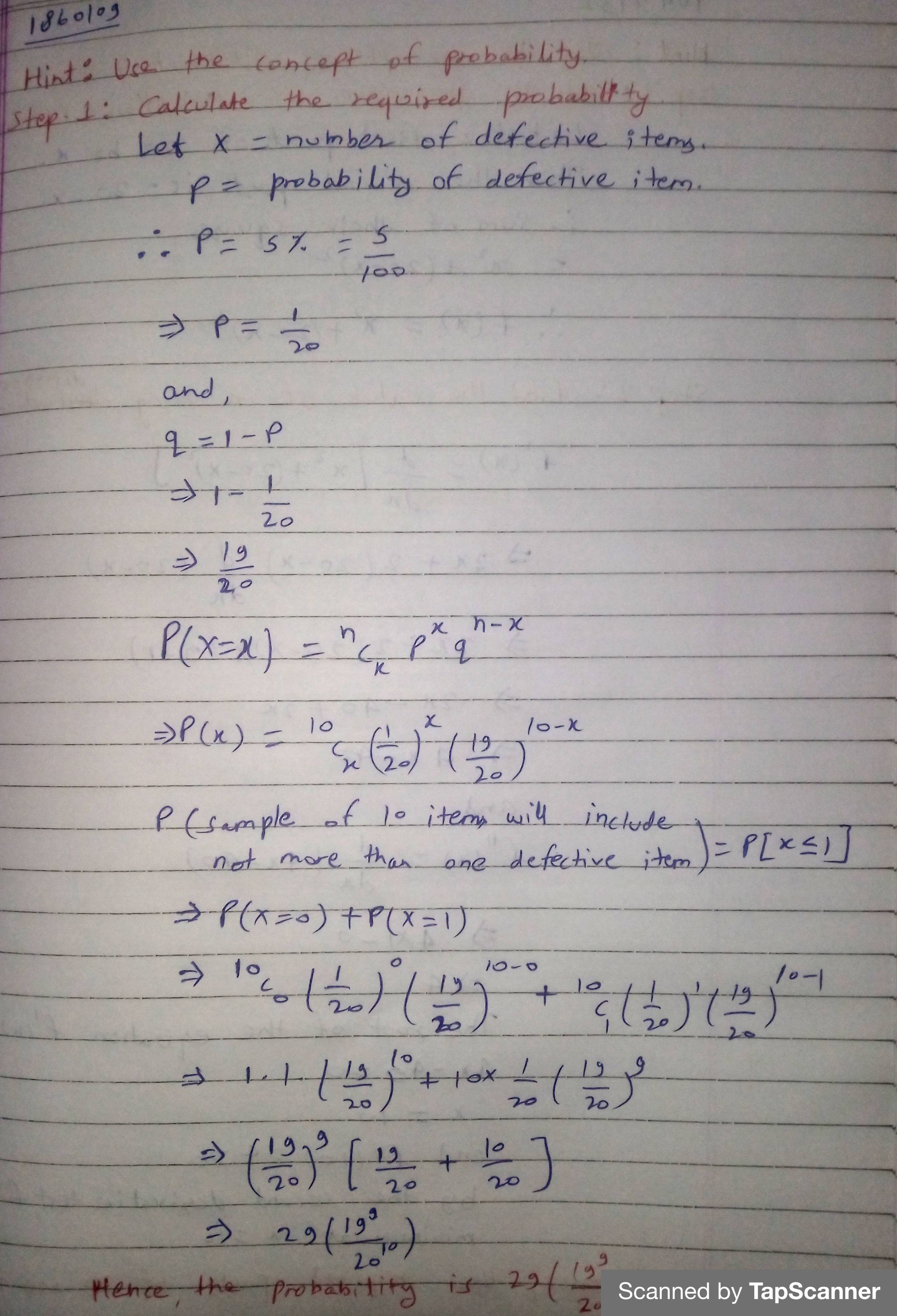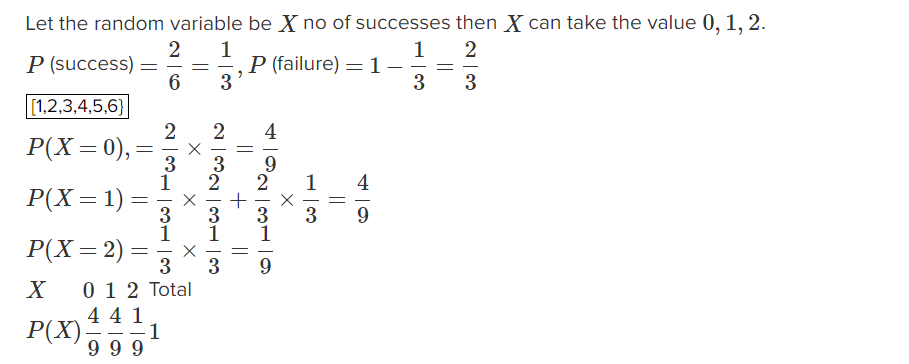Probability - Class 12 Commerce Maths - Extra Questions
Given that $$E$$ and $$F$$ are events such that $$P\left(E\right) = 0.6 , P\left(F\right) = 0.3$$ and $$P\left(E \cap F\right) = 0.2$$, find $$6P\left(F | E\right)$$.
Compute $$100\times P\left(A | B\right)$$, if $$P\left(B\right) = 0.5$$ and $$P\left(A \cap B\right) = 0.32$$.
If $$P\left( A \right) = \displaystyle\frac { 3 }{ 5 } $$ and $$P\left( B \right) = \displaystyle\frac { 1 }{ 5 } $$, find $$100P\left( A\cap B \right) $$ if $$A$$ and $$B$$ are independent events.
A card from a pack of $$52$$ cards is lost. From the remaining cards of the pack, two cards are drawn and are found to be both diamonds. If the probability of the lost card is a diamond is $$p$$ enter $$100p$$
A fair coin is tossed $$8$$ times. Find the probability that it shows heads at least once.
From a bag containing 2 one rupee and 3 two rupee coins a person is allowed to draw 2 coins indiscriminately; find the value of his expectation.
Find the probability distribution of the number of successes in two tosses of a die, where a success is defined as
(i) number greater than 4
(ii) six appears on at least one die
$$8p(\bar {A})$$
Find $$P(B/A)$$ when $$P(A)=\dfrac {5}{11},P(B)=\dfrac {6}{11}$$ and $$P(A \cup B)=\dfrac {7}{11}$$.
The probability that $$A$$ hit a target is $$1/4$$ and the probability that $$B$$ hits the target is $$1/3$$. If each of them fired once, what is the probability that the target will be hit atleast once?
Find the probability of successes in toss of a die, where a success is defined as
(i) Number greater than $$4$$
(ii) Six appears on die
Given $$3$$ identical boxes $$1,2,$$ & $$3$$. Each containing $$2$$ coins. In box $$1$$, both are gold coins & in box $$2$$ both are silver coins and in box 3 there is $$1$$ silver and $$1$$ gold coin. A person chooses a box at random and takes out the coin. If the coin is gold then what is the probability that it is coming from the first box?
A black and a red die are rolled together. Find the conditional probability of obtaining the sum $$8$$, given that the red die resulted in a number less than $$4$$.
Of the students in a school in a school , it is known that 30% have 100% attendance and 70% students are irregular . Previous year results report that 70% of all students who have 100% attendance attain A grade and 10% irregular students attain A grade in their annual examination . At the end of the year,one student is chosen at random from the school and he was found to have an A grade ,what is the probability that the student has 100% attendance?
For two events $$A$$ and $$B$$ with $$P(B)\ne 1$$ prove that $$P(A|B')=\dfrac{P(A)-P(A\cap B)}{1-P(B)}$$.
A n insurance company insured 2000 scoo terdrivers. 4000 car drivers and 6000 truck drivers , 7 he probeblitey of an accident involving a scooter. a and truck is $$\frac{1}{100},\frac{3}{100}and\frac{3}{20}$$ respectively. one of the insured persons meets with an accident. what is the probability that he is a scooter driver?
A card from pack of 52 cards is lost. From the remaining card of the pack, one card is drawn and is found to be heart, find the probability of missing card to be (I) heart (II) club.
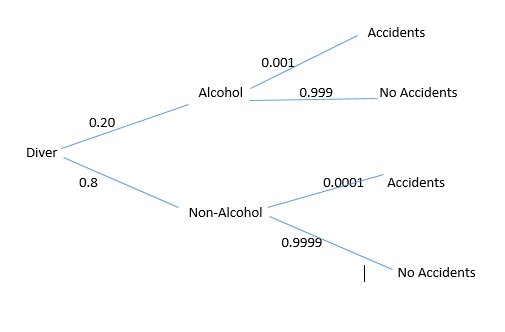
On a Saturday night $$20\%$$ of all divers is U.S.A. are under the influence of alcohol. The probability that a driver under the influence of alcohol will have an accident is $$0.001$$. The probability that a sober driver will have an accident is $$0.0001$$. If a car on a Saturday night smashed into a tree, the probability that the driver was under the influence of alcohol, is?
Hence, Probability that the diver was under the influence of alcohol when the accident happened- $$0.001\times 0.20 = 0.0002$$
A man is know to speak truth $$4$$ out of $$5$$ times. He tosses a coin and reports that it is head. Find the probability that it is actually head.
An urn contains 5 red and 2 black balls . Two balls are randomly drawn. Let X represent the number of black balls. What are the possible values of X ? Is X a random variable ?
A bag contains $$10$$ white and $$15$$ black balls. Two balls are drawn in succession without replacement. What is the probability that first is white and second is black?
An urn contains $$5$$ red and $$2$$ black balls. Two balls are randomly selected. If $$X$$ represents the number of black balls, what are the possible values of $$X$$?
| $$X=x$$ | $$-2$$ | $$-1$$ | $$0$$ | $$1$$ | $$2$$ | $$3$$ |
| $$P(X=x)$$ | $$0.1$$ | $$K$$ | $$0.2$$ | $$2K$$ | $$0.3$$ | $$K$$ |
A box contain 10 red balls , 20 yellow balls and 50 blue balls. If a ball is drwan at random from the box , find the probability that it will be
(i) a blue ball (ii) neither yellow nor blue
If two different numbers are taken from the set $$\{0,1,2,3............,10\}$$; then the probability that their sum as well as absolute different are both multiple of $$4$$ , is :
Compute $$P(A|B)$$ if $$P(B)=0.5$$ and $$P(A \cap B)=0.32$$.
50 plants were planted each school out of 10 schools. After a month, the number of planets that survived are given below:Find Mean and Variance
| School | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Number of planet survived | 40 | 35 | 32 | 45 | 35 | 30 | 45 | 40 | 35 | 25 |
IF $$P(A)=\dfrac{1}{3}, P(B)=\dfrac{1}{12}$$ and $$P(A \cap B)=\dfrac{1}{36}$$, are the events $$A$$ and $$B$$ independent ?
If 12 identical balls are to be placed in 3 different boxes, then the probability that one of the boxes contains excatly 3 balls, is :
Total outcomes =
$$ \{ (12,0,0), (11,1,0), (10,1,1), (10,2,0)$$
$$ (9,3,0), (9,2,1), (8,4,0), (8,3,1)$$
$$ (8,2,2),(7,5,0), (7,4,1)$$
$$(7,3,2),(6,6,0),(6,5,1),$$
$$ (6,4,2)(6,3,3)(5,5,2)(5,4,3)$$
$$(4,4,4)\} = 19$$
Favorable cost = 4
$$ \{ (3,9,0), (3,8,1), (3,7,2), (3,5,4)\}$$
Probability = $$ 4/19 $$
A number is chosen at random from numbers -3,-2, -1,0,1,2,What is the probability that |x| < 2.
Probability of getting 2 when we roll a dice.
If $$p \in = 0.6$$ and $$p ( E \cap F ) = 0.2$$ then find $$p ( F / E )$$
Bag $$B_{1}$$ contains $$4$$ white and $$2$$ black balls. Bag $$B_{2}$$ cantains $$3$$ white and $$4$$ black balls. A bag is drawn at random and a ball is chosen at random from it. What is the probability that the ball drawn is white?
Let E denote the event of drawing while ball
$$\Rightarrow P(E)=P(B_1)P(E/B_1)+P(B_2)P(E/B_2)$$
$$=\dfrac{1}{2}\times \dfrac{4}{6}+\dfrac{1}{2}\times \dfrac{3}{7}=\dfrac{1}{2}\left(\dfrac{2}{3}+\dfrac{3}{7}\right)=\dfrac{1}{2}\left(\dfrac{14+9}{21}\right)=\dfrac{23}{42}$$.
For the following probability density function (p. d. f.) of $$X$$, find: (i) $$P(X < 1)$$, (ii) $$P (|X| < 1)$$,
if $$\left \{\begin{matrix}f(x) = \dfrac{x^2}{18}, & -3 < x < 3 \\= 0, & \text{ otherwise} \end {matrix} \right.$$
A bag contains $$10$$ red balls and $$8$$ green balls. $$2$$ balls are drawn at random one by one with replacement. Find the probability that both the balls are green that a second year student is chosen.
A bag contains 6 red balls and 8 green balls. A ball is drawn at random . What is the probability that the ball is green
Chance that Sheela tells truth is 35% and for Ramesh is 75%. In what percent they likely to contradict each other in the same question?
A die is thrown once. If A is the event "the number appearing is a multiple of $$3"$$ and B is the event "the number appearing is even" Are the event A and B independent ?
Two event A and B are independent if $$P(A\cap B)=P(A).P(B)$$ A die is thrown.
$$S=\left \{ 1,2,3,4,5,6 \right \}$$
Let two events be
A: the number appear is a multiple of 3.
B: the number appearing is even.
A:[3,6]
$$P(A)=\frac{2}{6}=\frac{1}{3}$$
$$B:[2,4,6]$$
$$P(B)=\frac{3}{6}=\frac{1}{2}$$
$$A\cap B$$= the number appearing is even multiple of 3 = [3]
So, $$P(A\cap B)=\frac{1}{6}$$
Now, $$P(A).P(B)=\frac{1}{3}.\frac{1}{2}=\frac{1}{6}$$
Since, $$P(A\cap B)=P(A).P(B)$$
Therefore A and B are independent events.
A bag contains 4 balls.Two balls drawn at random without replacement and are found to be white. What is the probability that all balls are white?
Let A be the event of drawing 2 white balls.
from the bag containing 4 balls.
The remaining 2 balls of the bag has three options.
Let $$E_{1}$$ be the event that the remaining 2 balls of the bag are not white
Let $$E_{2}$$ be the event that are remaining 2 balls of the bag are one white and one not white.
Let $$E_{3}$$ be the event that rae remaining 2 balls of the bag are white.
$$\therefore P(E_{1})=P(E_{2})=P(E_{3})=\frac{1}{3}$$
$$P(A/E_{1})=P$$ (drawing 2 white balls from the bag contains 2 white and 2 not white)
$$=\frac{^{2}C_{2}}{^{4}C_{2}}=\frac{1}{6}$$
$$P(A/E_{2})=P$$ (drawing 2 white balls from the bag containing 2 white and 1 non-white)
$$=^{3}.C_{2}/^{4}.C_{2}=\frac{3}{6}=\frac{1}{2}$$
$$P(A/E_{3})=P$$ (drawing 2 white ball from bag containing 4 whire balls)
= 1.
$$P(E_{2}/A)=\frac{P(E_{2})(PA/E_{2})}{P(E_{1})P(A/E_{1})+P(E_{2})+P(E_{3})P(A/E_{3})}$$
$$=\frac{1}{3}\times \frac{1}{6}+\frac{1}{3}\times \frac{1}{2}+\frac{1}{3}.\frac{1}{1}$$
$$=\frac{1}{3}(\frac{1}{6}+\frac{1}{2}+1)$$
$$=\frac{1}{3}$$
$$P(E_{2}/A)=\frac{\frac{1}{3}.\frac{1}{2}}{\frac{1}{3}.\frac{5}{3}}=\frac{\frac{1}{6}}{\frac{5}{9}}$$
$$=\frac{1}{6}\times \frac{3}{5}=\frac{3}{10}$$
Compute $$P ( A | B ) ,$$ if $$P ( B ) = 0.25$$ and $$P ( A \cap B ) = 0.18$$.
Evaluate $$P(A \cup B)$$, if $$2P(A)=P(B)=\dfrac{5}{13}$$ and $$P(A/B)=\dfrac{2}{5}$$.
Find the expected number of boys in a family with 8 children,assuming the sex distribution to be equally probable.
Compute $$P ( A | B ) ,$$ if $$P ( B ) = 0.5$$ and $$P ( A \cap B ) = 0.32$$.
Compute $$P ( A | B ) ,$$ if $$P ( B ) = 0.5$$ and $$P ( A \cap B ) = 0.32$$.
The probability distribution function of a random variable $$X$$ is given by
| $$x_{i}$$: | 0 | 1 | 2 |
| $$p_{i}$$: | $$3c^{}$$ | $$10c$$ | $$5c-1$$ |
The probability of student $$A$$ passing an examination is $$\dfrac{2}{9}$$ and of students, $$B$$ passing is $$\dfrac{5}{9}$$. Assuming the two events: $$A$$ passes'. $$B$$ passes' as independent, find the probability of both passing the examination.
An urn contains $$10$$ black and $$5$$ white balls. Two balls are drawn from the urn one after the other without replacement. What is the probability that both drawn balls are black?
Two numbers are selected at random from integers $$1$$ through $$9$$. If the sum is even, find the probability that both the numbers are odd.
Kamal and Monika appeared for an interview for two vacancies. The probability of Kamal's selection is $$1/3$$ and that of Monika's selection is $$1/5$$. Find the probability that at least one of them will be selected.
Find the value of $$k$$ in the given probability distribution:
| $$x_{i}$$: | 2 | 3 | 4 |
| $$p_{i}$$: | 0.2 | $$k$$ | 0.3 |
The probability that it will rain tomorrow is $$0.85$$. What is the probability that it will not rain tomorrow ?
To know the opinion of the students about Mathematics, a survey of 200 students was conducted. The data is recorded in the following table:
| Opinion: | Like | Dislike |
| Number of students: | 135 | 65 |
A school gives awards to the student each class $$5$$ for bravery, $$3$$ for punctuality, $$3$$ for full attendance, $$4$$ for social services $$5$$ self confidence. An awarded student is selected at random. What is the probability that he /she is being awarded for self confidence.
A school gives awards to the student each class $$5$$ for bravery, $$3$$ for punctuality, $$3$$ for full attendance, $$4$$ for social services $$5$$ self confidence. An awarded student is selected at random. What is the probability that he /she is being awarded for punctuality
Match column I with column II
In a class $$30$$% students fail in English; $$20$$% students fail in Hindi and $$10$$% students fail in English and Hindi both. A student is chosen at random, then the probability that he will fail English if he has failed in Hindi is $$\dfrac { k }{ 2 } $$.The value of $$k$$ is
An urn contains 2 white and 2 black balls. A ball is drawn at random. If it is white it is not replaced into the urn. Otherwise it is along with another ball of same colour. The process is repeated. the probability that the third ball drawn is black is a/b (no common divisor), then b-a =
Two sets of candidates are competing for the positions on the board of directors of a company. The probabilities that first and second sets will win are 0.6 and 0.4 respectively. If the first set wins the probability of introducing a new product is 0.8 and the corresonding probability if the second set wins is 0.The probability that the new product will be introduced is $$0.1k$$. Find the value of $$k$$.
An urn contains five balls alike in every respect save colour. If three of these balls are white and two are black and we draw two balls at random from this urn without replacing them. If A is the event that the first ball drawn is white and B the event that the second ball drawn is black, are A and B independent? If A and B are independent then enter 1, else enter 0.
Suppose there are three urns containing 2 white and 3 black balls: 3 white and 2 black balls, and 4 white and one black ball respectively. There is equal probability of each urn being chosen. One ball is drawn from an urn chosen at random. The probability that a white ball is drawn is $$\displaystyle \frac{k}{15}$$. Find the value of $$k$$.
$$\displaystyle P\left ( A\cup B \right )=P\left ( A\cap B \right )$$ if and only if the ralation between $$P(A)$$ and $$P(B)$$ is $$P(A)+P(B)=2P(AB)$$. If this is true enter 1, else enter 0.
In a test an examine either gusses or copies or knows the answer to a multiple choice question with $$m$$ choices out of which exactly one is correct. The probability that he makes a guess is 1/3 and the probability that he copies the answer is 1/The probability that his answer is correct given that the copied it, is 1/If the probability that he knew the answer to the question given that he correctly answered it is 120/141, find $$m$$
One ticket is selected at random from 100 tickets numbered 00, 01, 02, ..., 98,If X and Y denote the sum and the product of the digits on the tickets, What is the value of $$57P(X=9|Y=0)$$?
A bag contains 3 red and 7 black balls. Two balls are selected at random one-by-one without replacement. The probability that the second selected ball happens to be red if the first selected ball is red, is $$\dfrac{2}{k}.$$ Find k.
A bag contains n+1 coins. It is known that one of these coins has heads on both sides, whereas the other coins are fair. One coin is selected at random and tossed. If the probability that the toss results in heads is 7/12, find n
A speaks truth $$3$$ out of $$4$$ times. He reported that Mohan Bagan has won the match. The probability that his report was correct is $$\displaystyle \frac { k }{ 5 } $$, then $$k=$$
The probability that an archer hits the target when it is windy is 0.4; when it is not windy, her probability of hitting the target is 0.On any shot, the probability of a gust of wind is 0.The probability that she hits the target on first shot is $$0.x1$$. Find $$x$$.
If three coins are tossed, represent the sample space and the event of getting atleast two heads, then find the number of elements in them.
Box-I contains $$5$$ red and $$4$$ white balls while box-II contains $$4$$ red and $$2$$ white balls. A fair die is thrown. If it turns up a multiple of $$3,$$ a ball is drawn, from box-I else a ball is drawn from box-II. The probability that the ball drawn is white is $$\dfrac{a}{27}$$. Find $$a$$.
$$A$$ speaks the truth '$$3$$ times out of $$4$$' and $$B$$ speaks the truth '$$2$$ times out of $$3$$', $$A$$ die is thrown. Both assert that the number turned up is $$2.$$ Find the probability of the truth of their assertion.
Cards of an ordinary deck of playing cards are placed into two heaps. Heap-I consists of all the red cards and heap-II consists of all the black cards. A heap is chosen at random and a card is drawn, find the probability that the card drawn is a king.
A fair die is rolled. Consider events $$E=\left\{ 1,3,5 \right\} ,F=\left\{ 2,3 \right\} $$ and $$G=\left\{ 2,3,4,5 \right\} $$ Find
(i) $$P\left( E|F \right) $$ and $$P\left( F|E \right) $$
(ii) $$P\left( E|G \right) $$ and $$P\left( G|E \right) $$
(iii) $$P\left( \left( E\cup F \right) |G \right) $$ and $$P\left( \left( E\cap F \right) |G \right) $$
Evaluate $$P\left( A \cup B \right)$$, if $$ 2 P\left( A \right) = P\left( B \right) = \displaystyle\frac { 5 }{ 13 }$$ and $$ P\left( A | B \right) = \displaystyle\frac { 2 }{ 5 } $$. Find $$P\left( A \cup B \right)\times 100$$
Mother, father and son line up at random for a family picture
$$E : $$ son on one end, $$F : $$ father in middle.
Determine $$P\left( E|F \right) $$
Determine $$P\left( E|F \right) $$
A die is thrown three times,
$$E\ :\ 4$$ appears on the third toss, $$F\ :\ 6$$ and $$5$$ appears respectively on first two tosses.
Determine $$36P$$ where $$ P\left( E|F \right) $$
If $$P\left(A\right) = 0.8, P\left(B\right) = 0.5$$ and $$P\left(B | A\right) = 0.4$$, find
(i) $$P\left(A \cap B\right)$$
(ii) $$P\left(A | B\right)$$
(iii) $$P\left(A \cup B\right)$$
Of the students in a college, it is known that $$60\%$$ reside in hostel and $$40\%$$ are day scholars (not residing in hostel). Previous year results report that $$30\%$$ of all students who reside in hostel attain $$A$$ grade and $$20\%$$ of day scholars attain $$A$$ grade in their annual examination. At the end of the year, one student is chosen at random from the college and he has an $$A$$ grade, what is the probability that the student is a hosteller?
A bag contains $$4$$ red and $$4$$ black balls, another bag contains $$2$$ red and $$6$$ black balls. One of the two bags is selected at random and a ball is drawn from the bag which is found to be red. Find the probability that the ball is drawn from the first bag.
Consider the experiment of throwing a die, if a multiple of $$3$$ comes up, throw the die again and if any other number comes, toss a coin. Find the conditional probability of the event 'the coin shows a tail', given that 'at least one die shows a $$3$$'.
Two cards are drawn at random and without replacement from a pack of $$52$$ playing cards. Find the probability that both the cards are black.
An instructor has a question bank consisting of $$300$$ easy True / False questions, $$200$$ difficult True / False questions, $$500$$ easy multiple choice questions and $$400$$ difficult multiple choice questions. If a question is selected at random from the question bank, what is the probability that it will be an easy question given that it is a multiple choice question ?
A box of oranges is inspected by examining three randomly selected oranges drawn without replacement. If all the three oranges are good, the box is approved for sale, otherwise, it is rejected. Find the probability that a box containing $$15$$ oranges out of which $$12$$ are good and $$3$$ are bad ones will be approved for sale.
In answering a question on a multiple-choice test, a student either knows the answer or guesses. Let $${ 3 }/{ 4 }$$ be the probability that he knows the answer and $${ 1 }/{ 4 }$$ be the probability that he guesses. Assuming that a student who guesses at the answer will be correct with probability $${ 1 }/{ 4 } $$. What is the probability that the student knows the answer given that he answered it correctly?
Two groups are competing for the position on the Board of directors of a corporation. The probabilities that the first and the second groups will win are $$0.6$$ and $$0.4$$ respectively. Further, if the first group wins, the probability of introducing a new product is $$0.7$$ and the corresponding probability is $$0.3$$ if the second group wins. Find the probability that the new product introduced was by the second group.
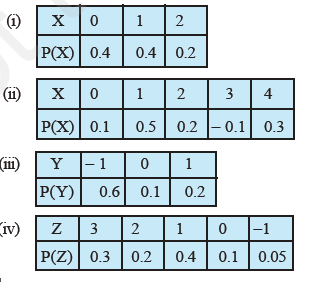
State which of the following are not the probability distributions of a random variable. Give reasons for your answer.
A manufacturer has three machine operators $$A, B$$ and $$C$$. The first operator $$A$$ produces $$1\%$$ defective items, whereas the other two operators $$B$$ and $$C$$ produce $$5\%$$ and $$7\%$$ defective items respectively. $$A$$ is on the job for $$50\%$$ of the time, $$B$$ is on the job for $$30\%$$ of the time and $$C$$ is on the job for $$20\%$$ of the time. A defective item is produced, what is the probability that it was produced by $$A$$?
Suppose a girl throws a die. If she gets a $$5$$ or $$6$$, she tosses a coin three times and notes the number of heads. If she gets $$1, 2, 3$$ or $$4$$, she tosses a coin once and notes whether a head or tail is obtained. If she obtained exactly one head, what is the probability that she threw $$1, 2, 3$$ or $$4$$ with the die ?
Find the probability distribution of
(i) number of heads in two tosses of a coin.
There are three coins. One is a two-headed coin another is a biased coin that comes up heads $$75$$% of the time and third is an unbiased coin. One of the three coins is chosen at random and tossed, it shows heads, what is the probability that it was the two-headed coin?
An insurance company insured $$2000$$ scooter drivers, $$4000$$ car drivers and $$6000$$ truck drivers. The probability of an accidents are $$0.01, 0.03$$ and $$0.15$$ respectively. One of the insured persons meets with an accident. What is the probability that he is a scooter driver ?
A factory has two machines $$A$$ and $$B$$. Past record shows that machine $$A$$ produced $$60\%$$ of the items of output and machine $$B$$ produced $$40\%$$ of the items. Further, $$2\%$$ of the items produced by machine $$A$$ were defective and $$1\%$$ produced by machine $$B$$ were defective. All the items are put into one stockpile and then one item is chosen at random from this and is found to be defective. What is the probability that it was produced by machine $$B$$?
A laboratory blood test is $$99\%$$ effective in detecting a certain disease when it is present. However, the test also yields a false-positive result for $$0.5\%$$ of the healthy person tested (i.e., if a healthy person is tested, then, with probability $$0.005$$, the test will imply he has the disease). If $$0.1$$ percent of the population actually has the disease, what is the probability that a person has the disease given that his test result is positive?
Two numbers are selected at random (without replacement) the first six positive integers. Let $$X$$ denote the larger of the two numbers obtained. Find $$E\left(X\right)$$.
An urn contains 25 balls of which 10 balls bear a mark $$'X'$$ and the remaining 15 bear a mark $$'Y'$$. A ball is drawn at random from the urn, its mark is noted down and it is replaced. If 6 balls are drawn in this way, find the probability that
(i) all will bear $$'X'$$ mark
(ii) not more than 2 will bear $$'Y'$$ mark
(iii) at least one ball will bear $$'Y'$$ mark
(iv) the number of balls with $$'X'$$ mark and $$'Y'$$ mark will be equal.
An experiment succeeds twice as often as it fails. Find the probability that in the next six trials, there will be atleast 4 successes.
Two dice are thrown simultaneously. If $$X$$ denotes the number of sixes, find the expectation of $$X$$.
The random variable $$X$$ has a probability distribution $$P\left(X\right)$$ of the following form, where $$k$$ is some number :
$$P\left(X\right) = \left\{k, if x = 0 \\ 2k, if x = 1 \\ 3k, if x = 2 \\ 0, otherwise\right\}$$
(a) Determine the value of $$k$$
(b) Find $$P\left(X < 2\right), P\left(X \le 2\right), P\left(X \ge 2\right)$$.
What is the minimum number of times must a man toss a fair coin so that the probability of having at least one head is more than $$90\%$$ ?
Bag $$I$$ contains $$3$$ red and $$4$$ black balls and Bag $$II$$ contains $$4$$ red and $$5$$ black balls. One ball is transferred from Bag $$I$$ and Bag $$II$$ and then a ball is drawn from Bag $$II$$. The ball so drawn is found to be red in colour. Find $$310$$ times the probability that the transferred ball is black.
In a hurdle race, a player has to cross $$10$$ hurdles. The probability that he will clear each hurdle is $$\displaystyle\frac { 5 }{ 6 } $$. What is the probability that he will knock down fewer than $$2$$ hurdles ?
In a game, a man wins a rupee for a six and loses a rupee for any other number when a fair die is thrown. The man decided to throw a die thrice but to quit as and when he gets a six. Find the expected value of the amount he win / loses.
Two different dice are tossed together. Find the probability that the product of the two numbers on the top of the dice is $$6$$.
Three cards are drawn successively with replacement from a well shuffled pack of $$52$$ cards. Find the probability distribution of the number of spades. Hence find the mean of the distribution.
An article manufactured by a company consists of two parts $$X$$ and $$Y$$. In the process of manufacture of the part $$X$$. $$9$$ out of $$100$$ parts may be defective. Similarly $$5$$ out of $$100$$ are likely to be defective in part $$Y$$. Calculate the probability that the assembled product will not be defective.
$$8p(\bar A \cup \bar B)$$
$$8p(\bar A \cap B)$$
If A and B are both random events.
$$p(A)=\dfrac{3}{8}$$; $$p(B)=\dfrac{1}{2}$$; $$p(A\ \cap\ B)=\dfrac{1}{4}$$
Calculate:
$$8p(\bar A \cap \bar B)$$
$$p(A)=\dfrac{3}{8}$$; $$p(B)=\dfrac{1}{2}$$; $$p(A\ \cap\ B)=\dfrac{1}{4}$$
Calculate:
$$4p(\bar {B})$$
$$8p( A \cap \bar B)$$
From a pack of $$52$$ cards, two cards are drawn randomly one by one without replacement. Find the probability that both of them are red.
A die is thrown twice and the sum of the numbers appearing is observed to be $$7$$. Find the conditional probability that the number $$3$$ has appeared at least once.
A bag contains 8 red and 5 white balls. Two successive draws of 3 balls are made at random from the bag without replacements. Find the probability that the first draw yields 3 white balls and the second draw 3 red balls.
Bag A contains 2 red and 3 black balls while another bag B contains 3 red and 4 black balls. One ball is drawn at random from one of the bag and it is found to be red. Find the probability that it was drawn from bag B.
Three boxes $${B}_{1},{B}_{2},{B}_{3}$$ contain balls with different colours as follows:
| White | Black | Red | |
| $${B}_{1}$$ | 2 | 1 | 2 |
| $${B}_{2}$$ | 3 | 2 | 4 |
| $${B}_{3}$$ | 4 | 3 | 2 |
Box-I contains 2 gold coins, while another Box-II contains 1 gold and 1 silver coin. A person choose a box at random and takes out a coin. If the coin is of gold, what is the probability that the order coin in the box is also of gold?
State and prove Bayes' theorem
If $$P(A)=\dfrac{4}{5}$$ and $$P(B/A)=\dfrac{2}{5}$$, find $$P(A\cap B).$$
If $$P(A)=0.8$$ and $$P(B|A)=0.4$$, then find $$P(A\cap B)$$.
Three boxes numbered I, II, III contains the balls as follows:
| White | Black | Red | |
| I | $$1$$ | $$2$$ | $$3$$ |
| II | $$2$$ | $$1$$ | $$1$$ |
| III | $$4$$ | $$5$$ | $$3$$ |
A person buys a lottery ticket in 50 lotteries in each of which his chance of winning a price is $$\dfrac{1}{100}$$. What is the probability that he will win a price exactly once?
In a factory, there are two machines $$A$$ and $$B$$ producing bulbs. Their contributions are respectively $$60\%$$ and $$40\%$$ of the total production. It is found that $$1\%$$ and $$3\%$$ of the items produced by these machines are defective. An item randomly chosen from a day's production was found to be defective. Find the probability that the defective item was produced by machine $$B$$.
There are two small boxes $$A$$ and $$B$$. In $$A$$ there are $$9$$ white beads and $$8 $$ black beads.
In $$B$$ there are $$7$$ white and $$8$$ black beads. We want to take a bead from a box.
(a) What is the probability of getting a white bead from each box?
(b) A white bead and a black bead are added to box $$B $$ an then a bead is taken from it.
What is probability of getting a white bead from it.
Find the probability distribution of number of heads in two tosses of a coin.
A coin is tossed twice. Find the probability distribution of the number of heads.
If $$P(A)=0.6, P(B)=0.7$$ and $$P(A\cup B)=0.9$$, then find $$P\left(\dfrac{A}{B}\right)$$ and $$P\left(\dfrac{B}{A}\right)$$.
If $$mn$$ coins have been distributed into na purses, n into each, find $$(1)$$ the chance that two specified coins will be found in the same purse; and $$(2)$$ what the chance becomes when $$r$$ purses have been examined and found not to contain either of the specified coins.
A certain stake is to be won by the first person who throws an ace with an octahedral die, if there are $$4$$ persons what is the chance of the last to win the stake?
A bag contain 6 Red and 4 White balls. 4 balls are drawn one by one without replacement and were found to be atleast 2 white. Then the probability that next draw of a ball from this bag will give a white ball.
$$10$$ witnesses each of whose probability of speaking the truth is $$\cfrac { 5 }{ 6 } $$. Asserts that the certain event took place, if the probability of this event before their statement is $$\cfrac { 1 }{ 1+{ 5 }^{ 9 } } $$, find the probability of the truth of their assertion.
A biased coin which comes up heads three times as often as tails is tossed. If it shows heads, a chip is drawn from urn-I which contains $$2$$ white chips and $$5$$ red chips. If the coin comes up tail, a chip is drawn from urn-II which contains $$7$$ white and $$4$$ red chips. Given that a red chip was drawn, what is the probability that the coin came up heads?
Suppose a girl throws a die. If she gets $$1$$ or $$2$$, she tosses a coin three times and notes the number of tails. If she gets $$3, 4, 5$$ or $$6$$, she tosses a coin once and notes whether a 'head' or 'tail' is obtained. If she obtained exactly one 'tail', what is the probability that she threw $$3, 4, 5$$ or $$6$$ with the die?
A is one of the $$6$$ horses entered for a race and is to be ridden by one of two jockeys B or C. It is $$2:1$$ that B rides A, in which case all the horses are equally likely to win; if C rides A, his chance is gets tripled. If the odds against his winning is $$\dfrac{p}{q}$$, where p and q are co-primes then find the value of $$ p+q$$.
There is a probability that 4 out of 10 students appearing in CA CPT exams will qualify for CA course after passing CA CPT exam. The probability that of 5 atudents all will qualify CA CPT exam.
From a lot of $$6$$ items containing $$2$$ defective items, a sample of $$4$$ items are drawn at random. Let the random variable X denote the number of defective items in the sample. If the sample is drawn without replacement, find the probability distribution of X.
If A and B are events such that $$P(A)=\displaystyle\frac{1}{2}$$, $$P(B)=\displaystyle\frac{1}{3}$$ and $$P(A\cap B)=\displaystyle\frac{1}{4}$$, then find $$P(B/A)$$.
If A and B are events such that $$P(A)=\displaystyle\frac{1}{2}$$, $$P(B)=\displaystyle\frac{1}{3}$$ and $$P(A\cap B)=\displaystyle\frac{1}{4}$$, then find $$P(A/B)$$.
Assume that the chances of a patient having a heart attack are $$40\%$$. It is also assumed that a meditation and yoga course reduce the risk of heart attack by $$30\%$$ and the prescription of certain drugs reduces its chances by $$25\%$$. At a time a patient can choose any one of the two options the patient selected at random suffers a heart attack. Find the probability that the patient followed a course of meditation and yoga?
A family has two children. What is the probability that both the children are boys, given that atleast one of them is a boy?
If $$P(A) = \dfrac {7}{13}, P(B) = \dfrac {9}{13}$$ and $$P(A\cap B) = \dfrac {4}{13}$$, find $$P(A/ B)$$.
Three fair coins are tossed simultaneously. If X denotes the number of heads, find the probability distribution of X.
A random variable $$X$$ has the following probability distribution:
| $$X$$ | $$0$$ | $$1$$ | $$2$$ | $$3$$ | $$4$$ |
| $$P(X)$$ | $$0.1$$ | $$k$$ | $$2k$$ | $$2k$$ | $$k$$ |
(i) $$k$$
(ii) $$P(X \geq 2)$$.
Five coins are tossed simultaneously. Find the probability of getting atleast onehead.
$$P(A)=\dfrac {1}{Z}$$
$$P(B)=\dfrac {1}{4}$$
$$P(A \cap B)=\dfrac {1}{5}$$
$$P(A^{}/B^{})=?$$
A is known to speak truth $$5$$ out of $$7$$ times. What is the probability that $$A$$ reports that it is a $$7$$ when a die is thrown?
A purse contains n coins of unknown value, a coin drawn at random is found to be a rupee, what is the chance that it is the only rupee in the purse? Assume all numbers of rupee coins in the purse to be equally likely.
Consider the experiment of throwing a die, if a multiple of $$3$$ comes up, thrown the die again and if any other number comes, toss a coin. Find the conditional probability of the event 'the coin shows a tail', given that 'at least one die shows a $$3$$'.
If $$A$$ ad $$B$$ are two events such that $$P(A)=\dfrac{1}{4}, P(B)=\dfrac{1}{3}$$ and $$P(A\cup B)=\dfrac{1}{2}$$, show that $$A$$ and $$B$$ are independent events
Find the value of K.
Consider rolling of die.
Find probability that a multiple of $$3$$ appear in third roll.
Two coins are tossed once. Let $$A=$$ Tail appears on one coin $$B=$$ coin show Head. Find $$P(A|B)$$.
In how many ways can $$10$$ people be made to sit around a circular table?
What is the probability that you will get admission in atleast two colleges?
A fair die is rolled. Consider the events $$E = \{1, 3, 5\}$$ and $$F = \{2, 3\}$$, find $$P(E| F)$$.
$$10\%$$ of the tools produced by a machine are defective. Find the probability distribution of the number of defective tools when $$3$$ tools are drawn one by one with replacement.
$$20\%$$ of the bulbs produced by a machine are defective. Find the probability distribution of the number of defective bulbs when $$4$$ bulbs are drawn one by one with replacement.
The probability that a bulb produced by a factory will fuse after 160 days of use is 0.Find the probability that out of 5 such bulbs, at the most one bulb will fuse after 160 days of use.
In a certain college, 65% of the students are fully time students 55% of the students are female, 35% of the students are male full times students, Find the probability that
i) a student chosen at random from all the students in the college is a part time student
ii) a student chosen at random from all the students in the college is female and a part time student
iii) a student chosen at random from all the female students in the college is a part time.
Find P(AUB) when 2P(A)=P(B)=$$ \frac { 5 }{ 13 } $$and P(A|B)=$$ \frac { 2 }{ 5 } $$.
There are two bags 1 and 2, containing $$3$$ red and $$4$$ white balls and $$2$$ red and $$3$$ white balls respectively. A bag is selected at random and a ball is drawn from it. If it is found to be a red ball, Find the probability that it is drawn from the first bag.
A family has two children. What is the probability that both the children are boys given that of them is a boy.
If $$P(A)=\dfrac{1}{4}, P(B)=\dfrac{1}{5}$$ and $$P(A\cap B)=\dfrac{1}{7}$$, find $$P(\overline{A}/\overline{B})$$.
A person goes to work by car, train or bus. The probabilities of person travelling by there modes are $$3/10,1/2$$ and $$1/5$$ respectively. It is found that chance of person being late for work are $$3/7,1/7$$ and $$5/7$$ by respective modes. Given that on particular day person reaches late, find the probability that on that day he had travelled by train.
Two cards are drawn from a well shuffled pack of $$52$$ acrds. Find the probability that one of them is a red card & the other is a queen.
Three bags contain $$2$$ silver, $$5$$ copper coins, and $$3$$ silver, $$4$$ copper coins and $$5$$ silver, $$2$$ copper coins respectively. A bag is chosen at random and a coin is drawn from it which happens to be silver. What is the probability that it has come from third bag?
What is the probability that the total of two dice will be greater than 9, given that the first die is a 5 ?
Assume that a factory has two machines $$A$$ and $$B$$. Past records shows that machine $$A$$ produces 60% of the items of output and machine $$B$$ produces 40% of the items. Further, 2% of the items produced by machine $$A$$ were defective and only 1% produced by machine $$B$$ were defective. If a detective item is drawn at random, what is the probability that it was produced by machine $$A$$?
A factory has three machines A,B and C, which produce $$100,200\ and\ 300 \ $$items of a particular type daily. The machines produce $$2\%, 3\%\ and \ 5\% $$ defective items respectively. One day when the production was over, an item was picked up randomly and it was found to be defective. Find the probability that it was produced by machine A.
In a bolt factory, three machines A,B, and C manufacture 25,35 and 40 percent of the total bolts respectively. Out of the total bolts manufactured by the machines 5,4 and 2 percent are defective from machine A, B & C respectively. A bolt is drawn at random and is found to be defective. Find the probability that it was manufactured by (i) Machine A or C (ii) Machine B.
There are 4 boys and 2 girls in Room no. 1 and 5 boys and 3 girls in room no 2 Find the probability that a girl from one of the two rooms laughed loudly was from Room no. 2?
State which of the following variables are continuous and which are discrete :
a)number of children in your class
b) distance traveled by a car
c) sizes of shoes
d) time
e) number of patients in a hospital
Obtain the probability distribution of the number of sixes in two tosses of a fair die .
Amit and Nisha apear for an interview for two vacancies in a company. The probability of amit's selection is $$1/5$$ and that Nisha's selection is $$1/6.$$ What is the probability that both of then selected?
In a certain university , the percentage of a Hindus, Muslim and Christians among student are 50, and 25 and 25 respectively. if 50% of Hindus, 90% of Muslim and 80% of Christians are smokers, Find the probability that a randomly selected smoker student in Muslim.
If the chance that any of $$5$$ telephone lines is busy at any instance is $$0.01$$. What is the probability that all the lines are busy? What is the probability that more than $$3$$ lines are busy?
A lot of 20 bulbs contain 4 defective ones. One bulb is selected at random from the lot. What is the probability that this bulb is defective? Suppose the bulb selected in the previous case is not defective and is not replaced. Now one bulb is selected at random from the rest. What is the probability that this bulb is not defective?
Find the probability success when a die is thrown , where a success is defined as
(i) number greater than $$4$$ (ii) six appears on the die
Three unbaised coins are tossed find the probability distribution of the number of heads occurring on the topmost faces.
A card from a pack 52 cards is lost. From the remaining card of the pack, one card is drawn and is found be heart, Find the probability that the lost cards were both hearts.
An integer is chosen at random from the first 200 numbers.What is the probability that the integer chosen is divisible by 6 or 8.
A card from a pack of 52 cards is lost. from the remaining cards of pack, two cards are drawn and are found to be both diamonds. Find the probability of the lost card being a diamond.
In a school, there are $$1000$$ student, out of which $$430$$ are girls. It is known that out of $$ 430, 10$$% of the girls study in class $$XII$$. What is the probability that a student chosen randomly studies in class $$XII$$ given that the chosen student is a girl?.
In a shop X, $$30$$ tin pure ghee and $$40$$ tin adultered ghee are kept for sale while in shop Y, $$50$$ tin pure ghee and $$60$$ tin adultered ghee are there. One tin of ghee is purchased from one of the shops randomly and it is found to be adultered. Find the probability that it is purchased from shop B.
A bag contains $$3$$ red and $$7$$ black balls. Two balls are drawn one by one at a time at random without replacement. If second drawn ball is red then what is the probability the first drawn ball is also red?
From three men and two women, environment committee of two person to be formed.
Condition for event $$A :$$ There must be at least one woman member.
Condition for event $$B :$$ One man, one woman committee to be formed.
Condition for event $$C :$$ There should not be a woman member.
A dice is manufactured in such a way that probability of getting an even number is twice likely to occur as an odd number. If the dice is tossed twice, find the probability distribution of the random variable representing the perfect square in the both tosses.
If dice is tossed twice, Then, probability of perfect square on both tossed are
Let X be denote the perfect square number
$$(1,1),(4,4)$$
$$P\left( {1,1} \right) = \frac{1}{{36}},P\left( {4,4} \right) = \frac{1}{{36}}$$
Probability distribution
Find the probability distribution of number of doublets in three throws of a pair of dice.
Let X denotes the number of doublets. X can take the value 0,1,2 or 3.
Possible doublets are (1,1), (2,2), (3,3), (4,4), (5,5) and (6,6)
Probability of getting a doublet $$=\dfrac{6}{36}=\dfrac{1}{6}$$
Probability of not getting a doublet $$=1-\dfrac{1}{6}=\dfrac{5}{6}$$
Now,
$$P(X=0)=P(No\ doublet)$$
$$=\dfrac{5}{6}\times\dfrac{5}{6}\times\dfrac{5}{6}$$
$$=\dfrac{125}{216}$$
$$P(X=1)=P(One\ doublet\ and\ two\ non-doublet)$$
$$=\dfrac{1}{6}\times\dfrac{5}{6}\times\dfrac{5}{6}+\dfrac{5}{6}\times\dfrac{1}{6}\times\dfrac{5}{6}+\dfrac{5}{6}\times\dfrac{5}{6}\times\dfrac{1}{6}$$
$$=\dfrac{25}{216}+\dfrac{25}{216}+\dfrac{25}{216}$$
$$=\dfrac{75}{216}$$
$$P(X=2)=P(Two\ doublet\ and\ one\ non-doublet)$$
$$=\dfrac{1}{6}\times\dfrac{1}{6}\times\dfrac{5}{6}+\dfrac{1}{6}\times\dfrac{5}{6}\times\dfrac{1}{6}+\dfrac{5}{6}\times\dfrac{1}{6}\times\dfrac{1}{6}$$
$$=\dfrac{5}{216}+\dfrac{5}{216}+\dfrac{5}{216}$$
$$=\dfrac{15}{216}$$
$$P(X=3)=P(Three\ doublets)$$
$$=\dfrac{1}{6}\times\dfrac{1}{6}\times\dfrac{1}{6}$$
$$=\dfrac{1}{216}$$
$$\therefore$$ The required probabilities are shown in the figure.
A box contains $$150$$ oranges. If one orange. If one orange is taken out from the box at random the probabilty of its being rotten is $$0.06$$, then find the number of good oranges in the box.
Bag A contains 3 red and 2 white balls, and Bag B contains 2 red and 5 white balls. A bag selected at random, a ball is drawn and put into the other bag; then a ball is drawn from the second bag. Find the probability that both balls drawn are of the same colour.
Evaluate $$P\left( {A \cup B} \right),$$ if $$2P\left( A \right) = P\left( B \right) = \dfrac{5}{{13}}$$ and $$P\left( {A|B} \right) = \dfrac{2}{5}$$
Find the probability that in a year of $$22$$nd century chosen at a random, there will be $$53$$ sundays.
A company has two plants to manufacture televisions. The plant I manufacture $$70$$% of televisions and plant II manufacture $$30$$%. At plant I, $$80$$% of the televisions are rated as of standard quality and at plant II, $$90$$% of the televisions are rated as of standard quality. A television is chosen at random and is found to be of standard quality. The probability that it has come from plant II is
The probabilities of x, y and z becoming manager are$$\frac { 4 }{ 9 } ,\frac { 2 }{ 9 } \& \frac { 1 }{ 3 } $$ respectively. The probabilities that the bonus scheme will be introduced if x,y and z become managers are$$\frac { 3 }{ 10 } ,\frac { 1 }{ 2 } \& \frac { 2 }{ 5 } $$ respectively. Find (i) What is the probatility that the bonus scheme will be introduced? (ii) if the bonus scheme has teen introduced, What is the probability that the manager appointed wax x?
In a simultaneous throw of a pair of dice, if the probability of getting neither $$9$$ nor $$11$$ as the sum of the numbers on the faces is $$\dfrac{5}{a}.$$ Find $$a.$$
In a simultaneous throw of a pair of dice, if the probability of getting odd number on the first and $$6$$ on the second is $$\dfrac{1}{a}.$$ Find $$a.$$
In a simultaneous throw of a pair of dice, if the probability of getting a sum less then $$6$$ is $$\dfrac{5}{a}.$$ Find $$a.$$
In a simultaneous throw of a pair of dice, if the probability of getting a sum less than $$7$$ is $$\dfrac{a}{b}.$$ Find $$a+b.$$
In a simultaneous throw of a pair of dice, if the probability of getting a number greater than $$4$$ on each die is $$\dfrac{1}{a}.$$ Find $$a.$$
Cards marked with number $$2$$ to $$101$$ are placed in a box and mixed thoroughly. One card is drawn from this box. Find the probability that the number of the card is an even number.
$$3000$$ families with $$2$$ children each were selected randomly and the following date are recorded.
| No of girls | $$2$$ | $$1$$ | $$0$$ |
| No of familis | $$950$$ | $$1628$$ | $$422$$ |
Find the value of P for the following distribution whose mean is 10
| $$x_1$$ | 5 | 7 | 9 | 11 | 13 | 15 | 20 |
| $$f_i$$ | 4 | 4 | p | 7 | 3 | 2 | 1 |
$$x_if_i=20, 28, 9p, 77, 39, 30, 20$$
Mean$$=\dfrac{\sum x_if_i}{\sum f_i}=\dfrac{214+9p}{p+21}=10$$
$$\Rightarrow 9p+214=10p+210$$
$$\Rightarrow p=4$$.
A card is picked up from a deck of $$52$$ plying cards.
What is the even that the chosen card id black faces card?
Ten pairs of shoes are in a closet. Four shoes are selected at random. The probability that there will be at least one pair among the four shoes selected is
In a simultaneous throw of a pair of dice, if the probability of getting a total of $$9$$ or $$11$$ is $$\dfrac{1}{x}.$$ Find $$x.$$
Find the number of triangles whose vertices are at the vertices of an octagon but none of whose sides happen to come from the octagon .
A die is thrown twice and the sum of the numbers appearing is observed to beWhat is the conditional probability that the number 4 has appeared at least once?
Enter 1 if true else enter 0.In a simultaneous throw of a pair of dice, the probability of getting a total greater than $$8$$ is $$\dfrac {5}{18}$$
In a single throw of three dice, if the probability of getting a total of $$17$$ or $$18$$ is $$\dfrac{1}{a}$$. Find $$a.$$
A die is thrown three times, find the probability that $$4$$ appears on the third toss if it is given that $$6$$ and $$5$$ appear respectively on first two tosses.
How many coins are to be tossed at once to get $$64$$ outcomes in total?
If $$A$$ and $$B$$ are two events, such that $$P(A) = 0.4, P(B) = 0.8$$, and $$P(B/A) = 0.6 $$, then find $$P(A/B)$$.
Coin tossed 6 times ,find the probability it shows heads.
i) Exact 5 times. ii) Head in 1st four and tail in rest.
Let $$X$$ denote the number of hours you study during a randomly selected school day. The probability that $$X$$ can take the values of $$x$$, has the following form, where $$k$$ is some constant
$$P(X=x)=\begin{matrix} \begin{cases} 0,1 & \text{if }x=0 \\ Kx & \text{if }x=1 \text{ or } 2 \\ K(5-x) & \text{if } x = 3 \text{ or } 4 \\ 0 & \text{otherwise} \end{cases} \end{matrix}$$
What is the probability that you study.
For at least two hour.
Find the number of ways in which 5 boys and 5 girls be seated in a row so that no two girls may sit together.
Verify that the following function can be regarded as p.d.f for the random variable $$X$$
| $$x$$ | $$-1$$ | $$0$$ | $$1$$ |
| $$P(x)$$ | $$-0.2$$ | $$1$$ | $$0.2$$ |
Three machines $$E_{1}$$. $$ E_{2}, E_{3} $$ in a certain factory produce 50$$ \% $$ . 25$$ \% $$ and 25$$ \% $$ respectively of the total daily output of electric tubes. It is known that 4$$ \% $$ of the tube produced on each of machines $$E_{1}$$. and $$E_{2},$$are defective and that 5$$ \% $$ those produced on $$ E_{3} $$ are defective. If one is picked up at random from a day production, calculate the probability that it is defective.
Find the number of numbers of $$5$$ digits that can be formed with the digits $$0, 1, 2, 3, 4$$ if the digits can be repeated in the same number.
A die is rolled. If the outcome is an odd number, what is the probability that it is prime?
How many numbers of $$3$$ digits can be formed with the digits $$1, 2, 3, 4, 5$$ when digits may be repeated?
In a class of $$10$$ students there are $$3$$ girls $$A, B, C$$. In how many different ways can they be arranged in a row such that no two of the three girls are consecutive.
Find the number of ways in which $$5$$ boys and $$5$$ girls be seated in a row so that all the girls sit together and all the boys sit together.
In an examination hall there are four rows of chairs. Each row has $$8$$ chairs one behind the other. There are two classes sitting for the examination with $$16$$ students in each class. It is desired that in each row, all students belong to the same class and that no two adjacent rows are allotted to the same class. In how many ways can these $$32$$ students be seated?
A factory has two machines A and B. past records shows that machine A produced 60% of the items of output and machine B produced 40% of the items. Further, 2% of the items produced by machine A and 1% produced by machine B were defective. All the items are put into one stockpile and then one item is chosen at random from this and is found to be defective. What is the probability that it was produced by machine B?
Three urns have the following composition of balls:
Urn I : $$1$$ white, $$2$$ black
Urn II : $$2$$ white, $$1$$ black
Urn III : $$2$$ white, $$2$$ black
One of the urns is selected at random and a ball is drawn. It turns out to be white. Find the probability that it came from urn III.
How many even numbers are there with three digits such that if $$5$$ is one of the digits, then $$7$$ is the next digit?
A card is drawn from a pack of 52 cards. The card is drawn at random; find the probability that it is neither club nor queen?
How many different signals can be made by $$5$$ flags from $$8$$ flags of different colours?
How many times must a man toss a fair coin so that the probability of having at least one head is more than 90% ?
If $$x$$ is a random variable with probability distribution $$p\left(x = k\right) = \dfrac{\left(k + 1\right)C}{2^k}, k = 0,1,2,3,............$$, then find $$C.$$
A lot consists of $$144$$ ball pens of which $$20$$ are defective and the others are good. Nuri will buy a pen if it is good, but will not buy if it is defective. The shopkeeper draws one pen at random and gives it to her. What is the probability that
She will not buy it ?
How many numbers between $$400$$ and $$1000$$ can be formed with the digits $$0, 2, 3, 4, 5, 6,$$ if no digit is repeated in the same number?
Five defective bulbs are accidently mixed with 20 good ones. It is not possible to just look at a bulb and tell whether or not it is defective. Find the probability distribution from this lot.
Two cards are drawn (without replacement) from a well-shuffled deck of $$52$$ cards. Find the probability distribution table and mean.
Compute $$P ( A | B ) ,$$ if $$P ( B ) = 0.5$$ and $$P ( A \cap B ) = 0.32$$.
A $$4-$$ digit number is formed by the digits $$0, 1, 2, 5$$ and $$8$$ without repetition. Find the probability that the number is divisible by $$5$$.
Two persons $$A$$ and $$B$$ appear in an interview. The probability of $$A$$'s selection is $$\dfrac{1}{5}$$ and the probability of $$B$$'s selection is $$\dfrac{2}{7}$$. What is the probability that only one of them is selected?
If $$P{\left( A \right)} = \cfrac{7}{13}$$, $$P{\left( B \right)} = \cfrac{9}{13}$$ ,$$P{\left( A \cup B \right)} = \cfrac{12}{13}$$, then find (A|B).
If the height of $$300$$ students are normally distributed with mean $$64.5$$ inches and standard deviation $$3.3$$ inches,find the height below which $$99\%$$ of the student lie.
Let X denote the number of hours you study during a randomly selected school day. The probability that X can take the value 'x' has the following from, where 'k' is some unknown constant.
p = (X=x) = $$\begin{cases} 0.1,\quad \quad \quad \quad \quad \quad if\quad x=0 \\ kx,\quad \quad \quad \quad \quad \quad \quad if\quad x=1\quad or\quad 2\quad \\ k(5-x),\quad \quad \quad \quad if\quad x=3\quad or\quad 4 \\ 0,\quad \quad \quad \quad \quad \quad \quad \quad otherwise \end{cases}$$
(a) find the value of 'k'
(b) what is the probability that you study :
(i) at least two hours?
(ii) exactly two hours?
(iii) at most 2 hours?
Bag $$I$$ contains $$2$$ blacks and $$8$$ red balls, bag $$II $$contains $$7$$ black and $$3$$ red balls and bag $$III$$ contains $$5$$ black and $$5v$$ red balls. One bage is chosen at random and a ball is drawn from it which is found to bered. Find the probability that the ball is drawn from bag $$II$$
There are two boxes $$I$$ and $$II$$. Box $$I$$ contains $$3$$ red and $$6$$ black balls. Box $$II$$ contains $$5$$ red and 'n' black balls. One of the two boxes, box $$I$$ and box $$II$$ is selected at random and a ball is drawn at random. The ball drawn is found to be red. If the probability that this red ball comes out from box $$II$$ is $$\dfrac{3}{5}$$, find the value of 'n'.
Mother, father and son line up at random for a family photo. If $$A$$ and $$B$$ are two events given by $$A$$ = Son on one end, $$B$$ = Father in the middle, find $$P(A/B)$$ and $$P(B/A)$$.
A black and a red dice are rolled.
a) find the conditional probability of obtaining a sum greater then 9, given that the black die resulted in a 5.
Let $$X$$ be a random variable which assumes values $$x_1, x_2, x_3, x_4$$ such that $$2P(X = x_1) = 3P(X = x_2) = P(X = x_3) = 5P(X = x_4)$$.
Find the probability distribution of $$X$$.
In a factory there are three types of Machines $${M}_{1}$$ , $${M}_{2}$$ and $${M}_{3}$$ which produces $$25\%, 35\%$$ and $$40\%$$ of the total products respectively. $${M}_{1}$$ , $${M}_{2}$$ and $${M}_{3}$$ produces $$5\% , 4\%$$ and $$2\%$$ defective products, respectively. A bolt is drawn at random from the product and is found to be defective.What is the probability of that it is manufactured by machine $${M}_{2}$$?
----------
Two dice are thrown. Find the probability that the numbers appeared has the $$8$$, if it is known that the second die always exhibits $$4$$.
The probability distribution function of a random variable $$X$$ is given by
| $$x_{i}$$: | 0 | 1 | 2 |
| $$p_{i}$$: | $$3c^{}$$ | $$4c$$ | $$c-1$$ |
A random variable $$X$$ has the following probability distribution :
| Values of X: | -2 | -1 | 0 | 1 | 2 | 3 |
| P(X): | 0.1 | k | 0.2 | 2k | 0.3 | k |
Let $$X$$ be a random variable which assumes values $$x_{1},x_{2},x_{3},x_{4}$$ such that $$2P(X=x_{1})=3P(X=x_{2})=P(X=x_{3})=5P(X=x_{4})$$. Find the probability distribution of $$X$$.
A card is thrown from a pack of $$52$$ cards so that each card equally likely to be selected. Then find whether the events $$A$$ and $$B$$ independent?
$$A=$$the card drawn is spade, $$B=$$the card drawn in an ace.
$$A=$$the card drawn is spade, $$B=$$the card drawn in an ace.
Arun and Tarun appeared for an interview for two vacancies. The probability of Arun's selection is $$\dfrac{1}{4}$$ and that of Tarun's rejection is $$\dfrac23$$. Find the probability that at least one of them will be selected.
A random variable $$X$$ has the following probability distribution :
Values of X: 0 1 2 3 4 5 6 7 8 P(X): a 3a 5a 7a 9a 11a 13a 15a 17a
Determine the value of $$k$$, if $$a=\dfrac1k$$.
| Values of X: | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| P(X): | a | 3a | 5a | 7a | 9a | 11a | 13a | 15a | 17a |
The probability distribution function of a random variable $$X$$ is given by
| $$x_{i}$$: | 0 | 1 | 2 |
| $$p_{i}$$: | $$c/2$$ | $$c$$ | $$2c$$ |
Two cards are drawn simultaneously from a well-shuffled deck of 52 cards. Find the probability distribution of the number of successes, when getting a spade is considered a success.
An urn contains 4 red and 3 blue balls. Find the probability distribution of the number of blue balls in a random draw of 3 balls with replacement.
Five defective mangoes are accidently mixed with 15 good ones. Four mangoes are drawn at random from this lot. Find the probability distribution of the number of defective mangoes.
Find the probability distribution of the number of white balls drawn in a random draw of 3 balls without replacement, from a bag containing 4 white and 6 red balls.
A bag contains 2 white, 3 red and 4 blue balls. Two balls are drawn at random from the bag. If X denotes the number of white balls among the two balls drawn, describe the probability distribution of X.
Two cards are drawn successively with replacement from a well shuffled pack of 52 cards. Find the probability distribution of the number of kings.
The probability distribution of a random variable X is given below:
| X: | 0 | 1 | 2 | 3 |
| P(X): | k | $$\dfrac{k}{2}$$ | $$\dfrac{k}{4}$$ | $$\dfrac{k}{8}$$ |
Two balls are drawn at random with replacement from a box containing $$10$$ black and $$8$$ red balls. Find the probability that both the balls are red.
From a lot of 10 bulbs, which includes 3 detectives, a sample of 2 bulbs is drawn at random. Find the probability distribution of the number of defective bulbs.
Five defective bolts are accidentally mixed with twenty good ones. If four bolts are drawn at random from this lot, find the probability distribution of the number of defective bolts.
The probability distribution of a random variable X is given below:
| X: | 0 | 1 | 2 | 3 |
| P(X): | k | $$\dfrac{k}{2}$$ | $$\dfrac{k}{4}$$ | $$\dfrac{k}{8}$$ |
A fair coin is tossed four times. Let X denote the longest string of heads occurring. Find the probability distribution, mean and variance of X.
The probability distribution of a random variable X is given below:
| X: | 0 | 1 | 2 | 3 |
| P(X): | k | $$\dfrac{k}{2}$$ | $$\dfrac{k}{4}$$ | $$\dfrac{k}{8}$$ |
A box contains 13 bulbs, out of which 5 are defective. 3 bulbs are randomly drawn, one by one without replacement, from the box. Find the probability distribution of the number of defective bulbs.
A card is thrown from a pack of $$52$$ cards so that each cards equally likely to be selected. Determine whether in the following case are the events $$A$$ and $$B$$ independent.$$A=$$the card is drawn is a spade, $$B=$$the card is drawn in an ace.
$$A=$$the card is drawn is a spade, $$B=$$the card is drawn in an ace.
In a factory machine $$A$$ produce $$30\%$$ of the total output, machine $$B$$ produced $$25\%$$ and the machine $$C$$ produced the remaining output. If defective items produced by machine $$A, B$$ and $$C$$ are $$1\% ,\ 1.2\% ,\ 2\%$$ respectively. Three machine working together produced $$10000$$ item in a day. An item is drawn at random from a day's output and found to be defective.Find the probability that it was produced by machine $$B$$?
A discrete random variable X has the probability distribution given below:
| X: | 0.5 | 1 | 1.5 | 2 |
| P(X): | k | $$2k^{}$$ | $$3k^{}$$ | k |
A discrete random variable X has the probability distribution given below:
| X: | 0.5 | 1 | 1.5 | 2 |
| P(X): | k | $$k^{}$$ | $$2k^{}$$ | k |
Three cards are drawn at random (without replacement) from a well shuffled pack of 52 cards. Find the probability distribution of number of red cards. Hence find the mean of the distribution.
In a factory machine $$A$$ produce $$30\%$$ of the total output, machine $$B$$ produced $$25\%$$ and the machine $$C$$ produced the remaining output. If defective items produced by machine $$A, B$$ and $$C$$ are $$1\% ,\ 12\% ,\ 2\%$$ respectively. Three machine working together produced $$10000$$ item in a day. An item is drawn at random from a day's output and found to be defective. Find the probability that it was produced by machine $$B$$.
Two coins are tossed simultaneously 500 times with the following frequencies of different outcomes:
Two heads: 95 times
One tail: 290 times
No head: 115 times
Find the probability of occurrence of each of these events.
A die is thrown. Find the probability of getting:
a prime number
If $$A$$ and $$B$$ are two event such that
$$P(A)=\dfrac {6}{11},\ P(B)=\dfrac {5}{11}$$ and $$P(A\cup B)=\dfrac {7}{11}$$, find $$P(A\cap B), \ P(A/B),\ P(B/A)$$.
Three coins are tossed simultaneously 100 times with the following frequencies of different outcomes:
| Outcome: | No head | One head | Two heads | Three heads |
| Frequency | 14 | 38 | 36 | 12 |
Three coins are tossed simultaneously 100 times with the following frequencies of different outcomes:
| Outcome: | No head | One head | Two heads | Three heads |
| Frequency | 14 | 38 | 36 | 12 |
Three coins are tossed together. Find the probability of getting :
at least one head and one tail
A coin is tossed 1000 times with the following frequencies:
Head: 455, Tail: 545
Compute the probability for each event.
Enter 1 if true else enter 0.Three coins are tossed together. The probability of getting at least two heads is $$\dfrac{1}{2}$$
Enter 1 if true else enter 0.
Enter 1 if it is true else enter 0Three coins are tossed together. The probability of getting no tails is $$\dfrac{1}{8}$$.
A bag contains $$3$$ white and $$2$$ black balls and another bag contains $$2$$ white and $$4$$ black balls. One bag is chosen at random. From the selected bag, one ball is drawn. Find the probability that the ball drawn is white.
If a number $$x$$ is chosen at random from the numbers $$-3,-2,-1,0,1,2,3$$. What is probability that $$x^2\le 4$$?
A bag contains $$5$$ red balls and some blue balls. If the probability of drawing a blue ball at random from the bag is three times that of a red ball, find the number of blue balls in the bag.
Find the probability that 5 Sundays occurs in the month of November of a randomly selected year.
Enter 1 if it is true else enter 0.A bag contains $$3$$ red balls, $$5$$ black balls and $$4$$ white balls. A ball is drawn at random from the bag. The probability that the ball drawn is red is $$\dfrac{1}{4}$$.
Enter 1 if it is true else enter 0.
20% of the bulbs produced by a machine are defective.find the probability distribution of the numbers of defective bulbs in sample of 4 bulbs chosen at random.
In a shop $$X$$, 30 tins of ghee of Type A and 40 tins of ghee of Type B which look alike, are kept for sale while in shop $$Y$$, similar 50 tins of ghee of Type A and 60 tins of ghee of Type B are there. One tin of ghee is purchased from one of the randomly selected shops and is found to be of Type B. Find the probability that it is purchased from shop $$Y$$.
$$E_1 =$$ event of selecting shop $$X$$
$$E_2 = $$ event of selecting shop $$Y$$
$$E = $$ event of selecting type $$B$$ ghee
$$E_2 = $$ event of selecting shop $$Y$$
$$E = $$ event of selecting type $$B$$ ghee
Now,
$$P(E_1) = P(E_2) = \dfrac{1}{2}$$
$$P(E/E_1) = \dfrac{40}{70} = \dfrac{4}{7}$$ and $$P(E/E_2) = \dfrac{60}{110} = \dfrac{6}{11}$$
Now,
$$P(E_2/E) = \dfrac{P(E_2) . P(E/E_2)}{P(E_1) . P(E/E_1) + P(E_2) . P(E/E_2)}$$
$$P(E_2/E) = \dfrac{P(E_2) . P(E/E_2)}{P(E_1) . P(E/E_1) + P(E_2) . P(E/E_2)}$$
$$= \dfrac{\left(\dfrac{1}{2}\right) \times \left(\dfrac{6}{11}\right)}{\left(\dfrac{1}{2} \right) \left(\dfrac{4}{7} \right) + \left(\dfrac{1}{2} \right) \left(\dfrac{6}{11} \right)}$$
$$= \dfrac{42}{86} = \dfrac{21}{43}$$
A coin is tossed twice. If the outcome is at most one tail, what is the probability that both head and tail have appeared?
A dice is thrown twice and the sum of the numbers appearing is observed to be $$8$$. What is the conditional probability that the number $$5$$ has appeared at least once ?
There is a box containing $$30$$ bulbs of which $$5$$ are defective. If two bulbs are chosen at random from the box in succession without replacing the first, what is the probability that both the bulbs chosen are defective?
A coin is tossed 4 times. Let X denote the number of heads . Find the Probability distribution of X. also Find the mean and variance of X .
A machine operates only when all of its three components functions. The probability of the failures of the first, second and third components are $$0.14, 0.10$$ and $$0.05$$ respectively. What is the probability that the machine will fail?
A sample of $$3$$ bulbs is tested. A bulb is labelled as $$G$$ if it is good and $$D$$ if it is defective. Find the number of all possible outcomes.
A coin is tossed (m+n) times (m > n).Show that the probability of at least m consecutive heads is $$n+2/2^{m+1}$$
Assume that each born child is equally likely to be a boy or a girl . If a family has two children , what is the conditional probability that both are girls given that the youngest is a girl ?
For a biased die,the probability for the different face to turn up are given below:
This die is tossed and you are told that either face 1 or face 2 has turned up.Then the probability that it is face 1 is...................
In a village there are three mohallas A , B and C . In A , $$ 60 $$ % persons believe in honesty , while in B $$ 70 $$ % and in C , $$ 80 $$ % . A person is selected at random from village and found , he is honest . Find the probability that he belongs to mohalla B .
Assume that each born child is equally likely to be a boy or a girl . If a family has two children , what is the conditional probability that both are girls given that at least one is a girl ?
A person wants to construct a hospital in a village for welfare. The probabilities are $$ 0.40 $$ that some bad elements opposite this work , $$ 0.80 $$ that the hospital will be completed if there is not any oppose of any bad elements and $$ 0.30 $$ that the hospital will be completed if bad elements oppose. Determine the probability that the construction of hospital will be completed .
In a survey it was found that $$30\%$$ of the population is using non-biodegradable products while the remaining is using biodegradable products. What is the probability that a person at random uses non biodegradable products?
Which type of products should be used in a society for its proper development biodegradable o non-biodegradable? Justify your answer?
A number $$x$$ is selected at random from the numbers $$1,2,3$$ and $$4$$. Another number $$y$$ is selected at random from the numbers $$1,4,9$$ and $$16$$. Find the probability that product of $$x$$ and $$y$$ is less than $$16$$.
Two dice are thrown together and the total score is noted. The events $$ E, F $$ and $$ G $$are 'a total of 4 ', 'a total of 9 or more', and 'a total divisible by 5 ', respectively. Calculate $$ P(E), P(F) $$ and $$ P(G) $$ and decide which pairs of events, if any, are independent.
A factory produces bulbs. The probability that any one bulb is defective is $$ \dfrac{1}{50} $$ and they are packed in boxes of $$ 10 . $$ From a single box, find the probability that
(i) none of the bulbs is defective
For a loaded die, the probabilities of outcomes are given as under:
$$ P(1)=P(2)=0.2, P(3)=P(5)=P(6)=0.1 $$ and $$ P(4)=0.3 $$
If the die were fair, determine whether or not the events A and B are independent.
The probability distribution of a random variable X is given below:
$$\begin{array}{|l|l|l|l|l|}\hline \mathrm{X} & 0 & 1 & 2 & 3 \\\hline \mathrm{P}(\mathrm{X}) & k & \dfrac{k}{2} & \dfrac{k}{4} & \dfrac{k}{8} \\\hline\end{array}$$
(ii) Determine $$ P(X \leq 2) $$ and $$ P(X>2) $$
A factory produces bulbs. The probability that any one bulb is defective is $$ \dfrac{1}{50} $$ and they are packed in boxes of $$ 10 . $$ From a single box, find the probability that
(ii) exactly two bulbs are defective
A discrete random variable X has the probability distribution given as below:
$$\begin{array}{|l|ll|l|l|}\hline \mathrm{X} &0.5 & 1 & 1.5 & 2 \\\hline \mathrm{P(X)}& k & k^2 & 2k^2 & k \\\hline\end{array}$$
(i) Find the value of k
A factory produces bulbs. The probability that any one bulb is defective is $$ \dfrac{1}{50} $$ and they are packed in boxes of $$ 10 . $$ From a single box, find the probability that
(iii) more than 8 bulbs work properly
Out of $$400$$ bulbs in a box, $$15$$ bulbs are defective. One bulb is taken out at random from the box. Find the probability that the drawn bulb is not defective.
For the following probability distribution determine standard deviation of the random variable X.
$$\begin{array}{|l|l|l|l|}\hline \mathrm{X} & 2 & 3 & 4 \\\hline \mathrm{P}(\mathrm{X}) & 0.2 & 0.5 & 0.3 \\\hline\end{array}$$
Two biased dice are thrown together. For the first die $$ P(6)=\dfrac{1}{2}, $$ the other scores being equally likely while for the second die, $$ P(1)=\dfrac{2}{5} $$ and the other scores are equally likely. Find the probability distribution of 'the number of one seen'.
Two dice are tossed. Find whether the following two events A and B areindependent:$$ A=\{(x, y): x+y=11\} $$ and $$ B=\{(x, y): x \neq 5\}, $$ Where $$ (x, y) $$ denotes a typical sample point.
An item is manufactured by three machines A, B and C. Out of the total number of items manufactured during a specified period, 50% are manufactured on A, 30% on B and 20% on C. 2% of the items produced on A and 2% of items produced on B are defective, and 3% of these produced on C are defective. All the items are stored at one godown. One item is drawn at random and is found to be defective. What is the probability that it was manufactured on machine A?
Two natural numbers $$ \mathbf{r}, $$ s are drawn one at a time, without replacement from the set $$ S=\{1,2,3, \ldots, n\} $$. Find $$ \mathrm{P}[\mathrm{r} \leq \mathrm{p} \mid \mathrm{s} \leq \mathrm{p}] $$, where $$ p \in S $$
The probability distribution of a random variable x is given as under:
$$P(X = x) = {\begin{matrix}kx^{2} & for \space x = 1, 2, 3 \\ 2kx & for \space x = 4, 5, 6\\ 0 & otherwise \end{matrix}}$$
Where k is a constant. Calculate
(i) E(X)
(ii) $$E(3X^{2})$$
(iii) $$P(X \geq 4)$$
We know that, $$\sum P_i = 1$$
$$\Rightarrow 44k = 1 \Rightarrow k = \frac{1} {44}$$
$$\therefore \sum XP(X) = k + 8k + 27k + 32k + 50k + 72k + 0$$
$$190k = 190 \times \frac{1} {44} = \frac{95} {22}$$
(i) So, $$E(X) = \sum XP(X) = \frac{95} {22} = 4.32$$
(ii) Also, $$ E(X^{2}) = \sum X^{2}P(X) = k + 16k + 81k + 128k + 250k + 432k $$
$$= 908k = 908 \times \frac{1} {44}$$ $$\left[ \therefore k = \frac{1} {44} \right]$$
$$= 20.636 = 20.64(approx)$$
$$ E(3X^{2}) = 3E (X^{2}) = 3 \times 20.64 = 61.92 = 61.9 $$
(iii) $$P(X \geq 4) = P(X = 4) + P(X = 5) + P(X = 6)$$
$$= 8k + 10k + 12k = 30k = 30k = 30 \cdot \frac {1} {44} = \frac {15} {22}$$
The probability distribution of a random variable X is given below:
$$\begin{array}{|l|l|l|l|l|}\hline \mathrm{X} & 0 & 1 & 2 & 3 \\\hline \mathrm{P}(\mathrm{X}) & k & \dfrac{k}{2} & \dfrac{k}{4} & \dfrac{k}{8} \\\hline\end{array}$$
(iii) Find $$ P(X \leq 2)+P(X>2) $$
Find the probability distribution of
(iii) number of heads in four tosses of a coin
There are $$5\%$$ defective items in a large of items. What is the probability that a sample of $$10$$ items will include not more than one defective item?
Find the probability distribution of
(ii) number of tails in the simultaneous tosses of three coins
Let A and B be two events. If P(A/B) = P(A), then A is _________ of B.
In a bundle of $$50$$ shirts, $$44$$ are good, $$4$$ have minor defects and $$2$$ have major defects. What is the probability that it is acceptable to a trader who accepts only a good shirt?
In a hockey team, there are 6 defenders, 4 offenders, and 1 goalie. Out of these, one player is to be selected randomly as a captain. Find the probability of the selection that -A defender will be selected.
In a bundle of $$50$$ shirts, $$44$$ are good, $$4$$ have minor defects and $$2$$ have major defects. What is the probability that it is acceptable to a trader who rejects only a shirt with major defects?
It is known that $$10\%$$ of certain articles manufactured are defective. What is the probability that in a random sample of $$12$$ such articles $$9$$ are defective?
(i) A lot of 20 bulbs contain 4 defective ones. One bulb is drawn at random from the lot. What is the probability that the bulb is defective?
(ii) Suppose the bulb drawn in (i) is not defective and is not replaced. Now one bulb is drawn at random from the rest. What is the probability that this bulb is not defective?
$$4$$ rotten oranges are mixed accidently with $$16$$ good oranges. Find the probability distribution of the number of rotten oranges in a draw of two oranges.
Find the probability distribution of the number of successes in two tosses of a die, where a success is defined as
i) number greater than $$4$$
A die is thrown twice and the sum of the numbers appearing is observed to be $$6$$. What is the conditional probability that the number $$4$$ has appeared at least once?
Consider the experiment of tossing a coin. If the coin shows head, toss it again but if it shows tail, then throw a die. Find the conditional probability of the event that 'the die shows a number greater that 4' given that 'there is at least one tail?
Find which of the following probability distribution is possible for a random variable:
(i)
| $$X:$$ | 0 | 1 | 2 |
| $$P(X):$$ | $$0.4$$ | $$0.4$$ | $$0.2$$ |
| $$X:$$ | 0 | 1 | 2 |
| $$P(X):$$ | $$0.6$$ | $$0.1$$ | $$0.2$$ |
| $$X:$$ | 0 | 1 | 2 | 3 | 4 |
| $$P(X):$$ | $$0.1$$ | $$0.5$$ | $$0.2$$ | $$-0.1$$ | $$0.3$$ |
Find the probability distribution of the number of successes in two tosses of a die, where a success is defined as
ii) Six appears on at least one die
The probability of picking a non - defective items from a sample is $$ \dfrac{7}{12}. $$ Find the probability of picking a defective item.
A random variable $$X$$ can take al non-negative values and the probability that $$X$$ take the value $$r$$ is proportional to $$ar$$ where $$(0< a< 1)$$. Find $$P(X=0)$$
Let $$X$$ be random variable which assumes value $${x}_{1},{x}_{2},{x}_{3},{x}_{4}$$ such that
$$2P(X={x}_{1})=3P(X={x}_{2})=4P(X={x}_{3})=5P(X={x}_{4})$$
Find the probability distribution of $$X$$.
From a lot of $$10$$ items containing $$3$$ detectives, a sample of $$4$$ items is drawn at random. Let the random variable $$X$$ denote the number of defective items in the sample. If the sample is drawn randomly, find
(i) the probability distribution of $$X$$
(ii) $$P(x\le 1)$$
(iii) $$P(x< 1)$$
(iv) $$P(0< x< 2)$$
An urn contains $$4$$ white and $$3$$ red balls. Find the probability distribution of the number of red balls if $$3$$ balls are drawn at random.
Ten eggs are drawn successively, with replacement, from a lot containing $$10$$% defective eggs. Find the probability that there is at least one defective egg.
An equipment will work only when its three components A ,B and C are in working condition . Probability that A will not work is 0 . 15 and (M) 5 of B and 0 .10 to C .What is the probability that equipment will not be in working condition before year ending ?
There are 48 mobile phones in a group out of which 42 are good, 3 are some defective and other 3 are largely defected. Varnika will purchase the mobile phone only when it is good, but a businessman will buy the mobile phone only when there is defective largely. A phone is chosen at random from these. What is the probability that the chosen phone is:
(i) Accepted by Varnika
(ii) Accepted by businessman.
By chance 12 defected pens are mixed into 132 good pens. On seeing them it cannot be decided which pen is defected and which is good. If at random one pen is drawn out them, what is the probability that pen is good?
A die is manufactured in a such a way that an even number is twice likely to occur as an odd number. If the die is tossed twice, find the probability distribution of the random variable $$X$$ representing the perfect square in the two tosses.
20 ball pens are defective among a heap of 144 ball pens. You would like to buy a good pen not bad. The shopkeeper takes out a ball pen at random from these and gives you. What is the probability that:
(i) You will buy that ball pen.
(ii) You will not buy that ball pen.
(i) Among 20 bulbs, 4 bulbs are defective. A bulb is drawn at random from these. What is the probability that the bulb drawn will be defective?
(ii) Let the bulb drawn is neither defective not it is mixed with the remaining bulbs again. Now a bulb is taken out from these remaining bulbs. What is the probability of the bulb drawn is not defective?
To explain the computation of conditional probability of a given event $$B$$ when event $$A$$ has already occurred.
Fifteen coupons are numbered from 1 toSeven coupons are selected at random one at a time with replacement. The probability that the largest number appearing on a selected coupon is 9, is
Die $$A$$ has $$4$$ red and $$2$$ white faces whereas die $$B$$ has $$2$$ red and $$4$$ white faces. A coin is flipped once. If it shows a head, the game continues by throwing die $$A$$, if it shows tail, then die $$B$$ is to be used. If the probability that die $$A$$ is used is $$\displaystyle\frac{64}{66} $$ where it is given that red turns up every time in first n throws, then $$n$$ is
A lot contains $$20$$ articles. The probability that the lot contains exactly $$2$$ defective articles is $$0\cdot4$$ and that lot contains exactly $$3$$ defective articles is $$0\cdot6$$. Articles are drawn from the lot at random one by one without replacement and are tested till all defective articles are found. The probability that testing procedure ends at the twelfth testing is $$\cfrac {11k}{1900}$$. Find the value of $$k$$ ?
The probability that the total is $$6$$ is $$\cfrac{k}{108}$$.Find $$k$$ ?
A man takes a step forward with probability $$0.4$$ and backward with probability $$0.6$$. Let $$k$$ be the probability that at the end of eleven steps he is one step away from the starting point.Find the first digit after the decimal of $$k$$ ?
A lot contains $$20$$ articles. The probability that the lot contains exactly $$2$$ defective articles is $$0.4$$ and the probability that the lot contains exactly $$3$$ defective articles is $$0.6$$. Article are drawn from the lot at random one by one without replacement and are tested till all defective articles are found. What is the probability that the testing procedure ends at the twelfth testing?
A box contains $$2$$ fifty paise coins, $$5$$ twenty five paise coins and a certain fixed number $$n(\ge 2)$$ of ten and five paise coins. Five coins are taken out of the box at random.The probability that the total value of these five coins is less than Re.$$1$$ & $$50$$ paise is $$1-\left\{ \cfrac { 10(k+n) }{ { _{ }^{ n+7 }{ C } }_{ 5 } } \right\} $$.Find $$k$$?
Four small squares on a chess board are selected at random. the probability that they form a square of the size 2 X 2 is $$ \dfrac{a}{b} $$, where HCF of a and b is 1, then $$a+b=?$$
There is $$30$$% chance that it rains on any particular day. What is the probability that there is at least one rainy day within a period of $$7$$ days? Given that there is at least one rainy day, The probability that these are at least two rainy days is $$(1-{ \left( 0.7 \right) }^{ 7 });\cfrac { 1-k{ \left( 0.7 \right) }^{ 7 } }{ 1-{ \left( 0.7 \right) }^{ 7 } } $$. Find the value of $$k$$.
In a test an examinee either guesses or copies or knows the answer to a multiple choice question with 4 choices. The probability that he makes a guess is 1/3 & the probability that he copies the answer is 1/The probability that his answer is correct given that he copied it, is 1/Find the probability that he knew the answer to the question given that he correctly answered it.
If expressed in the form of $$a/b$$ (simplest form), $$b-a = ?$$
If two events $$A$$ and $$B$$ such that $$P({ A }^{ c })=0.3,P(B)=0.4$$ and $$P(A\cap { B }^{ c })=0.5$$, $$P[B/A\cup { B }^{ c })]=\frac{1}{k}$$,then value of k is
The probabilities of three events $$A,B$$ and $$C$$ are $$P(A)=0.6, P(B)=0.4$$ and $$P(C)=0.5$$. If $$P(A\cup B)=0.8, P(A\cap C)=0.3, P(A\cap B \cap C)=0.2$$ and $$P(A\cup B \cup C) \ge 0.85$$, $$0.04k \le P(B\cap C) \le 0.07k$$. Find the value of $$k$$.
An urn contairis 2 white and 2 black balls. A ball is drawn at random.If it is white, it is not replaced into the urn, otherwise it is replaced along with another ball of the same colour.The process is repeated.The probability that the third ball drawn is black is $$1-\displaystyle \frac{k}{30}$$. Find the value of $$k$$.
An urn contains five balls. Two balls are drawn and are found to be white. The probability that all the balls are white is $$\displaystyle \frac{1}{k}$$. Find the value of $$k$$.
It is known that an urn containing altogether 10 balls was filled in the following manner: A coin was tossed 10 times, and according as it showed heads or tails, one white or on black ball was put into the urn. Balls are drawn from this urn one at a time, 10 times in succession (with replacements) and every one turns out to be white. The chance that the urn contains nothing but white balls is $$\displaystyle \frac{1}{2^{k}}$$. Find the value of $$k$$.
A box contains $$100$$ tickets, numbered $$1, 2, ...., 100$$. Two tickets are chosen at random. It is given that the maximum number on the two chosen tickets is not more thanThe minimum number of them is $$2$$ with probability $$(15-k)/15$$. Find the value of $$k.$$
A bag $$A$$ contains $$2$$ white and $$3$$ red balls and a bag $$B$$ contains $$4$$ white and $$5$$ red balls. One ball is drawn at random from one of the bags and is found to be red. The probability that it was drawn from bag $$B$$ is $$\dfrac {25}X$$, then find the value of X.
A lot contains 20 articles. The probability that the lot contains exactly 2 defective articles is 0.4 and the probability that the lot contains exactly 3 defective articles is 0.Articles are drawn from the lot at random one by one without replacement and tested till all the defective articles are found. The probability that the testing procedure ends at the twelfth testing $$ \displaystyle \frac{100-k}{1900}$$. Find the value of $$k$$.
Let 0.8 the probability that a man aged 90 years will die in a year., If p is the probability that out of 4 men $$A_1, A_2, A_3$$ and $$A_4$$ each aged 90, $$A_1$$ will die in a year and will be the first to die, find 10000p
Two integers $$r$$ and $$s$$ are drawn one at a time without replacement from the set $$1, 2, .... n$$. If $$p_k=P(r\leq k\ |\ s\leq k)$$, find $$4p_7$$ if $$n=25$$
Two numbers are selected at random from the number $$1, 2, ..., n$$. Let $$p$$ denote the probability that the difference between the first and second is not less than $$m$$ (where $$0 < m < n$$). If $$n=25$$ and $$m=10$$, find $$5p$$
A certain drug, manufactured by a Company is tested chemically for its toxic nature. Let the event "THE DRUG IS TOXIC" be denoted by H & the event "THE CHEMICAL TEST REVEALS THAT THE DRUG IS TOXIC" be denoted by S. Let $$P(H) = a, P(S/H) = P (\overline S / H) = 1 - a$$. Then show that the probability that the drug is not toxic given that the chemical test reveals that it is toxic, is $$\displaystyle \frac{k_1}{k_2} $$ (HCF of k_1 and k_2 is 1) then find the value of $$k_1+k_2$$ for $$a=3$$, for
Consider the experiment of tossing a coin. If the coin shows head, toss it again, but if it shows tail, then throw a die. Find the conditional probability of the event that 'the die shows a number greater than 4' given that 'there is at least one tail'.
A man is known to speak the truth $$3$$ out of $$5$$ times. He throws a die and reports that it is $$ '6'$$. The probability that it is actually '$$6$$' is $$\dfrac{3}{k}$$. Find the value of $$k$$.
A prisoner escapes from a jail and is equally likely to choose one of the four roads I, II, III or IV to reach away from the hands of law. If he choose I road, he is successful with probability 1/6 and for II, III and IV this is 1/8, 1/10 and 1/If the prisoner is successful, the probability that he chose road
Match the follwoing
A random variable $$X$$ has the following probability distribution:
| $$X$$ | $$0$$ | $$1$$ | $$2$$ | $$3$$ | $$4$$ | $$5$$ | $$6$$ | $$7$$ |
| $$P(X)$$ | $$0$$ | $$k$$ | $$2k$$ | $$2k$$ | $$3k$$ | $$k^{2}$$ | $$2k^{2}$$ | $$7k^{2}+k$$ |
(i) $$k$$
(ii) $$P\left ( X< 3 \right )$$
(iii) $$P\left ( X>6 \right )$$
(iv) $$P\left ( 0< X< 3 \right )$$
A family has three children. Event $$A$$ is that family has at most one boy, Event $$'B'$$ is that family has at least one boy and one girl, Event $$'C'$$ is that the family has at most one girl. Find whether events $$'A'$$ and $$'B'$$ are independent. Also find whether $$A, B, C$$ are independent or not.
An urn contains $$5$$ red and $$5$$ black balls. A ball is drawn at random, its colour is noted and is returned to the urn. Moreover, $$2$$ additional balls of the colour drawn are put in the urn and then a ball is drawn at random. What is the probability that the second ball is red ?
One card is drawn at random from a well-shuffled deck of $$52$$ cards. In how many of the following cases are the events $$E$$ and $$F$$ independent?
(i) $$ E: $$ 'the card drawn is a spade'
$$ F: $$ 'the card is drawn is an ace'
(ii) $$ E: $$ 'the card drawn is black'
$$ F: $$ 'the card drawn is a king'
(iii) $$ E: $$ 'the card drawn is a king or queen'
$$ F: $$ 'the card drawn is a queen or jack'.
A random variable $$X$$ has the following probability distribution:
Determine
(i) $$k$$
(ii) $$P\left(X < 3\right)$$
(iii) $$P\left(X > 6\right)$$
(iv) $$P\left(0 < X < 3\right)$$
Suppose we have four boxes $$A, B, C$$ and $$D$$ containing colored marbles as given :
One of the boxes has been selected at random and a single marble is drawn from it. If the marble is red, what is the probability that it was drawn from box $$A$$, box $$B$$, box $$C$$ ?
Assume that the chances of a patient having a heart attack is 40%. It is also assumed that a meditation and yoga course reduce the risk of heart attack by 30% and prescription of certain drug reduces its chances by 25%. At a time a patient can choose any one of the two options with equal probabilities. It is given that after going through one of the two options the patient selected at random suffers a heart attack. Find the probability that the patient followed a course of meditation and yoga?
An urn contains $$3$$ white and $$6$$ red balls. Four balls are drawn one by one with replacement from the urn. Find the probability distribution of the number of red balls drawn. Also find mean and variance of the distribution
$$P\left( w \right) =\dfrac{3}{9}=\dfrac{1}{3}$$
$$P\left( R \right) =\dfrac{6}{9}=\dfrac{2}{3}$$
Probability distribution of number of red balls.
$$\Rightarrow$$ Mean $$=\sum { xP\left( x \right) } =nP$$ ( in case of binomial distribution )
$$\Rightarrow \mu =4\times \dfrac{2}{3}=\dfrac{8}{3}$$
Variance $$\left( { \sigma }^{ 2 } \right) =\sum x^2P\left(x\right) -\left[ \sum { xP\left( x \right) } \right] ^{ 2 }=npq$$ ( in case of binomial distribution )
$$=4\times \dfrac{1}{3}\times \dfrac{2}{3}$$
$$=\dfrac{8}{9}$$
Hence, the answer is $$\dfrac{8}{9}.$$
Of the students in a college, it is known that $$60$$% reside in hostel and $$40$$% are day scholars .Previous year results report that $$30$$% of all students who reside in hostel attain 'A' grade and $$20$$% of day scholars attain 'A' grade in their annual examination. At the end of the year, one student is chose at random from the college and he has an 'A' grade, what is the probability that the student is a hostlier?
Assume that the chances of a patient having a heart attack is 40%. Assuming that a meditation and yoga course reduces the risk of heart attack by 30% and prescription of certain drug reduces its chance by 25%. At a time a patient can choose any one of the two options with equal probabilities. It is given that after going through one of the two options, the patient selected at random suffers a heart attack. Find the probability that the patient followed a course of meditation
The given table categorises the house types and the number of bedrooms.
Development Houses 2 Br 3 Br 4 Br TotalSingle-Family 5 19 34 58Townhouse 24 42 30 96Total 29 61 64 154
A daycare centre is planning to distribute pamphlets to the families with children living houses with three or more bedrooms, due to budget. In addition to sending out flyers, it also decides to send out invitations for a free day of daycare, to the family residing in two categories with the most houses. If a house that already received a flyer is chosen at random to receive the second stage of the marketing, then the probability that the house belongs to one of these two groups is $$\dfrac pq$$, where $$p,q$$ are co-primes. What is the value of $$q-p$$?
A bag $$X$$ contains $$4$$ white balls and $$2$$ black balls, while another bag $$Y$$ contains $$3$$ white balls and $$3$$ black balls. Two balls are drawn (without replacement) at random from one of the bags and were found to be one white and one black. Find the probability that the balls were drawn from bag $$Y.$$
Bag I contains $$3$$ red and $$4$$ black balls and Bag II contains $$4$$ red and $$5$$ black balls. Two balls are transferred at random from Bag I to Bag II and then a ball is drawn from Bag II. The ball so drawn is found to be red in colour. Find the probability that the transferred balls were both black
In a factory which manufactures bolts, machines A, B and C manufacture $$30 \%, 50 \%$$ and $$20 \%$$ of the bolts respectively. Of their output $$3 \% ,4 \%$$ and $$1 \%$$ respectively are defective bolts. A bolt is drawn at random from the product and is found to be defective. Find the probability that this is not manufactured by machine B.
Assume that the chances of a patient having a heart attack is 40%. Assuming that a mediation and yoga course reduces the risk of heart attack by 30% and prescription of certain drug reduces its chance by 25%. At a time a patient can choose any one of the two options with equal possibilities. It is given that after going through one of the two options, the patient selected at random suffers a heart attack. Find the probability that the patient followed a course of mediation and yoga. Interpret the result and state which of the above stated methods is more beneficial for the patient.
There are three coins. One is a two-headed coin (having head on both faces), another is a biased coin that comes up heads $$75$$% of the times and third is also a biased coin that comes up tails $$40$$% of the times. One of the three coins is chosen at random and tossed, and it shows heads. What is the probability that it was the two-headed coin?
Assume that each born child is equally likely to be a boy or a girl. If a family has two children, what is the conditional probability that both are girls? Given that :
(i) the youngest is a girl.
(ii) at least one is a girl.
A card from a pack of $$52$$ playing cards is lost. From the remaining cards of the pack three cards are drawn at random (without replacement) and are found to be all spades. Find the probability of the lost card being a spade.
What is the probability that if you roll a standard die three times, you will get three different numbers?
In an automobile factory, certain parts are to be fixed into the chassis in a section before it moves into another section. On a given day, one of the three persons $$A,B$$ and $$C$$ carries out this task. $$A$$ has $$45$$% chance, $$B$$ has $$35$$% chance and $$C$$ has $$20$$% chance of doing the task. The probability that $$A,B$$ and $$C$$ will take more than the allotted time is $$\cfrac { 1 }{ 6 } ,\cfrac { 1 }{ 10 } $$ and $$\cfrac{1}{20}$$ respectively. If it is found that the time taken is more than the allotted time, what is the probability that $$A$$ has done the task?
For A, B, and C, the chances of being selected as the manager of a firm are 4 : 1 : 2 respectively. The probabilities for them to introduce a radical change in the marketing strategy are 0.3, 0.8 and 0.5 respectively. If a change takes place; find the probability that it is due to the appointment of B.
An urn contains $$2$$ white and $$2$$ black balls. A ball is drawn at random. If it is white, it is not replaced into the urn. Otherwise, it is replaced with another ball of the same colour. The process is repeated. Find the probability that the third ball drawn is black.
In a bolt factory, three machines $$A, B$$ and $$C$$ manufacture $$25$$%, $$35$$% and $$40$$% of the total production respectively. Of their respective outputs, $$5$$%, $$4$$% and $$2$$% are defective. A bolt is drawn at random from the total production and it is found to be defective. Find the probability that it was manufactured by machine $$C$$.
Box I contains two white and three black balls. Box II contains four white and one black balls and box III contains three white and four black balls. A dice having three red, two yellow and one green face, is thrown to select the box. If red face turns up, we pick up box I, if a yellow face turns up we pick up box II, otherwise, we pick up box III. Then, we draw a ball from the selected box. If the ball drawn is white, what is the probability that the dice had turned up with a red face?
From a lot of 30 bulbs which include 6 defectives, a sample of 2 bulbs are drawn at random with replacement. Find the probability distribution of the number of defective bulbs.
A fair die is rolled. If face $$1$$ turns up, a ball is drawn from Bag $$A$$. If face $$2$$ or $$3$$ turns up, a ball is drawn from Bag $$B$$. If face $$4$$ or $$5$$ or $$6$$ turns up, a ball is drawn from Bag $$C$$. Bag $$A$$ contains $$3$$ red and $$2$$ white balls, Bag $$B$$ contains $$3$$ red and $$4$$ white balls and Bag $$C$$ contains $$4$$ red and $$5$$ white balls. The die is rolled, a Bag is picked up and a ball is drawn. If the drawn ball is red; what is the probability that it is drawn from Bag $$B$$?
State and prove Baye's theorem.
An experiment succeeds twice as often as it fails. Find the probability that in the next six trials, there will at least $$4$$ successes.
In a class of 75 students, 15 are above average, 45 are average and the rest below average achievers. The probability that an above average achieving student fails is 0.005, that an average achieving student fails is 0.05 and the probability of a below average achieving student failing is 0.If a student is know to have passed, what is the probability that he is a below average achiever?
A dice is thrown twice. A success is an even number on each throw. Find the probability distribution of the number of successes.
A bag contain 6 Red and 4 White balls. 4 balls are drawn one by one without replacement and were found to be atleast 2 white. If the next draw of a ball from this bag will give a white ball then the probability that the drawn of four balls initially contain two white and two red balls.
The range of a random variable $$X$$ is $$\left\{ 0,1,2 \right\} $$ and given that $$P(X=0)=3{ c }^{ 3 },\quad P(X=1)=4c-10{ c }^{ 2 },\quad P(X=2)=5c-1$$, find (i) the value of $$c$$
(ii) $$P(X<1),\quad P(1<X\le 2),\quad P(0<X\le 3)\quad $$
A fair coin is tossed $$9$$ times. Find the probability that it shows head exactly $$5$$ times.
Suppose a girl throws a die. If she gets a $$5$$ or $$6$$, she tosses a coin $$3$$ times and notes the number of heads. If she gets $$1, 2, 3$$ and $$4$$ she tosses a coin once and notes whether a head or tail is obtained. If she obtained exactly one head. What is the probability that she threw $$1, 2, 3$$ or $$4$$ with the die?
Consider the experiment of tossing a coin. If the coin shows head, toss it again, but if it shows tail, then throw a die. Find the conditional probability of the event that 'the die shows a number greater than $$4$$', given that 'there is atleast one tail'.
Bag I contains 1 white, 2 black and 3 red balls; Bag II contains 2 white, 1 black and 1 red balls; Bag III contains 4 white, 3 black and 2 red balls. A bag is chosen at random and two balls are drawn from it with replacement. They happen to be one white and one red. What is the probability that they came from Bag III.
Thirty-two player ranked $$1$$ to $$32$$ are play knockout tournament. Assume that in every match between any two players the better ranked player wins, the probability that ranked $$1$$ and ranked $$2$$ players are winner and runner up respectively is $$p$$, then the value of $$[2/p]$$ is, where [.] represents the greatest integer function.
A bas contains $$4$$ white, $$7$$ black and $$5$$ red balls. Three balls are drawn one after the other without replacement. Find the probability that the balls drawn are white, black and red respectively.
$$10$$ boys and $$5$$ girls study in a class. Three students are selected at random, one after the other. Find probability that,
(1) First two are boys and the third is a girl,
(2) First and third are boys and second is a girl
For the following p.d.f.s of X, find $$P(X < 1)$$ and $$P(|x| < 1)$$
$$f(x)=\dfrac{x^2}{18}$$, $$-3 < x < 3$$;
$$=0$$, otherwise.
If a fair coin is tossed $$10$$ times find the probability of (a) exactly six head
(b) At least six heads
(c) at most six heads.
If $$P(not\ A)=0.7,P(B)=0.7$$ and $$P(B/A)=0.5$$, find$$P\left(A\bigcup B \right)$$.
A family has two children. What is the probability that both the children are boys given that at least one of them is a boy?
In a class of $$60$$ boys and $$20$$ girls, half of the boys and half of the girls know cricket. Find the probability of the event that a person selected from the class is either a boy or a girl who knows cricket.
Box - $$1$$ contains $$5$$ red and $$2$$ blue balls white box - $$2$$ contains $$2$$ red and $$6$$ blue balls. A fair coin is tossed if it turns up head, a ball is drawn from the box - $$1$$, else a ball is drawn from the box - $$2$$. Find the probability of each of the following:- A red ball is drawn
- Ball drawn is from box-$$1$$ if it is blue
- A red ball is drawn
- Ball drawn is from box-$$1$$ if it is blue
Following is the distribution function F (x) of a discrete r. v. X
| x | 1 | 2 | 3 | 4 | 5 | 6 |
| F(x) | 0.2 | 0.37 | 0.48 | 0.62 | 0.85 | 1 |
(ii) Find P (x $$\leq$$3), (2 < x < 5)
Probability distribution of x
$$\begin{array}{l} P\left( { x\le 3 } \right) \\ \Rightarrow P\left( { x\le 3 } \right) =P\left( { x=3 } \right) +P\left( { x=2 } \right) +P\left({x=1}\right) \\ \Rightarrow P\left( { x\le 3 } \right) =0.48+0.37+0.2=0.87 \end{array}$$
In a bulb factory, three machines $$A,B,C$$ manufacture $$60\%,25\%$$ and $$15\%$$ of the total production respectively. Of their respective outputs $$1\%,2\%$$ and $$1\%$$ are defective. A bulb is drawn at random from the total product and it is found to be defective. Find the probability that it was manufactured by machine $$C$$.
A letter is known to have come either from TATANAGAR or CALCUTTA. On the envelop just two consecutive letter TA are visible. What is the probability that the letter has come from CALCUTTA?
There are 3 boxes, the first one containing 1 white, 2 red and 3 black balls; the second one containing 2 white, 3 red and 1 black ball and the third one containing 3 white, 1 red and 2 black balls. A box is chosen at random and from it two balls are drawn at random. One ball is red and the other, white. What is the probability that they come from the second box?
Two cards are selected at random from a box which contains five cards numbered 1,1,2,2, andLet X denote the sum and Y the maximum of the two numbers drawn. Find the probability distribution, mean and variance of X and Y.
A die is tossed 180 times. Find the expected value $$(\mu )$$, variance $$(q^{2})$$ and S.D $$(\sigma )$$ of number of times the face 3 will appear.
Let E be event of getting face $$3$$ in a single throw of dice
Let $$p=p(E)$$
Since these are total $$6$$ possible outcomes $$(1, 2, 3, 4, 5, 6)$$ and $$1$$ favourable outcomes i.e., $$3$$.
$$p=p(t)=\dfrac{1}{6}$$
$$p(\bar{E})=1-p=1-\dfrac{1}{6}=\dfrac{5}{6}$$
Mean$$=$$np
Variance $$=np(1-p)$$
Standard deviation$$=\sqrt{np(1-p)}$$
Mean$$=180\times \dfrac{1}{6}30$$
Variance $$=180\times \dfrac{1}{6}\left(1-\dfrac{1}{6}\right)=25$$
Standard deviation$$=\sqrt{180\times \dfrac{1}{6}\left(1-\dfrac{1}{6}\right)}=\sqrt{25}=5$$.
Four balls are to be drawn without replacement from a box containing 8 red and 4 white balls. If X denotes the number of red balls drawn, find the probability distribution of X.
By examining the chest X-ray , the probability that TB is detected when a person is actually suffering from it is $$0.99$$ . The probability of an healthy person diagnosed to having TB is $$0.001$$ . In a certain city $$1$$ in $$1000$$ people suffers from TB . A person is selected at random and is diagnosed to have TB . What is the probability that he/she actually have TB ?
Three numbers are selected at random (without replacement) from first six positive integers . If X denotes the smallest of the three numbers obtained , find the probability distribution of X . Also , find the mean and variance of the distribution.
Class 12 Commerce Maths Extra Questions
- Application Of Derivatives Extra Questions
- Application Of Integrals Extra Questions
- Continuity And Differentiability Extra Questions
- Determinants Extra Questions
- Differential Equations Extra Questions
- Integrals Extra Questions
- Inverse Trigonometric Functions Extra Questions
- Linear Programming Extra Questions
- Matrices Extra Questions
- Probability Extra Questions
- Relations And Functions Extra Questions
- Three Dimensional Geometry Extra Questions
- Vector Algebra Extra Questions