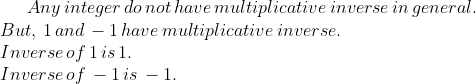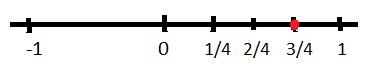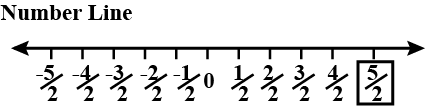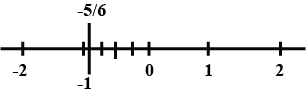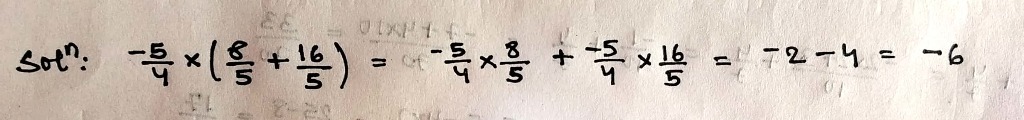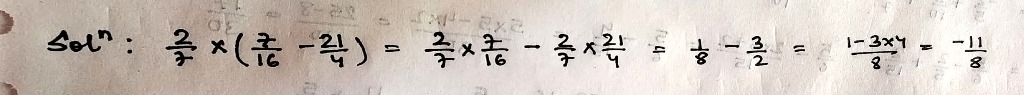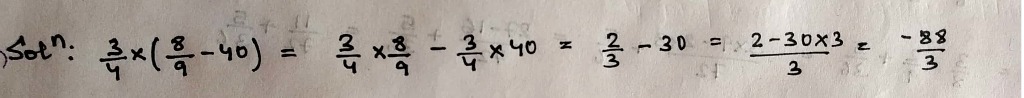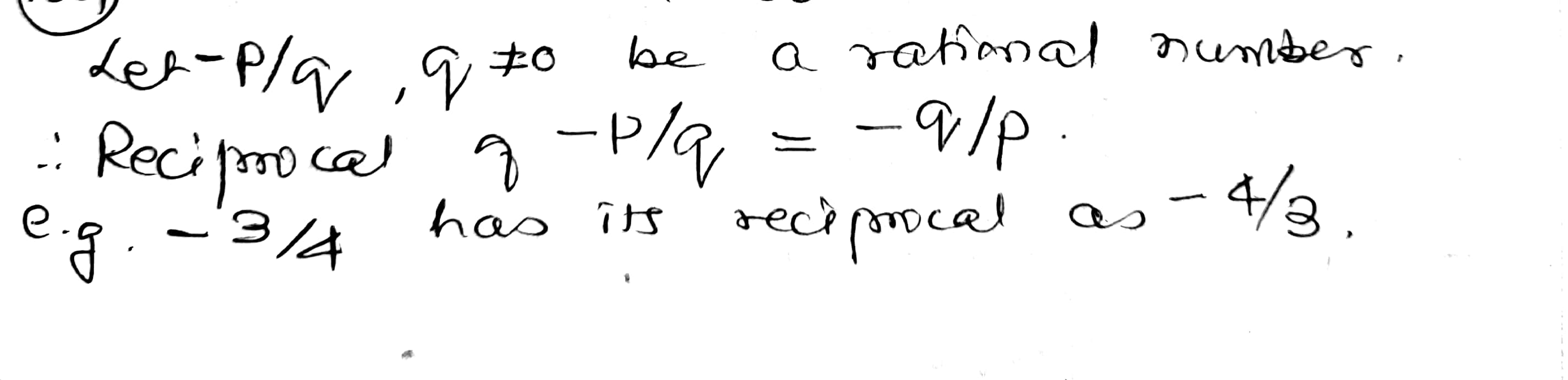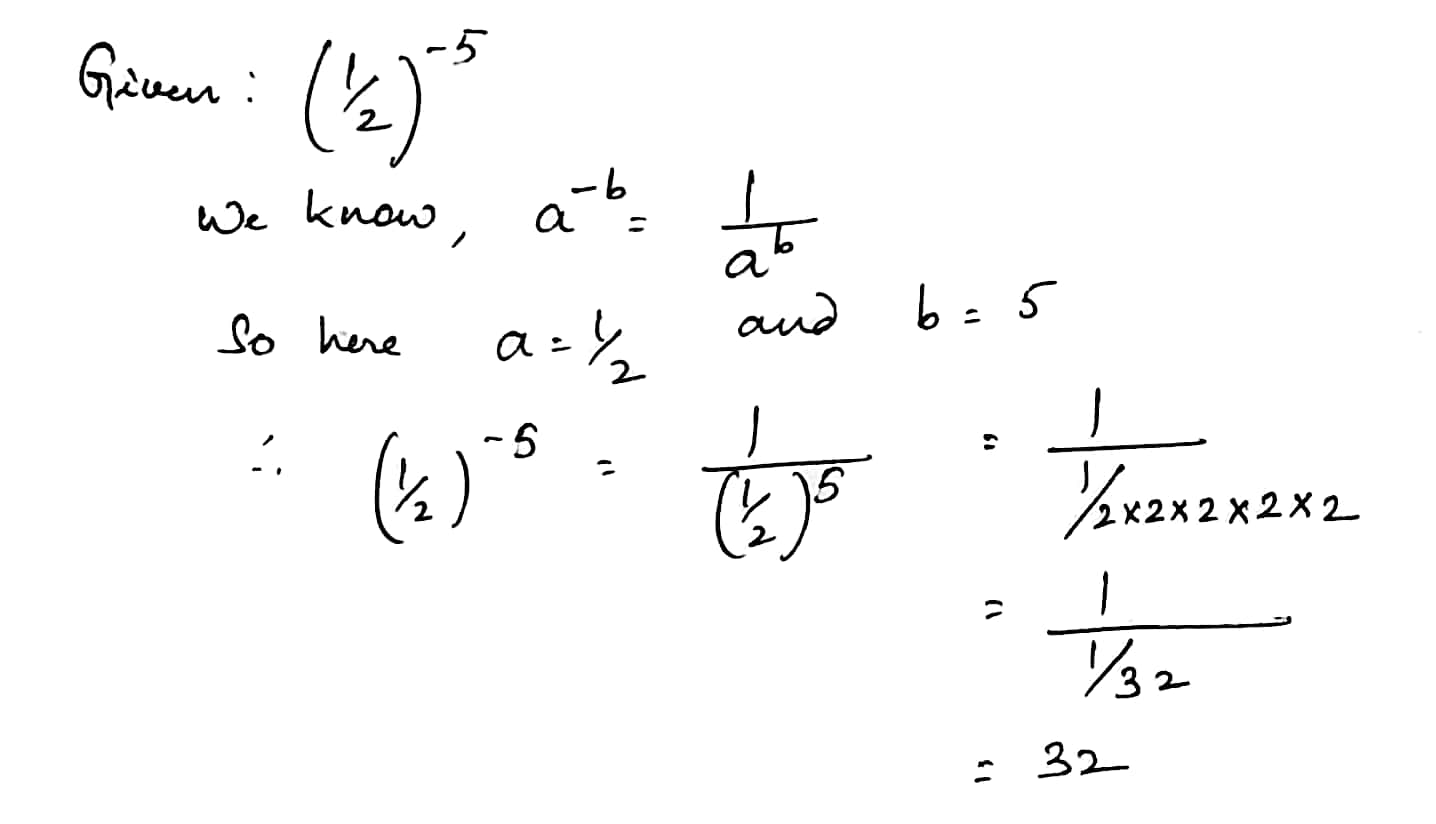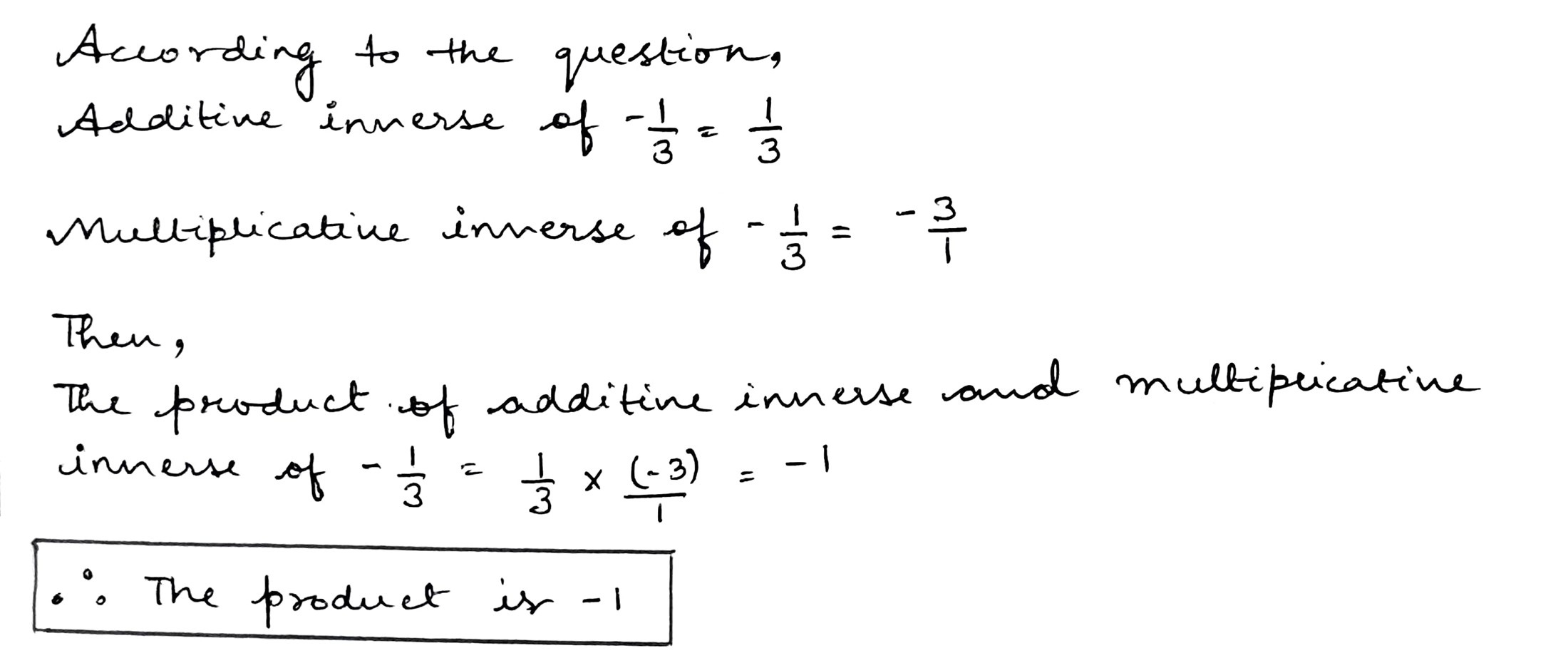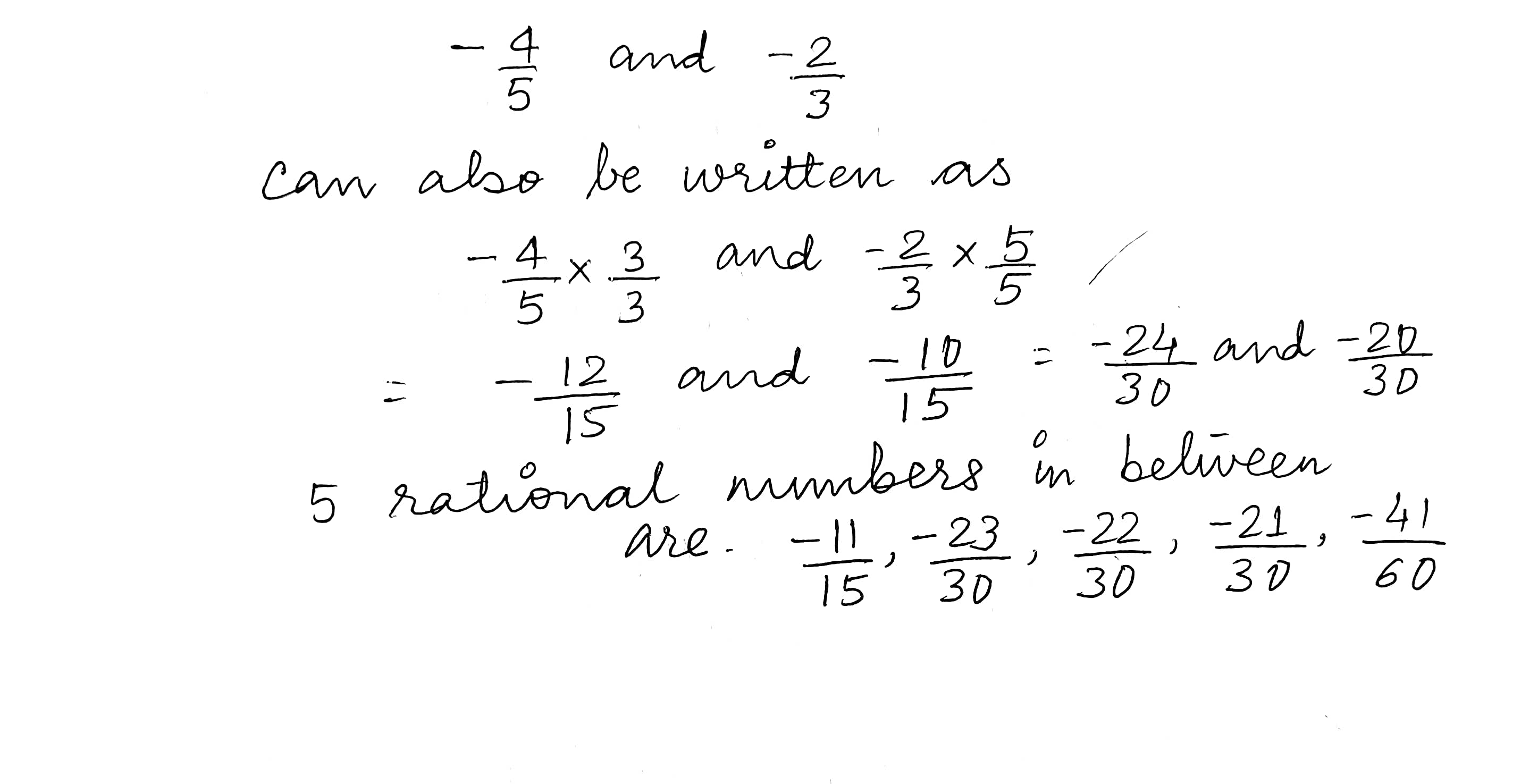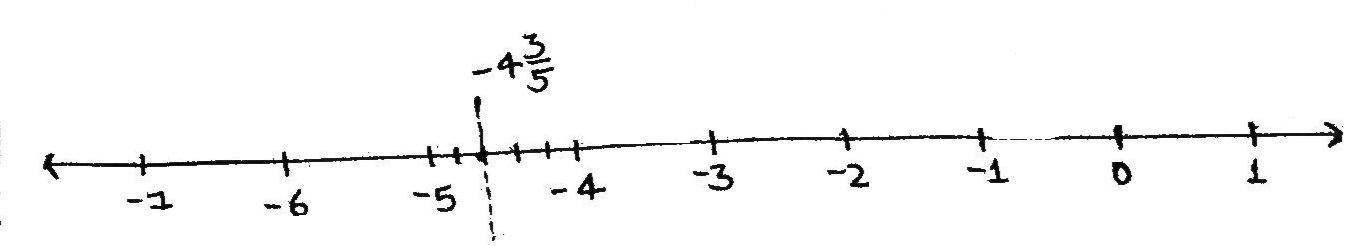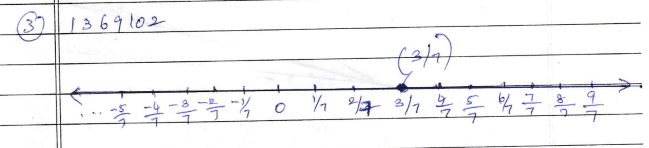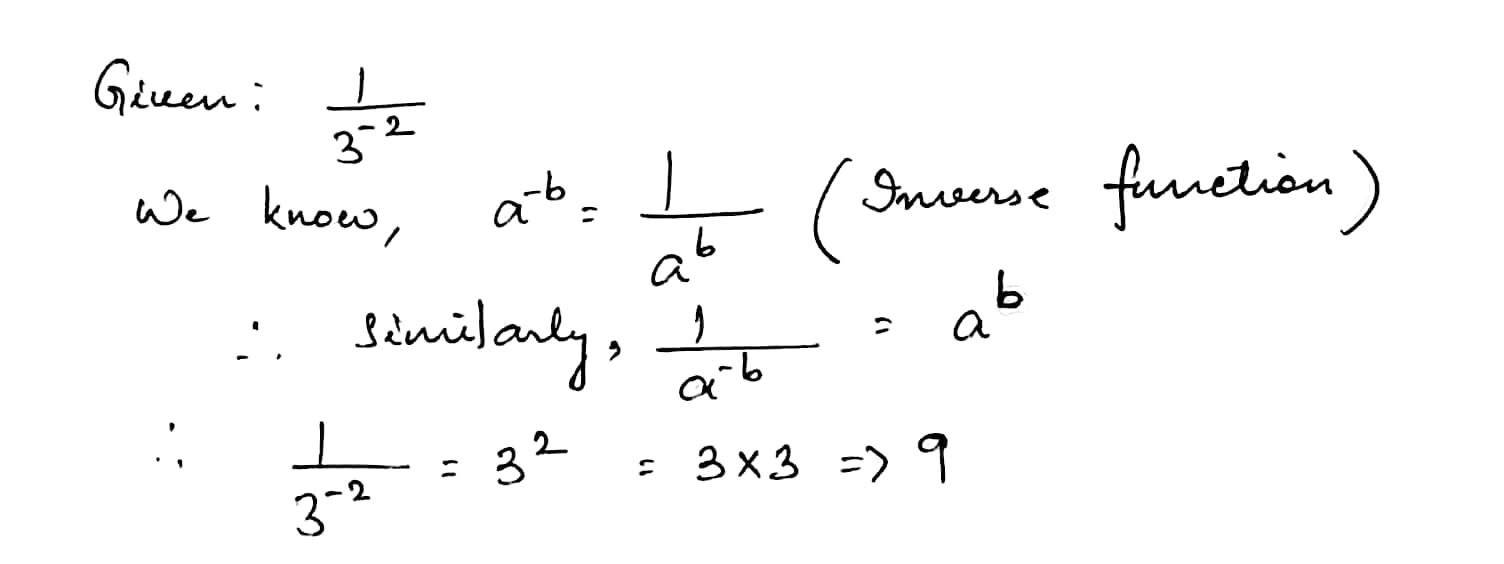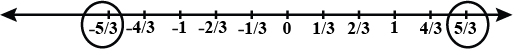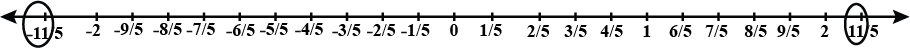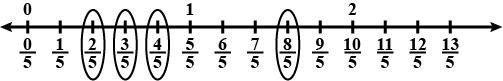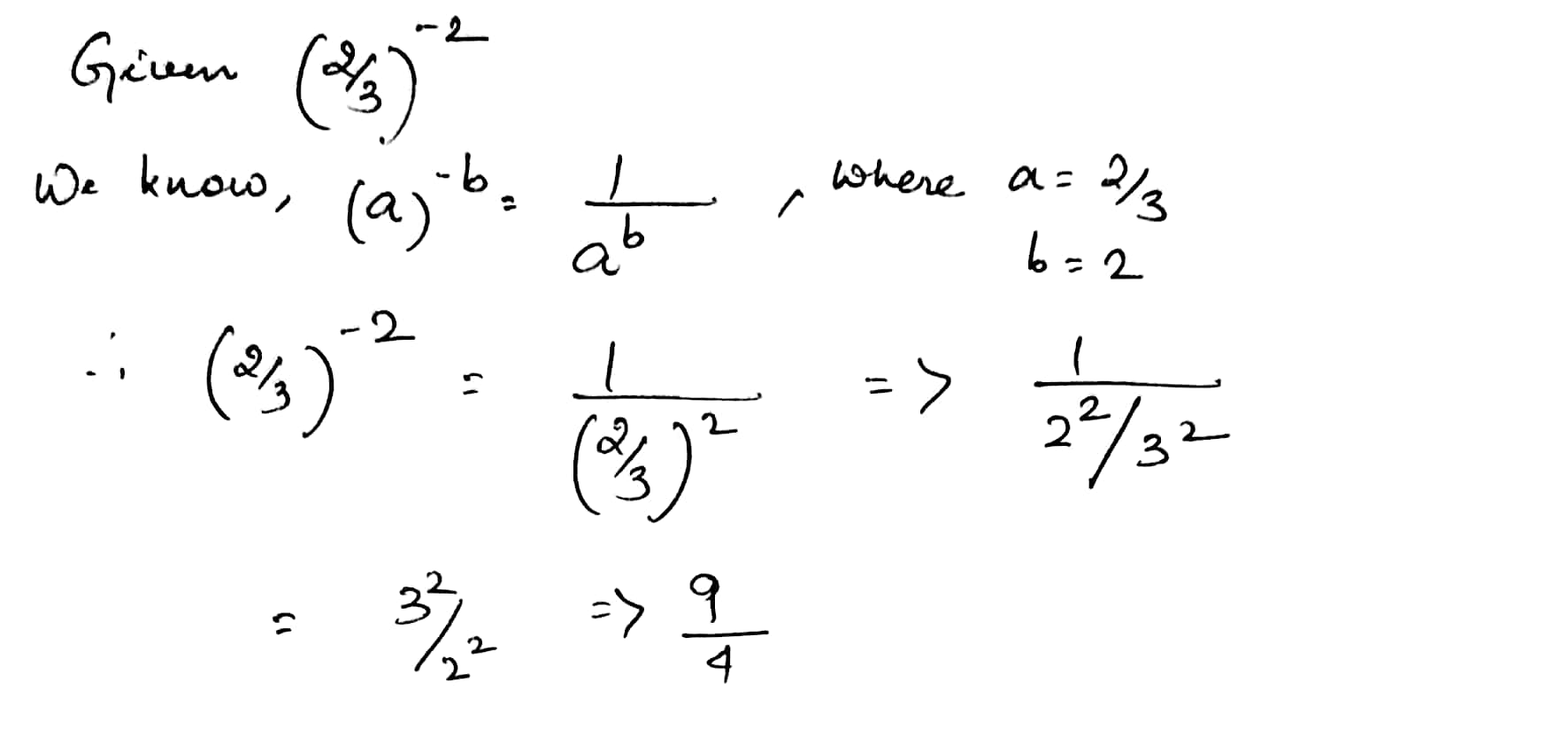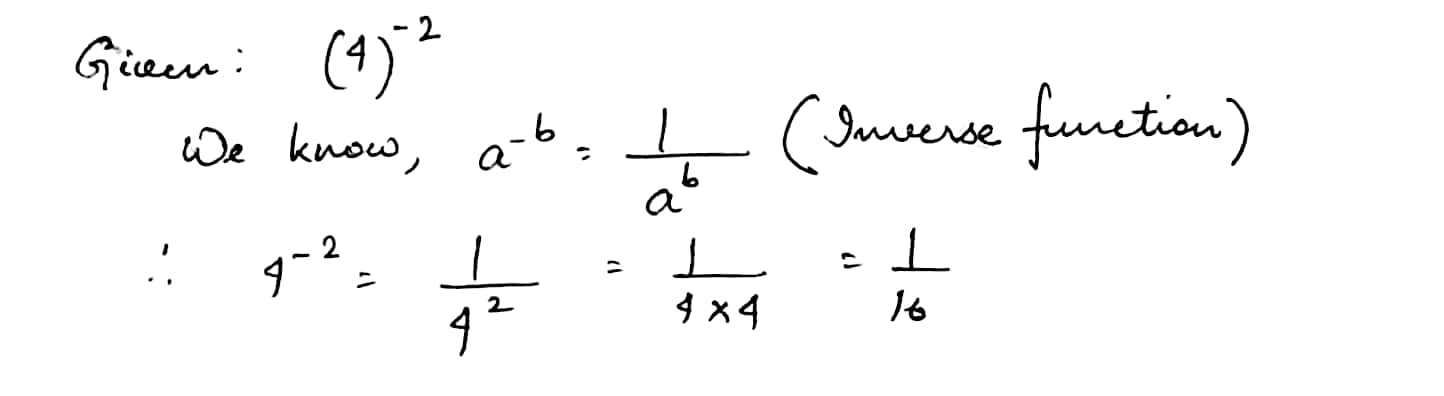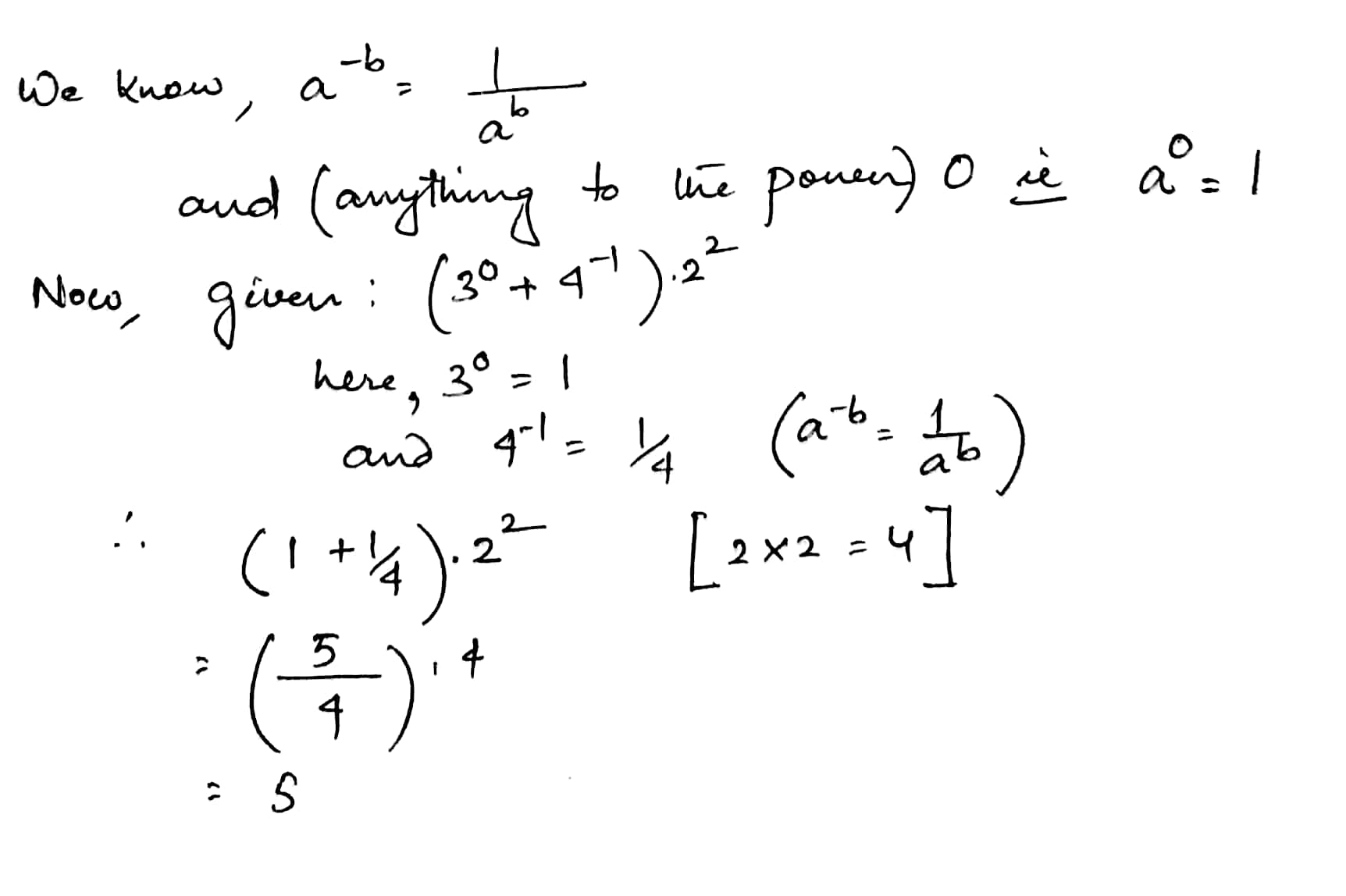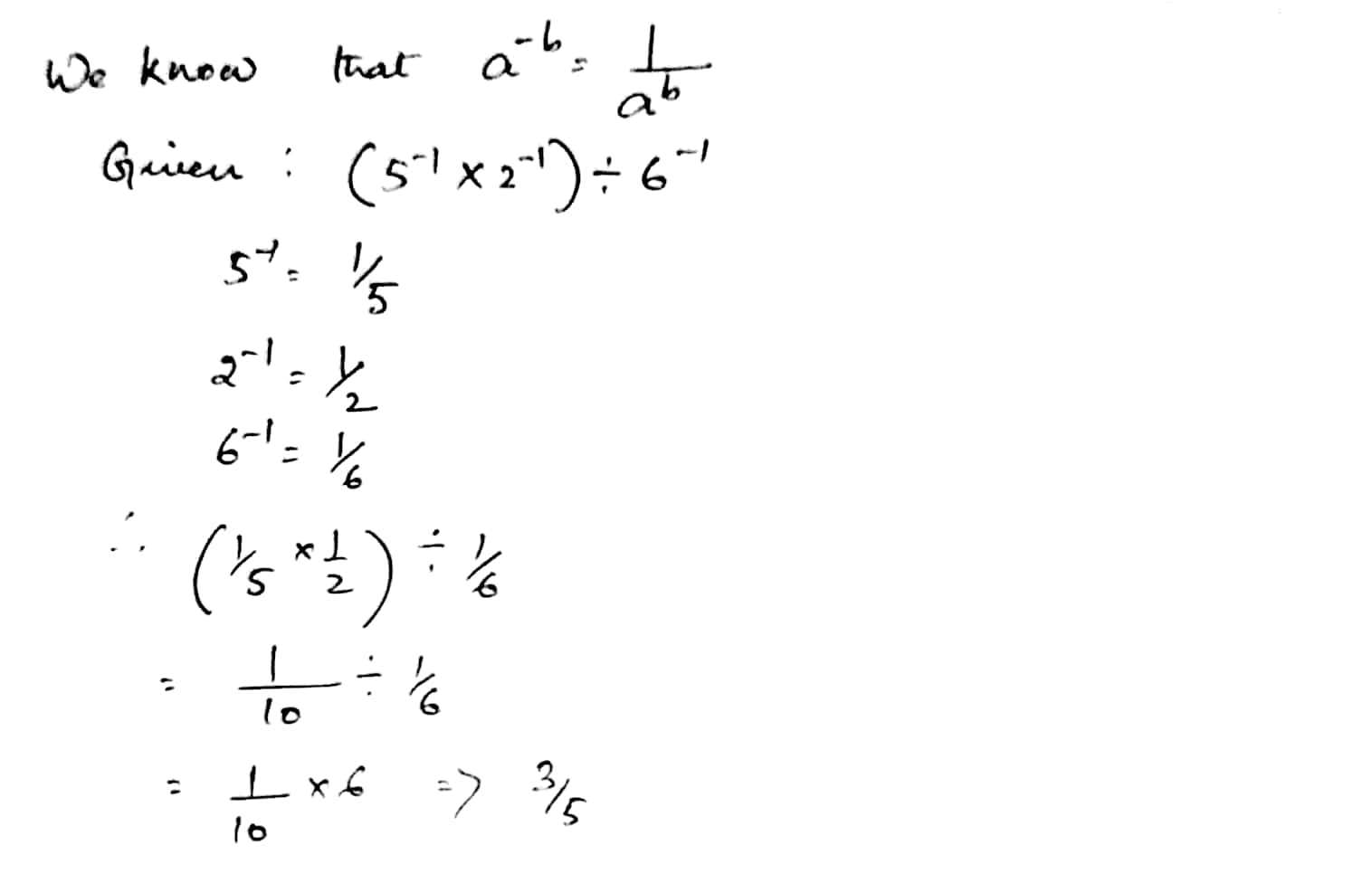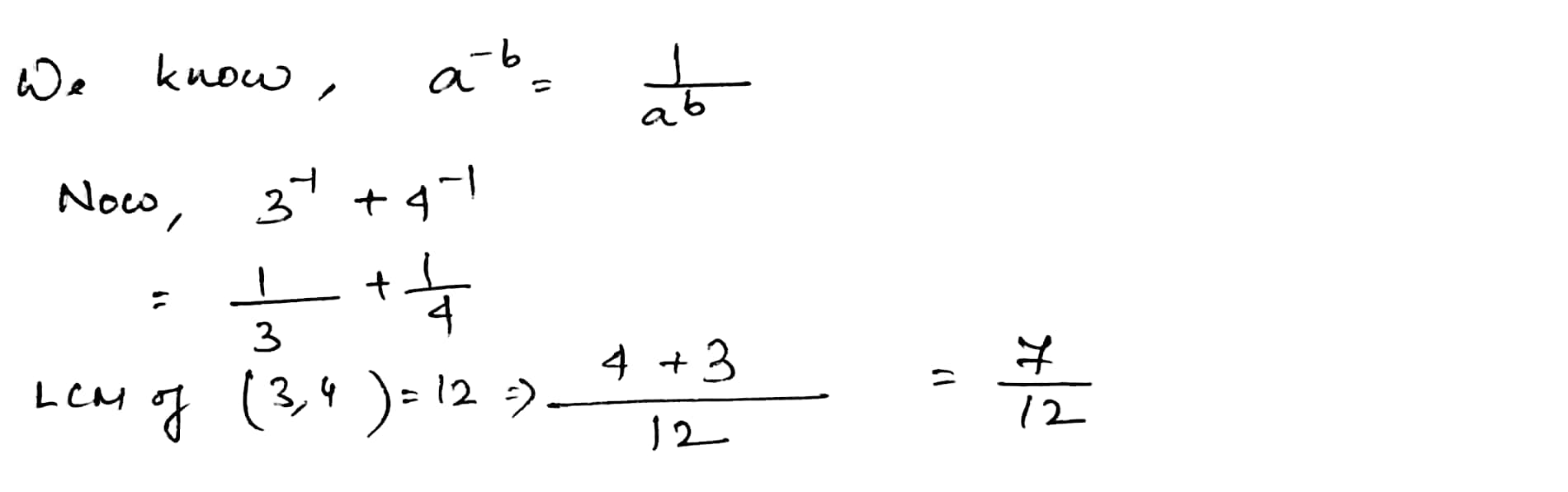Rational Numbers - Class 8 Maths - Extra Questions
Write the additive inverse of each of the following rational numbers:
$$\dfrac{3}{-11}$$.
If it is $$\dfrac{3}{11}$$ enter $$1$$ else enter $$0$$
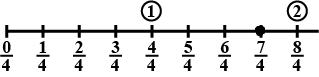
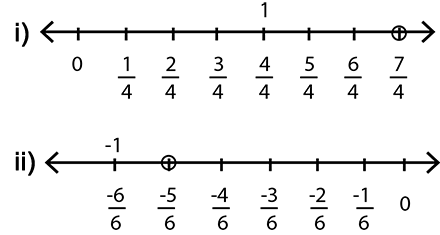
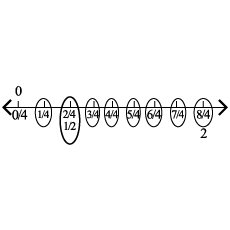
Represent $$\dfrac{7}{4}$$ on the number line.
Write the additive inverse of each of the following rational numbers:
$$\dfrac{-2}{17}$$
By what number should $$\left( 5\right) ^{ -5 }$$ be multiplied so that the product is 1?
Write the negative (additive inverse) of each of the following:
$$\dfrac{-2}{5}$$
Write the additive inverse of $$\dfrac{-11}{-25}$$
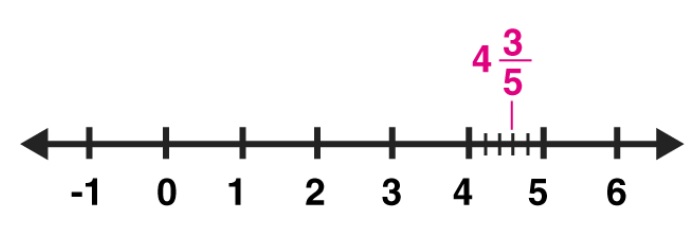
Represent the following rational numbers on the number line.
$$4\dfrac {3}{5}$$.
Represent the following rational numbers on the number line.
$$-9/7$$.
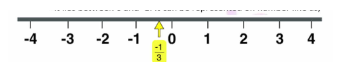
Write the additive inverse (negative ) of :
$$ - \dfrac{1}{3}$$
Fill in the blanks :
$$ \dfrac{5}{8} $$ and $$ \dfrac{-3}{10} $$ are on the ............ sides of zero.
Write the negative (additive inverse) of $$\dfrac{7}{-9}$$.
If the answer is $$\dfrac ab$$, then the value of $$(a+b)$$ is:-
Fill in the blank:
$$(-5) \times (......) = 0$$
Find the multiplicative inverse (i.e. reciprocal of :
$$-1$$.
Represents each of the following rational numbers on the number line:
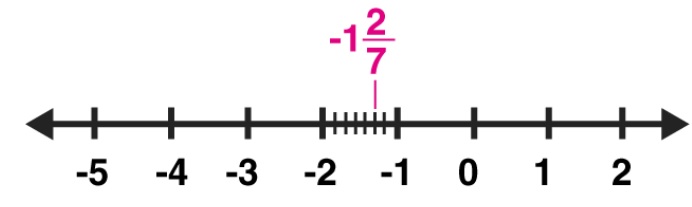
$$(-1/3)$$
Find the additive inverse of:
$$\cfrac3{14}$$
Represents each of the following rational numbers on the number line:
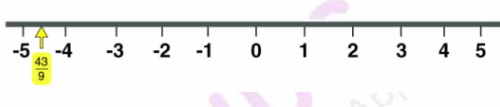
$$\cfrac{-43}9$$
Represents each of the following rational numbers on the number line:
$$(37/8)$$
Find the additive inverse of:
$$\cfrac{-11}{15}$$
Find the additive inverse of:
$$\cfrac{15}{-4}$$
Find the additive inverse of:
$$\cfrac{-18}{-13}$$
Fill the additive inverse of:
$$-9$$
Represents each of the following rational numbers on the number line:
$$\cfrac{36}{-5}$$
Find the additive inverse of:
$$5$$
Find the additive inverse of:
$$\cfrac{1}{-6}$$
Fill in the blanks to make the statements true.
Additive inverse of $$\dfrac{2}{3}$$ is ________.
Fill in the blanks to make the statements true.
On a number line, $$\dfrac{4}{3}$$ is to the ________ of zero $$(0)$$.
Fill in the blanks to make the statements true.
On a number line, $$\dfrac{-1}{2}$$ is to the ________ of zero $$(0).$$
Find a rational number exactly halfway between:
$$\dfrac{-1}{3}$$ and $$\dfrac{1}{3}$$
Find the multiplicative inverse or reciprocal of each of the following:
$$0$$
How many rational number p/q are there between 0 and 1 for which q<P ?
Which integers have a multiplication inverse?
Fill n the blanks :
$$ - \dfrac{-5}{-12} + $$ its Additive inverse = _____
Write the additive inverse (negative ) of :
$$ \dfrac{-3}{1}$$
Write the additive inverse (negative ) of :
$$ \dfrac{4}{13}$$
Write the additive inverse (negative ) of :
$$ \dfrac{-7}{5}$$
Fill n the blanks :
If $$ \dfrac{a}{b} $$ is additive inverse of $$ \dfrac{-c}{d'}$$ then $$\dfrac{-c}{d} $$ is additive inverese of ________ ?
Find the additive inverse of each of the following:
$$-18$$.
Find the additive inverse of the following:
$$\dfrac {1}{3}$$
Fill in the blank:
$$\{(-5) \times 3\} (-6)= (......) \times \{3 \times (-6)\}$$
Find the multiplicative inverse of $$\dfrac02.$$
Write the additive inverse (negative) of:
0
Enter 1 if true else enter 0.
The numbers $$1$$ and $$ -1$$ are their own reciprocals.
Can you find a rational number whose multiplicative inverse is $$-1$$ ?
Find the multiplicative inverse (i.e. reciprocal of :
$$-1/8$$.
Fill n the blanks :
Additive inverse of $$ \dfrac{-5}{-12}$$ = ________
$$\displaystyle\frac{2}{3}\times\displaystyle\frac{6}{21}=\displaystyle\frac{6}{21}\times$$ $$\displaystyle\frac{2}{3}$$
If true then enter $$1$$ and if false then enter $$0$$
If true then enter $$1$$ and if false then enter $$0$$
The addition of rational numbers is commutative.
If true then enter $$1$$ and if false then enter $$0$$.
$$\displaystyle\frac{7}{8}\times\begin{pmatrix}\displaystyle\frac{17}{13}+\displaystyle\frac{14}{13}\end{pmatrix}=\begin{pmatrix}\displaystyle\frac{7}{8}\times\displaystyle\frac{14}{13}\end{pmatrix}+\begin{pmatrix}\displaystyle\frac{7}{8}\times\displaystyle\frac{17}{13}\end{pmatrix}$$
If true then enter $$1$$ and if false then enter $$0$$
If $$\cfrac{-5}{9}$$ is additive inverse of $$\cfrac{5}{p}$$, then $$p$$ is equal to
The additive inverse of $$\dfrac{2}{8}$$ is $$\dfrac{-2}{q}$$ , $$q$$ is
The rational number that is equal to its negative.
Represent the number on the number line: $$\dfrac{7}{4}$$
Verify that: $$-(-x)=x$$ for $$x=\displaystyle\frac{11}{15}$$.
Substraction of rational numbers is associative.
If true then enter $$1$$ and if false then enter $$0$$
$$\displaystyle\frac{18}{29}\times\displaystyle\frac{44}{35}=\displaystyle\frac{-44}{35}\times\displaystyle\frac{18}{29}$$
If true then enter $$1$$ and if false then enter $$0$$
$$\displaystyle\frac{9}{-13}+\displaystyle\frac{4}{-16}=\displaystyle\frac{4}{-16}+$$ $$\displaystyle\frac{9}{-13}$$.
If true then enter $$1$$ and if false then enter $$0$$
Multiplication distributes over substraction of rational numbers.
If true then enter $$1$$ and if false then enter $$0$$
If $$\begin{pmatrix}\displaystyle\frac{-11}{14}\times\displaystyle\frac{6}{13}\end{pmatrix}+\begin{pmatrix}\displaystyle\frac{-11}{14}\times\displaystyle\frac{7}{13}\end{pmatrix}=\dfrac{m}{14}$$.Then find $$-m$$
$$\displaystyle\frac{-17}{18}\times\displaystyle\frac{18}{-17}=...........$$.
$$\begin{pmatrix}\displaystyle\frac{-9}{13}\times\displaystyle\frac{5}{6}\end{pmatrix}-\begin{pmatrix}\displaystyle\frac{-9}{13}\times\displaystyle\frac{4}{6}\end{pmatrix}= \displaystyle\frac{-9}{13} \times\begin{pmatrix}\displaystyle\frac{5}{6}-\displaystyle\frac{4}{6}\end{pmatrix}$$.
If true then enter $$1$$ and if false then enter $$0$$
Check whether the following statements are true or false. If true, then state the property illustrated by the statement.
$$\displaystyle\frac{-2}{3}+0=0+\begin{pmatrix}\displaystyle\frac{-2}{3}\end{pmatrix}=\displaystyle\frac{-2}{3}$$
$$\displaystyle\frac{-4}{5}+\displaystyle\frac{7}{8}=\displaystyle\frac{7}{8}+\begin{pmatrix}\displaystyle\frac{-4}{5}\end{pmatrix}$$
If true then enter $$1$$ and if false then enter $$0$$
The reciprocal of a positive rational number is negative.
If true then enter $$1$$ and if false then enter $$0$$
If additive inverse of $$\dfrac{4}{18}$$ is added to it then the result will be ___.
Find the multiplicative inverse of the following.
(i) $$-13$$
(ii) $$\dfrac{1}{5}$$
(iii) $$\dfrac{-5}{8}\times\dfrac{-3}{7}$$
(iv) $$-1\times\dfrac{-2}{5}$$
(v) $$-1$$
State what property allows you to compute $$\dfrac{1}{3}\times\begin{pmatrix}6\times\dfrac{4}{3}\end{pmatrix}$$ as $$\begin{pmatrix}\dfrac{1}{3}\times6\end{pmatrix}\times\dfrac{4}{3}$$.
Is $$0.3$$ the multiplicative inverse of $$3\dfrac{1}{3}$$? Why or why not?
Name the property indicated in the following:
$$\dfrac {8}{17} + \dfrac {-8}{17} = 0$$
Identify the property in the following statements:
$$2 \cdot 8 = 8\cdot 2$$
Identify the property in the following statements:
$$2 + (3 + 4) = (2 + 3) + 4$$
Represent $$\dfrac{-2}{11}$$, $$\dfrac{-5}{11}$$, $$\dfrac{-9}{11}$$ on the number line.
Check the commutative property of multiplication for $$\dfrac {-7}{13}, \dfrac {25}{27}$$
Prove that $$(-1)\times (-1)=1$$
Write the rational number that does not have any reciprocal.
Check the commutative property of multiplication for the following pairs:
$$\dfrac {-8}{9}, \dfrac {-17}{19}$$
Check the commutative property of addition for $$\dfrac {-7}{9}, \dfrac {-18}{19}$$
Find the additive inverse of each of the following numbers:
$$\dfrac {8}{5}, \dfrac {6}{10}, \dfrac {-3}{8}, \dfrac {-16}{3}, \dfrac {-4}{1}$$
Check the commutative property of multiplication for $$\dfrac {22}{4}, \dfrac {3}{4}$$
Write the additive inverse of the given rational number:$$\dfrac{-2}{-3}$$
Write the additive inverse of $$\dfrac{7}{-13}$$.
Mark the following rational numbers on the number line.
$$\cfrac { 10 }{ 3 } $$
Mark the following rational numbers on the number line.
$$\cfrac { 3 }{ 2 } $$
Name the property used in each of the following:
$$\dfrac {-1}{2}+0=\dfrac {-1}{2}=0+\dfrac {-1}{2}$$
Mark the following rational numbers on the number line.
$$\cfrac { 3 }{ 4 } $$
Write the multiplicate inverse of
$$\dfrac { 3 }{ 2 } $$
Are rational number always closed under subtraction?
Write the additive inverse of $$\left( \dfrac { -3 }{ 10 } +\dfrac { 6 }{ 10 } \right)$$
Write the multiplicate inverse of:
$$-5\dfrac { 6 }{ 7 }$$
Tell what property allows you to compute $$\frac{1}{3} \times \left( {6 \times \frac{4}{3}} \right)$$ as $$\left( {\frac{1}{3} \times 6} \right) \times \frac{1}{4}$$
Verify the following:
$$\left( \dfrac { -9 }{ 5 } \times \dfrac { -10 }{ 3 } \right) \times \dfrac { 21 }{ -4 } =\dfrac { -9 }{ 5 } \times \left( \dfrac { -10 }{ 3 } \times \dfrac { 21 }{ -4 } \right) $$
Find six rational numbers between $$ - \dfrac{1}{4}$$ and $$ - \dfrac{1}{2}$$.
Mark the following rational number on the number line.
$$\dfrac { 5 }{ 2 }$$
Write the multiplicate inverse of $$-5-\dfrac { 1 }{ -5 }$$
Verify the following:
$$\left( \dfrac { 5 }{ 7 } \times \dfrac { 12 }{ 13 } \right) \times \dfrac { 7 }{ 18 } =\dfrac { 5 }{ 7 } \left( \dfrac { 12 }{ 13 } \times \dfrac { 7 }{ 18 } \right) $$
Insert two rational numbers between $$1$$ and $$2$$
Find $$12$$ rational number between $$-1$$ and $$2$$ ?
Find the multiplicative inverse of $$3$$ and $$-7$$.
Represents these number on number line
$$\dfrac {-5}{6}$$
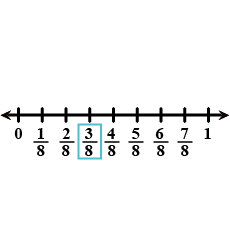
Write the additive inverse of the $$\dfrac{3}{8}$$
Find six rational numbers between $$\dfrac {3}{7}$$ and $$\dfrac {4}{8}$$
Write three rational numbers that lie between the two given numbers.
$$\dfrac{2}{7}, \dfrac{6}{7}$$
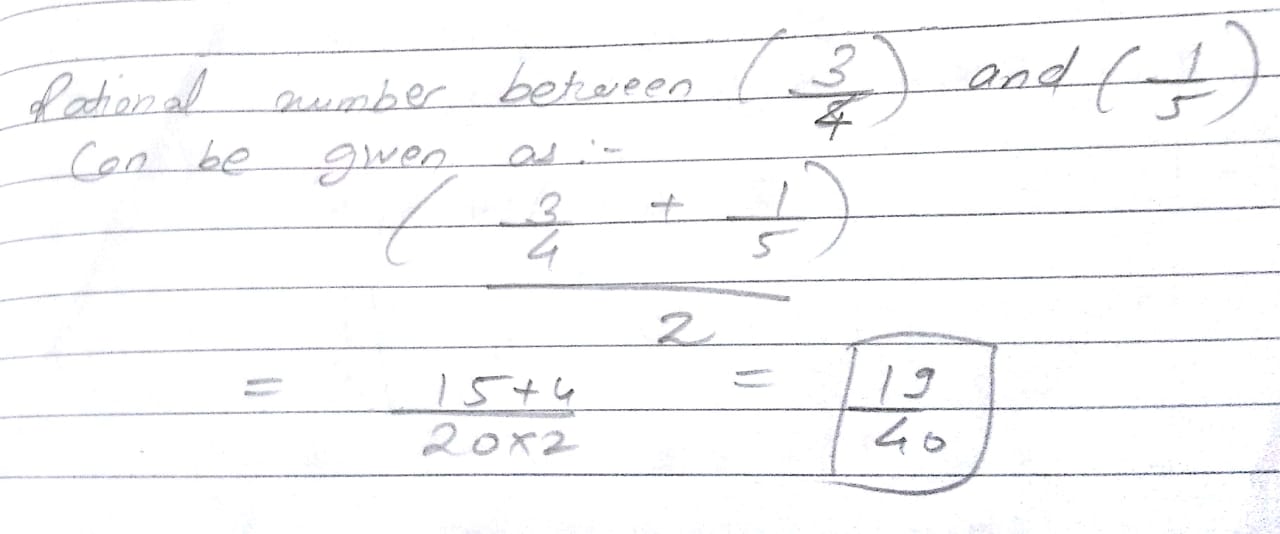
Find a rational number between $$\dfrac{1}{5}$$ and $$\dfrac{3}{4}$$
Insert the rational number between $$7$$ and $$8$$.
Fill in the blanks
Multiplicative inverse of $$2^{-16}$$ is _____ .
Find a rational number between $$\dfrac {1}{4}$$ and $$\dfrac {1}{3}$$
Write a rational number which does not lie between the rational numbers $$-\dfrac{2}{3}$$ and $$-\dfrac{1}{5}$$.
Fill in the blank:
The quotient when a rational number is divided by its additive inverse is ________
Verify the following $$\dfrac { 1 } { 2 } - \left( \dfrac { 3 } { 4 } - \dfrac { 5 } { 4 } \right)= \left(\dfrac { 1 } { 2 } - \dfrac { 3 } { 4 } \right)- \left(\dfrac { 5 } { 4 } \right)$$
Find 1 rational numbers between 2.1 and 2.2
How many rational numbers are there in between two given rational numbers?
Find the additive inverse of the number $$\dfrac{2}{8}$$.
Represent each of the following number on the number line:
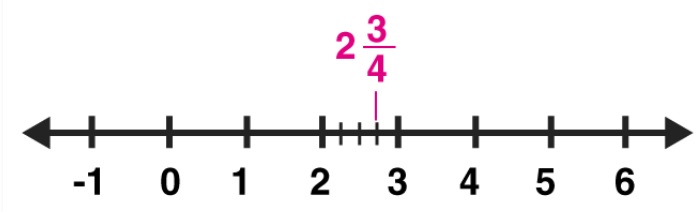
$$1\dfrac {3}{4}$$.
Name the property used in each of the following:
$$\dfrac {-3}{2}+\left(\dfrac {1}{3}+\dfrac {4}{7}\right)=\left(\dfrac {-3}{5}+\dfrac {1}{3}\right)+\dfrac {4}{7}$$
Using commutativity and associativity of addition of rational numbers, express each of the following as a rational number:
$$\dfrac{2}{5}+\dfrac{8}{3}+\dfrac{-11}{15}+\dfrac{4}{5}+\dfrac{-2}{3}$$
Write the negative (additive inverse) of $$1$$
Using commutativity and associativity of addition of rational numbers, express each of the following as a rational number:
$$\dfrac{3}{7}+\dfrac{-4}{9}+\dfrac{-11}{7}+\dfrac{7}{9}$$
Write the negative (additive inverse) of each of the following:
$$\dfrac{-16}{13}$$
Use the distributivity of multiplication of rational numbers over their addition to simplify:
$$\dfrac{-5}{4}\times\left(\dfrac{8}{5}+\dfrac{16}{5}\right)$$
Write the negative (additive inverse) of each of the following:
$$\dfrac{-5}{1}$$
Write the negative (additive inverse) of each of the following:
$$-1$$
Using commutativity and associativity of addition of rational numbers, express each of the following as a rational number:
$$\dfrac{4}{7}+0+\dfrac{-8}{9}+\dfrac{-13}{7}+\dfrac{17}{21}$$
Using commutativity and associativity of addition of rational numbers, express each of the following as a rational number:
$$\dfrac{2}{5}+\dfrac{7}{3}+\dfrac{-4}{5}+\dfrac{-1}{3}$$
Write the negative (additive inverse) of each of the following:
$$0$$
In each of the following cases, write the rational number whose numerator and denominator are respectively as under:
$$25+15$$ and $$81 \div 40$$
Use the distributivity of multiplication of rational numbers over their addition to simplify:
$$\dfrac{2}{7}\times\left(\dfrac{7}{16}-\dfrac{21}{4}\right)$$
Find a rational number exactly halfway between:
$$\dfrac{5}{-13}$$ and $$\dfrac{-7}{9}$$
Find a rational number exactly halfway between:
$$\dfrac{1}{15}$$ and $$\dfrac{1}{12}$$
Represent the following number on the number line:
$$-3$$.
Use the distributivity of multiplication of rational numbers over their addition to simplify:
$$\dfrac{3}{4}\times\left(\dfrac{8}{9}-40\right)$$
Fill in the blanks to make the statement true:
The negative of a negative rational number is always a ............... rational number.
Fill in the blanks to make the statement true:
The rational numbers $$\dfrac{1}{3}$$ and $$\dfrac{-1}{3}$$ are on the ........... sides of zero on the number line.
Fill in the blanks to make the statement true:
Rational numbers can be added or multiplied in any ..............
Tell which property allows you to compute
$$\dfrac{1}{5} \times \left[ \dfrac{5}{6} \times \dfrac{7}{9} \right]$$ as $$\left[\dfrac{1}{5} \times \dfrac{5}{6}\right] \times \dfrac{7}{9}$$
Find the multiplicative inverse of $$-1 \dfrac{1}{8}$$
Name the property used in the following-
$$\dfrac{1}{3} + \left[\dfrac{4}{9} + \left(\dfrac{-4}{3} \right)\right] = \left[\dfrac{-2}{3} + \dfrac{4}{9} \right] + \left(\dfrac{-4}{3}\right)$$
Name the property used in the following-
$$\dfrac{3}{8} \times 1 = 1 \times \dfrac{3}{8} = \dfrac{3}{8}$$
Name the property used in the following-
$$\dfrac{-2}{3} \times \left[\dfrac{3}{4} + \dfrac{-1}{4} \right] = \left[\dfrac{-2}{3} \times \dfrac{3}{4} \right] + \left[\dfrac{-2}{3} \times \dfrac{-1}{4} \right]$$
Find the multiplicative inverse of $$3\dfrac{1}{3}$$
Name the property used in the following-
$$\dfrac{-2}{7} + 0 = 0 + \dfrac{2}{7} = \dfrac{-2}{7}$$
Tell which property allows you to compare
$$\dfrac{2}{3} \times \left[\dfrac{3}{4} \times \dfrac{5}{7}\right]$$ as $$\left[\dfrac{2}{3} \times \dfrac{5}{7}\right] \times \dfrac{3}{4}$$
Name the property used in the following-
$$-\dfrac{7}{11} \times \dfrac{-3}{5} = \dfrac{-3}{5} \times \dfrac{-7}{11}$$
Find the sum of additive inverse and multiplicative inverse of $$7$$.
Enter 1 if it is true else enter 0.
The multiplicative inverse of $$-3\dfrac{1}{5}$$ is $$\dfrac{-5}{16}$$.
Verify commutative property of addition for the following pairs of rational numbers.
$$9/11$$ and $$2/13$$.
Enter 1 if true else enter 0.The rational number $$\dfrac{-5}{11}$$ lies to the left of zero on the number line
Find the additive inverse of the following rational numbers:
$$2/-3$$.
Enter 1 if true else enter 0.
The number $$\dfrac{-4}{7}$$ lies to the left of zero on the number line.
Verify commutative property of addition for the following pairs of rational numbers.
$$-4/3$$ and $$3/7$$.
Using the appropriate properties of operations of rational numbers, evaluate the following:
$$2/5\times - 3/7 - 1/14 - 3/7 \times 3/5$$.
Verify commutative property of multiplication for the following pairs of rational numbers:
$$-7/-20$$ and $$5/-14$$.
Find the additive inverse of the following rational number:
$$\dfrac{-7}{-12}$$
Verify commutative property of multiplication for the following pairs of rational numbers:
$$13\dfrac {1}{3}$$ and $$1\dfrac {1}{8}$$.
Verify the following and name the property:
$$5/9 \times (-3/2 + 7/5) = 5/9 \times -3/2 + 5/9\times 7/5$$.
Fill in the following blanks:
$$-8/9\times \left \{4/13 + 5/17\right \} = -8/9 \times 4/13 +$$ _______.
Using the appropriate properties of operations of rational numbers, evaluate the following:
$$8/9 \times 4/5 + 5/6 - 9/5 \times 8/9$$.
Find the product of additive inverse and multiplication inverse of $$-3/7$$.
Find the sum of additive inverse and multiplication inverse of $$9$$.
Represent the following rational numbers on the number line.
$$11/4$$.
Fill in the following blanks:
$$-6/13 \times \left \{8/9 - 4/7\right \} = -6/13 \times$$ ____ $$-(-6/13) \times (4/7)$$.
Fill in the following blanks:
$$3/7\times (-2/8\times$$ _____$$) = (3/7 \times -2/8) \times 5/9$$.
Using distributivity, find
$$\left \{9/16 \times 4/12\right \} + \left \{9/16 \times (-3/9)\right \}$$.
Using distributivity, find
$$\left \{7/5 \times (-3/12) \right \} + \left \{7/5 + 5/12\right \}$$.
For each pair of , verify commutative property of addition of rational numbers.
$$ 3 and \dfrac{-2}{7} $$
Write the additive inverse (negative ) of :
1
Fill in the blanks :
$$ \dfrac{-5}{8} $$ and $$ \dfrac{3}{10} $$ are on the ............ sides of zero.
Fill in the blanks :
$$ \dfrac{-5}{8} $$ and $$ \dfrac{-3}{10} $$ are on the ............ sides of zero.
For each pair of , verify commutative property of addition of rational numbers.
$$ \dfrac{-4}{5} and \dfrac{-13}{-15} $$
Fill in the blanks :
$$ \dfrac{5}{8} $$ and $$ \dfrac{3}{10} $$ are on the .............. side of zero.
Represent the following rational numbers on the number line.
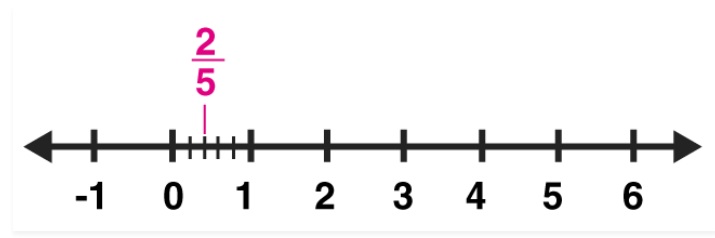
$$\dfrac{2}{5}$$.
What is the multiplicative inverse if $$1$$?
Write any three rational numbers between the two numbers given below.
1) $$0.3$$ and $$-0.5$$
2) $$-2.3$$ and $$-2.33$$
3) $$5.2$$ and $$5.3$$
4) $$-4.5$$ and $$-4.6$$
Name the property under multiplication used in each of the following:
i) $$\cfrac{-4}{5}\times1=1\times\cfrac{-4}{5}=-\cfrac{4}{5}$$ii) $$-\cfrac{13}{17}\times\cfrac{-2}{7}=\cfrac{-2}{7}\times\cfrac{-13}{17}$$iii) $$\cfrac{-19}{29}\times\cfrac{29}{-19}=1$$
List three rational numbers between -2 and -1
Use the method of mean to find $$3$$ rational numbers between $$-1$$ and $$-2$$.
Using appropriate properties, find
(i) $$-\dfrac{2}{3}\times\dfrac{3}{5}+\dfrac{5}{2}-\dfrac{3}{5}\times\dfrac{1}{6}\\$$
(ii) $$\dfrac25\times\left(-\dfrac37\right) - \dfrac16\times\dfrac32 + \dfrac1{14}\times\dfrac25$$
Write the additive inverse of each of the following.
(i) $$\dfrac{2}{8}$$ (ii) $$\dfrac{-5}{9}$$ (iii) $$\dfrac{-6}{-5}$$ (iv) $$\dfrac{2}{-9}$$ (v) $$\dfrac{19}{-6}$$
Fill in the blanks.
(i) Zero has _________ reciprocal.
(ii) The numbers ___________ and __________ are their own reciprocals.
(iii) The reciprocal of $$-5$$ is _________.
(iv) Reciprocal of $$\dfrac{1}{x}$$, where $$x\neq0$$ is _________.
(v) The product of two rational numbers is always a ______________.
(vi) The reciprocal of a positive rational number is _______________.
Find five rational numbers between $$\displaystyle\frac{3}{5}$$ and $$\displaystyle\frac{4}{5}$$.
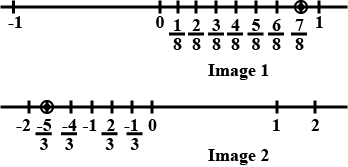
Represent these numbers on the number line. (i) $$\dfrac{7}{4}$$ (ii) $$\dfrac{-5}{6}$$
Find five rational numbers between $$3$$ and $$4$$.
Is $$\dfrac{8}{9}$$ the multiplicative inverse of $$-1\dfrac{1}{8}$$? Why or why not?
Name the property under multiplication used in each of the following.
(i) $$\dfrac{-4}{5}\times1=1\times\dfrac{-4}{5}=-\dfrac{4}{5}$$
(ii) $$-\dfrac{13}{17}\times\dfrac{-2}{7}=\dfrac{-2}{7}\times\dfrac{-13}{17}$$
(iii) $$\dfrac{-19}{29}\times\dfrac{29}{-19}=1$$
Name the property indicated in the following:
$$315 + 115 = 430$$
Which property is illustrated by the following statement?
$$(16+18)+20=(18+16)+20$$
Name the property indicated in the following:
$$\dfrac {3}{4} \cdot \dfrac {9}{5} = \dfrac {27}{20}$$
What are the properties of $$R$$ used in the following? $$a+(\pi + e)=(a+\pi)+e$$
Name the property indicated in the following:
$$\dfrac {8}{9}\times 1 = \dfrac {8}{9}$$
Check the distributive property for the stated triples of rational numbers:
$$\dfrac {3}{8}, 0, \dfrac {13}{7}$$
Check the commutative property of addition for $$\dfrac {-8}{13}, \dfrac {23}{27}$$
What are the properties of $$R$$ used in the following? $$8\times 7 = 7\times 8$$
Suppose $$\dfrac{m}{n}$$ and $$\dfrac{p}{q}$$ are two positive rational numbers. Where do $$\dfrac{m + p}{n + q} lie,$$ with respect to $$\dfrac{m}{n}$$ and $$\dfrac{p}{q}$$?
Check the distributive property for the stated triples of rational numbers:
$$\dfrac {1}{8}, \dfrac {1}{9}, \dfrac {1}{10}$$
Check the distributive property for the stated triples of rational numbers:
$$\dfrac {-4}{9}, \dfrac {6}{5}, \dfrac {11}{10}$$
Check the commutative property of addition for $$\dfrac {102}{201}, \dfrac {3}{4}$$
Find the multiplicative inverse of each of the following numbers:
$$2, \dfrac {6}{11}, \dfrac {-8}{15}, \dfrac {19}{18}, \dfrac {1}{1000}$$
Represent $$-\dfrac {3}{4}$$ on number line
What are the properties of $$R$$ used in the following? $$\pi \times 1 = \pi$$
Find the additive inverse of: $$7+\sqrt[4]{2}$$
Find the additive inverse of $$\sqrt{5}.$$
Find the additive inverse of: $$-\frac{3}{\sqrt{\pi}}$$
Find the additive inverse of: $$1+\pi$$
Find the additive inverse of each of the following: $$(-3+\sqrt{3})^2$$
Write the reciprocal of a negative rational number.
Find two rational numbers between $$\dfrac {-3}{4}$$ and $$\dfrac {1}{2}$$
Find any two rational numbers $$\displaystyle\frac{1}{4}$$ and $$\displaystyle\frac{3}{4}$$.
Represent $$\dfrac {8}{5}$$ and $$\dfrac {-8}{5}$$ on a numberline
If a/b is the additive inverse of c/d, then find the value of $$
\dfrac{a}
{b} + \dfrac{c}
{d}
$$
Find a rational number and also an irrational number lying between the numbers $$0.401001000100001000001........$$ and $$0.404004000400004000004..........$$.
a. Write additive inverse of $$\frac{2}{8}and\frac{{ - 6}}{{ - 5}}$$
b. Write multiplicative inverse of $$ - 13{\rm{ and }}\frac{{ - 13}}{{19}}$$
Write a multiple of $$\dfrac{-6}{3}$$ rational number.
Write $$5$$ rational numbers between $$3$$ and $$\cfrac { 3 }{ 10 } $$
Mark the following rational number on number line.
$$\dfrac { 4 }{ 5 }$$
I am a number between $$20$$ and $$30$$. If you divide $$47$$ and $$92$$ by me, the remainders are $$3$$ and $$4$$ respectively what number am I?
Represented $$\dfrac {-3}{4}$$ & $$\dfrac {1}{8}$$ on the number line
Find five fractions between $$\dfrac {2}{3}$$ and $$\dfrac {4}{5}$$.
Let * be a binary operation on the set $$Q$$ of rational numbers as follows:
$$a*b=a-b$$
Find which of the binary operations are commutative and which are associative.
Verify the following:
$$\dfrac { -13 }{ 24 } \times \left( \dfrac { -12 }{ 5 } \times \dfrac { 35 }{ 36 } \right) =\left( \dfrac { -13 }{ 24 } \times \dfrac { -12 }{ 5 } \right) \times \dfrac { 35 }{ 36 } $$
Write three rational numbers that lie between the two given numbers
$$\dfrac {4}{5},\dfrac {2}{3}$$
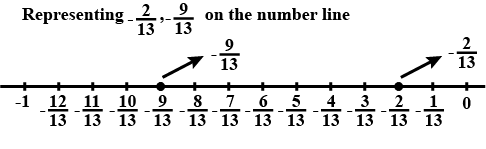
Represent $$-\cfrac { 2 }{ 13 } $$ and $$\cfrac { -9 }{ 13 }$$ on the number line.
Find two rational no between $$3$$ & $$4$$.
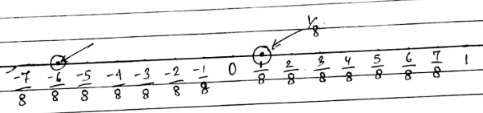
Represent these number on number line: $$\dfrac {7}{8},\dfrac {-5}{3}$$
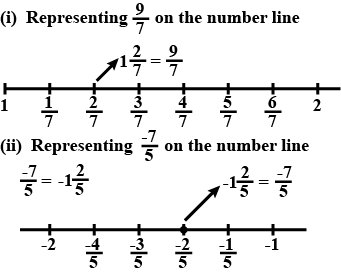
Represent this numbers on number line:(1) $$\dfrac { 9 }{ 7 }$$(2) $$-\dfrac { 7 }{ 5 } $$
Find a rational number between the following rational numbers:
(i)$$\frac { 3 } { 4 } \text { and } \frac { 4 } { 3 }$$
(ii) $$5 \text { and } 6$$
(iii)$$- \frac { 3 } { 4 } \text { and } \frac { 1 } { 3 }$$
Find 3 rational numbers between $$\dfrac{1}{2}\;$$ and $$\dfrac{1}{3}$$
Express the each of the following as a rational number of the form $$\dfrac {p}{q}$$, where $$p$$ and $$q$$ are integers and $$q\neq 0$$:
$$\left (\dfrac {1}{2}\right)^{-5}$$
Prove that the associative property hold true for the addition $$\left( \dfrac { 7 } { 8 } + \dfrac { 2 } { 5 } \right) + \dfrac { 8 } { 3 }$$
The multiplicative inverse of
$${\left( {\dfrac{1}{2}} \right)^4} \div {\left( {\dfrac{1}{3}} \right)^4} + {\left( { - \dfrac{1}{2}} \right)^{^3}}\;{\text{is}}$$
Find the product of additive inverse and multiplicative inverse of $$-\dfrac{1}{3}$$.
Fill in the blank:
The multiplicative inverse of $$0$$ _______
Find 5 rational numbers between $$-4/5\quad and\quad -2/3$$
Write any two rational numbers which are between $$2.3$$ and $$2.4$$.
Find any two rational numbers between $$\dfrac{-1}{2}$$ and $$\dfrac{-2}{3}$$
Represent on number line
$$\dfrac {2}{3} $$
Represent on number line
$$\dfrac {1}{6} $$
Represent each of the following numbers on the number line:
$$-4\dfrac {3}{5}$$.
Represent $$\dfrac {3}{7} $$ on a number line.
Represent each of the following numbers on the number line:
$$\dfrac {-3}{4}$$
Represent on number line
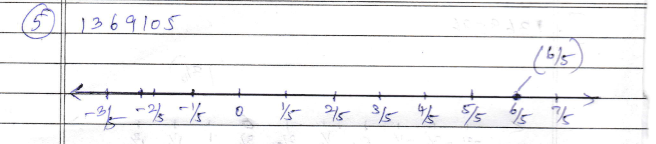
$$\dfrac {6}{5} $$
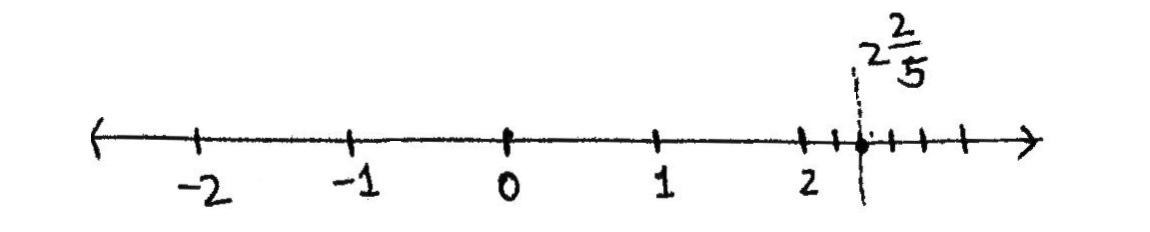
Represent each of the following numbers on the number line:
$$2\dfrac {2}{5}$$.
Draw number lines and locate the points on them.
$$\displaystyle \frac{1}{2},\frac{1}{4},\frac{3}{4},\frac{4}{4}$$
Express the each of the following as a rational number of the form $$\dfrac {p}{q}$$, where $$p$$ and $$q$$ are integers and $$q\neq 0$$:
$$\dfrac {1}{3^{-2}}$$
Find three rational numbers between $$-3$$ and $$5$$.
Represent $$\dfrac53$$ and $$\dfrac{-5}3$$ on the number line.
What is the sum of additive inverse and multiplicative inverse of $$-7$$.
Represent $$\dfrac{-11}{5}$$ and $$\dfrac{11}{5}$$ on the number line
Draw number lines and locate the points on them:
$$\displaystyle \frac{2}{5},\frac{3}{5},\frac{8}{5},\frac{4}{5}$$
Write the additive inverse and multiplicative inverse of a rational number.
The multiplicative inverse of 5 will be
Draw the number line and represent the following rational number on it:
$$\cfrac{-5}{8}$$
Draw the number line and represent the following rational number on it:
$$\cfrac{7}{8}$$
By what number should $$\left( 2\right) ^{ -7 }$$ be multiplied so that the product is $$1.$$
Express the each of the following as a rational number of the form $$\dfrac {p}{q}$$, where $$p$$ and $$q$$ are integers and $$q\neq 0$$:
$$\left (\dfrac {2}{3}\right)^{-2}$$
Express the each of the following as a rational number of the form $$\dfrac {p}{q}$$, where $$p$$ and $$q$$ are integers and $$q\neq 0$$:
$$(-4)^2$$
The points $$P,Q,R,S,T,U,A$$ and $$B$$ on the number line are such that $$TR=RS=SU$$ and $$AP=PQ=QB$$. Name the rational numbers represented by $$P,Q,R,S$$

Verify commutativity of addition of rational number for each of the following pairs of rational numbers:
$$\dfrac{-11}{5}$$ and $$\dfrac{4}{7}$$
Verify commutativity of addition of rational number for the following pair of rational numbers:
$$-4$$ and $$\dfrac{4}{-7}$$
Verify the property: $$x\times y=y\times x$$ by taking:
$$x=-\dfrac{1}{3}, y=\dfrac{2}{7}$$
Find the value of each of the following:
$$(3^0 +4^{-1})\times 2^2$$
Verify commutativity of addition of rational number for each of the following pairs of rational numbers:
$$\dfrac{-3}{5}$$ and $$\dfrac{-2}{-15}$$
Verify commutativity of addition of rational number for each of the following pairs of rational numbers:
$$\dfrac{4}{9}$$ and $$\dfrac{7}{-12}$$
Find the value of each of the following:
$$(5^{-1}\times 2^{-1})\div 6^{-1}$$
Verify commutativity of addition of rational number for each of the following pairs of rational numbers:
$$\dfrac{2}{-7}$$ and $$\dfrac{12}{-35}$$
Write the additive inverse of the following rational number:
$$\dfrac{-17}{5}$$
If the answer is $$\dfrac ab$$, then the value of $$(a+b)$$ will be what?
Find the value of each of the following:
$$3^{-1}+4^{-1}$$
Find a rational number between $$-3$$ and $$1$$.
Name the property of multiplication of rational number illustrated by the following statements:
$$\dfrac{-3}{2}\times\dfrac{5}{4}+\dfrac{-3}{2}\times \dfrac{-7}{6}=\dfrac{-3}{2}\times\left(\dfrac{5}{4}+\dfrac{-7}{6}\right)$$
Name the property of multiplication of rational number illustrated by the following statements:
$$\dfrac{-5}{16}\times \dfrac{8}{15}=\dfrac{8}{5}\times \dfrac{-5}{16}$$
Name the property of multiplication of rational number illustrated by the following statements:
$$\dfrac{-11}{6}\times \dfrac{16}{-11}=1$$
Name the property of multiplication of rational number illustrated by the following statements:
$$\dfrac{13}{-17}\times 1= \dfrac{13}{-17}=1\times \dfrac{13}{-17}$$
Use the distributivity of multiplication of rational numbers over their addition to simplify:
$$\dfrac{3}{5}\times\left(\dfrac{35}{24}+\dfrac{10}{1}\right)$$
Draw the number line and represent the following rational number on it: $$\dfrac{3}{8}$$
Find two rational numbers between $$\dfrac{-2}{9}$$ and $$\dfrac{5}{9}$$
Name the property of multiplication of rational number illustrated by the following statements:
$$\dfrac{-5}{9}\times \left(\dfrac{4}{15}\times \dfrac{-9}{8}\right)=\left(\dfrac{-5}{9}\times \dfrac{4}{15}\right)\times \dfrac{-9}{8}$$
Name the property of multiplication of rational number illustrated by the following statements:
$$\dfrac{-17}{5}\times 9=9\times \dfrac{-17}{5}$$
Draw the number line and represent the following rational numbers on it : $$-\dfrac{22}{7}$$
Draw the number line and represent the following rational numbers on it : $$-\dfrac{7}{3}$$
Draw the number line and represent the following rational numbers on it:
$$\dfrac{-5}{8}$$
Draw the number line and represent the following rational numbers on it : $$\dfrac{-31}{3}$$
Represent the following rational number on the number line.
$$-\dfrac{23}{6}$$.
Find a rational number between $$\dfrac{3}{8}$$ and $$\dfrac{2}{5}$$.
Find a rational number between $$-\dfrac{3}{4}$$ and $$-\dfrac{2}{5}$$.
Represent each of the following numbers on the number line:
$$3\dfrac {1}{2}$$.
Represent each of the following numbers on the number line:
$$8$$.
Represent $$\dfrac{5}{7}$$ rational number on the number line.
Find the additive inverse of each of the following:
$$\dfrac {-17}{8}$$.
Find the additive inverse of each of the following:
$$\dfrac {-3}{11}$$.
Represent each of the following numbers on the number line:
$$-2\dfrac56$$.
Find the additive inverse of each of the following:
$$\dfrac {23}{9}$$.
Find the additive inverse of each of the following:
$$\dfrac {-16}{-5}$$.
Find the additive inverse of each of the following:
$$\dfrac {15}{-4}$$.
i. Which rational number is its own additive inverse?
ii. Is the difference of two rational numbers are rational number?
iii. Is addition commutative on rational numbers?
iv. Is addition associative on rational numbers?
v. Is subtraction commutative on rational numbers?
vi. Is subtraction associative on rational numbers?
vii. What is the negative of a negative rational number?
Find the multiplicative inverse (i.e. reciprocal of :
$$18$$.
Find the multiplicative inverse (i.e. reciprocal of :
$$(-3) / (-5)$$.
Find the multiplicative inverse (i.e. reciprocal of :
$$-16$$.
Find the multiplicative inverse of $$\dfrac{-17}{12}$$
Find the additive inverse of each of the following:
$$\dfrac {19}{-6}$$.
Find the additive inverse of each of the following:
$$0$$.
Find the additive inverse of each of the following:
$$\dfrac {-8}{-7}$$.
Find the multiplicative inverse (i.e. reciprocal of:
$$13/25$$.
Find the multiplicative inverse (i.e. reciprocal of:
$$-7/24$$.
Find the multiplicative inverse (i.e. reciprocal of :
$$\dfrac {2}{-5}$$.
Fill in the blank:
$$(-8) \times (-9) = (-9) \times (.....)$$
Fill in the blank:
$$7 \times (-3) = (-3) \times (.....)$$
Fill in the blank:
$$(-6) \times (.....) = 6$$
Fill in the blank:
$$(-18) \times (.....) = (-18)$$
Find a rational number exactly halfway between:
$$\dfrac{1}{6}$$ and $$\dfrac{1}{9}$$
Fill in the blanks to make the statement true:
The two rational numbers lying between $$-2$$ and $$-5$$ with denominator as $$1$$ are .......................... and .................
Fill in the blanks to make the statement true:
The multiplicative inverse of $$\dfrac{4}{3}$$ is ..........
Give one example each to show that the rational numbers are closed under addition, subtraction, and multiplication. Are rational numbers closed under division ? Give one example in support of your answer.
Verify $$- (-x) = x$$ for $$x = \dfrac{3}{5}$$
Verify the property $$x \times y = y \times x$$ of rational numbers by using
$$x = \dfrac{2}{3}$$ and $$y = \dfrac{9}{4}$$
Verify the property $$x + y = y + x$$ of rational numbers by taking
$$x = \dfrac{1}{2}, y = \dfrac{1}{2}$$
Verify the property $$x \times y = y \times x$$ of rational numbers by using
$$x = 7$$ and $$y = \dfrac{1}{2}$$
Verify the property $$x + y = y + x$$ of rational numbers by taking
$$x = \dfrac{-3}{7}, y = \dfrac{-20}{21}$$
Verify the property $$x + y = y + x$$ of rational numbers by taking
$$x = \dfrac{-2}{3}, y = \dfrac{-5}{6}$$
Verify the property $$x \times y = y \times x$$ of rational numbers by using
$$x = \dfrac{-5}{7}$$ and $$y = \dfrac{14}{15}$$
Simplify the following by using suitable property. Also name the property.
$$\left[ \dfrac{1}{2} \times \dfrac{1}{4} \right] + \left[ \dfrac{1}{2} \times 6\right]$$
Simplify the following by using suitable property. Also name the property.
$$\dfrac{-3}{5} \times \left \{ \dfrac{3}{7} + \left(\dfrac{-5}{6}\right) \right \}$$
Verify the property $$x \times y = y \times x$$ of rational numbers by using
$$x = \dfrac{-3}{8}$$ and $$y = \dfrac{-4}{9}$$
Verify the property $$x + y = y + x$$ of rational numbers by taking
$$x = \dfrac{-2}{5}, y = \dfrac{-9}{10}$$
Verify the property $$x \times (y + z) = x \times y + x \times z$$ of rational numbers by taking
$$x = \dfrac{-1}{2}, y = \dfrac{2}{3}, z = \dfrac{3}{4}$$
Verify the property $$x \times (y + z) = x \times y + x \times z$$ of rational numbers by taking
$$x = \dfrac{-1}{2}, y = \dfrac{3}{4}, z = \dfrac{1}{4}$$
Verify the property $$x \times (y + z) = x \times y + x \times z$$ of rational numbers by taking
$$x = \dfrac{-1}{5}, y = \dfrac{2}{15}, z = \dfrac{-3}{10}$$
Verify the property $$x \times (y + z) = x \times y + x \times z$$ of rational numbers by taking
$$x = \dfrac{-2}{3}, y = \dfrac{-4}{6}, z = \dfrac{-7}{9}$$
Use the distributive of multiplication of rational numbers over addition to simplify
$$\dfrac{-5}{4} \times \left[\dfrac{8}{5} + \dfrac{16}{15}\right]$$
Verify the property $$x \times (y \times z) = (x \times y) \times z$$ of rational numbers by using
$$x = \dfrac{2}{3}, y = \dfrac{-3}{7}, z = \dfrac{1}{2}$$
Verify the property $$x \times (y \times z) = (x \times y) \times z$$ of rational numbers by using
$$x = 1, y = \dfrac{-1}{2}, z = \dfrac{1}{4}$$
Verify the property $$x \times (y \times z) = (x \times y) \times z$$ of rational numbers by using
$$x = 0, y = \dfrac{1}{2}$$
The multiplicative inverse of $$10^{10}$$ is
Verify the property $$x \times (y \times z) = (x \times y) \times z$$ of rational numbers by using
$$x = \dfrac{-2}{7}, y = \dfrac{-5}{6}, z = \dfrac{1}{4}$$
Draw a
number line and represent the following rational numbers on it:
(i)$$\dfrac{3}{8}$$
(ii) $$\dfrac{-3}{4}$$
(iii) $$\dfrac{-7}{8}$$
(iv) $$\dfrac{-17}{8}$$
Represent the following numbers on the number line:
$$7, 7.2, \dfrac {-3}{2}, \dfrac {-12}{5}$$.
Find the multiplicative inverse of $$(-7)^{-2}\div (90)^{-1}$$.
Find three rational numbers between:
$$0.1$$ and $$0.11$$.
Verify commutative property of multiplication for the following pairs of rational numbers:
$$\dfrac{4}{5}$$ and $$\dfrac{-7}{8}$$
Find the multiplication inverse of the following:
$$\left(\dfrac{81}{16}\right)^{-\tfrac{3}{4}}$$
Find the multiplication inverse of the following:
$$\left(\dfrac 57\right)^{-2}\times \left(\dfrac 57\right)^4 \div \left(\dfrac 57\right)^3$$
Show that the set of all non-zero rational numbers is not closed under addition.
Mark the following pairs of rational numbers on the number line :
$$ \dfrac{2}{5} $$ and $$ \dfrac{-4}{5} $$
Find the multiplication inverse of the following:
$$\left\{(-3/2)^{-4}\right\}^{1/2}$$
Write the rational numbers for each point labeled with a letter.

Mark the following pairs of rational numbers on the number line:
$$ \dfrac{2}{5} $$ and $$ \dfrac{-3}{5} $$
Mark the following pairs of rational numbers on the number line:
$$ \dfrac{5}{6} $$ and $$ \dfrac{-2}{6} $$
Write the rational numbers for each point labeled with a letter.

For each pair of , verify commutative property of addition of rational numbers.
$$ \dfrac{5}{9} and \dfrac{5}{-12}$$
Find the multiplicative inverse of the following rational numbers.
$$\displaystyle \frac { 8 }{ 13 } ,\frac { -13 }{ 11 } ,\frac { 12 }{ 17 } ,\frac { -101 }{ 100 } ,\frac { 26 }{ 23 } $$
For each set of rational numbers , given below , verify the associative property of addition of rational numbers .
$$ \dfrac{-2}{5} , \dfrac{4}{15} and \dfrac{-7}{10} $$
Write the additive inverse (negative ) of :
$$ \dfrac{-3}{8}$$
For each set of rational numbers , given below , verify the associative property of addition of rational numbers .
$$ - 1 \dfrac{5}{6} and \dfrac{-2}{3} $$
For each pair of , verify commutative property of addition of rational numbers.
$$ - 2 and \dfrac{3}{-5} $$
For each pair of , verify commutative property of addition of rational numbers.
$$ \dfrac{2}{-5} + \dfrac{11}{-15} = \dfrac{11}{-15} + \dfrac{2}{-5} $$
For each set of rational numbers , given below , verify the associative property of addition of rational numbers .
$$ \dfrac{-7}{9} , \dfrac{2}{-3} and \dfrac{-5}{18}$$
For the given pair of rational numbers, verify commutative property of addition of rational numbers.
$$ 3 $$ and $$ \dfrac{-2}{7} $$
For each set of rational numbers , given below , verify the associative property of addition of rational numbers .
$$ \dfrac{1}{2} , \dfrac{2}{3} and -\dfrac{1}{6}$$
Write the additive inverse (negative ) of :
$$ \dfrac{4}{-9}$$
Write the additive inverse (negative ) of :
-2
Class 8 Maths Extra Questions
- Algebraic Expressions And Identities Extra Questions
- Comparing Quantities Extra Questions
- Cubes And Cube Roots Extra Questions
- Data Handling Extra Questions
- Direct And Inverse Proportions Extra Questions
- Exponents And Powers Extra Questions
- Factorisation Extra Questions
- Introduction To Graphs Extra Questions
- Linear Equations In One Variable Extra Questions
- Mensuration Extra Questions
- Playing With Numbers Extra Questions
- Practical Geometry Extra Questions
- Rational Numbers Extra Questions
- Squares And Square Roots Extra Questions
- Understanding Quadrilaterals Extra Questions
- Visualising Solid Shapes Extra Questions