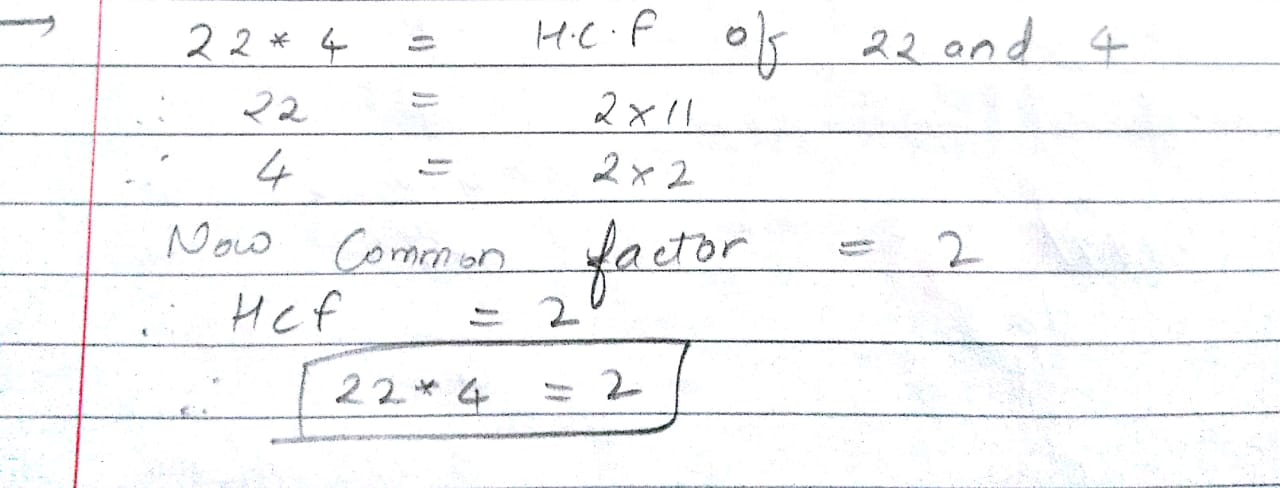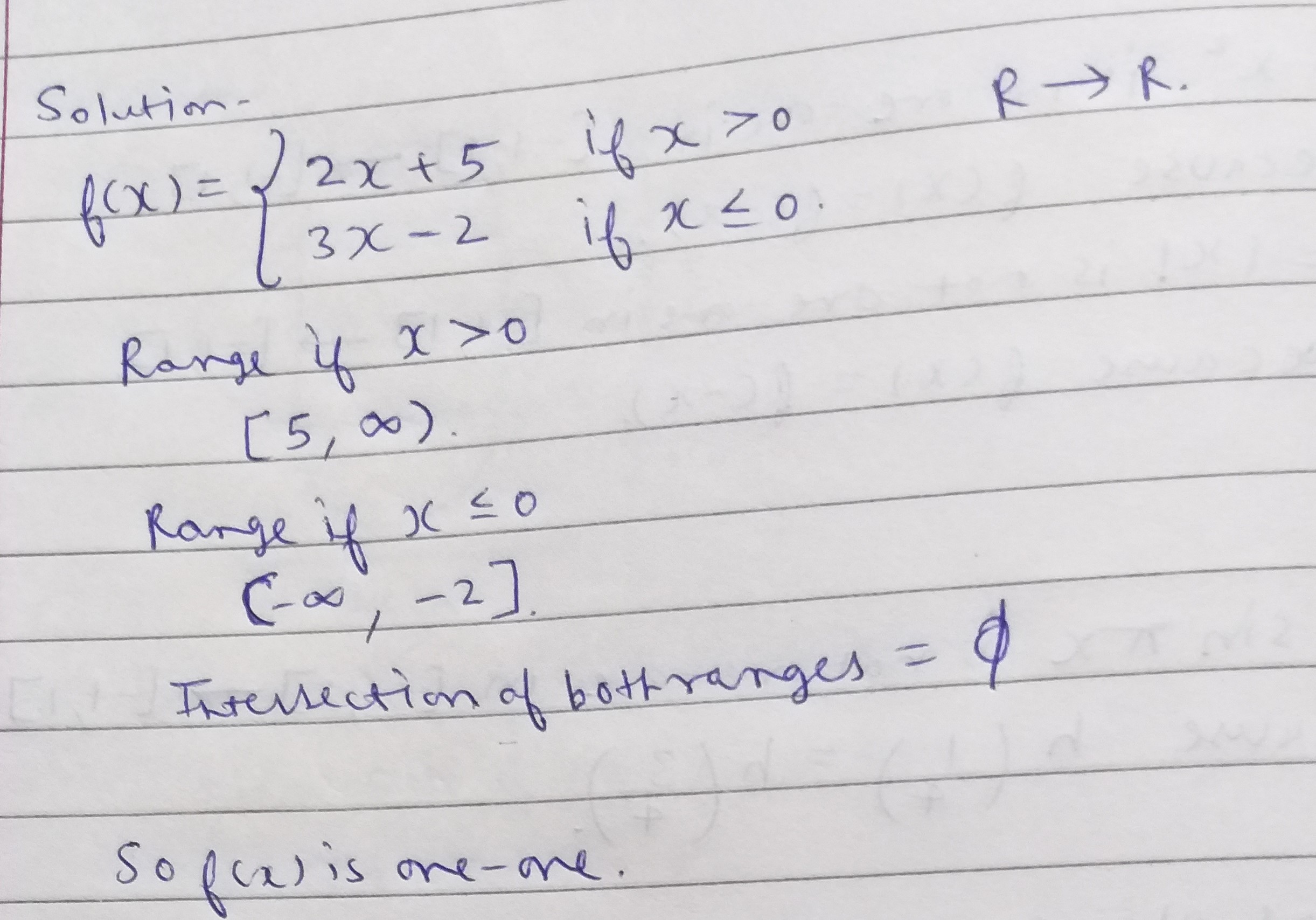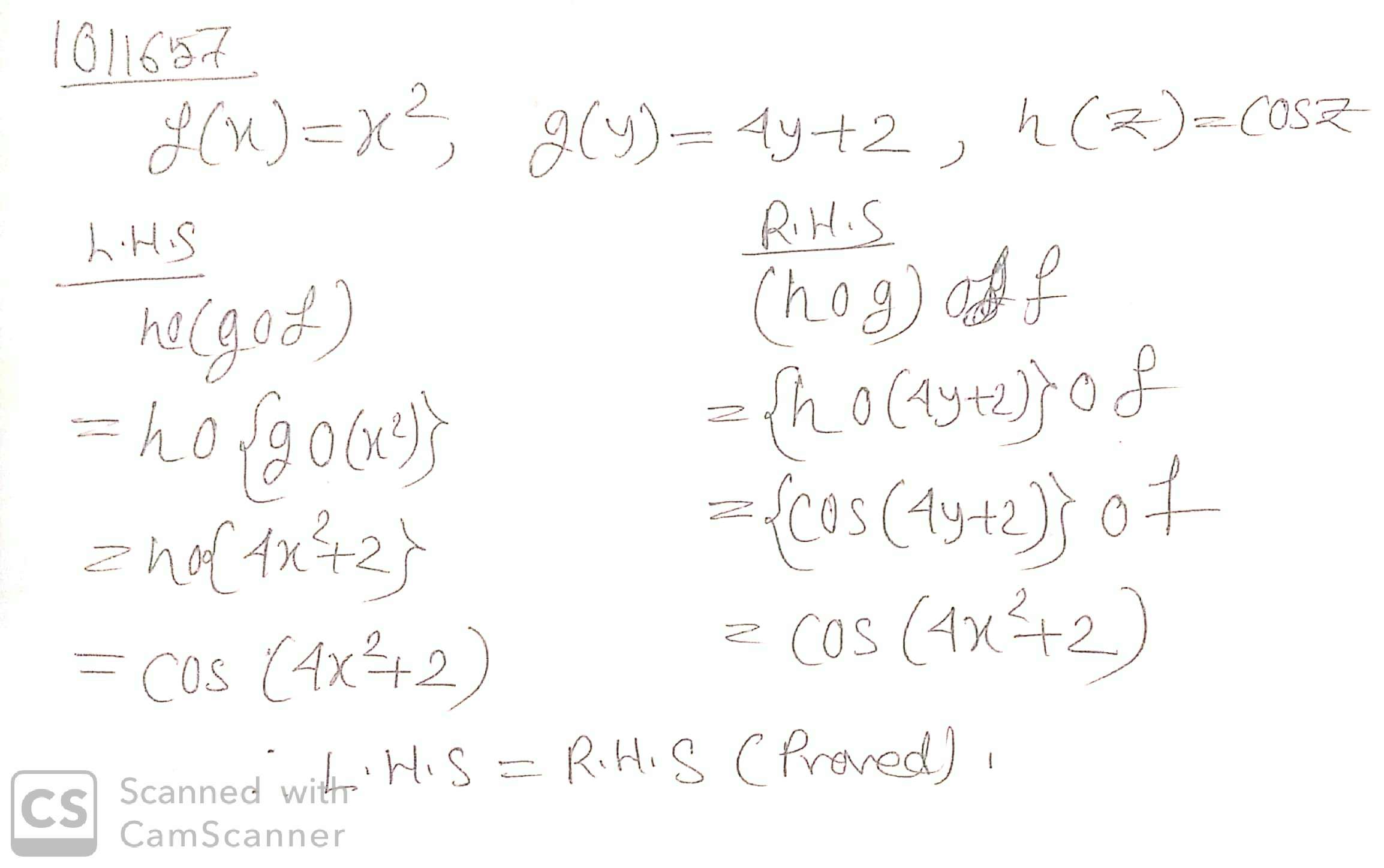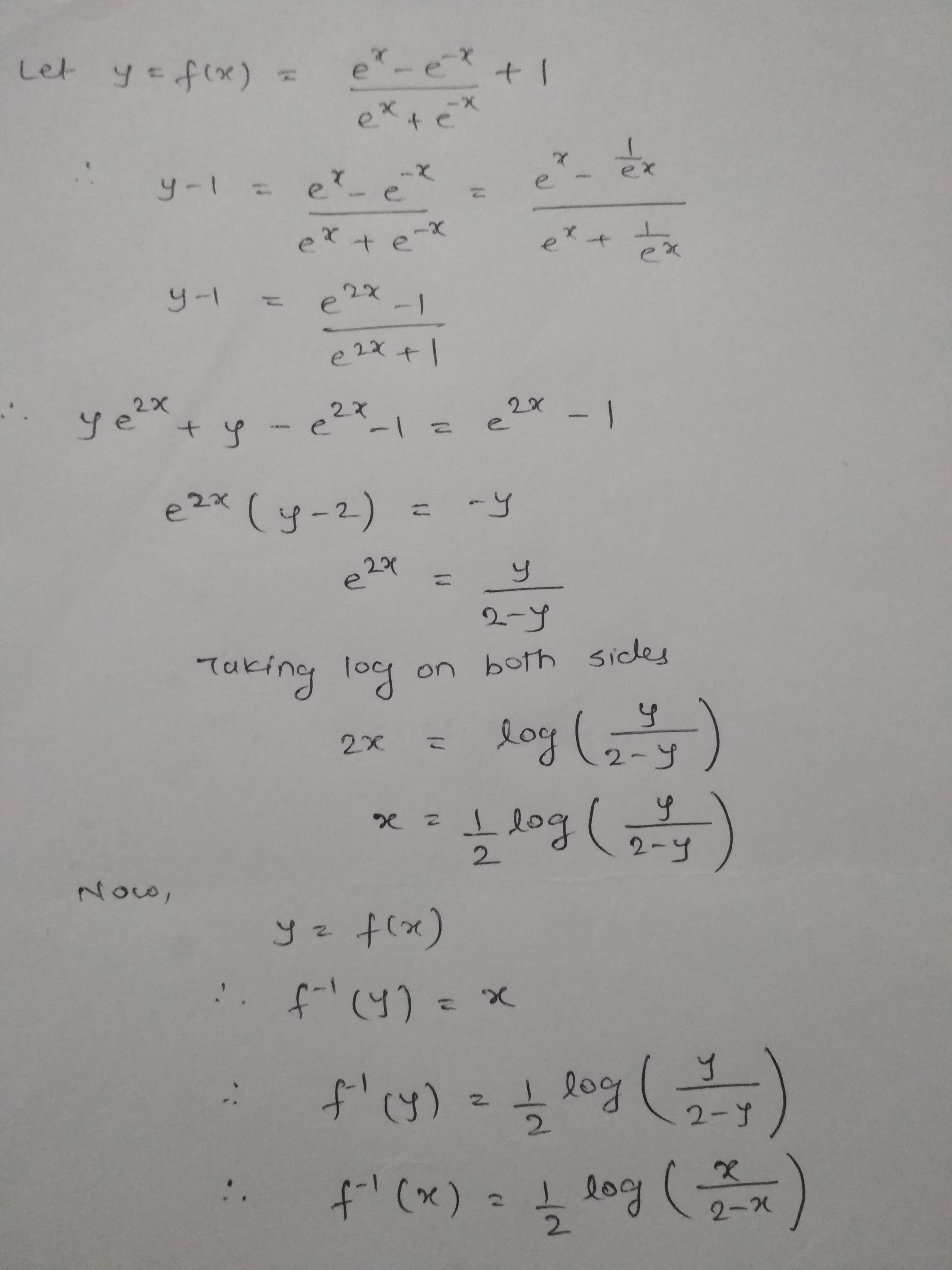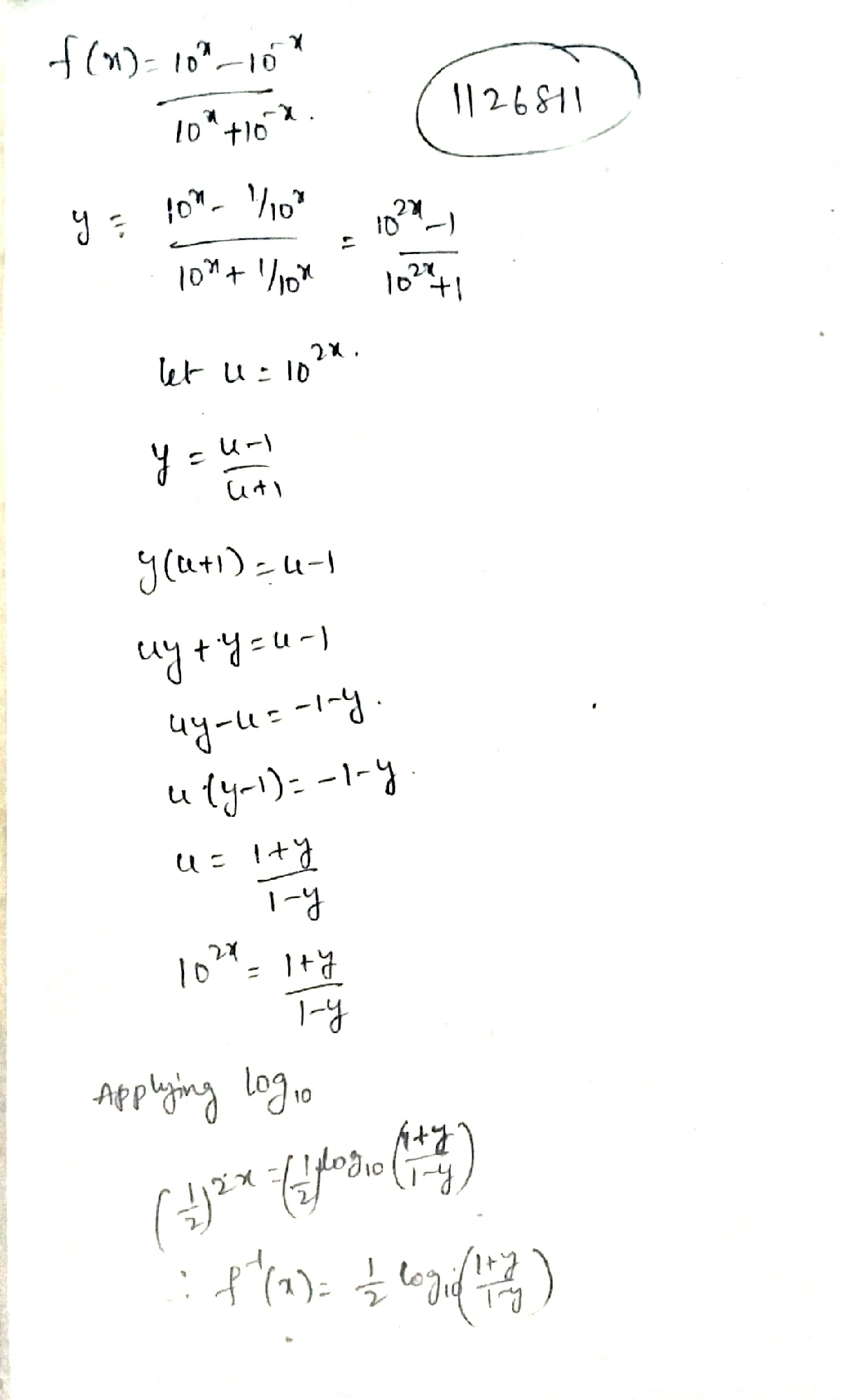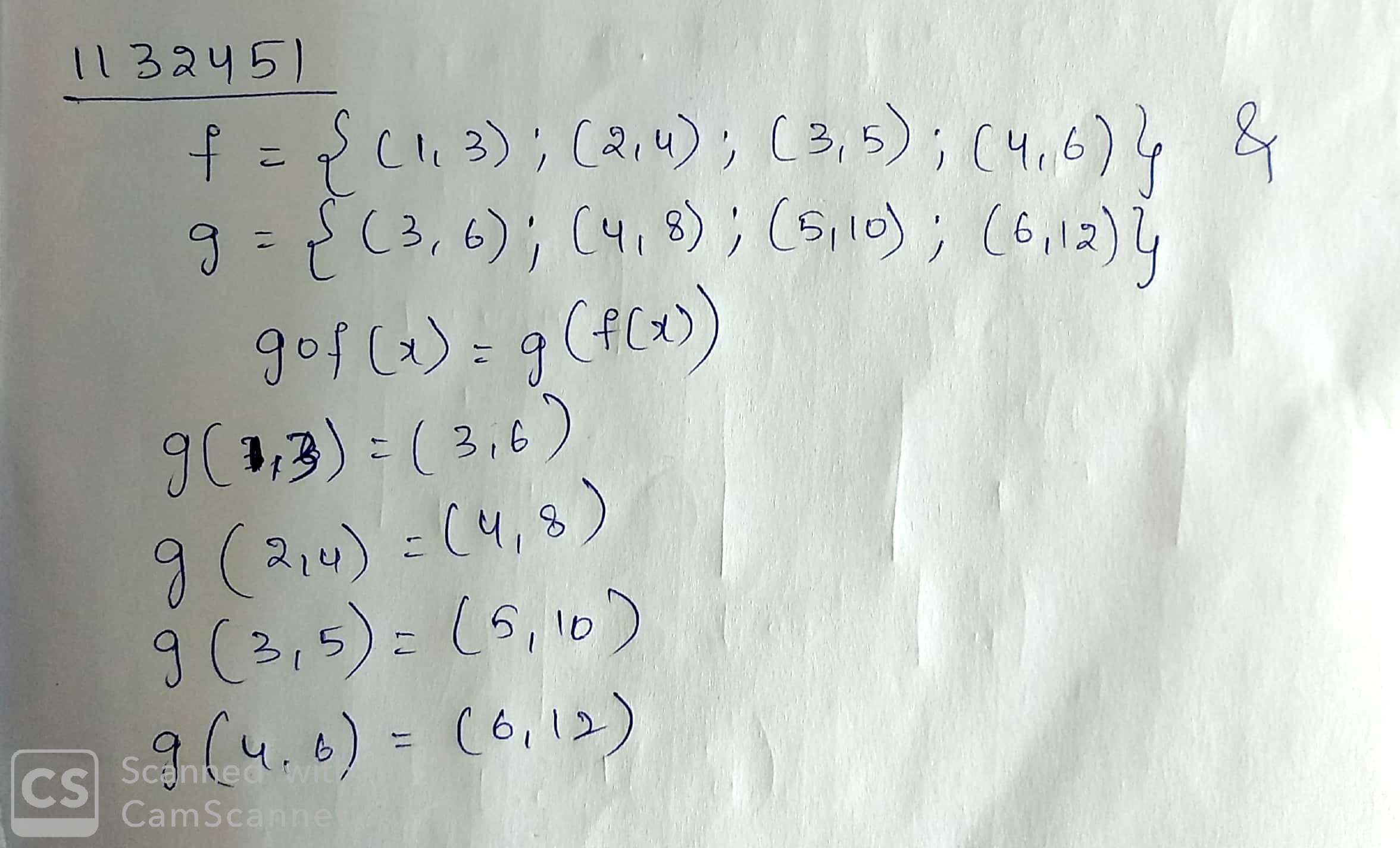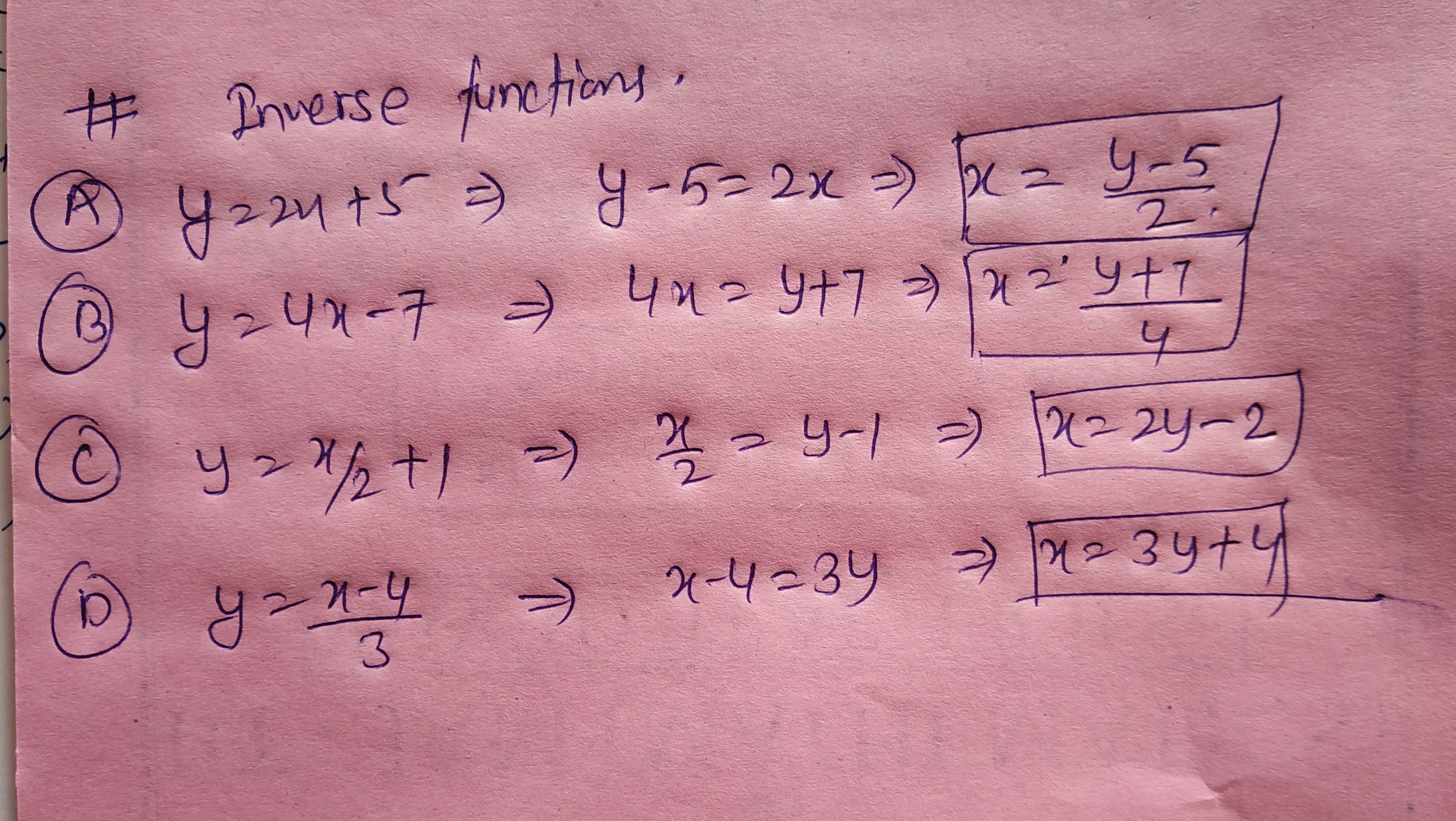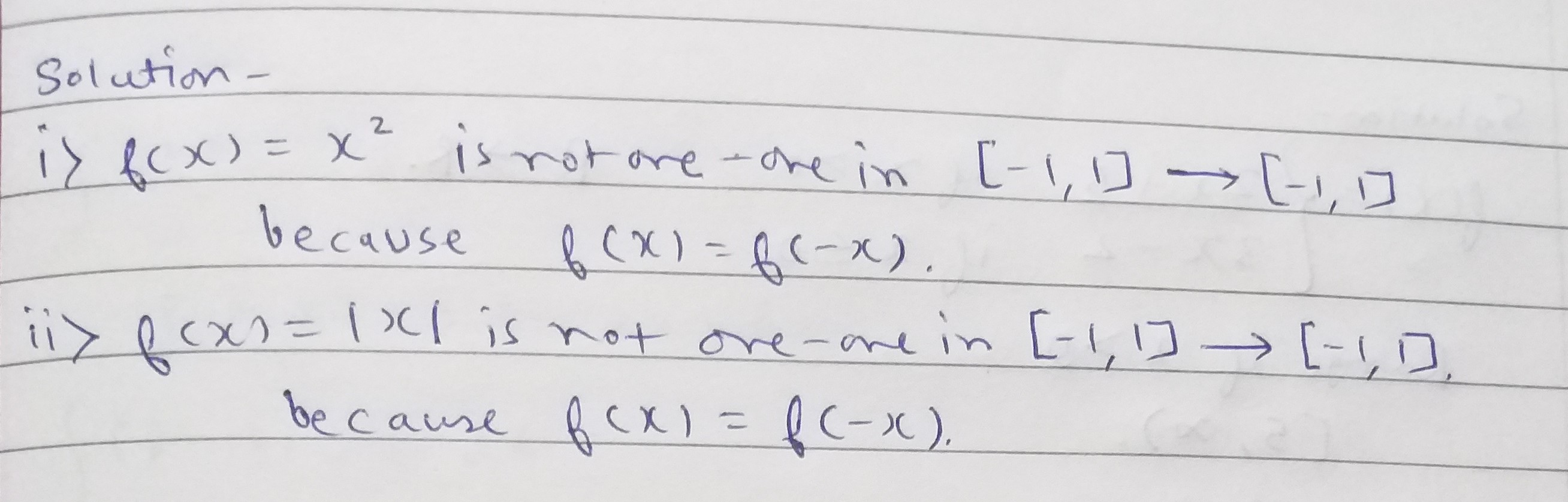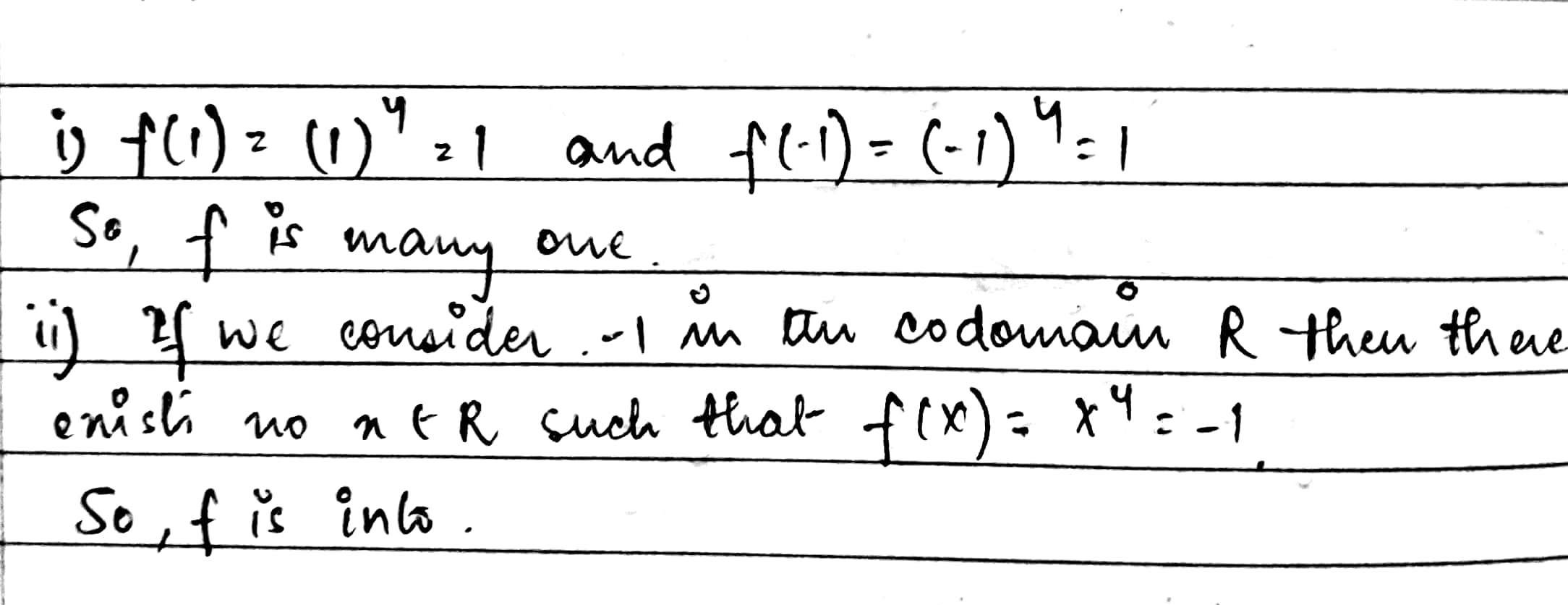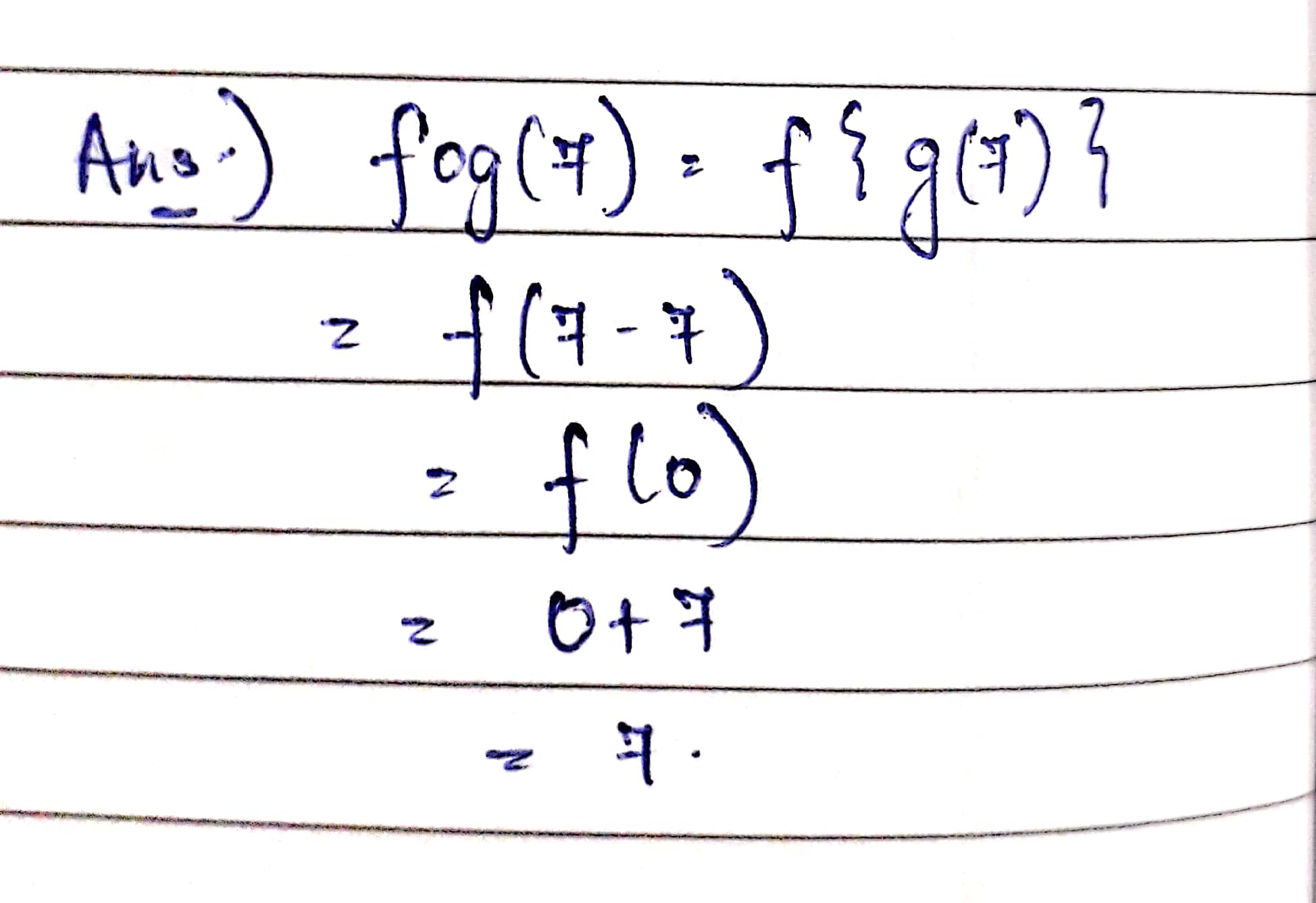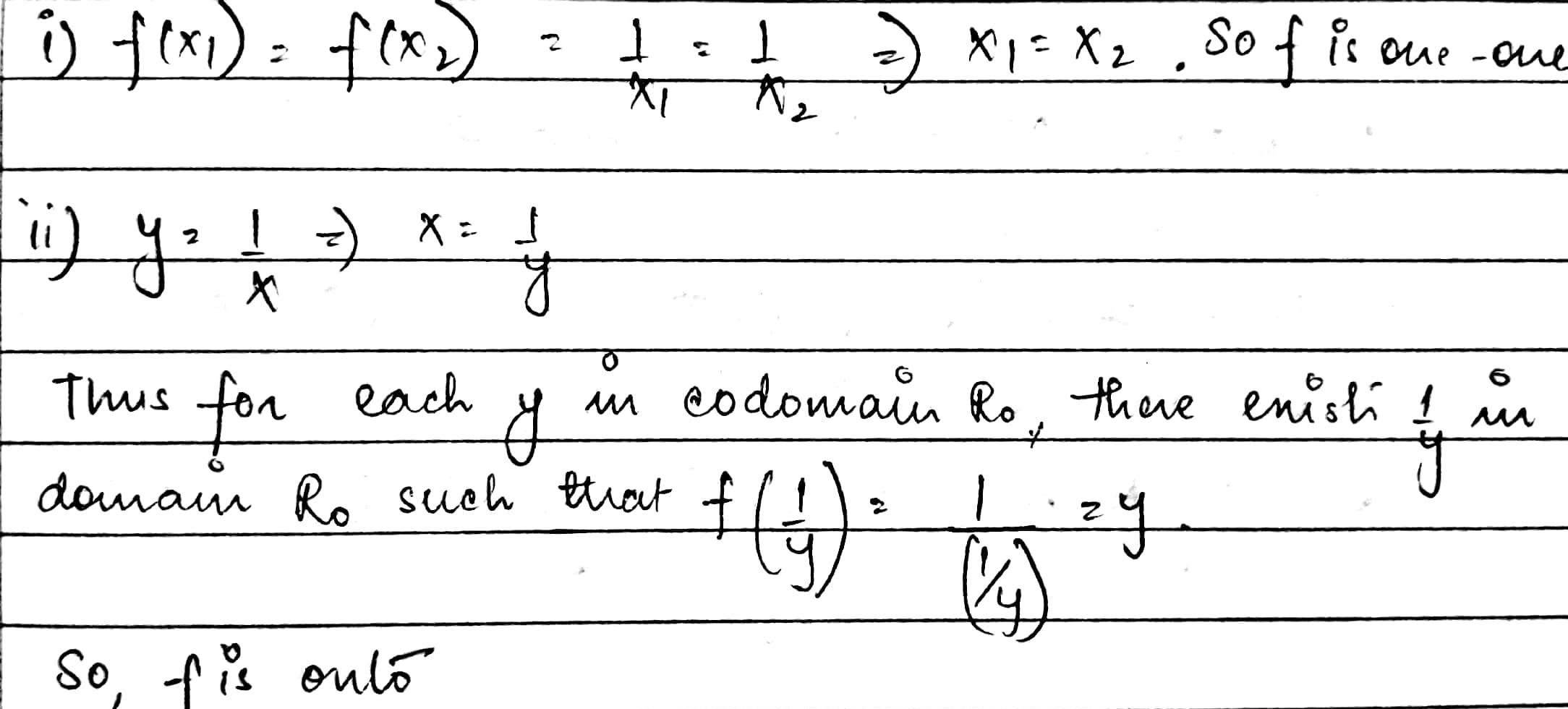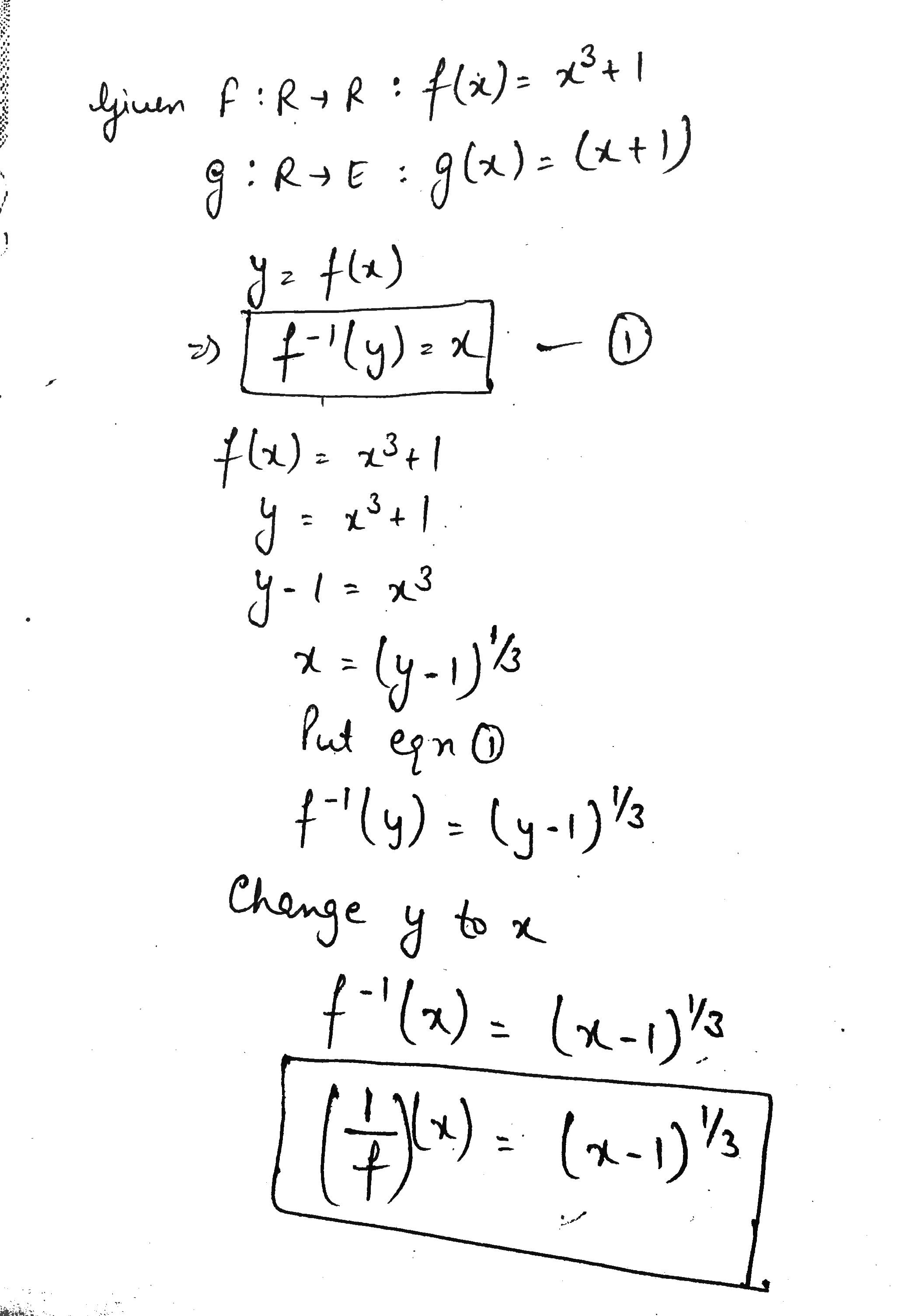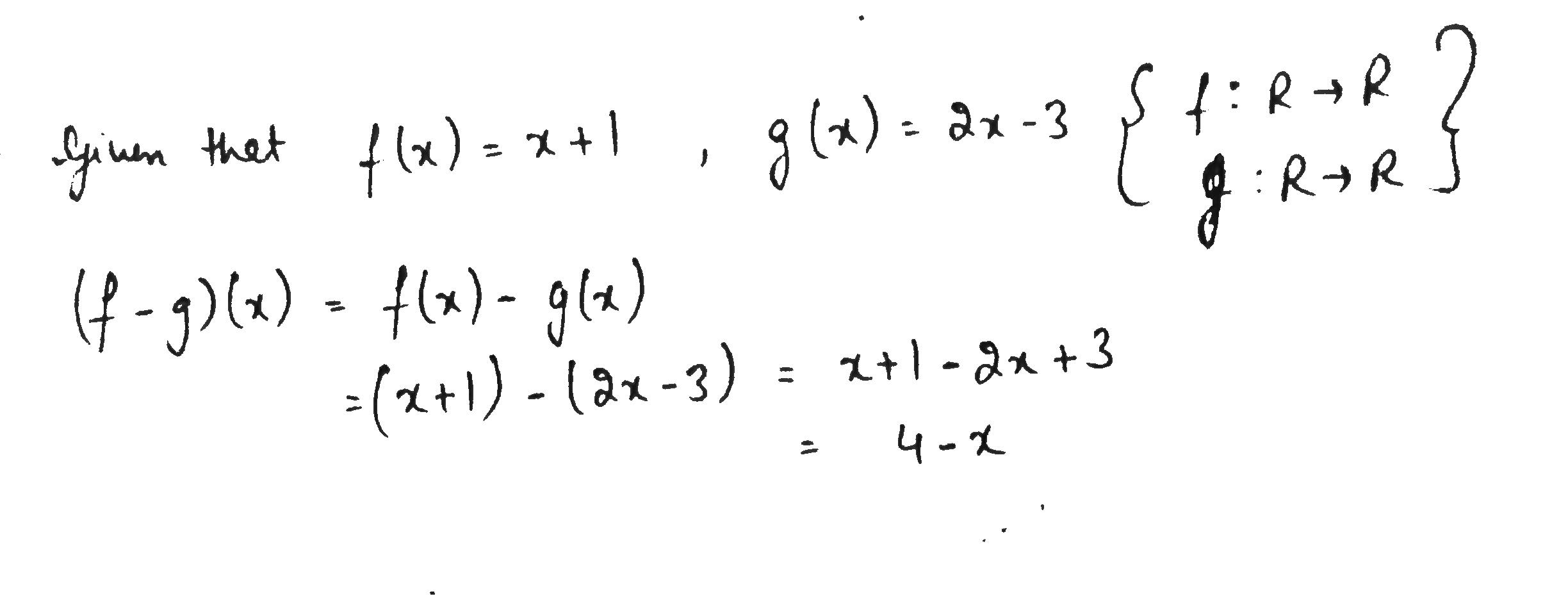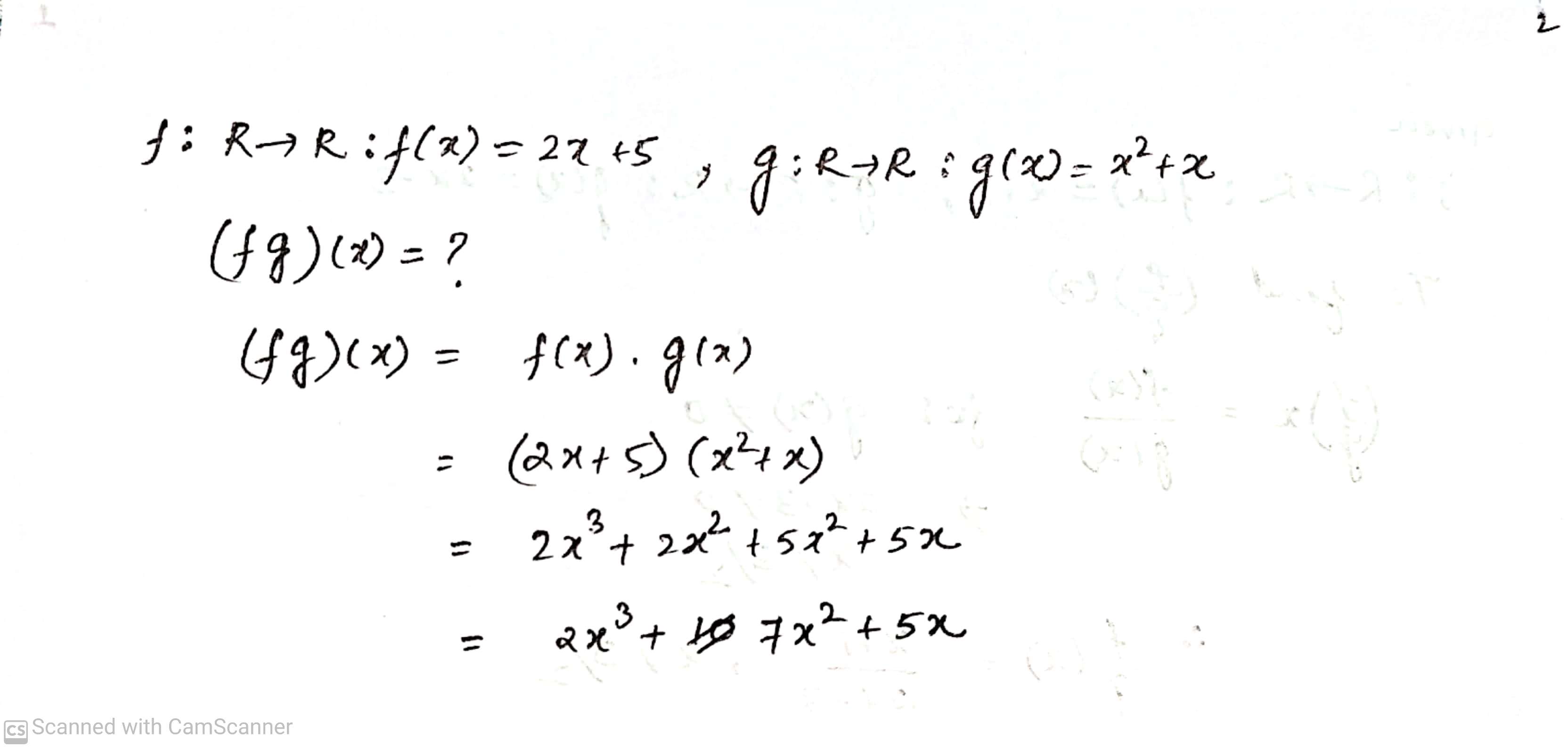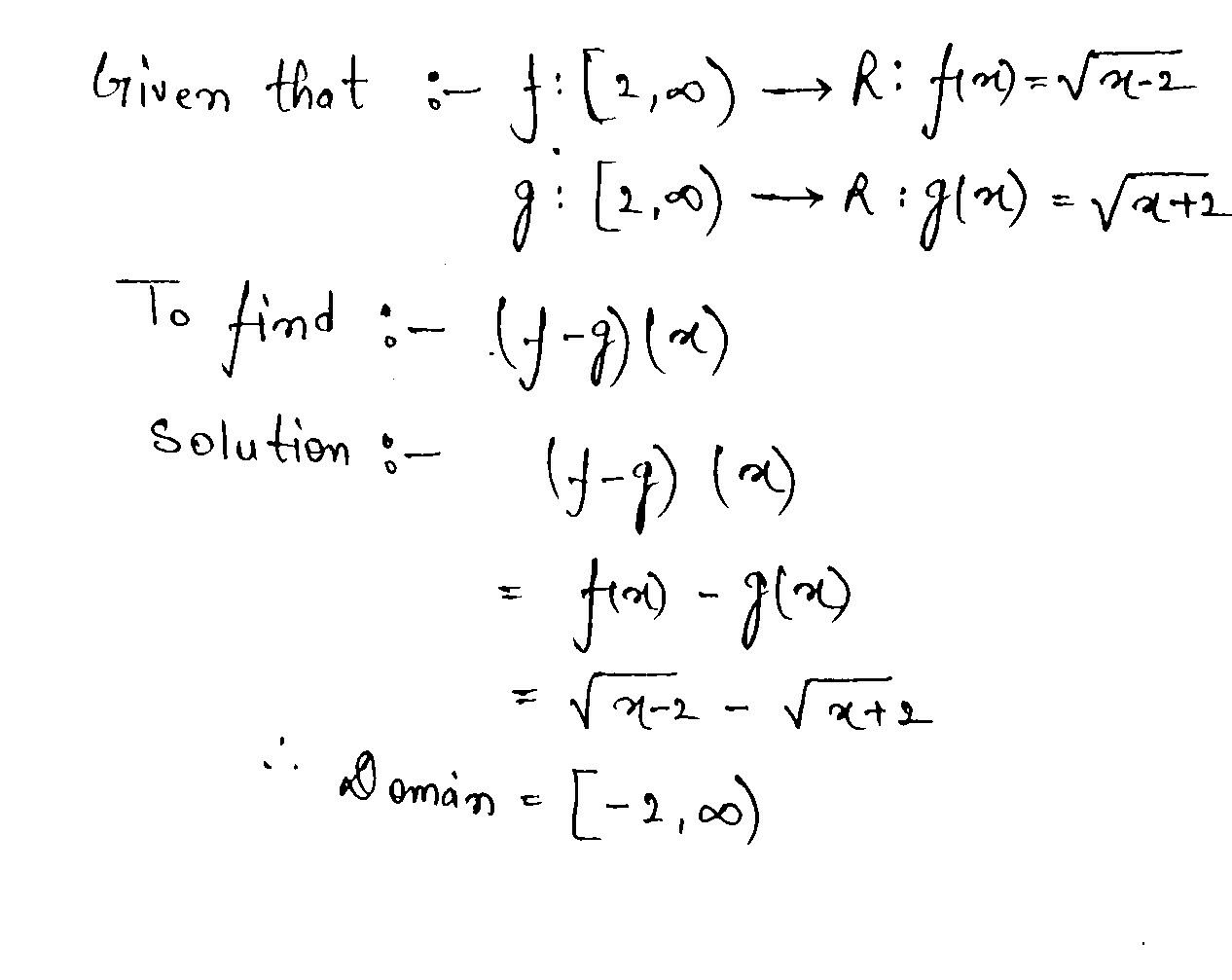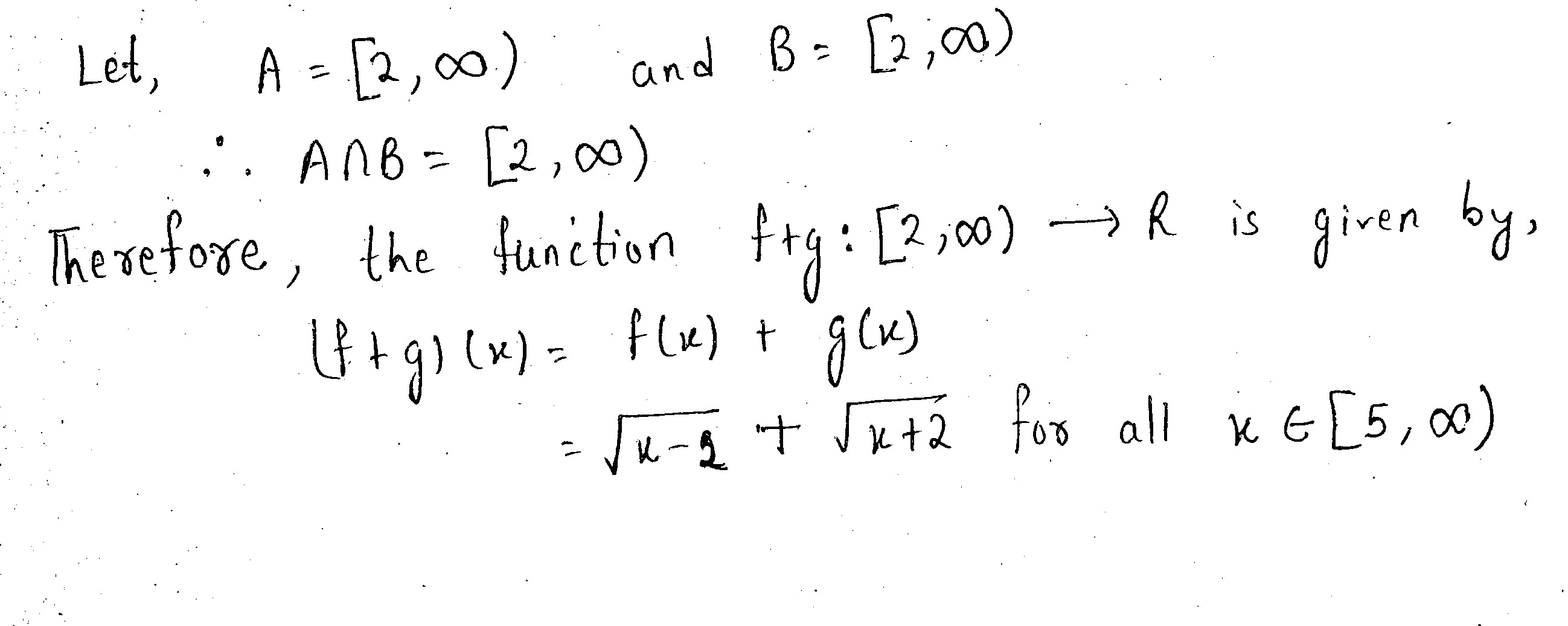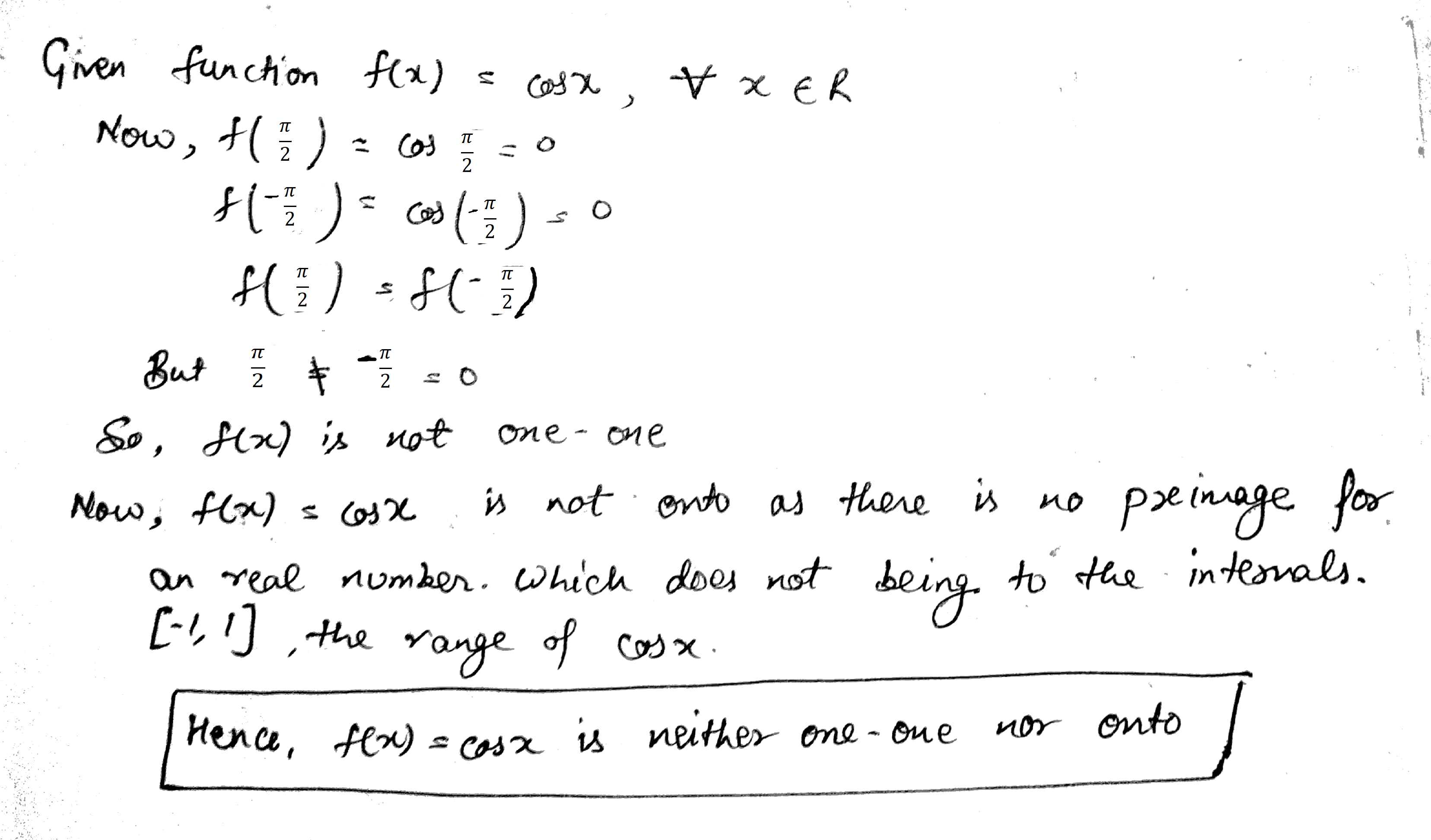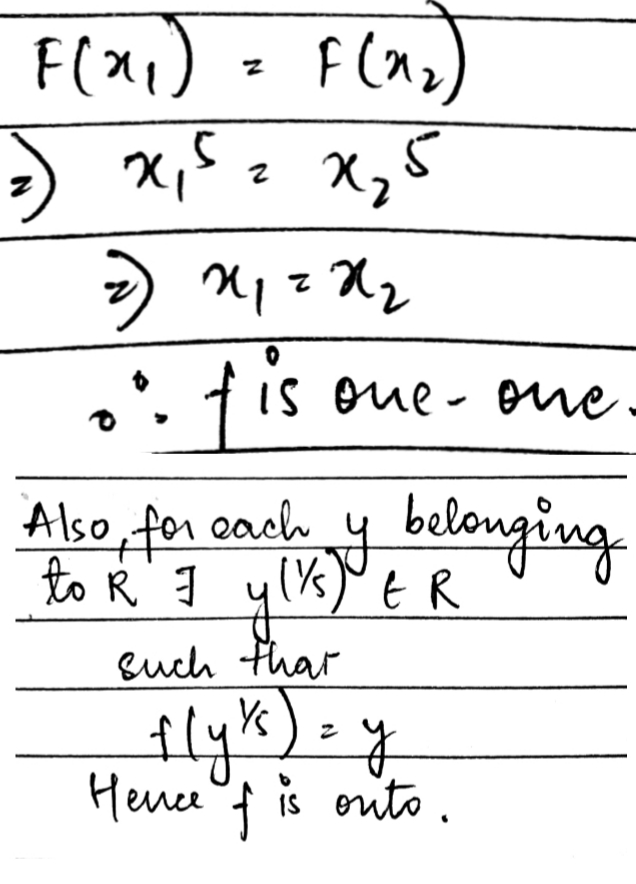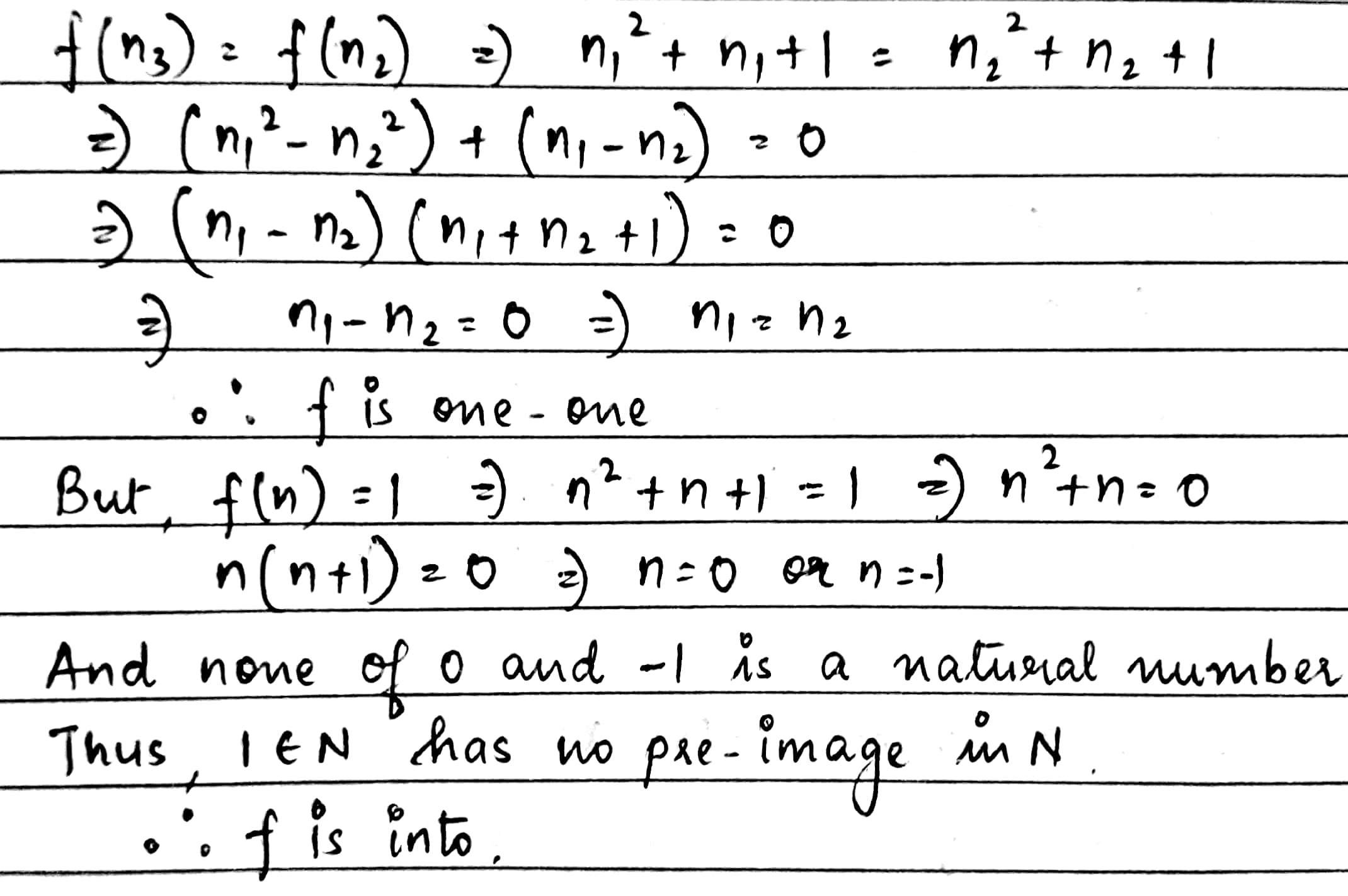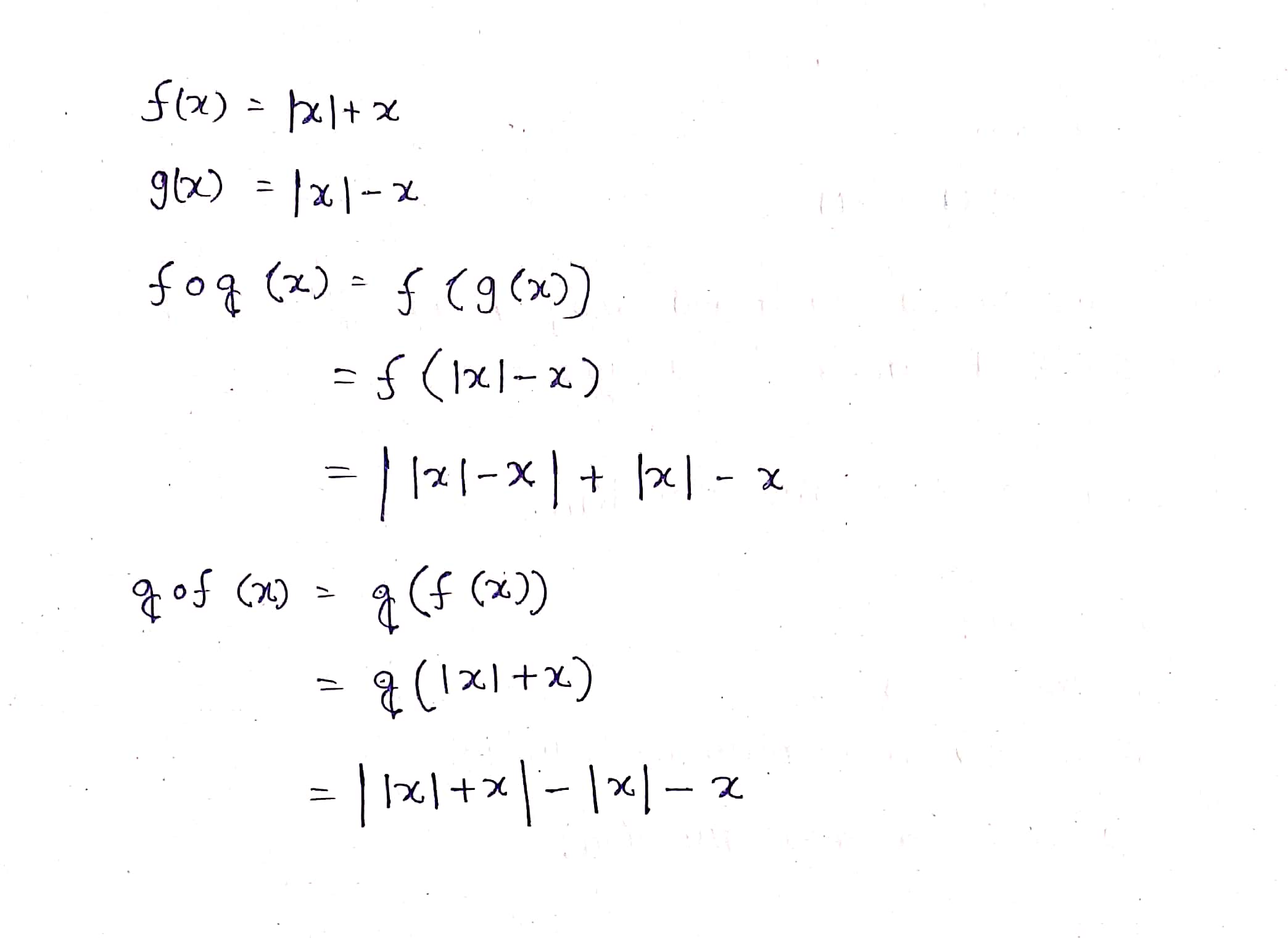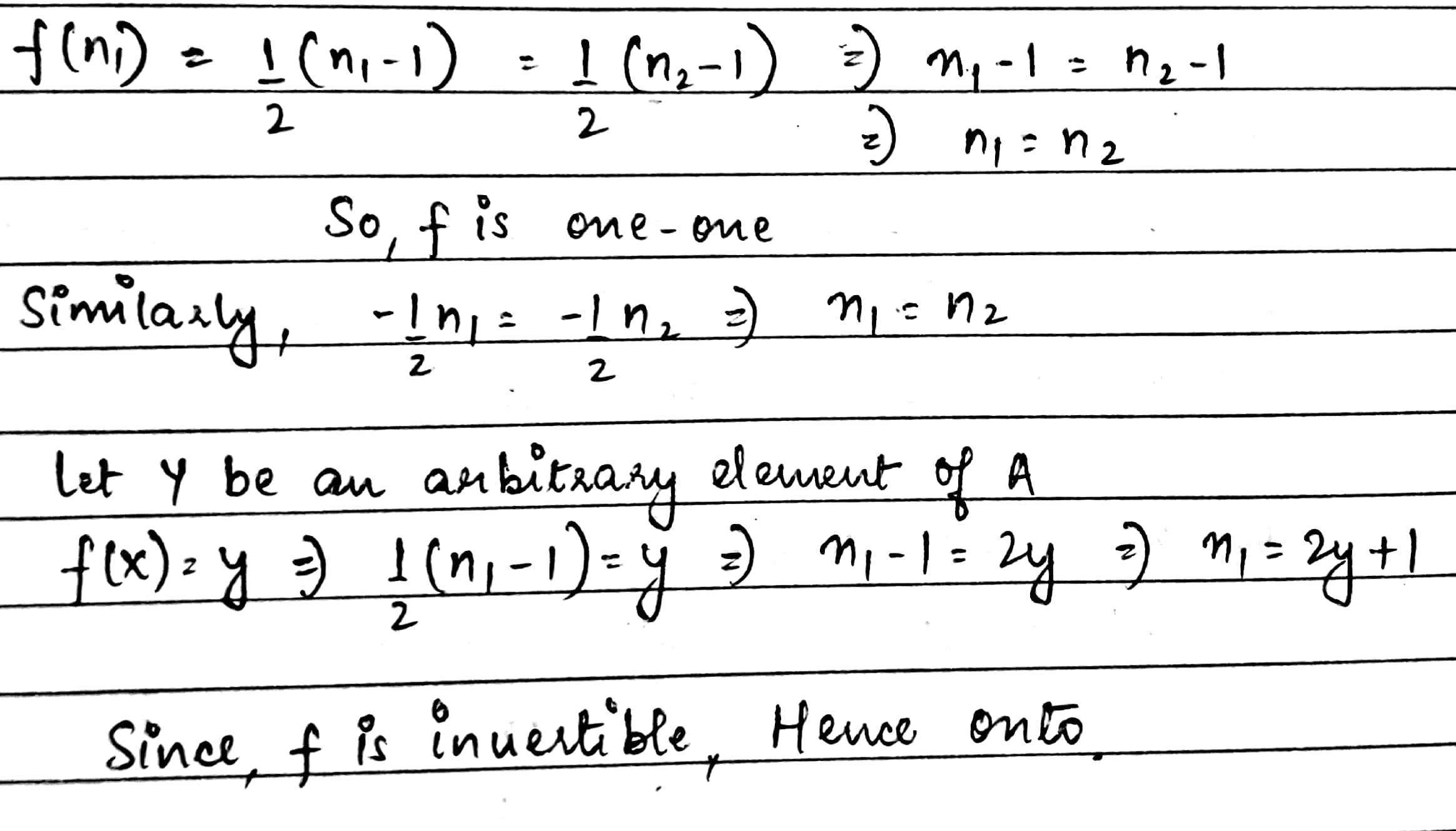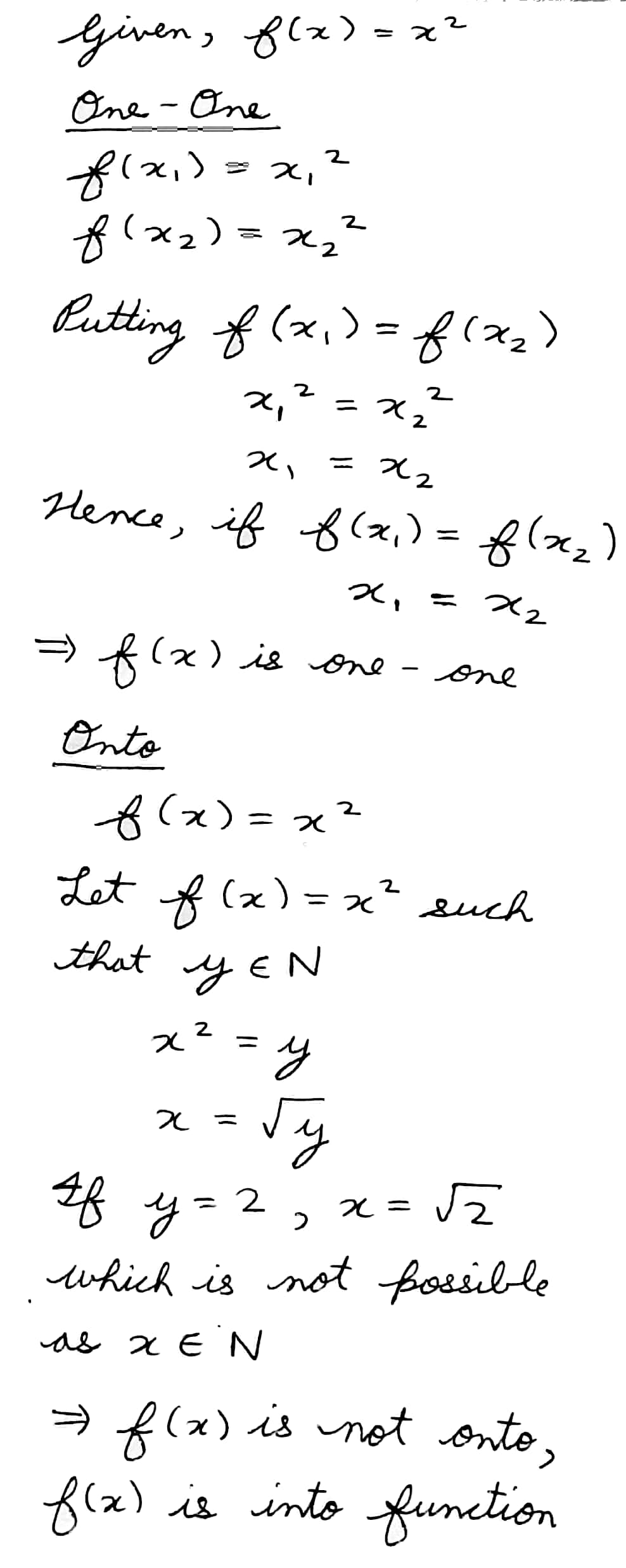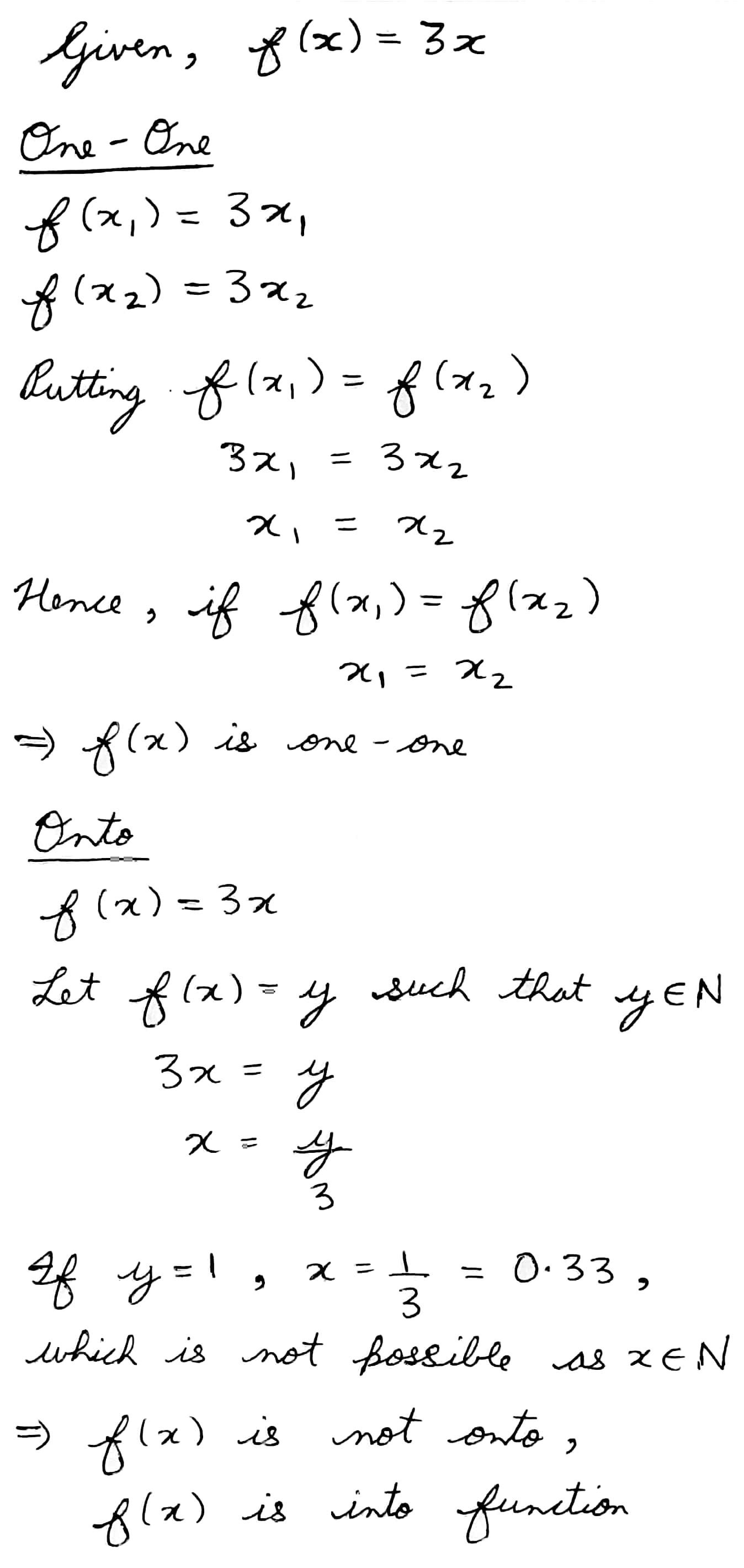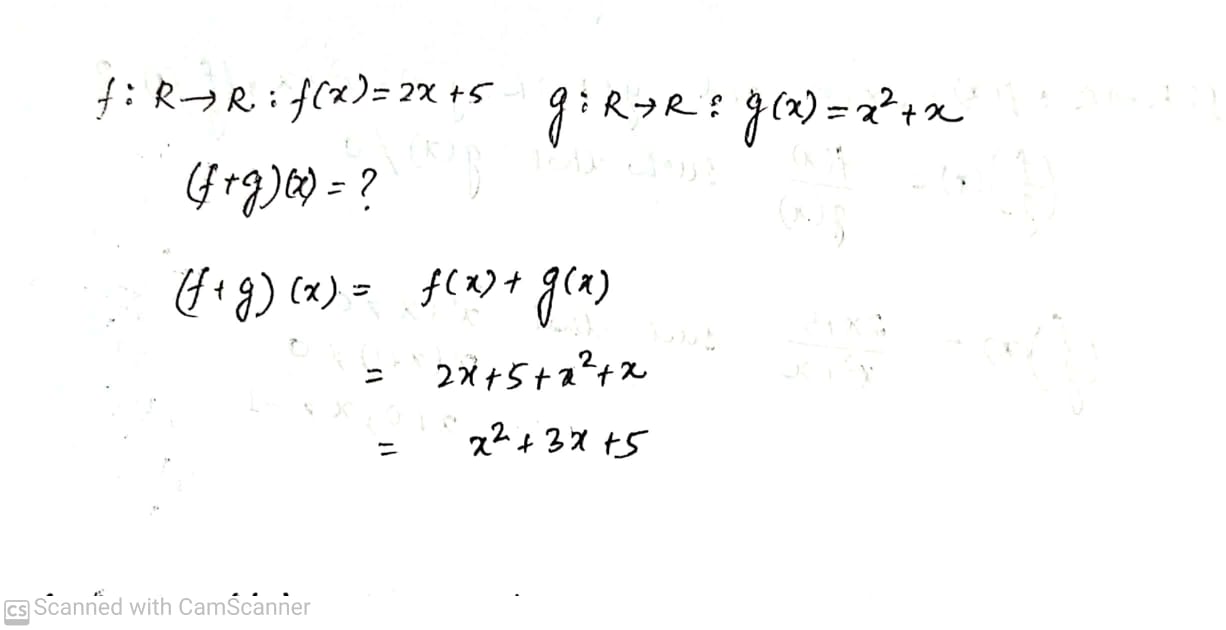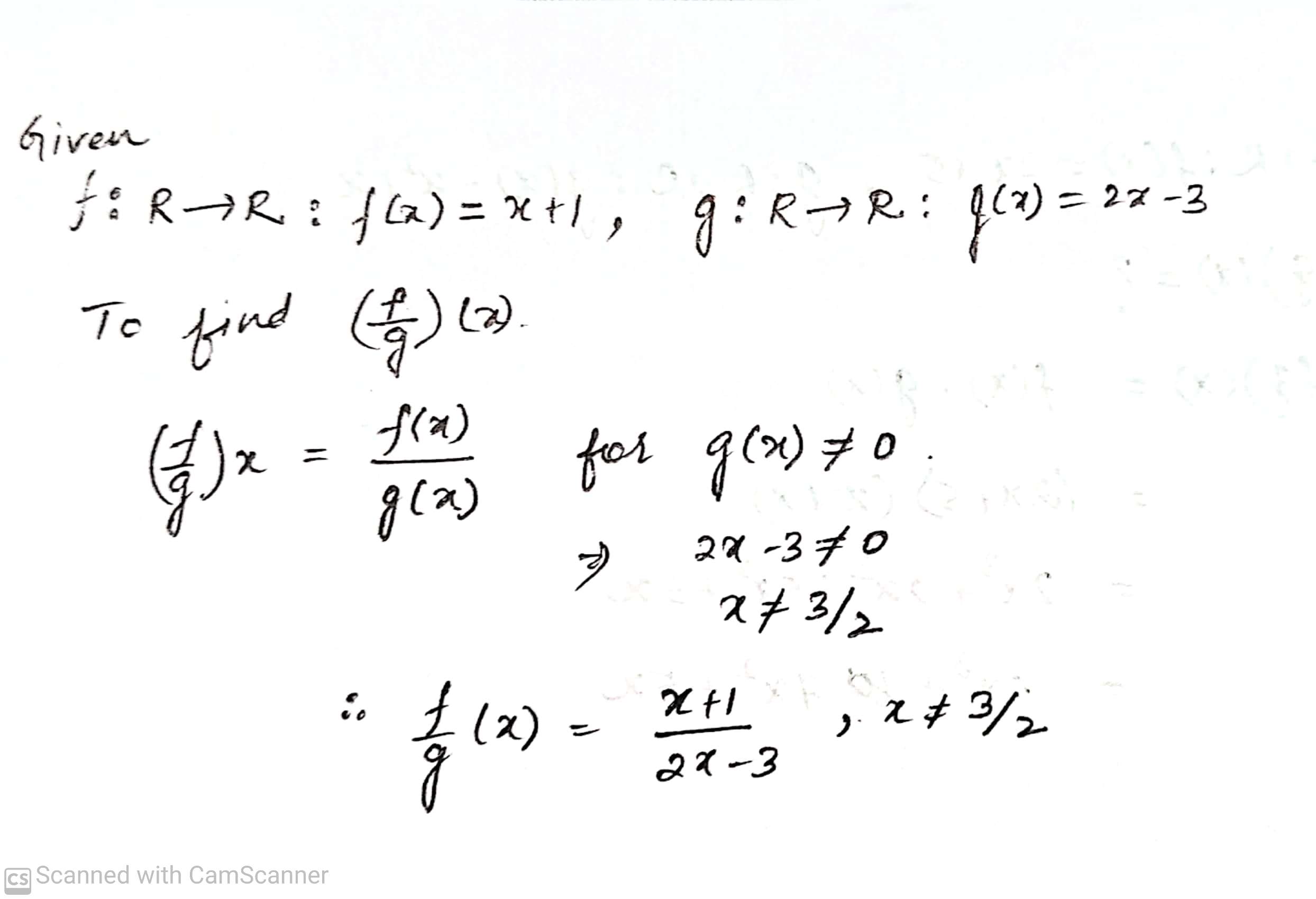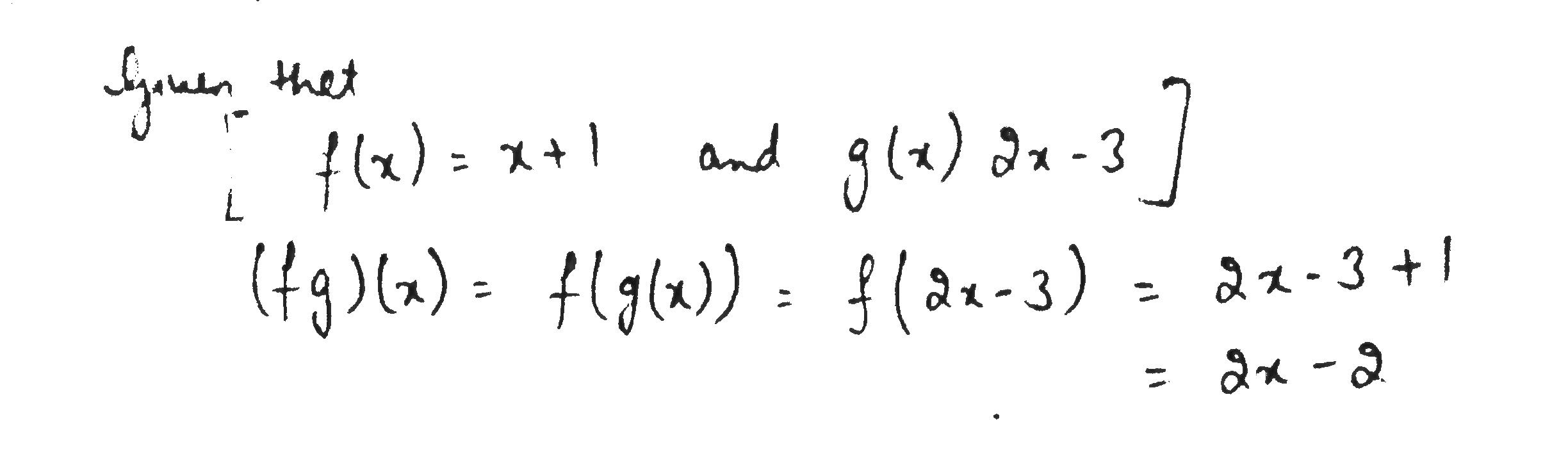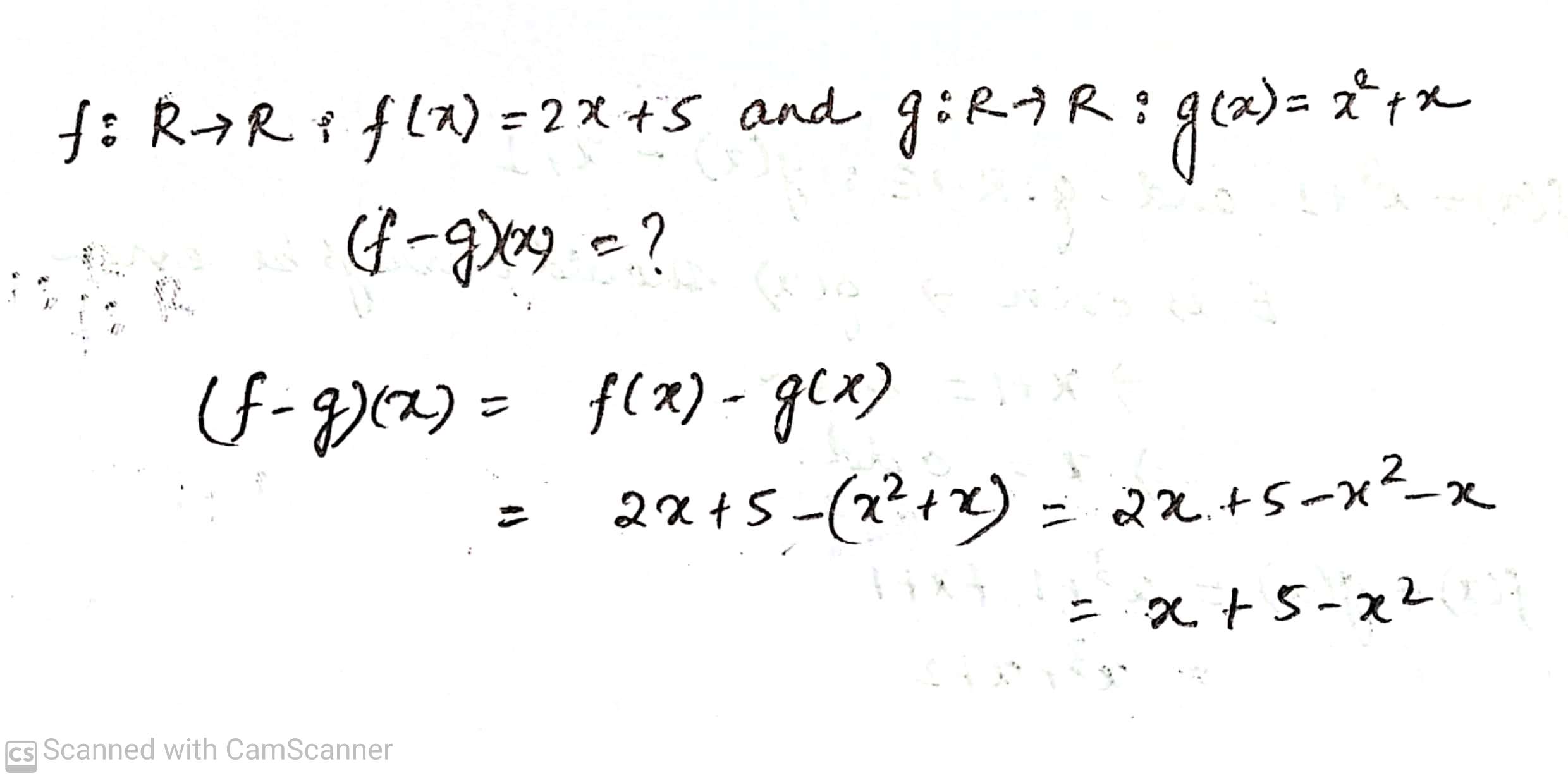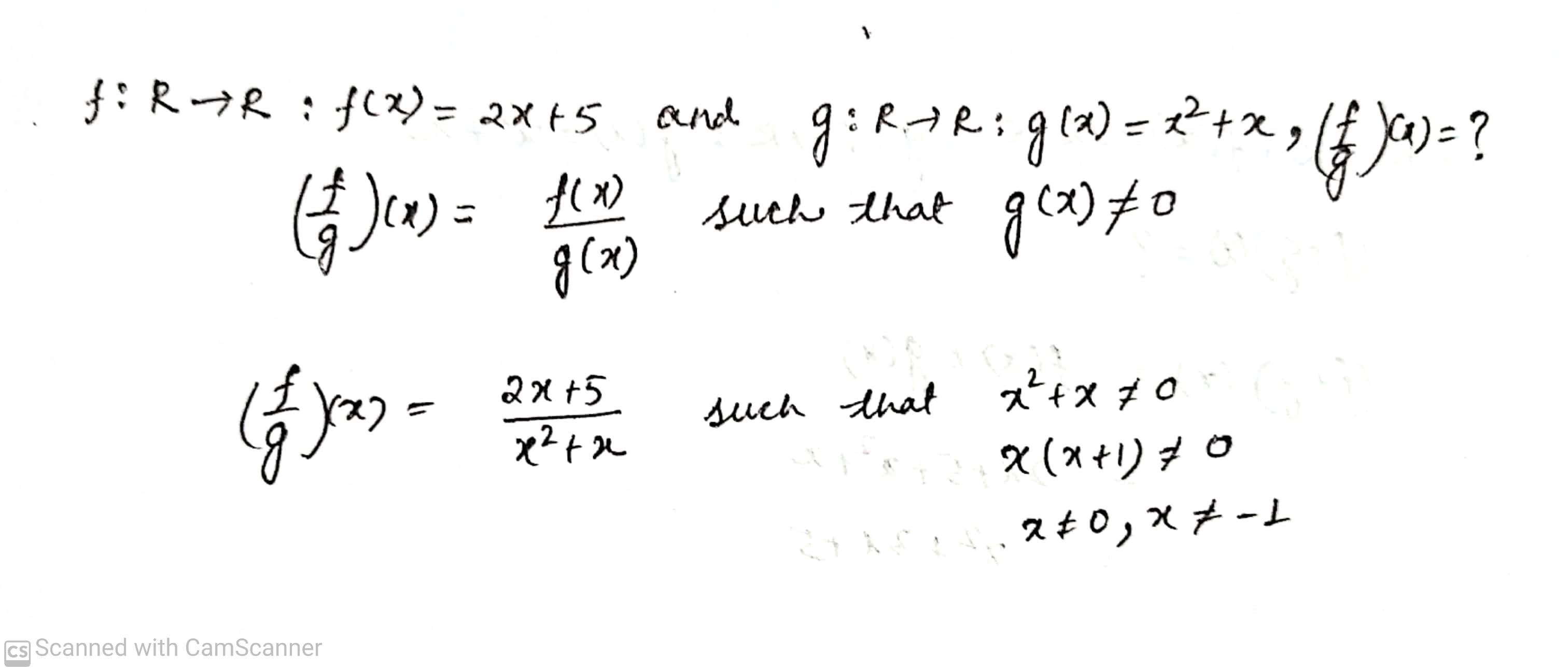Relations And Functions - Class 12 Commerce Maths - Extra Questions
Let the functions $$f: (-1, 1) \rightarrow R$$ and $$g: (-1, 1) \rightarrow (-1, 1)$$ be defined by $$f(x) = |2x - 1| + |2x + 1| $$ and $$g(x) = x - [x]$$, where $$[x]$$ denotes the greatest integer less than or equal to x. Let $$f \circ g : (-1, 1) \rightarrow R$$ be the composite function defined by $$(f \circ g) (x) = f(g(x))$$. Suppose c is the number of points in the interval $$(−1, 1) $$ at which $$f \circ g$$ is NOT continuous, and suppose d is the number of points in the interval $$(−1, 1)$$ at which $$f \circ g$$ is NOT differentiable. Then the value of $$c + d$$ is _____.
Let $$A=\left \{ 2, 3, 5, 7, 10 \right \}$$ show that the relation
(i) $$R_{1}$$ is A defined as "is equal to" is an identify relation. (ii) $$R_{2}$$ is A defined as "difference is an integer" is the universal relation in A.
If the function $$\displaystyle f(x)=\left\{\begin{matrix} x,&x<1\\x^{2},&1\leq x\leq 4\\8\sqrt{x},&x>4 \end {matrix}\right.$$
then find $$\displaystyle f^{-1}(9)= $$
If $$\displaystyle f\left ( x \right )=x^{6}+3x^{3}+1$$ then find $$\displaystyle f\left ( \frac{1}{x} \right )$$ in terms of f(x)
Is function $$g$$ defined by
$$g(x)=\left\{ () \right\} $$
a one to one function?
If $$f(x) = 3x - 1$$ and $$g(x)= 4x + 2$$, what if the value of $$g(f(0) + 2)$$?
If a function $$f:R\rightarrow R$$ is defined by $$f(x)=3x+4$$ show that $${f}^{-1}$$ (the inverse function of $$f$$) exists and find it.
If $$f(x) = \log x$$ and $$g(x) =x^3$$ find $$fog(a) + fog(b)$$.
Let A = { 1, 2, 3, 4, 5 }, B = N and $$f: A \rightarrow B$$ be defined by$$f(x)=x^2$$.
Find the range of f. Identify the type of function.
Given $$f(x)=\dfrac{8}{x}, x\neq 0$$ and $$\text{fog}(x)=4x$$, find the (i) $$g(x)$$ (ii) the value of $$x$$, when $$\text{gof} (x)=3$$.
Given the function $$f(x) =\dfrac{x-2}{5}$$ and $$\text{gof}(x)=x-3$$. Find the component function $$g$$.
Let $$*$$ be a operation defined on the set of rational numbers by $$a*b=\dfrac{ab}{4}$$, find the identity element.
Let $$f : N\rightarrow Y$$ be a function defined as $$f(x) = 4x + 3$$, where, $$Y = \left \{y\epsilon N : y = 4x + 3 \text {for some}x\epsilon N\right \}$$. Show that $$f$$ is invertible. Find the inverse function
If function $$f : R\rightarrow R$$ and $$g : R\rightarrow R$$ are given by $$f(x) = |x|$$ and $$g(x) = [x]$$, (where $$[x]$$ is greatest integer function) find $$f\circ g\left(-\dfrac{1}{2}\right)$$ and $$g\circ f \left(-\dfrac{1}{2}\right)$$.
An equation $$*$$ on $$Z^+$$ (the set of all non-negative integers) is defined as $$a*b=a-b, \forall a, b \in Z^+$$. Is $$*$$ a binary operation on $$Z^+$$ ?
Let $$\ast$$ be an operation such that $$a \ast b = $$LCM of $$a$$ and $$b$$ defined on the set $$A = \left\{ 1,2,3,4,5 \right\}$$. Is $$ \ast$$ a binary operation? Justify your answer.
If $$g:N\rightarrow N$$ is given by $$g(n)=2n+3$$, and $$f:N\rightarrow N$$ is given by $$f(n)=n+1$$, then find $$g\circ f$$, $$f\circ g$$ and $$g\circ g$$
Find $$gof\left( x \right)$$, if $$ f\left( x \right) =8{ x }^{ 3 }$$ and $$g\left( x \right) ={ x }^{ { 1 }/{ 3 } }$$.
If $$a\ast b$$ denotes the larger of $$'a'$$ and $$'b' $$ and if $$aob=(a\ast b) +3,$$ then write the value of $$(5$$ $$o$$ $$10),$$ where $$\ast$$ and $$o$$ are binary operations.
Let $$f:N\rightarrow R$$ be a function defined as $$f(x)=4{x}^{2}+12x+15$$ that $$f:N\rightarrow S$$ where $$S$$ is range of $${f}_{a}$$ is invariable. Find the inverse $$f(x)$$.
Prove that the function $$f(x)=x+|x|$$, $$x\in \mathbb{R}$$. is not injective.
If $$a\ast b=\cfrac { ab }{ 10 } $$ on $${Q}^{+}$$, then find the identity for $$\ast$$.
The function $$f:\mathbb{R}\to \mathbb{R}$$ be defined by $$f(x)=(x^2+1)^{35}$$. Prove that the function $$f(x)$$ is not one-one.
If $$h(x)=2x, g(x)=x^2, f(x)=2$$, then find $$(f \circ g \circ h)(x).$$
Define a binary operation on a set.
Consider functions f and g such that composite gof is defined and is one are g both necessarily one-one.
Given that $$f(x) = {\left( {a - {x^n}} \right)^{\cfrac{1}{n}}};2 > 0,n \in N$$, show that $$f\left( {f(x)} \right) = x$$.
If $$f : R \rightarrow R$$ defined by $$f(x) = (3 - x^3)^{\dfrac{1}{3}}$$, then find $$(fof) (x).$$
Show that the function $$f$$ in A =$$R = \dfrac{2}{3}$$ defined by $$f\left( x \right) = \dfrac{{3x + 2}}{{5x + 3}},$$ $$ \ne \dfrac{{ - 3}}{5}$$ is one-one and onto.Hence find $${f^{ - 1}}\left( x \right)$$
Let $$\ast$$ be a binary operation on the set of all non zero real numbers, given by $$a\ast b=\cfrac{ab}{5}\forall a,b\in R-\left\{ 0 \right\} $$, find the value of $$x$$, given that $$2\ast(x\ast 5)=10$$
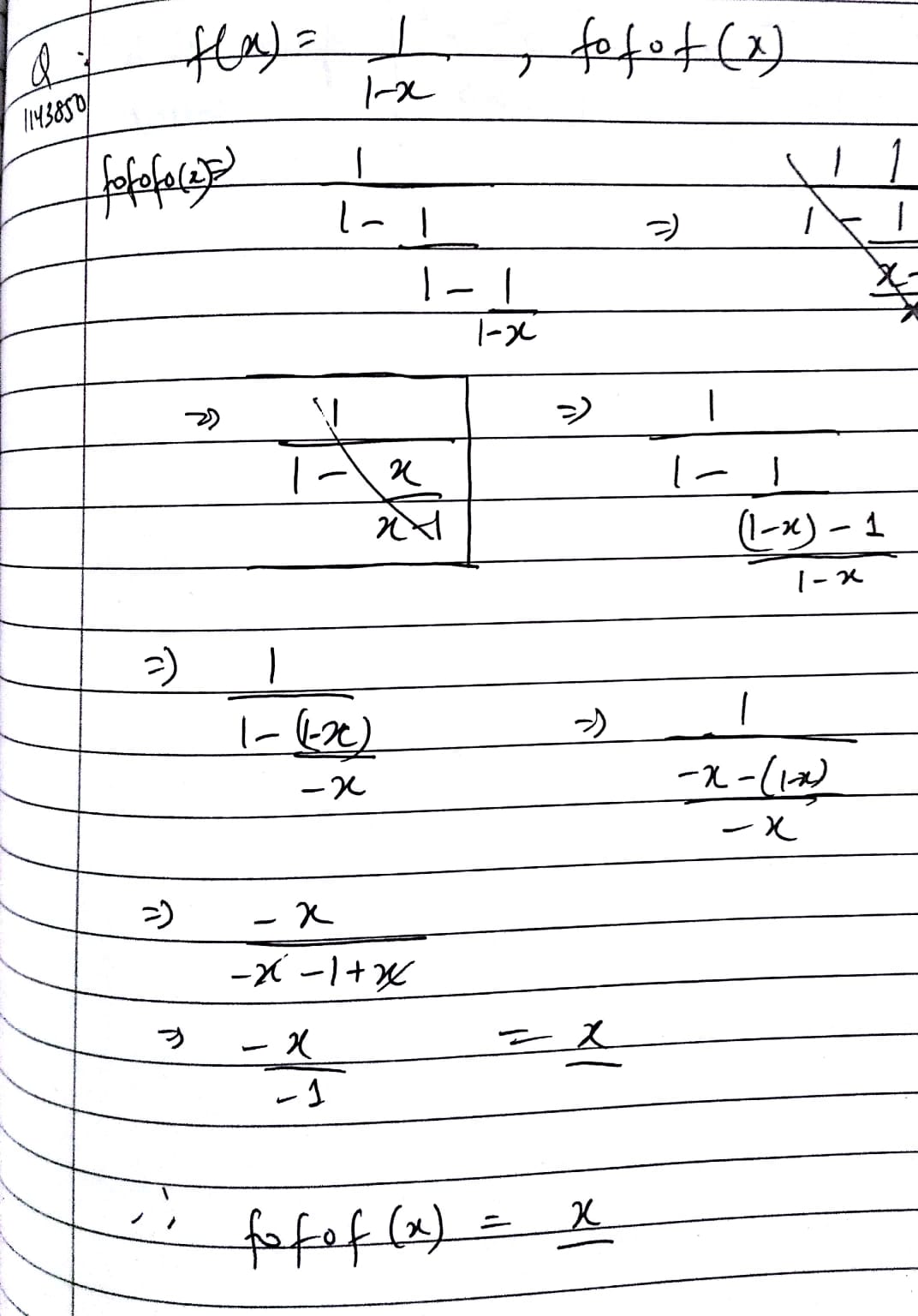
If $$f(x) = \dfrac{1}{1-x}$$, then $$(f \,o \,f \, o \,f)(x)$$ is
If $$f ( x ) = \dfrac { x + 1 } { x - 1 } ,$$ then show that $$f ( x ) + f \left( \begin{array} { l } { 1 } \\ { x } \end{array} \right) = 0$$.
If $$f ( x ) = 2 x + 1$$ and $$g ( x ) = x - 3 $$ find $$fog$$.
Let $$*$$ be $$a$$ binary operation on $$N$$ given by $$a*b=HCF*(a,b)$$ find $$22*4$$
Solve: If $$f(x)=(x-1)(2x+1)$$ Find $$f(1),f(2)$$and $$f(-3)$$
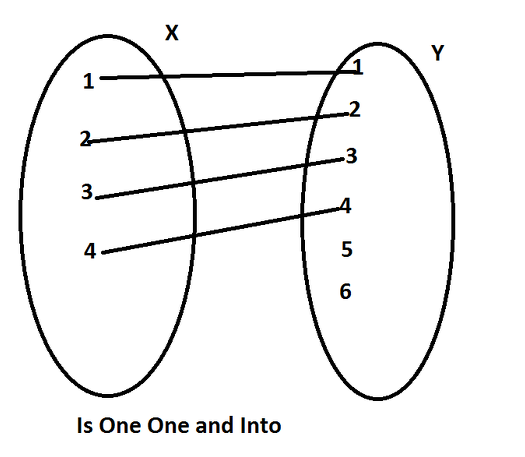
Show that the function $$f:N\rightarrow N$$, given by $$f(1)=f(2)=1$$ and $$f(x)=x-1$$ for every $$x>2$$, is onto but not one-one.
$$f$$ from $$R$$ into $$R$$ is defined as
$$f\left( x \right) = \left\{ \begin{array}{l}2x + 5,\,\,if\,x > 0\\3x - 2,\,if\,x \le 0\end{array} \right.$$ Show that $$F$$ is one -one.
Let $$*:R\times R \rightarrow R$$ given by $$(a,b)\rightarrow a+4b^2$$ is a binary operation, compute $$(-5)*(2*0)$$.
If f(x) =$$x^{ 2 }$$ and $$g(x)=2x+1$$ be two real valued function. Find $$f\left(g\left(x\right)\right)$$ and $$\dfrac{f\left(x\right)}{g\left(x\right)}$$
Let '$$o$$' be a binary operation on the set $$Q_{0}$$ of all non-zero rational numbers defined by $$a\, o\, b= \dfrac{ab}{2}$$, for all $$a,b \in Q_{0}$$. Show that '$$o$$' is commutative.
For what value of k, the matrix $$\begin{bmatrix} 2-k & 4 \\ -5 & 1 \end{bmatrix}$$ is not invertible?
Let $$A= R_{0}\times R$$, where $$R_{0}$$ denote the set of all non-zero real numbers. A binary operation 'O' is defined on A as follows: $$(a,b)O(c,d)= (ac, bc+d)$$ for all $$(a,b)(c,d)\in R_{0}\times R$$
Find the invertible elements in A.
Check the commutativity and associativity of the following binary operation:
$$'\ast '$$ on $$Q$$ defined by $$a \ast b= ab+1$$ for all $$a,b \in Q$$.
If $$f(x)=\left [4-(x-7)^3 \right]$$, then $$f^{-1}(x)=$$ .......
Using the definition, prove that the function $$f:A\to B$$ is invertible if and only if $$f$$ is both one-one and onto.
Let $$R$$ be the set of real numbers and $$^*be$$ the binary operation defined on $$R$$ as $$a^*b=a+b-ab \ \forall\ a,b\ \in R$$ Then, the identity element with respect to the binary operation $$*$$ is _______.
State how many of $$(1, 0)\ (-2, -1)\ (7, -6)\ (-3, 4)\ (0, 2) \left (\dfrac{-1}{2}, \dfrac{1}{2} \right )$$ are not the elements of the relation:
$$\left \{ (x, y):y=1-\left | x \right |; x, y\in Q \right \}$$
A mapping is defined as $$f: R\rightarrow R, f(x)= \cos x$$. Show that it is neither one-one nor surjective.
$$\displaystyle f:R\rightarrow R$$ defined as under: $$\displaystyle f\left ( x \right )=\left\{\begin{matrix}x-4, &x< -9 \\x^{2}-1, &x\epsilon \left [ -9, 9 \right ] \\2x+5 &x> 9 \end{matrix}\right.$$ Evaluate $$\displaystyle \left ( f\: o\: f \right )5$$
if $$\displaystyle f\left ( x \right )=\left\{\begin{matrix}1+x; &0\leq x\leq 2 \\3-x; &2< x\leq 3 \end{matrix}\right.$$ then determine $$\displaystyle \left ( fof \right )(2).$$
If the functions $$\displaystyle f:R\rightarrow R $$ and $$\displaystyle g:R\rightarrow R $$ be defined by $$\displaystyle f\left ( x \right )= 2x+1,g\left ( x \right )=x^{2}-2$$Find the formulae for $$f o g$$.(2)
$$\displaystyle y= \frac{1}{\sqrt{\left ( 4+3\cos x \right )}}$$ Is the function one-one ? Explain
Let A = {1, 2, 3, 4} and B = {a, b, c}. State, which of the given are relations from A to B.
{ (1, a), (1, b), (2, b), (3, c), (4, c) }
Given A={2,3,4}, B={2,5,6,7}.
A mapping from A to B $$\displaystyle g= \left \{ \left ( 2,2 \right ), \left ( 3,5 \right ), \left ( 4,2 \right ) \right \}$$.
Is it one-one
Let A = {1, 2, 3, 4} and B = {a, b, c}. State, which of the given are relations from A to B.
{ (1, 2), (1, 3), (2, 3), (2, 4), (3, 4), (3, 1) }.
Let A = {1, 2, 3, 4} and B = {a, b, c}. State, which of the given are relations from A to B.
{ (a, 1), (b, 2), (c, 3), (b, 3), (b, 4) }
Let A = {1, 2, 3, 4} and B = {a, b, c}. State, which of the given are relations from A to B.
{ (a, b), (a, c), (b, a), (b, c), (c, a) }
Let A = {a, b, c} and B = {5, 7, 9}. State, which of the given are relations from B to A.
{ (a, 5), (a, 7), (b, 7), (c, 9) }
Let A = {a, b, c} and B = {5, 7, 9}. State, which of the given are relations from B to A.
{ (5, b), (7, c), (7, a), (9, b) }
If $$f\left ( x \right )=\sin ^{2}x+\sin ^{2}\left ( x+\dfrac{\pi}3 \right )+\cos x\cos \left ( x+\dfrac{\pi}3 \right )$$ and $$g\left(\dfrac54\right)=1,$$ then $$gof(x)$$ is equal to
Let A = {a, b, c} and B = {5, 7, 9}. State, which of the given are relations from B to A.
{ (5, 7), (9, 9), (7, 5) }
Given A = {3, 4, 5, 6} and B = {8, 9}. State, giving reason, whether { (3, 8), (4, 9), (5, 8) } is a mapping from A to B or not. Type 1 if it is a mapping and 0 if it is not
If $$f\left( x \right)=\left| x-2 \right| $$ and $$g\left( x \right)=f\left( f\left( x \right) \right) $$, then $$g'\left( x \right) $$ for $$x>2$$ is
Let A = {a, b, c} and B = {5, 7, 9}. State, which of the given are relations from B to A.
{ (5, a), (5, b), (5, c) }
Let two functions are defined as $$\displaystyle g(x)= \left\{\begin{matrix} x^{2}, &-1\leq x\leq 2\\x+2, &2 \leq x \leq 3\end{matrix}\right.,$$ and $$f(x)=\left\{\begin{matrix}x+1&x\leq 1\\2x+1&1<x\leq 2,\end{matrix}\right.$$ then find $$g of$$(1)
Let $$A = \{1, 2, 3, 4\}, B = \{ 1, 5, 9, 11, 15, 16\}$$ and $$f = \{(1, 5), (2, 9), (3, 1), (4, 5), (2, 11)\}$$ Are the following true?
(i) $$f$$ is a relation from $$A$$ to $$B$$
(ii) $$f$$ is a function from $$A$$ to $$B$$
Justify your answer in each case
Let $$f: {1,3,4} \rightarrow {1,2,5}$$ and $$g: {1,2,5}\rightarrow {1,3}$$ be given by $$f={(1,2), (3,5), (4,1)}$$ and $$g= {(1,3), (2,3), (5,1)}$$. Write down $$gof$$.
Show that the Signum function $$f:R \rightarrow R$$, given by
$$\displaystyle f(x)=\begin{cases}1,\ if\ x > 0 \\0,\ if\ x = 0 \\ -1,\ if\ x < 0 \end{cases}$$is neither one-one nor onto.
Let $$A=$${$$1,2,3$$}, $$B=$${$$4,5,6,7$$} and let $$f={(1,4), (2,5),(3,6)}$$ be a function from $$A$$ to $$B$$. Show that $$f$$ is one-one.
Let $$f,g$$ and $$h$$ be functions from $$R$$ to $$R$$. Show that
(i) $$(f+g)oh=foh+goh$$
(ii) $$(f.g)oh=(foh).(goh)$$
Find $$gof$$ and $$fog$$, if $$(i)$$ $$f(x)=|x|$$ and $$g(x)=|5x-2|$$
ii)$$f(x)=8x^3$$ and $$\displaystyle g(x)=x^{\frac {1}{3}}$$
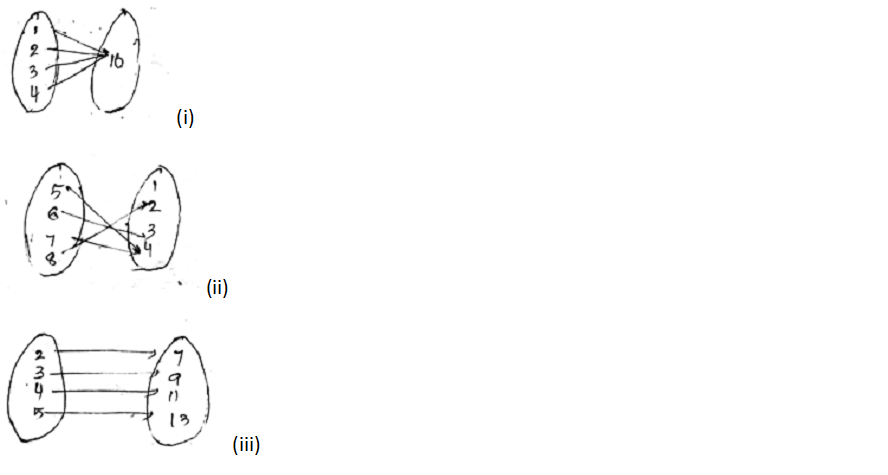
State with reason whether following functions have inverse
(i) $$f:\left \{1, 2, 3, 4\right \}\rightarrow \left \{10\right \}$$ with
$$f = \left \{(1, 10), (2, 10), (3, 10), (4, 10)\right \}$$
(ii) $$g: \left \{5, 6, 7, 8\right \}\rightarrow \left \{1, 2, 3, 4\right \}$$ with
$$g = \left \{(5, 4), (6, 3), (7, 4), (8, 2)\right \}$$
(iii) $$h: \left \{2, 3, 4, 5\right \}\rightarrow \left \{7, 9, 11, 13\right \}$$ with
$$h = \left \{(2, 7), (3, 9), (4, 11), (5, 13)\right \}$$
If $$f(x) = \dfrac {4x + 3}{6x - 4}, x\neq \dfrac {2}{3}$$, show that $$fof (x) = x$$, for all $$x\neq \dfrac {2}{3}$$. What is the inverse of $$f$$?
Let $$f: X\rightarrow Y$$ be an invertible function. Show that $$f$$ has unique inverse
Consider $$f: R^{+} \in [-5, \infty)$$ given by $$f(x) = 9x^{2} + 6x - 5$$. Show that $$f$$ is invertible with $$f^{-1} (y) = \left (\dfrac {(\sqrt {y + 6})- 1}{3}\right )$$
If $$g(x)=3x+\sqrt {x}$$, find $$g({d}^{2}+6d+9)$$.
Given a non-empty set $$X$$, consider the binary operation $$* : P(X) \times P(X) \rightarrow P(X)$$ given by $$A * B = A\cap B\forall A, B$$ in $$P(X)$$, where $$P(X)$$ is the power set of $$X$$. Show that $$X$$ is the identity element for this operation and $$X$$ is the only invertible element in $$P(X)$$ with respect to the operation $$*$$
Show that the function $$f: R\rightarrow R$$ given by $$f(x) = x^{3}$$ is injective
Let $$f: W\rightarrow W$$ be defined as $$f(x) = x - 1$$, if $$x$$ is odd and $$f(x) = x + 1$$, if n is even. Show that $$f$$ is invertible. Find the inverse of $$f,$$ where, $$W$$ is the set of all whole numbers.
Consider $$f: \left \{1, 2, 3\right \}\rightarrow \left \{a, b, c\right \}$$ given by $$f(1) = a, f(2) = b$$ and $$f(3) = c$$. Find $$f^{-1}$$ and show that $$(f^{-1})^{-1} = f$$
Let $$f: X \rightarrow Y$$ be an invertible function. Show that the inverse of $$f^{-1}$$ is $$f$$, i.e., $$(f^{-1})^{-1} = f$$
Give examples of two functions $$f: N \rightarrow Z$$ and $$g: Z \rightarrow Z$$ such that gof is injective but $$g$$ is not injective
Given a non-empty set $$X$$, let $$*: P(X) \times P(X) \rightarrow P(X)$$ be defined as $$A * B = (A - B) \cup (B - A), \forall A, B\epsilon P(X)$$. Show that the empty set $$\phi$$ is the identity for the operation $$*$$ and all the elements $$A$$ of $$P(X)$$ are invertible with $$A^{-1} = A$$
Let $$S = \left \{a, b, c\right \}$$ and $$T = \left \{1, 2, 3\right \}$$. Find $$F^{-1}$$ of the following functions $$F$$ from $$S$$ to $$T$$, if it exists
(i) $$F = \left \{(a, 3), (b, 2), (c, 1)\right \}$$ (ii) $$F = \left \{(a, 2), (b, 1), (c, 1)\right \}$$
Give examples of two functions $$f: N\rightarrow N$$ and $$g: N\rightarrow N$$ such that gof is onto but $$f$$ is not onto
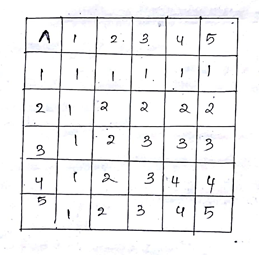
Consider the binary operation $$\wedge$$ on the set $$\left \{1, 2, 3, 4, 5\right \}$$ defined by $$a\wedge b = min \left \{a, b\right \}$$. Write the operation table of the operation $$\wedge$$
Is $$\ast$$ defined on the set $$\left \{1, 2, 3, 4, 5\right \}$$ by $$a\ast b = L.C.M.$$ of $$a$$ and $$ba$$ binary operation? Justify your answer
Let $$\ast'$$ be the binary operation on the set $$\left \{1, 2, 3, 4, 5\right \}$$ defined by $$a\ast' b = H.C.F.$$ of $$a$$ and $$b$$. Is the operation $$\ast'$$$ same as the operation $$\ast$$ defined in above? Justify your answer
If the inverse of the rational function $$f(x)=\dfrac{x+1}{x-1}$$ is $$\dfrac{x+m}{x-m}$$.Find the value of $$m$$
Let $$\ast$$ be a 'binary' operation of $$N$$ given by $$a\ast b = LCM (a, b)$$ for all $$a, b\in N$$. Find $$5\ast 7.$$
If the function $$f : R\rightarrow R$$ be given by $$f(x) = x^{2} + 2$$ and $$g : R\rightarrow R$$ be given by $$g(x) = \dfrac {x}{x - 1}, x\neq 1$$, find fog and gof and hence find $$fog(2)$$ and $$gof(-3)$$
Let $$A = Q \times Q$$, where Q is the set of all rational numbers, and * be a binary operation on $$A$$ defined by $$(a, b) * (c, d) = (ac, b + ad)$$ for $$(a, b), (c, d)$$ $$\epsilon$$ $$A.$$ Then find
(i) The identify element of $$*$$ in $$A.$$
(ii) Invertible elements of $$A$$, and hence write the inverse of elements $$(5, 3)$$ and $$\left ( \dfrac{1}{4}, 4 \right )$$.
Consider $$f:R^{+} \rightarrow [-9, \infty]$$ given by $$f(x) = 5x^2 + 6x - 9$$. Prove that $$f$$ is invertible with $$f'(y) =(\dfrac{\sqrt{54+5y}-3}{5})$$.
Show that $$f : N\rightarrow N$$, given by$$f(x) = \begin{cases}x + 1, \ \ \ \text{if} \ x \ \text{is} \ \text{odd} \\ x - 1, \ \ \ \text{if} \ x \ \text{is} \ \text{even} \end{cases}$$ is both one-one and onto.
Let $$\ast$$ be binary operation on the set of all non-zero real numbers, given by $$a\ast b = \dfrac {ab}{5}$$ for all $$a, b, \in R - \left \{0\right \}$$. Find the value of $$x,$$ given that $$2\ast (x \ast 5) = 10.$$
Given $$f: x\rightarrow 2x+p$$ and $$f^{-1} : x \rightarrow m (4x + 3)$$, where $$p$$ and $$m$$ are constants. Find the value of $$p$$ and value of $$m$$.
$$(f\circ f)(x)$$
If $$x\ \lambda\ y = 2x - y$$ and $$x\nu y = 3x \times y$$, then $$(5\ \nu\ 2)\lambda\ 9$$
Consider $$f : R \rightarrow R$$ given by $$f(x) = 2x + 3$$. Show that f is invertible. Find also the inverse of function f.
A function $$f : (-3, 7)\rightarrow R$$ is defined as follows:
$$f(x) = \left\{\begin{matrix} 4x^{2} -1;& -3 \leq x < 2\\ 3x - 2; & 2\leq x \leq 4\\ 2x - 3; & 4 < x \leq 6\end{matrix}\right.$$
Find: $$f(5) + f(6)$$
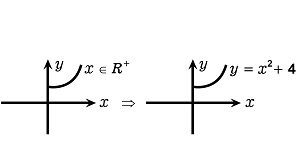
Let $$R_+$$ be the set of all non-negative real numbers. Show that the function $$f:R_+ \rightarrow [4, \infty)$$ given by $$f(x)=x^2+4$$ is invertible and write the inverse of $$f$$.
A function f : [3, 7) $$\rightarrow$$ R is defined as follows
$$f(x) = \left\{\begin{matrix}4x^2 - 1; &-3 \le x < 2 \\ 3x - 2; & 2 \leq x \leq 4\\ 2x -3; & 4 < x < 7\end{matrix}\right.$$
Find $$f(-2) - f(4)$$
Let $$f,g,h$$ are functions defined by $$f(x)=x; \,g(x)=1-x; \,h(x)=x+1$$; then show that $$h\circ (g\circ f)=(h\circ g)\circ f$$.
Find g o f and f o g if $$f : R\rightarrow R$$ and $$g: R\rightarrow R$$ are given by $$f(x)=\cos x$$ and $$g(x) = 3x^2$$. Show that g o f $$\ne$$ f o g.
Prove that the function $$f:N\rightarrow Y$$ defined by $$f(x)=4x+3$$, where $$Y={y=4x+3, x\epsilon N}$$ is invertible. Also write the inverse of $$f(x)$$.
Let $$f: \left \{x, y, z\right \} \rightarrow \left \{a, b, c\right \}$$ be an one-one function. It is known that only one of the following statements is true:
(i) $$f(x) \neq b$$ (ii) $$f(y) = b$$ (iii) $$f(z) \neq a$$.
Find the function $$f$$.
Show that the function $$f: R_{\ast} \rightarrow R_{\ast}$$ defined by $$f(x) = \dfrac {1}{x}$$ is one-one, where $$R_{\ast}$$ is the set of all non-zero real numbers. Is the result true, if the domain $$R_{\ast}$$ is replaced by $$N$$ with co-domain being same as $$R_{\ast}$$?
The binary operation $$\ast$$ : R $$\times$$ R $$\rightarrow$$ R is defined as a $$a\ast b=2a+b$$. Find $$(2\ast 3)\ast 4$$.
Solve the equation. f'(x) \, g'(x) if $$f(x) \, = \, 3 \, + \, 2x^2 \, and \, g(x) \, 3x^2 \, - \, (5x \, - \, 3)\, (2 \, - \, x)$$
If $$f(x) = 4x+2, g(x) = 3x^2, h(x) = 3x -2$$ such that $$fo(goh) = (fog)o h$$
Let f : [0,3] is defined by $$f(x) = {x^2} + x + 1$$ then $${f^{ - 1}}(x)$$
$$ f: N \rightarrow N, g: N \rightarrow N$$, and $$ h: N \rightarrow R$$ defined and $$f(x) = x^2, g(y) = 4y+2, h(z) = \ cosz $$ such that $$ ho(gof) = (hog)of$$
Let $$f : R \rightarrow R$$ be defined by $$f(x) = 3x + 4$$, $$x \epsilon R$$. Is $$f$$ invertible? If so, give a formula for $$f^{-1}$$.
Let $$f\left( x \right) =\left[ x \right] $$ and $$g\left( x \right) =\left| x \right| $$, find $$(g+f)(2.3)$$
If $$f:R \to \left( {0,2} \right)$$ defined by $$f\left( x \right) = \dfrac{{{e^x} - {e^{ - x}}}}{{{e^x} + {e^{ - x}}}} + 1$$ is invertible, find $${f^{ - 1}}$$
Show that if $$f: A \rightarrow B$$ and $$g: B \rightarrow C$$ are $$1-1$$, then $$gof:A \rightarrow C$$ is also $$1-1$$
Show that the function $$ f: R \rightarrow R$$ is defined by $$f(x) = 4x+3$$ is invertible. Hence write the inverse of $$f$$.
Let $$f(x+\frac{1}{2}) =f(x)$$. If f(2)= 5 and $$f(\frac{9}{4}) =2$$. Find f(-3) and $$f(\frac{1}{4})$$.
Let * be a binary operation on the set $$Q$$ of rational numbers as follows:
$$a*b={ \left( a-b \right) }^{ 2 }$$
Find which of the binary operations are commutative and which are associative.
Let * be a binary operation on the set $$Q$$ of rational numbers as follows:
$$a*b={ ab }^{ 2 }$$
Find which of the binary operations are commutative and which are associative.
Let * be a binary operation on the set $$Q$$ of rational numbers as follows:
$$a*b=a+ab$$
Find which of the binary operations are commutative and which are associative.
Let * be a binary operation on the set $$Q$$ of rational numbers as follows:
$$a*b=\dfrac { ab }{ 4 }$$
Find which of the binary operations are commutative and which are associative.
Let $$F(x)={x}^{3}-3x+1$$
find no. of real soln, of $$F(F(x))=0$$.
$$f(x)=3x^{4}+17x^{3}+9x^{2}-7x-10; g(x)=x+5$$
If $$f(x)=\dfrac{3x+2}{4x-1}$$ and $$g(x)=\dfrac{x+2}{4x-3}$$, prove that $$(gof)(x)=(fog)(x)=x$$.
Let $$F(x)$$=$${x^3} - 3x + 1$$
Find no of real solutions of $$F\left( {F\left( x \right)} \right) = 0$$
$$f:R \rightarrow R,f(x)=x^{2},g:R \rightarrow R,g(x)=2^{x}$$, then $${x|(fog)(x)=(gof))(x)}=.........$$
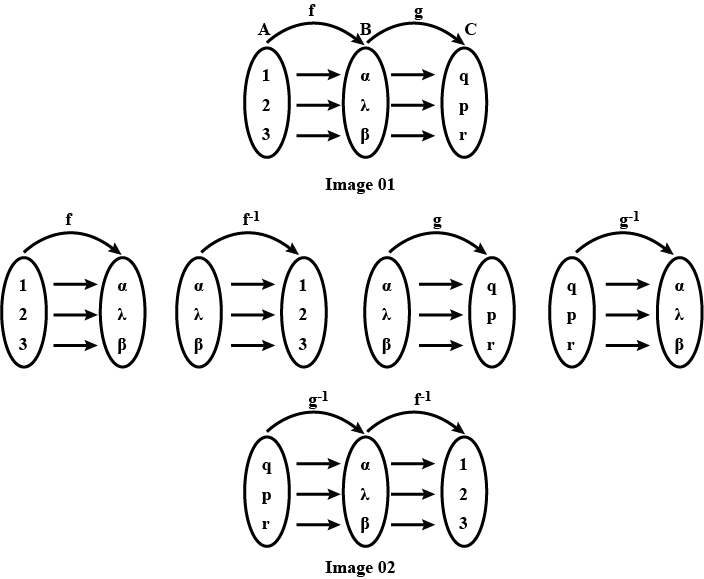
If $$A = \{ 1,2,3\} ,B = \{ \alpha ,\beta ,\lambda \} C = \{ p,q,r\} $$ and $$f:A \to B,\,g:B \to C$$ are defined by $$f = \left\{ {\left( {1,\alpha } \right),\left( {2,\lambda } \right)\left( {3,\beta } \right)} \right\}$$ and $$g = \left\{ {\left( {\alpha ,q} \right),\left( {\beta ,r} \right),\left( {\lambda ,p} \right)} \right\}$$ Show that $$f$$ and $$g$$ are bijective functions and $${\left( {gof} \right)^{ - 1}} = {f^{ - 1}}o{g^{ - 1}}$$
Find composite of $$f$$ and $$g$$ and express it by formula :
$$f=\{(1,3),(2,4),(3,5),(4,6)\}$$
$$g=\{(3,6),(4,8),(5,10),(6,12)\}$$
$$f : R\rightarrow (-1, 1), f(x) = \dfrac {10^{x} - 10^{-x}}{10^{x} + 10^{-x}}$$. Find $$f^{-1}$$, if it exists.
If the binary operation on the set of integers Z, defined by $$a\times b=a+3{ b }^{ 2 }$$, then find the value of $$8\times 3$$.
If $$f(x)=\dfrac {1}{(1-x)}$$ find $$(fofof)(x)=?$$
If $$f:R\rightarrow R$$ be given by $$f\left( x \right) =\left( 3-{ x }^{ 3 } \right) $$, find the value of $$fof\left( x \right) $$
If $$g\ {(x)}={e}^{2x}+{e}^{x}-{1}$$ and $$h\ {(x)}={3x}^{2}-{1}$$, the value of $$g\ {(h(0))}$$ is
Find composite function $$g \, o f(x)$$ of $$f$$ and $$g$$.
$$f = \{(1,3) ; (2, 4) ; (3, 5) ; (4, 6) \}$$ & $$g = \{(3, 6) ; (4, 8); (5, 10) ; (6, 12)\}$$.
If $$f:R\rightarrow R$$ is given by $$f(x)=(3-x^3)^{1/3}$$, find $$fof(x)$$.
If f (x) =$$\cfrac{x^{2}-x}{x^{2}+2x}$$, find the domain of $$f(x)$$. Show that f is one-one.
(ii) Let $$ * $$ be the binary operation on N given by a * b= ab
(a) Find 20 $$ * $$16
(b) Find the identity of $$ * $$ in N
Find inverse function of $$\,f(x) = 9{x^2} + 6x - 5$$
$$f:R \to R\;$$given by f$$\left( x \right) = 4x + 3$$, show that $$f$$ is invertable. Find the inverse of $$f$$.
Show that subtraction are not binary operation on natural number N
If $$y=f(x)=\dfrac{px+q}{px-p}$$, then find $$f(y)$$ in terms of $$x$$.
Let $$A$$ be a finite set, If $$f:A \to A$$ is onto. Show that $$f$$ is one-one
Work out the inverse function for each equation.a)$$y = 2 x + 5$$b)$$y = 4 x - 7$$c)$$y = \frac { x } { 2 } + 1$$d)$$y = \frac { x - 4 } { 3 }$$
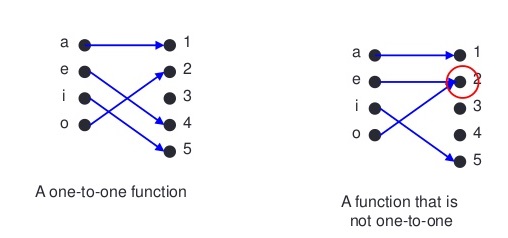
Give one example for One one function.
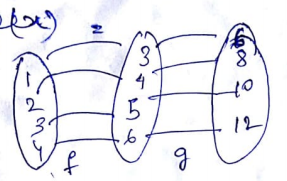
If $$f= \{(2,4)(3,6)(4,8)(5,10)(6,12)\},$$
$$g=\{(4,13)(6,19)(8,25)(10,31)(12,37)\},$$
Find $$(gof) $$ ?
Let $$A=B=[-1,1].$$ State whether the following functions from $$A$$ into $$B$$ are one-one.
i)$$f\left( x \right) = {x^2}$$
ii)$$g\left( x \right) = \left| x \right|$$
Prove that the function $$f:R\to R$$ be defined by $$f(x)=(x^2+1)^{35}$$ is not one one.
Prove that the function $$f(x)=x+|x|$$, $$x\in R$$ is not one-one.
If the functions f and g are given by f =$${(1,2)(3,5)(4,1)}$$ & $$g={(2,3)(5,1)(1,3)}$$. Find the range of f and g . Also find fog(2).
If $$*$$ is a binary operation on set $$N$$,of natural no defined as $$a*b=HCF$$ of $$(a,b)$$. Evaluate $$3*(2*5)$$.
A binary operation * on the set {0,1,2,3,4,5} is defined as
$$a*b = \left\{ \matrix{ a + b{\rm{\ , if\ a + b < 6}} \hfill \cr {\rm{a + b - 6\, if\ a + b}} \ge {\rm{6}} \hfill \cr} \right\}$$ show that zero is the identity element of this operational each element 'a' of the set is invertible with 6-a being the inverse of 'a'
Find the inverse of the following functions.
$$f:R\rightarrow (0,\infty)$$ defined by $$f(x)=5^{x}$$.
Prove that the function $$f : R \rightarrow R$$ defined by $$f ( x ) = 4 x + 3 ,$$ is invertible and find the inverse of $$f .$$
If $$y=f(x)=\dfrac{x-5}{5x-1}$$, show that $$f(y)=x$$.
Show that the function $$f:R \rightarrow R$$ defined by $$f(x) = \dfrac{x}{{x}^{2}+1}$$ for all $$x\in R$$ is neither one-one nor onto.
Examine whether the binary operation $$*$$ defined on R by $$a*b=ab+1$$ is associative or not.
Find the equation of two straight lines through the point (4,5) which makes an acute angle of 45 degree with 2x-y+7=0.
On the set W of all non-negative integers $$*$$ is defined by $$a*b=a^b$$. Prove that $$*$$ is not a binary operation on W.
If $$*$$ is defined on the set R of all real numbers by $$a*b=\sqrt{a^2+b^2}$$, find the identity element in R with respect to $$*$$.
If the function $$f : R \rightarrow R$$ be given by $$f(x) = {x}^{2}+2$$ and $$g : R → R$$ be given $$g(x) =\dfrac{x}{x-1},\,\, x \neq 1$$, find $$f. g$$ and $$g.f$$ and hence $$fog\left(2\right)$$ and $$gof\left(-3\right)$$.
$$f(x) = \dfrac{1}{x^{3}}$$ then $$f^{'}(x)=$$
If $$f(x)=x+1$$ and $$g(x)=x^{2}$$ Find
$$Fog\ (1)$$
$$Gof\ (-1)$$
$$Fog\ (2)$$
$$Gof\ (3)$$
If f(x)=x, g(x)=x$$^2$$ and h(x)=x$$^3$$, then find [(hog) of] (x).
Is the binary operation $$*$$ defined on the set of integer $$z$$ by the rule $$a * b = a - b + 2$$ commutative ?
Check whatever there is a direct or an inverse proportion in the following cases. Give reason to support your answer.i) Number of water bottles and their costii) Time taken and the distance covered at a uniform speed of vehicleiii) Distance traveled and there fare charge for itiv) Number of person and the number of days for which the food should last
Let $$A=\left\{1,2,3\right\},B=\left\{4,5,6,7\right\}$$ and let $$f=\left\{\left(1,4\right),\left(2,5\right),\left(3,6\right)\right\}$$ be a function from $$A$$ to $$B$$.Show that $$f$$ is one-one.
Let $$f(x)=3x^2-5$$ and $$g(x)=\dfrac{x}{x^2+1}$$. Then find $$(gof)(x)$$.
The function $$f$$ is defined for $$x\le 0$$ by $$f\left( x \right) =\frac { { x }^{ 2 }-1 }{ { x }^{ 2 }+1 } $$. Find its inverse
If $$f\left( x \right) ={ x }^{ 2 }$$ and $$g\left( x \right) =2x+1$$ be two real valued function. Find $$\left( fg \right) \left( x \right) $$ and $$\left( \dfrac { f }{ g } \right) \left( x \right) .$$
Let $$f : N \rightarrow N$$ be a function defined as $$f(x) =4x^2+12x+15$$. Show that $$f : N \rightarrow S$$ is invertible, where $$S$$ is range of $$f$$. Also find the inverse of $$f$$.
Let $$x$$ be non-empty set. $$P ( x )$$ be its power set. Let * be an operation defined on element of $$P ( x ) b y , A * B =$$
$$A \cap B \forall A , B \in P ( x ) .$$ Then
(i) Prove that * is a binary operation in $$P ( x )$$
(ii) is * associative?
(iii) Is * commutative?
Let $$f(x)=3x+1$$ and $$g(x)=x^2+2$$ then find $$fog$$.
Show that function $$ f : N \rightarrow N $$ given by $$f ( x ) = 3 x $$ is one-one but not onto.
The function $$f$$ and $$g$$ as defined for $$x \ge 0$$ by
$$f (x) = 2x^2 + 3$$,
$$g(x) = 3x+2$$.
Show that $$g(f(x)) = 6x^2 + 11$$
Show that function $$f:R\rightarrow R, f(x)=\frac { 2x+5 }{ 8 } $$ is invertible. Also find inverse of f.
Given an example to show that $$\ast : N\times N \rightarrow N$$, given by $$(a, b) = a - b$$ is not a binary operation.
Give examples of two one-one functions $${f}_{1}$$ and $${f}_{2}$$ from $$R$$ to $$R$$ such that $${f}_{1}+{f}_{2}:R\rightarrow R$$, defined by $$({f}_{1}+{f}_{2})(x)={f}_{1}(x)+{f}_{2}(x)$$ is not one-one.
Find the number of all onto functions from the set $$A=\left\{ 1,2,3,....n \right\} $$ to itself.
If $$f:A\rightarrow B$$ and $$g:B\rightarrow C$$ are one-one functions, show that $$g\circ f$$ is a one-one function.
Let $$A=\left\{ 1,2,3 \right\} $$. Write all one-one from $$A$$ to itself.
Let $$f=\left\{ \left( 3,1 \right) ,\left( 9,3 \right) ,\left( 12,4 \right) \right\} $$ and $$g=\left\{ \left( 1,3 \right) ,\left( 3,3 \right) ,\left( 4,9 \right) ,\left( 5,9 \right) \right\} $$. Show that $$g\circ f$$ and $$f\circ g$$ are both defined. Also, find $$f\circ g$$ and $$g\circ f$$.
Show that if $${f}_{1}$$ and $${f}_{2}$$ are one-one maps from $$R$$ to $$R$$, then the product $${f}_{1}\times {f}_{2}:R\rightarrow R$$ defined by $$({f}_{1}\times {f}_{2})(x)={f}_{1}(x){f}_{2}(x)$$ need not be one-one.
Give examples of two functions $$f:N\rightarrow N$$ and $$g:N\rightarrow N$$ such that $$g\circ f$$ is onto, but $$f$$ is not onto.
Show that the exponential function $$f:R\rightarrow R$$, given by $$f(x)={e}^{x}$$, is one-one but not onto. What happens, if the co-domain is replaced by $${R}_{0}^{+}$$ (Set of all positive real numbers)?
Prove that the function $$F:N\rightarrow N$$, defined by $$f(x)={x}^{2}+x+1$$ is one-one but not onto.
Let $$f=\left\{ \left( 1,-1 \right) ,\left( 4,-2 \right) ,\left( 9.-3 \right) ,\left( 16,4 \right) \right\} $$ and $$g=\left\{ \left( -1,-2 \right) ,\left( -2,-4 \right) ,\left( -3,-6 \right) ,\left( 4,8 \right) \right\} $$. Show that $$g\circ f$$ is defined while $$f\circ g$$ is not defined. Also, find $$g\circ f$$.
Consider $$f:R\rightarrow R$$ given by $$f(x)=4x+3$$. Show that $$f$$ is invertible. Find the inverse $$f$$.
Determine whether the operation $$'\ast '$$ on $$N$$ defined by $$a\ast b = a^{b}$$ for all $$a,b \in N$$ is a binary operation or not :
If $$f:R\rightarrow (-1,1)$$ defined by $$f(x)=\cfrac{{10}^{x}-{10}^{-x}}{{10}^{x}+{10}^{-x}}$$ is invertible, find $${f}^{-1}$$.
Let $$f(x)={x}^{2}+x+1$$ and $$g(x)=\sin x$$. Show that $$f\circ g\ne g\circ f$$.
If $$f(x)=\left| x \right| $$, prove that $$f\circ f=f$$.
Let $$f:[-1,\infty)\rightarrow [-1,\infty)$$ is given by $$f(x)={(x+1)}^{2}-1$$. Show that $$f$$ is invertible. Also, find the set $$S\left\{ x:f(x)={ f }^{ -1 }(x) \right\} $$.
Let $$f$$ be a function from $$R$$ to $$R$$, such that $$f(x)=\cos(x+2)$$. Is $$f$$ invertible? Justify your answer.
If $$f(x)=\cfrac{4x+3}{6x-4},x\ne \cfrac{2}{3}$$, show that $$f\circ f(x)=x$$ for all $$x\ne \cfrac{2}{3}$$. What is the inverse of $$f$$?
Determine whether the operation $$'O '$$ on $$Z$$ defined by $$aO b = a^{b}$$ for all $$a,b \in Z$$ is a binary operation or not :
If $$f:R\rightarrow (0,2)$$ is defined by $$f(x)=\cfrac{{e}^{x}-{e}^{-x}}{{e}^{x}+{e}^{-x}}$$ is invertible, then find $${f}^{-1}$$.
Determine whether the following operation define a binary operation on the given set or not :
$$'x_{6}'$$ on $$S=\left \{ 1,2,3,4,5 \right \}$$ defined by $$a\times _{6}b=$$ Remainder when $$ab$$ is divided by $$6$$.
Let $$\ast $$ be a binary operation on the set $$I$$ of integers, defined by $$a\ast b= 2a+b-3$$. Find the value of $$3\ast 4$$.
Determine whether or not the definition of $$\ast $$ On $$Z^{+}$$, define $$\ast $$ by $$a\ast b= a$$. gives a binary operation.If the event that $$\ast $$ is not a binary operation give justification of this.
Determine whether or not the definition of $$\ast $$ On $$Z^{+}$$ define $$\ast $$ by $$a\ast b= \left | a-b \right |$$ gives a binary operation. If the event that $$\ast $$ is not a binary operation give justification of this.
Determine whether the following operation define a binary operation on the given set or not:
$$'\bigodot '$$ on $$N$$ defined by $$a\bigodot b= a^{b}+b^{a}$$ for all $$a,b \in N$$.
Determine whether or not the definition of $$\ast $$ On $$Z^{+}$$, defined by $$a\ast b= ab$$. gives a binary operation. If the event is not a binary operation give justification of this.
Determine whether the operation $$'\ast '$$ on $$N$$ defined by $$a\ast b = a+b-2$$ for all $$a,b \in N$$ is a binary operation or not :
Determine whether the following operation define a binary operation on the given set or not:
$$'\ast '$$ on $$Q$$ defined by $$a\ast b= \dfrac{a-1}{b+1}$$ for all $$a,b \in Q$$.
Determine whether or not the definition of $$\ast $$ On $$Z^{+}$$, defined by $$a\ast b= a-b$$ gives a binary operation. If the event $$\ast $$ is not a binary operation give justification of this.
Determine whether or not the definition of $$\ast $$ On $$R$$, defined by $$a\ast b= ab^{2}$$. gives a binary operation. If the event that $$\ast $$ is not a binary operation give justification of this.
Write the total number of one-one functions from set $$A=\left\{ 1,2,3,4 \right\} $$ to set $$B=\left\{ a,b,c \right\} $$.
Let $$S$$ be the set of all rational number of the form $$\dfrac{m}{n}$$, where $$m\in Z$$ and $$n= 1,2,3$$. Prove that $$\ast $$ on S defined by $$a\ast b=ab$$ is not a binary operation.
If $$f:R\rightarrow R$$ is given by $$f(x)={x}^{3}$$, write $${f}^{-1}(1)$$.
Find the total number of binary operations on $$\left \{ a,b \right \}$$.
If $$A=\left\{ a,b,c \right\} $$ and $$B=\left\{ -2,-1,0,1,2 \right\} $$, write total number of one-one functions from $$A$$ to $$B$$.
If $$f:R\rightarrow R$$ is defined by $$f(x)={x}^{2}$$, write $${f}^{-1}(25)$$.
The binary operation $$\ast : R\times R\rightarrow R$$ is defined as $$a\ast b= 2a+b$$. Find $$(2\ast 3)\ast 4$$.
Let $$\ast $$ be a binary operation on $$N$$ given by $$a\ast b= \text{LCM}(a,b)$$ for all $$a,b \in N$$. Find $$5\ast 7$$.
Let $$S= \left \{ a,b,c \right \}$$. Find the total number of binary operations on $$S$$.
Which one of the given graphs represents a one-one function?

Check the commutativity and associativity of the following binary operation:
$$'\ast '$$ on $$Q$$ defined by $$a \ast b= ab^{2}$$ for all $$a,b \in Q$$.
Let $$A=\left\{ 1,2,3,4 \right\} $$ and $$B=\left\{ a,b \right\} $$ be two sets. Write total number of onto functions from $$A$$ to $$B$$.
Check the commutativity and associativity of the following binary operation:
$$'\ast '$$ on $$Q$$ defined by $$a \ast b= (a-b)^{2}$$ for all $$a,b \in Q$$.
Let $$'\ast '$$ be a binary operation on $$N$$ defined by $$a\ast b= \text{LCM}(a,b)$$ for all $$a,b \in N$$. Find $$2\ast 4, 3\ast 5, 1\ast 6$$.
Check the commutativity and associativity of the following binary operation:
$$'\ast '$$ on $$Z $$ $$a \ast b= a-b$$ for all $$a,b \in Z$$.
Check the commutativity and associativity of the following binary operation:
$$'\ast '$$ on $$N$$, defined by $$a \ast b= a^{b}$$ for all $$a,b \in N$$.
Let $$f$$ be an invertible real function. Write $$({f}^{-1} \circ f)(1)+({f}^{-1} \circ f(2)+.....+({f}^{-1} \circ f)(100)$$.
Check the commutativity and associativity of the following binary operation:
$$'\ast '$$ on $$R$$ defined by $$a \ast b= a+b-7$$ for all $$a,b \in Q$$.
Check the commutativity and associativity of the following binary operation:
$$'\ast '$$ on $$Q$$ defined by $$a \ast b= a+ab$$ for all $$a,b \in Q$$.
Check the commutativity and associativity of the following binary operation:
$$'o '$$ on $$Q$$ defined by $$a o b= \dfrac{ab}{2}$$ for all $$a,b \in Q$$.
Check the commutativity and associativity of the following binary operation:
$$'\ast '$$ on $$Q$$ defined by $$a \ast b= \dfrac{ab}{4}$$ for all $$a,b \in Q$$.
Let $$A=\left\{ 1,2,3 \right\} $$, $$B=\left\{ 4,5,6,7 \right\} $$ and let $$f=\left\{ \left( 1,4 \right) ,\left( 2,5 \right) ,\left( 3,6 \right) \right\} $$ be a function from $$A$$ to $$B$$. State whether $$f$$ is one-one or not.
If $$f:R\rightarrow R$$ be defined by $$f(x)={(3-{x}^{3})}^{1/3}$$, then find $$f\circ f(x)$$.
If $$f:R\rightarrow R$$ be defined by $$f(x)=3x+2$$, find $$f(f(x))$$.
Let $$\ast $$ be a binary operation on $$Z$$ defined by $$a\ast b= a+b-4$$ for all $$a,b\in Z$$. Find the invertible elements in $$Z$$.
Let $$f,g:R\rightarrow R$$ be defined by $$f(x)=2x+1$$ and $$g(x)={x}^{2}-2$$ for all $$x\in R$$, respectively. Then, find $$g\circ f$$.
If $$f(x)=x+7$$ and $$g(x)=x-7, x\in R$$, write $$f\circ g(7)$$.
Let $$S$$ be the set of all rational numbers except $$1$$ and $$\ast $$ be defined on S by $$a\ast b= a+b- ab$$, for all $$a,b \in S$$. Prove that $$\ast $$ is commutative as well as associative.
Let $$S$$ be the set of all rational numbers except $$1$$ and $$\ast $$ be defined on $$S$$ by $$a\ast b= a+b- ab$$, for all $$a,b \in S$$. Prove that $$\ast $$ is a binary operation on $$S$$.
Let $$\ast $$ be a binary operation on $$Z$$ defined by $$a\ast b= a+b-4$$ for all $$a,b\in Z$$.
Show that $$'\ast '$$ is commutative.
For the binary operation $$\times _{7}$$ on set $$S=\left \{ 1,2,3,4,5,6 \right \}$$, compute $$3^{-1}\times _{7}4$$.
Let $$R_{0}$$ denote the set of all non-zero real numbers and let $$A= R_{0}\times R_{0}$$. If $$'\ast '$$ is a binary operation on A defined by $$(a,b)\ast (c,d)= (ac, bd)$$ for all $$(a,b)(c,d) \in A$$.
Show that $$'\ast '$$ is both commutative and associative on A
Let '$$o$$' be a binary operation on the set $$Q_{0}$$ of all non-zero rational numbers defined by $$a\, o\, b= \dfrac{ab}{2}$$, for all $$a,b \in Q_{0}$$. Find the invertible elements of $$Q_{0}$$.
Let $$\ast $$ a binary operation on $$Q-\left \{ -1 \right \}$$ defined by $$a\ast b= a+b+ab$$ for all $$a,b \in Q -\left \{ -1 \right \}$$.
Then, show that $$'\ast '$$ is commutative on $$Q-\left \{ -1 \right \}$$.
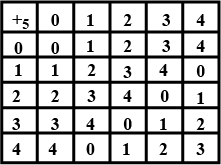
Construct the composition table for $$+_{5}$$ on set $$S= \left \{ 0,1,2,3,4 \right \}$$.
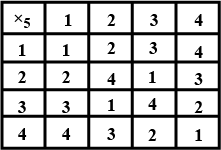
Construct the composition table for $$\times_{5}$$ on $$Z= \left \{ 1,2,3,4 \right \}$$.
Let $$R_{0}$$ denote the set of all non-zero real numbers and let $$A= R_{0}\times R_{0}$$. If $$'\ast '$$ is a binary operation on A defined by $$(a,b)\ast (c,d)= (ac, bd)$$ for all $$(a,b)(c,d) \in A$$.
Find the invertible element in A.
Find $$f\circ g$$ and $$g\circ f$$, if $$f(x)={x}^{2},g(x)=\cos x$$.
Find $$f\circ g$$ and $$g\circ f$$, if $$f(x)=\sin ^{ -1 }{ x } $$, $$g(x)={x}^{2}$$.
Find $$f\circ g$$ and $$g\circ f$$, if $$f(x)=c,c\in R$$, $$g(x)=\sin {x}^{2}$$.
For the relation $$R_1$$ defined on $$R$$ by the rule $$(a, b)\in R_1\Leftrightarrow 1+ab > 0$$. Prove that: $$(a, b)\in R_1$$ and $$(b, c)\in R_1\Rightarrow (a, c)\in R_1$$ is not true for all $$a, b, c \in$$ R.
Find $$g\circ f$$ and $$f\circ g$$ when $$f:R\rightarrow R$$ and $$g:R\rightarrow R$$ are defined by $$f(x)=8{x}^{3}$$ and $$g(x)={x}^{1/3}$$.
Find $$f\circ g$$ and $$g\circ f$$, if $$f(x)={x}^{2}-2$$, $$g(x)=1-\cfrac{1}{1-x}$$.
Find $$f\circ g$$ and $$g\circ f$$, if $$f(x)={e}^{x},g(x)=\log _{ e }{ x } $$.
Find $$f\circ g$$ and $$g\circ f$$, if $$f(x)=x+1$$, $$g(x)=2x+3$$.
Find $$f\circ g$$ and $$g\circ f$$, if $$f(x)=\left| x \right| $$, $$g(x)=\sin x$$.
Find $$f\circ g$$ and $$g\circ f$$, if $$f(x)=x+1$$; $$g(x)={e}^{x}$$.
Give an example of a function which is one-one and onto.
If $$f(x) = \dfrac{4x + 3}{6x -4}, \, x \neq \dfrac{2}{3}$$, then show that $$(fof) (x) = x$$, for all $$x \neq \dfrac{2}{3}$$. Also, write inverse of $$f$$.
Give an example of a function which is one-one but not onto.
Show that the function $$f: R\rightarrow R: f(x)=x^4$$ is neither one-one nor onto.
Let R be a relation on $$N\times N$$ defined by $$(a, b) R(c, d)\Leftrightarrow a+d=b+c$$ for all $$(a, b), (c, d)\in N\times N$$
Show that $$(a, b) R (a, b)$$ for all $$(a, b)\in N\times N$$.
Show that the function $$f: N\rightarrow N:f(x)=x^2$$ is one-one into.
The binary operation $$^\star$$ on R is defined by $$a^{\star} b=2a+b$$. Find $$(2^{\star} 3)\star 4$$.
Let $$f(x)=x+7$$ and $$g(x)=x-7$$, $$x\in R$$. Find $$(f o g)(7)$$.
Let $$R_0$$ be the set of all non zero real numbers. Then, show that the function $$f: R_0\rightarrow R_0:f(x)=\dfrac{1}{x}$$ is one-one and onto.
Let $$f: R\rightarrow R:f(x)=(3-x^3)^{1/3}$$. Find $$f o f$$.
Let $$\star$$ be a binary operation on the set I of all integers, defined by $$a^{\star}b=3a+4b-2$$. Find the value of $$4\star 5$$.
Let $$^{\star}$$ be a binary operation on the set of all non zero real numbers, defined by $$a^{\star}b=\dfrac{ab}{5}$$. Find the value of x given that $$2^{\star}(x^{\star}5)=10$$.
Let $$A=\{1, 2, 3\}$$, $$B=\{4, 5, 6, 7\}$$ and let $$f=\{(1, 4), (2, 5), (3, 6)\}$$ be a function from A to B. State whether f is one-one.
Let $$f: R\rightarrow R$$ and $$g: R\rightarrow R$$ defined by $$f(x)=x^2$$ and $$g(x)=(x+1)$$. Show that $$g o f\neq f o g$$.
Let $$^{\star}: R\times R\rightarrow R$$ be a binary operation given by $$a^{\star}b=a+4b^2$$. Then, compute $$(-5)^{\star}(2^{\star}0)$$.
Show that $$\star$$ on $$Z^+$$ defined by $$a\star b=|a-b|$$ is not a binary operation.
Let $$ F : R \rightarrow R : f(x) = x^3 + 1 $$ and $$ g: R \rightarrow E : g (x) = (x+ 1) $$.
Find $$ ( \frac {1}{f})(x) $$.
Let $$ f : R \rightarrow R : f(x) =x +1 $$ and $$ g : R \rightarrow R : g(x) = 2x -3 $$.
Find $$(f -g)(x) $$.
Let $$^{\star}$$ be a binary operation on the set Q of all rational numbers given as $$a^{\star}b=(2a-b)^2$$ for all a, b$$\in$$Q. Find $$3^{\star}5$$ and $$5^{\star}3$$. Is $$3^{\star}5=5^{\star}3$$?
Let $$Q^+$$ be the set of all positive rational numbers. Show that the operation $$\star$$ on $$Q^+$$ defined by $$a\star b=\dfrac{1}{2}(a+b)$$ is a binary operation.
If $$\star$$ be the binary operation on the set Z of all integers defined by $$a^{\star}b=(a+3b^2)$$, find $$2^{\star}4$$.
Let $$ f : R \rightarrow R : f(x) = 2x +5 $$ and $$ g : R \rightarrow R : g(x) =x^2 + x.$$
Find ($$fg$$)($$x$$).
Let $$A=N\times N$$. Define $$\star$$ on A by $$(a, b)\star (c, d)=(a+c, b+d)$$. Show that A is closed for $$\star$$.
Let $$f(x)$$ and $$g(x)$$ be two continuous functions and h(x) $$=\underset{h\rightarrow \infty }{\lim}\dfrac{x^{2n}f(x)+x^{2n}g(x)}{(x^{2n}+1)}$$ if limit of h(x) exists $$x=1$$ then one root of $$f(x)-g(x)=0$$ is
Let $$ f : [ 2 , \infty ) \rightarrow R : f(x) = \sqrt {x-2} $$ and $$ g: [2, \infty) \rightarrow R : g (x) = \sqrt {x +2} $$
Find $$(f-g)(x)$$.
Let $$ f : [ 2 , \infty ) \rightarrow R : f(x) = \sqrt {x-2} $$ and $$ g: [2, \infty) \rightarrow R : g (x) = \sqrt {x +2} $$
Find $$( f+g)(x)$$.
Find the set of values for which the function $$ f(x) = x +3 $$ and $$ g(x) = 3x^2 -1 $$ are equal.
Given $$f(\dfrac{1}{e})=0$$ $$\dfrac{\int_{f(y)}^{f(y)}e'dt}{\int_{y}^{x}(1/2)dt}=1,\forall x,y\epsilon (\dfrac{1}{e^{2}}\infty ) $$ Where f(x) is Continuous and differentiable function and $$f\left ( \dfrac{1}{e} \right )=0$$ if then the value of K' for which $$f(g(x))$$ is continuous $$\forall x\epsilon R^{+}$$ is
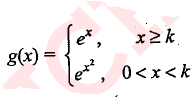
Let $$f : R\to R$$ be the function defined by $$f(x)=2x-3, \forall c \in R.$$ write $$f^{-1}$$.
A table of values of $$ \mathrm{f}, \mathrm{g}, \mathrm{f}^{\prime} $$ and $$ \mathrm{g}^{\prime} $$ is given :
If $$ \mathrm{r}(\mathrm{x})=\mathrm{f}[\mathrm{g}(\mathrm{x})] $$ find $$ \mathrm{r}^{\prime}(2) $$
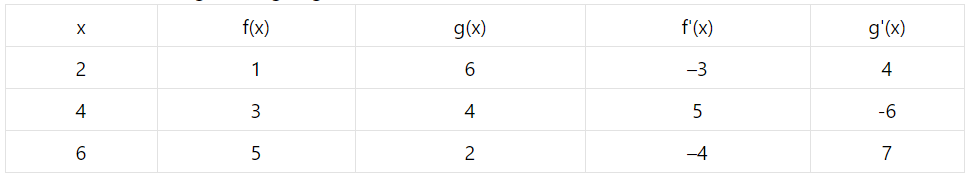
Let $$f, g:R\to R$$ be defined by $$f(x)=2x+1$$ and $$g(x)=x^2 -2$$ respectively.
Then find $$g\ o\ f$$.
A table of values of $$ \mathrm{f}, \mathrm{g}, \mathrm{f}^{\prime} $$ and $$ \mathrm{g}^{\prime} $$ is given:
If $$ \mathrm{R}(\mathrm{x})=\mathrm{g}[3+\mathrm{f}(\mathrm{x})] $$ find $$ \mathrm{R}^{\prime}(4) $$
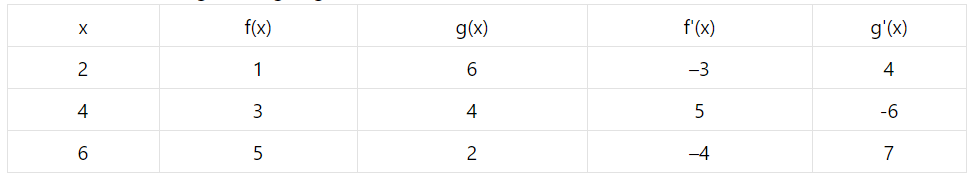
If $$A=\left\{a,b,c,d \right\}$$ and the function $$f=\left\{(a,b),(b,d),(c,a),(d,c) \right\}$$, write $$f^{-1}$$.
Consider the binary operation $$*$$ on the set {$$1,2,3,4,5$$} defined by $$a*b=min$$. {$$a,b$$}. Write the operation table of the operation $$*$$.
If $$ f(x)=x^{3}+x-2, $$ find $$ \left(f^{-1}\right)^{\prime}(-2) $$
Determine whether or not each of the definitions given below gives a binary operation. In the event that is not a binary operation, give justification for this.
$$OnZ^+,*$$ defined by $$a*b=|a-b|$$
Determine whether or not each of the definition of given below gives a binary operation. In the even that is not a binary operation, give justification for this.
$$On\ R,*$$ defined by $$a*b=ab^2$$
Determine whether or not each of the definition of given below gives a binary operation. In the even that is not a binary operation, give justification for this.
$$OnZ^+,*$$ defined by $$a*b=ab$$
Determine whether or not each of the definition of given below gives a binary operation. In the even that is not a binary operation, give justification for this.
$$OnZ^+,*$$ defined by $$a*b=a$$
Determine whether or not each of the definition of given below gives a binary operation. In the even that is not a binary operation, give justification for this.
$$OnZ^+,*$$ defined by $$a*b=a-b$$
A table of values of $$ f, g, f^{\prime} $$ and $$ g^{\prime} $$ is given:
If $$ S(x)=g[g(x)] $$ find $$ S^{\prime}(6) $$
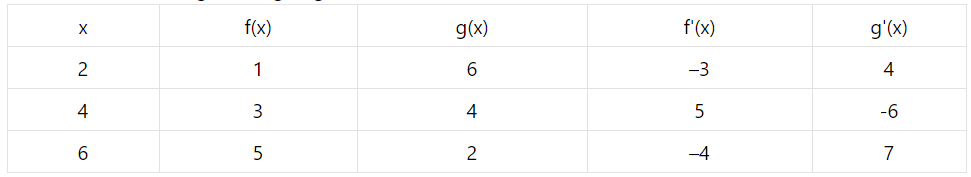
If $$ h(x)=\sqrt{4 f(x)+3 g(x)}, f(1)=4, g(1)=3, f \prime(1)=3, g \prime(1)=4, $$ find $$ h ^{\prime}(1) $$
A table of values of $$ f, g, f^{\prime} $$ and $$ g^{\prime} $$ is given:
If $$ s(x)=f[9-f(x)] $$ find $$ s^{\prime}(4) $$
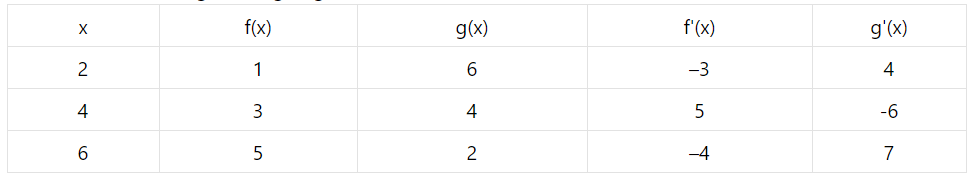
Let $$S= \left\{a,b,c\right\}$$ and $$T=\left\{1,2,3,\right\}$$ Find $$F^{-1}$$ of the folowing function $$F$$ from $$S$$ to $$T$$ if it exists.
$$F=\left\{(a,2), (i,1), (c,1) \right\}$$
Let $$S= \left\{a,b,c\right\}$$ and $$T=\left\{1,2,3,\right\}$$ Find $$F^{-1}$$ of the folowing function $$F$$ from $$S$$ to $$T$$ if it exists.
$$F=\left\{(a,3), (b,2), (c,1) \right\}$$
Consider a binary $$*$$ operation on the set $${1,2,3,4,5}$$ given by the following multiplication table
Compute $$(2*3)*4$$ and $$2*(3*4)$$
| $$*$$ | $$1$$ | $$2$$ | $$3$$ | $$4$$ | $$5$$ |
| $$1$$ | $$1$$ | $$1$$ | $$1$$ | $$1$$ | $$1$$ |
| $$2$$ | $$1$$ | $$2$$ | $$1$$ | $$2$$ | $$1$$ |
| $$3$$ | $$1$$ | $$1$$ | $$3$$ | $$1$$ | $$1$$ |
| $$4$$ | $$1$$ | $$2$$ | $$1$$ | $$4$$ | $$1$$ |
| $$5$$ | $$1$$ | $$1$$ | $$1$$ | $$1$$ | $$5$$ |
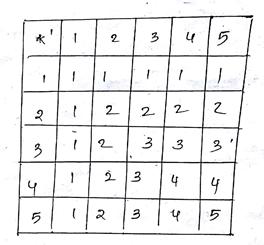
Consider a binary $$*$$ operation on the set $${1,2,3,4,5}$$ given by the following multiplication table
Compute $$(2*3)*(4*5)$$ .
| $$*$$ | $$1$$ | $$2$$ | $$3$$ | $$4$$ | $$5$$ |
| $$1$$ | $$1$$ | $$1$$ | $$1$$ | $$1$$ | $$1$$ |
| $$2$$ | $$1$$ | $$2$$ | $$1$$ | $$2$$ | $$1$$ |
| $$3$$ | $$1$$ | $$1$$ | $$3$$ | $$1$$ | $$1$$ |
| $$4$$ | $$1$$ | $$2$$ | $$1$$ | $$4$$ | $$1$$ |
| $$5$$ | $$1$$ | $$1$$ | $$1$$ | $$1$$ | $$5$$ |
Consider $$f:\left\{1,2,3\right\}\rightarrow \left\{a, b, c\right\}$$ given by $$f(1)=a, f(2)=b$$ and $$f(3)=c$$. Find $$f^{-1}$$ and show that $$(f^{-1})^{-1}=f$$.
$$*'$$ Let be the binary operation on the set $${1,2,3,4,5}$$ defined by $$a*'b=H.C.F$$ of $$a$$ band $$b$$. Is the $$*'$$ operation same as the $$*$$ operation defined in Exercise $$4$$ above? Justify your answer.
Consider a binary $$*$$ operation on the set $${1,2,3,4,5}$$ given by the following multiplication table
$$*$$ Is commutative?
| $$*$$ | $$1$$ | $$2$$ | $$3$$ | $$4$$ | $$5$$ |
| $$1$$ | $$1$$ | $$1$$ | $$1$$ | $$1$$ | $$1$$ |
| $$2$$ | $$1$$ | $$2$$ | $$1$$ | $$2$$ | $$1$$ |
| $$3$$ | $$1$$ | $$1$$ | $$3$$ | $$1$$ | $$1$$ |
| $$4$$ | $$1$$ | $$2$$ | $$1$$ | $$4$$ | $$1$$ |
| $$5$$ | $$1$$ | $$1$$ | $$1$$ | $$1$$ | $$5$$ |
Let $$f: W \rightarrow W$$ be defined as $$f(n)=-1$$ i f$$n$$ is odd and $$f(n)=n-1$$, if $$n$$ is even. Show that
$$f$$ is invertible. Find the inverse of $$f$$. Here, $$W$$ is the set of all whole numbers.
Let $$A= \left\{-1,0,1,2 \right\},\ B=\left\{-4,-2,0,2 \right\}$$ and $$f, g : A \rightarrow B$$ be functions defined by
$$f(x)=x^2-x, x \in A$$ and $$g(x)=-1, x \in A$$ Are $$f$$ and $$g$$ equal? Justify your answer.
Consider the binary $$\wedge $$ operation on the set $$\left\{1,2,3,4,5\right\}$$
defined by a $$\wedge b=min\left\{a,b\right\}$$. Write operation table of the operation $$\wedge$$
Determine whether each of the following operation define a binary on the given set or not. Also, Justify your answer.
$$a*b =a+3b$$, on $$N$$
Define a relation.
Determine whether each of the following operation define a binary on the given set or not. Also, Justify your answer.
$$a*b =a$$, on $$N$$
Determine whether each of the following operation define a binary on the given set or not. Also, Justify your answer.
$$a*b =a/b$$, on $$Q$$
Let $$f, g: R\to R$$ be defined, respectively by $$f(x)=x+1, g(x)=2x-3$$ Find $$f+g, f-g$$ and $$\cfrac{f}{g}$$
Show that the function $$f: R \rightarrow R$$ defined by $$f(n)=\dfrac{2n-1}{3}, n \in R$$ is one-one onto function. Also find the inverse of $$f$$
Determine whether each of the following operation define a binary on the given set or not. Also, Justify your answer.
$$a*b =a+b-3$$, on $$N$$
Let $$f(x)=\sqrt x$$ and $$g(x)=x$$ be two function defined over the set of non-negative real numbers. Find $$f(+g)(x), (f-g)(x)(fg)(x)$$ and $$\left( \dfrac fg \right)(x)$$
State whether the following statements are true or false. Justify.
For an arbitrary binary operation $$*$$ on a set $$N,a*a=a \forall a\epsilon N$$
If $$A=\left\{ -1, 1\right\}f$$ and $$g$$ are two functions defined on $$A$$, where $$f(x)=x^2, g(x)=\sin ( \pi x/2)$$, prove that $$g^{-1}$$ exists but $$f^{-1}$$ does not exist, also find $$g^{-1}$$.
Give one example of each of the following function :
One-one into
Four function are defined on set $$R_0$$. Such that,
$$f_1(x)=x, f_2(x)=-x, f_3(x)=1/x, f_4(x)=-1/x$$ Construct the composition table for the composition of functions $$f_1, f_2, f_3, f_4$$. Also find identify element and inverse of every element.
If $$f:R\rightarrow R,f(x)=\cos (x+2)$$, is $$f^{-1}$$ exists.
Determine whether each of the following operation define a binary on the given set or not. Also, Justify your answer.
$$a*b =a-b$$, on $$R$$
If $$ f : C \rightarrow C , f ( x + iy) = ( x - iy) $$ , then prove that if is an one-one onto function.
Verify the associative law for the composite function of following three functions:
$$f:N \to Z_0, f(x)=2x$$
$$g: Z_0 \to Q, g(x)=1/x$$
$$h: Q \to R, h(x)=e_x$$
Give one example of each of the following function :
Onto but not one-one
Verify or prove whether the given functions are inverses of each other or not:
$$f(x)=4x-2$$ and $$g(x)=\dfrac{x+2}{4}$$
Let $$A=\{a,b,c\},B=\{u,v,w\}$$ and $$f $$ and $$g$$ be two function from $$A$$ to $$B$$ and from $$B$$ to $$A $$ respectively defined as $$f = \{(a,v),(b,u),(c,w)\} $$ and $$g=\{(u,b),(v,a),(w,c)\}$$.
Show that $$f $$ and $$g$$ both are bijections and find $$fog $$ and $$gof.$$
Give one example of each of the following function :
One - one but not onto
If the function $${f}({x})={x}^{3}+{e}^{{x}/2}$$ and $${g}({x})={f}^{-1}({x})$$, then the value of $${g}'(1)$$ is
Let $$f(x)=x+\dfrac{1}{x}$$ and $$g(x)=\dfrac{x+1}{x+2}$$
Determine whether or not each of the definition of $$*$$ given below gives a binary operation. In the event that $$*$$ is not a binary operation, given justification for this
(i) On $$Z^{+}$$, define $$*$$ by $$a * b = a - b$$
(ii) On $$Z^{+}$$, define $$*$$ by $$a * b = ab$$
(iii) On $$R$$, define $$*$$ by $$a * b = ab^{2}$$
(iv) On $$Z^{+}$$, define $$*$$ by $$a * b = |a - b|$$
On $$Z^{+}$$, define $$*$$ by $$a * b = a$$
Find the inverse of the rational function $$f$$.
$$f(x)=\dfrac2x$$
If the function $$ f:R\rightarrow A,$$ given by $$\displaystyle f(x)=\frac{x^{2}}{x^{2}+1}$$ is surjection, then $$ A\in [k,m)$$. Find $$k+m$$.
If the function $$ f:R\rightarrow A,$$ given by $$\displaystyle f(x)=\frac{e^{x}-e^{-\left|x\right|}}{e^{x}+e^{\left|x\right|}}$$ is surjection,then $$\displaystyle A\in \left[ m,k.\right)$$,Find 2(m+k) ?
Let $$\displaystyle A=R\times R$$ and $$\displaystyle *$$ be a binary operation on A defined by
$$\displaystyle \left( a,b \right) \ast \left( c,d \right) =\left( a+c,b+d \right) $$
Show that $$\displaystyle *$$ is commutative and associative. Find the identity element for $$\displaystyle *$$ on A. Also find the inverse of every element $$\displaystyle \left( a,b \right) \in A$$.
Show that the function $$f$$ in $$A=R-$$$$\left\{\dfrac{2}{3}\right\}$$ defined as $$f(x)=\dfrac{4x+3}{6x-4}$$ is one-one and onto. Hence find $$f^{-1}$$.
The binary operation $$\ast : R\times R \rightarrow R$$ is defined as $$a\ast b = 2a + b$$. Find $$(2\ast 3)\ast 4.$$
Consider $$f:R+\rightarrow [4, \infty]$$ given by $$f(x) = x^2+4$$. Show
that $$f$$ is invertible with the inverse $$f^{-1}$$ of $$f$$ given by $$f^{-1}(y) = \sqrt{y-4}$$ where $$R_+$$ is the set of all non-negative real numbers.
Consider the binary operations $$\ast : R\times R \rightarrow R$$ and $$o : R\times R \rightarrow R$$ defined as $$a\ast b = |a - b|$$ and $$aob = a$$ for all $$a, b\in R$$. Show that $$'\ast'$$ is commutative but not associative, 'o' is associative but not commutative.
If $$f(x) = \sqrt{x^2+1}, g(x)=\dfrac{x+1}{x^2+1}$$ and $$h(x) = 2x - 3,$$ then find $$f'[h'|g'(x)|]$$.
Let $$f,g,h$$ are functions defined by $$f(x)=x-1,g(x)={ x }^{ 2 }-2$$ and $$h(x)={ x }^{ 3 }-3$$, show that $$\left( f\circ g \right) \circ h=f\circ \left( g\circ h \right) $$.
If $$f:R-\left\{ 3 \right\} \rightarrow R$$ is defined by $$f(x)=\cfrac { x+3 }{ x-3 } $$, show that $$f\left[ \cfrac { 3x+3 }{ x-1 } \right] =x$$ for $$x\ne 1$$.
If functions $$f, g : R \rightarrow R$$ are defined as $$f(x) = x^{2} + 1, g(x) = 2x - 3$$, then find $$f\ o\ g(x), g\ o\ f(x)$$ and $$g\ o\ g(3)$$
If $$f(x)={x}^{2}$$ and $$g(x)=2x-6$$, find the following functions:
$$(f+g)(x), (f\times g)(x), (f\circ g)(x), (f\circ f)(x), {g}^{-1}(x)$$
Let $$f:A \to B$$ and $$g:B \to C$$ be one-one onto functions. prove that $$\left( {gof} \right):A \to C$$ which is one-one onto
Let $$f:[0,\infty )\rightarrow R$$ be a function defined by $$f(x)=9{ x }^{ 2 }+6x-5$$. Prove that $$f$$ is not invertible and then find its inverse.
Let $$f:\left\{1,3,4\right\} \rightarrow \left\{1,2,5\right\}$$ and $$g:\left\{1,2,5\right\} \rightarrow \left\{1,3\right\}$$
given by $$f=\left\{(1,2),(3,5),(4,1)\right\}$$ and $$g=\left\{(1,3),(2,3),(5,1)\right\}$$ write down $$gof$$
If $$f(x)=(a-x^n)^{\dfrac{1}{n}}$$ then $$fof(x)$$ is?
Let $$f:W\longrightarrow W$$ be defined as $$f(x)=x-1$$, if $$x$$ is odd and $$f(x)=x+1$$, if $$x$$ is even, then show that $$f$$ is invertible. Also, find the inverse of $$f$$, where $$W$$ is the set of all whole numbers.
Let $$f:R\rightarrow R$$ be defined by $$f\left( x \right) =2x+\left| x \right|$$ Then prove that $$f\left( 2x \right) +f\left( -x \right) -f\left( x \right) =2\left| x \right|$$.
If $$f\left( x \right)=\dfrac { 2x-1 }{ x-2 }$$
what is the inverse function of $$f\left( x \right)$$
Show that the binary operation on $$Q - \{1\}$$, defined by $$a \times b = a + b - ab$$ for all $$a, b \in Q - \{1\}$$ satisfies (i) the closure property, (ii) the associative law
(iii) the commutative law
(iv) What is the identity element ?
(v) For each $$a \in Q - \{1\}$$, find the inverse of $$a$$.
If $$f\left( x \right) =2{ x }^{ 2 }-3x-1$$, Find $$f\left( x+2 \right)$$
Given $$f(x)=x+2,g(x)=2x+3,h(x)=3x^4$$ for $$x \epsilon R$$ . Find
$$fo(goh)$$
Let $$*$$ be the binary operation on $$N$$ , given by $$a * b = L C M$$ of $$a$$ and $$b$$ . Find $$20 * 16$$.
$$0.25\ (4-f-3)=0.05\ (10f-9)$$
Let $$A=Z\times Z$$ and * be a binary operation on $$A$$ defined by $$(a, b)*(c, d)=(ad+bc, bd)$$.
Find the identity element for * in the set $$A$$.
If $$f(x)=3x-2$$ and $$(gof)^{-1}(x)=x-2$$, then find the function $$g(x)$$
$$A,B,C$$ are three sets such that $$n(A)=2$$,$$n(B)=3$$,$$n(C)=4$$, If $$P(x)$$ denotes power set of $$X$$,$$k=\dfrac{n\left(P\left(P\left(C\right)\right)\right)}{n\left(P\left(P\left(A\right)\right)\right)\times n\left(P\left(P\left(B\right)\right)\right)}$$.then find the Sum of digits of $$k$$
Let the function f:$$R\longrightarrow R$$ be defined by $$f(x)=\cos { x } ,\forall x\in R$$. Show hat f is neither one-one nor onto.
Let $$A=Q\times Q$$ and let* be a binary operation on A defined by $$\left( a,b \right) *\left( c,d \right) =\left( ac,b+ad \right) for\left( a,b \right) ,\left( c,d \right) \epsilon A.$$ Determine, whether * is commutative and associative. Then, with respect to * on A
Find the invertible elements of A.
Find $${f}^{-1}$$, if it exists:$$f:A\rightarrow B$$, where
(i) $$A=\left\{ 0,-1,-3,2 \right\} ;B=\left\{ -9,-3,0,6 \right\} $$ and $$f(x)=3x$$
(ii) $$A=\left\{ 1,3,5,7,9 \right\} ;B=\left\{ 0,1,9,25,49,81 \right\} $$ and $$f(x)={x}^{2}$$
State with reasons whether given functions have inverse:
(i) $$f:\left\{ 1,2,3,4 \right\} \rightarrow \left\{ 10 \right\} $$ with $$f=\left\{ \left( 1,10 \right) ,\left( 2,10 \right) ,\left( 3,10 \right) ,\left( 4,10 \right) \right\} $$
(ii) $$g:\left\{ 5,6,7,8 \right\} \rightarrow \left\{ 1,2,3,4 \right\} $$ with $$g=\left\{ \left( 5,4 \right) ,\left( 6,3 \right) ,\left( 7,4 \right) ,\left( 8,2 \right) \right\} $$
(iii) $$h:\left\{ 2,3,4,5 \right\} \rightarrow \left\{7,9,11,13 \right\} $$ with $$h=\left\{ \left( 2,7 \right) ,\left( 3,9 \right) ,\left( 4,11 \right) ,\left( 5,13 \right) \right\} $$
Let $$f:R\rightarrow R$$ and $$g:R\rightarrow R$$ be defined by $$f(x)={x}^{2}$$ and $$g(x)=x+1$$. Show that $$f\circ g\ne g\circ f$$.
Show that the function $$f:Q\rightarrow Q$$ defined by $$f(x)=3x+5$$ is invertible. Also, find $${f}^{-1}$$.
Which of the following functions from $$A$$ to $$B$$ are one-one and onto?
(i) $${f}_{1}=\left\{ \left( 1,3 \right) ,\left( 2,5 \right) ,\left( 3,7 \right) \right\} $$; $$A=\left\{ 1,2,3 \right\} ,B=\left\{ 3,5,7 \right\} $$
(ii) $${f}_{2}=\left\{ \left( 2,a \right) ,\left( 3,b \right) ,\left( 4,c \right) \right\} $$; $$A=\left\{ 2,3,4 \right\} ,B=\left\{ a,b,c \right\} $$
(iii) $${f}_{3}=\left\{ \left( a,x \right) ,\left( b,x \right) ,\left( c,z \right) \right\} $$; $$A=\left\{ a,b,c,d \right\} ;B=\left\{ x,y,z \right\} $$
Suppose $${f}_{1}$$ and $${f}_{2}$$ are non-zero one-one functions from $$R$$ to $$R$$. Is $$\cfrac{{f}_{1}}{{f}_{2}}$$ necessarily one-one. Justify your answer. Here $$\cfrac{{f}_{1}}{{f}_{2}}:R\rightarrow R$$ is given by $$\left( \cfrac { { f }_{ 1 } }{ { f }_{ 2 } } \right) \left( x \right) =\cfrac { { f }_{ 1 }(x) }{ { f }_{ 2 }(x) } $$ for all $$x\in R$$.
Let $$f:R\rightarrow R$$ and $$g:R\rightarrow R$$ be defined by $$f(x)=x+1$$ and $$g(x)=x-1$$. Show that $$f\circ g=g\circ f={R}_{R}$$.
Let $$f(x)=\begin{cases} 1+x,\quad 0\le x\le 2 \\ 3-x,\quad 2<x\le 3 \end{cases}$$. Find $$f\circ f$$.
Consider the function $$f:{R}^{+}\rightarrow [-9,\infty)$$ given by $$f(x)=5{x}^{2}+6x-9$$. Prove that $$f$$ is invertible with $${f}^{-1}(y)=\cfrac { \sqrt { 54-5y } -3 }{ 5 } $$.
Let $$A=R-\left\{ 3 \right\} $$ and $$B=R-\left\{ 1 \right\} $$. Consider the function $$f:A\rightarrow B$$ defined by $$f(x)=\cfrac{x-2}{x-3}$$. Show that $$f$$ is one-one and onto and hence find $${f}^{-1}$$.
Consider $$f:{R}^{+}\rightarrow [-5,\infty)$$ given by $$f(x)=9{x}^{2}+6x-5$$. Show that $$f$$ is invertible with $${f}^{-1}(x)=\cfrac{\sqrt{x+6}-1}{3}$$.
Show that the function $$f: R\rightarrow R:f(x)=x^5$$ is one-one and onto.
Show that the function $$f: Z\rightarrow Z:f(x)=x^3$$ is one-one into.
Prove that the function $$f: N\rightarrow N:f(n)=(n^2+n+1)$$ is one-one but not onto.
If the mapping $$f:\left\{ 1,3,4 \right\} \rightarrow \left\{ 1,2,5 \right\} $$ and $$g:\left\{ 1,2,5 \right\} \rightarrow \left\{ 1,3 \right\} $$, given by $$f=\left\{ \left( 1,2 \right) ,\left( 3,5 \right) ,\left( 4,1 \right) \right\} $$ and $$g=\left\{ \left( 2,3 \right) ,\left( 5,1 \right) ,\left( 1,3 \right) \right\} $$, write $$f\circ g$$.
Consider $$f:{R}^{+}\rightarrow [4,\infty)$$ given by $$f(x)={x}^{2}+4$$. Show that $$f$$ is invertible with inverse $${f}^{-1}$$ of $$f$$ given by $${f}^{-1}(x)=\sqrt{x-4}$$, where $${R}^{+}$$ is the set of all non-negative real numbers.
Let $$f:\left[0, \dfrac{\pi}{2}\right]\rightarrow R:f(x)=\sin x$$ and $$g:\left[0, \dfrac{\pi}{2}\right]\rightarrow R: g(x)=\cos x$$. Show that each one of $$f$$ and $$g$$ is one-one but $$(f+g)$$ is not one-one.
Show that the function $$f: N\rightarrow N:f(x)=x^3$$ is one-one into.
Let $$A=\{1, 2, 3, 4\}$$ and $$f=\{(1, 4), (2, 1), (3, 3), (4, 2)\}$$. Write down $$(f o f)$$.
Let $$f(x)=8x^3$$ and $$g(x)=x^{1/3}$$. Find g o f and f o g.
Let f and g be two functions from R into R, defined by $$f(x)=|x|+x$$ and $$g(x)=|x|-x$$ for all $$x\in R$$. Find f o g and g o f.
Show that the function $$f:Z\rightarrow Z:f(x)=x^3$$ is one-one and into.
Let $$f=\{(1, 2), (3, 5), (4, 1)\}$$ and $$g=\{(1, 3), (2, 3), (5, 1)\}$$. Write down g o f.
Prove that the function $$f: R\rightarrow R: f(x)=2x$$ is one-one and onto.
Show that the function $$f: N\rightarrow Z$$, defined by
$$f(n)=\left\{\begin{matrix} \dfrac{1}{2}(n-1), & \text{when} \,n \,\text{is odd}\\ -\dfrac{1}{2}n, & \text{when} \, n \, \text{is even}\end{matrix}\right.$$ is both one-one and onto.
Show that the function $$f: N\rightarrow N:f(x)=x^2$$ is one-one and into.
Prove that the function $$f: N\rightarrow N:f(x)=3x$$ is one-one and into.
Let Q be the set of all rational numbers. Define an operation $$\star$$ on $$Q-\{-1\}$$ by $$a\star b=a+b+ab$$.
Show that $$\star$$ is a binary operation on $$Q-\{-1\}$$.
Let $$ f : R \rightarrow R : f(x) = 2x +5 $$ and $$ g : R \rightarrow R : g(x) =x^2 + x.$$
Find $$(f +g)(x) $$.
Let $$ f : R \rightarrow R : f(x) =x +1 $$ and $$ g : R \rightarrow R : g(x) = 2x -3 $$.
Find $$ (\frac {f}{g} )(x) $$.
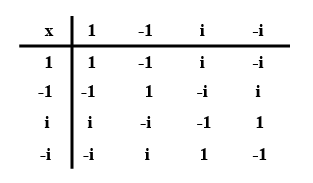
Let $$A=\{1, -1, i, -i\}$$ be the set of four $$4$$th roots of unity. Prepare the composition table for multiplication on A and show that
(i) A is closed for multiplication,
(ii) multiplication is associative on A,
(iii) multiplication is commutative on A,
(iv) $$1$$ is the multiplication identity,
(v) every element in A has its multiplicative inverse.
Let $$ f : R \rightarrow R : f(x) =x +1 $$ and $$ g : R \rightarrow R : g(x) = 2x -3 $$. Find ($$fg$$)($$x$$).
Let $$ f : R \rightarrow R : f(x) = 2x +5 $$ and $$ g : R \rightarrow R : g(x) =x^2 + x.$$
Find $$ (f-g)(x)$$.
Find the set of values for which the function $$ f(x) = 1 -3x $$ and $$ g(x) = 2x^2 -1 $$ are equal.
Let $$ f : R \rightarrow R : f(x) = 2x +5 $$ and $$ g : R \rightarrow R : g(x) =x^2 + x.$$
Find $$ ( \frac {f}{g})(x) $$.
Let $$ F : R \rightarrow R : f(x) = x^3 + 1 $$ and $$ g: R \rightarrow E : g (x) = (x+ 1) $$.
Find $$(f +g)(x)$$
Let $$\displaystyle A = \{3, 5 \}$$ and $$\displaystyle B = \{ 7, 9 \}$$. Let $$\displaystyle R = \{ (a, b) : a \in A, b \in B$$ and $$\displaystyle (a - b)$$ is odd $$\displaystyle \}$$.
Show that $$\displaystyle R$$ is an empty relation from $$\displaystyle A $$ to $$\displaystyle B$$.
Let $$ F : R \rightarrow R : f(x) = x^3 + 1 $$ and $$ g: R \rightarrow E : g (x) = (x+ 1) $$.
Find $$ ( \frac {f}{g} ) (x) $$.
Let $$ f : [ 2 , \infty ) \rightarrow R : f(x) = \sqrt {x-2} $$ and $$ g: [2, \infty) \rightarrow R : g (x) = \sqrt {x +2} $$
Find $$(fg)(x).$$
Let $$ F : R \rightarrow R : f(x) = x^3 + 1 $$ and $$ g: R \rightarrow E : g (x) = (x+ 1) $$.
Find $$(f-g)(x)$$.
Consider the set $$A$$ containing $$n$$ elements. Then, the total number of injective functions from $$A$$ onto itself is _______.
Class 12 Commerce Maths Extra Questions
- Application Of Derivatives Extra Questions
- Application Of Integrals Extra Questions
- Continuity And Differentiability Extra Questions
- Determinants Extra Questions
- Differential Equations Extra Questions
- Integrals Extra Questions
- Inverse Trigonometric Functions Extra Questions
- Linear Programming Extra Questions
- Matrices Extra Questions
- Probability Extra Questions
- Relations And Functions Extra Questions
- Three Dimensional Geometry Extra Questions
- Vector Algebra Extra Questions