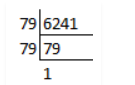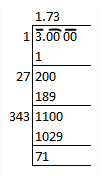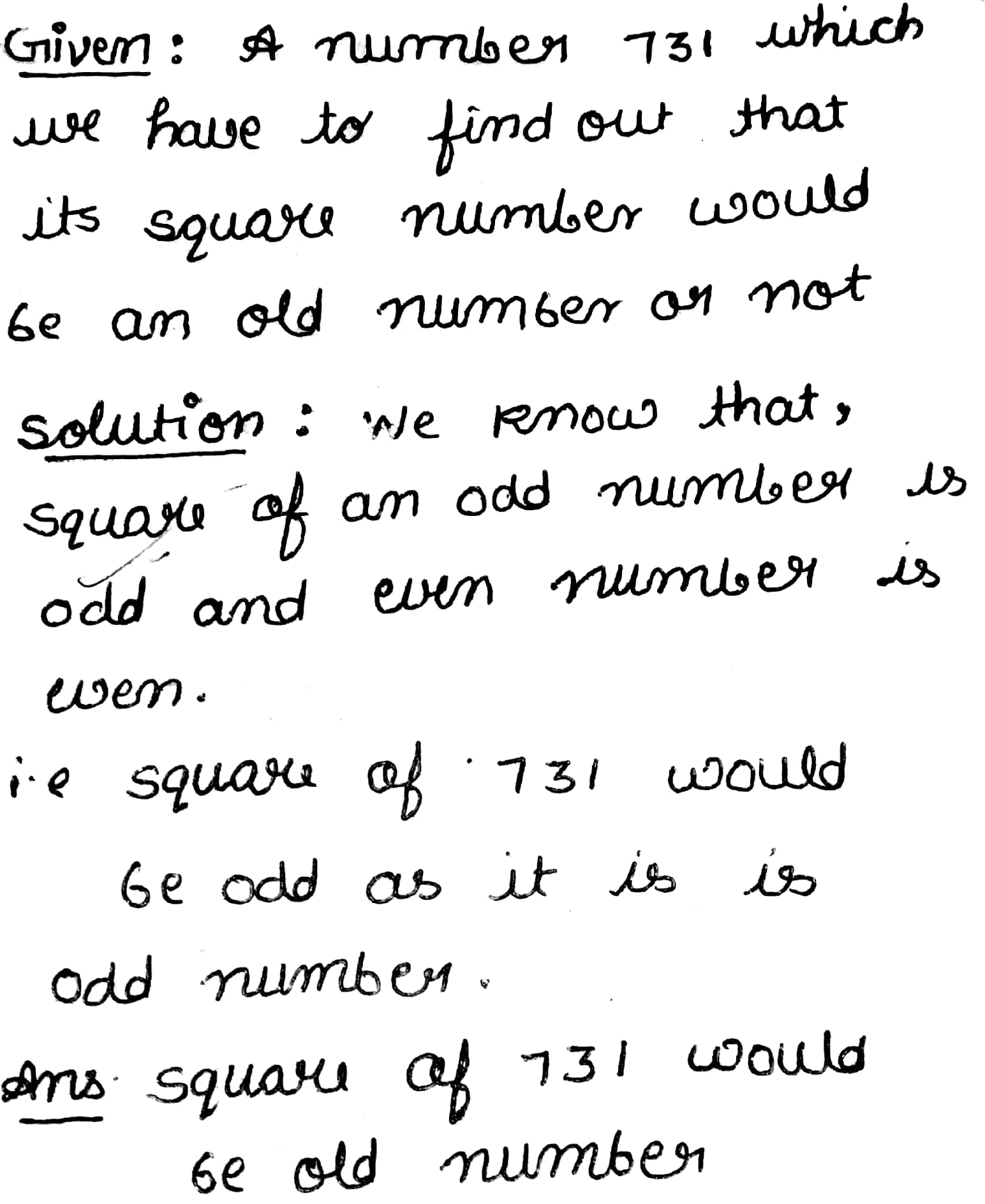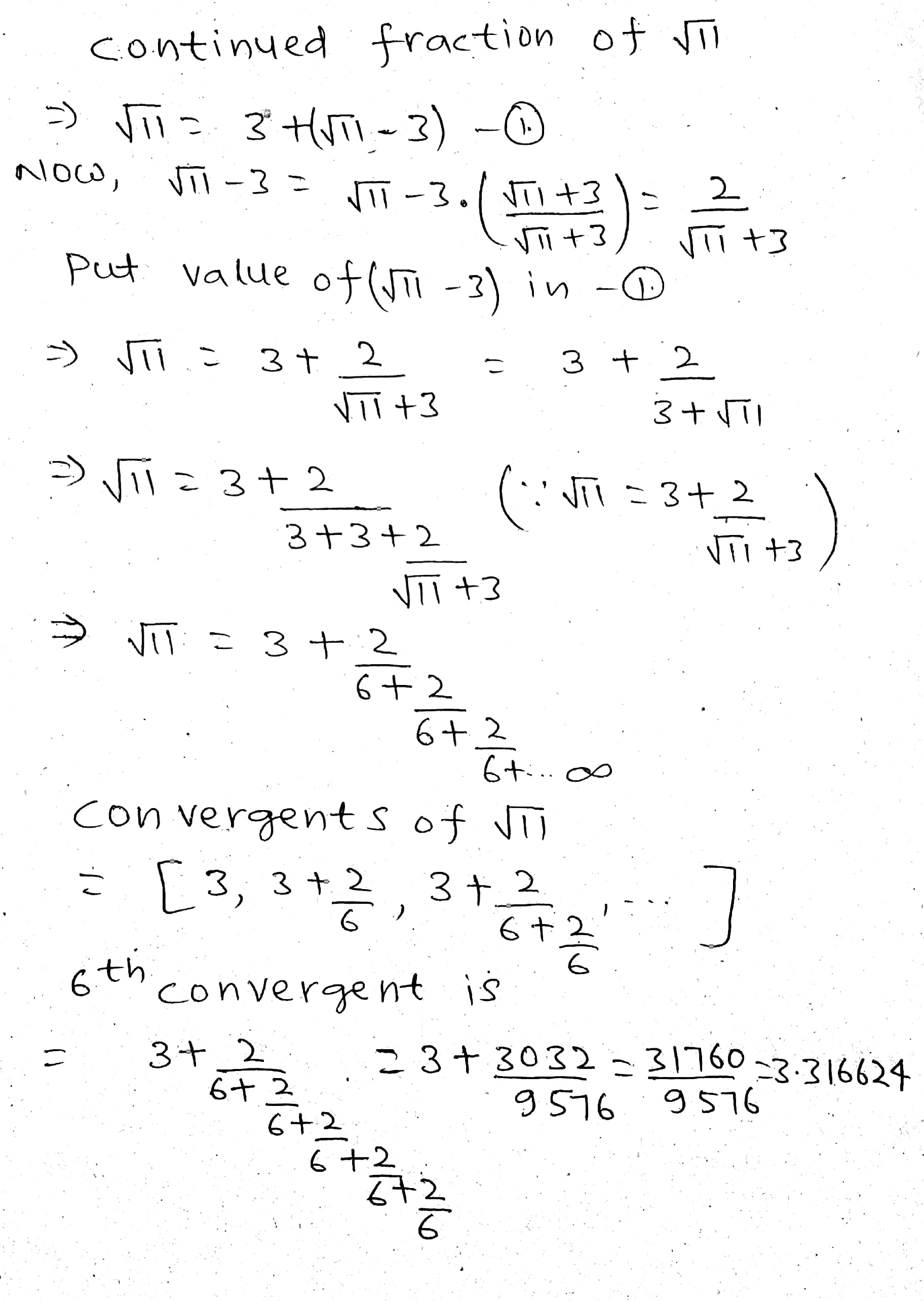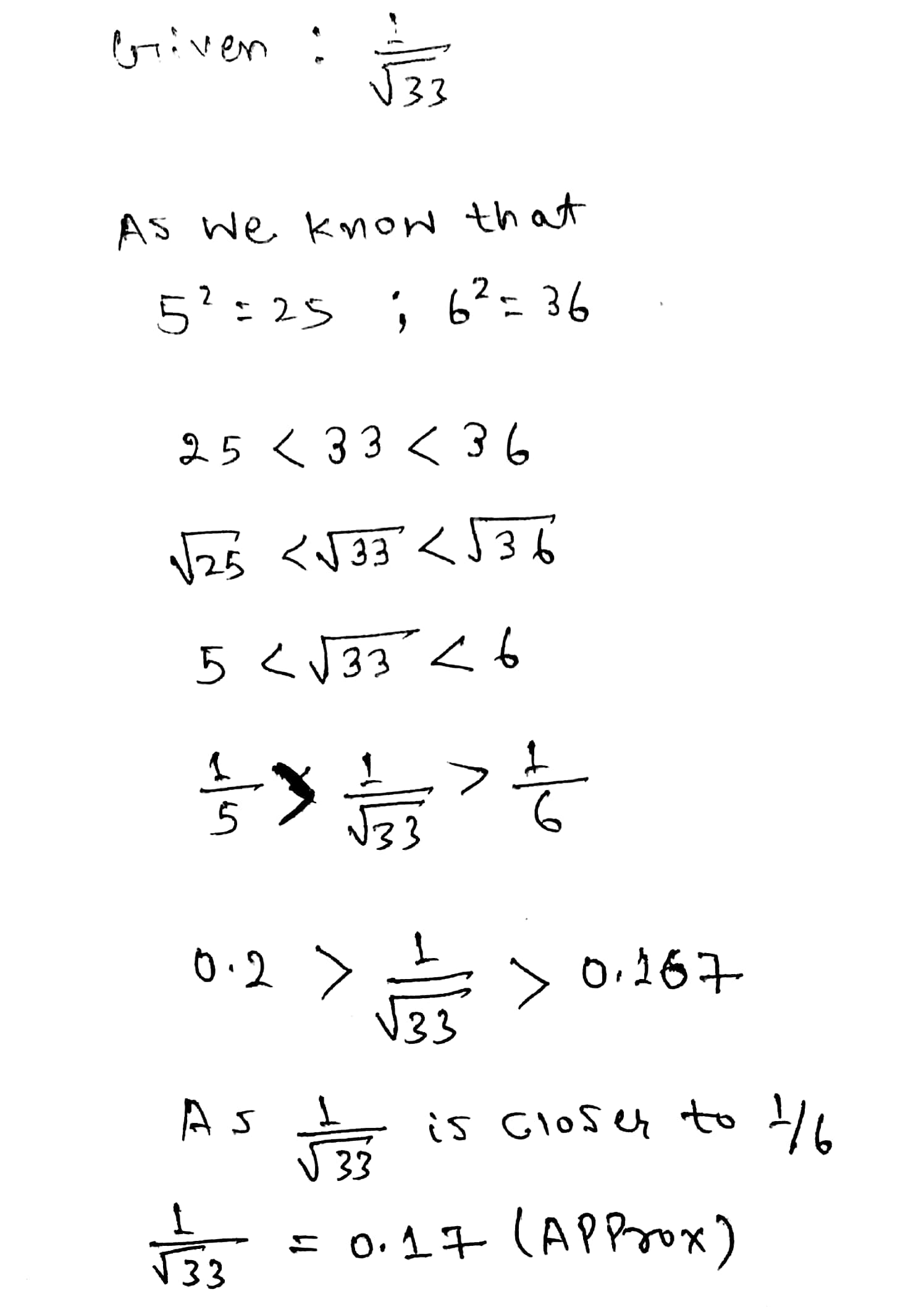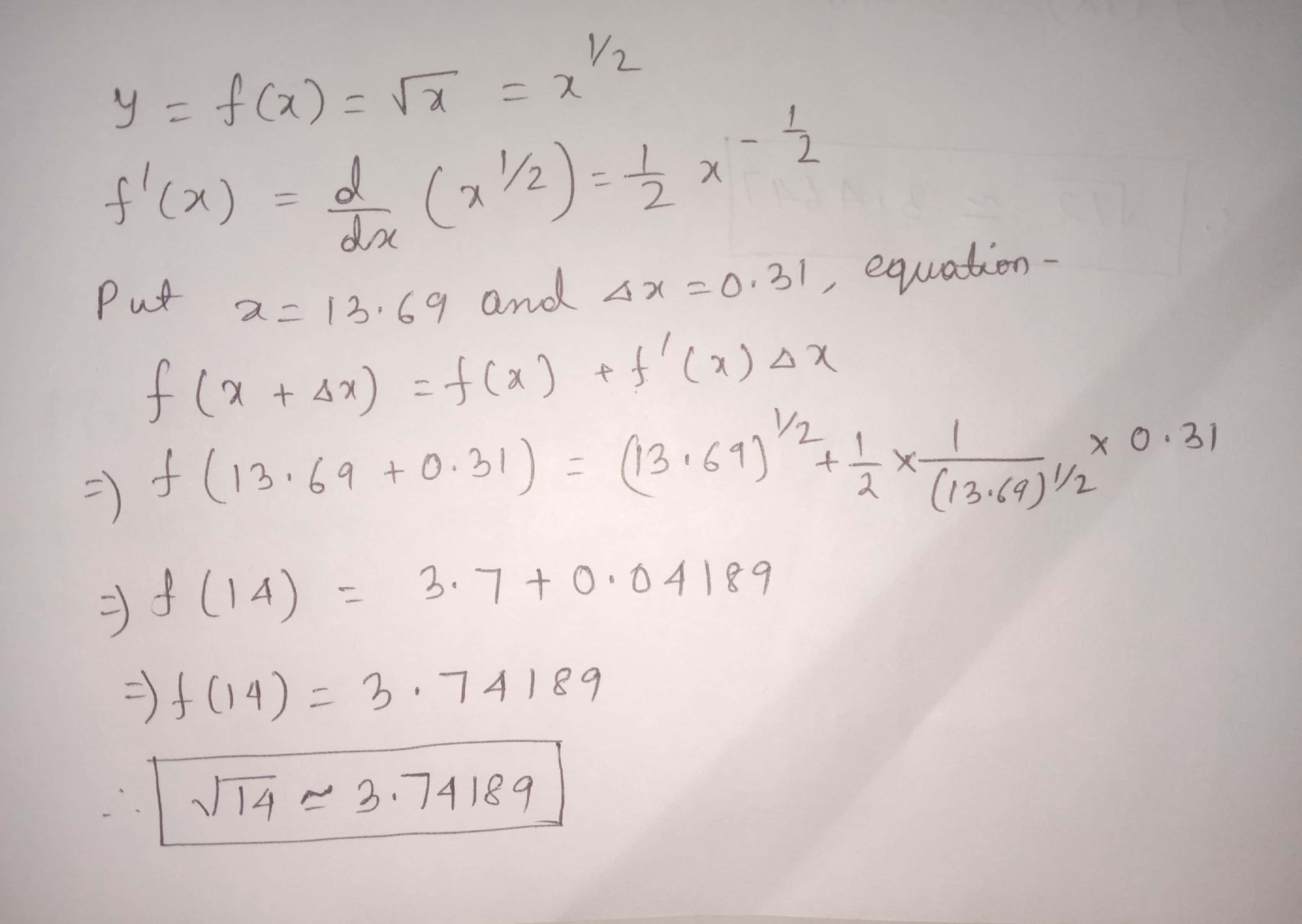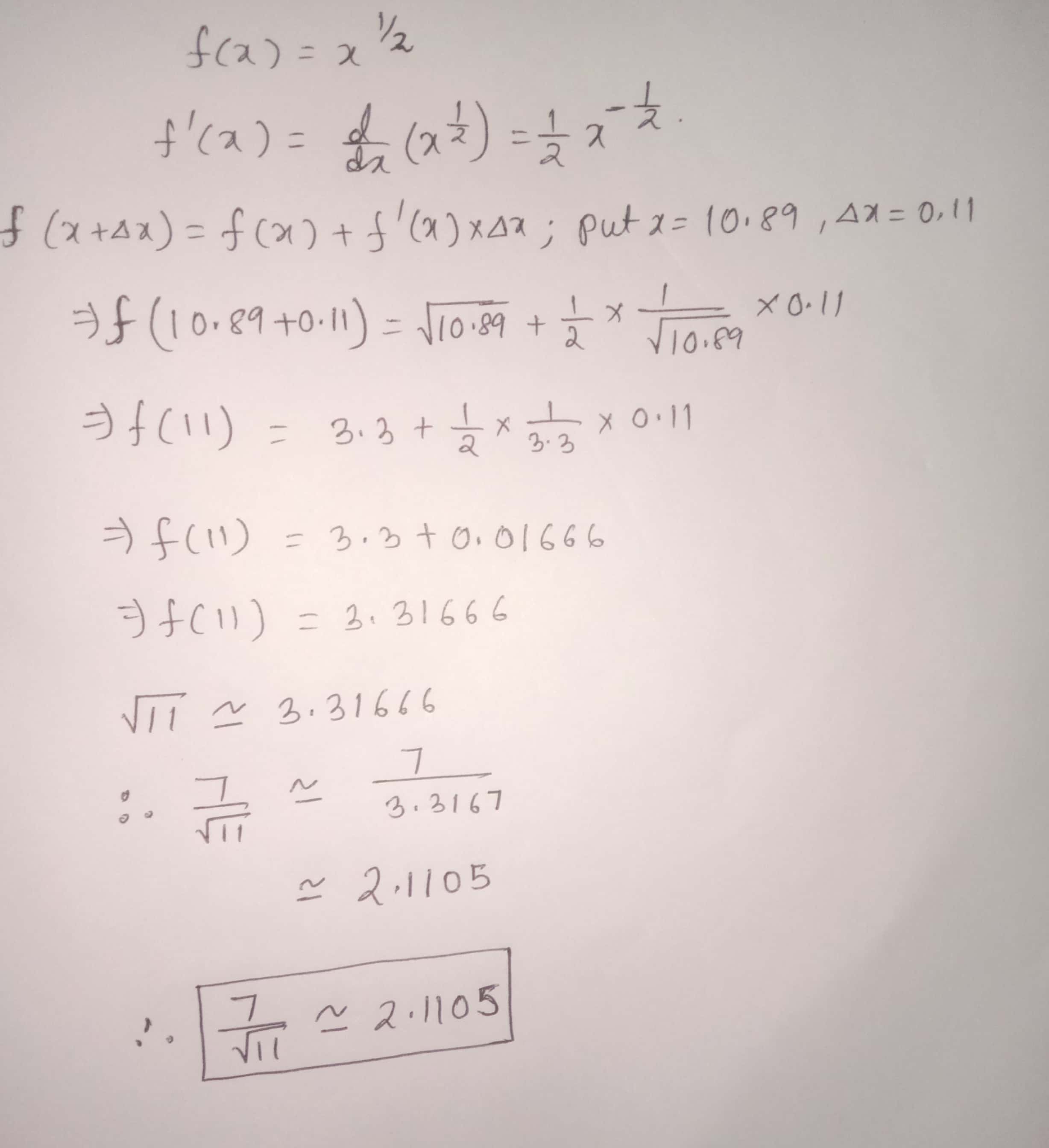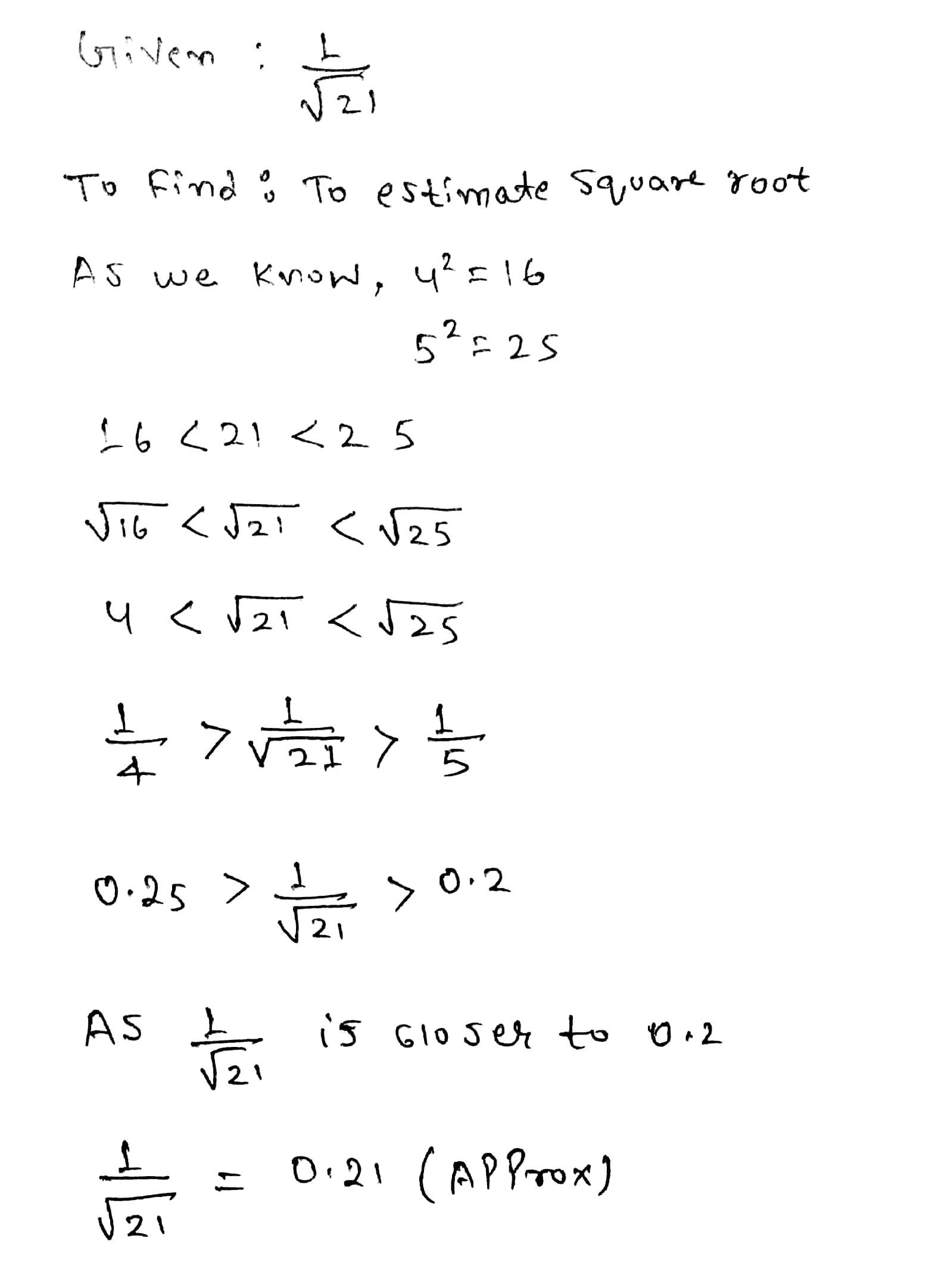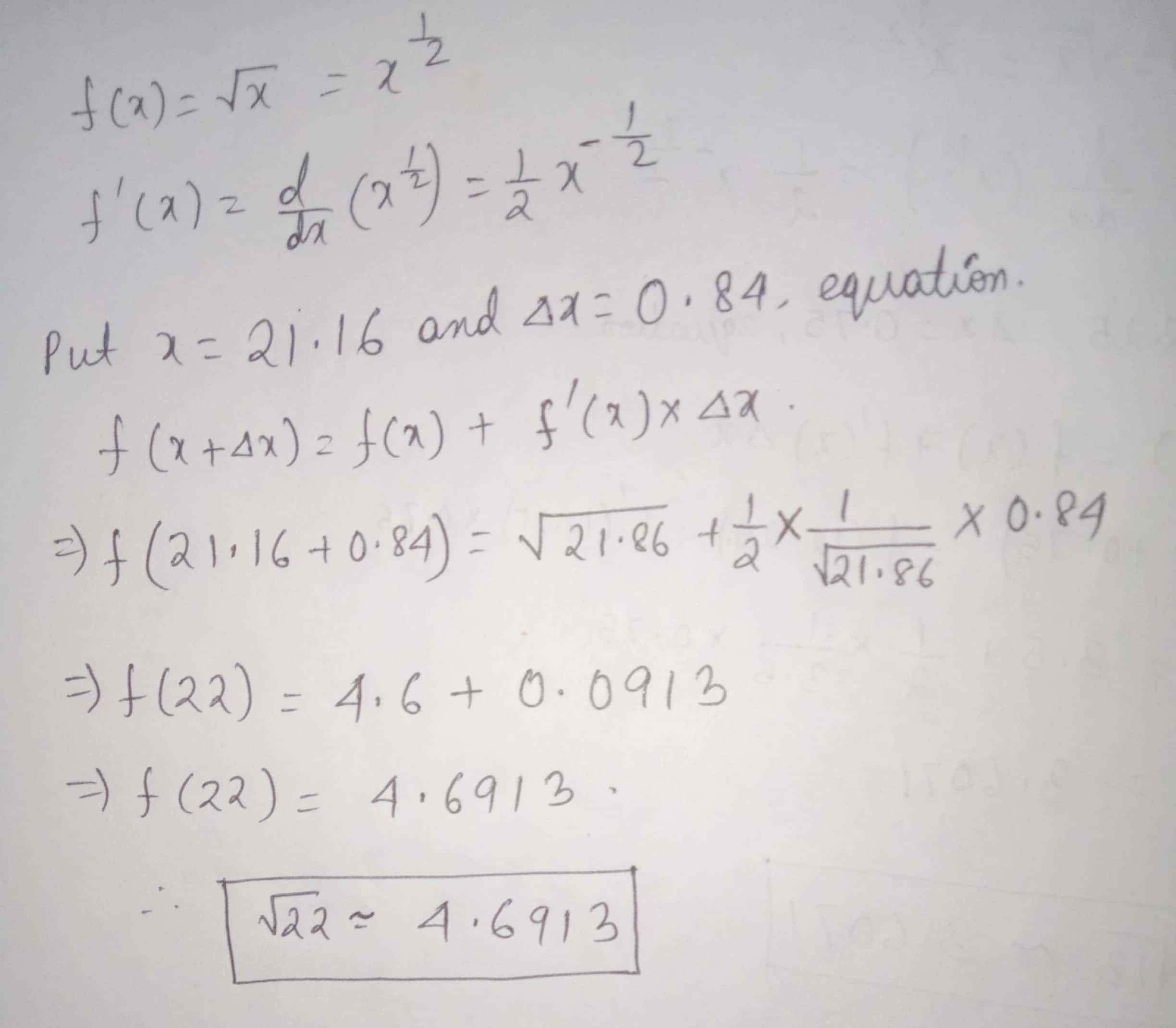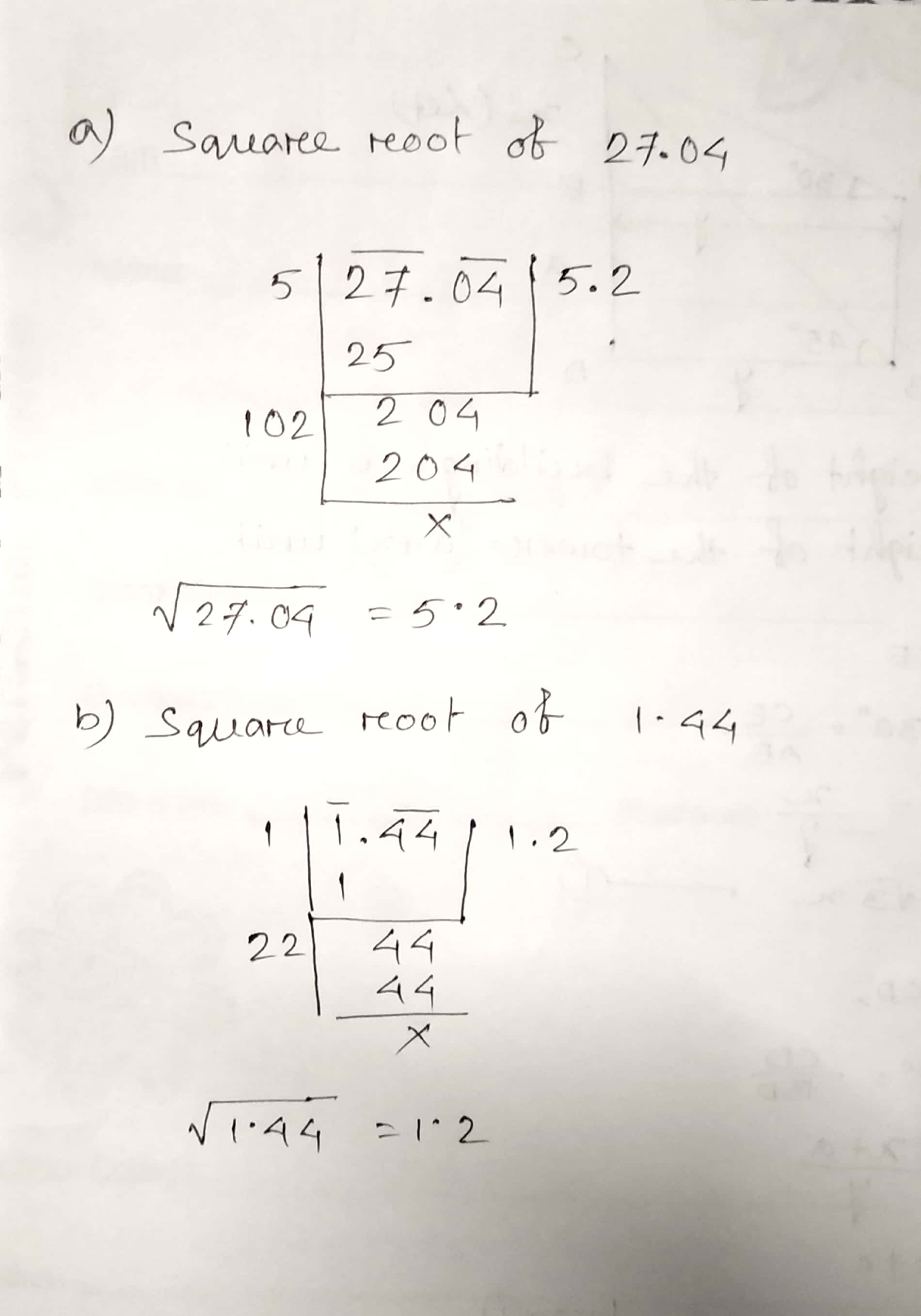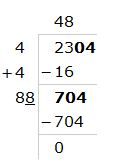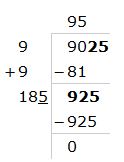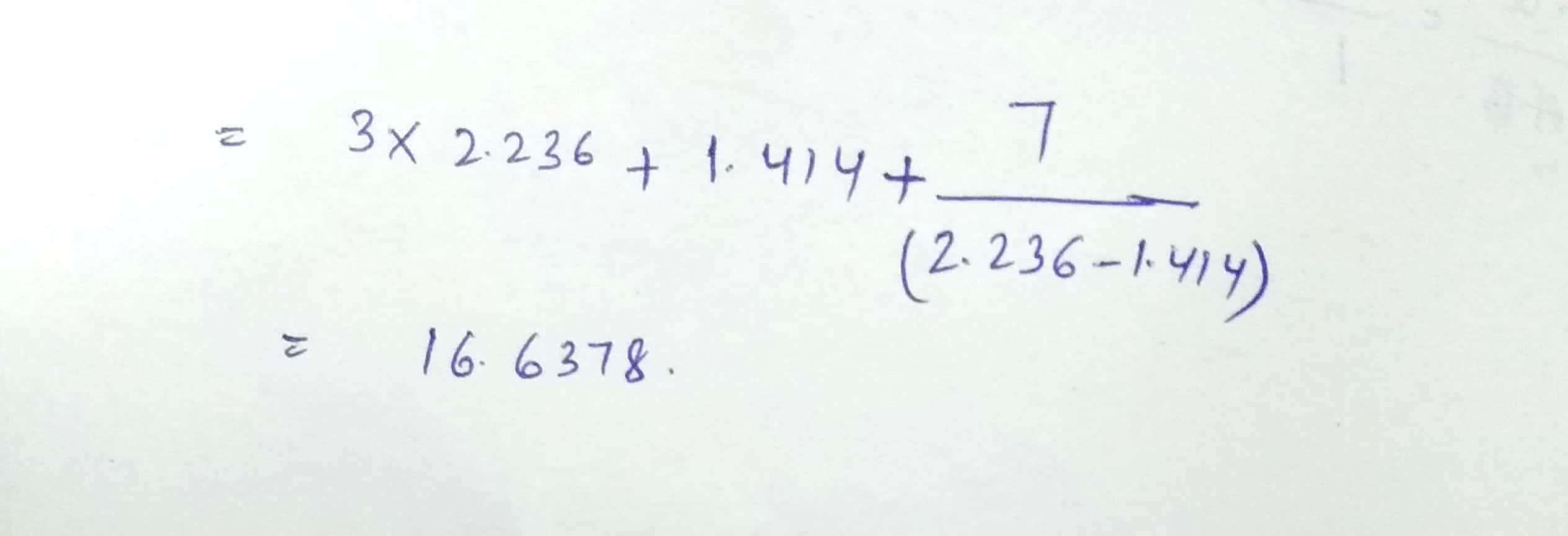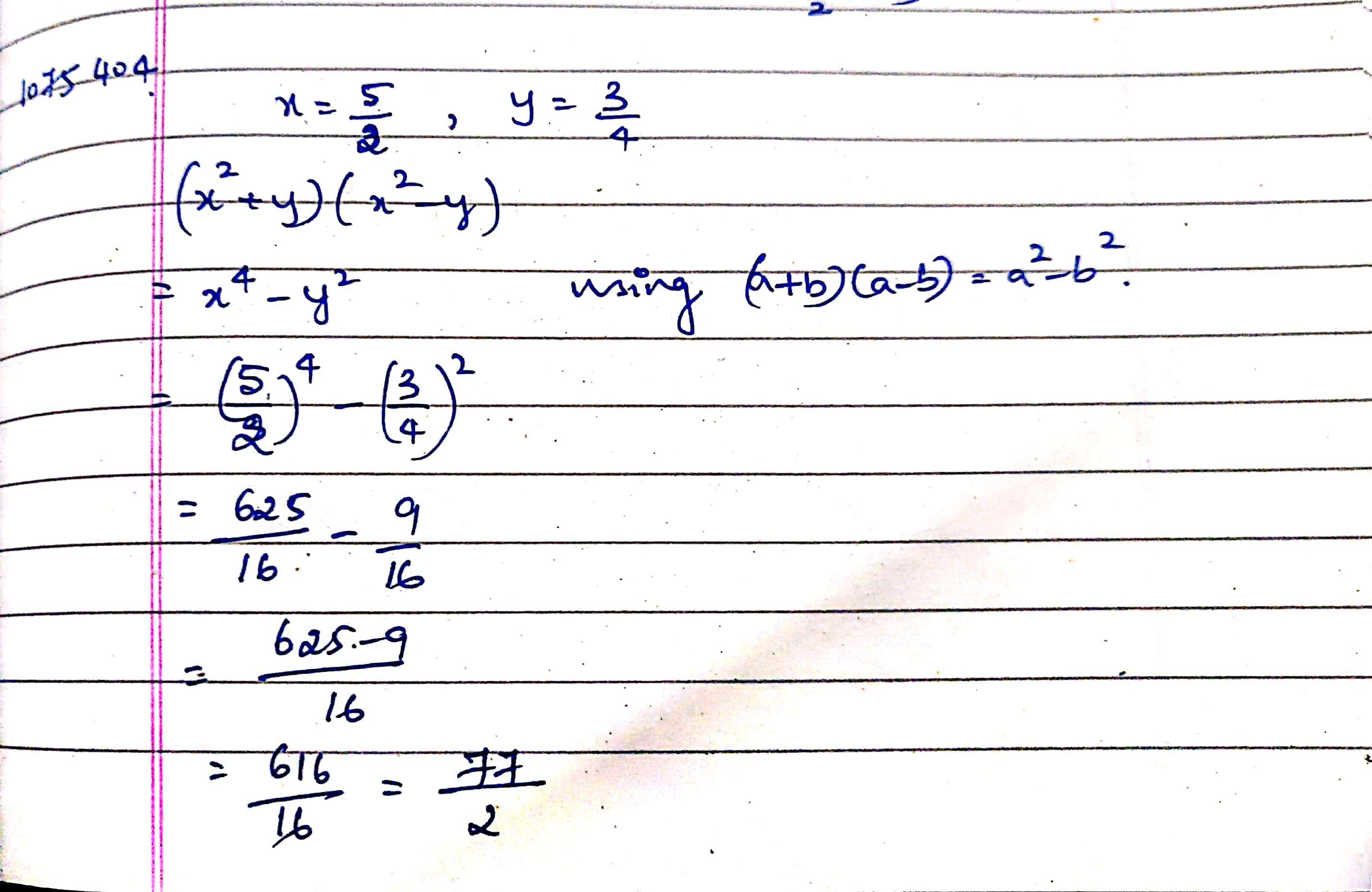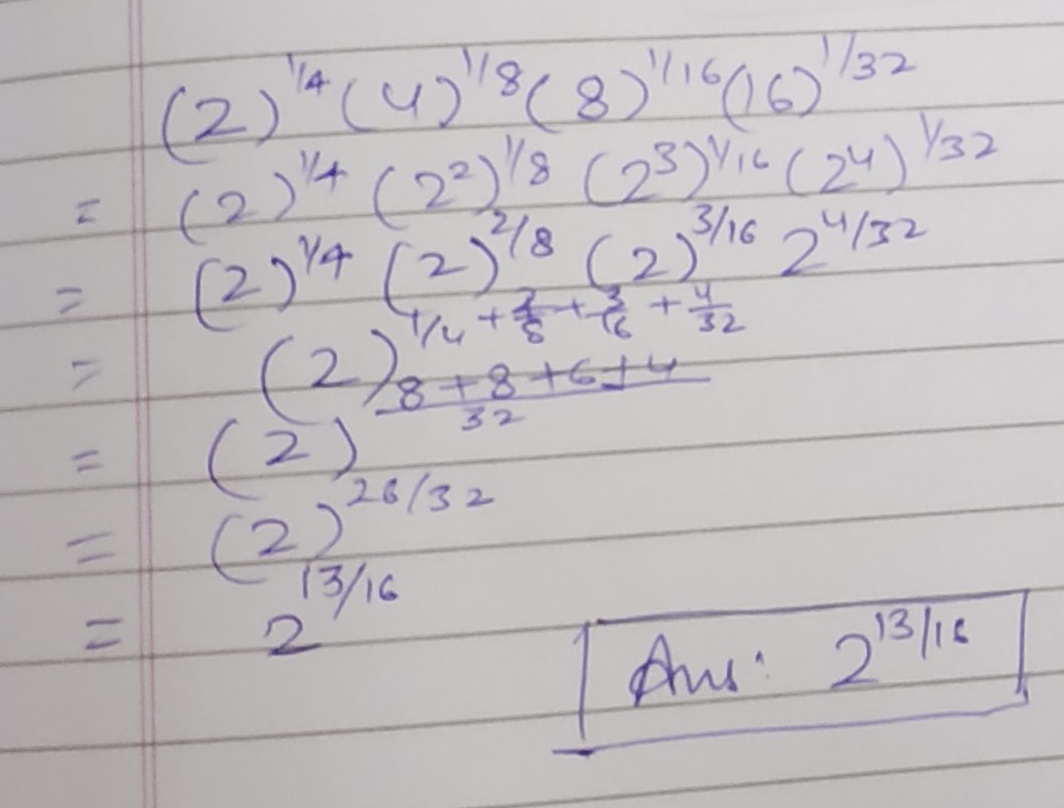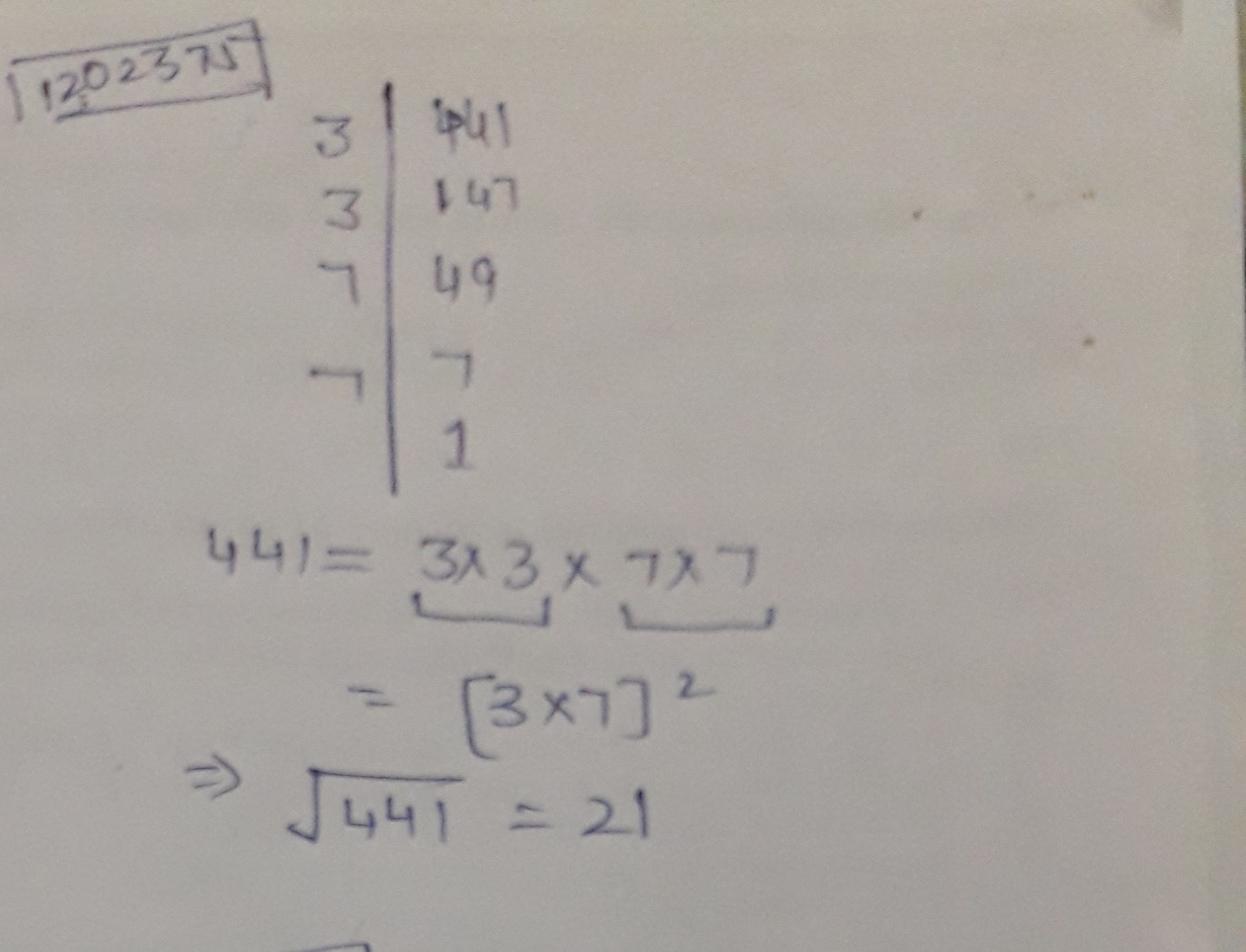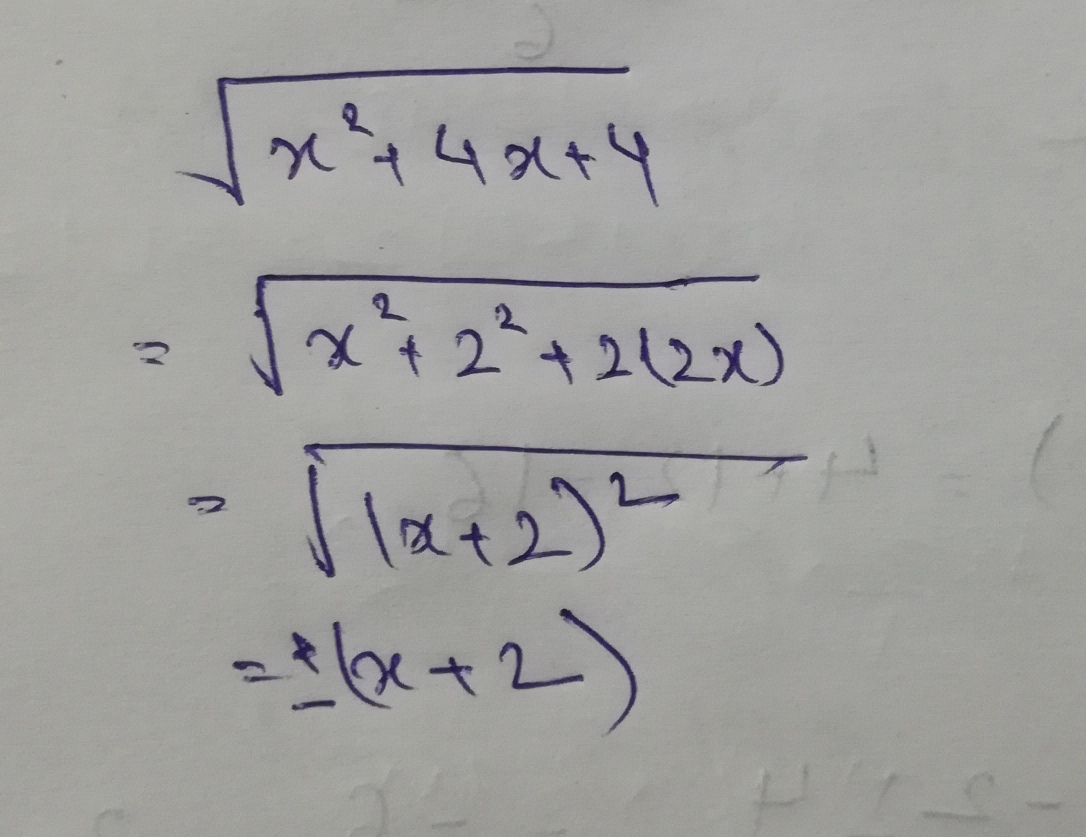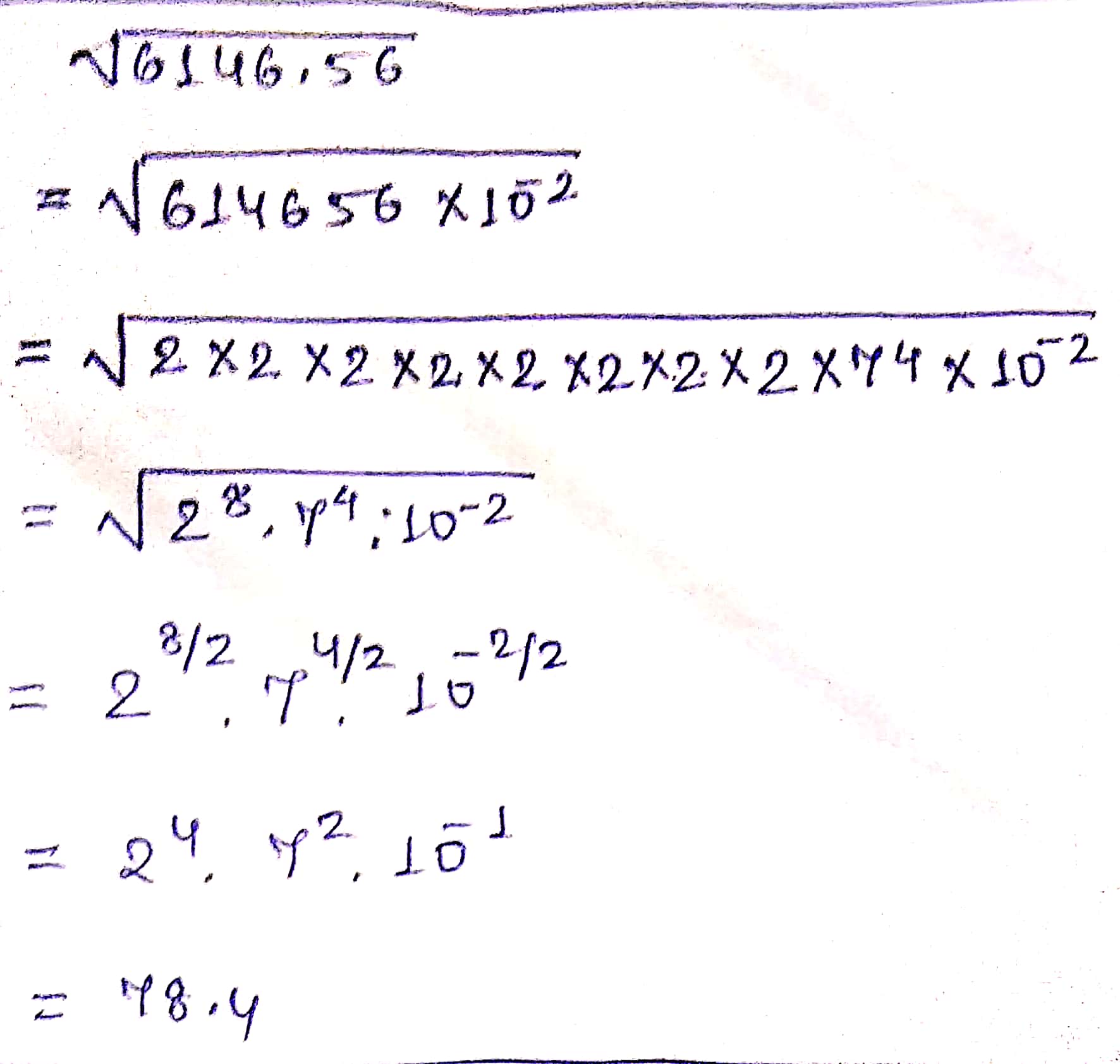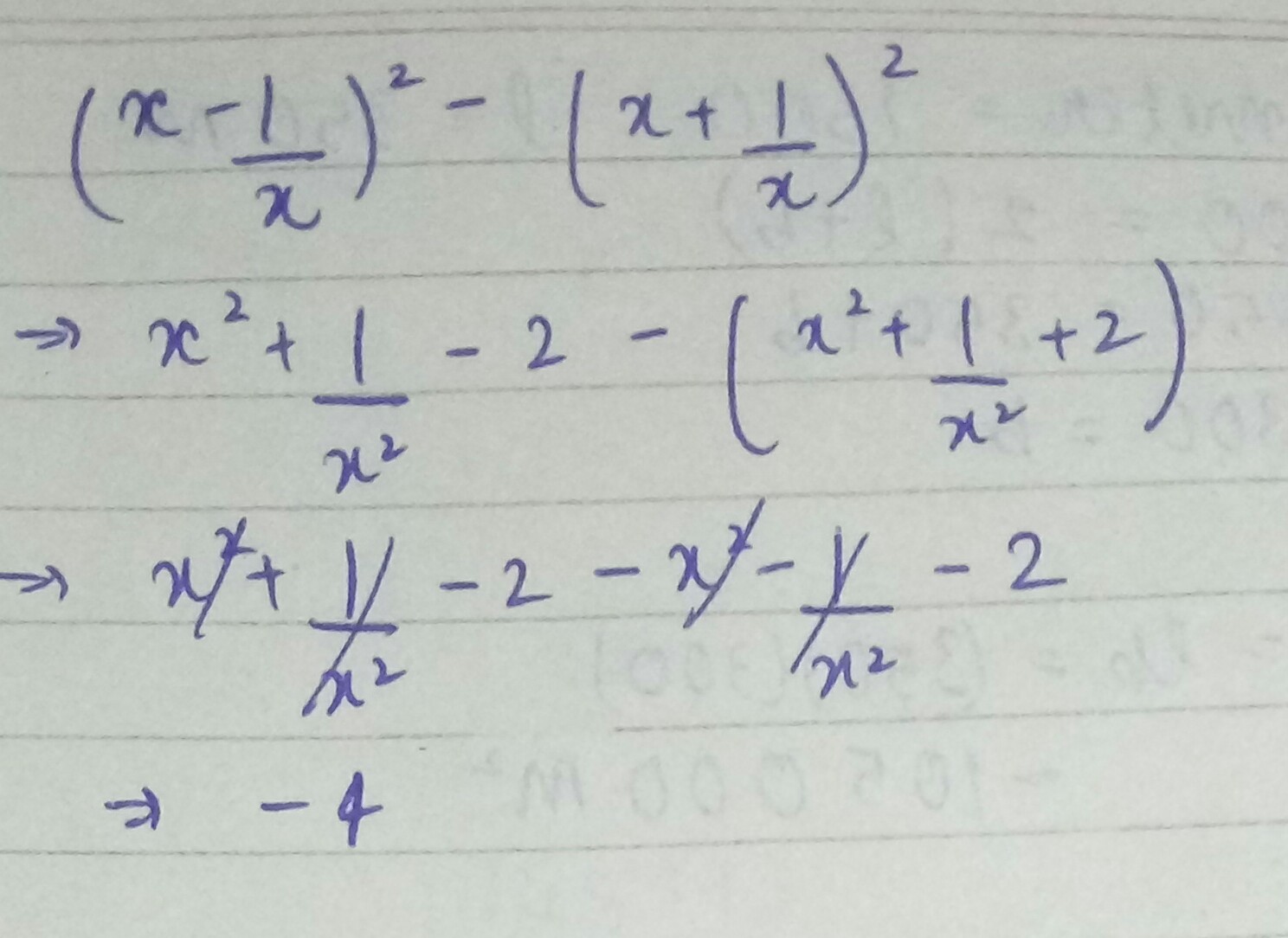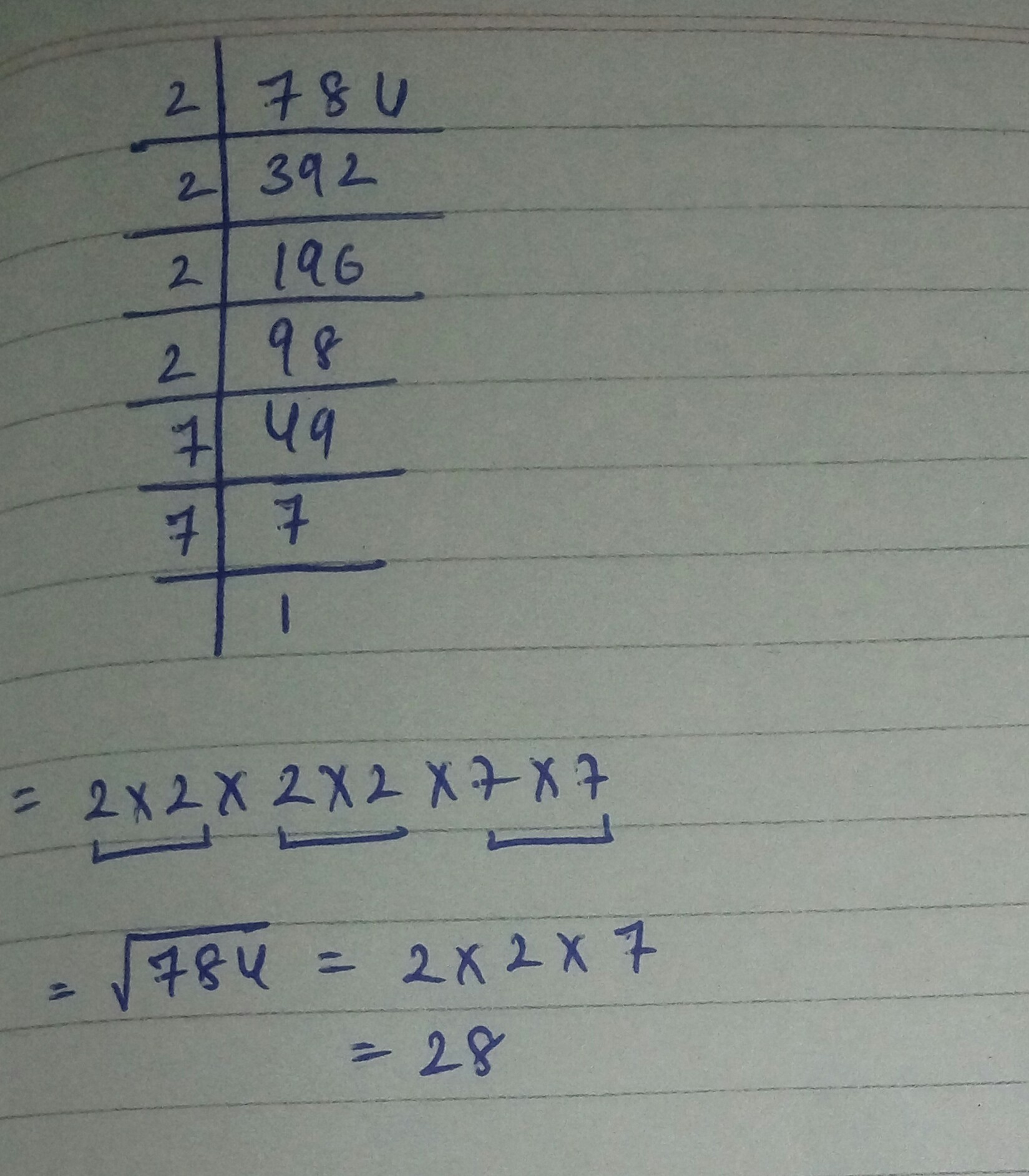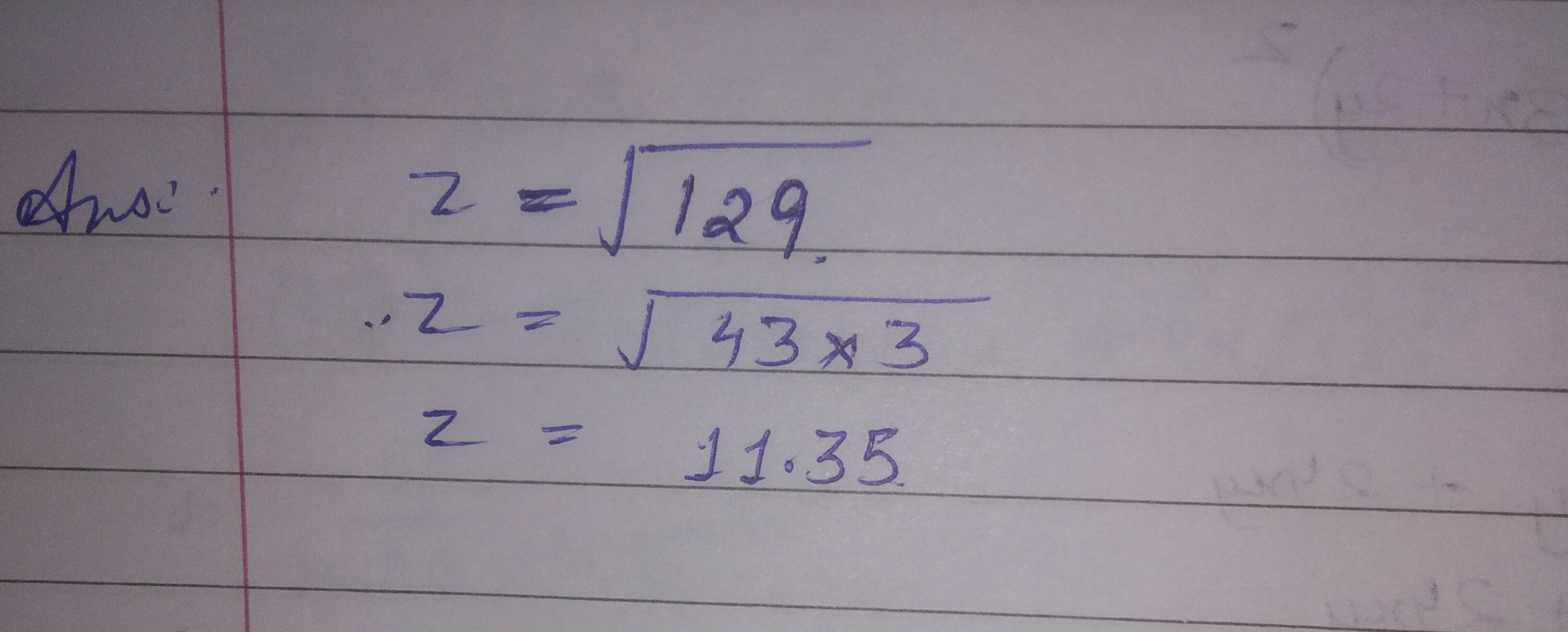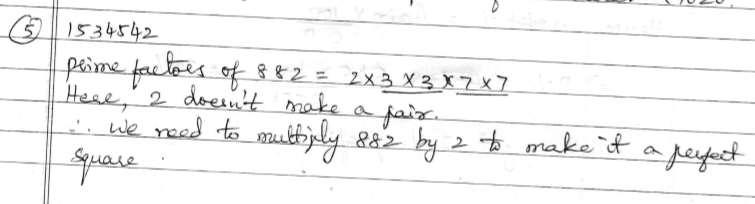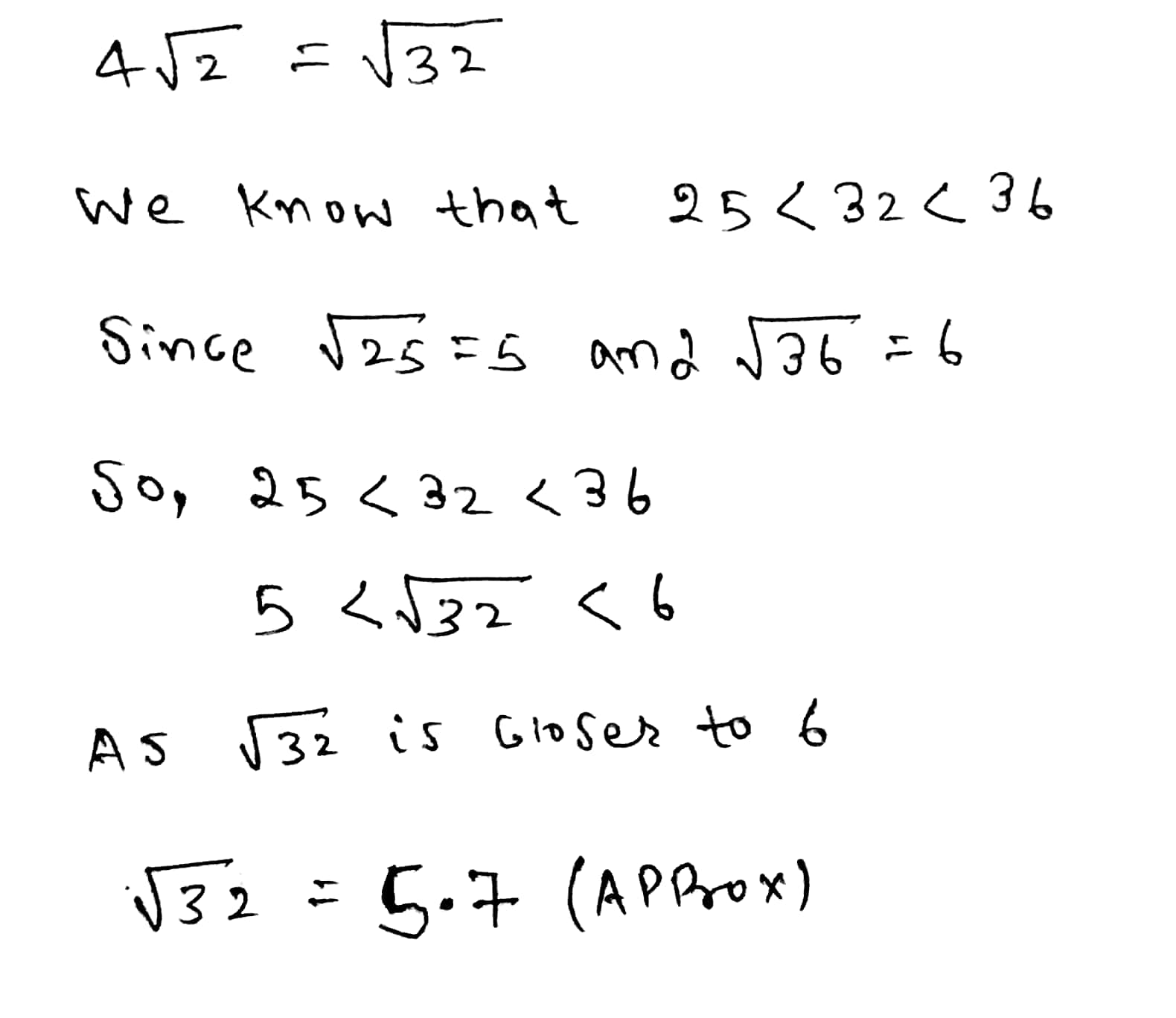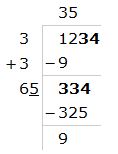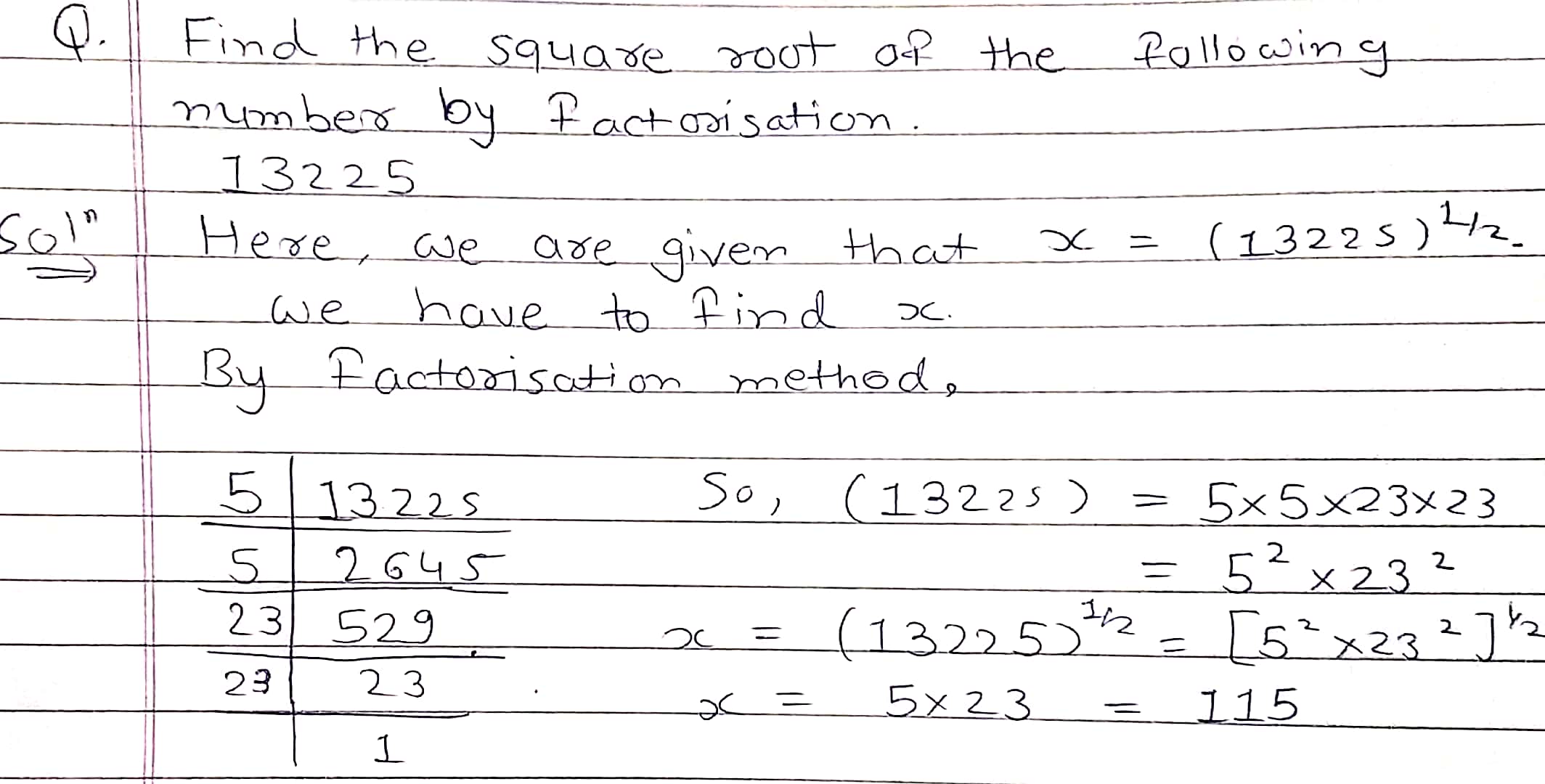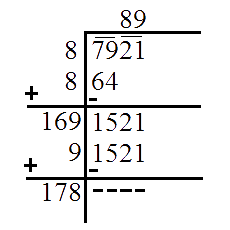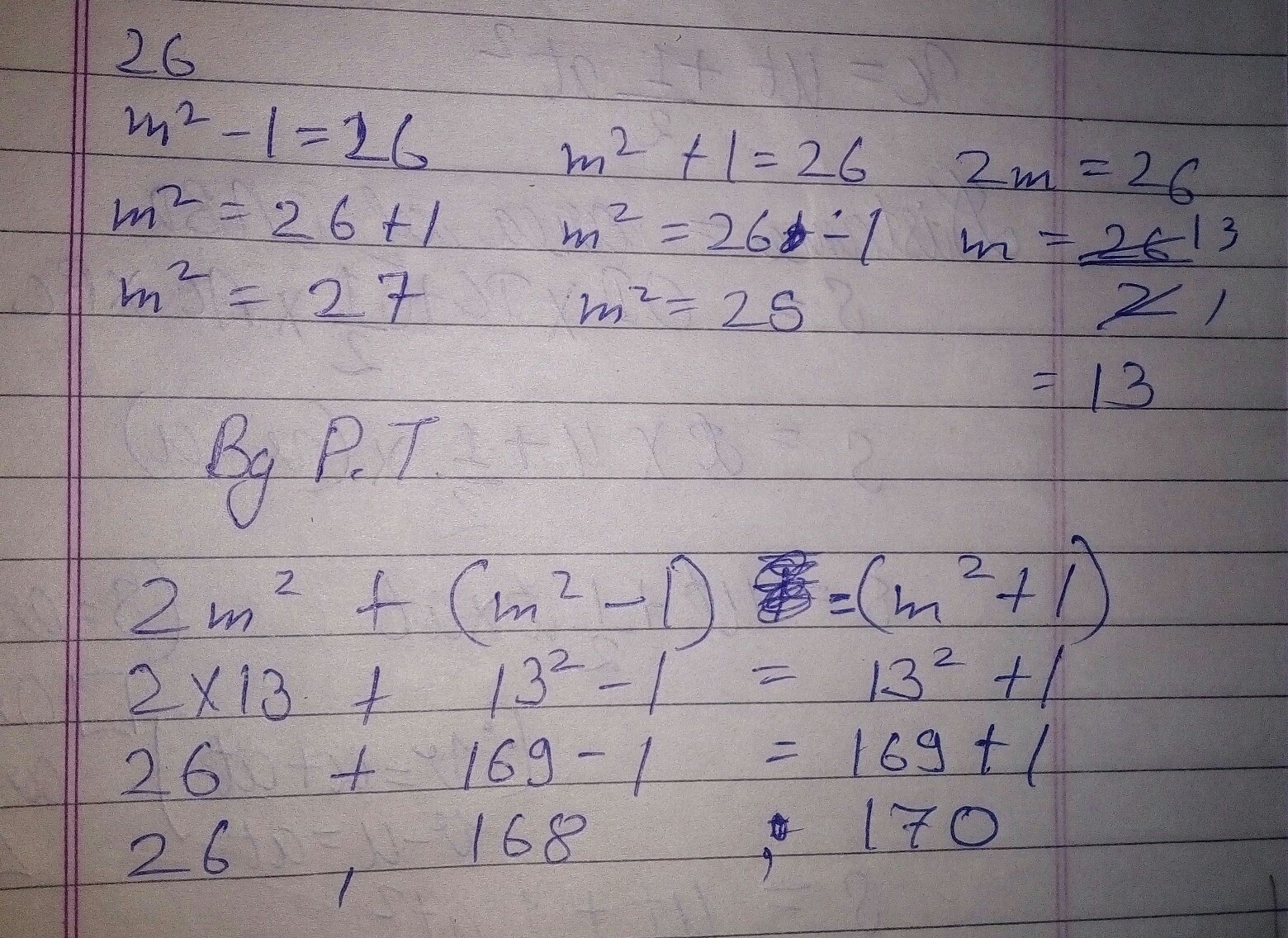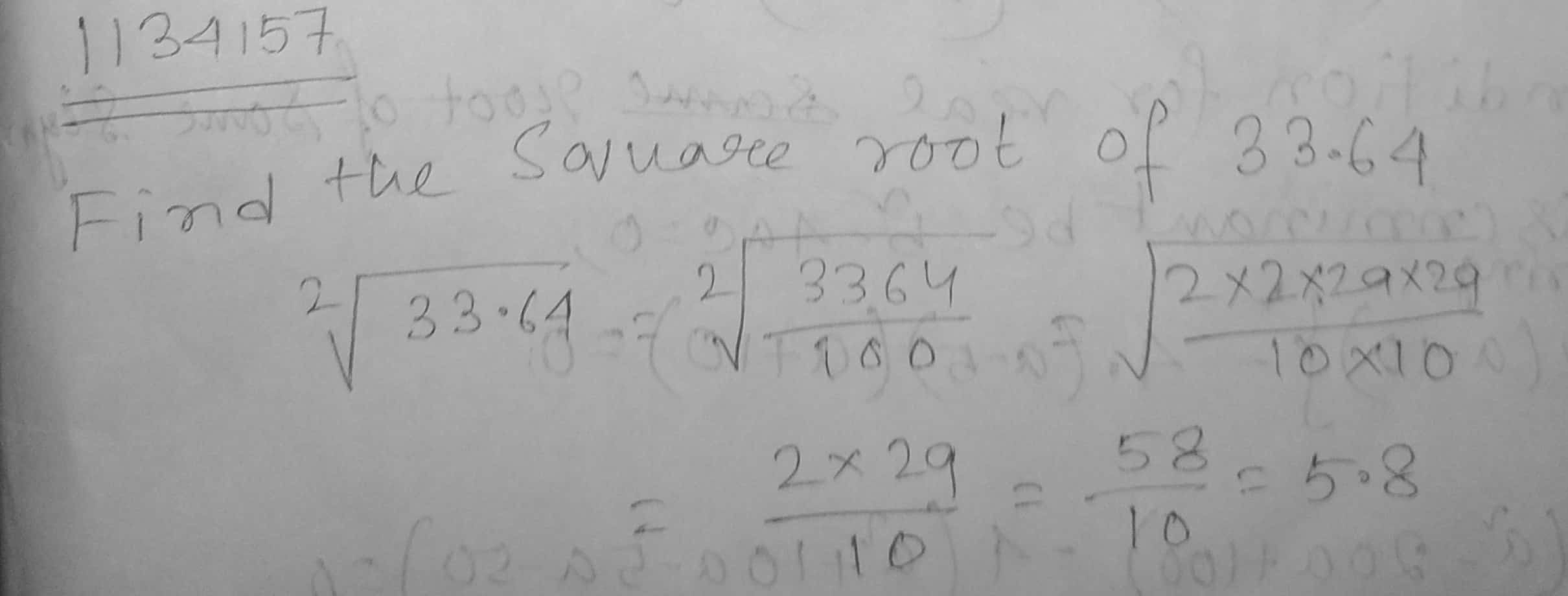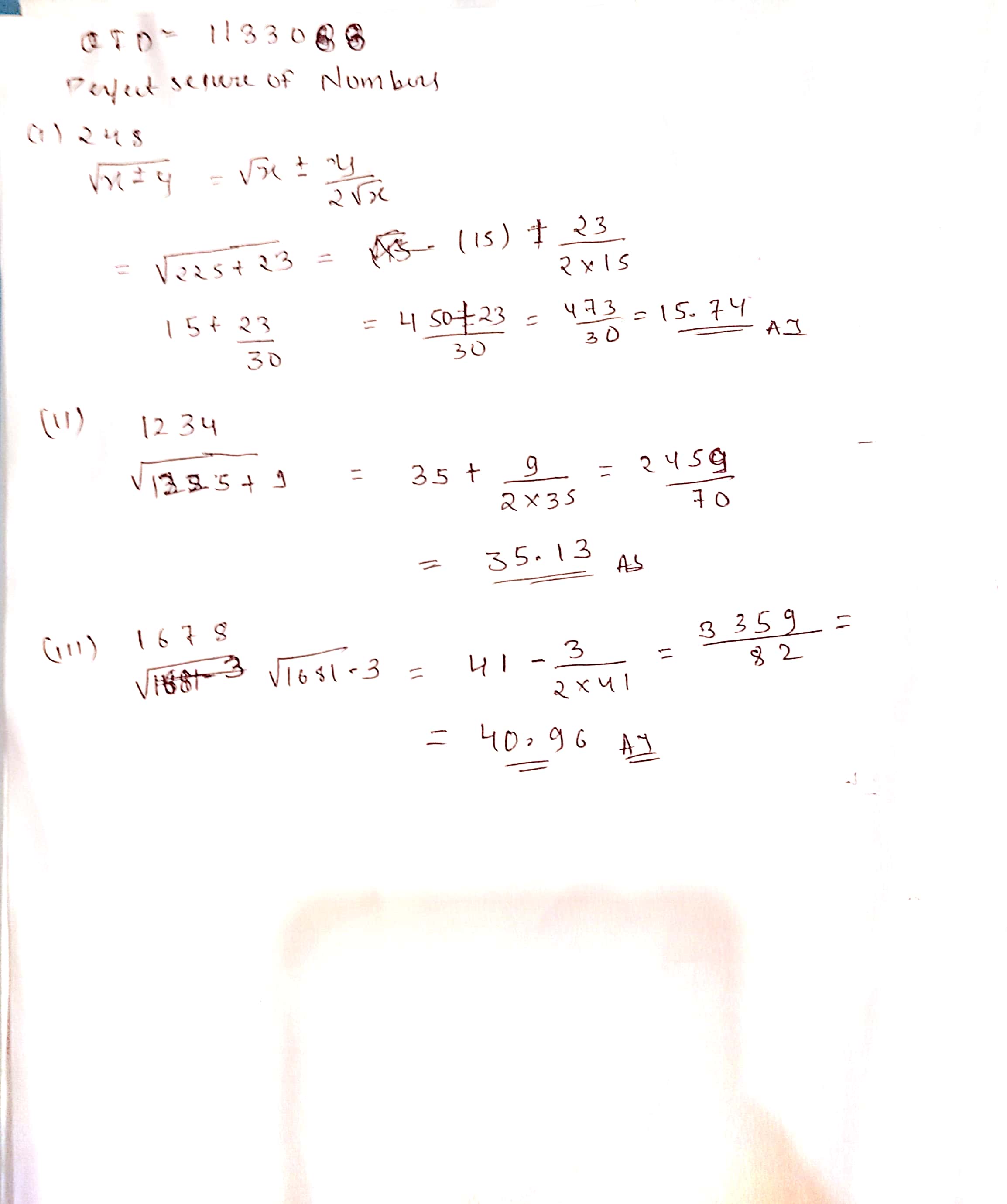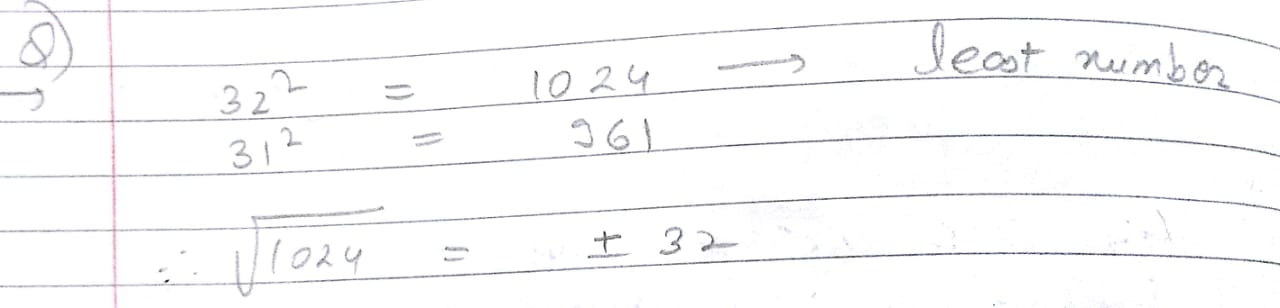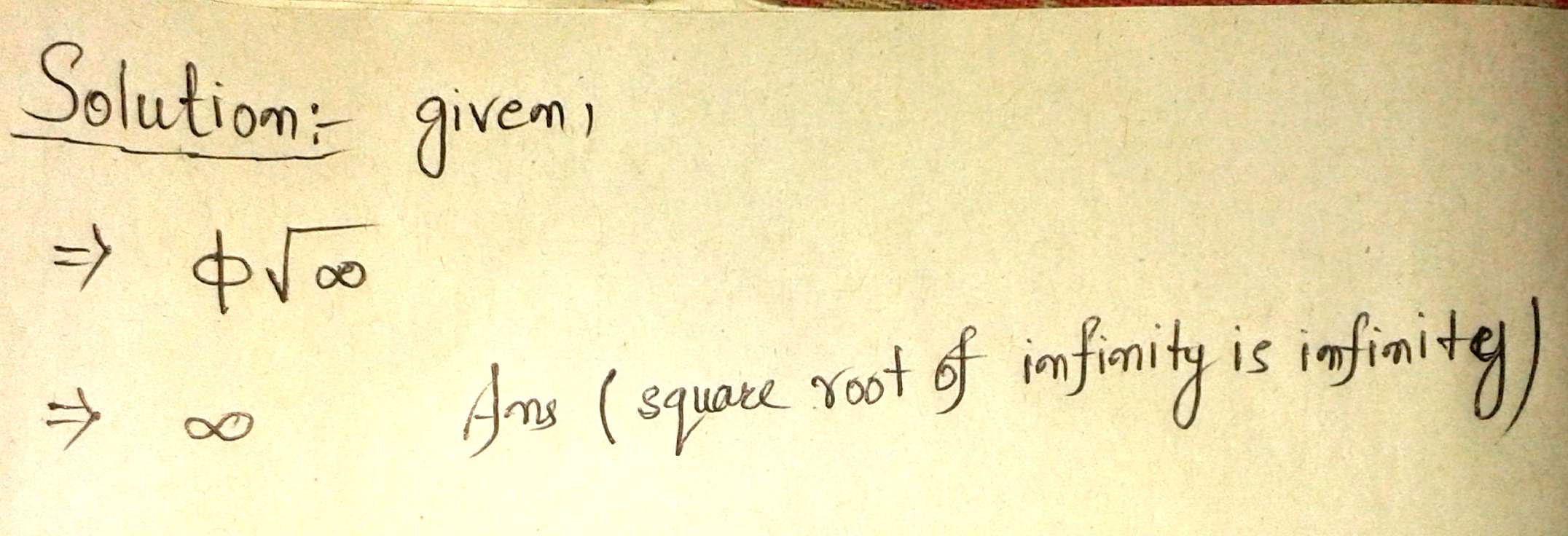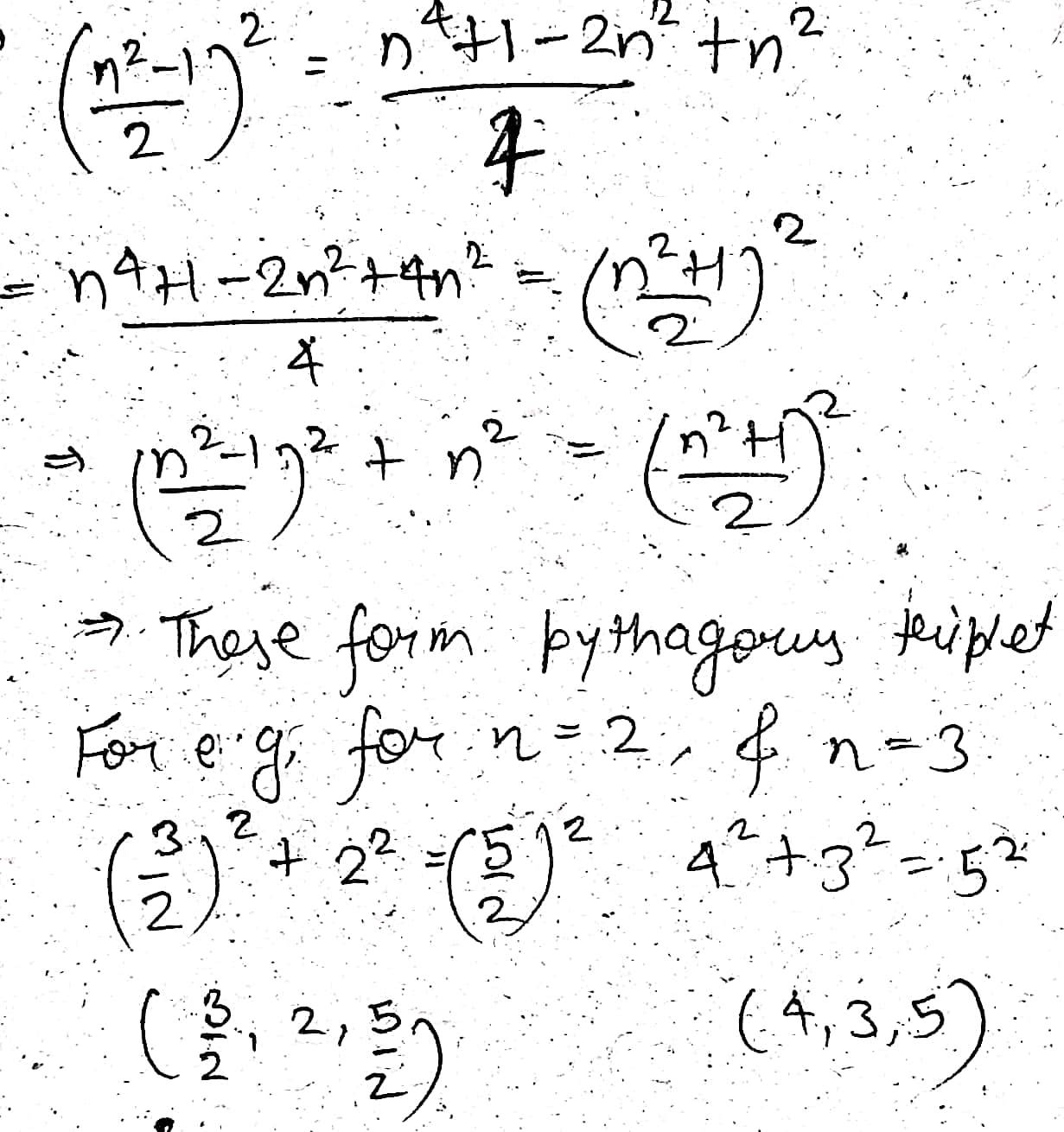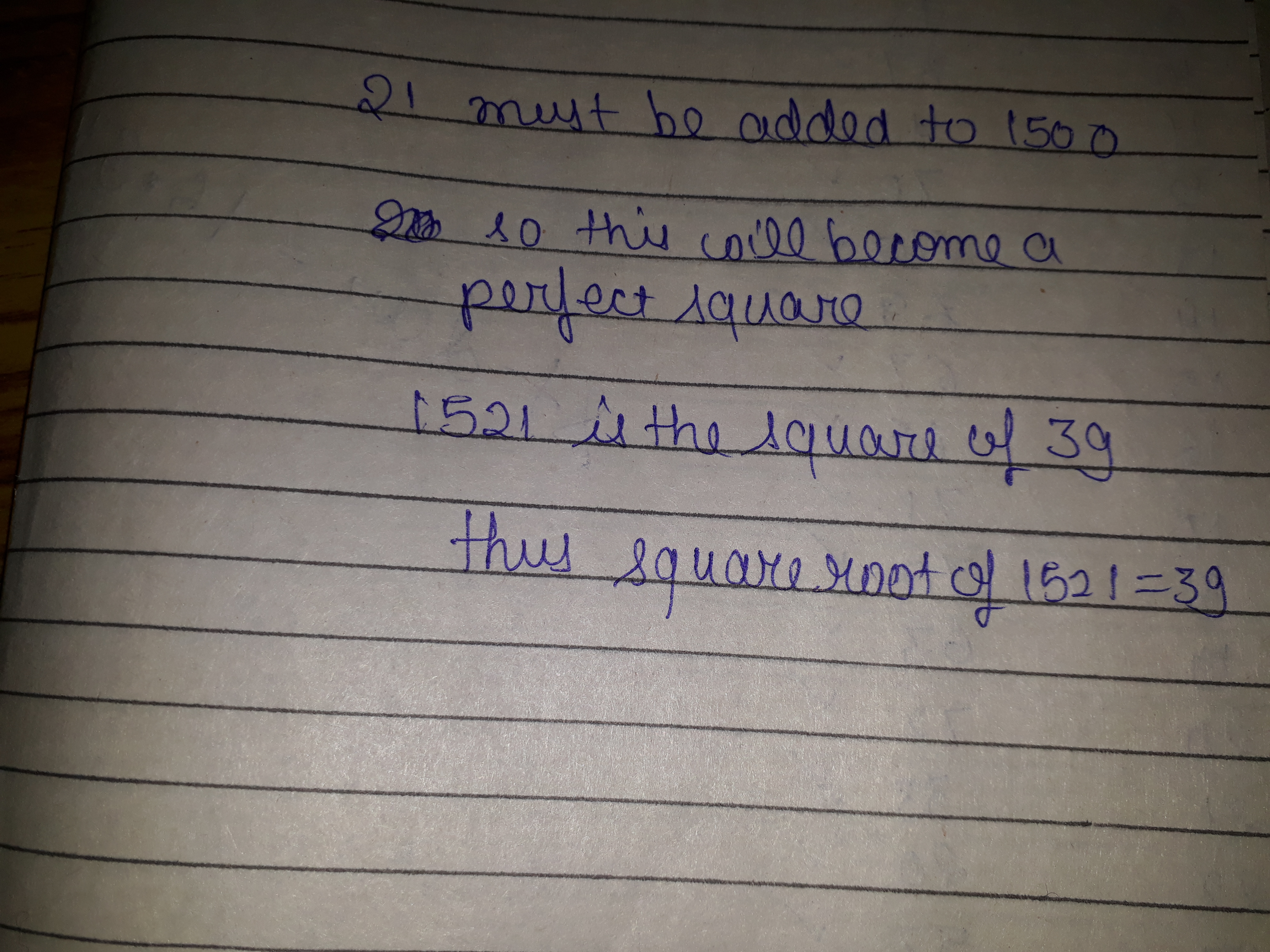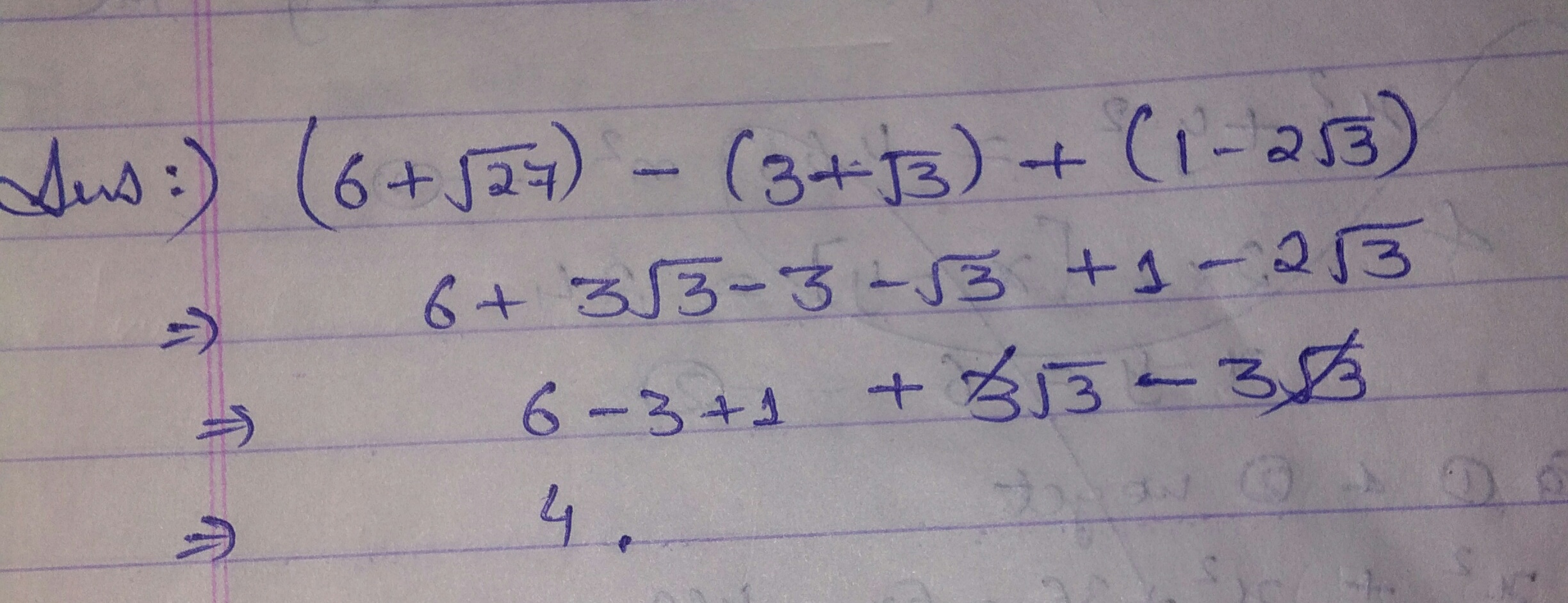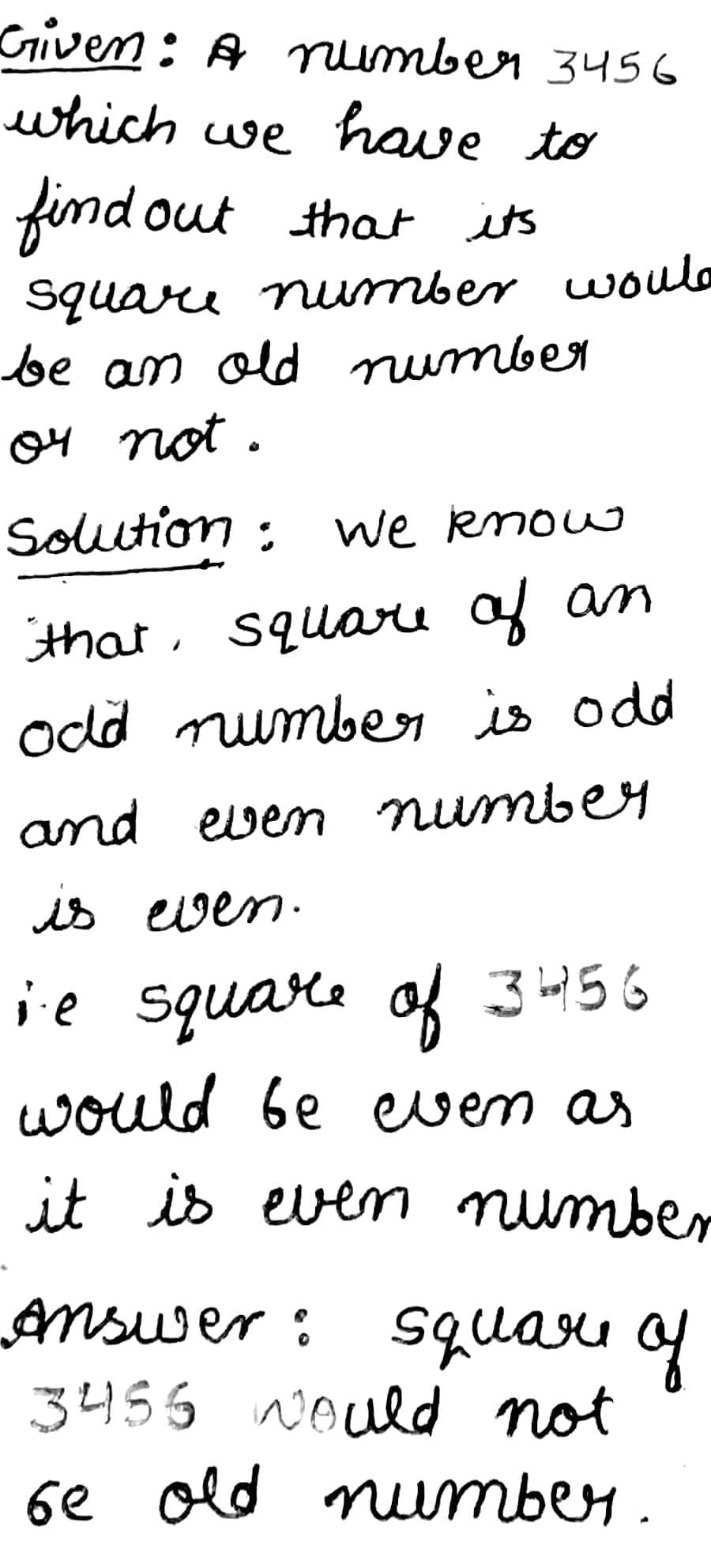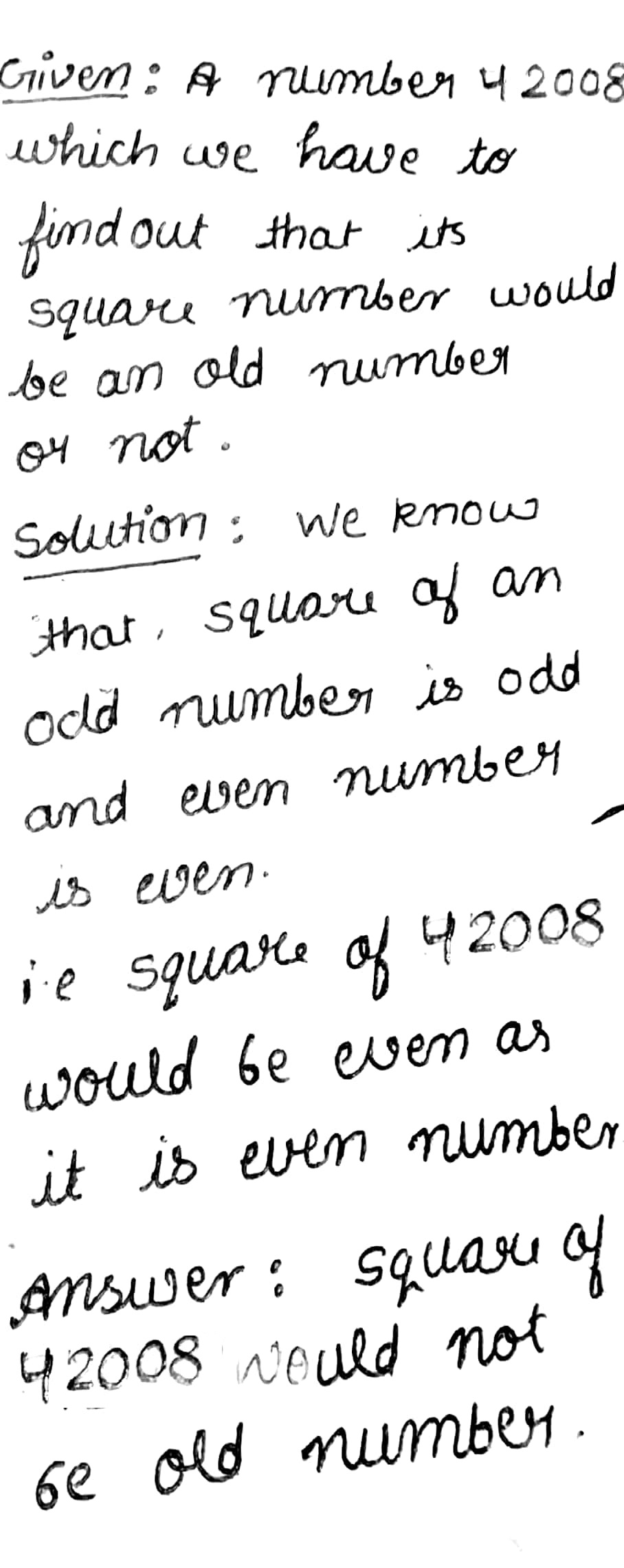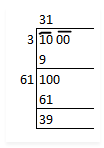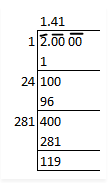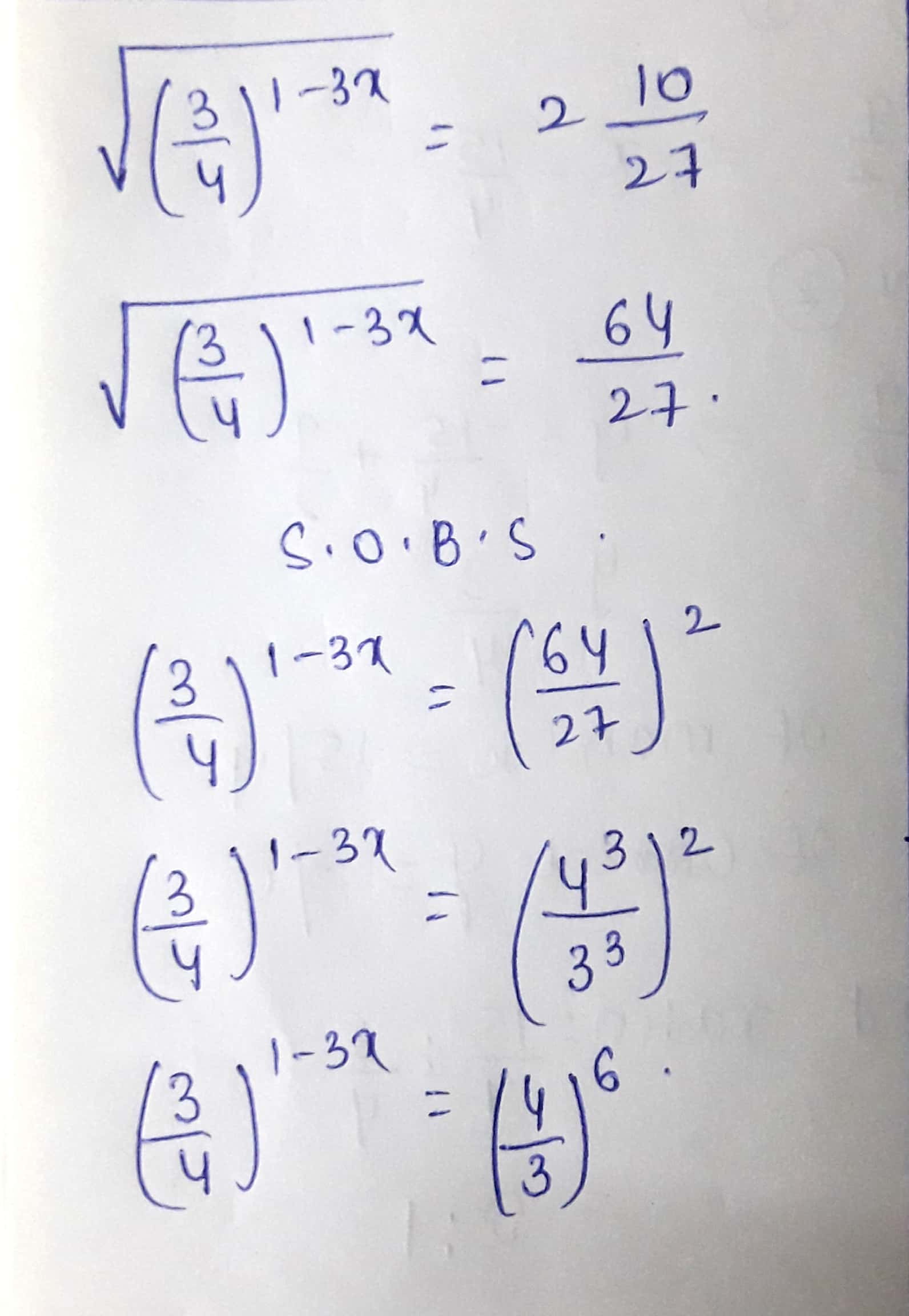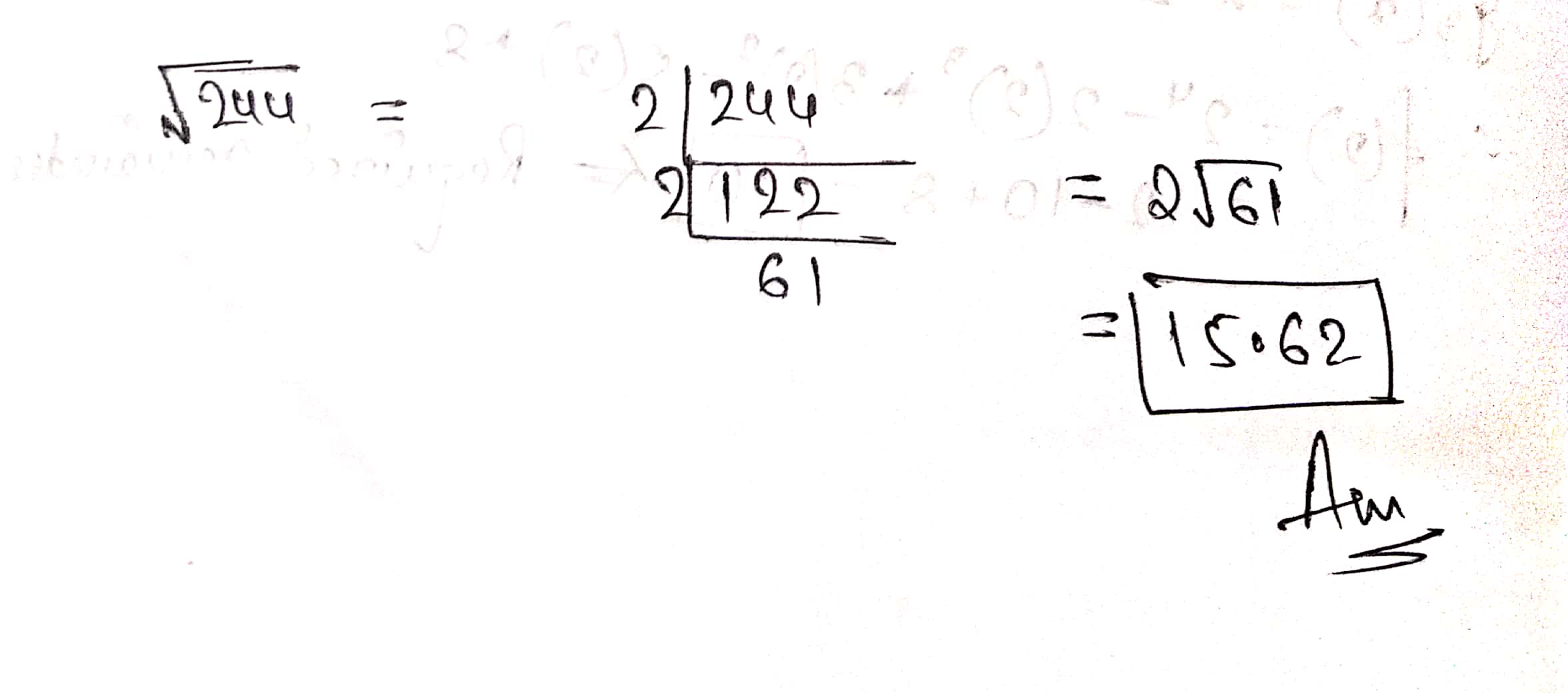Squares And Square Roots - Class 8 Maths - Extra Questions
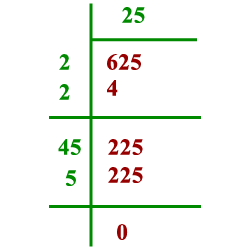
Find the square root of the following numbers correct to two decimal places:
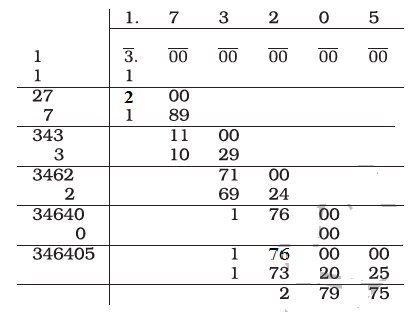
$$5.462$$
Find the square root of the following decimal numbers by division method:
$$18.4041$$
Find the square root of the following numbers by prime factorization method:
$$1849$$
Find the square root of the following numbers correct to two decimal places:
$$645.8$$
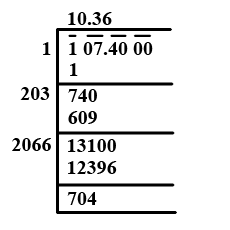
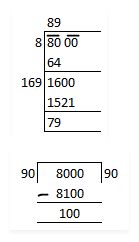
Find the square root of the following numbers correct to two decimal places:
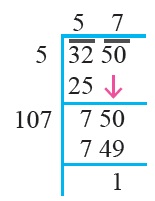
$$107.45$$
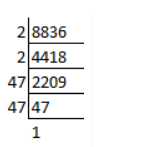
Find the square root of the following numbers by prime factorization method:
$$6241$$
Find the square root of the following decimal numbers by division method:
$$5.774409$$
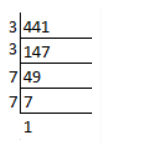
Find the square root of the following numbers by prime factorization method:
$$441$$
Find the square root of the following numbers by prime factorization method:
$$784$$
Find the square root of the following numbers by prime factorization method:
$$4356$$
Find the square root of the following numbers correct to two decimal places:
$$3$$
Find the square root of the following numbers by prime factorization method:
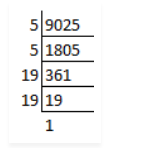
$$9025$$
Find the square root of the following number by prime factorization method:
$$8281$$
Which of the following natural numbers are perfect squares? Give reasons in support of your answer.
$$5488$$
Which of the following natural numbers are perfect squares? Give reasons in support of your answer.
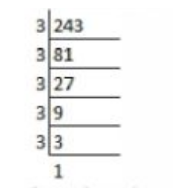
$$243$$
Find the square root of the following numbers by prime factorization method:
$$0.0064$$
Show that each of the following numbers is a perfect square. Also, find the number whose square is the given number.
$$7056$$
Find numbers from $$100$$ to $$400$$ that end with $$0, 1, 4, 5, 6$$ or $$9$$, which are perfect squares.
Find the square root of the following numbers by factorization $$256$$
Find the smallest positive integer with which one has to multiply $$847$$ to get a perfect square.
Find the square root by prime factorization method $$1156$$
Find the square root of $$10404$$ by prime factorization method.
Simplify: $$\sqrt{169} \times \sqrt{361}$$
Simplify: $$\sqrt{1764} - \sqrt{1444}$$
Simplify: $$\sqrt{1360 + 9} $$
Find the square root by prime factorization method $$13225$$
Simplify $$\sqrt{2704} + \sqrt{144} + \sqrt{289}$$
Simplify: $$\sqrt{225} - \sqrt{25}$$
Simplify $$\sqrt{100} + \sqrt{36}$$
Find the largest perfect square factor of $$48$$
Find the largest perfect square factor in the number $$1352$$.
Find the smallest positive integer with which one has to multiply $$450$$ to get a perfect square.
Find the smallest positive integer with which one has to multiply to $$1445$$ to get a perfect square.
Find the smallest positive integer with which $$1352$$ be multiplied to get a perfect square.
Find the nearest integer to the square root of $$232$$.
Find the nearest integer to the square root of $$824.$$
Find the largest perfect square factor in $$729$$
If the area of a square is $$90$$ cm$$^2$$, what is its side-length, rounded to the nearest integer?
A square piece of land has area 112 m$$^2$$. What is the closest integer which approximates the perimeter of the land?
Find the square root of 0.017424.
Find the square root of the following numbers by the factorisation numbers : 82944
Explain with reason whether the given number is perfect square or not: $$2433$$
Find whether the square of the given number is even or odd: 8204
Explain with reason whether the given number is perfect square or not: $$6098$$
What will be the units digit of the square of the given number:$$8742$$
Find the square root of $$1296$$ by Prime Factorization
How many numbers lie between the square of the given numbers: $$25$$ and $$26$$
Find the square roots of the given number by Prime factorization method: 441
Explain with reason whether the given number is perfect square or not: 4592
Find the square root of
$$24+4\sqrt { 15 } -4\sqrt { 21 } -2\sqrt { 35 } $$
Express the following square numbers as the sum of two odd numbers.i)$$81$$ ii)$$144$$
A society collected $$\text{Rs. }9,216$$ wherein, each member contributed as many rupees as there were members in the society. Find the number of members.
Find the smallest whole number by which $$1458$$ should be multiplied, so as to get a perfect square number.
For the following number, find the smallest whole number by which it should be multiplied so as to get a perfect square number.
252
Find the least number that must be added to $$1300$$ so as to get a perfect square. Also find the square root of the perfect square.
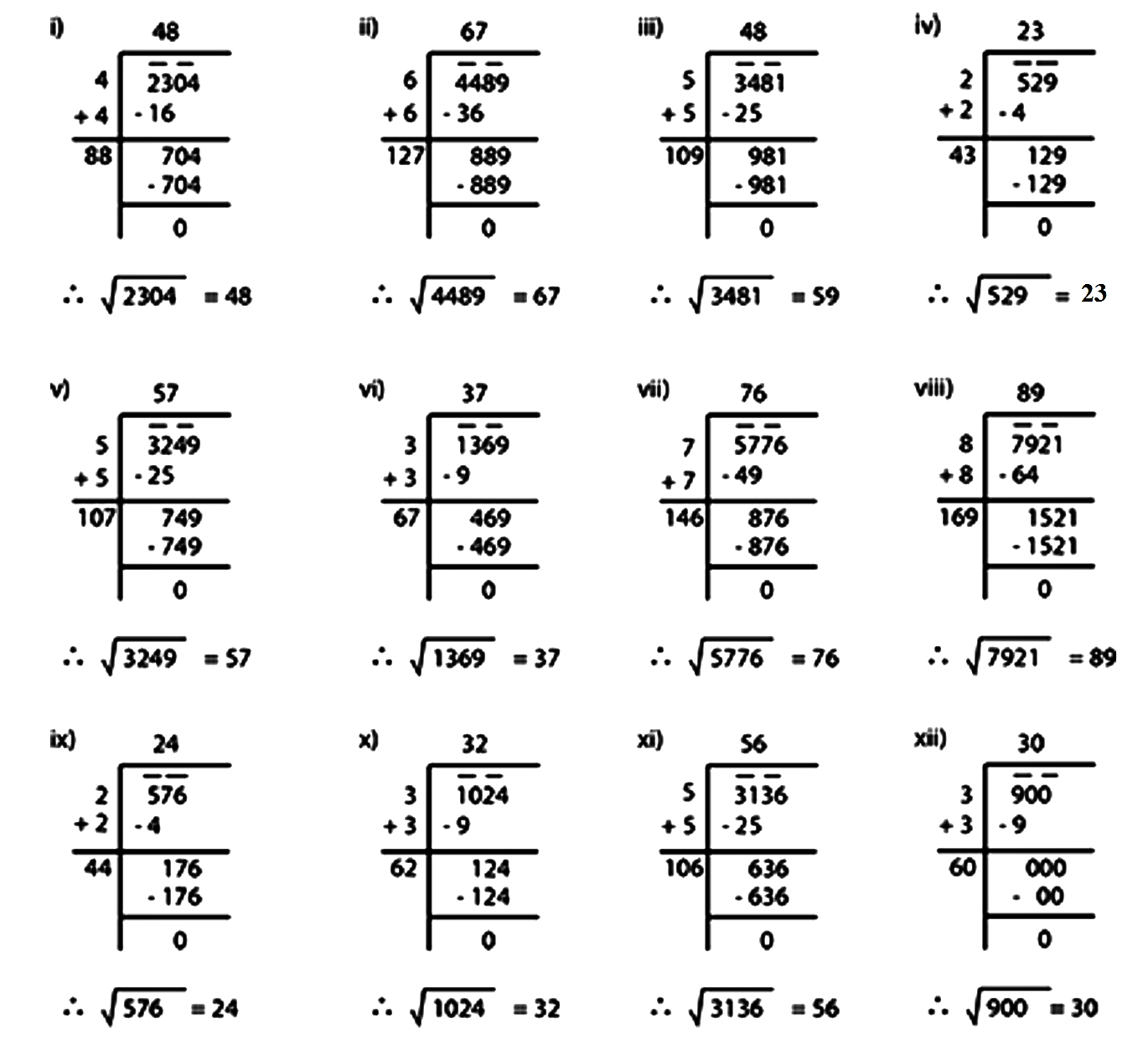
Find the square root of each of the following by Long division method:
(i) $$2304$$ (ii) $$4489$$
(iii) $$3481$$ (iv) $$529$$
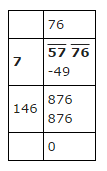
(v) $$3249$$ (vi) $$1369$$
(vii) $$5776$$ (viii) $$7921$$
(ix) $$576$$ (x) $$3136$$
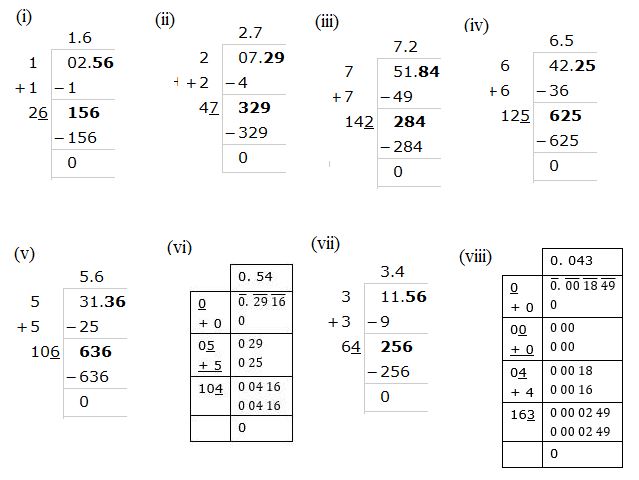
Find the square root of the following decimal numbers:
(i) $$2.56$$ (ii) $$7.29$$
(iii) $$51.84$$ (iv) $$42.25$$
(v) $$31.36$$ (vi) $$0.2916$$
(vii) $$11.56$$ (viii) $$0.001849$$
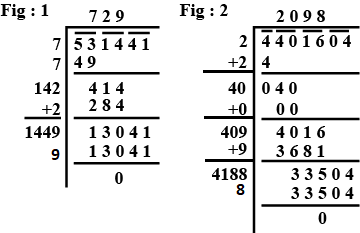
Find the square root of the following numbers by long division method:
531441
4401604
Find the square root of each of the following numbers by using the method of prime factorization:
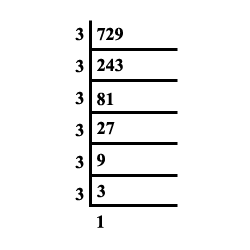
$$729$$
Find the square root of each of the following numbers by using the method of prime factorization:
$$4096$$
Find the square root of each of the following numbers by using the method of prime factorization:
$$7056$$
Find the square root of each of the following numbers by using the method of prime factorization:
$$2025$$
Find the square root of each of the following numbers by using the method of prime factorization:
$$8100$$
Write a Pythagorean triplet whose smallest number is
$$20$$
Write a Pythagorean triplet whose smallest number is
$$14$$
Find the least square number which exactly divisible by each of the numbers $$8,12,15$$ and $$20$$
Find the largest number of $$3$$ digits which is perfect square.
Evaluate:
$$\surd 576$$
Write a Pythagorean triplet whose number is
$$63$$
Find the square root of the following decimal numbers by division method:
$$42.25$$
Find the square root of each of the following by division method:
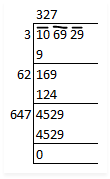
$$106929$$
Write a Pythagorean triplet whose number is
$$8$$
Find the square root of 1764 by the prime factorisation method.
Evaluate :
$$\sqrt { 92416 } $$
Find the unit digit in the square of the numbers $$81$$ and $$79$$.
Show that the following number is not perfect square:
$$22453$$
The square of which of the following numbers would be an odd number?
$$731$$
Show that the following number is not a perfect square. Give reason.
$$8948$$
Show that the following number is not perfect square:
$$4058$$
Show that the following number is not a perfect square. Give reason.
$$333333$$
What will be the units digit of the squares of the following numbers?
$$977$$
What will be the units digit of the squares of the following number?
$$53924$$
What will be the units digit of the squares of the following numbers?
$$4583$$
What will be the units digit of the squares of the following numbers?
$$52698$$
What will be the units digit of the squares of the following numbers?
$$12796$$
What will be the units digit of the squares of the following numbers?
$$99880$$
Check whether the following triplet is Pythagorean?$$(18, 80, 82)$$
What will be the unit's digit of the square of the following number?
$$78367$$
What will be the units digit of the squares of the following numbers?
$$52$$
What will be the units digit of the squares of the following numbers?
$$55555$$
The number $$1023$$ is a perfect square.Type 1 if above statement is true, otherwise 0.
Write five numbers which you cannot decide whether they are square just by looking at the unit’s digit.
The number $$1027$$ is a perfect square.Type 1 if above statement is true, otherwise 0.
Find the square root of the following number by division method.$$2304$$.
Find the square root of the following number by factorisation.
$$1156$$
Check whether the following triplet is Pythagorean?$$(12, 35, 38)$$
The number $$1027$$ is a perfect square.Type 1 if above statement is true, otherwise 0.
Type 1 if above statement is true, otherwise 0.
Find the square root of each of the following by long division method:
$$1471369$$
Write the prime factorization of the following number and hence find its square root:
$$5929$$
Express the following surds as continued fraction, and find the sixth convergent to each
$$\sqrt 11$$
Estimate the square root : $$\dfrac {1}{\sqrt {33}}$$
Estimate the value of square root : $$\sqrt {14}$$
Give reason to show that none of the numbers given below is a perfect square:
$$360$$
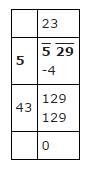
Find the square root of 5929 by the prime factorisation method.
Find the square root of the number 729 by the prime factorisation method.
The difference of two perfect squares is a perfect square.
If true then enter $$1$$ and if false then enter $$0$$
The product of two perfect squares is a perfect square.
If true then enter $$1$$ and if false then enter $$0$$
The number of digits in a perfect square is even.
If true then enter $$1$$ and if false then enter $$0$$
Find the square root of the $$196$$ by factorisation.
Find the square root of the following in the form of a binomial surd.
$$8+2\sqrt{7}$$.
Find the greatest number of three digit which is a perfect square.
Estimate the square root : $${\dfrac {7}{\sqrt {11}}}$$
Estimate the square root : $$\dfrac {1}{\sqrt {21}}$$
Express the following surds as continued fraction, and find the sixth convergent to each:
$$\sqrt 5$$
Find limits of the error when $$\dfrac {208}{65}$$ is taken for $$\sqrt {17}$$
Estimate the value of square root : $$\sqrt 22$$
Find the square root of the following in the form of a binomial surd.
$$14+6\sqrt{5}$$.
Give reason to show that none of the numbers given below is a perfect square:
$$5963$$
Give reason to show that none of the numbers given below is a perfect square:
$$64000$$
Give reason to show that none of the numbers given below is a perfect square:
$$8457$$
Find limits of the error when $$\dfrac {916}{191}$$ is taken for $$\sqrt {23}$$.
Which of the following squares are squares of even number?
$$196$$
Give reason to show that none of the numbers given below is a perfect square:
$$9468$$
Give reason to show that none of the numbers given below is a perfect square:
$$5372$$
Fill in the blanks to make the statements true.
The square of 0.7 is _________.
Fill in the blanks to make the statements true.
The digit at the ones place of $$57^2$$ is _________.
Fill in the blanks to make the statements true.
The square root of $$24025$$ will have _______ digits.
Write a Pythagorean triplet whose number is
$$80$$
Find the square of the following number containing $$5$$ in unit's place:
$$305$$
Find the square root of each of the following by division method:
$$167281$$
Find the square of the following number containing $$5$$ in unit's place:
$$525$$
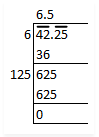
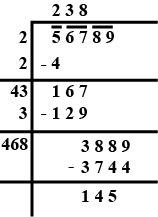
Find the square root of $$13.69$$?
Write two Pythagorean triplets each having one of the numbers as $$5$$.
Find the square root of the following by long division method.
a) $$27.04$$
b) $$1.44$$
Write the first five square numbers.
Write five number which you can decide by looking at their one's digit that they are not square numbers.
The following numbers are obviously not perfect. Give reason.
$$5298$$
Find the square root of the following decimal numbers by division method:
$$51.84$$
Find the square root of 2304 by long division method.
Find the square root of 529 by long division method.
Find the square root of 3481 by long division method.
Find the square root of 400 by prime factorisation method.
Find the smallest positive integer with which one has to divide 336 to get a perfect square.
What could be the possible 'one's' digits of the square root of the following number?
$$657666025$$
Solve : $$3\sqrt{25 \times 6 \times 30 \times 6}$$
Find:
$$\sqrt {4096} $$
Find the square root of $$9216$$
If $$\sqrt { 2 } =1.414$$, then find the value of $$\cfrac { 1 }{ 1-\sqrt { 2 } } $$
Find the least number which must be subtracted to get a perfect square from $$1000$$.
Find the square root of a number $$529$$ by prime factorisation method.
For each of the following numbers, find the smallest whole number by which it should be divided so as to get a perfect square number. Also, find the square root of the square number obtained.
(i) $$252$$ (ii) $$2925$$ (iii) $$396$$ (iv) $$2645$$ (v) $$2800$$ (vi) $$1620$$
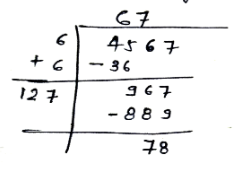
Find $$\sqrt{96.04}$$.
Find the square root of $$2025$$.
Find the square root of 42.25 using division method.
Find the square root of $$8281$$
Find the square root of $$7744$$ by the prime factorisation method.
What will be the unit digit of the square of $$3853$$?
What will be the unit digit of the square $$12796$$?
What will be the unit digit of the square of $$799$$?
What will be the unit digit of the square of $$52698$$?
What will be the unit digit of the square of $$81$$?
What will be the unit digit of the square of $$26387$$?
What will be the unit digit of the square of $$272$$?
What will be the unit digit of the square of $$99880$$?
Find the square root of 1369 by long division method.
Find the square root of 4489 by long division method.
Find the square root of 5776 by long division method.
Find the square root by long-division method:
$$3249$$
For the following number, find the smallest whole number by which it should be divided so as to get a perfect square. Also, find the square root of the square number so obtained.
$$252$$
$$2925$$
One of the following number is not a perfect square, state the number.
$$2453, 2500$$
What will be the unit digit of the square of the number $$26387$$?
What will be the unit digit of the square of the number $$12796$$?
What will be the unit digit of the square of the number $$52698$$?
What will be the unit digit of the square of the number $$272$$?
State whether $$1335$$ is a perfect square or not.
Find the square root of the following decimal numbers
$$(i) 2.56 (ii) 7.29 (iii) 51.84 (iv) 42.25 (v) 31.36$$
Find the square root of $$1057$$.
Is $$676$$ a perfect square? If yes, explain why?
The following numbers are obviously not perfect squares. Give reason.
(i) 1057
(ii) 23453
(iii) 7928
(iv) 222222
(v) 64000
(vi) 89722
(vii) 222000
(viii) 505050
Make a list of all perfect squares from $$1$$ to $$500$$.
Find the smallest integer larger than 1 which is a perfect square as well as a perfect cube.
Find the least number to be added to 9300 to get a perfect square.
Find the square root of the following numbers by the factorisation numbers : 19881
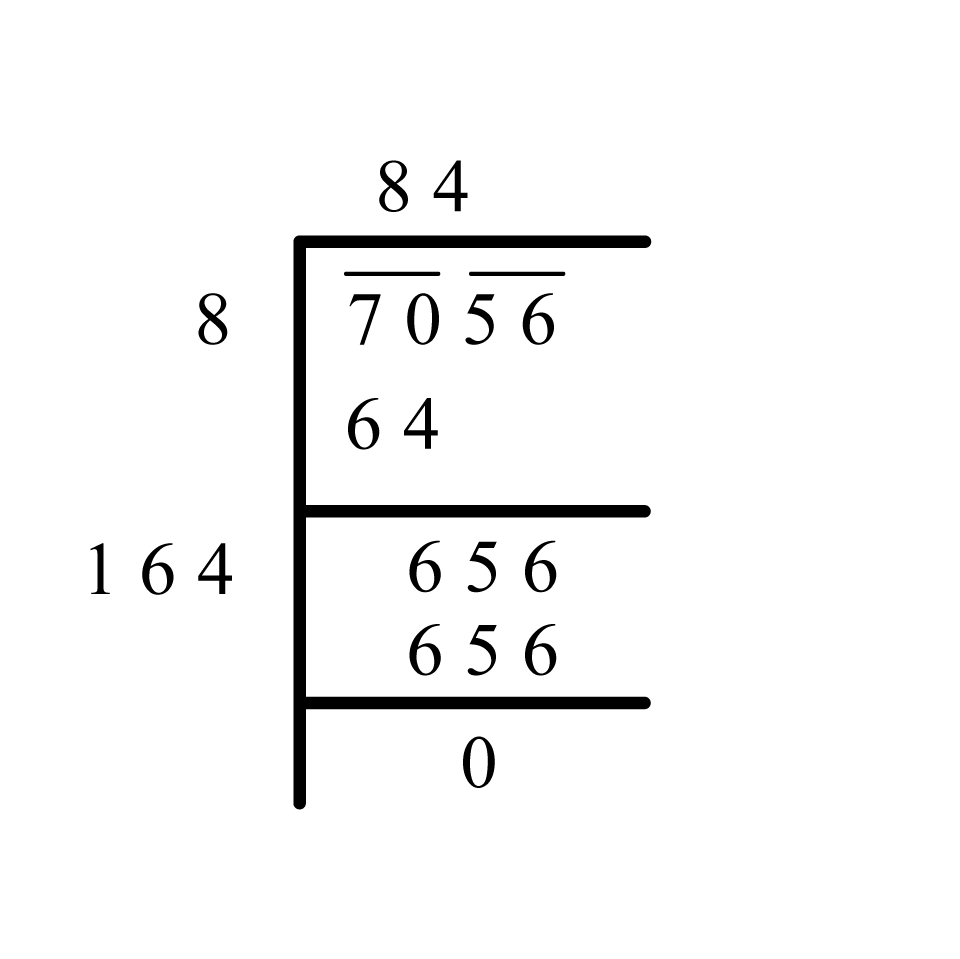
Find the square root of 70.56.
Find the least number to be subtracted from 2011 to get a perfect square.
Find the square root of the following numbers by the factorisation numbers : 34596
Find the square root of the following numbers by the factorisation numbers : 76176
Find the approximation of $$\sqrt{3.11}$$ both from below and above to 3 decimal places.
Find the square root of the following number correct to 2 decimal places: 12
Round off following number to 3 decimal places : 14.56789
Round off following number to $$3$$ decimal places : $$1.5678$$
Find the square root of the following number correct to 2 decimal places: 234.234
Find the square root of the following number correct to 2 decimal places: 12.34
Round off following number to 3 decimal places : 2.84671
Find the square root of the following number correct to 2 decimal places: 1.8
Round off following numbers to 3 decimal places : 3.3333567
Find the square roots of the given number by Prime factorization method: 784
Which of the following numbers are perfect squares?
(i) 121 (ii) 1136 (iii) 256 (iv) 321 (v) 600
Find the square root of the following numbers by the factorization method:
(i) $$729$$ (ii) $$400$$
(iii) $$1764$$ (iv) $$4096$$
(v) $$7744$$ (vi) $$9604$$
(vii) $$5929$$ (viii) $$9216$$
(ix) $$529$$ (x) $$8100$$
Find the square root of the given decimal number: $$84.64$$
Find the square roots of the given number by Prime factorization method: 7056
Find the square root of the given number by division method: $$1089$$
Find the square root of the given number by division method: 2304
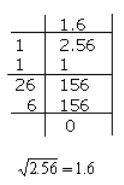
Find the square root of the given decimal number: $$2.56$$
Find the square root of each expression given below:
(i) $$3\times 3\times 4\times 4$$
(ii) $$2\times 2\times 5\times 5$$
(iii) $$3\times 3\times 3\times 3\times 3\times 3$$
(iv) $$5\times 5\times 11\times 11\times 7\times 7$$
Write down the unit digits of the following:
(i) $$78^{2}$$
(ii) $$27^{2}$$
(iii) $$41^{2}$$
(iv) $$35^{2}$$
(v) $$42^{2}$$
Find the square roots of the given number by Prime factorization method: 4096
Find the square root of the given number by division method: $$9025$$
Find the square root of $$5929$$
Find the least number by which $$384$$ must be divided to make it a perfect square
Write down the unit digits of the squares of the following numbers:
(i) $$24$$ (ii) $$78$$ (iii) $$35$$
Find the square root of $$529$$ using long division method
Find the least number by which $$200$$ must be multiplied to make it a perfect square
By observing the units digits, which of the numbers $$3136, 867$$ and $$4413$$ cannot be perfect squares?
Find the square root of $$169$$
Find the square root of $$64$$
Find $$\sqrt {3969}$$ by the long division method
Find the square root of $$12.25$$
Find the square root of
$$6+\sqrt { 12 } -\sqrt { 24 } -\sqrt { 8 } $$
Solve the following equation.$$16x^2-24x+9=0$$
Verify the validity of the identity
$$(a + b + c)^2 = a^2 + b^2 + c^2 + 2ab + 2bc + 2ca$$
for the following given values.
$$a = 2$$ $$b = 4$$ $$c = 6$$
$$a = 5$$ $$ b = -2$$ $$c = 3$$
$$a = -2$$ $$b = 3 $$ $$c =-4$$
Find the square root of the following in the form of a binomial surd.
$$n+\sqrt{n^2-1}$$.
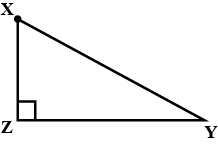
Triangle $$XYZ$$ is right-angled at vertex $$Z$$. Calculate the length of $$YZ$$, if $$XY=13$$ and $$XZ=12$$
Find the least number, which must be subtracted from $$3250$$ to make it a perfect square
Find the square root of $$-7-24\sqrt { -1 } $$.
Find a square of a natural number between 75 and 90.
Check if the following number is perfect square.
1243
Evaluate: $$\dfrac{\sqrt{32} + \sqrt{48}}{\sqrt{8} + \sqrt{12}}$$
Check if the following number is perfect square.
3300
Find the square root of a given number by prime factorization method.
3136
Find the value of $$\dfrac { 3 }{ \sqrt { 5 } +\sqrt { 2 } } +\dfrac { 7 }{ \sqrt { 5 } -\sqrt { 2 } } \sqrt { 5 } =2.236$$ and $$\sqrt { 2 } =1.414$$ ?
Find the value of $$\sqrt {3}$$
Number of solutions of $$2^{x} + 3^{x} + 4^{x} = 5^{x}$$ is
A General wishes to draw up his $$7500$$ soldiers in the form of a largest square. After arranging, he found out that some of them are left out. How many soldiers were left out?
Find the square root of $$11 + 2\sqrt {30} $$
Solve the problem:-
$$\sqrt 5 = ?$$
Find the square root of $$\left(x+\dfrac{1}{x}\right)^2-4\left(x-\dfrac{1}{x}\right)$$.
Prove the followings,i) $$(a+b)^2+(a-b)^2=2(a^2+b^2)$$ii) $$(a+b)^2-(a-b)^2=4ab$$
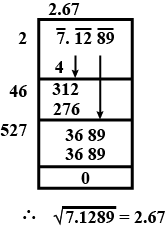
Find square root of $$= 7.1289$$ by long division method.
Find the greatest five digit number which is a perfect square. Also, find the square root of the number so obtained.
Find the square root of $$361201$$ by long division method
Find the smallest number by which $$2400$$ is to be multiplied to get a perfect square and also find the square root of the resulting number.
Find whether the square of the following numbers are even or odd?
$$2826$$.
Find square root of $$625$$ by long divison method.
Find the square of $$\dfrac{-12}{13}$$
Solve:$$25{\left( {2x + y} \right)^2} - 16{\left( {x - y} \right)^2}$$
Rajini says $$1\ sq\ m=100^{2}\ sq\ cm$$. Do you agree? Explain.
If $$x=\dfrac{5}{2}, y=\dfrac{3}{4}$$ then find the value of $$(x^2+y^1)(x^2-y^1)$$.
If $$\sqrt {15625}=125$$, then find the value of $$\sqrt {15625}+\sqrt {15625}+\sqrt {0.015625}$$
Write a Pythagorean triplet whose one member is $$(i)6$$$$(ii)14$$$$(iii)16$$$$(iv)18$$
Find the square root of $$529$$
Find the square roots of $$6084$$ by division method.
What could be the possible 'one's' digits of the square root of the following number?
$$99856$$
Find the square roots of the following decimal numbers.
i) $$2.56$$ ii) $$18.49$$ iii) $$68.89$$ iv) $$84.64$$
What could be the possible 'one's' digits of the square root of the following numbers?
$$9801$$
Simplify: $$(2)^{\dfrac{1}{4}}.(4)^{\dfrac{1}{8}}.(8)^{\dfrac{1}{16}}.(16)^{\dfrac{1}{32}}$$.
Evaluate : $${\left( {{{17}^2} - {8^2}} \right)^{\frac{1}{2}}}$$
Simplify $$\sqrt { 10 \frac { 151 } { 225 } }$$.
Which of $$77^2,82^2,161^2,109^2$$ will end with the digit $$1$$?
Solve $$\sqrt{444}$$
simplify $$\sqrt {98} $$
A rational number whose square is $$\dfrac { 81 }{ 64 } $$ is ______ .
Square of $$-\dfrac { 13 }{ 17 } $$ is_____
The approximate value of $$\sqrt { 50 }$$ is
Solve:-
$$\dfrac{2\sqrt{6}-\sqrt{5}}{3\sqrt{5}-2\sqrt{6}}$$
Find the square roots of the following numbers by prime factorization method.
$$441$$
Find the square roots of the following numbers by prime factorization method.
$$784$$
Find the square roots of the following numbers by prime factorization method.
$$4096$$
Find the square roots of the following numbers by prime factorization method.
$$7056$$
Find the square of the following :
$$7\frac{1}{2}$$
Find $$\sqrt{1276}$$
Find:
$$5\sqrt {25} + \sqrt {25} - 5\sqrt {25} = .......$$
Find the square root of $$(x^{2}+4x+4)$$.
Solve : $$20\sqrt { 15 } $$
What is the square root of $$18$$?
Solve
$$5^{2}+6^{2}+7^{2}+...+20^{2}$$
Find the last $$4$$ digit no which is a perfect square.
Expression the following as the product of expression through prime factorization
$$144$$
Identify with reason whether the following are Pythagoras triplet $$ 24, 70, 74$$.
Evaluate : $$\sqrt{5.38\times 0.47}$$
Evaluate: $$\sqrt { 616225 } $$
Find answer
$$\sqrt {5x}\times \sqrt {5x}=$$
Find the square roots of $$11\dfrac {9}{18}$$
Simplify:$$\sqrt { \dfrac { 35.87\times 0.0914 }{ 0.0578 } }$$
Evaluate :
$$\sqrt{\dfrac{2809}{4096}}$$
Find the following .
$$\sqrt{6146.56}$$
Evaluate $$\left( x-\dfrac { 1 }{ x } \right) ^{ 2 }-\left( x+\dfrac { 1 }{ x } \right) ^{ 2 }$$
$$\sqrt { 784 } $$ by long division method
$$\sqrt {129}=z$$. Find the value of $$z$$.
Write the Pythagorean triplet whose one member is
$$\left(i\right)16$$
$$\left(ii\right)14$$
What is the value of $$3^{2} +4^{2} ?$$
Find the smallest number by which $$882$$ be multiplied so that the product becomes a perfect square.
$$\sqrt{0.6}$$
Estimate the square root : $$4\sqrt {10}$$
Estimate the square root : $$3\sqrt 5$$
Estimate the square root : $$2\sqrt 3$$
Estimate the square root : $$4\sqrt 2$$
Write down the cube root of $$64$$
$$\sqrt{401}$$
Find the smallest whole number by which $$1458$$ should be multiplied so as to get a perfect square number.
$$2025$$ plants are to be planted in a garden in such a way that each row contains as many plants as the number of rows. Find the number of plants in each row.
Determine all pairs of positive integers (m, n) for which $$2^{m}+3^{n}$$ is a perfect square.
A man, after a tour, finds that he had spent every day as many rupees as the number of days he had been on tour. How long did his tour last, if he had spent in all $$Rs.\ 1,296$$?
Out of 745 students, maximum are to be arranged in the school field for a P.T. display, such that the number of rows is equal to the number of columns. Find the number of rows if 16 students were left out after the arrangement.
State true or false.
The square root of 739.461 correct to two decimal places is 27.193.
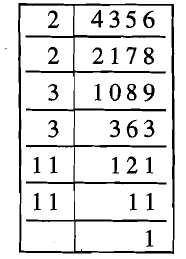
Find the square root of $$4356$$ by prime factorization method.
The following numbers are not perfect squares. Give reason
$$1057$$
$$23453$$
$$7928$$
What will be the unit digit of the squares of the following numbers?
$$81$$
$$272$$
$$799$$
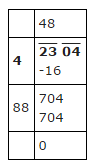
Evaluate $$\sqrt{7056}$$.
Find the greatest $$4$$-digit number, which is a perfect square. Find its square root.
Estimate the square root of $$140$$ to the nearest integer.
$$5929$$ students are sitting in an auditorium in such a manner that there are as many students in a row as there are rows in the auditorium. How many rows are there in the auditorium?
If $$ABC x CBA = 65125$$ where $$A, B$$ and $$C$$ are single digits the $$A + B + C =$$ ?
Find the square root of a number $$400$$ by the prime factorisation method.
For the following number, find the smallest whole number by which it should be multiplied so as to get a perfect square number.
$$2028$$
Find the square root of a number $$4096$$ by prime factorisation method.
Find the square root of the following number by the prime factorisation method.
$$9216$$
Find the smallest whole number by which $$180$$ should be multiplied, so as to get a perfect square number.
Find the smallest whole number by which $$768$$ should be multiplied, so as to get a perfect square number.
Find the square root of a number $$1764$$ by the prime factorisation method.
For the following number, find the smallest whole number by which it should be multiplied so as to get a perfect square number.
$$1008$$
Find the smallest whole number by which $$2645$$ should be multiplied so as to get a perfect square number.
Find the smallest whole number by which $$252$$ should be divided, so as to get a perfect square.
Find the smallest whole number by which $$396$$ should be multiplied, so as to get a perfect square number.
Find the square root of the number 729 by the prime factorisation method.
Find the square root of 7744.
Find the square of the integer just greater than the square root of the following number:
540
Find the square of the integer just less than the square root of the following number:
5500
For each of the following numbers find the smallest whole number by which it should be multiplied so as to get a perfect square number. Also find the square root of the square number so obtained .
(i) 252 (ii) 180(iii) 1008 (iv) 2028 (v) 1458 (vi) 768
(i) 252
Find the least number that must be subtracted from $$5607$$ so as to get a perfect square. Also, find the square root of the perfect square.
State whether $$7927$$ is a perfect square or not.
Find the square root of $$33453$$.
Find the square root of $$22222$$
State whether $$23453$$ is a perfect square or not.
Find the square root of $$1058$$.
Estimate square root of $$447$$.
Using prime factorization method, find the square root of the following:
(i) $$390625$$ (ii) $$119025$$ (iii) $$193600$$
Find the square root of the following numbers:
(i) $$1444$$ (ii) $$1849$$ (iii) $$5776$$ (iv) $$7921$$
Find the smallest number that must be added to get a perfect square.
(i) $$2361$$ (ii) $$4931$$ (iii) $$18265$$ (iv) $$390700$$
Find the square roots of the following numbers correct to two places of decimal:
(i) $$1.7$$ (ii) $$23.1$$ (iii) $$5$$ (iv) $$20$$ (v) $$0.1$$
Find the least numbers which must be subtracted from the following numbers so as to leave a perfect square:
(i) $$2361$$ (ii) $$4931$$ (iii) $$18265$$ (iv) $$390700$$
Write true (T) or false (F) for the following statements:
(i) $$\sqrt{0.9} = 0.3$$
(ii) If $$a$$ is a natural number, then $$\sqrt{a}$$ is a rational number.
(iii) If $$a$$ is negative, then $${a}^{2}$$ is also negative.
(iv) If $$p$$ and $$q$$ are perfect squares, then $$\sqrt{\displaystyle\frac{p}{q}}$$ is a rational number.
(v) The square root of a prime number may be obtained approximately, but never exactly.
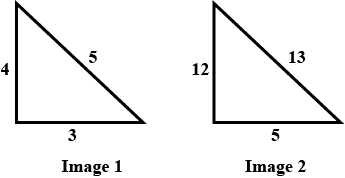
What is the Pythagorean Triples using the values, $$m = 3$$ and $$n = 5$$?
Find the Pythagorean Triples using the values, $$m = 4$$ and $$n = 8$$.
What is the Pythagorean Triples using the values, $$m = 1$$ and $$n = 5$$?
Find the Pythagorean Triples using the values, $$m = 2$$ and $$n = 3$$.
Find whether the following lengths are Pythagorean triples: $$3, 7$$ and $$1$$.
Find whether the following lengths are Pythagorean triples: $$6, 1$$ and $$7$$.
Check if the following lengths are Pythagorean triples: $$8, 15$$ and $$17$$.
What is the Pythagorean Triples using the values, $$m = 0$$ and $$n = 2$$?
Check if the following lengths are Pythagorean triples: $$60, 61$$ and $$11$$.
Determine if the following lengths are Pythagorean triples: $$9, 40$$ and $$41$$.
Evaluate using long division method: $$\sqrt{6241}$$
Evaluate using long division method: $$\sqrt{7056}$$
Find the square root of $$9.61$$ using long division method.
Find the square root of $$79.21$$ using long division method.
What is the square root of $$96.04$$ using long division method?
Find the square root of $$2.89$$ using long division method.
For each of the following number, find the smallest whole number by which it should be multiplied so as to get a perfect square number. Also find the square root of the square number so obtained.
$$(i)\ 252$$ $$(ii)\ 180$$ $$(iii)\ 1008$$ $$(iv)\ 2028$$ $$(v)\ 1458$$ $$(vi)\ 768$$
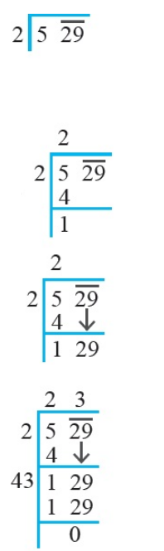
How many numbers lie between squares of the following numbers ?
(i) $$12$$ and $$13$$
(ii)$$25$$ and $$26$$
(iii) $$99$$ and $$100$$
What will be the unit digit of the squares of the following number ?
(i) 81 (ii) 272 (iii) 799 (iv) 3853 (v) 1234
(vi) 26387 (vii) 52698 (viii) 99880 (ix) 12796 (x) 55555
Without doing calculation, find the numbers which are surely not perfect squares.
$$(i) 153\
(ii) 257 \
(iii) 408 \
(iv) 441$$
The square of which of the following number will be odd numbers?
(i) 431
(ii) 2826
(iii) 7779
(iv) 82004
What could be possible one's digit of the square root of each of the following numbers?
(i) 9801
(ii) 99856
(iii) 998001
(iv) 657666025
Find the square root of the following number by prime factorisation method
(i) 729
(ii) 400
(iii) 1764
(iv) 4096
(v) 7744
(vi) 9604
(vii) 5929
(viii) 9216
(ix) 529
(x) 8100
Let n be a product of four consecutive positive integers then n is never a perfect square
Find square root of each of the following no. by division method
$$(i)\ 2304$$ $$(ii)\ 4489$$ $$(iii)\ 3481$$ $$(iv)\ 529$$ $$(v)\ 3249$$ $$ (vi)\ 1369$$ $$(vii)\ 5776$$ $$(viii)\ 7921$$ $$(ix)\ 576$$ $$(x)\ 1024$$ $$(xi)\ 3136$$ $$(xii)\ 900$$
Identify the perfect squares among the following numbers:
$$1, 2, 3, 8, 36, 49, 65, 67, 71, 81, 169, 625, 125, 900, 100, 1000, 100000$$
Find the number of digits in the square root of each of the following number.
$$(i)\ 64$$ $$(ii)\ 144$$ $$(iii)\ 4489$$ $$(iv)\ 27225$$ $$(v)\ 390625$$
Find the least number which must be added from each of the following so as to get a perfect square. Also find the square root of the perfect square so obtained.
$$(i)\ 525$$ $$(ii)\ 1750$$ $$(iii)\ 252$$ $$(iv)\ 1825$$ $$(v)\ 6412 $$
Write $$3$$-digit numbers ending with $$0, 1, 4, 5, 6, 9$$ one for each digit, but none of them is a perfect square.
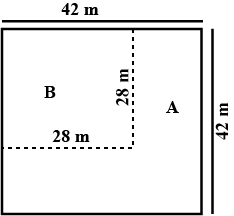
A square yard has area $$1764$$ m$$^2$$. From a corner of this yard, another square part of area $$784$$ m$$^2$$ is taken out for public utility. The remaining portion is divided in to $$5$$ equal square parts. What is the perimeter of each of these equal parts?
Find the largest perfect square factor of each of $$11280$$
Find the smallest square no. which is divisible by each of the numbers $$4,9$$ and $$10$$.
Find the square root of the following numbers by the factorisation numbers : 1296
Find the nearest integer to the square root of $$728.$$
Find the square root of 19.5364
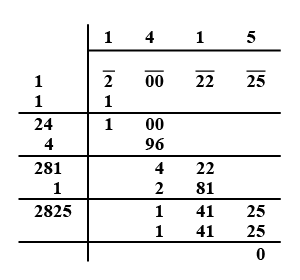
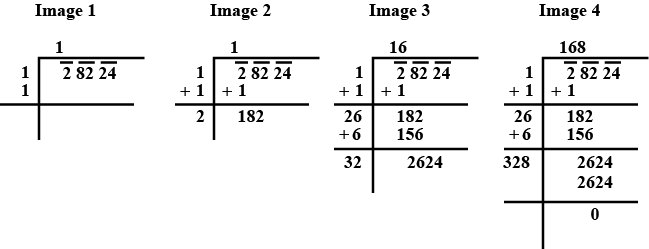
Find the square root of $$2002225$$.
Find the nearest integer to the square root of $$1729.$$
The nearest integer to the square root of $$600$$ is ___.
Find the square root of 96721.
Find the square root of $$5329$$ by division method
A square-field has area 3.32,929$$m^2$$. It has to be fenced using barbed wire, The barbed wire should go round the field 5 times. The barbed wire is available in bundles of 100 m length. The vendor sells the wire only in complete bundles. How many bundles have to be bought?
Find the square root of the following numbers: $$184.96$$
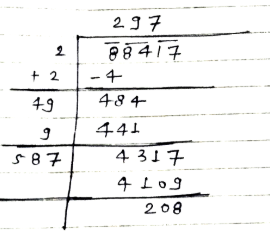
Find the least number to be added to get a perfect square: 88417
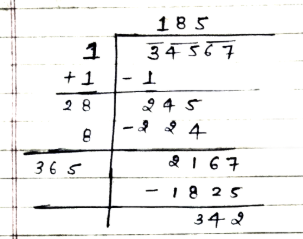
Find the least number to be subtracted from the following number to get a perfect square: 34567
Find the square root of the following number by division method: $$186624$$
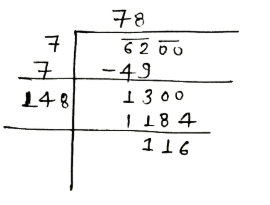
Find the least number to be added to get a perfect square: 6200
Find the consecutive perfect squares between which the following numbers lie: 56789
Find the consecutive perfect squares between which the following numbers lie: 4567
Find the square root of the following number by division method: 28224
Find the least number to be subtracted from $$1234$$ to get a perfect square.
Check whether the following numbers form Pythagorean triplet.
$$6,8,10$$
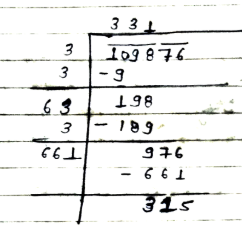
Find the least number to be subtracted from the following numbers to get a perfect square: 109876
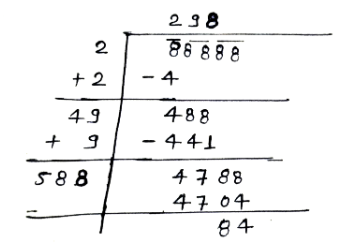
Find the consecutive perfect squares between which the following numbers lie: 88888
How many digits are there after the decimal points in the following : $$(1.234)^2$$
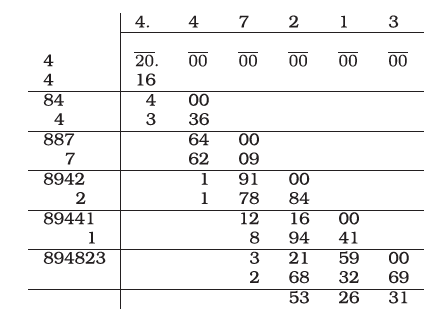
Find the square root of the following numbers using division method: 651.7809
If $$a$$ is the side of an equilateral triangle, then its area is given by $$\dfrac{\sqrt{3}}{4}a^2$$. Given that the area of an equilateral triangle is $$5\sqrt{3}$$ units, find its side correct to 4 decimal ploaces
Find approximations from below to 4 decimal places to the square root of the following number: 5
A square garden has area 900 $$m^2$$. Additional land measuring equal area, surrounding it, has been added to it. If the resulting plot is also in the form of a square, what is its side correct to 2 decimal places?
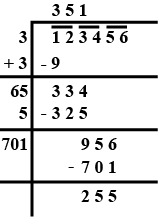
Find the consecutive perfect squares between which the following numbers lie: 123456
Find the square root of 3 and also correct it to 4 decimal places.
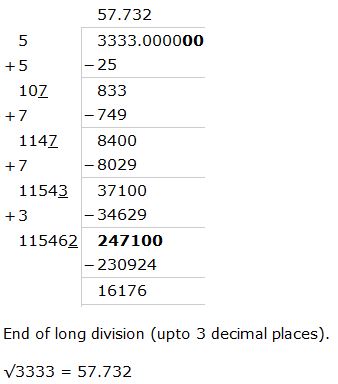
Find the square root of the following number correct to 3 decimal places: 3333
How many digits are there after the decimal points in the following : $$(3.16)^2$$
Find approximations from below to 4 decimal places to the square root of the following number: 8
Explain with reason whether the given number is perfect square or not: 257
Find the value of
$${ \left( 26+15\sqrt { 3 } \right) }^{ \dfrac { 2 }{ 3 } }-{ \left( 26+15\sqrt { 3 } \right) }^{ -\dfrac { 2 }{ 3 } }$$
Which of the following numbers are perfect squares?$$3, 5, 23, 25, 36, 26, 40$$
To find the value of $$\sqrt [ 4 ]{ -64{ a }^{ 4 } } $$.
$$\sqrt { 4{ x }^{ 4 }-12{ x }^{ 3 }+25{ x }^{ 2 }-24x+16 } =?$$
Solve the following equations.
$$\displaystyle\, \frac{x}{\sqrt{1 \, + \, x^2}}\, + \, \frac{x}{\sqrt{1 \, - \, x^2}}\, = \, 0$$
Find the square root of
$$5-\sqrt { 10 } -\sqrt { 15 } +\sqrt { 6 } $$
Write a Pythagorean triplet whose one member is $$6$$$$14$$$$16$$
Find the square root of a given number by prime factorization method.
2304
Which of the following are Pythagorean triplets?
i) (9, 8, 10)
ii) (4, 3, 5)
iii) (6, 8, 10)
Show that each of the following number is a perfect square. In each case find the number whose square is the given number.
(i) $$2025$$ (ii) $$6561$$ (iii) $$38416$$ (iv) $$7921$$ (v) $$1444$$ (vi) $$5776$$
Find the square root of a given number by the prime factorization method.
$$900$$
Suppose m and n are any two numbers. If $${ m }^{ 2 }-{ n }^{ 2 },2mn$$ and $${ m }^{ 2 }+{ n }^{ 2 }$$ are the three sides of a triangle, then show that it is a right angled triangle and hence write any two pairs of Pythagorean triplet
Find the square root of 2025
$$\sqrt{\sqrt{50} + \sqrt{48}} = k(\sqrt{3} + \sqrt{2})$$, then k =
A student writes the formula $$\sqrt{ab} \, = \, \sqrt{a} \sqrt{b}$$. Then substitutes a = -1 and b = -1 finds 1 = -Explain where he is wrong.
solve: $$\sqrt {2 + \sqrt {2 + \sqrt {2 + \sqrt {2\,\,\,...........} } } } $$
What is the smallest natural number that should be multiplied with $$840$$ to make it a perfect square?
Find the fifty-sixth square number.
Find smallest No: by which $$3645$$ must be $$\div$$ to make it a per.square
$$\sqrt{1806336}$$=
Find the value:$$\sqrt { 8+\sqrt { 773+\sqrt { 116+\sqrt { 2+\sqrt { 520+81 } } } } } $$
$$(1035 + x)$$ chairs are placed in an auditorium in such way that the number of rows is equal to number of columns. Find the least value of $$x$$.
Find whether the square of the following numbers are even or odd?
$$431$$.
Find the square root of the following number by the prime factorisation method.
$$5625$$
Find the square roots of the following numbers by Prime factorization method.(i)441(ii)784(iii)4096(iv)7056
Find whether the square of the following numbers are even or odd?
$$9999$$
Find the smallest number by which $$7776$$ is to be divided to get a perfect square.
Find the smallest number by which $$3645$$ must be multiplied to get a perfect square.
Find whether the square of the following numbers are even or odd?
$$17779$$
Find whether the square of the following numbers are even or odd?
$$8204$$
Find the square root of the following number by the prime factorisation method.
$$1\dfrac{17}{64}$$
Find the square root of the following number by the prime factorisation method.
$$4096$$
Find the largest number of $$6$$ digits which is a perfect square.
Find the square root of the following number by factorisation.
$$256$$
Find the square root of the following number by the prime factorisation method.
$$1936$$
Find the square root of the following number by the prime factorisation method.
$$7744$$
Find the square root of the following number by the prime factorisation method.
$$6\dfrac{1}{4}$$
Find the square root of the following number by the prime factorisation method.
$$4356$$
Find the square root of the following number by the prime factorisation method.
$$1521$$
Find the square root of the following number by the prime factorisation method.
$$5929$$
Three-eighth of the students of a class opted for visiting an old age home. Sixteen students opted for having a nature walk. Square root of total number of students in the class opted for tree plantation in the school. The number of students who visited the old age home is same as the number of students who went for a nature walk and did tree plantation. Find the total number of students. What values are inculcated in students through such activities?
Find the square root of the following number by factorisation.
$$13225$$
Find the square root of the following number by the prime factorisation method.
$$\dfrac{289}{144}$$
Estimate the value of the following numbers to the nearest whole number
(i) $$\sqrt{97}$$
(ii) $$\sqrt{250}$$
(iii) $$\sqrt{780}$$
Find the square root of the following number by factorisation.
$$10404$$
Find the square root of the following number by factorisation.
$$196$$
Write a Pythagorean triplet whose one member is $$14$$.
Find the square root by long-division method:
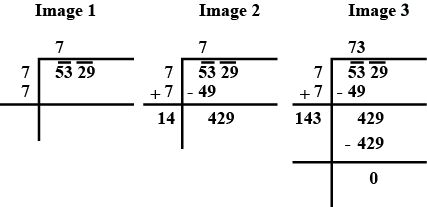
$$7921$$
Find the square root of the following number by long division method.
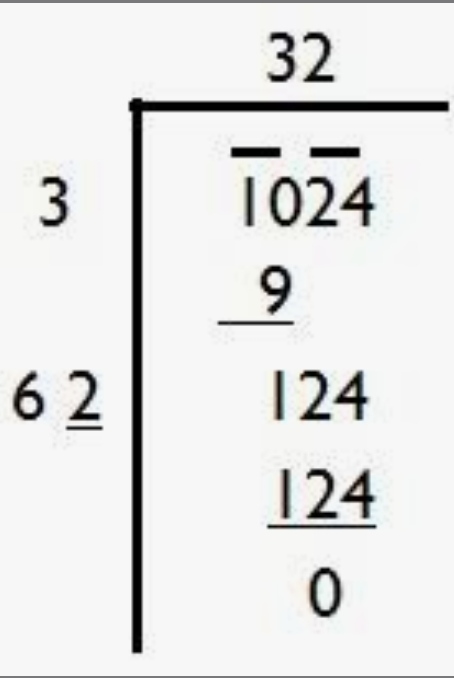
$$1024$$
Find the square root of the following number by division method.
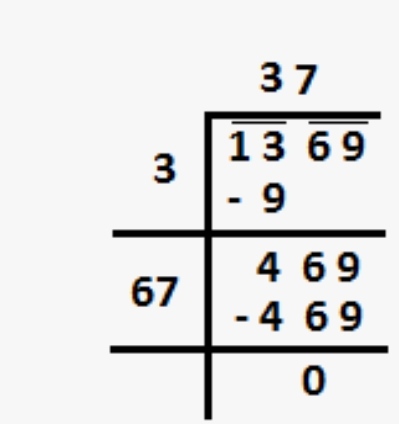
$$1369$$
Find the square root of the following number by division method.
$$3249$$
Write a Pythagorean triplet whose one member is $$16$$.
Find the square root of the following number by long division method.
$$576$$
Find the square root of the following number by Division method.
$$3481$$
Find the square root of the following number by long division method.
$$529$$
Find the square root of following surds:
$$a+\sqrt{a^{2}-b^{2}}$$
Find the square root of the following number by Division method.
$$4489$$
Find the square root of the following number by long division method.
$$3136$$
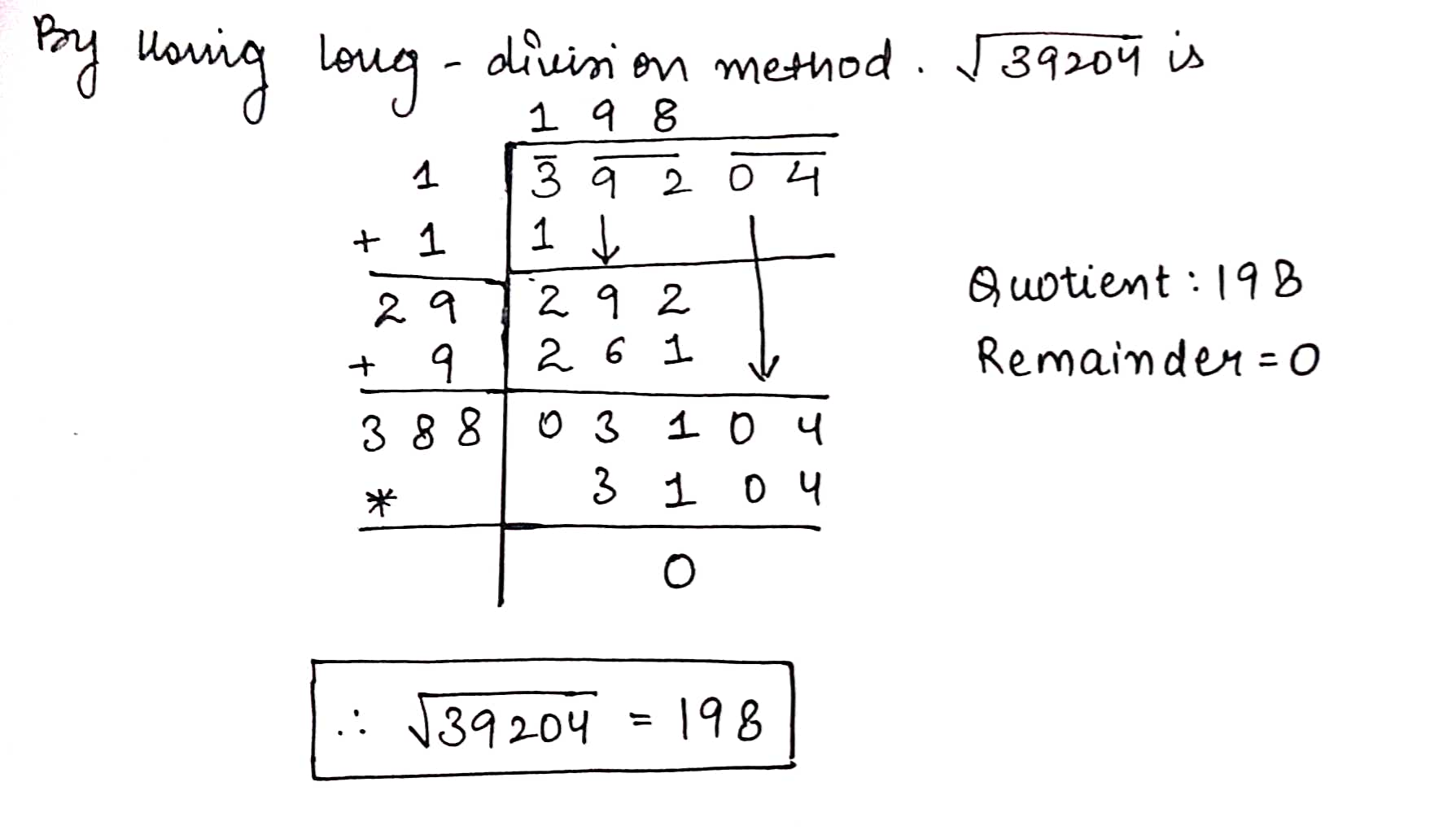
Find the $$\,\sqrt {39204} $$
Find the value of $$\sqrt {73441} $$ and evaluate $$\sqrt {734.41} \times \sqrt {7.3441} $$
The students of $$8^{th}$$ class of a school donate $$Rs.2401$$ in all for Prime Minister National Relief Fund. Each student donates as many rupees as the no. of students in the class. Find the no. of students in the class.
What will be the unit digit of the squares of the following numbers?
$$(i) 81 \quad
\quad(ii) 272 \quad(iii) 799
\quad(iv) 243 \quad(v) 26387 \quad(vi) 52698
\quad(vii) 2796 \quad(viii) 55555$$
Find the square root of the following number by long division method.
$$900$$
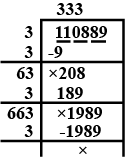
Find the value of $$\sqrt {110889} $$ and hence find the value of $$\sqrt {11.0889} + \sqrt {1108.89} $$
Mr. Khanna has $$1200$$ plants. He wants to plant these in such a way that the number of rows and the number of column remain the same.
a) What is the minimum number of plants he needs more for this purpose ?
b) Which value is depicted by Mr. Khanna ?
What will be the unit digit of the square of the following numbers?
$$81$$
Find the square root by long-division method:
$$5776$$.
Find the value of $$\sqrt{2401}$$ using prime factorization method.
Find the square root of following surd :
$$7+\sqrt{48}$$
Estimate the value of the given number to the nearest whole number: $$\sqrt{112}$$ ?
Find the square root of:
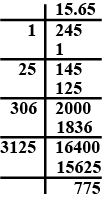
$$245$$ correct to two places of decimal
Find the least number which must be added to $$4931$$ to make it a perfect square ?
Find the square root of $$256$$.
Find the square root of $$1024$$. Hence find the value of $$\sqrt{10.24}+\sqrt{0.1024}+\sqrt{10240000}$$.
What will be the unit digit of the square of the following numbers?
$$1234$$
What will be the unit digit of the square of the following numbers?
$$55555$$
What will be the unit digit of the square of the following numbers?
$$26387$$
Find the smallest number by which $$98$$ should be multiplied to make it a perfect square.
What will be the unit digit of the square of the following numbers?
$$52698$$
What will be the unit digit of the square of the following numbers?
$$99880$$
Write a phythogorean triphlets whose one of the member is 26.
What will be the unit digit of the square of the following numbers?
$$799$$
What will be the unit digit of the square of the following numbers?
$$3853$$
Find the square root of the following in the form of a binomial surd.
$$12+2\sqrt{35}$$.
Find the square root of: $$33.64$$
Find the square root of the following in the form of a binomial surd.
$$2+\dfrac{2}{3}\sqrt{5}$$.
Find the square root of following surds:
$$8-3\sqrt{7}$$
What is the closest perfect square root of following numbers?
(i) $$248$$ (ii) $$1234$$ (iii) $$1678$$.
Solve $$\sqrt{\dfrac{2\times (9\times 10^9)(1.6\times 10^{-19})(47)(1.6\times 10^{-19})}{(1.67\times 10^{-27})(2.5\times 10^{-14})}}$$
Do the following numbers make Pythagorean triplets?
(i) $$8,\ 10,\ 17$$
(ii) $$8,\ 10,\ 12$$
How many square tiles of side $$9 \,cm$$ will be needed to fit in a square floor of a bathroom of side $$720 \,cm$$? Find the cost of tilling at the rate of $$Rs. 7.50$$ per tile.
Find the least number of $$4$$ digits which is a perfect square. Find the square roots of this number.
Solve : $$\sqrt{\frac{1+e^{x}}{1-e^{x}}}$$
Value $$\phi \sqrt \infty $$
A group of boys collected 256 marbles for some project. The contribution of each boy was equal to the number of boys in the group.How many boys were in the group?
Find the square roots of the following perfect squares using the long division method :
a) $$357096609$$
b) $$159.7696$$
Estimate each root, to the nearest whole number.
(a) $$\sqrt{171}$$
(b) $$\sqrt{35}$$
(c) $$\sqrt{407}$$
(d) $$\sqrt{292}$$
Solve the term:-
$$1^{2},\ 3^{2},\ 5^{2},\ 7^{2},\ ......$$
If $$\sqrt{6}=2.55$$, then the value of $$\sqrt{\dfrac{2}{3}}+3\sqrt{\dfrac{3}{2}}$$ is
What is a Pythagorean triplet? Give some examples.
If $$'n'$$ is odd no & $$n> 1$$, them prove that $$\left(n,\dfrac{n^2-1}{2},\dfrac{n^2+1}{2}\right)$$ is a Pythagorean, triplet. Write two Pythagorean triplet taking suitable value of $$'n'$$.
How many non-perfect square numbers lie between $$n^2$$ and $$(n+1)^2$$?
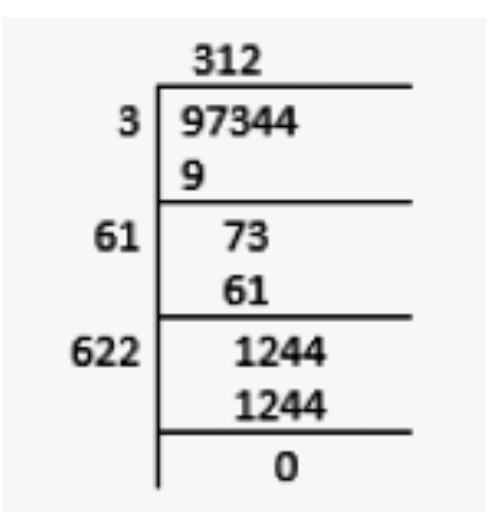
Find the square root of $$97344$$ by prime factorization method.
Find the value of $$\sqrt{8 + \sqrt{289}}$$:
In $$n$$ is an odd number and n > 1, then prove that $$\left(n,\dfrac{n^{2}-1}{2},\dfrac{n^{2}+1}{2}\right)$$ is a Pythagorean triplet. Write two Pythagorean triplet making suitable value of $$n$$.
what will be the units digits of the square of the following number? 39, 297, 5125, 7286
Find the least number that must be added to 1500 so as to get a perfect square. Also find the square root of the perfect square.
Check whether the following numbers form Pythagorean triplet
$$9,10,11$$
Check whether the following numbers form Pythagorean triplet:-
$$2,3,4$$
Is $$2352$$ a perfect square? If not, find the smallest number that should be multiplied to $$2352$$ to make a perfect square. Find the square root of the new numbers.
Solve:$$\sqrt{27^{x+1}}=9^{x-2}$$
Find the square root of $$12+2\sqrt{35}$$.
Check whether the following numbers form a Pythagorean triplet.
$$8,15,17$$
Find the pythagorean triplet whose smallest number is $$16$$
Solve:
$$\sqrt{6\sqrt{6\sqrt{6}}}$$
Expression the following as the product of expression through prime factorization
$$36$$
Expression the following as the product of expression through prime factorization
$$1125$$
Express the following as the product of expression through prime factorization
$$288$$
Which of the following triplets are Pythagorean ?
$$( 3,4,5 ) , ( 6,7,8 ) , ( 10,24,26 ) , ( 2,3,4 ).$$
Square root of $$375$$ is -
Find the least number that should be subtracted from $$1,300$$ to get perfect square.
by what smallest number should $$10584$$ be multiplied so that product may be a perfect square ? also find the square root of the new number.
Find the square root of the following decimal fraction :
$$0.09$$
Simplify:
$$3\sqrt {45}-\sqrt {125}+\sqrt {200}-81\sqrt {30}$$
Simplify :-
$$\sqrt { 9\times { 6 }^{ 3 }\times 24 } $$
$$625$$ is a perfect square number.If above statement is true, type $$1$$ otherwise $$0$$.
Which of the following numbers are perfect square?
$$2500$$
$$576$$ is a perfect square number.If above statement is true, type $$1$$ otherwise $$0$$.
Find the square root of $$1296$$ by prime factorization method.
Simplify :$$\sqrt{41-\sqrt{21+\sqrt{19-\sqrt{9}}}}$$
Evaluate: $$(6+\sqrt {27})-(3+\sqrt 3)+(1-2\sqrt 3)$$
$$941$$ is a perfect square number.If above statement is true, type $$1$$ otherwise $$0$$.
Find the Pythagorean triplets from among the following set of numbers.
$$3, 4, 5$$.
$$484$$ is a perfect square number.If above statement is true, type $$1$$ otherwise $$0$$.
$$961$$ is a perfect square number.If above statement is true, type $$1$$ otherwise $$0$$.
Which of the following numbers are perfect square?
$$11, 12, 16, 32, 36, 50, 64, 79, 81, 111, 121$$
Using prime factorization method, find which of the following numbers are perfect square?
$$189, 225, 2048, 343, 441, 2916, 11025, 3549$$
Find the number whose square is the given following number:
$$4761$$
The following number is not perfect square. Give reason.
$$45743$$
Find the number whose square is the given number.
$$1156$$
Find the number whose square is the given number.
$$14641$$
Find the greatest number of two digits which is a perfect square.
The following number is a perfect square. Give reason.
$$1547$$
Find the least number of three digits which is perfect square.
Find the number whose square is the given number:
$$2025$$
The square of which of the following numbers would be an odd number?
$$3456$$
Show that the following number is not perfect square:
$$9327$$
The square of which of the following numbers would be an odd number?
$$5559$$
Show that the following number is not perfect square:
$$743522$$
The square of the following number would be an odd number?
$$42008$$
The number $$1027$$ is a perfect square.Type 1 if above statement is true, otherwise 0.
Check whether the following triplet is Pythagorean?$$(10, 24, 26 )$$
Check whether the following triplet is Pythagorean?$$(14, 48, 51)$$
Check whether the following triplet is Pythagorean?$$(16, 63, 65 )$$
By just examining the units digits, can you tell whether the following can be whole square?
$$1024$$
Find the square root of the following number by prime factorization:
$$11664$$
Find the square root of the following number by prime factorization:
$$47089$$
Find the square root of the following number by prime factorization:
$$7056$$
Find the square root of the following number by prime factorization:
$$196$$
Find the square root of the following number by prime factorization:
$$8281$$
Using the prime factorization method, find if the following number is a perfect square:
$$441$$
Give reason to show that none of the numbers given below is a perfect square:
$$2500000$$
Find the square root of the following number by prime factorization:
$$4096$$
Find the square root of the following number by prime factorization:
$$1764$$
Find the square root of the following number by prime factorization:
$$1156$$
Find the square root of the following number by prime factorization:
$$441$$
Find the square root of the following number by prime factorization:
$$529$$
Find the least number of $$4$$ digits which is a perfect.
Write the prime factorization of the following number and hence find its square root:
$$7056$$
Find the square root of the following by prime factorization:
$$27225$$
Find the square root of the following by long division method:
$$97344$$
Find the square root of the following by long division method:
$$12544$$
Write the prime factorization of the following number and hence find its square root:
$$7744$$
Find the square root of the following by prime factorization:
$$24336$$
Write the prime factorization of the following number and hence find its square root:
$$9604$$
Using the prime factorization method, find if the following number is a perfect square:
$$9075$$
Using the prime factorization method, find if the following number is a perfect square:
$$1176$$
Which of the following squares are squares of even number?
$$900$$
Which of the following squares are squares of even number?
$$324$$
Using the prime factorization method, find if the following number is a perfect square:
$$11025$$
Using the prime factorization method, find if the following number is a perfect square:
$$4225$$
Using the prime factorization method, find if the following number is a perfect square:
$$5625$$
Which of the following are squares of even number?
$$441$$
Using the prime factorization method, find if the following number is a perfect square:
$$576$$
Which of the following are squares of even number?
$$625$$
Using the prime factorization method, find if the following number is a perfect square:
$$1089$$
Find the square root of each of the following numbers by using the method of prime factorization:
$$9216$$
Find the square root of each of the following numbers by using the method of prime factorization:
$$225$$
Find the square root of each of the following numbers by using the method of prime factorization:
$$1296$$
Find the square root of each of the following numbers by using the method of prime factorization:
$$441$$
By what least number should the given number be multiplied to get a perfect square number ? Also find the number, whose square is the new number.
$$9075$$
By what least number should the given number be multiplied to get a perfect square number ? In the case, find the number whose square is the new number.
$$2925$$
By what least number should the given number be multiplied to get a perfect square number ? In the case, find the number whose square is the new number.
$$3332$$
By what least number should the given number be multiplied to get a perfect square number ? In the case, find the number whose square is the new number.
$$2156$$
Find the smallest number by which $$252$$ must be multiplied to get a perfect square. Also, find the square root of the perfect square so obtained.
By what least number should the given number be multiplied to get a perfect square number ? In the case, find the number whose square is the new number.
$$3675$$
Find the square root of each of the following numbers by using the method of prime factorization:
$$11025$$
Find the square root of each of the following numbers by using the method of prime factorization:
$$17424$$
Write a Pythagorean triplet whose smallest number is
$$6$$
Find the square root of each of the following numbers by using the method of prime factorization:
$$15876$$
By what least number should the given number be divided to get a perfect square number?
In the case, find the number of square is the new number
$$9075$$
By what least number should the given number be divided to get a perfect square number?
In the case, find the number of square is the new number
$$3380$$
By what least number should the given number be divided to get a perfect square number?
In the case, find the number of square is the new number
$$4851$$
Write a Pythagorean triplet whose smallest number is
$$16$$
By what least number should $$2475$$ be multiplied to get a perfect square number ? In the case, find the number whose square is the new number.
By what least number should the given number be multiplied to get a perfect square number? Also, find the number whose square is the new number.
$$7623$$
By what least number should the given number be divided to get a perfect square number?
In the case, find the number of square is the new number
$$1575$$
By what least number should the given number be multiplied to get a perfect square number ? In the case, find the number whose square is the new number.
$$3380$$
Evaluate:
$$\surd 6241$$
Evaluate:
$$\sqrt{ 1444}$$
Write a Pythagorean triplet whose number is
$$15$$
By what least number should the given number be divided to get a perfect square number?
In the case, find the number of square is the new number
$$7776$$
By what least number should the given number be divided to get a perfect square number?
In the case, find the number of square is the new number
$$4056$$
By what least number should the given number be divided to get a perfect square number?
In that case, find the new number which is a square number.
$$8820$$
By what least number should the given number be divided to get a perfect square number?
In the case, find the number of square is the new number
$$4500$$
Evaluate:
$$\surd 4489$$
Evaluate:
$$\surd 10404$$
Evaluate: $$\sqrt {9025}$$
Evaluate:
$$\surd 7056$$
Evaluate:
$$\sqrt {14161}$$
Fill in the blanks to make the statements true.
There are ________ perfect squares between 1 and 100.
The unit digit in the square of $$1294$$ is _______.
Fill in the blanks:
The square of an even number is.......... .
Fill in the blanks:
The square of an odd number is.......... .
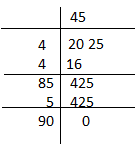
Using prime factorisation, find the square roots of
a) 11025
b) 4761
Find the square root of the following by long division method.
a) 1369
b) 5625
Show that $$500$$ is not a perfect square.
Write the Pythagorean triplet whose one of the numbers is 4.
By what smallest number should 216 be divided so that the quotient is a perfect square? Also find the square root of the quotient.
Are 176 a perfect square? If not, find find the smallest number by which it should be multiplied to get a perfect square.
What is the least number that should be subtracted from 1385 to get a perfect square? Also find the square root of the perfect square.
A perfect square number has four digits, none of which is zero. The digits from left to right have values that are: even, even. odd, even. Find the number.
Find the greatest number of three digits which is a perfect square.
Find the decimal fraction which when multiplied by itself $$84.64$$.
Find the least number of four digits that is a perfect square.
Find the least square number which is exactly divisible by 3, 4, 5, 6 and 8.
A decimal number is multiplied by itself. If the product is 51.84, find the number.
What is the least number that should be added to 6200 to make it a perfect square?
Find the smallest square number divisible by each one of the numbers 8, 9 and 10.
What will be the unit digit of the squares of the following numbers?
$$951$$
What will be the unit digit of the squares of the following numbers?
$$7625$$
The following numbers are obviously not perfect. Give reason.
$$567$$
What will be the unit digit of the squares of the following numbers?
$$5124$$
What will be the unit digit of the squares of the following numbers?
$$502$$
What will be the unit digit of the squares of the following numbers?
$$329$$
What will be the unit digit of the squares of the following numbers?
$$12796$$
What will be the unit digit of the squares of the following numbers?
$$95628$$
What will be the unit digit of the squares of the following numbers?
$$99880$$
What will be the unit digit of the squares of the following numbers?
$$68327$$
What will be the unit digit of the squares of the following numbers?
$$643$$
Find the square root of each of the following by division method:
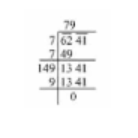
$$2401$$
The following numbers are obviously not perfect. Give reason.
$$74000$$
Find the square root of each of the following by division method:
$$4489$$
The following numbers are obviously not perfect. Give reason.
$$2453$$
The square of which of the following numbers would be an odd number or an even number? Why?
$$8267$$
The following numbers are obviously not perfect. Give reason.
$$46292$$
The square of which of the following numbers would be an odd number or an even number? Why?
$$37916$$
The square of the following number would be an odd number or an even number? Why?
$$573$$
The square of which of the following numbers would be an odd number or an even number? Why?
$$4096$$
Find the smallest four- digit number which is a perfect square.
Find the least number which must be added to each of the following numbers to make them a perfect square. Also, find the square root of the perfect square number so obtained:
$$8000$$
Find the square root of the following numbers correct to two decimal places:
$$2$$
Find the square root of the following numbers by prime factorization method:
$$17 \dfrac{13}{ 36} $$
Find the square root of the following numbers by prime factorization method:
$$1.96$$
Find the square root of the following numbers by prime factorization method:
$$9\dfrac{67}{121}$$
Find the square root of the following numbers by prime factorization method:
$$8836$$
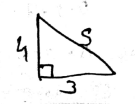
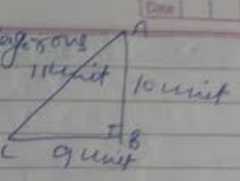
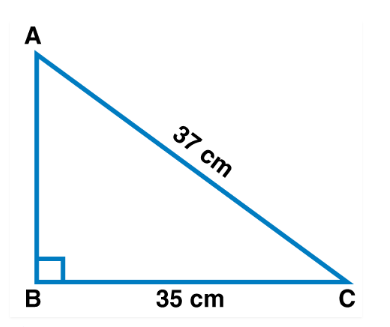
In a right triangle $$ABC, \angle B=90^{o}$$
If $$AC=37\ cm, BC=35\ cm$$, find $$AB$$
Show that each of the following numbers is a perfect square. Also, find the number whose square is the given number.
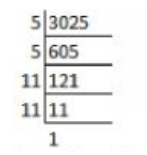
$$3025$$
Which of the following natural numbers are perfect squares? Give reasons in support of your answer.
$$1024$$
check if the following natural number is a perfect square? Give reasons in support of your answer.
$$729$$
Show that each of the following numbers is a perfect square. Also, find the number whose square is the given number.
$$1764$$
Show that each of the following numbers is a perfect square. Also, find the number whose square is the given number.
$$1296$$
Find the smallest number by which $$2592$$ be multiplied so that the product is a perfect square.
Find the smallest perfect square divisible by $$3, 4, 5$$ and $$6.$$
Find the square root of:
$$4761$$
Identify , with reason , if the following is a pythagoran triplet .
$$(4,9,12)$$
Identify , with reason , if the following is a pythagoran triplet .
$$(3,5, 4)$$
Identify, with reason, if the following is a Pythagorean triplet.
$$(5,12,13)$$
By splitting into prime factors, find the square root of:
$$396900$$
Find the square root of:
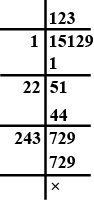
$$15129$$
Show that each of the following numbers is a perfect square. Also, find the number whose square is the given number.
$$3969$$
Find the smallest number by which $$10368$$ be divided so that the result is a perfect square. Also, find the square root of the resulting numbers.
Divide, and write the answer in simplest form.
$$\sqrt{310}\div\sqrt{5}$$
Divide and write in simplest form.
$$\sqrt{54}\div\sqrt{27}$$
Identify , with reason , if the following is a pythagoran triplet .
$$(24,70,74)$$
Write the digit in units place when the following numbers are squared.
$$ 4, 5, 9, 24, 17, 76, 34, 52, 33, 2319, 18, 3458,$$
Identify , with reason , if the following is a pythagoran triplet .
$$(10,24,27)$$
Identify , with reason , if the following is a pythagoran triplet .
$$(11,60,61)$$
Find the sum of the digits of
$$ (111111111)^{2} $$
Can $$1010$$ be written as a difference of two perfect squares ?
What is the least perfect square which leaves the remainder $$1$$ when divided by $$7$$ as well as by $$11$$ ?
What are the remainders when a perfect cube is divided by $$7$$ ?
Find the value of $$\sqrt{30}$$ upto $$4$$ places of decimal.
$$\sqrt{0.0037}$$
Write all the numbers from $$400$$ to $$425$$ which end in $$2 , 3 , 7 $$ or $$8$$. Check if any of these in a perfect square.
What is the objective of the school administration behind such an arrangement?
Find the square root of perfect square number $$10329796$$.
A natural number $$n$$ is chosen strictly between two consecutive perfect squares. The smaller of these two squares is obtained by subtracting $$k$$ from $$n$$ and the larger one is obtained by adding $$l$$ to $$n$$. Prove that $$ n kl $$ is a perfect square.
Find the square root of the following.
$$10.0489$$
Find the $$\sqrt {39204} $$.
Prove that $$\dfrac{1}{3 -\sqrt{8}} - \dfrac{1}{\sqrt{8} - \sqrt{7}} + \dfrac{1}{\sqrt{7} - \sqrt{6}} - \dfrac{1}{\sqrt{6} - \sqrt{5}} + \dfrac{1}{ \sqrt{5} - 2} = 5$$
What will be the unit digit of the square of the following numbers?
$$272$$
What will be the unit digit of the square of the following numbers?
$$12796$$
Find the square root of following surd :
$$6+4\sqrt{2}$$
Find the square root of following surds:
$$5+\sqrt{21}$$
Solve:
$$\sqrt{\left(\dfrac{3}{4}\right)^{1-3x}}=2\dfrac{10}{27}$$
By what smallest number must $$180$$ be multiplied so that it becomes a perfect square? Also, find the square root of the number so obtained.
Find the least number which must be added to each of the following numbers to make them a perfect square. Also find the square root's of the perfect square number so obtained.
$$1750$$
Square root of $$\sqrt{5-\sqrt{21}}$$.
$$\sqrt{244}=?$$
Verify that the following numbers represent Pythagorean triplet.
$$27, 36, 45$$.
Find the value of :
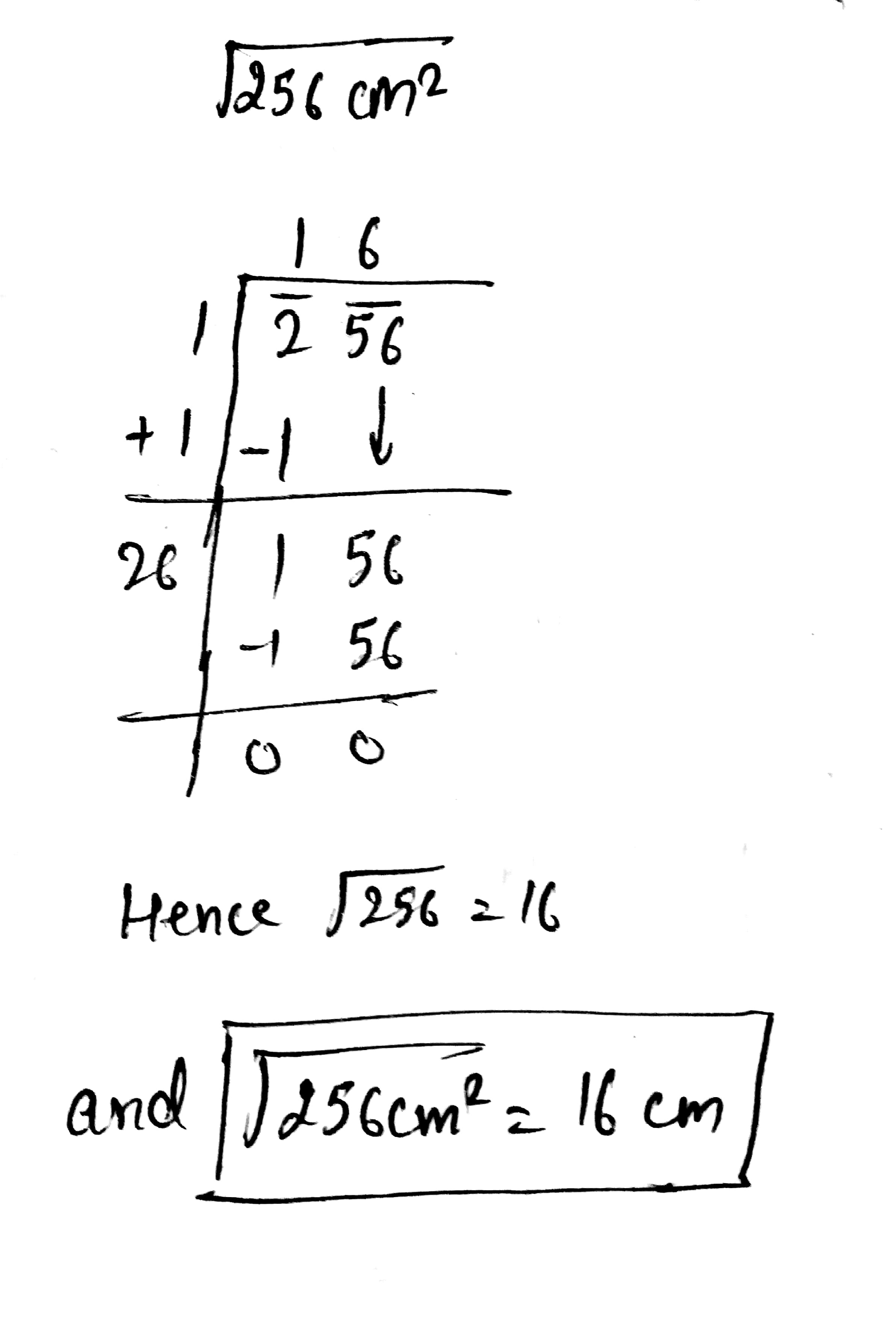
$$\sqrt{256cm^2}$$
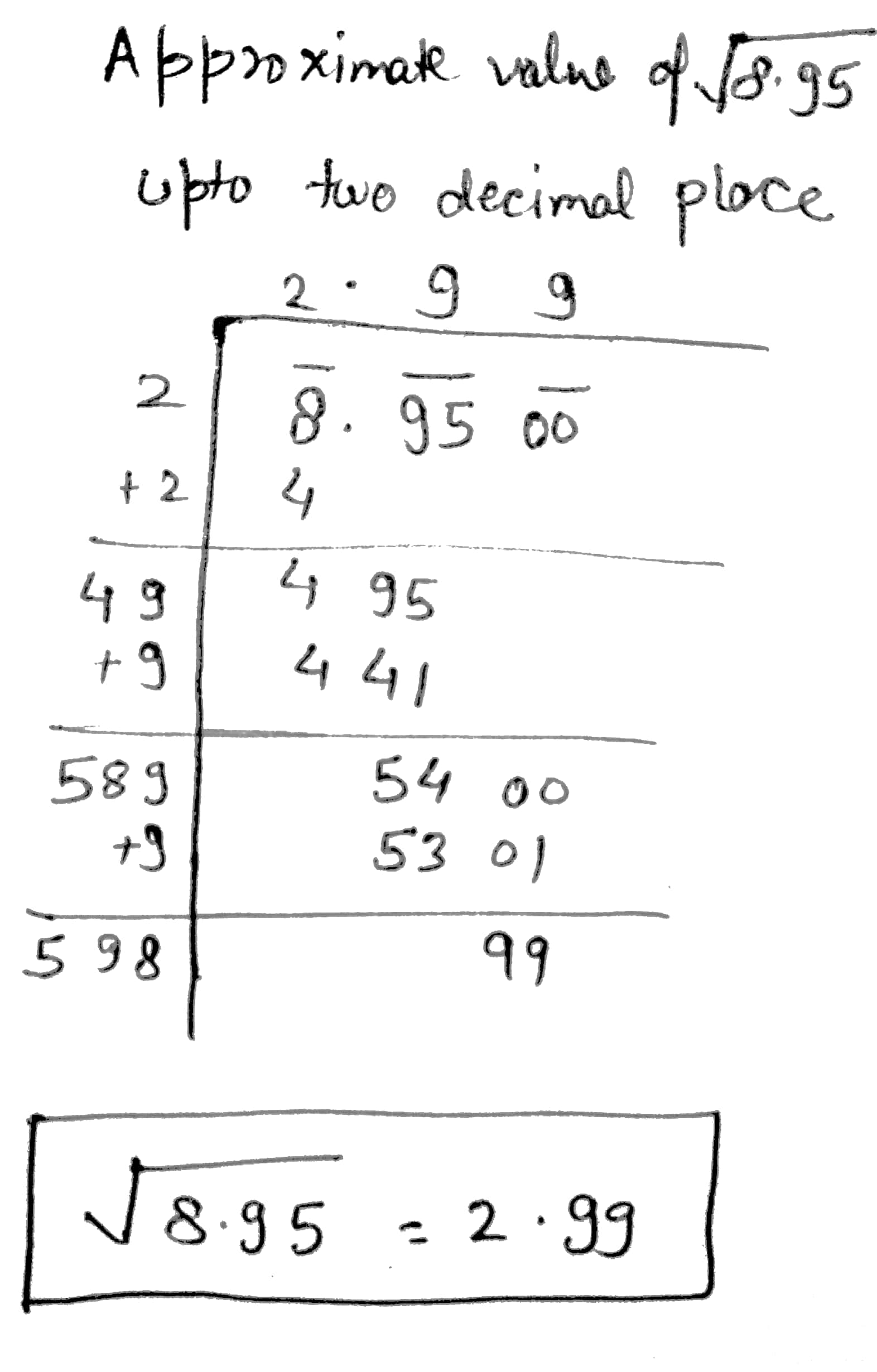
Find the approximate value of $$\sqrt { 8.95 }$$
Find the least 8 digit number which is a perfect square.
Verify that the following numbers represent Pythagorean triplet.
$$12, 35, 37$$.
Verify that the following numbers represent Pythagorean triplet.
$$7, 24, 25$$.
Find the smallest number by which $$2925$$ must be multiplied to get a perfect square. Also, find the square root of the perfect square so obtained.
Estimate square root : $$\sqrt {13}$$
Verify that the following numbers represent Pythagorean triplet.
$$15, 36, 39$$.
Class 8 Maths Extra Questions
- Algebraic Expressions And Identities Extra Questions
- Comparing Quantities Extra Questions
- Cubes And Cube Roots Extra Questions
- Data Handling Extra Questions
- Direct And Inverse Proportions Extra Questions
- Exponents And Powers Extra Questions
- Factorisation Extra Questions
- Introduction To Graphs Extra Questions
- Linear Equations In One Variable Extra Questions
- Mensuration Extra Questions
- Playing With Numbers Extra Questions
- Practical Geometry Extra Questions
- Rational Numbers Extra Questions
- Squares And Square Roots Extra Questions
- Understanding Quadrilaterals Extra Questions
- Visualising Solid Shapes Extra Questions