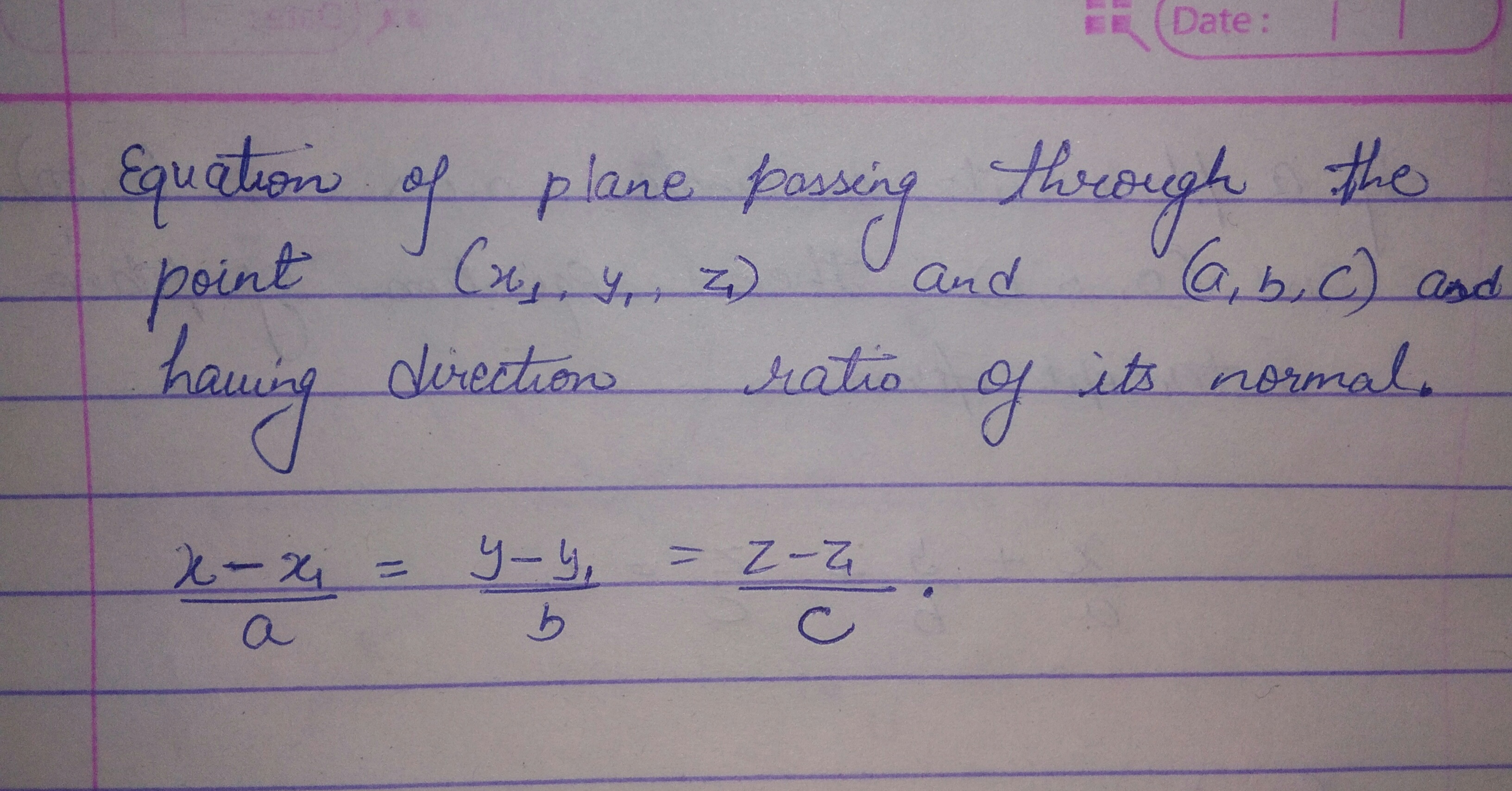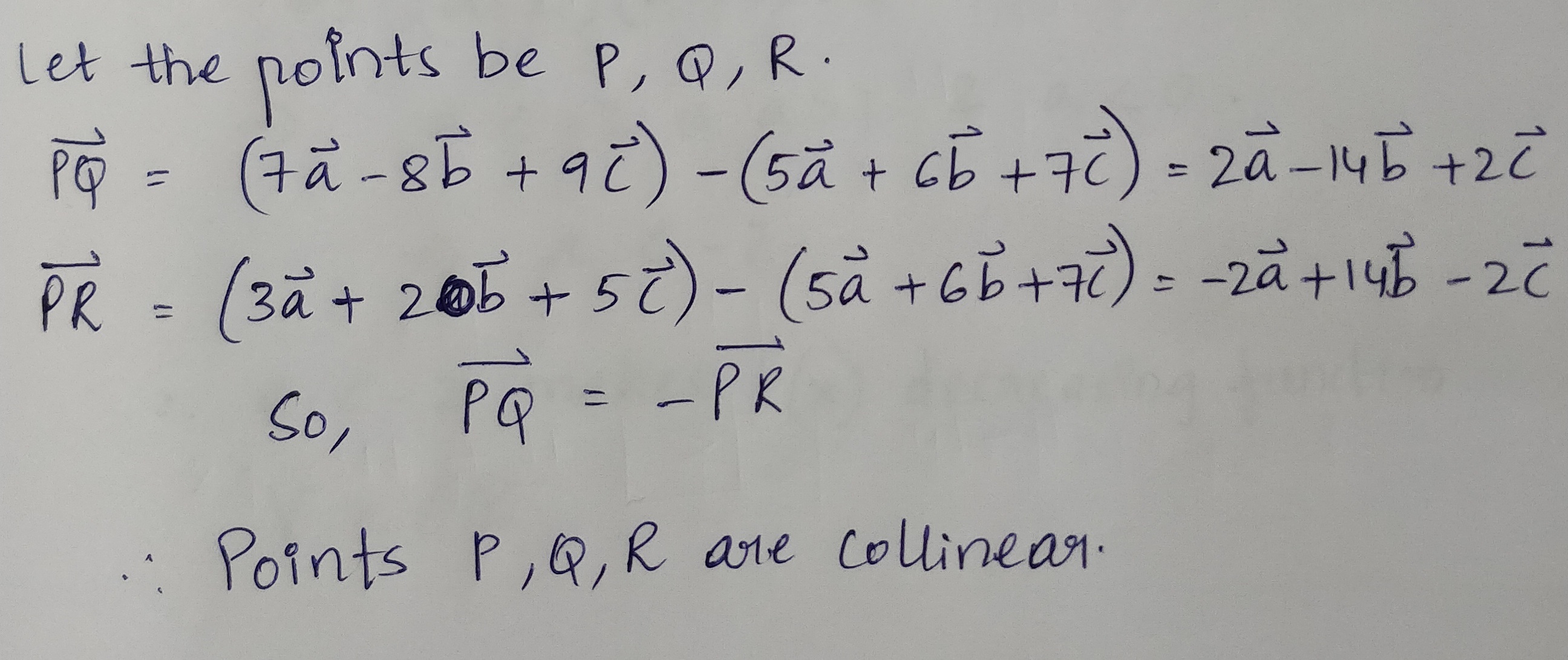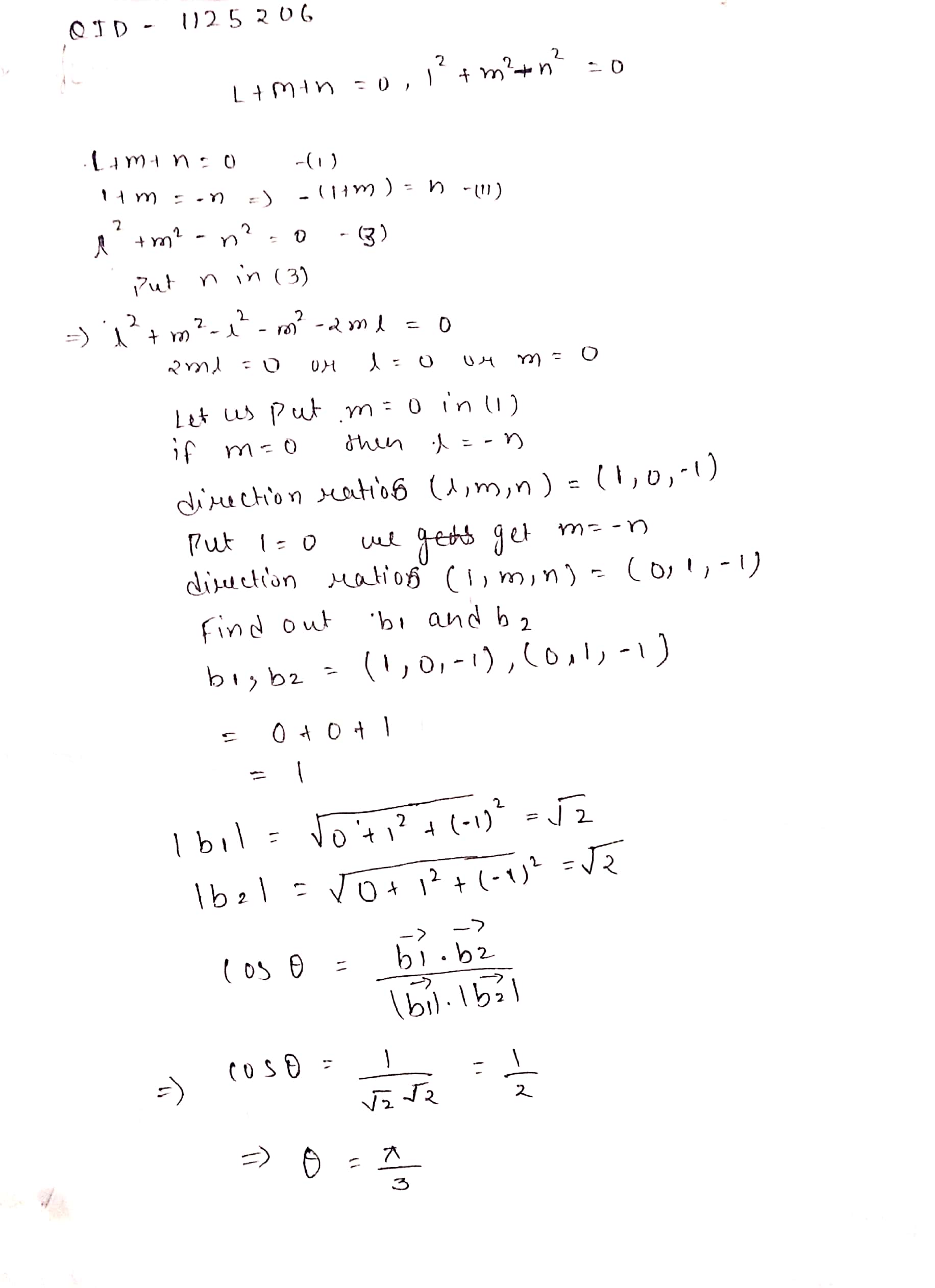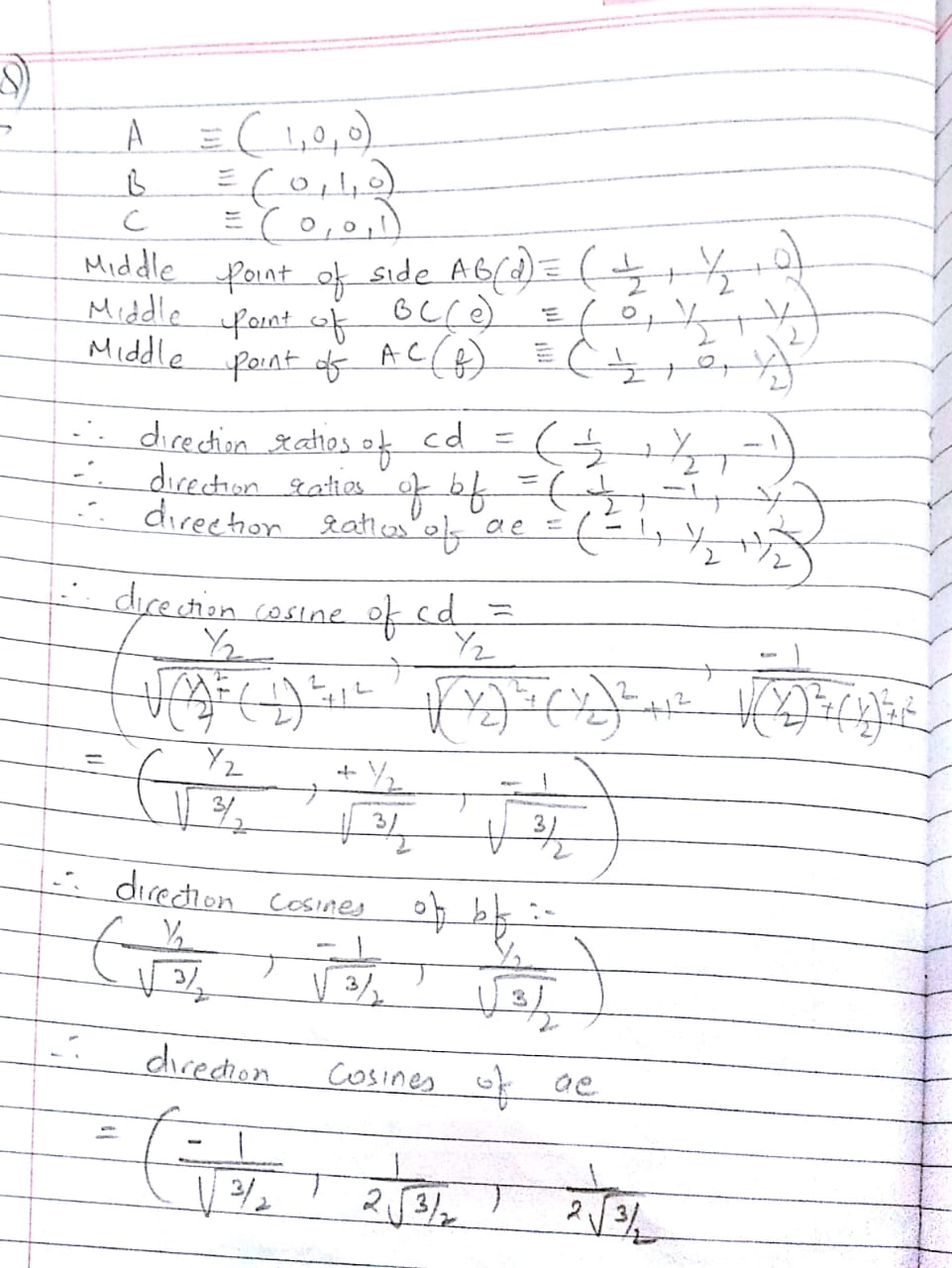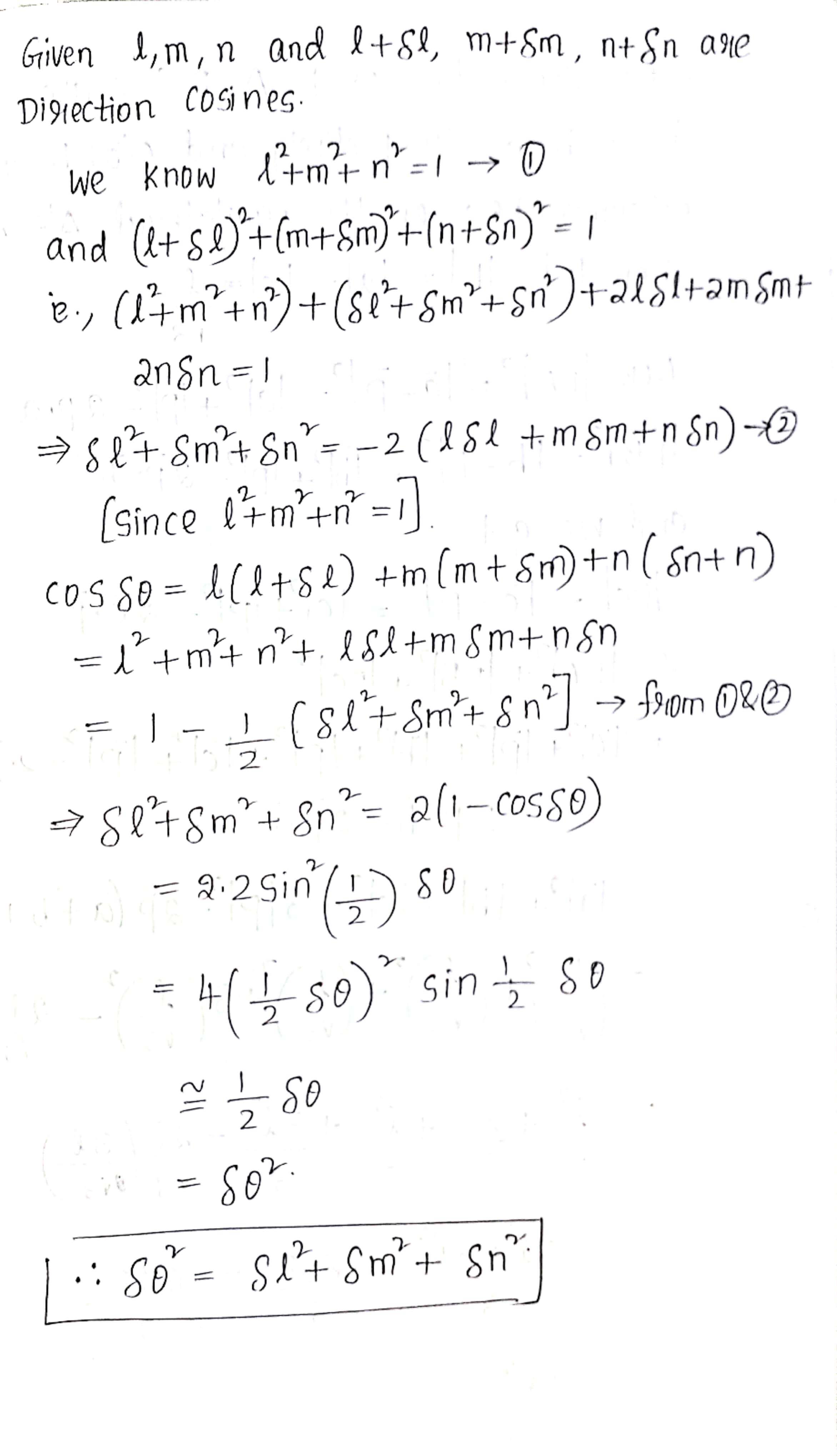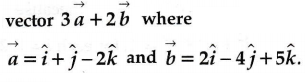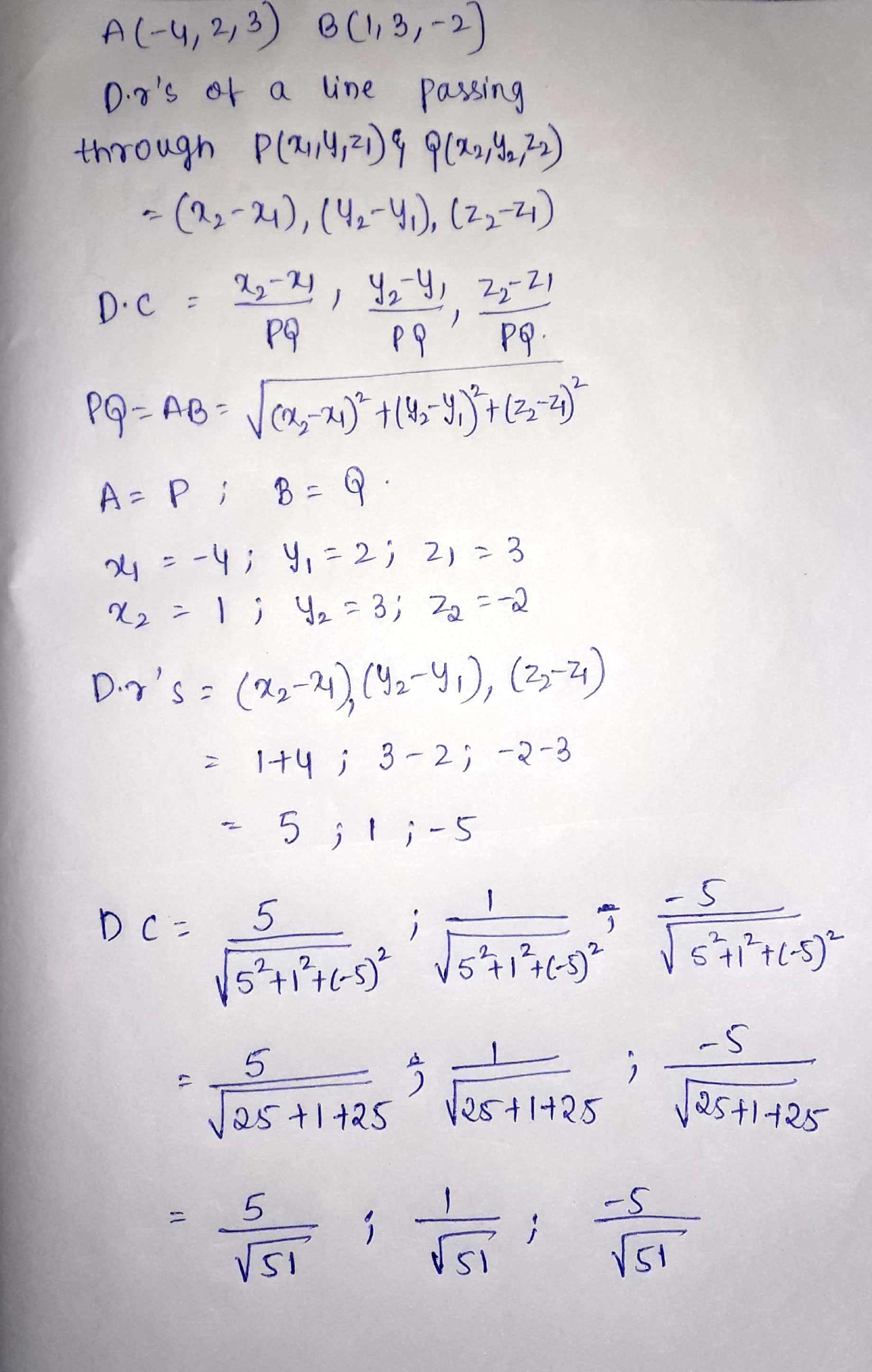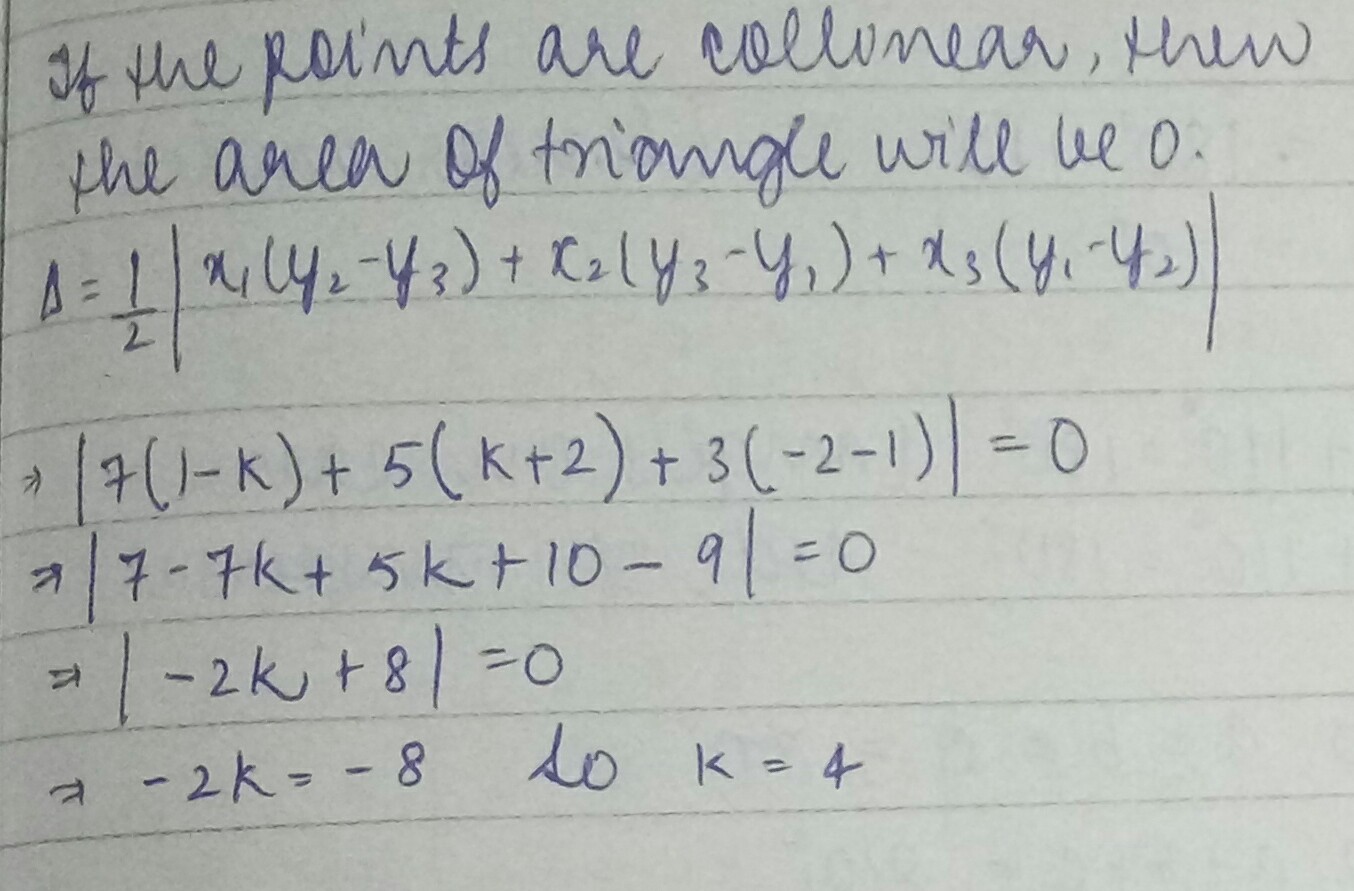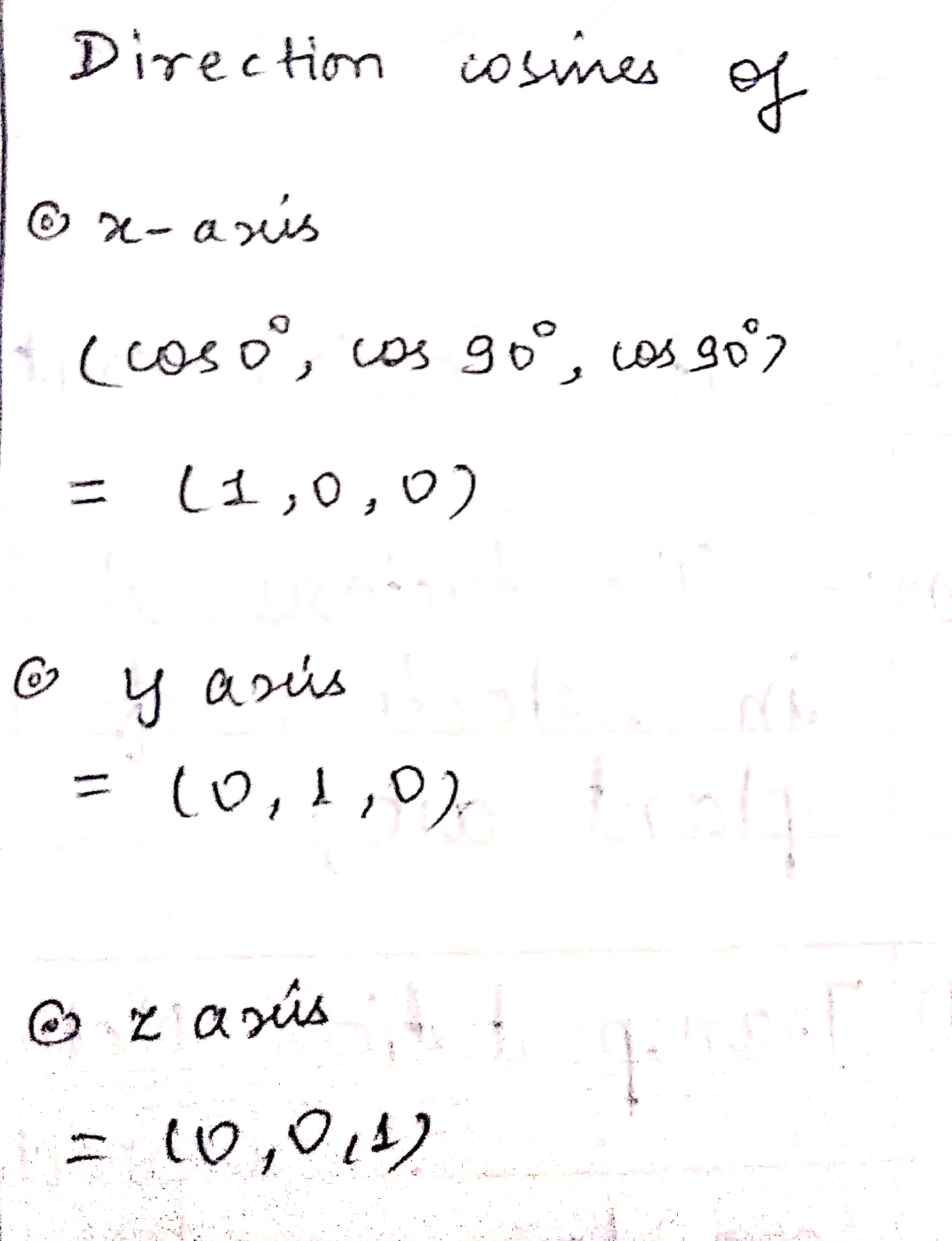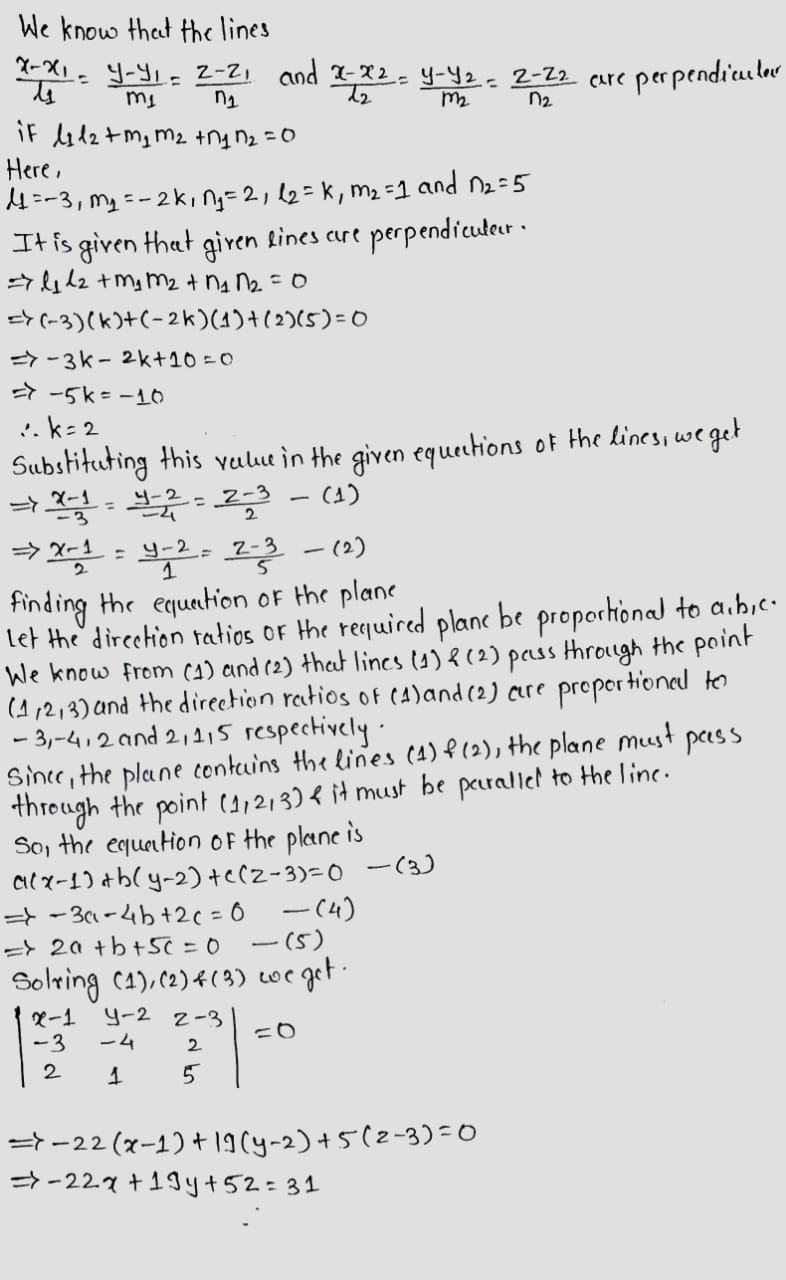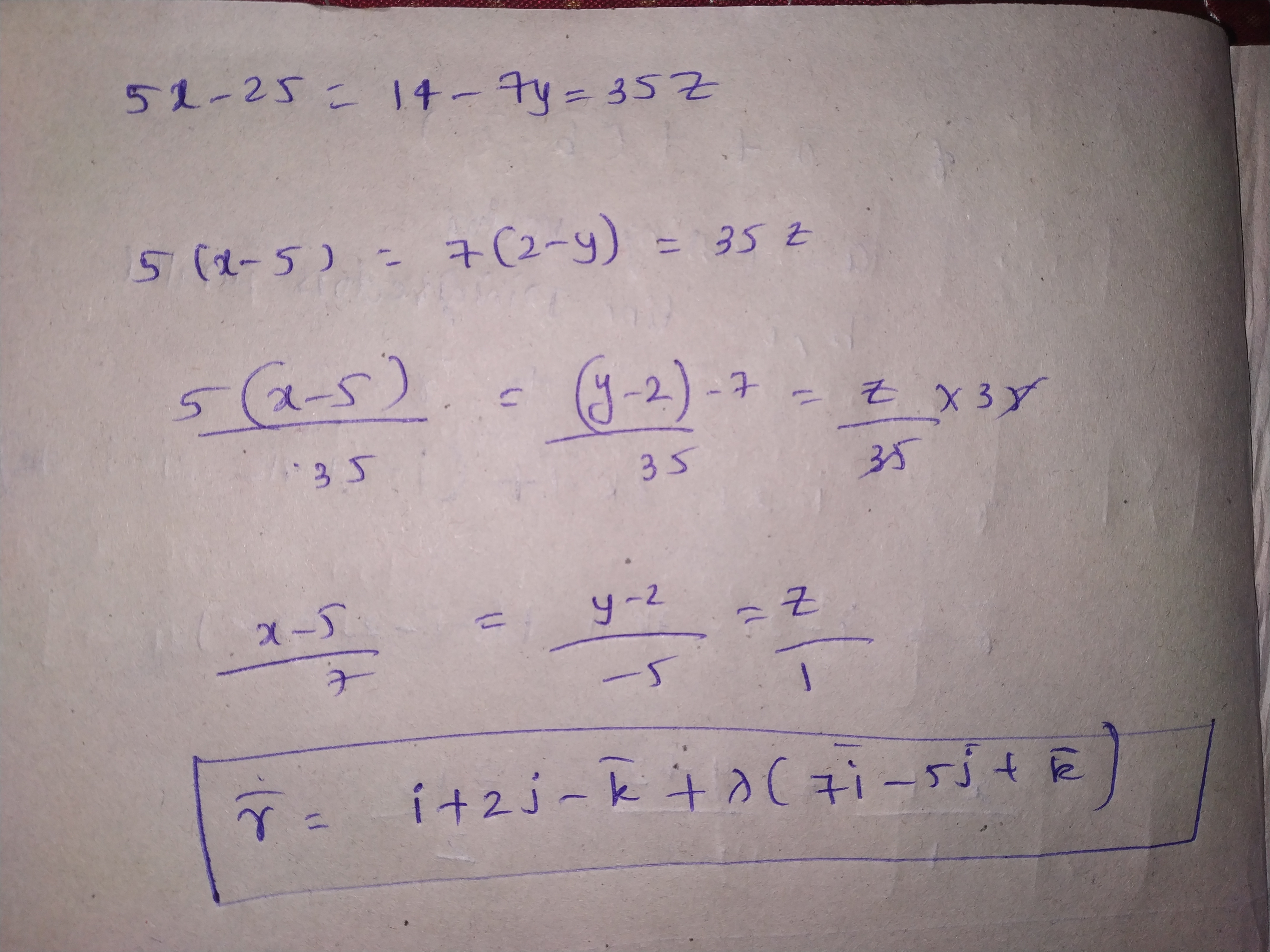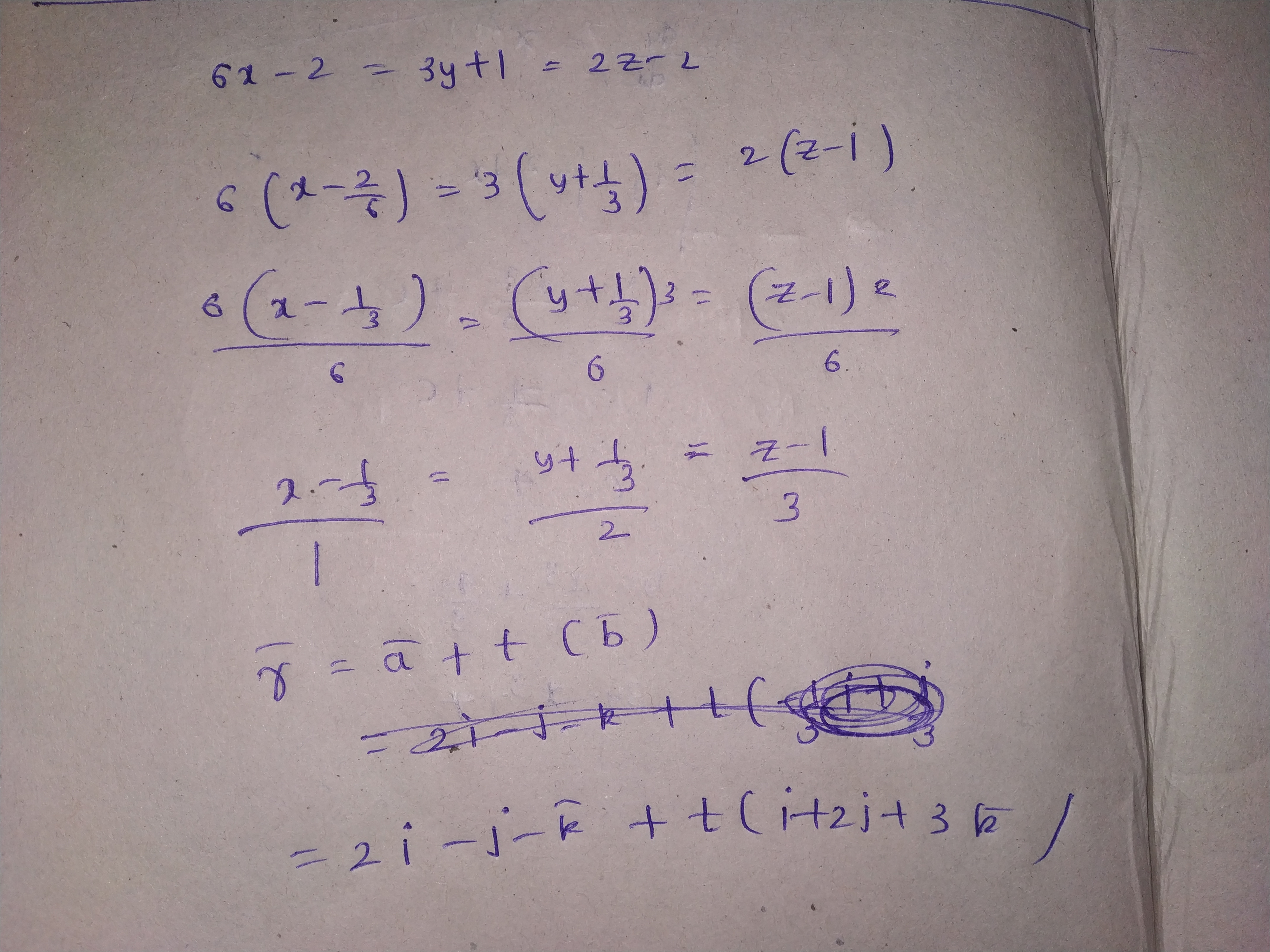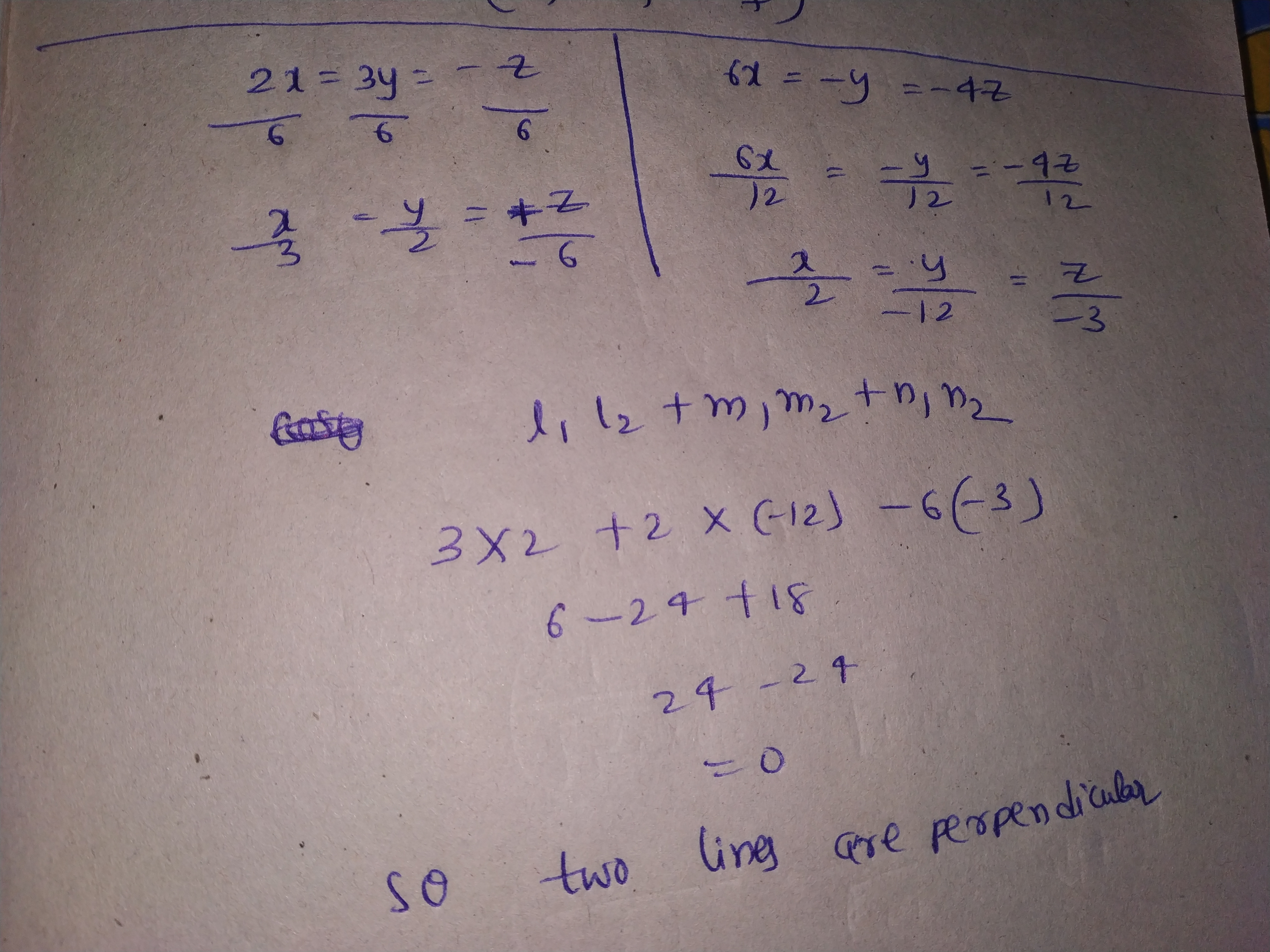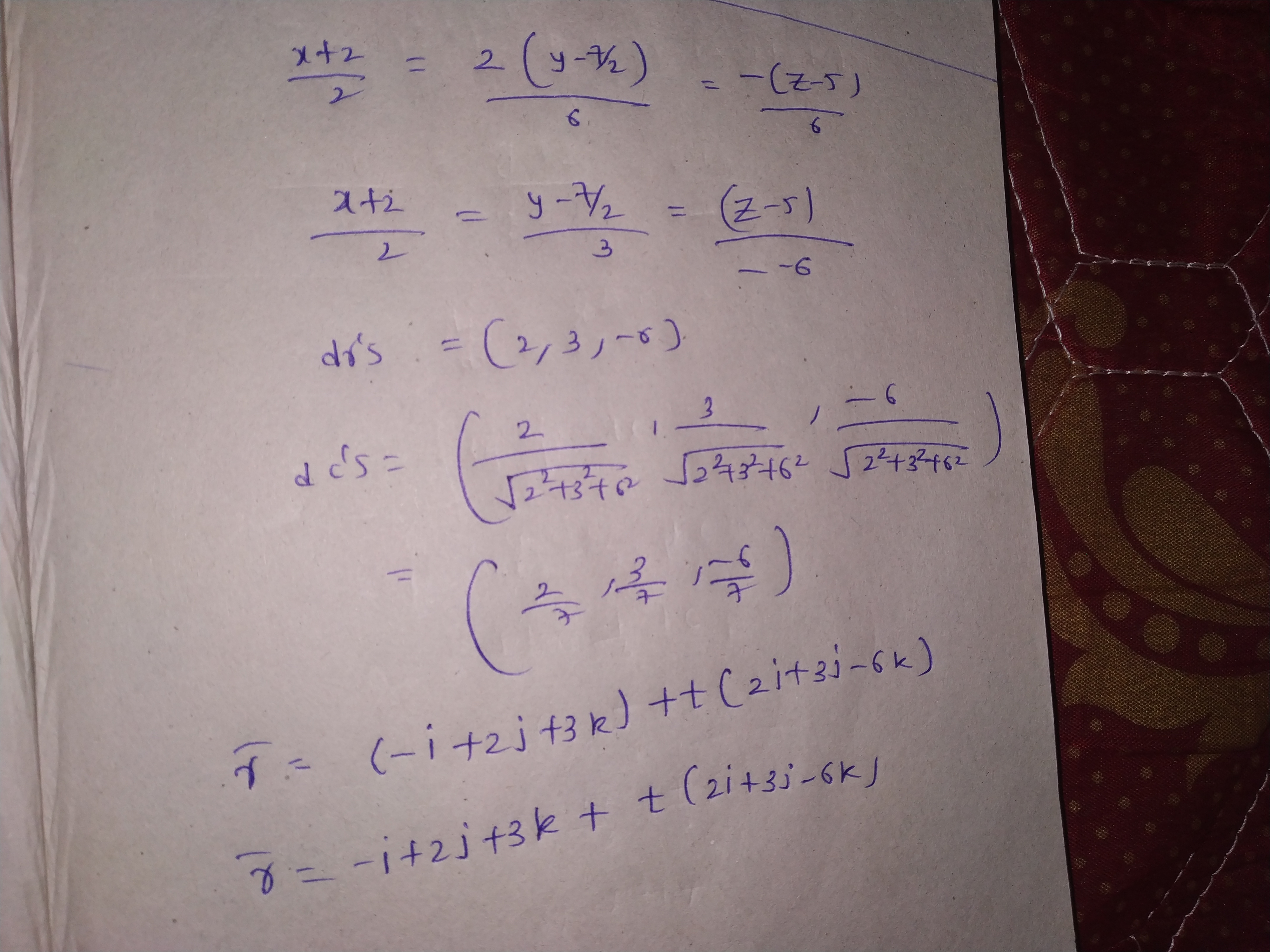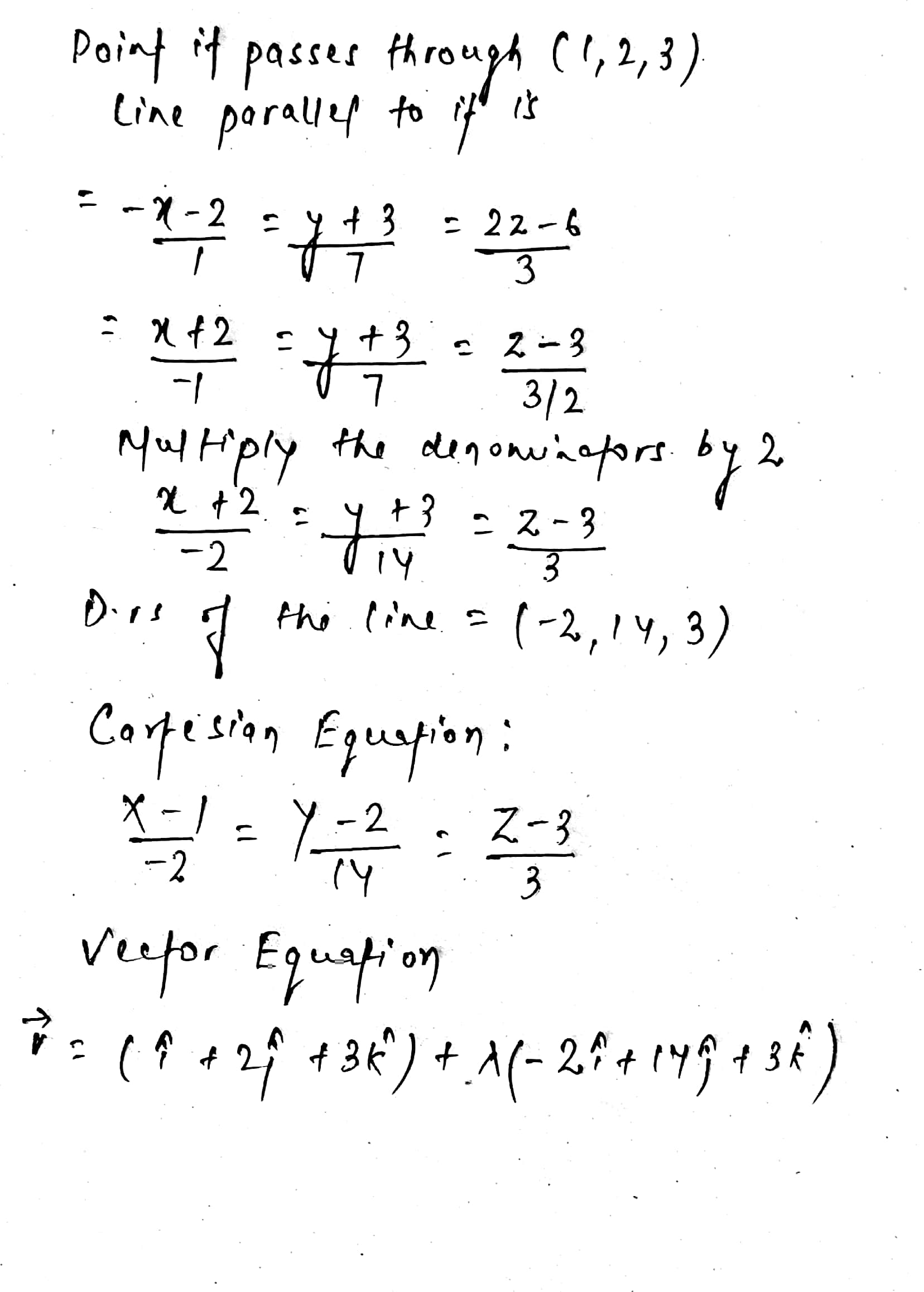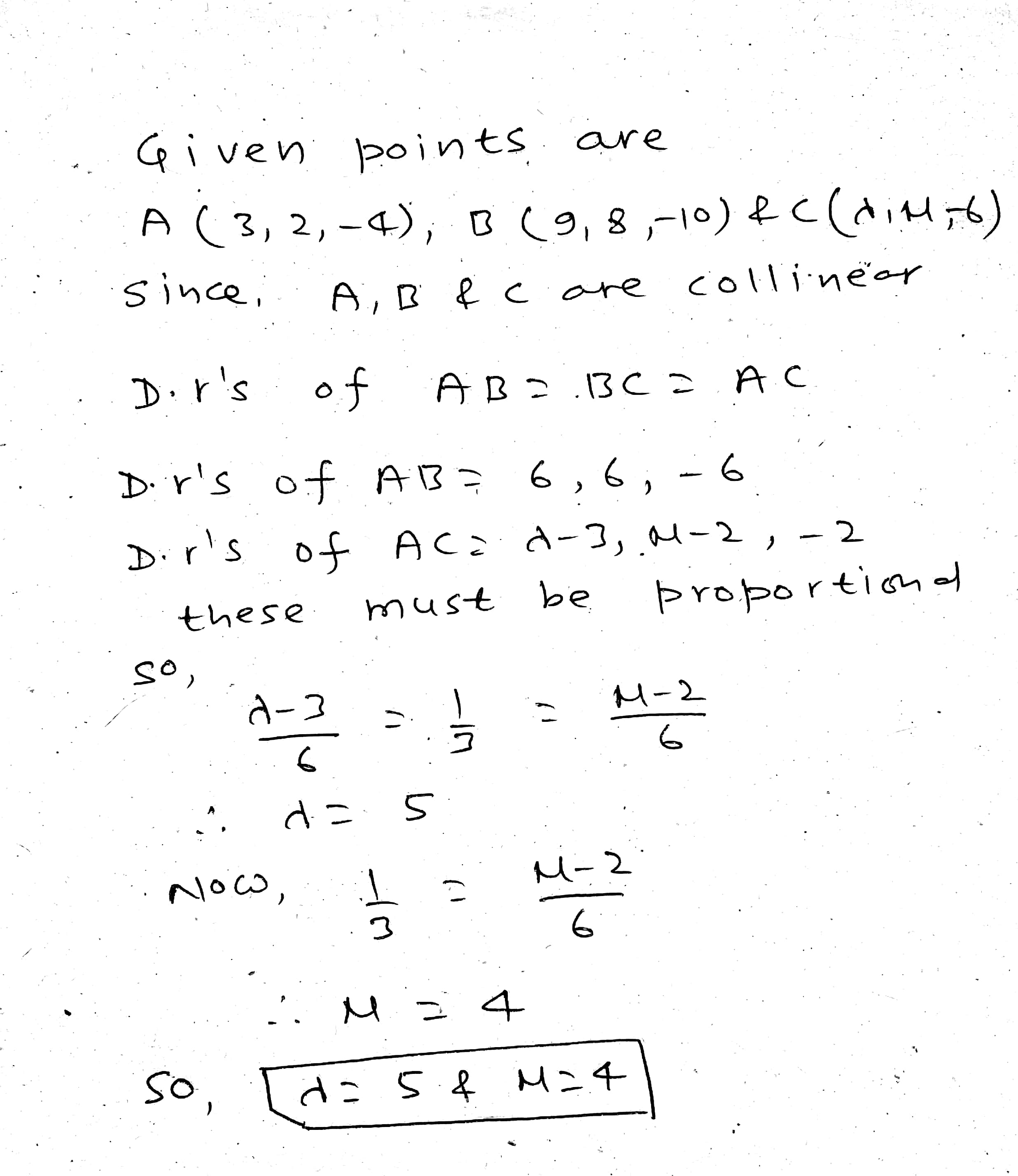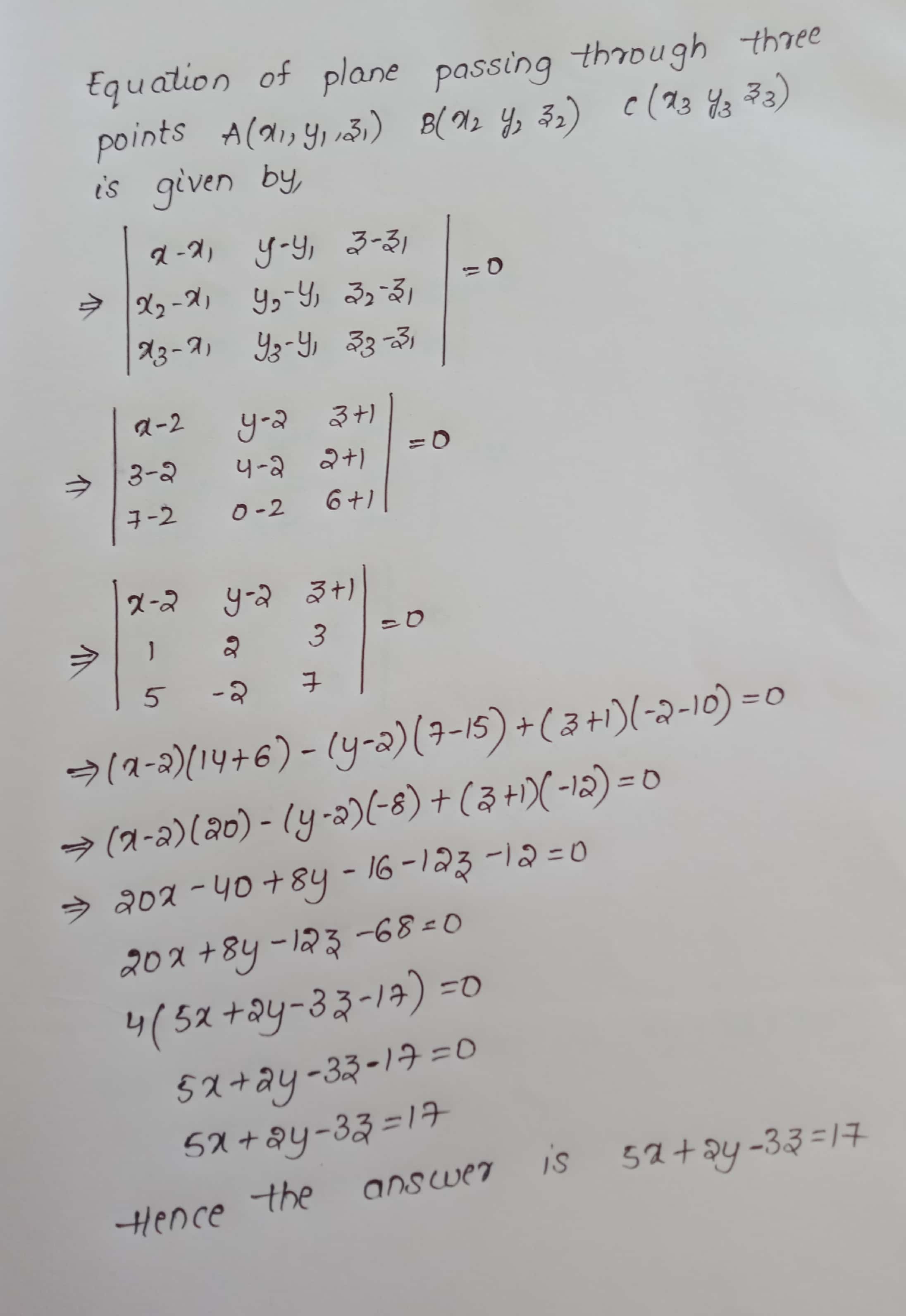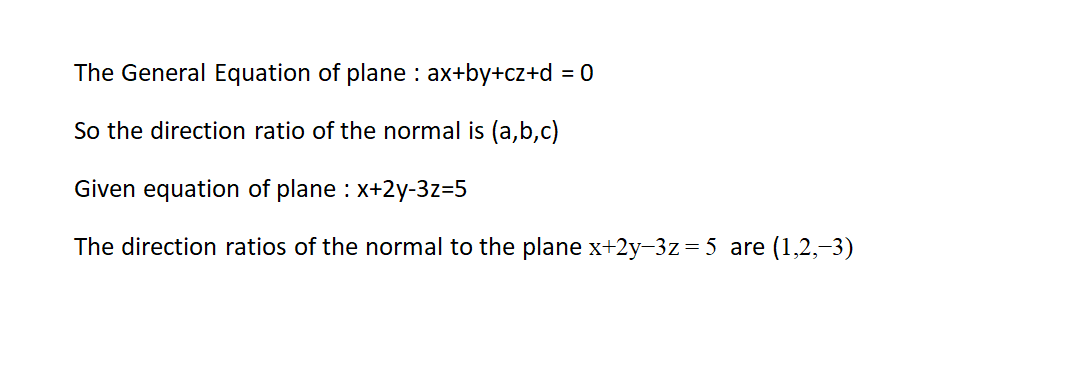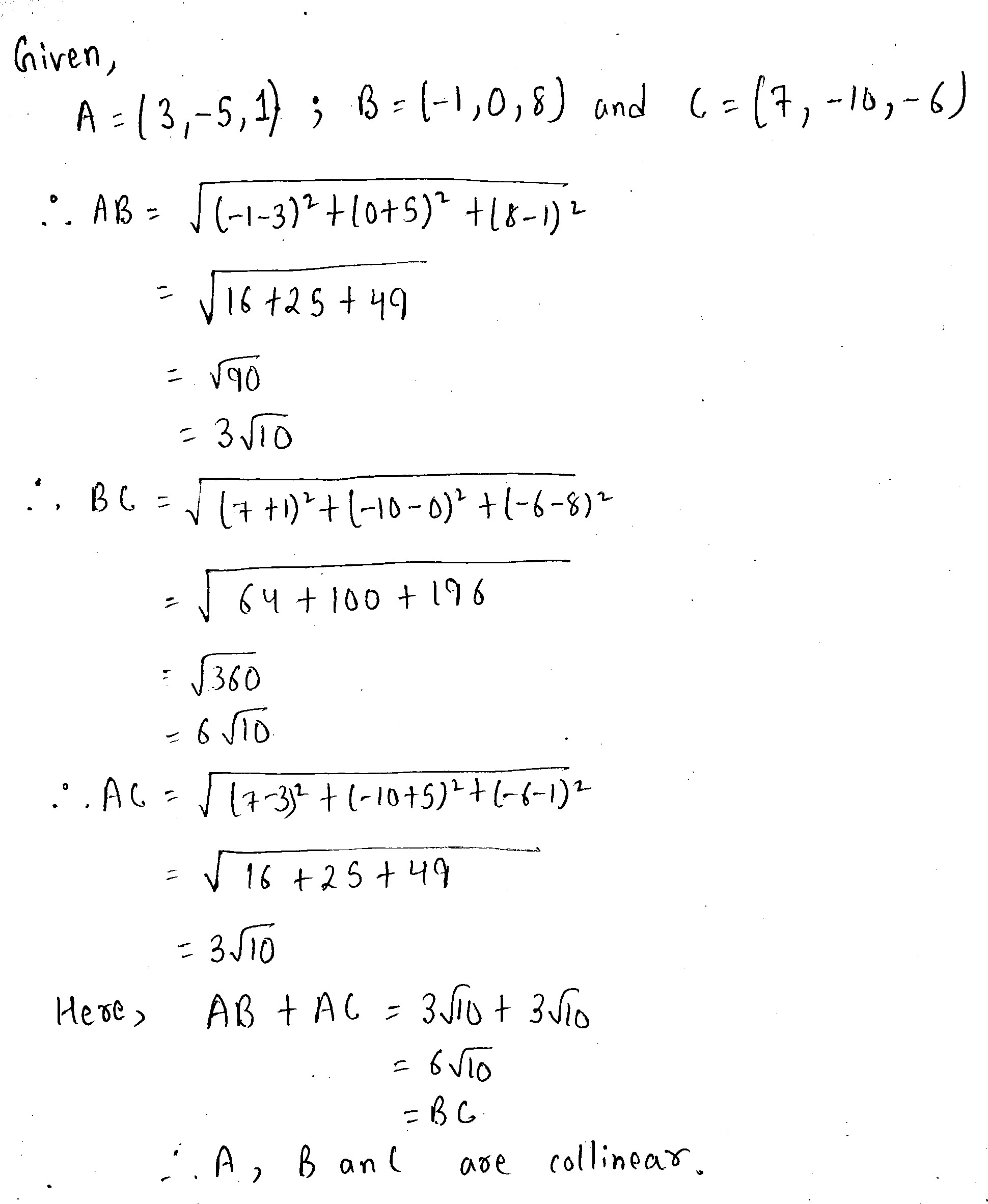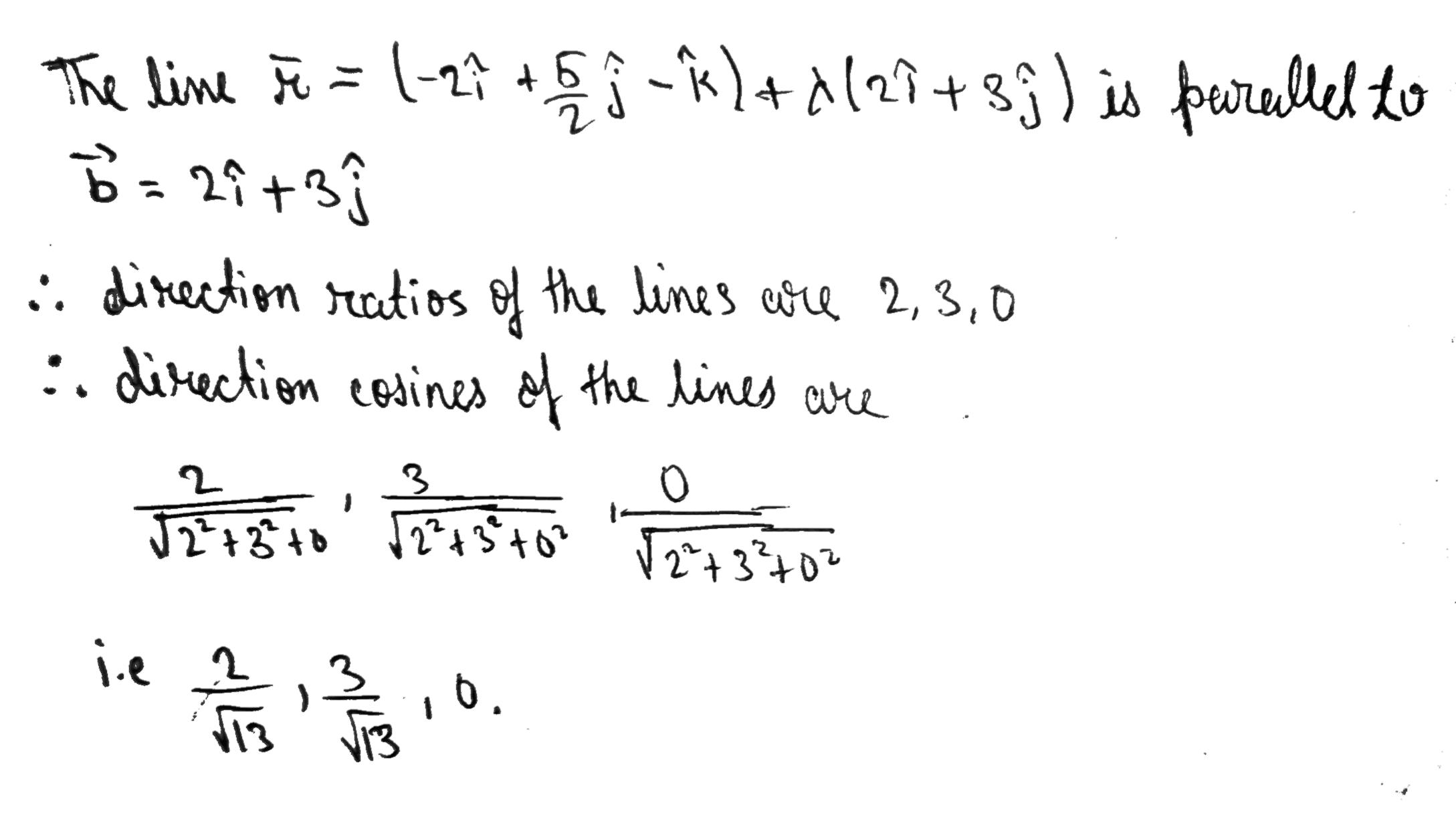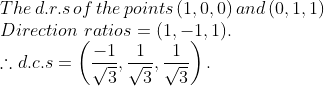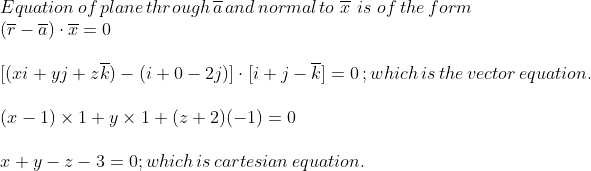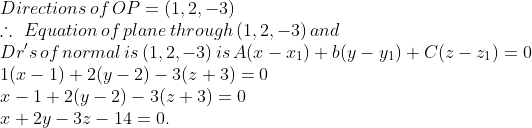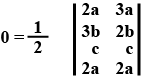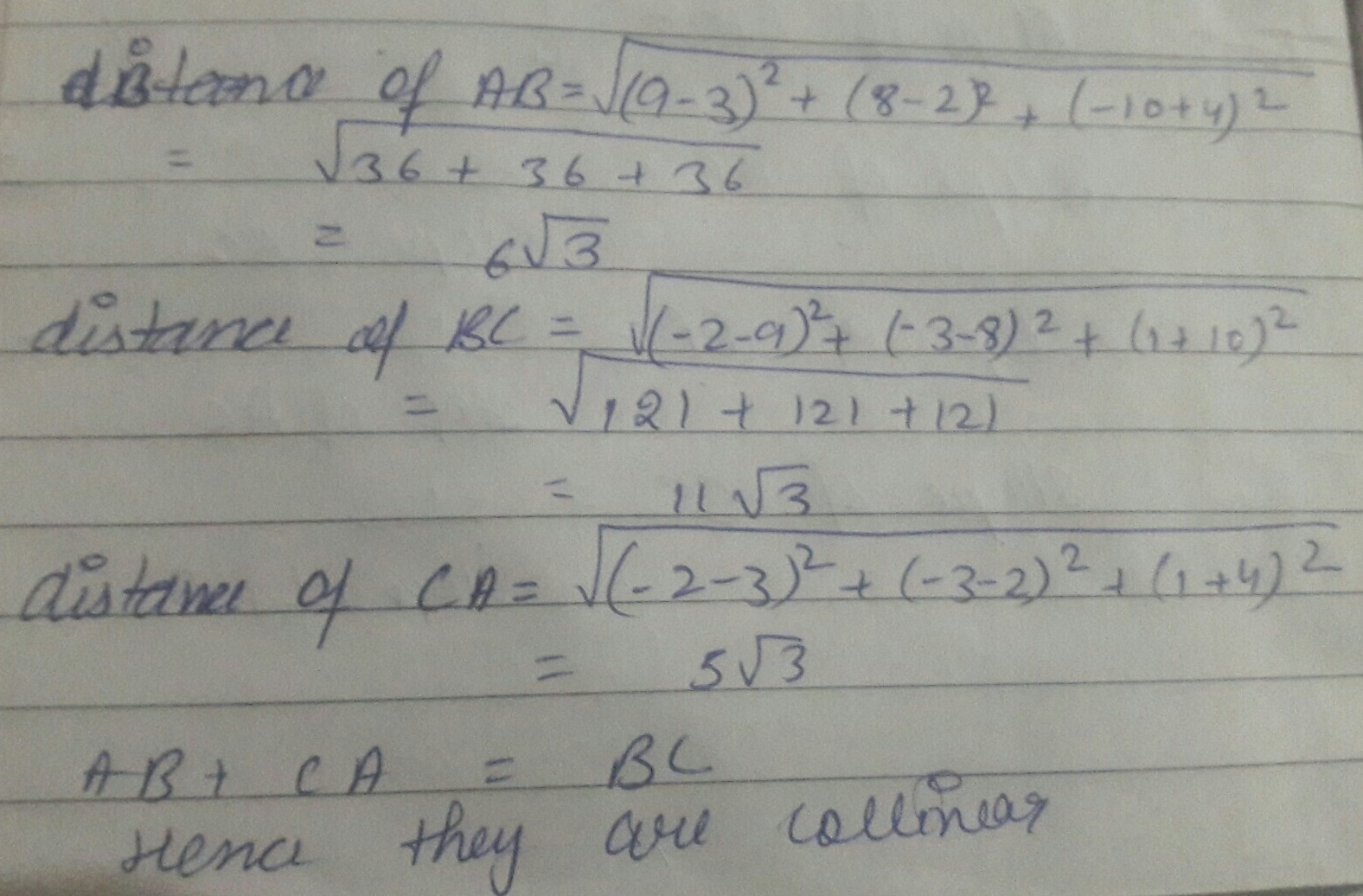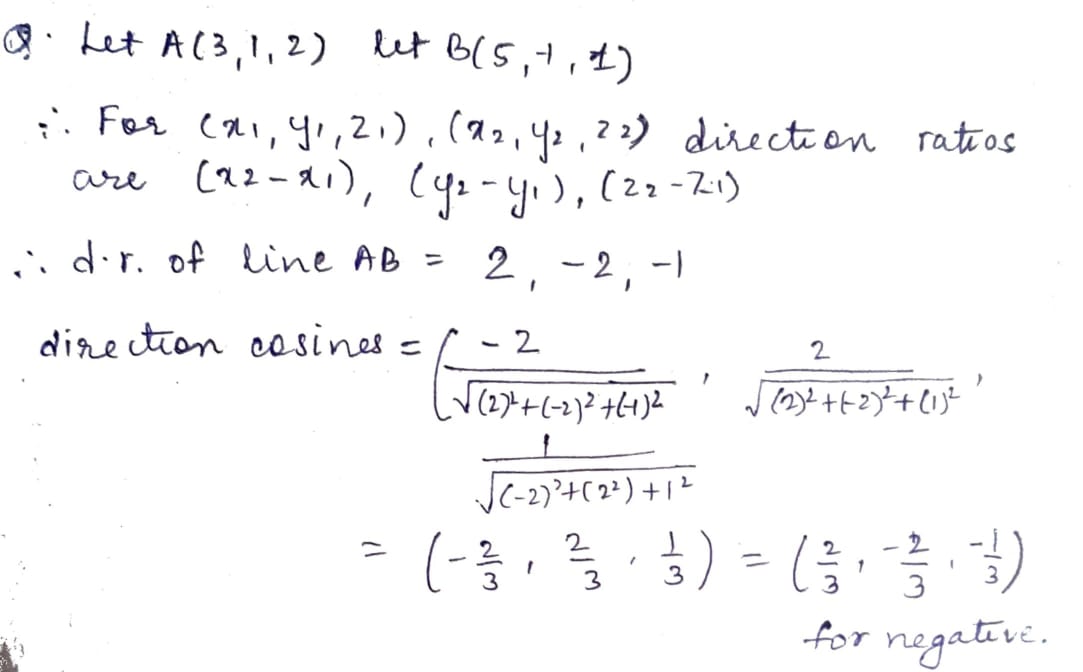Three Dimensional Geometry - Class 12 Commerce Maths - Extra Questions
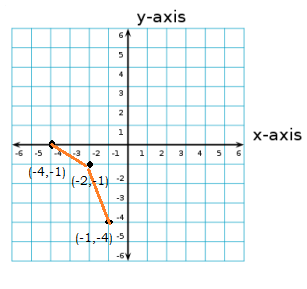
(-2, -1), (-1, -4) and (-4,-1)
No, they are not collinear as they do not lie on one single straight line.
Find the values of $$p$$ so the line $$\cfrac{1-x}{3}=\cfrac{7y-14}{2p}=\cfrac{z-3}{2}$$ and $$\cfrac{7-7x}{3p}=\cfrac{y-5}{1}=\cfrac{6-z}{5}$$ are at right angles.
Find the direction cosines of the vector joining the points $$A (1, 2, -3)$$ and $$B (-1, -2, 1)$$ directed from $$A$$ to $$B$$.
If $$O$$ be the origin and the coordinates of $$P$$ be $$(1,2,-3)$$, then find the equation of the plane passing through $$P$$ and perpendicular to $$OP$$.
If a line makes angles $$90^{\circ}, 135^{\circ}, 45^{\circ}$$ with the $$x, y$$ and $$Z-\text{axes}$$ respectively, find its direction cosines.
Find the equation plane passing $$(a, b, c)$$ and parallel to the plane $$\vec {r} \cdot (\hat {i} + \hat {j} + \hat {k}) = 2$$.
Find the direction cosines of the vector $$\hat {i}+2\hat {j}+3\hat {k}$$.
Find the angle between the lines whose direction ratios are $$a,b,c$$ and $$b-c, c-a, a-b$$
Find the vector and the Cartesian equations of the lines that pass through the origin and $$(5, -2, 3)$$
Show that the points $$A (1, 2, 7), B (2, 6, 3)$$ and $$C (3, 10, -1)$$ are collinear .
The equation of a line is $$5x-3=15y+7=3-10z$$. Write the direction cosines of the line.
The acute angle between the planes $$2x-y+z=6$$ and $$x+y+2z=3$$ is _____.
Write the direction cosines of $$x$$-axis.
Determine the direction cosines of the line through the points $$(2,0,3)$$ and $$(4,1,1)$$
The Cartesian equation of a line is: $$2x-3=3y+1=5-6z$$. Find the vector equation of a line passing through $$(7, -5, 0)$$ and parallel to the given line.
Find the acute angle between the lines passing through (-3 , -1 , 0), (2, -3 , 1) and (1 , 2 , 3),(-1 ,4 , -2) respectively.
Find direction cosine line $$x=3z+2,y=2-5z$$.
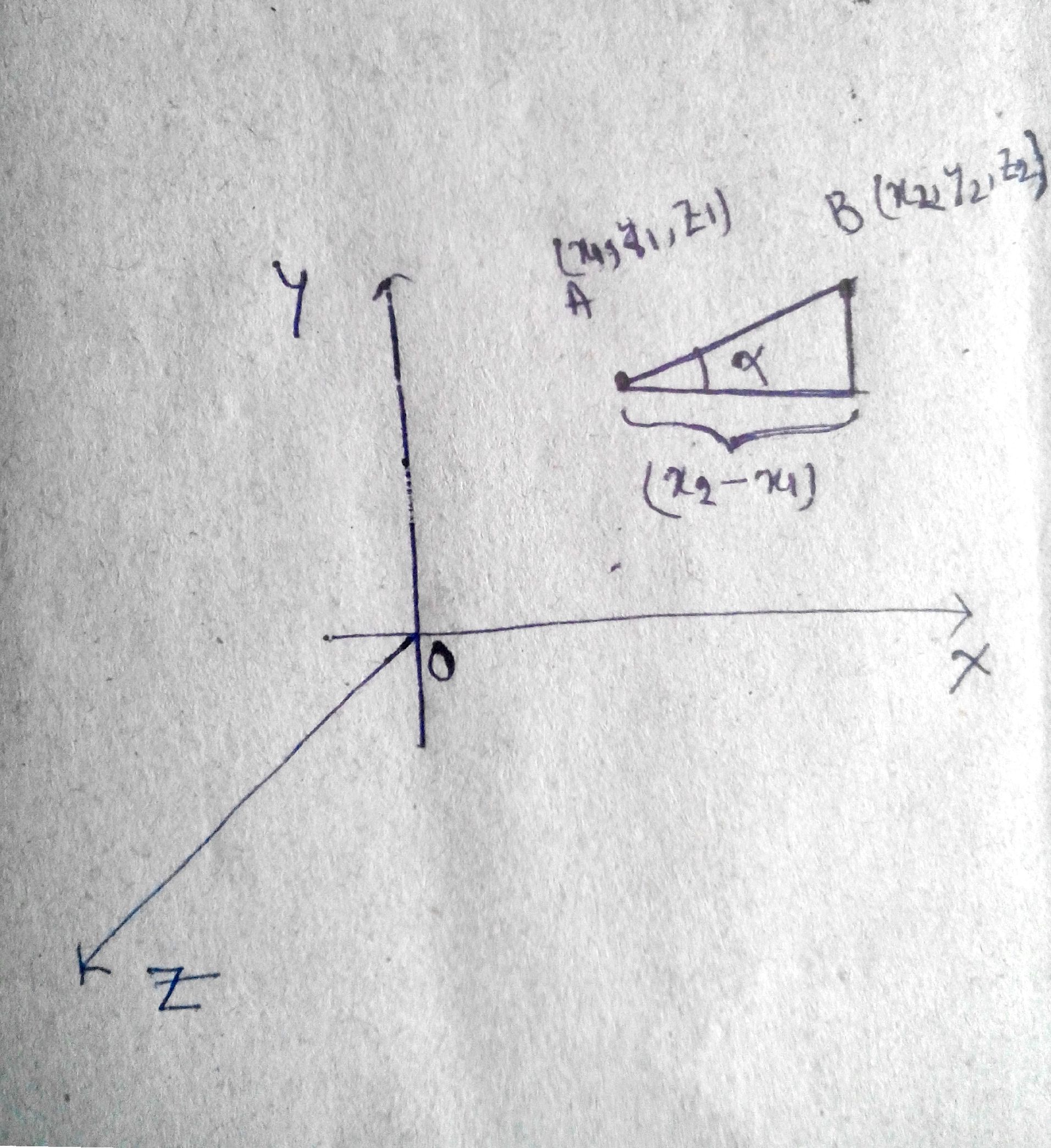
If $$A\left( { x }_{ 1 },{ y }_{ 1 },{ z }_{ 1 } \right)$$ and $$B\left( { x }_{ 2 },{ y }_{ 2 },{ z }_{ 2 } \right)$$ are two points such that the direction cosines of $$\bar { AB }$$ are $$l$$, $$m$$, $$n$$ then
$$l=\dfrac { { x }_{ 2 }-{ x }_{ 1 } }{ \left| \bar { AB } \right| }$$, $$m=\dfrac { { y }_{ 2 }-{ y }_{ 1 } }{ \left| \bar { AB } \right| }$$, $$n=\dfrac { { z }_{ 2 }-z_{ 1 } }{ \left| \bar { AB } \right| }$$.
Direction cosines of $$\overline{AB}$$ is the cosines of angles made by the line with the positive direction of $$x$$- axis, $$y$$-axis and $$z$$- axis respectively.
Let, $$\alpha$$, $$\beta$$, $$\gamma$$ be the angles made by the line with the positive direction of $$x$$-axis, $$y$$-axis and $$z$$-axis.
Then $$l=\cos \alpha=\large{\frac{x_2-x_1}{\sqrt{(x_2-x_1)^2+(y_2-y_1)^2+(z_2-z_1)^2}}}=\frac{(x_2-x_1)}{|\overline{AB}|}.$$
and $$m=\cos \beta=\large{\frac{y_2-y_1}{\sqrt{(x_2-x_1)^2+(y_2-y_1)^2+(z_2-z_1)^2}}}=\frac{(y_2-y_1)}{|\overline{AB}|}.$$
and $$n=\cos \alpha=\large{\frac{z_2-z_1}{\sqrt{(x_2-x_1)^2+(y_2-y_1)^2+(z_2-z_1)^2}}}=\frac{(z_2-z_1)}{|\overline{AB}|}.$$
Find the direction collinear of a line which makes equal angles with the positive co-ordinate axes.
Find the length of the perpendicular drawn from the origin to the plane $$2x-3y+6z+21=0$$.
Find the value of $$\beta$$ so that the line $$\dfrac {x - 2}{6} = \dfrac {y - 1}{\beta} = \dfrac {z + 5}{-4}$$ is perpendicular to the plane $$3x - y - 2z = 7$$.
Find the direction cosines of the line $$\dfrac{{x + 2}}{2} = \dfrac{{2y - 5}}{3};z = - 1$$. Also, find the vector equation of the line.
Find the vector equation of the line through $$A(3,4,-7)$$ and $$B(6,-1,1)$$. Also find the cartesian form.
Show that the lines whose d.c.s are given by $$l + m + n = 0 , 2mn + 3ln - 5lm = 0$$ are perpendicular to each other.
If a line is making same angle $$\theta$$ with the positive direction of $$X-,Y-$$ and $$Z-$$axes, then show that $$\theta=\cos^{-1}(\dfrac {1}{\sqrt {3}}$$.
Find the equation of the line in vector and in cartesion form that passes through the point with position vector $$2\hat {i}-\hat{j}+4\ \hat {k}$$ and is in the direction $$\hat {i}+2\hat {j}-\hat {k}$$.
Find the direction cosines of the lines , connected by the relations: l + m + n = 0 and 2lm + 2ln - mn = 0.
If the lines through the points $$(4, 1, 2)$$ and $$(5, k, 0)$$ is parallel to the line through the points $$(2, 1, 1)$$ and $$(3, 3, 1)$$, find $$k$$.
If the d.c's of a line are $$\left( {\dfrac{1}{c}\,,\,\dfrac{1}{c}\,,\,\dfrac{1}{c}} \right)$$ , find c.
find the angle between the lines whose direction cosines satisfy the equation $$\ell + m + n = 0,\,\,{\ell ^2} + {m^2} - {n^2} = 0$$
Find the co-ordinate of the pt. $$p$$, if $$ \ell \left( PQ \right) =21$$, $$ Q\equiv \left( -2,1,-8 \right) $$ and directional cosines of $$PQ$$ are $$(6/7), (2/7), (3/7)$$?
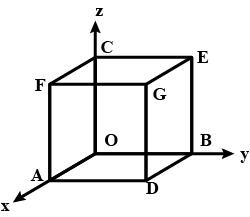
A line makes angle $$\theta_{1}, \theta_{2}, \theta_{3}, \theta_{4}$$ with the diagonals of the cube. Show that $$\cos^{2}\theta_{1} + \cos^{2}\theta_{2} + \cos^{2}\theta_{3} + \cos^{2}\theta_{4} = \dfrac{4}{3} $$?
Let side of cube be 'a'
Dr's of a diagonal OG = a ,a ,a
Dr's of a diagonal CD = a ,a , - a
Dr's of a diagonal BE = a , - a ,a
Dr's of a diagonal AF = - a ,a ,a
$$now\,\,Dc's\,\,of\,diagonal\,\,OG = \left( {\frac{1}{{\sqrt 3 }},\,\,\frac{1}{{\sqrt 3 }}\,,\,\frac{1}{{\sqrt 3 }}} \right)$$
$$now\,\,Dc's\,\,of\,diagonal\,\,CD = \left( {\frac{1}{{\sqrt 3 }},\,\,\frac{1}{{\sqrt 3 }}\,,\,\frac{ -1}{{\sqrt 3 }}} \right)$$
$$now\,\,Dc's\,\,of\,diagonal\,\,BE = \left( {\frac{1}{{\sqrt 3 }},\,\,\frac{ - 1}{{\sqrt 3 }}\,,\,\frac{1}{{\sqrt 3 }}} \right)$$
$$now\,\,Dc's\,\,of\,diagonal\,\,AF = \left( {\frac{ - 1}{{\sqrt 3 }},\,\,\frac{1}{{\sqrt 3 }}\,,\,\frac{1}{{\sqrt 3 }}} \right)$$
lets dcs of given line which is making
$${ \theta _{ 1 } },{ \theta _{ 2 } },{ \theta _{ 3 } },{ \theta _{ 4 } },$$ with the diagonal be l, m, n now applying between two angle
so
\begin{array}{l} cos{ \theta _{ 1 } }=l\left( { \frac { 1 }{ { \sqrt { 3 } } } } \right) +m\, \left( { \frac { 1 }{ { \sqrt { 3 } } } } \right) \, +n\, \left( { \frac { 1 }{ { \sqrt { 3 } } } } \right) \to \left( 1 \right) \\ cos{ \theta _{ 2 } }=l\left( { \frac { 1 }{ { \sqrt { 3 } } } } \right) -m\, \left( { \frac { 1 }{ { \sqrt { 3 } } } } \right) \, +n\, \left( { \frac { 1 }{ { \sqrt { 3 } } } } \right) \to \left( 2 \right) \\ cos{ \theta _{ 3 } }=l\left( { \frac { 1 }{ { \sqrt { 3 } } } } \right) +m\, \left( { \frac { 1 }{ { \sqrt { 3 } } } } \right) \, -n\, \left( { \frac { 1 }{ { \sqrt { 3 } } } } \right) \to \left( 3 \right) \\ cos{ \theta _{ 4 } }=-l\left( { \frac { 1 }{ { \sqrt { 3 } } } } \right) +m\, \left( { \frac { 1 }{ { \sqrt { 3 } } } } \right) \, +n\, \left( { \frac { 1 }{ { \sqrt { 3 } } } } \right) \to \left( 4 \right) \end{array}
squaring and adding equation (1), (2) , (3) (4)
$$co{s^2}{\theta _1} + co{s^2}{\theta _2} + co{s^2}{\theta _3} + co{s^2}{\theta _4} = $$
$$\frac { 1 }{ 3 } \left[ { { l^{ 2 } }+{ m^{ 2 } }+{ n^{ 2 } }+2lm+2mn+2\ln { + } { l^{ 2 } }+{ m^{ 2 } }+{ n^{ 2 } }+2lm-2mn-2\ln { + } { l^{ 2 } }+{ m^{ 2 } }+{ n^{ 2 } }-2lm-2mn+2\ln { + } { l^{ 2 } }+{ m^{ 2 } }+{ n^{ 2 } }-2lm+2mn-2\ln { } } \right] $$
$$\frac { 1 }{ 3 } \left[ { 4\left( { { l^{ 2 } }+{ m^{ 2 } }+{ n^{ 2 } } } \right) } \right] $$
$$\frac { 1 }{ 3 } \left( 4 \right) \, \, \, \, \, \, \to \left( { { l^{ 2 } }+{ m^{ 2 } }+{ n^{ 2 } } } \right) =1$$
$$\frac { 4 }{ 3 } $$
$$co{ s^{ 2 } }{ \theta _{ 1 } }+co{ s^{ 2 } }{ \theta _{ 2 } }+co{ s^{ 2 } }{ \theta _{ 3 } }+co{ s^{ 2 } }{ \theta _{ 4 } }=\frac { 4 }{ 3 } $$
Find the vector equation of the line joining $$(1,2,3)$$ and $$(-3,4,3)$$ and show pependicular to the z-axis
The cartesian equation of a line is $$\dfrac{{x + 3}}{2} = \dfrac{{y - 5}}{4} = \dfrac{{z + 6}}{2}$$ find the vector equation of the line?
If the d.c's of a line are $$ \left( {\frac{1}{c},\,\frac{1}{c},\,\frac{1}{c}} \right) $$, find c.
If a line makes angles $$\alpha,\beta,\gamma$$ with positive directions of X,Y,Z-axes, what is the value of $${sin}^{2}{\alpha}\ +\ {sin}^{2}{\beta} +\ {sin}^{2}{\gamma}$$?
Given , A line make a angle $$\alpha ,\beta ,\chi ,$$ with x , y , z axis , then
let length of line be $$\left| r \right|$$ x , y , z be the intercept mode by line on the three coordinates axis
So $$\cos \alpha = \frac{x}{r}\,\,\,\,\,\,\cos \beta = \frac{y}{r}\,\,\,\,\cos \chi = \frac{z}{r}$$
$${\cos ^2}\alpha + {\cos ^2}\beta + {\cos ^2}\chi = \frac{{{r^2}}}{{{r^2}}}$$
$${\cos ^2}\alpha + {\cos ^2}\beta + {\cos ^2}\chi = 1$$
$$1 - {\sin ^2}\alpha + 1 - {\sin ^2}\beta + 1 - {\sin ^2}\chi = 1$$
$$\therefore \,\,\,{\sin ^2}\alpha + {\sin ^2}\beta + {\sin ^2}\chi = 2$$
so answer is 2
Find the direction ratio of the line $$\dfrac{x-1}{2}=3y=\dfrac{2z+3}{4}$$
If a line makes angle $$\left( {\alpha ,\,\beta ,\,\gamma } \right)$$ with the co-ordinates axes. Prove that $${\sin ^2}\alpha \, + \,{\sin ^2}\beta \, - \,{\cos ^2}\gamma \, = \,1$$
Find the equation of line passing through $$(5, 0, 5)$$ & $$(2, 1, 3)$$. Also show that $$(5, 0, 5), (2, 1, 3)$$ & $$(-4, 3, -1)$$ are collinear.
Find the vector equation of the line joining points $$2\hat i + \hat j + 3\hat k$$ and $$ - 4\hat i + 3\hat j - \hat k$$ .
Find the measure of the angle between two lines if their direction cosines $$\ell, m, n$$ satisfy $$\ell+m-n=0, \ell^{2}+m^{2}-n^{2}=0$$.
The angle between the lines whose direction cosines satisfy the equations $$l+m+n=0$$ and $$l^2=m^2+n^2$$ is?
Find the direction cosines of the vector $$\vec{r}=(6\hat{i}+2\hat{j}-3\hat{k})$$.
Given three points whose position are vectors $$x\hat i + y\hat j + z\hat k$$ and $$ - \hat i - \hat j$$. Find the condition for the points to be collinear.
Using vectors, find the value of $$\lambda$$ such that the points $$(\lambda, -10, 3), (1, -1, 3)$$ and $$(3, 5, 3)$$ are collinear.
Find the vector equation of the line passing through the points $$2\hat i + 3\hat j + \hat k$$ and parallel to the vector $$4\hat i - 2\hat j + 3\hat k$$ .
Show that points $$A\left( a,b+c \right), B\left( b,c+a \right), C\left( c,a+b \right)$$ are collinear.
The number of straight line that are equally inclined to the three dimensional co- ordinate axes , is
$$4$$ lines.
If a unit vector $$\overrightarrow { a } $$ makes angles $$\cfrac{\pi}{3}$$ with $$\hat { i } $$, $$\cfrac{\pi}{4}$$ with $$\hat { j } $$ and an acute angle $$\theta$$ with $$\hat { k } $$, then find $$\theta$$ and hence, the components of $$\overrightarrow { a } $$
Find the equation of plane passing through the point $$(3,2,4)$$ and perpendicular to the $$X-$$axis.
The direction cosines of a line are $$\dfrac{1}{2}, \dfrac{1}{2}, k$$ and $$k > 0$$, then $$k=?$$
The cartasian equation of a line is $$\dfrac {x-5}{3}=\dfrac {y+4}{7}=\dfrac {z-6}{2}$$. Find its vector equation.
Show that the points $$A(-2\hat{i}+3\hat{j}+5\hat{k}), B(\hat{i}+2\hat{j}+3\hat{k})$$ and $$C(7\hat{i}-\hat{k})$$ are collinear.
Show that the points with position vectors $$\overrightarrow{a}+\overrightarrow{b}, \overrightarrow{a}-\overrightarrow{b}$$ and $$\overrightarrow{a}+k\overrightarrow{b}$$ are collinear for all values of $$k$$.
Find the equation of plane passing through the point $$(2-1,3)$$ and perpendicular to the $$X-$$axis.
Show that
$$A(1,-2,-8),B(5,0,-2)$$ and $$C(11,3,7)$$ are collinear.
If the direction cosines of a line are $$\left(\dfrac{1}{2},0,n\right)$$ and $$n<0$$. Then find $$n$$.
Determine whether the points are collinear.
$$P(-2,3),B(1,2),C(4,1)$$
Slope of PB $$ = \dfrac{2-3}{1-(-2)} $$
$$ = \dfrac{-1}{3} $$
Slope of BC $$ = \dfrac{1-2}{4-1} $$
$$ = \dfrac{-1}{3} $$
Since slope are Equal
Points are colliner.
The position vectors $$\vec {a},\vec {b},\vec {c}$$ of three points satisfy the relation $$2\vec {a}+7\vec {b}+5\vec {c}=\vec {0}$$. Are these points collinear?
$$ 2\vec{a}+7\vec{b}+5\vec{c} = 0 $$
$$ \therefore 7\vec{b} = -5\vec{c}-2\vec{a} $$
$$ \therefore \vec{b} = \dfrac{5\vec{c}-2\vec{a}}{7} $$
$$ \therefore \vec{b} = -\dfrac{(5\vec{c}+2\vec{a})}{7} $$
Above indicates
$$ \vec{b} $$ divides $$ \vec{c} $$ and $$ \vec{a} $$ internally
in ratio $$ 5:2 $$
Hence points are collinear.
If a line makes angles $$\alpha ,\beta$$ & $$\gamma$$ with $$OX,OY$$ & $$OZ$$ respectively Prove that: (i) $$\sin ^{ 2 }{ \alpha } +\sin ^{ 2 }{ \beta } +\sin ^{ 2 }{ \gamma } =2$$
The direction ratios of a vector are $$2, -3, 4$$ . Find its direction cosines
Obtain the equation of the plane which passes through (3, 4, -5) and (1, 2, 3) and parallel to Z axis.
Prove that the points $$A(4,-3,-1), B(5,-7,6)$$ and $$C(3,1,-8)$$ are collinear.
Find the angle between the pairs of lines with direction ratios proportional to
(i)$$5 , - 12,13 \text { and } - 3,4,5$$
(ii)$$2,2,1 \text { and } 4,1,8$$
(iii)$$1,2 , - 2 \text { and } - 2,2,1$$
(iv)$$a , b , c \text { and } b - c , c - a , a - b$$
Find the value of p so the line $$\dfrac{1-x}{3}=\dfrac{7y-14}{2p}=\dfrac{z-3}{2}$$ and $$\dfrac{7-7x}{3p}=\dfrac{y-5}{1}=\dfrac{6-z}{5}$$ are at right angles.
If a line makes $$\theta _ { 1 } , \theta _ { 2 } , \theta _ { 3 }$$ angles with the co-ordinates axes, then prove that $$\cos 2 \theta _ { 1 } + \cos 2 \theta _ { 2 } + \cos 2 \theta _ { 3 } + 1 = 0$$
Show that each of the given three vectors is a unit vector:
$$\frac{1}{7}(2\bar{i}+3\bar{j}+6\bar{k},) $$ $$\frac{1}{7}(3\bar{i}+6\bar{j}+\bar2{k}), $$ $$\frac{1}{7}(6\bar{i}+2\bar{j}+3\bar{k})$$
Find the vector equation of the line through A(3,4,-7) and B(6,-1,1).
If a line makes angles $$90^{o}, 135^{o}, 45^{o}$$ with x, y and z-axis respectively, find its direction cosines.
Find the angles at which the normal vector to the plane $$4x+8y+z=5$$ is inclined to the coordinate axes.
Write the equation of the plane passing through the point $$\left({x}_{1},{y}_{1},{z}_{1}\right)$$ and having $$a, b, c$$, as direction ratios of its normal.
Equation of plane passing through the point $$(x_1 , y_1 , z_1)$$ and (a,b,c)
and having direction ratio of its normal.
$$ \frac{x-x_1}{a} = \frac{y-y_1}{b} = \frac{z-z_1}{c}$$
If $$\vec{PO}+\vec{OQ}=\vec{QO}+\vec{OR}$$, prove that the points $$P, Q, R$$ are collinear.
A ray makes angles $$\dfrac{\pi}{3},\dfrac{\pi}{3}$$ with $$\overrightarrow { OX }$$ and $$\overrightarrow { OY }$$ respectively. Find the angle made by it with $$\overrightarrow { OZ }$$.
Find the equation of the line passing through the point $$(-1, 2, 1)$$ and parallel to the line $$\dfrac {2x - 1}{4} = \dfrac {3y + 5}{2} = \dfrac {2 - z}{3}$$.
Find the vector equation of the coordinates planes.
Find the equation of the line joining the points $$(-1,3)$$ and $$(4,-2)$$.
The foot of the perpendicular drawn from the origin to the plane is $$(4,2,6)$$. Find the equation of the plane.
Find a normal to the plane $$x+2y+3z-6=0$$
Find the direction cosines if the passing through two points $$(-2,4,-5)$$ and $$(1,2,3).$$
Find the equation of the plane passing through the point $$(2,3,1)$$ given that the direction ratios of normal to the plane are proportional to $$5, 3,2$$
If a line has direction ratio $$2,-1,-2,$$ determine its direction cosines.
Let $$l_i,m_i,n_i$$ $$i = 1,2,3$$ be the direction cosines of three mutually perpendicular vectors in space. Show that $$A A ^ { ' } = I _ { 3 } ,$$ where $$A = \left[ \begin{array} { l l l } { l _ { 1 } } & { m _ { 1 } } & { n _ { 1 } } \\ { l _ { 2 } } & { m _ { 2 } } & { n _ { 2 } } \\ { l _ { 3 } } & { m _ { 3 } } & { n _ { 3 } } \end{array} \right].$$
Find the vector equation of the line passing through the point $$(1, 2, -4)$$ and parallel to the line $$\dfrac {x - 3}{4} = \dfrac {y - 5}{2} = \dfrac {z + 1}{3}$$.
Find the vector equation of a plane which is at 42 unit distance from the origin and which is normal to the vector $$2\hat{i}+\hat{j}-2\hat{k}$$
Write the vector equation of a line whose Cartesian equations are $$\cfrac{x-5}{3}=\cfrac{y+4}{7}=\cfrac{6-z}{2}$$
Find the vector equation of the line passing through the point vector $$\hat{i}+\hat{j}+\hat{k}$$ and $$2\hat{i}-\hat{j}+\hat{k}$$
Show that the points $$A(2,3,4),B(-1,-2,1)$$ and $$C(5,8,7)$$ are collinear.
Find the equation of the line passing through the point $$(2, -1, 3)$$ and parallel to the line $$\vec {r} = (\hat {i} - 2\hat {j} + \hat {k}) + \lambda (2\hat {i} + 3\hat {j} - 5\hat {k})$$.
Find the vector equation of the line passing through the point having position vector $$-2\hat{i} + \hat{j}+\hat{k}$$ and parallel to vector $$4\hat{i}-\hat{j}+2\hat{k}$$
The direction ratios of two lines are 1,-3, 4 and -2, 0,The direction cosines of a line perpendicular to both the lines are
State True or False.The following position vectors are collinear.$$a-2b+3c$$,$$ 2a+3b-4c$$, $$-7b+10c$$.
State True or False.
The following position vectors are collinear.
Test the co-linearity of the set of points with the following position vectors: If they are co-linear then write 1 otherwise write 0.$$5a+4b+2c, \ 6a+2b-c, \ 7a+b-c.$$
The directions cosines of the joins of the following pairs of vectors :
(i) $$(6,3,2), (5,1,4)$$ be $$\dfrac{k}{3}, \dfrac{m}{3}, -\dfrac{m}{3}$$(ii) $$(3,-4,7), (0,2,5)$$ be $$\dfrac{n}{7},\dfrac{l}{7},\dfrac{m}{7}$$
Find $$k+m+n+l$$ ?
Find $$k+m+n+l$$ ?
If $$A(1, 2, 1), B(2, 6, 2)$$ and $$C(\lambda, 14, 4)$$ are collinear, then value of $$\lambda$$ is
Find the direction cosines of the line $$\displaystyle{\frac{x + 2}{2}}$$ = $$\displaystyle{\frac{2y - 7}{6}}$$ = $$\displaystyle{\frac{5 - z}{6}}$$. then the vector equation of the line through the point A(1, 2, 3) and parallel to the given line can be expressed as $$\vec{r} = \hat{i} + 2\hat{j}+ 3\hat{k} + \lambda (2\hat{i} +3\hat{j} - 6\hat{k} )$$, where $$\lambda$$ is real.
If true enter 1 else enter 0
The cartesian equation of a line is $$\dfrac {x - 5}{3} = \dfrac {y + 4}{7} = \dfrac {z - 6}{2}$$ write its vector form.
If a line has the direction ratios $$-18, 12,- 4$$, then what are its direction cosines?
The angle between the following pair of lines:
$$\cfrac{x}{2}=\cfrac{y}{2}=\cfrac{z}{1}$$ and $$\cfrac{x-5}{4}=\cfrac{y-2}{1}=\cfrac{z-3}{8}$$ is $$\theta = \cos^{-1}\dfrac{a}{3}$$ then $$a=$$
Find the equation of the line in vector and in cartesian form that passes through the point with position vector $$2\hat {i} - \hat {j} + 4\hat {k}$$ and is in the direction $$\hat {i} + 2\hat {j} - \hat {k}$$.
Find the Cartesian equation of the line which passes through the point $$(-2, 4, -5)$$ and parallel to the line given by $$\cfrac{x+3}{3}=\cfrac{y-4}{5}=\cfrac{z+8}{6}$$
Show that the points $$(-2, 3, 5), (1, 2, 3)$$ and $$(7, 0, -1)$$ are collinear.
Find the direction cosines of a line which makes equal angles with the coordinate axes.
$$x+y+z=1$$
Find the equation of the line which passes through the point $$(1, 2, 3)$$ and is parallel to the vector $$(3\hat {i} + 2\hat {j} - 2\hat {k}$$.
Find the vector and the Cartesian equations of the line that passes through the points $$(3, -2, -5), (3, -2,6)$$
Find the distance of the point $$(-1,-5,-10)$$ from the point of intersection of the line $$\vec { r } =\left( 2\hat { i } -\hat { j } +2\hat { k } \right) +\lambda \left( 3\hat { i } +4\hat { j } +2\hat { k } \right) $$ and the plane $$\vec { r } .\left( \hat { i } -\hat { j } +\hat { k } \right) =5$$
Find the coordinates of the foot of the perpendicular drawn from the origin to the plane $$5y + 8 = 0$$.
Find the vector and Catesian equation of the plane that passes through the point $$(1,4,6)$$ and the normal vector to the plane is $$\hat { i } -2\hat { j } +\hat { k } $$
Find the vector and Catesian equation of the plane that passes through the point $$(1,0,-2)$$ and the normal to the plane is $$\hat { i } +\hat { j } -\hat { k } $$
Show that points
A (a, b + c), B (b, c + a), C (c, a + b) are collinear
In the following cases, find the coordinates of the foot of the perpendicular drawn from the origin.
$$x + y + z = 1$$.
Find the equation of a line parallel to x-axis and passing through the origin
Show that the vector $$\hat {i}+\hat {j}+\hat {k}$$ is equally inclined to the axes $$OX, OY$$ and $$OZ$$.
Find the vector equation of a plane which is at a distance of $$5$$ units from the origin and its normal vector is $$2\hat i - 3\hat j + 6\hat k$$
If a line makes angles $$90^o, 60^0$$ and $$\theta$$ with $$x, y$$ and $$z-$$ axis respectively, where $$\theta$$ is acute, then find $$\theta$$.
Find the Cartesian equation of the line which passes through the point $$(-2, 4, -5)$$ and is parallel to the line $$\displaystyle \frac{x+3}{3}=\frac{4-y}{5}=\frac{z+8}{6}$$
Find the vector equation of the plane passing through a point having position vector $$3\hat {i} - 2\hat {j} + \hat {k}$$ and perpendicular to the vector $$4\hat {i} + 3\hat {j} + 2\hat {k}$$
If a line makes angles $$90^{\circ}, 60^{\circ}$$ and $$30^{\circ}$$ with the positive direction of $$x, y$$ and z-axes respectively, find its direction cosines
Find the direction cosines of the unit vector perpendicular to the plane $$\overrightarrow { r } .\left( 6\hat { i } -3\hat { j } -2\hat { k } \right) +1=0$$
Find vector equation of line passing through the point whose position vector is
$$3\hat { i } -4\hat { j } +\hat { k } $$ and parallel to the vector $$2\hat { i } +\hat { j } -3\hat { k } $$. Also write the equation in Cartesian form.
If the points $$(a,1),(1,2)$$ and $$(0,b+1)$$ are collinear, then show that $$\cfrac{1}{a}+\cfrac{1}{b}=1$$
Find the angle between the two lines whose direction cosines are given by equations $$l+m+n=0$$ and $$2l+2m-nm=0$$.
Write the vector equation of the line equation
$$\cfrac { x-1 }{ 2 } =\cfrac { y-2 }{ 3 } =\cfrac { z-3 }{ 4 } $$
If $$l, m, n$$ are the direction cosines of a line, then prove that $$l^{2} + m^{2} + n^{2} = 1$$. Hence find the direction angle of the line with the $$X$$ axis which makes direction angles of $$135^{\circ}$$ and $$45^{\circ}$$ with $$Y$$ and $$Z$$ axes respectively
If from a point $$Q(a, b, c)$$ perpendiculars $$QA$$ and $$QB$$ are drawn to the $$YZ$$ and $$ZX$$ planes respectively, then find the vector equation of the plane $$OAB$$.
Drive the equation of a plane perpendicular to a given vector and passing through a given point both in vector and Cartesian form.
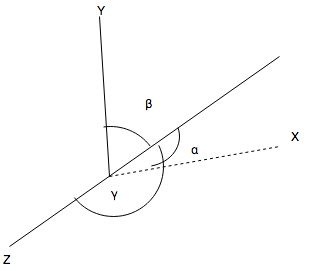
If $$\cos \alpha, \cos \beta, \cos \gamma$$ are direction-cosines of any straight line, then prove that:
$$\cos 2\alpha + \cos 2\beta + \cos 2\gamma = -1$$
Find the equation to the plane through the point $$(-1,3,2)$$ and perpendicular to the planes $$x+2y+2z=11$$ and $$3x+3y+2z=15$$.
Find the equation of the plane passing through the point $$(1, -2, 1)$$ and perpendicular to the line joining the points $$A(3, 2, 1)$$ and $$B(1, 4, 2)$$.
The direction cosines of two lines are determined by the relation $$l-5m+3n=0$$ and $$7l^2+5m^2-3n^2=0$$, find them.
Find the vector and Cartesian equation of the line that passes through the points (3 , -2 , -5) and (3 , -2 , 6).
Find the equation of plane through the points $$(2, 2, 1)$$ and $$(9, 3, 6)$$ and perpendicular to the plane $$2x+6y+6z=9$$
Show that the points $$(3, 3), (h, 0)$$ and $$(0, k)$$ are collinear, if $$\dfrac {1}{n} + \dfrac {1}{k} = \dfrac {1}{3}$$.
The foot of the perpendicular drawn from the origin to the plane is $$(4, -2, -5)$$, then find the vector equation of plane.
Prove that the points $$(4, 5, -5), (0, -11, 3)$$ and $$(2, -3, -1)$$ are collinear.
Find the position vector of a point $$R$$ which divides the line joining two points $$P$$ and $$Q$$ whose position vectors are $$(2\vec {a} + \vec {b})$$ and $$(\vec {a} - 3\vec {b})$$ externally in the ratio $$1 : 2$$. Also, show that $$P$$ is the mid point of the line segment $$RQ$$.
The direction cosines of $$\bar { AB } $$ are $$-2,2,1$$. If $$A\equiv (4,1,5)$$ and $$l(AB)=6$$units, find the coordinates of $$B$$.
Find a vector $$\vec { r } $$ of magnitude $$3\sqrt { 2 } $$ units which makes and angle $$\cfrac { \pi }{ 4 } $$ and $$\cfrac { \pi }{ 2 } $$ with $$y$$ and z-axis respectively
Find the vector equation of a line passing through the point $$A$$ whose position vector is $$3\overline{i}+\overline{j}-\overline{k}$$ and which is parallel to the vector $$2\overline{i}-\overline{j}+2\overline{k}$$.If $$P$$ is a point of this line such that $$AP=15$$,find the position vector of $$P$$.
If $$\vec a, \vec b$$ and $$\vec c$$ are mutually perpendicular vectors of equal magnitudes, If the angles which the vector $$2\vec a+\vec b+2\vec c$$ makes with the vectors $$\vec a$$ is $$\cos^{-1}\sqrt{\dfrac{2}{m}}$$. Find $$m$$
Find the direction cosines (d.cs) of directed line $$OP$$ if coordinates of $$P$$ is $$(2, 3, 7)$$, $$O$$ being the origin.
If a directed line $$OP$$ makes angles $$45^o, 60^o$$ & $$60^o$$ with $$+ve$$ direction of $$x, y, z$$ axis respectively then find d.cs of $$OP$$
Find the direction cosines of the sides of the triangle whose vertices are $$(3,5,-4)$$ and $$(-1,1,2)$$ and $$(-5,-5,-2)$$ what type of triangle is it.
Can a line have direction angles as $$45^o, 45^o$$ & $$60^o$$.
Find angle in degrees between the line joining the points $$(2,1,3)$$ and $$(1,-1,2)$$ and the line having direction ratios $$2,1 ,-1$$.
Write the equation of the line passing through $$(2 , -6, 3) $$ & having D.R.'s $$\propto$$ $$1, 5, 9$$.
Write the vector equation of the line $$\dfrac {x - 5}{3} = \dfrac {y + 4}{7} = \dfrac {z - 6}{2}$$.
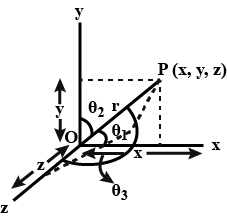
If $$P(x, y, z)$$ is point in the space at a distance $$r$$ from the origin $$O$$, then direction cosines of the line $$OP$$ are
Show that the lines whose d.c's are given by $$2l + 2m - n = 0,\,mn + nl + lm = 0$$ are perpendicular to each other.
If $$l_1, m_1, n_1$$ and $$l_2, m_2, n_2$$ are the direction cosines of two lines, then show that the direction cosines of the line perpendicular to them are proportional to $$m_1n_2-m_2n_1$$, $$n_1l_2-n_2l_1$$, $$l_1m_2-l_2m_1$$.
If a line makes angles $$90^{\circ}$$, $$135^{\circ}$$, $$45^{\circ}$$ with the X, Y, and Z axes respectively, then find its product direction cosines.
The cartesian equation of a line are $$3x - 1=6y + 2=1 - z $$. Find the direction ratios and writes its equation in vector form.
If a line makes angles $$\alpha, \beta, \gamma$$ with coordinate axes, Find the value of $$\sin^{2} \alpha + \sin^{2}\beta + \sin^{2} \gamma $$
Find the angles between the lines whose direction cosines are given by the equations.$$l+m+n=0$$$$l^2+m^2+n^2=0$$
Show that angles between any two diagonals $$\theta= \cos^{-1} \left(\dfrac{1}{3}\right)$$
Directions of $$OG,AE,CD,FB$$
$$OG=1,1,1$$$$AE=-1,1,1$$
$$CD=1,1,-1$$
$$FB=-1,1,-1$$
let angle between $$OG$$ and $$AE$$ be
$$\therefore \cos { \theta } =\cfrac { \left| x \right| +\left| x \right| +\left| x \right| }{ \sqrt { { 1 }^{ 2 }+{ 1 }^{ 2 }+{ 1 }^{ 2 } } \sqrt { { -1 }^{ 2 }+{ 1 }^{ 2 }+{ 1 }^{ 2 } } } =\cfrac { 1 }{ 3 } $$
Clearly,
$$ \cos { \theta } =\cfrac { 1 }{ 3 } $$ for any two diagonals.
$$ \therefore \theta =\cos ^{ -1 }{ (\cfrac { 1 }{ 3 } ) } $$ is angle between any two diagonals.
If a line makes angles $$\alpha, \beta, \gamma$$ with coordinate axes, find
$$\cos^{2}\alpha + \cos^{2}\beta + \cos^{2}\gamma +1$$
Find the perpendicular distance from the origin to the plane passing through the points $$(1, -2, 5), (0, -5, -1)$$ and $$(-3, 5,0)$$.
A mirror and a source of light are situated at a origin $$O$$ and a point on $$OX$$ , respectively. A ray of light from the source strikes the mirror and is reflected . If the direction ratios of the normal to the plane are $$1 ,-1, 1$$, then find the $$DCs$$ of the reflected ray.
Find the direction cosines of the sides of the triangle whose vertices are $$(3, 5, -2),(-1, 1 , 2)$$ and $$(-5 , -5, -2)$$. What type of triangle is it?
Show that the straight lines whose direction cosines are given by $$2l+2m−n=0$$ and $$mn+nl+lm=0$$ are at right angles.
Find the equation of the plane if the perpendicular from the origin to the plane is (2, 3, -5).
Let the point of plane be $$p(2,3,-5)$$
$$ \therefore$$ the equation of plane through $$p(2,3,-5)$$ is
$$a\left( {n - 2} \right) + b\left( {y - 3} \right) + c\left( {z - \left( { - 5} \right)} \right) = 0\left( {0,0,0} \right)$$
The disection ratios of the line through the point $$0(0,0,0)$$ and $$(2,3,-5)$$ are
$$2-0,3-0,-5-0$$
$$ \therefore$$ the line op with disection -ratios $$4,3,2$$ is normal to the plane $$(i)$$
$$ \therefore$$ equation (i) of plane becomes
$$\begin{array}{l} 2\left( { x-2 } \right) +3\left( { y-3 } \right) +\left( { -5 } \right) \left( { z-\left( { -5 } \right) } \right) =0 \\ \Rightarrow 2x-2+3y-9-5z-25=0\, \, \left[ { \frac { a }{ 2 } =\frac { b }{ 3 } =\frac { c }{ { -5 } } } \right] \\ \Rightarrow 2x+3y-5z-38=0 \end{array}$$
Find the vector equation of the line joining the points $$2i+j+3k$$ and $$-4i+3j-k$$ $$(2i+j+3k) + \lambda (pi-2j+4k)$$ then p =
Find the equation of the line through the origin which intersect the line $$\frac{{x - 3}}{2} = \frac{{y - 3}}{1} = \frac{z}{1}$$ at an angle of $$\dfrac{\pi}{2}$$ and $$\frac{{x - 3}}{1} = \frac{{y - 3}}{2} = \frac{z}{1}$$ at an angle of $$\dfrac{\pi}{2}$$
Find the direction cosines of a line which makes equal angles with the positive coordinate axes.
Find the direction cosines of the line PQ joining the points $$P(2, 3, 4)$$ and $$Q(2, 1, 1)$$.
Find the angle between the lines whose direction ratios are $$3, 2, -6$$ and $$1, 2, 2$$.
Show that the following poionts are collinear
(i) $$A(3,2,-4), \ B(9,8,-10), \ C(-2,-3,1)$$
(ii) $$P(4,5,2),\ Q(3,2,4), \ R(5,8,0)$$
Let 'k' is distance of the plane through (1, 1, 1) and perpendicular to the line $$\dfrac{x - 1}{3} = \dfrac{y - 1}{0} = \dfrac{z - 1}{4}$$ from the origin, then value of 5 k is __
Find direction cosines of line given by $$x=ay+b,\ z=cy+d.$$
Prove that the points whose position vectors are $$5\vec{a}+6\vec{b}+7\vec{c}, 7\vec{a}-8\vec{b}+9\vec{c}, 3\vec{a}+20\vec{b}+5\vec{c}$$ are collinear.
Let the points be P,Q,R.
$$\vec{PQ}=(7\vec{a}-8\vec{b}+9\vec{c})-(5\vec{a}+6\vec{b}+7\vec{c})=2\vec{a}-14\vec{b}+2\vec{c}$$
$$\vec{PR}=(3\vec{a}+2\vec{b}+5\vec{c})-(5\vec{a}+6\vec{b}+7\vec{c})=-2\vec{a}+14\vec{b}-2\vec{c}$$
So, $$\vec{PQ}= -\vec{PR}$$
$$\therefore $$ Points P,Q,R are collinear.
If $$\vec P\left( {1,5,4} \right)$$ and $$\vec Q\left( {4, - 1, - 2} \right)$$, find the direction ratio of $${\vec {{PQ}}}$$
Find the direction cosines of a line whose direction ratios are $$2, -6, 3$$.
If a line makes angles $$90^{o}$$ and $$60^{o}$$ respectively with the positive directions of $$x$$ and $$y$$ axes, find the angle which it makes with the positive direction of $$z-$$axis.
Find the equation of the plane which is perpendicular to $$x - axis$$ and that passes through the point $$\left( {2, - 1,3} \right)$$.
If $$ {\cos ^4}\theta + {\cos ^2}\theta = 1 ,$$ then show that : $$ {\sec ^4}\theta - {\sec ^2}\theta = 1 $$.
Obtain the equation of the line passing through $$(1, 1, 2)$$ and $$(2, 1, 2)$$ in the vector form.
Lines $$\dfrac{x-1}{2}=\dfrac{y-1}{2}=\dfrac{z-2}{3}$$ and $$\dfrac{x-1}{2}=\dfrac{y-2}{2}=\dfrac{z-3}{-2}$$
(Check whether the lines are parallel, mutually perpendicular or intersecting in acute angle)
Direction ratio of $$\dfrac{3-x}{1}=\dfrac{y-2}{5}=\dfrac{2z-3}{1} are.......$$
If a line makes angles $$\alpha,\ \beta,\ \gamma$$ with coordinate axes, prove that
$$\cos{2\alpha}+\cos{2\beta}+\cos{2\gamma}+1=0$$
The direction $$cosines\ l,m,m$$ of two lines satisfy $$l+m+n=0,\ { l }^{ 2 }+n^{ 2 }{ =m }^{ 2 }$$. Find the measure of the angle between the lines.
Write the equation of the line passing through A$$(1, 2, 3)$$ and having the direction in $$(1, 1, 1)$$ the vector form and also in the symmetric form.
Write the equation of a line through $$(1, 2, 3)$$ and parallel to $$\overline {r} . (\hat {i} - \hat {j} + 3\hat {k}) = 5$$.
Find the direction cosines of the line: $$\displaystyle \frac { x-1 }{ 2 } =-y=\frac { z+1 }{ 2 }$$
If $$O$$ is origin $$OP = 3$$ with direction ratios proportional to $$-1, 2, -2$$ then what are the coordinates of $$P$$?
Show that the points $$A(1,-2,-8),B(5,0,-2)$$ and $$C(11,3,7)$$ are collinear, and find the ratio in which $$B$$ divides $$AC$$.
$$A= (1,-2,-8)$$
$$B= (5,0,-2)$$
$$C=(11,3,7)$$
A,B,C are collinear if
$$\left | \vec{AB} \right |+\left | \vec{BC} \right |=\left | \vec{AC} \right |$$
$$\vec{AB}= (5-1)\hat{i}+(0+2)\hat{j}+(-2+8)\hat{k}= 4\hat{i}+2\hat{j}+6\hat{k}$$
$$\left | \vec{AB} \right |= \sqrt{16+4+36}= 2\sqrt{14}$$
$$\vec{BC}= (11-5)\hat{i}+(3-0)\hat{j}+(7+2)\hat{k}= 6\hat{i}+3\hat{j}+9\hat{k}$$
$$\left | \vec{BC} \right |=\sqrt{36+9+81}= 3\sqrt{14}$$
$$\vec{AC}=(11-1)\hat{i}+(3+2)\hat{j}+(7+8)\hat{k}= 10\hat{i}+5\hat{j}+15\hat{k}$$
$$\left | \vec{AC} \right |= \sqrt{100+25+225}= 5\sqrt{14}$$
Thus $$\left | \vec{AB} \right |+\left | \vec{BC} \right |=\left | \vec{AC} \right |$$
let B divide AC in k:1
then
$$(5,0,-2)= \dfrac{k(11,3,7)+1(1,-2,-8)}{k+1}$$
$$=\dfrac{(11k+1, 3k-2, 7k-8)}{k+1}$$
$$\Rightarrow k= 2/3\Rightarrow k:1\Rightarrow 2:3$$
$$\Rightarrow $$ B divide AC in 2:3.
To find the vector and the Cartesian equation in symmetric form of line passing through the points, $$(2, 0, -3)$$ and $$(7, 3, -10)$$.
Show that the following set of point are collinear ?
$$(2,3,-4),(-1,0,5),(3,4,-7)$$
If the vectors $$x\hat{i}+\hat{j}+\hat{k},\hat{i}+y\hat{j}+\hat{k}$$ and $$\hat{i}+\hat{j}+z\hat{k}$$ are co-planar where $$x\neq 1,y\neq 1,z\neq 1$$, then prove that $$\dfrac{1}{1-x}+\dfrac{1}{1-y}+\dfrac{1}{1-z}=1$$.
Find the equation of the line passing through the points $$A(3, 2, -1)$$ and $$B (4, -1, 3)$$.
If the vectors $$a\hat{i}+\hat{j}+\hat{k},\hat{i}+b\hat{j}+\hat{k},\hat{i}+\hat{j}+c\hat{k} \left(a\neq 1 ,b\neq 1,c\neq 1\right)$$ are coplanar, then the value of $$\dfrac{1}{1-a}+\dfrac{1}{1-b}+\dfrac{1}{1-c}$$
Show that the three lines with direction cosines
$$\frac{12}{13},\frac{-3}{13},\frac{-4}{13}:\frac{4}{13},\frac{12}{13},\frac{3}{13};\frac{-4}{13},\frac{12}{13}$$ are mutually perpendicular
$$P$$ and $$Q$$ are the points $$(-1,2,1)$$ and $$(4,3,5)$$ respectively. Find the projection of $$PQ$$ on a line which makes angles of $$120^{o}$$ and $$135^{o}$$ with $$y$$ and $$z$$ axes respectively and an acute with $$x-axis$$ ?
Find the direction cosines of the line passing through the two points $$(-2,4,-5)$$ and $$(1,2,3)$$
A vector $$\vec {r}$$ is inclined at equal angles to the three axes. If the magnitude of $$\vec {r}$$ is $$2\sqrt {3}$$ units, find $$\vec {r}$$.
A triangle is formed by joining the points $$(1,0,0),(0,1,0)$$ and $$(0,0,1)$$. Find the direction cosines of the medians.
$$ A \equiv (1,0,0) $$
$$ B \equiv (0,1,0) $$
$$ C \equiv (0,0,1) $$
Middle point of side $$ \displaystyle AB (d) \equiv (\frac{1}{2},\frac{1}{2},0) $$
Middle point of $$ \displaystyle BC (e) \equiv (0,\frac{1}{2},\frac{1}{2}) $$
Middle point of $$ \displaystyle AC (f) \equiv (\frac{1}{2},0,\frac{1}{2}) $$
$$ \therefore $$ direction ratio of cd $$\displaystyle = (\frac{1}{2},\frac{1}{2},-1) $$
$$ \therefore $$ direction ratio of bf $$\displaystyle = (\frac{1}{2},-1,\frac{1}{2}) $$
$$ \therefore $$ direction ratio of ae $$ \displaystyle = (-1,\frac{1}{2},\frac{11}{2}) $$
$$ \therefore $$ direction cosine of cd =
$$\displaystyle (\frac{1/2}{\sqrt({\frac{1}{2})^{2}+(\frac{1}{2})^{2}}+1^{2}},\frac{1/2}{\sqrt{(\frac{1}{2})^{2}+(\frac{1}{2})^{2}}+1^{2}},\frac{-1}{\sqrt{(\frac{1}{2})^{2}+(\frac{1}{2})^{2}}+1^{2}}) $$
$$\displaystyle = (\frac{1/2}{\sqrt{3/2}},\frac{+1/2}{\sqrt{3/2}},\frac{-1}{\sqrt{3/2}}) $$
$$ \displaystyle \therefore $$ direction cosines of bf $$ :- $$
$$\displaystyle (\frac{1/2}{\sqrt{3/2}},\frac{-1}{\sqrt{3/2}},\frac{1/2}{\sqrt{3/2}}) $$
$$ \therefore $$ direction cosines of ae
$$ \displaystyle = (\frac{-1}{\sqrt{3/2}},\frac{1}{2\sqrt{3/2}},\frac{1}{2\sqrt{3/2}}) $$
Find the direction cosines of two lines which are connected by the relations $$l+m+n=0$$ and $$mn-2nl-2lm=0.$$
Show that the points $$(2,3,4,)(-1,-,2,1),(5,8,7)$$ are collinear.
Find the vector of magnitude (5/2) units which is parallel to the vector $$3\hat i + 4\hat j$$
Find the direction cosines of the sides of the triangle whose vertices are $$(3, 5, -4), (-1, 1, 2) $$ and $$(-5, -5, -2)$$.
Find the direction cosine $$l,m,n$$ of line which are connected by the relations $$l + m + n = 0.$$,$$2mn + 2ml - nl = 0$$
Find the equation of the plane which contains the line of intersection of the planes $$\overrightarrow r .\left( {\widehat i + 2\widehat j + 3\widehat k} \right) - 4 = 0,\overrightarrow {r.} \left( {2\widehat i + \widehat j - \widehat k} \right) + 5 = 0$$ and which is perpendicular to the plane $$\overrightarrow {r.} \left( {5\widehat i + 3\widehat j - 6\widehat k} \right) + 8 = 0.$$
Find the vector equation of the line passing through the point $$(3,1,2)$$ and perpendicular to the plane $$\vec r.\left( {2\widehat i - \widehat j + \widehat k} \right) = 8$$ Also .find the point of intersection of line and plane.
The points A(4, 5, 10), B(2, 3, 4) and C(1, 2, - 1) are three vertices of a parallelogram ABCD. Find the vector equations of the sides AB and BC and also find the coordinates of point D.
Find the equation of line passing through points
(i) $$(3\hat i + 2\hat j - 8\hat k)$$,$$(5,2, - 4)$$
If a variable line in two adjacent position has direction cosines $$l,\ m,\ n$$ and $$l+\delta l,\ m+\delta m,\ n+\delta n$$ show that the small angle $$\delta \theta$$ between two positions is given by $$(\delta \theta)^{2}$$=$$(\delta l)^{2}+(\delta m)^{2}+(\delta n)^{2}$$.
If a line makes $${90 ^\circ}$$ and $${60 ^\circ}$$ with x & y axis, find angle it make with z-axis.
If the points $$(p, q) (m, n)$$ and $$(p-m, q-n)$$ are collinear, Determine the relation between $$p, q, n $$ and $$m$$.
Find vector equation of line passing through point $$\hat i + 2\hat j + 3\hat k$$ and perpendicular to vector $$\hat i + \hat j + \hat k$$ and $$2\hat i + \hat j + 3\hat k$$
Find the direction cosines of the sides of the triangles whose vertices are $$(3,5,-4),(-1,1,2)$$ and $$(-5,-5,-2)$$.
What are the direction cosines of a line that passes through the points $$P ( 6 , - 7 , - 1 )$$ and $$Q ( 2 , - 3,1 )$$
Direction ratio of $$\overrightarrow {PQ} = - 4\widehat i + 4\widehat j + 2\widehat k$$
Now,
Direction cosine $$ = \frac{{ - 4\widehat i + 4\widehat j + 2\widehat k}}{{\sqrt {{{\left( { - 4} \right)}^2} + {{\left( 4 \right)}^2} + {{\left( 2 \right)}^2}} }}$$
$$ = \frac{{ - 4\widehat i + 4\widehat j + 2\widehat k}}{6}$$
$$ = \frac{{ - 2}}{3}\widehat i + \frac{2}{3}\widehat j + \frac{1}{3}\widehat k$$
Hence, the direction cosine is $$\left( {\frac{{ - 2}}{3},\frac{2}{3},\frac{1}{3}} \right)$$
The position vectors of the points A, B, C are respectively $$(1,1,1) ; (1,-1,2) ; (0,2,-1)$$. Find a unit vector parallel to the plane determined by ABC and perpendicular to the vector $$(1,0,1)$$
Show that the lines whose d.c's are proportional to $$(2,1,1), (4, \sqrt{3}-1,-\sqrt{3} -1)$$ are inclined to one another at angle $$\dfrac{\pi}{3}$$.
Find the equation of a line passing through the point $$(2,0,1)$$ and parellel to the whose equation is $$\vec { r } =(2\lambda +3)\hat i+(7\lambda -1)\hat j+(-3\lambda +2)\hat k$$
Show that the points $$O(0,0), A(2,-3,3), B(-2,3,-3)$$ are collinear. Find the ratio in which each point divides the segment joining the other two.
Show that the points $$(1,2,3), (7,0,1)$$ and $$(-2,3,4)$$ are collinear.
The equation of the plane through the point $$(4,4,0)$$ and perpendicular to the plane $$x+2y +2z-5 = 0$$ and $$3x+3y +2z -8 =0$$ is
If the direction ratios of two parallel lines $$4, -3, -1$$ and $$p+q, 1+q, 2$$ then find the values of $$p$$ and $$q$$.
If $$l_{1}, m_{1}, n_{1}$$ and $$l_{2}, m_{2}, n_{2}$$ are the direction cosines of two mutually perpendicular lines, show that the direction cosines of the line perpendicular to both of these are $$m_{1}n_{2} - m_{2}n_{1}, n_{1}l_{2} - n_{2}l_{1},l_{1}m_{2} - l_{2}m_{1}$$.
Write the direction ratio of the vector $$3\vec{a}+2\vec{b}$$ where $$\vec{a}=\hat{i}+\hat{j}-2\hat{k}$$ and $$\vec{b}=2\hat{i}-4\hat{j}+5\hat{k}$$
If the three point $$A=(2,0,1);B=(x,0,3);C=(4,0,4)$$ are collineas .Find the value of x and y.
A line makes angles of measure $$45^{\circ}$$ and $$60^{\circ}$$ with the positive direction of the Y and Z axes respectively. Find the angle made by line with the positive directions of X-axis.
Can $$\dfrac { 2 }{ \sqrt { 3 } } ,\dfrac { -2 }{ \sqrt { 3 } } ,\dfrac { -1 }{ \sqrt { 3 } }$$ be the direction ratios of any directed line? Justify your answer.
Find the angle between the lines $$\dfrac{-x+2}{-2}=\dfrac{y-1}{7}=\dfrac{z+3}{-3}$$ and $$\dfrac{x+2}{-1}=\dfrac{2y-8}{4}=\dfrac{z-5}{4}$$. Check if they are parallel or perpendicular.
The equation of the plane through $$( 3,1 , - 3 )$$ and $$( 1 , - 2,2 )$$ and parallel to the line with dr's $$1,1 , - 2$$ is
Find the equation of the line passing through the point $$(1 , 1 , 1)$$ and intersects the line $$\frac { ( x - 1 ) } { 2 } = \frac { ( y - 2 ) } { 3 } = \frac { ( z - 3 ) } { 4 }$$ and $$\frac { ( x + 2 ) } { 1 } = \frac { ( y - 3 ) } { 2 } = \frac { ( z + 1 ) } { 4 }$$
$$A(-1,\ 2,\ 3),\ B(5,\ 0,\ -6),\ C(0,\ 4,\ -1)$$ are three points. Show that the direction cosines of the bisectors of $$\angle BAC$$ are proportional to $$(25,\ 8,\ 5)$$ and $$(-11,\ 20,\ 23)$$.
Find the direction cosines of a line which is perpendicular to the lines whose direction ratios are $$(1,-1,2)$$ and $$(2,1,-1).$$
If the direction ratios of two parallel lines are $$4, -3, -1$$ and $$p+q, 1+q, 2$$ then find the values of p and q.
Find the angle between the line whose direction cosines are given by $$l+m+n=0$$ and $$ { l }^{ 2 }+{ m }^{ 2 }={ n }^{ 2 }$$
Show that $$2x+3y+7=0$$ represents a plane perpendicular to $$XY$$-plane.
Find the equation of the plane through the point $$(1, 1, 1)$$ and perpendicular to the line $$x - 2 y + z = 2,4 x + 3 y - z + 1 = 0$$
Directions ratio of two lines are $$3, -2, k$$ and $$-2, k, 4$$ . Find k if the lines are perpendicular to each other.
Draw five two- dimensional and five three- dimensional objects your choice, and label them.
What is the direction cosine of angle which the vector $$\sqrt {2\hat i} + \hat j + \hat k\;makes\;with\;y - axis\;?$$
For a vector
$$ai+bj+ck$$
direction cosines are given by
$$t=\dfrac{a}{\sqrt{a^2+b^2+c^2}}, m=\dfrac{b}{\sqrt{a^2+b^2+c^2}}, n=\dfrac{c}{\sqrt{a^2+b^2+c^2}}$$
$$L=\cos \alpha, m=\cos\beta, n=\cos\gamma$$
Where
$$\alpha, \beta, \gamma$$
are angles made by the vectors with x-axis, y-axis and z-axis respectively for the given vector $$\sqrt{2i}+j+k$$
$$m=\cos\beta =\dfrac{1}{\sqrt{2+1+1}}=\dfrac{1}{\sqrt{4}}=\dfrac{1}{2}$$
$$\therefore \beta =\dfrac{\pi}{3}$$.
Find the equations of the straight line perpendicular to the lines $$\dfrac{x+1}{-3}=\dfrac{y-3}{2}=\dfrac{z+2}{1}; \dfrac{x}{1}=\dfrac{y-7}{-3}=\dfrac{z+7}{2}$$
Find the angle between the lines joining the points $$\left( 1,4,2\right ) , \left( - 2,1,2\right)$$ and $$\left( 1,2,3\right ) , \left( 2,5,1\right )$$
Find the vector equation of the plane through the points $$( 2,1 , - 1 )$$ and $$( - 1,3,4 )$$ and perpendicular to the plane $$x - 2 y + 4 z = 10$$.
Find the direction cosine of the line passing through the points $$A(-4,2,3)$$ and $$B(1,3,-2)$$
$$ A\,(-4,2,3) \: B\,(1,3,-2)$$
D.r's of a line passing through $$ P(x_1,y_1,z_1)$$ & $$Q(x_2,y_2,z_2)$$
$$ = (x_2 - x_1), (y_2 - y_1), (z_2 - z_1)$$
$$ D.C = \frac{x_2 - x_1}{PQ}, \frac{y_2 - y_1}{PQ} , \frac{z_2 - z_1}{PQ}$$
$$ PQ = AB = \sqrt{(x_2 - x_1)^{2} + (y_2 - y_1)^{2} + (z_2 - z_1)^{2}}$$
$$ A=P; \, B=Q$$
$$ x_1 = -4; y_1 = 2; z_1 = 3 $$
$$ x_2 = 1; y_2 = 3; z_2 = -2 $$
$$ D.r's = (x_2 - x_1), (y_2 - y_1),(z_2 - z_1)$$
$$ = 1+4; \,3-2; \, -2-3$$
$$= 5; \,1; \, -5 $$
$$ DC = \frac{5}{\sqrt{5^{2} + 1^{2} + (-5)^{2}}}$$; $$ \frac{1}{\sqrt{5^{2} + 1^{2} + (-5)^{2}}}$$; $$ \frac{-5}{\sqrt{5^{2} + 1^{2} + (-5)^{2}}}$$
$$ = \frac{5}{\sqrt{25 + 1 + 25}};\, \frac{1}{\sqrt{25+1+25}};\, \frac{-5}{\sqrt{25+1+25}}$$
$$ = \frac{5}{\sqrt{51}};\, \frac{1}{\sqrt{51}};\, \frac{-5}{\sqrt{51}}$$
Equation of the plane passing through the three points $$P(2,3,1), Q(2,1,2)$$ and $$R(3,6,-1)$$ is
Prove that $$1,1,1$$ cannot be direction cosines of a straight line
Do you think the points $$(3,5),(6,8)$$ and $$(10,12)$$ are straight line? Given reasons for your answer.
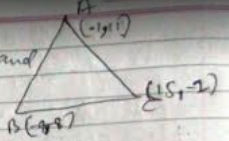
Prove that the circumcenter, orthocenter, incenter and centroid of the triangle formed by the points $$A(-1,11)$$ $$B(-9,-8)$$ and $$C(15,-2)$$ are collinear, without actually finding any of them.
Distance of AB, BC and CA
$$\begin{array}{l} \Rightarrow AB=\sqrt { { { \left( { -8 } \right) }^{ 2 } }+{ { \left( { 19 } \right) }^{ 2 } } } \\ \Rightarrow AB=\sqrt { 64+361 } =\sqrt { 425 } \, \, unit \\ \Rightarrow BC=\sqrt { { { \left( { 15+9 } \right) }^{ 2 } }+{ { \left( { -6 } \right) }^{ 2 } } } =\sqrt { { { \left( { 24 } \right) }^{ 2 } }+36 } =\sqrt { 612 } \, \, unit \\ \Rightarrow and\, \, AC=\sqrt { { { \left( { 16 } \right) }^{ 2 } }+{ { \left( { 13 } \right) }^{ 2 } } } =\sqrt { 256+109 } =\sqrt { 425 } \, \, unit \end{array}$$
$$\therefore \Delta ABC$$ are Isosceles triangle
Hence, centroid, orthocentre, incentre and circumcentre lie on same line.
For what value of m , the points (3 , 5) , (m , 6) and $$ \left ( \dfrac{1}{2} , \dfrac{15}{2}\right ) $$ are collinear ?
Find the value of $$K$$ for which the points $$(7,-2) ,(5,1)$$ and $$(3,K)$$ are collinear.
If the points are collinear then the area of triangle will be O.
$$\Delta =\frac {1}{2}|x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)|$$
$$\Rightarrow |7(1-k) +5 (k+2)+3 (-2-1)|=0$$
$$\Rightarrow |7 -7k+5k+10-9|=0$$
$$\Rightarrow |-2k +8|=0$$
$$\Rightarrow -2k =-8 $$ so $$k=4$$
Find the shortest distance between the skew lines :$$l_{1} : \dfrac{x-1}{2}=\dfrac{y+1}{1}=\dfrac{z-2}{4}$$
$$l_{2} : \dfrac{x+2}{4}=\dfrac{y-0}{-3}=\dfrac{z+1}{1}$$
Find the equation of the plane that passes through $$x -$$ axis and point $$( 3,2,4 )$$.
Find the equation of the plane passing through the point (1,-1,2) having 2,3,2 as direction ratios of normal to the plane.
The foot of the perpendicular drawn from the origin to the plane is $$( 2,5,7 ) .$$ Find the equation of the plane.
Show that the points having position vectors, $$\bar a, \bar b$$ and $$3\bar a-2\bar b$$ are colliera, where $$\bar a , \bar b , \bar c$$ any vectors.
Let given vectors $$\underset{A}{\bar{a}}, \underset{B}{\bar{b}}, \underset{C}{3\bar{a} - 2\bar{b}}$$
$$\overline{AB} = \bar{b} - \bar{a}$$
$$\overline{AC} = 3\bar{a} - 2\bar{b} - \bar{a} = 2\bar{a} - 2\bar{b}$$
$$\overline{AC} = -2\overline{AB}$$
Here $$\bar{a}, \bar{b}, 3\bar{a} - 2\bar{b}$$ are collinear
Find the directions cosines of $$x,y$$ and $$z$$ axis.
Direction cosines of
a-axis
$$(cos0^{\circ},cos90^{\circ},cos90^{\circ})$$
=(1,0,0)
(2)y axis
= (0,1,0)
(3)z axis
=(0,0,1)
If a line makes angles $$\alpha ,\beta$$ and $$\gamma$$ with three-dimensional coordinate axes, respectively, then find the value of $$\cos 2\alpha +\cos 2\beta+\cos 2\gamma$$.
[a]l$$ =cos\alpha $$
$$ m=cos\beta $$
$$ n=cos\gamma $$
we now ,
$$l^{2}+m^{2}+n^{2}=1$$
$$cos^{2}\alpha +cos^{2}\beta +cos^{2}\gamma =1$$
$$we know cos^{2}\theta =2cos^{2}\theta -1$$
so,
$$\frac({1-cos^{2}\alpha }{2})+(\frac{1-cos^{2}\beta }{2})+(\frac{1-cos^{2}\gamma }{2})=1$$
$$= (1-cos^{2}\alpha )+(1-cos^{2}\beta )+(1-cos^{2}\gamma )=2$$
$$=-1= cos^{2}= cos^{2}\alpha +cos^{2}\beta +cos^{2}\gamma $$
Hence value is -1
Find the direction cosines of the line $$\dfrac{{x + 2}}{2} = \dfrac{{2y - 5}}{3};z = - 1$$.
Show that the points $$( 1,0 ) , ( 6,0 ), (0,0)$$ are collinear
Prove that points $$A, B, C$$ having positions vectors $$\vec { a } ,\vec { b } ,\vec { c } $$ are collinear, if $$\left[\vec { b } \times \vec { c } +\vec { c } \times \vec { a } +\vec { a } \times \vec { b } \right]=\vec { 0 } $$
If$$A = ( 4,1,5 )$$ and $$B=(3,4,5)$$ The direction ratios of $$\overline { A B }$$ are
Find the vector equation of the line passing through $$(1, 2, 3)$$ and perpendicular to the plane $$\vec {r} \cdot (\hat {i} + 2\hat {j} - 5\hat {k}) + 9 = 0$$.
Using direction ratio show that the points $$ A(2,3,-4), B(1,-2,3)$$ and $$ C(3,8,-11)$$ are collinear.
Find the intercepts made on the coordinates axes by the plane $$2x+y-2z=3$$ and find also the direction cosines of the normal to the plane.
If the lines $$\dfrac {x - 1}{-3} = \dfrac {y - 2}{-2k} = \dfrac {z - 3}{2}, \dfrac {x - 1}{K} = \dfrac {y - 2}{1} = \dfrac {z - 3}{5}$$ are $$\perp^{r}$$, find $$K$$.
The coordinates of the foot of the perpendicular drawn from of the origin to a plane are $$(12, -4, 3)$$. Find the equation of the plane.
If a line has the direction ratios $$-18, 12, -4$$, then what are its direction cosines ?
If $$O$$ be the origin and the coordinates of $$P$$ be $$(1,2,-3)$$, then find the equation of the plane passing through $$P$$ and perpendicular to $$OP$$
Find the cartesian equation of a line passing through $$(1, -1, 2)$$ and parallel to the line whose equation are $$\dfrac {x - 3}{1} = \dfrac {y - 1}{2} = \dfrac {z + 1}{-2}$$. Also, reduce the equation obtained in vector form.
Find the equation of the plane that bisects the line segment joining points $$(1,2,3)$$ and $$(3,4,5)$$ and is at right angle to it.
Find the vector equation of plane which is at a distance of $$3$$ units form the origin and has $$\hat{k}$$ as the unit vector normal to it.
Write the normal form of the equation of the plane $$2x-3y+6z+14=0$$.
Find the vector equation of the plane passing through the point $$A(a,0,0), B(0, b, 0)$$ and that $$C(0,0,c)$$. Reduce it to normal form. If plane $$ABC$$ is at distance $$p$$ from the origin, prove that $$\dfrac{1}{p^{2}}=\dfrac{1}{a^{2}}+\dfrac{1}{b^{2}}+\dfrac{1}{c^{2}}$$.
Find the vector and cartesian equation of the plane which passes through the point $$(5, 2, -4)$$ and perpendicular to the line with direction ratios $$2, 3, -1$$
Find the vector equation of the line passing through the point$$A(1, 2, -1)$$ and parallel to the line $$5x - 25 = 14 - 7y = 35z$$.
Find the direction cosines of the line $$\dfrac {4 - x}{2} = \dfrac {y}{6} = \dfrac {1 - z}{3}$$. Also, reduce it to vector form.
Reduce the equation $$2x-3y-6z=14$$ to the normal form and hence find the length of perpendicular from the origin to the plane. Also, find the direction cosines of the normal to the plane.
Using vectors, find the value of $$ \lambda $$ such that the points $$ (\lambda , -10, 3), (1, -1, 3)$$ and $$ (3,5,3)$$ are collinear.
Find the vector equation of the line passing through the point $$(2, -1, -1)$$ which is parallel to the line $$6x - 2 = 3y + 1 = 2z - 2$$.
If the equations of a line $$AB$$ are $$\dfrac {3 - x}{1} = \dfrac {y + 2}{-2} = \dfrac {z - 5}{4}$$, write the direction ratios of a line parallel to $$AB$$.
Cartesian equations of a line $$AB$$ are $$\dfrac {2x - 1}{2} = \dfrac {4 - y}{7} = \dfrac {z + 1}{2}$$. Write the direction cosines of a line parallel to $$AB$$.
Write the direction cosines of the line whose cartesian equations are $$2x = 3y = -z$$.
Write the angle between the lines $$2x = 3y = -z$$ and $$6x = -y = -4z$$.
Write the direction cosines of the line $$\dfrac {x - 2}{2} = \dfrac {2y - 5}{-3}, z = 2$$.
Find the direction cosines of the line $$\dfrac {x + 2}{2} = \dfrac {2y - 7}{6} = \dfrac {5 - z}{6}$$. Also, find the vector equation of the line through the point $$A(-1, 2, 3)$$ and parallel to the given line.
Write the direction cosines of the line, whose cartesian equations are $$6x - 2 = 3y + 1 = 2z - 4$$.
Write the angle between the lines $$\dfrac {x - 5}{7} = \dfrac {y + 2}{-5} = \dfrac {z - 2}{1}$$ and $$\dfrac {x - 1}{1} = \dfrac {y}{2} = \dfrac {z - 1}{3}$$.
Find the value of $$p$$ for which the points $$A(-1,3,2),B(-4,2,-2)$$ and $$C(5,5,p)$$ are collinear.
Find the direction ratios and the direction cosines of the line segment joining the points:
(i) $$A(1,0,0)$$ and $$B(0,1,1)$$
(ii) $$A(5,6,-3)$$ and $$B(1,-6,3)$$
(iii) $$A(-5,7,-9)$$ and $$B(-3,4,-6)$$
A passes through the point $$(3,4,5)$$ and is parallel to the vector $$\left( 2\hat { i } +2\hat { j } -3\hat { k } \right) $$. Find the equations of the line in the vector as well as Cartesian forms.
The equations of a line are given by $$\dfrac {4 - x}{3} = \dfrac {y + 3}{3} = \dfrac {z + 2}{6}$$. Write the direction cosines of a line parallel to this line.
Write the coordinates of the foot of the perpendicular from the point $$(1,2,3)$$ on y-axis. Mark 1 if the answer is $$(0,2,0)$$ otherwise mark 0.
Show that the points $$A(2,3,-4),B(1,-2,3)$$ and $$C(3,8,-11)$$ are collinear.
Find the vector equation of a line passing through the point $$A(3,-2,1)$$ and parallel to the line joining the points $$B(-2,4,2)$$ and $$C(2,3,3)$$. Also, find the Cartesian equations of the line.
Find the value of $$\lambda$$ for which the points $$A(2,5,1),B(1,2,-1)$$ and $$C(3,\lambda,3)$$ are collinear.
Show that the points $$A(2,1,3), B(5,0,5)$$ and $$C(-4,3,-1)$$ are collinear.
Find the Cartesian equations of the line which passes through the point $$(1,3,-2)$$ and is parallel to the line given by
$$\cfrac { x+1 }{ 3 } =\cfrac { y-4 }{ 5 } =\cfrac { z+3 }{ -6 } $$.
Also, find the vector form of the equations so obtained.
Find the equations of the line passing through the point $$(1,-2,3)$$ and parallel to the line $$\cfrac { x-6 }{ 3 } =\cfrac { y-2 }{ -4 } =\cfrac { z+7 }{ 5 } $$.
Also find the vector form of this equation so obtained.
Find the vector equation of a line passing through the point having the position vector $$\left( \hat { i } +2\hat { j } -3\hat { k } \right) $$ and parallel to the line joining the points with position vecgtors $$\left( \hat { i } -\hat { j } +5\hat { k } \right) $$ and $$\left( 2\hat { i } +3\hat { j } -4\hat { k } \right) $$. Also, find the Cartesian equivalents of this equation.
Find the vector equation of the line passing through the point with position vector $$\left( 2\hat { i } +\hat { j } -5\hat { k } \right) $$ and parallel to the vector $$\left( \hat { i } +3\hat { j } -\hat { k } \right) $$. Deduce the Cartesian equations of the line.
Find the equations of the line passing through the point $$(1,-2,3)$$ and parallel to the line $$\cfrac { x-3 }{ 2 } =\cfrac { y+2 }{ -5 } =\cfrac { z-6 }{ 4 } $$
Also find the vector form of this equation so obtained
Find the Cartesian and vector equations of a line which passes through the point $$(1,2,3)$$ and is parallel to the line.
$$\cfrac { -x-2 }{ 1 } =\cfrac { y+3 }{ 7 } =\cfrac { 2z-6 }{ 3 } $$
Find the angle between each of the following pairs of lines:
$$\vec { r } =\left(3 \hat { i } +\hat { j } -2\hat { k } \right) +\lambda \left( \hat { i } -\hat { j } -2\hat { k } \right) $$ and $$\vec { r } =\left( 2\hat { i } -\hat { j } -5\hat { k } \right) +\mu \left( 3\hat { i } -5\hat { j } -4\hat { k } \right) $$
Find the angle between each of the following pairs of lines:
$$\vec { r } =\left( 3\hat { i } -4\hat { j } +2\hat { k } \right) +\mu \left( \hat { i } +3\hat { k } \right) $$ and $$\vec { r } =\left( 5\hat { i } \right) +\mu \left( -\hat { i } +\hat { j } +\hat { k } \right) $$
Find the angle between each of the following pairs of lines:
$$\vec { r } =\left( \hat { i } -2\hat { j } \right) +\mu \left(2 \hat { i } -2\hat { j } +\hat { k } \right) $$ and $$\vec { r } =\left( 3\hat { k } \right) +\mu \left( \hat { i } +2\hat { j } -2\hat { k } \right) $$
Find the values of $$\lambda$$ and $$\mu$$ so that the points $$A(3,2,-4),B(9,8,-10)$$ and $$C(\lambda, \mu, -6)$$ are collinear.
Find the values of $$\lambda$$ and $$\mu$$ so that the points $$A(-1,4,-2), B(\lambda, \mu, 1)$$ and $$C(0,2,-1)$$ are collinear.
Find the angle between each of the following pairs of lines:
$$\cfrac{x+1}{1}=\cfrac{y-4}{1}=\cfrac{z-5}{2}$$ and $$\cfrac{x+3}{3}=\cfrac{y-2}{5}=\cfrac{z+5}{4}$$
Find the angle between each of the following pairs of lines:
$$\cfrac{5-x}{3}=\cfrac{y+3}{-2},z=5$$ and $$\cfrac{x-1}{1}=\cfrac{1-y}{3}=\cfrac{z-5}{2}$$
Find the angle between each of the following pairs of lines:
$$\cfrac{3-x}{-2}=\cfrac{y+5}{1}=\cfrac{1-z}{3}$$ and $$\cfrac{x}{3}=\cfrac{1-y}{-2}=\cfrac{x+2}{-1}$$
Find the angle between each of the following pairs of lines:
$$\cfrac{x}{1}=\cfrac{z}{-1},y=0$$ and $$\cfrac{x}{3}=\cfrac{y}{4}=\cfrac{z}{5}$$
The position vectors of three points $$A,B,C$$ are $$\left(-4 \hat { i } +2\hat { j } -3\hat { k } \right) ,\left( \hat { i } +3\hat { j } -2\hat { k } \right) $$ and $$\left(-9 \hat { i } +\hat { j } -4\hat { k } \right) $$ . respectively. Show that the points $$A,B$$ and $$C$$ are collinear.
If $$P(1,5,4)$$ and $$Q(4,1,-2)$$ be two given points, find the direction ratios of $$PQ$$.
The direction ratios of a line are $$2,6,-9$$. What are its direction cosines?
The Cartesian equations of a line are $$\cfrac{x-1}{2}=\cfrac{y+2}{3}=\cfrac{5-z}{1}$$. Find its vetor equation.
A line makes angles $${90}^{o},{135}^{o}$$ and $${45}^{o}$$ with positive directions of x-axis, y-axis and z-axis respectively. What are the direction cosines of the line?
The equations of a line are $$\cfrac{4-x}{2}=\cfrac{y+3}{2}=\cfrac{z+2}{1}$$. Find the direction cosines of a line parallel to this line.
Write the vector equation of a line passing through the point $$(1,-1,2)$$ and parallel to the line whose equations are $$\cfrac{x-3}{1}=\cfrac{y-1}{2}=\cfrac{z+1}{-2}$$.
Write the equations of line parallel to the line $$\cfrac{x-2}{-3}=\cfrac{y+3}{2}=\cfrac{z+5}{6}$$ and passing through the point $$(1,-2,3)$$.
If the equations of a line are $$\cfrac{3-x}{-3}=\cfrac{y+2}{-2}=\cfrac{z+2}{6}$$, find the direction cosines of a line parallel to the given line.
If $$A(1,2,3),B(4,5,7),C(-4,3,-6)$$ and $$D(2,9,2)$$ are four given points then find the angle between the lines $$AB$$ and $$CD$$.
Find the vector equation of a line passing through the point $$(1,2,3)$$ and parallel to the vector $$\left( 3\hat { i } +2\hat { j } -2\hat { k } \right) $$
What are the direction cosines of the y-axis?
Find the Cartesian and vector equations of a plane passing through the point $$(1, 2, 3)$$ and perpendicular to the line with direction ratios $$2, 3, -4$$.
Find the equation of the plane passing through group of points.
$$A(2, 2, -1), B(3, 4, 2)$$ and $$C(7, 0, 6)$$.
If O be the origin and $$P(1, 2, -3)$$ be a given point, then find the equation of the plane passing through P and perpendicular to OP.
Find the equation of the plane passing through group of points.
$$A(-2, 6, -6), B(-3, 10, -9)$$ and $$C(-5, 0, -6)$$.
Find the equation of the plane passing through group of points.
$$A(0, -1, -1), B(4, 5, 1)$$ and $$C(3, 9, 4)$$.
For the following planes, find the direction cosines of the normal to the plane and the distance of the plane from the origin.
$$z=3$$.
Find the vector and Cartesian equations of a plane which is at a distance of $$\dfrac{6}{\sqrt{29}}$$ from the origin and whose normal vector from the origin is $$(2\hat{i}-3\hat{j}+4\hat{k})$$.
Find the vector and Cartesian equations of a plane which is at a distance of $$5$$ units from the origin and which has $$3\hat{i}-2\hat{j}+6\hat{k}$$ as the unit vector normal to it.
Find the vector and Cartesian equations of a plane which is at a distance of $$7$$ units from the origin and whose normal vector from the origin is $$(3\hat{i}+5\hat{j}-6\hat{k})$$.
Find the vector equation of a plane whose Cartesian equation is $$5x-7y+2z+4=0$$.
Find the direction cosines of the normal to the plane $$3x-6y+2z=7$$.
Find a unit vector normal to the plane $$x-2y+2z=6$$.
Find the vector and cartesian equations of the planes that passes through the point $$(1, 4, 6)$$ and the normal vector to the plane is $$\hat {i} - 2\hat {j} + \hat {k}$$.
For the following planes, find the direction cosines of the normal to the plane and the distance of the plane from the origin.
$$2x+3y-z=5$$.
Find the equation of a plane passing through the points $$A(a, 0, 0), B(0, b, 0)$$ and $$C(0, 0, c)$$.
Find the direction cosines of the normal to the plane $$y=3$$.
Find the direction ratios of the normal to the plane $$x+2y-3z=5$$.
Find the direction cosines of the perpendicular from the origin to the plane $$\vec{r}\cdot(6\hat{i}-3\hat{j}-2\hat{k})+1=0$$.
For the following planes, find the direction cosines of the normal to the plane and the distance of the plane from the origin.
$$3y+5=0$$.
Find the direction cosines of the normal to the plane $$3x+4=0$$.
A vector $$\vec{n}$$ of magnitude $$8$$ units is inclined to the x-axis is $$45^o$$, y-axis at $$60^o$$ and an acute angle with the z-axis. If a plane passes through a point $$(\sqrt{2}, -1, 1)$$ and is normal to $$\vec{n}$$, find its equation in vector form.
Prove that the normals to the planes $$4x+11y+2z+3=0$$ and $$3x-2y+5z=8$$ are perpendicular to each other.
Find the direction cosines of the normal to the plane $$2x+3y-z=4$$.
Show that points $$A(a, b+c), B(b, c+a)$$ and $$C(c, a+b)$$ are collinear.
Show that the following points are collinear:
$$A(3, -5, 1), B(-1, 0, 8)$$ and $$C(7, -10, -6)$$.
If the equation of a line AB is $$\dfrac{x - 3}{1} = \dfrac{y + 2}{-2} = \dfrac{z - 5}{4}$$. Then find the direction ratios of line parallel to AB.
Write the cartesian equation of a plane, bisecting the line segment joining the points $$A (2, 3, 5)$$ and $$B(4, 5, 7)$$ at right angles.
Show that the points $$A(2, 3, -4), B(1, -2, 3)$$ and $$C(3, 8, -11)$$ are collinear.
Find the angle between the lines $$2x = 3y = -z$$ and $$6x = -y = -4z.$$
Write the direction ratios of a line parallel to $$AB:\dfrac{2x - 1}{2} = \dfrac{4 - y}{7} = \dfrac{x - 1}{2}$$
Find the direction cosines of the line passing through two points $$(-2, 4, -5)$$ and $$(1, 2, 3).$$
Find the angle between the pair of lines given by
$$\vec{r} = 3i + 2j - 4k + \lambda (i + 2j + 2k)$$ and $$\vec{r} = 5i - 2j + \mu(3 i + 2 j + 6 k)$$
If a line makes an angle $$30^\circ, 60^\circ, 90^\circ$$ with the positive direction of $$x, y, z$$ axes respectively, then find its direction cosines.
Find the value of p, so that the lines $$l_1 = \dfrac{1 - x}{3} = \dfrac{7y - 14}{p} = \dfrac{z - 3}{2}$$ and $$l_2: \dfrac{7 - 7x}{3p} = \dfrac{y - 5}{1} = \dfrac{6 - z}{5}$$ are perpendicular to each other. Also find the equations of a line passing through a point $$(3, 2, -4)$$ and parallel to line $$l_1.$$
What are the direction consines of a line , which makes equal angles with the co-ordinates axes?
Find the vector and cartesian equations of the plane which bisects the line joining the points $$(3, -2, 1)$$ and $$(1, 4, -3)$$ at right angles.
Find the vector equation of the line passing through the point $$A(1, 2, -1)$$ and parallel to the line $$5x - 25 = 14 - 7y = 35z.$$
The direction cosines of the vector $$ (2 \hat{i}+2 \hat{j}-\hat{k}) $$ are ____.
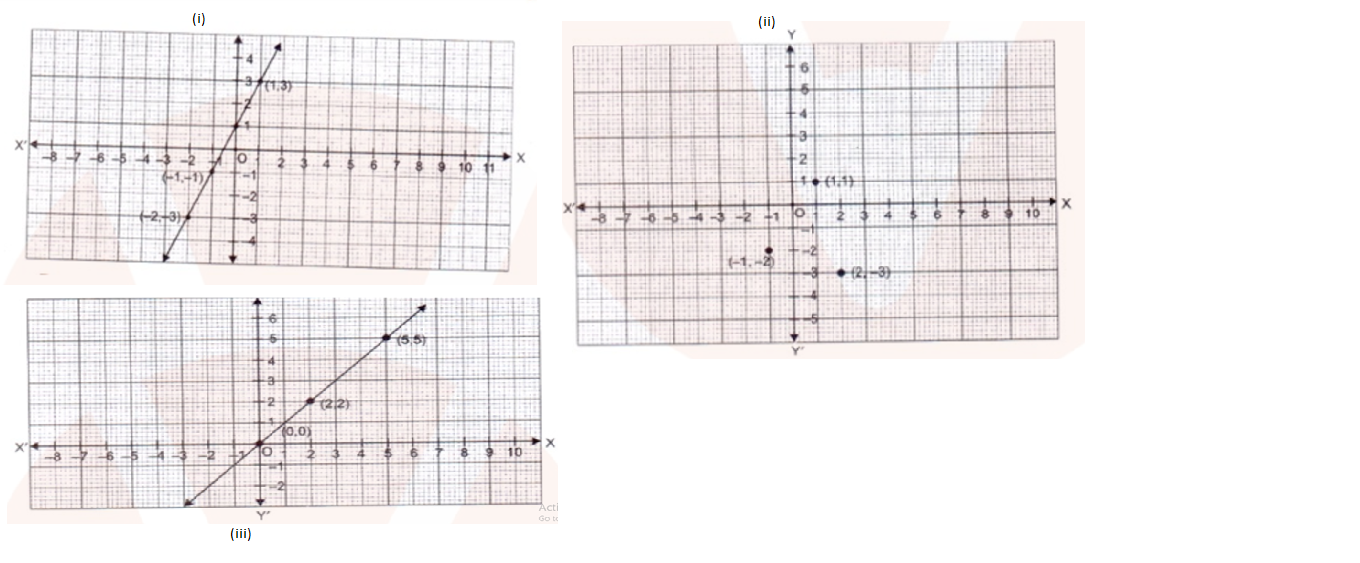
Plot the following points and check whether they are collinear or not :
$$(i) \left(1,3\right), \left(-1 ,-1\right), \left(-2, -3\right)$$
$$(ii) \left(1,1\right), \left(2 ,-3\right), \left(-1, -2\right)$$
$$(iii) \left(0,0\right), \left(2 ,2\right), \left(5, 5\right)$$
(i) From the graph, we find that all the three points lie on the same straight line. Hence, the given points are collinear.
(ii) From the graph, we find that all the three points do not lie on the same straight line. Hence, the given points are not collinear.
(iii) From the graph, we find that all the three points lie on the same straight line. Hence, the given points are collinear.
If the points $$(-1, -1, 2), (2,m,5)$$ and $$(3,11,6)$$ are collinear, find the value of $$m$$.
The plane $$ ax+b y=0 $$ is rotated about its line of intersection with the plane $$ z=0 $$ through an angle $$ \alpha . $$ Prove that the equation of the plane in its new position is $$ a x+b y \pm(\sqrt{a^{2}+b^{2}} \tan \alpha) z=0 $$
Show that the straight lines whose direction cosines are given by the equations $$ a l+b m+c n=0 $$ and $$ u l^{2}+v m^{2}+w n^{2}=0 $$ are parallel or perpendicular as $$ \dfrac{a^{2}}{u}+\dfrac{b^{2}}{v}+\dfrac{c^{2}}{w}=0 $$ or $$ a^{2}(v+w)+b^{2}(w+u)+c^{2}(u+v)=0 $$
Find the vector equation of the line which is parallel to the vector $$ 3 \hat{i}-2 \hat{j}+6 \hat{k} $$ and which passes through the point $$(1,-2,3)$$.
If a line makes angles $$90^{o}, 135^{o}, 45^{o}$$ with the $$X-, Y-$$ and $$Z-$$ axes respectively, then find its direction cosines.
If $$\bar {AB}=2\hat i-4\hat j+7\hat k$$ and initial $$A(1,5,0)$$. Find the terminal point $$B$$.
If a vector has direction angles $$45^{o}$$ and $$60^{o}$$, find the third direction angle.
If a line has the direction ratios $$4, -12, 18$$, then find its direction cosines.
Show that the following points are collinear:
$$P=(4,5,2),Q=(3,2,4),R=(5,8,0)$$.
If the points $$A(3,0,p), B(-1,q, 3)$$ and $$C(-3,3,0)$$ are collinear, then find
the values of $$p$$ and $$q$$.
Find the value of $$\lambda $$ so thta the lines $$\dfrac{1-x}{3}=\dfrac{7y-14}{\lambda }=\dfrac{z-3}{2} and \dfrac{7-7x}{3\lambda }=\dfrac{y-5}{1}=\dfrac{6-z}{5} $$ are at riht angles.
Find the vector equation of the line which passes through the point ( 3 , 2 , 1 ) and is parallel to the vector $$2\hat{i}+2\hat{j}-3\hat{k}$$
Find the vector equation of the line passing through point through point through points having position vector $$3\hat{i}+4\hat{j}-7\hat{k} and 6\hat{i} - \hat{j}-+\hat{k}$$
Find the vector equation of the plane passing through the point having position vector $$\hat{i}+\hat{j}+\hat{k}$$ and perpendicular to the vector $$4\hat{i}+5\hat{j}+6\hat{k}$$
Find the vector equation of the line passing through the point having position vector
$$-\hat{i}-\hat{j}+2\hat{k}$$and parallel to the line $$\bar{r}=(\hat{i}+2\hat{j}+3\hat{k})+\lambda (3\hat{i}+2\hat{j}+\hat{k})$$
Find the vector equation of line passing through the point having vector $$5\hat{i}+4\hat{j}+3\hat{k}$$ and having direction ratios $$-3,4,2$$
Find the acute between the lines x = y , z = 0 and x = 0 , z = 0
Reduce the vector equation $$\bar{r} \cdot (3\hat{i}+4\hat{j}+12\hat{k})$$ to normal
form and hence find the length of the perpendicular from the origin to
the plane.
Find the direction cosines of the lines $$\bar{r}=(-2\hat{i}+\frac{5}{2}\hat{j}-\hat{k})+\lambda (2\hat{i}+3\hat{j})$$
Show that the points $$(2, 3, 4), (-1, -2, 1), (5, 8, 7)$$ are collinear.
Find the vector equation of the plane which is at a distance of 5 units from the origin and which is normal to the vector $$2\hat{i}+\hat{j}+2\hat{k}$$
Show that the line through the points $$(4, 7, 8), (2, 3, 4)$$ is parallel to the line through the points $$(-1, -2, 1), (1, 2, 5)$$.
Find the direction cosines of the sides of the triangle whose vertices are $$(3, 5, -4), (-1, 1, 2)$$ and $$(-5, -5, -2)$$.
Find the cartesian equation of the line which passes through the point $$(-2, 4, -5)$$ are parallel to the line given by $$\dfrac {x + 3}{3} = \dfrac {y - 4}{5} = \dfrac {z + 8}{6}$$.
Find the vector equations of the plane passing through the point $$A (1 , 92 , 1 ) , B ( 2 , 91 , 93 ) and ( C ( 0 , 1 , 5) $$
Write the dc's of the line joining the points $$(1, 0, 0)$$ and $$(0, 1, 1)$$.
Find the vector and cartesian equations of the planes that passes through the point $$(1, 0, -2)$$ and the normal to the plane is $$\hat {i} + \hat {j} - \hat {k}$$.
Find the direction cosines of the vctor joining the points $$ A(1, 2 , -3) $$ and $$ B ( -1, -2, 1) $$directed from $$ A $$ to $$ B $$.
Find the vector equation of a plane which is at a distance of $$7$$ units from the origin and normal to the vector $$6i+3j-2k$$
Find the vector equation of a plane which is at a distance of $$7$$ unit from the origin and has $$\hat i$$ as the unit vector normal to it.
If the coordinates of the points $$A, B, C, D$$ be $$(1, 2, 3), (4, 5, 7), (-4, 3, -6)$$ and $$(2, 9, 2)$$ respectively, then find the angle between the lines $$AB$$ and $$CD$$.
Find the equations of the planes that passes through three points.
$$(1, 1, 0), (1, 2, 1), (-2, 2, -1)$$.
Find the direction of the line joining two points $$(4,2,3)$$ and $$(4,5,7)$$
Find the equations of the planes that passes through three points.
$$(1, 1, -1), (6, 4, -5), (-4, -2, 3)$$.
If O be the origin and the coordinates of P be (1, 2, -3), then find the equation of the plane passing through P and perpendicular to OP.
Find the equation of the line which passes through the points $$(5,7,9)$$ and is parallel to the following axis:
$$Y-$$axis
Find the equation of plane perpendicular of the origin from the plant is $$13$$ and direction ratios of this perpendicular are $$4,-3,12$$
Projection of a line on axis are $$-3,4,-12$$. Find length of line segment and direction cosines.
Find the equation of the line which passes through the points $$(5,7,9)$$ and is parallel to the following axis:
$$X-$$axis
Find the vector equation of the line that passes through point $$(2, 3, 2)$$ and is parallel to the line $$\vec r=( -2\hat i +3\hat j)+\mu (2\hat i -3\hat j +6\hat k)$$.
Find the vector equation of a plane which is at a direction of $$4$$ units from the origin and direction cosines of the normal to the plane are $$2,-1,2.$$
Find a unit normal vector to the plane $$x+y+z-3=0$$
Find the vector equation of the line which passes through the point $$(3, 4, 5)$$ and is parallel to the vector $$2\hat{ i} + 2\hat{ j} – 3\hat{k}$$.
Find the equation of the line parallel to the vector
$$2\hat i-\hat j+3\hat k$$
and passes through the point $$(5,-2,4)$$.
Find the equation of a line in vector and Cartesian form that passes through the point with position vector
$$2\hat i-\hat j+4\hat k$$
and in the direction
$$\hat i+2\hat j-\hat k$$.
Find the equation of the line which passes through the points $$(5,7,9)$$ and is parallel to the following axis:
$$Z-$$axis
Find an equation passes through $$(1,2,3)$$ and is parallel to the vector.
$$(3\hat i+2\hat j-2\hat k)$$.
Find the equation of the line cartesian from which passes through $$(1,2,3)$$ and is parallel to $$\dfrac {-x-2}{1}=\dfrac {y+3}{7}=\dfrac {2z-6}{3}$$.
Find the equation of the line passes through the point $$(2,-1,1)$$ and is parallel to the line $$\dfrac {x-3}{2}=\dfrac {y+1}{7}=\dfrac {z-2}{-3}$$.
Find the Cartesian equation of line passes through the point $$(-2,4,-5)$$ and is parallel to
$$\dfrac {x+3}{3}=\dfrac {y-4}{5}=\dfrac {z+8}{6}$$.
Find the equation of the line vector and in certesian form that passes through the point with vector
$$2\hat i-3\hat j-4\hat k$$
and
$$3\hat i+4\hat j-5\hat k$$
is parallel to the vector.
Let the equation of the plane containing the straight line $$\displaystyle \frac{x - 1}{2} = \frac{y + 2}{-3} = \frac{z}{5}$$ are perpendicular to the plane $$x - y + z + 2 = 0$$ be $$kx + ny + z + 4 = m$$. Find $$k+n$$ ?
Find the direction cosine of the line $$\dfrac{x}{4} = \dfrac{y}{7} = \dfrac{z}{4}$$
Find the acute angle between the lines whose direction ratios are $$(5,12,-13)$$ and $$(3,-4,5)$$.
If a.b.c are noncoplanar find the point of intersection of the line passing through the points $$2a+3b-c , \,3a+4b-2c$$ with the line joining the points $$a-2b+3c,\, d-6b+bc$$
Find the direction cosines of the line which is perpendicular to the lines which direction cosines proportional to 1, -2, -2 and 0, 2, 1.
Find the value of $$k$$, if the points $$(k, 3), (6, -2)$$ and $$(-3, 4)$$ are collinear.
If l, m, n are the direction cosines of a straight line, then prove that $$l^2+m^2+n^2=1$$.
Let $$OP$$ be any line through the origin $$O$$ which has direction cosines $$l,m,n$$.
Let $$P$$ be the point having coordinates $$(x,y,z)$$ and $$OP=r$$.
Then $$OP^2=x^2+y^2+z^2=r^2 \quad ...(1)$$
From $$P$$ draw $$PA,PB,PC$$ perpendicular on the coordinate axes, so that $$OA=x,OB=y,OC=z$$
Also, $$\angle POA=\alpha, \angle POB= \beta, \angle POC= \gamma$$
From triangle $$AOP, l=cos\:\alpha=\dfrac{x}{r}\Rightarrow x=lr$$
Similarly, $$y=mr, z=nr$$
Adding all we get$$x^2+y^2+z^2=r^2(l^2+m^2+n^2)$$
$$\Rightarrow r^2=r^2(l^2+m^2+n^2)$$
$$\Rightarrow l^2+m^2+n^2=1$$
Find the orthocentre of the triangle whose vertices are $$A\left(a,0,0\right),\,B\left(0,b,0\right),\,C\left(0,0,c\right)$$
The plane of the triangle is $$x/a+y/b+z/c=1$$
Let $$O(\alpha,\beta,y)$$ be the orthocenter
drs of OA are $$\alpha-a,\beta,y$$
drs of BC are $$o,-b,c$$
$$OA \bot BC \Rightarrow \beta b=yc$$
$$OB \bot CA \Rightarrow \alpha a=yc$$
$$\therefore \alpha a=\beta b=yc=k^2(say)$$
$$o(\alpha ,\beta,y)$$ lies on the plane
$$\therefore \dfrac{\alpha}{a}+\dfrac{\beta}{b}+\dfrac{y}{c}=1\Rightarrow\dfrac{1}{k^2}=\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}$$
The orthocentre is $$\left(\dfrac{{k}^{2}}{a},\dfrac{{k}^{2}}{b},\dfrac{{k}^{2}}{c}\right)$$
Find the vector equation of the line which passes through the point with position vector $$4\hat {i} - \hat {j} + 2\hat {k}$$ and is in the direction of $$-2\hat {i} + \hat {j} + \hat {k}$$.
The direction ratios of $$\vec{ AB } $$ are $$(-2, 2, 1)$$ If $$A=(4, 1, 5)$$ and $$l$$(AB)$$=6$$ units, find the coordinates of $$B.$$
Find the vector equation of the passing through the point $$2i+3j+k$$ and parallel to the vector $$4i-2j+3k$$.
The points with the co-ordinates $$(2a, 3a)$$, $$(3b, 2b)$$ & $$(c, c)$$ are collinear.
If the area of triangle is $$0$$, then there will be no triangle, the points will be collinear,
$$=4ab+3bc-2ac-9ab-2bc-2ac$$
$$=4ab-3bc-2b-9ab$$
$$=4ab-9ab+bc$$
$$=-5ab+bc$$
$$5ab=bc$$
$$5a=c$$.
Find the equation of the plane which passes through the point $$(3, 2, 0)$$ and the line $$\dfrac{x-4}{1}=\dfrac{y-6}{5}=\dfrac{z-4}{4}$$ is?
The direction cosine of the two lines are determined by the relations $$l-5m+3n=0$$ and $$7{l}^{2}+5{m}^{2}-3{n}^{2}=0$$.Find the solution.
If the line passing through the origin makes angles $$\theta_{1},\theta_{2},\theta_{3}$$ with the planes $$XOY,XOZ$$ and $$ZOX$$ respectively, then prove that $$\cos^{2}\theta_{1}+\cos^{2}\theta_{2}+\cos^{2}\theta_{3}=2.$$
Direction cosine are given as $$\cos \theta_1, \cos\theta_2, \cos\theta_3$$
Here $$P(x, y, z)$$ & $$0(0, 0, 0)$$
$$OP=\sqrt{(x-0)^2+(y-0)^2+(z-0)^2}$$
$$OP=\sqrt{x^2+y^2+z^2}$$
$$r=x^2+y^2+z^2$$
According to diagonal
$$\cos\theta_1=\dfrac{x}{r}$$ $$\cos\theta_2=\dfrac{y}{r}$$ $$\cos\theta_3=\dfrac{z}{r}$$
$$x=r\cos\theta_1$$ $$y=r\cos\theta_2$$ $$z=r\cos\theta_3$$
Square & add
$$x^2+y^2+z^2=r^2(\cos^2\theta_1+\cos^2\theta_2+\cos^2\theta_3)$$
$$r^2=r^2\cos^2\theta_1+\cos^2\theta_2+\cos^2\theta_3$$
So $$\boxed{\cos^2\theta_1+\cos^2\theta_2+\cos^2\theta_3=1}$$.
If $$\vec {n}$$ is a vector of magnitude $$\sqrt{3}$$ and is equally inclined with an acute angle with the coordinate axes. Find the vector and cartesian forms of equation of a plane which passes through $$(2,1,-1)$$ and is normal to $$\vec {n}$$.
Find the equation of the plane passing through $$(-2,1,3)$$ and having $$(3,-5,4)$$ as $$d.r's$$ of its normal.
Find the direction cosines of two lines if they satisfy $$l+3n=5m$$ and $$7l^2+5m^2=3n^2$$.
Show that the points are collinear
(1)$$A(3,2,-4), B(9,8,-10), C(-2,-3,1)$$
The direction cosines l, m, n of two lines satisfy $$l+m+n=0$$, $$l^2+m^2=n^2$$. Find the measure of the angle between the lines.
Find the direction cosines of perpendicular from the origin to the plane $$\bar{r}(2\hat{i}+3\hat{j}+6\hat{k})+7=0$$
The direction cosines of two lines are given by $$al+bm+cn=0,\,\,u{l}^{2}+v{m}^{2}+w{n}^{2}=0$$.Find the conition for the lines to be parallel.
Find the direction cosines and direction ratios of the line joining the points
$$A(5,6,-3), B(1,-6,3)$$
Find the direction cosines and direction ratios of the line joining the points
$$A(0,0,0,), B(4,8,-8)$$
Find the direction cosines of a line that pass through the point $$P\left(1,4,6\right)$$ and $$Q\left(5,1,11\right)$$ and is so directed that it make an acute angle with the positive direction of $$y-axis$$
Find the direction cosines and direction ratios of the line joining the points
$$A(4,2,-6), B(-2,1,3)$$
Find the direction cosines and direction ratios of the line joining the points
$$A(1,3,5), B(-1,0,-1)$$
Find the direction ratio of a line perpendicular to the two lines whose direction ratios are
$$-2,1,-1$$ and $$-3,-4,1$$
Find the vector equation for the line passing through the points $$(-1,0,2)$$ and $$(3,4,6)$$.
Find the equation of the plane passing through $$(1,2-4)$$ and perpendicular to the line $$\cfrac{x+1}{3}=\cfrac{y}{-1}=\cfrac{z-8}{4}$$. Also find the distance of the point $$(3,-1,4)$$ from the plane.
Find the vector and cartesian equations of the plane passing through the point $$(2, -1, 1)$$ and perpendicular to the line having direction ratios $$4, 2, -3$$.
A line passes through the points (3,1, 2) and (5 , - 1, 1), find the direction ratios and direction cosines of the line.
Show that the following points are collinear:
$$P(3, -2, 4), Q(1, 1, 1)$$ and $$R(-1, 4, 2)$$.
Find the equation of the plane passing through the point $$(-1, 2, 1)$$ and perpendicular to the line joining the points $$(-3, 1, 2)$$ and $$(2, 3, 4)$$. Also, find the perpendicular distance of the origin from this plane.
Class 12 Commerce Maths Extra Questions
- Application Of Derivatives Extra Questions
- Application Of Integrals Extra Questions
- Continuity And Differentiability Extra Questions
- Determinants Extra Questions
- Differential Equations Extra Questions
- Integrals Extra Questions
- Inverse Trigonometric Functions Extra Questions
- Linear Programming Extra Questions
- Matrices Extra Questions
- Probability Extra Questions
- Relations And Functions Extra Questions
- Three Dimensional Geometry Extra Questions
- Vector Algebra Extra Questions