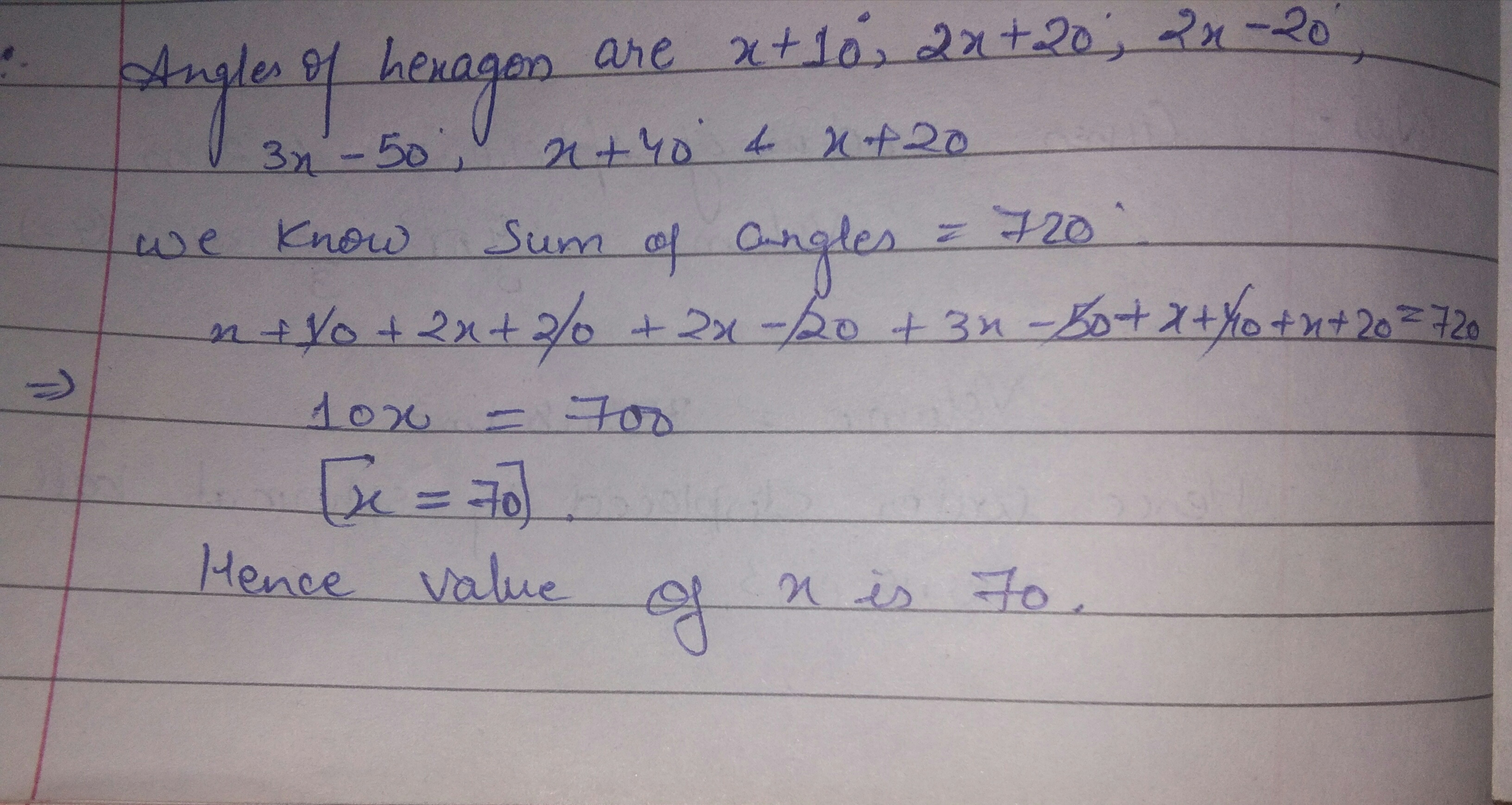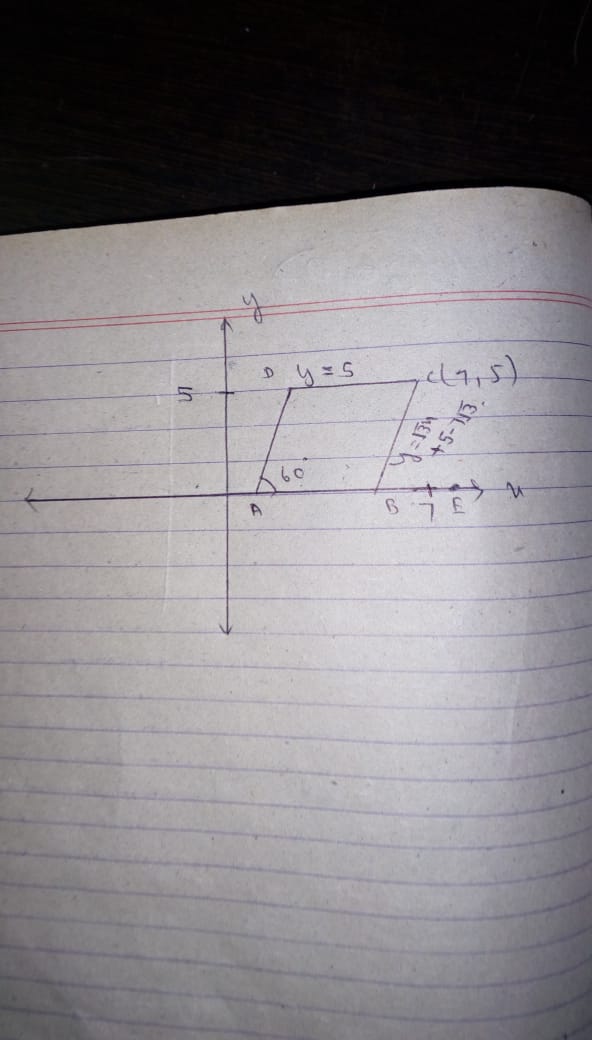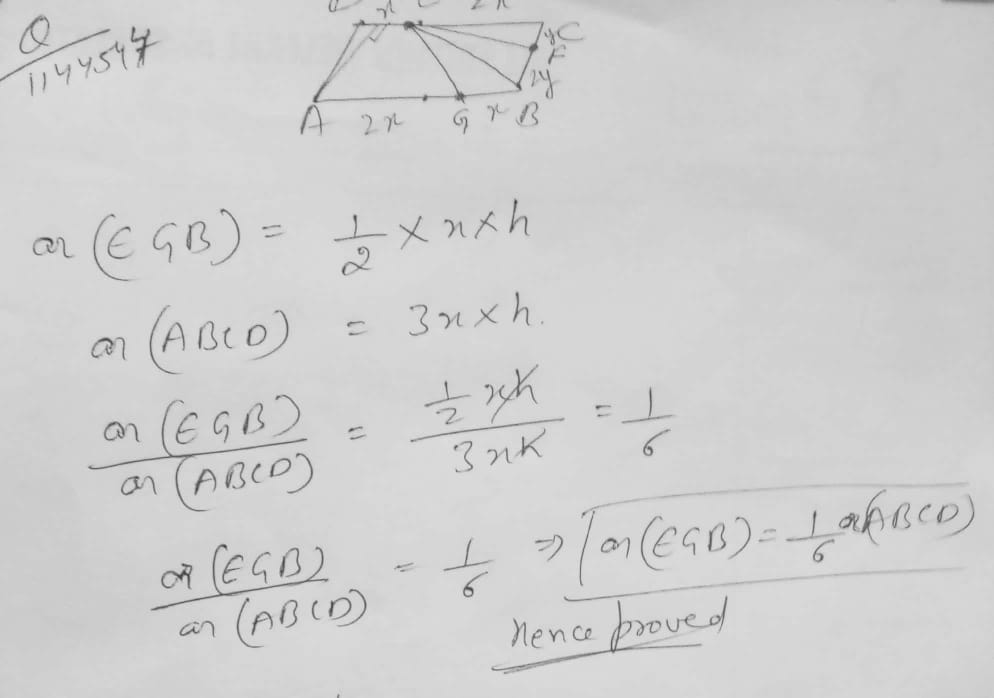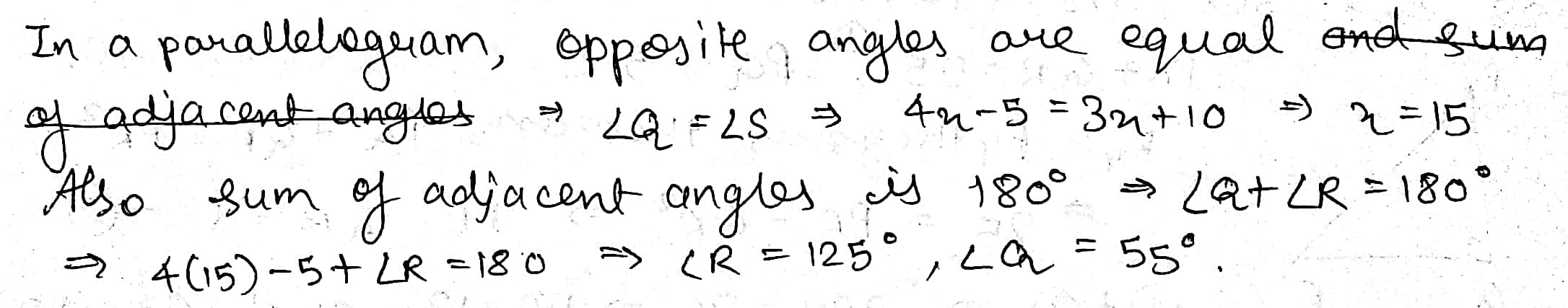Sum of interior angles of pentagon is 540
Understanding Quadrilaterals - Class 8 Maths - Extra Questions
Find the perimeter of a parallelogram with sides $$9\ cm$$ and $$5\ cm$$
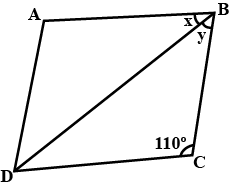
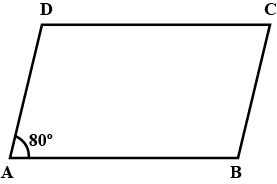
A, B, C, D is a parallelogram angle be $$80^o$$ find remain angles.
Justify the given statement: Rhombus is a parallelogram
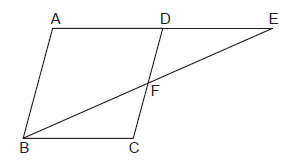
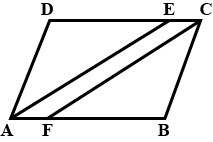
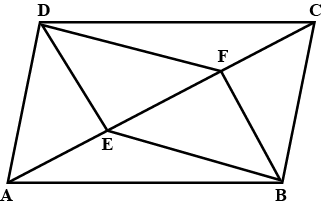
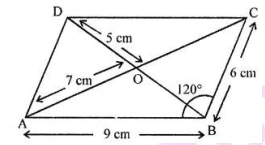
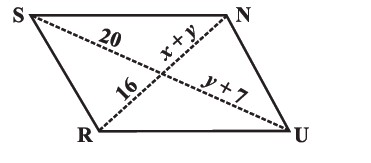
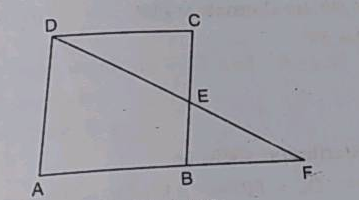
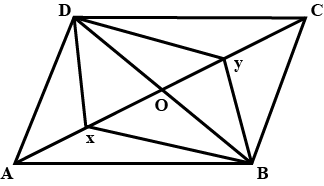
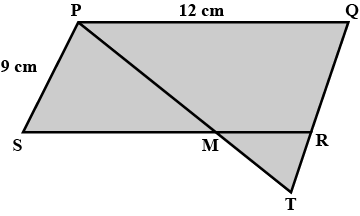
The following figure is a parallelogram.
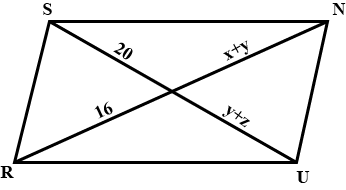
Find $$x + y$$. (Lengths are in cm)
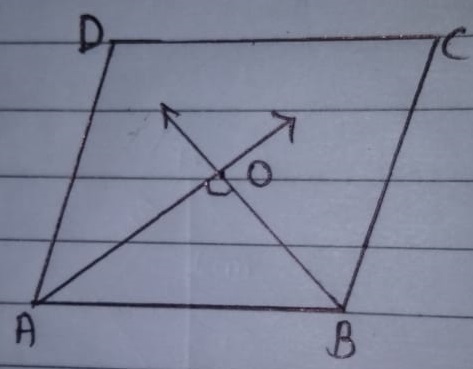
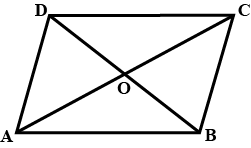
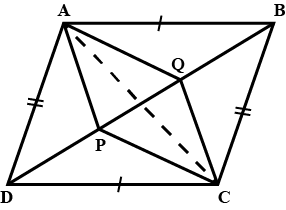
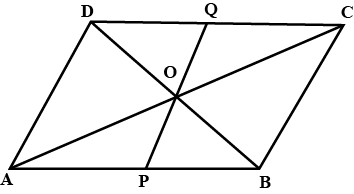
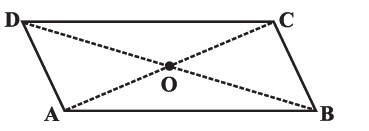
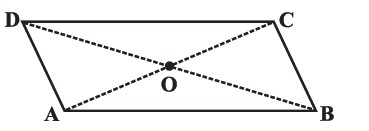
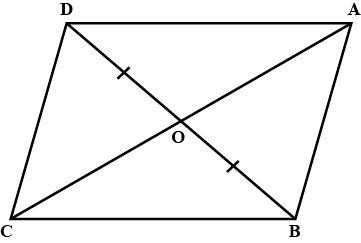
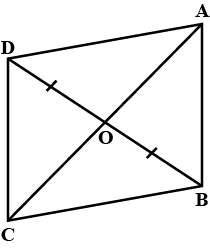
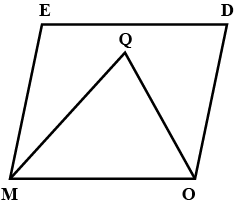
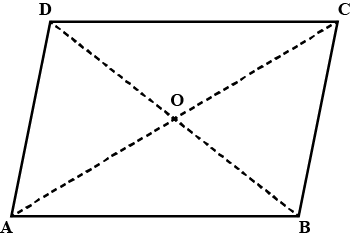
Given a parallelogram ABCD. Prove that $$OC = OA$$
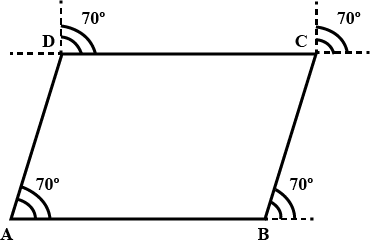
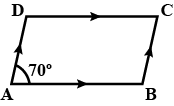
If one angle of a parallelogram is of measure $$70^{\circ}$$, find the measures of all the angles of the parallelogram.
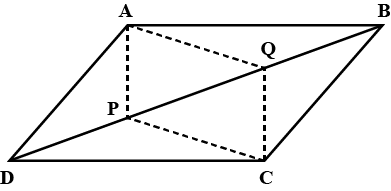
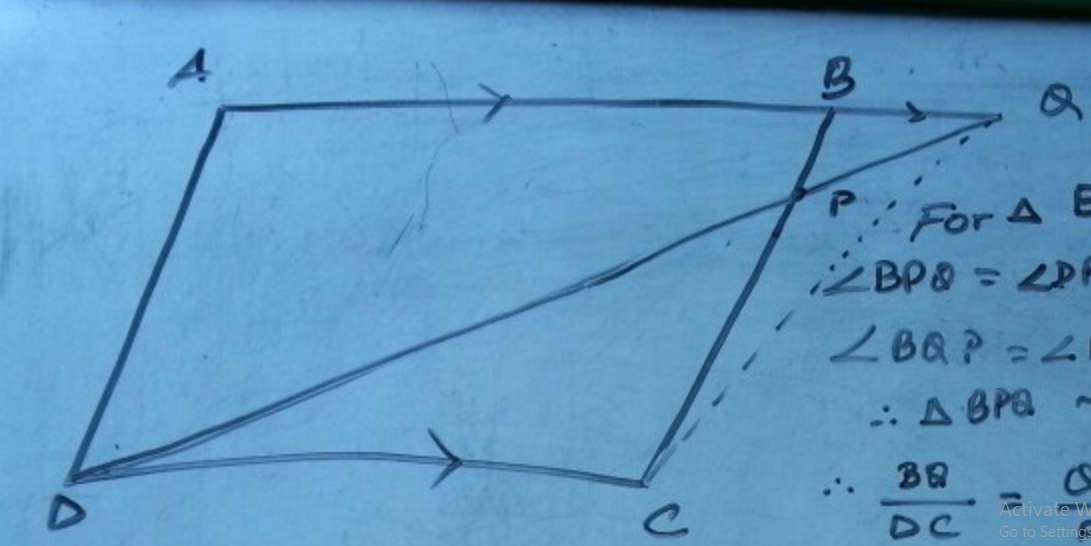
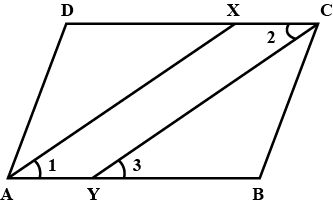
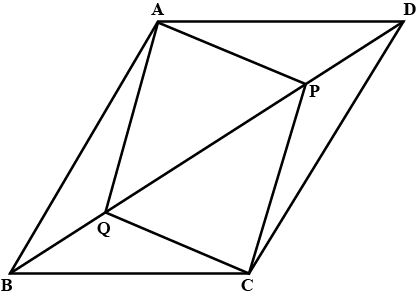
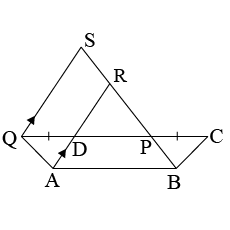
$$ABCD$$ is a parallelogram, a line through $$A$$ cuts $$DC$$ at point $$P$$ and $$BC$$ produced at $$Q$$ .
Prove that triangle $$BCP$$ is equal in area to triangle $$DPQ$$.
Given: In parallelogram $$ABCD,$$ $$AB\parallel CD$$ and $$AD\parallel BC$$
Now, join a line from $$A$$ to $$C$$
We get $$\triangle APC$$
We get $$\triangle APC$$
Here, $$\triangle ACP$$ and $$\triangle BCP$$ lie on the same base $$CP$$ and between the same parallels $$AB$$ and $$CP$$
Hence $$Area\left(\triangle ACP \right) =Area\left(\triangle BCP \right) $$ $$...(1)$$
Also, $$\triangle ADQ$$ and $$\triangle ADC$$ lie on the same base $$AD$$ and lie between the same parallels $$AD$$ and $$BC$$
$$\therefore \ \ Area\left( \triangle ADQ \right) =Area\left(\triangle ADC \right) $$ $$...(2)$$
$$\Rightarrow Area(\triangle ADQ)-Area(\triangle ADP) =Area\left(\triangle ADC \right) -Area\left(\triangle ADP \right) $$
$$\Rightarrow Area\left(\triangle APC \right) =Area\left(\triangle DPQ \right) $$ $$...(3)$$
From $$(1)$$ and $$(3),$$ we get
$$\Rightarrow Area\left( \triangle BPC \right) =Area\left(\triangle DPQ \right) $$
Explain why a rectangle is a convex quadrilateral.
$$ABCD$$ is a parallelogram and $$\angle A = 60^{\circ}$$. Find the remaining angles
Given : $$ABCD$$ is a parallelogram and $$\angle A=60^{\circ}$$
Solution :
We know that opposites angles of a parallelogram are equal.
Therefore,
$$\angle A=\angle C=60^{\circ}$$
Also, we know that $$\angle A+\angle B=180^{\circ}$$
$$60^{\circ}+\angle B=180^{\circ}$$
$$\angle B=120^{\circ}$$
$$\angle B=\angle D=120^{\circ}$$ (opposite angles of parallelogram)
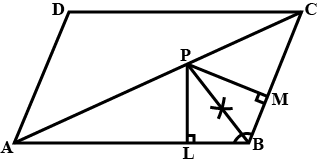
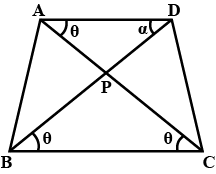
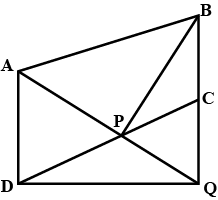
In the figure, $$ABCD$$ is a parallelogram in which the angle bisectors of $$\angle A$$ and $$\angle B$$ intersect at the point $$P$$. Prove that $$\angle APB = 90^{\circ}$$
Since, $$ABCD$$ is a Parallelogram.
Therefore,
$$AD || BC $$
$$AB$$ is a transversal.
Therefore,
$$A + B = 180°. [ Consecutive\ interior\ angles]$$
Multiply both sides by $$\dfrac{1}{2}$$,
$$\dfrac{1}{2} A + \dfrac{1}{2} B = \dfrac{1}{2}\times (180^0) $$
$$\dfrac{1}{2} A + \dfrac{1}{2} B = 90^0$$ $$..........(1)$$
Since, $$AP$$ and $$PB$$ are angle bisectors of $$A$$ and $$B$$.
Therefore,
$$\angle 1 = \dfrac{A}{2}$$
$$\angle 2 = \dfrac{B}{2}$$
Substitute the values in
$$\angle 1 + \angle 2 = 90^0$$ $$.........(2)$$
Now, in $$\triangle APB$$,
$$1 + APB + 2 = 180^0$$
$$90^0 + APB = 180^0$$ $$From\ equation\ (2)$$
$$\angle APB = 90^0$$
Hence, Proved.
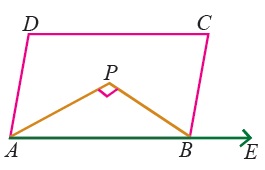
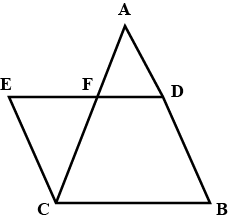
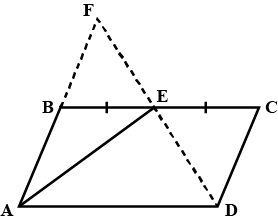
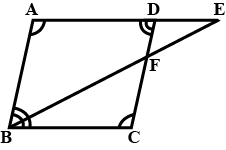
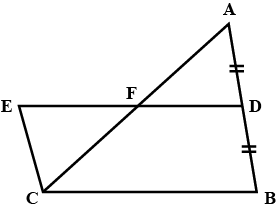
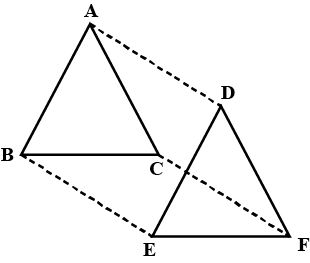
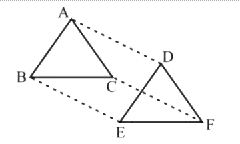
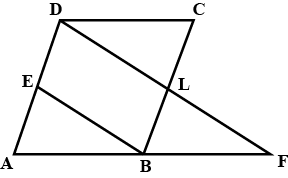
In $$\triangle^{s}ABC$$ and $$DEF, AB\parallel DE; BC = EF$$ and $$BC\parallel EF$$. Vertices, $$A, B$$ and $$C$$ are joined to vertices $$D, E$$ and $$F$$ respectively (see figure). Show that
quadrilateral $$BCFE$$ is a parallelogram
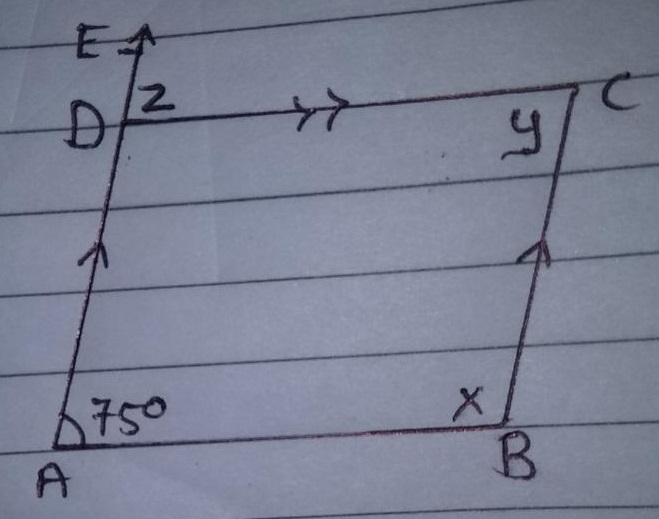
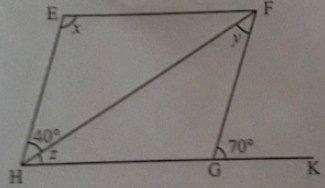
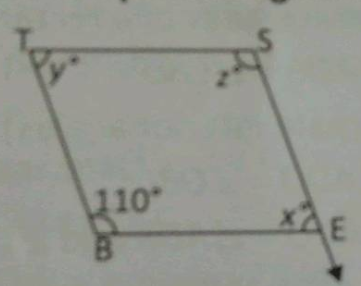
In figure, $$BEST$$ is a parallelogram. Find the values of $$x,\ y,\ z$$.
Name the type of quadrilateral formed by the points $$(4,5),(7,6),(4,3),(1,2)$$.
Point $$X$$ and $$Y$$ are taken on the sides $$QR$$ and $$RS$$, respectively of a parallelogram $$PQRS$$, so that $$QX = 4\ XR$$ and $$\vec {RY} = 4\vec {YS}$$. The line $$XY$$ cuts the line $$PR$$ at $$Z$$. Prove that $$\vec {PZ} = \left (\dfrac {21}{25}\right )\vec {PR}$$.
Let point P be taken as origin & $$\vec{q}\cdot \vec{r}$$ are the position vectors of Q & S points respectively.
$$\vec{PR}=\vec{q}+\vec{r}$$
Position vector of $$x=\dfrac{\vec{9}+4(\vec{q}+\vec{s})}{5}$$
$$=\dfrac{5\vec{q}+4\vec{s}}{5}$$
Position vector of $$y=\dfrac{4\vec{s}+\vec{q}+\vec{s}}{5}=\dfrac{\vec{q}+5\vec{s}}{5}$$
Let $$\dfrac{PZ}{ZR}=\dfrac{1}{\lambda}$$ & $$\dfrac{YZ}{ZX}=\mu$$
Position vector of $$P=\dfrac{\vec{q}+\vec{s}}{\lambda +1}=\dfrac{\mu\left(\vec{q}+\dfrac{4}{5}\vec{s}\right)+\left(\dfrac{\vec{q}}{5}+\vec{s}\right)}{\mu +1}$$
$$\Rightarrow \dfrac{1}{\lambda +1}=\dfrac{\mu +\dfrac{1}{5}}{\mu +1}$$ ........(i)
$$\Rightarrow \dfrac{1}{\lambda +1}=\dfrac{\dfrac{4\mu}{5}+1}{\mu +1}$$ ........(ii)
From eq (i) & eq (ii) we get
$$\mu =4$$ & $$\lambda =\dfrac{4}{21}$$
$$\Rightarrow \dfrac{PZ}{ZR}=\dfrac{21}{4}$$
$$\Rightarrow \dfrac{PZ}{PR}=\dfrac{21}{25}$$.
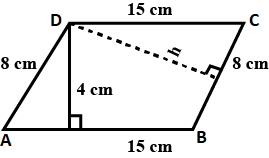
The adjacent side of a parallelogram are $$15\text{ cm}$$ and $$8\text{ cm}$$. If the distance between the longer sides is $$4\text{ cm}$$, find the distance between the shorter sides.
Let ABCD be a paralleogram
Given is that the adjacent sides of $$||$$gm are $$15 \text{ cm}$$ and $$8\text{ cm}$$.Area of parallelogram$$=15\times4=60\text{ cm }^{ 2 }$$
$$\because$$ (Area of parallelogram $$=$$ base$$\times$$height)
Similarly using the shorter side as base we can find area of the parallelogram to be
$$8\times h=60$$
$$\Rightarrow h=\cfrac { 15 }{ 2 } =7.5\text{ cm }$$
ABCD is a parallelogram, and AE and CF bisect $$\angle A $$ and $$\angle C$$ respectively. Prove that AE || FC.
Find the value of $$x,y$$ and $$z$$ from the given parallelograms.
Quadrilateral $$ABCD$$ is a parallelogram. Find the value of $$x$$ and measure of all the angles.
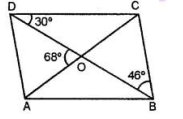
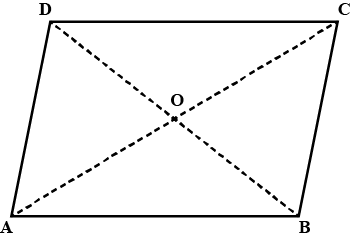
In a parallelogram $$ABCD,$$ the bisectors of $$\angle A$$ and $$\angle B$$ bisect at $$O.$$ Find $$\angle AOB.$$
We know that sum of adjacent angles in a parallelogram is $$180^o$$
$$\therefore$$ $$\angle A+\angle B=180^o$$
$$\Rightarrow$$ $$2x+2y=180^o$$
$$\therefore$$ $$x+y=90^o$$ ---- ( 1 )
In $$\triangle AOB,$$
$$\Rightarrow$$ $$x+y+\angle AOB=180^o$$ [ Sum of angles in a triangles is $$180^o$$ ]
$$\Rightarrow$$ $$90^o+\angle AOB=180^o$$ [ From ( 1 ) ]
$$\therefore$$ $$\angle AOB=90^o$$
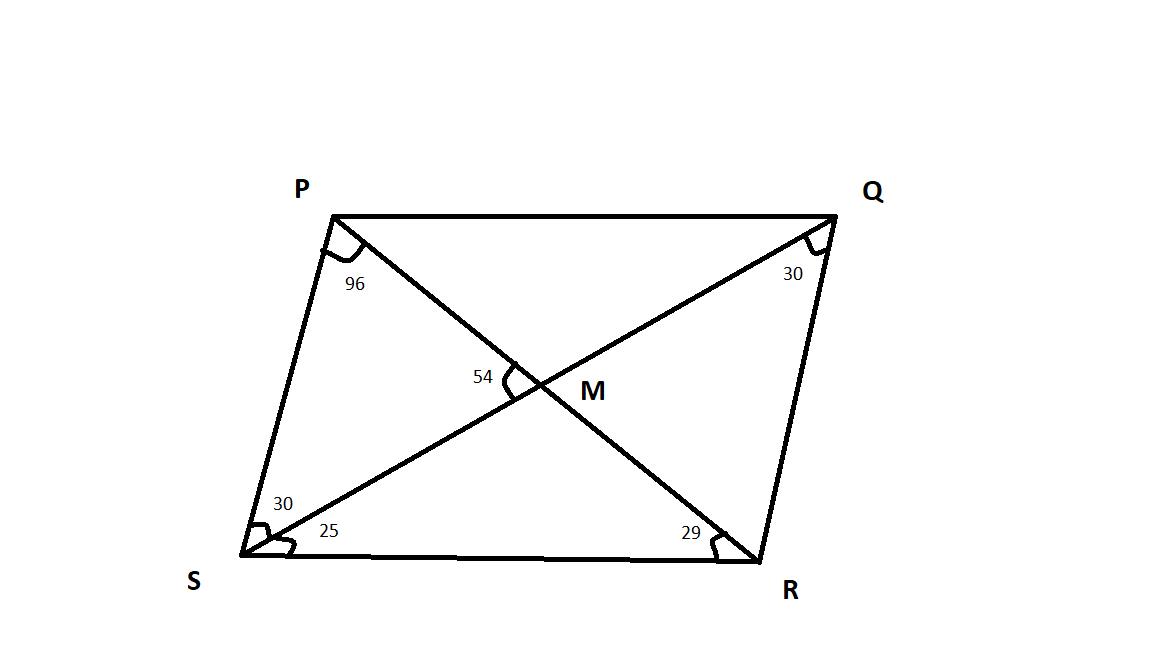
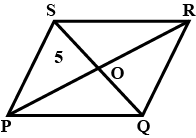
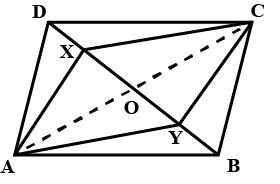
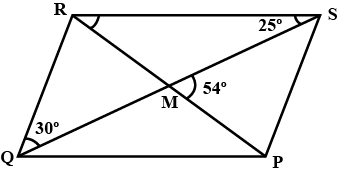
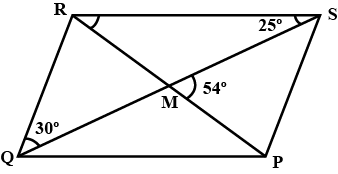
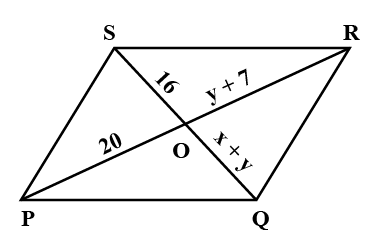
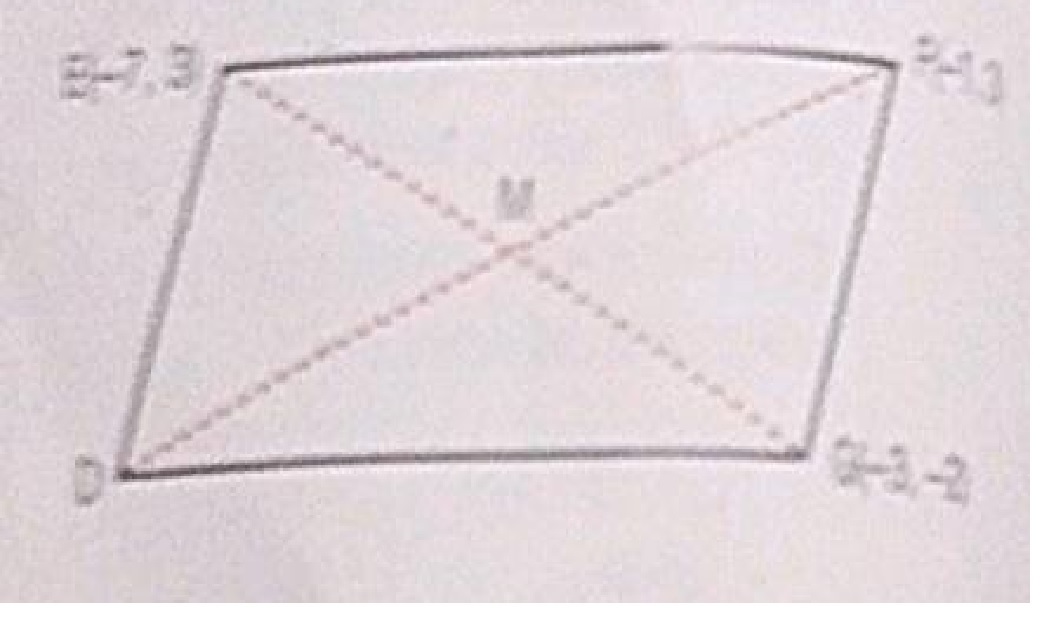
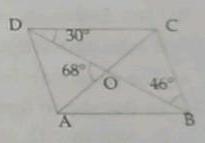
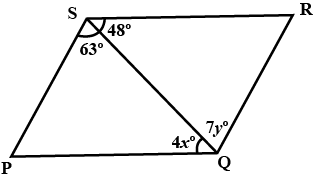
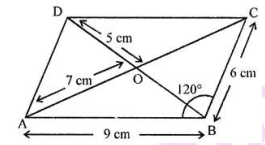
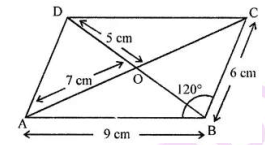
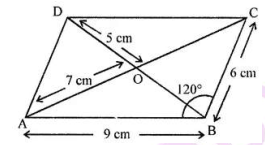
$$PQRS$$ is a parallelogram whose diagonals intersect at $$M$$.
If $$\angle PMS=54^{o}, \angle QSR=25^{o}$$ and $$\angle SQR=30^{o}$$; find:
i) $$\angle RPS$$
ii) $$\angle PRS$$
iii) $$\angle PSR$$.
we know that for this parallelogram;
$$\angle PMS =\angle QSR+\angle PRS;\\ \angle SQR= \angle PSQ;\\ \angle RPS+ \angle PMS+ \angle PSM=180^{\circ}\\ \implies \angle RPS=96^{\circ};\\ \angle PRS=29^{\circ} \\ \angle PSR= 55^{\circ}$$
In figure $$HELP$$ is parallelogram. if $$OE=4\ cm$$ and $$HL$$, is $$5\ cm$$ more then $$PE$$ Find $$OH$$.
we know that the diagonals of the parallelogram bisect each other.
$$OE=4$$
$$HL = 5+PE$$
$$PE=2OE,HL=2OH$$
$$2OH=5+2OE=5+8=13$$
$$OH=6.5\ cm$$
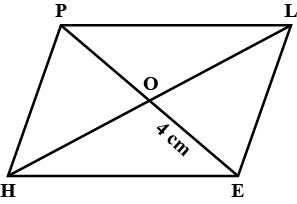
Figure given below, $$PQRS$$ is parallelogram, find the value $$x$$ and $$y$$.
$$PQRS$$ is a parallelogram.
So, opposite sides of parallelogram are parallel and equal.
$$\therefore$$ $$PQ=SR$$
$$\Rightarrow$$ $$5x=25$$
$$\therefore$$ $$x=5$$
$$\Rightarrow$$ $$3y-1=47$$
$$\Rightarrow$$ $$3y=48$$
$$\Rightarrow$$ $$y=16$$
$$\therefore$$ We get $$x=5$$ and $$y=16$$
The sum of two opposite angles of a parallelogram is $$130^o$$. Find the measure of each of its angles.
$$ABCD$$ is a parallelogram.
$$\angle B+\angle D=130^{\circ}$$
$$\angle B=\angle D$$ (opposite angles of a parallelogram are equal)
$$\angle B=\angle B=130^{\circ}$$
$$2\angle B=130^{\circ}$$
$$\angle B=\dfrac{130^{\circ}}{2}$$
$$\angle B=65^{\circ}$$
Now $$\angle B+\angle C=180^{\circ}$$ (adjacent angles of a parallelogram are supplementary )
$$\angle C=180^{\circ}-\angle B=180^{\circ}-65^{\circ}$$
$$\angle C=115^{\circ}$$
$$\therefore \angle A=\angle C=115^{\circ}$$ (opp. angles of parallelogram are equal)
$$\therefore \angle B=\angle D=65^{\circ}$$ and $$\angle A=\angle C=115^{\circ}$$
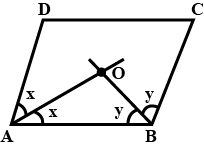
In a parallelogram $$ABCD,$$ the bisectors $$\angle A$$ and $$\angle B$$ meet at $$O.$$ Find $$\angle AOB.$$
$$\Rightarrow$$ $$\angle A+\angle B=180^o$$ [ Sum of adjacent angles of parallelogram are supplementary ]
$$\Rightarrow$$ $$\dfrac{1}{2}\angle A+\dfrac{1}{2}\angle B=\dfrac{180^o}{2}$$
$$\Rightarrow$$ $$\angle OAB+\angle OBA=90^o$$
In $$\triangle AOB$$
$$\Rightarrow$$ $$\angle OAB+\angle AOB+\angle OBA=180^o$$
$$\Rightarrow$$ $$\angle AOB=180^o-(\angle OAB+\angle OBA)$$
$$\Rightarrow$$ $$\angle AOB=180^o-(\angle OAB+\angle OBA)$$
$$\Rightarrow$$ $$\angle AOB=180^o-90^o$$
$$\therefore$$ $$\angle AOB=90^o$$
The adjacent figure ABCD is parallelogram
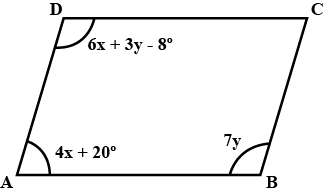
$$\angle A = 3\left( {x - 5} \right)$$, $$\angle B = \dfrac{x}{4}$$, $$\angle C = 2\left( {x + 22\frac{1}{2}} \right)$$ then show that $$\angle A + \angle B = {180^o}$$
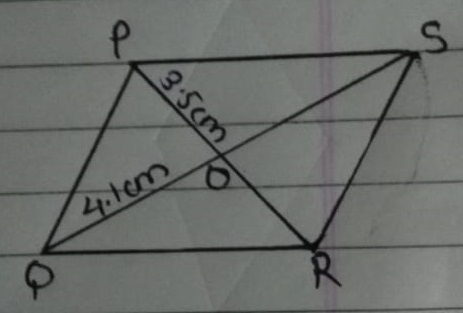
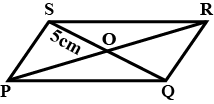
PQRS is a parallelogram and diagonals PR and SQ bisect at O. If PO$$=3.5$$cm and OQ$$=4.1$$ cm. What is the length of the diagonals?
$$PQRS$$ is a parallelogram where $$PR$$ and $$SQ$$ are diagonals.
$$PR$$ and $$SQ$$ bisect at $$O$$
$$PO=3.5\,cm$$ and $$OQ=4.1\,cm$$
$$\Rightarrow$$ $$PR=2\times PO=2\times 3.5\,cm=7\,cm$$
$$\Rightarrow$$ $$SQ=2\times OQ=2\times 4.1\,cm=8.2\,cm$$
$$\therefore$$ The length of the diagonals are $$7\,cm$$ and $$8.2\,cm$$
Two lines that are cut by a transversal are parallel, if the sum of any pair of interior angles on the same side on the transversal is _________?
In the given figure, the bisectors of $$\angle A$$ and $$\angle B$$ of parallelogram $$ABCD$$ meet at $$O$$. Find the measure of $$\angle AOB$$.
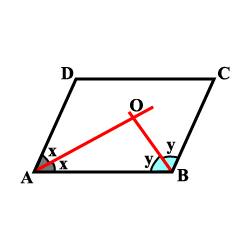
In a parallelogram PQRS, if $$\angle$$P is thrice $$\angle$$Q, find the angles.
We know that sum of adjacent sides of parallelogram is $$180^o.$$
$$\angle P+\angle Q=180^o$$
$$3x+x=180^o$$
$$4x=180^o$$
$$x=45^o$$
$$\Rightarrow$$ $$\angle Q=45^o$$
$$\Rightarrow$$ $$\angle P=3\times 45^o=135^o$$
We know that, opposite angles of a parallelogram are equal.
$$\therefore$$ $$\angle P=\angle R=135^o$$
$$\therefore$$ $$\angle Q=\angle S=45^o$$
In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP$$=$$BQ. Show that $$\Delta$$AQB$$\cong\Delta$$CPD.
Here, $$ABCD$$ is a parallelogram.
$$AB\parallel DC$$ and $$BD$$ is a transversal.
$$\therefore$$ $$\angle ABQ=\angle CDP$$ [ Alternate angles ] ---- ( 1 )
In $$\triangle AQB$$ and $$\triangle CPD,$$
$$\Rightarrow$$ $$AB=CD$$ [ Opposite sides of parallelogram are equal ]
$$\Rightarrow$$ $$\angle ABQ=\angle CDP$$ [ From ( 1 ) ]
$$\Rightarrow$$ $$BQ=DP$$ [ Given ]
$$\therefore$$ $$\triangle AQB\cong \triangle CPD$$ [ By SAS congruence ]
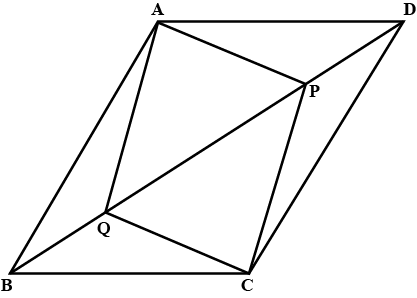
$$P$$ and $$Q$$ are the points of trisection of the diagonal $$BD$$ of a parallelogram $$ABCD$$. Prove that $$CQ$$ is parallel to $$AP$$.
In $$\triangle DPC$$ and $$\triangle BQA$$
$$DP=BQ$$
$$AB=CD$$
$$\angle CDP=\angle ABQ$$
$$\triangle DPC\cong \triangle BQA$$
$$\therefore CP=AQ,AP=CQ$$
$$\implies APCQ$$ is a parallelogram
$$\implies AP\parallel CQ$$
Two adjecnt angles of a parallelogram are equal measure. Find the measure of each angle.
Find x, y and z in the given parallelogram.
$$ABCD$$ is a given parallelogram, where $$AB\parallel CD$$ and $$AD\parallel BC$$
$$\Rightarrow$$ $$\angle A+\angle B=180^o$$ [ In parallelogram sum of adjacent angles is supplementary ]
$$\Rightarrow$$ $$75^o+x=180^o$$
$$\Rightarrow$$ $$x=105^o$$
$$\Rightarrow$$ $$\angle B=\angle D=105^o$$$$ [ In parallelogram opposite angles are equal ]
$$\Rightarrow$$ $$\angle A=\angle C=75^o$$ [ In parallelogram opposite angles are equal ]
$$\therefore$$ $$y=75^o$$
$$\Rightarrow$$ $$\angle ADC+\angle EDC=180^o$$ [ Linear pair ]
$$\Rightarrow$$ $$105^o+z=180^o$$
$$\Rightarrow$$ $$z=75^o$$
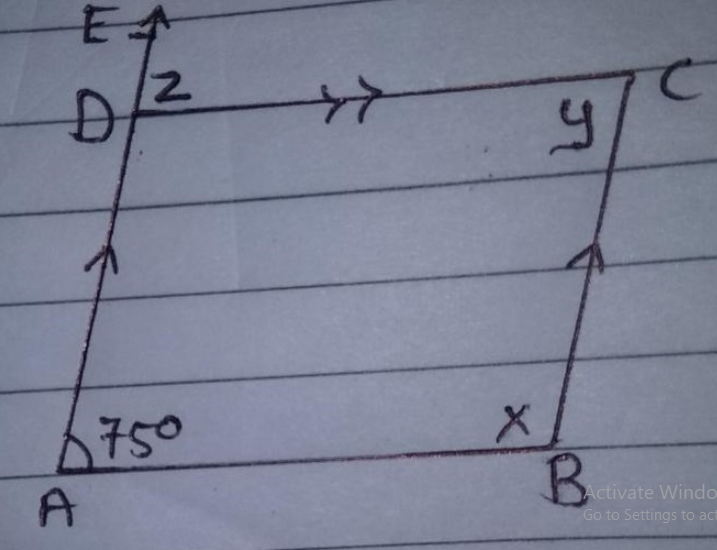
$$\Delta ABP$$ and parallelogram ABCD are on the same base AB and between the same parallels AB and PC.
Prove that $$ar(\Delta ABP) = \dfrac{1}{2} ar (ABCD)$$.
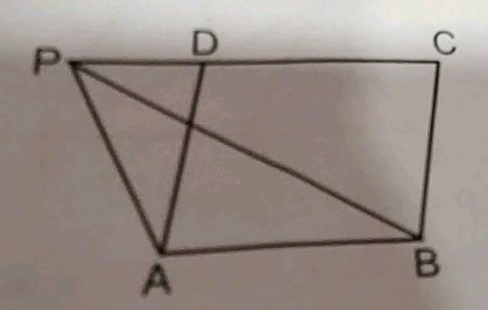
Find the measure of each angle of a $$parallelogram$$, one its angle is $$30$$ less than twice the smaller angle.
$$\Rightarrow$$ $$\angle A+\angle B=180^o$$ [ Sum of adjacent angles in parallelogram is supplementary ]
$$\Rightarrow$$ $$x+(2x-30)=180^o$$
$$\Rightarrow$$ $$3x-30=180^o$$
$$\Rightarrow$$ $$3x=210^o$$
$$\Rightarrow$$ $$x=70^o$$
$$\Rightarrow$$ $$\angle A=x=70^o$$
$$\Rightarrow$$ $$\angle B=(2x-30)^o=(2\times 70-30)^o=110^o$$
We know that opposite angles are equal in parallelogram
$$\therefore$$ $$\angle A=\angle C=70^o$$
$$\therefore$$ $$\angle B=\angle D=110^o$$
In a parallelogram $$ABCD$$, determine the sum of $$\angle C$$ and $$\angle D$$.
What is the length of side $$BD$$ in the parallelogram $$ABCD$$ ?
REF.Image.
Properties of parallelogram
opposite sides are congruent & equal, so
so,since AC = 85 cm
$$ \therefore BD \Rightarrow 85 cm $$
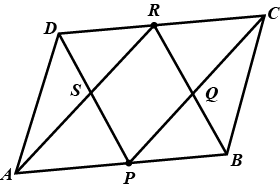
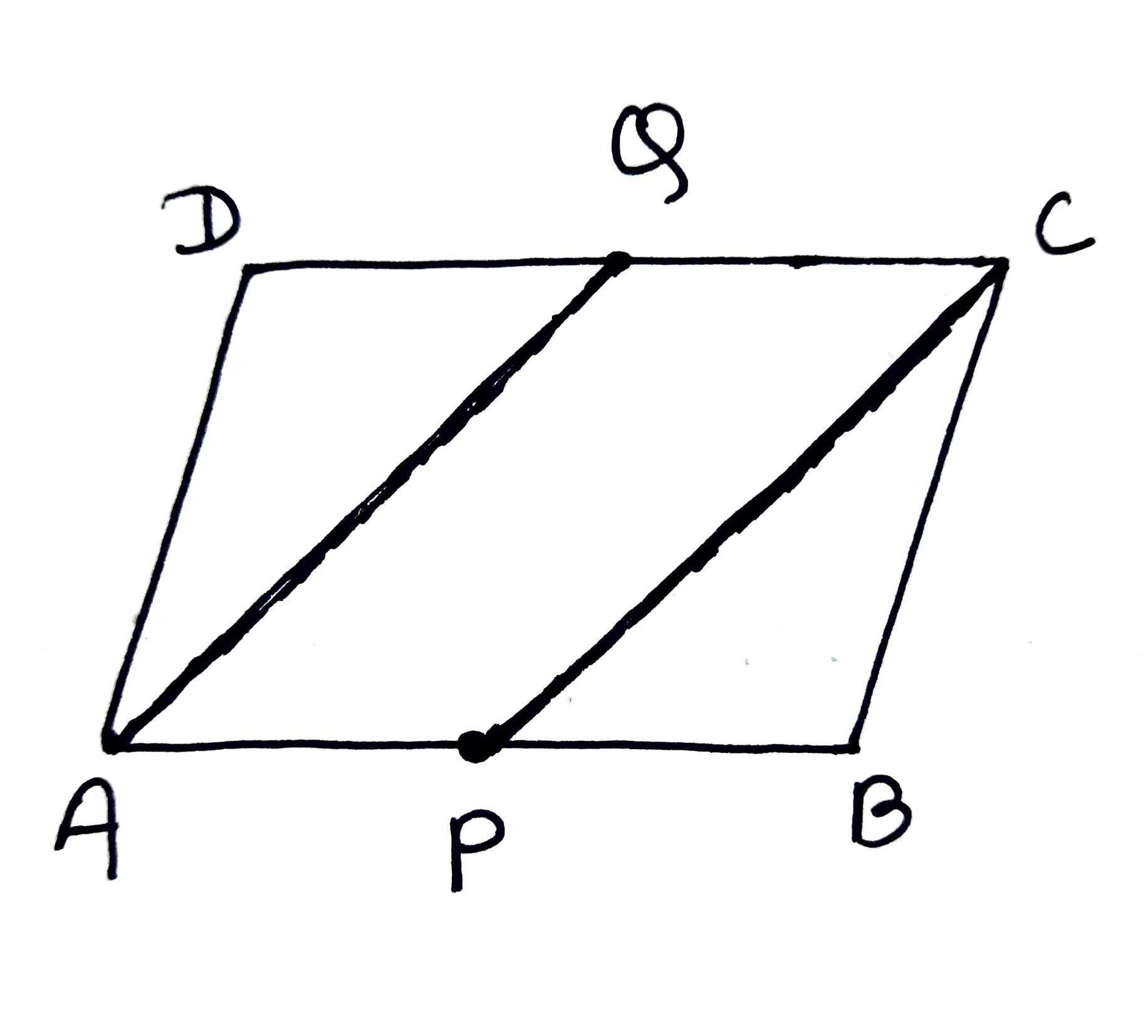
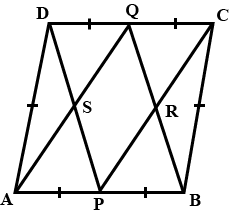
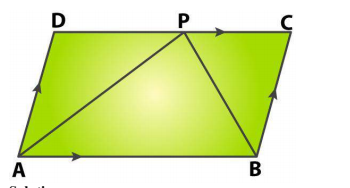
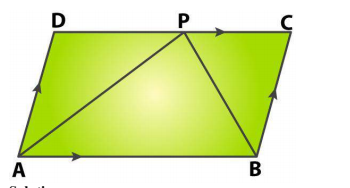
ABCD is a parallelogram. P is the mid-point of AB and R is the midpoint of DC as shown in the figure. Lines AR and DP intersect at S and lines PC and BR intersect at Q. Show that PQRS is a parallelogram.
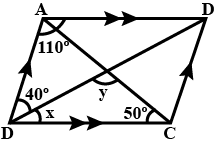
In the following parallelogram $$ABCD$$, find the values of $$x$$ and $$y$$. Mention the property used.
$$ABCD$$ is a parallelogram, with diagonals $$AC$$ and $$BD$$ intersect at point $$O$$.
$$\Rightarrow$$ $$\angle A+\angle B=180^o$$ [ Sum of adjacent angles are supplementary in parallel ]
$$\Rightarrow$$ $$110^o+(40^o+x)=180^o$$
$$\Rightarrow$$ $$150^o+x=180^o$$
$$\Rightarrow$$ $$x=30^o$$
In $$\triangle OBC,$$
$$\Rightarrow$$ $$\angle OBC+\angle BCO+\angle COB=180^o$$
$$\Rightarrow$$ $$x+50^o+y=180^o$$
$$\Rightarrow$$ $$30^o+50^o+y=180^o$$
$$\Rightarrow$$ $$80^o+y=180^o$$
$$\therefore$$ $$y=100^o$$
$$\therefore$$ $$x=30^o,y=100^o$$
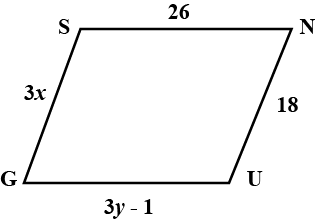
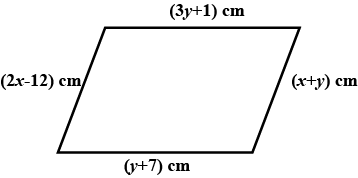
Find parameters of given parallelogram
In the following figures, find the area of the shaded portions.
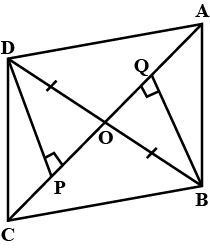
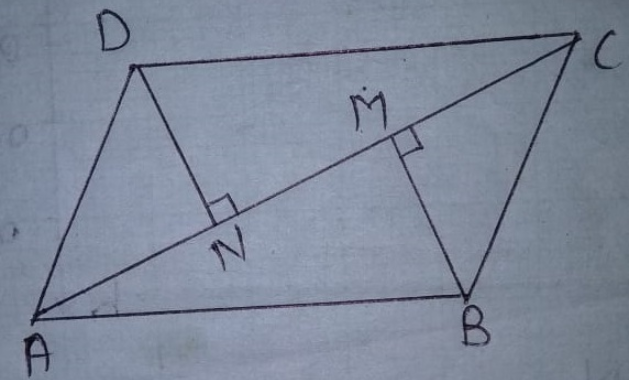
In the adjoining figure, $$ABCD$$ is a parallelogram.
$$BM \bot\ AC\ and \ DN \bot\ AC$$.
Prove that:
$$ \Delta\ BMC\cong \Delta\ DNA$$
$$BM=DN$$
$$ABCD$$ is a parallelogram then,
$$AD\parallel BC$$ and $$AC$$ is a transversal.
$$\therefore$$ $$\angle BCA=\angle DAC$$ [ Alternate angles ]
i.e. $$\angle BCM=\angle DAN$$ ---- ( 1 )
In $$\triangle BMC$$ and $$\triangle DNA$$$$\Rightarrow$$ $$BC=AD$$ [ Opposite sides of parallelogram are equal ]
$$\Rightarrow$$ $$\angle BCM=\angle DAN$$ [ From ( 1 ) ]
$$\Rightarrow$$ $$\angle BMC=\angle DNA$$ [ Both $$90^o.$$ ]
$$\therefore$$ $$\triangle BMC\cong \triangle DNA$$ [ By $$SAA$$ congruence rule ]
$$\therefore$$ $$BM=DN$$ [ By CPCT ]
In the figure given below, $$E$$ and $$F$$ are points on diagonal $$AC$$ of a parallelogram $$ABCD$$ such that $$AE=CF$$. Show that $$BFDE$$ is a parallelogram.
Join $$BD,$$ meet $$AC$$ at point $$O.$$
Since, diagonals of a parallelogram bisect each other.
$$\therefore$$ $$OA=OC$$
and $$OD=OB$$
Now, $$OA=OC$$
and $$AE=CF$$ [ Given ]
$$\Rightarrow$$ $$OA-AE=OC-CF$$
$$\Rightarrow$$ $$OE=OF$$
Thus, $$BFDE$$ is a quadrilateral whose diagonals bisect each other.
Hence, $$BFDE$$ is a parallelogram.
If one angle of a parallelogram is $$65 ^ { \circ } ,$$ find the measure of other angles.
As we know,
Opposite angles of a parallelogram are equal.
$$\implies \angle A =\angle C =65^{\circ } $$
and let us say that, $$\angle B = \angle D =\theta$$
$$\\65^{\circ}+\theta+65^{\circ}+\theta=360^{\circ}\\ 2\theta+130^{\circ}=360^{\circ}\\2\theta=230^{\circ}\\\therefore\theta=(\frac{230^{\circ}}{2})=115^{\circ}$$
$$\text{So angles are } 65^{\circ},65^{\circ},115^{\circ} $$and$$ 115^{\circ}$$.
The adjacent angles of a parallelogram are in the ratio $$2:1$$. Find the measure of all angles.
We know that the sum of the interior angles of a triangle is $${180^ \circ }$$ . show that the sum of the interior angles of polygons with $$3,4,5,6,\dots$$ sides form an arithmetic progression. find the sum of the interior angles for a $$21$$ sided polygon.
Given figure $$\text{ABCD}$$ is a parallelogram, $$\text{P}~\text{and}~\text{Q}$$ are midpoints of sides $$\text{AB}\ $$and $$\text{DC}$$ respectively, then prove that$$\text{ APCQ}$$ is a parallelogram.
$$P,Q$$ are mid-point of $$AB$$ and $$CD$$ respectively.
since $$AB\parallel DC$$ [ Opposite sides of parallelogram are parallel ]
$$\Rightarrow$$ $$AP\parallel QC$$ [ Parts of parallel lines are parallel ]
since $$AB=CD$$ [ Opposite sides of parallelogram are equal ]
$$\Rightarrow$$ $$\dfrac{1}{2}AB=\dfrac{1}{2}CD$$
$$\Rightarrow$$ $$AP=QC$$ [ $$P$$ is mid-point of $$AB$$ and $$Q$$ is mid-point of $$DC$$ ]
Since $$AP\parallel QC$$ and $$AP=QC$$
One pair of opposite sides of $$APCQ$$ is equal and parallel.
One pair of opposite sides of $$APCQ$$ is equal and parallel.
$$\therefore$$ $$APCQ$$ is a parallelogram.
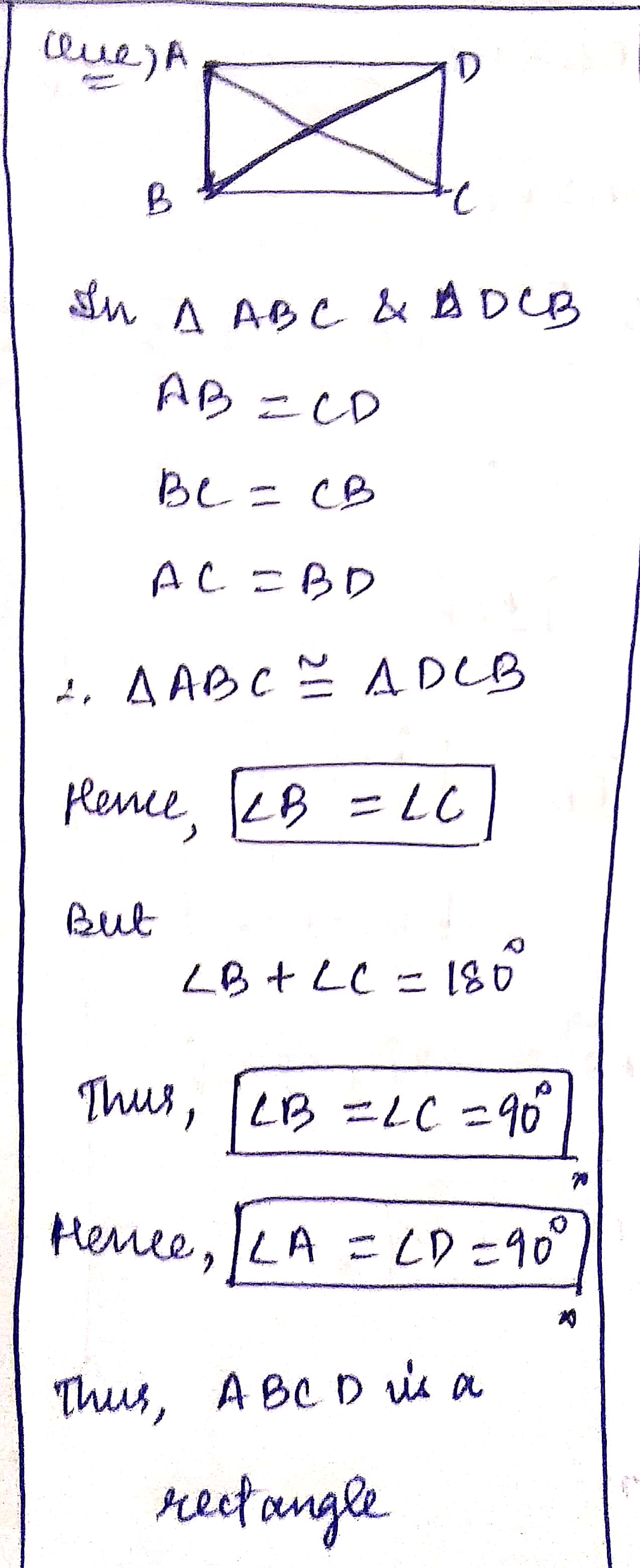
If the diagonals of a parallelogram are equal, then show that it is a rectangular.
Ref.Image
$$ \square $$ ABCD is a parallelogram
consider $$ \Delta $$ ACD and $$\Delta $$ ABD
AC = BD .... (given)
AB = DC .... (opposite sides of parallelogram)
AD = AD .... (common side)
$$ \therefore \Delta $$ ACD $$\cong \Delta $$ ABD (sss test of congruence)
$$\angle $$ BAD = $$ \angle $$ CDA .... (cpct)
$$\angle BAD+\angle CDA=180^{\circ}.$$ [Adjacent angles of parallelogram are supplementary]
so $$ \angle $$ BAD and $$\angle $$ CDA are right angles as they are congruent and supplementary.
Therefor, $$\square $$ ABCD is a rectangle since a
parallelogram with one right interior angle is a rectangle.
Two adjacent angles of a parallelogram are equal. What is the measure of each angle?
Fill in the blank
A quadrilateral with exactly one side parallel is a _______
The measure of one angle of a parallelogram is $$80^{\circ}$$. What are the measures of the remaining angles?
The opposite angles of a parallelogram are (3x-2) and (x+48) Find the measure of each angle of the parallelogram .
Draw and define a parallelogram. What would you call it if all its four sides are equal?
Parallelogram : It is a closed figure with two opposite sides parallel to one another.
The diagonals of a parallelogram bisect each other.
If all the four sides are equal, them the parallelogram is known as rhombus.
Prove that a diagonals of a parallelogram divides it into two congruent triangles.
Similarly another pair can also be shown congruent by drawing another diagonal and using same criteria of congruence
Two angles of a polygon are right angles and the remaining are $$120^{\circ}$$ each. Find the number of sides in it.
Given 2 angle is polygon are = $$90^{\circ}$$
remaining are = $$120^{\circ}$$
Let n be no. of sides in polygon
$$2\times 90^{\circ}\times +(n-2)\times 120^{\circ}=(2n-4)90^{\circ}$$
$$180+120n-240=180n-360$$
$$60n=540-240=300$$
$$[n=5]$$
If the diagonals of a parallelogram are equal, prove that it is rectangle.
R.E.F image
$$ In \bigtriangleup$$ ABC &$$ \bigtriangleup DCB $$
AB=CD
BC=CB
AC=BD
$$\therefore $$ $$\bigtriangleup ABC \cong \bigtriangleup DCB$$
Hence, $$[\angle B=\angle c]$$
But
$$ \angle B+\angle C=180^{\circ}$$
$$ Thus,[\angle B= \angle C=90^{\circ} ]$$
$$ Hence,[\angle A=\angle D=90^{\circ}]$$
Thus, ABCD is a rectangle
Fill in the blank
All rectangle, squares and rhombus are _________ but a trapezium is not.
Fill in the blank
The diagonal of this quadrilateral are equal but not perpendicular. The quadrilateral is a _______
Show that A (-1, 0), B(3,1), C(2,2) and D(-2,1) are the vertices of a parallelogram ABCD.
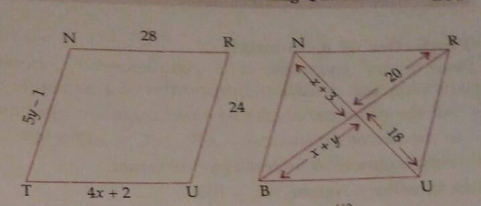
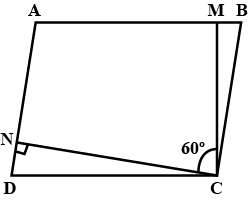
In the adjoining figures $$TURN$$ and $$BURN$$ are parallelograms. Find the measures of $$x$$ and $$y$$ where the lengths are in centimeter.
All rectangles are parallelograms, but all parallelograms are not rectangles. Justify this statement.
Write two properties of parallelogram.
Find the measure of each interior angle of a regular polygon of
$$9\ sides$$
The opposite of a parallelogram $$ (3x-2)$$ and $$(x+48)$$. Find the measure of each angle at the parallelogram.
ABCD is a parallelogram .if $$\angle A=60^{\circ}$$Find other angles
Define:
Convex polygon and concave polygon
If the sum of opposite angles of a paarallelogram is $$120^{\circ}$$ Find the all its angles.
Sum of opposite angles of parallelogram is $$120$$
Let x be opposite angle of parallelogram. [opp 2s of parallelograms are equal]
$$2x=120$$
$$[x=60^o]$$
Now two angle of Parallelogram are $$=60^o$$ each
Now, let y be adjacent angle of parallelogram to $$60^o$$, then
$$60^o+y=180$$
$$[y=120^o]$$
$$\therefore$$ Angles of parallelogram are $$60^o, 60^o, 120^o$$ & $$120^o$$.
One angle of a pentagon is $$140^{o}$$. If the remaining angles are in the ratio $$1:2:3:4$$. What is the size of the largest angle?
The angles of a hexagon are $$x+$$$$10^{\circ}$$, $$2x$$ $$ +20^{\circ}, 2x-20^{\circ},3x-50^{\circ},x+40^{\circ}$$ and $$x+20^{\circ}. $$Find $$x.$$
$$\therefore $$ Angles of hexagon are $$x+10^{\circ},2x+20^{\circ},2x-20^{\circ}$$
3x-50,x+40 & x+20
We know sum of angles = 720
x+10+2x+20+2x-20+3x-50+x+40+x+20=720
$$\Rightarrow 10x=700$$
x=70
Hence value of x is 70.
In the following figure , ABCD is a parallelogram . Find the value x,y and z .
Fill in the blanks to make the statements true.
Adjacent angles of a parallelogram are ________ .
State whether the following statements are true (T) or false (F):
The diagonal of a parallelogram are equal.
State whether the following statements are true (T) or false (F):
All sides of a parallelogram are equal in length.
Solve the following :
The adjacent of a parallelogram are $$ (2x - 4)^{\circ} $$ and $$ (3x - 1)^{\circ} $$ . Find the measures of all angles of the parallelogram.
In the given figure, $$ A B C D $$ is a parallelogram. Complete each statement along with the definition or property used.
$$ \mathrm{AD}=\ldots \ldots \ldots \ldots $$
Fill in the blanks the statements are true.
A trapezium with 3 equal sides and one side double the equal side can be divided into ________ equilateral triangles of ________ area.
3, equal
Let ABCD is a trapezium in which
AD=DC=BC= a and AB = 2a
Draw medians through the vertices D and C on the side AB
AE=EB=a
Now in parallelogrma ADCE, we have
AD= EC= a and AE = CD=a
{ parallelogram has equal opposite sides}
In triangle ADE and DEC,
AD= EC, AE= CD, DE=BC
Thus, the triangles ADE and DEC are equilateral triangles having equal sides, which means trapezium can be divided into 3 equilateral triangles of equal area.
In the given figure, $$ A B C D $$ is a parallelogram. Complete each statement along with the definition or property used.
$$ \mathrm{DC}=\ldots \ldots \ldots $$
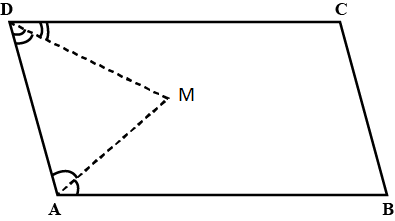
In parallelogram $$ABCD$$, side $$AB$$ is greater than side $$BC$$ and $$P$$ is a point in $$AC$$ such that $$PB$$ bisects angle $$B$$. Prove that $$P$$ is eqidistant from $$AB$$ and $$BC$$.
Construction: From $$P$$, draw $$PL\bot AB$$ And $$PM\bot BC$$
Proof: In $$\triangle PLB$$ and $$\triangle PMB$$
$$\angle PLB=\angle PMB$$ (Each $${ 90 }^{ o }$$)
$$\angle PBL =\angle PBM$$ (Given)
$$PB=PB$$ (Common)
Thus, by AAS criterion of congruence
$$\triangle PLB\cong \triangle PMB$$
And, by Corresponding Parts of Congruent Triangle (CPCT)
$$PL=PM$$
Therefore, $$P$$ is equidistant from $$AB$$ and $$AC$$
Proof: In $$\triangle PLB$$ and $$\triangle PMB$$
$$\angle PLB=\angle PMB$$ (Each $${ 90 }^{ o }$$)
$$\angle PBL =\angle PBM$$ (Given)
$$PB=PB$$ (Common)
Thus, by AAS criterion of congruence
$$\triangle PLB\cong \triangle PMB$$
And, by Corresponding Parts of Congruent Triangle (CPCT)
$$PL=PM$$
Therefore, $$P$$ is equidistant from $$AB$$ and $$AC$$
Solve the following :
Two adjacent angles of a parallelogram are in the ratio $$ 1 : 3 $$ . Find its angles.
If the diagonals of a parallelogram are equal lengths, the parallelogram is a rectangle. Prove it.
Given : parallelogram $$ABCD$$ in which $$AC=BD$$
To prove: $$ABCD$$ is rectangle
Proof: In $$\Delta ABC$$ and $$\Delta ABD$$
$$AB=AB$$ (Common)
$$AC=BD$$ (given)
$$BC=AD$$ (opposite sides of parallelogram)
$$\triangle ABC=\triangle ABD\ (s.s.s.rule)$$
$$\angle A=\angle B$$
But $$AD//BC$$ (opp. sides of || Gm are
$$\angle A+\angle B=180^{0}$$
$$\angle A=\angle B=90^{o}$$
Similarly $$\angle D=\angle C=90^{o}$$
Hence $$ABCD$$ is a rectangle.
To prove: $$ABCD$$ is rectangle
Proof: In $$\Delta ABC$$ and $$\Delta ABD$$
$$AB=AB$$ (Common)
$$AC=BD$$ (given)
$$BC=AD$$ (opposite sides of parallelogram)
$$\triangle ABC=\triangle ABD\ (s.s.s.rule)$$
$$\angle A=\angle B$$
But $$AD//BC$$ (opp. sides of || Gm are
$$\angle A+\angle B=180^{0}$$
$$\angle A=\angle B=90^{o}$$
Similarly $$\angle D=\angle C=90^{o}$$
Hence $$ABCD$$ is a rectangle.
In a parallelogram $$ABCD$$, if $$\angle\,C = {80^ \circ }$$ then what is the measure of $$\angle\,A?$$
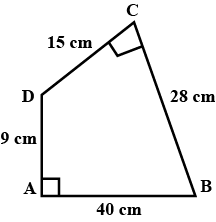
A parallelogram AXZ has two sides 60 m and 25 m and a diagonal 65 m long. Find z.
Given a parallelogram ABCD. Prove that $$\angle DCB=\angle DAB$$
A parallelogram has two sides 60 m and 25 m and a diagonal 65 m long. Find z
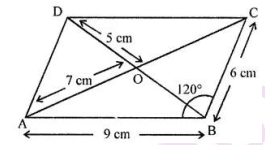
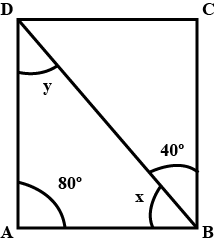
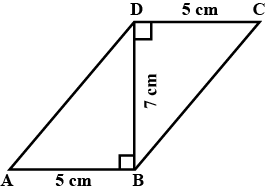
The following figure is a parallelogram.
Find $$x + y$$. (Lengths are in cm)
Given a parallelogram ABCD. Prove that $$ AD = BC$$
A parallelogram has two sides 60 m and 25 m and a diagonal 65 m long. Find z.
$$ Let\quad us\quad rename\quad the\quad given\quad figure\quad as\quad ABCD\quad when\\ \angle A=x,\quad \\ \angle B=suppimentery\quad of\quad the\quad external\quad angle\quad z,\quad (linear\quad pair),\\ \angle C=y,\quad \\ \angle D={ 50 }^{ o }.\\ Now\quad \angle B=\angle D\quad \& \quad \angle A=\angle C\quad (opposite\quad angles\quad of\quad a\quad parallelogram\quad are\quad equal).....(i)\\ \quad \therefore \quad \angle B={ 50 }^{ o }\Longrightarrow z={ 180 }^{ o }-{ 50 }^{ o }={ 130 }^{ o }\\ Again\quad AB\parallel DC.\quad i.e\quad \angle A+\angle D={ 180 }^{ o }\quad \quad (sum\quad of\quad the\quad same\quad sided\quad internal\quad angles={ 180 }^{ o }.)\\ \therefore \quad \angle A=x={ 180 }^{ o }-{ 50 }^{ o }={ 130 }^{ o }.....(ii)\\ But\quad by\quad (i)\quad \angle A=\angle C.\quad i.e\quad x=y.\\ or\quad y={ 130 }^{ o }\quad (from\quad ii).\\ So\quad x={ 130 }^{ o },\quad y={ 130 }^{ o },\quad z={ 130 }^{ o }.\\ Ans-x={ 130 }^{ o },\quad y={ 130 }^{ o },\quad z={ 130 }^{ o }.\quad \\ \\ $$
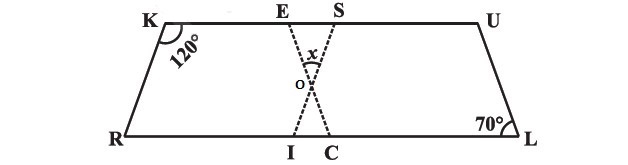
In the above figure, both $$RISK$$ and $$CLUE$$ are parallelograms. Find the value of $$x.$$
The measures of two adjacent angles of a parallelogram are in the ratio $$3 : 2$$. Find the measure of smallest of the angles of the parallelogram(in degree).
In a parallelogram PQRS , OS$$=5$$cm and PR is $$6$$cm more than QS. Find OP.
Given
$$OS=5\ cm$$
$$QS=2(OS)$$
$$QS=10\ cm$$
$$PR=QS+6=16\ cm$$
$$OP=\dfrac{1}{2}(PR)=\dfrac{1}{2}(16)=8\ cm$$
$$OP=8 \ cm$$
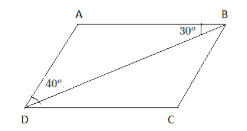
In figure, $$\square$$ABCD is a parallelogram. $$\angle ADB = 40^o, \angle ABD = 30^o$$, find the measure of $$\angle BAD- \angle DCB+ \angle ADC-\angle ABC$$
The three vertices of a parallelogram taken in order are $$(-1, 0)$$, $$(3, 1)$$ and $$(2, 2)$$ respectively. Find the coordinates of the fourth vertex.
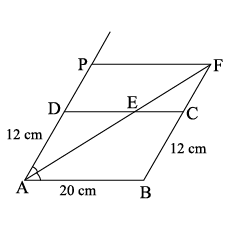
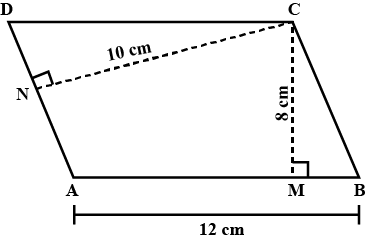
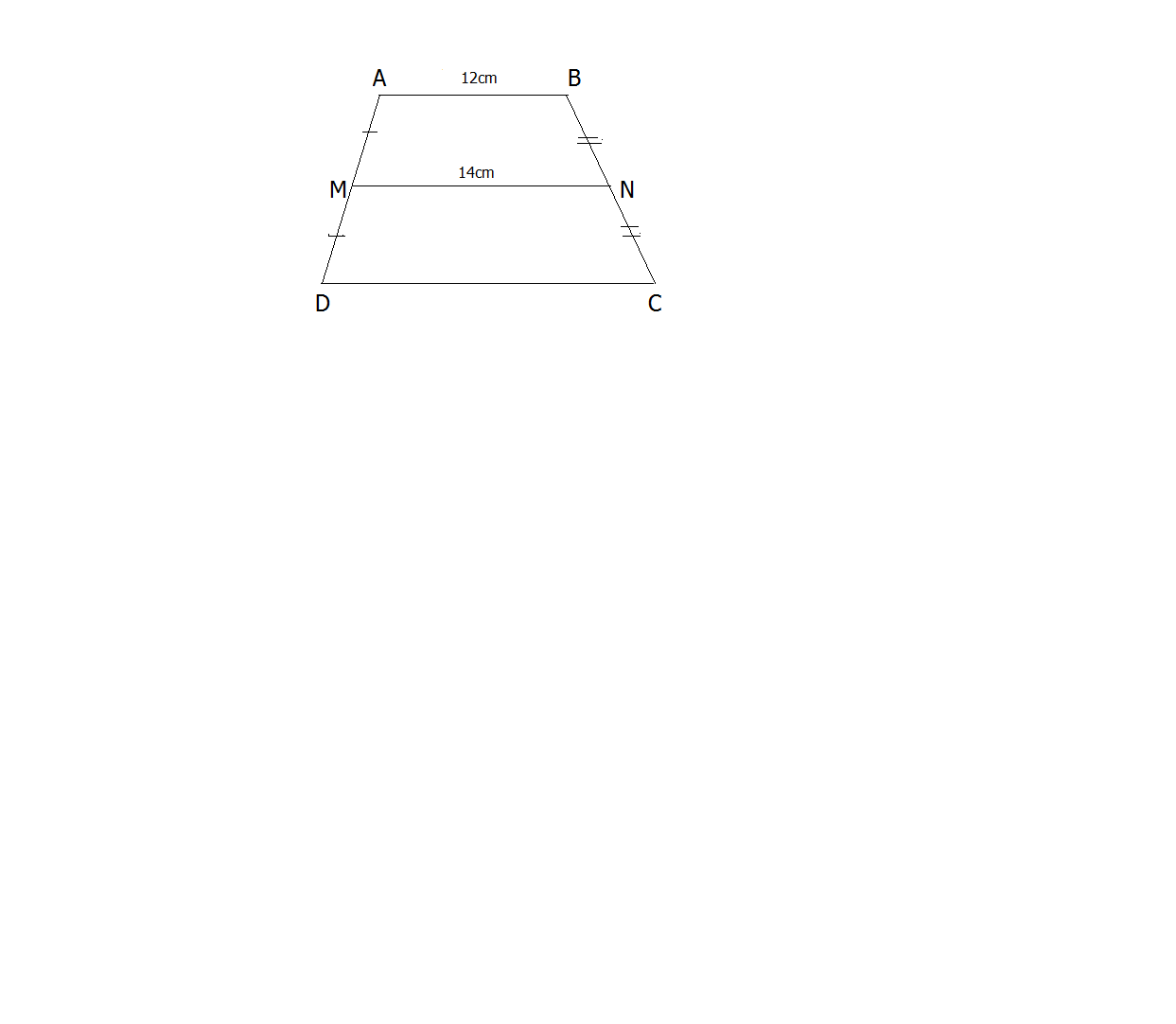
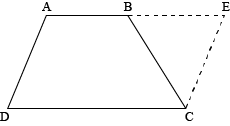
$$ABCD$$ is a trapezium in which $$AB || DC$$. $$M$$ and $$N$$ are mid-points of side $$AD$$ and side $$BC$$ respectively. If $$AB= 12\ cm $$and $$MN =14\ cm$$ , find $$CD$$
One side of a parallelogram is $$4.8$$ cm and the other side is $$\displaystyle \frac{3}{2}$$ times the first side, find the perimeter of the parallelogram
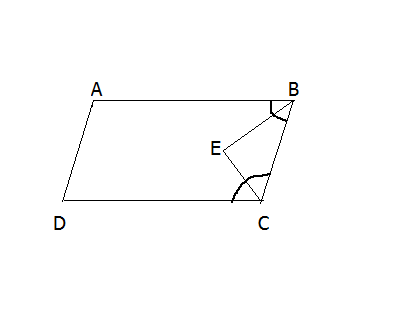
In a parallelogram ABCD, the bisectors of angles at B and C intersect each other at point E. Prove that angle BEC is equal to a right angle.
$$
Given\quad ABCD\quad is\quad a\quad parallelogram.$$
Given\quad ABCD\quad is\quad a\quad parallelogram.$$
$$\angle B\quad \& \quad \angle C\quad are\quad adjacent\quad angles\quad in\quad the\quad parallelogram $$
$$so,\quad \angle B+\angle C={ 180 }^{ 0 }\Rightarrow \angle B={ 180 }^{ 0 }-\angle C\quad ---\left( 1 \right) $$
$$Given\quad that\quad EB\quad \& \quad EC\quad are\quad angle\quad bisectors\quad for\quad \angle B\quad \& \quad \angle C\quad respectively.$$
$$So,\quad \angle EBC=\dfrac { 1 }{ 2 } \angle B\quad \& \quad \angle ECB=\dfrac { 1 }{ 2 } \angle C$$
$$ Now\quad in\quad \triangle BEC,\quad \angle EBC+\angle ECB+\angle CEB={ 180 }^{ 0 }$$
$$ \Rightarrow \dfrac { 1 }{ 2 } \angle B+\dfrac { 1 }{ 2 } \angle C+\angle CEB=180$$
$$ \Rightarrow \angle CEB+\dfrac { 1 }{ 2 } \left( \angle B+\angle C \right) =180\\ \Rightarrow \angle CEB+\dfrac { 1 }{ 2 } \times 180={ 180 }^{ 0 }\quad \left\{ from\quad (1) \right\} $$
$$\Rightarrow \angle CEB+{ 90 }^{ 0 }={ 180 }^{ 0 }$$
$$ \Rightarrow \angle CEB={ 90 }^{ 0 }$$
$$ \Rightarrow \angle CEB\quad is\quad a\quad right\quad angle.\\
$$
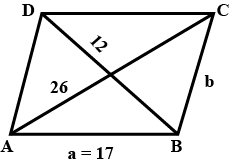
$$
Adjacent sides of a parallelogram are $$11\text{ cm}$$ and $$17\text{ cm}$$. If the length of one of its diagonals is $$26\text{ cm}$$. Find the length of the other.
Two adjacent angles of a parallelogram have equal measure. Find the measure of each of the angles of the parallelogram.
In a parallelogram $$ABCD$$, $$P$$ is a point on side $$AD$$ such that $$3AP = AD$$ and $$Q$$ is a point on $$BC$$ such that $$3CQ = BC$$. Prove that $$AQCP$$ is a parallelogram.If true answer is 1,else 0
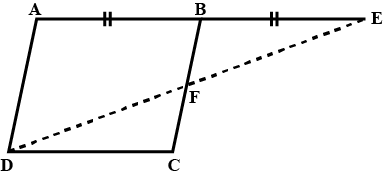
In quadrilateral ABCD, AB=DC and AD= BC, and the side AB and DC are parallel to each other.
If the above statement is true for any such quadrilateral to exist then mention the answer as 1, else mention 0 if false.
In the given figure, $$D$$ is mid-point of side $$AB$$ of $$\bigtriangleup \: ABC$$ and $$BDEC$$ is a parallelogram.
Prove that:
$$Area \: of \:\bigtriangleup \:ABC \: = \: Area \: of\: || \ gm \:BDEC $$.
D is the mid point of side AB of $$\triangle ABC$$
BDEC is a parallelogram.
$$AD=DB$$ (D is the mid point of AB)
Also,
$$DB=CE$$ (opposite side of parallelogram)
$$\therefore AD=CE$$
and $$\triangle ADF \cong \triangle CFE$$
$$\therefore Area of \triangle ADF=Area of \triangle CFE$$
$$=>Area of \triangle ADF+Area of quadrilateral CBDF=Area of \triangle CFE+Area of quadrilateral CBDF$$
$$=>Area of \triangle ABC=Area of parallelogram BDEC$$
BDEC is a parallelogram.
$$AD=DB$$ (D is the mid point of AB)
Also,
$$DB=CE$$ (opposite side of parallelogram)
$$\therefore AD=CE$$
and $$\triangle ADF \cong \triangle CFE$$
$$\therefore Area of \triangle ADF=Area of \triangle CFE$$
$$=>Area of \triangle ADF+Area of quadrilateral CBDF=Area of \triangle CFE+Area of quadrilateral CBDF$$
$$=>Area of \triangle ABC=Area of parallelogram BDEC$$
The sum of the interior angles and the sum of exterior angles of a polygon are in the ratio $$9 : 2$$. Find the number of sides in the polygon.
In parallelogram $$ABCD$$, $$AB = (3x - 4)$$ cm, $$BC = (y - 1) $$ cm, $$CD = (y + 5)$$ cm and $$AD = (2x + 5) $$ cm, find the ratio $$AB : BC$$.
Answer: $$41 : 35$$
Mention answer as 1 if true else mention 0 if false
parallelogram ABED;
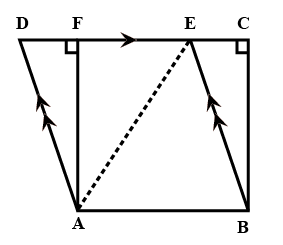
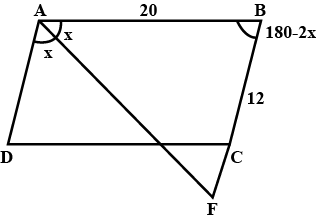
In a parallelogram ABCD, AB = 20 cm and AD = 12 cm. The bisector of angle A meets DC at E and BC produced at F. Find the length of CF.
Given $$ AB = 20 cm, AD = 12 cm $$
$$ DC = AB = 20 cm $$ and $$ AD = BC = 12 cm $$
Given that bisector of $$ \angle A $$ intersects $$ DC$$ at $$E$$ and $$BC$$ produced at $$F$$.
Draw $$ PF \parallel CD $$
From the figure, $$ CD \parallel FP $$ and $$ CF \parallel DP $$
Hence $$ PDCF $$ is a parallelogram.
$$ AB \parallel FP $$ and $$ AP \parallel BF $$
$$ABFP$$ is also a parallelogram
Consider $$ \triangle APF $$ and $$ \triangle ABF $$
$$ \angle APF = \angle ABF $$ [Since opposite angles of a parallelogram are equal]
$$ AF = AF $$ (Common side)
$$ \angle PAF = \angle AFB $$ (Alternate angles)
$$ \triangle PAF \cong \triangle BFA $$ (By ASA congruence criterion)
$$ DC = AB = 20 cm $$ and $$ AD = BC = 12 cm $$
Given that bisector of $$ \angle A $$ intersects $$ DC$$ at $$E$$ and $$BC$$ produced at $$F$$.
Draw $$ PF \parallel CD $$
From the figure, $$ CD \parallel FP $$ and $$ CF \parallel DP $$
Hence $$ PDCF $$ is a parallelogram.
$$ AB \parallel FP $$ and $$ AP \parallel BF $$
$$ABFP$$ is also a parallelogram
Consider $$ \triangle APF $$ and $$ \triangle ABF $$
$$ \angle APF = \angle ABF $$ [Since opposite angles of a parallelogram are equal]
$$ AF = AF $$ (Common side)
$$ \angle PAF = \angle AFB $$ (Alternate angles)
$$ \triangle PAF \cong \triangle BFA $$ (By ASA congruence criterion)
$$ AB = AP $$
$$ AB = AD + DP $$
$$ = AD + CF $$ [Since $$DCFP$$ is a parallelogram]
$$ CF = AB - AD $$
$$ = (20 -12) cm = 8 cm $$
$$ AB = AD + DP $$
$$ = AD + CF $$ [Since $$DCFP$$ is a parallelogram]
$$ CF = AB - AD $$
$$ = (20 -12) cm = 8 cm $$
Consider the following parallelograms. Find the values of the unknowns : $$x,y,z$$.
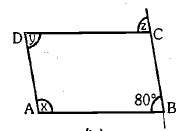
The adjacent figure HOPE is a parallelogram. find the angle measures $$x, y$$ and $$z$$. State the properties you use to find them.
$$\textbf{Step 1: Calculating y and z}$$
$$\text{HE || OP and HO || EP }$$
$$\text{Considering the parallel lines HE and OP}$$
$$\angle EHO = \angle POX -----\text{Corresponding angles are equal}$$
$$\implies40+z=70$$
$$\implies z=30$$
$$\angle EHP = \angle HPO ----\text{Interior alternate angles are equal}$$
$$\implies y=40$$
$$\textbf{Step 2: Calculating x}$$
$$\text{Considering the parallel line HO and EP}$$
$$\angle PEH + \angle EHO = 180 ----\text{Interior angles on the same side of transversal are supplementary}$$
$$\implies 70+x=180$$
$$\implies x=110$$
$$\textbf{Therefore, the angles x,y and z measure }\mathbf{110 ,40}\textbf{ and }\mathbf{ 30}\textbf{ respectively}$$
In the given fig ABCD is a quadrilateral P, Q,R,and S are the points of trisection of the sides of AB,BC,CD< and DA, respectively Prove that PQRS is a parallelogram
In the given figure (not to scale) ABC is an isosceles triangle in which AB = AC. AEDC is parallelogram. If $$\displaystyle \angle CDF = 70^{\circ}$$ and $$\displaystyle \angle BFE = 100^{\circ}$$ then find $$\displaystyle \angle FBA$$.
Three vertices of a parallelogram $$ABCD$$ are $$A (3, -1, 2), B(1, 2, -4)$$ and $$C (-1, 1, 2)$$. Find the coordinates of the fourth vertex.
The measures of two adjacent angles of a parallelogram are in the ratio $$3 : 2$$. Find the measure of each of the angles of the parallelogram.
In a quadrilateral $$ABCD, \angle A$$ and $$\angle C$$ are of of equal measure; $$\angle B$$ is supplementary to $$\angle D$$. Find the measure of $$\angle A$$ and $$\angle C$$
In the given Figure, diagonals $$AC$$ and $$BD$$ of quadrilateral $$ABCD$$ intersect at $$O$$ such that $$OB = OD$$. If $$AB = CD$$, then show that :
(i) $$ar(DOC) = ar(AOB)$$
(ii) $$ar(DCB) = ar(ACB)$$
(iii) $$DA\parallel CB$$ or $$ABCD$$ is a parallelogram.
Construction:
Draw $$DE \bot AC$$ and $$BF \bot AC$$.
In $$\triangle DEO$$ and $$\triangle BFO$$
$$\angle DEO= \angle BFO$$ ....By construction
$$\angle DOE= \angle BOF$$ ....Vertically opposite angles
$$OD = OB$$ .....Given
$$\triangle DOE \cong \triangle BOF$$ ...SAA test of congruence ....(1)
$$\therefore DE=BF$$ .... CSCT ....(2)
and
$$OE = OF$$ ... CSCT ....(3)
In $$\triangle DCE$$ and $$\triangle BFA$$
$$\angle DEC= \angle BFA$$ ..... By construction
$$DC = AB$$ ....Given
$$DE = BF$$ ....From (2)
$$\triangle DEC \cong \triangle BFA$$ .....(RHS) Right Hypotenuse Side test ....(4)
$$\therefore EC = AF$$ ......C.S.C.T. ....(5)
Similarly, we can prove $$\triangle DOA \cong \triangle BOC$$ ....(6)
Adding (1) and (2), we get
$$OE+EC = OF+AF$$
$$\therefore OC = OA$$ .....(7)
(i) Adding (1) & (4), we get,
$$A(\triangle DOE) + A (\triangle DEC) = A (\triangle BOF) + A (\triangle BFA) $$
$$\therefore A(\triangle DOC) = A (\triangle BOA)$$ ....(8)
(ii) Adding (6) and (8), we get
$$A (\triangle DOC) + A (\triangle DOA) = A (\triangle BOA) + A (\triangle BOC) $$
$$\Rightarrow A (\triangle ACD) = A (\triangle ACB)$$
(iii) So, from (7) and given,
$$ \Box ABCD$$ is a parallelogram .....(Diagonals bisect each other)
and $$DA \parallel CB$$ ....Opp. sides of parallelogram are parallel to each other
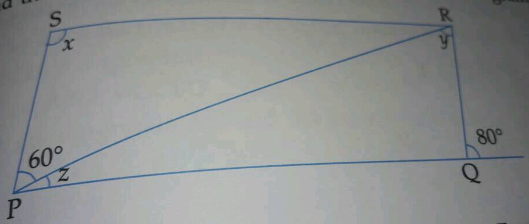
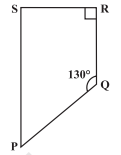
Find the measure of $$\angle P$$ and $$\angle S$$ if $$\overline {SP}\parallel \overline {RQ}$$ & in Fig.
(If you find $$m\angle R$$, is there more than one method to find $$m\angle P?$$)
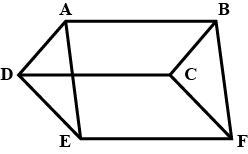
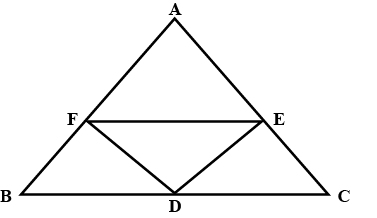
$$D, E$$ and $$F$$ are respectively the mid-points of the sides $$BC, CA$$ and $$AB$$ of a $$\triangle ABC$$. Show that
(i) $$BDEF$$ is a parallelogram
(ii) $$ar(DEF) = \dfrac {1}{4} ar(ABC)$$
(iii) $$ar(BDEF) = \dfrac {1}{2} ar(ABC)$$
In $$\Delta ABC$$,
E and F are midpoints of side AC and AB
Therefore, $$EF\parallel BC$$ and $$EF= \dfrac{1}{2} BC$$
Similarly, $$ED \parallel AB$$ and $$ED= \dfrac{1}{2} AB$$
Since, $$EF \parallel BC$$ $$\Rightarrow EF||BD$$ and $$ED \parallel FB$$
$$\therefore \Box BDEF $$ is a parallelogram.
Similarly, $$ED \parallel AB$$ and $$ED= \dfrac{1}{2} AB$$
Since, $$EF \parallel BC$$ $$\Rightarrow EF||BD$$ and $$ED \parallel FB$$
$$\therefore \Box BDEF $$ is a parallelogram.
(ii)Using above concept , we will have BDEF, CDFE,DFAE, are parallelogram ,
And as we know that diagonal of parallelogram divides it into two triangles of equal area
$$\therefore A(\Delta BDF) = A(\Delta DFE) = A(\Delta CDE) = A(\Delta AFE)$$
$$A(\Delta BDF) + A(\Delta DFE) + A(\Delta CDE) + A(\Delta AFE) = A(\Delta ABC)$$
$$A(\Delta DFE)= \dfrac{1}{4} A(\Delta ABC)$$
(iii) Using the relation in (ii), we have
$$A(\Box BDEF)= A(\Delta DBF)+ A(\Delta DFE)$$
$$A(\Box BDEF)= A(\Delta DBF)+ A(\Delta DFE)$$
and $$A(\Delta BDF) = A(\Delta DFE) = A(\Delta CDE) = A(\Delta AFE) = \dfrac{1}{4} A(\Delta ABC)$$
$$A(\Delta BDEF)= A(\Delta DBF)+ A(\Delta DFE) = \dfrac{1}{4} A(\Delta ABC)+\dfrac{1}{4} A(\Delta ABC) = \dfrac{1}{2} A(\Delta ABC) $$
In the given Figure, $$ABCD, DCFE$$ and $$ABFE$$ are parallelograms. Show that $$ar(ADE) = ar(BCF)$$.
The adjacent angles of a parallelogram are in the ratio $$2 : 1$$. Find the measures of all the angles
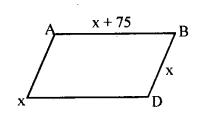
A field is in the form of a parallelogram, whose perimeter is $$450\ m$$ and one of its sides is larger than the other by $$75\ m$$. Find the lengths of all sides
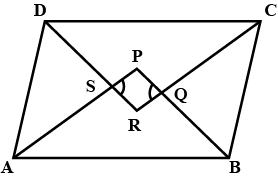
Prove that the quadrilateral formed by the bisectors of the four angles of a parallelogram is a rectangle.
Given: A quadrilateral $$ABCD$$ in which bisector of angles $$A,B,C,D$$ intersect at $$P,Q,R,S$$ to from a quadrilateral $$PQRS$$
Refer image,
To prove: $$PQRS$$ is a rectangle.
Proof: Since $$ABCD$$ is a parallelogram.
Therefore, $$AB||DC$$
Now, $$AB||DC$$ and transversal $$AD$$ intersect them at $$D$$ and $$A$$ respectively.
Therefore,
$$\angle A+\angle D=180^0$$ ($$\because$$ Sum of consecutive interior angles is $$180^0$$)
$$\Rightarrow \dfrac{1}{2}\angle A+\dfrac{1}{2}\angle D=90^0$$
$$\angle DAS+\angle ADS=90^0....(i)$$
($$\because$$ $$DS$$ and $$AS$$ are bisectors of $$\angle A$$ and $$\angle D$$ respectively)
But, in $$\Delta DAS$$, we have
$$\angle DAS+\angle ASD+\angle ADS=180^0$$ ($$\because$$ Sum of the angles of a triangle is $$180^0$$)
$$\Rightarrow \angle ASD+90^0=180^0$$ [Using (1)]
$$\Rightarrow \angle ASD=90^0$$
$$\Rightarrow \angle PSR=90^0$$ [$$\because \angle ASD$$ and $$\angle PSR$$ are vertically opposite angles $$\therefore \angle PSR=\angle ASD$$]
Similarly, we can prove that
$$\angle SRQ=90^0,\angle RQP=90^0$$ and $$\angle SPQ=90^0$$
Hence, $$PQRS$$ is a rectangles.
Prove logically the diagonals of a parallelogram bisect each other. Show conversely that a quadrilateral in which diagonals bisect each other is a parallelogram
We have to prove that the diagonals bisect each other in a parallelogram $$ABCD.$$
$$\angle ABE\simeq \angle CDE$$ ( by alternate interior angles )
$$\angle DEC\simeq \angle BAE$$ ( alternate interior angles )
$$\angle ABE\simeq \angle CDE$$ by ASA
$$\Rightarrow \left\{ AE=CE\\ BE=CE \right\} $$ coordinate sides of $$\cong $$ triangle
$$\angle CED\cong \angle BEA$$ [ vertical angles ]
$$\triangle AEB\cong \triangle DEC$$ [ by $$SAS\cong A's$$ ]
$$\angle CDE\cong \angle BAE$$ [ coordinate angles of $$\cong $$ triangles. ]
$$\therefore AB\parallel CD$$ by alternate interior angles $$\cong$$ of parallel lines.
$$\angle AEC\cong \angle DEB$$ ( vertical angles )
$$\triangle AEC\cong \triangle DEB$$ ( by SAS )
$$\angle CAE\cong \angle BDE$$ [ coordinate angle ]
$$\therefore AC \parallel BC$$ by alternate interior angles
Theorm :
A quadrilateral is a parallelogram if and only if the diagonals bisect each other.
Hence, the answer proved.
Suppose $$ABCD$$ is a parallelogram and the diagonals intersect at $$E$$. Let $$PEQ$$ be a line segment with $$P$$ on $$AB$$ and $$Q$$ on $$CD$$. Prove that $$PE = EQ$$.
$$ABCD$$ is a parallelogram and the diagonals intersect at $$E$$.
Let $$PEQ$$ be a line segment with $$P$$ on $$AB$$ and $$Q$$ on $$CD$$.
Consider the triangles $$PEB$$ and $$DEQ$$.
$$∠PEB = ∠DEQ$$ [Vertically opposite angles]
$$DE = BE$$ [Diagonals of a parallelogram bisect each other.]
$$∠EDQ = ∠EBP$$ [Alternate angles]
$$∴ ΔPEB ≅ ΔDEQ$$
$$⇒ PE = EQ$$ [CPCT]
Hence proved.
In a quadrilateral $$ABCD$$, suppose $$AB = CD$$ and $$AD = BC$$. prove that $$ABCD$$ is a parallelogram.
In quadrilateral ABCD, we have $$AB= CD$$ and $$AD=BC$$
$$\Rightarrow$$ Now, join segment AC.
$$\Rightarrow$$ In $$\triangle ABC$$ and $$\triangle ACD$$, we have
$$\Rightarrow$$ AB = CD [Given]
$$\Rightarrow$$ AD = BC [Given]
$$\Rightarrow$$ AC = AC [Common side]
So, by SSS criteria,
$$\Rightarrow$$ $$\triangle ABC \cong \triangle ACD$$
$$\therefore$$ $$\angle$$DAC = $$\angle$$BCA [By CPCT]
$$\therefore$$ $$CD\parallel AB$$ [$$\because$$ Alternate angles are equal] ---- ( 1 )
$$\Rightarrow$$ $$\angle DCA = \angle CAB$$ [By CPCT]
$$\therefore$$ $$AD\parallel BC$$ [$$\because$$ Alternate angles are equal] --- ( 2 )
From ( 1 ) and ( 2 ) we get that opposite sides of quadrilateral are parallel.
$$\therefore$$ ABCD is a parallelogram.
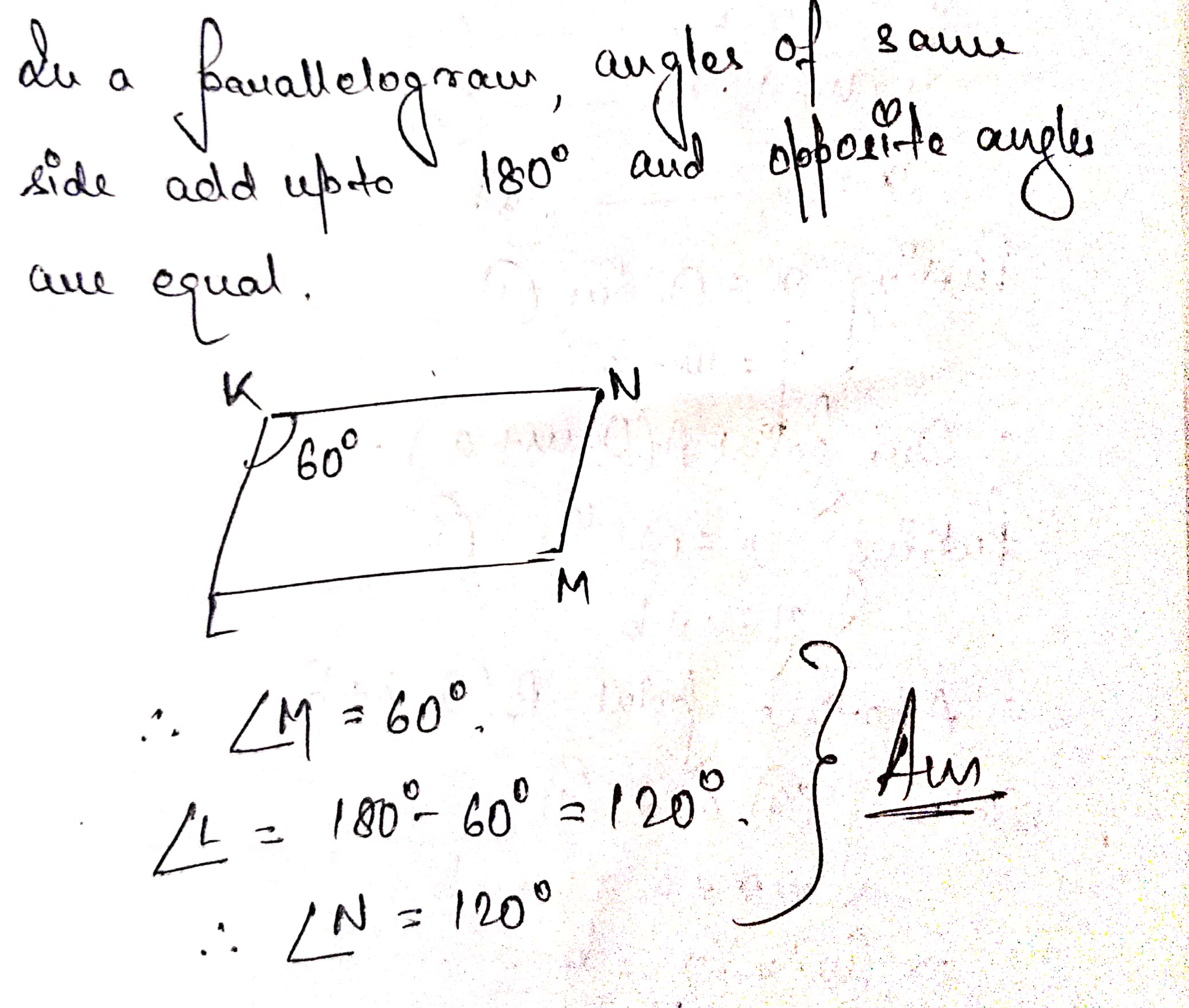
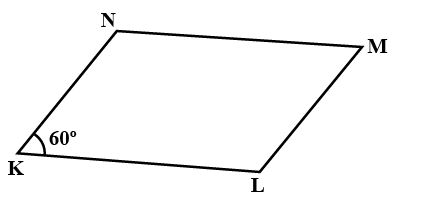
In a parallelogram $$KLMN, \angle K = 60^{\circ}$$. Find the measures of all the angles.
$$\Rightarrow$$ In parallelogram $$KLMN$$, $$\angle K=60^\circ$$ [Given]
$$\Rightarrow$$ $$\angle K = \angle M$$ [Opposite angles of parallelogram are equal]
$$\Rightarrow$$ So, $$\angle K=\angle M=60^\circ$$ ---- ( 1 )
$$\Rightarrow$$ $$\angle K+\angle N =180^\circ$$ [Sum of adjacent angles of parallelogram is supplementary]
$$\Rightarrow$$ $$60^\circ + \angle N = 180^\circ$$
$$\therefore$$ $$\angle N = 120^\circ$$
$$\Rightarrow$$ $$\angle N = \angle L $$ [Opposite angles of parallelogram are equal]
$$\Rightarrow$$ So, $$\angle N =\angle L=120^\circ$$ ---- ( 2 )
From ( 1 ) and ( 2 ) we get,
$$\angle K = 60^\circ , \angle L =120^\circ, \angle M = 60^\circ\, and\, \angle N = 120^\circ$$.
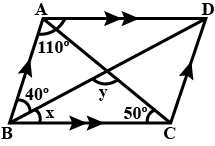
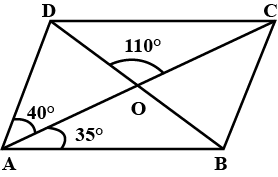
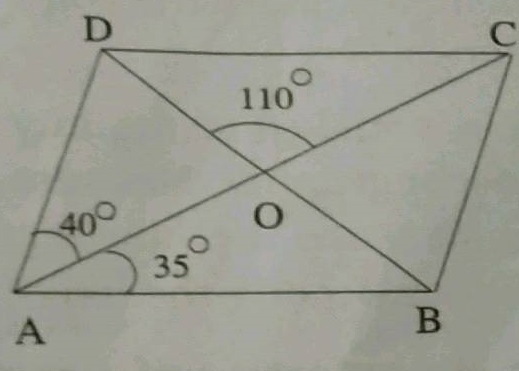
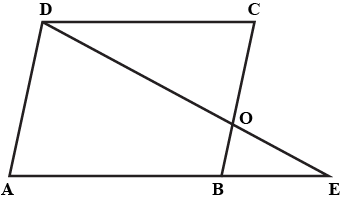
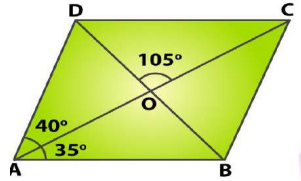
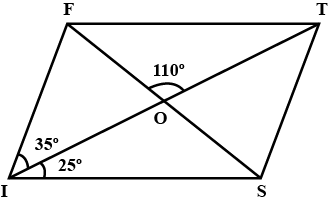
In the figure, $$ABCD$$ is a parallogram. The diagonals $$AC$$ and $$BD$$ intersect at $$O$$; and $$\angle DAC = 40^{\circ}, \angle CAB = 35^{\circ}$$; and $$\angle DOC = 110^{\circ}$$. Calculate the $$\angle ABO, \angle ADC, \angle ACB$$, and $$\angle CBD$$
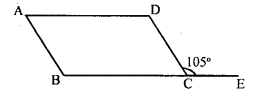
In a parallelogram $$ABCD$$, the side $$DC$$ is produced to $$E$$ and $$\angle BCE = 105^{\circ}$$. Calculate $$\angle A, \angle B, \angle C$$, and $$\angle D$$.
In the adjoining figure, $$PQRS$$ is a parallelogram. Find $$x$$ and $$y$$ in $$cm$$
$$ABCD$$ is a parallelogram, $$G$$ is the point on $$AB$$ such that $$AG=2GB, E$$ is a point of $$DC$$ such that $$CE = 2DE$$ and F is the point of BC such that $$BF = 2FC$$. Prove
that: $$ar(ADEG) = ar(GBCE)$$
Prove that if the opposite sides of a quadrilateral are equal, the quadrilateral is a parallelogram.
Given: Quadrilateral ABCD in which AB = DC and AD = BC$$
To prove: ABCD is a parallelogram.
Construction: Draw diagonal AC.
Proof: Some statements and reasons for their validity are given below:
It follows that ABCD is a parallelogram.
To prove: ABCD is a parallelogram.
Construction: Draw diagonal AC.
Proof: Some statements and reasons for their validity are given below:
| Statement | Reason |
| AD=BC | Given |
| AB=CD | Given |
| AC=AC | Common |
| $$\triangle CBA \cong \triangle ADC$$ $$\quad$$ | By SSS postulate |
| $$\angle DCA = \angle BAC$$ | Corresponding angles of congruent triangles |
| $$DC\parallel AB$$ | Alternate angles are equal. |
| $$\angle DAC = \angle BCA$$ | Corresponding angles of congruent triangles |
| $$AD \parallel BC$$ | Alternate angles are equal. |
Let $$ABCD$$ be a parallelogram. Let $$BP$$ and $$DQ$$ be perpendiculars respectively from $$B$$ and $$D$$ on to $$AC$$. Prove that $$BP = DQ$$.
It is given that in parallelogram $$ABCD$$, $$BP$$ is perpendicular to $$AC$$ and $$DQ$$ is perpendicular to $$AC$$.
In $$ΔADQ$$ and $$ΔCBP$$,
$$AD = CD$$ (Opposite sides of a parallelogram)
$$\angle DAQ=\angle BCP$$ and $$AD||BC,AC$$ (Transversal alternate angles)
$$\angle DQA=\angle BPC=90^0$$ (Given)
$$⸫ ΔADQ = ΔCBP$$ (SAA)
$$⸫BP = DQ$$ (C.P.C.T)
Hence proved.
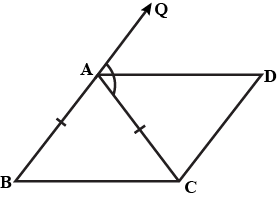
$$ABC$$ is an isosceles triangle in which $$AB = AC. AD$$ bisects exterior angle $$QAC$$ and $$CD\parallel BA$$ as shown in the figure. Show that:
(i) $$\angle DAC = \angle BCA$$
(ii) $$ABCD$$ is a parallelogram
In right triangle $$ABC$$, right angle is at $$C, M$$ is the mid-point of hypotenuse $$AB, C$$ is joined to $$M$$ and produced to a point $$D$$ such that $$DM = CM$$. Point $$D$$ is joined to point $$B$$. Show that:
$$CM = \dfrac {1}{2}AB$$
Prove that if the diagonals of a parallelogram are equal then it is a rectangle.
$$\textbf{Step 1: Show that the triangles ABC and DCB are congruent.}$$
$$\text{Let }ABCD$$ $$\text{be a parallelogram in which }AC=DB$$.
$$\text{To show that }ABCD$$ $$\text{is a rectangle, we have to prove that one of its interior angles is }90^{\circ}$$.
$$\text{In }ΔABC$$ $$\text{and }ΔDCB$$,
$$AB = DC$$ $$\textbf{(Opposite sides of a parallelogram are equal)}$$
$$BC = BC$$ $$\text{(Common side)}$$
$$AC = DB$$ $$\text{(Given)}$$
$$∴ ΔABC ≅ ΔDCB$$ $$\textbf{(By SSS Congruence rule)}$$
$$\textbf{Step 2: Show that angle between any two sides is 90}\,^\circ.$$
$$∠ABC = ∠DCB........(1)$$ $$\textbf{[By CPCT]}$$
$$\text{It is known that the sum of two adjacent angles of a parallelogram is }180^{\circ}$$.
$$∠ABC + ∠DCB = 180^{\circ}$$
$$⇒ ∠ABC + ∠ABC = 180^{\circ}$$ [from $$(1)$$]
$$⇒ 2∠ABC = 180^{\circ}$$
$$⇒ ∠ABC = 90^{\circ}$$
$$\text{Since }ABCD$$ $$\text{is a parallelogram and one of its interior angles is }90^{\circ}$$.
$$\textbf{Hence, ABCD is a rectangle.}$$
Let $$ABCD$$ be a quadrilateral in which $$\triangle ABD \cong \triangle BAC$$. Prove that $$ABCD$$ is a parallelogram.
Given: $$ABCD$$ is a Quadrilateral
$$ΔABD ≅ ΔBAC$$
To prove: $$ABCD$$ is a parallelogram
$$BD = AC$$ (CPCT)
Therefore, Area of $$ΔABD =$$ Area of $$ΔBAC$$
And both the triangles stand on same base $$AB$$.
$$⸫ DC | | AB$$
But $$AD | | BC$$
$$⸫ AD | | BC$$
Therefore, opposite sides are parallel
Hence, $$ABCD$$ is a parallelogram
In a parallelogram $$ABCD, \angle DAB = 40^{\circ}$$ find the other angles of the parallelogram.
ABCD is a parallelogram
Given: $$\angle DAB=\angle BCD=40^{0}$$ and $$AD\parallel BC$$
We know that the sum of consecutive angle are $$180^{0}$$
$$\angle CBA+\angle DAB=180^{0}$$
$$\therefore \angle CBA=180-40=140^{0}$$
We know that in parallelogram opposite angles are equal.
Therefore, $$\angle ADC=\angle CBA=140^{0}$$
So angles of parallelogram are $$40^{0},140^{0},40^{0},140^{0}$$
Adjacent sides of a parallelogram are $$11\ \text{cm}$$ and $$17\ \text{cm}$$. If the length of one of its diagonal $$26\ \text{cm}$$, find the length of the other.
Let $$ABCD$$ be a parallelogram.
$$\therefore AB=17\ cm, BC = 11\ cm$$ and $$AC =26\ cm$$
Let its diagonal $$AC$$ and $$BD$$ bisect each other at point $$O$$.
$$AO=\cfrac{1}{2}\times AC$$
$$=\cfrac{1}{2}\times 26$$
$$=13 ~cm$$
and $$BO=\cfrac{1}{2} BD$$
In $$\Delta ABC$$, $$BO$$ is a median.
$$\therefore (AB)^2+(BC)^2=2(BO)^2+2(AO)^2$$ (by Apollonius theorem)
$$(17)^2+(11)^2=2BO^2+2(13)^2$$
$$289 + 121=2BO^2+338$$
$$2BO^2=72$$
$$BO^2=\cfrac{72}{2}=36$$
$$BO=\sqrt{36}$$
$$=6 \,cm$$
$$\therefore AB=17\ cm, BC = 11\ cm$$ and $$AC =26\ cm$$
Let its diagonal $$AC$$ and $$BD$$ bisect each other at point $$O$$.
$$AO=\cfrac{1}{2}\times AC$$
$$=\cfrac{1}{2}\times 26$$
$$=13 ~cm$$
and $$BO=\cfrac{1}{2} BD$$
In $$\Delta ABC$$, $$BO$$ is a median.
$$\therefore (AB)^2+(BC)^2=2(BO)^2+2(AO)^2$$ (by Apollonius theorem)
$$(17)^2+(11)^2=2BO^2+2(13)^2$$
$$289 + 121=2BO^2+338$$
$$2BO^2=72$$
$$BO^2=\cfrac{72}{2}=36$$
$$BO=\sqrt{36}$$
$$=6 \,cm$$
$$\therefore$$ length of diagonal $$= 2\times 6 = 12\ cm$$
The three vertices of a parallelogram taken in order are $$(-1, 0), (3, 1)$$ and $$(2, 2)$$ respectively. Find coordinates of the fourth vertex.
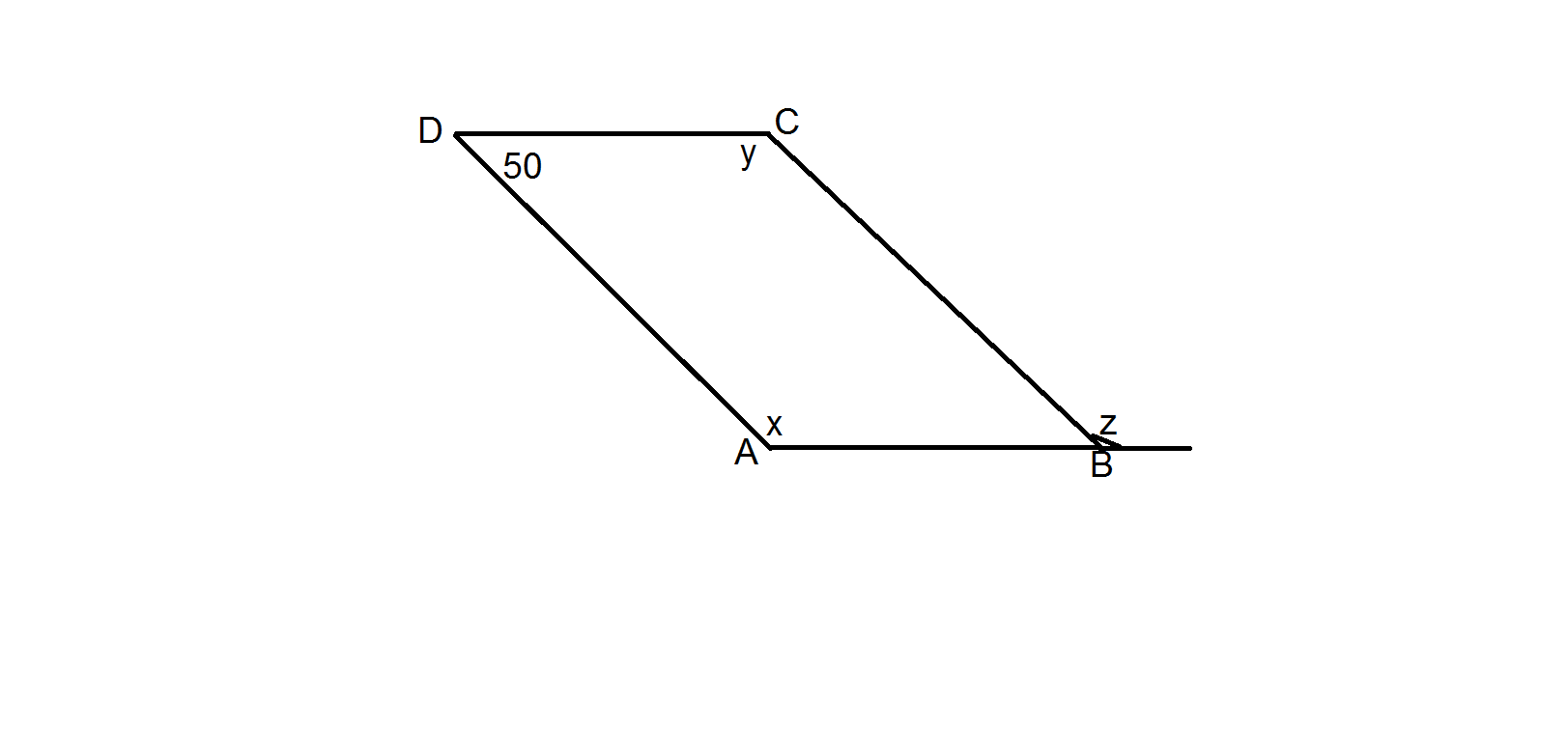
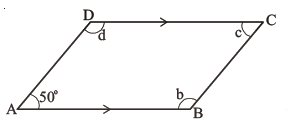
ABCD is a quadrilateral in which $$AB || DC$$ and $$DC || BC$$. Find $$\angle b, \angle c\ and\ \angle d$$.
Two adjacent sides of a parallelogram are $$4.5$$ cm and $$3$$ cm. Find its perimeter
In parallelogram $$ABCD$$, its diagonals $$\overline {AC}$$ and $$\overline {BD}$$ intersect at $$O$$. If $$AO = 5\ cm$$ then $$AC =$$ ____________ cm.
$$ABCD$$ is a parallelogram.
$$AC$$ and $$BD$$ bisect each other at point $$O.$$
Where, $$AO= 5\,cm$$
Then, $$AO=CO$$
$$\therefore$$ $$AC=AO+CO$$
$$\Rightarrow$$ $$AC=5+5$$
$$\therefore$$ $$AC=10\,cm$$
Is quadrilateral $$ABCD$$ a parallelogram, if $$\angle A = 70^{\circ}$$ and $$\angle C = 65^{\circ}$$? Give reason.
A parallelogram in which one angle is $$90^{\circ}$$ and two adjacent sides are equal is a ________________.
In $$\triangle ABC$$ and $$\triangle DEF, AB = DE, AB\parallel DE, BC = EF$$ and $$BC\parallel EF$$. Vertices $$A, B$$ and $$C$$ are joined to vertices $$D, E$$ and $$F$$ respectively. Show that
(i) quadrilateral $$ABED$$ is a parallelogram
(ii) quadrilateral $$BEFC$$ is a parallelogram
(iii) $$AD \parallel CF$$ and $$AD = CF$$
(iv) quadrilateral $$ACFD$$ is a parallelogram
(v) $$AC = DF$$
(vi) $$\triangle ABC = \triangle DEF$$.
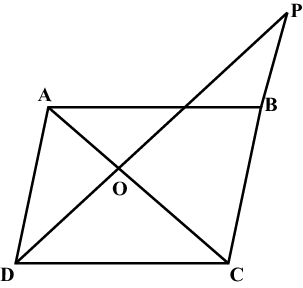
The given figure shows a parallelogram $$ABCD. BC$$ is extended to the point $$P. PC$$ is joined intersecting $$AC$$ to $$O$$.
Show that: $$DO\times CP = OP \times BC$$.
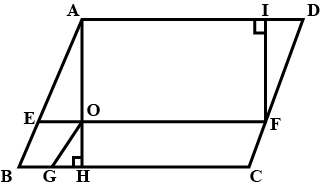
$$ABCD$$ is a parallelogram. If $$E$$ is mid-point of $$BC$$ and $$AE$$ is the bisector of $$\angle A$$, prove that $$AB=\dfrac { 1 }{ 2 } AD$$.
$$\Rightarrow$$ $$ABCD$$ is a parallelogram. Mid-point of $$BC$$ is $$E$$
$$\Rightarrow$$ Join $$A$$ to $$E$$, $$\angle EAD = \angle EAB$$ ----- ( 1 )
$$\Rightarrow$$ $$AD$$ is parallel to $$BC$$ and $$AE$$ is a transversal
$$\therefore$$ $$\angle EAD = \angle BEA$$ ----- ( 2 ) [Alternate angle]
$$\Rightarrow$$ $$\angle EAB = \angle BEA$$ [From ( 1 ) and ( 2 )]
$$\therefore$$ $$AB = BE $$ ---- ( 3 )
$$\Rightarrow$$ But $$BE=\dfrac{BC}{2}=\dfrac{AD}{2}$$ ---- ( 4 )
$$\Rightarrow$$ Put value of BE in equation ( 3 )
$$\therefore$$ $$AB=AD\dfrac{1}{2}$$ [Proved]
In the given figure, $$ABCD$$ and $$BGOE$$ are parallelograms. If $$AO=2OH, AH$$ $$\bot BC$$ and $$FI \bot AD$$, the ratio of $$ar(BGOE)$$ to $$ar(\Delta DIF)$$ is equal to $$m:n$$, then find $$m+n$$.
$$E$$ is a point on the side $$AD$$ produced of a parallelogram $$ABCD$$ and $$BE$$ intersects $$CD$$ at $$F$$. Show that $$\Delta ABE\sim \Delta CFB$$.
In a parallelogram, opposite angles are equal to each other. Then find the relation between angles of both triangles to show them similar.
If two angles of a triangle are respectively equal to two angles of another triangle, then Triangles are similar (because by the angle sum property of a triangle their third angle will also be equal ) and it is called AA similarity criterion.
In Δ$$ABE$$ and Δ$$CFB,$$
$$∠A = ∠C$$ (Opposite angles of a parallelogram)
$$∠AEB = ∠CBF$$ (Alternate interior angles as AE || BC)
∴ $$ΔABE \sim ΔCFB$$ (By AAA similarity criterion)
$$ABCD$$ is a quadrilateral with $$\angle A = 80^{\circ}, \angle B = 40^{\circ}, \angle C = 140^{\circ}, \angle D = 100^{\circ}$$.
(i) Is $$ABCD$$ is trapezium? (ii) Is $$ABCD$$ is parallelogram?
Justify your answer.
ABCD is neither a parallelogram nor a trapezium . It can be justified using basic sum property of co-interior angles to be 180 of parallel lines .
$$ABCD$$ is parallelogram. $$L$$ and $$M$$ are points on $$AB$$ and $$DC$$ respectively such that $$AL = CM$$. The diagonal $$BD$$ intersects $$LM$$ at point $$O$$. If $$AB = 14 text{ cm}, AD = 9 \text{ cm}$$ and $$LO = 5 \text{ cm}$$, find the length of $$MO$$.
Given : $$ ABCD $$ is a parallelogram and $$AL=CM$$
To find : The length of $$MO$$
Solution:
$$AB=CD$$ (opposite sides of parallelogram)
Subtracting $$AL$$ from both sides
$$AB-AL=CD-AL$$
$$AB-AL=CD-CM$$ (because $$AL=CM$$)
$$LB=DM$$
In triangles $$BLO$$ and $$MDO$$,
$$\angle MDO = \angle LBO $$ (because $$AB||CD$$ and taking $$DB$$ as transversal)
$$LB=DM$$
$$\angle OMD = \angle OLB $$ (because $$AB||CD$$ and taking $$ML$$ as transversal)
So, by A.S.A criterion of congruency, triangle $$BLO$$ is congruent to triangle $$MDO.$$
Therefore,
$$MO=LO=5\text{ cm}$$ (By CPCT)
Given ABCD is a parallelogram, find the measure of $$x -2y+ z$$ in degrees form the following figure.
In given figure through the mid-point $$M$$ of the side $$CD$$ of a parallelogram $$ABCD$$, the line $$BM$$ is drawn intersecting $$AC$$ in $$L$$ and $$AD$$ produced in $$E$$. Prove that $$EL=2BL$$.
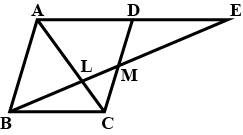
Through the mid point M of the side CD of a parallelogram ABCD, the line BM is drawn intersecting AC at L and AD produced at E. Prove EL=2BL.
In $$\bigtriangleup BMC$$ and $$\bigtriangleup EMD$$
$$\angle BMC=\angle EMD$$ [Vertically opposite]
$$MC=DM$$ [Given]
$$\angle BCM=\angle EDM$$ [Alternate angles]
$$\therefore \bigtriangleup BMC\cong \bigtriangleup EMD$$ [By ASA]
Hence, $$BC=DE$$ [By CPCT] $$\rightarrow (1)$$
$$AE=AD+DE=BC+BC=2BC$$ $$\rightarrow (2)$$
Now, $$\bigtriangleup BLC\sim \bigtriangleup ELA$$ (AA Similarly)
$$\dfrac{BL}{EL}=\dfrac{BC}{AE}$$ [By CPCT]
$$\dfrac{BL}{EL}=\dfrac{BC}{2BC}$$
$$\dfrac{BL}{EL}=\dfrac{1}{2}$$
$$EL=2BL$$
$$\angle BMC=\angle EMD$$ [Vertically opposite]
$$MC=DM$$ [Given]
$$\angle BCM=\angle EDM$$ [Alternate angles]
$$\therefore \bigtriangleup BMC\cong \bigtriangleup EMD$$ [By ASA]
Hence, $$BC=DE$$ [By CPCT] $$\rightarrow (1)$$
$$AE=AD+DE=BC+BC=2BC$$ $$\rightarrow (2)$$
Now, $$\bigtriangleup BLC\sim \bigtriangleup ELA$$ (AA Similarly)
$$\dfrac{BL}{EL}=\dfrac{BC}{AE}$$ [By CPCT]
$$\dfrac{BL}{EL}=\dfrac{BC}{2BC}$$
$$\dfrac{BL}{EL}=\dfrac{1}{2}$$
$$EL=2BL$$
The three vertices of a parallelogram taken in order are (-1, 0), (3, 1) and (2, 2) respectively.Find the coordinates of the fourth vertex.
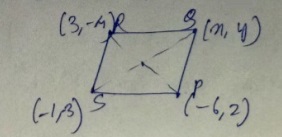
If A(-2, -1), B(a, 0), C(4, b) and D(1, 2) are the vertices of a parallelogram, find the values of a and b.
In a parallelogram ABCD, from vertex D, a line is draw which intersects produced BA and BC at E and F respectively. prove $$\frac{AD}{AE} = \frac{EB}{BE} = \frac{FC}{CD}$$
In $$\bigtriangleup EAD$$ and $$\bigtriangleup DCF$$
$$\angle 1=\angle 2 [AB\parallel CD]$$
$$\angle 3=\angle 4 [AD\parallel BC]$$
$$\therefore \bigtriangleup EAD\sim \bigtriangleup DCF$$
[By AA similarity]
$$\frac{EA}{DC}=\frac{AD}{CF}=\frac{DE}{FD}$$ [BySSS]
$$\frac{AD}{AE}=\frac{CF}{CD}\rightarrow (2)$$
In $$\bigtriangleup EAD$$ and $$\bigtriangleup EBF$$
$$\angle 1=\angle 1 $$ (common
$$\angle 3=\angle 4 [AD\parallel BC]$$
$$\therefore \bigtriangleup EAD\sim \bigtriangleup EBF$$ [By AA similarity]
$$\frac{EA}{EB}=\frac{AD}{BF}=\frac{DE}{EF}$$ [By SSS]
$$\frac{AD}{AE}=\frac{FB}{BE}\rightarrow (2)$$
From (1) and (2) , $$\frac{AD}{AE}=\frac{FB}{BE}=\frac{CF}{CD}$$
Find the radian measure of the interior angle of a regular (i) Pentagon (ii) Hexagon (iii) Octagon
In the parallelogram, $$ABCD$$ the bisectors of $$\angle A$$ and $$\angle B$$ meet at $$O.$$ Find $$\angle AOB.$$
In parallelogram $$ABCD,$$ $$AO$$ and $$BO$$ are angles bisector of $$A$$ and $$B$$.
As we know that, the sum of the adjacent angles of a parallelogram is equal to $$180^\circ.$$ So,
$$2x+2y=180^{\circ}$$
$$\Rightarrow x+y=90^\circ$$
Now, by using angle sum property in $$\triangle AOB,$$
$$90^{\circ}+\angle AOB=180^{\circ}$$
$$\Rightarrow \angle AOB=90^{\circ}$$
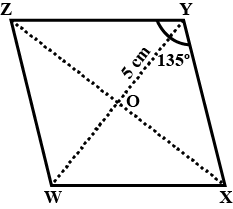
Parallelogram $$HEAR$$
$$HE=5\ cm$$
$$EA=6\ cm$$
$$\angle R ={85}^{o}$$
Let us consider,
Parallelogram $$HEAR$$
In which $$HE \parallel AR$$
and in which $$\angle R=85^{\circ}$$
$$\angle E=\angle R$$ (opposite angles of parallelogram are equal)
Therefore, $$\angle E=85^{\circ}$$
Now,
$$\angle A+\angle R=180^{\circ}$$ (sum of co-interiors angle are $$180$$)
Hence $$\angle A=180^{\circ}-85^{\circ}$$
Therefore, $$\angle A=95^{\circ}$$
and $$\angle H=\angle A$$ (opposite angles of parallelogram)
$$\angle H=95^{\circ}$$
and $$HE=AR$$ (opposite sides of parallelogram are equal and parallel)
$$AR=5\;cm$$
and $$EA=HR$$ (opposite sides of parallelogram are equal and parallel)
Hence, $$HR=6\;cm$$
$$AE$$ is the bisector of $$\angle{CAD}$$. Also , $$BA\parallel CE$$ and $$AB=AC$$. Prove that $$\angle {EAC}=\angle {ACB}$$ and $$ABCD$$ is a parallelogram.
Prove that the bisector of interior angles of a parallelogram form a rectangle.
To prove: MNOP is a rectangle.
In parallelogram $$ABCD$$
$$\angle A=\angle D=90^{\circ}$$ [they form a straight line]
$$\therefore IN \triangle AMD, \angle M=90^{\circ}$$
$$\angle M=\angle N =90^{\circ}$$ [they form a straight line]
Similarly,
$$\angle M=\angle P =90^{\circ}$$
And
$$\angle P=\angle O =90^{\circ}$$
$$\therefore \angle MPO=\angle PON\angle ONM=\angle NMO=90^{\circ}$$
$$\therefore $$ MNOP is a rectangle. [A rectangle is a parallelogram with one angle $$90^{\circ}$$]
In given figure $$AB\parallel DC$$. Find the value of $$x$$ .
If all the angles of a parallelogram are equal. Prove that it is a rectangle.
Let $$ABCD$$ be a parallelogram when $$AC=BC$$
To prove that ABCD is a rectangle, prove rectangle is a parallelogram with one of its interior angle is $${90^ \circ }$$ in $$\vartriangle ABC$$ and $$\vartriangle DCB$$
$$AB = DC$$
$$BC = BC$$
$$AC = DB$$
$$\therefore ABC \cong DCB$$
$$\angle ABC = \angle DCB$$
Now
$$\begin{matrix} AC\parallel DC \\ \angle B+\angle C={ 180^{ \circ } } \\ \angle B+\angle B={ 180^{ \circ } } \\ 2\angle B={ 180^{ \circ } } \\ \angle B={ 90^{ \circ } } \\ \end{matrix}$$
$$ABCD$$ is a parallelogram with one angle $${90^ \circ }$$ which implies all other angles are $$90^0$$
Hence,
$$ABCD$$ must be a rectangle.
The following figure shows a parallelogram $$ABCD$$ whose side $$AB$$ is parallel to $$x-axis$$, $$\angle{A}={60}^{o}$$ and vertex $$C=(7, 5)$$. Find the equations of $$BC$$ and $$CD$$.
Given $$C(7,5)$$ and $$\angle BAD=60^{\circ}$$
$$AB \parallel x-axis$$
consider th problem.
$$\angle DAB=\angle CBE$$
Hence, $$\angle CBE=60^{\circ}$$ (corresponding angles of parallelogram $$ABCD$$)
Now, slope for the line $$BC(m)=\tan 60^{\circ}=\sqrt 3$$
Therefore, equation for the line $$BC$$ by point-slope formula.
$$y-y_1=m(x=x_1)$$
$$y-5=\sqrt 3(x-7)$$
$$y=\sqrt 3x+5-7\sqrt 3$$
Now, for equation of line $$CD$$
Slope $$(m_1)=\tan 0^{\circ}=0$$, and passing through the points $$(7,5)$$
$$y-y_1=m_1(x-x_1)$$
$$y-5=0(x-7)$$
$$y=5$$
Hence the equation of sides $$BC$$ and $$CD$$ are $$y=\sqrt 3x+5-7\sqrt 3$$ and $$y=5$$ respectively.
ABC is an isosceles triangle in which $$AB=AC$$. $$AD$$ is the bisector of exterior angle $$PAC$$ and $$CD$$ is parallel to $$AB$$. Prove that
(i) $$\angle DAC = \angle BCA$$
(ii) $$ABCD$$ is parallelogram.
AD bisects $$\angle PAC$$, then
$$\angle PAD = \angle DAC = \dfrac{1}{2}\angle PAC .............. (1)$$
Also $$AB=AC$$
$$\therefore \angle BCA= \angle ABC ...........(2)$$
In $$\bigtriangleup$$ ABC, $$\angle PAC$$ is an exterior angle.
$$\angle PAC = \angle ABC+ \angle BCA$$
$$\angle PAC = \angle BCA+ \angle BCA$$ [from (2)]
$$\angle PAC= 2\angle BCA$$
$$\angle BCA = \dfrac{1}{2} \angle PAC$$
$$\angle BCA = \angle DAC$$ [from (1)]
$$(ii)$$ For lines $$BC$$ and $$AD$$ , $$AC$$ is transversal & $$\angle DAC $$ &
$$\angle BCA$$ are alternate interior angles and are equal. Therefore $$BC \parallel AD$$. In ABCD, $$BC \parallel AD$$ & $$AB \parallel CD$$ .
Since, opposite sides are parallel. ABCD is a parallelogram.
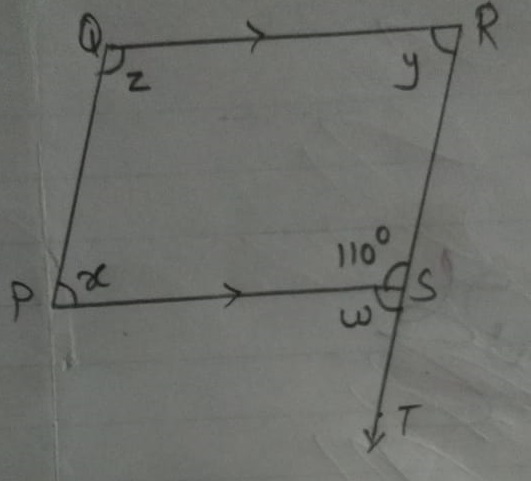
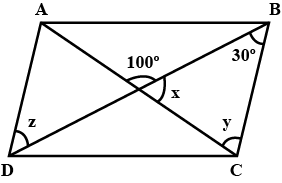
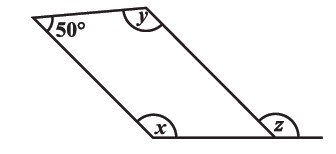
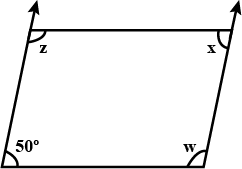
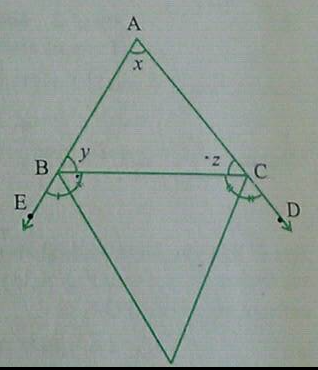
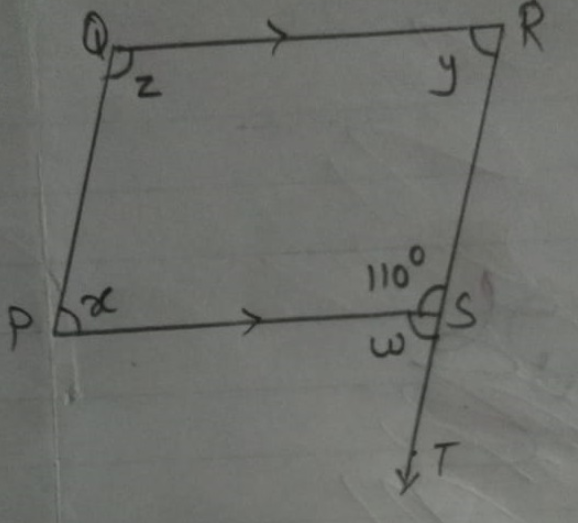
Find $$\angle z$$ ,$$\angle w$$ $$\angle x$$ ?
In case of a parallelogram prove that:
(i) the bisector of any two adjacent angles intersect at $${90}^{\circ}.$$
(ii) the bisector of opposite angle are parallel to each other.
i) Given: $$ ABCD$$ is a parallelogram
We know
$$\Rightarrow \angle DAB+\angle ABC=180^{\circ}$$ [ corresponding Interior angles]
$$\Rightarrow \dfrac{1}{2} \angle DAB+\dfrac{1}{2}=\angle ABC=90^{\circ}$$ [Multiplying $$\dfrac{1}{2}$$ on both sides]
$$\Rightarrow \angle DAB+\angle OBA=90^{o}\rightarrow (1)$$
In $$\triangle AOB,$$
$$\Rightarrow \angle AOB+\angle OAB+\angle OBA=180^{o}$$ [Angle sum property]
$$\Rightarrow \angle AOB+90^{o}=180^{o}$$ [from $$(1)$$]
$$\therefore \angle AOB=90^{o}$$
Hence proved
ii) Given: $$AE$$ is the bisector of $$\angle DAB$$
and $$CF$$ is the bisector of $$\angle DCB$$
$$\Rightarrow \angle A=\angle C $$ [Opposite angle of parallelogram are equal]
$$\Rightarrow \dfrac{1}{2}\angle A=\dfrac{1}{2}\angle C$$ [ Multiply by $$\dfrac{1}{2}$$]
$$\Rightarrow \angle EAB=\angle DCF$$ [$$AE$$ & $$CF$$ are bisector] $$...(1)$$
$$\Rightarrow \angle DCF=\angle CFB$$ [ Alternate interior angles are equal] $$...(2)$$
$$\therefore \angle EAB=\angle CFB$$ [ from $$(1)$$ and $$(2)$$]
$$\therefore AB\parallel CF$$ [ Corresponding angles are equal]
Hence proved
In a parallelogram $$ABCD,$$ the bisectors $$\angle A$$ and $$\angle B$$ and at $$0.$$ Find $$\angle AOB.$$
$$\angle A+\angle B=180^o$$
$$2x+2y=180^o$$
$$x+y=90^o$$
$$\triangle AOB\ \Rightarrow \ x+y+\angle AOB=180^o$$
$$90^o +\angle AOB=180^o$$
$$\angle AOB=90^o$$
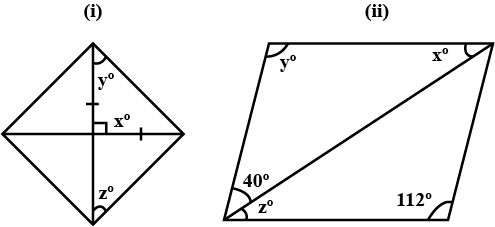
In the following parallelograms, find the values of $$x,y,z$$(both figures)(in degrees)
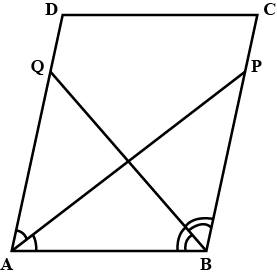
In the given figure, $$AP$$ is bisector of $$\angle A$$ and $$CQ$$ is bisector of $$\angle C$$ of parallelogram $$ABCD$$. Prove that $$APCQ$$ is a parallelogram
Join $$AC$$ and show that diagonals $$AC$$ and $$PQ$$ bisect each other.
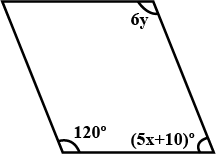
The adjacent angle of a parallelogram are $${(2x+7)}^{o}$$ and $$(3x-2)^{o}$$. Find all the angles.
The ratio of two adjacent sides of a parallelogram is $$5:4$$. Its perimeter is $$8\text{ cm}$$ then, what is the length of the adjacent sides.
Find the measure of all the angles of a parallelogram, if one angle is $${24}^{o}$$ less than twice the smallest angle.
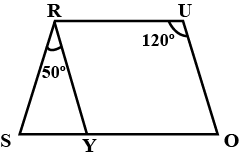
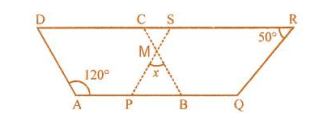
In the given parallelogram YOUR, $$\angle$$RUO $$=120^o$$ and OY is extended to point S such that $$\angle$$SRY$$=50^o$$. Find $$\angle$$YSR.
$$YOUR$$ is a parallelogram.
$$\angle RUO=120^o$$
$$\Rightarrow$$ $$RUO=\angle RYO$$ [ Opposite angles in parallelogram are equal ]
$$\therefore$$ $$\angle RYO=120^o$$
$$\Rightarrow$$ $$\angle RYS+\angle RYO=180^o$$ [ Linear pair ]
$$\Rightarrow$$ $$120^o+\angle RYO=180^o$$
$$\therefore$$ $$\angle RYO=60^o$$
In $$\triangle RSY,$$
$$\Rightarrow$$ $$\angle SRY+\angle RYS+\angle YSR=180^o$$ [ Sum of angles in triangle is $$180^o$$ ]
$$\Rightarrow$$ $$50^o+60^o+\angle YSR=180^o$$
$$\Rightarrow$$ $$110^o+\angle YSR=180^o$$
$$\therefore$$ $$\angle YSR=70^o$$.
In a parallelogram $$ABCD, \angle B$$ is $${50}^{o}$$ more than $$\angle A$$. What is the measure of all the angles of parallelogram, $$ABCD$$?
Measure of opposite angle of a parallelogram are $${(3x-2)}^{o}$$ and $${(50-x)}^{o}$$. Find the measure of its each angle.
Points $$P$$ and $$Q$$ have been taken on opposite sides $$AB$$ and $$CD$$, respectively of a parallelogram $$ABCD$$ such that $$AP = CQ$$. Show that $$AC$$ and $$PQ$$ disect each other.
In $$ \triangle APO$$ and $$\triangle OQC$$
$$ \angle OAP = \angle OCQ $$ ( taking $$AC$$ as transversal then angles are on opposites sides of transversal)
$$AP = CQ $$ (given )
$$ \angle OPA = \angle OQC $$ ( taking $$PQ$$ as transversal then angles are on opposites sides of transversal )
By $$ASA$$ criterion of congruency ,$$\triangle APO$$ is congruent to $$\triangle OQC $$.
$$PO = OQ, AO=OC$$ ( Corresponding parts of a congruent triangle are equal )
Hence $$AC$$ and $$PQ$$ bisect each other.
Prove that the sum of the squares of the diagonals of a parallelogram is equal to the sum of squares of its sides.
$$AB=CD$$ and $$BC=AD$$
Draw perpendiculars from $$C$$ and $$D$$ on $$AB$$ as shown.
In right angled $$\triangle AEC,$$
$$\Rightarrow$$ $$(AC)^2=(AE)^2+(CE)^2$$ [ By Pythagoras theorem ]
$$\Rightarrow$$ $$(AC)^2=(AB+BE)^2+(CE)^2$$
$$\Rightarrow$$ $$(AC)^2=(AB)^2+(BE)^2+2\times AB\times BE+(CE)^2$$ ----- ( 1 )
From the figure $$CD=EF$$ [ Since $$CDFE$$ is a rectangle ]
But $$CD=AB$$
$$\Rightarrow$$ $$AB=CD=EF$$
Also $$CE=DF$$ [ Distance between two parallel lines
$$\Rightarrow$$ $$\triangle AFD\cong \triangle BEC$$ [ RHS congruence rule ]
$$\Rightarrow$$ $$AF=BE$$ [ CPCT ]
Considering right angled $$\triangle DFB$$
$$\Rightarrow$$ $$(BD)^2=(BF)^2+(DF)^2$$ [ By Pythagoras theorem ]
$$\Rightarrow$$ $$(BD)^2=(EF-BE)^2+(CE)^2$$ [ Since $$DF=CE$$ ]
$$\Rightarrow$$ $$(BD)^2=(AB-BE)^2+(CE)^2$$ [ Since $$EF=AB$$ ]
$$\Rightarrow$$ $$(BD)^2=(AB)^2+(BE)^2-2\times AB\times BE+(CE)^2$$ ----- ( 2 )
Adding ( 1 ) and ( 2 ), we get
$$(AC)^2+(BD)^2=(AB)^2+(BE)^2+2\times AB\times BE+(CE)^2+(AB)^2+(BE)^2-2\times AB\times BE+(CE)^2$$
$$\Rightarrow$$ $$(AC)^2+(BD)^2=2(AB)^2+2(BE)^2+2(CE)^2$$
$$\Rightarrow$$ $$(AC)^2+(BD)^2=2(AB)^2+2[(BE)^2+(CE)^2]$$ ---- ( 3 )
In right angled $$\triangle BEC,$$
$$\Rightarrow$$ $$(BC)^2=(BE)^2+(CE)^2$$ [ By Pythagoras theorem ]
Hence equation ( 3 ) becomes,
$$\Rightarrow$$ $$(AC)^2+(BD)^2=2(AB)^2+2(BC)^2$$
$$\Rightarrow$$ $$(AC)^2+(BD)^2=(AB)^2+(AB)^2+(BC)^2+(BC)^2$$
$$\therefore$$ $$(AC)^2+(BD)^2=(AB)^2+(BC)^2+(CD)^2+(AD)^2$$
$$\therefore$$ The sum of the squares of the diagonals of a parallelogram is equal to the sum of squares of its sides.
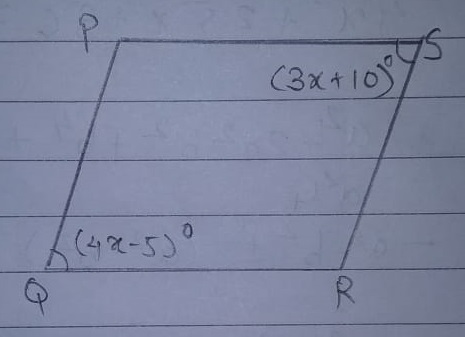
In parallelogram PQRS, $$\angle$$Q$$=(4x-5)^o$$ and $$\angle$$S$$=(3x+10)^o$$. Calculate: $$\angle$$Q and $$\angle$$R.
$$\therefore$$ $$\angle Q=\angle S$$
$$\Rightarrow$$ $$4x-5=3x+10$$
$$\Rightarrow$$ $$4x-3x=10+5$$
$$\Rightarrow$$ $$x=15$$
$$\Rightarrow$$ $$\angle Q=(4x-5)^o=(4\times 15-5)^o=55^o$$
We know that, sum of adjacent angles of parallelogram is $$180^o$$
$$\Rightarrow$$ $$\angle Q+\angle R=180^o$$
$$\Rightarrow$$ $$55^o+\angle R=180^o$$
$$\therefore$$ $$\angle R=125^o$$
Two opposite angles of a parallelogram are $$(5x+1)^{o}$$ and $$(49-3x)^{o}$$. Find the measure of these opposite angles of the parallelogram.
In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP$$=$$BQ. Show that AQ$$=$$CP.
Here, $$ABCD$$ is a parallelogram.
$$AB\parallel DC$$ and $$BD$$ is a transversal.
$$\therefore$$ $$\angle ABQ=\angle CDP$$ [ Alternate angles ] ---- ( 1 )
In $$\triangle AQB$$ and $$\triangle CPD,$$
$$\Rightarrow$$ $$AB=CD$$ [ Opposite sides of parallelogram are equal ]
$$\Rightarrow$$ $$\angle ABQ=\angle CDP$$ [ From ( 1 ) ]
$$\Rightarrow$$ $$BQ=DP$$ [ Given ]
$$\therefore$$ $$\triangle AQB\cong \triangle CPD$$ [ By SAS congruence ]
$$\Rightarrow$$ $$AQ=CP$$ [ CPCT ]
In fig. the sides$$ AB$$ and $$AC$$ of $$\Delta ABC $$ are produced to points $$E$$ and $$D$$ respectively. If bisectors $$BO$$ and $$CO$$ of $$\angle CBE \, and \, \angle BCD$$ respectively meet at point $$O$$, then prove that $$\angle BOC = 90^o - \dfrac{1}{2} \angle BAC$$.
Prove that, opposite sides of a parallelogram are equal.
R.E.F image
In triangle ADC and ABC,
$$ \angle DAC = \angle ACB (AB\parallel CD $$ and taking AC as transversal)
$$ AC = AC $$ (common)
$$ \angle DCA = \angle BAC (AB\parallel CD $$ taking AC as transversal)
By ASA criterion of concurrency triangle ADC is congruent to triangle ABC.
$$ AD = BC $$ (By CPCT)
$$ AB = CD $$ (By CPCT)
In parallelogram $$ABCD,E$$ is the mid-point of side $$AB$$ and $$CE$$ bisects angle $$BCD$$. Prove that$$:$$
$$(I)AE=AD$$
$$(II)DE$$ bisects $$\angle ADC$$ and
$$(III) \angle DEC$$ is a right angle.
In $$\triangle CBE,\angle ECB+\angle CBE+\angle BEC=180^{\circ}$$
$$\implies \dfrac{C}{2}+180^{\circ}-C+\alpha=180^{\circ}\implies \alpha =\dfrac{C}{2}$$
$$\implies \triangle CBE$$ is an isosceles triangle $$\implies b=\dfrac{a}{2}$$
$$\implies AE=AD$$
$$\triangle AED $$ is also an isosceles triangle $$(\because AE=AD)$$
$$\implies \angle AED=\angle ADE=\theta$$
$$\angle AED+\angle ADE+\angle DAE=180^{\circ}$$
$$\theta +\theta +C=180^{\circ}\implies \theta =90^{\circ}-\dfrac{C}{2}$$
$$\angle EDC=180^{\circ}-{C}-\angle ADE=90^{\circ}-\dfrac{C}{2}=\angle ADE$$
$$\implies DE$$ bisects $$\angle ADC$$
From figure ,$$\theta +\alpha+\angle DEC=180^{\circ}$$
$$\implies 90^{\circ}-\dfrac{C}{2}+\dfrac{C}{2}+\angle DEC=180^{\circ}\implies \angle DEC=90^{\circ}$$
P is mid point of the side $$CD$$ of a parallelogram ABCD. A line through $$C$$ parallel to $$PA$$ intersect $$AB$$ at $$Q$$ and $$DA$$ produced at $$R.$$ Prove that $$DA=AR$$ and $$CQ=QR.$$
Refer attached image, given ABCD is a parallelogram
$$AP\parallel CR$$
$$CP=PD$$
Since, $$\triangle APD\sim \triangle RCD\quad \quad (AAA)$$
$$\Rightarrow \dfrac { DA }{ DR } =\dfrac { DP }{ DC } \quad \quad \quad \quad \quad \quad (CPCT)$$
$$\Rightarrow \dfrac { DA }{ DR } =\dfrac { 1 }{ 2 } \quad \quad \quad \quad \quad \quad (As\quad P\quad is\quad the\quad midpoint\quad of\quad CD)$$
$$\Rightarrow 2DA=DR$$
$$\Rightarrow 2DA=DA+AR$$
$$\Rightarrow DA=AR$$
Hence Proved DA=AR
Again as, $$\angle APD=\angle QCD\quad \& \quad \angle BQC=\angle APD\quad (AP\parallel QC)$$,
$$\Rightarrow \angle APD=\angle QCD=\angle BQC$$
&
$$\angle RDC=\angle CBQ\quad \quad \quad (Opposite\quad of\quad \angle \quad is\quad \parallel gm)$$
&
$$\angle BCQ=\angle CRD\quad \quad \quad (Properties\quad of\quad \parallel gm)$$
$$\Rightarrow \triangle BQC\sim \triangle DCR\quad \quad (AAA)$$
Now,
As,
$$\Rightarrow \triangle APD\cong \triangle CBQ$$
$$PD=BQ$$
or $$\dfrac { CD }{ 2 } =BQ\quad \quad \quad (As\quad P\quad is\quad the\quad midpoint\quad of\quad CD)$$
or $$\dfrac { AB }{ 2 } =BQ\quad \quad \quad (In\quad \parallel gm\quad AB=CD)$$
$$\Rightarrow $$ Q is the mid-point of AB
Again,
as,
$$\triangle BQC\sim \triangle DCR$$
$$\dfrac { BQ }{ CQ } =\dfrac { CD }{ CR } $$
$$\Rightarrow 2CQ=CR\quad (As\quad CD=2BQ)$$
$$\Rightarrow 2CQ=CQ+QR$$
$$\Rightarrow CQ=QR$$
Hence Proved CQ=QR
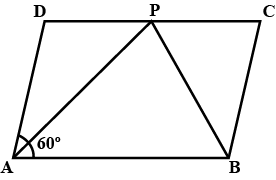
In figure, ABCD is a parallelogram in which $$\angle$$A $$=60^o$$. If the bisectors of $$\angle$$A and $$\angle$$B meet at P, prove that AD$$=$$DP, PC$$=$$BC and DC$$=2$$AD.
Then, $$\angle DAP=\angle PAB=30^o$$ ------ ( 1 )
We know that in parallelogram adjacent angles are supplementary
$$\therefore$$ $$\angle A+\angle B=180^o$$
$$\Rightarrow$$ $$60^o+\angle B=180^o$$
$$\therefore$$ $$\angle B=120^o.$$
$$BP$$ bisects $$\angle B$$
Then, $$\angle PAB=\angle PBC=60^o$$ ---- ( 2 )
$$\Rightarrow$$ $$\angle PAB=\angle APD=30^o$$ [ Alternate angles ] ---- ( 3 )
$$\therefore$$ $$\angle DAP=\angle APD=30^o$$ [ From ( 1 ) and ( 3 ) ]
$$\therefore$$ $$AD=DP$$ [ Since base angles are equal ]
Similarly, $$\angle PBA=\angle BPC=60^o$$ [ Alternate angles ] --- ( 4 )
$$\Rightarrow$$ $$\angle PBC=\angle BPC=60^o$$ [ From ( 2 ) and ( 4 ) ]
$$\therefore$$ $$PC=BC$$ [ Since base angles are equal
$$\Rightarrow$$ $$DC=DP+PC$$
$$\Rightarrow$$ $$DC=AD+BC$$ [ Since, $$DP=AD,PC=BC$$ ]
$$\Rightarrow$$ $$DC=AD+AD$$ [ Opposite sides of parallelogram are equal ]
$$\therefore$$ $$DC=2AD$$
Two adjacent sides of a parallelogram are in the ratio 5 :If the perimeter of parallelogram is 72 cm. find the length of its sides.
$$ABCD$$ is a trapezium in which $$AB ||CD$$ and $$AD=BC$$. Show that $$\angle A=\angle B$$.
Given that ABCD is a trapezium,
$$AB\parallel CD$$ and $$AD=BC$$
To prove: $$\angle A=\angle B$$
Construction: Draw $$CE\parallel AD$$ and extend AB to intersect CE at E.
Poof: As AECD is a parallelogram.
By constriction, CE is parallel to AD and AE is parallel to CD,
$$\therefore \,\,AD=EC$$
But, AD=BC (Given)
$$\therefore \,\,BC=EC$$
$$\Rightarrow \,\angle 3=\angle 4$$ (Angle opposite to equal side are equal)
Now, $$\angle 1+\angle 4={{180}^{0}}$$ (consecutive interior angle of parallelogram )
And $$\angle 2+\angle 3={{180}^{0}}$$ (linear pair )
$$\Rightarrow \angle 1+\angle 4=\angle 2+\angle 3$$ $$\Rightarrow \angle 1=\angle 2\,\,\,\,\,\,\,\,\,\,\,\,\because \angle 3=\angle 4$$ (so get cancelled with each other )
$$\Rightarrow \,\angle A=\angle B$$
Hence, proved .
In parallelogram PQRS, find $$x, y, z$$ and $$w$$.
We know that, sum of adjacent angles of parallelogram is $$180^o.$$
$$\therefore$$ $$\angle QPS+\angle PSR=180^o$$
$$\Rightarrow$$ $$x+110^o=180^o$$
$$\Rightarrow$$ $$x=70^o$$
We know that, opposite angles of a parallelogram are equal.
$$\therefore$$ $$x=y=70^o$$ and $$z=110^o$$
$$\Rightarrow$$ $$\angle PSR+\angle PST=180^o$$ [ Linear pair ]
$$\Rightarrow$$ $$110^o+w=180^o$$
$$\Rightarrow$$ $$w=70^o$$
We get, $$x=70^o,y=70^o,z=110^o$$ and $$w=70^o$$
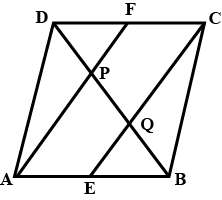
In a parallelogram $$ABCD,E$$ and $$F$$ are the mid-point of sides $$AB$$ and $$CD$$ respectively. Show that the line segment $$AF$$ and $$EC$$ trisect the diagonal $$BD$$.
Show that the points $$\left( {2, - 2} \right),\left( {8,4} \right),\left( {5,7} \right)$$ and $$\left( { - 1,1} \right)$$ taken in order constitute the vertices of a Rectangle.
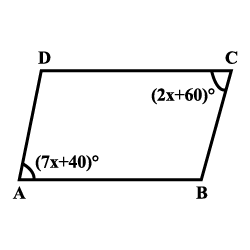
In a parallelogram $$ABCD,$$ $$m\angle A=({ 7x+40 })^{ o }$$ and $$m\angle C=({ 2x+60 })^{ o }$$. Find the measures of $$\angle B$$ and $$\angle D?$$
Here, $$ABCD$$ is a parallelogram.
$$\angle A=\angle C$$ [Opposite angles are equal in parallelogram ]
$$\Rightarrow$$ $$7x+40^o=2x+60^o$$
$$\Rightarrow$$ $$5x=20^o$$
$$\Rightarrow$$ $$x=4^o$$
Now, measure of $$\angle A$$ will be,
$$m\angle A=(7x+40)^o$$
$$=(7\times 4+40)^o$$
$$=68^o$$
Also, sum of adjacent angles in a parallelogram is equal to $$180^o,$$
$$\angle A+\angle B=180^o$$
$$\Rightarrow 68^o+\angle B=180^o$$
$$\Rightarrow \angle B=112^o$$
$$\Rightarrow$$ $$\angle B=\angle D=112^o$$ [Opposite angles are equal in parallelogram ]
The measure of $$\angle B$$ and $$\angle D$$ is $$112^o$$.
In a parallelogram $$RING$$, if $$m\angle R=70^{o}$$, find all the other angles.
We have,
A parallelogram $$RING$$, if $$\angle R={{70}^{o}}$$
Then, solve that,
$$ \angle I=? $$
$$ \angle N=? $$
$$ \angle G=? $$
We know that,
Adjacent angles of parallelogram is supplementary.
Then,
$$ \angle R+\angle I={{180}^{o}} $$
$$ {{70}^{o}}+\angle I={{180}^{o}} $$
$$ \angle I={{180}^{o}}-{{70}^{o}} $$
$$ \angle I={{110}^{o}} $$
But we know that,
Opposite angles of parallelogram are equal.
Then,
$$ \angle R=\angle N $$
$$ {{70}^{o}}=\angle N $$
$$ \angle N={{70}^{o}} $$
And
$$ \angle I=\angle G $$
$$ {{110}^{o}}=\angle G $$
$$ \angle G={{110}^{o}} $$
Hence, this is the answer.
Prove that the points $$(-7,-3)$$ $$(5,10)$$ $$(15,8)$$ and $$(3,-5)$$ taken in order are the corner of a parallelogram
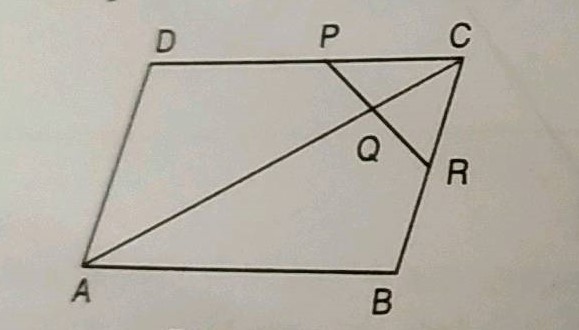
In the fig, $$\Box PQRS$$ and $$\Box ABCR$$ are two parallelograms.
If $$\angle P = 110^o$$ then find the measures of all angles of $$\Box ABCR$$.
Given:- $$PQRS$$ and $$ABCR$$ are parallelograme
$$\angle P=110^0$$
$$\Rightarrow \angle SRQ=110^0$$ (opposite angle of a parallelogram. are equal).
$$\Rightarrow \angle ARC=110^0$$
if $$\angle=ARC=110^0$$
$$\Rightarrow \angle ABC=110^0$$ (opposite of angle of $$\angle ARC$$ of parallelogram $$ABCR$$)
Sum of adjunct angles of a parallelogram $$=180^0$$
$$\angle ABC+\angle BCR=180^0$$ ......(1)
$$\angle ABC+\angle BAR=180^0$$ ......(2)
$$\angle BCR=180-\angle ABC=180-110=70^0$$
$$\angle BAR=180-\angle ABC=180-110=70^0$$
$$\therefore $$ in parallelogram $$ABCR$$
$$\angle A=70^0, \angle B=110^0, \angle C=70^0, \angle R=110^0$$
In $$\Box {ABCD}$$, side $$BC\parallel $$ side $$AD$$. Diagonals $$AC$$ and $$BD$$ intersect each other at $$P$$. If $$AP=\cfrac{1}{3}AC$$, then prove that $$DP=\cfrac{1}{2}BP$$.
Clearly, $$\triangle APD \sim \triangle CPB$$
$$\Rightarrow \ \dfrac {AP}{CP}=\dfrac {PD}{PB}$$
$$\Rightarrow \ \dfrac {AP}{AC-AP}=\dfrac {PD}{PB}$$
$$\Rightarrow \ \dfrac {1}{\dfrac {AC}{AP}-1}=\dfrac {PD}{PB}$$
$$\Rightarrow \ \dfrac {1}{3-1}=\dfrac {PD}{PB}$$
$$\therefore \ DP=\dfrac {1}{2}BP$$
In the given figure, ABCD is a parallelogram. P is the mid-point of AB. Prove that ACBM is a parallelogram.
(i) $$ABCD$$ is parallellogram
(ii) $$P$$ is midpoint pf $$CM$$.
$$ABCD$$ is parfallellogram
$$\therefore AD||BC$$ .
$$\angle MAB=\angle CBA$$ ,,,(1) (interior opposite angle of tranversal AB)
$$\boxed{\angle CPB=\angle ABM}$$ ...(2) (vertical opposite angle)
In $$\Delta CPB$$ and $$\Delta ABM$$
from (1) and (2) $$\boxed{\angle BCP=\angle PMA}$$
$$\boxed{CP+PM=\frac{CM}{2}}$$ ...(4) (P is mid point )
from (2), (3) and (4)
$$\boxed{\Delta CPB\cong \Delta MPA}$$
$$\therefore \boxed{CB=AM}$$
We know $$CB$$ is parallel to $$AM$$
$$\therefore \boxed{\angle AMB \text{is a parallelllogram since}\, CB||AM\, and \, CB=AM}$$
In a parallelogram $$ABCD$$, if $$\angle B = 135^{\circ}$$, determine the measures of its other angles.
$$ABCD$$ is a parallelogram, $$\angle B= 135^o$$.
In parallelogram sum of adjacent angles supplementary.
$$\Rightarrow$$ $$\angle A+\angle B=180^o$$
$$\Rightarrow$$ $$\angle A+135^o=180^o$$
$$\Rightarrow$$ $$\angle A=180^o-135^o$$
$$\Rightarrow$$ $$\angle A=45^o$$
In parallelogram opposite angles are equal.
$$\therefore$$ $$\angle A=\angle C=45^o$$
And $$\angle B=\angle D=135^o$$
ABCD is a parallelogram and X is mid-point of AB. If $$ar (AXCD) = 24 \, cm^2$$, then $$ar (\Delta ABC) = 24 \, cm^2$$. Write if it is true or false and justify your answer.
$$ar(AXCD)=24cm^2$$
$$AX=XB=\dfrac{1}{2}AB$$
area $$(ABCD)=AB\times h$$ (h = height of ABCD)
area of $$\Delta XBC=\dfrac{1}{2}\times XB\times h$$
$$=\dfrac{1}{2}\times \dfrac{AB}{2}\times h$$
area of $$(\Delta XBC)=\dfrac{area(ABCD)}{4} $$
area $$(AXCD)=ar(ABCD)$$ $$-ar \Delta XBC$$
$$=ar(ABCD)-\dfrac{ar(ABCD)}{4}$$
$$\boxed{ar(AXCD)=\dfrac{3ar(ABCD)}{4}}=24cm^2$$ (Given)
$$ar(ABCD)=4 \times \dfrac{24}{3}=32cm^2$$
$$ar(\Delta ABC)=\dfrac{1}{2}ar(ABCD)=\dfrac{1}{2}(32)=16cm^2$$
[diagonal divides parallelogram to two equal areas].
$$\therefore ar(\Delta ABC)=16cm^2$$
So the answer is false.
$$EFGH$$ is a parallelogram. Find the values of $$x,y$$ and $$z$$.
$$\because EFGH$$ is a parallelogram.
$$\Rightarrow$$ $$\angle FGH+\angle FGK=180^o$$ [ Linear pair ]
$$\Rightarrow$$ $$\angle FGH+70^o=180^0$$
$$\therefore$$ $$\angle FGH=110^o$$
$$\Rightarrow$$ $$\angle FGH=\angle FEH=110^o$$ [ Opposite angles of a parallelogram are equal ]
$$\therefore$$ $$x=110^o$$
Now, $$\angle EHG+\angle FGH=180^o$$ [ Sum of adjacent angles of parallelogram is $$180^o.$$ ]
$$\Rightarrow$$ $$\angle EHF+\angle FHG+\angle FGH=180^o$$
$$\Rightarrow$$ $$40^o+z+110^o=180^o$$
$$\Rightarrow$$ $$z+150^o=180^o$$
$$\therefore$$ $$z=30^o$$
$$\Rightarrow$$ $$\angle EHG=40^o+z$$
$$=40^o+30^o$$
$$\Rightarrow \angle EHG=70^o$$
$$\Rightarrow$$ $$\angle FHG+\angle HGF+\angle GFH=180^o$$ [ Sum of angles of triangle is $$180^o$$ ]
$$\Rightarrow$$ $$30^o+110^o+y=180^o$$
$$\Rightarrow$$ $$140^o+y=180^o$$
$$\therefore$$ $$y=40^o$$
We get, $$x=110^o,y=40^o,z=30^o$$
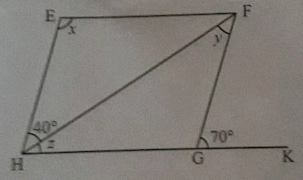
$$ABCD$$ is a parallelogram in which $$\angle A={ 110 }^{ \circ }$$, Find the measure of angle $$\angle C$$ ?
If the three successive vertices of a parallelogram have the position vectors as, $$A (-3,-2,0) ; B(3,-3,1) $$ and $$ C ( 5,0,2) . $$ Then find :
a vector having the same direction as that of $$\vec{AB}$$ but magnitude equal to $$ \vec{AC}$$
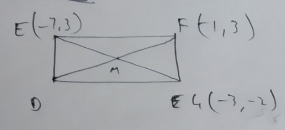
The diagram shows a parallelogram DEFG. The point M is the midpoint of the diagonals DF and EG. Calculate the coordinates of M.
$$M$$ is mid point
$$M=\left(\dfrac{-7-3}{2}, \dfrac{3-2}{2}\right)=\left(\dfrac{10}{2}, \dfrac{+1}{2}\right)$$
$$=\left(-5, \dfrac{1}{2}\right)$$
The opposite angles of a parallelogram are $$\left (3\ x - 2\right)^{o}$$ and $$\left ( x + 48\right)^{o}$$. Find the measure of each angle of the parallelogram.
ABCD is a parallelogram, G is the point on AB such that $$AG=2GB$$. E is a point on DC such that $$CE=2DE$$ and F is a point of BC such that $$BF=2FC$$. Prove that
$$ar{(\triangle EFC)}=\dfrac {1}{2}ar(\triangle EBF)$$
Given$$ABCD$$ is a parallelogram in which $$AG=2GB,CE=2DE$$ and $$BF=2FC$$
$$1)$$ Since $$ABCD$$ is a parallelogram we have $$AB\parallel CD$$ and $$AB=CD$$
$$\therefore BG=\dfrac{1}{3}AB$$ and $$DE=\dfrac{1}{3}AB$$
$$\therefore BG=DE$$
$$\therefore ADEH$$ is a parallelogram (since $$AH\parallel DE$$ and $$AD\parallel HE$$)
Area of parallelogram $$ADEH$$=area of parallelogram $$BCIG$$ ....$$\left(1\right)$$
Since $$DE=BG$$ and $$AD=BC$$ parallelogram with corresponding sides are equal
we have area$$\left(\triangle{HEG}\right)=$$area$$\left(\triangle{EGI}\right)$$ ....$$\left(2\right)$$
Diagonals of a parallelogram divide it into two equal areas.
From $$\left(1\right)$$ and $$\left(2\right)$$ we get
Area of parallelogram $$ADEH+$$area$$\left(\triangle{HEG}\right)=$$area of parallelogram $$BCIG+$$area$$\left(\triangle{EGI}\right)$$
$$\therefore$$ Area of parallelogram $$ADEG=$$Area of parallelogram $$GBCE$$
$$2)$$Height of parallelogram $$ABCD$$ and $$\triangle{EGB}$$ is the same
Base of $$\triangle{EGB}=\dfrac{1}{3}AB$$
Area of parallelogram $$ABCD=h\times AB$$ area$$\left(\triangle{EGB}\right)=\dfrac{1}{2}\times h\times\dfrac{1}{3}AB=\dfrac{1}{6}h\times AB$$
Area$$\left(\triangle{EGB}\right)=\dfrac{1}{6}$$Area of parallelogram $$ABCD$$
$$3)$$Let the distance between $$EH$$ and $$CB=x$$
area$$\left(\triangle{EBF}\right)=\dfrac{1}{2}\times BF\times x=\dfrac{1}{2}\times\dfrac{2}{3}BC\times x=\dfrac{1}{3}\times BC\times x$$
and area$$\left(\triangle{EFC}\right)=\dfrac{1}{2}\times CF\times x=\dfrac{1}{2}\times\dfrac{1}{3}BC\times x=\dfrac{1}{2}$$Area of $$\left(\triangle{EBF}\right)$$
$$\Rightarrow$$ Area$$\left(\triangle{EFC}\right)=\dfrac{1}{2}\times$$Area$$\left(\triangle{EBF}\right)$$
A point P is taken on side CD of a parallelogram ABCD and CD is produced to Q making DQ = CP. The line through Q parallel to AD meets BP produced at S and AD is produced to meet BS at R. Prove that ARSQ is a parallelogram.
$$QD=CP$$ [ Given ] ---- ( 1 )
$$AB=CD$$ [ Opposite sides of parallelogram ]
$$\Rightarrow$$ $$AB=CP+DP$$
$$\Rightarrow$$ $$AB=QD+DP$$ [ From ( 1 ) ]
$$\Rightarrow$$ $$AB=QP$$
$$\therefore$$ $$AB\parallel QP$$ [ Since, $$AB\parallel CD$$ ]
$$\therefore$$ $$ABPQ$$ is a parallelogram.
$$\therefore$$ $$AQ\parallel BP$$
As $$SR$$ is extended part of $$BP$$
$$\Rightarrow$$ $$AQ\parallel SR$$
$$\Rightarrow$$ $$AQ\parallel RP$$
$$\Rightarrow$$ $$QS\parallel AR$$
$$\therefore$$ $$ARSQ$$ is a parallelogram.
If the three successive vertices of a parallelogram have the position vectors as, $$A (-3,-2,0) ; B(3,-3,1) $$ and $$ C ( 5,0,2) . $$ Then find :
the angle between $$ \vec{AC} $$ and $$ \vec{BD} $$
$$A(-3, -2, 0)\ B(3, -3, 1)\ C(2, 0, 2)$$
same $$ABCD$$ is a parallelogram
$$D_x=A_x+C_x+B_x$$
$$\Rightarrow \ D=((-3+5-3),\ (-2+10. (9)), D(2, 1))$$
$$D=(-1,1,1)$$
angle between $$\vec {AC} $$ and $$\vec {BC}$$:
$$\vec {AC}=\vec {OC}-\vec {OA}=(5 \hat i+2\hat k)-(-3\hat i-2\hat j)$$
$$\vec {AC}=8\hat i+2\hat j+2\hat k$$
$$\vec {BD}=\vec {OD}-\vec {OB}=(-\hat i +\hat j+\hat k)-(3\hat i-3\hat j+\hat k)$$
$$=(4\hat i+4\hat j)$$
$$|\vec {AC}+\vec {BD}|=(8\hat i+2\hat j+2\hat k)+(-4\hat i+4\hat j)$$
$$=(4\hat i-\hat j+2\hat k)$$
$$(\vec {AC}+\vec {BD})^2=|\vec {AC}|^2+|\vec {BD}|^2+2|AC| |\vec {BD}| \cos (\vec {AC},\ \vec {BD})$$
$$|AC|=\sqrt {64+4+4}=\sqrt {72}$$
$$|BD|=\sqrt {16+16}=-\sqrt {32}$$
$$|\vec {AC}+\vec {BD}|=\sqrt {16+36+7}=\sqrt {56}$$
$$(\sqrt {56})^2=(\sqrt {72})^2+(\sqrt {32})^2+2\sqrt {(32)(72)}\cos \theta$$
$$56=72+32+2\sqrt {(64)(36)}\cos \theta$$
$$-48=2\times 8\times 6\cos \theta$$
$$\cos \theta =-1/2$$
$$\boxed {\theta =120^o}$$
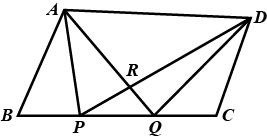
ABCD is a parallelogram in which P and Q are mid-points of opposite sides AB and CD . If AQ intersects DP at S and BQ intersects CP at R, show that ;
i) APCQ is a parallelogram
ii) DPBQ is a parallelogram
iii) PSQR is a parallelogram
The sum of opposite angles of a parallelogram is $$ 160^ \circ$$ find the measure of the angles in parallelogram.
In the given figure, ABCD is a parallelogram. Points P and Q on BC trisect BC.
Prove that :
i) $$ar (\Delta APR) = ar (\Delta DRQ)$$
ii) $$ar (\Delta DPQ) = \dfrac{1}{6} ar (ABCD)$$
iii) $$ar(ARPB) = ar(DRQC)$$
$$BP=PQ+QC=\dfrac{1}{3}BC$$
$$ABCD$$ is a parallelogram.
(i) $$ar(\triangle APR)=ar(\triangle DRQ)$$.
ina parallellogram, triangle inscribed with the
same bak have equal access.
$$\Rightarrow ar(\triangle APD)=ar(\triangle AQD)$$
$$\Rightarrow ar(\triangle ARD)+ar(\triangle APR)=ar(\triangle ARD)+ar(\triangle QRD)$$
$$\boxed{ar(\triangle APR)=ar(DRQ)}$$.....(1)
$$\Rightarrow (\triangle DPQ)\dfrac{1}{2}\times h\times (PQ)=\dfrac{1}{2}\times hr(\dfrac{BC}{3})$$
h=height of parallelogram.
$$\boxed{ar(\triangle DPQ)\dfrac{(h\times BC)}{6}}$$
area of parallellogram $$ABCD=(h\times BC)$$
$$\therefore \boxed{\Rightarrow ar(\triangle DPQ)\dfrac{1}{6}\times ar(ABCD)}$$
(iii) $$ar(\triangle ABP)=\dfrac{1}{2}\times h\times PB=\dfrac{1}{2}\times h\times \dfrac{BC}{3}=\dfrac{1}{6}(h\times BC)$$
$$ ar(\triangle DQC)\dfrac{1}{2}\times h\times (QC)=\dfrac{1}{2}\times h\times \dfrac{BC}{3}=\dfrac{1}{6}(h\times BC)$$
$$\Rightarrow ar(\triangle ABP)=\dfrac{1}{6}(h\times BC)=ar(\triangle DQC)$$
$$\boxed{ar(\triangle ABP)=ar(\triangle DQC)}$$....(3)
add (1) and (3)
$$ar(ABP)ar(\triangle APR)=ar(\triangle DQC)+ar(DQR)$$
$$\boxed{ar(ARPB)=ar(DRQC)}$$
Two adjacent angle of a parallelogram have equal measure. Find the measure of each of the angle of parallelogram.
$$\measuredangle a=\measuredangle b$$
$$\measuredangle a+\measuredangle b=180°$$ (co-interior angles)
$$\therefore \measuredangle a=90°\Rightarrow \measuredangle b=90°$$
Write the properties of parallelogram.
ABCD is a parallelogram. If L, M be the middle points of BC and CD, express $$\bar{AL}$$ and $$\bar{AM}$$ in terms of $$\bar{AB}$$ and $$\bar{AC}$$ also show that $$\bar{AL}+\bar{AM}=\left(\dfrac{3}{2}\right)\bar{AC}$$.
Given $$ABCD$$ is a parallelogram and $$L,M $$ are the mid points of $$BC$$ and $$CD$$ respectively.
In $$\triangle ALC$$
$$\vec{AL}+\vec{LC}=\vec{AC}$$
Since $$L$$ is the mid point of $$BC$$,
$$\vec{LC}=\cfrac{1}{2}\vec{BC}$$
$$\implies \vec{AL}+\cfrac{1}{2}\vec{BC}=\vec{AC}$$
$$\implies \vec{AL}=-\cfrac{1}{2}\vec{BC}+\vec{AC}$$
In $$\triangle AMC$$
$$\vec{AM}+\vec{MC}=\vec{AC}$$
Since $$M$$ is the mid point of $$DC$$,
$$\vec{MC}=\cfrac{1}{2}\vec{DC}$$
$$\implies \vec{AL}+\cfrac{1}{2}\vec{DC}=\vec{AC}$$
$$\implies \vec{AL}=-\cfrac{1}{2}\vec{DC}+\vec{AC}$$
Hence $$\vec{AL}+\vec{AM}=-\cfrac{1}{2}(\vec{DC}+\vec{BC})+2\vec{AC}$$
Since $$ABCD$$ is a parallelogram, $$\vec{DC}=\vec{AB}$$
$$\vec{AL}+\vec{AM}=-\cfrac{1}{2}(\vec{AB}+\vec{BC})+2\vec{AC}$$
From triangular law of addition in $$\triangle ABC$$
$$\vec{AB}+\vec{BC}=\vec{AC}$$
Hence,
$$\implies\vec{AL}+\vec{AM}=-\cfrac{1}{2}(\vec{AC})+2\vec{AC}$$
$$\implies\vec{AL}+\vec{AM}=\cfrac{3}{2}\vec{AC}$$
Hence proved.
$$A(1,1),B(5,4),C(3,8),D(-1,2)$$ are the vertices of $$\Box ABCD$$. If $$P,Q,R,S$$ are the mid-points of $$\overline {AB},\overline {BC},\overline {CD},\overline {DA}$$ respectiely, show that $$PQRS$$ is parallelogram.
$$ABCD$$ is a parallelogram so co-ordinates of $$P$$
$$\Rightarrow \left( \dfrac{1+5}{2}, \dfrac{1+9}{2} \right)$$
$$P\left( 3,\dfrac{5}{2} \right)$$
$$Q= \left( \dfrac{5+3}{2}, \dfrac{4+8}{2} \right) \Rightarrow (4,6)$$
$$R= \left( \dfrac{3+ (-1)}{2}, \dfrac{4+8}{2} \right) \Rightarrow (1,5)$$
$$S= \left( \dfrac{-1+1}{2}, \dfrac{2+1}{2} \right) \Rightarrow \left( 0,\dfrac{3}{2} \right)$$
$$PQ= \sqrt{(4-3)^{2} + \left( 6-\dfrac{5}{2}^{2} \right) }$$
$$=\sqrt{1^{2}+ \left( \dfrac{7}{2}^{2} \right)} \Rightarrow \sqrt{\dfrac{53}{4}}$$
$$QR= \sqrt{ (1-4)^{2}+ (5-6)^{2}}$$
$$=\sqrt{(-3)^{2} + (-1)^{2} } = \sqrt{10}$$
$$RS= \sqrt{ (0-1)^{2} + \left( \dfrac{3}{2} -5 \right)^{2} }$$
$$=\sqrt{(-1)^{2}+ \left( \dfrac{-7}{2} \right)^{2}}= \sqrt{\dfrac{53}{4}}$$
$$SP= \sqrt{ (3-0)^{2} + \left( \dfrac{5}{2}, \dfrac{-3}{2} \right)^{2} }$$
$$=\sqrt{(3)^{2}+ (1)^{2}}= \sqrt{10}$$
So $$PQ= RS$$ and $$QR= SP$$ as in parallelogram opposite sides are equal.
$$\therefore PQRS$$ is parallelogram
Hence showed.
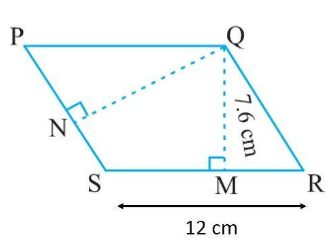
$$PQRS$$ is a parallelogram (Fig $$11.23$$). $$QM$$ is the height from $$Q$$ to $$SR$$ and $$QN$$ is the height from $$Q$$ to $$PS$$. If $$SR=12\ cm$$ and $$QM=7.6\ cm$$. Find:
(a) the area of the parallelogram $$PQRS$$
(b) $$QN$$, if $$PS=8\ cm$$
The diagram shows a parallelogram DEFG. The point M is the midpoint of the diagonals DF and EG. Calculate the coordinates of the vertex D.
In $$ ||gm$$ $$ABCD,E$$ and $$F$$ are mid-points of sides $$AB$$ and $$BC,$$ if $$ar(BEF) = 10 cm^2 $$ then $$ ar(||gmABCD) = $$
Find the value of every interior angle of that regular polygon which has $$10$$ side.
If the points $$A(-2,-1), B(1,0) , C(x,3)$$ and $$D(1,y) $$ are the vertices of a parallelogram, find the values of $$x$$ and $$y$$.
For the parallelogram given above, find the values of x and y.
ABCD is a parallelogram, G is the point on AB such that $$AG=2GB$$. E is a point on DC such that $$CE=2DE$$ and F is a point of BC such that $$BF=2FC$$. Prove that
$$ar{(\delta EGB)}=\dfrac {1}{6}ar(ABCD)$$
REF.Image.
$$ ar(EGB) = \dfrac{1}{2}\times x \times h $$
$$ ar(ABCD) = 3x \times h $$
$$ \dfrac{ar(EGB)}{ar(ABCD)} = \dfrac{\dfrac{1}{2}xh}{3xh} = \dfrac{1}{6}$$
$$ \dfrac{ar(EGB)}{ar(ABCD)} = \dfrac{1}{6} \Rightarrow ar (EGB) = \dfrac{1}{6}ar(ABCD)$$
Hence proved
In the adjoining figure, ABCD is a parallelogram. P is a point on BC such that BP$$:$$PC$$=1:2$$. DP produced meets AB produced at Q. Given ar($$\Delta$$CPQ)$$=20cm^2$$. Calculate ar($$\Delta$$CDP).
For $$\triangle{BPQ}$$ and $$\triangle{DCP}$$
$$\angle{BPQ}=\angle{DPC}\,\,\,\because\,of\,vertically\,opposite\,angles$$
$$\angle{BQP}=\angle{PDC}\,\,\,\because\,of\,alternate\,angles$$
$$\therefore\,\triangle{BPQ}\sim\triangle{DCP}$$
$$\therefore\,\dfrac{BQ}{DC}=\dfrac{QP}{PD}=\dfrac{BP}{PC}$$
Given:$$BP:PC=1:2$$
$$\Rightarrow\,\dfrac{BP}{PC}=\dfrac{1}{2}$$
$$\therefore\,\dfrac{QP}{PD}=\dfrac{1}{2}$$
For $$\triangle{CPQ}$$ and $$\triangle{CDQ}$$ are on the same base at vertex $$C$$
$$\dfrac{Area\,of\,\triangle{CPQ}}{Area\,of\,\triangle{CDP}}=\dfrac{Qp}{PD}=\dfrac{1}{2}$$
$$\therefore\,\dfrac{20}{Area\,of\,\triangle{CDP}}=\dfrac{1}{2}$$
$$\therefore\,Area\,of\,\triangle{CDP}=40\,sq.cm$$
In a parallelogram $$ABCD, AB = 20\ cm$$ and $$AD = 12\ cm$$. The bisector of angle $$A$$ meets $$DC$$ at $$E$$ and $$BC$$ produced at $$F$$. Find the length of $$CF$$.
$$\therefore$$ $$DC=AB=20\,cm$$
$$\Rightarrow$$ $$AD=BC=12\,cm$$
Bisector of $$\angle A$$ meets $$DE$$ on $$E.$$ Produced $$AE$$ and $$BC$$ to meet at point $$F.$$ Extend $$AD$$ to $$G.$$ From $$F$$ draw $$HF\parallel CD.$$
We have $$CD\parallel FH$$ and $$CF\parallel DH.$$
$$\therefore$$ $$DCFH$$ is a parallelogram.
Also, $$AB\parallel FH$$ and $$AH\parallel BF$$
$$\therefore$$ $$ABFH$$ is also parallelogram.
In $$\triangle AHF$$ and $$\triangle ABF$$
$$\Rightarrow$$ $$\angle AHF=\angle ABF$$ [ Opposite angles are equal ]
$$\Rightarrow$$ $$AF=AF$$ [ Common side ]
$$\Rightarrow$$ $$\angle HAF=\angle FAB$$ [ Since, $$AF$$ divides $$\angle HAB$$ ]
$$\Rightarrow$$ $$\triangle AFH\cong\triangle ABF$$ [ By AAS congruence ]
$$\Rightarrow$$ $$AB=AH$$ [ CPCT ]
$$\Rightarrow$$ $$AB=AH=AD+DH=AD+CF$$ [ Since, $$DAFH$$ is a parallelogram ]
$$\therefore$$ $$CF=AB-AD=(20-12)\ cm=8\,cm$$
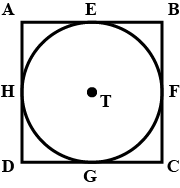
In fig. $$\square ABCD$$ is a parallelogram. It circumscribes the circle with centre $$T$$. Point $$E, F, G, H$$ are touching point are touching points. If $$AE = 4.5, EB 5.5$$. Find $$AD$$.
In the figure, diagonals $$AC$$ and $$BD$$ of a quadrilateral $$ABCD$$ intersect at $$O$$ such that $$OB=OD$$, show that $$ar(\Delta DOC)=ar(\Delta AOB)$$
$$BO=OD$$
Since $$BO=OD$$ is the mid point
we know thta $$a$$ mid point of a $$\triangle $$ divides it into two $$\triangle $$ of equal areas
$$CO$$ is medpoint of $$\triangle BCD$$
i.e., $$ar (\triangle COD)=ar (\triangle COB)---(1)$$
$$AO$$ is a medpoint of $$\triangle ABD$$
i.e. $$ar(\triangle AOD) =ar (\triangle AOB)---(2)$$
from $$(I)$$ & $$(II)$$ we have
$$ar (\triangle COD)+ar (\triangle AOD)=ar (\triangle COB)+ar (\triangle AOB)$$
$$ar (\triangle ADC)= ar (\triangle ABC)$$
The diagonals of a parallelogram are perpend cular to each other. Is this statement true? Gives reason for your answer.
A farmer was a having a field in the form of a parallelogram $$PQRS$$. He took a point $$A$$ on $$RS$$ and joined it to point $$P$$ and $$Q$$. In how many parts the field is divided? What are the shapes of these parts? The farmer want to sow wheat and pulses in equal portions of the field separately. How should he do it?
The field is divided in three triangles.
Since $$\triangle{APQ}$$ and parallelogram $$PQRS$$ are on the same base $$PQ$$ and between the same parallels $$PQ$$ and $$RS$$.
$$\therefore ar{\left( APQ \right)} = \cfrac{1}{2} ar{\left( PQRS \right)}$$
$$2ar{\left( APQ \right)} = ar{\left( PQRS \right)}$$
But,
$$ar{\left( PQRS \right)} = ar{\left( APQ \right)} + ar{\left( PSA \right)} + ar{\left( ARQ \right)} \; \left( \text{From fig.} \right)$$
$$2 ar{\left( APQ \right)} = ar{\left( APQ \right)} + ar{\left( PSA \right)} + ar{\left( ARQ \right)}$$
$$ar{\left( APQ \right)} = ar{\left( PSA \right)} + ar{\left( ARQ \right)}$$
Thus, $$\text{area of } \triangle{APQ} = \text{area of } \triangle{PSA} + \text{area of } \triangle{ARQ}$$
To sow wheat and pulses in equal portions of the field separately, farmer should sow wheat in $$\triangle{APQ}$$ and pulses in other two triangles or pulses in $$\triangle{APQ}$$ and wheat in other two triangles.
$$ABCD$$ is a paralleogram. If its diagonals are equal, then find the value of $$\angle ABC$$
In fig 14.36, ABCD is a parallelogram and E is the mid-point of side BC. IF DE and AB when produced meet at F, prove that AF = 2AB.
Solution :-
in the figure
$$ \triangle DCE$$ and BFE
any DEC = any BEF (vertically opp any)
$$EC = BE$$ ($$E$$ is the mid point)
$$\angle DCB = \angle EBF$$ (alternate angle DC parallel to AF)
So $$ \triangle DCE$$ congruent to $$ \triangle BFE $$
Therefore $$ DC = BF$$ ...(1)
now CD = AB (ABCD is a parallelogram)
$$so AF = AB + BF$$
$$= AB + DC$$ from $$(1)$$
$$= AB + AB$$
$$= 2AB$$
The ratio of an exterior angle and interior angle of a regular polygon is $$2:7$$. Find
(i) Each exterior angle of the regular polygon.
(ii) Number of the sides in the polygon.
in $$\Delta ABC$$ and $$\Delta DEF$$, $$AB = DE, \, AB || DE, \, BC = EF$$ and $$BC || EF$$. Vertices$$ A,\ B$$ and $$C$$ are joined to vertices $$D,\ E$$ and $$F$$ respectively. Show that
(i) quadrilateral $$ABED$$ is parallelogram
(ii) quadrilateral $$BEFC$$ is a parallelogram
(iii) $$AD || CF$$ and $$AD = CF$$
(iv) quadrilateral $$ACFD$$ is a parallelogram
(v) $$AC = DF$$
(vi) $$\Delta ABC \cong \Delta DEF$$
Two adjacent angles of a parallelogram are $$\left(3x-4\right)^{o}$$ and $$\left(3x+10\right)^{o}$$. Find the angles of the parallelograms.
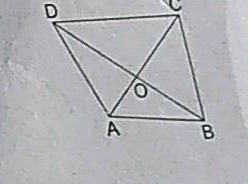
In the adjoining figure, $$ABCD$$ is a parallelogram and diagonals intersect at $$O$$. Find
(i)$$\angle CAD$$
(ii)$$\angle ACD$$
(iii)$$\angle ADC$$.
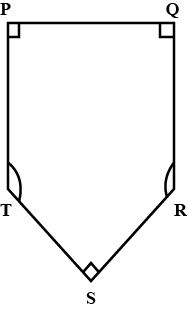
A field is in the shape of a pentagon as shown in the figure. Three of the interior angles of the pentagon are right angles. The remaining two interior angles are congruent. What is the measure of each angle?
In a parallelogram $$PQRS$$ of the given figure, the bisectors of $$\angle P$$ and $$\angle Q$$ meet $$SR$$ at $$O$$. Show that $$\angle POQ=90^{o}$$
In parallelogram ABCD, E and F are mid point of the sides AB and CD respectively.The line segment AF and BF meet the line segment ED and EC at point G and H respectively prove that :
(i) Triangle HEB and FHC are congruent
(ii) GEHF is a parallelogram.
Given, $$ABCD$$ is a parallelogram. Since, $$E$$ and $$F$$ are midpoints of the sides $$AB$$ and $$CD$$ respectively,
$$\therefore AE=BE=DF=CF$$
$$(1)$$
Here, for $$\triangle HEB$$ and $$\triangle FHC$$,
$$\angle EHB=\angle FHC\quad \quad \left[ \because vertically\quad opposite\quad angles \right] \\ \angle HFC=\angle HBE\quad \quad \left[ Alternate\quad interior\quad angles\quad of\quad the\quad lines\quad AB\parallel CD\quad and\quad BF\quad is\quad transversal \right] \\ BE=CF\\ \therefore \triangle HEB\cong \triangle FHC\quad \quad \left[ by\quad Angle-Angle-Side\quad property \right] \\ $$
$$(2)$$
In quadrilateral $$AECF,$$
$$AE=CF$$
and $$AE\parallel CF\quad \left( as\quad AB\parallel CD \right) $$
$$\therefore AECF\quad is\quad a\quad parallelogram\quad \left[ in\quad a\quad quadrilateral,if\quad a\quad pair\quad of\quad opposite\quad sides\quad is\quad equal\quad and\quad parallel\quad then\quad it\quad is\quad a\quad parallelogram \right] $$
So, $$EC\parallel AF\\ \Rightarrow EH\parallel GF\quad \quad \longrightarrow (1)$$
In quadrilateral $$BEDF,$$
$$BE=DF$$
and $$BE\parallel DF\quad \left( as\quad AB\parallel CD \right) $$
$$\therefore BEDF\quad is\quad parallelogram$$
So, $$BF\parallel ED\\ \Rightarrow HF\parallel GE\quad \quad \longrightarrow (2)$$
From $$(1)$$ and $$(2)$$ we get,
$$GEHF$$ is a parallelogram.
$$PQRS$$ is a parallelogram. $$PS$$ is produced to meet $$M$$ so that $$SM=SR$$ and $$MR$$ is produced to meet $$PQ$$ produced at $$N$$. Prove that $$QN=QR.$$
$$\Rightarrow$$ $$SM=SR$$ [ Given ]
$$\therefore$$ $$\angle SMR=\angle SRM$$ [ Angles opposite to equal sides are equal ]
Let $$\angle SMR=\angle SRM=x$$ ----- ( 1 )
As $$\angle PSR$$ is an exterior angle of $$\triangle SMR$$
$$\Rightarrow$$ So, $$\angle PSR=\angle SMR+\angle SRM$$
$$\Rightarrow$$ $$\angle PSR=x+x=2x$$ ---- ( 2 )
$$\Rightarrow$$ $$\angle PSR=\angle PQR$$ [ Opposite angles of parallelogram $$PQRS$$ ]
$$\Rightarrow$$ So, $$\angle PQR=2x$$ ----- ( 3 )
As $$PM\parallel QR$$
$$\Rightarrow$$ So, $$\angle PSR+\angle QRS=180^o.$$
$$\Rightarrow$$ $$2x+\angle QRS=180^o.$$
$$\Rightarrow$$ $$\angle QRS=180^o-2x$$ ----- ( 4 )
As, $$\angle QRS+\angle SRM+\angle QRN=180^o$$
$$\Rightarrow$$ $$(180^o-2x)+x+\angle QRN=180^o$$ [ From ( 1 ) and ( 4 ) ]
$$\Rightarrow$$ $$(180^o-x)+\angle QRN=180^o$$
$$\Rightarrow$$ $$\angle QRN=x$$ ---- ( 5 )
Also, $$\angle PQR$$ is an exterior angle of $$\triangle QRM$$
So, $$\angle PQR=\angle QRN+\angle QNR$$
$$\Rightarrow$$ $$2x=x+\angle QNR$$ [ From ( 5 ) and ( 3 ) ]
$$\Rightarrow$$ $$\angle QNR=x$$ ---- ( 6 )
In $$\triangle QNR,$$
$$\Rightarrow$$ $$\angle QRN=\angle QNR$$ [ From ( 5 ) and ( 6 ) ]
$$\therefore$$ $$QR=QN$$ [ Angles opposite to sides are equal ]
Find $$\angle ADC$$ from the given figure.
Join $$AC$$,
Now consider $$\Delta ABC$$
$$\angle B+\angle BAC+\angle BCA=180^{\circ}$$
$$50^o+(\angle BAD+\angle DAC)+(\angle BCD+\angle DCA)=180^{\circ}$$
$$30^o+\angle DAC+55^o+\angle DCA=130^{\circ}$$
$$\angle DAC+\angle DCA=45^{\circ}$$.......................................$$(1)$$
$$\angle DAC+\angle DCA+\angle ADC=180^{\circ}$$
$$45+\angle ADC=180^{\circ}$$
Thus,
$$\angle ADC=135^{\circ}$$
ABCD is a parallelogram.In which side AB to produced to E so that BE=AB.prove that ED bisects BC
REF.Image.
As, $$AB = BE$$
$$B$$ is mid point of $$AE$$
Consider $$ \triangle EAD $$
From midpoint Theorem
$$ BM = \dfrac{1}{2}AD $$ (As$$ AD \parallel BM)$$ & B is mid point of AE
$$ \Rightarrow = \dfrac{1}{2}BC $$ (As AD = BC for parallelogram)
$$ \Rightarrow $$ M is midpoint of BC
Hence $$ED$$ bisects $$BC$$
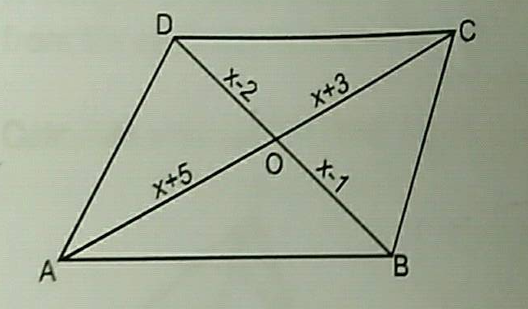
Diagonals AC and BD of a parallelogram ABCD intersect each other at O. If $$OA=3$$cm and $$OD=2$$cm determine the lengths of AC and BD.
$$OA=3\,cm$$ and $$OD=2\,cm$$
We know that, diagonals of a parallelogram bisect each other.
$$\therefore$$ $$AO=OC$$ and $$BO=OD$$
$$\Rightarrow$$ $$AC=2\times OA=2\times 3\,cm=6\,cm$$
$$\Rightarrow$$ $$BD=2\times OD=2\times 2\,cm=4\,cm$$
$$\therefore$$ The length of the diagonals $$AC$$ and $$BD$$ are $$6\,cm$$ and $$4\,cm.$$
$$\Box ABCD$$ is a parallelogram. The ratio of $$\angle A$$ and $$\angle B$$ of this parallelogram is $$5 : 4$$. Find the measure of $$\angle B$$.
Here, $$ABCD$$ is a parallelogram.
Let the measure of $$\angle A$$ and $$\angle B$$ be $$5x$$ and $$4x$$.
We know that in parallelogram sum of measure of adjacent angles is supplementary.
$$\therefore$$ $$\angle A+\angle B=180^o$$
$$\Rightarrow$$ $$5x+4x=180^o$$
$$\Rightarrow$$ $$9x=180^o.$$
$$\Rightarrow$$ $$x=20^o.$$
Measure of $$\angle B=4x=4\times 20^o=80^o.$$
XY is parallel to the side BC of triangle ABC. If BE || AC and CF ||AB meet XY at E and F respectively, show that ar(ABE)=ar(ACF)
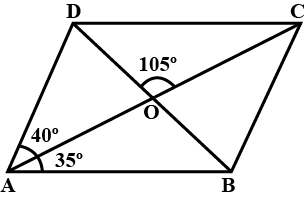
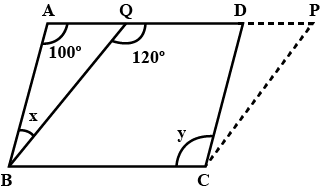
In the adjoining figure, $$ABCD$$ is a parallelogram in which $$\angle CAD = {40^ \circ },\,\angle BAC = {35^ \circ }$$ and $$\angle COD = {65^ \circ }$$. Calculate (i) $$\angle ABD$$ (ii) $$\angle BDC$$ (iii) $$\angle CBD$$
The base and the corresponding altitude of a parallelogram are $$35\ \text{cm}$$ and $$42\ \text{cm}$$ respectively. If the other altitudes is $$30\ \text{cm}$$, find the length of the other pair of parallel sides.
Find the measure of each interior angle of a regular $$15 -gon.$$
$$P$$ and $$Q$$ are any two points lying on the sides $$DC$$ and $$AD$$ respectively of a parallelogram $$ABCD$$. Show that $$ar(APB)=ar(BQC)$$
ABCD is a parallelogram
So, $$AB||CD$$ and $$AD||BC$$ [Opposite sides of parallelogram are parallel]
$$\triangle{APB}$$ and parallelogram ABCD lie on the same base AB and are between the same parallel lines AB and DC
$$Area\ (\triangle{APB})=\dfrac{1}{2}Area\ (ABCD)........(1)$$ [Area of triangle is half of parallelogram if they have same base and parallels]
$$\triangle{QBC}$$ and parallelogram ABCD lie on the same base BC and are between the same parallel lines AD and BC
$$Area\ (\triangle{BQC})=\dfrac{1}{2}Area\ (ABCD)........(2)$$ [Area of triangle is half of parallelogram if they have same base and parallels]
From (1) and (2)
$$Area\ (\triangle{APB})=Area\ (\triangle{BQC})$$
Hence proved.
If the ratio of measures of two adjacent angle of a parallelogram is $$1:2$$ find the measure of all angles of the parallelogram
$$ABCD$$ is a parallelogram and $$X, Y$$ are the points on diagonal $$BD$$ such that $$DX=BY$$. Prove that $$CXAY$$ is a parallelogram.
$$ABCD$$ is a parallelogram.
We know that the diagonals of a parallelogram bisect each other.
So, $$OA=OC$$ and $$OD=OB$$
$$\Rightarrow$$ $$OD=OB$$ ---- ( 1 )
$$\Rightarrow$$ $$DX=BY$$ ---- ( 2 ) [ Given ]
Subtracting ( 2 ) from ( 1 ), we get
$$\Rightarrow$$ $$OD-DX=OB-BY$$
$$\Rightarrow$$ $$OX=OY$$
$$CXAY$$ is a quadrilateral whose diagonals bisect each other.
$$\therefore$$ $$CXAY$$ is a parallelogram.
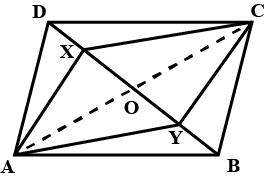
In quadrilateral $$ABCD$$ of the given figure $$X$$ and $$Y$$ are point on diagonal $$AC$$ such that $$AX=CY $$ & $$BXDY$$ is a parallelogram. Show that $$ABCD$$ is a parallelogram.
$$ABCD$$ is a parallelogram with area is $$12\ \text{cm}^2$$. If $$BD$$ is one of the diagonals of $$ABCD$$, find as $$(\triangle ABD)$$
Area of parallelogram $$ABCD=$$ twice the area of a triangle $$ABD$$
$$\Rightarrow$$ Area of $$\Delta ABD=\dfrac { 1 }{ 2 } \times $$ Area of parallelogram $$ABCD$$
$$=\dfrac { 1 }{ 2 } \times 12=6{ cm }^{ 2 }$$
Find the size of the angle of a parallelogram if one angle is $$20^{0}$$ less than twice the smallest angle
The angle of a quadrilateral are in the ratio $$2:3:4:6$$. Find the measure of each of the four angles.
Write 4 conditions for a quadrilateral to be a parallelogram.
The points $$(3,-4)$$ and $$(-6,2)$$ are the extremities of a diagonal of a parallelogram. If the third vertex is $$(-1,-3)$$. Find the coordinates of the fourth vertex.
Let the fourth vertex be $$(x,y)$$
The two diagonals of a parallelogram bisect each other.
So, mid-point of $$PR=$$ Mid-point of $$QS$$
$$(\cfrac{3-6}{2},\cfrac{-4+2}{2})=(\cfrac{x-1}{2},\cfrac{y-3}{2})$$
$$(\cfrac{-3}{2},-1)=(\cfrac{x-1}{2},\cfrac{y-3}{2})$$
Comparing,
$$\cfrac{x-1}{2}=\cfrac{-3}{2}$$
$$x=-2$$
$$\cfrac{y-3}{2}=-1$$
$$y=1$$
$$\therefore (x,y)=(-2,1)$$
In a parallelogram $$ABCD$$, If $$\angle A = {\left( {3x + 12} \right)^ \circ },$$ $$\angle B = {\left( {2x - 32} \right)^ \circ }$$ then find the value of $$x$$ and then find the measures of $$\angle C$$ and $$\angle D$$.
$$\angle A=(3x+12)^o$$
$$\angle B=(2x-32)^o$$
Now sum of adjacent angles of a parallelogram is $$180^o$$.
$$\Rightarrow \angle A + \angle B=180^o$$
$$\Rightarrow 3x+12+2x-32=180$$
$$\Rightarrow 5x-20=180$$
$$\Rightarrow 5x=200$$
$$\Rightarrow x=40$$
So
$$\angle A=(3(40)+12)^o=132^o$$
$$\angle B=(2(40)-32)^o=48^o$$
Now opposite angles in a parallelogram are equal
$$\Rightarrow \angle A=\angle C$$ and $$\angle B=\angle D$$
$$\therefore \angle C=132^o$$ and $$\angle D=48^o$$.
If in a quadrilateral each pair of opposite angle is equal then prove that it is a parallelogram
$$\left. \begin{matrix} \angle B=\angle D \\ \, \angle A=\angle C \\ \end{matrix} \right| given \\ \angle A+\angle B + \angle C +\angle D=360^\circ \\ \angle A+\angle B={ 180^{ 0 } }\} condition\, \, of\, \, parallelogram \\ \, \therefore It\, would\, be\, a\, parallelogram \\ $$
In the given figure, ABCD is parallelogram and E is the mid-point of AD. A line through D, drawn parallel to EB, meets AB produced at F and BC at L. Prove that
$$(i) AF=2DC$$
$$(ii) DF=2DL$$
Given, $$E$$ is mid point of $$AD$$
Also $$EB \parallel DF$$
$$\Rightarrow$$ $$B$$ is mid point of $$AF$$ [mid--point theorem]
so, $$AF=2AB$$ (1)
Since, $$ABCD$$ is a parallelogram,
$$CD=AB$$
$$\Rightarrow AF=2CD$$
$$AD \parallel BC\Rightarrow LB \parallel AD$$
In $$\Delta FDA$$
$$\Rightarrow LB \parallel AD$$
$$\Rightarrow \dfrac{LF}{LD}=\dfrac{FB}{AB}=1$$ from (1)
$$\Rightarrow LF=LD$$
so, $$DF=2DL$$
$$ABCD$$ is parallelogram whose diagonals intersect at $$O$$. If $$OD=9\ cm, OB=x+y\ cm, OA=x-y$$, and $$OC=5\ cm$$, find $$x$$ and $$y$$.
Since diagonals of a parallelogram bisect each other.
$$\implies OA=OC$$ and $$OB=OD$$
$$\implies x+y=9$$ ---------(i)
$$\implies x-y=5$$ ---------(ii)
solving both we get
$$2x=14 \Rightarrow x=7$$cm
$$\implies 7-y=5$$
$$\implies y=2$$cm
$$\therefore x=7$$cm and $$y=2$$cm
In a parallelogram $$ABCD, \angle D=115^{o}$$, determine the measure of $$\angle A$$ and $$\angle B$$.
In triangle $$ABC$$, angle $$B$$ is obtuse. $$D$$ and $$E$$ are mid-points of sides $$AB$$ and $$BC$$ respectively and $$F$$ is a point on side $$AC$$ such that $$EF$$ is parallel to $$AB$$. Show that $$BEFD$$ is a parallelogram.
Show that the bisector of angles of a parallelogram from a rectangle.
Let a parallelogram $$ABCD$$
we know that
$$\angle PAS=\angle RAB=\dfrac{1}{2}< PAB$$..............(1)
Similarly
$$\angle CBQ=\angle QBA=\dfrac{1}{2}< CBA$$..............(2)
So
$$AD||BC$$ then
$$\angle OAB+\angle CAB=180^0$$
$$\dfrac{1}{2}\angle DAB+\dfrac{1}{2}\angle CAB=90^0$$
$$\angle RAB+\angle RBA=180^0$$
Now In $$\Delta le$$ $$ RAB$$
$$\angle RAB+\angle RBA_\angle ARB=180^0$$
$$90^0+\angle ARB=180^0$$
$$\boxed{\angle ARB=90^0}$$
Similarly
$$\boxed{\angle DPC=90^0}$$
So opposite angles are $$90^0$$, so
It is a rectangle.
The first line of solution should be
In a parallelogram $$ABCD$$, $$\angle D = 135 ^ { \circ }$$, determine the measures of $$\angle A$$ and $$\angle B$$
1) Opposite angles in a parallelogram are equal.
2) Adjacent angles in a parallelogram are supplementary $$(sum\,is \,180^0)$$
$$\therefore \angle B=\angle D=135^0$$ (opposite angles)
$$\angle A+\angle B=180^0$$ (adjacent angles)
$$\angle A=180-135$$
$$\angle A=45^0$$
In the figure, $$\square\ ABCD$$ is parallelogram. Point $$E$$ is on the ray $$AB$$ such that $$BE = AB$$, then prove that line $$ED$$ bisects seg $$BC$$ at point F.
$$ABCD$$ is a parallelogram in which $$\angle A = 70 ^ { \circ }$$. Compute $$\angle B , \angle C \text { and } \angle D$$
$$\angle B+70^0=180^0$$
$$\angle B=110^0$$
$$\angle A$$ and $$\angle D$$ are internal angles on same side of the line.
$$\therefore \angle A+\angle D=180^0$$
$$\angle D=180-70=110^0$$
Similarly $$\angle B+\angle C=180^0$$
$$\angle C=70^0$$
$$\angle A,\angle C=70^0$$ and $$\angle B,\angle D=110^0$$
Prove that AE$$||$$FC.
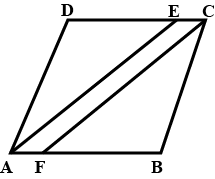
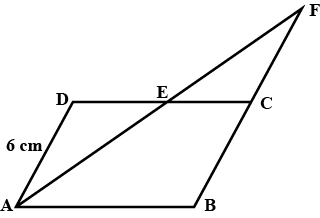
Let ABCD be a parallelogram of area 124 cm$$^2$$. If E and F are the mid-points of side .
Find the area of parallelogram AEFD.
$$ABCD$$ is a parallelogram in which bisectors of $$\angle A$$ and $$\angle C$$ meet the diagonal $$BD$$ at $$P$$ and $$Q$$ respectively. Prove $$PCQA$$ is a parallelogram.
ABCD is a parallelogram in which in bisectors of $$\angle A$$ and $$\angle C$$ meet diagonal BD at P and Q respectively prove PCQA is a parallelogram.
Given : $$ABCD$$ is parallelogram
To prove: $$PCQA$$ is parallelogram
i) $$\angle BAP=\dfrac{1}{2}\angle A$$ .. AP is angle bisector of $$\angle A$$
ii) $$\angle DCQ=\dfrac{1}{2}\angle C $$ .......CQ is angle bisector of $$\angle C$$
iii) $$\angle BAP=\angle DCQ$$ .........[since $$\angle A=\angle C,\because ABCD\, is \, ||gm$$]
iv) $$\angle BAC =\angle DCA$$ ....[average angles , since $$AB||DC$$]
v) $$\angle BAP-\angle BAC=\angle DCQ-\angle DCA$$ [(4)-(3)]
Vi) $$\angle CAP=\angle ACQ$$ [result of (V)] from fig
vii) $$\therefore AP||AQ$$
$$\therefore $$ from vii) and viii) PCQA is a parallelogram.
If $$E,F,G$$ and $$H$$ are respectively the mid-points of the sides of parallelogram $$ABCD$$, show that $$ar(EFGH)=\dfrac {1}{3}ar(ABCD)$$.
Given, $$E, F, G, H$$ are respectively the mid points of sides of parallelogram $$ABCD$$
Construction: Draw a line $$HF$$ which should be parallel to $$CD$$ and $$AB$$
To prove: $$Ar(EFGH)=\cfrac{1}{2} Ar(ABCD)$$
proof: We know $$AB$$ is parallel to $$HF$$. Hence $$ABHF$$ is parallelogram. (opp.sides of parallelogram are equal)
now
$$Ar(DEFH)=\cfrac{1}{2} Ar. (ABFH).....(1)$$
Also $$HF$$ is parallel and equal to $$DC$$
So, $$DCHF$$ is parallelogram
Hence $$Ar (DGFH)=\cfrac{1}{2} Ar(DCFH)$$
(parallelogram $$DCFH$$ and $$DGFH$$ lie on same base $$HF$$ and between same parallel $$DC$$ and $$HF$$)
from eq (1) and (2) we get
$$Ar.(DEFH)+Ar(DGFH)=\cfrac{1}{2}[Ar(ABFH)+Ar(DCFH)]$$
$$Ar(EFGH)=\cfrac { 1 }{ 2 } \left[ Ar(ABCD) \right] $$
ABCD is a parallelogram. E is a point on BC and the diagonal BD intersects AE at F. Prove that DF x FE = FB x FA.
Given that, the diagonal $$BO$$ of parallelogram $$ABCD$$ intersects the segment $$AE$$ at $$F,$$ where $$E$$ is any point on $$BC$$.
To prove: $$DF\times EF=FB\times FA$$
Based on the given information, we can draw the figure shown above.
Now, in $$\triangle AFD$$ and $$\triangle BFE$$,
$$\Rightarrow$$ $$\angle FAD=\angle FEB$$ [ Alternate angles ]
$$\Rightarrow$$ $$\angle AFD=\angle BFE$$ [ Vertically opposite angles ]
$$\therefore$$ $$\triangle ADF\sim\triangle BFE$$ [ By $$AA$$ similarity ]
$$\therefore$$ $$\dfrac{DF}{FA}=\dfrac{FB}{EF}$$
$$\therefore \ DF\times EF=FB\times FA\quad \quad [Hence\ proved]$$
In given figure, PQRS is a parallelogram RT and QT are bisectors of $$\angle R$$ and $$\angle Q$$ respectively meeting at T. find the measure of $$\angle T$$
In parallelogram $$\angle R + \angle Q = 180^{\circ}$$ (sum of adjacent angles in a parallelogram is $$180^{\circ}$$ -----(1)
$$\angle 1 = \angle 2$$ and $$\angle 3 = \angle 4$$ [RT and QT are angle bisectors]
From (1)
$$ \angle 1 + \angle 2 + \angle 3 + \angle 4 = 180^{\circ}$$
$$\implies 2\angle 1+2\angle 3=180^{\circ}$$
$$\therefore \angle 1 + \angle 3 = 90^{\circ}$$
$$\therefore \angle T = 180 - 90^{\circ} = 90^{\circ}$$ [sum of angles in a triangle $$=180^{\circ}$$ ]
The measure of the angles of a pentagon are $$(x-5)^0,(x-6)^0,(2x-7)^0,x^0$$ and $$(2x-2)^0.$$ Find value of $$x$$.
If the diagonal $$AC$$ of a parallelogram $$ABCD$$ bisects $$\angle$$ $$A$$, Show that $$ABED$$ is a rhombus.
Given $$AC$$ bisects $$C$$
$$\angle 1=\angle 2$$
T.P:- ABCD is rhombus
Sol:
$$\angle 1=\angle 2$$
$$\angle 2=\angle 3$$ (alternate opposite)
$$\angle 1=\angle 4$$
$$\Rightarrow \angle 3=\angle 4$$
i.e., $$\angle ACD=\angle CAD$$
$$AD=CD$$ (opposite sides of equal angle in a triangle are equal)
but $$AB=CD$$ & $$AD=BC$$
$$\Rightarrow AB=BC=CD=DA$$
Thus $$ABCD$$ is a rhombus.
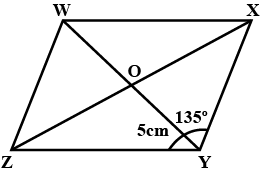
Diagonals of a parallelogram $$WXYZ$$ intersect each other at point $$O$$ . If $$\angle XYZ = 135^0$$, then what is the measure $$\angle XWZ $$ and $$\angle YZW$$ ?
If $$l(OY) = 5\ cm$$ then $$l(WY) =?$$
R.E.F.Image.
In a parallelogram, diagonal bisect each other
$$ \therefore OY = OW = 5 cm$$
$$ \angle XYZ + \angle YZW = 180^{\circ}$$ [$$\therefore $$ interior angles]
$$ 135^{\circ}+\angle YZW = 180^{\circ}$$
$$ \angle YZW = 45^{\circ}$$
In a parallelogram, opposite angles are equal
$$ \angle XYZ = \angle XWZ = 135^{\circ}$$
and OY = 5 cm then WY = OY + OW
$$ 5+5 = 10\, cm $$ [opposite diagonal]
Is it possible to have a regular polygon each of whose interior angles is $$100^0$$?
Find the measure of each angle (in degrees) of a regular octagon.
If each diagonal of a quadrilateral divides it into two triangles to equal areas then prove that quadrilateral is a parallelogram.
Proof:
With respect to diagonal $$AC,$$
$$\Rightarrow$$ $$ar(\triangle ABC)=ar(\triangle ACD)\quad\quad\quad\dots(i)$$
$$\Rightarrow$$ $$ar(\triangle ABC)+ar(\triangle ACD)=ar(ABCD)\quad\quad\quad\dots(ii)$$
From $$(i )$$ and $$( ii ),$$
$$\Rightarrow 2ar(\triangle ABC)=ar(ABCD)\quad\quad\quad\dots(iii)$$
With respect to diagonal $$BD,$$
$$\Rightarrow ar(\triangle ABD)=ar(\triangle BCD)\quad\quad\quad\dots(iv)$$
$$\Rightarrow$$ $$ar(\triangle ABD)+ar(\triangle BCD)=ar(ABCD)\quad\quad\quad\dots(v)$$
From $$( iv )$$ and $$( v ),$$
$$\Rightarrow 2ar(\triangle ABD)=ar(ABCD)\quad\quad\quad\dots(vi)$$
From $$( iii )$$ and $$( vi )$$ we get,
$$\Rightarrow 2ar(\triangle ABC)=2ar(\triangle ABD)$$
$$\Rightarrow ar(\triangle ABC)=ar(\triangle ABD)$$
Since $$\triangle ABC$$ and $$\triangle ABD$$ are on the same base $$AB$$ and have equal area. Therefore, they must have equal corresponding altitudes.
i.e. Altitude from $$C$$ of $$\triangle ABC=$$ Altitude from $$D$$ of $$\triangle ABD$$
$$\Rightarrow$$ $$DC\parallel AB$$
Similarly, we can prove that $$AD\parallel BC.$$
So, opposite sides of quadrilateral $$ABCD$$ are parallel which implies that $$ABCD$$ is a parallelogram.
In parallelogram $$ABCD$$, two points $$P$$ and $$Q$$ are taken on diagonal $$BD$$ such that $$D P = B Q$$. Show that:
$$\Delta APD \cong \Delta CQB$$
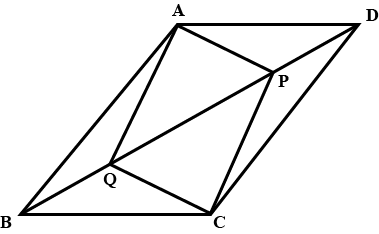
The given figure is a parallelogram. Find $$x$$ and $$y$$
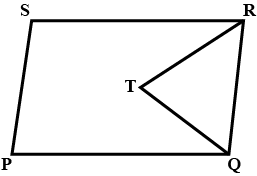
PQRS and ABRS are parallelogram and x is any point on the side BR. show that
(I) ar(PQRS) = ar(ABRS)
(ii) ar$$(\Delta AXS) =\dfrac{1}{2} ar(PQRS)$$
R.E.F.Image.
As $$ AB\parallel PQ \parallel RS $$
$$ \Rightarrow $$ any perpendicular from
PQ to RS would have same
length as that given AB to RS
As $$ ar(PQRS) = base \times height = RS \times height$$
& $$ ar (ABRS) = base \times height = RS \times height$$
$$ \Rightarrow ar (PQRS) = ar(ABRS)$$
NOW, $$ ar (AXS) = \frac{1}{2}\times Base \times height = \frac{1}{2}\times AS\times MX$$
& $$ ar (ABRS) = ar(PQRS) = base\times height = (MX) \times (AS)$$
$$ \Rightarrow ar (AXS) = \frac{1}{2}ar(PQRS)$$
In a parallelogram, ABCD, find the measure of all the angles if one of its angles is $${15^ \circ }$$ less then twice the smallest angle.
Two angles of a hexagon are $$90^{o}$$ and $$10^{o}$$ remaining four angles are equal, find each equal angle.
In a trapezium $$ABCD, AB \parallel CD$$. If $$\angle A=95^{o}$$ then $$\angle D=$$?
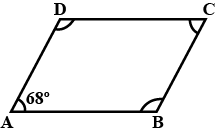
In a parallelogram $$ABCD$$ find the measure of all the angles if one angle measures $${68^\circ}.$$
In parallelogram $$ABCD,$$ let the measure of $$\angle A$$ be $$68^{\circ}.$$
As, the sum of the adjacent angles in a parallelogram is equal to $$180^{\circ}$$. So,
$$ \angle A +\angle B =180^{\circ}$$
$$\Rightarrow \angle B = 180^{\circ}-68^{\circ}$$
$$\Rightarrow \angle B=112^{\circ}$$
Also, opposite angles of a parallelogram are equal so,
$$ \angle B = \angle D = 112^{\circ}$$
$$ \angle A = \angle C = 68^{\circ}$$
Two opposite angles of a parallelogram are $$100^{o}$$ each. Find each of the other two opposite angles.
Given two opposite angles of a parallelogram are $$100^0$$ each
$$\because $$ Adjacent angles of a parallelogram are supplementary.
$$\begin{matrix} \therefore \angle A+\angle B={ 180^{ 0 } } \\ \Rightarrow { 100^{ 0 } }+\angle B={ 180^{ 0 } } \\ \Rightarrow \angle B={ 180^{ 0 } }-{ 100^{ 0 } } \\ \end{matrix}$$
$$ \Rightarrow \angle B = {80^0}$$
Also,
Opposite angles of parallelogram are equal
$$\begin{matrix} \therefore \angle D=\angle B={ 80^{ 0 } } \\ \therefore \angle B=\angle D={ 80^{ 0 } } \\ \end{matrix}$$
$$ABCD$$ is a parallelogram and $$AP$$ and $$CQ$$ are perpendiculars from vertices $$A$$ and $$C$$ on diagonal.
$$\mathrm { BD } ($$ see Fig.$$) .$$ Show that $$\mathrm { AP } = \mathrm { CQ }$$.
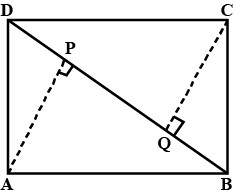
ABCD is a parallelogram . AB is divided at P and CD at Q so that AP : PB = 3 : 2 and CQ : QD = 4 : 1 . If PQ meets AC at R then prove that AR = $$\dfrac{3}{7}$$AC .
Let, AB$$=$$CD$$=5x$$ according to the parallelogram definition that opposite sides are equal.
$$AP=3x, PB=2x$$ and $$CQ=4x$$, $$QD=x$$
$$\Rightarrow ARP\sim CRQ$$
$$\dfrac{3x}{4x}=\dfrac{AR}{RC}$$
$$\dfrac{AR}{RC}=\dfrac{3}{4}$$
According to this fraction, we have
$$AR=3$$ & $$RC=4$$ so that $$AC=3+4=7$$
Finally, $$\dfrac{AR}{AC}=\dfrac{3}{7}$$
$$\therefore AR=\dfrac{3}{7}AC$$.
$$E$$ is a point on the side $$AD$$ produced of a parallelogram $$ABCD$$ and $$BE$$ intersects $$CD$$ at $$F$$. Show that $$\Delta ABE\sim \Delta CFB$$.
$$\begin{array}{l} In\, ABCD \\ \angle A=\angle C\, \, \& \, \, AD\parallel BC\to (i) \\ since,\, \, AE\, \, is\, \, AD\, \, extended \\ \therefore AE\parallel BC\, and \end{array}$$
BE is the transversal
$$\begin{array}{l} \therefore \angle AEB=\angle CBF\to (ii) \\ In\, \Delta ABE\, \, \& \, \, \Delta CBF \\ \angle FDE=\angle FCB (alternate\ angles) \\ \angle DFE=\angle BFC (opposite\ angle ) \\ \angle AEB=\angle CBF\, \, \left( { from\, \, (ii) } \right) \\ \therefore \Delta ABE\sim \Delta CFB\, \, \left( { AAA\, \, criteria } \right) \end{array}$$
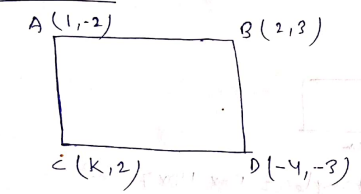
The points $$A(1, -2), B(2, 3), C(k, 2)$$ and $$D(-4, -3)$$ are the vertices of a parallelogram. Find the value of $$k$$.
$$\begin{array}{l} AB=CD \\ u\sin g\, \, dis\tan ce\, \, formula \\ \sqrt { { { \left( { 2-1 } \right) }^{ 2 } }+{ { \left( { 3+2 } \right) }^{ 2 } } } =\sqrt { { { \left( { k+4 } \right) }^{ 2 } }+{ { \left( { 3-2 } \right) }^{ 2 } } } \\ \sqrt { 26 } \, \, \, \, =\, \, \sqrt { { k^{ 2 } }+8k+41 } \\ squaring\, \, both\, \, side \\ 26={ k^{ 2 } }+8k+41 \\ { k^{ 2 } }+8k+15=0 \\ k\left( { k+5 } \right) +3\left( { k+5 } \right) =0 \\ k=\left( { -3,-5 } \right) \end{array}$$
Five angles of a hexagon are each $$115^{o}$$. Calculate the measure of the sixth angle.
The area of the parallelogram ABCD is 90 cm(see Fig.5) Find
(i) ar (ABEF)
(ii) ar (ABD)
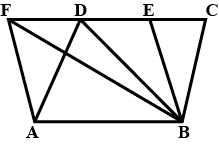
Show that a diagonal of a parallelogram divides into two congruent triangles and hence prove that the opposite sides of a parallelogram are equal.
REF. Image.
consider $$\Delta $$ ABC and $$\Delta $$ ACD
Since the line segments AB+CD are parallel
to each other and AC is a transversal
$$\angle $$ ACB = $$\angle $$ CAD.
AC = AC (common side)
$$\angle $$CAB = $$\angle $$ ACD.
Thus, by ASA criteria
$$ \Delta $$ABC $$\cong $$ $$ \Delta $$ACD
The corresponding part of the congruent
triangle are congruent
AB = CD + AD = BC
In the following figure, $$ABCD$$ is a parallelogram and $$EFCD$$ is a rectangle. Also, $$AL\bot DC$$. Prove that
(i) $$ar(ABCD) = ar(EFCD)$$
(ii) $$ar(ABCD) = DC \times AL$$.
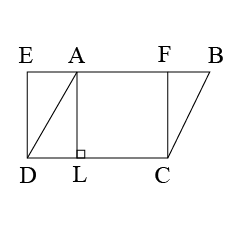
In the following figure both $$ABCD$$ and $$PQRS$$ are parallelogram find the value of $$x.$$
Find the co-ordinates of the point where the diagonals of the parallelogram formed by joining the points $$(-2,-1),(1,0),(4,3)$$ and $$(1,2)$$ meet.
$$M$$ is the midpoint of the side $$A B$$ of a parallelogram $$A B C D .$$ If $$a r (A M C D)=24{ cm }^{ { 2 } },$$ find $$a r ( \Delta A B C ).$$
Find the measure of interior angle. Also name the polygon.
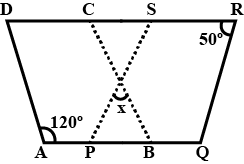
In the given figure, $$ABCD$$ is a rhombus in which $$\angle BCD=110^{o}$$, find $$(x+y)$$.
The measures of two adjacent angles of a parallelogram are in the ratio of 3:Find the measure of each of the angles of the parallelogram.
$${\textbf{Step -1: Draw a parallelogram ABCD.}}$$ 
$${\text{The measurement of two adjacent angles of a parallelogram are in the ratio of 3:2}}{\text{.}}$$
$${\text{Let two adjacent angles be A and B. }}$$
$${\text{Let}}$$ $$\angle A = 3x$$ $${\text{and}}$$ $$\angle B = 2x$$ $$\quad \quad \text{......eqn(i)}$$
$${\text{Since angles}}$$ $$A$$ $${\text{and}}$$ $$B$$ $${\text{are}}$$ $${\text{Supplementary angles}}{\text{.}}$$
$$\therefore \angle A + \angle B = {180^\circ }$$
$$ \Rightarrow 3x + 2x = {180^\circ }$$
$$ \Rightarrow 5x = {180^\circ }$$
$$ \Rightarrow x = \dfrac{{{{180}^\circ }}}{5}$$
$$ \Rightarrow x = {36^\circ }$$
$${\textbf{Step -2: Find the values of angles }}$$ $$\mathbf A$$ $${\textbf{and}}$$ $$\mathbf B$$ $${\textbf{using the value of}}$$ $$\mathbf x.$$
$$\angle A = 3\times{{{36}^\circ }}$$ $$\quad \textbf{[from eqn(i)]}$$
$$ \Rightarrow \angle A = {108^\circ }$$
$${\text{and}}$$ $$\angle B = 2\times {{{36}^\circ }}$$ $$\quad \textbf{[from eqn(i)]}$$
$$ \Rightarrow \angle B = {72^\circ }$$
$${\text{As we know that opposite angles in a parallelogram are equal}}{\text{.}}$$
$$ \Rightarrow \angle C = {108^\circ } = \angle A$$ $$\quad \left[ {\mathbf \because {\textbf{ Opposite angles of parallelogram}}} \right]$$
$$ \Rightarrow \angle D = {72^\circ } = \angle B$$ $$\quad \quad \left[ {\because {\textbf{Opposite angles of parallelogram}}} \right]$$
$${\textbf{Hence, angles of the parallelogram
are 10}}{{\textbf{8}}^\mathbf {\circ} }\mathbf{,{72\boldsymbol{^\circ} },}{\textbf{10}}{{\textbf{8}}^\mathbf\circ }$$ $${\textbf{and 7}}{{\textbf{2}}^\circ }\textbf.$$
In a polygon, there are $$5$$ right angles and the remaining angles are equal to $$195^{o}$$ each., Find the number of sides in the polygon.
In the given fig. $$ABCD$$ is a parallelogram. Find the angles $$x$$ and $$y$$.
If each pair of opposite sides of a quadrilateral is equal the it is a parallelogram.
Given:- A quadrilateral $$ABCD$$ in which $$AB = CD$$ and $$AD = BC$$.
To prove:- $$AB \parallel CD$$ and $$AD \parallel BC$$
Construction:- Joi $$A$$ and $$C$$.
Proof:-
In $$\triangle{ABC}$$ and $$\triangle{CDA}$$,
$$AB = CD \quad \left( \text{Given} \right)$$
$$AD = BC \quad \left( \text{Given} \right)$$
$$AC = AC \quad \left( \text{Common} \right)$$
$$\therefore \triangle{ABC} \cong \triangle{CDA} \quad \left( \text{By SSS} \right)$$
Therefore, by CPCTC,
$$\angle{ACD} = \angle{BAC}$$
$$\angle{DAC} = \angle{ACB}$$
Since alternate anglea are equal, thus the ines are parallel.
Therefore,
$$AB \parallel CD$$ and $$AD \parallel BC$$
Since both the pairs of opposite sides of quadrilateral are parallel, $$ABCD$$ is a parallelogram.
Hence proved.
Three angles of a seven sided polygon are $$132^{o}$$ each and the remaining four angles are equal. Find the value of each equal angle.
The areas of parallelogram and a rectangle are same. The rectangle measures $$10cm\ \times 8cm$$. If one side of the parallelogram is $$16cm$$, Find the corresponding height..
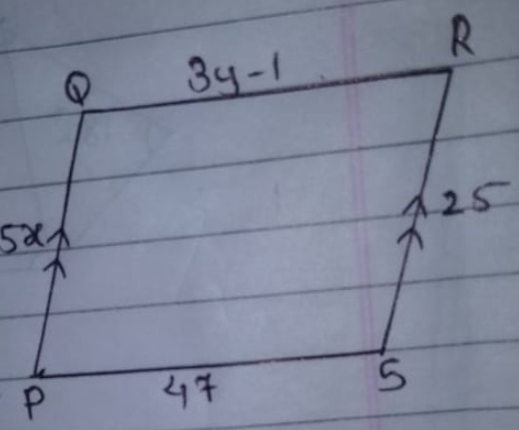
$$PQRS$$ is a parallelogram. From the information given in the figure, find the values of $$x$$ and $$y$$.
Name each of the following parallelograms.
(i) The diagonals are equal and the adjacent sides are unequal.
(ii) The diagonals are equal and the adjacent sides are equal.
(iii) The diagonals are unequal and the adjacent sides are equal.
$$(i)$$ The diagonals are equal and the adjacent sides are unequal.
$$\Rightarrow$$ Rectangle is the name of parallelogram which diagonal are equal and adjacent side are unequal.
$$(ii)$$ The diagonals are equal and the adjacent sides are equal.
$$\Rightarrow$$ Square is the name of parallelogram in which diagonals are equal and the adjacent sides are equal.
$$(iii)$$ The diagonals are unequal and the adjacent sides are equal.
$$\Rightarrow$$ Rhombus is the name of parallelogram in which diagonals are unequal and the adjacent sides are equal.
The three vertices of a parallelogram $$ABCD$$ are $$A(3, -4), B(-1, -3) $$ and $$C(-6, 2)$$. Find the coordinate of vertex $$D$$.
If the diagonals of a parallelogram are equal in length, then prove that the parallelogram is a rectangle.
Given $$ABCD$$ is parallelogram.
$$AC$$ and $$BD$$ are diagonals of parallelogram such that $$AC=BD$$
In $$ \triangle ABD \ \& \ \triangle ACD$$
$$AC = BD$$
$$AB = DC$$ (opposite sides of parallelogram)
$$AD = AD$$ (common side)
$$ \therefore $$$$ \Delta ABD $$ $$\cong $$ $$\Delta DCA $$ (by $$SSS$$ criterion )
$$ \angle BAD $$ = $$ \angle CDA $$ (Corresponding parts of congruent triangles are equal)
$$ \angle BAD+ \angle CDA = 180^{\circ}$$(adjacent angles)
$$\implies \angle BAD = \angle CDA = 90^o$$ ( as they are congruent and supplementary.)
Parallelogram $$ABCD$$ is a rectangle since any parallelogram with one right interior angle is rectangle.
Two consecutive angles of a parallelogram are in the ratio $$1:3$$. Find the smallest angle.
$$ABCD$$ is a parellelogram, $$AB$$ is divided at $$P$$ and $$CD$$ divided at $$Q$$. So that $$AP:PB=3:2$$ and $$CQ:QD=4:1$$. If $$PQ$$ intersect $$AC$$ at$$R$$, then prove that $$AR=3/7AC$$.
If the three vertices of a parallelogram are $$\left(1,3\right),\left(2,4\right)$$ and $$\left(5,3\right)$$,find the fourth vertex.
$$ABCD$$ is a parallelogram.Compute the values $$x$$ and $$y$$
In a parallelogram $$ABCD,$$ prove that sum of any two consecutive angles is $${180}^{\circ}$$
Since $$ABCD$$ is a parallelogram, $$AD\parallel BC$$
Now,$$AD\parallel BC$$ and transversal $$AB$$ intersects them at $$A$$ and $$B$$ respectively.
$$\therefore \angle{A}+\angle{B}={180}^{\circ}$$
$$\because$$ Sum of the interior angles on the same side of the transversal is $${180}^{\circ}$$
Since $$ABCD$$ is a parallelogram, $$AB\parallel DC$$
Now,$$AB\parallel DC$$ and transversal $$AC$$ intersects them at $$A$$ and $$C$$ respectively.
$$\therefore \angle{C}+\angle{D}={180}^{\circ}$$
$$\because$$ Sum of the interior angles on the same side of the transversal is $${180}^{\circ}$$
Now,$$AD\parallel BC$$ and transversal $$AC$$ intersects them at $$A$$ and $$C$$ respectively.
$$\therefore \angle{A}+\angle{D}={180}^{\circ}$$
$$\because$$ Sum of the interior angles on the same side of the transversal is $${180}^{\circ}$$
Now,$$DC\parallel AB$$ and transversal $$BD$$ intersects them at $$B$$ and $$D$$ respectively.
$$\therefore \angle{B}+\angle{D}={180}^{\circ}$$
$$\because$$ Sum of the interior angles on the same side of the transversal is $${180}^{\circ}$$
Hence proved.
If the three vertices of a parallelogram are $$\left(-2,-1\right),\left(1,0\right)$$ and $$\left(4,3\right)$$,find the fourth vertex.
If the three vertices of a parallelogram are $$\left(1,3\right),\left(4,2\right)$$ and $$\left(3,5\right)$$, then find the fourth vertex.
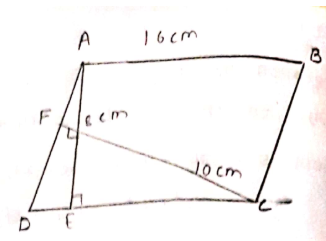
In the figure, $$ABCD$$ is a paralle-logram, $$AE \bot DC$$ and $$CF \bot AD$$. If $$AB = 16$$ cm, $$AE = 8$$ cm and $$CF = 10$$ cm, find $$AD$$.
If the three vertices of a parallelogram are $$\left(-1,-3\right),\left(2,4\right)$$ and $$\left(3,5\right)$$,find the fourth vertex.
If the three vertices of a parallelogram are $$\left(1,3\right),\left(2,4\right)$$ and $$\left(3,5\right)$$,find the fourth vertex.
The following figure shows a parallelogram ABCD whose side AB is parallel to the x-axis, $$\angle A={ 60 }^{ \circ }$$ and vertex C = (7, 5). Find the equations of BC and CD.
A farmer has distributed his field in the shape of parallelogram $$ABCD$$ amongst his son and daughter according to the given figure $$Ar (BEC)$$ of the land was given to the son and combined lands comprising of $$ar(AEB)$$ to his daughter.
Is the distribution of land between son and daughter are equal? Justify your answer.
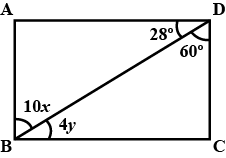
In parallelogram FIST, find $$\angle SFT,$$ $$\angle OST$$ and $$\angle STO.$$
$$ABCD$$ is a parallelogram $$m\angle A=(2x+50)$$ and $$m\angle C=(3x+40)$$, then find the value of $$x$$.
In a parallelogram, opposite angles are equal
$$\Rightarrow \angle A = \angle C \Rightarrow 2x+50 = 3x + 40 \Rightarrow x = 10$$
In a parallelogram $$KLMN, \angle K=60^{o}$$. Find the measures of all the angles.
See the figure aboveFind its perimeter.
In parallelogram $$PQRS, \angle Q=(4x-5)^{o}$$ and $$\angle S=(3x+10)^{o}$$, then find $$\angle Q$$ and $$\angle R$$.
In a parallelogram, opposite angle are equal
$$\Rightarrow \angle Q = \angle s \Rightarrow 4x - 5 = 3x + 10 \Rightarrow x = 15$$
Also sum of adjacent angles is $$180^o \Rightarrow \angle Q + \angle R = 180^o$$
$$\Rightarrow 4(15) - 5 + \angle R = 180$$
$$\Rightarrow \angle R = 125^o$$, $$\angle Q = 55^o$$
In the above figure ABCD is a parallelogram in which P is the midpoint of DC and Q is a point on AC such that CQ =$$ \frac { 1 } { 4 }$$ AC. If PQ produced meets BC at R, prove that R is the midpoint of BC.
The angles of a hexagon are $$(2x+5)^{o},(3x-5)^{o},(x+40)^{o},(2x+20)^{o},(2x+35)^{o}$$. Find the value of $$x$$.Hence find the angles.
The perimeter of a parallelogram is 140 cm. If one of the sides is longer than the other by 10 cm,find the length of each of its sides.
If the diagonals of a parllelogram are equal, then show that it is a rectangle.
Three consecutive vertices of a parallelogram $$ABCD$$ are $$A\left(-1,2,4\right),\,B\left(-3,2,1\right)$$ and $$C\left(-2,-3,4\right)$$.Find the fourth vertex $$D$$
The measure of two adjacent angles of a parallelogram are in the ratio 4 :Find the measure of each angle of the parallelogram.
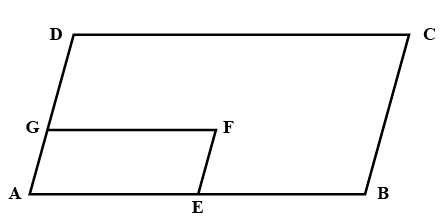
In the below figure, it is given that BDEF and FDEC are parallelograms. Can you say that BD=CD? Why or why not?
In the above right sided figure, ABCD and AEFG are two parallelograms. If $$\angle C={ 55 }^{ 0 }$$, determine $$\angle F$$.
In the figure, ABCD is a parallelogram. The diagonals AC and $$ B D $$ intersect at $$ O; $$ and $$ \angle D A C=40^{\circ}, \angle C A B=35^{\circ} ; $$ and$$ \angle D O C=110^{\circ} $$ . Calculate the measure of $$ \angle A B O, \angle A D C, \angle A C B $$and $$ \angle C B D $$ .
Five angles of a hexagon have measures $${ 100 }^{ \circ },{ 110 }^{ \circ },{ 120 }^{ \circ },{ 130 }^{ \circ }$$ and $${ 140 }^{ \circ }$$. What is the measure of the remaining angle?
ABCD is a parallelogram, $$AE \bot DC$$ and $$CF \bot AD$$. If $$AB=16$$ cm , $$AE=8 cm$$ and $$CF=10 $$ cm, find $$AD$$.
REF.image
Area of a parallelogram
=Base $$\times $$ Altitude.
For ABCD,
$$\therefore AE\perp DC$$
$$\therefore$$ AE is the altitude,DC is the base.
Area of a parallelogram $$=Base\times Altitude$$
$$=DC\times AE$$
$$=AB\times AE$$ (opp.sides of parallelogram are equal ).
$$=16\times 8----(1)$$
For ABCD,
$$\therefore CF \perp AD $$
$$\therefore $$ CF is the altitude AD is the base
Area of a parallelogram= $$base\times Altitude$$
$$=AD\times CF$$
$$=AD\times 10----(2)$$
From (1) & (2)
$$16\times 8=AD\times 10$$
$$\Rightarrow AD=\dfrac{16 \times 8}{10}$$
$$\Rightarrow AD=12.8cm$$
$$\therefore$$ Thus,the length of AS is $$12.8 \, cm$$.
$$ABCD$$ is a quadrilateral in which $$AB$$ and $$CD$$ are smallest and longest sides respectively.
Prove that $$\angle A > \angle C\,and\,\angle B > \angle D.$$
REF.image
Given
AB is the smallest side -----(1)
CD is the largest side -----(2)
To prove $$ :< A> \angle C,< B> \angle D$$
Proof:
Join A and c,and mark the angles
In $$\bigtriangleup ABC,$$
$$\therefore BC > AB $$$$................. (from (1))$$
$$\therefore \angle 1 =\angle 2$$
Angle opposite to the longer side greater.
In$$\bigtriangleup ADC,$$
$$CD> AD..................... (from(2))$$
$$\therefore \angle 3=\angle 4$$
Angle opposite to the longer side is greater.
Adding equation
$$\angle 1+\angle 3> \angle 2+\angle 4$$
Now ,solving for $$\angle B> \angle D$$
Join B and d, and mark the angles.
In $$\bigtriangleup ABD$$,
$$ AD> AB...................(from(1))$$
$$\therefore \angle 5=\angle 6$$
In $$\bigtriangleup CBD,$$
$$ CD> BC ...............(from(2))$$
$$\therefore \angle 7=\angle 8$$
Adding equations
$$\angle 5+\angle7> \angle6+\angle8$$
$$\Rightarrow \angle B> \angle D$$
Hence proved.
In the adjoining figure, show that $$ABCD$$ is a parallelogram.
$$\square ABCD$$ is a parallelogram. The ratio of $$\angle A$$ and $$\angle B$$ of this parallelogram is $$5:4$$. Find the measure of $$\,\angle B$$.
D,E and F are respectively the mid-point of the side BC,CA and AB of a $$\Delta ABC$$ show that
(i) BDEF is a parallelogram.
(ii) ar $$\left( {DEF} \right) = \frac{1}{4}\,\,ar\left( {ABC} \right)$$
Two angles of hexagon are $${90^0}$$ and $${110^0}$$. If the remaining four angles are equal, find each equal angle.
In a parallelogram, $$ABCD$$, if $$AD=10\,cm,\,CF=8\,cm$$, then find $$AB$$.
In $$\Delta ABC\,\,and\,\,\,\Delta DEF,AB = DE,AB\parallel DE,BC = EF\,\,\,and\,\,\,BC\parallel EF.$$ vertices A,B and C are joined to vertices D,E and F respectively in figure show that.
Quadrilateral ABED is a parallelogram
Quadrilateral BEFC is a parallelogram
$$AD\parallel CF\,\,and\,\,AD = CF$$
Quadrilateral ACFD is a parallelogram$$AC=DF$$
$$\Delta ABC \cong \Delta DEF.$$
Quadrilateral ABED is a parallelogram
Quadrilateral BEFC is a parallelogram
$$AD\parallel CF\,\,and\,\,AD = CF$$
Quadrilateral ACFD is a parallelogram
The diagonals of a parallelogram $$ABCD$$ intersect at a point $$O$$. Through $$O$$, a line is drawn to intersect $$AD$$ at $$P$$ and $$BC$$ at $$Q$$. Show that $$PQ$$ divides the parallelogram into two equal parts.
$$\because AC$$ is a diagonal of the || gm $$ABCD$$
Refer image,
$$\therefore ar(\Delta ACD)=\dfrac{1}{2}ar(gmABCD)$$.......(1)
Now, in $$\Delta AOP$$ and $$\Delta COQ$$
$$AO=CO$$ [$$\because$$ Diagonals of || gm bisects each other]
$$\angle AOP=\angle COQ$$ [Vert, opp $$\angle s$$]
$$\angle OAP=\angle OCQ$$ [Alt. $$\angle s;AB||CD$$]
$$\Delta AOP\cong$$ $$\Delta COQ$$ [By ASA cong. Rule]
Hence, $$ar(\Delta AOP)=$$ $$ar(\Delta COQ)$$ [Cong. Area axiom]......(2)
Adding ar(quad.$$AOQD)$$ to both sides of (2), we get
$$ar(quad.AOQD)+ar(\Delta AOP)=ar(quad.AOQD)+ar(\Delta COQ)$$
$$\Rightarrow ar(quad.APQD)=ar(\Delta ACD)$$
But, $$ar(\Delta ACD)=\dfrac{1}{2}ar||(gm ABCD)$$ [From (1)]
Hence, $$ar(quad.APQD)=\dfrac{1}{2}ar(||gmABCD)$$
So, $$PQ$$ divides the parallelogram into two parts of equal area.
The difference between the two adjacent angles of a parallelogram is $${ 20 }^{ \circ }.$$ Find measures of all the angles of the parallelogram.
In the adjoining figure, area of $$\triangle ABE$$ is equal to the area of parallelogram $$ABCD$$. If altitude $$EF$$ is $$16cm$$ long, find the length of altitude of the parallelogram to base $$AB$$ of length $$10cm$$. What is the area of $$\triangle AMD$$, where $$M$$ is mid-point of side $$DC$$ ?
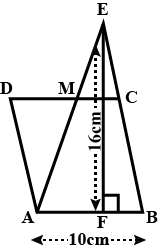
Find the number of sides in a regular polygon. If its each interior angle is $${ 160 }^{ \circ }$$.
Find the number of sides in a regular polygon. If its each interior angle is $${ 150 }^{ \circ }$$.
In Fig. diagonals $$AC$$ and $$BD$$ of quadrilateral $$ABCD$$ intersect at $$O$$ such that $$OB=OD$$. If $$AB=CD$$, then show that :i) ar$$(\triangle DOC) =$$ ar($$\triangle AOB)$$ii) ar$$(\triangle DCB) =$$ ar$$(\triangle ACB)$$iii) $$DA\parallel CB$$ or $$ABCD$$ is parallelogram.
(i) $$ar(DOC)=ar(AOB)$$
Given: A quadrilateral ABCD where $$OB=OD$$ & $$AB=CD.$$
To prove: $$ar(DOC)=ar(AOB)$$
Proof: Let us draw $$OP \perp AC $$ and $$BQ\perp AC$$:
In $$\Delta$$DOP and $$\Delta$$BOQ,
$$\angle DPO=\angle BQO$$ (Both $$90^\circ$$)
$$\angle DOP=\angle BOQ$$ (vertically opposite angles)
$$OD=OB$$ (Given)
$$\Delta DOP\cong \Delta BOQ$$(ASS congruence rule)
$$\therefore$$ $$DP=BQ$$(CPT) ………$$(1)$$
and ar($$DOP$$)=ar($$BOQ$$)$$ ……………..$$(2)$$
(Area of congruent triangles are equal)
In $$\Delta COP$$ and $$\Delta ABQ,$$
$$\angle CPD=\angle AQB$$ (Both $$90^o$$)
$$CP=AB$$ (Given)
$$DP=BQ$$(from $$(1)$$)
$$\therefore \Delta CDP\cong \Delta ABQ$$ (RHS congruence rule)
$$\Rightarrow ar(CDP)=ar(ABQ)$$ …………$$(3)$$
(Area of congruent triangles are equal)
Adding $$(2)$$ & $$(3)$$:
$$ar(DOP)+ar(CPD)=ar(BOQ)+ar(ABQ)$$
$$ar(DOC)=ar(AOB)$$
Hence proved.
(ii) $$ar(DCB)=ar(ACB)$$
In part (i) we proved that
$$ar(DOC)=Ar(AOB)$$
Adding $$ar(OCB)$$ both sides
$$ar(DOC)+ar(OCB)=ar(AOB)+ar(OCB)$$
$$\Rightarrow ar(DCB)=ar(ACB)$$.
(iii) In part (ii) we proved
$$ar(\Delta DBC)=ar(\Delta ABC)$$
We know that two trinagles having same base & equal areas, lie between same parallels.
Here $$\Delta DBC$$ & $$\Delta ABC$$ are on the same base BC & are equal in area.
So, these triangles lie between the same parallels $$DA$$ and $$CB$$.
$$\therefore DA||CB$$.
Now,
In $$\Delta DOA$$ & $$\Delta BOC$$
$$\angle DOA=\angle BOC$$ (vertically opposite angles)
$$\angle DAO=\angle BCO$$
($$DA||BC, AC$$ traversal, alternate angles equal)
$$OB=OB$$ (Given)
$$\therefore \Delta DOA\cong \Delta BOC$$ (ASA congruency)
$$DA=BC$$ (CPCT)
So, in $$ABCD$$, since $$DA||CB$$ and $$DA=CB$$.
One pair of opposite sides of quadrilateral $$ABCD$$ is equal and parallel.
$$\therefore$$ $$ABCD$$ is a parallelogram.
Hence proved.
In a parallelogram $$ABCD$$, the bisector of $$\angle A$$ meets $$DC$$ in $$E$$ and $$AB = 2 \,AD$$. Prove that:
(i) $$BE$$ bisects $$\angle B$$
(ii) $$\angle AEB$$ is a right angle
If angles A,B,C and D of the quadrilateral ABCD, taken in order, are in the ratio 3:7:6:4, then name type of quadrilateral ABCD.
P and Q are the mid-points of the opposite sides AB and CD of a parallelogram ABCD. AQ intersects DP at S and BQ intersects CP at R. Show that PQRS is a parallelogram.
$$ABCD$$ is a parallelogram and $$P$$ is the point of intersection of its diagonals. If $$O$$ is the origin of reference, show that $$ \overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD} = 4\,\overrightarrow{OP} $$
P is the point of intersection of diagonals
ABCD is a parallelogram
so, diagonals bisect each other
$$\therefore \vec{OD}=\dfrac{\vec{OA}+\vec{OC}}{2}$$
$$\Rightarrow \vec{OA}+\vec{OC}=2\vec{OP}$$ ....$$(1)$$
Also, $$\vec{OP}=\dfrac{\vec{OB}+\vec{OD}}{2}$$
$$\Rightarrow \vec{OB}+\vec{OD}=2\vec{OP}$$ ........$$(2)$$
Adding $$(1)$$ & $$(2)$$
$$\vec{OA}+\vec{OB}+\vec{OC}+\vec{OD}=2\vec{OP}+2\vec{OP}$$
$$=4\vec{OP}$$
$$\therefore \vec{OA}+\vec{OB}+\vec{OC}+\vec{OD}=4\vec{OP}$$.
Let $$ \vec{a}, \vec{b}, \vec{c}, \vec{d}$$ be the position vectors of the four distinct points $$A, B, C, D$$. If $$ \vec{b}-\vec{a}=\vec{c}-\vec{d},$$ then show that $$ABCD$$ is parallelogram.
Diagonals of parallelogram $$ABCD$$ intersect at $$O$$ as shown in Fig. $$XY$$ contains $$O$$, and $$X, Y$$ are points on opposite sides of the parallelogram. Give reasons for each of the following:
$$OB = OD$$.
Now, state if $$XY$$ is bisected at $$O$$.
In a parallelogram $$ABCD, AB = 10\ cm, AD = 6\ cm$$. The bisector of $$\angle A$$ meets, $$DE$$ in $$E, AE$$ and $$BC$$ produced meet at $$F$$. Find the length $$CF$$.
$$ABCD$$ is a parallelogram , in which $$AB=10cm$$ and $$AD=6cm$$. The bisector of $$\angle A$$ meets $$DC$$ in $$E.AE$$ and $$BC$$ produced meet at $$F$$
Refer image,
$$\angle BAE=\angle EAD$$.........(1) [bisect of $$\angle A$$]
$$\angle EAD=\angle EFB$$.........(2) [Alt. $$\angle s$$]
$$\Rightarrow \angle BAE=\angle EFB$$.........(2) [From (1) and (2)]
$$\therefore BF=AB$$ [$$\because$$ Sides opposite to equal $$\angle s$$ are equal]
$$\Rightarrow BF=10cm[\because AB=10cm$$
$$\Rightarrow BC+CF=10cm\Rightarrow 6cm+CF=10cm$$ [$$\because BC=AD=6cm$$, opposite sides of a ||gm]
$$\Rightarrow CF=10-6cm=4cm$$
In the figure, $$ABCD$$ is a parallelogram in which $$\angle A={60}^{o}$$. If the bisectors $$\angle A$$ and $$\angle B$$ meet $$DC$$ at $$P$$, prove that $$\angle APB={90}^{o}$$
In the figure, $$ABCD$$ is a parallelogram in which $$\angle A={60}^{o}$$. If the bisectors $$\angle A$$ and $$\angle B$$ meet $$DC$$ at $$P$$, prove that $$DC=2AD$$
In the figure, $$ABCD$$ is a parallelogram in which $$\angle BAO={35}^{o},\angle DAO={40}^{o}$$ and $$\angle COD={105}^{o}$$. Calculate $$\angle ABO$$.
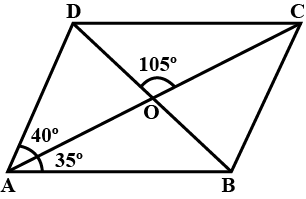
In the figure, $$ABCD$$ is a parallelogram in which $$\angle BAO={35}^{o},\angle DAO={40}^{o}$$ and $$\angle COD={105}^{o}$$. Calculate $$\angle ODC$$
In the figure, $$M$$ is the midpoint of side $$BC$$ of a parallelogram $$ABCD$$ such that $$\angle BAM=\angle DAM$$. Prove that $$AD=2CD$$
In the figure, $$ABCD$$ is a parallelogram in which $$\angle A={60}^{o}$$. If the bisectors $$\angle A$$ and $$\angle B$$ meet $$DC$$ at $$P$$, prove that $$AD=DP$$ and $$PB=PC=BC$$
The angle between two altitudes of a parallelogram through the vertex of an obtuse angle fo the parallelogram is $${60}^{o}$$. Find the angles of the parallelogram.
In the figure, $$ABCD$$ is a parallelogram whose diagonals intersect each other at $$O$$. A line segment $$EOF$$ is drawn to meet $$AB$$ at $$E$$ and $$DC$$ at $$F$$. Prove that $$OE=OF$$.
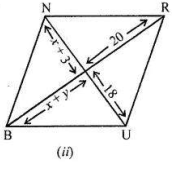
In the given figure BURN is parallelograms. Find the measures of $$ x $$ and $$ y $$ (lengths are in $$ \mathrm{cm} $$ ).
In a parallelogram $$ABCD$$, if $$\angle A={(2x+5)}^{o}$$ and $$\angle B={(3x-5)}^{o}$$, find the value of $$x$$ and the measure of each angle of the parallelogram.
A $$\triangle ABC$$ is given. If lines are drawn through $$AB,B,C$$ parallel respectively to the sides $$BC,CA$$ and $$AB$$ forming $$\triangle PQR$$, as shown in the figure, show that $$BC=\cfrac{1}{2}QR$$
$$ABCD$$ is a parallelogram in which $$AB=9.5cm$$ and its perimeter is $$30cm$$. Find the length of each side of the parallelogram.
In the figure, $$ABCD$$ is a parallelogram in which $$AB$$ is produced to $$E$$ so that $$BE=AB$$. Prove that $$ED$$ bisects $$BC$$
$$P,Q,R$$ and $$S$$ are respectively the midpoints of the sides $$AB,BC,CD$$ and $$DA$$ of a quadrilateral $$ABCD$$. Show that $$PQRS$$ is a parallelogram
In the figure, $$ABCD$$ is a parallelogram. If $$P$$ and $$Q$$ are points on $$AD$$ and $$BC$$ respecetively such that $$AP=\dfrac{1}{3}AD$$ and $$CQ=\dfrac{1}{3}BC$$, prove that $$AQCP$$ is a parallelogram.
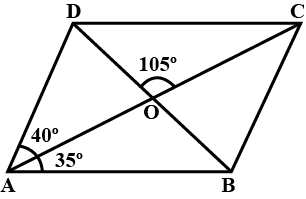
In the figure, $$ABCD$$ is a parallelogram in which $$\angle BAO={35}^{o},\angle DAO={40}^{o}$$ and $$\angle COD={105}^{o}$$. Calculate $$\angle ACB$$
In the given figure, $$ A B C D $$ is a parallelogram. Complete each statement along with the definition or property used.
(viii) $$ \mathrm{m} \angle \mathrm{DAB}+\mathrm{m} \angle \mathrm{CDA}=\ldots \ldots $$
In the figure, $$ABCD$$ is a parallelogram in which $$\angle BAO={35}^{o},\angle DAO={40}^{o}$$ and $$\angle COD={105}^{o}$$. Calculate $$\angle CBD$$
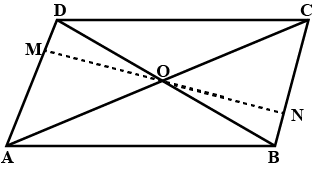
$$M$$ and $$N$$ are points on opposite sides $$AD$$ and $$BC$$ of a parallelogram $$ABCD$$ such that $$MN$$ passes through the point of intersection $$O$$ of its diagonals $$AC$$ and $$BD$$. Show that $$MN$$ is bisected at $$O$$.
Is it possible to have a regular polygon each of whose interior angles is $$100^o$$?
Find the measure of each angle of a parallelogram, if one of its angle is $${30}^{o}$$ less than twice the smallest angle.
Prove that the diagonals of the parallelogram formed by the four straight lines
$$\sqrt{3x} + y = 0, \sqrt{3y} + x = 0, \sqrt{3x} + y = 1$$, and $$\sqrt{3y} + x = 1$$
are at right angles to one another.
$$ABCD$$ is a parallelogram in which $$\angle {110^{o}}.$$ Find the measure of each of angles $$\angle B,\ \angle C$$ and $$\angle D.$$
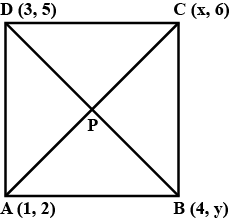
If $$(1,2),(4, y),(x, 6)$$ and (3,5) are the vertices of a parallelogram taken in order, then find $$x$$ and $$y$$.
Find the sum of interior angles of a polygon with:
$$16$$ sides
In the figure, $$ABCD$$ is a parallelogram in which $$E$$ and $$F$$ are the midpoints of $$AB$$ and $$CD$$ respectively. If $$GH$$ is a line segment that cuts $$AD, EF$$ and $$BC$$ at $$G, P$$ and $$H$$ respectively, prove that $$GP=PH$$.
From the figure we know that $$AD, EF$$ and $$BC$$ are three line segment and $$DC$$ and $$AB$$ are the two transversal
We know that the intercepts made by the line on $$AB$$ and $$CD$$ are equal
so we get
$$AE=EB$$ and $$DF=FC$$
Let us prove that $$FE$$ is parallel to $$AD$$ by using the method of contradiction
Assume $$FE$$ is not parallel to $$AD$$
Construct $$FR$$ parallel to $$AD$$
Based on the Intercept theorem
We get $$AR=RB$$ as $$DF=FC$$
It is given that $$AE=EB$$
$$AB$$ cannot have two midpoints ie. $$R$$ and $$E$$
so our assumption is not correct
We know that $$AD\parallel EF\parallel BC$$
By using the Intercept theorem
$$GP=PH$$
So we know that $$GH$$ is a transversal and the intercepts made by $$AD, EF$$ and $$BC$$ on $$GH$$ are equal as $$DF=FC$$.
Therefore it is proved that $$GP=PH$$
In a parallelogram $$PQRS$$, $$PQ=12\ \text{cm}$$ and $$PS=9\ \text{cm}$$. The bisector of $$\angle P$$ meets $$SR$$ in $$M$$. $$PM$$ and $$QR$$ both when produced meet at $$T$$. Find length of $$RT$$.
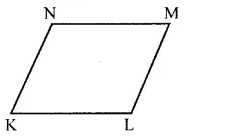
Draw a rough sketch of a quadrilateral $$KLMN$$. State,
two pairs of opposite sides
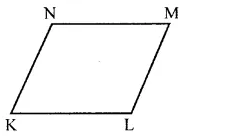
Draw a rough sketch of a quadrilateral $$KLMN$$. State,
Two pairs of adjacent sides
Draw a rough sketch of a quadrilateral $$KLMN$$. State,
Fill in the blanks to make the statements true.
The measure of _________ angle of concave quadrilateral is more than $$ 180^{\circ} $$.
Solve the following :
In parallelogram $$ABCD$$ , find $$ \angle B , \angle C$$ and $$ \angle D$$.
Solve the following :
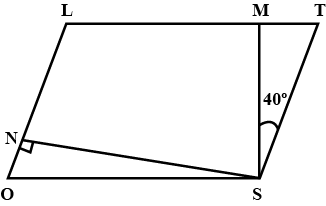
In parallelogram $$LOST$$ , $$SN$$ $$ \perp $$ $$OL$$ and $$SM$$ $$ \perp LT$$. Find $$ \angle STM , \angle SON$$ and $$ \angle NSM$$
Solve the following :
In parallelogram FIST , find $$ \angle $$ SFT , $$ \angle $$OST and $$ \angle $$ STO .
Solve the following :
Find the values of $$x$$ and $$y$$ in the following parallelogram.
$$ABCD$$ is a parallelogram . Points $$P$$ and $$Q$$ are taken on the sides $$AB$$ and $$CD$$ respectively and the parallelogram $$PRQA$$ is formed . If $$ \angle C = 45^{\circ} $$ , find $$ \angle R$$ .
A diagonal of a parallelogram bisects an angle . Will it also bisect the other angle ? Give reason.
Consider
a parallelogram $$ABCD$$ where diagonal $$AC$$ bisects $$\angle A$$
Here,
$$AB$$ is parallel to $$CD$$ and $$AC$$ is the transversal.
$$\therefore \angle \, 1 = \angle \, 4\quad...(i) \qquad$$[Alternate interior angle]
and, $$ \angle \,2 = \angle \, 3 \quad...(ii)\qquad$$[Alternate interior angle]
Now given that,
$$ \angle \, 1 = \angle \, 2 $$
$$\Rightarrow \angle \, 3 = \angle \, 4 $$ [From equation $$(i)$$ and $$(ii)$$]
If $$56x 32y$$ is divisible by $$18$$, find the least value of $$y$$.
The angle between the two altitudes of a parallelogram through the vertex of an obtuse angle of the parallelogram is $$ 45^{\circ} $$. Find the angles of the parallelogram.
Let $$ABCD$$ be a parallelogram where $$BE$$ and $$BF$$ are the perpendiculars through the vertex $$B$$ to the sides $$DC$$ and $$AD$$ respectively.
Let,
$$ \angle A= \angle C= x $$
$$ \angle B = \angle D = y $$
Now,
$$ \angle A + \angle B = 180^{\circ} \qquad$$ [Adjacent angles]
$$ \Rightarrow \, x + \angle ABF + \angle FBE + \angle EBC = 180^{\circ} $$
$$ \Rightarrow \, x + (90^{\circ} - x) + 45^{\circ} + (90^{\circ} - x) = 180^{\circ} $$
$$ \Rightarrow \, x-x-x +90^{\circ}+90^{\circ}+45^\circ= 180^{\circ} $$
$$ \Rightarrow \, -x = 180^{\circ} -225^{\circ} $$
$$ \Rightarrow \, x = 45^{\circ} $$
$$ \therefore \, \angle A = \angle C = 45^{\circ} $$
$$\begin{aligned}{}\angle B& = \left( {{{90}^\circ } - {{45}^\circ }} \right) + {45^\circ } + \left( {{{90}^\circ } - {{45}^\circ }} \right)\\ &= {45^\circ } + {45^\circ } + {45^\circ }\\ &= {135^\circ }\\&=\angle D\end{aligned}$$
Hence, the angles of the parallelogram are $$ 45^{\circ} , 135^{\circ} , 45^{\circ} $$ and $$ 135^{\circ} .$$
Perpendicular dropped on the base of a parallelogram from the opposite vertex is known as the corresponding ______ of the base.
Perpendicular dropped on the base of a parallelogram from the opposite vertex is known as the corresponding Height/Altitude of the base.
The angles of a pentagon are in the ratio 4 : 8 : 6 : 4 : 5 .Find each angle of the pentagon.
Solve the following :
In parallelogram MODE , the bisector of $$ \angle $$ M and $$ \angle $$ O meet at Q , find the measure of $$ \angle $$ MQO.
$$ABCD$$ is a parallelogram. The bisector of $$\angle A$$ intersects $$CD$$ at $$X$$ and bisector of $$\angle C$$ intersects $$AB$$ at $$Y$$. Is $$AXCY$$ a parallelogram ? Give reason.
Given
$$ABCD$$ is a parallelogram.
Then, $$ \angle A = \angle C $$
$$\Rightarrow \dfrac{\angle A}{2} = \dfrac{\angle C}{2} $$
$$\Rightarrow \angle \, 1 = \angle \, 2 \quad...(i)$$
Now, $$AB \parallel CD$$ and $$CY$$ is transverse
$$\therefore \angle \,2 = \angle \,3 $$ [Alternate interior angle]
$$\Rightarrow \angle \,1 = \angle \,3 $$ [Using $$(i)$$]
$$\Rightarrow AX \parallel YC\quad...(a)$$
In parallelogram $$ABCD$$,
$$AB\parallel AC$$
$$\Rightarrow AY \parallel XC\quad.. (b)$$
Hence, from $$(a)$$ and $$(b)$$,
$$AXCY$$ is a parallelogram.
Solve the following :
In the following figure of a ship , ABDH and CEFG are two parallelogram. Find the value of $$ x $$.
In the given figure, $$ A B C D $$ is a parallelogram. Complete each statement along with the definition or property used.
$$ \mathrm{OB}=\ldots \ldots \ldots $$
In the given figure, $$ A B C D $$ is a parallelogram. Complete each statement along with the definition or property used.
$$ \angle \mathrm{ADC}=\ldots \ldots \ldots $$
In the given figure, $$ A B C D $$ is a parallelogram. Complete each statement along with the definition or property used.
$$ \angle \mathrm{DAB}=\ldots \ldots \ldots \ldots $$
In the given figure , if PQRS is a parallelogram and AB || PS , then prove that OC || SR.
In the given figure, $$ A B C D $$ is a parallelogram. Complete each statement along with the definition or property used.
$$ \angle \mathrm{DCB}=\ldots \ldots \ldots $$
In the given figure, $$ A B C D $$ is a parallelogram. Complete each statement along with the definition or property used.
$$ \mathrm{OC}=\ldots \ldots \ldots . $$
State 'true' or 'false'
The diagonals of a parallelogram bisect each other at right angle.
False
consider a rectangle as shown below,
It is a parallelogram . However ,the diagonals of a rectangle do not intersects at right angles , even though they bisects each other .
consider a rectangle as shown below,
It is a parallelogram . However ,the diagonals of a rectangle do not intersects at right angles , even though they bisects each other .
The measure of two adjacent angles of a parallelogram is in the ratio $$ 4: 5 . $$ Find the measure of each angle of the parallelogram.
Consider the parallelogram PQRS, From the question it is given that, The measure of two adjacent angles of a parallelogram is in the ratio 4: 5
$$\mathrm{So}, \angle \mathrm{P}: \angle \mathrm{Q}=4: 5$$
Let us assume the $$ \angle P=4 $$ y and $$ \angle Q=5 y $$
Then, we know that, $$ \angle P+\angle Q=180^{\circ} $$
$$\begin{array}{l}\begin{array}{c}4 y+5 y=180^{\circ} \\9 y=180^{\circ} \\y=180^{\circ} / 9 \\y=20^{\circ}\end{array} \\\text { Therefore, } \angle P=4 y=4 \times 20^{\circ}=80^{\circ} \text { and } \angle Q=5 y=\left(5 \times 20^{\circ}\right)=100^{\circ}\end{array}$$
In parallelogram opposite angles are equal,
$$ \begin{aligned} So, \angle R &=\angle P=80^{\circ} \\ \angle S &=\angle Q=100^{\circ} \end{aligned} $$
$$\mathrm{So}, \angle \mathrm{P}: \angle \mathrm{Q}=4: 5$$
Let us assume the $$ \angle P=4 $$ y and $$ \angle Q=5 y $$
Then, we know that, $$ \angle P+\angle Q=180^{\circ} $$
$$\begin{array}{l}\begin{array}{c}4 y+5 y=180^{\circ} \\9 y=180^{\circ} \\y=180^{\circ} / 9 \\y=20^{\circ}\end{array} \\\text { Therefore, } \angle P=4 y=4 \times 20^{\circ}=80^{\circ} \text { and } \angle Q=5 y=\left(5 \times 20^{\circ}\right)=100^{\circ}\end{array}$$
In parallelogram opposite angles are equal,
$$ \begin{aligned} So, \angle R &=\angle P=80^{\circ} \\ \angle S &=\angle Q=100^{\circ} \end{aligned} $$
Can a quadrilateral $$ABCD$$ be a parallelogram, give reasons in support of your answer.
(i) $$ \angle \mathrm{A}+\angle \mathrm{C}=180^{\circ} ? $$
(ii) $$ \mathrm{AD}=\mathrm{BC}=6 \mathrm{cm}, \mathrm{AB}=5 \mathrm{cm}, \mathrm{DC}=4.5 \mathrm{cm} ? $$
(iii) $$ \angle \mathrm{B}=80^{\circ}, \angle \mathrm{D}=70^{\circ} ? $$
(iv) $$ \angle \mathrm{B}+\angle \mathrm{C}=180^{\circ} ? $$
From the question it is given that, quadrilateral $$ABCD$$ can be a parallelogram.
We know that in a parallelogram opposite sides are equal and opposites angles are equal.
$$ \mathrm{So}, \mathrm{AB}=\mathrm{DC} $$ and $$ \mathrm{AD}=\mathrm{BC} $$ also $$ \angle \mathrm{A}=\angle \mathrm{C} $$ and $$ \angle \mathrm{B}=\angle \mathrm{D} $$
(i) $$ \angle \mathrm{A}+\angle \mathrm{C}=180^{\circ} $$
(ii) $$ \mathrm{AD}=\mathrm{BC}=6 \mathrm{cm}, \mathrm{AB}=5 \mathrm{cm}, \mathrm{DC}=4.5 \mathrm{cm} $$
The above dimensions can not form a parallelogram.
Because $$ \mathrm{AB} \neq \mathrm{DC} $$
(iii) $$ \angle \mathrm{B}=80^{\circ}, \angle \mathrm{D}=70^{\circ} $$
The above dimensions can not form a parallelogram.
Because $$ \angle \mathrm{B} \neq \angle \mathrm{D} $$
(iv) $$ \angle \mathrm{B}+\angle \mathrm{C}=180^{\circ} $$
We know that in a parallelogram opposite sides are equal and opposites angles are equal.
$$ \mathrm{So}, \mathrm{AB}=\mathrm{DC} $$ and $$ \mathrm{AD}=\mathrm{BC} $$ also $$ \angle \mathrm{A}=\angle \mathrm{C} $$ and $$ \angle \mathrm{B}=\angle \mathrm{D} $$
(i) $$ \angle \mathrm{A}+\angle \mathrm{C}=180^{\circ} $$
It is not a necessary condition for parallelogram.
So, from the above condition it may or may not be a parallelogram.
So, from the above condition it may or may not be a parallelogram.
(ii) $$ \mathrm{AD}=\mathrm{BC}=6 \mathrm{cm}, \mathrm{AB}=5 \mathrm{cm}, \mathrm{DC}=4.5 \mathrm{cm} $$
The above dimensions can not form a parallelogram.
Because $$ \mathrm{AB} \neq \mathrm{DC} $$
(iii) $$ \angle \mathrm{B}=80^{\circ}, \angle \mathrm{D}=70^{\circ} $$
The above dimensions can not form a parallelogram.
Because $$ \angle \mathrm{B} \neq \angle \mathrm{D} $$
(iv) $$ \angle \mathrm{B}+\angle \mathrm{C}=180^{\circ} $$
It is a necessary condition but $$ABCD$$ can be a parallelogram if opposite sides are equal.
From the above condition it may or may not be a parallelogram.
From the above condition it may or may not be a parallelogram.
In the given figure, $$ \mathrm{ABCD}, $$ is a parallelogram and diagonals intersect at $$ \mathrm{O} $$. Find :
(i) $$ \angle \mathrm{CAD} $$
(ii) $$ \angle \mathrm{ACD} $$
(iii) $$ \angle \mathrm{ADC} $$
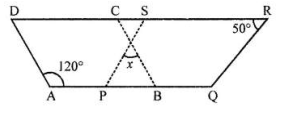
In the following figure, both $$ A B C D $$ and PQRS are parallelograms. Find the value of $$ x . $$
From the figure, it is given that, $$ A B C D $$ and $$PQRS$$ are two parallelograms.
$$ \angle A=120^{\circ} $$ and $$ \angle R=50^{\circ} $$
We know that, $$ \angle \mathrm{A}+\angle \mathrm{B}=180^{\circ} $$
$$\begin{array}{l}120^{\circ}+\angle B=180^{\circ} \\\angle B=180^{\circ}-120^{\circ} \\\angle B=60^{\circ}\end{array}$$
In parallelogram opposite angles are equal.
$$ \angle A=120^{\circ} $$ and $$ \angle R=50^{\circ} $$
We know that, $$ \angle \mathrm{A}+\angle \mathrm{B}=180^{\circ} $$
$$\begin{array}{l}120^{\circ}+\angle B=180^{\circ} \\\angle B=180^{\circ}-120^{\circ} \\\angle B=60^{\circ}\end{array}$$
In parallelogram opposite angles are equal.
$$\Rightarrow \angle P=50^o$$
Then, consider the triangle $$MPB$$ we know that the sum of measures of interior angles of the triangle is equal to $$ 180^{\circ} $$.
$$\begin{array}{l}\angle PMB+\angle P+\angle B=180^{\circ} \\x+50^{\circ}+60^{\circ}=180^{\circ} \\x+110^{\circ}=180^{\circ}\end{array}$$
By transposing we get,
$$x=180^{\circ}-110^{\circ}$$
Therefore, value of $$ x=70^{\circ} $$
$$\begin{array}{l}\angle PMB+\angle P+\angle B=180^{\circ} \\x+50^{\circ}+60^{\circ}=180^{\circ} \\x+110^{\circ}=180^{\circ}\end{array}$$
By transposing we get,
$$x=180^{\circ}-110^{\circ}$$
Therefore, value of $$ x=70^{\circ} $$
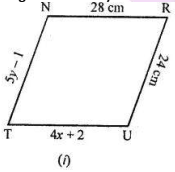
In the given figure TURN is are parallelograms. Find the measures of $$ x $$ and $$ y $$ (lengths are in $$ \mathrm{cm} $$ ).
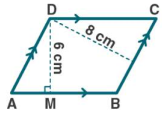
In the given figure, $$ABCD$$ is a parallelogram. $$CB$$ is produced to E such that $$BE=BC$$. Prove that $$AEBD$$ is a parallelogram.
Given $$ABCD$$ is a $$||$$ gm in which $$CB$$ is produced to $$E$$ such that $$BE = BC$$
$$BD$$ and $$AE$$ are joined
To prove: $$AEBD$$ is a parallelogram
Proof:
In $$\triangle AEB$$ and $$\triangle BDC$$
$$EB = BC$$ [Given]
$$\angle ABE = \angle DCB$$ [Corresponding angles]
$$AB = DC$$ [Opposite sides of $$||$$ gm]
Thus, $$\triangle AEB \cong \triangle BDC$$ by S.A.S axiom
So, by C.P.C.T
But, $$AD = CB = BE$$ [Given]
As the opposite sides are equal and $$\angle AEB = \angle DBC$$
But these are corresponding angles
Hence, $$AEBD$$ is a parallelogram.
$$BD$$ and $$AE$$ are joined
To prove: $$AEBD$$ is a parallelogram
Proof:
In $$\triangle AEB$$ and $$\triangle BDC$$
$$EB = BC$$ [Given]
$$\angle ABE = \angle DCB$$ [Corresponding angles]
$$AB = DC$$ [Opposite sides of $$||$$ gm]
Thus, $$\triangle AEB \cong \triangle BDC$$ by S.A.S axiom
So, by C.P.C.T
But, $$AD = CB = BE$$ [Given]
As the opposite sides are equal and $$\angle AEB = \angle DBC$$
But these are corresponding angles
Hence, $$AEBD$$ is a parallelogram.
Two adjacent sides of a parallelogram are in the ratio $$ 5: 7 . $$ If the perimeter of a parallelogram is $$ 72 \mathrm{cm}, $$ find the length of its sides.
Consider the parallelogram PQRS, From the question it is given that, two adjacent sides of a parallelogram are in the ratio 5: 7
Perimeter of parallelogram $$ =72 \mathrm{cm} $$
$$\begin{array}{l}2(S P+R Q)=72 \mathrm{cm} \\S P+R Q=72 / 2 \\S P+R Q=36 \mathrm{cm}\end{array}$$
Let us assume the length of side $$ \mathrm{SP}=5 \mathrm{y} $$ and $$ \mathrm{RQ}=7 \mathrm{y} $$
$$5 y+7 y=36$$
$$\begin{array}{l}12 y=36 \\y=36 / 12 \\y=3\end{array}$$
Therefore, $$ \mathrm{SP}=5 \mathrm{y}=5 \times 3=15 \mathrm{cm} $$
$$\mathrm{RQ}=7 \mathrm{y}=7 \times 3=21 \mathrm{cm}$$
Perimeter of parallelogram $$ =72 \mathrm{cm} $$
$$\begin{array}{l}2(S P+R Q)=72 \mathrm{cm} \\S P+R Q=72 / 2 \\S P+R Q=36 \mathrm{cm}\end{array}$$
Let us assume the length of side $$ \mathrm{SP}=5 \mathrm{y} $$ and $$ \mathrm{RQ}=7 \mathrm{y} $$
$$5 y+7 y=36$$
$$\begin{array}{l}12 y=36 \\y=36 / 12 \\y=3\end{array}$$
Therefore, $$ \mathrm{SP}=5 \mathrm{y}=5 \times 3=15 \mathrm{cm} $$
$$\mathrm{RQ}=7 \mathrm{y}=7 \times 3=21 \mathrm{cm}$$
$$ABCD$$ is a parallelogram. If the diagonal $$AC$$ bisects $$CA$$, then prove that:
(i) $$AC$$ bisects $$\angle C$$
(ii) $$ABCD$$ is a rhombus
(iii) $$AC \bot BD$$.
Is it possible to have a polygon, whose number of interior angles is $$1030^o$$.
If all the angles of an octagon are equal, find the measure of each angle.
$$P$$ and $$Q$$ are points on opposite sides $$AD$$ and $$BC$$ of a parallelogram $$ABCD$$ such that $$PQ$$ passes through the point of intersection $$O$$ of its diagonals $$AC$$ and $$BD$$. Show that $$PQ$$ is bisected at $$O$$.
To prove :
Diagonals of $$\parallel$$ gm $$ABCD$$ bisect each other at $$O$$
So, $$AO = OC$$ and $$BO = OD$$
Now, in $$\triangle AOP$$ and $$\triangle COQ$$ we have
$$AO = OC$$ and $$BO = OD$$
Now, in $$\triangle AOP$$ and $$\triangle COQ$$
$$AO = OC$$ [Proved]
$$\angle OAP=\angle OCQ$$ [Alternate angles]
$$\angle AOP=\angle COQ$$ [Vertically opposite angles]
So, $$\triangle AOP \cong \triangle COQ$$ by S.A.S axiom
Thus, by C.P.C.T
$$OP=OQ$$
Hence, $$O$$ bisects $$PQ$$.
Diagonals of $$\parallel$$ gm $$ABCD$$ bisect each other at $$O$$
So, $$AO = OC$$ and $$BO = OD$$
Now, in $$\triangle AOP$$ and $$\triangle COQ$$ we have
$$AO = OC$$ and $$BO = OD$$
Now, in $$\triangle AOP$$ and $$\triangle COQ$$
$$AO = OC$$ [Proved]
$$\angle OAP=\angle OCQ$$ [Alternate angles]
$$\angle AOP=\angle COQ$$ [Vertically opposite angles]
So, $$\triangle AOP \cong \triangle COQ$$ by S.A.S axiom
Thus, by C.P.C.T
$$OP=OQ$$
Hence, $$O$$ bisects $$PQ$$.
$$ABCD$$ is a parallelogram, bisectors of angles $$A$$ and $$B$$ meet at $$E$$ which lie on $$DC$$. Prove that $$AB=3AD$$.
Given: $$ABCD$$ is a parallelogram in which bisector of $$\angle A$$ and $$\angle B$$ meets $$DC$$ in $$E$$
To prove: $$AB = 2 AD$$
Proof:
In parallelogram $$ABCD$$, we have $$AB||DC$$
$$\angle 1=\angle 5$$ [Alternate angles, $$AE$$ is transversal]
$$\angle 1 = \angle 2$$ [AE is bisector, $$\angle A$$ given]
Thus,
$$\angle 2=\angle 5 ...(i)$$
Now, in $$\Delta AED$$
$$DE=AD$$ [Sides opposite to equal angles are equal]
$$\angle 3 = \angle 6$$ [Alternate angles]
$$\angle 3=\angle 4$$ [Since, $$BE$$ is bisector of $$\angle B$$ (given)]
Thus, $$\angle 4=\angle 6...(ii)$$
In $$\Delta BCE$$, we have
$$BC=EC$$ [Sides opposite to equal angles are equal]
$$AD=BC$$[Opposite sides of $$|| \,gm$$ are equal]
$$AD=DE=EC$$ [From (i) and (ii)]
$$AB=DC$$ [Opposite sides of $$|| \,gm$$ are equal]
$$AB=DE+EC$$
$$=AD+AD$$
Hence,
$$AB=2AD$$
To prove: $$AB = 2 AD$$
Proof:
In parallelogram $$ABCD$$, we have $$AB||DC$$
$$\angle 1=\angle 5$$ [Alternate angles, $$AE$$ is transversal]
$$\angle 1 = \angle 2$$ [AE is bisector, $$\angle A$$ given]
Thus,
$$\angle 2=\angle 5 ...(i)$$
Now, in $$\Delta AED$$
$$DE=AD$$ [Sides opposite to equal angles are equal]
$$\angle 3 = \angle 6$$ [Alternate angles]
$$\angle 3=\angle 4$$ [Since, $$BE$$ is bisector of $$\angle B$$ (given)]
Thus, $$\angle 4=\angle 6...(ii)$$
In $$\Delta BCE$$, we have
$$BC=EC$$ [Sides opposite to equal angles are equal]
$$AD=BC$$[Opposite sides of $$|| \,gm$$ are equal]
$$AD=DE=EC$$ [From (i) and (ii)]
$$AB=DC$$ [Opposite sides of $$|| \,gm$$ are equal]
$$AB=DE+EC$$
$$=AD+AD$$
Hence,
$$AB=2AD$$
Two adjacent side of a parallelogram are 15 cm. If the distance between the longer sides is 8 cm , find the ares of the parallelogram. Also find the distance between shorter sides.
Find the number of sides of a polygon, if the sum of its interior angles is:
$$1620^o$$
If all the angles of a hexagon arc equal, find the measure of each angle.
In quadrilateral $$ABCD, \angle A + \angle D = 180^\circ$$. What special name can be given to the quadrilateral?
(a) In the figure ( 1 ) given below, the perimeter of parallelogram is $$ 42 \mathrm{cm} $$. Calculate the lengths of the sides of the parallelogram.
(a) Given:
The perimeter of parallelogram $$ \mathrm{ABCD}=42 \mathrm{cm} $$
To find:
Lengths of the sides of the parallelogram ABCD. From fig (1) We know that, $$ A B=P $$
Then, perimeter of $$ \| \mathrm{gm} \mathrm{ABCD}=2(\mathrm{AB}+\mathrm{BC}) $$
$$\begin{array}{l}42=2(\mathrm{P}+\mathrm{BC}) \\42 / 2=\mathrm{P}+\mathrm{BC} \\21=\mathrm{P}+\mathrm{BC} \\\mathrm{BC}=21-\mathrm{P} \\\text { So, ar }(\| \mathrm{gm} \mathrm{ABCD})=\mathrm{AB} \times \mathrm{DM} \\=\mathrm{P} \times 6 \\=6 \mathrm{P} \ldots \ldots \ldots(1)\end{array}$$
Again, ar $$ (\| \mathrm{gm} \mathrm{ABCD})=\mathrm{BC} \times \mathrm{DN} $$
$$ =(21-\mathrm{P}) \times 8 $$
$$ =8(21-\mathrm{P}) \ldots \ldots \ldots $$(2)
From ( 1 ) and $$ (2), $$ we get
$$ 6 P=8(21-P) $$
$$ 6 P=168-8 P $$
$$ 6 P+8 P=168 $$
$$ 14 P=168 $$
$$ P=168 / 14 $$
$$ =12 $$
Hence, sides of $$ \| \mathrm{gm} $$ are
$$ \mathrm{AB}=12 \mathrm{cm} $$ and $$ \mathrm{BC}=(21-12) \mathrm{cm}=9 \mathrm{cm} $$
The perimeter of parallelogram $$ \mathrm{ABCD}=42 \mathrm{cm} $$
To find:
Lengths of the sides of the parallelogram ABCD. From fig (1) We know that, $$ A B=P $$
Then, perimeter of $$ \| \mathrm{gm} \mathrm{ABCD}=2(\mathrm{AB}+\mathrm{BC}) $$
$$\begin{array}{l}42=2(\mathrm{P}+\mathrm{BC}) \\42 / 2=\mathrm{P}+\mathrm{BC} \\21=\mathrm{P}+\mathrm{BC} \\\mathrm{BC}=21-\mathrm{P} \\\text { So, ar }(\| \mathrm{gm} \mathrm{ABCD})=\mathrm{AB} \times \mathrm{DM} \\=\mathrm{P} \times 6 \\=6 \mathrm{P} \ldots \ldots \ldots(1)\end{array}$$
Again, ar $$ (\| \mathrm{gm} \mathrm{ABCD})=\mathrm{BC} \times \mathrm{DN} $$
$$ =(21-\mathrm{P}) \times 8 $$
$$ =8(21-\mathrm{P}) \ldots \ldots \ldots $$(2)
From ( 1 ) and $$ (2), $$ we get
$$ 6 P=8(21-P) $$
$$ 6 P=168-8 P $$
$$ 6 P+8 P=168 $$
$$ 14 P=168 $$
$$ P=168 / 14 $$
$$ =12 $$
Hence, sides of $$ \| \mathrm{gm} $$ are
$$ \mathrm{AB}=12 \mathrm{cm} $$ and $$ \mathrm{BC}=(21-12) \mathrm{cm}=9 \mathrm{cm} $$
Find the number of sides of a polygon, if the sum of its interior angles is:
$$1440^o$$
The angles of a pentagon are in the ratio $$5:4:5:7:6$$; find each angle of the pentagon.
In a parallelogram $$ABCD, \angle A=90^o$$
What is the measure of angle $$B$$.
Given
In a parallelogram $$ABCD, \angle A=90^o$$
We know that
In a parallelogram, adjacent angles are supplementary
Hence,
$$\angle A+\angle B=180^o$$
$$90^o+\angle B=180^o$$
$$\angle B=180^o -90^o$$
We get,
$$\angle B=90^o$$
Therefore, the measure of $$\angle B=90^o$$
If one angle of a pentagon is $$120^o$$ and each of the remaining four angles is $$x^o$$, find the magnitude of $$x$$.
In a parallelogram $$ABCD$$. Its diagonals $$AC$$ and $$BD$$ intersect each other at point $$O$$.
If $$AC=12\ cm$$ and $$BD=9\ cm$$; find lengths of $$OA$$ and $$OB$$.
Two adjacent angles of a parallelogram are $$70^o$$ and $$110^o$$ respectively. Find the other two angles of it.
Given
Two adjacent angles of a parallelogram are $$70^o$$ and $$100^o$$ respectively.
We know that,
Opposite angles of a parallelogram are equal.
Hence, $$\angle C=\angle A=70^o$$ and $$\angle D=\angle B=110^o$$
In a parallelogram $$ABCD, \angle A=90^o$$
Write the special name of the parallelogram.
Given
In a parallelogram $$ABCD, \angle A=90^o$$
Since all the angles of a given parallelogram is right angle.
Hence the given parallelogram is a rectangle.
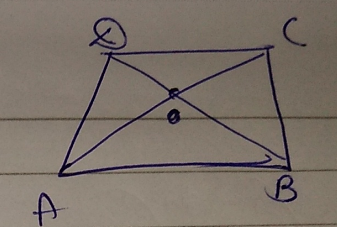
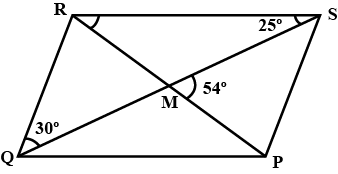
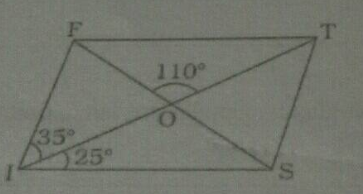
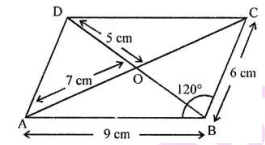
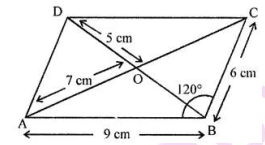
$$PQRS$$ is a parallelogram whose diagonals intersect at $$M.$$
$$\angle PMS=54^{0},\angle QSR=25^{0}$$ and $$\angle SQR=30^{0}$$;
$$\angle RPS$$
Given: Parallelogram $$PQRS$$ in which diagonals $$PR QS$$ intersect at $$M.$$
$$\angle PSM=54^{o};\angle OSR=25^{0}$$ and $$\angle SQR=30^{o}$$
To find: $$\angle RPS$$
proof: $$QR\parallel PS$$
$$\Rightarrow \angle PSQ=\angle SQR$$ (Alternate $$\angle S$$)
But $$\angle SQR=30^{o}$$
$$\angle PSQ=30^{o}$$
In $$\triangle SMP,$$
$$\angle PMS+\angle PSM+\angle MPS=180^{o}$$ or $$54^{o}+30^{o}+\angle RPS=180^{o}$$
$$\angle RPS=180^{o}-84^{o}=96^{o}$$
Now,$$\angle PRS+\angle RSQ=\angle PMS$$
$$\angle PRS+25^{o}=54^{0}$$
$$\angle PRS=54^{o}-25^{o}=29^{o}$$
$$\angle PSR=\angle PSQ+\angle RSQ=30^{o}+25^{o}=55^{o}$$
Hence $$\angle RPS=96^{o}$$
The angle $$A, B, C$$ and $$D$$ of a quadrilateral are in the ratio $$2:3:2:3$$. Show this quadrilateral is a parallelogram.
In a parallelogram $$ABCD$$. Its diagonals intersect at point $$O$$. If $$OA=6\ cm$$ and $$OB=7.5\ cm$$, find the lengths of $$AC$$ and $$BD$$.
Two opposite angles of a parallelogram are $$100^o$$ each. Find each of the other two opposite angles.
Given two opposite angles of a parallelogram are $$100^o$$ each
The sum of adjacent angles of a parallelogram $$=180^o$$
Hence,
$$\angle A+\angle B=180^o$$
$$100^o+\angle B=180^o$$
$$\angle B=180^o -100^o$$
We get,
$$\angle B=80^o$$
We know that
The opposite angles of a parallelogram are equal
$$\angle D=\angle B=80^o$$
Therefore, th eother opposite angles $$\angle D=\angle B=80^o$$
$$PQRS$$ is a parallelogram whose diagonals intersect at $$M.$$
$$\angle PMS=54^{0},\angle OSR=25^{0}$$ and $$\angle SOR=30^{0}$$;
$$\angle PSR$$
Given: Parallelogram $$PQRS$$ in which diagonals $$PR \ and \ QS$$ intersect at $$M.$$
$$\angle PSM=54^{o};\angle QSR=25^{0}$$ and $$\angle SQR=30^{o}$$
To find: $$\angle RPS$$
proof: $$QR\parallel PS$$
$$\Rightarrow >PSQ=\angle SQR$$ (Alternate $$\angle S$$)
But $$\angle SQR=30^{o}$$
$$\angle PSQ=30^{o}$$
In $$\triangle SMP,$$
$$\angle PMS+\angle PSM+\angle MPS=180^{o}$$ or
$$54^{o}+30^{o}+\angle RPS=180^{o}$$
$$\angle RSP=180^{o}-84^{o}=96^{o}$$
Now,$$\angle PRS+\angle RSQ=\angle PMS$$
$$\angle PRS+25^{o}=54^{0}$$
$$\angle PRS=54^{o}-25^{o}=29^{o}$$
$$\angle PSR=\angle PSQ+\angle RSQ=30^{o}+25^{o}=55^{o}$$
Hence $$\angle PSR=55^{o}$$
$$ABCD$$ is a parallelogram. What kind of quadrilateral is it if:
$$AC$$ is perpendicular to $$BD$$ but is not equal to it?
$$AC\bot BD$$ (Given)
But $$AC$$ & $$BD$$ are not equal
$$\therefore ABCD$$ is a Rhombus.
$$ABCD$$ is a parallelogram. What kind of quadrilateral is it if:
$$AC=BD$$ and $$AC$$ is not perpendicular to $$BD$$?
$$AC=BD$$ but $$AC$$ & $$BD$$ are not $$\bot\ r$$ to each other.
$$\therefore ABCD$$ is a Rectangle.
The sum of the interior angles of a polygon is four times the sum of its exterior angles . Find the number of sides in the polygon .
$$PQRS$$ is a parallelogram whose diagonals intersect at $$M.$$
$$\angle PMS=54^{0},\angle OSR=25^{0}$$ and $$\angle SOR=30^{0}$$;
$$\angle PRS$$
Given: Parallelogram $$PQRS$$ in which diagonals $$PR = QS$$ intersect at $$M.$$
$$\angle PSM=54^{o};\angle OSR=25^{0}$$ and $$\angle SQR=30^{o}$$
To find: $$\angle PRS$$
proof: $$QR\parallel PS$$
$$\Rightarrow >PSQ=\angle SQR$$ (Alternate $$\angle S$$)
But $$\angle SOR=30^{o}$$
$$\angle PSQ=30^{o}$$
In $$\triangle SMP,$$
$$\angle PMS+\angle PSM+\angle MPS=180^{o}$$ or $$54^{o}+30^{o}+\angle RPS=180^{o}$$
$$\angle RSP=180^{o}-84^{o}=96^{o}$$
Now,$$\angle PRS+\angle RSQ=\angle PMS$$
$$\angle PRS+25^{o}=54^{0}$$
$$\angle PRS=54^{o}-25^{o}=29^{o}$$
$$\angle PSR=\angle PSQ+\angle RSQ=30^{o}+25^{o}=55^{o}$$
Hence $$\angle PRS=29^{o}$$
$$\angle PSM=54^{o};\angle OSR=25^{0}$$ and $$\angle SQR=30^{o}$$
To find: $$\angle PRS$$
proof: $$QR\parallel PS$$
$$\Rightarrow >PSQ=\angle SQR$$ (Alternate $$\angle S$$)
But $$\angle SOR=30^{o}$$
$$\angle PSQ=30^{o}$$
In $$\triangle SMP,$$
$$\angle PMS+\angle PSM+\angle MPS=180^{o}$$ or $$54^{o}+30^{o}+\angle RPS=180^{o}$$
$$\angle RSP=180^{o}-84^{o}=96^{o}$$
Now,$$\angle PRS+\angle RSQ=\angle PMS$$
$$\angle PRS+25^{o}=54^{0}$$
$$\angle PRS=54^{o}-25^{o}=29^{o}$$
$$\angle PSR=\angle PSQ+\angle RSQ=30^{o}+25^{o}=55^{o}$$
Hence $$\angle PRS=29^{o}$$
$$ABCD$$ is a parallelogram. What kind of quadrilateral is it if:
$$AC=BD$$ and $$AC$$ is perpendicular to $$BD$$?
$$AC=BD$$ (Given)
&$$AC \bot BD$$ (Given)
i.e. Diagonals of quadrilateral are equal and they
Are perpendicular to each other.
$$\therefore ABCD$$ is square.
In a polygon . there are 5 right angles and the remaining angles are equal to $$ 195^{o}$$ each .Find the number of sides in the polygon .
AB ,BC and CD are the three consecutive sides of a regular polygon .If $$ \angle BAC = 15^{o}$$
Find,
Number of sides of the polygon.
In a pentagon ABCDE , AB is parallel to DC and angles A : E : D = 3 : 4 :Find angle E .
The ratio between an exterior angles and an interior angles of a regular polygoin is 2 : 3 . Find the number of sides in the polygon.
Two angles of eight sided polygon are $$ 142^{o} and 176 ^{o}$$ .If the remaining angles are equal to each other : find the magnitude of each of the equal angles .
Three angles of a seven sided polygon are $$132 ^{o} $$ each and the remaining four angles are equal . Find the value of each equal angle.
AB ,BC and CD are the three consecutive sides of a regular polygon .If $$ \angle BAC = 15^{o}$$
Find,
Each interior angle of the polygon.
Two alternate side of regular polygon , when produce , meet at right angle .Find :
The number of sides in the polygon.
One angles of a six - added polygon is $$ 140^{o}$$ and the other angles are equal . Find the measure of each equal angle.
In the figure given above, AM bisects angle A and DM bisects angle D of parallelogram ABCD. Prove that : $$ \angle AMD = 90^{o} $$.
In the given figure , ABCD is a parallelogram in which AP bisects angle A and BQ bisects angle B . Prove that :
AQ = BP
PQ = CD
ABPQ is a parallelogram
Join PQ .
Consider the $$ \Delta AOQ and \Delta BOP $$
$$ \angle AOQ = \angle BOP $$ [opposite angles]
$$ \angle OAQ = \angle BPO $$ [alternate angles]
$$\Rightarrow \Delta AOQ \cong \Delta BOP $$ [AA test]
Hence AQ = BP Consider the$$ \Delta QOP and\Delta AOB$$
$$ \angle AOB = \angle QOP $$ [opposite angles]
$$ \angle OAQ = \angle BPO $$ [alternate angles]
$$\Rightarrow \Delta AOQ \cong \Delta BOP $$ [AA test]
Consider the quadrilateral QPCD
DQ = CP and DQ || CP [ since AD = BC and AD ||BC]
Hence quadrilateral QPCD is a parallelogram.
Consider the $$ \Delta AOQ and \Delta BOP $$
$$ \angle AOQ = \angle BOP $$ [opposite angles]
$$ \angle OAQ = \angle BPO $$ [alternate angles]
$$\Rightarrow \Delta AOQ \cong \Delta BOP $$ [AA test]
Hence AQ = BP Consider the$$ \Delta QOP and\Delta AOB$$
$$ \angle AOB = \angle QOP $$ [opposite angles]
$$ \angle OAQ = \angle BPO $$ [alternate angles]
$$\Rightarrow \Delta AOQ \cong \Delta BOP $$ [AA test]
Consider the quadrilateral QPCD
DQ = CP and DQ || CP [ since AD = BC and AD ||BC]
Hence quadrilateral QPCD is a parallelogram.
The diagonal BD of a parallelogram ABCD bisects angles B and D . Prove that ABCD is a rhombus.
Given
ABCD is parallelogram where the diagonal BD bisects
Parallelogram ABCD at $$\angle B$$ and $$\angle D$$
To prove :
ABCD is a rhombus
Proof
Let us draw a parallelogram ABCD where the diagonal BD bisects the parallelogram and B and D
Construction :
Let us join AC as a diagonal of the parallelogram ABCD
Since ABCD is a parallelogram
Therefore,
AB = DC
AD = BC
Diagonal BD bisects and B and D
So $$ \angle COD = \angle DOA $$
Again AC also bisects at A and C
Therefore $$ \angle AOB = \angle BOC $$
Thus ABCD is a rhombus
Hence proved
ABCD is parallelogram where the diagonal BD bisects
Parallelogram ABCD at $$\angle B$$ and $$\angle D$$
To prove :
ABCD is a rhombus
Proof
Let us draw a parallelogram ABCD where the diagonal BD bisects the parallelogram and B and D
Construction :
Let us join AC as a diagonal of the parallelogram ABCD
Since ABCD is a parallelogram
Therefore,
AB = DC
AD = BC
Diagonal BD bisects and B and D
So $$ \angle COD = \angle DOA $$
Again AC also bisects at A and C
Therefore $$ \angle AOB = \angle BOC $$
Thus ABCD is a rhombus
Hence proved
prove that the bisector of opposite angles of a parallelogram are parallel .
Given ABCD is a parallelogram. The bisectors of $$ \angle ADC and \angle BCD $$ meet at E.
The bisectors of $$ \angle ABC\ and\ \angle BCD $$ meet at F
From the parallelogram ABCD we have
$$ \angle ADC + \angle BCD = 180^{o}$$ [sum of adjacent angles of parallelogram]
$$ \Rightarrow \dfrac{\angle ADC }{2} + \dfrac{\angle BCD}{2} = 90^{o}$$
In triangle ECD sum of angles $$= 180^{o} $$
$$ \Rightarrow \angle EDC + \angle BCD + \angle CBD =180^{o}$$
$$\Rightarrow CED = 90^{o}$$
Therefore the lines DE are parallel
Hence proved.
The bisectors of $$ \angle ABC\ and\ \angle BCD $$ meet at F
From the parallelogram ABCD we have
$$ \angle ADC + \angle BCD = 180^{o}$$ [sum of adjacent angles of parallelogram]
$$ \Rightarrow \dfrac{\angle ADC }{2} + \dfrac{\angle BCD}{2} = 90^{o}$$
In triangle ECD sum of angles $$= 180^{o} $$
$$ \Rightarrow \angle EDC + \angle BCD + \angle CBD =180^{o}$$
$$\Rightarrow CED = 90^{o}$$
Therefore the lines DE are parallel
Hence proved.
State 'true or False
Every parallelogram is a rhombus
Prove that a quadrilateral is a parallelogram if and only if its diagonal bisect each other.
Let $$\bar{a}, \bar{b}, \bar{c}$$ and $$\bar{d}$$ be respectively the position vectors of the vertices $$A, B, C$$ and $$D$$ of the parallelogram $$ABCD$$.
Then $$AB=DC$$ and side $$AB\parallel$$ side $$DC$$.
$$\therefore \bar{AB}=\bar{DC}$$
$$\therefore \bar{b}-\bar{a}=\bar{c}-\bar{d}$$
$$\therefore \bar{a}+\bar{c}=\bar{b}\bar{d}$$
$$\therefore \dfrac{\bar{a}+\bar{c}}{2}=\dfrac{\bar{b}+\bar{d}}{2}$$ ....(1)
The position vectors of the midpoints of the diagonals $$AC$$ and $$BD$$ are $$\dfrac{\bar{a}+\bar{c}}{2}$$ and $$\dfrac{\bar{b}+\bar{d}}{2}$$.
By $$(1)$$, they are equal.
$$\therefore$$ the midpoint of the diagonal $$AC$$ and $$BD$$ are the same.
This shows that the diagonals $$AC$$ and $$BD$$ bisect each other.
(ii) Conversely, suppose that the diagonals $$AC$$ and $$BC$$ of $$\square ABCD$$ bisect each other,
i.e. they have the same midpoint.
$$\therefore$$ the position vectors of these midpoints are equal.
$$\therefore \dfrac{\bar{a}+\bar{c}}{2}=\dfrac{\bar{b}+\bar{d}}{2}$$
$$\therefore \bar{a}+\bar{c}=\bar{b}+\bar{d}$$
$$\therefore \bar{b}-\bar{a}=\bar{c}-\bar{d}$$
$$\therefore \bar{AB}=\bar{DC}$$
$$\therefore \bar{AB}\parallel \bar{DC}$$ and $$|\bar{AB}|=|\bar{DC}|$$
$$\therefore$$ side $$AB\parallel$$ side $$DC$$ and $$AB=DC$$
$$\therefore \square ABCD$$ is a parallelogram.
Then $$AB=DC$$ and side $$AB\parallel$$ side $$DC$$.
$$\therefore \bar{AB}=\bar{DC}$$
$$\therefore \bar{b}-\bar{a}=\bar{c}-\bar{d}$$
$$\therefore \bar{a}+\bar{c}=\bar{b}\bar{d}$$
$$\therefore \dfrac{\bar{a}+\bar{c}}{2}=\dfrac{\bar{b}+\bar{d}}{2}$$ ....(1)
The position vectors of the midpoints of the diagonals $$AC$$ and $$BD$$ are $$\dfrac{\bar{a}+\bar{c}}{2}$$ and $$\dfrac{\bar{b}+\bar{d}}{2}$$.
By $$(1)$$, they are equal.
$$\therefore$$ the midpoint of the diagonal $$AC$$ and $$BD$$ are the same.
This shows that the diagonals $$AC$$ and $$BD$$ bisect each other.
(ii) Conversely, suppose that the diagonals $$AC$$ and $$BC$$ of $$\square ABCD$$ bisect each other,
i.e. they have the same midpoint.
$$\therefore$$ the position vectors of these midpoints are equal.
$$\therefore \dfrac{\bar{a}+\bar{c}}{2}=\dfrac{\bar{b}+\bar{d}}{2}$$
$$\therefore \bar{a}+\bar{c}=\bar{b}+\bar{d}$$
$$\therefore \bar{b}-\bar{a}=\bar{c}-\bar{d}$$
$$\therefore \bar{AB}=\bar{DC}$$
$$\therefore \bar{AB}\parallel \bar{DC}$$ and $$|\bar{AB}|=|\bar{DC}|$$
$$\therefore$$ side $$AB\parallel$$ side $$DC$$ and $$AB=DC$$
$$\therefore \square ABCD$$ is a parallelogram.
State 'true or 'False'
If two adjacent side of a parallelogram are equal it is rhombus,
In the following figure , AE and BC are equal and parallel and the three sides AB ,CD and DE are equal to one another . If angle A is $$ 102 ^{o}$$ , find the angles AEC ad BCD .
According to the question,
Given that AE = BC
We have to find $$ \angle AEC,\angle BCD $$
Let us join EC and BD.
In the quadrilateral AECB
AE = BC and AB = EC
Aslo AE || BC
AB ||EC
So quadrilateral is a parallelogram
In parallelogram consecutive angles are supplementary
$$ \Rightarrow \angle A + \angle B = 180^{o}$$
$$ \Rightarrow 102^{o} +\angle B = 180^{o}$$
$$\Rightarrow \angle B = 78^{o}$$
In parallelogram opposite angles are equal
$$ \Rightarrow \angle A = \angle BEC and \angle B = \angle AEC $$
$$ \Rightarrow BEC = 102^{o} and \angle AEC = 78^{o}$$ Now consider $$ \Delta ECD $$
EC = ED = CD [since AB = EC]
Therefore $$ \Delta ECD $$ is an equilateral triangle . $$\Rightarrow \angle ECD = 60^{o}$$
$$ \angle BCD = \angle BEC + \angle ECD $$
$$\Rightarrow BCD = 102^{o} + 60^{o}$$
$$\Rightarrow \angle BCD = 162^{o}$$
THerefore $$ \angle AEC = 78^{o} and \angle BCD = 162^{o}$$
Given that AE = BC
We have to find $$ \angle AEC,\angle BCD $$
Let us join EC and BD.
In the quadrilateral AECB
AE = BC and AB = EC
Aslo AE || BC
AB ||EC
So quadrilateral is a parallelogram
In parallelogram consecutive angles are supplementary
$$ \Rightarrow \angle A + \angle B = 180^{o}$$
$$ \Rightarrow 102^{o} +\angle B = 180^{o}$$
$$\Rightarrow \angle B = 78^{o}$$
In parallelogram opposite angles are equal
$$ \Rightarrow \angle A = \angle BEC and \angle B = \angle AEC $$
$$ \Rightarrow BEC = 102^{o} and \angle AEC = 78^{o}$$ Now consider $$ \Delta ECD $$
EC = ED = CD [since AB = EC]
Therefore $$ \Delta ECD $$ is an equilateral triangle . $$\Rightarrow \angle ECD = 60^{o}$$
$$ \angle BCD = \angle BEC + \angle ECD $$
$$\Rightarrow BCD = 102^{o} + 60^{o}$$
$$\Rightarrow \angle BCD = 162^{o}$$
THerefore $$ \angle AEC = 78^{o} and \angle BCD = 162^{o}$$
In figure, $$ABCD$$ and $$AEFG$$ are both parallelograms. If $$\angle C= 55^\circ$$ then find the value of $$\angle F$$.
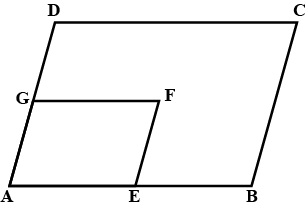
The given figure shows a parallelogram $$ABCD$$ in which $$AE = EF = FC$$ . Prove that $$DE$$ is parallel to $$FB$$.
Given that,
$$ABCD$$ is a parallelogram,
$$AE=EF=FC....(i)$$
Construct:
Join $$DF$$ and $$EB$$
Join diagonal $$BD$$
$$AC$$ and $$BD$$ intersect each other at $$O$$.
Since diagonal of a parallelogram bisect each other.
$$OA = OC.....(ii)$$
and $$OB = OD.....(iii)$$
Also , from $$(i)$$,
$$AE = FC$$
Now , $$OA = OC$$ and $$AE = FC$$
$$ \Rightarrow OA - AE = OC - FC $$
$$\Rightarrow OE = OF .....(iv)$$
Thus , in quadrilateral $$DEFB$$ , we have
$$OB = OD$$ and $$OE = OF$$
So, diagonals of quadrilateral $$BDEF$$ bisect each other.
$$\Rightarrow$$ $$BDEF$$ is a parallelogram.
$$\Rightarrow $$ $$DE$$ is parallel to $$FB$$, as they are opposite sides of a paralllelogram.($$Hence\ proved$$)
In a parallelogram ABCD , AB = 20 cm and AD = 12 cm. The bisectors of angles A meet DC at E and BC produce at F . Find the length of CE.
Given AB = 20 cm and AD = 12 cm
From the above figure
Its evident that ABF is an isosceles triangle with angle BAF = angle BFA = x
So $$AB = BF = 20$$
$$BF = 20$$
$$BC + CF = 20$$
$$CF = 20 - 12 = 8$$ cm
From the above figure
Its evident that ABF is an isosceles triangle with angle BAF = angle BFA = x
So $$AB = BF = 20$$
$$BF = 20$$
$$BC + CF = 20$$
$$CF = 20 - 12 = 8$$ cm
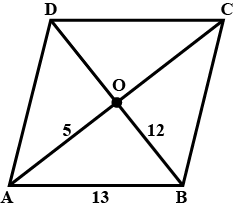
Diagonals of a parallelogram intersect each other at point $$\text{O}.$$ If $$\text{AO} = 5\text{ cm}$$, $$\text{BO} = 12\text{ cm}$$ and $$\text{AB} = 13\text{ cm}$$ then show that
$$\text{ABCD}$$ is a rhombus.
In $$\Delta AOB$$,
$$AO = 5 \text{ cm}$$
$$OB = 12 \text{ cm}$$
$$AB = 13 \text{ cm}$$
$$5, 12$$ and $$13$$ form a Pythagorean triplet.
Thus, $$\Delta$$AOB is a right angle triangle, right angled at O.
$$\because ~~ABCD$$ is a parallelogram.
So, diagonal bisect each other.
$$\Rightarrow$$ $$AO = OC = 5 \text{ cm}$$
Also, $$OB = OD = 12 \text{ cm}$$
Thus, in parallelogram $$ABCD,$$ diagonals bisect at right angles.
Hence, $$ABCD$$ is a rhombus.
$$AO = 5 \text{ cm}$$
$$OB = 12 \text{ cm}$$
$$AB = 13 \text{ cm}$$
$$5, 12$$ and $$13$$ form a Pythagorean triplet.
Thus, $$\Delta$$AOB is a right angle triangle, right angled at O.
$$\because ~~ABCD$$ is a parallelogram.
So, diagonal bisect each other.
$$\Rightarrow$$ $$AO = OC = 5 \text{ cm}$$
Also, $$OB = OD = 12 \text{ cm}$$
Thus, in parallelogram $$ABCD,$$ diagonals bisect at right angles.
Hence, $$ABCD$$ is a rhombus.
In the given figure, G is the point of concurrence of medians of $$ \Delta $$ DEF. Take point $$ \mathrm{H} $$ on ray DG such that $$ \mathrm{D}-\mathrm{G} - \mathrm{H} $$ and $$ \mathrm{DG}=\mathrm{GH}, $$ then prove that $$ \square $$ GEHF is a parallelogram.
G is the point of concurrence of the medians of $$ \Delta $$ DEF.
Let the point where the median divides EF into two equal parts be A.
Thus, $$ E A=A F \ldots$$(1)
we know that the point of concurrence of the medians divides each median in the ratio 2: 1.
So, let $$ \mathrm{DG}=2 \mathrm{x} $$ and $$ \mathrm{GA}=\mathrm{x} $$
Given that $$ D G=G H $$
$$ \mathrm{So}, \mathrm{GA}=\mathrm{AH}=\mathrm{x} $$
Thus, point A divides $$EF$$ and $$GH$$ into two equal parts.
Hence, $$ \square $$ GEHF is a parallelogram as the diagonals $$ \mathrm{EF} $$ and $$ \mathrm{GH} $$ bisect each other.
Let the point where the median divides EF into two equal parts be A.
Thus, $$ E A=A F \ldots$$(1)
we know that the point of concurrence of the medians divides each median in the ratio 2: 1.
So, let $$ \mathrm{DG}=2 \mathrm{x} $$ and $$ \mathrm{GA}=\mathrm{x} $$
Given that $$ D G=G H $$
$$ \mathrm{So}, \mathrm{GA}=\mathrm{AH}=\mathrm{x} $$
Thus, point A divides $$EF$$ and $$GH$$ into two equal parts.
Hence, $$ \square $$ GEHF is a parallelogram as the diagonals $$ \mathrm{EF} $$ and $$ \mathrm{GH} $$ bisect each other.
Sum, of the square of adjacent sides of a parallelogram is 130 sq. cm and length of one of its diagonals is 14 cm . Find the length of the other diagonals
It is given that
$$AB^{2} + AD ^{2} = 130 sq. cm $$
$$BD = 14 cm $$
Diagonals of a parallelogram bisect each other . i.e. O is the mid point of AC and BD .
$$In \bigtriangleup ABD, $$
point O is the midpoint of side BD .
$$BO = OD = \dfrac{1}{2}BD = 7 cm $$
$$AB^{2} + AD ^{2}=2AO^{2}+2BO^{2}$$
( by Apollonius theorem)
$$\Rightarrow 130 = 2 AO^{2} + 2 (7)^{2} $$
$$\Rightarrow 130 = 2AO ^{2}+ 2 \times 49 $$
$$\Rightarrow 130 = 2AO^{2} + 98 $$
$$\Rightarrow 2AO^{2}= 130 -98$$
$$\Rightarrow 2AO^{2}= 32 $$
$$\Rightarrow AO^{2}= 16 $$
$$\Rightarrow AO = 4 cm $$
Since, point O is the midpoint of side AC.
$$\therefore AC = 2AO = 8cm $$ Hence, the length of the other diagonal is 8 cm
Prove that the sum of the squares of the diagonals of a parallelogram is equal to the sum of the squares of its sides.
Diagonal of a parallelogram bisect each other . i.e. O is the mid point of AC and BD.
In $$\bigtriangleup ABD,$$ point O is the midpoint of side BD
$$BO = OD= \dfrac{1}{2} BD$$
$$AB^{2} + AD^{2} = 2AO^{2} + 2BO^{2} $$ (by Apollonius theorem )...(1)
$$In \bigtriangleup CBD $$ ,
point O is the midpoint of side BD
$$BO = OD = \dfrac{1}{2}BD$$
$$CB^{2} + CD^{2} = 2CO^{2} + 2BO^{2} $$ (by Apollonius theorem)....(2)
Adding (1) and (2), we get
$$AB^{2} + AD^{2} + CB ^{2} + CD ^{2} = 2 AO ^{2}+ 2 BO ^{2} +2 CO^{2} + 2BO ^{2} $$
$$\Rightarrow AB ^{2} + AD ^{2} + CB ^{2} + CD^{2}= 2AO^{2} + 4BO^{2} + 2AO^{2}(\because OC = OA)$$
$$\Rightarrow AB^{2} + AD^{2}+ CB ^{2} + CB ^{2} = 4AO^{2} + 4BO ^{2}$$
$$\Rightarrow AB^{2} + AD^{2}+ CB ^{2} + CB ^{2} = (2AO)^{2} + (2BO) ^{2}$$
$$\Rightarrow AB^{2} + AD ^{2}+ CB ^{2} + CD ^{2} = ( AC)^{2} + (BD)^{2}$$
$$\Rightarrow AB ^{2}+ AD ^{2} + CB ^{2} + CD^{2}= AC ^{2}+ BD ^{2} $$
Hence, the sum of the squares of the diagonal of a parallelogram is equal to the sum of the squares of its sides
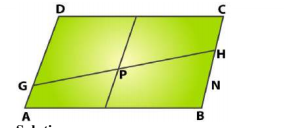
Prove that quadrilateral formed by the intersection of angle bisectors of all angles of a parallelogram is a rectangle.(shown in the given figure)
Using opposite angles test for a parallelogram, prove that every rectangle is a parallelogram.
$$ \square ABCD $$ is a parallelogram point E is on side BC .Line DE intersects ray AB in point T . Prove that $$ DE \times BE = CE \times TE. $$
Diagonals of a parallelogram WXYZ intersect each other at point O. If $$\angle XYZ = 135^o$$ then what is the measure of $$\angle$$ XWZ and $$\angle$$ YZW?Also, If $$l(OY) = 5 \text{ cm}$$ then $$l(WY) = ?$$
In a parallelogram, opposite angles are equal.
$$\angle XYZ = \angle XWZ = 135^o$$
Also, WX || ZY
So, $$\angle YZW + \angle XWZ = 180^o$$
(Since, interior angles on the same side of the transversal are supplementary)
$$\Rightarrow \angle YZW + 135^o = 180^o$$
$$\Rightarrow \angle YZW = 180^o - 135^o$$
$$\implies \angle YZW = 45^o$$
Now $$l(OY) = 5\text{ cm}$$
we know that diagonals of a parallelogram bisect each other.
So, $$l(WY) = 2 \times OY = 2 \times 5 = 10 \text{ cm}$$
$$\angle XYZ = \angle XWZ = 135^o$$
Also, WX || ZY
So, $$\angle YZW + \angle XWZ = 180^o$$
(Since, interior angles on the same side of the transversal are supplementary)
$$\Rightarrow \angle YZW + 135^o = 180^o$$
$$\Rightarrow \angle YZW = 180^o - 135^o$$
$$\implies \angle YZW = 45^o$$
Now $$l(OY) = 5\text{ cm}$$
we know that diagonals of a parallelogram bisect each other.
So, $$l(WY) = 2 \times OY = 2 \times 5 = 10 \text{ cm}$$
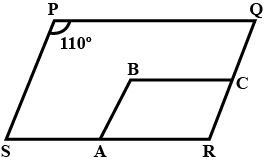
In the given figure, $$\square$$ PQRS and $$\square$$ ABCR are two parrallelograms. If $$\angle P = 110^o$$ then find the measures of all angles of $$\square ABCR$$.
Let $$ABCD$$ be a parallelogram, what special name will you give if.
$$AB=BC$$ and $$\angle BAD=90^o$$
Ratio of two adjacent sides of a parallelogram is $$ 3: 4, $$ and its perimeter is $$ 112 \mathrm{cm} $$. Find the length of its each side.
A field is in the form of a parallelogram whose perimeter is $$450m$$ and one of its sides is larger than the other by $$75$$ m. Find the lengths of all sides
Let one side be $$x$$, then the other side is
$$x+75$$
Perimeter $$=450$$
$$x+(x+75)+x+(x+75)=450$$
$$4x=450$$
$$4x=450-150$$
$$4x=300$$
$$x=\dfrac{300}{4}=75$$
$$x=75m$$
$$x+75=75+75=150\ m$$
$$\therefore $$ The four sides are $$75m,150m,75m,150m$$
$$x+75$$
Perimeter $$=450$$
$$x+(x+75)+x+(x+75)=450$$
$$4x=450$$
$$4x=450-150$$
$$4x=300$$
$$x=\dfrac{300}{4}=75$$
$$x=75m$$
$$x+75=75+75=150\ m$$
$$\therefore $$ The four sides are $$75m,150m,75m,150m$$
In Fig, diagonals $$AC$$ and $$BD$$ of quadrilateral $$ABCD$$ intersect at $$O$$ such that $$OB=OD$$. If $$AB=CD$$, then show that:
$$DA\parallel CB$$ or $$ABCD$$ is a parallelogram.
[Hint: From $$D$$ and $$B$$, draw perpendiculars to $$AC$$.]
Data: Diagonals $$AC$$ and $$BD$$ of a quadrilateral $$ABCD$$ intersect at $$O$$ such that $$OB=OD$$. If $$AB=CD$$,
To prove:
(i) $$ar.(\triangle DOC)=ar.(\triangle AOB)$$
(ii) $$ar.(\triangle DCB)=ar.(\triangle ACD)$$
(iii) $$DA\parallel CB$$ or $$ABCD$$ is a parallelogram
Construction:Draw $$DM\bot AC$$ and $$BN\bot AC$$
To prove:
(i) $$ar.(\triangle DOC)=ar.(\triangle AOB)$$
(ii) $$ar.(\triangle DCB)=ar.(\triangle ACD)$$
(iii) $$DA\parallel CB$$ or $$ABCD$$ is a parallelogram
Construction:Draw $$DM\bot AC$$ and $$BN\bot AC$$
Proof:
(i) $$DM\bot CO, BN\bot AO$$.
In $$\triangle DOM$$ and $$\triangle BON$$
$$DO=BO$$ (data)
$$\angle DMP=\angle BNO=90^o$$ (Construction)
$$\angle DOM=\angle BON$$ (Vertically opposite angles)
$$\therefore \triangle DOM \cong \triangle BON$$ (AAS Postulate)
$$\therefore DM=BN$$
$$\therefore ar.(\triangle DOM)=ar.(\triangle BON)$$ .........(i)
In $$\triangle DMC$$, and $$\triangle BNA$$,
$$\angle DMC=\angle BNA=90^{o}$$
$$DC=AB$$ (Data)
$$DM=BN$$ (Proved)
$$\therefore \bot \triangle DMC=\bot \triangle BNA$$
$$\therefore ar.(\triangle DMC)=ar,(\triangle BNA)$$ ........(ii)
Adding $$(i)$$ and $$(ii)$$,
$$ar.(\triangle DOM)+ar.(\triangle DMC)=ar.(\triangle BON)+ar.(\triangle BNA)$$
$$\therefore (\triangle DOC)=(\triangle AOB)$$ .........(iii)
(i) $$DM\bot CO, BN\bot AO$$.
In $$\triangle DOM$$ and $$\triangle BON$$
$$DO=BO$$ (data)
$$\angle DMP=\angle BNO=90^o$$ (Construction)
$$\angle DOM=\angle BON$$ (Vertically opposite angles)
$$\therefore \triangle DOM \cong \triangle BON$$ (AAS Postulate)
$$\therefore DM=BN$$
$$\therefore ar.(\triangle DOM)=ar.(\triangle BON)$$ .........(i)
In $$\triangle DMC$$, and $$\triangle BNA$$,
$$\angle DMC=\angle BNA=90^{o}$$
$$DC=AB$$ (Data)
$$DM=BN$$ (Proved)
$$\therefore \bot \triangle DMC=\bot \triangle BNA$$
$$\therefore ar.(\triangle DMC)=ar,(\triangle BNA)$$ ........(ii)
Adding $$(i)$$ and $$(ii)$$,
$$ar.(\triangle DOM)+ar.(\triangle DMC)=ar.(\triangle BON)+ar.(\triangle BNA)$$
$$\therefore (\triangle DOC)=(\triangle AOB)$$ .........(iii)
Proof:
(ii) $$(\triangle DOC)=(\triangle AOB)$$ (Proved)
Adding $$\triangle BOC$$ to both sides,
$$\triangle DOC+\triangle BOC=\triangle AOB+\triangle BOC$$
$$\therefore \triangle DCB=\triangle ACB$$.
(ii) $$(\triangle DOC)=(\triangle AOB)$$ (Proved)
Adding $$\triangle BOC$$ to both sides,
$$\triangle DOC+\triangle BOC=\triangle AOB+\triangle BOC$$
$$\therefore \triangle DCB=\triangle ACB$$.
.
Proof:
(iii) From equation (ii), $$\triangle DMC=\angle BNA$$
$$\therefore \angle DCM=\angle BAN$$
These are pair of alternate angles.
$$\therefore AB\parallel BC$$
and also $$AB=DC$$ (Data)
$$\therefore ABCD$$ is a parallelogram OR $$DA\parallel CB$$.
Proof:
(iii) From equation (ii), $$\triangle DMC=\angle BNA$$
$$\therefore \angle DCM=\angle BAN$$
These are pair of alternate angles.
$$\therefore AB\parallel BC$$
and also $$AB=DC$$ (Data)
$$\therefore ABCD$$ is a parallelogram OR $$DA\parallel CB$$.
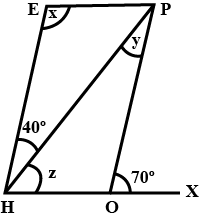
A farmer was having a field in the form of a parallelogram $$PQRS$$. She took any point $$A$$ on $$RS$$ and joined it to points $$P$$ and $$Q$$. In how many parts the fields is divided? What are the shapes of these parts? The farmer wants to sow wheat and pulses in equal portions of the field separately. How should she do it?
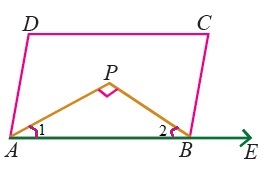
Let $$ABCD$$ be a parallelogram and suppose the bisector of $$\angle A$$ and $$\angle B$$ meet at $$P$$ prove that $$\angle APB=90^o$$
$$\angle A+\angle B=180^o$$
[ Adjacent angles of a parallelogram]
$$\dfrac 12 \angle A+\dfrac 12 \angle B=\dfrac{1}{2}.180^o$$ [ Multiplying by $$\dfrac 12$$]
$$\angle PAB+\angle PBA =90^o[AP$$ and $$BP$$ are angular bisectors]
$$\angle PAB+\angle PBA +\angle APB=180^o$$ [ Angle sum property of a triangle]
$$90+\angle APB=180^o$$
$$\angle APB=180-90$$
$$\angle APB=90^o$$
In the given figure, if points $$ \mathrm{P}, \mathrm{Q}, \mathrm{R}, \mathrm{S} $$ are on the sides of parallelogram such that $$ \mathrm{AP}=\mathrm{BQ}=\mathrm{CR}=\mathrm{DS} $$ then prove that $$ \square $$ PQRS is a parallelogram.
Three angles of a quadrilateral $$ABCD$$ are equal. Is is it a parallelogram? Why or why not?
$$ABCD$$ is a parallelogram. $$P$$ is any point on side $$BC$$ of parallelogram. If $$DP$$ and $$AB$$ produced, meet at $$L$$ then prove that
(i) $$\cfrac{DP}{PL}=\cfrac{DC}{BL}$$
(ii) $$\cfrac{DL}{DP}=\cfrac{AL}{DC}$$
To prove: $$\cfrac{DP}{PL}=\cfrac{DC}{BL}$$
Proof: In $$\triangle LDA$$
$$BP\parallel AD$$
$$\cfrac{LP}{DP}=\cfrac{LB}{AB}...(i)$$ (By B.P theorem)
or $$\cfrac{DP}{PL}=\cfrac{DC}{BL}$$
$$\cfrac{DP}{PL}=\cfrac{DC}{BL}$$
(ii) to prove
$$\cfrac{DL}{DP}=\cfrac{AL}{DC}$$
From equation (1) $$\cfrac{LP}{DP}=\cfrac{LB}{AB}$$
$$\cfrac{LP}{DP}+1=\cfrac{LB}{AB}+1$$
$$\cfrac{LP+DP}{DP}=\cfrac{LB+AB}{AB}$$
$$\cfrac{DL}{DP}=\cfrac{AL}{AB}$$
$$\cfrac{DL}{DP}=\cfrac{AL}{CD}$$ ($$\because AD=CD$$)
Proof: In $$\triangle LDA$$
$$BP\parallel AD$$
$$\cfrac{LP}{DP}=\cfrac{LB}{AB}...(i)$$ (By B.P theorem)
or $$\cfrac{DP}{PL}=\cfrac{DC}{BL}$$
$$\cfrac{DP}{PL}=\cfrac{DC}{BL}$$
(ii) to prove
$$\cfrac{DL}{DP}=\cfrac{AL}{DC}$$
From equation (1) $$\cfrac{LP}{DP}=\cfrac{LB}{AB}$$
$$\cfrac{LP}{DP}+1=\cfrac{LB}{AB}+1$$
$$\cfrac{LP+DP}{DP}=\cfrac{LB+AB}{AB}$$
$$\cfrac{DL}{DP}=\cfrac{AL}{AB}$$
$$\cfrac{DL}{DP}=\cfrac{AL}{CD}$$ ($$\because AD=CD$$)
In a parallelogram $$ABCD$$, the side $$DC$$ is produced to $$E$$ and $$\angle BCE=105^o$$ calculate $$\angle A,\angle E,\angle C$$ and $$\angle D$$.
$$\angle DCB+\angle DCE=180^o$$[Linear pair ]$$|DCB+1050=180^o$$
$$\angle DCB=180-105$$
$$\angle DCB=75^o$$
$$\angle A=\angle C=75^o$$
[Opposite angles of a parallelogram]
$$\angle A+\angle B=180^o$$
[adjacent angles of a parallelogram]
$$75^o+\angle B=180^o$$
$$\angle B=180+75$$
$$\angle B=105^o$$
$$\angle B=\angle D=105^o$$
[Opposite angles of a parallelogram]
$$\angle DCB=180-105$$
$$\angle DCB=75^o$$
$$\angle A=\angle C=75^o$$
[Opposite angles of a parallelogram]
$$\angle A+\angle B=180^o$$
[adjacent angles of a parallelogram]
$$75^o+\angle B=180^o$$
$$\angle B=180+75$$
$$\angle B=105^o$$
$$\angle B=\angle D=105^o$$
[Opposite angles of a parallelogram]
The diagonals of a quadrilateral bisect each other. Prove that this quadrilateral is parallelogram.
Given, A quadrilateral ABCD whose diagonals AC and BD bisects at point O. i.e., OA = OC and OB = OD.
To prove : ABCD is a parallelogram.
Proof:
$$\Delta$$AOB and $$\Delta$$COD
OA = OC (Given)
$$\angle$$AOB = $$\angle$$ COD (Vertically opposite angles)
and OB = OD (given)
$$\Delta AOB \cong \Delta COD$$ (By ASA rule)
$$\Rightarrow \angle OAB = \angle OCD$$ (CPCT)
$$\Rightarrow \angle CAB = \angle ACD$$
But these are alternate angles made by transversal at lines AB and CD. Hence AB || CD.
Similarly, AD || BC
Hence, ABCD is a parallelogram.
To prove : ABCD is a parallelogram.
Proof:
$$\Delta$$AOB and $$\Delta$$COD
OA = OC (Given)
$$\angle$$AOB = $$\angle$$ COD (Vertically opposite angles)
and OB = OD (given)
$$\Delta AOB \cong \Delta COD$$ (By ASA rule)
$$\Rightarrow \angle OAB = \angle OCD$$ (CPCT)
$$\Rightarrow \angle CAB = \angle ACD$$
But these are alternate angles made by transversal at lines AB and CD. Hence AB || CD.
Similarly, AD || BC
Hence, ABCD is a parallelogram.
A regular polygon has 8 sides, then
Find the measure of each interior angle.
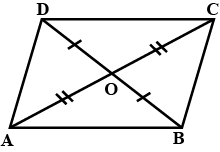
Let $$ABCD$$ be a quadrilateral with diagonals $$AC$$ and $$BD$$. Prove the following statement
$$AB+BC+CD + DA > AC+BD$$
In figure, $$ABCD$$ is a parallelogram and lines $$AQ$$ and $$CP$$ are the bisector of $$\angle A - \angle C$$ respectively. Prove the $$APCQ$$ is a parallelogram.
A regular polygon has 8 sides, then
Find the sum of all interior angles.
Can there exist a regular polygon whose interior angle is $$ 137^{\circ} $$?
The sum of the interior angles of a polygon is $$ 2160^{\circ} $$, find the number of sides in the polygon.
The sum of interior angles of a polygon is 10 right angles. Find the number of sides.
The four angles of a pentagon are $$40^o, $$ $$75^o, $$ $$125^o, $$ and $$135^o $$ respectively. Find the fifth angle.
In the given figure, $$BCPQ$$ and $$BCDA$$ are two parallelograms on the same base $$BC$$. Find the value of $$x+y$$.
A regular polygon has 12 sides, find the measure of each of its interior angles.
In the given figure, $$PQRS$$ is a parallelogram in which $$PQ$$ is produced to $$T$$ such that $$QT= PQ$$. Prove that $$ST$$ bisects $$RQ$$.
Find the magnitude of an interior angle of a regular hexagon.
(i) in degree
(ii) in radians
Write the measurements of exterior and interior angles of regular pentagon
(i) in degrees
(ii) in radian
In parallelogram $$ABCD, AB= 12 \ cm$$. The altitudes corresponding to the two sides $$AB$$ and $$AD$$ are $$8 \ cm$$ and $$10 \ cm$$ respectively. Compute $$BC$$.
Area of parallelogram $$ABCD= AB\times CM= 12 \ cm \times 8 \ cm= 96 \ cm^2$$
Again area of parallelogram $$ABCD= BC \times CN$$
$$\implies 96 = BC \times 10$$
$$\implies BC= 9.6 \ cm$$
Again area of parallelogram $$ABCD= BC \times CN$$
$$\implies 96 = BC \times 10$$
$$\implies BC= 9.6 \ cm$$
Determine the number of sides the polygon for which the ratio of the sum of the interior angles to the sum of the exterior angle is 5: 1.
ABCD is a parallelogram.
Write down
the sum of the interior angles of ABCD.
In figure, $$ABCD$$ is a parallelogram, $$AE \perp DC$$ and $$CF \perp AD$$. If $$AB= 16 \ cm, AE= 8 \ cm$$ and $$CF= 10 \ cm$$, find $$AD$$.
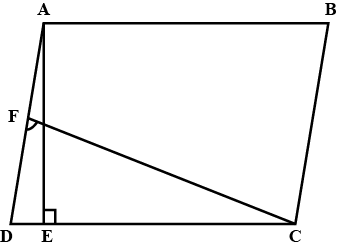
Prove that, if the diagonals of a parallelogram are perpendicular to each other, the parallelogram is a rhombus.
Since the diagonals of a parallelogram bisect each other,
$$BE$$ and $$DE$$ are congruent and $$AE$$ is congruent to itself.
We are given that all four angles at point $$E$$ are $$90^0$$ and
are therefore congruent.
Triangles $$ABE$$ and $$ADE$$ are congruent by side-angle-side,
Therefore, $$AB$$ and $$AD$$ are congruent.
Since opposite sides of a parallelogram are congruent,
$$AD$$ and $$BC$$ are congruent, and $$AB$$ and $$CD$$ are congruent.
So all four sides are congruent.
Hence, $$ABCD$$ is a rhombus.
The adjacent angles in a parallelogram are $$\left(3x+10\right)^{}$$ and $$\left(x+20\right)^{}$$ then, find the measures of the four angles.
The area of a square and a parallelogram is the same. If the side of the square is $$60 \ cm$$ and base of the parallelogram is $$120 \ cm$$, find the corresponding height of the parallelogram.
ABCD is a parallelogram. AE and AF are bisectors of interior and exterior angles respectively at A and BE and BF are bisectors of interior and exterior angles respectively at B. Show that AFBE is a parallelogram.
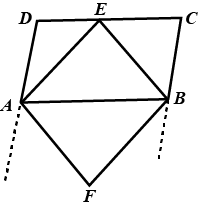
If $$D,E,F$$ are midpoints of $$AB,BC,AC$$ respectively prove that $$BDEF$$ is a $$||\ gm$$
In $$\triangle ABC, D, E$$ and $$F$$ are midpoints of $$BC, AC$$ and $$AB$$ respectively.
$$\because \ E$$ and $$F$$ are mid point of $$AC$$ and $$AB$$ respectively
$$\therefore \ FE||BC\Rightarrow FE||BD---(1) $$
Similarly $$DE++AB \Rightarrow DE||FB-----(2)$$
Now, from $$(1)$$ and $$(2)$$,
opposite pairs are parallel
$$\therefore \ BDEF$$ is a parallelogram -----proved.
If bisectors of $$\angle A$$ and $$ \angle B$$ of a quadrilateral $$ABCD$$ intersect each other at $$P,$$ of $$\angle B$$ and $$ \angle C$$ at $$Q.$$ $$\angle C$$ and $$ \angle D$$ at $$R ,$$ $$\angle D$$ and $$ \angle A$$ at $$S$$ then show that $$PQRS$$ is a quadrilateral whose opposite angle are supplementary
To Prove:
$$\angle PSR+\angle PQR=180^\circ\\ \angle SPQ+\angle SRQ=180^\circ$$
Apply angle sum property in $$\triangle DSA,$$
$$\angle DAS+\angle ADS+\angle DSA=180^\circ$$
$$\Rightarrow \cfrac { 1 }{ 2 } \angle A+\cfrac { 1 }{ 2 } \angle D+\angle DSA=180^\circ$$
$$\Rightarrow \angle DSA=180^\circ-\cfrac { 1 }{ 2 } \angle A-\cfrac { 1 }{ 2 } \angle D$$
As, $$\angle DSA$$ and $$\angle PSR$$ are vertically opposite angle,
$$\angle PSR=180^\circ-\cfrac { 1 }{ 2 } \angle A-\cfrac { 1 }{ 2 } \angle D\quad\quad\quad\dots(i)$$
Similarly, in $$\triangle CQB,$$
$$\angle PQR=180^\circ-\cfrac { 1 }{ 2 } \angle C-\cfrac { 1 }{ 2 } \angle B\quad\quad\quad\dots(ii)$$
On adding equations $$(i)$$ and $$(ii),$$ we get,
$$\begin{aligned}{}\angle PSR + \angle PQR &= {180^\circ } - \frac{1}{2}\angle C - \frac{1}{2}\angle B + {180^\circ } - \frac{1}{2}\angle A - \frac{1}{2}\angle D\\& = {360^\circ } - \frac{1}{2} \times \left( {\angle A + \angle B + \angle C + \angle D} \right)\\& = {360^\circ } - \frac{1}{2} \times {360^\circ }\\ &= {180^\circ }\end{aligned}$$
$$\therefore \angle PSR + \angle PQR =180^\circ$$
In quadrilateral $$PQRS,$$
$$\angle SPQ+\angle SRQ+\angle PSR+\angle PQR=360^\circ$$
$$\Rightarrow \angle SPQ+\angle SRQ+180^\circ=360^\circ$$
$$\Rightarrow \angle SPQ+\angle SRQ=180^\circ$$
Hence, proved that opposite angles of $$PQRS$$ are supplementary.
In a parallelogram RISE if Olis equal to $$4$$ cm and Rs $$1$$ equal to $$6$$ CM more then EI then FIND RO
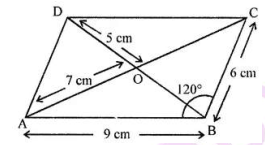
The length of one side of a parallelogram is $$17\ cm.$$ If the length of its diagonals is $$12\ cm$$ and $$26\ cm$$, then find the length of the other side of a parallelogram.
In parallelogram $$ABCD,$$
$$\begin{aligned}{}d_1^2 + d_2^2 &= 2\left( {{a^2} + {b^2}} \right)\\{26^2} + {12^2} &= 2\left( {{{17}^2} + {b^2}} \right)\\676 + 144& = 2\left( {289 + {b^2}} \right)\\{b^2} + 289 &= \frac{{820}}{2}\\{b^2}& = 410 - 289\\{b^2} &= 121\\b &= \sqrt {121} \\& = 11\;cm\end{aligned}$$
Hence, the length of the other side of the parallelogram is equal to $$11\ cm.$$
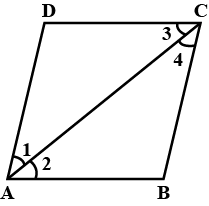
Diagonal $$AC$$ of a parallelogram $$ABCD$$ bisects $$\angle$$ $$A$$. Show that
(i) it bisects $$\angle$$ $$C$$ also,
(ii) $$ABCD$$ is a rhombus.
diagonal $$AC$$ of $$||gm \, ABCD$$ bisects $$\angle A$$
Also given, to show that, it bisects $$\angle C$$
Let us first know, what is a parallelogram "A quadrilant in which both pairs of opposite sides are parallel is called a parallelogram"
And theoretically Rhombus is a "Quadrilateral in which all four sides are equal to both pairs of opposite sides are parallel is called rhombus".
as given: $$\overline{AC}$$ diagonal bisects $$\angle A$$ in $$ABCD ||$$ & $$\angle CAD = \angle CAB$$ (as given)
required to prove: (i) it bisects $$\angle C$$.
let us now consider.
proof: (i) In $$\Delta AOC$$ & $$\Delta CBA$$
$$AD = CB $$ ($$\because$$ common & opposite sides of $$||gm$$)
$$DC = BA$$ ($$\because$$ opposite sides of $$||gm$$)
$$AC = CA$$ ($$\because $$ common side)
$$\therefore \Delta ADC \cong \Delta CBA$$ [$$\because$$ by SSS congruency rule]
$$\angle ADC = \angle CBA$$
$$\Rightarrow \angle ACD = \angle CAB $$ ...(1) ($$\because $$ common angle)
$$\angle BCA = \angle CAD$$ ...(2) ($$\because$$ common angle)
$$\angle CAB = \angle CAD$$ ...(3) ($$\because$$ common angle)
from eq. (1), (2) & (3) we get,
$$\angle ACD = \angle BCA$$
$$\therefore AC$$ diagonal bisects $$\angle C$$.
Hence proved
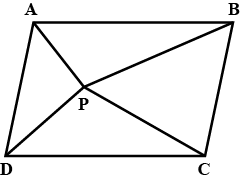
In Fig. $$9.16$$ $$P$$ is a point in the interior of a parallelogram $$ABCD.$$ Show that
$$(i)\,ar\left( {APB} \right) + ar\left( {PCD} \right) = \frac{1}{2}ar\left( {ABCD} \right)$$
$$(ii)\,ar\left( {APD} \right) + ar\left( {PBC} \right) = ar\left( {APB} \right)ar\left( {PCD} \right)$$
[Hint: Through $$P,$$ draw a line parallel to $$AB.$$ ]
Assume two lines $$EF$$ and $$GH$$ such that $$EF \parallel AB$$ and $$GH\parallel AD.$$
In $$\parallel gm \;AEFB;\;ar \left( APB\right) =\dfrac{1}{2}ar \left( AEFB\right) \longrightarrow \left(1\right)$$
In $$\parallel\;g, EFCD;\;ar \left(DPC\right)=\dfrac{1}{2} ar \left( EFCD\right)\longrightarrow \left(2\right)$$
From $$\left(1\right)$$ and $$\left(2\right)$$ (adding )
$$\Rightarrow ar\left( APB\right)+ar \left(PDC\right)=\dfrac{1}{2}\left[ ar \left( AEFB\right) +ar\left( EFCD\right)\right]$$
$$\Rightarrow ar \left(APB\right)+ar \left( PDC\right)=\dfrac{1}{2}ar \left( ABCD\right) -$$
In $$\parallel\;gm\; AGHD;\;ar \left(APD\right) =\dfrac{1}{2} ar \left( AGHD\right) \longrightarrow \left(3\right)$$
In $$\parallel \;gm \;GBCH;\; ar \left( PBC\right) =\dfrac{1}{2}ar \left( GBCH\right)\longrightarrow \left(4\right)$$
Adding $$\left(3\right)$$ and $$\left(4\right)$$
$$\Rightarrow ar\left( APD\right)+ar \left(PBC\right)=\dfrac{1}{2}\left[ ar \left(AGHD\right) +ar\left( GBCH\right)\right]$$
$$\Rightarrow ar \left(APD\right) +ar \left( PBC\right) =\dfrac{1}{2}ar \left(ABCD\right)$$
From previous part -
$$\Rightarrow ar \left(APD\right)+ar \left( PBC\right)=ar \left( APB\right) +ar \left( PCD\right).$$
Hence, solved.
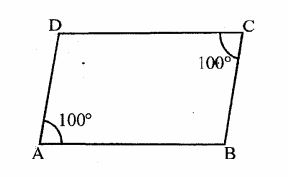
In the given figure, ABCD is a parallelogram in which $$\angle =70^0.$$ Calculate $$\angle B,\angle C$$ and $$\angle D.$$
In a parallelogram, opposite angles are always equal.
$$\Rightarrow \angle A=\angle C$$ and $$\angle B=\angle D$$
as $$\angle A=70^o\Rightarrow \angle C=70^o$$
Also $$\angle A+\angle B+\angle C+\angle D=360^o$$
$$\Rightarrow \angle B+\angle D=360^o-140^o$$
$$\Rightarrow 2\angle B=220^o$$
$$\Rightarrow \angle B=110^o$$
$$\Rightarrow D=110^o$$
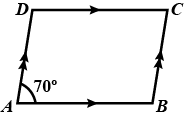
If the adjacent sides of a parallelogram are in the ratio $$2 : 3$$ and the sum of all the sides is $$50\ \mathrm{cm}$$, find the measure of the sides of the parallelogram.
Three consecutive vertices of a parallelogram $$ABCD$$ are $$A\left(-1,2\right),\,B\left(3,5\right)$$ and $$C\left(2,3\right)$$.Find the fourth vertex $$D$$
In parallelogram PQRS, PQ = 10 cm. The altitudes corresponding to the sides PQ and SP are respectively 6 cm and 8 cm. Find SP.
Equations of pairs of opposite sides of a parallelogram are $$ x ^ { 2 } - 7 x + 6 = 0 $$ and $$ y ^ { 2 } - 14 y + 40 = 0 . $$ Find the joint equation of its diagonals.
Class 8 Maths Extra Questions
- Algebraic Expressions And Identities Extra Questions
- Comparing Quantities Extra Questions
- Cubes And Cube Roots Extra Questions
- Data Handling Extra Questions
- Direct And Inverse Proportions Extra Questions
- Exponents And Powers Extra Questions
- Factorisation Extra Questions
- Introduction To Graphs Extra Questions
- Linear Equations In One Variable Extra Questions
- Mensuration Extra Questions
- Playing With Numbers Extra Questions
- Practical Geometry Extra Questions
- Rational Numbers Extra Questions
- Squares And Square Roots Extra Questions
- Understanding Quadrilaterals Extra Questions
- Visualising Solid Shapes Extra Questions