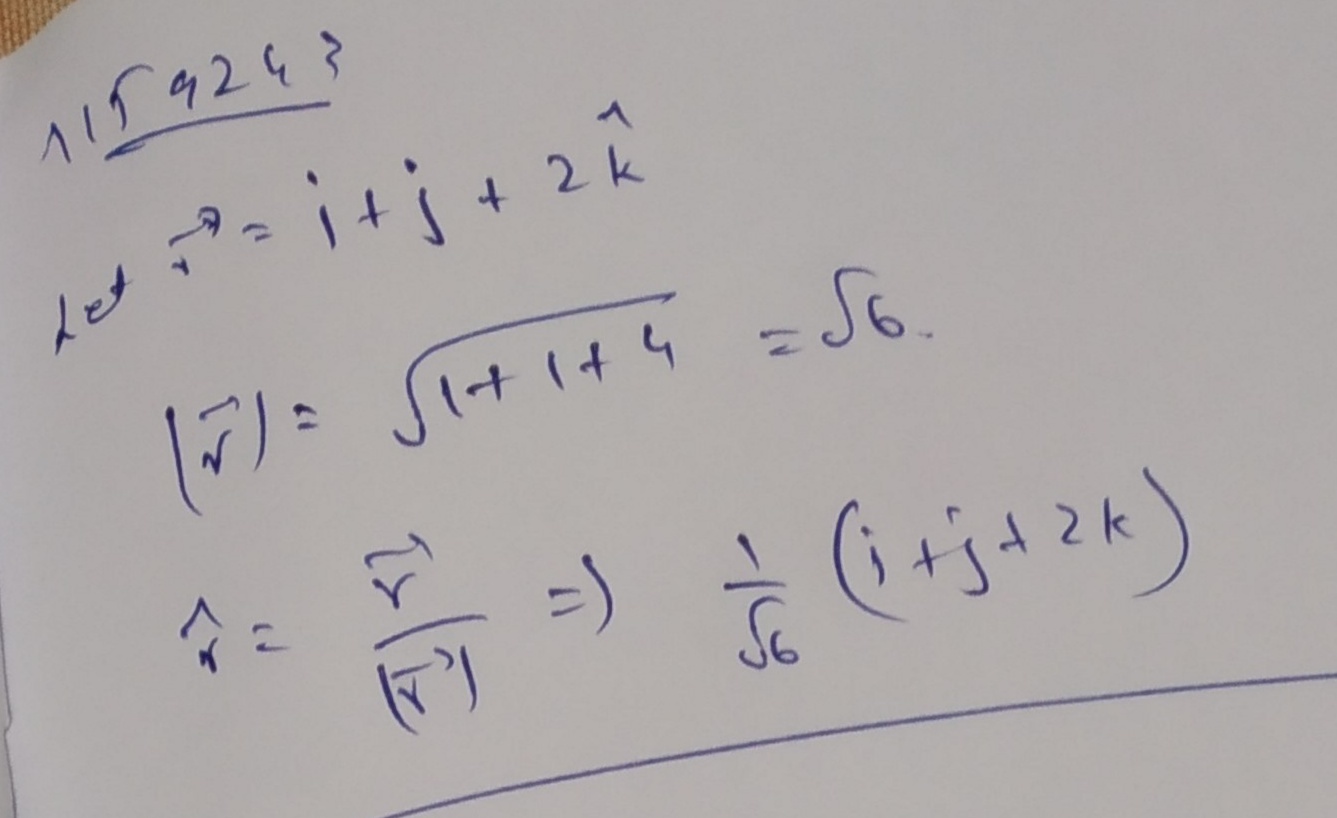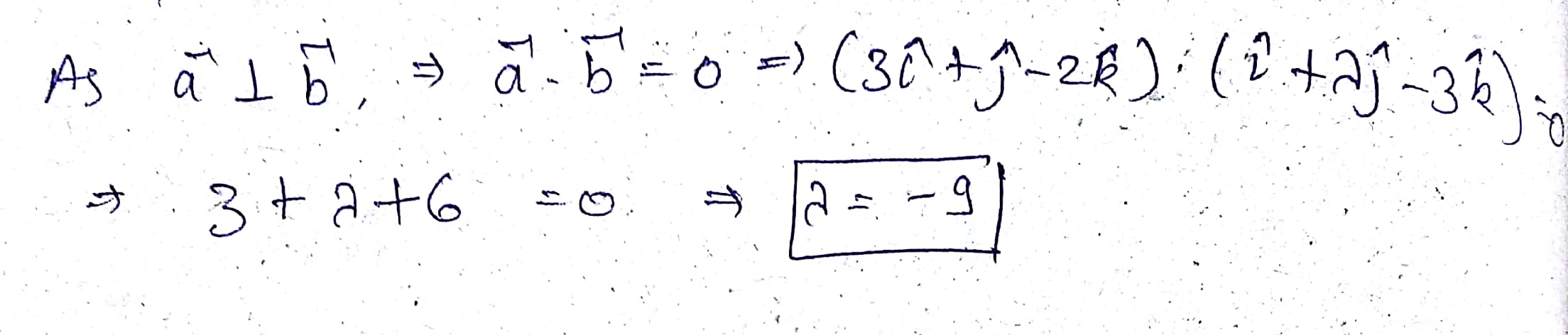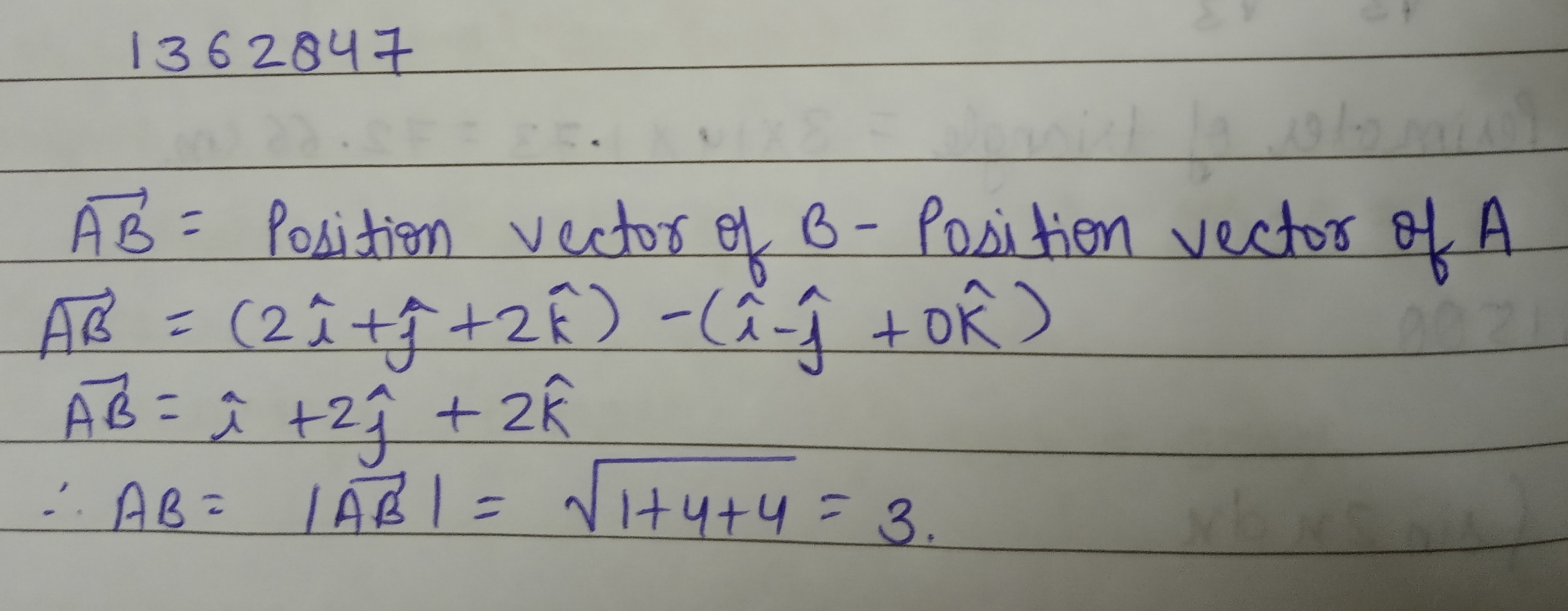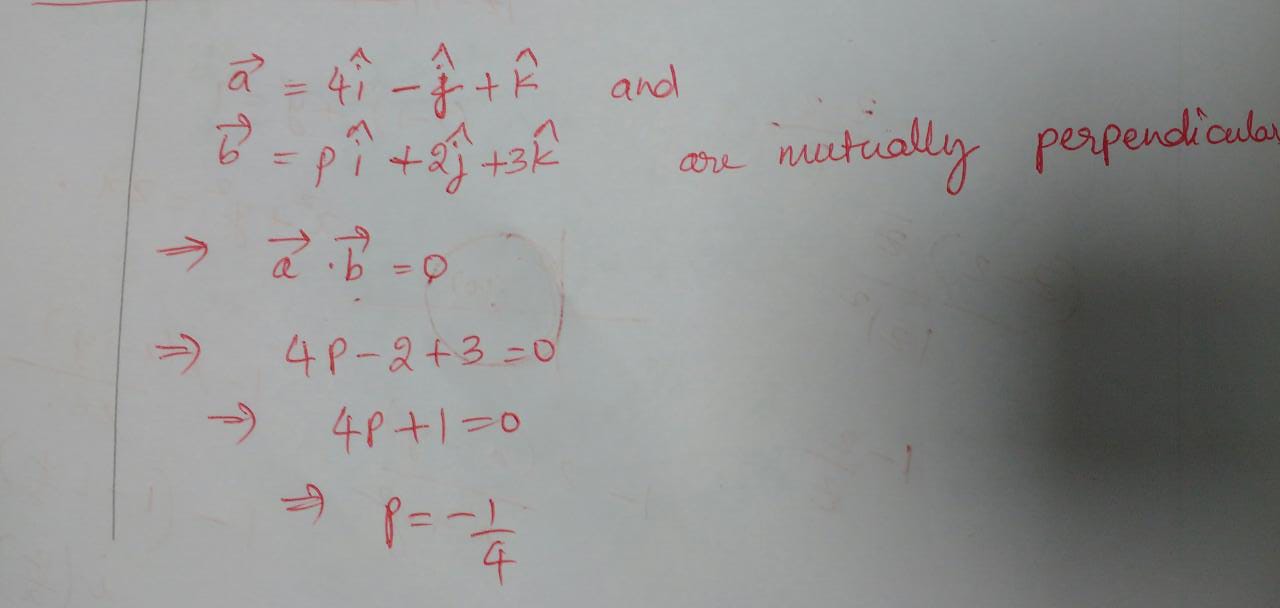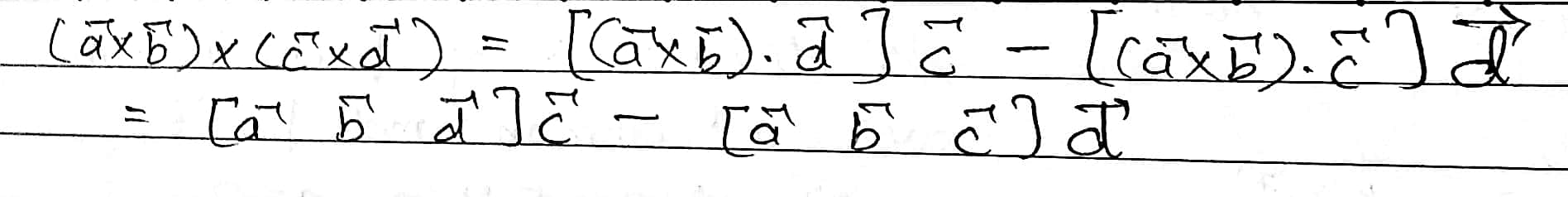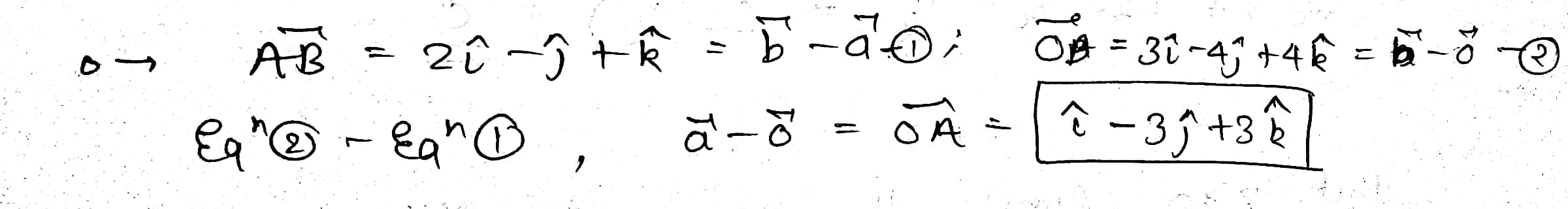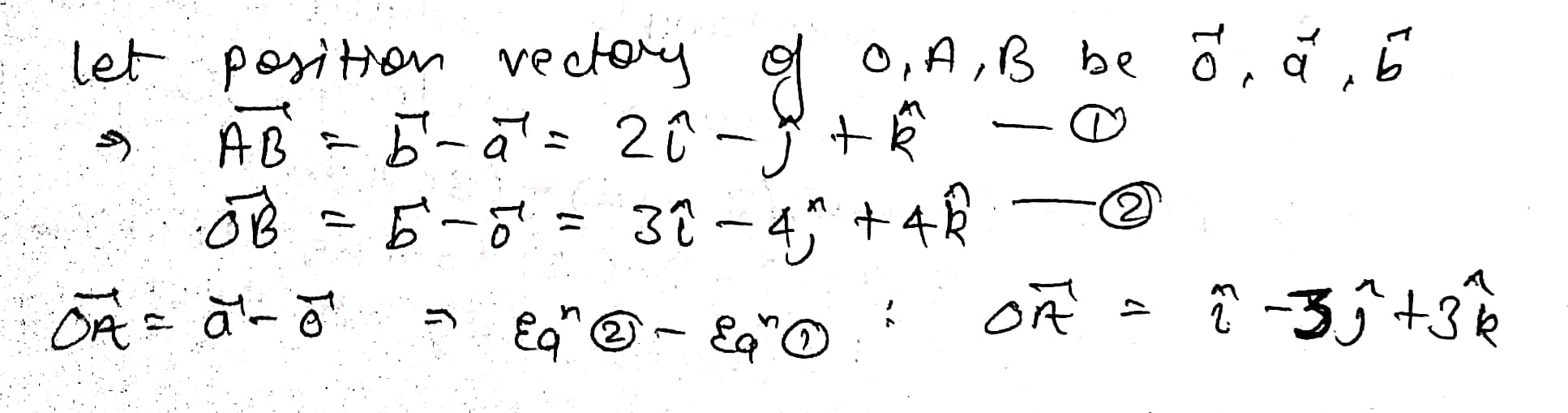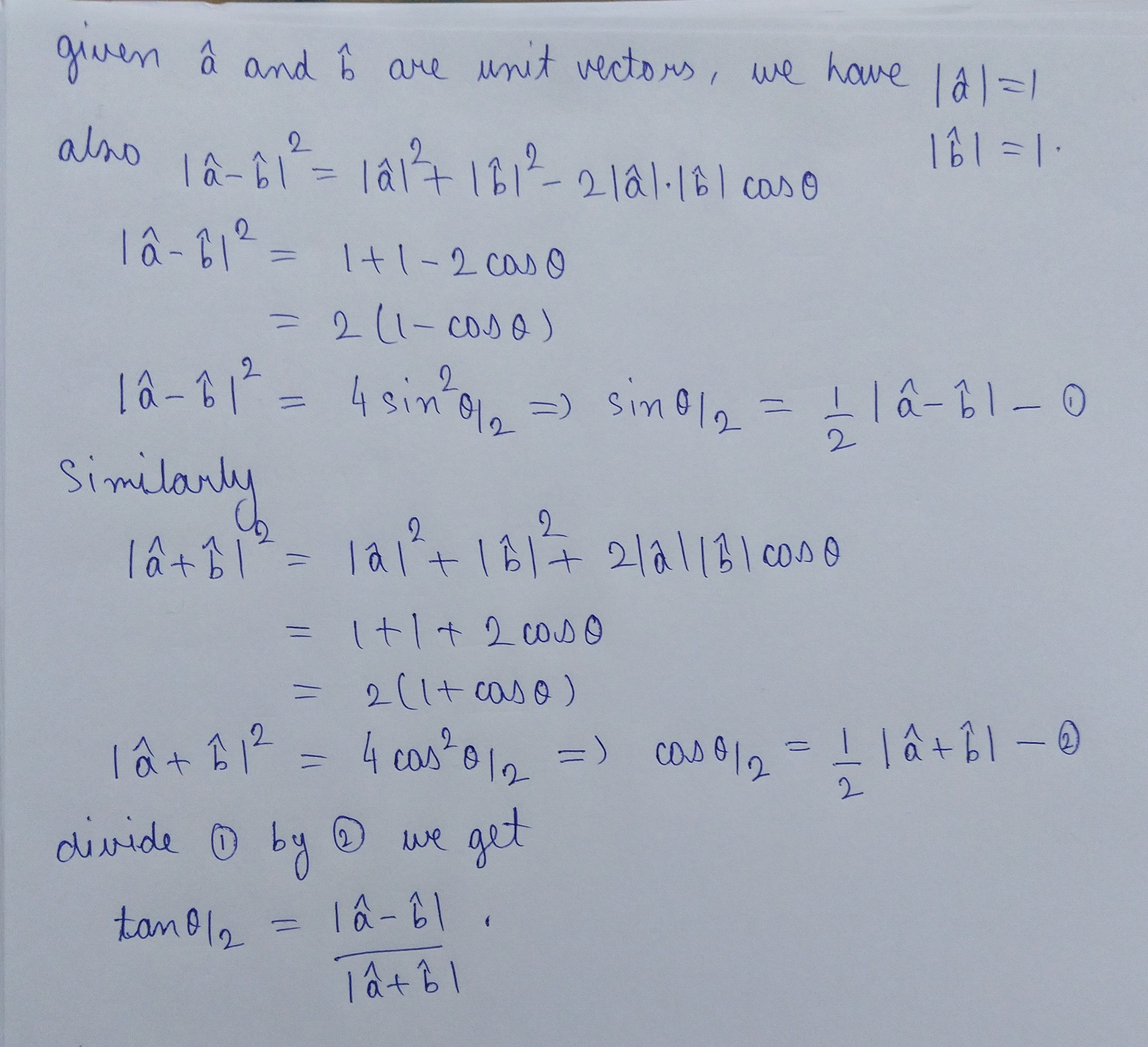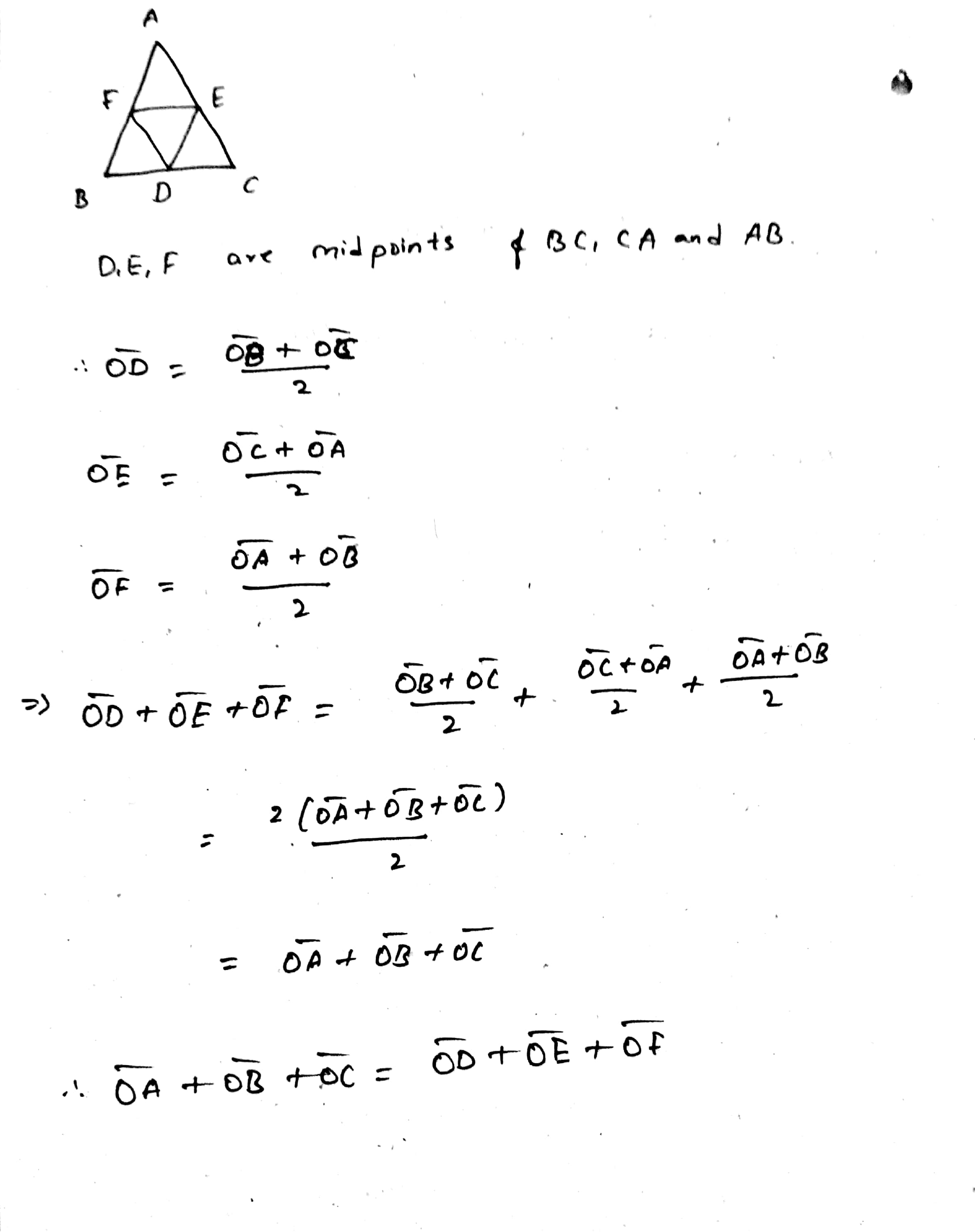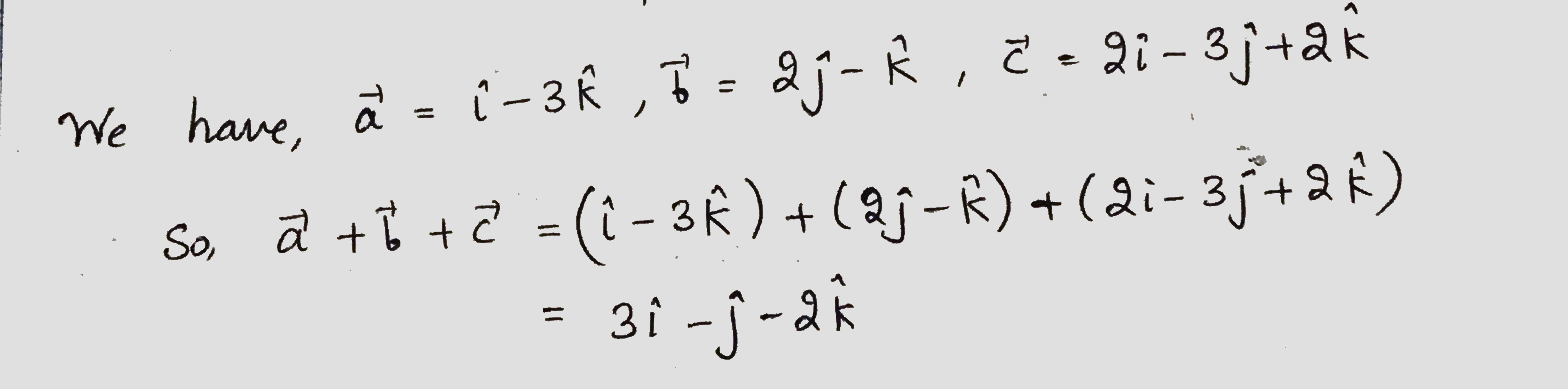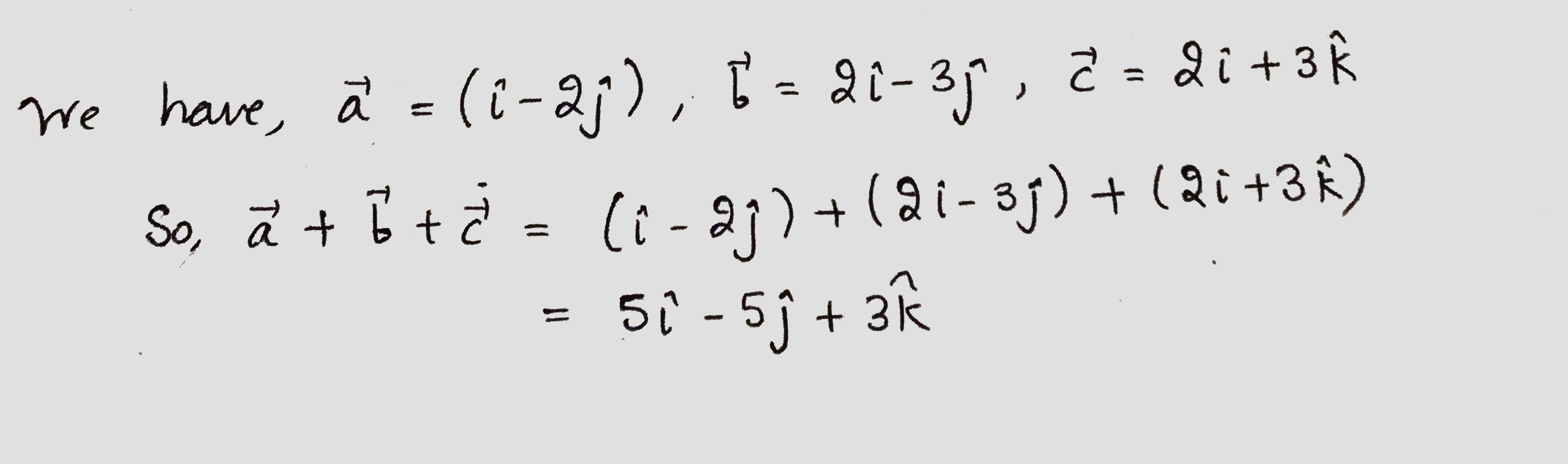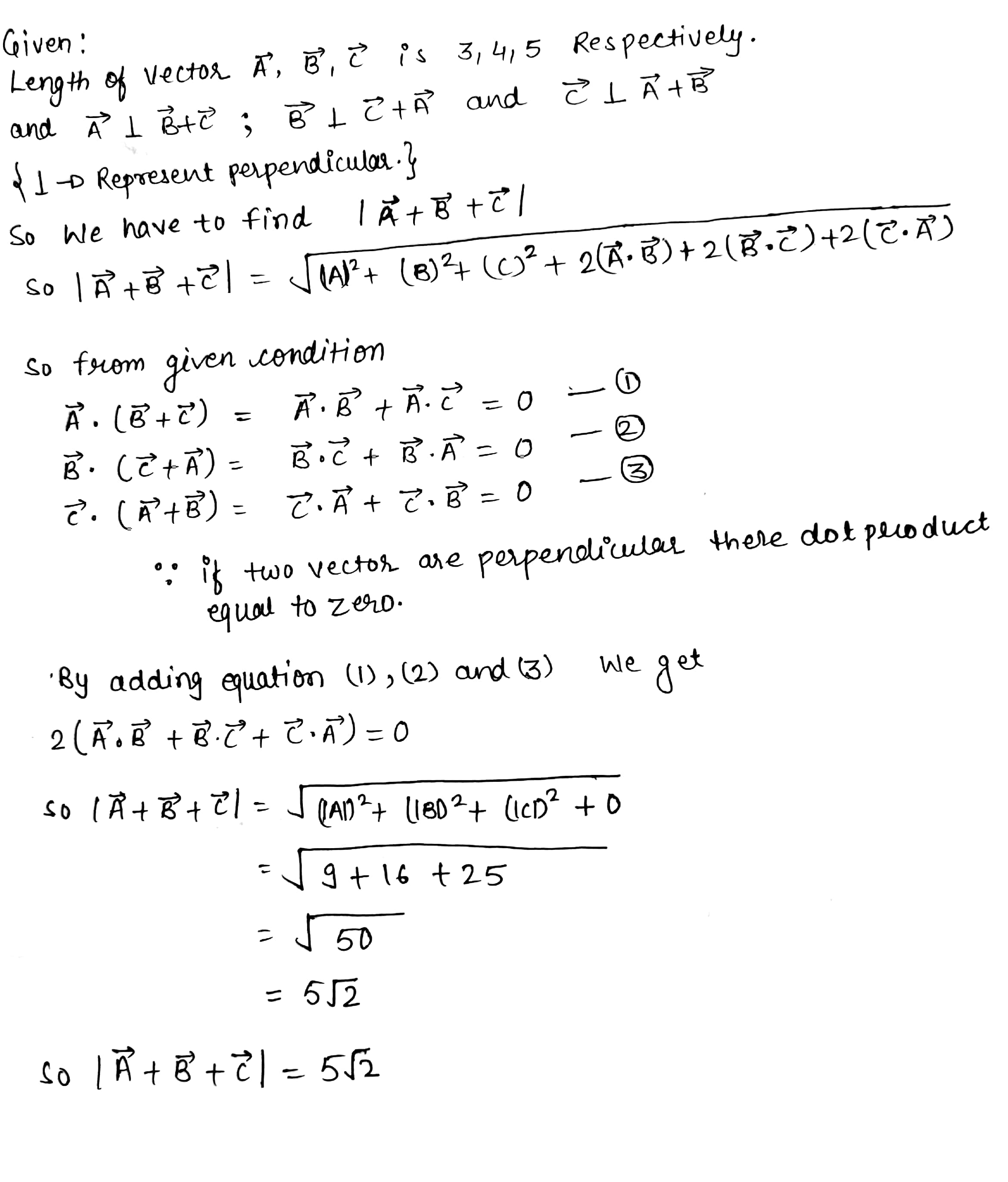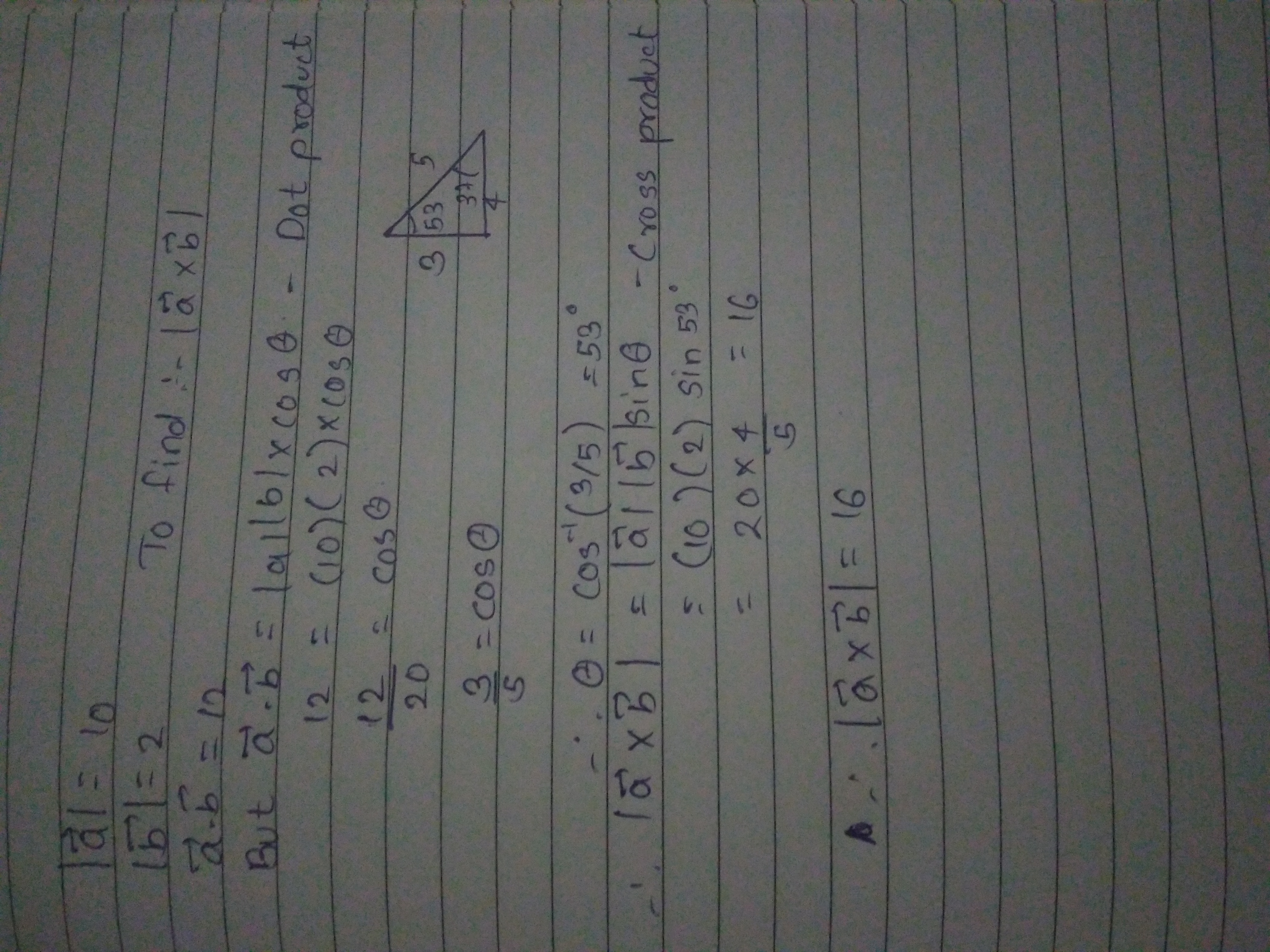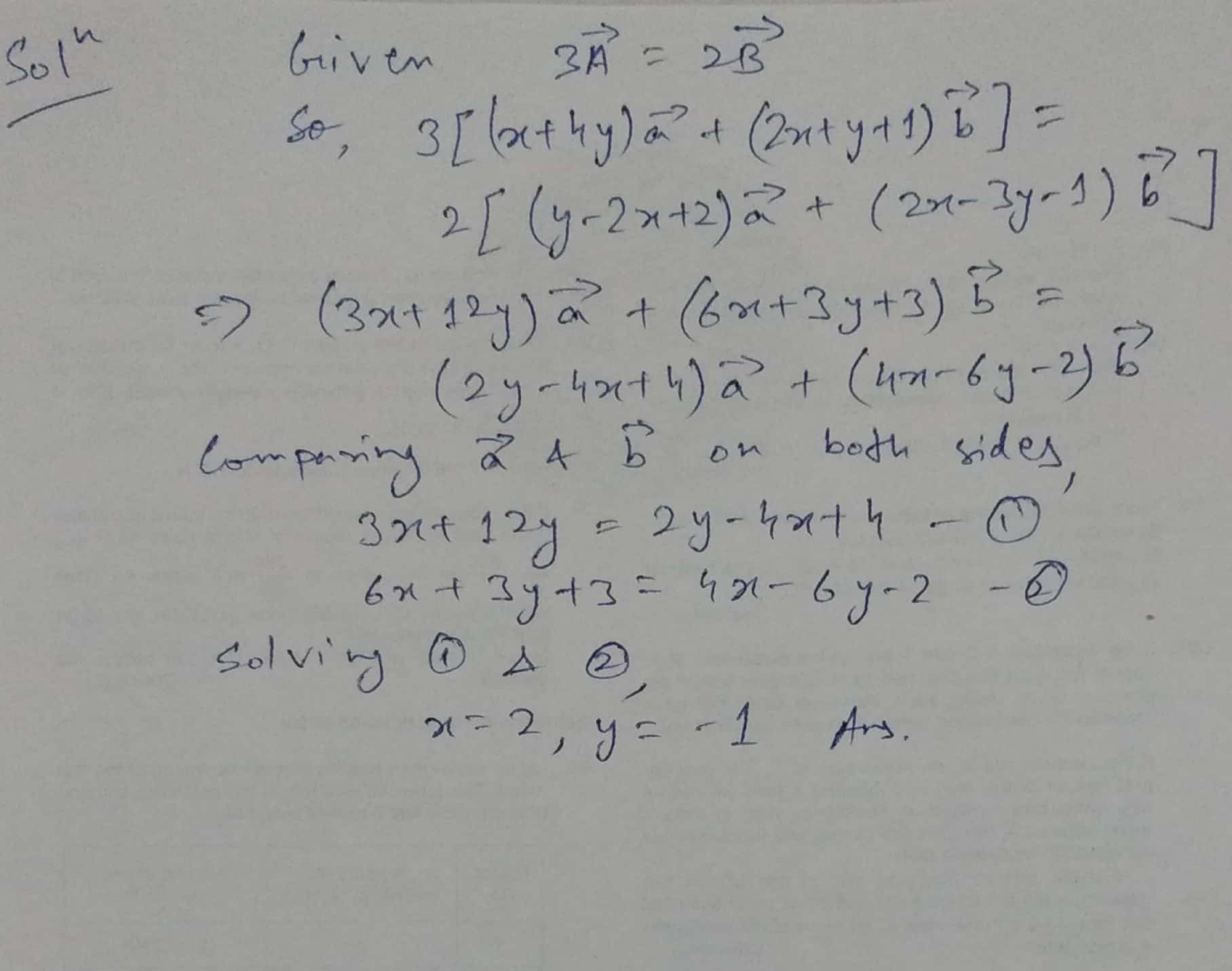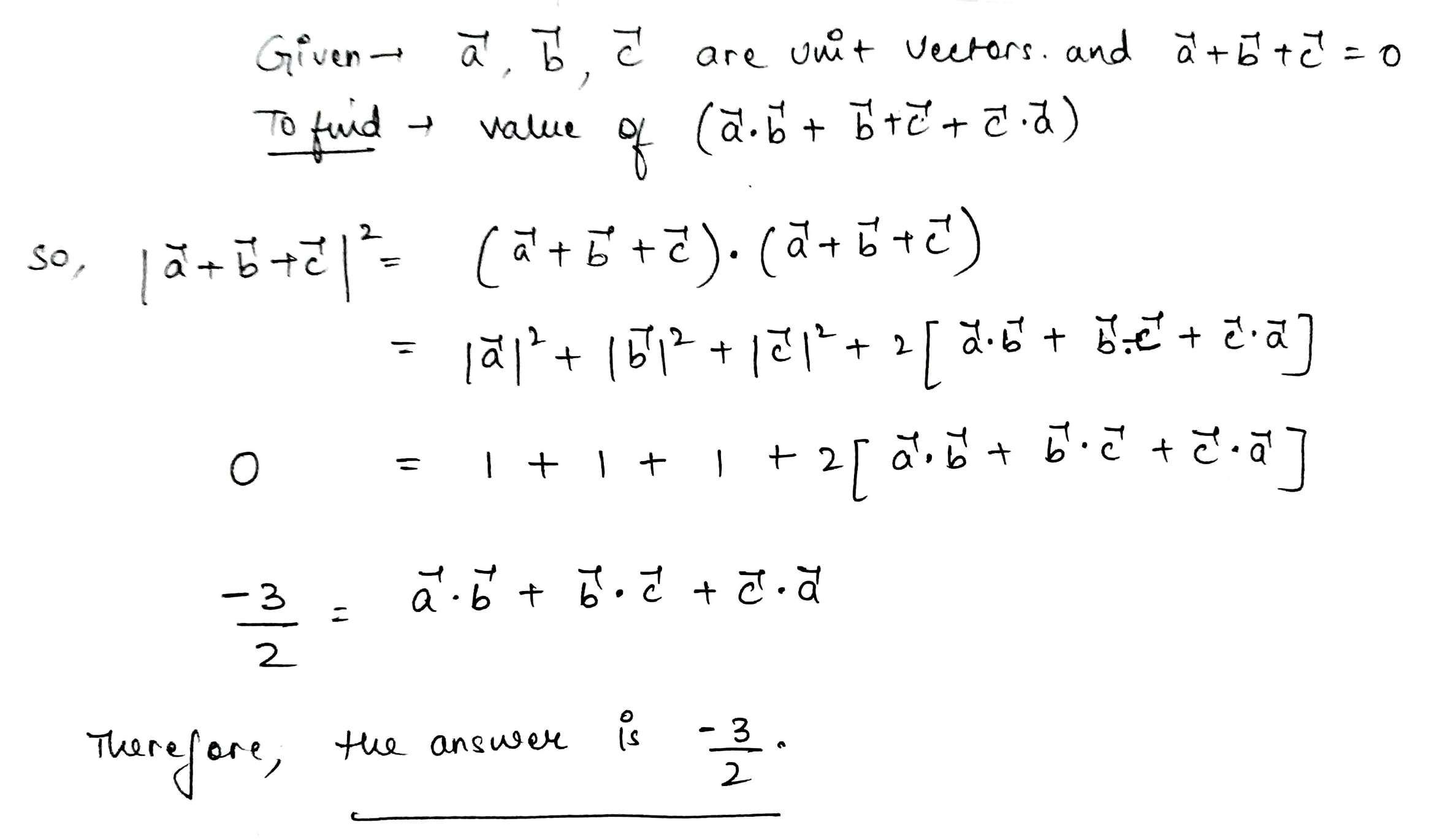Vector Algebra - Class 12 Commerce Maths - Extra Questions
Match the column
A point is on the $$x$$-axis. What are its $$y$$-coordinate and $$z$$-coordinates?
Find the projection of the vector $$\hat {i}+3\hat {j}+7\hat {k}$$ on the vector $$7\hat {i}-\hat {j}+8\hat {k}$$ .
If either vector $$\vec {a}=\vec {0}$$ or $$\vec {b}=\vec {0}$$, then $$\vec {a}\cdot \vec {b}=0$$. But the converse need not be true. Justify your answer with an example.
Find the sum of the vectors $$\vec {a}=\hat {i}-2\hat {j}+\hat {k}, \vec {b}=-2\hat {i}+4\hat {j}+5\hat {k}$$ and $$\vec {c}=\hat {i}-6\hat {j}-7\hat {k}$$.
Find $$|\vec {x}|$$, if for a unit vector $$\vec {a}, (\vec {x}-\vec {a})\cdot (\vec {x}+\vec {a})=12$$
Answer required
If $$\vec {a}, \vec {b}, \vec {c}$$ are unit vectors such that $$\vec {a}+\vec {b}+\vec {c}=\vec {0}$$, find the value of $$\vec {a}\cdot \vec {b}+\vec {b}\cdot \vec {c}+\vec {c}\cdot \vec {a}$$
If $$\vec{a}=-\hat{i}-\hat{j}+\hat{k}$$ and $$\vec{b}=-\hat{i}+\hat{j}-\hat{k}$$, then find the value of $$|\vec{a}\cdot \vec{b}|$$.
Projection of $$\vec{b}$$ in the direction of $$\vec{a}$$ ___________.
If vectors $$\vec{a}=\hat{i}-\hat{j}+\hat{k}$$ and $$\vec{b}=\hat{i}+\hat{j}+\hat{k}$$, then find the value of $$\vec{a}\cdot\vec{b}$$.
For any two vectors $$\vec { a } ,\vec { b } $$, prove that $${ \left| \vec { a } \times \vec { b } \right| }^{ 2 }=\begin{vmatrix} \vec { a } .\vec { a } & \vec { a } .\vec { b } \\ \vec { b } .\vec { a } & \vec { b }.\vec { b } \end{vmatrix}$$
If $$\bar{OA} = 3 \hat{i} + \hat{j} - 2\hat{k}$$ and $$\bar{OB} = 5 \hat{i} + 4 \hat{j} - \hat{k}$$ then find the value of $$\bar{AB}$$
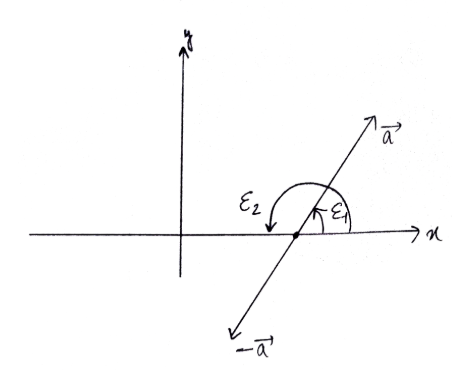
Let $$\varepsilon_1$$ and $$\varepsilon_2$$ be the angles made by $$\vec{A}$$ and $$-\overrightarrow{A}$$ with the positive X-axis. Show that $$\tan \varepsilon_1=\tan\varepsilon_2$$. Thus, given $$\tan\varepsilon$$ does not uniquely determine the direction of $$\overrightarrow{A}$$.
Now, $$\varepsilon_{2}=\varepsilon_{1}+180^{\circ}$$
$$\Rightarrow \tan \varepsilon_{2}=\tan (\varepsilon_{1}+180^{\circ})$$
$$\Rightarrow \tan \varepsilon_{2}=\tan \varepsilon_{1}$$
$$\therefore \tan \varepsilon_{1}=\tan \varepsilon_{2}$$
$$\rightarrow $$ So $$\tan$$ (of angle made by the vector with $$x-$$axis ) does not uniquely determine the direction of the vector as the negative of a given vector has reverse direction with respect to given vector.
Calculate the scalar product of the following vectors$$\displaystyle a \, = \, 3i \, + \, 2j \, + \, 2k \, and \, b \, = \, 18i \, - \, 22j \, - \, 5k$$
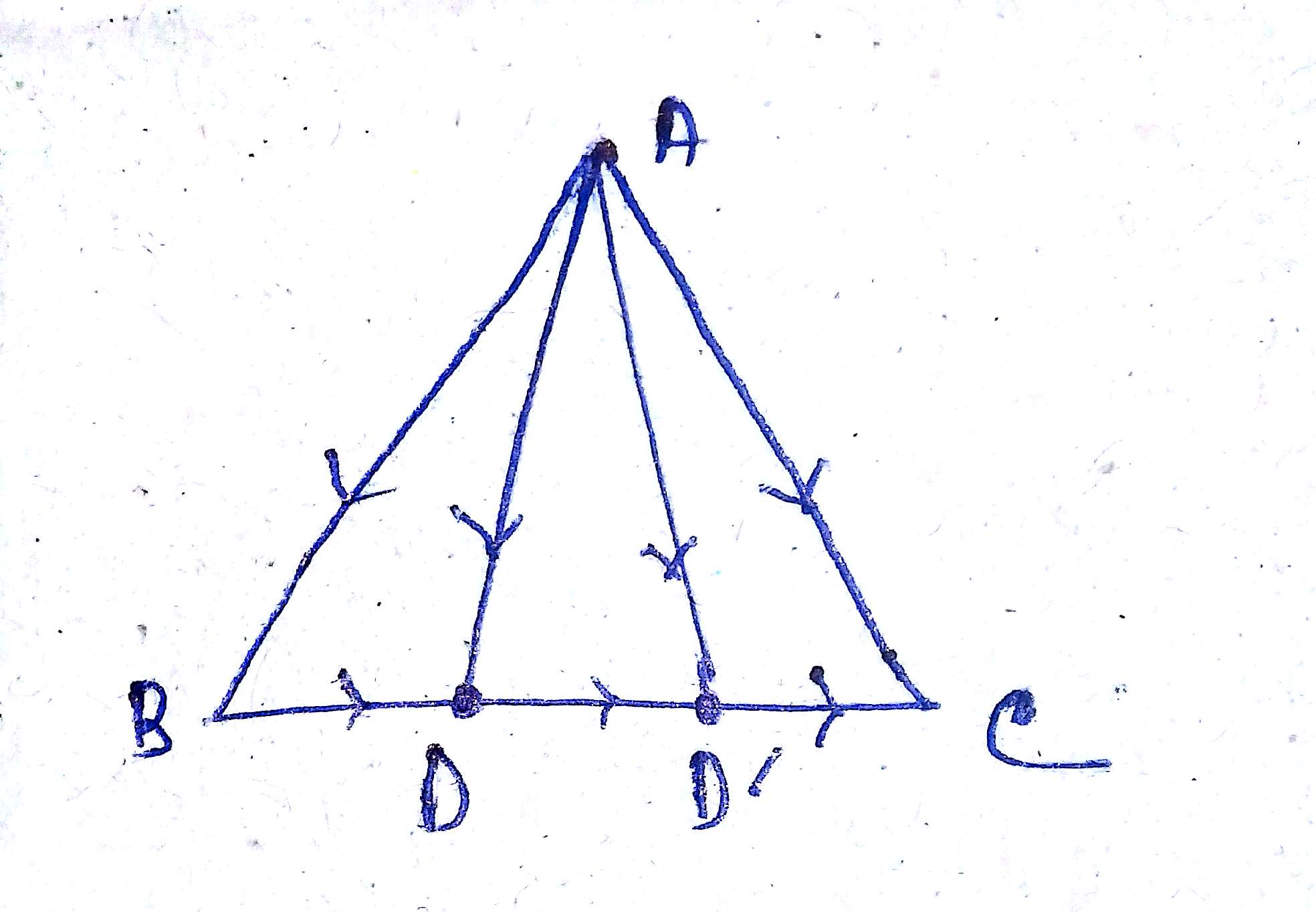
In a $$\Delta$$ ABC, $$\vec{AB}=6\vec{i}+3\vec{j}+3\vec{k}$$ ; $$\vec{AC}=3\vec{i}-3\vec{j}+6\vec{k}$$. D and D' are points of tri-sections of sides BC. Find $$\vec{AD}$$ and $$\vec{AD'}$$.
We have
$$\vec{BC}=\vec{AC}-\vec{AB}$$
or, $$\vec{BC}=(3\hat{i}-3\hat{j}+6\hat{k})$$$$-(6\hat{i}+3\hat{j}+3\hat{k})=-3\hat{i}-6\hat{j}+3\hat{k}$$.
Now, according to the problem,
$$\vec{BD}=\vec{D'C}=\dfrac{1}{3}\vec{BC}=(-\hat{i}-2\hat{j}+\hat{k})$$.
$$\therefore \vec{AD}=\vec{BD}-\vec{BA}=\vec{BD}+\vec{AB}=5\hat{i}+\hat{j}+4\hat{k}$$.
And $$\vec{AD'}=\vec{AC}-\vec{D'C}=4\hat{i}-\hat{j}+5\hat{k}$$.
Given $$\vec{AB} = 3i + 2j - k \, , \vec{OB} = i + 2j + k$$. find $$\vec{OA}$$
If vector $$\vec a = {a_1}\hat i + {a_2}\hat j + {a_3}\hat k$$ then, find unit vector.
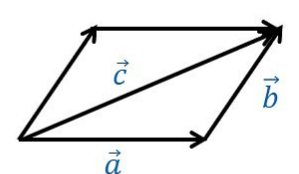
The sides of a parallelogram are $$2\hat i - 4\hat j +5\hat k$$ and $$\hat i - 2\hat j - 3\hat k$$ . Find the unit vectors parallel to the diagonals and also find the Area of parallelogram.
If $$r=t^2i-tj+(2t+1)k$$, find $$|dr/dt|$$.
If a vector $$\vec{AB}=2\hat{i}-\hat{j}+\hat{k}$$ and $$\vec{OB}=3\hat{i}-4\hat{j}+4\hat{k}$$ find the position vector $$\vec{OA}$$.
Show that:
$$[\bar{a} \times \bar{b} \, \bar{b} \times \bar{c} \,\bar{c} \times \bar{a}] = [abc]^2$$
Points X & Y are taken on the sides QR & RS respectively of a parallelogram PQRS, so that $$\vec{QX}=4\vec{XR}$$ & $$\vec{RY}=4\vec{YS}$$. The line XY cuts the line PR at Z. Prove that $$\vec{PZ}=\left(\dfrac{21}{25}\right)\vec{PR}$$.
Component of $$(1,1)$$ along $$(3,4)$$ is ?
Find the component of $$\overline i + \overline k \,on\,\overline i - \overline j $$ and its magnitude.
If $$\overline a = \left( {1, - 1} \right)$$ and $$\overline b = \left( {1,0} \right)$$ then comp $$\overline a \overline b = ..........$$
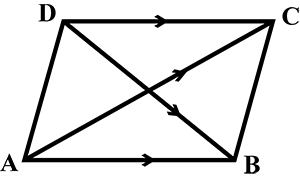
ABCD is parallelogram. If $$\vec { AB } =\vec { a } ,\vec { BC } =\vec { b }$$ then show that $$\vec { AB } =\vec { a } ,+\vec { b }$$ and $$\vec { BD } =\vec { b } ,-\vec { a }$$ ?
Given ABCD is a parallalogaram and
\begin{array}{l} \overline { AB } =\overline { a } \, \, ,\, \, \overline { BC } =\overline { b } \\ Here\, \, ,\, \overline { AC } \, \, is\, \, the\, result\, \, of\, \overline { AE } \, and\, \overline { EC } \\ so \\ \, \, \, \, \, \, \, \left| { \overline { AC } } \right| =\, \left| { \overline { AE } } \right| +\left| { \overline { EC } } \right| \\ \, \, \, \, \, \, \, =\sqrt { { { \left( { a+b\cos \theta } \right) }^{ 2 } }+{ { \left( { b\sin \theta } \right) }^{ 2 } } } \\ \, \, \, \, \, \, \, \, \sqrt { { a^{ 2 } }+{ b^{ 2 } }{ { \cos }^{ 2 } }\theta +2ab\cos \theta +{ b^{ 2 } }{ { \sin }^{ 2 } }\theta } \\ \, \, \, \, \, \, \, \, \sqrt { { a^{ 2 } }+{ b^{ 2 } }+2ab\cos \theta } \\ \, \, \, \, \, \, \, \, \, \, \left| { a+b } \right| \\ \, \, \, \, \, \, \, \, \, \, \overline { AB } =\overline { a } +\overline { b } \\ \, \, \, \, \, \, \, \, \, \, similerily\, \, \, \, \, \, \, \, \overline { BD } =\overline { b } -\overline { a } \\ \, \, \, \, \, \, \, \, \, \, \end{array}
Find the value or values of $$m$$ for which $$m\left( \hat { i } +\hat { j } +\hat { k } \right) $$ is a unit vector.
If $$\vec{a}$$ and $$\vec{b}$$ are position vectors of point s A and B respectively, then the position vector of points of trisection of AB
Find a unit vector which is along the direction of vector $$\hat{i}+\hat{j}+2\hat{k}$$.
Let $$\vec{r}=i+j+2\hat{k}$$
$$|\vec{r}|=\sqrt{1+1+4}=\sqrt{6}$$
$$\hat{r}=\dfrac{\vec{r}}{|\vec{r}|}$$
$$\Rightarrow \dfrac{1}{\sqrt{6}}(i+j+2k)$$.
If $$\vec{a}||\vec{b}\times \vec{c}$$ then $$\left(\vec{a}\times \vec{b}\right)\cdot (\vec{a}\times \vec{c})$$ is equal to?
Find the projection of $$(a,b,c)$$ on X-axis and its magnitude.
Let $$a=i+2j+3k$$ and $$b=3i+j$$. Find the unit vector in the direction of $$a+b$$.
If $$\vec {a}=\vec {b}+\vec {c}$$, then is true that $$|\vec {a}|=|\vec {b}|+|\vec {c}|$$? Justify your answer.
If the projections of the line segment $$\underset{PQ}{\rightarrow}$$ on the axes are 3,4,12 then the length of $$\underset{PQ}{\rightarrow}$$ is
Length of $$\vec{PQ}=\sqrt{3^2+4^2+12^2}$$
$$=\sqrt{5^2+12^2}$$
$$=\sqrt{13^2}$$
$$=13$$
$$($$since, projection of $$\vec{PQ}$$ on x-axis is $$|\vec{PQ}|=\cos\alpha =3$$
projection of $$\vec{PQ}$$ on y-axis is $$|\vec{PQ}|\cos \beta =4$$
projection of $$\vec{PQ}$$ on z-axis is $$|\vec{PQ}|\cos\gamma =12$$
$$\cos^2\alpha +\cos^2\beta +\cos^2\gamma =1)$$.
If $$\hat { \mathbf { a } }$$ is a unit vector and $$( x - \hat { a } ) \cdot ( \vec { x } + \hat { a } ) = 1.5 $$ then find the value of $$ | \vec { x } |$$.
Find $$a\times (b\times c)$$ and $$(a\times b)\times c$$ where $$a=(1, -1, -6), b=(1, -3, 4), c=(2, -5, 3)$$.
Find a unit vector in the direction of $$\hat { i } + \hat { j }$$.
The vector product of two vector is $$\sqrt{3}$$ times of their of two scalar produced. The angle between the two vector is-
Write the unit vector in the direction of $$\overset { \rightarrow }{ A } =5\overset { \rightarrow }{ i } + \overset { \rightarrow }{ j } - 2\overset { \rightarrow }{ k } $$.
Find the value of $$\lambda$$, so that the vectors $$\overrightarrow a =3\widehat{i}+2\widehat{j}+9\widehat{k}$$ and $$\overrightarrow b =\widehat{i}+\lambda \widehat{j}+3\widehat{k}$$ are perpendicular to each other.
Simplify:
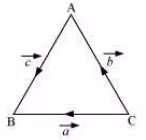
(i)$$\vec { D E }$$+$$( - \vec { B E } )$$
(ii)$$\vec { AC }$$+$$( - \vec { B C })$$(iii)$$\vec { C D }$$+$$\vec { B A }$$$$( - \vec { B D } )$$
Find the sum of the vectors :
$$\overrightarrow a = \widehat i - 3\widehat k\,,\,\overrightarrow b = 2\widehat j - \widehat k\,,\,\overrightarrow c = 2\widehat i - 3\widehat j\, + 2\widehat k$$
The dot product of a vector with vectors $$\hat{i}+\hat{j}-3\hat{k}$$, $$\hat{ i}+ 3\hat{ j}-2\hat{k}$$ ,$$2\hat{i} + \hat{j} + 4k$$ are $$0,5$$ and $$8$$ respectively. Find the vector .
Let vertor be $$a\hat{i}+b\hat{j}+c\hat{k}$$
Dot product with $$\hat{i}+\hat{j}-3\hat{k}=a+b-3c=0$$ …………$$(1)$$
Dot product with $$\hat{i}+3\hat{j}-2\hat{k}=a+3b-2c=5$$ ……….$$(2)$$
Dot product with $$2\hat{i}+\hat{j}+4\hat{k}=2a+b+4c=8$$ ……………$$(3)$$
Equation $$(2)$$ -Equation $$(1)$$
$$\Rightarrow a+3b-2c-a-b+3c=5-0$$
$$\Rightarrow 2b+c=5$$ ………..$$(4)$$
Equation $$(3)$$-$$2\times$$ equation $$(2)$$
$$\Rightarrow 2a+b+4c-2a-6b+4c=8-10$$
$$-5b+8c=-2$$ …………..$$(5)$$
Equation $$(5)$$ - $$4\times$$ equation $$(4)$$
$$\Rightarrow -5b+8c-16b-8c=-2-40$$
$$\Rightarrow -21b=-42$$
$$\therefore b=\dfrac{-42}{-21}=2$$
Put $$b=2$$ in $$(4)$$ we get $$c=5-2b$$
$$c=5-2\times 2=5-4$$
$$\therefore c=1$$
Put $$b=2$$, $$c=1$$ in $$(1)$$
$$a+2-3\times 1=0$$
$$a+2-3=0$$
$$\therefore a-1=0$$
(or) $$a=1$$
Hence the verctor is $$\hat{i}+2\hat{j}+\hat{k}$$.
Forces measuring $$5,3$$ and $$1$$ unit act in the directions $$(6,2,3),(3,-2,6)$$ and $$(5,-1,1)$$. Find the resultant force.
$$\overrightarrow { a } =3\hat { i } +\hat { j } -2\hat { k } ;\overrightarrow { b } =\hat { i } +\lambda \hat { j } -3\hat { k } $$
$$\overrightarrow { a } \bot \overrightarrow { b } $$, find value of $$\lambda$$.
As $$ \vec{a}\perp \vec{b}, \Rightarrow \vec{a}-\vec{b} = 0 \Rightarrow (3\hat{i}+\hat{j}-\hat{2k})(\hat{i}+\lambda \hat{j}-3\hat{k}) = 0 $$
$$ \Rightarrow 3+\lambda +6 = 0 \Rightarrow \lambda = -9 $$
Find $$\vec{a}.\vec{b}$$, when $$\vec{a}=\hat{j}+2\hat{k}$$ and $$\vec{b}=2\hat{i}+\hat{k}$$.
Find the projection of the vector $$\widehat{i}-\widehat{j}$$ on the vector $$\widehat{i}+\widehat{j}$$.
Find the dot product of the following vectors:$$\vec{a}=2\hat{i}+\hat{j}+3\hat{k}$$ and $$\vec{b}=3\hat{i}+5\hat{j}-2\hat{k}$$.
Compute the magnitude of the following vector :$$\overrightarrow a = 2\widehat{i}-7\widehat{j}-3\widehat{k}$$
Find the value of x for which $$x(\widehat{i}+\widehat{j}+\widehat{k})$$ is a unit vector.
Find the distance between the points A and B whose position vectors $$\widehat{i}-\widehat{j}$$ and $$2\widehat{i}+\widehat{j}+2\widehat{k}$$.
If $$\vec a =a_1\hat i +a_2\hat j+a_3\hat k, \, \, \vec b=b_1\hat i+b_2\hat j+b_3\hat k$$ and $$\vec c=c_1\hat i+c_2\hat j+c_3\hat k$$, than verify that $$\vec a \times (\vec b +\vec c)=\vec a \times \vec b +\vec a\times \vec c$$
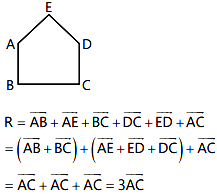
$$ ABCDE $$ is a pentagon, then prove that $$\overrightarrow{AB}+\overrightarrow{AE}+\overrightarrow{BC}+\overrightarrow{DC}+\overrightarrow{ED}+\overrightarrow{AC} = 3\,\overrightarrow{AC} $$.
If $$\vec a , \vec b , \vec c$$ are three unit vector such that $$\vec a\times \vec b=\vec c, \vec b\times \vec c=\vec a, \vec c\times \vec a=\vec b$$. Show that $$\vec a , \vec b , \vec c$$ from an orthogonal right handed tried of unit vectors.
Answer the following as true or false:
Zero vector is unique.
Find the projection of the vector $$7\widehat{i}+\widehat{j}-4\widehat{k}$$ and $$2\widehat{i}+6\widehat{j}+3\widehat{k}$$.
Enter $$1$$ if true else $$0$$.
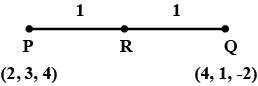
$$ 3\hat{i}+2\hat{j}+\hat{k} $$ is the position vector of the mid-point of the vector joining the points $$ P(2,3,4) $$ and $$ Q(4,1,-2). $$
If $$ a\hat{i}+b\hat{j}+c\hat{k} $$ is the position vector of the mid - point of the vector joining the points $$ P(2\hat{i}-3\hat{j}+4\hat{k}) $$ and $$ Q(4\hat{i}+\hat{j}-2\hat{k}) $$ then $$a+b+c$$ is equal to ___.
$$\hat{a} \space and \space \hat{b}$$ form the consecutive sides of a regular hexagon ABCDEF.
Find the projection of the vector $$\displaystyle i-2j+k$$ on the vector $$\displaystyle 4i-4j+7k$$
If $$\displaystyle r=xi+yj+zk$$ then show that r can also be expressed as $$\displaystyle r= \left ( r.i \right )i+\left ( r.j \right )j+\left ( r.k \right )k$$.
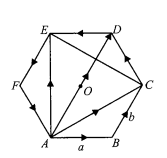
If $$\displaystyle \vec{a}\:and\:\vec{b}$$ are the vectors $$\displaystyle \overrightarrow{AB}\:and\:\overrightarrow{BC}$$ determined by the adjacent sides of a regular hexagon. What are the vectors determined by the other sides taken in order?
Given:
$$\overrightarrow { AB } =\overrightarrow { a } \\ \overrightarrow { BC } =\overrightarrow { b } $$
EF is parallel to BC and equal to its length
hence ,
$$\overrightarrow { FE } =\overrightarrow { b } $$
and ED vector is also eqaul to AB
$$\overrightarrow { ED } =\overrightarrow { a } $$
let the center point is O
then $$\overrightarrow { BO } =\overrightarrow { BC } +\overrightarrow { CO } =\overrightarrow { b } -\overrightarrow { a } $$
now $$\overrightarrow { AF } $$ is parallel to $$\overrightarrow { BO } $$
hence , $$\overrightarrow { AF } =\overrightarrow { b } -\overrightarrow { a } $$
And $$\overrightarrow { CD } $$ vector is also equal to $$\overrightarrow { BO } $$
Hence, $$\overrightarrow { CD } =\overrightarrow { b } -\overrightarrow { a } $$
If $$D, \ E, \ F$$ are the midpoints of the sides $$BC, \ CA, \ AB,$$ respectively, of a triangle $$ABC$$ and $$O$$ is any point, then
Write the three times of the projection of the vector $$\overset{\rightarrow}{a} = 2\hat{i} - \hat{j} + \hat{k}$$ on the vector $$\overset{\rightarrow}{b} = \hat{i} + 2\hat{j} + 2\hat{k}$$
Evaluate the product $$(3\vec {a}-5\vec {b})\cdot (2\vec {a}+7\vec {b})$$ .
If $$\vec {a}=\vec {b}+\vec {c}$$, then is it true that $$|\vec {a}|=|\vec {b}|+|\vec {c}|$$? Justify your answer.
In $$\Delta ABC$$, let $$\vec {CB}=\vec {a}, \vec {CA}=\vec {b}$$, and
$$\vec {AB}=\vec {c}$$ (as shown in the following figure).
Now, by the triangle law of vector addition, we have $$\vec {a}=\vec {b}+\vec {c}$$.
It is clearly known that $$|\vec {a}|, |\vec {b}|$$, and $$|\vec {c}|$$ represent the sides of $$\Delta ABC$$.
Also, it is known that the sum of the lengths of any two sides of a triangle is greater than the third side.
$$\therefore |\vec {a}| < |\vec {b}| + |\vec {c}|$$
Hence, it is not true that $$|\vec {a}| = |\vec {b}| + |\vec {c}|$$.
Now, by the triangle law of vector addition, we have $$\vec {a}=\vec {b}+\vec {c}$$.
It is clearly known that $$|\vec {a}|, |\vec {b}|$$, and $$|\vec {c}|$$ represent the sides of $$\Delta ABC$$.
Also, it is known that the sum of the lengths of any two sides of a triangle is greater than the third side.
$$\therefore |\vec {a}| < |\vec {b}| + |\vec {c}|$$
Hence, it is not true that $$|\vec {a}| = |\vec {b}| + |\vec {c}|$$.
Find the projection of the vector $$\hat {i}-\hat {j}$$ on the vector $$\hat {i}+\hat {j}$$ .
If $$\displaystyle \overrightarrow { a } =4\hat { i } -\hat { j } +\hat k$$ and $$\displaystyle \overrightarrow { b } =2\hat { i } -2\hat { j } +\hat k$$, then find a unit vector parallel to the vector $$\displaystyle \overrightarrow { a } +\overrightarrow { b } $$.
The two vectors $$\hat j + \hat k$$ and $$3\hat i - \hat j + 4\hat k$$ represent the two sides $$AB$$ and $$AC$$, respectively of a $$\triangle ABC$$. Find the length of the median through $$A$$
Find $$'\lambda'$$ when the projection of $$\vec {a} = \lambda \hat{i} + \hat{j} + 4\hat{k}$$ on $$\vec{b} = 2\hat{i} + 6\hat{j} + 3\hat{k}$$ is 4 units.
A and B are two points with position vectors $$2\overrightarrow{a}-3\overrightarrow{b}$$ and $$6\overrightarrow{b}-\overrightarrow{a}$$ respectively. Write the position vector of a point P which divides the line segment AB internally in the ratio 1:2.
$$P$$ and $$Q$$ are two points with position vectors $$3\overrightarrow{a}-2\overrightarrow{b}$$ and $$\overrightarrow{a}+\overrightarrow{b}$$ respectively. Write the position vector of a point R which divides the line segment $$PQ$$ in the ratio $$2:1$$ externally.
Position vector of $$P =$$ $$3\overrightarrow{a} -2\overrightarrow{b}$$
Position vector of $$Q =$$ $$\overrightarrow{a} +\overrightarrow{b}$$
Point R divides segment PQ in ratio 2:1 externally.
Position vector of $$R =$$ $$\dfrac{(Position \space\ of \space\ P)1-(Position \space\ of \space\ Q)2}{1-2}$$
Position vector of $$R =$$ $$\dfrac{(3\overrightarrow{a} -2\overrightarrow{b})1-(\overrightarrow{a} +\overrightarrow{b})2}{-1}=\dfrac{\overrightarrow{a}-4\overrightarrow{b}}{-1}$$
Therefore, position vector of $$R =$$ $$4\overrightarrow{b}-\overrightarrow{a}.$$
L and M are two points with position vectors $$2\overrightarrow{a}-\overrightarrow{b}$$ and $$\overrightarrow{a}+2\overrightarrow{b}$$ respectively. Write the position vector of a point N which divides the line segment LM in the ratio 2 : 1 externally.
Find the scalar projection of the vector $$\hat {i} + 3\hat {j} + 7\hat {k}$$ on the vector $$2\hat {i} - 3\hat {j} + 6\hat {k}.$$
If point $$C(\overline c)$$ divides the segment joining the point $$A(\overline a)$$ and $$B(\overline b)$$ internally in the ratio $$m : n$$, then prove that $$\overline c = \dfrac{m \overline b + n \overline a}{m + n}$$
Find the projection of vector $$\overrightarrow { a } =2\hat { i } +3\hat { j } +2\hat { k } $$ on a vector $$\overrightarrow { b } =\hat { i } +2\hat { j } +\hat { k } $$
If $$\overline { a } ,\overline { b } ,\overline { c } $$ are the position vectors of the points $$A,B,C$$ respectively and $$3\overline { a } +4\overline { b } -7\overline { c } =\overline { 0 } $$, find the ratio in which point $$B$$ divides the segment $$AC$$.
If $$\vec {a}$$ is a non-zero vector of modulus $$a$$ and $$m$$ is a non-zero scalar then $$m\vec {a}$$ is a unit vector if
$$AC$$ and $$BD$$ are the diagonals of a quadrilateral $$ABCD$$, prove that: $$\vec{AB}+\vec{DC}=\vec{AC}+\vec{DB}$$.
Let $$ABCD$$ be a rectangle, $$AC$$ and $$BD$$ its diagonals.
In $$\Delta ABC$$,
$$\vec{AB}+\vec{BC}=\vec{AC}$$
$$\vec{AB}=\vec{AC}-\vec{BC}$$ ...........(i)
In $$\Delta BCD$$ by vector law of addition
$$\vec{DC}=\vec{DB}+\vec{BC}$$ ......(ii)
by adding (i) and (ii), we get
$$\vec{AB}+\vec{DC}=\vec{AC}-\vec{BC}+\vec{DB}+\vec{BC}$$
$$\vec{AB}+\vec{DC}=\vec{AC}+\vec{DB}$$
In $$\Delta ABC$$,
$$\vec{AB}+\vec{BC}=\vec{AC}$$
$$\vec{AB}=\vec{AC}-\vec{BC}$$ ...........(i)
In $$\Delta BCD$$ by vector law of addition
$$\vec{DC}=\vec{DB}+\vec{BC}$$ ......(ii)
by adding (i) and (ii), we get
$$\vec{AB}+\vec{DC}=\vec{AC}-\vec{BC}+\vec{DB}+\vec{BC}$$
$$\vec{AB}+\vec{DC}=\vec{AC}+\vec{DB}$$
Prove that $$[\overrightarrow{a}. \overrightarrow{b}. \overrightarrow{c} + \overrightarrow{d}] = [\overrightarrow{a} . \overrightarrow{b} . \overrightarrow{c}]+[\overrightarrow{a} . \overrightarrow{b} . \overrightarrow{d}]$$.
In a triangle $$ABC, D, E, F$$ are the mid-points of the sides $$BC, CA$$ and $$AB$$ respectively then prove that, $$\vec {AD} = - (\vec {BE} + \vec {CF})$$.
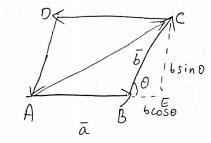
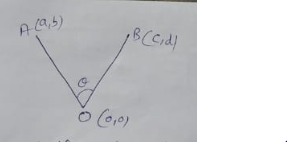
If the line segments joining the points $$A(a,b)$$ and $$B(c,d)$$ subtends and angle $$\theta$$ at the origin, then find $$\cos{\theta}$$
$$\vec {OB}=c\hat i +d \hat j$$
$$|\vec {OA}|=\sqrt{a^2+b^2}$$
$$|\vec {OB}|=\sqrt {c^2+d^2}$$
$$\cos \theta = \dfrac{{\overrightarrow {OA} \cdot \overrightarrow {OB} }}{{|\overrightarrow {OA} ||\overrightarrow {OB} |}} = \dfrac{{ac + bd}}{{\sqrt {{a^2} + {b^2}} \sqrt {{c^2} + {d^2}} }}$$
Write the associative law for addition of vectors.
Calculate the scalar product of the following vectors:
$$\displaystyle a \, = \, \left \{ 2, 4, 1 \right \} \, and\ \, b \, = \, \left \{ 3, 5, 7 \right \}$$
Three forces $$2\hat { i } -\hat { j } +3\hat { k } ,\hat { j } +\hat { k } $$ and $$-2\hat { i } -2\hat { j } +\hat { k } $$ are applied on a body. Is the body in equilibrium?
Find the value $$\left[ \hat { i } \quad \hat { j } \quad \hat { k } \right] $$.
Find the magnitude of each of the two vectors $$\overset{\rightarrow}{a}$$ and $$\overset{\rightarrow}{b}$$, having the same magnitude such that the angle between them is $$60^o$$ and their scalar product is $$\displaystyle\frac{9}{2}$$.
Evaluate $$\overset { \wedge }{ j } \left( \overset { \wedge }{ i } +\overset { \wedge }{ k } \right) $$
Prove that:$$\vec{P}\times \vec{Q}=(\hat{k})P_xQ_y+(-\hat{j})P_xQ_z+(-\hat{k})P_yQ_x+O+\hat{i}P_yQ_z+(\hat{j})P_zQ_x+(-\hat{i})P_zQ_y$$.
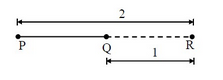
Find the position vector of a point $$R$$ which divides the line joining two points $$P$$ and $$Q$$ whose position vectors are $$\hat { i } +2\hat { j } -\hat { k } $$ and $$-\hat { i } +\hat { j } +\hat { k } $$ respectively in the ratio $$2:1$$ (i) Internally (ii) externally
A triangle is specified by the coordinates of its vertices A (3, 2, -3), B (5, 1, -1), and C (1, -2, 1). Calculate the coordinates of the vector a which is of the same direction as the vector $$\displaystyle \overrightarrow{AB}$$ and has the same length as the vector $$\displaystyle \overrightarrow{AC}.$$
Calculate the scalar product of the following vectors.
Given a triangle ABC. The lengths of the vectors $$\displaystyle \overrightarrow{CB}, \overrightarrow{CA}, \, and \, \overrightarrow{AB}$$ are a, b, and c respectively. Find the scalar product of the vectors $$\displaystyle \overrightarrow{CA} \, and \, \overrightarrow{CD},$$ where [CD] is the median of the triangle ABC.
Find the projection of the vector $$\hat {i} + 3\hat {j} + \hat {k}$$ on the vector $$7\hat {i} - \hat {j} + 8\hat {k}$$.
Let $$\vec a$$ & $$\vec b$$ be two non-zero perpendicular vectors. If a vector $$\vec x$$ satisfying the equation $$\vec x$$ x $$\vec b$$ = $$\vec a$$ is $$\vec x$$ = $$\beta \vec b - {1 \over {{{\left| {\vec b} \right|}^2}}}$$$$\vec a$$ x $$\vec b$$ then $$\beta $$ can be
If $$\vec{r}.\hat{i} = \vec{r}.\hat{j} = \vec{r}.\hat{k}$$ and $$|\vec{r}| = 3$$, then find vector $$\vec{r}$$.
Find all $$\lambda \in R$$such that $$\left( {x,y,z} \right) \ne \left( {0,0,0} \right)$$ and $$\left( {\hat i + \hat j + \hat k} \right)x + \left( {3\hat i - 3\hat j + \hat k} \right)y + \left( { - 4\hat i + 5\hat j} \right)z = \lambda \left( {x\hat i + y\hat j + z\hat k} \right)$$
Show that magnitude of vector product of two vectors is numerically equal to the area of a parallelogram formed by two vectors.
$$Formula\quad for\quad area\quad of\quad parallelogram$$
$$ =base\times height$$
$$ =\left| \overline { a } \right| .h$$
$$ h=\left| \overline { b } \right| \sin { \theta } $$
$$ \therefore Area=\left| \overline { a } \right| .\left| \overline { b } \right| \sin { \theta } $$
$$ We\quad know\quad \left| \overline { a } \times \overline { b } \right| =\left| \overline { a } \right| .\left| \overline { b } \right| \sin { \theta } $$
$$ Hence\quad proved.$$
If $${\vec x}$$ satisfying the conditions $${\vec b}$$.$${\vec x}$$ = $$\beta $$ & $${\vec b}$$ x $${\vec x}$$ = $${\vec a}$$ is $$\vec x = {{\left( {{\beta ^2} - 12} \right)\vec b} \over {{{\left| {\vec b} \right|}^2}}} + {{\vec a \times \vec b} \over {{{\left| {\vec b} \right|}^2}}}$$ then $$\beta $$ can be
Establish the following vector inequalities geometrically or
otherwise:
(a) $$\left| {a + b} \right| \le \left| a \right| + \left| b \right|$$
(b) $$\left| {a + b} \right| \ge \left| {\left| a \right| - \left| b \right|} \right|$$
(a) Find the unit vector which is parallel to the vector $$\overrightarrow {\rm{A}} {\rm{ = 2}}\widehat {\rm{i}}{\rm{ + 2}}\widehat {\rm{j}}{\rm{ - 2}}\widehat {\rm{k}}$$
(b) Find the unit vector which is perpendicular to both of the
vector $$\overrightarrow {\rm{A}} {\rm{ = 2}}\widehat {\rm{i}}\;{\rm{and}}\;\overrightarrow B {\rm{ = 3}}\widehat {\rm{i}}{\rm{ + 4}}\widehat {\rm{j}}{\rm{ + 12}}\widehat {\rm{k}}$$
Suppose the vectors $$\overrightarrow a ,\overrightarrow {\rm{b}} ,\overrightarrow {\rm{c}} $$ on a plane satisfy the condition that $$|\overrightarrow a | = |\overrightarrow {\rm{b}} | = |\overrightarrow {\rm{c}} | = |\overrightarrow {\rm{a}} + \overrightarrow b | = 1{\rm{ }};{\rm{ }}\overrightarrow {\rm{c}} $$ is perpendicular to $$\overrightarrow {\rm{a}} $$ and $$\overrightarrow {\rm{b}} {\rm{.}}\overrightarrow {\rm{c}} {\rm{ > 0}}$$, then
Let $$\overrightarrow a = 2\widehat i + 3\widehat i + 2\widehat k$$ and $$\overrightarrow b = \widehat i + 2\widehat i + \widehat k$$.
Find the projection of
1.$$\overrightarrow a$$ on $$\overrightarrow b$$
2. $$\overrightarrow b$$ on $$\overrightarrow a$$
Find the projection of the vector $$\vec {a}=4\hat {i}-2\hat {j}+\hat {k}$$ on the vector $$\vec {b}=3\hat {i}+6\hat {j}+2\hat {k}$$. Also find component of $$\vec {a}$$ along $$\vec {b}$$ and perpendicular to $$\vec {b}$$.
If $$\overrightarrow a $$ is a unit vector and $$\left( {\overrightarrow x - \overrightarrow a } \right)$$, $$\left( {\overrightarrow x - \overrightarrow b } \right)$$=35, then the $$\left| {\overline x } \right|$$.
Solve the equation $${x^4} - 8{x^3} + 24{x^2} - 32x + 20 = 0$$ if 3+1 is a root.
For any two vectors $$\vec{a}$$ and $$\vec{b}$$, If $$(\vec{a}+\vec{b})\cdot (\vec{a}-\vec{b})=0.$$
Then $$ | \vec{a}|-|\vec{b}|=?$$.
Find the value of $$\lambda$$ such that points $$P(1, 2), Q(-2, 3)$$ and $$R(\lambda +1, \lambda)$$ are not forming a triangle?
Prove that $$\left[ {\vec a\,\,\vec b\,\,\vec c\,\, + \,\,\vec d} \right] = \left[ {\vec a\,\,\vec b\,\,\vec c\,} \right] + \left[ {\vec a\,\,\vec b\,\,\vec d\,} \right]$$
Show that vectors $$\left| {\overline a } \right|\left| {\overline a + } \right|\overline a \left| {\overline b } \right.$$ and $$\left| b \right|\overline a - \left| a \right.\left| {\overline b } \right.$$ are orthogonal.
Two vertices of a triangle are at $$-\hat{i}+3\hat{j}$$ and $$2\hat{i}+5\hat{j}$$ and its orthocentre is at $$\hat{i}+2\hat{j}$$. Find the position vector of thrid vertex.
We know that
$$AB \perp CD$$ and $$AC \perp BF$$
$$BC \perp AE$$ and $$m_{1},m_{2}=-1$$ for two lines which are $$ \perp $$
$$\therefore AB \perp CH \Rightarrow \dfrac{(5-3)}{(2-(-1))}\left(\dfrac{y-2}{x-1}\right)=-1$$
$$2y-4=3-3x$$
$$3x+2y-7=0$$ ______(1)
$$BH \perp AC\Rightarrow \dfrac{(5-2)}{(2-1)}\left(\dfrac{y-3}{x+1}\right)=-1$$
$$3y-9=-x-1$$
$$x+3y-8=0$$ _____ (2)
solving equations (1) and (2)
$$(1)-3\times (2)$$
$$3x+2y-7-3x-9y+24=0$$
$$-7y+17=0$$
$$y=\dfrac{17}{7}$$
$$\therefore x=8-\dfrac{3\times 7}{7}=\dfrac{5}{7}$$
$$\therefore C\equiv \dfrac{5}{7}\hat{i}+\dfrac{17}{7}\hat{j}$$
Angle between $$\overrightarrow{a}$$ & $$\overrightarrow{b}$$. Find a vector along the angle bisector of $$\overrightarrow{a}$$ & $$\overrightarrow{b}$$.
Let $$\overset { \rightarrow }{ a } =2\overset { \wedge }{ i } +3\overset { \wedge }{ j } +2\overset { \wedge }{ k } $$ and $$\overset { \rightarrow }{ b } =\overset { \wedge }{ i } +2\overset { \wedge }{ j } +\overset { \wedge }{ k } $$.Find the component of $$\overset { \rightarrow }{ b } $$ on $$ \overset { \rightarrow }{ a }$$.
Find the projection of $$3\hat i + 4\hat j + \hat k$$ on $$\hat i + \hat j - \hat k$$ and its magnitude.
If $$\hat { a }$$ and $$\hat { b }$$ are unit vector and $$\theta$$ is the angle between them, show that $$\cos { \left( \dfrac { \pi }{ 4 } -\dfrac { \theta }{ 2 } \right) } =\dfrac { 1 }{ 2\sqrt { 2 } } \left( \left| \hat { a } -\hat { b } \right| +\left| \hat { a } +\hat { b } \right| \right)$$
If $$\ \overline r = \left( {x + y + 2} \right)\overline i + \left( {2x - y + 3} \right)\overline j + \left( {x + 2y + 7} \right)\overline k $$ where $$\overline r .\overline i = 3,\overline r .\overline j = 5$$ then $$\overline r .\overline k = $$
A line passes through the points whose position vectors are $$ \hat { i } + \hat { j } - 2 \hat { k } $$ and $$ \hat { i } - 3 \hat { j } + \hat { k } $$. The position vector of a point on it at unit distance from the first point is
If $$C$$ is the midpoint of $$AB$$ and $$P$$ is any point outside $$AB$$, then $$\overrightarrow{PA}+\overrightarrow{PB}=$$
Let $$\vec {a}=\hat {i}+4\hat {j}+2\hat {k},\,\vec b=3\hat i-2\hat j+7\hat k$$ and $$\vec {c}=2\hat {i}-\hat j+4\hat {k}$$. Find a vector $$\vec d$$ which is perpendicular to both $$\vec {a}$$ and $$\vec {b}$$, and $$\vec {c}\cdot \vec {d}=15$$.
Find the position vector of the midpoint of the vector joining the points $$P(2, 3, 4)$$ and $$Q(4, 1, -2)$$.
Let the midpoint of $$PQ$$ be $$R$$
Position vector of $$P=(2-0)\hat i+(3-0)\hat j+(4-0)\hat k$$
$$\vec{OP}=2\hat i+3\hat j+4\hat k$$
Position vector of $$Q=(4-0)\hat i+(1-0)\hat j+(-2-0)\hat k$$
$$\vec{OQ}=4\hat i+\hat j-2\hat k$$
Now,
Position vector of $$R=\dfrac{\vec {OQ}+\vec {OP}}{2}$$
$$\vec {OR}=\dfrac{(4\hat i+\hat j -2\hat k)+(2\hat i+3\hat j+4\hat k)}{2}$$
$$\vec {OR}=\dfrac{(4+2)\hat i+(1+3)\hat j+(-2+4)\hat k}{2}$$
$$\vec {OR}=\dfrac{6\hat i+4\hat j+2\hat k}{2}$$
$$\vec {OR}=\dfrac{2(3\hat i+2\hat j+\hat k)}{2}$$
$$\vec {OR}=3\hat i+2\hat j+\hat k$$
Therefore, position vector of midpoint of $$PQ$$ is $$3\hat i+2\hat j+\hat k$$
If $$A, B, C$$ and $$D$$ are any four points E and F are the middle points of $$AC$$ and $$BD$$, respectively then prove that $$\vec{CB}+\vec{CD}+\vec{AD}+\vec{AB}=4\vec{EF}$$.
if $$\overline{a},\overline{b},\overline{c}$$ are co planarProve that :
$$[\overline {a}\ \ \ \ \overline {b}+\overline {c}\ \ \ \ \overline {a}+\overline {b}+\overline {c}]=0$$
$$[\overline {a}\ \ \ \ \overline {b}+\overline {c}\ \ \ \ \overline {a}+\overline {b}+\overline {c}]=0$$
$$ [\bar{a}\bar{b}+\bar{c}\, \bar{a}+\bar{b}+\bar{c}]$$
$$ (\bar{a}+\bar{b}+\bar{c}). (\bar{a}\times \bar{b}+\bar{a}\times \bar{c})$$
Since $$ \bar{a},\bar{b}\bar{c}$$ are co planar
$$ \bar{a}+\bar{b}+\bar{c}$$ and $$\bar{a}\times \bar{b}+\bar{a}\times\bar{c}$$ are $$ \perp$$ to each other
so $$ (\bar{a}+\bar{b}+\bar{c}).(\bar{a}\times \bar{b}+\bar{a}\times \bar{c}) = 0$$
If $$\vec{a} +\vec{b}+\vec{c}=\vec{0}$$, $$|\vec{a}|=3 .|\vec{b}|=\vec|c|=5$$ find $$\vec {a}.\vec{b}+\vec{b}.\vec{c}+\vec{c}.\vec{a}$$
If $$\vec{a}=\vec{i}+\vec{j}+2\vec{k}, \vec{b}=3\vec{i}+2\vec{j}-\vec{k}$$ find $$(\vec{a}+3\vec{b}).(2\vec{a}-\vec{b}).(\vec{a}+3\vec{b})$$.
For any vector $$\vec { r }$$ prove that $$\vec { r }=$$ $$\left(\vec { r }.\vec { i }\right) \vec { r }+\left(\vec { r } .\vec { j }\right) \vec { j }+\left(\vec { r }.\vec { k }\right)\vec { k }$$
To prove : $$ \vec{r} = (\vec{r}.\vec{c})\vec{r}+(\vec{r}.\vec{j})\vec{j}+(\vec{r}.\vec{k})\vec{k}$$
Solving R.H.S $$ \vec{r} = (x\hat{i}+y\hat{j}+z\hat{k})$$
So,$$ (\vec{r},\vec{i}) = [(x\hat{i}+y\hat{j}+z\hat{k}).\hat{i}]\hat{i}+[(x\hat{i}+y\hat{j}+z\hat{k}).\hat{j}] \hat{j}+[(x\hat{i}+y\hat{j}+z\hat{k}).\hat{k}]\hat{k}$$
$$=[x\hat{i},\hat{i}+y\hat{j}.\hat{i}+z\hat{k}.\hat{i}]\hat{i}+[x\hat{i}.\hat{j}+y\hat{j}.\hat{j+2\hat{k}.\hat{j}}]\hat{i}+[x\hat{i}.\hat{k}+y\hat{j}.\hat{k}+2\hat{k}.\hat{k}]\hat{k}$$
$$ = [\because \hat{i}.\hat{i}=1=\hat{j}.\hat{j} = \hat{k}.\hat{k}$$ & $$ \hat{i}.\hat{j}= \hat{j},\hat{k} = \hat{k}.\hat{i} = 0]$$
$$ = x\hat{i} +y\hat{j}+z\hat{k}$$
$$ = r = R.H.S$$
$$ \Rightarrow L.H.S = R.H.S $$
Hence proved.
If $$\bar{x},\bar{y},\bar{z}$$ are mutually perpendicular vectors of eqaul magnitude, then find the measure of an angle that $$\bar{x}+\bar{y}+\bar{z}$$ makes with any of the three vectors.
Let $$\overrightarrow{A}=2\hat{i}+\hat{k},\overrightarrow{B}=\hat{i}+\hat{j}+\hat{k}$$ and $$\overrightarrow{C}=4\hat{i}-3\hat{j}+7\hat{k}$$.Determine a vector $$\overrightarrow{R}$$ satisfying $$\overrightarrow{R}.\overrightarrow{A}=0$$ and $$\overrightarrow{R}\times \overrightarrow{B}=\overrightarrow{C}\times \overrightarrow{B}$$
Let $$\overrightarrow{b}=4\hat{i}+3\hat{j}$$ and $$\overrightarrow{c}$$ be two vectors perpendicular to each other in the $$xy-$$plane.Find all vectors in the same plane having projections $$1$$ and $$2$$ along $$\overrightarrow{b}$$ and $$\overrightarrow{c}$$ respectively.
if the sum of two vectors is a unit vector , prove that the magnitude of their difference $$\sqrt 3 $$.
Find the position vector of the midpoint of the vector joining the points $$P(2,2,4)$$ and $$Q(4,1,-2)$$.
Find the projection of $$\vec a = \hat i - 3\hat k$$ on $$\vec b = 3\hat i + \hat j - 4\hat k$$
Find vector $$\vec { c }$$ such that $$\vec { c } \cdot \hat { i } = \vec { c } \cdot \hat { j } = \vec { c } \cdot \hat { k }$$ and $$| \vec { c } | = 100$$
Find the projection of vector $$2\hat i + \hat j$$ on the vector $$\hat i + 2\hat j$$ .
in $$\triangle ABC$$ if $$A=2\hat {i}+4\hat {j}-\hat {k},B=4\hat {i}+\hat {j}+\hat {k}$$ and $$C=3\hat {i}+6\hat {j}-3\hat {k}$$ and $$D$$ is mid point of the side $$BC$$,then the length of $$AD$$ is $$\sqrt m$$/2 then m=
undefined
Find unit vector in the direction of vector $$a=2i+3j+k$$.
unit vector $$ \hat{a} = \frac{\vec{a}}{\left | \vec{a} \right |} $$
Given $$ \vec{a} = 2\hat{i}+3\hat{j}+\hat{k} $$
$$ \left | \vec{a} \right | = \sqrt{2^{2}+3^{2}+1} $$
$$ = \sqrt{14} $$
unit vector $$ \hat{a} = \frac{2\hat{i}+3\hat{j}+\hat{k}}{\sqrt{14}} $$
$$ = \frac{2}{\sqrt{14}}\hat{i}+\frac{3}{\sqrt{14}}\hat{j}+\frac{1}{\sqrt{14}}\hat{k} $$
zero vector $$ \vec{0} = 0\hat{i}+0\hat{j}+0\hat{k} $$
$$\vec{a}=4\hat{i}-\hat{j}+\hat{k} \quad and \quad \vec{b}=p\hat{i}+2\hat{j}+3\hat{k}$$ are mutually perpendicular , then find the value of p.
$$\vec{a}=4\hat{i}-\hat{j}+\hat{k}$$ and $$\vec{b}=p\hat{i}+2\hat{j}+3\hat{k}$$ are initially perpendicular
$$\Rightarrow \vec{a}\cdot \vec{b}=0$$
$$\Rightarrow 4p-2+3=0$$
$$\Rightarrow 4p+1=0$$
$$\Rightarrow p=-\dfrac{1}{4}$$.
If $$\left| \overline { a } \right| =2,\left| \overline { b } \right| =7$$ and $$\overline { a } \times \overline { b } =3\overline { i } +2\overline { j } +6\overline { k } $$ then $$\overline { a }.\overline { b }=$$
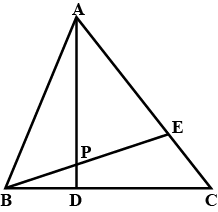
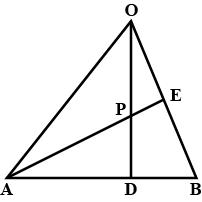
In a $$\Delta A B O , E$$ is the midpoint of $$\overline { O B }$$ and $$D$$ is a point on $$AB$$ such that $$A D : D B = 2:1$$ if $$\overline { O D }$$ and $$\overline { A E }$$ intersect at $$P$$ then $$\overline { O P } : \overline { P D } =$$
If the vector $$- \hat i + \hat j - \hat k$$ bisects the angle between the vector c and the vector$$3\hat i + 4\hat j$$,then the unit vector in the direction of c,is
$$A ( 1 , - 1 , - 3 ) , B ( 2,1 , - 2 ) \quad \& \quad C ( - 5,2 , - 6 )$$ are the position vectors of the vertices of a triangle $$ABC$$, then the length of the bisector of its internal angle $$A$$ is
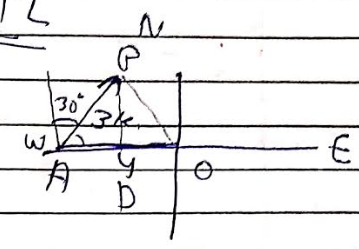
A girl walks $$4\ km$$ towards west, then she walks $$3\ k$$ in the direction of $$30$$ east of north and stops. Determine the girl's displacement from her initial point of departure.
$$\begin{array}{l} BAO={ 90^{ 0 } }-{ 30^{ 0 } }={ 60^{ 0 } } & \\ \sin { 60^{ 0 } } =\frac { { BD } }{ { 3kn } } & \\ \frac { { \sqrt { 3 } } }{ 2 } =\frac { { BD } }{ 3 } & \\ BD=\frac { { 3\sqrt { 3 } } }{ 2 } & \\ \cos { 60^{ 0 } } =\frac { { AD } }{ 3 } & OD=OA-AD \\ AD=\frac { 3 }{ 2 } & =4\frac { { -3 } }{ 2 } =\frac { 5 }{ 2 } \\ O{ B^{ 2 } }=B{ D^{ 2 } }+O{ D^{ 2 } } & \\ ={ \left( { \frac { { 3\sqrt { 3 } } }{ 2 } } \right) ^{ 2 } }+{ \left( { \frac { 5 }{ 2 } } \right) ^{ 2 } } & \\ =\frac { { 9\times 3 } }{ 4 } +\frac { { 25 } }{ 4 } =\frac { { 52 } }{ 4 } =13 & \\ OB=\sqrt { 13 } & \end{array}$$
If A , B , C and D are any four points E and F are the middle points of AC and BD, respectively then prove that $$\underset{CB}{\rightarrow}+\underset{CD}{\rightarrow}+\underset{AD}{\rightarrow}+\underset{AB}{\rightarrow}=4 \underset{EF}{\rightarrow}$$
$$\vec {AB}+\vec {AD}+\vec {CB}=4\vec {CF}$$
$$AB+AD=2AF----(1)$$
$$CB+CD=2CF---(2)$$
$$AB+AD+CB+CD=(AF+CF)$$
$$AB+AD+CB+CD=2(\vec {FA}+\vec {CF})$$
$$AB+AD+CB+CD=-2(2FC)$$
$$AB+AD+CB+CD=4EF$$
Let $$\vec{a}$$ be an unit vector and $$m$$ being a scalar then find the value of $$m$$ from the equation $$|m\vec{a}|=2$$.
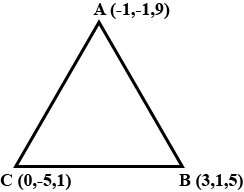
Find by vector method the perimeter of the triangle whose vectors are $$( - 1 , - 1,9 ) , ( 3,1,5 )$$ and $$( 0 , - 5,1 ) .$$
$$AB=(1-,1-,9)-(3,1,5)=(-4,-2,4)\\ \left| AB \right| =\sqrt { { 4 }^{ 2 }+{ 2 }^{ 2 }+{ 4 }^{ 2 } } =6\\ BC=(3,1,5)-(0,-5,1)=(3,6,4)\\ \left| BC \right| =\sqrt { 9+36+16 } =\sqrt { 61 } \\ CA=(0,-5,1)-(-1,-1,9)=(1,-4,-8)\\ \left| CA \right| =\sqrt { { 1 }^{ 2 }+{ 4 }^{ 2 }+{ 8 }^{ 2 } } =\sqrt { 64+16+1 } =9$$
Perimeter$$=\left| AB \right| +\left| BC \right| +\left| CA \right| $$
$$=6+\sqrt { 61 } +9\\ =15+7.81\\ =22.81$$
1.Find the projection of the vector i-j on the vector i+j.
2.Find the projection of the vector $$2\widehat i + 3\widehat j + 2\widehat k$$ on the vector
$$\widehat i + 2\widehat j + \widehat k.$$.
3.Find the projection of $$\overrightarrow a = \widehat i + 3\widehat j + \widehat k\,along\,\overrightarrow b = 2\widehat i - 3\widehat j + 6\widehat k.$$
Find the position vectors of a point $$R$$ which divides the line joining two points $$P$$ and $$Q$$ whose position vectors are $$2\vec{a}+3\vec{b}$$ and $$\vec{a}-3\vec{b}$$ respectively, externally in the ratio $$1:2$$. Also, show that $$P$$ is the midpoint of the line segment $$R$$.
For what value of $$\lambda ,$$ the vector $$i - \lambda j + 2k$$ and $$8i + 6j - k$$ are at right angles?
Using vector method, if $$Q$$ is the point of concurrence of the medians of the triangle $$ABC$$,then prove that $$\vec {QA} + \vec{QB}+\vec{QC} = \vec { 0 }$$
If $$\vec { DA } =\vec { a } $$, $$\vec { AB } =\vec { b } $$, $$\vec { CB } =\vec { ka } $$ where $$k>0$$ X, Y are the mid points of DB and AC respectively, such that $$\left| \vec { a } \right| =17$$ and $$\left| \vec { XY } \right| =4$$, then k equal to ?
Let D be origin $$\vec{DA}=\vec{A}-\vec{D}=\vec{a}$$
$$\Rightarrow \vec{A}=\vec{a}$$
$$\vec{AB}=\vec{B}-\vec{A}=\vec{b}$$
$$\Rightarrow \vec{B}=\vec{a}+\vec{b}$$
$$\vec{CB}=\vec{B}-\vec{C}=k\vec{a}$$
$$\Rightarrow \vec{C}=\vec{a}+\vec{b}-k\vec{a}$$
$$\vec{x}=\dfrac{\vec{a}+\vec{b}}{2}$$, $$\vec{y}=\dfrac{2\vec{a}+\vec{b}-k\vec{a}}{2}$$
$$\vec{xy}=\dfrac{\vec{a}-k\vec{a}}{2}=\left(\dfrac{1-k}{2}\right)\vec{a}$$
$$(\vec{xy})=\left(\dfrac{1-k}{2}\right)|\vec{a}|$$
$$\Rightarrow 4=\left(\dfrac{1-k}{2}\right)17$$
$$\Rightarrow 1-k=\dfrac{8}{17}$$
$$\Rightarrow k=\dfrac{9}{17}$$.
Get the area of $$\triangle ABC$$ for $$A(1,1,2),B(2,3,5),C(1,3,4)$$ by use of vectors.
Let $$\vec {a},\vec {b},\vec {c}$$ be three non-zero vectors such that $$\vec {c}$$ is a unit vectors perpendicular is both $$\vec {a}$$ and $$\vec {b} $$. If the angle between $$\vec {a}$$ and $$\vec {b}$$ is $$\dfrac {\pi}{6}$$, prove that $$[ \vec {a}\ \vec {b}\ \vec {c} ]^{2}=\dfrac {1}{4}|\vec {a}|^{2}|\vec {b}|^{2}$$.
A man walks $$2a-b\ km$$ due North from a fixed point $$O$$ and then walks a distance of $$3a+2b\ km$$ due South. What is his final position with regard to $$O$$.
R.E.F image
On walking north, he reaches $$(2a-b)$$ units due north to $$A$$.
He moves $$3a + 2b$$ due south from $$A$$.
So, subtract $$3a + 2b$$ from $$2a -b$$.
$$\therefore 2a - b - 3a - 2b = -a - 3b$$
$$\therefore$$ He is $$(a+3b)$$ distance due south of O.
Prove that
$$\vec ({ a } \vec { b })\times (\vec { c } \vec { d }) = [\vec ({ a } \vec { b } \vec { d }] \vec [{ a } \vec { b } \vec { c }] \vec { d }$$
$$(\vec{a}\times\vec{b})\times (\vec{c}\times \vec{d})=[(\vec{a}\times \vec{b})\cdot \vec{d}]\vec{c}-[(\vec{a}\times \vec{b})\cdot \vec{c}]\vec{d}=[\vec{a}\vec{b}\vec{d}]\vec{c}-[\vec{a}\vec{b}\vec{c}]\vec{d}$$.
If A, B, C, D are the points with position vectors $$\hat{i} - \hat{j} + \hat{k}, 2 \hat{i} - \hat{j} + 3 \hat{k}, 2 \hat{i} - 3 \hat{k}, 3 \hat{i} - 2 hat{j} + \hat{k}$$, respectively, find the projection of $$\overline{AB}$$ along $$\overline{CD}$$
If $$\vec {a}=\hat {i}+\hat {j}+2\hat {k}$$ and $$\vec {b}=3\hat {i}+2\hat {j}-\hat {k}$$, find the value of $$(\vec {a}+3\vec {b}).(2\vec {a}-\vec {b})$$
If P and Q are the midpoints of the diagonals AC and BD respectively of a quadrilateral ABCD, prove that $$\overline { AB } +\overline { AD } +\overline { CB } +\overline { CD } =4\overline { PQ } $$.
Show that vectors $$2\hat{i}-\hat{k},\hat{i}-3\hat{j}-5\hat{k}$$ and $$3\hat{i}-4\hat{j}-4\hat{k}$$ form the vertices of the triangle.
Let $$u=(2,4,-5)$$ and $$v=(1,-6,9)$$ then find $$3u-5v$$.
Show that the points $$A(2, 1, -1)$$, $$B(0, -1, 0)$$, $$C(4, 0, 4)$$ and $$D(2, 0, 1)$$ are coplanar.
The two adjacent sides of a parallelogram, $$\vec{a}=2i+4j-5k$$ and $$\vec{b}=i+2j+3k$$, then find the unit vector parallel to its diagonal.
Let $$u=(1,-2,3)$$ and $$v=(4,5,-1)$$ find $$u.v$$.
Find the angle between two vectors $$\overrightarrow a$$ and $$\overrightarrow b$$ with magnitude $$\sqrt{3}$$ and $$2$$, respectively having $$\overrightarrow a . \overrightarrow b=\sqrt{6}$$.
Using the vector equation of the straight line passing through two points, prove that the points whose vectors are $$a, b$$ and $$(3a-2b)$$ are collinear.
If vector $$\vec {AB}=2\hat {i}-\hat {j}+\hat {k}$$ and $$\vec {OB}=3\hat {i}-4\hat {j}+4\hat {k}$$ find the position vector $$\vec {OA}$$
$$\vec{AB}=2\hat{i}-\hat{j}+\hat{k}=\vec{b}-\vec{a}$$….$$(1)$$;
$$\vec{OA}=3\hat{i}-4\hat{j}+4\hat{k}=\vec{a}-\vec{0}$$ …………$$(2)$$
Equation $$(2)$$- Equation $$(1)$$
$$\vec{a}-\vec{0}=\vec{OA}=\hat{i}-3\hat{j}+3\hat{k}$$.
If vector $$\vec{AB}=2\hat{i}-\hat{j}+\hat{k}$$ and $$\vec{OB}=3\hat{i}-4\hat{j}+4\hat{k}$$, find the position vector $$\vec{OA}$$
Let position vector of $$O, A, B$$ be $$\vec{O}, \vec {a}, \vec{b}$$
$$\Rightarrow \overrightarrow{AB} - \vec{b} - \vec{a} = 2\hat{i} - \hat{j} + \hat{k}$$ ...(1)
$$\overrightarrow{OB} = \vec{b} - \vec{O} = 3\hat{j}-4\hat{j} + 4\hat{k}$$ ...(2)
$$\overrightarrow{OA} = \vec{a} - \vec{O} $$
Eqn. (2) - eqn. (1)
$$overline{OA} = \hat{i} - 3\hat{j} + 3\hat{k}$$
Write the position vector of the point which divides the join of points with position vectors $$3 \vec { a } - 2 \vec { b } $$ and $$2 \vec { a } + 3 \vec { b }$$ in the ratio $$2 : 1.$$
Find the position vector of a point R which divides the line joining two points P and Q whose position vectors are $$\hat { i } +2\hat { j } -\hat { k } $$ and $$\hat { -i } +\hat { j } +\hat { k } $$ respectively, in the ratio 2 :externally
Dot product of a vector with $$\hat{i}+\hat{j}-3\hat{k},\hat{i}+3\hat{j}-2\hat{k}$$ and $$2\hat{i}+\hat{j}+4\hat{k}$$ are $$0,5$$ and $$8$$ respectively. Find the vector.
Find $$\vec{a}.\vec{b}$$, when $$\vec{a}=\hat{i}-2\hat{j}+\hat{k}$$ and $$\vec{b}=4\hat{i}-4\hat{j}+7\hat{k}$$.
If $$\hat{a}$$ and $$\hat{b}$$ are unit vectors inclined at an angle $$\theta $$, then prove that
$$tan \dfrac{\theta }{2}=\dfrac{\left | \hat{a}-\hat{b} \right |}{\left | \hat{a}+\hat{b} \right |}$$
If $$\hat{a}$$ and $$\hat{b}$$ are unit vectors inclined at an angle $$\theta $$, then prove that
$$cos \dfrac{\theta }{2}=\dfrac{1}{2}\left | \hat{a}+\hat{b} \right |$$
Find $$|\overrightarrow a |$$ and $$|\overrightarrow b|$$, if $$(\overrightarrow a -\overrightarrow b).(\overrightarrow a +\overrightarrow b)=27$$ and $$|\overrightarrow a |=2|\overrightarrow b|$$.
Show that the four points A,B,C,D with position vectors $$\vec{a},\vec{b}, \vec{c}, \vec{d}$$ respectively such that $$ 3\vec{a}-2\vec{b}+5\vec{c}-6\vec{d} = \vec{0},$$ are coplanar. Also find the position vector of the point of intersection of the line segments AC and BD.
A, B, C, D has position vectors $$\vec{a}, \vec{b}, \vec{c}, \vec{d}$$
$$3\vec{a}-2\vec{b}+5\vec{c}-6\vec{d}=0$$
$$\Rightarrow 3\vec{a}+5\vec{c}=2\vec{b}+\vec{d}$$
$$\Rightarrow 3\vec{OA}+5\vec{OC}=2\vec{OB}+6\vec{OD}$$
$$\Rightarrow \dfrac{3\vec{OA}+5\vec{OC}}{8}=\dfrac{2\vec{OB}+6\vec{OD}}{8}$$
$$\vec{OQ}$$ be the point which divides AC in the ratio $$5:3$$
$$\therefore \vec{OQ}=\dfrac{3\vec{OA}+5\vec{OC}}{8}=\dfrac{2\vec{OB}+6\vec{OD}}{8}$$
so, Q also divides BD in the ratio $$6:2$$
$$\therefore$$ Q also lies on Bd
$$\therefore$$ Q is the point of intersection of AC and BD
$$\therefore$$ Point of intersection
$$=\dfrac{3\vec{a}+5\vec{c}}{8}$$ (or) $$\dfrac{2\vec{b}+6\vec{c}}{8}$$.
$$ ABCDE $$ is a pentagon, then prove that $$\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CD}+\overrightarrow{DE}+\overrightarrow{EA} = \vec{0} $$.
If O is a point in space, ABC is a triangle and D,E,F are the mid-points of the sides BC,CA and AB respectively of the triangle,prove that $$ \overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC} = \overrightarrow{OD}+\overrightarrow{OE}+\overrightarrow{OF}. $$
Find the position vector of a point $$R$$ which divides the line joining the two points $$P$$ and $$Q$$ with position vectors $$ \vec{OP} = 2\vec{a}+b $$ and $$ \vec{OQ}=\vec{a}-2\vec{b},$$ respectively in the ratio $$1:2$$ internally and externally.
If P is a point and ABCD is a quadrilateral and $$ \overrightarrow{AP}+\overrightarrow{PB}+\overrightarrow{PD} = \overrightarrow{PC}, $$ show that ABCD is a paralleogram.
The projection of the line segment joining the points $$(1, -1, 3)$$ and $$(2, -4, 11)$$ on the line joining the points $$(-1, 2, 3)$$ and $$(3, -2, 10)$$ is _________.
Given points.
$$A(1, -1, 3) \, B(2, -4, 11)$$
$$\overline{AB} = (2 - 1, -4 + 1, 11 - 3)$$$$\equiv (1, -3 , 8)$$
$$C (-1, 2, 3) \, D(3, -2, 10)$$
$$\overline{CD} = (3 + 1 , -2-2, 10 - 3)$$$$\equiv(4, -4 , 7)$$ -Direction ratios.
Projection of $$\overline{AB} $$ on $$\overline{CD}$$
Ref. image
$$= \dfrac{\overline{AB} . \overline{CD}}{|\overline{CD}|}$$
$$= \dfrac{(1 \times 4) + (-3 \times - 4) +(8 \times 7)}{\sqrt{4^2 + 4^2 + 7^2}}$$
$$= \dfrac{4 + 12 + 56}{\sqrt{81}}$$
$$= \dfrac{72}{9}$$
$$= 8$$
Find the projection of $$\vec{b}+\vec{c}$$ on $$\vec{a}$$, where $$\vec{a}=2\hat{i}-2\hat{j}+\hat{k}, \vec{b}=\hat{i}+2\hat{j}-2\hat{k}$$ and $$\vec{c}=2\hat{i}-\hat{j}+4\hat{k}$$.
The two vectors $$ \hat{j}+\hat{i} $$ and $$ 3\hat{i}-\hat{j}+4\hat{k} $$ represent the sides $$ \overrightarrow{AB} $$ and $$ \overrightarrow{AC} $$ respectively of triangle $$ABC$$. Find the length of the median through $$A$$.
$$\vec{AB}=\hat{i}+\hat{j}$$
$$\vec{AC}=3\hat{i}-\hat{j}+4\hat{k}$$
Median through A is $$\vec{AD}$$
$$=\dfrac{\vec{AB}+\vec{AC}}{2}$$
$$=\dfrac{(\hat{i}+\hat{j})+(3\hat{i}-\hat{j}+4\hat{k})}{2}$$
$$=\dfrac{(4\hat{i}+4\hat{k})}{2}$$
$$\vec{AD}=2\hat{i}+2\hat{k}$$
$$\therefore$$ Length of Median $$=|\vec{AD}|=\sqrt{4^2+4^2}=\sqrt{8}$$
$$=2\sqrt{2}$$.
Find the vector sum of $$N$$ coplanar forces, each of magnitude $$F$$, When each force makes an angle $$2\pi /N$$ with that preceding it.
Consider a regular polygon of N sides. Each side of the polygon is same. C is the centre of polygon (Fig. 2.60).
$$\theta = \frac{2\pi}{N} \rightarrow \theta$$ is the angle subtended at the centre of polygon by any one side.
We can prove that $$\alpha = \theta$$ as
$$\angle ABC + \angle CBD + \alpha = 180^0$$ .......(i)
But $$ \angle ABC= \angle CBD = 90^0 - \frac{\theta}{2}$$ ........(ii)
From Eqs. (i) and (ii), we get $$\alpha = \theta$$
$$\Rightarrow \alpha = \frac{2\pi}{N}$$
So if we have N vectors of equal magnitude and they are arrangged in such a way that each vector makes an angle $$\frac{2\pi}{N} (=\alpha)$$ with its preceding vector, we find that the head of the last vector will coincide with the tail of the first vector. Hence, the resultant of all these vectors becomes zero.
$$\theta = \frac{2\pi}{N} \rightarrow \theta$$ is the angle subtended at the centre of polygon by any one side.
We can prove that $$\alpha = \theta$$ as
$$\angle ABC + \angle CBD + \alpha = 180^0$$ .......(i)
But $$ \angle ABC= \angle CBD = 90^0 - \frac{\theta}{2}$$ ........(ii)
From Eqs. (i) and (ii), we get $$\alpha = \theta$$
$$\Rightarrow \alpha = \frac{2\pi}{N}$$
So if we have N vectors of equal magnitude and they are arrangged in such a way that each vector makes an angle $$\frac{2\pi}{N} (=\alpha)$$ with its preceding vector, we find that the head of the last vector will coincide with the tail of the first vector. Hence, the resultant of all these vectors becomes zero.
The vector equation of a line which passes through the points $$(3, 4 , -7)$$ and $$(1,-1, 6)$$ is ______.
Find the sum of the vectors $$\vec{a}=(\hat{i}-3\hat{k})$$, $$\vec{b}=(2\hat{j}-\hat{k})$$ and $$\vec{c}=(2\hat{i}-3\hat{j}+2\hat{k})$$.
Find the sum of the vectors $$\vec{a}=(\hat{i}-2\hat{j}), \vec{b}=(2\hat{i}-3\hat{j})$$ and $$\vec{c}=(2\hat{i}+3\hat{k})$$.
If $$ \left| \overrightarrow { a } \right| =\sqrt { 3 } ,\left| \overrightarrow { b } \right| =2 $$ and angle between $$ \overrightarrow{a} $$ and $$ \overrightarrow{b} $$ is $$ 60^o $$ , Then find $$ \overrightarrow{a}.\overrightarrow{b}. $$
Find the projection of $$ \overrightarrow{a} $$ on $$ \overrightarrow{b}, $$ if $$ \over $$ and $$ \overrightarrow{a}.\overrightarrow{b}.=8 $$ and $$ \overrightarrow{b}=2\hat{i} +6 \hat{j} + 3\hat{k} $$.
If $$ \overrightarrow {a} , \overrightarrow {b} , \overrightarrow {c} $$ are three vectors such that $$ | \overrightarrow {a} | = 5 , | \overrightarrow {b} |= 12 $$ and $$ | \overrightarrow {c} | = 13 $$ and $$ \overrightarrow {a} + \overrightarrow {b} +\overrightarrow {c} = \overrightarrow {0} $$ then find the value of $$ \overrightarrow {a}.\overrightarrow {b} + \overrightarrow {b}.\overrightarrow {c} + \overrightarrow {c} . \overrightarrow {a}. $$
Find the sum of the vectors.
$$ \overrightarrow{a}=\hat{i} - 2\hat{j} + \hat{k}=\overrightarrow{b}-2\hat{i}+4\hat{j} + 5k $$ and $$ \overrightarrow{c} = \hat{i}-6\hat{j}-7\hat{k} $$.
Find the value of $$ \overrightarrow{a}. \overrightarrow{b} $$ if $$ \left| \overrightarrow { a } \right| =10,\left| \overrightarrow { b } \right| =2 $$ and $$ \left| \overrightarrow { a } \times \overrightarrow { b } \right| =16 $$
Find the position vector of a point $$ R $$ which divides the line joining two points $$ P $$ and $$ Q $$, whose position vectors are $$ (2 \overrightarrow{a}+\overrightarrow{b}) $$ and $$ ( \overrightarrow{a}-3\overrightarrow{b}) $$ respectively, externally in the ratio $$ 1:2 $$ Also, show that $$ P $$ is the mid point of the segment $$ RQ $$.
If $$ \overrightarrow{a}, \overrightarrow{b},\overrightarrow{c} $$ are three vectors such that $$ \overrightarrow{a}.\overrightarrow{b}=\overrightarrow{a}.\overrightarrow{c} $$ and $$ \overrightarrow{a} \times \overrightarrow{b}=\overrightarrow{a} \times \overrightarrow{c},\overrightarrow{a} \neq 0 $$, then show that $$ \overrightarrow{b}=\overrightarrow{c} $$.
If $$\vec{A} \space and \space \vec{B}$$ be two vectors and k be any scalar quantity greater than zero, then prove that $$|\vec{A} + \vec{B}|^2 \leq (1 + k) |\vec{A}|^2 + \left( 1 + \dfrac{1}{k}\right) |\vec{B}|^2$$.
If $$ \vec{a} $$ and $$ \vec{b} $$ are any two unit vectors, then find the greatest positive integer in the range of $$ \dfrac{3|\vec{a}+\vec{b}|}{2}+2|\vec{a}-\vec{b}| $$
Let $$ \vec{u} $$ be a vector on rectangular coordinate system with sloping angle $$ 60^{\circ} $$. Suppose that $$ |\vec{u}-\hat{i} | $$ is geometric mean of $$ |\vec{u}| $$ and $$ |\vec{u}-2 \hat{i}|, $$ where $$ \hat{i} $$ is the unit vector along $$ x $$ -axis. Then find the value of $$ (\sqrt{2}+1)|\vec{u}| $$
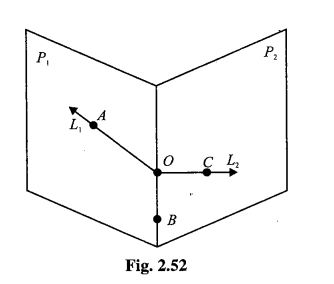
$$ P_{1} $$ and $$ P_{2} $$ are planes passing through origin. $$ L_{1} $$ and $$ L_{2} $$ are two lines on $$ P_{1} $$ and $$ P_{2} $$, respectively, such that their intersection is the origin. Show that there exist points $$ A, B $$ and $$ C, $$ whose permutation $$ A^{\prime}, B^{\prime} $$ and $$ C^{\prime}, $$ respectively, can be chosen such that
(i) $$ \mathrm{A} $$ is on $$ L_{1}, B $$ on $$ P_{1} $$ but not on $$ L_{1} $$ and $$ C $$ not on $$ P_{1} $$
(ii) $$ A^{\prime} $$ is on $$ L_{2}, B^{\prime} $$ on $$ P_{2} $$ but not on $$ L_{2} $$ and $$ C^{\prime} $$ not on $$ P_{2} $$
The following figure shows the possible situation for planes $$ P_{1} $$ and $$ P_{2} $$ and the lines $$ L_{1} $$ and $$ L_{2} $$
Now if we choose points $$ A, B $$ and $$ C $$ as $$ A $$ on $$ L_{1}, B $$ on the line of intersection of $$ P_{1} $$ and $$ P_{2} $$ but other than the origin and $$ C $$ on $$ L_{2} $$ again other than the origin, then we can consider
$$ A $$ corresponds to one of $$ A^{\prime}, B^{\prime}, C^{\prime} $$
$$ B $$ corresponds to one of the remaining of $$ A^{\prime}, B^{\prime} $$ and $$ C^{\prime} $$
$$ C $$ corresponds to third of $$ A^{\prime}, B^{\prime} $$ and $$ C^{\prime}, $$ e.g., $$ A^{\prime} \equiv C ; B^{\prime} \equiv B ; C^{\prime} \equiv A $$
Hence one permutation of $$ [A B C] $$ is $$ [C B A] . $$ Hence proved.
Let $$ \vec{A}, \vec{B} $$ and $$ \vec{C} $$ be vectors of length, 3,4 and 5, respectively. Let $$ \vec{A} $$ be perpendicular to $$ \vec{B}+\vec{C}, \vec{B} $$ to $$ \vec{C}+\vec{A} $$ and $$ \vec{C} $$ to $$ \vec{A}+\vec{B} $$. Then the length of vector $$ \vec{A}+\vec{B}+\vec{C} $$ is______________
If $$ c $$ be a given non-zero scalar, and $$ \vec{A} $$ and $$ \vec{B} $$ be given non-zero vectors such that $$ \vec{A} \perp \vec{B} $$, find the vector $$ \vec{X} $$ which satisfies the equations $$ \vec{A} \cdot \vec{X}=c $$ and $$ \vec{A} \times \vec{X}=\vec{B} $$.
Prove that : $$ | \overrightarrow {a} \times \overrightarrow {b}|^2 = \begin{vmatrix} \overrightarrow {a}. \overrightarrow {a} & \overrightarrow {a}. \overrightarrow {b} \\ \overrightarrow {a}. \overrightarrow {b} & \overrightarrow {b} . \overrightarrow {b} \end{vmatrix} $$
Find three-dimensional vectors $$ \vec{v}_{1}, \vec{v}_{2} $$ and $$ \vec{v}_{3} $$ satisfying $$ \vec{v}_{1} \cdot \vec{v}_{1}=4, \vec{v}_{1} \cdot \vec{v}_{2}=-2, \vec{v}_{1} \cdot \vec{v}_{3}=6, \vec{v}_{2} \cdot \vec{v}_{2}=2, $$$$ \vec{v}_{2} \cdot \vec{v}_{3}=-5, \vec{v}_{3} \cdot \vec{v}_{3}=29 $$
Prove by vector method that the diagonals of a parallelogram bisect each other.
We draw a parallelogram with one diagonal coincident to x-axis and the intersect of two diagonals is on origin. One diagonal into divided into $$\overrightarrow{a}$$
and $$m\overrightarrow{a}$$, the other is $$\overrightarrow{b}$$ and $$n\overrightarrow{b}$$.
Now,
$$\Rightarrow \overrightarrow{a}$$ +$$\overrightarrow{l}$$ =$$\overrightarrow{b}$$ and $$\overrightarrow{l}$$ +$$m\overrightarrow{a}$$ =$$n\overrightarrow{b}$$
(where m and n are scalars)
$$\Rightarrow \overrightarrow{a}$$ -$$\overrightarrow{b}$$ =$$m\overrightarrow{a}$$ -$$n\overrightarrow{b}$$
$$\Rightarrow (m-1)\overrightarrow{a}$$ =$$(n-1)\overrightarrow{b}$$
So,
$$\overrightarrow{a}$$ =$$\begin{pmatrix}
|a|\\
0
\end{pmatrix}$$
$$\overrightarrow{b}$$ =$$\begin{pmatrix}
|b|cos\ \theta\\
|b|sin\ \theta
\end{pmatrix}$$
y direction:
$$0=(n−1)|b|sin\ \theta$$
In the parallelogram, $$\theta>0$$ and $$|b|>0$$
$$\therefore n=1$$ and $$\overrightarrow{b} =n\overrightarrow{b}$$
Hence, diagonal $$b$$ is bisected.
and since, $$\overrightarrow {a}=m\overrightarrow {a}$$
diagonal $$a$$ is bisected.
Let $$ \vec{b}=4 \hat{i}+3 \hat{j} $$ and $$ \vec{c} $$ be two vectors perpendicular to each other in the $$ x y $$ -plane. All vectors in the same plane having projections 1 and 2 along $$ \vec{b} $$ and $$ \vec{c}, $$ respectively, are given by______________
Find a vector a magnitude $$11$$ in the direction opposite to that of $$\bar{PQ}$$, where $$P$$ and $$Q$$ are the points $$(1,3,2)$$ and $$(-1, 0, 8)$$, respectively.
Find the position vector of a point $$R$$ which divides the line joining the two points $$P$$ and $$Q$$ with position vectors $$\bar{OP}=2\bar{a}+\bar{b}$$ and $$\bar{OQ}=\bar{a}-2\bar{b}$$, respectively, in the ratio $$1:2$$ externally.
If $$\vec a$$ is any non zero vector, then $$(\vec a, \hat i)\hat i+(\vec a, \hat j)\hat j +(\vec a, \hat k)\hat k$$ equals ______ .
The value of the expression $$|\vec a\times \vec b|^2 +(\vec a, \vec b)^2$$ is _______ .
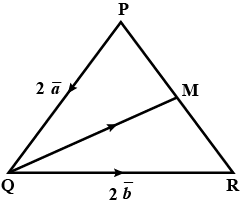
In the triangle $$PQR,\bar {PQ}=\bar {2a},\bar {QR}=\bar{2b}$$. The midpoint of $$PR$$ is $$M$$. Find the following vectors in terms of $$\bar a$$ and $$\bar b$$:
(i) $$\bar {PR}$$ (ii) $$\bar {PM}$$ (iii) $$\bar {QM}$$.
$$\bar{PQ}=\bar{2a},\bar{QR}=\bar{2b}$$
(i) $$\bar{PR}=\bar{PQ}+\bar{QR}$$
$$=2\bar a+2\bar b$$
(ii) $$\because M$$ is the midpoint of $$PR$$
$$\\bar{PM}=\dfrac{1}{2}\bar{PR}=\dfrac{1}{2}[2\bar a+2\bar b]$$
$$=\bar a+\bar b$$
(iii) $$\bar{RM}=\dfrac{1}{2}(\bar{RP})=-\dfrac{1}{2}\bar{PR}=-\dfrac{1}{2}(2\bar a+2\bar b)$$
$$=-\bar a-\bar b$$
$$\therefore \bar{QM}=\bar{QR}+\bar{RM}$$
$$=2\bar b-\bar a-\bar b$$
$$=\bar b-\bar a$$
[note: point (i) answer in the textbook is incorrect.]
(i) $$\bar{PR}=\bar{PQ}+\bar{QR}$$
$$=2\bar a+2\bar b$$
(ii) $$\because M$$ is the midpoint of $$PR$$
$$\\bar{PM}=\dfrac{1}{2}\bar{PR}=\dfrac{1}{2}[2\bar a+2\bar b]$$
$$=\bar a+\bar b$$
(iii) $$\bar{RM}=\dfrac{1}{2}(\bar{RP})=-\dfrac{1}{2}\bar{PR}=-\dfrac{1}{2}(2\bar a+2\bar b)$$
$$=-\bar a-\bar b$$
$$\therefore \bar{QM}=\bar{QR}+\bar{RM}$$
$$=2\bar b-\bar a-\bar b$$
$$=\bar b-\bar a$$
[note: point (i) answer in the textbook is incorrect.]
If $$\bar{p}, \bar{q}$$ and $$\bar{r}$$ are unit vectors and forms a triangle, find $$\bar{p}. \bar{r}$$.
If $$\bar{p}, \bar{q}$$ and $$\bar{r}$$ are unit vectors and forms a triangle, find $$\bar{p}.\bar{q}$$.
Show that the sum of the length of projections of $$p\hat{i}+q\hat{j}+r\hat{k}$$ on the coordinates axes, where $$p=2, q=3$$ and $$r=4$$ is $$9$$.
$$D$$ and $$E$$ divide sides $$BC$$ and $$CA$$ of a triangle $$ABC$$ in the ratio $$2:3$$ each. Find the positive vector of the point of intersection of $$AD$$ and $$BE$$ and the ratio in which this point divides $$AD$$ and $$BE$$.
Let $$AD$$ and $$BE$$ intersect at $$P$$.
Let $$A, B, C, D, E, P$$ have position vectos $$\bar{a}, \bar{b}, \bar{c}, \bar{d}, \bar{e}, \bar{p}$$ respectively.
$$D$$ and $$E$$ divide segment $$BC$$ and $$CA$$ internally in the ratio $$2:3$$.
By the section formula for internal division,
$$\bar{d}=\dfrac{2\bar{c}+3\bar{b}}{2+3}$$
$$\therefore 5\bar{d}=2\bar{c}+3\bar{b}$$ ....(1)
and $$\bar{e}=\dfrac{2\bar{a}+3\bar{c}}{2+3}$$
$$\therefore 5\bar{e}=2\bar{a}+3\bar{c}$$ .....(2)
From $$(1), 5\bar{d}-3\bar{b}=2\bar{c}\therefore 15\bar{d}-9\bar{b}=6\bar{c}$$
From $$(2), 5\bar{e}-2\bar{a}=3\bar{c}\therefore 10\bar{e}-4\bar{a}=6\bar{c}$$
Equating both values of $$6\bar{c}$$, we get
$$15\bar{d}-9\bar{b}=10\bar{e}-4\bar{a}$$
$$\therefore 15\bar{d}+4\bar{a}=10\bar{e}+9\bar{b}$$
$$\therefore \dfrac{15\bar{d}+4\bar{a}}{15+4}=\dfrac{10\bar{e}+9\bar{b}}{10+9}$$
$$LHS$$ is the position vector of the point which divides segment $$AD$$ internally in the ration $$15:4$$.
$$RHS$$ is the position vector of the point which divides segment $$BE$$ internally in the ratio $$10:9$$.
But $$P$$ is the point of intersection of $$AD$$ and $$BE$$.
$$\therefore P$$ divides $$AD$$ internally in the ratio $$15:4$$ and $$P$$ divides $$BE$$ internally in the ratio $$10:9$$.
Hence, the position vector of the point of interaction of $$AD$$ and $$BE$$ is
$$\bar{p}=\dfrac{15\bar{d}+4\bar{a}}{19}=\dfrac{10\bar{e}+9\bar{b}}{19}$$
and it divides $$AD$$ internally in the ratio $$15:4$$ and $$BE$$ internally in the ratio $$10:9$$.
Let $$A, B, C, D, E, P$$ have position vectos $$\bar{a}, \bar{b}, \bar{c}, \bar{d}, \bar{e}, \bar{p}$$ respectively.
$$D$$ and $$E$$ divide segment $$BC$$ and $$CA$$ internally in the ratio $$2:3$$.
By the section formula for internal division,
$$\bar{d}=\dfrac{2\bar{c}+3\bar{b}}{2+3}$$
$$\therefore 5\bar{d}=2\bar{c}+3\bar{b}$$ ....(1)
and $$\bar{e}=\dfrac{2\bar{a}+3\bar{c}}{2+3}$$
$$\therefore 5\bar{e}=2\bar{a}+3\bar{c}$$ .....(2)
From $$(1), 5\bar{d}-3\bar{b}=2\bar{c}\therefore 15\bar{d}-9\bar{b}=6\bar{c}$$
From $$(2), 5\bar{e}-2\bar{a}=3\bar{c}\therefore 10\bar{e}-4\bar{a}=6\bar{c}$$
Equating both values of $$6\bar{c}$$, we get
$$15\bar{d}-9\bar{b}=10\bar{e}-4\bar{a}$$
$$\therefore 15\bar{d}+4\bar{a}=10\bar{e}+9\bar{b}$$
$$\therefore \dfrac{15\bar{d}+4\bar{a}}{15+4}=\dfrac{10\bar{e}+9\bar{b}}{10+9}$$
$$LHS$$ is the position vector of the point which divides segment $$AD$$ internally in the ration $$15:4$$.
$$RHS$$ is the position vector of the point which divides segment $$BE$$ internally in the ratio $$10:9$$.
But $$P$$ is the point of intersection of $$AD$$ and $$BE$$.
$$\therefore P$$ divides $$AD$$ internally in the ratio $$15:4$$ and $$P$$ divides $$BE$$ internally in the ratio $$10:9$$.
Hence, the position vector of the point of interaction of $$AD$$ and $$BE$$ is
$$\bar{p}=\dfrac{15\bar{d}+4\bar{a}}{19}=\dfrac{10\bar{e}+9\bar{b}}{19}$$
and it divides $$AD$$ internally in the ratio $$15:4$$ and $$BE$$ internally in the ratio $$10:9$$.
Find the position vector of point $$R$$ which divides the line joining the points $$P$$ and $$Q$$ whose position vectors are $$2\hat{i}-\hat{j}-3\hat{k}$$ and $$-5\hat{i}+2\hat{j}-5\hat{k}$$ in the ratio $$3:2$$ is internally.
In $$\triangle OAB, E$$ is the midpoint of $$OB$$ and $$D$$ is the point on $$AB$$ such that $$AD: DB= 2:1$$. If $$OD$$ and $$AE$$ intersect at $$P$$, then determine the ratio $$OP:PD$$ using vector methods.
Let $$A,\ B,\ D,\ E,\ P$$ have position vectors $$\bar {a},\bar {b},\bar {d},\bar {e},\bar {p}$$
w.r.t $$O.$$
$$\because AD:DB=2:1$$
$$\therefore D$$ divides $$AB$$ internally in the ratio $$2:1.$$
Using section formula for internal division, we get
$$\bar {d} = \dfrac {2\bar {b}+\bar {a}}{2+1}$$
$$\bar {d} = 2\bar {b}+\bar {a}$$ .......$$(1)$$
Since $$E$$ is the midpoint of $$OB,\ \bar {e}= \bar {OE} = \dfrac {1}{2}\bar {OB}=\dfrac {\bar {b}}{2}$$
$$\therefore \bar {b} = 2 \bar {e}$$.....$$(2)$$
$$\therefore$$ from $$(1),$$
$$3\bar {d} = 2 (2\bar {e}) + \bar {a}$$.....$$[By\ (2)]$$
$$4\bar {e} + \bar {a} \\ \therefore \dfrac {3\bar {d}+2.\bar {0}}{3+2} = \dfrac {4\bar {e}+\bar {a}}{4+1}$$
$$LHS$$ is the poistion vector of the point which divides $$OD$$ internally in the ration $$3:2.$$
$$RHS$$ is the position vector of the point which divides $$AE$$ internally in the ration $$4:1.$$
But $$OD$$ and $$AE$$ intersect at $$P$$
$$\therefore P$$ divides $$OD$$ internally in the ration $$3:2.$$
Hence, $$OP:PD=3:2.$$
w.r.t $$O.$$
$$\because AD:DB=2:1$$
$$\therefore D$$ divides $$AB$$ internally in the ratio $$2:1.$$
Using section formula for internal division, we get
$$\bar {d} = \dfrac {2\bar {b}+\bar {a}}{2+1}$$
$$\bar {d} = 2\bar {b}+\bar {a}$$ .......$$(1)$$
Since $$E$$ is the midpoint of $$OB,\ \bar {e}= \bar {OE} = \dfrac {1}{2}\bar {OB}=\dfrac {\bar {b}}{2}$$
$$\therefore \bar {b} = 2 \bar {e}$$.....$$(2)$$
$$\therefore$$ from $$(1),$$
$$3\bar {d} = 2 (2\bar {e}) + \bar {a}$$.....$$[By\ (2)]$$
$$4\bar {e} + \bar {a} \\ \therefore \dfrac {3\bar {d}+2.\bar {0}}{3+2} = \dfrac {4\bar {e}+\bar {a}}{4+1}$$
$$LHS$$ is the poistion vector of the point which divides $$OD$$ internally in the ration $$3:2.$$
$$RHS$$ is the position vector of the point which divides $$AE$$ internally in the ration $$4:1.$$
But $$OD$$ and $$AE$$ intersect at $$P$$
$$\therefore P$$ divides $$OD$$ internally in the ration $$3:2.$$
Hence, $$OP:PD=3:2.$$
Find the position vector of point $$R$$ which divides the line joining the points $$P$$ and $$Q$$ whose position vectors are $$2\hat{i}-\hat{j}-3\hat{k}$$ and $$-5\hat{i}+2\hat{j}-5\hat{k}$$ in the ratio $$3:2$$ is externally.
Find the position vector of midpoint $$M$$ joining the points $$L(7,-6,12)$$ and $$N(5,4,-2)$$.
The position vector of points $$A$$ and $$B$$ are $$6\bar{a}+2\bar{b}$$ and $$\bar{a}-3\bar{b}$$. If the point $$C$$ divides $$AB$$ in the ratio $$3:2$$, show that the position vector of $$C$$ is $$3\bar{a}-\bar{b}$$.
Find $$\bar u.\bar v$$ if $$|\bar u|=2, |\bar v|=5,|\bar u\times \bar n|=8$$
Prove that $$\left[\bar{a}\ \ \ \ \bar{b}+\bar{c}\ \ \ \ \ \bar{a}+\bar{b}+\bar{c}\right]=0$$
Find $$\bar{a}. (\bar{b}\times \bar{c})$$ if $$\bar{a}=3\hat{i}-\hat{j}+4\hat{k}, \bar{b}=2\hat{i}+3\hat{j}-\hat{k}$$ and $$\bar{c}=-5\hat{i}+2\hat{j}+3\hat{k}$$
If $$\bar a=\hat i+\hat j+\hat k$$ and $$\bar c=\hat j-\hat k$$, find $$\bar a$$ vector $$\bar b$$ satisfying $$\bar a\times \bar b=\bar c$$ and $$\bar a.\bar b=3$$
If $$\bar{u}=\hat{i}-2\hat{j}+\hat{k}, \bar{r}=3\hat{i}+\hat{k}$$ and $$\bar{w}=\hat{j}-\hat{k}$$ are given vectors, then find $$(\bar{u}+\bar{w}).\left[(\bar{u}\times \bar{r})\times (\bar{r}\times \bar{w})\right]$$
If $$\bar{a}=\hat{i}+2\hat{j}+3\hat{k}, \bar{b}=3\hat{i}+2\hat{j}$$ and $$\bar{c}=2\hat{i}+\hat{j}+3\hat{k}$$, then verify that $$\bar{a}\times (\bar{b}\times \bar{c})=(\bar{a}.\bar{c})\bar{b}-(\bar{a}.\bar{b})\bar{c}$$
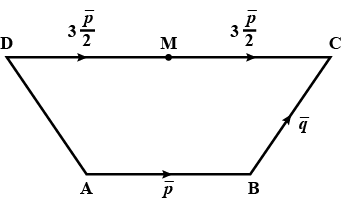
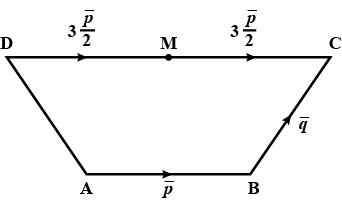
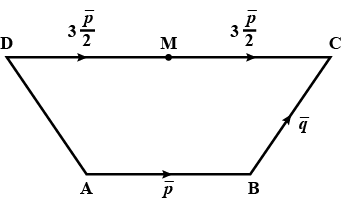
$$ABCD$$ is a trapezium with $$AB$$ parallel to $$DC$$ and $
$$DC=3AB$$. $$M$$ is the midpoint of $$DC.\ \overline {AB}=
\overline {p},\ \overline {BC}=\overline {q}.$$Find in terms of $$\overline {p}$$ and $$\overline {q}$$:$$\overline {DA}$$
$$DC$$ is parallel to $$AB$$ and $$DC=3AB$$
$$\because \overline {AB} = \overline {p}\ \therefore \overline {DC}=3AB.$$
$$M$$ is the midpoint of $$DC$$
$$\therefore \overline {DM} = \overline {MC} = \dfrac {1}{2} \overline {DC}=\dfrac {3}{2} \overline {p}$$
$$(i)\ \overline {AM} = \overline {AM}+\overline {BC}+\overline {CM}$$
$$\overline {AB}+\overline {BC}-\overline {MC}$$
$$\overline {p}+\overline {q}-\overline {\dfrac {3p}{2}}$$
$$\overline {q}-\dfrac {1}{2}\overline {p}$$
$$(iv)\ \overline {DA}=\overline {DC}+\overline {CB}+\overline {BA}=\overline {DC}-\overline {BC}-\overline {AB}=3\overline {p}-\overline {q}-\overline {p}=2\overline {p}-\overline {q}$$
$$\because \overline {AB} = \overline {p}\ \therefore \overline {DC}=3AB.$$
$$M$$ is the midpoint of $$DC$$
$$\therefore \overline {DM} = \overline {MC} = \dfrac {1}{2} \overline {DC}=\dfrac {3}{2} \overline {p}$$
$$(i)\ \overline {AM} = \overline {AM}+\overline {BC}+\overline {CM}$$
$$\overline {AB}+\overline {BC}-\overline {MC}$$
$$\overline {p}+\overline {q}-\overline {\dfrac {3p}{2}}$$
$$\overline {q}-\dfrac {1}{2}\overline {p}$$
$$(iv)\ \overline {DA}=\overline {DC}+\overline {CB}+\overline {BA}=\overline {DC}-\overline {BC}-\overline {AB}=3\overline {p}-\overline {q}-\overline {p}=2\overline {p}-\overline {q}$$
$$ABCD$$ is a trapezium with $$AB$$ parallel to $$DC$$ and
$$DC=3AB$$. $$M$$ is the midpoint of $$DC.\ \overline {AB}=
\overline {p},\ \overline {BC}=\overline {q}.$$Find in terms of $$\overline {p}$$ and $$\overline {q}$$:$$\overline {MB}$$
$$DC$$ is parallel to $$AB$$ and $$DC=3AB$$
$$\because \overline {AB} = \overline {p}\ \therefore \overline {DC}=3AB.$$
$$M$$ is the midpoint of $$DC$$
$$\therefore \overline {DM} = \overline {MC} = \dfrac {1}{2} \overline {DC}=\dfrac {3}{2} \overline {p}$$
$$(i)\ \overline {AM} = \overline {AM}+\overline {BC}+\overline {CM}$$
$$\overline {AB}+\overline {BC}-\overline {MC}$$
$$\overline {p}+\overline {q}-\overline {\dfrac {3p}{2}}$$
$$\overline {q}-\dfrac {1}{2}\overline {p}$$
$$(iii)\ \overline {MB}=\overline {MC}+\overline {CB}=\overline {MC}-\overline {BC}=\dfrac {3}{2}\overline {p}-\overline {q}$$
$$\because \overline {AB} = \overline {p}\ \therefore \overline {DC}=3AB.$$
$$M$$ is the midpoint of $$DC$$
$$\therefore \overline {DM} = \overline {MC} = \dfrac {1}{2} \overline {DC}=\dfrac {3}{2} \overline {p}$$
$$(i)\ \overline {AM} = \overline {AM}+\overline {BC}+\overline {CM}$$
$$\overline {AB}+\overline {BC}-\overline {MC}$$
$$\overline {p}+\overline {q}-\overline {\dfrac {3p}{2}}$$
$$\overline {q}-\dfrac {1}{2}\overline {p}$$
$$(iii)\ \overline {MB}=\overline {MC}+\overline {CB}=\overline {MC}-\overline {BC}=\dfrac {3}{2}\overline {p}-\overline {q}$$
If $$\bar {a},\ \bar {b},\ \bar {c}$$ are unit vectors such that $$\bar
{a}+\bar {b}+\bar {c}=\bar {0},$$ then find the value of $$\bar {a}.
\bar {b}+\bar {b}.\bar {c}+\bar {c}.\bar {a}.$$
In a parallelogram $$ABCD,$$ diagonal vectors are $$\overline
{AC}=2\hat {i}+3\hat {j}+4\hat {k}$$ and $$\overline {BD}=-6\hat
{i}+7\hat {j}-2\hat {k}$$ then find the adjacent side vectors $$
\overline {AB}$$ and $$\overline {AD}$$.
$$ABCD$$ is a parallelogram.
$$\therefore \overline {AB}=\overline {DC},\ \overline {AD}=\overline {BC}$$
$$\overline {AC}=\overline {AB}+\overline {BC}$$
$$\overline {AB}+\overline {AD} ...(1)$$
$$\overline {BD}=\overline {BA}+\overline {AD}=-\overline {AB}+\overline {AD} ...(2)$$
Adding $$(1)$$ and $$(2)$$, we get
$$2\overline {AD}=\overline {AC}+\overline {BD}= (2\overline {i}+3\overline {j}+4\overline {k})+(-6\overline {i}+7\overline {j}-2\overline {k})$$
$$=-4\overline {i}+10\overline {j}+2\overline {k}$$
$$\therefore \overline {AD}=\dfrac {1}{2}(-4\overline {i}+10\overline {j}+2\overline {k})$$
$$=-2\overline {i}+5\overline {j}+\overline {k}$$
From $$(1),\ \overline {AB}=\overline {AC}-\overline {AD}$$
$$=(2\overline {i}+3\overline {j}+4\overline {k})-(-2\overline {i}+5\overline {j}+\overline {k})$$
$$=4\overline {i}-2\overline {j}+3\overline {k}$$
$$\therefore \overline {AB}=\overline {DC},\ \overline {AD}=\overline {BC}$$
$$\overline {AC}=\overline {AB}+\overline {BC}$$
$$\overline {AB}+\overline {AD} ...(1)$$
$$\overline {BD}=\overline {BA}+\overline {AD}=-\overline {AB}+\overline {AD} ...(2)$$
Adding $$(1)$$ and $$(2)$$, we get
$$2\overline {AD}=\overline {AC}+\overline {BD}= (2\overline {i}+3\overline {j}+4\overline {k})+(-6\overline {i}+7\overline {j}-2\overline {k})$$
$$=-4\overline {i}+10\overline {j}+2\overline {k}$$
$$\therefore \overline {AD}=\dfrac {1}{2}(-4\overline {i}+10\overline {j}+2\overline {k})$$
$$=-2\overline {i}+5\overline {j}+\overline {k}$$
From $$(1),\ \overline {AB}=\overline {AC}-\overline {AD}$$
$$=(2\overline {i}+3\overline {j}+4\overline {k})-(-2\overline {i}+5\overline {j}+\overline {k})$$
$$=4\overline {i}-2\overline {j}+3\overline {k}$$
A point $$P$$ with position vector $$\dfrac {-14\hat {i}+39\hat
{j}+28\hat {k}}{5}$$ divides the line joining $$A\ (1,\ 6,\ 5)$$ and
$$B$$ in the ration $$3:2,$$ then find the point $$B.$$
State whether the expression is meaningful. If not, explain why? If so,
state whether it is a vector or a scalar :$$\overline {a}. (\overline {b} . \overline {c})$$
If $$\left| \bar { a } \right| = \left| \bar { b } \right| =1,\ \bar{a}.\bar
{b}=0,\ \bar{a}+\bar{b}+\bar{c}=\bar{0},$$ find $$\left| \bar { c }
\right|.$$
State whether the expression is meaningful. If not, explain why? If so,
state whether it is a vector or a scalar :$$\overline {a}.(\overline {b} \times \overline {c})$$
$$ABCD$$ is a trapezium with $$AB$$ parallel to $$DC$$ and $$DC=3AB$$. $$M$$ is the midpoint of $$DC.\ \overline {AB}=\overline {p},\ \overline {BC}=\overline {q}.$$Find in terms of $$\overline {p}$$ and $$\overline {q}$$:$$\overline {BD}$$
$$DC$$ is parallel to $$AB$$ and $$DC=3AB$$
$$\because \overline {AB} = \overline {p}\ \therefore \overline {DC}=3AB.$$
$$M$$ is the midpoint of $$DC$$
$$\therefore \overline {DM} = \overline {MC} = \dfrac {1}{2} \overline {DC}=\dfrac {3}{2} \overline {p}$$
$$(i)\ \overline {AM} = \overline {AM}+\overline {BC}+\overline {CM}$$
$$\overline {AB}+\overline {BC}-\overline {MC}$$
$$\overline {p}+\overline {q}-\overline {\dfrac {3p}{2}}$$
$$\overline {q}-\dfrac {1}{2}\overline {p}$$
$$(ii)\ \overline {BD}=\overline {BC}+\overline {CD}=\overline {BC}-\overline {CD}=\overline {q}-3\overline {p}$$
$$\because \overline {AB} = \overline {p}\ \therefore \overline {DC}=3AB.$$
$$M$$ is the midpoint of $$DC$$
$$\therefore \overline {DM} = \overline {MC} = \dfrac {1}{2} \overline {DC}=\dfrac {3}{2} \overline {p}$$
$$(i)\ \overline {AM} = \overline {AM}+\overline {BC}+\overline {CM}$$
$$\overline {AB}+\overline {BC}-\overline {MC}$$
$$\overline {p}+\overline {q}-\overline {\dfrac {3p}{2}}$$
$$\overline {q}-\dfrac {1}{2}\overline {p}$$
$$(ii)\ \overline {BD}=\overline {BC}+\overline {CD}=\overline {BC}-\overline {CD}=\overline {q}-3\overline {p}$$
If $$D,\ E,\ F$$ are the midpoints of the sides $$BC,\ CA,\ AB$$ of a
triangle $$ABC,$$ prove that $$\overline {AD}+\overline {BE}+
\overline {CF}=\overline {0}.$$
State whether the expression is meaningful. If not, explain why? If so,
state whether it is a vector or a scalar :$$\left| \bar { a } \right| (\overline {b} . \overline {c})$$
State whether the expression is meaningful. If not, explain why? If so,
state whether it is a vector or a scalar :$$\bar { a }.\bar { b }+\bar { c }$$
State whether the expression is meaningful. If not, explain why? If so,
state whether it is a vector or a scalar :$$(\overline {a} . \overline {b}). \overline {c}$$
Prove that $$(\overline {a} \times \overline {b}).(\overline {c} \times
\overline {d}) = \begin{vmatrix} \bar { a } .\bar { c } & \bar { b } .\bar
{ c } \\ \bar { a } .\bar { d } & \bar { b } .\bar { d } \end{vmatrix}.$$
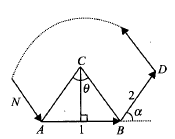
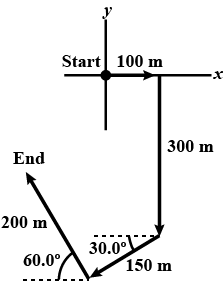
A person going for a walk follows the path shown in above figure. The total trip consists of four straight line paths. At the end of the walk, what is the persons resultant displacement measured from the starting point.
On our version of the diagram we have drawn in the resultant from the tail of the first arrow to the head of the last arrow.
The resultant displacement $$\vec{R}$$ is equal to the sum of the four individual displacements,
$$\vec{R}=\vec{d}_{1}+\vec{d}_{2}+\vec{d}_{3}+\vec{d}_{4}$$. We translate from the pictorial representation to a mathematical representation by writing the individual displacements in
unit-vector notation:
$$\vec{d}_{1} = 100\hat{i} m$$
$$\vec{d}_{2}= −300\hat{j} m$$
$$\vec{d}_{3} = (−150 \cos 30^{0})\hat{i} m+ ( − 150 \sin 30^{0})\hat{j} m = –130\hat{i} m − 75\hat{j} m$$
$$\vec{d}_{4}= (− 200 \cos60^{0})\hat{i} m + (200 \sin60^{0})\hat{j} m = − 100\hat{i} m + 173\hat{j} m$$
Summing the components together, we find
$$R_{x} = d_{1x} + d_{2x} + d_{3x} + d_{4x} = (100 + 0 − 130 − 100) m = − 130m$$
$$R_{y} = d_{1y} + d_{2y} + d_{3y} + d_{4y} = (0 − 300 − 75 + 173) m = –202 m$$
so altogether
$$\vec{R}=\vec{d}_{1}+\vec{d}_{2}+\vec{d}_{3}+\vec{d}_{4} = (−130\hat{i} − 202\hat{j})m$$
Its magnitude is
$$|\vec{R}|=\sqrt{(-130)^{2}+(-202)^{2}}=240m$$
We calculate the angle $$\phi=\tan^{-1}\left ( \dfrac{R_{y}}{R_{x}} \right )=\tan^{-1}\left ( \dfrac{-202}{-130} \right )=57.2^{0}$$
The resultant points into the third quadrant instead of the first quadrant. The angle counter clockwise from the $$+x$$ axis is
$$\theta = 180 +\phi = 237^{0}$$
The resultant displacement $$\vec{R}$$ is equal to the sum of the four individual displacements,
$$\vec{R}=\vec{d}_{1}+\vec{d}_{2}+\vec{d}_{3}+\vec{d}_{4}$$. We translate from the pictorial representation to a mathematical representation by writing the individual displacements in
unit-vector notation:
$$\vec{d}_{1} = 100\hat{i} m$$
$$\vec{d}_{2}= −300\hat{j} m$$
$$\vec{d}_{3} = (−150 \cos 30^{0})\hat{i} m+ ( − 150 \sin 30^{0})\hat{j} m = –130\hat{i} m − 75\hat{j} m$$
$$\vec{d}_{4}= (− 200 \cos60^{0})\hat{i} m + (200 \sin60^{0})\hat{j} m = − 100\hat{i} m + 173\hat{j} m$$
Summing the components together, we find
$$R_{x} = d_{1x} + d_{2x} + d_{3x} + d_{4x} = (100 + 0 − 130 − 100) m = − 130m$$
$$R_{y} = d_{1y} + d_{2y} + d_{3y} + d_{4y} = (0 − 300 − 75 + 173) m = –202 m$$
so altogether
$$\vec{R}=\vec{d}_{1}+\vec{d}_{2}+\vec{d}_{3}+\vec{d}_{4} = (−130\hat{i} − 202\hat{j})m$$
Its magnitude is
$$|\vec{R}|=\sqrt{(-130)^{2}+(-202)^{2}}=240m$$
We calculate the angle $$\phi=\tan^{-1}\left ( \dfrac{R_{y}}{R_{x}} \right )=\tan^{-1}\left ( \dfrac{-202}{-130} \right )=57.2^{0}$$
The resultant points into the third quadrant instead of the first quadrant. The angle counter clockwise from the $$+x$$ axis is
$$\theta = 180 +\phi = 237^{0}$$
Suppose $$\overline {a}\neq \overline {0}:$$ If $$\overline {a}.\overline {b}=\overline {a}.\overline {c},$$ then is
$$\overline {b}=\overline {c} \ ?$$.
State whether the expression is meaningful. If not, explain why? If so,
state whether it is a vector or a scalar :$$(\overline {a} \times \overline {b}) . (\overline {c} \times \overline
{d})$$
State whether the expression is meaningful. If not, explain why? If so,
state whether it is a vector or a scalar :$$(\overline {a} . \overline {b}) \overline {c}$$
State whether the expression is meaningful. If not, explain why? If so,
state whether it is a vector or a scalar :$$\bar { a }.(\overline {b} + \overline {c})$$
Suppose $$\overline {a}=\overline {0}:$$If $$\overline {a}.\overline {b}=\overline {a}.\overline {c},$$ and $$
\overline {a}\times \overline {b}=\overline {a}\times \overline {c}$$
then is $$\overline {b}=\overline {c} \ ?$$.
Find the sum of the vector
$$ \overrightarrow {a} = \hat {i} - 2 \hat {j} + \hat {k},\ \ \overrightarrow {b} = -2\hat {i} + 4 \hat {j} + 5 \hat {k} $$ and $$ \overrightarrow {c} = \hat {i} - 6 \hat {j} - 7 \hat {k} $$
Find the position vector of a vector of a point R which divides the line joining two points P and Q whose position vectors are $$ ( 2a + b) $$ and $$ 9 \overrightarrow {a} - 3 \overrightarrow {b}) $$ externally in the ratio $$ 1 : 2 $$ also show that P is the mid point of the line segment $$ RQ $$
$$ ( 2a + \bar {b}) \quad \quad ( \bar {a} - 3 \bar {b}) $$
$$ \frac { 1( 7bar {a} - 3 \bar {b}) - 2( 2 \bar {a} + \bar {b}) }{ 1 -2 } , \frac { -3 \bar {a} - 5 \bar {b} }{-1} = 3 \bar {a} + 5 \bar {b} $$
$$ \therefore $$ p.v. of R $$ ( 3 \bar {a} + 5 \bar {b} ) $$
$$ \frac { 1( 7bar {a} - 3 \bar {b}) - 2( 2 \bar {a} + \bar {b}) }{ 1 -2 } , \frac { -3 \bar {a} - 5 \bar {b} }{-1} = 3 \bar {a} + 5 \bar {b} $$
$$ \therefore $$ p.v. of R $$ ( 3 \bar {a} + 5 \bar {b} ) $$
Find $$ | \overrightarrow {a} | $$ and $$ | \overrightarrow {b} | $$ , if $$ ( \overrightarrow {a} + \overrightarrow {b} ) . ( \overrightarrow {a} - \overrightarrow {b} ) = 8 $$ and $$ | \overrightarrow {a} | = 8 | \overrightarrow {b} | $$
$$ \overrightarrow {a} = \overrightarrow {b} + \overrightarrow {c} $$ then is it true that $$ | \overrightarrow {a} | = | \overrightarrow {b} |+ | \overrightarrow {c} | $$ justify your answer.
$${\textbf{Step-1: Find relation with help of diagram.}}$$
$${\text{Given,}}$$
$${\text{In}}$$ $$ΔABC,$$ $${\text{let}}$$ $$\bar CB=\bar a, \bar CA=\bar b,$$ $${\text{and}}$$ $$\bar AB=\bar c$$ $${\text{(as shown in the following figure).}}$$
$${\text{Now, by the triangle law of vector addition, we have}}$$ $$\bar a= \bar b+\bar c.$$
$${\textbf{Step-2: Show true or false for that given condition.}}$$
$${\text{It is clearly known that}}$$ $$∣\bar a∣,∣\bar b∣,$$ $${\text{and}}$$ $$∣\bar c∣$$ $${\text{represent the sides of ΔABC.}}$$
$${\text{Also, it is known that the sum of the lengths of any two sides}}$$
$${\text{of a triangle is greater than the third side.}}$$
$$∴∣\bar a∣<∣\bar b∣+∣\bar c|$$
$${\text{Hence, it is not true that}}$$ $$∣\bar a∣=∣\bar b∣+∣\bar c∣.$$
$${\textbf{ Hence, it is not true that}}$$ $${\mathbf{∣\bar a∣=∣\bar b∣+∣\bar c∣.}}$$
if either vector $$ \overrightarrow {a} = \overrightarrow {0} $$ or $$ \overrightarrow {b} = \overrightarrow {0} $$ then $$ \overrightarrow {a}. \overrightarrow {b} = \overrightarrow {0} $$ but the converse need not be true. justify your answer with an example.
Given that $$ \overrightarrow {a} . \overrightarrow {b} = 0 $$ and $$ \overrightarrow {a} \times \overrightarrow {b} = \overrightarrow {0 } $$ when can you conclude about the vectors $$ \overrightarrow {a} $$ and $$ \overrightarrow {b} $$
Evaluate the product
$$ (3\overrightarrow { a } -5\overrightarrow { b } ).(2\overrightarrow { a } +7\overrightarrow { b } )$$
Find the $$| \overrightarrow {x} | $$ if a is a unit vector $$ \overrightarrow {a} , ( \overrightarrow {x} - \overrightarrow {a} ) $$ . $$ ( \overrightarrow {x} + \overrightarrow {a}) = 12 $$
If magnitude of two vectors be $$4$$ and $$5$$ units, then find scalar product of them, where angle between them be:
$$60^{o}$$
Find $$\overrightarrow {a}. \vec{b}$$, if $$\overrightarrow{a}$$ and $$\vec{b}$$ are as follows:
$$5\hat{i}+\hat{j}-2\hat{k}; 2\hat{i}-3\hat{j}$$
Find $$ \bar {a}. \bar {b} $$ of $$ | \bar {a}| = 3 , | \bar {b} | = 4 , | \bar {a} \times b| = 6 $$
Find $$\overrightarrow {a}. \vec{b}$$, if $$\overrightarrow{a}$$ and $$\vec{b}$$ are as follows:
$$4\hat{i}+3\hat{k}; \hat{i}-\hat{j}+\hat{k}$$
If magnitude of two vectors be $$4$$ and $$5$$ units, then find scalar product of them, where angle between them be:
$$90^{o}$$
Write the projection of $$ i - j $$ on $$ i + j $$
Write the value of $$ ( i \times j) . \bar {k} + i . j $$
If magnitude of two vectors be $$4$$ and $$5$$ units, then find scalar product of them, where angle between them be:
$$30^{o}$$
Find $$\overrightarrow {a}. \vec{b}$$, if $$\overrightarrow{a}$$ and $$\vec{b}$$ are as follows:
$$2\hat{i}+5\hat{j}; 3\hat{i}-2\hat{j}$$
Prove that:
$$|\vec{a}.\vec{b}|^{2}\le |\vec{a}|^{2} |\vec{b}|^{2}$$
If $$\vec{a}=0$$ or $$\vec{b}=0$$, then
identify $$|\vec{a}.\vec{b}|=0=|\vec{a}||\vec{b}|$$
But here let $$|\vec{a}|\neq 0\neq |\vec{b}|$$
Then we know that
$$\vec{a}.\vec{b}=|\vec{a}||\vec{b}|\cos \theta$$
[where $$\theta$$ be the angle between $$\vec{a}$$ and $$\vec{b}$$]
or $$\dfrac{|\vec{a}.\vec{b}|}{|\vec{a}||\vec{b}|}=|\cos \theta|\le 1[\because -1\le \cos \theta \le 1]$$
$$\therefore |\vec{a}.\vec{b}|\le |\vec{a}||\vec{b}|$$
Squaring on both sides
$$|\vec{a}.\vec{b}|^{2}\le |\vec{a}|^{2}|\vec{b}|^{2}$$
identify $$|\vec{a}.\vec{b}|=0=|\vec{a}||\vec{b}|$$
But here let $$|\vec{a}|\neq 0\neq |\vec{b}|$$
Then we know that
$$\vec{a}.\vec{b}=|\vec{a}||\vec{b}|\cos \theta$$
[where $$\theta$$ be the angle between $$\vec{a}$$ and $$\vec{b}$$]
or $$\dfrac{|\vec{a}.\vec{b}|}{|\vec{a}||\vec{b}|}=|\cos \theta|\le 1[\because -1\le \cos \theta \le 1]$$
$$\therefore |\vec{a}.\vec{b}|\le |\vec{a}||\vec{b}|$$
Squaring on both sides
$$|\vec{a}.\vec{b}|^{2}\le |\vec{a}|^{2}|\vec{b}|^{2}$$
Prove that
$$\begin{bmatrix} \hat i & \hat j & \hat k\end{bmatrix}+\begin{bmatrix} \hat i & \hat k & \hat j\end{bmatrix}=0$$
If for a vetoer $$\vec a, (\vec x-\vec a). (\vec x +\vec a)=12$$, then $$|\vec x|$$.
If vertices $$\vec a, \vec b, \vec c$$ are such that
$$\vec a+\vec b+\vec c=\vec 0$$
then, find the value of $$\vec a. \vec b+\vec b. \vec c+\vec c. \vec a$$.
Find the projection of the vector
$$4\hat{i}-2\hat{j}+\hat{k}$$
on the vector
$$3\hat{i}+6\hat{j}-2\hat{k}$$
Find projection vector on vector
$$\hat i +3\hat j +7\hat k$$
on vector
$$7\hat i -\hat j+8\hat k$$
Find the value of
$$(3\vec a -5\vec b). (2\vec a +7\vec b)$$
Find the projection of vector
$$\hat i-\hat j$$ on $$\hat i +\hat j$$
Use vectors to prove the sum of square of diagonal of a parallelogram is equal to be the sum of square of their side.
Let $$OACB$$ is a parallelogram. Taking $$O$$ as origin, the position vectors of $$A$$ and $$B$$ are $$\vec{a}$$ and $$\vec{b}$$ respectively.
Let $$\vec{OA}=\vec{BC}=\vec{a}$$
and $$\vec{OB}=\vec{AC}=\vec{b}$$
then $$\vec{AB}=\vec{b}-\vec{a}$$
$$\vec{OC}=\vec{a}+\vec{b}$$
$$\therefore \vec{OC}^{2}+\vec{AB}^{2}=(\vec{a}+\vec{b})^{2}+(\vec{b}-\vec{a})^{2}$$
$$=2(\vec{a^{2}}+\vec{b^{2}})$$
$$=(\vec{OA^{2}}+\vec{BC^{2}})+(\vec{OB^{2}}+\vec{AC^{2}})$$
$$\therefore$$ Sum of the squares of diagonals= sum of the squares of sides.
Hence the sum of square of diagonals of a parallelogram is equal to the sum of the square of their sides.
Let $$\vec{OA}=\vec{BC}=\vec{a}$$
and $$\vec{OB}=\vec{AC}=\vec{b}$$
then $$\vec{AB}=\vec{b}-\vec{a}$$
$$\vec{OC}=\vec{a}+\vec{b}$$
$$\therefore \vec{OC}^{2}+\vec{AB}^{2}=(\vec{a}+\vec{b})^{2}+(\vec{b}-\vec{a})^{2}$$
$$=2(\vec{a^{2}}+\vec{b^{2}})$$
$$=(\vec{OA^{2}}+\vec{BC^{2}})+(\vec{OB^{2}}+\vec{AC^{2}})$$
$$\therefore$$ Sum of the squares of diagonals= sum of the squares of sides.
Hence the sum of square of diagonals of a parallelogram is equal to the sum of the square of their sides.
For any vector $$\vec{a}$$, prove that
$$\vec{a}=(\vec{a}.\hat{i})\hat{i}+(\vec{a}.\hat{j})\hat{j}+(\vec{a}.\hat{k})\hat{k}$$.
Prove that
$$\begin{bmatrix} 2\hat i & \hat j & \hat k\end{bmatrix}+\begin{bmatrix} \hat i & \hat k & \hat j\end{bmatrix}+\begin{bmatrix} \hat k & \hat j & 2\hat i\end{bmatrix}=0$$
If $$ \vec{a} = 7 \hat{i} + \hat{j} - 4 \hat{k} $$ and $$ \vec{b} = 2 \hat{i} + 6 \hat{j} + 3 \hat{k} $$, then find the projection of $$ \vec{a}$$ on $$ \vec{b}$$.
If two adjacent sides of a triangle are represented by vectors
$$\hat i+2\hat j+2\hat k$$
and
$$3\hat i-2\hat j+\hat k$$,
then find the area of triangle.
For any vector $$\vec a$$, prove that
$$|\vec a\times \hat i|^2+|\vec a\times \hat j|^2+|\vec a\times \hat k|^2=2|\vec a|^2$$
If $$\vec a=2\hat i -3\hat j +4\hat k, \vec b=\hat i+2\hat j -\hat k$$ and $$\vec c=3\hat i -\hat j+2\hat k$$, then find $$\begin{bmatrix} \vec a & \vec b & \vec c \end{bmatrix}$$.
Match the statement of Column I with values of Column II.
$$\vec{a}$$ and $$\vec{b}$$ form the consecutive sides of a regular hexagon ABCDEF.
$$\vec{AB} = \vec{a}, \vec{BC} = \vec{b}$$
$$\vec{AB} = \vec{a}, \vec{BC} = \vec{b}$$
$$\vec{AC} =\vec{AB} + \vec{BC} = \vec{a} + \vec{a}$$ (i)
$$\vec{AD} = 2 \vec{BC} = 2 \vec{b}$$ (ii)
(because AD is parallel to BC and twice its length).
$$\vec{CD} = \vec{AD} - \vec{AC} = 2 \vec{b} - (\vec{a} + \vec{b}) = \vec{b} -\vec{a}$$
$$\vec{FA} = - \vec{CD} = \vec{a} - \vec{b}$$ (iii)
$$\vec{DE} = - \vec{AB} = - \vec{a}$$ (iv)
$$\vec{EF} = - \vec{BC} = -\vec{b}$$ (v)
$$\vec{AE} = \vec{AD} + \vec{DE} = 2 \vec{b} - \vec{a}$$ (vi)
$$\vec{CE} = \vec{CD} + \vec{DE} = \vec{b} - \vec{A} - \vec{A} = \vec{b} - 2 \vec{a}$$ (vii)
$$\vec{AC} =\vec{AB} + \vec{BC} = \vec{a} + \vec{a}$$ (i)
$$\vec{AD} = 2 \vec{BC} = 2 \vec{b}$$ (ii)
(because AD is parallel to BC and twice its length).
$$\vec{CD} = \vec{AD} - \vec{AC} = 2 \vec{b} - (\vec{a} + \vec{b}) = \vec{b} -\vec{a}$$
$$\vec{FA} = - \vec{CD} = \vec{a} - \vec{b}$$ (iii)
$$\vec{DE} = - \vec{AB} = - \vec{a}$$ (iv)
$$\vec{EF} = - \vec{BC} = -\vec{b}$$ (v)
$$\vec{AE} = \vec{AD} + \vec{DE} = 2 \vec{b} - \vec{a}$$ (vi)
$$\vec{CE} = \vec{CD} + \vec{DE} = \vec{b} - \vec{A} - \vec{A} = \vec{b} - 2 \vec{a}$$ (vii)
Write unit vector in the direction of the sum of vectors:
$$\overrightarrow{a}=2\hat{i}-\hat{j}+2\hat{k}$$ and $$\overrightarrow{b} =-\hat{i}+\hat{j}+3\hat{k}$$.
Find the shortest distance between the lines $$\overrightarrow{r}=\hat{i}+2\hat{j}+3\hat{k}+\lambda (2\hat{i}+3\hat{j}+4\hat{k})$$ and $$\overrightarrow{r}=2\hat{i}+4\hat{j}+5\hat{k}+\mu (4\hat{i}+6\hat{j}+8\hat{k})$$.
If $$a+b+c=\alpha d, b+c+d=\beta a$$ and a, b, c are non-coplanar vectors, then show the $$a+b+c+d=0$$.
Show that the line joining the points P and Q with position vectors $$\vec { p } ={ p }_{ 1 }\hat { l } +{ p }_{ 2 }\hat { j } +{ p }_{ 3 }\hat { k }\ and\ \vec { q } ={ q }_{ 1 }\hat { i } +{ q }_{ 2 }\hat { j } +{ q }_{ 3 }\hat { k }$$ passes through the origin if $$\vec { p } \cdot \vec { q } =\left| \vec { p } \right| \left| \vec { q } \right|. $$
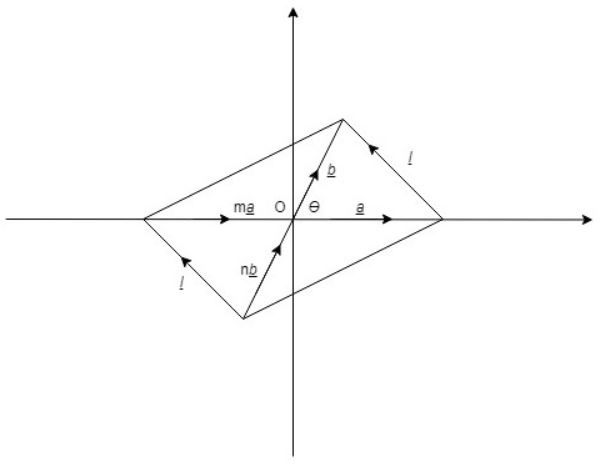
Find $$\, | a \, - \, b |$$ if the vectors a and b makes an angle of $$\displaystyle 120^{\circ} \,and \ | a | \, = \, 3, \, and \, | b | \, = \, 5 \,. $$
Calculate the scalar product of the following vectors.
$$\displaystyle a \, = \, \left \{- 2, 3, 11 \right \} \, and \, b \, = \, \left \{ 5, 7, -4 \right \}$$
Find the value of $$\displaystyle (2\alpha \, + \, 3\beta) \, . \, (4\alpha \, - \, 6\beta), \, where \, \alpha, \, \beta$$ are mutually perpendicular unit vectors.
Find the sin angle between the vectors $$A = 3i - 4j + 5k$$ and $$B = i - j + k$$?
Prove that for any three vectors a, b, c [b + c c + a a + b] = 2 [abc].
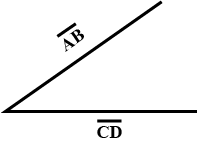
If $$\hat {i}+\hat {j}+\hat {k},\ 2\hat {i}+5\hat {j},\ 3\hat {i}+2\hat {j}-3\hat {k}$$ and $$\hat {i}-6\hat {j}-\hat {k}$$ are the position vectors of points $$A,B,C$$ and $$D$$ respectively, then find the angel between $$\overline {AB}$$ and $$\overline {CD}$$. Deduce that $$\overline {AB}$$ and $$\overline {CD}$$ are collinear.
Find $$|\vec{a}\times \vec{b}|$$ if $$|\vec{a}|=10$$, $$|\vec{b}|=2$$ and $$\vec{a}\cdot \vec{b}=12$$.
If $$\vec { a }$$ and $$\vec { b }$$ are non-collinear and $$\overline { A } = ( x + 4 y ) \overline { a } + ( 2 x + y + 1 ) \vec { b }$$ and $$\vec { \mathrm { B } } = ( y - 2 x + 2 ) \vec { a } + ( 2 x - 3 y - 1 )b $$ Find $$x$$ and $$y$$ such that $$3 \vec { A } = 2 \vec { B }$$
The values of $$\lambda$$ such than $$(x,y,z)\neq (0,0,0)\\ $$ and $$(\hat { i+ } \hat { j } +3\hat { k } )x+(3\hat { i } -3\hat { j } +\hat { k } )y+(-4\hat { i } +5\hat { j } )z=\lambda (x\hat { i } +y\hat { j } +z\hat { k } )$$ are
If $$ \overline{a}, \vec{b}, \vec{c} $$ are unit vectors such that $$ \overline{a}+ \vec{b}+ \vec{c} $$, find the value of $$ \vec{a} \cdot \vec{b}+\vec{b} \cdot \vec{c}+\overline{c} \cdot \vec{c} $$.
Prove that: $$ \left[ \begin{array} { l l l } { \overline { x } + \overline { y } } & { \overline { y } + \overline { z } } & { \overline { z } + \overline { x } } \end{array} \right] = 2 \left[ \begin{array} { l l } { \overline { x } \overline { y } \overline { z } } \end{array} \right] $$
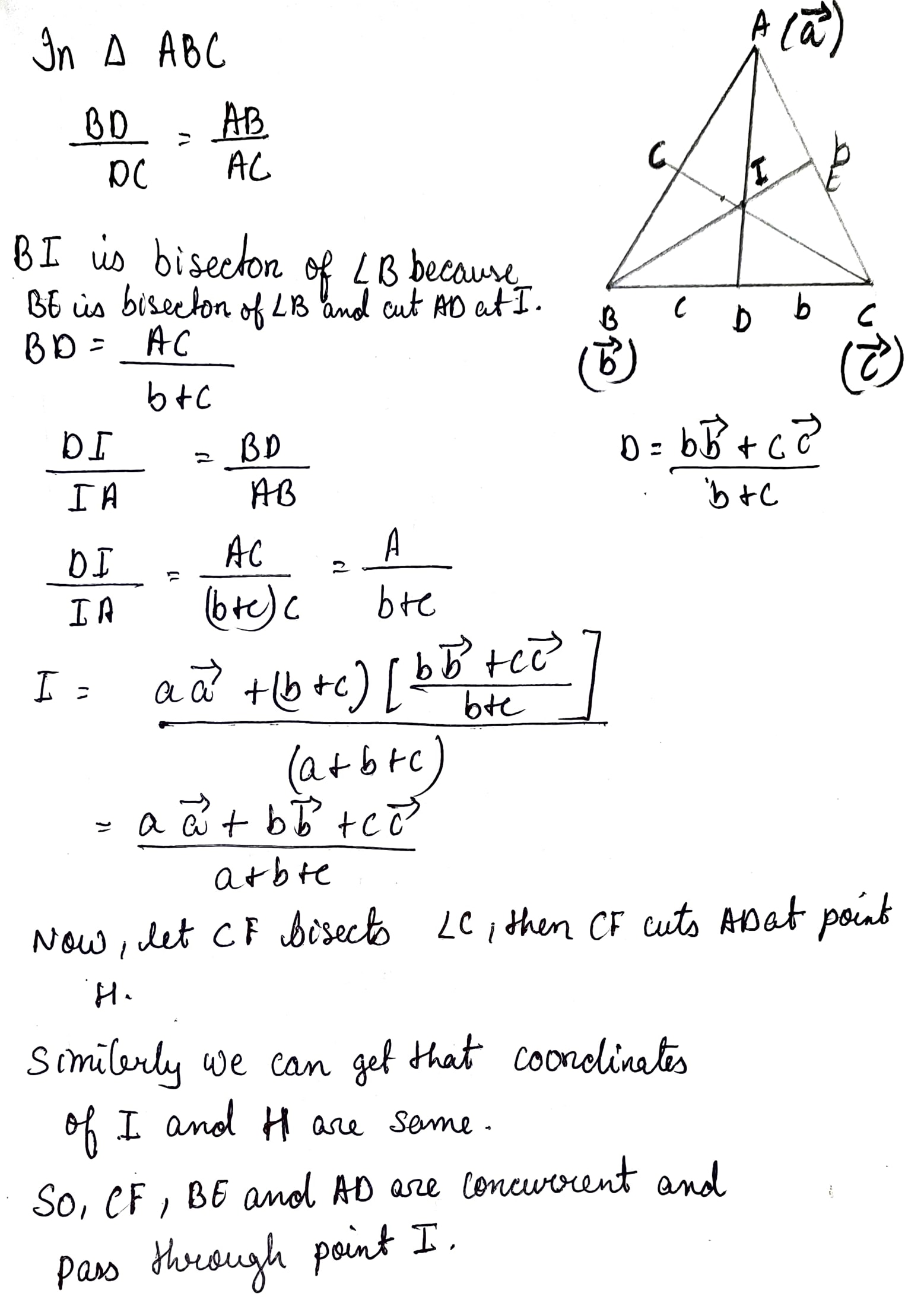
Show, by vector method, that the angular bisectors of a triangle are concurrent and find an expression for the position vector of the point of concurrency in terms of the position vectors of the vertices.
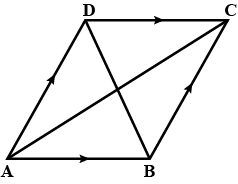
Let OACB be a parallelogram with O at the origin and OC a diagonal. Let D be the midpoint of OA Using vector methods prove that BD and CO intersect in the same ratio. Determine this ratio. (IIT - JEE, 1993)
Show that the four points P, Q, R, S with position vectors $$\vec{p},\vec{q},\vec{r},\vec{s}$$ respectively such that $$5\vec{p}-2\vec{q}+6\vec{r}-9\vec{s} = \vec{0},$$ are coplanar. Also, find the position vector of the point of intersection of the line segments PR and QS.
If $$\vec{a}, \vec{b}$$ are the position vectors of A, B respectively, find the position vector of a point C in AB produced such that AC = 3 AB and that a point D in BA produced such that BD = 2 BA.
Prove, by vector method or otherwice, that the point of intersection of the diagonals of a trapezium lies on the line passing through the midpoint of the parallel sides (you may assume that the trapezium is not a parallelogram)
If $$\vec{e}_1, \vec{e}_2, \vec{e}_3$$ and $$\vec{E}_1, \vec{E}_2, \vec{E}_3$$ are two sets of vectors such that $$\vec{e}_i . \vec{E}_j$$, if i = j and $$\vec{e}_i . \vec{E}_j = 0$$ and if $$i \neq j$$, then prove that $$[\vec{e}_1 \vec{e}_2 \vec{e}_3][\vec{E}_1 \vec{E}_2 \vec{E}_3] = 1$$
Find the vector equation of the plane passing through the points $$\hat{i}+\hat{j}-3\hat{k},\hat{i}+2\hat{j}+\hat{k},2\hat{i}-\hat{j}+\hat{k}$$
Class 12 Commerce Maths Extra Questions
- Application Of Derivatives Extra Questions
- Application Of Integrals Extra Questions
- Continuity And Differentiability Extra Questions
- Determinants Extra Questions
- Differential Equations Extra Questions
- Integrals Extra Questions
- Inverse Trigonometric Functions Extra Questions
- Linear Programming Extra Questions
- Matrices Extra Questions
- Probability Extra Questions
- Relations And Functions Extra Questions
- Three Dimensional Geometry Extra Questions
- Vector Algebra Extra Questions