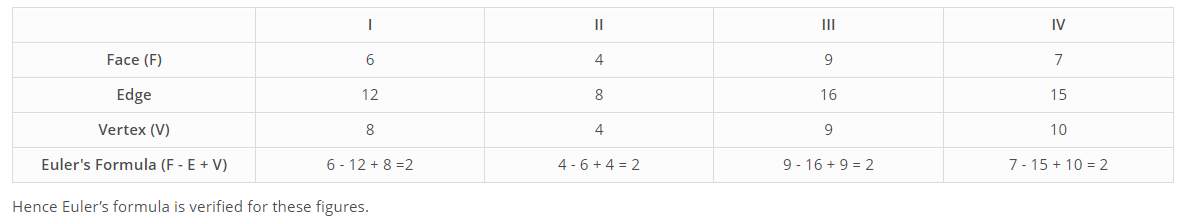Visualising Solid Shapes - Class 8 Maths - Extra Questions
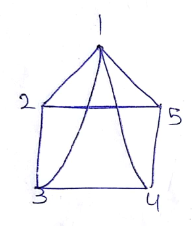
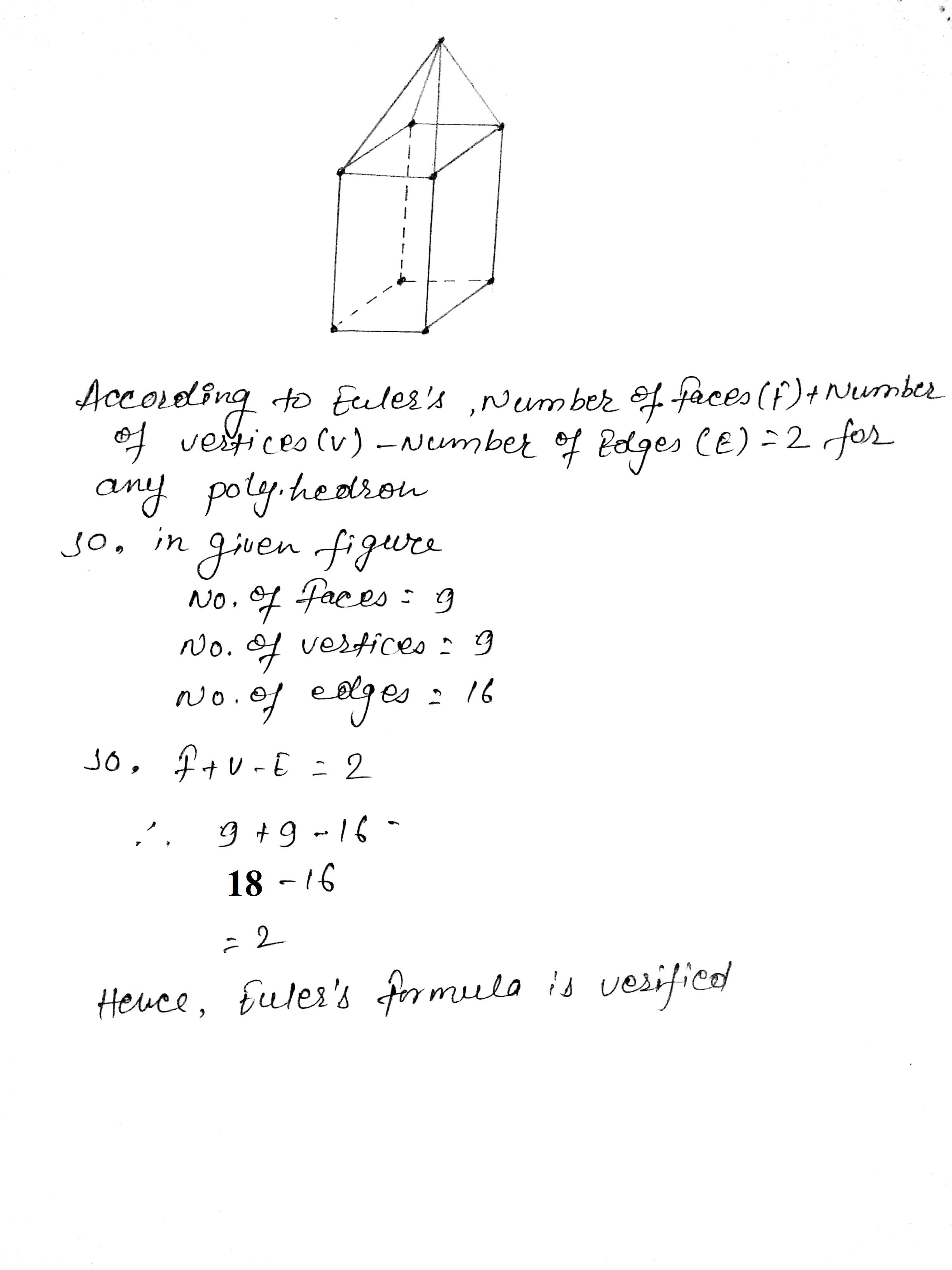
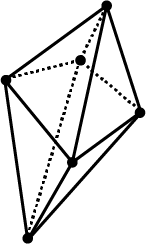
Verify Euler's formula for the solid.
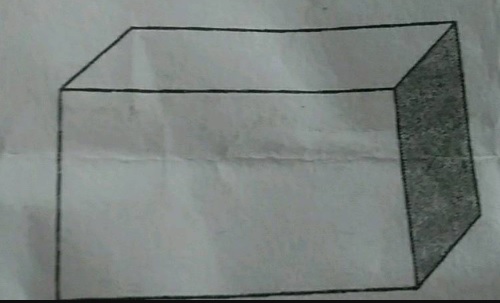
For any polyhedron if $$V = 10, \:E = 18$$, then find $$F$$.
Suppose that for a polyhedron $$F = 14, \:V = 24$$ then find $$E$$.
If the number of lateral surfaces of a right prism is equal to 9, then the number of edges of the base of the prism is
According to Euler's formula, $$F+V-E = k$$. Find the value of $$k$$.
Define regular polyhedron.
What are convex polyhedrons?
If $$F = 6, V = 8$$. Using Euler's formula, find the value of $$E$$.
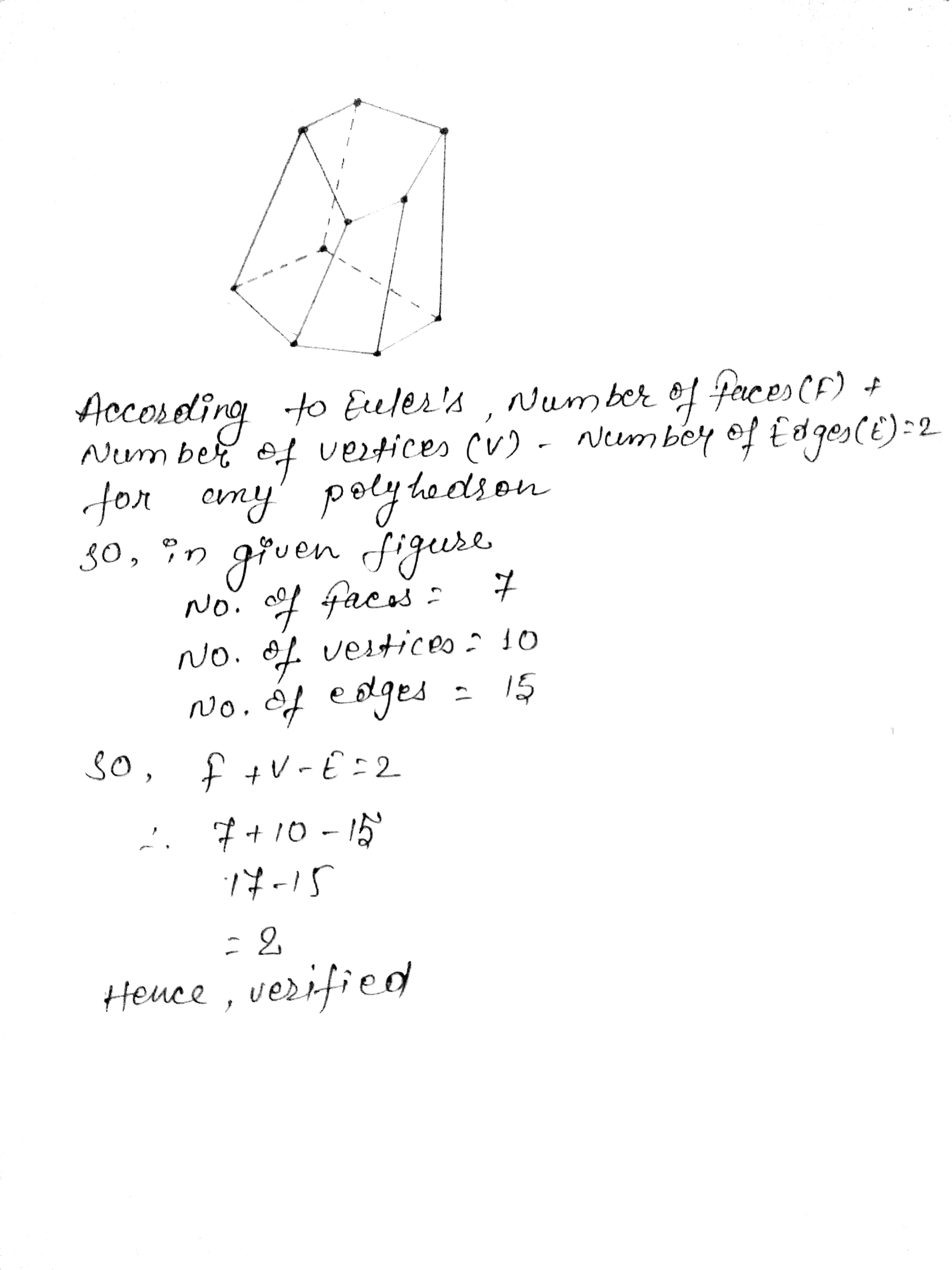
Verify Euler's formula for the given solid.
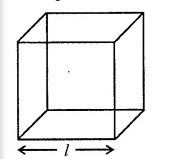
The length of an edge of a cube is $$l$$. Find the formula for the sum of lengths of all the edges of the cube.
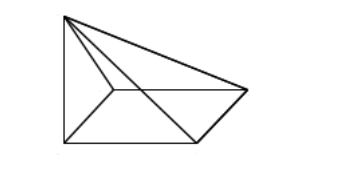
Can a polyhedron have for its faces:
$$3$$ triangles ?
A rectangular pyramid has ..... faces, ..... edges and ....... vertices.
Look at the shape given below and state if it is a Polyhedra using Euler's formula.

Look at the shape given below and state if it is a Polyhedra using Euler's formula.
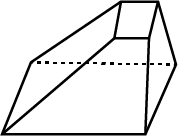
Look at the shape given below and state if it is a Polyhedron using Euler's formula.
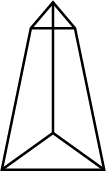
Look at the shape given below and state if it is a Polyhedra using Euler's formula.
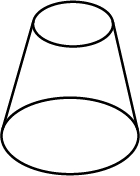
Look at the shape given below and state if it is a Polyhedra using Euler's formula.
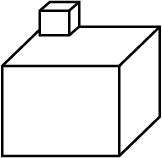
Look at the shape given below and state if it is a Polyhedra using Euler's formula.
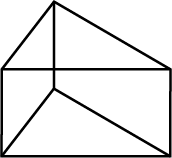
Look at the shape given below and state if it is a Polyhedra using Euler's formula.
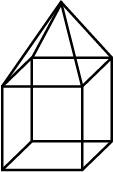
Look at the shape given below and state if it is a Polyhedra using Euler's formula.
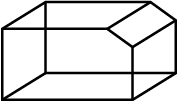
Draw a figure that represents your mathematics textbook. What is the name of this figure? Is it a prism?
A solid has forty faces and, sixty edges. Find the number of vertices of the solid.
Using Euler's formula, find the value of unknown $$x, y, z, p, q, r,$$ in the following table.
(i) (ii) (iii) (iv) (v) (vi) Faces $$ 7$$ $$ y$$ $$9$$ $$ p$$ $$ 6$$ $$8 $$ Vertices $$ 10$$ $$ 12$$ $$z$$ $$6$$ $$ q$$ $$11 $$ Edges $$ x$$ $$ 18$$ $$ 16$$ $$ 12$$ $$12 $$ $$ r$$
| (i) | (ii) | (iii) | (iv) | (v) | (vi) | |
| Faces | $$ 7$$ | $$ y$$ | $$9$$ | $$ p$$ | $$ 6$$ | $$8 $$ |
| Vertices | $$ 10$$ | $$ 12$$ | $$z$$ | $$6$$ | $$ q$$ | $$11 $$ |
| Edges | $$ x$$ | $$ 18$$ | $$ 16$$ | $$ 12$$ | $$12 $$ | $$ r$$ |
Look at the shape given below and state if it is a Polyhedra using Euler's formula.
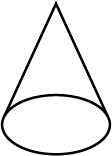
Look at the shape given below and state if it is a Polyhedra using Euler's formula.
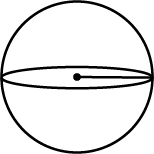
Look at the shape given below and state if it is a Polyhedra using Euler's formula.
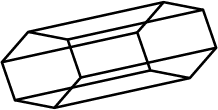
Look at the shape given below and state if it is a Polyhedra using Euler's formula.
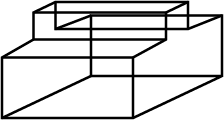
Look at the shape given below and state if it is a Polyhedra using Euler's formula.
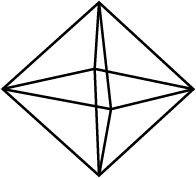
Can a polyhedron have V = F = 9 and E = 16? If yes, draw its figure.
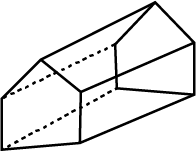
Look at the solid, shown in the figure, and fill the given chart.
| Polyhedron | Faces(F) | Vertices(V) | Edges(E) | F-E+V |
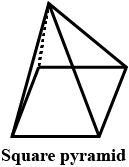
| Square Pyramid |
The side of a square board is 50 cm. A student has to draw its image in her notebook. If the drawing of the square board in the notebook has perimeter of 40 cm, then by which scale the figure has been drawn?
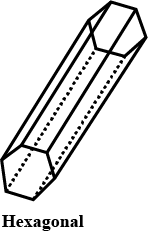
Look at the solid, shown in the figure, and fill the given chart.
| Polyhedron | Faces(F) | Vertices(V) | Edges(E) | F-E+V |
| Hexagonal Prism |
Verily Euler’s formula for the following three dimensional figures:
Verily Euler’s formula for the following three dimensional figures:
Find the scaleActual size $$12$$ $$m$$ Drawing size $$3$$ $$cm$$
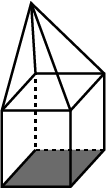
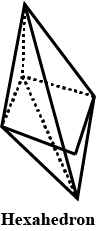
Look at the solid, shown in the figure, and fill the given chart.
| Polyhedron | Faces(F) | Vertices(V) | Edges(E) | F-E+V |
| Hexahedron |
The actual length of a painting was 2 m. What is its length in the photograph if the scale used in 1 mm: 20 cm.

A photographer uses a computer program to enlarge a photograph. What is the scale according to which the width has enlarged?
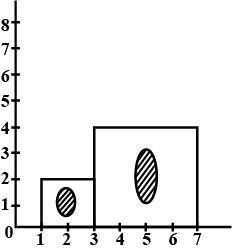
Look at the solid, drawn below, and fill the given chart.
| Polyhedron | Faces(F) | Vertices(V) | Edges(E) | F-E+V |
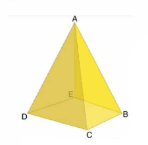
| Triangular Pyramid |
Faces Vertices Edges (i) $$x$$ 15 20 (ii) 6 $$y$$ 8 (iii) 14 26 $$z$$
Using Euler’s formula, find the values of $$x, y, z$$.
| Faces | Vertices | Edges | |
| (i) | $$x$$ | 15 | 20 |
| (ii) | 6 | $$y$$ | 8 |
| (iii) | 14 | 26 | $$z$$ |
Using Euler's formula, find $$V$$, if $$E = 30, \:F = 12$$
Polyhedra are solid figures made up of .......... .
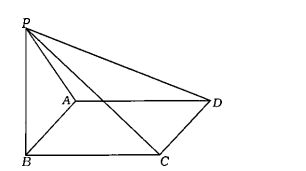
In a given tetrahedron ABCD let K and L be the centers of edges AB and CD respectively. Prove that every plane that contains the line KL divides the tetrahedron into two parts of equal volume
Count the number of faces, vertices, and edges of given polyhedra and verify Euler's formula. The maximum value of V+F is:

Classify the following solids in to regular and irregular prisms.
Rectangular-based prism
Equilateral traingle-based prism
Square-based prism
Cube
Right-traingle-based prism
Scalene traingle-based prism
Number of the polyhedron which has $$12$$ edges
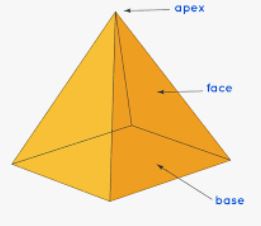
How many faces are there in square pyramid
Using Euler's formula, find $$V$$ if $$E = 10, F=6$$.
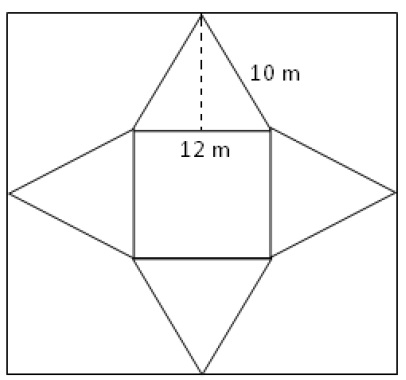
Figure below shows the diagram drawn on a square sheet of paper for constructing a square pyramid.
What is the length of a side of the square sheet of paper taken?
The figure drawn in the square paper is cut out and folded to make a square pyramid.
What would be the height of that pyramid?
A________ can also be called a square prism.
Cont the number of faces, vertices and edges of given polyhedra and verify Euler's formula
Find the volume of a tetrahedron whose vertices are A $$( - 1,2,3)$$ ,B $$(3,-2,1)$$, C $$(2,1,3)$$ and D $$(-1,-2,4)$$.
The number of vertices in a square pyramid are_______
The number of vertices in a right prism which has $$24$$ edges are ________
Use Euler's formula to find the value of $$a,b$$ and $$c$$
| Faces | Vertices | Edges | |
| (i) | 8 | a | 12 |
| (ii) | b | 6 | 9 |
| (iii) | 20 | 12 | c |
Solid Geometry. Problems on Proof.
Prove that two triangular pyramids are equal or symmetric; if their respective edges are equal.
The diagram shows a net of a solid.
Write down the mathematical name of the solid.
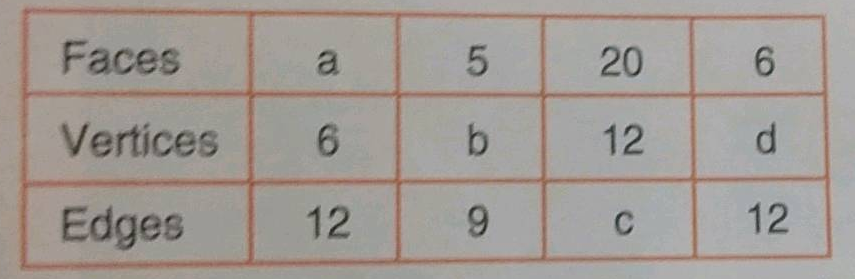
Using Euler's formula, find the values of a, b, c and d.
A model of a ship is made to a scale of $$1 : 250$$ calculate:
(i) The length of the ship, if the length of model is $$1.6\ m$$.
(ii) The area of the deck of the ship, if the area of the deck of model is $$2.4\ m^{2}$$.
(iii) The volume of the model, if the volume of the ship is $$1\ km^{3}$$.
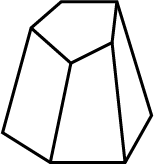
Verify Euler's formula for each of the following polyhedrons:
The perimeter of the base of a square pyramid is $$96cm$$ and its height is $$16cm$$,
a. What is the length of a base edge?
b. What is the slant height?
c. Find the lateral surface area.
Write down the number of faces of each of the following figures:
Square pyramid
Verify Euler's formula for each of the following polyhedrons:
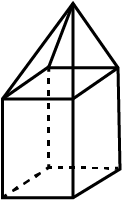
Verify Euler's formula for each of the following polyhedrons:

Complete the following table and verify Euler's formula in each case.

Write down the number of faces in a Triangular prism
Verify Euler's formula for each of the following polyhedrons:
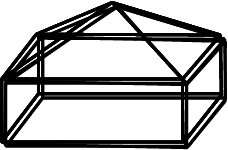
How many edges are there in a Square pyramid
Define Euler's relation between the number faces, number of edges and number of vertices for various $$3-$$ dimensional figures.
Fill in the blanks :
A triangular prism has ..... triangular faces, ........ rectangular faces, ...... edges, and ...... vertices.
Square prism is also called a ______.
Rectangular prism is also called a ______.
Total number of faces in a pyramid which has eight edges is ____.
A pyramid on an n sided polygon has _____ faces.
If a solid shape has $$12$$ faces and $$20$$ vertices, then the number of edges in this solid is _____.
If a pyramid has a hexagonal base, then the number of vertices it will have, is ______.
A pentagonal prism has ______ faces.
Total number of regular polyhedron is _____.
Check whether a polyhedron can have $$V =12, E = 6$$ and $$F =8$$.
How many edges do the following solid have?
Octagonal Pyramid
How many edges do the following solid have?
Hexagonal Prism
How many vertices does the following solid have?
Hexagonal Prism
In a town, an ice cream parlour has displayed an ice cream sculpture of height $$360$$ cm. The parlour claims that these ice creams and the sculpture are in the scale $$1:30$$. What is the height of the ice creams served?
If a polyhedron has $$7$$ faces and $$10$$ vertices, find the number of edges.
Verify Eulers formula for these solids:
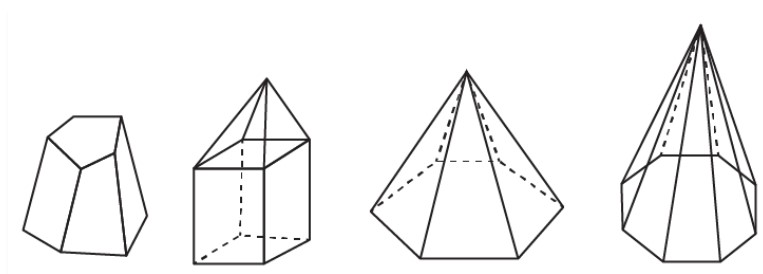
Using Euler’s formula, complete the following table:
Faces | Vertices | Edges | |
(i) | $$6$$ | __ | $$ 12$$ |
(ii) | __ | $$5$$ | $$8$$ |
(iii) | $$14$$ | $$24$$ | __ |
(iv) | __ | $$16$$ | $$30$$ |
(v) | $$16$$ | __ | $$42$$ |
(vi) | $$19$$ | $$19$$ | __ |
If a polyhedron has $$8$$ faces and $$8$$ vertices, find the number of edges.
| Faces | Vertices | Edges | |
| (i) | $$x$$ | 15 | 20 |
| (ii) | 6 | $$y$$ | 8 |
| (iii) | 14 | 26 | $$z$$ |
If a polyhedron has 8 faces and 8 vertices, find the number of edges in it.
Verily Euler's formula for the following three dimensional figure :
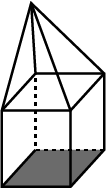
Faces Vertices Edges (i) $$x$$ 15 20 (ii) 6 $$y$$ 8 (iii) 14 26 $$z$$
Using Euler’s formula, find the values of $$x, y, z$$.
| Faces | Vertices | Edges | |
| (i) | $$x$$ | 15 | 20 |
| (ii) | 6 | $$y$$ | 8 |
| (iii) | 14 | 26 | $$z$$ |
Solve :
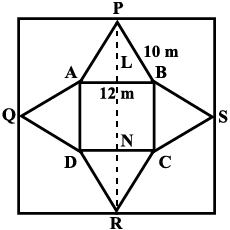
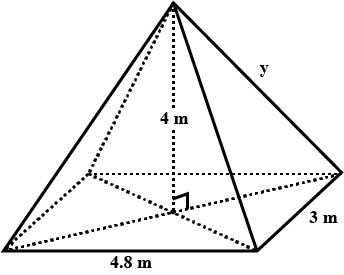
The diagram shows a pyramid with a horizontal rectangular base.
The rectangular base length $$4.8\ m $$ and width $$3\ m$$ and the height of the pyramid is $$4\ m $$
Calculate
(i) $$y$$ , the length of a sloping edge of the pyramid.
(ii) the angle between a sloping edge and the rectangular base of the pyramid.
The solid with six faces, six vertices and ten edges is a __________
Differentiate between the given types of prism:
Right prism and oblique prism
Height and slant height of a pyramid
Prism and pyramid
Solid Geometry. Problems on Proof.
How many planes of symmetry can a triangular pyramid. have?
Give two new examples of each of the following three dimensional shapes:
Pyramid
Class 8 Maths Extra Questions
- Algebraic Expressions And Identities Extra Questions
- Comparing Quantities Extra Questions
- Cubes And Cube Roots Extra Questions
- Data Handling Extra Questions
- Direct And Inverse Proportions Extra Questions
- Exponents And Powers Extra Questions
- Factorisation Extra Questions
- Introduction To Graphs Extra Questions
- Linear Equations In One Variable Extra Questions
- Mensuration Extra Questions
- Playing With Numbers Extra Questions
- Practical Geometry Extra Questions
- Rational Numbers Extra Questions
- Squares And Square Roots Extra Questions
- Understanding Quadrilaterals Extra Questions
- Visualising Solid Shapes Extra Questions