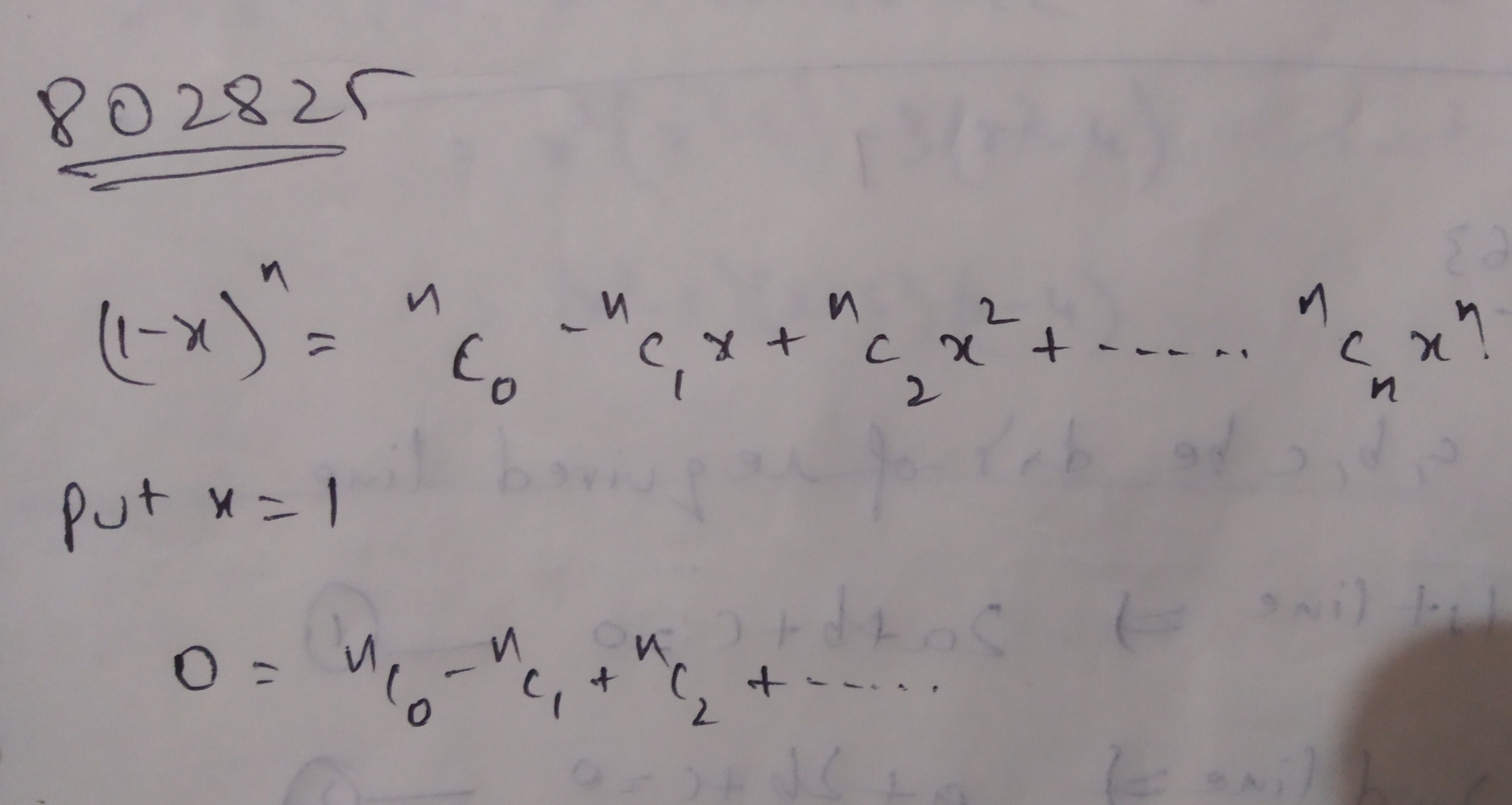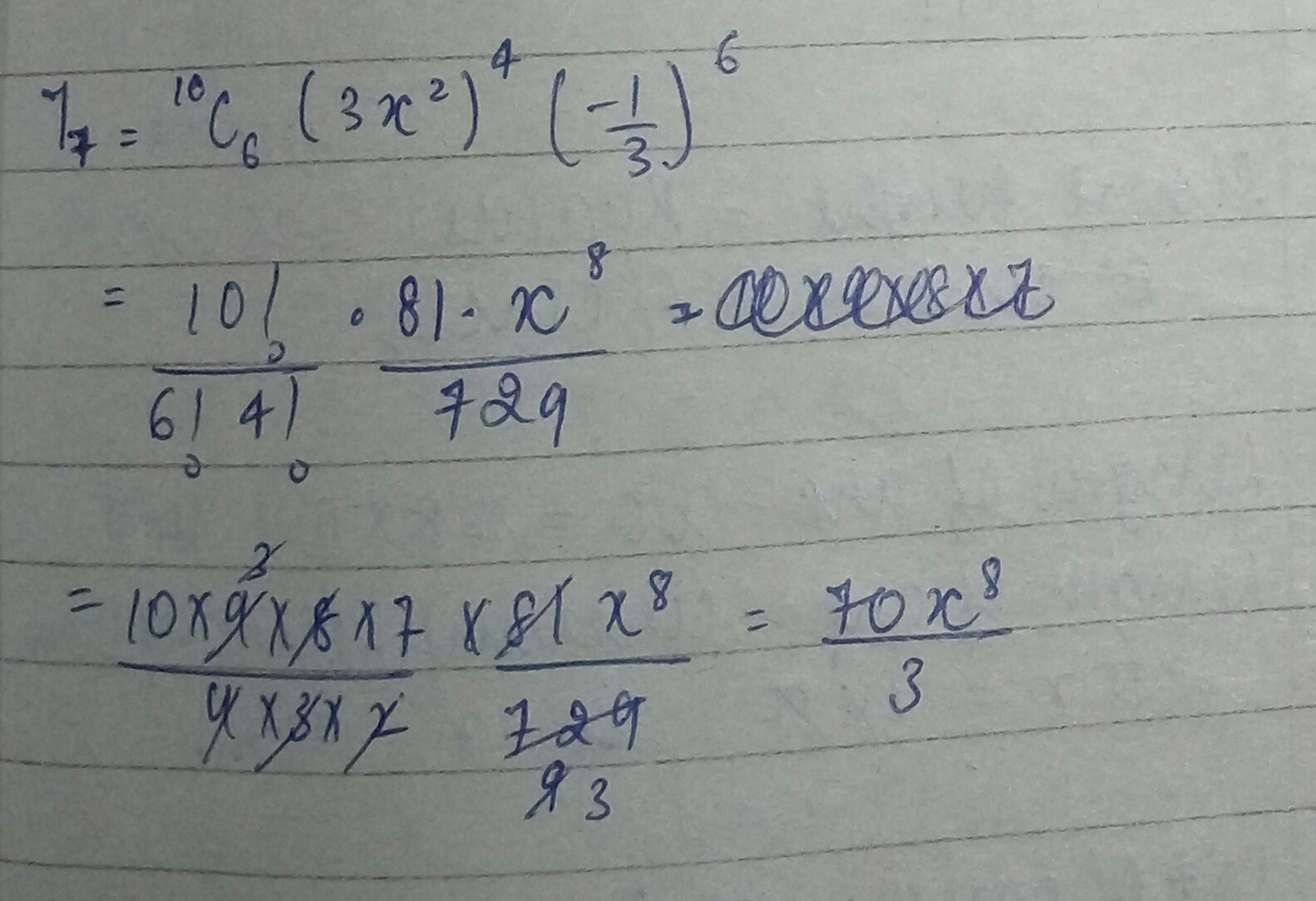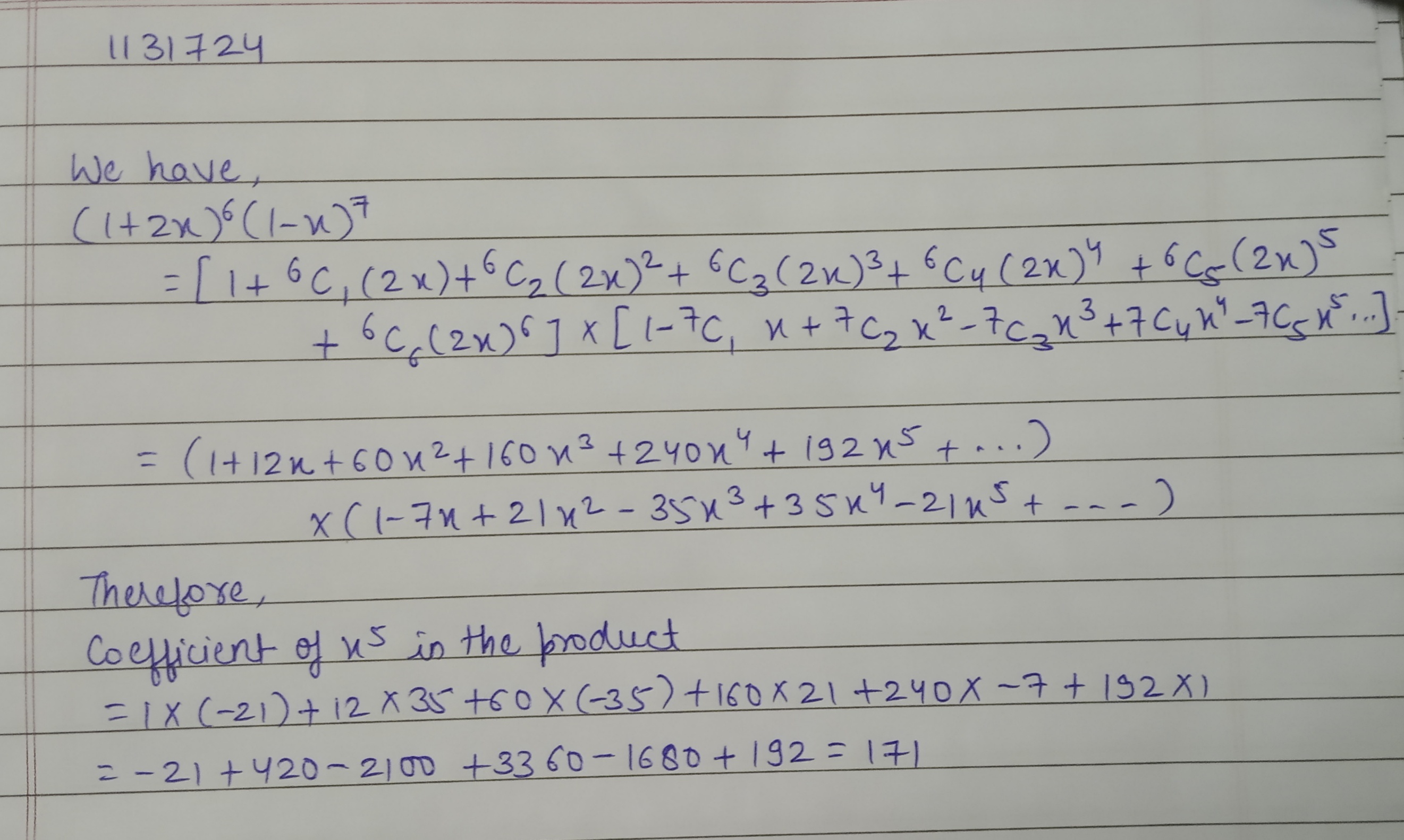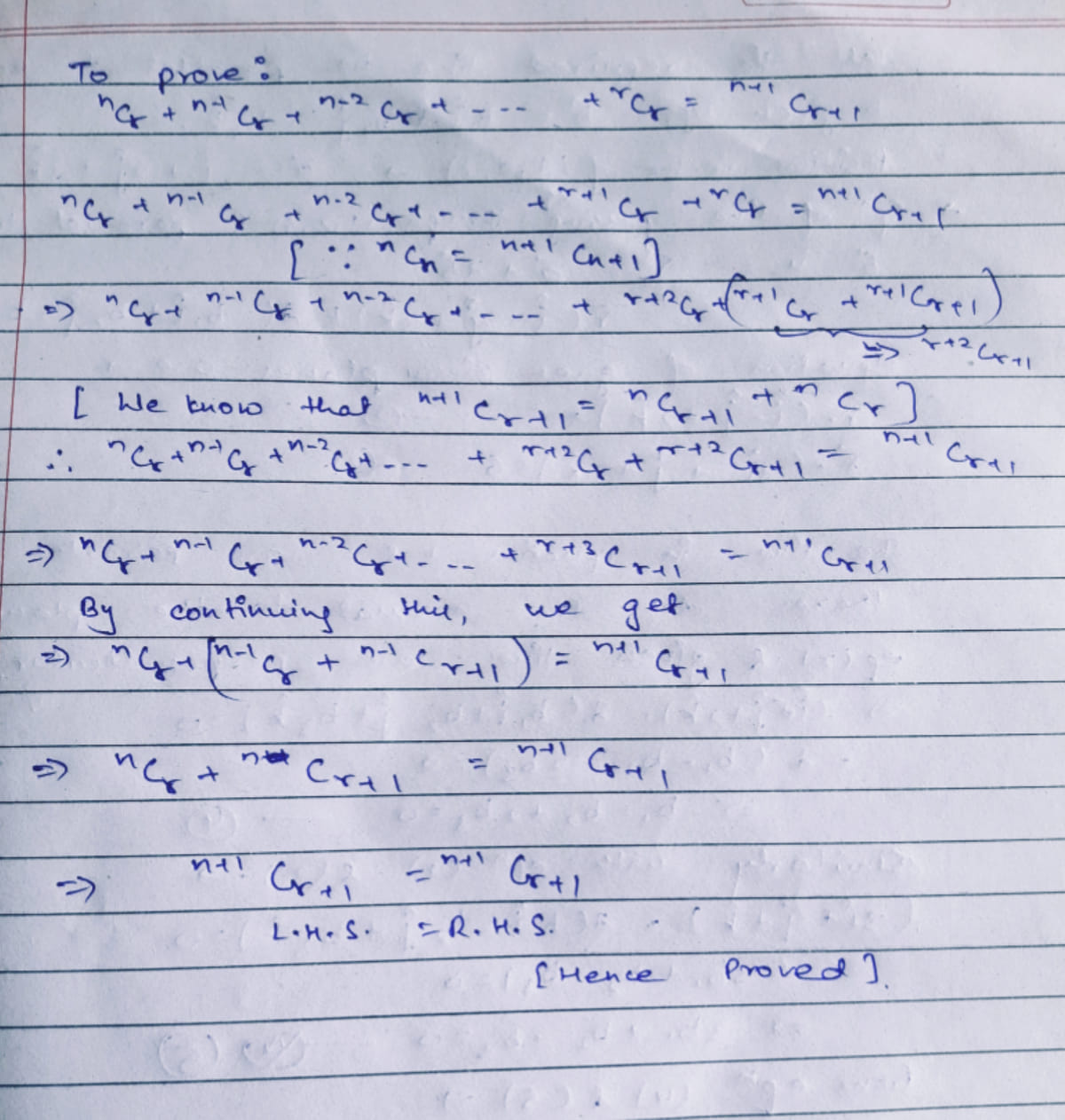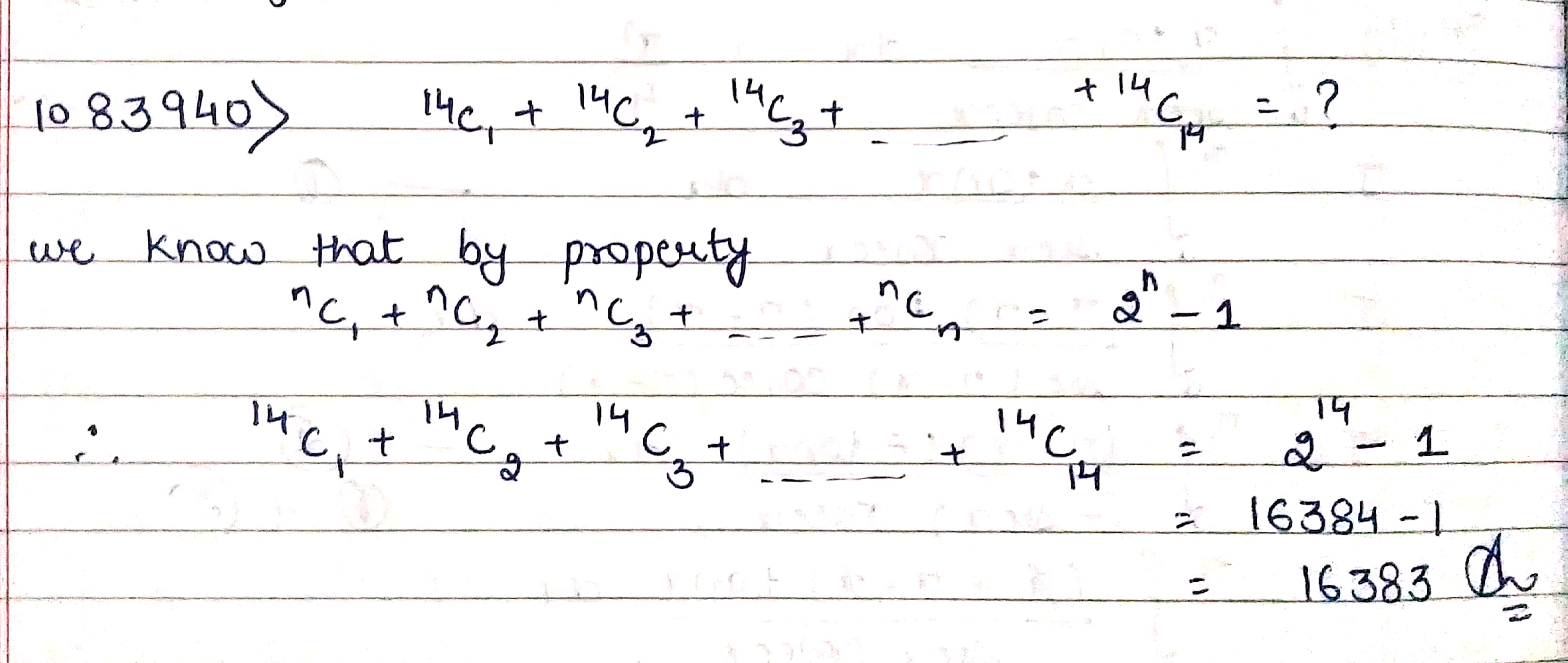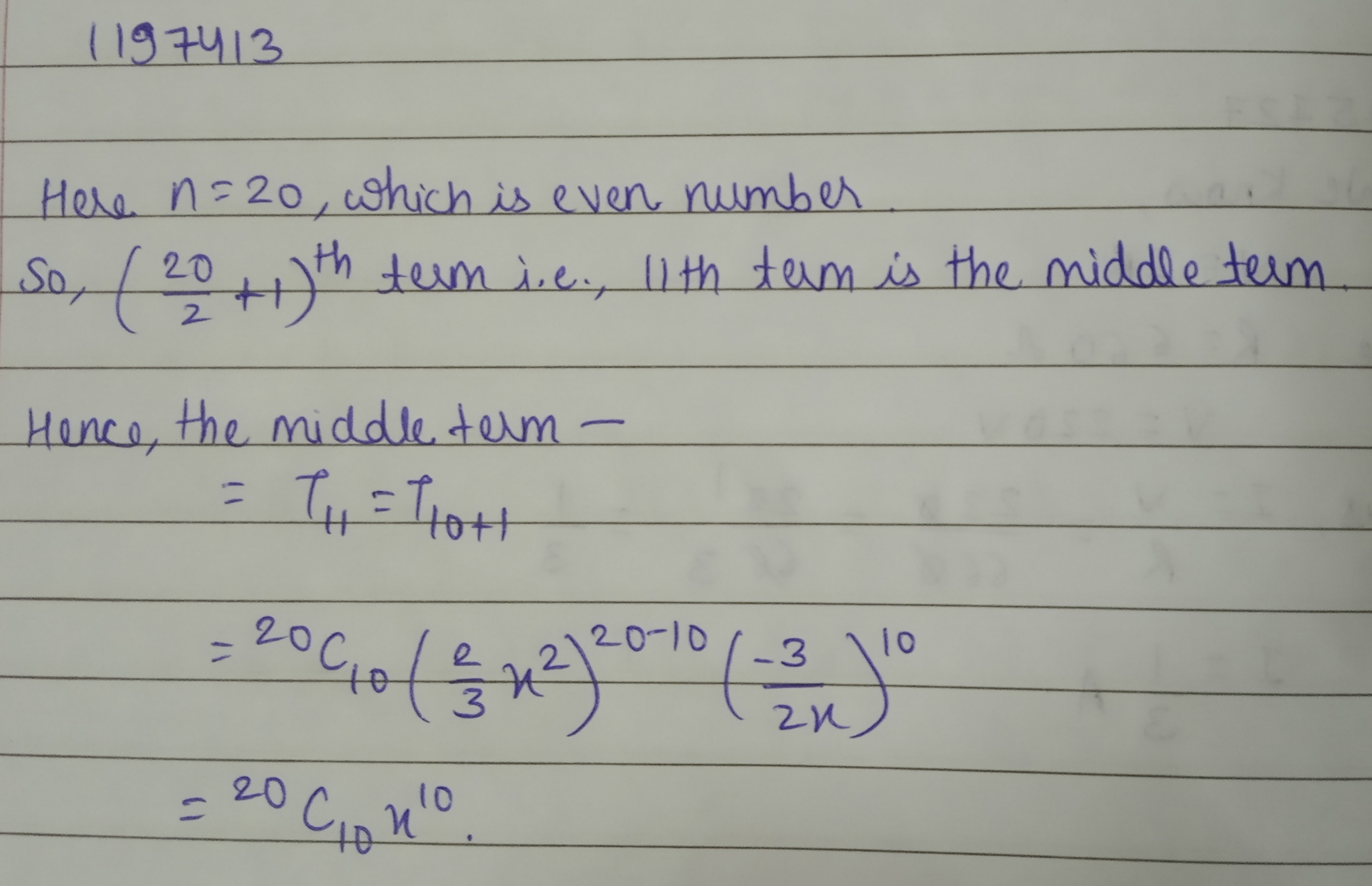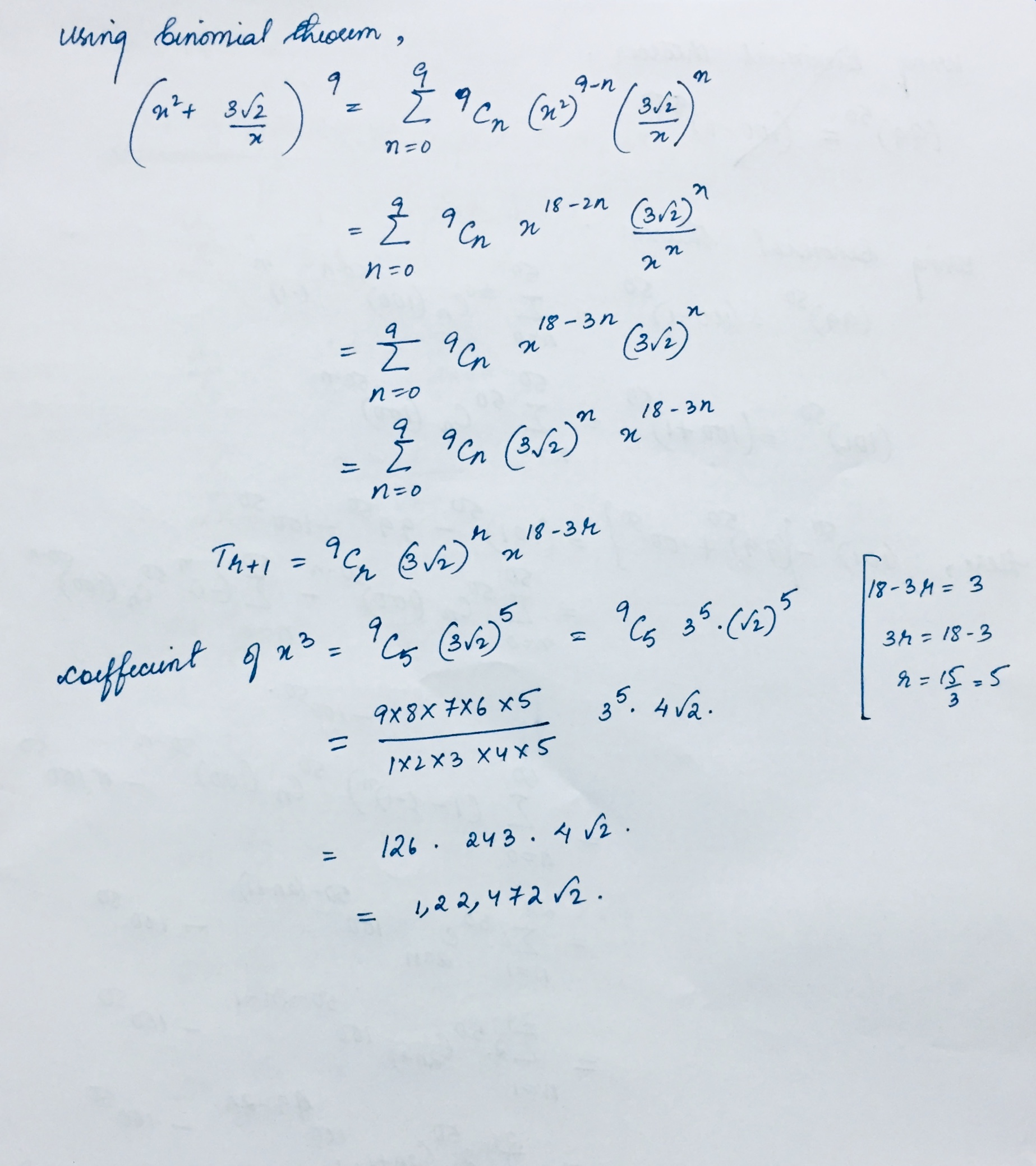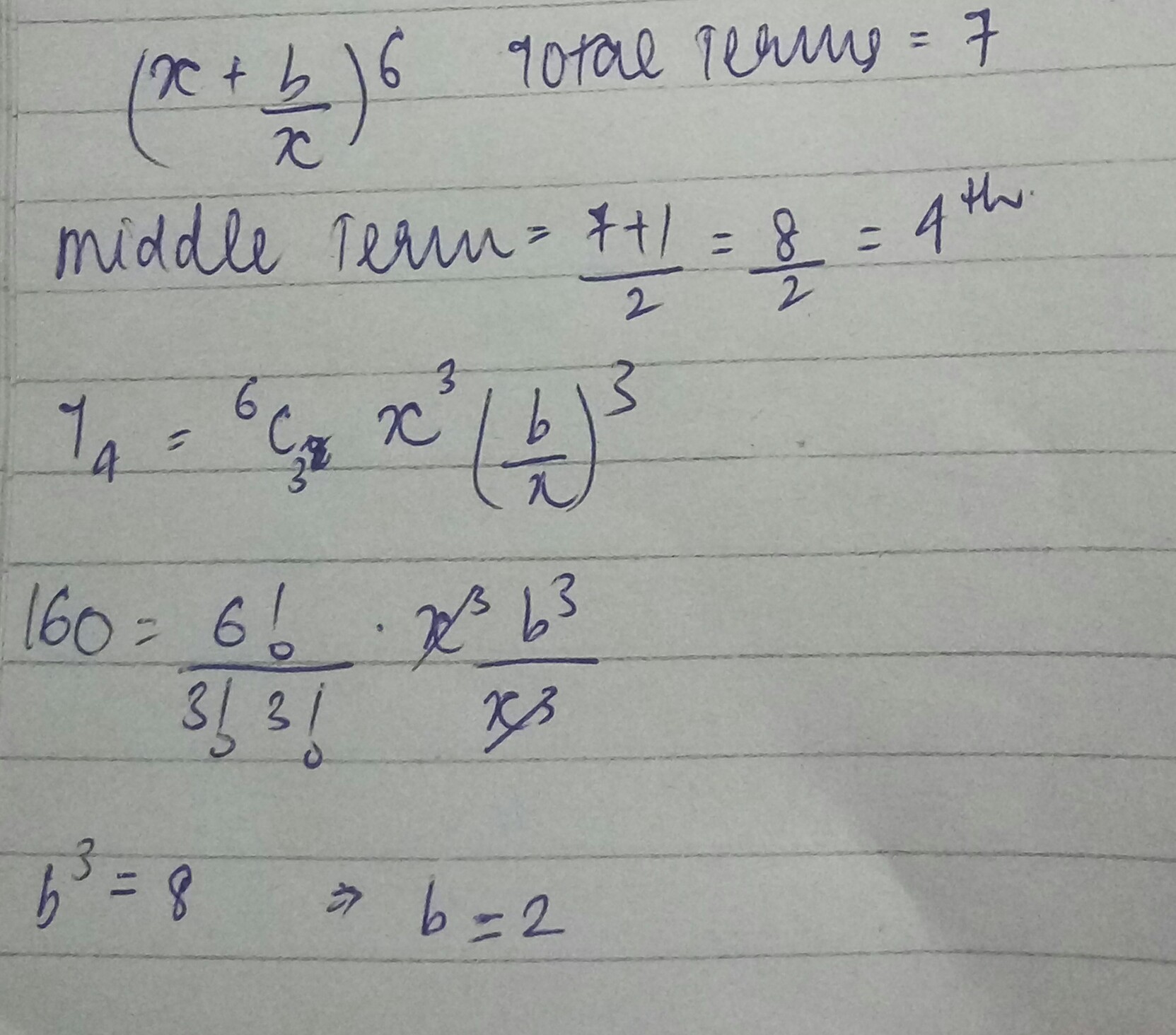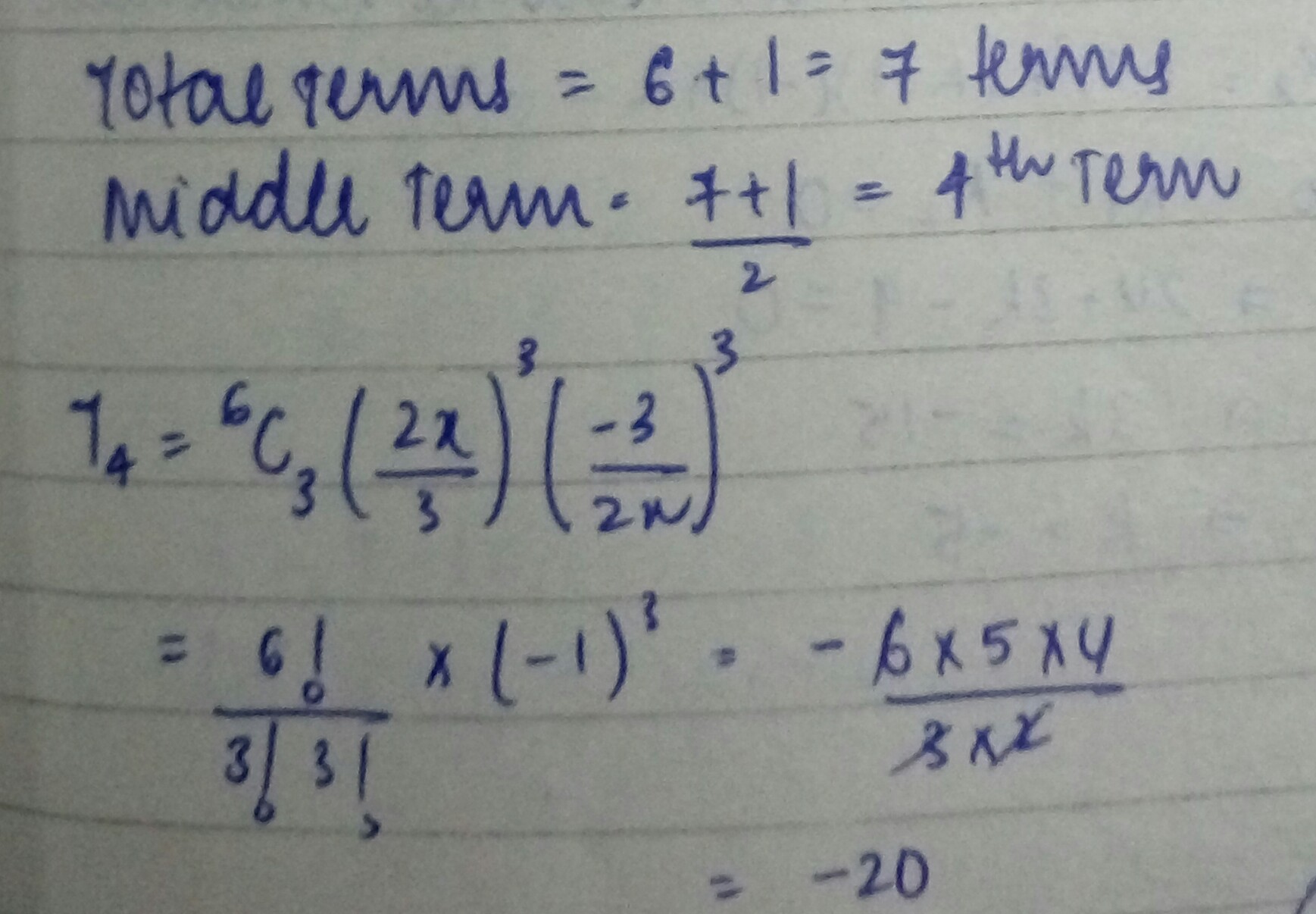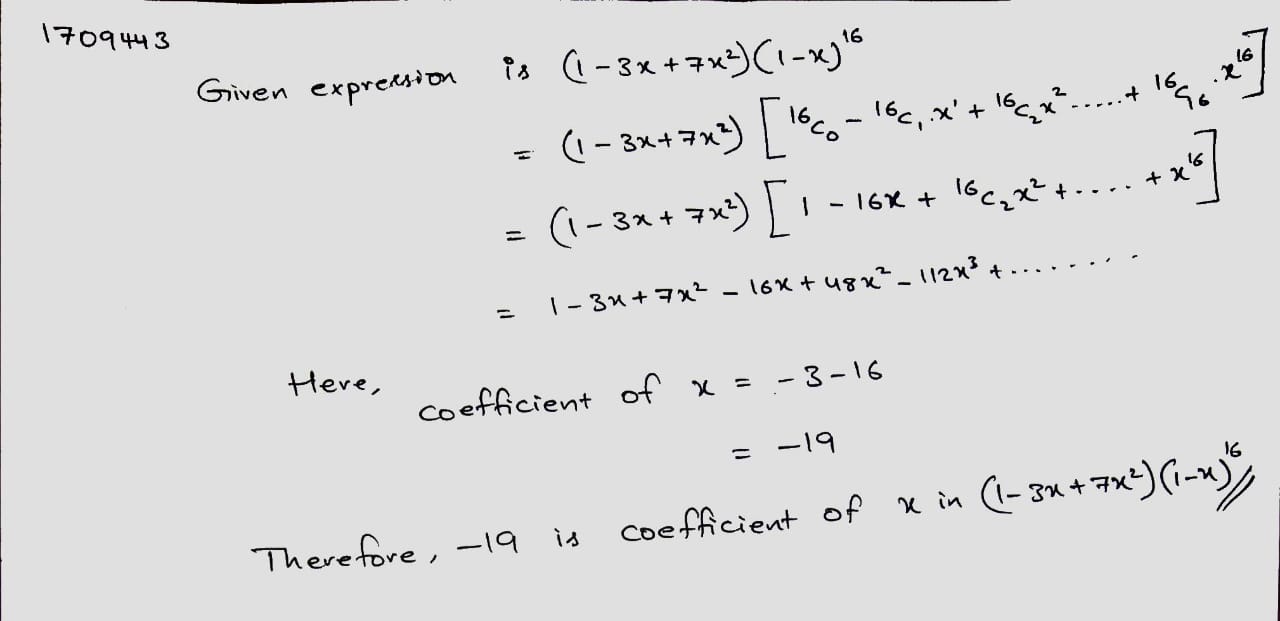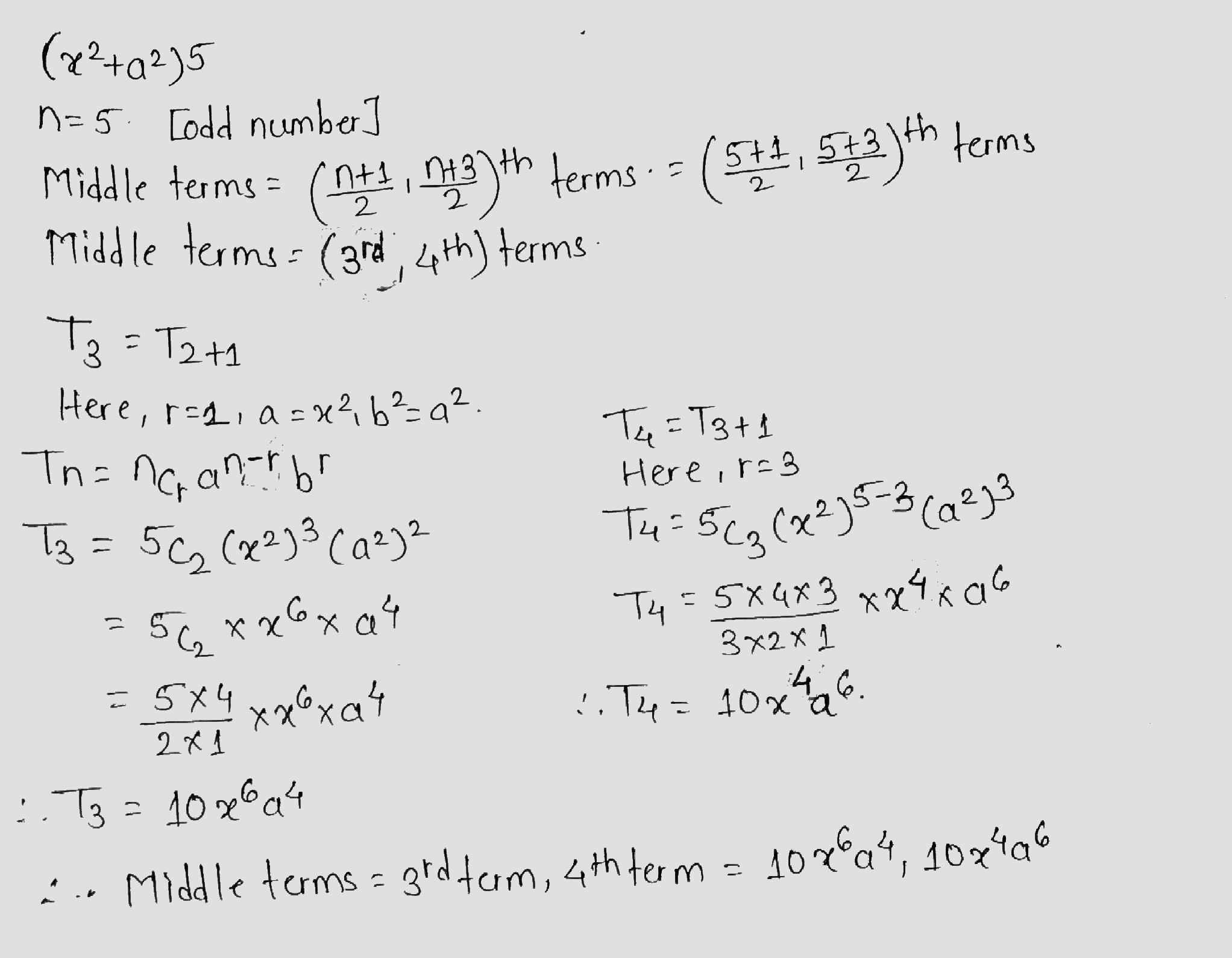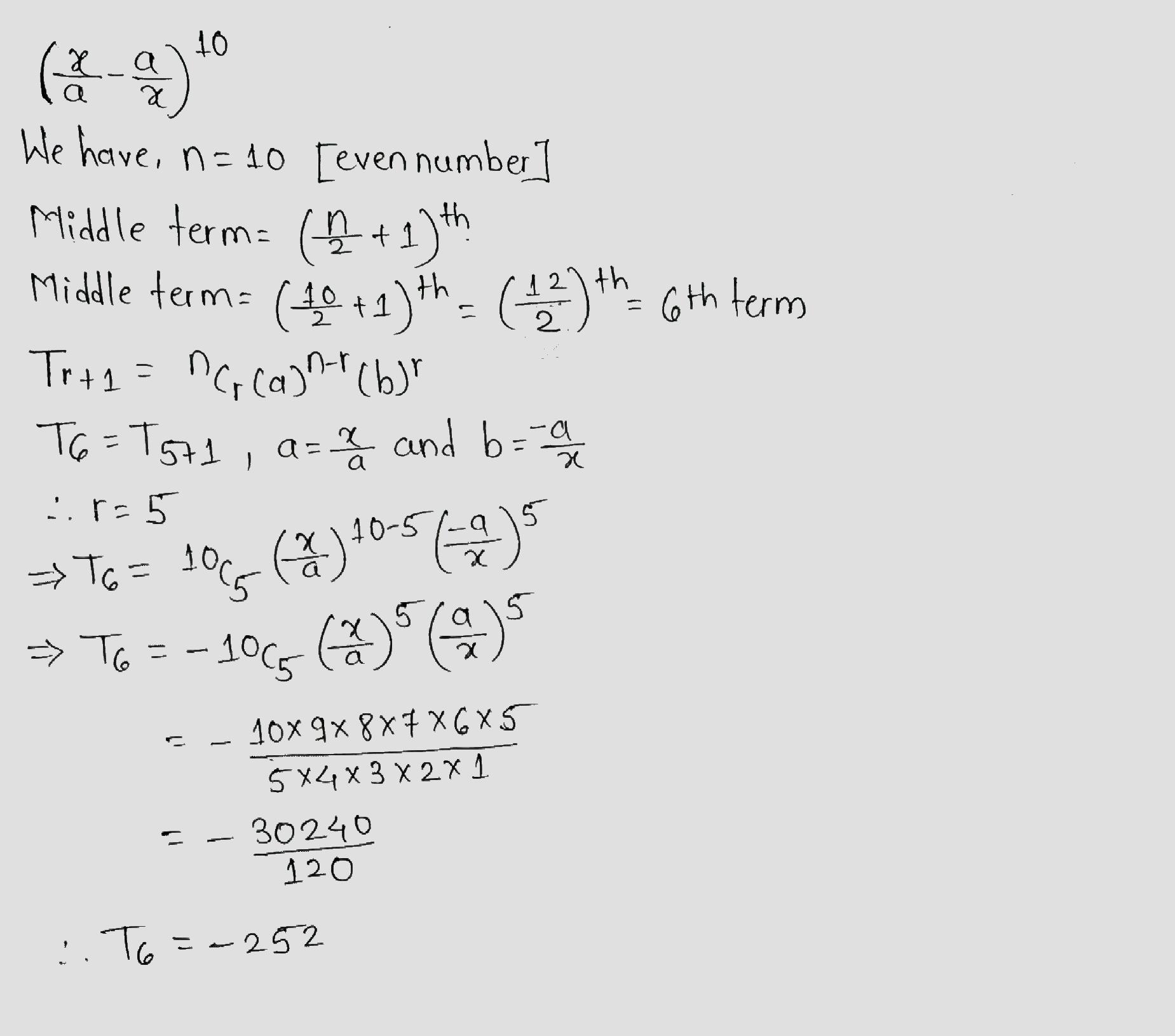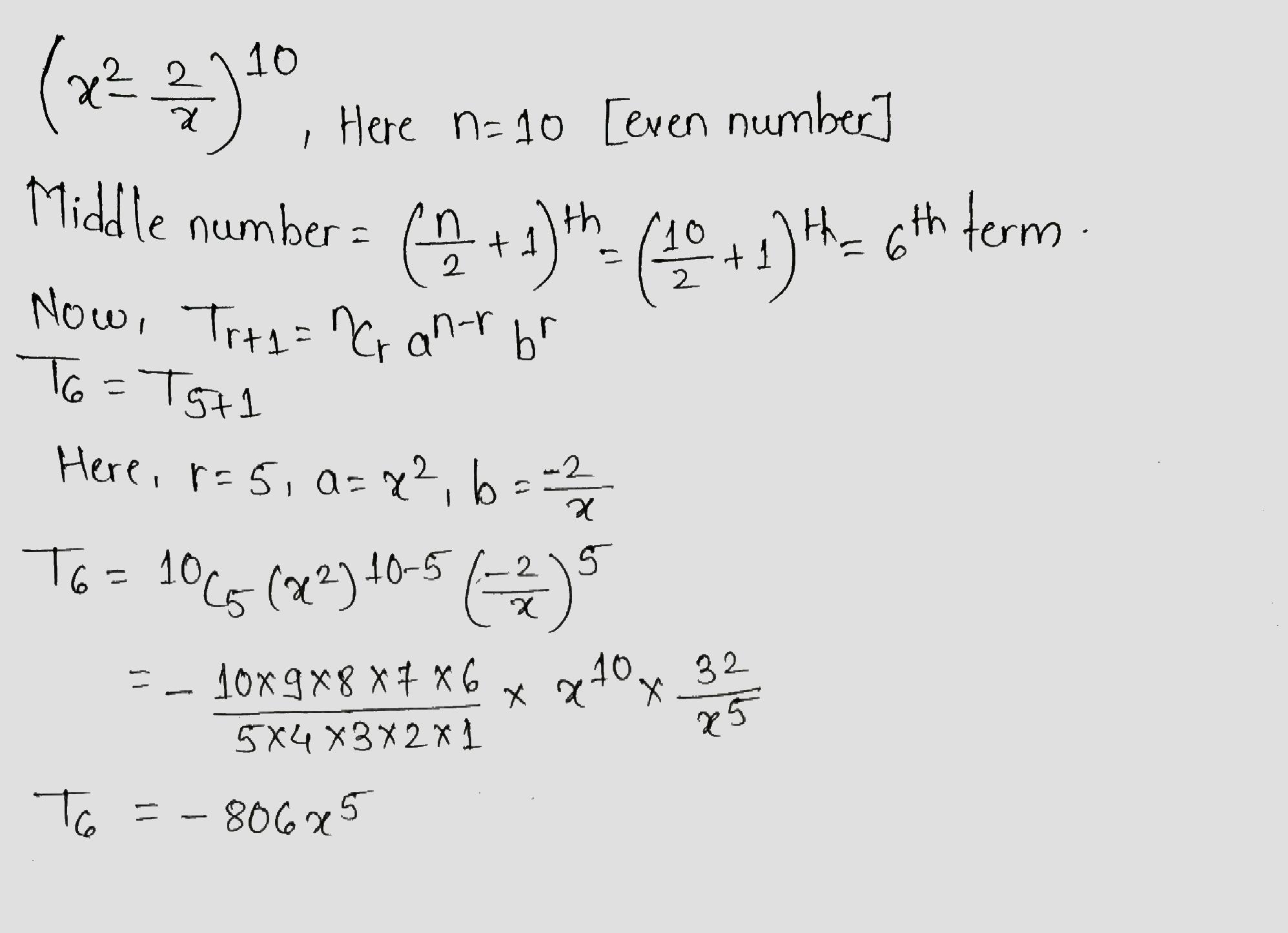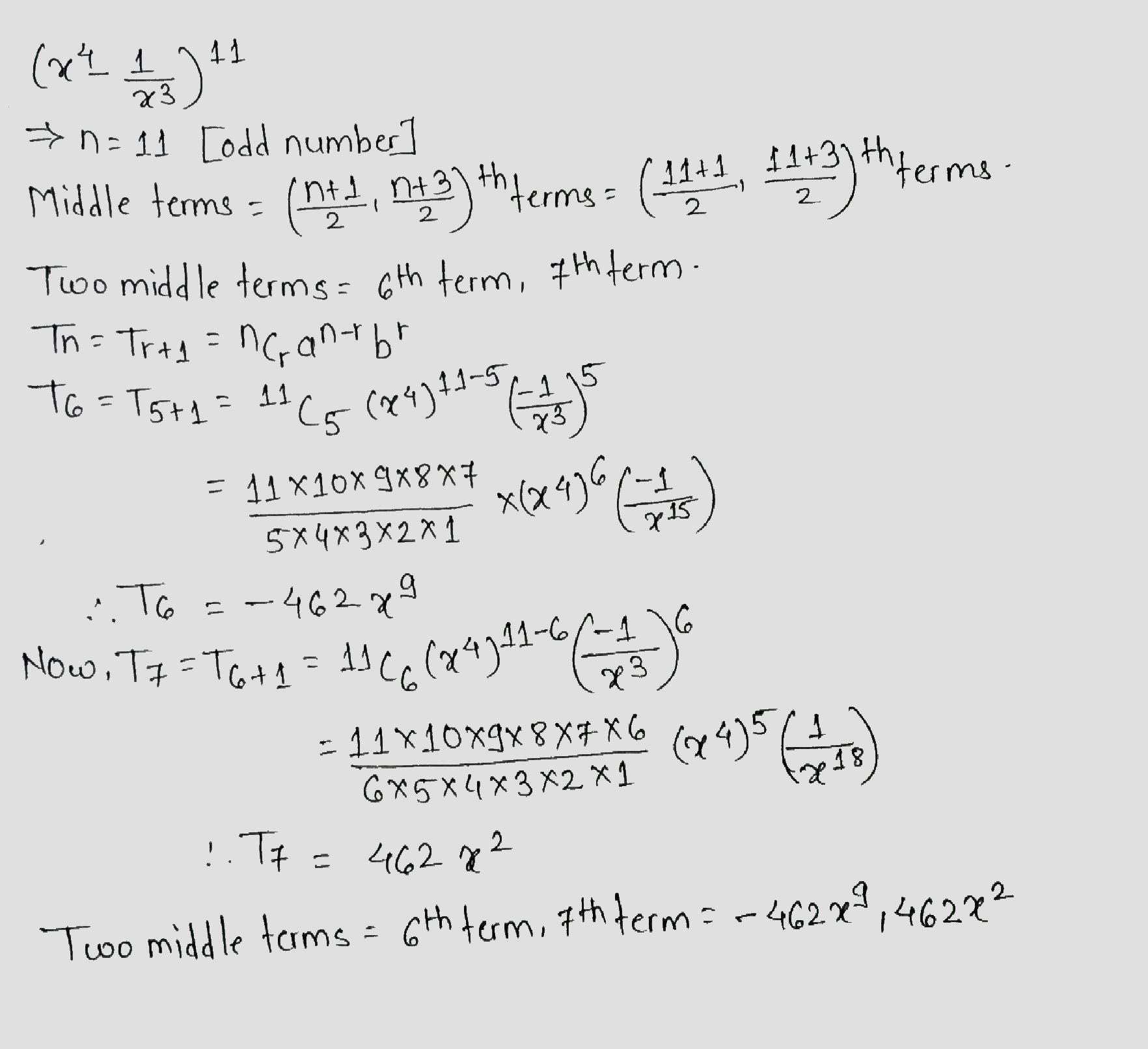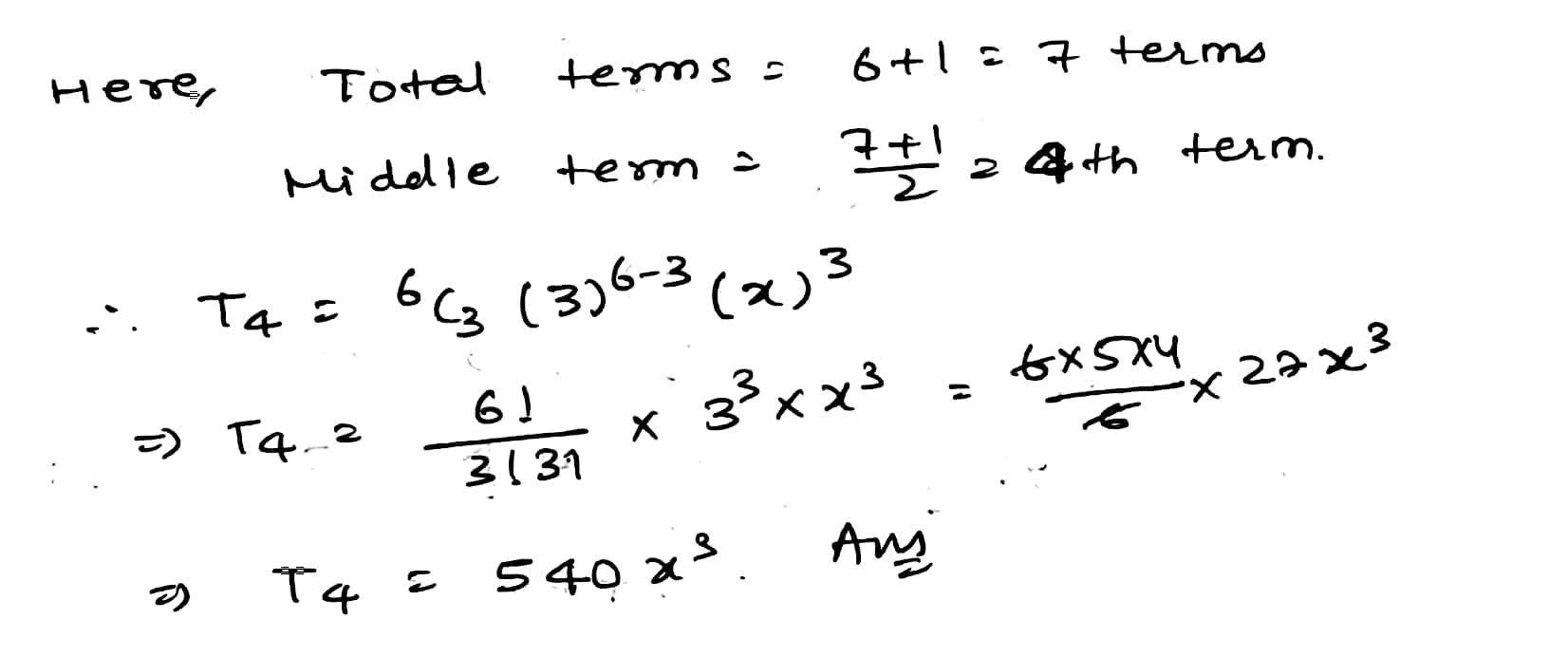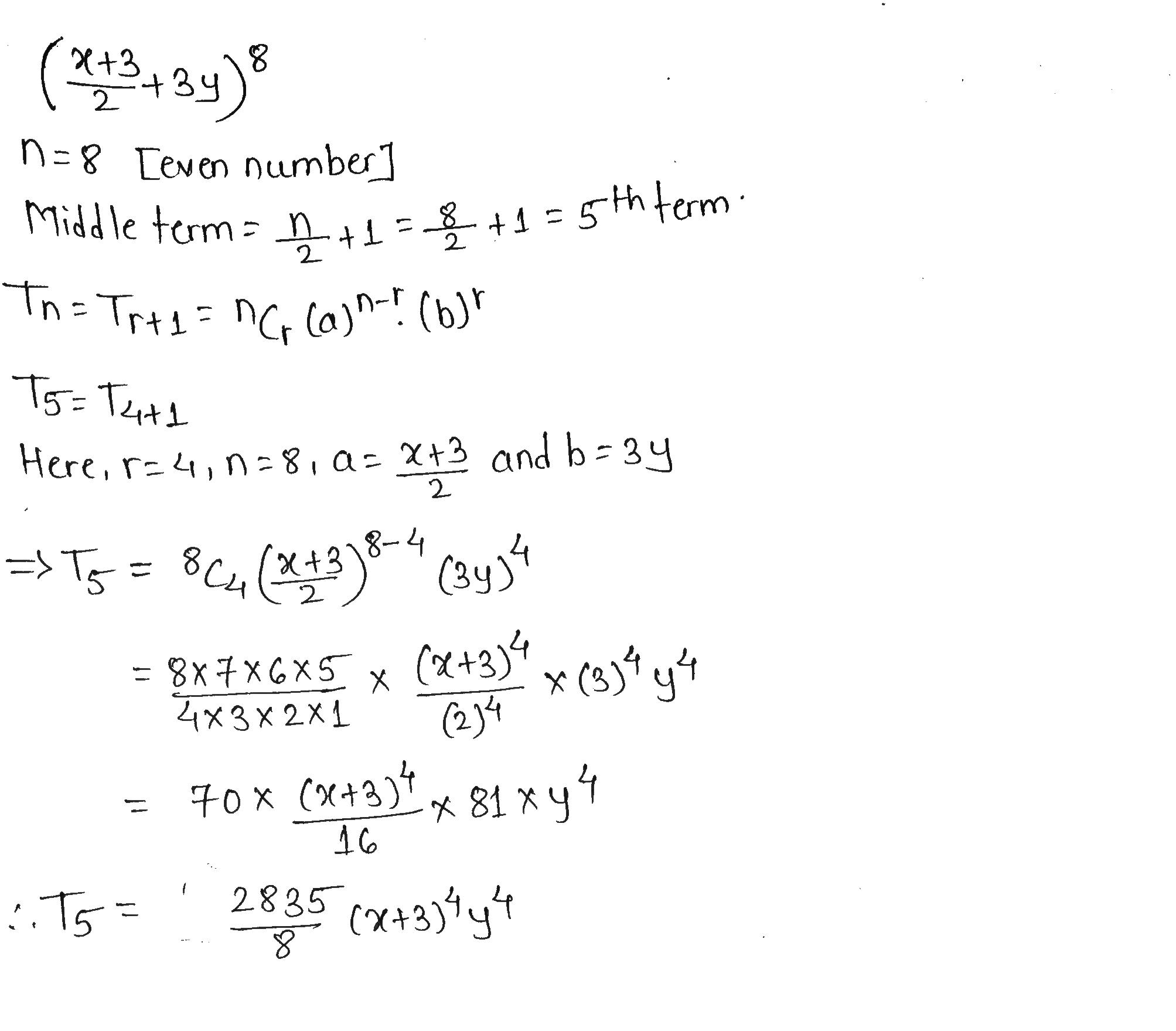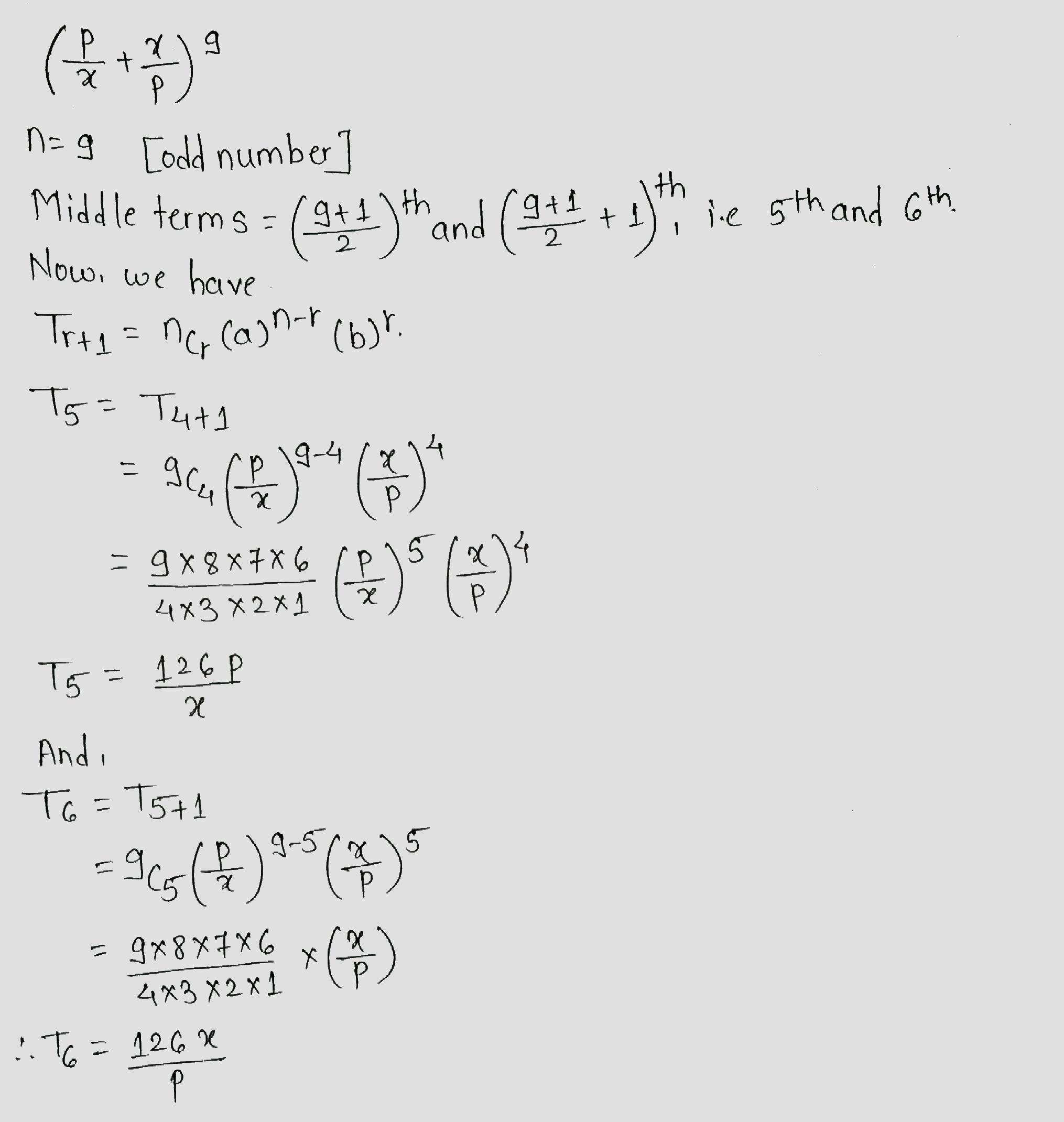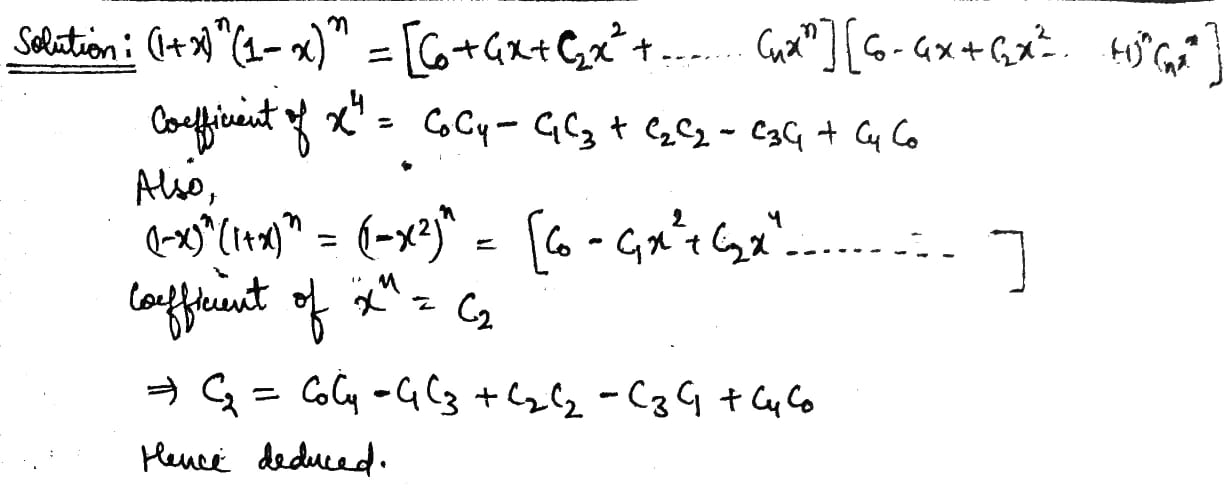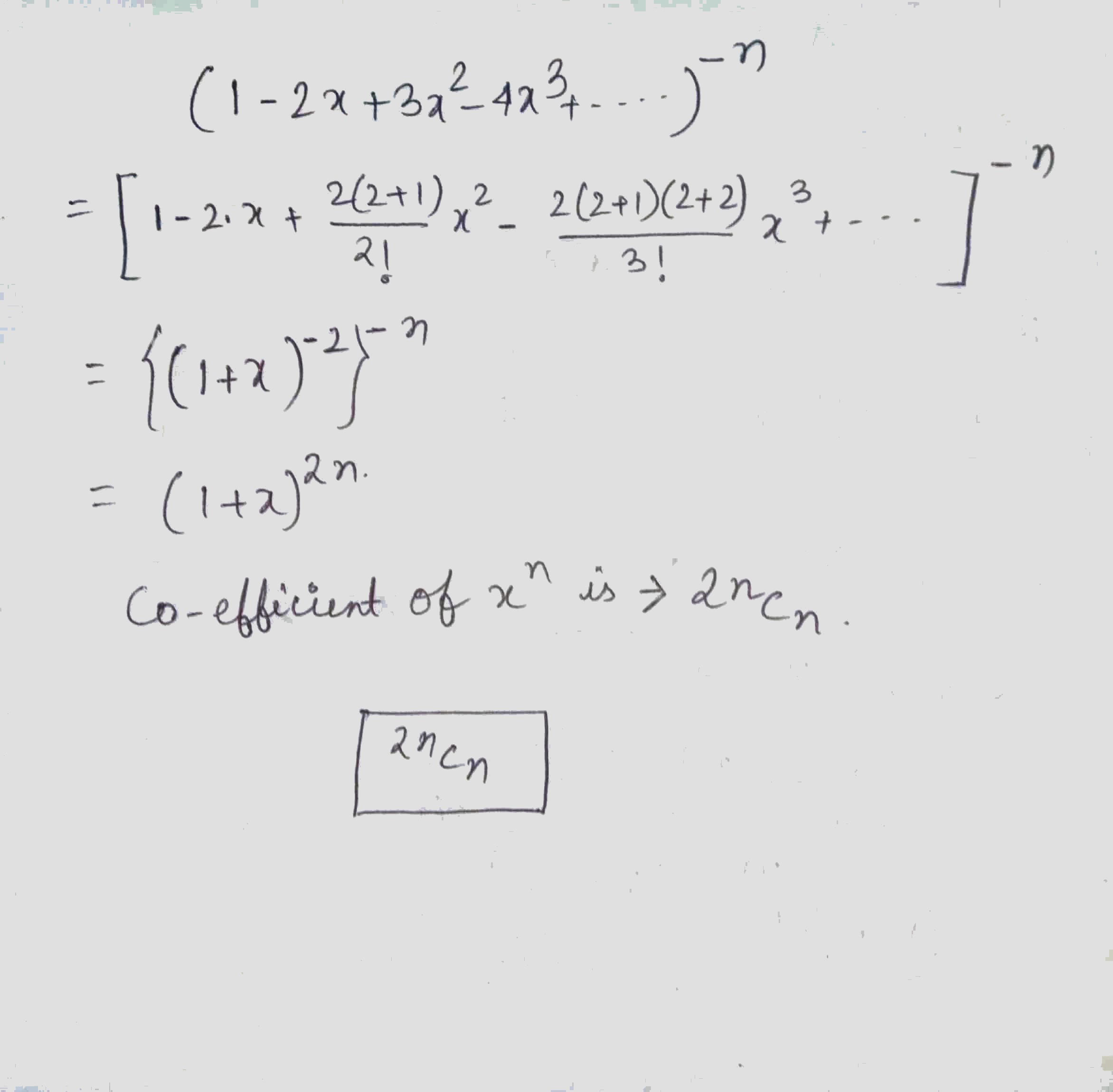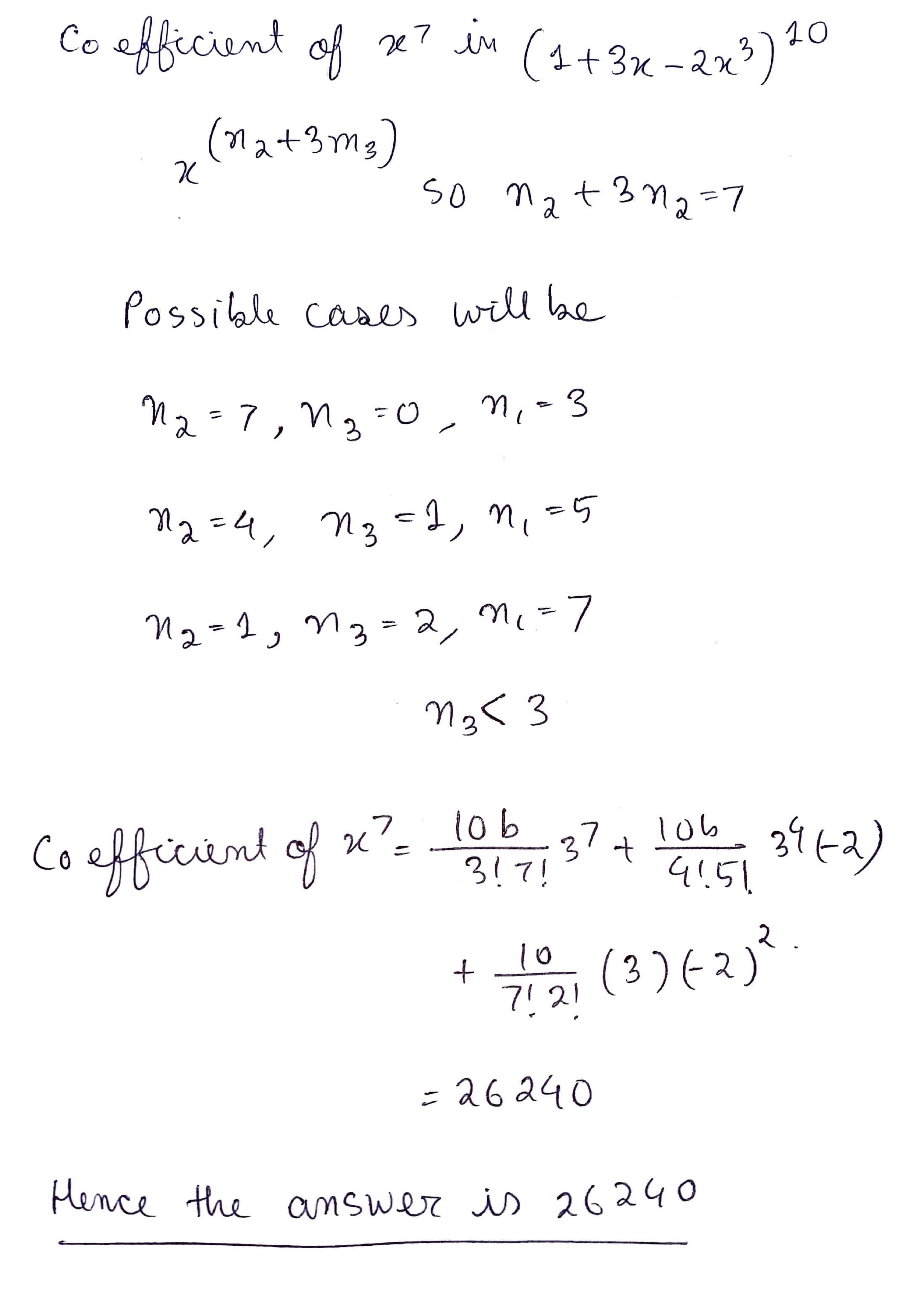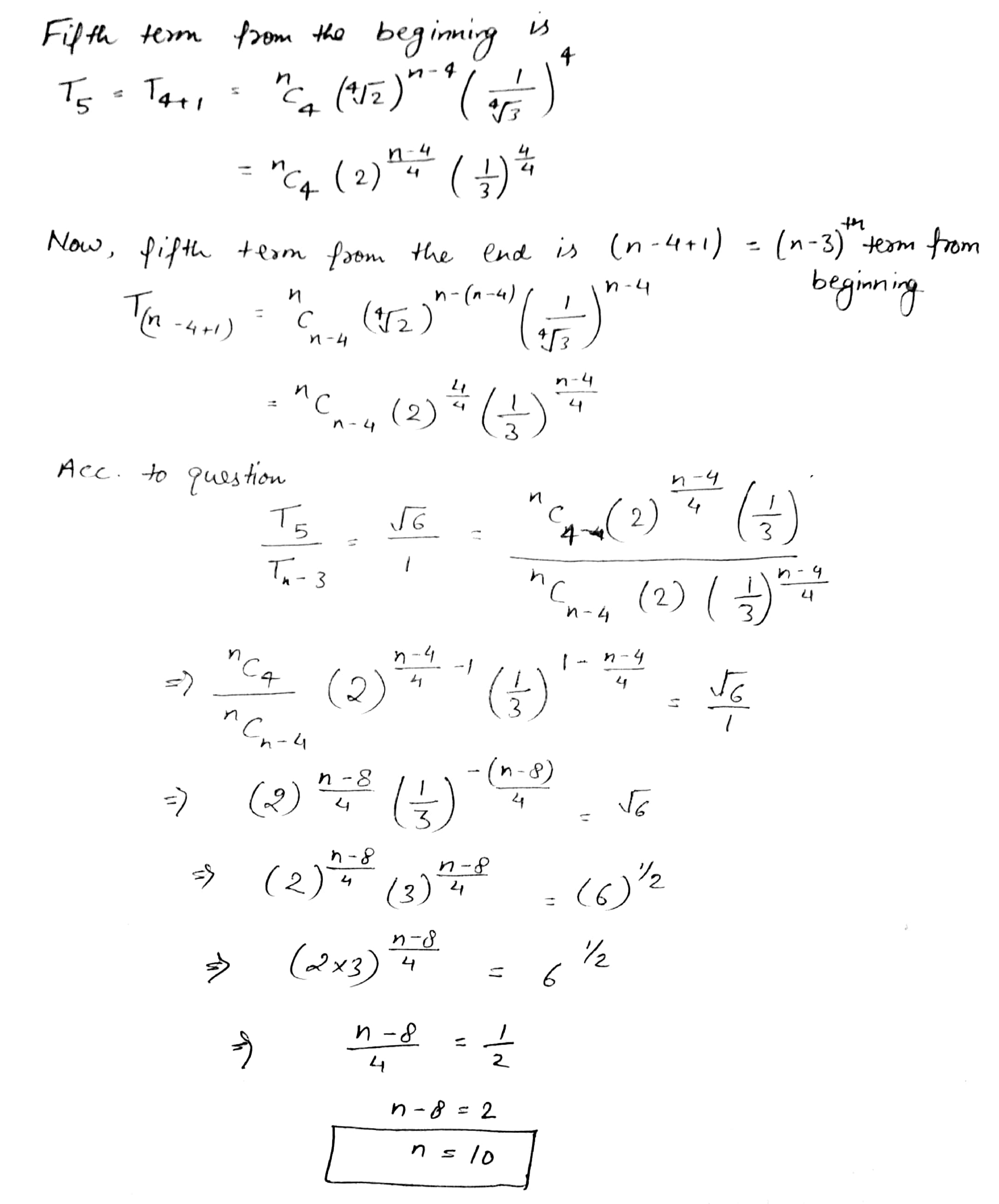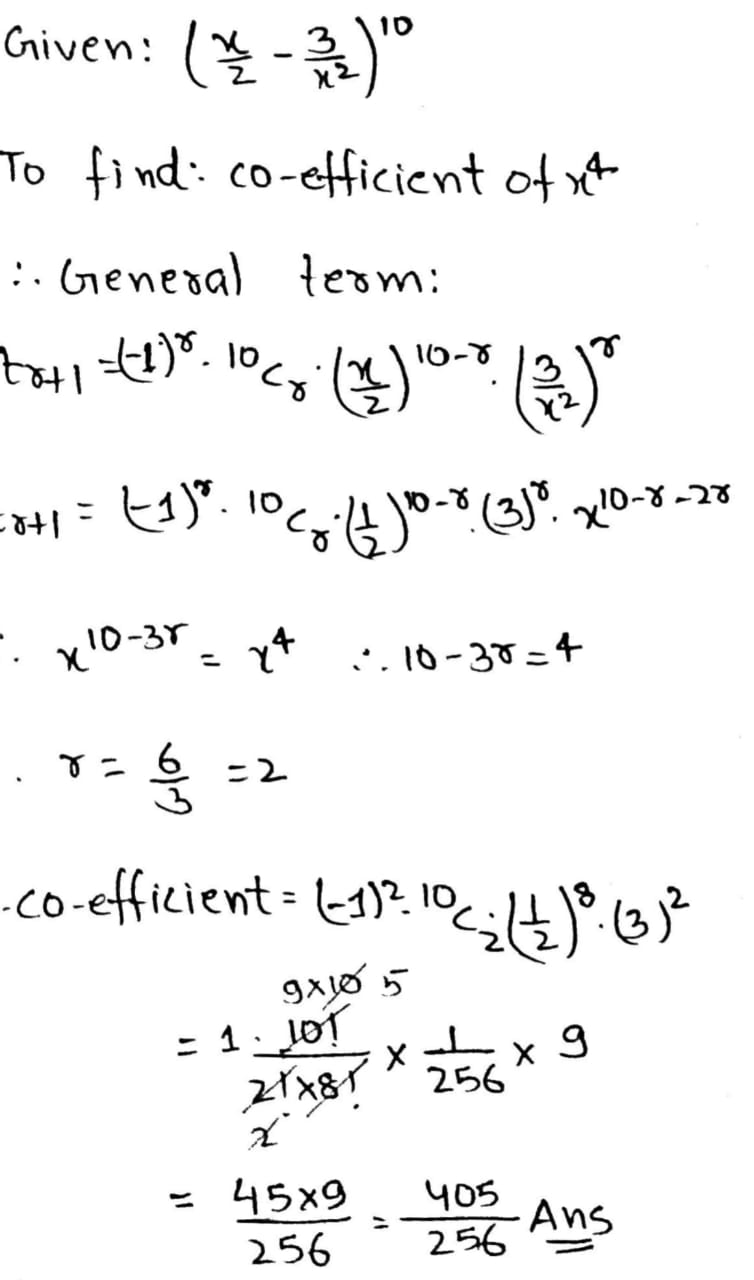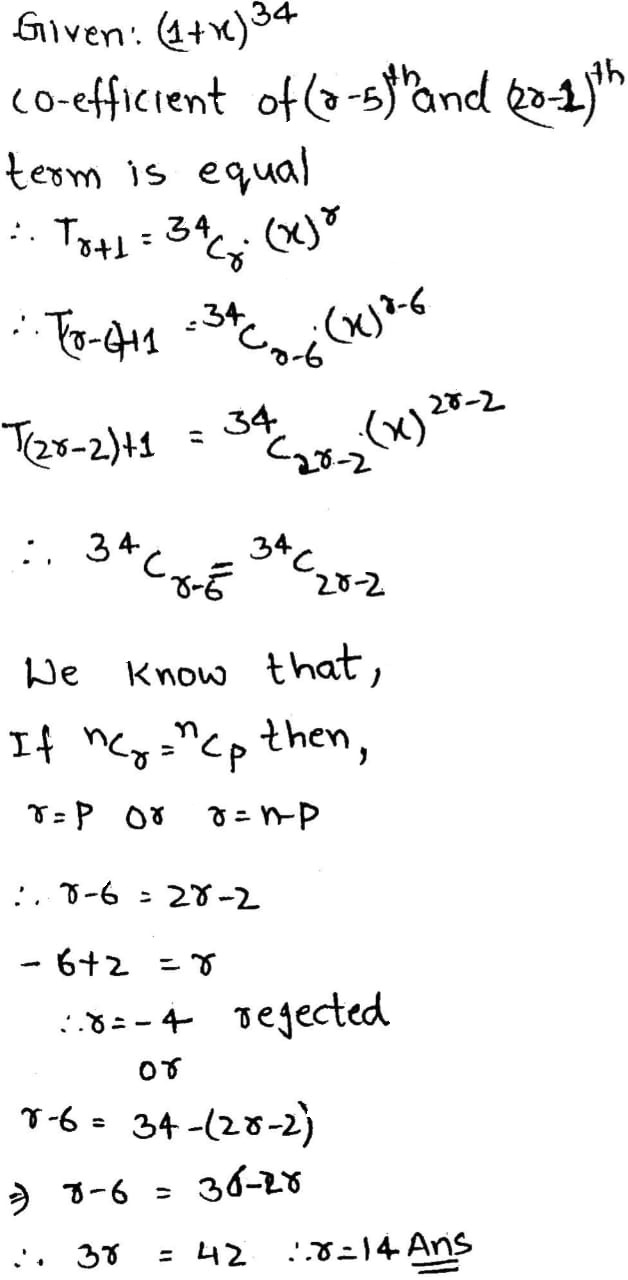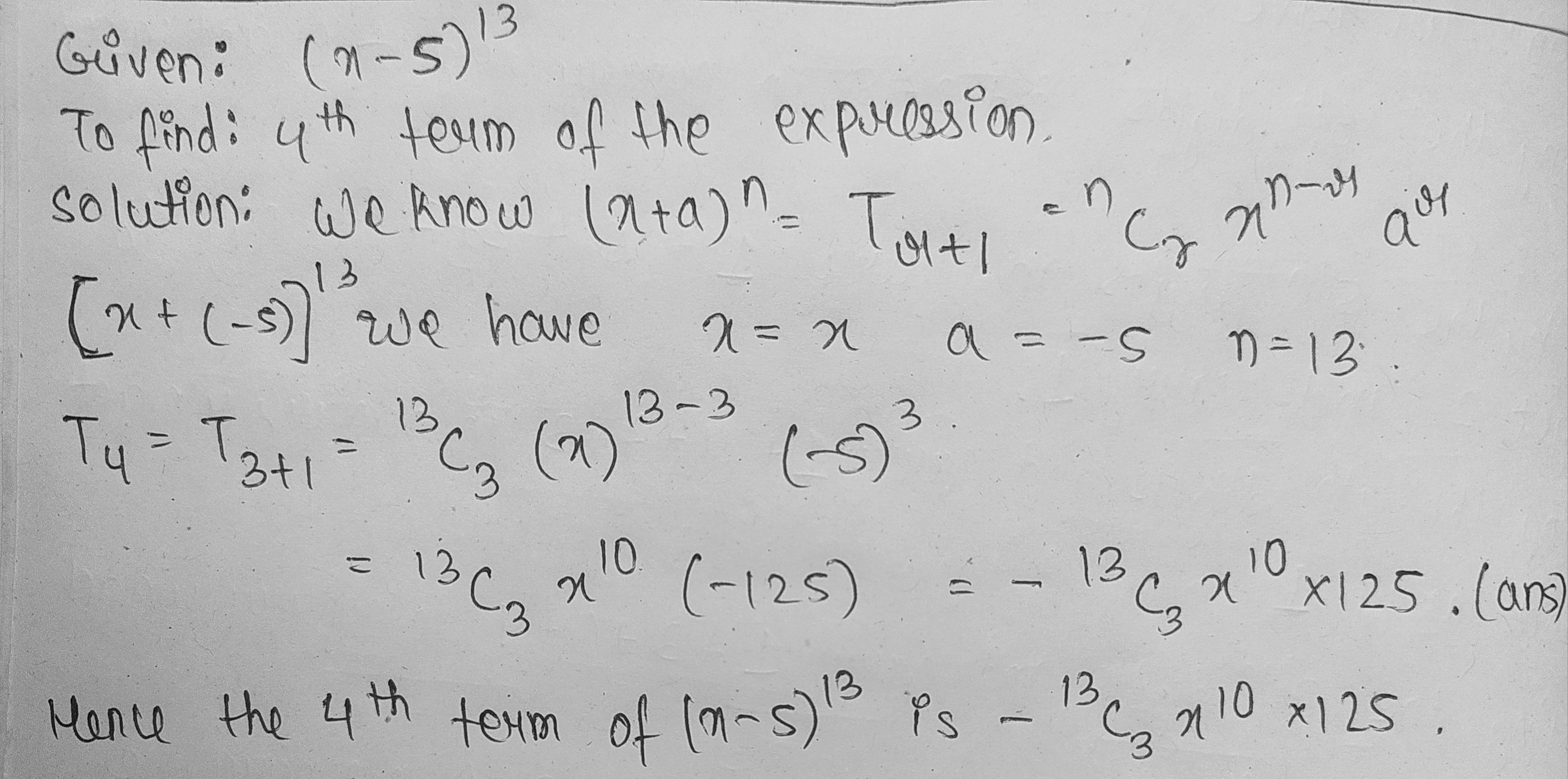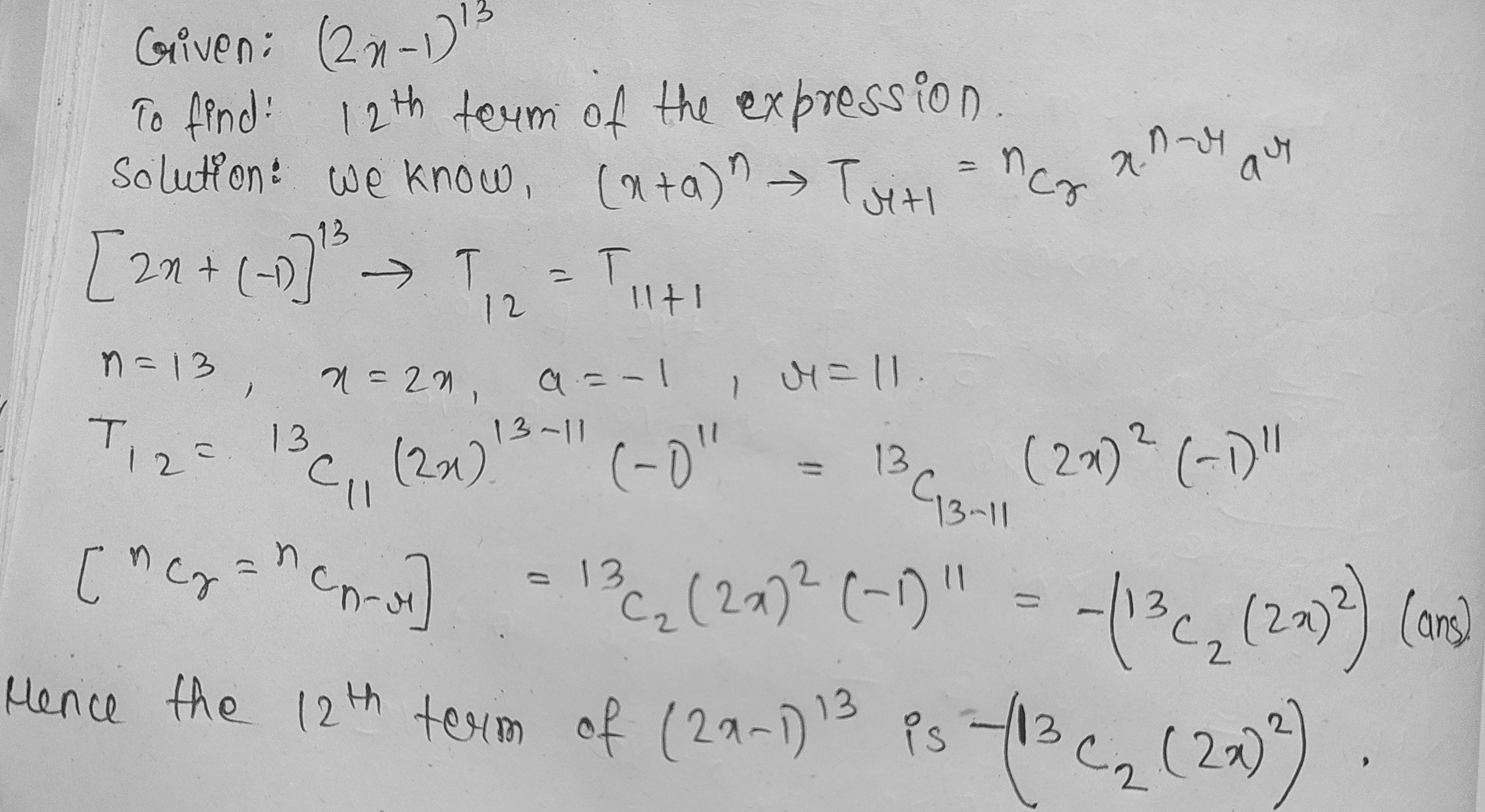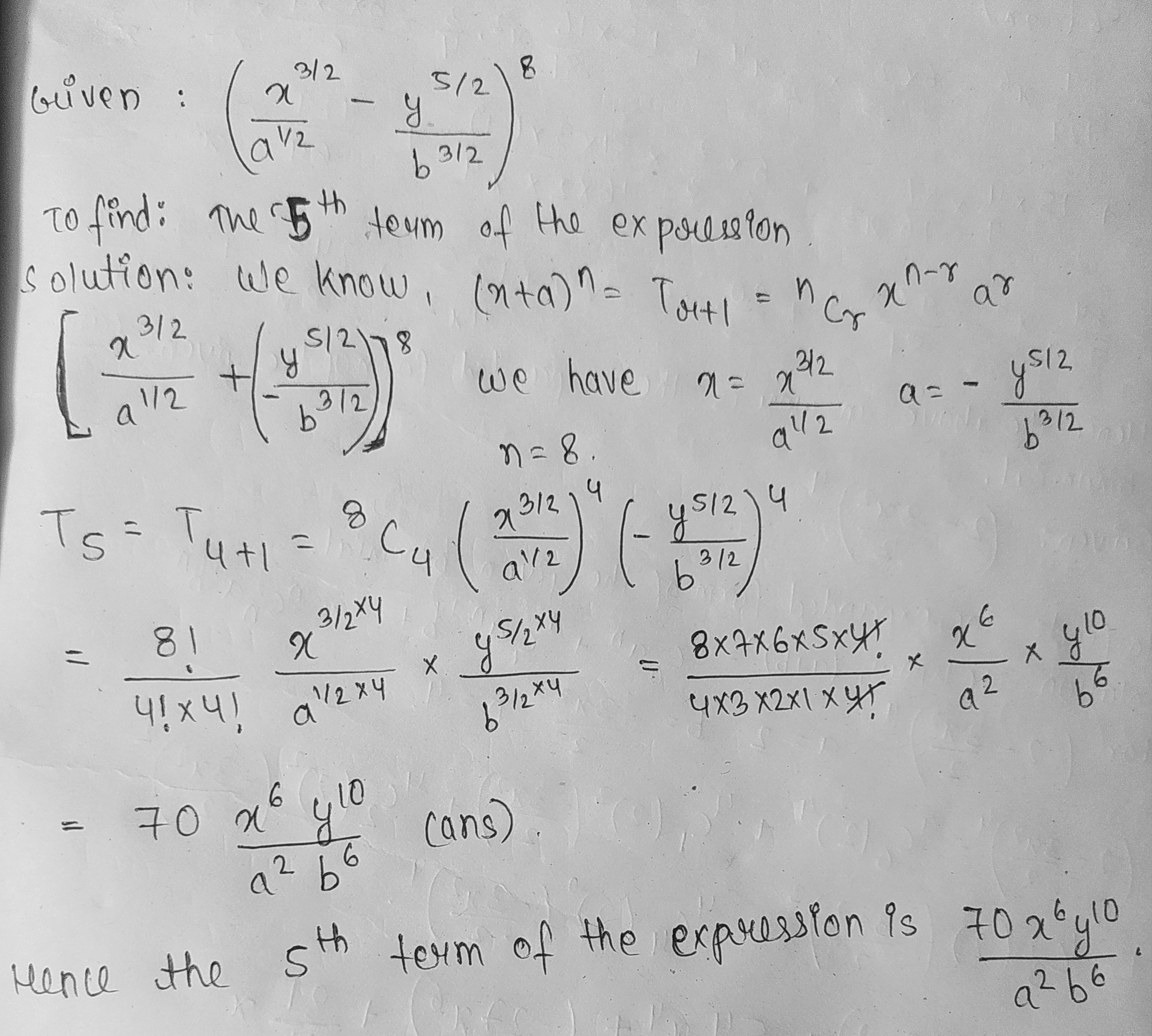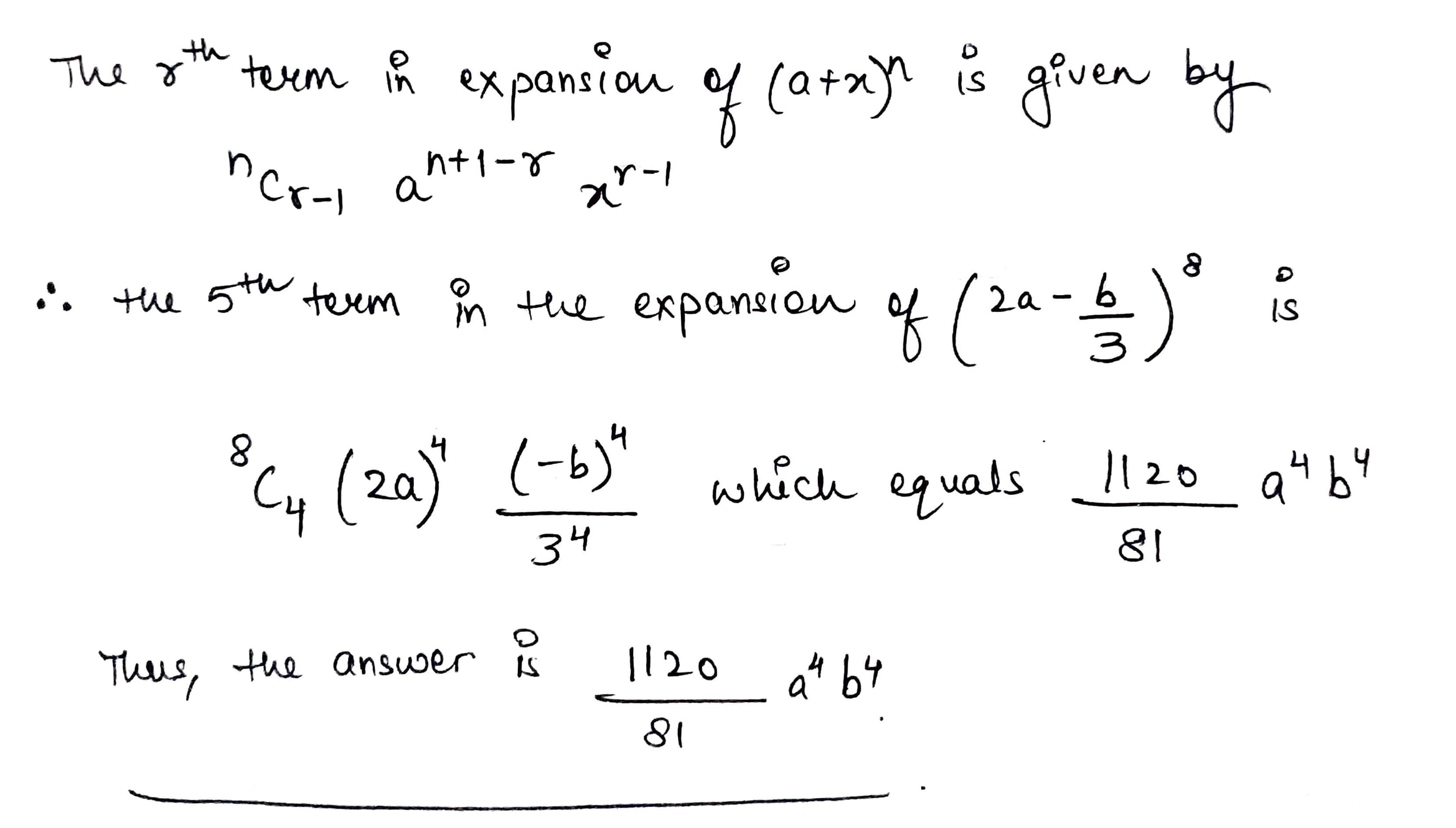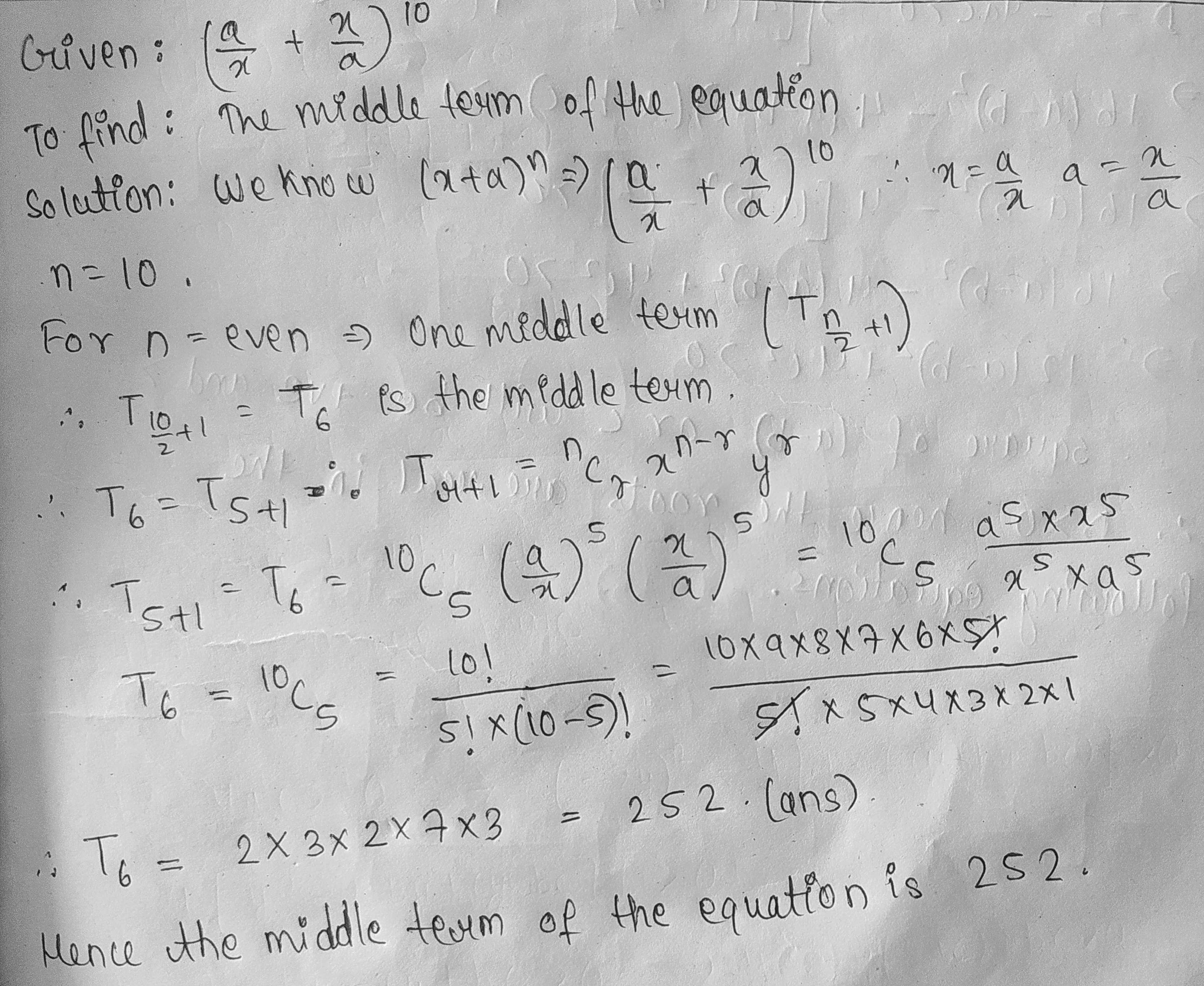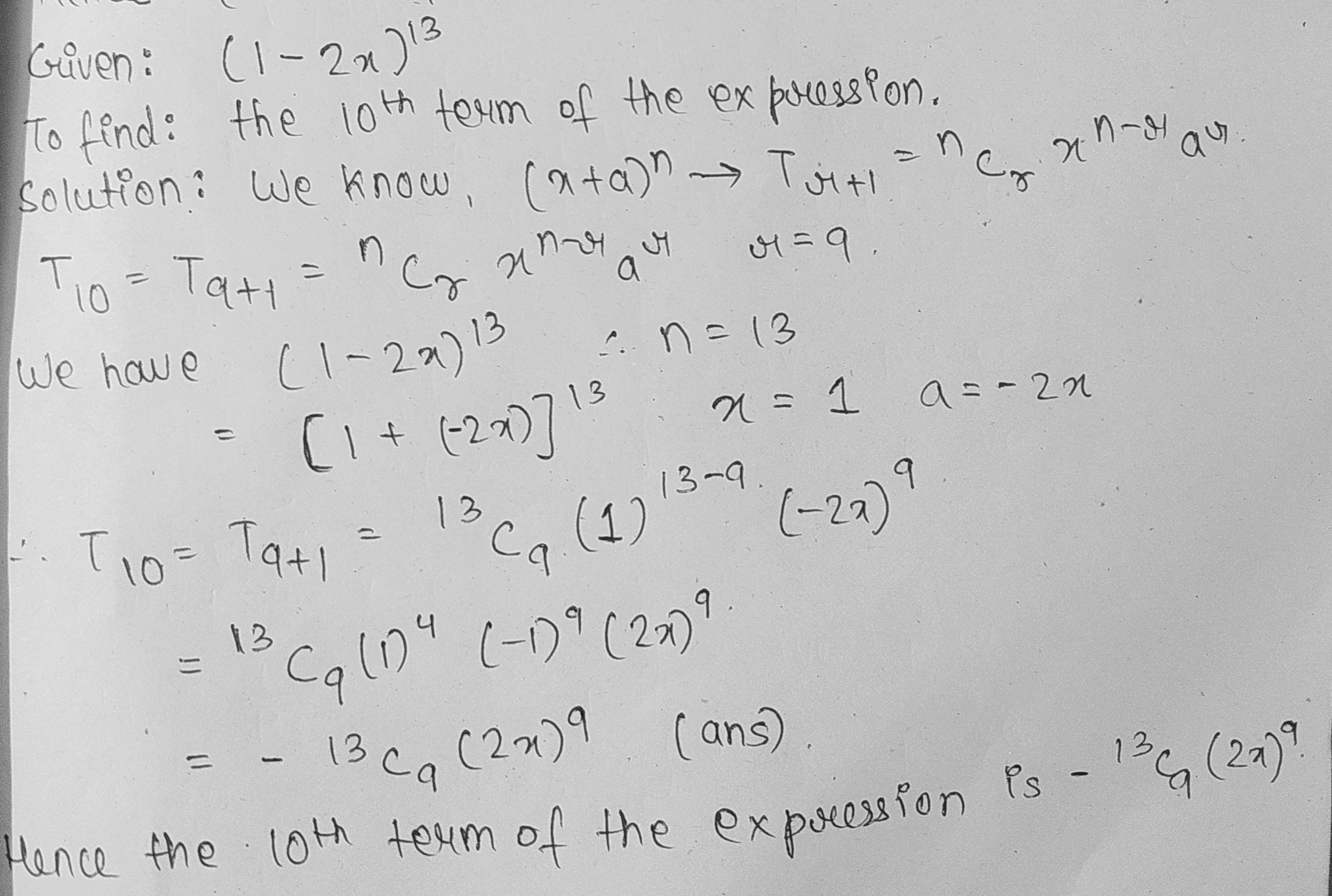Binomial Theorem - Class 11 Engineering Maths - Extra Questions
Find the middle terms in the expansion of $$(5x-7y)^7$$.
Find the 28th term of $$(5x+8y)^{30}$$.
Show that the expansion of $$\left( x^2 + \dfrac{1}{x} \right)^{12}$$ does not contain any term involving $$x^{-1}$$.
General term is
$$ T_{r} = ^{n}C_{r}\,x^{r}\,a^{n-r} $$
in $$ (x+a)r_{n}(r\epsilon z) $$
$$ \therefore T_{r} = ^{12}C_{r}(x^{2})^{r}\left ( \dfrac{1}{x} \right )^{12-r} $$
$$ \Rightarrow T_{r} = ^{12}C_{r}\,x^{3r-12} $$
for $$ x^{-1}$$ term $$ 3r-12 = -1 $$
$$ \Rightarrow \boxed{r = \dfrac{11}{3}} $$ not possible
Find the middle term in the expansion $${ \left( \cfrac { x }{ a } +\cfrac { y }{ b } \right) }^{ 6 }$$.
Write down and simplify:
The 4th term of $${ \left( x-5 \right) }^{ 13 }$$
Find the $$13^{th}$$ term in the expansion of $${ \left( 9x-\cfrac { 1 }{ 3\sqrt { x } } \right) }^{18 }$$.
The sum of the coefficients in the first three terms of the expansion of $$\displaystyle\, \left ( x^2 - \frac{2}{x} \right )^m$$ is equal to $$97$$. Find the term of the expansion containing $$x^4$$.
Write general term of this:-
$$2x{\left( {3 + 2{x^2}} \right)^{20}}$$
Find the middle term of $${ \left( \cfrac { a }{ x } +\cfrac { x }{ a } \right) }^{ 10 }$$.
Show that $$\displaystyle ^{ n }C_{ 0 } -\ ^{ n }C_{ 1 }+^{ n }C_{ 2 }\ -.....=0$$
$$ (1-x)^{n} = ^{n}C_{0}-^{n}C_{1}x+^{n}C_{2}x^{2}+....^{n}C_{n}x^{4} $$
Put $$ x = 1 $$
$$ 0 = ^{n}C_{0}-^{n}C_{1}+^{n}C_{2}+.... $$
Write down and simplify:
The 7th term of $${ \left( \cfrac { 4x }{ 5 } -\cfrac { 5 }{ 2x } \right) }^{ 9 }\quad $$
Find the sum $$\displaystyle \sum_{r=1}^{n}\dfrac {r {^{n}C_{r}}}{{^{n}C_{r-1}}}$$.
Find the $$7 ^ { th }$$ term of $$\left( 3 x ^ { 2 } - \frac { 1 } { 3 } \right) ^ { 10 }$$.
$$ 7_{7}= ^{10}C_{6}(3x^{2})^{4}(\frac{-1}{3})^{6}$$
$$ = \frac{10!}{6!4!}.\frac{81.x^{8}}{729}$$
$$ = \frac{10\times 9\times 8\times 7}{9\times 3\times 2}\times \frac{81x^{8}}{729} = \frac{70x^{8}}{3}$$
If $$4^{th}$$ term in the expansion of $$\left(ax+\dfrac{1}{x}\right)^n$$ is $$\dfrac{5}{2}$$, then find the value of $$a$$ and $$n$$.
Find the coefficient of $$x^5$$ in the expansion of the product $$(1+2x)^6(1-x)^7$$.
$$^{ 15 }{ C_{ 3 } }{ +^{ 15 } }{ C_{ 5 } }+.......{ +^{ 15 } }{ C_{ 15 } }$$
Show that the middle term in the expansion of $$(1 + x)^{n}$$ is $$ 6x^2$$ if $$n=4$$
The sum of the rational terms in the expansion of $$(\sqrt{2}+3^{1/5})^{10}$$ is _______.
The sum of the coefficient of the polynomial $$(1+x-3x^{2})^{2163}$$ is______
Find the coefficient of $$x^{2}$$ in $$(x^{2}+\dfrac{1}{x^{3}})^{6}$$.
If the middle term in the expansion of $$\left(\dfrac{x}{2}+2\right)^{8}$$ is $$1120$$; then the sum of possible real values of $$x$$ is
Find the middle terms in the expansion of $$\left(x^{2}+\dfrac {1}{x}\right)^{7}$$.
General term, $$T_{r+1}={^7C_r}(x^2)^r\left(\dfrac{1}{x}\right)^{7-r}={^7C_r}\cdot x^{2r-7+r}$$
$$={^7C_r.x^{3r-7}}$$
As total number of terms are $$(n+1)=8$$
$$\Rightarrow$$ Middle terms would be $$\left(\dfrac{n}{2}\right.$$ and $$\left.\dfrac{n}{2}+1\right)^{th}$$
$$\Rightarrow 4^{th}$$ and $$5^{th}$$
$$\Rightarrow 4^{th}$$ term $$r=3\Rightarrow T_4={^{7}C_3.x^2}$$
$$5^{th}$$ term $$r=4$$ $$\Rightarrow T_5={^7C_4x^5}$$.
Find the coefficient of $$x^3$$ in the expansion of $$(2+5x)(1-2x)^2$$.
The number of integral terms in the expansion of $${ \left( { 5 }^{ 1/2 }+{ 7 }^{ 1/8 } \right) }^{ 1024 }$$ is................
If the second term in the expansion $${ \left( { a }^{ 1/13 }+{ a }^{ 3/2 } \right) }^{ n }$$ is $$14{ a }^{ 5/2 }$$, then the value of $$\cfrac { { _{ }^{ n }{ C } }_{ 3 } }{ { _{ }^{ n }{ C } }_{ 2 } } $$ is .........
If $$n$$ is odd natural number, then $$\sum _{ r=0 }^{ n }{ \cfrac { { \left( -1 \right) }^{ r } }{ { _{ }^{ n }{ C } }_{ r } } } $$ equals................
Coefficient of $$x^3$$ and $$x^4$$ in $${ \left( 1+x+{ x }^{ 2 }+{ x }^{ 3 }+{ x }^{ 4 } \right) }^{ 199 }{ \left( x-1 \right) }^{ 201 }$$ are .
2.
If the sum of the coefficients in the expansion of $${(x+y)}^{n}$$ is $$4096$$, find the greatest coefficient in the expansion.
The greatest binomial coefficient in the expansion of $$\displaystyle \left ( a+b \right )^{n}$$ is $$\displaystyle ^{k}C_{m}$$ given that the sum of all the coefficients is equal to $$4096$$. Find $$k-m$$ ?
Following question contains statements given in two columns which have to be matched The statements in Column-I are labelled as A, B, C and D while the statements in Column-II are labelled as p, q, r and s Any given statement in Column-I can have correct matching with ONE statement in Column-II
| Column-I | Column-II |
If $$\displaystyle \left ( 1\times x \right )\left ( 1 +x+x^{2} \right )\left ( 1+x+x^{2}+x^{3} \right ).....\left ( 1+x+x^{2}+x^{3}+......+x^{n} \right )\equiv $$$$a_{0}+a_{1}x+a_{2}x^{2}+a_{3}x^{3}+.......a_{m}x^{m}$$ then $$\displaystyle \sum_{r=0}^{m}a_{r}$$ has the value equal to $$\displaystyle \left ( n+k \right )!$$ .Find $$k$$ ?
Find the negative of middle term in the expansion of$$\displaystyle \left ( \frac{2x}{3}-\frac{3}{2x} \right )^{6}$$
If $$\displaystyle ^{n+1}C_{2}+2\left ( ^2C_{2}+^3C_{2}+^4C_{2}+.....+^nC_{2} \right )=1^{2}+2^{2}+3^{2}+....+100^{2}$$ then find sum of digits of n ?
Number of terms in the expansion of $$(x^{1/3} + x^{2/5})^{40}$$ with integral power of x is equal to
Find the middle term in the expansion of $$(5x\, -\, 7y)^7$$.
Find the 7th term of $$\left (\dfrac {4x}{5}-\dfrac {5}{2x}\right )^9$$.
Find the number of rational terms in the expansion of $$\left ( 9^{1/4}+8^{1/6} \right )^{1000}.$$
$$\displaystyle \left ( 3a-\frac{a^{3}}{6} \right )^{9}$$
Find the middle term in the expansion of $$(2x + 3y)$$$$^8$$.
Find the middle term(s) in the expansion of:
$$\left (1-\dfrac {x^2}{2}\right )^{14}$$
Find the middle term(s) in the expansion of
$$\displaystyle \left ( 1-\frac{x^{2}}{2} \right )^{14}$$
Find the $$13^{th}$$ term in the expansion of $$\left ( 9x - \dfrac{1}{3\sqrt x} \right )^{18}, x \neq 0$$
Write the general term in the expansion of $$(x^2 - y)^6$$
Find the $$4^{th}$$ term in the expansion of $$(x-2y)^{12}$$
Find the middle terms in the expansion of $$\left (3- \dfrac{x^3}{6} \right )^7$$
Find the middle terms in the expansion of $$\left (\dfrac {x}{3}+ 9y\right)^{10}$$
Write the middle terms in the expansion of $$\left(\dfrac{3x}{7}-2y\right)^{10}$$.
If $$P$$ and $$Q$$ are the sum of odd terms and the sum of even terms respectively, in the expansion of $$(x + a)^{n}$$ then prove that
(i) $$P^{2} - Q^{2} = (x^{2} - a^{2})^{n}$$(ii) $$4PQ = (x + a)^{2n} - (x - a)^{2n}$$
Prove that $$C_0 +C_1 +C_2 +C_3 + ...... + 2^n . C_n = 3^n$$.
Find the fifth term of $${ \left( a+{ 2x }^{ 3 } \right) }^{ 17 }$$.
Write down and simplify:
The 10th term of $${ \left( 1-2x \right) }^{ 12 }$$
Find the fourteenth term of $${ \left( 3-a \right) }^{ 15 }$$.
Find the middle term of $${ \left( 1-\cfrac { { x }^{ 2 } }{ 2 } \right) }^{ 14 }$$.
Expand $$\cfrac { 7+x }{ \left( 1+x \right) \left( 1+{ x }^{ 2 } \right) } $$ in ascending powers of $$x$$ and find the general term.
The 2nd, 3rd and 4th terms in the expansion of $${(x+y)}^{n}$$ are $$240,720, 1080$$ respectively; find $$x,y,n$$.
Write down and simplify:
The 4th term of $${ { \left( \cfrac { a }{ 3 } +9b \right) }^{ 10 } }$$.
Show that the middle term in the expansion of $${ \left( 1+x \right) }^{ 2n }$$ is
$$\cfrac { 1.3.5....(2n-1) }{ |\underline { n } } { 2 }^{ n }{ x }^{ n }$$.
Find the$$(p+2)$$th term from the end in $${ \left( x-\cfrac { 1 }{ x } \right) }^{ 2n+1 }$$.
Find the rth term from the end in $${ \left( x+a \right) }^{ n }$$.
Write down and simplify:
The 25th term of $${ \left( 5x+8y \right) }^{ 30 }$$
Write down and simplify:
The 12th term of $${ \left( 2x-1 \right) }^{ 13 }$$.
Write down and simplify:
The 5th term of $${ \left( 2a-\cfrac { b }{ 3 } \right) }^{ 8 }$$.
If $$(1+x)^n=c_0+c_1x+c_2x^2+....+c_nx^n$$, find the value of $$1^2c_1+2^2c_2+3^2c_3+.....+n^2c_n$$.
$$2.C_0+5.C_1 +8.C_2 + ...+ (3n+2)C_n = (3n+4)2^{n-1}$$
$$\sum_{k=1}^{3n} 6 ^nC_{2\, k-1}(-3)^k$$ is equal to:
Prove that $$^{n}C_{r} + ^{n - 1}C_{r} + ^{n - 2}C_{r} + ..... + ^{r}C_{r} = ^{n + 1}C_{r + 1}$$.
To prove:
$$^nC_r+{^{n-1}C_r}+{^{n-2}C_r}+......+{^rC_r}={^{n+1}C_{r+1}}$$
$$^nC_r+{^{n-1}C_r}+{^{n-2}C_r}+.....+{^{r+1}C_r}+{^rC_r}={^{n+1}C_{r+1}}$$
$$[\because {^{n}C_n}={^{n+1}C_{n+1}}]$$
$$\Rightarrow {^{n}C_r}+{^{n-1}C_r}+{^{n-2}C_r}+......+{^{r+2}C_r}+({^{r+1}C_r}+{^{r+1}C_{r+1}})$$
$$\Rightarrow {^{r+2}C_{r+1}}$$
[We know that $$^{n+1}C_{r+1}={^nC_{r+1}+{^nC_r}}$$]
$$\therefore ^nC_r+{^{n-1}C_r}+{^{n-2}C_r}+......+{^{r+2}C_r}+{^{r+2}C_{r+1}}={^{n+1}C_{r+1}}$$
$$\Rightarrow ^nC_r+{^n-1}C_r+{^{n-2}C_r}+......+{^{r+3}C_{r+1}}={^{n+1}C_{r+1}}$$
By continuing this, we get
$$\Rightarrow ^nC_r+({^{n-1}C_r}+{^{n-1}C_{r+1}})={^{n+1}C_{r+1}}$$
$$\Rightarrow ^nC_r+{^nC_{r+1}}={^{n+1}C_{r+1}}$$
$$\Rightarrow {^{n+1}C_{r+1}}={^{n+1}C_{r+1}}$$
L.H.S$$=$$R.H.S
[Hence proved].
Write down and simplify $$6^{th}$$ term in the expansion of $$\displaystyle \left( \frac{2x}{3} + \frac{3y}{2} \right)^9$$.
The last term in $$(2^{1/3} \, + \, 2^{-1/2})^n \, is \, \left(\dfrac{1}{3(9)^{1/3}}\right)^{log_33}$$ then show that the fifth term is 210
If '$$n$$' is a positive integer and '$$x$$' is any non-zero number, then prove that
$$\displaystyle C_0 + C_1 . \frac{x}{2} + C_2 . \frac{x^2}{3} + ..... + C_n . \frac{x^n}{n+1} = \frac{(1+x)^{n+1} - 1}{(n+1)x}$$
Find the third term of the expansion of $$\displaystyle\, \left ( z^2 + \frac{1}{z} \sqrt[3]{z} \right )^n$$, if the sum of all the binomial coefficients is equal to 2048.
Find the middle term of the expansion of $$\displaystyle\, \left ( \sqrt{x} - \frac{1}{x} \right )^6$$
Find the second term of the binomial expansion of $$\displaystyle\, \left ( \sqrt[13]{a} + \frac{a}{\sqrt{a^{-1}}} \right )^m$$, if $$\displaystyle\, C_{3}^{m} : C_{2}^{m} = 4 : 1$$
if $$a_0 \, , \, a_1 \, , \, a_2$$....be the coefficients in the expansion of (1 + x + x$$^2)^n$$ in ascending powers of x , then prove that
$$a_{0}^{2} \, - \, a_{1}^{2} \, + \, a_{2}^{2} \, - \, a_{3}^{2} \, + \, ......+ \, (- 1)^{n \, - \, 1} \, a_{n \, - \, 1}^{2} $$
$$ = \, \dfrac{1}{2}a_n(1 \, -(- 1)^n \, a_n)$$
If the coefficient of $$a^{r-1}, a^r$$ and $$a^{r + 1}$$ in the expansion of $$(1 + a)^n$$ are in arithmetic progression, prove that $$n^2 - n(4r + 1) + 4r^2 - 2 = 0$$.
In the expansion of $$(7^{1/3} \, + \, 11^{1/9})^{6561}$$ prove that three will be only $$730$$ term which are free from radicals
If $$a_0 \, , \, a_1 \, , \, a_2$$....be the coefficients in the expansion of $$(1 + x + x$$$$^2)^n$$ in ascending powers $$x$$ , then prove that :
$$a_r \, = \, a_{2n \, - \, r}$$
Find the middle term(s) of $$(\frac{x^{3/2}y}{2} + \frac{2}{xy^{3/2}})^{13}$$
$${ C }_{ 0 }+\dfrac { 3 }{ 2 } .{ C }_{ 1 }+\dfrac { 9 }{ 3 } .{ C }_{ 2 }+\dfrac { 27 }{ 4 } .{ C }_{ 3 }+...........+\dfrac { { 3 }^{ n } }{ n+1 } .{ C }_{ n }=\dfrac { { 4 }^{ n+1 }-1 }{ 3\left( n+1 \right) } $$.Is it true ?If true enter 1 else 0.
Find the coefficient of $$x^{25}$$ in expansion of expression $$\displaystyle \sum_{r = 0}^{50} {^{50}C}_r (2x - 3)^r (2 - x)^{50 -r}$$.
Find the middle term:
(i) $$\left[3x - \dfrac{2}{x}\right]^{15}$$
If n is odd
$$\left(\dfrac{n+1}{2}\right)^{th}$$ & $$\left(\dfrac{n+1}{2}+1\right)^{th}$$ term are middle terms.
$$\Rightarrow (3x\dfrac{-2}{x})^{15}$$
$$\therefore n=odd=15$$
Middle terms $$=\left(\dfrac{15+1}{2}\right)^{th}=8^{th}$$ term & $$\left(\dfrac{15+1}{2}+1\right)^{th}=9^{th}$$ term
Term $$8^{th}$$ Here $$a=3x, b=\dfrac{-2}{x}, n=15, r=7$$
Tern $$8^{th}$$ $$={^{15}C_7}(3x)^{15-7}\left(\dfrac{-2}{x}\right)^{7}$$
$$\Rightarrow {^{15}C_7}3^8x^8\times \dfrac{(-2)^7}{x^7}$$
$$\Rightarrow -{^{15}C_7}3^8\times 2^7x$$.
Term $$9^{th}$$ Here $$a=3x, b=\dfrac{-2}{x}, n=15, r=8$$
Term $$9^{th}={^{15}C_8}(3x)^{15-8}\left(\dfrac{-2}{x}\right)^8$$
$$\Rightarrow {^{15}C_8}3^7\times x^7\times \dfrac{(-2)^8}{x^8}$$
$$\Rightarrow {^{15}C_8}3^7\times 2^8\times x$$.
Find the coefficient of $$a^4$$ in the product $$(1 + 2a)^4 (2 - a)^5$$ using binomial theorem.
$$\Rightarrow $$(1+2a)^4$$
$$\Rightarrow ^{4}C_1+{^{4}C_1}(2a)+{^{4}C_2}(2a)^2+{^{4}C_3}(2a)^3+{^{4}C_4}(2a)^4$$
$$\Rightarrow 1+8a+24a^2+32a^3+16a^4$$
$$(2-a)^5$$
$$\Rightarrow {^{5}C_0}2^5-{^{5}C_1}2^4(a)+{^{5}C_2}2^3(a)^2-{^{5}C_3}2^2a^3+{^{5}C_4}2a^4-{^{5}C_5}a^5$$
$$\Rightarrow 32-80a+80a^3+10a^4-a^5$$
$$\therefore$$ Coefficient of $$a^4$$ is $$\Rightarrow 1\times 10a^4+(8a)(80a^3)+32a^3(-80a)+16a^4(32)$$
$$\Rightarrow 10a^4+640a^4-2560a^4+512a^4$$
$$\Rightarrow -1.398x^4$$.
Evaluate $${(\sqrt{3}+\sqrt{2})}^{6} -{(\sqrt{3}-\sqrt{2})}^{6}.$$
In the expansion of $${\left( {{x^3} - \dfrac{1}{{{x^2}}}} \right)^2}$$, where n is a positive integer, the sum of the coefficients of $${x^6}$$ is $$1.$$
Find the sum $$\sum _{ r=1 }^{ n }{ \overset { n+r }{ \underset { \quad \quad r }{ C }}} $$.
Find the sum of $$\sum _{ 0\le i\le j\le n } \sum { j\overset { n }{ \underset { \quad i }{ C } } } $$
In the expansion of $${\left( {\dfrac{3}{2} + \dfrac{7}{3}} \right)^n}$$ when $$x = \dfrac{1}{2}$$ if is known that $${6^{th}}$$ term is the greatest term the find the possible integral value of n.
Find the sum $$\sum _{ r=1 }^{ n }{ \dfrac { r\overset { n }{ \underset { \quad \quad r }{ C } } }{ \overset { n }{ \underset { \quad \quad r-1 }{ C } } } } $$
Find the middle term in the expansion of $$\left ( \dfrac{x}{y}-\dfrac{y}{x} \right )^7$$.
Write the following form in expanded form:-
(A) $${\left( {2a + 3b} \right)^3}$$
(B) $${\left( {5x - 3y} \right)^3}$$
Show that the middle term in the expansion of $${(1 + x)^{2n}}$$ is $$\frac{{1.3.5.....(2n - 1)}}{{n!}}$$ $${2^n}{x^n}$$; where n is a positive integer.
If sum of coefficient in expansion of $$(2+3cx+c^2x^2)^{12}$$ is $$0$$. Then find the value of $$c$$.
Evaluate:$$\sum\limits_{r=0}^{20}\ ^{20}C_r$$.
$$^{14}C_1+$$ $$^{14}C_2+$$ $$^{14}C_3+$$...$$+$$ $$^{14}C_{14}=?$$
Is $$x^5$$ in the expansion of $$\left[2x^3 - \dfrac{1}{3x^3}\right]^{10}$$.
Find the $$24th$$ term in the sequence whose nth term $${a_n} = \dfrac{{n\left( {n - 2} \right)}}{{n + 3}}$$ . using binomial theorem , Evaluate $${\left( {102} \right)^3}$$
Find the $$7$$th term in the expansion of $$\left(\dfrac{4x}{5}-\dfrac{5}{2x}\right)^9$$.
Find the coefficient of $$x^4$$ in $$(1 + 2x)^4 (2 -x)^5$$
Find the middle terms in the expansions of
i) $$\left(3 - \dfrac{x^3}{6} \right)^7$$
ii) $$\left(\dfrac{x}{3} + 9y \right)^{10}$$
Find the coeifficient of
(i) $$x^{6}y^{3}in (x+y)^{9}$$
Show that the middle term in the expansion of $$(1+x)^{2n}$$ is $$\dfrac{1.3.5...(2n-1)}{n!}$$ $$2^nx^n$$, where n is a positive integer.
Find the coefficient of $$x^{15}$$ in
$$(1 + x)^{15} + (1 + x)^{16} + .... (1 + x)^{30}$$.
If the coefficients of $$\left( r-5 \right) $$th and $$\left( 2r-1 \right)$$th terms in the expansion of $${ \left( 1+x \right) }^{ 34 }$$ are equal, then write the value of $$r$$
Find the $$8th$$ term in the expansion of $${ \left( { x }^{ 3/2 }{ y }^{ 1/2 }-{ x }^{ 1/2 }{ y }^{ 3/2 } \right) }^{ 10 }$$
$$ (a+b)^{n} \Rightarrow $$ General term $$ \Rightarrow T_{r} = ^{n}C_{r} a^{n-r} b^{r}$$
$$ \therefore 8^{th} $$ term in $$ (x^{3/2} y^{1/2}-x^{1/2}y^{3/2})^{10}$$
$$ T_8 \Rightarrow ^{10}c_{7}(x^{3/2}y^{1/2})^{1/2}(-1)(x^{1/2}y^{3/2})^{7}$$
$$ = \dfrac{10 \times 8 \times 9 (-1)}{3 \times 2} (x^{1/2}y^{3/2}) (x^{3/2} y^{2/2} )$$
$$ = -10 \times 4 \times 3 (x^{9/2+7/2}) (y^{3/2+4/2})$$
$$ = -120 (x^{16/2}y^{24/2})$$
$$ T_{8} = -120x^{8}y^{12}$$
Prove that there is no term involving $$x^6$$ in the expansion of $$\left (2x^2-\dfrac{3}{x}\right)^{11}$$, where $$r\neq 0$$.
If the coefficients of $$x$$ and $${x}^{2}$$ in the expansion of $${(1+x)}^{m}{(1-x)}^{n}$$ are $$3$$ and $$-6$$ respectively. Find the values of $$m$$ and $$n$$.
Find the coefficient of x$$^{13}$$ in the expansion of $$(1-x)^{5}x(1+x+x^{2}+x^{3})^{4}$$
$$(1-x)^5x(1+x+x^2+x^3)^4$$ sum of $$4$$ terms of G.P$$=1+x+x^2+x^3=1\dfrac{(1-x^4)}{1-x}$$
$$=(1-x)^5x\left(\dfrac{1-x^4}{1-x}\right)^4$$
$$=(1-x)^5x\dfrac{(1-x^4)^4}{(1-x)^4}$$
$$=(1-x)x(1-x^4)^4$$
Coefficient of $$x^{13}$$ in $$(1-x)x(1-x^4)^4$$
$$=$$Coefficient of $$x^{12}$$ in $$(1-x)(1-x^4)^4$$
$$=$$Coefficient of $$x^{12}$$ in $$(1-x^4)^4-x(1-x^4)^4$$
$$=$$Coefficient of $$x^{12}$$ in $$(1-x^4)^4-$$coefficient of $$x^{12}$$ in $$x(1-x^4)^4$$
$$=$$Coefficient of $$x^{12}$$ in $$(1-x^4)^4-0$$ ($$x^{12}$$ term is not possible in $$x(1-x^4)^4$$)
$$={^{4}C_3}(-1)^3$$ $$(\because (1-x^4)^4={^{4}C_0}-{^{4}C_1}x^4+{^{4}C_2}x^8-{^{4}C_3}x^{12}+{^{4}C_4}x^{16})$$
$$=-4$$
$$\therefore$$ Coefficient of $$(1-x)^5x(1+x+x^2+x^3)^4=-4$$.
The sum of the coefficients of first three terms in the expansion of $${ \left( x-\cfrac { 3 }{ { x }^{ 2 } } \right) }^{ m },x\neq 0$$, $$m$$ being a natural number, is $$559$$. Find the term of the expansion containing $${x}^{3}$$.
If $${x}^{p}$$ occurs in the expansion of $$\quad { \left( { x }^{ 2 }+\cfrac { 1 }{ x } \right) }^{ 2n }$$, prove that its coefficient is $$\quad \left[ \cfrac { \left( 2n \right) ! }{ \left( \cfrac { 4n-p }{ 3 } \right) !\left( \cfrac { 2n+p }{ 3 } \right) ! } \right] $$
The value of $$\sum_{r=1}^{15}r^{2}(\frac{^{15}Cr}{^{15}Cr-1})$$ is equal to:
$$\displaystyle\sum^{15}_{r=1}r^2\left(\dfrac{^{15}C_r}{^{15}C_{r-1}}\right)$$
$$\dfrac{^{n}C_r}{^{n}C_{r-1}}=\dfrac{n-r+1}{r}$$
$$\dfrac{^{15}C_r}{^{15}C_{r-1}}=\dfrac{15-r+1}{r}=\dfrac{16-r}{r}$$
$$\displaystyle\sum^{15}_{r=1}r^2\left(\dfrac{^{15}C_r}{^{15}C_{r-1}}\right)=\displaystyle\sum^{15}_{r=1}r^2\left(\dfrac{16-r}{r}\right)$$
$$=\displaystyle\sum^{15}_{r=1}16r-r^2$$
$$=16\displaystyle\sum^{15}_{r=1}r-\displaystyle\sum^{15}_{r=1}r^2$$
$$\displaystyle\sum^n_{r=1}r=\dfrac{n(n+1)}{2}$$
$$\displaystyle\sum^n_{r=1}r^2=\dfrac{n(n+1)(2n+1)}{6}$$
$$=16\left(\dfrac{15(15+1)}{2}\right)-\dfrac{15(15+1)(2(15)+1)}{6}$$
$$=15(16)\left[8-\dfrac{31}{6}\right]=15(16)\dfrac{17}{6}$$
$$=5\times 8\times 17=40\times 17$$
$$=680$$.
The coefficient of x$$^{10}$$ in the expansion of (1+x)$$^{2}$$
If the coefficients of $$r$$th, $$(r+1)$$th and $$(r+2)$$nd terms in the expansion of $${(1+x)}^{n}$$ are in A.P, then show that $${n}^{2}-(4r+1)n+4{r}^{2}-2=0$$.
If $$\displaystyle \sum_{r = 1}^{n} {^{n}C_{r}} 3^{r}$$ is equal to $$4095$$ then $$n$$ equals.
The coefficent of $$x^{10}$$ in the expansion $$(x+10)^{10}$$
Find the middle term in the expansion of $$\left (\dfrac{2}{3}x^2-\dfrac{3}{2x}\right )^{20}$$.
Find the middle term of $$\left(x-\dfrac {1}{2x}\right)^{10}$$
Find the middle term in term expansion of $${\left(1+x\right)}^{2n}$$
If the sum of the coefficients of $$x^7 and \ x^4$$ in the expansion of $$\left(\dfrac{x^2}{a} - \dfrac{b}{x}\right)^{11}$$ is zero, then ab=
Find general term in the expansion of $$\left( x _ { 1 } + x _ { 2 } + \ldots . + x _ { p } \right) ^ { n }$$
In the expansion of $$\left( 5 ^ { \dfrac { 1 } { 2 } } + 2 ^ { \dfrac { 1 } { 8 } } \right) ^ { 1024 },$$ the number of integral terms is
Find the coefficient of $${ x }^{ 3 }$$ in the expansion of $${ \left( { x }^{ 2 }+\dfrac { 3\sqrt { 2 } }{ x } \right) }^{ 9 }$$
using binomial therm
$$(x^{2}+\frac{3\sqrt{2}}{x^{9}}) $$ $$\sum_{n=0}^{9}$$ $$^{9}C_{n}$$ $$(x^{2})^{9-n}(\frac{3\sqrt{2}}{x})^{n}$$
$$ \sum_{n=0}^{9} $$ $$^{9}C_{n}$$ $$x^{18-2n}$$ $$\frac{(3\sqrt{2})^{n}}{x^{n}}$$
$$ = \sum_{n=0}^{9} $$ $$^{9}C_{n}$$ $$x^{18-3n}$$ $$(3\sqrt{2})^{n}$$
$$ =\sum_{n=0}^{9} $$ $$^{9}C_{n}$$ $$x^{18-2n}$$ $$x^{18-2n}$$
$$ T_{n+1} = ^{9}C_{n} (3\sqrt{2})^{n} x^{18-3n}$$
coefficient of $$ x^{3} = ^{9}C_{5} (3\sqrt{2})^{5} = ^{9}C_{5} 3^{5}. (\sqrt{2})^{5} [18+3n = 3 3n=18-3 n =\frac{15}{3}=5$$
$$ = \frac{9\times 8\times 7\times 6\times 5}{1\times 2\times 3\times 4\times 5} 3^{5}.4\sqrt{2}$$
$$ = 126. 243 . 4\sqrt{2} .$$
$$ = 422,472\sqrt{2}.$$
Find the coefficient $${ x }^{ 8 }$$ in the product $$\left( 1+2x \right) ^{ 6 }\left( 1-x \right) ^{ 7 }$$ using binomial therm.
If the middle term in the expansion of $$\left(x+\dfrac {b}{x}\right)^{6}$$ is $$160$$, find $$b$$.
$$\left(x+\dfrac{b}{x}\right)^{6}$$ Total term$$=7$$
middle term=$$\dfrac{7+1}{2}=\dfrac{8}{2}=4^{th}$$
$$ T_{4}$$ $$= ^{6}C_{3}$$ $$ x^{3}$$ $$\left(\dfrac{b}{x}\right)^{3}$$
$$160=\dfrac{6!}{3!3!}.x^{3}\dfrac{b^{3}}{x^{3}}$$
$$b^{3}=8$$
$$\Rightarrow b=2$$.
Find the sum of coefficients of odd powers of $$x$$ in the expansion $${\left(1+x\right)}^{50}$$
The coefficient of $$x ^ { 10 }$$ in the expansion of $$( 1 + x ) ^ { 2 } \left( 1 + x ^ { 2 } \right) ^ { 3 } \left( 1 + x ^ { 3 } \right) ^ { 4 }$$ is equal to :
The middle term in the expansion of $$(5x-7y)^{7}$$.
Fidn the $${ 7 }^{ th }$$ term from the end in the expansion of $${ \left( 9x-\dfrac { 1 }{ 3\sqrt { x } } \right) }^{ 18 },x\neq 0$$.
$$\left(9x-\dfrac{1}{3\sqrt{x}}\right)^{18}=7^{th}$$ term from end
$$11^{th}$$ term from start
$$T_{11}={^{18}C_{11}(9x)^{11}}\left(\dfrac{1}{3\sqrt{x}}\right)^{18-11}$$.
In expansion of $$(1+x)^3$$ , the second term is 240 , find $$x$$
Find the middle term in the expansion of
$$\left( \dfrac { 2x }{ 3 } -\dfrac { 3 }{ 2x } \right) ^{ 6 }$$
Total terms $$=6+1=7$$ terms
Middle terms $$=\dfrac{7+1}{2}=4^{th}$$ term
$$T_4={^{6}C_3}\left(\dfrac{2x}{3}\right)^3\left(\dfrac{-3}{2x}\right)^3$$
$$=\dfrac{6!}{3!3!}\times (-1)^3=\dfrac{-6\times 5\times 4}{3\times 2}$$
$$=-20$$.
Find the middle term in the expansion of $$\left( \dfrac { { 2x }^{ 2 } }{ 3 } -\dfrac { 3 }{ 2x } \right) ^{ 12 }$$.
Find the 8th term of $${\left( {1 - \frac{{5x}}{2}} \right)^{ - 3/5}}$$
Find the $${ 7 }^{ th }$$ term in $${ \left( \dfrac { 4 }{ { x }^{ 3 } } +\dfrac { { x }^{ 2 } }{ 2 } \right) }^{ 14 }$$
$$\left(\dfrac{4}{x^3}+\dfrac{x^2}{2}\right)^{14}$$
$$T_7={^{14}C_6}\left(\dfrac{4}{x^3}\right)^8\left(\dfrac{x^2}{2}\right)^6$$
$$=\dfrac{14!}{6!8!}\times \dfrac{4^8}{x^{24}}\times \dfrac{x^{12}}{2^6}$$
$$=\dfrac{14\times 13\times 12\times 10\times 9}{6\times 5\times 3\times 2}\times \dfrac{2^{16}}{2^6}\times \dfrac{1}{x^{12}}$$
$$=\dfrac{14\times 13\times 6\times 2^{10}}{x^{12}}$$
$$=\dfrac{1118208}{x^{12}}$$.
Prove that the coefficient of $${x^n}$$ in the expression of $${\left( {1 + x} \right)^{2n}}$$ is twice the coefficient of $${x^n}$$ in the expression of $${\left( {1 + x} \right)^{2n - 1}}$$.
We know that
General term of $$(a+b)^n$$ is
$$T_{r+1}={^{n}C_r}a^{n-r}, b^r$$
For $$(1+x)^{2n}$$
General term of $$(1+x)^{2n}$$
Putting $$a=1, b=x, n=2n$$
$$T_{r+1}={^{2n}C_r}1^{2n-r}(x)^r$$
$$T_{r+1}={^{2n}C_r}x^r$$ …………….$$(1)$$
For coefficient of $$x^n$$
Putting $$r=n$$ in $$(1)$$
$$T_{r+1}={^{2n}C_n}x^n$$
Coefficient of $$x^n={^{2n}C_n}$$
For $$(1+x)^{2n-1}$$
General term of $$(1+x)^{2n-1}$$
Putting $$a=1, b=x, n=2n-1$$
$$T_{r+1}{^{2n-1}C_n}x^n$$
Coefficient of $$x^n={^{2n-1}C_n}$$
We have to prove
Coefficient of $$x^n$$ in $$(1+x)^{2n}=2x$$, coefficient of $$x^n$$ in $$(1+x)^{2n-1}$$
i.e., $${^{2n}C_n}={^{2n-1}C_n}$$
L.H.S R.H.S
$$^{2n}C_n$$ $$2\times {^{2n-1}C_n}$$
$$=\dfrac{2n!}{n!(2n-n)!}$$ $$=2\times \dfrac{(2n-1)!}{n!(2n-1-n)!}$$
$$=\dfrac{2n!}{n!\cdot n!}$$ $$=2\times \dfrac{(2n-1)!}{n!(n-1)!}$$
Multiply & divide by n
$$=2\times \dfrac{(2n-1)!}{n!(n-1)!}\times \dfrac{n}{n}$$
$$=\dfrac{2n(2n-1)!}{n!n(n-1)!}$$
$$=\dfrac{2n!}{n!n!}$$
Hence L.H.S$$=$$R.H.S
We proved.
Find the middle term in the expansion of :
$$\left(\dfrac{x}{a}-\dfrac{a}{x}\right)^{10}$$
Find the coefficient of $$x^3$$ in the expansion of $$(3x + 1)(2 - x)^6$$
Find the coefficient of $$x^2$$ and $$x^3$$ in the expansion of $$(1-2x)^3$$.
Show that the expansion of $$ (2x^2 - \frac {1}{x} )^{20} $$ does not contain any term involving $$x^9 $$
Show that the term containing $$ x^3 $$ does not exist in the expansion of $$ (3 x -\frac {1}{2x})^8 $$.
Find the coefficient of $$ x^{-15} $$ in the expansion of $$ (3x^2 - \frac {a}{3x^3} )^{10} $$.
Find the coefficient of x in the expansion of $$ ( 1 -3x +7x^2)(1-x)^{16}. $$
Write the general term in the expansion of $$ ( x^2 -y)^6 $$
Find the coefficient of $$ x^5 $$ in the expansion of $$ (x+ 3)^8 $$.
Find the coefficient of $$x^6 $$ in the expansion of $$ (3x^2 - \frac {1}{3x})^9 $$.
Find the two middle terms in the expansion of $$ ( x^2 +a^2)^5 $$
Find the middle term in the expansion of :
$$ (\frac {x}{a} - \frac {a}{x})^{10} $$
Find the middle term in the expansion of :
$$ ( x^2 - \frac {2}{x})^{10} $$
Find the 4th term from the end in expansion of $$ ( \frac {4x}{5} - \frac {5}{2x})^9 $$
Find the two middle terms in the expansion of $$ ( 3x - \frac {x^3}{6})^9 $$
Find the two middle terms in the expansion of $$( x^4 - \frac {1}{x^3})^{11} $$
Find the 5th term from the end in expansion of $$ ( x- \frac {1}{x})^{12} $$.
Find the middle term in the expansion of $$ ( 3+ x)^6 $$
Find the middle term in the expansion of $$ (\frac {x+ 3}2 +3y)^8 $$
Find the two middle terms in the expansion of $$ (\frac {p}{x} + \frac {x}{p})^9 $$
Find the coefficient of $$ x^4 $$ in the expansion of $$ ( 1+ x)^n(1 -x)^n. $$ deduce that $$ C_2 = C_0C_4 - C_1C_3 +C_2C_2 - C_3C_1 +C_4C_0, $$ where $$ C_r $$ stands for$$ ^nC_r. $$
Find a and b so that the $$n^{th}$$ term in the expansion of $$\dfrac {a + bx}{(1 - x)^2}$$ may be $$(3n - 2)x ^{n - 1}.$$
The larger of $$99^{50}+100^{50}$$ is $$101^{50}$$ is ________.
If $$(1+ax)^{n}=1+8x+24x^{2}+....$$ then $$a=$$ _______ and $$n=$$ _______
Find $$a , b , c$$ so that the coefficient of $$x^{n}$$ in the expansion of $$\dfrac {a + bx + cx^2}{(1 - x)^3}$$ may be $$n^2 + 1.$$
Prove that the sum of the coefficient of the odd powers of x the expansion of $$(1+x+x^2+x^3+x^4)^{n-1}$$, when $$n$$ is a prime number other than $$5,$$ is divisible by $$n.$$
Match the statements $$a,b,c,d$$ in column I with statements $$p,q,r,s$$ in column II.
Shew that the middle term in the expansion of $$(1+x)^{2n}$$ is $$\dfrac{1.3.5...(2n-1)}{(n)!}2^nx^n$$.
Find the coefficient of $$x^n$$ in the expansion of
$$(1 - 2x + 3x^2 - 4x^3 + \dots)^{-n}$$.
Find n, if the ratio of fifth term from the beginning to the fifth term from the end in the expansion of $$\left ( \sqrt[4]{2} + \cfrac{1}{\sqrt[4]{3}} \right )^{n} \text {is} \sqrt{6} : 1$$
Find the $$4^{th}$$ term in the expansion of $$(x - 2y)^{12}.$$
In the following expansions, find the term as stated:
$$9th$$ term of $$\Bigg(\dfrac{x}{y} - \dfrac{3y}{x^2}\Bigg)^{12}$$
In the following expansions, find the term as stated :
$$5th$$ term of $$(a + 2x^3)^{17}$$
Find $$a$$, if the $$17^{th}$$ and $$18^{th}$$ terms of the expansion $$(2 + a)^{50}$$ are equal.
Find the middle terms in the expansions of
(i) $$\left (3 - \cfrac{x^{3}}{6} \right )^{7}$$
(ii)$$\left (\cfrac{x}{3} + 9 y \right)^{10}$$
Expand the following Binomials upto fourth term: $$(1+x^2)^{-2}$$
Find the $$13^{th}$$ term in the expansion of
$$\left ( 9x - \dfrac{1}{3\sqrt{x}} \right )^{18}, x \neq 0$$
Find the general term of the following expansions:
$$(1 x)^{-p/q}$$
Find the coefficient of $$x^6$$ in the expansion of $$(a + 2bx^2)^{-3}$$.
Find the middle term in the following expansions.
$$\bigg(\dfrac{x}{2}+2y\bigg)^6$$
Find the required terms in the following expansions:
Eighth term of $$(1+2x)^{-1/2}$$
Expand the following Binomials upto fourth term $$\bigg(1-\dfrac{x}{2}\bigg)^{1/2}$$.
Expand the following Binomials upto fourth term: $$(3-2x^2)^{-2/3}$$
Expand the following Binomials upto fourth term: $$\dfrac{1}{\sqrt{5+4x}}$$.
Find the middle term in the following expansions.
$$\bigg(x+\dfrac{1}{x}\bigg)^{2n}$$
Find the required terms in the following expansions:
Seventh term of $$(1+x)^{5/2}$$
Find the required terms in the following expansions: Fourth term of $$(1 3x)^{-1/3}$$.
The ratio of fifth term from the beginning to the fifth term from the end in the expansion of $$ \left(\sqrt[4]{2} + \dfrac{1}{\sqrt[4]{3}}\right)^{n}$$ is $$\sqrt{6} : 1$$. If $$n = \dfrac{20}{\lambda}$$, find the value of $$ \lambda$$.
Find the coefficient of $${ x }^{ 50 }$$ in the polynomials after parenthesis have been removed and like terms have been collected in the expansion
$${ \left( 1+x \right) }^{ 1000 }+x{ \left( 1+x \right) }^{ 999 }+{ x }^{ 2 }{ \left( 1+x \right) }^{ 998 }+....+{ x }^{ 1000 }$$
If $${ \left( 1+x \right) }^{ n }={ C }_{ 0 }+{ C }_{ 1 }x+{ C }_{ 2 }{ x }^{ 2 }+....+{ C }_{ n }{ x }^{ n } $$, then find the sum of the series
$$\cfrac { { C }_{ 0 } }{ 2 } -\cfrac { { C }_{ 1 } }{ 6 } +\cfrac { { C }_{ 2 } }{ 10 } -\cfrac { { C }_{ 3 } }{ 14 } +........+\cfrac { { \left( -1 \right) }^{ n }{ C }_{ n } }{ 4n+2 } $$
For $$n\ge 2$$, let $${ C }_{ r }=\begin{pmatrix} n \\ r \end{pmatrix}$$ and $${ a }_{ n }=\sum _{ r=0 }^{ n }{ \cfrac { 1 }{ { C }_{ r } } } $$
Match the entries in column I with entries in column II
If the 2nd,3rd and 4th terms in the expansion of $${(a+x)}^{n}$$ are respectively $$240,720,1080$$, find $$a,x,n$$.
Find the middle term in the expansion of $${\left(\dfrac{a}{x}+bx\right)}^{12}$$
If $${c}_{0},{c}_{1},{c}_{2},.......{c}_{n}$$ denote the coefficients in the expansion of $${(1+x)}^{n}$$, prove that
$$\cfrac { { c }_{ 1 } }{ { c }_{ 0 } } +\cfrac { 2{ c }_{ 2 } }{ { c }_{ 1 } } +\cfrac { 3{ c }_{ 3 } }{ { c }_{ 2 } } +...\cfrac { n{ c }_{ n } }{ { c }_{ n-1 } } =\cfrac { n(n+1) }{ 2 } $$.
Find the two middle terms of $${ \left( 3a-\cfrac { { a }^{ 3 } }{ 6 } \right) }^{ 9 }$$.
If $$p$$ is a prime number, show that the coefficients of the terms of $$(1 + x)^{p - 1}$$ are alternately greater and less by unity than some multiple of $$p$$.
If $$ c_0 , c_1 , c_2 , ...... c_n $$ are the coefficients in the expansion $$ (1+x)^n , $$ where $$n$$ is a positive integer, shew that
$$ c_1 - \dfrac {c_2}{2} + \dfrac{c_3}{3} - ...... + \dfrac { (-1)^{n-1} c_n }{n} = 1 + \dfrac {1}{2} + \dfrac {1}{3} + .... \dfrac {1}{n} $$
If $${c}_{0},{c}_{1},{c}_{2},.......{c}_{n}$$ denote the coefficients in the expansion of $${(1+x)}^{n}$$, prove that
$${ c }_{ 0 }+\cfrac { { c }_{ 1 } }{ 2 } +\cfrac { { c }_{ 2 } }{ 3 } +......+\cfrac { { c }_{ n } }{ n+1 } =\cfrac { { 2 }^{ n+1 }-1 }{ n+1 } $$.
If $${x}^{p}$$ occurs in the equation $${ \left( { x }^{ 2 }+\cfrac { 1 }{ x } \right) }^{ 2n }$$., prove that its coefficient is $$\cfrac { |\underline { 2n } }{ |\underline { \cfrac { 1 }{ 3 } (4n-p) } \quad |\underline { \cfrac { 1 }{ 3 } (2n+p) } } $$.
If $${c}_{0},{c}_{1},{c}_{2},.......{c}_{n}$$ denote the coefficients in the expansion of $${(1+x)}^{n}$$, prove that
$$({c}_{0}+{c}_{1})({c}_{1}+{c}_{2}).......({c}_{n-1}+{c}_{n})=\cfrac { { c }_{ 1 }{ c }_{ 2 }...{ c }_{ n }{ (n+1) }^{ n } }{ |\underline { n } } $$.
Find the middle term(s) in the expansion of $$(1+3x+3x^2+x^3)^{2n}$$.
Find the middle terms in the expansion of $${ \left( { x }^{ 2 }+\dfrac { 1 }{ x } \right) }^{ 11 }$$
Prove that: $$\sum_{r \, = \, 0}^{n} \, r(n \, - \, r)C_r^2 \, = \, n^2(^{2n \, - \, 2}C_n)$$
If $$(1+x)^n=C_0+C_1x+C_2x^2+...+C_nx^n$$, then the value of $$C_0+C_2+C_4+....$$ is?
If $${\left(x+\dfrac{1}{x}+1\right)}^{6}={a}_{0}+\left({a}_{1}x+\dfrac{{b}_{1}}{x}\right)+\left({a}_{2}{x}^{2}+\dfrac{{b}_{2}}{{x}^{2}}\right)+...+\left({a}_{6}{x}^{6}+\dfrac{{b}_{6}}{{x}^{6}}\right)$$ then find the value of $${a}_{0}$$
Find the integral part of $$(3 + \sqrt {7})^{5}$$.
$$Let\,\,n \in N;{S_n} = \sum\limits_{r = 0}^{3n} {\left( {^{3n}{C_{3r}}} \right)} .\,\,Find\,\,\left| {{S_n} - 3{T_n}} \right|.$$
If log 1001= 3.000434, find the number of digits in $${1001^{101}}$$
Find the sum of coefficient of the expression
$${(x+2y+4z)}^{10}$$
In the expansion of $${ \left( { 7 }^{ 1/3 }+{ 11 }^{ 1/9 } \right) }^{ 6561 }$$, prove that there will be only $$730$$ terms which are free from radicals.
Find the term containing $$x^{2}$$, if any, in the expansion of $$(3x-\dfrac{1}{2x})^{8}$$
The coefficient of $$x^{4}$$ in the expansion of $$(\frac{x}{2}-\frac{3}{x^{2}})^{10}$$ is equal to:
Prove that
$$C_{1}+2 C_{2}+3 C_{3}+4 C_{4}+.+ ^nC_{n}=n.2^{n-1}$$
In the expansion of $${\left({3}^{\tfrac{-x}{4}}+{3}^{\tfrac{5x}{4}}\right)}^{n},$$ if the sum of the binomial coefficeints is $$64$$ and the term with the greatest binomial coefficient exceeds the third by $$\left(n-1\right)$$,then the value of $$x$$ is
Show that, if the greatest term in the expansion of $${\left(1+x\right)}^{2n}$$ has also the greatest coefficient , then $$x$$ lies between $$\dfrac{n}{n+1}$$ and $$\dfrac{n+1}{n}$$
The numerically greatest term in the expansion of $${\left(2+3x\right)}^{9}$$ when $$x=\dfrac{3}{2}$$ is
Coefficient of $${x}^{7} $$ in the expansion of $$ \left( {1+3x-{2x}^{3}} \right )^{10} $$
Find $$a$$ if the coefficients of $${x}^{2}$$ and $${x}^{3}$$ in the expansion of $${\left(3+ax\right)}^{3}$$ are equal.
Find the coefficient of $$x^5$$ in the product $${\left(1+2x\right)}^{6}{\left(1-x\right)}^{7}$$ using binomial theorem.
Find $$a, b$$ and $$n$$ in the expression of $$(a+b)^n$$ if the first three terms of the expansion are $$729, 7290$$ and $$30375$$ respectively.
Find n, if the ratio of the fifth term from the beginning to the fifth term from the end in the expansion of $$ \left( \sqrt [ 4 ] { 2 } + \frac { 1 } { \sqrt [ 4 ] { 3 } } \right) ^ { ( n ) } $$ is $$ \sqrt { 6 } : 1 $$
Show that the middle term in the expansion of $$(x - \frac{1}{x})^2n$$ is $$\frac{1.3.5.....(2n-1)}{n;} (-2)^n$$
Find the coefficient of $$ x^5 $$ in the expansion of $$ ( 1+ x)^3(1-x)^6 $$.
Show that the coefficient of $$ x^4 $$ in the expansion of $$ ( \frac {x}{2} - \frac {3}{x^2} )^{10} $$ is $$ \frac {405}{256} $$
If the 17th and 18th terms in the expansion of $$ ( 2+a )^{50} $$ are equal , find the value of a.
Find the 9th term in the expansion of $$ ( \frac {a}{b} - \frac {b}{2a^2})^{12} $$
Find the term independent of $$x$$ in the expansion of the following expressions:
$$(1+x+2x^{3})\left(\dfrac{3}{2}x^{2}-\dfrac{1}{3x}\right)^{9}$$
Enter 1 if answer is $$\dfrac {17}{54}$$ otherwise enter 0.
If the middle term in the expansion of $$ ( \frac {p}{2} + 2 )^8 $$ is 1120, find p.
Find the sixth term in the expansion $$(y^{1/2}+x^{1/3})^{n}$$, if the binomial coefficient of the third term from the ends is $$45$$.
Find the 6th term if expansion $$ ( y^{1/2} + x^{ 1/3} )^n $$ , if the binominal coefficient of 3rd term form the end is 45.
Show that the middle term in the expansion of $$ ( \frac {2x^3}{3} + \frac {3}{2x^2} )^{10} $$ is 252
Show that the coefficient of $$ x^{-3}$$ in the expansion of $$ ( x -\frac {1}{x} )^{11} $$is -330
Write the number of terms in the expansion of $$ (\sqrt {2} + 1)^5 +( \sqrt {2} -1)^5 $$.
If the coefficient of $$ (r-5)^{th}$$ and $$(2r -1)^{th} $$ terms in the expansion of $$ (1+ x)^{34} $$ are equal, find the value of $$r.$$
Write the coefficient of $$ x^7y^2 $$ in the expansion of $$ (x +2y)^9 $$.
Prove that there is no term involving $$ x^6 $$ in the expansion $$ (2x^2 - \frac {3}{x})^{11} $$.
Show that the coefficient of $$ x^4 $$ in the expansion of $$ ( 1+ 2x+ x^2)^5 $$ is 210.
Write the coefficient of the middle term in the expansion of $$ ( 1 +x)^{2n} .$$
Write down and simplify:
The $$4^{th}$$ term of $$(x-5)^{13}$$.
Write down and simplify:
The $$12^{th}$$ term of $$(2x-1)^{13}$$.
Write down and simplify:
The $$5^{th}$$ term of $$\left(\frac{x^{\frac{3}{2}}}{a^{\frac{1}{2}}}-\frac{y^{\frac{5}{2}}}{b^{\frac{3}{2}}}\right)^8$$.
Write down and simplify:
The $$5^{th}$$ term of $$\left(2a-\dfrac{b}{3}\right)^8$$.
Find the $$13^{th}$$ term of $$\left(9x-\dfrac{1}{3\sqrt{x}}\right)^{18}$$.
Find the middle term of $$\left(\dfrac{a}{x}+\dfrac{x}{a}\right)^{10}$$.
Write down and simplify:
The $$7^{th}$$ term of $$\left(\dfrac{4x}{5}-\dfrac{5}{2x}\right)^9$$.
Write down and simplify:
The $$10^{th}$$ term of $$(1-2x)^{13}$$.
Write down and simplify:
The $$28^{th}$$ term of $$(5x+8y)^{30}$$.
Write down and simplify:
The $$4^{th}$$ term of $$\left(\dfrac{a}{3}+9b\right)^{10}$$.
Prove that the coefficient of $$x^n$$ in the expansion $$\dfrac{1}{1 + x+ x^2}$$ is $$1, 0, -1$$ according as $$n$$ is of the form $$3m, \ 3m-1, or \ 3m+1$$.
Class 11 Engineering Maths Extra Questions
- Binomial Theorem Extra Questions
- Complex Numbers And Quadratic Equations Extra Questions
- Conic Sections Extra Questions
- Introduction To Three Dimensional Geometry Extra Questions
- Limits And Derivatives Extra Questions
- Linear Inequalities Extra Questions
- Mathematical Reasoning Extra Questions
- Permutations And Combinations Extra Questions
- Principle Of Mathematical Induction Extra Questions
- Probability Extra Questions
- Relations And Functions Extra Questions
- Sequences And Series Extra Questions
- Sets Extra Questions
- Statistics Extra Questions
- Straight Lines Extra Questions
- Trigonometric Functions Extra Questions