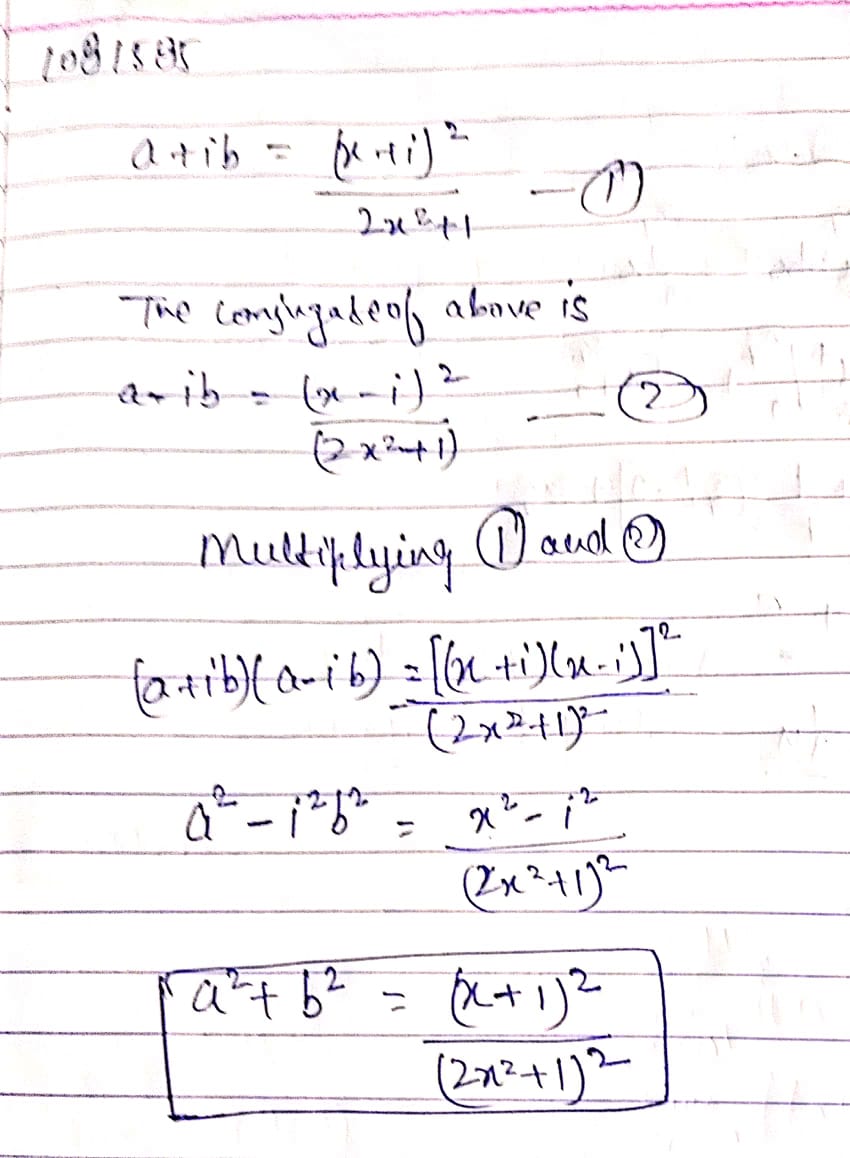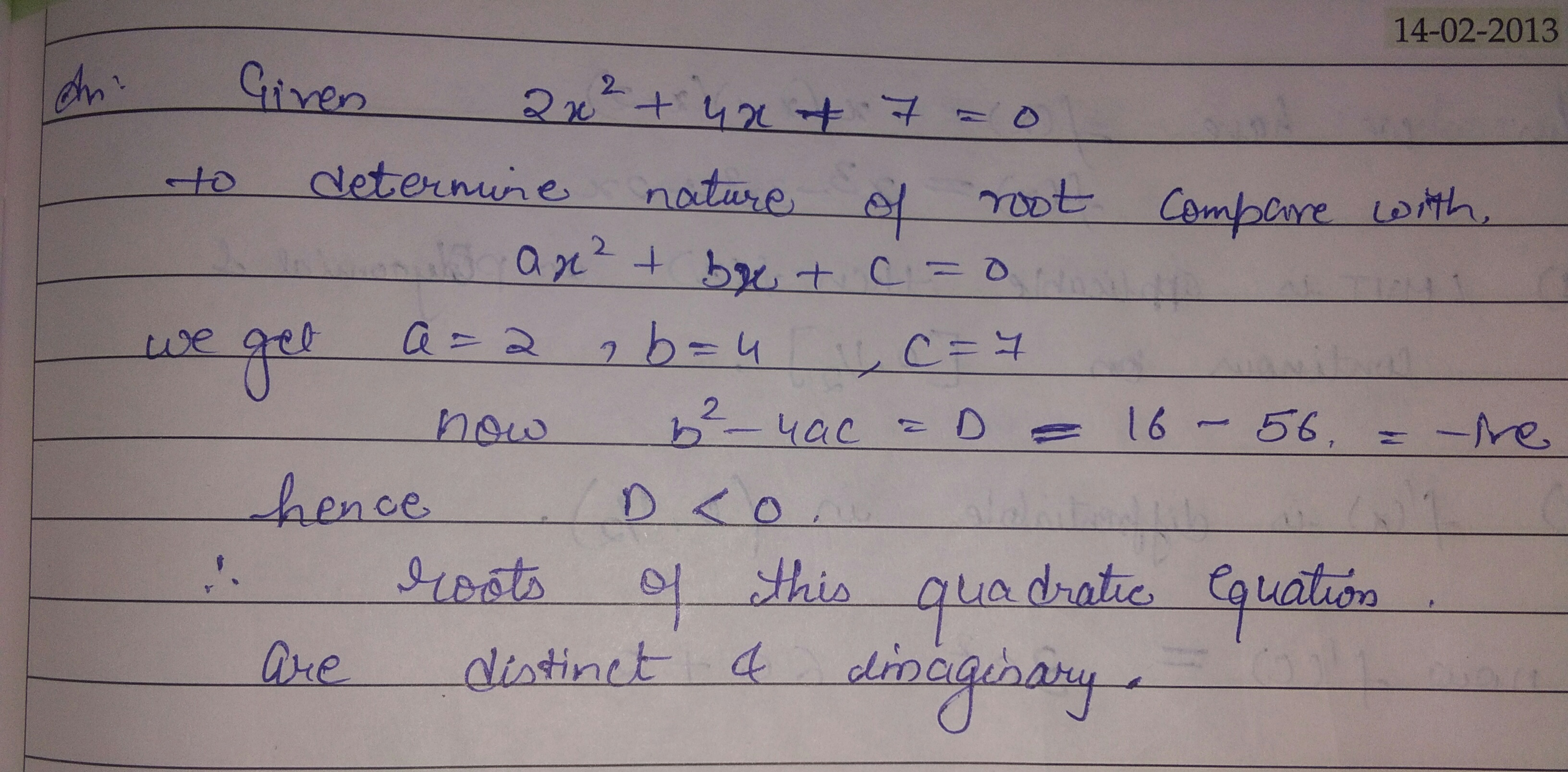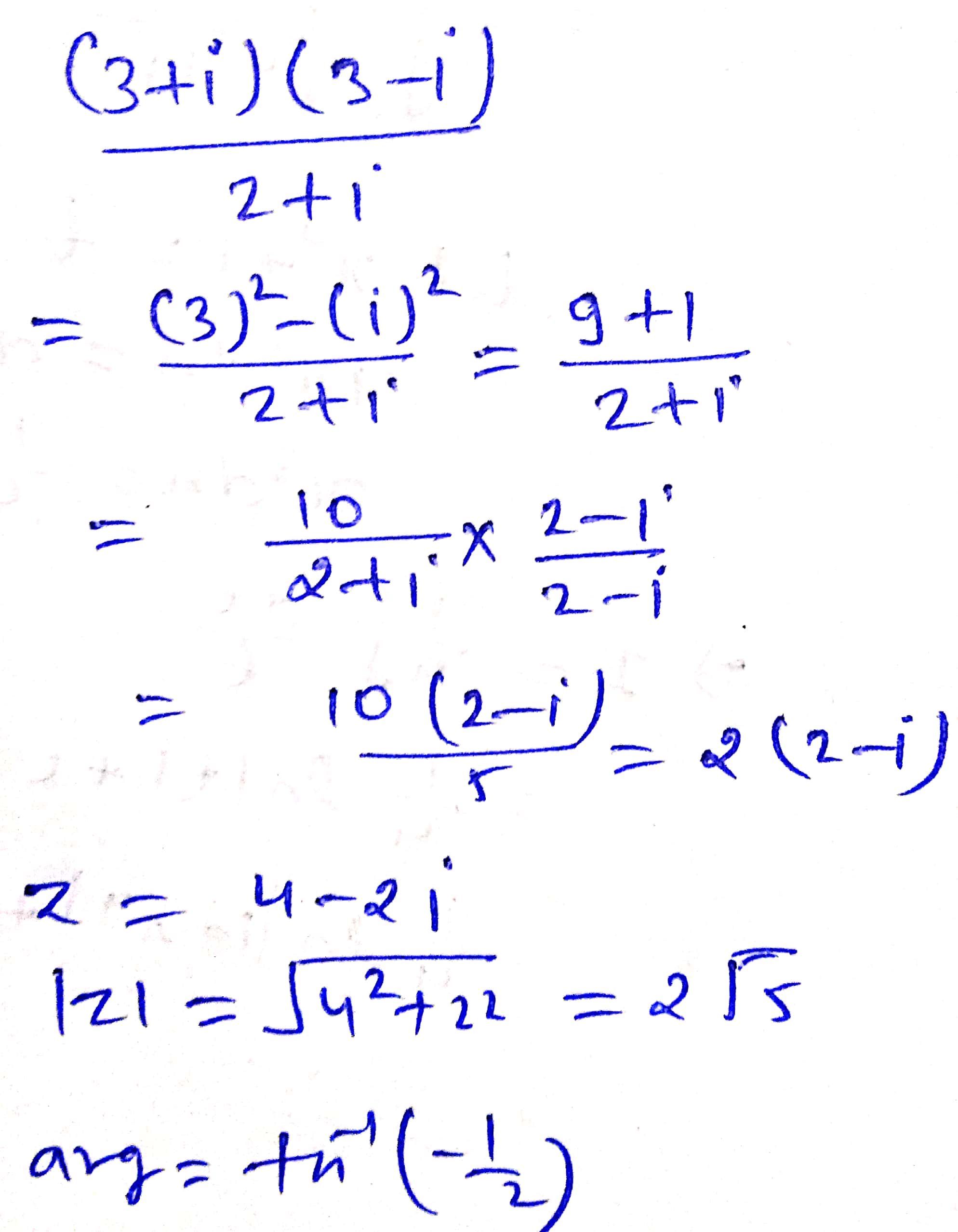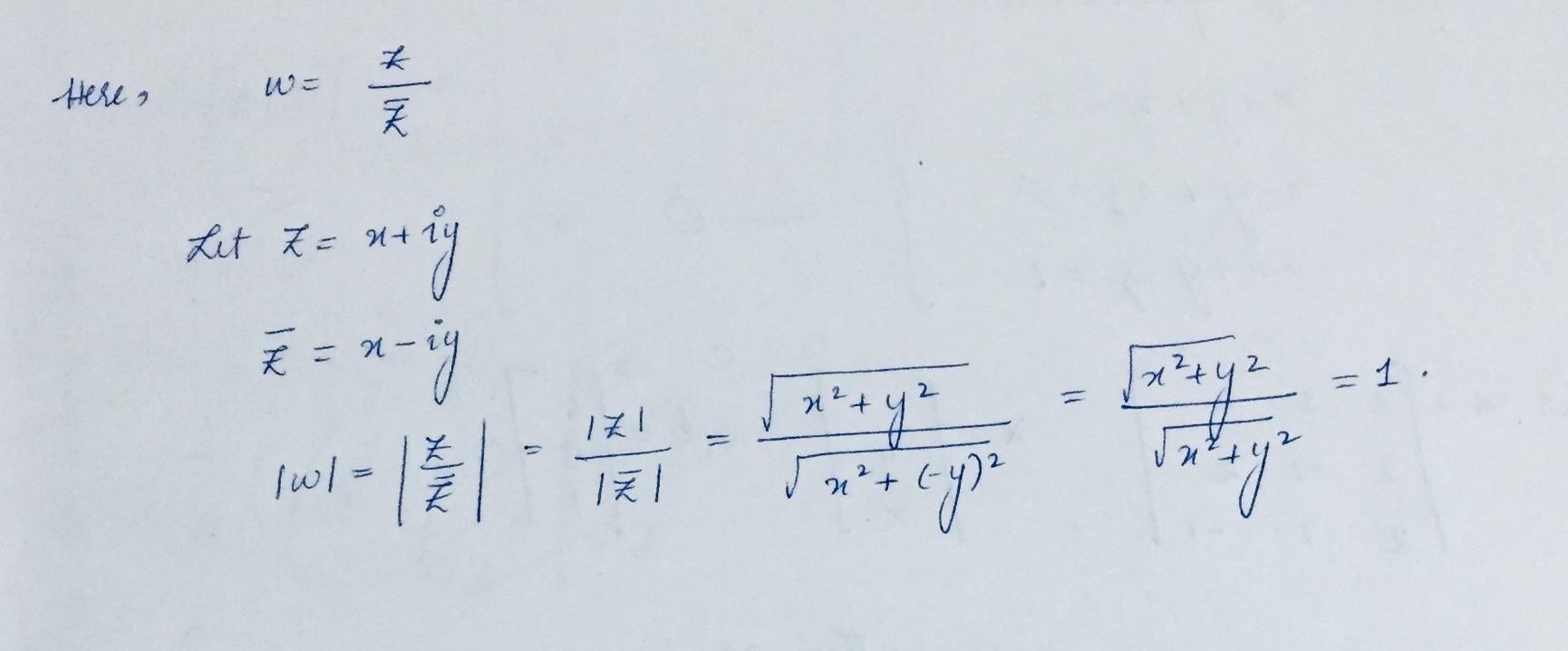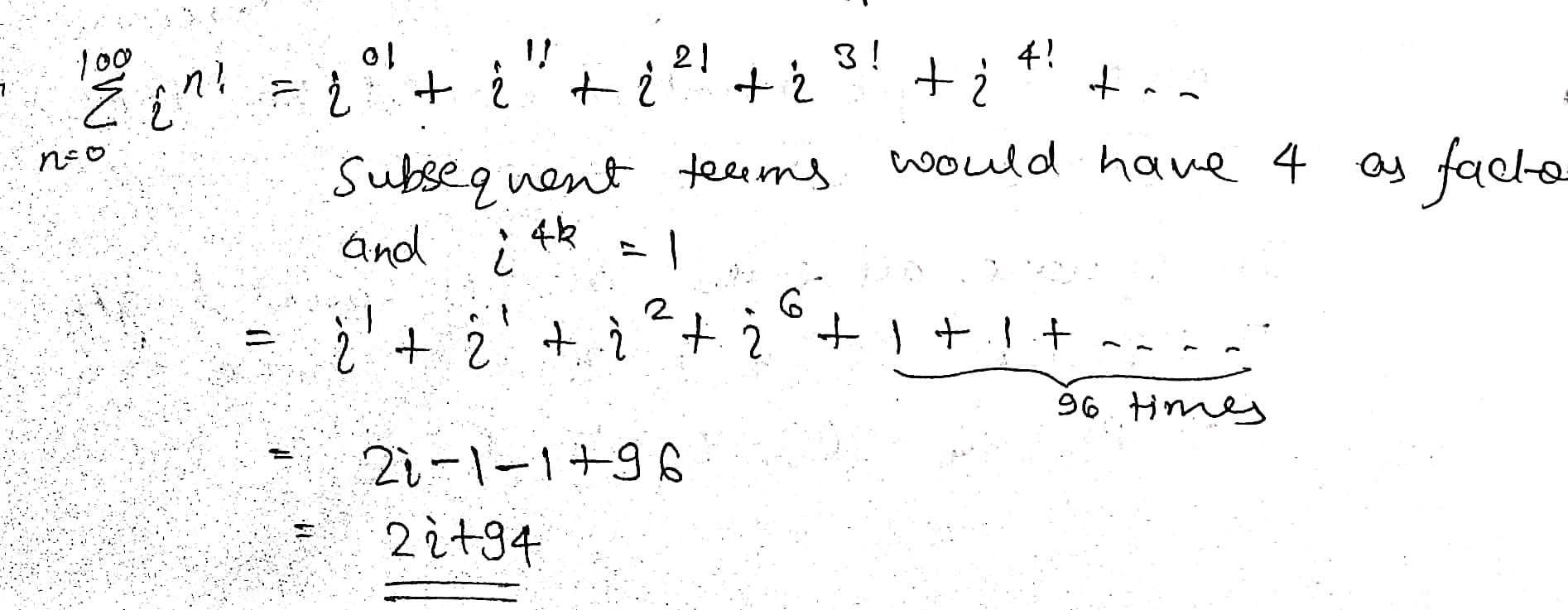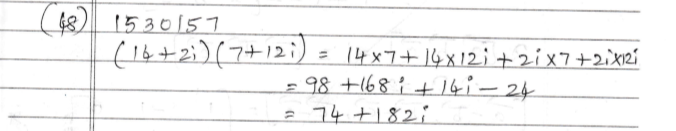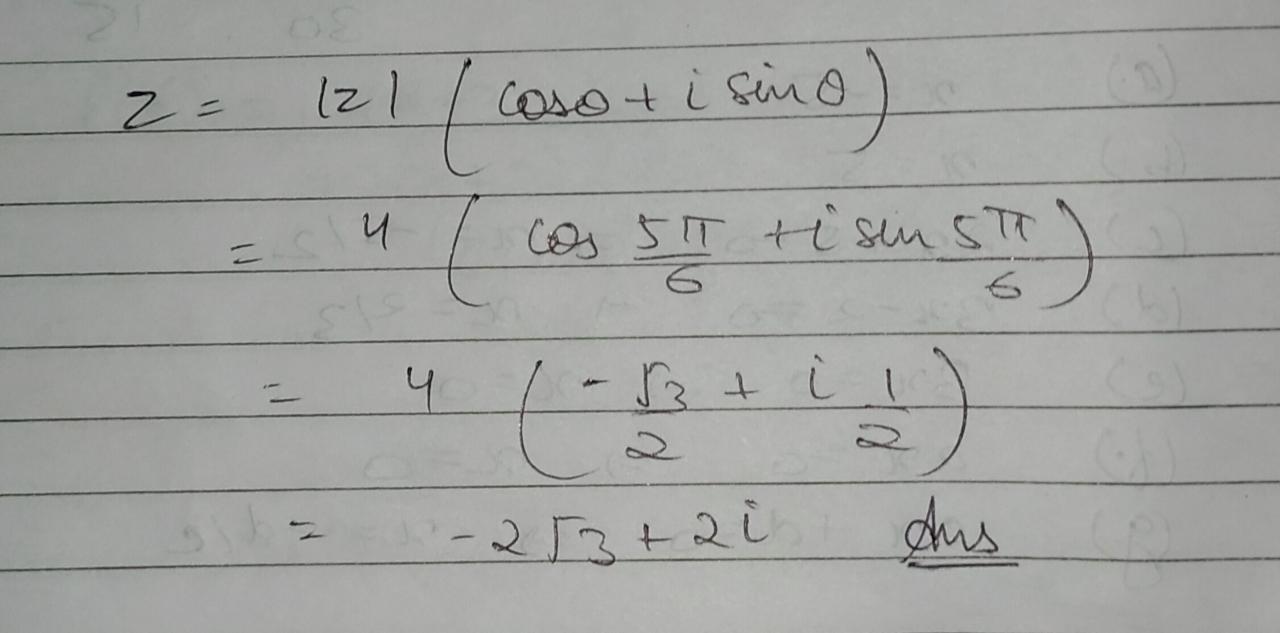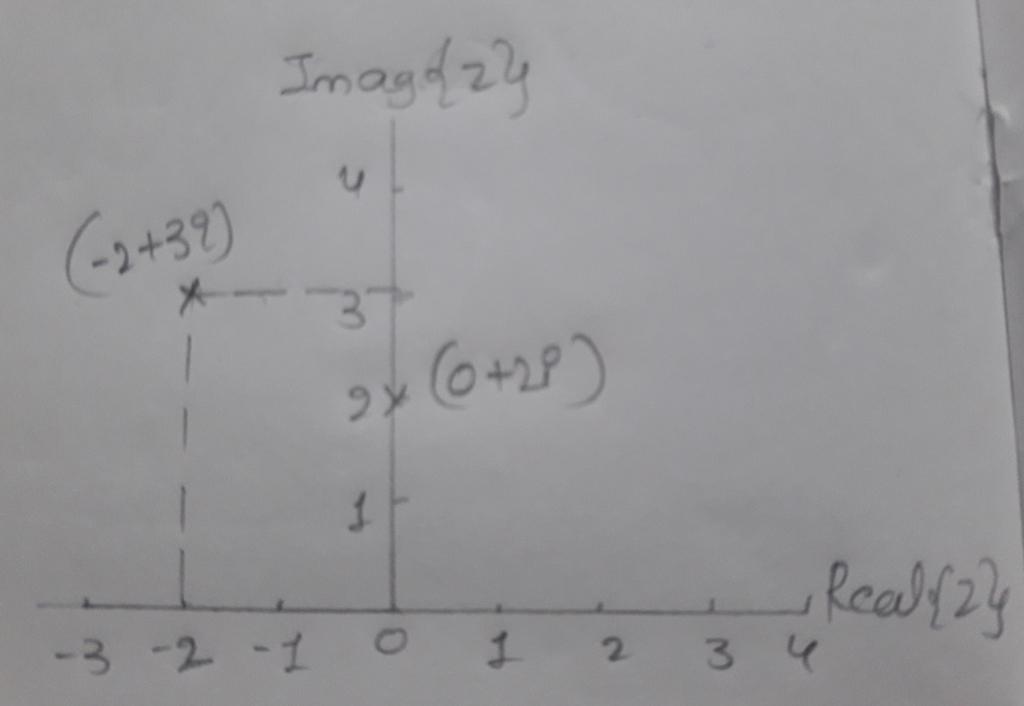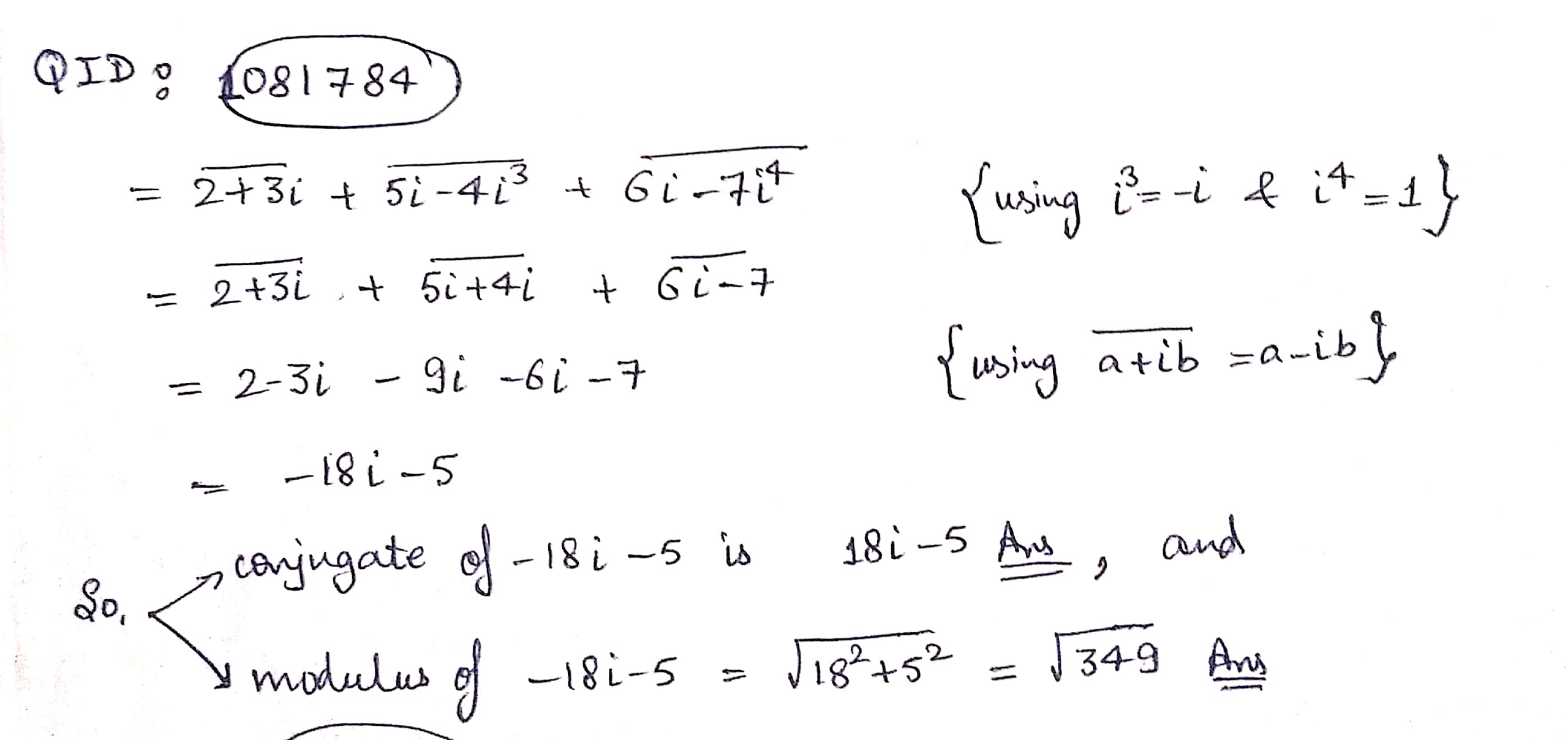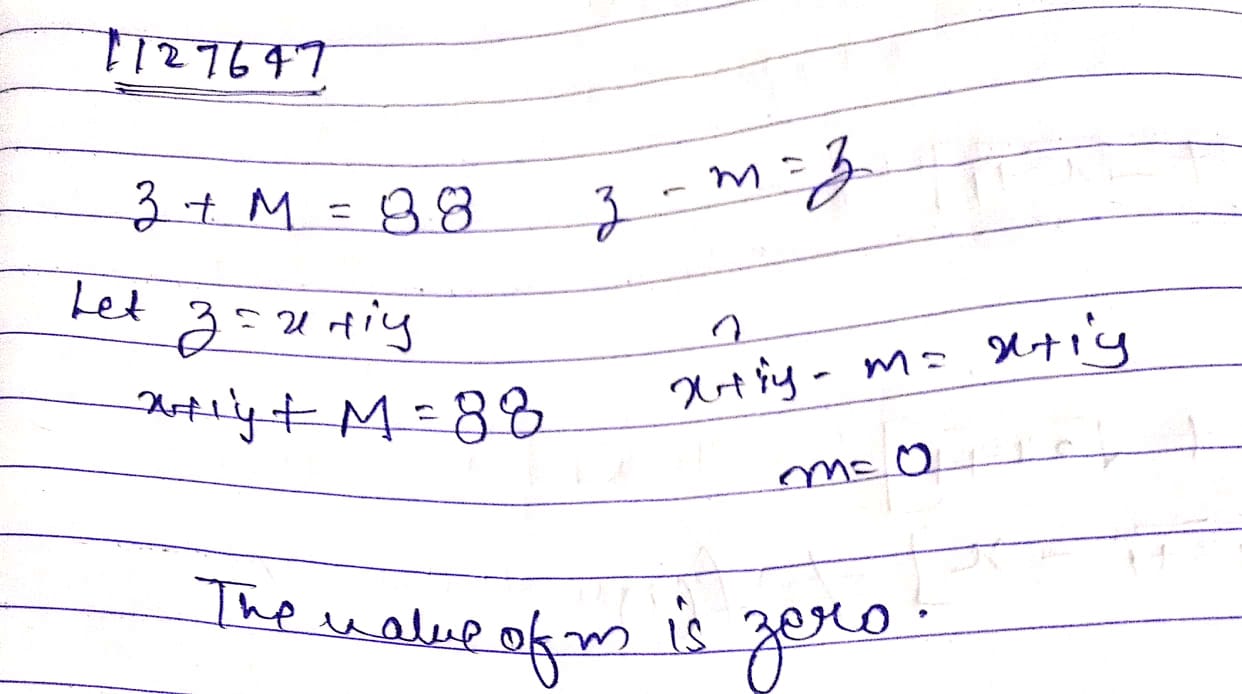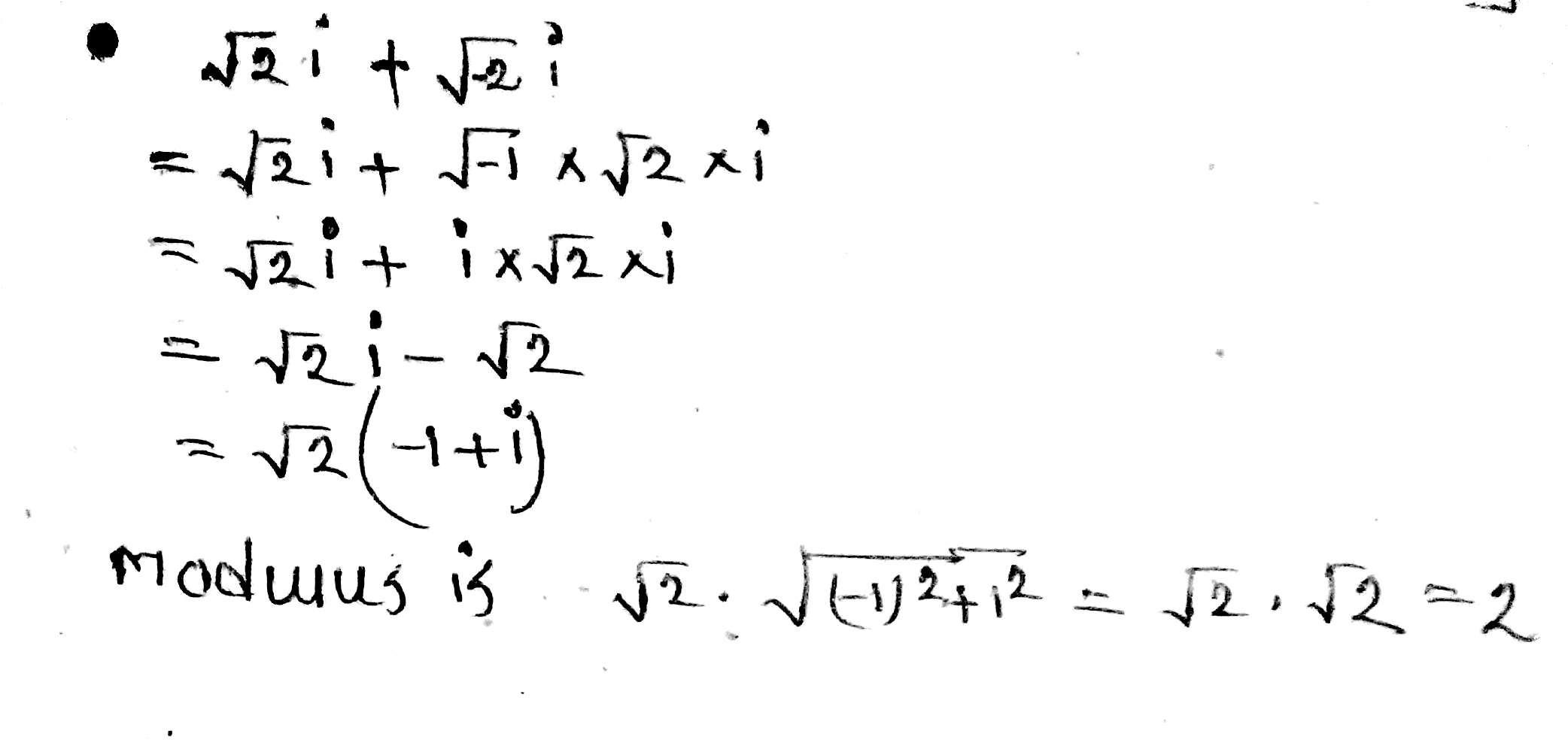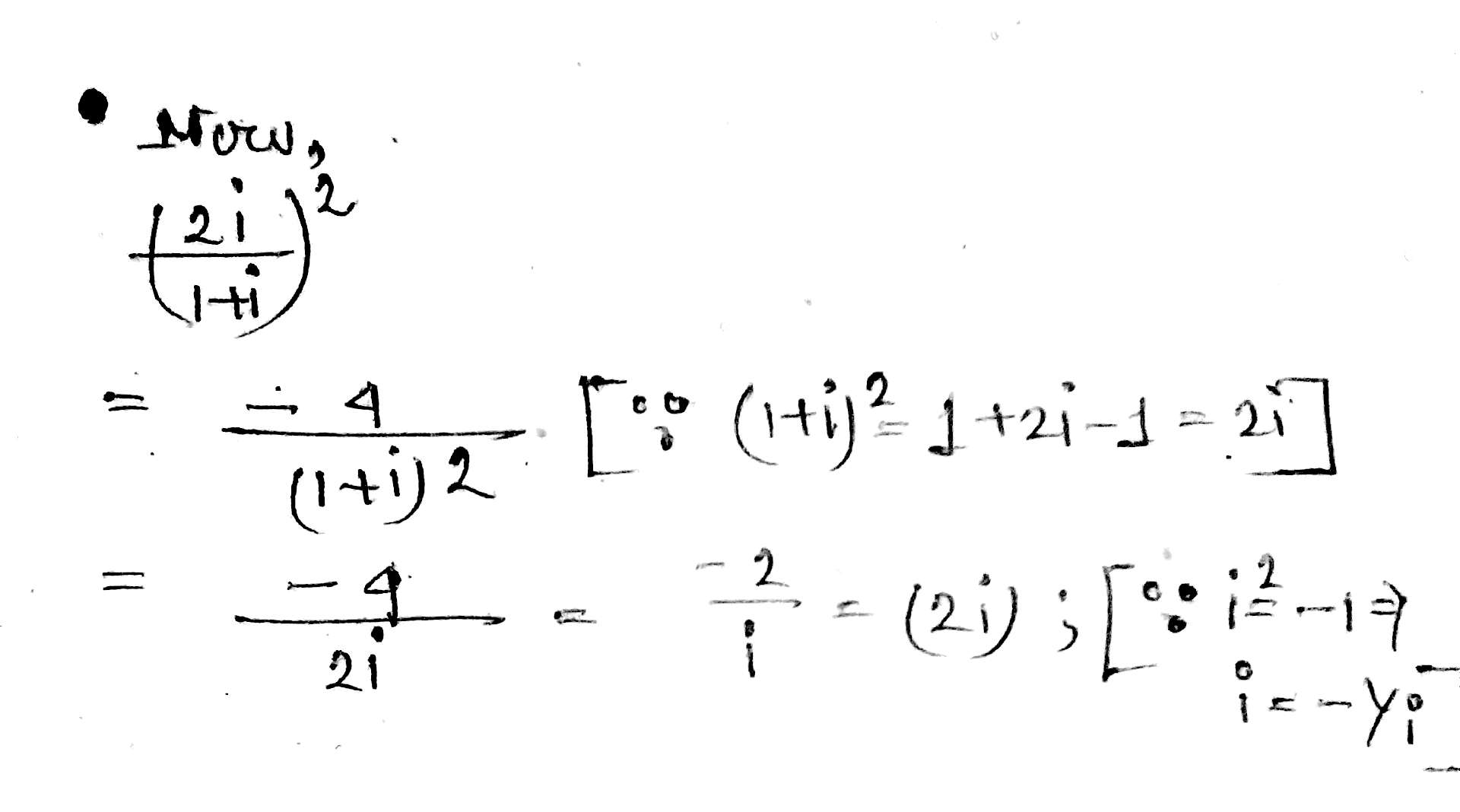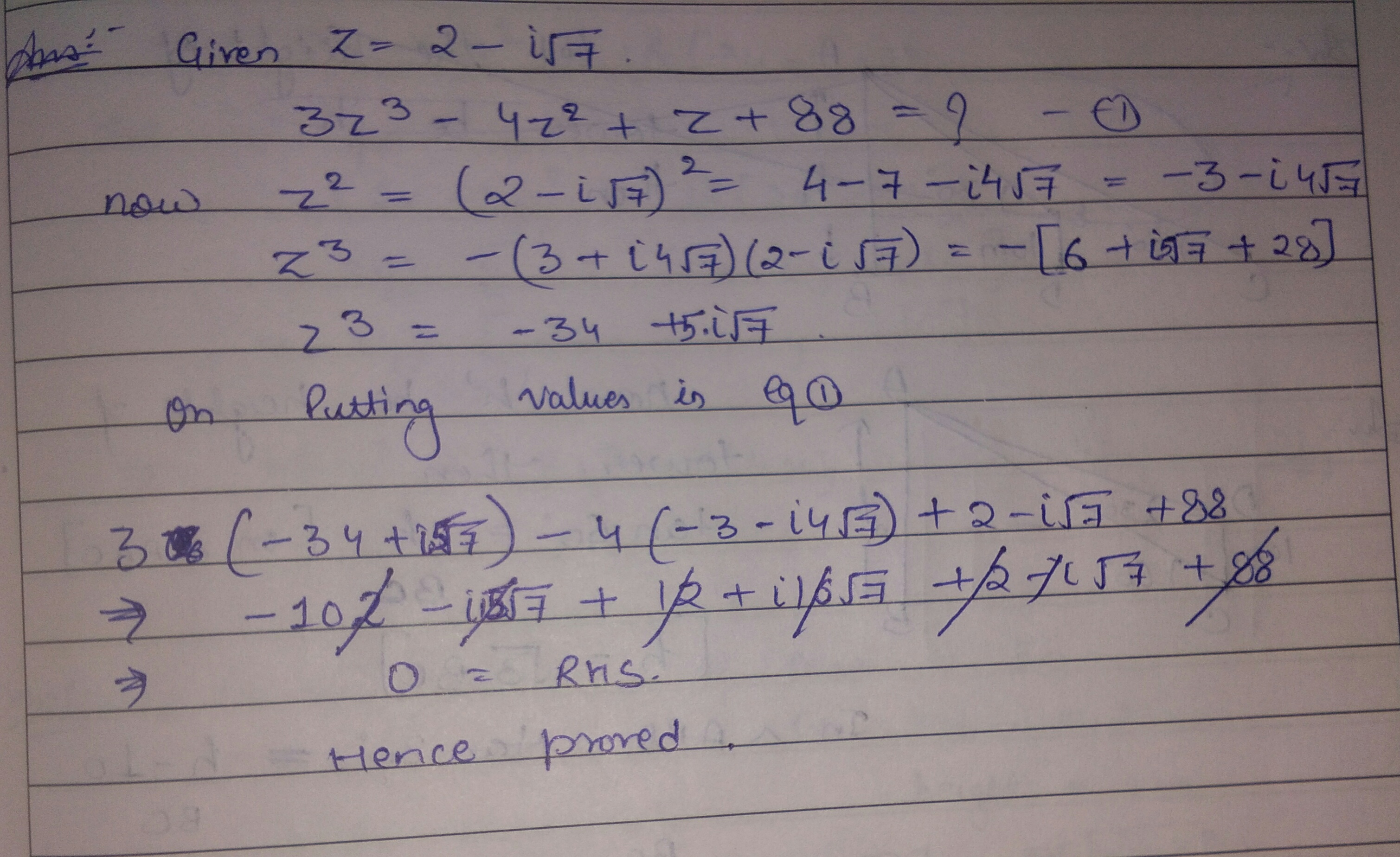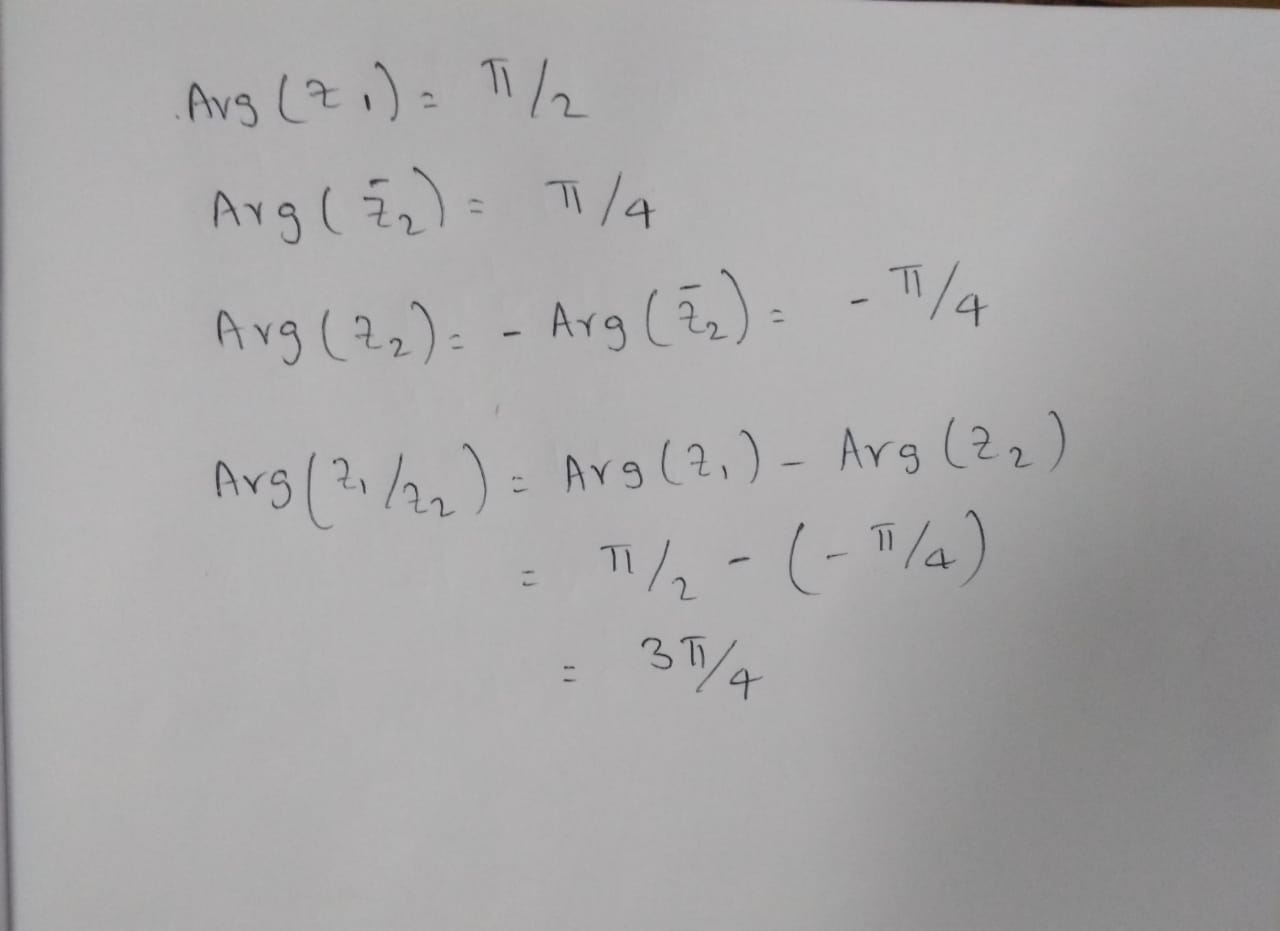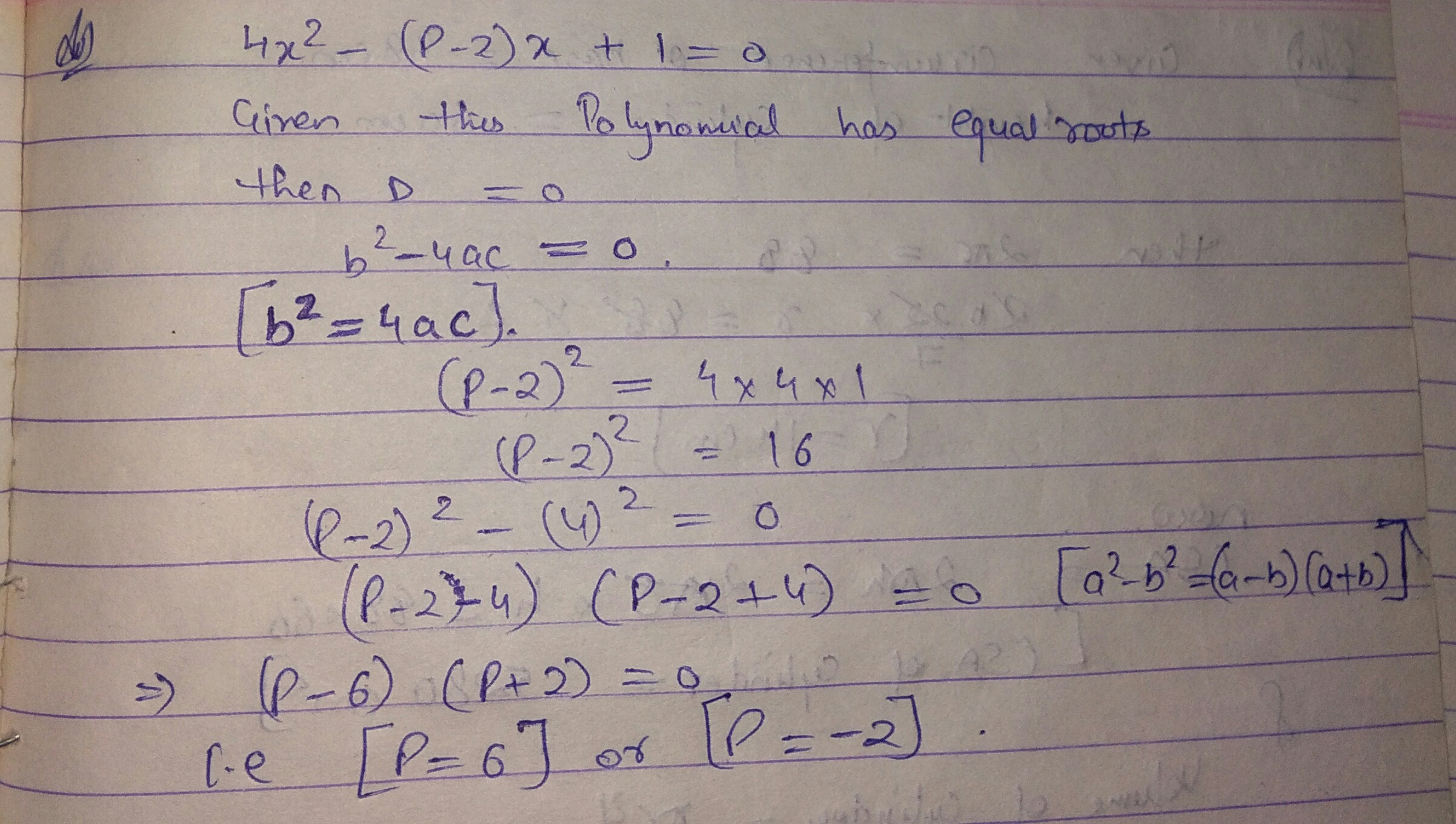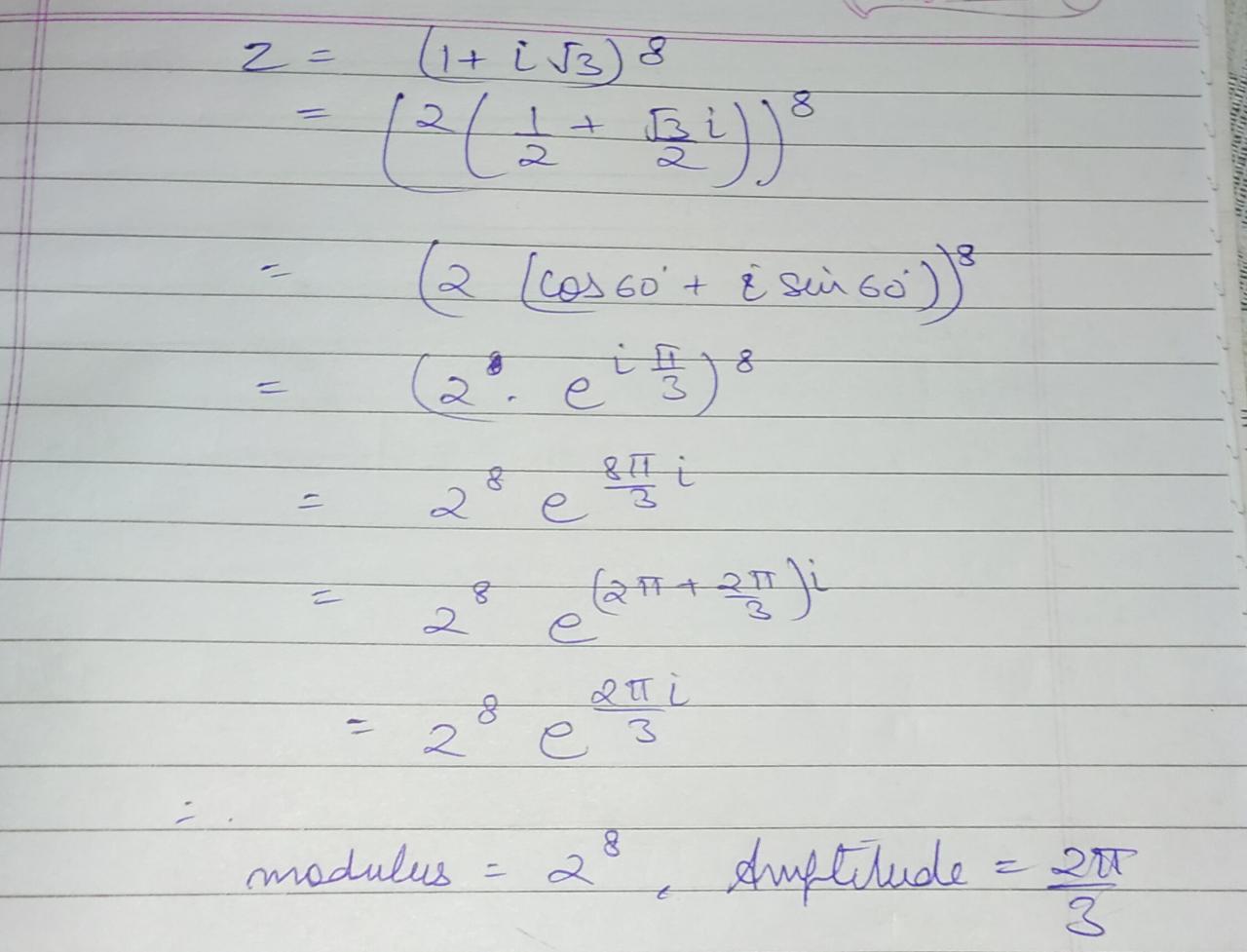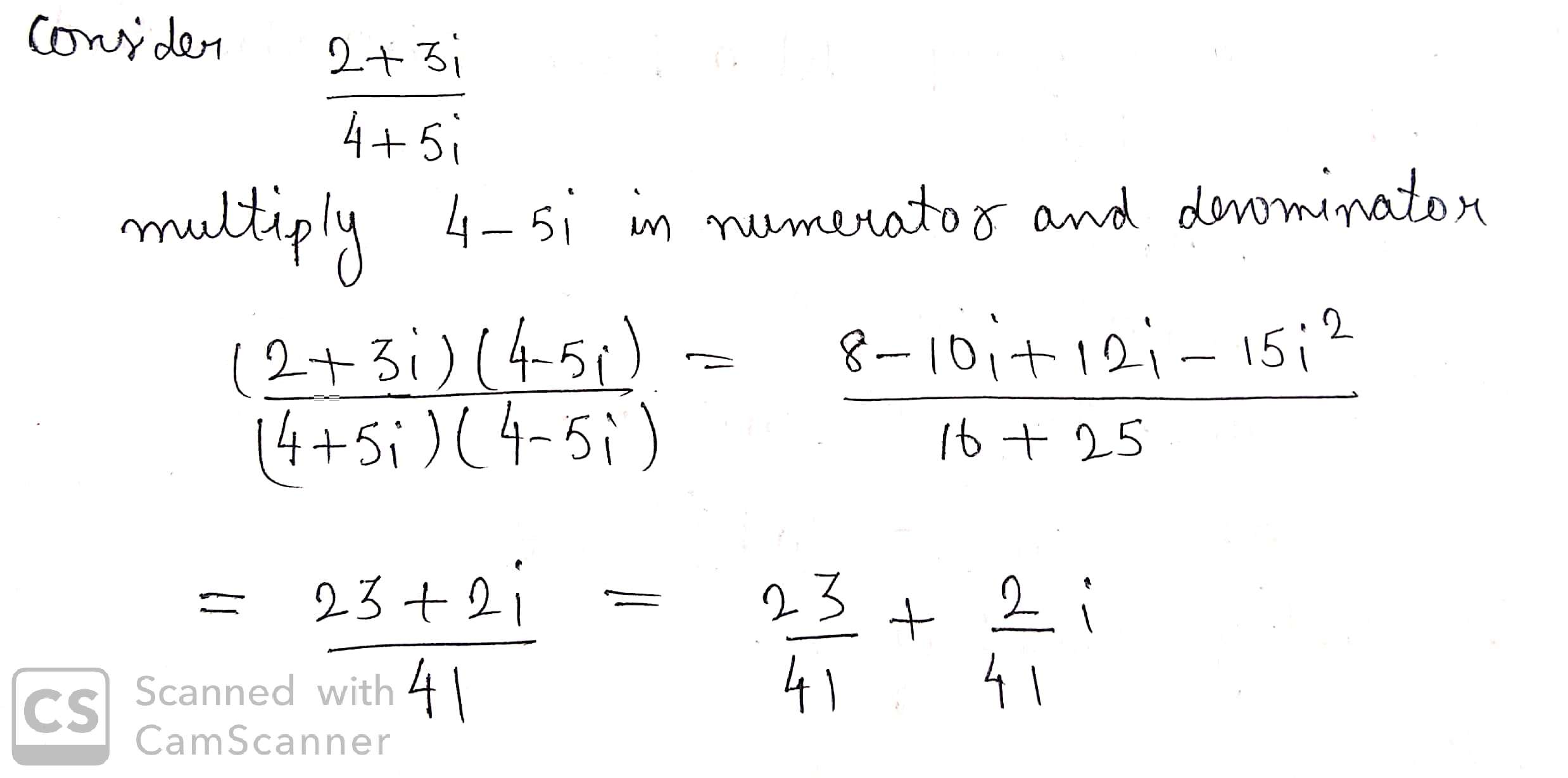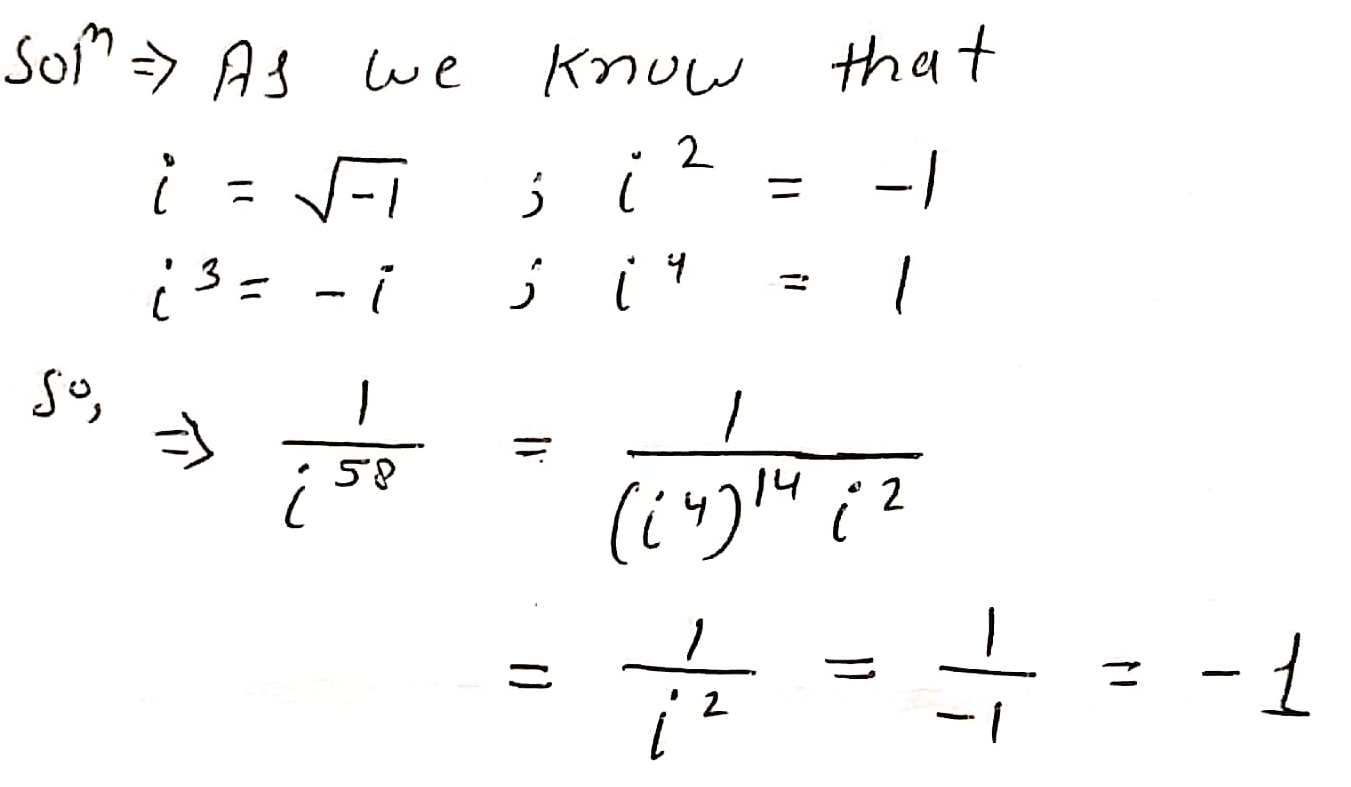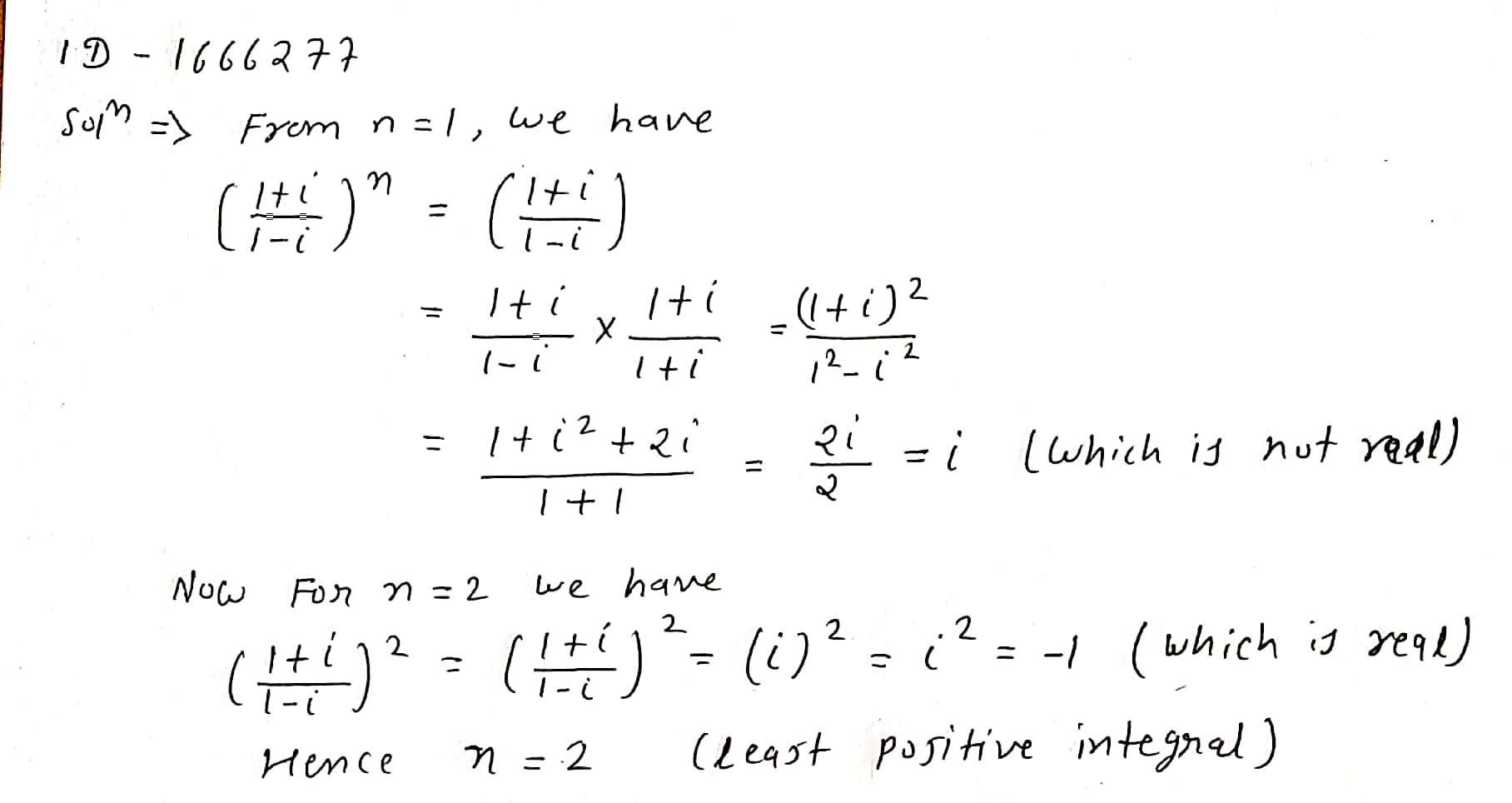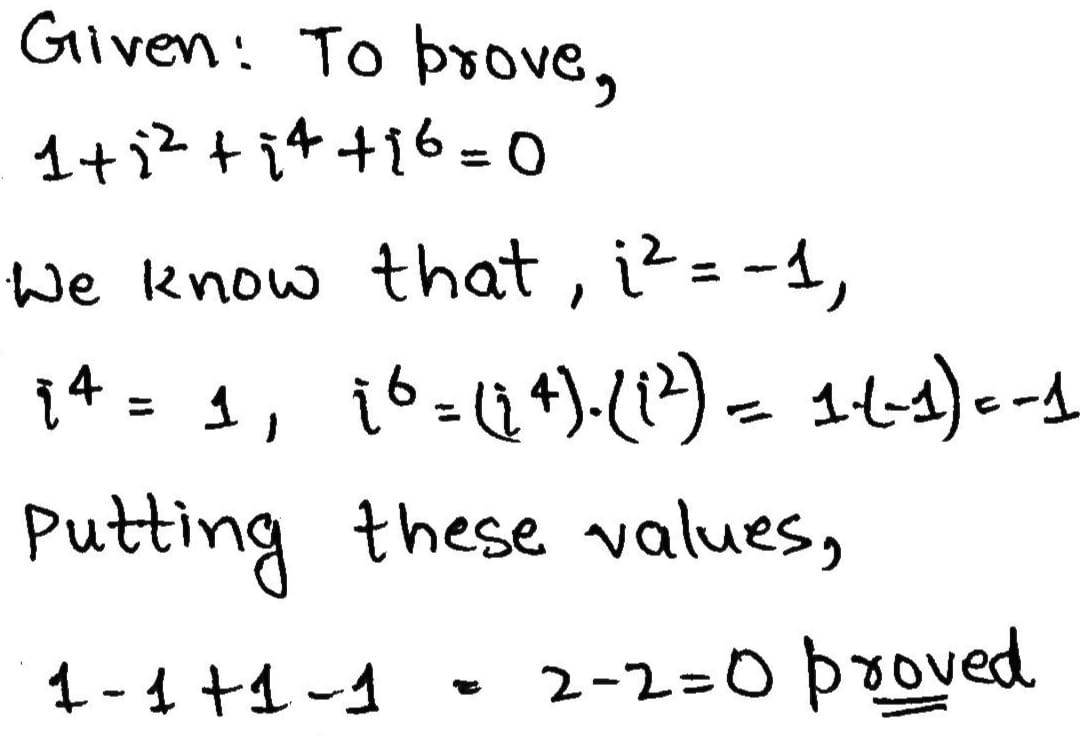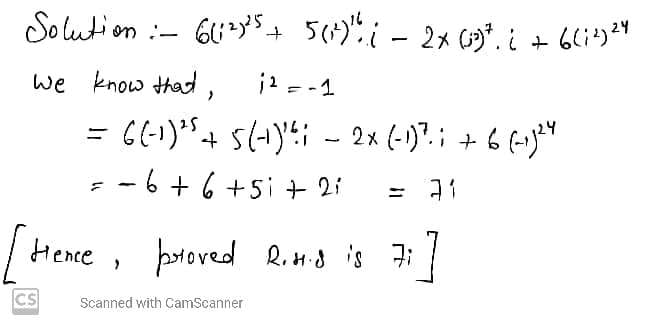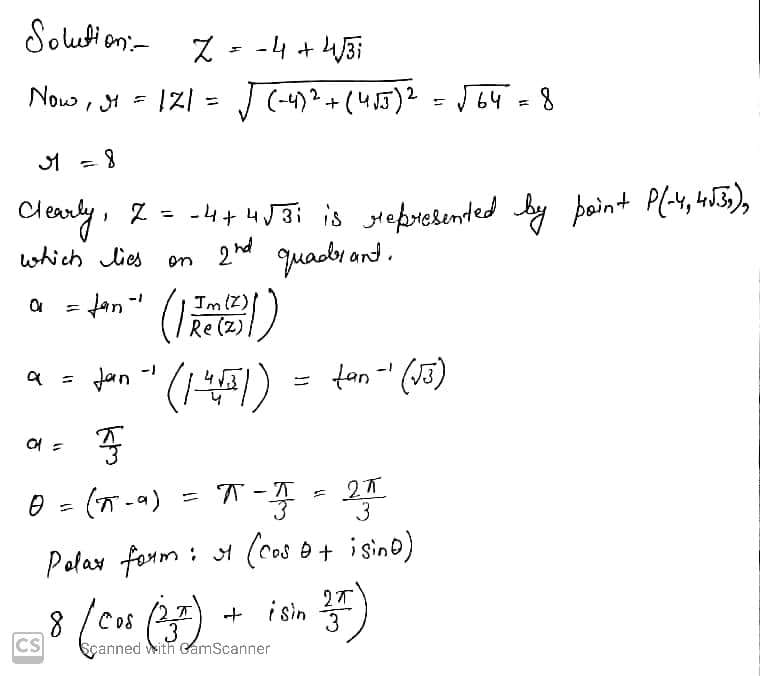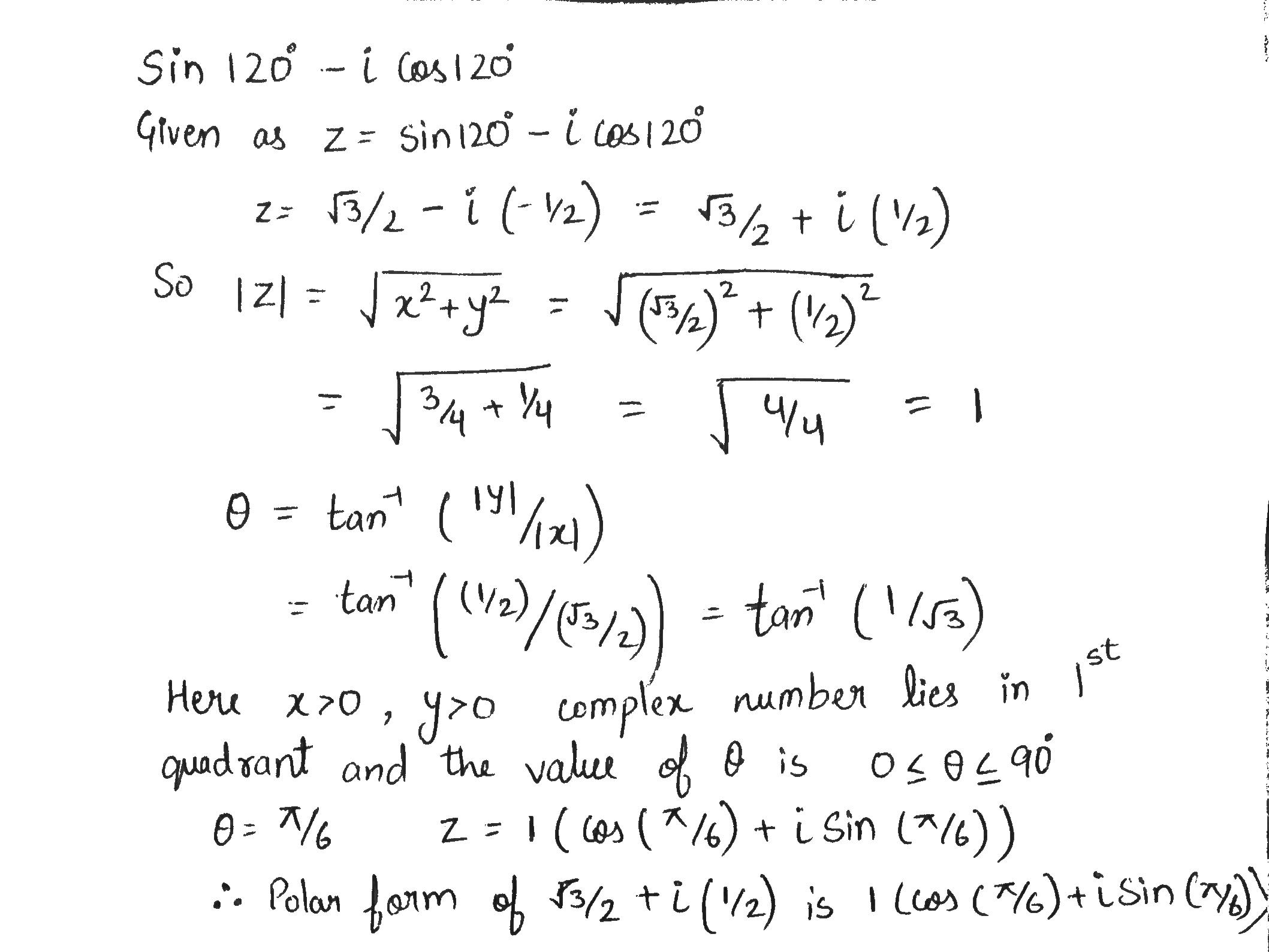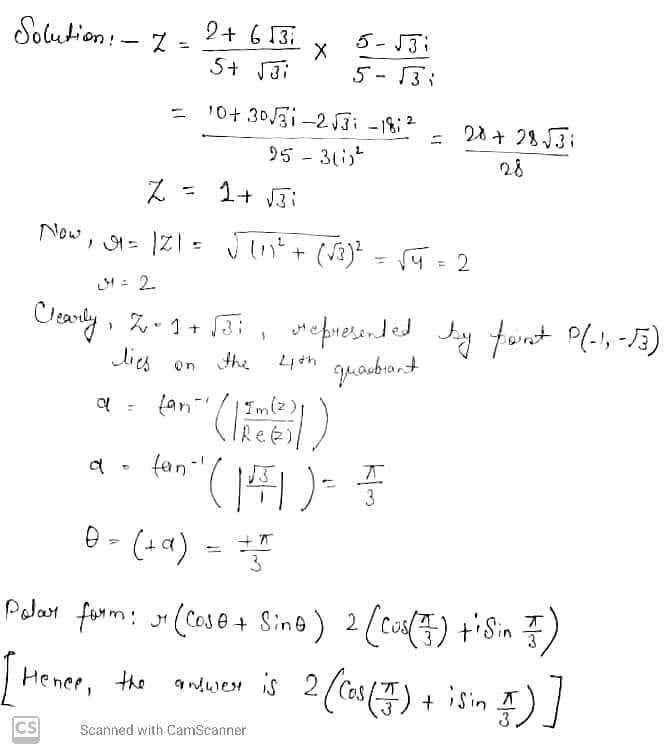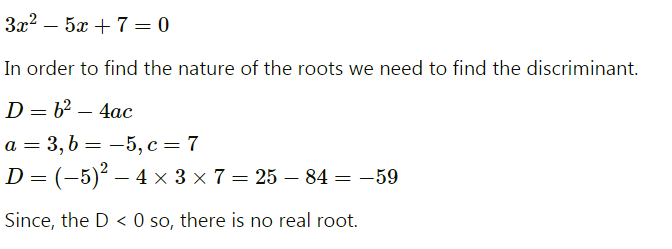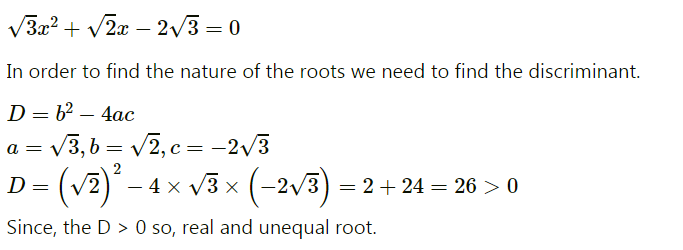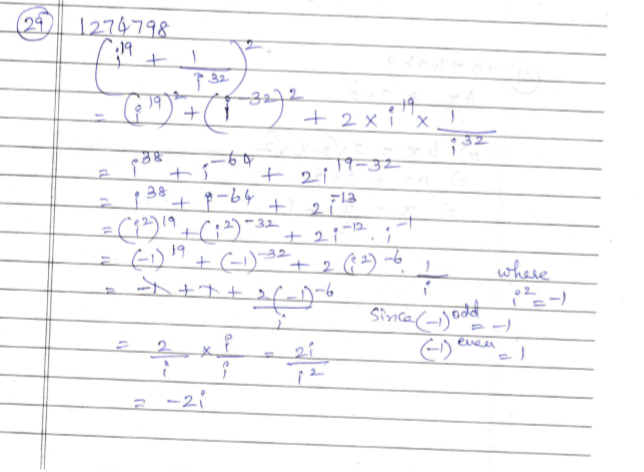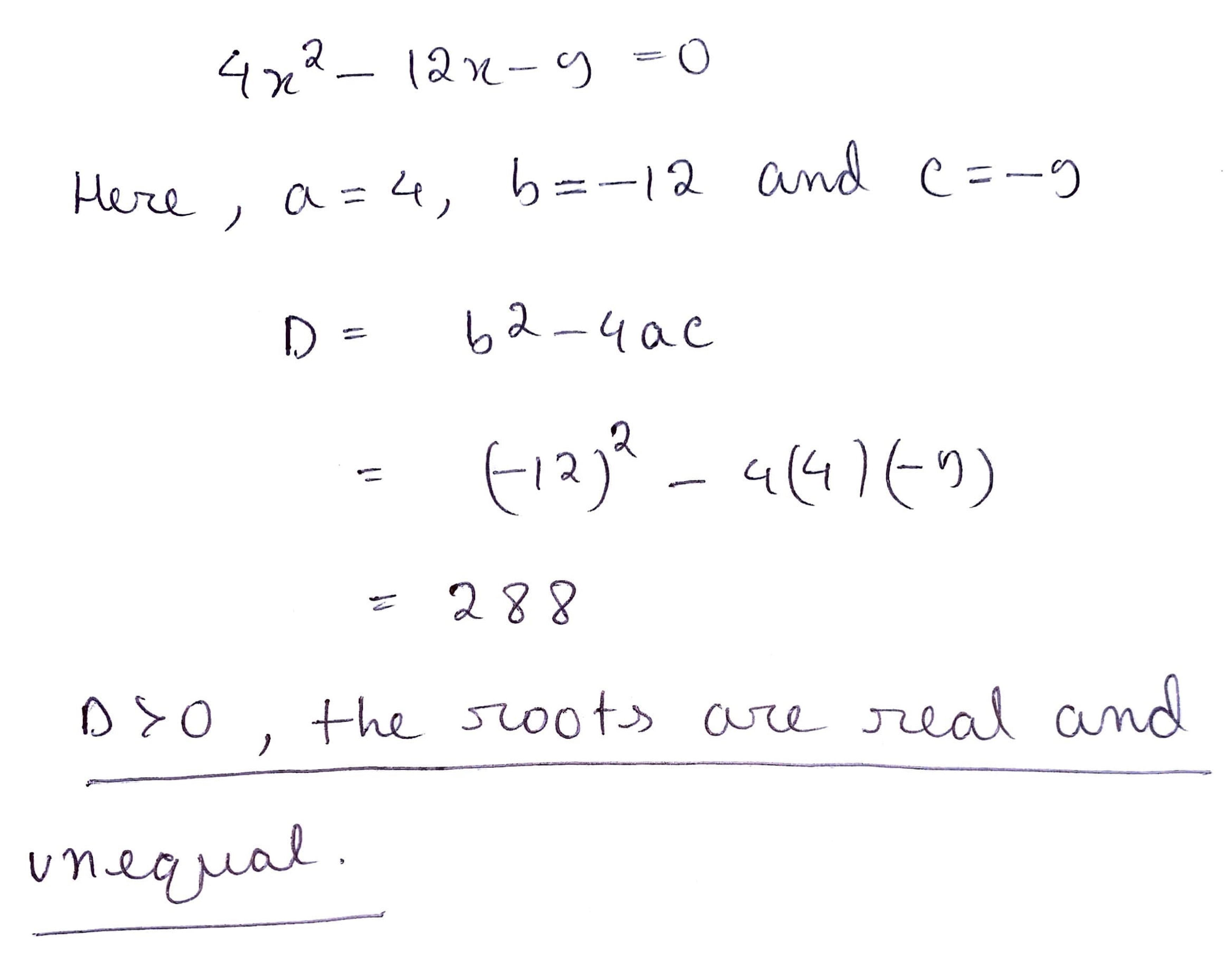Complex Numbers And Quadratic Equations - Class 11 Engineering Maths - Extra Questions
Number of roots of the quadratic equation $$\displaystyle 8\sec ^{2}x-6\sec x+1= 0$$ is/are:
$$\left | z \right |\leq 5$$ & $$Arg\left ( z-1-i \right )> \pi /6$$
$$Arg \left ( z-1-i \right )\geq \pi /3$$
Multiply $$2\sqrt { -3 } +3\sqrt { -2 } $$ by $$4\sqrt { -3 } -5\sqrt { -2 } $$
If the value of the discriminant of the quadratic equation $$a{ x }^{ 2 }+bx+c=0$$ is less than $$0$$, then the nature of the roots is ____
If $${Z}_{1}=-1$$ and $${Z}_{2}=i$$, then find $$Arg\left( \cfrac { { Z }_{ 1 } }{ { Z }_{ 2 } } \right) $$
Write an example for a quadratic polynomial that has no real zeroes.
Without solving the following quadratic equation, find the value of $$m$$ for which the given equation has real and equal roots.
$$x^2+2(m-1)x+(m+5)=0$$
Calculate $$\displaystyle \sqrt{i}$$
What is $$cis\ 0$$?
Find the value of $$k$$ so that the following equation has equal roots.
$$2x^{2} - (k - 2) x+1 = 0$$
Calculate $$\displaystyle \sqrt[3]{- \, i}$$
Represent $$(-1-\sqrt 3i)$$ in the polar form.
For the real numbers x and y, if $$(x-iy)(3+5i)$$ is the conjugate of $$-6-24i$$ then find the value of $$x$$ and $$y$$.
Indicate the point of the complex plane $$z$$ which satisfy the following equation.
$$\displaystyle z^2 \, + \, | \, \overline{z} \, | \, = \, 0$$
Find the values of p for which the quadratic equation $$4x^2+px+3=0$$ has equal roots.
Find the modulus of the complex number $$2-5!$$.
Determine the nature of the roots of the following quadratic equation
$$2x^2+ 6x + 3 = 0$$
Find the length of the segments connecting the points represented by the following pairs of numbers :
3, -4i
locate the point representing the complex numbers $$z$$ on the Argand diagram for which
$$\left| z \right| \ge 3,$$
Simplify the following :
$$\dfrac{3 \, - \, i}{2 \, + \, i} \, + \, \dfrac{3 \, + \, i}{2 \, - \, i}$$
Find the length of the segments connecting the points represented by the following pairs of numbers :
-1 - i, 2 + 3i
$$x \, +\, i \sqrt x^\, 4 \, +, x^2 \, +\, 1$$
Find the discriminant of the following quadratic equations and hence determine the nature of the roots of the equation :
$${x^2} = 9$$
What is value of $$(-i)^{12}$$
In the given, determine whether the given quadratic equation has real roots and if so, find the roots.
$${ x }^{ 2 }+5x+5=0$$
Determine the nature of the roots of the given quadratic equation
$$2{ x }^{ 2 }+x-1=0$$
Determine the nature of the roots of the given quadratic equation
$$4{ x }^{ 2 }-4x+1=0\quad $$
Solve$$z = \left( {2 + i} \right)+\left( {1 - 3i} \right)$$
Find the modulus of: (i) $${{21} \over 5} - {{12} \over 5}i$$ (ii) 3+4i
Find the value of $$(1+i)(1+{i}^{2})(1+{i}^{3})(1+{i}^{4})$$.
Find the amplitude and modulus of following(i) $$\displaystyle {{21} \over 5} - {{12} \over 5}i$$ (ii) $$3 + 4{\rm{ i}}$$
Express the given complex number $$3(7+i7)+i(7+i7)$$ in the form $$a+ib$$,
Find the amplitude of $$-4$$.
Find modulus and argument of $$i$$
Write the nature of roots of the quadratic equation $$5x^2-2x+3=0$$.
Write the argument of $$(1+\sqrt {3})(1+i)(\cos \theta+i\sin \theta)$$.
The values of $$x$$ and $$y$$ satisfying the equation $$\dfrac{(1+i)x - 2i}{3+ i} + \dfrac{(2 -3i)y + i}{3 - i} = i$$, are
Solve for $$x$$ : $$4\sqrt 3 x^{2} + 5x-2\sqrt 3 = 0$$ Write about the nature of roots.
Express $$(1-i)-(1+i6)$$ as $$a+ib$$
If $$\dfrac {a-ib}{a+ib}=\dfrac {1+i}{1-i}$$, then prove that $$a+b=0$$
Solve the equation $$\left| z \right| + z = 2 + i$$
Convert the given complex number into the polar form:$$z = -3$$
If $${z_1} = 1 + i = \sqrt 3 + i$$, then the principle arg $$\left( {\frac{{{z_1}}}{{{z_2}}}} \right)$$
If $$a+ib=\cfrac { { (x+i) }^{ 2 } }{ 2{ x }^{ 2 }+1 } $$, prove that $${ a }^{ 2 }+{ b }^{ 2 }=\cfrac { { (x+i) }^{ 2 } }{ { (2{ x }^{ 2 }+1) }^{ 2 } } $$.
Solve the problem:-
$$\left( {\frac{1}{5} + i\frac{2}{5}} \right) - \left( {4 + i\frac{5}{2}} \right)$$
For what value of $$k$$, the equation $$kx^2 - 6x - 2 = 0$$ has equal roots.
Evaluate: $$\left[i^{18}+\left(\dfrac{1}{i}\right)^{25}\right]^3$$.
If $$z=x+iy$$ and $$z_1=1+2i$$, determine the region in the complex plane represented by $$1 < |z-z_1 |< 3$$. Represent it on the Argand plane.
Determine the nature of roots of the following quadratic equation :$$2x^2+5x+5=0$$
If $$z_1=2-i, z_2=1+i$$, find $$\left|\dfrac{z_1+z_2+1}{z_1-z_2+i}\right|$$.
Find the values of the following:
$${ \left( 1+i\sqrt { 3 } \right) }^{ 3 }$$
Solve $$(3-7i)+(-2+4i)$$.
If $$\alpha$$ and $$\beta$$ are the zeroes of the equation $$6{x^2} + x - 2 = 0$$, find $$\dfrac{\alpha }{\beta } + \dfrac{\beta }{\alpha }$$
$$\dfrac{2+5i}{3-2i}+\dfrac{2-5i}{3+2i}$$.
Write principal argument of $$\dfrac {-\sqrt {11}i}{17}$$.
Since Real part = 0
Argument $$ 90^{\circ}(\pi/2)$$
Find the modulus:
$$-4-4i$$
If $$a=\frac { -1+\sqrt { 3i } }{ 2 } ,b=\frac { -1-\sqrt { 3i } }{ 2 }$$ then show that $${a}^{2}=b$$ and $${b}^{2}=a$$.
Represent following complex numbers $$z_1=1+2i$$ and $$z_2=5-7i$$ by points in Argand's diagram and determine their amplitudes approximately.
R.E.F image
Argand plane
$$ amp(z_{1}) = tan^{-1}2 = 1.107 $$
$$ amp(z_{2}) = tan^{-1}(\dfrac{-7}{5}) $$
$$ = -0.95 $$
If $$g\left( x \right) ={ x }^{ 4 }{ -x }^{ 3 }+{ x }^{ 2 }+3x-5$$, find $$g(2+3i)$$
$$g(x)=x^4-x^3+x^2+3x-5$$
$$=x^2(x^2+1)-x(x^2-3)-5$$
$$x=2+3i$$
$$x^2=4-3+12i=1+12i$$
$$=(1+12i)(2+12i)-(1+12i)(-2+12i)-5$$
$$=2+12i+24i-144+2+24i-12i+144-5$$
$$=-1+48i$$.
What will be the nature of roots of the quadratic equation $$2{x^2} + 4x + 7 = 0$$.
Find the modulus of $$\dfrac {3 -4i}{5 + 7i}$$.
Write the nature of roots of quadratic equation $$4{ x }^{ 2 }+6x+3=0$$
Find the amplitude of $$ 1 + i \sqrt{3}$$.
Find the modulus of the complex number $$z=2+3i$$.
Find discriminant of the equation $$5x - 6 = \dfrac{1}{x}$$.
If $$a+ib=\dfrac{c+i}{c-i}$$, where $$c$$ is a real number, then prove that : $$a^{2}+b^{2}=1$$ and $$\dfrac{b}{a}=\dfrac{2c}{c^{2}-1}$$.
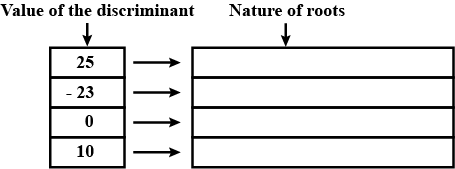
Write the nature of roots from the given values of the discriminants and complete the activity.
Find the modulus and amplitude of $$4+3i$$.
Write (i) $$-1 -i$$ (ii) $$1 - i$$ in polar form.
Simplify and hence find the modulus and argument $$ \dfrac {(3 + i)(3 - i)}{2 + i} $$.
$$\dfrac{(3+i)(3-i)}{2+i}$$
$$=\dfrac{(3)^2-(i)^2}{2+i}=\dfrac{9+1}{2+i}$$
$$=\dfrac{10}{2+i}\times \dfrac{2-i}{2-i}$$
$$=\dfrac{10(2-i)}{5}$$
$$=2(2-i)$$
$$z=4-2i$$
$$|z|=\sqrt{4^2+22}=2\sqrt{5}$$
$$arg=+n^{-1}\left(-\dfrac{1}{2}\right)$$.
In $$-3+3i$$, find amplitude and modulus
If the discriminant is 13, how many solutions and of what type?
Express $$\dfrac{-1+i}{\sqrt{2}}$$ in the polar form
If $$z=(\cos \theta, \sin \theta))$$, find $$\left(z-\dfrac{1}{z}\right)$$
Find the nature of roots of the quadratic equation $${ y }^{ 2 }-7y+2=0$$.
Simplify: $$\left(\dfrac{1}{3}+3i\right)^{3}$$
If $$\omega =\frac { Z }{ \bar { Z } } $$, then $$|\omega |=$$
Here, $$\omega =\frac{z}{z}$$
Let z = x+iy
$$\bar{z}=x-iy$$
$$\left | \omega \right |=\left | \frac{z}{z} \right |\frac{\left | z \right |}{\left | z \right |}=\frac{\sqrt{x^{2}+y^{2}}}{\sqrt{x^{2}+(-y)^{2}}}=\frac{\sqrt{x^{2}+y^{2}}}{\sqrt{x^{2}+y^{2}}}=1$$
If $$z_1=5+3i\\z_2=2-3i$$ Find $$z_1+z_2$$
$$3 \sqrt { 2 } x ^ { 2 } - 2 \sqrt { 6 } x + 2$$ find the nature of roots.
Check whether the following equation will have two distinct real or imaginary or two real equal roots.$$x^2-3x+5=0$$.
Prove that the roots of the following quadratic equation has two real distinct roots.$$2x^2-6x+3=0$$.
Find the condition for which the roots of the equation $$ax^{2}+bx+c=0$$ be real and distinct.
Find the value of $$\displaystyle \sum^{100}_{n=0}i^{n!}$$ $$(where, i=\sqrt {-1})$$
$$\displaystyle \sum_{n = 0}^{100} i^{n!} = i^{0!} +i ^{1!}+ i^{2!} + i^{3!} + i ^{4!} + ...$$
subsequent terms would have 4 as factor and $$i^{4k}=1$$
$$=i^1 + i^1 + i^2 + i^6 + \underbrace{1 + 1 + ....}_{96 \, times}$$
$$ = 2i -1-1+96$$
$$= 2i + 94$$
Check whether the roots of the following quadratic equations are real or not?$$3x^2-4\sqrt{3}x+4=0$$.
Evaluate : $$i^{373}$$
Simplify:$$\left(14+ 2i\right)\left(7 + 12i\right)$$ where $$i=\sqrt{-1}$$
$$(14+2i)(7+12i)=14\times 7+14\times 12i+2i\times 7+2i\times 12i$$
$$=98+168 i+14i-24$$
$$=74+182i$$
Find the modulus of $$ \dfrac{1+i}{1-i}-\dfrac{1-i}{1+i}$$
Express the complex number $$1 + i \sqrt{3}$$ in modulus amplitude form.
Simplify the following
$$(2-5i)+(-3+4i)+(8-3i)$$
Find z if , $$\left| z \right| = 4$$ and arg (z ) = $${{5\pi } \over 6}$$
$$ x^{2}-2x-1=0$$Find the nature of roots
Evaluate $$\dfrac{1}{i^{78}}$$
Determine the nature of root of the quadratic equation.
$$m^{2} + 2m + 1 = 0$$
Find the modulus of the following ;
$$ -2-3i $$
If $$-5$$ is a root of the quadratic equation $$2{x}^{2}+px-15=0$$ and the quadratic equation $$p({x}^{2}+x)+k=0$$ has equal roots, then find the value of $$k$$.
For what value of $$k$$, is $$3$$ a root of the equation $$2{x}^{2}+x+k=0$$?
Evaluate : $$i^{-50}$$
Find the nature of the roots of the following quadratic equation. If the real roots exist, find them:
$$3{x}^{2}-4\sqrt { 3x } +4=0$$
Find the values of $$k$$ for which the quadratic equation $$9{x}^{2}-3kx+k=0$$ has equal roots.
Find the nature of the roots of the following quadratic equation. If the real roots exist, find them:
$$2{x}^{2}-6x+3=0$$
Find the modulus of the following ;
$$ (4+i) $$
If $$a$$ and $$b$$ are real, then show that the principal value of arg $$a$$ is $$0$$ or $$\pi$$ according to $$a$$ is positive or negative and that of arg $$b$$ is $$\pi$$/2 or $$-\pi$$/2 according to $$b$$ is positive or negative.
If $$ z = 4 + i\sqrt{7}$$, then find the value of $$|z^3 - 4z^2 - 9z + 91|$$.
The number of complex numbers $$z$$ satisfies $$Re(z^2) = 0, \left|z\right| = \sqrt{3}.$$
If Arg $$(z + i)\, -$$ Arg $$(z - i)$$ $$= \dfrac{\pi}{2}$$, then $$z$$ lies on a circle.
If statement is True, enter $$1$$, else enter $$0$$
Prove that he expression $$\displaystyle \frac{\sqrt{(1 + m)} +i \sqrt{(1 - m)}}{\sqrt{(1 + m)} - i\sqrt{(1 - m)}} - \frac{\sqrt{(1 - m)} + i \sqrt{(1 + m)}}{\sqrt{(1 - m)} -i \sqrt{(1 + m)}} (m \in R)$$ simplifies to 2m.
Write the correct letter from column II against the entry number in column I in your answer book, z $$\neq$$ 0 is a complex number
If $$x = a + bi$$ is a complex number such that $$x^2 = 3 + 4i$$ and $$x^3 = 2 + 11i$$, where $$i = \sqrt{-1}$$, then $$(a+ b)$$ equal to
Let z and w be two nonzero complex numbers such that $$\left|z\right| = \left|w\right|$$ and $$arg(z) + arg(w) = \pi$$. Then prove that $$z = -\overline{w}$$.
Solve $$\displaystyle \sin 2x+ \cos 4x=2$$
Solve the equation $$ { 5 }^{ 2x }-24.{ 5 }^{ x }-25=0$$
find the number of roots .
State true or false:$$\displaystyle \sqrt{-2}.\sqrt{-3}= \sqrt{\left ( -2 \right )\left ( -3 \right )}= \sqrt{6}$$.
For false type 0 and for true type 1
Let $$k$$ be the value of $$\lambda $$ for which the given equation will have equal roots : $$\displaystyle x^{2}+2\left ( 3\lambda +5 \right )x+2\left ( 9\lambda ^{2}+25 \right )=0$$.Find $$6k$$ ?
What is the square of the modulus of the complex number 2+3$$i$$
The equation $$\displaystyle ax^{2}+bx+c=0$$ where a, b, c are real numbers connected by the relation 4a+2b+c= 0 and ab > 0 has real roots.If you think this is true write 1 otherwise write 0 ?
Find the value of the sum $$\displaystyle \sum_{n=1}^5(i^n+i^{n+2})$$, where $$i=\sqrt {-1}$$
Find the modulus and the argument of the complex number $$\displaystyle z=-1-i\sqrt { 3 } $$
Convert the given complex number in polar form : $$\displaystyle -1+i$$
Convert the given complex number in polar form: $$i$$
Convert the given complex number in polar form : $$\displaystyle 1-i$$
If $$\displaystyle \alpha $$ and $$\displaystyle \beta $$ are different complex numbers with $$\displaystyle \left| \beta \right| = 1$$, then find $$\displaystyle \left| \frac { \beta -\alpha }{ 1-\bar { \alpha } \beta } \right| $$.
Find the modulus and argument of the complex number $$\displaystyle \frac { 1+2i }{ 1-3i } $$
Find the modulus and the argument of the complex number $$\displaystyle z=-\sqrt { 3 } +i$$
Find the modulus of : $$\displaystyle \frac { 1+i }{ 1-i } -\frac { 1-i }{ 1+i } $$
Find the nature of the roots of the following quadratic equations. If the real roots exist, find them:
(i) $$\displaystyle 2{ x }^{ 2 }-3x+5=0$$
(ii) $$\displaystyle 3{ x }^{ 2 }-4\sqrt { 3 } x+4=0$$
(iii) $$\displaystyle 2{ x }^{ 2 }-6x+3=0$$
Find the values of k for each of the following quadratic equations, so that they have two equal roots.
(i) $$\displaystyle 2{ x }^{ 2 }+kx+3=0$$
(ii) $$\displaystyle kx\left( x-2 \right) +6=0$$
Represent the complex number $$2 + 3i$$ in argand plane
If $${ b }^{ 2 }-4ac> 0$$ in $$a{ x }^{ 2 }+bx+c=0$$, then what can you say about roots of the equation? ($$a\ne 0$$)
Show that the roots of the equation $${x}^{2}-2px+{p}^{2}-{q}^{2}+2qr-{r}^{2}=0$$ are rational.
Show that the equation $$2{x}^{2}-6x+7=0$$ cannot be satisfied by any real values of $$x$$.
Simplify equation: $$\quad \cfrac { 1 }{ x } -\cfrac { 1 }{ (x+1) } =\cfrac { 1 }{ (x+2) } -\cfrac { 1 }{ (x+4) } $$ to get a quadratic equation. Find the nature of roots. Solve the equation using the formula.
Simplify $$\dfrac { 2 }{ i } +\dfrac { 3 }{ { i }^{ 3 } } +\dfrac { 4 }{ { i }^{ 4 } } +\dfrac { 5 }{ { i }^{ 5 } }$$ in the form of $$a+ib$$ & represent graphically & find modulus & amplitude.
Given $$\dfrac { 2 }{ i } +\dfrac { 3 }{ { i }^{ 3 } } +\dfrac { 4 }{ { i }^{ 4 } } +\dfrac { 5 }{ { i }^{ 5 } } =a+ib$$
$$\Rightarrow { i }^{ 2 }=-1$$ $${ i }^{ 3 }=--i$$
$${ i }^{ 4 }=-1$$ $${ i }^{ 5 }=-i$$
$$\Rightarrow \dfrac { -2\times -2 }{ i } +\dfrac { 3 }{ \left( -i \right) } +4+\dfrac { 5 }{ { i } } =a+ib$$
$$\Rightarrow -2i+3i+4-5i=a+ib$$
$$4-4i=a+ib$$
$$\Rightarrow a=4,$$ $$b=-4$$
$$\Rightarrow \left| a+ib \right| =\sqrt { { 4 }^{ 2 }+{ 4 }^{ 2 } } =4\sqrt { 2 } $$
$$\Rightarrow arg \left( a+ib \right) =-\tan { \left( \dfrac { 4 }{ 4 } \right) } $$ ( as it is 4th quadrant )
$$\Rightarrow arg \left( a+ib \right) =\dfrac { -\pi }{ 4 } $$
Hence, the answer is $$\dfrac { -\pi }{ 4 }. $$
Find the value of the principal argument of the complex number $$z = \dfrac {(1 + i\sqrt {3})^{2}}{(1 - i)^{3}}$$.
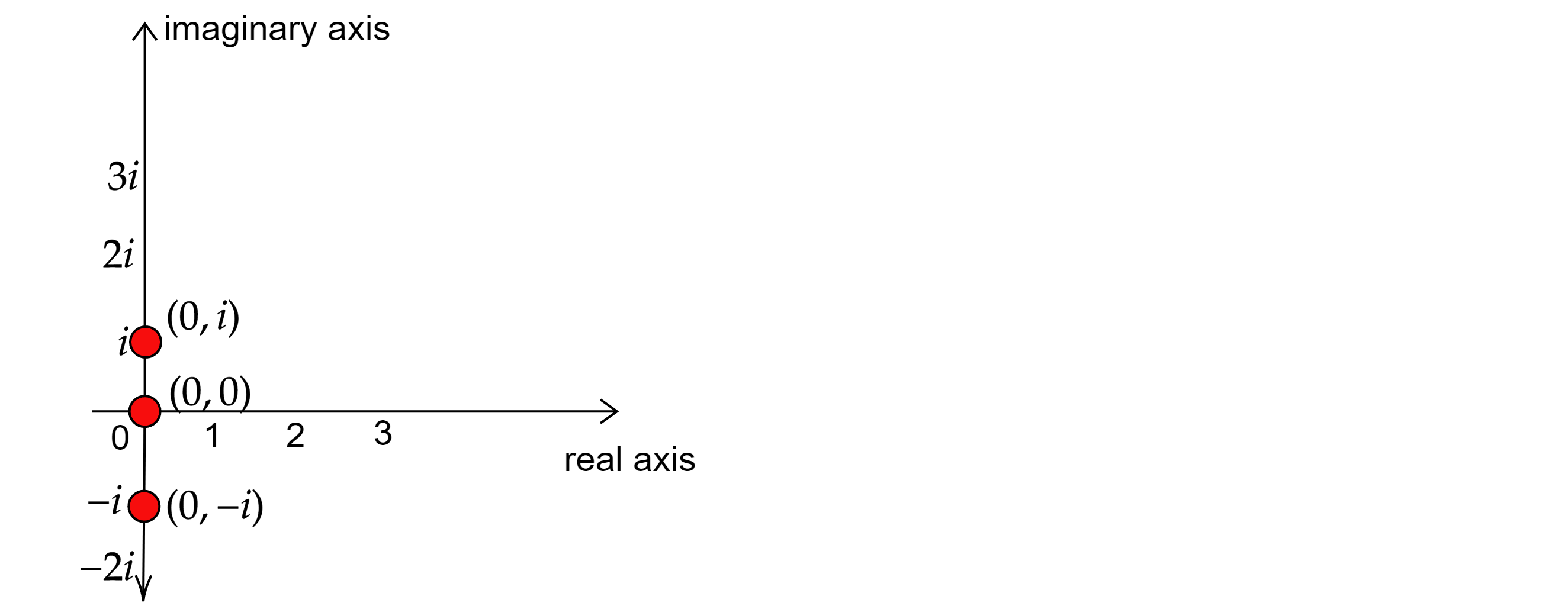
Indicate the point of the complex plane $$z$$ which satisfy the following equation.
$$\displaystyle z^2 \, + \, | \, z \, | \, = \, 0$$
Then, $$z^2+|z|=0$$
$$\implies (x+iy)^2+\sqrt{x^2+y^2}=0$$
$$\implies x^2-y^2+2xyi+\sqrt{x^2+y^2}=0+0i$$
By comparing real an imaginary parts:
$$x^2-y^2+\sqrt{x^2+y^2}=0$$..........[1] or
$$2xy=0\implies x=0$$ or $$y=0$$
Case$$1$$: if $$y=0$$, from eq. $$1$$
$$x^2+\sqrt{x^2}=0\implies x^2+|x|=0$$..........[2]
Now if $$x>0$$, then $$x^2+x$$ will not be $$0$$(sum of two positive numbers can't be $$0$$).
So, for $$x<0$$; $$x^2-x=0\implies x=0,1$$. But $$x=1$$ doesn't satisfy eq. 2.
So only point that satisfies is $$y=0,x=0$$
Case$$2$$: if $$x=0$$, from eq. $$1$$
$$-y^2+\sqrt{y^2}=0\implies -y^2+|y|=0$$..........[3]
Now if $$y<0$$, then $$-y^2-y=0\implies y=0,-1$$
So, for $$y>0$$; $$-y^2+y=0\implies y=0,1$$. But $$y=1,0$$ both satisfies eq. 3.
So the points that satisfy case$$2$$ are $$y=0,x=0$$ and $$x=0, y=1$$ and $$x=0, y=-1$$
Hence all points which satisfies the given equation $$z^2+|z|=0$$ is $$(0,0),(0,1)$$ and $$(0,-1)$$
So,
$$z=0+0i=0$$
$$z=0+1i=i$$
$$z=0-1i=-i$$
Indicate the point of the complex plane $$z$$ which satisfy the following equation.
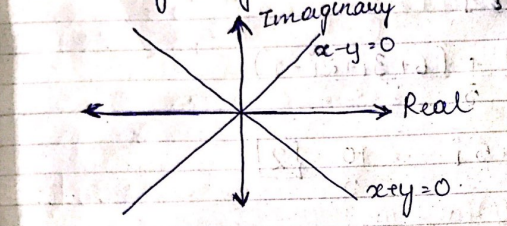
Im $$z^2 = 0$$
Let $$z=x+iy\\ \implies { z }^{ 2 }={ \left( x+iy \right) }^{ 2 }\\\implies={ x }^{ 2 }-{ y }^{ 2 }+2ixy\\ Im\left( { z }^{ 2 } \right) =0\\ \therefore \quad xy=0$$
Indicate the point of the complex plane $$z$$ which satisfy the following equation.
$$\displaystyle | \, z \, |^3 \, + \, z \, = \, 0$$
Indicate the point of the complex plane $$z$$ which satisfy the following equation.
$$\displaystyle Re \, z^2 \, = \, 0$$
Let $$z=x+iy\\ \implies { z }^{ 2 }={ \left( x+iy \right) }^{ 2 }\\\implies={ x }^{ 2 }-{ y }^{ 2 }+2ixy\\ Re\left( { z }^{ 2 } \right) =0\\ \therefore \quad { x }^{ 2 }-{ y }^{ 2 }=0\\ \implies (x+ y)(x-y)=0$$
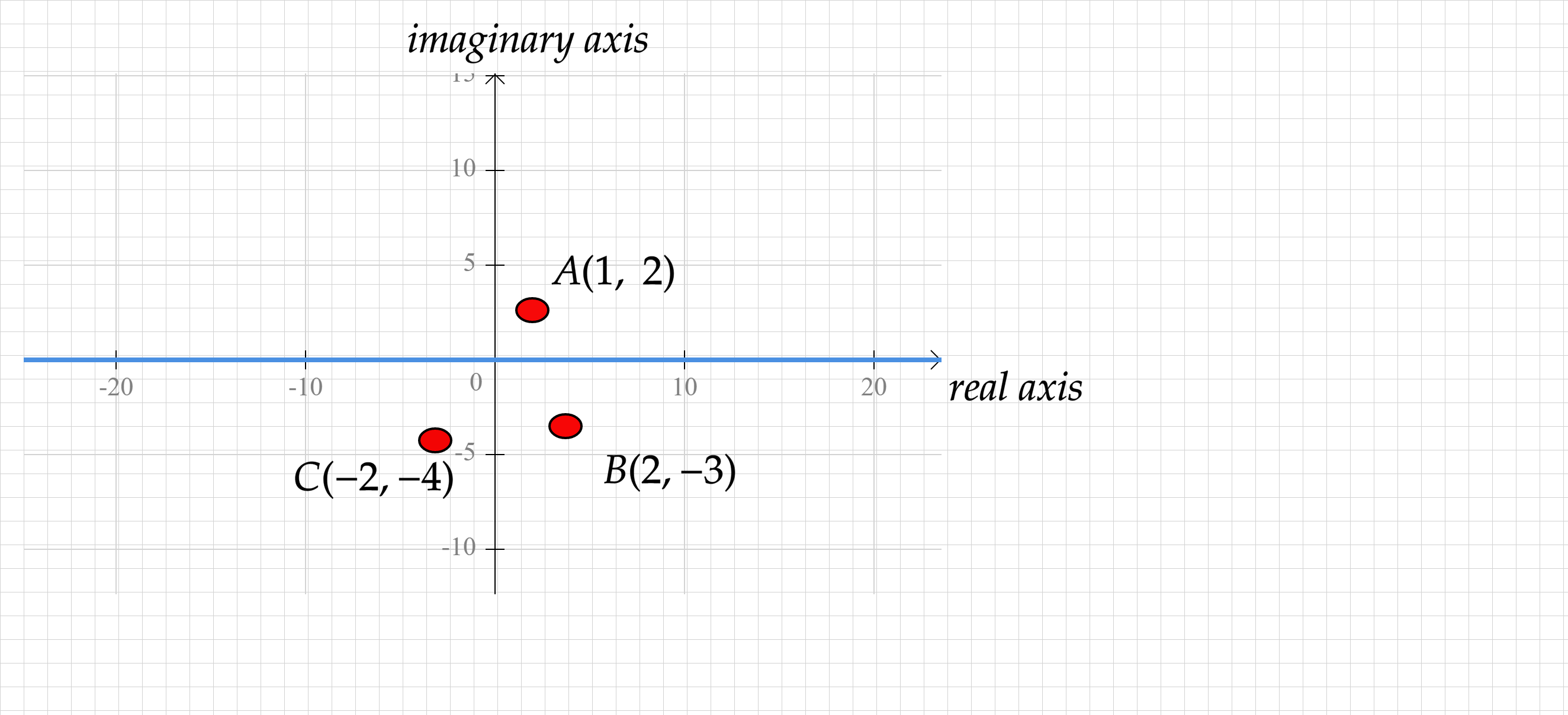
Indicate the point of the complex planea) $$1+2i$$b)$$2-3i$$c)$$-2-4i$$
Calculate $$\displaystyle \sqrt[3]{- \, 1}$$
Calculate, $$\displaystyle \sqrt[4]{- \, 1 \, \frac{1}{2} \, - \, i \, \frac{\sqrt{3}}{2}}.$$
Indicate the point of the complex plane $$z$$ which satisfy the following equation.
$$\displaystyle | \, z \, | \, + \, z \, = \, 0$$
Let $$z=x+iy$$
$$|z|=\sqrt{x^2+y^2}$$
$$|z|+z=0$$
$$\sqrt{x^2+y^2}$$ $$+x+iy=0$$
$$\sqrt{x^2+y^2}$$ $$+x=0$$ and $$y=0$$
$$\implies \sqrt x^2+x=0$$
$$\implies 2x=0$$
$$\implies x=0$$
Find the values of $$k$$ for which the given quadratic equation has real and distinct roots
$$kx^2 + 2x + 1 = 0$$
Prove the following inequalities:
$$ \left| z-1 \right| \le \left| \left| z \right| -1 \right| +\left| z \right| \left| \arg\ z \right|$$
(a) For any two non-zero complex numbers $${z}_{1}$$ and $${z}_{2}$$ if $$\left| { z }_{ 1 }+{ z }_{ 2 } \right| =\left| { z }_{ 1 } \right| +\left| { z }_{ 2 } \right|$$, then prove that $$arg\ {z}_{1}-arg\ {z}_{2}$$ is zero.
(b) Prove the above result if we have$$\left| { z }_{ 1 }-{ z }_{ 2 } \right| =\left| { z }_{ 1 } \right| -\left| { z }_{ 2 } \right|$$
Put the following in the form A + iB :
$$\dfrac{(1 \, + \, i)^2}{3 \, - \, i}$$
Simplify the following :
$$\dfrac{3}{1 \, + \, i} \, - \, \dfrac{2}{2 \, - \, i} \, + \, \dfrac{2}{1 \, - \, i}$$
If a, b, c are real numbers such that ac $$\neq$$ 0, then show that at least one of the equations $$ax^2$$ + bx + c = 0 and - $$ax^2$$ + bx + c = 0 has real roots.
Find the length of the segments connecting the points represented by the following pairs of numbers :
3 - 2i, 3 + 5i
locate the point representing the complex numbers $$z$$ on the Argand diagram for which
$$ \left| z+i \right| =\left| z-2 \right|$$
If $${z}_{1},{z}_{2},{z}_{3}$$ are three complex numbers, prove that
$${ z }_{ 1 }Im\left(\bar { { z }_{ 2 } } { z }_{ 3 } \right) +{ z }_{ 2 }Im\left(\bar { { z }_{ 3 } } { z }_{ 1 } \right) +{ z }_{ 3 }Im\left(\bar { { z }_{ 1 } } { z }_{ 2 } \right) =0$$ where $$Im(w)=$$ imaginary part of $$w,w$$ being a complex number.
Solve the following equations:
x-1= $$\sqrt{a-x^{2}}$$
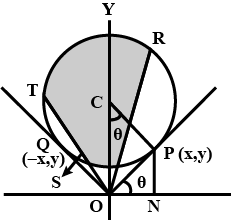
Among the complex numbers $$z$$ which satisfy the condition $$\left| z-25i \right| \le 15,$$ find the number having the least positive and greatest positive argument.
The complex numbers $$z$$ satisfying the condition
$$\left|z-25i \right| \le 15$$
are represented by the points inside and
on this circle of radius $$15$$ and centre at the point $$C
(0,25)$$. From the figure, it is clear that the complex number $$z$$ satisfying $$(1)$$ and having least positive argument correspond to the point $$P(x,y)$$ which is the point of contact
ofa ray issuing from the origin and lying in the first quadrant
to the above circle. The positive argument of all other points
which and on the circle is greater than the argument of $$P$$
From figure, we have
$$OC=25,\ CP=radius=15$$
and $$\angle\ CPO=90$$
Hence $$OP=\sqrt { { OC }^{ 2 }-{ CP }^{ 2 } } =\sqrt { { 25 }^{
2 }-{ 15 }^{ 2 } } =20$$.
If $$\angle\ PCO=\theta$$, then $$\angle\ PON=\theta$$, Also
$$cos\theta =\dfrac { PC }{ OC } =\dfrac { 15 }{ 25 } =\dfrac { 3
}{ 5 } ,$$
$$\therefore x=ON=OP\cos \theta =20\times (3/5)=12,$$
and $$y=PN=OP\sin \theta =20\times (4/5)=16,$$.
Hence $$P$$ represents the complex number $$z=x+iy=12+16i$$ which
is therefore the required value of $$z$$ satisfying the given
conditions. The corresponding point $$Q$$ on the other tangent
from $$O$$ will have greatest $$+ive$$ argument. It will be $$-
12+16i$$ whose argument is $$\pi -\theta$$.
$$\left|z-25i \right| \le 15$$
are represented by the points inside and
on this circle of radius $$15$$ and centre at the point $$C
(0,25)$$. From the figure, it is clear that the complex number $$z$$ satisfying $$(1)$$ and having least positive argument correspond to the point $$P(x,y)$$ which is the point of contact
ofa ray issuing from the origin and lying in the first quadrant
to the above circle. The positive argument of all other points
which and on the circle is greater than the argument of $$P$$
From figure, we have
$$OC=25,\ CP=radius=15$$
and $$\angle\ CPO=90$$
Hence $$OP=\sqrt { { OC }^{ 2 }-{ CP }^{ 2 } } =\sqrt { { 25 }^{
2 }-{ 15 }^{ 2 } } =20$$.
If $$\angle\ PCO=\theta$$, then $$\angle\ PON=\theta$$, Also
$$cos\theta =\dfrac { PC }{ OC } =\dfrac { 15 }{ 25 } =\dfrac { 3
}{ 5 } ,$$
$$\therefore x=ON=OP\cos \theta =20\times (3/5)=12,$$
and $$y=PN=OP\sin \theta =20\times (4/5)=16,$$.
Hence $$P$$ represents the complex number $$z=x+iy=12+16i$$ which
is therefore the required value of $$z$$ satisfying the given
conditions. The corresponding point $$Q$$ on the other tangent
from $$O$$ will have greatest $$+ive$$ argument. It will be $$-
12+16i$$ whose argument is $$\pi -\theta$$.
Locate the complex numbers $$z=x+iy$$ such that
$$ \left| z-i \right| =1,\arg\dfrac { z }{ z+i } =\dfrac { \pi }{ 2 }.$$
Here are two conditions to satisfied.
$$\left| z-i \right| =1\Rightarrow { x }^{ 2 }+\left( y-1 \right) ^{ 2 }=1$$ ......$$(1)$$
It represents a circle with centre at $$(0,1)$$ and radius $$1$$. It clearly touches $$x-$$axis as $$r=k=1$$. Hence all points on the boundary of this circle are the solutions of this.
Again $$\arg\dfrac { z }{ z+i } =\dfrac { \pi }{ 2 }$$
$$\therefore\quad \dfrac { z }{ z+i } =r\left( \cos { \dfrac { \pi }{ 2 } } +i\sin { \dfrac { \pi }{ 2 } } \right)$$
$$0+ir$$
$$\therefore\quad R.P.=0$$, $$I.P.=r=+ive$$ ......$$(2)$$
Now $$\dfrac { z }{ z+i } =\dfrac { x+iy }{ x+i\left( y+1 \right) } .\dfrac { x-i\left( y+1 \right) }{ x-i\left( y+1 \right) }$$
$$=\dfrac { x^{ 2 }+{ y }^{ 2 }+y-ix }{ { x }^{ 2 }+\left( y+1 \right) ^{ 2 } }$$
Condition $$\left( 2 \right) \Rightarrow { x }^{ 2 }+{ y }^{ 2 }+y=0$$
It represents a circle with centre at $$\left( 0,-\dfrac { 1 }{ 2 } \right)$$ and radius $$\dfrac { 1 }{ 2 }$$, i.e. $${ x }^{ 2 }+\left( y+\dfrac { 1 }{ 2 } \right) ^{ 2 }=\left( \dfrac { 1 }{ 2 } \right) ^{ 2 }$$
Also I.P. $$=-x>0$$ or $$x<0$$
Thus we have two circles $$x^{ 2 }+(y-1)^{ 2 }=1^{ 2 }$$
and $$ x^{ 2 }+\left( y+\dfrac { 1 }{ 2 } \right) ^{ 2 }=\left( \dfrac { 1 }{ 2 } \right) ^{ 2 }$$ with $$x<0$$
Because of the condition $$x<0$$, only left hand portion of the second circle will be valid except the points $$P$$ and $$Q$$ as for both $$x=0$$. Also $$P(0,0)$$ does not satisfy 1st circle.
$$\left| z-i \right| =1\Rightarrow { x }^{ 2 }+\left( y-1 \right) ^{ 2 }=1$$ ......$$(1)$$
It represents a circle with centre at $$(0,1)$$ and radius $$1$$. It clearly touches $$x-$$axis as $$r=k=1$$. Hence all points on the boundary of this circle are the solutions of this.
Again $$\arg\dfrac { z }{ z+i } =\dfrac { \pi }{ 2 }$$
$$\therefore\quad \dfrac { z }{ z+i } =r\left( \cos { \dfrac { \pi }{ 2 } } +i\sin { \dfrac { \pi }{ 2 } } \right)$$
$$0+ir$$
$$\therefore\quad R.P.=0$$, $$I.P.=r=+ive$$ ......$$(2)$$
Now $$\dfrac { z }{ z+i } =\dfrac { x+iy }{ x+i\left( y+1 \right) } .\dfrac { x-i\left( y+1 \right) }{ x-i\left( y+1 \right) }$$
$$=\dfrac { x^{ 2 }+{ y }^{ 2 }+y-ix }{ { x }^{ 2 }+\left( y+1 \right) ^{ 2 } }$$
Condition $$\left( 2 \right) \Rightarrow { x }^{ 2 }+{ y }^{ 2 }+y=0$$
It represents a circle with centre at $$\left( 0,-\dfrac { 1 }{ 2 } \right)$$ and radius $$\dfrac { 1 }{ 2 }$$, i.e. $${ x }^{ 2 }+\left( y+\dfrac { 1 }{ 2 } \right) ^{ 2 }=\left( \dfrac { 1 }{ 2 } \right) ^{ 2 }$$
Also I.P. $$=-x>0$$ or $$x<0$$
Thus we have two circles $$x^{ 2 }+(y-1)^{ 2 }=1^{ 2 }$$
and $$ x^{ 2 }+\left( y+\dfrac { 1 }{ 2 } \right) ^{ 2 }=\left( \dfrac { 1 }{ 2 } \right) ^{ 2 }$$ with $$x<0$$
Because of the condition $$x<0$$, only left hand portion of the second circle will be valid except the points $$P$$ and $$Q$$ as for both $$x=0$$. Also $$P(0,0)$$ does not satisfy 1st circle.
locate the point representing the complex numbers $$z$$ on the Argand diagram for which
$$ \left| z-1 \right| =\left| z-3 \right| =\left| z-i \right| ,$$
$$\left| z-1 \right| ^{ 2 }=\left| z-3 \right| ^{ 2 }=\left| z-i
\right| ^{ 2 }$$ on squaring
$$\therefore \left( x-1 \right) ^{ 2 }+y^{ 2 }=\left( x-3 \right)
^{ 2 }+y^{ 2 }=x^{ 2 }+\left( y-1 \right) ^{ 2 }$$
$$I$$ $$II$$ $$III$$
From $$I$$ and $$II$$, $$2(2x-4)=0$$ $$\therefore x=2$$
From $$I$$ and $$III$$, $$-2x=-2y$$ $$\therefore x=y=2$$
$$\therefore z=x+i\ y=2+2i$$
Remarks: Geometric speaking, the equation $$(1)$$ means that $$z
$$ is a point equidistant from the point representing the number
$$1,3,i$$, that is, equidistant from the points $$A(1,0)$$, $$B
(3,0)$$ and $$C(0,1)$$. It is therefore the circumcentre of $$
\Delta ABC$$.
So it is the intersection of perpendicular bisectors $$FP$$ and$$EP$$ of segment $$AB$$ and $$AC$$, that is, the intersection $$P$$ of the lines represented by the equation $$x=2$$ and $$y=x$$. So we get $$x=y=2$$ as before. (See fig.).
\right| ^{ 2 }$$ on squaring
$$\therefore \left( x-1 \right) ^{ 2 }+y^{ 2 }=\left( x-3 \right)
^{ 2 }+y^{ 2 }=x^{ 2 }+\left( y-1 \right) ^{ 2 }$$
$$I$$ $$II$$ $$III$$
From $$I$$ and $$II$$, $$2(2x-4)=0$$ $$\therefore x=2$$
From $$I$$ and $$III$$, $$-2x=-2y$$ $$\therefore x=y=2$$
$$\therefore z=x+i\ y=2+2i$$
Remarks: Geometric speaking, the equation $$(1)$$ means that $$z
$$ is a point equidistant from the point representing the number
$$1,3,i$$, that is, equidistant from the points $$A(1,0)$$, $$B
(3,0)$$ and $$C(0,1)$$. It is therefore the circumcentre of $$
\Delta ABC$$.
So it is the intersection of perpendicular bisectors $$FP$$ and$$EP$$ of segment $$AB$$ and $$AC$$, that is, the intersection $$P$$ of the lines represented by the equation $$x=2$$ and $$y=x$$. So we get $$x=y=2$$ as before. (See fig.).
If $$z_1 \, , \, z_2 \, , \,z_3 \, , \,z_4 $$ be the vertices of rhombus in argand palne and $$\angle CBA \, = \, \pi/3$$ , then prove that
$$2\, z_2 \, = \, z_1(1 \, + \, i\sqrt3) \, + \, z_3(1 \, - \, i\sqrt3)$$
and $$2\, z_4 \, = \, z_1(1 \, - \, i\sqrt3) \, + \, z_3(1 \, + \, i\sqrt3)$$
locate the point representing the complex numbers $$z$$ on the Argand diagram for which
$$\left| z \right| -4=\left| z-i \right| -\left| z+5i \right| =0$$
Find the range of $$k$$ for which the equation $${ x }^{ 2 }-4x+k=0$$ has distinct real roots.
Find the value(s) of $$k$$ for which the equation $${ x }^{ 2 }+5kx+16=0$$ has no real roots.
Determine whether the given quadratic equation has real roots and if so, find the roots.
$$2{ x }^{ 2 }+5\sqrt { 3 } x+6=0\quad $$
If $$p,q,r$$ and $$s$$ are real numbers such that $$pr=2(q+s)$$, then show that at least one of the equations $${ x }^{ 2 }+px+q=0$$ and $${ x }^{ 2 }+rx+s=0$$ has real roots.
For each of the quadratic equations below, convert them into the standard form $$ax^2+bx+c=0$$ and determine the value of '$$b^2-4ac$$. Comment on the nature of roots from the value of '$$b^2-4ac$$
(i) $$5x^2=6x-7$$
(ii) $$4x^2+16=-16x$$
(iii) $$2x^2+6x+3=0$$
Solve$$(\cfrac { 1 }{ 5 } +i\cfrac { 2 }{ 5 } )-(4+i\cfrac { 5 }{ 2 } )$$
Express the following complex numbers in the form $$r\left( {\cos \theta + i\sin \theta } \right)$$ :
1 + i tan$$\alpha $$
What is the value of $${i^i}$$
Where $$i = \sqrt { - 1} $$
Find the discriminant of the following quadratic equations and hence determine the nature of the roots of the equation :
$$5{x^2} - 6x + 2 = 0$$
Given that $$iz^{2}$$ =$$ 1 + \frac{2}{z} + \frac{3}{z^{2}} +\frac{4}{z^{3}} +\frac{5}{z^{4}}+ ....$$ and $$z= n\pm\sqrt{-i}$$, find $$\left \lfloor 100n \right \rfloor$$
Find the discriminant of the following quadratic equations and hence determine the nature of the roots of the equation :
$$x(x - 5) = 36$$
Find modulus of following(i)$$ \pm \left( {4 + 3i} \right)$$ (ii) $$ \pm \sqrt 2 + 0i$$ (iii) $$0 \pm \sqrt 2 i$$
Find the discriminant of the following quadratic equations and hence determine the nature of the roots of the equation :
$$5{x^2} - 4\sqrt 5 x + 4 = 0$$
Find the discriminant of the following quadratic equations and hence determine the nature of the roots of the equation :
$$3{x^2} - 18x + 27 = 0$$
Find the discriminant of the following quadratic equations and hence determine the nature of the roots of the equation :
$${x^2} + x - 3 = 0$$
Find the discriminant of the following quadratic equations and hence determine the nature of the roots of the equation :
$${x^2} + x + {1 \over 4} = 0$$
Find the discriminant of the following quadratic equations and hence determine the nature of the roots of the equation :
$$4{x^2} - 6x + 2 = 0$$
Find the value of $$ i^{i}$$
Find the modulus of $$-15-8i$$.
Find the discriminant of the following quadratic equations and hence determine the nature of the roots of the equation :
$${x^2} - 2x - 15 = 0$$
Simplify $${ \left[ i^{17}+{ \left( \dfrac { 1 }{ i} \right) }^{ 25 } \right] }^{ 3 }$$
Represent the following complex numbers by point in Aegand's dialogram.
$$(i)$$ $$0-2+3i$$
$$(ii)$$ $$2i$$
The number of integral values that $$k$$ can take if $$x^{2}+kx-k^{2}+5k > 0$$ for all $$x \in R$$, is
Find the real values of $$x$$ and $$y$$, if
$$(x+iy)(2-3i)=4+i$$
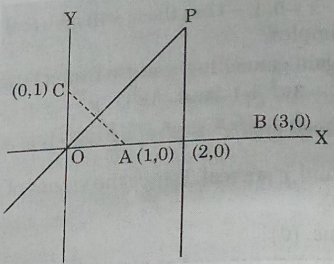
If $$Arg\left( {\frac{{z + 1}}{{z - 1}}} \right) = \frac{\pi }{6}$$ , then find the locus of z.
Let $$z=x+iy$$ and $$|(2z-3)|=|(z-6)|$$ then prove that $$x^2+y^2=3$$.
Let $$z=x+iy$$. If $$\dfrac{z-1}{z+1}$$ is purely imaginary then prove that $$|z|=1$$.
Evaluate : $$\sqrt { - 16} + 3\sqrt { - 25} + \sqrt { - 36} - \sqrt { - 625} $$
Find the arguments of each of the complex numbers.
$$z = -1 - i\sqrt{3}$$
$$z = -\sqrt{3} + i$$$$z=1+i\sqrt{3}$$
Find the principal argument of the complex number $$\sin \dfrac{6\pi}{5} + i(1 + \cos\dfrac{6\pi}{5})$$
Find the modulus and amplitude for each of the following complex numbers.
i) $$7 - 5i $$ vi) $$\sqrt{3} - i$$
ii) $$\sqrt{3} + \sqrt{2 i}$$ vii) $$3$$
iii) $$-8 + 15 i $$ viii) $$1 + i$$
iv) $$-3 (l - i) $$ ix) $$1 + i \sqrt{3}$$
v) $$-4 - 4i $$ x) $$(1 + 2i)^2 (1 - i)$$
Solve the equation $${z}^{2}+|z|=0$$, where $$z$$ is a complex number.
Find the modulus, argument and the principal argument of the complex numbers.
$$-2(\cos 30^o+i\sin 30^o)$$
Let $$a=\dfrac{1+i}{2}$$ then prove that $$a^6+a^4+a^2+1=0$$.
Find the modulus, argument and the principal argument of the complex numbers.
$$6(\cos 310^o-i\sin 310^o)$$
If $$i{z^3} + {z^2} - z + i = 0$$, then find $$\left| z \right|$$.
Find the number of $$a$$ for which given equation have equal roots$$x^2+3x-(a^2+a-2)=0$$
If $$\dfrac {a+3l}{2+ib}=1-1$$, show that $$(5a-7b)=0$$
Find the modulus of $$\dfrac{{\left( {1 + 3i} \right)\left( {2 - 5i} \right)}}{{\left( {2 - \sqrt 6 i} \right)\left( { - 3 + 2\sqrt 5 i} \right)}}$$
Convert the complex number $$z=\dfrac { i-1 }{ \cos { \dfrac { \pi }{ 3 } +i } \sin { \dfrac { \pi }{ 3 } } }$$ in the polar from and hence find the modulus and the argument of $$x$$.
Find the modulus of $$\dfrac{1+2i}{1-3i}$$
Solve: $$\left(\dfrac{1}{1 - 2i} + \dfrac{3}{1 + i}\right)\left(\dfrac{3 + 4i}{2 - 4i}\right)$$.
If $$Z=\cos \theta+i\sin \theta$$ find the complex representation of $$\dfrac {Z}{1-2Z{}}$$.
Solve:$$\sqrt[4]{-81}$$.
For $$z=x+iy$$ find the real and imaginary part of $$e^z$$.
Let $${x_1}$$ and $${x_2}$$ be two complex numbers such that $$\left| {{x_1} + {x_2}} \right| = \left| {{x_1}} \right| + \left| {{x_2}} \right|$$. show that arg$$\left( {{x_1}} \right) - \arg \left( {{x_2}} \right) = 0$$
Let $$x_{1}=a_{1}+ib_{1}$$
$$x_{2}=a_{2}+ib_{2}$$
$$\left | x_{1} \right |+\left | x_{2} \right |=\left | x_{1}+x_{2} \right |$$
$$\sqrt{a_{1}^{2}+b_{1}^{2}}+\sqrt{a_{2}^{2}+b_{2}^{2}}=\sqrt{(a_{1}+a_{2})^{2}+(b_{1}+b_{2})^{2}}$$
square both sides
$$2\sqrt{(a_{1}^{2}+b_{1}^{2})(a_{2}^{2}+b_{2}^{2})}=2a_{1}a_{2}+2b_{1}b_{2}$$
$$\dfrac{b_{1}}{a_{1}}=\dfrac{b_{2}}{a_{2}}$$
$$arg(x_{1})=arg(x_{2})=\dfrac{b_{1}}{a_{1}}=\dfrac{b_{2}}{a_{2}}$$
$$arg(x_{1})-arg(x_{2})=0$$
find the modulus and argument of the complex numbers.
$$\frac{{2 + 14i}}{{{{\left( {2 - i} \right)}^2}}}$$
For what values of $$a$$, that the roots of the equation $$x^2 + 2 (3a + 5) x + 2 (9a^2 + 25) = 0$$ are complex
Find the modulus and argument of the complex numbers.
$$\dfrac{{5 - i}}{{2 - 3i}}$$
If $$\left| {\dfrac{{z - 5i}}{{z + 5i}} } \right|=1$$, prove that $$z$$ is real.
Find the modulus of the complex number $$\dfrac{i}{1-i}$$.
Number of real roots of $$2\sqrt{2x+1}=2x-1$$
Comment on the nature of the roots of the Quadratic equation $$3\sqrt{3}x^2+10x+\sqrt{3}=0$$.
Find the conjugate and modulus of the following complex numbers.
$$\overline{(2+3i)}+\overline{(5i-4i^3)}+\overline{(6i-7i^4)}$$.
Show that the roots of the equation $${x}^{2}+2(3a+5)x+2(9{a}^{2}+25)=0$$ are complex unless $$a=\cfrac{5}{3}$$
If $$\left| Z \right| =2$$ and $$arg(Z)=\cfrac{\pi}{4}$$ then write $$Z$$.
What is the nature of roots of quadratic equation $$5{x^2} - 7x + 2 = 0?$$
Find the modulus are arguments $$z = -\sqrt{3} + i$$
If $$z_1=6+i$$ $$z_2=3-4i$$ then find $$z_1z_2$$
Find the Modulas and argument of $$\dfrac{1+i}{1-i}$$
If $$z+m=88$$ & $$z-m=z$$, then $$m=______$$
Which terms of the $$8\vec {i},\ 7-4\vec {i},\ 6-2\vec {i}$$,.... is purely imaginary
If z = x + yi and $$\dfrac{\left| z - 1 -i\right| + 4}{3 \left| z - 1 -i\right| -2} = 1$$, show that $$ x^2 + y^2 - 2x - 2y - 7 = 0$$.
$$\dfrac{\left| z - 1 -i\right| + 4}{3 \left| z - 1 -i\right| -2} = 1$$
Put $$ z = x + yi $$
$$ \dfrac{|x+iy-1-i|+4}{3|x+iy-1-i|-2} = 1 $$
$$ \dfrac{|(x-1)+i(y-1)|+4}{3|(x-1)+i(y-1)-2} = 1 $$
$$ \dfrac{\sqrt{(x-1)^{2}+(y-1)^{2}}+4}{3\sqrt{(x-1)^{2}+(y-1)^{2}}-2} = 1 $$
$$ \sqrt{(x-1)^{2}+(y+1)^{2}+4} = 3\sqrt{(x-1)^{2}+(y-1)^{2}}-2 $$
$$ 2\sqrt{(x-1)^{2}+(y-1)^{2}} = 6 $$
$$ \sqrt{(x-1)^{2}+(y-1)^{2}} = 3 $$
$$ \sqrt{(x^{2}+1-2x+y^{2}+1-2y)} = 9 $$
$$ x^{2}+y^{2}-2x-2y -7 = 0 $$ Hence proved
Find the values of $$m$$ for which the quadrilateral equation $${x}^{2}-m\left(2x-8\right)-15=0$$ has
(i) equal roots
(ii) both roots positive.
if $$z=r \cos \theta$$ then find the value $$|e^{iz}|.$$
If $$a > 0,|z| =a$$, then find the real part of $$\left ( \dfrac{z-a}{z+a} \right )$$.
In the Argand plane ,the vector $$OP$$,where $$O$$ is the origin and $$P$$ represents the complex number $$z=4-3i$$ ,is turned in the clockwise sense through $${180^ \circ }$$ and streched $$3$$ times. the complex number represented by the new vector is -----.
Solve the equation $$z^{2}=\overline {z}$$
If $$g(x)=x^{4}-x^{3}\div x^{2}+3x-5$$, find $$g(2+3i)$$ ?
If $$1 + \dfrac{1}{i} = A + iB,$$ then find the value of B.
Represent follow complex no. in polar form.
$$z=-1+\sqrt3i$$
Find the real and imaginary part of $$\dfrac{{3 - 2i}}{{7 + 4i}}$$
If the quadratic equation $$(b^2+c^2)x^2-2(a+b)c x+(c^2+a^2)=0$$ has equal roots. Then find a relation between $$a,b,c$$.
Find the modulus of the complex number, $$\sqrt{2}i+\sqrt{-2}i$$.
$$\sqrt{2}i+\sqrt{2}i$$
$$=\sqrt{2}i+\sqrt{-1}\times \sqrt{2}\times i$$
$$=\sqrt{2}i+i\times \sqrt{2}\times i$$
$$=\sqrt{2}i-\sqrt{2}$$
$$=\sqrt{2}(-1+i)$$.
Modulus is $$\sqrt{2}\cdot \sqrt{(-1)^2+i^2}=\sqrt{2}\cdot \sqrt{2}=2$$.
Find the value of $$\left(\dfrac{2i}{1+i}\right)^2$$
Now,
$$\left(\dfrac{2i}{1+i}\right)^2$$
$$=\dfrac{-4}{(1+i)^2}$$ $$[\because (1+i)^2=1+2i-1=2i]$$
$$=\dfrac{-4}{2i}=\dfrac{-2}{i}=(2i);$$ $$[\because i^2=-1\Rightarrow i=-yi]$$
The equation $$(\cos\:p - 1) x^2 +(\cos \: p)x+\sin \:p=0$$ has real roots, then 'P' can take any value in the interval
If $$z = 2 - i \sqrt 7$$, then show that $$3z^3 - 4z^2 + z + 88 = 0.$$
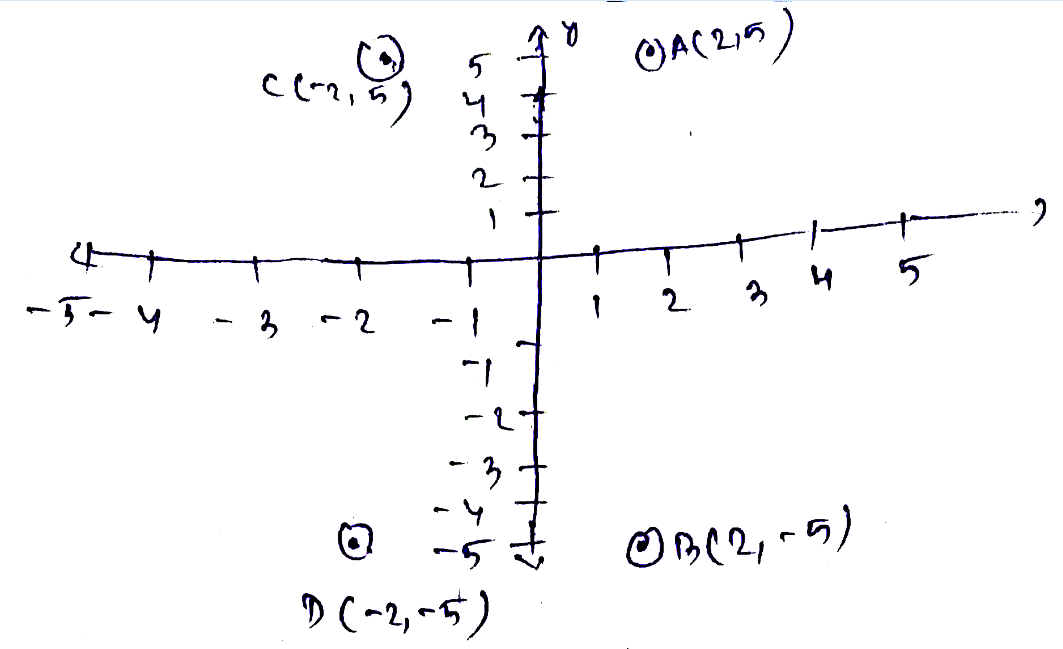
Represent the complex number $$2+5i,2-5i,-2+5i$$ and $$-2-5i$$ in Argand's diagram.
If $$z=\sqrt{20i-21}+\sqrt{21+20i}$$ then principal value of arg z can not be
If $$\alpha , \beta$$ are the roots of $$x ^ { 2 } - 8 x + A = 0$$ and $$\gamma , \delta$$ are the roots of $$x ^ { 2 } - 72 x + B = 0 ,$$ if $$\alpha < \beta < \gamma < \delta$$ are in GP, then find the value of $$A + B .$$
Let $$x-iy=\sqrt{\dfrac{a-ib}{c-id}}$$ then prove that $$(x^2+y^2)^2=\dfrac{a^2+b^2}{c^2+d^2}$$.
If $$a,b,c\ \in\ R^{+}$$ and $$2b=a+c$$, then check the nature of roots of equation $$ax^{2}+2bx+c=0$$.
If $$\pi/2\ and\ \pi/4$$ are respectively the arguments nof $$Z_1 and\ \overline{Z_2}$$, what is the value of arg$$(z_1/z_2)$$
$$Arg(z_1)=\dfrac{\pi}{2}$$
$$Arg(\bar{z_2})=\dfrac{\pi}{4}$$
$$Arg(z_2)=-Arg(\bar{z_2})=-\dfrac{\pi}{4}$$
$$Arg(z_1/z_2)=Arg(z_1)-Arg(z_2)$$
$$=\dfrac{\pi}{2}-\left(-\pi/4\right)$$
$$=3\pi/4$$.
$$x^{2}+6x+9=0$$
$$x=?$$
If the discriminant of $$3x^2+2x+a=0$$ is double the discriminant of $$x^2-4x+2$$, then find the value of a.
Discriminant of $$-x^{2}+\frac{1}{2}x+\frac{1}{2}=0$$ is
If $$z _ { 1 } = 9 + 5 i$$ and $$z _ { 2 } = 3 + 5 i$$ and if $$arg \left( \dfrac { z - z _ { 1 } } { z - z _ { 2 } } \right) = \dfrac { \pi } { 4 }$$ then $$| z - 6 - 8 i | = 3 \sqrt { 2 }.$$
Express: $$Z=\dfrac {i-1}{\cos \dfrac {\pi}{3}+i\sin \dfrac {\pi}{3}}$$ in polar form.
$$ Z = \frac{i-1}{cos\frac{\pi }{3}+isin\frac{\pi }{3}}$$
$$ = \frac{i -1}{(\frac{1}{2}+i\frac{\sqrt{3}}{2})} \times \frac{(\frac{1}{2}-\frac{i\sqrt{3}}{2})}{(\frac{1}{2}-\frac{\sqrt{3}i}{2}}$$
$$ = \frac{\frac{i}{2}+\frac{\sqrt{3}}{2}-\frac{1}{2}+\frac{\sqrt{3}i}{2}}{\frac{1}{4}+\frac{3}{4}}$$
$$ = (\frac{\sqrt{3}}{2}-\frac{1}{2})+i(\frac{1}{2}+\frac{\sqrt{3}}{2})$$
polor from
$$z = r (cos\theta +isin\theta )$$
$$ rcos\theta = \frac{\sqrt{3}-1}{2}, rsin\theta = \frac{\sqrt{3}+1}{2}.$$
squaring and adding
$$ \therefore r^{2} = \frac{3-2\sqrt{3}+1+3+2\sqrt{3}+1}{4} = 2$$
$$\therefore r =\sqrt{2}$$
$$ cos\theta = \frac{\sqrt{3}-1}{2\sqrt{2}} = \frac{\sqrt{3}}{2}\times \frac{1}{\sqrt{2}}-\frac{1}{2}\times \frac{1}{\sqrt{2}}$$
$$ =cos \frac{\pi }{6}. cos(\frac{\pi }{4}) - sin\frac{\pi }{6}.sin\frac{\pi }{4}$$
$$ cos\theta = cos(\frac{\pi }{6}+\frac{\pi }{4})$$
$$ \therefore \theta = \frac{5\pi }{12} (cos(A+B)) =cosA.cosB - sinA sinB)$$
Hence, required poloar from
$$z = \sqrt{2} (cos \frac{5\pi }{12}+isin \frac{5\pi }{12} )$$
Simplify:$$\left(\dfrac{2i}{1+i}\right)^2$$
If $$a+ib=\dfrac{p+i}{2q-i}$$, prove that $$a^2+b^2=\dfrac{(p^2+1)}{4q^2+1}$$
Simplify and hence find the modulus and argument of $$\frac{{3 + 2i}}{{2 - 5i}} + \frac{{3 - 2i}}{{2 + 5i}}$$ and $$\frac{{(3 + i)(3 - i)}}{{2 + i}}$$.
Simplify : $$\dfrac {(\cos \theta+i\sin \theta)^{4}}{(\cos \theta+i\sin \theta)^{5}}$$
$$\dfrac{(\cos\theta +i\sin\theta)4}{(\cos\theta +i\sin\theta)5}=\dfrac{1}{(\cos\theta +i\sin\theta)}$$
$$\Rightarrow \dfrac{1(\cos\theta -i\sin\theta)}{(\cos\theta +i\sin\theta)(\cos\theta -i\sin\theta)}$$
$$\Rightarrow\dfrac{\cos\theta -i\sin\theta}{(\cos^2\theta -i\sin^2\theta)}=\dfrac{\cos\theta -i\sin\theta}{\cos^2\theta +\sin^2\theta)}$$
$$=\cos\theta -i\sin\theta$$.
Represent the complex number $$Z = 1 + i$$, $$Z = -1 + i$$ in the Argand's diagram and find their arguments.
For what value of $$k,\left( 4-k \right) { x }^{ 2 }+\left( 2k+4 \right) x+\left( 8k+1 \right) =0$$ is a perfect square:
Locate the complex number $$z$$ such that $$\log_{\cos\dfrac{\pi}{6}}\dfrac{|z-2|+5}{4|z-2|-4}<2$$
Express each of the complex number given in the Exercises $$1$$ to $$10$$ in the form $$a+ib$$.
$$(5i)\left(-\dfrac{3}{5}i\right)$$
Convert the given complex number in polar form: $$- 1 - i$$.
Express :
$$\dfrac{(a+ib)^{2}}{a-ib}-\dfrac{(a-ib)^{2}}{a+ib}$$
in the forum $$x+iy$$
Find the value of P so that the quadratic equation px(x-3)+9=0 has two equal roots.
If $$y=\log { \left( \dfrac { \sqrt { \left( x+1 \right) } -1 }{ \sqrt { \left( x+1 \right) } +1 } \right) } +\dfrac { \sqrt { x } }{ \sqrt { \left( x+1 \right) } } $$ the by using substitution $$x=\tan^{2}\theta,y$$ reduces to
Find the arguments of $${z}_{1}=5+5i,\,{z}_{2}=-4+4i,\,{z}_{3}=-3-3i$$ and $${z}_{4}=2-2i,$$ where $$i=\sqrt{-1}$$
Find the condition on the complex constants $$\alpha ,\beta $$ if $${ z }^{ 2 }+\alpha z+\beta =0$$ has two distinct roots on the line Re(z)= 1.
Find the nature of the roots of the quadratic equation $$4x^{2}-5x+3=0$$.
Let $$z$$ and $$\omega$$ be the complex numbers.If $$Rs\left(z\right)=\left|z-2\right|$$,$$Re\left(\omega\right)=\left|\omega-2\right|$$ and $$arg\left(z-\omega\right)=\dfrac{\pi}{3},$$ find the value of $$Im\left(z+\omega\right)$$
Explain the nature of roots of a quadratic equation $$x^2-x-2=0$$.
Does there exist a quadratic equation whose coefficients are rational but both of its roots are irrational ? Justify your answer.
Find the value of k for which the given quadratic equation $$ x^{2}-4 x+k=0 $$distinct real roots.
Find the nature of the roots of the quadratic equation $$(b-c)x^2+2(c-a)x+(a-b)=0$$.
Simplify: $$\dfrac{1}{i+1} + \dfrac{1}{i-1}$$
Simplify:$$\dfrac{\sqrt{2+3i}}{\sqrt{2-3i}}$$
Compare the quadratic equation $$\sqrt 3 {x^2} + 2\sqrt 3 = 0\,\,to\,\,a{x^2} + bx + c = 0$$ and find the value of discriminant and hence write the nature of the roots.
For what value of $$k$$ are the roots of the quadratic equation $$kx^{2}+1=-4x$$ equal and real?
If $$a=\dfrac{1+i}{\sqrt{2}}$$ then show that $$a^6+a^4+a^2+1=0$$.
If the roots of the quadratic equation $$kx\left(x+2\right)+6=0$$ are real and equal.then find the value of $$k$$
Find the value of $$k$$ for the quadratic equation $$3{y}^{2}+ky+12=0$$ has two equal roots.
$$\dfrac { 3\sqrt { -2 } +2\left( -5 \right) }{ 3\sqrt { -2 } -2\sqrt { -2 } } $$
Express the following in the form of a = ib, a,b$$\epsilon$$R $$i = \sqrt{-1}$$. State the values of a and b.$$(1+i)^{3}$$
Express the following in the form of a = ib, a,b$$\epsilon$$R $$i = \sqrt{-1}$$. State the values of a and b.
If $$a=\dfrac { -1+i\sqrt { 3} }{ 2 } ,b=\dfrac { -1-i\sqrt { 3 } }{ 2 } $$ then show that $${ a }^{ 2 }=b $$ and $${ b }^{ 2 }=a.$$
Write the real and imaginary part of $${ (i-\sqrt { 3 } ) }^{ 3 }$$.
1) Express the following in the form of a = ib, a,b$$\epsilon$$R $$i = \sqrt{-1}$$. State the values of a and b. $$(2+3i)(2-3i)$$
Show that $$\dfrac{\sqrt 5 + i\sqrt 2}{\sqrt 5 - i\sqrt 2} + \dfrac{\sqrt 5 - i\sqrt 2}{\sqrt 5 + i\sqrt 2}$$ is real.
Show that $$\dfrac{\sqrt 7 + i\sqrt 3}{\sqrt 7 - i\sqrt 3} + \dfrac{\sqrt 7 - i\sqrt 3}{\sqrt 7 + i\sqrt 3}$$ is real.
Simplify: $$\left( -\sqrt { 3 } +\sqrt { -2 } \right) \left( 2\sqrt { 3 } -i \right) $$
Find the value of $$p$$ if the following quadratic equation has equal roots :
$${ 4x }^{ 2 }-(p-2)x+1=0$$
Find the modulus of $$\dfrac{{i + 1}}{{1 - i}}$$.
First we solve $$\frac{1+i}{1-i}$$
Let $$z=\frac{1+i}{1-i}$$
Rationalizing the same
$$=\frac{1+i}{1-i}\times \frac{1+i}{1+i}$$
$$=\frac{(1+i)(1+i)}{(1-i)(1+i)}$$
Using $$(a+b)(a-b)=a^{2}-b^{2}$$
$$=\frac{(1+i)^{2}}{1^{2}-i^{2}}$$
Using $$(a+b)^{2}=a^{2}+2ab+b^{2}$$
$$=\frac{(1)^{2}+(i)^{2}+2.1.i}{(1)^{2}-i^{2}}$$
$$=\frac{1+i+2i}{(1)^{2}-(i)^{2}}$$
$$\left( 3k+1 \right) { x }^{ 2 }-2\left( k+1 \right) x+1=0$$ has equal and real roots.
$$(3k+1)x^{2}-2(k+1)x+1=0$$
when D=0,then the equation real equal roots.
$$D=b^{2}-4ac=0$$
$$\Rightarrow (-2(k+1))^{2}-4(3k+1)(1)=0$$
$$\Rightarrow 4(k+1)^{2}-4(3k+1)=0$$
$$\Rightarrow k^{2}+1+2k-3k-1=0$$
$$\Rightarrow k^{2}-k=0$$
$$\Rightarrow k(k-1)=0$$
so k=0 or k=1
If arg$$\left(z\right)<0$$ then find arg$$\left(-z\right)-$$arg$$\left(z\right)$$
The modulus and amplitude of $$(1+i\sqrt { 3 } )^{ 8 }$$ are respectively.
Express the following complex numbers in the standard from $$ a+ib$$ :
$$ \dfrac{2+3i}{4+5i}$$
Evaluate the following:
$$ \dfrac{1}{i^{58}}$$
Find the modulus of $$(1-i)^{10}$$
Find the least positive integral value of n for which
$$ \left ( \dfrac{1+i}{1-i} \right )^{n}$$ is real.
Give three examples from your environment of Points.
Find the modulus and argument of the following complex numbers and hence express each of them in the polar form:
$$\dfrac{-16}{1+i\sqrt{3}}$$
Find the real values of $$ \theta $$ for which the complex number $$ \dfrac{1+i\, cos \,\theta}{1-2\, i\, cos \, \theta }$$ is purely real.
Find the modulus of the following complex number
$$\sin\, 120^{\circ}-i\, \cos\, 120^{\circ}$$
Find the modulus and argument of the following complex numbers and hence express each of them in the polar form:
$$\sqrt{3}+i$$
Evaluate : $$(\sqrt{-1})^{30}$$
Evaluate : $$i^{62}$$
Evaluate : $$(\sqrt{-1})^{192}$$
Evaluate $$i^{19}$$
Evaluate : $$i^{-131}$$
Evaluate : $$\left(i^{41}+\dfrac{1}{i^{71}}\right)$$
Evaluate : $$i^{-9}$$
Evaluate : $$(\sqrt{-1})^{93}$$
Evaluate : $$\left(i^{53}+\dfrac{1}{i^{53}}\right)$$
Find the modulus and argument of the following complex numbers and hence express each of them in polar form:
$$2i$$
Prove that:
$$1+i^{2}+i^{4}+i^{6}=0$$
Find the modulus and argument of the following complex numbers and hence express each of them in polar form:
$$\sqrt 3+i$$
Prove that:
$$(1+i^{10}+i^{20}+i^{30})$$ is a real number.
Find the modulus and argument of the following complex numbers and hence express each of them in polar form:
$$4$$
Find the modulus and argument of the following complex numbers and hence express each of them in polar form:
$$1-i$$
Prove that:
$$\dfrac{1}{i}-\dfrac{1}{i^{2}}+\dfrac{1}{i^{3}}-\dfrac{1}{i^{4}}=0$$
Prove that:
$$6i^{50}+5i^{33}-2i^{15}+6i^{48}=7i$$
Find the modulus and argument of the following complex numbers and hence express each of them in polar form:
$$-1+\sqrt 3 i$$
Find the modulus and argument of the following complex numbers and hence express each of them in polar form:
$$-2$$
Find the modulus of the following :
$$(3+\sqrt {-5})$$
Find the modulus of the following :
$$(7+24i)$$
Find the modulus and argument of the following complex numbers and hence express each of them in polar form:
$$\dfrac{1+i}{1-i}$$
Find the modulus and argument of the following complex numbers and hence express each of them in polar form:
$$\dfrac{1-3i}{1+2i}$$
Find the modulus and argument of the following complex numbers and hence express each of them in polar form:
$$-4+4\sqrt 3 i$$
Find the modulus of the following :
$$(-3-4i)$$
Find the modulus and argument of the following complex numbers and hence express each of them in polar form:
$$\dfrac{1+3i}{1-2i}$$
Find the modulus and argument of the following complex numbers and hence express each of them in polar form:
$$\dfrac{5-i}{2-3i}$$
Find the modulus and argument of the following complex numbers and hence express each of them in polar form:
$$2-2i$$
Find the modulus and argument of the following complex numbers and hence express each of them in polar form:
$$-3\sqrt 2+3\sqrt 2 i$$
Find the modulus of the following :
$$5$$
Evaluate $$(i^{57}+i^{70}+i^{91}+i^{101}+i^{108})$$
Find the modulus and argument of the following complex numbers and hence express each of them in polar form:
$$-\sqrt 3-i$$
Find the modulus of the following :
$$\dfrac {(3+2i)^2}{(4-3i)}$$
Find the modulus of the following :
$$3i$$
Find the modulus of each of the following :
$$(1+2i) (i-1)$$
Find the modulus of the following :
$$\dfrac {(2-i)(1+i)}{(1+i)}$$
Find the modulus and argument of the following complex numbers and hence express each of them in polar form:
$$(\sin 120^o-i\cos 120^o)$$
Find the modulus and argument of the following complex numbers and hence express each of them in polar form:
$$\dfrac{2+6\sqrt 3 i}{5+\sqrt 3 i}$$
Find the modulus and argument of the following complex numbers and hence express each of them in polar form:
$$(i^{25})^3$$
Write the principal argument of $$(1+i\sqrt{3})^{2}$$
Evaluate $$\left(\dfrac{i^{180}+i^{178}+i^{176}+i^{174}+i^{172}}{i^{170}+i^{168}+i^{166}+i^{164}+i^{162}}\right)$$
Find the sum $$(i^{n}+i^{n+1}+i^{n+2}+i^{n+3})$$, where $$n\in N$$
Evaluate $$(i^{40+1}-i^{4n-1})$$
Find the principal argument of $$(-2i)$$
Find the value of $$p$$ for which the quadratic equation
$$\left( 2p+1 \right) { x }^{ 2 }.\left( 7p+2 \right) x+\left( 7p-3 \right) =0$$ has equal roots. Also find these roots.
Find the value(s) of p for which the equation $$2 x^{2}+3 x+p=0$$ has real roots.
If 'a' is a complex number such that $$\mid a \mid$$ = 1, find arg(a), so that equation $$az^2 + z + 1 = 0$$ has one purely imaginary root.
State whether the following quadratic equation has two distinct real roots. Justify your answer.
$$ 2x^2 - 6x + \dfrac{9}{2}= 0$$
Convert the following in the polar form:
$$\dfrac{1+7i}{(2-i)^{2}}$$
Convert the following in the polar form:
$$\dfrac{1+3i}{1-2i}$$
Convert the given complex number in polar form : $$\sqrt 3+i$$
Find the modulus and argument of the complex number $$\dfrac {1 + 2i}{1 - 3i}$$.
State whether the following quadratic equation has two distinct real roots. Justify your answer.
$$2x^2 + x - 1 = 0$$
Find the modulus of $$\dfrac{1+i}{1-i}-\dfrac{1-i}{1+i}$$
Find whether the following quadratic equations have a repeated root: $$16y^2-40y+25=0$$
Find whether the following quadratic equations have a repeated root: $$x^2+6x+9=0$$
Find whether the following quadratic equations have a repeated root: $$y^2-6y+6=0$$
Find whether the following quadratic equations have a repeated root: $$9x^2+4x+6=0$$
Examine whether the following quadratic equations have real roots or not: $$x^2-10x+2=0$$
Find whether the following quadratic equations have a repeated root: $$9x^2-12x+4=0$$
Examine whether the following quadratic equations have real roots or not: $$x^2+x-1=0$$
Examine whether the following quadratic equations have real roots or not: $$7x^2+8x-1=0$$
Examine whether the following quadratic equations have real roots or not: $$2x^2+3x+4=0$$
Examine whether the following quadratic equations have real roots or not: $$x^2-12x-16=0$$
Without solving, determine whether the following equations have real roots or not.If yes,find them: $$2x^2-4x+3=0$$
Without solving, determine whether the following equations have real roots or not.If yes,find them: $$y^2-\dfrac{2}{3}y+\dfrac{1}{9}=0$$
Comment upon the nature of roots of the following equations: $$x^2+10x+39=0$$
Without finding the roots,comment upon the nature of roots of each of the following quadratic equations : $$2x^2-5x-3=0$$
Comment upon the nature of roots of the following equations: $$4x^2+7x+2=0$$
Without finding the roots,comment upon the nature of roots of each of the following quadratic equations : $$2x^2-6x+3=0$$
Find the value of k for which the following quadratic equation has equal roots.$$9x^2+8kx+16=0$$
Find the value of k for which the quadratic equation $$4x^2-2(k+1)x+(k+4)=0$$ has equal roots.
If -5 is root of the quadratic equation $$2x^2+2px=15=0$$ and the quadratic equation $$p(x^2+x)+k=0$$ has equal roots,find the value of k.
Define the addition of two complex numbers.
Determine the nature of roots of the following quadratic equation.
$$2y^{2} - 7y + 2 = 0$$
Determine the nature of roots of the following quadratic equation.
$$m^{2} + 2m + 9 = 0$$
Determine the nature of roots of the following quadratic equation.
$$x^{2} - 4x + 4 = 0$$
Choose the correct answer for the following question.
$$\sqrt{5}m^{2} - \sqrt{5}m + \sqrt{5}$$ which of the following statement is true for this given equation?
Real and unequal roots
Real and equal roots
Roots are not real
Three roots
Define a complex number.
Determine the nature of root of the quadratic equation.
$$3x^{2} - 5x + 7 = 0$$
Determine the nature of root of the quadratic equation.
$$\sqrt{3}x^{2} + \sqrt{2}x - 2\sqrt{3}= 0$$
Find the values of k,for which the given equation has real roots: $$kx^2+4x+1=0$$
Define purely real and purely imaginary numbers.
Define multiplication numbers.
Define the division of two complex numbers.
Define the modulus of a complex number.
Write down the modulus of $$(-1-i)^3$$
Find the modulus and the arguments of the following:
1
Write down the modulus of $$3+\sqrt{-3}$$
Define the difference of two complex numbers.
Find the modulus and the arguments of the following:
-3
Write down the modulus of i
Find the modulus of $$z=\dfrac{1+i}{1-i}-\dfrac{1-i}{1+i}$$
Find the modulus and the arguments of the following:
$$\dfrac{1+2i}{1-3i}$$
Find the modulus and the arguments of the following:
i
Find the modulus and the arguments of the following:
$$\dfrac{1+i}{1-i}$$
Find the modulus and the arguments of the following:
$$ -8 i $$
Write the formula to find the nature of roots?
Find the modulus and the arguments of the following:
$$ -\sqrt{3}+i $$
Find the modulus and the arguments of the following:
$$ 1+\mathrm{i} $$
Find the modulus and the arguments of the following:
$$\dfrac{1}{1+i}$$
Find the modulus and the arguments of the following:
$$ \sqrt{3}-i $$
Find the modulus and the arguments of the following:
$$ -1-i \sqrt{3} $$
Find the modulus of the following ;
$$ \dfrac1{(3-2i)}$$
Find the arguments of the following numbers :
$$ \frac { 1 + i}{ 1 - i} $$
Write the principle argument of $$ -2 $$
Find the arguments of the following numbers :
$$ \frac { 5 + i \sqrt {3} }{4 - i 2 \sqrt {3} } $$
Find the arguments of the following numbers :
$$ -1+ \sqrt {3} i $$
Let $$z = 9 + bi$$, where $$b$$ is nonzero real and $$i^2 = -1$$. If the imaginary part of $$z^2$$ and $$z^3$$ are equal, then find the value of $$\dfrac{b}{3}$$.
Solve the following equation for x $$ { \left( 15+4\sqrt { 14 } \right) }^{ t }+{ \left( 15-4\sqrt { 14 } \right) }^{ t }=30$$ where $$ t={ x }^{ 2 }-2\left| x \right| $$
find the number of roots of the equation.
show that: The modulus and argument of the complex number $$\displaystyle z_{1}=z^{2}-z,\space$$ if $$z=\cos \phi +i\sin \phi .$$ is $$2|\sin \phi/2|, \left (\displaystyle \dfrac{3\pi+3\phi }{2} \right )$$.
Express the complex number $$\dfrac {(1 + \sqrt {3}i)^{2}}{\sqrt {3} - i}$$ in the form of $$a + ib$$. Hence, find the modulus and argument of the complex number
Find the modulus, argument and the principal argument of the complex numbers.
$$\dfrac{2+i}{4i+(1+i)^2}$$
Convert the complex number $$\dfrac {-16}{1+i\sqrt {3}}$$ into polar form.
Find the modulus and argument of the complex number:
$$\dfrac{1+i}{1-i}$$
Express the complex number given in the form $$a+ib$$.
$$i^{-39}$$.
Express the complex number given in the form $$a+ib$$.
$$i^9+i^{19}$$.
Find the modulus and argument of $$z=\dfrac{3+2i}{-2+i}$$.
Prove that the equation $${x}^{2}+px-1=0$$ has real and distinct roots for all real values of $$p$$.
If $$(2+i)(2+2i)(2+3i).....(2+ni)=x+iy$$ then the value of $$5.8.13.....(4+n^2)$$.
Real numbers $$x$$ and $$y$$ satisfy the equation
$$\dfrac{x}{1+i}+\dfrac{y}{1-i}=\dfrac{148}{12+2i}.$$
What is the value of $$xy$$ ?
Evaluate : $$ [i^{19}+(\frac {1}{i}^{32}]^2 $$
Find the real value of $$\theta$$ such that $$\dfrac{3+2i\sin{\theta}}{1-2i\sin{\theta}}$$, where $$i=\sqrt{-1}$$ is $$(i)$$purely real$$(ii)$$ Purely imaginary.
Find the value of $$k$$ for which the equation $$x ^ { 2 } + k ( 2 x + k - 1 ) + 2 = 0$$ has real and equal roots.
What is the nature of the roots of the quadratic equation $$ 4 x^{2}-12 x-9=0? $$
Class 11 Engineering Maths Extra Questions
- Binomial Theorem Extra Questions
- Complex Numbers And Quadratic Equations Extra Questions
- Conic Sections Extra Questions
- Introduction To Three Dimensional Geometry Extra Questions
- Limits And Derivatives Extra Questions
- Linear Inequalities Extra Questions
- Mathematical Reasoning Extra Questions
- Permutations And Combinations Extra Questions
- Principle Of Mathematical Induction Extra Questions
- Probability Extra Questions
- Relations And Functions Extra Questions
- Sequences And Series Extra Questions
- Sets Extra Questions
- Statistics Extra Questions
- Straight Lines Extra Questions
- Trigonometric Functions Extra Questions