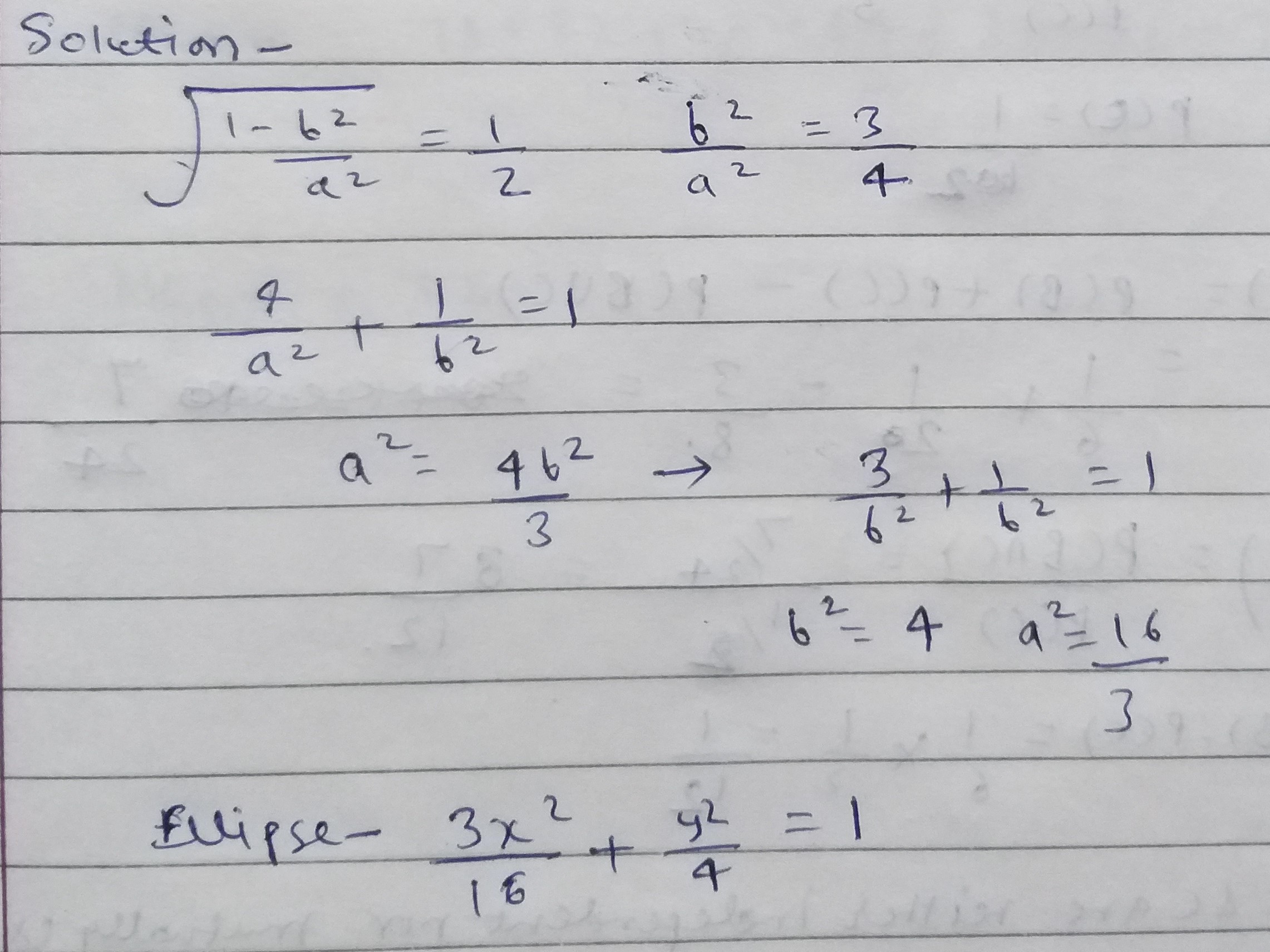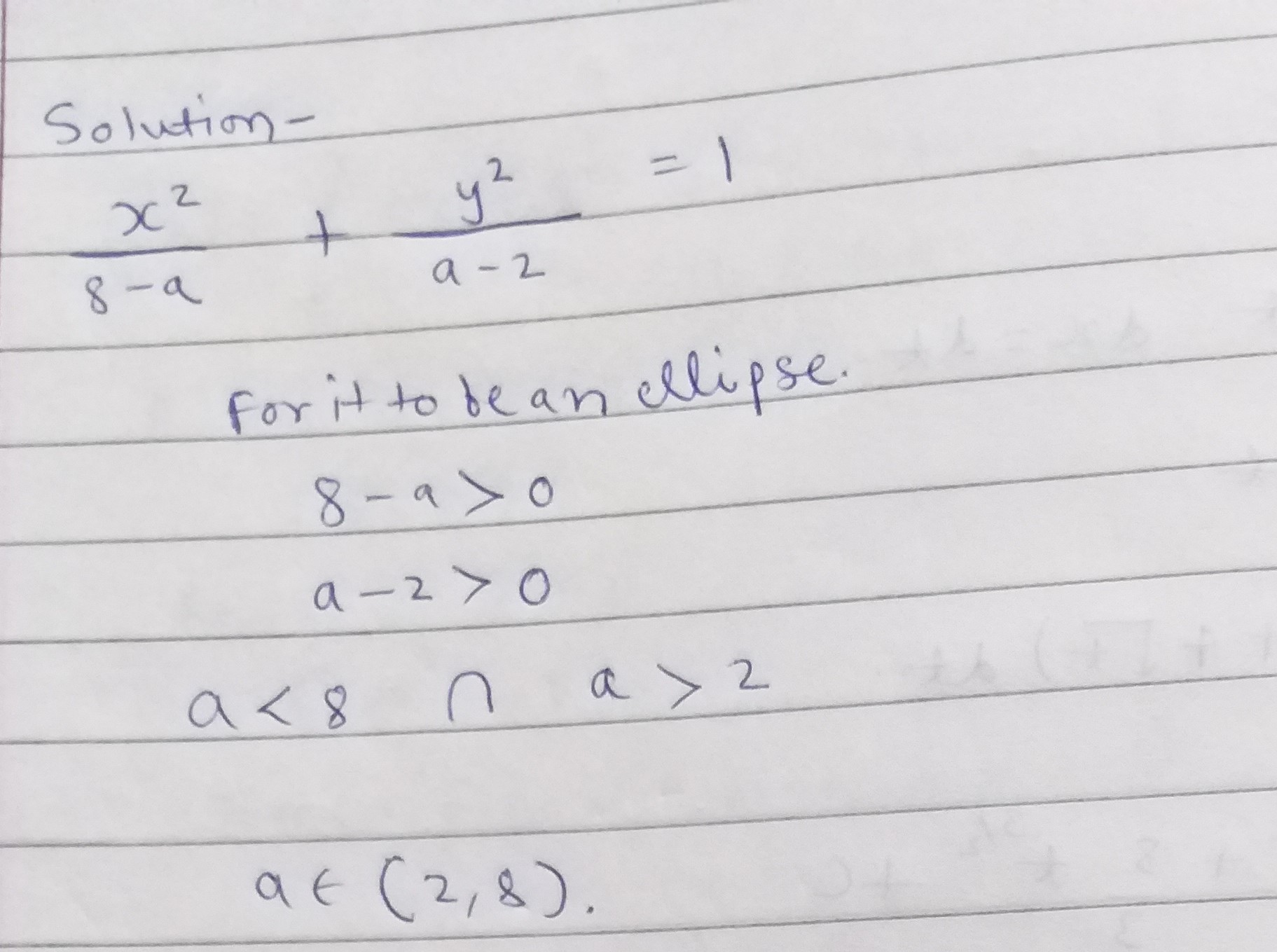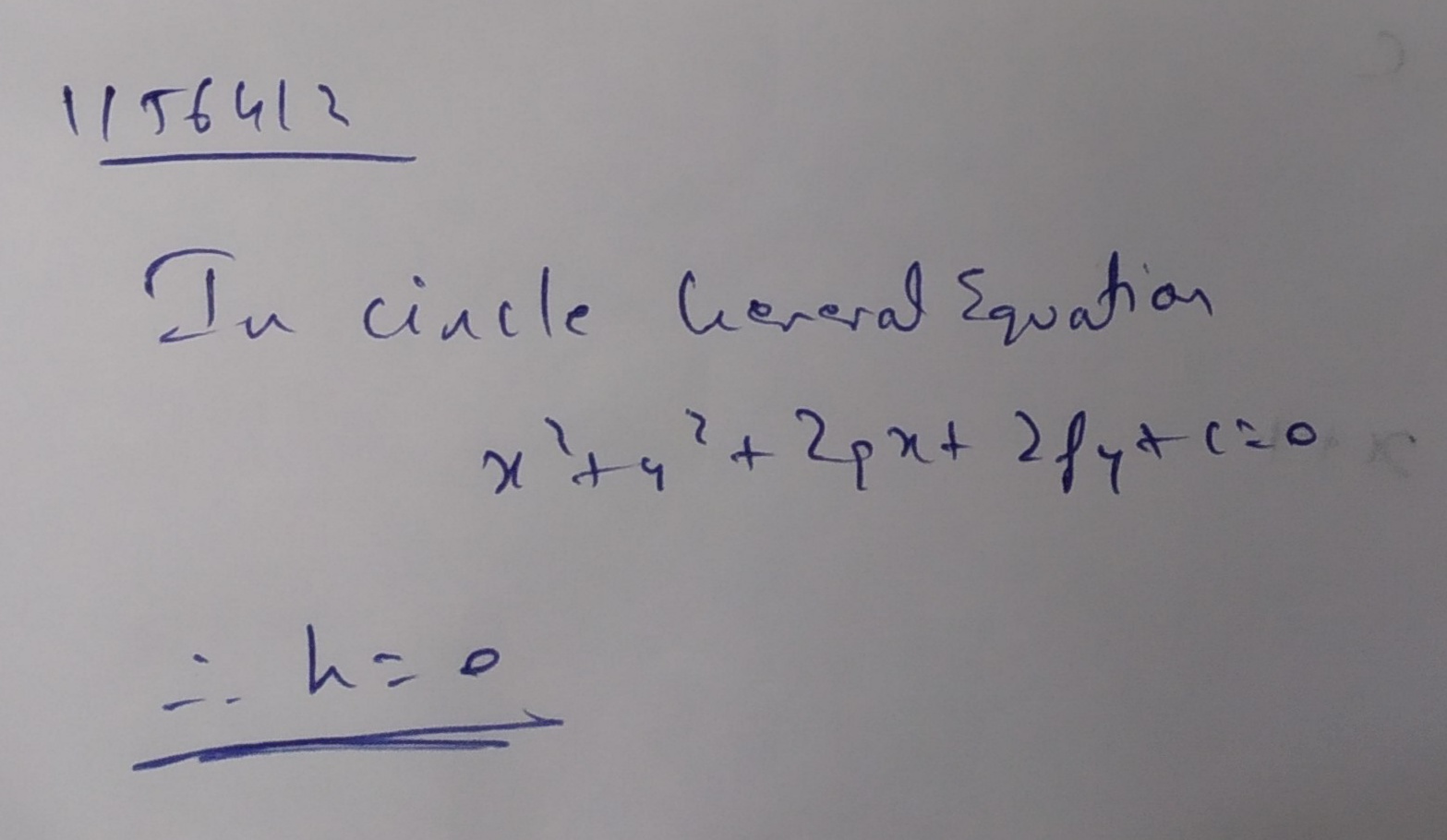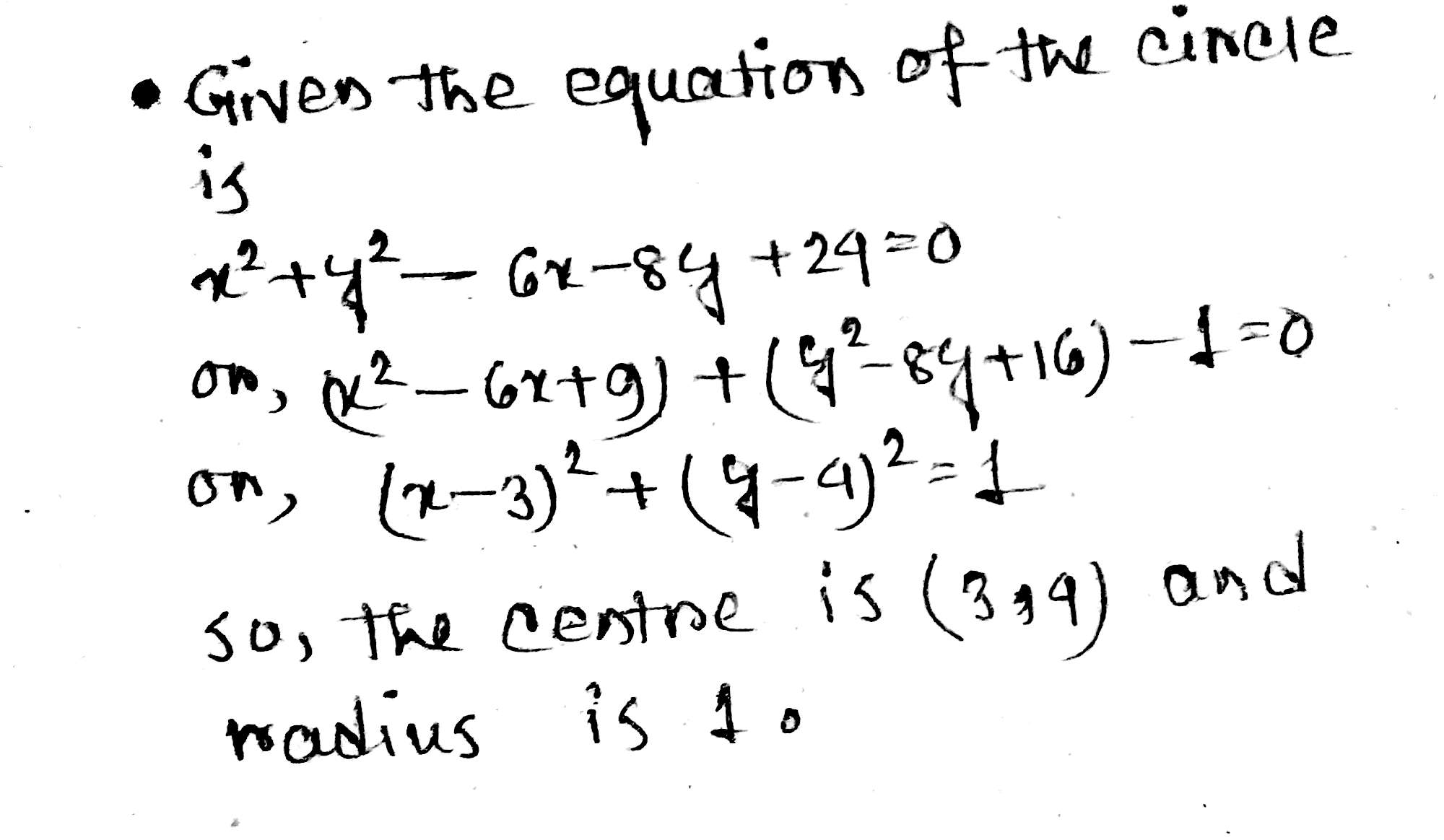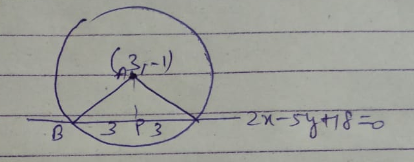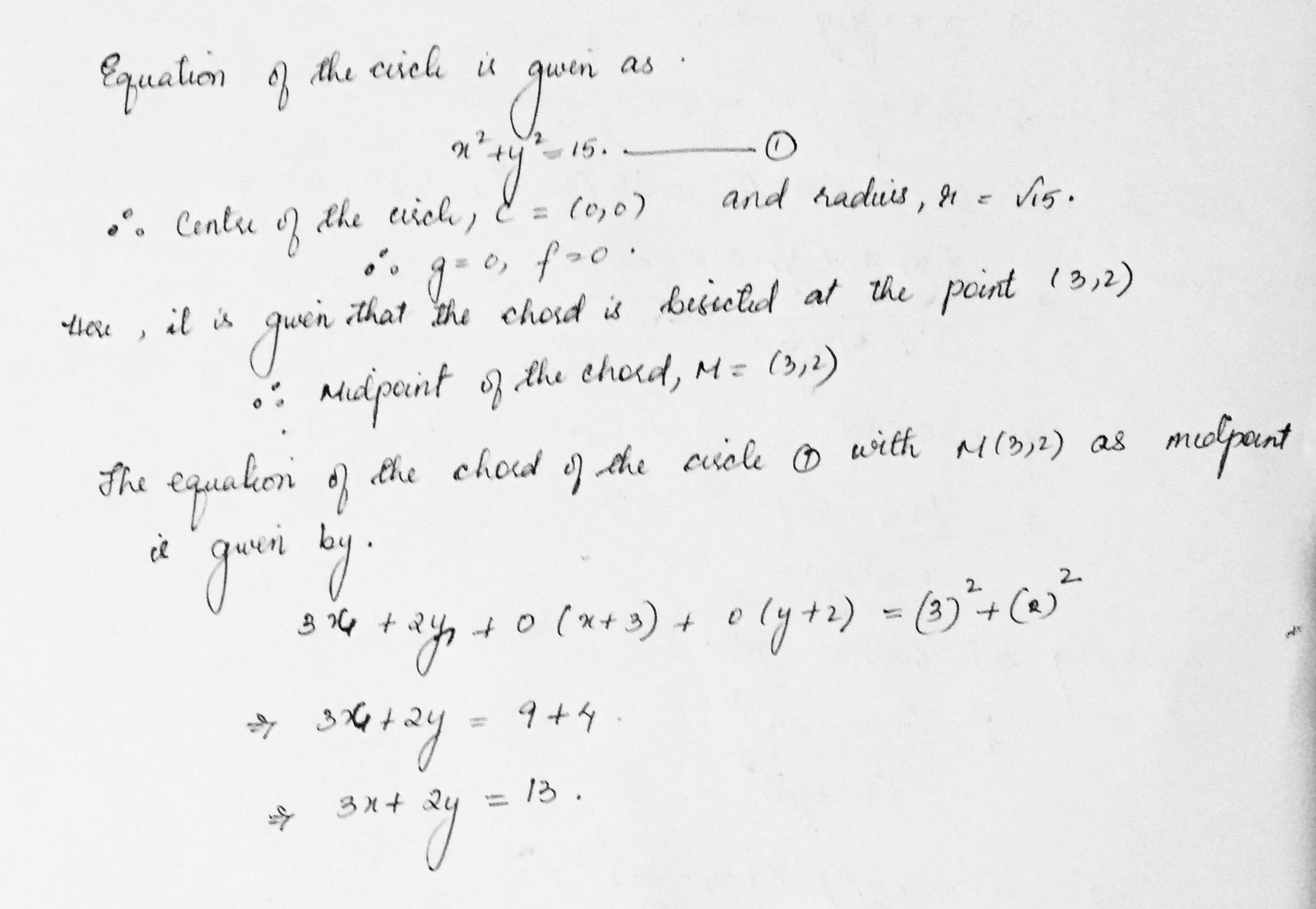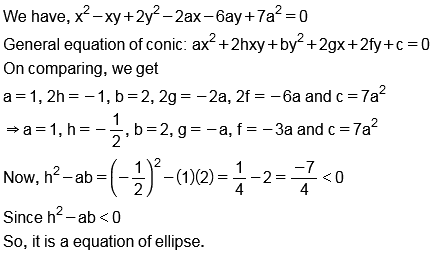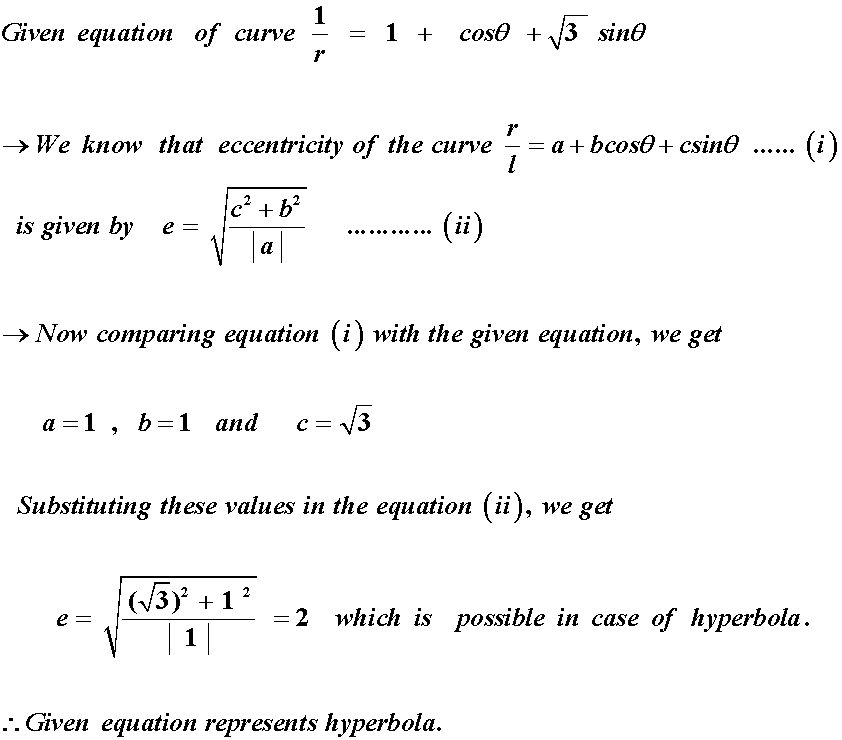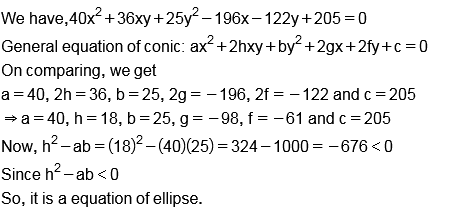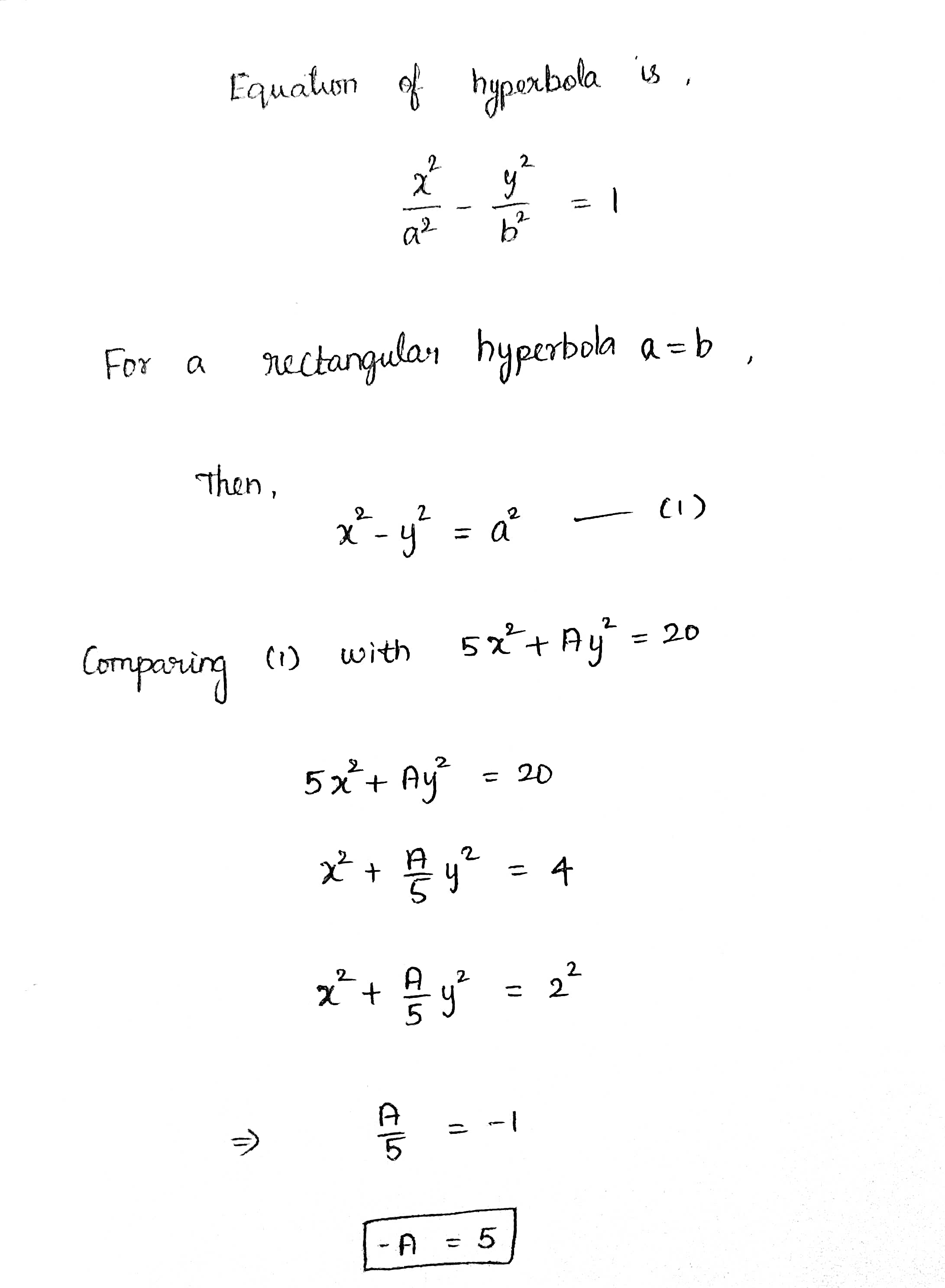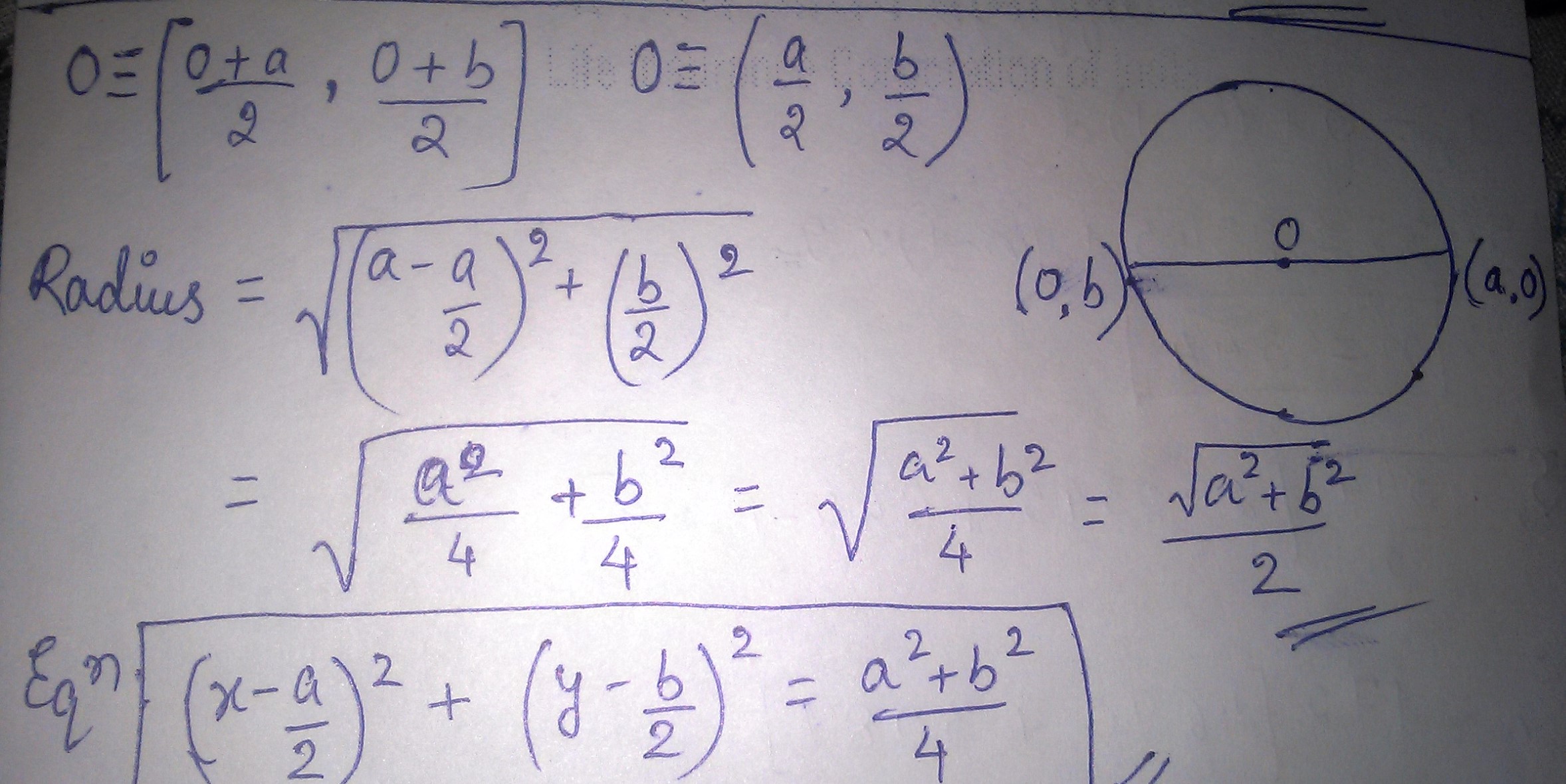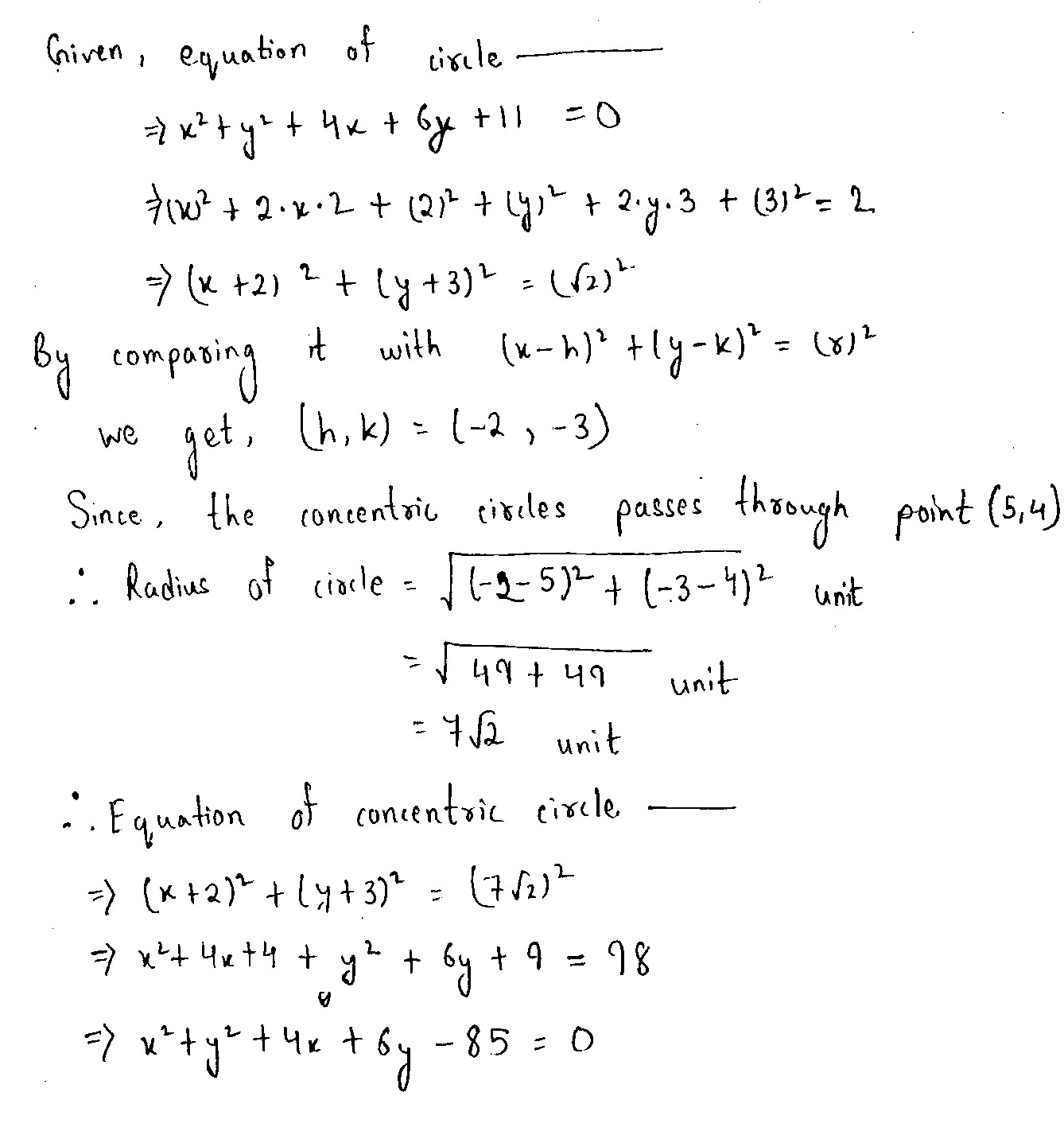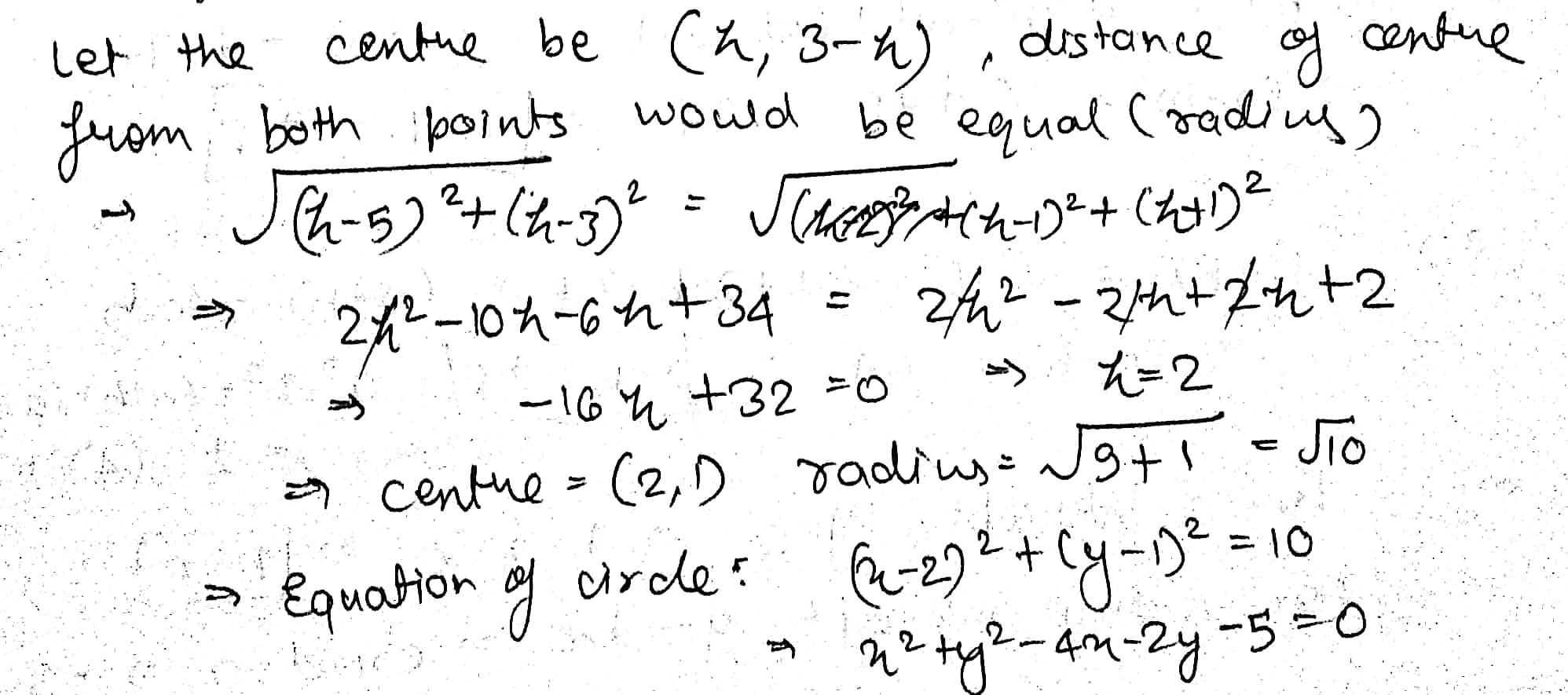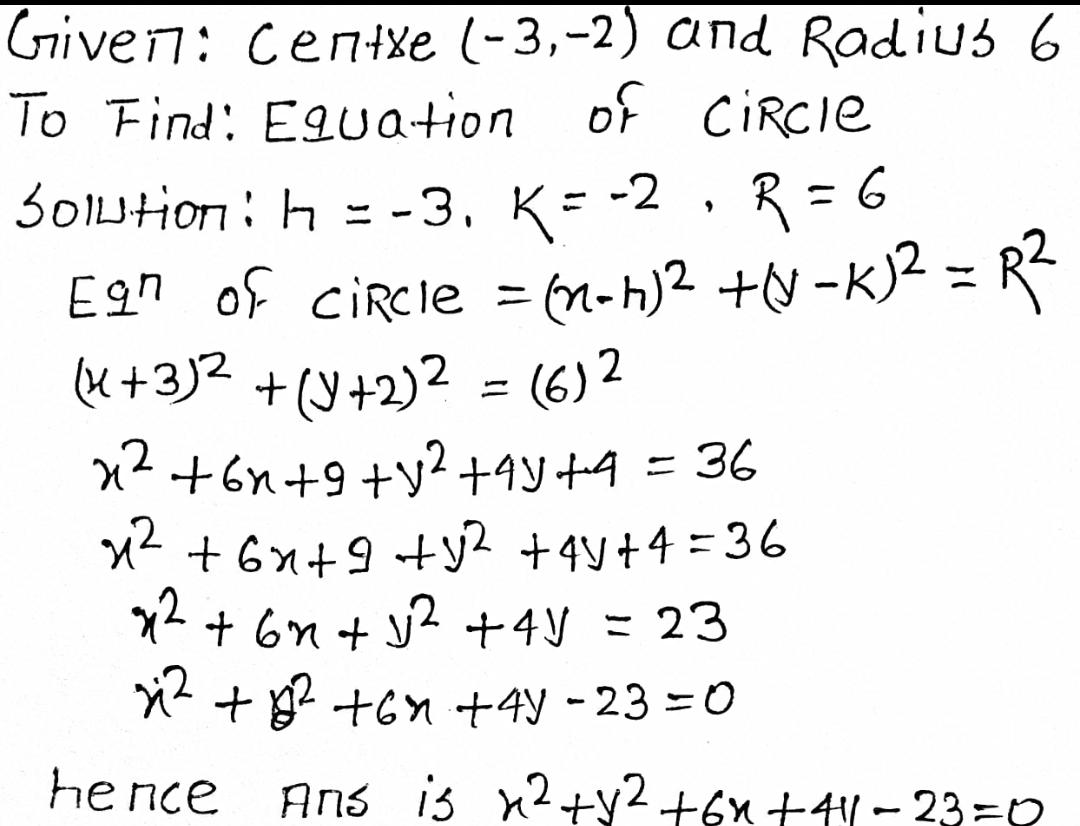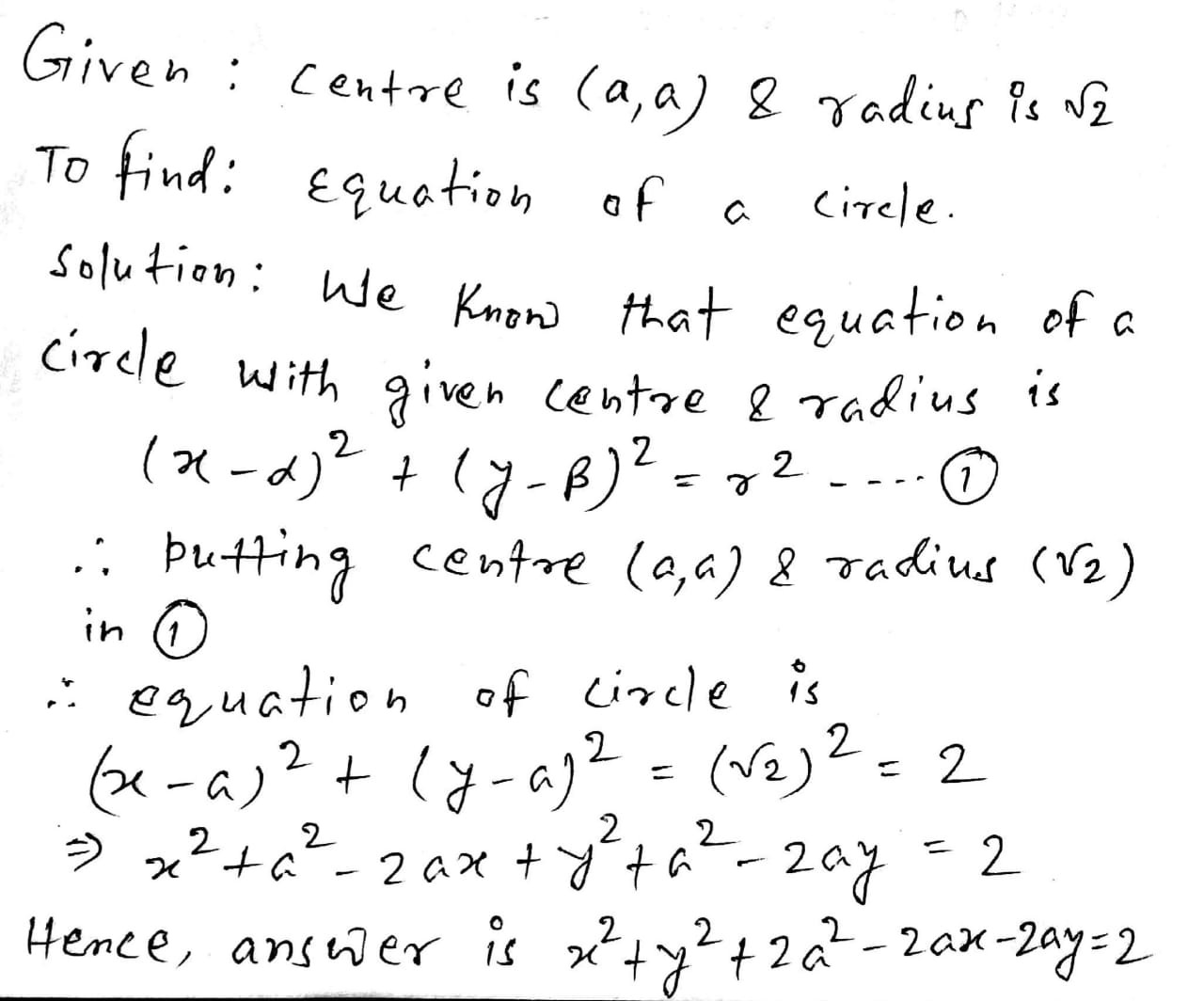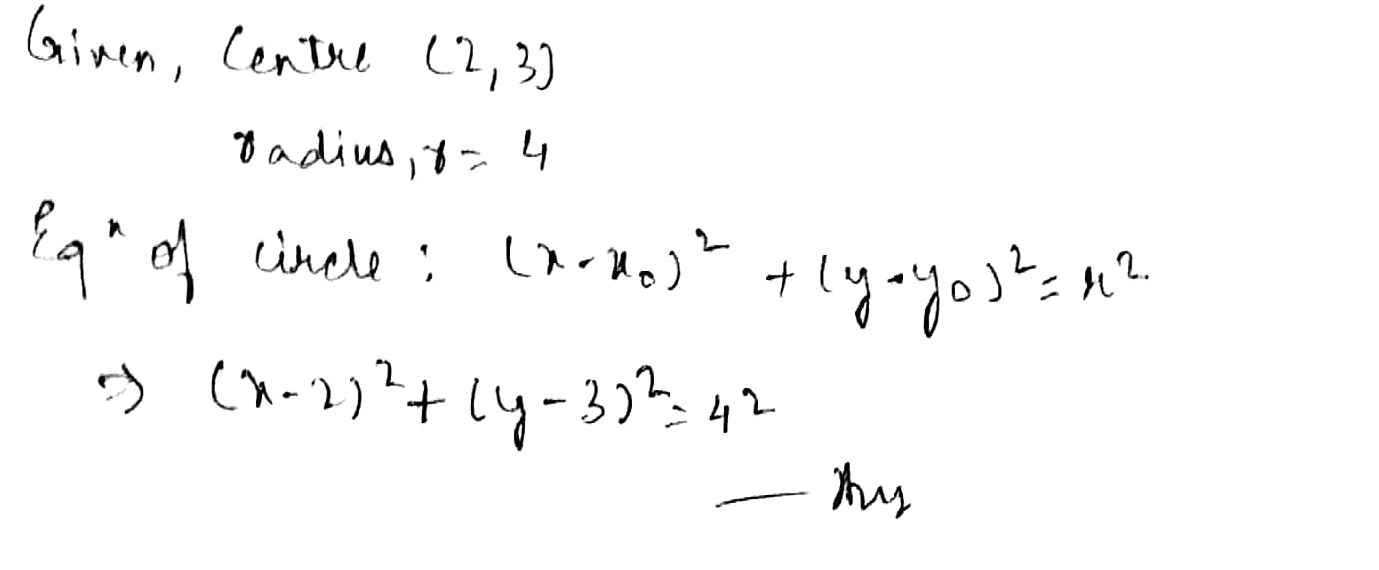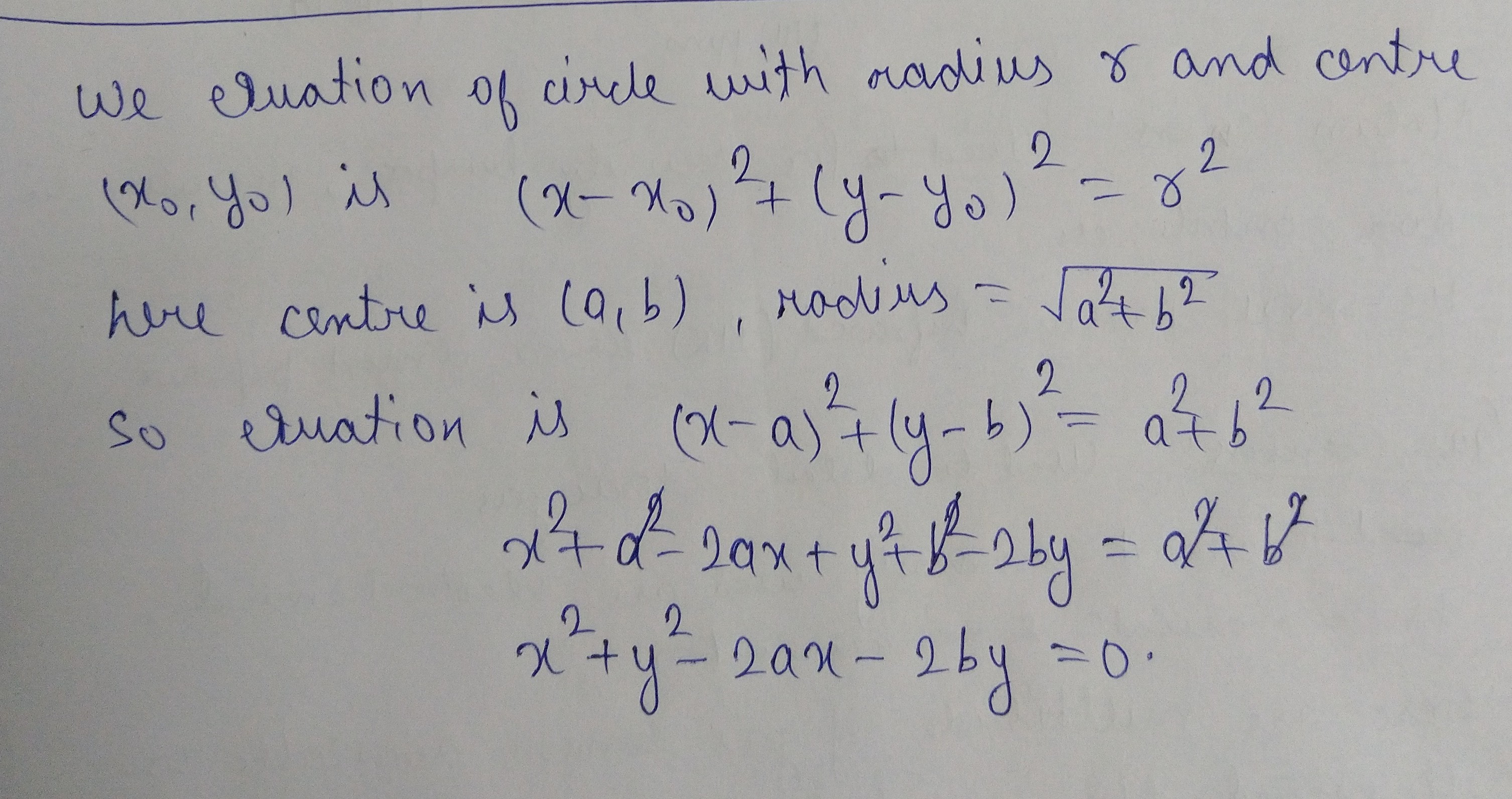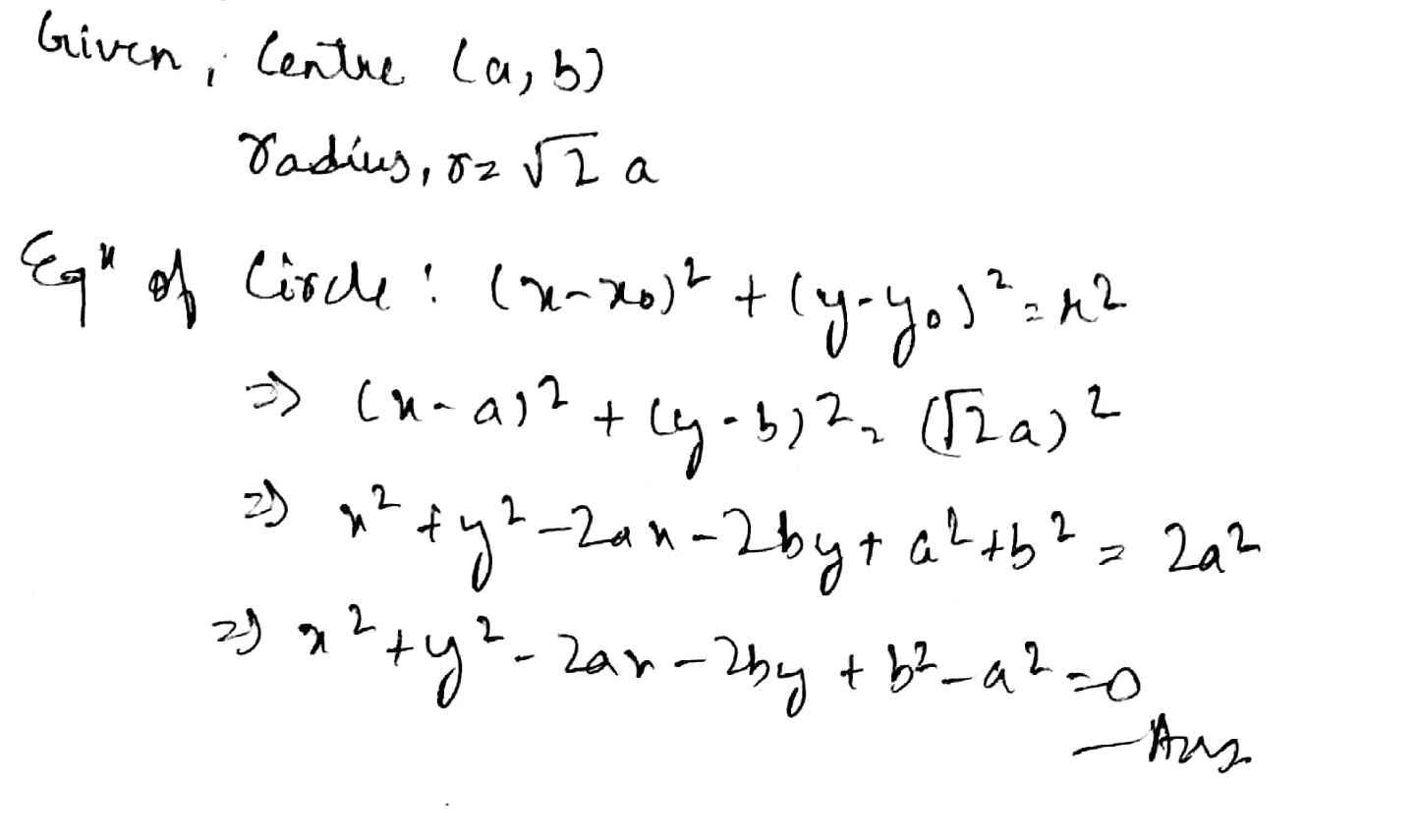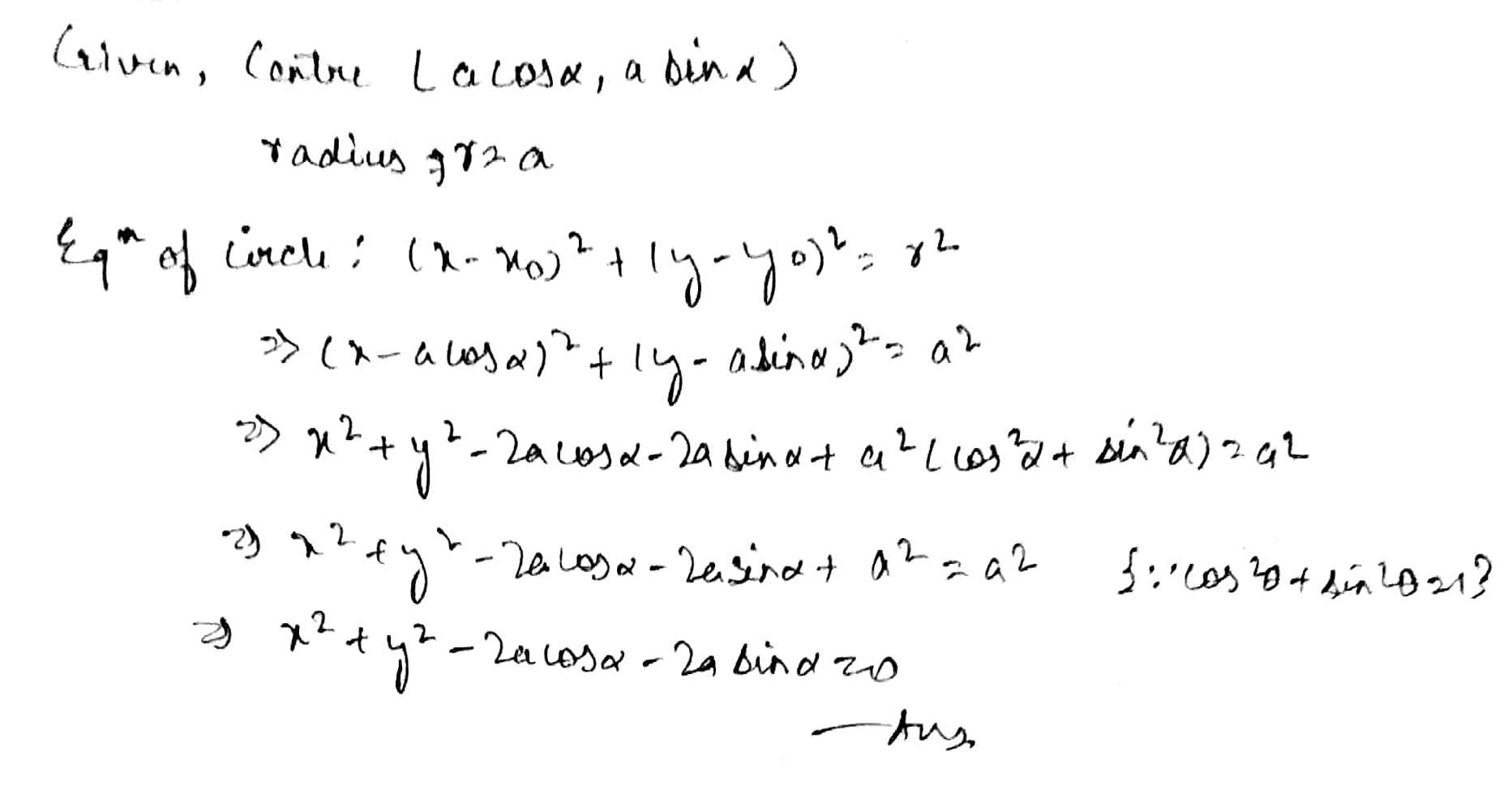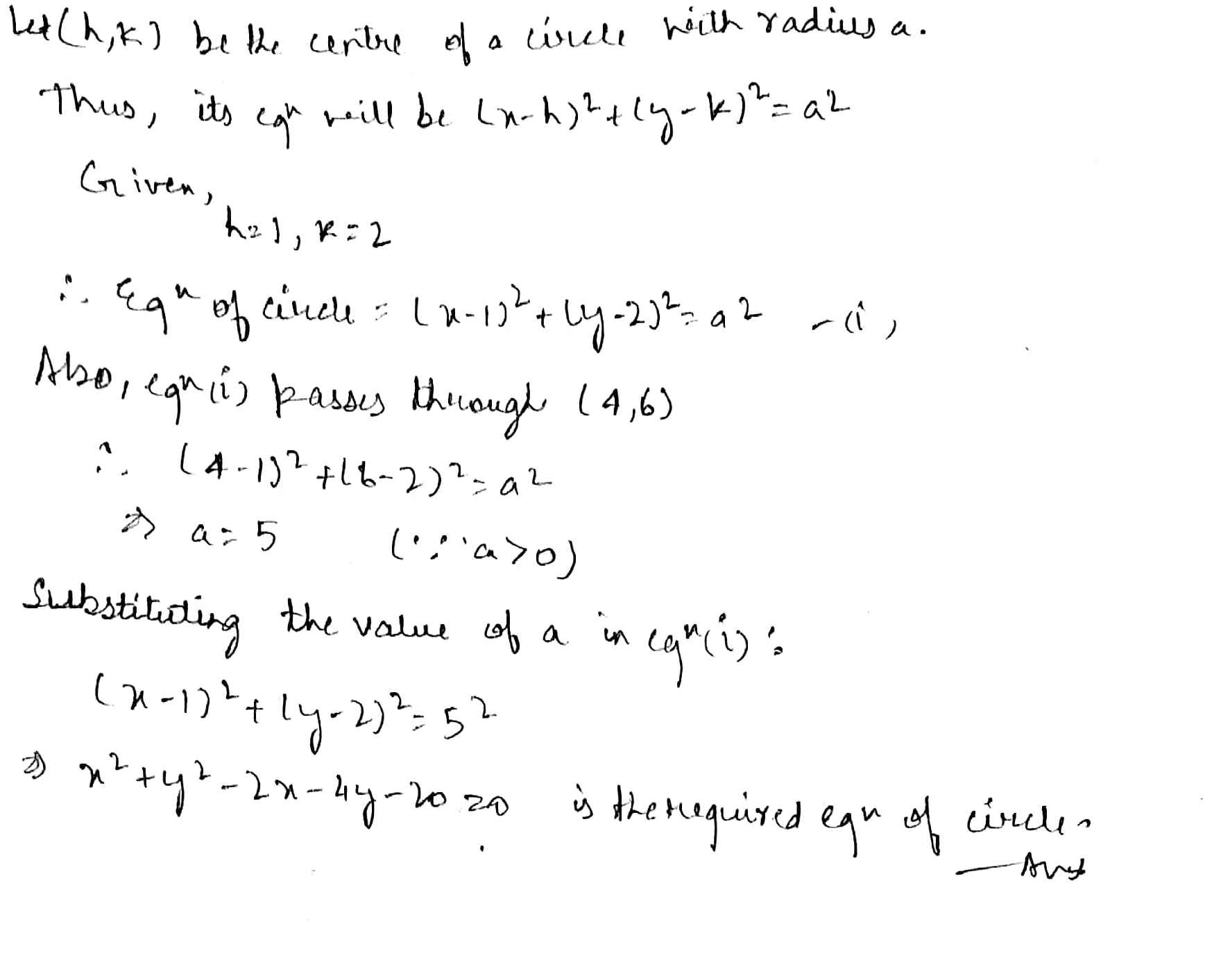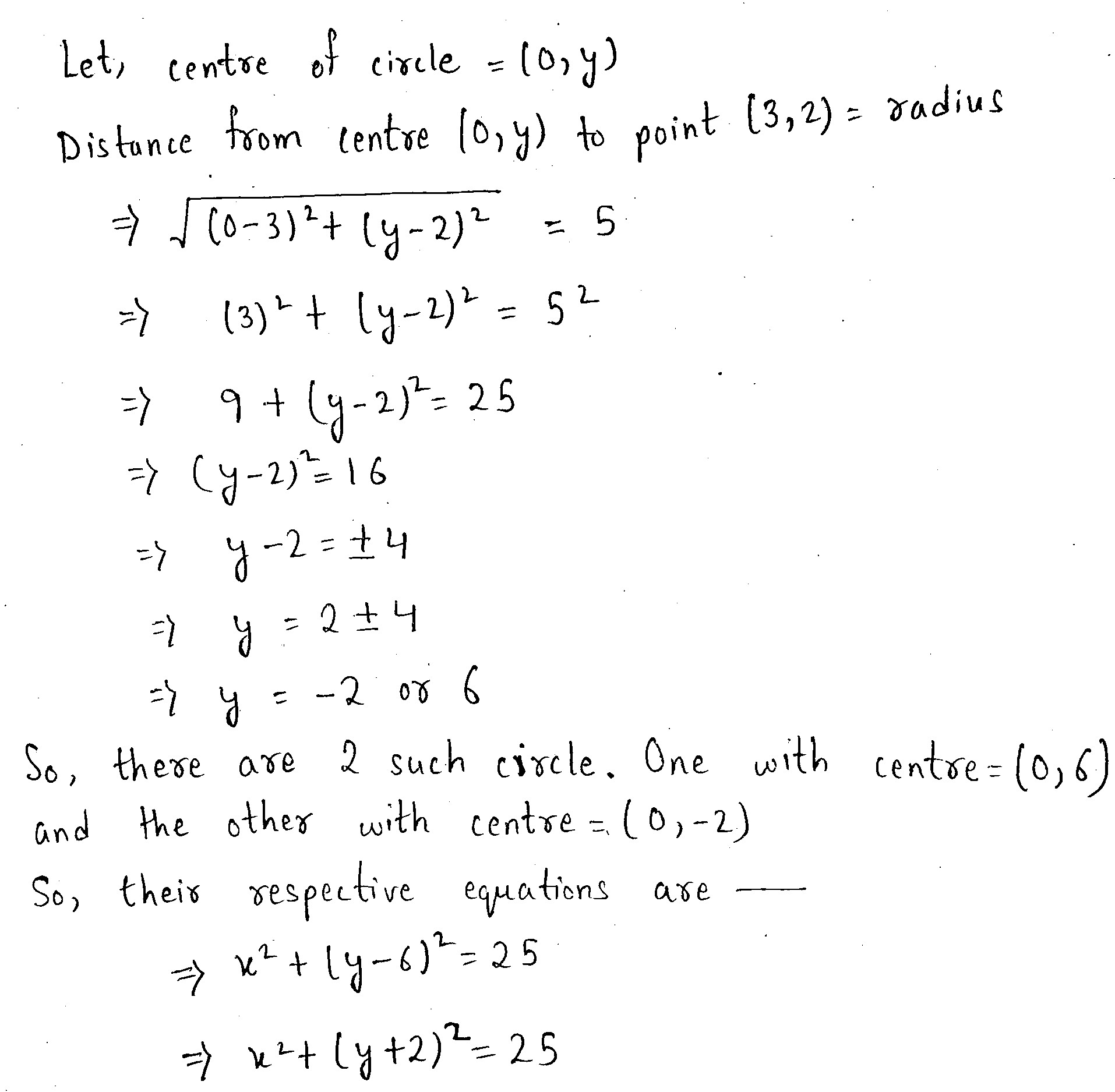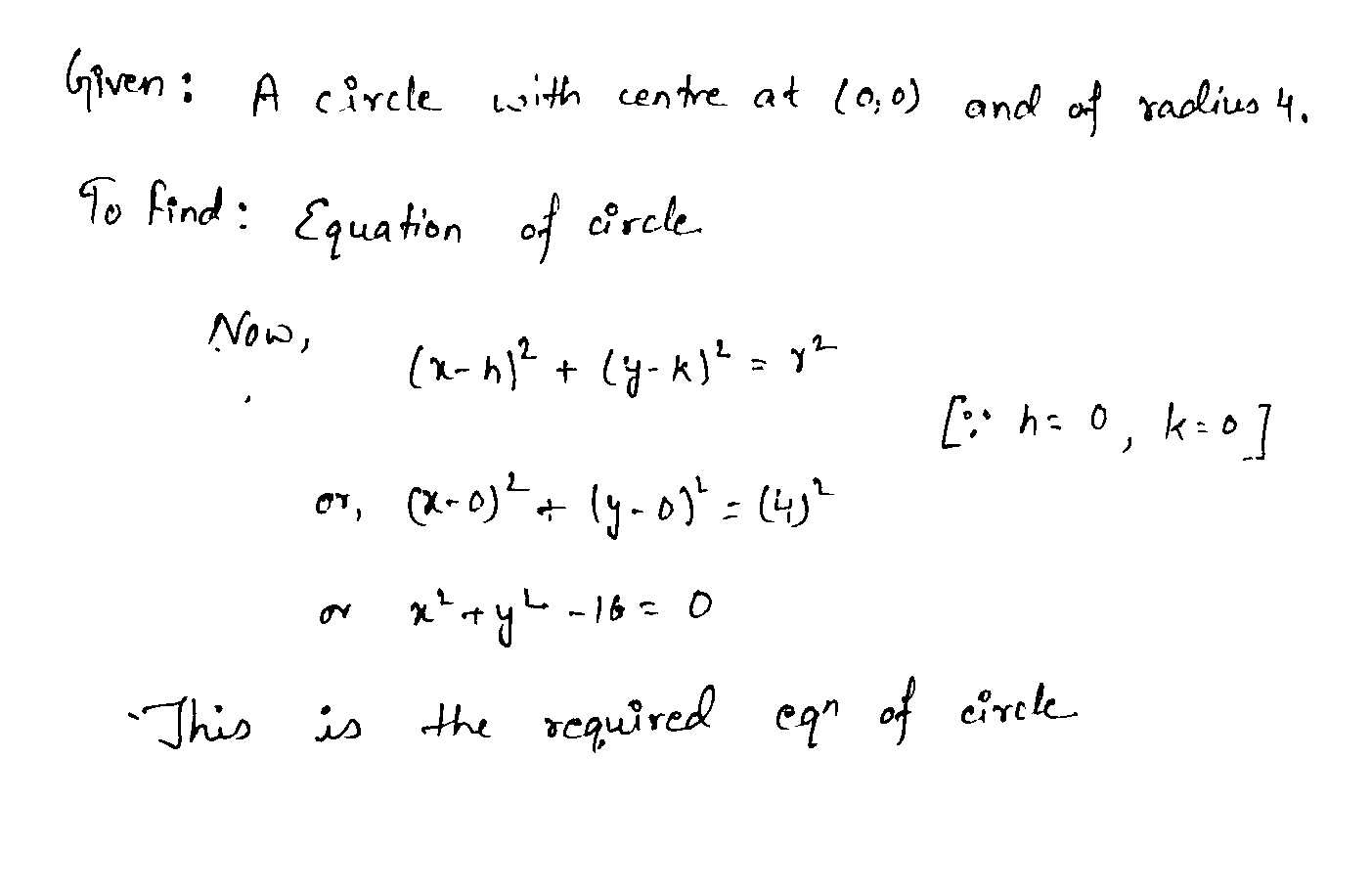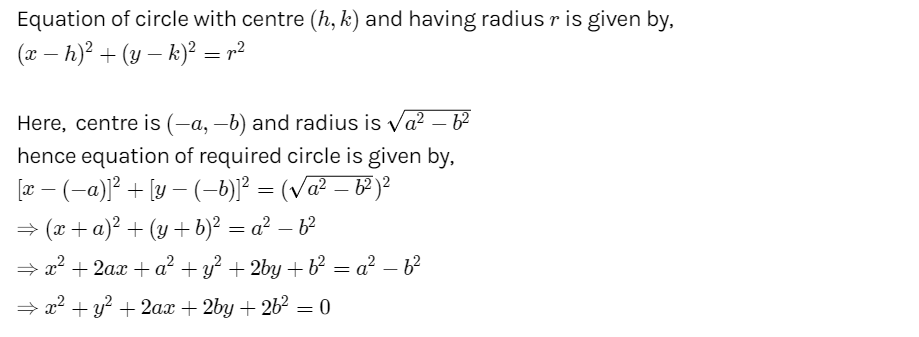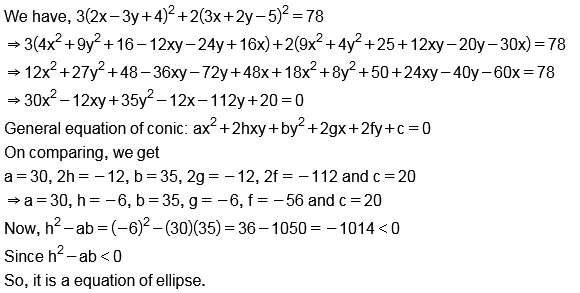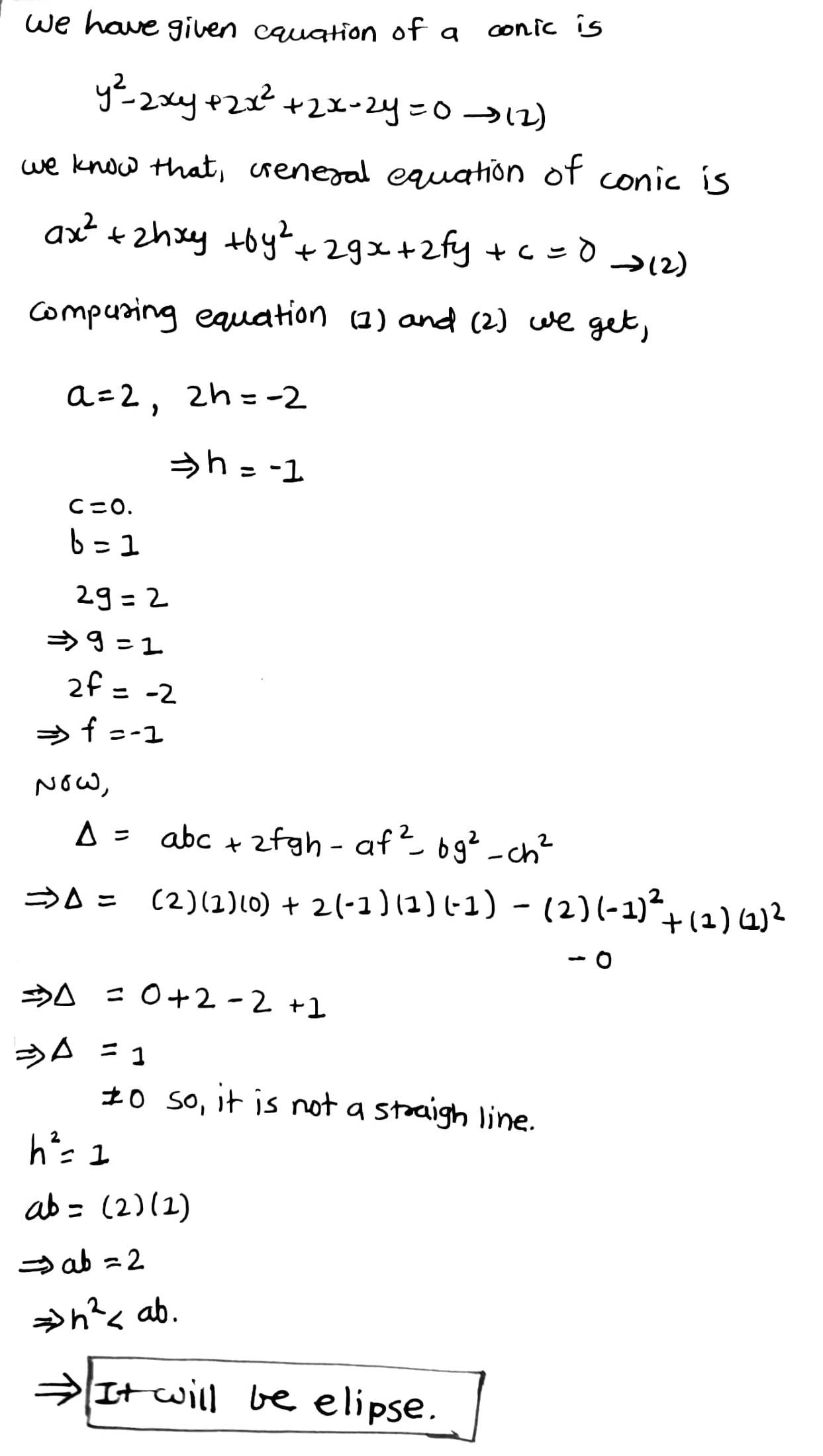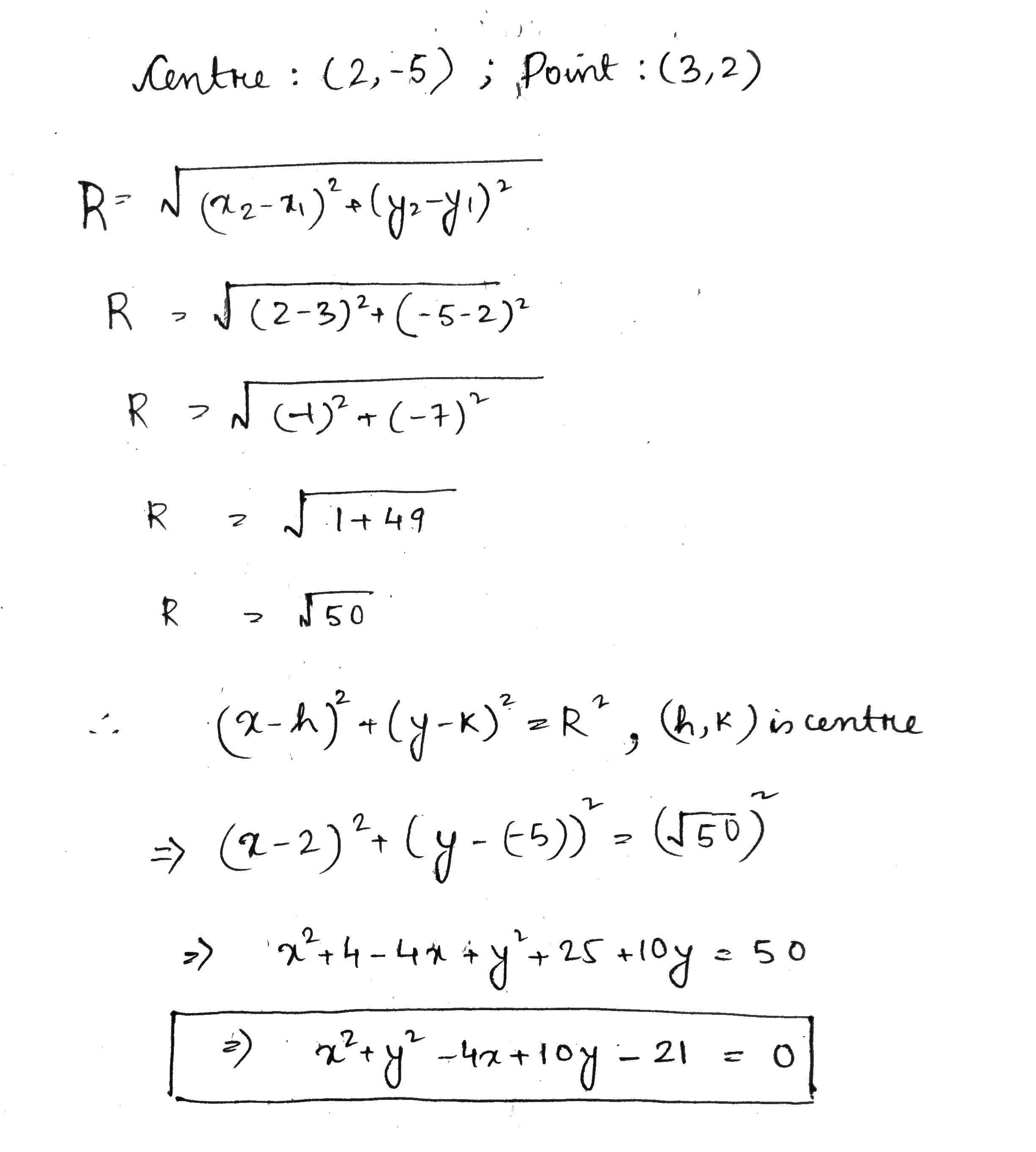Class 11 Engineering Maths - Conic Sections

Find the locus of a point which is at a distance of 5 units from (-1 , -2)

Let, P(x, y) be any point on locus and the given point be A(-1, -2)
Given that, AP = 5 units
i.e.

$\displaystyle \sqrt{(x-(-1))^{2} + (y - (-2))^{2}} = 5$

$\displaystyle \Rightarrow \sqrt{(x + 1)^{2} + (y + 2)^{2}} = 5$

$\displaystyle \Rightarrow x^{2} + 2x +1 +y^{2} + 4y + 4 = 5$

$\displaystyle \Rightarrow x^{2} + y^{2} + 2x + 4y = 0$

$\displaystyle \therefore$ The required locus is

$\displaystyle x^{2} + y^{2} + 2x + 4y = 0$

Find the equation of the circle with centre $(0, 2)$ and radius $2$

The equation of a circle with centre

$(h, k)$ and radius

$r$ is given by,

$(x - h)\displaystyle ^{2} + (y - k)\displaystyle ^{2} = r\displaystyle ^{2}$
Here it is given that centre

$(h, k) = (0, 2)$ and radius

$r = 2$
Therefore the equation of required circle is,

$(x - 0)^{2} + (y - 2)^{2} = 2^{2}$

$\Rightarrow x\displaystyle^{2} + y\displaystyle ^{2} + 4 - 4 y = 4$

$\Rightarrow x\displaystyle^{2} + y\displaystyle ^{2} - 4y = 0$

Find the equation of the circle with centre $\displaystyle \left ( \frac{1}{2},\frac{1}{4} \right )$ and radius $\displaystyle \frac{1}{12}$

Here it is given that centre

$(h, k) = \displaystyle \left ( \frac{1}{2},\frac{1}{4} \right )$ and radius

$r = \displaystyle \frac{1}{2}$
Therefore the equation of the circle is

$\displaystyle \left ( x -\frac{1}{2} \right )^{2}+ \left ( y - \frac{1}{4} \right )^{2} = \left ( \frac{1}{12} \right )^{2}$

$\displaystyle\Rightarrow x^{2}-x +\frac{1}{4}+y^{2}-\frac{y}{2}+\frac{1}{16}=\frac{1}{144}$

$\Rightarrow \displaystyle x^{2}-x +\frac{1}{4}+y^{2}-\frac{y}{2}+\frac{1}{16}-\frac{1}{144} = 0$

$\Rightarrow 144x\displaystyle ^{2} -144x + 36 + 144y\displaystyle ^{2} - 72y + 9 - 1 = 0$

$\Rightarrow 36x\displaystyle ^{2} + 36y\displaystyle ^{2} - 36x - 18y + 11 = 0$

Find the equation of the circle with centre $(-2, 3)$ and radius $4$

Here it is given that centre

$(h, k) = (-2, 3)$ and radius

$r = 4$
Therefore the equation of the circle is

$(x + 2)\displaystyle ^{2} + (y - 3)\displaystyle ^{2} = (4)\displaystyle ^{2}$

$\Rightarrow x\displaystyle ^{2} + 4x + 4 + y\displaystyle ^{2} - 6y + 9 = 16$

$\Rightarrow x\displaystyle ^{2} + y\displaystyle ^{2} + 4x - 6y - 3 = 0$

The point at which the hyperbola intersects the transverse axis are called the ................. of the hyperbola.

From the figure, the points

$A$ and

$A'$ where the curve meets the line joining the foci

$S$ and

$S'$ i.e. the point at which the hyperbola intersects the transverse axis are called vertices of the hyperbola.

Find the equation of the circle with centre $(1, 1)$ and radius $\displaystyle \sqrt{2}$

Here it is given that centre

$(h, k) = ( 1, 1 )$ and radius

$r = \displaystyle \sqrt{2}$
Therefore the equation of the circle is

$\displaystyle \left ( x - 1 \right )^{2} +\left ( y - 1 \right )^{2}=\left ( \sqrt{2} \right )^{2}$

$\Rightarrow \displaystyle x^{2}-2x + 1 + y^{2}- 2y + 1 = 2$

$\displaystyle \Rightarrow x^{2}+y^{2}-2x - 2y = 0$

Find the centre and radius of the circle $(x + 5)\displaystyle ^{2} + (y - 3)\displaystyle ^{2} = 36$

The equation of the given circle is,

$(x + 5)\displaystyle ^{2} + (y - 3)\displaystyle ^{2} = 36$

$\displaystyle \Rightarrow \left \{ x - \left ( - 5 \right ) \right \}^{2}+ \left ( y - 3 \right )^{2}=6^{2}$
which is of the form

$(x - h)\displaystyle ^{2} + (y - k)\displaystyle ^{2} = r\displaystyle ^{2}$
where

$h = - 5, k = 3$ and

$r = 6$
Thus the centre of the given circle is

$(-5, 3)$ while its radius is

$6$

Derive the standard form of the parabola

Parabola is defined as distance of each point on it is equidistant from a fixed line,point.

Consider Line

$x=-a,point(a,0)$

Let

$(x,y)$ be any ordinary point on parabola

$|x+a|=\sqrt { { (x-a) }^{ 2 }+{ (y-0) }^{ 2 } }$

${ |x+a| }^{ 2 }={ (x-a) }^{ 2 }+{ (y-0) }^{ 2 }$

${ y }^{ 2 }={ (x+a) }^{ 2 }-{ (x-a) }^{ 2 }$

Hence

${ y }^{ 2 }=4ax$

${ y }^{ 2 }=4ax$ is standard form of the parabola

Find the value of p when the parabola $y^2=4px$ goes through the point (i) (3, - 2) and (ii) (9, - 12).

parabola

$y^{2}=4px$

(i) P (3 , -2)

parabola passes thorugh this point ,
point satisfy the given equation

$(-2)^{2}=4p\times 3$

$4=4p\times 3$

$\therefore p = \dfrac{1}{3}$

(i) P (9 , -12)

parabola passes thorugh this point ,
point satisfy the given equation

$(-12)^{2}=4p\times 9$

$(4)^{2}=4p$

$\therefore p =4$

Find the equation to the conic passing through the origin and the points $\left( 1,1 \right) ,\left( -1,1 \right) ,\left( 2,0 \right)$ , and $\left( 3,-2 \right)$ . Determine its species.

General Equation of a conic:

$Ax^2+By^2+2Cx+2Dy+2Hxy+G=0$

The following points satisfies it:

$(0,0)$

$\implies G=0$

$\therefore Ax^2+By^2+2Cx+2Dy+2Hxy=0$

is the new equation.

$(2,0)$

$\implies A+C=0$

$\therefore Ax^2+By^2-2Ax+2Dy+2Hxy=0$

is the new equation.

$(1,1)\ and\ (-1,1)$

$A+B-2A+2D+2H=0$

$A+B+2A+2D-2H=0$

Subtracting both,

$A=H$

Adding both,

$A+B+2D=0 \rightarrow (1)$

$\therefore Ax^2+By^2-2Ax+2Dy+2Axy=0$

is the new equation.

$(3,-2)$

$9A+4B-6A-4D-12A=0$

$\implies 4B-4D-9A=0 \rightarrow(2)$

Using (1) and (2),

$D=\dfrac{-13A}{12}$

$B=\dfrac{7A}{6}$

$\therefore Ax^2+\dfrac{7A}{6}y^2-2Ax-\dfrac{13A}{6}y+2Axy=0$

is the new equation.

which is nothing but,

$\therefore x^2+\dfrac{7}{6}y^2-2x-\dfrac{13}{6}y+2xy=0$

$6{ x }^{ 2 }+12xy+7{ y }^{ 2 }-12x-13y=0$ .

An Ellipse

Draw the circles whose equation are
$x^2 + y^2 = 2ay.$

Given equation of circle is

$x^2 + y^2 = 2ay.$

Making perfect square, we get

$(x-0)^2+(y-a)^2=a^2$

So, centre of the circle is

$C(0,a)$ and radius

$r=a$

Now draw a circle with radius

$a$ and centre

$(0,a)$ .

Find the eccentricity and length of latus rectum of hyperbola
$\cfrac { { x }^{ 2 } }{ 25 } -\cfrac { { y }^{ 2 } }{ 9 } =1$

The equation of the hyperbola is

$\cfrac { { x }^{ 2 } }{ 25 } -\cfrac { { y }^{ 2 } }{ 9 } =1$
There,

${ a }^{ 2 }=25\Rightarrow a=5$
and

${ b }^{ 2 }=9\Rightarrow b=3$
We know

${ b }^{ 2 }={ a }^{ 2 }({ e }^{ 2 }-1)\quad$

$\Rightarrow 9=25({ e }^{ 2 }-1)$

$\Rightarrow { e }^{ 2 }-1=\cfrac { 9 }{ 25 }$

$\Rightarrow { e }^{ 2 }=\cfrac { 9 }{ 25 } +1=\cfrac { 34 }{ 25 }$

$\Rightarrow e=\sqrt { \cfrac { 34 }{ 25 } } =\cfrac { \sqrt { 34 } }{ 5 }$
Length of latus rectum

$=\cfrac { 2{ b }^{ 2 } }{ a }$

$=2\times \cfrac{9}{5}=\cfrac{18}{5}$ units

Draw the circles whose equation are
$3x^{2} + 3y^{2} = 4x$ .

The given equation of circle is

$3x^2 + 3y^2 = 4x .$

Making perfect square, the equation of circle becomes

$\left(x-\cfrac{2}{3}\right)^2+(y-0)^2=\left(\cfrac{2}{3}\right)^2$

Centre is

$\left(\dfrac{2}{3},0\right)$ and radius is

$\dfrac{2}{3}$

What are represented by the equation $(x^2 - a^2)^2 - y^4 =$

${ ({ x }^{ 2 }-{ a }^{ 2 }) }^{ 2 }-{ y }^{ 4 }\\ { ({ x }^{ 2 }-{ a }^{ 2 }) }^{ 2 }-{ ({ y }^{ 2 }) }^{ 2 }=0$

Factorising the equation

$({ x }^{ 2 }-{ a }^{ 2 }+{ y }^{ 2 })({ x }^{ 2 }-{ a }^{ 2 }-{ y }^{ 2 })=0$

Then, either

${ x }^{ 2 }-{ a }^{ 2 }+{ y }^{ 2 }=0$ or

${ x }^{ 2 }-{ a }^{ 2 }-{ y }^{ 2 }=0$

${ x }^{ 2 }-{ a }^{ 2 }+{ y }^{ 2 }=0$

${ x }^{ 2 }+{ y }^{ 2 }={ a }^{ 2 }$

represents a circle centred at origin and radius

$a$

${ x }^{ 2 }-{ a }^{ 2 }-{ y }^{ 2 }=0$

${ x }^{ 2 }-{ y }^{ 2 }={ a }^{ 2 }$

represents a rectangular hyperbola.

Thus the combined equation represents a circle and a rectangular hyperbola.

Find the equation of the circle drawn on the intercept made by the line $2x+3y=6$ between the coordinate axes as diameter.

The line

$2x+3y=6$ meets

$x$ and

$y-axis$ at

$A(3,0)$ and

$B(0,2)$ respectively. Taking

$AB$ as a diameter, the equation of the required circle is :

$(x-3)(x-0)+(y-0)(y-2)=0$

$x^2+y^2-3x-2y=0$

A circle of radius $5$ units touches the coordinate axes in the first quadrant. If the circle makes one complete roll on x-axis along the positive direction of x-axis, find its equation in new position.

Here

$(5,5)$ is the center of circle which is touching both the coordinate axes in first quadrant and

$5$ is the radius of circle, then

$(x-5)^2+(y-5)^2=5^2.$ is the equation of the circle

Now it makes one complete roll along positive

$X$ axis,hence its

$x$ coordinate of center will change its position to

$5 + 10\pi$ while

$y$ coordinate will remain the same.

$\therefore$ The final equation will be,

$(x-(5+10\pi))^2+(y-5)^2=5^2.$

If the line $lx+my+n=0$ touches the circle $x^2+y^2=a^2$ , then prove that $(l^2+m^2)a^2=n^2$ .

If the line

$lx+my+n=0$ touches the circle

$x^2+y^2=a^2$ , then length of the perpendicular from its centre

$O(0,0)$ is equal to its radius a.

Therefore,

$|\dfrac{l \times 0 + m \times 0 +n}{\sqrt{l^2+m^2}}|=a$

$(l^2+m^2)a^2=n^2$ , which is the required condition.

Find the centre and radius of the circle $x^2+y^2+2ax\cos \theta-2ay\sin \theta-3a^2=0$ .

Given the equation of circle is

$x^2+y^2+2ax\cos \theta-2ay\sin \theta-3a^2=0$ . The equation can be written as

$x^2+2ax\cos \theta+a^2\cos^2\theta+y^2-2ay\sin \theta+a^2\sin^2\theta-3a^2-a^2=0$ [Since

$\sin^2\theta+\cos^2\theta=1$ ]

or,

$(x+a\cos \theta)^2+(y-a\sin\theta)^2=(2a)^2$

From this equation we have the centere of the circle is

$(-a\cos\theta,a\sin\theta)$ and radius is

$2a$ units.

If the line $lx+my+n=0$ touches the parabola $y^2=4ax$ , prove that $ln=am^2$ .

The x-coordinates of the points of intersection of the line

$lx+my+n=0$ or

$y=-(\dfrac{lx+n}{m})$ and the parabola

$y^2=4ax$ are roots of the equation

$[-(\dfrac{lx+n}{n})]^2=4ax$

$l^2x^2+2x(ln-2am^2)+n^2=0$

If the line

$lx+my+n=0$ touches the parabola

$y^2=4ax$ , then this equation has equal roots.

Therefore,

$4(ln-2am^2)^2-4l^2n^2=0$

$-4alm^2n+4a^2m^4=0$

$ln=am^2$

Find the area of a quadrant of a circle whose circumference is $44$ cm.

Circumference of circle

$=2\pi r$

Given,

$2\pi r=44$

$\Rightarrow r=\dfrac { 44 }{ 2\pi } =\dfrac { 22 }{ \pi }$

Area of quadrant

$=\dfrac { \pi { r }^{ 2 } }{ 4 }$

$\Rightarrow A=\dfrac { \pi { \left( \dfrac { 22 }{ \pi } \right) }^{ 2 } }{ 4 } \\ \Rightarrow A=\dfrac { \pi \times 22\times 22 }{ \pi \times \pi \times 4 } \\ \Rightarrow A=\dfrac { 121 }{ \pi }$

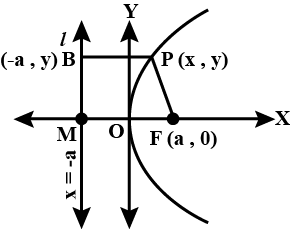
Find the locus of coordinates of A and B which are two points in place so that $PA - PB =$ constant.

In this case the locus will be

$\dfrac{x^2}{k^2} \, - \, \dfrac{y^2}{a^2-k^2} \, = \, 1$
which is hyperbola if

$a^2 \, - \, k^2 \, > \, 0$

Find the equation of the circle whose two end points of diameter are $(4,-2),(-1,3)$ .

The equation of the circle whose two end points of diameter are

$(4,-2),(-1,3)$ is

$(x-4)(x+1)+(y+2)(y-3)=0$

or,

$x^2-3x-4+y^2-y-6=0$

or,

$x^2+y^2-3x-2y=10$ .

Determine the equation of the circle which touches the line x - y = 0 at the origin and bisects the circumference of the circle $x^2 \, + \, y^2 \,+\, 2y \, \, - \, 3 \,= \,0$

The line x - y = 0 touches at (0,0)

$S_1 \, \Rightarrow \, x^2 \, + \, y^2 \, + \, \lambda \, (x - y ) \, = \, 0$ .......(1)

$S_2 \, \Rightarrow \, x^2 \, + \, y^2 \, + \, 2y \,- \, 3 \, = \, 0$ .............(2)

$S_1$ bisects the circumference of

$S_2$ .
Common chord

$S_1 \, - \, S_2 \, = \, 0$ passes through the centre (0,-1) of

$S_2$ .

$\therefore \, \lambda \, (x - y) \, - \, 2y \, + \, 3 \, = \, 0$

$\lambda \, + \, 2 \, + \, 3 \, = \, 0 \, \Rightarrow \, \lambda \, = \, -5$

$\therefore$ put in (1)

$x^2 \, + \, y^2 \, - \, 5x \, + \, 5y \, = \, 0$

Find the equation of circle with centre $(-3, 2)$ & radius $4$

Given the centre of the circle is

$(-3,2)$ and radius is

$4$ .

Let

$(x,y)$ be any point on the circle now the equation of the circle is

$(x+3)^2+(y-2)^2=4^2$ .

Find the equation of circle on which the co-ordinates of any point are $\left ( 2 \, + \, 4 \, cos \theta , \, - \, 1 \, + \, 4 \, sin \, \theta \right ), \, \theta$ being the parameter.

$x = 2 + 4 cos$

$\theta$ ,

$y = - 1 + 4 sin \theta$
clearly

$(x - 2)^2 + (y + 1)^2$

$= 16(cos^2 \theta \, + \, sin^2 \, \theta ) = 16$
Above represents a circle with centre

$(2 , - 1)$ and radius

$4$

Find the equation of circle with centre at $(0, 0)$ & radius $r$ .

Given the centre of the circle is

$(0,0)$ and the radius is

$r$ .

Then the equation of the circle is

$(x-0)^2+(y-0)^2=r^2$ or

$x^2+y^2=r^2$ .

Find equation of the circle which touch the ordinate axes at a distance of unit $5$ from the origin.

As the circle is given to touch the ordinate axes at a distance

$5$ units for the origin. Then its centre is at

$(5,5)$ and radius being

$5$ units.

Then the equation of the circle is

$(x-5)^2+(y-5)^2=5^2$ .

Find the equation of parabola with vertex $(0, 0)$ & focus at $(0, 2)$ .

Given the vertex of the parabola is

$(0,0)$ and focus is at

$(0,2)$ .

This gives the axis of the parabola is the positive

$y-$ axis.

Then the equation of the parabola will be

$x^2=4ay$ where

$a=2$ .

So the equation of the parabola is

$x^2=8y$ .

Find the equation of circle if centre $(-a , -b)$ and radius $\sqrt{a^2 - b^2}$ .

centre =

$(-a,-b)$ radius =

$\sqrt{a^{2}-b^{2}}=r$

$\therefore$ equation of circle =

$(x-(-a))^{2}+(y-(-b))^{2}=r^{2}$

$(x+a)^{2}+(y+b)^{2}=a^{2}-b^{2}$

$x^{2}+2ax+a^{2}+y^{2}+2by+b^{2}=a^{2}-b^{2}$

$x^{2}+y^{2}+2ax+2by+2b^{2}=0$

$\therefore$ equation of circle is

$x^{2}+y^{2}+2ax+2by-2b^{2}=0$

The length of the diameter of the circle $x^2+y^2-4x-6y+4=0$ is -

Given circle equation is:

$x^2+y^2-4x-6y+4=0 .........(1)$

Since we know that general equation of circle is

$x^2+y^2+2gx+2fy+c=0.......(2)$ and radius of circle is

$\sqrt{g^2+f^2-c}$ .

Now, compairing euation 1 and 2.

$g=-2, f=-3, \& c=4$ .

Radius=

$\sqrt{(-2)^2+(-3)^2-4}$

Radius=

$\sqrt{9}$

Radius of given circle is

$3$ .

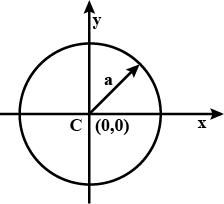
Show that ${x^2} + {y^2} = {a^2}$ represent the standard equation of a circle whose centre at $(0,0)$ and radius is $a$ .

$\rightarrow$ co-ordinate of centre

$(0,0)$

$\rightarrow$ Take B pt

$(x,y)$ on circle

$\rightarrow$ and Radius is

$''a''$

So by the distance formula .

$BC^2=(x-0)^2+(y-0)^2$

$\boxed{BC=a}$

$\boxed{x^2+y^2=a^2}$

1055532_1110548_ans_a6fc399d708c412481e9dbd6405a8723.png

Find the equation of the ellipse in the standard form given $e = \dfrac{1}{2}$ and it passes through $\left( {2,\,1} \right)$

Solution -

$\sqrt{1-\frac{b^{2}}{a^{2}}} = \frac{1}{2}$

$\frac{b^{2}}{a^{2}} = \frac{3}{4}$

$\frac{4}{a^{2}}+\frac{1}{b^{2}} = 1$

$a^{2} = \frac{4b^{2}}{3} \rightarrow \frac{3}{6^{2}}+\frac{1}{6^{2}} = 1$

$b^{2} = 4$

$a^{2} = \frac{16}{3}$

Ellipse -

$\frac{3x^{2}}{16}+\frac{y^{2}}{4} = 1$

1100663_1187815_ans_113df837a37148e88d8af629840b57ee.jpg

Define Ellipse?

in mathematics, an ellipse is a curve in a plane surrounding two focal points such that the sum of the distances to the two focal points is constant for every point on the curve. As such, it is a generalization of a circle, which is a special type of an ellipse having both focal points at the same location.

Find the equation of the parabola with
(i) vertex $(0,0)$ and focus $(3,0)$

Equation of a parabola

$y^2=4ax$ ,

$a$ is the distance from origin to the focus and here it is

$3$ . And we have the equation of parabola

$y^2=12x$

$\dfrac{{{x^2}}}{{8 - a}} + \dfrac{{{y^2}}}{{a - 2}} = 1$ represents an ellipse .Then find range of 'a'

Solution -

$\frac{x^{2}}{8-a}+\frac{y^{2}}{a-2} = 1$

For it to be an ellipse.

$8-a> 0$

$a-2> 0$

$a< 8 \bigcap a> 2$

$a\epsilon (2,8).$

1103988_1188902_ans_b8cc4e13a82848e38c6acc0075dbcf41.jpg

What is Coefficient of $\text{xy}$ i.e., $h$ in circle

In circle general equation

$x^2+y^2+2px+2py+c=0$

$\therefore h=0$ .

1241160_1156412_ans_71f7177f61194ae4b8b2cf67e9f1e0e4.jpg

Find the equation of centre $(1, 1)$ and radius $\sqrt{2}$ .

centre (1,1) (p,a)

radius

$\sqrt{2}$ =r

$(x-p)^{2}+(y-q)^{2}=r^{2}$

$\Rightarrow (x-1)^{2}+(y-1)^{2}=(\sqrt{2})^{2}$

$\Rightarrow x^{2}+1+2x+y^{2}+1+2y=2$

$\Rightarrow x^{2}+y^{2}+2x+2y=0$

Define Lateral Section?

A section formed by a plane cutting through an object, usually at right angles to an axis.

The D on of family of circles with radius = 5 & and center on y = 2 is __.

$(x - x - (y - 2) \dfrac{dy}{dx} )^2 + (y - 2)^2 = 5^2$

$(y - 2)^2 \left(\dfrac{dy}{dx} \right)^2 + (y - 2)^2 = 5^2$

$(y - x)^2 \left( \left(\dfrac{dy}{dx} \right)^2 + 1 \right) = 0$

Find the centre and radius of the circle: $x^{2}+y^{2}-6x-8y+24=0$

Given the equation of the circle is

$x^2+y^2-6x-8y+24=0$

or,

$(x^2-6x+9)+(y^2-8y+16)-1=0$

or,

$(x-3)^2+(y-4)^2=1$

So, the centre is

$(3, 4)$ and radius is

$1$ .

1180400_1195854_ans_0af68663737147aa84769ffd09e4ed26.jpg

Find the coordinates of the focus, equation of the directrix and the latus rectum of
$3y^{2}+7x=0$ .

Given,

$3y^2+7x=0$

$\Rightarrow y^2=-\dfrac{7}{3}x$

General equation:

$y^2=-4ax$

Focus:

$(-a,0)=\left ( \dfrac{7}{3},0 \right )$

Directrix:

$x=a\rightarrow x=-\dfrac{7}{3}\Rightarrow x+\dfrac{7}{3}=0$

Latus rectum:

$4a\rightarrow 4\left ( -\dfrac{7}{3} \right )=-\dfrac{28}{3}$

Find the area of the circle $4{x^2} + 4{y^2} = 9$

Equation of circle is

$4x^2+4y^2=9\\x^2+y^2=\dfrac{9}{4}$

So the radius of circle is

$\sqrt{\dfrac{9}{4}}=\dfrac 32$

Area of circle is

$\pi r^2=\dfrac {22}{7}\times \dfrac 32 \times \dfrac 32=7.065$

Find the equation of the circle with centre at $(3, -1)$ and which cuts off a chord of length $6$ on the line $2x - 5y + 18 = 0$

We have

$2x-5y+18=0$

$AP$ (Length of perpendicular force $$

$\frac{{12 \times 3 - 5\left( { - 1} \right) + 81}}{{\sqrt {4 + 25} }} = \sqrt {29}$

$r = AB = \sqrt {9 + {{\left( {AP} \right)}^2}} = \sqrt {38}$

${\left( {x - 3} \right)^2} - \left( {y + 1} \right) = 38$

Hence, the equation of the circle is

${x^2} + {y^2} - 6x + 2y = 28$

1202063_1278217_ans_865d99c0f1f24567ab46069b69c74d8f.PNG

If the equation of two diameters of a circle are $2x + y = 6$ and $3x + 2y = 4$ equation of circle.

Given the equation of two diameters of a circle are

$2x+y=6$ and

$3x+2y=4$ and radius is

$10$ ,
we have to find equation of circle solving 2x+y=6 .....(1) and 3x+2y=4 .......(2)
we get to the center of circle
=> now multiple (1) by

$2$
we get 4x +2y = 12 ........(3)
Now subtract

$2$ from

$3$ we get

$(4x +2y ) -(3x +2y) = 12-4$
=>

$x = 8$
Putting the value of

$x$ in (1) we get
=>

$2×8 +y = 6$
=>

$16+y = 6$
=>

$y = -10$
Here centre of circle

$= (8,-10)$ .

Equation of circle

$= (x-h)² + (y-k)² = r²$ .
where

$(h,k)$ is the center of circle and

$r$ is the radius
=>

$(x-8)² + (y+10)² = 10²$
=>

$x² +64 -16x +y² +100 +20y = 100$
=>

$x² +y² -16x +20y +64=0$

Hence

$x² +y² -16x +20y +64=0$ is the required equation of circle.

Conswing line $x + y = 5$ and the circle ${x^2} + {y^2} - 2x - 4y+3 = 0$ then

$\begin{array}{l} Given\, line:\, x+y-5=0 \\ circle\, \, equ:{ x^{ 2 } }+{ y^{ 2 } }-2x-4y+3=0 \\ we\, \, take, \\ 2gx=-2x \\ g=-1 \\ 2fy=-4y \\ f=-2 \\ centre\, (-g-f)=(1,2) \\ radius:\, \sqrt { { g^{ 2 } }+{ f^{ 2 } }-c } =\sqrt { 1+4-30 } =\sqrt { 2 } \\ Now,perpendicular\, from\, centre\, to\, x+y-5=0equal\, to\, radius\, of\, circle. \\ P=\frac { { \left| { 1+2-5 } \right| } }{ { \sqrt { 2 } } } =\frac { 2 }{ { \sqrt { 2 } } } =\sqrt { 2 } \, \, \, hence,\, the\, \, line\, touches\, in\, the\, circle. \\ let\, the\, \, point\, (h,k)\, \, and\, \, \, centre\, \, be\, \, C, \\ so,PC\, \bot \, to\, x+y-5=0\, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \left| { PC=\frac { { k-2 } }{ { h-1 } } } \right. \\ \Rightarrow y=-x+5=-1 \\ \Rightarrow \frac { { k-2 } }{ { h-1 } } \times -1=-1 \\ \Rightarrow k-2=h-1 \\ \Rightarrow k-h=1----------(I) \\ also\, h,k\, lie\, on\, the\, line,so: \\ h+k=5----------(2) \\ solving\, equ\, (1)\, \, \& (2) \\ 2k=6 \\ k=3\, \, ,h=2 \\ Hence,\, po{ { int } }\, is\, P(2,3) \\ \, \, \end{array}$

Find the equation of the circle passing through the points
$(1,2),(3,-4)$ and $(5,-6)$

$x^2+y^2+2gy+2fy+c=0$

passing from

$(1,2)$ then

$1+4+2g+4f+c=0$

$=2g+4f+c=-5$ .....................

$(1)$

from

$(3,-4)$

$9+16+8f+c=0$

$6g-8f+c=-25$ ...............

$(2)$

from

$(5,-6)$

$25+36+10g-12f+c=0$

$10g-12f+c==61$ ............

$(3)$

on substituting equation

$(1)$ and

$(2)$

hence, we have

$-4g+12f=20$

$-g+3f=5$ ..................

$(4)$

on substituting equation

$2$ and

$3$

we get

$-4g+4f=36$

$-g+f=9$ ............

$(5)$

on substituting equation

$4$ and

$5$

we get

$2f=-4$

$f=-2$

$\therefore g==11$

and

$c=25$

putting in the equation

we get

$x^2+y^2-22x-4f+25=0$

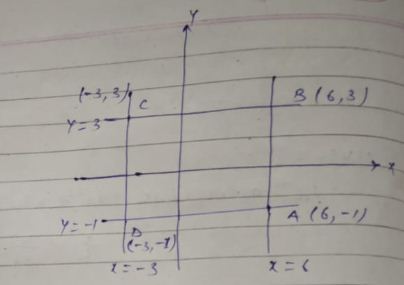
Find the equation of the circle circumscribing the rectangle formed by the lines x =6, x= -3, y = 3 and y = -1.

Let

$,$

$AC$ is the diameter of the circle which quadranant is

$\left( {6, - 1} \right)$ and

$\left( { - 3,3} \right)$

$,$ equation of circle

$:$

$\left( {x - 6} \right)\left( {x + 3} \right) + \left( {y + 1} \right)\left( {y - 3} \right) = 0$

1217944_1303611_ans_3b9d491efac846a08873a78f6316c5a6.JPG

Find the equation of that chord of the circle ${ x }^{ 2 }+{ y }^{ 2 }=15$ Which is bisected at the point (3,2).

Equation of the circle is given as

$x^2+y^2=15$ …………..

$(1)$

$\therefore$ Centre of the circle,

$C=(0, 0)$ and radius,

$r=\sqrt{15}$

$\therefore g=0, f=0$

Here, it is given that the chord is bisected at the point

$(3, 2)$

$\therefore$ Midpoint of the chord,

$M=(3, 2)$

The equation of the chord of the circle

$(1)$ with

$M(3, 2)$ as midpoint is given by

$3x+2y+0(x+3)+0(y+2)=(3)^2+(2)^2$

$\Rightarrow 3x+2y=9+4$

$\Rightarrow 3x+2y=13$ .

1215688_1301097_ans_aa36c66d44ba42dca2fa581ff8e6d9eb.JPG

Show that the equation $x^{2}+y^{2}-3x+3y+10=0$ is not circle.

We have,

$x^2+y^2-3x+3y+0=0$

Compare with general equation of circle

$x^2+y^2+2gx+fy+c=0$

$g = \dfrac{{ - 3}}{2},f = \dfrac{3}{2},c = 10$

Radius

$= \sqrt {{9^2} + {6^2} - c}$

$\begin{array}{l} =\sqrt { \dfrac { 9 }{ 4 } +\dfrac { 9 }{ 4 } -10 } \\ =\sqrt { 4.5-10 } \\ =\sqrt { -5.5 } \end{array}$

imaginary, so it is not a circle.

The equation of the circle passing through the point (1,0) and (0,1) and having the smallest radius is.

We have,

$\left( {{x}_{1}},{{y}_{1}} \right)=\left( 1,0 \right)$

$\left( {{x}_{2}},{{y}_{2}} \right)=\left( 0,1 \right)$

Then,

Equation of circle is

$\left( x-{{x}_{1}} \right)\left( x-{{x}_{2}} \right)+\left( y-{{y}_{1}} \right)\left( y-{{y}_{2}} \right)=0$

$\Rightarrow \left( x-1 \right)\left( x-0 \right)+\left( y-0 \right)\left( y-1 \right)=0$

$\Rightarrow x\left( x-1 \right)+y\left( y-1 \right)=0$

$\Rightarrow {{x}^{2}}-x+{{y}^{2}}-y=0$

$\Rightarrow {{x}^{2}}+{{y}^{2}}-x-y=0$

Hence, this is the answer.

Find the centre and radius of the circle $x^{2}+y^{2}=36$ .

Given, the equation of the circle,

$x^2+y^2=36$

or,

$x^2+y^2=6^2$

From the equation of the circle it is clear that the center is

$(0,0)$ and radius is

$6$ .

Find the equation of the circle whose diameters are along the lines $2x-3y+12=0$ and $x+4y-5=0$ and whose area is $154\ sq$ . units.

$\begin{array}{l} Let\, centre\, \left( { g,t } \right) \, and\, \, radius\, \, r. \\ then\, according\ to\ the\ problem, \\ 2h-3k+12=0\, \, \, \, \, ---\left( i \right) \\ h+4k-5=0\, \, \, \, \, \, \, \, \, \, \, ---\left( { ii } \right) \\ subtracting\, \left( i \right) -\left( { ii } \right) \, we\, get \\ \left( { 2h-3k+12 } \right) -\left( { 2h+8k-10 } \right) =0 \\ -3k-8k+12+10=0 \\ -11k=-22 \\ \therefore k=2 \\ h=-3 \\ \therefore centre=\left( { -3,2 } \right) \\ Now, \\ Area=154 \\ \pi { r^{ 2 } }=154 \\ \frac { { 22 } }{ 7 } .{ r^{ 2 } }=154 \\ { r^{ 2 } }=49 \\ \therefore r=7\, cm \\ Hence, \\ eq{ u^{ n } }\, of\, \, circle: \\ { \left( { x+3 } \right) ^{ 2 } }+{ \left( { y-2 } \right) ^{ 2 } }={ 7^{ 2 } } \\ { \left( { x+3 } \right) ^{ 2 } }+{ \left( { y-2 } \right) ^{ 2 } }=49 \end{array}$

Which is the required answer.

Find the Equation of the circle whose centre is $( - 2,3 )$ which passes through the point $( 4,5 )$

The equation of circle be

$(x-h)^2+(y-k)^2=r^2$

center

$(-2,3)$

$\implies (x+2)^2+(y-3)^2=r^2$

It passes through

$(4,5)$

$\implies (4+2)^2+(5-3)^2=r^2\\6^2+2^2=r^2\\r^2=36+4\\r^2=40$

So the equation of circle is

$(x+2)^2+(y-3)^2=40$

Find the equation of circle with center $(3,4)$ and radius 5

Center of circle

$(3,4)$

Radius of circel

$5$

The equation of circle is given as

$(x-3)^2+(y-4)^2=5^2\\x^2-6x+9+y^2-8y+16=25\\x^2+y^2-6x-8y$

Find the equation of the circle passing through the points $(0,-1)$ and $(2,0)$ and whose centre lies on the line $3x+y=5$ .

Let A= (0,-1) B= (2,0)

The midpoint of segment AB is M =

$\frac{A+B}{2}$

$=(\frac{0+2}{2},\frac{0-1}{2})$

$M=(1,-\frac{1}{2})$

equation of

$\perp$ bisector of AB is

$y+\frac{1}{2}=2(x-1)$

$2x-y=\frac{5}{2}$

$4x-2y=5$ ________ (1)

The center must be intersaction of equation (1) and 3x+y=5 _______ (2) in which center lie.

4x-2y=5 radius =

$\sqrt{(\frac{3}{2}-0)^{2}+(\frac{1}{2}+1)^{2}}=\frac{3}{\sqrt{2}}$

6x+2y=10

_________

10x= 15

$[x=\frac{3}{2}]$ and

$[y=\frac{1}{2}]$

equation of circle with center

$(\frac{3}{2},\frac{1}{2})$ & radius

$(x-\frac{3}{2})^{2}+(y-\frac{1}{2})^{2}=\frac{9}{4}$ _____ (3)

1199736_1380170_ans_007c9c0055b5472ea2f68f2d6388cfe9.JPG

Find the centre and radius of circle :
$2x^2+2y^2-x=0$

The equation of the given circle is

$2x^2+2y^2-x=0$

$(2x^2-x)+2y^2=0$

$2[(x^2-\dfrac{x}{2})+y^2]=0$

$[x^2-2x(\dfrac{1}{4})+(\dfrac{1}{4})^2]+y^2-(\dfrac{1}{4})^2=0$

$(x-\dfrac{1}{4})^2+(y-0)^2=(\dfrac{1}{4})^2$

Thus, the centre of the given circle is

$(\dfrac{1}{4},0)$ while its radius is

$\dfrac{1}{4}$ .

Find the equation of the circle whose centre is $(-1, 2)$ and which passes through $(5, 6)$ .

Equation of circle with center

$(-1,2)$ is :

$(x+1)^{2}+(y-2)^{2}=r^{2}$

It passes through

$(5,6)$

$\Rightarrow (5+1)^{2}+(6-2)^{2}=r^{2}$

$\Rightarrow r=\sqrt {52}$

$\Rightarrow$ equation of circle :

$(x+1)^{2}+(y-2)^{2}=52$

Find the equation of the ellipse referred to its centre
whose latus rectum is $5$ and whose eccentricity is $\dfrac {2}{3}$ ,
whose minor axis is equal to the distance between the foci and whose latus rectum is $10$ ,
whose foci are the points $(4, 0)$ and $(-4, 0)$ and whose eccentricity is $\dfrac {1}{3}$ .

1570653_1741399_ans_b57ff00c336143f6b26848cabe625faa.jpg

Find the equation of circle with center $(1,4)$ and radius $5$ .

As we know that the equation of circle with center at

$\left( h, k \right)$ ad radius

$r$ is given as-

${\left( x - h \right)}^{2} + {\left( y - k \right)}^{2} = {r}^{2}$

Given that the centre of circle is

$\left( 1, 4 \right)$ and radius is

$5$ .

Therefore the equation of circle is-

${\left( x - 1 \right)}^{2} + {\left( y - 4 \right)}^{2} = {\left( 5 \right)}^{2}$

At what point of the parabola $x^{2}=9y$ is the abscissa three times the ordinate?

Let the required point be

$\left( 3a, a \right)$ .

Now since the point lies on the parabola

${x}^{2} = 9y$ .

Therefore,

${\left( 3a \right)}^{2} = 9 \cdot a$

$9{a}^{2} = 9a$

$\Rightarrow a = 1$

Hence the required point is

$\left( 3, 1 \right)$ .

Find the equation of the circle center at origin and having radus $7cm$

The equation of circle having radius

$r$ and center at origin is

$x^2+y^2=r^2$

The equation of circle having radius

$7$ and center at origin is

$x^2+y^2=7^2\\$

$x^2+y^2=49$

Find the co-ordinates of centre and radius of circle.
$4(x^{2}+y^{2})=1$

Given the equation of the circle is

$4(x^{2}+y^{2})=1$

or,

$x^2+y^2=\dfrac{1}{4}$

or,

$x^2+y^2=\left(\dfrac{1}{2}\right)^2$ .

From this equation it is clear that the center of the circle is

$(0,0)$ and radius is

$\dfrac{1}{2}$ units.

Find the equation of a circle which passes through $(4, 1), (6, 5)$ and having the centre on:
$4x + 3y - 24 = 0$ .

Let

$\left( h, k \right)$ be the centre of circle.

Since the centre of circle lies on the line

$4x + 3y - 24 = 0$

Therefore,

$4h + 3k - 24 = 0 ..... \left( 1 \right)$

Given that the points

$\left( 4, 1 \right)$ and

$\left( 6, 5 \right)$ lies on the circle.

Therefore,

$\sqrt{{\left( 4 - h \right)}^{2} + {\left( 1 - k \right)}^{2}} = \sqrt{{\left( 6 - h \right)}^{2} + {\left( 5 - k \right)}^{2}}$

$\sqrt{16 + {h}^{2} - 8h + 1 + {k}^{2} - 2k} = \sqrt{36 + {h}^{2} - 12h + 25 + {k}^{2} - 10k}$

$\sqrt{{h}^{2} + {k}^{2} - 8h - 2k + 17} = \sqrt{{h}^{2} + {k}^{2} - 12h - 10k + 61}$

Squaring both sides, we get

${h}^{2} + {k}^{2} - 8h - 2k + 17 = {h}^{2} + {k}^{2} - 12h - 10k + 61$

$8h + 2k - 17 = 12h + 10k - 61$

$4h + 8k - 44 = 0 ..... \left( 2 \right)$

Subtracting equation

$\left( 1 \right)$ from

$\left( 2 \right)$ , we have

$\left( 4h + 8k - 44 \right) - \left( 4h + 3k - 24 \right) = 0$

$5k - 20 = 0$

$\Rightarrow k = 4$

Substituting the value of

$k$ in equation $$\left( 2 \right)$4, we have

$4h + 8 \times 4 - 44 = 0$

$h = \cfrac{12}{4} = 3$

Thus the centre of circle is

$\left( 3, 4 \right)$ .

Now,

Radius of circle

$= \sqrt{{\left( 4 - 3 \right)}^{2} + {\left( 1 - 4 \right)}^{2}} = \sqrt{1 + 9} = \sqrt{10}$

Therefore,

Equation of circle is-

${\left( x - 3 \right)}^{2} + {\left( y - 4 \right)}^{2} = {\left( \sqrt{10} \right)}^{2}$

Hence the equation of circle is

${\left( x - 3 \right)}^{2} + {\left( y - 4 \right)}^{2} = 10$ .

Find the equation of the circle with centre $(-a, -b)$ and radius $\sqrt { a^2 - b^2}$

The equation of a circle with centre

$(h , k)$ and radius

$r$ is given as

$(x - h)^2 + (y - k)^2 = r^2$
It is given that centre

$(h, k) = (-a, -b)$ and radius

$(r) = \sqrt{a^2 - b^2}.$
Therefore, the equation of the circle is

$(x + a)^2 + (y + b)^2 = (\sqrt{a^2 - b^2})^2$

$x^2 + 2ax + a^2 + y^2 + 2by + b^2 = a^2 - b^2$

$x^2 + y^2 + 2ax + 2by + 2b^2 = 0$

Trace the following central conics
$x^{2}-xy+2y^{2}-2ax-6ay+7a^{2}=0$

1574565_1741771_ans_c62e1eb35ad84315a9044fc57657f928.png

What are represent by the equation
$\dfrac{1}{r}=1+\cos\theta+\sqrt{3}\sin\theta$

1568773_1741718_ans_a8fc039d79aa4beabbc9d9b8caf662bd.gif

Prove that the equation to the circle of curvature of the conic $ax^2+2hxy+by^2=2y$ at the origin is $a(x^2+y^2)=2y$ .

1569058_1741880_ans_f4e26cb268fa40ac90caafd87541fee0.jpg

Trace the following central conics
$40x^{2}+36xy+25y^{2}-196x-122y+205=0$

1574562_1741765_ans_16a986788b8641f4a4ec995b42514e82.png

Find the coordinates of the focus, axis of the parabola, the equation of directrix and the length of the latus rectum for $y^2 = -8x.$

The given equation is

$y^2 = -8x.$
Here, the coefficient of x is negative. Hence, the parabola opens towards the left.
On comparing this equation with

$y^2 = -4ax,$ we obtain

$-4a = 8 \Rightarrow a = 2$

$\therefore$ Coordinates of the focus

$= (-a, 0) = (-2, 0)$
Since the given equation involves

$y^2,$ the axis of the parabola is the x-axis.
Equation of directrix,

$x = a$ i.e.,

$x = 2$
Length of latus rectum

$= 4a = 8$

Find the coordinates of the focus, axis of the parabola, the equation of directrix and the length of the latus rectum for $x^2 = -9y$

The given equation is

$x^2 = -9y.$
Here, the coefficient of y is negative. Hence, the parabola opens downwards.
On comparing this equation with

$x^2 = -4ay,$ we obtain

$-4a = -9 \Rightarrow b = \dfrac{9}{4}$

$\therefore$ Coordinates of the focus

$= (0, -a) = \left ( 0, -\dfrac{9}{4} \right )$
Since the equation involves

$x^2,$ the axis of the parabola is the y-axis.
Equation of the directrix,

$y = -a$ i.e.,

$y = \dfrac{9}{4}$
Length of latus rectum

$= 4a = 9$

Find the locus of the middle points of chords of an ellipse which are drawn through the positive end of the minor axis.

1570654_1741403_ans_f045bd695417441395b551d6e86e858e.jpg

The constant ratio denoted by $'e'=\sqrt{1-\dfrac{b^m}{a^m}},\, a>b$ is the eccentricity of an ellipse. Find $m$ .

$\displaystyle 2x^{2}+y^{2}-8x-2y+1=0.$
Find the square of the Latus Rectum for the given ellipse.

Given equation

$\displaystyle 2{ x }^{ 2 }+{ y }^{ 2 }-8x-2y+1=0$ .

By simplifying we get

$\displaystyle 2{ (x-2) }^{ 2 }+{ (y-1) }^{ 2 }=8\quad or\quad \frac { { (x-2) }^{ 2 } }{ 4 } +\frac { { (y-1) }^{ 2 } }{ 8 } =1$ or

$\dfrac { { X }^{ 2 } }{ 4 } +\dfrac { { Y }^{ 2 } }{ 8 } =1$ ,where

$\displaystyle X=(x-2) ,Y=(y-1),{b}^{2}=8,{a}^{2}=4$
Here Y-axis is major axis,now length of L.R is given by

$\displaystyle \frac { 2{ a }^{ 2 } }{ b } =\frac { 8 }{ \sqrt { 8 } } =2\sqrt { 2 }$
Square of it is equal to

$\displaystyle 8$ .

$\displaystyle x^{2}+y^{2}+2x-4y+k=0$ passes through

A) For

$k=0$

${ x }^{ 2 }+{ y }^{ 2 }+2x-4y+k=0\Rightarrow { x }^{ 2 }+{ y }^{ 2 }+2x-4y=0\\ \Rightarrow { x }^{ 2 }+{ y }^{ 2 }+2x-4y+1+4-1-4\Rightarrow { \left( x+1 \right) }^{ 2 }+{ \left( y-2 \right) }^{ 2 }=5$
Point

$\left( 0,0 \right)$ and

$\left( 0,4 \right)$ satisfies this

B) For

$k=1$

${ x }^{ 2 }+{ y }^{ 2 }+2x-4y+k=0\Rightarrow { x }^{ 2 }+{ y }^{ 2 }+2x-4y+1=0\\ \Rightarrow { x }^{ 2 }+{ y }^{ 2 }+2x-4y+1+4-4\Rightarrow { \left( x+1 \right) }^{ 2 }+{ \left( y-2 \right) }^{ 2 }=4$
Point

$\left( 1,2 \right)$ satisfies this

C) For

$k=-15$

${ x }^{ 2 }+{ y }^{ 2 }+2x-4y+k=0\Rightarrow { x }^{ 2 }+{ y }^{ 2 }+2x-4y-15=0\\ \Rightarrow { x }^{ 2 }+{ y }^{ 2 }+2x-4y+1+4-20\Rightarrow { \left( x+1 \right) }^{ 2 }+{ \left( y-2 \right) }^{ 2 }=20$
Point

$\left( 3,4 \right)$ satisfies this

D) For

$k=2$

${ x }^{ 2 }+{ y }^{ 2 }+2x-4y+k=0\Rightarrow { x }^{ 2 }+{ y }^{ 2 }+2x-4y-1=0\\ \Rightarrow { x }^{ 2 }+{ y }^{ 2 }+2x-4y+1+4-6\Rightarrow { \left( x+1 \right) }^{ 2 }+{ \left( y-2 \right) }^{ 2 }=2$
Point (0, 1) satisfies

The area cut off by the parabola $\displaystyle y^{2}=4ax$ and its latus rectum is.........., if $a=3$

$A=2\int _{ 0 }^{ a }{ 2\sqrt { ax } =24 }$ where,

$a=3$

Coordinates of a focus

1) For

$\cfrac {x^{2}}{25}+\cfrac {y^{2}}{21}=1$ , coordinates of a focus are (ae, 0) where

$a^{2}=25$

$\displaystyle e^{2}=\cfrac{25-21}{25}=\frac{4}{25}$
So that the required coordinates are

$(2, 0)$ .

2)

$xy=1$ is the equation of a rectangular hyperbola, referred to its asymptotes as the axes of coordinates.
So, if we rotate the axis through an angle

$\cfrac {\pi}{4}$ we get

$\displaystyle X=x\cos 45^{\circ}+y\sin 45^{\circ}=\frac{x+y}{\sqrt{2}}$
and

$\displaystyle Y=-x\sin 45^{\circ}+y\cos 45^{\circ}=\frac{y-x}{\sqrt{2}}$ .
So that

${ X }^{ 2 }-{ Y }^{ 2 }=1/2.4xy=2$ which is a rectangular hyperbola whose focus is

$X=ae, Y=0.$
where

$a^{2}=2$ ,

$\displaystyle e^{2}=\frac{2+2}{2}=2$

$\Rightarrow$

$X=\sqrt{2}\times \sqrt{2}$ ,

$Y=0$

$\Rightarrow$

$\displaystyle \frac{x+y}{\sqrt{2}}=2$ and

$\displaystyle \frac{y-x}{\sqrt{2}}=0\Rightarrow y=x=\sqrt{2}$
Coordinates of focus of xy=1 are

$\left ( \sqrt{2}, \sqrt{2} \right )$

3)

$y^{2}-4y-8x+28=0$

$\Rightarrow$

$\left ( y-2 \right )^{2}=8x-24=8\left ( x-3 \right )$
which represents the parabola

$Y^{2}=4aX$ where

$Y=y-2$ ,

$X+x-3$ and

$4a=8$ .

The coordinates of the focus are

$(X=a, Y=0)=(x-3=2, y-2=0)=(5, 2)$ .

4)

$\displaystyle 21x^{2}-4y^{2}=84\Rightarrow \frac{x^{2}}{4}-\frac{y^{2}}{21}=1$
which is a hyperbola with eccentricity

$\displaystyle e^{2}=\frac{4+21}{4}=\frac{25}{4}\Rightarrow e=\frac{5}{2}$ and the coordinates of a focus are

$(ae, 0)(a=2)=(5, 0)$

The length of the latus rectum of the parabola $x=a{ y }^{ 2 }+by+c$ is $\displaystyle\frac { k }{ a }$ . Find $k$

$\displaystyle x=a\left( { y }^{ 2 }+\frac { b }{ a } y+\frac { { b }^{ 2 } }{ 4{ a }^{ 2 } } \right) -\frac { { b }^{ 2 } }{ 4{ a }^{ 2 } } +c$

$\displaystyle \Rightarrow a{ \left( y+\frac { b }{ 2a } \right) }^{ 2 }=x+\frac { { b }^{ 2 } }{ 4a } -c$

$\displaystyle \Rightarrow { \left( y+\frac { b }{ 2a } \right) }^{ 2 }=\frac { 1 }{ a } \left( x+\frac { { b }^{ 2 }-4ac }{ 4a } \right)$

$\therefore$ the latus rectum

$\displaystyle =\frac { 1 }{ a }$

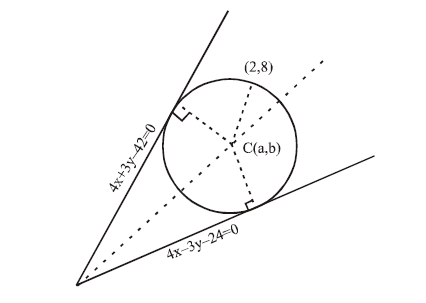
Find the equation of the circles passing through the point $(2,8)$ touching the line $4x-3y-24=0$ and $4x+3y-42=0$ and having $x$ coordinate of the centre of the circle less than or equal to $8$ .

Let the centre of the circle be

$(a,b)$

${(a-b)}^{2}+{(b-8)}^{2}={r}^{2}..........(i)$

$\left| \cfrac { 4a-3b-24 }{ 5 } \right| =\left| \cfrac { 4a+3b-42 }{ 5 } \right| =r......(ii)$

$\Rightarrow$

$4a-3b-24=\pm (4a+3b-42).......(iii)$

$6b=18$

$\Rightarrow$

$b=3$
from

$(i)$

${(a-2)}^{2}={r}^{2}-25$
from

$(ii)$

$4a-3b-24=5r$

$4a=5r+33$

${(a-2)}^{2}={ \left( \cfrac { 4a-33 }{ 5 } \right) }^{ 2 }-25$

${(a-2)}^{2}={ \left( \cfrac { 4a-33 }{ 5 } -5 \right) }\left( \cfrac { 4a-33 }{ 5 } +5 \right)$

${(a-2)}^{2}={ \left( \cfrac { 4a-58 }{ 5 } \right) }\left( \cfrac { 4a-8 }{ 5 } \right) \quad$

$25{(a-2)}^{2}=4.2(2a-29)(a-2)$

$25(a-2)=8(2a-29)$ or

$a-2=0$

$\Rightarrow$

$a=2$
Also

$9a=-182$

$a=\cfrac{=182}{9}$

$\therefore$

$a=2, b=3, r=5$
and

$a=\cfrac{-182}{9}, b=3, r=\cfrac{205}{9}$
(from -ve sign in

$(iii)$

$8a=66$

$\Rightarrow$

$a=33/4 >8$

Find the equations of the following curves in cartesian form. Also find the centre and radius of the circle $\displaystyle x=a+c\cos \theta ,y=b+c\sin \theta$

We have

$\displaystyle x=a+c\cos \theta ,y=b+c\sin \theta$

$\displaystyle \Rightarrow \cos \theta =\frac{x-a}{c},\sin \theta =\frac{y-b}{c}$

$\displaystyle \Rightarrow \left ( \frac{x-a}{c} \right )^{2}+\left ( \frac{y-b}{c} \right )^{2}=\cos ^{2}\theta +\sin ^{2}\theta \Rightarrow \left ( x-a \right )^{2}+\left ( y-b \right )^{2}=c^{2}$
Clearly it is a circle with centre at (a, b) and radius c

Find the equation of the circle whose centre is (1, -2) and radius is 4

The equation of the circle is

$\displaystyle \left ( x-1 \right )^{2}+\left ( y-\left ( -2 \right ) \right )^{2}=4^{2}$

$\displaystyle \Rightarrow \left ( x-1 \right )^{2}+\left ( y+2 \right )^{2}=16$

$\displaystyle \Rightarrow x^{2}+y^{2}-2x+4y-11=0$

Find the equation of the circle passing through the point (2, 1) and touching the line x + 2y - 1 = 0 at the point (3, -1)

Equation of circle is

$\displaystyle (x-3)^{2}+(y+1)^{2}+\lambda (x+2y-1)=0$
Since it passes through the point

$(2, 1), 1 + 4 +$

$\lambda$ (2 + 2 - 1) = 0

$\displaystyle \Rightarrow \lambda =-\frac{5}{3}$

$\displaystyle \therefore circle \: is\: (x-3)^{2}+(y+1)^{2}-\frac{5}{3}(x+2y-1)=0$

$\displaystyle \Rightarrow 3x^{2}+3y^{2}-23x-4y+35=0$

Find the equation of a circle with centre $(2, 2)$ and passes through the point $(4, 5)$ .

The centre of the circle is given as

$(h, k) = (2, 2)$
Since the circle passes through point

$(4, 5)$ the radius

$(r)$ of the circle is the distance between the point

$(2, 2)$ and

$(4, 5)$

$\displaystyle \therefore r = \sqrt{\left ( 2 - 4 \right )^{2}+\left ( 2 - 5 \right )^{2}}= \sqrt{\left ( -2 \right )^{2}+\left ( -3 \right )^{2}=}$

$\displaystyle \sqrt{4 + 9} =\sqrt{13}$
Thus the equation of the circle is

$\displaystyle \left ( x - h \right )^{2} +\left ( y - k \right )^{2} = r^{2}$

$\displaystyle \left ( x - 2 \right )^{2}+\left ( y - 2 \right )^{2}=\left ( \sqrt{13} \right )^{2}$

$\displaystyle x^{2}-4x + 4 + y^{2}- 4y + 4 = 13$

$\displaystyle x^{2}+y^{2} - 4x - 4y - 5 = 0$

Find the centre and radius of the circle $\displaystyle x^{2}+y^{2}-8x +10y - 12 = 0$

$\displaystyle x^{2}+y^{2}-8x +10y - 12 = 0$

$\displaystyle \Rightarrow \left ( x^{2}-8x \right )+\left ( y^{2}+10y \right )= 12$

$\displaystyle \Rightarrow \left \{ x^{2}-2\left ( x \right )\left ( 4 \right ) +4^{2}\right \}+\left \{ y^{2}+2\left ( y \right ) \left ( 5 \right )+5^{2}\right \}- 16 - 25 = 12$

$\displaystyle \Rightarrow \left ( x - 4 \right )^{2}+\left ( y +5 \right )^{2}= 53$

$\displaystyle \Rightarrow \left ( x -4 \right )^{2}+\left \{ y -\left ( -5 \right ) \right \}^{2}= \left ( \sqrt{53} \right )^{2}$

which is of the form

$\displaystyle \left ( x - h \right )^{2}+\left ( y - k \right )^{2}= r^{2}$

where

$h= 4, k = -5$ and

$r = \displaystyle \sqrt{53}$

Thus the centre of the given circle is

$(4, -5)$ while its radius is

$\displaystyle \sqrt{53}$

Find the equation of the circle with radius $5$ whose centre lies on $x$ -axis and passes through the point $(2, 3)$

Given a circle of radius

$r=5$
Given center lies on

$x$ -axis.

So, let the center be

$(h,0)$
Equation of circle is

$(x-h)^2+y^2=25$ ....(1)
Since, it passes through

$(2,3)$

$\Rightarrow (2-h)^2+3^2=25$

$\Rightarrow (2-h)^2=16$

$\Rightarrow 2-h=\pm 4$

$\Rightarrow h=-2, h=6$

When

$h=-2$ , the equation of circle is

$(x+2)^2+y^2=25$

$\Rightarrow x^2+4x+4+y^2=25$

$\Rightarrow x^2+y^2+4x-21=0$

When

$h=6$ , the equation of circle is

$(x-6)^2+y^2=25$

$\Rightarrow x^2-12x+36+y^2=25$

$\Rightarrow x^2+y^2-12x+11=0$

Find the equation of the circle passing through $(0, 0)$ and making intercepts $a$ and $b$ on the coordinate axes.

Let the equation of the required circle be

$(x - h) ^{2} + (y - k)^{2} = r ^{2}$
Since the circle passes through

$(0, 0)$

$(0 - h) ^{2} + ( 0 - k) ^{2} = r \displaystyle ^{2}$

$\displaystyle \Rightarrow h^{2}+k^{2}= r^{2}$
So, the equation of the circle becomes

$(x - h) ^{2} + (y - k)\ ^{2} = h^{2} + k ^{2}$

Given that the circle makes intercepts

$a$ and

$b$ on the coordinate axes.

This means that the circle passes through points

$(a, 0)$ and

$(0, b)$ .

Therefore,

$(a - h) ^{2} + (0 - k) ^{2} = h ^{2} + k^{2}$ ...(1)

$(0 - h) ^{2} + (b - k) ^{2}$

$= h ^{2} + k^{2}$ ...(2)
From equation (1) we obtain

$\displaystyle a^{2} - 2ah + h ^{2} + k^{2} = h \displaystyle ^{2} + k^{2}$

$\displaystyle \Rightarrow a^{2}-2ah = 0$

$\displaystyle \Rightarrow a(a - 2h) = 0$

$\displaystyle \Rightarrow a = 0 or (a - 2h) = 0$
But since

$\displaystyle a\neq 0$

Hence

$(a - 2h) = 0 \Rightarrow a=2h$

$\displaystyle \Rightarrow h = \frac{a}{2}$

From equation (2) we obtain,

$\displaystyle h^{2} + b^{2} - 2bk +k ^{2} = h^{2} + k^{2}$

$\displaystyle \Rightarrow b ^{2} - 2bk = 0$

$\displaystyle \Rightarrow b (b - 2k) = 0$

$\displaystyle \Rightarrow b = 0 or (b - 2k) = 0$
But since

$\displaystyle b\neq 0$

Hence

$(b - 2k) = 0 \Rightarrow b=2k$

$\displaystyle \Rightarrow k = \cfrac{b}{2}$
Thus the equation of the required circle is

$\displaystyle \left ( x-\frac{a}{2} \right )^{2}+\left ( y-\frac{b}{2} \right )^{2}=\left ( \frac{a}{2} \right )^{2}+\left ( \frac{b}{2} \right )^{2}$

$\displaystyle \Rightarrow \left ( \frac{2x - a}{2} \right )^{2}+\left ( \frac{2y - b}{2} \right )^{2}= \frac{a^{2}+b^{2}}{4}$

$\displaystyle \Rightarrow 4x^{2}-4ax+ a^{2}+4y^{2}-4by + b^{2}= a^{2}+b^{2}$

$\displaystyle \Rightarrow 4x^{2}+4y^{2}- 4ax-4by = 0$

$\displaystyle \Rightarrow x^{2}+y^{2}-ax - by = 0$

Find the center and radius of the circle $\displaystyle x^{2}+y^{2}-4x - 8y - 45 = 0$

$\displaystyle x^{2}+y^{2}-4x - 8y - 45 = 0$

$\displaystyle \Rightarrow \left ( x^{2}- 4x \right ) + \left ( y^{2} - 8y\right )=45$

$\displaystyle \Rightarrow$

$\displaystyle \left \{ x^{2}-2\left ( x \right )\left ( 2 \right )+2^{2} \right \}+\left \{ y^{2} - 2\left ( y \right )\left ( 4 \right )+4^{2} \right \}- 4 - 16 = 45$

$\displaystyle \Rightarrow \left ( x - 2 \right )^{2}+ \left ( y- 4 \right )^{2} = 65$

$\displaystyle \Rightarrow$

$\displaystyle \left ( x - 2 \right )^{2}+\left ( y - 4 \right )^{2}=\left ( \sqrt{65} \right )^{2}$
Which is of the form

$\displaystyle \left ( x - h \right )^{2}+\left ( y - k^{2} \right )= r^{2}$
where

$h = 2, k = 4$ and

$r = \displaystyle \sqrt{65}$
Thus the centre of the given circle is

$(2, 4)$ while its radius is

$\displaystyle \sqrt{65}$

Find the equation of the circle passing through the points $(2, 3)$ and $(-1, 1)$ and whose centre is on the line $x - 3y - 11 = 0$

Let the equation of circle be

$x^2+y^2+2gx+2fy+c=0$ .....(1)

where

$(-g,-f)$ is center and

$g^2+f^2-c$ is the radius.

Since, the circle passes through

$(2,3)$ , so it satisfies eqn (1)

$\Rightarrow 4+9+4g+6f+c=0$

$\Rightarrow 4g+6f+c=-13$ .....(2)

Since, the circle passes through

$(-1,1)$ , so it satisfies eqn (1)

$\Rightarrow 1+1-2g+2f+c=0$

$\Rightarrow -2g+2f+c=-2$ .....(3)

Subtracting eqn (3) from eqn (2), we get

$6g+4f=-11$ ....(4)

Given center lies on the line

$x-3y-11=0$

Since, center

$(-g,-f)$ satisfies this equation.

$\Rightarrow -g+3f=11$ ....(5)

Solving eqn (4) and (5), we get

$g=\cfrac{-7}{2}, f=\cfrac{5}{2}$

Put this value in (2), we get

$c=-14$

Substituting these values in (1),

$x^2+y^2-7x+5y-14=0$

which is the equation of required circle.

If $5x^2 + Ay^2 = 20$ represents a rectangular hyperbola, then $-A$ equals

1958980_355963_ans_da123c5e48b3495e9e3571c9f2db7051.jpg

Find the centre and radius of the circle $\displaystyle 2x^{2}+2y^{2}-x = 0$

Given

$\displaystyle 2x^{2}+2y^{2}-x = 0$

$\displaystyle \Rightarrow (2x^{2}-x)+2y^{2}= 0$

$\displaystyle \Rightarrow 2\left [ \left ( x^{2} -\frac{x}{2}\right )+y^{2} \right ]=0$

$\displaystyle \Rightarrow \left \{ x^{2}-2x\left ( \frac{1}{4} \right )+\left ( \frac{1}{4} \right )^{2} \right \} +y^{2}-\left ( \frac{1}{4} \right )^{2} = 0$

$\displaystyle \Rightarrow \left ( x -\frac{1}{4} \right )^{2}+\left ( y - 0 \right )^{2}=\left ( \frac{1}{4} \right )^{2}$
which is of the form

$\displaystyle \left ( x - h \right )^{2}+\left ( y - k \right )^{2}= r^{2}$
where

$h = \displaystyle \frac{1}{4}$ ,

$k = 0$ and

$r = \displaystyle \frac{1}{4}$
Thus the centre of the given circle is

$\displaystyle \left ( \frac{1}{4},0 \right )$ while its radius is

$\displaystyle \frac{1}{4}$ .

Find the equation of the circle with centre $(-a, -b)$ and radius $\displaystyle \sqrt{a^{2}-b^{2}}$

Here it is given that centre

$(h, k) = (-a, -b)$ and radius

$r = \displaystyle \sqrt{a^{2}-b^{2}}$
Therefore the equation of the circle is

$\displaystyle \left ( x + a \right )^{2}+ \left ( y + b \right )^{2}= \left ( \sqrt{a^{2}-b^{2}} \right )^{2}$

$\Rightarrow \displaystyle x^{2}+ 2ax + a^{2}+ y^{2} + 2by + b^{2}= a^{2} - b^{2}$

$\displaystyle\Rightarrow x^{2}+ y^{2}+ 2ax + 2by + 2b^{2} = 0$

Find the equation of the parabola that satisfies the following conditions: Focus $(6, 0)$ ; directrix $x = -6$

Focus

$=(6, 0)$ ; directrix

$x = -6$
Since the focus lies on the

$x$ -axis and directrix is to the left of

$y$ -axis.
So, the axis of the parabola is

$x$ -axis
Therefore the equation of the parabola is either of the form

$\displaystyle y^{2} = 4ax$
Here ,

$a = 6$
Thus, the equation of the parabola is

$\displaystyle y^{2} = 24x$

Find the equation of the parabola that satisfies the following conditions: Focus $(0,-3)$ ; directrix $y = 3$

Focus

$S= (0, -3)$ ; directrix

$y = 3$
Since, the focus lies on the

$y$ -axis and directrix

$y = 3$ is above the

$x$ -axis.
So, the axis of the parabola is

$y$ -axis.
Therefore, the equation of the parabola is either of the form

$\displaystyle x^{2} = - 4ay$
Here

$a = 3$
Thus, the equation of the parabola is

$\displaystyle x^{2} = - 12y$

Find the coordinates of the focus, axis of the parabola ,the equation of directrix and the length of the latus rectum for $x\displaystyle ^{2} = -9y$

The given equation is

$\displaystyle x^{2} = -9y$
Here the coefficient of

$y$ is negative.
Hence, the parabola opens downwards
On comparing this equation with

$\displaystyle x^{2} = - 4ay$ , we get

$-4a = -9$

$\displaystyle \Rightarrow a = \displaystyle \frac{9}{4}$

$\displaystyle \therefore$ Coordinates of the focus

$= (0, -a) = \displaystyle \left ( 0,-\frac{9}{4} \right )$
Axis of the parabola is the

$y$ -axis i.e

$x=0$
Equation of directrix

$y = a$ i.e.

$y = \displaystyle \frac{9}{4}$
Length of latus rectum

$= 4a = 9$

Find the coordinates of the focus axis of the parabola, the equation of directrix and the length of the latus rectum for the parabola $x\displaystyle ^{2}$ $= - 16y$ .

The given equation is

$\displaystyle x^{2} = - 16y$
Here, the coefficient of

$y$ is negative.
Hence the parabola opens downwards.
On comparing this equation with

$\displaystyle x^{2} = - 4ay$

$-4a = - 16$

$\displaystyle \Rightarrow a = 4$

$\displaystyle \therefore$ Coordinates of the focus

$= (0, -a) = (0, -4)$
Axis of the parabola is the

$y$ -axis i.e

$x=0$
Equation of directrix

$y = a$ i.e.,

$y = 4$
Length of latus rectum

$= 4a = 16$

Find the coordinates of the focus, axis of the parabola, the equation of directrix and the length of the rectum for $\displaystyle y^{2} = 12x$

The given equation is

$\displaystyle y^{2} = 12x$
Here the coefficient of

$x$ is positive.
Hence the parabola opens right
On comparing this equation with

$\displaystyle y^{2} = 4ax$ ,

$4a =12$

$\displaystyle \Rightarrow a =3$

$\displaystyle \therefore$ Coordinates of the focus

$= (a, 0) =(3,0)$
Since the given equation involves

$\displaystyle y^{2}$ , the axis of the parabola is the

$x$ -axis
Equation of directrix

$x = -a$ i.e.

$x = - 3$
Length of latus rectum

$= 4a = 12$

Find the equation of the parabola that satisfies the following conditions: Vertex $(0, 0)$ passing through $(2, 3)$ and axis is along $x$ -axis

Since the vertex

$A$ is

$(0, 0)$ and the axis of the parabola is the

$x$ -axis.
Equation of the parabola is either of the form

$\displaystyle y^{2} = 4ax$ or

$\displaystyle y^{2} = - 4ax$
The parabola passes through point

$(2, 3)$ which lies in the first quadrant
Therefore, the equation of the parabola is of the form

$\displaystyle y^{2} = 4ax$
Point

$(2, 3)$ must satisfy the equation

$\displaystyle y^{2} = 4ax$

$\displaystyle \therefore 3^{2}= 4a\left ( 2 \right )$

$\Rightarrow a =\cfrac{9}{8}$
Thus, the equation of the parabola is

$\displaystyle y^{2}= 4\left ( \frac{9}{8} \right )x$

$\displaystyle y^{2}= \frac{9}{2}x$

$\displaystyle 2y^{2}=9x$

Find the coordinates of the focus, axis of the parabola ,the equation of directrix and the length of the latus reactum for $x$ $\displaystyle ^{2} = 6y$

The given equation is

$\displaystyle x^{2} = 6y$
Here the coefficient of

$y$ is positive.
Hence the parabola opens upwards
On comparing this equation with

$\displaystyle x^{2} = 4ay$ ,

$4a = 6$

$\displaystyle \Rightarrow a = \displaystyle \frac{3}{2}$

$\displaystyle \therefore$ Coordinates of the focus

$= (0, a) = \displaystyle \left ( 0,\frac{3}{2} \right )$
Since the given equation involves

$\displaystyle x^{2}$ , the axis of the parabola is the

$y$ -axis
Equation of directrix

$y = -a$ i.e.

$y = - \displaystyle \frac{3}{2}$
Length of latus rectum

$= 4a = 6$

Find the equation of the parabola that satisfies the following conditions: Vertex $(0, 0)$ ; focus $(3, 0)$

Vertex

$A(0, 0)$ ; focus

$S(3, 0)$
Since, the vertex of the parabola is

$(0, 0)$ and the focus lies on the positive

$x$ -axis , so the axis of the parabola is

$x$ -axis.
Equation of the parabola is of the form

$\displaystyle y^{2} = 4ax$
Since, the focus is

$(3, 0)$ , so

$a = 3$
Thus, the equation of the parabola is

$\displaystyle y^{2} = 12x$

Find the coordinates of the focus axis of the parabola the equation of directrix and the length of the latus rectum for $y\displaystyle ^{2}$ $= - 8x$

The given equation is

$\displaystyle y^{2} = -8x$
Here the coefficient of

$x$ is negative.
Hence the parabola opens towards the left.
On comparing this equation with

$\displaystyle y^{2} = -4ax$

$-4a = -8$

$\displaystyle \Rightarrow a = 2$

$\displaystyle \therefore$ Coordinates of the focus

$= (-a, 0) = (-2, 0)$
Axis of the parabola is the

$x$ -axis i.e.

$y=0$
Equation of directrix

$x = a$ i.e.,

$x = 2$
Length of latus rectum

$= 4a = 8$

Find the coordinates of the focus axis of the parabola the equation of directrix and the length of the latus rectum for y $\displaystyle ^{2} = 10x$

The given equation is

$\displaystyle y^{2} = 10x$
Here the coefficient of

$x$ is positive.
Hence the parabola opens towards the right
On comparing this equation with

$\displaystyle y^{2} = 4ax$ , we get

$4a = 10$

$\displaystyle \Rightarrow a = \displaystyle \frac{5}{2}$

$\displaystyle \therefore$ Coordinates of the focus

$= (a, 0) = \displaystyle \left ( \frac{5}{2},0 \right )$
Axis of the parabola is the

$x$ -axis i.e

$y=0$
Equation of directrix

$x = -a$ i.e.

$x = - \displaystyle \frac{5}{2}$
Length of latus rectum

$= 4a = 10$

Find the coordinates of the foci, the vertices, the length of major axis, the minor axis, the eccentricity and the length of the latus rectum of the ellipse $\displaystyle 36x^{2}+ 4y^{2}= 144$

The given equation is

$\displaystyle 36x^{2}+ 4y^{2}= 144$
It can be written as

$\displaystyle 36x^{2}+ 4y^{2}= 144$

$\displaystyle \frac{x^{2}}{4}+\frac{y^{2}}{36}= 1$

$\displaystyle \frac{x^{2}}{2^{2}}+\frac{y^{2}}{6^{2}}= 1$ ...(1)
Here the donominator of

$\displaystyle \frac{y^{2}}{6^{2}}$ is greater than the denominator of

$\displaystyle \frac{x^{2}}{2^{2}}$
Therefore, the major axis is along the

$y$ -axis while the minor axis is along the

$x$ -axis.
On comparing equation (1) with

$\displaystyle \frac{x^{2}}{b^{2}}+\frac{y^{2}}{a^{2}}= 1$ , we obtain

$b = 2$ and

$a = 6$

$\displaystyle \therefore ae=c = \sqrt{a^{2}-b^{2}}=\sqrt{36 - 4}= \sqrt{32}= 4\sqrt{2}$
Therefore, the coordinates of the foci are

$\displaystyle \left ( 0, \pm 4\sqrt{2} \right )$
The coordinates of the vertices are (0,

$\displaystyle \pm 6)$
Length of major axis

$= 2a = 12$
Length of minor axis

$= 2b = 4$
Eccentricity

$e =$

$\displaystyle \frac{c}{a}=\frac{4\sqrt{2}}{6}=\frac{2\sqrt{2}}{3}$
Length of latus rectum

$=$

$\displaystyle \frac{2b^{2}}{a}=\frac{2 \times 4}{6}= \frac{4}{3}$

Find the coordinates of the foci. the vertices the eccentricity and the length of the latus rectum of the hyperbola $\displaystyle 49y^{2}-16x^{2}= 784$

The given equation is

$\displaystyle 49y^{2}-16x^{2}= 784$
It can be written as

$\displaystyle 49y^{2}-16x^{2}= 784$

$\displaystyle \frac{y^{2}}{16}-\frac{x^{2}}{49}= 1$

$\displaystyle \frac{y^{2}}{4^{2}}-\frac{x^{2}}{7^{2}}= 1$ ...(1)
On comparing equation (1) with the standard equation of hyperbola
i.e.,

$\displaystyle \frac{y^{2}}{a^{2}}-\frac{x^{2}}{b^{2}}= 1$
we obtain

$a = 4$ and

$b = 7$
We know that

$\displaystyle a^{2}+b^{2}= c^{2},$ where

$c=ae$

$\displaystyle \therefore c^{2}= 16 + 49 = 65$

$\displaystyle \Rightarrow c = \sqrt{65}$
Therefore, the coordinates of the foci are

$\displaystyle \left ( 0, \pm \sqrt{65} \right )$
The coordinates of the vertices are

$\displaystyle \left ( 0, \pm 4 \right )$
Eccentricity

$e = \displaystyle \frac{c}{a}=\frac{\sqrt{65}}{4}$
Length of latus rectum

$=$

$\displaystyle \frac{2b^{2}}{a}= \frac{2\times 49}{4}= \frac{49}{2}$

Find the coordinates of the foci, the vertices the length of major axis, the minor axis, the eccentricity and the length of the latus rectum of the ellipse $\displaystyle \frac{x^{2}}{4}+\frac{y^{2}}{25}= 1$

Given equation of ellipse is

$\displaystyle \frac{x^{2}}{4} +\frac{y^{2}}{25} = 1$
On comparing the given equation with

$\displaystyle \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}= 1$ , we get

$a=2, b=5$
Since,

$b>a$ ,therefore the major axis is along the

$y$ -axis while the minor axis is along the

$x$ -axis.
Length of major axis

$= 2b = 10$
Length of minor axis

$= 2a = 4$
Eccentricity

$\displaystyle e = \sqrt{1-\frac{a^{2}}{b^{2}}} = \sqrt{\frac{25 -4}{25}}= \frac{\sqrt{21}}{5}$

Coordinates of the foci are

$\displaystyle \left ( 0,\sqrt{21} \right )\,$ and

$\left ( 0,-\sqrt{21} \right )$
The coordinates of the vertices are

$(0, 5)$ and

$(0, -5)$
Length of latus rectum =

$\displaystyle \frac{2a^{2}}{b}= \frac{2 \times 4}{5}= \frac{8}{5}$

Find the coordinates of the foci, the vertices the eccentricity and the length of latus rectum of the hyperbola $\displaystyle 16x^{2}- 9y^{2}= 576$

We have,

$\displaystyle 16x^{2}- 9y^{2}= 576$

$\displaystyle \Rightarrow \frac{x^{2}}{36}-\frac{y^{2}}{64} = 1$

$\displaystyle \Rightarrow \frac{x^{2}}{6^{2}}-\frac{y^{2}}{8^{2}}= 1 ...(1)$
On comparing equation (1) with the standard equation of hyperbola,

$\displaystyle \frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}= 1$ ,
we obtain

$a = 6, b = 8\Rightarrow e =\sqrt{1+\cfrac{b^2}{a^2}}=\sqrt{1+\cfrac{64}{36}}=\cfrac{5}{3}$
Therefore, the coordinates of the foci are

$\displaystyle \left ( \pm 10, 0 \right )$
The coordinates of the vertices are

$\displaystyle \left ( \pm 6, 0 \right )$
Eccentricity

$e = \dfrac{5}{3}$
Length of latus rectum

$=$

$\displaystyle \frac{2b^{2}}{a}=\frac{2\times 64}{6}=\frac{64}{3}$

Find the coordinates of the foci, the vertices, the length of major axis, the minor axis, the eccentricity and the length of the latus rectum of the ellipse $\displaystyle \frac{x^{2}}{36} +\frac{y^{2}}{16} = 1.$

Given equation of ellipse is

$\displaystyle \frac{x^{2}}{36} +\frac{y^{2}}{16} = 1$
On comparing the given equation with

$\displaystyle \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}= 1$ , we get

$a=6, b=4$
Since,

$a>b$ ,therefore the major axis is along the

$x$ -axis while the minor axis is along the

$y$ -axis.
Length of major axis

$= 2a = 12$
Length of minor axis

$= 2b = 8$
Eccentricity

$\displaystyle e = \sqrt{1-\frac{b^{2}}{a^{2}}} = \sqrt{\frac{36 -16}{36}}= \frac{\sqrt{20}}{6}=\cfrac{\sqrt{5}}{3}$

Coordinates of the foci are

$\displaystyle \left ( 2\sqrt{5},0 \right )\,$ and

$\left ( -2\sqrt{5},0 \right )$
The coordinates of the vertices are

$(6, 0)$ and

$(-6, 0)$
Length of latus rectum =

$\displaystyle \frac{2b^{2}}{a}= \frac{2 \times 16}{6}= \frac{16}{3}$

Find the equation of the parabola that satisfies the following conditions: Vertex $(0, 0)$ passing through $(5, 2)$ and symmetric with respect to $y$ - axis

Since the vertex is

$(0, 0)$ and the parabola is symmetric about the

$y$ -axis. Equation of the parabola is either of the form

$\displaystyle x^{2} = 4ay$ or

$\displaystyle x^{2} = -4ay$
The parabola passes through point

$(5, 2)$ which lies in the first quadrant
Therefore, the equation of the parabola is of the form

$\displaystyle x^{2} = 4ay$
Point

$(5, 2)$ must satisfy the equation

$\displaystyle x^{2}= 4ay$

$\displaystyle \therefore \left ( 5 \right )^{2}= 4\times a\times 2$

$\Rightarrow 25= 8a$

$\Rightarrow \displaystyle a=\frac{25}{8}$
Thus, the equation of the parabola is

$\displaystyle x^{2}= 4\left ( \frac{25}{8} \right )y$

$\displaystyle 2x^{2}= 25y$

Find the equation of the hyperbola satisfying the give conditions: Vertices $\displaystyle \left ( 0, \pm 5 \right )$ foci $\displaystyle \left ( 0, \pm 8 \right )$

We have vertices

$\displaystyle \left ( 0, \pm 5 \right )$ foci

$\displaystyle \left ( 0, \pm 8 \right )$
Here the vertices are on the

$y$ -axis
Therefore, the equation of the hyperbola is of the form

$\displaystyle \frac{y^{2}}{a^{2}}-\frac{x^{2}}{b^{2}}= 1$
Since the vertices are

$\displaystyle \left ( 0, \pm 5 \right )\Rightarrow a = 5$
And the foci are

$\displaystyle \left ( 0, \pm 8 \right )\Rightarrow ae = 8$
We know that

$\displaystyle b^{2}= a^2(e^2-1)=a^2e^2-a^2=64-25=39$
Thus the equation of the hyperbola is

$\displaystyle \frac{y^{2}}{25}-\frac{x^{2}}{39}= 1$

Find the coordinates of the foci, the vertices the eccentricity and the length of latus rectum of the hyperbola $\displaystyle 9y^{2}-4x^{2}= 36$

The given equation is

$\displaystyle 9y^{2}-4x^{2}= 36$
It can be written as

$\displaystyle 9y^{2}-4x^{2}= 36$

$\displaystyle \frac{y^{2}}{4}-\frac{x^{2}}{9}= 1$

$\displaystyle \frac{y^{2}}{2^{2}}-\frac{x^{2}}{3^{2}}= 1 ...(1)$
On comparing equation (1) with the standard equation of hyperbola
i.e.,

$\displaystyle \frac{y^{2}}{a^{2}}-\frac{x^{2}}{b^{2}}= 1$
we obtain

$a = 2$ and

$b = 3$
We know that

$\displaystyle a^{2}+b^{2}= c^{2},$ where

$c=ae$

$\displaystyle \therefore c^{2}= 4 + 9 = 13$

$\displaystyle \Rightarrow c = \sqrt{13}$
Therefore, the coordinates of the foci are

$\displaystyle \left ( 0, \pm \sqrt{13} \right )$
The coordinates of the vertices are

$\displaystyle \left ( 0, \pm 2 \right )$
Eccentricity

$e$

$\displaystyle = \frac{c}{a}=\frac{\sqrt{13}}{2}$
Length of latus rectum

$=$

$\displaystyle \frac{2b^{2}}{a}=\frac{2\times 9}{2}= 9$

Find the length of major axis, the eccentricity the latus rectum, the coordinate of the centre, the foci, the vertices and the equation of the directrices of following ellipse:
$\displaystyle 16x^{2}+y^{2}= 16.$

The given equation is

$\displaystyle 16x^{2}+y^{2}= 16$
It can be written as

$\displaystyle 16x^{2}+y^{2}= 16$

$\displaystyle \frac{x^{2}}{1}+\frac{y^{2}}{16}= 1$

$\displaystyle \frac{x^{2}}{1^{2}}+\frac{y^{2}}{4^{2}}= 1 ...(1)$
Herethe denominator of

$\displaystyle \frac{y^{2}}{4^{2}}$ is greater than the denominator of

$\displaystyle \frac{x^{2}}{1^{2}}$
Therefore, the major axis is along the

$y$ -axis while the minor axis is along the

$x$ -axis.
On comparing equation (1) with

$\displaystyle \frac{x^{2}}{b^{2}}+\frac{y^{2}}{a^{2}}= 1$ , we obtain

$b = 1$ and

$a = 4$

$\displaystyle \therefore ae=c = \sqrt{a^{2}-b^{2}}=\sqrt{16 - 1}=\sqrt{15}$
Therefore, the coordinates of the foci are

$\displaystyle \left ( 0, \pm \sqrt{15} \right )$
The coordinates of the vertices are

$\displaystyle \left ( 0, \pm 4 \right )$
Length of major axis

$= 2a = 8$
Length of minor axis

$= 2b = 2$
Eccentricity

$e =$

$\displaystyle \frac{c}{a}=\frac{\sqrt{15}}{4}$
Length of latus rectum

$=$

$\displaystyle \frac{2b^{2}}{a}=\frac{2\times 1}{4}=\frac{1}{2}$

Find the coordinates of the foci, the vertices the eccentricity and the length of the latus rectum of the hyperbola $\displaystyle 5y^{2}-9x^{2}= 36$

The given equation is

$\displaystyle 5y^{2}-9x^{2}= 36$

$\displaystyle \Rightarrow$

$\displaystyle \frac{y^{2}}{\left ( \frac{36}{5} \right )}-\frac{x^{2}}{4}= 1$

$\displaystyle \Rightarrow \frac{y^{2}}{\left ( \frac{6}{\sqrt{5}} \right )^{2}} - \frac{x^{2}}{2^{2}} = 1 ...(1)$
On comparing equation (1) with the standard equation of hyperbola

i.e.,

$\displaystyle \frac{y^{2}}{a^{2}}-\frac{x^{2}}{b^{2}}= 1$ ,
we obtain

$a = \displaystyle \frac{6}{\sqrt{5}}$ and

$b = 2$
We know that

$\displaystyle a^{2}+ b^{2}= c^{2},$ where

$c=ae$

$\displaystyle \therefore c^{2}=\frac{36}{5}+ 4 = \frac{56}{5}$

$\displaystyle \Rightarrow c = \sqrt{\frac{56}{5}}= \frac{2\sqrt{14}}{\sqrt{5}}$
Therefore, the coordinates of the foci are

$\displaystyle \left ( 0, \pm \frac{2\sqrt{14}}{\sqrt{5}} \right )$
The coordinates of the vertices are

$\displaystyle \left ( 0, \pm \frac{6}{\sqrt{5}} \right )$
Eccentricity

$e =$

$\displaystyle \frac{c}{a}=\frac{\left ( \frac{2\sqrt{14}}{\sqrt{5}} \right )}{\left ( \frac{6}{\sqrt{5}} \right )}=\frac{\sqrt{14}}{3}$
Length of latus rectum

$=$

$\displaystyle \frac{2b^{2}}{a}=\frac{2\times 4}{\left ( \frac{6}{\sqrt{5}} \right )}= \frac{4\sqrt{5}}{3}$

Find the equation of the hyperbola satisfying the given conditions: Foci $\displaystyle \left ( \pm 3\sqrt{5}, 0 \right )$ the latus rectum is of length $8$

Here the foci are on the

$x$ -axis
Therefore, the equation of the hyperbola is of the form

$\displaystyle \frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}= 1$
Since the foci are

$\displaystyle \left ( \pm 3\sqrt{5}, 0 \right )\Rightarrow ae= c = \displaystyle \pm 3\sqrt{5}$
Length of latus rectum

$= 8$

$\displaystyle \Rightarrow \frac{2b^{2}}{a}= 8$

$\displaystyle \Rightarrow$

$\displaystyle b^{2}= 4a$
We know that

$\displaystyle a^{2}+b^{2}= c^{2}$

$\displaystyle \therefore a^{2}+4a = 45$

$\displaystyle \Rightarrow a^{2}+4a - 45 = 0$

$\displaystyle \Rightarrow a^{2}+ 9a - 5a - 45 = 0$

$\displaystyle \Rightarrow (a + 9) (a - 5) = 0$

$\displaystyle \Rightarrow a = -9, 5$
Since a in non-negative

$a = 5$

$\displaystyle \therefore b^{2}= 4a = 4\times 5 = 20$
Thus the equation of the hyperbola is

$\displaystyle \frac{x^{2}}{25}-\frac{y^{2}}{20}= 1$

A rod of length $12$ cm moves with it ends always touching the coordinate axes. Dertermine the equation of the locus of a point $P$ on the rod which is $3$ cm from the end in contact with the $x$ -axis

Let

$AB$ be the rod making an angle

$\displaystyle \theta$ with positive direction of

$x$ -axis and

$P (x, y)$ be the point on it such that

$AP= 3cm$

Now,

$PB = AB - AP = (12 - 3) cm = 9 cm$

$\displaystyle \left (AB = 12 cm \right)$

Draw

$\displaystyle PQ \perp OY$ and

$\displaystyle PR\perp OX$

$\displaystyle \bigtriangleup PBQ$ ,

$\displaystyle \cos \theta =\dfrac{PQ}{PB}= \dfrac{x}{9}$

$\displaystyle \bigtriangleup PRA$ ,

$\displaystyle \sin \theta =\frac{PR}{PA}= \frac{y}{3}$

Since

$\displaystyle \sin ^{2}\theta +\cos ^{2}\theta = 1$

$\Rightarrow \displaystyle \left ( \dfrac{y}{3} \right )^{2}+\left ( \dfrac{x}{9} \right )^{2}= 1$

$\Rightarrow \displaystyle \dfrac{x^{2}}{81}+\dfrac{y^{2}}{9}= 1$

Thus the equation of the locus of point

$P$ on the rod is

$\displaystyle \dfrac{x^{2}}{81}+\dfrac{y^{2}}{9}= 1$

Find the equation of the hyperbola satisfying the give conditions: Foci $\displaystyle \left ( 0, \pm 13 \right )$ the conjugate axis is of length $24$

It is given that, foci

$\displaystyle \left ( 0, \pm 13 \right ),$ the conjugate axis is of length

$24$
Here the foci are on the

$y$ -axis.
Therefore, the equation of the hyperbola is of the form

$\displaystyle \frac{y^{2}}{a^{2}}-\frac{x^{2}}{ b^{2}}= 1$
Since the foci are

$\displaystyle \left ( 0, \pm 13 \right )\Rightarrow ae=c = 13$
Since the length of the conjugate axis is

$24$ ,

$\Rightarrow 2b = 24\Rightarrow b = 12$
We know that

$\displaystyle a^{2}+b^{2}= c^2$

$\displaystyle \therefore a^{2}+12^{2}=13^{2}$

$\displaystyle \Rightarrow a^{2}=169 - 144 = 25$
Thus the equation of the hyperbola is

$\displaystyle \frac{y^{2}}{25}-\frac{x^{2}}{144}= 1$

Find the center and radius of the circle whose equation is given by ${(x-2)}^{2}+{(y+5)}^{2}=13$

An equation of the circle with center

$(h,k)$ and radius

$r$ is

$(x-h)^{ 2 }+(y-k)^{ 2 }=r^{ 2 }$

So, comparing

$(x-2)^2+(y+5)^2=13$ that is

$(x-2)^2+(y-(5))^2=13$ with the above equation of circle we get:

$h=2$ ,

$k=-5$ and

$r=\sqrt { 13 }$

Therefore, center of the circle is

$(2,-5)$ and radius of the circle is

$r=\sqrt { 13 }$ .

Find the center and radius of the circle whose equation is given by ${(5-x)}^{2}+{(y-1)}^{2}=4$

An equation of the circle with center

$(h,k)$ and radius

$r$ is

$(x-h)^{ 2 }+(y-k)^{ 2 }=r^{ 2 }$

So, comparing

$(5-x)^2+(y-1)^2=4$ that is

$(x-5)^2+(y-1)^2=4$ with the above equation of circle we get:

$h=5$ ,

$k=1$ and

$r=2$

Therefore, center of the circle is

$(5,1)$ and radius of the circle is

$r=2$ .

Find the equation of the hyperbola whose Transverse and Conjugate axes are the $x$ and $y$ axes respectively, given that the length of conjugate axis is $5$ and distance between the foci is $13$ .

Let equation of hyperbola be

$\dfrac{x^2}{a^2} - \dfrac{y^2}{b^2} = 1$ ...... (i)
According to question,

$2b = 5 \Rightarrow b = 5/2$

$2ae = 13 \Rightarrow ae = 13/2$
Also,

$b^2 = a^2 e^2 - a^2$

$\left( \dfrac{5}{2} \right )^2 = \left ( \dfrac{13}{2} \right )^2 - a^2$

$\Rightarrow a^2 = \left( \dfrac{13}{2} \right )^2 - \left ( \dfrac{5}{2} \right )^2$

$\Rightarrow a^2 = 36$
Substituting values of

$a^2$ and

$b^2$ in equation (i),

$\dfrac{x^2}{36} - \dfrac{y^2}{\dfrac{25}{4}} = 1$

$\Rightarrow \dfrac{x^2}{36} - \dfrac{4y^2}{25} = 1$

$\Rightarrow \dfrac{25x^2 - 144y^2}{900} = 1 \Rightarrow 25x^2 - 144y^2 = 900$

From the following information, find the equation of Hyperbola and the equation of its Transverse Axis:
Focus : $(-2, 1),$ Directrix : $2x - 3y + 1, e = \dfrac{2}{\sqrt 3}$

The focus of the hyperbola is (-2, 1), the corresponding directrix is

$2x - 3y + 1 = 0$ and

$e = \dfrac{2}{\sqrt 3}$

Let P(x, y) be any point on the hyperbola and |MP| be the perpendicular distance from P to the directrix, then by definition of hyperbola

$|FP| = e|MP|$

$\sqrt{(x + 2)^2 + (y - 1)^2} = \dfrac{2}{\sqrt 3} . \dfrac{2x - 3y + 1}{\sqrt{(2)^2 + (-3)^2}}$

$\Rightarrow x^2 + 3x + 4 + y^2 - 2y + 1 = \dfrac{4}{39} (4x^2 + 9y^2 + 1 - 12 xy - 6y + 4x)$

$\Rightarrow 39x^2 + 156 x + 156 + 39y^2 - 78y + 39 = 16x^2 + 36y^2 + 4 - 48 xy - 24 y + 16 x$

$\Rightarrow 23x^2 + 48xy + 3y^2 + 140x - 54y + 191 = 0$
Which is the required equation of the hyperbola.

Transverse axis

$\bot$ directrix
Equation of transverse axis be

$3x + 2y + k = 0$

Focus (-2, 1) lies on transverse axis

$\therefore 3 \times (-2) + 2 \times 1 + k = 0$

$-4 + k = 0$

$\Rightarrow k = 4$

$\therefore$ Equation of transverse axis is

$3x + 2y + 4 = 0$

Find the eccentricity, foci, length of the Latus rectum and the equations of directrices of the ellipse $9x^2 + 16y^2 = 144$ .

Given equation can be written in standard form as

$\dfrac{x^2}{16}+\dfrac{y^2}{9}=1$

$\Rightarrow a^2=16, b^2=9\Rightarrow a=4, b=3$

So eccentricity

$,e=\sqrt{1-\dfrac{b^2}{a^2}}=\sqrt{1-\dfrac{9}{16}}=\dfrac{\sqrt 7}{4}$

Thus foci

$=(\pm ae,0)=(\pm \sqrt 7,0)$

Length of latus rectum

$=\dfrac{2b^2}{a}=\dfrac{2\cdot 9}{4}=\dfrac{9}{2}$

And equation of directrices are

$x=\pm \dfrac{a}{e}=\pm \dfrac{16}{\sqrt 7}$

If the abscissae of points $A, B$ are the roots of the equation $x^{2} + 2ax - b^{2} = 0$ and ordinates of $A, B$ are roots of $y^{2} + 2py - q^{2} = 0$ , then find the equation of a circle for which $\overline {AB}$ is a diameter

Let

$x_{1},x_{2}$ be the roots of the equation

$x^{2}+2ax-b^{2}=0$ . Then

$x_{1}+x_{2}=-2a$ and

$(x_{1}-x_{2})=\sqrt{(x_{1}+x_{2})^{2}-4x_{1}x_{2}}=\sqrt{4a^{2}+4b^{2}}$
Similarly
Let

$y_{1},y_{2}$ be the roots of the equation

$x^{2}+2px-q^{2}=0$ . Then

$y_{1}+y_{2}=-2p$ and

$(y_{1}-y_{2})=\sqrt{(y_{1}+y_{2})^{2}-4y_{1}y_{2}}=\sqrt{4p^{2}+4q^{2}}$

Hence the centre of the circle with diameter AB is

$C=\left(\dfrac{x_{1}+x_{2}}{2},\dfrac{y_{1}+y_{2}}{2}\right)$

$=\left(\dfrac{-2a}{2},\dfrac{-2p}{2}\right)$

$=(-a,-p)$

And the radius of the circle is given by

$\dfrac{AB}{2}=0.5\sqrt{(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}}$

$=0.5\sqrt{4a^{2}-4b^{2}+4p^{2}-4q^{2}}$

$=\sqrt{a^{2}+p^{2}-b^{2}-q^{2}}$
Hence the equation of the circle is

$(x+a)^{2}+(y+p)^{2}=a^{2}+p^{2}-b^{2}-q^{2}$

$x^{2}+y^{2}+2ax+2py+a^{2}+p^{2}=a^{2}+p^{2}-b^{2}-q^{2}$

$x^{2}+y^{2}+2ax+2py+b^{2}+q^{2}=0$

Find the equation of the parabola whose focus is $(-2, 3)$ and directrix is the line $2x+3y-4=0$ . Also find the length of the Latus rectum and equation of the axis of parabola.

In parabola directrix is at $2a$ distance from focus

So $2a=d(P,L)$

$=\dfrac { |a{ x }_{ 1 }+b{ y }_{ 1 }+c| }{ \sqrt { { a }^{ 2 }+{ b }^{ 2 } } }$

$=\dfrac { |2\times (-2)+3\times 3-4| }{ \sqrt { { 2 }^{ 2 }+{ 3 }^{ 2 } } } =\dfrac { 1 }{ \sqrt { 5 } }$

So $4a=\dfrac { 2 }{ \sqrt { 5 } }$

So length of latus rectum $=4a=\dfrac { 2 }{ \sqrt { 5 } }$ units

The axis is perpendicular to directrix

For $ax+by+c=0$ perpendicular is of the form $bx-ay+k=0$

So axis is of the form $3x-2y+k=0$

As the focus lies on the axis $3(-2)-2(3)+k=0$

Hence $k=12$

So axis is $3x-2y+12=0$

Find the eccentricity and length of latus rectum of the ellipse $9{ x }^{ 2 }+16{ y }^{ 2 }-36x+32y-92=0$ .

We have

$9x^2+16y^2-36x+32y-92=0$

$\Rightarrow 9(x^2-4x)+16(y^2+2y)=92$

$\Rightarrow 9(x^2-4x+4)+16(y^2+2y+1)=92+36+16=144$

$\Rightarrow 9(x-2)^2+16(y+1)^2=144$

$\Rightarrow \dfrac{(x-2)^2}{16}+\dfrac{(y+1)^2}{9}=1$

$\Rightarrow a^2=16, b^2=9$

Thus eccentricity,

$e=\sqrt{1-\dfrac{b^2}{a^2}}=\sqrt{1-\dfrac{9}{16}}=\dfrac{\sqrt 7}{4}$

and length of latus rectum

$=\dfrac{2b^2}{a}=\dfrac{9}{2}$

Find the equation of the ellipse in the standard form whose distance between foci is $2$ and the length of latus rectum is $\dfrac { 15 }{ 2 }$ .

Given distance between foci

$=2ae=2\Rightarrow ae=1$

And length of latus rectum

$=\dfrac{2b^2}{a}=\dfrac{15}{2}$

$\Rightarrow \dfrac{b^2}{a^2}=\dfrac{15}{4a}=\dfrac{15e}{4}$

Now use

$e^2=1-\dfrac{b^2}{a^2}$

$\Rightarrow e^2=1-\dfrac{15e}{4}$

$\Rightarrow 4e^2+15e-4=0$

$\Rightarrow e=\dfrac{1}{4}$

$a=4$ and

$b=\sqrt {15}$

Hence standard equation of ellipse is given by

$\dfrac{x^2}{16}+\dfrac{y^2}{15}=1$

Find the equation to the circle :
Whose radius is a + b and whose centre is (a, - b).

Fact:

Equation of circle with centre

$(h,k)$ and having radius

$r$ is given by,

$(x-h)^2+(y-k)^2=r^2$

Here, centre is

$(a,-b)$ and radius is

$a+b$

hence equation of required circle is given by,

$(x-a)^2+[y-(-b)]^2=(a+b)^2$

$\Rightarrow (x-a)^2+(y+b)^2=a^2+b^2+2ab$

$\Rightarrow x^2-2ax+a^2+y^2+2by+b^2=a^2+b^2+2ab$

$\Rightarrow x^2+y^2-2ax+2by=2ab$

Find the equation to the circle :
Whose radius is 10 and whose centre is ( - 5, - 6).

Fact:

Equation of circle with centre

$(h,k)$ and having radius

$r$ is given by,

$(x-h)^2+(y-k)^2=r^2$

Here, centre is

$(-5,-6)$ and radius is

$10$

Hence equation of required circle is given by,

$[x-(-5)]^2+[y-(-6)]^2=10^2$

$\Rightarrow (x+5)^2+(y+6)^2=100$

$\Rightarrow x^2+10x+25+y^2+12y+36=100$

$\Rightarrow x^2+y^2+10x+12y=39$

Find the equation to the circle :
Whose radius is 3 and whose centre is ( - 1, 2).

Fact:

Equation of circle with centre

$(h,k)$ and having radius

$r$ is given by,

$(x-h)^2+(y-k)^2=r^2$

Here, centre is

$(-1,2)$ and radius is

$3$

hence equation of required circle is given by,

$[x-(-1)]^2+(y-2)^2=3^2$

$\Rightarrow (x+1)^2+(y-2)^2=9$

$\Rightarrow x^2+2x+1+y^2-4y+4=9$

$\Rightarrow x^2+y^2+2x-4y-4=0$

Prove that the sum of the distances from the focus of the points in which a conic is intersected by any circle, whose centre is at a fixed point on the transverse axis, is constant.

The equation to any circle having its center on the traverse axis, say

$\left( R,O \right)$ and radius 'a' will be

${ r }^{ 2 }-2rR\cos { \theta } +{ R }^{ 2 }-{ a }^{ 2 }=0$ .....(2)
Let the equation of the conic be

$\cfrac { l }{ r } =1-e\cos { \theta }$ ....(2)
To get the points of intersection, we have to eliminate

$\theta$ from (1) and (2).
So eliminating

$\theta$ from

$1$ and

$2$ , we get

$\cfrac { e.\left( { r }^{ 2 }+{ R }^{ 2 }-{ a }^{ 2 } \right) }{ 2Rr } =\cfrac { r-1 }{ r }$

$e{ r }^{ 2 }-2Rr+e\left( { R }^{ 2 }-{ a }^{ 2 } \right) +2Rl=0$
Let

${ r }_{ 1 }$ and

${ r }_{ 2 }$ be its roots, then

${ r }_{ 1 }+{ r }_{ 2 }=\cfrac { 2R }{ e }$
which is a constant

A straight line drawn through the common focus S' of a number of conics meets them in the points $P_1 , P_2 , .... ;$ on it is taken a point Q such that the reciprocal of SQ is equal to the sum of the reciprocals of $SP_1 , SP_2 , ...$ Prove that the locus of Q is a conic section whose focus is O, and show that the reciprocal of its latus rectum is equal to the sum of the reciprocals of the latera recta of the given conics.

Equation of a conic in polar form is

$\dfrac { l }{ r } =1-e\cos { \theta }$

Let the eccentricities of the conies be ${ e }_{ 1 },{ e }_{ 2 },{ e }_{ 3 }....$ and latustrecum ${ l }_{ 1 },l_{ 2 },{ l }_{ 3 }....$ . Let the axes be inclined at angle ${ \alpha }_{ 1 },\alpha _{ 2 },{ \alpha }_{ 3 }....$ then

$\dfrac { l }{ { SP }_{ 1 } } =1-{ e }_{ 1 }\cos { (\theta -{ \alpha }_{ 1 }) } \\ \Rightarrow \dfrac { 1 }{ { SP }_{ 1 } } =\dfrac { 1-{ e }_{ 1 }\cos { (\theta -{ \alpha }_{ 1 }) } }{ l }$

Similarly $\dfrac { l }{ { SP }_{ 2 } } =1-{ e }_{ 2 }\cos { (\theta -{ \alpha }_{ 2 }) }$

$\Rightarrow \dfrac { 1 }{ { SP }_{ 2 } } =\dfrac { 1-{ e }_{ 2 }\cos { (\theta -{ \alpha }_{ 2 }) } }{ l }$

Given $\dfrac { 1 }{ SQ } =\dfrac { 1 }{ { SP }_{ 1 } } +\dfrac { 1 }{ { SP }_{ 2 } } ......$

$\Rightarrow \dfrac { 1 }{ SQ } =\dfrac { 1-{ e }_{ 1 }\cos { (\theta -{ \alpha }_{ 1 }) } }{ { l }_{ 1 } } +\dfrac { 1-{ e }_{ 2 }\cos { (\theta -{ \alpha }_{ 2 }) } }{ { l }_{ 2 } } ......\\ \Rightarrow \dfrac { 1 }{ SQ } =\left( \dfrac { 1 }{ { l }_{ 1 } } +\dfrac { 1 }{ { l }_{ 2 } } ..... \right) -\left( \dfrac { { e }_{ 1 } }{ { l }_{ 1 } } \cos { (\theta -{ \alpha }_{ 1 }) } +\dfrac { { e }_{ 2 } }{ { l }_{ 2 } } \cos { (\theta -{ \alpha }_{ 2 }) } ...... \right)$

This is equation of form $\dfrac { 1 }{ r } =\dfrac { 1 }{ l } -\dfrac { e }{ l } \cos { (\theta -\alpha ) }$

Hence it represents a conic with focus $S'$ and latusrectum $L$

where $\dfrac { 1 }{ L } =\dfrac { 1 }{ { l }_{ 1 } } +\dfrac { 1 }{ { l }_{ 2 } } +\dfrac { 1 }{ { l }_{ 3 } } .....$

Hence proved

Find the equation to the circle :
Whose radius is $\sqrt {a^2 - b^2}$ and whose center is (-a, -b) .

Fact:

Equation of circle with centre

$(h,k)$ and having radius

$r$ is given by,

$(x-h)^2+(y-k)^2=r^2$

Here, centre is

$(-a,-b)$ and radius is

$\sqrt{a^2-b^2}$

hence equation of required circle is given by,

$[x-(-a)]^2+[y-(-b)]^2=(\sqrt{a^2-b^2})^2$

$\Rightarrow (x+a)^2+(y+b)^2=a^2-b^2$

$\Rightarrow x^2+2ax+a^2+y^2+2by+b^2=a^2-b^2$

$\Rightarrow x^2+y^2+2ax+2by+2b^2=0$

Find the eccentricity of an ellipse, if its latus rectum be equal to one half its minor axis.

$\textbf{Step-1: Finding relation between a and b}$

$\text{Latus rectum of ellipse is half of the minor axis}$

$\Rightarrow \text{L.R} = \dfrac{{2{b^2}}}{a} = {b}$

$\Rightarrow \dfrac{b}{a} = \dfrac{1}{2}$ $\dots(1)$

$\textbf{Step-2: Eccentricity of ellipse is given as-}$

$e = \sqrt {1 - {{\left( {\dfrac{b}{a}} \right)}^2}}$ $\dots(2)$

$\textbf{Step-3: Putting values (1) in (2)}$

$e = \sqrt {1 - {{\left( {\dfrac{b}{a}} \right)}^2}}$

$= \sqrt {1 - {{\left( {\dfrac{1}{2}} \right)}^2}}$

$= \sqrt {1 - \dfrac{1}{{4}}}$

$= \sqrt {\dfrac{{3}}{{4}}}$

$\textbf{ So, the eccentricity of ellipse is given by}$ $\mathbf{{\dfrac{{\sqrt3}}{{2}}}}.$

Find the equation to the parabola with focus (a, b) and directrix $\frac {x}{a}+ \frac {y}{b} = 1 .$

Let

$P(x,y)$ be a point on the parabola with the directrix M:

$\dfrac{x}{a} +\dfrac{y}{b} =1$ and focus S:(a,b)

we know that ,

$SP^2=PM^2$

$(x-a)^2+(y-b)^2$ =

$\dfrac{(\dfrac{x}{a}+\dfrac{y}{b}-1)}{\dfrac{1}{a^2}+\dfrac{1}{b^2}}^2$

After rearranging the terms in both sides,we get

$a^2x^2+b^2y^2+a^2y^2+b^2x^2-2a^3x-2yba^2-2axb^2-2yb^3+a^4+2a^2b^2+b^4$ =

$a^2y^2+b^2x^2+a^2b^2+2abxy-2b^2xa-2a^2yb$

After simplifying both sides,we get

$(ax-by)^2-2a^3x-2b^3y+a^4+a^2b^2+b^4=0$

Find the equation to the ellipses, whose centres are the origin, whose axes are the axes of coordinates, and which pass through $(\alpha)$ the points $(2, 2)$ , and $(3, 1)$ and $(\beta)$ the points $(1, 4)$ and $(-6, 1)$ .

We will have general equation of ellipse for centre at

$(0,0)$

$\dfrac { x^{ 2 } }{ a^{ 2 } } +\dfrac { y^{ 2 } }{ b^{ 2 } } =1$

Putting

$(2,2),(3,1)$

$\dfrac { 4 }{ a^{ 2 } } +\dfrac { 4 }{ b^{ 2 } } =1$

$\dfrac { 9 }{ a^{ 2 } } +\dfrac { 1 }{ b^{ 2 } } =1$

We have,

$\dfrac { 1 }{ a^{ 2 } } =\dfrac { 3 }{ 32 } ,\dfrac { 1 }{ b^{ 2 } } =\dfrac { 5 }{ 32 }$

We get,

$3x^2+5y^2=32$

For second part,

Putting

$(1,4),(-6,1)$

$\dfrac { x^{ 2 } }{ a^{ 2 } } +\dfrac { y^{ 2 } }{ b^{ 2 } } =1$

$\dfrac { 1 }{ a^{ 2 } } +\dfrac { 16 }{ b^{ 2 } } =1$

$\dfrac { 36 }{ a^{ 2 } } +\dfrac { 1 }{ b^{ 2 } } =1$

We have

$\dfrac { 1 }{ a^{ 2 } } =\dfrac { 3 }{ 115 } ,\dfrac { 1 }{ b^{ 2 } } =\dfrac { 7 }{ 115 }$

We get,

$3x^2+7y^2=115$

Find the equation to the parabola with focus (3, -4) and directrix 6x - 7y + 5 = 0.

Given the focus of the parabola as S:

$(3,-4)$ and directrix M:

$6x-7y+5$ =0.

Let P

$(x,y)$ be the point on the parabola,such that

$SP^2$ =

$PM^2$ .

$(x-3)^2+(y+4)^2$ =

$\dfrac{(6x-7y+5)^2}{6^2+7^2}$

on simplifying both sides,we get

$(7x+6y)^2-216x-294x-60x+288y+492y+70y+(9\times36+49\times9+49\times16+36\times16)-25$ =

$0$

After adding alike terms,we get

$(7x+6y)^2-570x+750y+2100$ =

$0$

Therefore the required equation of the parabola is

$(7x+6y)^2-570x+750y+2100$ =

$0$ .

What are represented by the equation $x^3 + y^3 +(x+y)(xy-ax-ay) = 0 .$

${ x }^{ 3 }+{ y }^{ 3 }+(x+y)(xy-ax-ay)=0$

Factorising the equation

$(x+y)({ x }^{ 2 }+{ y }^{ 2 }-xy)+(x+y)(xy-ax-ay)=0\\ (x+y)({ x }^{ 2 }+{ y }^{ 2 }-xy+xy-ax-ay)=0$

$(x+y)({ x }^{ 2 }+{ y }^{ 2 }-ax-ay)=0$

Then, either

$(x+y)=0$ or

$({ x }^{ 2 }+{ y }^{ 2 }-ax-ay)=0$

$x+y=0$ represents a straight line passing through origin.

${ x }^{ 2 }+{ y }^{ 2 }-ax-ay=0$

represents a circle with centre

$\left( \dfrac { a }{ 2 } ,\dfrac { a }{ 2 } \right)$ and radius

$\dfrac { a }{ \sqrt { 2 } }$

So, the combined equation represents a circle and a straight line.

A point moves so that the sum of the squares of its distances from $n$ fixed points is given. Prove that its locus is a circle.

Let the points be

$(x_1,y_1),(x_2,y_2),(x_3,y_3)....(x_n,y_n)$ and let the given sum of distances be t

The point is given by (x,y)

$(x-x_1)^2+(y-y_1)^2+(x-x_2)^2+(y-y_2)^2+(x-x_3)^2+(y-y_3)^2+...=t$

$\Rightarrow \ n x^2 +ny^2-2(x_1+x_2+x_3+...x_n)x -2(y_1+y_2+y_3+...y_n)y+$

$(x_1^2+x_2^2+x_3^2+...)+(y_1^2+y_2^2+y_3^2...)=t$

$\Rightarrow x^2+y^2-\cfrac{2}{n}(x_1+x_2+x_3+....)-\cfrac{2}{n}(y_1+y_2+y_3+....)+\cfrac{(x_1+x_2+x_3+...)^2}{n^2}+\cfrac{(y_1+y_2+y_3+...)^2}{n^2} \\ = \cfrac{t}{n}- \cfrac{(x_1^2+x_2^2+x_3^2+...)}{n}-\cfrac{(y_1^2+y_2^2+y_3^2+...)}{n}+\cfrac{(x_1+x_2+x_3+...)^2}{n^2}+\cfrac{(y_1+y_2+y_3...)^2}{n^2}$

$\Rightarrow \left(x-\cfrac{(x_1+x_2+x_3+...)}{n}\right)^2+\left(y-\cfrac{(y_1+y_2+y_3+...)}{n}\right)^2=\cfrac{t}{n}-\cfrac{(x_1^2+x_2^2+...)}{n}-\cfrac{(y_1^2+y_2^2+..)}{n}+ \\ \cfrac{(x_1+x_2+...)^2}{n^2}+\cfrac{(y_1+y_2+...)^{2}}{n^2}$

This is an equation of circle with centre at

$\left(\cfrac{x_1+x_2+x_3+...}{n},\cfrac{y_1+y_2+y_3+...}{n}\right)$

Hence proved, the locus of the point is a circle.

Trace the following central conics.
$x^2 + xy + y^2 + x + y + 1=0 .$

${ x }^{ 2 }+xy+{ y }^{ 2 }+x+y+1=0$

General eqn of a conic :

${ ax }^{ 2 }+2hxy+{ by }^{ 2 }+2gx+2fy+c=0$

Comparing both equations,

$a=1,\quad 2h=1,\quad b=1,\quad 2g=1,\quad 2f=1,c=1$

${ h }^{ 2 }=1/4$ and

$ab=1$

${ h }^{ 2 }<ab$

Hence, conic is an ellipse.

If ${ a }^{ 2 }+{ b }^{ 2 }=1$ , and ${ x }^{ 2 }+{y}^{2}=1$ , show that $ax+by< 1$ .

Correct relation is

$ax + by \leq 1$

Solving this question using parametric equation of circle.

Since

$a^2 + b^2 = 1$ and

$x^2 + y^2 = 1$ both are equations of circle so let say

$a = \cos \theta$ and

$x = \cos \alpha$ then

$b = \sin \theta$ and

$y = \sin \alpha$

$ax + by = \{\cos \theta\} \{\cos \alpha\} + \{\sin \theta\} \{\sin \alpha\}$

$=\cos \{ \theta - \alpha\}$

And as we know

$\cos \{ \theta - \alpha\} \leq 1$ so

$ax + by \leq 1$ .

Show that the latus rectum of the parabola $( a^2 + b^2) (x^2 + y^2) = (bx + ay - ab)^2$ is $2ab \div \sqrt{a^2 + b^2} .$

Given equation of the parabola:

$(a^2+b^2)(x^2+y^2)=(bx+ay-ab)^2$

Standard equation of parabola is of the form:

$(distance\, from\, Axis)^2=\pm(Latus\, Rectum)\times(distance\, from\, tangent\, at\, Vertex)...eqnI$ , where Axis and tangent at Vertex are equations of some

$mutually\, perpendicular$ lines.

$(a^2+b^2)(x^2+y^2)=(bx+ay-ab)^2$

$\Rightarrow a^2x^2+a^2y^2+b^2x^2+b^2y^2=b^2x^2+a^2y^2+a^2b^2+2abxy-2a^2by-2ab^2x$

$\Rightarrow a^2x^2+b^2y^2-2abxy=a^2b^2-2a^2by-2ab^2x$

$\Rightarrow (ax-by)^2=-ab(2bx+2ay-ab)$

$\Rightarrow \left(a^2+b^2\right)\times\left(\dfrac{ax-by}{\sqrt{a^2+b^2}}\right)^2=-ab\times2\left(\sqrt{a^2+b^2}\right)\times\left(\dfrac{2bx+2ay-ab}{\sqrt{\left(2b\right)^2+\left(2a\right)^2}}\right)$

$\Rightarrow \left(\dfrac{ax-by}{\sqrt{a^2+b^2}}\right)^2=-\dfrac{2ab}{\left(\sqrt{a^2+b^2}\right)}\times\left(\dfrac{2bx+2ay-ab}{\sqrt{\left(2b\right)^2+\left(2a\right)^2}}\right)...eqnII$

Comparing

$eqnI\, and\, eqnII$ gives,

$Latus\,Rectum=\dfrac{2ab}{\sqrt{a^2+b^2}}$

Find the eccentricity, coordinates of foci, length of latus recturm and equation of directrix of the hyperbola $3{ x }^{ 2 }-{ y }^{ 2 }=4$ .

Equation of the given hyperbola in standard form is:

$\dfrac{x^2}{\dfrac{4}{3}} - \dfrac{y^2}{4} = 1$

Comparing with the form:

$\dfrac{x^2}{a^2} - \dfrac{y^2}{b^2} = 1$

we get:

$a^2 = \dfrac43, \ b^2 = 4$

Thus, eccentricity:

$e = \sqrt{1+\dfrac{b^2}{a^2}} = 2$

Foci are at:

$(\pm ae,0) = (\pm \dfrac{4}{\sqrt{3}},0)$

Length of latus rectum:

$\dfrac{2b^2}{a} = 4\sqrt{3}$

Equation of directrix:

$x = \pm \dfrac{a}{e} \Rightarrow x = \pm \dfrac{1}{\sqrt{3}}$

Find the coordinates of the point of intersection of the axis and the directrix of the parabola whose focus is $(3,3)$ and directrix is $3x-4y=2$ . Put your answer only as the length of the latus-rectum.

Parabola with focus :

$(3,3)$

Directrix ;

$3x-4y=2 ................(1)$

$=>y=\cfrac { 3 }{ 4 } x-\cfrac { 1 }{ 2 } \quad ................(2)$

Slope of Direction

$=>{ m }_{ 1 }=\cfrac { 3 }{ 4 }$

Slope of axis must be

${ m }_{ 2 }=-\cfrac { 1 }{ { m }_{ 1 } } \quad =>{ m }_{ 2 }=\cfrac { -4 }{ 3 } \quad (as\quad axis\quad is\quad \bot \quad to\quad directrix)$

Equation of axis,

$y=-\cfrac { 4 }{ 3 } x+c\quad ...............(3)$

As axis passes through focus,

$(3,3)$ must satisfy equation

$(3)$ ,

$=>3=-\cfrac { 4 }{ 3 } (3)+c$

$=>c=7$

Then equation of axis is,

$3y+4x-21=0 .................(4)$

Point of intersection of axis and directrix, equation

$(2)$ and

$(4)$ ,

$M=>(\cfrac { 18 }{ 5 } ,\cfrac { 11 }{ 5 } )\quad .......................(5)$

$LR= 2\times($ distance between point of intersection of axis and directrix and focus

$)$

$=2\times \sqrt { ({ \cfrac { 18 }{ 5 } -3 })^{ 2 }+({ \cfrac { 11 }{ 5 } -3 })^{ 2 } }$

$=2\times\sqrt { \cfrac { 1 }{ 25 } (9+16) }$

$=2\times\sqrt { \cfrac { 25 }{ 25 } }$

$=2\quad unit\quad length.$

If parabola ${ y }^{ 2 }=4ax$ passes through the point $\left( 9,-12 \right)$ then find the length of latus rectum and coordinates of focus.

$\because\ y^2=4ax\ passes\ through\ (9,-12)$

$(-12)^2=4a(9)$

$a=\dfrac{144}{36}\Rightarrow 4$

$\Rightarrow\ focus\ of\ parabola\ be\ (a,0)$

$\therefore\ focus\ =(4,0)$

Length of latus Rectum

$= 4a$

$=4\times 4$

$=\ 16\ Units$

A straight line and a point not lying on it are given on a plane. Find the set of points which are equidistant from the given straight line and the given point.

The set of points which are equidistant from a given line and a given point form a parabola with the point as its focus and the line as its directrix

Find the equation of a circle with centre $(2,2)$ and passes through the point $(4,5)$ .

${\mathbf{Step}}\;1:\;{\mathbf{Finding}}\;{\mathbf{the}}\;{\mathbf{radius}}\;{\mathbf{of}}\;{\mathbf{the}}\;{\mathbf{circle}}$

${\text{Centre}}: \left( {2,2} \right)$

${\text{Circle passes through }}\left( {4,5} \right).$

$\Rightarrow {\text{Radius of the circle}} = {\text{ Distance between }}\left( {2,2} \right){\text{ and }}\left( {4,5} \right).$

${\text{Therefore}},$

$=\sqrt{ (4-2)^2 + (5-2)^2 }$

$= \sqrt{ (4 + 9)}$

$= \sqrt {13}$

${\mathbf{Step}}\;2 :{\mathbf{Finding}}\;{\mathbf{the}}\;{\mathbf{equation}}\;{\mathbf{of}}\;{\mathbf{the}}\;{\mathbf{circle}}$

${\text{We know}},$

${\text{ The equation of the circle is}}:$

${({\text{x}} - {\text{h}})^2} + {\left( {{\text{y }} - {\text{ k}}} \right)^2}{\text{ }} ={{\text{r}}^2}$

${\left( {x - 2} \right)^2} + {\left( {{\text{y}} - 2} \right)^2}= {\left( {\sqrt {13} } \right)^2}$

${{\text{x}}^2} - \text{4x +4} + {{\text{y}}^2} - 4{\text{y}} + 4{\text{ }} = 13$

${{\text{x}}^2} + {{\text{y}}^2} -\text{4x} - 4{\text{ y }} - 5 = 0$

${\mathbf{Hence}},{\mathbf{the}}\;{\mathbf{equation}}\;{\mathbf{of}}\;{\mathbf{the}}\;{\mathbf{circle}}\;{\mathbf{is}}\;{{\boldsymbol{ x^2 + y^2 - 4x - 4y -5 = 0}}}$

The sides of a square are parallel to coordinate axes and it is inscribed in the circle ${x}^{2}+{y}^{2}-2x+4y-93=0$ . Find the coordinates of the vertices of the square.

The given circle is

$(1,-2)$ and

$7\sqrt { 2 }$ . The sides are parallel to axes. Diagonal

$AC$ will be making an angle of

${45}^{o}$ and

$BD$ will make an angle

${135}^{o}$ with

$x-axis$ .

$A$ and

$C$ will lie on

$\dfrac { x-1 }{ \cos { \theta } } =\dfrac { y+2 }{ \sin { \theta } } =\begin{matrix} 7\sqrt { 2 } \\ C \end{matrix},\begin{matrix} -7\sqrt { 2 } \\ A \end{matrix}$
Put

$\theta ={45}^{o}$

$\therefore\quad C$ and

$A$ are

$(8,5)$ and

$(-6,-9)$

$B$ and

$D$ will lie on

$\dfrac { x-1 }{ \cos { \theta } } =\dfrac { y+2 }{ \sin { \theta } } =\begin{matrix} 7\sqrt { 2 } \\ B \end{matrix},\begin{matrix} -7\sqrt { 2 } \\ D \end{matrix}$
Put

$\theta ={135}^{o}$

$\therefore\quad B$ and

$D$ are

$(-6,5)$ and

$(8,-9)$

Find the locus of a point which moves in such a way that the sum of its distances from(4,3) and (4,1) is 5.

Let the moving or variable point be

$P(x,y)$ and the given points be

$A(4,3)$ and

$B(4,1)$

By the conditions of the problem,

$PA+PB=5$

$PA=5-PB$

$\Rightarrow \sqrt { { \left( x-4 \right) }^{ 2 }+{ \left( y-3 \right) }^{ 2 } } =5-\sqrt { { \left( x-4 \right) }^{ 2 }+{ \left( y-1 \right) }^{ 2 } }$

$\Rightarrow { \left( x-4 \right) }^{ 2 }+{ \left( y-3 \right) }^{ 2 }=25+{ \left( x-4 \right) }^{ 2 }+{ \left( y-1 \right) }^{ 2 }-10\sqrt { { \left( x-4 \right) }^{ 2 }+{ \left( y-1 \right) }^{ 2 } }$

$\Rightarrow { y }^{ 2 }-6y+9=25+{ y }^{ 2 }-2y+1-10\sqrt { { \left( x-4 \right) }^{ 2 }+{ \left( y-1 \right) }^{ 2 } }$

$\Rightarrow 10\sqrt { { \left( x-4 \right) }^{ 2 }+{ \left( y-1 \right) }^{ 2 } } =4y+17$

Squaring both sides again

$100\left( { x }^{ 2 }-8x+16+{ y }^{ 2 }-2y+1 \right) ={ \left( 4y+17 \right) }^{ 2 }$

$\Rightarrow 100\left( { x }^{ 2 }+{ y }^{ 2 }-8x-2y+17 \right) =16{ y }^{ 2 }+136y+284$

$\Rightarrow { 100x }^{ 2 }+{ 100y }^{ 2 }-{ 16y }^{ 2 }-800x-200y-136y+1700-284=0$

${ 100x }^{ 2 }+84{ y }^{ 2 }-800x-336y+1411=0$

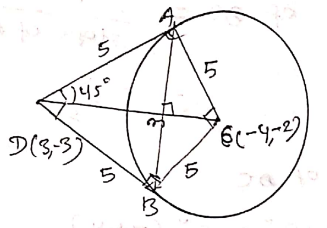
The circle $OAB$ where $O$ is origin and $A, B$ are points on the co-ordinate axes is drawn such that the distances of points $A$ and $B$ from the tangent to the circle at origin are $p$ and $q$ respectively. Prove that the diameter of the circle is $p + q$ and its centre is $\left [\dfrac {1}{2} \sqrt {p(p + q)}, \dfrac {1}{2}\sqrt {q(p + q)}\right ]$ .

Circle

$OAB$ is

$x^{2} + y^{2} - ax - by = 0$
Tangent at

$(0, 0)$ is

$ax + by = 0$

$\therefore p = \dfrac {a^{2}}{\sqrt {(a^{2} + b^{2})}}, q = \dfrac {b^{2}}{\sqrt {(a^{2} + b^{2})}}$

$\therefore p + q = \sqrt {(a^{2} + b^{2})} = diameter\ AB$

$\therefore a^{2} = p \sqrt {(a^{2} + b^{2})} = p(p + q)$ ,

$b^{2} = q(p + q)$

$\therefore$ Centre is

$\left (\dfrac {1}{2}a, \dfrac {1}{2}b\right )$ etc.
922630_1006849_ans_854a5d0b56ea4668ae32a477fbcab381.jpg

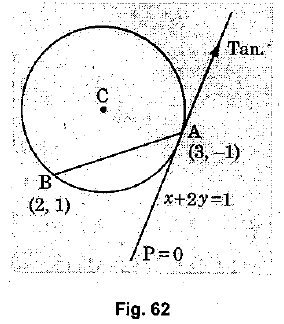
A circle passes through the point (2,1) and the line x + 2y = 1 is a tangent to it at the point (3,-1) Determine its equation.

The required circle will be

$(x-3)^2 \, + \, (y+1)^2 \, + \, \lambda \, (x+2y-1) \, = \, 0$ ......(1)
It passes through (2,1)

$5 \, + \, 3\lambda \, = \, 0 \,\, \therefore \,\, \lambda \, = \, -5/3$
Putting in (1) , the required circle is

$3(x^2 + y^2) \, - \, 23x \, - \, 4y \, + \, 35 \, = \, 0$
1083666_1007387_ans_2ba7e58312a2443ca64e13ff56d25d33.png

Find the equation of circle passing through the points where the circles
$x^{2} + y^{2} + 6x - 8y - 11 = 0$ and
$x^{2} + y^{2} - 8x + 14y + 56 = 0$ subtend equal angles and cut the first of these circles orthogonally.

The given circles are

$C_{1}(-3, 4), r_{1} = 6$

$C_{2} (4, -7), r_{2} = 3$
The circles subtend equal angles at the points from where common tangents are drawn. These points divide the line of centres in the ratio of the radii internally and externally. These are easily found to be

$A(11, -18), B\left (\dfrac {5}{3}, -\dfrac {10}{3}\right )$ .
If the required circle be

$x^{2} + y^{2} + 2gx + 2fy + c = 0$
Since it passes through the points

$A$ and

$B$ , we have

$22g - 36f + c = -445 ......(1)$

$\dfrac {10}{3}g - \dfrac {20}{3}f + c = -\dfrac {125}{9} .....(2)$
Also condition of orthogonality with the first gives

$6g - 8f - c = -11$
Adding

$(1)$ and

$(3)$ and then

$(2)$ and

$(3)$ thus eliminating

$c$ , we get

$7g - 11f = -144$ and

$7g - 11f = -\dfrac {56}{3}$
These are inconsistent. Hence no such circle exists.

Find the equation of the circle of minimum radius which contains the three circles
$S_1\equiv x^2 \, + \, y^2 \, - \, 4y \, - \, 5 \, = \, 0$
$S_2\equiv x^2 \, + \, y^2 \, + \, 12x \, + \, 4y \, + \, 31 \, = \, 0$
and $S_2\equiv x^2 \, + \, y^2 \, + \, 6x \, + \, 12y \, + \, 36 \, = \, 0$

The given circles are

$S_1$ (0, 2), 3

$S_2$ (-6, - 2), 3 and

$S_3$ (- 3, - 6), 3. In other words all the three circles are of same radius. Let the required circle be (h, k),r. The circle is to contain the three given circles and should be of minimum radius. Hence the given circles should touch the required circle internally so that the distance between the centres is equal to difference of radii, i.e.,

$r - 3, r - 3, r -3$ as all circles are of equal radius

$\therefore \, \,h^2 + (k - 2)^2 = (h - 6)^2 + (k + 2)^2 = (h + 3)^2 + (k+ 6)^2 = (r - 3)^2$

$\therefore \, 6h + 16k + 41 = 0$ and

$6h - 8k -5 = 0$

Solving, we get (h, k) =

$\left ( \, - \, \dfrac {31}{18} , - \, \dfrac{23}{12}\right)$ and

$(r-3)^2$ =

$h^2 + (k- 2)^2 = \left ( - \dfrac {31}{18}\right)^2 \, + \,\left(- \dfrac {47}{12}\right)^2$

$= \, \dfrac {1}{(36)^2} \, (23725) \, = \, \dfrac {25 \, \times \,949}{(36)^2}$

$\therefore r-3 = \dfrac {5}{36}\sqrt{949}$ or

$r = 3 + \, \dfrac{5}{36} \sqrt{949}$

Hence,

the required circle is

$(x- h)^2 + (y - k)^2 = r^2$

1103142_1007402_ans_ac8a381b34d440119e0ae59d6e3d4603.png

If the equations of the circles whose radii are $r$ and $R$ be respectively $S = 0$ and $S' = 0$ , then prove that the circles $\dfrac {S}{r} \pm \dfrac {S'}{R} = 0$ will cut orthogonally.

For the sake of convenience let the line of centres be chosen as axis of

$x$ and distance between them be

$2a$ and mid-point of the centres be chosen as origin so that the centres are

$(a, 0)$ , radius

$r$ for

$S$ and

$(-a, 0)$ , radius

$R$ for

$S'$ .

$\therefore S = (x - a)^{2} + y^{2} = r^{2}$
or

$x^{2} + y^{2} - 2ax + a^{2} - r^{2} = 0$

$S' = (x + a)^{2} + y^{2} = R^{2}$
or

$x^{2} + y^{2} + 2ax + a^{2} - R^{2} = 0$ .
The two circles are

$\dfrac {S}{r} \pm \dfrac {S'}{R} = 0$ or

$RS \pm rS' = 0$
Circle

$RS + rS' = 0$ becomes

$(R + r)(x^{2} + y^{2} + a^{2}) - 2ax (R - r) - rR (r + R) = 0$
or

$x^{2} + y^{2} - 2a \dfrac {R - r}{R + r} x + (a^{2} - rR) = 0 ..... (1)$
Replacing

$r$ by

$-r$ the circle

$RS - rS' = 0$ becomes

$x^{2} + y^{2} - 2a \dfrac {R + r}{R - r} x + (a^{2} + rR) = 0 .....(2)$
The circle

$(1)$ and

$(2)$ will cut orthogonally if

$2g_{1}g_{2} + 2f_{1}f_{2} = c_{1} + c_{2}$
i.e.

$2\left \{-a\dfrac {R - r}{R + r}\right \}\left \{-a \dfrac {R + r}{R - r}\right \} + 0 = (a^{2} - rR) + (a^{2} + rR)$
or

$2a^{2} = 2a^{2}$ which is true.
Hence the circles

$\dfrac {S}{r} \pm \dfrac {S'}{R}$ cut each other orthogonally.

The equation of the circle which touches both the axes and the line $\dfrac{x}{3}+\dfrac{y}{4}=1$ and lies in the first quadrant is $(x-c)^{2}+(y-c)^{2}=c^{2}$ where $c$ is

After comparing this (x-c)²+(y-c)²=c²

we will get c=6

1311450_1043331_ans_659c920858534769836153d05c98e1cc.jpg

Find the equation of a circle passing through point $(1, 2)$ and $(3, 4)$ and touching the line $3x+y-3=0$

Circle

$(1,2)$ and

$(3,4)-3x+y-3=0\Rightarrow (0,1)(1,0)$

Let

$(x,y)$ be centre of circle

$\Rightarrow$ Radius is equal both points.

$\sqrt{(x+1)^2+(y-2)^2}=\sqrt{(x-3)^2(y-2)^2}$ ....(1)

$x^2+1-2x+y^2+4-4y=x^2+9-6x+y^2+16-8y$

$-20+4x+4y=0\Rightarrow x+y=5\Rightarrow y=5-x$ ......(2)

distance from center of circle is same as radius.

$\dfrac{|3x+y-3|}{(3)^2+(1)^2}=\dfrac{|3x+5-x-3|}{\sqrt{10}}=\dfrac{|2x+2|}{\sqrt{10}}$ ....(3)

Substituting

$(2)$ in

$(1) \, 4$ equality to

$3$

$\sqrt{(x-1)^2+(3-x)^2}=\dfrac{|2x+2|}{\sqrt{10}}\Rightarrow (x-1)^2+(3-x)^2=\dfrac{(2x+2)^2}{10}$

$x^2+1-2x+9+x^2-6x=4x^2+4\dfrac{x}{10}$

$16x^2-88x+96=0$

Solving form

$=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}=\dfrac{88+\pm\sqrt{(88)^2-4\times 16\times 96}}{2\times 16}=\dfrac{88\pm 40}{32}$

$x_1=\dfrac{86+40}{32},x_2=\dfrac{88-40}{32}$

$x_1=4,x_2=1.5$

Substituting

$x_1$ and

$x_2$ in (2)

$y_1=1,y_2=3.5$

we get two circle with center

$(4,1)$ and

$(1.5,3.5)$

Radius of circle

$C_1=(4-1)^2+(3-4)^2=\sqrt{10}$

$C_2=(1.5-1)^2+(3-1.5)^2=\sqrt{2.5}$

$\boxed{C_1\Rightarrow (x-y)^2+(y-1)^2=10\,\,\,C_2\Rightarrow (x-1.5)^2+(y-3.5)^2=2.5}$

Find the equation of the circle whose centre is the point of intersection of the lines 2x -3y +4 =0 and 3x + 4y - 5 = 0 and passes through the origin.

Intersection point of

$2x - 3y + 4 = 0$ and

$3x + 4y - 5 = 0$ -

$2x - 3y + 4 = 0$

Multiplying above equation by

$4$ , we get

$8x - 12y + 16 = 0 ..... \left( 1 \right)$

$3x + 4y - 5 = 0$

Multiplying above equation by

$3$ , we get

$9x + 12y - 15 = 0 ..... \left( 2 \right)$

Adding

${eq}^{n} \left( 1 \right) \& \left( 2 \right)$ , we have

$\left( 4x - 12y + 16 \right) + \left( 9x + 12y - 15 \right) = 0$

$\Rightarrow 13x = -1$

$\Rightarrow x = \cfrac{-1}{17}$

Substituting the value of

$x$ in

${eq}^{n} \left( 1 \right)$ , we have

$\cfrac{-4}{17} - 12y + 16 = 0$

$\Rightarrow 12y = \cfrac{264}{17}$

$\Rightarrow y = \cfrac{22}{17}$

Hence the centre of circle will be

$\left( \cfrac{-1}{17}, \cfrac{22}{17} \right)$ .

As the circle touches the origin, hence the distance between the centre of circle to the origin will be the radius of circle.

$\therefore r = \sqrt{{\left( \cfrac{-1}{17} - 0 \right)}^{2} + {\left( \cfrac{22}{17} - 0 \right)}^{2}}$

$\Rightarrow r = \sqrt{\cfrac{1}{289} + \cfrac{484}{289}}$

$\Rightarrow {r}^{2} = \cfrac{485}{289}$

As we know that equation of a circle whose centre at

$\left( h, k \right)$ and radius

$r$ is given by-

${\left( x - h \right)}^{2} + {\left( y - k \right)}^{2} = {r}^{2}$

Therefore, equation of the given circle will be-

${\left( x - \left( \cfrac{-1}{17} \right) \right)}^{2} + {\left( y - \cfrac{22}{17} \right)}^{2} = \cfrac{485}{289}$

$\Rightarrow {\left( x + \cfrac{1}{17} \right)}^{2} + {\left( y - \cfrac{22}{17} \right)}^{2} = \cfrac{485}{289}$

$\Rightarrow {\left( 17x + 1 \right)}^{2} + {\left( 17y - 22 \right)}^{2} = 485$

Hence the required answer is

${\left( 17x + 1 \right)}^{2} + {\left( 17y - 22 \right)}^{2} = 485$ .

Find the equation of tangents to the hyperbola $3x^2 - 4y^2 = 12$ , which make equal intercepts on the axes.

Equation of the hyperbola is,

$3x^{2}-4y^{2}=12$ ........ (1)

Tangent of the hyperbola makes equal intercepts on the axes. So the tangent is of the form

$x+y=a$

To find the point of contact of the tangent, substitute

$y=a-x$ in equation (1).

$3x^{2}-4(a-x)^{2}=12$

$3x^{2}-4a^{2}-4x^{2}+8ax=12$

$x^{2}-8ax+4a^{2}+12=0$

Because the tangent will touch on a point, there will be single solution for the above Quadratic equation

$b^{2}-4ac=0$

$64a^{2}-4\left ( 4a^{2}+12 \right )=0$

$48a^{2}-48=0$

$a=\pm 1$

So the tangents are

$x+y=1$ and

$x+y=-1$

Find k, if one of the lines given by $kx^{2} + 10xy + 8y^{2} = 0$ is perpendicular to the line $2x - y =5$ .

The slope of

$2x-y=5$ is

$2$ .

So the slope of a perpendicular line is

$\dfrac{-1}{2}$

$kx^2+10xy+8y^2=0$ is supposed to be the intersection of

$2$ straight lines so, lets solve it for

$y.$

$\Rightarrow$

$y=\dfrac{-10x\pm\sqrt{100x^2-32kx^2}}{16}$

$=\dfrac{-10x\pm x\sqrt{100-68k}}{16}$

$=\dfrac{x(-10\pm\sqrt{100-32k})}{16}$

So the slope of the two lines is

$\dfrac{(-10\pm\sqrt{100-32k})}{16}$

$\therefore$

$\dfrac{(-10\pm\sqrt{100-32k})}{16}=\dfrac{-1}{2}$

$\Rightarrow$

$-20\pm 2\sqrt{100-32k}=-16$

$\Rightarrow$

$\pm 2\sqrt{100-32k}=4$

$\Rightarrow$

$\pm\sqrt{100-32k}=2$

$\Rightarrow$

$100-32k=4$ [ Squaring both sides ]

$\Rightarrow$

$32k=96$

$\therefore$

$k=3$

(a) If the equation $\lambda {x^2}4xy + {y^2} + \lambda x + 3y + 2 = 0$ represents a parabola then find
(b) Find the length of latus rectum of the parabola $169\{ {(x - 1)^2} + {\left( {y - 3} \right)^2}\} = {(5x - 12y + 17)^2}.$

Length of latus rectum of parabola is generally given by :

$L.R=4a$ , where :

$a=\dfrac{1}{2}$ ( Distance between focus and Directrix)

Now equation of parabola is given as:

$(x-1)^2+(y-3)^2=\left(\dfrac{5x-12y+17}{13}\right)^2$

This means the distance of point

$1, 3$ is same as its perpendicular distance from line

$5x-12y+17$ which means its focus lies at

$(1, 3)$

and equation of directrix :

$5x-12y+17$

$a=\dfrac{1}{2}\left|\dfrac{5(1)-12(3)+17}{13}\right|$

$=\dfrac{1}{2}\left|\dfrac{-14}{13}\right|$

$a=\dfrac{7}{13}$

$\therefore$ Length of latus rectum,

$LR=4a$

$=\dfrac{4\times 7}{13}$

$=\dfrac{28}{13}$

Find the equation of circles which touch $2x-3y+1=0$ at $(1,1)$ and having radius $\sqrt {13}$

Let the equation of the circle.

$(x-h)^2+(y-k)^2=r^2$ ----- (1)

$(h,k)$ is the coordinate of center, radius

$\sqrt{13}$ and it is touches by the line

$2x-3y+1=0$ at

$(1,1)$

By distance formula

$\sqrt{(h-1)^2-(k-1)^2}=\sqrt{13}$

$h^2=13-k^2+2k+2h-2$ ------- (2)

Now,

Tangent is always perpendicular to the radius

Slope of the line

$2x-3y+1\;(m_1)=\frac{2}{3}$

Slope of the radius

$m_2=-\frac{3}{2}$

Also the slope of of radius

$m_2=\frac{k-1}{h-1}=-\frac{3}{2}$

$3h+2k=-5$ ------- (3)

$h=\frac{2k-5}{3}$ ----- (4)

squaring on both side on equation (3)

$9h^2+4k^2=25$

From (2) and (4)

$5k^2-6k-104$

$(5k-26)(k+4)=0$

$k=-4,\frac{26}{5}$

Therefore,

$h=-\frac{13}{3},\frac{27}{15}$

Hence the point of center

$(-4,-\frac{13}{3}),(\frac{26}{5},\frac{27}{15})$

Hence the equation of circle are,

$(x-(-4))^2+(y-(-\frac{13}{3}))^2=(\sqrt{13})^2$

$(x-\frac{26}{5})^2+(y-\frac{27}{5})^2=(\sqrt{13})^2$

Find the equation of a circle if:
(i)center (a,b) and radius $\sqrt{a^2+b^2}$
(ii)center $(a \sec{\alpha},b \tan{\alpha})$ and radius $\sqrt { { a }^{ 2 }\sec ^{ 2 }{ \alpha } +{ b }^{ 2 }\sec ^{ 2 }{ \alpha } } \\$

$\left(i\right){r}^{2}={\left(x-a\right)}^{2}+{\left(y-b\right)}^{2}$

$r=\sqrt{{a}^{2}+{b}^{2}}$ (given)

$\Rightarrow {x}^{2}+{a}^{2}-2ax+{y}^{2}+{b}^{2}-2by={a}^{2}+{b}^{2}$

$\Rightarrow {x}^{2}-2ax-2by+{y}^{2}=0$ is the required equation of the circle.

$\left(ii\right)$ Center

$\left(a\sec{\alpha},b\tan{\alpha}\right)$

$r=\sqrt{{a}^{2}{\sec}^{2}{\alpha}+{b}^{2}{\tan}^{2}{\alpha}}$

${\left(x-a\sec{\alpha}\right)}^{2}+{\left(y-b\tan{\alpha}\right)}^{2}={a}^{2}{\sec}^{2}{\alpha}+{b}^{2}{\tan}^{2}{\alpha}$

On simplifying we get

${x}^{2}+{y}^{2}-2ax\sec{\alpha}-2by\tan{\alpha}=0$ is the required equation of the circle.

Define Latus rectum of the parabola.

$\underline {Latus\ Rectum:}$

$Latus\ Rectum$ . The line segment through a focus of a conic section, perpendicular to the major axis, which has both endpoint on the curve. The length of a

$parabola's\ latus\ rectum$ is

$4$ , where

$p$ is the distance from the focus to the vertex.

Find the equation of the circle which passes through the point $(2, -2)$ and $(3, 4)$ and whose centre lies on the line $x + y = 2$ .

We know that the equation of a circle with center at $\left( h,k \right)$ is,

${{\left( x-h \right)}^{2}}+{{\left( y-k \right)}^{2}}={{r}^{2}}$

Now, this circle passes through $\left( 2,-2 \right)$ . Then

${{\left( 2-h \right)}^{2}}+{{\left( -2-k \right)}^{2}}={{r}^{2}}$

${{h}^{2}}+{{k}^{2}}-4h+4k+8={{r}^{2}}$

Again, this circle passes through $\left( 3,4 \right)$ . Then

${{\left( 3-h \right)}^{2}}+{{\left( 4-k \right)}^{2}}={{r}^{2}}$

${{h}^{2}}+{{k}^{2}}-6h-8k+25={{r}^{2}}$

Subtracting the above results, we have

$2h+12k=17$ …… (1)

Now, the center lies on $x+y=2$ . So,

$h+k=2$ ….. (2)

Solving equations (1) and (2), we get

$h=\dfrac{7}{10}$ and $k=\dfrac{13}{10}$

Put values of $\left( h,k \right)$ in the first expression.

${{\left( 2-\dfrac{7}{10} \right)}^{2}}+{{\left( -2-\dfrac{13}{10} \right)}^{2}}={{r}^{2}}$

${{r}^{2}}=\dfrac{169+1089}{100}$

$r=\dfrac{\sqrt{1258}}{10}$

Therefore, equation of the circle is,

${{\left( x-\dfrac{7}{10} \right)}^{2}}+{{\left( y-\dfrac{13}{10} \right)}^{2}}=\dfrac{1258}{100}$

Hence, this is the required equation.

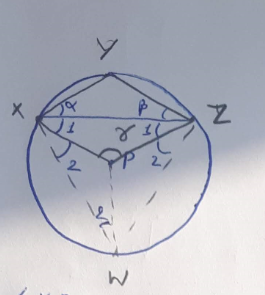
In the Fig. P is the centre of the circle. Prove that: $\angle XPZ = 2\left( {\angle XZY + \angle YXZ} \right)$ .

Conservation: draw line joining

$XW$ and

$ZW$ where

$W$ is equidistance from

$X$ and

$Z$ along circle

To prove:

$\angle XPZ=2(\angle XAY+\angle YXZ)$ , or

$r=2(\alpha +\beta)$

Now

$\because \ XYZW$ is a quadrilateral inside a circle opposite angles add to

$180^o$

$\angle YXW+\angle YZW=180---(1)$

also

$\because PX=PZ\ \angle PXZ=\angle PZX=\angle 1\quad$ (equal side stand equal angle)

similarly

$PX=PW=PZ \Rightarrow \angle WXP=\angle WZP =\angle PWX= \angle 2$

then in

$\triangle PXW$

$2\angle 2+\angle XPW=180$

and

$\because \ \angle XPW=\angle WPZ=360-r$

$\angle 2=\left (180-180+\dfrac {r}{2}\right) \dfrac {-1}{2}=\dfrac {r}{4}-----(2)$

also in

$\triangle XPZ$

$2\angle 1+\angle r=180$

$\Rightarrow \ \angle 1=90-\dfrac {r}{2}===(3)$

using

$(2)$ and

$(3)$ in

$(1)$

$\alpha +\angle 1+\angle 2+\beta +\angle 1+\angle 2=180$

$\Rightarrow \ \alpha +\beta +\dfrac {r}{2}+180-r=180$

$\alpha +\beta =\dfrac {r}{2}$

$\Rightarrow \ r=2(\alpha +\beta)$

1420994_1075157_ans_8ac96d6e5fd344608ecd988e65c8149d.png

The centre of a circle is $(-2,3)$ and it touches the straight line $4x+3y+2=0$ . Then find the equation of the circle.

Given the centre of the circle is

$(-2,3)$ .

Also given the circle touches the line

$4x+3y+2=0$ ......(1).

So line (1) is a tangent to the circle.

So the distance between the centre

$(-2,3)$ and the line (1) is the radius of the circle.

So the radius is

$\left|\dfrac{4.-2+3.3+2}{\sqrt{4^2+3^2}}\right|=\dfrac{3}{5}$ units.

Now, the equation of the circle is

$(x+2)^2+(y-3)^2=\left(\dfrac{3}{5}\right)^2$ .

Find the equation of the circle whose centre is at $(-1,3)$ and radius is $2$ .

Given the centre is at

$(-1,3)$ and radius is

$2$ .

Then the equation of the circle will be

$(x+1)^2+(y-3)^2=2^2$

or,

$x^2+2x+y^2-6y+6=0$ .

The centre of a circle is $(2a-1,a).$ Find the value of $a,$ if the circle passes through the point $(10,-2)$ and has diameter $10\sqrt 2$ units.

Here diameter

$\begin{array}{l}2r = 10\sqrt 2 \\r = 5\sqrt 2 \\OA = r = 5\sqrt 2 \\ = \sqrt {\left( {2a - 1 - 10} \right) + {{\left( {a + 2} \right)}^2}} = 5\sqrt 2 \\{\left( {2a - 11} \right)^2} + {\left( {a + 2} \right)^2} = 50\\4{a^2} - 44a + 121 + {a^2} + 4a + 4 = 50\\5{a^2} - 40a + 75 = 0\\{a^2} - 8a + 15 = 0\\a - 5a - 3a + 15 = 0\\\left( {a - 5a} \right)\left( {a - 3} \right) = 0\\a = 5\,or\,3\end{array}$

Find the equation of the circle each of which has radius $5$ and has tangent as the line $3x-4y+5=0$ at $(1,2)$ .

The tangent is line

$3x-4y+5=0$ at

$(1,2)$ of the circle

Let the equation of circle be

${ x }^{ 2 }+{ y }^{ 2 }+2gx+2fy+c=0$

Hence the centre of circle

$=(-g,-f)$

and radius of circle

$=\sqrt { { g }^{ 2 }+{ f }^{ 2 }-c }$

The distance from centre of circle to the line

$3x-4y+5=0$ is

$5$

By equation

$3x-4y+5=0\\ \Rightarrow y=\dfrac { 3 }{ 4 } x+\dfrac { 5 }{ 4 }$

slope of tangent

$=\dfrac { 3 }{ 4 }$

therefore slope of normal

$=\dfrac { -4 }{ 3 }$

$\Rightarrow \dfrac { 2-(-f) }{ 1-(-g) } =\dfrac { -4 }{ 3 } \\ \Rightarrow 3f+4g=-10\longrightarrow \left( 2 \right)$

solving

$(1)$ and

$(2)$ we get,

$g=4\quad and\quad f=2\quad \\ then,\quad r=\sqrt { { \left( -4 \right) }^{ 2 }+{ 2 }^{ 2 }-c } \\ \Rightarrow 5=\sqrt { { \left( -4 \right) }^{ 2 }+{ 2 }^{ 2 }-c } \\ \Rightarrow c=-5$

therefore equation of circle is given as;

${ x }^{ 2 }+{ y }^{ 2 }-8x+4y-5=0$

The graph of $x^2-4x+y^2+6y=0$ in the xy-plane is a circle. What is the radius of the circle?

Given,

$x^2-4x+y^2+6y=0$

$x^2-4x+4-4+y^2+6y+9-9=0$

$(x-2)^2+(y+3)^2-13=0$

$(x-2)^2+(y+3)^2=13$

Equation of circle ,

$(x-h)^2+(y-k)^2=r^2$

by comparing

$r^2=13$

$r=$

$\sqrt { 13 }$

so , radius of circle is

$\sqrt { 13 }$

Form the differential equation of the family of circles touches the X-axis at the origin.

Since the circle touches the

$x-axis$ at origin.

The center will be on the

$y-axis$

So,

$x$ - coordinate of the center

i.e.,

$a=0$

since,center=

$(0,b)$

So,

equation of circle

$=>(x-0)^2+(y-b)^2=b^2$

$=>x^2+(y-b)^2=b^2$

$=>x^2+y^2+b^2-2yb=b^2$

$=>x^2+y^2=2yb--------------(i)$

Since,there is variable we differentiate once

Differentiate w.r.t

$x$ we get

$=>2x+2y\dfrac{dy}{dx}=2b\times \dfrac{dy}{dx}$

$=>x+yy'=by'$

$=>b=[\dfrac{x+yy'}{y'}]$

Putting the value of b in

$(i)$ we get

$=>x^2+y^2=2y[\dfrac{x+yy'}{y'}]$

$=>(x^2+y^2)y'=2y(x+yy')$

$=>x^2y'+y^2y'=2yx+2 y^2y'$

$=>y'(x^2-y^2)=2xy$

$=>y'=\dfrac{2xy}{x^2-y^2}$

The equation of circle circumscribing the triangle whose sides are $L_1=0,L_2=0$ and $L_2=0$
$L_1L_2+\lambda L_2L_3+\mu L_3 L_1=0$
Where $\lambda$ and $\mu$ are real constants to be determined by
(a)coefficient of $x^2=$ coefficient of $y^2\neq 0$
(b)coefficient of $xy=0$

1356666_1126785_ans_4950718a4a87411abefe5d1581e71413.jpg

Find the equation of the parabola with
(a) Focus at $F\left( { - 1,\ - 3} \right)$ and the line $y = 1$ as the directrix.

REF .Image

V is the vector of

parabola which

will he the midpoint

of (-1,1) and (-1,3)

$\therefore V(-1, -1)(h,k)$

So, equation of parabola will be

$(x+1)^{2} = -4a (y+1)$

where a = distance between vertex and focus

$\therefore a = 2$

$\therefore$ equation of parabola

$\Rightarrow \boxed{(x+1)^2 = -8(y+1)}$

1181327_1103426_ans_590392f048314aadb815e7a1ed71d440.jpg

Find the equation of the circle passing through the points $\left( {2,3} \right)$ and $( - 1,1)$ and whose centre is on the line $x - 3y - 11 = 0$ .

The equation of circle

$(x-h)62+(y-k)^2=r^2 ...(i)$
According to question, circle passes through the point

$(2,3)$ and

$(-1,1)$
Thus

$(2-h)62+(3-k)^2=r^2$

$\Rightarrow 4+h^2-4h+9+k^2-6k=r^2$
and

$(-1-h)^2+(1-k)^2 =r^2$

$\Rightarrow 1+h^2+2h+1+k^2-2k=r^2$
Again

$h^2+k^2-4h-6k+12=r^2 ..(ii)$
and

$h^2+k^2+2h-2k+2-r^2..(iii)$
Since centre of circle

$(h,k)$ lie on line

$x-3y-11=0$
Thus

$h-3k-11-0$

$\Rightarrow h-3k-11...(iv)$
Subtraction eq

$(iii)$ from

$(ii)$ ,

$\dfrac { \begin{matrix} h^2+k^2-4h-6k+12=r^2 \\ h^2+k^2+2h-2k+2=r^2 \end{matrix}\\ \begin{matrix} - \ -\ -\ +\ -\ - \\ \end{matrix} }{ \begin{matrix} -6h-4k+11=0 \\ -6h-4k=-11 \end{matrix}\\ \begin{matrix} 6h+4k=11 \\ \end{matrix} ...(iv)}$
Multiply eq.

$(iv)$ by

$4$ and eq.

$(v)$ by

$3$ and then adding

$4h-12k=44$

$18h+12k=33$

$22h=77$

$\Rightarrow h=\dfrac{77}{22}$

$\therefore h=\dfrac{7}{2}$
Put the value of

$h$ in equation

$(iv)$ ,

$\dfrac{7}{2}-3k=11$

$\Rightarrow 3k=\dfrac{7}{2}-11$

$\Rightarrow 3k=\dfrac{7-22}{2}$

$\Rightarrow 3k=-\dfrac{15}{2}$

$\Rightarrow k=-\dfrac{15}{2 \times 3}$

$\therefore K=- \dfrac{5}{2}$
Put the values of

$h$ and

$k$ in equation

$(ii)$ ,

$\left( \dfrac{7}{2}\right)^2 + \left( -\dfrac{5}{2}\right)^2-4 \times \dfrac{7}{2}-6 \times \left( -\dfrac{5}{2}\right)+12=r^2$

$\Rightarrow \dfrac{49}{4}+\dfrac{25}{4}-14+15+13=r^2$

$\Rightarrow \dfrac{74}{4}+14=r^2$

$\Rightarrow \dfrac{74+56}{4}=r^2$

$\Rightarrow r62 =\dfrac{130}{4}$

$\Rightarrow r=\sqrt{\dfrac{130}{4}}$
Put teh values of

$h, k$ and

$r$ in equation

$(i)$

$\left( x-\dfrac{7}{2}\right)^2+ \left[ y - \left( -\dfrac{5}{2}\right) \right]^2= \left( \sqrt{\dfrac{130}{4} }\right)^2$

$\Rightarrow \left( x-\dfrac{7}{2}\right)^2 + \left( y + \dfrac{5}{2}\right)^2 =\dfrac{130}{4}$

$\Rightarrow x^2+ \dfrac{49}{4}-2 \times x \times \dfrac{7}{2}+y^2+\dfrac{25}{4}+2 \times \dfrac{5}{2}\times y=\dfrac{130}{4}$

$\Rightarrow x^2+y^2-7x+5y+\dfrac{49}{4}+\dfrac{25}{4}=\dfrac{130}{4}$

$\Rightarrow x^2+y^2-7x+5y+\dfrac{74}{4}-\dfrac{130}{4}=0$

$\Rightarrow x^2+y^2-7x+5y+\dfrac{-56}{4}=0$

$\Rightarrow x^2+y^2-7x+5y+-14=0$
Thus, required equation of circle

$x^2+y^2-7x+5y+-14=0$

Show that the points $A(1,,0) , B(2, -7), C(8, 1) \, and \, D(9, -6)$ all lie on the same circle. Find the equation of this circle, its centre and radius.

$A(1,0)B(2,-7),C(8,1)D(9,-6)$ . Let Centre

$(x,y)$

$\sqrt{(x-1)^2(y-0)^2}=\sqrt{(x-2)^2+(y+7)^2}=\sqrt{(x-8)^2+(y-1)^2}$

$(x-1)^2+y^2=(x-2)+(y+7)^2\Rightarrow x^2+1-2x+y^2+y^2=x^2+4-4x+y^2+49+14y-52+2x-14y$ ......(1)

$x^2+y-42+y^2+49+14y=x^2+6y-16x+y^2+1-2y$

$\Rightarrow -12+12x+16y=0$ ......(2)

Solving (1) and (2)

$\Rightarrow 12x-14y=52\times 6$

$12x+16y=12$

- - -

$\overline{\quad\quad-100y=300}\Rightarrow y=-3$

$-12+12x-48=0\Rightarrow 12x=60\Rightarrow x=5$

Centre

$(5,-3)$

$radius=\sqrt{(5-1)^2+(-3)^2}=5$

eq. of circle

$=(x-5)^2+(y+3)^2=25$

Now,

$'D'$ should be this circle

$(9.-6)$

$(9-5)^2+(-6+3)^2=4^2+3^2=25$

Equation of parabola whose vertex is $\left( {2,5} \right)$ and focus $\left( {2,2} \right)$ is

1125110_1098940_ans_22a28d15184a4c569bf7073051e809cc.jpg

Let $C$ be any circle with centre $(0, \sqrt{2})$ . Prove that at the most two rational points can be there on $C$ . (A rational point is a point both of whose co-ordinates are rational numbers).

Equation of any circle with centre at

$(0, \sqrt{2})$ is given by

$(x-0)^{2}+(y-\sqrt{2})=r^{2}$

$x^{2}+y^{2}-2\sqrt{2}=r^{2}-2$ ........

$(1)$

where

$r>0$

Let

$p(x_{1} y_{1}) Q(x_{2}y_{2}) R(x_{3}y_{3})$ be three destinct rational points on

$(1)$ since a straight line meet a circle in at most two point either

$y_{1}\neq y_{2}$

$P, Q, R$ lie on

$(1)$

$x_{1}^{2}+y_{1}^{2}-2\sqrt{2}y_{1}=r^{2}-2$ .......

$(2)$

$x_{2}^{2}+y_{2}^{2}-2\sqrt{2}y_{2}=r^{2}-2$ .........

$(3)$

$x_{3}^{2}+y_{3}^{2}-2\sqrt{2}y_{3}=r^{2}-2$ .......

$(4)$

$a_{1}-\sqrt{2}b_{1}=0$ .........

$(5)$

$a_{2}-\sqrt{2}b_{2}=0$ ........

$(6)$

where

$a_{1}=x_{2}^{2}+y_{2}^{2}-x_{1}^{2}-y_{1}^{2}$

$a_{2}=x_{3}^{2}+y_{3}^{2}-x_{1}^{2}-y_{1}^{2}$

$b_{1}=y_{2}-y_{1}$

$b_{2}=y_{3}-y_{1}$

Note that

$a_{1}, a_{2}, a_{3}$ are rational no. Also either

$b_{1}\neq 0$ or

$b_{2}\neq 0$

Suppose

$b_{1}\neq 0$ then

$\sqrt{2}=a_{1}/b_{1}$

$\Rightarrow \sqrt{2}$ is a rational no.

This is a contradiction.

Find the equation of the circle having $(a, 0)$ and $(0, b)$ as the extremities of the diameter.

$\left( { if\, enterprises\, \, \left( { o,\, \, h } \right) (a,o } \right) \\ diameter\, \, of\, \, a\, \, circle\, \, are\, \, given) \\ Then,\, equation\, \, of\, \, circle \\ \Rightarrow \left( { x-0 } \right) \left( { x-a } \right) +\left( { y-b } \right) \left( { y-0 } \right) =0 \\ \Rightarrow { x^{ 2 } }-ax+{ y^{ 2 } }-by=0 \\ \Rightarrow { x^{ 2 } }+{ y^{ 2 } }ax-by=0\, \, Ans.$

Prove that the points $\left(7,-9\right)$ and $\left(11,3\right)$ lie on a circle with centre at the origin. Also its equation.

Given

$(7 , -9)d (11,3)$ and center

$(0,0)$ calculating distance between the center

$(0,0)$ and

$(7,-9)$ using distance formula,

$D= \sqrt{(0-7)^{2}+ (0+9)^{2}} = \sqrt{49+81} = \sqrt{130}$

Circles equation is

$(x-0)^{2}+ (y-0)^{2}= \sqrt{130}$

$x^{2}+ y^{2}= \sqrt{130}$ ------

$(1)$

Now putting

$p + (11, 3)$ in the above

$eq^{n} \ (1)$

$(11)^{2}+ (3)^{2} - (\sqrt{130})^{2}$

$121+9 = (\sqrt{130})^{2}$

$130=130$

Since the equation is true, that point is also on the circle.

$\therefore$ both the points lies on a circle with center at the origin.

Also, the equation is

$x^{2}+y^{2}= (\sqrt{130})^{2}$

$x^{2} + y^{2} = 130$

A circle passing through $(0,0)$ has its centre on $y = x,$ If it cuts ${x^2} + {y^2} - 4x - 6y = 10,$ orthongly find its equation.

Let center of the circle is at

$(-g,-f)$

with radius

$=\sqrt{g^{2}+f^{2}}$ because it passes from

$(0,0)$

$(x+g)^{2}+(y+f)^{2}=g^{2}+f^{2}$

$x^{2}+y^{2}+2gx+2fy=0$ ...(1)

For orthogonaly with circle

$x^{2}+y^{2}-4x-6y=10$

$(x-2)^{2}+(y-3)^{2}=23$

$(x-2)^{2}+(y-3)^{2}-23=0$

$g'=2, f'=-3$

$2gg'+2ff'+c+c'$

$-4g-6f=-23$

Because center is on line

$y=x$

$g=f$

$-10g=-23$

$g=\dfrac{23}{10}, \,f=\dfrac{23}{10}$

Equation of circle will be

$x^{2}+y^{2}+\dfrac{23}{5}x+\dfrac{23}{5}y=0$

Show that the points $\left( 5,5 \right)$ , $\left( 6,4 \right)$ , $\left( -2,4 \right)$ and $\left( 7,1 \right)$ Concyclic find its equation, centre and radius.

consider the problem

If four points are concyclic then

${4^{th}}$ point must satisfy equation of circle passing through other three points.

Let,

${x^2} + {y^2} + 2gx + 2fy + c = 0$ be equation of circle

$(5,6),(6,4),\;and\;(7,1)$ must satisfy circle

$\begin{array}{l} \left( { 5,5 } \right) \to 25+25+10g+10f+c=0 \\ \Rightarrow 10g+10f+c=-50\left( i \right) \\ \end{array}$

$\begin{array}{l} \left( { 6,4 } \right) \to 36+16+12g+8f+c=0 \\ \Rightarrow 12g+8f+c=-52\left( { ii } \right) \end{array}$

$\begin{array}{l} \left( { 7,1 } \right) \to 49+1+14g+2f+c=0 \\ \Rightarrow 14g+2f+c=-50\left( { iii } \right) \end{array}$

And

$(ii)-(i)$

$\Rightarrow 2g - 2f = - 2 \ldots \left( {iv} \right)$

$(iii)-(ii)$

$\Rightarrow 2g - 6f = 2 \ldots \left( v \right)$

$(iv)-(v)$

$\begin{array}{l} 2g-2f-2g+6f=-2-2 \\ \Rightarrow 4f=-4 \\ \Rightarrow f=-1 \end{array}$

Put in

$(iv)$

$\begin{array}{l} 2g+2=-2 \\ \Rightarrow g=-2 \end{array}$

$10g + 10f + c = - 50$

Put in

$(i)$

$\begin{array}{l} -20-10+c=-50 \\ \Rightarrow c=-20 \end{array}$

Therefore, equation is

${x^2} + {y^2} - 4x - 2y - 20 = 0$

Now, put

$(-2,4)$ in

$R.H.S$

$4+16+8-8-20=28-28=0$

Therefore,

$(-2,4)$ satisfies circle passing through

$(5,5),(6,4)\; and \;(7,1)$

Hence,

$(5,5),(6,4),(-2,4)\;and\;(7,1)$ are concyclic

Center is

$(2,1)$

And Radius is

$\begin{array}{l} =\sqrt { 4+1-\left( { -20 } \right) } \\ =\sqrt { 25 } \\ =5 \end{array}$

Express the following equation of the curve in cartesian form. If the curve is a circle find its center and radius
i) $x = 5\cos \theta ,y = 5\sin \theta$
ii) $x = 2 + 3\cos \theta ,y = 3 - 3\sin \theta$

$x=5 \cos \theta \,\, y=5 \sin \theta$

$x^{2}+y^{2}=25(\cos^{2}\theta +\sin^{2}\theta )$

$x^{2}+y^{2}=25$

Center

$(0,0)$ Radius

$=\sqrt{25}=5$

ii)

$x=2+3 \cos\theta \,\, y=3-3 \sin\theta$

$(x-2)^{2}+(y-3)^{2}=9(\cos^{2}\theta +\sin^{2}\theta )$

$(x-2)^{2}+(y-3)^{2}=9$

Center

$(2,3)$ Radius

$\sqrt{9}=3$

Find the vertex, axis, focus, directrix,lastusrectum of the parabola. $x^{2}-2x+4y+9=0$

$x^{2}-2x+4y+9=0$

$\therefore \left(x^{2}-2x+1\right)+4y+8=0$

$\therefore \left(x-1\right)^{2}+4\left(y+2\right)=0$

$\therefore \left(x-1\right)^{2}=-4\left(y+2\right)$

$\therefore \left(x-1\right)^{2}=4\left(-y-2\right)$

$\therefore$ Vertex :-

$\left(x-1\right)^{2}=0$

$\left(-y-2\right)=0$

$\therefore$ Vertex:- \left(1,-2\right)

Axis

$\left(x-1\right)^{2}=0$

$\therefore \boxed{x=1}$

Direction :-

$-y-2=-1$

$\therefore \boxed{y=-1}$

Latus rectum

$\boxed{4}$

Find the length of the latus rectum, the eccentricity and the coordinates of the foci of the ellipse
$5x^{2}+4y^{2}=1$

$5x^2+4y^2=1$

$\dfrac{x^2}{4}+\dfrac{y^2}{5}=\dfrac{1}{20}$ or

$\dfrac{x^2}{1/5}+\dfrac{y^2}{1/4}=1$

$a^2=1/5\quad b^2=1/4$

$a=1/\sqrt 5\quad b=\dfrac{1}{2}$

$e=\sqrt{1-\dfrac{a^2}{b^2}}\Rightarrow e=\dfrac{1}{\sqrt{5}}$

coordinate of foci

$=(0, \pm be)$

$=\left(0, \dfrac{\pm 2}{2\sqrt 5}\right)$

Length of Latus rectum

$=\dfrac{2a^2}{b}=\dfrac{4}{5}$

Find equation of the circle, which passes through the origin, has its centre on the line $x + y = 4$ and cuts the circle ${x^2} + {y^2} - 4x + 2y + 4 = 0$ orthogonally

Circle passes through origin

centre lies on

$x + y = 4$

cuts the circle

$x^2 + y^2 - 4x + 2y + 4 = 0$ orthogonally

Let circle be

$x^2 + y^2 + 29 x + 2 fy + C = 0$

with centre

$(-g , -f)$

$(0,0)$ satisfies it

$C = 0$ ___(1)

$-g - f = 4$ ____(2)

for orthogonality,

$2g \, g' + 2 f \, f' = c + c'$

$-4g + 2f = 4$ ____(3)

$g = -2 \, f = -2$ . [on solving (2), (3)]

circle :

$x^2 + y^2 - 4x - 4y = 0$

find the equation of the circle which cuts the circles ${x^2} + {y^2} - 9x + 14 = 0$ and ${x^2} + {y^2} - 15x + 14 = 0$ orthogonally and passes through the piont $(2,5)$ .

circle passes through

$(2,5)$

cuts orthogonally

$x^{2}+y^{2}-9x+14=0$

cuts orthoganally

$x^{2}+y^{2}-15x+14=0$

let circle is

$x^{2}+y^{2}+2gx+2fy+c=0$

with centre

$(-9,-8)$

$4+25+4g+10f+c=0$

$4g+10f+c=-29.....(i)$

$-9g=c+14.....(ii)$

$-15g=c+14.....(iii)$

$g=0,c=-14,B=3/2.$

circle :

$x^{2}+y^{2}+37-14=0$

Find the equation of a circle which touches the line $2x-y=4$ at the point $(1, -2)$ and
Radius $=5$

General form of a circle triangle

$x-y-4=\theta$

$(1-x)$ as given by

$(x-1)^2+(y+2)^2+\lambda (2x-y-4)=0$

$\Rightarrow \ x^2+y^2+x(2\lambda -2)+y(4-\lambda)+5-4\lambda =0$

$r=5$

$\Rightarrow \ g^2+f^2-c=25$

$\Rightarrow \ (\lambda -1)^2+\left (\dfrac {4-\lambda}{c}\right)+4\lambda -5=25$

$\Rightarrow \ 4\lambda^2+4-8\lambda +\lambda^2-8\lambda +16+16\lambda -20=100$

$\Rightarrow \ 5\lambda^2=100$

$\Rightarrow \ \lambda^2=20$

$\Rightarrow \ \lambda =\pm 2\sqrt {5}$

$\lambda =2\sqrt {5}$

Equation of circle is

$x^2+y^2+x(4\sqrt 5-2)+y(4-2\sqrt 5)+5-8\sqrt {5}=0$

$\lambda =2\sqrt 5$

Equation of circle is

$x^2+y^2-x(4\sqrt 5+2)+y(4+2\sqrt 5)+5+8\sqrt {5}=0$

Find the equation of the following curve in cartesian form $x = - 1 + 2\sin \theta ,y = 1 + 2\cos \theta .$ find the centre and radius of circle.

$x=-1+2sin\theta$

$y=1+2cos\theta$

$(x+1)^{2}+(y-1)^{2}=4sin^{2}\theta +4cos^{2}\theta$

$(x+1)^{2}+(y-1)^{2}=4(sin^{2\theta }+cos^{2}\theta )$

$(x+1)^{2}+(y-1)^{2}=4$

$(x+1)^{2}+(y-1)^{2}=2^{2}$

centre

$(-1,1)$ , Radius=

$2$ .

Find the equation of a circle of radius 5 units, whose centre lies on the x-axis and which passes through the point $\left( {2,3} \right)$ .

Radius

$=5$ units

Centre

$(a,0)$ pt.

$(2,3)$

$(x-a)^2+y^2=5^2$

$(2-a)^2+3^2=5^2$

$(2-a)^2=25-4=16=4^2$

$2-a=\pm 4\Rightarrow a=2\mp4\Rightarrow a=-2,6$

$\therefore$ equation of circle :

$(x+2)^2+y^2=5^2$ Or

$(x-6)^2+y^2=5^2$

2128777_1176089_ans_9014014bca924f63a99b0c83e94d3b7b.png

Find the equation of the circle whose centre is on the line $2x-y=3$ and which passes through $(3,-2)$ and $(-2,0)$ .

Let center of circle is

$(h,k)$
So equation of circle

${ \left( x-h \right) }^{ 2 }+{ \left( y-k \right) }^{ 2 }={ r }^{ 2 }$
So,

$\left( 3,-2 \right)$ &

$\left( -2,0 \right)$ satisfies the above equation

${ \left( 3-h \right) }^{ 2 }+{ \left( -2-k \right) }^{ 2 }={ r }^{ 2 }\rightarrow i$

${ \left( -2-k \right) }^{ 2 }+{ \left( -k \right) }^{ 2 }={ r }^{ 2 }\rightarrow ii$
As,

${ r }^{ 2 }={ r }^{ 2 }$ so, from

$i$ and

$ii$

${ \left( 3-h \right) }^{ 2 }+{ \left( 2+k \right) }^{ 2 }={ \left( 2+h \right) }^{ 2 }+{ k }^{ 2 }$

$9-6h+{ h }^{ 2 }+4+4k+{ k }^{ 2 }-4+4h+{ h }^{ 2 }+{ k }^{ 2 }$

$=9+4k=10h\rightarrow iii$
As,

$\left( h,k \right)$ lies in

$2x-y=3$

$2h-k=3\rightarrow iv$

$k=2h-3$

Solving

$iii$ and

$iv$

$9+4\left( 2h-3 \right) =10h$

$9+8h-12=10h$

$-3=2h$

$h=-\cfrac { 3 }{ 2 }$
So,

$k=2\left( -\cfrac { 3 }{ 2 } \right) -3$

$=-3-3=-6$
Equation of circle

$={ \left( x+\cfrac { 3 }{ 2 } \right) }^{ 2 }+{ \left( y+6 \right) }^{ 2 }={ r }^{ 2 }$

As (-2,0) lies on the circle, Substituting it.

${ \left( -2+\cfrac { 3 }{ 2 } \right) }^{ 2 }+{ 6 }^{ 2 }={ r }^{ 2 }$

${ r }^{ 2 }=\cfrac { 1 }{ 4 } +{ 6 }^{ 2 }$

$r=\sqrt { 36.25 }$

So,

${ \left( x+\cfrac { 3 }{ 2 } \right) }^{ 2 }+{ \left( y+6 \right) }^{ 2 }=36.25$

Find the equation of the circle whose diameters are along the lines $2x-3y+12=0$ and $x+4y-5=0$ and whose area is $154$ sq. units.

Equation of diameter given are

$2x-3y=-12$ and

$x+4y=5$

Let us solve these two equation to get the centre of the circle.

$2x-3y=-12.....(1)$

$x+4y=5(\times 2)$

$2x+8y=10.....(2)$

Subtracting (1) from (2), we get

$\Rightarrow2x+8y-2x+3y=10-(-12)$

$\Rightarrow11y=22$

$\Rightarrow y=2$

Putting y=2 in (1), we get

$\Rightarrow2x-3(2)=-12$

$\Rightarrow2x=-6$

$\Rightarrow x=-3$

Hence the coordinate of the centre are (-3,2)

Area of the circle is given as 154 sq.units

$\Rightarrow\pi r^2=154$

$\Rightarrow r^2=\dfrac{154\times7}{22}$

$\Rightarrow r=7$

Hence the equation of the circle is

$\Rightarrow(x+3)^2+(y-2)^2=7^2$

$\Rightarrow x^2+9+6x+y^2+4-4y=7^2$

$\Rightarrow x^2+y^2+6x-4y-36=0$

This is the required equation of the circle.

Centre at $(0,0)$ and which passes through the points $(3,2)$ and $(1,6)$ .

Let equation of circle whose centre is at

$(0, 0)$ be

$(x-0)^2+(y-0)^2=r^2$ ['r' being its radius]

or,

$x^2+y^2=r^2$

Given the circle passes through

$(3, 2)$ then we have,

$3^2+2^2=r^2$

$r^2=13$

So equation of the circle is

$x^2+y^2=13$ .

1175728_1194972_ans_2400d390534f4f449320358e5edbdd1d.jpg

The centre of those circle which touch the circle $x^{2}+y^{2}+8x-8y-4=0$ , externally and also touch the x-axis , lie on:

Construction

$x^2+y^2+8x-8y-4=0$

$\rightarrow$ radius

$=\sqrt{4^2+4^2+4}=\sqrt{36}=6$

center

$(-4, 4)$

construct a line parallel to

$x=0$ at a distance of

$6$ units from it as shown

$\dfrac{CP}{PM}=\dfrac{r+6}{r+6}=1$

$\Rightarrow \dfrac{CP}{PM}=1$

$\Rightarrow$ P is a point whose distance from fixed point 'C' and its distance from fixed line

$'L_1'$ are equal

From locus definition P(center) lies on parabola.

1188524_1195027_ans_746ed62703ea423d9e4fbedb81af3be4.jpg

The points $\left( {0,\,4} \right)$ and $\left( {0,\,2} \right)$ are respectively the vertex and focus of a parabola. Then find the equation of the parabola.

The coordinates of the vertex is (0,4)

The coordinates of the focus is (0,2)

It is clear that the vertex and the focus lies on the positive side of the y-axis.

Hence the curve is open downwards.

The equation of the form

$(x−h)^2=4a(y−k)$

i.e.

$(x−0)^2=−4×2(y−4)$

On simplifying we get,

$x^2=−8(y−4)$

$\Rightarrow x^2=−8y+32$

$x^2+8y−32=0$ is the required equation of the parabola.

An ellipse passes through the point $( 4 , - 1 )$ and touches the line $x + 4 y - 10 = 0 .$ Find its equation if its axes coincide with the coordinate axes.

consider equation of ellipse as

$\cfrac { { x }^{ 2 } }{ { a }^{ 2 } } +\cfrac { { y }^{ 2 } }{ { b }^{ 2 } } =1$

Putting

$(4,-1)$ as it lies on it

$\cfrac{16}{{a}^{2}}+\cfrac{1}{{b}^{2}}=1......(1)$

equation of tangent of ellipse is

$y=mx\pm \sqrt { { a }^{ 2 }m^{ 2 }+{ b }^{ 2 } }$

compare it with given one

$y=\cfrac{x}{4}+\cfrac{5}{2}$

$\cfrac{5}{2}=\sqrt { { a }^{ 2 }m^{ 2 }+{ b }^{ 2 } }$ where

$m=\cfrac{1}{4}$

$\cfrac{25}{4}=\cfrac{{a}^{2}}{16}+{b}^{2}.....(2)$

$\cfrac{16}{2}=1-\cfrac{1}{{b}^{2}}$ from (1)

$\cfrac{{a}^{2}}{16}=\cfrac{1}{1-\cfrac{1}{{b}^{2}}}=\cfrac{25}{4}-{b}^{2}$

${b}^{2}=(\cfrac{25}{4}-{b}^{2})({b}^{2}-1)$

Let

${b}^{2}=t$

$t=(\cfrac{25}{4}-t)(t-1)$

$t=\cfrac{25}{4}t-{t}^{2}-\cfrac{25}{4}+t$

$4{t}^{2}-25t+25=0$

$4{t}^{2}-20t-5t+25=0$

$4t(t-5)-5(t-5)=0$

$t=\cfrac{5}{4},t=5$

${b}^{2}=\cfrac{5}{4},5$

Substituting value of

${b}^{2}$ in (1)

we get

${a}^{2}=20,80$ for

${b}^{2}$

$=5,\cfrac{3}{4}$ respectively

Thus equation of ellipse is

$\cfrac{{x}^{2}}{20}+\cfrac{{y}^{2}}{5}=1$ and

$\cfrac{{x}^{2}}{80}+\cfrac{{y}^{2}}{5/4}=1$

Find the equation of the circle concentric with $x^{2}+y^{2}-4x-6y-3=0$ and which touches the $y-$ axis.

$\begin{array}{l} { x^{ 2 } }+{ y^{ 2 } }-4x-6y-3=0\, \, \& \, \, touches\, \, y-axis \\ { x^{ 2 } }+{ y^{ 2 } }+2yx+2yy+c=0 \\ 2g=-4 \\ g=-2 \\ 2f=-6 \\ f=-3 \\ radius=\sqrt { { g^{ 2 } }+{ f^{ 2 } }-c } \\ =\sqrt { 16+9-3 } \\ =\sqrt { 25-3 } \\ =\sqrt { 22 } \\ Centre=\left( { -g,-f } \right) \\ =\left( { 2,3 } \right) \\ So,\, \, radius=2 \\ Now \\ { \left( { x-2 } \right) ^{ 2 } }+{ \left( { y-3 } \right) ^{ 2 } }={ \left( 2 \right) ^{ 2 } } \\ { x^{ 2 } }-4x+4+{ y^{ 2 } }-6y+9=4 \\ { x^{ 2 } }-4x+{ y^{ 2 } }-6y+9=0 \end{array}$

Find equation of circle which is concentric to circle $x^2+y^2-6x+7=0$ and touches the line $x+y+3=0$ .

The two circles are concentric so they have the same centre. Centre of the given circle-

${ x }^{ 2 }-6x+9-9+{ y }^{ 2 }+7=0$

$\Rightarrow \quad { \left( x-3 \right) }^{ 2 }+{ \left( y-0 \right) }^{ 2 }={ \left( \sqrt { 2 } \right) }^{ 2 }$

$\therefore$ Centre is

$(3,0)$

Equation of the required circle is

${ \left( x-3 \right) }^{ 2 }+{ y }^{ 2 }={ a }^{ 2 }$

$\Rightarrow { x }^{ 2 }+9-6x+{ y }^{ 2 }={ a }^{ 2 }$

Whose centre is

$(3,0)$ and radius is a unit.

$x+y+3=0$ is a tangent to it, so distance of line from centre

$=$ its radius.

i.e.

$\dfrac { \left| 3+0+3 \right| }{ \sqrt { 1+1 } } =a$

$\Rightarrow \dfrac { 6 }{ \sqrt { 2 } } =a\Rightarrow \dfrac { 2\times 3 }{ \sqrt { 2 } } =a$

$\Rightarrow a=3\sqrt { 2 }$ units.

$\therefore$ equation of circle is

${ \left( x-3 \right) }^{ 2 }+{ y }^{ 2 }={ \left( 3\sqrt { 2 } \right) }^{ 2 }$

$\Rightarrow { x }^{ 2 }+9-6x+{ y }^{ 2 }=18$

$\Rightarrow { x }^{ 2 }+{ y }^{ 2 }-6x-9=0$

Find the equation of the circle whose two end points of the diameter are $(4,-2)$ and $(-1,3)$ .

Given the two end points of the diameter of the circle is

$(4,-2)$ and

$(-1,3)$ .

Then the equation of the circle is

$(x-4)(x+1)+(y+2)(y-3)=0$

or,

$x^2+y^2-3x-y-10=0$

or,

$x^2+y^2-3x-y=10$ .

Find the equation of the circle which cuts the circle $x^{2}+y^{2}-14x-8y+64=0$ and the coordinate axes orthogonally.

$x^2+y^2-14x-8y+64=0$

$(g, f)=(7, 4)$ ;

$c_1=64$

Let

$x^2+y^2=a^2$

$\Rightarrow x^2+y^2-a^2=0$

$(g, f)=(0, 0)$ ;

$c_2=-a^2$

$2g_1g_2+2f_1f_2=c_1+c_2$

$0+0=64+(-a^2)$

$a^2=64$

i.e;

$x^2+y^2=64$ .

Equation of a circle whose centre is origin and radius is equal to the distance between the lines $x =1$ and $x = -1$ is

Distance between lines

$x = 1$ and

$x = -1$

$r - 2$ units

centre ,

$0 \equiv (h , k) \equiv (0, 0)$

Equation :

$(x - h)^2 + (y - k)^2 = r^2$

$(x - 0)^2 + (y - 0)^2 = 2^2$

$\therefore x^2 + y^2 = 4$

Find the equation of the circle passing through the points $(5,5),(3,7)$ and has its center on the line $x-4y+11=0$

equation of circle (?)

A-(5, 5), B(3,7)

center of circle is A,B

$\rightarrow$ the center of circle has to lie on the perpendicular

bisector of line AB.

$\rightarrow$ slop of AB =

$\frac{7-5}{3-5} = -1$

$\rightarrow$ Also the perpendicular bisector of AB has

to pass through mid point of AB.

$= (\frac{3+5}{2})(\frac{5+7}{2})$

$= (\frac{8}{2}, \frac{12}{2})$

$= (4, 6)$

$\rightarrow$ so, equation of perpendicular bisector

$\frac{y-6}{x-4} = I$

$y-6 = x-4$

$\therefore y = x+2$

$\rightarrow$ so, now we know the center of the circle passes

through two line.

$x-4y = 1$ &

$y = x+2$

$\rightarrow$ solving equation

$x = -3, y = -1$

$\rightarrow$ the circle pass through (5, 5) so the radius

$= \sqrt{5-(-3)^{2})+(5-(-1))^{2}} = \sqrt{64+36} = \sqrt{100} = 10$

$\rightarrow$ so equation of circle

$(x-(-3)^{2})+(y-(-1))^{2} = r^{2}$

$\therefore (x+3)^{2}+(y+1)^{2} = 100$

1166404_1247984_ans_81dedac2570a4458895f54f1d6ae8e66.jpg

If the points $(1,0),(-2,3),(1,4),(2,k)$ all lie on the same circle, find the value of $'k'$ .

Let the equation of a circle passing through the point

$\left(1,0\right),\left(-2,3\right),\left(1,4\right)$ and

$\left( 2,k\right)$ be

$x^2+y^2+2gx+2fy+c=0$

$......\left(1\right)$

Since these point lie on the circle, therefore must satisfy the above equation of circle.

Hence putting

$\left(1,0\right)$ we get

$\Rightarrow 1+2g+c=0$

$2g+c=-1$

$...........\left(2\right)$

Putting

$\left( -2,3\right)$ in

$\left(1\right)$ we get

$\Rightarrow 4+9-4g+6f+c=0$

$\Rightarrow 4g-6f-c=13$

$......\left(3\right)$

Putting

$\left(1,4\right)$ in

$\left(1\right)$ we get

$\Rightarrow 1+16+2g+8f+c=0$

$\Rightarrow 2g+8f+c=-17.....\left(4\right)$

combining

$\left(2\right)\;\&\;\left(4\right)$ we get

$\Rightarrow 8f-1=-17$

$\Rightarrow 8f=-16$

$\Rightarrow f=-2$

$......\left( 5\right)$

Putting

$\left(5\right)$ in

$\left(3\right)$ we get

$\Rightarrow 4g-c=1$

$.........\left(6\right)$

Solving

$\left(2\right)$

$\&$

$\left(6\right)$ simultaneously we get

$\Rightarrow 9=0$ and

$c=-1$

$\therefore$ the equation of circle is

$x^2+y^2-4y-1=0$

now putting

$\left( 2,k\right)$ in the above equation

$\Rightarrow 4+k^2-4k-1=0$

$\Rightarrow k^2-4k+3=0$

$\Rightarrow \left(k-3\right) \left(k-1\right)=0$

$\therefore k=3$ or

$k=1$

Hence, the answer is

$3\;or\;1.$

A variable circle passes through the point $A(2,1)$ and touches the x-axis. Locus of the other end of the diameter through $A$ is a parabola.
(i) Find the length of the rectum of the parabola.

We have,

A variable circle passes through the point $A\left( 2,1 \right)$ and touches the X-axis.

So,

In a circle AB is a diameter where the coordinate of point A is (2,1) and let the coordinate of B is $\left( {{x}_{1}},{{y}_{1}} \right)$ .

Now, we know that,

Equation of circle in diameter from is

$\left( x-{{x}_{1}} \right)\left( x-2 \right)+\left( y-{{y}_{1}} \right)\left( y-1 \right)=0$

And it touches X-axis so $y=0$

$\left( x-{{x}_{1}} \right)\left( x-2 \right)+\left( 0-{{y}_{1}} \right)\left( 0-1 \right)=0$

$\Rightarrow {{x}^{2}}-x{{x}_{1}}-2x+2{{x}_{1}}+{{y}_{1}}=0$

$\Rightarrow {{x}^{2}}+\left( -2-{{x}_{1}} \right)x+2{{x}_{1}}+{{y}_{1}}=0$

Also, the discriminate of above equation will be equal to zero,

Because circle touches X-axis.

${{\left( -2-{{x}_{1}} \right)}^{2}}=4\left( 2{{x}_{1}}+{{y}_{1}} \right)$

$\Rightarrow 4+4{{x}_{1}}+{{x}_{1}}^{2}=8{{x}_{1}}+4{{y}_{1}}$

$\Rightarrow 4-4{{x}_{1}}+{{x}_{1}}^{2}=4{{y}_{1}}^{2}$

$\Rightarrow {{\left( {{x}_{1}}-2 \right)}^{2}}=4{{y}_{1}}^{2}$

Hence, the locus of end pint of diameter.

This is the answer.

The equation of the circle whose diameters have the end points (a,0) and (0,b).

REF.Image

$O\equiv [\frac{O+a}{2},\frac{O+b}{2}]$

$O\equiv (\frac{a}{2},\frac{b}{2})$

Radius =

$\sqrt{(a-\frac{a}{2})^{2}+(\frac{b}{2})^{2}}$

$=\sqrt{\frac{a^{2}}{4}+\frac{b^{2}}{4}}= \sqrt{\frac{a^{2}+b^{2}}{4}}= \frac{\sqrt{a^{2}+b^{2}}}{2}$

$Eq^{n}(x-\frac{a}{2})^{2}+(y-\frac{b}{2})^{2}= \frac{a^{2}+b^{2}}{4}$

1133996_1249554_ans_7bd0b774b8c5427498420abd975f6c1d.jpg

Find the coordinate of the centre and radius of the following circle.
$2x^2+2y^2-3x+5y=7$ .

we know general equation of circle is

$x^2+y^2+2gx+2fy+c=0$

with centre

$(-g, -f)$ and radius

$=\sqrt{g^2+f^2-c}$

consider

$2x^2+2y^2-3x+5y=7$

$x^2+y^2-\dfrac{3}{2}x+\dfrac{5}{2}y-\dfrac{7}{2}=0$

centre

$\left(\dfrac{3}{4}, \dfrac{-5}{4}\right)$ radius

$=\sqrt{\left(\dfrac{3}{4}\right)^2+\left(\dfrac{-5}{4}\right)^2+\dfrac{7}{2}}$

$=\sqrt{\dfrac{9}{10}+\dfrac{25}{16}+\dfrac{7}{2}}=\sqrt{\dfrac{90}{16}}=\dfrac{3\sqrt{10}}{4}$

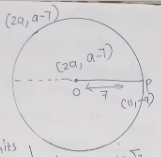
The centre of a circle is $(2a, a - 7)$ . Find the values of a if the circle passes through the point $(11, -9)$ and has diameter $10 \sqrt{2}$ units.

the centre of the circle

$(0)=(2a,a-7)$

Point

$(P)=(11,-9)$

diameter

$(D)=10\sqrt{2}$ units

Also given, to find out the values of

$a$

from figure, we get

$\overline { OP } =7$ units

$\therefore$

$OP=\sqrt { { \left( { x }_{ 2 }-{ x }_{ 1 } \right) }^{ 2 }+{ \left( { y }_{ 2 }-{ y }_{ 1 } \right) }^{ 2 } }$

$O=(2a,a-7)$ ,

$P(11,-9)$

$\Rightarrow$

$7=\sqrt { { \left( 11-2 \right) }^{ 2 }+{ \left( -9-(a-7) \right) }^{ 2 } }$

$7=\sqrt { 121+4{ a }^{ 2 }-44a+{ \left( -9-a+7 \right) }^{ 2 } }$

$7=\sqrt { 121+4{ a }^{ 2 }-44a+{ a }^{ 2 }+4a+4 }$

$7=\sqrt { { 5a }^{ 2 }-40a+125 }$

s.o.b/s we get

$49={ 5a }^{ 2 }-40a+125$

$\Rightarrow { 5a }^{ 2 }-40a+76=0$

We know that

$\cfrac { -b\pm \sqrt { { b }^{ 2 }-4ac } }{ 2a }$ is used to findroots for quadratic equation

we get

${ 5a }^{ 2 }-40a+76=0\quad ;\quad \cfrac { -b\pm \sqrt { { b }^{ 2 }-4ac } }{ 2a }$

$\quad b=-40;a=5;c=76$

$\Rightarrow \cfrac { -(-40)\pm \sqrt { { (-40) }^{ 2 }-4(5)(76) } }{ 2\times 5 } =\cfrac { 40\pm \sqrt { 1600-1520 } }{ 10 }$

$=\cfrac { 40\pm \sqrt { 80 } }{ 10 } =\cfrac { 40\pm 4\sqrt { 5 } }{ 10 } =\cfrac { 4(10\pm \sqrt { 5 } ) }{ 10 } =\cfrac { 2(10\pm \sqrt { 5 } ) }{ 5 }$

$\therefore a=\cfrac { 2\left( 10+\sqrt { 5 } \right) }{ 5 } ;a=\cfrac { 2\left( 10-\sqrt { 5 } \right) }{ 5 }$

$a=10.89=11;a=3.10=3$

$\therefore a=11,3$

1343357_1251345_ans_cefb6574798d49369d97d91803853251.PNG

Find the equation of the circle passing through the points $\left(4,1\right)$ and $\left(6,5\right)$ whose center is on the line $4x+y=16$ .

Let the equation of required circle be

$(x - b)^2 + (y - k)^2 = r^2$ .. (1)

It gives that circle passes through

$A(4, 1)$ &

$B (6, 5)$

$(4, h)^2 + (1 - k)^2 = r^2 \, \& \, (6 - h)^2 + (5 - k)^2 = r^2$

$(4 - h)^2 + (1 - k)^2 = (6 - h)^2 + (5 - k)^2$

$16 - 8h + h^2 + 1 - 2k + k^2 = 36 - 12 h + h^2 + 25 - 10 k + k^2$

$16 - 8h + 1 - 2k = 36 - 12h + 25 - 10k$

$4h + 8k = 44$

$h + 2k = 11$ ... (2)

Given that center lies on circle line

$4x + y = 16$

$\therefore 4h + k = 16$ ... (3)

Solving (2) & (3)

$-7k = -28$

$k = 4$

i.e;

$4h + 4 = 16 \rightarrow h = 3$

substitute h, k in (1)

$(4 - 3)^2 + (1 + 4)^2 = r^2$

$1^2 + (-3)^2 = r^2$

$r^2 = 10$ or

$r = \sqrt{10}$

Hence the equation of circle is

$(x - 3)^3 + (y - 4)^2 = (\sqrt{10})^2$

$x^2 - 6x + 9 + y^2 - 8y + 16 = 10$

$x^2 + y^2 - 6x - 8y + 15 = 0$

is the required equation of circle.

Find the radius and centre of the circle $x^{2}+y^{2}-24y+128=0$ .

Given the equation of the circle is

$x^2+y^2-24y+128=0$

$x^2+y^2-24y+144=16$

or,

$x^2+(y-12)^2=4^2$ .

From this equation it is clear that the centre is

$(0,12)$ and radius is

$4$ units.

General second degree equation in X and y is ${ ax }^{ 2 }+2hxy+{ by }^{ 2 }+2gx+2fy+c=0$ , Where a,h,b,g,f and c are constats.
Prove that condition for it to be a circle is: $a=b$ and $h=0$

General second-degree equation in

$X$ and

$Y$ is

$ax^2+2hxy+by^2+2gx+2fy+c=0$ , Where

$a,h,b,g,t$ and

$c$ are constants. If a

$a=b(\neq 0)$ and

$h=0$ , then the alone equation

becomes:

$ax^2+ay^2+2gx+2fy=0$

$=x^2+y^2+2gx+2fy=0+c$

$\Rightarrow x^2+y^2+2.\dfrac{g}{a}x+2.\dfrac{f}{a}y+\dfrac{c}{a}=0$ (since

$a\neq 0$ )

$\Rightarrow x^2+2.x.\dfrac{g}{a}+\dfrac{g^2}{a^2}+y^2+2.y.\dfrac{f}{a}+\dfrac{f^2}{a^2}=\dfrac{g^2}{a^2}+\dfrac{f^2}{a^2}-\dfrac{c}{a}$

$\Rightarrow (x+\dfrac{g}{a})^2+(y+\dfrac{f}{a})^2=(\dfrac{1}{a}\sqrt{g^2+f^2-Ca})^2$

Which represents the equation of a circle having centre at

$(\dfrac{-g}{a},\dfrac{-f}{a})$ and radius

$=\dfrac{1}{a}\sqrt{g^2+f^2-Ca}$

$\therefore$ the general second degree equation in

$X$ and

$Y$

represents a circle if coefficient of

$x^2(i.e,a)$ =coefficient of

$y^2(i.e.b)$ and coefficient of

$xy(i,e.h)=0$

Find the equation of circle where centre in $(3,\ -2)$ and which cuts of an intercept of length $6$ on the line $4x-3y+2=0$ .

We have,

Equation of line is $4x-3y+2=0\,\,\,.......\,\,\left( 1 \right)$

Now,

The length of perpendicular from $\left( 3,-2 \right)$ to given line $4x-3y+2=0$

So,

$\text{Length}\,\,=\,\,P\,\,=\,\left| \dfrac{4x-3y+2}{\sqrt{{{4}^{2}}+{{\left( -3 \right)}^{2}}}} \right|$

At point $\left( 3,-2 \right)$

So,

$P=\left| \dfrac{4\times 3-3\times \left( -2 \right)+2}{5} \right|$

$P=\dfrac{20}{5}=4\,\,unit\,$

Now, As circle cuts off an intercepts of length 6,

So, it intercepts at a distance of 3 on each so, from foot of perpendicular.

Hence, the radius of circle is

$=\sqrt{{{4}^{2}}+{{3}^{2}}}$

$\sqrt{16+9}=\sqrt{25}=5$

Hence, equation of circle is

${{\left( x-3 \right)}^{2}}+{{\left( y+2 \right)}^{2}}=5$

$or\,\,{{x}^{2}}+9-6x+{{y}^{2}}+4+4y=5$

$\Rightarrow {{x}^{2}}+{{y}^{2}}-6x+4y+13-5=0$

$\Rightarrow {{x}^{2}}+{{y}^{2}}-6x+4y+8=0$

Hence, this is the answer.

Find the equations of the circle having the pair of lines $x^{2}+2xy+3x+6y=0$ its normals and having the size just sufficient to contain the circle $x(x-4)+y(y-3)=0$

$\begin{array}{l} { x^{ 2 } }+2xy+3x+6y=0 \\ { x^{ 2 } }+3x+2xy+6y=0 \\ x\left( { 3+x } \right) +2y\left( { x+3 } \right) =0 \\ \left( { x+2y } \right) \left( { x+3 } \right) =0 \\ x=-3 \\ or\, \, x=-2y,y=\frac { 3 }{ 2 } \\ x\left( { x-4 } \right) +y\left( { y-3 } \right) =0 \end{array}$

Points on circle is

$[4,3]$

then equation of circle

$\begin{array}{l} \left( { x+3 } \right) \left( { x-4 } \right) +\left( { y-\frac { 3 }{ 2 } } \right) \left( { y-3 } \right) =1 \\ { x^{ 2 } }-x-12+{ y^{ 2 } }-\frac { { 9y } }{ 2 } +\frac { 9 }{ 2 } =0 \\ { x^{ 2 } }+{ y^{ 2 } }-x-\frac { { 9y } }{ 2 } =\frac { { 15 } }{ 2 } \end{array}$

Find the equation of the circle which pass through the origin and cut off intercepts $a$ and $b$ respectively from the $x$ and $y$ axes.

General equation of circle

$x^{2}+y^{2}+2gx+2fy+c=0$

Points lie on the circle are

$(0,0) \,;(a,0)$ &

$(0,b).$

by putting (0,0) we get c = 0 ;

by putting (a,0) we get

$a^{2}+2ga = 0$

by putting (0,b) we get

$b^{2}+2fb = 0$

Hence

$a = -2g ;\, b = -2f$

$\therefore$ equation of circle will be

$x^{2}+y^{2}-ax-by=0$

1208483_1283810_ans_bd95e7aef1944c5e872f8d0138182058.jpg

The circle $x^{2}-y^{2}-2x+1=0$ is method angle the positive direction of $x-$ axis and makes one complete roll. Find its equation in new position.

$\begin{array}{l} { x^{ 2 } }-{ y^{ 2 } }-2x+1=0 \\ \Rightarrow { x^{ 2 } }-2x+1-{ y^{ 2 } }=0 \\ \Rightarrow { \left( { x-1 } \right) ^{ 2 } }+1-{ y^{ 2 } }=1 \\ \Rightarrow { \left( { x-1 } \right) ^{ 2 } }+y\left( { 1-y } \right) =1,r=1 \end{array}$

New equation of circle

$\Rightarrow { \left\{ { x-\left( { 1+2\pi } \right) } \right\} ^{ 2 } }+{ \left( { y-1 } \right) ^{ 2 } }=1$

1213459_1283682_ans_d1ee3075c0ea4b56b9941d848a0bfe3e.PNG

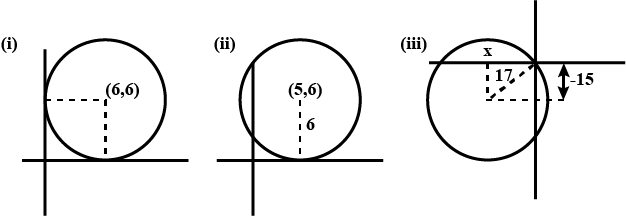
Find the equation of a circle.
(i) Which touches both the axes at a distance of $6$ units from the origin.
(ii) Which touches x-axis at a distance $5$ from the origin and radius $6$ units.
(iii) Which touches both the origin, radius $17$ and ordinate of the centre is $-15$ .
(iv) Passing through the origin, radius $17$ and ordinate of the centre is $-15$ .

(i) R.E.F image

Center : (6,6)

radius = 6 units

$\therefore Eq^{n} (x-6)^{2} + (y - 6)^2= 36.$

(ii) R.E.F image

Center : (5,6)

radius : 6 units

$Eq^{n} : (x-5)^{2}+(y-6)^{2} = 36.$

(iii) R.E.F image

$x = \sqrt{17^{2}-15^{2}} = 8$

Center : (-8,-15)

radius : 17

$Eq^{n} : (x+8)^{2}+(y+15)^{2} = 17^{2}$ } same equation for (iv).

1141048_1276529_ans_801cc6de5bb74998846150be6e6594f5.png

Find the equation of the circle whose radius is $3$ and which touches the circle $x^{2}+y^{2}-4x-6y-12=0$ internally at the point $(-1,\ -1)$

Now,

$\begin{array}{l} { x^{ 2 } }+{ y^{ 2 } }-4x-6y-12=0 \\ 2g=-4\, \, ,2f=-6\, \, ,c=-12 \\ g=-2\, \, \, ,f=-3 \\ Centre\, \, \left( { -g,-f } \right) \Rightarrow \left( { 2,3 } \right) \\ radius\, \, =\sqrt { { g^{ 2 } }+{ f^{ 2 } }-c } \\ =\sqrt { 13+12 } \\ =5\, unit. \\ Let\, \, centre\, \, \left( { h,k } \right) \, \, and\, \, radius\, \, is\, \, 3 \\ { \left( { h+1 } \right) ^{ 2 } }+{ \left( { k+1 } \right) ^{ 2 } }=9 \\ { h^{ 2 } }+{ k^{ 2 } }+2h+2k+2=9 \\ { h^{ 2 } }+{ k^{ 2 } }+2h+2h=7..........\left( 1 \right) \\ { \left( { h-1 } \right) ^{ 2 } }+{ \left( { k-5 } \right) ^{ 2 } }=4 \\ { h^{ 2 } }+{ k^{ 2 } }-4h-6k=9.............\left( 2 \right) \\ 2{ h^{ 2 } }+2{ k^{ 2 } }-2h-4k=16 \\ { h^{ 2 } }+{ k^{ 2 } }-h-2k=8 \\ { x^{ 2 } }+{ y^{ 2 } }-x-2y-8=0 \end{array}$

A circle touches both the $x-$ axis and the line $4x-3y+4=0$ . Its centre is in the third quadrant and lies on the line $x-y-1=0$ . Find the equation of the circle.

We have,

Line $4x-3y+4=0$ ….. (1)

Line $x-y-1=0$ …… (2)

From equation (1) and (2) to and we get,

$x=-7\,and\,y=-8$

Then,

Centre of circle $\left( h,k \right)=\left( -7,-8 \right)$

But centre lies third quadrant.

So,

centre $\left( h,k \right)=\left( -7,8 \right)$

so,

Equation of circle

${{\left( x-h \right)}^{2}}+{{\left( y-k \right)}^{2}}={{r}^{2}}$

$\Rightarrow {{\left( x+7 \right)}^{2}}+{{\left( y-8 \right)}^{2}}={{\left( -7 \right)}^{2}}\,\,\,\left( \therefore \,x-axis\,so,\,radius\,of\,circle\,=Abssicissa \right)$

$\Rightarrow {{x}^{2}}+49+14x+{{y}^{2}}+64-16y=49$

$\Rightarrow {{x}^{2}}+{{y}^{2}}+14x-16y+64=0$

Hence, the required equation of circle.

Find the centre and radius of the circle:
$\dfrac{1}{2}(x^2 + y^2) + X cos\theta + y sin \theta - 4 = 0$

Given circle

$\frac{(x^{2}+y^{2})}{2}+x cos \theta + y sin \theta -4=0$

$\Rightarrow x^{2}+y^{2}+2x cos\theta +2 y sin \theta -8=0$

center =

$(- cos\theta , - sin\theta )$

radius =

$\sqrt{(-cos \theta )^{2}+(- sin \theta )^{2}+8}$

$=\sqrt{cos^{2}\theta + sin^{2}\theta +8}$

$=\sqrt{1+8}=\sqrt{9}=3$

$\therefore$ radius of circle = 3 units

1173866_1293525_ans_5597eabfc79f42a5a65aed44abcfea04.jpeg

Find the coordinates of the focus, equation of the directrix and the latus rectum of
$2x^{2}+3y=0$

We have,

$\begin{array}{l} 2{ x^{ 2 } }+3y=0 \\ 2{ x^{ 2 } }=-3y \\ { x^{ 2 } }=\cfrac { { -3 } }{ 2 } y \end{array}$

Since, above equation include

${x^2}$ so, it axis is

$x- axis$ . Also, coefficient of

$y$ is positive

$\left( -{\dfrac{{ 3}}{2}} \right)$ . hence,

$\begin{array}{l} { x^{ 2 } }=-4ay \\ \therefore -4a=-\dfrac { { 3 } }{ 2 } \\ a=\dfrac { 3 }{ 8 } \\ focus=\left( { 0,-a } \right) =\left( { 0,\dfrac { { -3 } }{ 8 } } \right) \\ equation\, \, of\, \, directrix=y=a=\dfrac { 3 }{ 8 } \\ latus\, \, rectum=-4a=\dfrac { 3 }{ 2 } \end{array}$

Hence, this is the answer.

Find vertex and focus for the equation $y^{2}-8y-x+19=0$

$\begin{array}{l} { y^{ 2 } -}8y-x+19=0 \\ { y^{ 2 } }-2\left( 4 \right) y+16+3=x \\ { \left( { y-4 } \right) ^{ 2 } }=\left( { x-3 } \right) \, \, \, \, \, \, \, \, \, \, \left[ \begin{array}{l} { y^{ 2 } }=4ax \\ A=\frac { 1 }{ 4 } \end{array} \right] \\ y=y-4 \\ x=x-3 \\ x=3 \\ y=4 \\ vertex=\, \, \left( { 3,4 } \right) \\ focus:\, \\ x-3=\frac { 1 }{ 4 } \\ x=\frac { { 13 } }{ 4 } \\ y=4 \end{array}$

Show that the tangents to the parabola $y^{2}=4ax$ at the ends of its latus rectum meet at its directrix.

take the parabola as $y^2=4ax$

now coordinates of its end of latus rectum are $(a,2a) ; (a,-2a)$ .

Now tangent at any point $(x`,y`)$ on parabola is $yy`=2a(x+x`)$ .

Tangent at point $(a,2a)$ is $2ay=2ax+2a^2$ and at $(a,-2a)$ is $-2ay=2ax+2a^2$ .

By solving this linear equation in two unknown, we get point of intersection of tangent $y=0$ and $x=-a$ ;

so the point of intersection is $(-a,0)$ and it clearly lie on directrix.

Prove that the sum of the squares of the reciprocals of two perpendicular diameter of an ellipse is constant.

1569861_1306641_ans_79a0b85ec6674740a9e5ab289e82d77e.jpg

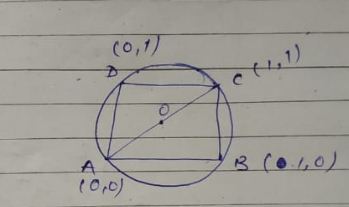
Find the equation of the circle circumscribing a square ABCD with side l and AB and AD as coordinate axes

centre

$'o' = \left( {\frac{1}{2},\frac{1}{2}} \right)$

$AC: - \sqrt 2$

$AO: - \frac{1}{{\sqrt 2 }}$

$e{q^n}\,of\,circle\,{\left( {x - \frac{1}{2}} \right)^2} + {\left( {y - \frac{1}{2}} \right)^2} = {\left( {\frac{1}{{\sqrt 2 }}} \right)^2}$

${\left( {x - \frac{1}{2}} \right)^2} + {\left( {y - \frac{1}{2}} \right)^2} = \frac{1}{2}$ Answer.

1217907_1302818_ans_569cf05778d844fa95d76555e8020378.JPG

Find the equation circle if the equations of two diameters are $2x + y = 6$ and $3x + 2y = 4$ . When radius of circle is $9$ .

Intersection of equation of diameter gives centre

$3x + 2y = 4$

$2x + y = 6 \rightarrow \times 2$

$3x + 2y = 4$

$4x + 2y = 12$

$-x = -8$

$x = 8$

$2x + y = 6$

$16 + y = 6$

$y = -10$

Centre

$C(8, -10)$

$Radius = r = 9$

Equation of circle

$C = (8, -10), r = 9$

$(x - 8)^{2} + (y + 10)^{2} = (9)^{2}$

$x^{2} - 16x + 1 64 + y^{2} + 20y + 100 = 81$

$x^{2} + y^{2} - 16x + 20y + 83 = 0$ .

Find the equation of normal to the parabola $y ^ { 2 }=4ax$ which passes through the point $(-6a,0).$ and suspended at $60^o$ .

$\[ \begin{array}{l} y-\left( { -6a } \right) =m\left( { 1-0 } \right) \\ y=mx-6a \\ { y^{ 2 } }=4ax \\ { y^{ 2 } }=4ax\left( { \frac { { y-mx } }{ { -6a } } } \right) \\ { y^{ 2 } }=-\frac { 2 }{ 3 } yx+\frac { 2 }{ 3 } m{ x^{ 2 } }. \\ { y^{ 2 } }+\frac { 2 }{ 3 } yx-\frac { 2 }{ 3 } m{ x^{ 2 } }=0 \\ 3{ y^{ 2 } }-2yx-2m{ x^{ 2 } }=0 \\ 3\left( { \frac { { { y^{ 2 } } } }{ { { x^{ 2 } } } } } \right) -\frac { { 2y } }{ x } -2m=0 \\ 3{ m^{ 2 } }-2{ m^{ 1 } }-2n=0 \\ Now, \\ \tan \theta =\left| { \frac { { { m_{ 1 } }-{ m_{ 2 } } } }{ { 1-{ m_{ 1 } }{ m_{ 2 } } } } } \right| \\ 1=\left| { \frac { { \sqrt { { { \left( { { m_{ 1 } }+{ m_{ 2 } } } \right) }^{ 2 } }-4{ m_{ 1 } }{ m_{ 2 } } } } }{ { 1+{ m_{ 1 } }{ m_{ 2 } } } } } \right| \\ 1=\left| { \frac { { \sqrt { \frac { 4 }{ 9 } +4.\frac { { 2m } }{ 3 } } } }{ { 1-\frac { { 2m } }{ 3 } } } } \right| \\ { \left( { 1-\frac { { 2m } }{ 3 } } \right) ^{ 2 } }=\frac { 4 }{ 9 } +\frac { { 8m } }{ 3 } \\ 1-\frac { { 4m } }{ 3 } +\frac { { 4{ m^{ 2 } } } }{ 9 } =\frac { 4 }{ 9 } ++\frac { { 8m } }{ 3 } \\ \frac { { 4{ m^{ 2 } } } }{ 4 } -4m+\frac { 5 }{ 9 } =0 \\ 4{ m^{ 2 } }-36m+5=0 \\ m=\frac { { 36\pm \sqrt { { { 36 }^{ 2 } }-4\times 4\times 5 } } }{ { 2\times 4 } } \\ on\, solving\, we\, get \\ m=\frac { { 9-\sqrt { 76 } } }{ 2 } \, \, ,\, \frac { { 9+\sqrt { 76 } } }{ 2 } \, \, \, \end{array}$

Find the equation of the parabola with focus (6, 0) and directrix x = -Also find the length of latus-rectum

We have,

Equation of parabola

${{y}^{2}}=4ax$

Focus has positive x co ordinate.

So,

Co ordinate of focus $=\left( a,0 \right)$

$\left( a,0 \right)=\left( 6,0 \right)$

$a=6$

Hence, equation of parabola is

${{y}^{2}}=4ax$

${{y}^{2}}=4\times 6x$

${{y}^{2}}=24x$

Then,

Latus rectum $=4a=4\times 6=24$

Hence, this is the answer.

Find the vertex focus, equation of directrix and equation of axis of the $y^{2}-x+4y+5=0$ .

$\begin{array}{l} { y^{ 2 } }+4y-x+5=0 \\ { y^{ 2 } }+4y+4=x-5 \\ { \left( { y+2 } \right) ^{ 2 } }=\left( { x-5 } \right) \\ { { standard } }\, \, form\, \, of\, \, equation. \\ { \left( { y-b } \right) ^{ 2 } }=2P\left( { x-a } \right) \\ \therefore b=-2\, \, \, \, a=5\, \, \, 2P=1\, \, \, \, \Rightarrow p=\frac { 1 }{ 2 } \\ vertex\, \, is\, \, \left( { a,b } \right) \Rightarrow \left( { 5,-2 } \right) \\ focus\, \, is\, \, \left( { a+\frac { P }{ 2 } ,b } \right) \, \, \Rightarrow \left( { 5+\frac { 1 }{ { \frac { 2 }{ 2 } } } ,-2 } \right) =\left( { \frac { { 21 } }{ 4 } ;-2 } \right) \\ directrix\, \, is\, \, x=a-\frac { P }{ 2 } =5-\frac { 1 }{ 4 } =\frac { { 19 } }{ 4 } \end{array}$

Find the Equation of tangent which passes through Point $( 0,1 )$ and line touches touches the Parabola $9 x ^ { 2 } + 12 x + 18 y - 14 = 0.$

$\begin{array}{l} 9{ x^{ 2 } }+12x+18y-14=0 \\ equation\, of\, \tan gent\, with\, slope\, m\, \, \, to\, \, parabola\, and\, passes\, through\, \left( { 0,\, 1 } \right) \\ y-1=m\left( { x-0 } \right) \\ \Rightarrow y-1=mx \\ \therefore y=mx+1 \\ solve\, \tan gent\, and\, parabola \\ 9{ x^{ 2 } }+12x+18\left( { mx+1 } \right) -14=0 \\ \Rightarrow 9{ x^{ 2 } }+12x+18mx+18-14=0 \\ \Rightarrow 9{ x^{ 2 } }+\left( { 12+18m } \right) x+4=0 \\ i.e\, \, line\, touch\, \\ i.e\, equal\, roots \\ D=0 \\ { b^{ 2 } }-4ac=0 \\ { \left( { 12+18m } \right) ^{ 2 } }-4\times 9\times 4=0 \\ 36{ \left( { 2+3m } \right) ^{ 2 } }-4\times 36=0 \\ 4+9{ m^{ 2 } }+12m-4=0 \\ 9{ m^{ 2 } }+12m=0 \\ \therefore m\left( { 9m+12 } \right) =0 \\ \therefore m=0,\, \, \, \, \, m=\frac { { -12 } }{ 9 } =\frac { { -4 } }{ 3 } \\ \end{array}$

If the line $2x-y+1=0$ touches the circle at the point $(2,5)$ and the centre of the circle on the line $x+y-9=0$ . Find the equation of the circle.

$\begin{array}{l} { \left( { x-2 } \right) ^{ 2 } }+{ \left( { y-5 } \right) ^{ 2 } }+\lambda \left[ { 2x-y+1 } \right] =0 \\ { x^{ 2 } }+{ y^{ 2 } }+29-4x-10y+\lambda \left( { 2x-y+1 } \right) =0 \\ { x^{ 2 } }+{ y^{ 2 } }+x\left( { 2\lambda -4 } \right) +y\left( { -\lambda -10 } \right) +\left( { 29+\lambda } \right) =0 \\ \\ Centre:\, \, \left( { 2-\lambda ,\, \, 5+\frac { \lambda }{ 2 } } \right) \\ 2-\lambda +5+\frac { \lambda }{ 2 } -9=0 \\ -2-\frac { \lambda }{ 2 } =0 \\ \frac { \lambda }{ 2 } =-2 \\ \therefore \lambda =-4 \\ Hence, \\ Equation\, of\, circle:{ x^{ 2 } }+{ y^{ 2 } }-12x-6y+25=0 \end{array}$

Find the equation of the circle concentric with the circle ${ x }^{ 2 }+{ y }^{ 2 }+4x+6y+11=0$ and passing through the point p(5,4)

1846290_1330721_ans_31520eb1585b4455940f160315d91f76.jpg

Find the equation of a circle of radius $5$ whose centre lies on $x-axis$ and passes through the point $(2, 3)$ .

Since the centre lies on

$x$ -axis, let the coordinates of centre be

$\left( h, 0 \right)$ .

Also, radius of circle

$= 5$

Equation of circle-

${\left( x - h \right)}^{2} + {\left( y - 0 \right)}^{2} = {5}^{2}$

${\left( x - h \right)}^{2}+ {y}^{2} = 25$

Also the circle passes through the point

$\left( 2, 3 \right)$ .

Therefore,

${\left( 2 - h \right)}^{2} + {3}^{2} = 25$

$\Rightarrow 4 + {h}^{2} - 4h = 25 - 9$

${h}^{2} - 4h - 12 = 0$

${h}^{2} - 6h + 2h - 12 = 0$

$\left( h - 6 \right) \left( h + 2 \right) = 0$

$\Rightarrow h = 6$ or

$h = -2$

Case I:-

$h = 6$

Equation of circle-

${\left( x - 6 \right)}^{2} + {y}^{2} = 25$

${x}^{2} - 12x + {y}^{2} + 11 = 0$

Case II:-

$h = -2$

Equation of circle-

${\left( x + 2 \right)}^{2} + {y}^{2} = 25$

${x}^{2} + 4x + {y}^{2} - 21 = 0$

Find the equation of circle with centre at $(-2,3)$ and touching the X-axis

The equation of circle is

$x^2+y^2+2gx+2fy+c=0\\$

The center of circle is

$(-g,-f)$ comparing it with

$(-2,3)$

$\implies g=2,f=-3$

The equation with center

$(-2,3)$ is

$x^2+y^2+4x-6y+c=0$

The equation touches X axis

$\Rightarrow g^2=c\Rightarrow c=4$

So the required equation of circle is

$x^2+y^2+4x-6y+4=0$

Find the center and the radius of the circle $x^ {2}+y^ {2}+8x+10y-8=0$

Given equation of circle-

${x}^{2} + {y}^{2} + 8x + 10y - 8 = 0 ..... \left( 1 \right)$

General form of equation of circle-

${x}^{2} + {y}^{2} + 2gx + 2fy + c = 0 ..... \left( 2 \right)$

Comparing equation

$\left( 1 \right)$ and

$\left( 2 \right)$ , we have

$g = 4$

$f = 5$

$c = -8$

Therefore,

Radius of circle

$= \sqrt{{g}^{2} + {f}^{2} - c} \\ = \sqrt{{4}^{2} + {5}^{2} - \left( -8 \right)} \\ = \sqrt{16 + 25 + 8} = \sqrt{49} = 7$

Centre of circle

$= \left( -g, -f \right) \\ = \left( -4, -5 \right)$

Find the equation of the parabola with focus $\left(8,0\right)$ and directrix $x=-8$ .Also find the length of the latus rectum.

The focus of the parabola is

$F\left(8,0\right)$ and its directrix is the line

$x=-8$ i.e.,

$x+8=0$

Let

$P\left(x,y\right)$ be any point in the plane of directrix and focus, and

$MP$ be the perpendicular distance from

$P$ to the directrix,then

$P$ lies on parabola iff

$FP=MP$

$\Rightarrow\,\sqrt{{\left(x-8\right)}^{2}+{\left(y-0\right)}^{2}}=\dfrac{\left|x+8\right|}{1}$

$\Rightarrow\,{x}^{2}-16x+64+{y}^{2}={x}^{2}+16x+64$

$\Rightarrow \, -16x+{y}^{2}=16x$

$\Rightarrow \,{y}^{2}=32x$ which is the required equation of the parabola.

Comparing it with

${y}^{2}=4ax$ we get

$4a=32\Rightarrow\,a=\dfrac{32}{4}=8$

$\therefore\,$ Length of the latus rectum

$=4a=4\times 8=32$

Find the equation of the parabola with focus $\left(5,0\right)$ and directrix $x=-5$ .Also find the length of the latus rectum.

The focus of the parabola is

$F\left(5,0\right)$ and its directrix is the line

$x=-5$ i.e.,

$x+5=0$

Let

$P\left(x,y\right)$ be any point in the plane of directrix and focus, and

$MP$ be the perpendicular distance from

$P$ to the directrix,then

$P$ lies on parabola iff

$FP=MP$

$\Rightarrow\,\sqrt{{\left(x-5\right)}^{2}+{\left(y-0\right)}^{2}}=\dfrac{\left|x+5\right|}{1}$

$\Rightarrow\,{x}^{2}-10x+25+{y}^{2}={x}^{2}+10x+25$

$\Rightarrow \, -10x+{y}^{2}=10x$

$\Rightarrow \,{y}^{2}=20x$ which is the required equation of the parabola.

Comparing it with

${y}^{2}=4ax$ we get

$4a=20\Rightarrow\,a=\dfrac{20}{4}=5$

$\therefore\,$ Length of the latus rectum

$=4a=4\times 5=20$

Find the equation of the parabola with focus $\left(3,0\right)$ and directrix $x=-3$ .Also find the length of the latus rectum.

The focus of the parabola is

$F\left(3,0\right)$ and its directrix is the line

$x=-3$ i.e.,

$x+3=0$

Let

$P\left(x,y\right)$ be any point in the plane of directrix and focus, and

$MP$ be the perpendicular distance from

$P$ to the directrix,then

$P$ lies on parabola iff

$FP=MP$

$\Rightarrow\,\sqrt{{\left(x-3\right)}^{2}+{\left(y-0\right)}^{2}}=\dfrac{\left|x+3\right|}{1}$

$\Rightarrow\,{x}^{2}-6x+9+{y}^{2}={x}^{2}+6x+9$

$\Rightarrow \, -6x+{y}^{2}=6x$

$\Rightarrow \,{y}^{2}=12x$ which is the required equation of the parabola.

Comparing it with

${y}^{2}=4ax$ we get

$4a=12\Rightarrow\,a=\dfrac{12}{4}=3$

$\therefore\,$ Length of the latus rectum

$=4a=4\times 3=12$

Find the equation of the parabola with focus $\left(6,0\right)$ and directrix $x=-6$ .Also find the length of the latus rectum.

The focus of the parabola is

$F\left(6,0\right)$ and its directrix is the line

$x=-6$ i.e.,

$x+6=0$

Let

$P\left(x,y\right)$ be any point in the plane of directrix and focus, and

$MP$ be the perpendicular distance from

$P$ to the directrix,then

$P$ lies on parabola iff

$FP=MP$

$\Rightarrow\,\sqrt{{\left(x-6\right)}^{2}+{\left(y-0\right)}^{2}}=\dfrac{\left|x+6\right|}{1}$

$\Rightarrow\,{x}^{2}-12x+36+{y}^{2}={x}^{2}+12x+36$

$\Rightarrow \, -12x+{y}^{2}=12x$

$\Rightarrow \,{y}^{2}=24x$ which is the required equation of the parabola.

Comparing it with

${y}^{2}=4ax$ we get

$4a=24\Rightarrow\,a=\dfrac{24}{4}=6$

$\therefore\,$ Length of the latus rectum

$=4a=4\times 6=24$

Find the equation to the circle which has its centre at the point $(1, -3)$ and touches the straight line $2x - y - 4 = 0$ .

Give, the centre of the circle is

$(1,-3)$ and the equation of the line that it touches is

$2x-y-4=0$

Therefore, radius of the circle is,

$\left|\dfrac{2\times 1-(-3)-4}{\sqrt{(2^{2}+1)}}\right|=\dfrac{1}{\sqrt{5}}$

Therefore, the equation of the circle is

$(x-1)^{2}+(y+3)^{2}=\left (\frac{1}{\sqrt{5}} \right )^{2}\\\Rightarrow 5x^{2}+5y^{2}-10x+30y+49=0$

Find the equation of the parabola with focus $\left(2,0\right)$ and directrix $x=-2$ .Also find the length of the latus rectum.

The focus of the parabola is

$F\left(2,0\right)$ and its directrix is the line

$x=-2$ i.e.,

$x+2=0$

Let

$P\left(x,y\right)$ be any point in the plane of directrix and focus, and

$MP$ be the perpendicular distance from

$P$ to the directrix,then

$P$ lies on parabola iff

$FP=MP$

$\Rightarrow\,\sqrt{{\left(x-2\right)}^{2}+{\left(y-0\right)}^{2}}=\dfrac{\left|x+2\right|}{1}$

$\Rightarrow\,{x}^{2}-4x+4+{y}^{2}={x}^{2}+4x+4$

$\Rightarrow \, -4x+{y}^{2}=4x$

$\Rightarrow \,{y}^{2}=8x$ which is the required equation of the parabola.

Comparing it with

${y}^{2}=4ax$ we get

$4a=8\Rightarrow\,a=\dfrac{8}{4}=2$

$\therefore\,$ Length of the latus rectum

$=4a=4\times 2=8$

Find the equation of the parabola with vertex at origin, symmetric with respect to $y-$ axis and passing through $\left(1,-5\right)$

The vertex of the parabola is at origin and it is symmetric with respect to

$y-$ axis

Also, it passes through

$\left(1,-5\right)$ , a point in the fourth quadrant.

Let its equation be

${x}^{2}=-4ay$ ........

$(1)$

As it passes through

$\left(1,-5\right)$ , we get

${1}^{2}=-4a\times -5\Rightarrow\,a=\dfrac{1}{20}$

Substituting this value of

$a$ in

$(1)$ , the equation of the parabola is

${x}^{2}=-4\times\dfrac{1}{20}y$

$5{x}^{2}=-y$

Find the equation of the parabola with vertex $\left(0,0\right)$ and focus at $\left(-\dfrac{1}{2},0\right)$

Since the focus of the parabola is

$F\left(-\dfrac{1}{2},0\right)$ which lies on

$x-$ axis itself is the axis of the parabola.

Also, the vertex of the parabola is at

$O\left(0,0\right)\,\,\,\,\therefore,$ the parabola is of the form

${y}^{2}=-4ax$ with

$a=\dfrac{1}{2}$

Hence the required equation of the parabola is

${y}^{2}=-4\times \dfrac{1}{2}x=-2x$

Find the equation of the parabola with vertex $\left(0,0\right)$ and focus at $\left(-2,0\right)$

Since the focus of the parabola is

$F\left(-2,0\right)$ which lies on

$x-$ axis itself is the axis of the parabola.

Also, the vertex of the parabola is at

$O\left(0,0\right)\,\,\,\,\therefore,$ the parabola is of the form

${y}^{2}=-4ax$ with

$a=2$

Hence the required equation of the parabola is

${y}^{2}=-4\times 2x=-8x$

Find the equation of the parabola with vertex at origin, symmetric with respect to $y-$ axis and passing through $\left(2,-2\right)$

The vertex of the parabola is at origin and it is symmetric with respect to

$y-$ axis

Also, it passes through

$\left(2,-2\right)$ , a point in the fourth quadrant.

Let its equation be

${x}^{2}=-4ay$ ........

$(1)$

As it passes through

$\left(2,-2\right)$ , we get

${2}^{2}=-4a\times -2\Rightarrow\,a=\dfrac{1}{2}$

Substituting this value of

$a$ in

$(1)$ , the equation of the parabola is

${x}^{2}=-4\times\dfrac{1}{2}y$

${x}^{2}=-2y$

Find the equation of the parabola with vertex at origin, symmetric with respect to $y-$ axis and passing through $\left(3,-3\right)$

The vertex of the parabola is at origin and it is symmetric with respect to

$y-$ axis

Also, it passes through

$\left(3,-3\right)$ , a point in the fourth quadrant.

Let its equation be

${x}^{2}=-4ay$ ........

$(1)$

As it passes through

$\left(3,-3\right)$ , we get

${3}^{2}=-4a\times -3\Rightarrow\,a=\dfrac{3}{4}$

Substituting this value of

$a$ in

$(1)$ , the equation of the parabola is

${x}^{2}=-4\times\dfrac{3}{4}y$

${x}^{2}=-3y$

Find the equation of the parabola with vertex $\left(0,0\right)$ and focus at $\left(-3,0\right)$

Since the focus of the parabola is

$F\left(-3,0\right)$ which lies on

$x-$ axis itself is the axis of the parabola.

Also, the vertex of the parabola is at

$O\left(0,0\right)\,\,\,\,\therefore,$ the parabola is of the form

${y}^{2}=-4ax$ with

$a=-3$

Hence the required equation of the parabola is

${y}^{2}=-4\times 3x=-12x$

Find the equation of the parabola with vertex $\left(0,0\right)$ and focus at $\left(-4,0\right)$

Since the focus of the parabola is

$F\left(-4,0\right)$ which lies on

$x-$ axis itself is the axis of the parabola.

Also, the vertex of the parabola is at

$O\left(0,0\right)\,\,\,\,\therefore,$ the parabola is of the form

${y}^{2}=-4ax$ with

$a=4$

Hence the required equation of the parabola is

${y}^{2}=-4\times 4x=-16x$

Find the equation of the parabola with vertex at the origin, symmetric with respect to $y-$ axis and passing through $\left(3,-5\right)$ .

The vertex of the parabola is at origin and it is symmetric with respect to

$y-$ axis

Also, it passes through

$\left(3,-5\right)$ , a point in the fourth quadrant.

Let its equation be

${x}^{2}=-4ay$ ........

$(1)$

As it passes through

$\left(3,-5\right)$ , we get

${3}^{2}=-4a\times -5\Rightarrow\,a=\dfrac{9}{20}$

Substituting this value of

$a$ in

$(1)$ , the equation of the parabola is

${x}^{2}=-4\times\dfrac{9}{20}y$

$5{x}^{2}=-9y$

Find the equation of the parabola with vertex $\left(0,0\right)$ and focus at $\left(-5,0\right)$

Since the focus of the parabola is

$F\left(-5,0\right)$ which lies on

$x-$ axis itself is the axis of the parabola.

Also, the vertex of the parabola is at

$O\left(0,0\right)\,\,\,\,\therefore,$ the parabola is of the form

${y}^{2}=-4ax$ with

$a=5$

Hence the required equation of the parabola is

${y}^{2}=-4\times 5x=-20x$

Find the equation of the circle with centre $\left(-2,3\right)$ and radius $4$

Since the centre of the circle is

$\left(-2,3\right)$ and its radius

$4\,\,\,\,\,$

$\therefore$ the equation of the circle is

${\left(x-\left(-2\right)\right)}^{2}+{\left(y-3\right)}^{2}={4}^{2}$

$\Rightarrow\,{\left(x+2\right)}^{2}+{\left(y-3\right)}^{2}=16$

$\Rightarrow\,{x}^{2}+4x+4+{y}^{2}-6y+9-16=0$

$\Rightarrow \,{x}^{2}+{y}^{2}+4x-6y-3=0$

Find the equation of the circle with centre $\left(-7,-5\right)$ and radius $6$

Since the centre of the circle is

$\left(-4,-5\right)$ and its radius $$6\$$

Then, the equation of the circle is

${\left(x-\left(-7\right)\right)}^{2}+{\left(y-\left(-5\right)\right)}^{2}={6}^{2}$

$\Rightarrow\,{\left(x+7\right)}^{2}+{\left(y+5\right)}^{2}=36$

$\Rightarrow\,{x}^{2}+14x+49+{y}^{2}+10y+25-36=0$

$\Rightarrow \,{x}^{2}+{y}^{2}+14x+10y+38=0$

Find the equation of the circle with centre $\left(-4,-5\right)$ and radius $6$

Since the centre of the circle is

$\left(-4,-5\right)$ and its radius

$=6$

Then, the equation of the circle is

$\Rightarrow {\left(x-\left(-4\right)\right)}^{2}+{\left(y-\left(-5\right)\right)}^{2}={6}^{2}$

$\Rightarrow\,{\left(x+4\right)}^{2}+{\left(y+5\right)}^{2}=36$

$\Rightarrow\,{x}^{2}+8x+16+{y}^{2}+10y+25-36=0$

$\Rightarrow \,{x}^{2}+{y}^{2}+8x+10y+5=0$

Find the co-ordinates of the foci, the vertices, the length of major axis, latus rectum and the eccentricity of the conic represented by the equation $3{x}^{2}+5{y}^{2}=15$

The equation of the given conic is

$3{x}^{2}+5{y}^{2}=15$

It can be written as

$\dfrac{{x}^{2}}{5}+\dfrac{{y}^{2}}{3}=1$ ........

$(1)$

which is comparable with

$\dfrac{{x}^{2}}{{a}^{2}}+\dfrac{{y}^{2}}{{b}^{2}}=1$

$(1)$ represents an ellipse

Here

${a}^{2}=5,\,{b}^{2}=3\Rightarrow a=\sqrt{5},\,b=\sqrt{3}$

We know that

$c=\sqrt{{a}^{2}-{b}^{2}}=\sqrt{5-3}=\sqrt{2}$

$\therefore\,$ the coordinates of foci are

$\left(-c,0\right)$ and

$\left(c,0\right)$

i.e.,

$\left(-\sqrt{2},0\right)$ and

$\left(\sqrt{2},0\right)$

The co-ordinate of vertices are

$\left(-a,0\right)$ and

$\left(a,0\right)$

i.e.,

$\left(-\sqrt{5},0\right)$ and

$\left(\sqrt{5},0\right)$

Length of major axis

$=2a=2\times \sqrt{5}=2\sqrt{5}$

Length of minor axis

$=2b=2\times \sqrt{3}=2\sqrt{3}$

Length of latus rectum

$=\dfrac{2{b}^{2}}{a}=\dfrac{2\times{\left(\sqrt{3}\right)}^{2}}{\sqrt{5}}=\dfrac{2\times 3}{\sqrt{5}}=\dfrac{6}{\sqrt{5}}$

Eccentricity

$=\dfrac{c}{a}=\dfrac{\sqrt{2}}{\sqrt{5}}=\sqrt{\dfrac{2}{5}}$

Find the equation of the circle with centre $\left(-3,2\right)$ and radius $5$

Since the centre of the circle is

$\left(-3,2\right)$ and its radius

$5\,\,\,\,\,\therefore,$ the equation of the circle is

${\left(x-\left(-3\right)\right)}^{2}+{\left(y-2\right)}^{2}={5}^{2}$

$\Rightarrow\,{\left(x+3\right)}^{2}+{\left(y-2\right)}^{2}=25$

$\Rightarrow\,{x}^{2}+6x+9+{y}^{2}-4y+4-25=0$

$\Rightarrow \,{x}^{2}+{y}^{2}+6x-4y-12=0$

Find the equation of the circle with centre $\left(-3,-2\right)$ and radius $7$

Since the centre of the circle is

$\left(-3,-2\right)$ and its radius

$7\,\,\,\,\,$

$\therefore$ The equation of the circle is

${\left(x-\left(-3\right)\right)}^{2}+{\left(y-\left(-2\right)\right)}^{2}={7}^{2}$

$\Rightarrow\,{\left(x+3\right)}^{2}+{\left(y+2\right)}^{2}=49$

$\Rightarrow\,{x}^{2}+6x+9+{y}^{2}+4y+4-49=0$

$\Rightarrow \,{x}^{2}+{y}^{2}+6x+4y-36=0$

Find the equation of the circle with centre $\left(3,5\right)$ and radius $6$

Since the centre of the circle is

$\left(3,5\right)$ and its radius

$6$

Then, the equation of the circle is

${\left(x-3\right)}^{2}+{\left(y-5\right)}^{2}={6}^{2}$

$\Rightarrow\,{\left(x-3\right)}^{2}+{\left(y-5\right)}^{2}=36$

$\Rightarrow\,{x}^{2}-6x+9+{y}^{2}-10y+25-36=0$

$\Rightarrow \,{x}^{2}+{y}^{2}-6x-10y-2=0$

Find the equation of the circle with centre $\left(-3,4\right)$ and radius $5$

Since the centre of the circle is

$\left(-3,4\right)$ and its radius

$5\,\,\,\,\$

$\therefore$ the equation of the circle is

${\left(x-\left(-3\right)\right)}^{2}+{\left(y-4\right)}^{2}={5}^{2}$

$\Rightarrow\,{\left(x+3\right)}^{2}+{\left(y-4\right)}^{2}=25$

$\Rightarrow\,{x}^{2}+6x+9+{y}^{2}-8y+16-25=0$

$\Rightarrow \,{x}^{2}+{y}^{2}+6x-8y=0$

Find the equation of a parabola with focus at $\left(-1,-2\right)$ and directrix $x-2y+3=0$

The focus of the parabola is

$F\left(-1,-2\right)$ and directrix is the line

$x-2y+3=0$

Let

$P\left(x,y\right)$ be any point in the plane of focus and directrix, and

$MP$ be the perpendicular distance from

$P$ to the directrix, then

$P$ lies on the parabola iff

$FP=MP$

$\Rightarrow\sqrt{{\left(x+1\right)}^{2}+{\left(y+2\right)}^{2}}=\dfrac{\left|x-2y+3\right|}{\sqrt{{1}^{2}+{\left(-2\right)}^{2}}}$

$\Rightarrow\sqrt{{\left(x+1\right)}^{2}+{\left(y+2\right)}^{2}}=\dfrac{\left|x-2y+3\right|}{\sqrt{1+4}}$

$\Rightarrow\sqrt{{\left(x+1\right)}^{2}+{\left(y+2\right)}^{2}}=\dfrac{\left|x-2y+3\right|}{\sqrt{5}}$

$\Rightarrow\,5\left[{\left(x+1\right)}^{2}+{\left(y+2\right)}^{2}\right]={\left(x-2y+3\right)}^{2}$

$\Rightarrow\,5\left[{x}^{2}+2x+1+{y}^{2}+4y+4\right]={x}^{2}+4{y}^{2}+9-4xy-12y+6x$

$\Rightarrow \,5\left[{x}^{2}+2x+{y}^{2}+4y+5\right]={x}^{2}+4{y}^{2}+9-4xy-12y+6x$

$\Rightarrow \,5{x}^{2}+10x+5{y}^{2}+20y+25-{x}^{2}-4{y}^{2}-9+4xy+12y-6x=0$

$\Rightarrow \,4{x}^{2}+{y}^{2}+4xy+4x+32y+16=0$ is the required equation of the parabola.

Find the equation of the circle with centre $\left(-5,-7\right)$ and radius $9$

Since the centre of the circle is

$\left(-5,-7\right)$ and its radius

$9\,\,\,\,\,$

$\therefore$ the equation of the circle is

${\left(x-\left(-5\right)\right)}^{2}+{\left(y-\left(-7\right)\right)}^{2}={9}^{2}$

$\Rightarrow\,{\left(x+5\right)}^{2}+{\left(y+7\right)}^{2}=81$

$\Rightarrow\,{x}^{2}+10x+25+{y}^{2}+14y+49-81=0$

$\Rightarrow \,{x}^{2}+{y}^{2}+10x+14y-7=0$

Find the equation of the ellipse whose vertices are $\left(\pm\,3,0\right)$ and foci are $\left(\pm\,2,0\right)$

Since the foci of the ellipse are

${F}_{1}\left(-2,0\right)$ and

${F}_{2}\left(2,0\right)$ which lie on the

$x-$ axis and the mid-point of the line segment

${F}_{1}{F}_{2}$ is

$\left(0,0\right),\,\,\,\therefore,$ origin is the centre of the ellipse and the major axis lies along

$x-$ axis.

Hence the equation of the ellipse can be taken as

$\dfrac{{x}^{2}}{{a}^{2}}+\dfrac{{y}^{2}}{{b}^{2}}=1$ .........

$(1)$

As the vertices are

$\left(\pm\,3,0\right)$ . So,

$a=3$

Also,

$c=2$

We know that

${b}^{2}={a}^{2}-{c}^{2}={3}^{2}-{2}^{2}=9-4=5$

From equation

$(1)$ , the equation of the ellipse is

$\dfrac{{x}^{2}}{9}+\dfrac{{y}^{2}}{5}=1$

Find the equation of the circle with centre $\left(-1,-2\right)$ and radius $5$

Since the centre of the circle is

$\left(-1,-2\right)$ and its radius

$5\,\,\,\,\,$

$\therefore$ the equation of the circle is

${\left(x-\left(-1\right)\right)}^{2}+{\left(y-\left(-2\right)\right)}^{2}={5}^{2}$

$\Rightarrow\,{\left(x+1\right)}^{2}+{\left(y+2\right)}^{2}=25$

$\Rightarrow\,{x}^{2}+2x+1+{y}^{2}+4y+4-25=0$

$\Rightarrow \,{x}^{2}+{y}^{2}+2x+4y-20=0$

Find the equation of the circle with centre $\left(-1,-1\right)$ and radius $3$

Since the centre of the circle is

$\left(-1,-1\right)$ and its radius

$3\,\,\,\,\,$

$\therefore,$ the equation of the circle is

${\left(x-\left(-1\right)\right)}^{2}+{\left(y-\left(-1\right)\right)}^{2}={3}^{2}$

$\Rightarrow\,{\left(x+1\right)}^{2}+{\left(y+1\right)}^{2}=9$

$\Rightarrow\,{x}^{2}+2x+1+{y}^{2}+2y+1-9=0$

$\Rightarrow \,{x}^{2}+{y}^{2}+2x+2y-7=0$

Find the equation of a circle having $\left(1,-2\right)$ as its centre and passing through the intersection of the lines $3x+y=14$ and $2x+5y=18$

Given lines are:

$3x+y=14$ ..........

$(1)$

and

$2x+5y=18$ .......

$(2)$

Substitute

$y=14-3x$ from in

$(2)$ we get

$2x+5\left(14-3x\right)=18$

$\Rightarrow 2x+70-15x=18$

$\Rightarrow -13x=18-70=-52$

$\Rightarrow \,x=\dfrac{-52}{-13}=4$

$\therefore\,x=4$

Put

$x=4$ in

$y=14-3x$

$y=14-3\times 4=14-12$

$y=2$

$\therefore\,x=4,\,y=2$

Since the centre of the circle is

$C\left(1,-2\right)$ and it passes through the point

$P\left(4,2\right)$

Its radius

$=\sqrt{{\left(4-1\right)}^{2}+{\left(2+2\right)}^{2}}=\sqrt{9+16}=\sqrt{25}=5$

$\therefore\,$ The equation of the circle is

${\left(x-1\right)}^{2}+{\left(y+2\right)}^{2}={5}^{2}$

$\Rightarrow {x}^{2}-2x+1+{y}^{2}+4y+4-25=0$

$\Rightarrow {x}^{2}+{y}^{2}-2x+4y-20=0$

Find the equation of the ellipse whose vertices are $\left(\pm\,6,0\right)$ and foci are $\left(\pm\,4,0\right)$

Since the foci of the ellipse are

${F}_{1}\left(-4,0\right)$ and

${F}_{2}\left(4,0\right)$ which lie on the

$x-$ axis and the mid-point of the line segment

${F}_{1}{F}_{2}$ is

$\left(0,0\right),\,\,\,\therefore,$ origin is the centre of the ellipse and the major axis lies along

$x-$ axis.

Hence the equation of the ellipse can be taken as

$\dfrac{{x}^{2}}{{a}^{2}}+\dfrac{{y}^{2}}{{b}^{2}}=1$ .........

$(1)$

As the vertices are

$\left(\pm\,6,0\right)$ .So,

$a=6$

Also,

$c=4$

We know that

${b}^{2}={a}^{2}-{c}^{2}={6}^{2}-{4}^{2}=36-16=20$

From equation

$(1)$ , the equation of the ellipse is

$\dfrac{{x}^{2}}{36}+\dfrac{{y}^{2}}{20}=1$

Find the equation of the circle when the end points of a diameter are $A\left(2,3\right)$ and $B\left(3,5\right)$

Using diameter form,the equation of the circle having

$A\left(2,3\right)$ and

$B\left(3,5\right)$ as the end points of a diameter is

$\left(x-2\right)\left(x-3\right)+\left(y-3\right)\left(y-5\right)=0$

$\Rightarrow {x}^{2}-2x-3x+6+{y}^{2}-3y-5y+15=0$

$\Rightarrow {x}^{2}+{y}^{2}-5x-8y+21=0$ is the required equation of the circle.

Find the equation of the ellipse whose vertices are $\left(\pm\,7,0\right)$ and foci are $\left(\pm\,6,0\right)$

Since the foci of the ellipse are

${F}_{1}\left(-6,0\right)$ and

${F}_{2}\left(6,0\right)$ which lie on the

$x-$ axis and the mid-point of the line segment

${F}_{1}{F}_{2}$ is

$\left(0,0\right),\,\,\,\therefore,$ origin is thhe centre of the ellipse and the major axis lies along

$x-$ axis.

Hence the equation of the ellipse can be taken as

$\dfrac{{x}^{2}}{{a}^{2}}+\dfrac{{y}^{2}}{{b}^{2}}=1$ .........

$(1)$

As the vertices are

$\left(\pm\,7,0\right)$ .So,

$a=7$

Also,

$c=6$

We know that

${b}^{2}={a}^{2}-{c}^{2}={7}^{2}-{6}^{2}=49-36=13$

From equation

$(1)$ , the equation of the ellipse is

$\dfrac{{x}^{2}}{49}+\dfrac{{y}^{2}}{13}=1$

Find the equation of a circle having $\left(-1,2\right)$ as its centre and passing through the intersection of the lines $3x-y=7$ and $2x-5y=9$

Given lines are:

$3x-y=7$ ..........

$(1)$

and

$2x-5y=9$ .......

$(2)$

Substitute

$y=3x-7$ from in

$(2)$ we get

$2x-5\left(3x-7\right)=9$

$\Rightarrow 2x-15x+35=9$

$\Rightarrow -13x=9-35=-26$

$\Rightarrow \,x=\dfrac{-26}{-13}=2$

$\therefore\,x=2$

Put

$x=2$ we get

$y=3x-7=3\times 2-7=6-7=-1$

$\therefore\,x=2,\,y=-1$

Since the centre of the circle is

$C\left(-1,2\right)$ and it passes through the point

$P\left(2,-1\right)$

Its radius

$=CP=\sqrt{{\left(2+1\right)}^{2}+{\left(-1-2\right)}^{2}}=\sqrt{9+9}=\sqrt{18}=3\sqrt{2}$

$\therefore\,$ The equation of the circle is

${\left(x-1\right)}^{2}+{\left(y+2\right)}^{2}={\left(3\sqrt{2}\right)}^{2}$

${x}^{2}-2x+1+{y}^{2}+4y+4=18$

${x}^{2}+{y}^{2}-2x+4y+5-18=0$

${x}^{2}+{y}^{2}-2x+4y-13=0$

Find the equation of the ellipse whose foci are $\left(0,\,\pm\, 6\right)$ and length of the minor axis is $16$

Since the foci of the ellipse are

${F}_{1}\left(0,-6\right)$ and

${F}_{2}\left(0,6\right)$ which lie on the

$y-$ axis and the mid-point of the line segment

${F}_{1}{F}_{2}$ is

$\left(0,0\right)$

$\therefore$ origin is the centre of the ellipse and the major axis lies along

$y-$ axis.

Hence the equation of the ellipse can be taken as

$\dfrac{{x}^{2}}{{b}^{2}}+\dfrac{{y}^{2}}{{a}^{2}}=1$ .........

$(1)$

Here

$c=6$

Also, the length of the minor axis is

$16$

$\Rightarrow\,2b=16$

$\Rightarrow\,b=\dfrac{16}{2}=8$

We know that

${b}^{2}={a}^{2}-{c}^{2}$

$\Rightarrow\,{8}^{2}={a}^{2}-{6}^{2}$

$\Rightarrow \,{a}^{2}=64+36=100$

From

$(1)$ , the equation of the ellipse is

$\dfrac{{x}^{2}}{64}+\dfrac{{y}^{2}}{100}=1$

Find the equation of the ellipse whose vertices are $\left(\pm\,5,0\right)$ and foci are $\left(\pm\,1,0\right)$

Since the foci of the ellipse are

${F}_{1}\left(-1,0\right)$ and

${F}_{2}\left(1,0\right)$ which lie on the

$x-$ axis and the mid-point of the line segment

${F}_{1}{F}_{2}$ is

$\left(0,0\right),\,\,\,\therefore,$ origin is the centre of the ellipse and the major axis lies along

$x-$ axis.

Hence the equation of the ellipse can be taken as

$\dfrac{{x}^{2}}{{a}^{2}}+\dfrac{{y}^{2}}{{b}^{2}}=1$ .........

$(1)$

As the vertices are

$\left(\pm\,5,0\right)$ .So,

$a=5$

Also,

$c=1$

We know that

${b}^{2}={a}^{2}-{c}^{2}={5}^{2}-{1}^{2}=25-1=24$

From equation

$(1)$ , the equation of the ellipse is

$\dfrac{{x}^{2}}{25}+\dfrac{{y}^{2}}{24}=1$

Find the equation of the ellipse whose vertices are $\left(\pm\,2,0\right)$ and foci are $\left(\pm\,1,0\right)$

Since the foci of the ellipse are

${F}_{1}\left(-1,0\right)$ and

${F}_{2}\left(1,0\right)$ which lie on the

$x-$ axis and the mid-point of the line segment

${F}_{1}{F}_{2}$ is

$\left(0,0\right),\,\,\,\therefore,$ origin is the centre of the ellipse and the major axis lies along

$x-$ axis.

Hence the equation of the ellipse can be taken as

$\dfrac{{x}^{2}}{{a}^{2}}+\dfrac{{y}^{2}}{{b}^{2}}=1$ .........

$(1)$

As the vertices are

$\left(\pm\,2,0\right)$ .So,

$a=2$

Also,

$c=1$

We know that

${b}^{2}={a}^{2}-{c}^{2}={2}^{2}-{1}^{2}=4-1=3$

From equation

$(1)$ , the equation of the ellipse is

$\dfrac{{x}^{2}}{4}+\dfrac{{y}^{2}}{3}=1$

Find the equation of the ellipse whose foci are $\left(0,\,\pm\, 3\right)$ and length of the minor axis is $16$

Since the foci of the ellipse are

${F}_{1}\left(0,-3\right)$ and

${F}_{2}\left(0,3\right)$ which lie on the

$y-$ axis and the mid-point of the line segment.

${F}_{1}{F}_{2}$ is

$\left(0,0\right),\,\,\,\therefore,$ origin is the centre of the ellipse and the major axis lies along

$y-$ axis.

Hence the equation of the ellipse can be taken as

$\dfrac{{x}^{2}}{{b}^{2}}+\dfrac{{y}^{2}}{{a}^{2}}=1$ .........

$(1)$

Here

$c=3$

Also, the length of the minor axis is

$16$

$\Rightarrow\,2b=16$

$\Rightarrow\,b=\dfrac{16}{2}=8$

We know that

${b}^{2}={a}^{2}-{c}^{2}$

$\Rightarrow\,{8}^{2}={a}^{2}-{3}^{2}$

$\Rightarrow \,{a}^{2}=64+9=73$

From

$(1)$ , the equation of the ellipse is

$\dfrac{{x}^{2}}{64}+\dfrac{{y}^{2}}{73}=1$

Find the equation of the ellipse whose vertices are $\left(\pm\,5,0\right)$ and foci are $\left(\pm\,3,0\right)$

Since the foci of the ellipse are

${F}_{1}\left(-3,0\right)$ and

${F}_{2}\left(3,0\right)$ which lie on the

$x-$ axis and the mid-point of the line segment

${F}_{1}{F}_{2}$ is

$\left(0,0\right),\,\,\,\therefore,$ origin is the centre of the ellipse and the major axis lies along

$x-$ axis.

Hence the equation of the ellipse can be taken as

$\dfrac{{x}^{2}}{{a}^{2}}+\dfrac{{y}^{2}}{{b}^{2}}=1$ .........

$(1)$

As the vertices are

$\left(\pm\,5,0\right)$ .So,

$a=5$

Also,

$c=3$

We know that

${b}^{2}={a}^{2}-{c}^{2}={5}^{2}-{3}^{2}=25-9=16$

From equation

$(1)$ , the equation of the ellipse is

$\dfrac{{x}^{2}}{25}+\dfrac{{y}^{2}}{16}=1$

Find the equation of the ellipse whose vertices are $\left(\pm\,9,0\right)$ and foci are $\left(\pm\,5,0\right)$

Since the foci of the ellipse are

${F}_{1}\left(-5,0\right)$ and

${F}_{2}\left(5,0\right)$ which lie on the

$x-$ axis and the mid-point of the line segment

${F}_{1}{F}_{2}$ is

$\left(0,0\right),\,\,\,$

$\therefore$ origin is the center of the ellipse and the major axis lies along with

$x-$ axis.

Hence the equation of the ellipse can be taken as

$\dfrac{{x}^{2}}{{a}^{2}}+\dfrac{{y}^{2}}{{b}^{2}}=1$ .........

$(1)$

As the vertices are

$\left(\pm\,9,0\right)$ .So,

$a=9$

Also,

$c=5$

We know that

${b}^{2}={a}^{2}-{c}^{2}={9}^{2}-{5}^{2}=81-25=56$

From equation

$(1)$ , the equation of the ellipse is

$\dfrac{{x}^{2}}{81}+\dfrac{{y}^{2}}{56}=1$

Find the equation of the ellipse whose foci are $\left(0,\,\pm\, 1\right)$ and length of the minor axis is $12$

Since the foci of the ellipse are

${F}_{1}\left(0,-1\right)$ and

${F}_{2}\left(0,1\right)$ which lie on the

$y-$ axis and the mid-point of the line segment

${F}_{1}{F}_{2}$ is

$\left(0,0\right),\,\,\,\therefore,$ origin is the centre of the ellipse and the major axis lies along

$y-$ axis.

Hence the equation of the ellipse can be taken as

$\dfrac{{x}^{2}}{{b}^{2}}+\dfrac{{y}^{2}}{{a}^{2}}=1$ .........

$(1)$

Here

$c=1$

Also, length of the minor axis is

$12$

$\Rightarrow\,2b=12$

$\Rightarrow\,b=\dfrac{12}{2}=6$

We know that

${b}^{2}={a}^{2}-{c}^{2}$

$\Rightarrow\,{6}^{2}={a}^{2}-{1}^{2}$

$\Rightarrow \,{a}^{2}=36+1=37$

From

$(1)$ , the equation of the ellipse is

$\dfrac{{x}^{2}}{36}+\dfrac{{y}^{2}}{37}=1$

Find the equation of the ellipse whose vertices are $\left(\pm\,8,0\right)$ and foci are $\left(\pm\,3,0\right)$

Since the foci of the ellipse are

${F}_{1}\left(-3,0\right)$ and

${F}_{2}\left(3,0\right)$ which lie on the

$x-$ axis and the mid-point of the line segment

${F}_{1}{F}_{2}$ is

$\left(0,0\right),\,\,\,\therefore,$ origin is the centre of the ellipse and the major axis lies along

$x-$ axis.

Hence the equation of the ellipse can be taken as

$\dfrac{{x}^{2}}{{a}^{2}}+\dfrac{{y}^{2}}{{b}^{2}}=1$ .........

$(1)$

As the vertices are

$\left(\pm\,8,0\right)$ .So,

$a=8$

Also,

$c=3$

We know that

${b}^{2}={a}^{2}-{c}^{2}={8}^{2}-{3}^{2}=64-9=55$

From equation

$(1)$ , the equation of the ellipse is

$\dfrac{{x}^{2}}{64}+\dfrac{{y}^{2}}{55}=1$

Find the equation of the ellipse whose foci are $\left(0,\,\pm\, 5\right)$ and length of the minor axis is $24$

Since the foci of the ellipse are

${F}_{1}\left(0,-5\right)$ and

${F}_{2}\left(0,5\right)$ which lie on the

$y-$ axis and the mid-point of the line segment

${F}_{1}{F}_{2}$ is

$\left(0,0\right),\,\,\,\therefore,$ origin is the centre of the ellipse and the major axis lies along

$y-$ axis.

Hence the equation of the ellipse can be taken as

$\dfrac{{x}^{2}}{{b}^{2}}+\dfrac{{y}^{2}}{{a}^{2}}=1$ .........

$(1)$

Here

$c=5$

Also, the length of the minor axis is

$24$

$\Rightarrow\,2b=24$

$\Rightarrow\,b=\dfrac{24}{2}=12$

We know that

${b}^{2}={a}^{2}-{c}^{2}$

$\Rightarrow\,{12}^{2}={a}^{2}-{5}^{2}$

$\Rightarrow \,{a}^{2}=144+25=169$

From

$(1)$ , the equation of the ellipse is

$\dfrac{{x}^{2}}{144}+\dfrac{{y}^{2}}{169}=1$

Find the equation of the ellipse whose foci are $\left(0,\,\pm\, 7\right)$ and length of the minor axis is $30$

Since the foci of the ellipse are

${F}_{1}\left(0,-7\right)$ and

${F}_{2}\left(0,7\right)$ which lie on the

$y-$ axis and the mid-point of the line segment

${F}_{1}{F}_{2}$ is

$\left(0,0\right)$

$\therefore$ origin is the centre of the ellipse and the major axis lies along

$y-$ axis.

Hence the equation of the ellipse can be taken as

$\dfrac{{x}^{2}}{{b}^{2}}+\dfrac{{y}^{2}}{{a}^{2}}=1$ .........

$(1)$

Here

$c=7$

Also, length of the minor axis is

$30$

$\Rightarrow\,2b=30$

$\Rightarrow\,b=\dfrac{30}{2}=15$

We know that

${b}^{2}={a}^{2}-{c}^{2}$

$\Rightarrow\,{15}^{2}={a}^{2}-{7}^{2}$

$\Rightarrow \,{a}^{2}=225+49=274$

From

$(1)$ , the equation of the ellipse is

$\dfrac{{x}^{2}}{225}+\dfrac{{y}^{2}}{274}=1$

Find the equation of the circle which passes through the points $(5,0)$ and $(1,4)$ whose centre lies on the line $x+y-3=0$ .

Let the centre be

$(h, 3-h)$ , distance of centre from both points would be equal (radius)

$\Rightarrow \sqrt{(h-5)^2+(h-3)^2}=\sqrt{(h-1)^2+(h+1)^2}$

$\Rightarrow 2h^2-10h-6h+34$

$=2h^2-2h+2h+2$

$\Rightarrow -16h+32=0$

$\Rightarrow h=2$

$\Rightarrow$ Centre

$=(2, 1)$

Radius

$=\sqrt{9+1}=\sqrt{10}$

$\Rightarrow$ Equation of circle

$=(x-2)^2+(y-)^2=10$

$\Rightarrow x^2+y^2-4x-2y-5=0$ .

1214490_1396209_ans_ef173dfab616464d80e225ac38350281.jpg

Find the centre and radius of the circles.
$2x^{2}+2y^{2}-x=0$

Given the equation of the circle is

$2x^{2}+2y^{2}-x=0$

or,

$x^2+y^2-\dfrac{x}{2}=0$

or,

$x^2-2.x.\dfrac{1}{4}+\dfrac{1}{4^2}+y^2=\dfrac{1}{4^2}$

or,

$\left(x-\dfrac{1}{4}\right)^2+y^2=\dfrac{1}{4^2}$ .

From this equation we've the center is

$\left(\dfrac{1}{4},0\right)$ and radius is

$\dfrac{1}{4}$ .

Find the equation of the ellipse whose foci are $\left(0,\,\pm\, 5\right)$ and length of the minor axis is $20$

Since the foci of the ellipse are

${F}_{1}\left(0,-5\right)$ and

${F}_{2}\left(0,5\right)$ which lie on the

$y-$ axis and the mid-point of the line segment

${F}_{1}{F}_{2}$ is

$\left(0,0\right),\,\,\,\therefore,$ origin is the centre of the ellipse and the major axis lies along

$y-$ axis.

Hence the equation of the ellipse can be taken as

$\dfrac{{x}^{2}}{{b}^{2}}+\dfrac{{y}^{2}}{{a}^{2}}=1$ .........

$(1)$

Here

$c=5$

Also, the length of the minor axis is

$20$

$\Rightarrow\,2b=20$

$\Rightarrow\,b=\dfrac{20}{2}=10$

We know that

${b}^{2}={a}^{2}-{c}^{2}$

$\Rightarrow\,{10}^{2}={a}^{2}-{5}^{2}$

$\Rightarrow \,{a}^{2}=100+25=125$

From

$(1)$ , the equation of the ellipse is

$\dfrac{{x}^{2}}{100}+\dfrac{{y}^{2}}{125}=1$

Find the equation of the ellipse whose foci are $\left(0,\,\pm\, 6\right)$ and length of the minor axis is $22$

Since the foci of the ellipse are

${F}_{1}\left(0,-6\right)$ and

${F}_{2}\left(0,6\right)$ which lie on the

$y-$ axis and the mid-point of the line segment

${F}_{1}{F}_{2}$ is

$\left(0,0\right),\,\,\,\therefore,$ origin is the centre of the ellipse and the major axis lies along

$y-$ axis.

Hence the equation of the ellipse can be taken as

$\dfrac{{x}^{2}}{{b}^{2}}+\dfrac{{y}^{2}}{{a}^{2}}=1$ .........

$(1)$

Here

$c=6$

Also, length of the minor axis is

$22$

$\Rightarrow\,2b=22$

$\Rightarrow\,b=\dfrac{22}{2}=11$

We know that

${b}^{2}={a}^{2}-{c}^{2}$

$\Rightarrow\,{11}^{2}={a}^{2}-{6}^{2}$

$\Rightarrow \,{a}^{2}=121+36=157$

From

$(1)$ , the equation of the ellipse is

$\dfrac{{x}^{2}}{121}+\dfrac{{y}^{2}}{157}=1$

Find the equation of the ellipse with centre at the origin, one vertex at $(4,0)$ and which passes through the point P $\left ( 2, \dfrac{\sqrt{3}}{2} \right )$

Let general equation of ellipse with centre at origin is

$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$ ………..

$(1)$

Given ellipse passes through

$\left(2, \dfrac{\sqrt{3}}{2}\right)$ and having

$[a=4]$

From equation

$(1)$

$\dfrac{(2)^2}{(4)^2}+\dfrac{(\sqrt{3}/2)^2}{b^2}=1$

$\dfrac{3}{4b^2}=1-\dfrac{1}{4}=\dfrac{3}{4}$

$b^2=1$

$\Rightarrow [b=1]$

From equation

$(1)$

$[a=4]$ &

$[b=1]$

Equation of ellipse is

$\dfrac{x^2}{16}+\dfrac{y^2}{1}=1$ .

1204149_1399164_ans_bbbe45568464494e8d7c157e925edb52.JPG

Derive the equation of parabola $y^{2}=4x$ in standard forms.

Standard form of given parabola is :

$(y-0)^{2}=4(x-0)$

Here focus =

$(1,0)$

Vertex =

$(0,0)$

Find the equation of the ellipse whose foci are $\left(0,\,\pm\, 4\right)$ and length of the minor axis is $18$

Since the foci of the ellipse are

${F}_{1}\left(0,-4\right)$ and

${F}_{2}\left(0,4\right)$ which lie on the

$y-$ axis and the mid-point of the line segment

${F}_{1}{F}_{2}$ is

$\left(0,0\right)$

$\therefore$ origin is the centre of the ellipse and the major axis lies along

$y-$ axis.

Hence the equation of the ellipse can be taken as

$\dfrac{{x}^{2}}{{b}^{2}}+\dfrac{{y}^{2}}{{a}^{2}}=1$ .........

$(1)$

Here

$c=4$

Also, the length of the minor axis is

$18$

$\Rightarrow\,2b=18$

$\Rightarrow\,b=\dfrac{18}{2}=9$

We know that

${b}^{2}={a}^{2}-{c}^{2}$

$\Rightarrow\,{9}^{2}={a}^{2}-{4}^{2}$

$\Rightarrow \,{a}^{2}=81+16=97$

From

$(1)$ , the equation of the ellipse is

$\dfrac{{x}^{2}}{81}+\dfrac{{y}^{2}}{97}=1$

Find the equation of the ellipse if its foci are $\left(\pm\,2,0\right)$ and the length of the latus rectum is $\dfrac{10}{3}$

Since the foci of the ellipse are

${F}_{1}\left(-2,0\right)$ and

${F}_{2}\left(2,0\right)$ which lie on

$x-$ axis and the mid-point of the line segment

${F}_{1}{F}_{2}$

$\therefore$ origin is the centre of the ellipse and the major axis lies along

$x-$ axis.

Hence the equation of the ellipse can be taken as

$\dfrac{{x}^{2}}{{a}^{2}}+\dfrac{{y}^{2}}{{b}^{2}}=1$ .....

$(1)$

Here

$c=2$

Also, the length of the latus rectum is

$\dfrac{10}{3}\Rightarrow\dfrac{2{b}^{2}}{a}=\dfrac{10}{3}$

$\Rightarrow \dfrac{{b}^{2}}{a}=\dfrac{5}{3}$

$\Rightarrow\,{b}^{2}=\dfrac{5}{3}a$

$\Rightarrow\,{a}^{2}-{c}^{2}=\dfrac{5a}{3}$

$\Rightarrow\,{a}^{2}-{2}^{2}=\dfrac{5a}{3}$

$\Rightarrow\,{a}^{2}-4-\dfrac{5a}{3}=0$

$\Rightarrow\,3{a}^{2}-5a-12=0$

$\Rightarrow\,3{a}^{2}-9a+4a-12=0$

$\Rightarrow\,3a\left(a-3\right)+4\left(a-3\right)=0$

$\Rightarrow\,\left(3a+4\right)\left(a-3\right)=0$

$\therefore\,a=\dfrac{-4}{3},\,3$

But

$a>0,\,\,\,\therefore\,a=3$

$\therefore\,{b}^{2}=\dfrac{5a}{3}=\dfrac{5\times 3}{3}=5$

From

$(1)$ equation of the ellipse is

$\dfrac{{x}^{2}}{9}+\dfrac{{y}^{2}}{5}=1$

Find the equation of the parabola whose-
Vertex $(0,0)$ ; Focus $(3,0)$

Vertex is

$(0,0)$ and focus is

$(3,0)$

The distance between focus and vertex

$(a)=\sqrt{(3-0)^2+(0-0)^2}\\\sqrt {9+0}=3$

The equation of parabola is given as

$(y-0)^2=4(3)(x-0)\\y^2=12x$

Find the equation of circle which cuts x-axis at a distance $+3$ from origin and cuts an intercept at y-axis of length $6$ units.

Let circle touches

$x-$ axis at point

$E$ and cuts

$AB$
intercepts at

$y-$ axis.
According to questions,
Let

$C$ is centre of the circle. Draw

$CD \bot AB$ . Then

$CD=OE=3$ and

$AD=\dfrac{AB}{2}=\dfrac{6}{2}=3$
In right angled triangle

$ACD$ ,

$CA^2=AD^2+CD^2$

$=3^2+3^2=9+9+=18$

$=2 \times 9 =3\sqrt 2$

$\therefore$ Radius of circle

$a=CA=3 \sqrt 2$
whereas

$CE=CA=3 \sqrt 2$
Thus, centre of circle will be

$(3,3 \sqrt 2)$
Equation of circle,

$(x-3)^2-(y-3 \sqrt 2)^2=(3 \sqrt 2)^2$

$\Rightarrow x^2+9-6x+y^2+18-6 \sqrt 2=18$

$\Rightarrow x^2+y^2-6x-6 \sqrt 2+9=0$
Similarly circle will be in

$IInd, IIIrd$ and

$IVth$ quadrant whose centres will be

$(-3,3\sqrt 2),(-3,-3\sqrt 2),(3,-3\sqrt 2)$

$x^2+y^2-6x-6\sqrt {2y}+9=0$

$x^2+y^2+6x-6\sqrt {2y}+9=0$
and

$x^2+y^2-6x-6\sqrt {2}+9=0$
Thus, total four circles are possible whose equations is

$x^2+y^2 \pm 6x \pm 6\sqrt {2y}+9=0$
1954251_1402601_ans_723122d9441f4434a2e53f053c992f2f.png

If the eccentricity of an ellipse is $\dfrac{5}{8}$ and the distance between its foci is $10$ , then find latus-rectum of the ellipse.

According to the given,

$2c=10\Rightarrow\,c=\dfrac{10}{2}=5$

We know that eccentricity

$=\dfrac{c}{a}$

$\Rightarrow\,\dfrac{5}{8}=\dfrac{5}{a}\Rightarrow\,a=8$

Also,

${c}^{2}={a}^{2}-{b}^{2}$

$\Rightarrow\,{b}^{2}={a}^{2}-{c}^{2}={8}^{2}-{5}^{2}=64-25=39$

Length of the latus- rectum

$=\dfrac{2{b}^{2}}{a}=\dfrac{2\times 39}{8}=\dfrac{39}{4}$

A circle is drawn with its centre of the line $(4,5)$ and pass through point $(0,1)$ . Find its equation.

Equation of circle center at

$(4,5)$ is given as

$(x-4)^2+(y-5)^2=r^2$

It passes through

$(0,1)$

$\implies 4^2+(1-5)^2=r^2\\16+16=r^2\\r^2=32$

So the equation is

$(x-4)^2+(y-5)^2=32\\x^2+y^2-8x-10y+9=0$

If the latus rectum of an ellipse is equal to half of minor axis, then find its eccentricity.

According to given,

$\dfrac{2{b}^{2}}{a}=b\Rightarrow\,2b=a$

$\Rightarrow\,b=\dfrac{a}{2}$

We know that

${c}^{2}={a}^{2}-{b}^{2}={a}^{2}-\dfrac{{a}^{2}}{4}=\dfrac{4{a}^{2}-{a}^{2}}{4}=\dfrac{3{a}^{2}}{4}$

$\Rightarrow\,\dfrac{{c}^{2}}{{a}^{2}}=\dfrac{3}{4}$

$\Rightarrow\,\dfrac{c}{a}=\dfrac{\sqrt{3}}{2}$

Hence, the eccentricity of the ellipse

$=\dfrac{\sqrt{3}}{2}$

The asymptotes of a hyperbola having centre at the point $(1, 2)$ are parallel to the lines $3x +4y= 0$ and $4x+5y= 0$ . If the hyperbola passes through the point $(3,5)$ , Find the equation of the hyperbola.

Let the asymptotes be

$3x+4y+{c}_{1}=0$ and

$4x+5y+{c}_{2}=0$

Since, the asymptotes passes through the centre

$(1,2)$ of the hyperbola.

$\therefore,\,3+8+{c}_{1}=0$ and

$4+10+{c}_{2}=0$

$\Rightarrow \,{c}_{1}=-11,\,\,{c}_{2}=-14$

Thus, the equations of the asymptotes are

$3x+4y-11= 0$ and

$4x +5y-14= 0$

Let the equation of the hyperbola be

$\left(3x+4y-11\right)\left(4x +5y-14\right)+\lambda=0$ ........

$(1)$

It passes through

$(3,5)$ .

$\therefore,\left(9+20-11\right)\left(12+25-14\right)+\lambda=0$

$\Rightarrow\,18\times 23+\lambda=0$

$\Rightarrow 414‬+\lambda=0$

$\Rightarrow \lambda=-414‬$

Putting the value of

$\lambda$ in

$(1)$ , we obtain

$\left(3x+4y-11\right)\left(4x +5y-14\right)-414=0$

This is the equation of the required hyperbola.

Find the equation of a circle which touches y-axis and cuts an intercept of length 2 l on $x$ -axis.

In the Standard equation of circle put

$k=\sqrt{r^2-l^2}$ and

$h=r$ . Thus
Equation of circle

$(x-r)^2+ (y-\sqrt{r^2-l^2})^2=r^2$

$\Rightarrow x^2+r^2-2rx+y^2+(r^2-l^2)-2y \sqrt{r^2-l^2} -r^2=0$

$\Rightarrow x^2+y^2-2rx-2y \sqrt{r^2-l^2}+ (r^2-l^2)=0$

The given equation represents a____
$y=\sqrt { 1-{ x }^{ 2 } }$

$y=\sqrt{1-{x}^{2}}$

$\Rightarrow {y}^{2}=1-{x}^{2}$ by squaring both sides

$\Rightarrow {x}^{2}+{y}^{2}=1$ is the equation of the circle

Find the number of circle having radius $5$ and passing through the points $(-2,0)$ and $(4,0)$

let center of circle is

$\left(h,k\right)$

${\left(h+2\right)}^{2} +{k}^{2}=25$ .......

$\left(1\right)$

and

${\left(h-4\right)}^{2}+{k}^{2}=25$ .......

$\left(2\right)$

From equation

$\left(1\right)$ and

$\left(2\right)$

${\left(h+2\right)}^{2} +{k}^{2}={\left(h-4\right)}^{2}+{k}^{2}$

$\Rightarrow {\left(h+2\right)}^{2}={\left(h-4\right)}^{2}$

$\Rightarrow {\left(h+2\right)}^{2}-{\left(h-4\right)}^{2}=0$ is of the form

${a}^{2}-{b}^{2}$

$\Rightarrow \left(h+2+h-4\right)\left(h+2-h+4\right)=0$ where

${a}^{2}-{b}^{2}=\left(a+b\right)\left(a-b\right)$

$\Rightarrow 6\left(2h-2\right)=0$ or

$h=1$

Substituting

$h=1$ in eqn

$\left(1\right)$ we get

${\left(h+2\right)}^{2}+{k}^{2}=25$

$\Rightarrow {3}^{2}+{k}^{2}=25$

$\Rightarrow {k}^{2}=25-9=16$

$\Rightarrow k=\pm 4$

So two circles are possible.

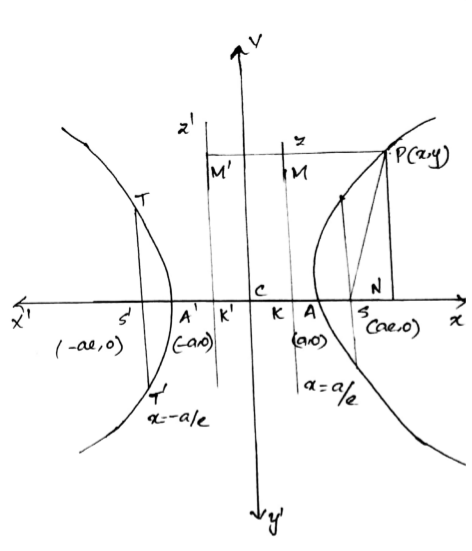
Derive the equation of parabola in the standard from $y^2=4ax$ with diagram.

Consider the above diagram, we take a point

$P(x, y)$ on the parabola such that,

$PF = PB$ … (1) … where

$PB$ is perpendicular to

$l$ . The coordinates of the point

$B$ are

$(- a, y)$ . Also, by the distance formula, we know that

$PF = \sqrt{(x – a)^2 + y^2}$

Also,

$PB = \sqrt{(x + a)^2}$

Since,

$PF = PB$ [from eq. (1)], we get

$\sqrt{(x – a)^2 + y^2} = \sqrt{(x + a)^2}$

So, by squaring both sides, we have

$(x – a)^2 + y^2 = (x + a)^2$ or,

$x^2 – 2ax + a^2 + y^2 = x^2 + 2ax + a^2$ . Further, by the solving the equation, we have

$y^2 = 4ax$ … where

$a > 0$ . Therefore, we can say that any point on the parabola satisfies the equation:

$y^2 = 4ax$ … (2)

Let’s look at the converse situation now. If

$P(x, y)$ satisfies equation (2), then

$PF = \sqrt{(x – a)^2 + y^2}$

$= \sqrt{(x – a)^2 + 4ax}$ … using the RHS of equation (2)

$= \sqrt{(x^2 – 2ax + a^2) + 4ax} = \sqrt{x^2 + 2ax + a^2}$

$= \sqrt{(x + a)^2} = PB$ … (3)

Hence, we conclude that the point

$P(x, y)$ satisfying eq. (2) lies on the parabola. Also, equations (2) and (3) prove that the equation to the parabola with vertex at the origin, focus at

$(a, 0)$ and directrix

$x = – a$ , is

$y^2 = 4ax$ .

1181850_1435885_ans_ca71bc22ae214dbf95c9181845652f15.png

If the equations of the two diameters of a circle are $x + y = 6$ and $x + 2y = 4$ and the radius of the circle is $10$ , find the equation of the circle.

Here radius of the circle

$= 10$

Equations of two diameters of the circle are

$x + y = 6$ ....

$(1)$

$x + 2y = 4$ ....

$(2)$

Solving

$(1)$ and

$(2)$ we get

$(1)\Rightarrow\,y=6-x$

Substituting

$y=6-x$ in

$(2)$ we get

$x+2\left(6-x\right)=4$

$\Rightarrow\,x+12-2x=4$

$\Rightarrow\,-x=4-12=-8$

$\therefore\,x=8$

substitute

$x=8$ in

$y=6-x$

we get

$y=6-8=-2$

Hence centre of the circle is

$(8, – 2)$

Now the equation of the required circle is

${\left(x-8\right)}^{2}+{\left(y+2\right)}^{2}={10}^{2}$

${x}^{2}-16x+64+{y}^{2}+4y+4-100=0$

${x}^{2}+{y}^{2}-16x+4y-32=0$

Find the co-ordinates of the point from which tangents drawn to the circle ${x}^{2}+{y}^{2}–6x– 8y+3=0$ such that the mid point of its chord of contact is $(1, 1)$ .

Let the required point be

$P\left({x}_{1},{y}_{1}\right)$ . The equation of the chord of contact

$P$ with respect to the given circle is

$x{x}_{1}+y{y}_{1}+g\left(x+{x}_{1}\right)+f\left(y+{y}_{1}\right)+c=0$

$\Rightarrow \,2g=-6\Rightarrow\,g=-3$ and

$2f=-8\Rightarrow\,f=-4$

The equation of the chord with mid-point

$\left({x}_{1},{y}_{1}\right)=(1, 1)$ is

$x+y-3\left(x+1\right)-2\left(y+1\right)+3=0$

$\Rightarrow\,x+y-3x-3-2y-2+3=0$

$\Rightarrow\,-2x-y-2=0$

$\Rightarrow 2x+y=3$

Equating the ratios of the coefficients of

$x, y$ and the constant terms and solving for

$x, y$ we get

${x}_{1}=-1,\,{y}_{1}=0$

Find the radius and centre of the circle represented by the equation:
$2x^2+2y^2-x=0$

Given

$2x^{2}+2y^{2}-x=0$ ______(1)

we need to make this form

$(x-h)^{2}+(y-k)^{2}=r^{2}$

From (i)

$2x^{2}+2y^{2}-x=0$

$2(x^{2}+y^{2}-\dfrac{x}{2})=0$

$\Rightarrow x^{2}+y^{2}-\dfrac{x}{2}=\dfrac{0}{2}$

$\Rightarrow x^{2}-\dfrac{x}{2}+y^{2}=0$

$\Rightarrow (x)^{2}-2.\times .(\dfrac{1}{4})x+y^{2}=0$

$\Rightarrow .(x^{2})-2.(\dfrac{1}{4})x+(\dfrac{1}{4})x+y^{2}=0$

$\Rightarrow [x^{2}-2.(\dfrac{1}{4})x+(\dfrac{1}{4})^{2}]-(\dfrac{1}{4})^{2}+y^{2}=0$

$\Rightarrow [x^{2}-2.(\dfrac{1}{4})^{2}]-(\dfrac{1}{4})^{2}+y^{2}=0$

Using

$(a-b)^{2}=a^{2}-2ab+b^{2}$

$(x-\dfrac{1}{4})^{2}-(\dfrac{1}{4})^{2}=0$

$(x-\dfrac{1}{4})^{2}+(y-0)^{2}=(\dfrac{1}{4})^{2}$ ________ (2)

comparing (2) with

$(x-b)^{2}+(y-k)^{2}=r^{2}$

$h=\dfrac{1}{4}, k=0 ; r=\dfrac{1}{4}$

Hence center of circle

$(\dfrac{1}{4} \& \,\, 0)$

Radius of circle =

$r=\dfrac{1}{4}$

Find the equation of a circle of radius $5$ which is touching another circle $x^2+y^2-2x-4y-20=0$ at the point $(5,5)$ .

1894542_1473377_ans_3d2a9a99d0eb4eb489162cef8bbdcf76.jpg

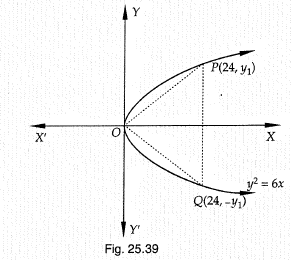
Find the equations of the joining are vertex of the parabola ${ y }^{ 2 }=6x$ to the point on inwhich have abscissa 24.

The parabola

$y^{2}=6x$ is symmetric about

$x-$ axis. So, for a given abscissa there will be two points on the parabola as shown in Fig

$25.39$ .

Let

$P$ and

$Q$ be two points on the parabola whose absicssa is

$24$ . Let their coordinates be

$(24, y_{1})$ and

$(24, -y_{1})$ respectively.

Since

$P(24,y_{1})$ lies on

$y^{2}=6x$ .

$\therefore y_{1}^{2}=6\times 24\Rightarrow y_{1}=12$

So, the coordinates of

$P$ and

$Q$ are

$(24,12)$ and

$(24, -12)$ respectivety.

The equation

$OP$ and

$OQ$ are

$y-0=\dfrac{12-0}{24-0}(x-0)$ and

$y-0=\dfrac{-12-0}{24-0}(x-0)$
or,

$x=2y$ and

$x=-2y$ respectively.

1406714_1464913_ans_0bbb23648ff54d45b4b1a434eb214086.png

Find the direction cosines of the unit vector perpendicular to the plane $\vec { r } .(6\hat { i } -3\hat { j } -2k)+1=0$ passing through the origin.

The equation of the plane is

$\vec{r}.(6\hat{i}-3\hat{j}-2\hat{k})+1=0$ . To find the direction cosines of the normal through the origin, we must write the equation in normal form as follows.

$\vec{r}.(6\hat{i}-3\hat{j}-2\hat{k})+1=0$

$\Rightarrow \vec{r}.(-6\hat{i}+3\hat{j}+2\hat{k})=1$

$\Rightarrow \vec{r}.\dfrac{(-6\hat{i}+3\hat{j}+2\hat{k})}{\sqrt{36+9+4}}=\dfrac{1}{\sqrt{36+9+4}}\Rightarrow \vec{r}\left(-\dfrac{6}{7}\hat{i}+\dfrac{3}{7}\hat{j}+\dfrac{2}{7}\hat{k}\right)=\dfrac{1}{7}$
Hence,m direction cosines of the normal vector through the origin are

$-\dfrac{6}{7}, \dfrac{3}{7}, \dfrac{2}{7}$ .

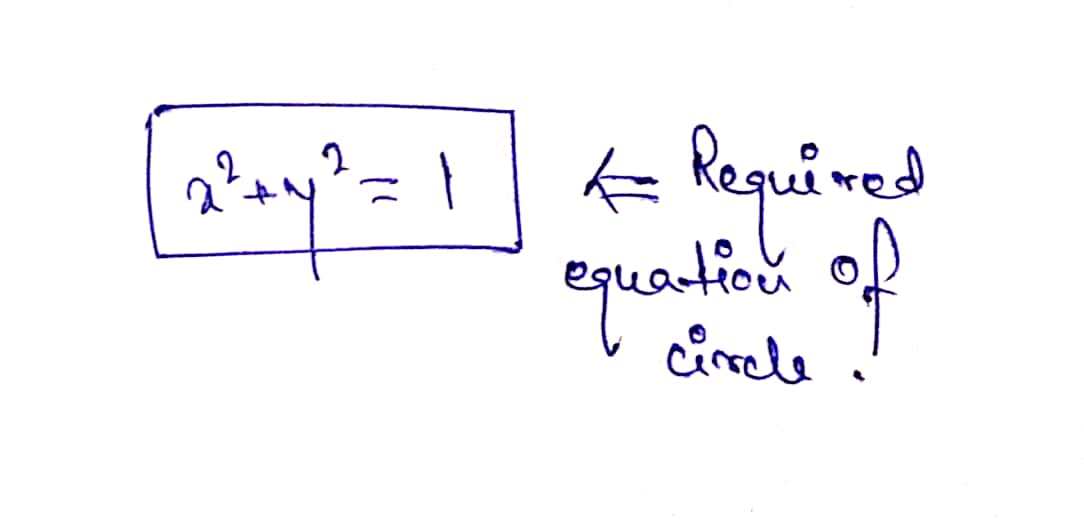
Find the equation of a unit circle whose centre is at the origin.

1318986_1586184_ans_11dde994e73241e09bf3958ece87b18c.jpg

What is the vertex, focus, directrix, and the equation of the axis of the parabola
$\displaystyle (x+5)^{2}=-4(y+1)$ ?

This parabola is of the form

$( x-h)^{2}=4c(y-k)$

with

$\displaystyle (h,k)=(-5,-1)$ and

$\displaystyle c=-1$

then

$\displaystyle Vertex:(-5,-1);Focus:(-5,-1+c)=(-5,-2)$

Directrix

$\displaystyle y=k-c\Longrightarrow y=0$

Axis

$\displaystyle x=h\Longrightarrow x=-5$

$ABCD$ is a square whose side is $a$ ; taking $AB$ and $AD$ as axes, prove that the equation of the circle circumscribing the square is ${ x }^{ 2 }+{ y }^{ 2 }-a(x+y)=0$ .

Given that we need to find the equation of the circle which circumscribes the square ABCD of side a.

It is also told that AB and AD are assumed as x and y - axes.

Assuming A as origin, We get the points $B(a,0)\ and\ D(0,a)$ .

So, we need to find the circle which is passing through the points $A(0,0), B(a,0)\ and\ D(0,a)$ .

We know that the standard form of the equation of the circle is given by:

$\Rightarrow x^2+y^2+2fx+2gy+c=0$ $........(1)$

$Substituting\ A(0,0)\ in\ (1),\ we\ get,$

$0^2+0^2+2f(0)+2g(0)+c=0$

$\Rightarrow c=0$ $........(2)$

$Substituting\ B(a,0)\ in\ (1),\ we\ get,$

$a^2+0^2+2f(a)+2g(0)+c=0$

$\Rightarrow a^2+2fa=0$ $........(3)$

$Substituting\ D(0,a)\ in\ (1),\ we\ get,$

$0^2+a^2+2f(0)+2g(a)+c=0$

$\Rightarrow a^2+2ga=0$ $.......(4)$

$On\ solving\ (2),\ (3)\ and\ (4)\ we\ get,$

⇒

$Substituting\ these\ values\ in\ (1),\ we\ get$

⇒

$\Rightarrow x^2+y^2-ax-ay=0$

$\Rightarrow x^2+y^2-a(x+y)=0$

∴Thus proved.

The perpendicular distance of a line from the origin is 5 units and its slope is-Find the equation of the line.

1412364_1592915_ans_bada8c06304d4cc9b88d82ee11d1df7b.jpg

Find the equation of a circle with radius $5$ and whose centre lies on $x$ -axis and passes through the point $( 2,3 ).$

$\textbf{Step 1: Use equation of circle with given centre and radius}$

$\text{According to question, centre of circle lies on $$x-$$axis. let centre of circle (h,0) and radius=5 units}$

$\text{So equation of the circle}$

$(x-h)^2+(y)^2=5^2.....(i)$

$\Rightarrow (x-h)^2+y^2=25$

$\text{circle passes through point (2,3)}$

$\text{Then}$

$(2-h)^2+3^2=25$

$\Rightarrow 4+h^2-4h+9=25$

$\textbf{Step 2: Simplify to get required unknown}$

$\Rightarrow h^2-4h+13-25=0$

$\Rightarrow h^2-4h-12=0$

$\Rightarrow h^2-(6-2)h-12=0$

$\Rightarrow h^2-6h+1h-12=0$

$\Rightarrow h(h-6)+2(h-6)=0$

$\Rightarrow (h-6)(h+2)=0$

$\Rightarrow h=6$ or

$h=-2$

$\text{so the centre is }$

$(6,0)$

$\text{or }$

$(-2,0)$

$\text{Put}$

$h=6$

$\text{in equation (i)}$ ,

$\text{the equation of circle}$

$(x-6)^2+y^2=25$

$x^2+36-12x+y^2=25$

$x^2+y^2-12x+36--25=0$

$x^2+y^2-12x+11=0$

$\text{Again, putting}$

$h=-2$

$\text{in equation (i) }$

$\text{equation of circle}$

$(x-(-2)^2)^2+y^2=25$

$\Rightarrow (x+2)^2+y^2=25$

$\Rightarrow x^2+4x+4+y^2=25$

$\Rightarrow x^2+y^2+4x+4-25=0$

$\Rightarrow x^2+y^2+4x-21=0$

$\textbf{Thus, required equation of circle is}$

$\mathbf{x^2+y^2-12x+11=0\ }$

$\mathbf{ or\ x^2+y^2+4x-21=0}$

Find the vertex, focus, axis and, directrix of the following parabola
$y^2-4y-8x-28=0$

We will complete squares to find the shape of the parabola equation then

$\displaystyle y^{2}-4y-8x-28=(y-2)^{2}-4=8x+28\Longrightarrow (y-2)^{2}=8x+32$

So the equation of parabola is

$\displaystyle \dfrac{1}{8}(y-2)^{2}=(x+4)$

Then Vertex is at

$\displaystyle (-4,2) \ and\ \displaystyle c=\frac{1}{32}$

Then focus is

$\displaystyle (-4+c,2)=(-\frac{127}{32},2)$

The axis is

$\displaystyle y=2$ and directrix is

$\displaystyle x=-c=-\frac{1}{32}$

Find the equation of the circle circumscribing the rectangle whose sides are $x - 3y = 4$ , $3x + y = 22$ , $x - 3y = 14$ , $3x + y = 62$ .

The given sides of the rectangle are:

$x - 3y = 4$ ...(1)

$3x +y = 22$ ...(2)

$x - 3y = 14$ ...(3)

$3x + y = 62$ ...(4)

On solving (1) and (2) we get,

$X = 7, y = 1$

i.e intersection of (1) and (2) is

$(7, 1)$

On solving (2) and (3) we get,

$x=8\, y=-2$

i.e intersection of (2) and (3) is

$(8, -2)$

On solving (3) and (4) we get,

$x=20, \, y=2$

i.e intersection of (3) and (4) is

$(20,2)$

On solving (1) and (4) we get,

$x=19, \, y=5$

i.e intersection of (1) and (4) is

$(19,5)$

Hence, the curtics of rectangle are

$(7, +1), (8,-2), (20,2)$ and

$(19,5)$

The, cutics of the diagonals are

$(7, 1), (20, 2)$ and

$(19, 5), (8, -2)$

Thus, the required equation of the circle is

$(x-7)(x-20)+(y-1)(y-2) = 0$

$x^2 + y^2 - 27x - 3y + 142 = 0$

Find the eccentricity of the ellipse which meets the straight line $2x-3y=6$ on the x-axis and the straight line $4x+5y=20$ on the y-axis and whose axes lie along the coordinates axes.

$\dfrac{x}{3} - \dfrac{y}{2} = 1 , \dfrac{x}{5} + \dfrac{y}{4} = 1$

$(3 , 0)$

$(0 , 4)$

$\dfrac{x^{2}}{9} + \dfrac{y^2}{16} = 1$

$b > a$

$a^{2} = b^{2} (1 - e^{2})$

$\dfrac{a}{16} = 1 - e^{2}$

$e^{2} = \dfrac{7}{16}$

$e= \dfrac{\sqrt{7}}{4}$

Form the differential equation representing the family of ellipses having centre at the origin and foci on x-axis.

The equation of the family of ellipses having centre at the origin and foci on x-axis is

$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$ …….(i)

It is a two parameter family of curves.

Differentiating (i) twice with respect to x, we get

$\dfrac{2x}{a^2}+\dfrac{2y}{b^2}\dfrac{dy}{dx}=0$ and

$\dfrac{2}{a^2}+\dfrac{2}{b^2}\left(\dfrac{dy}{dx}\right)^2+\dfrac{2y}{b^2}\dfrac{d^2y}{dx^2}=0$

$\Rightarrow \dfrac{x}{a^2}+\dfrac{y}{b^2}\dfrac{dy}{dx}=0$ ……..(ii) and,

$\dfrac{1}{a^2}+\dfrac{1}{b^2}\left(\dfrac{dy}{dx}\right)^2+\dfrac{y}{b^2}\dfrac{d^2y}{dx^2}=0$ ……(iii)

Multiplying (iii) by x and subtracting from (ii), we get

$\dfrac{1}{b^2}\left\{y\dfrac{dy}{dx}-x\left(\dfrac{dy}{dx}\right)^2-xy\dfrac{d^2y}{dx^2}\right\}=0\Rightarrow xy\dfrac{d^2y}{dx^2}+x\left(\dfrac{dy}{dx}\right)^2-y\dfrac{dy}{dx}=0$

This is the required differential equation.

Find the area bounded by the ellipse $\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1$ and the ordinates $x=0$ and $x=ae$ , where $b^{2}=a^{2}(1-e^{2})$ and $e<1$

Required area

$A$ is given by

$A=2$ (Area of shaded region in first quadrant)

$\Rightarrow A=2 \displaystyle\int_{0}^{ae}|y|\ dx=2\displaystyle\int_{0}^{ae}y\ dx$

$[\because y\ge 0\therefore |y|=y]$

$\Rightarrow A=2\dfrac{b}{a}\left[\displaystyle\int_{0}^{ae}\sqrt{a^{2}-x^{2}}dx\right]$

$\Rightarrow A=\dfrac{2b}{a}\left[\dfrac{1}{2}x\times \sqrt{a^{2}-x^{2}}+\dfrac{1}{2}a^{2}\sin^{-1}\dfrac{x}{a}\right]_{0}^{ae}$

$\Rightarrow A=\dfrac{2b}{a}\left[\dfrac{ae}{2}\sqrt{a^{2}-a^{2}e^{2}}+\dfrac{1}{2}a^{2}\sin^{-1}e\right]$

$\Rightarrow A=\dfrac{b}{a}\left(a^{2}e\sqrt{1-e^{2}}+a^{2}\sin^{-1}e\right)=ab\left(e\sqrt{1-e^{2}}+\sin^{-1}e\right)$

Find the equation of a circle with centre $(-3, -2)$ and radius $6$ .

1846247_1595109_ans_d03e62658a084e11a28094453ce020e8.jpeg

Find the equation of a circle with centre (a, a) and radius $\sqrt{2}$ .

1847342_1595110_ans_a67230359eb2458f9858bf8866b8bd13.jpeg

Find the equation of the circle with:
Centre $(2, 3)$ and radius $4$

1412377_1667079_ans_5c6e0523bc2c42c4bc99aa6eaddc5850.jpg

Find the equation of the parabola, is
the focus is at $(-6,-6)$ and the vertex is at $(-2,2)$

1413430_1667135_ans_97415d1eee1841ab965f6fd61a75695b.jpg

Find the centre and radius of each of the following circles:
$(x-1)^2+y^2=4$

Given,

$(x-1)^2+y^2=4$ ------(i)

standard eqn of circle :

$(x-x_0)^2+(y-y_0)^2=r^2$ ------(ii)

where

$(x_0, y_0)$ is the centre and

$x$ is the radius

eqn (i) can be written as

$(x-1)^2+(y-0)^2=2^2$

comparing eqn (i) and (ii), we get

$x_0=1, y_0=0$

$r=2$

$\therefore$ centre

$= (1, 0)$

radius

$=2$

Find the equation of the circle with centre $(a, b)$ and radius $\sqrt {a^2 +b^2}$

1428709_1667083_ans_ea6099ec7ebe46e39b7d501201c6c25c.jpg

Find the equation of the parabola, is
the focus is at $(0,-3)$ and the vertex is at $(0,0)$

1413431_1667140_ans_d9242c92eb63494a9de8d7dc6831bbb7.jpg

Find the equation of the circle with:
Centre $(a, b)$ and radius $\sqrt {2} a$

1412380_1667085_ans_3d8f7145625b4f07b26d138dcbd7dea7.jpg

Find the equation of the circle with:
Centre $(a \cos \alpha, a\sin \alpha)$ and radius $a$ .

1412381_1667088_ans_45d5d326f6504fe19b38febfbb984d94.jpg

Find the equation of the parabola, is
the focus is at $(0,-3)$ and the vertex is at $(-1, -3)$

1413456_1667141_ans_4c23891623444c99a8e8ad0e20e895f9.jpg

Find the equation of the circle which passes through the points $(3, -2), (-2, 0)$ and has its centre on the line $2x-y=3$

1413268_1667194_ans_af7af5cf77ab4bcb95a4997080299087.jpg

Find the equation of the circle which passes through the points $(3, 7),\ (5, 5)$ and has its centre on the line $x-4y=1$ .

1413269_1667195_ans_7f90026c9d0b496cafe925c774bfd63c.jpg

Find the equation of the circle whose centre is $(1, 2)$ and which passes through the point $(4, 6)$ .

1412393_1667102_ans_b7461b2285d74795974c58e73a21c588.jpg

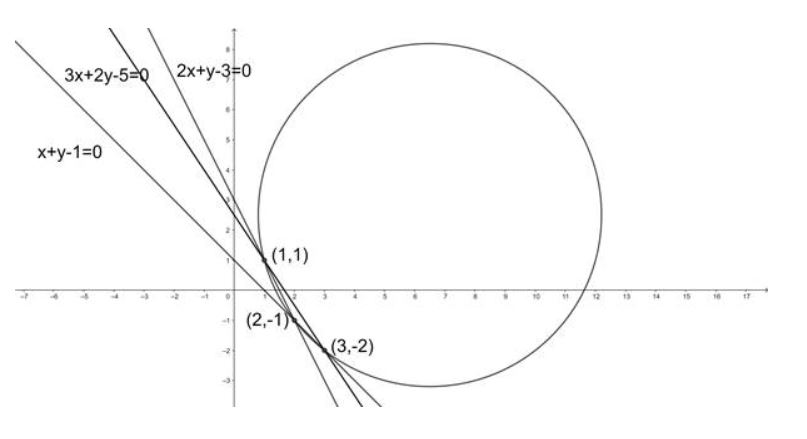
Find the equations of the circle which circumscribes the triangle formed by the lines
$2x+y-3=0,\ x+y-1=0$ and $3x+2y-5=0$

We are given the following equations:

$\Rightarrow 2x + y - 3 = 0$

$\Rightarrow x + y - 1 = 0$

$\Rightarrow 3x + 2y - 5 = 0$

On solving these lines we get the intersection points

$A(2, - 1)$ ,

$B(3, - 2)$ ,

$C(1,1)$

We know that the standard form of the equation of a circle is given by:

$\Rightarrow x^2 + y^2 + 2ax + 2by + c = 0$

$.....(1)$

Substituting

$(2, - 1)$ in

$(1)$ , we get

$\Rightarrow 2^2 + (- 1)^2 + 2a(2) + 2b(- 1) + c = 0$

$\Rightarrow 4 + 1 + 4a - 2b + c = 0$

$\Rightarrow 4a - 2b + c + 5 = 0$

$..... (2)$

Substituting

$(3, - 2)$ in

$(1)$ , we get

$\Rightarrow 3^2 + (- 2)^2 + 2a(3) + 2b(- 2) + c = 0$

$\Rightarrow 9 + 4 + 6a - 4b + c = 0$

$\Rightarrow 6a - 4b + c + 13 = 0$

$..... (3)$

Substituting

$(1,1)$ in

$(1)$ , we get

$\Rightarrow 1^2 + 1^2 + 2a(1) + 2b(1) + c = 0$

$\Rightarrow 1 + 1 + 2a + 2b + c = 0$

$\Rightarrow 2a + 2b + c + 2 = 0$

$..... (4)$

Solving

$(2), (3), (4)$ we get

$\Rightarrow a=\dfrac{-13}{2} , b=\dfrac{-5}{2}, c=16$ .

Substituting these values in

$(1)$ , we get

$\Rightarrow x^2+y^2+2(\dfrac{-13}{2})x+2(\dfrac{-5}{2})y+16=0$

$\Rightarrow x^2 + y^2 - 13x - 5y + 16 = 0$

Hecne, the equation of the circle is

$x^2 + y^2 - 13x - 5y + 16 = 0$
1611569_1667210_ans_9d63a6b49fc6437dab64451345a8b4c4.JPG

If the distance between the foci of an ellipse is equal to the length of the latus-rectum, write the eccentricity of the ellipse.

For ellipse

$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$ , length of latus-rectum is

$\dfrac{2b^2}{a}\\$ and distance between foci is

$2ae$ , where

$e$ is eccentricity of an ellipse.

According to given condition,

$2ae=\dfrac{2b^2}{a}\\$

$e=\dfrac{b^2}{a^2}\\$ ....

$(1)$

Eccentricity of ellipse

$e=\sqrt{1-\dfrac{b^2}{a^2}}\\$

$\therefore e=\sqrt{1-e}\\$ .....from

$(1)$

$\Rightarrow e^2=1-e\\$

$\Rightarrow e^2+e-1=0\\$

$\Rightarrow e=\dfrac{-1\pm \sqrt{1+4}}{2}\\$

$\Rightarrow e=\dfrac{-1\pm \sqrt{5}}{2}\\$

Negative eccentricity is not possible

$\therefore e=\dfrac{-1+ \sqrt{5}}{2}\\$

$\therefore e=\dfrac{ \sqrt{5}-1}{2}\\$

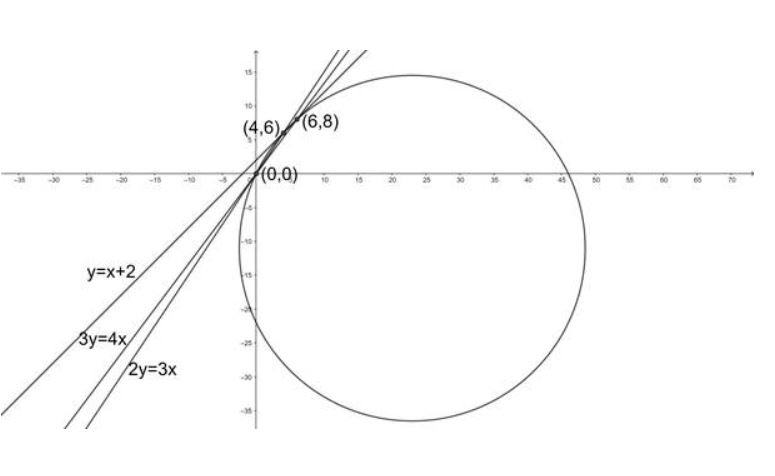
Find the equations of the circle which circumscribes the triangle formed by the lines
$y=x+2,\ 3y=4x$ and $2y=3x$

Given that we need to find the equation of the circle formed by the lines:

$\Rightarrow y = x + 2$

$\Rightarrow 3y = 4x$

$\Rightarrow 2y = 3x$

On solving these lines we get the intersection points

$A(6,8), B(0,0), C(4,6)$

We know that the standard form of the equation of a circle is given by:

$\Rightarrow x^2 + y^2 + 2ax + 2by + c = 0$

$.....(1)$

Substituting

$(6,8)$ in

$(1)$ , we get

$\Rightarrow 6^2 + 8^2 + 2a(6) + 2b(8) + c = 0$

$\Rightarrow 36 + 64 + 12a + 16b + c = 0$

$\Rightarrow 12a + 16b + c + 100 = 0$

$......(2)$

Substituting

$(0,0)$ in

$(1)$ , we get

$\Rightarrow 0^2 + 0^2 + 2a(0) + 2b(0) + c = 0$

$\Rightarrow 0 + 0 + 0a + 0b + c = 0$

$\Rightarrow c = 0$

$.....(3)$

Substituting

$(4,6)$ in

$(1)$ , we get

$\Rightarrow 4^2 + 6^2 + 2a(4) + 2b(6) + c = 0$

$\Rightarrow 16 + 36 + 8a + 12b + c = 0$

$\Rightarrow 8a + 12b + c + 52 = 0$

$..... (4)$

Solving

$(2), (3), (4)$ we get

$\Rightarrow a = - 23, b = 11,c = 0$

Substituting these values in

$(1)$ , we get

$\Rightarrow x^2 + y^2 + 2(- 23)x + 2(11)y + 0 = 0$

$\Rightarrow x^2 + y^2 - 46x + 22y = 0$

Hence the equation of the circle is

$x^2 + y^2 - 46x + 22y = 0$
1611580_1667214_ans_456dbf7cc285415b80214e866f86e84b.JPG

If the minor axis of an ellipse subtends an equilateral triangle with vertex at one end of major axis, then write the eccentricity of the ellipse.

For ellipse

$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$ , distance of minor axis is

$2b$

So,

$2b$ will be length of side of equilateral triangle.

And semi-major axis will be height of this triangle.

We know that height of equilateral triangle is

$\dfrac{\sqrt{3}}{2}$ times its side.

So, According to given condition,

$a=\dfrac{\sqrt{3}}{2}{2b}\\$

$\therefore \dfrac{a}{b}=\sqrt{3}\\$

$\therefore \dfrac{b}{a}=\dfrac{1}{\sqrt{3}}\\$ ....

$(1)$

Eccentricity of ellipse

$e=\sqrt{1-\dfrac{b^2}{a^2}}\\$

$e=\sqrt{1-\dfrac{1}{3}}\\$ ..............from

$(1)$

$\therefore e=\sqrt{\dfrac{2}{3}}\\$

If $S$ and $S'$ are two foci of the ellipse $\dfrac {x^{2}}{a^{2}} + \dfrac {y^{2}}{b^{2}} = 1$ and $B$ is an end of the minor axis such that $\triangle BSS'$ is equilateral, then write the eccentricity of the ellipse.

For ellipse

$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$ , distance between foci is

$2ae$ , where

$e$ is eccentricity of an ellipse.

So,

$2ae$ will be length of side of equilateral triangle

$\Delta BSS'$

And semi minor axis will be height of this triangle.

We know that height of equilateral triangle is

$\dfrac{\sqrt{3}}{2}$ time s its side.

So, According to given condition,

$b=\dfrac{\sqrt{3}}{2}{2ae}\\$

$\therefore \dfrac{b}{a}=\sqrt{3}e\\$ ....

$(1)$

Eccentricity of ellipse

$e=\sqrt{1-\dfrac{b^2}{a^2}}\\$

$e=\sqrt{1-3e^2}\\$ ..............from

$(1)$

$\Rightarrow e^2=1-3e^2\\$

$\Rightarrow 4e^2=1\\$

$\Rightarrow e^2=\dfrac{1}{4}\\$

$\Rightarrow e=\pm\dfrac{1}{2}\\$

Negative eccentricity is not possible

$\therefore e=\dfrac{1}{2}$

Write the centre and eccentricity of the ellipse $3x^{2} + 4y^{2} - 6x + 8y - 5 = 0$ .

Equation of an ellipse is

$3x^{2} + 4y^{2} - 6x + 8y - 5 = 0$

$\therefore 3x^{2}-6x + 4y^{2} + 8y - 5 = 0\\$

$\Rightarrow 3x^{2}-6x+3-3 + 4y^{2} + 8y+4-4 - 5 = 0\\$

$\Rightarrow 3x^{2}-6x+3 + 4y^{2} + 8y+4-12 = 0\\$

$\Rightarrow 3(x^{2}-2x+1 )+ 4(y^{2} +2 y+1)-12 = 0\\$

$\Rightarrow 3(x^{2}-2x+1 )+ 4(y^{2} +2 y+1) = 12\\$

$\Rightarrow \dfrac{(x^{2}-2x+1 )}{4}+\dfrac{(y^{2} +2 y+1)}{3} = 1\\$

$\Rightarrow \dfrac{(x-1)^2}{4}+\dfrac{(y+1)^2}{3} = 1\\$

Comparing it with

$\Rightarrow \dfrac{(x-h)^2}{a^2}+\dfrac{(y-k)^2}{b^2} = 1$

We get,

$h=1,y=-1,a=2,b=\sqrt3\\$

So center of ellipse is

$(1,-1)$ ,

For eccentricity

$e$ ,

$e=\sqrt{1-\dfrac{b^2}{a^2}}\\$

$e=\sqrt{1-\dfrac{3}{4}}\\$

$\therefore e=\dfrac{1}{2}$

Write the eccentricity of the ellipse $9x^{2} + 5y^{2} - 18x - 2y - 16 = 0$ .

$9x^{2} + 5y^{2} - 18x - 2y - 16 = 0\\$

$(3x)^2-2\cdot 3x\cdot 3+9-9+({\sqrt{5}y})^2-2\cdot \sqrt{5}y\cdot \dfrac{1}{\sqrt{5}}+\dfrac{1}{5}-\dfrac{1}{5}-16=0\\$

$(3x)^2-2\cdot 3x\cdot 3+3^2+({\sqrt{5}y})^2-2\cdot \sqrt{5}y\cdot \dfrac{1}{\sqrt{5}}+(\dfrac{1}{\sqrt 5})^2-\dfrac{1}{5}-16-9=0\\$

$(3x^2-3)^2+({\sqrt{5}y}-\dfrac{1}{\sqrt 5})^2-\dfrac{1}{5}-25=0\\$

$(3x^2-3)^2+({\sqrt{5}y}-\dfrac{1}{\sqrt 5})^2-\dfrac{126}{5}=0\\$

$(3x^2-3)^2+({\sqrt{5}y}-\dfrac{1}{\sqrt 5})^2=\dfrac{126}{5}\\$

$9(x^2-1)^2+5({y}-\dfrac{1}{5})^2=\dfrac{126}{5}\\$

$\dfrac{9(x^2-1)^2}{\dfrac{126}{5}}+\dfrac{5({y}-\dfrac{1}{5})^2}{\dfrac{126}{5}}=1\\$

$\dfrac{(x^2-1)^2}{\dfrac{14}{5}}+\dfrac{({y}-\dfrac{1}{5})^2}{\dfrac{126}{25}}=1\\$

Comparing it with

$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$ , we get

$a^2=\dfrac{14}{5},\ b^2=\dfrac{126}{25}$

Here,

$b>a$

$\therefore$ Eccentricity is given by

$e=\sqrt{1-\dfrac{a^2}{b^2}}\\$

$e=\sqrt{1-\dfrac{\dfrac{14}{5}}{\dfrac{126}{25}}}\\$

$e=\sqrt{1-{\dfrac{14}{5}}\times{\dfrac{25}{126}}}\\$

$e=\sqrt{1-{\dfrac{5}{9}}}\\$

$e=\sqrt{{\dfrac{4}{9}}}\\$

$e={\dfrac{2}{3}}\\$

Therefore, eccentricity of given ellipse is

$\dfrac{2}{3}$

Find the equation of the circle which passes through the points $(1, 1)(2, 2)$ and whose radius is $1$ . Show that there are two such circles.

1413293_1667225_ans_b0f0452dc455476aace7274715fcdcc6.jpg

Write the eccentricity of an ellipse, whose latus-rectum is one half of the minor axis.

For ellipse

$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$ , length of latus-rectum is

$\dfrac{2b^2}{a}\\$

Condition:Latus-rectum is one half of the minor axis.

$\therefore \dfrac{2b^2}{a}=\dfrac{1}{2}{2b}\\$

$\therefore \dfrac{b}{a}=\dfrac{1}{2}\\$

Eccentricity is given by,

$e=\sqrt{1-\dfrac{b^2}{a^2}}\\$

$e=\sqrt{1-\dfrac{1}{4}}\\$

$e=\sqrt{\dfrac{3}{4}}\\$

$e={\dfrac{\sqrt 3}{2}}\\$

Find the equations of the circle which circumscribes the triangle formed by the lines
$x+y=2,\ 3x-4y=6$ and $x-y=0$

Suppose that in

$\Delta$ ABC

Line AB is represented by

$x+y=2------(1)$

Line BC is represented by

$3x-4y=6-----(2)$

Line AC is represented by

$x-y=0------(3)$

Now, we know that the intersection of two lines will give a point of triangle.

So,

Intersection point of equation(1) and equation (2) is

$(2,0)$ .

Intersection point of equation(2) and equation (3)is

$(-6,-6)$ .

Intersection point of equation(1) and equation (3) is

$(1,1)$ .

Therefore, the coordinates of A, B, and C are

$(2,0), (-6,-6)$ and

$(1,,)$ respectively.

Now, let the equation of the circle which circumscribes the triangle ABC is

$x^2+y^2+2gx+2fy+c=0----------------(4)$

The circle will pass through points A, B, and C, then each point will satisfy equation (4).

Point A(2,0) satisfies equation(4)-

$4+4g+c=0-----(5)$

Point B(-6,-6) satisfies equation(4)-

$72-12g-12f+c=0-----(6)$

Point C(1,1) satisfies equation(4)-

$2+2g+2f+c=0-------(7)$

Now, Substract equation (6) from(5)-

$68-16g-12f=0--------(8)$

Now, Substarct equation (7) from (5)-

$2+2g-2f=0-----(9)$

Now, Soving equation (8) and (9), we get-

$g=2,\, f=3$ .

Now putting the value of g in equation (5) we get-

$c=-12$ .

So, equation (4) will be-

$x^2+y^2+4x+6y-12=0$

Which is our required equation of circle.

If a latus-rectum of an ellipse subtends a right angle at the centre of the ellipse, then write the eccentricity of the ellipse.

For ellipse

$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$ , length of latus-rectum is

$\dfrac{2b^2}{a}\\$ and

$e$ is eccentricity of an ellipse.

Height

$'h'$ of right angle triangle divides hypotenous in two parts

$p$ and

$q$ such that

$h^2=pq$

In this right angle triangle formed by latus-rectum,

$ae$ (

$x$ co-ordinate of latus rectum

$) is height and length$

$\dfrac{2b^2}{a}$ $ is hypotenous.

According to above condition,

$h=ae, p=q=\dfrac{b^2}{a}$

$\Rightarrow a^2e^2=\dfrac{b^4}{a^2}\\$

$\Rightarrow e^2=\dfrac{b^4}{a^4}\\$

$\Rightarrow e=\pm\dfrac{b^2}{a^2}\\$

But, negative is not possible because

$a$ and

$b$ are both positive and

$e$ can't be negative

$\therefore e=\dfrac{b^2}{a^2}\\$ .....

$(1)$

Eccentricity of ellipse

$e=\sqrt{1-\dfrac{b^2}{a^2}}\\$

$\therefore e=\sqrt{1-e}\\$ .....from

$(1)$

$\Rightarrow e^2=1-e\\$

$\Rightarrow e^2+e-1=0\\$

$\Rightarrow e=\dfrac{-1\pm \sqrt{1+4}}{2}\\$

$\Rightarrow e=\dfrac{-1\pm \sqrt{5}}{2}\\$

Negative eccentricity is not possible

$\therefore e=\dfrac{-1+ \sqrt{5}}{2}\\$

$\therefore e=\dfrac{ \sqrt{5}-1}{2}\\$

Find the area lying in first quadrant and included between the circle ${ x }^{ 2 }+{ y }^{ 2 }=8$ and $x$ axis.

Given circle

$x^2+y^2=8$

$y^2=8-x^2$

$y=\sqrt {8-x^2}$

Radius of Circle

$\sqrt 8=2\sqrt 2$

The area is given as

$\displaystyle \int _0^{2\sqrt 2} \sqrt {8-x^2}\quad dx$

$\displaystyle \int \sqrt {a^2-x^2} dx=\dfrac x2\sqrt {a^2-x^2}+\dfrac {a^2}2\sin ^{-1}\dfrac xa +c$

$\displaystyle \int _0^{2\sqrt 2} \sqrt {8-x^2}dx=\left.\dfrac x2\sqrt {8-x^2}+\dfrac 82\sin^{-1}\dfrac x{2\sqrt 2}\right|_0^{2\sqrt 2}$

$=\dfrac {2\sqrt 2}2\sqrt {8-{(2\sqrt 2)}^2} +\dfrac 82\sin^{-1} \dfrac {2\sqrt 2}{2\sqrt 2}$

$-\dfrac 02$

$\sqrt {8-0} -\dfrac 82\sin^{-1} \dfrac 0{2\sqrt 2}$

$=4$

Find the equation of a circle with Center (2,4) and radius 5.

1847163_1709984_ans_e49710cc64204c758b285ea0ca7a6329.jpeg

Find the equation of circle of radius 5 cm, whose center lies on the y axis and which passes through the point (3,2).

1847301_1709995_ans_a98b667e1a864358a352c3ad78175ec6.jpg

Find the equation of the circle whose center is ( 2, -3) and which passes through the intersection of the lines 3x +2y = 11 and 2x +3y = 4.

1847303_1709996_ans_db323e8710514a2e8b112f302ca687ab.jpg

The perimeter of a certain sector of a circle is $10$ feet ; if the radius of the circle be $3$ feet, find the area of the sector.[Assume that $\pi = 3.14159....,\dfrac{1}{\pi}=.31831$ and $\log \pi =.49715$ ]

1596905_1734436_ans_ca6bb1d5f3a44e38bf5ca72233ff0b5a.jpg

Find the equation of a circle with center at the origin and radius 4.

1847170_1709986_ans_078d3c2c323d46479de399e5cf49cb63.jpeg

Find the equation of the circle passing through the point ( -1, 3) and having its center at the point of intersection of the lines x -2y = 4 and 2x +5y +1 =0 $$

1849828_1709997_ans_0b0be8de990d4ed39bf0315429bc2645.jpg

The axes being inclined at $60^{\circ}$ , find the equation to the circle whose centre is the point $(-3, -5)$ and whose radius is $6$ .

1686942_1740721_ans_fd7c08b7ae8244f0a27f961ccc16e7dd.jpg

Find the equation to the circle whose radius is $\sqrt {a^{2} - b^{2}}$ and centre is $(-a, -b)$ .

1565007_1740580_ans_521b91bcaeba4408ac2fd35ca41c12fd.png

What are represented by the equation
$(r\cos\theta-a)(r-a\cos\theta)=0$

Given

$\left ( rcos\Theta -a \right )\left ( r-acos\Theta \right )=0\\$

$= > rcos\Theta -a = 0\\$

$= > rcos\Theta =a$ (i)

and

$= > r-acos\Theta = 0\\$

$= > r=acos\Theta$ (ii)

We know the parametric form

$x=rcos\Theta,y=rsin\Theta,r=\sqrt{x^{2}+y^{2}}$

From equation (i)

=>x=a

Now, eq(ii) can be written as

$= > r=acos\Theta\\$

$= > r^{2}=arcos\Theta\\$

$= > x^{2}+y^{2}=ax$

Therefore, from the above equation it is cleared that the given expression represent a circle with centre

$\left ( \dfrac{a}{2},0 \right )\\$ and radius

$\ \dfrac{a}{2}$

Find the equation to the circle whose radius is $3$ and whose centre is $(-1, 2)$ .

1564995_1740577_ans_806f234837954e5783455cc4b855349a.png

Find the equation to the circle whose radius is $10$ and whose centre is $(-5, -6)$ .

1564999_1740578_ans_2d34d92b788b46d5af44b48532ecbdb2.png

Find the equation to the circle whose radius is $a + b$ and whose centre is $(a, -b)$ .

1565004_1740579_ans_d6c951c87571446591770f780c1ceef7.png

Show that the latus rectum of the parabola
$(a^{2}+b^{2})(x^{2}+y^{2})=(bx+ay-ab)^{2}$
$2ab\div \sqrt{a^{2}+b^{2}}$ is

1753682_1741808_ans_0f76e3f647b345c19da53054009ee525.jpg

Prove that the area of the triangle formed by three points on an ellipse, whose eccentric angles are $\theta, \phi$ , and $\psi$ , is
$\dfrac {1}{2} ab\sin \dfrac {\phi - \psi}{2}\sin \dfrac {\psi - \theta}{2} \sin \dfrac {\theta - \phi}{2}$ .
Prove also that its area is to the area of the triangle formed by the corresponding points on the auxiliary circle as $b : a$ , and hence that its area is a maximum when the latter triangle is equilateral, i.e. when $\phi - \theta = \psi - \phi = \dfrac {2\pi}{3}$ .

1570660_1741407_ans_6de4533422fc4a299c777b338ca970a1.jpg

$Q$ is the point on the auxiliary circle corresponding to $P$ on the ellipse; $PLM$ is drawn parallel to $CQ$ to meet the axes in $L$ and $M$ ; prove that $PL = b$ and $PM = a$ .

1570656_1741405_ans_e625b436dc104671819b7560ab0248df.jpg

Trace the following central conics
$3(2x-3y+4)^{2}+2(3x+2y-5)^{2}=78$

1574583_1741777_ans_d682dfc2759f4697a5d7bddc4a85a138.png

A circle of radius 5 units has diameter along the angle bisector of the lines $x+y=2$ and $x-y=2 .$ If chord of contact from origin makes an angle of $45^{\circ}$ with the positive direction of $x$ -axis, find the equation of the circle.

Obviously angle bisectors are

$x=2$ and

$y=0$

Now centre cannot lies on

$y=0$ because their chord of contact from origin will always be parallel to

$y$ -axis.

So Iet the centre

$(2, \alpha),$ then equation of circle will be

$(x-2)^{2}+(y-\alpha)^{2} =5^{2}$

$\Rightarrow x^{2}+y^{2}-4 x-2 \alpha y-21 \alpha^{2} =0$

Now chord of contact is

$-4 \dfrac{x}{2}-2 \alpha \dfrac{y}{2}+\alpha^{2}-21=0 \Rightarrow 2 x+\alpha y-\alpha^{2}+21=0$

Now,

$-\dfrac{2}{\alpha}=1 \Rightarrow \alpha=-2$

So equation of circle is

$(x-2)^{2}+(y+2)^{2}=5^{2}$

$S$ is a circle having centre at $(0, a)$ and radius $b(b<a)$
A variable circle centred at $(a, 0)$ and touching circle $S,$ meets the $X$ -axis at $M$ and $N .$
Find a point $P$ on the $Y$ -axis, such that $\angle M P N$ is a constant for any choice of $\alpha$ .

Let radius

$=r$

$\therefore$ From figure

$\quad \sqrt{\alpha^{2}+a^{2}}=b+r \qquad\qquad\qquad(1)$

Consider a point

$P(0, k)$ on the

$y$ -axis

$M(\alpha-r, 0) \text { and } N(\alpha+r, 0)$

$\text { Now, slope of } \quad M P=\dfrac{-k}{\alpha-r}, \text { slope } N P=\dfrac{-k}{\alpha+r}$

$\angle M P N=\theta$

$\tan \theta =\left|\dfrac{\dfrac{k}{\alpha-r}-\dfrac{k}{\alpha+r}}{1+\dfrac{k^{2}}{\alpha^{2}-r^{2}}}\right|$

$=\left|\dfrac{2 k r}{\alpha^{2}-r^{2}+k^{2}}\right|$

According to the given condition,

$\theta$ is a constant for any choice

$\alpha$

$\dfrac{2 k r}{\alpha^{2}-r^{2}+k^{2}}=\text { constant }$

$\text { i.e., } \quad \dfrac{r}{\alpha^{2}-r^{2}+k^{2}}=\text { constant }$

$\text { i.e., } \dfrac{\sqrt{\alpha^{2}+a^{2}}-b}{\alpha^{2}-\left(\sqrt{\alpha^{2}+a^{2}}-b^{2}\right)+k^{2}}=\text { constant }$

(From Eq.1)

$\text { i.e., } \dfrac{\sqrt{\alpha^{2}+a^{2}}-b}{2 b \sqrt{\alpha^{2}+a^{2}-a^{2}-b^{2}+k^{2}}}=\text { constant }$

$\qquad \dfrac{\sqrt{\alpha^{2}+a^{2}}-b}{\sqrt{\alpha^{2}+a^{2}-\lambda}}=\text { constant }$

$\text { where }\left\{\dfrac{\alpha^{2}+b^{2}-k^{2}}{2 b}\right\}=\lambda$

which is possible only, if

$\lambda=b$

$\therefore \dfrac{a^{2}+b^{2}-k^{2}}{2 b} =b \Rightarrow k=\pm \sqrt{a^{2}-b^{2}}$

$P \equiv(0, \pm \sqrt{a^{2}-b^{2}})$

1618376_1765828_ans_36c6f72108cd44c7a8642fcd65bc9cb4.png

If the length of the latus rectum of the parabola $169\{(x \left.-1)^{2}+(y-3)^{2}\right\}=(5 x-12 y+17)^{2}$ is $L$ then the value of $\dfrac{13 L}{4}$ is

Here,

$(x-1)^{2}+(y-3)^{2}=\left\{\dfrac{5 x-12 y+17}{\sqrt{5^{2}+(-12)^{2}}}\right\}^{2}$

$\therefore$ the focus

$=(1,3)$ and the directrix is

$5 x-12 y+17 =0$

The distance of the focus from the directrix

$=\left|\dfrac{5 \times 1-12 \times 3+17}{\sqrt{5^{2}+(-12)^{2}}}\right|=\dfrac{14}{13}$

$\therefore$ latus rectum

$=2 \times \dfrac{14}{13}=\dfrac{28}{13}$

$\dfrac{13 L}{4} =7$

Find the equation of the circle whose:
Centre $(a,b)$ and radius is $a-b$

According to question,
centre of circle

$(h,k)=(a,b)$
and Radius of circle

$r=(a-b)\ unit$
Then, equation of circle From formula

$(x-h)^2+(y-k)^2=r^2$

$[x-a]^2+ (y-b)^2=(a-b)^2$

$\Rightarrow (x-a)^2+(y-b)^2 =(a-b)62$

$\Rightarrow x^2+a^2-2ax+y^2+b^2-2by=a^2+b^2-2ab$

$\Rightarrow x^2+a^2-2ax-2by+a^2+b^2-a^2-b^2+2ab=0$

$\Rightarrow x^2+y^2-lax-2by+2ab=0$

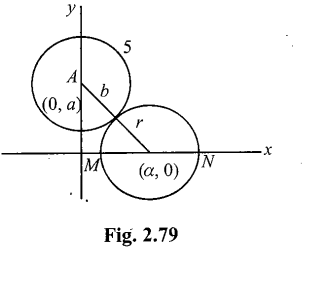
Find the equation of circle with radius $r,$ whose centre lies in $1st$ quadrant and touches $y-$ axis at a distance of $h$ from the origin. Find the equation of other tangent which passes through origin.

1977693_1898123_ans_23d6ff0f6c2e4999accdb1d9fae3d2da.jpg

If the point $P(x, y)$ lie on a circle with the center (3,-2) and radius 3 unit, then prove that $x^{2}+y^{2}-6 x+4 y+4=0$

Let center of circle

$C(3,-2)$ and point

$P(x, y)$ lie on a circle.
Given: radius of circle

$\mathrm{CP}=3$

$\Rightarrow \sqrt{(x-3)^{2}+(y+2)^{2}}=3$
Squaring both sides

$\Rightarrow(x-3)^{2}+(y+2)^{2}=9$

$\Rightarrow x^{2}+9-6 x+y^{2}+4+4 y=9$

$\Rightarrow x^{2}+y^{2}-6 x+4 y+4=0$
1860533_1877632_ans_86bfb16d0a25478c9e059a261a1592a8.png

Match the Column
The answers to these questions have to be appropriately doubled

Consider D,
All the three equations are parallel lines.
Hence they will not have any solution.
Consider C

$sin^{-1}(sin4)$

$=\pi-4$
And

$cos^{-1}(cos4)$

$=2\pi-4$
Hence

$3x^{2}+8x<2\pi-8-2\pi+4$

$3x^{2}+8x<-4$

$3x^{2}+8x+4<0$

$3x^{2}+6x+2x+4<0$

$3x(x+2)+2(x+2)<0$

$(3x+2)(x+2)<0$
Hence

$x\epsilon(-2,\dfrac{-2}{3})$
Hence one integral solution.
Consider B.
Let the point of contact of the tangent be

$P(2cos^{3}\theta,2sin^{3}\theta)$

$y=2sin^{3}\theta.$

$x=2cos^{3}\theta$

$\dfrac{dy}{dx}=-tan\theta$
Therefore

$(y-2sin^{3}\theta)=-tan\theta(x-2cos^{3}\theta)$

$\dfrac{y}{2sin\theta}+\dfrac{x}{2\cos\theta}=1$
Hence length of intercepts is

$(2cos^{2}\theta+2sin^{2}\theta)$

$=2$
Hence the answer key is

$A-3,B-2,C-1,D-0$

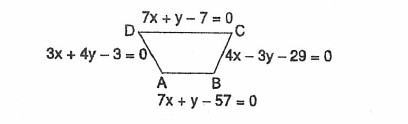
The radius of the circle circumscribing the quadrilateral formed by the lines $7x + y - 57 = 0, 4x - 3y - 29 = 0, 7x + y - 7 = 0$ and $3x + 4y - 3 = 0$ in order is

Let the equation of the circumcircie of the quadrilateral be

$(7x+y-57)(7x+y-7)+\lambda (4x-3y-29)(3x+4y-3)=0$

$\therefore$ coefficient of

$x^{2}=$ coefficient of

$y^{2}$

$\Rightarrow 49+12\lambda =1-12\, \lambda \Rightarrow \lambda =-2$

$\therefore$ equation (1) becomes 25

$(x^{2}+y^{2})-250x+150y+225=0$
i.e.,

$x^{2}+y^{2}-10x+6y+9=0$
Hence the radius =

$\sqrt{5^{2}+(-3)^{2}-9}=5$

Find the center and radius of the circle whose equation is given by: ${(-4-x)}^{2}+{(-y+11)}^{2}=9$

An equation of the circle with center

$(h,k)$ and radius

$r$ is

$(x-h)^{ 2 }+(y-k)^{ 2 }=r^{ 2 }$

So, comparing

$(-4-x)^2+(-y+11)^2=9$ that is

$(x-(-4))^2+(y-11)^2=9$ with the above equation of circle we get:

$h=-4$ ,

$k=11$ and

$r=3$

Therefore, center of the circle is

$(-4,11)$ and radius of the circle is

$r=3$ .

Find the equation of the circle passing through the three points (1, 2), (3, -4), (5, -6).

Let point

$(1,2)$ be

$A$ ,

$(3,-4)$ be

$B$ and

$(5,-6)$ be

$C$

Let the mid point of

$AB$ be

$D = (2,-1)$ and the midpoint of

$BC$ be

$E=(4,-5)$

The equation of line passing through

$D$ and perpendicular to

$AB$ is

$x-3y=5$

The equation of line passing through

$E$ and perpendicular to

$BC$ is

$x-y=9$

The center of circle is the point of intersection of above two lines which is equal to

$(11,2)$

The radius of circle is

$10$

Therefore the equation of circle is

${(x-11)}^{2}+{(y-2)}^{2}=100$

Find the inclinations of the axes so that the following equations may represent circles, and in each case find the radius and centre;
$x^{2} - xy + y^{2} - 2gx - 2fy = 0$ .

When the axes are inclined at an angle

$\omega$ , the general equation of a circle with center

$(h,k)$ and radius

$r$ can be written as

$x^2 + y^2 + 2xy\cos{\omega} - 2(h + k\cos{\omega})x - 2(k + h\cos{\omega}) y + h^2 + k^2 + 2hk\cos{\omega} - r^2 = 0$
When compared this equation with the equation of circle as given, we have

$2\cos{\omega} = -1$ or

$\cos{\omega} = \cfrac{-1}{2}$

$\therefore \omega = 120^o$
Also,

$h + k\cos{\omega} = h - \cfrac{k}{2} = g \ \ ...(1)$

$k - \cfrac{h}{2} = f \ \ ...(2)$ and

$h^2 + k^2 - hk = r^2$
Multiplying equation

$(1)$ by

$2$ and adding that to equation

$(2)$ , we get

$\cfrac{3h}{2} = 2g + f$ or

$h = \cfrac{2(2g + f)}{3}$

$\Rightarrow k = \cfrac{h}{2} + f = \cfrac{2g + f}{3} + f = \cfrac{2(g + 2f)}{3}$
Also,

$r^2 = \cfrac{4(4g^2 + f^2 + 4fg) + 4(g^2 + 4f^2 + 4fg) - 4(2g^2 + 2f^2 + 5fg)}{9} = \cfrac{4(3g^2 + 3f^2 + 3fg)}{9} = \cfrac{4(f^2 + g^2 + fg)}{3}$
Center

$= \left ( \cfrac{2(f + 2g)}{3}, \cfrac{2(g + 2f)}{3} \right )$
Radius

$= \sqrt{\cfrac{4(f^2 + g^2 + fg)}{3}}$

Find the equation of the hyperbola whose foci are $(0, \pm \sqrt{10})$ and passing through the point $(2, 3)$ .

Since, the foci of the given hyperbola are

$F'(0,-\sqrt{10})$ and

$F(0,\sqrt{10})$ which lie on the X-axis and mid-point of the segment

$F'F$ is

$(0,0)$ . Therefore origin is the centre of the hyperbola and its transverse axis lies along Y-axis, hence the equation of the hyperbola can be taken as

$\dfrac{y^2}{a^2}-\dfrac{x^2}{b^2}=1$ .........(i)

As the foci are

$(0, \pm \sqrt{10})$
So,

$ae = \sqrt{10}$

We know that

$b^2=a^2e^2-a^2$

$\Rightarrow b^2=10-a^2$ .........(ii)

Substituting this value of

$b^2$ in (i), we get

$\dfrac{y^2}{a^2}-\dfrac{x^2}{10-a^2}=1$

Since the hyperbola passes through the point

$(2,3)$ , we get

$\dfrac{9}{a^2}-\dfrac{4}{10-a^2}=1$

$9(10-a^2)-4a^2=a^2(10-a^2)$

$\Rightarrow 90-13a^2=10a^2-a^4$

$\Rightarrow a^4-23a^2+90=0$

$\Rightarrow (a^2-5)(a^2-18)=0$

$\Rightarrow a^2=5, 18$

$a^2=5, b^2=10-a^2=10-5=5$

$a^2=18, b^2=10-18=-8$ (not possible)

So, we get

$a^2=5, b^=5$

Hence from (i), the equation of the hyperbola is

$\dfrac{y^2}{5}-\dfrac{x^2}{5}=1$
i.e.,

$y^2-x^2=5$ .

The tangents at two points, P and Q, of a conic meet in T, and S is the focus ; prove that if the conic be a parabola, then $ST^2 = SP . SQ.$

Equation of parabola in polar form is

$\dfrac { 2a }{ r } =1-\cos { \theta }$

$\Rightarrow \dfrac { 2a }{ r } =2\sin ^{ 2 }{ \dfrac { \theta }{ 2 } } \\ \Rightarrow r=a\csc ^{ 2 }{ \dfrac { \theta }{ 2 } }$

Let the vectorical angle of $P$ and $Q$ be $\alpha$ and $\beta$ respectively

$\Rightarrow SP=a\csc ^{ 2 }{ \dfrac { \alpha }{ 2 } }$ and $SQ=a\csc ^{ 2 }{ \dfrac { \beta }{ 2 } } ........(i)$

Tangents at $P$ and $Q$ intersect at $T$ , let its polar coordinates be $(r',\phi)$

$\Rightarrow \dfrac { 2a }{ r } =\cos { (\phi -\alpha ) } -\cos { \phi } ......(ii)\\ \Rightarrow \dfrac { 2a }{ r } =\cos { (\phi -\beta ) } -\cos { \phi } ......(iii)$

substracting $(ii)$ and $(iii)$ $

$\Rightarrow \cos { (\phi -\alpha ) } =\cos { (\phi -\beta ) } \\ \Rightarrow \phi -\alpha =\phi -\beta \\ \Rightarrow \phi =\dfrac { \alpha +\beta }{ 2 }$

substituting in $(ii)$

$\Rightarrow \dfrac { 2a }{ r' } =\cos { \left( \dfrac { \alpha +\beta }{ 2 } -\alpha \right) } -\cos { \dfrac { \alpha +\beta }{ 2 } } \\ \Rightarrow \dfrac { 2a }{ r' } =\cos { \dfrac { \alpha -\beta }{ 2 } } -\cos { \dfrac { \alpha +\beta }{ 2 } } \\ \Rightarrow \dfrac { 2a }{ r' } =2\sin { \dfrac { \alpha }{ 2 } } \sin { \dfrac { \beta }{ 2 } } \\ \Rightarrow \dfrac { a }{ ST } =\sin { \dfrac { \alpha }{ 2 } } \sin { \dfrac { \beta }{ 2 } } \\ \Rightarrow ST=a\csc { \dfrac { \alpha }{ 2 } } \csc { \dfrac { \beta }{ 2 } } \\ \Rightarrow { ST }^{ 2 }={ a }^{ 2 }\csc ^{ 2 }{ \dfrac { \alpha }{ 2 } } \csc ^{ 2 }{ \dfrac { \beta }{ 2 } } \\ \Rightarrow { ST }^{ 2 }=\left( a\csc ^{ 2 }{ \dfrac { \alpha }{ 2 } } \right) \left( a\csc ^{ 2 }{ \dfrac { \beta }{ 2 } } \right)$

using $(i)$

$\Rightarrow { ST }=SP.SQ$

Hence proved.

Show that the equation of the parabola in standard from is $y^2 = 4ax$ .

Solution:

Let

$S$ be the focus,ZM the directrix and P the moving point.

Draw

$SZ$ perpendicular from

$S$ on the directrix. Then

$SZ$ is the axis of the parabola. Now the middle point of

$SZ$ ,say

$A$ , will lie on the locus of

$P$ , i.e.,

$AS=AZ$ . Take A as the origin, the x-axis along

$AS$ , and the y-axis along the perpendicular to

$AS$ at

$A$ , as in the figure.

Let

$AS=a$ , so that

$ZA$ also

$a$ , Let

$(x,y)$ be the coordinates of the moving point

$P$ . Then

$MP=ZN=ZA+AN=a+x$ . But by definition

$MP=PS\Longrightarrow MP^2=PS^2$

so that,

$(a+x)^2=(x-a)^2+y^2.$

Hence, the standard equation of the parabola is

$y^2=4ax$ .

Prove that the equation to a circle whose radius is $a$ and which touches the axes of coordinates, which are inclined at an angle $\omega$ , is
$x^{2} + 2xy\cos \omega + y^{2} - 2a (x + y) \cot \dfrac {\omega}{2} + a^{2}\cot^{2} \dfrac {\omega}{2} = 0$ .

If the circle touches both the axis, the center may be taken as

$(h,h)$ . If a us the radius

$a=h\sin { \omega }$ or

$h=a\csc { \omega }$

$\therefore$ Center

$\left( a\csc { \omega } ,a\csc { \omega } \right)$ and radius 'a'
Putting these values in the general equation , we get

${ x }^{ 2 }+{ y }^{ 2 }+2xy\cos { \omega } -2x\left( a\csc { \omega } +a\csc { \omega } \cos { \omega } \right) -2y\left( a\csc { \omega } +a\csc { \omega } \cos { \omega } \right) +{ a }^{ 2 }\csc ^{ 2 }{ \omega } +$

${ a }^{ 2 }\csc ^{ 2 }{ \omega } +2{ a }^{ 2 }\csc ^{ 2 }{ \omega } \cos { \omega } -{ a }^{ 2 }=0$
or

${ x }^{ 2 }+{ y }^{ 2 }+2xy\cos { \omega } -2xa\csc { \omega } \left( 1+\cos { \omega } \right) -2ya\csc { \omega } \left( 1+\cos { \omega } \right) +2{ a }^{ 2 }\csc ^{ 2 }{ \omega } \left( 1+\cos { \omega } \right) -{ a }^{ 2 }=0.....1$

$\csc { \omega } \left( 1+\cos { \omega } \right) =\cfrac { 2\csc ^{ 2 }{ { \omega }/{ 2 } } }{ 2\sin { { \omega }/{ 2 } } \cos { { \omega }/{ 2 } } } =\cot { \cfrac { \omega }{ 2 } }$
and

$2{ a }^{ 2 }\csc ^{ 2 }{ \omega } \left( 1+\cos { \omega } \right) -{ a }^{ 2 }$

$={ a }^{ 2 }\left[ 2\cfrac { 2\csc ^{ 2 }{ { \omega }/{ 2 } } }{ 4\csc ^{ 2 }{ { \omega }/{ 2 } } \sin ^{ 2 }{ { \omega }/{ 2 } } } -1 \right]$

$={ a }^{ 2 }\left[ \csc ^{ 2 }{ \cfrac { \omega }{ 2 } } -1 \right]$

$={ a }^{ 2 }\cot ^{ 2 }{ \cfrac { \omega }{ 2 } }$
Putting these values in

$1$ , we get

${ x }^{ 2 }+{ y }^{ 2 }+2xy\cos { \omega } -2a\left( x+y \right) \cot { \cfrac { \omega }{ 2 } } +{ a }^{ 2 }\cot ^{ 2 }{ \cfrac { \omega }{ 2 } } =0$

If radius of the circle which passes through the focus of the parabola $x^2=4y$ and touches it at the point (6 , 9 ) is $k\sqrt{10}$ .Then $k$ is equal to

1444620_708547_ans_86ab908d4c8e42a9ab1683d172a7f057.jpeg

A point moving around circle $(x+ 4)^2 + (y +2)^2 = 25$ with centre C broke away from it either at the point A or point B on the circle and moved along a tangent to the circle passing through the point D(3, -3). Find the following.
(i) Equation of the tangents at A and B
(ii) Coordinates of the points A and B
(iii) Angle ADB and the maximum and minimum distances of the point D from the circle.
(iv) Area of quadrilateral ABCD and the $\triangle{DAB}$
(v) Equation of the circle circumscribing the $\triangle{DAB}$ and also the intercepts made by this circle on the coordinate axes.

$(i)$

$\begin{array}{l} CD=\sqrt { 45+1 } =\sqrt { 50 } & & \\ AD=\sqrt { C{ D^{ 2 } }+A{ C^{ 2 } } } & & \\ =\sqrt { 50-25 } =5 & & \\ Hence & & \\ AC=BC=BD=AD=5 & & \\ \angle ADC=\angle BDC=45^{ \circ } & & \\ Let & & \\ Slope\, \, of\, \, AD={ m_{ 1 } } & & \\ Slope\, \, of\, \, BD={ m_{ 2 } } & & \\ Slope\, \, of\, \, CD=\frac { { -2+3 } }{ { -4-3 } } =\frac { { -1 } }{ 7 } & & \\ \frac { \pi }{ 4 } =\left| { \frac { { m+\frac { 1 }{ 7 } } }{ { 1-m\frac { 1 }{ 7 } } } } \right| & & \\ \frac { \pi }{ 4 } =\left| { \frac { { m+\frac { 1 }{ 7 } } }{ { 1-\frac { m }{ 7 } } } } \right| & & \\ Taking\, \, +ve & & Taking\, \, -ve \\ \left( { 1-\frac { m }{ 7 } } \right) =\left( { \frac { 1 }{ 7 } +m } \right) & & -1+\frac { m }{ 7 } =m+\frac { 1 }{ 7 } \\ m=\frac { 3 }{ 4 } & & m=\frac { { -4 } }{ 3 } \\ Equation\, \, of\, \, line & & Equation\, \, of\, \, line \\ y+3=\frac { 3 }{ 4 } \left( { x-3 } \right) & & y+3=\frac { { -4 } }{ 3 } \left( { x-3 } \right) \\ 4y-3x+21=0 & & 3y+4x-3=0 \end{array}$

$(ii)$

$\begin{array}{l} Slope\, \, of\, \, DC=\frac { { -1 } }{ { slope\, \, of\, \, AD } } & & Slope\, \, of\, \, BC=\frac { { -1 } }{ { Stage\, \, of\, \, BD } } \\ =\frac { { -4 } }{ 3 } & & =\frac { 3 }{ 4 } \\ Equation\, \, of\, \, AC & & Equation\, \, of\, BC \\ y+2^{ \circ }=\frac { { -4 } }{ 3 } \left( { x+4 } \right) & & y+2=\frac { 3 }{ 4 } \left( { x+4 } \right) \\ 3y+6=-4x-16 & & 4y+8=3x+12 \\ 4x+3y+22=0 & & 3x-4y+4=0 \end{array}$

For point

$A$ , intersection of

$AC$ and

$AD$

For point

$B$ , intersection of

$BC$ and

$BD$

Point

$A = (0, 1)$

$B = (-1, -6)$

$(iii)$

Minimum distance =

$= 5\sqrt 2 - 5$

Maximum distance =

$= 5\sqrt 2 + 5$

$(iv)$

Area of quadrilateral

$ABBC = {5^2} = 25$

Area of

$ODAB = \frac{1}{2} \times 25 = 12.5$

$(v)$

Mid point of

$CD = \left( {\frac{{ - 1}}{2},\,\,\frac{{ - 5}}{2}} \right)$

Equation of circle

$\begin{array}{l} { \left( { x+\frac { 1 }{ 2 } } \right) ^{ 2 } }+{ \left( { y+\frac { 5 }{ 2 } } \right) ^{ 2 } }={ \left( { \frac { { 5\sqrt { 2 } } }{ 2 } } \right) ^{ 2 } } \\ { x^{ 2 } }+{ y^{ 2 } }+x+5y-6=0 \end{array}$

1202142_793498_ans_9ac82dc2984e4bf99e292532b2901edc.PNG

Given below are Matching type questions, with two columns(each having some items) each.Each item of column $I$ has to be matched with the items of column $II$ , by enclosing the correct match.
Note $:$ An item of column $I$ can be matched with more than one items of column $II$ .All the items of column $II$ have to be matched.
The equation of conics represented by the general equation of second degree $a{x}^{2}+2hxy+b{y}^{2}+2gx+2fy+c=0$
and the discriminant of above equation is represented by $\triangle$ , where $\triangle=abc+2fgh-a{f}^{2}-b{g}^{2}-c{h}^{2}$ or $\left( \begin{matrix} a & h & g \\ h & b & f \\ g & f & c \end{matrix} \right)$
Now, match the entries from the following two columns

(A)

$\because \sqrt{\dfrac{x}{a}}+\sqrt{\dfrac{y}{b}}=1$
On squaring both sides, we get

$\dfrac{x}{a}+\dfrac{y}{b}+2\sqrt{\dfrac{xy}{ab}}=1$
or

$\dfrac{x}{a}+\dfrac{y}{b}-1=2\sqrt{\dfrac{xy}{ab}}$
Again squaring both sides, we get

$\dfrac{{x}^{2}}{{a}^{2}}+\dfrac{{y}^{2}}{{b}^{2}}+1+\dfrac{2xy}{ab}-\dfrac{2y}{b}-\dfrac{2x}{a}=4\left(\dfrac{xy}{ab}\right)$

$\Rightarrow \dfrac{{x}^{2}}{{a}^{2}}+\dfrac{{y}^{2}}{{b}^{2}}-2\left(\dfrac{xy}{ab}\right)+1-\dfrac{2y}{b}-\dfrac{2x}{a}=0$ .......

$\left(1\right)$
Now, comparing

$\left(1\right)$ with

$A{x}^{2}+2Hxy+B{y}^{2}+2Gx+2Fy+C=0$ then

$A=\dfrac{1}{{a}^{2}} , H=-\dfrac{1}{ab}, B=\dfrac{1}{{b}^{2}} , G=-\dfrac{1}{a} , F=-\dfrac{1}{b} , C=1$
On substituting the above values in the below condition,

$\triangle=ABC+2FGH-A{F}^{2}-B{B}^{2}-C{H}^{2}$

$=\dfrac{1}{{a}^{2}{b}^{2}}-\dfrac{2}{{a}^{2}{b}^{2}}-\dfrac{1}{{a}^{2}{b}^{2}}-\dfrac{1}{{a}^{2}{b}^{2}}-\dfrac{1}{{a}^{2}{b}^{2}}$

$=\dfrac{-4}{{a}^{2}{b}^{2}}\neq0$
and

${H}^{2}=AB$

$\because \triangle\neq0,{H}^{2}=AB$

$\therefore$ conic is non-degenerate and a parabola.

(B)Now comparing

$3{x}^{2}+10xy+3{y}^{2}-15x-21y+18=0$
with

$a{x}^{2}+2hxy+b{y}^{2}+2gx+2fy+c=0$ we get

$a=3,h=5,b=3,g=\dfrac{-15}{2} , f=\dfrac{-21}{2} , c=18$ ,
On substituting the above values in below condition, we get

$=\triangle=abc+2fgh-a{f}^{2}-b{g}^{2}-c{h}^{2}$

$=3\times3\times18+2\times\dfrac{-21}{2}\times\dfrac{-15}{2}\times5-3\times{\left(\dfrac{-21}{2}\right)}^{2}-3\times{\left(\dfrac{-15}{2}\right)}^{2}-18\times{\left(5\right)}^{2}$

$=162+288-450=450-450=0$
and

${h}^{2}\neq{ab}$

$\because \triangle=0,{h}^{2}\neq{ab}$ the conic is degenerate and a pair of intersecting straight lines.

(C)Now comparing

$8{x}^{2}-4xy+5{y}^{2}-16x-14y+17=0$ with

$a{x}^{2}+2hxy+b{y}^{2}+2gx+2fy+c=0$ we get

$a=8, h=-2 , b=5, g=-8 , f=-7 , c=17$
On substituting the above values in below condition, we get

$\triangle=abc+2fgh-a{f}^{2}-b{g}^{2}-c{h}^{2}$

$=8\times5\times17+2\times-7\times-8\times-2-8\times{\left(-7\right)}^{2}-5\times{\left(-8\right)}^{2}-17\times{\left(-2\right)}^{2}$

$=255-224-147-320-68=-504\neq{0}$
and

${h}^{2}<ab$

$\therefore \triangle \neq{0}$ and

${h}^{2}<ab$ then conic is non-degenerate and an ellipse.

Find the equation of a circle which touches the lines $7x^2-18xy+7y^2=0$ and the circle $x^2+y^2-8x-8y=0$ and is contained in the given circle.

Lines

$\Rightarrow7x^2-18xy+7y^2$ ........(1)

Coefficient of

$x=y\Rightarrow$ both lines through origin

- center of circle is on angle bisector of lines.

- Angle bisectors are ether

$(x+y)$ or

$(x-y)$

$\Rightarrow$ If is

$(x-y)$ , as the

$\underset {\underset{x^2+y^2-8x-8y=u}{\downarrow} }{contained}$ circle lies in

$1st$ quadrant

$\Rightarrow$ so center lies on

$y=x,\Rightarrow (a,a)$

$(x-a)^2+(y-a)^2=c^2$ ..........(2)

$1st$ distance from center to tangent = Radius

Let tangent

$\Rightarrow y=mx\Rightarrow \dfrac{|y-m^2|}{\sqrt{1+m^2}}=R\Rightarrow \dfrac{a-ma}{\sqrt{1+m^2}}=R$

$\Rightarrow R^2(m^2+1)=a^2(1+m^2-2m)\Rightarrow R^2m^2+R^2=a^2+a^2m^2-2ma^2$

$\Rightarrow m^2(R^2-a^2)=a^2-R^2-2ma^2$

$m^2=\dfrac{(a+R)(a+R)}{(R+a)(R-a)}-\dfrac{2ma^2}{(R^2-a^2)}$

Company with

$(1)$ sum of roots.

$\dfrac{2a^2}{R^2-a^2}=\dfrac{-18}{7}\Rightarrow 14a^2=-18R^2+18a^2\Rightarrow 4a^2=18R^2$

$\Rightarrow a=\dfrac{3}{\sqrt 2}Ror\dfrac{3}{\sqrt 2}C$

Radius of given

$\Rightarrow (x-y)^2(y-y)^2=(4\sqrt )^2$

$R-R_1=CC_1$

$\Rightarrow (4\sqrt 2-R)^2=\left(4-\dfrac{3R}{\sqrt 2}\right)^2\times 2\Rightarrow 4\sqrt 2-R=-\sqrt 2\left(4\dfrac{-3R}{\sqrt 2}\right)$

$\Rightarrow 8\sqrt 2=4R\Rightarrow R=2\sqrt2 \Rightarrow a=\dfrac{3}{\sqrt 4}\times 2\sqrt 2\Rightarrow a=6$

Center

$=(6,6)$ . Radius

$=2\sqrt 2$

Circle equation

$\Rightarrow (x-6)^2+(y-6)^2=(2\sqrt 2)^2$

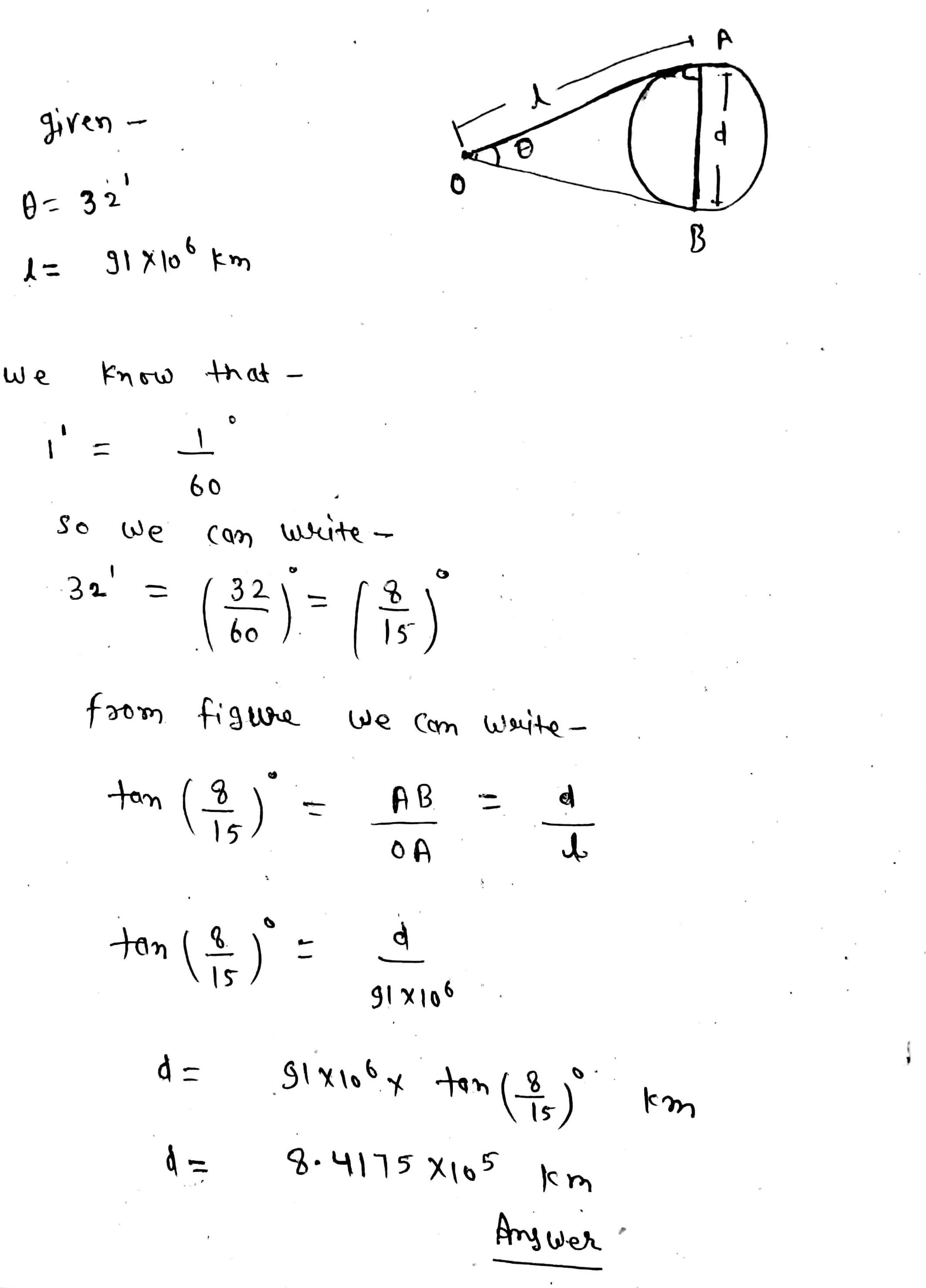
Estimate the diameter of the sun supposing that it subtends an angle of 32' at the eye of an observer. Given that the distance of the sun is $91 \times 10^6 km.$ Take $\pi = \dfrac{22}{7}$

1403155_1034529_ans_9f8537ff413d4c1daf60d3e6d04c4403.jpg

Find the equation of the circle which passes through the points $(1,-2)$ and $(4,-3)$ and which has its centre on the straight line $3x+4y=0$

2042673_1168538_ans_47eeb3c43b494cca875569607b297e0b.png

Find the equation of the circle which passes through $(2, 3)$ and $(4, 5)$ and the centre lies on the straight line $y-4x+3=0$

let the center of circle

$(-g,-f)$ and which passes through points

$(2,3)$ and

$(4,5)$

We know that,

Equation of circle whose center

$(-g,-f)$

$x^{2}+y^{2}+2gx+2fy+c=0---------(A)$

Now, passes through

$(2,3)$

Then,

$2^{2}+3^{2}+2g(2)+2f(3)+c=0$

$4+9+4g+6f+c=0$

$4g+6f+c+13=0-------(1)$

Now passes through

$(4,5)$

$4^{2}+5^{2}+2g(4)+2f(5)+c=0$

$16+25+8g+10f+c=0$

$8g+10f+c+c41=0-------(2)$

Equation of line (Given)

$y-4x+3=0$

passes through center

$(-g-f)$

$-f-4(-g)+3=0$

$4g-f+3=0----------(3)$

From equation

$(3)$

$4g-f+3=0$

$f=4g+3$

put the equation

$(1)$ and

$(2)$ and weget,

$4g+6(4g+3)+c+13=0$

4g+24g+18+c+13=0$$

$28g+c+31=0---------(4)$

$8g+10(4g+3)+c+41=0$

$8g+45g+30+c+41=0$

$48g+c+c71=0-----------(5)$

Solving equation

$(4)$ and

$(5)$ to

$28g+c+31=0\\ 48g+c+71=0\\ -\quad \quad -\quad \quad -\\ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \\ -20g-40=0$

on subtracting

$20g=-40$

now,

$f=4g+3$

$f=4(-2)+3$ (put the value of

$g$ )

$f=-8+3$

$f=-5$

put the value of

$(f)$ and

$(g)$ in equation

$(1)$ and weget,

$4g+6f+c+13=0$

$4x(-2)+6(-5)+c+13=0$

$-8-30+13+x=0$

$-38+13+c=0$

$c=-25$

Substitute the value of

$(f), (g)$ and

$(c)$ in equation

$(A)$ and weget,

$x^{2}+y^{2}+2gx+2fy+c=0$

$x^{2}+y^{2}+2(-2)x+2(-5)y+(-25)=0$

$x^{2}+y^{2}-4x-10y-25=0$

Hence, this is reprises equation.

Find the area of the region $\left\{(x,y): x^{2}+y^{2}\le 1\le x+y \right\}$

$x^2+y^2\le 1$ represents the area with in a circle of radius

$1$ with centre of origin ( shaded black )

$x+y \ge 1$ represents the region outside the line

$x+y=1,$ ( shaded blue)

$\therefore$ Area of region bounded by the curves

$x^2+y^2\le 1$

$\&$

$x+y\ge 1$

$=$ area of quadrent

$-$ area of

$\triangle OAB$

$=\dfrac{\pi \left(1\right)^2}{4}-\dfrac{1}{2}\times 1\times 1$

$=\dfrac{\pi}{4}-\dfrac{1}{2}$

$=\dfrac{\pi-2}{4}$

$=\dfrac{1.142}{4}$

$=0.285\;unit^2.$

Hence, the answer is

$0.285.$

1172146_1259898_ans_7847d92080994c89a75faac08f7eef2b.png

Find the coordinates of the focus, equation of the directrix and the latus rectum of
$x^{2}=-2y$

${x^2} = - 2y$

Since, above equation include

${x^2}$ , so, its axis is x-axis

Also coeficient of y is positive (-2)

hence,

${x^2} = - 4ay$

$\begin{array}{l} \therefore -2y=-4ay\Rightarrow -2=-4a\Rightarrow a=\frac { 1 }{ 2 } \\ focus\, is\, \, \left( { a,-a } \right) =\left( { 0,-\frac { 1 }{ 2 } } \right) \\ Equation\, \, of\, \, directrix\, \, is\, \, Y=a=\frac { 1 }{ 2 } \\ latus\, \, rectum=4a=2 \end{array}$

Find the equation of the circle which passes through the points $A(1, 1)$ and $B(2, 2)$ and whose radius is $1$ . Show that there are two such circles.

Let C is the center of circle with coordinates

$C\left( h,k \right)$

Coordinates of A are

$A\left( 1,2 \right)$

Coordinates of point B are

$B\left( 2,2 \right)$

As points A and B lie on circle, AC and BC are radii of circle.

By distance formula,

$AC=r=\sqrt { { \left( h-1 \right) }^{ 2 }+{ \left( k-2 \right) }^{ 2 } }$

$\therefore { r }^{ 2 }={ \left( h-1 \right) }^{ 2 }+{ \left( k-2 \right) }^{ 2 }$

$\therefore { \left( h-1 \right) }^{ 2 }+{ \left( k-2 \right) }^{ 2 }=1$ Equation (1)

Similarly,

$BC=r=\sqrt { { \left( h-2 \right) }^{ 2 }+{ \left( k-2 \right) }^{ 2 } }$

$\therefore { r }^{ 2 }={ \left( h-2 \right) }^{ 2 }+{ \left( k-2 \right) }^{ 2 }$

$\therefore { \left( h-2 \right) }^{ 2 }+{ \left( k-2 \right) }^{ 2 }=1$ Equation (2)

Perform Equation (1) - Equation (2),

${ \left( h-1 \right) }^{ 2 }-{ \left( h-2 \right) }^{ 2 }=0$

$\therefore \left( { h }^{ 2 }-2h+1 \right) -\left( { h }^{ 2 }-4h+4 \right) =0$

$\therefore { h }^{ 2 }-2h+1-{ h }^{ 2 }+4h-4=0$

$\therefore 2h-3=0$

$\therefore h=\frac { 3 }{ 2 }$

Put this value in equation (2),

${ \left( \frac { 3 }{ 2 } -2 \right) }^{ 2 }+{ \left( k-2 \right) }^{ 2 }=1$

${ \left( \frac { -1 }{ 2 } \right) }^{ 2 }+{ k }^{ 2 }-4k+4=1$

$\frac { 1 }{ 4 } +{ k }^{ 2 }-4k+4=1$

${ k }^{ 2 }-4k+\frac { 13 }{ 4 } =0$

Multiply both sides by 4, we get,

$4{ k }^{ 2 }-16k+13=0$

$\therefore k=\frac { -\left( -16 \right) \pm \sqrt { { \left( -16 \right) }^{ 2 }-4\times 4\times 13 } }{ 2\times 4 }$

$\therefore k=\frac { 16\pm \sqrt { 256-208 } }{ 8 }$

$\therefore k=\frac { 16\pm \sqrt { 48 } }{ 8 }$

$\therefore k=\frac { 16\pm 4\sqrt { 3 } }{ 8 }$

$\therefore k=\frac { 4\left( 4\pm \sqrt { 3 } \right) }{ 8 }$

$\therefore k=\frac { \left( 4\pm \sqrt { 3 } \right) }{ 2 }$

$\therefore k=\frac { \left( 4+\sqrt { 3 } \right) }{ 2 }$ and

$\therefore k=\frac { \left( 4-\sqrt { 3 } \right) }{ 2 }$

Thus, there are two centers of circle i.e.

${ C }_{ 1 }\left( \frac { 3 }{ 2 } ,\frac { \left( 4+\sqrt { 3 } \right) }{ 2 } \right)$ and

${ C }_{ 1 }\left( \frac { 3 }{ 2 } ,\frac { \left( 4-\sqrt { 3 } \right) }{ 2 } \right)$

Thus, there are two such circles.

Find the equation of the ellipse whose vertices are $\left(\pm\,7,0\right)$ and foci are $\left(\pm\,4,0\right)$

Since the foci of the ellipse are

${F}_{1}\left(-4,0\right)$ and

${F}_{2}\left(4,0\right)$ which lie on the

$x-$ axis and the mid-point of the line segment

${F}_{1}{F}_{2}$ is

$\left(0,0\right),\,\,\,\therefore,$ origin is the centre of the ellipse and the major axis lies along

$x-$ axis.

Hence the equation of the ellipse can be taken as

$\dfrac{{x}^{2}}{{a}^{2}}+\dfrac{{y}^{2}}{{b}^{2}}=1$ .........

$(1)$

As the vertices are

$\left(\pm\,7,0\right)$ .So,

$a=7$

Also,

$c=4$

We know that

${b}^{2}={a}^{2}-{c}^{2}={7}^{2}-{4}^{2}=49-16=33$

From equation

$(1)$ , the equation of the ellipse is

$\dfrac{{x}^{2}}{49}+\dfrac{{y}^{2}}{33}=1$

The equation $\dfrac{x^2}{2-r}+\dfrac{y^2}{r-5}+1=0$ represents an ellipse, if

Equating the equation of the ellipse with the second-degree equation

$A{x}^{2}+Bxy+C{y}^{2}+Dx+Ey+F=0$ with

$\dfrac{{x}^{2}}{2-r}+\dfrac{{y}^{2}}{r-5}+1=0$

we get

$A=\dfrac{1}{2-r}, B=0, C=\dfrac{1}{r-5},D=0,E=0$ and

$F=1$

For the second degree equation to represent an ellipse, the coefficients must satisfy the discriminant condition

${B}^{2}-4AC<0$ and also

$A\neq C$

$\Rightarrow {\left(0\right)}^{2}-4\left(\dfrac{1}{2-r}\right)\left(\dfrac{1}{r-5}\right)<0$

$\Rightarrow -4\left(\dfrac{1}{2-r}\right)\left(\dfrac{1}{r-5}\right)<0$

$\Rightarrow \left(\dfrac{1}{2-r}\right)\left(\dfrac{1}{r-5}\right)>0$

$\Rightarrow \left(2-r\right)\left(r-5\right)<0$

$\Rightarrow \left(r-2\right)\left(r-5\right)>0$

$\Rightarrow r>2$ and

$r>5$

The lines 2 x - 3 y = 5 and 3 x - 4 y = 7 are diameters of a circle having area as 154 sq unit Then, the equation of the circle is.

2041263_1458086_ans_f06e0185d7eb444482099838f5c41263.jpg

Find the equation of the circle passing through the point ( 6,3 ) and touching the coordinate axes.

2041292_1458555_ans_7ec88d2704c44d0881f26de5549be61e.jpg

The lines 2 x - 3 y = 5 and 3 x - 4 y = 7 are diameters of a circle

having area as 154 sq unit Then, the equation of the circle is.

2041287_1458372_ans_d384b6b77a604b3aa1bd59530a2267fe.jpg

The length of the latus rectum of the parabola $x = a y ^ { 2 } + b y + c$ is $\frac { k } { a } .$ Find $k$

2044542_1565960_ans_cc8bed120df44773b57b1bbc674ac8e4.JPG

Trace the following central conics
$y^{2}-2xy+2x^{2}+2x-2y=0$

1990726_1741756_ans_5136aa4cb25e4b1faf945d3402ea1f6a.jpg

Trace the following central conics
$x^{2}-2xy\,cosec \,2a+y^{2}=a^{2}$

2008000_1741749_ans_91a5494396074a368991cacc5749dd96.jpg

Find the equation of the circle concentric with the circle $x^2 +y^2 -6x +12y +15 =0$ and of double its area.

1948214_1710081_ans_92c807c1d67f4052ba48a9e92e527eac.jpg

Show that the points $(5, 5),\ (6, 4),\ (-2, 4)$ and $(7, 1)$ all lie on a circle , and find its equation, centre and radius.

Given four points are

$( 5, 5 ), ( 6, 4 ), ( -2, 4 )$ &

$(7, 1 )$

If the points are concyclic, then the

$4^{th}$ point must satisfy the equation of circle formed by any of the three points.

We, know that general form of a circle given by

$x^2+y^2+Dx+Ey+F=0$

Let's find value of variable

$D, E, F$ by putting value of points

$( 5, 5 ), ( 6, 4 ), ( -2, 4 )$

Using the point

$( 5, 5)$ we get

$5^2+5^2+5D+5E+F=0$

$\Rightarrow\ 5D + 5E + F + 50 = 0$ ......................................(eqn 1)

Using the point

$(6 , 4 )$ we get

$6^2+4^2+6D+4E+F=0$

$\Rightarrow\ 6D + 4E + F + 52 = 0$ ......................................(eqn 2)

Using the point

$( -2,4 )$ we get

$(-2)^2+4^2+(-2)D+4E+F=0$

$\Rightarrow-2D + 4E + F + 20 = 0$ ......................................(eqn 3)

Now, by simplifying these

$3$ equations we get the values of

$D, E, F$

Subtracting eqn

$(1)$ from eqn

$(2)$ we get,

$D - E + 2 = 0$ ................(eqn 4)

Subtracting eqn

$(3)$ from eqn

$(2)$ we get,

$8D + 32 = 0 \Rightarrow D = \dfrac{-32}{8} \Rightarrow D = -4$

Putting this value in eqn

$(4)$ we get,

$-4 - E + 2 = 0 \Rightarrow E = -4 + 2 \Rightarrow E = -2$

By substituting the values of

$D$ and

$E$ in eqn

$(1)$ we get,

$5(-4) + 5(-2) + F + 50 = 0$

$\Rightarrow -20 -10 + F + 50 = 0$

$\Rightarrow F = -50 + 30 \Rightarrow F = -20$

So, the equation of our circle is

$x^2+y^2-4x-2y-20=0$

Now substituting the coordinates of

$4^{th}$ point, we get

$L.H.S = x^2+y^2-4x-2y-20\\\ \ \ \ \ \ \ \ \ \ \ \ = 7^2+1^2-4\times7-2\times1-20\\\ \ \ \ \ \ \ \ \ \ \ \ =49+1-28-2-20\\\ \ \ \ \ \ \ \ \ \ \ \ =0=RHS\\$

Hence, the given points are concyclic.

We, know that the standard equation of circle is given by

$(x-h)^2+(y-k)^2=r^2$ where (

$h, k )$ is coordinate of center of the circle and

$r$ is radius of circle.

Now, lets convert the equation of circle to standard equation of circle using Completing the square method.

$x^2+y^2-4x-2y-20=0\\ (2^2\:and\: 1^2\: is\: added \:and\: subtracted\: to\: complete\: the\: square)\\\implies x^2+y^2-4x-2y+2^2-2^2+1^2-1^2-20=0\\\implies (x^2-4x+2^2)+(y^2-2y+1^2)-2^2-1^2-20=0\\\implies (x-2)^2+(y-1)^2-4-1-20 = 0\\\implies (x-2)^2+(y-1)^2 = 25\\\implies (x-2)^2+(y-1)^2 = 5^2$

By comparing with the standard equation,

Coordinate of center of the circle is

$( 2, 1 )$ and radius of circle is

$5$ unit.

Trace the following central conics
$xy=a(x+y)$

undefined

1990722_1741750_ans_6264db3839d149b5ae6e8a30f76960ae.jpg

Find the equation of the circle whose center is (2, -5) and which passes through the point (3,2) .

1969593_1709993_ans_b8f6e1af846a4ede91b7038e9c1c2fc1.jpg

Find the equation of the circle which passes through the points $(2,3)$ and $(4, 5)$ and the centre lies on the straight line $y-4x+3=0$ .

Let the equation of circle is

$x² + y² + 2gx + 2fy + c = 0$ where

$(-g, -f)$ is the centre of the circle
According to the question to question, the circle passes through the points

$(2, 3)$ and

$(4, 5)$

So, Putting the point

$(2,3$ in the equation we get

$\Rightarrow 2² + 3² + 2g(2) + 2f(3) + c = 0$

$\Rightarrow 4g + 6f + c + 13 = 0$ .......

$(1)$

And putting the point

$(4,5)$ we get:

$\Rightarrow 4² + 5² + 2g(4) + 2f(5) + c = 0$

$\Rightarrow 8g + 10f + c + 41 = 0$ .........

$(2)$

Solving the equations

$(1)$ and

$(2)$ we get,

$4g + 4f + 28 = 0$ (By subtracting equation

$1$ from equation

$2$ )

$g + f + 7 = 0$ ..........

$(3)$

Since it is given that the centre of the circle lies on the line

$y - 4x + 3 = 0$ .

Hence,

$(-g, -f)$ must satisfy the equation of the line
e.g.,

$-f +4g + 3 = 0$ .......

$(4)$

On solving equations

$(3)$ and

$(4)$ we get,

$\Rightarrow 5g + 10 = 0$ (By adding equations

$3$ and

$4$ )

$\Rightarrow g = -2$

Using this value of

$g$ we get

$f = -7 - g = -5$

Hence, the centre of the circle is

$(-2, -5)$

Using the values of

$f$ and

$g$ in the equation

$1$ we get

$c = 25$

So the radius of circle is

$\sqrt{g² + f² - c}$

$\Rightarrow \sqrt{2² + 5² - 25} = 2$

Hence, the radius of the circle is

$2$ units

Trace the following central conics
$x^{2}-2xy\cos 2x+y^{2}=2a^{2}$

1990720_1741748_ans_06d452df2a374ea199c50b675f188e16.jpg

Trace the following central conics
$xy-y^{2}=a^{2}$

2007514_1741752_ans_7bf8c4f38768412ea14972c7d2775da7.jpg

What conics do the following equations represent? When possible, find their centres, and their equation referred to the centre.
$13x^{2}-18xy+37y^{2}+2x+14y-2=0$

1754068_1741592_ans_afb464f27bfc48dcbaa3cd11dab96adc.jpg

Conic Sections - Class 11 Engineering Maths - Extra Questions

Find the locus of a point which is at a distance of 5 units from (-1 , -2)

Find the equation of the circle with centre (0, 2)(0, 2) and radius 22

Find the equation of the circle with centre \displaystyle \left ( \frac{1}{2},\frac{1}{4} \right )\displaystyle \left ( \frac{1}{2},\frac{1}{4} \right ) and radius \displaystyle \frac{1}{12}\displaystyle \frac{1}{12}

Find the equation of the circle with centre (-2, 3)(-2, 3) and radius 44

The point at which the hyperbola intersects the transverse axis are called the ................. of the hyperbola.

Find the equation of the circle with centre (1, 1)(1, 1) and radius \displaystyle \sqrt{2}\displaystyle \sqrt{2}

Find the centre and radius of the circle (x + 5)\displaystyle ^{2} + (y - 3)\displaystyle ^{2} = 36(x + 5)\displaystyle ^{2} + (y - 3)\displaystyle ^{2} = 36

Derive the standard form of the parabola

Find the value of p when the parabola y^2=4pxy^2=4px goes through the point (i) (3, - 2) and (ii) (9, - 12).

Find the equation to the conic passing through the origin and the points \left( 1,1 \right) ,\left( -1,1 \right) ,\left( 2,0 \right) \left( 1,1 \right) ,\left( -1,1 \right) ,\left( 2,0 \right) , and \left( 3,-2 \right) \left( 3,-2 \right) . Determine its species.

Draw the circles whose equation are x^2 + y^2 = 2ay. x^2 + y^2 = 2ay.

Find the eccentricity and length of latus rectum of hyperbola\cfrac { { x }^{ 2 } }{ 25 } -\cfrac { { y }^{ 2 } }{ 9 } =1\cfrac { { x }^{ 2 } }{ 25 } -\cfrac { { y }^{ 2 } }{ 9 } =1

Draw the circles whose equation are 3x^{2} + 3y^{2} = 4x3x^{2} + 3y^{2} = 4x.

What are represented by the equation (x^2 - a^2)^2 - y^4 = (x^2 - a^2)^2 - y^4 =

Find the equation of the circle drawn on the intercept made by the line 2x+3y=62x+3y=6 between the coordinate axes as diameter.

A circle of radius 55 units touches the coordinate axes in the first quadrant. If the circle makes one complete roll on x-axis along the positive direction of x-axis, find its equation in new position.

If the line lx+my+n=0lx+my+n=0 touches the circle x^2+y^2=a^2x^2+y^2=a^2, then prove that (l^2+m^2)a^2=n^2(l^2+m^2)a^2=n^2.

Find the centre and radius of the circle x^2+y^2+2ax\cos \theta-2ay\sin \theta-3a^2=0x^2+y^2+2ax\cos \theta-2ay\sin \theta-3a^2=0.

If the line lx+my+n=0lx+my+n=0 touches the parabola y^2=4axy^2=4ax, prove that ln=am^2ln=am^2.

Find the area of a quadrant of a circle whose circumference is 4444 cm.

Find the locus of coordinates of A and B which are two points in place so that PA - PB =PA - PB = constant.

Find the equation of the circle whose two end points of diameter are (4,-2),(-1,3)(4,-2),(-1,3).

Determine the equation of the circle which touches the line x - y = 0 at the origin and bisects the circumference of the circle x^2 \, + \, y^2 \,+\, 2y \, \, - \, 3 \,= \,0x^2 \, + \, y^2 \,+\, 2y \, \, - \, 3 \,= \,0

Find the equation of circle with centre (-3, 2)(-3, 2) & radius 44

Find the equation of circle on which the co-ordinates of any point are \left ( 2 \, + \, 4 \, cos \theta , \, - \, 1 \, + \, 4 \, sin \, \theta \right ), \, \theta\left ( 2 \, + \, 4 \, cos \theta , \, - \, 1 \, + \, 4 \, sin \, \theta \right ), \, \theta being the parameter.

Find the equation of circle with centre at (0, 0)(0, 0) & radius rr.

Find equation of the circle which touch the ordinate axes at a distance of unit 55 from the origin.

Find the equation of parabola with vertex (0, 0)(0, 0) & focus at (0, 2)(0, 2).

Find the equation of circle if centre (-a , -b) (-a , -b) and radius \sqrt{a^2 - b^2}\sqrt{a^2 - b^2}.

The length of the diameter of the circle x^2+y^2-4x-6y+4=0x^2+y^2-4x-6y+4=0 is -

Show that {x^2} + {y^2} = {a^2}{x^2} + {y^2} = {a^2} represent the standard equation of a circle whose centre at (0,0)(0,0) and radius is aa.

Find the equation of the ellipse in the standard form given e = \dfrac{1}{2}e = \dfrac{1}{2} and it passes through \left( {2,\,1} \right)\left( {2,\,1} \right)

Define Ellipse?

Find the equation of the parabola with(i) vertex (0,0)(0,0) and focus (3,0)(3,0)

\dfrac{{{x^2}}}{{8 - a}} + \dfrac{{{y^2}}}{{a - 2}} = 1\dfrac{{{x^2}}}{{8 - a}} + \dfrac{{{y^2}}}{{a - 2}} = 1 represents an ellipse .Then find range of 'a'

What is Coefficient of \text{xy} \text{xy} i.e., hh in circle

Find the equation of centre (1, 1)(1, 1) and radius \sqrt{2}\sqrt{2}.

Define Lateral Section?

The D on of family of circles with radius = 5 & and center on y = 2 is __.

Find the centre and radius of the circle: x^{2}+y^{2}-6x-8y+24=0x^{2}+y^{2}-6x-8y+24=0

Find the coordinates of the focus, equation of the directrix and the latus rectum of 3y^{2}+7x=03y^{2}+7x=0.

Find the area of the circle 4{x^2} + 4{y^2} = 94{x^2} + 4{y^2} = 9

Find the equation of the circle with centre at (3, -1)(3, -1) and which cuts off a chord of length 66 on the line 2x - 5y + 18 = 02x - 5y + 18 = 0

If the equation of two diameters of a circle are 2x + y = 62x + y = 6 and 3x + 2y = 43x + 2y = 4 equation of circle.

Conswing line x + y = 5x + y = 5 and the circle {x^2} + {y^2} - 2x - 4y+3 = 0{x^2} + {y^2} - 2x - 4y+3 = 0 then

Find the equation of the circle passing through the points (1,2),(3,-4)(1,2),(3,-4) and (5,-6)(5,-6)

Find the equation of the circle circumscribing the rectangle formed by the lines x =6, x= -3, y = 3 and y = -1.

Find the equation of that chord of the circle { x }^{ 2 }+{ y }^{ 2 }=15{ x }^{ 2 }+{ y }^{ 2 }=15 Which is bisected at the point (3,2).

Show that the equation x^{2}+y^{2}-3x+3y+10=0x^{2}+y^{2}-3x+3y+10=0 is not circle.

The equation of the circle passing through the point (1,0) and (0,1) and having the smallest radius is.

Find the centre and radius of the circle x^{2}+y^{2}=36x^{2}+y^{2}=36.

Find the equation of the circle whose diameters are along the lines 2x-3y+12=02x-3y+12=0 and x+4y-5=0x+4y-5=0 and whose area is 154\ sq154\ sq. units.

Find the Equation of the circle whose centre is ( - 2,3 )( - 2,3 ) which passes through the point ( 4,5 )( 4,5 )

Find the equation of circle with center (3,4)(3,4) and radius 5

Find the equation of the circle passing through the points (0,-1)(0,-1) and (2,0)(2,0) and whose centre lies on the line 3x+y=53x+y=5.

Find the centre and radius of circle :2x^2+2y^2-x=02x^2+2y^2-x=0

Find the equation of the circle whose centre is (-1, 2)(-1, 2) and which passes through (5, 6)(5, 6).

Find the equation of circle with center (1,4)(1,4) and radius 55.

At what point of the parabola x^{2}=9yx^{2}=9y is the abscissa three times the ordinate?

Find the equation of the circle center at origin and having radus 7cm7cm

Find the co-ordinates of centre and radius of circle.4(x^{2}+y^{2})=14(x^{2}+y^{2})=1

Find the equation of a circle which passes through (4, 1), (6, 5)(4, 1), (6, 5) and having the centre on:4x + 3y - 24 = 04x + 3y - 24 = 0.

Find the equation of the circle with centre (-a, -b)(-a, -b) and radius \sqrt { a^2 - b^2}\sqrt { a^2 - b^2}

Trace the following central conicsx^{2}-xy+2y^{2}-2ax-6ay+7a^{2}=0x^{2}-xy+2y^{2}-2ax-6ay+7a^{2}=0

What are represent by the equation\dfrac{1}{r}=1+\cos\theta+\sqrt{3}\sin\theta\dfrac{1}{r}=1+\cos\theta+\sqrt{3}\sin\theta

Prove that the equation to the circle of curvature of the conic ax^2+2hxy+by^2=2yax^2+2hxy+by^2=2y at the origin is a(x^2+y^2)=2ya(x^2+y^2)=2y.

Trace the following central conics40x^{2}+36xy+25y^{2}-196x-122y+205=040x^{2}+36xy+25y^{2}-196x-122y+205=0

Find the coordinates of the focus, axis of the parabola, the equation of directrix and the length of the latus rectum for y^2 = -8x.y^2 = -8x.

Find the coordinates of the focus, axis of the parabola, the equation of directrix and the length of the latus rectum for x^2 = -9yx^2 = -9y

Find the locus of the middle points of chords of an ellipse which are drawn through the positive end of the minor axis.

The constant ratio denoted by 'e'=\sqrt{1-\dfrac{b^m}{a^m}},\, a>b 'e'=\sqrt{1-\dfrac{b^m}{a^m}},\, a>b is the eccentricity of an ellipse. Find mm.

\displaystyle 2x^{2}+y^{2}-8x-2y+1=0.\displaystyle 2x^{2}+y^{2}-8x-2y+1=0.Find the square of the Latus Rectum for the given ellipse.

\displaystyle x^{2}+y^{2}+2x-4y+k=0\displaystyle x^{2}+y^{2}+2x-4y+k=0 passes through

The area cut off by the parabola \displaystyle y^{2}=4ax\displaystyle y^{2}=4ax and its latus rectum is.........., if a=3a=3

Coordinates of a focus

The length of the latus rectum of the parabola x=a{ y }^{ 2 }+by+cx=a{ y }^{ 2 }+by+c is \displaystyle\frac { k }{ a } \displaystyle\frac { k }{ a } . Find kk

Find the equation of the circles passing through the point (2,8)(2,8) touching the line 4x-3y-24=04x-3y-24=0 and 4x+3y-42=04x+3y-42=0 and having xx coordinate of the centre of the circle less than or equal to 88.

Find the equations of the following curves in cartesian form. Also find the centre and radius of the circle \displaystyle x=a+c\cos \theta ,y=b+c\sin \theta \displaystyle x=a+c\cos \theta ,y=b+c\sin \theta

Find the equation of the circle whose centre is (1, -2) and radius is 4

Find the equation of the circle with centre $(0, 2)$ and radius $2$

Find the equation of the circle with centre $\displaystyle \left ( \frac{1}{2},\frac{1}{4} \right )$ and radius $\displaystyle \frac{1}{12}$

Find the equation of the circle with centre $(-2, 3)$ and radius $4$

Find the equation of the circle with centre $(1, 1)$ and radius $\displaystyle \sqrt{2}$

Find the centre and radius of the circle $(x + 5)\displaystyle ^{2} + (y - 3)\displaystyle ^{2} = 36$

Find the value of p when the parabola $y^2=4px$ goes through the point (i) (3, - 2) and (ii) (9, - 12).

Find the equation to the conic passing through the origin and the points $\left( 1,1 \right) ,\left( -1,1 \right) ,\left( 2,0 \right)$ , and $\left( 3,-2 \right)$ . Determine its species.

Draw the circles whose equation are
$x^2 + y^2 = 2ay.$

Find the eccentricity and length of latus rectum of hyperbola
$\cfrac { { x }^{ 2 } }{ 25 } -\cfrac { { y }^{ 2 } }{ 9 } =1$

Draw the circles whose equation are
$3x^{2} + 3y^{2} = 4x$ .

What are represented by the equation $(x^2 - a^2)^2 - y^4 =$

Find the equation of the circle drawn on the intercept made by the line $2x+3y=6$ between the coordinate axes as diameter.

A circle of radius $5$ units touches the coordinate axes in the first quadrant. If the circle makes one complete roll on x-axis along the positive direction of x-axis, find its equation in new position.

If the line $lx+my+n=0$ touches the circle $x^2+y^2=a^2$ , then prove that $(l^2+m^2)a^2=n^2$ .

Find the centre and radius of the circle $x^2+y^2+2ax\cos \theta-2ay\sin \theta-3a^2=0$ .

If the line $lx+my+n=0$ touches the parabola $y^2=4ax$ , prove that $ln=am^2$ .

Find the area of a quadrant of a circle whose circumference is $44$ cm.

Find the locus of coordinates of A and B which are two points in place so that $PA - PB =$ constant.

Find the equation of the circle whose two end points of diameter are $(4,-2),(-1,3)$ .

Determine the equation of the circle which touches the line x - y = 0 at the origin and bisects the circumference of the circle $x^2 \, + \, y^2 \,+\, 2y \, \, - \, 3 \,= \,0$

Find the equation of circle with centre $(-3, 2)$ & radius $4$

Find the equation of circle on which the co-ordinates of any point are $\left ( 2 \, + \, 4 \, cos \theta , \, - \, 1 \, + \, 4 \, sin \, \theta \right ), \, \theta$ being the parameter.

Find the equation of circle with centre at $(0, 0)$ & radius $r$ .

Find equation of the circle which touch the ordinate axes at a distance of unit $5$ from the origin.

Find the equation of parabola with vertex $(0, 0)$ & focus at $(0, 2)$ .

Find the equation of circle if centre $(-a , -b)$ and radius $\sqrt{a^2 - b^2}$ .

The length of the diameter of the circle $x^2+y^2-4x-6y+4=0$ is -

Show that ${x^2} + {y^2} = {a^2}$ represent the standard equation of a circle whose centre at $(0,0)$ and radius is $a$ .

Find the equation of the ellipse in the standard form given $e = \dfrac{1}{2}$ and it passes through $\left( {2,\,1} \right)$

Find the equation of the parabola with
(i) vertex $(0,0)$ and focus $(3,0)$

$\dfrac{{{x^2}}}{{8 - a}} + \dfrac{{{y^2}}}{{a - 2}} = 1$ represents an ellipse .Then find range of 'a'

What is Coefficient of $\text{xy}$ i.e., $h$ in circle

Find the equation of centre $(1, 1)$ and radius $\sqrt{2}$ .

Find the centre and radius of the circle: $x^{2}+y^{2}-6x-8y+24=0$

Find the coordinates of the focus, equation of the directrix and the latus rectum of
$3y^{2}+7x=0$ .

Find the area of the circle $4{x^2} + 4{y^2} = 9$

Find the equation of the circle with centre at $(3, -1)$ and which cuts off a chord of length $6$ on the line $2x - 5y + 18 = 0$

If the equation of two diameters of a circle are $2x + y = 6$ and $3x + 2y = 4$ equation of circle.

Conswing line $x + y = 5$ and the circle ${x^2} + {y^2} - 2x - 4y+3 = 0$ then

Find the equation of the circle passing through the points
$(1,2),(3,-4)$ and $(5,-6)$

Find the equation of that chord of the circle ${ x }^{ 2 }+{ y }^{ 2 }=15$ Which is bisected at the point (3,2).

Show that the equation $x^{2}+y^{2}-3x+3y+10=0$ is not circle.

Find the centre and radius of the circle $x^{2}+y^{2}=36$ .

Find the equation of the circle whose diameters are along the lines $2x-3y+12=0$ and $x+4y-5=0$ and whose area is $154\ sq$ . units.

Find the Equation of the circle whose centre is $( - 2,3 )$ which passes through the point $( 4,5 )$

Find the equation of circle with center $(3,4)$ and radius 5

Find the equation of the circle passing through the points $(0,-1)$ and $(2,0)$ and whose centre lies on the line $3x+y=5$ .

Find the centre and radius of circle :
$2x^2+2y^2-x=0$

Find the equation of the circle whose centre is $(-1, 2)$ and which passes through $(5, 6)$ .

Find the equation of circle with center $(1,4)$ and radius $5$ .

At what point of the parabola $x^{2}=9y$ is the abscissa three times the ordinate?

Find the equation of the circle center at origin and having radus $7cm$

Find the co-ordinates of centre and radius of circle.
$4(x^{2}+y^{2})=1$

Find the equation of a circle which passes through $(4, 1), (6, 5)$ and having the centre on:
$4x + 3y - 24 = 0$ .

Find the equation of the circle with centre $(-a, -b)$ and radius $\sqrt { a^2 - b^2}$

Trace the following central conics
$x^{2}-xy+2y^{2}-2ax-6ay+7a^{2}=0$

What are represent by the equation
$\dfrac{1}{r}=1+\cos\theta+\sqrt{3}\sin\theta$

Prove that the equation to the circle of curvature of the conic $ax^2+2hxy+by^2=2y$ at the origin is $a(x^2+y^2)=2y$ .

Trace the following central conics
$40x^{2}+36xy+25y^{2}-196x-122y+205=0$

Find the coordinates of the focus, axis of the parabola, the equation of directrix and the length of the latus rectum for $y^2 = -8x.$

Find the coordinates of the focus, axis of the parabola, the equation of directrix and the length of the latus rectum for $x^2 = -9y$

The constant ratio denoted by $'e'=\sqrt{1-\dfrac{b^m}{a^m}},\, a>b$ is the eccentricity of an ellipse. Find $m$ .

$\displaystyle 2x^{2}+y^{2}-8x-2y+1=0.$
Find the square of the Latus Rectum for the given ellipse.

$\displaystyle x^{2}+y^{2}+2x-4y+k=0$ passes through

The area cut off by the parabola $\displaystyle y^{2}=4ax$ and its latus rectum is.........., if $a=3$

The length of the latus rectum of the parabola $x=a{ y }^{ 2 }+by+c$ is $\displaystyle\frac { k }{ a }$ . Find $k$

Find the equation of the circles passing through the point $(2,8)$ touching the line $4x-3y-24=0$ and $4x+3y-42=0$ and having $x$ coordinate of the centre of the circle less than or equal to $8$ .

Find the equations of the following curves in cartesian form. Also find the centre and radius of the circle $\displaystyle x=a+c\cos \theta ,y=b+c\sin \theta$

Find the equation of a circle with centre $(2, 2)$ and passes through the point $(4, 5)$ .

Find the centre and radius of the circle $\displaystyle x^{2}+y^{2}-8x +10y - 12 = 0$

Find the equation of the circle with radius $5$ whose centre lies on $x$ -axis and passes through the point $(2, 3)$

Find the equation of the circle passing through $(0, 0)$ and making intercepts $a$ and $b$ on the coordinate axes.

Find the center and radius of the circle $\displaystyle x^{2}+y^{2}-4x - 8y - 45 = 0$

Find the equation of the circle passing through the points $(2, 3)$ and $(-1, 1)$ and whose centre is on the line $x - 3y - 11 = 0$

If $5x^2 + Ay^2 = 20$ represents a rectangular hyperbola, then $-A$ equals

Find the centre and radius of the circle $\displaystyle 2x^{2}+2y^{2}-x = 0$

Find the equation of the circle with centre $(-a, -b)$ and radius $\displaystyle \sqrt{a^{2}-b^{2}}$

Find the equation of the parabola that satisfies the following conditions: Focus $(6, 0)$ ; directrix $x = -6$

Find the equation of the parabola that satisfies the following conditions: Focus $(0,-3)$ ; directrix $y = 3$

Find the coordinates of the focus, axis of the parabola ,the equation of directrix and the length of the latus rectum for $x\displaystyle ^{2} = -9y$