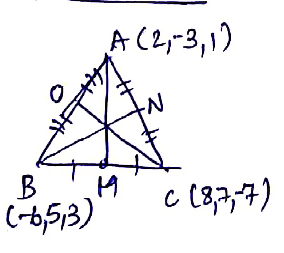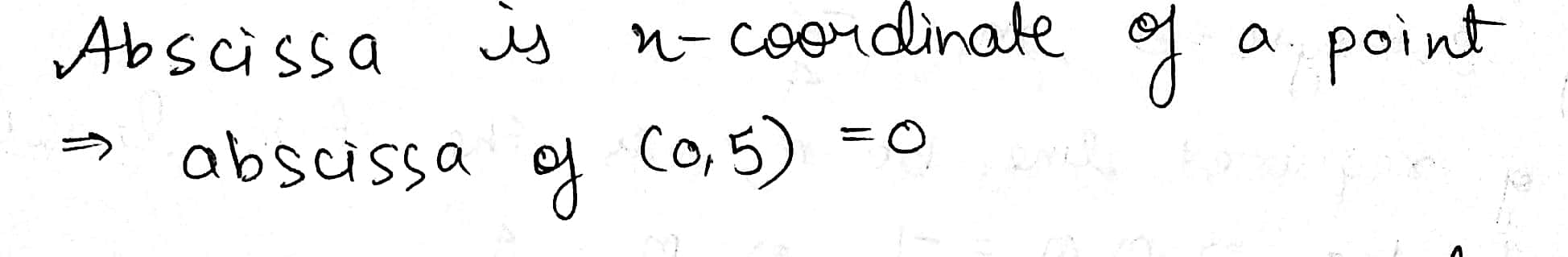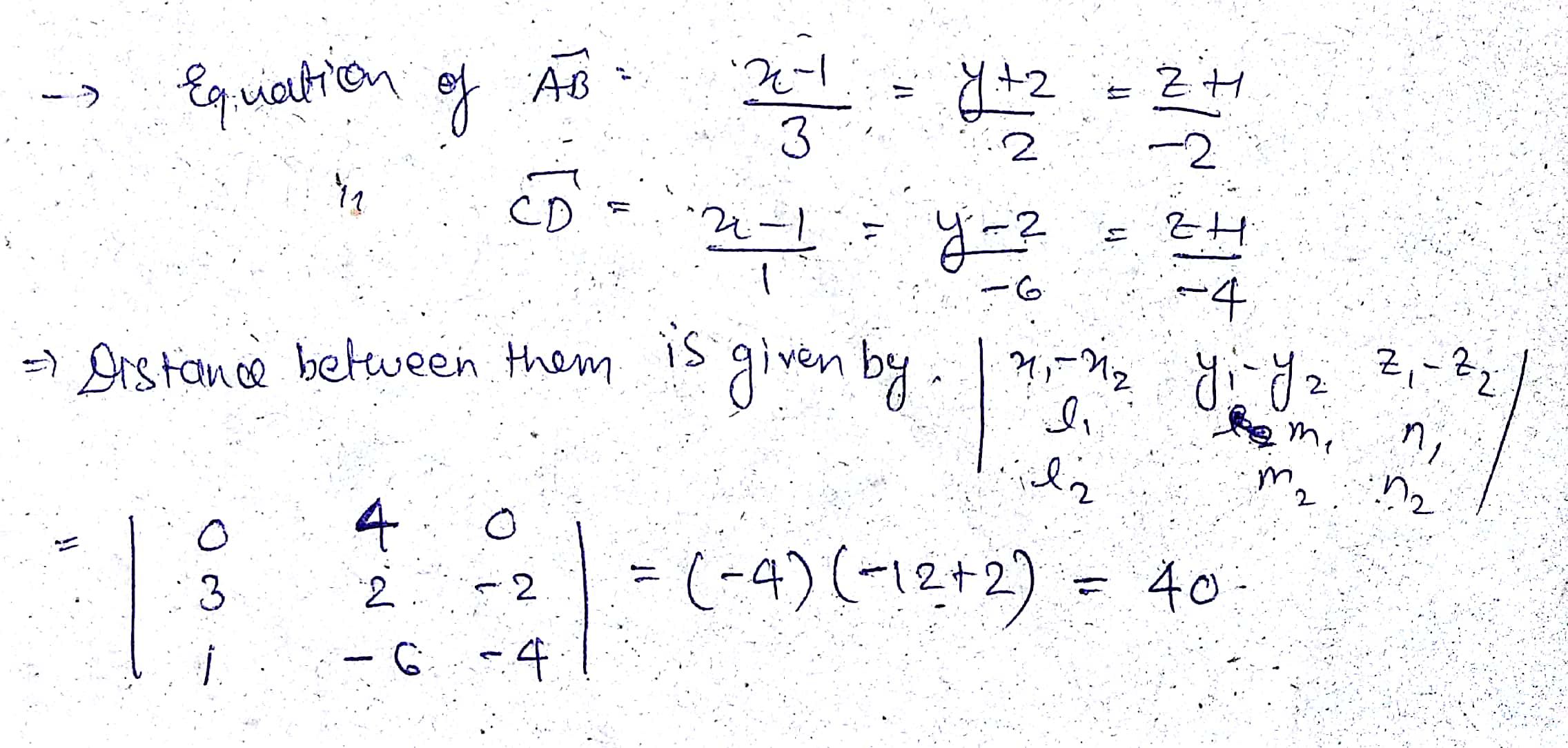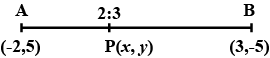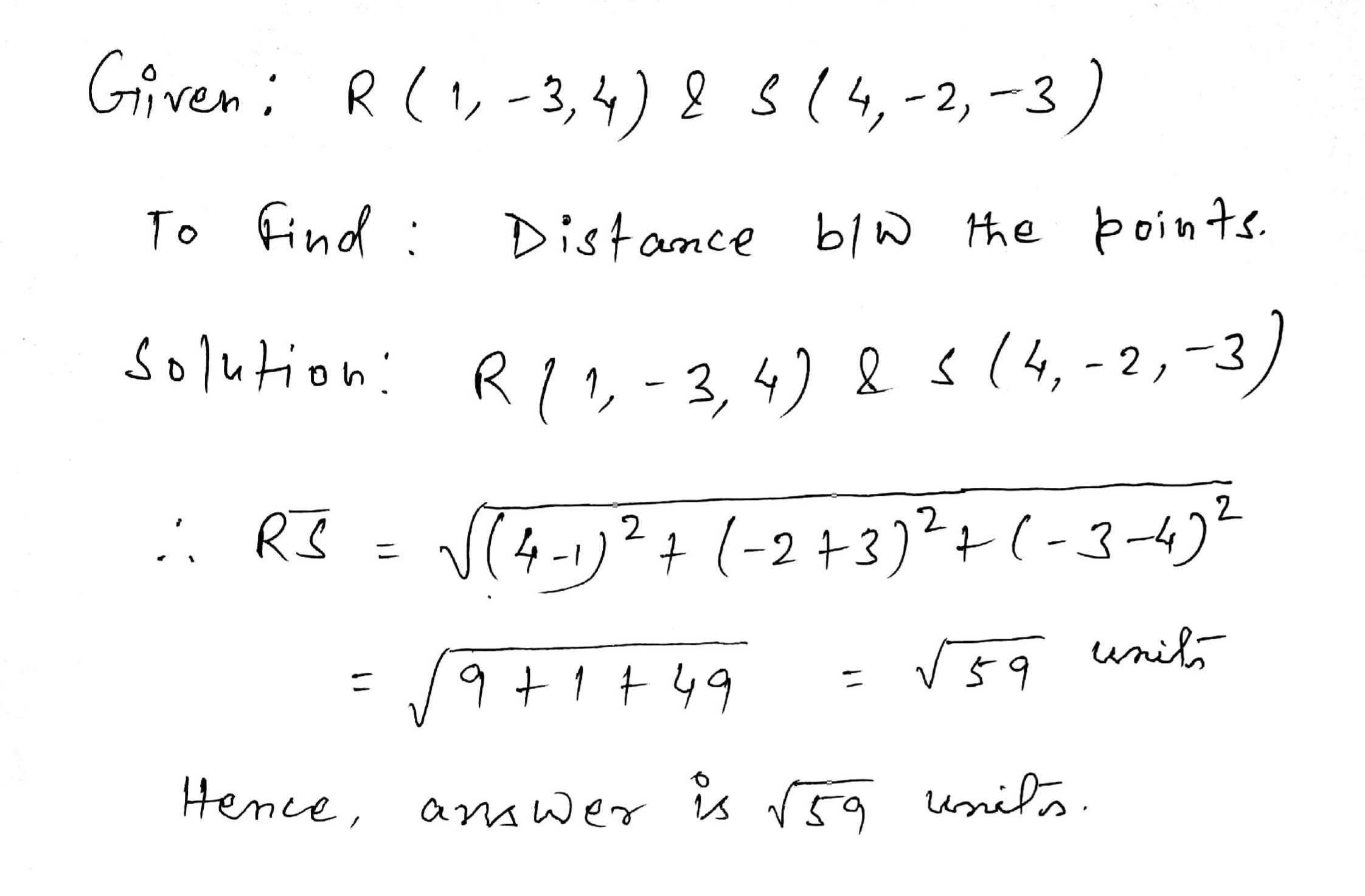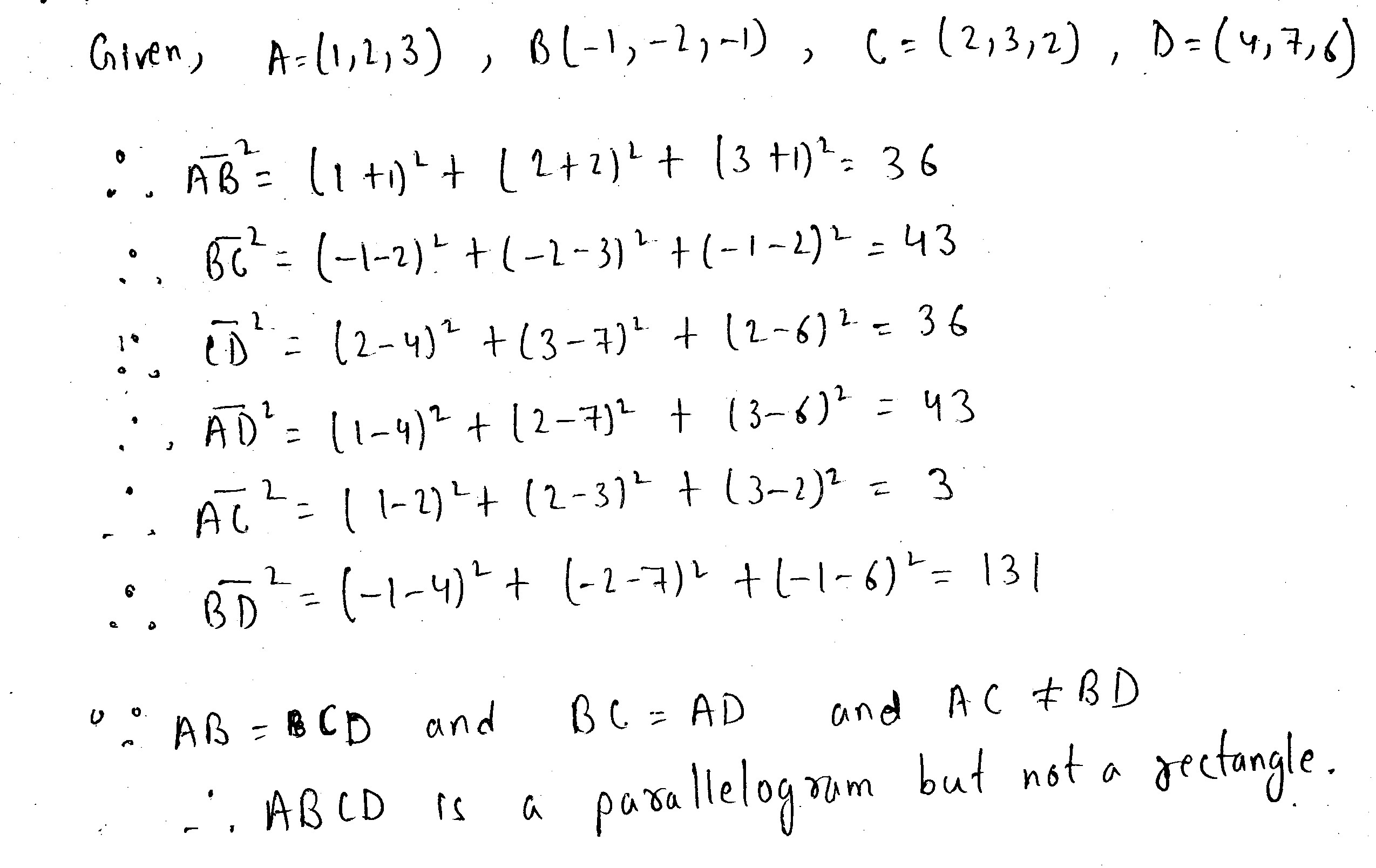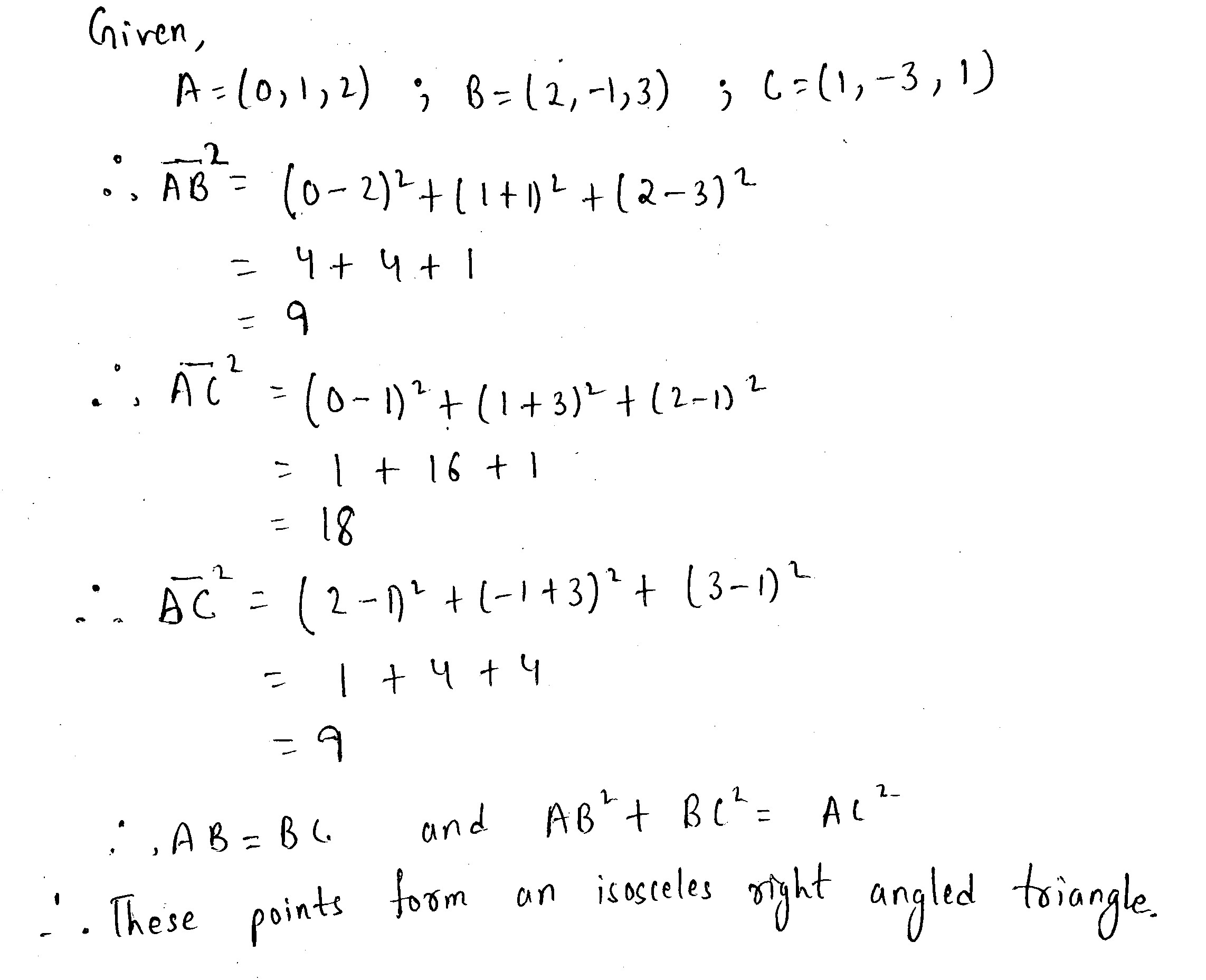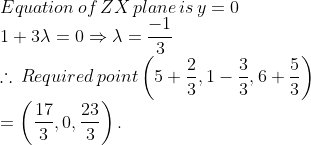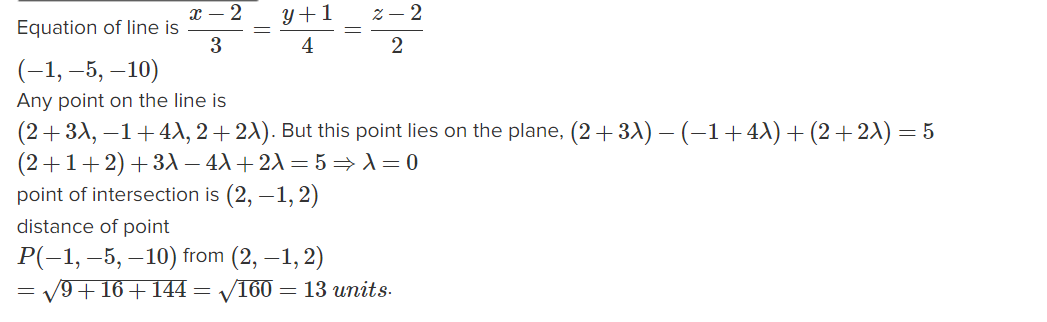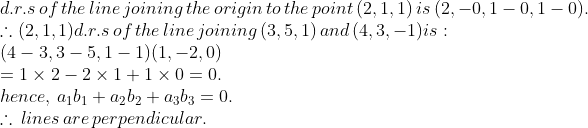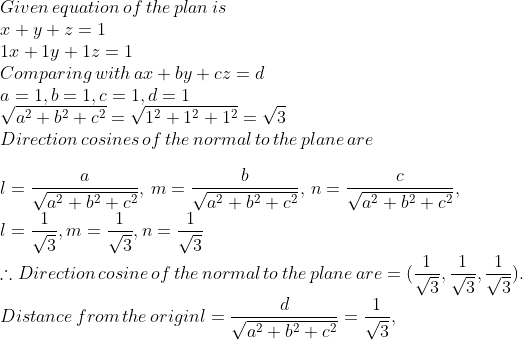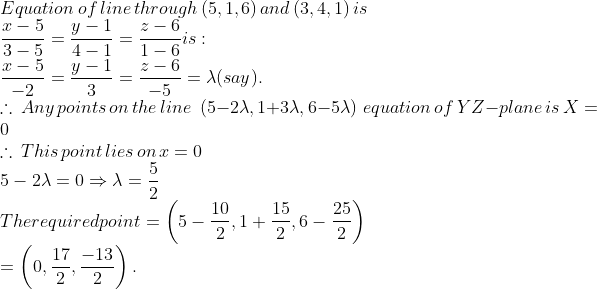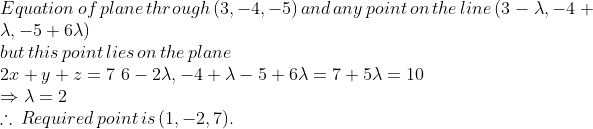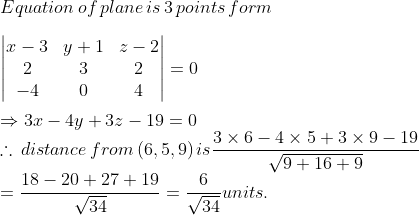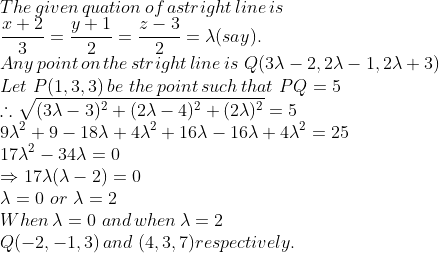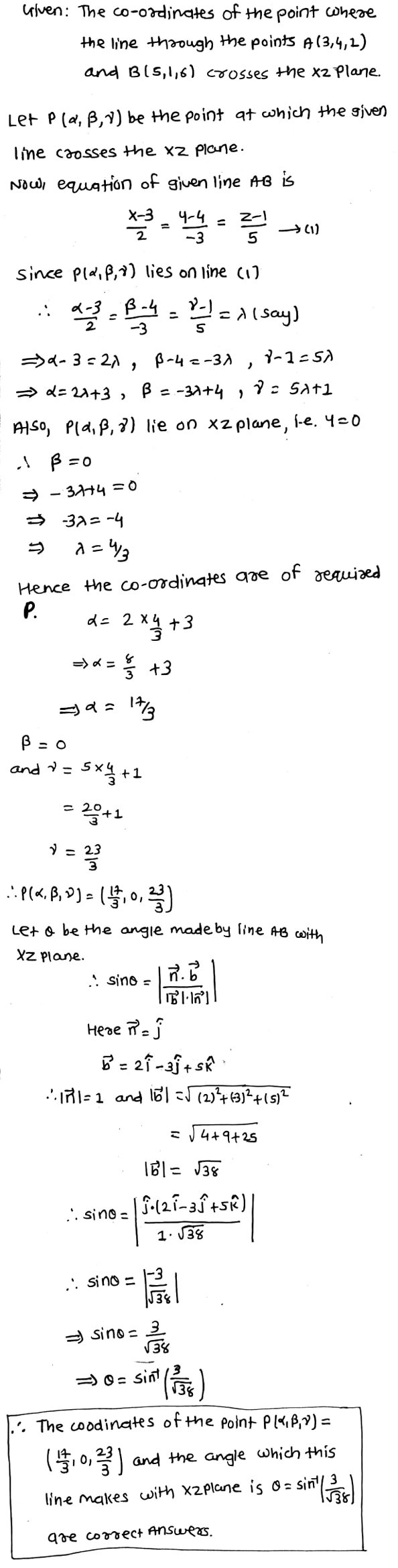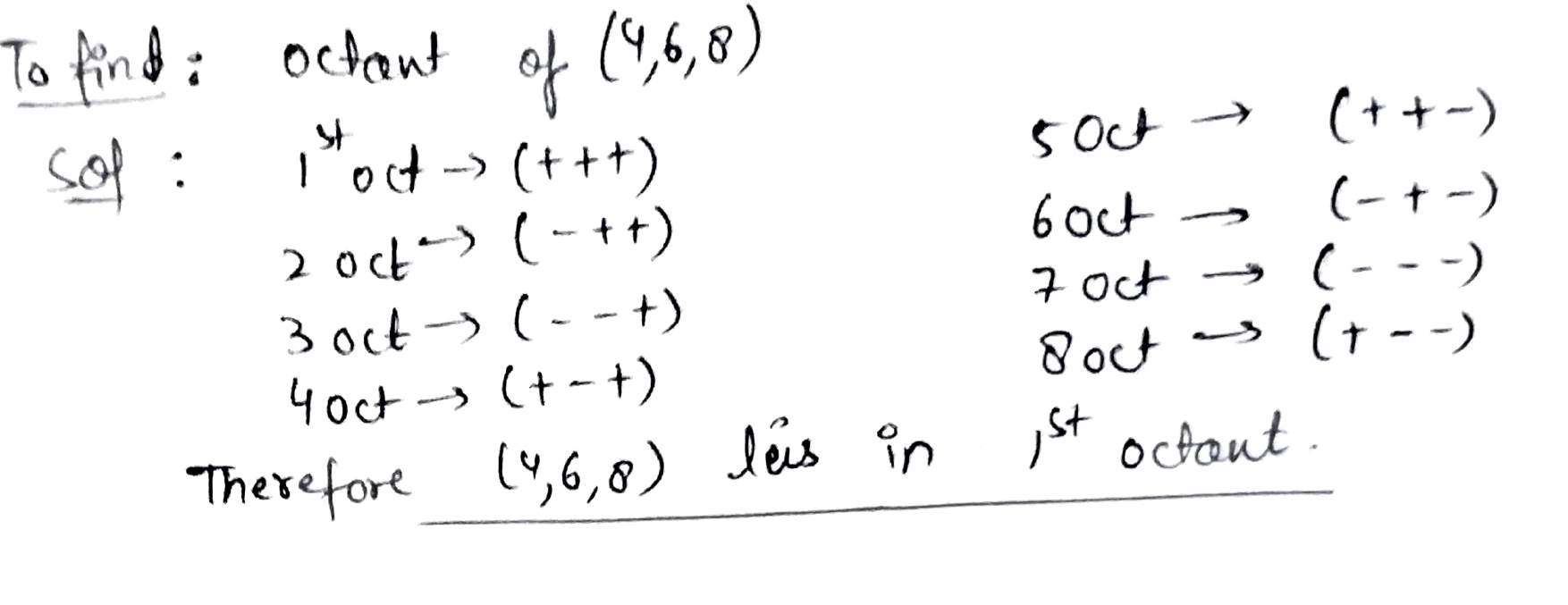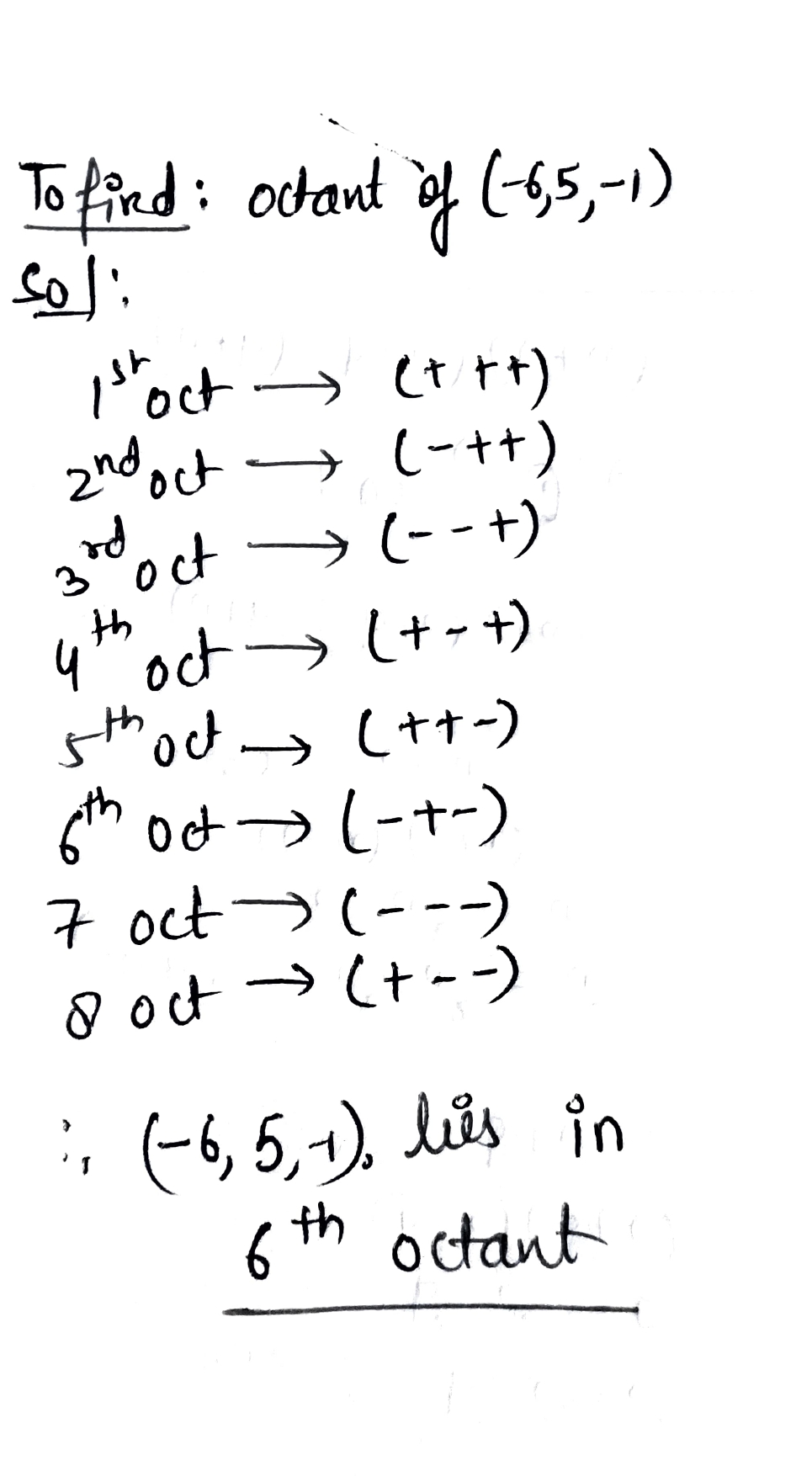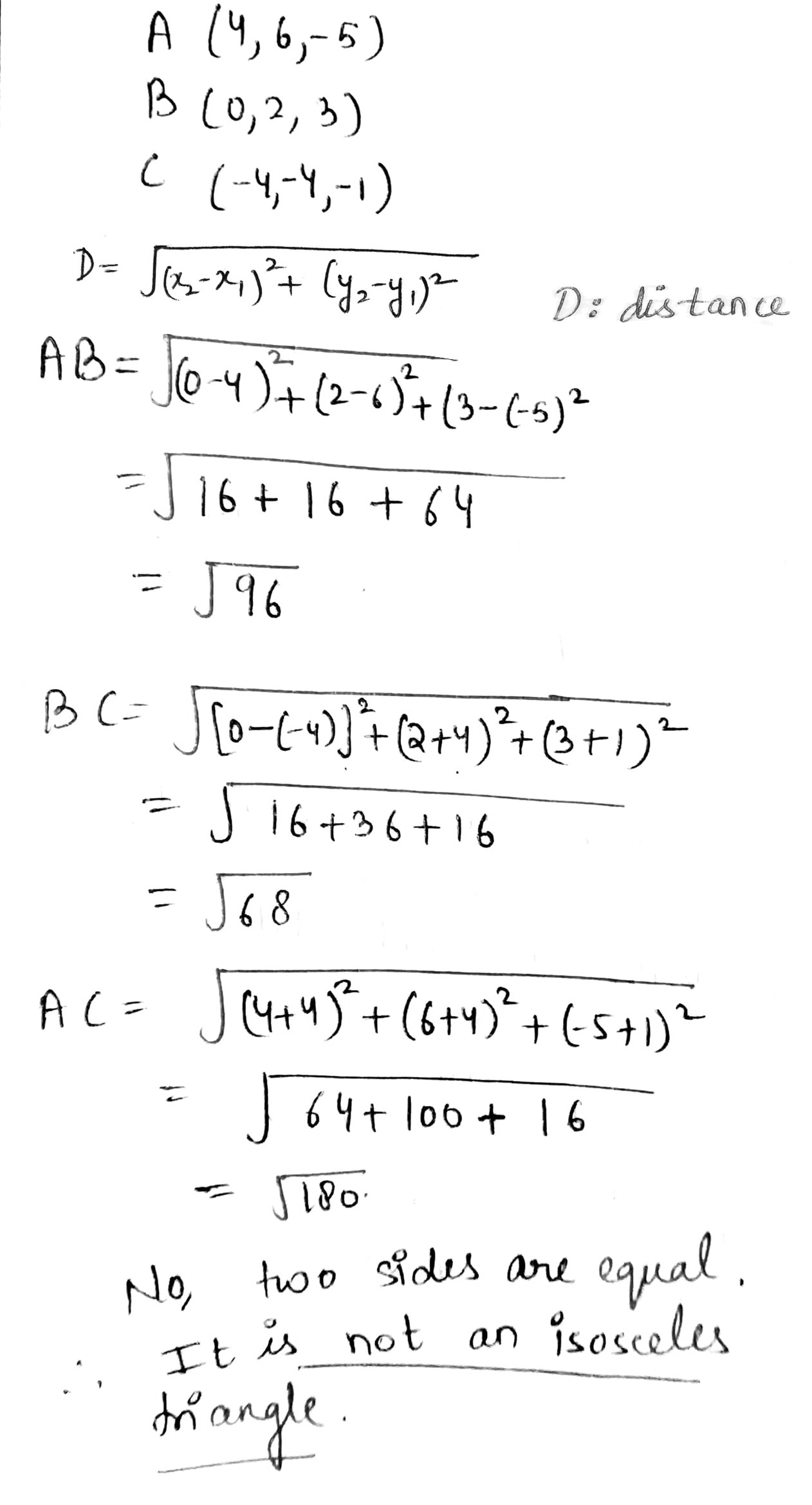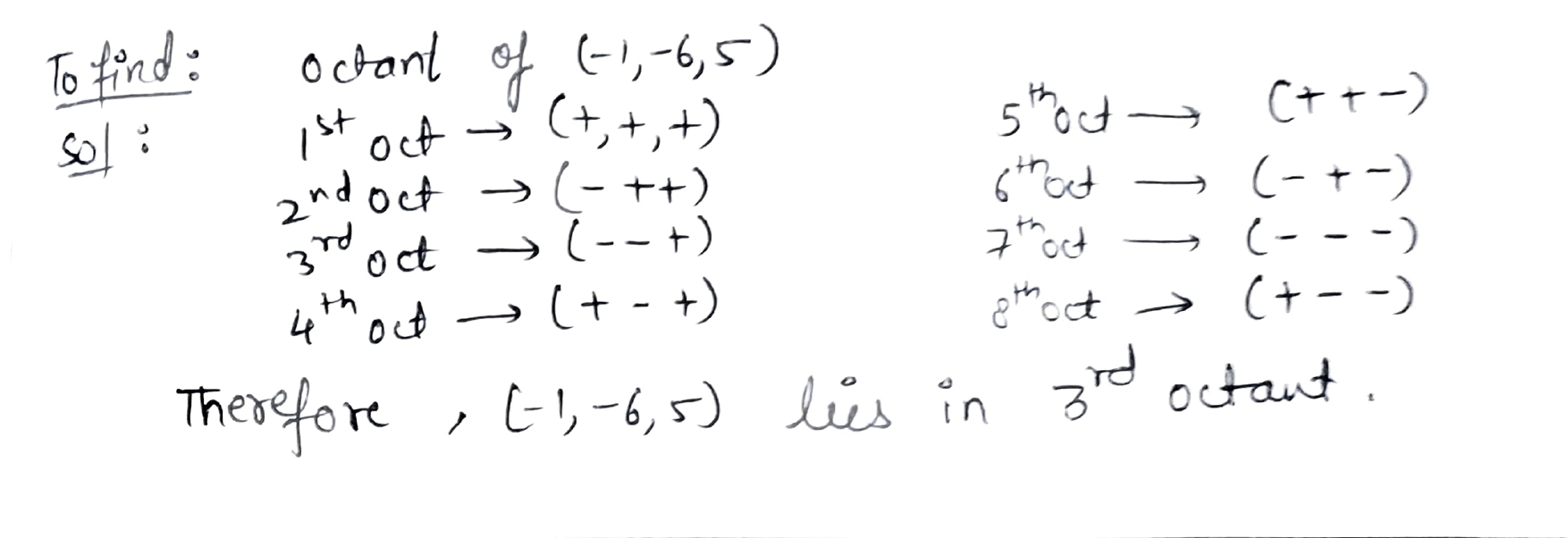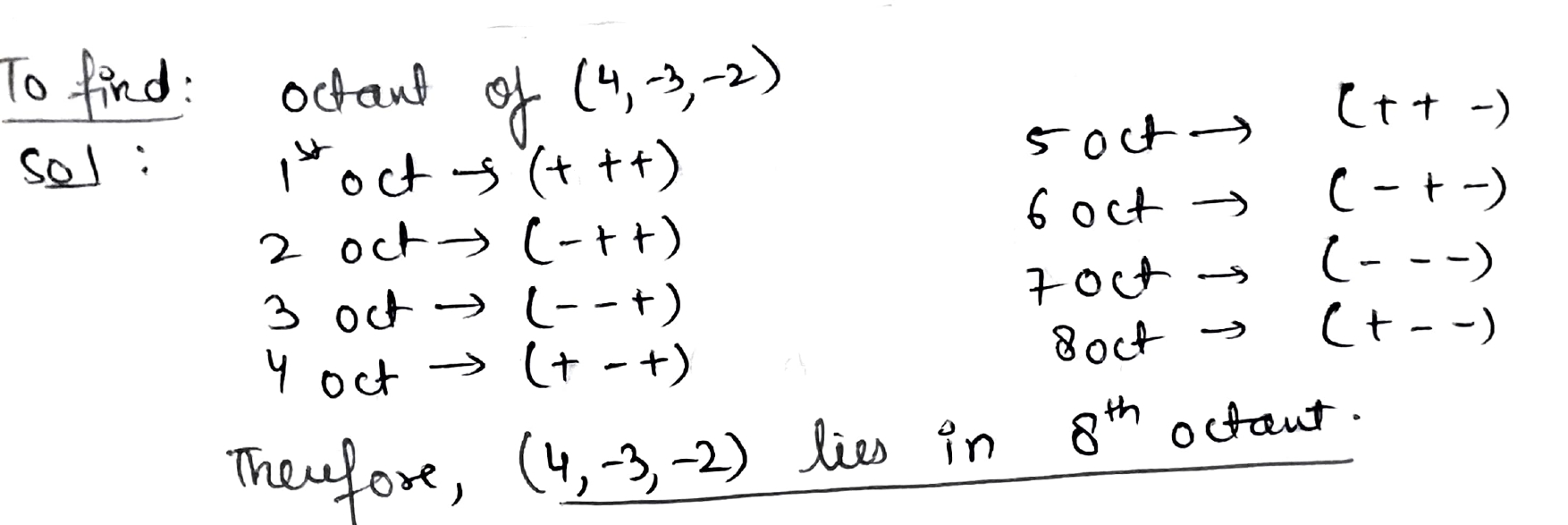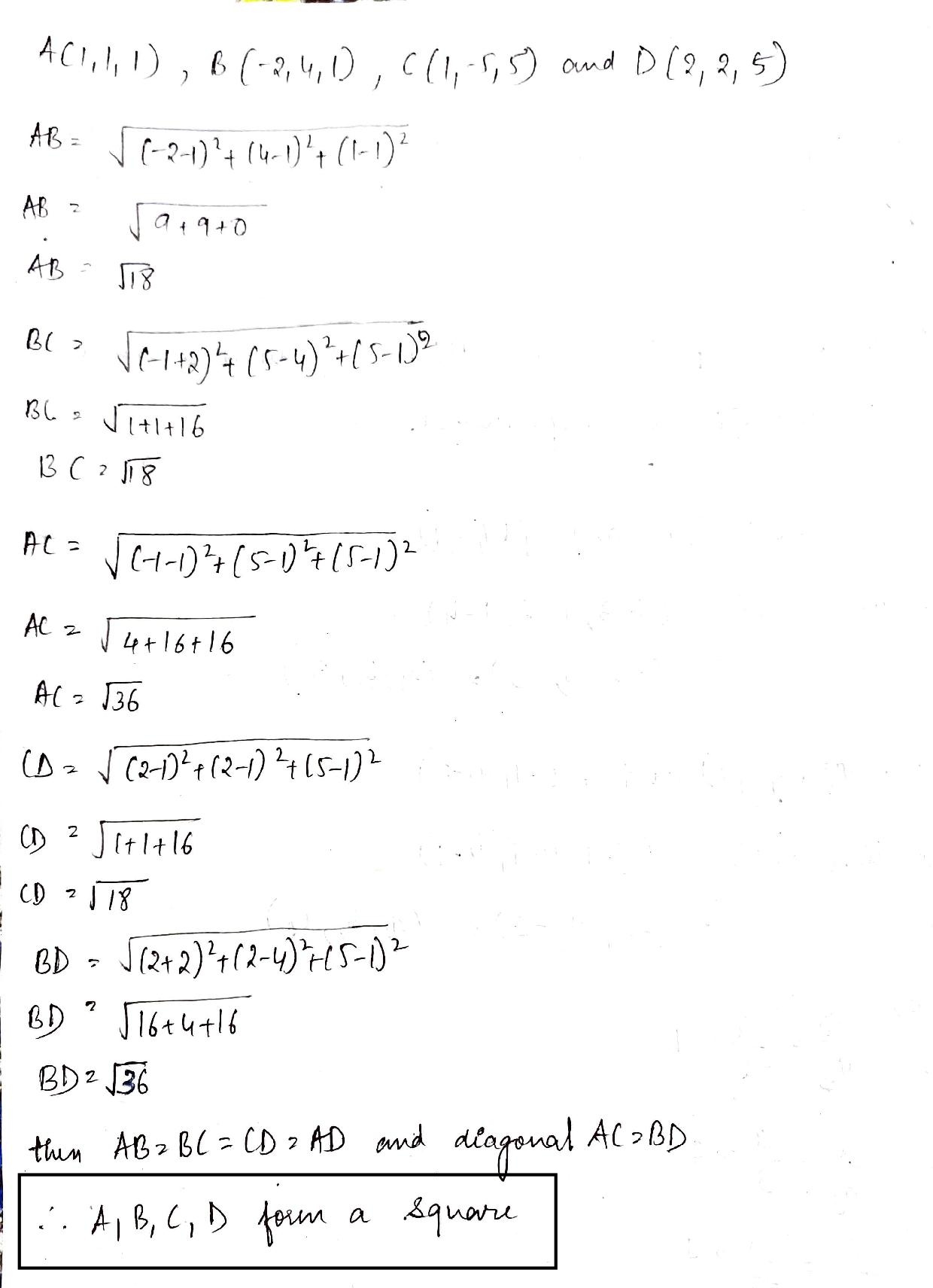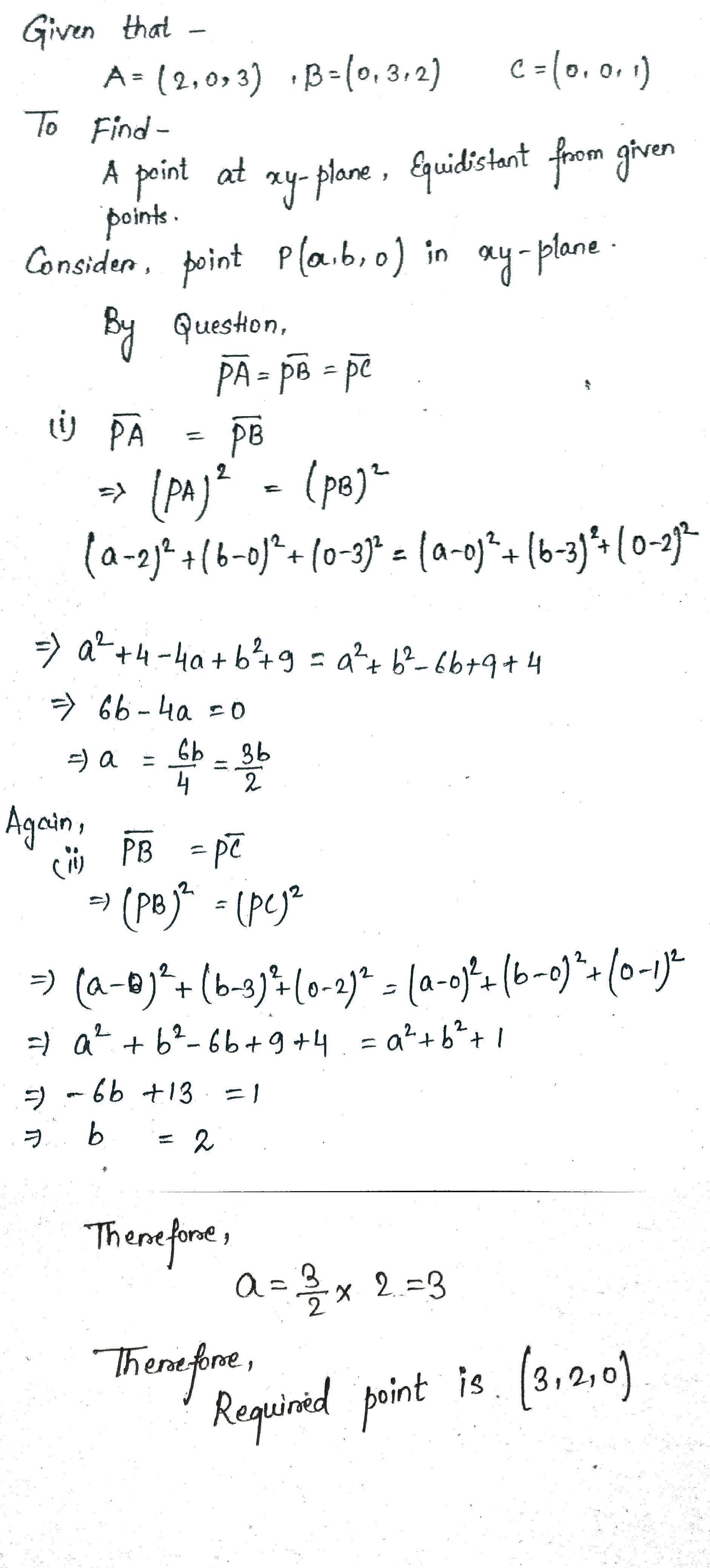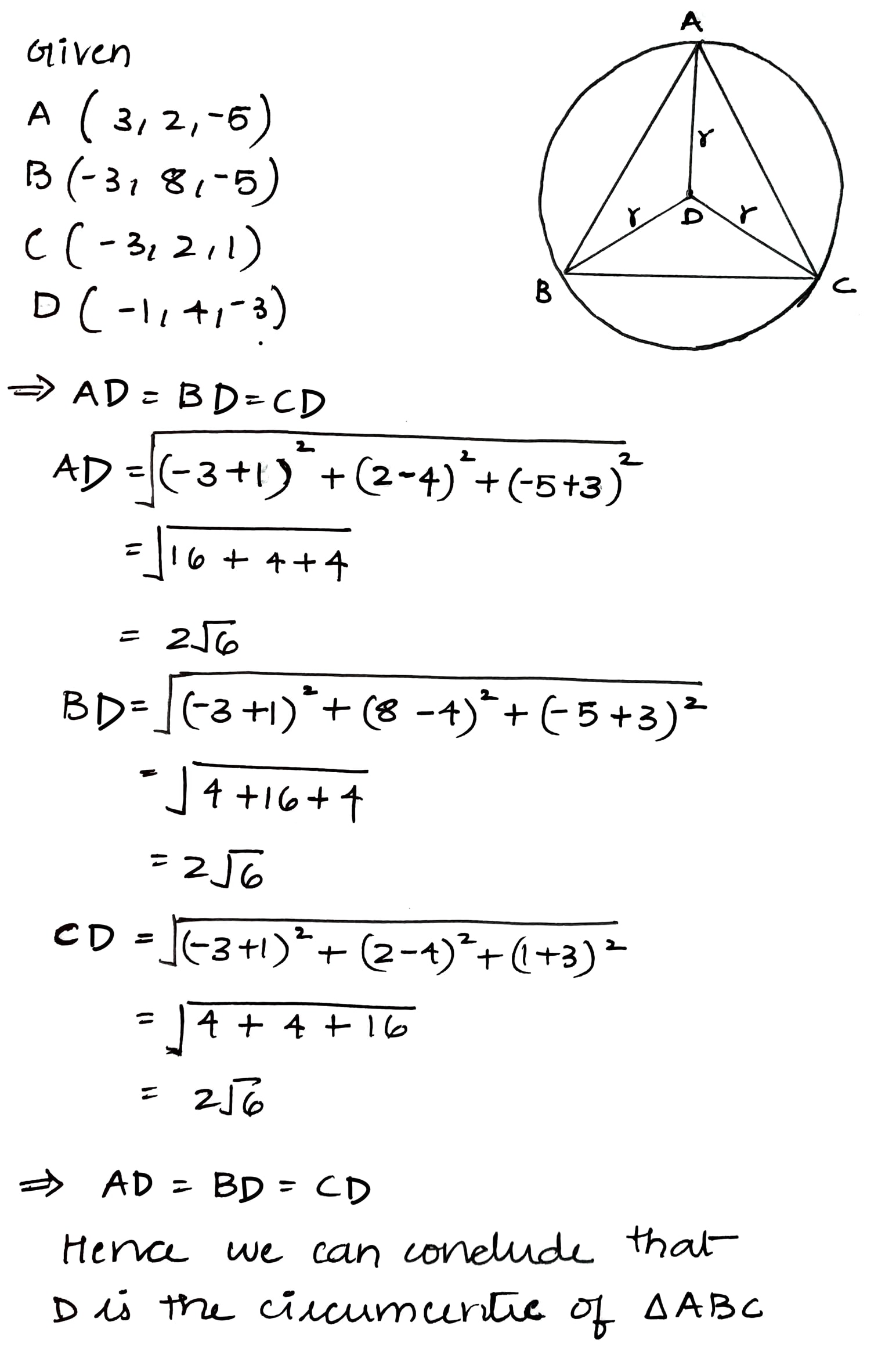Introduction To Three Dimensional Geometry - Class 11 Engineering Maths - Extra Questions
If a point is in the $$XZ$$-plane. What can you say about its $$y$$-coordinate?
Find the square of the distance between the points whose cartesian coordinates are:
$$(-1,1,3), (0,5,6);$$
Find the distance between the following pairs of points:
(i) $$(2, 3, 5)$$ and $$(4, 3, 1)$$
(ii)$$ (-3, 7, 2)$$and $$((2, 4, -1)$$
(iii) $$(-1, 3, -4)$$ and $$(1, -3, 4)$$
(iv) $$(2, -1, 3)$$ and $$(-2, 1, 3)$$
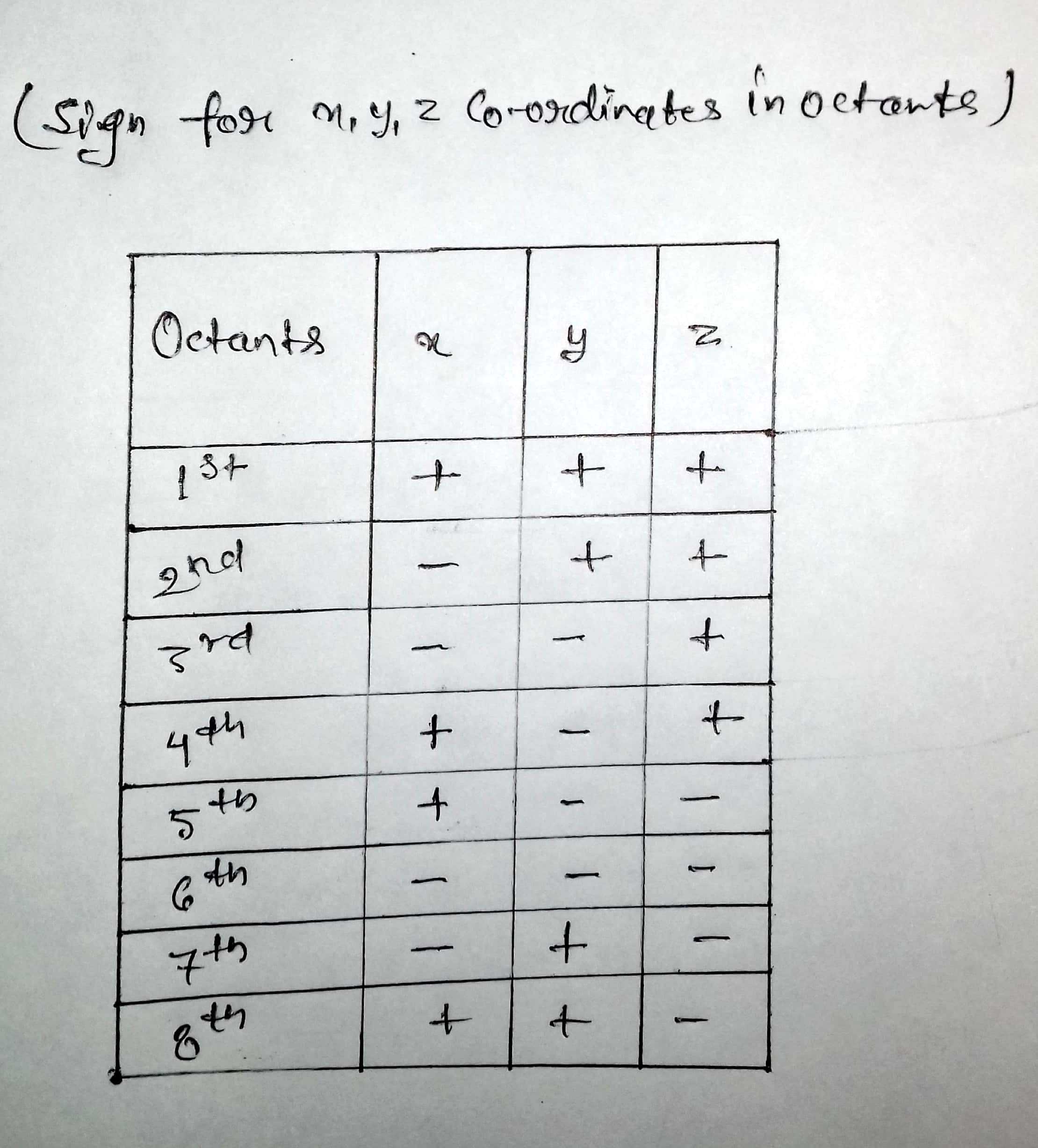
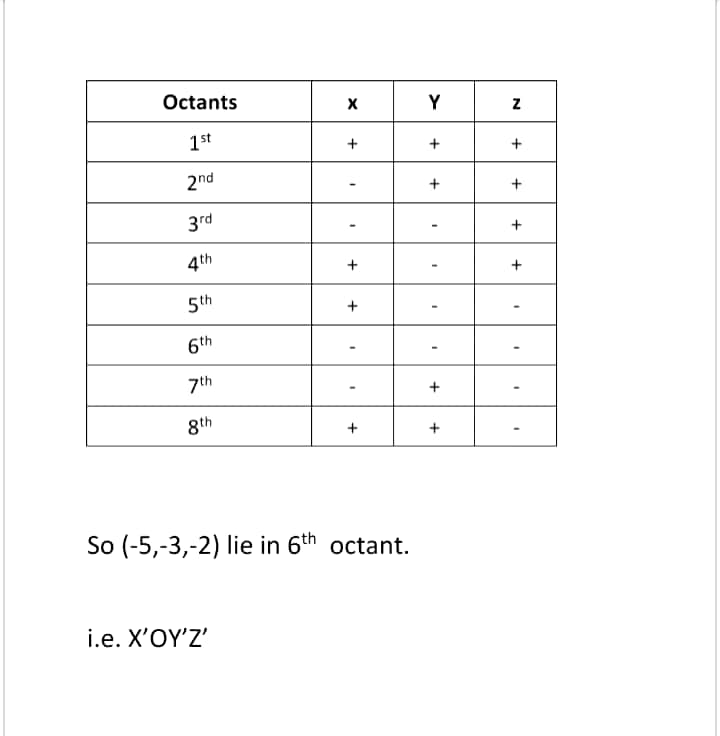
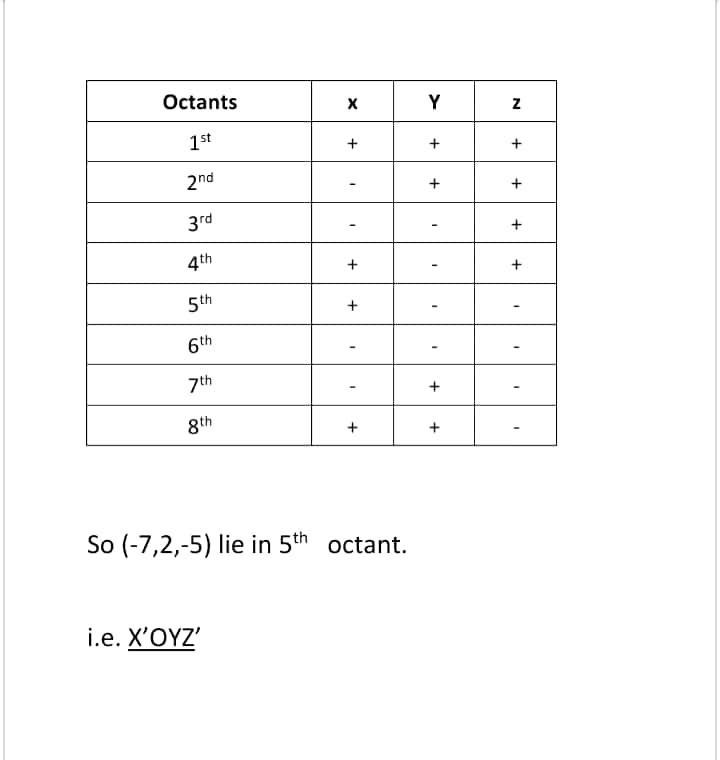
Name the octants in which the following points lie:
$$(1, 2, 3), (4, -2, 3) (4, -2, -5), (4, 2, -5), (-4, 2, -5), (-4, 2, 5), (-3, -1, 6), (2, -4, -7) $$
Find the coordinates of the points which trisect the line segment joining the points $$P (4, 2, -6)$$ and $$Q (10, -16, 6)$$
Fill in the blanks:
(i) The $$x$$-axis and $$y$$-axis taken together determine a plane known as______
(ii) The coordinates of points in the $$XY$$-plane are of the form_____
(iii) Coordinate planes divide the space into_____ octants
In what ratio, the line joining $$(-1, 1)$$ and $$(5, 7)$$ is divided by the line $$x + y \displaystyle = 4$$?
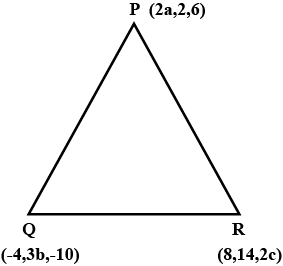
If the origin is the centroid of the triangle $$PQR$$ with vertices $$P (2a, 2, 6), Q (-4, 3b, -10)$$ and $$R (8, 14, 2c),$$ then find the values of $$a, b$$ and $$c$$
Find the coordinates of a point on $$y$$-axis which are at a distance of $$\displaystyle 5\sqrt{2}$$ from the point $$P (3, -2, 5)$$
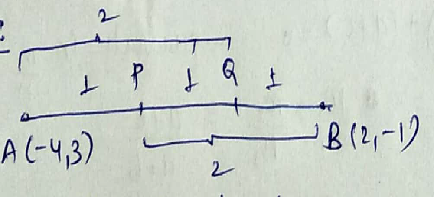
Find the coordinates of the points of trisection of the line segment joining the points $$A(-4, 3)$$ and $$B (2, -1)$$.
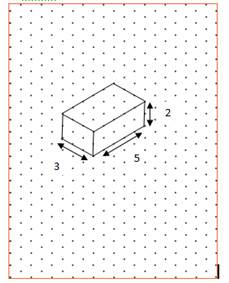
Draw a cuboid on the isometric dot sheet with the measurements 5 units $$\times$$ 3 units $$\times$$ 2 units
Draw the following 3-D figure on isometric dot sheet.
Show that LHS=RHS i.e. $$\dfrac {2}{9}\times 3 = \dfrac {2}{9} \times \dfrac {3}{1} = \dfrac {2\times 3}{9\times 1} = \dfrac {6}{9} = \dfrac {2}{3}$$.
The point P(3,4) is reflected to $$P^{'}_{}$$ in the x-axis and $$O^{'}_{}$$ is the image of O(the origin) when reflected in the line $$PP^{'}_{}$$. Using Graph paper give :
1) The coordinates of $$P^{'}_{}$$ and $$O^{'}_{}$$
2) The length of segments $$PP^{'}_{}$$ and $$OO^{'}_{}$$
3) The perimeter of the quadrilateral $$POP^{'}_{}O^{'}_{}$$
4) Geometrical name of the figure $$POP^{'}_{}O^{'}_{}$$
Find a, b, c if $$a(1, 3, 2)+b(1, -5, 6)+c(2, 1, -2)=(4,10, -8)$$.
Find the distance between the points $$(3,4,-2),(1,0,7)$$
Find the coordinates of point which divides the line joining the points $$(3,4)$$ and $$(6,1)$$ in the ratio of $$1:2$$
A policeman and a thief are equidistant from the jewel box, upon considering jewel box as origin, the position of the policeman is (0,5). If the ordinate of the position of the thief is zero, then write the coordinates of the position of the thief.
Find $$x$$ so that the point $$(6, 5, -3)$$ is at a distance of $$13$$ from the point $$(x , -7 , 0)$$
Find the coordinate of the points which trisect the line segment joining the points $$A(2, 1, -3)$$ and $$B(5, -8, 3)$$.
The three point $$A(0,0,0),B(2,-3,3),C(-2,3,-3)$$ are collinear. Find in what ratio each point divides the segment joining other two.
Find the length of the median of the whose vertices are $$A(2,-3,1),B(-6,5,3),C(8,7,-7)$$
Find the ratios in which the following straight lines divide the line segments joining the given points. State whether the points lie on the same side or on either side of the straight line.
$$2x+3y=5$$; $$(0, 0)$$ and $$(-2, 1)$$.
Find the distance between the points $$R\left( {-3,\, 0} \right),\,S\left( {0,\,\dfrac{5}{2}} \right)$$
Find the distance between the points $$A \left(x, \dfrac{1}{x} \right) $$ and $$ B \left(\dfrac{1}{x} , x \right)$$
Find the coordinates of the point which trisect $$AB$$ given that $$A(2,1,-3)$$ and $$B(5,-8,3)$$.
Prove that $$A(1, 2, 0), B(3, 1, 1), C(7, -1, 3)$$ are collinear.
Using section formula prove that the point $$(0.7.-7), (1,4,-5)$$ and $$(-1,10,-9)$$ are collinear.
Find m if the point on the $$x$$-axis which is equidistant from $$(7,6)$$ and $$(3,4)$$ is $$\left (\dfrac {m}{2},0\right)$$
Determine if the points $$(5,-1,1), (7,-4,7), (1,-8,10)$$ and $$(-1,-3,4)$$ are the vertices of a rhombus or a square.
Show that the points $$A\left( -3\hat { i } +3\hat { j } +5\hat { k } \right) ,B\left( \hat { i } +2\hat { j } +3\hat { k } \right) ,C\left( 7\hat { i } -\hat { j } \right) $$ are collinear.
Show that the points $$A(1,1,1),B(1,2,3)$$ and $$C(2,-1,1)$$ are vertices of an isosceles triangle.
In general if two points are on $$x-$$axis, which formula do you apply for distance between them and if two points are on $$y-$$axis, which formula do you apply for distance between them and why?
Plot the following numbers graph:
$$P(3, -5), Q(0, -8), R(4, 0)$$
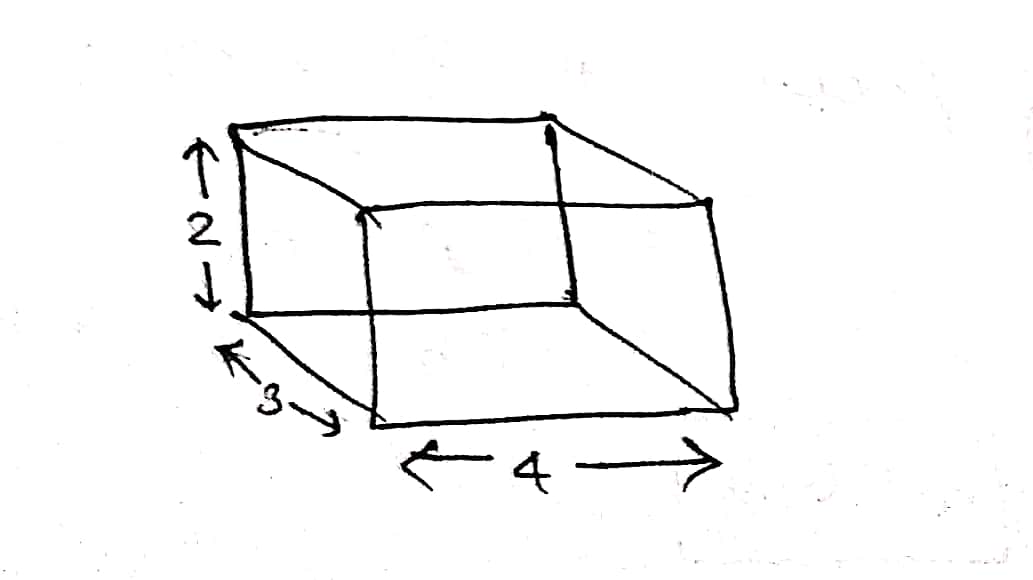
Draw an isometric rough sketch for a cuboid of dimensions $$4\times 3\times 2$$.
Find the coordinates of the point which divides the line segment joining the points $$(-2, 3, 5)$$ and $$(1, -4, 6)$$ in the ratio
(i) $$2 : 3$$ internally (ii) $$2 : 3$$ externally.
Find the point on y-axis whose distance from the points $$A(6,7)$$ and $$B(4,-3)$$ are in the ratio $$1:2$$
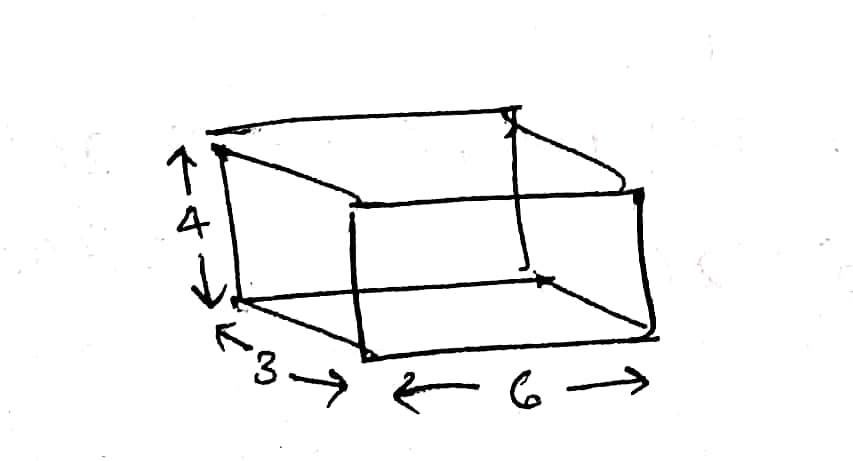
Draw an isometric rough sketch for a cuboid of dimensions $$6\times 3\times 4$$.
Find the distance between the points $$A ( 2,1,5 )$$ and $$B ( 3,4,3 )$$
What is the distance of the point $$(p,q,r)$$ from the $$x-$$ axis.
In which plane does the point $$(4, -3, 0)$$ lie?
Write the abscissa of the following point:
$$(0,5)$$
Calculate the distance between the points $$P(2,2)$$ and $$Q(5,4) $$ correct to three significant figures.
If the origin is the centroid of the triangle PQR with vertices $$P(2a, 2, 6), Q(-4, 3b, -10)$$ and $$R(8, 14, 2c).$$ then find the values of a, b and c.
Find the coordinates of the points which trisect the line segment joining the points $$P(4, 2, -6)$$ and $$Q(10, -16, 6).$$
Find the ratio in which the YZ-plane divides the line segment formed by joining the points $$(-2, 4, 7)$$ and $$(3, -5, 8)$$
Given that $$P(3, 2, -4), Q(5, 4, -6)$$ and $$R(9, 8, -10)$$ are collinear. Find the ratio in which Q divides PR.
Let the distance between the pairs of points whose cartesian coordinates are:
(i) $$(-1,1,3) , (0,5,6)$$ be $$\displaystyle \sqrt{k}$$
(ii) $$(2,3,-1), (2,6,2)$$. be $$\displaystyle 3\sqrt{m}$$
Find $$\cfrac km$$ ?
A rectangular parallelopiped is formed by drawing planes through the point $$(-1,2,5)$$ and $$(1,-1,-1)$$ and parallel to the coordinates planes. The length of the diagonal of the parallelopiped is
The distance between the following vectors $$\displaystyle \sqrt{2}i,-\sqrt{3}k$$ is m. Find $${m}^{2}$$ ?
The ratio in which the surface $${ x }^{ 2 }+{ y }^{ 2 }+{ z }^{ 2 }=25$$ divides the line joining $$(0,1,2)$$ and $$(3,4,5)$$ is $$\displaystyle \frac { a\pm \sqrt { b } }{ c } $$ then $$a+b+c=$$
Verify the following
(i) $$(0, 7, -10 ), (1, 6, -6)$$ and $$(4, 9, -6)$$ are the vertices of an isosceles triangle
(ii) $$(0, 7, 10), (-1, 6, 6)$$ and $$(-4, 9, 6)$$ are the vertices of a right angled triangle
(iii) $$(-1, 2, 1), (1, -2, 5), (4, -7, 8)$$ and $$(2, -3, 4)$$ are the vertices of a parallelogram
Find $$a$$, if the distance between the points $$P(11, -2)$$ and $$Q(a, 1)$$ is $$5$$ units.
Given that $$P (3, 2, -4), Q (5, 4, -6)$$ and $$R (9, 8, -10)$$ are collinear. Find the ratio in which $$Q$$ divides $$PR$$.
Find the coordinates of the point which divides the line segment joining the points $$(-2, 3, 5)$$ and $$(1, -4, 6)$$ in the ratio
(i) $$2:3$$ internally
(ii) $$2:3$$ externally
Find the equation of the set of points $$P$$, the sum of whose distances from $$A (4,0,0)$$ and $$B (-4, 0, 0)$$ is equal to $$10$$.
Find the equation of the set of points which are equidistant from the points $$(1, 2, 3)$$ and $$(3, 2, -1)$$
Find the coordinate of the point $$P$$ where the line through $$A(3, -4, -5)$$ and $$B(2, -3, 1)$$ crosses the plane passing through three points $$L(2, 2, 1), M(3, 0, 1)$$ and $$N(4, -1, 0)$$. Also, find the ratio in which $$P$$ divides the line segment $$AB$$.
Using section formula show that the points $$A\ (2, -3, 4), B\ (-1, 2, 1)$$ and $$\displaystyle C\left ( 0,\dfrac{1}{3},2 \right )$$ are collinear.
Find the ratio in which the $$YZ$$-plane divides the line segment formed by joining the points $$(-2, 4, 7)$$ and $$(3, -5, 8) $$
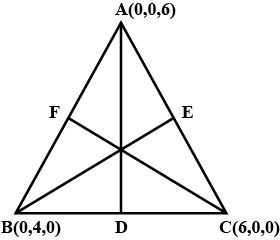
Find the lengths of the medians of the triangle with vertices $$A (0, 0, 6), B (0, 4, 0)$$ and $$(6, 0, 0).$$
A point $$R$$ with $$x$$-coordinate $$4$$ lies on the line segment joining the points $$P (2, -3, 4)$$ and $$Q (8, 0, 10)$$. Find the coordinates of the point $$R$$.
If $$A$$ and $$B$$ be the points $$(3, 4, 5)$$ and $$(-1, 3, -7)$$ respectively. Find the equation of the set of points $$P$$ such that $$PA^2$$ +$$PB^2$$ $$ =K\displaystyle ^{2}$$, where $$K$$ is a constant
Write the equations for the $$x$$-and $$y$$-axes.
Find the distance of the point P$$(3,4,4)$$ from the point, where the line joining the point A$$(3,-4,-5)$$ and B$$(2,-3,1)$$ intersects the plane $$2x+y+z = 7$$.
Using vector method, find the incentre of the triangle whose vertices are $$P(0, 4, 0), Q (0, 0, 3)$$ and $$R(0, 4, 3)$$
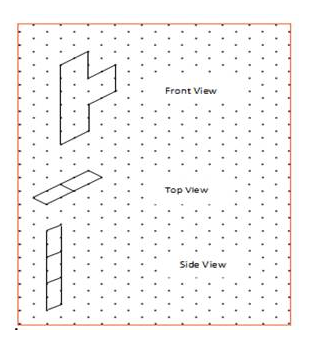
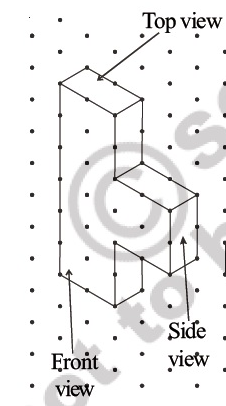
Consider the distance between two consecutive dots to be 1 cm and draw the front view, side view and top view of the following 3-D figures.
Find the area of the triangle whose vertices are $$A(1, 1, 1), B(1, 2, 3)$$ and $$C(2, 3, 3)$$
If the origin is the centroid of the triangle whose vertices are $$A(2, p, -3), B(q, -2, 5)$$ and $$R(-5, 1, r)$$, then find the values of $$p, q, r$$.
Find the equations to the straight lines which are conjugate to the coordinate axes with respect to the conic $$A{ x }^{ 2 }+2Hxy+B{ y }^{ 2 }=1$$.
Find the condition that they may coincide, and interpret the result.
Find the equation of the set of points P, the sum of whose distances from $$A\left( 4,0,0 \right)$$ and $$B\left( -4,0,0 \right)$$ is equal to 10.
Derive the coordinates of the points $$R(x,y,z)$$ dividing the line joining the points $$P\left( { x }_{ 1 },{ y }_{ 1 },{ z }_{ 1 } \right) $$ and $$Q\left( { x }_{ 2 },{ y }_{ 2 },{ z }_{ 2 } \right) $$ internally in the ratio $$m:n$$.
Find the distance of the point $$(2,12,5)$$ from the point of intersection of the line $$\vec { r } =2\hat { i } -4\hat { j } +2\hat { k } +\lambda \left( 3\hat { i } +4\hat { j } +2\hat { k } \right) $$ and the plane $$\vec { r } \left( \hat { i } -2\hat { j } +\hat { k } \right) =0$$
The points A and B have co-ordinate $$(1,2,4)$$ and $$(-1,3,5)$$ respectively. Find $$AB$$ and its magnitude.
Find the ratio in which the YZ-plane divides the line segment formed by joining the points $$(-2,4,7)$$ and $$(3,-5,8)$$.
Use analytical geometry to prove that the mid-point of the hypotenuse of a right-angled triangle is equidistant from its vertices.
$$P$$ is a variable point which moves such that $$3PA=2PB$$. If $$A=(-2, 2, 3)$$ and $$B=(13, -3, 13)$$ prove that $$P$$ satisfies the equation $${x}^{2}+{y}^{2}+{z}^{2}+28x-12y+10z-247=0$$.
If the ratio in which XY-plane divides the line segment joining $$A(2, 4, 5)$$ and $$B(3, 6, -4)$$ is $$m:n$$.Find $$m+n$$
In what ratio does the plane $$2x + y - z = 3$$ divide line segment joining the point $$a = (2, 1, 3), b = (9, -2, 5)$$.
Verify the following:
$$(0,7,-10),(1,6,-6)$$ and $$(4,9,-6)$$ are the vertices of an isosceles triangle.
Show that the points $$A(1, 2, 3)$$, $$B(-1, -2, -3)$$, $$C(2, 3, 2)$$ and $$D(4, 7, 3)$$ are the vertices of a parallelogram.
Find the values of $$a$$ and $$b$$ so that the points $$(a, b, 3), (2, 0, -1)$$ and $$(1, -1, -3)$$ are collinear.
If A(2,1, 3), B(2, -3, 4) , C(-1, 2 , 7) are the three points ; find a point D such that $$|\overrightarrow { AB } |=\frac { 1 }{ 2 } |\overrightarrow { CD } | \, and \, AB||CD.$$
Find the co-ordinates of a point, which is at a distance of $$21$$ units from the point $$A=(1, -3, 4)$$ in the direction of vectors $$2\hat i-3\hat j-6\hat k$$
Find the centroid of a triangle, mid-points of whose sides are $$(1, 2, -3), (3, 0, 1)$$ and $$(-1, 1, -4)$$.
Find the coordinates of the point , which divides the line segment joining the points $$A(2,-6,8)$$ and $$B(-1,3,-4)$$, externally in the ratio $$1:3$$.
Prove the $$A(-5,4), B(-1,-2), C(5,2)$$ are the vertices of n isosceles right angled triangle ?
Find the coordinates of the points which divides the line joining the points $$(2,-4,3),(-4,5,-6)$$ in the ratio $$(i) 1:-4$$
$$(ii) 2:1$$
$$(ii) 2:1$$
Show that $$A(1, 1, 2), B(2, 1, 3)$$ and $$C(1, 3, 5)$$ are not collinear.
Find the value of $$k$$ if the pts $$A\equiv (1,2,-1), B\equiv(4,-2,4)$$ and $$C\equiv (0,0,k)$$ form a triangle right angled at $$C$$.
The points $$P\ (3,2, - 4),Q\ (5,4, - 6)$$ and $$R\ (9,8, - 10)$$ are collinear. If the ratio in which $$Q$$ divides $$PR$$ is $$1:a$$, then $$a$$ is equal to____ .
Show that the points $$(2, -1, 3), (4, 3, 1)$$ and $$(3, 1, 2)$$ are collinear.
Find the volume of a tetrahedron whose vertices are $$A(-1,2,3), B(3,-2,1), C(2,1,3)$$ and $$D(-1,-2,4)$$
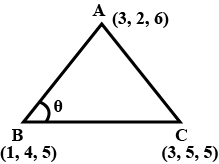
If $$A(3,2,6),\ B(1,4,5)$$ and $$C(3,5,5)$$ are the vertices of $$\Delta ABC$$, then find $$m\angle ABC$$
Find the point on Z-axis which are at a distance $$\sqrt{21}$$ unit from the point$$(1,2,3)$$
Find the coordinates of a point equidistant from four points $$O(0,0,0),A(\ell,0,0),B(0,m,0)$$ and $$C(0,0,n)$$.
Find the distance of the point $$(-1,-5,-10)$$ from the point of intersection of the line
$$\overline { r } =2\overline { i } -\overline { j } +2\overline { k } +\overline { \lambda } \left( 3\overline { i } +4\overline { j } +2\overline { k } \right) $$ and the plane $$\overline { r } .\left( \overline { i } -\overline { j } +\overline { k } \right) =5$$
Find the coordinates of those points on the line $$\dfrac{x+1}{2}=\dfrac{y+2}{3}=\dfrac{z-3}{6}$$ which is at a distance of $$3$$ units from the point $$(1,-2,3)$$
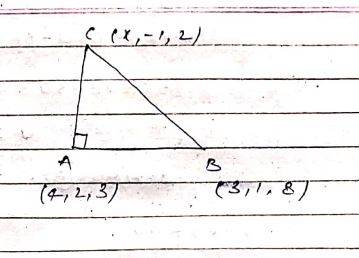
Find $$x$$, if $$\triangle ABC$$ is right-angled at $$A$$, where $$A\equiv (4, 2, 3), B \equiv (3, 1, 8), C \equiv (x, -1, 2)$$.
Find the ratio in which the XY - plane divides AB if is (1,2,3) and B is (-3,4,-5). Also find the positive vector of the point of division.
Find the magnitude of the shortage distance between the lines ,$$\frac{{x - 8}}{3} = \frac{{y + 9}}{{ - 16}} = \frac{{z - 10}}{7};\frac{{x - 15}}{3} = \frac{{y - 29}}{8} = \frac{{z - 5}}{{ - 5}}$$
Find the points on the line $$\dfrac {x + 2}{3} = \dfrac {y + 1}{2} = \dfrac {z - 3}{2}$$ at a distance of $$5$$ units from the points $$(1, 3, 3)$$.
The points $$A(6, -7,0) , B(16, -19, -4), C(0,3,-6)$$ and $$D(2,-5,10)$$ are such that AB and CD intersect at the point $$P(1,-1,2).$$ If true enter 1 or else 0.
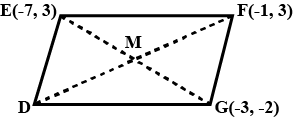
The diagram shows a parallelogram DEFG.
the point M is the midpoint of the diagonals DF and EG.
calculate .
a) the coordinate of M
b) the coordinate of the vertex D.
Find the ratio in which $$C(0,1,3)$$ divides $$A(1,2,3),\ E(-1,4,2)$$
Find the distance of point $$(-2,\ 3,\ -4)$$ from the line $$\dfrac {x+2}{3}=\dfrac {2y+3}{4}=\dfrac {3z+4}{5}$$ measured parallel to the plane $$4x+12y-3z+1=0$$.
Show that the points $$A(3,2,-4), B(5,4,-6)$$ and $$C(9,8,-10)$$ are collinear, find the ratio in which $$B$$ divides $$\overline { AC } $$.
If $$A(1,2,-1), B(4,0,-3), C(1,2,-1), D(2,-4,-5)$$, find the distance between $$AB$$ and $$CD$$.
If $$A(1,-2,-1), B(4,0,-3), C(1,2,-1), D(2,-4,-5)$$, find the distance between $$AB$$ and $$CD$$.
Find the co-ordinates of the points of trisection of the line joining the points $$(-3,0)$$ and $$(6,6).$$
what is the distance of the point (p,q,r) from the x-axis ?
A plane makes intercept $$1,2,3$$ on the co-ordinate axes. If the distance from origin is $$p$$ then find the value of $$p$$.
Find the coordinates of the point $$P$$, which divides the join of $$A(-2,5)$$ and $$B(3,-5)$$ in the ratio $$2:3$$.
Find the ratio in which the line segment joining the points $$(4,8,10)$$ and $$(6,10,-8)$$ is divided by the $$YZ-$$ plane.
A parallelepiped is formed by planes drawn through the points $$P\left(6,8,10\right)$$ and $$Q\left(3,4,8\right)$$ parallel to the coordinate planes. Find the length of edges and diagonals of the parallelepiped.
Find the distance between the following pairs of points
$$(-5, 7)$$ and $$(-1, 3)$$
Find the distance between the following pairs of points
$$(-2, -3)$$ and $$(3, 2)$$
A parallelepiped is formed by planes drawn through the point $$P\left(6,8,10\right)$$ and $$Q\left(3,4,8\right)$$ parallel to the coordinate planes. Find the length of edges and edges and diagonals of the parallelepiped.
The centroid of Tetraheadron $$(3,4,5),(2,5,9),(5,2,8),(2,5,2)$$ is
By using the section formula, show that the points $$(1, 2), (2, 5)$$ and $$(5, 8)$$ are collinear .
Find the distance of the point $$(-1,5,-5)$$ from the origin.
Derive the equation of the locus of a point equivalent from the points (1,-2,3) and (-3,4,2)
If the points $$A\left(2,1,-5\right),\,B\left(-2,p,q\right)$$ and $$C\left(-4,8,5\right)$$ are collinear,find the values of $$p$$ and $$q$$
Find distance of a point $$(3,4)$$ from the origin.
If $$P ( - 3 , - 1,6 )$$ be any point in space, then find the
(a ) distance of $$P$$ from $$Y$$-axis.
(b ) distance of $$P$$ from $$X Z$$-plane.
(c ) Image of $$P$$ with respect to $$X Y$$-plane.
(d ) Octant in which $$P$$ lies.
In what ratio is the line segment joining the points $$\left(-2,4,7\right)$$ and $$\left(3,-5,8\right)$$ is divided by the $$YZ$$ plane ?Also, find the co-ordinates of the point of division.
Name the octants in which the following points lie: $$(-5,4,3)$$
Name the octants in which the following points lie: $$(5,2,3)$$
Fill in the blanks:
The perpendicular distance of a point $$(5, 12, 13)$$ from Y-axis is _______
In which ratio does the $$YZ$$ plane divide the line joining the points $$(-2, 4, 7)$$ and $$(3, -5, 8)$$
Derive the equation of the locus of a point twice as far from (-2,3,4) as from (3,-1,-2).
Prove that the points having position vectors $$ \hat{i}+2\hat{j}+3\hat{k},\,4\hat{j}+7\hat{k}, -3\hat{i}-2\hat{j}-5\hat{k}$$ are non-collinear.
Name the octants in which the following points lie:
$$(2,-5,-7)$$
Name the octants in which the following points lie:
$$(-5,-4,7)$$
Name the octants in which the following points lie: $$(4,-3,5)$$
Name the octants in which the following points lie: $$(7,4,-3)$$
$$d=$$ distance between the points $$P$$ and $$Q$$ having coordinates $$P(-2,3,1)$$ and $$Q(2,1,2)$$.
Find value of $$d^2.$$
Verify the following:
$$(-1,2,1),(1,-2,5),(4,-7,8)$$ and $$(2,-3,4)$$ are vertices of a parallelogram.
Name the octants in which the following points lie:
$$(-5,-3,-2)$$
Name the octants in which the following points lie:
$$(-7,2,-5)$$
Find the distance between the points :
$$A(5, 1, 2)$$ and $$B(4, 6, -1)$$.
Find the coordinates of the foot of the perpendicular drawn from the origin to the plane $$2x+3y+4z-12=0$$.
From the point $$P(1, 2, 4)$$ a perpendicular is drawn on the plane $$2x+y-2z+3=0$$. Find the equation, the length and the coordinates of the foot of the perpendicular.
Find the co-ordinate of the foot of $$\perp^{r}$$ and the perpendicular distance of the point $$P(3, 2, 1)$$ from the plane $$2x - y + z + 1 = 0$$. Find also the image of the point in the plane.
Find the coordinates of the foot of the perpendicular drawn from the point $$A(1,8,4)$$ to the line joining the points $$B(0,-1,3)$$ and $$C(2,-3,-1)$$
Find the distance between the points :
$$R(1, -3, 4)$$ and $$S(4, -2, -3)$$.
Find the coordinates of the foot of the perpendicular drawn from the point $$A(1,2,1)$$ to the line joining the points $$B(1,4,6)$$ and $$C(5,4,4)$$
Find the distance between the points :
$$P(1, -1, 3)$$ and $$Q(2, 3, -5)$$.
Find the point on the $$z-axis$$ which is equidistant from the points $$A(1, 5, 7)$$ and $$B(5, 1, -4)$$.
Find the point on the $$y-axis$$ which is equidistant from the points $$A(3, 1, 2)$$ and $$B(5, 5, 2)$$.
Find the coordinates of the point which divides the join $$A(3, 2, 5)$$ and $$B(-4, 2, -2)$$ in the ratio $$4 : 3$$.
Find the point in $$yz-plane$$ which is equidistant from the points $$A(3, 2, -1), B(1, -1, 0)$$ and $$C(2, 1, 2)$$.
Show that the points $$A(1, 2, 3), B(-1, -2, -1), C(2, 3, 2)$$ and $$D(4, 7, 6)$$ are the vertices of a parallelogram. Show that $$ABCD$$ is not a rectangle.
Find the coordinates of the point that divides the join of $$A(-2, 4, 7)$$ and $$B(3, -5, 8)$$ extremally in the ratio $$2 : 1$$.
Find the distance between the points :
$$C(9, -12, -8)$$ and the origin.
Show that the points $$A(0, 1, 2), B(2, -1, 3)$$ and $$C(1, -3, 1)$$ are the vertices of an isosceles right-angled triangle.
Let $$A(2, 1, -3)$$ and $$B(5, -8, 3)$$ be two given points. Find the coordinates of the points of trisection of the line segment $$AB$$.
Show that the points $$A(1, -1, -5), B(3, 1, 3)$$ and $$C(9, 1, -3)$$ are the vertices of an equilateral triangle.
Two vertices of a triangle $$ABC$$ are $$A(2, -4, 3)$$ and $$B(3, -1, -2)$$, and its centroid is $$(1, 0, 3)$$. Find its third vertex $$C$$.
The midpoint of the sides of a triangle are $$(1, 5, -1), (0, 4, -2)$$ and $$(2, 3, 4)$$. Find its vertices.
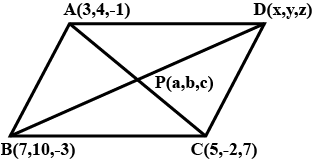
If the three consecutive vertices of a parallelogram be $$A(3, 4, -1), B(7, 10, -3)$$ and $$C(5, -2, 7)$$, find the fourth vertex $$D$$.
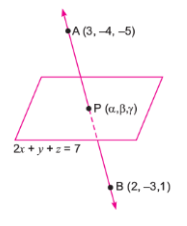
Find the coordinates of the point where the line through the points $$(3, -4, -5)$$ and $$(2, -3, 1)$$ crosses the plane $$2x + y + z = 7.$$
The points $$A(4, 5, 10), B(2, 3, 4)$$ and $$C(1, 2, -1)$$ are three vertices of a parallelogram ABCD. Find the vector equations of the sides AB and BC and also find the coordinates of point D.
The equation of motion of a point in space is $$x = 2t, y = -4t, z = 4t$$ where $$t$$ measured in hour and the co-ordinates of moving point in kilometers. Find the distance of the point from the starting point $$O (0, 0, 0)$$ in $$10$$ hours.
The vertices of a triangle $$ABC$$ are $$A(3, 2, 0), B(5, 3, 2)$$ and $$C(-9, 6, -3)$$. The bisector $$AD$$ of $$\angle A$$ meets $$BC$$ at $$D$$. Find the coordinates of $$D$$.
The points $$A(x_1 , y_1) , B(x_2 , y_2) $$ and $$C(x_3 , y_3) $$ are the vertices of $$ \Delta $$ ABC.
What are the coordinates of the centroid of the $$ \Delta $$ ABC ?
Find the area of the triangle with vertices $$(1,1,0),(1,0,1)$$ and $$(0,1,1)$$.
If the centroid of a tetrahedron $$OABC$$ is $$(1,2,-1)$$ where $$A(a, 2,3), B(1,b,2), C(2,1,c)$$, find the distance of $$P(a, b, c)$$ from origin.
Find the lengths of the sides of the triangle and also determine the type
of a triangle:$$L(3,\ -2,\ -3),\ M(7,\ 0,\ 1),\ N\ (1,\ 2,\ 1)$$
Find the lengths of the sides of the triangle and also determine the type
of a triangle:$$A(2,\ -1,\ 0),\ B(4,\ 1,\ 1),\ C(4,\ -5,\ 4)$$
If the points $$A(3,0,p), B(-1,q, 3)$$ and $$C(-3,3,0)$$ are collinear, then find
the ratio in which the point $$C$$ divides the line segment $$AB$$
Find the coordinate of the point P where the line through $$A(3, -4, -5)$$ and $$B(2, -3, 1)$$ crosses the plane passing through three points $$L(2, 2, 1), M(3, 0, 1)$$ and $$N(4, -1, 0).$$ Also, find the ratio in which $$P$$ divides the line segment AB.
Find the centroid of tetrahedron with vertices $$K(5,-7, 0), L(1,5,3), M(4,-6,3), N(6,-4,2)$$
In each of the following cases, determine the direction cosines of the normal to the plane and the distance from the origin,
$$z = 2$$.
Find the coordinates of the point where the line through $$(5, 1, 6)$$ and $$(3, 4, 1)$$ crosses the $$ZX-plane$$.
Show that the line through the points $$(1, 1, -2), (3, 4, -2)$$ is perpendicular to the line through the points $$(0, 3, 2)$$ and $$(3, 5, 6)$$.
Find the distance of the point $$(-1, -5, -10)$$ from the point of intersection of the line $$\vec {r} = 2\hat {i} - \hat {j} + 2\hat {k} + \lambda (3\hat {i} + 4\hat {j} + 2\hat {k})$$ and plane $$\vec {r} \cdot (\hat {i} - \hat {j} + \hat {k}) = 5$$.
In the following cases, find the distance of each of the given points from the corresponding given plane.
$$(2, 3, -5), x + 2y - 2z = 9$$.
Show that the line joining the origin to the point $$(2, 1, 1)$$ is perpendicular to the line determined by the points $$(3, 5, -1), (4, 3, -1)$$.
In each of the following cases, determine the direction cosines of the normal to the plane and the distance from the origin,
$$x + y + z = 1$$.
Find the coordinates of the point where the line through $$(5, 1, 6)$$ and $$(3, 4, 1)$$, crosses the $$YZ - plane$$.
Find the coordinates of the point where the line through $$(3, -4, -5)$$ and $$(2, -3, 1)$$ crosses the plane $$2x + y + z = 7$$.
If $$A\ (3,\ 2,\ 1),\ B\ (-2,\ 2,\ -3),\ C\ (3,\ 5,\ -2),\ D\ (-2,\ 5,\ -4)$$
then verify that the points are the vertices of a parallelogram.
Find the distance of the point $$P(6, 5, 9)$$ from the plane determined by the points $$A(3, -1, 2), B(5, 2, 4)$$ and $$C(-1, -1, -6)$$.
Find the distance between the point $$(-1, -5, -10)$$ and the point of intersection of the line $$ \dfrac{x - 2}{3} = \dfrac{y + 1}{4} = \dfrac{z - 2}{12} $$ and the plane $$x - y + z = 5 $$.
Coordinates of three vertices of parallelogram $$ABCD$$ are $$A(4,5,10), B(2,3,4)$$ and $$C(1,2,-1)$$. Find vector and cartesian equation of $$AB$$ and $$AC$$. Also Find coordinates of $$D$$.
Find the points on the line $$\dfrac {x + 2}{3} = \dfrac {y + 1}{2} = \dfrac {z - 3}{2}$$ at a distance of $$5$$ units from the point $$(1, 3, 5)$$.
The plane $$P;ax+by+cz+d=0$$ divides the line joining $$\left( { x }_{ 1 },{ y }_{ 1 },{ z }_{ 1 } \right) $$ and $$\left( { x }_{ 2 },{ y }_{ 2 },{ z }_{ 2 } \right) $$ in the ratio of $$\displaystyle \left( -\frac { { ax }_{ 1 }+{ by }_{ 1 }+{ cz }_{ 1 }+d }{ { ax }_{ 2 }+{ by }_{ 2 }+{ cz }_{ 2 }+d } \right) =-\frac { { p }_{ 1 } }{ { p }_{ 2 } } $$; where $${ P }_{ 1 }={ ax }_{ 1 }+{ by }_{ 1 }+{ cz }_{ 1 }+d$$ and $${ P }_{ 2 }={ ax }_{ 2 }+{ by }_{ 2 }+{ cz }_{ 2 }+d$$. If true enter 1 else 0
Find the ratio in which YZ-plane divides the line joining $$A(2,4,5)$$ and $$B(3,5,-4)$$. Also find the point of intersection.
Show that the point whose distance from $$y-axis$$ is thrice its distance from $$(1,2,-1)$$ satisfies the equation $$8x^2+9y^2+8z^2-18x-36y+18z+54=0$$
Find the point on the line $$\dfrac{x+2}{3} = \dfrac{y+1}{2} = \dfrac{z-3}{2}$$ at a distance $$3\sqrt{2}$$ from the point $$(1, 2, 3)$$
A point $$R$$ with $$x-$$coordinate $$4$$ lies on the line segment joining the points $$P\left(2,-3,4\right)$$ and $$Q\left(8,0,10\right)$$.Find the coordinates of the point $$R$$
Find the coordinates of the point where the line through the points A(3,4,1) and B(5,1,6) crosses the XZ plane.Also find the angle which this line makes with the XZ plane.
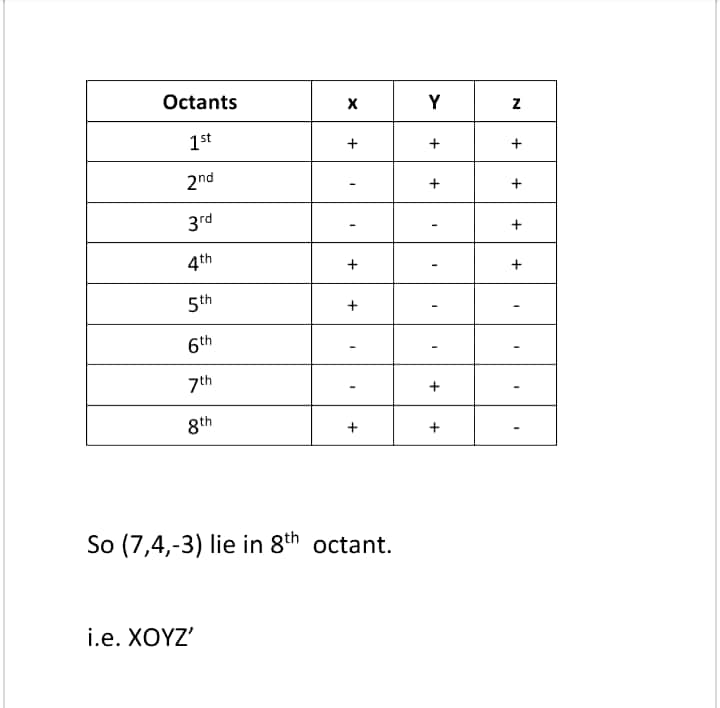
In which octant does the given point lie?
$$(4, 6, 8)$$.
Show that the points $$P(2, 3, 5), Q(-4, 7, -7), R(-2, 1, -10)$$ and $$S(4, -3, 2)$$ are the vertices of a rectangle.
In which octant does the given point lie?
$$(-6, 5, -1)$$.
Show that the points $$A(4, 6, -5), B(0, 2, 3)$$ and $$C(-4, -4, -1)$$ form the vertices of an isosceles triangle.
In which octant does the given point lie?
$$(-1, -6, 5)$$.
Show that the points $$P(1, 3, 4), Q(-1, 6, 10), R(-7, 4, 7)$$ and $$S(-5, 1, 1)$$ are the vertices of a rhombus.
In which octant does each of the given points lie?
$$(-4, -1, -6)$$.
In which octant does the given point lie?
$$(2, 3, -4)$$.
In which octant does the given point lie?
$$(4, -3, -2)$$.
Show that the points $$A(1, 1, 1), B(-2, 4, 1), C(1, -5, 5)$$ and $$D(2, 2, 5)$$ are the vertices of a square.
Find the point in $$xy-plane$$ which is equidistant from the points $$A(2, 0, 3), B(0, 3, 2)$$ and $$C(0, 0, 1)$$.
Show that $$D(-1, 4, -3)$$ is the circumcentre of triangle $$ABC$$ with vertices $$A(3, 2, -5), B(-3, 8, -5)$$ and $$C(-3, 2, 1)$$.
Class 11 Engineering Maths Extra Questions
- Binomial Theorem Extra Questions
- Complex Numbers And Quadratic Equations Extra Questions
- Conic Sections Extra Questions
- Introduction To Three Dimensional Geometry Extra Questions
- Limits And Derivatives Extra Questions
- Linear Inequalities Extra Questions
- Mathematical Reasoning Extra Questions
- Permutations And Combinations Extra Questions
- Principle Of Mathematical Induction Extra Questions
- Probability Extra Questions
- Relations And Functions Extra Questions
- Sequences And Series Extra Questions
- Sets Extra Questions
- Statistics Extra Questions
- Straight Lines Extra Questions
- Trigonometric Functions Extra Questions