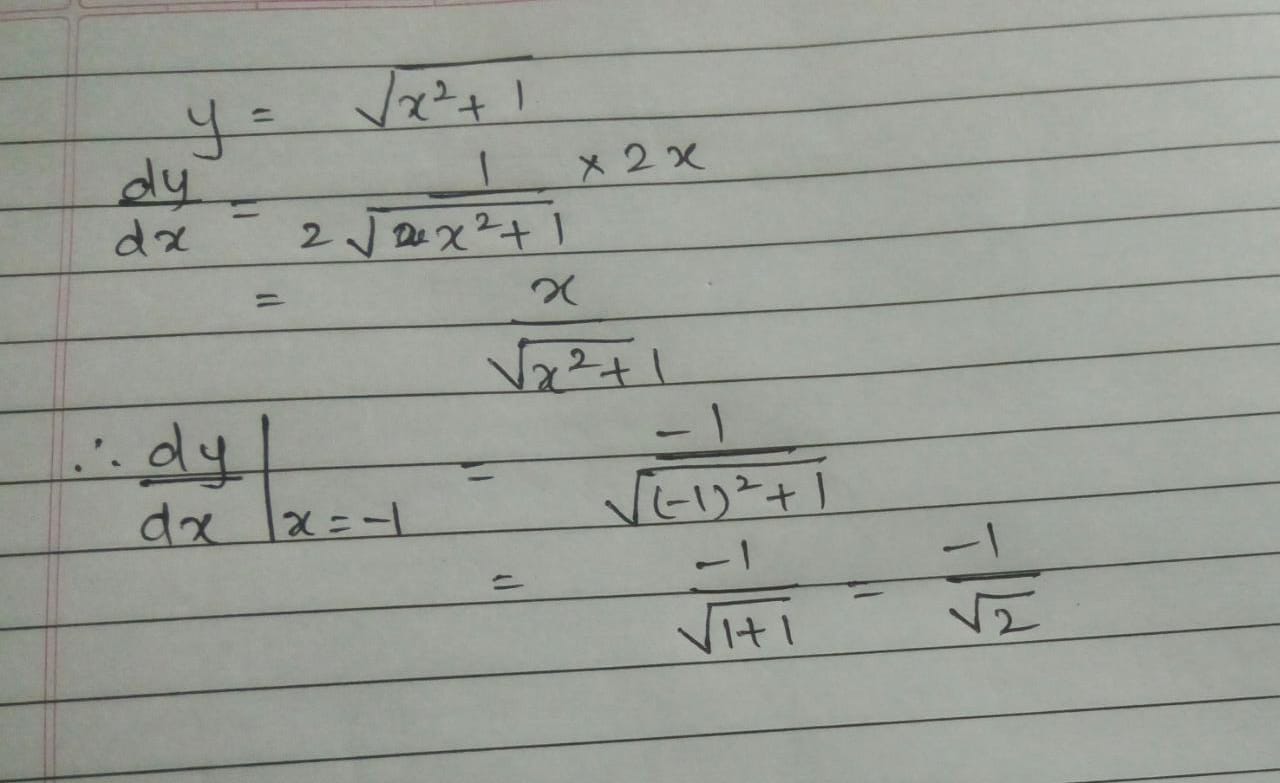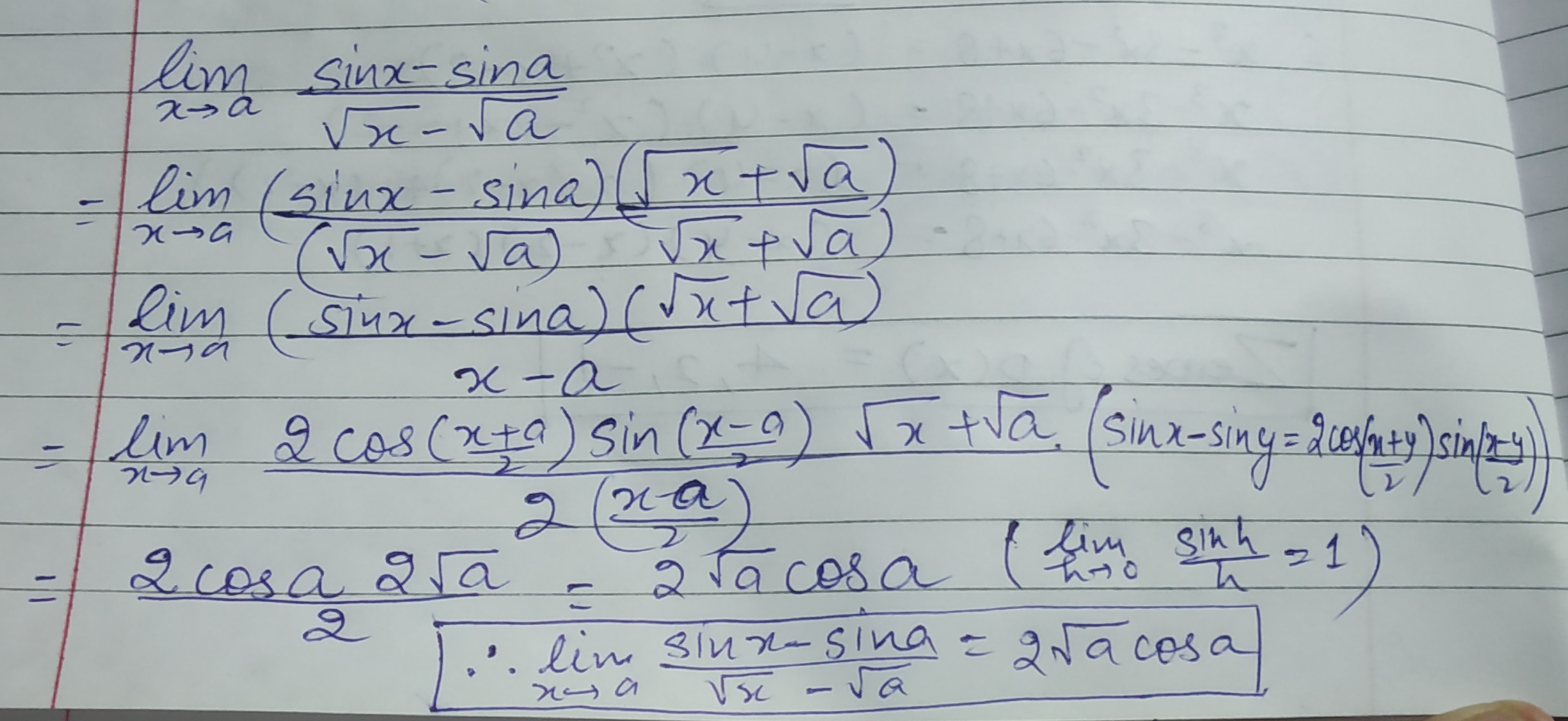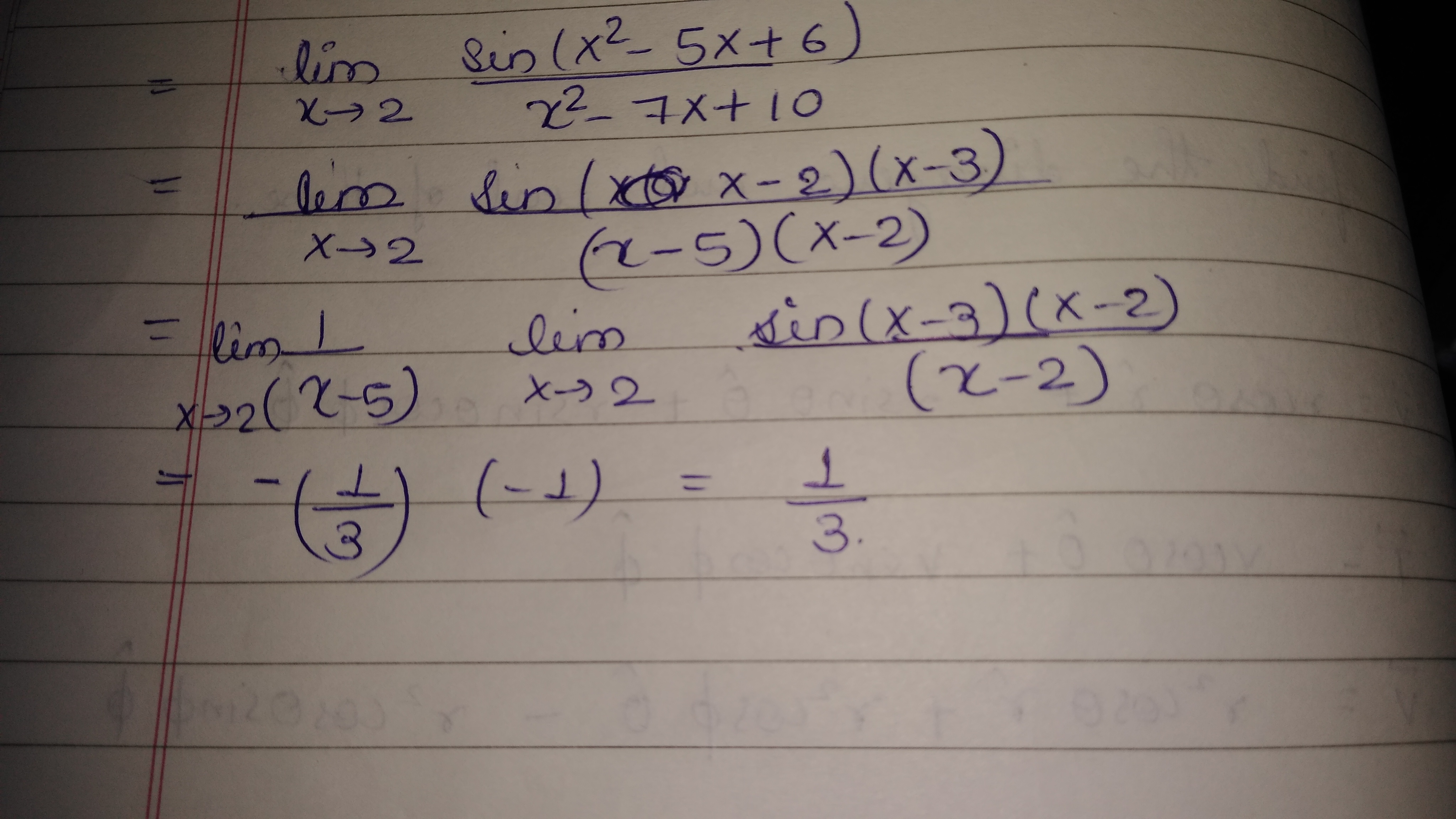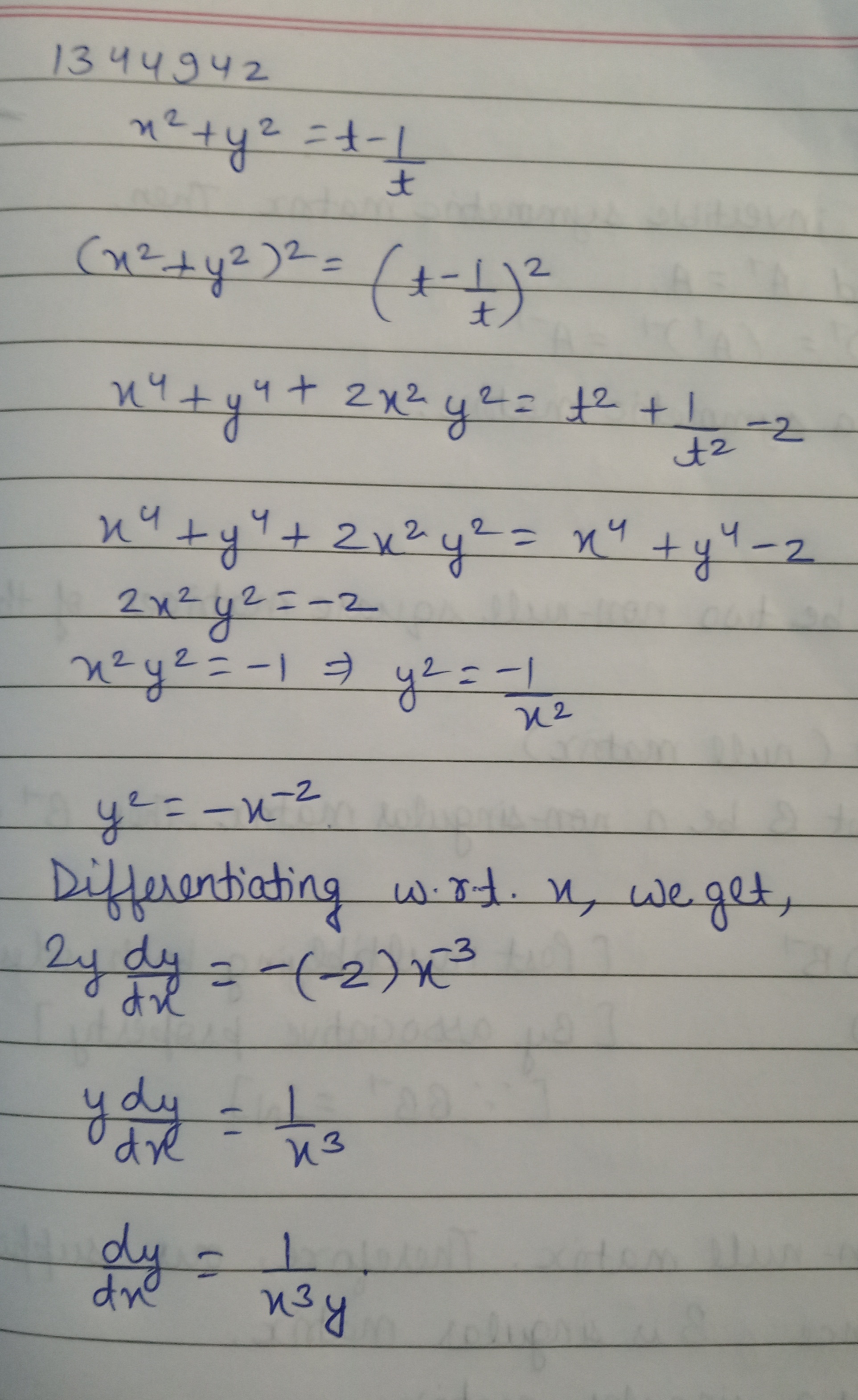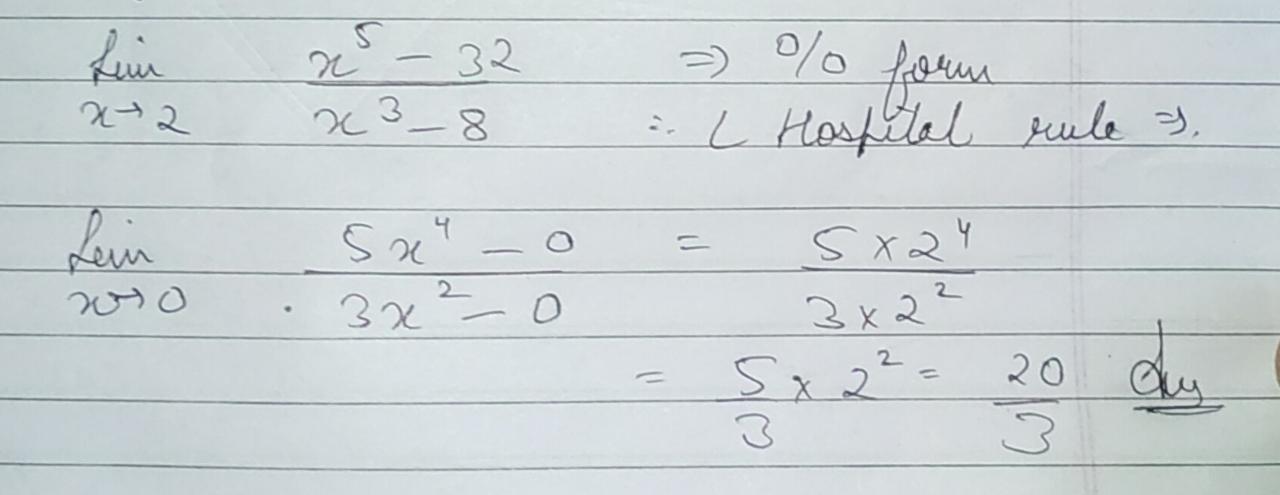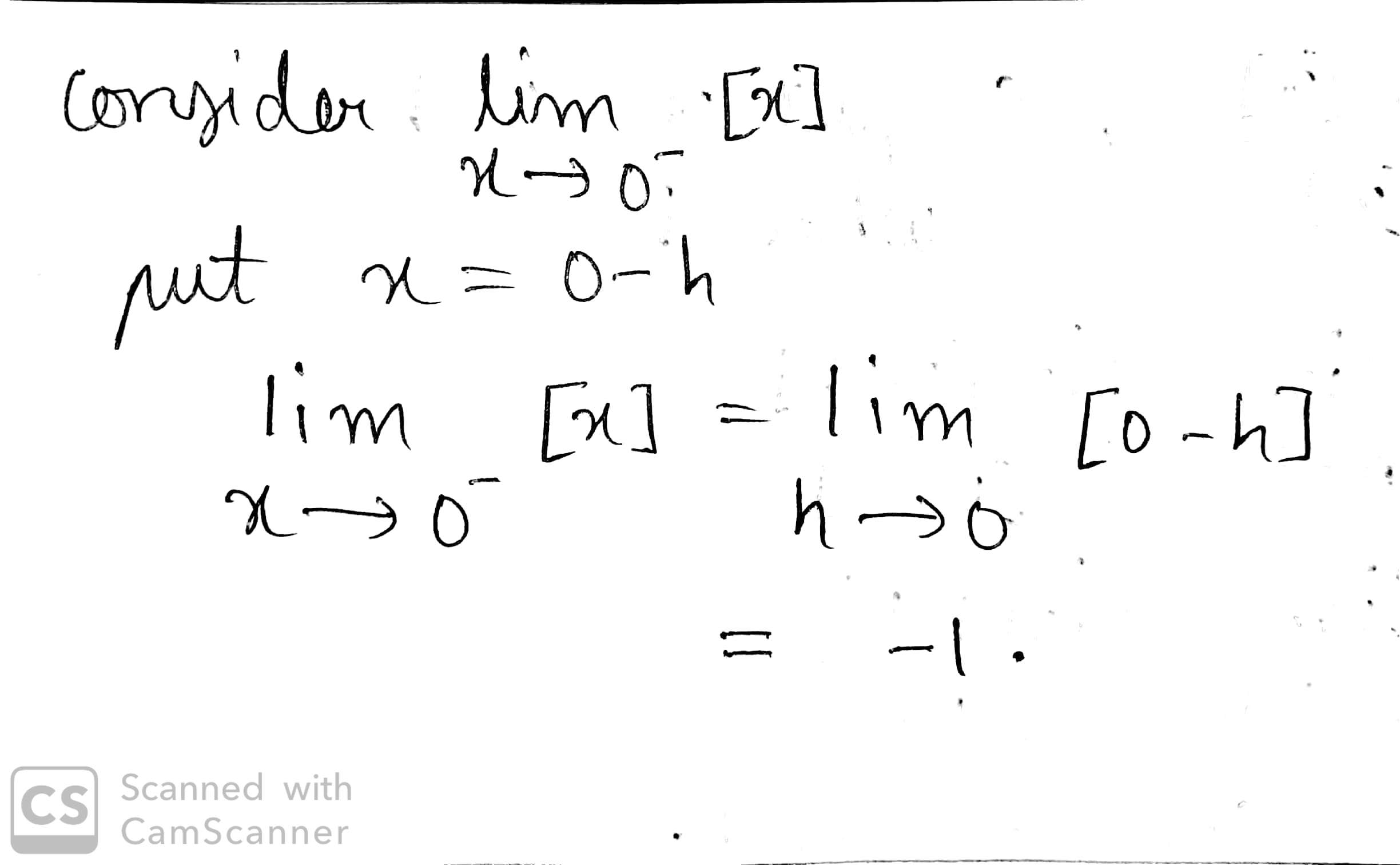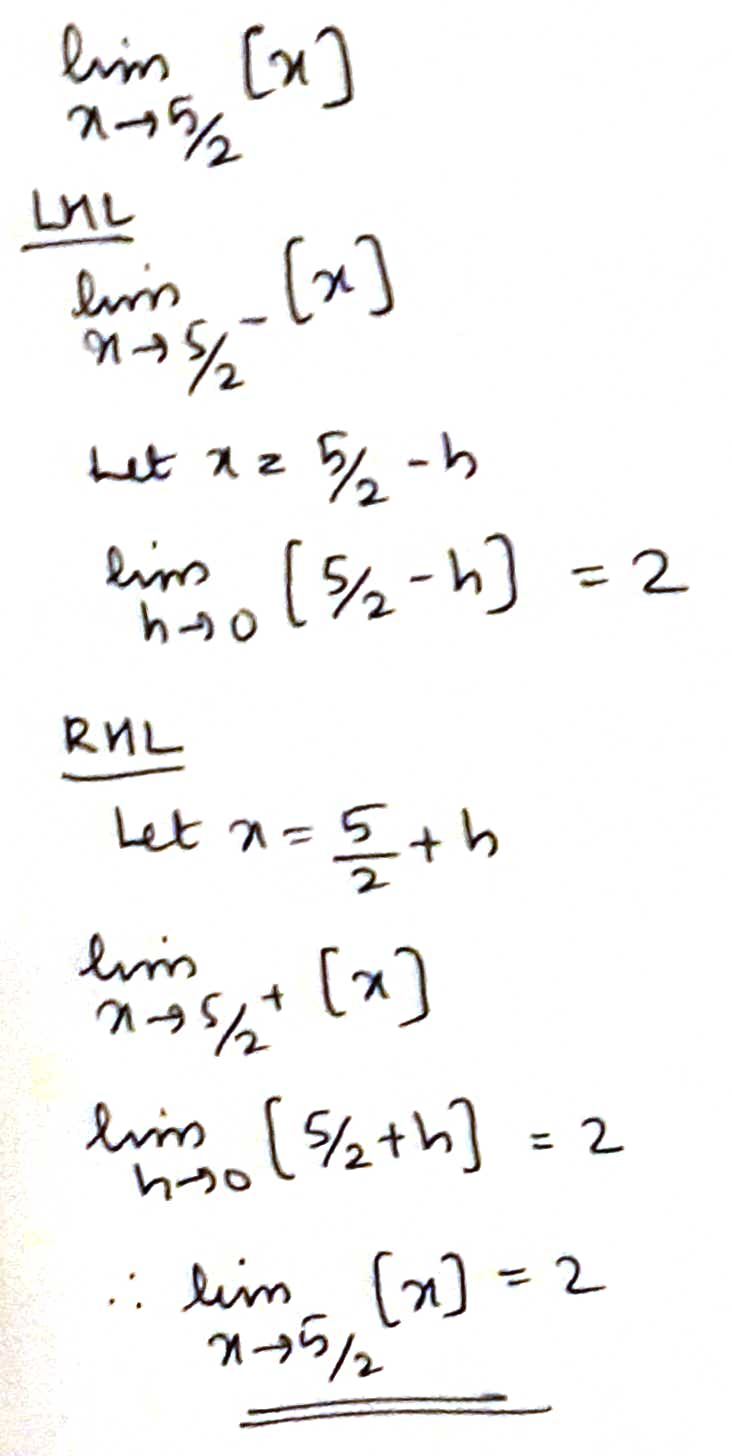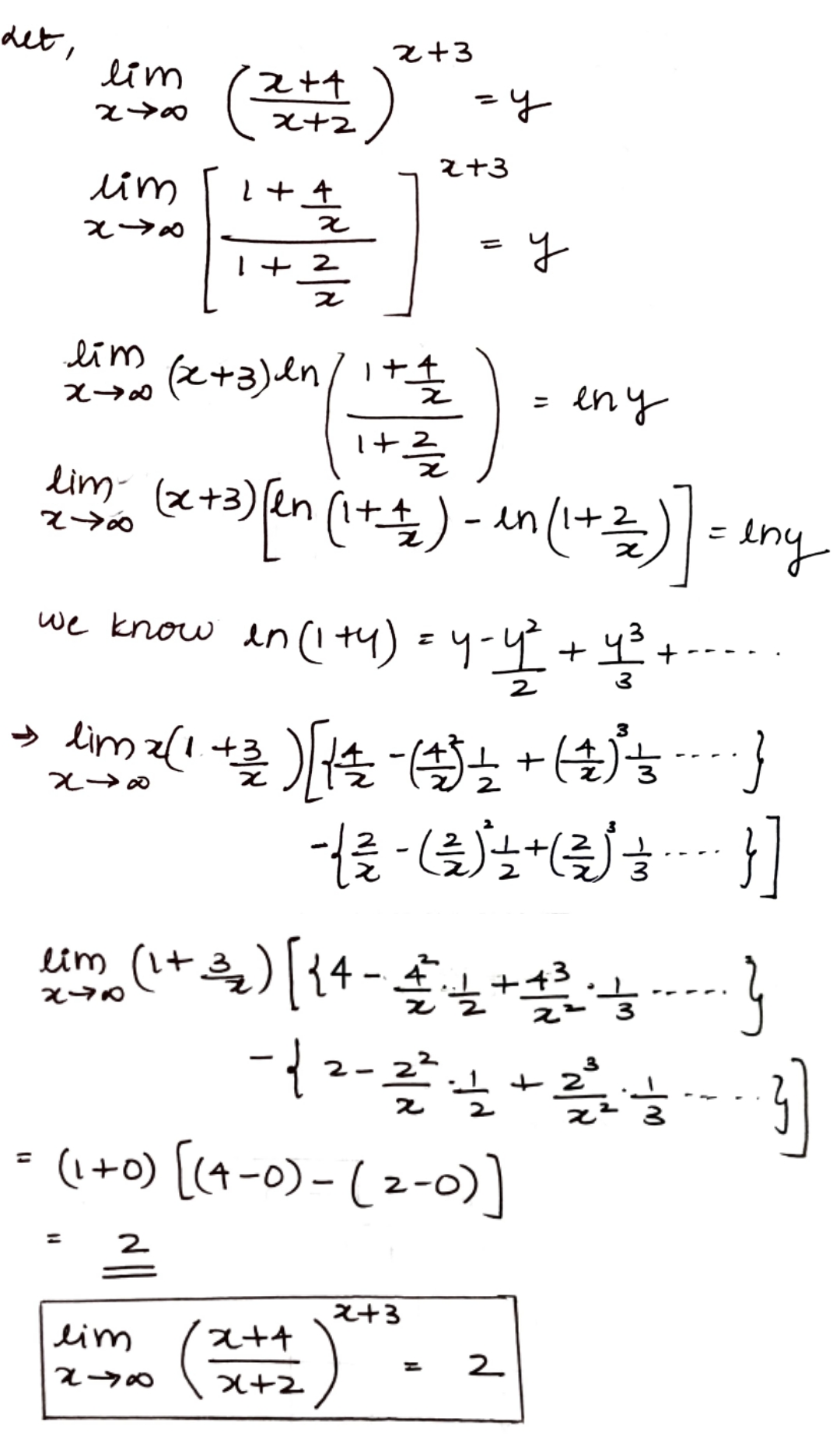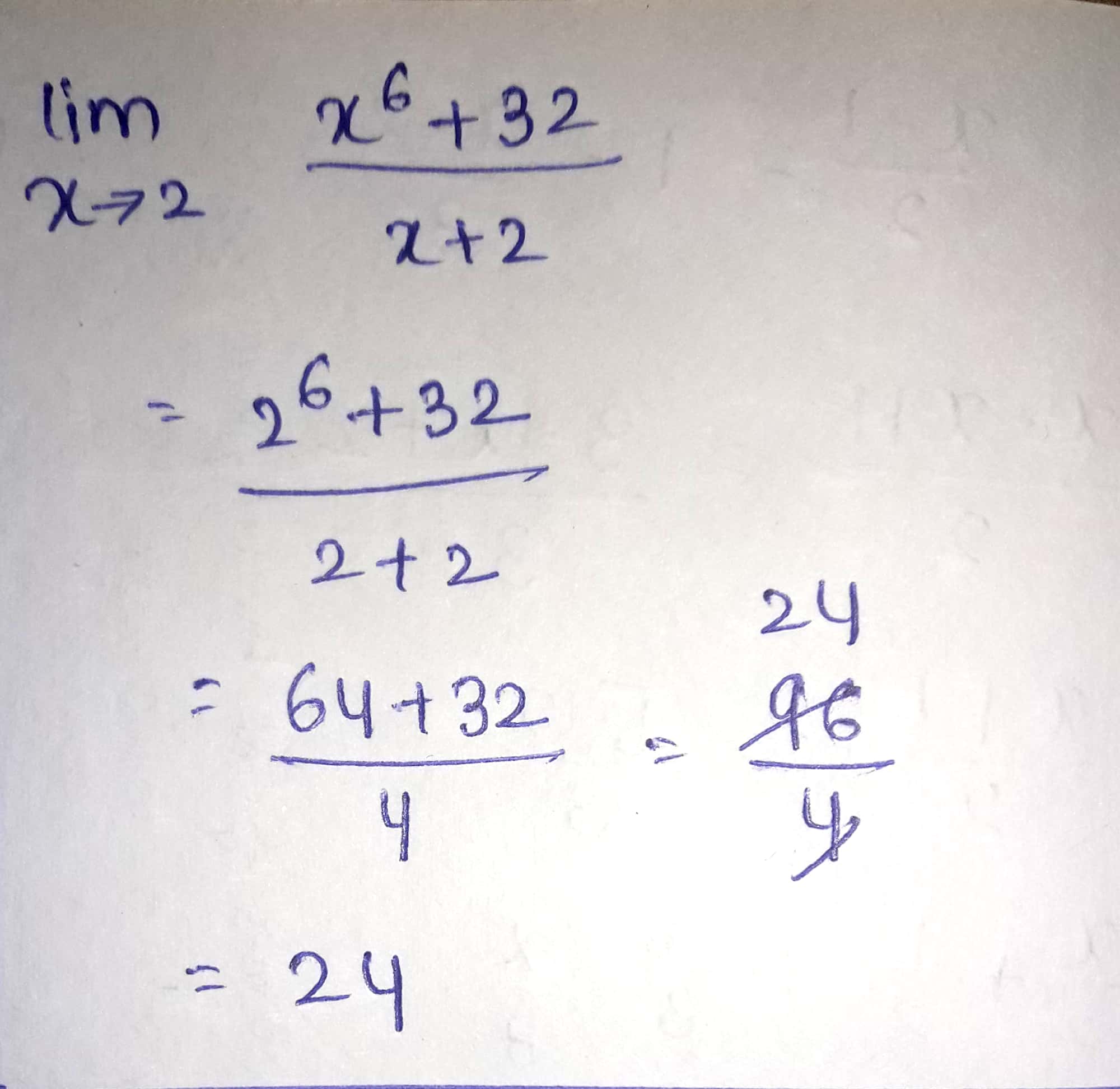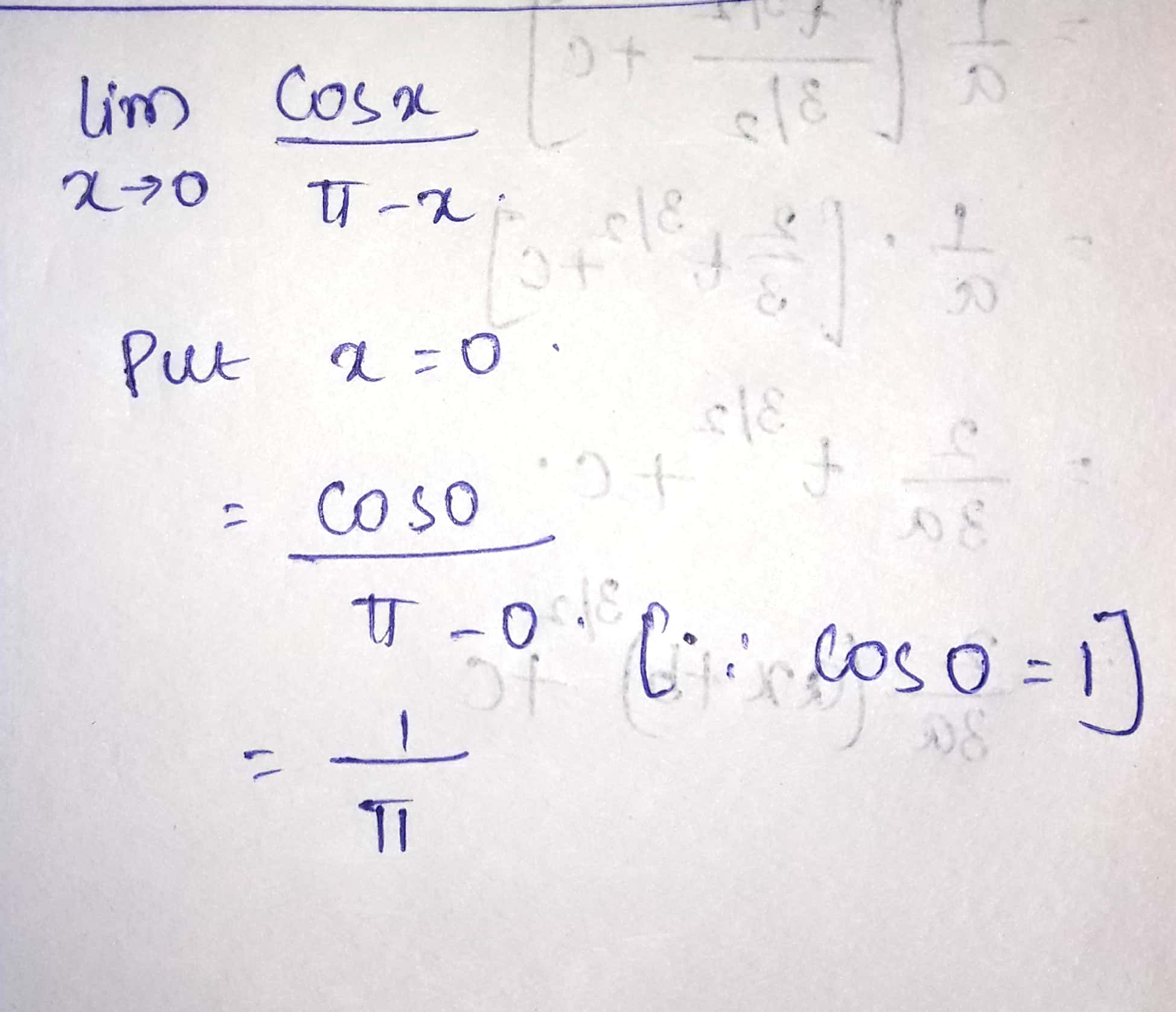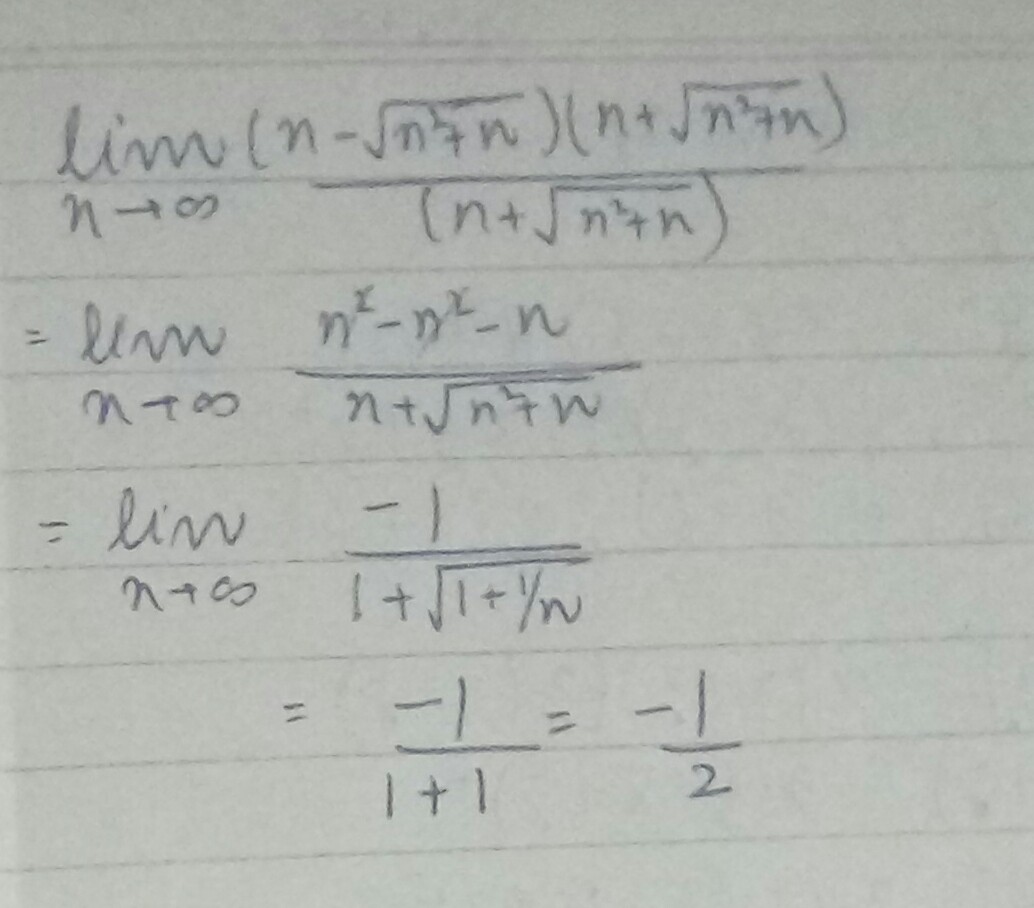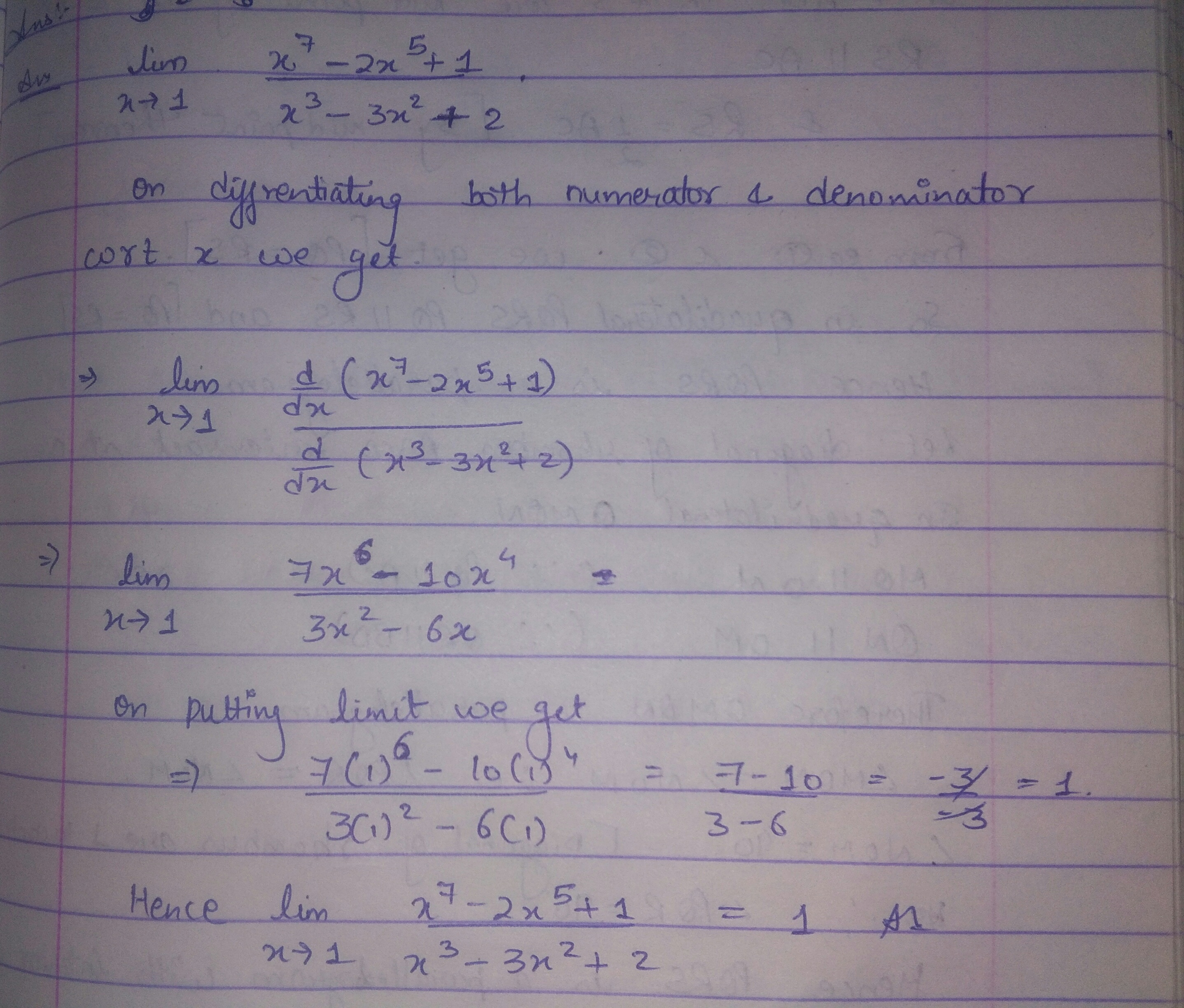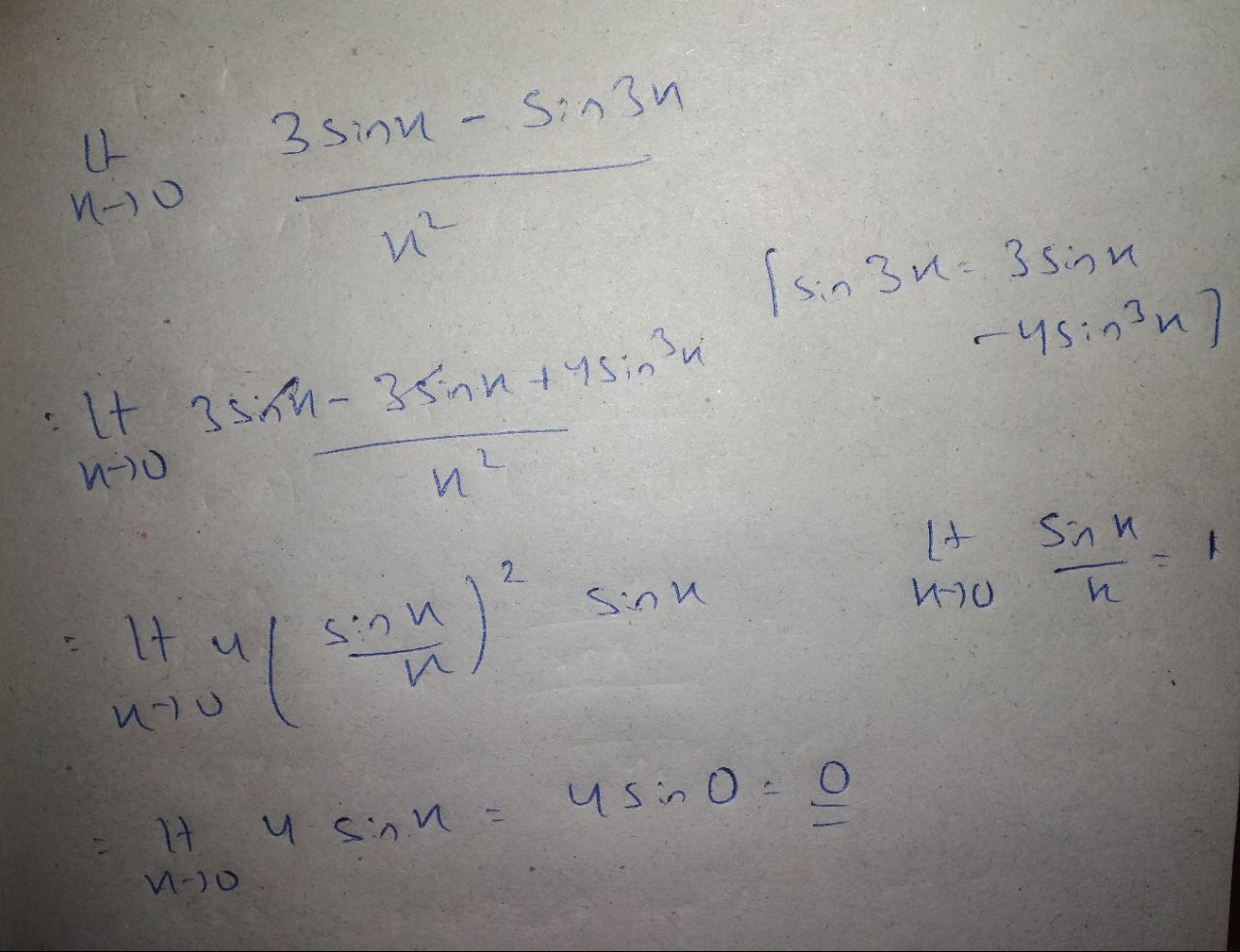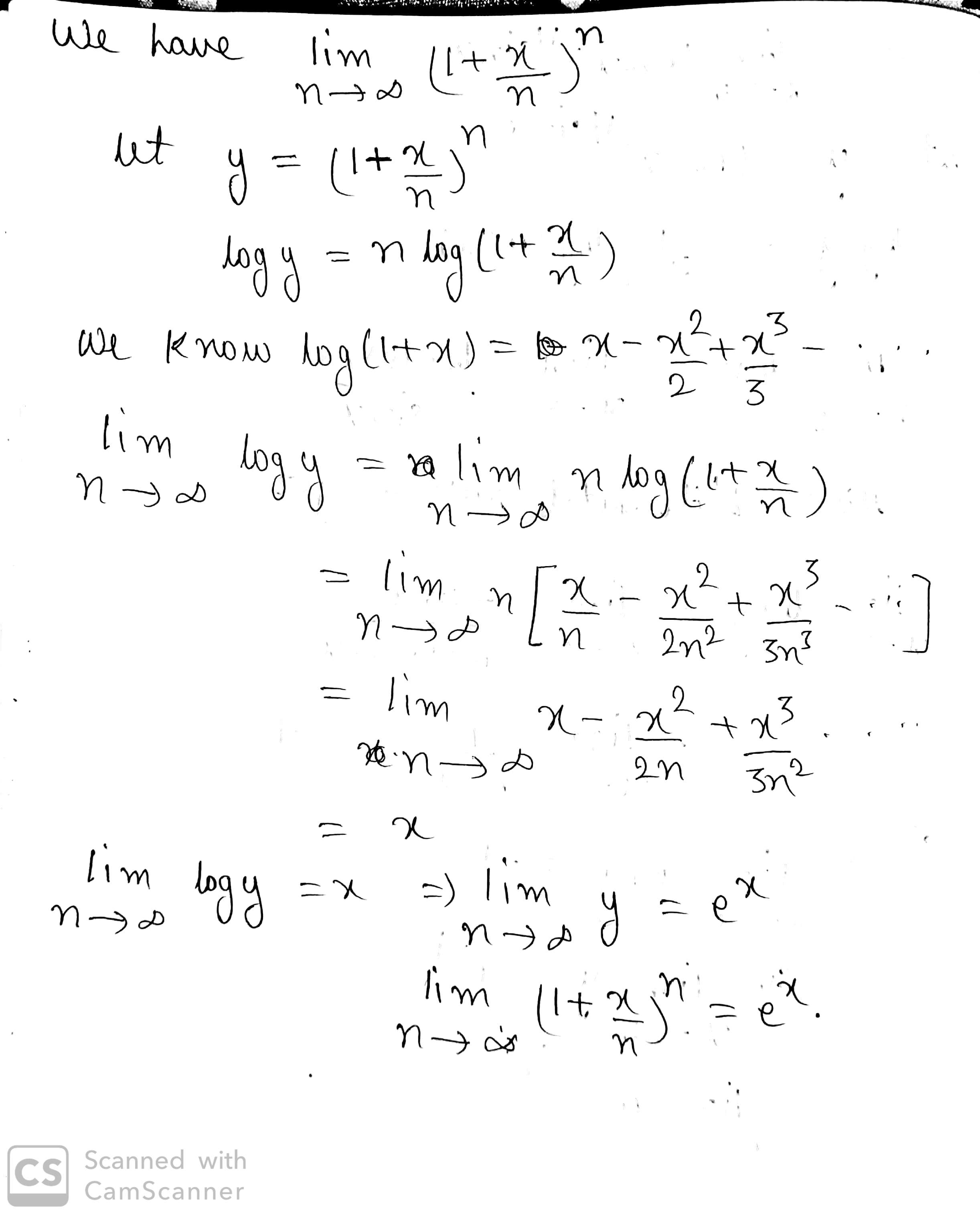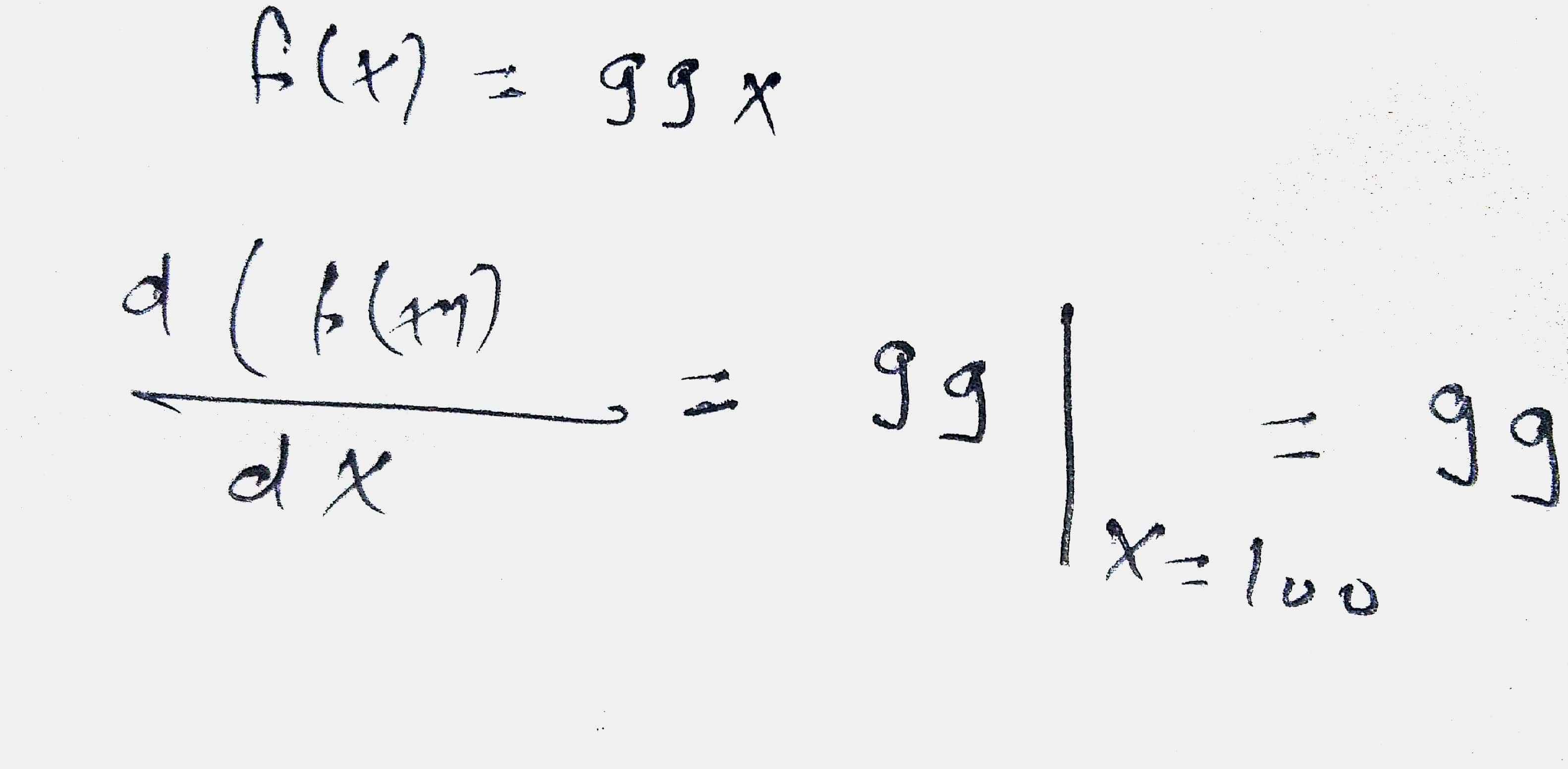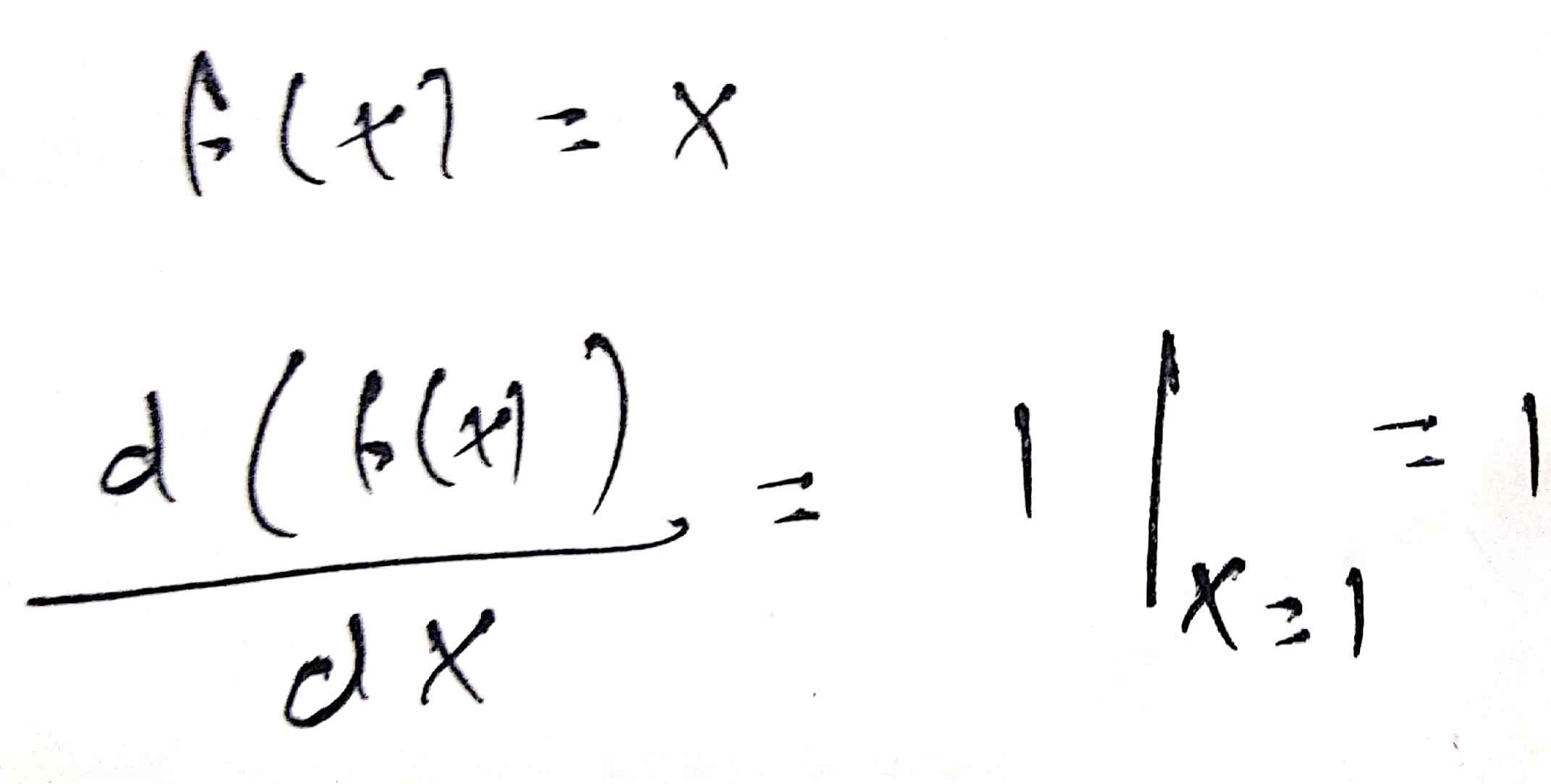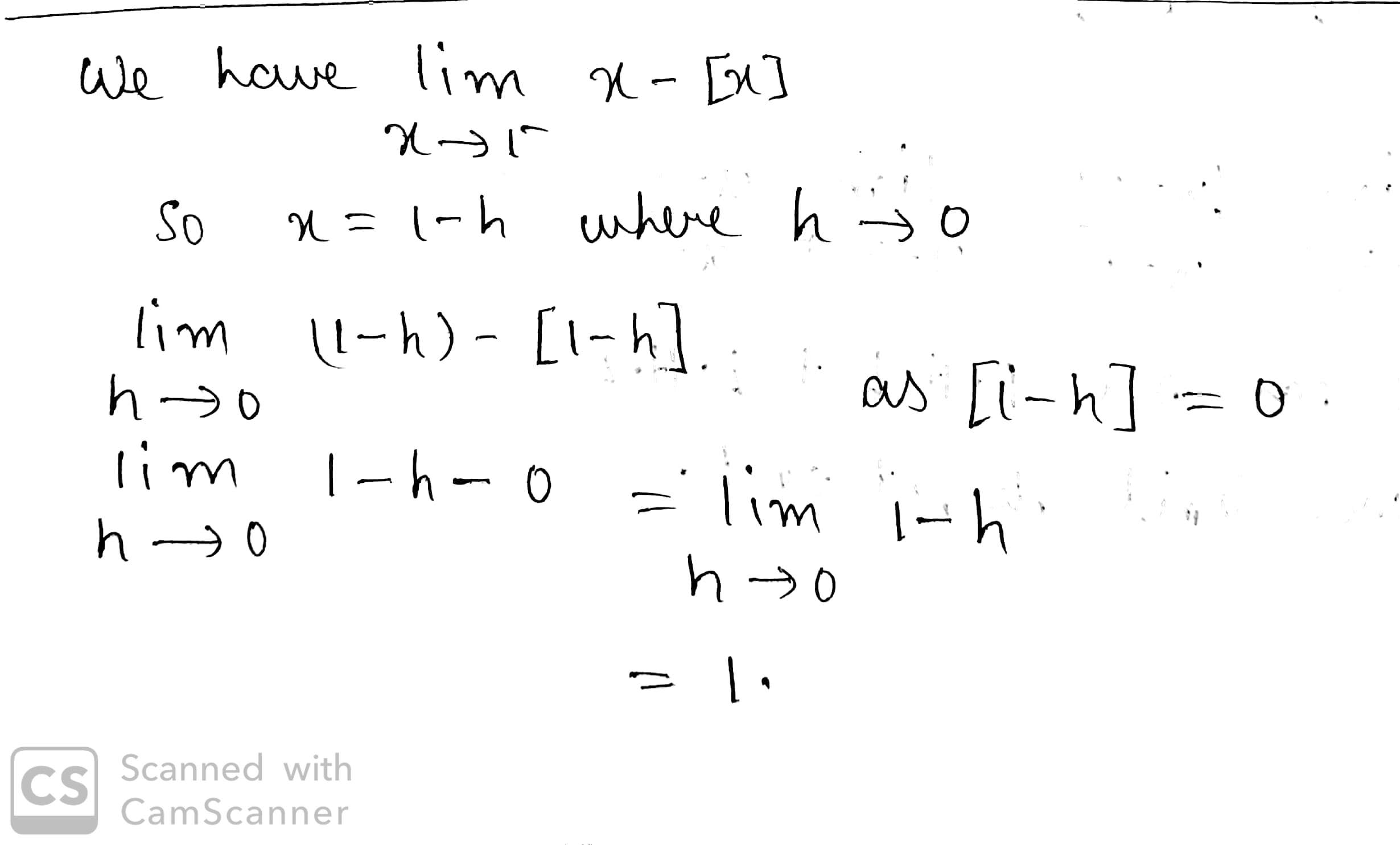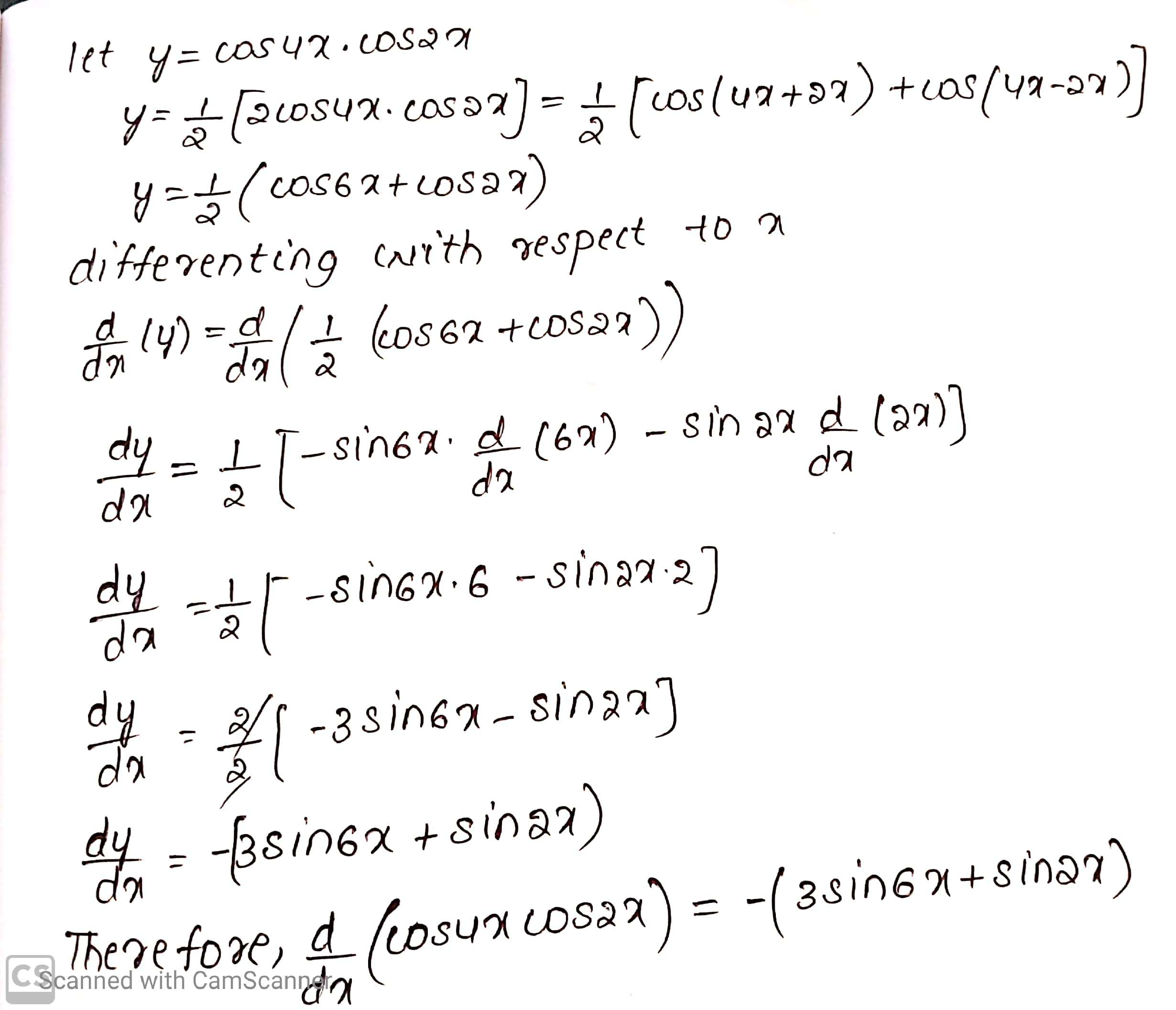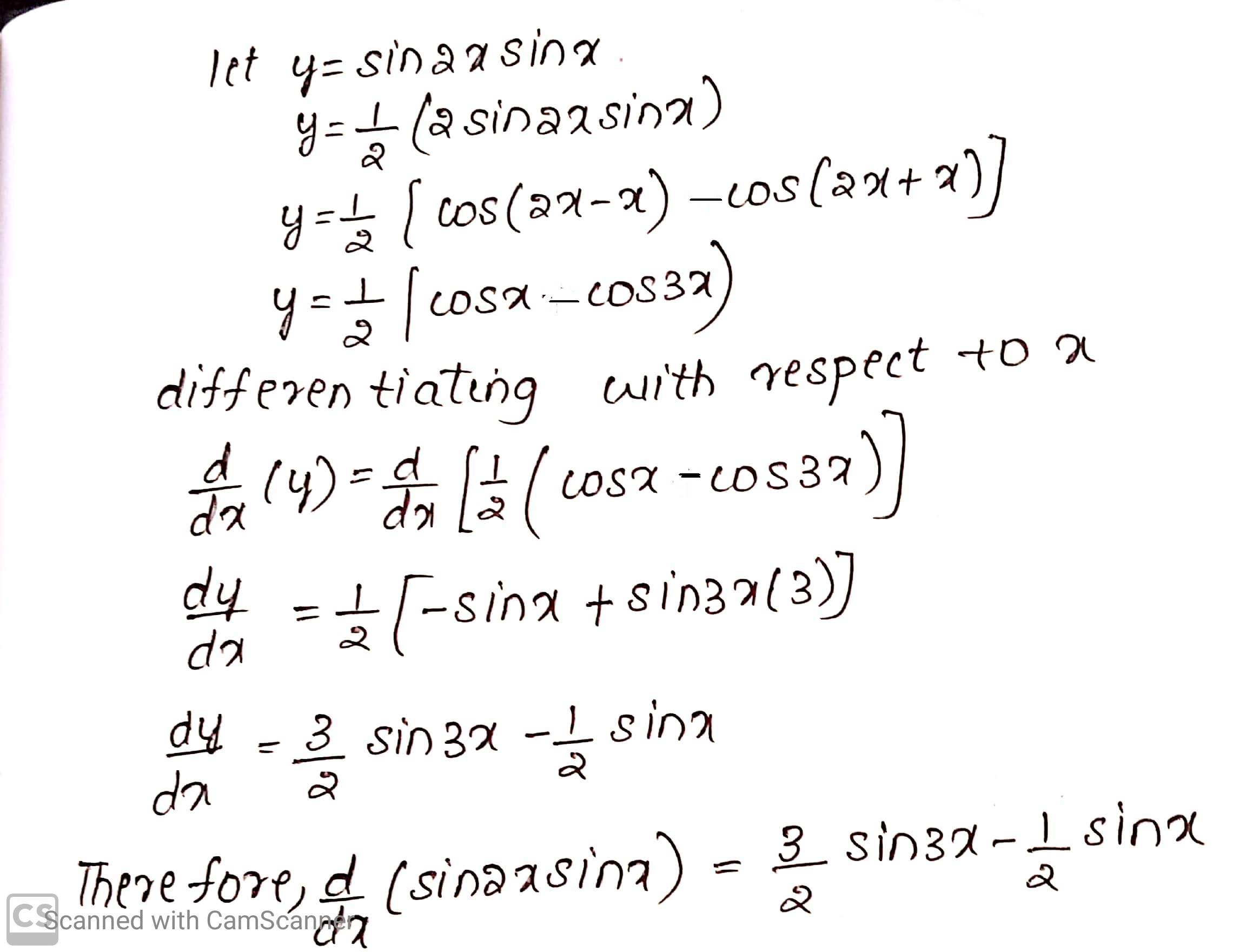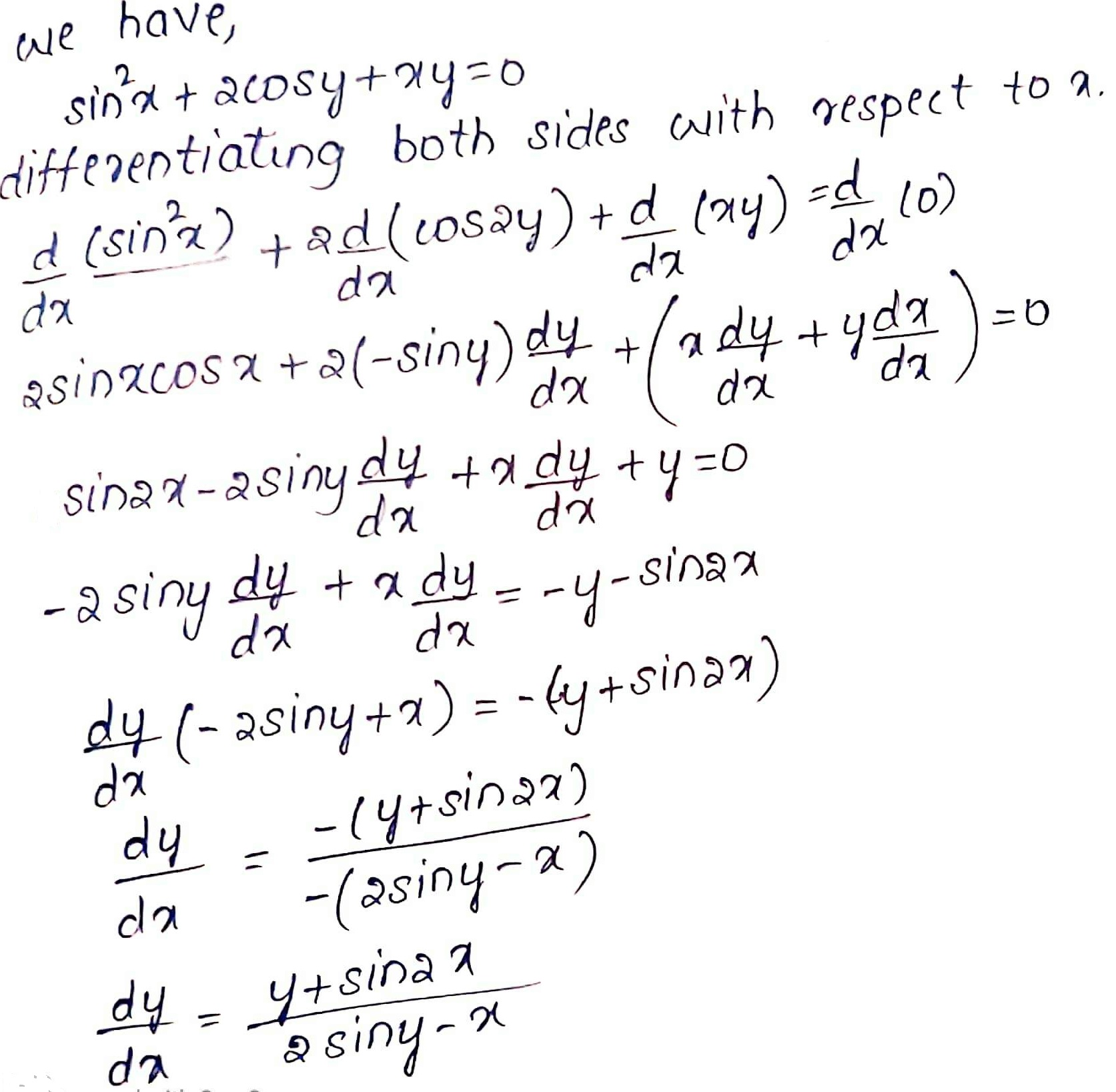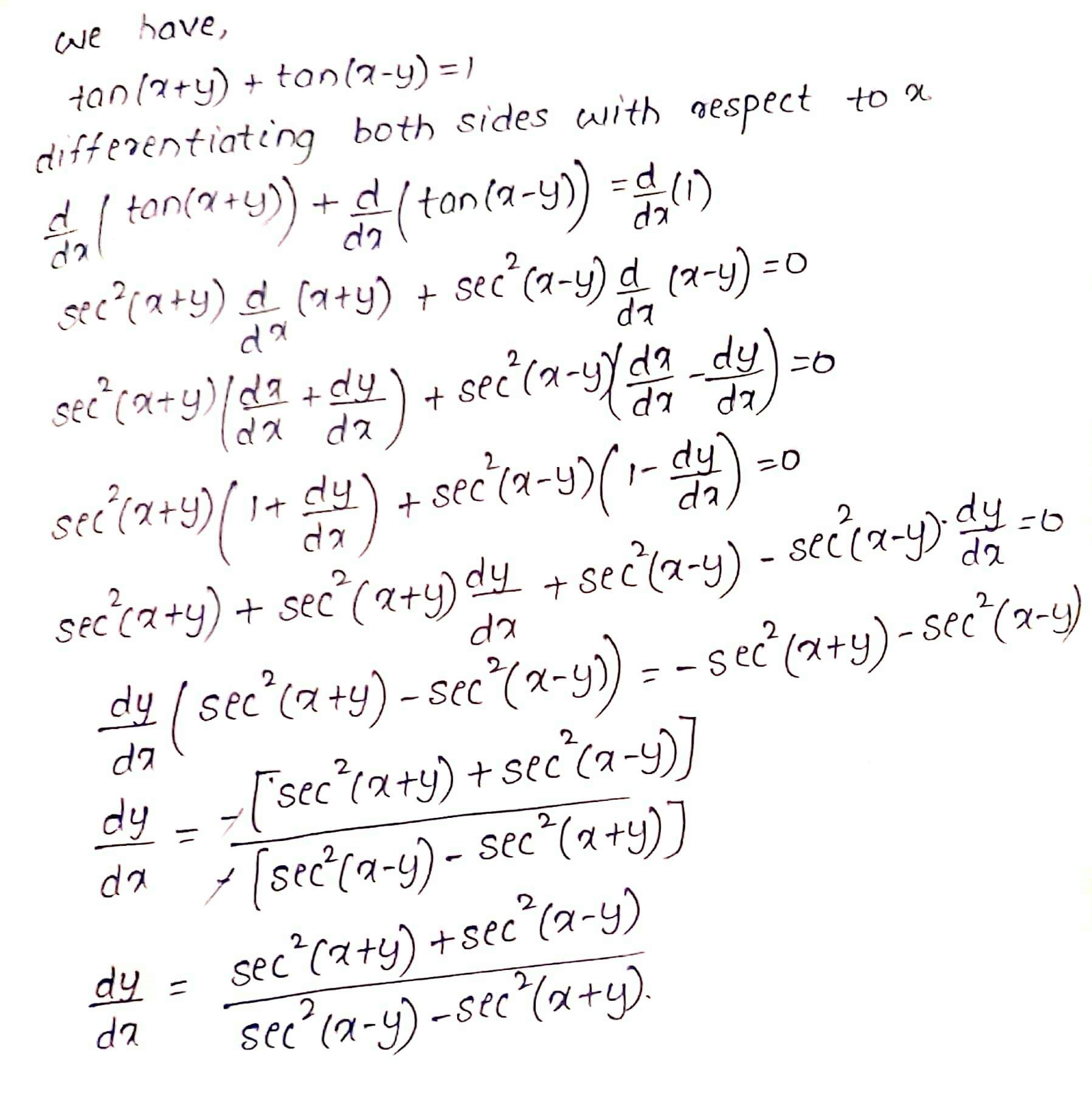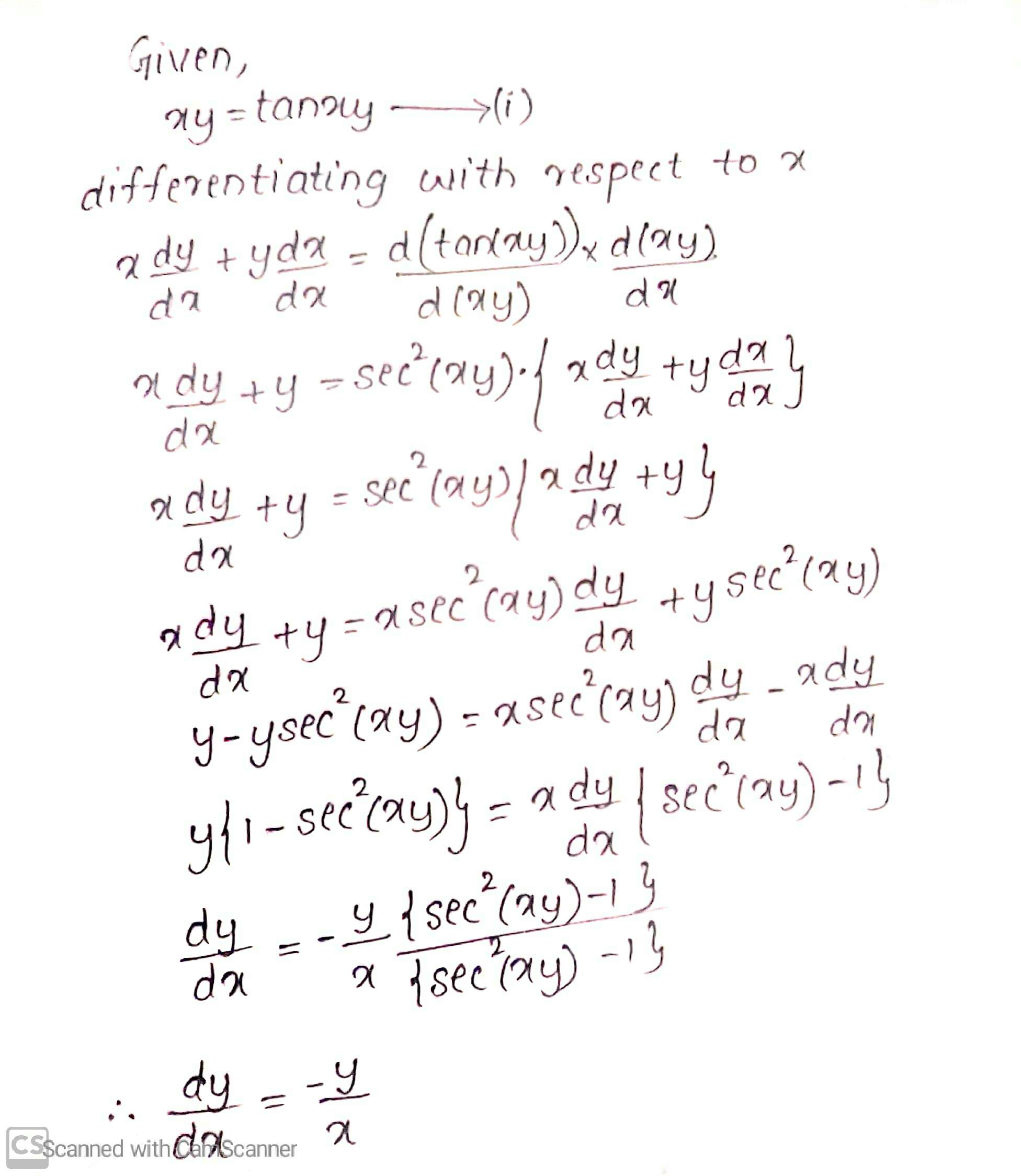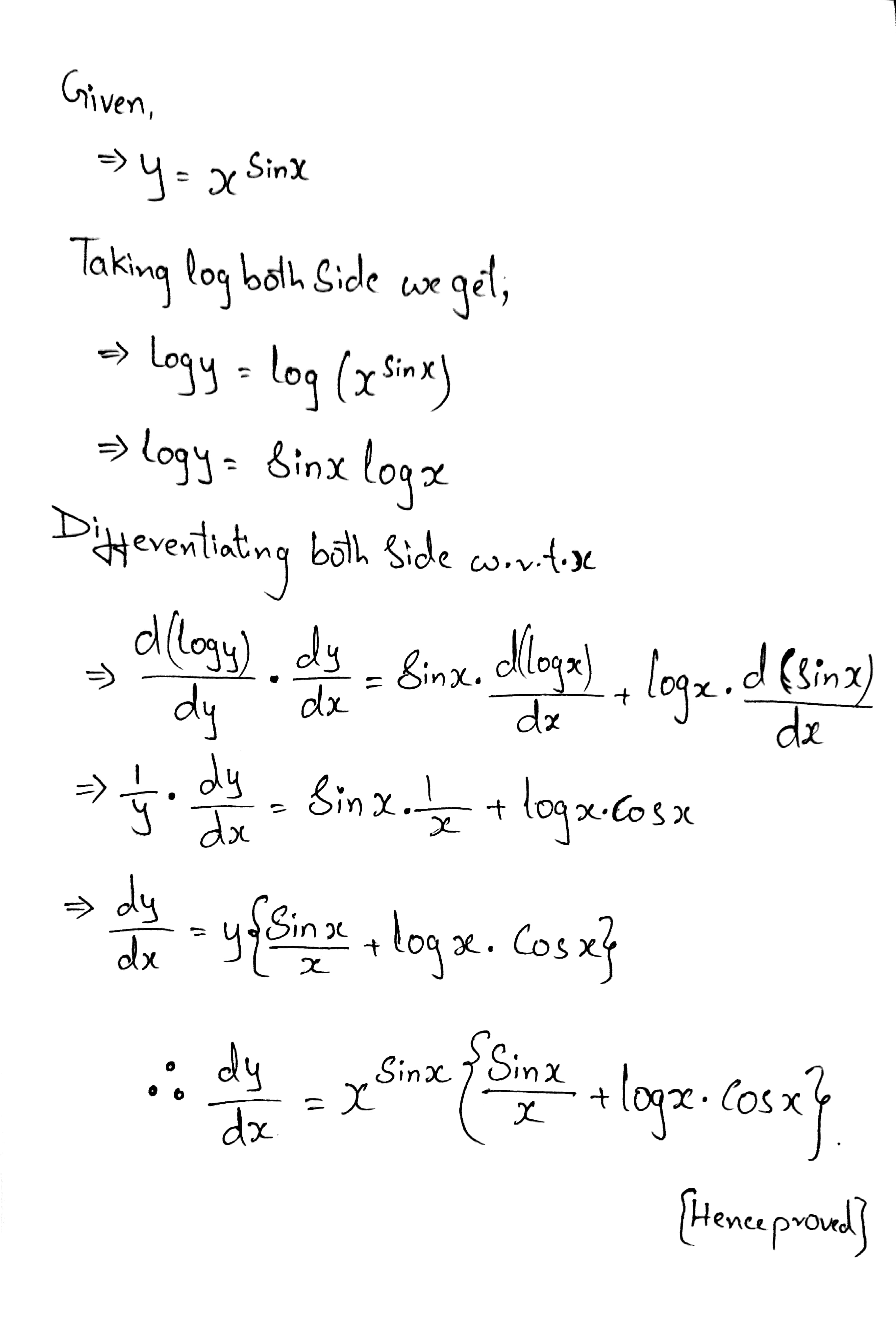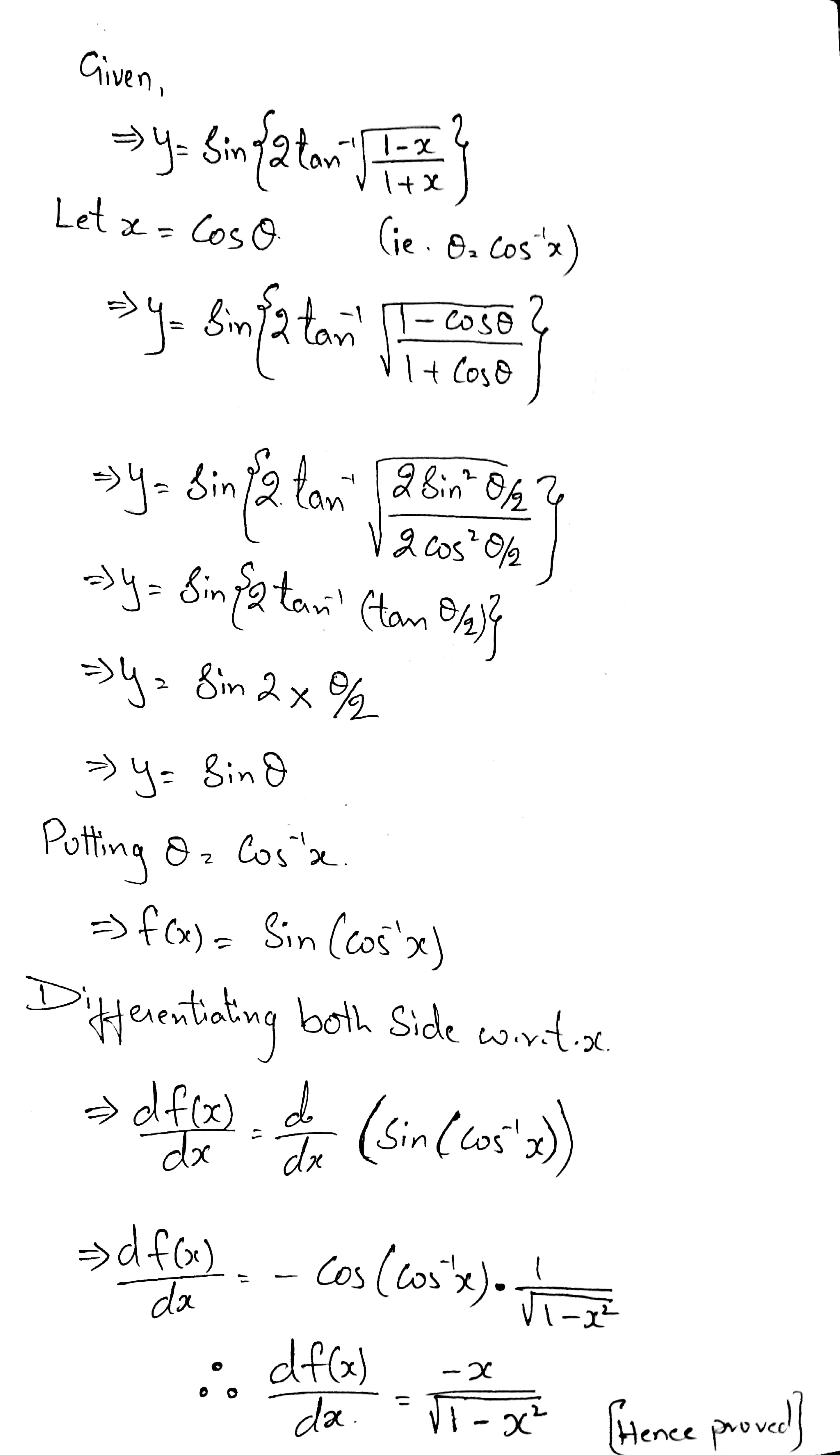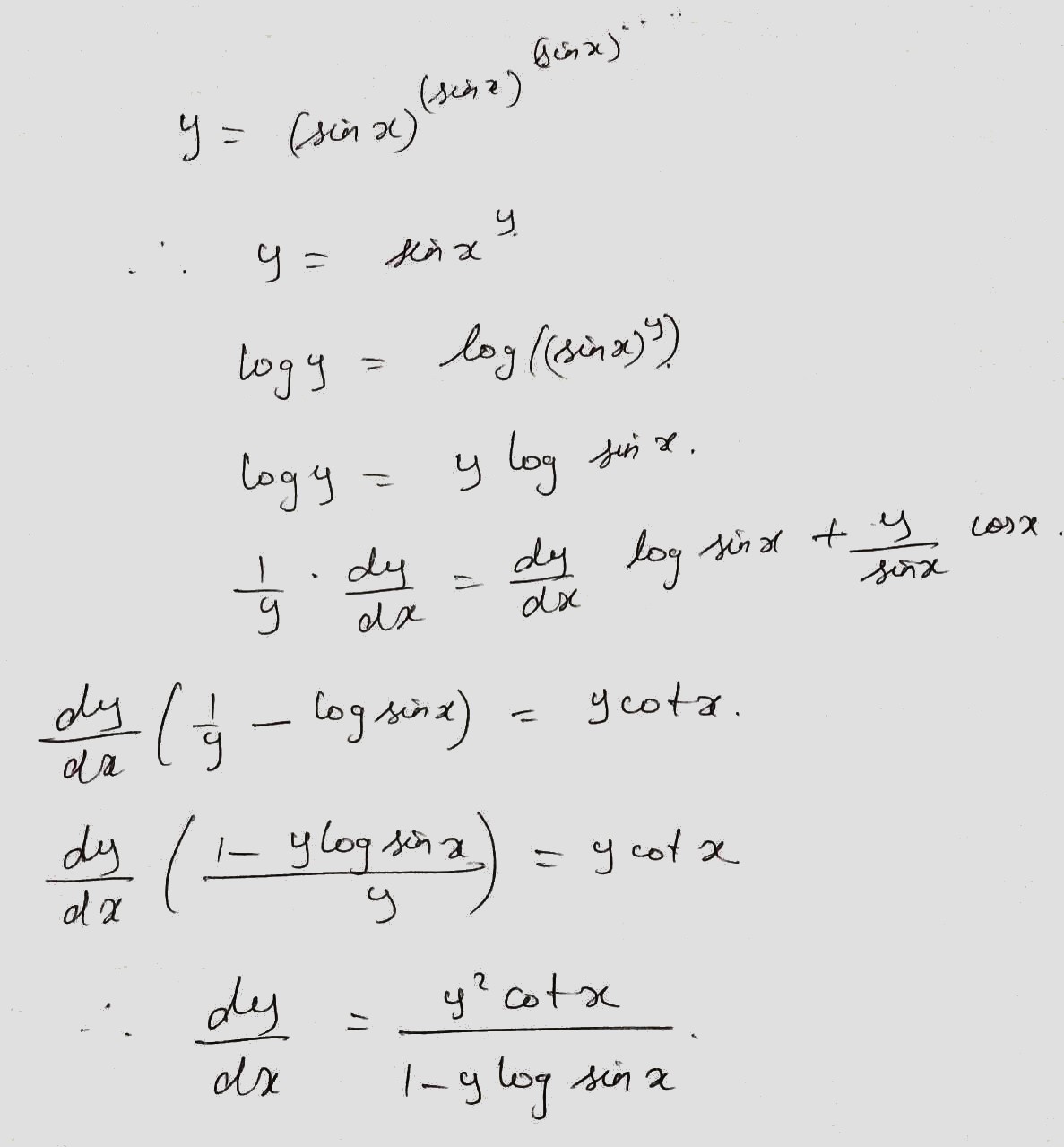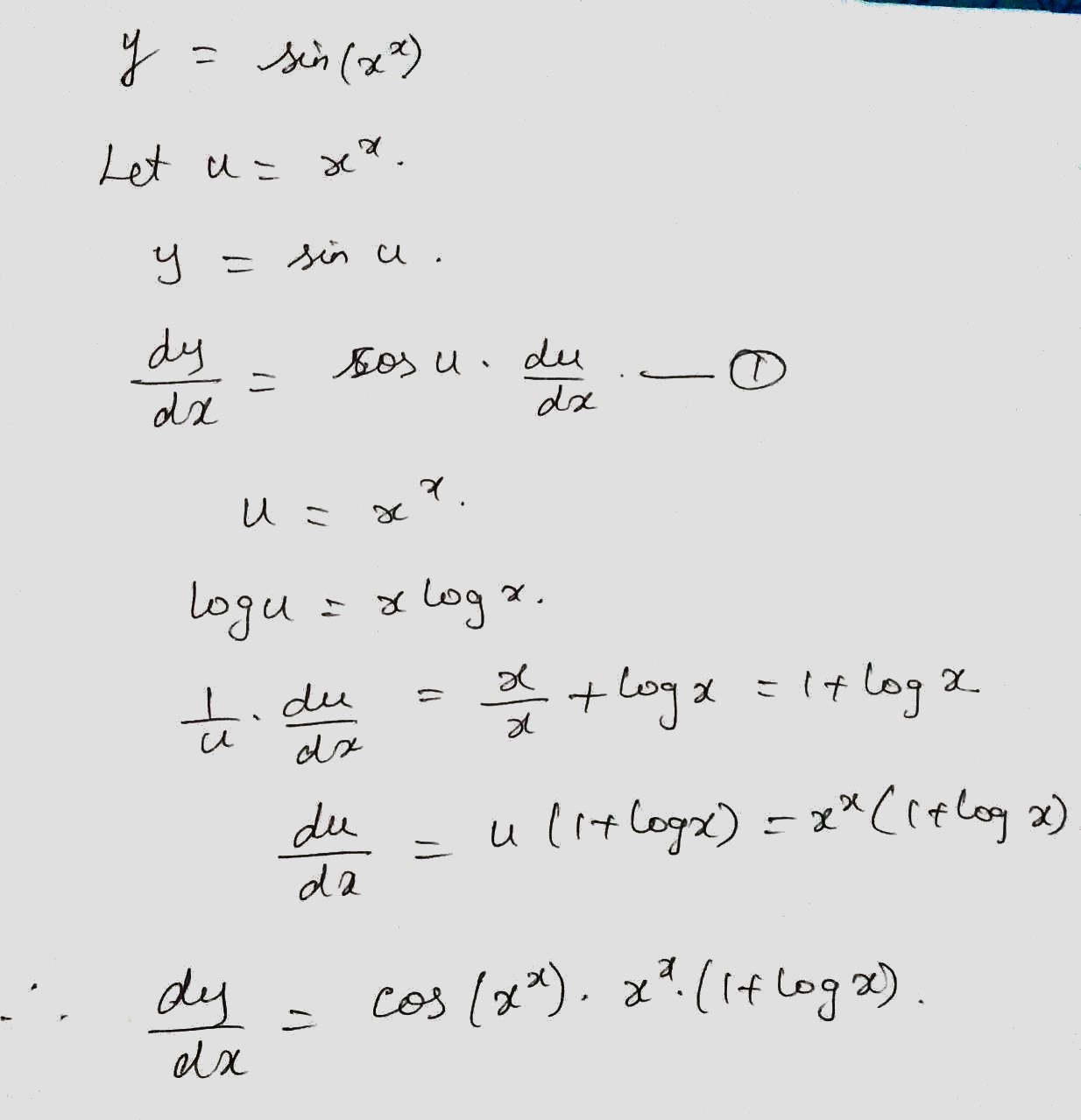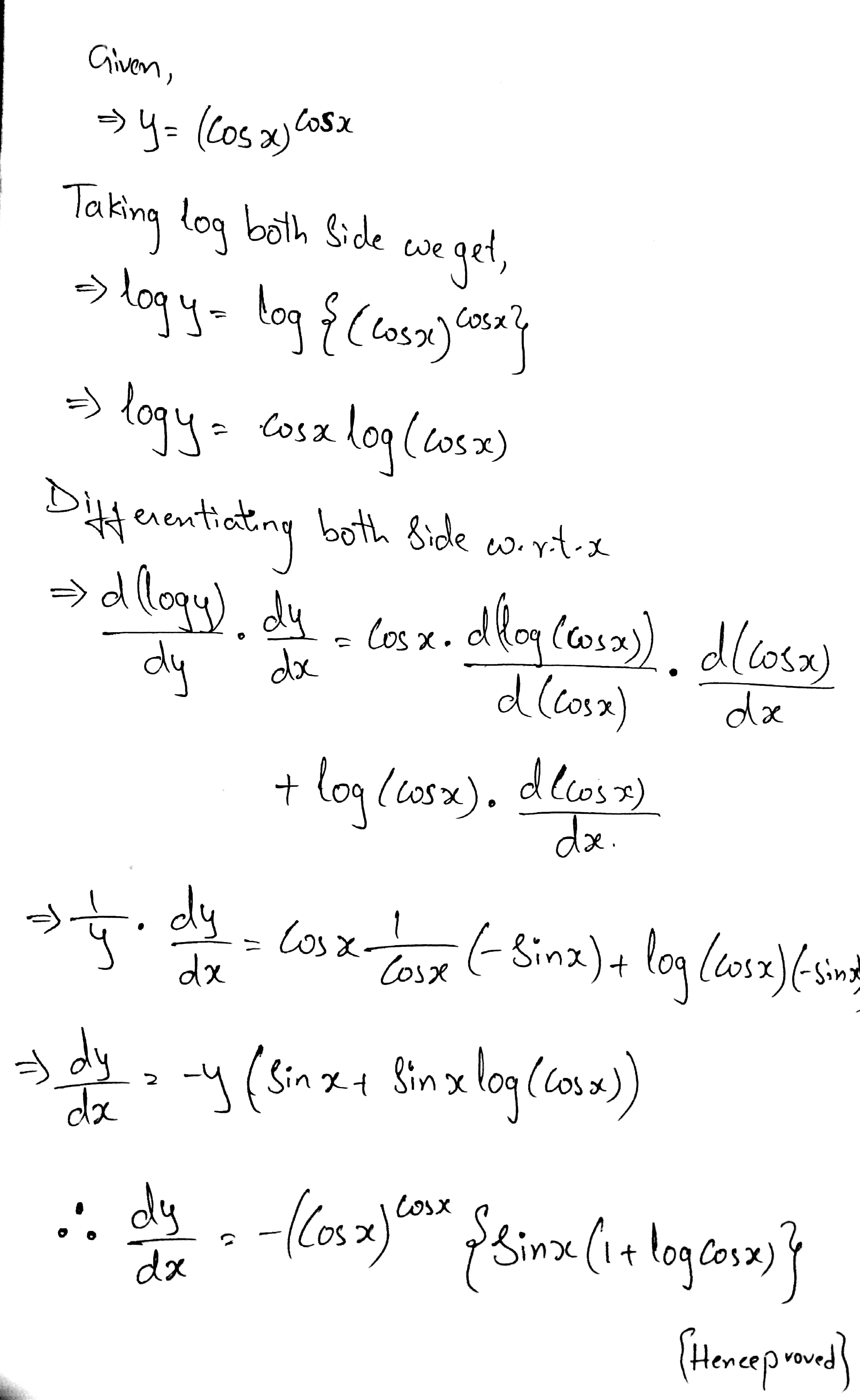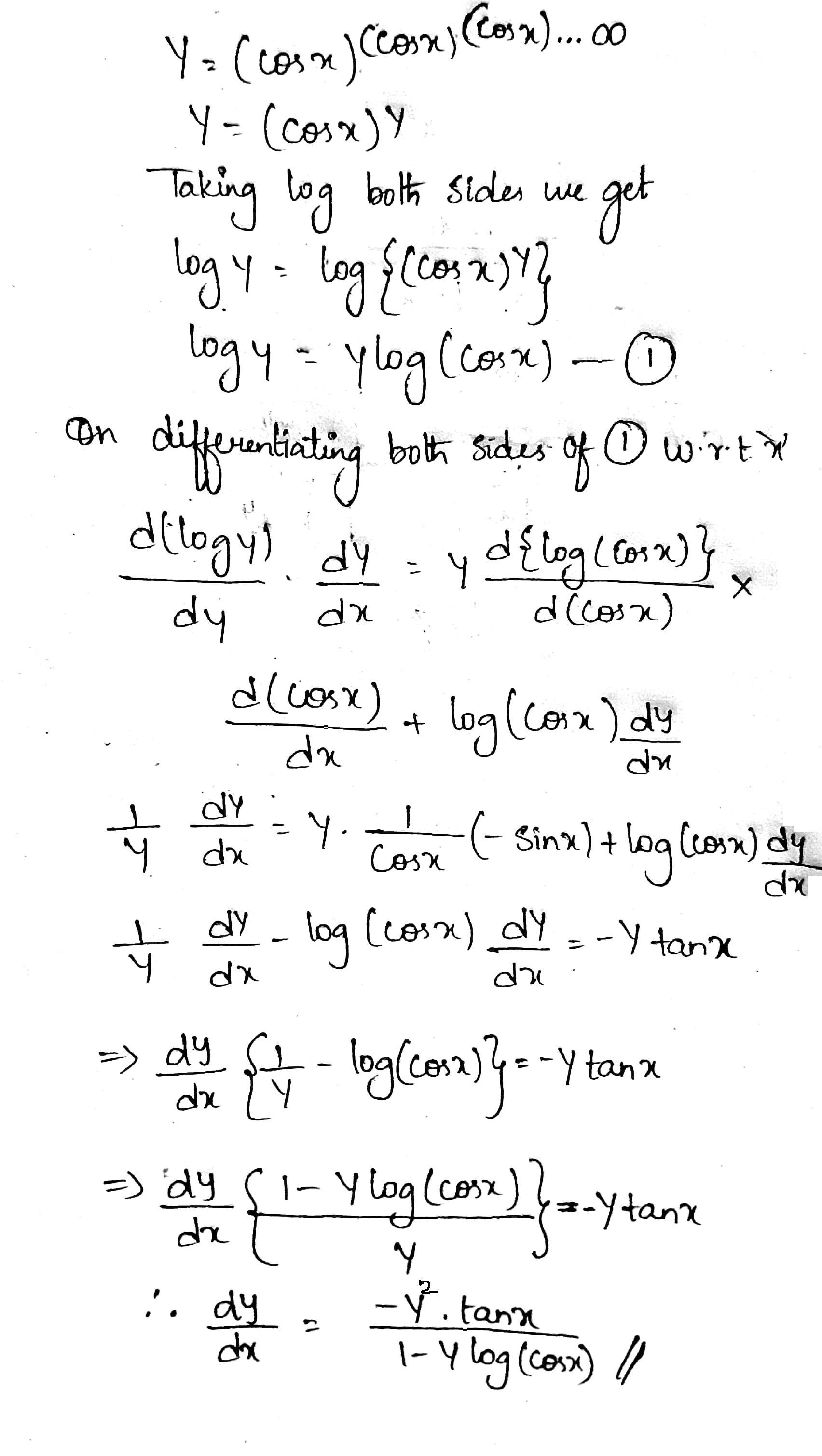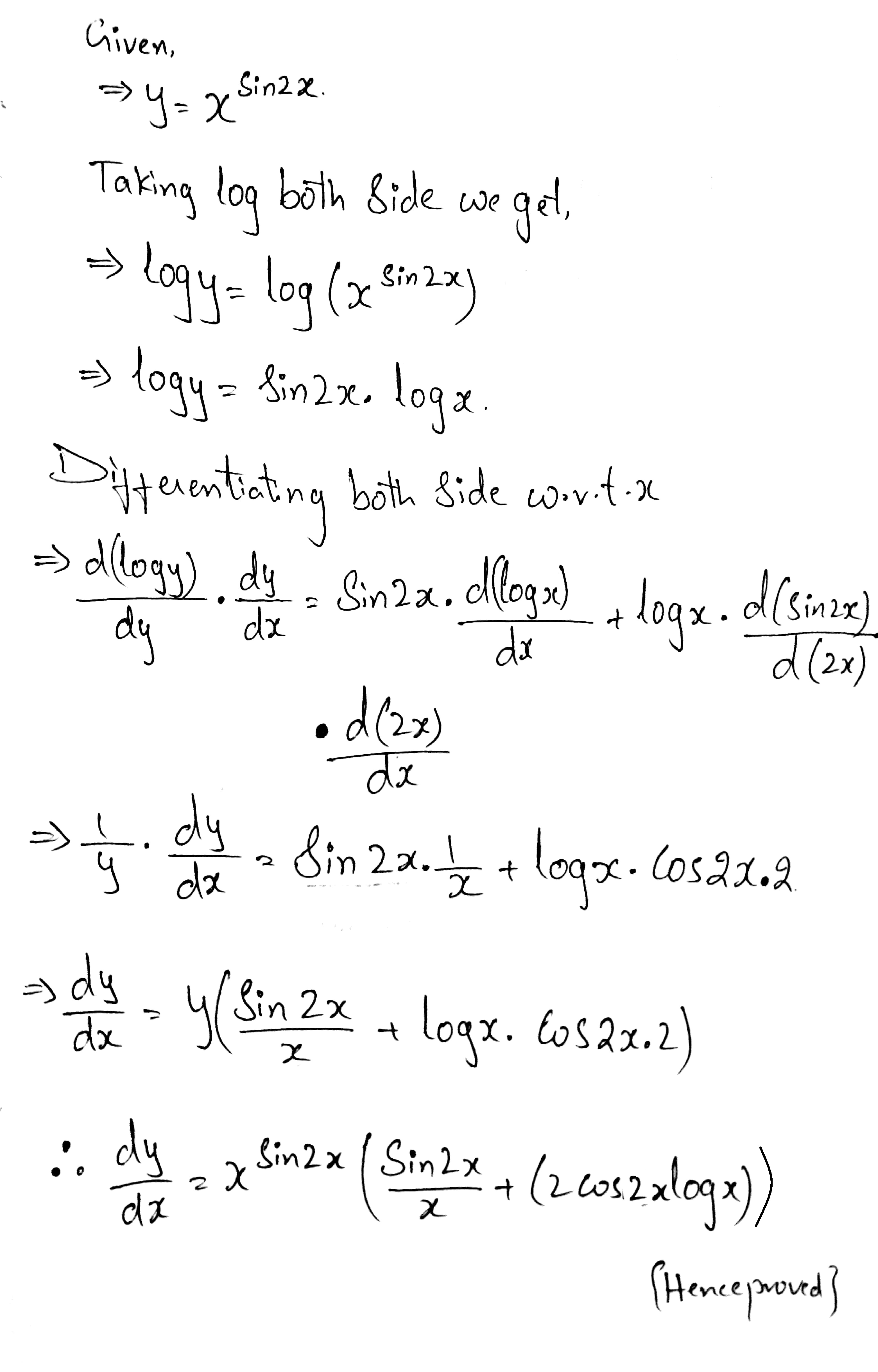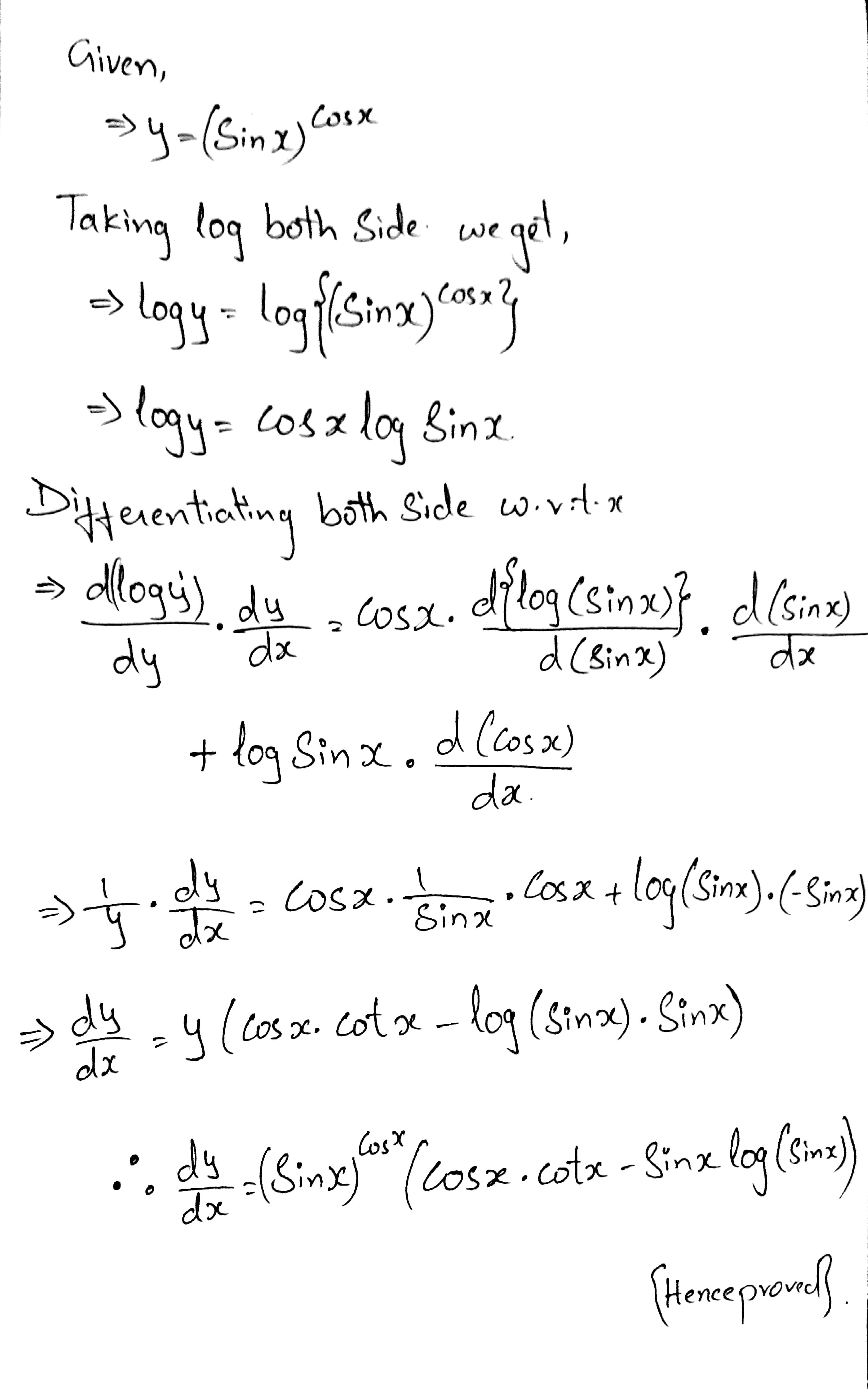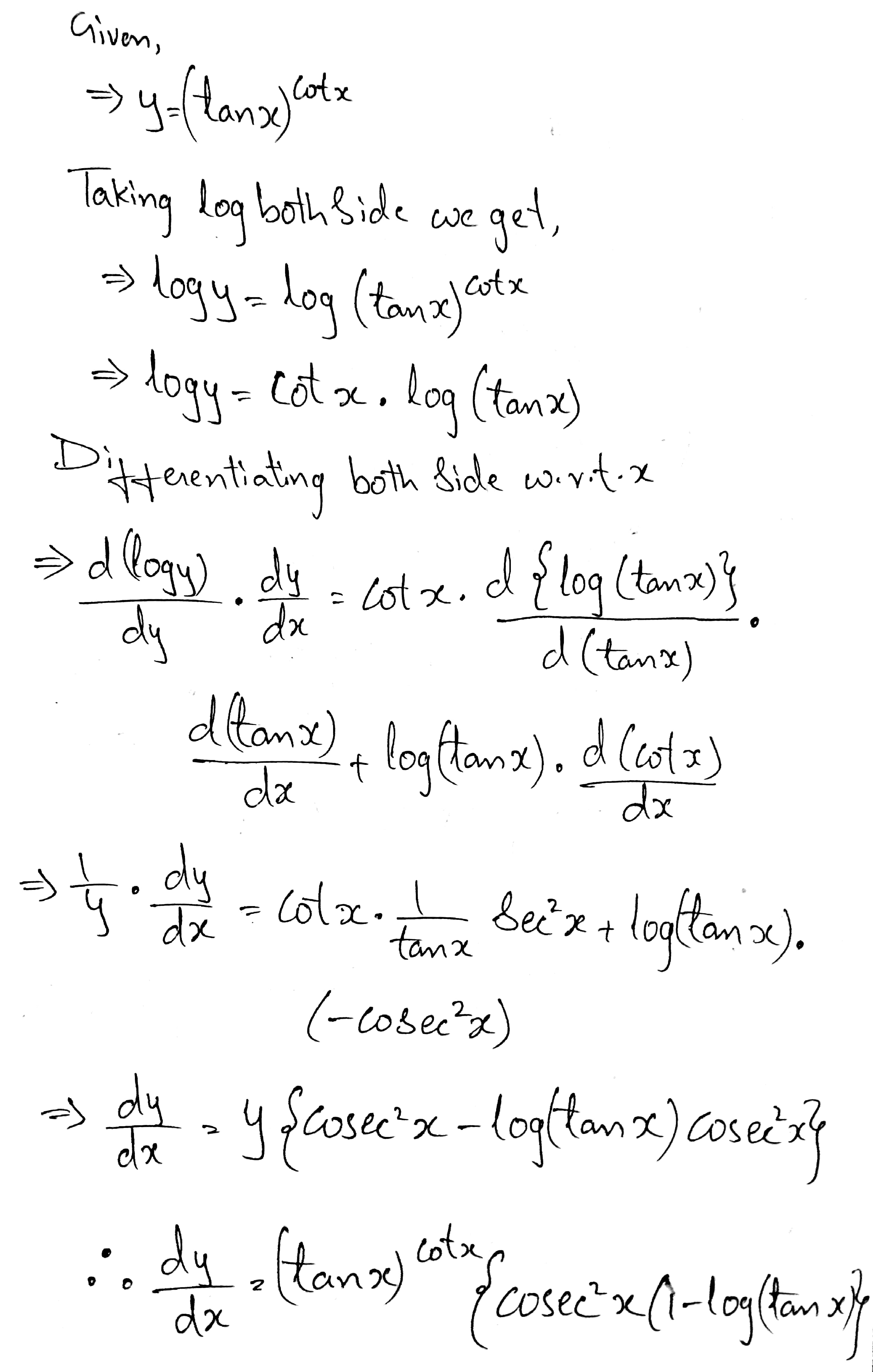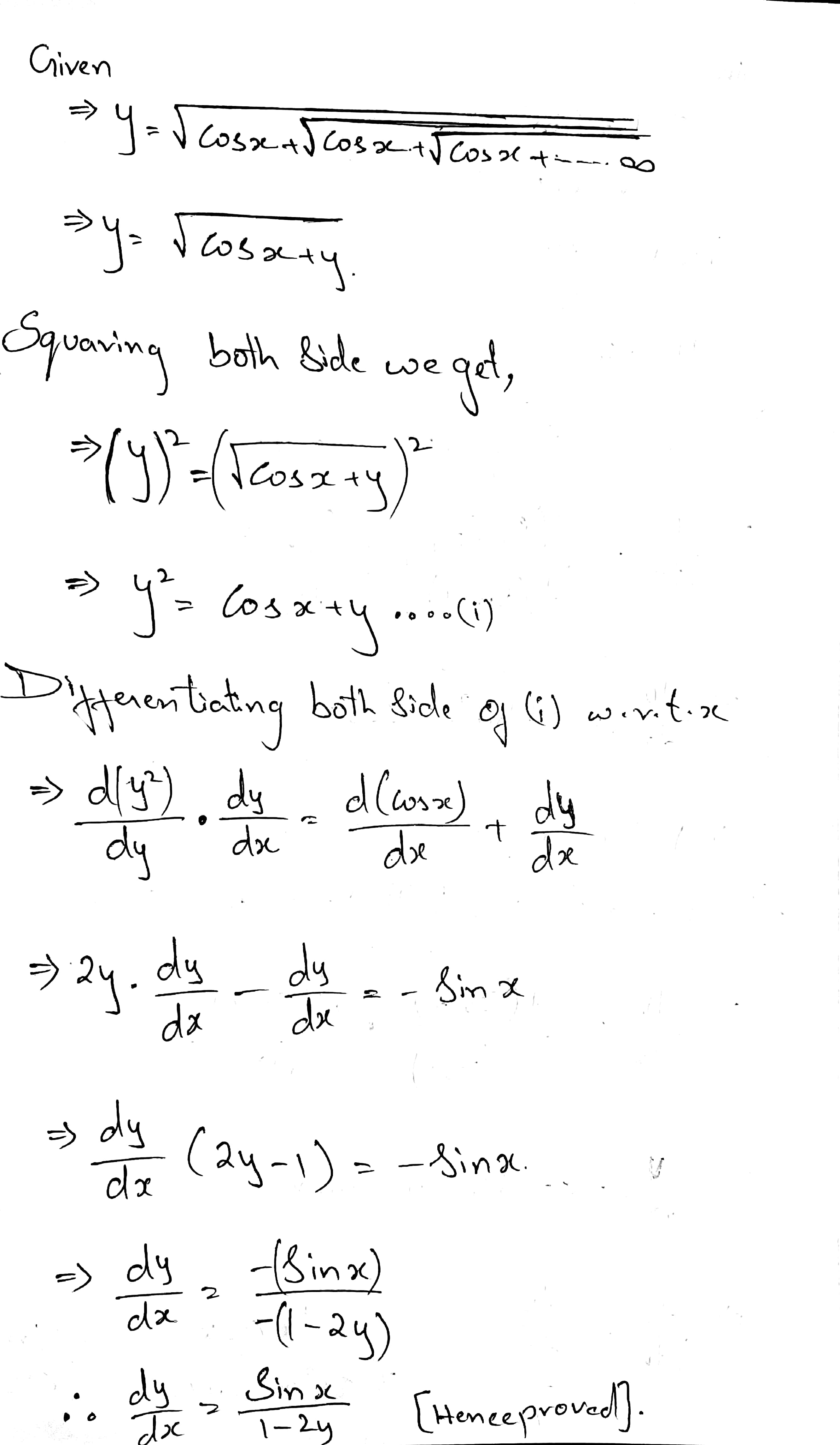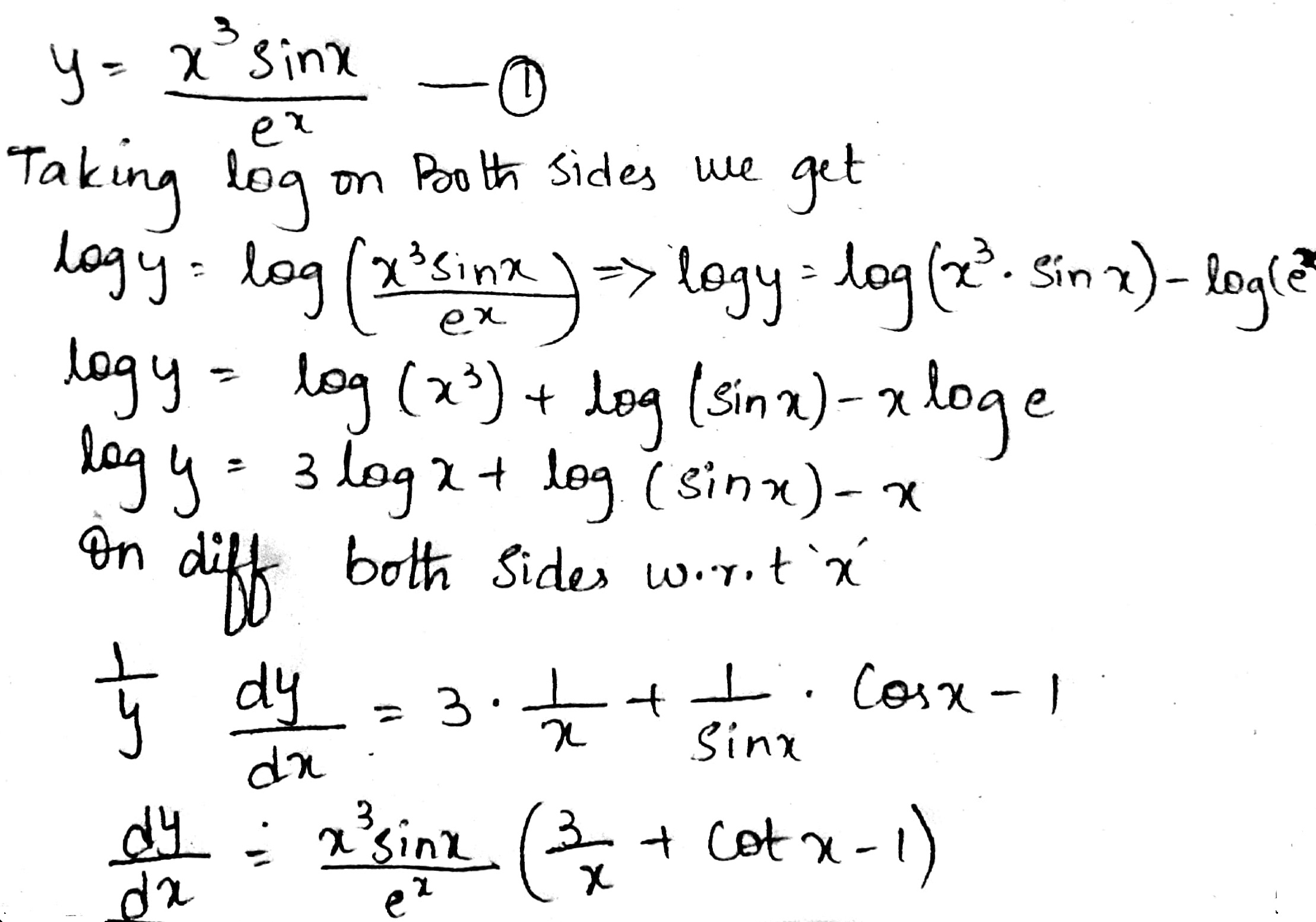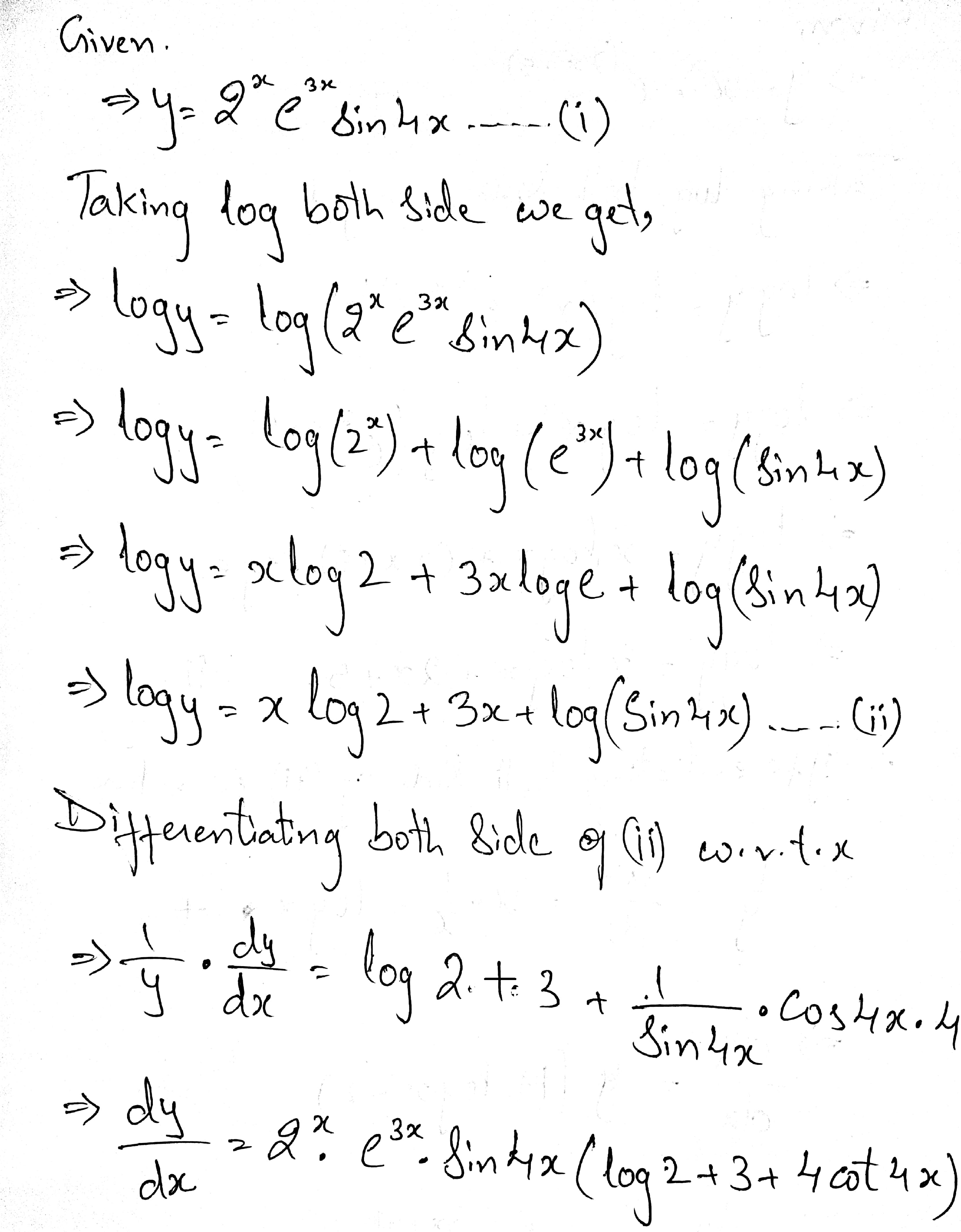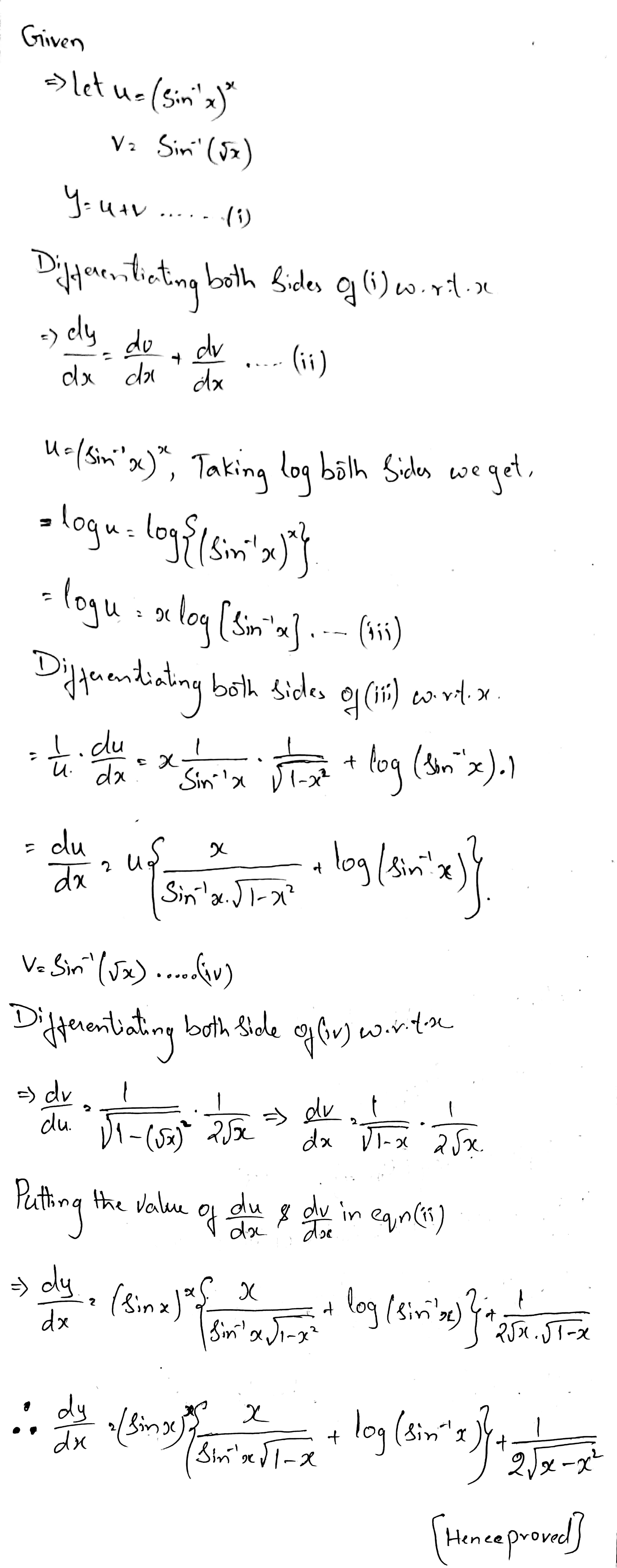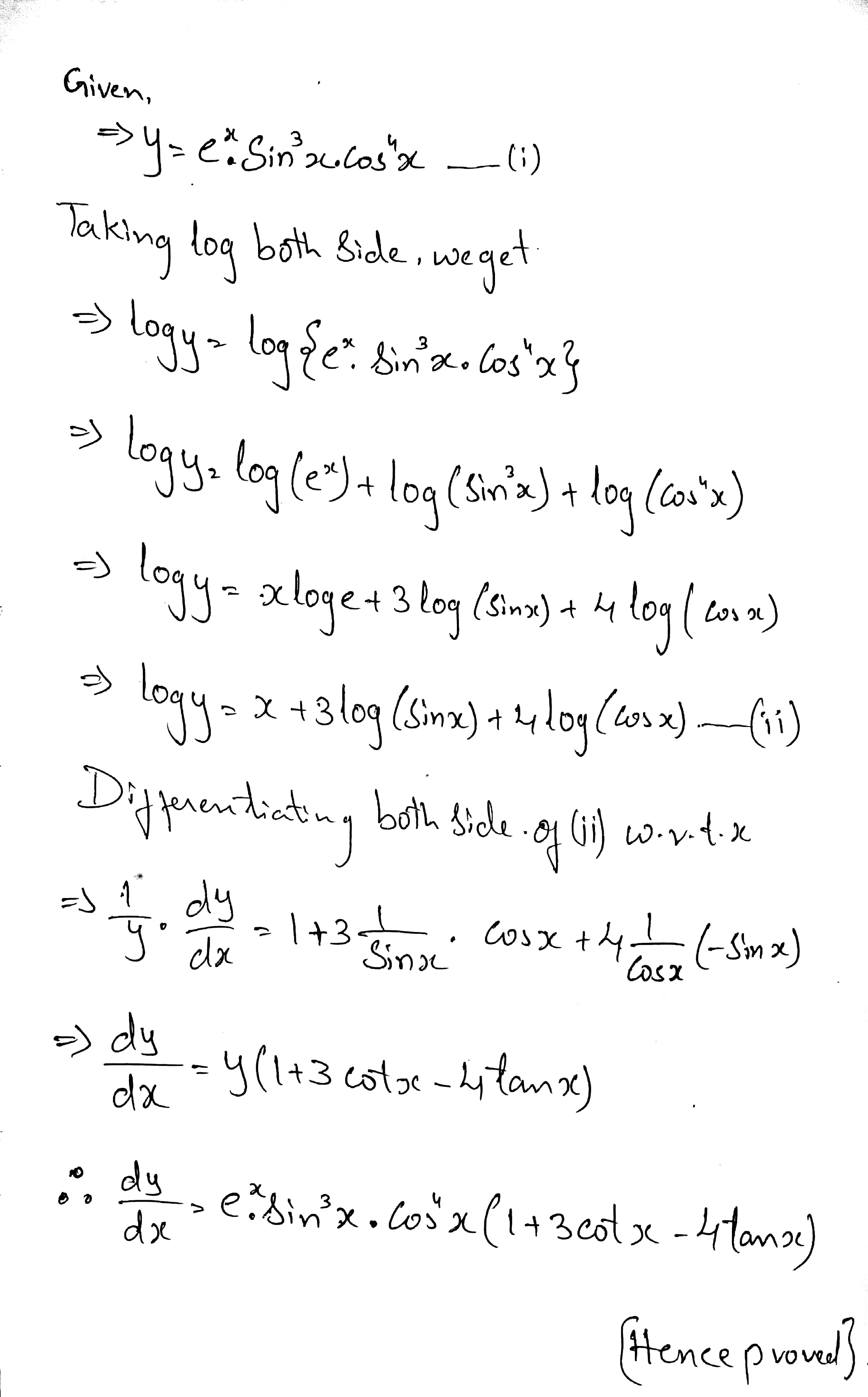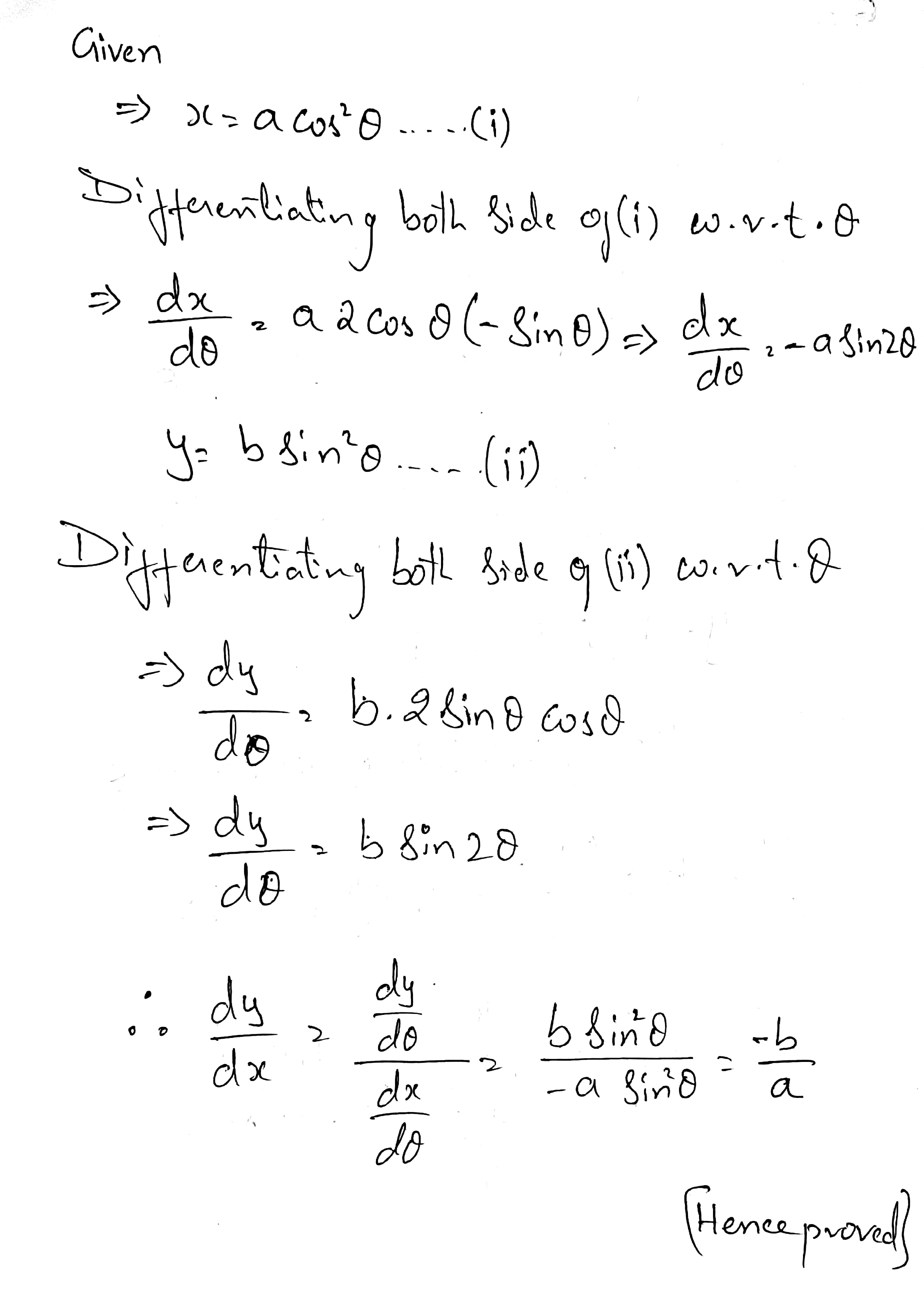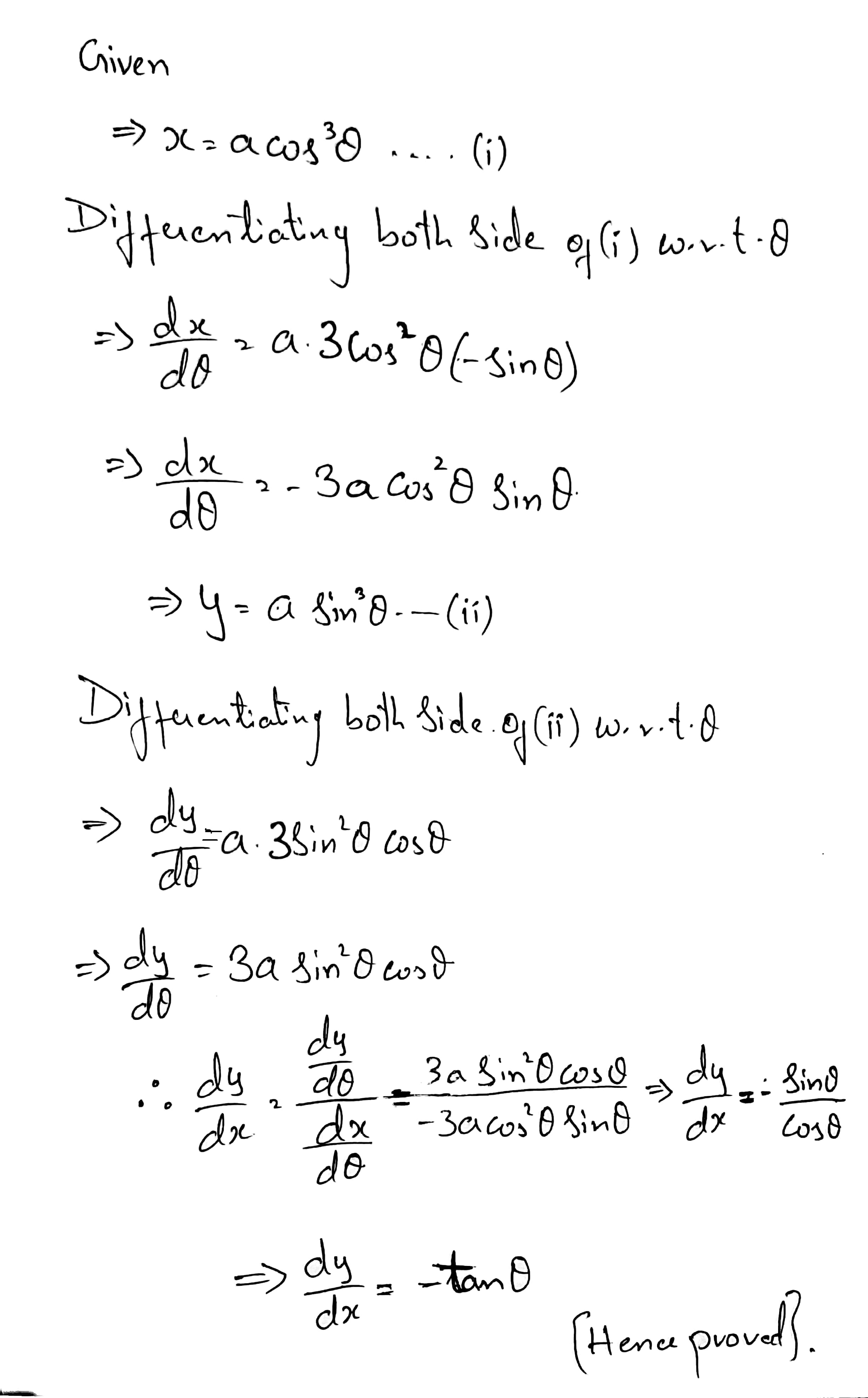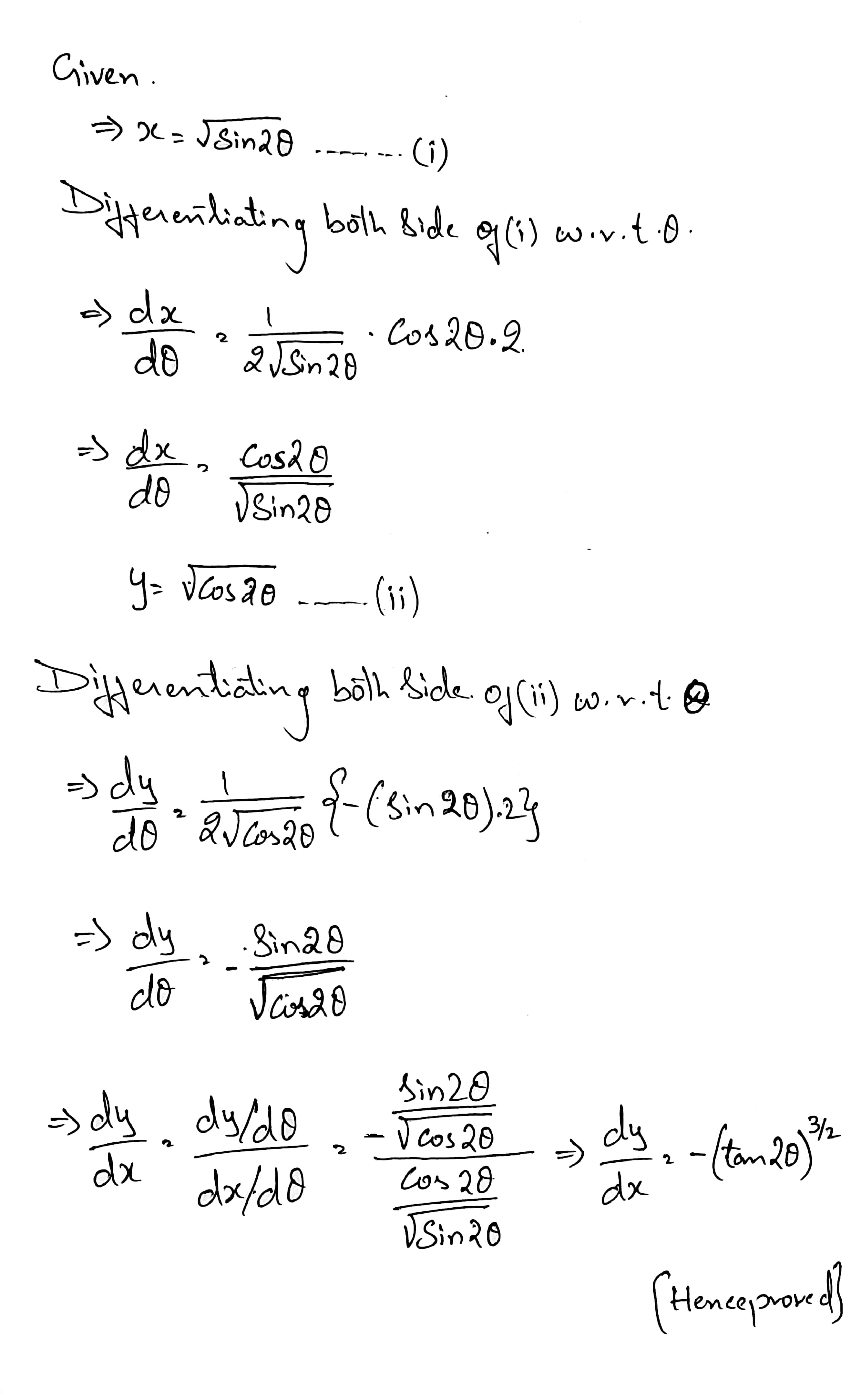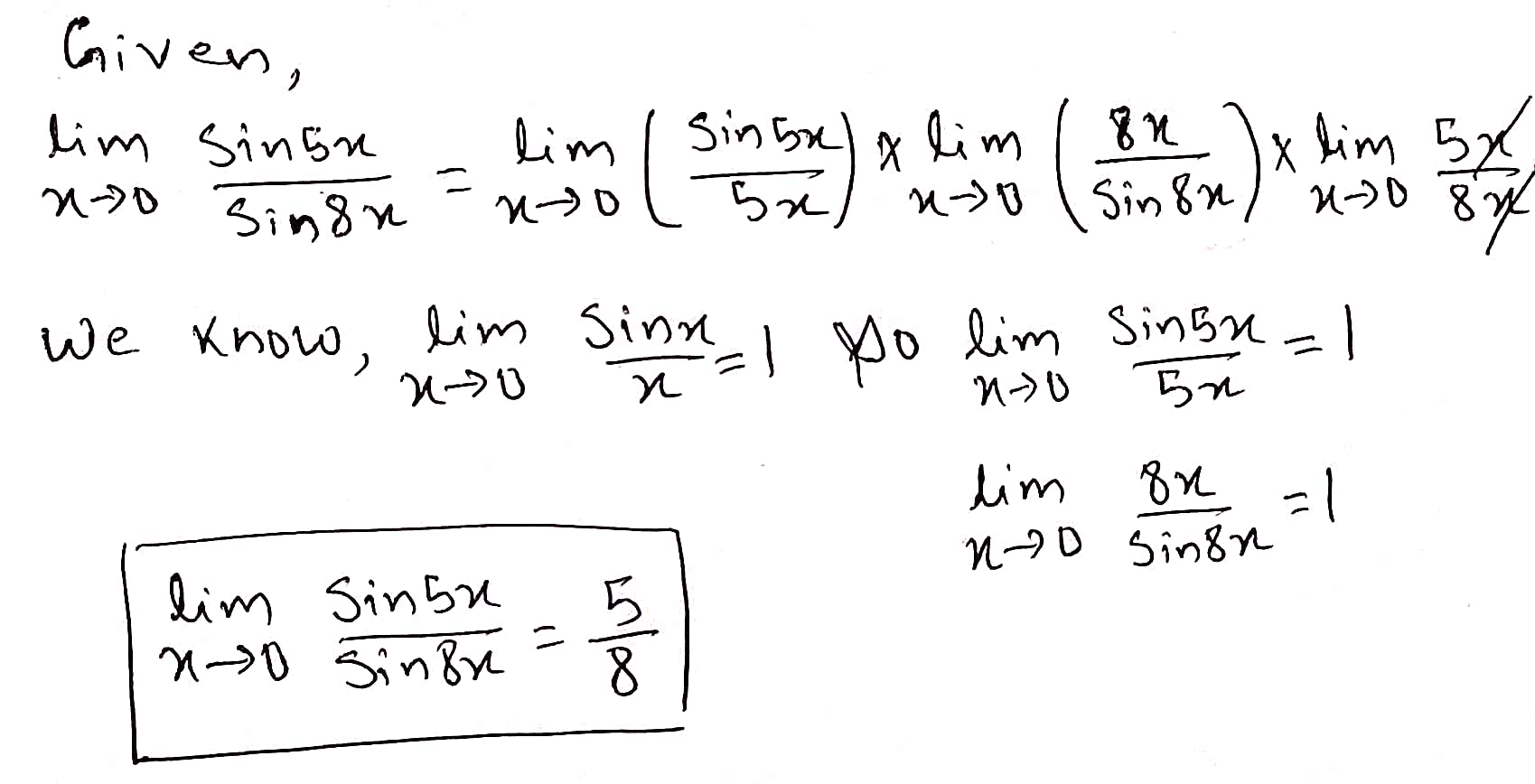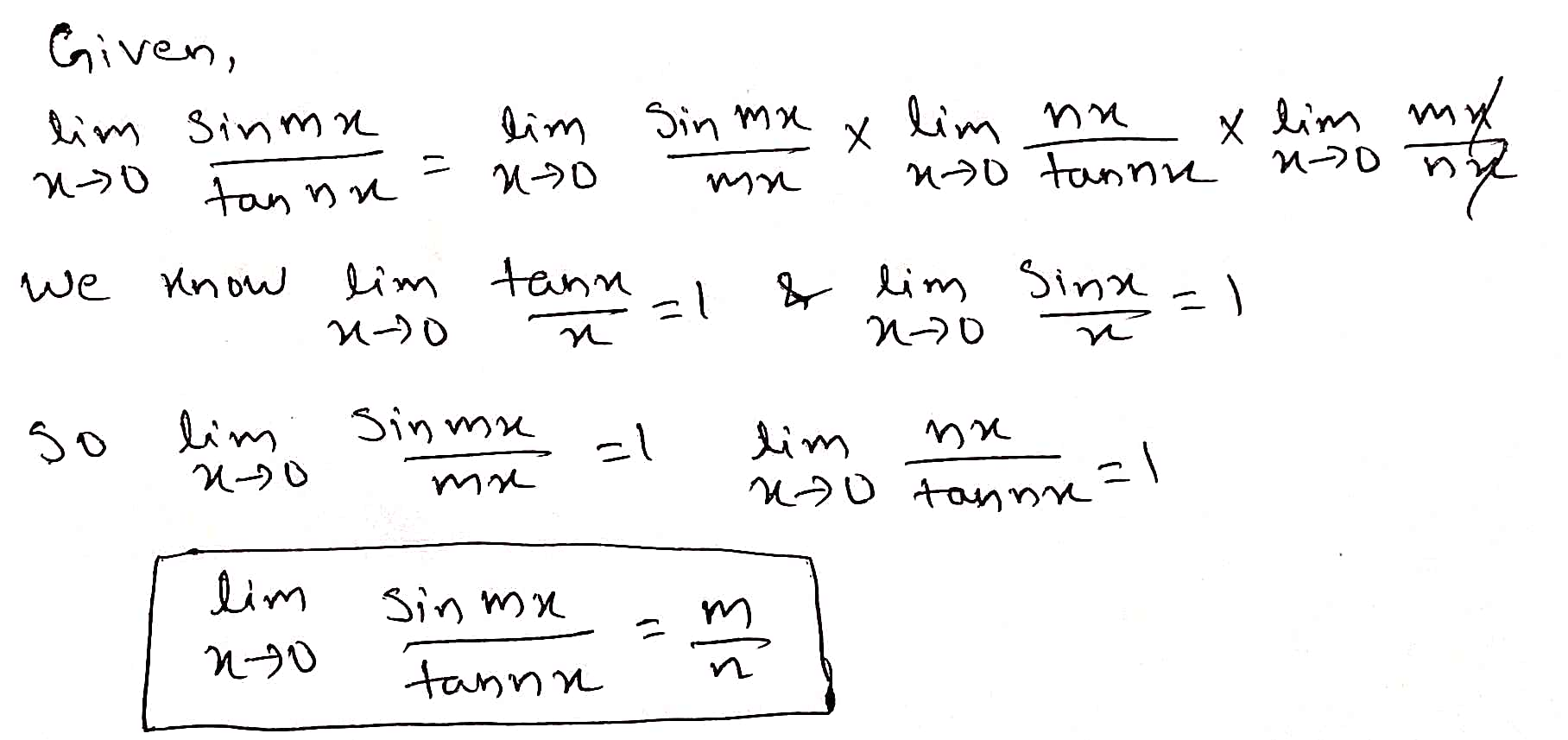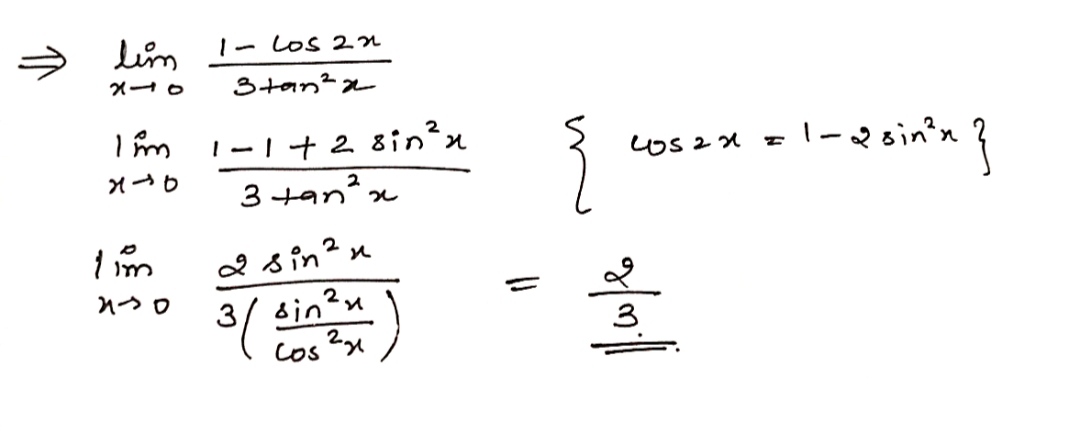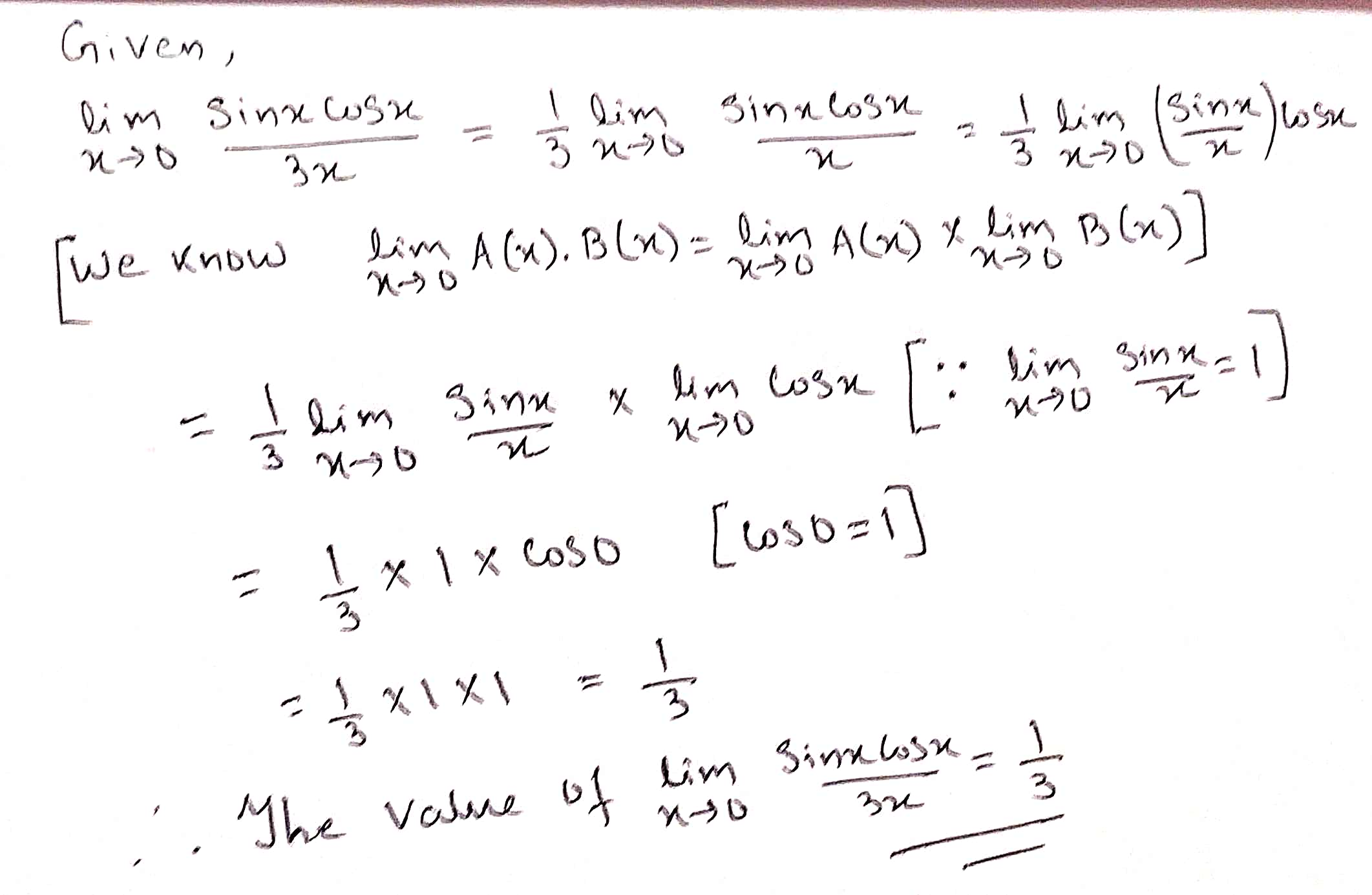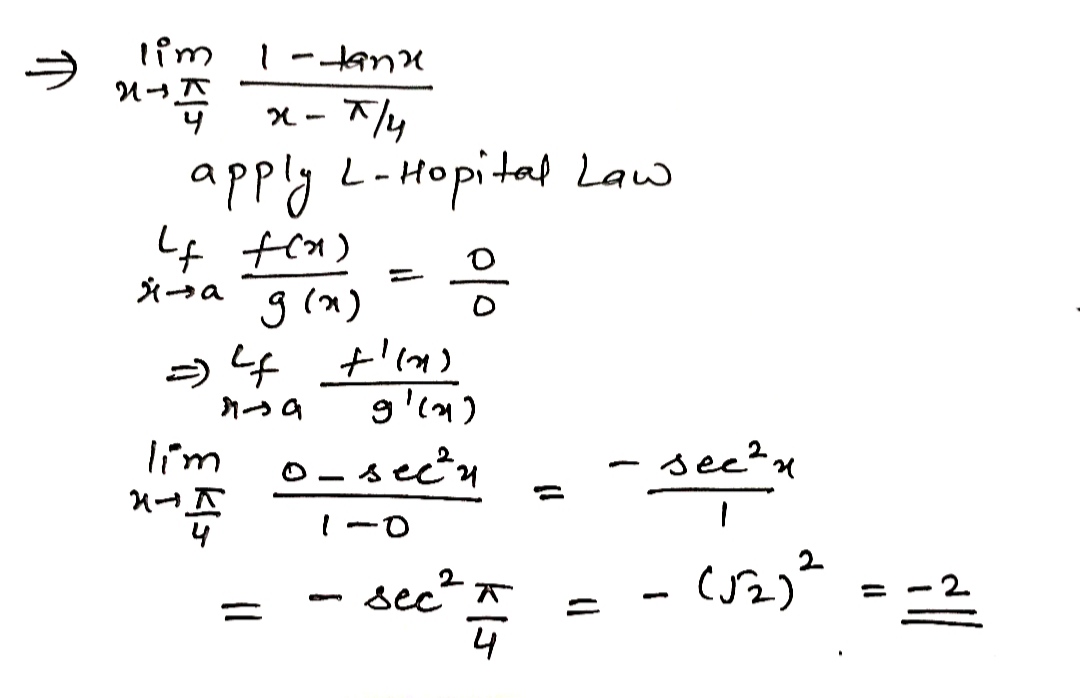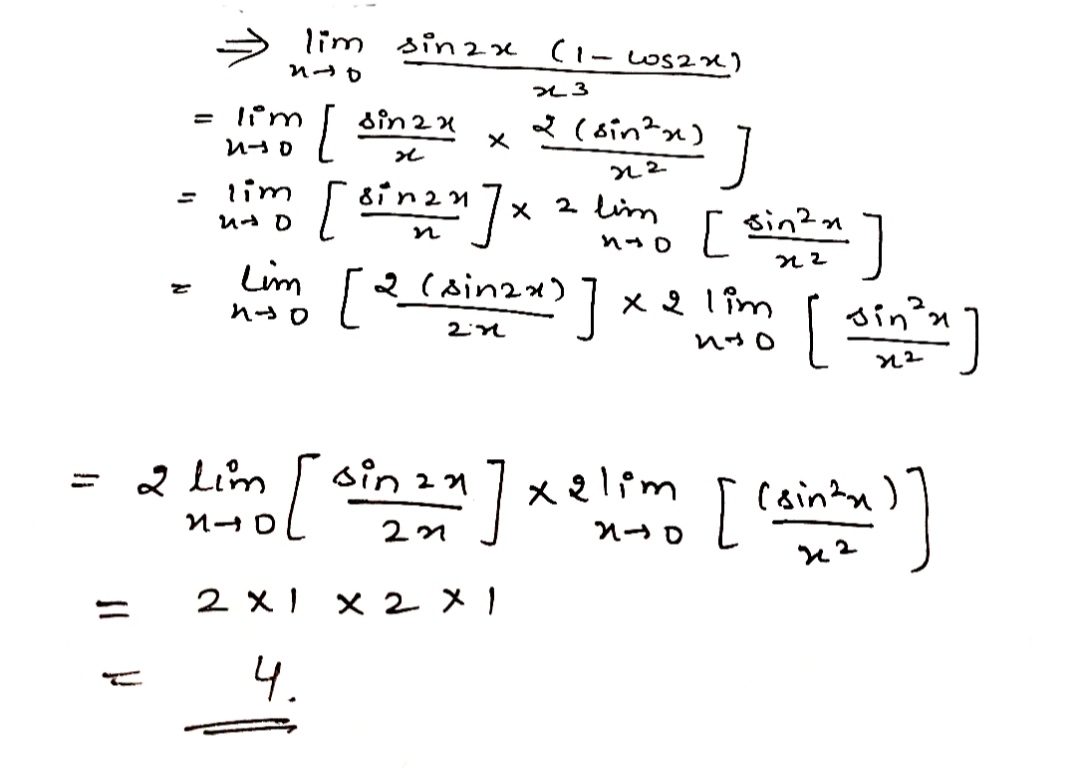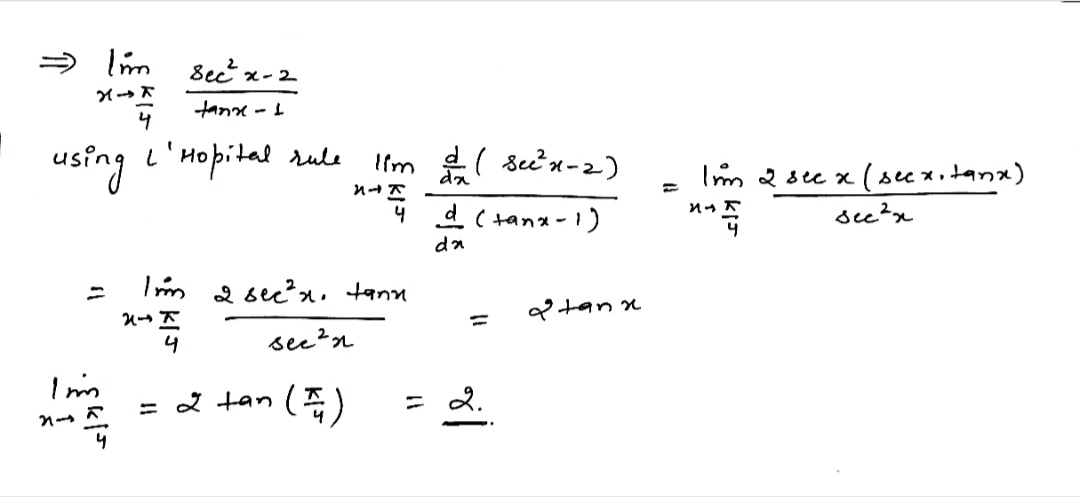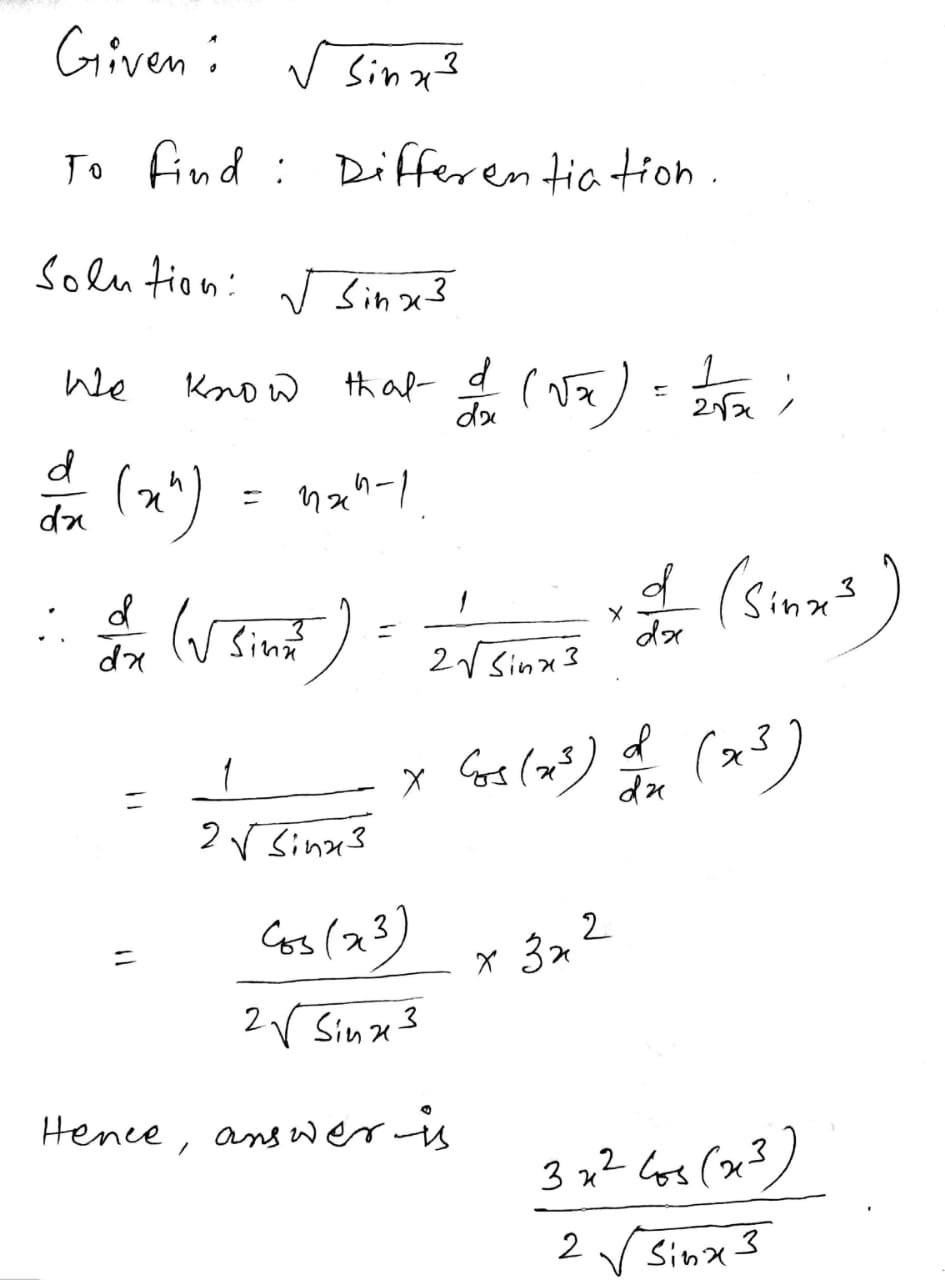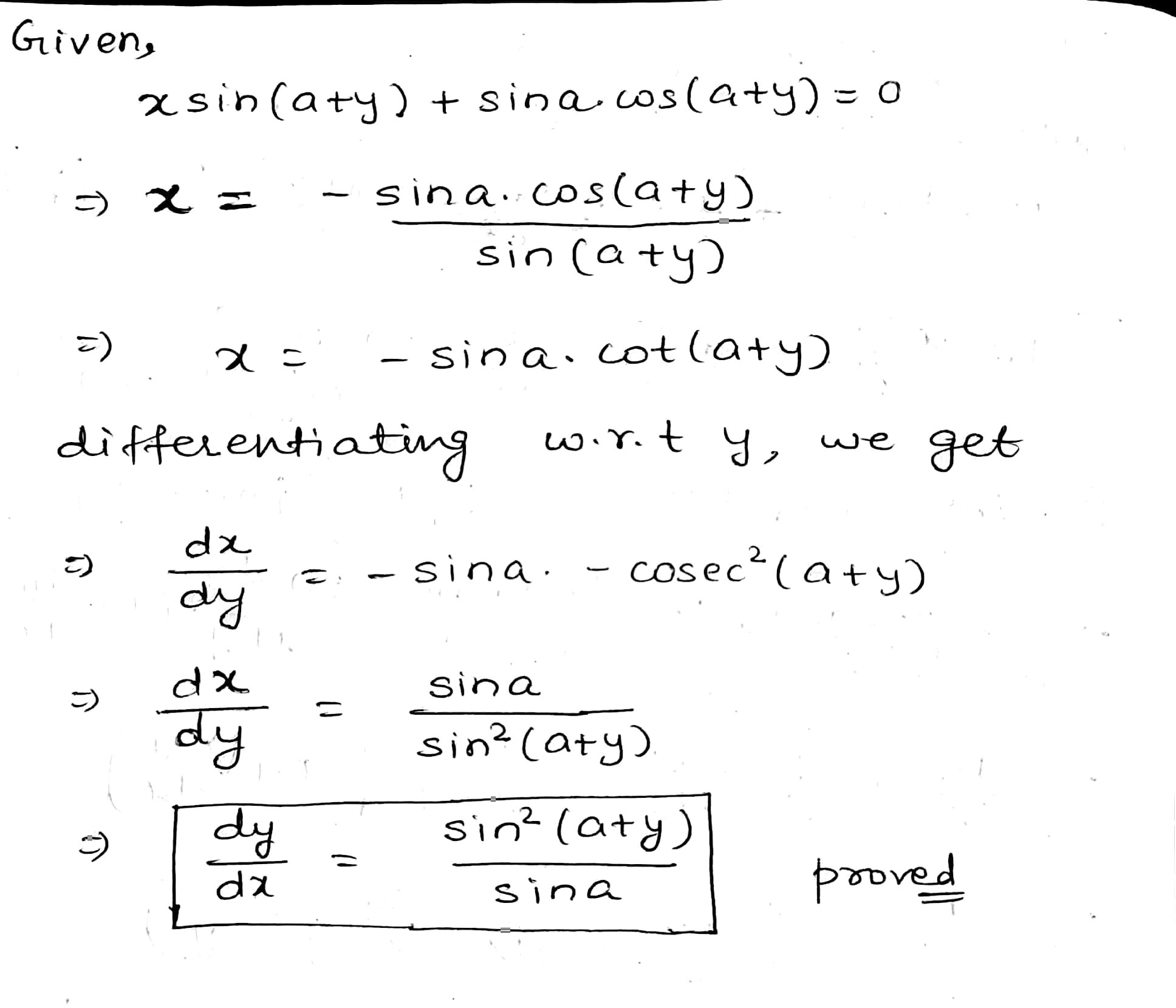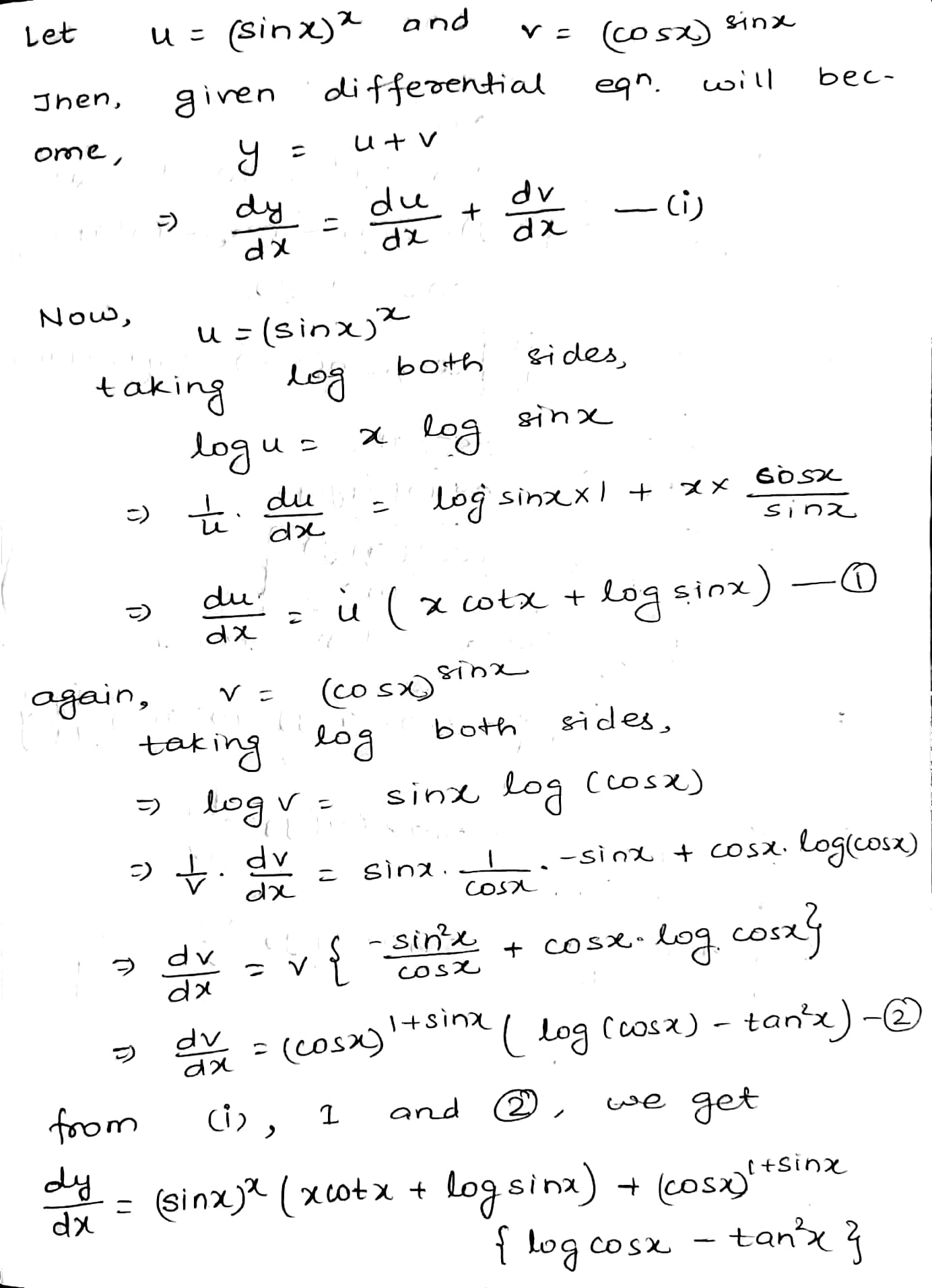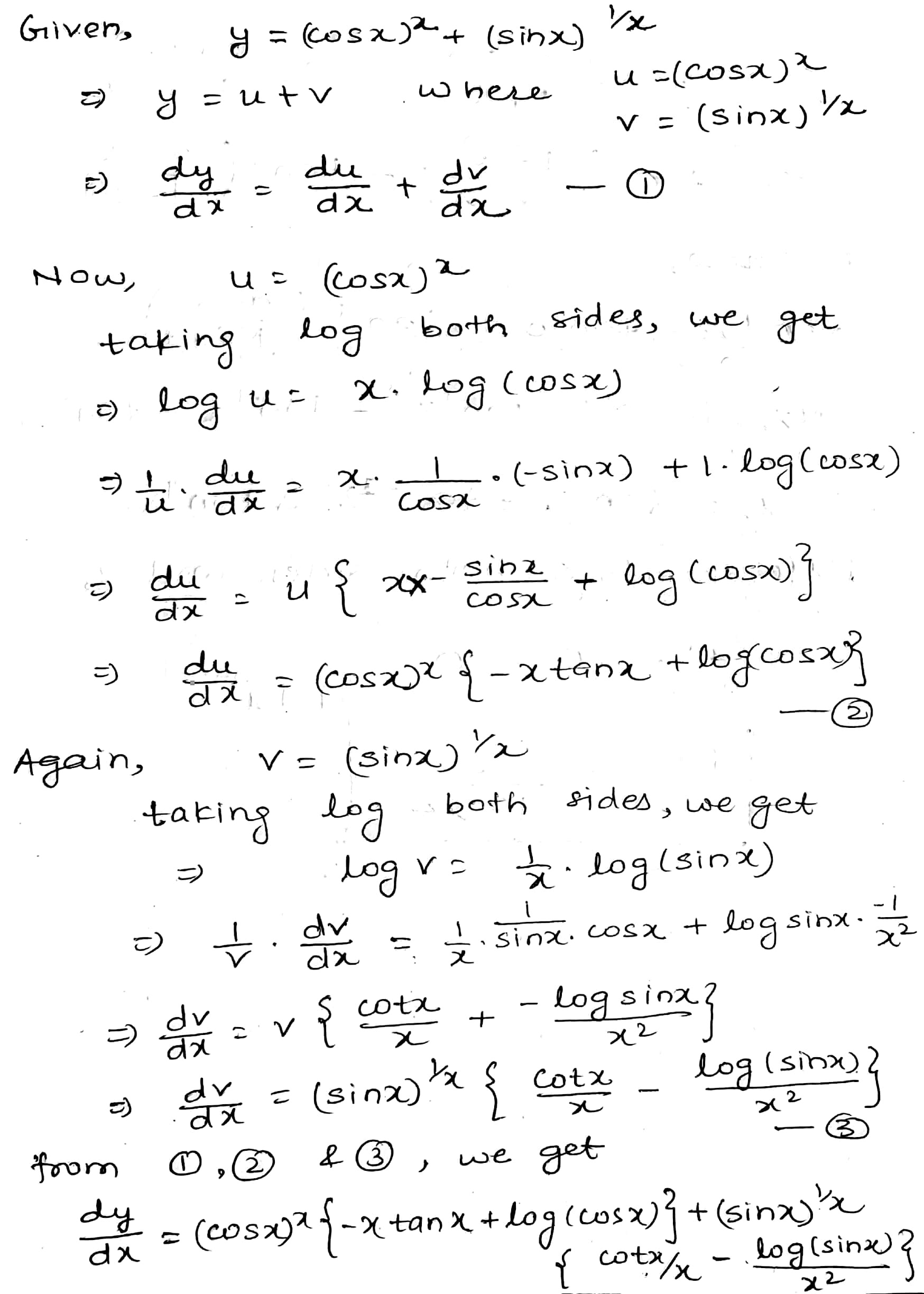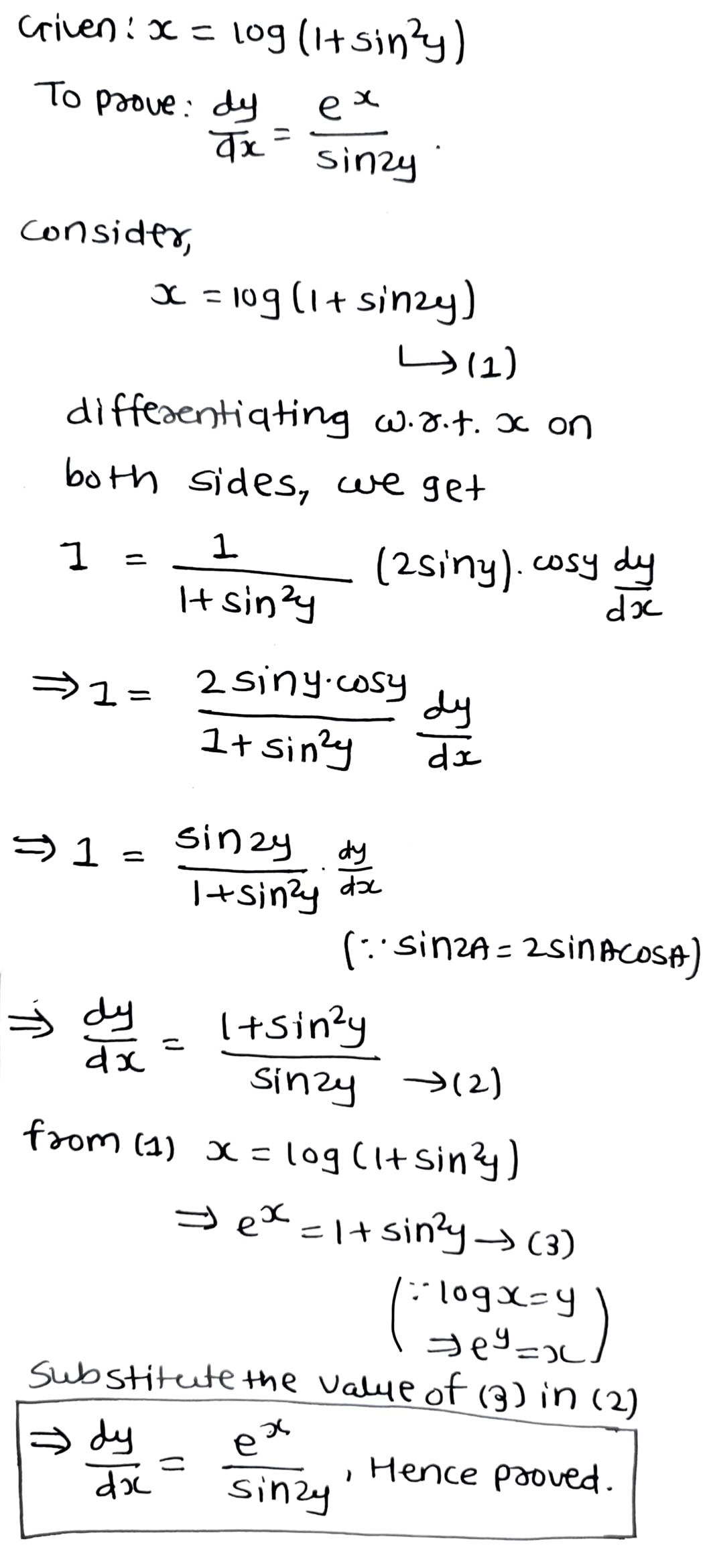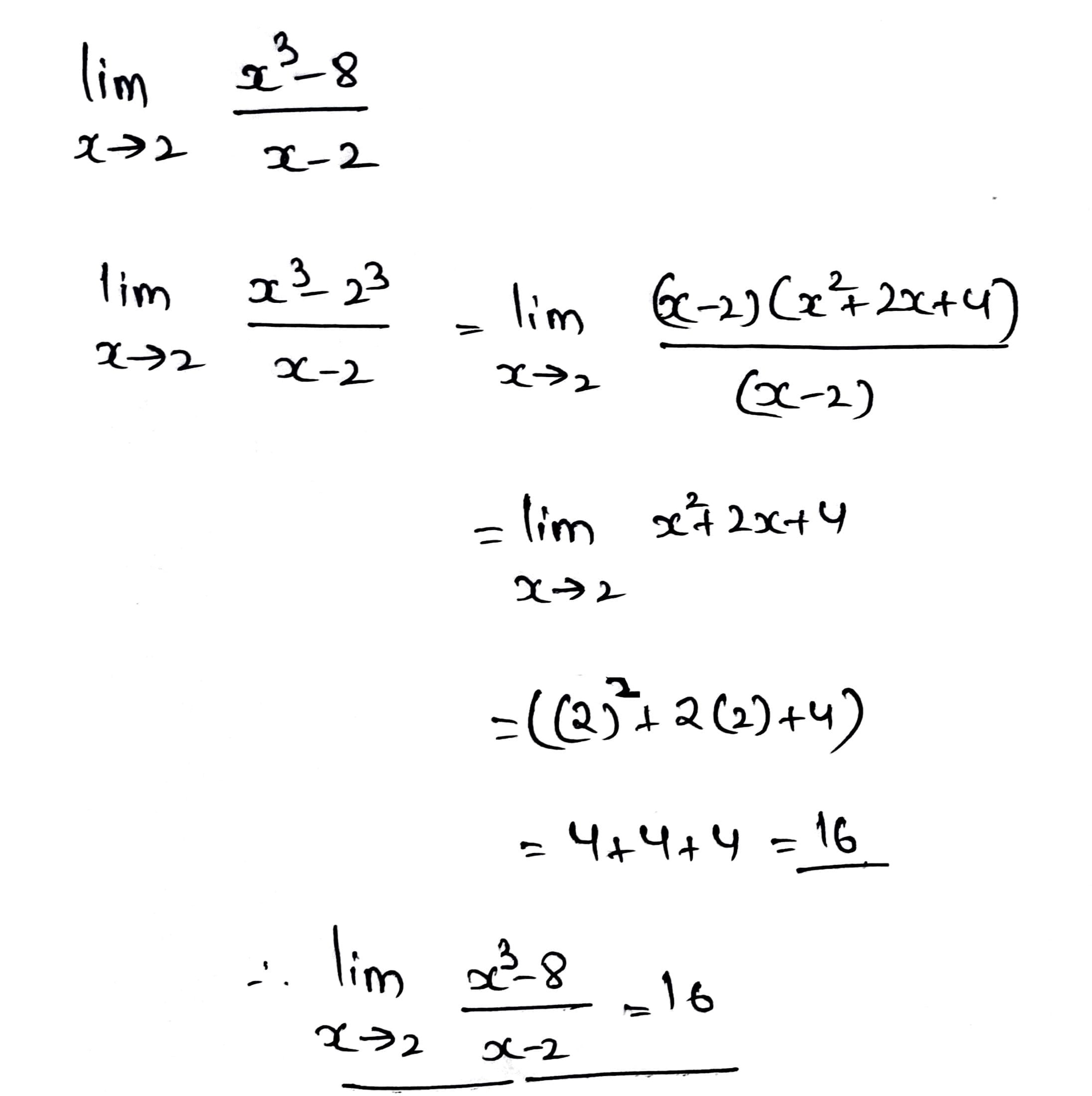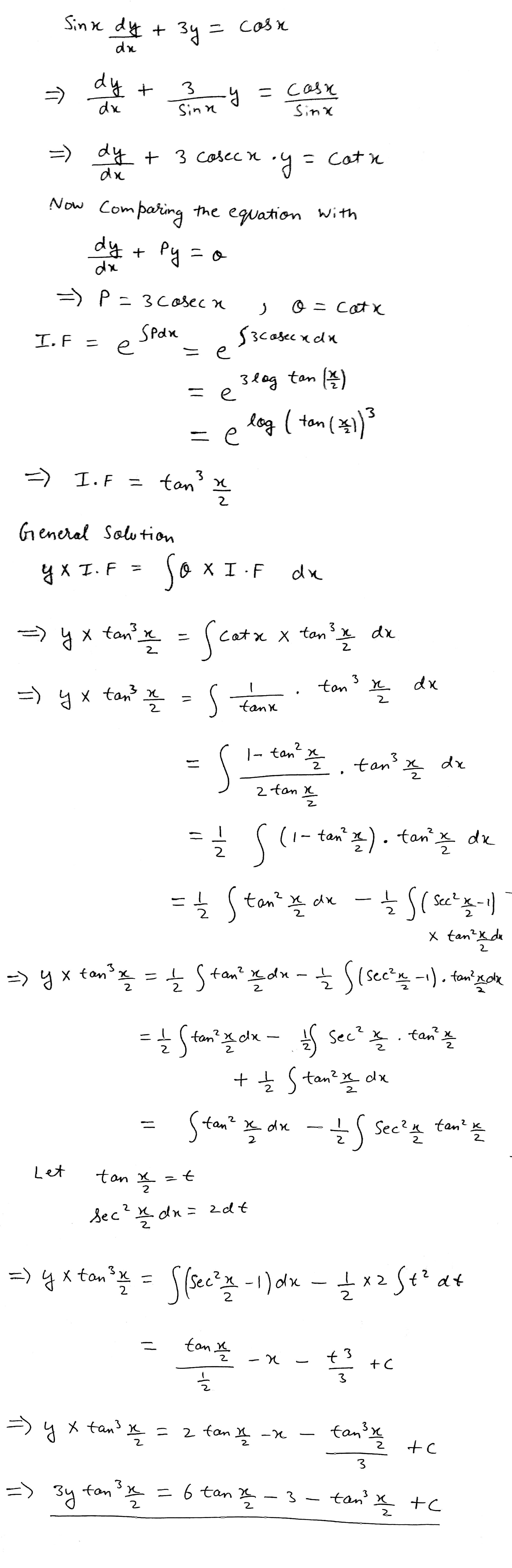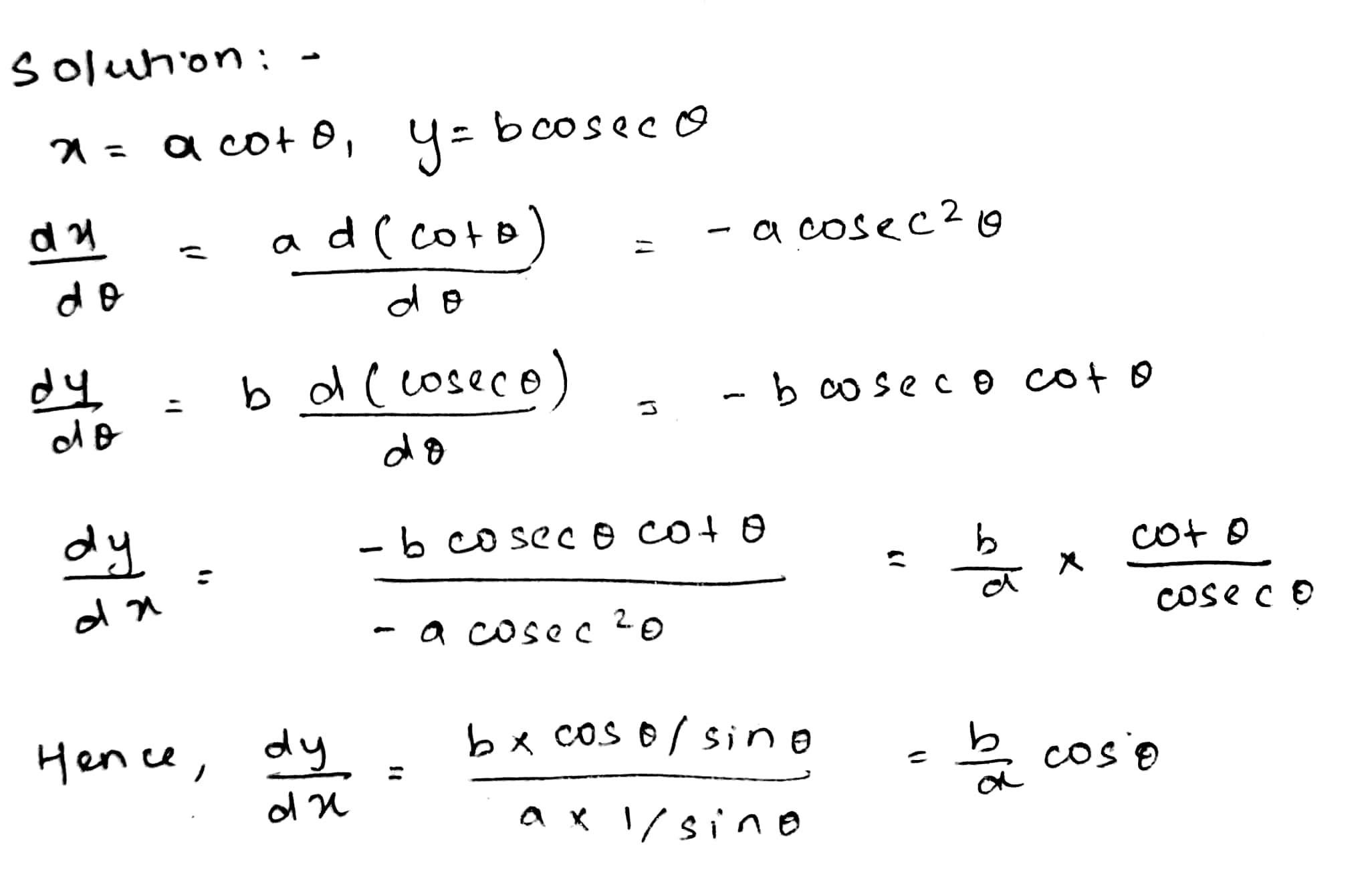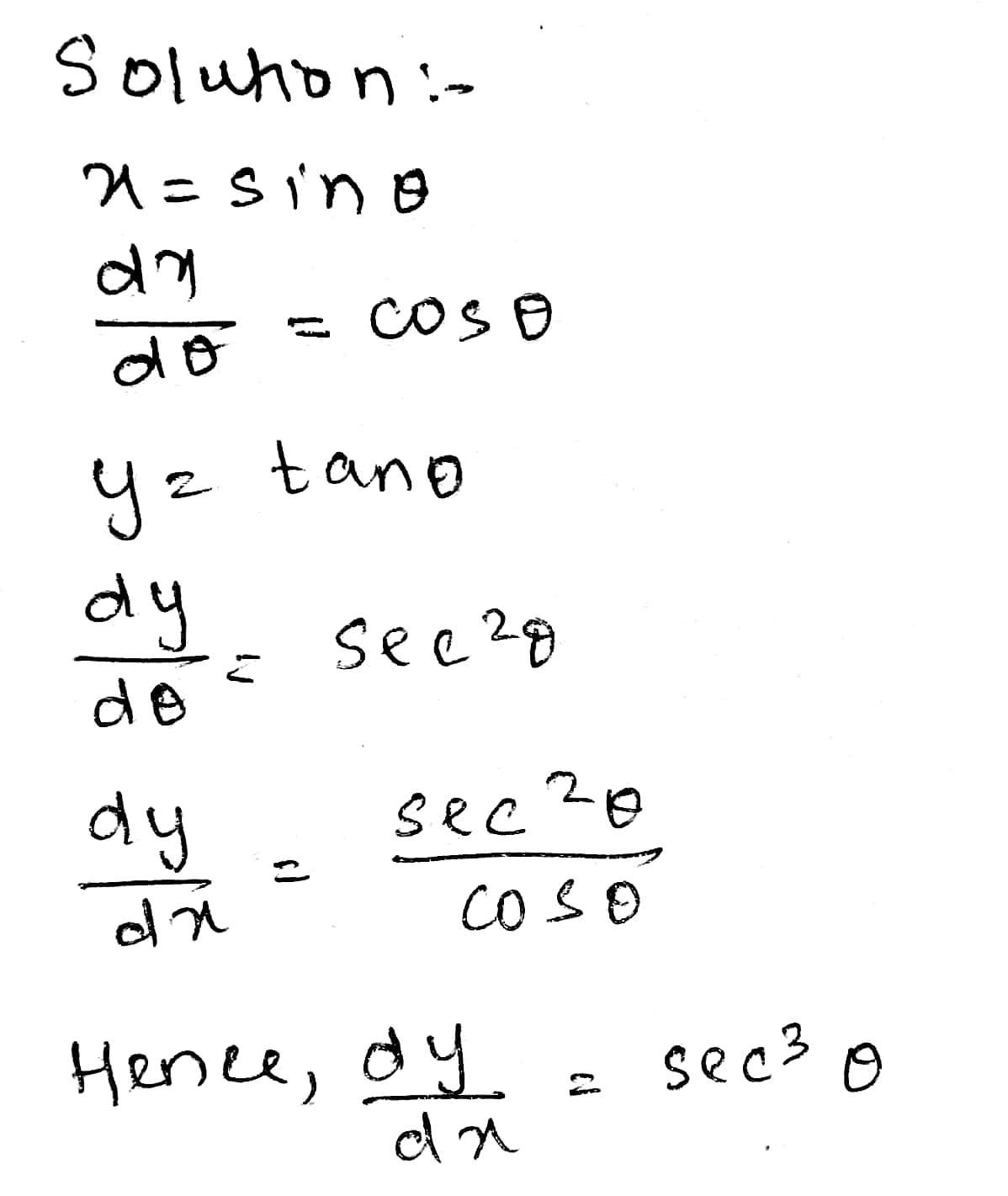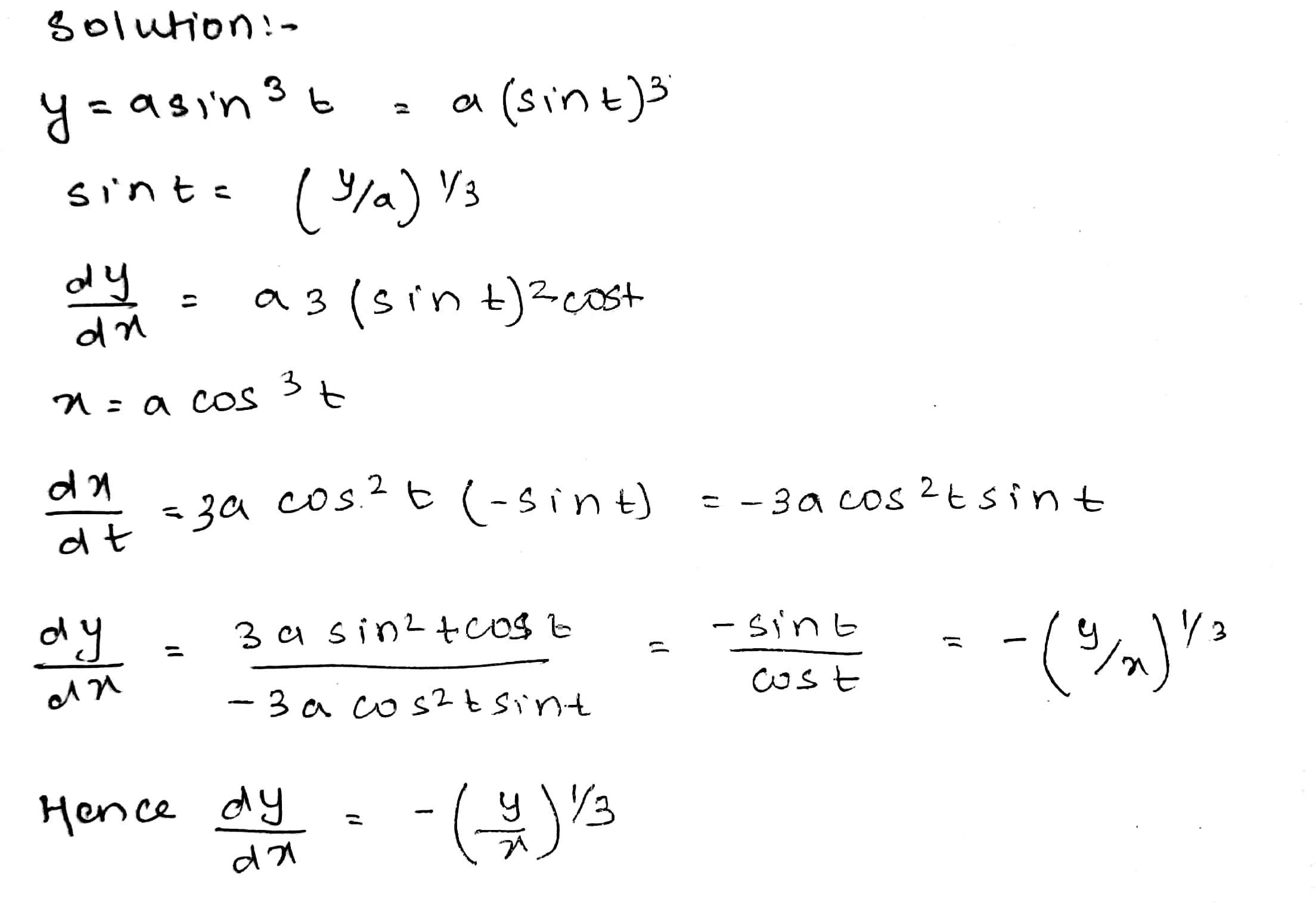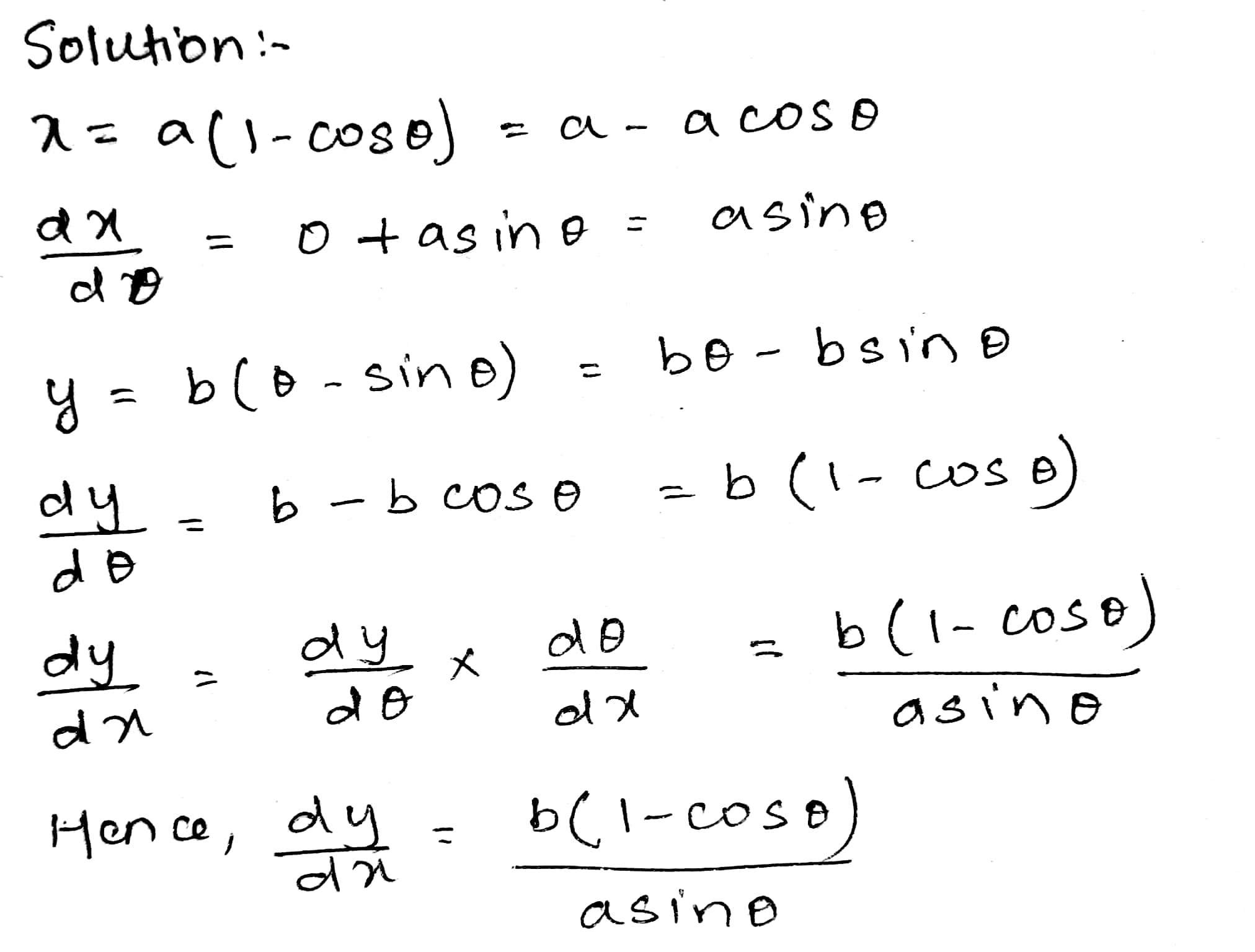Limits And Derivatives - Class 11 Engineering Maths - Extra Questions
The value of the limit $$\underset{x \rightarrow \dfrac{\pi}{2}}{\lim} \dfrac{4 \sqrt{2} (\sin 3x + \sin x)}{\left(2 \sin 2x \sin \dfrac{3x}{2} + \cos \dfrac{5x}{2} \right) - \left(\sqrt{2} + \sqrt{2} \cos 2x + \cos \dfrac{3x}{2}\right)}$$ is ______.
State whether the following statement is true or false.Enter $$1$$ for true and $$0$$ for false$$f(x)$$ is differentiable at a point $$P$$, if there exists a unique tangent at point $$P$$.
State whether the following statement is true or false.
Enter $$1$$ for true and $$0$$ for false
Find the derivative of the following functions from first principle:
$$\displaystyle \cos \left ( x-\frac{\pi }{8} \right )$$
Evaluate the Given limit: $$\displaystyle \lim_{x\rightarrow \pi}\frac{\sin \left ( \pi -x \right )}{\pi \left ( \pi -x \right )}$$
Evaluate : $$\displaystyle \underset{n\, \rightarrow \,
\infty }{Lt} \frac{1}{2^n}$$
Evaluate the given limit: $$\displaystyle \lim_{x\rightarrow 0}\frac{\cos \,x}{\pi -x}$$
Find $$ \displaystyle \frac{dy}{dx} $$ of $$2x + 3y = \sin x$$
Find the derivative of the following functions from first principle:
$$\sin (x + 1) $$
If the derivative of the function $$\displaystyle 4\sqrt{x}-2$$ is $$\dfrac{a}{\sqrt{x}}.$$ Find the value of $$a$$.
Find the derivative of $$\displaystyle 2x-\frac{3}{4}$$
$$\lim_\limits{x\to\frac{\pi}{4}} \dfrac{\sqrt{1-\sqrt{\sin 2x}}}{\pi-4x}=-\dfrac{1}{m}$$.Find $$m$$
Evaluate $$\displaystyle \lim_{x \rightarrow 1}\left( \dfrac{1}{x^2 + x - 2} - \dfrac{x}{x^3 - 1}\right)$$
Differentiate $$\sec x$$ by first principle.
$$\displaystyle\lim _{ x\rightarrow 0 }{ \left[ \dfrac { 8\sin { x } +x\sin { x } }{ 3\tan { x } +{ x }^{ 2 } } \right] } $$ is equal to
If y = log(logx) + $$2sinx$$, find $$\frac{dy}{dx}$$
If $$f(x)=\tan x$$, find $$f'(x)$$ and hence find $$f'\left(\dfrac{\pi}{4}\right)$$.
If $$x = a(\theta + \sin \theta)$$ and $$y = a(1 - \cos \theta)$$, find $$dy/ dx$$.
Write the negation of "some continuous functions are differentiable".
$$Find \ \dfrac{{dy}}{{dx}}\,in\,the\,following:$$
1)$$2x + 3y = \sin x$$
2)$$ax + b{y^2} = \cos x$$
3)$${x^3} + xy + y = 100$$
Differentiate the function with respect to $$x$$.
$$f(x)=$$ $$x^{2/3} + 7e^x - \dfrac{5}{x} + 7\tan x$$
Find $$\dfrac{dy}{dx}$$; $$y=4-x^2$$
Find the integrals of the function :
$$\sin^{2}(2x+5)$$
$$\underset {x\rightarrow 0}{\lim}\dfrac{x-\sin\,x}{x+\cos^2\,x}=$$
If $$y=\sqrt{x^2+1}$$, find $$\dfrac{dy}{dx}$$ at $$x=-1$$
If $$f\left( x \right) = \sin 2x - \cos 2x,$$ find $$f'\left( {\dfrac{\pi}{6}} \right)$$
Evaluate the following: $$\underset{n \rightarrow \infty}{\lim}\dfrac{\cos n + \sin n}{n^2}$$,
Find $$\dfrac{dy}{dx}$$, if $$y = \sin^3 x \, \cos^5 x$$.
Evaluate :$$lim_{x\rightarrow \infty} \dfrac{3x^2+4x+5}{4x^2+7}$$
$$\lim\limits_{x \to 0}\dfrac{\sin x^o}{x}=$$
Find $$\displaystyle \lim_{x \rightarrow \frac {\pi}{2}}[\sin x]$$ where $$[x]$$ indicates greatest integer function
Find the derivative of $$f(x)$$ from the first principles, where $$f(x)$$ is
$$\sin x+\cos x$$
$$\mathop {\lim }\limits_{x \to 1} \left( {1 - x} \right)\tan \left( {\frac{{\pi x}}{2}} \right)$$
$$ \lim_{x\rightarrow 1} f(x) = (1-x) tan(\frac{x\pi }{2}) = f(1) $$
$$ \lim_{x\rightarrow 1} sin(\frac{\pi x}{2}) \frac{1-x}{\frac{cosx\pi }{2}} = \lim_{x\rightarrow 1} sin\frac{\pi x}{2} \lim_{x\rightarrow 1} \frac{1-x}{\frac{cos\pi x}{2}} $$
$$ \Rightarrow (1) \lim_{x\rightarrow 1} \frac{-1}{\frac{-\pi }{2}sin\frac{\pi x}{2}} = \frac{2}{\pi } = f(1) $$
Derivative of :$$(x+1)^2$$
Evaluate $$\underset{x \rightarrow a}{\lim} \dfrac{\sin x - \sin a}{\sqrt{x} - \sqrt{a}}$$
$$ \lim_{x\rightarrow a} \frac{sinx-sina}{\sqrt{x}-\sqrt{a}} $$
$$= \lim_{x\rightarrow a} \frac{(sinx-sina)(\sqrt{x}+\sqrt{a})}{(\sqrt{x}-\sqrt{a})(\sqrt{x}+\sqrt{a})} $$
$$= \lim_{x\rightarrow a} \frac{(sinx-sina)(\sqrt{x}+\sqrt{a})}{x-a} $$
$$= \lim_{x\rightarrow a} \frac{2cos(\frac{x+a}{2})sin(\frac{x-a}{2})\sqrt{x}+\sqrt{a}}{2(\frac{x-a}{2})} $$ $$ (sinx-siny = 2cos(\frac{x+y}{2})sin(\frac{x-y}{2})) $$
$$ = \frac{2cosa2\sqrt{a}}{2} = 2\sqrt{a}cosa(\lim_{x\rightarrow a} \frac{sinx}{x} = 1) $$
$$ \therefore \lim_{x\rightarrow a} \frac{sinx-sina}{\sqrt{x}-\sqrt{a}} = 2\sqrt{a}cosa $$
If $$y = \dfrac {1}{4} (x\pm A)^{2} $$Hence prove: $$y_{1}^{2} = y$$.
Differentiate with respect to $$x$$, where $$y = x - x^2.$$
Solve $$\mathop {\lim }\limits_{x \to 0} \dfrac{{\cos x}}{{\pi - x}}$$
Evaluate $$\underset { x\rightarrow 0 }{ lim\quad } log\frac { sinx }{ x } \\ $$
Find $$\dfrac{dy}{dx}$$
$$y = - x ^ { 3 } + x$$ ...
Find the derivatives of the following:
$$\sin x\cos x$$.
Evaluate :$$\mathop {\lim }\limits_{x \to 0} \cfrac{{{2^x} - 1}}{{{{(1 + x)}^{1/2}} - 1}}$$
$$\mathop {\lim }\limits_{x \to 0} \dfrac{{{e^x} - {e^5}}}{{x - 5}}$$
Evaluate $$\lim_{x\rightarrow \pi/2} \dfrac {\cos x}{\pi-2x}$$
Find the derivative of $$x^{2}$$ - 2 at x = 10
Let $$y=x^2-2$$
$$\dfrac{dy}{dx}=2x$$
$$\dfrac{dy}{dx}$$ at $$x=10$$ is $$2(10)=20$$.
Evaluate $$\mathop {\lim }\limits_{x \to \infty } \dfrac{{5{x^2} + 4}}{{\sqrt {2{x^4} + 1} }}$$
Find the derivative of the following functions:
(i) tan$$x$$cos$$x$$
(ii) sec$$x$$
Evaluate: $$\displaystyle{\lim}_{x\rightarrow2}\dfrac{\sin(x^{2}-5x+6)}{x^{2}-7x+10}$$
$$ = \lim_{x\rightarrow 2} \dfrac{sin(x^{2}-5x+6)}{x^{2}-7x+10} $$
$$ = \lim_{x\rightarrow 2} \dfrac{sin(x-2)(x-3)}{(x-5)(x-2)} $$
$$ = \lim_{x\rightarrow 2} \dfrac{1}{(x-5)} \lim_{x\rightarrow 2} \dfrac{sin(x-3)(x-2)}{(x-2)} $$
$$ = -(\dfrac{1}{3})(-1) = \dfrac{1}{3} $$
$$\mathop {\lim }\limits_{x \to 0} \cfrac{{\sin \left( {\pi {{\cos }^2}x} \right)}}{{{x^2}}}$$
Evaluate : $$\displaystyle \lim _ { x \rightarrow 3 } \dfrac { \sqrt [ 4 ] { x } - \sqrt [ 4 ] { 3 } } { \sqrt [ 3 ] { x } - \sqrt [ 3 ] { 3 } }$$
$$\lim _{ x\rightarrow 0 }{ \dfrac { \tan { x }-\cos x }{ x} } $$ is p then$${p}$$ =
Solve:
$$\lim_{x\to\ 3}\dfrac{x^2-9}{x-3}$$
Find the value of $$\displaystyle x\xrightarrow { lim } 1\frac{\sqrt{x-1}+\sqrt{x}-1}{\sqrt{{x}^{2}-1}}$$
If $$x^2+y^2=t-\dfrac{1}{t}$$ and $$x^4+y^4=t^2+\dfrac{1}{t^2}$$, then prove that $$\dfrac{dy}{dx}=\dfrac{1}{x^3y}$$.
Find the derivative of $$f(x)$$ from the first principle.
$$\sin x\div \cos x$$
Find the derivative by first principle
$$\cos 5 x$$
Evaluate $$\underset { x\rightarrow 0 }{ lim } f(x)$$, where $$f(x)=\{ \overset { { |x| } ,\quad \quad x\neq 0 }{ \underset { 0,\quad \quad x=0 }{ x } } $$
$$\lim _{ x\rightarrow \pi /2 }{ \frac { \sin ^{ }{ x } }{ x } } $$
Find the derivative by first principle in examples to $$( 8 )$$
$$ \cos x $$
If $$y=x^2+5x$$ find $$\dfrac {dy}{dx}$$
$$\dfrac{dy}{dx}=\cos x +\sin x $$
Find $$\dfrac {dy}{dx}$$ if $$y=\dfrac {x^2+x}2$$
$$\displaystyle \lim_{x\rightarrow 0} \tan \left(\dfrac {\pi}{4}+x\right)$$
$$y=\sin x \cos x $$ find $$\dfrac{dy}{dx}$$
If $$y=e^x+\sec x$$, then find $$\dfrac{dy}{dx}$$.
$$\displaystyle \lim _{ x\rightarrow 0 } \left(\dfrac{a}{b}+\dfrac{\cos{x}}{b}\right)$$
Differentiate with respect to $$x$$:
$$3x^2-e^{-3x}+\sec x$$
Find $$\frac { d y } { d x } ,$$ if $$y = \log \left( \sqrt { x } - \frac { 1 } { \sqrt { x } } \right)$$
Differentiate with respect to $$x$$:
$$\cos x+\sin 2x$$
Find $$\dfrac{dy}{dx}$$ if $$y=3x^2+2$$
A curve has equation $$y=(2x-1)^{-1}+2x$$. $$x\neq\dfrac{1}{2}$$
Find $$\dfrac{dy}{dx}$$ and $$\dfrac{d^2y}{dx^2}$$.
$$\lim_{x\rightarrow 3} x^2-3x+1$$
Evaluate $$lim_{ x_\rightarrow 2} \,\dfrac { x ^ { 5 } - 32 } { x ^ { 3 } - 8 } $$
Evaluate $$\lim_{x\rightarrow 2}{(x)^{3}}$$.
Differentiate $$e^x+e^{-x}$$ with respect to x.
$$y=\dfrac{6}{x^2}+2x$$, then find $$\dfrac{dy}{dx}$$.
Differentiate w.r.t. $$x$$:$$y=2x^2-\log x +(x+1)^2$$
If $$y=a^x +\log x +3x^2$$, find $$\dfrac{dy}{dx}$$.
Differentiate with respect to $$x$$:
$$y=e^{-3x}+\sin 2x$$
If $$y=e^x+e^{-x}+\log x^2$$, find $$\dfrac{dy}{dx}$$.
If $$y=2x^3+\dfrac{3}{x^2}$$, then find $$\dfrac{dy}{dx}$$.
Differentiate w.r.t. $$x$$:$$\log e^x+\sin 3x-8$$
If $$y=e^x+x^2+\log x$$, then find $$\dfrac{dy}{dx}$$.
Differentiate with respect to $$x$$:
$$y=\cos x + \sin 2x$$
Differentiate $$e^x+e^{x^2}+....+e^{x^5}$$ w.r.t. $$x$$.
Evaluate the following limits.
$$\displaystyle\lim_{x\rightarrow a}a^3x$$
Answer the following question in one word or one sentence or as per exact requirement of the question.
If the value of $$\displaystyle\lim_{x\rightarrow -\infty}(3x+\sqrt{9x^2-x})$$$$=\dfrac{1}{6b}$$. Find the value of $$b$$?
Answer the following question in one word or one sentence or as per exact requirement of the question.
Write the value of $$\displaystyle\lim_{n\rightarrow \infty}\dfrac{n!+(n-1)!}{(n+1)!+(n+2)!}$$.
Evaluate the following:
$$\displaystyle\lim_{x\rightarrow 0}x^2-3 $$
Differentiate each of the following w.r.t. $$x$$ :
$$\sin 4x$$
Evaluate the following question:$$\displaystyle\lim_{x\rightarrow 2}2x+5 $$
Answer the following question in one word or one sentence or as per exact requirement of the question.
Write the value of $$\displaystyle\lim_{x\rightarrow 0^-}[x]$$.
Evaluate the following limit:
$$\displaystyle\lim_{h\rightarrow 0}\dfrac{\sqrt{x+h}-\sqrt{x}}{h}, x\neq 0$$.
$$\displaystyle\lim_{h\rightarrow 0}\dfrac{\sqrt{x+h}-\sqrt{x}}{h}, x\neq 0$$.
Differentiate
$$ \left ( \dfrac{sec\,x - 1}{sec\,x + 1} \right ) $$
Find derivative of $$ sec\, x $$ by first principle
Differentiate the following w.r.t.x: $$ \sin ^{2} x^{2}-\cos ^{2} x^{2} $$
Find the derivative of following functions w.r.t. $$x$$:
$$\sec x^o$$
If $$\displaystyle \underset{x\rightarrow a}{lim} f\left ( x \right )g\left ( x \right )$$ exists, then does it imply that $$\displaystyle \underset{x\rightarrow a}{lim} f\left ( x \right )$$ and $$\displaystyle \underset{x\rightarrow a}{lim}\ g\left ( x \right )$$ also exist? Yes =5 No=7
Find $$m+n$$
$$\displaystyle \underset{x\rightarrow \infty }{lim} \frac{2\sqrt{x}+3\sqrt[3]{x}+5\sqrt[5]{x}}{\sqrt{\left ( 5x-2 \right )}+\sqrt[3]{\left ( 3x-2 \right )}}$$ is $$\dfrac{m}{\sqrt{n}}$$
Find the value of $$\displaystyle \lim_{x\rightarrow 1}e\left ( 1+\sin \pi x \right )^{\cot \pi x}$$
Match the columns
Extending the functions in col. 1 as $$\lim _{ x\rightarrow \pi }{ f(x)}$$
Let $$\displaystyle f(x)=x+\dfrac {1}{2x+\dfrac {1}{2x+\dfrac {1}{2x+.....\infty}}}$$
Compute the value of $$f(100).f'(100).$$
If the function$$f(x)$$ satisfies $$\displaystyle \lim_{x\rightarrow 1}\frac{f\left ( x \right )-2}{x^{2}-1}=\pi $$ evaluate $$\displaystyle \lim_{x\rightarrow 1}f\left ( x \right )$$
Evaluate the Given limit: $$\displaystyle \lim_{x\rightarrow 0}\frac{\sin \,ax}{bx}$$
Find the derivative of the following functions:$$\displaystyle 2\tan x-7\sec x$$
For some constant $$a$$ and $$b$$, find the derivative of the following functions:
$$(ax^{2} + b)^{2}$$.
Find the derivatives of the following:
$$\sec x$$.
Find $$ \displaystyle \frac{dy}{dx}$$, if $$\displaystyle y = \sin^{-1} x + \sin^{-1} \sqrt{1 - x^2} , - 1 \leq t \leq 1$$
Find the derivatives of the following:
$$3\cot x + 5 cosec x$$.
Find $$\dfrac{dy}{dx}$$ if $$x=a(\cos \theta + \theta \sin \theta)$$. and $$y=a(\sin \theta - \theta \cos \theta)$$.
If $$y + \sin y = \cos x$$, find $$\dfrac{dy}{dx}$$.
Show that when $$n$$ is infinite the limit of $$nx^{n}$$ tends to $$0$$, when $$x> 1$$.
If $$y=\sin ^{ -1 }{ (3x) } +\sec ^{ -1 }{ \left( \cfrac { 1 }{ 3x } \right) } $$, find $$\cfrac { dy }{ dx } $$
If $$x = a sin$$ $$\theta$$ $$+ b cos$$ $$\theta$$, $$y= a cos$$ $$\theta$$ $$- b sin$$ $$\theta$$ , then show that $$(ax + ay)^2$$ + $$(bx - ay)^2$$ = $$(a^2 + b^2)^2$$.
$$\displaystyle \lim _{ x\rightarrow 1 }{ { \left( 2-x+a\left[ x-1 \right] +b\left[ 1+x \right] \right) } } $$ =exists
So find $$a,b$$
Find the following limit:
$$\displaystyle \lim_{x \, \rightarrow \, -2 } \, \frac{x^4 \, + \, 5x^3 \, + \, 6x^2}{x^2 \, - \, 3x \, - \, 10}$$
Calculate the following limits.
$$\displaystyle \lim_{n \, \rightarrow \, \infty} \, \frac{n^2}{1 \, - \, 9n^2}, \, n \, \epsilon \, N.$$
Find the derivative of $$\displaystyle\, y \, =\, (2 \, -\, x^2)\, \cos\, x \, +\, 2x \, \sin\, x$$
Find the following limit:
$$\displaystyle \lim_{x \, \rightarrow \, 1 } \, \left [ \, \left (\frac{x^3 \, - \, 4x}{x^3 \, - \, 8} \right )^{-1} \, - \, \left (\frac{x \, + \, \sqrt{2x}}{x \, - \, 2} \, - \, \frac{\sqrt{2}}{\sqrt{x} \, - \, \sqrt{2}} \right )^{-1} \, \right]$$
Evaluate $$\displaystyle \lim_{x\rightarrow 0} \dfrac {a^{\sin x} - 1}{\sin x}$$.
Find the following limit:
$$\displaystyle \lim_{x \, \rightarrow \, \infty } \, \frac{x^2 \, + \, 3x \, - \, 4}{1 \, - \, 3x^2}.$$
Find the derivative of $$\displaystyle\, y \, =\, \frac{1}{x} \, +\, \frac{1}{x^2} \, +\, \frac{3}{x^3}$$
Find the following limit.
$$\displaystyle \lim_{x \, \rightarrow \, 1 } \, \frac{x^4 \, - \, 2x^2 \, + \, 1}{x^3 \, - \, 1}.$$
Find the following limit.
$$\displaystyle \lim_{x \, \rightarrow \, 0 } \, \frac{(1 \, + \, x) \, (x \, + \, 2x) \, (1 \, + \, 3x) \, - \, 1}{x}.$$
Find the value of $$x$$ for which the derivative of the function $$\displaystyle\, f(x) = 20\, \cos \, 3x + 12\, \cos\, 5x - 15\, \cos\, 4x$$ is equal to zero?
Find the slope of the tangent to the curve $$y = x^{3} - x$$ at $$x = 2$$.
Find the derivative of $$\sin {x}$$ with respect to $$x$$ from first principles.
Find the derivatives of the following functions.
(a) $$\cot^3 \, x$$ (b) $$\sin \, \sqrt{x}$$
Find the derivatives of the following functions at the indicated points.
$$\displaystyle\, f(x) \, = \, sin \, 4x \, cos \, 4x, \, f' \, (\pi/3) \, = \, ?$$
Find the derivative of
$$f(x)=(x^2-5)(x^3-2x+3)$$
Find $$\dfrac{dy}{dx}$$ when $$x$$ and $$y$$ are connected by the relation given:
$$\sin (xy)+\dfrac{x}{y}=x^2-y$$
$$(3x^4-x^3+4)^{5/2}$$ differentiate w.r.t x.
Differentiate $$3x^{1/3} + \frac{6}{7} x^{7/6} +3x^{2/3} +C$$
solve: $$x - \ sin x + C$$
Differentiate$$ \frac{2}{3} x^{3} + \frac{3}{2} x^{2} +C$$
Differentiate$$ \sqrt{2x^{3/2} - 5x^{4/5}}$$
Differentiate$$ \dfrac{ x^4 }{4} - \dfrac{x^{-3}}{3} - \dfrac{2}{x} +C$$
(a) Differentiate $$y = {\cos ^{ - 1}}\left( {\frac{{1 - {x^2}}}{{1 + {x^2}}}} \right)$$ with respect to $$x,0<x<1$$,
(b) Differentiate $${x^x} - {2^{\sin x}}$$ with respect to $$x$$
Solve $$\lim _{ x\rightarrow a }{ \{ \dfrac { { (x+2) }^{ 5/3 }-{ (a+2) }^{ 5/3 } }{ x-a } } \}$$
The value of $$\lim\limits_{x\to 0}\left[\dfrac{\tan x}{x}+\dfrac{\sin x}{x}\right]$$ is
$$y={e}^{x}+{e}^{-x}$$ prove that $$\dfrac { dy }{ dx } =\sqrt { { y }^{ 2 }-4 }$$
$$\lim _{ n\rightarrow \infty }{ \dfrac { \cos { x } +\cos { 3x } +\cos { 5x } +\cos { \left( 2n-1 \right) } x }{ n } } $$ where $$x\neq k\pi ,k\epsilon $$
Differentiate with respect to $$x$$$$y=\sin{2x}-4{e}^{3}x$$
If $$y = \dfrac{{\sin \left( {x + 9} \right)}}{{\cos x}}$$, then $$\dfrac{dy}{{dx}}$$ at $$x = 0$$, is
Solve $$\lim_{x \rightarrow \infty}(\sqrt{x^{2} +ax + a^{2}} - \sqrt{x^{2} + a^{2}})$$ =
Solve: $$\underset{x \rightarrow 0}{lim}\left(\dfrac{1}{x^2} - \cot^2 x\right)$$.
Solve $$x=a(\theta -\sin \theta),y=a(1+\cos \theta )$$ find $$\dfrac{dy}{dx}$$ ?
Examine the graph of $$y=f(x)$$ as shown and evaluate the following limits
(i) $$\lim_\limits{x \to1}f(x)$$
(ii) $$\lim_\limits{x \to2}f(x)$$
(iii) $$\lim_\limits{x \to3}f(x)$$
(iv) $$\lim_\limits{x \to199}f(x)$$
(v) $$\lim_\limits{x \to3^+}f(x)$$
If $${f}_{1}(x)=\cfrac{x}{2}+10\forall x\in R$$ and $${f}_{n}(x)={f}_{1}({f}_{n-1}(x))\forall n\ge 2,n \in N$$, then evaluate $$\lim _{ n\rightarrow \infty }{ { f }_{ n }(x) } $$
$$x=e^{\theta}(\sin\theta+\cos\theta)$$, $$y=e^{\theta}(\sin\theta-\cos\theta)$$Fine $$\dfrac{dy}{dx}$$.
Find the derivative of $$f(x)$$ from the first principles, where $$f(x)$$ is:
$$x \sin x$$
Given a function and we have to find its derivative by the definition. Consider the expression
and find its limit for
The second summand has the limit because
is continuous for any
The first summand has the limit (by the definition of the derivative
Differentiate $$\sqrt {\dfrac{{1 - \tan x}}{{1 + \tan x}}} $$
Find the derivative of $$\sin \left( {x + 1} \right)$$, with respect to $$x$$, from first principle.
Solve: $$\displaystyle\lim_{x\rightarrow \dfrac {3\pi}{4}} \dfrac {2 + \tan x}{5 + 4\tan x}$$.
$$\displaystyle \lim_{x \to 0} \sin \dfrac{\pi}{x}$$
Find
$$\displaystyle \lim_{x \rightarrow \dfrac {5}{2}}[x]$$
$$\lim_{x\rightarrow o}\frac{4sin^{2(x/_{2})cos^{2}(x/_{2})}}{sin^{2}(x/_{2})}=K$$
$$\displaystyle\lim_{x\rightarrow\infty}\dfrac{\cos x+\sin^2x}{x+1}$$.
$$f(x)=\sec x-\cos x,x \epsilon (0,\pi/2)$$find f'(x)
Which of the following limits vanish ?
Solve: $$\underset{x \rightarrow 2}{\lim} \dfrac{(1 - 3^x - 4^x + 12^x)}{\sqrt{(2 \cos x + 7)} - }$$
Solve the equation:-
$$\overset{lim}{n\rightarrow 20}\displaystyle\int_{r=0}^{n-1}\dfrac{n}{n^{1}+r^{2}}$$
Find the limit :-
$$\mathop {\lim }\limits_{x \to 1} \,\,\dfrac{{1 - \dfrac{1}{x}}}{{\sin \,\pi (x - 1)}}$$
$$\lim_{x\rightarrow o}cos\left ( \sqrt{1+x} \right )-cos\sqrt{x}$$.
$$\dfrac{sin2x}{a cos^{2}x+b sin ^{2}x}$$
Solve: $$\displaystyle \int^{1}_{-1} \frac{dx}{x^2 + 2x + 5}$$
Evaluate the following limits
$$\mathop {\lim }\limits_{x \to 0} \left( {\frac{{{e^x} - \sin x}}{x}} \right)$$
$$y = \sin \left( {\pi /6{e^{xy}}} \right){\text{putting}}\;x = 0\;{\text{than}}\dfrac{{dy}}{{dx}}$$
Solve $$\mathop {\lim }\limits_{x \to \infty } {\left( {\frac{{x + 4}}{{x + 2}}} \right)^{x + 3}}$$
Evaluate :
$$\mathop {\lim }\limits_{x \to 0} \frac{{x - \sin x\cos x}}{{{x^3}}}.$$
Solution -
$$ \lim_{x\rightarrow 0} \frac{x-sin\,xcos\,x}{x^{3}} $$
$$ = \lim_{x\rightarrow 0} \frac{1-cos\,x}{x^{2}} $$ because $$ \lim_{x\rightarrow 0} \frac{sin\,x}{x} = 1 $$
Apply L Hospital Rule twice
$$ = \lim_{x\rightarrow 0} \frac{sin\,x}{2x} $$
$$ = \lim_{x\rightarrow 0} \frac{cos\,x}{2} $$
$$ = \frac{1}{2} $$
$$y=6{{x}^{3}}+3{{x}^{2}}+4x+5$$
Find the value of $$\dfrac{dy}{dx}$$?$$\lim_{x\rightarrow 2}\frac{\sum 32x}{x^{3}-p}$$
Solve
$$\mathop {\lim }\limits_{x \to 0} \,\,\dfrac{{\tan 8x}}{{\sin 2x}}$$
Solve the equation:-
$$\lim_{{x\rightarrow \pi/2}}\ \ \dfrac{\tan\ 2x}{x-\pi/2}$$
$$\lim _ { x \rightarrow 0 } \dfrac { 1 - \cos ^ { 3 } x } { x \sin 2 x }$$
$$\displaystyle\lim_{x\rightarrow \frac{\pi}{2}}\dfrac{\tan 2x}{x-\dfrac{\pi}{2}}$$.
Solve $$\lim _ { x \rightarrow 0 } \dfrac { \sqrt { 2 + x } - \sqrt { 2 } } { x }$$
Find differentiation of $$\sec ^ { - 1 } \tan x$$.
Find the diffrentiation of $$xsinx$$.
Solve $$\underset { x\rightarrow 1 }{ \lim } \dfrac { { x }^{ 3 }+{ 3x }^{ 2 }-6x+2 }{ { x }^{ 3 }+{ 3x }^{ 2 }-3x-1 } $$
Find the derivative of $$cosec^2\:x$$, by using first principle of derivatives ?
Let $$y=$$$$\sqrt { x } + 2 x ^ { \dfrac { 3 } { 4 } } + 3 x ^ { \dfrac { 5 } { 6 } } ( x > 0 )$$. Find the derivative of $$y$$ with respect to $$x$$.
Differentiate:
$$y = c ^ { 2 } + \dfrac { c } { x }$$
Solve:
$$\underset { x\rightarrow 0 }{ lim } \dfrac { sin3x }{ x } $$
Evaluate $$ \lim_{x\rightarrow 0}\dfrac { { x }^{ 2 }-\tan 2x }{ \tan x } $$
If $$y=\tan x +\cot x$$ find $$\dfrac{dy}{dx}$$
Evaluate:$$\mathop {\lim }\limits_{x \to \tfrac{\pi }{3}} \dfrac{{\sin \left( {\frac{\pi }{3} - x} \right)}}{{2\cos x - 1}}$$
$$\lim\limits_{x \rightarrow 0}\dfrac{\sin (\pi\, \cos^2\,x)}{x^2}$$=
If $$y=\cos^{-1}\left\{\dfrac{2x-3\sqrt{1-x^{2}}}{\sqrt{13}}\right\}$$, find $$\dfrac{dy}{dx}$$.
Evaluate: $$\lim _{x\to 0}\:\dfrac{e^{\alpha x}-e^{\beta x}}{sin\:\alpha x-sin\:\beta x}$$
Differentiate w.r.t $$x$$
$$e ^ { x }\cos ^ { 3 } x\sin ^ { 2 } x$$
$$lim_{x \rightarrow 1}\dfrac{sin\, \pi\,x}{x-1}$$ is
Solve $$\mathop {\lim }\limits_{x \to 2} \,f\left( x \right) = \mathop {\lim }\limits_{x \to 2} \,\dfrac{{\left( {{x^2} - 4} \right)}}{{\left( {x - 2} \right)}}$$
If $$\dfrac{3}{2}+y^{3}=3axy$$, then find $$ \dfrac {dy}{dx} $$
If $$y = \log \left( {{e^{3x}}{{\left( {\frac{{x - 4}}{{x + 3}}} \right)}^{\frac{2}{3}}}} \right)$$, then find $$\dfrac{{dy}}{{dx}} $$
Find $$\dfrac{dy}{dx}$$, if $$x=a(\theta-\sin \theta)$$ and $$y=a(1-\cos \theta)$$.
Solve:
$$\displaystyle \lim_{n\rightarrow \infty}{\dfrac{1.n+2(n-1)+3(n-2)+.....+n.1}{n^{3}}}$$
$$lim_{x \rightarrow 3}\dfrac{x^5-243}{x^2-9}$$
verify that the function y= $$\sqrt{a^2 - x^2}, x\epsilon (-a,a_)$$ is a solution of the diffrential equation x + y $$\dfrac{dy}{dx}=0, (y \neq 0)$$
$$\dfrac{dy}{dx}=\dfrac{-2x}{2\sqrt{a^2-x^2}}=\dfrac{-x}{\sqrt{a^2-x^2}}$$
$$\Rightarrow x+y\dfrac{dy}{dx}=x-\dfrac{xy}{\sqrt{a^2-x^2}}=x-2$$
$$=0$$.
$$\begin{matrix} lim \\x \xrightarrow\quad 1 \end{matrix}$$ $$\left(\dfrac{1}{x-1} - \dfrac{2}{x^2 - 1}\right)$$
$$\frac{1}{x-1}-\frac{2}{(x+1)(x-1)}=\frac{x+1-2}{(x+1)(x-1)}=\frac{x-1}{(x+1)(x-1)}=\frac{1}{x+1}$$
$$\lim_{x-1} \frac{1}{x+1}=\frac{1}{2}$$
Solve:
$$\displaystyle \lim _{ \theta \rightarrow \pi }{ \dfrac {\pi -\theta}{\sqrt {\cos \theta +1}} } $$
Solve :
$$\displaystyle\lim _{ x\rightarrow 1 }{ \left[ \dfrac { 3 }{ { x }^{ 2 }+x-2 } -\dfrac { 4 }{ { x }^{ 2 }+2x-3 } \right] } $$
Solve:
$$\displaystyle\lim _{ x\rightarrow 2 }{ \dfrac { { x }^{ 6 }+32 }{ x+2 } } $$
$$\displaystyle \lim_{x\rightarrow 2} \frac{x^{6}+32}{x+2}$$
$$ = \frac{2^{6}+32}{2+2}$$
$$ = \frac{64+32}{4} = \frac{96}{4}$$
$$ = 24 $$
$$\lim_{x\rightarrow\ 0}\dfrac{\cos\ x}{\pi-x}$$
$$\lim_{x\rightarrow 0} \frac{cos \, x}{\pi -x}$$
Put x = 0
= $$\frac{cos \,0 }{\pi - 0}$$ $$[\because cos \, 0 = 1]$$
$$= \frac{1}{\pi }$$
Evaluate: $$\displaystyle\lim_{n\rightarrow \infty}(n-\sqrt{n^2+n})$$.
$$\displaystyle\lim_{n\rightarrow \infty}\dfrac{(n-\sqrt{n^2+n})(n+\sqrt{n^2+n})}{(n+\sqrt{n^2+n})}$$
$$=\displaystyle\lim_{n\rightarrow \infty}\dfrac{n^2-n^2-n}{n+\sqrt{n^2+n}}$$
$$=\displaystyle\lim_{n\rightarrow \infty}\dfrac{-1}{1+\sqrt{1+1/n}}$$
$$=\dfrac{-1}{1+1}=\dfrac{-1}{2}$$.
$$\underset { x\rightarrow 3 }{ lim } \left( [x-3] \right) +[3-x]-x$$
Evaluate : $$\underset { x\rightarrow 0 }{ lim } \frac { { 3 }^{ x }-1 }{ \sqrt { 1+x } -1 } $$.
solve $$\underset { x\rightarrow 0 }{ lim } \cfrac { { 5 }^{ x }-{ 4 }^{ x } }{ x } $$
If $$y=\dfrac{(ax+b)(cx+d)}{(ax-b)(cx-d)}, x \neq \dfrac{b}{a}, \dfrac{d}{c}$$ then find $$\dfrac{dy}{dx}$$.
$$\underset { x\rightarrow 1 }{ lim } \cfrac { (\log { (1+x) } -\log { 2 } )(3.{ 4 }^{ x-1 }-3x) }{ \{ { (7+x) }_{ 3 }^{ 1 })-{ (1+3x) }^{ \cfrac { 1 }{ 2 } })\} \sin { \pi x } } $$
$$lim_{x\to \infty} (10e^{3x} +8)^{5/x}$$
$$\displaystyle\lim_{x\rightarrow \infty}(10 e^{3x}+8)^{5/x}$$
$$\Rightarrow \lim_{x\rightarrow \infty} exp(log ((10e^{3x}+8)^{5/x}))$$
$$=\displaystyle\lim_{x\rightarrow \infty} exp\left[\dfrac{s log(10 e^{3x}+8)}{x}\right]$$
$$\Rightarrow exp\left[\displaystyle\lim_{x\rightarrow \infty}\left(\dfrac{s log(10e^{3x}+8)}{x}\right)\right]$$
$$=exp\left[5 \displaystyle\lim_{x\rightarrow \infty}\left(\dfrac{log (10 e^{3x})+log \left(\dfrac{4e^{-3x}}{5}+1\right)}{x}\right)\right]$$
but $$\displaystyle\lim_{x\rightarrow \infty} log\left(\dfrac{4e^{-3x}}{5}+1\right)=0$$
$$\Rightarrow exp\left[5\displaystyle\lim_{x\rightarrow \infty}\left(\dfrac{log(10 e^{3x})}{x}\right)\right]$$
Applying L' Hospital's rule
$$exp\left[5\displaystyle\lim_{x\rightarrow 0}\dfrac{d}{dx}\dfrac{log(10 e^{3x})}{\dfrac{dx}{dx}}\right]$$
$$=exp\left(5\displaystyle\lim_{x\rightarrow \infty}\dfrac{3}{1}\right)=exp(5\times 3)=e^{15}$$.
$$\underset { x\rightarrow 0 }{ lim } \dfrac { { sin(\pi cos }^{ 2 }x) }{ { x }^{ 2 } } $$ is equal to
Find $$\dfrac{dy}{dx}$$, if $$x^{y}+y^{x}=1$$
Let $$b(x. y)=x^y+y^x-1$$
$$b'=0$$
$$b'xdx+b'ydy=0$$
$$b'x+b'y\dfrac{dy}{dx}=0$$
$$\dfrac{dy}{dx}=\dfrac{-b'x}{b'y}=-\dfrac{yx^{y-1}+y^x10y}{xy^{x-1}+x^y10x}$$.
If $$y = \cos ^ { - 1 } \left( \dfrac { 5 \cos x - 12 \sin x } { 13 } \right) , x \in \left( 0 , \dfrac { \pi } { 2 } \right) ,$$ then find the value of $$dy/dx .$$
Solve: $$\underset{x \rightarrow 0}{lim} \dfrac{(x + 1)^5 -1}{x}$$
$$\displaystyle x\xrightarrow { lim } 0\frac{log(2+x)-log(2-x)}{x}$$
Evaluate $$\displaystyle x\xrightarrow { lim }a\, \frac{{x}^{7}-{a}{7}}{x-a} $$
Evaluate$$\lim_{x\rightarrow 0}\dfrac{cos(2x^3)-cos(5x^3)}{xsin^2(2x)tan^3(3x)}$$
Find $$\dfrac{dy}{dx}$$ for $$y=x^{10}+10^x+10x+10$$.
Solve:
$$\displaystyle\lim _{ x\rightarrow 5 }{ \dfrac { x-5 }{ \sqrt { 6x-5 } -\sqrt { 4x+5 } } } $$
Solve:
$$\displaystyle \lim_{x\rightarrow 8}\dfrac {\sqrt {1+\sqrt {1+x}}-2}{x-8}$$
Evaluate : $$\lim_{x-1}\frac{x^{7}-2x^{5}+1}{x^{3}-3x^{2}+2}$$
$$\displaystyle\lim_{x\rightarrow 1}\dfrac{x^{7}-2x^{5}+1}{x^{3}-3x^{2}+2}$$
on differentiating both numertor & denomitator w.r.t x we get
$$\Rightarrow \displaystyle\lim_{x\rightarrow 1} \dfrac{\dfrac{d}{dx}(x^{7}-2x^{5}+1)}{\dfrac{d}{dx}(x^{3}-3x^{2}+2)}$$
$$\Rightarrow \displaystyle\lim_{x\rightarrow 1}\dfrac{7x^{6}-10x^{4}}{3x^{2}-6x}$$
on putting limit we get
$$\Rightarrow \dfrac{7(1)^{6}-10(1)^{4}}{3(1)^{2}-6(1)}$$
$$\dfrac{7-1}{3-6}$$
$$=\dfrac{-3}{-3}$$ $$=1$$
Hence $$\displaystyle\lim_{x\rightarrow 1} \dfrac{x^{7}-2x^{5}+1}{x^{3}-3x^{2}+2}$$
$$=1$$
Hence $$\displaystyle\lim_{x\rightarrow 1} \dfrac{x^{7}-2x^{5}1}{x^{3}-3x^{2}+2}=1$$.
if $$\displaystyle \lim_{x\rightarrow 2}\dfrac{ x^5-32}{x^2-4}$$
Evaluate $$\displaystyle \lim _{ x\rightarrow 0 } \dfrac{3\sin{x}-\sin{3x}}{x^{2}}$$
$$\underset{x\rightarrow 0}{Lt}\dfrac{3\sin x-\sin 3x}{x^2}$$
$$\underset{x\rightarrow 0}{Lt}\dfrac{3\sin x-3\sin x+4\sin^3x}{x^2}$$ $$[\sin 3x=3\sin x-4\sin^3x]$$
$$=\underset{x\rightarrow 0}{Lt}4\left(\dfrac{\sin x}{x}\right)^2\sin x$$
$$\underset{x\rightarrow 0}{Lt}\dfrac{\sin x}{x}=1$$
$$=\underset{x\rightarrow 0}{Lt}4\sin x=4\sin 0=0$$.
$$\text{Show that}$$ $$f\left(x\right)=\dfrac{x\tan{2x}}{\sin{3x}\sin{5x}}$$ for $$x\neq \,0, f(0)=\dfrac{2}{17} \, \text{is discontinuous at x=0}$$.
$$\displaystyle \lim_{x\rightarrow 1}\left(\dfrac{1}{1-x}-\dfrac{3}{1-x^{3}}\right)$$ is equal to
Find the slope of tangent to the curve $$y=3x^{2}-6$$ at the point on it whose x-coordinate is 2.
Differentiate $$y=\sin{b{x}^{2}}$$ w.r.t $$x$$
Differentiate $$y=\left(x+a\right)\left({x}^{2}+{a}^{2}\right)$$ w.r.t $$x$$
Given:
$$y = {\tan ^{ - 1}}\left( {\dfrac{{3x - {x^3}}}{{1 - 3{x^2}}}} \right), - \dfrac{1}{{\sqrt 3 }} < x < \dfrac{1}{{\sqrt 3 }}.$$ Then find $$\dfrac{dy}{dx}$$.
Find $$\dfrac{dy}{dx}$$ $$( x + y ) \frac { d y } { d x } = 1$$
If $$y=\dfrac { { 2x }^{ 9 } }{ 3 } -\dfrac { 5 }{ 7 } { x }^{ 7 }+6{ x }^{ 3 }$$ find $$\dfrac { dy }{ dx } $$ at x =1
Differentiate : y = 5 sin x + 3 cos x
Find the derivative of $${\csc}^{2}{x}$$, by using first principle of derivatives.
Using the $$\in -\delta $$ definition prove that $$\underset { x\rightarrow 1 }{ lim } \left( 2x-1 \right) =1$$
The function $$f(x)=2x-1$$ is a polynomial and as such it is continuous for every $$x\in R$$. Then $$\displaystyle\lim_{x\rightarrow 1}f(x)=f(1)=2\times 1-1=2-1=1$$
To prove it by using the definition of limit,
$$|f(x)-1|=|2x-1-1|=2|x-1|$$
For $$x\in (1-f, 1+f)$$ with $$f > 0$$, we have
$$|f(x)-1|=2|x-1|< 2f$$
Given any $$\in > 0$$, choose $$f_{\in} < \in/2$$ s.t
$$x\in (1-f_{\in}, 1+f_{\in})$$
$$\Rightarrow |f(x)-1| < 2f_{\in} < \in$$
which proves the result.
Differentiate $$ \dfrac { 1 }{ 3 } { \tan }^{ 3 }{x}-\tan{x}+x$$ w.r.t $$x$$
Find the derivative of $$ \sin \sqrt{x} $$ from the first principle.
Prove that the limit of $$f\left(x\right)=2x-3$$ as $$x$$ approaches $$5$$ is $$7$$ using the $$\epsilon-\delta$$ proof.
The function $$f(x)=2x-3$$ is a polynomial and as such it is continuous for every $$x\in R$$. Then, $$\displaystyle\lim_{x\rightarrow 5}f(x)=f(5)=2\times 5-3=10-3=7$$
To prove it using the definition of limit,
$$|f(x)-7|=|2x-3-7|=|2x-10|=2|x-5|$$
For $$x\in (5-f, 5+f)$$ with $$f > 0$$ then we have $$|f(x)-7|=2|x-5| < 2f$$
Given any $$\in > 0$$, choose $$f_{\in} < \in/2$$ s.t
$$x\in (5-f_{in}, 5+f_{\in})$$
$$\Rightarrow |f(x)-7| < 2f_{\in} < \in$$
which proves the limit.
$$\int { \dfrac { dx }{ { x }^{ 2 }+1 } } $$
If $$x=a\sin { 2t(1+\cos { 2t } ) } $$ and $$y=b\cos { 2t } (1-\cos { 2t } )$$, find $$\dfrac { dy }{ dx } $$ at $$t=\dfrac { \pi }{ 4 } $$.
Differentiate the following functions with respect to $$x$$
$$(x \cos x)^x +(x\sin x)^{1/x}$$
Differentiate the following functions with respect to $$x$$:
$$\log (3x-2)-x^2 \log (2x-1)$$
Differentiate with respect to $$x$$:
$$e^{3x}-6x^3+\tan x$$
If $$y=e^{-x}+\log x -\sec^2x$$, then find $$\dfrac{dy}{dx}$$.
Find the intervals in which the following functions are increasing or decreasing
$$f(x)=10-6x-2{ x }^{ 2 }$$
Differentiate with respect to $$x$$:
$$e^{-x}+\log x+\sin 2x$$
Differentiate the following functions with respect to $$x$$:
$$x\sin 2x+5^x +k^k +(\tan^2 x)^2$$
Differentiate the following functions with respect to $$x$$:
$$\cos^{-1}\left\{\dfrac {x}{\sqrt {x^2 + a^2}}\right\}$$
Find $$\dfrac{dy}{dx}$$, if $$y=e^{3x}+\sin (2x^5)$$.
Evaluate the following limits.
$$\displaystyle\lim_{x\rightarrow 1}\dfrac{\sqrt{x+8}}{\sqrt{x}}$$.
Solve the following differential equation.
$$\dfrac{dy}{dx}=x^2$$.
Show that $$f(x)=x-\sin x$$ is increasing for all $$x\in R$$
Evaluate the following limits.
$$\displaystyle\lim_{x\rightarrow 0}9$$.
Evaluate the following limits.
$$\displaystyle\lim_{x\rightarrow 2}(3-x)$$.
Evaluate the following limits.
$$\displaystyle\lim_{x\rightarrow 3}\dfrac{\sqrt{2x+3}}{x+3}$$.
If $$\displaystyle\lim_{x\rightarrow 2}\dfrac{\sqrt{3-x}-1}{2-x}$$ $$=\dfrac 1 a$$, then $$a$$ is equal to ____.
Evaluate the following limits.
$$\displaystyle\lim_{x\rightarrow 1}\dfrac{1-x^{-1/3}}{1-x^{-2/3}}$$.
Evaluate the following limits.
$$\displaystyle\lim_{x\rightarrow 3}\dfrac{x^4-81}{x^2-9}$$.
Evaluate the following limits.
$$\displaystyle\lim_{x\rightarrow 1}\dfrac{\sqrt{5x-4}-\sqrt{x}}{x-1}$$.
If $$\displaystyle\lim_{x\rightarrow 0}\dfrac{\sqrt{1+x}-\sqrt{1-x}}{2x}$$$$=\dfrac 1 a$$, then $$a$$ is equal to ____.
Evaluate the following limits.
$$\displaystyle\lim_{x\rightarrow 3}\dfrac{x-3}{\sqrt{x-2}-\sqrt{4-x}}$$.
Evaluate the following limits.
$$\displaystyle\lim_{x\rightarrow 0}\dfrac{x}{\sqrt{1+x}-\sqrt{1-x}}$$.
If $$\displaystyle\lim_{x\rightarrow 7}\dfrac{4-\sqrt{9+x}}{1-\sqrt{8-x}}$$$$=\dfrac 1 a$$, then $$a$$ is equal to ____.
Evaluate the following limits.
$$\displaystyle\lim_{x\rightarrow 0}\dfrac{\sqrt{1+3x}-\sqrt{1-3x}}{x}$$.
Evaluate the following limits.
$$\displaystyle\lim_{x\rightarrow 5}\dfrac{x-5}{\sqrt{6x-5}-\sqrt{4x+5}}$$.
If $$\displaystyle\lim_{x\rightarrow 0}\dfrac{\sqrt{1+x}-1}{x}$$$$=\dfrac 1 a$$, then $$a$$ is equal to ____.
Evaluate: $$\displaystyle\lim_{h\rightarrow 0}\dfrac{\sqrt{x+h}-\sqrt{x}}{h}, x\neq 0$$.
Evaluate the following limits.
$$\displaystyle\lim_{n\rightarrow \infty}\left(1+\dfrac{x}{n}\right)^n$$$$=e^{ax}$$. Find the value of $$a?$$
Differentiate the following function with respect to x.$$\dfrac{ax+b}{px^2+qx+r}$$.
If $$\displaystyle\lim_{x\rightarrow 3}\dfrac{x^n-3^n}{x-3}=108$$, find the value of n.
Evaluate the following limits.
$$\displaystyle\lim_{x\rightarrow 0}\dfrac{e^x-x-1}{2}$$.
Evaluate the following question:
$$\displaystyle\lim_{x\rightarrow 0}x^2-3 $$
Evaluate the following limit:-
$$\displaystyle\lim_{x\rightarrow 0}\dfrac{ax+x\cos x}{b\sin x}$$.
Evaluate the following limits.
$$\displaystyle\lim_{x\rightarrow 0}\dfrac{\cos 2x-1}{\cos x-1}$$.
Find the derivative of $$f(x)=99x$$ at $$x=100$$.
Differentiate the following function with respect to x.$$\dfrac{1}{\sin x}$$.
Find the derivative of $$f(x)=x$$ at $$x=1$$.
Answer the following question in one word or one sentence or as per exact requirement of the question.
Write the value of $$\displaystyle\lim_{x\rightarrow 1^-}x-[x]$$.
Answer the following question in one word or one sentence or as per exact requirement of the question.
Write the value of $$\displaystyle\lim_{x\rightarrow 2}\dfrac{|x-2|}{x-2}$$.
Write the value of $$\displaystyle\lim_{x\rightarrow \infty}\dfrac{1+2+3+...…+n}{n^2}$$.
Differentiate the following function with respect to x.$$\dfrac{x+\cos x}{\tan x}$$.
Differentiate the following function with respect to x.
$$\dfrac{x^n}{\sin x}$$.
Differentiate the following from first principle.
$$\cos\left(x-\dfrac{\pi}{8}\right)$$.
Differentiate the following w.r.t. $$x$$ :
$$\cos 4x \cos 2x$$
Differentiate the following w.r.t. $$x$$ :
$$\sin 5x \cos 3x$$
Find $$\dfrac {dy}{dx}$$, where $$y \sec x + \tan x +x^2 y=0$$.
Differentiate using first principle
$$\sqrt {cosec\ (x^3 +1)}$$
Differentiate the following function with respect to x.
$$\dfrac{4x+5\sin x}{3x+7\cos x}$$.
Differentiate the following w.r.t. $$x$$ :
$$\sin 2x \sin x$$
Find $$\dfrac {dy}{dx}$$, where $$\sin^2 x+2\cos y+xy =0$$.
Find $$\dfrac {dy}{dx}$$, where $$x \sin 2y= y\cos 2x$$.
Answer the following question in one word or one sentence or as per exact requirement of the question.
If $$\dfrac{\pi}{2} < x <\pi$$, then find $$\dfrac{d}{dx}\left(\sqrt{\dfrac{1+\cos 2x}{2}}\right)$$.
Find $$\dfrac {dy}{dx}$$, when $$y=(\tan x)^{1/x}$$.
If $$\cos y=x\cos (y+a)$$, prove that $$\dfrac {dy}{dx}=\dfrac {\cos^2 (y+a)}{\sin a}$$.
Find $$\dfrac {dy}{dx}$$, where :
$$\tan (x+y)+\tan (x-y)=1$$
If $$xy=\tan (xy)$$, show that $$\dfrac {dy}{dx}=\dfrac {-y}{x}$$
Differentiate the following w.r.t.$$x$$:
$$e^{\cot x}$$
Find $$\dfrac {dy}{dx}$$, where $$y\tan x-y^2 \cos x +2x =0$$
Find $$\dfrac {dy}{dx}$$, when $$y=x^{\sin x}$$.
Find $$\dfrac {dy}{dx}$$, where $$\cot (xy)+xy =y$$.
Different the following w.r.t.$$x$$:
$$e^{\sqrt{\sin x}}$$
If $$y=\sin\left\{2\tan^{-1}\left(\sqrt{\dfrac{1-x}{1+x}}\right)\right\}$$. show that $$\dfrac{dy}{dx}=\dfrac{-x}{\sqrt{1-x^{2}}}$$
If $$y=(\sin x)^{(\sin x)^{(\sin x) ...... \infty}}$$, prove that $$\dfrac{dy}{dx}=\dfrac{y^{2}\cot x}{(1-y\log \sin x)}$$
Find $$\dfrac {dy}{dx}$$, when $$y=(\tan x)^{\sin x}$$.
Find $$\dfrac {dy}{dx}$$, when $$y=\sin (x^x)$$.
Find $$\dfrac {dy}{dx}$$, when $$y=\cos x \cos 2x \cos 3x$$.
Find $$\dfrac {dy}{dx}$$, when $$y=(\cos x)^{\cos x}$$.
If $$y=(\cos x)^{(\cos x)^{(\cos x).....\infty}}$$, prove that $$\dfrac{dy}{dx}=\dfrac{-y^{2}\tan x}{(1-y\log \cos x)}$$
Find $$\dfrac {dy}{dx}$$, when $$y=x^{\sin 2x}$$.
Find $$\dfrac {dy}{dx}$$, when $$y=\sin 2x \sin 3x \sin 4x$$.
Find $$\dfrac {dy}{dx}$$, when $$y=(\sin x)^{\cos x}$$.
Find $$\dfrac {dy}{dx}$$, when $$y=(\tan x)^{\cot x}$$.
If $$y=\sqrt{\cos x+\sqrt{\cos x+\sqrt{\cos x+.......\infty}}}$$, prove that $$\dfrac{dy}{dx}=\dfrac{\sin x}{(1-2y)}$$
Find $$\dfrac {dy}{dx}$$, when :
$$y=x^{\sin x}+(\sin x)^{\cos x}$$
Find $$\dfrac {dy}{dx}$$, when $$y=\dfrac {x^3 \sin x}{e^x}$$.
Find $$\dfrac {dy}{dx}$$, when :
$$y=(x \cos x)^x +(x \sin x)^{1/x}$$
Differentiate $$e^{\sin x}$$ with respect to $$\cos x$$.
Find $$\dfrac {dy}{dx}$$, when $$y=2^x . e^{3x} \sin 4x$$.
Find $$\dfrac {dy}{dx}$$, when $$y=x^{x\cos x} +\left (\dfrac {x^2 +1}{x^2 -1}\right)$$.
Find $$\dfrac {dy}{dx}$$, when :
$$y=(\sin x)^x +\sin^{-1}\sqrt x$$
Find $$\dfrac {dy}{dx}$$, when $$y=e^x \sin^3 x\cos^4 x$$.
Differentiate $$\sin^3 x $$ with respect to $$\cos^3x$$.
Find $$\dfrac {dy}{dx}$$, when $$(\tan x)^y =(\tan y)^x$$
Find $$\dfrac {dy}{dx}$$, when $$(\cos x)^y =(\cos y)^x$$
Find $$\dfrac{dy}{dx}$$, when $$x=a\cos^2\theta, y=b\sin^2\theta$$.
Find $$\dfrac{dy}{dx}$$, when $$x=\cos \theta+\cos 2\theta, y=\sin \theta+\sin 2\theta$$.
Find $$\dfrac{dy}{dx}$$, when $$x=a\cos^3\theta, y=a\sin^3\theta$$.
Find $$\dfrac{dy}{dx}$$, when $$x=a(1-\cos \theta), y=a(\theta+\sin \theta)$$.
Find $$\dfrac{dy}{dx}$$, when $$x=a\cos \theta, y=b\sin \theta$$.
Find $$\dfrac{dy}{dx}$$, when $$x=\sqrt{\sin 2\theta}, y=\sqrt{\cos 2\theta}$$.
If $$y=\sqrt{\tan x+\sqrt{\tan x+\sqrt{\tan x+.......\infty}}}$$, prove that $$\dfrac{dy}{dx}=\dfrac{\sec^{2}x }{(2y-1)}$$
If $$y=e^{\sin x}+(\tan x)^x$$, prove that. $$\dfrac {dy}{dx}=e^{\sin x}\cos x+(\tan x)^x [2x\ \text cosec 2x+\log \tan x]$$.
Evaluate the following limit:
$$\displaystyle \lim_{x\rightarrow 0}{\dfrac{\tan 3x}{\tan 5x}}$$
Evaluate the following limit:
$$\displaystyle \lim_{x\rightarrow 0}{\dfrac{\sin 5x}{\sin 8x}}$$
Evaluate the following limit:
$$\displaystyle \lim_{x\rightarrow 0}{\dfrac{\tan \alpha x}{\tan \beta x}}$$
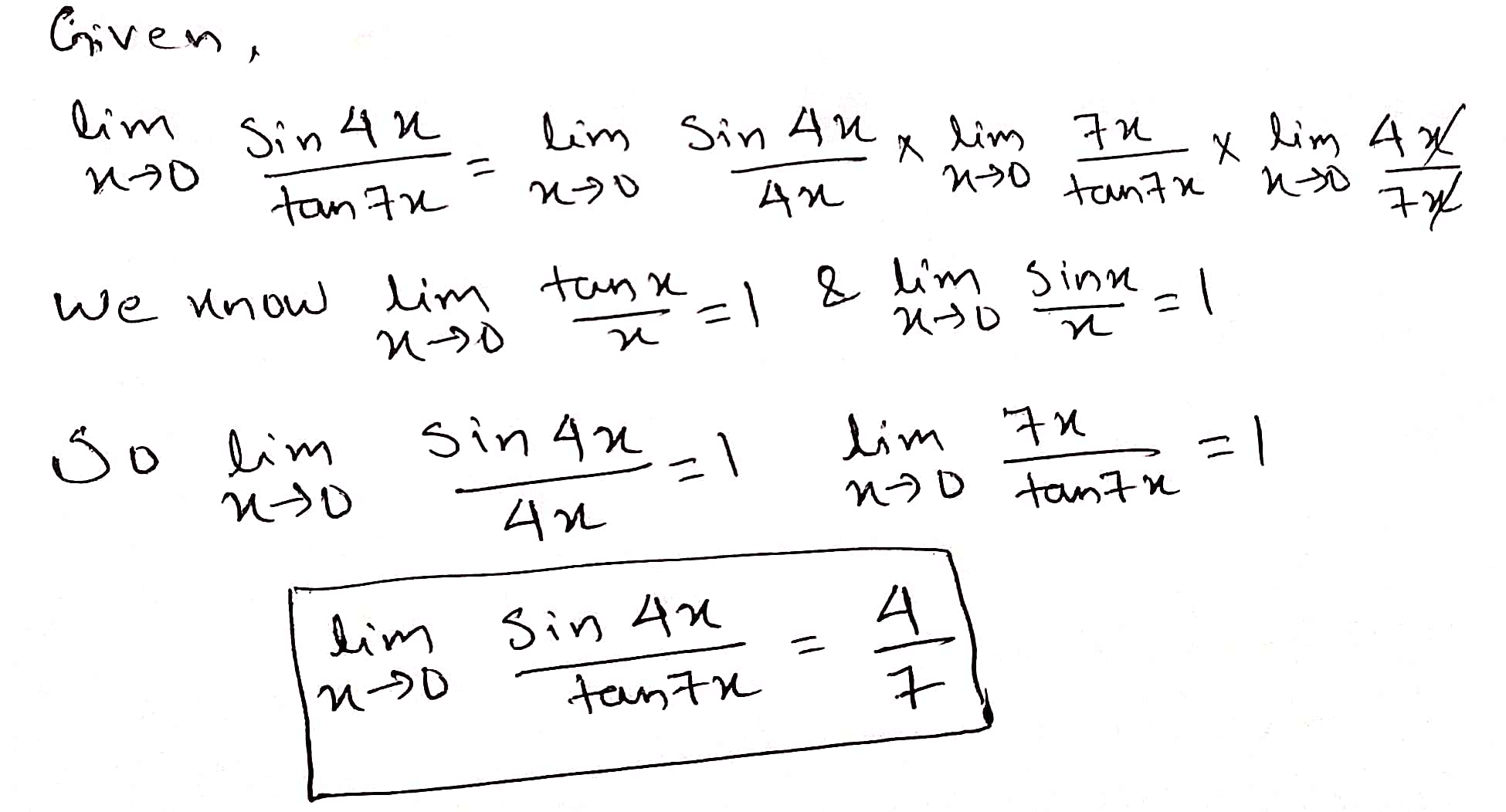
Evaluate the following limit:
$$\displaystyle \lim_{x\rightarrow 0}{\dfrac{\sin 4x}{\tan 7x}}$$
Evaluate the following limit:
$$\displaystyle \lim_{x\rightarrow 0}{\dfrac{(x\cos x+\sin x)}{(x^2+\tan x)}}$$
Evaluate the following limit:
$$\displaystyle \lim_{x\rightarrow 0}{\dfrac{(\tan 2x-x)}{(3x-\tan x)}}$$
Evaluate the following limit:
$$\displaystyle \lim_{x\rightarrow 0}{\dfrac{\sin mx}{\tan nx}}$$
Evaluate the following limit:
$$\displaystyle \lim_{x\rightarrow 0}{\dfrac{(\tan x-\sin x)}{\sin^3x}}$$
Evaluate the following limit:
$$\displaystyle \lim_{x\rightarrow 0}{(x\csc x)}$$
Evaluate the following limit:
$$\displaystyle \lim_{x\rightarrow 0}{\dfrac{(x^2-\tan 2x)}{\tan x}}$$
Evaluate the following limit:
$$\displaystyle \lim_{x\rightarrow 0}{\dfrac{\tan 3x}{\sin 4x}}$$
Evaluate the following limit:
$$\displaystyle \lim_{x\rightarrow \dfrac{\pi}{6}}{\dfrac{(2\sin^2x+\sin x-1)}{(2\sin^2x-3\sin x+1)}}$$
Evaluate the following limit:
$$\displaystyle \lim_{x\rightarrow 0}{\dfrac{(\sin 2x+3x)}{(2x+\sin 3x)}}$$
Evaluate the following limit:
$$\displaystyle \lim_{x\rightarrow 0}{(x\cot 2x)}$$
Evaluate the following limit:
$$\displaystyle \lim_{x\rightarrow 0}{\dfrac{(\tan x-\sin x)}{x^3}}$$
Evaluate the following limit:
$$\displaystyle \lim_{x\rightarrow 0}{\dfrac{(1-\cos 4x)}{(1-\cos 6x)}}$$
Evaluate the following limit:
$$\displaystyle \lim_{x\rightarrow 0}{\dfrac{(1-\cos x)}{\sin^2x}}$$
Evaluate the following limit:
$$\displaystyle \lim_{x\rightarrow 0}{\dfrac{(2\sin x-\sin 2x)}{x^3}}$$
Evaluate the following limit:
$$\displaystyle \lim_{x\rightarrow 0}{\dfrac{(1-\cos mx)}{(1-\cos nx)}}$$
Evaluate the following limit:
$$\displaystyle \lim_{x\rightarrow 0}{\dfrac{(\tan 2x-\sin 2x)}{x^3}}$$
Evaluate the following limit:
$$\displaystyle \lim_{x\rightarrow 0}{\dfrac{(1-\cos 2x)}{\sin^2 2x}}$$
Evaluate the following limit:
$$\displaystyle \lim_{x\rightarrow 0}{\dfrac{(1-\cos 2x)}{3\tan^2x}}$$
Evaluate the following limit:
$$\displaystyle \lim_{x\rightarrow 0}{\dfrac{(\csc x-\cot x)}{x}}$$
Evaluate the following limit:
$$\displaystyle \lim_{x\rightarrow 0}{\dfrac{\sin x \cos x}{3x}}$$
Evaluate the following limit:
$$\displaystyle \lim_{x\rightarrow \dfrac{\pi}{4}}{\dfrac{(1-\tan x)}{\left(x-\dfrac{\pi}{4}\right)}}$$
Evaluate the following limit:
$$\displaystyle \lim_{x\rightarrow a}{\dfrac{(\cos x-\cos a)}{(x-a)}}$$
Evaluate the following limit:
$$\displaystyle \lim_{x\rightarrow 0}{\dfrac{\sin 2x(1-\cos 2x)}{x^3}}$$
Evaluate the following limit:
$$\displaystyle \lim_{x\rightarrow a}{\dfrac{(\sin x-\sin a)}{(x-a)}}$$
Evaluate the following limit:
$$\displaystyle \lim_{x\rightarrow \dfrac{\pi}{2}}{\dfrac{(1+\cos 2x)}{(\pi-2x)^2}}$$
Evaluate the following limit:
$$\displaystyle \lim_{x\rightarrow 0}{\dfrac{(\sin 5x-\sin 3x)}{\sin x}}$$
Evaluate the following limit:
$$\displaystyle \lim_{x\rightarrow 0\dfrac{\pi}{4}}{\dfrac{(\csc^2x-2)}{(\cot x-1)}}$$
Evaluate the following limit:
$$\displaystyle \lim_{x\rightarrow \pi}{\dfrac{(\sin 3x-3\sin x)}{(\pi-x)^3}}$$
Evaluate the following limit:
$$\displaystyle \lim_{x\rightarrow \dfrac{\pi}{4}}{\dfrac{(\sec^2x-2)}{(\tan x-1)}}$$
Evaluate the following limit:
$$\displaystyle \lim_{x\rightarrow a}{\dfrac{(\sin x-\sin a)}{(\sqrt x-\sqrt a)}}$$
Evaluate the following limit:
$$\displaystyle \lim_{x\rightarrow \dfrac{\pi}{2}}{\left(\dfrac{\pi}{2}-x\right)}\tan x$$
Evaluate the following limit:
$$\displaystyle \lim_{x\rightarrow 0}{\dfrac{(\sqrt{1+2x}-\sqrt{1-2x})}{\sin x}}$$
Evaluate the following limit:
$$\displaystyle \lim_{x\rightarrow 0}{\dfrac{(1-\cos 2x)}{(\cos 2x-\cos 8x)}}$$
Evaluate the following limit:
$$\displaystyle \lim_{x\rightarrow 0}{\dfrac{[\sin (2+x)-\sin (2-x)]}{x}}$$
Evaluate the following limit:
$$\displaystyle \lim_{x\rightarrow 0}{\dfrac{\sin ax+bx}{ax+\sin bx}}$$, where $$a, b, a+b \neq 0$$
Evaluate the following limit:
$$\displaystyle \lim_{h\rightarrow 0}{\dfrac{(a+h)^2\sin (a+h)-a^2\sin a}{h}}$$
Evaluate the following limit:
$$\displaystyle \lim_{x\rightarrow 0}{\dfrac{(\cos 3x-\cos 5x)}{x^2}}$$
Evaluate the following limit:
$$\displaystyle \lim_{x\rightarrow 0}{\dfrac{\sin (\pi-x)}{\pi (\pi-x)}}$$
Evaluate the following limit:
$$\displaystyle \lim_{x\rightarrow 0}{\dfrac{(\sin 3x+\sin 5x)}{(\sin 6x-\sin 4x)}}$$
Evaluate the following limit:
$$\displaystyle \lim_{x\rightarrow 0}{\dfrac{(e^{\tan x}-1)}{\tan x}}$$
Evaluate the following limit:
$$\displaystyle \lim_{x\rightarrow 0}{\dfrac{1-\cos mx}{1-\cos nx}}$$
Evaluate the following limit:
$$\displaystyle \lim_{x\rightarrow 0}{\dfrac{\sqrt 2-\sqrt{1+\cos x}}{\sin^2x}}$$
Evaluate the following limit:
$$\displaystyle \lim_{x\rightarrow \dfrac{\pi}{2}}{\dfrac{\tan 2x}{x-\dfrac{\pi}{2}}}$$
Evaluate the following limit:
$$\displaystyle \lim_{x\rightarrow 0}{\dfrac{1-\cos 2mx}{1-\cos 2nx}}$$
Evaluate the following limit:
$$\displaystyle \lim_{x\rightarrow 0}{\dfrac{\sec 4x-\sec 2x}{\sec 3x-\sec x}}$$
Evaluate the following limit:
$$\displaystyle \lim_{x\rightarrow 0}{\dfrac{\sin^2 mx}{\sin^2 nx}}$$
Evaluate the following limit:
$$\displaystyle \lim_{x\rightarrow 0}{\dfrac{\sin 2x+\sin 3x}{2x+\sin 3x}}$$
Evaluate the following limit:
$$\displaystyle \lim_{x\rightarrow \dfrac{\pi}{6}}{\dfrac{2-\sqrt 3\cos x-\sin x}{(6x-\pi)^2}}$$
Evaluate the following limit:
$$\displaystyle \lim_{x\rightarrow 0}{(\csc x-\cot x)}$$
Evaluate the following limit:
$$\displaystyle \lim_{x\rightarrow 0}{\dfrac{\sqrt{1+\sin x}-\sqrt{1-\sin x}}{x}}$$
Evaluate the following limit:
$$\displaystyle \lim_{x\rightarrow \dfrac{\pi}{4}}{\dfrac{\tan^3x-\tan x}{\cos \left(x+\dfrac{\pi}{4}\right)}}$$
Evaluate the following limit:
$$\displaystyle \lim_{x\rightarrow 0}{\dfrac{\cos ax-\cos bx}{\cos cx -1}}$$
Evaluate the following limit:
$$\displaystyle \lim_{x\rightarrow \pi}{\dfrac{\sqrt{2+\cos x}-1}{(\pi -x)^2}}$$
Differentiate the following function :
$$\dfrac {x-4}{2\sqrt x}$$
Evaluate the following limit:
$$\displaystyle \lim_{x\rightarrow \dfrac{\pi}{6}}{\dfrac{2\sin^2x+\sin x-1}{2\sin^2x-3\sin x+1}}$$
Evaluate the following limit:
$$\displaystyle \lim_{x\rightarrow \dfrac{\pi}{6}}{\dfrac{\cot^2x-3}{\csc x-2}}$$
Evaluate the following limit:
$$\displaystyle \lim_{x\rightarrow \dfrac{\pi}{2}}{\dfrac{\sqrt 2-\sqrt{1+\sin x}}{\sqrt 2 \cos^2x}}$$
Evaluate the following limit:
$$\displaystyle \lim_{x\rightarrow \dfrac{\pi}{4}}{\dfrac{1-\tan x}{1-\sqrt 2\sin x}}$$
If $$y=6x^5 -4x^4 -2x^2+5x-9$$, find $$\dfrac {dy}{dx}$$ at $$x=-1$$
Evaluate the following limit:
$$\displaystyle \lim_{x\rightarrow 0}{\dfrac{\cos x-\cos a}{\cot x-\cot a}}$$
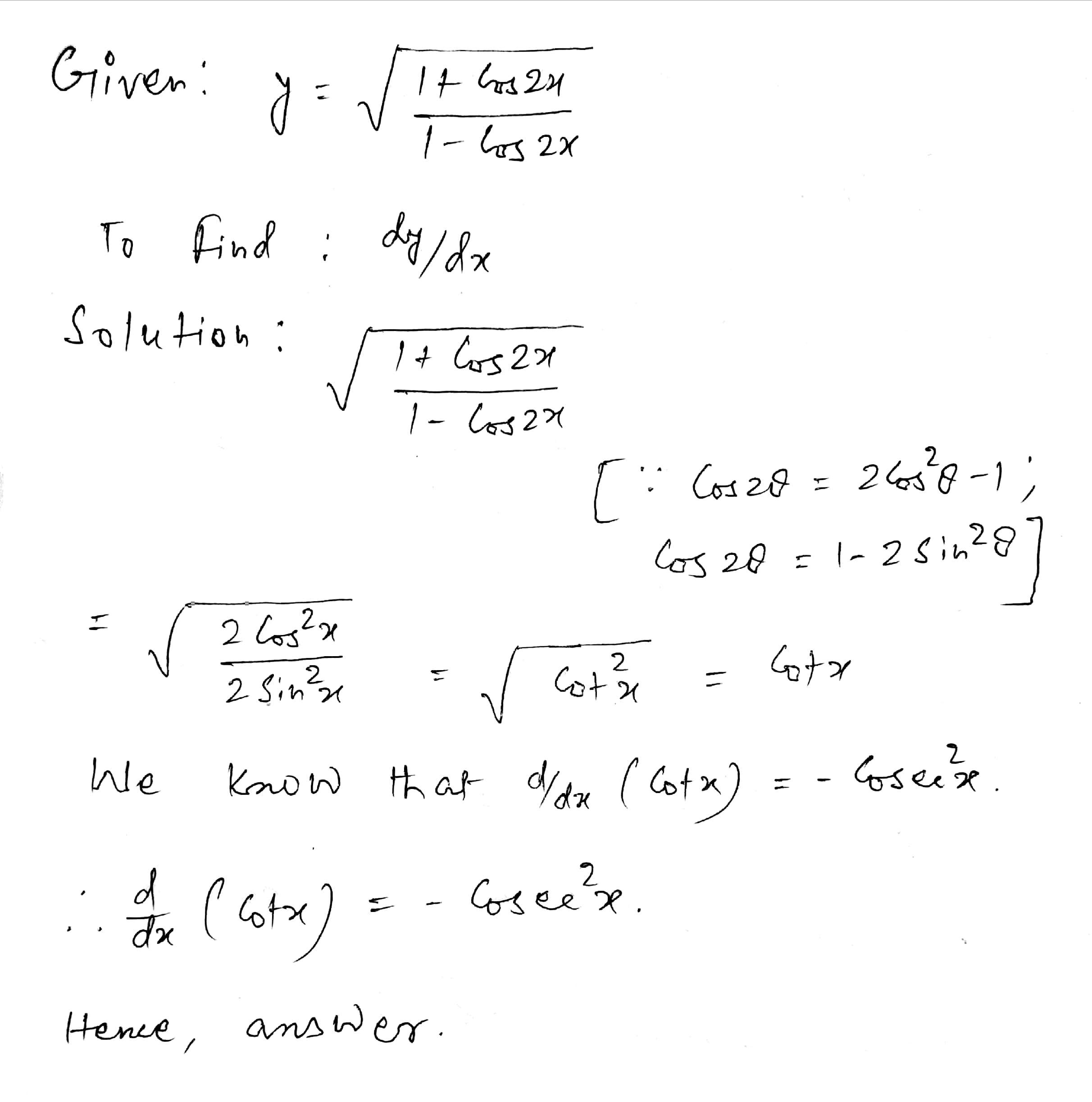
If $$y=\sqrt {\dfrac {1+\cos 2x}{1-\cos 2x}}$$, find $$\dfrac {dy}{dx}$$.
Differentiate:
$$\dfrac{x\tan x}{(\sec x+\tan x)}$$
Differentiate the following with respect to $$x$$:
$$\sqrt{\sin x^3}$$
Differentiate:
$$\cot x$$
Differentiate the following with respect to $$x$$:
$$\tan^3 x$$
Differentiate the following with respect to $$x$$:
$$\sin^2 (2x+3)$$
Differentiate the following with respect to $$x$$:
$$\cos^2 x^3$$
Differentiate the following with respect to $$x$$:
$$e^{\cot x}$$
Differentiate the following with respect to $$x$$:
$$\sqrt{\sin x}$$
Differentiate the following with respect to $$x$$:
$$\cot^2 x$$
Differentiate:
$$\sec x$$
Differentiate the following with respect to $$x$$:
$$\cos (\sin \sqrt{ax+b})$$
Differentiate the following with respect to $$x$$:
$$\cos 3x\sin 5x$$
Differentiate the following with respect to $$x$$:
$$e^{(x\sin x+\cos x)}$$
Differentiate the following with respect to $$x$$:
$$e^{2x}\sin 3x$$
Differentiate the following with respect to $$x$$:
$$\sqrt{\cot \sqrt x}$$
Differentiate the following with respect to $$x$$:
$$\sqrt{x\sin x}$$
Differentiate the following with respect to $$x$$:
$$\sin x\sin 2x$$
Differentiate the following with respect to $$x$$:
$$\cos (x^3.e^x)$$
If $$\sin y = x \sin (a + y),$$ then prove that $$\dfrac{dy}{dx} = \dfrac{\sin ^{2}(a + y)}{\sin a}$$.
If $$(\cos x)^{y} = (\cos y)^{x}$$, then find $$\dfrac{dy}{dx}$$.
Find derivative of
$$ \dfrac{x \, sin x}{1 + cos} $$
If $$x \sin (a + y) + \sin a \cos (a + y) = 0$$, then prove that $$\dfrac{dy}{dx} = \dfrac{\sin ^{2} (a + y)}{\sin a}$$
Differentiate $$ tan \,x $$ from first principle.
Find the derivative of the function $$ f(x) = 2x^2 + 3x - 5 $$ at $$ x = -1 $$. Also show that $$ f' (0) + 3\, f' (-1) = 0 $$
Differentiate the following with respect to x :
$$(\sin x)^{x} + (\cos x)^{\sin x}$$
Evaluate $$ \underset {x \rightarrow 0} {\lim} \dfrac{ax + x \, cos \,x}{b\, sin \,x} $$
Find $$\dfrac{dy}{dx}$$ if $$y = (\cos x)^{x} + (\sin x)^{1/x}$$.
Find $$\dfrac{dy}{dx} : y = \left ( \sin x \right )^{x} + \left ( \cos x \right )^{\tan x}$$.
Evaluate $$ \underset { x \rightarrow \dfrac{\pi}{4}} {\lim} \dfrac{sin \, x - cos \, x}{ \left ( x - \dfrac{\pi}{4} \right )} $$
Differentiate the following function with respect to X:
$$y = (\sin x)^{x} + \sin ^{-1} \sqrt{x}$$
If $$f(x,y)=\dfrac{1}{\sqrt {x^{2}+y^{2}}}$$ then, prove that $$x \dfrac{\partial f}{\partial x}+y \dfrac{\partial f}{\partial y}=-f$$
Differentiate the following w.r.t.x: $$ \cos \left(x^{2}+a^{2}\right) $$
Differentiate the following w.r.t.x: $$ \cos ^{2}\left[\log \left(x^{2}+7\right)\right] $$
Differentiate the following w.r.t.x: $$ e^{3 \sin ^{2} x-2 \cos ^{2} x} $$
The derivative of $$\sin x$$ w.r.t. $$\cos x$$ is ___________.
Differentiate the following w.r.t.x: $$ \operatorname{cosec}(\sqrt{\cos x}) $$
Differentiate
$$ \left ( \dfrac{a}{x^4} \right ) - \dfrac{b}{x^2} + cos x $$
Differentiate the following w.r.t.x: $$ 5^{\sin ^{3} x+3} $$
Differentiate the following w.r.t.x: $$ \sqrt{\tan \sqrt{x}} $$
Differentiate the following w.r.t.x: $$ \left(\sqrt{\dfrac{1+\cos \left(\dfrac{5 x}{2}\right)}{1-\cos \left(\dfrac{5 x}{2}\right)}}\right) $$
Differentiate the following w.r.t.x: $$ \sqrt{\cos x}+\sqrt{\cos \sqrt{x}} $$
Differentiate the following w.r.t.x: $$ \dfrac{1+\sin x^{\circ}}{1-\sin x^{\circ}} $$
Differentiate the following w.r.t.x: $$ \sec \left[\tan \left(x^{4}+4\right)\right] $$
Differentiate the following w.r.t.x: $$ \left(1+\sin ^{2} x\right)^{2}\left(1+\cos ^{2} x\right)^{3} $$
Differentiate the following w.r.t.x: $$ \tan [\cos (\sin x)] $$
Differentiate $$ x^{\mathrm{X}} $$ w.r.t. $$ \mathrm{x}^{\mathrm{Six} } $$
Find $$ \dfrac{dy}{dx} $$ in the following
$$ 2 x + 3 y = \sin y $$
Find $$ \dfrac{dy}{dx} $$ for the following
$$ 2 x + 3 y = \sin x $$
Differentiate the following w.r.t.x: $$ \sin \sqrt{\sin \sqrt{x}} $$
Differentiable the functions given in Exercises 1 to 11 w.r.t .x.
$$ \cos x . \cos 2x . \cos 3x $$
Solve:
$$\int \displaystyle \tan^3 2x \sec 2x \ dx$$
Find $$ \dfrac{dy}{dx} $$ in the following
$$ \sin^{2} y + \cos xy = \pi $$
Find $$ \dfrac{dy}{dx} $$ in the following
$$ sin^{2} x + \cos^{2} y = 1 $$
Solve:
$$\displaystyle\int \dfrac{1-\cos x}{1+\cos x}dx$$
Find $$ \dfrac{dy}{dx} $$ in the following
$$ ax + by^{2} = \cos y $$
Differentiable the functions given in Exercises 1 to 11 w.r.t .x.
$$ (x \cos x)^{x} + (x \sin x)^{\tfrac{1}{x}} $$
Differentiate the function w.r.t .x.
$$ x ^{x} - 2^{\sin x}$$
Solve:
$$\cfrac{\cos x-\sin x}{1+\sin 2 x}$$
Find $$ \dfrac{dy}{dx} $$ in the following
$$ ax + by^{2} = \tan x + y $$
Find the derivative of following functions w.r.t. $$x$$:
$$\dfrac{\sec x-1}{\sec x+1}$$
Find the derivative of following functions w.r.t. $$x$$:
$$\sin \left\{\cos (x^2)\right\}$$
Differentiate w.r.t.x.
$$ \sin^{3} x + \cos^{6}x $$
Find $$ \dfrac{dy}{dx} $$ of $$ (\cos x)^{y} = (cos y)^{x}$$
Find the derivative of following functions w.r.t. $$x$$:
$$\sin (x^2)$$
Differentiate w.r.t.x the function in Exercise 1 to 11 .
$$ (5x)^{3 \cos 2x}$$
Using the fact that $$ \sin (A + B ) = \sin A \cos B + \cos A \sin B $$ and the differentiation , obtain the sum formula for cosines.
If $$ y = \sqrt{\sin x + \sqrt{\sin x + \sqrt{\sin x +.........\infty }}} $$
prove that $$(2y - 1)$$ $$\dfrac{dy}{dx} = \cos x $$
Find the derivative of following functions w.r.t. $$x$$:
$$\tan (2x+3)$$
If $$ y = 5\cos x - 3 \sin x $$ ,prove that $$ \dfrac{d^{2}y}{dx^{2}} + y = 0 $$
$$\displaystyle \lim_{x \rightarrow 0} \dfrac {e^{x} + e^{-x} - 2\cos x}{x\sin x}$$.
Find $$\dfrac{dy}{dx}$$ of following functions:
$$\sin (xy)+ \dfrac{x}{y}=x^2-y$$
$$\displaystyle \lim_{x\rightarrow 0} \dfrac {x(e^{x} - 1)}{1 - \cos x}$$.
Find the derivative of following functions w.r.t. $$x$$:
$$\sin ^3x. \sin 3x$$
Find $$\dfrac{dy}{dx}$$ of following functions:
$$\tan (x+y)+ \tan (x-y)=4$$
Solve the following differential equation$$\dfrac {dy}{dx}=\sec (x+y)$$
$$\displaystyle \lim_{x\rightarrow \infty} \sqrt {\dfrac {x + \sin x}{x - \cos x}}$$.
Find $$\dfrac{dy}{dx}$$ of following functions:
$$\sin x +2 \cos^2y+xy=0$$
Find the derivative of following functions w.r.t. $$x$$:
$$\sin x^o$$
Find the derivative of following functions w.r.t. $$x$$:
$$a \tan 3x$$
Differentiate $$x^{\sin x} + (\sin x)^{\cos x}$$ with respect to x.
Prove that if the function is differentiable at a point C then it is also continuous at that point.
If $$y = x^{3} \cdot e^{x} \sin x$$, then find $$\dfrac {dy}{dx}$$.
The largest value of the non-negative integer $$a$$ for which $$\displaystyle \lim_{x \rightarrow 1} \displaystyle \left \{ \dfrac{-ax + \sin (x-1)+ a}{x+\sin (x-1)-1} \right \}^{\dfrac{1-x}{1-\sqrt{x}}} = \dfrac{1}{4} $$ is ................
Consider the function f defined by f(x) =x-x(x),where x is a positive variable,and (x) denotes the integral part of x and show that it is discontinuous for integral values of x,and continuous for all others. Is the function periodic? If periodic,what is its period? Draw its graph.
From the desfinition fo the function it follows that $$\displaystyle f\left ( x \right )=x-\left ( n-1 \right )for n-1< x< n. ...\left ( 1 \right )$$ $$\displaystyle f\left ( x \right )=0 for x=n, ...\left ( 2 \right )$$ $$\displaystyle f\left ( x \right )=x-n for n< x< n+1 ...\left ( 3 \right )$$ where n is an integer.We test the function for continuity at x=n.We have $$\displaystyle f\left ( n \right )=0.$$ by (2) $$\displaystyle f\left ( n -0\right )=\lim_{x\rightarrow n-0}\left [ x-\left ( n-1 \right ) \right ]$$ $$\displaystyle L=\lim_{h\rightarrow 0}\left [ \left ( n-h \right )-\left ( n-1 \right ) \right ]=1 by \left ( 1 \right )$$ and $$\displaystyle f\left ( n+0 \right )=\lim_{x\rightarrow n+0}\left ( x-n \right )$$ $$\displaystyle R=\lim_{h\rightarrow0 }\left ( n+h-n \right )=0,by\left ( 3 \right )$$ Hence f is discontinuous at x=n i.e. for all integral values ofx.It is obviously contin uous for all other values.Since x is positive variable, putting n=1,2,3,4,5,... We see that the graph consists of the following: $$\displaystyle \begin{matrix}y=x &when &0< x< 1 \\y=0 &when &x=1 \\y=x-1 &when &1< x< 2 \\y=0 &when &x=2 \\y=x-2 &when &2< x< 3 \\y=0 &when &x=3 \\y=x-3 &when &3< x< 4 \\y=0 &when &x=4 \end{matrix}$$
and so on. The graph is shown by thick lines from x=0 to x=4.
Remark : From the graph the following facts are evident :
(i) The function is discountinuous for all integral values and continuous for all others.
(ii) In every range which includes an integer, it is bouned between 0 and 1
.(iii) The lower bound zero is attained but the upper bound 1 is not attained since $$\displaystyle f\left ( x \right )\neq 1$$ for any value of x whatsoever.
The graphs of $$f$$ and $$g$$ are given. Use them to evaluate each limit.
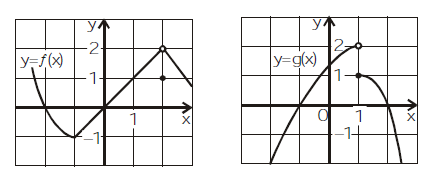
Let $$\displaystyle f_{p}\left ( \beta \right )=\left ( \cos \frac{\beta }{p^{2}}+i\sin \frac{\beta }{p^{2}} \right )+\displaystyle \left ( \cos \frac{2\beta }{p^{2}}+i\sin \frac{2\beta }{p^{2}} \right )\cdots \\ \cdots\displaystyle\left ( \cos \frac{\beta(p-1) }{p^2}+i\sin \frac{\beta(p-1) }{p^2} \right )+\left ( \cos \frac{\beta }{p}+i\sin \frac{\beta }{p} \right )$$
then $$\displaystyle \lim_{n\rightarrow \infty } 1/f_{n}\left ( \pi \right )=$$.
If $$ \displaystyle f\left ( x \right )=\cos ^{2}x+\cos ^{2}\left ( \frac{\pi }{3}+x \right )-\cos x\cos \left ( \frac{\pi }{3} +x\right ) $$ then $$ \displaystyle 4f\left ( \dfrac{\pi}8 \right ) $$ is equal to
Integrate $$\int{\frac{1}{{\sin}^{4}x+{\cos}^{4}x}}dx$$
Find the derivative of $$\displaystyle\, y \, =\, \frac{1}{x} \, +\, \frac{1}{\sqrt{x}} \, +\, \frac{1}{\sqrt[3]{x}}$$
Let $$S_{n}, n = 1, 2, 3....,$$ be sum of infinite geometric series whose first term is $$n$$ and the common ratio is $$\dfrac {1}{n +1}$$. Evaluate
$$\displaystyle \lim_{n\rightarrow \infty} \dfrac {S_{1}S_{n} + S_{2}S_{n - 1} + S_{3}S_{n - 2} + .... + S_{n}S_{1}}{S_{1}^{2} + S_{2}^{2} + .... + S_{n}^{2}}$$.
If $$\sqrt{1-x^2}+\sqrt{1-y^2}=a(x-y)$$, prove that $$\dfrac{dy}{dx}=\sqrt{\dfrac{1-y^2}{1-x^2}}$$
Solve :
$$\displaystyle \lim _{ h\rightarrow 0 }{ \frac { \sin { \left( x+h \right) } -\sin { \left( x-h \right) } }{ h } } $$
$$\displaystyle\lim _{ x\rightarrow 2 }{ \cfrac { 2x+5 }{ 8-{ x }^{ 3 } } } $$
For each of the differential equations in Exercises from $$11$$ to $$15$$, find the particular solutions satisfying the given condition:
$$x^{2}dy+(xy+y^{2})dx=0; y=1$$ when $$x=1$$
$$\underset { x\rightarrow \frac { \pi }{ 4 } }{ lim } \dfrac{1 - tan x}{1 - \sqrt2 sin x}$$
As $$sin\pi /4=\frac{1}{\sqrt{2}}, tan\pi /4=1\Rightarrow $$ limit is of $$\frac{0}{0}$$ form,
applying l'opital, $$\lim_{x\rightarrow \pi /4}-\frac{-sec^{2}x}{-\sqrt{x}cos x}=\lim_{x\rightarrow \frac{\pi }{4}}sec^{3}x$$
$$=(\sqrt{2})^{3}=2^{3/2}$$
Evaluate$$lim_{x\to -3} (\dfrac{1}{x^2+4x+3} + \dfrac{1}{x^2 +8x+15})$$
If $$y={ \left( sinx \right) }^{ cosx }+{ \left( cosx \right) }^{ sinx },find\dfrac { dy }{ dx } $$
Solve $$lim_{x\to 0} |x|^{sin x}$$
$$ifx=log\left( 1+{ sin }^{ 2 }y \right) show\quad that\quad \frac { dy }{ dx } =\frac { { e }^{ x } }{ sin\quad 2y } $$
Solve:
$$\lim_{x \rightarrow 2}{\dfrac{x^3-8}{x-2}}$$
Find the particular solution of differential equation : $$\frac{dy}{dx}$$ = $$- \frac{x+y cos x}{1 + sin x}$$ given that y = 1 when x = 0.
$$\sin x \frac { d y } { d x } + 3 y = \cos x$$
Find the derivative of following function:$$y = x / \sin ^ { n } x$$
$$lim_{x \rightarrow 0} \frac{ \sqrt[3]{1+x^2}- \sqrt[4]{1-2x}}{x+x^2}$$ is equal to
Differentiate:
$$\left(\dfrac{\sin x-x\cos x}{x\sin x+\cos x}\right)$$
If $$y=\left (\sqrt x +\dfrac {1}{\sqrt x} \right)$$, show that $$2x. \dfrac {dy}{dx}+y=2\sqrt x$$.
Find $$\dfrac {dy}{dx}$$, where :
$$x^n +y^n =a^n$$
Differentiate the following with respect to $$x$$:
$$\dfrac{e^{2x}+x^3}{\csc 2x}$$
undefined
Find : $$\displaystyle \lim_{x\rightarrow 0} \dfrac {\cot 2x - cosec 2x}{x}$$.
Find $$\dfrac {dy}{dx}$$, when $$y=x^x -2^{\sin x}$$.
Find $$\frac{dy}{dx}$$, if tan(x+y)+tan(x-y)=1
Find $$ \dfrac{d y}{d x} $$ if $$ x=a \cot \theta, y=b \operatorname{cosec} \theta $$
Find the derivative of y with respect to x, where $$y = \left ( x \right )^{\sin x} + (\sin x)^{x}$$
DIfferentiate $$ x \sin x $$ w.r.t. $$ \tan x $$
Find $$ \dfrac{d y}{d x}, $$ if $$ : x=\sin \theta, y=\tan \theta $$
If $$ x=a \cos ^{3} t, y=a \sin ^{3} t, $$ show that $$ \dfrac{d y}{d x}=-\left(\dfrac{y}{x}\right)^{3} $$
If $$ x=2 \cos ^{4}(t+3), y=3 \sin ^{4}(t+3), $$ show that $$ \dfrac{d y}{d x}=-\sqrt{\dfrac{3 y}{2 x}} $$
Find $$ \dfrac{d y}{d x}, $$ if $$ : x=a(1-\cos \theta), y=b(\theta-\sin \theta) $$
Class 11 Engineering Maths Extra Questions
- Binomial Theorem Extra Questions
- Complex Numbers And Quadratic Equations Extra Questions
- Conic Sections Extra Questions
- Introduction To Three Dimensional Geometry Extra Questions
- Limits And Derivatives Extra Questions
- Linear Inequalities Extra Questions
- Mathematical Reasoning Extra Questions
- Permutations And Combinations Extra Questions
- Principle Of Mathematical Induction Extra Questions
- Probability Extra Questions
- Relations And Functions Extra Questions
- Sequences And Series Extra Questions
- Sets Extra Questions
- Statistics Extra Questions
- Straight Lines Extra Questions
- Trigonometric Functions Extra Questions