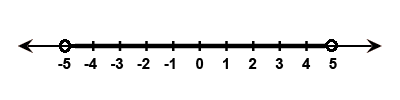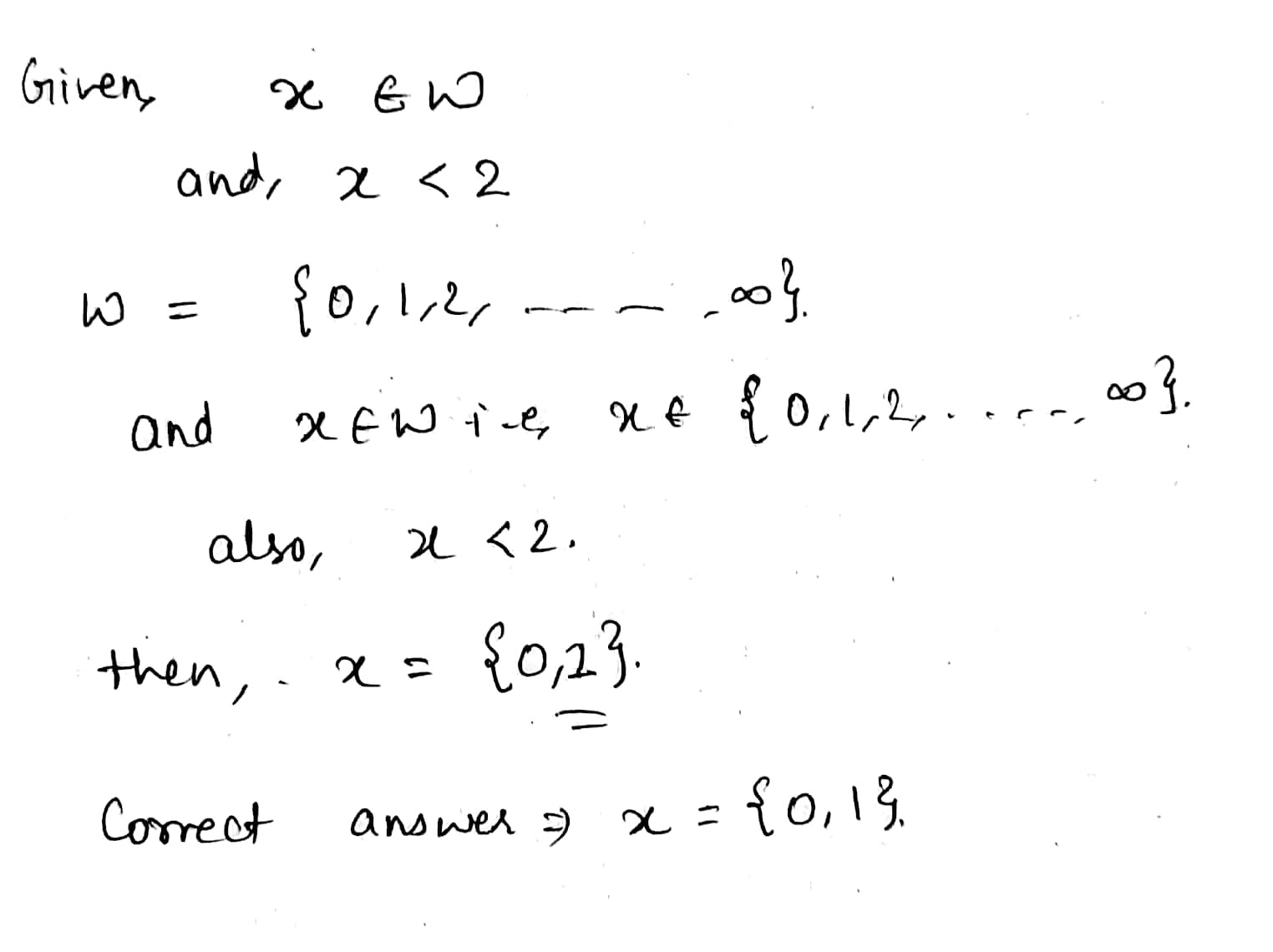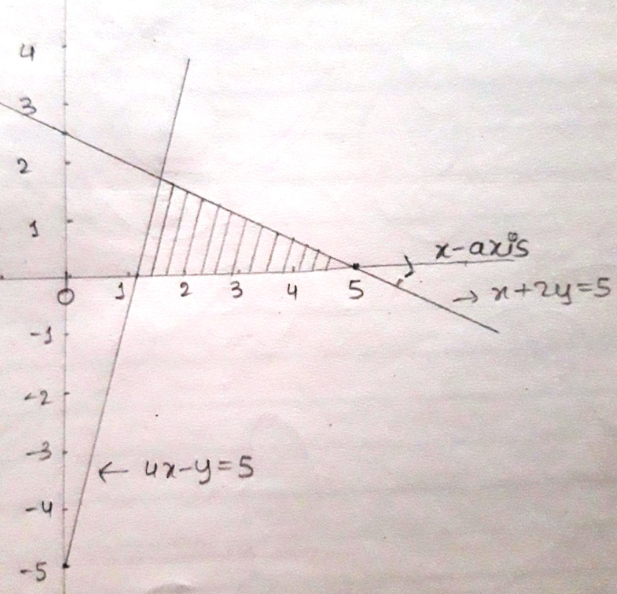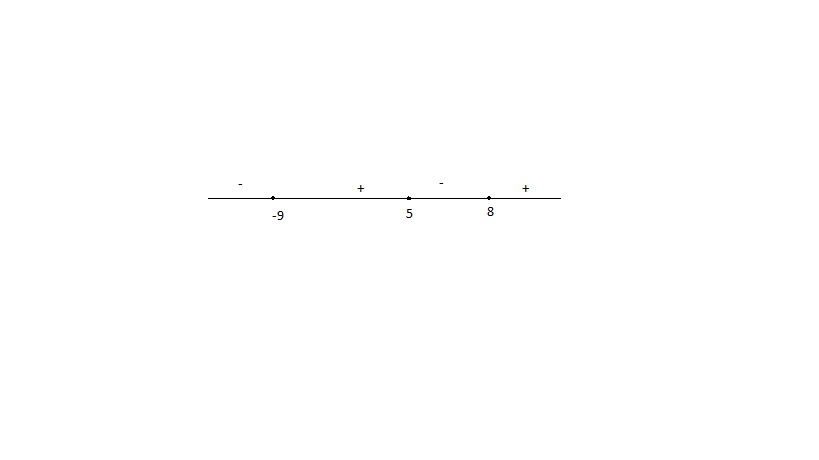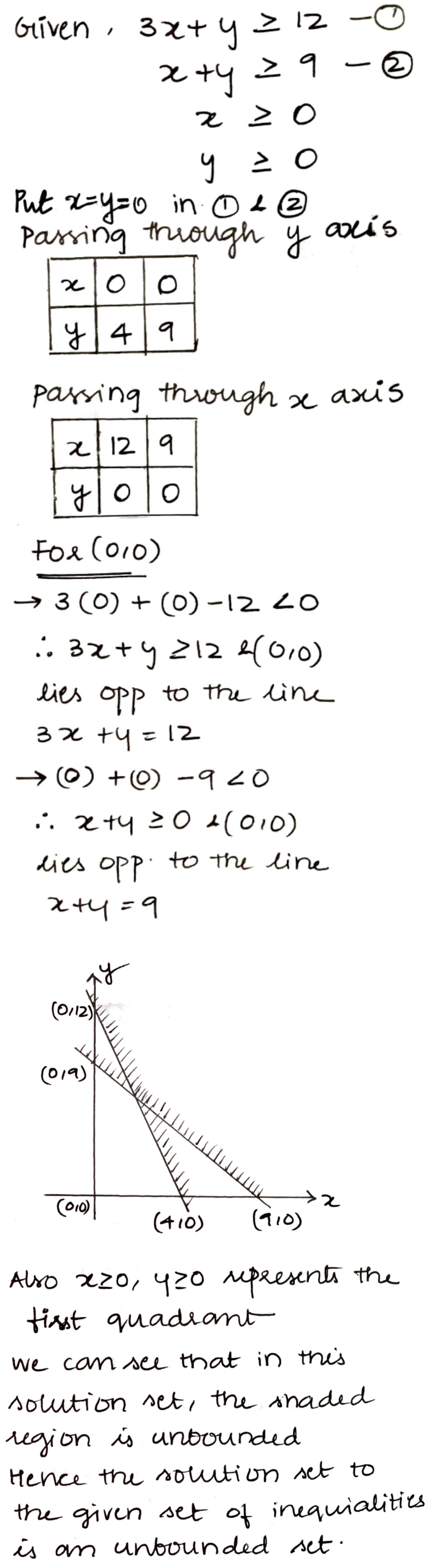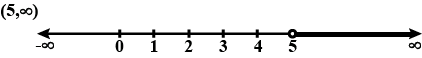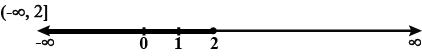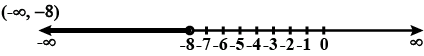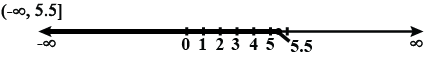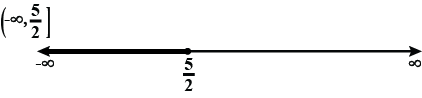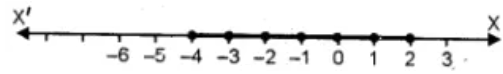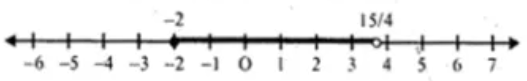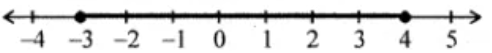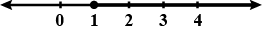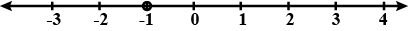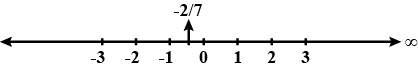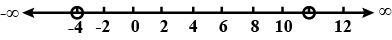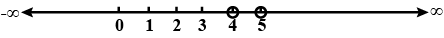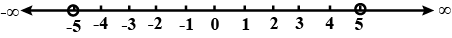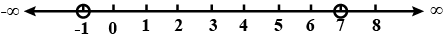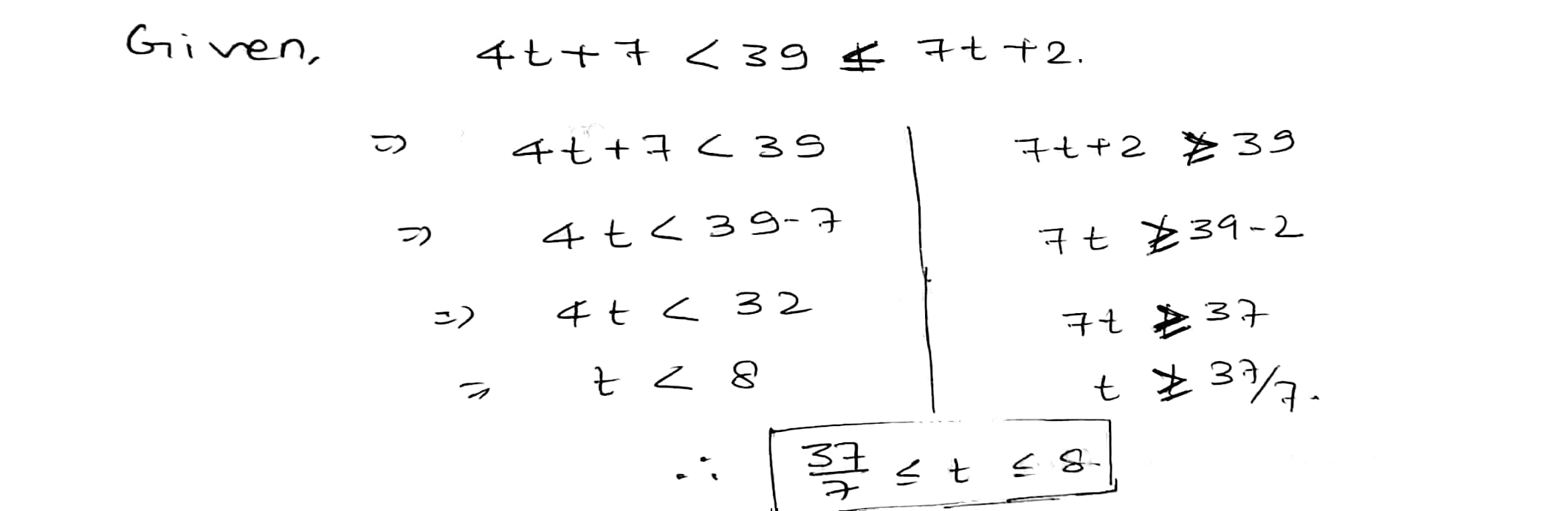Linear Inequalities - Class 11 Engineering Maths - Extra Questions
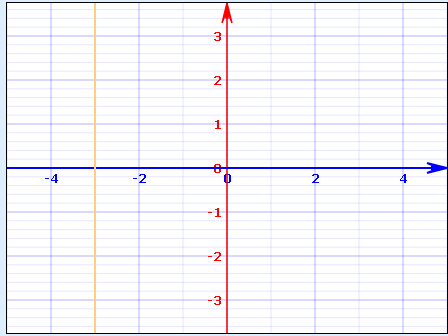
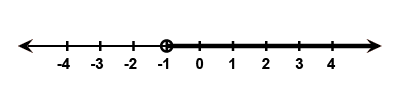
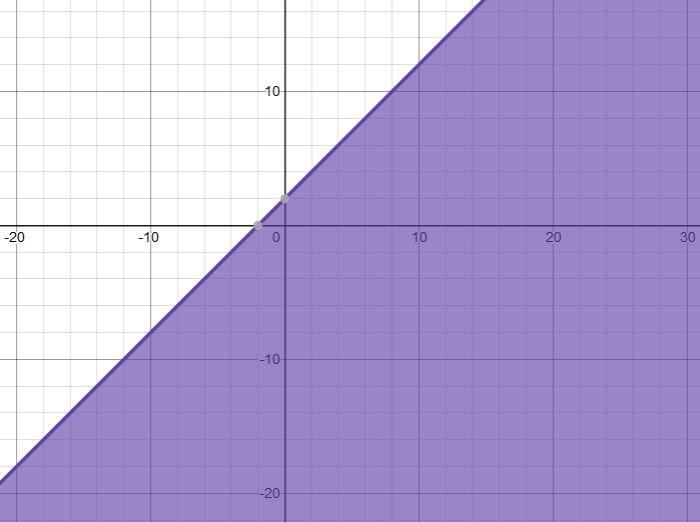
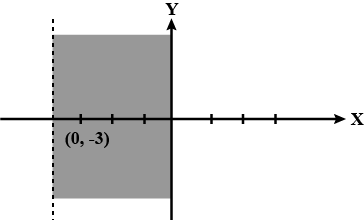
Solve the following inequalities graphically in two-dimensional plane:$$x >- 3$$
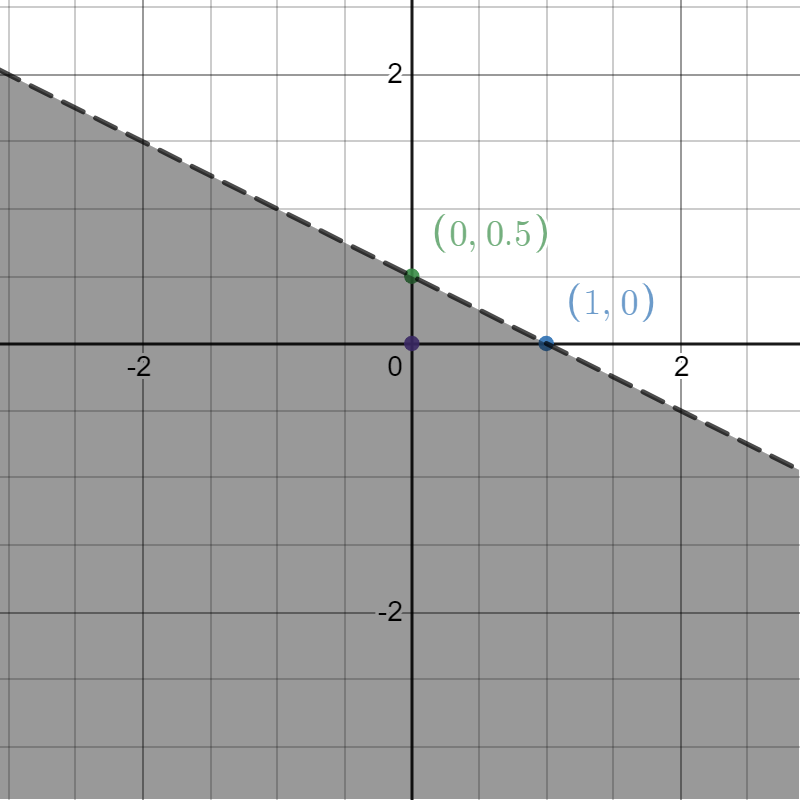
Solve 4x - 12 $$\displaystyle \geq $$ 0 graphically in two dimensional plane
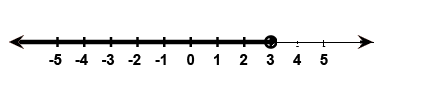
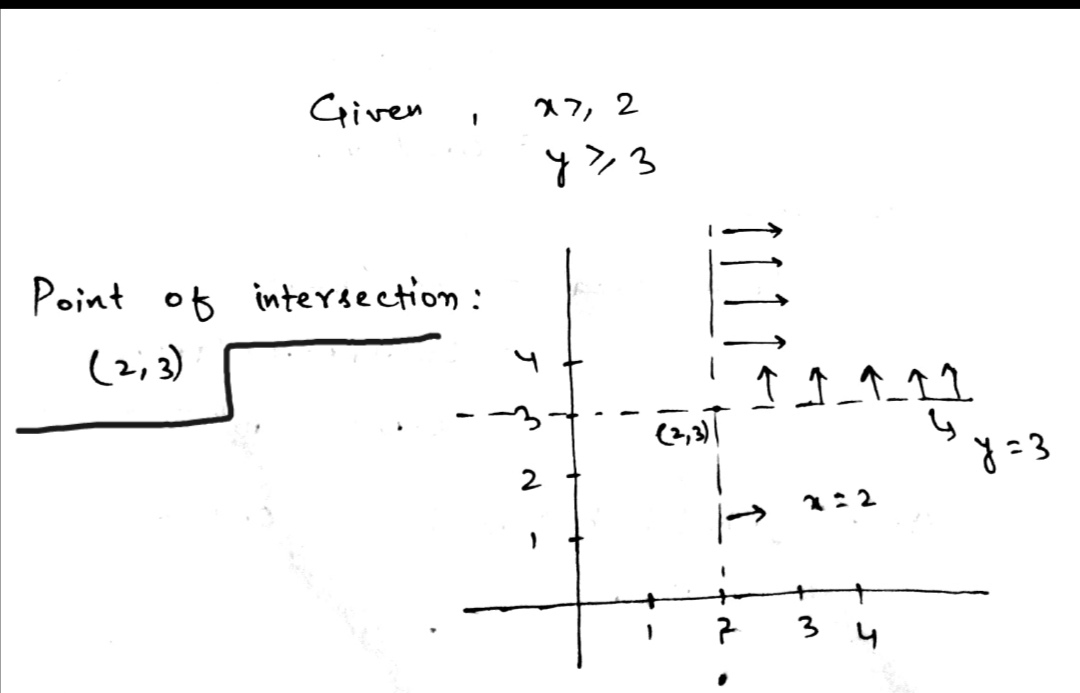
Solve the given inequalities graphically:$$x {\geq} 3, y {\geq} 2$$
Solve the inequalities and represent the solution graphically on number line.
$$5x+1 > -24, 5x-1 < 24$$
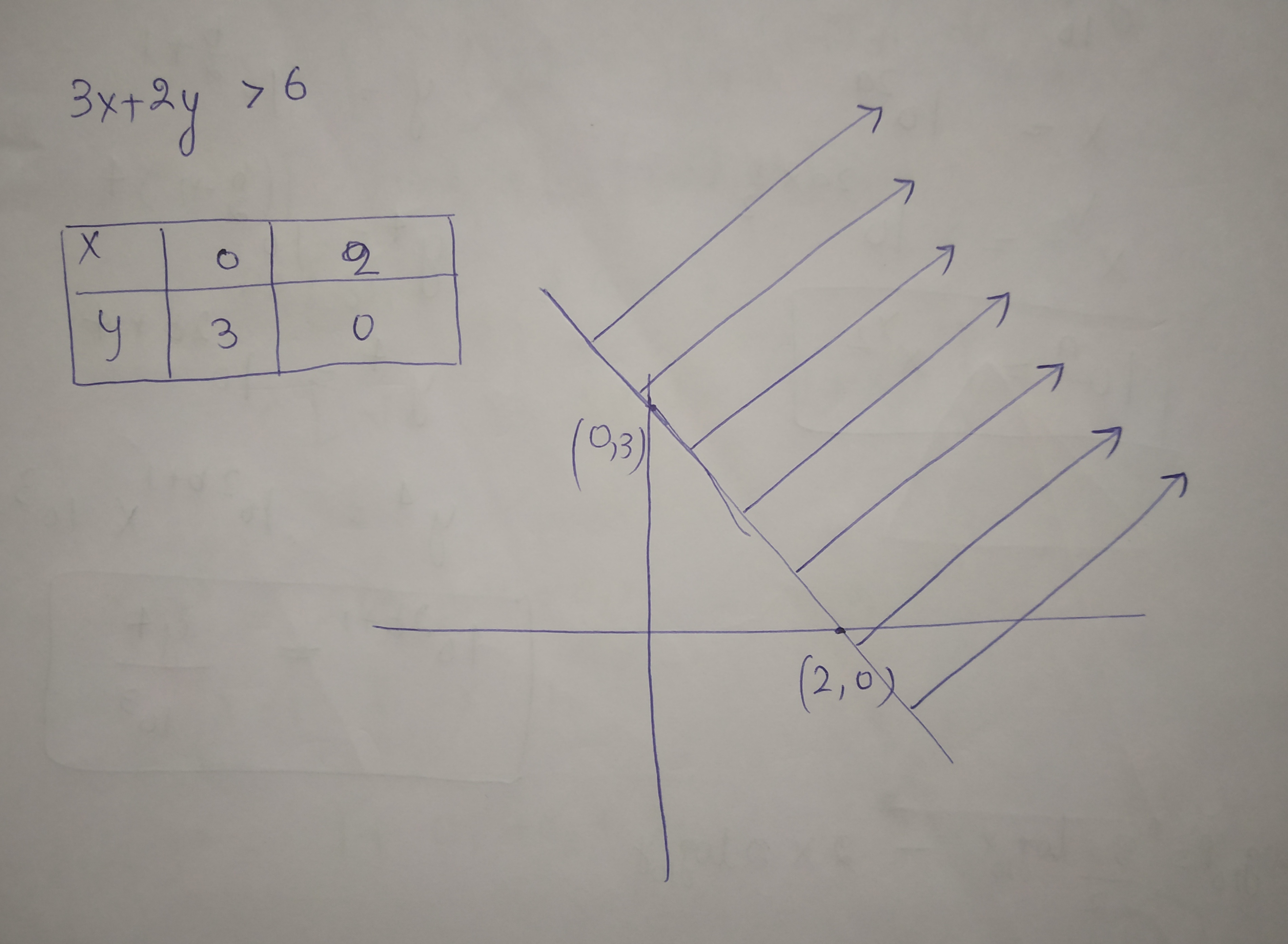
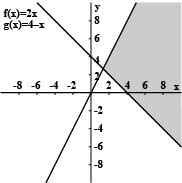
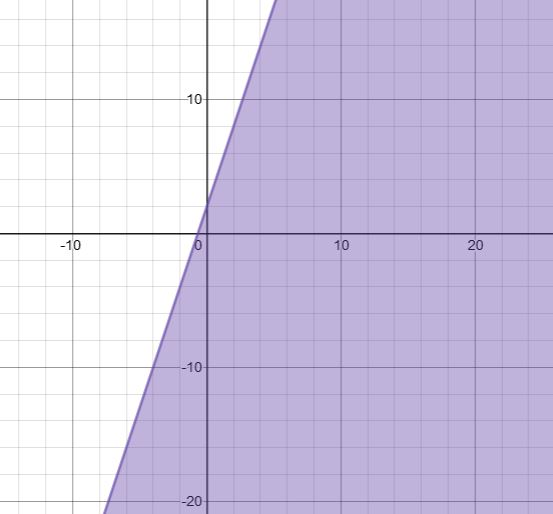
Solve $$3x+2y>6$$ graphically.
State which of the following are equation (with variable). Given reasons for your an mention which variable is used from the equation with a variable.
$$9n-9>5$$
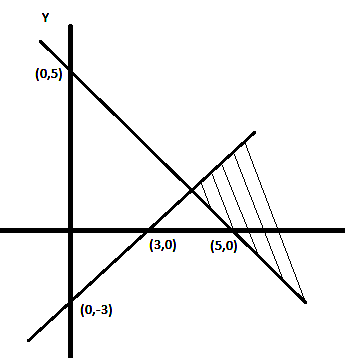
Solve: $$|2x-5|< 1$$.
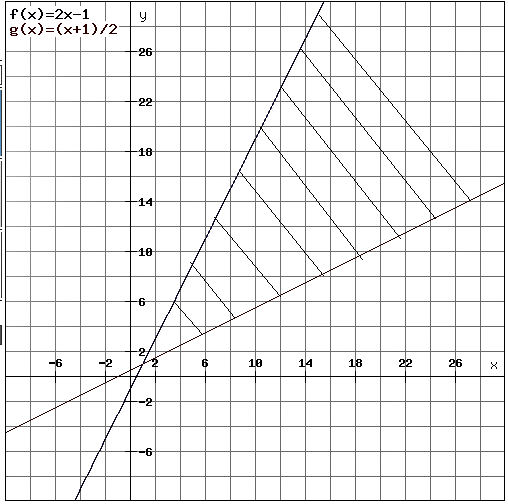
Find the solution of the inequality $$3\left( 1-x \right) <2\left( x+4 \right) $$ and draw on the number line.
Solve: $$-(x-2)+4 > - 3x+10$$.
Fill in the blank with $$>,\ <$$ or $$=$$ sign
$$(-25)-(-42)$$________$$(-42)-(-25)$$
Fill in the blank with $$>,\ <$$ or $$=$$ sign
$$45-(-11)$$________$$57+(-4)$$
Solve $$\dfrac{3}{x-2}<1$$, when $$x\in R$$
Solve :
$$3x-2y=1$$$$2x+y=3$$
State True or False and write the correct statement.
In the cartesian plane the horizontal line is called Y-axis.
In the cartesian plane the vertical line is called Y-axis.
The point which lies both the axes is called origin.
The point $$(2,-3)$$ lies in the third quadrant.
$$(-5,-8)$$ lies in the fourth quadrant.
The point (-x,-y) lies in the first quadrant where $$x<0, y,0.$$
Solve the inequalities for real $$x$$ -
$$3\left( 2-x \right) \ge 2\left( 1-x \right) $$
Find the pairs of consecutive even positive integers, both of which are larger than $$5$$ such that their sum is less than $$23$$.
Solve the following inequation and represent the solution set on a number line
$$-8\cfrac{1}{2}< -\cfrac{1}{2}-4x\le 7\cfrac{1}{2},x\in 1$$
Represent the following inequalities on real number line:
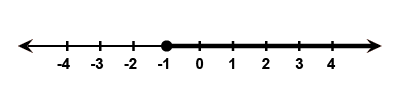
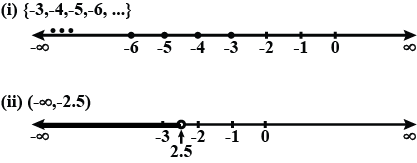
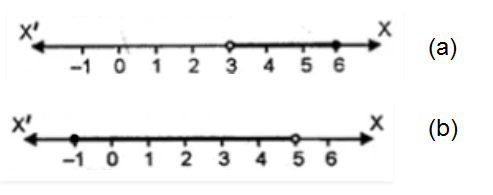
$$ -5<x \leq-1 $$
Enter 1 if it is true else enter 0.If $$x\, \epsilon\, W$$, then the solution set of $$x<2$$ is $$x = \{0,1\}$$
Fill in the blanks with correct inequality sign $$(>, <, \ge, \le )$$.
$$p-q=-3\Rightarrow p.....q$$
Solve $$2(x – 3) < 1, x ∈ {1, 2, 3, …. 10}$$
Solve the equation
$$ 7 \leq \dfrac{3 x+11}{2} \leq 11 $$
If $$x \in I$$, find the smallest value of $$x$$ which satisfies the inequation $$2x+\dfrac{5}{2}>\dfrac{5x}{3}+2$$
Solve the inequation $$- 3 \le 3 - 2x < 9, x \in R.$$ Represent your solution on a number line.
$$Solve:$$ $$4x + 3 < 5x + 7$$
Solve the inequality and show the graph of the solution on number line:
$$3 (1 -x) < 2 (x + 4)$$
Solve & graph the solution set of $$3x + 6 \geq 9$$ and $$-5x > -15$$, $$x \in R$$.
Solve & graph the solution set of $$\displaystyle 3x+6\geq 9$$ and -5x > -15 $$\displaystyle x\: \epsilon \: R$$
Solve $$24 x < 100$$, when $$x$$ is a natural number.
Solve the inequality and show the graph of the solution on number line:
$$3x- 2 < 2x + 1$$
Solve the inequality and show the graph of the solution on number line:
$$\displaystyle {\frac{x}{2}\geq \frac{(5x-2)}{3}-\frac{(7x-3)}{5}}$$
Solve the inequality and show the graph of the solution on number line:
$$5x -3 \geq 3x- 5$$
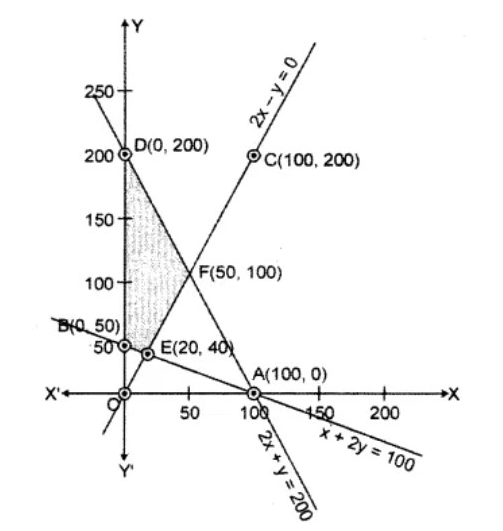
Solve the following system of inequalities graphically
$$\displaystyle x+2y\leq 8 $$ ......(1)
$$\displaystyle 2x+y\leq 8 $$ ......(2)
$$\displaystyle x\geq 0 $$ ......(3)
$$\displaystyle y\geq 0 $$ ......(4)
Find x satisfying | x - 5 | $$\displaystyle \leq $$ 3
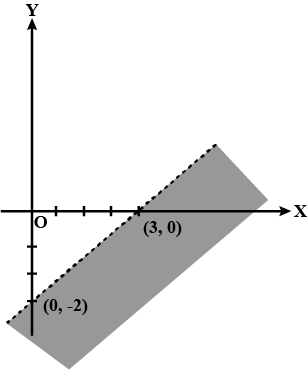
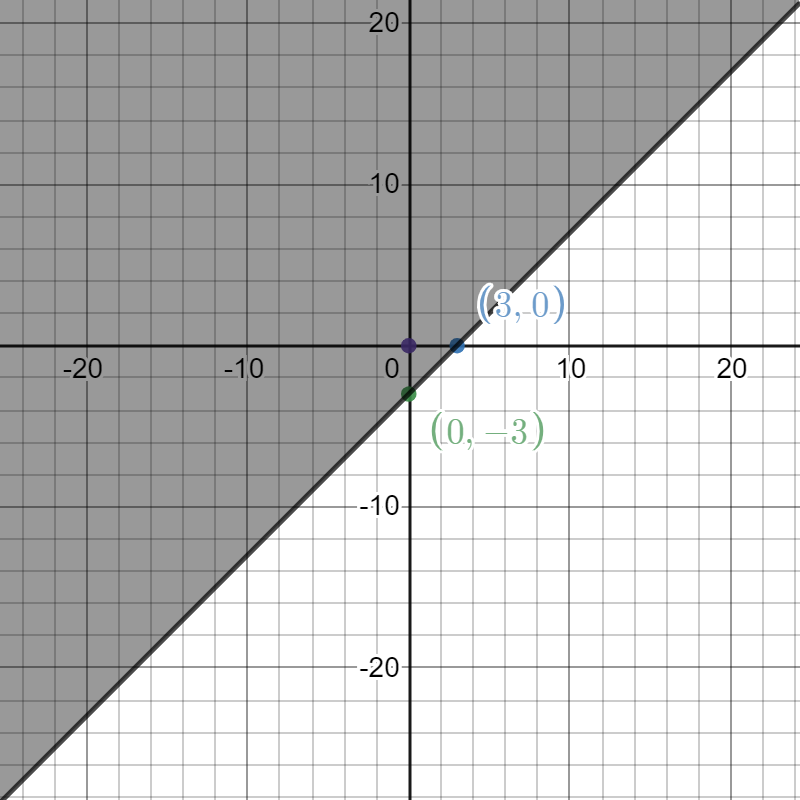
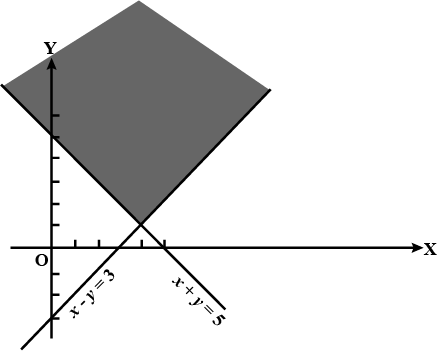
Solve the following inequalities graphically in two-dimensional plane:
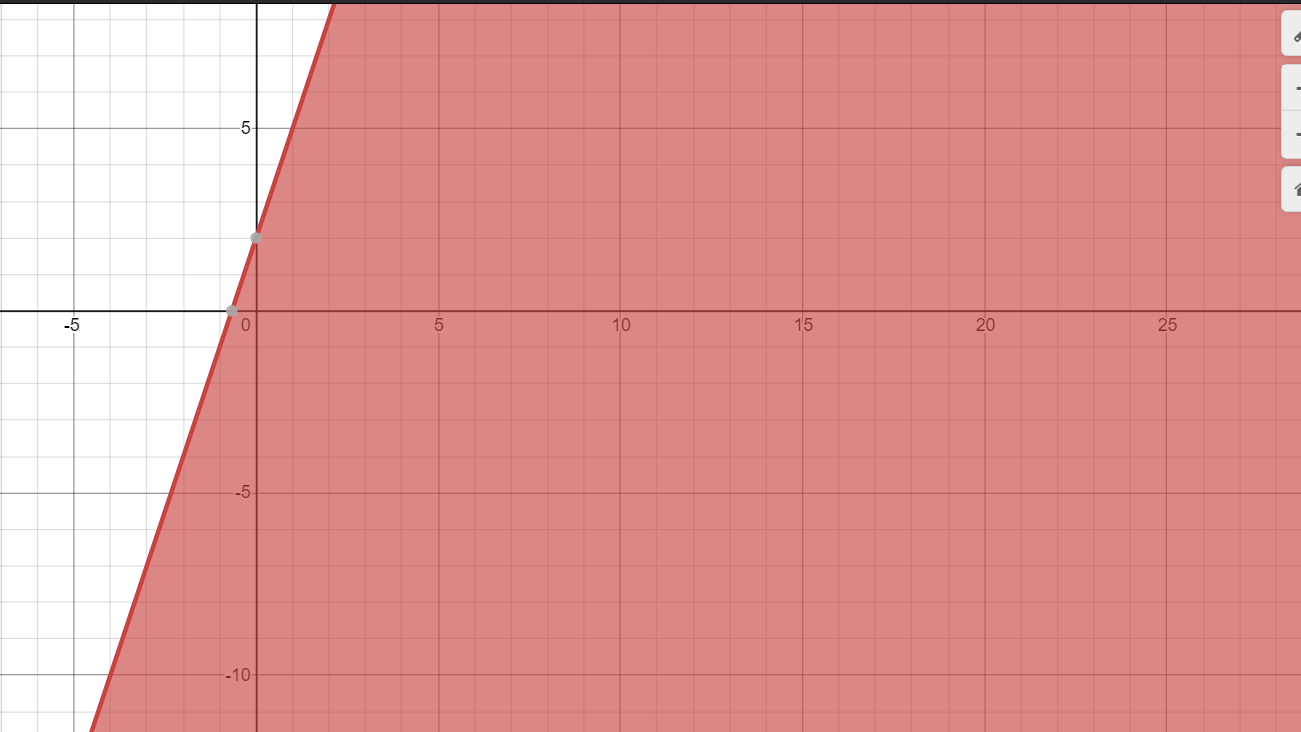
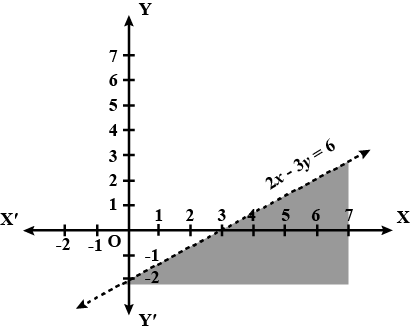
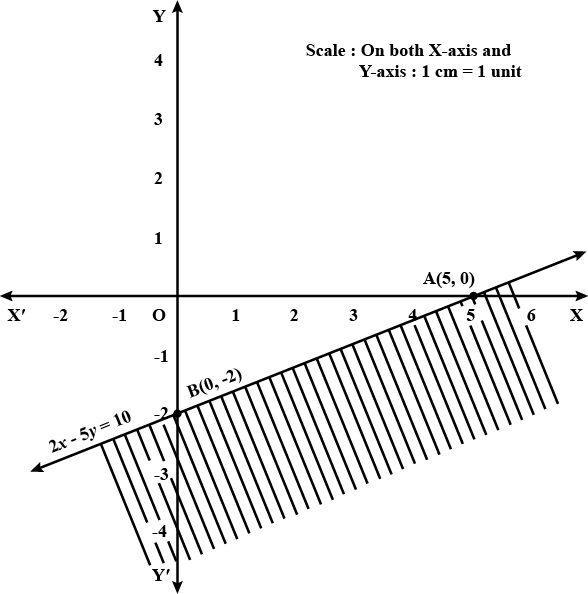
$$2x -3y > 6$$
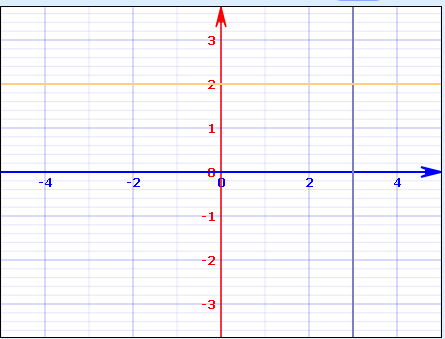
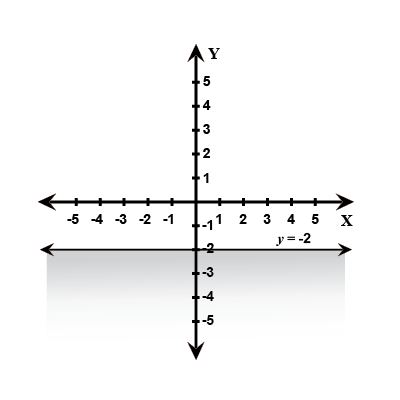
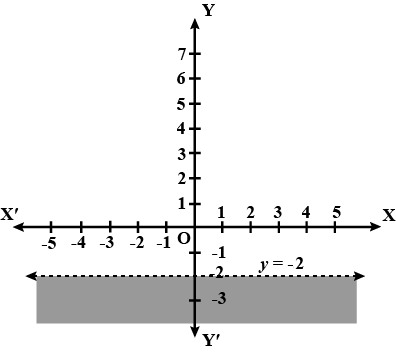
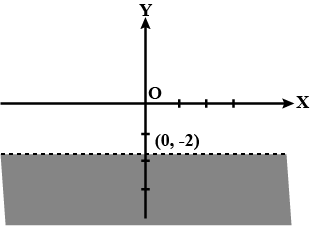
Solve the following inequalities graphically in two-dimensional plane:$$y < -2$$
Solve the following inequalities graphically in two-dimensional plane:
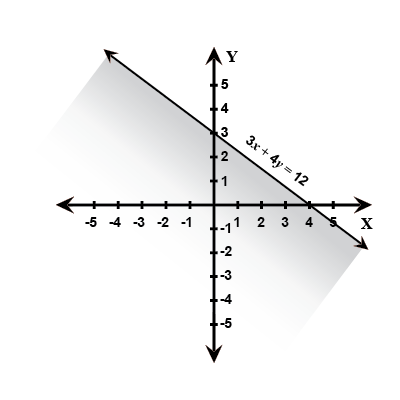
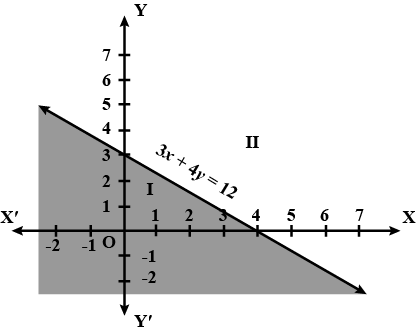
3x + 4y$${ \leq}$$ 12
Solve the following inequalities graphically in two-dimensional plane:
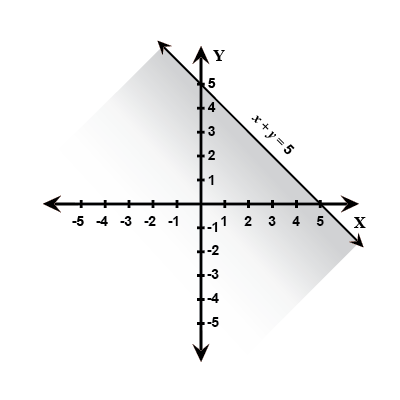
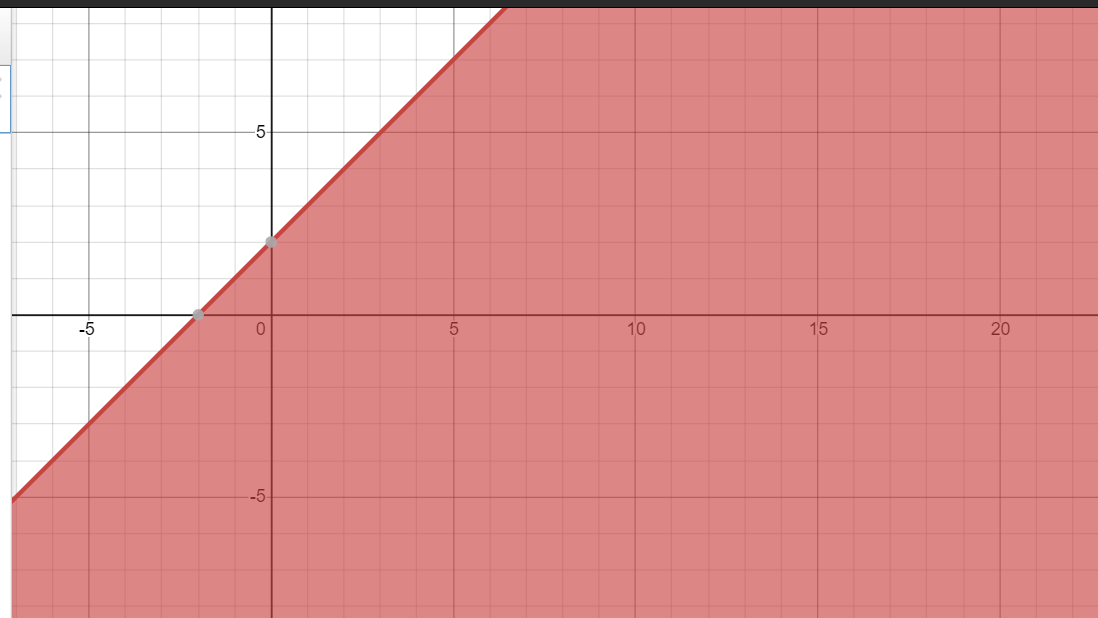
$$x + y < 5$$
Find all pairs of consecutive even positive integers, both of which are larger than 5 such that their sum is less than 23
Solve the following inequalities graphically in two-dimensional plane:
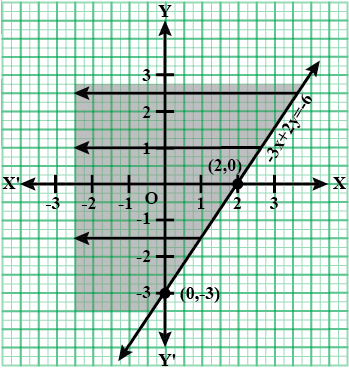
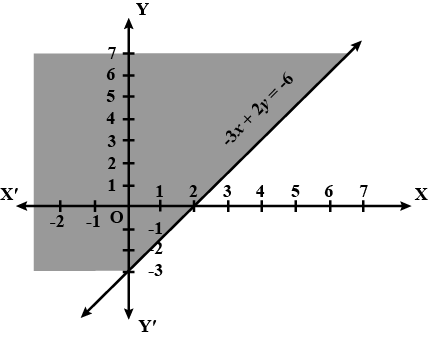
$$-3x + 2y {\geq} -6$$
Solve the following inequalities graphically in two-dimensional plane:
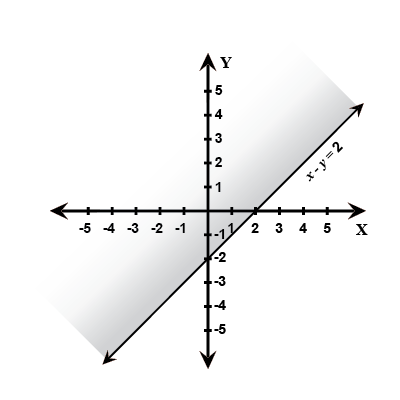
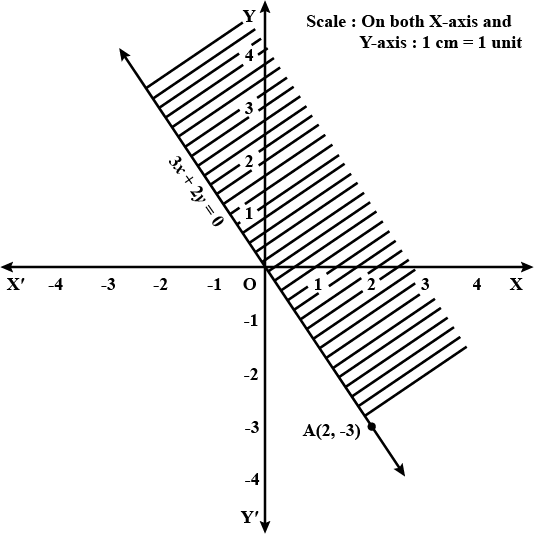
$$x -y {\leq} 2$$
The longest side of a triangle is $$3$$ times the shortest side and the third side is $$2$$ cm shorter than the longest side. If the perimeter of the triangle is at least $$61$$ cm, find the minimum length in cm. of the shortest side.
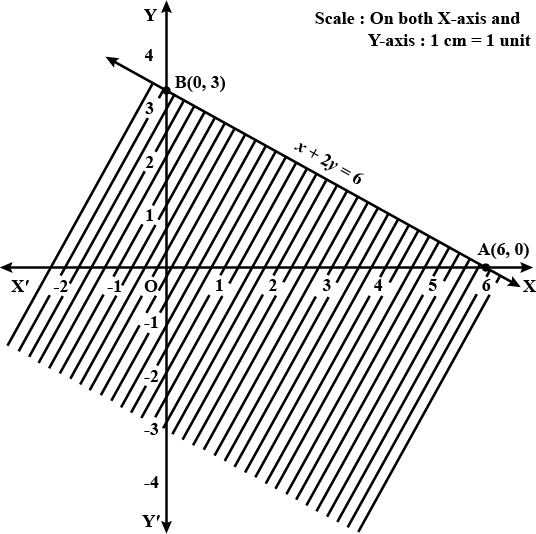
Solve the following inequalities graphically in two-dimensional plane: $$2x + y {\geq} 6$$
Solve the following inequalities graphically in two-dimensional plane:
$$y + 8 {\geq}2x $$
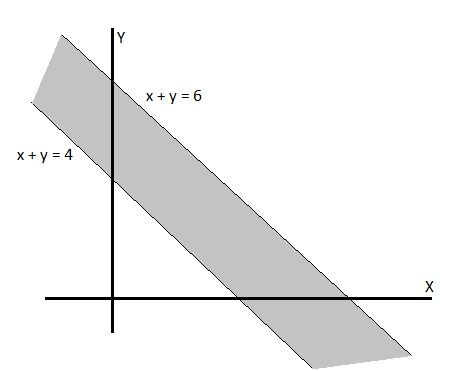
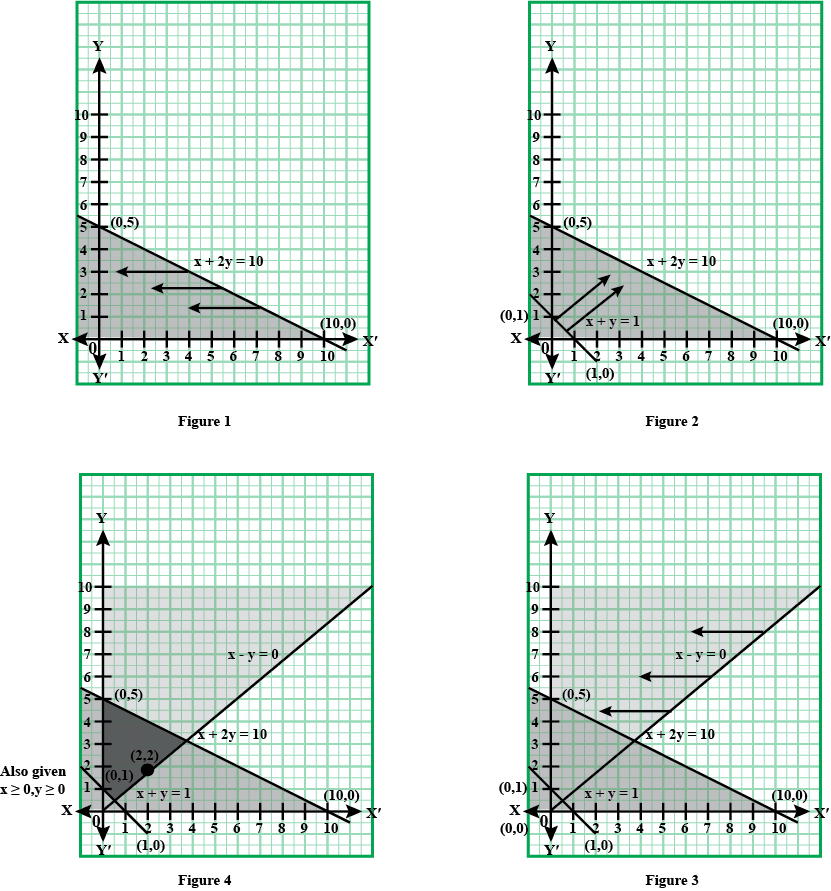
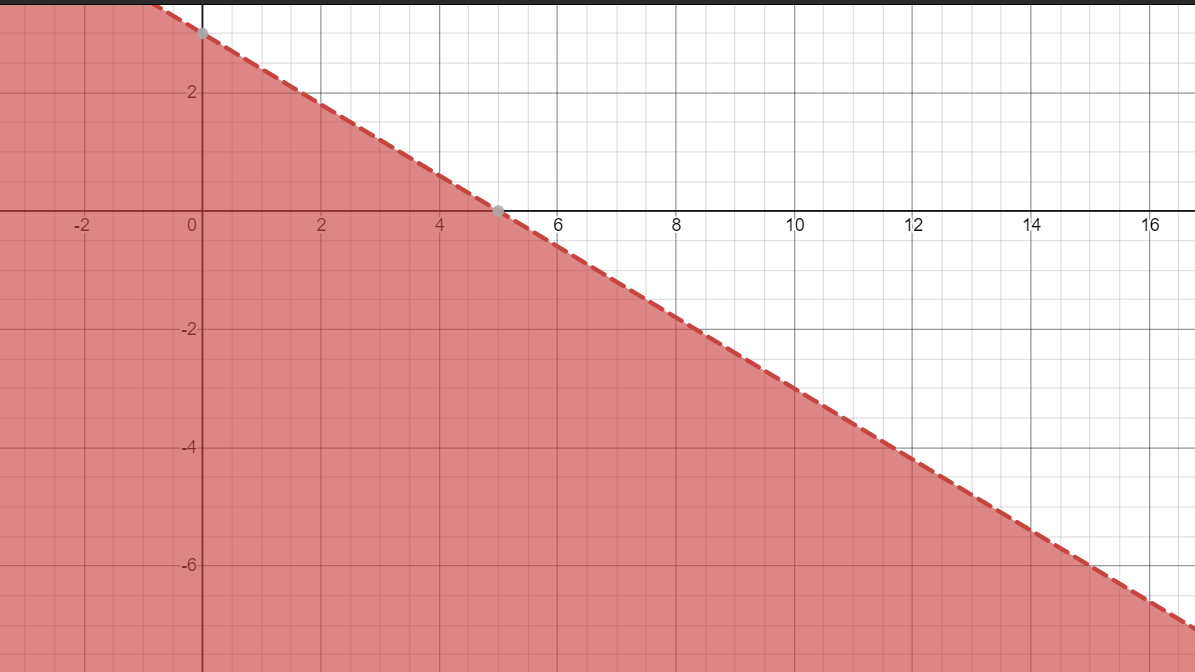
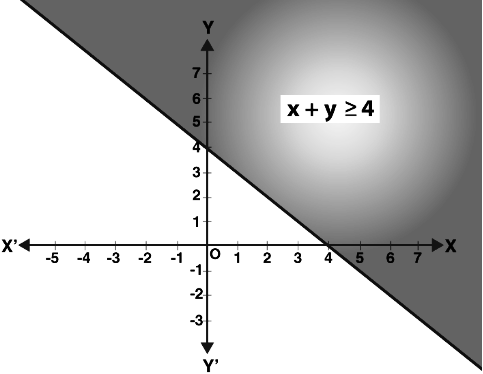
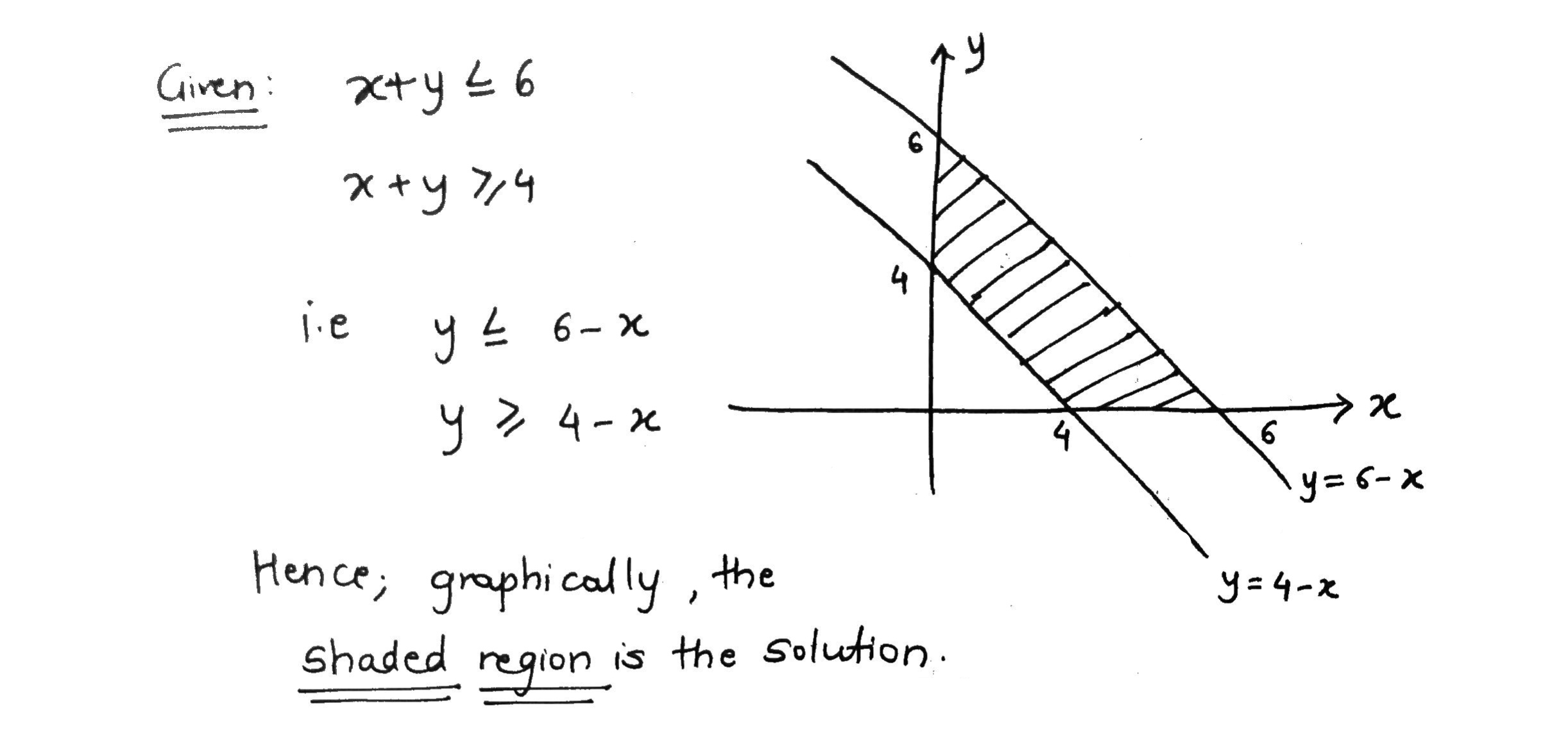
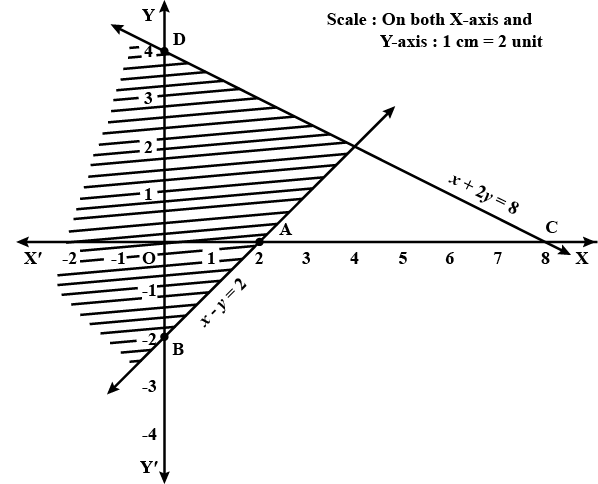
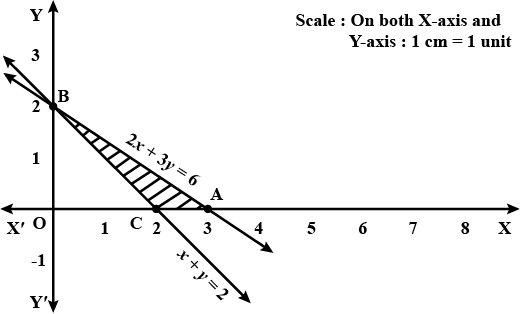
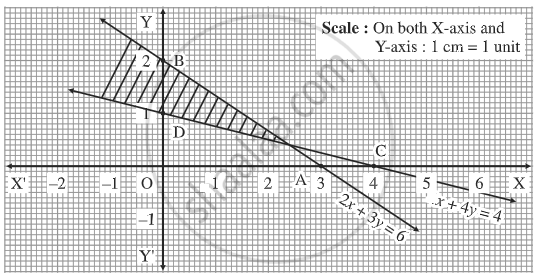
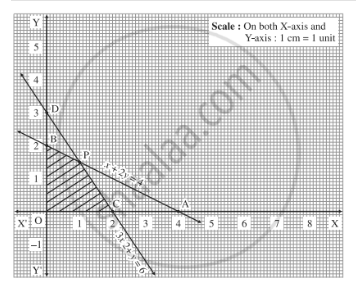
Solve the given inequalities graphically:$$x + y $$$${\leq}$$ $$6, x + y$$ $${\geq}$$ $$4$$
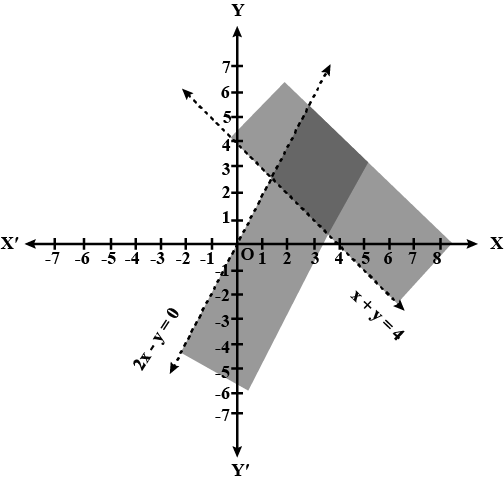
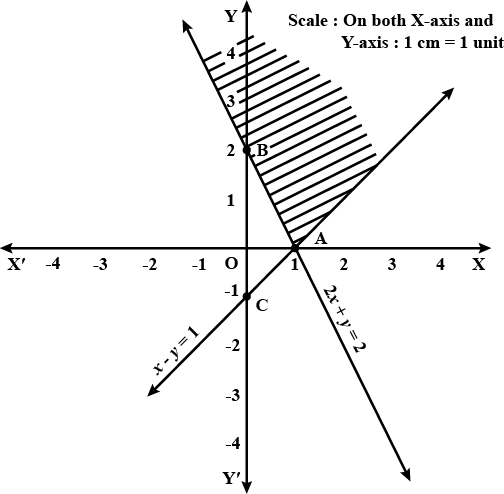
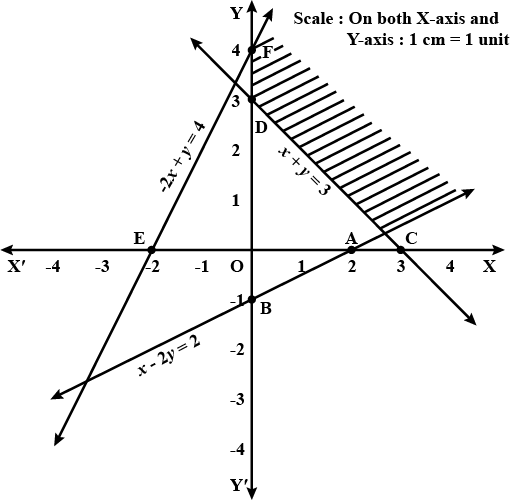
Solve the given inequalities graphically:$$x + y $$$${\geq}$$ $$4$$ and $$ 2x -y > 0$$
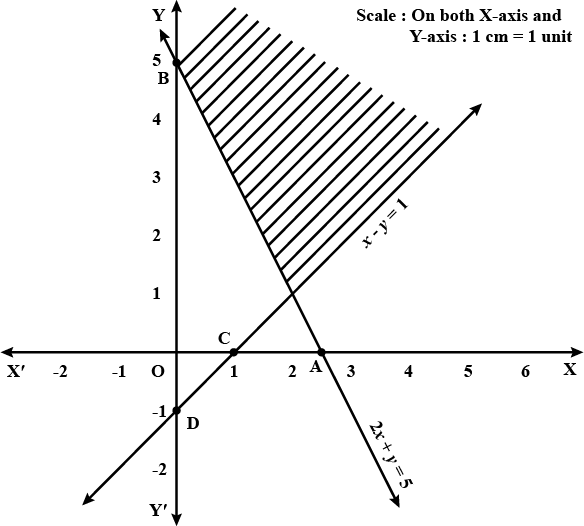
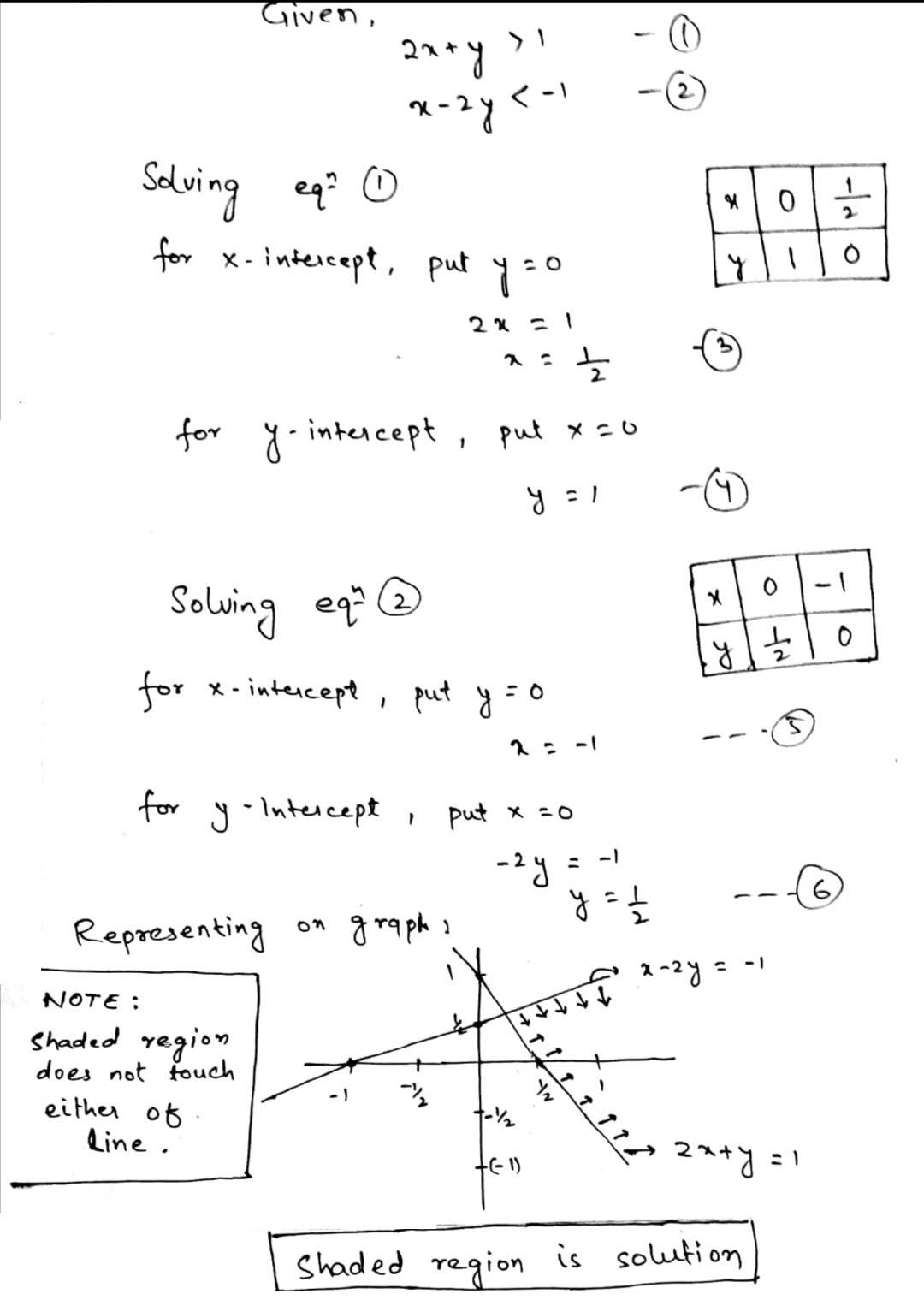
Solve the following inequations graphically:$$2x- y >1, x -2y < -1$$
Solve the system of inequalities graphically:$$2x + y $$$${\geq}$$ $$4, x + y $$$${\leq}$$$$ 3, 2x- 3y $$$${\leq}$$ $$6$$
Solve the system of inequalities graphically:$${x- 2y \leq 3, 3x + 4y \geq 12, x \geq 0 , y \geq 1}$$
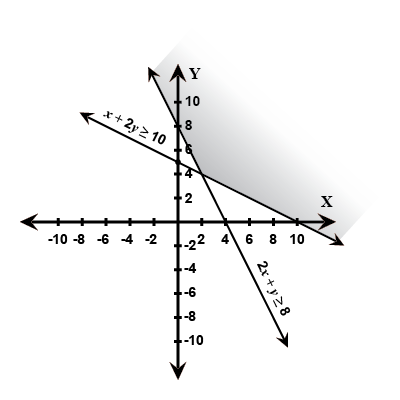
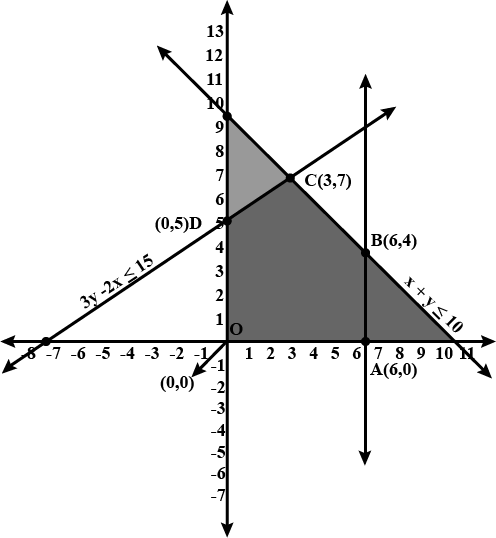
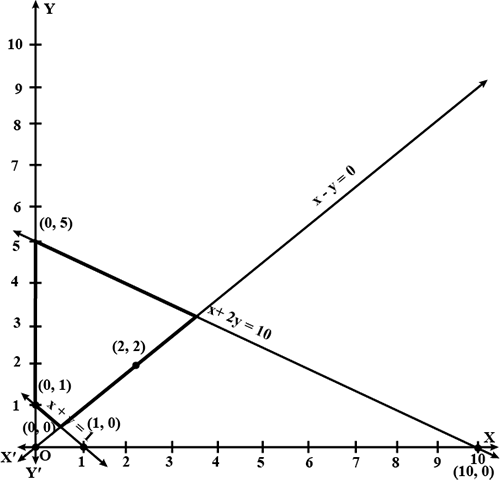
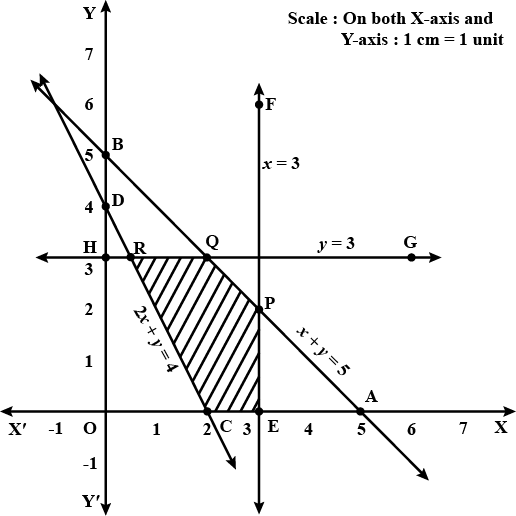
Solve the given inequalities graphically:$$2x + y$$ $${\geq}$$ $$8, x + 2y $$$${\geq}$$$$ 10$$
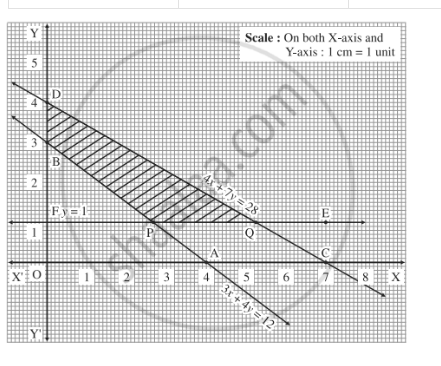
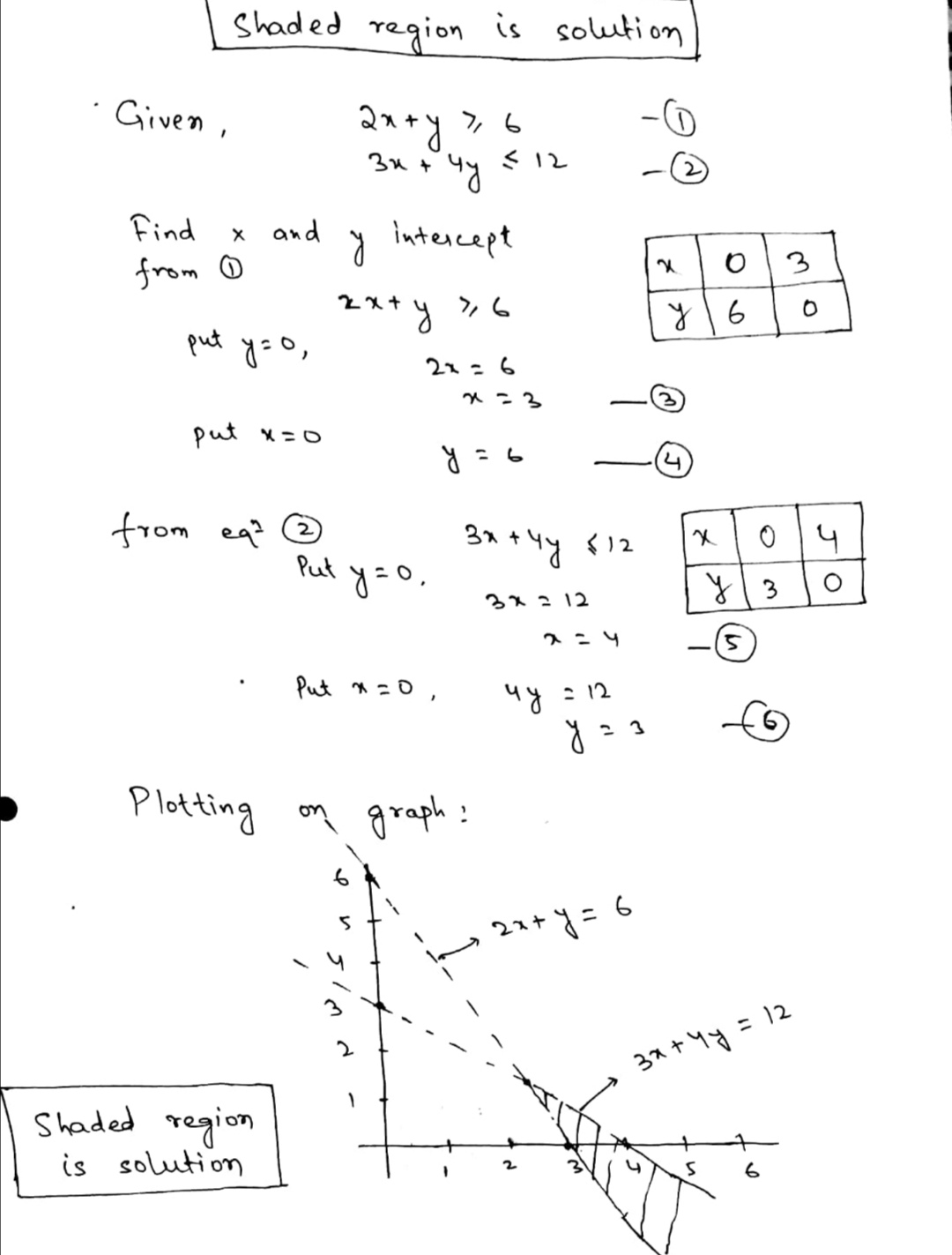
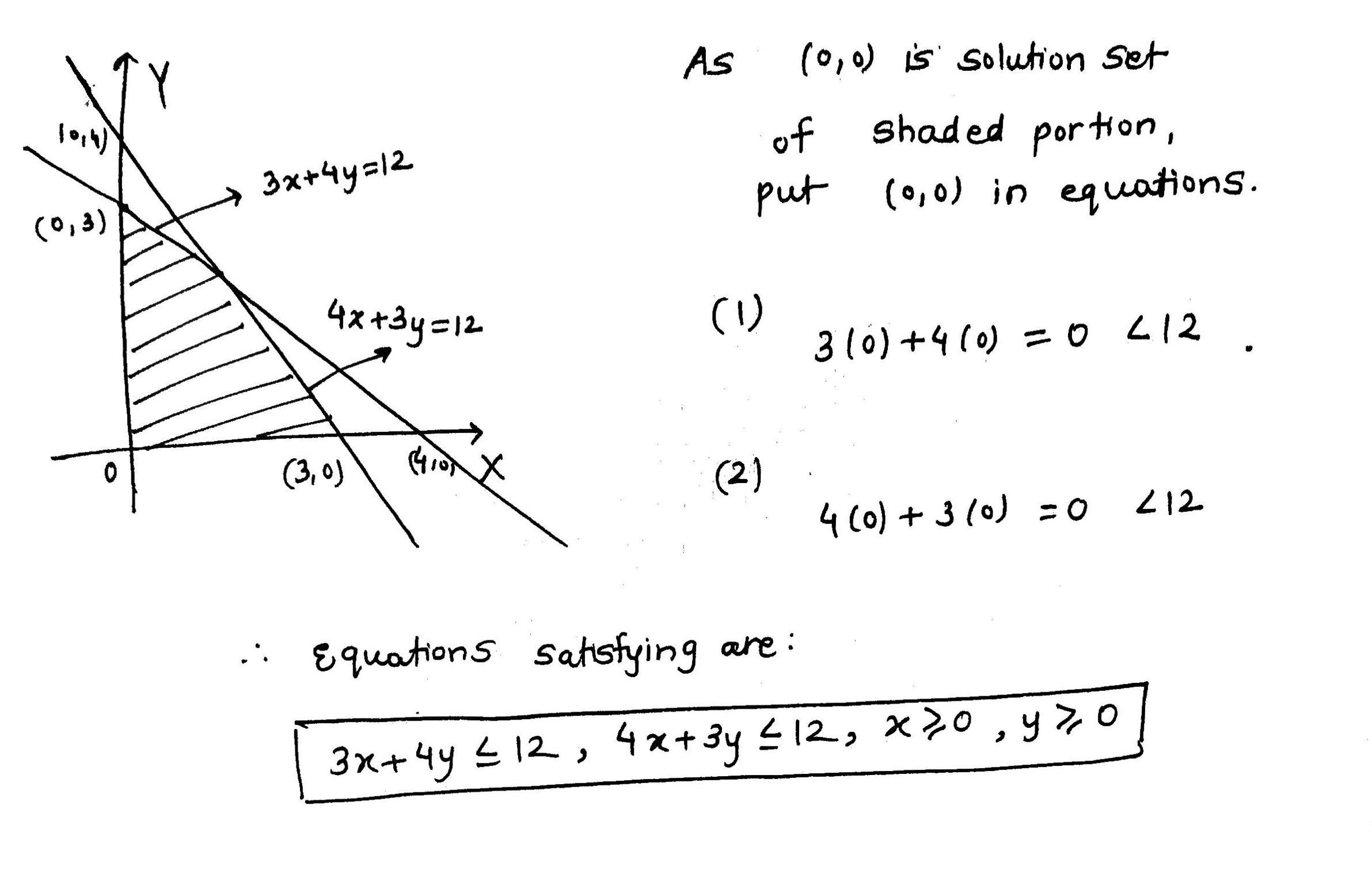
Solve the given inequalities graphically:$$2x + y$$ $${\geq}$$ $$6$$ and $$3x + 4y$$ $${\leq}$$ $$12$$
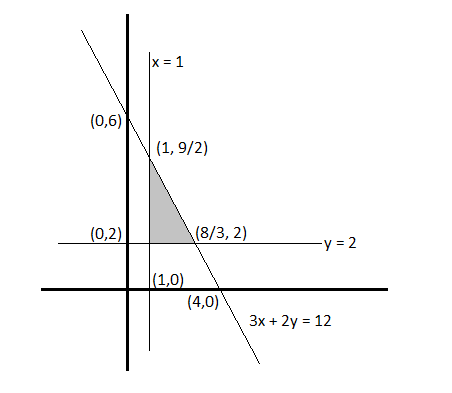
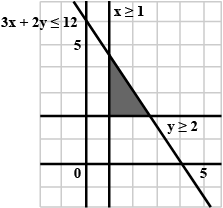
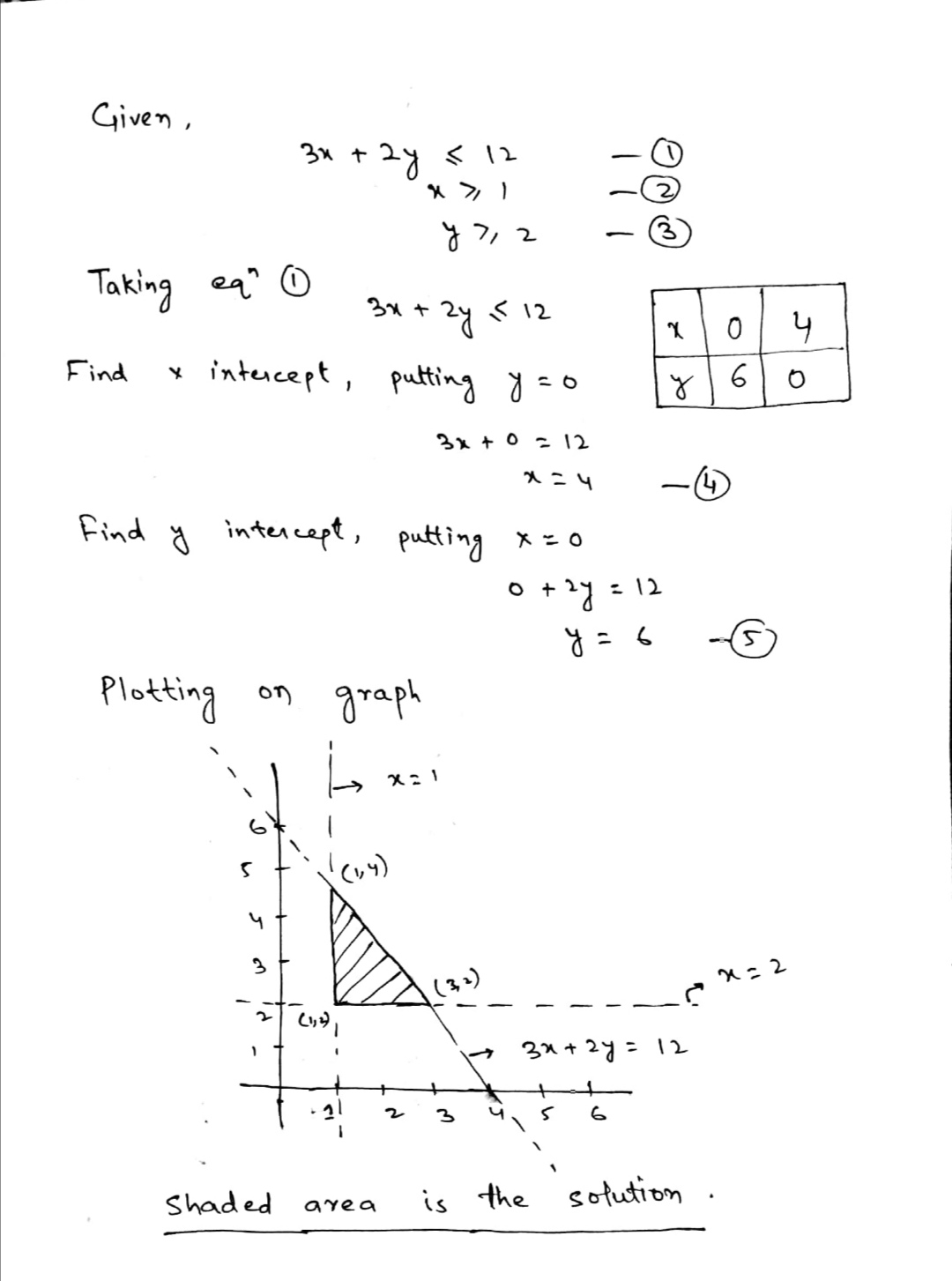
Solve the given inequalities graphically:$$3x + 2y$$ $${\leq}$$ $$12, x$$ $${\geq}$$ $$1, y$$ $${\geq}$$$$ 2$$
Solve the system of inequalities graphically:$$5x + 4y $$$${\leq}$$ $$20, x $$$${\geq}$$$$1, y$$ $${\geq}$$$$ 2$$
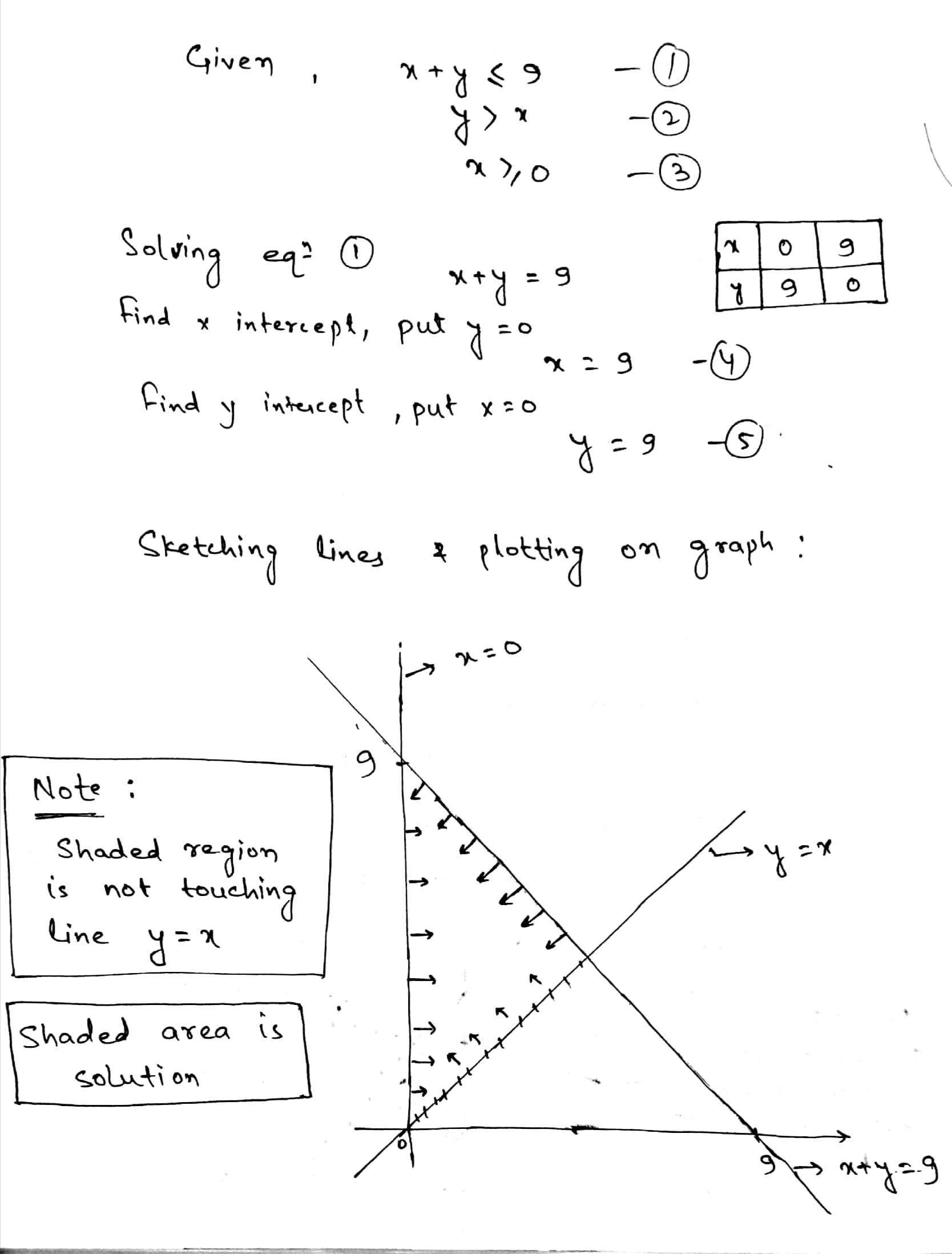
Solve the given inequalities graphically:$$x + y {\leq} 9, y > x, x {\geq} 0$$
Solve, and express the answer graphically.
$$\displaystyle\frac{4x+4}{x-4} \le 0$$
Solve the inequalities and represent the solution graphically on number line.
$$3x-7 >2(x-6), 6-x> 11-2x$$
Solve the system of inequalities graphically$${3x + 2y \leq 150, x + 4y \leq 80, x \leq 15, y \geq 0, x \geq 0}$$
Solve the given inequalities graphically:$${x + 2y \leq 10, x + y \geq 1, x- y \leq 0, x \geq 0, y \geq 0}$$
Solve the following inequality$$\displaystyle \frac{-2x+5}{x+6}>-2$$
Solve the inequality and represent the solution graphically on number line.
$$2(x-1)< x+5, 3(x+2)> 2-x$$
Solve the inequality and represent the solution graphically on number line.
$$5(2x-7)-3(2x+3)\le 0, 2x+19\le 6x+47$$
A solution is to be kept between $$68^{o}F $$ and $$77^{o}F$$ . What is the range in temperature in degree Celsius (C) if the Celsius / Fahrenheit (F) conversion formula is given by $$F=\dfrac{9}{5}C+32?$$
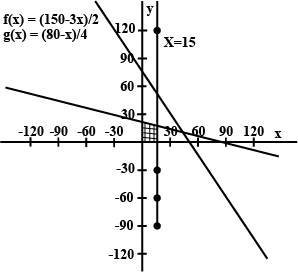
A solution of 8% boric acid is to be diluted by adding a 2% boric acid solution to it. The resulting mixture is to be more than 4% but less than 6% boric acid. If we have 640 litres of the 8% solution, how many litres of the 2% solution will have to be added?
How many litres of water will have to be added to $$1125$$ litres of the $$45\% $$ solution of acid so that the resulting mixture will contain more than $$25\%$$ but less than $$30\% $$ acid content?
Find the values of $$x$$, which satisfy the inequation $$-2\dfrac {5}{6} < \dfrac {1}{2} - \dfrac {2x}{3} \leq 2, x \in W$$.
Solve the following inequation and write the solution set :
$$13x - 5 < 15x + 4 < 7x + 12, x \in R$$
Represent the solution on a real number line.
Solve the following inequation and represent the solution set on the number line:
$$4x-19<\dfrac{3x}{5}-2\le-\dfrac{2}{5}+x,\,\,\,\,\,\, x\in R$$
Solve the following inequation, write the solution set and represent it on the number line.
$$-3 (x - 7)\geq 15 - 7x > \dfrac {x + 1}{3}, x\in R$$
Solve the following inequation, write the solution set and represent it on the number line: $$-\displaystyle\frac{x}{3}\leq \frac{x}{2}-1\frac{1}{3} < \frac{1}{6}, x\in R$$.
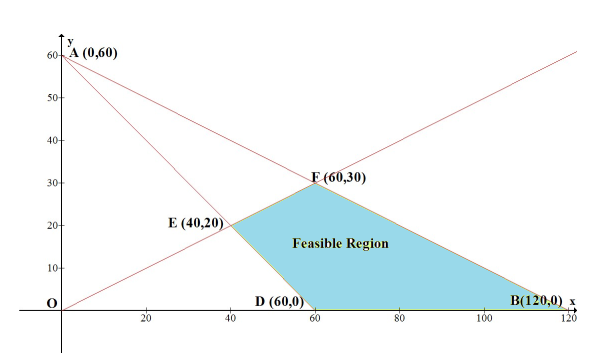
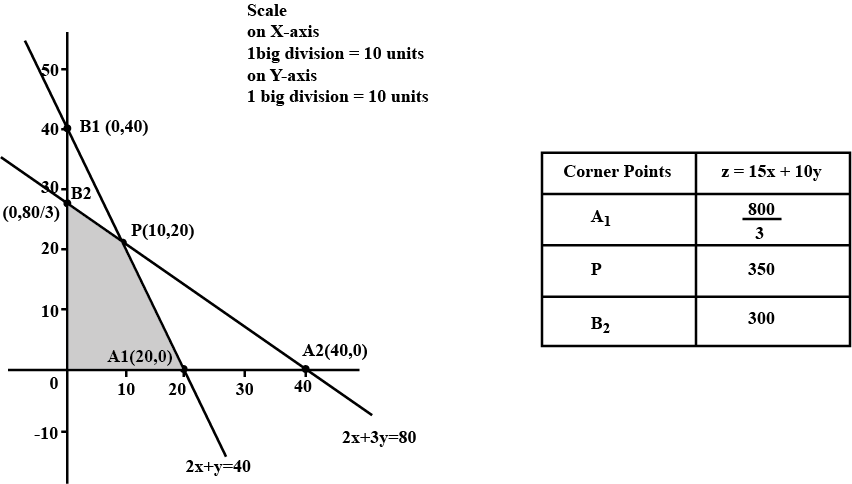
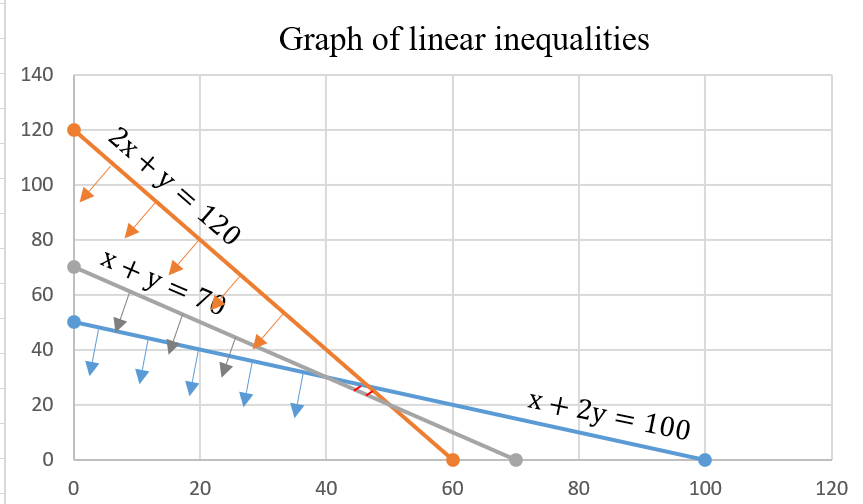
Minimize and maximize $$z=5x+10y$$
subject to the constraints
$$x+2y \le 120$$
$$x+y\ge 60$$
$$x-2y\ge 0$$ and $$x \ge 0,\, y \ge 0$$ by graphical method.
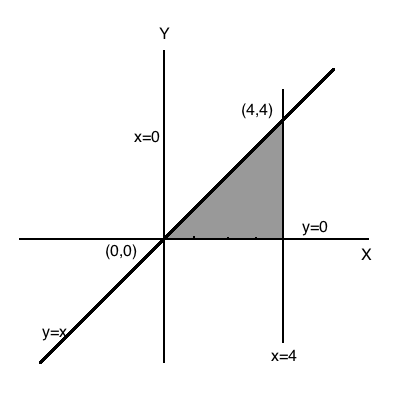
Solve by graphical method $$x+y \geq 5, x-y \leq 3$$
Indicate the polygonal region represented by the system of inequations
$$x\ge 0, y≥0, x\le 4, x\ge y$$.
Solve: $$5x-7 < 3(x+3), 1-\displaystyle\frac{3x}{2} \geq x-4$$.
Solve the following inequalities.
$$\displaystyle\, \frac{2 \, - \, 5x \, }{x \, + \, 1}\, > \, 2$$
Solve by graphical method: $$y-2x\leq 1, x+y\leq 3, x\geq 0, y\geq 0$$.
Show triangle formed x + 2y = 5 and 4x - y = 5 and x-axis graphically.
Represent the solution of the following inequality on the real number line:
$${\dfrac{2x + 5}{3}} > 3x - 3$$
Represent $$x$$ on number line or find $$x$$$$\dfrac{3x - 2} {5} > \dfrac{4x - 3}{2}$$
Solve the following equation:
$$- 8 < - (3x - 5) < 13$$
Find the largest value of x for which $$2(x - 1) \le 9 - x$$ and $$x \in W$$.
Solve the following and find $$x$$$$3x + 9 \ge - x + 19$$
$$x \in $$ {real numbers} and $$ - 1 < 3 - 2x \le 7$$, evaluate x and represent it on a number line.
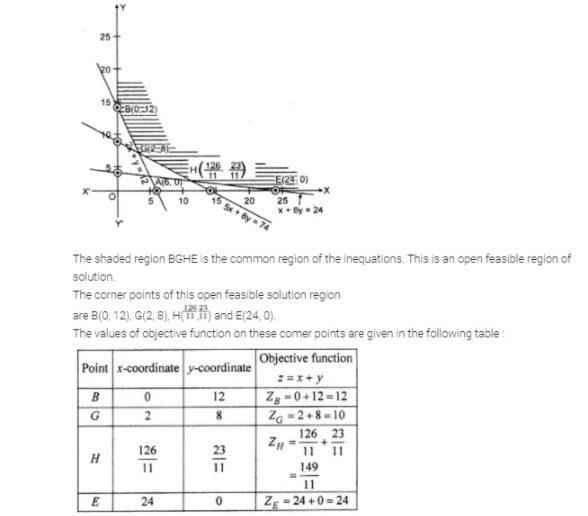
Maximize $$z=x+y$$ subject to $$x+y \le 10,3y-2x \le 15,x \le 6,x,y \ge 0$$. Find the maximum value.
Solve the inequalities for real $$x$$.
$$\dfrac {x}{3}>\dfrac {x}{2}+1$$
Find $$x$$$$\dfrac{5x}{2} + \dfrac{3x}{4} \ge \dfrac{39} {4}$$
Solve the following system of inequalities graphically
$$3x+2y\le 12, x\ge 1, y\ge 2$$
Minimize $$z = 6x + 2y,$$ Subject to $$x + 2y \ge 3, x + 4y \ge 4 , 3x + y \ge 3 , x \ge 0, y \ge 0$$.
Solve the inequalities for real $$x$$.
$$\dfrac { 3\left( x-2 \right) }{ 5 } \le \dfrac { 5\left( 2-x \right) }{ 3 } $$
Find $$x$$$$ - \left( {x - 3} \right) + 4 < 5 - 2x$$
Find $$x$$$$\dfrac{3} {x - 2} < 1$$
Solve the inequalities for real $$x$$.
$$2(2x+3)-10 < 6(x-2)$$
Solve the inequalities for real $$x$$.
$$37-(3x+5) \ge 9x-8(x-3)$$
Solve the inequalities for real $$x$$.
$$\dfrac { x }{ 4 } <\dfrac { \left( 5x-2 \right) }{ 3 } -\dfrac { \left( 7x-3 \right) }{ 5 } $$
Solve the system of in equations
$$ \dfrac { x }{ 2x+1 } \ge \dfrac { 1 }{ 4 } ;\dfrac { 6x }{ 4x-1 } <\dfrac { 1 }{ 2 }$$
Solve:$$10 \le - 5(x - 2) < 20$$
Solve the following inequation:
$$(x-5)(x+9)(x-8)< 0$$
Solve the inequalities for real $$x$$ -
$$\dfrac { 3\left( x-2 \right) }{ 5 } \le \dfrac { 5\left( 2-x \right) }{ 3 } $$
Solve the inequalities for real $$x$$.
$$\dfrac { \left( 2x-1 \right) }{ 3 } \ge \dfrac { \left( 3x-1 \right) }{ 4 } -\dfrac { \left( 2-x \right) }{ 5 } $$
Solve $$\dfrac{\left| x-3 \right|}{x^{2}-5x+6}\ge 2$$
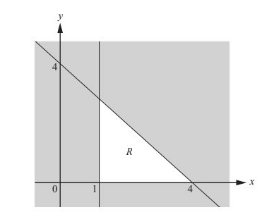
Write down the three inequalities that define the unshaded region, R.
Solve $$\frac{1}{2}\left( {\frac{{3x}}{5} + 4} \right) \ge \frac{1}{3}\left( {x - 6} \right)$$.
Graph the solution sets of the following inequations :
$$x - y \leq 3$$.
Solve:$$2\left(2x+3\right)-10<6\left(x-2\right)$$
Graph the solution sets of the following inequations :
$$x + 2y > 1$$.
Graph the solution sets of the following inequations :
$$x + y \geq 4$$.
Solve the following inequalities graphically in two-dimensional plane:
$$3y-5x<30$$
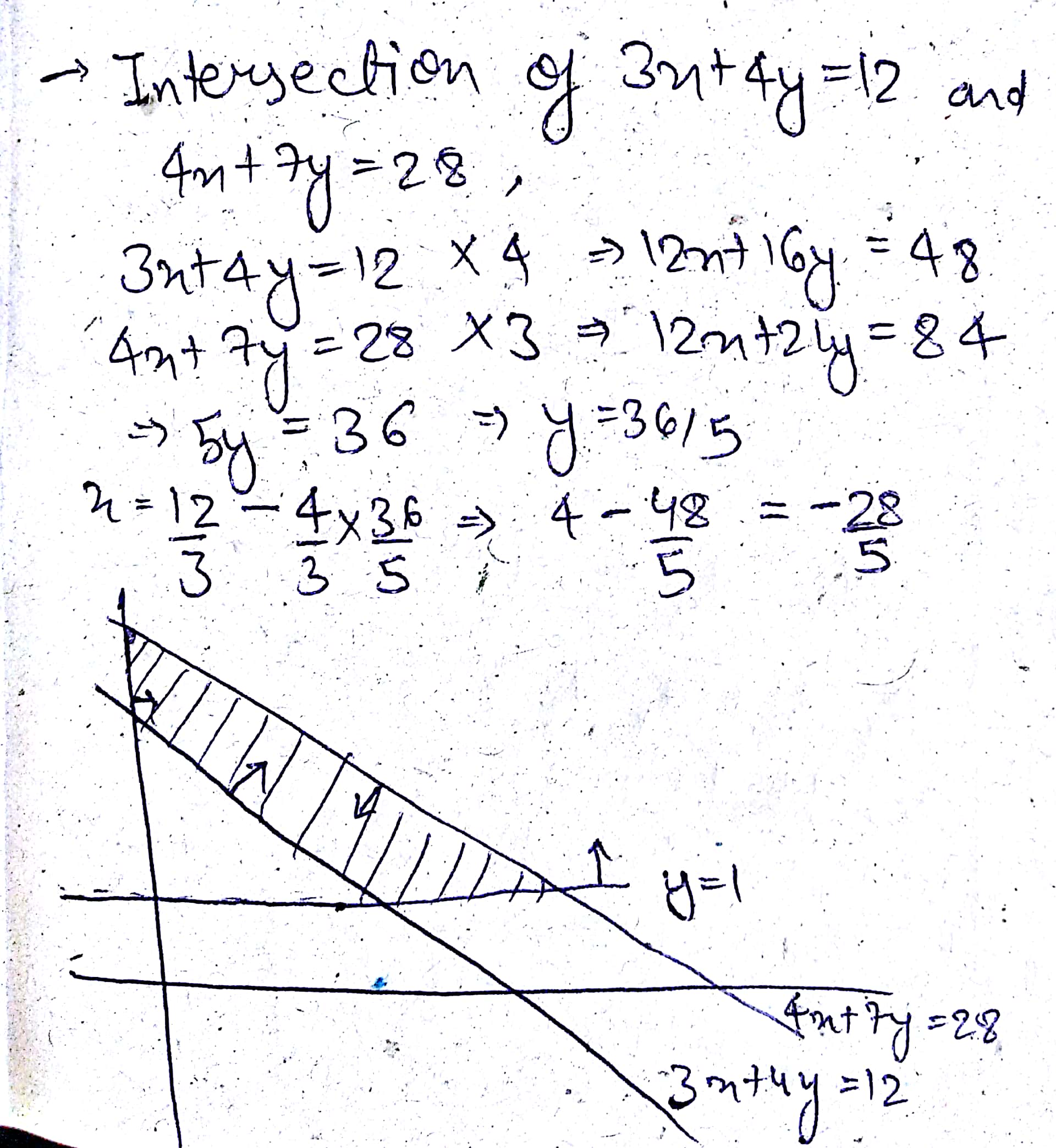
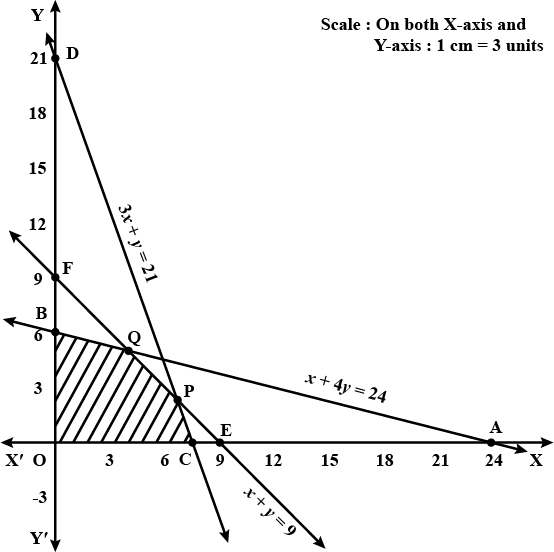
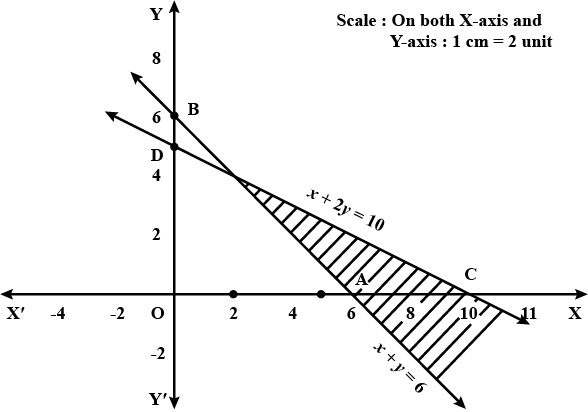
Solve: $$3x+4y\ge 12,\:x\ge 0,\:y\ge 1$$ and $$4x+7y\le 28$$
Maximize: $$z = 3x + 5y$$
Subject to: $$x + 4y \leq 24, \\ 3x + y \leq 21, \\ x + y \leq 9, \\ x \geq 0, y \geq 0$$
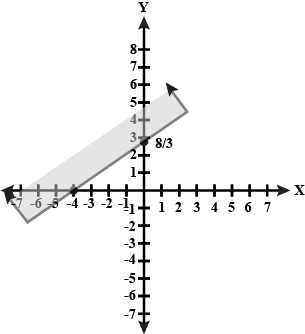
Draw the graph of the solution set of the following inequations: $$ 3x+2y> 6 $$
Graph the solution sets of the following inequations :
$$2x - 3y < 4$$.
Draw the graph of the solution set of the following inequations: $$ x-y\leq 3 $$
Draw the graph of the solution set of the following inequations: $$ x\geq y-2 $$
Draw the graph of the solution set of the following inequations: $$ 3x+5y< 15 $$
Graph the solution sets of the following inequations :
$$x \geq y - 2$$.
Draw the graph of the solution set of the following inequations: $$ x+y\geq 4 $$
Draw the graph of the solution set of the following inequations: $$ y-2\leq 3x$$
Solve the following system of inequations graphically:$$ x\geq 2,y\geq 3$$
Graph the solution sets of the following inequations :
$$y - 2 \leq 3x$$.
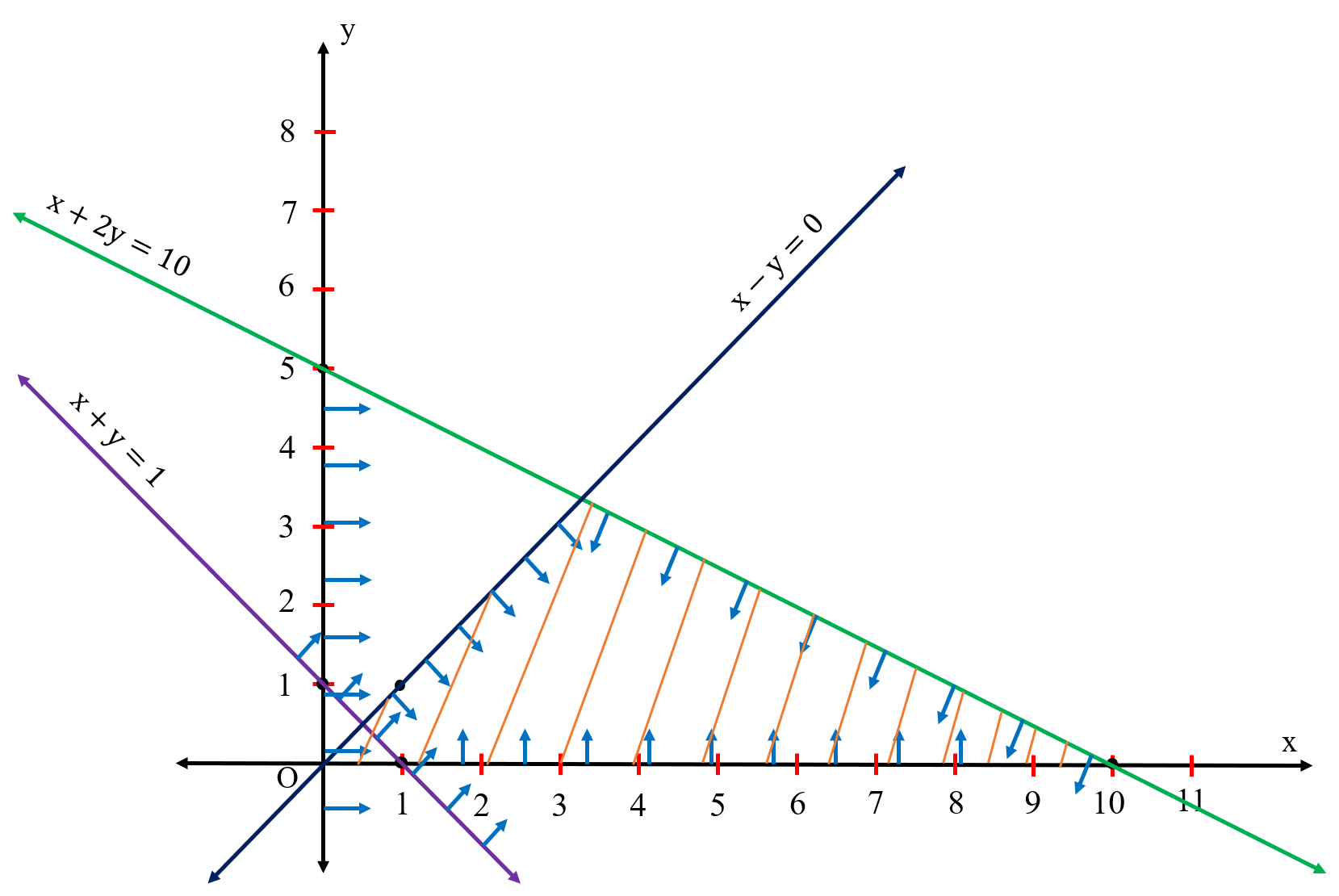
Find the solution set of the inequation $$\dfrac{x+1}{x+2}>1$$
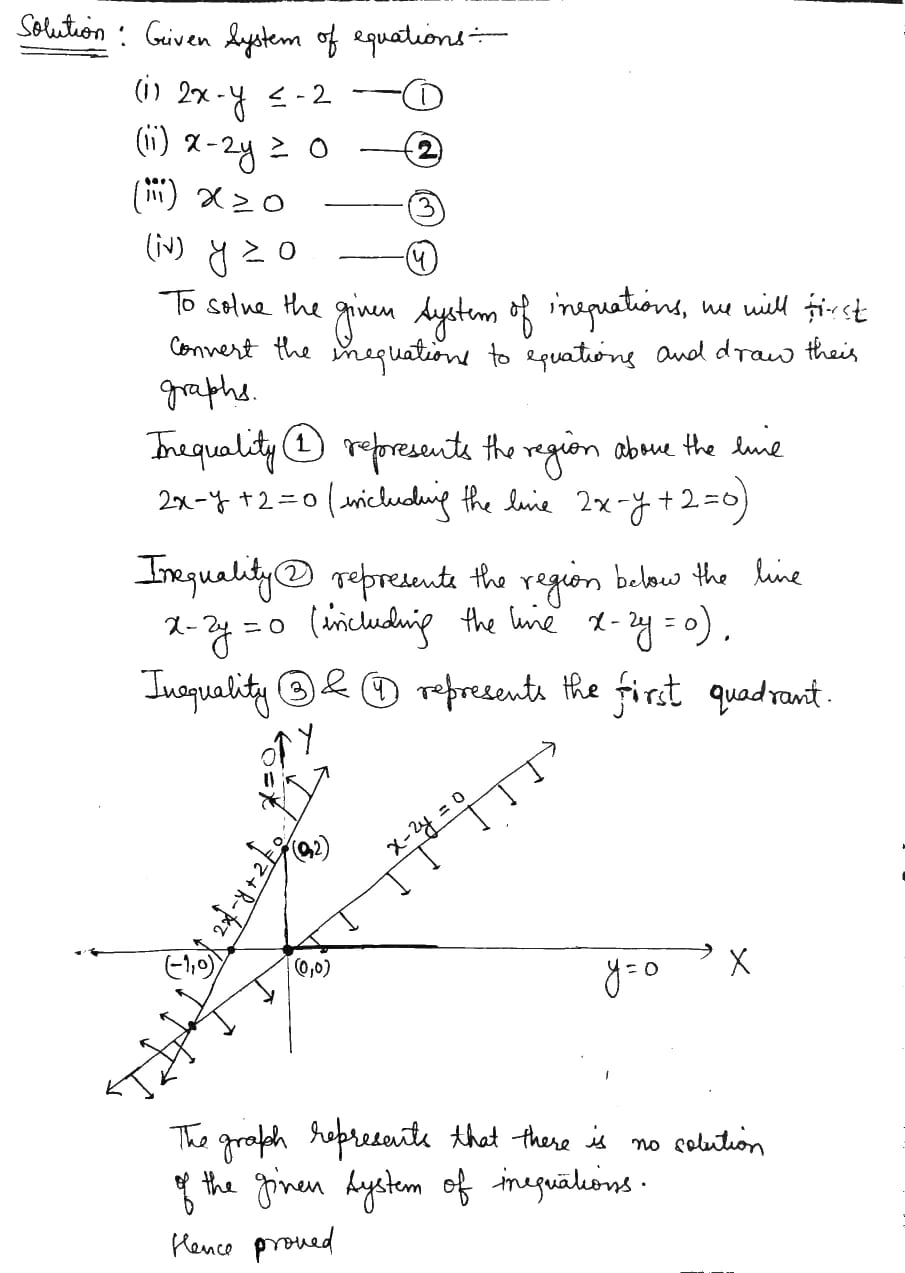
Show that each of the following systems of linear inequations has no solution: $$ 3x+2y\geq 24,3x+y\leq 15,x\geq 4 $$
Solve the following system of inequations graphically: $$ 2x+y\geq 4,x+y\leq 3,2x-3y\leq 6 $$
Solve the following system of inequations graphically: $$ 3x+4y\leq 60,x+3y\leq 30,x\geq 0,y\geq 0$$
Find the solution set of the inequation $$\dfrac{[x-2]}{(x-2)}>0,x\neq 2$$
Solve the following system of inequations graphically: $$ 5x+4y\leq 20,x\geq 1,y\geq 2 $$
Show that each of the following systems of linear inequations has no solution: $$ 2x-y\leq -2,x-2y\geq 0,x\geq 0,y\geq 0 $$
Solve the following system of inequations graphically: $$ x+y\leq 6,x+y\geq 4 $$
Show that the solution set of the following system of inequations is an unbounded set: $$ 3x+y\geq 12,x+y\geq 9,x\geq 0,y\geq 0 $$
Find the solution set of the inequation $$\dfrac{1}{x-2}<0$$
Fill in the blanks with correct inequality sign $$(>, <, \ge, \le )$$.
$$-6x\le -18\Rightarrow x.....3$$
Solve $$|x|<4$$, where $$x\in R$$
Solve $$|x|>4$$, where $$x\in R$$
Solve $$\dfrac{x}{x-5}>\dfrac{1}{2}$$, when $$x\in R$$
Fill in the blanks with correct inequality sign $$(>, <, \ge, \le )$$.
$$-3x>9\Rightarrow x.....-3$$
Fill in the blanks with correct inequality sign $$(>, <, \ge, \le )$$.
$$4x>-16\Rightarrow x.....-4$$
Solve the system of inequation $$x-2\ge 0,2x-5\le 3$$
Solve $$-4x>16$$, when $$x\in R$$
Solve $$x+5>4x-10$$, when $$x\in R$$
Fill in the blanks with correct inequality sign $$(>, <, \ge, \le )$$.
$$5x<20\Rightarrow x.....4$$
Fill in the blanks with correct inequality sign $$(>, <, \ge, \le )$$.
$$a<b$$ and $$c<0\Rightarrow \dfrac{a}{c}.....\dfrac{b}{c}$$
Fill in the blanks with correct inequality sign $$(>, <, \ge, \le )$$.
$$u-v=2\Rightarrow u.....v$$
Solve the following inequations and represent the solution set on the number line.
$$-2x>5$$, where $$(i)x\in Z, (ii) x\in R$$.
Solve the following inequations and represent the solution set on the number line.
$$3x-4>x+6$$, where $$x\in R$$.
Solve the following inequations and represent the solution set on the number line.
$$3-2x\ge 4x-9$$, where $$x\in R$$.
Solve the following inequations and represent the solution set on the number line.
$$\dfrac{5x}{4}-\dfrac{4x-1}{3}>1$$, where $$x\in R$$.
Solve the following inequations and represent the solution set on the number line.
$$\dfrac{1}{4}\left(\dfrac{2}{3}x+1\right)\ge \dfrac{1}{3}(x-2)$$, where $$x\in R$$.
Solve the following inequations and represent the solution set on the number line.
$$\dfrac{5x-8}{3}\ge \dfrac{4x-7}{2}$$, where $$x\in R$$.
Solve the following inequations and represent the solution set on the number line.
$$3x+8>2$$, where $$(i) x\in Z, (ii) x\in R$$.
Fill in the blanks with correct inequality sign $$(>, <, \ge, \le )$$.
$$x>-3\Rightarrow -2x.....6$$
Solve the following inequations and represent the solution set on the number line.
$$\dfrac{(2x-1)}{3}\ge \dfrac{(3x-2)}{4}-\dfrac{(2-x)}{5}$$, where $$x\in R$$.
Solve:
$$\dfrac{x-7}{x-2}\ge 0, x\in R$$
Solve:
$$\dfrac{1}{x-1}\le 2, x\in R$$
Solve:
$$\dfrac{x-3}{x+4}>0, x\in R$$
Solve:
$$\dfrac{x-3}{x+1}<0, x\in R$$
Solve the following inequations and represent the solution set on the number line.
$$\dfrac{2x-1}{12}-\dfrac{x-1}{3}< \dfrac{3x+1}{4}$$, where $$x\in R$$.
Solve:
$$\dfrac{3}{x-2}> 2, x\in R$$
Solve:
$$\dfrac{5x+8}{4-x}< 2, x\in R$$
Solve:
$$\dfrac{2x-3}{3x-7}>0, x\in R$$
Solve the following inequations and represent the solution set on the number line.
$$\dfrac{x}{4}<\dfrac{(5x-2)}{3}-\dfrac{(7x-3)}{5}$$, where $$x\in R$$.
Solve the inequation, $$3x 11 < 3$$ where $$x \in \{1, 2, 3,, 10\}$$. Also, represent its solution on a number line.
Solve:
$$|5-2x| \le 3, x\in R$$.
Solve:
$$|4x-5| \le \dfrac{1}{3}, x\in R$$.
List the solution set of $$30 4 (2x 1) < 30,$$ given that $$ x$$ is a positive integer.
Solve: $$ \dfrac{(2x – 3)}4 ≥ \dfrac12 , x \in \{0, 1, 2,…,8\}$$
Solve $$5 -4x > 2 - 3x, x \in W$$. Also represent its solution on the number line.
Solve:
$$|3x-7| > 4, x\in R$$.
If $$x$$ is a negative integer, find the solution set of $$\dfrac23 + \dfrac13 (x + 1) > 0$$.
Solve: $$2 (x – 2) < 3x – 2, x \in \{– 3, – 2, – 1, 0, 1, 2, 3\}.$$
If $$x\epsilon Z$$, solve : $$2 + 4x < 2x - 5 \leq 3x$$. Also, represent its solution on the real number line.
Given that $$x \in I$$, solve the inequation and graph the solution on the number line: $$3 \ge \dfrac{(x 4)}2 + \dfrac x3 \ge 2$$
Given $$A = \{x: x \in I, – 4 ≤ x ≤ 4\}$$, solve $$2x - 3 < 3$$ where $$x$$ has the domain A. Graph the solution set on the number line.
If $$x\in W$$, find the solution set of $$\dfrac35 x - \dfrac{2x 1}3 > 1.$$ Also graph the solution set on the number line, if possible.
Solve $$ x 3 (2 + x) > 2 (3x 1), x { 3, 2, 1, 0, 1, 2, 3}. $$ Also represent its solution on the number line.
Find the values of $$x$$, which satisfy the inequation :
$$-2 \leq \dfrac{1}{2}-\dfrac{2x}{3} \leq1\dfrac{5}{6}$$ , $$x \in N.$$ Graph the solution set on the number line.
Given $$x \in \{1, 2, 3, 4, 5, 6, 7, 9\}$$ solve $$x - 3 < 2x - 1$$.
Solve:
(i) $$\dfrac x2 + 5 \le \dfrac x3 + 6$$ , where $$x$$ is a positive odd integer.
(ii) $$\dfrac{(2x + 3)}3 ≥ \dfrac{(3x – 1)}4$$ , where $$x$$ is positive even integer.
Given $$x \in \{1, 2, 3, 4, 5, 6, 7, \},$$ find the values of $$x$$ for which $$-3 < 2x – 1 < x + 4.$$
List the solution set of the inequation
$$\dfrac12 + 8x > 5x -\dfrac32, x \in Z$$
Solve the following inequation and represent the solution set on the number line:
$$-3<-\dfrac{1}{2}-\dfrac{2x}{3}\leq \dfrac{5}{6},xR$$
Solve the inequation $$12 + 1\dfrac{5}{6}x 5 + 3x, x R$$. Represent the solution on a number
$$A = \{x \ ;\ 11x - 5 > 7x + 3, x \in R\}$$ and $$B = \{x\ ;\ 18x - 9 ≥ 15 + 12x, x \in R\}$$. Find the range of set $$A \cap B$$ and represent it on a number line.
If $$P$$ is the solution set of $$-3x + 4 < 2x - 3, x \in N$$ and $$Q$$ is the solution set of $$4x - 5 < 12, x \in W$$, find
(i) $$P \cap Q$$
(ii) $$Q – P$$
Solve $$2 2x 3 5, x R$$ and mark it on a number line.
Given that $$x \in R$$, solve the following inequation and graph the solution on the number line: $$-1 \leq 3 + 4x < 23$$
Solve: (4x 10)/3 (5x 7)/2, x R and represent the solution set on the number line.
Solve $$\dfrac{2x+1}{2}+2(x-3)\geq 7,xR$$. Also graph the solution set on the number line
Solve 3x/5 (2x 1)/3 > 1, x R and represent the solution set on the number line.
Solve the following inequation and graph the solution on the number line.
$$-2\dfrac{2}{3}\leq x+\dfrac{1}{3}<3+\dfrac{1}{3} , x \in R$$
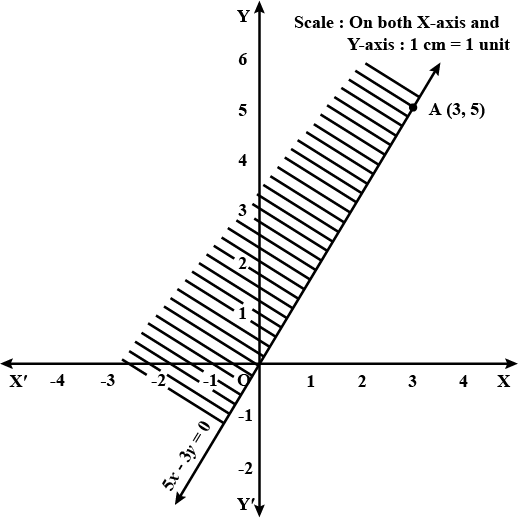
$$2x-5>11$$ is an equation
Solve the inequation:
$$\dfrac{5x+1}{7}-4\left(\dfrac{x}{7}+\dfrac{2}{5}\right)\leq 1\dfrac{3}{5}+\dfrac{3x-1}{7},xR$$
Solve the inequation: $$5x 2 3 (3 x)$$ where $$x \left\{-2, -1, 0, 1, 2, 3, 4\right\}$$. Also represent its solution on the number line.
Find the solution set of the inequation x + 5 2x + 3; x R
Graph the solution set on the number line.
Solve the inequation: 6x 5 < 3x + 4, x I
Given 20 – 5 x < 5 (x + 8), find the smallest value of x, when
$$(i) x ∈ I$$
$$(ii) x ∈ W$$
$$(iii) x ∈ N.$$
One-third of a bamboo pole is buried in mud, one-sixth of it is in water and the part above the water is greater than or equal to 3 metres. Find the length of the shortest pole.
Find the greatest integer which is such that if $$7$$ is added to its double, the resulting number becomes greater than three times the integer.
Solve the inequation and represent the solution set on the number line.
$$-3+x\leq \dfrac{8x}{3}+2 <\dfrac{14}{3}+2x,\text{ where }x\in I$$
Given: $$P= \{x : 5 < 2x - 1 ≤ 11, x \in R\}$$ and $$Q =\{x \ :\ - 1 ≤ 3 + 4x < 23, x \in I\}$$ where R = (real numbers), I = (integers)
Represent $$P$$ and $$Q$$ on the number line. Write down the elements of $$P \cap Q$$.
Solve the inequality $$2\le 3x-4\le 5$$
Solve the inequality $$-15 < \dfrac {3(x-2)}{5}\le 0$$
Solve the inequalities
$$2(x-1)< x+5, 3(x+2) > 2-x$$
Solve the inequality $$-12 < 4-\dfrac {3x}{-5}\le 2$$
Solve the inequalities
$$3x-7 > 2(x-6), 6-x > 11-2x$$
Solve the inequality $$7\le \dfrac {(3x+11)}{2}\le 11$$
Solve the inequality $$6\le -3(2x-4) < 12$$
Solve the inequality $$-3\le 4-\dfrac {7x}{2} \le 18$$
Solve the inequalities
$$5(2x-7)-3(2x+3)\le 0, 2x+19\le 6x+47$$
Solve the inequality
$$5x+1 > -24, 5x-1 < 24$$
Solve the given inequality graphically in two-dimensional plane: $$2x-3y > 6$$
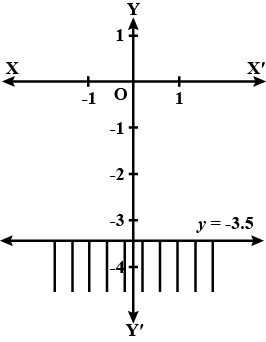
Solve the given inequality graphically in two-dimensional plane: $$y < -2$$
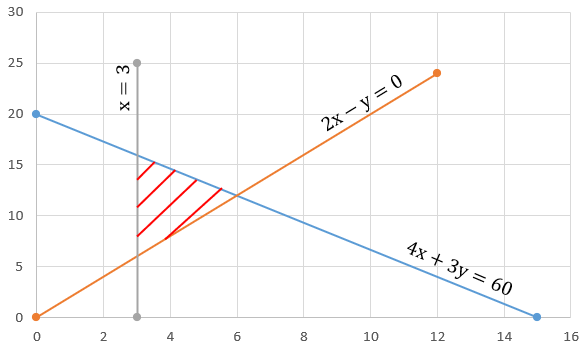
Solver the following system of inequalities graphically : $$3x+2y \ge 12, x\ge 1, y \ge 2$$
Solve the given inequality graphically in two-dimensional plane: $$-3x+2y \ge -6$$
Solve the following system of inequalities graphically : $$4x+3y \le 60, y \ge 2x, x \ge 3, x,x \ge 0$$
Solve the following system of inequalities graphically : $$x-2y \le 3, 3x +4y \ge 12, x \ge 0, y \ge 1$$
Solve the following system of inequalities graphically : $$x+y \ge 4, 2x-y > 0$$
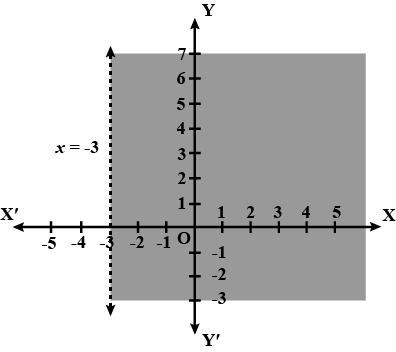
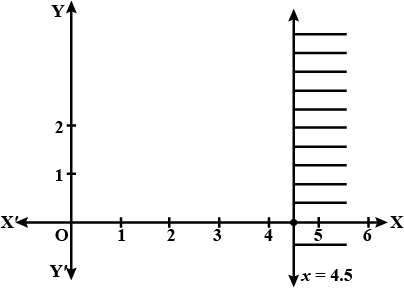
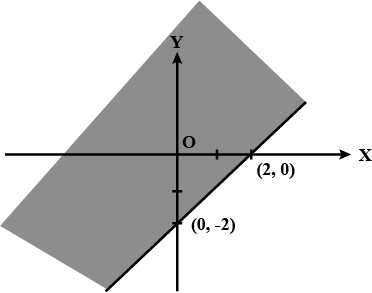
Solve the given inequality graphically in two-dimensional plane: $$x > -3$$
Solver the following system of inequalities graphically : $$2x-y > 1, x-2y < -1$$
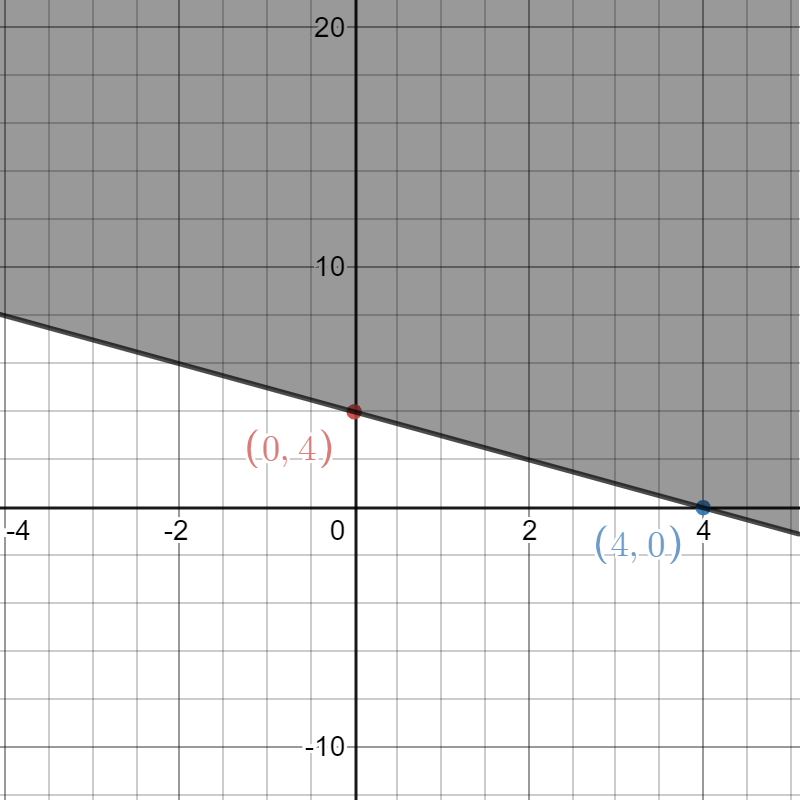
Solve the given inequality graphically in two-dimensional plane: $$3x+4y \ge 12$$
Solve the following system of inequalities graphically : $$x+2y \le 10, x+y \ge 1, x-y \le 0 , x\ge 0, y \ge 0$$
Solve $$24x < 100$$, when
$$x$$ is an integer.
Solve $$5x-3 < 7$$, when
$$x$$ is a real number
Solve $$-12x > 30$$, when
$$x$$ is an integer
Solve $$-12x > 30$$, when
$$x$$ is a natural number
Solve the following system of inequalities graphically : $$3x+2y \le 150, x+4y=80, x \le 15, y \ge 0, x \ge 0$$
Solve $$5x-3 < 7$$, when
$$x$$ is an integer
Solve $$3x+8 > 2$$, when
$$x$$ is an integer
Solve $$24x < 100$$, when
$$x$$ is a natural number
Solve $$3x+8 > 2$$, when
$$x$$ is a real number
Solve the given inequality for real $$x:3x-7> 5x-1$$
Solve the given inequality for real $$x:3(2-x)\ge (1-x)$$
Solve the given inequality for real $$x:\dfrac{1}{2}\left(\dfrac{3x}{5}+4\right)\ge \dfrac{1}{3}(x-6)$$
Solve the given inequality for real $$x:37-(3x+5)\ge 9x-8(x-3)$$
Solve the given inequality for real $$x:\dfrac{3(x-2)}{5}\le \dfrac{5(2-x)}{3}$$
Solve the given inequality $$x:2(2x+3)-10 < 6(x-2)$$
Solve the given inequality for real $$x:\dfrac{x}{3} > \dfrac{x}{2}+1$$
Solve the given inequality for real $$x:3(x-1) \le 2(x-3)$$
Solve the given inequality for real $$x:4x+3 < 5x+7$$
Solve the given inequality for real $$x:x+\dfrac{x}{2}+\dfrac{x}{3} < 11$$
Solve the given inequality for real $$x:\dfrac{(2x-1)}{3} \ge \dfrac{(3x-2)}{4}-\dfrac{(2-x)}{5}$$
Solve the given inequality and show the graph of the solution on number line:
$$5x-3\ge 3x-5$$
To receive Grade $$A$$ in a course, one must obtain an average of $$90$$ marks or more in five examinations (each of $$100$$ marks). If Sunita's marks in first four examination are $$87, 92, 94$$ and $$95$$, find minimum marks that sunita must obtain in fifth examination to get grade $$'A'$$ in the course.
Find all pairs of consecutive even positive integers, both of which are larger than $$5$$ such that their sum is less than $$23$$.
Solve the given inequality and show that graph of the solution on number line:
$$\dfrac{x}{2} > \dfrac{(5x-2)}{3}-\dfrac{(7x-3)}{5}$$
Solve the given inequality and show the graph of the solution on number line:
$$3(1-x) < 2 (x+4)$$
Find all pairs of consecutive odd positive integers both which are smaller than $$10$$ such that their sum is more than $$11$$.
Ravi obtained $$70$$ and $$75$$ marks in the first two-unit test. Find the minimum marks he should get in the third test to have an average of at least $$60$$ marks.
Solve the given inequality for real $$x:\dfrac{x}{4} < \dfrac{(5x-2)}{3}-\dfrac{(7x-3)}{5}$$
Solve the given inequality and show the graph of the solution on number line:
$$3x-2 < 2x+1$$
Solve $$-7< 4x + 1 \leq 23, x \, \epsilon\, l$$
Represent the solution of the following inequalities graphically :
$$ x \leq 4 , x\, \varepsilon \, N $$
Solve $$3 - 4x < x - 12, x\, \epsilon\, {-1, 0, 1, 2, 3, 4, 5, 6, 7}$$
Solve the following inequations and represent their solution on a number line:
(i) $$\dfrac{2x - 1}{3} \leq 2 \dfrac{1}{2}, x \epsilon W$$
(ii) $$ -1 < \dfrac{2x}{3} + 1 \leq 4, x\, \epsilon\, l $$
Represent the solution of the following inequalities graphically :
$$ x < 5 , x \, \varepsilon\, W $$
A man wants to cut three from a single piece of board of length $$91\ cm$$, The second length is to be $$3\ cm$$ longer than the shortest and the third length is to be twice as long as the shortest. What are the possible lengths of the shortest board if the third piece is to be at lest $$5\ cm$$ longer than the second?
Represent the following inequations graphically:
(i) $$x \leq 3, x \epsilon N$$
(ii) $$x<4, x \epsilon W$$
(iii) $$-2 \leq x< 4, x \epsilon l$$
(iv) $$-3 \leq x \leq 2, x \epsilon l$$
Solve the following inequations.
(i)$$ 4 - x > -2, x\, \epsilon\, N$$
(ii) $$3x + 1 \leq 8, x\, \epsilon\, W$$
Also represent their solutions on the number line.
Solve the following inequations and graph their solutions on a number line
$$ -1 < \dfrac{x}{2} + 1 \leq 3 , x \, \varepsilon\, I $$
If the replacement set is $$ \left \{ - 3 , -2 , -1 , 0 , 1 , 2 , 3 \right \} $$ solve the inequation $$ \dfrac{3x - 1}{2} < 2 $$ . Represent its solution on the number line.
Solve the following inequation :
$$ \dfrac{2}{3}p + 5 < 9 , p\, \varepsilon \, W $$
Solve the following inequations and graph their solutions on a number line
$$ -4 \leq 4x < 14 , x \, \varepsilon \, N $$
Solve $$ \dfrac{x}{3} + \dfrac{1}{4} < \dfrac{x}{6} + \dfrac{1}{2} , x \, \varepsilon\, W $$ . Also represent its solution on the number line.
Represent the solution of the following inequalities graphically :
$$ -3 \leq x < 3 , x \, \varepsilon \, 1 $$
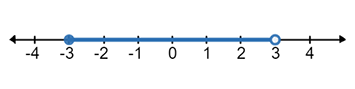
If the replacement set is $$ \left \{-6 , -4 , -2 , 0 , 2 , 4 , 6 \right \}$$ ; then represent the solution set of the inequality $$ -4 \leq x < 4 $$ graphically
If $$ 25-4 x \leq 16, $$ find the smallest value of $$ \mathbf{x}, $$ when $$ \mathbf{x} $$ is a real number.
Represent the following inequalities on real number line:
$$ 8 \geq x>-3 $$
Represent the following inequalities on the real number line:
$$ 2 x-1<5 $$
Represent the following inequality on real number line:
$$ -4<x<4 $$
Represent the following inequality on real number line:
$$ 3 x+1 \geq-5 $$
Solve the inequation:
$$ 3-2 \mathbf{x} \geq \mathbf{x}-12 $$ given that $$ \mathbf{x} \in \mathbf{N} $$
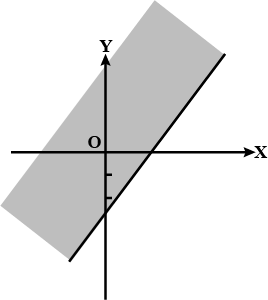
For given graph alongside, write an inequation taking $$ \mathbf{x} $$ as the variable:

If $$ 25-4 x \leq 16, $$ find the smallest value of $$ x $$, when $$ x $$ is an integer.
Represent the following inequalities on real number line:
$$ -2 \leq x<5$$
Represent the following inequality on real number line:
$$ 2(2 x-3) \leq 6 $$
For the given graph alongside, write an inequation taking $$ \mathbf{x} $$ as the variable.

For the given graph alongside, write an inequation taking $$ \mathbf{x} $$ as the variable.

Represent the solution of each of the following inequations on the real number line:
$$ x+3 \leq 2 x+9 $$
For the following inequation, graph the solution set on the real number line:
$$ -4 \leq 3 x-1<8 $$
For the following inequation, graph the solution set on the real number line:
$$ x-1<3-x \leq 5 $$
Represent the solution of each of the following inequations on the real number line:
$$ 7-x \leq 2-6 x $$
Represent the solution of each of the following inequations on the real number line:
$$ 4 x-1>x+11 $$
Represent the solution of each of the following inequations on the real number line:
$$ 1+x \geq 5 x-11 $$
For the given graph alongside, write an inequation taking $$ \mathbf{x} $$ as the variable.

Represent the solution of each of the following inequations on the real number line:
$$2-3 x>7-5 x$$
Solve and graph the solution set of:
$$ x+5 \geq 4(x-1) $$ and $$ 3-2 x<-7, x \in R $$
Find the range of values of $$ x $$ which satisfies
$$ -2 \dfrac{2}{3} \leq x+\dfrac{1}{3}<3 \dfrac{1}{3} ; x \in R $$
Graph these values of $$ x $$ on the number line.
$$\mathrm{x} \in\{\text { real numbers }\} $$ and $$ -1<3-2 x \leq 7 $$, evaluate $$ x $$ and represent it on a number line.
Solve and graph the solution set of:
$$ 2 x-9<7 $$ and $$ 3 x+9 \leq 25, x \in R $$
Given $$ \mathbf{x} \in\{\text { real numbers }\} $$, find the range of values of $$ \mathbf{x} $$ for which $$ -5 \leq 2 x-3<x+2 $$ and represent it on a real number line.
Solve and graph the solution set of:
$$ 2 x-9 \leq 7 $$ and $$ 3 x+9>25, x \in \mathbf{I} $$
Solve and graph the solution set of:
$$ 3 x-2>19 $$ or $$ 3-2 x \geq-7, x \in R $$
Solve the following inequation and graph the solution set on the number line:
$$ 2 x-3<x+2 \leq 3 x+5, x \in R $$
Find the values of $$ x $$, which satisfy the equation:
$$ -2 \leq \dfrac{1}{2}-\dfrac{2 x}{3} \leq 1 \dfrac{5}{6}, x \in N $$
Graph the solution on the number line.
Represent the solution of each of the following inequations on the real number line:
$$ (2 x+5) / 3>3 x-3 $$
Solve and graph the solution set of:
$$ 5>\mathrm{p}-1>2 $$ or $$ 7 \leq 2 \mathrm{p}-\leq 17, \mathrm{p} \in \mathrm{R} $$
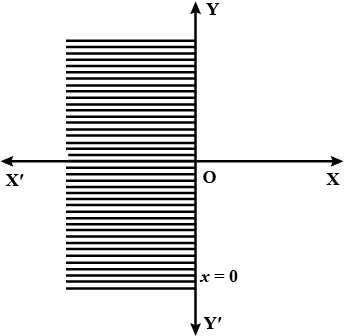
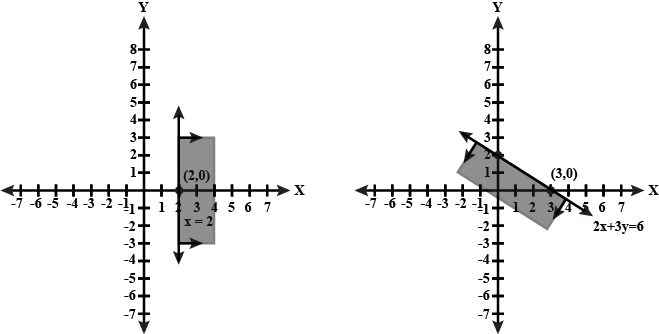
Draw graph of : $$x \geq 0$$
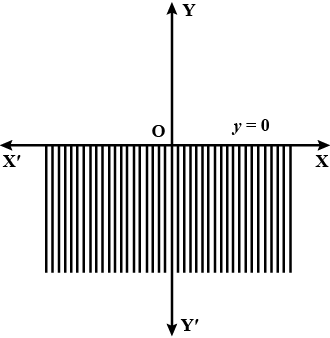
Solve graphically : $$y \leq 0$$
Solve the graph the solution set on a number line:
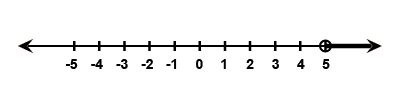
$$x-5 < -2; x\in N$$
Draw graph of : $$y \geq 0$$
Solve graphically : $$x \leq 0$$
Solve: $$3+x < 2, x\in N$$
Solve the inequation $$8-2x > x-5; x\in N$$
Solve the inequality $$18-3(2x-5) > 12; x\in W$$
Solve: $$\dfrac{2x+1}{3}+15 < 17; x\in W$$
Solve graphically : $$3x + 4 \leq 0$$
Solve graphically : $$2x - 5y \geq 10$$
Solve graphically : $$x \geq 0$$ and $$y \geq 0$$
Solve graphically : $$2y - 5 \geq 0$$
Solve graphically : $$x \leq 0$$ and $$y \leq 0$$
Solve graphically : $$x + 2y \leq 6$$
Solve graphically : $$2x - 3 \geq 0$$
Solve graphically : $$5y + 3 \leq 0$$
Solve graphically : $$5x - 3y \leq 0$$
Solve graphically : $$3x + 2y \geq 0$$
Solve graphically : $$x - y \leq 2$$ and $$x + 2y \leq 8$$
Find the feasible solution for the following system of linear inequations:
$$0 \leq * \leq 3, 0 \leq y \leq 3, x + y \leq 5, 2x + y \geq 4$$
Solve graphically : $$2x + y \geq 2$$ and $$x - y \leq 1$$
Find the feasible solution of the following inequation:
$$2x + 3y \leq 6, x + y \geq 2, x \geq 0, y \geq 0$$
Solve graphically : $$2x + y \geq 5$$ and $$x - y \leq 1$$
Find the feasible solution of the following inequations:
$$x - 2y \leq 2, x + y \geq 3, -2x + y \leq 4, x \geq 0, y \geq 0$$
Find the feasible solution of the following inequation:
$$3x + 4y \geq 12, 4x + 7y \leq 28, y \leq 1, x \leq 0$$
Solve graphically : $$2x + 3y \leq 6$$ and $$x + 4y \geq 4$$
Find the feasible solution of the following inequation:
$$x + 4y \leq 24, 3x + y \leq 21, x + y \leq 9, x \geq 0, y \geq 0$$
Solve graphically : $$x + y \geq 6$$ and $$x + 2y \leq 10$$
$$5y -12 \geq 0$$
x is a natural number.
Find graphical solution for the following system of linear in equation:
$$3x + 4y \leq 12, x - 2y \geq 2, y \geq -1$$
x is an integer.
$$4x - 18 \geq 0$$
$$y \leq -3.5$$
A company produces two types of articles A and B which require silver and gold. Each unit of A requires 3 gm of silver and 1 gm of gold, while each unit of B requires 2 gm of silver and 2 gm of gold. The company has 6 gm of silver and 4 gm of gold. Construct the inequations and find feasible solution graphically.
$$- 11x - 55 \leq 0$$
$$x$$ is a real number
$$x$$ $$\epsilon$$ $$N$$
$$x$$ is an integer
x is an integer
$$x$$ is a real number.
Solve: $$4x + 3 < 6x + 7$$
$$x$$ $$\epsilon$$ $$Z$$
Solve: $$3x - 7 > 5x - 1$$
x is a real number.
Solve: $$37 - (3x + 5) \geq 9x - 8(x - 3)$$
Solve: $$3(2 - x) > 2(1 - x)$$
Solve : $$x+\cfrac{x}{2}+ \cfrac{x}{3}<11$$
Solve:
$$\cfrac{2 x-1}{3} \geq \cfrac{3 x-2}{4}- \cfrac{2-x}{5}$$
Solve:
$$\cfrac{x}{3}>\cfrac{x}{2} + 1$$
$$3x - 2 < 2x + 1$$
Solve: $$\frac{3(x - 2)}{5} \leq \frac{5(2 - x)}{3}$$
Solve: $$3(x - 1) < 2 (x - 3)$$
Solve: $$\cfrac{5 - 2 x}{3} \leq \cfrac{x}{6} - 5$$
Solve:
$$\cfrac{x}{4} <\cfrac{5 x - 2}{3} - \cfrac{7 x-3}{5}$$
x > -3
Solve the following system of inequalities graphically.
$$x \geq 3, y \geq 2$$
$$5x - 3 \geq 3x - 5$$
$$7x + 3 < 5x + 9$$
y < -2
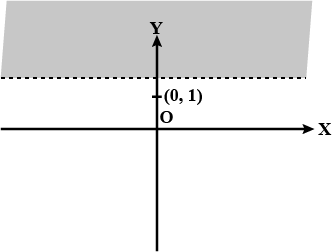
y > 2
3x + 2y > 6
$$\cfrac{3 x-4}{2} \geq \cfrac{x+1}{4} - 1$$
$$3(1 - x) < 2(x + 4)$$
$$\cfrac{x}{2} \geq \cfrac{5 x-2}{3} - \cfrac{7 x-3}{5}$$
Solve the following system of inequalities graphically.
$$2x + y \geq 8, x + 2y \geq 10$$
2x + y > 6
3x + 4y < 12
Solve the following system of inequalities graphically.
$$x + y \geq 4, 2x - y > 0$$
Solve the following system of inequalities graphically.
$$2x + y \geq 6, 3x + 4y\leq 12$$
Solve the following system of inequalities graphically.
$$x + y \leq 6, x + y \geq 4$$
Solve the following system of inequalities graphically.
$$2x - y > 1, x - 2y < -1$$
3x - 6 > 0
Solve the following system of inequalities graphically.
$$8x + 3y \leq 100, x \geq 0, y \geq 0$$
Solve the following system of inequalities graphically.
$$x+y \geq 3, x-y \geq 2$$
Solve the following system of inequalities graphically.
$$5x + 4y \leq 20, x \geq 1, y \geq 2$$
Solve the following system of inequalities graphically.
$$x + 2y \leq 8, 2x + y \leq 8, x \geq 0, y \geq 0$$
Solve the following system of inequalities graphically.
$$3x + 4y \leq 60, x + 3y \leq 30, x \geq 0, y \geq 0$$
Solve the following system of inequalities graphically.
$$3x + 2y \leq 12, x \geq 1, y \geq 2$$
Solve the following system of inequalities graphically.
$$5x + 4y \leq 40, x \geq 0, y \geq 0$$
x - y < 2
Solve the following system of inequalities graphically.
$$2x + y \geq 4, x + y \leq 3, 2x - 3y \leq 6$$
Solve the following system of inequalities graphically.
$$x + y \leq 9, y > x, x \geq 0$$
y + 8 > 2x
Solve the following system of inequalities graphically.
$$x - 2y \leq 3, 3x + 4y \geq 12, x \geq 0, y \geq 0$$
Solve the following system of inequalities graphically.
$$x + 2y \leq 10, x + y \geq x - y \leq 0, x \geq 0, y \geq 0$$
Solve the following system of inequalities graphically.
$$3x + 2y \leq 150, x + 4y \leq 80, x \leq 15, y \geq 0, x \geq 0$$
Solve the following system of inequalities graphically.
$$4x + 3y \leq 60, y \geq 2x, x \geq 3, y \geq 0$$
Solve the equations.
$$-5 \leq \frac{5 - 3x} {2} \leq 8$$
-3x + 2y > -6
Solve the equations.
$$6 < -3 \left(2JC - 4 \right) < 12$$
Solve the equations.
$$-15 \leq \frac{3 \left(x - 2 \right)} {5} \leq 0$$
Solve the equations.
$$-3 \leq 4 - \frac{7x} {2} \leq 18$$
Solve the equations.
$$2 \leq 3x - 4 \leq 5$$
Solve the equations.
$$-8 \leq 5x - 3 < 7$$
A solution of $$ 8 \% $$ boric acid to be diluted by. adding a $$ 2 \% $$ boric acid solution to it. The resulting mixture is to be more than $$ 4 \% $$ but less than $$ 6 \% $$ boric acid. If we have 640 liters of the $$ 8 \% $$solution, how many liters of the $$ 2 \% $$ solution will have to be added?
Solve the inequalities and represent the solution graphically on the number line:
$$ 5(2 x-7)-3(2 x+3) \leq 0,2 x+19 \leq 6 x+47 $$
Solve the inequalities and represent the solution graphically on the number line:
$$ 3 x-7>2(x-6), 6-x>11 .-2 x $$
Solve the inequalities and represent the solution graphically on the number line:
$$ 5 x+1>-24,5 x-1<24 $$
A manufacturer has 600 liters of $$ 12 \% $$ solution of acid. How many liters of a $$ 30 \% $$ acid solution must be added to it so that acid content in the resulting mixture will be more than $$ 15 \% $$ but less than $$ 18 \%? $$
Solve the inequalities and represent the solution graphically on the number line:
$$ 2(x-1)<x+5,3(x+2)>2-x $$
Solve the inequalities and represent the solution graphically on the number line:
$$ 3 x-7<5+x, 11-5 x \leq 1 $$
Solve the equations.
$$ -12<4-\dfrac{3 x}{-5} \leq 2 $$
Solve the equations.
$$-12 < 4 - \frac{3x} {-5} \leq 2$$
Solve the equations.
$$7 \leq \frac{3x + 11} {2} \leq 11$$
Find the integer values of $$t$$ which satisfy the inequalities.
$$4t + 7 < 39 \nless 7t + 2 $$
Solve the following inequalities, graphically :
$$| x - y | \geq 1$$
Solve the following inequalities, graphically :
$$3x - 2y \leq x + y - 8$$
Solve the following linear programming problem by graphical method :
Minimize and maximize $$Z = x + 2y$$
Subject to the constraints,
$$x + 2y \geq 100$$
$$2x y \leq 0$$
$$2x + y \leq 200$$
and $$x \geq 0,y \geq 0$$
By graphical method, show the solution set of the following inequalities :
(i) $$x \geq 2$$
(ii) $$2x + 3y \leq 6$$
Maximise $$Z = x + 2y$$
subject to the constraints
$$x + 2y \geq 100$$
$$2x - y \leq 0$$
$$2x + y \leq 200$$
$$x, y \geq 0$$
Solve the above LPP graphically.
A manufacturer has employed $$5$$ skilled men and $$10$$ semi-skilled men and makes two models $$A$$ and $$B$$ of an article. The making of one item of model $$A$$ requires 2 hours work by a skilled man and 2 hours work by a semi-skilled man. One item of model $$B$$ requires 1 hour by a skilled man and 3 hours by a semi-skilled man. No man is expected to work more than 8 hours per day. The manufacturers profit on an item of model A is Rs. 15 and on an item of model $$B$$ is Rs. How many of items of each model should be made per day in order to maximize daily profit? Formulate the above LPP and solve it graphically and find the maximum profit.
How many liters of water will have to be added to 1125 liters of the $$ 45 \% $$ solution of acid so that the resulting mixture will contain more than $$ 25 \% $$ but less than $$ 30 \% $$ acid content?
Solve the following inequalities, graphically :
$$|x | \leq 3$$
If $$(xy)^{a-1}=z$$
$$(yz)^{b-1}=x$$
$$(zx)^{c-1}=y$$
then $$ab+bc+ca=?$$
Solve the following system of inequations graphically: $$ 2x+y> 1,x-2y< -1 $$
Solve the following system of inequations graphically: $$ x+y\leq 9,y> x,x\geq 0 $$
Solve the following systems of inequations graphically: $$ x+2y\leq 100,2x+y\leq 120,x+y\leq 70,x\geq 0,y\geq 0 $$
Solve the following system of inequations graphically: $$ 3x+2y\leq 12,x\geq 1,y\geq 2 $$
Solve the following system of inequations graphically: $$ 4x+3y\leq 60,y\geq 2x,x\geq 3,x\geq 0,y\geq 0 $$
Solve the following system of inequations graphically: $$ x+2y\leq 10,x+y\geq 1,x-y\leq 0,x\geq 0,y\geq 0 $$
Solve the following systems of inequations graphically: $$ x-2y\leq 2,x+y\geq 3,-2x+y\leq 4,x\geq 0,y\geq 0 $$
Solve the following system of inequations graphically: $$ 2x+y\geq 6,3x+4y\leq 12 $$
Solve the following systems of inequations graphically: $$ x+2y\leq 2000,x+y\leq 1500,y\leq 600,x\geq 0,y\geq 0 $$
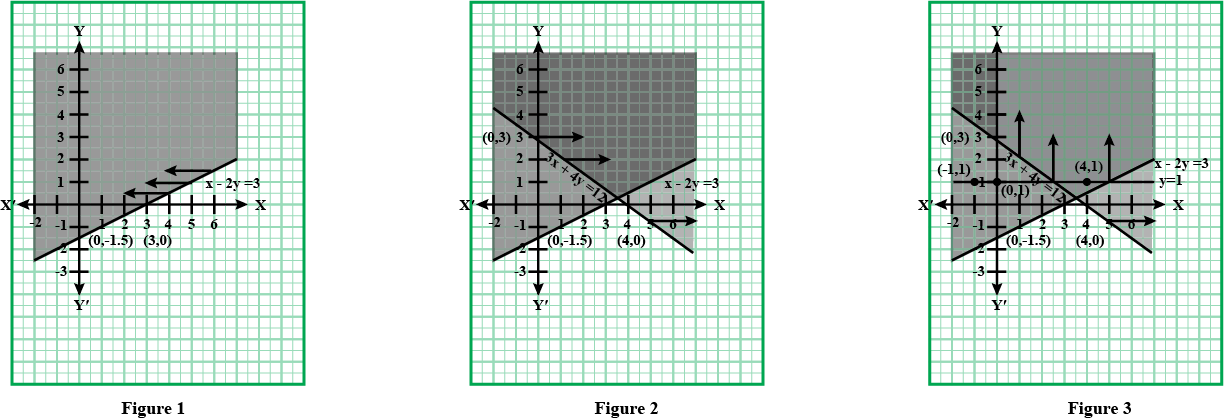
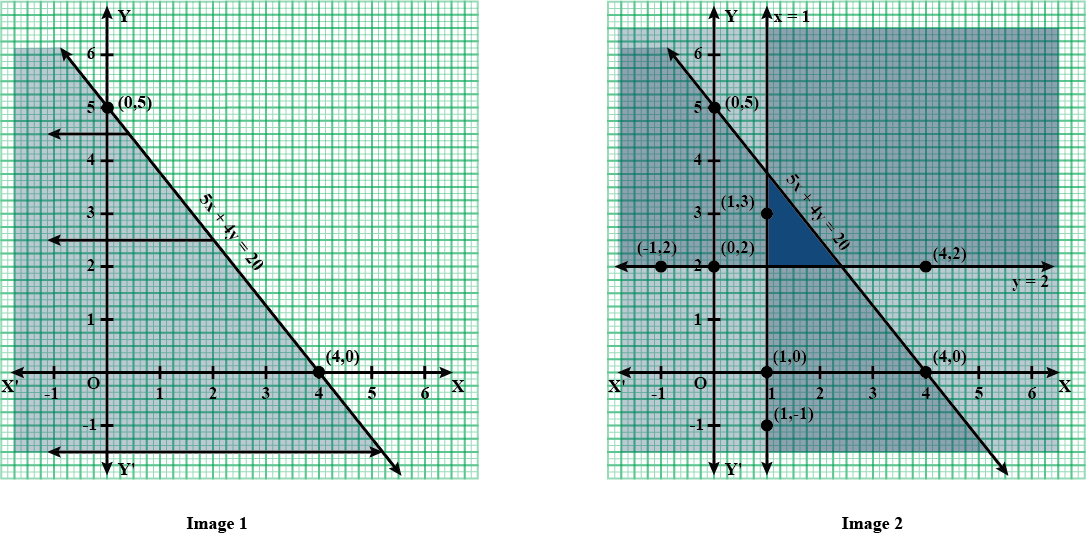
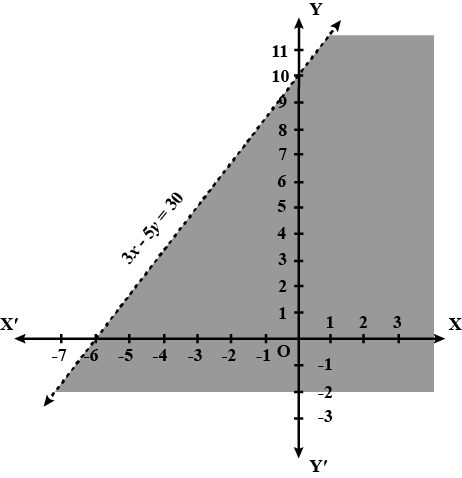
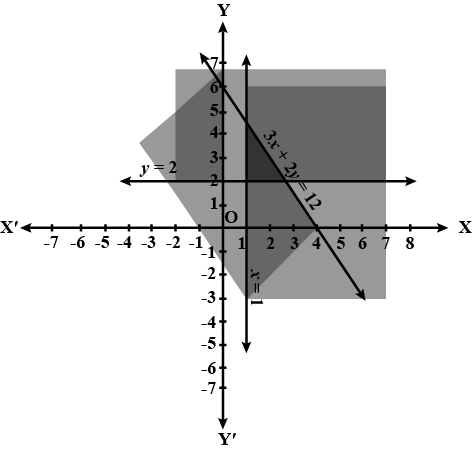
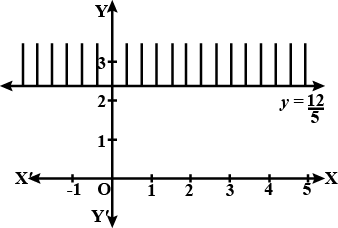
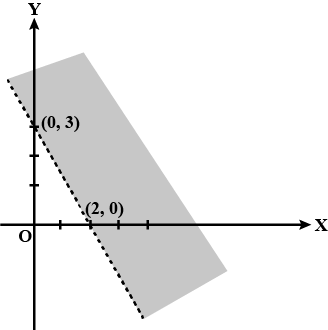
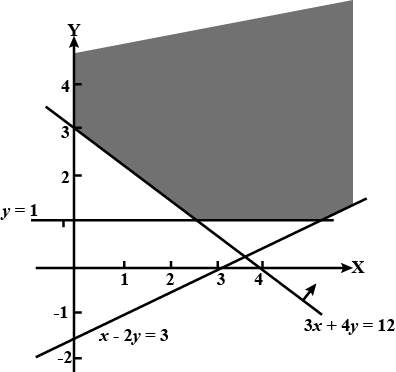
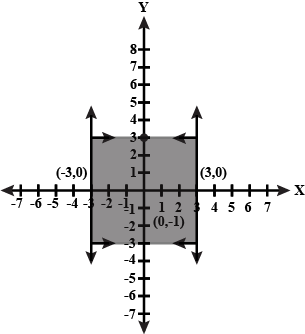
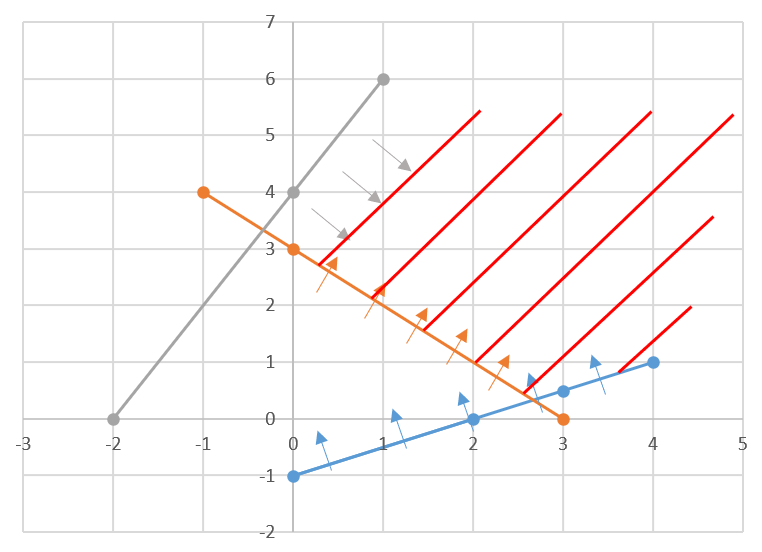
Find the linear inequations for which the shaded area is the solution set in the figure given below.
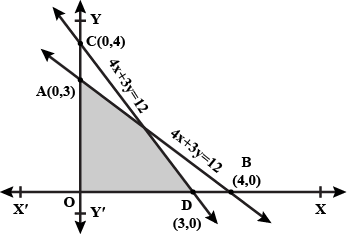
Find the linear inequations for which the shaded area in the figure given below, is the solution set.
A firm manufactures headache pills in two sizes A and B. Size A contains $$2$$ grams of aspirin $$5$$ grams of bicarbonate and $$1$$ gram of caffeine; size B contains $$1$$ gram of aspirin of $$8$$ grams of bicarbonate and $$6$$ grains of caffeine. It has been found by users that it requires at least $$12$$ grams of aspirin $$74$$ grams of bicarbonate and $$24$$ grams of caffeine for providing immediate effects. Determine graphically the least number of pills a patient should have to get immediate relief.
Class 11 Engineering Maths Extra Questions
- Binomial Theorem Extra Questions
- Complex Numbers And Quadratic Equations Extra Questions
- Conic Sections Extra Questions
- Introduction To Three Dimensional Geometry Extra Questions
- Limits And Derivatives Extra Questions
- Linear Inequalities Extra Questions
- Mathematical Reasoning Extra Questions
- Permutations And Combinations Extra Questions
- Principle Of Mathematical Induction Extra Questions
- Probability Extra Questions
- Relations And Functions Extra Questions
- Sequences And Series Extra Questions
- Sets Extra Questions
- Statistics Extra Questions
- Straight Lines Extra Questions
- Trigonometric Functions Extra Questions