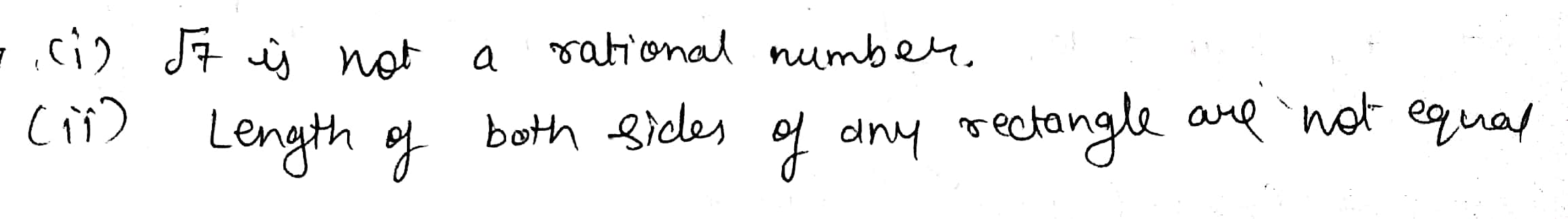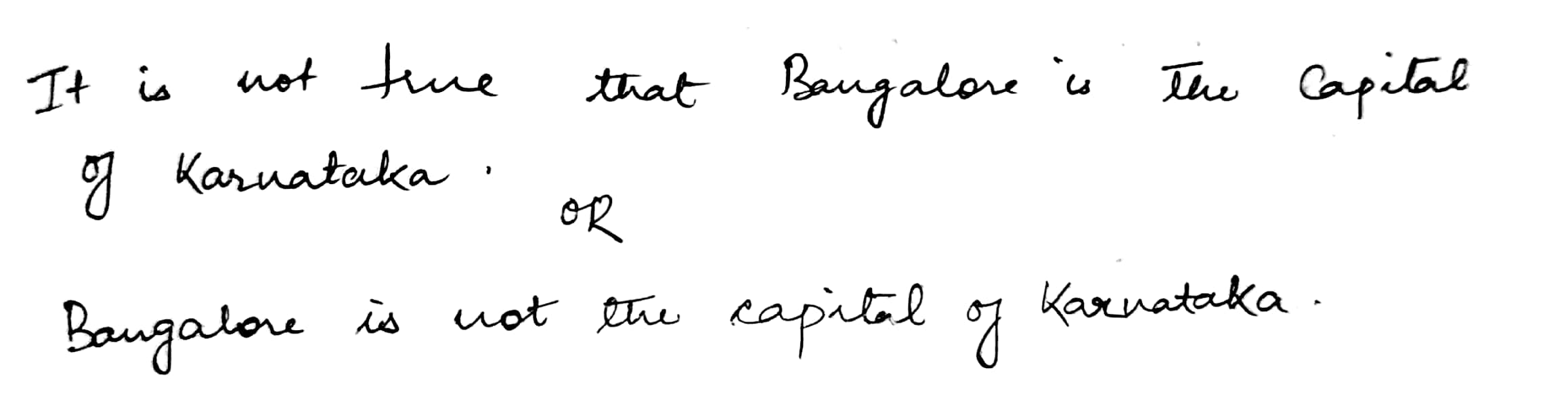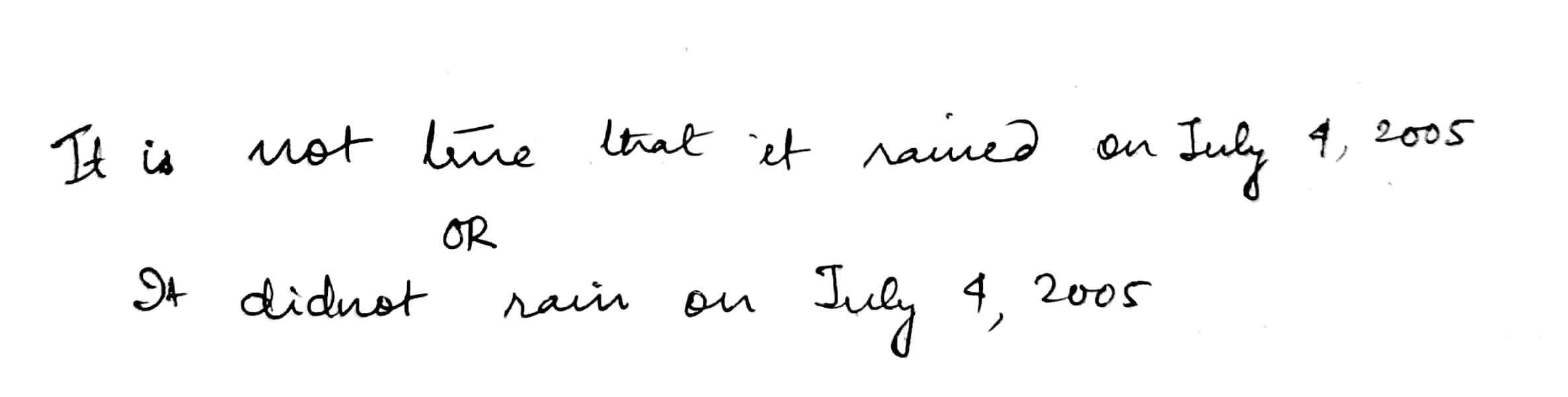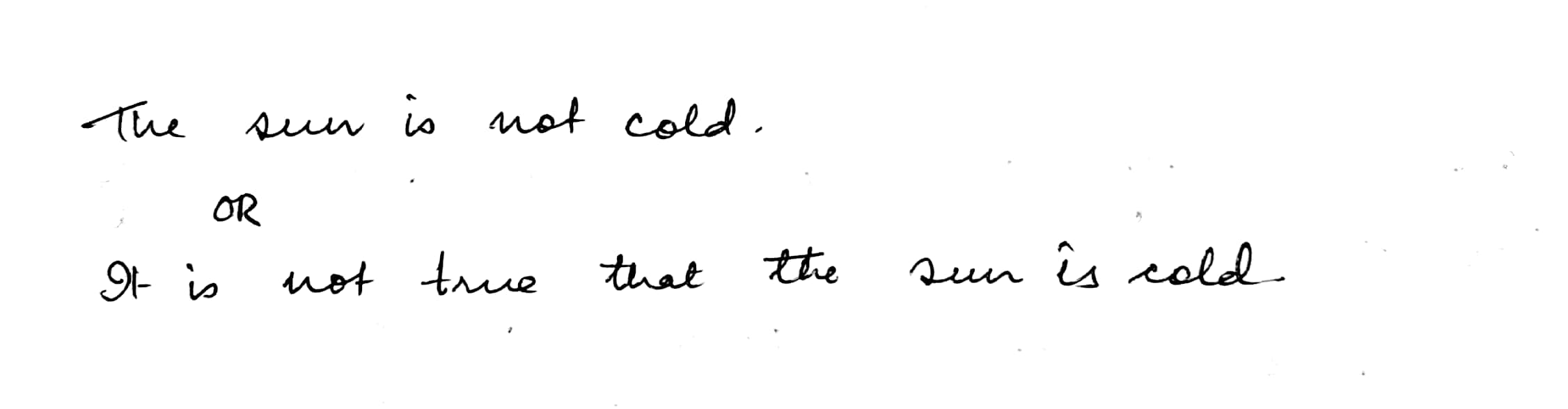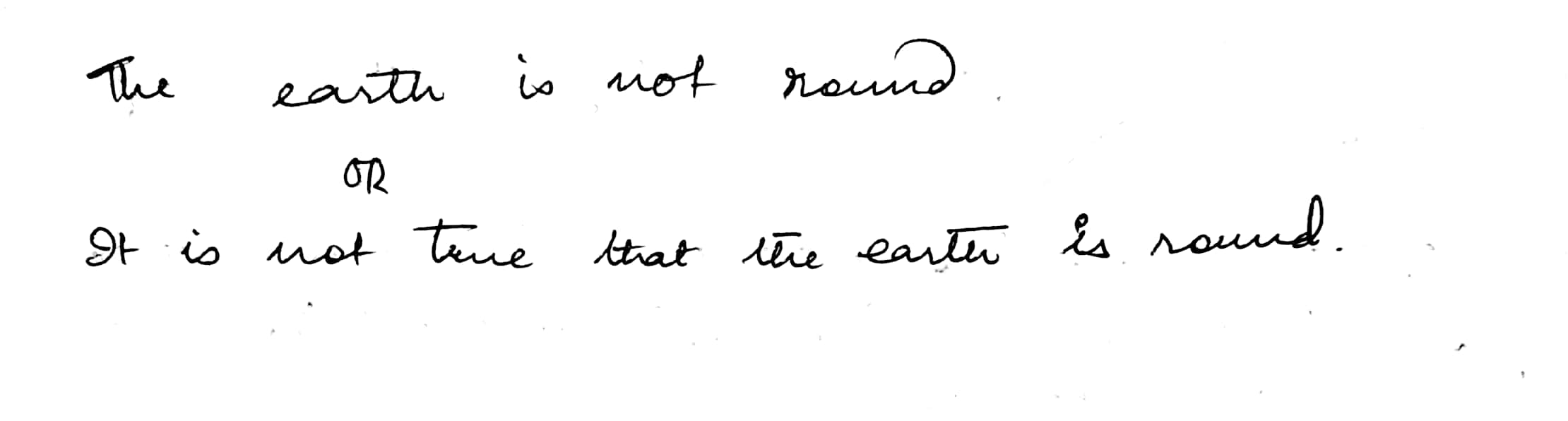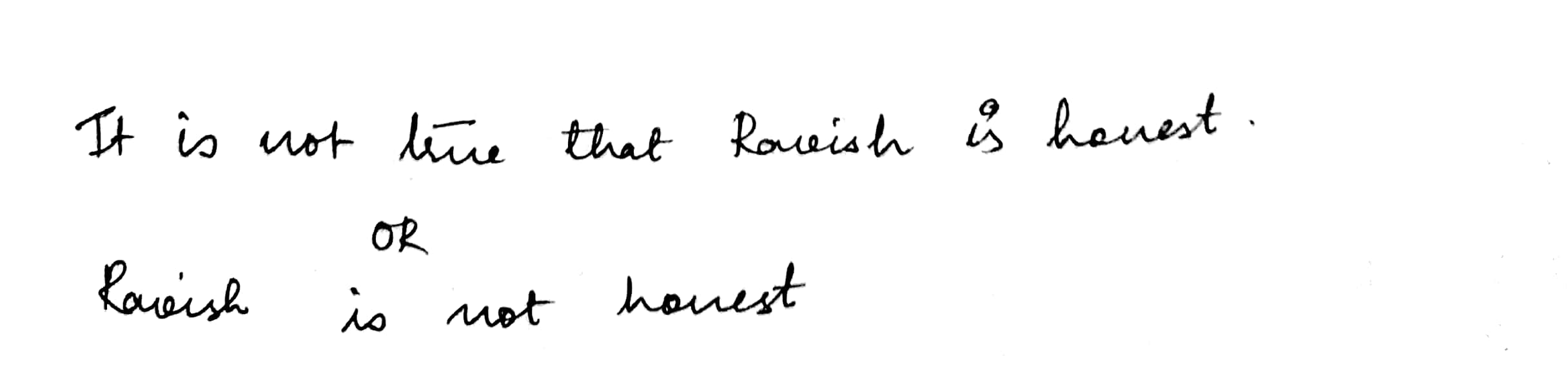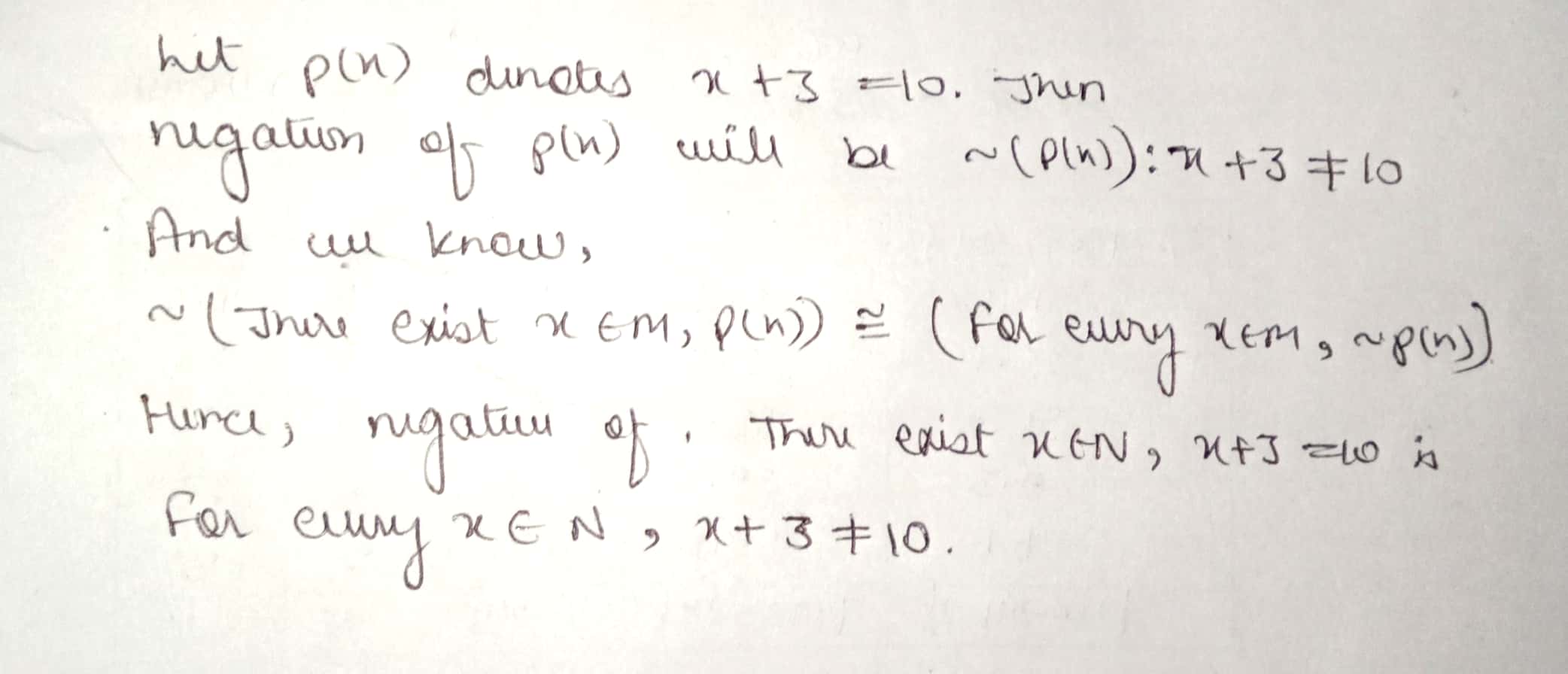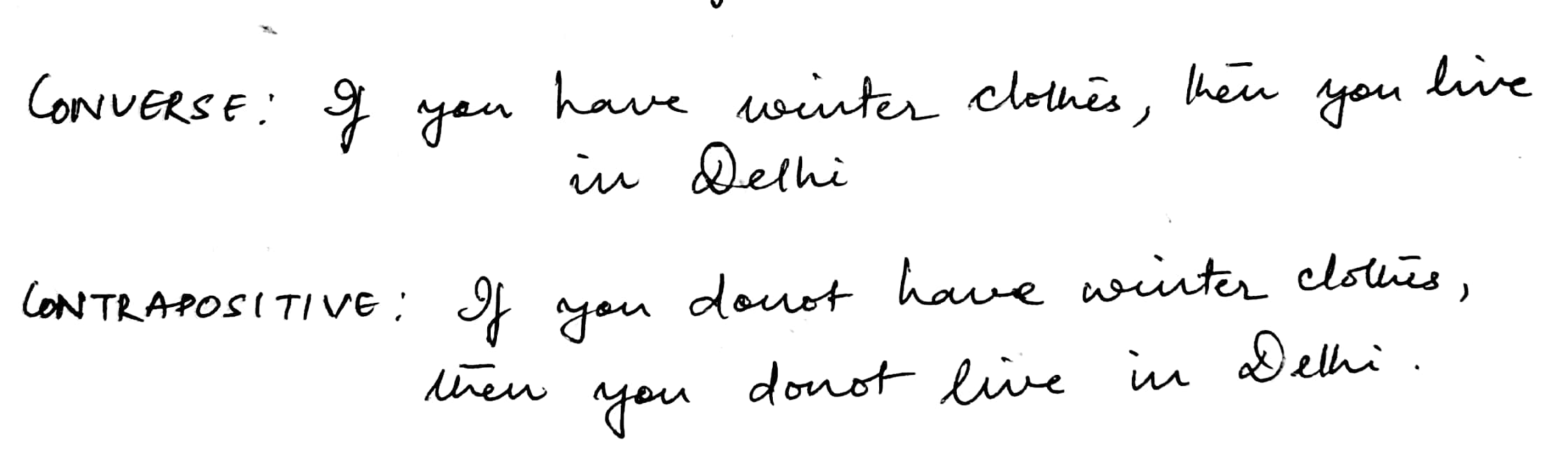Mathematical Reasoning - Class 11 Engineering Maths - Extra Questions

Are the following pairs of statements negations of each other?
(i) The number $$x$$ is not a rational number
The number $$x$$ is not an irrational number
(ii) The number $$x$$ is a rational number
The number $$x$$ is an irrational number

(i) Let $$p:$$ the number $$x$$ is not a rational number
The negation of $$p$$ is "the number $$x$$ is a rational number"
This is same as the second statement as if a number is not an irrational number then it is a rational number
Therefore the given statements are negations of each other

(ii) Let $$p:$$ the number $$x$$ is a rational number
The negation of the first statement is "the number $$x$$ is not a rational number" .
This means that the number $$x$$ is an irrational number which is the same as the second statement
Therefore the given statements are negations of each other


Find the component statements of the following compound statements and check whether they are true or false
(i) Number $$3$$ is prime or it is odd
(ii) All integers are positive or negative
(iii)$$ 100$$ is divisible by $$3, 11$$ and $$5$$

(i) The component statements are as follows
$$p$$ : Number $$3$$ is prime
$$q$$ : Number $$3$$ is odd
Both the statements are true
(ii) The component statements are as follows
$$p$$ : All integers are positive
$$q$$ : All integers are negative
Both the statements are false
(iii) The component statements are as follows
$$p$$ :$$100$$ is divisible by $$3$$
$$q$$ : $$100$$ is divisible by $$11$$
$$r$$ : $$100$$ is divisible by $$5$$
Here the statements $$p$$ and $$q$$ are false and statement $$r$$ is true


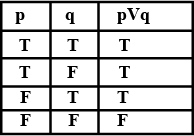
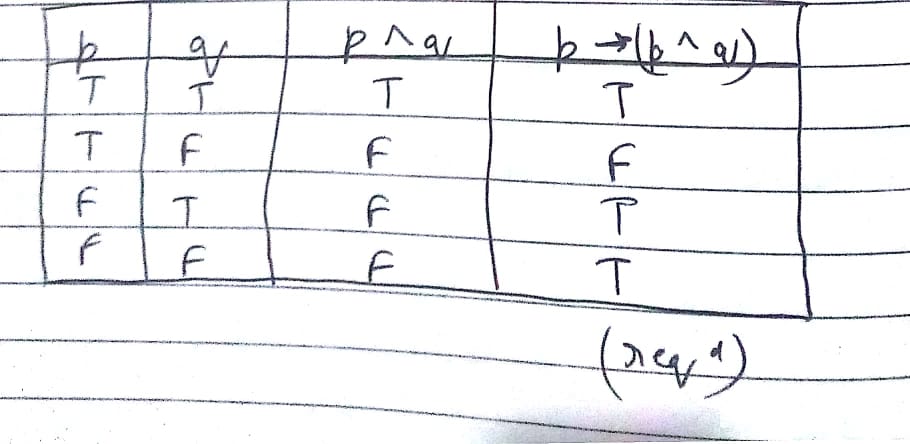
Write the truth table of $$p\Rightarrow(p\wedge q)$$

Truth table of $$p\Rightarrow(p\wedge q)$$:

p 
q
$$p\wedge q$$
   $$p\Rightarrow(p\wedge q)$$
T
T
T
 T
T
F   
F      
F
F
T
F
F
F
F
F
T


$$p\Rightarrow p\vee q$$ is a

Truth table of $$p\Rightarrow p\vee q$$:

p
 q
 $$p\vee q$$ 
$$p\Rightarrow p\vee q$$
T
 T
T
T
T
 F
T
T
F
 T 
T
T
F 
F
F 
T

Since $$p\Rightarrow p\vee q$$ is always true, $$p\Rightarrow p\vee q$$ is a tautology.


State whether True or False. Correct that are false.
(i) A point whose x coordinate is zero and y-coordinate is non-zero will lie on the y-axis.
(ii) A point whose y coordinate is zero and x-coordinate is $$5$$ will lie on y-axis.
(iii) The coordinates of the origin are $$(0,\,0)$$

i) $$y-$$axis coordinates are given by $$( 0, y)$$ , $$x-$$coordinate is always zero for the point which is lying on $$y-$$axis, so statement is True.

ii) As explained above for a point to be on $$y-$$axis, its $$x-$$ coordinate must be zero, so the statement is false
Correct statement: A point whose $$y$$ coordinate is zero and $$x-$$ coordinate is $$5$$ will lie on $$x-$$axis.

iii) Origin is the point where both $$x$$ and $$y$$ coordinates are zero, so statement is True.


State whether the following sentences are always true, always false or ambiguous. Justify your answer.
There are $$27$$ days in a month.

Always false. There are minimum $$27$$ days in a month. Usually we have months of $$30$$ and $$31$$ days.


State whether the following sentence is always true, always false or ambiguous. Justify your answer.
February has only $$28$$ days.

Ambiguous, because in leap year the February has only $$28$$ days. 


State whether the following statements are true or false. Give reasons for your answers.
Square numbers can be written as the sum of two odd numbers.

The square number can written as sum of odd number is false. 
For example $$9=4+5$$ 
In these one number is even and other is odd.
Then this proves that the square of a number is not the sum of two odd numbers. 


State whether the following sentence is always true, always false or ambiguous. 
The temperature in Hyderabad is $$2^o$$C.

The given sentences is ambiguous. 
Because some time in winter, there can be a possibility that some place of India have $$2^{0}$$ temperature.


Write the converse and contrapositive of the statement
"If two traingles are congruent, then their areas are equal."

Converse: 'If areas of two triangles are equal, then they are congruent.'
Contrapositive: 'If areas of two triangles are not equal, then they are not congruent.'


State whether the following sentence is always true, always false or ambiguous. Justify your answer.
Makarasankranthi falls on a Friday.

Ambiguous : In given year, Makarsankranthi Fot falls on Friday but is falls on Sunday, then Makarsankranthi may or may not fall on friday.


State whether the following sentence is always true, always false or ambiguous. Justify your answer.
Dogs can fly.

Always false. Only birds can fly but dog can not fly. 


Using truth tables, examine whether the statement pattern $$(p\wedge q)\vee (p\wedge r)$$ is a tautology, contradiction or contingency

$$ p$$ $$q$$$$ r$$ $$p\wedge q$$ $$p\wedge r$$$$(p\wedge q)\vee (p\wedge r)$$ 
 T TT  T T T
 TT F  T F T
 TF T  F T T
 TF F  F F F
 FT T  F F F
 FF T  F F F
 FT F  F F F
 FF F  F F F
From the truth table it is neither a tautology nor a contradiction, hence can be termed as contingency.


Write the converse and contrapositive of the statement "If the two lines are parallel then they do not intersects in the same plane".

Contrapositive: "If the two lines intersect in the same plane then they are not parallel"
Converse: If two lines do not intersect in the same plane then they are parallel 


Prepare the truth table for the following statement pattern
$$\left( p\vee \sim q \right) \rightarrow \left( r\wedge p \right) $$

$$p$$         $$q$$          $$r$$         $$\sim q$$         $$\left( p\vee \sim q \right) $$         $$\left( r\wedge p \right) $$       $$\left( p\vee \sim q \right) \rightarrow \left( r\wedge p \right) $$     
TTTFTTT
TTFFTFF
TFTTTTT
TFFTTFF
FTTFFFT
FTFFFFT
FFTTTFF
FFFTTFF


If a compound statement is made up of three simple statements, then the number of rows in the truth table is

Fact: If a compound statement is made up of $$n$$ simple statements then number of roes in the truth table will be $$2^n$$

Here $$n=3$$, so required number of rows $$=2^3=8$$


Write down the negations for the following:
(a) If the diagonals of a parallelogram are perpendicular then it is a rhombus.
(b) Kanchanganga is in India and Everest is in Nepal.
(c) The Sun is a star or the Jupiter is a planet.

(a) If the diagonals of a parallelogram are not perpendicular then it is not rhombus.
(b) Kanchanganga is not in India or Everest is not in Nepal.
(c) The sun is not a star and the Jupiter is not a planet.


Write the negation of the statement "$$\sqrt {7}$$ is irrational"

Consider $$p$$ as the statement $$\sqrt { 7 } $$ is irrational 
$$\therefore\quad \sim p$$ is $$\sqrt { 7 } $$ is not irrational.


Do you think the reverse is also true ., is  the sum of any two consecutive positive integers is perfect square of a number ? Given example to support your answer.

No it is not always true
For an  example
1) 5+6=11 which is not perfect square
2)21+22=43 which is not perfect square


Write opposite of the following:
a)$$30 \,km$$ north
b)Increase in weight
c)Loss of $$Rs. 700$$
d)$$100 \,m$$ a bove sea level

a) $$30$$km south
b) Decrease in weight
c) Profit of Rs. $$700$$
d) $$100$$m below sea level.


$$Y$$ is to the East of $$X$$, which is to the North of $$Z$$. if  $$P$$ is to the South of $$Z$$ , then $$P$$ is in which direction with respect to  $$Y$$ ?

 P is in the south with respect to y.
1171349_1051280_ans_0e62e73d7d9b434dac163f8c7f739855.png


Negation of the statement $$p$$ : for every real number, either $$x > 1$$ or $$x < 1$$ is 

$$ \sim P:$$ there exist a real number $$x$$ such that neither $$x>1$$ nor $$x<1$$.


Write the compound statement of the following compound statement and check whether the compound statement is true or false : "Zero is less than every positive integer and every negative integer" 

Compound statements are
$$p : 0$$ is less than every positive integer
$$q : 0$$ is less than every negative integer.
We know that so p is true and q is false.
The connecting word is "and".
Hence compound statement is false.

1193303_1326150_ans_f4408aa52a274f128c24386c19b4aae2.jpg


Write the converse and contropositive of 'If a parallelogram is a square , then it is a rhombus'.

If a parallelogram is a square, then it is a rhombus.
then,
it is a rhombus.
Converse: if a parallelogram is a rhombus.
If a parallelogram is not a rhombus, then it is not a square.


Find the truth value of $$14$$ is a composite number or $$15$$ is a prime no.

Since, 14 is a composite number so its truth value is 1.
Since, 15 is not prime number so its truth value is 0.


Write the negation of the following statements
i) $$\sqrt{7}$$ is a rational number.
ii) Length of both diagonals of any rectangle are equal.

(i) $$\sqrt{7}$$ is not a rational number.
(ii) Length of both sides of any rectangle are not equal.

1214851_1396555_ans_b5ade3598ae2455c9fed9eee2fa6d5fd.jpg


Write the converse, inverse and contrapositive of the following statement :
A family becomes literate if the women in it are literate.

Let p: The woman in the family is literate.
Let q: A family becomes literate.
Then the symbolic form of the given statement is $$ p \rightarrow q$$.
Converse: $$ q \rightarrow p$$ is the converse of $$ p \rightarrow q$$.
i.e., If a family becomes literate, then the woman in it is literate.
Inverse: $$ \sim p \rightarrow \, \sim q$$ is the inverse of $$ p \rightarrow q$$.
i.e., If the woman in the family does not become literate.
Contrapositive: $$ \sim q \rightarrow \, \sim p$$ is the contrapositive of $$ p \rightarrow q$$.
i.e., If a family does not become literate, then the woman in it is not literate.


Fill in the blank.
The sum of the measure of complementary angle is _______

Complimentary angles are angles
 whose sum is $$90^{\circ}$$
where as
supplementary angles we angles whose sum is $$ 180^{\circ}$$


Prathyusha stated that "the average of first $$10$$ odd numbers is also $$10$$". Do you agree with her? Justify your answer.

First $$10$$ odd numbers-
$$1, 3, 5, 7, 9, 11, 13, 15, 17, 19$$
The above series forms an A.P. with first term and common difference of $$1$$ and $$2$$.
As we know that sum of $$n$$ terms in an A.P. is given as-
$${S}_{n} = \cfrac{n}{2} \left( a + l \right)$$
Whereas, $$a$$ and $$l$$ are first and last term.
Sum of first $$10$$ odd numbers-
$$\therefore {S}_{10} = \cfrac{10}{2} \left( 1 + 19 \right)$$
$$\Rightarrow {S}_{10} = 5 \times 20 = 100$$
Now, average of first $$10$$ odd numbers-
Av. $$= \cfrac{{S}_{n}}{n} \\ = \cfrac{100}{10} = 10$$
Thus the average of first $$10$$ odd numbers is $$10$$.
Hence I agree with Pratyusha as the average of first $$10$$ odd numbers is $$10$$.


Verify the property $$a\times (b+c)=(a\times b)+(a\times c)$$ When $$a=\frac { 1 }{ 2 } ,b=\frac { 3 }{ 7 } \quad \quad \& \quad c=\frac { 5 }{ 14 } $$.

$$a\times (b+c)$$
$$=\dfrac{1}{2} \times (\dfrac{3}{7} +\dfrac{5}{14})$$

$$=\dfrac{1}{2} \times \dfrac{11}{14}$$

$$=\dfrac{11}{28}$$

And,
$$(a\times b)+(a\times c)$$

$$=(\dfrac{1}{2} \times \dfrac{3}{7})+(\dfrac{1}{2} \times \dfrac{5}{14})$$

$$=\dfrac{3}{14}+\dfrac{5}{28}$$

$$=\dfrac{11}{28}$$

Hence, $$a\times (b+c) = (a\times b)+(a\times c)$$


Tell whether the following is certain to happen, impossible can happen but not certain.
You are older today than yesterday.

It is certain to happen. As you are always older than than your yesterday.


If $$ \vec{a},\vec{b} $$ are two vectors, then write the truth value of the following statement:
$$\vec{a} = -\vec{b} \Rightarrow |\vec{a}|=|\vec{b}| $$  


1404571_1662201_ans_6243c66b0b504cba9543670f9719f44e.jpg


If $$ \vec{a},\vec{b} $$ are two vectors, then write the truth value of the following statement:
$$ |\vec{a}| = |\vec{b}|\Rightarrow \vec{a} = \pm \vec{b} $$  


1404573_1662203_ans_db80c6d83bb249858b22ebb036d50d9f.jpg


If $$ \vec{a},\vec{b} $$ are two vectors, then write the truth value of the following statement :
$$ |\vec{a}| = |\vec{b}|\Rightarrow \vec{a} = \vec{b} $$ 

$$\vec{a}, \vec{b}$$ are two vectors,
$$|\vec{a}|=|\vec{b}|$$

Magnitudes of $$\vec{a}$$ & $$\vec{b}$$ are equal.

They may have different directions.

So, statement is false.


Write the negation of the following statement and check whether the resulting statement is true.
The sum of $$2$$ and $$5$$ is $$9$$.

The negation of the given statement is :

The sum of 2 and 5 is not equal to 9.

We know that $$2+5=7 \neq 9$$. So, this statement is true.


Find out which of the following sentences are statement and which are not. Justify your answer.
Mathematics is difficult.


1423874_1667821_ans_81014ca03c474210b198965c14a5f88b.jpg


Write the negative of the following statements:
Banglore is the capital of Karnataka.


1423900_1667830_ans_8a9159ecf9b943998f5d7442b712aa13.jpg


Write the negative of the following statements:
$$r:$$ There exists a number $$x$$ such that $$0<x<1$$.


1423995_1667854_ans_8e74d54a8ed7421eaca1576d25330651.jpg


Write the negative of the following statements:
It rained on July $$4, 2005$$


1423901_1667832_ans_cc725be6c60e409fb02bd1da93d96e78.jpg


Find out which of the following sentences are statement and which are not Justify your answer.
Is the earth round?


1423994_1667827_ans_a11f0e86d6174cf589afeaaf62d08448.jpg


Write the negative of the following statements:
The sun is cold.


1423904_1667835_ans_daf16f827e6e4d75adc3ffad360594a7.jpg


Find out which of the following sentences are statement and which are not Justify your answer.
The product of $$(-1)$$ and $$8$$ is $$8$$

The product of $$(-1)$$ and $$8$$ is $$8$$
It is an assertive sentence; therefore it is a statement. But $$-1\times 8=-8$$; therefore the statement is false.


Write the negative of the following statements:
The earth is round


1423903_1667834_ans_2c2a21c6ad0340819b57ab7c36e8ca9c.jpg


Write the negative of the following statement:
'I will not go to school'.


1423912_1667841_ans_fa6e955016c14baa877f230a6ce38e0c.jpg


Write the negative of the following statements:
Ravish is honest.


1423902_1667833_ans_56ce8fb7f1f44d579f70744607869098.jpg


Write the negative of the following statements:
$$p:$$ For every positive real number $$x$$, the number $$(x-1)$$ is also positive.

Negation of statement $$P$$:
There exist a positive real number $$x$$, such that $$x-1$$ is not positive.`


Find the components statement of the following compound statements:
The sky is blue and the grass is green.


1423998_1667864_ans_532feea678034e7c853c625eb5e142d3.jpg


Determine the contrapositive of  the following statements:
If it snows, then they do not drive the car.

Let $$p :$$ it snows .
$$q :$$ they do not drive the car.

The given statement is of the form "if $$p$$, then $$q$$".

And , contra-positive of "if $$p$$, then $$q$$" is "if $$\sim q$$, then $$\sim p$$".

Thus, the contra-positive of the given statement is,
If they drive the car, then there is no snow.


Determine the contrapositve of each of the following statements:
If Mohan is a poet, then he is poor


1428118_1667955_ans_64b8f2c2d37e41bca7e8009aede30c01.jpg


Find the components statement of the following compound statements:
The earth is round or the sun is cols.


1423999_1667866_ans_fb921237d5f242e48bf3cf0f26441a8f.jpg


Find the components statement of the following compound statements:
$$25$$ is a multiple of $$5$$ and $$8$$


1424001_1667870_ans_1a42fc5957844a73bafb61d2cc6cab27.jpg


Write the component statement of the following compounds statements and check whether the compound statement is true or false:
$$x=2$$ and $$x=3$$ are the roots of the equation $$3x^{2}-x-10=0$$


1424019_1667886_ans_c73b580ac2d24311812a3f763a80e205.jpg


Write each of the following statements in the form if ..... then;
When a number is a multiple of $$9$$, it is necessarily a multiple of $$3$$

If a number is a multiple of $$9$$ , then it is a multiple of $$3$$.


Find the components statement of the following compound statements:
All rational numbers are real and all real numbers are complex.


1424000_1667867_ans_5a9c6af2e58e4de3bfa67606ad6e56c4.jpg


Statement the converse and contrapositive of each of the following statements:
If a quadrilateral is a parallelogram, then its diagonal bisect each other.


1428808_1667919_ans_46780de1a6c84c819aedbf7241b83d04.jpg


State which of the following is the statement. Justify. In case of a statement, state its truth value.
$$ x - 3 = 14 $$

It is an open sentence, hence it is not a statement.


State which of the following is the statement. Justify. In case of a statement, state its truth value.
Close the door

It is an imperative sentence, hence it is not a statement.


Write the negation of each of the following statement:
The sum of $$4$$ and $$5$$ is $$8$$.

The negation of given statement is 
It is false that the sum of $$4$$ and $$5$$ is $$8$$.


Write the negation of the following statements :
Every student has paid the fees.

At least one student has not paid the fees.


Write the negation of the following statements : 
The number $$ 2 $$ is greater than $$ 7 $$.

The number $$ 2 $$ is not greater than $$ 7 $$.


State which of the following is the statement. Justify. In case of a statement, state its truth value.
$$ 5 + 4 = 13 $$

It is a statement which is false, hence its truth value is 'F'.


State which of the following is the statement. Justify. In case of a statement, state its truth value.
Zero is a complex number. 

It is a statement which is true, hence its truth value is 'T'.


Write the negation of the following statements : 
Chennai is the capital of Tamil Nadu. 

Chennai is not the capital of Tamil Nadu.


Write the negation of the following statement :
None of the students of this class has passed.

At least one student of this class has passed.


State which of the following is the statement. Justify. In case of a statement, state its truth value. 
A quadratic equation cannot have more than two roots. 

It is a statement which is true, hence its truth value is 'T'.


State which of the following is the statement. Justify. In case of a statement, state its truth value. 
$$ x^2 = x $$ 

It is an open sentence, hence it is not a statement.


State which of the following is the statement. Justify. In case of a statement, state its truth value. 
The sum of cube roots of unity is zero. 

It is a statement which is true, hence its truth value is 'T'.


State which of the following is the statement. Justify. In case of a statement, state its truth value.
Please get me breakfast. 

It is an imperative sentence, hence it is not a statement.


State which of the following is the statement. Justify. In case of a statement, state its truth value. 
All real numbers are whole numbers. 

All whole numbers are real numbers but vice versa is not true hence, It is a statement which is false, hence its truth value is 'F'.


State which of the following is the statement. Justify. In case of a statement, state its truth value. 
The sun sets in the west

It is a statement which is true, hence its truth value is 'T'.


State which of the following is the statement. Justify. In case of a statement, state its truth value.
Congruent triangles are similar.

It is a statement which is true, hence its truth value is 'T'.


State which of the following is the statement. Justify. In case of a statement, state its truth value. 
$$ x^2 - 6x - 7 = 0 $$ , when $$ x = 7 $$ 

Putting $$x=7$$ in the equation we get:
$$\Rightarrow 7^2-6\times 7-7$$
$$\Rightarrow 49-42-7$$
$$\Rightarrow 0$$
Hence, It is a statement which is true, hence its truth value is 'T'.


State which of the following is the statement. Justify. In case of a statement, state its truth value. 
Can you speak in Marathi ? 

It is an interrogative sentence, hence it is not a statement.


State which of the following is the statement. Justify. In case of a statement, state its truth value. 
Do you like Mathematics ? 

It is an interrogative sentence, hence it is not a statement.


If the statement $$p , q $$ are true statement and $$ r , s $$ are false statement then determine the truth value of the following:
$$ (p \rightarrow q) \vee (r \rightarrow s) $$

Truth values of $$p$$ and $$q$$ are $$T$$ and truth values of $$r$$ and $$s$$ are $$F$$.
$$(p \rightarrow q) \vee (r \rightarrow s) \equiv (T \rightarrow T) \vee (F \rightarrow F) $$
                                 $$ \equiv T \vee T \equiv T $$
Hence the truth value of the given statement is true.


Write the truth values of the following 
Milk is white if and only if sky is blue.

Let $$p:$$ Milk is white.
Let $$q:$$ Sky is blue.
Then the symbolic form of the given statement is $$ p \leftrightarrow q$$.
The truth values of both $$p$$ and $$q$$ are $$T$$.
$$ \therefore $$ The truth value of $$ p \leftrightarrow q $$ is $$T$$ ........... $$[T \leftrightarrow T \equiv T]$$


State which of the following is the statement. Justify. In case of a statement, state its truth value. 
It rains heavily. 

It is an open sentence, hence it is not a statement.


Write the truth values of the following.
It is not true that $$5 - 3i $$ is a real number.

Let $$p:$$ $$ 5 - 3i$$ is a real number.
Then the symbolic form of given statement is $$ \sim p$$.
The truth values of $$p$$ is $$F$$.
$$ \therefore $$ The truth values of $$ \sim p$$ is $$T$$ ........... $$[\sim F \equiv T]$$


Write the truth values of the following.
$$24$$ is a composite number or $$17$$ is a prime number.

Let $$p:$$ $$24$$ is a composite number.
Let $$q:$$ $$17$$ is a prime number.
Then the symbolic form of a given statement is $$ p \vee q $$.
The truth values of both $$p$$ and $$q$$ are $$T$$.
$$ \therefore $$ The truth value of $$ p \vee q$$ is $$T$$ ........... $$[T \vee T \equiv T]$$


Write the truth values of the following 
$$4$$ is odd or $$1$$ is prime. 

Let $$p$$ : $$4$$ is odd.
Let $$q$$ : $$1$$ is prime.
Then the symbolic form of the given statement is $$ p \vee q $$.
The truth values of both $$p$$ and $$q$$ are $$F$$.
$$ \therefore $$ The truth value of $$p \vee q $$ is $$F$$ ......  $$[F \vee F \equiv F] $$


Write the truth values of the following.
$$5$$ is a prime number and $$7$$ divides $$94$$.

Let $$p:$$ $$5$$ is a prime number.
Let $$q :$$ $$7$$ divides $$94$$.
Then the symbolic form of the given statement is $$ p \wedge q$$.
The truth values of $$p$$ and $$q$$ are $$T$$ and $$F$$ respectively.
$$ \therefore $$ The truth value of $$p \wedge q $$ is $$F$$ ......... $$ [ T \wedge F \equiv F] $$.


Write the truth values of the following.
If $$ 3 \times 5 = 8 $$ then $$ 3 + 5 = 15 $$.

Let $$p:$$ $$ 3 \times 5 = 8 $$ 
Let $$q:$$ $$ 3 + 5 = 15 $$
Then the symbolic form of the given statement is $$ p \rightarrow q $$.
The truth values of both $$p$$ and $$q$$ are $$F$$.
$$ \therefore $$ The truth value of $$ p \rightarrow q $$ is $$ T$$ ........... $$[F \rightarrow F \equiv T]$$


If the statement $$p , q $$ are true statement and $$ r , s $$ are false statement then determine the truth value of the following:
$$(p \rightarrow q) \wedge \sim r $$ 

Truth values of $$p$$ and $$q$$ are $$T$$ and truth values of $$r$$ and $$s$$ are $$F$$.
$$ (p \rightarrow q) \wedge (\sim r) \equiv (T \rightarrow T) \wedge (\sim F) $$
                            $$ \equiv T \wedge T \equiv T $$ 
Hence the truth value of the given statement is true.


Write the truth values of the following.
$$64$$ is a perfect square and $$46$$ is a prime number. 

Let $$p$$ : $$64$$ is a perfect square.
Let $$q$$ : $$46$$ is a prime number.
Then the symbolic form of the given statement is $$ p \wedge q $$.
The truth values of $$p$$ and $$q$$ are $$T$$ and $$F$$ respectively.
$$ \therefore $$ The truth value of $$ p \wedge q $$ is $$F$$ .......... $$[T \wedge F \equiv F] $$


Write the negation of the following.
$$3$$ is not a root of the equation $$ x^2 + 3x - 18 = 0 $$ 

The negation of the given statement is:
$$3$$ is a root of the equation $$x^2 + 3x - 18 = 0 $$.


If the statement $$p , q $$ are true statement and $$ r , s $$ are false statement then determine the truth value of the following:
$$(\sim r \leftrightarrow p) \rightarrow \, \sim q $$ 

Truth values of $$p$$ and $$q$$ are $$T$$ and truth values of $$r$$ and $$s$$ are $$F$$.
$$(\sim r \leftrightarrow p) \rightarrow \, (\sim q) \equiv (\sim F \leftrightarrow T) \rightarrow (\sim T) $$ 
                                 $$ \equiv (T \leftrightarrow T) \rightarrow F $$ 
                                 $$ \equiv T \rightarrow F \equiv F $$  
Hence the truth value of the given statement is false.


Write the negation of the following.
Tirupati is in Andhra Pradesh. 

The negation of the given statement is:
Tirupati is not in Andhra Pradesh.


If the statement $$p , q $$ are true statement and $$ r , s $$ are false statement then determine the truth value of the following:
$$ [(\sim p \wedge q) \wedge \, \sim r] \vee [(q \rightarrow p) \rightarrow (\sim s \vee r)] $$ 

Truth values of $$p$$ and $$q$$ are $$T$$ and truth values of $$r$$ and $$s$$ are $$F$$.
$$ [(\sim p \wedge q) \wedge \, (\sim r)] \vee [(q \rightarrow p) \rightarrow (\sim s \vee r)] $$ 
$$ \equiv [(\sim T \wedge T) \wedge (\sim F)] \vee [(T \rightarrow T) \rightarrow (\sim F \vee F)] $$ 
$$ \equiv [(F \wedge T) \wedge T] \vee [T \rightarrow (T \vee F)] $$ 
$$ \equiv (F \wedge T) \vee (T \rightarrow T) $$ 
$$ \equiv F \vee T \equiv T $$ 
Hence the truth value of the given statement is true.


If $$ A = \left  \{3 , 5 , 7 , 9 , 11 , 12  \right  \} $$, determine the truth value of the following.
$$ \forall \, x \, \in \,A , x^2 + x $$ is an even number 

For each $$x \in A , x^2 + x $$ is an even number.
So the given statement is true, hence its truth value is T.


If the statement $$p , q $$ are true statement and $$ r , s $$ are false statement then determine the truth value of the following:
$$ [ \sim p \wedge (\sim q \wedge r)] \vee [(q \wedge r) \vee (p \wedge r)] $$ 

Truth values of $$p$$ and $$q$$ are $$T$$ and truth values of $$r$$ and $$s$$ are $$F$$.
$$ [ \sim p \wedge (\sim q \wedge r)] \vee [(q \wedge r) \vee (p \wedge r)] $$ 
$$ \equiv [\sim T \wedge (\sim T \wedge F)] \vee [(T \wedge F) \vee (T \wedge F)] $$ 
$$ \equiv [F \wedge (F \wedge F) ] \vee [F \vee F] $$ 
$$ \equiv (F \wedge F) \vee F $$ 
$$ \equiv F \vee F \equiv F $$
Hence the truth value of the given statement is false.


If $$ A = \left  \{3 , 5 , 7 , 9 , 11 , 12  \right  \} $$, determine the truth value of the following.
$$\displaystyle  \exists \, x \, \in  A $$ such that $$ x - 8 = 1 $$ 

Clearly $$ x = 9 \in A $$ satisfies $$ x - 8 = 1 $$. So the given statement is true, hence its truth value if T.


Write the negation of the following.
$$ \sqrt{2} $$ is a rational number. 

The negation of the given statement is:
$$ \sqrt{2} $$ is not a rational number.


Write the negation of the following.
$$ 7 + 3 > 5 $$ 

$$ 7 + 3 \ngtr 5 $$


Write the negation of the following.
Polygon ABCDE is a pentagon. 

The negation of the given statement is:
Polygon ABCDE is not a pentagon.


If $$ A = \left  \{3 , 5 , 7 , 9 , 11 , 12  \right  \} $$, determine the truth value of the following.
$$ \exists \, x \, \in  A $$ such that $$3x + 8 > 40 $$ 

Clearly $$x = 11 \in A $$ and $$x = 12 \in A $$ satisfies $$3x + 8 > 40$$.
So the given statement is true, hence its truth value is T.


Write the negation of the following.
$$ x + 8 > 11 $$ or $$ y - 3 = 6 $$ 

Let p: $$x + 8 > 11 $$,
Let q: $$y - 3 = 6 $$ 
Then the symbolic form of the given statement is $$p \vee q$$.
Since $$ \sim (p \vee q) \equiv \, \sim p \wedge \sim q$$, the negation of the given statement is:
$$ x + 8 \ngtr11 $$ and $$ y - 3 \neq 6 $$.
OR
$$x + 8 \leq 11 $$ and $$ y - 3 \neq 6 $$.


Write the negation of the following.
Quadrilateral is a square if and only if it is a rhombus.

Let $$p:$$ Quadrilateral is a square.
Let $$q:$$ It is a rhombus.
Then the symbolic form of the given statement is $$ p \leftrightarrow q$$.
Since $$ \sim (p \leftrightarrow q) \equiv (p \wedge \, \sim q) \vee (q \wedge \, \sim p) $$, the negation of the given statement is:
Quadrilateral is a square but it not a rhombus or quadrilateral is a rhombus but it is not a square.


Write the negation of the following.
$$ 11 < 15 $$ and $$ 25 > 20 $$ 

Let p: $$ 11 < 15 $$,
Let q: $$25 > 20$$
Then the symbolic form of the given statement is $$ p \wedge q$$.
Since $$ \sim (p \wedge q) \equiv \, \sim p \vee q$$, the negation of the given statement is:
$$ 11 \geq 15 $$ or $$ 25 \leq 20 $$


Write the negation of the following.
It is cold and raining.

Let $$p$$: It is cold.
Let $$q$$: It is raining.
Then the symbolic form of the given statement is $$p \wedge q$$.
Since $$ \sim (p \wedge q) \equiv \, \sim p \vee q$$, the negation of the given statement is:
It is not cold or not raining.


Write the negation of the following.
If it is raining then we will go and play football.

Let $$p:$$ It is raining.
Let $$q:$$ We will go.
Let $$r:$$ We play football.
Then the symbolic form of the given statement is $$ p \rightarrow (q \wedge r)$$.
Since $$ \sim [p \rightarrow (q \wedge r)] \equiv p \wedge \, \sim (q \wedge r) \equiv p \wedge (\sim q \, \vee \, \sim r) $$, the negation of the given statement is:
It is raining and we will not go or not play football.


If $$ A = \left  \{3 , 5 , 7 , 9 , 11 , 12  \right  \} $$, determine the truth value of the following.
$$ \forall \, x \in  A , 2x + 9 > 14 $$ 

For each $$x \in A, 2x + 9 > 14 $$.
So the given statement is true, hence its truth value is T.


If $$ A = \left  \{3 , 5 , 7 , 9 , 11 , 12  \right  \} $$, determine the truth value of the following.
$$ \exists \, x \, \in  \, A $$ such that $$ x^2 < 0 $$

There is no $$ x \in A $$ which satisfies $$x^2 < 0 $$.
So the given statement is false, hence its truth value is F.


Write the negation of the following.
All natural numbers are whole numbers.

The negation of the given statement is:
Some natural numbers are not whole numbers.


If $$ A = \left  \{3 , 5 , 7 , 9 , 11 , 12  \right  \} $$, determine the truth value of the following.
$$ \forall \, x \, \in \, A , x $$ is an even number 

$$x = 3 \in A , x = 5 \in A , x = 7 \in A , x = 9 \in A , x = 11 \in A $$ do not satisfy $$x$$ is an even number. 
So the given statement is false, hence its truth value is F.


Write converse , inverse and contrapositive of the following statements.
If voltage increases then current decreases.

Let $$p:$$ Voltage increases.
Let $$ q:$$ Current decreases.
Then the symbolic form of the given statement is $$ p \rightarrow q$$.
Converse: $$ q \rightarrow p $$ is the converse of $$ p \rightarrow q $$.
i.e., If current decreases, then voltage increases.
Inverse: $$ \sim p \rightarrow \sim q$$ is the inverse of $$ p \rightarrow q$$.
i.e., If voltage does not increase, then current does not decrease.
Contrapositive: $$ \sim q \rightarrow p$$, is the contrapositive of $$ p \rightarrow q$$.
i.e., If current does not decrease, then voltage does not increase.


Write the negation of the following.
$$ \exists \, x \in  N $$ such that $$ x - 17 < 20 $$ 

The negation of the given statement is:
$$ \forall \, x \in N , x - 17 \geq 20 $$


Using the rule of negation write the negation of the following with justification.
$$ (\sim p \, \vee \, \sim q) \vee (p\, \wedge \, \sim q) $$ 

The negation of $$ (\sim p \vee \, \sim q) \vee (p \wedge \, \sim q) $$ is 
$$ \sim [(\sim p \vee \sim q) \vee (p \wedge \, \sim q)] \equiv \, \sim (\sim p \vee \sim q) \wedge \, \sim (p \wedge \, \sim q) $$ ......... (Negation of disjunction) 
$$ \equiv [\sim (\sim p) \wedge \, \sim (\sim q)] \wedge [\sim p \vee \, \sim (\sim q)] $$ ........(Negation of disjunction and conjuction) 
$$ \equiv (p \wedge q) \wedge (\sim p \vee q) $$ ......... (Negation of negation)


Using the rule of negation write the negation of the following with justification.
$$ p\,  \vee \, \sim q $$ 

The negation of $$ p \vee \, \sim q $$ is 
$$ \sim (p \vee \, \sim q) \equiv \, \sim p \wedge \sim (\sim q) $$ ........
(Negation of disjunction) 
$$ \equiv \, \sim p \wedge q $$ .......... (Negation of negation)


Using the rule of negation write the negation of the following with justification.
$$ p \rightarrow (p \vee \, \sim q) $$ 

The negation of $$ p \rightarrow (p \vee \, \sim q) $$ is 
$$ \sim [p \rightarrow (p \vee \, \sim q)] \equiv p \wedge \sim (p \vee \sim q) $$ ........... 
(Negation of implication) 
$$ \equiv p \wedge [\sim p \wedge \, \sim (\sim q)]$$ ............(Negation of disjunction) 
$$ \equiv p \wedge (\sim p \wedge q) $$ ............ (Negation of negation)


Using the rule of negation write the negation of the following with justification.
$$ \sim q \rightarrow p $$ 

The negation of $$ \sim q \rightarrow p $$ is 
$$ \sim (\sim q \rightarrow p) \equiv \, \sim q \wedge \, \sim p $$ ...... (Negation of implication)


Using the rule of negation write the negation of the following with justification.
$$ (p\,  \vee \, \sim q) \rightarrow (p \, \wedge \sim q) $$ 

The negation of $$ (p \vee \, \sim q) \rightarrow (p \wedge \, \sim q) $$ is 
$$ \sim [(p \vee \, \sim q) \rightarrow (p \wedge \, \sim q)] \equiv (p \vee \, \sim q) \wedge \sim (p \wedge \sim q) $$ ......... (Negation of implication) 
$$ \equiv (p \vee \, \sim q) \wedge [ \sim p \vee \sim (\sim q)] $$ .......... (Negation of conjunction) 
$$ \equiv (p \vee \, \sim q) \wedge (\sim p \vee q) $$ ......... (Negation of negation)


Using the rule of negation write the negation of the following with justification.
$$(p \vee \, \sim q) \wedge r $$ 

The negation of $$ (p \vee \, \sim q) \wedge r $$ is 
$$ \sim [(p \vee \sim q) \wedge r] \equiv (p \vee \, \sim q) \vee \sim r $$ .............
(Negation of conjunction) 
$$ \equiv [\sim p \wedge \, \sim (\sim q)] \vee \, \sim r $$......... (Negation of disjunction) $$ \equiv (\sim p \wedge q) \vee \sim r $$ ...............
(Negation of negation)


Using the rule of negation write the negation of the following with justification.
$$ p \wedge \, \sim q $$ 

The negation of $$ p \wedge \sim q $$ is 
$$ \sim (p \wedge \sim q) \equiv \, \sim p \vee \, \sim (\sim q) $$ ............
(Negation of conjugation) 
$$ \equiv \, \sim p \vee q$$ .............. (Negation of negation)


Write the negation of the following.
$$ \forall \, n \in  N , n^2 + n + 2 $$ is divisible by $$4$$.

The negation of the given statement is:
$$ \exists \, n \in N$$, such that $$n^2 + n + 2 $$ is not divisible by $$4$$.


Without using the truth table show that 
$$ p \leftrightarrow q \equiv (p \wedge q) \vee (\sim p\, \wedge \sim q) $$ 

L.H.S $$ = p \leftrightarrow q $$ 
$$ \equiv (p \rightarrow q) \wedge (q \rightarrow p) $$ .............. (Biconditional Law) 
$$ \equiv (\sim p \vee q) \wedge (\sim q \vee p) $$ ............ (Conditional Law) 
$$ \equiv [\sim p \wedge (\sim q \vee p)] \vee [q \wedge (\sim q \vee p)] $$ ............. (Distributive Law) 
$$ \equiv [(\sim p \wedge \sim q)] \vee (\sim p \wedge p)] \vee [(q \wedge \sim q) \vee (q \wedge p)] $$ .......... (Distributive Law) 
$$ \equiv [( \sim p \wedge \, \sim q) \vee F] \vee [F \vee (q \wedge p)]$$ ........... (Completed Law) 
$$ \equiv (\sim p \wedge \sim q) \vee (q \wedge p) $$ ........... (Identity Law) 
$$ \equiv (\sim p \wedge \sim q) \vee (p \wedge q) $$ .......... (Commutative Law) 
$$ \equiv ( p \wedge q) \vee (\sim p \wedge \, \sim q) $$ ......... (Commutative Law) 
$$ \equiv $$ R.H.S.


Rewrite the following statement without using if ........ then.
If $$ f(2) = 0 $$ then $$ f(x) $$ is divisible by $$(x - 2) $$.

Since $$ p \rightarrow q \equiv \, \sim p \vee q $$, the given statement can be written as:
$$ f(2) \neq 0 $$ or $$ f(x) $$ is divisible by $$ (x - 2) $$.


Rewrite the following statement without using if ........ then.
If a man is a judge then he is honest. 

Since $$ p \rightarrow q \equiv \, \sim p \vee q $$, the given statement can be written as:
A man is not a judge or he is honest.


Rewrite the following statement without using if ........ then.
If $$2$$ is a rational number then $$ \sqrt{2} $$ is irrational number.

Since $$ p \rightarrow q \equiv \, \sim p \vee q $$, the given statement can be written as:
$$2$$ is not a rational number or $$ \sqrt{2} $$ is irrational number.


Which of the following sentence is the statement in logic ? Justify. Write down the truth value of the statement:
India is a country and Himalayas is a river.

It is a statement which is false, hence its truth value is '$$F$$'. ......... $$[T \wedge F \equiv F] $$


Which of the following sentence is the statement in logic ? Justify. Write down the truth value of the statement:
If $$x$$ is a whole number then $$ x + 6 = 0 $$.

It is a statement which is false, hence its truth value is 'F'. 
[Note: Answer in the textbook is incorrect]


Write the truth table value of the following statement:
$$ \sqrt{5} $$ is an irrational but $$ 3\sqrt{5} $$ is a complex number.

Let $$p:$$ $$5$$ is an irrational
Let $$q:$$ $$35$$ is a complex number.
Then the symbolic form of the given statement is $$ p \wedge q$$.
The truth value of $$p$$ and $$q$$ are $$T$$ and $$F$$ respectively.
$$ \therefore $$ The truth value of $$ p \wedge q $$ is $$F$$. ............. $$[T \wedge F \equiv F] $$
[Note: Answer in the textbook is incorrect]


Which of the following sentence is the statement in logic ? Justify. Write down the truth value of the statement:
$$ 4 ! = 24 $$ 

It is a statement which is true, hence its truth value is 'T'.


Which of the following sentence is the statement in logic ? Justify. Write down the truth value of the statement:
$$ \pi $$ is an irrational number.

It is a statement which is true, hence its truth value is 'T'.


Write the truth table value of the following statement:
In $$ \Delta$$ ABC if all sides are equal then its all angles are equal.

Let $$p:$$ ABC is a triangle and all its sides are equal.
Let $$q:$$ It's all angles are equal.
Then the symbolic form of the given statement is $$ p \rightarrow q$$.
If the truth value of $$p$$ is $$T$$, then the truth value of $$q$$ is $$T$$.
$$ \therefore $$ The truth value of $$ p \rightarrow $$ is $$T$$............ $$[T \rightarrow T \equiv T]$$


Which of the following sentence is the statement in logic ? Justify. Write down the truth value of the statement:
Please get me a glass of water.

It is an imperative sentence, hence it is not a statement.


Write the truth table value of the following statement:
The square of any even number is odd or the cube of any odd number is odd.

Let $$p:$$ The square of any even number is odd.
Let $$q:$$ The cube of any odd number is odd.
Then the symbolic form of the given statement is $$ p \vee q $$.
The truth values of $$p$$ and $$q$$ are $$F$$ and $$T$$ respectively.
$$ \therefore $$ The truth value of $$ p \vee q$$ is $$t$$............. $$[F \vee T \equiv T]$$


Write the truth table value of the following statement:
$$ \exists \, n \in N $$ such that $$ n + 5 > 10 $$.

$$ \exists \, n \in N $$ such that $$ n + 5 > 10 $$ is a true statement, hence its truth value is T.
(All $$ n \geq 6 $$, where $$ n \in N $$, satisfy $$ n + 5 > 10$$).


Which of the following sentence is the statement in logic ? Justify. Write down the truth value of the statement:
$$ \cos^2 \theta - \sin^2 \theta = \cos 2 \theta $$ for all $$ \theta \in R $$ 

It is a statement which is true, hence its truth value is 'T'.


If $$ A = \left  \{1 , 2 , 3 , 4 , 5 , 6 ,7 , 8 , 9  \right  \} $$, determine the truth value of the following statement:
$$ \forall \, x \in A , 3x \leq 25 $$.

$$ x = 9 \in A $$ does not satisfy $$ 3x \leq 25 $$. So the given statement is false, hence its truth value is F.


Write negation of the following:
Some triangles are equilateral triangle.

The negation of the given statement is:
All triangles are not equilateral triangles.


Write the truth table value of the following statement:
$$ \forall \, n \in N , n + 6 > 8 $$.

$$ \forall \, n \in N , n + 6 > 8 $$ is a false statement, hence its truth value is F.
$$(n = 1 \in N , n = 2 \in N $$ do not satisfy $$ n + 6 > 8)$$.


If $$ A = \left  \{1 , 2 , 3 , 4 , 5 , 6 ,7 , 8 , 9  \right  \} $$, determine the truth value of the following statement:
$$ \exists \, x \in A $$ , such that $$ x + 7 \geq 11 $$.

Clearly $$x = 1 \in A , x = 2 \in A $$ and $$x = 3 \in A $$ satisfies $$ x + 7 \geq 11 $$. So the given statement is true, hence its truth value is T.


Write negation of the following:
$$ \exists \, x \in A $$, such that $$ x + 9 \leq 15 $$.

The negation of the given equation is:
$$ \forall \, x \in A, x + 9 > 15 $$.


Write negation of the following:
$$ \forall \, n \in A , n + 7 > 6 $$.

The negation of the given statement is:
$$ \exists \, n \in A $$, such that $$ n + 7 \leq 6 $$.
OR
$$ \exists \, n \in A $$, such that $$ n + 7 \ngtr 6$$.


If $$ A = \left  \{1 , 2 , 3 , 4 , 5 , 6 ,7 , 8 , 9  \right  \} $$, determine the truth value of the following statement:
$$ \forall \, x \in A , x + 5 < 12 $$.

There is no $$ x \in A $$ which satisfies $$x + 5 < 12 $$. So the given statement is false, hence its truth value is F.


Determine the truth values of $$p$$ and $$q$$ in the following case:
$$(p \vee q) $$ is $$T$$ and $$ (p \wedge q) $$ is $$T$$

$$p\ \ \ $$$$q\ \ \ $$$$p \vee q\ \ \ $$$$p  \wedge q$$
TTTT
TFTF
FTTF
FFFF

 Since $$p \vee q $$ and $$ p \wedge q $$ both are T, from the table, the truth values of both $$p$$ and $$q$$ are T.


If $$ A = \left  \{1 , 2 , 3 , 4 , 5 , 6 ,7 , 8 , 9  \right  \} $$, determine the truth value of the following statement:
$$ \exists \, x \in A $$ such that $$ x + 8 = 15 $$

Clearly $$ x = 7 \in A $$ satisfies $$x + 8 = 15 $$. So the given statement is true, hence its truth value is T.


Determine the truth values of $$p$$ and $$q$$ in the following case:
$$ (p \wedge q) $$ is $$F$$ and $$(p \wedge q) \rightarrow q $$ is $$T$$

$$p\ \ \ $$$$q\ \ \ $$$$p \wedge q\ \ \ $$$$(p \wedge q)
\rightarrow
q\ \  \ $$
TTTT
TFFT
FTFT
FFFT

Since the truth values of $$(p \wedge q) $$ is F and $$(p \wedge q) \rightarrow q$$ is T, from the table, the truth values of p and q are either T and F respectively or F and T respectively or both F.


Write the converse of the following statement. If the sum of the digits of a number is divisible by $$3$$ then the number is divisible by $$3$$.

If the given number is divisible by 33, then the sum of the digits of the number is divisible by 33.


Write the following statement in conditional form. Angles in a linear pair are supplementary.

If the given two angles are forming a linear pair, then they are supplementary.


Write the converses of the following statement. The alternate angles formed by two parallel lines and their transversal are congruent.

If the alternate angles made by the transversal with the two lines are congruent, then the lines are parallel.


Write the converses of the following statement. If a pair of the interior angles made by a transversal of two lines are supplementary then the lines are parallel.

It is known that, two distinct lines intersect at one point. Hence, the correct answer is one.


Write the converse of the following statement. If the sum of measures of two angles is $$90^\circ$$ then they are the complement of each other.

If the given two angles are the complement of each other, then the sum of the measures of two angles is 90∘90∘.


Write the converses of the following statement. The diagonals of a rectangle are congruent.

It is known that, two distinct lines intersect at one point. Hence, the correct answer is one.


Write the following statement in conditional form. Every rhombus is a square.

If the given quadrilateral is a square, then it must be a rhombus


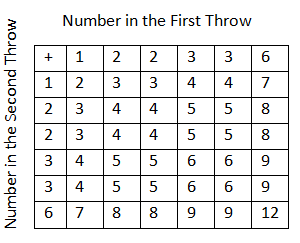
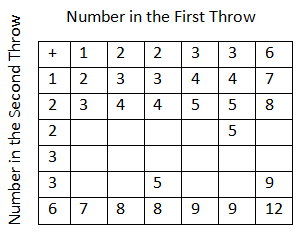
A die is numbered in such a way that its faces show the numbers 1,2,2,3,3,It is thrown two times and the total score in two throws is noted. Complete the following table which gives a few values of the total score on the two throws.
What is the probability that the total score is even
238240.png


  + Number

in the First Throw
1 2 2 3 3 6
Number  in

the  second    throw		 1 2 3 3 4 4 7
2 3 4 4 5 5 8
2 3 4 4 5 5 8
3 4 5 5 6 6 9
3 4 5 5 6 6 9
6 7 8 8 9 9 12

268641_238240_ans_d3bef907a9cd4d5d89140dfc55337cf5.png


Write the negation of the following statements:
(i) Chennai is the capital of Tamil Nadu
(ii) $$\displaystyle \sqrt{2}$$ is not a complex number 
(iii) All triangles are not equilateral triangle
(iv) The number $$2$$ is greater than $$7$$
(v) Every natural number is an integer

(i) Chennai is not the capital of Tamil Nadu
(ii) $$\displaystyle \sqrt{2}$$ is a complex number
(iii) All triangles are equilateral triangles
(iv) The number $$2$$ is not greater than $$7$$
(v) Every natural number is not an integer


Show that the following statement is true by the method of contrapositive
p : If $$x$$ is an integer and $$\displaystyle x^{2}$$ is even then $$x$$ is also even

$$p$$ : If $$x$$ is an integer and $$\displaystyle x^{2}$$ is even then $$x$$ is also even.
Let $$q$$ : $$x$$ is an integer and $$\displaystyle x^{2}$$ is even 
$$r$$ : $$x$$ is even
To prove that $$p$$ is true by contrapositive method we assume that $$r$$ is false and prove that $$q$$ is also false.
Let $$x$$ is not even
To prove that $$q$$ is false, it has to be proved that $$x$$ is not an integer or $$\displaystyle x^{2}$$ is not even.
$$x$$ is not even implies that $$\displaystyle x^{2}$$ is also not even.
Therefore statement $$q$$ is false.
Thus the given statement $$p$$ is true.


Given statements in (a) and (b) Identify the statements given below as contrapositive or converse of each other
(a) If you live in Delhi then you have winter clothes
(i) If you do not have winter clothes then you do not live in Delhi
(ii) If you have winter clothes then you live in Delhi
(b) If a quadrilateral is a parallelogram then its diagonals bisect each other
(i) If the diagonals of a quadrilateral do not bisect each other then the quadrilateral is not a parallelogram
(ii) If the diagonals of a quadrilateral bisect each other then it is a parallelogram

(a) (i) This is the contrapositive of the given statement (a)
(ii) This is the converse of the given statement (a)
(b) (i) This is the contapositive of the given statement (b)
(ii) This is the converse of the given statement (b)


Write the contrapositive and converse of the following statements
(i) If $$x$$ is a prime number then $$x$$ is odd
(ii) It the two lines are parallel then they do not intersect in the same plane
(iii) Something is cold implies that it has low temperature
(iv) You cannot comprehend geometry if you do not know how to reason deductively
(v) $$x$$ is an even number implies that $$x$$ is divisible by $$4$$

(i) The contrapositive is as follows
If a number $$x$$ is not odd then $$x$$ is not a prime number.
The converse is as follows
If a number $$x$$ is odd then it is a prime number.
(ii) The contrapositive is as follows
If two lines intersect in the same plane then they are not parallel.
The converse is as follows
If two lines do not intersect in the same plane then they are parallel.
(iii) The contrapositive is as follows
If something does not have low temperature then it is not cold.
The converse is as follows
If something is at low temperature then it is cold.
(iv) The contrapositive is as follows
If you know how to reason deductively then you can comprehend geometry.
The converse is as follows
If you do not know how to reason deductively then you cannot comprehend geometry.
(v) The given statement can be written as follows
If $$x$$ is an even number then $$x$$ is divisible by $$4$$.
The contrapositive is as follows
If $$x$$ is not divisible by $$4$$ then $$x$$ is not an even number.
The converse is follows
If $$x$$ is divisible by $$4$$ then $$x$$ is an even number.


Write each of the following statement in the form "if-then"
(i) You get a job implies that your credentials are good
(ii) The Banana trees will bloom if it stays warm for a month
(iii) A quadrilateral is a parallelogram if its diagonals bisect each other
(iv) To get $$\displaystyle A^{+}$$ in the class it is necessary that you do the exercises of the book 

(i) If you get a job then your credentials are good
(ii) If the Banana tree stays warm for a month then it will bloom
(iii) If the diagonals of a quadrilateral bisect each other then it is a parallelogram
(iv) If you want to get an $$\displaystyle A^{+}$$ in the class then you do all the exercises of the book


Write the negation of the following statements:
(i) p : For every positive real number $$x$$ the number $$x -1$$ is also positive
(ii) q : All cats scratch
(iii) r : For every real number $$x$$, either $$x > 1$$ or $$x < 1$$
(iv) s : There exist a number $$x$$ such that $$0 < x < 1$$

(i) The negation of statement $$p$$ is as follows
There exists a positive real number $$x$$ such that $$x - 1$$ is not positive

(ii) The negation of statement $$q$$ is as follows
There exists a cat that does not scratch

(iii) The negation of statement $$r$$ is as follows
There exists a real number $$x$$ such that neither $$x > 1$$ nor $$x < 1$$

(iv) The negation of statement s is as follows
There does not exist a number $$x$$ such that $$0 < x < 1$$


Write each of the statements in the form "if p then q"
(i) p : It is necessary to have a password to log on to the server
(ii) q : There is traffic jam whenever it rains
(iii) r : You can access the website only if you pay a subscription fee

(i) Statement $$p$$ can be written as follows
If you log on to the server then you have a password.
(ii) Statement $$q$$ can be written as follows
If it rains then there is a traffic jam.
(iii) Statement $$r$$ can be written as follows
If you can access the website then you pay a subscription fee.


Check whether the following pair of statements is negation of each other. Give reasons for the answer
(i) $$x + y = y + x$$  is true for every real numbers $$x$$ and $$y$$
(ii) There exists real number $$x$$ and $$y$$ for which $$x + y = y + x$$

The negation of statement (i) is as follows
There exists real number $$x$$ and $$y$$ for which $$x + y $$ $$\displaystyle \neq $$ $$y + x$$. This is not the same as statement (ii).
Thus the given statements are not the negation of each other 


Show that the statement
$$p$$ : "If $$x$$ is a real number such that $$\displaystyle x^{3}+4x=0$$ then $$x$$ is $$0$$" is true by 
(i) direct method
(ii) method of contradiction
(iii) method of contrapositive

$$p$$ : "If $$x$$ is a real number such that $$\displaystyle x^{3}+4x=0$$ then $$x$$ is $$0$$"
Let $$q : x$$ is a real number such that $$\displaystyle x^{3}+4x=0$$
$$r : x$$ is $$0$$
(i) To show that statement $$p$$ is true we assume that $$q$$ is true and then show that $$r$$ is true.
Therefore let statement $$q$$ be true.
$$\displaystyle \therefore x^{3}+4x=0$$
$$\displaystyle x\left ( x^{2} +4\right )=0$$
$$\displaystyle \Rightarrow x=0\,or\, x^{2}+4=0$$
However since$$x$$ is real it is $$0$$.
Thus statement $$r$$ is true
Therefore the given statement is true.
(ii) To show statement $$p$$ to be true by contradiction we assume that $$p$$ is not true.
Let $$x$$ be a real number such that $$\displaystyle x^{3}+4x=0$$ and let $$x$$ is not $$0$$.
Therefore $$\displaystyle x^{3}+4x=0$$
$$\displaystyle x\left ( x^{2}+4 \right )=0$$
$$x = 0$$ or $$\displaystyle x^{2}+4=0$$
$$x = 0$$ or $$\displaystyle x^{2}=-4$$
However $$x$$ is real. Therefore $$x = 0$$ which is a contradiction since we have assumed that $$x$$ is not $$0$$.
Thus the given statement p is true.
(iii) To prove statement $$p$$ to be true by contrapositive method we assume that $$r$$ is false and prove that $$q$$ must be false.
Here $$r$$ is false implies that it is required to consider the negation of statement $$r$$. This obtains the following statement,
$$\displaystyle \sim r:x\,is\,not\,0$$
It can be seen that $$\displaystyle \left ( x^{2}+4 \right )$$ will always be positive.
x$$\displaystyle \neq 0$$ implies that the product of any positive real number with $$x$$ is not zero.
Let us consider the product of $$x$$ with $$\displaystyle \left ( x^{2} +4\right )$$
$$\displaystyle \therefore x\left ( x^{2} +4\right )\neq 0$$
$$\displaystyle \Rightarrow x^{3}+4x\neq 0$$
This shows that statement $$q$$ is not true.
Thus it has been proved that 
$$\displaystyle \sim r\Rightarrow \sim q$$
Therefore the given statement $$p$$ is true.


State the converse and contrapositive of each of the following statements:
(i) p : A positive integer is prime only if it has no divisors other than $$1$$  and itself
(ii) q : I go to a beach whenever it is a sunny day
(iii) r : If it is hot outside then you feel thirsty

(i) Statement $$p$$ can be written as follows
If a positive integer is prime, then it has no divisors other than $$1$$ and itself.
The converse of the statement is as follows
If a positive integer has no divisors other than $$1$$ and itself then it is prime.
The contrapositive of the statement is as follows
If positive integer has divisors other than $$1$$ and itself it is not prime.
(ii) The given statement can be written as follows
If it is a sunny day then I go to a beach.
The converse of the statement is as follows
If I go to a beach then it is a sunny day.
The contrapositive of the statement is as  follows
If I do not go to a beach then it is not a sunny day.
(iii) The converse of statement $$r$$ is as follows
If you feel thirsty then it is hot outside.
The contrapositive of statement $$r$$ is as follows
If you do not feel thirsty then it is not hot outside.


Identify the quantifier in the following statements and write the negation of the statements
(i) There exists a number which is equal to its square
(ii) For every real number $$x, x$$ is less than $$x + 1$$
(iii) There exists a capital for every state in India

(i) The quantifier is "There exists"
The negation of this statement is as follows
There does not exist a number which is equal to its square
(ii) The quantifier is "For every"
The negation of this statement is as follows
There exist a real number $$x$$ such that $$x$$ is not less than $$x + 1$$
(iii) The quantifier is "There exists"
The negation of this statement is as follows
There exists a state in India which does not have a capital


Re write each of the following statements in the form "p if and only if q" 
(i) p : If you watch television then your mind is free and if your mind is free then you watch television
(ii) q : For you to get an A grade it is necessary and sufficient that you do all the homework regularly
(iii) r : If a quadrilateral is equiangular then it is a rectangle and if a quadrilateral is a rectangle then it is equiangular

(i) $$p\leftrightarrow q :$$ You watch television if and only if your mind is free.
(ii) $$p\leftrightarrow q :$$ You get an $$A$$ grade if and only if you do all the homework regularly.
(iii) $$p\leftrightarrow q :$$ A quadrilateral is equiangular if and only if it is a rectangle.


State whether the following sentences are always true, false or ambiguous. Justify your answer.
The earth is the only planet where life exist.

True
Earth is unique in the Solar System as being the only planet which is able to support life in all its forms: from basic living micro-organisms to highly sophisticated and intelligent human beings. There are many reasons why this happens.
Earth has a breathable atmosphere. Oxygen is the gas that is required for the life of most creatures. This is present in Earth's atmosphere and also in water. Oxygen is constantly put into the atmosphere by plants and trees. Then earth is the only planet where life exist.


Find the total surface area of a closed cylindrical petrol storage tank whose diameter 4.2 m and height 4.5 m.

Given :

Radius( r ) : $$\dfrac{4.2}{2} = 2.1 m $$

height(h) = 4.5 m 

We know total surface area of a cylinder is $$=2\pi$$$$r(h+r)$$

$$=2\times\dfrac{22}{7}\times 2.1(4.5 + 21 )$$

$$=87.12 $$$$ m^{3} $$

The total surface area of the closed cylindrical petrol storage tank is $$87.12$$$$m^{3}.$$ 



$$(x + 7)^2 = x^2 + 49$$


1306470_566787_ans_12a8c62988e648819a0ddcedc74b6945.jpg


Construct the truth table for $$(p \wedge q) \vee [\sim (p \wedge q)]$$.

$$p$$          $$q$$           $$p \wedge q$$        $$\sim (p \wedge q)$$            $$(p \wedge q) \vee [ \sim (p \wedge q)]$$
$$T$$$$T$$$$T$$$$F$$$$T$$
$$T$$$$F$$$$F$$$$T$$$$T$$
$$F$$$$T$$$$F$$$$T$$$$T$$
$$F$$$$F$$$$F$$$$T$$$$T$$


Prove: $$\sim (p\Rightarrow q)\equiv p\wedge (\sim q)$$.

 $$p$$ $$q$$$$\sim q$$ $$p\Longrightarrow q$$$$\sim(p\Longrightarrow q)$$ $$p\wedge(\sim q)$$ 
 $$T$$$$T$$ $$F$$  $$T$$ $$F$$ $$F$$
 $$T$$$$F$$ $$T$$ $$F$$ $$T$$$$T$$ 
 $$F$$$$T$$ $$F$$ $$T$$ $$F$$ $$F$$ 
$$F$$ $$F$$ $$T$$ $$T$$ $$F$$ $$F$$ 
So, from the truth table , $$\sim(p\Longrightarrow q)\equiv p\wedge(\sim q).$$


Prove that: $$\sim (p\Leftrightarrow q)\equiv \sim p\Leftrightarrow q$$.

To Prove:
$$\sim(p\Leftrightarrow q)\equiv\sim p\Leftrightarrow q$$

Solution:
$$p$$$$q$$ $$\sim q$$ $$p\Leftrightarrow q$$ $$\sim(p\Leftrightarrow q)$$ $$\sim p\Leftrightarrow q$$ 
$$T$$ $$T$$ $$F$$ $$T$$ $$F$$ $$F$$ 
$$T$$ $$F$$ $$F$$ $$F$$ $$T$$ $$T$$ 
$$F$$ $$T$$ $$T$$ $$F$$$$T$$ $$T$$ 
$$F$$ $$F$$ $$T$$ $$T$$  $$F$$$$F$$ 
Hence, from the truth table, $$\sim(p\Leftrightarrow q)\equiv\sim p\Leftrightarrow q.$$


Construct the truth table for the statement $$(p \wedge q) \vee r$$.

$$p$$            $$q$$              $$r$$                $$p \wedge q$$        $$(p \wedge q) \vee r$$
$$T$$$$T$$$$T$$$$T$$$$T$$
$$T$$$$T$$$$F$$$$T$$$$T$$
$$T$$$$F$$$$T$$$$F$$$$T$$
$$T$$$$F$$$$F$$$$F$$$$F$$
$$F$$$$T$$$$T$$$$F$$$$T$$
$$F$$$$T$$$$F$$$$F$$$$F$$
$$F$$$$F$$$$T$$$$F$$$$T$$
$$F$$$$F$$$$F$$$$F$$$$F$$


Prepare the truth table for the following.
$$\sim p\leftrightarrow q$$

Truth Table: $$\sim p \leftrightarrow q$$

$$p$$ $$q$$ $$\sim p$$ $$\sim p\leftrightarrow q$$ 
$$T$$ $$T$$ $$F$$ $$F$$ 
$$T$$ $$F$$ $$F$$ $$T$$ 
$$F$$ $$T$$ $$T$$ $$T$$ 
$$F$$ $$F$$ $$T$$ $$F$$ 



Write the converse and contrapositive of the following statement: 

If $$x+3 =9$$, then $$x=6$$.

$$\\The\>converse\>of\>p\>\to\>\>q\>is\>q\>\to\>p\\\>hence\>it\>would\>be\>\\If\>x=6,thenx+3=9\\The\>contrapositive\>of\>p\>\to\>q\>is\>\sim\>q\>\to\>\sim\>p\>\\\>hence\>would\>it\>be\>\\If\>x\neq\>6,then\>x+3\>\neq\>9$$



Write converse and inverse of the following statement:
"If Ravi is good in logic then Ravi is good in Mathematics."

S:-"If Ravi is good in logic, then Ravi is good in Math"
Let P=Ravi is good in logic
Q=Ravi is good in Math
$$\therefore S=P \rightarrow Q$$
Convere is $$Q \rightarrow P$$
Converse: "If Ravi is good in Math, then Ravi is good in logic"
Inverse is $$\sim P \rightarrow \sim Q$$
Inverse:"If Ravi is not good in logic, then he is not good in Math".


Prepare the truth table for the following.
$$\sim p\wedge q$$.

Truth Table $$\sim p \wedge q$$
 $$p$$$$q$$ $$\sim $$ $$\sim p \wedge q$$ 
$$T$$ $$T$$ $$F$$ $$F$$ 
$$T$$ $$F$$ $$F$$ $$F$$ 
$$F$$ $$T$$ $$T$$ $$T$$
 $$F$$$$F$$ $$T$$ $$F$$ 


Write converse, inverse and contrapositive of the following conditional statement:
If an angle is a right angle then its measure is $$90^{\circ}$$.

Given: If an angle is a right angle then its measure is $$90^0$$

Converse: If the measure of an angle is $$90^0$$ then it is a right angle.

Inverse: If an angle is not a right angle then its measure is not $$90^0$$.

Contrapositive: If the measure of the angle is not $$90^0$$ then it is not a right angle.


Find truth value of compound statement 'All natural number are even or odd''  

Truth table of compound statement :

Let  $$P$$ is an even number, $$\sim P$$ is an odd number

A Truth table of $$p,q$$ and $$pVq$$ :

Hence this is the answer.


1155613_1155572_ans_6ba80d050072481a9f02e03e734fa6e6.png


Prepare the truth tables for the following: 
$$p\rightarrow \left( p\wedge q \right)$$

 p q $$p\wedge q$$ $$p \rightarrow (p \wedge  q)$$
 T T T T
 T F F F
 F T F T
 F F F T
$$(req^d)$$
1147069_1144263_ans_fc605b7d098b44b7931d2dd657c4d580.jpg


The negation of $$q\vee \sim (p \wedge r)$$ is?

$$\begin{matrix} q\vee \sim (p\wedge r)=?\, \, \, \left[ { \because \sim (p\wedge r)=\left( { \sim p } \right) \vee \left( { \sim q } \right)  } \right]  \\ \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \left[ { \sim (p\vee r)=\left( { \sim p } \right) \wedge \left( { \sim q } \right)  } \right]  \\ by\, demorgan's\, law \\ \sim \left[ { q\wedge \sim (p\wedge r) } \right]  \\  \end{matrix}$$


prepare the truth table of the following statement patterns.
$$(i)\,\,\,[(p \to q) \wedge q] \to p$$
$$(ii)\,(p \wedge q) \to  \sim p$$
$$(iii)(p \to q) \leftrightarrow (\sim p \vee q)$$
$$(iv)\,(p \leftrightarrow r)\, \wedge (q \leftrightarrow p)$$
$$(v)\,(p\, \vee  \sim q) \to (r \wedge p)$$


1188490_1175746_ans_22854732517348a185a6bbd4abb86d72.jpg


Contrapositive of the statement 'If two number are not equal, then their squares are not equal', is: 


 If the squares of two numbers are equal, then the numbers are equal.


Write converse of statement. In $$\Delta ABC$$, if $$AB=AC$$ then $$\angle C=\angle B$$.

The converse of the statement given will be
" In $$\triangle ABC$$ if $$C=B$$ the $$AB=AC$$."


Write the converse, inverse and contrapositive of the following statements : "If a function is differentiable then it is continuous".

The Converse is like the conditional statement but the ifs and thens switch places. 
"If a function is differentiable, then it is continuous." 
Inverse is like the conditional statement but with not for the ifs and thens. 
"If a function is not continuous, then it is not differentiable." 
Contrapositive is like the converse but with not for the ifs and thens. 
"If a function is not differentiable, then it is not continuous."


Write the truth values of following statements 
(i) 9 is a perfect square but 11 is a prime number. 
(ii) Moscow is in Russia.
(iii) London is in France. 

(i) Since, 9 is a perfect square and 11 is a prime number so truth value is true(1).
(ii) Since, Moscow is in Russia so truth value is true(1).
(ii) Since, London is in England so truth value is False(0).


Prove that $$3+\sqrt{7}$$ is irrational number.

We have to prove that $$3+\sqrt{7}$$ is irrational.
Let us assume the opposite, that $$3+\sqrt{7}$$ is rational.
Hence $$3+\sqrt{7}$$ can be written in the form $$\dfrac{a}{b}$$ where $$a$$ and $$b$$ are co-prime and $$b\neq 0$$
Hence $$3+\sqrt{7}=\dfrac{a}{b}$$
$$\Rightarrow \sqrt{7}=\dfrac{a}{b}-3$$
$$\Rightarrow \sqrt{7}=\dfrac{a-3b}{b}$$
where $$\sqrt{7}$$ is irrational and $$\dfrac{a-3b}{b}$$ is rational.
Since,rational$$\neq$$ irrational.
This is a contradiction.
$$\therefore$$ Our assumption is incorrect.
Hence $$3+\sqrt{7}$$ is irrational.
Hence proved.


Consider the following three statements:
P     : 5 is a prime number.
Q     : 7 is a factor of 192.
R     : L. C. M. of 5 and 7 is 35.
Then the truth value of which one of the following statements is true ? 

$$P : True$$
$$Q : False$$
$$R : True$$


Are the following pairs of statements are negation of each other
(i)The number x is not a rational number.
The number x is not an irrational number.

The negation of the first statement is the number $$x$$ is a rational number.
This is same as the second statement. This is  if a because if a number is not an irrational number then it is a rational number.


State the converse, inverse and contrapositive of the following conditional statement:
If the teacher is absent, then the students are happy.

$$\textbf{Step 1: Write the converse, inverse, and contrapositive of the given statement.}$$
 
                $$\text{The given statement: " If the teacher is absent, then the students are happy".}$$

                $$\text{Let,}$$ $$p\rightarrow$$ $$\text{The teacher is absent.}$$
                         $$q\rightarrow$$ $$\text{The students are happy.}$$
                    $$\sim p\rightarrow$$ $$\text{The teacher is not absent.} $$
                    $$\sim q\rightarrow$$ $$\text{The students are not happy} $$

                $$\text{Converse:}$$ 
                $$q\rightarrow p$$ 

                $$\text{So, the converse statement: "If the students are happy, then the teacher is absent ".}$$

                $$\text{Inverse:}$$ 
                $$\sim p\rightarrow \sim q$$ 

                $$\text{So, the inverse statement: "If the teacher is not absent, then the students are not happy ".}$$

                $$\text{Contrapositive:}$$ 
                $$\sim q\rightarrow \sim p$$ 

                $$\text{So, the converse statement: "If the students are not happy, then the teacher is not absent ".}$$

$$\textbf{Hence, these are the required statements. }$$


when $$x\in R$$
Are the following pairs of the statement are negative of each other:
The number $$x$$ is an irrational number.
The number $$x$$ is a rational number.
If Yes put 1 else 0.

The negation of the given statement.
The number $$X$$ is not a rational number
which is same as second statement.
The number $$X$$ is an irrational number.
Hence the given pair are Negation of each other.
The given statement was True


Give three examples of sentence which are not statements. Give reasons for the answers.

The three examples of sentences, which are not statement are as follow
(i)He is a doctor
 As it is not evident from the sentence as to whom 'he' is referred to. Therefore, it is not a statement.
(ii) Geometry is difficult
It is not a statement, as for some people geometry is easy whereas for some people it is difficult.
(iii)Where is she going?
It is not a statement as it is a question.


Find out which of the following sentences are statement and which are not. Justify your answer.
There are $$35$$ days in a month.

There is a false declarative sentence as no month is having $$35$$ days. $$\therefore$$ its always false
And a statement says a declarative sentence which is either true or false but both at a time.
Hence the above sentence is a statement.


Find out which of the following sentences are statement and which are not Justify your answer.
All real numbers are complex numbers.

All real numbers can be written in the form of $$a+i\,o$$ (where 'a' is real number)
So, all real numbers are complex numbers
Hence, it is always True.
Hence, it is a statement.


Check whether the following pair of statement are negative of each other. Give reasons for your answer.
$$a+b=b+a$$ is true for every real number $$a$$ and $$b$$.There exist real numbers are a and b for which a+b = b+a.


1423996_1667857_ans_1a13dcb6c6be4841ad43140e495117f0.jpg


Tell whether the following is certain to happen, impossible can happen but not certain.
A tossed coin will land heads up.

It is possible to happen but not certain. as it lands whether from tail up or head up.


Write the negative of the following statement:
All birds sing.


1423907_1667837_ans_7da7c39614f94981802dcde338af5612.jpg


when $$x\in R$$
Are the following pairs of the statements are negative of each other:
The number $$x$$ is a rational number.
The number $$x$$ is not an irrational number.
If Yes put 1 else 0.

The negation of the given statement us 
The number $$x$$ is a rational number.
which is same as
The number $$x$$ is not irrational number.
Hence the given pairs are negation of each other.
So, the given statements are true


Write the component statement of the following compounds statements and check whether the compound statement is true or false:
The sand heats up quickly in the sun and does not cool down fast at night. 

The given compound statements are 

$$p$$ : The sand heats up quickly in the sun.
$$q $$: The sand does not cool down fast at night 

The compound statement uses and as the connective. For the compound statement to be true both the component statements must be true. The second component statement "Sand does not cool down fast at night is false. Sand cools fast at night.
Therefore, the compound statement is false.


Write the negative of the following statement:
All the students completed their homework.

Let $$p:$$ All the students completed their homework.
So , if we can find a student or some students who did not complete their work , will negates $$p$$ .
Hence negative of $$p:$$ All the students completed their homework is ,
There exists a student who did not complete his homework
Or
Some of the students did not complete their homework .


Write the negative of the following statement:
For every $$x\in N, x+3 < 10$$


1414723_1667896_ans_ea751768cba740248aef9ef30ee07534.jpg


Write the component statement of the following compounds statements and check whether the compound statement is true or false:
All rational number are real and all real number are not complex.

Here, 
$$p$$: all rational numbers are real .
$$q$$: all real numbers are not complex . 
So , here only $$p$$ is true and $$q$$ is false 
Therefore , the compound statement is false .
(Compound statement with "and" is true if all its component statements are true ) .


Write the component statement of the following compounds statements and check whether the compound statement is true or false:
Square of an integers is positive or negative.

Component statements are -
$$p :$$ square of an integer is positive .
$$q :$$ square of an integer is negative .
Clearly, $$p$$ is true whereas $$q$$ is false.
Thus compound statement is true .
(A compound statement with "or" is true when one component is true or both the component statements are true.)


Write the negative of the following statement:
There exists $$x\in N, x+3=10$$


1414726_1667897_ans_04379e3403e44a4fba61bf60c176edbb.jpg


Negate each of the following statements:
There exists a number which is equal to its square.

Negation : For every real number $$x,x^2\neq x$$


Statement the converse and contrapositive of each of the following statements:
If it is hot outside, then you feel thirsty.

CONVERSE : If you feel thirsty, then it is hot outside.
CONTRAPOSITIVE: If you do not feel thirsty, then it is not hot outside.


Determine the contrapositive of the following statement:
It never rains when it is cold.

Let $$p :$$ it is cold .

$$q :$$ it never rains.

The contrapositive of "if p, then q" is "if $$\sim q$$, then $$\sim p$$".

Hence, the contra-positive of the given statement is 
If it rains, then it is not cold.


Statement the converse and contrapositive of each of the following statements:
A positive integer is prime only if it has no divisors other than $$1$$ and itself.

CONVERSE: If an integer has no divisor other then I and itself, then it is prime.

CONTRAPOSITIVE: If an integer has some divisor other than I and itself, then it is not prime.


Determine the contrapositive of the following statement:
If she works, she will earn money.

Let $$p :$$ she works .
$$q :$$ she will earn money.

The given statement is of the form "if $$p$$, then $$q$$"
And we know contrapositive of "if p, then q" is "if $$\sim q$$, the $$\sim p$$"
 
Hence, contra-positive of the given statement is,
If she does not earn money, then she does not work.


Determine the contrapositive of the following statement:
If Ravish skis, then it snowed.

Let $$p:$$ Ravish skis.
$$q:$$ it snowed .

As we contrapositive of "if p then q " is "if $$\sim q$$ then $$\sim p$$ ".

Therefore contrapositive of "if Ravish skis, then it snowed" is 
If it did not snow, then Ravish will not ski. 


Statement the converse and contrapositive of each of the following statements:
If you live in Delhi, then you have winter clothes.


1428805_1667918_ans_0efaf77cc6cc4774a7cc60d21aab45b0.jpg


Statement the converse and contrapositive of each of the following statements:
I go to a beach whenever it is a sunny day.

CONVERSE : If I go to a beach, then it is a sunny day.
CONTRAPOSITIVE: If I don't go to beach, then it is not a sunny day.


Determine the contrapositve of each of the following statements:
If $$x$$ is less than zero, then $$x$$ is not positive.

Let $$p:$$ $$x$$ is less than zero .

$$q :$$ $$x$$ is not positive.

As we know contra-positive of "if $$p$$ then $$q$$" is "if $$\sim q$$ , then $$\sim p$$ ".

Hence , contra positive of " if $$x$$ is less than zero , then $$x$$ is positive " is, 
"If $$x$$ is positive , then $$x$$ is not less than zero ."


Determine the contrapositive of the following statement:
Only If Max studies will he pass the test.

Since given statement is of the form "p only if q" which is same as 
"if $$p$$, then $$q$$" . Therefore , let 
$$p:$$ he will pass the test .
$$q:$$ Max studies.
And we know contrapositive of "if $$p$$, then $$q$$" is "if $$\sim q$$, then $$\sim p$$"
Thus, contra-positive of the given statement is,
If Max does not study, then he will not pass the test.


Determine the contrapositive of the following statement:
Only if he does not tire will he win.

Let $$p :$$ he will win .
$$q :$$ he does not tire.

The given statement is of the form "$$p$$ only if $$q$$" which is same as 
"if $$p$$,then $$q$$". 

And contra positive of "if $$p$$, then $$q$$" is "if $$\sim q$$, then $$\sim p$$"

Hence, contra-positive of the given statement is, 
If he tires, then he will not win.


Determine the contrapositve of each of the following statements:
If he has courage he will win.

Let $$p :$$ he has courage.
$$q :$$ he will win.

As we know , contra positive of "if $$p$$ , then $$q$$ " is "if $$\sim q$$, then $$\sim p$$'.

Thus , contra-positive of " if he has courage he will win " is ,
If he does not win , then he does not have courage.


Determine the contrapositive of the following statement:
If $$x$$ is an integer and $$x^{2}$$ is odd, then $$x$$ is odd.

Let $$p:x$$ is an integer and $$x^2$$ is odd.

$$q:x$$ is odd.

The given statement is of the form. " If $$p$$, then $$q$$".

And contrapositive of " if $$p$$, then $$q$$" is " if $$\sim q$$, then $$\sim p$$".

Thus, contrapositive of given statement is,
if $$x$$ is even, then $$x^2$$ is even.


Determine the contrapositve of each of the following statements:
It is necessary to be strong in order to be a sailor.

Let $$p :$$ he is a sailor.
$$q :$$ he is strong .

The given statement is of the form "$$q$$ is necessary condition for $$p$$" which is same as "if $$p$$, then $$q$$ ".

And contra-positive of "if $$p$$, then $$q$$" is "if $$\sim q$$, then $$\sim p$$".
Hence , the contra-positive of the given statement is, 

If he is not strong , then he is not a sailor.



Comment if the following statement is true or false? And give a valid reason for saying so
$$\sqrt{11}$$ is a rational number

$$FALSE$$


Let as assume that $$\sqrt{11}$$ is a rational number.
A rational number can be written in the form of $$p/q$$  where $$q ≠ 0 \ and\ p , q \ are\ non\ negative\ number$$.

$$\sqrt{11}=\dfrac{p}{q}$$ ....( Where p and q are co prime number )

Squaring both side !

$$11 = \dfrac{p^2}{q^2}$$

$$11\ q^2 = p^2 \ \ \ \ \ ......( i )$$


$$p^2$$ is divisible by $$11$$
$$p$$ will be divisible by $$11$$


Let $$p = 11\ m$$ ( Where $$m$$ is any positive integer )

Squaring both side

$$p^2 = 121m^2$$


Putting in $$( i )$$

$$11 q^2 = 121m^2$$

$$q^2 = 11 m^2$$

$$q^2$$ is divisible by $$11$$

$$q$$ will also divisible by $$11$$

Since $$p\ and\ q$$ both are divisible by same number $$11$$

So, they are not co - prime .

Hence Our assumption is Wrong. Hence, $$\sqrt{11}$$ is an irrational number .


Write the given statement using numbers, literals and signs of basic operations. State what each letter represents.
The selling price equals the sum of the cost price and the profit.

Let
The cost price = $$C.P$$
The selling price = $$S.P$$
The profit = $$P$$ 
We know that the word 'sum' means ' addition'.
So, 
The selling price = sum of the cost price and the profit.
                              = cost price + profit
                    $$S.P$$ = $$C.P$$ + $$P$$ 


Show that the following statement is true by the method of contrapositive
$$p:$$ If $$x$$ is an integer and $$x^{2}$$ is odd, then $$x$$ is also odd

To do this, we must first state the contrapositive of what we set out to prove.

so

If $$x^2$$ is odd then $$x$$ is odd

now becomes

If $$x^2$$ is even then$$ x$$ is even

which is the contrapositive, the idea is that if we can prove that$$ x^2$$ is even for all$$ x$$ that is even, it stands to reason that $$x^2$$ can only be odd for all x that is odd.

The way to write this symbolically is $$~Q => ~P$$ so therefore $$P => Q$$.

So now we prove if $$x^2$$ is even then $$x$$ is even

$$x$$ is even so $$x=2y$$ for some integer y.

then $$x^2 = 2y(2y) = (4y^2) = 2(2y^2)$$ which is even.

Therefore if $$x^2$$ is even $$x$$ is even, so by contraposition, if $$x^2$$ is odd, $$x$$ is odd.


Write each of the following statements in the form if ..... then;
If a number is not a multiple of $$3$$, then it is not a multiple of $$6$$.

undefined
1982546_1710634_ans_175148c25932458f832fbc916c7b3791.jpg


Check whether the following sentence is a statement? In case of a statement mention whether it is true or false.
The sum of any two sides of a triangle is always greater than the third side.


1875336_1710629_ans_573d4f98c72b461db0675df9deddfa48.jpg


Check whether the following sentence is a statement? In case of a statement mention whether it is true or false.
$$\sqrt 7 $$ is an irrational number.


1877615_1710614_ans_aa7401443be44d3ea2961ab8aa7d5dc6.jpeg


Check whether the following sentence is statement? In case of a statement mention whether it is true or false.
The sun is a star. 


1877614_1710612_ans_9db6b14c93d7420393160a196594f70d.jpeg


Check whether the following sentence is a statement? In case of a statement mention whether it is true or false.
Every relation is a function.


1875310_1710626_ans_90428caf9da74d35bdcf5b8eddd2f155.jpg


Check whether the following sentence is a statement? In case of a statement mention whether it is true or false.
Ice is always cold.

It is scientifically proven the fact, therefore the sentence is always true.
1875313_1710620_ans_8ecd3e9738a84d7e940ff8b642005f87.jpg


Write each of the following statements in the form if ..... then;
You get a job implies that your credentials are good.

If you get a job, then your credentials are good.


State the converse, inverse and contrapositive of the conditional statement : 'If a sequence is bounded, then it is convergent.

$${\textbf{Step  - 1: Writing generalized rules}}$$

                    $${\text{Given statement: 'If a sequence is bounded, then it is convergent'}}$$

                    $${\text{Since, it is of the form: If P then Q, it can be written in symbol form as P}\rightarrow Q}$$

                    $$\text{where, P is 'a sequence is bounded' and Q is  'it is convergent.'}$$

                    $${\text{We know that for such statements, }}$$

                    $${\text{Converse: If Q then P }\Rightarrow \text{Q}\rightarrow \text{P}}$$

                    $${\text{Inverse: If not P then not Q }\Rightarrow \sim P \rightarrow \sim Q}$$

                    $${\text{Contrapositive: If not Q then not P}\Rightarrow \sim Q \rightarrow \sim P}$$

$${\textbf{Step  - 2: Writing converse, inverse and contrapositive for given statement}}$$

                    $${\text{Converse: If the sequence is convergent, then it is bounded}}$$

                    $${\text{Inverse: If a sequence is not bounded, then it is not convergent}}$$

                    $${\text{Contrapositive: If a sequence is not convergent then it is not bounded}}$$

$${\textbf{These are converse, inverse and contrapositive for the statement.}}$$



Write the following statements in the form if ..... then;
A rhombus is a square only if each of its angles measures $$90^{o}$$.

If each angle of a rhombus measures $$90^{o}$$, then is a multiple of $$3$$


Write the converse and contrapositive of the following:
If the diagonals of a quadrilateral bisect each other, then it is a parallelogram.



1886181_1710656_ans_72e7ed4cd98d48b0aba0763e1f5aebee.jpg


Check whether the following sentence is a statement? In case of a statement mention whether it is true or false.
$$(2+\sqrt 3)$$ is a complex number.


1886163_1710640_ans_db1f5788da8b4270804f79344358bc20.PNG


Write the converse and contrapositive of each of the following:
If a positive integer $$n$$ is divisible by $$9$$, then the sum of its digits is divisible by $$9$$

Converse: If the sum of the digits of a positive integer $$n$$ is not divisible by $$9$$, then it is divisible by $$9$$.
Contrapositive: If the sum of teh digits of a positive integer $$n$$ is not divisible by $$9$$, then it is not divisible by $$9$$, then it is not divisible by $$9$$.


Write the converse and contrapositive of each of the following:
If the two lines are parallel, then they do not intersect in the same plane.

Converse If the two lines do not intersect in the same plane, then they are parallel.
Contrapositive: If the two lines intersect in the same plane, then they are not parallel.


Check whether the following sentence is a statement? In case of a statement mention whether it is true or false.
Each prime number has exactly two factors.


1882331_1710636_ans_c50d789e488443018f218294957e7630.jpg


Write the converse and contrapositive of each of the following:
If $$x$$ is a prime number, then $$x$$ is odd.

Converse: If $$x$$ is an odd number, then it is prime.
Contrapositive If $$x$$ is not an odd number, then it is not prime.


Check whether the following sentence is a statement? In case of a statement mention whether it is true or false.
Every quadratic equation has at least one real root.


1886210_1710663_ans_c3e8c1b698f04cf4b6814d6fc4d1483d.jpg


Check whether the following sentence is a statement? In case of a statement mention whether it is true or false.
Pairs is in France.


1875270_1710635_ans_251add10a5d447ab9e5051f05855101d.jpg


Write the converse and contrapositive of each of the following:
If $$A$$ and $$B$$ are subsets of $$X$$ such that $$A\subseteq B$$, then $$(X-B)\subseteq (X-A)$$


1893789_1710658_ans_873273b987cc48cf9a2d8fc2b2e70652.jpg


Check whether the following sentences is a statement? In case of a statement mention whether it is true or false.
The angles opposite to the equal sides of an isosceles triangle are equal.


1886178_1710646_ans_c35fd91dbfd5477687849cd731632eff.jpg


Write the converse and contrapositive of each of the following:
If you were born in India, then you are a citizen of India.

Converse: If you are a citizen of India, then you were born in India.
Contrapositive: If you are not a citizen of India, then you were not born in India.


Write the converse and contrapositive of the following:
If it rains, then I stay at home

Converse: If I stay at home, then it rains.
Contrapositive If don't stay at home, then it does not rain.


Given below are pair of statements. Combine given pair using if and only is:
$$p:$$ If a quadrilateral is equiangular, then it is a rectangle.
$$q:$$ If a quadrilateral is a rectangle, then is equiangular.

A quadrilateral is a rectangle if and only if it equiangular.


Write the converse and contrapositive of each of the following:
If $$f(2)=0$$, then $$f(x)$$ is divisible by $$(x-2)$$

Converse: If $$f(x)$$ is divisible by $$(x-2)$$, then $$f(2)=0$$
Contrapositive: If $$f(x)$$ is not divisible by $$(x-2)$$, then $$f(2)$$ is not equal to $$0$$


Given below there is a pair of statement. Combine pair using if and only if:
$$p:$$ If $$f(a)=0$$, then $$(x-a)$$ is a factor of polynomial $$f(x)$$
$$q:$$ If $$(x-a)$$ is a factor of polynomial $$f(x)$$, then $$f(a)=0$$

Ans: $$(x-a)$$ is a factor of polynomial $$f(x)$$ is and only is $$f(a)=0$$
1888461_1710697_ans_e2755979529745259384bed7eab81399.jpg


Write the negation of each of the following statement:
The number $$6$$ is greater than $$4$$.

The negation of given statement is 
The number $$6$$ is not greater than $$4$$.


Given below there is a pair of statement. Combine pair using if and only if:
$$p:$$ If the sum of the digits of a number is divisible by $$3$$, then the number is divisible by $$3$$.
$$q:$$ If a number is divisible by $$3$$, then the sum of its digits is divisible by $$3$$.

A number is divisible by $$3$$ is and only if the sum of its digits is divisible by $$3$$
1887436_1710686_ans_1a847b09ba234135a3d9e54d07b3cf29.jpg


Write the negation of each of the following statement:
Both the diagonals of a rectangle are equal.

It is false that both the diagonals of a rectangle are equal.


Write the negation of each of the following statements :
Every natural number is an integer.

There exists a natural number which is not an integer.


Given below are some pairs of statements. Combine each pair using if and only is:
$$p:$$ A quadrilateral is a parallelogram is its diagonal bisect each other.
$$q:$$ If the diagonals of a quadrilateral bisect each other, then it is a parallelogram.

A quadrilateral is a parallelogram if and only if its diagonal bisect each other.


Write the negation of each of the following statement:
Every natural number is a greater than $$0$$

The negation of given statement is 
There exists a natural number which is not greater than $$0$$


Write the negation of the following statement :
The number $$-5$$ is a rational number.

The number $$-5$$ is not a rational number.


Write the negation of each of the following statements :
All cats scratch.

There exists a cat which does not scratch.


Given below there is a pair of statements. Combine each pair using if and only if.
$$p:$$ If a square matrix $$A$$ is invertible, then $$|A|$$ is nonzero.
$$q:$$ If $$A$$ is a square matrix such that $$|A|$$ is nonzero, then $$A$$ is invertible.


1893830_1710706_ans_d9cadafe56e34f279f368efef363520f.jpg


Use contradiction method to prove that:
$$p:\sqrt 3$$ is irrational is a true statment.

Given that - 
$$\sqrt{3}$$ is an irrational.

To find - 
Prove the statement using contradiction method.

Let p be the given mathematical statement:
i.e., $$p : \sqrt{3}$$ is irrational.

If possible let us assume that p is not true i.e., $$\sqrt{3}$$ is national, 
$$\Rightarrow \sqrt{3}$$ is $$\dfrac{x}{y}$$, where $$x$$ & $$y$$ are positive integers prime to each other & $$y > 1$$  [i.e., they have no common factor]
$$3 = \dfrac{x^2}{y^2}$$

$$\Rightarrow \dfrac{x^2}{y} = 3y$$ ____(1)

By assumption, $$x$$ & $$y$$ are prime positive to each other, hence, $$x^2$$ & $$y$$ are also prime to each other. $$y > 1$$.

Therefore, $$\dfrac{x^2}{y}$$ represents a positive real number which is not an integer. But $$2y$$ represents a positive integer.

$$\therefore$$ From (i), we get-
a positive number which is not integer = a positive integer.

Clearly, it is impossible. Hence, our assumption is not true, i.e., $$\sqrt{3} $$ is not rational.

Thus, $$\sqrt{3}$$ is irrational. (proved)


By giving a counter-example, show that the statement is false:
$$p$$: If $$n$$ is an odd positive integer, then $$n$$ is prime.


1855121_1710714_ans_ea64093f6bb148969fc882c296681961.jpg


Consider the statment:
$$q$$: For any real number $$a$$ and $$b, a^2=b^2\Rightarrow a=b$$.
By giving a counter-example, prove that $$q$$ is false.


1855124_1710713_ans_59c046b1ac9c493bb83844c0842c1a7b.jpg


Write the negation of each of the following statements :
There is some integer $$k$$ for which $$2k=6$$.


1893834_1710708_ans_8bd55c8d154947ca952f90eea4f73c8c.jpg


Write the following using 'if and only if'
If you watch television then your mind is free and if your mind is free then you watch television.


1893894_1710717_ans_6fe8c562b6c44fd89f8600a51a168b12.jpg


Write the negation of the following statements :
All students study mathematics at the elementary level. 

There exists a student who does not study mathematics at the elementary level. 


Write the following using 'if and only if':
In order to get $$A$$ grade, it is necessary and sufficient that you do all the homework regularly.


1893856_1710712_ans_b06feaddb1fe4e9e9ef3571337ee2e25.jpg


Write the contrapositive and converse of the following statements
You cannot comprehend geometry if you do not know how to reason deductively

The contrapositive is as follows
If you know how to reason deductively then you can comprehend geometry.
The converse is as follows
If you do not know how to reason deductively then you cannot comprehend geometry.


Write the opposite of the following : 
$$ 25^{\circ}\,C $$ above freezing point. 

The opposite of the given statement is $$ 25^{\circ} \,C $$ below freezing point. 


Write the negation of the following statements : 
All triangles are not equilateral triangle .

All triangles are equilateral triangle .


Write the contrapositive and converse of the following statements.
$$ x $$  is an even number implies that $$x$$ is divisible by $$ 4 $$.

The given statement can be written as follows.
If $$ x $$ is an even number , then $$ x $$ is divisible by $$ 4 $$.
The contrapositive is a s follows.
If $$ x $$ is not divisible by $$ 4 $$ , then $$ x $$ is not an even number. 
The converse is as follows.
If $$ x $$ is divisible by $$ 4 $$, then $$ x $$ is an even number.


By giving a counter-example, show that the following statement is false:
$$p:$$ If all the sides of a triangle are equal, then the triangle is obtuse angled.


1855182_1710719_ans_4fe5748d06f543a1baa0d7c61b8c7040.jpg


Write the opposite of the following statement:
Gaining a weight of $$5 kg$$.

The opposite statement of "gaining a weight of $$5 kg$$" is "losing a weight of $$5 kg.$$"


Identify the quantifier in the following statements and write the negation of the statements .
There exists a capital for every state in India.

The quantifier is "There exists".
The negation of this statement is as follows.
There exists a state in India which does not have a capital.


Write the contrapositive and converse of the following statements
Something is cold implies that it has low temperature

The contrapositive is as follows
If something does not have low temperature then it is not cold.
The converse is as follows
If something is at low temperature then it is cold.


Write the negation of the following statements : 
$$ \sqrt{2} $$ is not a complex number.

$$ \sqrt{2} $$ is a complex number.


By giving a counter example, show that the following statement is not true.
q : The equation $$  x^2 - 1 = 0 $$  does not have a root lying between $$ 0 $$ and $$ 2 $$ .

The given statement is as follows.
q : The equation $$  x^2 - 1 = 0 $$  does not have a root lying between $$ 0 $$ and $$ 2 $$ .
This statement has to be proved false. To show this a counter example is required.
Consider $$ x^2 - 1 = 0 $$ 
$$ x^2 = 1 $$ 
$$ x = \pm 1 $$ 
One root of the equation $$ x^2 - 1 = 0 $$ , i.e., the root $$ x = 1 $$ , lies between $$ 0 $$ and $$ 2 $$.
Thus the given statement is false.


If the statement $$p , q $$ are true statement and $$ r , s $$ are false statement then determine the truth value of the following:
$$ (q \wedge r) \vee (\sim p \wedge s) $$ 

Truth values of $$p$$ and $$q$$ are $$T$$ and truth values of $$r$$ and $$s$$ are $$F$$.
$$ (q \wedge r) \vee (\sim p \wedge s) \equiv (T \wedge F) \vee (\sim T \wedge F) $$ 
                                   $$ \equiv F \vee (F \wedge F) $$
                                  $$ \equiv F \vee F \equiv F $$
Hence the truth value of the given statement is false.


If the statement $$p , q $$ are true statement and $$ r , s $$ are false statement then determine the truth value of the following:
$$ p \vee (q \wedge r) $$ 

Truth values of $$p$$ and $$q$$ are $$T$$ and truth values of $$r$$ and $$s$$ are $$F$$.
$$ p \vee (q \wedge r) \equiv T \vee (T \wedge F) $$
                   $$ \equiv T \vee F \equiv T $$
Hence the truth value of the given statement is true.


If the statement $$p , q $$ are true statement and $$ r , s $$ are false statement then determine the truth value of the following:
$$ \sim [ (\sim p \wedge r) \vee (s \rightarrow \, \sim q)] \leftrightarrow (p \wedge r)$$ 

Truth value of $$p$$ and $$q$$ are $$T$$ and truth values of $$r$$ and $$s$$ are $$F$$.
$$ \sim [(\sim p \wedge r) \vee (s \rightarrow \, \sim q)] \leftrightarrow (p \wedge r) $$ 
$$ \equiv \, \sim [(\sim T \wedge F) \vee (F \rightarrow \, \sim T)] \leftrightarrow (T \wedge F) $$
$$ \equiv \, \sim [(F \wedge F) \vee (F \rightarrow F)] \leftrightarrow F $$
$$ \equiv \, \sim (F \vee T) \leftrightarrow F $$ 
$$ \equiv \, \sim T \leftrightarrow F $$ 
$$ \equiv F \leftrightarrow F \equiv T $$ 
Hence the truth value of the given statement is true.


Show that the statement 
p : If $$ x $$ is a real number such that $$ x^3 + 4x = 0 $$ , then $$ x $$ is $$ 0 $$ is true by 
method of contrapositive

p : If $$ x $$ is a real number such that $$ x^3 + 4x = 0 $$ , then $$ x $$ is $$ 0 $$.

Let q : $$ x $$ is a real number such that $$ x^3 + 4x = 0 $$
r : $$x $$ is $$ 0 $$.

To prove statement p to be true by contrapositive method , we assume that r is false and prove that q must be false.

Here, r is false implies that it is required to consider the negation of statement r. This obtains the following statement.
-r : $$ x $$ is not $$ 0 $$

I can be seen that $$ (x^2 + 4) $$ will always be positive 

$$ x = 0 $$ implies that the product of any positive real number with $$ x $$ is not zero.

Let us consider the product of $$ x $$ with $$ (x^2 _ 4) $$ 

$$ \therefore \, x(x^2 + 4) = 0 $$ 

$$ x^3 + 4x = 0 $$

This shows that statement q is not true.

Thus , it has been proved that 
-r $$ \Rightarrow $$ -q 

Therefore , the given statement p is true.


Check the validity of the statements given below by the method given against it. 
q : If $$ n $$ is a real number with $$ n > 3 $$ , then $$ n^2 > 9 $$ (by contradiction method).

The given statement , $$q$$ is as follows. 

If $$ n $$ is a real number with $$ n > 3 $$ , then $$ n^2 > 9 $$ . 

Let assume that $$ n $$ is a real number with $$ n > 3 $$ , but $$ n^2 > 9 $$ is not true.

That is , $$ n^2 < 9 $$ 

Then , $$ n > 3 $$ and $$ n $$ is a real number. 

Squaring both sides , we obtain 
$$ n^2 > (3)^2 $$ 

$$ \Rightarrow \, n^2 > 9 $$ , which is a contradiction , since we have assumed that $$ n^2 < 9 $$. 

Thus , the given statement is true. That is , if $$ n $$ is a real number with $$ n > 3 $$ , then $$ n^2 > 9 $$.


Show that the statement 
p : If $$ x $$ is a real number such that $$ x^3 + 4x = 0 $$ , then $$ x $$ is $$ 0 $$ is true by 
method of contradiction

p : If $$ x $$ is a real number such that $$ x^3 + 4x = 0 $$ , then $$ x $$ is $$ 0 $$.
Let q : $$ x $$ is a real number such that $$ x^3 + 4x = 0 $$
 r : $$x $$ is $$ 0 $$.

To show statement p to be true by contradiction , we assume that p is not true.
Let $$ x $$ be a real number such that $$ x^3 + 4x = 0 $$ and let $$ x $$ is not $$ 0 $$.
Therefore , $$ x^3 + 4x = 0 $$ 
$$ x(x^2 + 4) = 0 $$ 
$$ x = 0 $$ or $$ x^2 + 4 = 0 $$ 
$$ x = 0 $$ or $$ x^2 = -4 $$ 
However , $$ x $$ is real . Therefore , $$ x = 0 $$ , which is a contradiction since we have assumed that $$ x $$ is not $$ 0 $$.
Thus , the given statement p is true.


Check the validity of the statements given below by the method given against it. 
p : The sum of an irrational number and a rational number is irrational (by contradiction method)

The given statement is as follows,

p : the sum of an irrational number and a rational number is irrational

Let us assume that the given statement p is false. That is we assume that the sum of an irrational number and a rational number is rational.

Therefore , $$ \sqrt{a} + \dfrac{b}{c} = \dfrac{d}{e} $$ , when $$ \sqrt{a} $$ is irrational and $$ b , c , d , e $$ are integers.

$$ \dfrac{d}{e} - \dfrac{b}{c} $$ is a rational number and is an irrational number.

This is a contradiction. Therefore our assumption is wrong.

Therefore the sum of an irrational number and a rational number is rational

Thus the given statement is true.


Write the negation of the following statements :
r : For every real number $$ x $$ , either $$ x > 1 $$ or $$ x < 1 $$ .

The negation of statement r is as follows
There exists a real number $$ x $$  such that neither $$ x > 1 $$ nor $$ x < 1 $$.


Write the negation of the following statements:
s : There exists a number $$ x $$ such that $$ 0 < x < 1 $$.

The negation of statement s is as follows
There does not exist a number $$ x $$ , such that $$ 0 < x < 1 $$.


Write the converse of the following statement. If the corresponding angles formed by a transversal of two lines are congruent then the two lines are parallel.

f the given two lines are parallel, then the corresponding angles formed by a transversal of two lines are congruent.


Write the truth values of the following statement:
$$2$$ is a rational number and it is the only even prime number.

$$\textbf{Step 1: Find the truth value of individual statements. }$$
                $$\text{The given statement is:}$$
                $$\text{2 is a rational number and it is the only even prime number.}$$

                $$\text{We know, 2 is a rational number.}$$
                $$\text{So truth value of this statement : T}$$

                $$\text{Again, 2 is the only even prime number.}$$
                $$\text{So truth value of this statement : T}$$

$$\textbf{Step 2: Find truth value of the given statement. }$$

                $$\text{The elementary statements are joined with 'and'.}$$

                $$\text{So, truth value of the given statement =}\text{T}\cap\text{T}=\text{T}$$

$$\textbf{Hence, truth value of the given statement is T.}$$


Determine the truth values of $$p$$ and $$q$$ in the following case:
$$(p \vee q) $$ is $$T$$ and $$(p \vee q) \rightarrow q $$ is $$F$$

$$p\ \ \  $$$$q\ \ \ $$$$p \vee q\ \ \ $$$$(p \vee q)
\rightarrow
q$$
TTTT
TFTF
FTTT
FFFT

Since the truth values of $$p \vee q $$ is T and $$ (p \vee q) \rightarrow q $$ is F, from the table, the truth values of $$p$$ and $$q$$ are T and F respectively.


Write the converse of the following statement. If the sum of measures of angles in a figure is $$180^\circ$$, then the figure is a triangle.

If the given figure is a triangle, then the sum of the measures of its angles is  180∘180∘.


Write converse , inverse and contrapositive of the following statements.
If $$ x < y $$ then $$ x^2 < y^2 (x , y \in R) $$ 

Let $$p:$$ $$ x < y $$,
Let $$q:$$ $$ x^2 < y^2 $$ 
Then the symbolic form of the given statement is $$ p \rightarrow q$$.
Converse: $$ q \rightarrow p$$ is the converse of $$ p \rightarrow q$$.
i.e., If $$ x^2 < y^2 $$, then $$ x < y$$.
Inverse: $$ \sim p \rightarrow \, \sim q$$ is the inverse of $$p \rightarrow q$$.
i.e., If $$ x \geq y $$, then $$ x^2 \geq y^2 $$.
OR 
If $$ x \nless y $$, then $$ x^2 \nless y^2$$.
Contrapositive: $$ \sim q \rightarrow p $$ is the contrapositive of $$ p \rightarrow q$$.
i.e., If $$ x^2 \geq y^2 $$, then $$ x \geq y$$. 
OR 
If $$ x^2 \nless y^2 $$, then $$ x \nless y $$.


Write the following statement in conditional form. A number having only two divisors is called a prime number.

If the given number is having only two divisors, then it is a prime number.


Write the truth table value of the following statement:
$$ \forall \, n \in N , n^2 + n $$ is even number while $$n^2 - n $$ is an odd number.

Let $$p:$$ $$ \forall \, n \in N , n^2 + n $$ is an even number.
Let $$q:$$ $$ \forall \, n \in N , n^2 - n $$ is an odd number.
Then the symbolic form of the given statement is $$ p \wedge q$$.
The truth values of $$p$$ and $$q$$ are $$T$$ and $$F$$ respectively.
$$ \therefore $$ The truth value of $$ p \wedge q $$ is $$F$$. ............... $$[T \wedge F \equiv F]$$.


Write converse , inverse and contrapositive of the following statements.
If surfaces area decreases then pressure increases.

Let $$p:$$ The surface area decreases.
Let $$q:$$ The pressure increases.
Then the symbolic form of the given statement is $$ p \rightarrow q$$.
Converse: $$ q \rightarrow p $$ is the converse of $$ p \rightarrow q$$.
i.e., If the pressure increases, then the surface area decreases.
Inverse: $$ \sim p \rightarrow \, \sim q $$ is the inverse of $$ p \rightarrow q$$.
i.e., If the surface area does not decrease, then the pressure does not increase.
Contrapositive: $$ \sim q \rightarrow \, \sim p$$ is the contrapositive of $$ p \rightarrow q$$.
i.e., If the pressure does not increase, then the surface area does not decrease.


Write the following statement in conditional form. A triangle is a figure formed by three segments. 

If the given figure is a triangle, then it is formed by three segments..


Write the negations of the following statements:
(a) All students of this college live in the hostel.
(b) $$6$$ is an even number or $$36$$ is a perfect square.

$$(a)\: p:$$ All students of this college live in the hostel.

Negation: $$\sim p:$$ Some students of this college do not live in the hostel.

$$(b)\: p: 6$$ is an even number or $$q:36$$ is a perfect square.

Symbolic form: $$p \vee q$$

$$ \therefore \: \sim(p \vee q) \equiv \sim p \: \wedge \sim q$$

Negation: $$6$$ is not an even number and $$36$$ is not a perfect square.


Given P : 25 is a multiple of 5, q : 25 is a multiple ofWrite the compound statement connecting these two statements with "and", "or" in $$60^{th}$$ cases. Check the validity of the statement.

Compound statement using and -
1. $$25$$ is a multiple of $$5$$ and $$25$$ is a multiple of $$8.$$
   This statement is not valid since only one statement out of the two connected using and is valid.

2. using or 
   $$25$$ is a multiple of $$5$$ or $$25$$ is a multiple of $$8.$$
   The statement is valid since in case of or statement is valid if any one of the statements connected by or is valid.

Hence, solved. 


Prepare truth table of the following statement patterns.
(i) $$\sim p \rightarrow (q \leftrightarrow p)$$
(ii) $$(q \leftrightarrow p) \vee (\sim p \leftrightarrow q)$$
(iii) $$p \leftrightarrow [\sim(q \vee r)]$$

(3) $$p\leftrightarrow [\sim(q\vee r)]$$
 p q r $$q\vee$$ r$$\sim(q\vee r)$$ $$p\leftrightarrow [\sim(q\vee r)]$$ 
 0 00 0 1 0 
0 0 1 1 0 1 
0 1 0 10 1 
0 1  1 1 0 1
1  0 0 0 1 1
 1 01  1 0 0
1  1 0 1 0 0
 1 1 1 1 0 0
(2) $$(q\leftrightarrow p)\vee(\sim p\leftrightarrow q)$$
p  q $$q\leftrightarrow p$$$$ \sim p$$$$ \sim p\leftrightarrow q$$$$(q\leftrightarrow p)\vee(\sim p \leftrightarrow q)$$
 001 1 0 1 
01 0 1 1 1 
1 0 0 0 1 1 
1 1 1 0 0 1 
(1) $$\sim p\leftrightarrow\,\,\,q\leftrightarrow p$$
 p q $$\sim p$$$$q\leftrightarrow p$$  $$\sim p\rightarrow q\leftrightarrow p$$
001 1 1 
01 10 0 
1 00 0 1 
1 1 0 1 1


If a trigonometric ratio of an angle is known, we can find all remaining ratios.' Explain whether this statement is true or false.


2041291_1458521_ans_62d66983ed0f4cbf8349e953e99ee77f.jpg


Which of the following sentences are statements? In case of a statement mention whether it is true or false.
The equation $$x^2+5|x|+6=0$$ has no real roots.

undefined
1982547_1710639_ans_bb3afdb690ba4749ab483e8e0fd45e60.jpg


Let $$p$$: If $$x$$ is an integer and $$x^2$$ is even, then $$x$$ is even.Using the method of contrapositive, prove that $$p$$ is true.

Given :- A statement p, If $$x$$ is an integer and $$x^2$$ is even, then $$x$$ is also even.

To find :- The statement is true by the method of contrapositive.

Let $$q :$$ If $$x$$ is an integer and $$x^2$$ is even.
$$R : x$$ is even.

To show that p is true we will assume that r is false and prove that $$q$$ is also false.

Let $$x$$ is not even. To prove that $$q$$ is false it has to be proved that $$x$$ is not an integer or $$x^2$$ is not even.

If $$x$$ is not even i.e $$x$$ is odd.
ie $$x = 2n + 1$$

$$(x)^2 = (2n + 1)^2$$

$$x^2 = 2n^2 + 2 \times 2n \times 1 + (1)^2$$

$$x^2 = 4n^2 + 4n + 1$$

$$x^2 = 4 (n^2 + n) + 1$$

$$x^2$$ is odd.

Therefore $$q$$ is also false.
Thus the given statement $$p$$ is true.


Write the negation  of the following statements :
There exists a rational number $$x$$ such that $$x^2 =3$$.


1947882_1710701_ans_4ec04b1328394f46b1b12301ed5f6394.jpg


Class 11 Engineering Maths Extra Questions