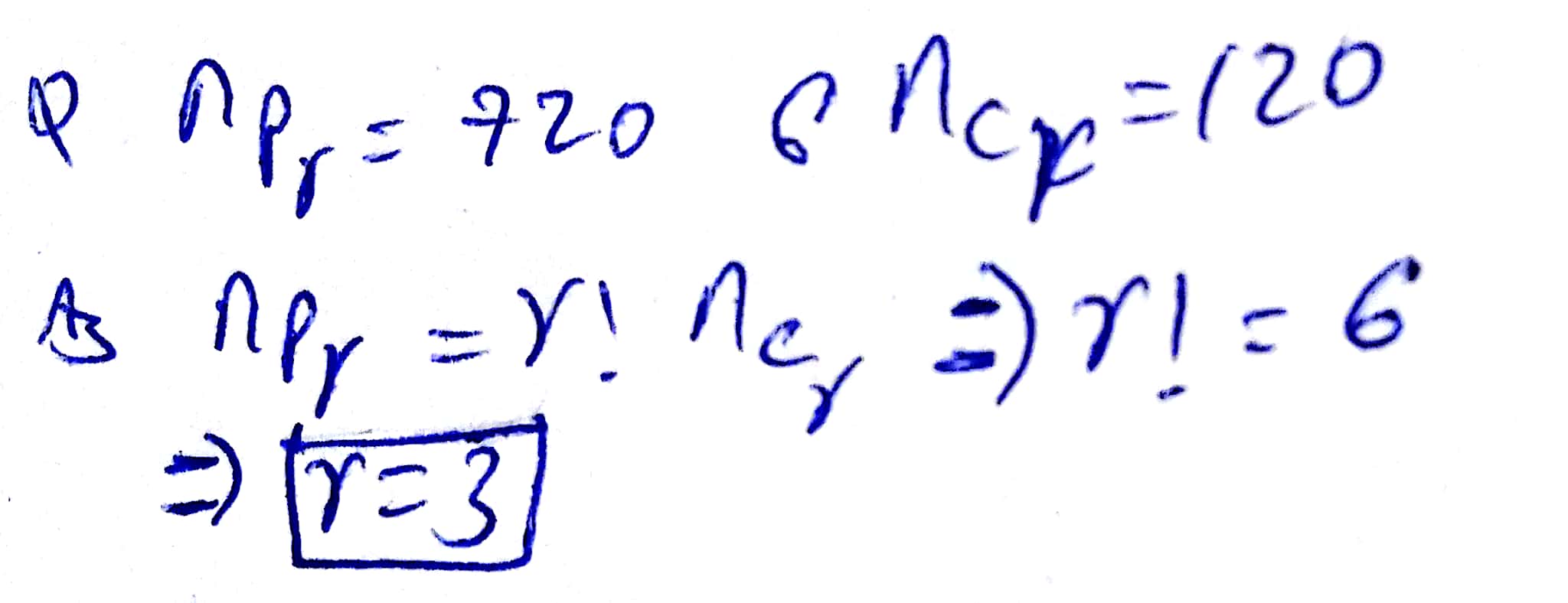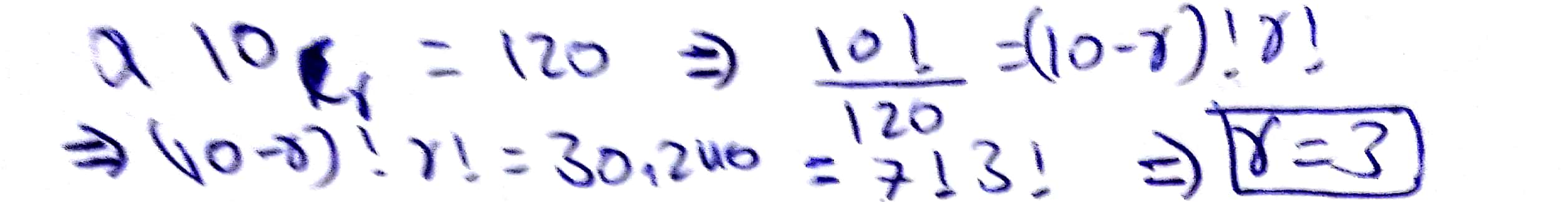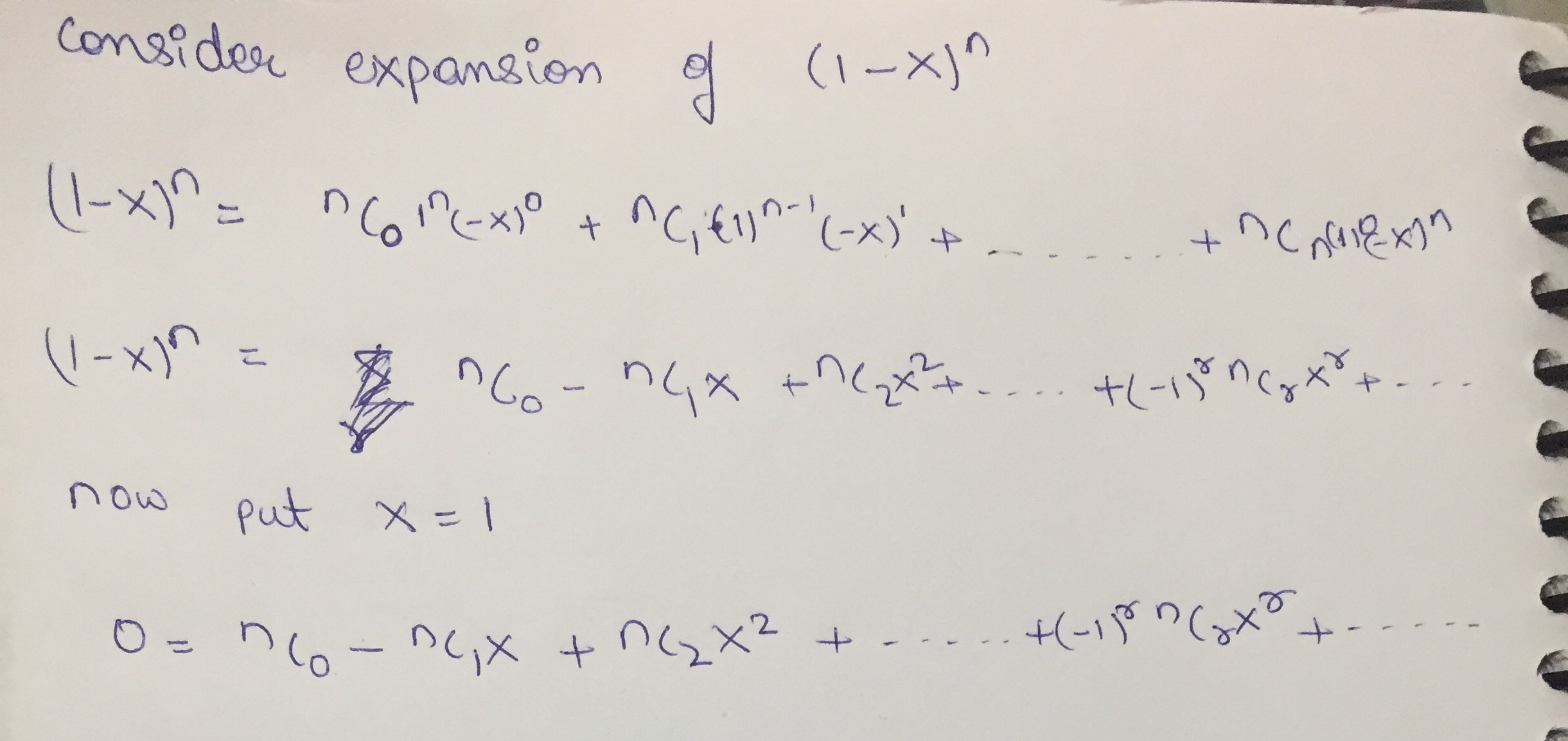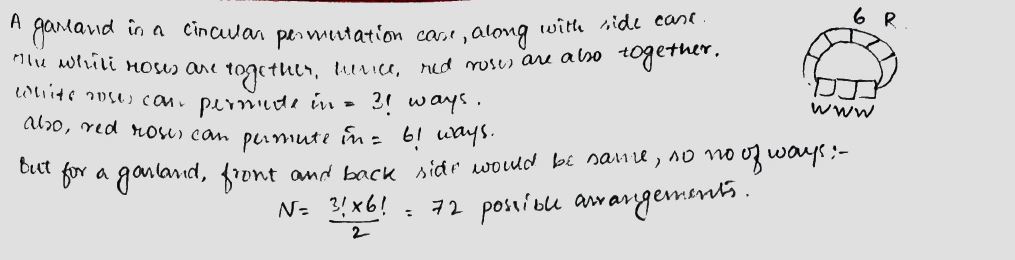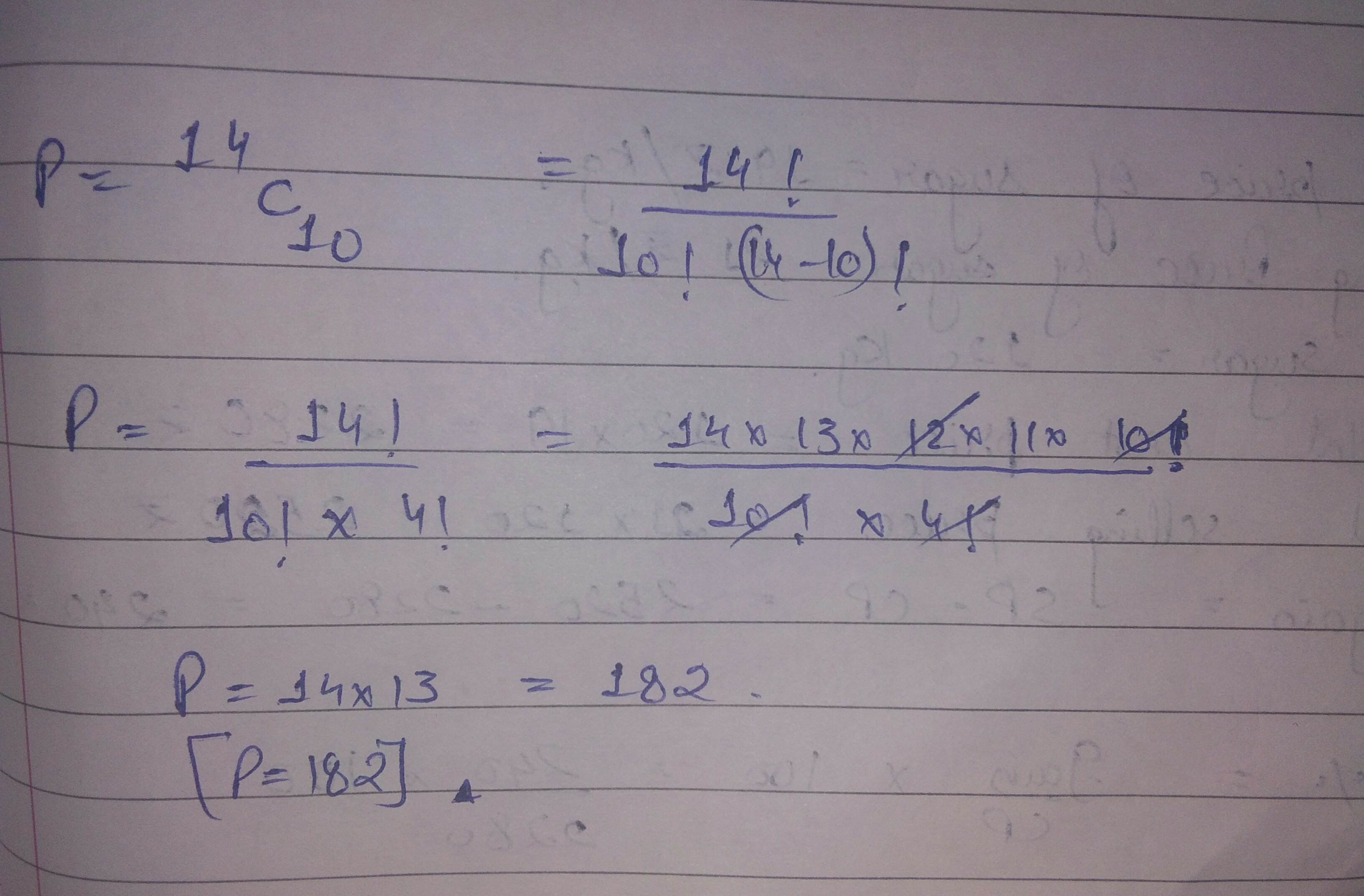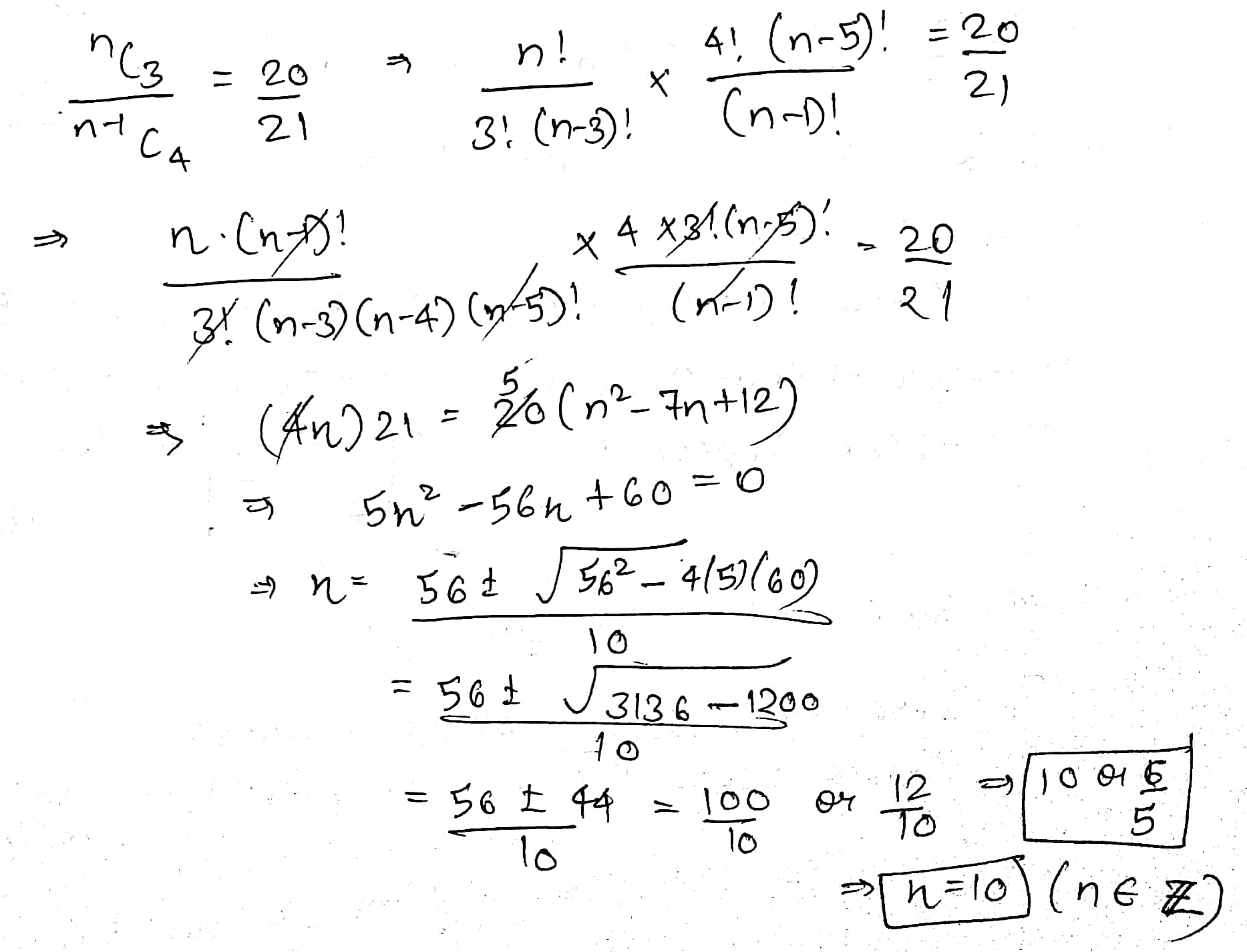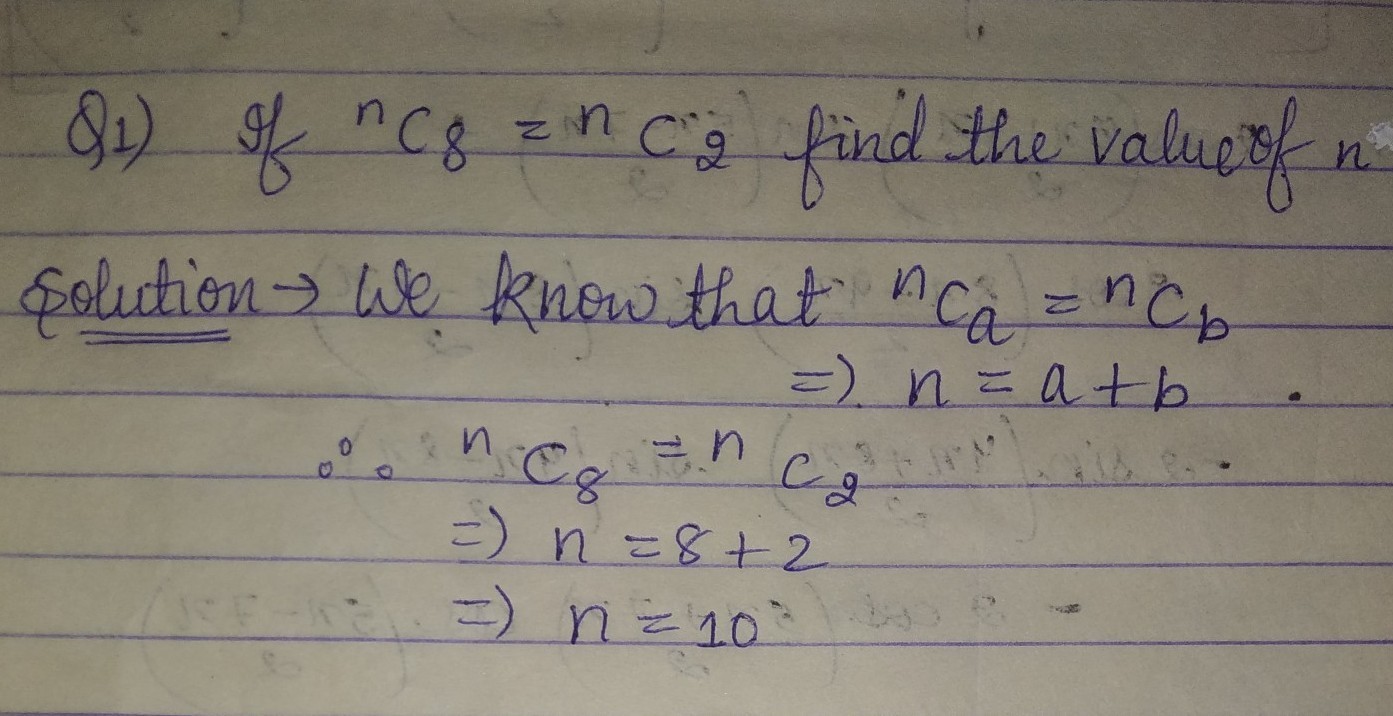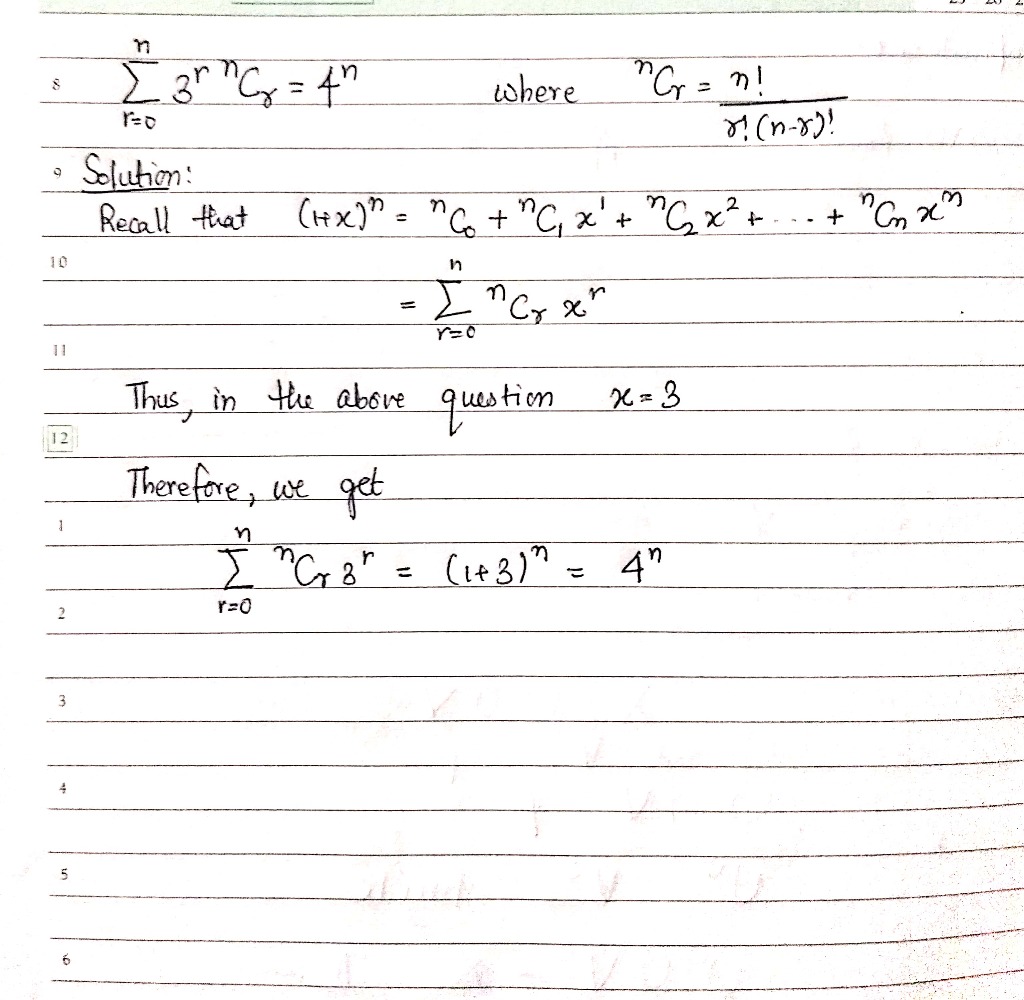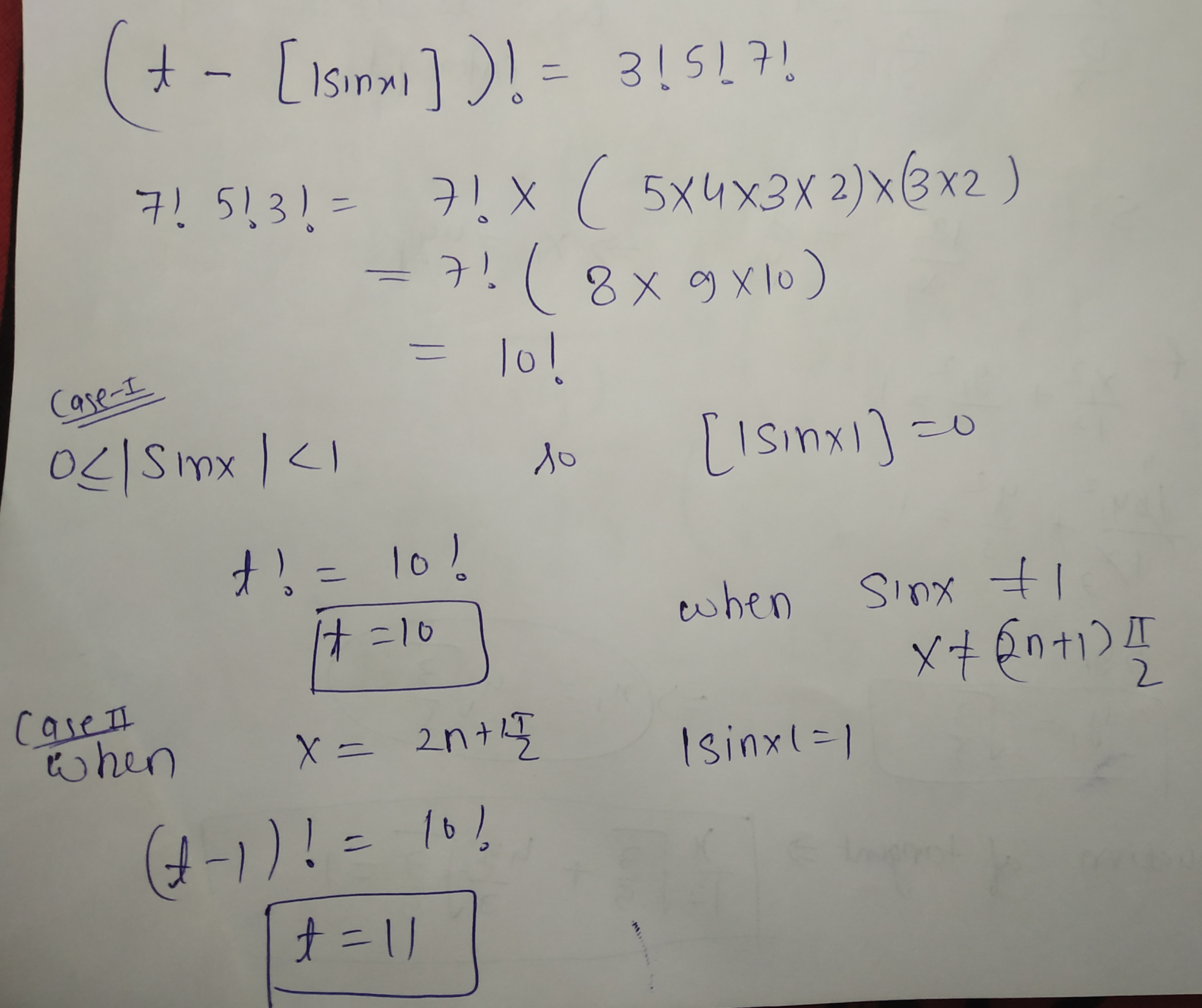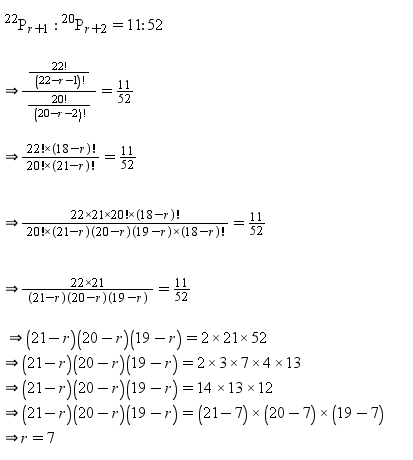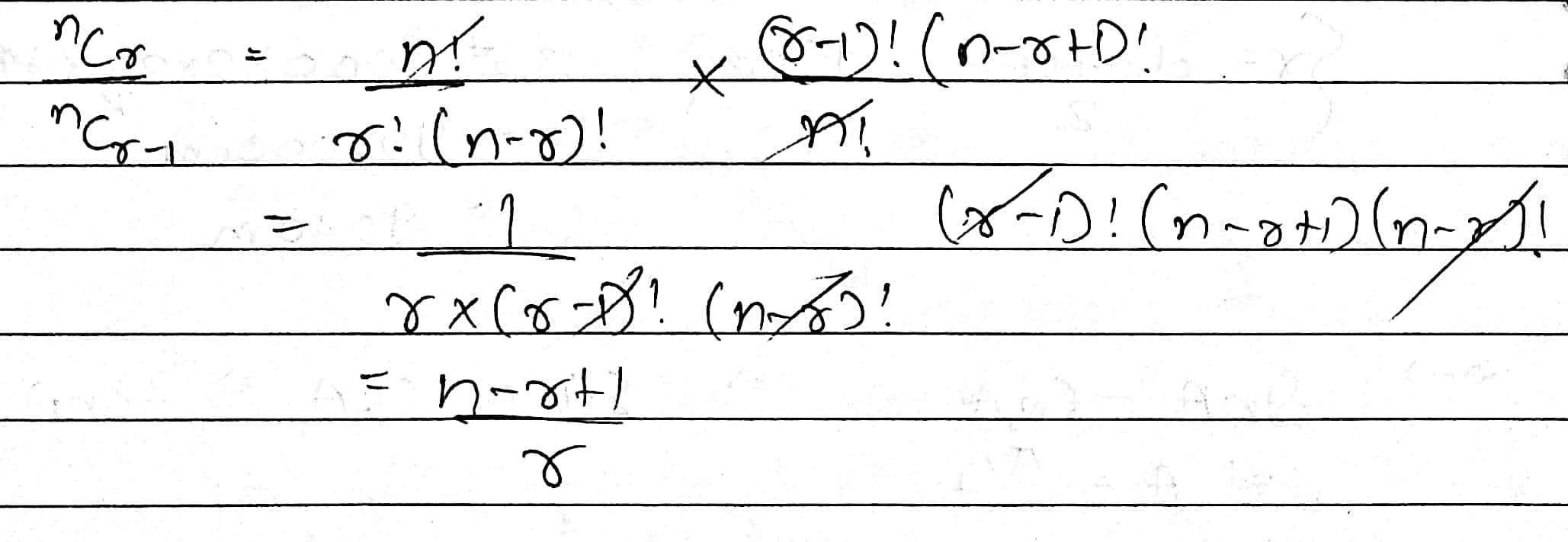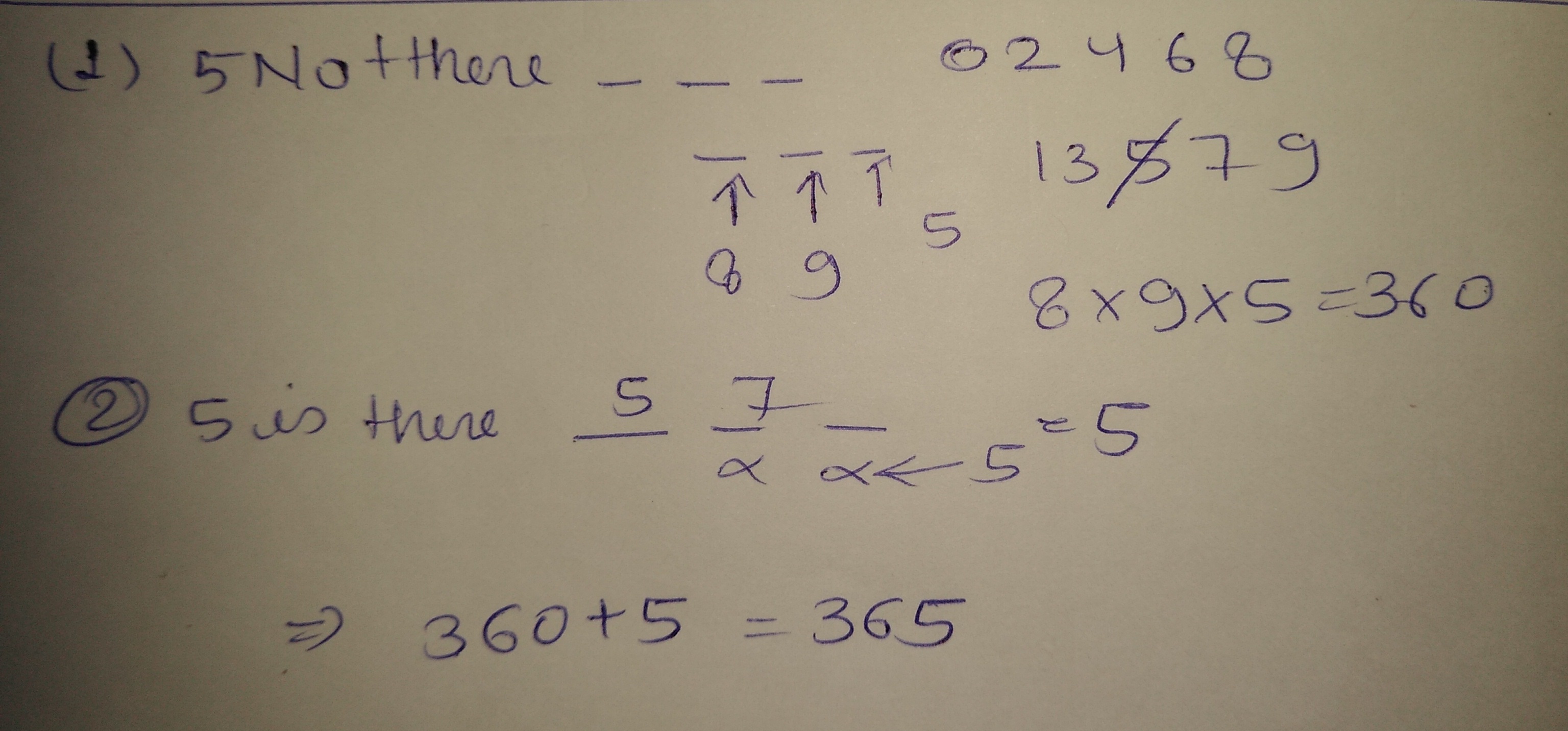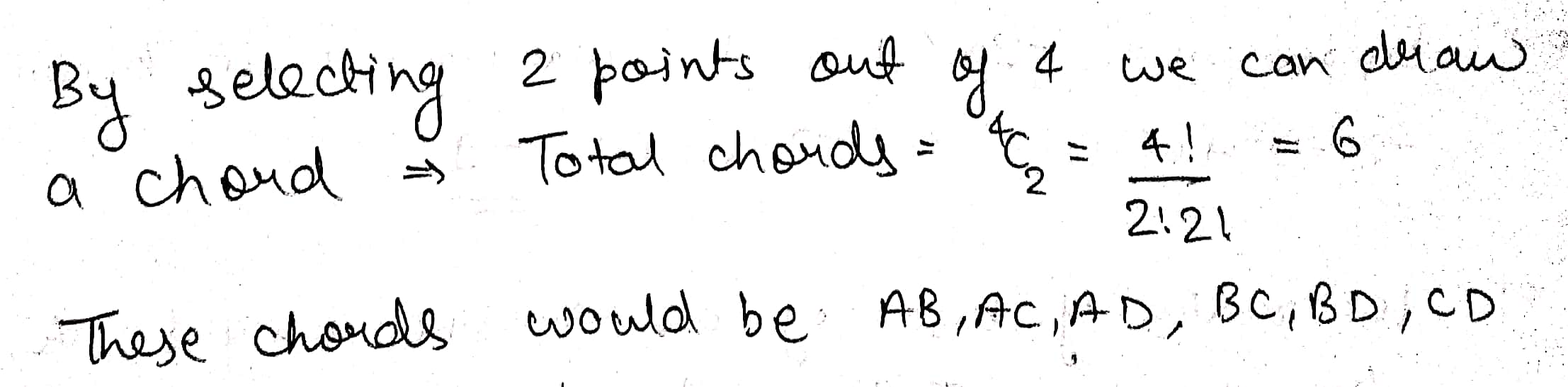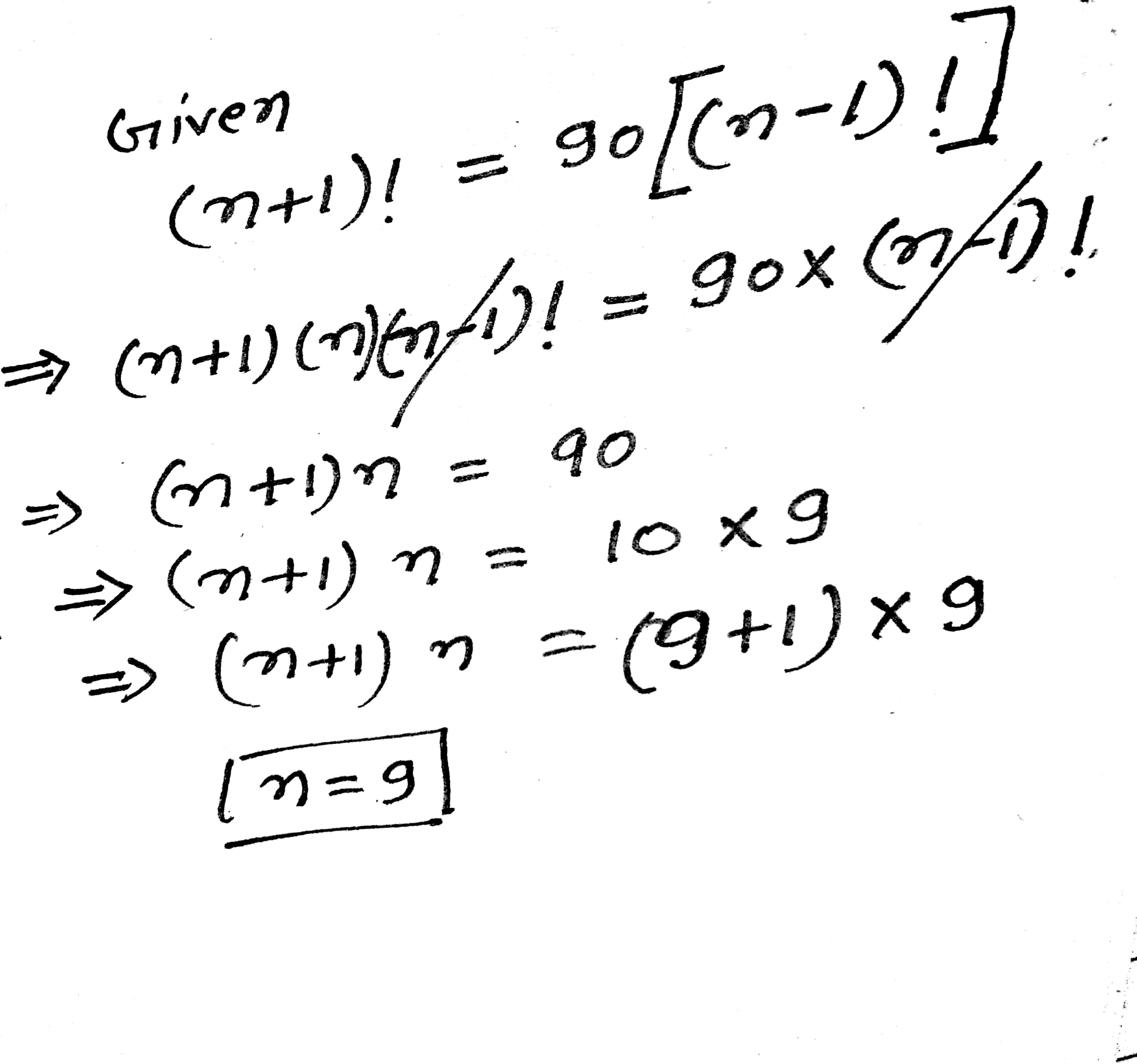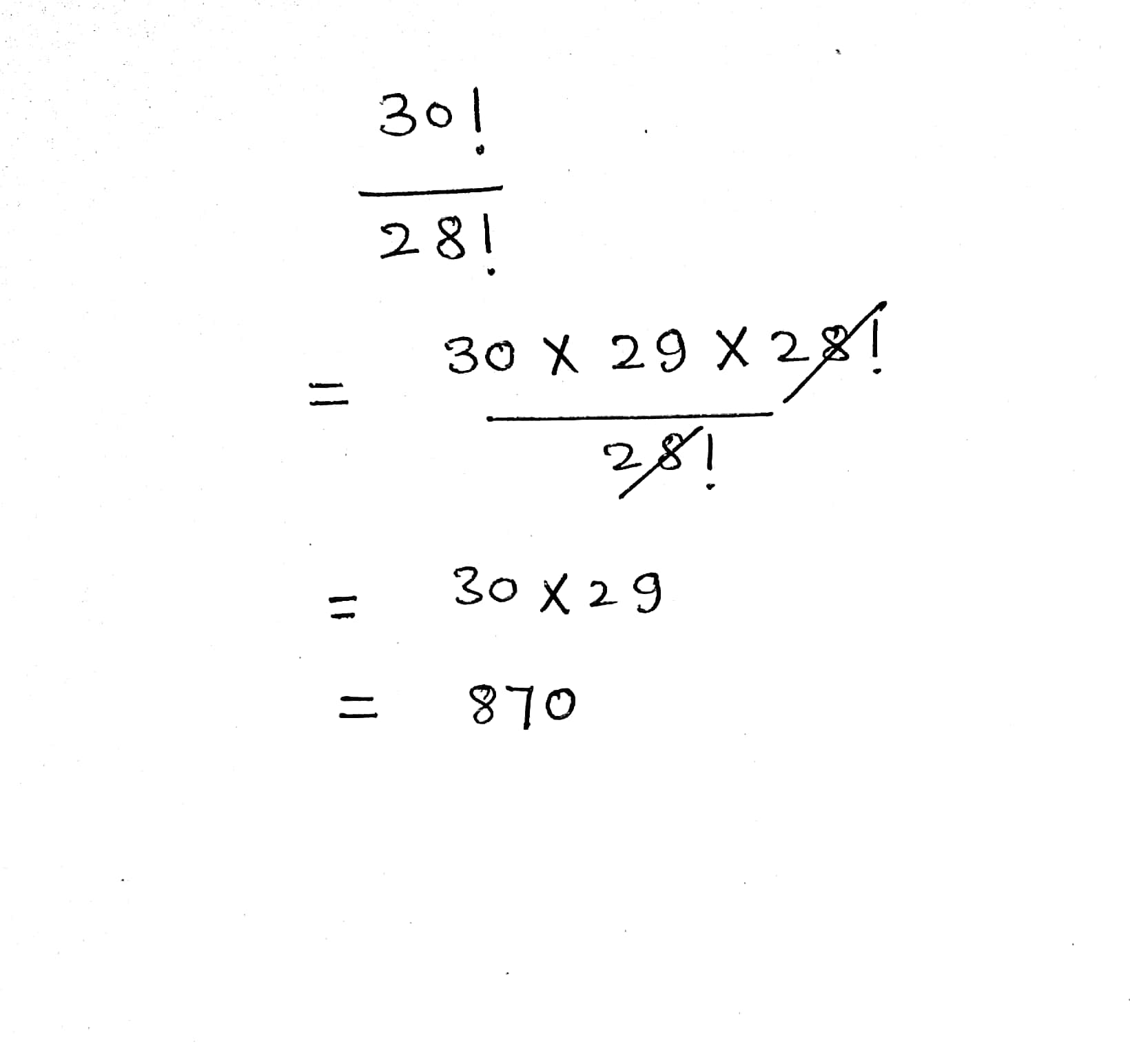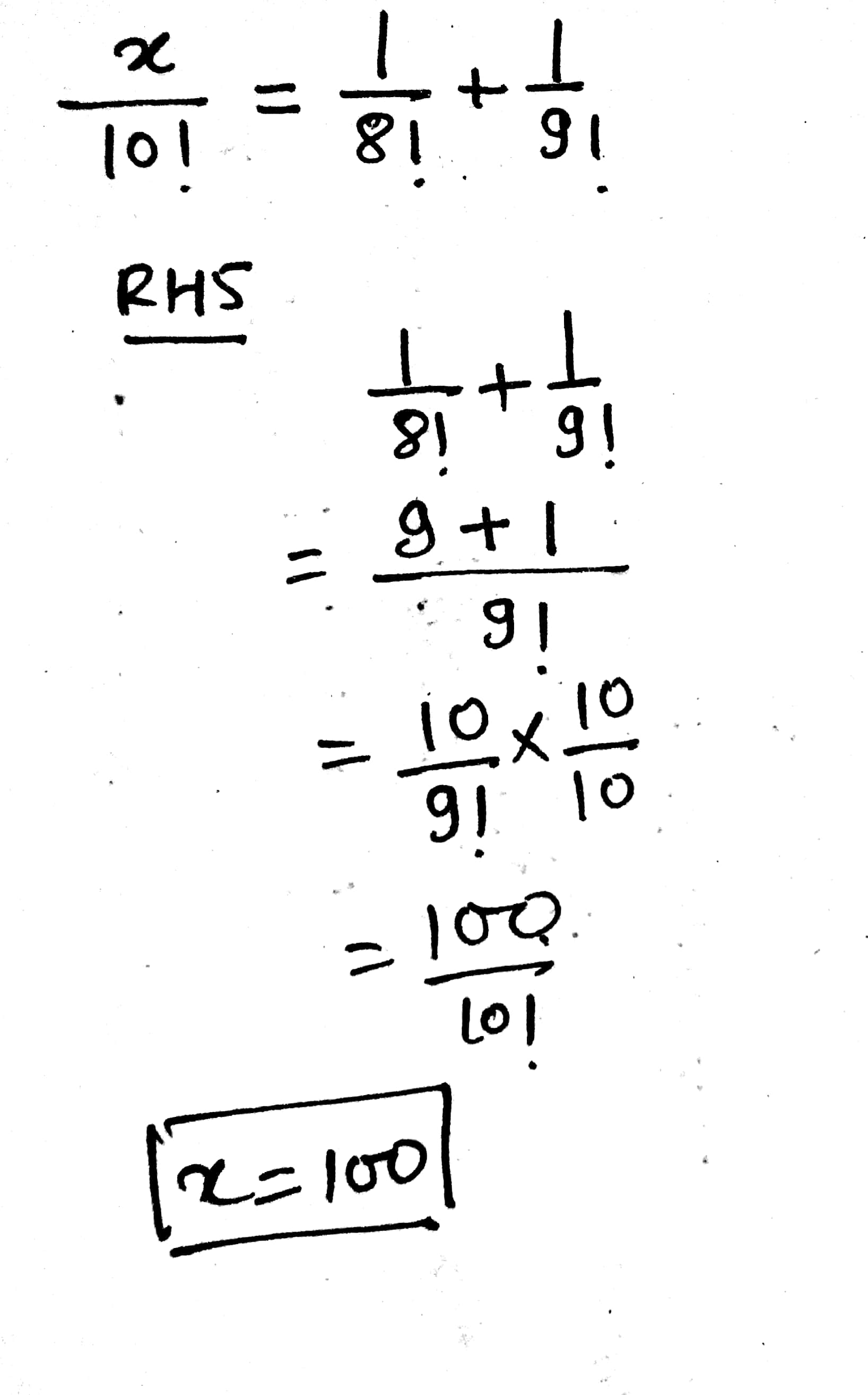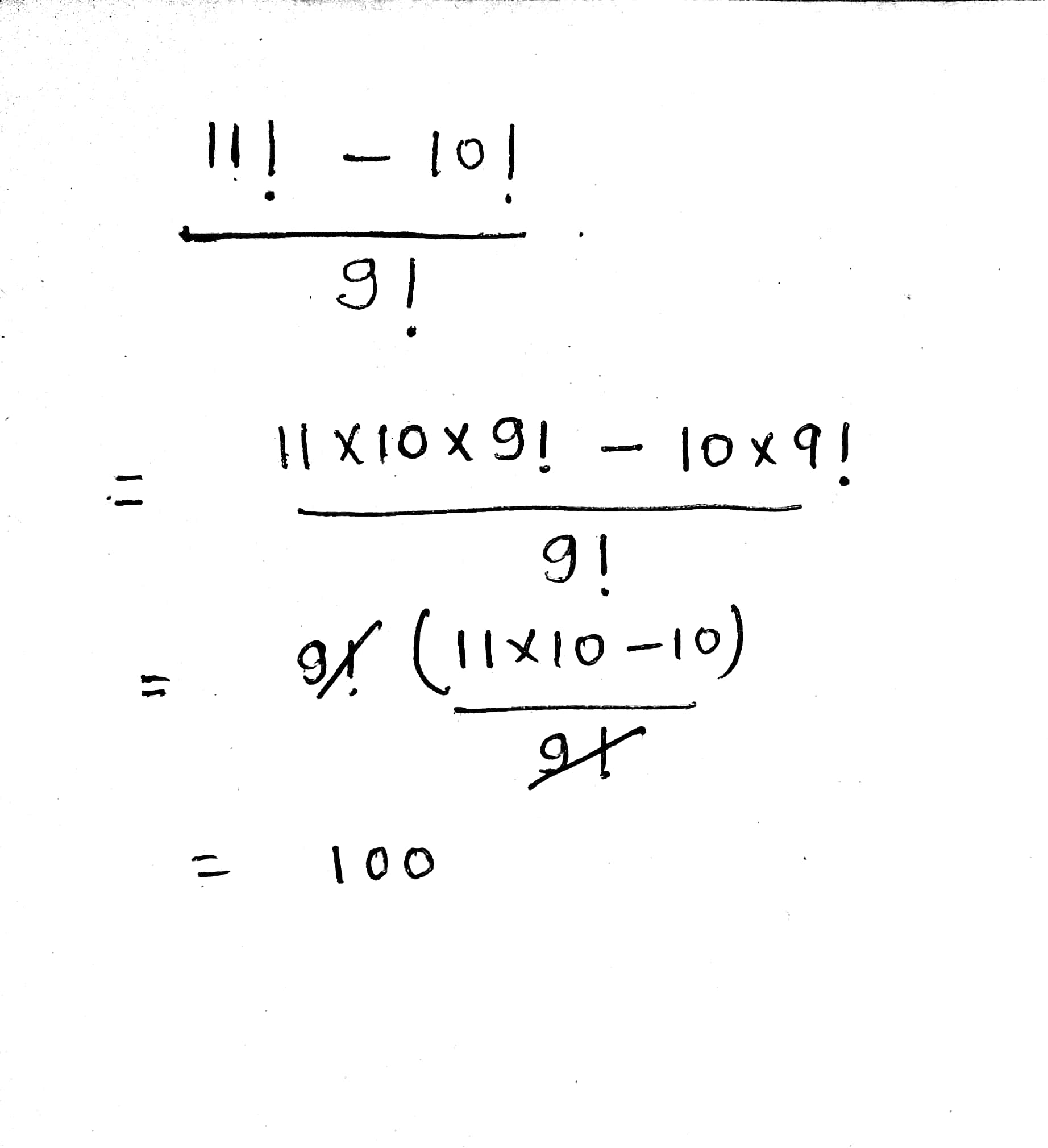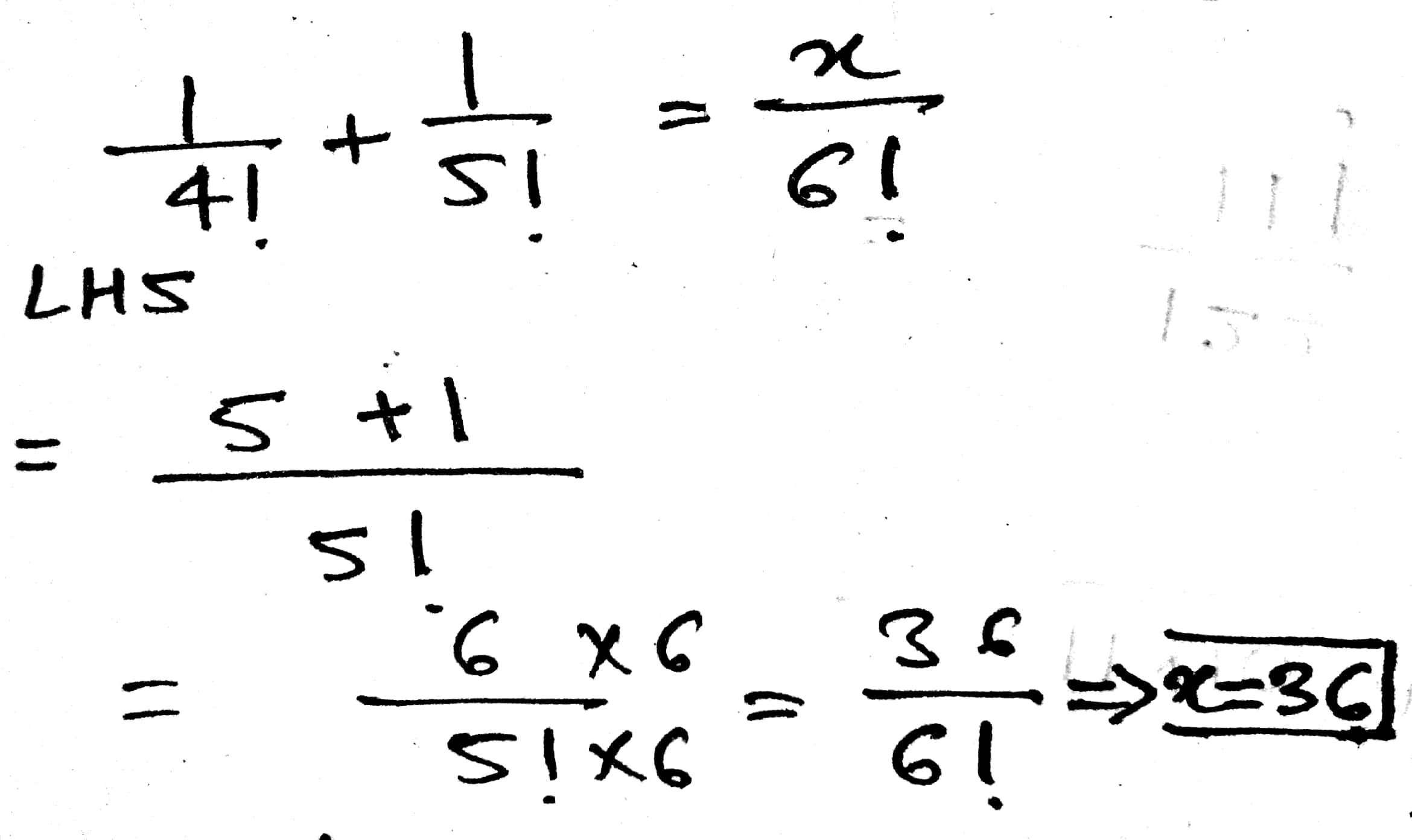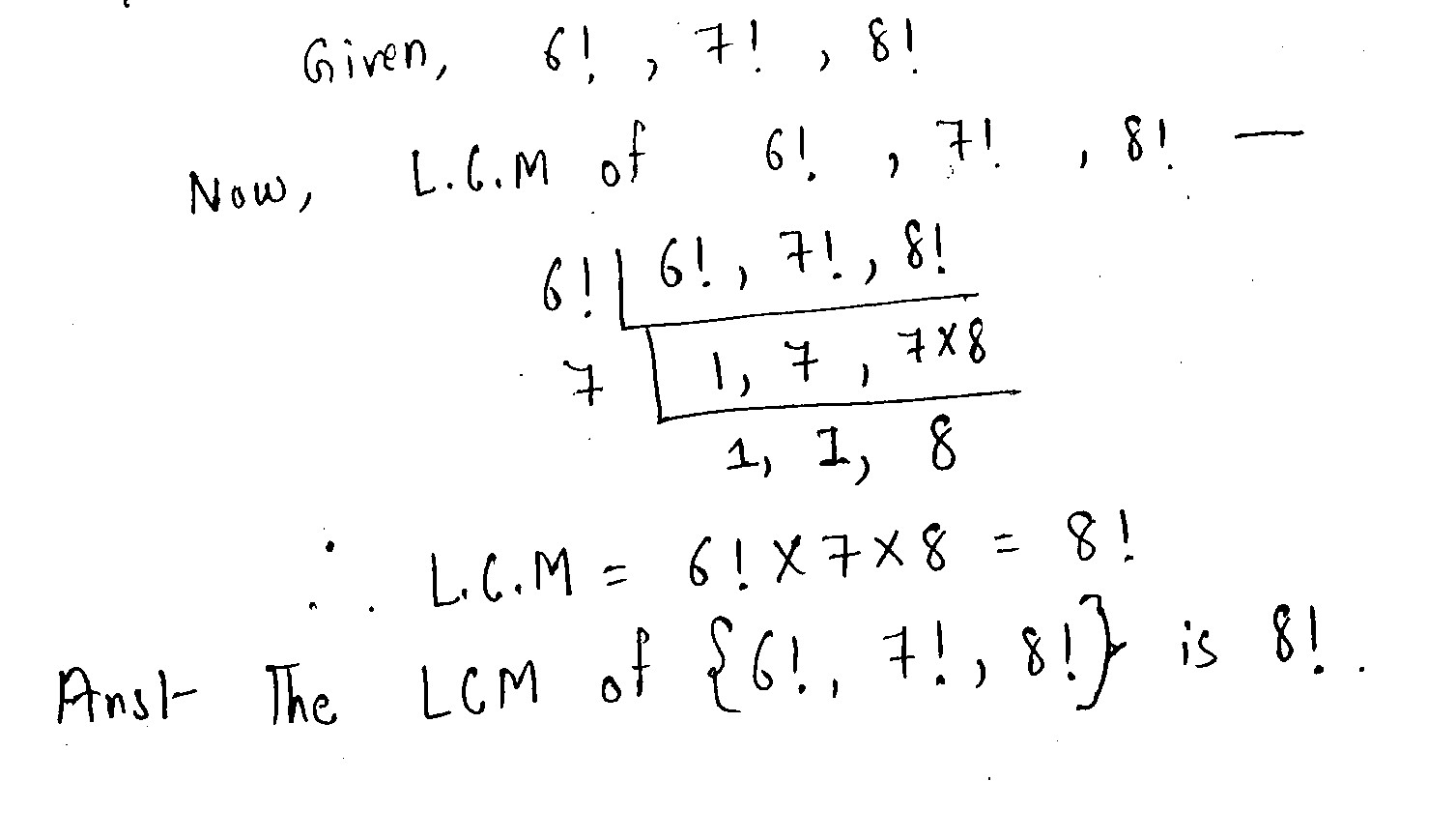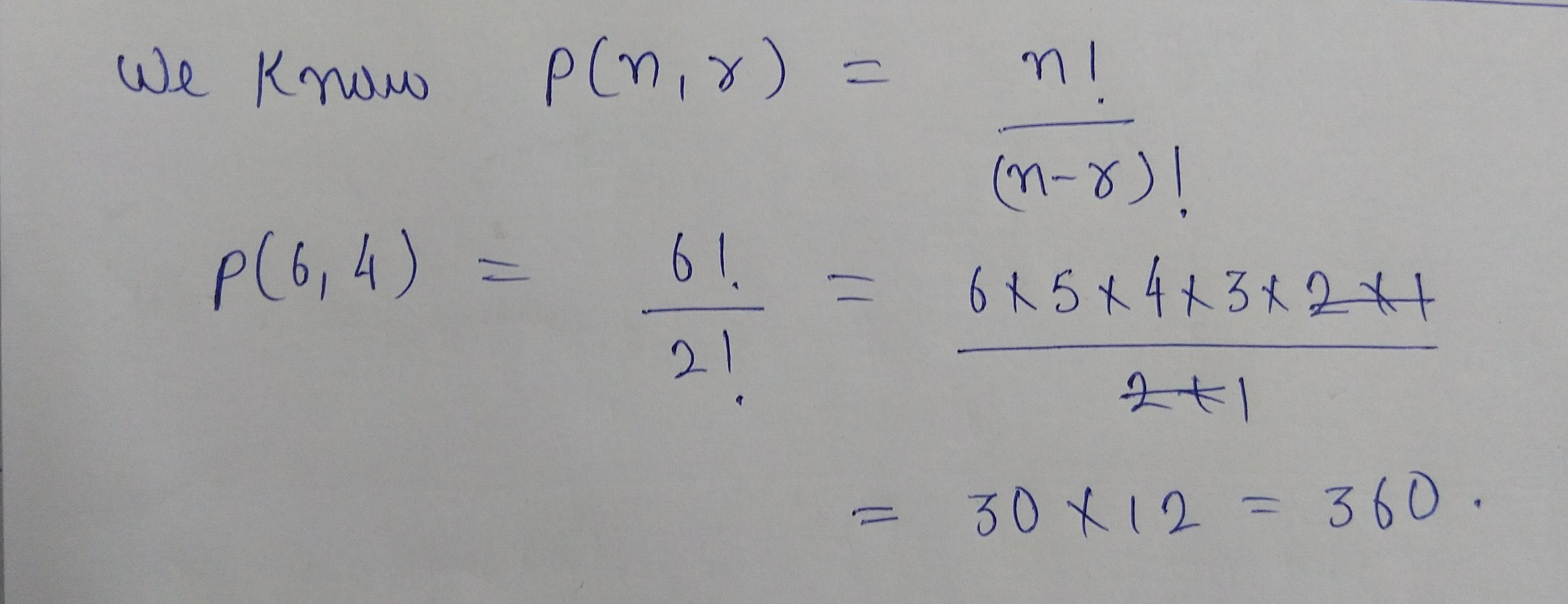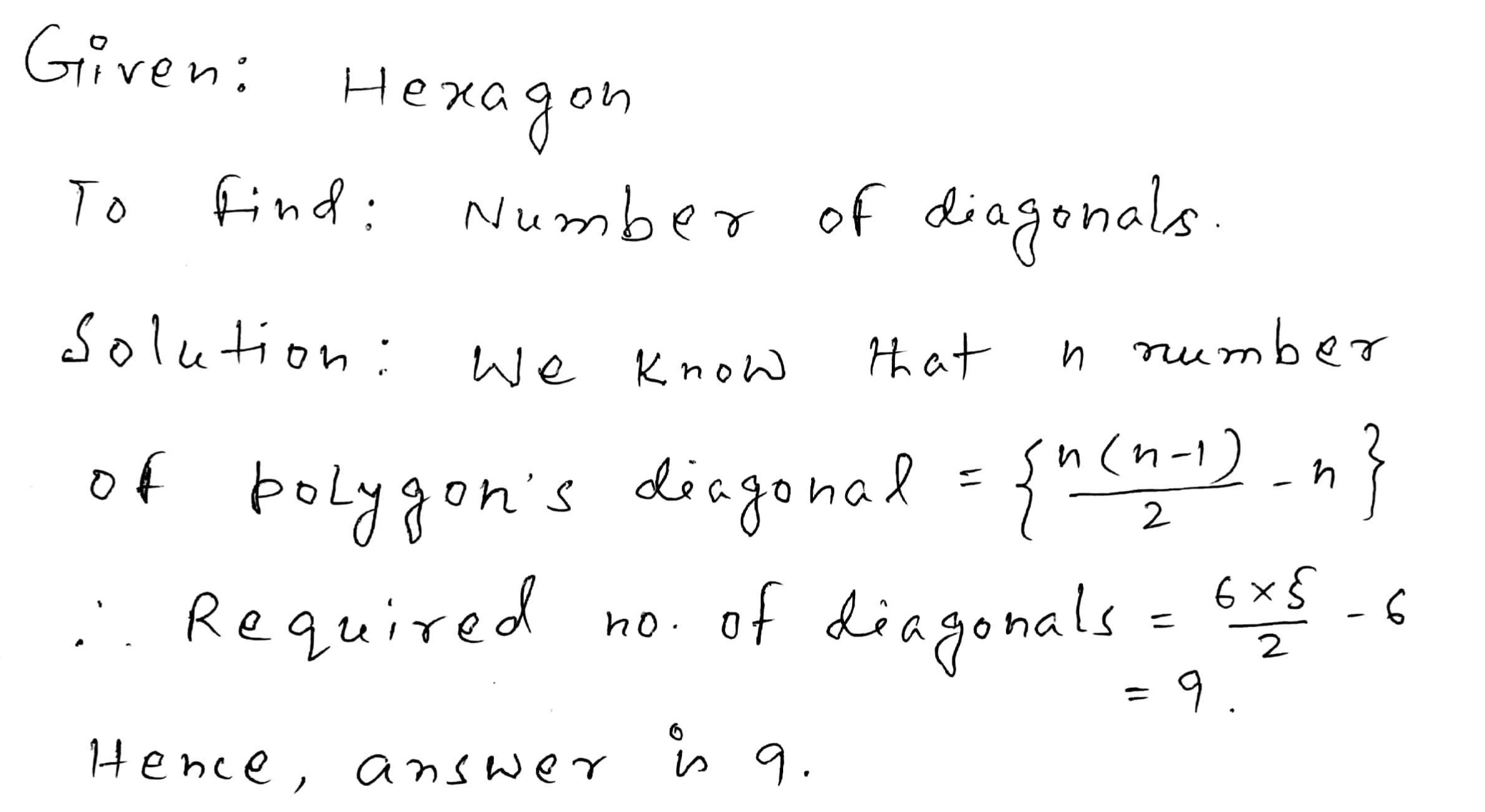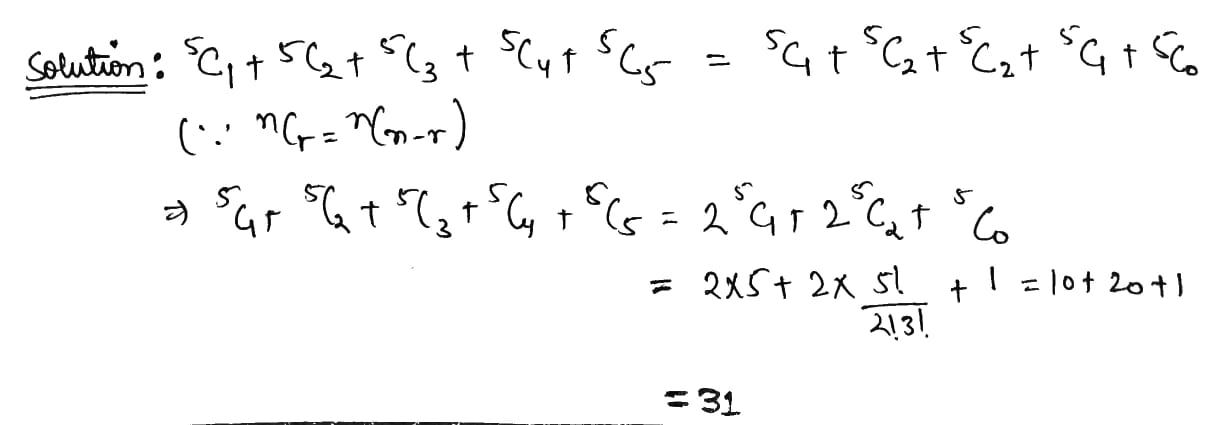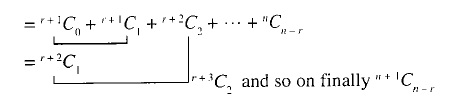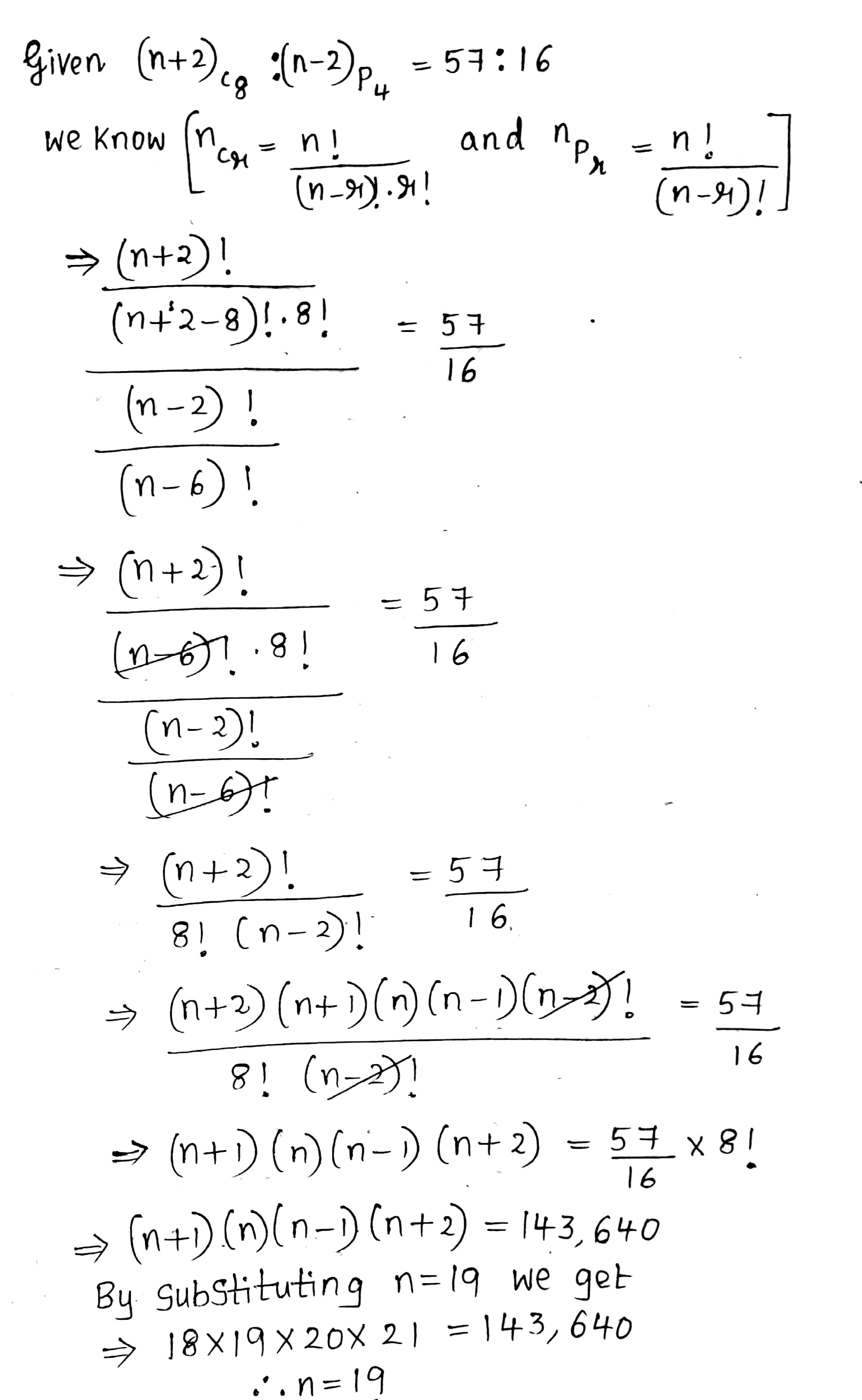Permutations And Combinations - Class 11 Engineering Maths - Extra Questions

Permutation of $$n$$ different things taken ____ at a time is denoted by $${ ^{ n }P }_{ 3 }$$.

Permutation is denoted by $$P$$ 
Total number of things $$A$$ 
Number of different things $$n$$ 
$$\Rightarrow $$ Permutation of $$n$$ different things 
Taken $$r$$ at a time = $${ ^{ n }P }_{ r }$$
Here $$r$$ is $$3$$
Hence, the answer is $$3$$.


Find $$^nC_r+^nC_{r-1}= .....$$ for $$n = r = 3$$

$${ ^{ n }C }_{ r }+{ ^{ n }C }_{ r-1 }=?$$

$$ { ^{ n }C }_{ r }=\dfrac { n! }{ r!(n-1)! } $$

$$ { ^{ n }C }_{ r-1 }=\dfrac { n! }{ (r-1)!(n-r+11)! } $$

$$ { ^{ n }C }_{ r }+{ ^{ n }C }_{ r-1 }=\dfrac { n! }{ r!(n-1)! } +\dfrac { n! }{ (r-1)!(n-r+1)! } $$

$$ =\dfrac { n! }{ (r-1)!(n-r+1)! } [\dfrac { 1 }{ r } +\dfrac { 1 }{ n-r+1 } ]$$

$$ =\dfrac { n! }{ (r-1)!(n-r+1)! } [\dfrac { n-r+1+r }{ r(n-r+1) } ]$$

$$ ==\dfrac { n! }{ (r-1)!(n-r+1)! } $$

$$ =  { ^{ n+1 }C }_{ r }$$

putting values we get $$ =  { ^{ 3+1 }C }_{ 3 } = 4$$



For $$0\leq r\leq n, ^nC_r=$$

$$0\le r\le n,$$      $${^nC_r}=\dfrac{n!}{r!(n-r)!}$$
Hence, the answer is $$\dfrac{n!}{r!(n-r)!}.$$


There are $$6$$ multiple choice questions on an examination. How many sequences of answers are possible, if the first three questions have $$4$$ choices each and the next three have $$5$$ each?

Each of teh first threee questions can be answered in $$4$$ ways.Each of the last three questions can be answered in $$5$$ ways.
By the fundamental principle of counting, sequences of answers are 
$$4\times 4\times 4\times 5\times 5\times 5\times =64\times 125$$
$$=8000$$


How many different numbers of two digits can be formed with the digits $$1, 2, 3, 4, 5, 6$$ no digits being repeated?

We have to fill up two places (since numbers are of two digits)
The first place can be filled up in $$6$$ ways, as any one of the six digits can be placed in the first place. 
The $$2^{nd}$$ place can be filled up in $$5$$ ways as no digit is to be repeated. 
Hence, both places can be filled up in $$6\times 5=30$$ ways.


A teacher of a class wants to set one question from each of two exercises in a book. If there are $$15$$ and $$12$$ questions in the two exercises respectively, then in how many ways can the two questions be selected?

Since the first exercise contains $$15$$ questions, the number of ways of choosing the first question is $$15$$.
Since the second exercise contains $$12$$ questions, the number of ways of choosing the second question is $$12$$.
Hence, by the fundamental principle, two question can be selected in $$=15\times 12=180$$ ways.


Evaluate 
(i) $$8 !$$ ii) $$4!-3!$$

i) $$8! =1\times 2\times 3\times 4\times 5\times 6\times 7\times 8=40320$$
ii) $$4!=1\times 2\times 3\times 4= 24$$
$$3!=1\times 2 \times 3=6$$
$$\therefore 4! -3!=24-6=18$$


Evaluate $$\cfrac {n!}{(n-r)!}$$, when
(i) $$n = 6, r = 2$$.
(ii) $$n=9, r=5$$

We need to find value of $$\displaystyle \frac {n!}{(n-r)!}$$
i) Given, $$n=6, r=2$$
$$\therefore \dfrac {n!}{(n-r)!}=\dfrac {6!}{(6-2)!}$$
$$=\dfrac {6!}{4!}$$
$$=\dfrac {6\times 5 \times 4!} {4!}=30$$
ii) Given, $$n=9, r=5$$
Therefore the value of $$\displaystyle \frac {n!}{(n-r)!}=\frac {9!}{(9-5)!}=\frac {9!}{4!}=\frac {9 \times 8 \times 7 \times 6 \times 5 \times 4!}{4!} $$
$$=9\times 8\times 7\times 6\times 5=15120$$


A man has 7 trousers and 10 shirts. How many different outfits can he wear?

Task 1: He may choose the trouser in 7 ways.
Task 2: He may choose the shirt in 10 ways.
According to the product, rule, the total number of different outfits is $$7\, \times\, 10$$ i.e. 70


Is $$3 ! + 4 ! = 7 ! $$ ?

$$3!=1\times 2\times 3=6$$ and $$4!=1\times 2 \times 3\times 4=24$$
$$\Rightarrow   3!+4!= 6+24=30$$
$$7!=1\times 2 \times 3\times 4 \times 5\times 6\times 7=5040$$
$$\therefore 4 ! + 3 ! \neq 7!$$


A group of $$10$$ close friends plans to take a photo for remembrance. Find the number of different ways they can be seated in a row for the photo session.

Total number of ways they can sit in a row $$=10!=3628800$$


If $$\displaystyle ^{ n }{ P }_{ r }=720$$ and $$\displaystyle ^{ n }{ C }_{ r }=120$$, then what is the value of 'r'.

$$ ^{n}P_{r} = 720 $$ & $$ ^{n}C_{r} = 120 $$
As $$ ^{n}P_{r} = r! ^{n}C_{r}\Rightarrow r! = 6 $$
$$ \boxed {r = 3} $$ 

1108254_518588_ans_a8619ebfc27a45a089da57729999366e.jpg


If $$\displaystyle ^{ 10 }{ C}_{ r }=120$$, find the value of r

$$ ^{10}C_{r} = 120\Rightarrow \dfrac{10!}{120} = (10-r)! r! $$
$$ \Rightarrow (10-r)r! = 30.240 = 7!3!\Rightarrow \boxed{r = 3} $$ 

1110016_518458_ans_c1c0287097f8466ca08d26a6fc44359b.jpg


Evaluate $$\cfrac {n!}{(n-r)!}$$, when.
$$n = 9, r = 5$$.

Given, $$n=9, r=5$$
Therefore the value of $$\displaystyle \frac {n!}{(n-r)!}=\frac {9!}{(9-5)!}=\frac {9!}{4!}=\frac {9 \times 8 \times 7 \times 6 \times 5 \times 4!}{4!} $$
$$=9\times 8\times 7\times 6\times 5=15120$$


In the expansion of $$ ( a+ b + c)^s $$ find (1) the number of terms, (2) the sum of the coefficients of the terms.

$$(a+b+c)^{8}$$
n = 8 , r =number of independent terms  in bracket = 3

number of terms = $$C^{n+r-1}_{r-1}=C^{10}_{2}=45$$

sum of coefficients = $$r^{n}$$

$$= 3^{8}=6561$$



If $${ \left( 1+x \right)  }^{ n }={ c }_{ 0 }+{ c }_{ 1 }{ x }^{  }+{ c }_{ 2 }{ x }^{ 2 }+.....+{ c }_{ n }{ x }^{ n }$$, then show that the sum of the products of the $$c$$'s taken two at a time, represented by $$\sum _{ 0\le i\le j\le n }^{  }{ { c }_{ i }{ c }_{ j } } $$, is equal to $${ 2 }^{ 2n-1 }-\cfrac { (2n)! }{ 2{ (n!) }^{ 2 } } $$


1691390_781837_ans_bf2d6f10516c4fd1938f353eb35746f6.PNG


Prove that $${ _{  }^{ n }{ C } }_{ n-r }-{ _{  }^{ n }{ C } }_{ r }=0$$.

Consider $${ }^{n}{C}_{n-r}-{ }^n{C}_{r}$$
                $$=\dfrac{n!}{(n-(n-r))!(n-r)!}-\dfrac{n!}{(n-r)!r!}$$

                $$=\dfrac{n!}{r!(n-r)!}-\dfrac{n!}{(n-r)!r!}$$
                $$=0$$

Hence, $${ }^{n}{C}_{n-r}-{ }^n{C}_{r}=0$$.


The value of $${ _{  }^{ n }{ C } }_{ 1 }$$ is _______

We know that:
$$^nC_r = \cfrac{n!}{(n-r)!r!}$$
$$\because r = 1$$

$$\therefore \ ^nC_1 = \cfrac{n!}{(n-1)!1!} = \cfrac{n}{1} = n$$


$$^{15}C_{3r} = ^{15}C_{r+3}$$, find r.

$$^{15}C_{3r} = ^{15}C_{r+3}$$
3r + r +3 = 15
4r = 12
r=3


Prove that $$\displaystyle ^{ n }C_{ 0 }\ -\ ^{ n }C_{ 1\  }+\ ^{ n }C_{ 2 }\ -\ ^{ n }C_{ 3 }\ +\ ...+{ \left( -1 \right)  }^{ r }\ ^{ n }C_{ r }\ +\ ...={ \left( -1 \right)  }^{ r-1 }\ ^{ n-1 }C_{ r-1 }$$

The statement given to prove is wrong as the L.H.S of the question evaluates to zero on solving. It does not depend on r.
1173460_802840_ans_692c107516904587b5e24196ed2b2419.jpg


How many 4-letter words, with or without meaning, can be formed out of the letters of the word, "LOGARITHMS", if repitition of letters is not allowed ?

There are 10 letters in the word $$"LOGARITHMS".$$
So, the number of 4-letter word = Number of arrangements of 10 letters, taken 4 at a time

$$=10_{P_4}=\dfrac{10!}{(10-4)!}=5040$$


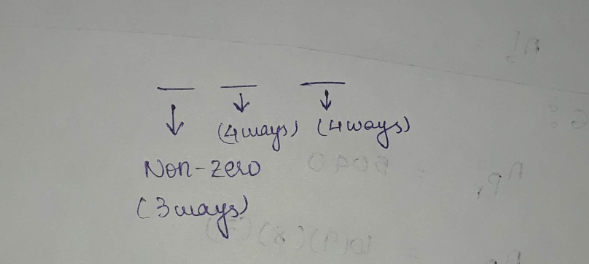
In how many ways three different rings can be worn in four fingers with at most one in each finger ?

The total number of ways is same as the number of arrangements of 4 fingers, taken 3 at a time.
So, required number of ways = $$4_{P_3}=\dfrac{4!}{(4-3)!}=\dfrac{4!}{1!}=4!=24$$


A parallelogram is cut by two sets of $$m$$ lines parallel to its sides. Find the number of parallelograms then formed.

The two sets of m parallel lines along with two sets
of 2 parallel lines of the given parallelogram will form two sets of m + 2 parallel lines. To form a parallelogram we have to choose sets of 2 parallel lines from each of the above.
Hence $$^{m + 2}C_{2} . ^{m + 2}C_{2} = (^{m + 2}C_{2})^{2}$$ is the required number of parallelograms.


In how many ways 7 pictures can be hung from 5 picture nails on a wall ?

The number of ways in which $$7$$ pictures can be hung from $$5$$ picture nails on a wall is the same as the number of arrangements of 7 things, taking 5 at a time.
Hence, the required number = $$7_{P_5}=\dfrac{7!}{(7-5)!}=\dfrac{7!}{2!}=2520$$


Solve the following equation:
$$\displaystyle\, C_{m + 1}^{n + 1} :  C_{m}^{n + 1} : C_{m -1}^{n + 1} = 5 : 5 : 3$$ 

$$^{n+1}C_{m+1}:^{n+1}C_{m}:^{n+1}C_{m-1}=5:5:3$$

$$\dfrac{1}{(m+1)m}:\dfrac{1}{m}:1=5:5:3$$

$$1:(m+1):m(m+1)=5:5:3$$

$$\implies \dfrac{1}{m+1}=1$$
$$\implies m=0$$


.
1059890_aac06b874a094b949c52a2dc2757f49f.jpg

$${{{M_1}{D_1}} \over {{W_1}}} = {{{M_2}{D_2}} \over {{W_2}}}$$

$${M_1} = Man,D = Days,W = work$$

$${M_1} = 100,{M_2} = 4$$

$${D_1} = 100,{D_2} = ?$$

$${W_1} = 100,{W_2} = 4$$

$${{100 \times 100} \over {100}} = {{4 \times {D_2}} \over 4}$$

$${D_2} = 100Days$$

A cat could kill 4 mice in 100 days .



Prove that $$^nC_r+^nC_{r-1}=^{n+1}C_r$$.

Now,
$$^nC_r+^nC_{r-1}$$
$$=\dfrac{n!}{r!(n-r)!}$$$$+\dfrac{n!}{(r-1)!(n-r+1)!}$$ [ Using the definition of $$^nC_r$$]
$$=\dfrac{n!}{(n-r)!(r-1)!}\left[\dfrac{1}{r}\right.$$$$\left.+\dfrac{1}{(n-r+1)}\right]$$
$$=\dfrac{n!}{(n-r)!(r-1)!}\left[\dfrac{(n+1)}{r(n+1-r)}\right]$$
$$=\dfrac{(n+1)!}{r!(n+1-r)!}$$
$$=^{n+1}C_r$$.


From $$4$$ officers and $$8$$ jawans , in how many ways can $$6$$ be chosen such that  to include exactly one officer .

$$1. ^4C_1=$$  no of ways $$1$$ officer can be selected
$$^8C_5=$$ no of ways $$5$$ jawans can be selected
Total no of ways  $$= ^4C_1 \times ^8C_5$$


How many $$3$$-digit even numbers are formed using the digits $$0,1,2,....,9,$$ if the repetition of digits is not allowed?

$$\begin{array}{l}0,{\rm{to,9}} \Rightarrow {\rm{10nos}}\\{\rm{8}} \times {\rm{9 = 72}}\\{\rm{8}} \times 8 \times 4 = 256\\72 + 256 = 328\end{array}$$


In an examination a candidate has to pass in each of four subject . In how many ways can he fails?

No. of ways in which one can pass or fail in the examination $$(m)=2^4=16$$24=16
To pass one has to pass in all the subjects $$(n)= 1\ way$$
Hence, the no. of ways in which one can fail $$=(m-n)$$
                                                                          $$=16-1$$
                                                                          $$=15\ ways$$


The least positive integer $${n}$$ such that $$(n-1){C}_{5}+(n-1){C}_{6}=n{C}_{7}$$ then the value $$n-7$$ is

Simplifying $${}^{n - 1}{C_5} + {}^{n - 1}{C_6} < {}^n{C_7}$$

$$\frac{{\left( {n - 1} \right)!}}{{5!\left( {n - 6} \right)!}} + \frac{{\left(n-1\right)!}}{{6!\left( {n - 7} \right)!}} = \frac{{n!}}{{7!\left( {n - 7} \right)!}}$$

$$\frac{{6\left( {n - 1} \right)! + \left( {n - 6} \right)\left( {n - 1} \right)!}}{{6!\left( {n - 6} \right)\left( {n - 7} \right)!}} = \frac{{n!}}{{7!\left( {n - 7} \right)!}}$$

$$\frac{{\left( {n - 1} \right)!\left( {6 + n - 6} \right)}}{{6!\left( {n - 6} \right)\left( {n - 7} \right)!}} = \frac{{n!}}{{7!\left( {n - 7} \right)!}}$$

$$\frac{1}{{n - 6}} = \frac{1}{7}$$

$$n - 6 = 7$$

$$n = 13$$

Therefore, the value of $$n - 7$$ is,

$$n - 7 = 13 - 7$$

$$ = 6$$



In how many ways we can select $$5$$ cards from a deck of $$52$$ cards, if each selection must include atleast one king.

Number of ways in which $$5$$cards can be selected $$=^{ 52 }C_{ 5 }$$
Number of ways in whcih no kings are selected $$=^{ 48 }C_{ 5 }$$
Number of ways in whcih atleast one king selected $$=^{ 52 }C_{ 5 }-^{ 48 }C_{ 5 }$$


Compute:
$$\frac{{10!}}{{5!}}$$

$$\dfrac{10!} {5!}$$

$$=\dfrac{10 \times 9 \times 8 \times 7 \times 6 \times 5!} {5!}$$

$$=6\times7\times8\times9\times10$$

$$=30240$$


Determine $$n$$ if $$^{2n}C_3 : ^nC_3 = 12 : 1$$.

We have,
$$\begin{array}{l} ^{ 2n }{ C_{ 3 } }{ :^{ n } }{ C_{ 3 } }=12:1 \\ \Rightarrow \dfrac { { ^{ 2n }{ C_{ 3 } } } }{ { ^{ n }{ C_{ 3 } } } } =\dfrac { { 12 } }{ 1 }  \\ \Rightarrow \dfrac { { 2n! } }{ { \left( { 2n-3 } \right) !3! } } .\dfrac { { \left( { n-3 } \right) !3! } }{ { n! } } =12 \\ \Rightarrow \dfrac { { 2!\left( { n-3 } \right) ! } }{ { \left( { 2n-3 } \right) !n! } } =12 \\ \Rightarrow \dfrac { { 2n\left( { 2n-1 } \right) \left( { 2n-2 } \right)  } }{ 6 } \times \frac { 6 }{ { n\left( { n-1 } \right) \left( { n-2 } \right)  } } =12 \\ \Rightarrow \dfrac { { 4\left( { 2n-1 } \right)  } }{ { \left( { n-2 } \right)  } } =12 \\ \Rightarrow 2n-4=12n-24 \\ \Rightarrow 4n=20 \\ \therefore n=5 \end{array}$$

Hence, this is the answer.


Find $$^ { \prime } n ^ { \prime }$$ if $$n C _ { 13 } = n C _ { 12 }$$.

$$nC_{13}=nC_{12}$$
$$\dfrac{n!}{13!(n-13)!}=\dfrac{n!}{12!(n-12)!}$$
$$\dfrac{1}{13!(n-13)!}=\dfrac{1}{12!(n-12)!}$$
$$\dfrac{1}{13\times 12!(n-13)!}=\dfrac{1}{12!(n-12)\times (n-13)!}$$
$$\dfrac{1}{13}=\dfrac{1}{n-12}$$
$$n-12=13$$
$$n=25$$


In a network of railways, a small island has $$15$$ stations. Find the number of different types of tickets to be printed for each class, if every stations must have tickets for other stations.

For each pair of stations, two different types of tickets are required.

Now, the number of selections of $$2$$ stations from $$15$$ stations $$=$$ $$^{15}C_2$$.

$$\therefore$$ Required number of types of tickets $$=2$$ 

$$^{15}C_2=2\dfrac{15!}{2!13!}$$ $$=15\times 14=210$$.


The number of way in which 6 red roses and 3 white roses (all rose different ) can from garland that all the white come together is -

REF.Image
A garland in a circular permutation case along with side cant
the white roses are together, hence, red roses are also together.
write roses can permute in = 3! ways.
also red roses can permute in = 6! ways.
but for a garland, front and back side would be same, so no of ways :-
$$ \displaystyle N = \frac{3!\times6!}{2} = 72 $$ possible arrangement.


1102757_1175596_ans_06f3d062f4cb4fff9231b607e47c7051.JPG


Suppose we have $$10\ points$$ in a plane forming a decagon.

How many triangles can be formed by joining them?

Number of vertices in a decagon $$= 10$$.

From these vertices, we will choose $$3$$ vertices to form a triangle.

Hence, number of ways to do this $$= ^{10}C_3=\dfrac {10!}{3!\cdot 7!}=\dfrac {10\times9\times8 }{3\times 2\times 1}=120$$ triangles



Find $$n$$ if $$\dfrac { ( 16 - n ) ! } { ( 14 - n ) ! } = 12$$

$$\dfrac{(16-n)!}{(14-n)!}=12$$

$$\dfrac{(16-n)(15-n)(14-n)!}{(14-n)!}=12$$

$$(16-n)(15-n)=4\times 3$$

$$16-n=4$$

$$n=16-4=12$$

n=12


If $$^{20}P_r = 13 \times ^{20}P_{r-1}$$, then the value of r is________.

$$\begin{array}{l} { \, ^{ 20 } }{ p_{ r } }\, =\left( { 13 } \right) { \, ^{ 20 } }{ p_{ r } }-1  \end{array}$$
$$\dfrac{20 !}{(20-r)!}=\dfrac{13\times 20!}{(20-r+1)!}\implies 21-r=13\implies r=8$$


Given $$5$$ flags of different colours how many different signals can be made if each signal requires the use of $$2$$ flags, one below the other.

First place can be filled up in $$5$$ ways.
After place ,we are left with $$4$$ flags.
$$ \therefore$$ The second place can be filled up in $$4$$ ways.
The total number of signals which can be generated $$=5 \times 4=20$$



Find WITHOUT assuming any formula, the permutations of $$35$$ different items taken $$13$$ at a time. (answer is factorial notation ).

1st item can be taken in 35 ways....
2nd item can be taken in 34 ways...
3rd item can be taken in 33 ways...
similarly.....
.
.
13th item can be taken in 23 ways...
so permutation of 35 items taken 13 at a time=$$35\ast 34\ast 33\ast \cdot \cdot \cdot \cdot \cdot \cdot \cdot \ast 23$$
multiplying 22! both in numerator and denominator we get
                                                                            =$$ \frac { 35\ast 34\ast 33\ast \cdot \cdot \cdot \cdot \cdot \cdot \cdot \ast 23\ast 22! }{ 22! }$$
                                                                            =$$\frac { 35! }{ 22! }$$                  (ans)


If the number of selections of $$3$$ difference letters  from the word $$SUMAN$$  is ________ .

No.of letters in word $$5$$
No. of letters to be selected $$3$$
No .of ways $$^5C_3=\dfrac{5!}{3!2!}=\dfrac{5\times 4}{2}=10$$


Find the value of: $$^{29}C_{9}$$

$$\begin{array}{l} ^{ 20 }{ C_{ r } }=\dfrac { { 20! } }{ { \left( { 20-r } \right) !r! } }  \\ ^{ 20 }{ C_{ 9 } }=\dfrac { { 20\times 19\times 18\times 17\times 16\times 15\times 14\times 13\times 12 } }{ { 8\times 7\times 6\times 5\times 4\times 3\times 2\times 1 } }  \\ Hence, \\ we\, get\,  \\ =83980 \end{array}$$


Find no of ways to put the $$3$$ book in the bookshelf.

$$3$$ books can be put in a bookshelf by $$3!$$ ways, i.e., $$3 \times 2 = 6$$ ways.


How many distinct positive integers are possible with the digits 1, 3, 5, 7 without repitition ?

Possible number of,

single-digit numbers = $$4$$

two-digit numbers = $$4\times 3=12$$

three-digit numbers = $$4\times 3\times 2=24$$

four-digit numbers = $$4\times 3\times 2\times 1 =24$$

Thus, total number of distinct positive integers without repitition = $$4+12+24+24=64$$.




How many different outcomes arise from first tossing a coin and then rolling a die ?

There are 2 possibilities (i.e., head or tail) for the first task ( tossing a coin) and after each of these outcomes there are 6 possibilities (i.e., any number from 1 to 6 ) for the second task ( rolling a dice ). Thus, by the product rule, there are $$2\times 6=12$$ possible outcomes, for the given compound task.


Find the number of divisors of $$16$$

$$16=2\times 2\times 2\times 2={2}^{4}$$

$$\therefore$$ No. of divisors =$$d\left(16\right)=4+1=5$$


Evaluate : $$^{14}C_{10}$$

$$ P = ^{14}C_{10} = \frac{14!}{10!(14-10)!}$$
$$ P = \frac{14!}{10!\times 4!} = \frac{14\times 13\times 12\times 11\times 10!}{10!\times 4!}$$
$$ P = 14\times 13 = 182.$$
$$ [P = 182]$$ 

1201943_1388818_ans_8d61aaae34b04f57b643e299cb4d83c5.JPG


If $$_{  }^{ n }{ { C }_{ 3 }:\ ^{n-1}   }{ C }_{ 4 }=20:21$$, then $$n$$ =

$$\dfrac{^{n}C_3}{^{n-1}C_4}=\dfrac{20}{21}$$
$$\Rightarrow \dfrac{n!}{3!(n-3)!}\times \dfrac{4!(n-5)!}{(n-1)!}=\dfrac{20}{21}$$
$$\Rightarrow \dfrac{n(n-1)!}{3!(n-3)(n-4)(n-5)!}\times \dfrac{4\times 3!(n-5)!}{(n-1)!}=\dfrac{20}{21}$$
$$\Rightarrow (4n)21=20(n^2-7n+12)$$
$$\Rightarrow 5n^2-56n+60=0$$
$$\Rightarrow n=\dfrac{56\pm \sqrt{56^2-4(5)(60)}}{10}$$
$$=\dfrac{56\pm \sqrt{3136-1200}}{10}$$
$$=\dfrac{56\pm 44}{10}=\dfrac{100}{10}$$ or $$\dfrac{12}{10}$$
$$\Rightarrow 10$$ or $$\dfrac{6}{5}$$
$$\Rightarrow n=10$$ $$(n\in Z)$$.

1216134_1397221_ans_426803f10daf4a45960740e2eb9280b6.jpg


Consider a, b, c, d. List all combintions taken 3 at a time.

The list includes abc, abd, acd, bcd.
Here abc, bca, cab are regarded the same as order is not important.
The number of combinations of n things taken r at a time is denoted by $${n_{C}}_{r}$$.


Find the value of $$4!$$

$$4!=4\times 3\times 2\times 1=24$$


Find the unit digit  of $$2\times 3\times 4\times ...\times 99$$

Multiple of $$99!$$ is multiple of $$3!$$

$$\therefore$$ units digit$$=0$$


There are $$7$$ men and $$8$$ women. In how many ways a committee of $$4$$ members can be made such that a particular woman is always included

Excluding the woman which is selected we have to select 3 members from the rest 15 
So total no. of ways = $$^{14}{c}_{3}$$ = $$\dfrac{14\times13\times12}{3\times2\times1}$$
=$$364$$


Find the value of 
(a) $$^{14}{C_5}$$
(b) $$^{90}{C_2}$$

(i) $${^{14}C_5}=\dfrac{14!}{5!(14-5)!}$$
$$=\dfrac{14!}{5!(9!)}$$
$$=\dfrac{14\times 13\times 12\times 11\times 10\times 9!}{5!\cdot 9!}=\dfrac{14\times 13\times 12\times 11\times 10}{5\times 4\times 3\times 2\times 1}$$
$$=7\times 13\times 11\times 2$$
$$=2,002$$

(ii) $${^{90}C_2}=\dfrac{90!}{2!(90-2)!}$$
$$=\dfrac{90!}{2!\cdot 88!}$$
$$=\dfrac{90\times 89\times 88!}{2!\cdot 88!}$$
$$=\dfrac{90\times 89}{2\times 1}$$
$$=4005$$.


If $$^{n}C_{8}=^{n}C_{2}$$, then find $$n$$.

If $$^{n}C_{8}=^{n}C_{2}$$ find the value of n 
solution $$\rightarrow $$ we know that $$^{n}C_{a}=^{n}C_{b}$$
$$\Rightarrow n=a+b$$
$$\therefore ^{n}C_{8}=^{n}C_{2}$$
$$\Rightarrow n=8+2$$
$$\Rightarrow n=10$$

1208937_1405628_ans_a4a58bed6724434281d5c3067a9e263b.jpg


If $${\,^n}{C_8} = \,{\,^n}{C_2}$$, then find $${\,^n}{C_2}.$$

Given $$^{n}C_8={^nC_2}$$
if $${^{n}C_r}={^{n}C_p}$$
Then either $$r=p$$ or $$r=n-p$$
Thus, $${^{n}C_8}={^{n}C_2}$$
$$8=n-2$$
$$10=n$$
$$\therefore n=10$$

Calculating $${^{n}C_2}$$

Put $$n=10$$
$${^{n}C_2}={^{10}C_2}$$
$$=\dfrac{10!}{2!(10-2)!}$$
$$=\dfrac{10\times 9\times 8!}{2\times 8!}$$
$$=\dfrac{10\times 9}{2}$$
$$=45$$
$$^{n}C_2=45$$.


How many even numbers greater then 300 can be formed with the digits 1,2,3,4,5 if repetitions of digits in a number is not allowed? 


Number of 3 digit even numbers = $$3\times 3$$(when ending with 2) + $$2\times 3$$(when ending with 4) $$=15$$
Number of 4 digit even numbers = $$2\times 3\times 4\times 2=48$$
Number of 5 digit even numbers = $$1\times 2 \times 3\times 4 \times 2=48$$
Therefore, total number of numbers = $$15+48+48=111$$


A word consists of $$9$$ letters, $$5$$ consonants and $$4$$ vowels. Three letters are chosen at random. Find the probability such that more than one vowel will be selected.

Given a word with $$9$$ letters, $$5$$ consonants and $$4$$ vowels

Three letters can be chosen out of 9 letters in $$9_{C_3}$$ ways.

Therefore, total number of elementary events = $$9_{C_3}$$

More than one vowels can be chosen in one of the following ways :

(i) 2 vowels and one consonant$$=4_{C_2} \times 5_{C_1}$$

(ii) 3 vowels$$=4_{C_3}$$

So, favourable number of elementary events = $$4_{C_2} \times 5_{C_1} +4_{C_3}$$

Hence, required probability = $$\dfrac{4_{C_2} \times 5_{C_1} +4_{C_3}}{9_{C_3}}=\dfrac{30+4}{84}=\dfrac{17}{42}$$


From a class of $$32$$ students, $$4$$ are to be chosen for a competition. In how many ways can this be done?

Out of 32 students, 4 students can be selected in $$32_{C_4}$$ ways.

Therefore, required number of ways = $$\dfrac{32!}{28!4!}=35960$$


In how many ways three different rings can be worn in four fingers with at most one in each finger?

The total number of ways is same as the number of arrangements of 4 fingers, taken 3 at a time.
So, required number of ways = $$4_{P_3}=\dfrac{4!}{(4-3)!}=4!=24$$


In how many ways can $$6$$ persons stand in a queue?

The number of ways in which 6 persons can stand in a queue is same as the number of arrangements of 6 different things taken all at a time.
Hence, the required number of ways = $$6_{P_6}=6!=720$$


Evaluate: $$^{16}C_{13}$$

As we know
$$^nC_r=\dfrac{n!}{r!(n-r)!}$$

$$^{16}C_{13}=\dfrac{16!}{13! \ 3!}=\dfrac{16 \times 15 \times 14}{3 \times 2}=560$$


$$Define\space permutations.$$

$$Permutation\space is\space an\space arrangement\space in\space definite\space order\space of\space a\space number\space of\space objects\space takens\space some\space or\space all\space at\space a\space time\space$$.


Evaluate: $$^{n+1}C_{n}$$

As we know
$$^nC_r=\dfrac{n!}{r!(n-r)!}$$

$$^{n+1}C_{n}=\dfrac{(n+1)!}{n! \ 1!}=n+1$$


Evaluate:
$$4! - 3! $$

$$4! - 3!  = ( 4 \times 3 \times 2 \times 1) - (3 \times 2 \times 1 ) = 24 - 6 = 18 $$


Write the following products in factorial notation:
$$6\times 7\times 8\times 9\times 10\times 11\times 12$$.

$$12!=12 \times11 \times 10\times 9\times 8\times 7\times 6\times 5\times 4\times 3\times 2\times 1 $$

$$6\times 7\times 8\times 9\times 10\times 11\times 12=\dfrac {12!}{5\times 4 \times 3 \times 2 \times 1}=\dfrac {12!}{5!}$$.


Find $$x$$ if,
$$ \dfrac{1}{6 !}+\cfrac{1}{7 !}=\cfrac{x}{8 !} $$

$$Given$$ : $$ \dfrac{1}{6 !}+\cfrac{1}{7 !}=\cfrac{x}{8 !} $$ 

$$multiplying\space by\space$$ $$8!$$, $$we\space get\space$$ 
 
$$ \dfrac{8!}{6!} + \dfrac{8!}{7!} = 8! \times \dfrac{x}{8!} $$ 

$$ \Rightarrow $$    $$ \dfrac{8 \times 7 \times 6!}{6!} + \dfrac{8 \times 7!}{7!} = x $$ 
$$ \Rightarrow $$   $$56 + 8 = x $$ 
$$ \Rightarrow $$    $$x = 64 $$


If the number of combination of $$n$$ dissimilar things taken $$r$$ at a time is given by $$\dfrac{n!}{r!(m)!}$$, then the value of $$m$$ for $$n=15$$ and $$r=3$$ is ____ .

To denote combination : $$C$$ 
Total number of things : $$n$$ 
No of selected things  : $$r$$

Required combination = $${ ^{n}C }_{ R }=\dfrac{n!}{r!(n-r)!}$$

Hence, the value of $$m$$ is $$n-r=15-3=12$$.


The students in a class are seated according to their marks in the previous examination.Once, it so happens that four of the students got equal marks and therefore the same rank To decide their seating arrangement, the teacher wants to write down all possible arrangements one in each of separate bits of paper in order to choose one of these by lots. How many bits of paper are required?

We are given that four students got equal marks. On one bit of paper, one arrangement of rank is to be written. 
Let the students be named as $$P, Q, R$$ and $$S$$. 
Now, $$P$$ can be treated as having rank I in $$4$$ ways.
$$Q$$ can be treated as having rank II in $$3$$ ways.
$$R$$ can be treated as having rank III in $$2$$ ways.
$$S$$ can be treated as having rank IV in $$1$$ ways.
Therefore, total number of bits of paper required for all arrangement
$$=4\times 3\times 2\times 1=24 $$


If $$^nC_x=\ ^nC_y$$, then x+y$$=$$

Given 
$${ ^{ n }{ C } }_{ x }={ ^{ n }{ C } }_{ y }........(1)$$
We Know that 
$${ ^{ n }{ C } }_{ r  }={ ^{ n }{ C } }_{ n-r }........(2)$$
Comparing (1) and (2)
$$r=x\quad \\ n-r=y$$
Now , 
$$x+y=r+n-r=n\quad \\ \Rightarrow x+y=n$$
Hence the value of $$x+y=n$$


A number lock on a suitcase has $$3$$ wheels each labeled with $$10$$ digits from $$0$$ to $$9$$. If the opening of the lock is a particular sequence of three digits with no repeats, how many such sequences will be possible?

On the first wheel, there can be $$10$$ digits. 

On the second wheel, there will be one of the $$9$$ digits and on the third wheel, there will be $$8$$ digits. 

Therefore, the number of numbers is $$10\times 9\times 8=720$$.


A code word is to consist of two English alphabets followed by two distinct numbers between $$1$$ and $$9$$. For example, $$CA23$$ is a code word. How many such code words are there? 

There are in all $$26$$ English alphabets. We have to choose $$2$$ distinct alphabets.
First alphabet can be selected in $$26$$ ways. Second alphabet can be selected in $$25$$ ways. Again out of $$9$$ Digits ($$1$$ to $$9$$), first digit can be selected in $$9$$ ways. second digit can be selected in $$8$$ ways.
Thus, the number of distinct codes 
$$=26\times 25\times 9\times 8$$
$$=46800$$


Three horses $$H_1, H_2, H_3$$ entered a field which has seven portions marked $$P_1, P_2, P_3, P_4,P_5, P_6 \ and\  P_7$$. If no two horses are allowed to enter the same portion of the field, in how many ways can the horses graze the grass of the field?

$$H_{1}$$ can graze the grass of either $$P_{1}$$ or $$P_{2}$$ or $$P_{3}$$... or $$P_{7}$$ that is, in $$7$$ ways.
After $$H_{1}$$ entered the field, there are six portions left for $$H_{2}$$ as no two can enter into the same portions left for $$H_{2}$$ as no two can enter into the same portion of the field.
After first two entered the field $$H_{3}$$ can enter the field in $$5$$ ways.
Therefore, by the fundamental principle of counting, the three horses can graze the grass of the field in 
$$7\times 6\times 5=210$$ ways


How many lines can be drawn through $$21$$ points on a circle?

We get a line by joining two points. If $$p$$ are the number of lines from $$21$$ points, then 
$$p=C(21, 2)=\dfrac{21!}{2!(21-2)!}$$
$$=\dfrac{21\times 20(19!)}{2\times 1(19!)}$$
$$=21\times 10=210$$ lines


 In how many combinations, a cricketer can make a century with fours and sixes only?

The possible combinations are: 
$$(25×4)$$,
$$(22×4+2×6)$$, 
$$(19×4+4×6)$$,
$$(16×4+6×6)$$,
$$(13×4+8×6)$$, 
$$(10×4+10×6)$$, 
$$(7×4+12×6)$$,
$$(4×4+14×6)$$,
$$(1×4+16×6)$$ 
Hence there are total 9 combinations.


A letter lock consists of 4 rings, each ring contains 9 non-zero digits. This lock can be opened by setting a 4 digit code with the proper combination of each of the 4 rings.Maximum how many codes can be formed to open the lock?

Given that the lock has $$4$$ rings  each ring contains $$9$$ digits.
To form a code we can use any of the $$9$$ digits on each ring i.e. we have $$9$$ choices for each ring.
$$\therefore$$ Total Possibilities $$=9\times9\times9\times9$$
                                  $$=9^4.$$
Hence, the answer is $$9^4.$$


Given that $$^nC_{n-r} + 3\space^nC_{n-r+1} + 3.\space^nC_{n-r+2} + \space^nC_{n-r+3} = \space ^xC_r$$. Let $$x=n+k$$, then find $$k$$ ?

We have 
$$\quad ^nC_{n-r} + 3\space^nC_{n-r+1} + 3.\space^nC_{n-r+2} + \space^nC_{n-r+3} = \space ^xC_r$$

$$\quad = (^nC_{n-r} + \space^nC_{n-r+1} ) + 2(\space^nC_{n-r+1} + \space^nC_{n-r+2}) + (\space^nC_{n-r+2} + \space^nC_{n-r+3}) = \space ^xC_r$$

$$\quad = \space ^{n+1}C_{n-r+1} + 2.\space^{n+1}C_{n-r+2} + \space^{n+1}C_{n-r+3} = \space ^xC_r$$

$$\quad = \space (^{n+1}C_{n-r+1} +\space^{n+1}C_{n-r+2}) + (\space^{n+1}C_{n-r+2} + \space^{n+1}C_{n-r+3}) = \space ^xC_r$$

$$\quad = \space ^{n+2}C_{n-r+2} + \space^{n+2}C_{n-r+3} = \space ^xC_r$$

$$\quad = \space ^{n+3}C_{n-r+3} = \space ^xC_r$$

$$\quad = \space ^{n+3}C_{r} = \space ^xC_r$$

Hence, $$x = n+3$$
$$\therefore\:k=3$$


$$8$$ different things are arranged around a circle. In how many ways can $$3$$ objects be selected when no two of the selected objects are consecutive.

Considering n different objects are to be arranged in a circle. The no of ways of selecting 3 such that no 2 of them are consecutive is
$$=\dfrac{n}{3} \:^{n-4}C_{2}$$

$$=\dfrac{n}{3}(\dfrac{(n-4)(n-5)}{2})$$

Substituting $$n=8$$ gives us
$$\dfrac{8}{3}(\dfrac{(8-4)(8-5)}{2})$$

$$=\dfrac{8}{6}(4\times 3)$$

$$=8\times 2$$

$$=16$$ ways.


Solve the equation $$3\space ^{x+1}C_2 + P_2 ^1.x = 4\space ^xP_2, \space x\in N$$. Find $$x$$ ?

We have 
$$\quad 3.\space ^{x+1}C_2 + P^1.x = 4\space^xP_2$$
$$\Leftrightarrow \quad \displaystyle\frac{3.(x+1)x}{1.2} + 2! x = 4.x(x-1)$$
$$\Leftrightarrow \quad 3x^2 + 3x + 4x = 8x^2 - 8x$$
$$\Leftrightarrow \quad 5x^2 - 15x = 0$$
$$\Leftrightarrow \quad 5x(x-3) = 0$$
$$\therefore \quad x\ne0$$
Hence $$x=3$$ is the solution of the given equation.


$$\left(\begin{matrix}18\\r-2\end{matrix}\right) + 2\left(\begin{matrix}18\\r-1\end{matrix}\right) + \left(\begin{matrix}18\\r\end{matrix}\right) \ge \left(\begin{matrix}20\\13\end{matrix}\right)$$. Find number of integer values $$r$$ can take ?

We have
$$\left(\begin{matrix}18\\r-2\end{matrix}\right) + 2\left(\begin{matrix}18\\r-1\end{matrix}\right) + \left(\begin{matrix}18\\r\end{matrix}\right) \ge \left(\begin{matrix}20\\13\end{matrix}\right)$$

It means that 
$$\quad ^{18}C_{r-2} + 2\space^{18}C_{r-1} + \space^{18}C_r \ge\space ^{20}C_{13}$$
$$\quad (^{18}C_{r-2} + \space^{18}C_{r-1}) + (\space^{18}C_{r-1} + \space^{18}C_r )\ge\space ^{20}C_{13}$$

$$\Leftrightarrow \quad ^{19}C_{r-1} + \space ^{19}C_r \ge \space ^{20}C_7$$
Or $$\quad ^{20}C_r \ge \space^{20}C_{13}$$
Hence $$7\le r \le 13$$
$$\therefore\quad  r = 7,8,9,10,11,12,13$$


A number of 18 guests have to be seated, half on each side of a long table. Four particular guests desire to sit on one particular side and three others on the other side. let the number of ways in which the sitting arrangements can be made is equal to $$^{11}C_k\times m!\times m!$$ arrangements. Find m+k ?

Out of 18 guests, 9 are to be seated on side A and rest 9 on side B.
Now

out of 18 guests, 4 particular guests desire to sit on one particular

side, say side A, and other 3 on other side B. Out of rest $$18-4-3=11$$

guests, we can select 5 more for side A and rest 6 can be seated on

side B. Selection of 5 out of 11 can be done in $$^{11}C_5$$ ways. Nine

guests on each side of table can be seated in $$9!\times 9!$$ ways.
Thus, there are total $$^{11}C_5\times 9!\times 9!$$ arrangements.


How many 4 digit numbers are there which contain not more than 2 different digits ?

Case 1 : When all digits are same : $$^9C_1$$ (excluding $$0$$)

Case 2: When digits are different and $$0$$ excluded.

(a) Selecting 2 numbers in $$^9C_2$$ ways
(b) Each digit can be filled in 2 ways hence $$2\, \, 2\, \, 2\, \, 2\, =\, 24$$ way
(c) Undesirable case : when a particular digit is same $$(2\, \, 1\, =\, 2$$ ways) 

(case 1)
$$\therefore\, ^9C_2\, (2^4\,- \, 2)$$ ways

Case 3: When digits are different and $$0$$ is included

(a) other digit can be chosen in $$^9C_1$$ ways

(b) 0 can't be placed at ten thousand's place, hence the selected digit should be fixed at this place remaining 3 digits can be filled with $$2\, \, 2\, \, 2\, =\, 2^3$$ ways.

(c) Undesirable case: When all the 4 digits gets filled with selected digit only (0 not included)= 1 way hence no. of ways will be: $$^9C_1\, (2^3\,- \, 1)$$

$$\therefore$$ Total desired ways :- $$^9C_1\, +\, ^9C_2\,(2^4\,- \, 2)\, +\,^9C_1\, (2^3\, -\, 1)\, =\, 576$$ ways


There are $$3$$ ways to go from $$A$$ to $$B$$, $$2$$ ways to go from $$B$$ to $$C$$ and $$1$$ way to go from $$A$$ to $$C$$. In how many ways can a person travel from $$A$$ to $$C ?$$

Travelling from $$A$$ to $$C$$ through $$B:$$
To travel from $$A$$ to $$B,$$ there are $$3$$ ways.
To travel from $$B$$ to $$C,$$ there are $$2$$ ways.
So, total ways of travelling from $$A$$ to $$C$$ through $$B=3\times 2=6$$ ways.
It is give that there is $$1$$ way to go from $$A$$ to $$C$$ directly.
$$\therefore$$  Total ways a person can travel from $$A$$ to $$C=6+1=7$$ ways. 


Find $$r$$ if $$^{15}C_{3r}\, =\, ^{15}C_{r\, +\, 3}$$ 

$$^{n}\textrm C_{r}=^{n}\textrm C_{n-r}$$$$^{n}\textrm C_{r}+^{n}\textrm C_{r-1}=^{(n+1)}\textrm C_{r}$$ If $$^{n}\textrm C_{r}=^{n}\textrm C_{s}$$then $$r=s$$ or $$r+s=n$$

Given, $$^{15}C_{3r}\, =\, ^{15}C_{r\, +\, 3}$$
$$\Rightarrow ^{15}C_{15-3r}\, =\, ^{15}C_{r\, +\, 3}$$
$$\Rightarrow 15-3r = r+3\Rightarrow 3r = 12\Rightarrow r = 3$$



There are $$8$$ buses running from Kota to Jaipur and $$10$$ buses running from Jaipur to Delhi. In how many ways a person can travel from Kota to Delhi via Jaipur by bus$$\: ?$$

Let $$E_{1}$$ be the event of travelling from Kota to Jaipur & $$E_{2}$$ be the event of travelling from Jaipur to Delhi by the person.
$$E_{1}$$ can happen in $$8$$ ways and $$E_{2}$$ can happen in $$10$$ ways.
Since both the events Eand Eare to be happened in order, simultaneously, the number of ways$$=8\times 10=80.$$


How many $$3$$-digit numbers can be formed from the digits $$1, 2, 3, 4$$ and $$5$$ assuming that repetition of the digits is not allowed?

A three digit number is to be formed from given $$5$$ digits $$1,2,3,4,5$$.

$$\Box \Box \Box \\ H T O$$

Now, there are $$5$$ ways to fill ones place.

Since, repetition is not allowed , so tens place can be filled by remaining $$4$$ digits.

So, tens place can be filled in $$4$$ ways.

Similarly, to fill hundreds place, we have $$3$$ digits remaining.

So,hundreds can be filled by $$3$$ ways.

So, required number of ways in which three digit numbers can be formed from the given digits is $$5\times 4\times 3=60$$


A man  has 7 trousers and 10 shirts How many different outfits can he wear?

Task 1: He may choose the trouser in $$7$$ ways
Task 2: He may choose the shirt in $$10$$ ways According to the Product Rule the total number of different outfits is $$7$$ $$\displaystyle\times 10 $$i.e. $$70$$


All letters are used but first letter is a vowel?

Total number of letters in the word MONDAY is $$6$$.
Number of vowels are $$2 (O, A )$$
Six letters word is to be formed.
$$\Box \Box \Box\Box \Box \Box$$
First letter should be a vowel. So, the rightmost place of the words formed can be filled only in $$2$$ ways.
Since the letters cannot be repeated , the second place can be filled by the remaining $$5$$ letters. So, second place can be done in $$5$$ ways
Similarly, third place in $$4$$ ways , fourth place in $$3$$ ways, fifth place in $$2$$ ways, sixth place in 1 way.

Hence, required number of words that can be formed using four letters of the given word is $$2\times 5\times 4\times 3 \times 2 \times 1 =240$$


How many $$3$$-digit even numbers can be formed from the digits $$1, 2, 3, 4, 5, 6$$ if the digits can be repeated?

A three digit even number is to be formed from given $$6$$ digits $$1,2,3,4,5,6$$.
$$\Box \Box \Box \\ H T O$$

Since, for the number is to be even , so ones place can be filled by $$ 2, 4$$ or $$6$$. So, there are $$3$$ ways to fill ones place.

Since, repetition is allowed , so tens place can also be filled by $$6$$ ways.

Similarly,hundreds place can also be filled by $$6$$ ways.

So, number of ways in which three digit even numbers can be formed from the given digits is $$6\times 6\times 3=108$$


In how many of the distinct permutations of the letters in MISSISSIPPI do the four I's not come together?

In the given word MISSISSIPPI, there are total $$11$$ letters.

$$I$$  appears $$4$$  times, $$S$$ appears $$4$$ times, $$P$$ appears $$2$$  times.

Therefore, number of distinct permutations of the letters in the given word 
$$=\cfrac {11!}{4!\times 4!\times 2!}$$

$$=\cfrac {11\times 10 \times 9\times 8\times 7\times 6\times 5\times 4! }{4!\times 4\times 3\times 2\times 1\times 2\times 1}$$

$$=\cfrac {11\times 10 \times 9\times 8\times 7\times 6\times 5}{4\times 3\times 2\times 1\times 2\times 1}$$

$$=34650$$

There are $$4$$  $$I's$$ in the given word. 

When they occur together, they are considered as a single object . This single object (letter) together with the remaining $$7$$ objects(letters) will give $$8$$ objects. 

These objects in which there are $$4 \ S's$$ and $$2\  P's$$ can be arranged in $$\cfrac {8!}{4!2!}$$ ways i.e.,$$840$$  ways.

Number of arrangements where all $$I's$$ occur together $$=840$$

Thus, number of distinct permutations of the letters in $$MISSISSIPPI$$  in which four $$I's$$  do not come together $$=34650-840=33810$$


There are 10 railway stations between a station x and another station y.
Find the number of different tickets that must be printed so as to enable a passenger to travel from any one station to any other.

Including $$x$$ and $$y$$ there are $$12$$ stations From any one station to any other we need $$11$$ different types of tickets Since there are $$12$$ stations the different tickets possible are $$(12)(11)=132$$


Find the number of factors of 324.

$$\displaystyle 324=18^{2}=3^{2}\times 2\times 3^{2}\times 2=3^{4}\times 2^{2}$$
 Number of factors = $$\displaystyle (4+1)(2+1)=15$$.


Find n if  $$^{n-1}P_3 : ^n P_4 = 1:9$$.

Given, $$^{n-1}P_3 :  ^n P_4 = 1:9$$

$$\displaystyle \Rightarrow \frac {^{n-1}P_3}{^nP_4}=\frac {1}{9}$$ 

$$\displaystyle \Rightarrow \dfrac{\dfrac{(n-1)!}{(n-1-3)!}}{\dfrac{n!}{(n-4)!}}=\frac{1}{9}$$

$$\displaystyle \Rightarrow \frac{(n-1)!}{(n-4)!}\cdot \frac{(n-4)!}{n!}=\frac{1}{9}$$

$$\displaystyle\Rightarrow \frac{1}{n}=\frac{1}{9}$$

$$ \Rightarrow
n=9$$


How many $$5$$ digit telephone numbers can be constructed using the digits $$0$$ to $$9$$ if each number starts with $$67$$ and no digit appears more than once?

It is given that the 5-digit telephone numbers always start with 67.
Therefore, there will be as many phone numbers as there as ways of filling 3 vacant places by the digits 0-9, keeping in mind that the digits cannot be repeated.
The unit place can be filled by any of the digits from 0-9, expect digits 6 and 7. 
Therefore, the unit place can be filled in 8 different ways following which, the tens place can be filled in by any of the  remaining 7 digits in 7 different ways, and the hundreds place can be filled in by any of the remaining 6 digits in 6 different ways.
Therefore, by the multiplication principle, the required number of  ways in which 5- digit telephone  numbers can be constructed is  $$ 8 \times 7 \times 6=336$$


In how many ways can be letters of word ASSASSINATION be arranged so that all the S's are together?

Considering all the S' together we get 

$$AAANNIITO(SSSS)$$

The above alphabets in which repetition of A is 3 times, N is 2 times and I is 2 times,can be arranged in 

$$\dfrac{10!}{3!2!2!}$$.... where all the S' remain as a pack.

$$=151200$$ ways.


If the different permutations of all the letter of the words $$EXAMINATION$$ are listed as in a dictionary, how many words are there in this list before the first word starting with $$E$$?

Arranging the words in dictionary order gives us 

$$AAEIINNMOTX$$

Hence consider the words starting with A

$$A - - - - - - - - - -$$

The remaining 10 places can be arranged in $$\dfrac{10!}{2!\cdot 2!\cdot 2!}$$ ( as there are $$2A,2I,2N$$)


The next letter that comes is $$E.$$

Hence the $$4,53,601^{st}$$ word will be starting with E.


How Many words, with or without meaning, each of $$2$$ vowels and $$3$$ consonants can be formed from the letters of the word $$DAUGHTER$$?

$${\textbf{Step -1: Identify how many vowels and consonant are  in the word DAUGHTER.}}$$

               $${\text{Vowels are A,U,E}}\left( {{\text{3 in number}}} \right)$$ $${\text{and}}$$

               $${\text{Consonant are D,G,H,T,R}}\left( {{\text{5 in number}}} \right)$$

$${\textbf{Step -2: Find number of ways to choose vowels.}}$$

                  $${\text{2 vowels can be chosen out of 3 different vowels in }}{}^3{{\text{C}}_2}$$ $${\text{ways}}{\text{.}}$$

               $$ \Rightarrow {\text{Number of ways to chose vowels}}$$$$ = {}^3{C_2}$$

               $$ \Rightarrow {\text{Number of ways to chose vowels}}$$ $$ = \dfrac{{3!}}{{2!\left( {3 - 2} \right)!}}$$  

               $$\left( \mathbf{{\text{using formula: }}{}^n{{\text{C}}_r} = \dfrac{{n!}}{{r!\left( {n - r} \right)!}}} \right)$$

               $$ \Rightarrow {\text{Number of ways to chose vowels}}$$ $$ = \dfrac{{3 \times 2!}}{{2!\left( 1 \right)!}}$$

               $$ \Rightarrow {\text{Number of ways to chose vowels}}$$$$ = 3$$

$${\textbf{Step -3: Find number of ways to choose consonant.}}$$

                 $${\text{3 consonant can be chosen out of 5 different consonant in }}{}^5{{\text{C}}_3}$$ $${\text{ways}}{\text{.}}$$

               $$ \Rightarrow {\text{Number of ways to chose consonant}}$$ $$ = {}^5{C_3}$$

               $$ \Rightarrow {\text{Number of ways to chose consonant}}$$ $$ = \dfrac{{5!}}{{3!\left( {5 - 3} \right)!}}$$  

               $$\left( \mathbf{{\text{using formula: }}{}^n{{\text{C}}_r} = \dfrac{{n!}}{{r!\left( {n - r} \right)!}}} \right)$$

               $$ \Rightarrow {\text{Number of ways to chose consonant}}$$$$ = \dfrac{{5 \times 4 \times 3!}}{{3!\left( 2 \right)!}}$$

               $$ \Rightarrow {\text{Number of ways to chose consonant}}$$$$ = 10$$

$${\textbf{Step -4: Find the total number of required words.}}$$

               $${\text{Use the multiplication formula find the ways to chose 2 vowels and 3 consonant}}{\text{.}}$$ 

               $$ \Rightarrow {\text{Required number of ways }}$$ $$ = 3 \times 10$$

               $${\text{Hence, 2 vowels out of 3 and 3 consonant out of 5 can be chosen in 30 ways}}{\text{.}}$$

               $${\text{Also, total number of ways of arranging 5 letters in each of the 30 group is}}$$ $$5!$$ 

               $${\text{i}}{\text{.e}}{\text{. it can be arrange in}}$$ $$5 \times 4 \times 3 \times 2 \times 1 = 120$$ $${\text{ways}}{\text{.}}$$

               $${\text{Therefore, the total number of words}}$$ $$ = 120 \times 30$$

               $$ \Rightarrow {\text{Required number of words}}$$ $$ = 3600$$

$${\textbf{Hence,Total 3600 word can be formed with or without meaning, each of}}$$ $$\textbf{2 vowels and 3 consonants can be formed from  the word }$$ $$\textbf{DAUGHTER.}$$ 



A committee of $$7$$ has to be formed from $$9$$ boys and $$4$$ girls. In how many ways can this be done when the committee consists of:
(i) exactly $$3$$ girls?
(ii) at least $$3$$ girls?
(iii) at most $$3$$ girls?

(i) exactly $$3$$ girls 

This means you have to choose $$3$$ girls from $$4$$ and $$4$$ boys from $$9$$ to form a committee of $$7$$. This can be done in 
$$^4{ C }_{ 3 }\times ^9{ C }_{ 4 }$$

(ii) At least $$3$$ girls 

This means girls can either be $$3$$ or $$4$$ 
So first choose $$3$$ girls and $$4$$ boys or $$4$$ girls and $$3$$ boys 
Total ways = $$^4{ C }_{ 3 }\times ^9{ C }_{ 4 }$$ + $$^4{ C }_{ 4 }\times ^9{ C }_{ 3 }$$

(iii) At most $$3$$ girls 

This means we have to choose $$1$$ or $$2$$ or $$3$$ girls 
So this can be done in 
$$^4C_0\times ^9C_7+^4{ C }_{ 1 }\times ^9{ C }_{ 6 }$$ + $$^4{ C }_{ 2 }\times ^9{ C }_{ 5 }$$ + $$^4{ C }_{ 3 }\times ^9{ C }_{ 4 }$$ ways.


If $$\displaystyle ^{ n }{ C }_{ 4 }=\dfrac{10}{6}\times ^{ n }{ C }_{ 2 }$$, find the value of "n".

$$\dfrac { { { n }_{ C } }_{ 4 } }{ { { n }_{ C } }_{ 2 } } =\dfrac { 10 }{ 6 } \\$$


$$ \dfrac { n(n-1)(n-2)(n-3)\times 2 }{ n(n-1)\times 24 } =\dfrac { 5 }{ 3 } \\$$

$$ (n-2)(n-3)=20\\$$

$$ n=7$$


A telegraph has $$5$$ arms and each arm is capable of $$4$$ distinct positions, including the position of rest. Find the total number of signals that can be made.

According to question ,
There are 4 positions for 5 arms

Therefore, total combination = $$4^5$$= $$1024$$

For including position of rest , we have to subtract this 1 from total.

Therefore total no. of signals=$$4^5-1=1024-1$$

=>$$1023$$


Four alphabets E, K, S and V, one in each, were purchased from a plastic warehouse. How many ordered pairs of alphabets, to be used as initials, can be formed from them?

 Total number of letters $$= 4$$
 Number of ordered pairs of letters that can be formed like (E, K) or (S, E) etc = $${ { 4 }_{ P } }_{ 2 }=\dfrac{4!}{2!}=\dfrac{24}{2}=12$$


The students in a class are seated according to their marks in the previous examination. Once, it so happens that four of the students got equal marks and therefore the same rank. To decide their seating arrangement, the teacher wants to write down all possible arrangements one in each of separate bits of paper in order to choose one of these by lots. How many bits of paper are required?

All 4 student secured equal marks  therefore same rank
So in order to write all possible arrangements one in each of separate paper in order to choose one of these lots=4!=24
It is basic thing  number of ways to arrange 4 things


Three horses $$\displaystyle { H }_{ 1 },{ H }_{ 2 },{ H }_{ 3 }$$ entered a field which has seven portions marked $$\displaystyle { P }_{ 1 },{ P }_{ 2 },{ P }_{ 3 },{ P }_{ 4 },{ P }_{ 5 },{ P }_{ 6 }$$ and $$\displaystyle { P }_{ 7 }$$. If no two horses are allowed to enter the same portion of the field, in-how many ways can the horses graze the grass of the field?

The horses who entered the field : h1 , h2 , h3

Number of horses who entered the field = 3

The given portions into which the horses are made to enter : p1 , p2 , p3 , p4 , p5 , p6 , p7

Total number of portions = 7

So, we need to find the number of ways in which the horses are made to enter the 7 portions given that no two horses can enter the same portion

Now, h1 horse can graze the grass in 7 ways

Also, h2 can graze the grass in 6 ways

And, h3 can graze the grass in 5 ways.

So, Total number of ways = 7 × 6 × 5

Hence, The total number of ways in which the horses can graze the grass of the field = 210



Find the value of  $$^{60}C_{60}$$

$$^{ 60 }C_{ 60 }=?$$
$$\left\lfloor ^{ n }C_{ r }=\dfrac { n! }{ r!(n-r)! }  \right\rfloor \\ \Rightarrow \dfrac { 60! }{ 60!\times 0! } =1\\ ^{ 60 }C_{ 60 }=1$$
Hence the correct answer is $$1$$


Find the value of $$\dfrac{n!}{(n-r)!}$$ when $$n=15$$ and $$r=2$$

Given $$n = 15$$ and $$r = 2$$
The value of $$\dfrac{n!}{(n-r)!} = \dfrac{15!}{(15!- 2!)}$$
                                       $$=\dfrac{15 \times 14 \times 13!}{13!}$$
Reducing $$13!$$ from fraction we get
$$\dfrac{n!}{(n-r)!}=15 \times 14 $$
                 $$=210$$
Hence, the answer is $$210$$.


Find the value of $$^{10}C_3$$

$$^{ 10 }C_{ 3 }=?$$
$$\left\lfloor ^{ n }C_{ r }=\dfrac { n! }{ r!(n-r)! }  \right\rfloor \\ \Rightarrow \dfrac { 10! }{ 3!\times 7! } =\dfrac { 10\times 9\times 8 }{ 3\times 2 } =120\\ \Rightarrow ^{ 10 }C_{ 3 }=120$$
Hence the correct answer is $$120$$


Verify that $$^8C_4+^8C_5=^9C_4$$

$$^{ 8 }C_{ 4 }+^{ 8 }C_{ 5 }=^{ 9 }C_{ 4 }\\  LHS=^{ 8 }C_{ 4 }+^{ 8 }C_{ 5 }\\ \Rightarrow \dfrac { 8! }{ 4!\quad 4! } +\dfrac { 8! }{ 5!\quad 3! } \\ \Rightarrow \dfrac { 8! }{ 4!\quad 3! } \left[ \dfrac { 1 }{ 4 } +\dfrac { 1 }{ 5 }  \right] \\ \Rightarrow \dfrac { 8! }{ 4!\quad 3! } \left[ \dfrac { 5+4 }{ 4!\quad 5! }  \right] \\ \Rightarrow \dfrac { 9! }{ 5!\quad 4! } =^{ 9 }C_{ 4 }=RHS$$

Hence verified as $$LHS = RHS$$



If $$^{2n}C_3:\,^nC_3=11:1$$, find n 

$$\dfrac { ^{ 2n }C_{ 3 } }{ ^{ n }C_{ 3 } } =\cfrac { 11 }{ 1 } \\ \Rightarrow \dfrac { \dfrac { 2n! }{ (2n-3)!3! }  }{ \dfrac { n! }{ (n-3)!3! }  } =\dfrac { 11 }{ 1 } \\ \Rightarrow \dfrac { 2n! }{ (2n-3)!3! } =\dfrac { 2n! }{ (2n-3)! } \times 11\\ \Rightarrow n=6$$
Hence the correct answer is $$6$$


Find the value of  $$\dfrac{n!}{(n-r)!r!}$$ when $$n=15$$ and $$r=2$$

Given $$n = 15$$ and $$r = 2$$
The value of  $$\dfrac{n!}{(n-r)!r!}$$ 
                  $$= \dfrac{15!}{(15- 2)!2!}$$
                  $$=\dfrac{15!}{13!(2!)}$$
                  $$=\dfrac{15 \times 14 \times 13!}{(13!)(2!)}$$
Reducing $$13!$$ from fraction we get
$$\dfrac{n!}{(n-r)! r!}=\dfrac{15 \times 14}{2 \times 1} $$
                    $$=\dfrac{210}{2}$$
                    $$=105$$
Hence, the answer is $$105$$.


Find the value of $$^{100}C_{97}$$

$$^{ 100 }C_{ 97 }=?\\ \left\lfloor ^{ n }C_{ r }=\dfrac { n! }{ r!(n-r)! }  \right\rfloor \\ ^{ 100 }C_{ 97 }=\dfrac { 100! }{ 97!\times 3! } \\ =\dfrac { 100\times 99\times 98 }{ 3\times 2\times 1 } \\ =161700\\ ^{ 60 }C_{ 60 }=161700$$
Hence the correct answer is $$ 161700$$


If $$^nC_4=^nC_7$$ find the $$n$$.

Given, 
$$^{ n }C_{ 4 }=^{ n }C_{ 7 }\\ \Rightarrow ^{ n }C_{ r }=^{ n }C_{ n-r }\\ \Rightarrow r+(n-r)=n\\ \Rightarrow 4+7=n\\ \Rightarrow n=11$$
Hence the correct answer is $$ 11$$


Prove that $$\dfrac{^nC_r}{^{n-1}C_{r-1}}=\dfrac{n}{r}$$ when $$1\le r \le n$$.

$$\dfrac { ^{ n }C_{ r } }{ ^{ n }C_{ n-r } } =\dfrac { n }{ r } \\ LHS=\dfrac { ^{ n }C_{ r } }{ ^{ n }C_{ n-r } } \\ \Rightarrow \dfrac { \dfrac { n! }{ (n-r)!r! }  }{ \dfrac { (n-1)! }{ (n-r)!(r-1)! }  } =\dfrac { n }{ r } $$

Hence proved as $$LHS=RHS$$



How many 3 - digit numbers can be formed from the digits 0, 1, 2, 3 and 4 with repetitions? 

$$0 , 1 ,2 , 3 $$
With repetition 
Three-digit number 

Therefore the total number of digits 
$$\Rightarrow 3\times 4\times 4$$
$$ \Rightarrow 48$$
Therefore $$48$$ Three digit numbers are possible 

853131_563027_ans_9da7969ddcfe4f4b858959bc0b560d38.PNG


If $$^nC_8 = { }^nC_{12}$$, find $$n$$

From the standard formula we get:
$$^nC_8 = { }^nC_{12}$$
$$^nC_8 = { }^nC_{n-12}$$           $$[\because { }^nC_r={ }^nC_{n-r}]$$
$$\implies 8=n-12$$    
$$\therefore n =12+8=20$$


If $${ _{  }^{ 12 }{ C } }_{ r+1 }={ _{  }^{ 12 }{ C } }_{ 3r-5 }$$, find $$r$$.

Fact:  If $$^nC_x=^nC_y$$ , then $$x=y$$ or $$x+y=n$$

Here  $$^{12}C_{r+1}=^{12}C_{3r-5}$$
$$\Rightarrow r+1=3r-5$$ or $$r+1+3r-5=12$$
$$\Rightarrow 2r=6$$ or $$4r=16$$
$$\Rightarrow r=3$$ or $$r=4$$


Find the sum of all four digit numbers that can be formed using the digits $$1,3,5,7,9$$.

A digit can be in a place in $$4\times 3\times 2$$ ways

So for digit $$k$$ sum of it's influence in all numbers $$=(k\times { 10 }^{ 3 }+k\times { 10 }^{ 2 }+k\times { 10 }+k)4\times 3\times 2$$

$$=k\times (1111)4\times 3\times 2$$

So for $$1,3,5,7,9$$

$$=(1111)\times 4\times 3\times 2(1+3+5+7+9)$$

$$=666600$$


Prove that $$\dfrac{^nC_r}{{ }^{n - 1}C_{r- 1}} = \dfrac{n}{r}$$ where $$1 \leq r \leq n$$

To prove:
$$\cfrac{{}^nC_r}{{}^{(n-1)}C_{r-1}}=\cfrac nr$$
Solution:
$$\cfrac{{}^nC_r}{{}^{(n-1)}C_{r-1}}=\cfrac{\cfrac{n!}{(n-r)!r!}}{\cfrac{(n-1)!}{(n-1-(r-1))!(r-1)!}}$$
$$=\cfrac{n!}{(n-r)!r!}\times \cfrac{(n-r)!(r-1)!}{(n-1)!}$$
$$=\cfrac{n!}{r!}\times\cfrac{(r-1)!}{(n-1)!}$$
$$=\cfrac{n(n-1)!}{r(r-1)!}\times\cfrac{(r-1)!}{(n-1)!}$$
$$=\cfrac nr$$
Hence, $$\cfrac{{}^nC_r}{{}^{(n-1)}C_{r-1}}=\cfrac nr$$


Find the number of $$4$$ letter words that can be formed using the letters of the word $$PISTON$$, in which at least one letter is repeated.

To find the number of $$4$$ letter words having at least one letter repeated, we find the total number of $$4$$ letter words possible and subtract from that the number of $$4$$ letter words having no repetition.
$$\therefore$$ we get the answer as $$6^4 - { }^6C_4$$


If $$^{n}P_{r} = 5040$$ and $$^{n}C_{r} = 210$$, then find $$n$$ and $$r$$.

We have,  $$^{n}P_{r} = 5040$$ and $$^{n}C_{r} = 210$$,

$$\dfrac{n!}{(n-r)!}=5040$$ and $$\dfrac{n!}{(n-r)!r!}=210$$
Divide both 
$$\Rightarrow r!=24\Rightarrow r=4$$
So $$\dfrac{n!}{(n-4)!}=5040$$
$$\Rightarrow \dfrac{n(n-1)(n-3)(n-4)!}{(n-4)!}=5040$$
$$\Rightarrow n(n-1)(n-2)(n-3)=5040$$
$$\Rightarrow n = 10$$


The value of $$^{ n }{ C }_{ r } -$$ $$^{ n }{ C }_{ n-r }=$$ ______________.

Consider $${ }^nC_{r}-{ }^{n}{C}_{n-r}$$
                $$=\dfrac{n!}{(n-r)!r!}-\dfrac{n!}{(n-(n-r))!(n-r)!}$$
                $$=\dfrac{n!}{(n-r)!r!}-\dfrac{n!}{r!(n-r)!}$$
                $$=0$$
Hence, $${ }^nC_{r}-{ }^{n}{C}_{n-r}=0$$.


How many different signals can be made by hoisting $$6$$ differently coloured flags one above the other, when any number of them may be hoisted at once?

No of ways for hoisting $$6$$ different flags out of $$6$$ given flags = $${ }^6P_6=720\text{ ways.}$$

No of ways for hoisting $$5$$ different flags out of $$6$$ given flags = $${ }^6P_5=720\text{ ways.}$$

No of ways for hoisting $$4$$ different flags out of $$6$$ given flags = $${ }^6P_4=360\text{ ways.}$$

No of ways for hoisting $$3$$ different flags out of $$6$$ given flags = $${ }^6P_3=120\text{ ways.}$$

No of ways for hoisting $$2$$ different flags out of $$6$$ given flags = $${ }^6P_2=30\text{ ways.}$$

No of ways for hoisting $$1$$ different flags out of $$6$$ given flags = $${ }^6P_1=6\text{ ways.}$$

Hence, total number of signals $$=720+720+360+120+30+6=1956\text{ ways.}$$


If $${ _{  }^{ n }{ C } }_{ 12 }={ _{  }^{ n }{ C } }_{ 8 }$$, find $${ _{  }^{ n }{ C } }_{ 17 },{ _{  }^{ 22 }{ C } }_{ 11 }$$

$$\dfrac{n!}{(n-12)!(12!)}=\dfrac{n!}{(n-8)!(8!)}$$
By solving above equation we get,
$$(n-8)(n-9)(n-10)(n-11) = 12\times 11 \times 10 \times 9 $$
So by comparing, we get $$n-8=12 \Rightarrow n=20$$
Now, 
$$^{20}{C}_{17}=\dfrac{20!}{3!\times17!}=1140$$
and,
$$^{22}{C}_{11}=705432$$


If $${ _{  }^{ 28 }{ C } }_{ 2r }:{ _{  }^{ 24 }{ C } }_{ 2r-4 }=225:11$$, find $$r$$.

$$\Longrightarrow \cfrac { 28! }{ \left( 2r \right) !\left( 28-2r \right) ! } \times \cfrac { \left( 2r-4 \right) !\left( 28-2r \right) ! }{ \left( 24 \right) ! } =\cfrac { 225 }{ 11 } $$

$$\Longrightarrow \cfrac { 28\times 27\times 26\times 25 }{ 2r\left( 2r-1 \right) \left( 2r-2 \right) \left( 2r-3 \right)  } =\cfrac { 225 }{ 11 } $$

$$\Longrightarrow 14\times 3\times 26\times 11=2r\left( 2r-1 \right) \left( 2r-2 \right) \left( 2r-3 \right) $$

$$\Longrightarrow 6006=\left( { r }^{ 2 }-r \right) \left( { 4r }^{ 2 }-8r+3 \right) $$
$$\Longrightarrow 6006={ 4r }^{ 4 }-12{ r }^{ 3 }+11r^{ 2 }-3r$$
$$\Longrightarrow { 4 }r^{ 4 }-{ 12 }r^{ 3 }+{ 11r }^{ 2 }-3r-6006=0$$
$$r=7$$  Other $$r$$  are complex and negative.


If $${ _{  }^{ 2n }{ C } }_{ 3 }:{ _{  }^{ n }{ C } }_{ 2 }=44:3$$, find $$n$$.

$${ _{  }^{ 2n }{ C } }_{ 3 }:{ _{  }^{ n }{ C } }_{ 2 }=44:3$$

$$\Longrightarrow \cfrac { \left( 2n \right) ! }{ \left( 2n-3 \right) !\times 3! } \times \cfrac { \left( n-2 \right) !\times 2! }{ n! } =\cfrac { 44 }{ 3 } $$

$$\Longrightarrow \cfrac { 2n\left( 2n-1 \right) \left( 2n-2 \right)  }{ n\left( n-1 \right) \times 3 } =\cfrac { 44 }{ 3 } $$

$$\Longrightarrow \cfrac { 2\left( 2n-1 \right) \left( n-1 \right)  }{ n-1 } =22$$

$$\Longrightarrow 2{ n }^{ 2 }-3n+1=11n-11$$

$$\Longrightarrow 2{ n }^{ 2 }-14n+12=0$$

$$\Longrightarrow \left( 2n-2 \right) \left( n-6 \right) =0$$

$$\Longrightarrow n=1,6$$

Since  $$^{ 1 }{ C }_{ 2 }$$  is not possible
$$\Longrightarrow \therefore \boxed { n=6 } $$


In a steamer there are stalls for $$12$$ animals, and there are cows, horses, and calves (not less than $$12$$ of each) ready to be shipped; in how many ways can the shipload be made?

$$\Longrightarrow $$ The number of arrangements of $$n$$ things (each consisting a valid amount ) into $$r$$ things is $${ n }^{ r }$$
$$\therefore 3$$ animals arranged over $$12$$ stalls in $${ 3 }^{ 12 }$$ ways
i.e. $$531441$$ no. of ways.


How many different selections can be made by taking four of the digits $$3,4,7,5,8,1$$? How many different numbers can be formed with four of these digits?

Total digits are $$6$$. 
(1) Number of ways of selecting $$4$$ digits out of $$6$$ digits is given by $$={}^{6}{C}_{4}=\dfrac{6!}{4!2!} = \dfrac{6\times5}{2}=15$$.

(2) Selected $$4$$ digits can be arranged in $$4$$ places to get different numbers i.e. $$={}^{6}{C}_{4}\times4!=15\times24=360$$.


If $${ _{  }^{ 18 }{ C } }_{ r }={ _{  }^{ 18 }{ C } }_{ r+2 }$$, find $${ _{  }^{ r }{ C } }_{ 5 }$$.

$$^{18}{C}_{r} = {}^{18}{C}_{r+2}$$

$$\Rightarrow \dfrac{18!}{(18-r)! r!} = \dfrac{18!}{(16-r)! (r+2)!}$$

By solving above equation we get, $$r=8$$
Using this $$r$$,
$$\Rightarrow {}^{8}{C}_{5}=56$$


In how many ways can $$n$$ things be given to $$p$$ persons, when there is no restriction as to the number of things each may receive?

Each person can receive a particular number of things in $$p$$ ways

$$\therefore $$ Total no. of ways of giving $$n$$ things to $$p$$ persons
$$=p\times p\times p.....n\left( times \right) $$
$$={ p }^{ n }$$


How many permutations of $$4$$ letters can be made out of the letters of the word examination?

$$\Longrightarrow $$  $$\underline { e } $$  $$\underline { x } $$  $$\underline { aa } $$  $$\underline { m } $$  $$\underline { ii } $$  $$\underline { nn } $$  $$\underline { t } $$  $$\underline { o } $$

Total number of single letters  $$=8$$  $$(e,x,a,m,i,n,t,o)$$
Duplicate letters  $$=3(aa,ii,nn)$$
Possible ways of selecting $$4$$ letters are :-
$$4$$ from single $$=^{ 8 }{ C }_{ 4 }\times 4!=1680$$
$$2$$ from single and $$1$$ pair of the duplicated letters $$={}^{ 3 }{ C }_{ 1 }\times{}^{ 7 }{ C }_{ 2 } \times \cfrac { 4! }{ 2! } =756$$
$$2$$ pair of duplicated letters $$={}^{ 3 }{ C }_{ 2 } \times \cfrac { 4! }{ 2!2! } =18$$
Total no. of ways $$=2454$$


A telegraph has $$5$$ arms and each arm is capable of $$4$$ distinct positions, including the position of first; what is the total number of signals that can be made?

Total number of position combinations $$={ 4 }^{ 5 }=1024$$
As we are not taking the position of first
$$\therefore $$ Total number of positions in which signals can be made $$=1024-1=1023$$


A letter lock consists of three rings each marked with fifteen different letters; find in how many ways it is possible to make an unsuccessful attempt to open the lock.

A letter lock contains three rings each marked with fifteen different letters
So, there can be $$15\times 15\times 15$$ number of attempts
$$\therefore $$  Total number of attempts $$=3375$$.
Now, there can be only one successful combination.
$$\therefore $$ Total number of wrong attempts $$=3375-1$$
$$=3374$$


The teacher distributes $$6$$ pencils per student. Can you find how many pencils are needed for the given number of students(use $$'z'$$ for the number of students).

Let the no. of students be z
Teacher distribute $$6$$ pencil per student then
$$1$$ student got $$6$$ pencil
$$2$$ students got $$12$$ pencil$$\Rightarrow 2\times 6$$
similarlt, z students got$$\Rightarrow 6z$$
that means $$6z$$ pencils are needed to distribute among z students.

1114984_701100_ans_56e83a74feba4095a520958605b1bf7e.PNG


Everybody in a function shakes hand with everybody else. The total number of handshakes areFind the number of persons in the function.

Let there be $$x$$ people in the function.
We name the people as $$1,2,3....,x-1,x$$
Take person 1: He can shake hands with $$(x-1)$$ people.
Take person 2: He can shake hands with $$(x-2)$$ people.
......
Take person $$x-1$$: He can shake hands with 1 people.
Adding them together:
$$(x-1)+(x-2)+...+1=4$$
$$\dfrac{x(x-1)}{2}=45$$
$$x=10$$
There were 10 people in the party.


If $$\dfrac{1}{1!10!}+\dfrac{1}{2!9!}+\dfrac{1}{3!10!}+.....+\dfrac{1}{1!10!}=\dfrac{2}{k!}(2^{k-1}-1)$$ then find the value of k.

Let $$S=\dfrac { 1 }{ 1!10! } +\dfrac { 1 }{ 2!9! } +\dfrac { 1 }{ 3!8! } +......+\dfrac { 1 }{ 10!1! } $$

$$\Rightarrow S\times 11!=\dfrac { 11! }{ 1!10! } +\dfrac { 11! }{ 2!9! } +\dfrac { 11! }{ 3!8! } +......+\dfrac { 11! }{ 10!1! }  $$

$$\Rightarrow S\times 11!+2=\dfrac { 11! }{ 0!11! } +\dfrac { 11! }{ 1!10! } +\dfrac { 11! }{ 2!9! } +\dfrac { 11! }{ 3!8! } +......+\dfrac { 11! }{ 10!1! } +\dfrac { 11! }{ 11!0! } $$

$$\Rightarrow S\times 11!+2=^{ 11 }{ { C }_{ 0 } }+^{ 11 }{ { C }_{ 1 } }+^{ 11 }{ { C }_{ 2 }+ }.......+^{ 11 }{ { C }_{ 11 } }$$     --------- where $$^{ n }{ { C }_{ r } }=\dfrac { n! }{ r!(n-r)! } $$

$$\Rightarrow S\times 11!+2={ 2 }^{ 11 }$$  ------ (Using $$^{ n }{ { C }_{ 0 } }+^{ n }{ { C }_{ 1 } }+^{ n }{ { C }_{ 2 } }+.......+^{ n }{ { C }_{ n } }={ 2 }^{ n }$$)

$$\Rightarrow S=\dfrac { 2 }{ 11! } ({ 2 }^{ 11-1 }-1)$$

Comparing this value of S with the expression in question, we get $$k=2$$.

 



In how many ways can five people be divided into three groups?

Five people can be divided into $$^5C_3$$
        So, $$\Rightarrow$$ $$\dfrac{5!}{3! \cdot 2!}$$
               $$\Rightarrow 10$$
So answer is $$10$$


How many different words can be formed with the letters of word $$INDIA$$? In how many of these
(a) Two $$I$$'s are always together?
(b) $$N$$ and $$A$$ are always together?

Total number of different words formed with the letters of word INDIA $$=\dfrac{5!}{2!}=60$$
Case a: If $$2$$ $$I$$'s are always together, then the number of words $$=4!=24$$
Case 2: $$N$$ and $$A$$ are together
 $$=\dfrac{4!2!}{2!}=24$$


In how many ways can five people be arranged in three different rooms if no room must be empty and each room has $$5$$ seats in a single row.

$$5$$ People are to arranged $$3$$ rooms given that no room is empty.
There are $$2$$ basic possibilities $$:$$
$$1. (2,2,1)$$      $$2. (3,1,1)$$
There are $$3$$ rearrangements (room rearrangement) for each possibility.
For $$1.$$ Since there are $$5$$ seats in each room 
$$\Rightarrow$$ Permutations $$={^5P_2}\times{^5P_2}\times{^5P_1}$$
                             $$={5^3\times4^2}$$
                             $$=4000.$$
$$\Rightarrow$$ For $$2.$$  $$={^5P_3}\times{^5P_1}\times{^5P_1}$$
                 $$={5^3\times4\times3}$$
                 $$=3000.$$
$$\Rightarrow$$ Total $$=3\times(4000+3000)$$
              $$=21000$$ ways.
Hence, the answer is $$21000.$$


In how many ways can the letter of the word "ARRANGE" be arranged so that
(i) the two R's are never together?
(ii) the two A's are together but not the two R's?
(iii) neither the two A's nor the two R's are together?

There are total 7 letters with 2 'A' and 2 'R'.

Total number of arrangements$$=\dfrac{7!}{2!2!}=1260$$

$$(i)$$  When two 'R' are together, taking both $$R$$ as one entity, number of different elements are $$7-2+1=6$$ and as two 'R' are same there will be no self arrangement within the entity.

Number of arrangement with 2 'R' together is $$\dfrac{6!}{2!}=360$$

Hence number of arrangement with no two 'R' together$$=1260-360=900$$

$$(ii)$$  The number of arrangement with two 'A' together is $$\dfrac{6!}{2!}=360$$

The number of arrangement of both two 'A' and two 'R' together is -

Take group of two 'A' as one and two 'R' as another entity .

Number of elements left is now $$7-4+2=5$$ and the 'R' and 'A' being same are not arranged within entity.

Number of arrangement with two 'A' together and two 'R" together is $$5!=120$$

Hence, number of arrangement with two 'A' together but two 'R' not together

= number of arrangement with 'A' together-number of arrangement with 'A' as well as 'R' together

$$=360-120=240$$

$$(iii)$$  Number of arrangement with neither 'A' nor 'R' together 

= total number of arrangement$$-$$number of arrangement with only 'A' together not 'R'$$-$$number of arrangement with only 'R' together not 'A'$$-$$ number of arrangement with both 'A' and 'R' together grouped

$$=1260-240-240-120$$

$$=660$$


In how many ways $$18$$ different objects can be divided into $$7$$ groups such that four groups contains $$3$$ objects each and three groups contains $$2$$ objects each.

Here total different objects are $$n=18$$
Four groups contains $$3$$ objects so $$\displaystyle^{18}C_{3}$$
Three groups contains $$2$$ objects so $$\displaystyle^{18}C_{2}$$
Hence No of ways $$=\dfrac{18!}{(\displaystyle^{18}C_{3})^4(\displaystyle^{18}C_{2})^3}$$


Prove that $$\displaystyle \sum _{r = 0}^n 3^r \text{ }^n\text{C}_r= 4^n$$

$$ \displaystyle \sum_{r =0 }^{n} $$  $$3^{r} $$ $$ ^{n}C_{r} = 4^{n} $$ where $$ ^{n}C_{r} = \dfrac{n!}{r!(n-r)!}$$
Solution :
Recall that $$ (1+x)^n = ^{n}C_{0}+^{n}C_{1}x^{1}+ ^{n}C_{2} x^2 + ...+ ^{n}C_{n}x^n $$
$$ \displaystyle = \sum_{r= 0}^{n}$$ $$ ^{n}C_{r} x^n $$
Thus, in the above question $$ x = 3$$
Therefore, we get
$$ \displaystyle \sum_{r=0}^{n}$$ $$ ^{n}C_{r} 3^r= (1+3)^n = 4^n $$

1179645_876975_ans_fade1ca9bc4b4892a777c5f0d0d64d04.jpg


Solve the following equation:

$$\displaystyle\, C_{3}^{x + 1} :  C_{4}^{x} = 6:5$$, then $$  x\, \epsilon \, N$$

$$\displaystyle^{x+1}C_{3}:^{x}C_{4}=6:5\implies \dfrac{(x+1)!}{(x-2)!3!}\times \dfrac{4!(x-4)!}{x!}=\dfrac{6}{5}\implies \dfrac{24(x+1)}{6(x-2)(x-3)}=\dfrac{6}{5}$$

$$\dfrac{x+1}{(x-2)(x-3)}=\dfrac{3}{10}\implies 3(x^{2}-5{x}+6)=10(x+1)\implies 3{x^{2}}-25{x}+8=0\implies x=8,\dfrac{1}{3}$$

$$\because x\in N, x=8$$


Solve the following equations.
$$\displaystyle\frac{C_{x +1}^{2x}}{C_{x - 1}^{2x + 1}} = \frac{2}{3}$$ , $$x\, \epsilon \, N$$

Given equation 
$$\dfrac{\displaystyle^{2x}C_{x+1}}{\displaystyle^{2x+1}C_{x-1}}=\dfrac{2}{3}$$
We know that $$\displaystyle^{n}C_{r}=\displaystyle^{n}C_{n-r}$$
And $$\displaystyle^{n}C_{r}=\dfrac{n}{r}\displaystyle^{n-1}C_{r-1}$$
Hence given equation can be written as 
$$\dfrac{\displaystyle^{2x}C_{2x-x-1}}{\dfrac{2x+1}{x-1}\displaystyle^{2x}C_{x-2}}=\dfrac{2}{3}$$

$$\Rightarrow \left (\dfrac{x-1}{2x+1}  \right )\left (\dfrac{\displaystyle^{2x}C_{x-1}}{\displaystyle^{2x}C_{x-2}}  \right )=\dfrac{2}{3}$$

We know that $$\dfrac{\displaystyle^{n}C_{r}}{\displaystyle^{n}C_{r-1}}=\dfrac{n-r+1}{r}$$

$$\Rightarrow \left (\dfrac{x-1}{2x+1}  \right )\left (\dfrac{2x-x+1+1}{x-1}  \right )=\dfrac{2}{3}$$

$$\Rightarrow \left (\dfrac{x+2}{2x+1}  \right )=\dfrac{2}{3}$$

$$\Rightarrow 3(x+2)=2(2x+1)$$

$$\Rightarrow 3x+6=4x+2$$

$$\Rightarrow x=4$$


Solve the following equation:
$$\displaystyle\, 11C_{3}^{x} = 24C_{2}^{x + 1}$$

$$11\dfrac { x! }{ 3!\left( x-3 \right) ! } =24\dfrac { \left( x+1 \right) ! }{ 2!(x-1)! } $$
$$\dfrac { 11 }{ 2\times 3 } (x-2)(x-1)x=\dfrac { 24 }{ 2 } x(x+1)$$
$${ 11(x }^{ 2 }-3x+2)=(24\times 3)(x+1)$$
$${ 11x }^{ 2 }-33x+22=72x+72$$
$$11{ x }^{ 2 }-105x-50=0$$
$$(x-10)(11x+5)=0$$
$$ x=10$$ or $$x=-\dfrac{5}{11}$$
since $$x$$ is natural number,hence the only possible value of $$x$$ is $$x=10$$


Solve the following equation:
$$\displaystyle\, C_{3}^{x} + C_{4}^{x} = 11 \cdot C_{2}^{x + 1}, \, x\, \epsilon \, N$$

$$\dfrac { x! }{ 3!\left( x-3 \right) ! } +\dfrac { x! }{ 4!\left( x-4 \right) ! } =11\times \dfrac { \left( x+1 \right) ! }{ 2!(x-1)! } $$
$$\dfrac { x! }{ 3!\left( x-3 \right) ! } \left[ \dfrac { 1 }{ x-3 } +\dfrac { 1 }{ 4 }  \right] =\dfrac { 11 }{ 2 } x\times \left( x+1 \right)  $$
$$ \dfrac { \left( x-3 \right) (x-2)(x-1)x }{ 3 } \left[ \dfrac { 4+x-3 }{ (x-3)(4) }  \right] =11x(x+1) $$
$$ \dfrac { (x-2)(x-1) }{ 3 } \left[ \dfrac { x+1 }{ 4 }  \right] =11(x+1) $$
$$(x-2)(x-1)=11\times 12  $$
$${ x }^{ 2 }-3x+2=132 $$
$$ { x }^{ 2 }-3x-130=0$$
$$ { x }^{ 2 }+10x-13x-130=0$$
$$x[x+10]-13[x+10]=0$$
$$(x-13)(x+10)=0$$
$$x=13$$ or $$x=-10$$
But x cannot be negative so $$x=13$$



Solve the following equation:
$$\displaystyle12C_{1}^{x} + C_{2}^{x + 4} = 162 , x\, \epsilon \, N$$

$$12\dfrac { x! }{ (x-1)! } +\dfrac { (x+4)! }{ 2!(x+4-2)! } =162$$
$$  12(x)+\dfrac { (x+4)! }{ 2\times (x+2)! } =162$$
$$  2(12x)+(x+3)(x+4)=162\times 2$$
$$24x+{ x }^{ 2 }+7x+12=324$$
$${ x }^{ 2 }+31x-312=0$$
$$x=\dfrac { -31\pm \sqrt { 961+1248 }  }{ 2 } $$
$$=\dfrac { -31\pm \sqrt { 2209 }  }{ 2 }$$ 
$$=\dfrac { -31\pm 47 }{ 2 }$$
 $$=\dfrac { -31+47 }{ 2 } =8$$
$$=\dfrac { -31-47 }{ 2 } =-39$$
Since $$x$$ have only positive value as $$C$$ is not defined for negative value.
$$x=8$$


Out of eight crew members three particular members can sit only on the left side.Another two particular members can sit only on the right side. Find the number of ways in which the crew can be arranged so that four men can sit on each side.

Out of $$8, 3$$ on left , $$2$$ on right remaining $$3$$ anywhere 
Choose $$1$$ out of $$3$$ remaining to fill the $$4^{th}$$ seat on left
By n$$3 ^{1}C_{1}$$
Now other two must fit on right arrange all.
$$3C_{1}  \times 4! \times 4!= 1728$$


Each of the six in squares in the strip, shown in figure, is to be coloured with anyone of $$10$$ different colours so that no two adjacent squares have the same colour. Find the number of ways of colouring the strip.
880344_81ecf0fcceb74025a560461e5f65c4f3.png

Now we are to colour the given six squares with $$10$$ colours, in such a manner that no two adjacent squares have same colour.
We have $$10$$ colours to colour the first square. 
But we have $$9$$ colour to colour the second box as we can't use the colour which we have used in first square.
Again to colour the third square we will have $$9$$ colours as we can use the colour of first square but not the colour of second.
In the same manner we will have $$9$$ colours to colour third, fourth,....., sixth square. And in this pattern no two square will have same colour.
Total number of ways =$$10\times 9\times9\times 9\times 9\times9=590490$$.


Prove that $$^nC_r = ^nC_{n-r}$$.

$$^nC_r = ^nC_{n-r}$$.
The number of combinations of n dissimilar things taken r at a time will be $$^nC_r $$. Now if we take out a group of r things, we are left with a group of (n-r) things. Hence the number of combinations of n things taken r at a time is equal to the number of combinations of n things taken (n-r) at a time.

$$\therefore $$  $$^nC_r = ^nC_{n-r}$$.

Alternative method :
$$^nC_r = \frac{n!}{r! (n-r)!}$$
$$ ^nC_{n-r} = \frac{n!}{(n-r)! (n-n+r)!} = \frac{n!}{r!(n-r)!}$$
$$\therefore $$  $$^nC_r = ^nC_{n-r}$$.
$$.


There are $$40$$ doctors in a surgical department. In how many ways can they be arranged to form the following teams: (a) a surgeon and an assistant; (b) a surgeon and four assistants?

a) first divide the doctors into 20 groups with 2 persons in each and then select one as a surgeon this can be done $$40!/20$$and other as an assistant, this can be done in $$2$$ ways
$$\therefore$$ total number of ways is $$40!/10$$
b) ) first divide the doctors into 8 groups with 5 persons in each and then select one as a surgeon this can be done $$40!/8$$and others as  assistants, this can be done in $$5$$ ways
$$\therefore$$ total number of ways is $$5\times 40!/8!$$


In how many ways can $$10$$ identical presents be distributed among $$6$$ children so that each child gets at least one present?

The number of ways of distributing $$N$$ identical objects among $$R$$ group such that each group can have any number of objects is given by:

$$C(N+R-1, R-1)= C( 10+6-1, 6-1)$$

$$=C(15,5)$$

$$=3003$$



How many five-digit numbers are there in whose notation each successive digit exceeds its predecessor?

the answer is the number of ways in which we can select 5 different digits out of 0 to 9 since if they are different we can make a single number in the ascending order but we have to consider that if we take 0 at first it will be a 4 digit number

from $$1$$ to $$9$$ we can select $$5$$ numbers in $${ 9 }_{ { C }_{ 5 } }=126$$ ways
now if we take 0 it must be kept at first according to the question so we shoulldnot take 0, therefore, the answer is 126


In a $$12$$-storey house $$9$$ people enter a lift cabin. It is. known that they will leave the lift in groups of $$2, 3$$ and $$4$$ people at different storeys. In how many ways can they do so if the lift does not stop at the second storey?

Given a $$12$$-storey  house in which a people enter a lift cabin$$.$$ They will leave in floor $$:$$ $$2,3$$ and $$4.$$
As the lift does not stop upto the $${2}^{nd}$$ storey$$,$$
hence no$$:$$ of possible stops in lift$$=12-2=10$$
No$$:$$ of ways of choosing $$3$$ stops $$={C}^{9}_{3}=\cfrac {9\cdot8\cdot7}{3\cdot2\cdot1}=84$$
For any particulars choice of steps$$,$$ no$$:$$ of ways for $$9$$ person to leave in $$3$$ groups$$=3\cdot2\cdot1=6$$
$$\therefore$$ Required no$$:$$ of ways$$=84\times6=504$$ ways$$.$$


If $$^nC_7 = ^nC_4$$. Find n.

$$C_{7}^{n}=C_{4}^{n}$$
We know that, $$C_{r}^{n}=C_{n-r}^{n}$$
$$\Rightarrow\,C_{7}^{n}=C_{n-7}^{n}=C_{4}^{n}$$
$$\Rightarrow n-7=4$$
$$\therefore n=11$$



Two variants of a test are suggested to twelve students. In how many ways can the students be placed in two rows so that there should be no identical variants side-by-side and that the students sitting one behind the other should have the same variant?

Consider the seat in the front row and the one behind it in the basic now$$.$$ So$$,$$ we choose there pair of seats for each variant$$.$$ 
No$$:$$ of seats paired from $$1$$ to $$6.$$
We have $$2$$ choices for the variant assigned to seat pair $$1.$$
Then if the variant is also assigned to seat$$.$$
Pair $$3$$ or $$5,$$ the remaining seat pair can be assigned in $$3$$ different ways$$.$$
Similarly it is also assigned to seat $$4$$ and $$6.$$
$$\Rightarrow 2(2.2+4+2)=20$$ different assignments
$$\Rightarrow 20\cdot{4!}^{3}=6!{4!}^{2}$$


If combinations of letters be formed by taking only 5 letters at a time out of the letters of the word "METAPHYSICS". In how many of them will letter $$T$$ occur?

There are 11 letters T,S,S and 8 all different since T is a must we have to select only 4 out of remaining S,S and 8 all different. Mind we have to find only combination are not words (arrangements not be considered) 
(a) $$2$$ alike $$(S,S), 2$$ different $$= {^2C}_1 . {^8C}_2 = 28$$

(b) $$1S, 3$$ different $$= {^8C}_3 = 56$$
 
(c)No $$S, 4$$ different $${^8C}_4 = 70$$

For (b), (c)
Now (b) and (c) would mean that we have to select 4 out of 9 different letters $${^9C}_4 = \dfrac{9.8.7.6}{1.2.3.4}$$

otherwise also $${^8C}_3 + {^8C}_4 = {^9C}_4$$

Hence total $$= 28 + 56 + 70 = 28 + 126 = 154$$ ways.


If $$^{28}C_{2r} : ^{24}C_{2r - 4} = 225 : 11$$, then find r

$$\cfrac{^{28}C_{2r}}{^{24}C_{2r-4}}=\cfrac{225}{11}$$
$$\Rightarrow\cfrac{\cfrac{28!}{2r!(28-2r)!}}{\cfrac{24!}{(2r-4)!(28-2r)!}}=\cfrac{225}{11}$$
$$\Rightarrow\cfrac{28\times24\times26\times 25}{2r\times2r-1\times2r-2\times 2r-3}=\cfrac{225}{11}$$
$$\Rightarrow 9(2r)(2r-1)(2r-2)(2r-3)=14\times2\times9\times3\times13\times2\times11$$
$$\Rightarrow(2r)(2r-1)(2r-2)(2r-3)=14\times13\times12\times11$$
$$\Rightarrow2r=14$$
$$\Rightarrow r=7$$


There are $$6$$ books of Economics, $$3$$ of Mathematics and $$2$$ of Accountancy. In how many ways  can these be placed on a shelf, if:
Books on the same subject are together ?
Books on the same subject are not together ?

For 1:  
We have $$6$$ books of Economics, $$3$$ of Mathematics and $$2$$ of Accountancy
Arranging the books within the branches:
Economics - $$6!$$
Maths - $$3!$$
Accountancy - $$2!$$
Thus the arranging branches are $$3!$$
Thus, total arrangement 
$$6!\times3!\times2!\times3!=32,400$$
For 2: We have to add all the books together then arrange it
$$6+3+2=11$$
Thus the total arrangement are:
$$11!$$
$$39,916,800$$



Prove that only 1422 different four letter words can be formed out of the letters of the word INEFFECTIVE.

Total $$(3e, 2f, 2i$$ rest 4 all different) i.e. 7 types.
(i) Al different $${^6P}_4 = 6 \times 5 \times 4 \times 3 = 360$$ .

(ii) Two different, two alike.
$${^2C}_1 \times {^5C}_2 \times \dfrac{4!}{2!} = 240$$

(iii) 3 alike, 1 different 
$${^1C}_1 \times {^5C}_1 \times \dfrac{4!}{3!} = 20$$

(iv) 2 alike of one type and 2 alike of other type.
$${^2C}_2 \times \dfrac{4!}{2!2!} = 6$$.

$$\therefore$$ Total number of words $$= 360 + 240 + 20 + 6 = 626$$.


If $$ ^nC_r  = { ^nC}_s$$ then prove that $$r =s$$ or $$n = r+s$$

$${ ^{ n }{ C } }_{ r }={ ^{ n }{ C } }_{ s }$$  Let $$r\neq s$$  $$\&$$  $$r>s$$  then $$n-r<n-s$$
As $$\dfrac { n! }{ \left( n-r \right) !r! } =\dfrac { n! }{ \left( n-s \right) !s! } $$
$$\Rightarrow \left( n-s \right) !s!=\left( n-r \right) !r!$$
$$\Rightarrow s!\left( s+1 \right) \left( s+2 \right) ........r\left( n-r \right) !=s!{ \left( n-r \right) !}{ \left( n-r+1 \right)  } { \left( n-r+2 \right)  }....{ \left( n-s \right)  }$$
$$\Rightarrow \left( s+1 \right) \left( s+2 \right)......r=\left( n-r+1 \right)\left( n-r+2 \right)......\left( n-s \right)$$
Since each side of this equation is a product of $$r-s$$ consecutive positive integers, we get $$r=n-s.$$
$$\Rightarrow r+s=n$$ Similarly if $$r<s,$$ the also we can prove that $$r+s=n.$$
$$\therefore$$ If $${ ^{ n }{ C } }_{ r }={ ^{ n }{ C } }_{ 5 }$$ there $$r=s$$ or $$r+s=n.$$
Hence, proved.


Prove that $${}^n{c_r}.r! = {}^n{p_r}$$

To prove $${ ^{ n }{ C } }_{ r }.r!={ ^{ n }{ P } }_{ r }$$
$$\Rightarrow \dfrac { n! }{ \left( n-r \right) !r! } ={ ^{ n }{ C } }_{ r }$$
and $${ ^{ n }{ P } }_{ r }=\dfrac { n! }{ \left( n-r \right) ! } $$
As $${ ^{ n }{ C } }_{ r }.r!=\dfrac { n! }{ \left( n-r \right) !r! } \times r!=\dfrac { n! }{ \left( n-r \right) ! }={ ^{ n }{ P } }_{ r }.$$
Hence, proved.


If $$^nC_{12} = ^nC_{8}$$, then find the value of $$^nC_{17}$$.

We have for $$^nC_r=^nC_{n-r}$$.
Now given
$$^nC_{12}=^nC_{8}$$
or, $$^nC_{n-12}=^nC_{8}$$
$$\Rightarrow n-12=8$$
or, $$n=20$$.
Then $$^nC_{17}$$
$$=^{20}C_{17}$$
$$=^{20}C_{20-17}$$
$$=^{20}C_{3}$$
$$=\dfrac{20.19.18}{3.2.1}$$
$$=20.57$$
$$=1140$$


Number of $$9$$ digits numbers divisible by nine using the digits from $$0$$ to $$9$$ if each digit is used almost once is $$K=8!$$, then K has the value equal to____

$$1+2+...3...9=\cfrac { 9\times 10 }{ 2 } =95$$
All the $$9$$ digit numbers using $$1$$ to $$9$$ are divisible by $$9$$
$$9!$$
The case when we use $$0$$ we must exclude $$9$$ from the number also $$0$$ can't be at the $${ 9 }^{ th }$$
$$8\times 8!$$
$$9!+8\times 8!=12\times 8!$$
$$K=17$$


If $$7$$ mercury lamp are there in a room. How many ways room can be lit?

there are $$7$$ mercury lamps

number of ways room can be lit=number of ways of selecting mercury lamps and liting them

if we assume all mercury lamps are identical then 

number of ways=number of mercury lamps selected 

$$=1+2+3+4+5+6+7=28$$ways


How many arrangements can be formed by letter of word "MISSIPPI"?

$$M=1\\I=3\\S=2\\P=2$$

Now, number of places are $$=8$$

So, number of arrangements are $$=\dfrac{8!}{3!2!1!2!}=1680$$


The value of $$t$$ which satisfy $$(t-[|\sin x|])!=3!5!7!$$ is/are . Where [.] is $$GIF$$  


1326512_1063326_ans_8b83ec4991364a62bc047feb0eea3e22.jpg


In a tennis tournament in which every pair has to play with every other pair, 10 players are playing. Find the number of games played.

Total number of players $$=10!$$

Numbers of game played= $$\dfrac { 10! }{ { (2! })^{ 5 }5! } =945$$


Find the numerically greatest term in the expansion $$(3-5x)^{15}$$ when $$x=\dfrac{1}{5}$$

Greatest digit to be find  $$(3-5x)^{15}$$ when $$x=\dfrac{1}{5}$$
$$T_x=^{15}C_r (3)^{15-r} (-5x)^{r}$$
$$T_x=^{15}C_r (3)^{15-r} (-1)^{r}$$
$$x=+\dfrac{1}{5}$$ and $$(-1)^r$$ will chnage sign.
$$T_x=^{15}C_r \quad 3^{15-r}$$
Maximum is obtained when both are maximum
Therefore,$$r=7$$
Maximum term=$$^{15}C_r \quad (3)^{15-r}$$
when r=7
$$T_x=^{15}C_7 \quad (3)^{15-7}$$
$$T_x=^{15}C_7 \quad (3)^{8}$$
$$T_x=42,220,035$$
$$T_x=4.2 \times 10^7$$


Find the number of ways of arranging six persons (having A, B, C and D among them) in a row so that A, B, C, and D are always in order ABCD (not necessarily together).

Choosing four position out of 6 and putting A B C D in order
_ _ _ _ _ _
A,B,c,D
Number of ways =$${ { 6 }_{ C } }_{ 4 }\times 2!=30$$


A question paper consists of $$11$$ question divided into two section $$1$$ and $$2$$. section $$1$$ consits of $$5$$ questions and section $$2$$ consists of 6 questions. In how many ways can a student select $$6$$ questions, taking at least $$2$$ questions from each section?

Total number of question =$$11$$

Part 1 contains$$ 5$$ questions and part $$2$$ contain $$6$$ questions.

A student has to select $$6$$ questions all in which there is at least $$2$$ questions from each part. 

Now different possibilities can occur.

   Part1 (5 questions)            Part2 (6 questions)

          $$ 3$$                                    $$3$$

           $$4$$                                   $$2$$

          $$ 2$$                                    $$4$$

Now total number of ways is

 =   (5C3 × 6C3 )+ ( 5C4 × 6C2 ) + ( 5C2× 6C4 )$$

= {(5×4×6×5)/ (2×3×2)+ {(5×6 ×5)/(2)} + {(5×4×6 ×5)/(2×2)}$$

= $$200$$ + $$75$$ + $$150$$

= $$425$$

So, the total number of ways a student can select the questions is $$425$$

Note: We have to take at least$$ 3$$ questions at once, not in different parts like first take$$ 3$$, then$$ 2$$, etc.

If we do so, then it is wrong because it is given in the question that we have to take at least 2 questions at once.

 

 

 



What is the number of the possible square matrix of order $$3$$ with each entry $$0$$ or $$1$$? If your answer is $$2^n$$ , then find $$n$$.

A square matrix of order $$3$$ with each entry $$0$$ or $$1$$
Now for each entry we have $$2$$ choices, i.e., it can be filled in $$2$$ ways.
And there are $$9$$ places as it is a $$3\times 3$$ matrix.
Thus the total number of ways of filling all the entries are
$$2\times 2\times 2\times 2\times 2\times 2\times 2\times 2\times 2\times =512$$
$$2^9=512$$
$$2^n=2^9$$
$$n=9$$.


How many automobile license plates can be made if each plate contains two different letters followed by three different digits?

There are 5 places to fill
2 places of alphabet(out of 26) can be filled in $$=26*25\ ways$$

3 places of digits(out of 10) can be filled in $$=10*9*8\ ways$$

No of different plates $$=26*25*10*9*8=468000$$


How many number greater than a million can be formed with the digits $$2, 3, 0, 7, 7, 3, 7,?$$

Here

One million $$=10,00,000.$$ given numbers are $$2,3,0,7,7,3,7$$

A number greater than $$1000000$$  has $$7$$  places, and all the digits are to be used. But $$7$$ is repeated thrice and $$3$$ is repeated twice.

Total number of ways arranging $$7$$  digits$$=\dfrac{7!}{2!\times 3!}=\dfrac{7\times 6\times 5\times 4\times 3!}{2\times 1\times 3!}=420$$

But the numbers begin with $$0$$ are no more $$7$$ digits numbers then reject those numbers.

Therefore, these can be arranged in $$\dfrac{6!}{2!\times 3!}=60$$

Then required number arrangements$$=420-60=360$$



Find the number of arrangements that can be formed by using all the letters of the word MATRIX, so that the vowels occupy even places.

$$Number\>of\>letters\>in\>MATRIX\>=6\>\\even\>positions=2nd,4th\>and\>6th\\two\>vowels\>A,I\\so\>two\>vowels\>in\>three\>places\>can\>be\>arranged\>in\>=\>3\times2=6\>ways\\Rest\>four\>positions\>can\>be\>filled\>by\>4\>letters\>in\>=\>4!\>ways\>=24\>ways\\\therefore\>Total\>permutation=24\times6\\144$$



Find the number of ways in which : (a) a selection (b) an arrangement, of four letters can be made from the letters of the word 'PROPORTION'.

Given word PROPORTION
$$P-2,R-2,0-3,T,I,N,$$
$$(i)$$ Words with all distinct letters $$= 6_{c4}=15 $$ways
Arrangement=$$6_{p4}=360$$ ways

$$(ii)$$ One letter repeat twice 
Selection $$=3_{c1}\times 5_{c2}$${i.e one from $$P/R/O$$ & $$2$$ from the $$5$$} 
Arrangement $$=3_{c1}\times 5_{c2}\times \dfrac{4!}{2!}=360$$ 

$$(iii)$$Two letter repeated twice 
Selection $$=3_{c2}=3$$ [i.e two from $$P/R/O$$]
Arrangement $$=3_{c2}\times \dfrac{4!}{2!.2!}=3\times 6=18$$

$$(iv)$$ Three letter some 
Selection $$=1_{c1}\times 5_{c1}=5$$ [i.e one from orther $$3$$ all $$'0"$$  ]
Arrangement$$=5\times\dfrac{4!}{3!}=20$$ 
$$\therefore$$ Total selection $$= 15+30+3+5$$
$$=53$$ ways
Total arrangement $$=360+360+18+20$$
$$=758$$ ways




















Evaluate
$$^{4}C_{3}+^{4}C_{4}=?$$

Given
$$\ ^4C_3+\ ^4C_4=\dfrac{4!}{3!(4-3)!}+\dfrac{4!}{4!(4-4)!}$$

                      $$=\dfrac{4\times3!}{3!}+1$$

                      $$=4+1$$

                      $$=5$$


Evaluate
$$^{21}C_{15}-^{10}C_{4}$$

Given
$$\ ^{21}C_{15}-\ ^{10}C_4=\dfrac{21!}{15!(21-15)!}-\dfrac{10!}{4!(10-4)!}$$

                          $$=\dfrac{21!}{15!6!}-\dfrac{10!}{4!6!}$$

                          $$=\dfrac{21\times20\times19\times18\times17\times16\times15!}{15!6!}-\dfrac{10\times9\times8\times6!}{4!6!}$$

                          $$=\dfrac{21\times20\times19\times18\times17\times16}{6!}-\dfrac{10\times9\times8\times7}{4!}$$

                          $$=\dfrac{39070080}{720}-\dfrac{5040}{24}$$

                          $$=54264-210$$

                          $$=54054$$


Every telephone number is of $$7$$ digits. How many telephone numbers are there which do not include any other digits but $$2, 3, 5 \& 7$$?

$$4$$ for each place $$\rightarrow \therefore 4\times 4\times ....$$
$$=4^{7}$$


In how many ways can $$3$$ people be seated in a row containing $$7$$ seats $$?$$

$$3$$ people to be seated in a row containing $$7$$ sectors
Total ways $$={^{7}C_3}\times 3!={^7P_3}=\dfrac{7!}{4!}$$
Total ways $$=\dfrac{7\times 6\times 5\times 4!}{4!}=210$$.


In how many ways can $$3$$ people be seated in a row containing $$7$$ seats $$?$$

No of People $$=3$$
No of seats $$=7$$

Hence, no of ways of arrangement of people $$= ^{7}P_3=\dfrac{7!}{(7-3)!}=210$$


There are $$2$$ gates to enter a school and $$3$$ staircases from first floor to the second floor. How many possible ways are there for a student to go from outside the  school to a classroom on the second floor and come back ?

From outside to class room on second floor:
Student can go into school at $$2$$ ways. He can go to second floor from first floor in $$3$$ ways.
Since, he has to do both,
No. of ways of going to class$$=2\times 3=6$$
In the same $$6$$ ways he can come back. Since, he has to go in and come back, total no. of ways$$=6\times 6=36$$.

1179472_1159128_ans_11256f2009934a7191782b8736f34e08.jpg


Find the exponent of $$10$$ in $$^{75}C_{25}$$

$$^{75}C_{25}=\dfrac{75!}{25!(75-25)!}$$
          $$=\dfrac{75!}{25!50!}$$
Now we have to count powers of 10 in $$75!,\ 25!,\ 50!$$
$$10=5\times2$$
Now number of powers of 5 will be deciding factor to obtain as exponent of 2 > Exponent of 5
Exponent of 5 in 75!
$$=\dfrac{75}{5}+\dfrac{75}{5^2}+\dfrac{75}{5^3}+........$$
$$=15+3+\dfrac{75}{125}$$
$$=15+3+0$$             [As x=0 when 0 $$\le$$ x < 1]
$$=18$$
Exponent of 5 in 50!
$$=\dfrac{50}{5}+\dfrac{50}{25}+\dfrac{50}{125}+........$$
$$=10+2+0$$
$$=12$$
Exponent of 5 in 25!
$$=\dfrac{25}{5}+\dfrac{25}{25}+\dfrac{25}{125}+........$$
$$=5+1+0$$
$$=6$$
Hence we have
$$\dfrac{10^{18}}{10^{12}\times10^{6}}=\dfrac{10^{18}}{10^{12+6}}=\dfrac{10^{18}}{10^{18}}=1=10^0$$
Hence exponent of 10 will be 0 in $$^{75}C_{25}$$


Find the number of parallelogram formed if 10 parallel lines in a plane are intersected by a family of 12 parallel lines.

A parallelogram is formed by choosing two straight lines 2 lines from the set of 10 lines and 2 lines from the set of 12 parallel lines.
Two parallel lines can be chosen from the set of 10 parallel lines in $$^{10}C_2$$ ways.
Two parallel lines can be chosen from the set of 12 parallel lines in $$^{12}C_2$$ ways.
Hence, the number of parallelogram formed $$=^{10}C_2\times^{12}C_2$$

                                                                           $$=\dfrac{10!}{2!8!}\times\dfrac{12!}{2!10!}$$

                                                                           $$=\dfrac{10\times9}{2}\times\dfrac{12\times11}{2}$$

                                                                           $$=2970$$


$${\text{Find the value of}}\;{\text{n,}}\;{\text{if}}\;{\text{(n + 1)!}}\;{\text{ = }}\;{\text{12}} \times {\text{(n - 1)!}}$$

$$(n+1)! = 12 \times (n-1)!$$

$$\Rightarrow (n+1) n (n-1) ! = 12 (n-1)!$$

$$\Rightarrow n^{2}+n=12$$

$$\Rightarrow n^{2}+n-12=0$$

$$\Rightarrow n^{2}+4n-3n-12=0$$
 
$$\Rightarrow n (n+4) - 3 (n+4)=0$$

$$\Rightarrow (n-3)(n+4)=0$$
 
$$\Rightarrow  n=3 \ \ n \neq-4 \because n$$ is $$(+)ve$$


How many ways are there to arrange the letters in the word $$GARDEN$$ with the vowels in alphabetical order ?

The word $$GARDEN$$ has 6 letters.
Therefore, all the ways of permuting the letters of $$GARDEN$$ are: $$6!$$

Now, the questions wants the vowels to appear in alphabetical order, this means that in all the words, $$A$$ must appear before $$E$$.
There are $$2!$$ ways of permuting $$A$$ and $$E$$ out of which we just want 1, so the final answer is: $$6!\cdot\dfrac{1}{2!} = \dfrac{720}{2} = \boxed{360}$$


If $$^{n+1}C_{r+1}:^{n}C_r:^{n-1}C_{r-1}=11:6:3,nr$$ is equal to

$${^{n+1}{C}_{r+1}} : {^{n}{C}_{r}} : {^{n-1}{C}_{r-1}} = 11 : 6 : 3$$
Therefore,
$$\cfrac{{^{n+1}{C}_{r+1}}}{{^{n}{C}_{r}}} = \cfrac{11}{6}$$
$$\because \cfrac{{^{n+1}{C}_{r+1}}}{{^{n}{C}_{r}}} = \cfrac{\left( n + 1 \right)!}{\left( r + 1 \right)! \left( n - r \right)!} \times \cfrac{r! \left( n - r \right)!}{n!} = \cfrac{n+1}{r+1}$$
$$\therefore \cfrac{n+1}{r+1} = \cfrac{11}{6} ..... \left( 1 \right)$$
Similarly,
$$\cfrac{{^{n}{C}_{r}}}{{^{n-1}{C}_{r-1}}} = \cfrac{n}{r} = \cfrac{6}{3}$$
$$n = 2r ..... \left( 2 \right)$$
Now from $${eq}^{n} \left( 1 \right) \& \left( 2 \right)$$, we have
$$\cfrac{2r + 1}{r + 1} = \cfrac{11}{6}$$
$$\Rightarrow 6 \left( 2r + 1 \right) = 11 \left( r + 1 \right)$$
$$\Rightarrow 12r + 6 = 11r + 11$$
$$\Rightarrow r = 5$$
Substituting the value of $$r$$ in $${eq}^{n} \left( 2 \right)$$, we have
$$n = 2r = 10$$
$$\therefore nr = 5 \times 10 = 50$$
Hence the value of $$nr$$ is $$50$$.


Evaluate:
$$1 ^ { 2 } c _ { 1 } + 2 ^ { 2 } c _ { 2 }+ 3 ^ { 2 } c _ { 3 }+ 4 ^ { 2 } c _ { 4 }+ ...... + n ^ { 2 } c _ { n }$$

$$s=1{^{2}C_1}+2{^2C_2}+3{^2C_3}+4{^2C_4}+.....+n{^{2}C_n}$$

$$(1+x)^n={^{n}C_0}+{^{n}C_1}x+{^{n}C_2x^2}+{^{n}C_3x^3}+.....+{^{n}C_nx^n}$$

Differentiable w.r.t. $$x$$

$$n(1+x)^{n-1}=0+{^{n}C_1}+2{^{n}C_2}x+3{^{n}C_3x^2+.....+n{^{n}C_x}x^{n-1}}$$

Multiply whole expression with x

$$nx(1+x)^{n-1}={^{n}C_1x}+2{^{n}C_2x^2}+3{^{n}C_3x^3}+...…+n{^{n}C_nx^n}$$

Differentiable w.r.t. $$x$$ again

$$n(1+x)^{n-1}+nx(n-1)(1+x)^{n-2}={^{n}C_1}+2^2{^{n}C_2}x+3^2{^{n}C_3x^2}+n{^{n}C_n}x^{n-1}$$

Put $$x=1$$

$$\Rightarrow S={^{n}C_1}+2^2{^{n}C_2}+3^2{^{n}C_3}+...….+n^2{^{n}C_n}$$

$$=n(1+1)^{n-1}+n.1.(n-1)(1+1)^{n-2}$$

$$=n2^{n-1}+n(n-1)2^{n-2}$$

$$=n2^{n-2}(2+(n-1))=n 2^{n-2}(n+1)$$.


Prove that:
$$^nC_r+\ ^nC_{r-1}=\ ^{n+1}C_r$$

$$\quad { _{  }^{ n }{ C } }_{ r }+={ _{  }^{ n }{ C } }_{ r-1 }$$
$$=\cfrac { n! }{ n!(n-r)! } +\cfrac { n! }{ (n-1)!(n-r+1)! } =\cfrac { n! }{ (r-1)!(n-r)! } \left[ \cfrac { 1 }{ r } +\cfrac { 1 }{ (n-r+1) }  \right] $$
$$=\cfrac { n! }{ (r-1)!(n-r)! } \left[ \cfrac { (n+1) }{ r(n-r+1) }  \right] =\cfrac { (n+1)! }{ r!(n-r+1)! } ={ _{  }^{ n+1 }{ C } }_{ r }$$


Find the number of ways in which a sum of $$10$$ can be obtained by throwing a dice thrice.

$$ a+b+c = 10 $$
Possible values of $$a,b,c$$ are where $$ 1\leq a,b,c\leq 6 $$

$$ (1,3,6)\rightarrow $$ can be arranged in $$3!$$ ways = $$6 $$

$$ (1,4,5)\rightarrow $$ can be arranged in $$3! $$ ways = $$6$$

$$ (2,3,5)\rightarrow $$ can be arranged in $$3! $$ ways = $$6$$

$$ (2,2,6)\rightarrow $$ can be arranged in $$\dfrac{3!}{2}$$ ways $$= 3$$ (As 2 is repeated twice)

$$ (2,4,4)\rightarrow $$ can be arranged in $$\dfrac{3!}{2}$$ ways $$= 3$$ (4 is repeated twice)

$$ (3,3,4)\rightarrow $$ can be arranged in $$\dfrac{3!}{2}$$ ways = $${3}$$ (3 is repeated twice)

So total $$27$$ ways.


If $$4$$ cards  are chosen from a pack of $$52$$ playing cards?
In how many of these four cards are of the same suit?

Numbers of ways of choosing $$4$$ cards is $$^{52}C_{4}$$

there will be $$13$$ cards of same suit 

Numbers of ways is $$4\times ^{13}C_{4}$$


Zeroes at the end of $$125!$$

Zeros at the end of $$125!$$
$$\Rightarrow x!=\left[ \dfrac{x}{5}\right] +\left[ \dfrac{x}{5^2}\right] +......$$
$$\left[ .\right]$$ is the box function
$$\Rightarrow 125!=\left[ \dfrac{125}{5}\right] +\left[ \dfrac{125}{5^2}\right] +\left[ \dfrac{125}{5^3}\right] +\left[ \dfrac{125}{5^4}\right]$$
              $$=25+5+1+0.....$$
              $$=31$$ zeros
Hence, the answer is $$31.$$



Find the number of ways of selecting 4 even numbers from the set of first 100 natural numbers. 

Even number in first $$160$$ natural number are: $$2,\ 4,\ 6,\ 8,........,100$$
Total numbers are $$=50$$
No. of ways of selrty $$4=\, ^{50}C_4$$


There are $$30$$ ways in which five distinct balls can be put into two distinct boxes so that no box remains empty.

No. of ways $$={ 5 }_{ { C }_{ 1 } }+{ 5 }_{ { C }_{ 2 } }+{ 5 }_{ { C }_{ 3 } }+{ 5 }_{ { C }_{ 4 } }$$
                    $$={ 2 }^{ 5 }-1-1=30$$
Hence the statement is true.


In how many ways can the following prizes be given away to a class of $$20$$ students, first and second in Mathematics, first and second in physics, first in Chemistry and first in English ?

First prize in mathematics can be given in $$=30$$ ways
second prize in mathematics $$=29$$ ways
First in physics $$=30$$ ways
second in physics $$=29$$ ways
First prize in chemistry can be given in $$=30$$ ways
similarly first in English $$=30$$ ways
All the $$6$$ prizes can be given in 
    $$=30\times 29\times 30\times 29\times 30\times 30$$ ways
    $$=681,210,000$$
Total number of ways to distribute all $$6$$ prizes
$$=681210000$$


Find $$x$$, if $$^nC_5=x.^nP_5$$ then x = $$\dfrac {1}{r!}$$ then r= 


1961081_1243553_ans_74b9def087214c2bafea4bb0a1976cb3.jpeg


How many numbers greater than 10,00,000 can be formed with the digits 0,1,2,1,2,2,3

Image 1
No. of numbers starting with $$1$$ are $$\cfrac { 6! }{ 3! } =6\times 5\times 4$$
$$=30\times 4$$
$$=120$$
No. of numbers starting with $$2$$ are (Image 2)
$$\cfrac { 6! }{ 2!2! } =\cfrac { 6\times 5\times 4\times 3 }{ 2 } =30\times 6=180$$
No. of numbers starting with $$3$$ are (Image 3)
$$\cfrac { 6! }{ 2!3! } =\cfrac { 6\times 5\times 4 }{ 2 } =6\times 5\times 2=60$$
$$\therefore $$Total no. of numbers are $$120+180+60$$
$$=300+60=360$$

1207206_1244597_ans_d3321e23225c450a8f0e70ca8bda743a.JPG


In how many ways $$5$$ different balls can be distributed into $$3$$ boxes so that no box remains empty?  

Lets fill each box with one ball.

So we are now left with 2 balls.

Now , let the boxes be labelled as A B C.

After each of them contains 1 ball each.

Possible ways of placing the remaining 2 balls:

Either both are placed in A or B or C -> 3 ways

Either (one placed in A and other in B ) or (one placed in B and other in C ) or (one placed in A and other in C ). -> 3 ways

Total , 6 ways.



Number of increasing permutations of  $$m$$  symbols are there from the  $$n$$  set numbers  $$\left\{ a _ { 1 } , a _ { 2 } , \dots , a _ { n } \right\}$$  where the order among the numbers is given by  $$a _ { 1 } < a _ { 2 } < a _ { 3 } < \ldots a _ { n - 1 } < a _ { n }$$  is :

No. of ways of choosing in things from an things $$={ n }_{ { C }_{ m } }$$
$$\therefore$$   No. of increasing permutations $$=\dfrac { n! }{ \left( n-m \right) !m! } $$


$$^{ 8 }{ P }_{ 5 }+5.^{ 8 }{ P }_{ 4 }=^{ 9 }{ P }{ _{ r } }$$

We  have,

 

We know that,

$$^{n}{{P}_{r}}=\dfrac{n!}{\left( n-r \right)!}$$

$$ now, $$

$$ ^{8}{{P}_{5}}+{{5.}^{8}}{{P}_{4}}{{=}^{9}}{{P}_{r}} $$

$$ \Rightarrow \dfrac{8!}{\left( 8-5 \right)!}+5\times \dfrac{8!}{\left( 8-4 \right)!}=\dfrac{9!}{\left( 9-r \right)!} $$

$$ \Rightarrow \dfrac{8!}{3!}+5\times \dfrac{8!}{4!}=\dfrac{9\times 8!}{\left( 9-r \right)!} $$

$$ \Rightarrow 8!\left( \dfrac{1}{6}+\dfrac{5}{24} \right)=\dfrac{9\times 8!}{\left( 9-r \right)!} $$

$$ \Rightarrow \dfrac{4+5}{24}=\dfrac{9}{\left( 9-r \right)!} $$

$$ \Rightarrow \dfrac{9}{24}=\dfrac{9}{\left( 9-r \right)!} $$

$$ \Rightarrow \dfrac{1}{24}=\dfrac{1}{\left( 9-r \right)!} $$

$$ \Rightarrow \left( 9-r \right)!=24 $$

$$ \Rightarrow \left( 9-r \right)!=3! $$

$$ \Rightarrow 9-r=3 $$

$$ \Rightarrow -r=3-9 $$

$$ \Rightarrow -r=-6 $$

$$ \Rightarrow r=6 $$

Hence, this is the answer.



The letters of the word $$ COCHIN$$  are permuted and all the permutations are arranged in an alphabetical order as in an English dictionary. The number of words that appear before the word  $$COCHIN$$  is

Total number of words starting with $$C=5!=120$$

It includes the word COCHIN also.

Therefore, the number of words that appears before the word COCHIN is less than $$120$$.

Total number of words starting with CO=$$4!=24$$

The other cases, the total words starting with CH,CI,CN is $$4!=24$$

Total numbe rof words starting with $$10=4 \times 24=9!=96$$

 



$$If\quad \overset { n }{ \underset { 8 }{ C }  } =\overset { n }{ \underset { 2 }{ C }  } $$ then find $$\overset { n }{ \underset { 2 }{ C }  } $$


1182698_1312499_ans_c75d97f77d794a77a5ee28b6efe5d453.jpg


$$^{ 22 }{ P }_{ r+1 }:^{ 20 }{ P }_{ r+2 }=11:52$$


1477135_1310485_ans_6d7553a785e84cc88346905375903e08.PNG


Four couples (husband and wife) decido to form a committee of four members. The number of different committees that can be formed in which no couple finds a place Is

There are four couples such that there are four men and four women.
$$\therefore$$ The number of committees of $$4$$ men$$={^{4}C_4}=1$$
The number of committees of $$3$$ men and $$1$$ women$$={^{4}C_3}{^{1}C_1}=4$$
The number of committees of $$2$$ men and $$2$$ women$$={^{4}C_2}{^{2}C_2}=6$$
The number of committees of $$1$$ men and $$3$$ women$$={^{4}C_1}{^{3}C_3}=4$$
The number of committees of $$4$$ women$$={^{4}C_4}=1$$
$$\therefore$$ The number of different committees that can be formed in which no couple finds a place$$=1+4+6+4+1$$
$$=16$$.

1188459_1315898_ans_f3a6c1b338e945d683e84855b278e938.JPG


Thew exponent of $$7$$ in $$_{  }^{ 100 }{ { C }_{ 50 } }$$ is_____

$$^{ 100 }{ { C }_{ 50 } }=\cfrac { 100! }{ 50!50! } $$
$$100!=k\times { 7 }^{ 16 }$$
For some no. k
Similarity $$50!=a\times { 7 }^{ 8 }$$
So, $$^{ 100 }{ { C }_{ 50 } }=\cfrac { k\times { 7 }^{ 16 } }{ { a }^{ 2 }\times { 7 }^{ 16 } } =\cfrac { k }{ { a }^{ 2 } } $$
Here $$\cfrac { k }{ { a }^{ 2 } } $$ is independent of factor of $$7$$
So, the exponent of $$7$$ in $$^{ 100 }{ { C }_{ 50 } }$$ is zero $$(0)$$


In how many ways a mixed double games can be arranged from $$8$$ married couples if no husband and wife play in the same game?

2 men are selected from 8 men in $$^{8}C_{2}$$ ways since no husband and wife should be in same game.
2 woman out of remaining 6 are chosen in $$^{6}C_{2}$$ ways.
Now one team can be chosen as $$(M_{1}, W_{1})$$ or $$(M_{1},W_{2})$$ in 2 ways.
$$\therefore $$ The required number of arrangements
$$=^{8}C_{2} \times  ^{6}C_{2} \times 2$$
$$\frac{8!}{6!2!}\times \frac{6!}{4!2!}\times 2$$
$$=\frac{8\times 7\times 6!}{6!\times 2!}\times \frac{6\times 5\times 4!}{4!\times 2!}\times 2$$
$$4\times 7\times 3\times 5\times 2$$
= 840

1257537_1330261_ans_6221938f0daa48c197d95d5e5f3d2539.PNG


Find the total number of ways in which $$30$$  distinct objects can be put into two different boxes so that no box remains empty.

These are 30 objects,, and each object  has 2
options i.e, either go in box A or in box 13.

Hence Total ways = $$2\times 2\times ---30$$ $$ times =2^{30}$$

Now in these $$2^{30}$$ ways, these would be one
particular instance when all objects would have gone to box A.
Also, there be one particular instance when all object would have gone to box B.
so these are 2 instance when one of the box would have been empty.

$$\Rightarrow $$ Required number of ways $$=2^{30}-2$$


Prove that $$2^{2}\dfrac{C_{0}}{1.2}+2^{3}\dfrac{C_{1}}{2.3}+2^{4}\dfrac{C_{2}}{3.4}+.........+2^{n+2}\dfrac{C_{n}}{(n+1)(n+2)}=\dfrac{3^{n+2}-2n-5}{(n+1)(n+2)}$$

Let $$S={ 2 }^{ 2 }\cfrac { { C }_{ 0 } }{ 1.2 } +{ 2 }^{ 3 }\cfrac { { C }_{ 1 } }{ 2.3 } +.....+{ 2 }^{ n+2 }\cfrac { { C }_{ n } }{ \left( n+1 \right) \left( n+2 \right)  } $$
$$S=\int { \left[ \int { { \left( 1+x \right)  }^{ n }dx }  \right] dx } $$ at $$x=2$$
$$S=\int { \cfrac { { \left( 1+x \right)  }^{ n+1 } }{ n+1 } dx } $$ at $$x=2$$
$$S=\cfrac { { \left( 1+x \right)  }^{ n+2 } }{ (n+1)(n+2) } $$ at $$x=2=\cfrac { { 3 }^{ n+2 } }{ (n+1)(n+2) } $$


A letter lock contains 3 rings, each ring containing 5 different letters. Determine the maximum number of false trials that can be made before the lock is opened.

$$\bar{5}\times \bar{5}\times \bar{5}$$
Each ring can be set in 5 different  
ways 
Hence total ways $$=5\times 5\times 5=125$$
unsuccessful attempt = 125 - 1
= 124 
[As one combination would be the correct one]


$$\displaystyle \frac{{C}_{0}}{1}+\frac{{C}_{2}}{3}+\frac{{C}_{4}}{5}+\frac{{C}_{6}}{7}......=$$

We know that 
$${ (1+x) }^{ n }={ C }_{ 0 }^{ n }+{ C }_{ 1 }^{ n }x+{ C }_{ 2 }^{ n }{ x }^{ 2 }+{ C }_{ 3 }^{ n }{ x }^{ 3 }.......+{ C }_{ n }^{ n }{ x }^{ n }\quad \quad -(1)\\ { (1-x) }^{ n }={ C }_{ 0 }^{ n }-{ C }_{ 1 }^{ n }x+{ C }_{ 2 }^{ n }{ x }^{ 2 }-{ C }_{ 3 }^{ n }{ x }^{ 3 }.......+{ (-1) }^{ n }{ C }_{ n }^{ n }{ x }^{ n }\quad -(2)$$
Integrating both sides of eq$$(1)$$ under limits $$0$$ to $$1$$ we get
$$\int _{ 0 }^{ 1 }{ { (1+x) }^{ n }dx } ={ C }_{ 0 }^{ n }\int _{ 0 }^{ 1 }{ dx } +{ C }_{ 1 }^{ n }\int _{ 0 }^{ 1 }{ xdx } +......+{ C }_{ n }^{ n }\int _{ 0 }^{ 1 }{ { x }^{ n }dx } \\ \Rightarrow { \cfrac { { (1+x) }^{ n+1 } }{ n+1 }  }_{ 0 }^{ 1 }={ C }_{ 0 }^{ n }+\cfrac { { C }_{ 1 }^{ n } }{ 2 } +\cfrac { { C }_{ 2 }^{ n } }{ 3 } +......+\cfrac { { C }_{ n }^{ n } }{ n+1 } \quad \quad -(3)$$
Integrating both sides of eq$$(2)$$ under limits $$0$$ to $$1$$ we get
$$\int _{ 0 }^{ 1 }{ { (1-x) }^{ n }dx } ={ C }_{ 0 }^{ n }\int _{ 0 }^{ 1 }{ dx } -{ C }_{ 1 }^{ n }\int _{ 0 }^{ 1 }{ xdx } +......{ (-1) }^{ n }\int _{ 0 }^{ 1 }{ { { C }_{ n }^{ n }x }^{ n }dx } \\ \Rightarrow { -\cfrac { { (1-x) }^{ n+1 } }{ n+1 }  }_{ 0 }^{ 1 }={ C }_{ 0 }^{ n }-\cfrac { { C }_{ 1 }^{ n } }{ 2 } +\cfrac { { C }_{ 2 }^{ n } }{ 3 } +......{ (-1) }^{ n }\cfrac { { C }_{ n }^{ n } }{ n+1 } \quad \quad -(4)$$
Adding $$(3)$$ & $$(4)$$ we get
$${ \Rightarrow \cfrac { { (1+x) }^{ n+1 } }{ n+1 }  }_{ 0 }^{ 1 }-{ \cfrac { { (1-x) }^{ n+1 } }{ n+1 }  }_{ 0 }^{ 1 }=2({ C }_{ 0 }^{ n }+\cfrac { { C }_{ 2 }^{ n } }{ 3 } +\cfrac { { C }_{ 4 }^{ n } }{ 5 } .......)\\ \Rightarrow \cfrac { { 2 }^{ n+1 }-1 }{ n+1 } +\cfrac { 1 }{ n+1 } =2({ C }_{ 0 }^{ n }+\cfrac { { C }_{ 2 }^{ n } }{ 3 } +\cfrac { { C }_{ 4 }^{ n } }{ 5 } .....)\\ \Rightarrow \cfrac { { 2 }^{ n+1 } }{ n+1 } =2({ C }_{ 0 }^{ n }+\cfrac { { C }_{ 2 }^{ n } }{ 3 } +\cfrac { { C }_{ 4 }^{ n } }{ 5 } .....)\\ \therefore \cfrac { { C }_{ 0 }^{ n } }{ 1 } +\cfrac { { C }_{ 2 }^{ n } }{ 3 } +\cfrac { { C }_{ 4 }^{ n } }{ 5 } .......=\cfrac { { 2 }^{ n } }{ n+1 } $$



Prove that : $$\dfrac{^{n}C_{r}}{^{n}C_{r-1}}=\dfrac{n-r+1}{r}$$

$$\dfrac{^{n}C_r}{^{n}C_{r-1}}=\dfrac{n!}{r!(n-r)!}\times \dfrac{(r-1)!}{n!}(n-r+1)!$$
$$=\dfrac{1}{r\times (r-1)!(n-r)!}$$  $$(r-1)!(n-r+1)(n-r)!$$
$$=\dfrac{n-r+1}{r}$$.

1208014_1392643_ans_231cf9d5b86e4f53905939daef3e2185.jpg


Find the value of $$\dfrac{6!}{3!}$$

$$\dfrac{6!}{3!}=\dfrac{6\times5\times4\times3!}{3!}=6\times5\times4=120$$



Find the value of : 
$$1\times 1!+2\times 2!+3\times 3!+.......+n\times n!$$

$$1\times 1! =\left(2-1\right)\times 1! =2 \times 1! -1\times 1!= 2!-1!$$
$$2\times2!=\left(3-1\right)\times 2!=3\times 2!-2!=3!-2!$$
$$3\times 3!=\left(4-1\right)\times 3! =4\times 3!-3! = 4!-3!$$
$$n\times n!=\left(n+1-1\right)\times n! =\left(n+1\right)\left(n!\right)-n!=\left(n+1\right)!-n!$$
Summing up all these terms, we get 
$$=2!-1!+3!-2!+4!-3!+...+\left(n+1\right)!-n!$$
$$=\left(n+1\right)! - 1!$$



How many even numbers are three digits such that if $$5$$ is one of the digits, then $$7$$ is the next digit?

(1)5 Not there ------0  2  4  6  8
               --- 13  5  7  9
                 $$8\times 9\times 5=360$$
(2)5in there 5  7    =5
$$\Rightarrow $$ 360+5=365.

1210853_1378692_ans_0757f981cb0c4504a4ad6b5238ab58b9.jpg


There are $$3$$ books on mathematics $$4$$ on physics and $$5$$ on english .How many different collections can be made such that each collections consists of : Atleast one book of english

All ways$$={2}^{3}\times{2}^{4}\times{2}^{5}$$
No of ways with at least one book of english $$={2}^{3}\times{2}^{4}\times{2}^{5}-{2}^{3}\times{2}^{4}$$
$$={2}^{3}\times{2}^{4}\left(32-1\right)$$
$$=8\times 16\times 31=3968$$


Find the number of ways to select $$3$$ pens from $$10$$ pens is 

The number of ways to select $$3$$ pens from $$10$$ pens is given as 

$$^{10}C_3\\\dfrac{10!}{3!7!}\\\dfrac{10\times 9\times 8}{3\times 2}=120$$


$$A, B, C$$ and $$D$$ are four point on a circle. How many chords can be drawn using only these points as the end points of the chord.
1396133_0db06dbf68fe452ba0e61755fa58bdda.png

By selecting $$2$$ points out of $$4$$ we can draw a chord $$\Rightarrow$$ Total chords $$={^4C_2}=\dfrac{4!}{2!2!}=6$$
These chords would be AB, AC, AD, BC, BD, CD.

1214476_1396133_ans_113755bb1c8f4d37987d214589260d53.jpg


If $$^n{C_9}{ = ^n}{C_{8,}}$$ then find $$^n{C_{17}}$$.

$$^{n}C_{9}= ^{n}C_{8}$$                $$\because ^{n}C_{r}=\dfrac{n!}{r!(n-r)!}$$
$$\dfrac{n!}{9(n-9)!}=\dfrac{n!}{8!(n-8)!}$$
$$\Rightarrow \dfrac{n!(n-8)!}{n!(n-9)!}=\dfrac{9!}{8!}$$
$$\Rightarrow \dfrac{(n-8)!}{(n-9)!}=\dfrac{9!}{8!}$$
$$\Rightarrow \dfrac{(n-8)(n-8-1)!}{(n-9)!}=\dfrac{9\times 8!}{8!}$$
$$\Rightarrow \dfrac{(n-8)(n-9)!}{(n-9)!}=9$$
$$\Rightarrow n-8=9$$
$$\Rightarrow n=17$$
$$^{n}C_{17}$$
putting n=17
$$=^{17}C_{17}$$
$$=\dfrac{17!}{17!(17-17)!}$$
$$=\dfrac{17!}{17!\times 0!}$$
$$=\dfrac{17!}{17!\times 1}$$
$$=\dfrac{1}{1}$$
$$\therefore ^{n}C_{17}=1$$


If $$^{ 9 }{ C }_{ 3 }+^{ 9 }{ C }_{ 5 }=^{ 10 }{ C }_{ r }$$ find 'r'.

$${\textbf{Hint: Recall properties of Binomial Coefficients.}}$$

$${\textbf{Step -1: Consider,}}$$$$\mathbf {{}^9{C_3}} \mathbf {\mathbf + {}^9{C_5}} = \mathbf {{}^{10}{C_r}} \ldots \left(\mathbf  1 \right)$$

               $${\text{As we know that,}}$$ $${}^n{C_r} = {}^n{C_{n - r}}$$

               $${\text{So, using this property we have,}}$$

               $${}^9{C_3} = {}^9{C_{9 - 3}} = {}^9{C_6}$$

               $${\text{substituting this value in equation 1 we get,}}$$                   

               $${}^9{C_6} + {}^9{C_5} = {}^{10}{C_r} \ldots \left( 2 \right)$$ 

$${\textbf{Step -2: Compare equation 2 with the property}}$$ $$\mathbf {{}^n{C_r} + {}^n{C_{r - 1}}} =\mathbf {{}^{n + 1}{C_r}.}$$

               $${}^9{C_6} + {}^9{C_{6 - 1}} = {}^{9 + 1}{C_6}$$

               $$\Rightarrow {}^9{C_6} + {}^9{C_5} = {}^{10}{C_6} \ldots \left( 3 \right)$$

               $${\text{Comparing equation 3 with equation 1 and 2 we get, }}$$

               $${}^{10}{C_r} = {}^{10}{C_6}$$

               $$\Rightarrow r = 6$$

$${\textbf{Hence, the value of r is 6.}}$$



Find the value of $$6!$$

$$6!=6\times 5\times 4\times 3\times 2\times 1$$
$$=720$$


Find the number of zeros at the end of $$100!$$

In terms of prime factors $$100!$$ Can be written as $${2}^{a}{3}^{b}{5}^{c}{7}^{d}…$$
Now,$${E}_{2}{\left(100!\right)}=\left[\dfrac{100}{2}\right]+\left[\dfrac{100}{{2}^{2}}\right]+\left[\dfrac{100}{{2}^{3}}\right]+\left[\dfrac{100}{{2}^{4}}\right]+\left[\dfrac{100}{{2}^{5}}\right]+\left[\dfrac{100}{{2}^{6}}\right]$$
$$=50+25+12+6+3+1=97$$
and $${E}_{5}{\left(100!\right)}=\left[\dfrac{100}{5}\right]+\left[\dfrac{100}{{5}^{2}}\right]$$
$$=20+4=24$$
$$\therefore\,100!={2}^{97}\times{3}^{b}\times{5}^{24}\times{7}^{d}\times...$$
$$={2}^{73}\times{\left(2\times 5\right)}^{24}\times{7}^{d}\times...$$
$$={10}^{24}\times{2}^{73}\times{3}^{b}\times{7}^{d}\times....$$
Thus, the number of zeros at the end of $$100!$$ is $$24$$.


Find the value of $$\dfrac{9!-6!}{4!}$$

$$\dfrac{9!-6!}{4!}$$

$$=\dfrac{9\times 8\times 7\times 6!-6!}{4!}$$

$$=\dfrac{\left(9\times 8\times 7-1\right)6!}{4!}$$

$$=\dfrac{\left(9\times 8\times 7-1\right)\times 6\times 5\times 4!}{4!}$$

$$=\left(9\times 8\times 7-1\right)\times 6\times 5$$

$$=\left(9\times 8\times 7-1\right)\times 30$$

$$=\left(504-1\right)\times 30$$

$$=503\times 30$$

$$=15,090‬$$


How many numbers greater than a million can be formed with the digits $$2, 3, 0, 3, 4, 2, 3$$?

Any number of greater than a million will contain all the seven digits.
Now, we have to arrange these seven digits, out of which $$2$$ occurs twice, $$3$$ occurs twice and the rest are distinct.
The number of such arrangements $$=\dfrac{7!}{2!\times 3!}=\dfrac{7\times 6\times 5\times 4\times 3!}{2!\times 3!} =7\times 6\times 5\times 2=420$$
These arrangements also include those numbers which contain $$0$$ at the million’s place.
Keeping $$0$$ fixed at the millionth place, we have $$6$$ digits out of which $$2$$ occurs twice, $$3$$ occurs thrice and the rest are distinct.
These arrangements also include those numbers which contain $$0$$ at the million’s place.
Keeping $$0$$ fixed at the millionth place, we have $$6$$ digits out of which $$2$$ occurs twice, $$3$$ occurs thrice and the rest are distinct.
These $$6$$ digits can be arranged in $$\dfrac{6!}{2!\times 3!}=\dfrac{6\times 5\times 4\times 3!}{2!\times 3!} =6\times 5\times 2=60$$  ways
Hence, the number of required numbers $$= 420 – 60 = 360$$.


Find number of words by using letters of word "ALLAHABAD"

There are $$9 $$ letter in given word , in which $$4A,2L $$ and other are different .
So by taking all letters , number of different words are 
$$ = \frac { (9)!}{(4)! \times (2) ! } $$
$$ = \frac {  9 \times 8 \times 7 \times 6 \times 5 \times (4)!}{ ( 4)! \times 2 \times  1} $$
$$ = \frac{ 9 \times  8 \times 7 \times 6 \times 5}{2} $$
$$ = 7560 $$
hence number of words are $$ 7560 $$.


If $$\ ^{n}C_{12}=\ ^{n}C_{5}$$, find the value of $$n$$.

We know that if

$$\ ^{n}C_{p}=\ ^{n}C_{q}$$ then one of the following condition need to be satisfied.

$$i) p=q$$

$$ii) n=p+q$$

From the problem, 

$$\ ^{n}C_{12}=\ ^{n}C_{5}$$

$$\therefore 12\neq 5$$

So, the condition $$(ii)$$ must be satisfied $$n=12+15=17$$

The value of $$n$$ is $$17$$


If $$(n+1)!=90 [(n-1)!]$$, find $$n$$.


1408937_1666386_ans_70e9e04bc1324acba98007e7e42b0312.jpg


Compute :
$$\dfrac {30!}{28!}$$


1407550_1666356_ans_6cc3dbb1358d451d882c9a943a880117.jpg


Find $$x$$ in each of the following:
$$\dfrac {x}{10!}=\dfrac {1}{8!}+\dfrac {1}{9!}$$


1407876_1666364_ans_f5f22b0efb6b40089fb116c34dbb2a57.jpg


Compute :
$$\dfrac {11!-10!}{9!}$$


1407555_1666357_ans_7a5e3a5956f34bffb193496a79391d8f.jpg


Find $$x$$ in each of the following:
$$\dfrac {1}{4!}+\dfrac {1}{5!}=\dfrac {x}{6!}$$


1407878_1666363_ans_21f536aaca5148d78bc86307aee733fd.jpg


Compute: $$\dfrac {32!}{29!}$$.

$$\dfrac {32!}{29!}=\dfrac{32 \times 31 \times 30 \times 29!}{29!}=32 \times 31 \times 30=29760$$.


A group consists of $$4$$ girls and $$7$$ boys. In how many ways can a team of $$5$$ members be selected is the team has no girl ?

Girls in the groups $$=4$$
Boys in the groups $$=5$$
If no girls is selected then all the candidates should be boys 
Total Number of ways $$=^4C_0 \times ^7C_5$$
$$=\dfrac {4!}{4!\times 1}\times \dfrac {7!}{2!\ 5!}$$
$$=21$$ ways.


The number of all $$3\times 3$$ matrices $$A$$, with enteries from the set $$\{-1, 0, 1\}$$ such that the sum of the diagonal elements of $$AA^T$$ is $$3$$, ______.

$$A = [a_{ij}]_{3\times 3}$$

$$tr(AA^T) = 3$$

$$a_{11}^2 + a_{12}^2 + a_{13}^2+ ...... + a_{33}^2=3$$

So out of $$9$$ elements $$(𝑎_{𝑖𝑗})’s,$$ $$3$$ elements must be equal to $$1$$ or $$−1$$ and rest elements must be $$0.$$ 

Possible cases

$$\left.\begin{matrix}  0,0,0,0,0,0,1,1,1 &\to &6(0's) \ and \ 3 (1's)\Rightarrow Total \ possibilities=^9C_6  \\ 0,0,0,0,0,0,-1,-1,-1 &\to  & 6(0's) \ and \ 3 (-1's)\Rightarrow Total \ possibilities=^9C_6 \\ 0,0,0,0,0,0,1,1,-1 & \to & 6(0's) \ and \ 2 (1's) \ and \ 1 \ (-1's)\Rightarrow Total \ possibilities=^9C_6 \times 3 \\ 0,0,0,0,0,0,-1,1,-1 & \to &6(0's) \ and \ 2 (-1's) \ and \ 1(1's)\Rightarrow Total \ Possibilities=^9C_6 \times 3\end{matrix}\right\}$$

$$\Rightarrow$$$$9_{C_6} \times (1 + 1 + 3 +3)$$

$$= 9_{C_6} \times 8$$

$$= 84 \times 8$$

$$= 672$$


Prove that $$\dfrac {1}{10!} + \dfrac {1}{11!} + \dfrac {1}{12!} = \dfrac {145}{12!}$$.

$$LHS = \left \{\dfrac {1}{10!} + \dfrac {1}{11\times (10!)}\right \} + \dfrac {1}{12!} $$

$$= \dfrac {(11 + 1)}{11\times (10!)} + \dfrac {1}{12\times (11!)}$$

$$= \dfrac {12}{11!} + \dfrac {1}{12\times (11!)} = \dfrac {(144 + 1)}{12\times (11!)} = \dfrac {145}{12!} = RHS$$.


Compute: $$\dfrac {9!}{(5!)\times (3!)}$$.

$$\dfrac {9!}{(5!) \times (3!)}=\dfrac{9 \times 8 \times 7 \times 6 \times 5!}{(5!) \times (3!)}=9 \times 8 \times 7=504$$


Prove that $$LCM \left \{6!, 7!, 8!\right \} = 8!$$.


1851364_1709014_ans_d9139ea4469445ada775a0f5a5ebe73c.jpg


Evaluate each of the following:
$$P(6, 4)$$


1421527_1666660_ans_7831eb6532cc498cbdfef5b8322e6a0f.jpg


Compute: $$\dfrac {(12!) - (10!)}{9!}$$.


 $$\dfrac {(12!) - (10!)}{9!}=\dfrac {(12 \times 11 \times 10 \times 9!) - (10\times 9!)}{9!}=\dfrac{9!\{ 12 \times 11 \times 10-10\}}{9!}=10(12 \times 11-1)=10 \times 131=1310$$


A group consists of $$4$$ girls and $$7$$ boys. In how many ways can a team of $$5$$ members be selected is the team has at least one boy and one girl ?

$$\textbf{Step-1: Apply combination to get the required unknown}$$
                 $$\text{Total number of girls in the group}$$ $$=4$$
                 $$\text{Total number of boys in the group}$$ $$=7$$
                 $$\text{Probability of selecting at least one boy and one girl =?}$$
                 $$\text{By considering following ways we can select}$$
                 $$\text{i)}$$ $$1$$ $$\text{girls}$$ $$+4$$ $$\text{boys}$$ $$\Rightarrow \ ^{4}C_{1}\times \ ^{7}C_{4}$$

                 $$\text{ii)}$$ $$2$$ $$\text{girls}$$ $$+3$$ $$\text{boys}$$ $$\Rightarrow \ ^{4}C_{2}\times \ ^{7}C_{3}$$

                 $$\text{iii)}$$ $$3$$ $$\text{girls}$$ $$+2$$ $$\text{boys}$$ $$\Rightarrow \ ^{4}C_{3}\times \ ^{7}C_{2}$$

                 $$\text{iv)}$$ $$4$$ $$\text{girls}$$ $$+1$$ $$\text{boy}$$ $$\Rightarrow \ ^{4}C_{4}\times \ ^{7}C_{1}$$
$$\textbf{Step-2: Use the above results & simplify}$$
                 $$\text{Total number of ways}$$ $$=(\ ^{4}C_{1}\times \ ^{7}C_{4})+(\ ^{4}C_{2}\times \ ^{7}C_{3})+(\ ^{4}C_{3}\times\ ^{7}C_{2})+(\ ^{4}C_{4}\times \ ^{7}C_{1})$$
                 $$=140+210+84+7$$
                 $$=441$$
$$\textbf{Hence, answer is 441}$$


Evaluate: $$^{90}C_{88}$$

As we know
$$^nC_r=\dfrac{n!}{r!(n-r)!}$$

$$^{90}C_{88}=\dfrac {90!}{2! \ 88!}=\dfrac{90 \times 89}{2}=45 \times 89=4005$$


Evaluate: $$^{71}C_{71}$$

$$^nC_r=\dfrac{n!}{r!(n-r)!}$$

$$^{71}C_71=\dfrac{71!}{0!71!}=1$$


Write the following products in factorial notation:
$$3\times 6\times 9\times 12\times 15$$.

$$3\times 6\times 9\times 12\times 15=3^5(1\times 2\times 3\times 4\times 5)=3^5 \times 5!$$


Evaluate $$\dfrac {n!}{(r!) \times (n - r)!}$$, when $$n = 15$$ and $$r = 12$$.

$$\dfrac {15!}{(12!) \times (3!)} = \dfrac {15\times 14\times 13\times (12!)}{6\times (12!)} = 455$$.


Prove that :
$$(n - r + 1) \cdot \dfrac {n!}{(n - r + 1)!} = \dfrac {n!}{(n - r)!}$$.

We know that $$(n - r + 1)! = (n - r + 1)\cdot (n - r)!$$.

$$(n - r + 1) \cdot \dfrac {n!}{(n - r + 1)!}=(n - r + 1) \cdot \dfrac {n!}{(n - r + 1) \times (n-r)!} =\dfrac{n!}{(n-r)!}$$


If $$^{n}C_{7} = ^{n}C_{5},$$ find $$n$$.

$$^{n}C_{7} = ^{n}C_{5}$$

$$\dfrac{n!}{7! \times (n-7)!}=\dfrac{n!}{5! \times (n-5)!}$$

$$\dfrac{1}{7 \times 6}=\dfrac{1}{(n-5)(n-6)}$$

comparing LHS and RHS we get, $$n=12$$


Evaluate: $$\displaystyle\sum_{r=1}^{6}$$ $$^{6}C_{r}$$

As we know
$$^nC_r=\dfrac{n!}{r!(n-r)!}$$

$$\displaystyle\sum_{r=1}^{6}$$ $$^{6}C_{r}=^{6}C_{1}+^{6}C_{2}+^{6}C_{3}+^{6}C_{4}+^{6}C_{5}+^{6}C_{6}=6+15+20+15+6+1=63$$


Verify that: $$ ^{10}C_{4}+^{10}C_{3} = ^{11}C_{4} $$ 

$$\dfrac{10!}{4! \times 6!}+\dfrac {10!}{3! \times 7!}=\dfrac {10!}{3! \times 6!} \times \left( \dfrac{1}{4}+\dfrac 17\right)=\dfrac {11 \times 10!}{3! \times  4 \times6! \times 7}=^{11}C_4 $$


Evaluate: $$^{20}C_{4}$$

As we know
$$^nC_r=\dfrac{n!}{r!(n-r)!}$$

 $$^{20}C_{4}=\dfrac{20!}{4! \ 16!}=\dfrac{20 \times 19 \times 18 \times 17 \times 16!}{16! \times  \ 4 \times 3 \times 2 }=4845$$


If $$(n + 2)! = 2550\times n!$$, find the value of $$n$$.

$$(n + 2)! = 2550\times n!$$

$$(n + 2)(n + 1)\times (n!) = 51\times 50\times (n!)$$

$$ \Rightarrow (n + 2)(n + 1) = 51 \times 50$$

Comparing we get,

$$\Rightarrow n + 1 = 50 \Rightarrow n = 49$$.


If $$\dfrac {1}{4!} + \dfrac {1}{5!} = \dfrac {x}{6!}$$, find the value of $$x$$.

$$\dfrac {1}{4!} + \dfrac {1}{5\times (4!)} = \dfrac {x}{(6\times 5)\times (4!)}$$

$$ \Rightarrow \dfrac {x}{30} = \left (1 + \dfrac {1}{5}\right ) = \dfrac {6}{5}$$

$$\Rightarrow x = \left (\dfrac {6}{5}\times 30\right ) = 36$$.


If $$^{20}C_{r} = ^{20}C_{r-10} $$ then find the value of $$ ^{17}C_{r}.$$

If $$^nC_x=^nC_y$$
then, $$n=x+y$$

According to question,
$$ r+r-10 = 20\Rightarrow r = 15.$$

So, $$ ^{17}C_{r} = ^{17}C_{15} = ^{17}C_{2}=\dfrac{17!}{2!\times 15!} = \dfrac{17\times 16}{2\times 1} = 136 $$


Find the number of diagonals of a hexagon 


1853419_1709818_ans_3f426cc30ba9467288f1bdc4949f1519.jpg


Find the number of diagonals of a decagon

In an $$10$$-sided polygon, total vertices are $$10.$$ Now, the $$10$$ vertices can be joined with each other by $$^{10}C_2$$ ways i.e. $$\dfrac{10!}{2! \cdot (10-2)!}=\dfrac{10 \times 9 \times 8!}{2 \cdot (8)!}=45$$ ways.

Now, there are $$45$$ diagonals possible for an $$10-$$sided polygon which includes its sides also. So, subtracting the sides will give the total diagonals contained by the polygon.

So, total diagonals contained within an $$10$$-sided polygon $$= 45 -10$$ i.e. $$35.$$


If $$ ^{n}C_{r-1} = 36,^{n}C_{r} = 84 $$ and $$ ^{n}C_{r+1} = 126, $$ find $$n$$ and $$r$$.

As we know,

$$\dfrac{^{n}C_{r-1}}{^{n}C_{r}} = \dfrac{r}{n-r+1}$$ and $$ \dfrac{^{n}C_{r}}{^{n}C_{r+1}} = \dfrac{r+1}{n-r} $$

$$\therefore \dfrac{r}{n-r+1} = \dfrac{36}{84}=\dfrac{3}{7}\Rightarrow 3n-3r+3=7r\Rightarrow 3n-10r=-3...(i)$$

and $$ \dfrac{r+1}{n-r}=\dfrac{84}{126}=\dfrac{2}{3}\Rightarrow 2n-2r=3r+3\Rightarrow 2n-5r=3 ...(ii) $$

$$(i)-2 \times (ii)$$
$$3n-10r-4n+10r=-3-6 \Rightarrow -n=-9 \Rightarrow \boxed {n=9}$$

putting value of $$n$$ in $$(i)$$, we get
$$27+3=10r \Rightarrow \boxed {r=3}$$


If $$^{20}C_{r+1} = ^{20}C_{r-1}$$ then find the value of $$^{10}C_{r}. $$

If $$^nC_x=^nC_y$$
then, $$n=x+y$$

According to question,
$$ r+1+r-1 = 20\Rightarrow r = 10.$$

As we know, $$^nC_r=\dfrac{n!}{r! \times (n-r)!}$$

So, $$^{10}C_{r} = ^{10}C_{10} = 1 $$


If $$ ^{n+1}C_{r+1}:^{n}C_{r} = 11:6 $$ and $$^{n}C_{r}:^{n-1}C_{r-1} = 6:3, $$ find $$n+r$$.

Use $$ \dfrac{^{n}C_{r}}{^{n-1}C_{r-1}} = \dfrac{n}{r} $$ and $$ \dfrac{^{n+1}C_{r+1}}{^{n}C_{r}} = \dfrac{n+1}{r+1}. $$

$$\therefore \dfrac{n}{r} = \dfrac{6}{3} = \dfrac{2}{1} $$ and $$ \dfrac{n+1}{r+1} = \dfrac{11}{6}\Rightarrow 6n+6 = 11r+11\Rightarrow 6n-11r = 5 $$

Solve $$n-2r = 0 $$ and $$ 6n-11r = 5 $$

Solving we get, $$n=10,r=5$$
$$\implies n+r=15$$


If $$^{2n}C_{3}:^{n}C_{3} = 12:1,$$ find $$n$$.

$$^{2n}C_{3}:^{n}C_{3} = 12:1$$

$$\Rightarrow \dfrac{\dfrac{2n!}{3! \ (2n-3)!}}{\dfrac{n!}{3! \ (n-3)!}}=\dfrac{12}{1}$$

$$\Rightarrow  \dfrac{2n(2n-1)(2n-2)}{3\times 2\times 1}\times \dfrac{3\times 2\times 1}{n(n-1)(n-2)} = \dfrac{12}{1} $$

$$\Rightarrow 4(2n-1) = 12(n-2)\Rightarrow 2n-1 = 3n-6\Rightarrow n=5.$$


How many triangle can be obtained by joining 12 points, four of which are collinear?


1854106_1709822_ans_fcb787721e4747f9933414e8d9f16fca.jpg


How many triangles can be formed in a decagon?


1854102_1709823_ans_1292c6e65cf54f9c8a0a564a0f1f8ea0.jpg


Find the values of  $$^{200}C_{198}. $$

As we know $$^nC_r=\dfrac{n!}{r! \cdot (n-r)!}$$

$$^{200}C_{198} = ^{200}C_{2} =\dfrac{200\times 199 \times 198!}{2! \times (200-2)!}= \dfrac{200\times 199}{2} = 19900.$$


Find the values of $$^{15}C_{15}.$$

As we know $$^nC_r=\dfrac{n!}{r! \cdot (n-r)!}$$

we know that $$0!=1$$

$$\therefore ^{15}C_{15} =\dfrac{15!}{15! \times (15-15)!}= \dfrac{15!}{15! \cdot 0!} = 1.$$


There are 12 points in a plane, out of which 3 points are collinear. How many straight lines can be drawn by joining two of them?

A line can be formed by joining any of two point. 
But we have to take care of that any line do not get counted twice.

Total no. of ways in which we can select 2 points out of 12 = $$^{12}C_2 = \dfrac{12!}{2!\times 10!} = 66$$

But since there are three points which are collinear we have counted some lines more than once. 
No. of times a single line got counted = $$^3C_2 = 3$$

So, we will subtract 3 from total value and instead add 1 because a line has to be counted only once.

Hence,
Final no. of ways = $$66-3+1=64$$

Hence, the correct answer is 64.


How many parallelograms can be formed from a set of 4 parallel lines intersecting set of 3 parallel lines?


1852738_1710546_ans_d30a9a2a02df402b8daf1e7d2c64ec9e.jpg


Find the number of diagonals in an n-sided polygon.

A polygon of n sides has n vertices. By joining any two vertices of a polygon, we obtain either a side or a diagonal of the polygon. Number of line segments obtained by joining the vertices of an n sided polygon taken two at a time
= Number of ways of selecting 2 out of n = $$n_{C_2}=\dfrac{n(n-1)}{2}$$

Out of these lines, n lines are the sides of the polygon.
Therefore, number of diagonals of the polygon = $$\dfrac{n(n-1)}{2}-n= \dfrac{n(n-3)}{2}$$.


Find the values of $$^{76}C_{0}$$

As we know $$^nC_r=\dfrac{n!}{r! \cdot (n-r)!}$$

we know that $$0!=1$$

$$\therefore ^{76}C_{0} =\dfrac{76!}{0! \times (76-0)!}= \dfrac{76!}{76!} = 1.$$


Write the value of $$(^{5}C_{1}+^{5}C_{2}+^{5}C_{3}+^{5}C_{4}+^{5}C_{5}). $$


1851410_1710354_ans_adfa4642e9bd46beae08f35830d165d5.jpeg


If $$^{n+1}C_{3} = 2(^{n}C_{2}),$$ find the value of n.

As we know, 
$$^nC_r=\dfrac {n!}{r! \cdot (n-r)!}$$

$$ ^{n+1}C_{3} = 2(^{n}C_{2})$$

$$\dfrac {(n+1)!}{3! \cdot (n-2)!}=2 \times \dfrac {n!}{2! \cdot (n-2)!}$$

$$\dfrac {(n+1) \cdot n!}{3 \cdot 2! \cdot (n-2)!}=2 \times \dfrac {n!}{2! \cdot (n-2)!}$$

$$\Rightarrow \dfrac{(n+1)}{6} =1\Rightarrow n+1 = 6\Rightarrow n = 5.$$


There person enter a railway compartment having 5 vacant seats. In how many ways can they seat themselves?

First can occupy any of the 5 seats, 2nd may occupy any of 4 seats and third may occupy any of 3 seats.
Required number of ways $$ = (5\times 4\times 3) = 60. $$


Let $$f(n) = \displaystyle \sum_{r = 0}^{n}\displaystyle \sum_{k = r}^{n} \binom{k}{r}$$. Find the total number of divisors of $$f(9)$$.

$$\displaystyle \sum_{k = r}^{n}\ ^{k}C_{r} + ^{r +1}C_{r} + ^{r + 2}C_{r} + ... + ^{n}C_{r}$$

$$= 1 + ^{r + 1}C_{1} + ^{r + 2}C_{2} + ^{r + 3}C_{3} + ... + ^{n}C_{n - r}$$

now, $$^{n + 1}C_{n - r} = ^{n + 1}C_{r + 1}$$

$$\therefore f(n) = \displaystyle \sum_{r = 0}^{n}\ ^{n + 1}C_{r + 1} = ^{n + 1}C_{1} + ^{n + 1}C_{2} + ^{n + 1}C_{3} + .... + ^{n + 1}C_{n + 1}$$

$$= ^{n + 1}C_{0} + ^{n + 1}C_{1} + ^{n + 1}C_{2} + ... + ^{n + 1}C_{n + 1} - 1$$

$$f(n) = (2^{n + 1}) - 1$$

$$f(9) = 2^{10} - 1 = 1023 = 3\cdot 11\cdot 31$$

hence number of divisors are $$(1 + 1)(1 + 1)(1 + 1) = 8$$.

1569214_1746792_ans_27bbf7879b50477f8453d047f4d0329d.jpg


There are $$2$$ women participating in a chest tournament. Every participant played $$2$$ games with the other participants. The number of games that the men played between themselves exceeded by $$66$$ as compared to the number of games that the men played with the women. Find the total number of participants.

There are $$2$$ women and let the number of men are $$n$$

According to question

$$2\times ^{n}C_{2} = 66 + 2 \times ^{n}C_{1} \times ^{2}C_{1}$$

$$\Rightarrow 2\cdot \dfrac {n(n - 1)}{2} = 2[33 + 2n]$$

$$\Rightarrow \dfrac {n(n - 1)}{1.2} = 33 + n(2)$$

$$\Rightarrow n^{2} - 5n - 66 = 0\Rightarrow (n - 11)(n + 6) = 0$$

$$\therefore n = 11 (\because sn > 0)$$

Total participants $$= 2 + 11 = 13$$.


Prove by combinatorial argument that $$^{n + 1}C_{r} = ^{n}C_{r} + ^{n}C_{r - 1}$$.

Consider $$n + 1$$ different toys Then,
(no. of ways of selecting $$r$$ toys out of $$(n + 1)$$ different toys) $$=$$ (no. of ways of selecting $$(r - 1)$$ toys out of $$n$$ toys when $$T_{0}$$ is always included) $$+$$ (no. of ways of selecting $$r$$ toys when $$T_{0}$$ is always excluded)
$$= ^{n}C_{r - 1} + ^{n}C_{r}$$
Hence, $$^{n + 1}C_{r} = ^{n}C_{r - 1} + ^{n}C_{r}$$.


If $$\ ^{n+2}C_{8}:\ ^{n-2}P_{4}=57:16$$, find $$n$$.


1575454_1746890_ans_e8114482e50d4cf189df2b0bf714f631.JPG


There are $$3$$ men and $$7$$ women taking a dance class. If $$N$$ is a number of different ways in which each man be paired with a women partner, and the four remaining women are paired into two pairs each of two, then find the value of $$\dfrac{N}{90}$$.

$$3$$ women can be selected in $$^{7}C_{3}$$ ways and can be paired with $$3$$ men in $$3!$$ ways.
Remaining $$4$$ women can be grouped into two couples in $$\dfrac {4!}{2! . 2! . 2!} = 3$$
$$\therefore Total = ^{7}C_{3} \cdot 3! \cdot 3 = 630\ N$$
Then the value of $$N/90$$ is $$7$$.


A person has $$'n'$$ friends. Find the minimum value of $$'n'$$ so that a person can invite a different pair of friends every day for four weeks in a row.

According to question ,
A person can invite a different pair of friends in every day of four week
Number of ways of selecting pair=$$^nC_2$$

For all 28 days he has to invite different pair 
so $$^nC_2$$=28
$$n(n-1)=56$$
$$n(n-1)=8\times 7$$
So n=8.
So Minimum number of friends is 8.


Determine
$$^{n}C_{17} $$, if $$^{n}C_{9} = ^{n}C_{8} $$

We have,
$$^{n}C_{9} = ^{n}C_{8} \Rightarrow n = 9 + 8 = 17 $$
$$ \therefore \, ^{n}C_{17} = ^{17}C_{17} = 1 $$ 


Compute:
$$ \cfrac{7 !}{5 !} $$

$$ \dfrac{7!}{5!} = \dfrac{7 \times 6 \times 5!}{5!} = 7 \times 6 = 42 $$


Compute:
$$ \cfrac{12 !}{10 ! \times 2 !} $$

$$ \dfrac{12 !}{10 ! \times 2 !} = \dfrac{12 \times 11 \times 10!}{10! \times 2 \times 1} = \dfrac{12 \times 11}{2} $$
   $$ = 6 \times 11 = 66 $$


Find the value of $$ n$$ whereas 
$$ ^{2n}C_3 : ^nC_3 = 11 : 1 $$

$$ ^{2n}C_3 : ^nC_3 = 11 : 1 $$
$$ \frac{^{2n}C_3}{^nC_3}=11 $$
$$ \frac{2n!}{(2n-3)! 3!}= 11 \times \frac{n!}{(n-3)!3! } $$
$$ \frac{2n(2n-1)(2n-2)(2n-3)!}{(2n-3)!}=\frac{11\times n(n-1)(n-2)(n-3)!}{(n-3)!} $$
$$ 2n(2n-1)(2n-2)=11n(n-1)(n-2) $$
$$ 4(2n-1)(n-1)=11(n-1)(n-2)$$
$$ 4)2n-1)=11(n-2) $$
$$ 8n-4=11n-22 $$
$$ 18=3n $$
$$ \therefore n=6 $$
Hence, value of $$ n=6 $$


Find the value of $$ n$$ whereas 
$$ ^{20}C_{n-2} = ^{20}C_{n+2}  $$

$$ ^{20}C_{n-2} = ^{20}C_{n+2}  $$
$$ \Rightarrow ^{20}C_{n-2}=^{20}C_{20-n-2} (\because ^nC_r=^nC_{n-r} )$$
$$ \Rightarrow ^{20}C_{n-2}=^{20}C_{18-n} $$
On comparing $$ n-2=18-n $$
$$ \Rightarrow n+n=18+2 $$
$$ \Rightarrow 2n=20 $$
$$ \Rightarrow n=\frac{20}{2}=10 $$
Hence, $$ n=10 $$


Show that $$^{n}C_{r} + ^{n}C_{T - x} = ^{n + 1}C_{r} $$.

We have 
LHS  $$ = ^{n}C_{r} + ^{n}C_{r - 1} $$ 

$$ = \dfrac{n!}{(n - r)r!} + \dfrac{n!}{(n - (r - 1))! (r - 1)!} $$ 

$$ = \dfrac{n!}{(n - r)r!} + \dfrac{n!}{(n - r + 1)(n - r)! (r - 1)!} $$ 

$$ = \dfrac{n!}{(n - r)! (r - 1)! } .\cdot \left  [ \dfrac{1}{r} + \dfrac{1}{n - r + 1}  \right  ] $$ 

$$ = \dfrac{n!}{(n - r)! (r - 1)!} \cdot \left  [ \dfrac{n - r + 1 + r}{r (n - r + 1)}  \right  ] $$ 

$$ = \dfrac{n!}{(n - r)! (r - 1)!}  \cdot \left  [\dfrac{(n + 1)}{(n - r + 1)r}  \right  ] $$ 

$$ = \dfrac{(n + 1)n !}{(n - r)! (n - r + 1)! r !} $$ 

$$ = \dfrac{(n + 1)!}{(n + 1 - r)! r !} $$      $$ \because (n + 1 - r) (n - r) = (n + 1 - r)! $$ 

$$ = ^{n + 1}C_{r} $$ = RHS 


State fundamental principle of counting (or multiplication principle) for three events.

Fundamental principle for three events states that " If an event can occur in m different ways, following which second even occur in n different ways, following third event can occur in p different ways, the the total number of occurrence of the events in the given order 


State fundamental principle of counting (or multiplication principle) for two events.

Fundamental principle for two events states that " If an event can occur in m different ways, following which another even occur in different ways, then the total number of occurrence of the events in the given order is $$ m \times n $$.


Prove that
$$\displaystyle\Sigma_{n = 0}^{n} \,y . c_{n} = 4$$

$$LHS = \overset{n}{\underset{r = 0}{\Sigma}} 3^{r} . ^{n}C_{r}$$
$$= \,^{n}C_{0} . 3^{0} + ^{n}C_{1}3^{1} + ^{n}C_{2} . 3^{2} + .... + ^{n}C_{n}3^{n}$$
$$= (1 + 3)^{n}$$
$$= 4^{n}$$
$$= RHS$$


Find $$x$$, if 
$$ \cfrac{1}{8 !}+\cfrac{1}{9 !}=\cfrac{x}{10 !} $$

Given : $$ \dfrac{1}{8 !}+\cfrac{1}{9 !}=\cfrac{x}{10 !} $$ multiplying by $$10!$$, we get 
 
$$ \dfrac{10!}{8!} + \dfrac{10!}{9!} = x $$

$$ \Rightarrow $$    $$ \dfrac{10 \times 9 \times 8!}{8!} + \dfrac{10 \times 9!}{9!} = x $$ 

$$ \Rightarrow $$   $$90 + 10 = x $$ 
$$ \Rightarrow $$    $$x = 100 $$


Find the value of $$ ^{50}C_{11} + ^{50}C_{12} +^{51}C_{13} -^{52}C_{13}$$

$$ ^{50}C_{11} + ^{50}C_{12} +^{51}C_{13} -^{52}C_{13}$$
=$$ (^{50}C_{12}+^{50}C_{11})+^{51}C_{13}-^{52}C_{13} $$
=$$ ^{50+1}C_{12}+^{51}C_{13}-^{52}C_{13} $$
$$( \because ^nC_r+^nC_{r-1}=^{n+1}C_r)$$
=$$ (^{51}C_{13}-^{51}C_{12})-^{52}C_{13} $$
=$$ ^{51+1}C_{13}-^{52}C_{13} \quad (\because ^nC_r+^nC_{r-1}=^{n+1}C_r)$$
=$$ ^{52}C_{13}-^{52}C_{13}=0 $$
Hence, $$ ^{50}C_{11}+^{50}C_{12}+^{51}C_{13}-^{52}C_{13}=0.$$


Find the value of $$ n$$ whereas 
$$ ^nC_{10} = ^nC_{15 } $$

$$ ^nC_{10} = ^nC_{15 } $$
$$ \Rightarrow ^nC_{10}=^nC_{n-15} \quad \quad     (\because ^nC_r=^nC_{n-r})$$
On comparing
$$ n-15=10 $$
$$ \Rightarrow n=10+15 $$
$$ \Rightarrow n=25.$$


if $$ ^nC_9 = ^nC_7 $$ then find $$^nC_{16} $$.

$$ ^nC_9 = ^nC_7 $$
$$ \Rightarrow ^nC_7 = ^nC_{n-7} ( \because ^nC_r = ^nC_{n-r} ) $$
On comparing 
$$  9 = n-7 $$
$$  \Rightarrow n = 9+7 = 16 $$
$$ \therefore ^nC_{16} = ^{16}C_{16} = 1 $$
hence $$ ^nC_{16} = 1 $$


Find the value of n
$$ ^{2n}C_3 :^nC_3 = 11 :1 $$

$$ ^{2n}C_3 : ^nC_3 = 11 : 1 $$
$$ ^{2n}C_3 = 11 \times ^nC_3 $$
$$ \frac { 2n!}{3!(2n-3)!} = \frac {n!}{3!(n-3)!} $$
$$ \frac {2n(2n-1)(2n-2)(2n-3)!}{(2n-3)!} = 11 \times  \frac { n(n-1)(n-2)(n-3)}{(n-3)!} $$
$$ 2n(n-1)(2n-2) = 11 \times n(n-1)(n-2) $$
$$ 2(4n^2 -2n-4n +2) = 11(n^2 -n-2n +2) $$
$$ 8n^2 - 12 n +4 = 11n^2 -33n +22 $$
$$ 3n^2 -21n +18 = 0 $$
$$n^2 - 7n + 6 = 0 $$
$$ (n-1)(n-6) = 0 $$
$$ n = 1  , n = 6 $$
hence value of $$ n = 6 $$


$$(i)$$ If $$\space ^{m+r}P_2 = 90$$ and $$\space ^{m-r}P_2 = 30$$.
$$(ii)$$ If $$\space ^nP_r = ^nP_{r+1}$$ and $$\space ^nC_r = \space ^nC_{r-1}$$.
Find $$m+n-r$$ ?

$$(i)$$ Since $$\space ^{m+r}P_2 = 90$$
$$\therefore \quad (m+r)(m+r-1) = 90$$
$$\Leftrightarrow\quad (m+r)^2 - (m+r) - 90 = 0$$
$$\therefore \quad m+r = 10$$ and $$m+r = -9$$
Hence $$m+r = 10,\quad m+r \ne -9\quad                                            ....(1)$$
$$\quad ^{m-r}P_2 = 30$$
$$\therefore \quad (m-r)(m-r-1) = 30$$
$$\therefore \quad (m-r)^2 - (m-r) - 30 = 0$$
$$\Leftrightarrow \quad m-r = 6, m-r = -5\quad                                        ....(2)$$
Solving $$(1)$$ and $$(2)$$, we get $$m=8$$ & $$r=2$$
Hence, $$(m,r) = (8,2)$$

$$(ii)$$ Given $$^nP_r = ^nP_{r+1}$$
$$\Leftrightarrow \quad            \displaystyle\frac{n!}{(n-r)!} = \displaystyle\frac{n!}{(n-r-1)!}$$
$$\Leftrightarrow \quad               (n-r)! = (n-r-1)!$$
$$\Leftrightarrow \quad               (n-r)(n-r-1)! - (n-r-1)! = 0$$
$$\Leftrightarrow \quad               (n-r-1)!(n-r-1) = 0$$
$$\quad               (n-r-1)! \ne 0 \quad \therefore \quad n-r-1 = 0$$
$$\quad                                                                 n-r = 1\quad                   ...(1)$$
and given $$\quad           ^nC_r = \space ^nC_{r-1} \quad               \left\{\because \quad ^nC_A = \space ^nC_B \Rightarrow n = A + B \space or \space A = B\right\}$$
$$\quad                n = r + (r-1)$$
$$\quad                  n - 2r = -1\quad                    ...(2)$$
Solving $$(1)$$ and $$(2)$$, we get
$$\quad r = 2$$ and $$ n = 3$$
$$\therefore\; m+n-r=9$$


Solve the inequality
$$^{x-1}C_4 - \space ^{x-1}C_3 - \displaystyle\frac{5}{4}\space^{x-2}C_2 < 0, \quad x\in N$$. Find difference of largest and smallest values x can take ?

`We have 
$$\quad ^{x-1}C_4 - \space ^{x-1}C_3 - \displaystyle\frac{5}{4}\space^{x-2}C_2 < 0$$

$$\Leftrightarrow \quad \displaystyle\frac{(x-1)(x-2)(x-3)(x-4)}{1.2.3.4} - \displaystyle\frac{(x-1)(x-2)(x-3)}{1.2.3} - \displaystyle\frac{5}{4}.(x-2)(x-3) < 0$$

$$\Leftrightarrow \quad (x-1)(x-2)(x-3)(x-4) - 4(x-1)(x-2)(x-3) - 30(x-2)(x-3) < 0$$

$$\Leftrightarrow \quad (x-2)(x-3)\left\{(x-1)(x-4) - 4(x-1) - 30\right\} < 0$$

$$\Leftrightarrow (x-2)(x-3)\left\{x^2 - 9x - 22\right\} < 0$$

$$\Leftrightarrow \quad (x-2)(x-3)(x+2)(x-11) < 0$$

From wavy curve method
$$\quad x\in (-2,2)\cup(3,11)$$
But $$x\in N$$
$$\therefore \quad x = 1,4,5,6,7,8,9,10 \quad ...(1)$$
From inequality,
$$\quad x-1 \ge 4, x-1 \ge 3, x-2 \ge 2$$
or $$\quad x\ge5, \space x\ge4, \space x\ge4$$
Hence $$\quad x\ge5 \quad ...(2)$$
From $$(1)$$ and $$(2)$$, solutions of the inequality
$$x=5,6,7,8,9,10$$
$$\therefore$$ the difference between the largest and smallest value of $$x$$ is $$5$$


From a class of $$25$$ students, $$10$$ are to be chosen for an excursion party. There are $$3$$ students who decide that their all of them will join or none of them will join. In how many ways can the excursion party be chosen?

We have 2 cases 
1) when the group of $$3$$ decides to join
Then we already have those $$3$$ and we need to select $$7$$ more from $$22$$ and that can be done in $$^{22}{ C }_{ 7 }$$ ways

Other case is 
2) When the group of $$3$$ decides not to join
Then we have to choose $$10$$ from remaining $$22$$ and that can be done in $$^{22}{ C }_{ 10 }$$ ways

So total number of ways are $$^{22}{ C }_{ 7 }$$ + $$^{22}{ C }_{ 10 }$$ ways


Prove that $$\dfrac{^{4n}C_{2n}}{^{2n}C_n} = \dfrac{1.3.5...... (4n - 1)}{\{ 1.3.5...... (2n - 1)\}^2}$$

$$\cfrac{^{4n}C_{2n}}{^{2n}C_n} = \cfrac{(4n)!(n)!(n)!}{(2n)!(2n)!(2n)!}$$
$$= \cfrac{(4n)!}{(2n)!} \times \cfrac{n!}{(2n)!} \times \cfrac{n!}{(2n)!}$$
$$= [1.3.5......(4n - 1)] \times \cfrac{1}{1.3.5.....(2n - 1)} \times \cfrac{1}{1.3.5.....(2n - 1)}$$
$$= \cfrac{1.3.5.....(4n - 1)}{\{ 1.3.5....(2n - 1) \}^2}$$


For $$r = 0, 1, 2, ...., n$$, prove that $$C_{0}\cdot C_{r} + C_{1}\cdot C_{r + 1} + C_{2} \cdot C_{r + 2} + .... + C_{n - r} \cdot C_{n} = \ ^{2n}C_{(n + r)}$$ and hence deduce that
i) $$C_{0}^{2} + C_{1}^{2} + C_{2}^{2} + ...... + C_{n}^{2} = \ ^{2n}C_{n}$$
ii) $$C_{0}\cdot C_{1} + C_{1}\cdot C_{2} + C_{2}\cdot C_{3} + ..... + C_{n - 1} \cdot C_{n} = \ ^{2n}C_{n + 1}$$

To prove:
$$C_0.C_r+C_1.C_{r+1}+C_2.C_{r+2}+......+C_{n-r}.C_n={}^{2n}{C}_{n+r}$$
$$i)C_0^2+C_1^2+C_2^2+........+C_n^2={}^{2n}{C}_{n}$$
$$ii)C_0.C_1+C_1.C_{2}+C_2.C_{3}+......+C_{n-1}.C_n={}^{2n}{C}_{n+1}$$
Solution:
We know that,
$$C_0+C_1x+C_2x^2+......+C_nx^n=(1+x)^n$$         $$...............(1)$$
$$C_0x^n+C_1x^{n-1}+C_2x^{n-2}+......+C_n=(x+1)^n$$         $$...............(2)$$
Multiplying eqn.$$(1)$$ and eqn.$$(2)$$ we get,
$$(C_0+C_1x+C_2x^2+......+C_nx^n)$$ $$(C_0x^n+C_1x^{n-1}+C_2x^{n-2}+......+C_n)=(1+x)^{2n}$$            $$.............(3)$$
Equating coeffiecients of $$x^{n-r}$$ from both sides of $$(3)$$ we get,
$$C_0.C_r+C_1.C_{r+1}+C_2.C_{r+2}+......+C_{n-r}.C_n={}^{2n}{C}_{n+r}$$     $$..........(4)$$
Now putting $$r=0$$ in eqn.$$(4)$$ we get,
$$C_0.C_0+C_1.C_{1}+C_2.C_{2}+......+C_{n}.C_n={}^{2n}{C}_{n}$$
or, $$C_0^2+C_1^2+C_2^2+........+C_n^2={}^{2n}{C}_{n}$$
Now putting $$r=1$$ in eqn.$$(4)$$ we get,
$$C_0.C_1+C_1.C_{2}+C_2.C_{3}+......+C_{n-1}.C_n={}^{2n}{C}_{n+1}$$


In how many ways fifteen different items my be given to $$A, B, C$$ such that$$ A$$ gets $$3$$, $$B$$ gets $$5$$ and remaining goes to $$C$$.

There are $$15$$ items, $$A$$ gets $$3, B$$ gets $$5,C$$ gets $$\left(15-3-5\right)=7$$
$$A$$ may get any $$3$$ of the $$15$$
$$= {^{15}C_3}$$
$$B$$ may get any $$5$$ of the remaining $$12$$
$$={^{12}C_5}$$
$$C$$ gets remaining $$7$$
$$={^{7}C_7}$$
$$\Rightarrow$$ Total $$={^{15}C_3}\times {^{12}C_5} \times {^{7}C_7}$$
               $$=\dfrac{15!\times5!}{3!7!}$$
Hence, the answer is $$\dfrac{15!\times5!}{3!7!}.$$


Solve the following inequalities.
$$C_{m - 2}^{13} > C_{m}^{18}, m\, \epsilon \, N$$

$$C^{18}_{m-2}> C_{m}^{18} > C_{m}^{18}\ \ \ m$$
Using the formula $$C_{r}^{n}=\dfrac{n!}{(n-r)!r!}$$
We have
$$C_{m-2}^{18} > C_{m}^{18}$$
$$\Rightarrow \dfrac{(18)!}{(m-2)!(18-m+2)!}> \dfrac{(18)!}{(m)!(18-m)!}$$
$$\Rightarrow \dfrac{1}{(m-2)!(18-m+1)(18-m+2)(18-m)!}>\dfrac{1}{(m)(m-1)(m-2)!}$$
$$\Rightarrow \dfrac{1}{(18+1-m)(18-m+2)}>\dfrac{1}{m(m-1)}$$
$$\Rightarrow m(m-1)> (19-m)(20-m)$$        (Cross multiply)
$$\Rightarrow m^{2}-m>(380+m^{2}-39m)$$ as $$m^{2}>0$$
$$\Rightarrow -m > 380-39\ m$$
$$\Rightarrow 39 m-m>380$$
$$\Rightarrow 38\ m > 380$$
$$\Rightarrow m >\dfrac{380}{380}$$
$$\Rightarrow m> 10$$


If $$^nC_6 : ^{n - 3}C_3 = 33 : 4$$, find n.

$$\cfrac{^nC_{6}}{^{n-3}C_{3}}=\cfrac{33}{4}$$
$$\Rightarrow\, \cfrac{\cfrac{n!}{(n-6)!6!}}{\cfrac{(n-3)!}{3!(n-6)!}}=\cfrac{33}{4}$$
$$\Rightarrow\, \cfrac{n!}{6!}\times\cfrac{ 3!}{(n-3)!}=\cfrac{33}{4}$$
$$\Rightarrow\,n(n-1)(n-2)=11\times3\times5\times2\times 3=11\times10\times9$$
$$\therefore\,n=11$$


How many $$4$$ letter words can be formed from the letters of the word $$'ANSWER'$$? How many of the words start with a vowel?

$$ANSWER$$
Case:1 Starts with $$A$$
$$5$$ Letters and $$3$$ Blanks
Number of ways $$=^{ 5 }{ C }_{ 3 }=\cfrac { 5\times 4 }{ 2 } =10$$ Ways 
Case: 2 starts with $$E$$
$$5$$ Letters and $$3$$ blanks 
Number of ways $$=^{ 5 }{ C }_{ 3 }=\cfrac { 5\times 4 }{ 2 } =10$$ Ways 
Hence total ways are $$20$$


If $$^nC_{r - 1} = 36, ^nC_r = 84$$ and $$^nC_{r + 1} = 126$$, find the values of n and r.

$$\cfrac{^nC_{r}}{^nC_{r-1}}=\cfrac{84}{36}$$
$$\Rightarrow\cfrac{\cfrac{n!}{r!(n-r)!}}{\cfrac{n!}{(r-1)!(n-r+1)!}}=\cfrac{84}{36}$$
$$\Rightarrow\cfrac{n-r+1}{r}=\cfrac{7}{3}$$
$$\Rightarrow 3n-3r+3=7r$$
$$\Rightarrow10r=3n+3$$---------------1
$$\cfrac{^nC_{r+1}}{^nC_{r}}=\cfrac{126}{84}$$
$$\Rightarrow\cfrac{\cfrac{n!}{(r+1)!(n-r-1)!}}{\cfrac{n!}{(r)!(n-r)!}}=\cfrac{3}{2}$$
$$\Rightarrow \cfrac{n-r}{r+1}=\cfrac{3}{2}$$
$$\Rightarrow 2n-2r=3r+3$$
$$\Rightarrow 5r=2n-3$$-------------------2
Dividing Equation 1 by Equation 2,
$$\cfrac{10r}{5r}=\cfrac{3n+3}{2n-3}$$
$$\Rightarrow2(2n-3)=3n+3$$
$$\Rightarrow4n-6=3n+3$$
$$\Rightarrow n=6+3$$
$$\Rightarrow n=9$$

$$10r=3n+3$$
$$\Rightarrow 3(9)+3=30$$
$$\Rightarrow 10r=30$$
$$\Rightarrow r=3$$

$$\therefore\, n=9,r=3$$



Three married couples are to be seated in a row having six seats in a cinema hall. If spouses are to be seated next to each other, in how many ways can they be seated? Find also the number of ways of their seating if all the ladies sit together.

Let us denote married couples by S1, S2, S3
Then the number of ways in which spouces can be seated next to each other is 3! = 6 ways.
 Again each couple can be seated in 2! ways. 
Thus the total number of seating arrangement so that spouces sit next to each other = 3! × 2! × 2! × 2! = 48. 


Again, if three ladies sit together, then necessarily three men must sit together. 
Thus, ladies and men can be arranged altogether among themselves in 3! ways. 
Therefore, the total number of ways where ladies sit together is 4! × 3! × 1! = 144


How many zeros in 100! ?

Given number is = 100!
Exponent or power of 5 in the expansion
of 100! is $$ = \left [ \dfrac{100}{5} \right ]+\left [ \dfrac{100}{5^2} \right ]+\left [ \dfrac{100}{5^3} \right ]+...$$
# using formula : Exponent of a point no . k
in the expansion of n! is $$= \left [ \dfrac{n}{k} \right ]+\left [ \dfrac{n}{k^2} \right ]+ \left [ \dfrac{n}{k^3} \right ]+...$$
where [0] is the greatest integer function
$$ \Rightarrow $$ Exponent of 5 $$ = [20]+[4]+[0.8]+...$$
$$ = 20+4+0 ...$$
$$ = 24 $$
similarly Exponent of 2 is $$ = \left [ \dfrac{100}{2} \right ] +\left [ \dfrac{100}{4} \right ]+\left [ \dfrac{100}{8} \right ]+\left [ \dfrac{100}{16} \right ]$$
$$ + \left [ \dfrac{100}{32} \right ]+\left [ \dfrac{100}{64} \right ]+\left [ \dfrac{100}{18} \right ]+...$$
$$ = 50+25+12+6+3+1 +0...$$
$$ = 97 $$
Now prime factor of 10 are 2 & 5 
$$ \Rightarrow (10)^1 = 2^{1} \times 5^{1}$$ which makes one zero at the and 
similarly $$ 100 = 2^2 \times 5^2 \Rightarrow $$ In zeroes.
$$ \Rightarrow 5^{24} \times 2^{24} = (10)^{24} \Rightarrow  24 $$ zeroes at the end in the expansion of 100!
$$ \Rightarrow Ans : 24 $$

1172662_877211_ans_2cb93f26746e4ab9955abba4656e6385.jpg


If $$^{15}C_r : ^{15}C_{r - 1} = 11 : 5$$, find r.

$$\cfrac{^{15}C_{r}}{^{15}C_{r-1}}=\cfrac{11}{5}$$
$$\Rightarrow\,\cfrac{\cfrac{15!}{r!(15-r)!}}{\cfrac{15!}{(r-1)!(15-r+1)}}=\cfrac{11}{5}$$
$$\Rightarrow\cfrac{(r-1)!\cdot\,15(15-r+1)!}{r!(15-r)!}=\cfrac{11}{5}$$
$$\Rightarrow\cfrac{15-r+1}{r}=\cfrac{11}{5}$$
$$\Rightarrow75-5r+5=11r$$
$$\Rightarrow 80=16r$$
$$\Rightarrow r=5$$



There are $$10$$ different books in a shelf. Find the number of ways in which $$3$$ books can be selected so that exactly two of them are consecutive.

$$\textbf{Step -1: When two consecutive books are selected from the end of the shelf.}$$

                   $$\text{Let }10\text{ different books in the shelf are }A_1,A_2,A_3,A_4,A_5,A_6,A_7,A_8,A_9,A_{10}.$$

                   $$\text{Two consecutive books chosen from the end are either }A_1,A_2\text{ or }A_9,A_{10}.$$

                   $$\text{If }A_1,A_2\text{ are selected then, the third book selected cannot be }A_3.$$

                   $$\text{And if }A_9,A_{10}\text{ are selected then, the third book selected cannot be }A_8.$$

                   $$\therefore\text{Number of ways of chosing two consecutive books from the end}=2$$

                   $$\text{Number of ways of chosing the third book}=7$$

                   $$\text{Total number of ways}=2\times7=14$$

$$\textbf{Step -2: When two consecutive books are selected from the middle of the shelf.}$$

                  $$\text{Two consecutive books selected from the middle can be one of the pair among:}$$

                  $$A_2A_3,A_3A_4,A_4A_5,A_5A_6,A_6A_7,A_7A_8,A_8A_9.$$

                  $$\text{And the third book selected cannot be the book placed either side of the chosen pair.}$$

                  $$\Rightarrow\text{If }A_2A_3\text{ pair is selected then the possible outcome for the third book are }A_5,A_6,A_7,A_8,A_9,A_{10}.$$

                  $$\therefore\text{Number of ways of chosing two consecutive books from the middle}=7$$

                  $$\text{Number of ways of chosing the third book}=6$$

                  $$\text{Total number of ways}=7\times6=42$$

$$\textbf{Step -3: Find the required number of ways.}$$

                  $$\text{The required number of ways}=14+42$$

                  $$=56$$

$$\textbf{Hence 56 number of ways in which 3 books can be selected so that exactly}$$ $$\textbf{two of them are consecutive.}$$



Find the value of $$^{61}C_{57}-^{60}C_{56}$$
i)  $$^{61}C_{58}$$
ii) $$^{60}C_{57}$$

Simplifying $${}^{61}{C_{57}} - {}^{60}{C_{56}}$$.

$${}^{61}{C_{57}} - {}^{60}{C_{56}} = \dfrac{{61!}}{{57!\left( {61 - 57} \right)!}} - \dfrac{{60!}}{{56!\left( {60 - 56} \right)!}}$$

$$ = \dfrac{{61!}}{{57!4!}} - \dfrac{{60!}}{{56!4!}}$$

$$ = 521855 - 487635$$

$$ = 34220$$

(i)

Simplifying $${}^{61}{C_{58}}$$.

$${}^{61}{C_{58}} = \dfrac{{61!}}{{58!\left( {61 - 58} \right)!}}$$

$$ = \dfrac{{61!}}{{58!3!}}$$

$$ = 35990$$

(ii)

Simplifying $${}^{60}{C_{57}}$$.

$${}^{60}{C_{57}} = \dfrac{{60!}}{{57!\left( {60 - 57} \right)!}}$$

$$ = \dfrac{{60!}}{{57!3!}}$$

$$ = 34220$$



If $$( 1 + x ) ^ { 15 } = C _ { 0 } + C _ { 1 } x + C _ { 2 } x ^ { 2 } + \ldots \ldots + C _ { 15 } x ^ { 15 } ,$$ find the value of $$C _ { 2 } + 2 C _ { 3 } + 3 C _ { 4 } + \ldots \ldots + 14 C _ { 15 }$$

$$\left( 1+x\right)^{15}=C_0+C_1 x+C_2 x^2...........+C_{15} x^{15}$$
so, $$C_2+2C_3+......14C_{15}$$ is the expansion of $$\dfrac{d}{dx}\left( \dfrac{\left(1+x\right)^{15}-1}{x}\right)$$ at $$x=1$$
so, $$\dfrac{d}{dx}\left( \dfrac{\left( 1+x\right)^{15}-1}{x}\right)=\dfrac{x\left( 15\left( 1+x\right)^{14}\right)-\left( \left( 1+x\right)^{15}-1\right)}{x^2}$$
at $$x=1,$$  this value tends to
$$\Rightarrow \dfrac{1\left( 15\left( 2\right)^{14}\right)-\left(2^{15}-1\right)}{1}$$
$$\Rightarrow \dfrac{2^{14}\left(13\right) +1}{1}$$
so, $$C_2+2C_3+3C_4+..........+14C_{15}=\dfrac{2^{14}\left(13\right)+1}{1}$$
Hence, the answer is $$\dfrac{2^{14}\left( 13\right)+1}{1}.$$



Prove:
$$C^2_0+\dfrac{C^2_1}{2}+\dfrac{C^2_2}{3}+......+\dfrac{C^2_n}{n+1}=\dfrac{(2n+1)!}{((n+1)!)^2}$$


2059353_1166079_ans_f3eb79fa1f9a4081afbb7dd5ca2bf18a.jpg


Find the value of $$_{  }^{ n }{ { C }_{ r-1 } }/_{  }^{ n }{ { C }_{ r } }$$

$$\cfrac{^{n}C_{r-1}}{^{n}C_{r}}$$
$$=\cfrac{\cfrac{n!}{(r-1)!(n-r+1)!}}{\cfrac{n!}{r!(n-r)!}}$$
$$=\cfrac{r!(n-r)!}{(r-1)!(n-r+1)!}$$
$$=\cfrac{r}{n-r+1}$$



Prove that $${ 2c }_{ 0 }+{ 5c }_{ 1 }+{ 8c }_{ 2 }+.....+\left( 3n+2 \right) { c }_{ n }=\left( 3n+4 \right) { 2 }^{ n-1 }$$


2040783_1327637_ans_50916b30a67a4fad978e2ce9ea124d7f.jpg


There are 720 permutations of the digits 1,2,3,4,5,suppose these permutations are arranged from smallest to largest numerical of values, beginning from 1 2 3 4 5 6 and ending with 6 5 4 3 2(a)what number falls on $${ 124 }^{ th }$$ position?  (b) what is the position of 321546? 


The set {$$1,2,3,4,5,6$$} has a total of $$6!$$ permutations
a. Of those $$6!$$ permutations, $$5!=120$$ begin with $$1$$. So first $$120$$ numbers would contain $$1$$ as the unit digit.
b. The next $$120$$, including the $$124$$th, would begin with $$'2'$$
c. Then of the $$5!$$ numbers beginning with $$2$$, there are $$4!=24$$ including the $$124$$th number, which have the second digit $$=1$$
d. Of these $$4!$$ permutations beginning with $$21$$, there are $$3!=6$$ including the $$124$$th permutation which have third digit $$3$$
e. Among these $$3!$$ permutations beginning with $$213$$, there are $$2$$ numbers with the fourth digit $$=4$$ ($$121$$th & $$122$$th), $$2$$ with fourth digit $$5$$ (numbers $$123$$ & $$124$$) and $$2$$ with fourth digit $$6$$ (numbers $$125$$ and $$126$$).
Lastly, of the $$2!$$ permutations beginning with $$2135$$, there is one with $$5$$th digit $$4$$ (number $$123$$) and one with $$5$$ digit $$6$$ (number $$124$$).
$$\therefore$$   The $$124$$th number is $$213564$$
Similarly reversing the above procedure we can determine the position of $$321546$$ to be $$267$$th on the list.


Verify that: $$^{15}C_{8}+^{15}C_{9}-^{15}C_{6}-^{15}C_{7} = 0 $$

We know that,
$${ n }_{ C_{ r } }=\displaystyle \frac { n! }{ r!\left( n-r \right) ! } $$

$$\therefore LHS={ { 15 }_{ { C }_{ 8 } } }+{ 15 }_{ { C }_{ 9 } }-{ 15 }_{ { C }_{ 6 } }-{ 15 }_{ { C }_{ 7 } }$$

$$\displaystyle =\dfrac { 15! }{ 8!\left( 15-8 \right) ! } +\frac { 15! }{ 9!\left( 15-9 \right) ! } -\frac { 15! }{ 6!\left( 15-6 \right) ! } -\frac { 15! }{ 7!\left( 15-7 \right) ! }$$

$$=\displaystyle \dfrac { 15! }{ 8!\times 7! } +\frac { 15! }{ 9!\times 6! } -\frac { 15! }{ 6!\times 9! } -\frac { 15! }{ 7!\times 8! } $$

$$=\displaystyle \left( \frac { 15! }{ 8!\times 7! } -\frac { 15! }{ 7!\times 8! }  \right) +\left( \frac { 15! }{ 9!\times 6! } -\frac { 15! }{ 6!\times 9! }  \right) $$

$$=\left( 0 \right) +\left( 0 \right) =0$$

$$=RHS$$


Prove that:
$$\dfrac {n!}{r!} = n(n - 1)(n - 2) ... (r + 1)$$.


1947874_1709075_ans_9413539845c04b9eb5ce49aca643f07d.jpg


If $$ ^{n}C_{14} = ^{n}C_{16},$$ find $$^{n}C_{28}$$.

Given, $${ n }_{ { C }_{ 14 } }={ n }_{ { C }_{ 16 } }$$

$$\therefore \dfrac { n! }{ 14!\left( n-14 \right) ! } =\dfrac { n! }{ 16!\left( n-16 \right) ! } $$

$$\therefore \dfrac { 1 }{ 14!\left( n-14 \right) \times \left( n-15 \right) \times \left( n-16 \right) ! } =\dfrac { 1 }{ 16\times 15\times 14!\left( n-16 \right) ! } $$

$$\displaystyle \therefore \frac { 1 }{ \left( n-14 \right) \times \left( n-15 \right)  } =\frac { 1 }{ 16\times 15 } $$

$$\displaystyle \therefore \left( n-14 \right) \times \left( n-15 \right) =16\times 15$$

$$\displaystyle \therefore { n }^{ 2 }-29n+210=240$$

$$\displaystyle \therefore { n }^{ 2 }-29n-30=0$$

$$\displaystyle \therefore { n }^{ 2 }-30n+n-30=0$$

$$\displaystyle \therefore n\left( n-30 \right) +1\left( n-30 \right) =0$$

$$\displaystyle \therefore \left( n+1 \right) \left( n-30 \right) =0$$

$$\therefore n=-1$$ or $$n=30$$

Consider only positive root
$$\therefore n=30$$

$${ n }_{ { C }_{ 28 } }={ 30 }_{ { C }_{ 28 } }$$

$$\displaystyle \therefore { 30 }_{ { C }_{ 28 } }=\frac { 30! }{ 28!\left( 30-28 \right) ! } $$

$$\displaystyle \therefore { 30 }_{ { C }_{ 28 } }=\frac { 30\times 29\times 28! }{ 28!\times 2! } $$

$$\displaystyle \therefore { 30 }_{ { C }_{ 28 } }=\frac { 30\times 29 }{ 2 } $$

$$\therefore { 30 }_{ { C }_{ 28 } }=15\times 29$$

$$\therefore { 30 }_{ { C }_{ 28 } }=435$$


Prove that $$\sum _{ r=0 }^{ n }{ ^nC_r } .3^r = 4^n $$


1855000_1709615_ans_8068fae3e70642829e355cd79c672d03.jpeg


If $$ ^{n}C_{16} = \ ^{n}C_{14},$$ find $$ ^{n}C_{27}$$.

Given $$\therefore n_{ { C }_{ 16 } }=n_{ { C }_{ 14 } }$$

$$\displaystyle \therefore \frac { n! }{ 16!\left( n-16 \right) ! } =\frac { n! }{ 14!\left( n-14 \right) ! } $$

$$\displaystyle \therefore \frac { 1 }{ 16\times 15\times 14!\left( n-16 \right) ! } =\frac { 1 }{ 14!\left( n-14 \right) \times \left( n-15 \right) \times \left( n-16 \right) ! } $$

$$\displaystyle \therefore \frac { 1 }{ 16\times 15 } =\frac { 1 }{ \left( n-14 \right) \times \left( n-15 \right)  } $$

$$\displaystyle \therefore \left( n-14 \right) \times \left( n-15 \right) =16\times 15$$

$$\displaystyle \therefore { n }^{ 2 }-29n+210=240$$

$$\displaystyle \therefore { n }^{ 2 }-29n-30=0$$

$$\therefore { n }^{ 2 }-30n+n-30=0$$

$$\therefore n\left( n-30 \right) +1\left( n-30 \right) =0$$

$$\therefore \left( n+1 \right) \left( n-30 \right) =0$$

$$\therefore n=-1$$ or $$n=30$$

Consider only positive root
$$\therefore n=30$$

$$\displaystyle \therefore { n }_{ { C }_{ 27 } }={ 30 }_{ { C }_{ 27 } }$$

$$\displaystyle \therefore { 30 }_{ { C }_{ 27 } }=\frac { 30! }{ 27!\left( 30-27 \right) ! } $$

$$\displaystyle \therefore { 30 }_{ { C }_{ 27 } }=\frac { 30\times 29\times 28\times 27! }{ 27!\times 3! } $$

$$ \displaystyle\therefore { 30 }_{ { C }_{ 27 } }=\frac { 30\times 29\times 28 }{ 6 } $$

$$\therefore { 30 }_{ { C }_{ 27 } }=5\times 29\times 28$$

$$\therefore { 30 }_{ { C }_{ 27 } }=4060$$


If $$ ^{18}C_{r} = ^{18}C_{r+2},$$ find $$ ^{r}C_{5}$$.

Given, $${ 18 }_{ { C }_{ r } }={ 18 }_{ { C }_{ r+2 } }$$

We know that if $${ n }_{ { C }_{ r } }={ n }_{ { C }_{ s } }$$, then
$$r=s$$ or $$r+s=n$$

In given problem, $$r=r$$ and $$s=r+2$$
$$\therefore s\neq r$$
 
Thus, $$r+s=n$$
$$\therefore r+r+2=18$$
$$\therefore 2r=16$$
$$\therefore r=8$$

$$\therefore { r }_{ { C }_{ 5 } }={ 8 }_{ { C }_{ 5 } }$$
$$\displaystyle =\frac { 8! }{ 5!\left( 8-5 \right) ! } $$

$$\displaystyle =\frac { 8! }{ 5!\times 3! } $$

$$\displaystyle =\frac { 8\times 7\times 6\times 5! }{ 5!\times 3! } $$

$$\displaystyle =\frac { 8\times 7\times 6 }{ 6 } $$

$$=8\times 7=56$$


There are 18 points in a plane of which 5 are collinear. How many straight lines can be formed by joining them?


1846314_1710082_ans_6a5d1f2ee9524d0981851ad3a18c5cbc.jpeg


Class 11 Engineering Maths Extra Questions