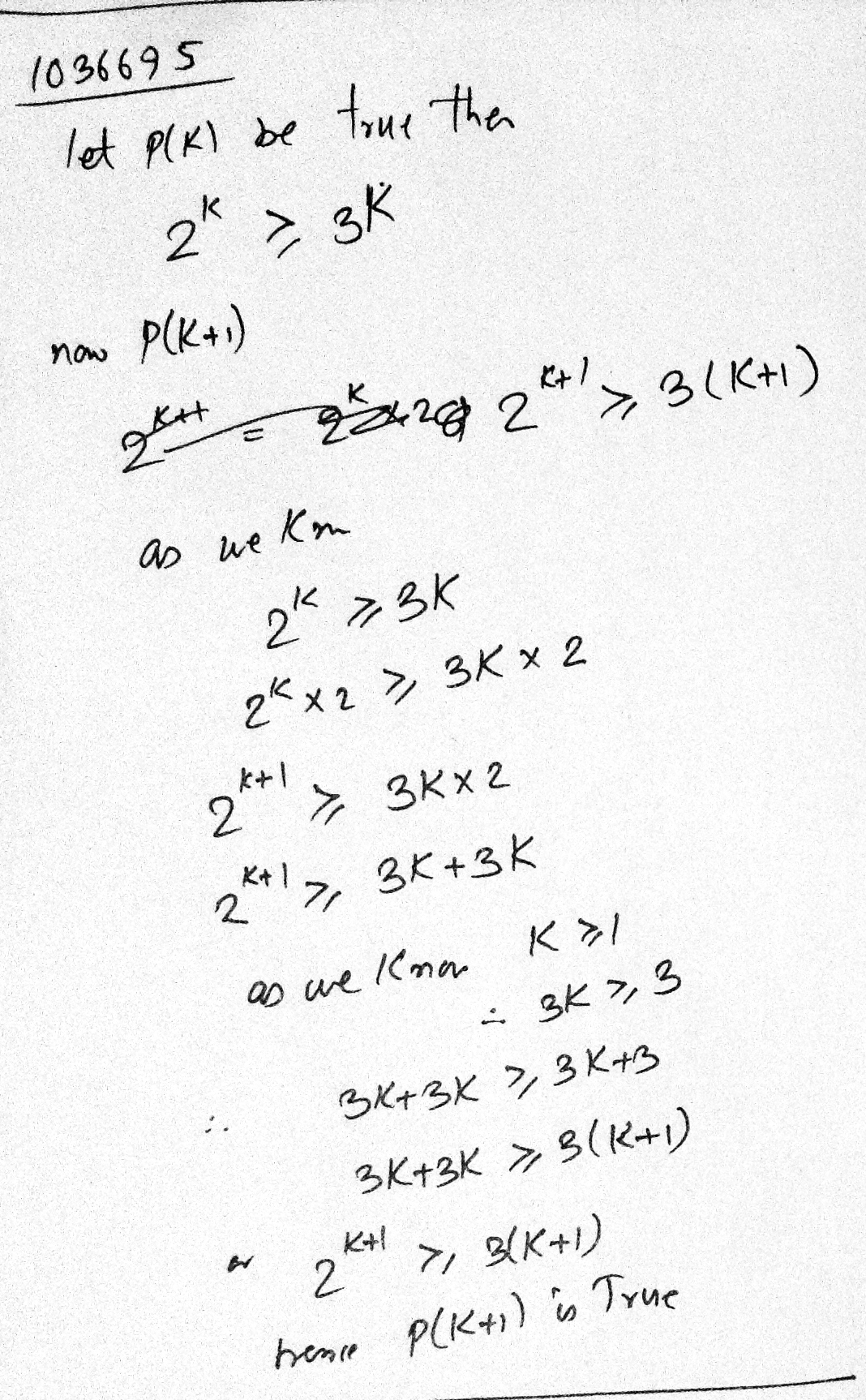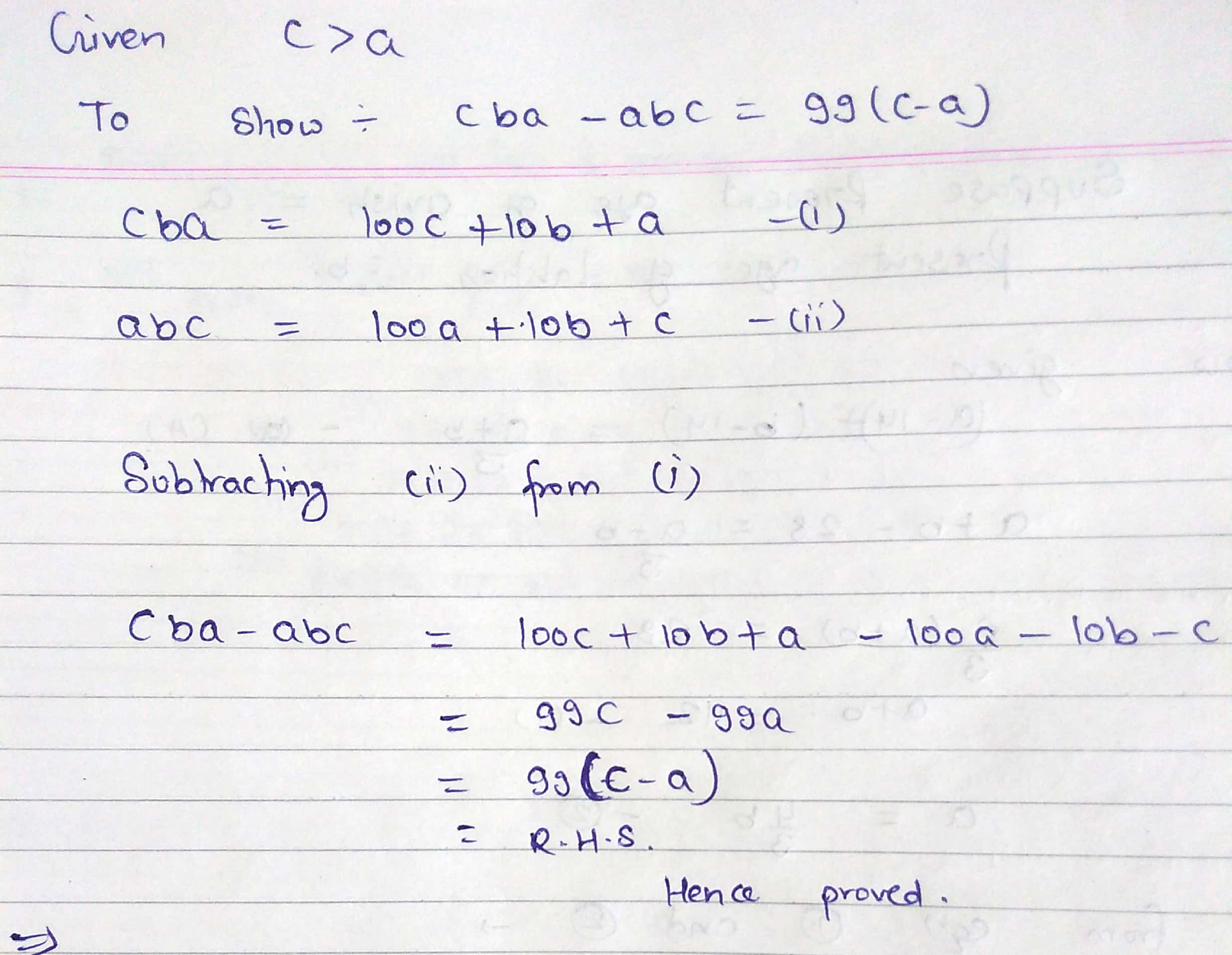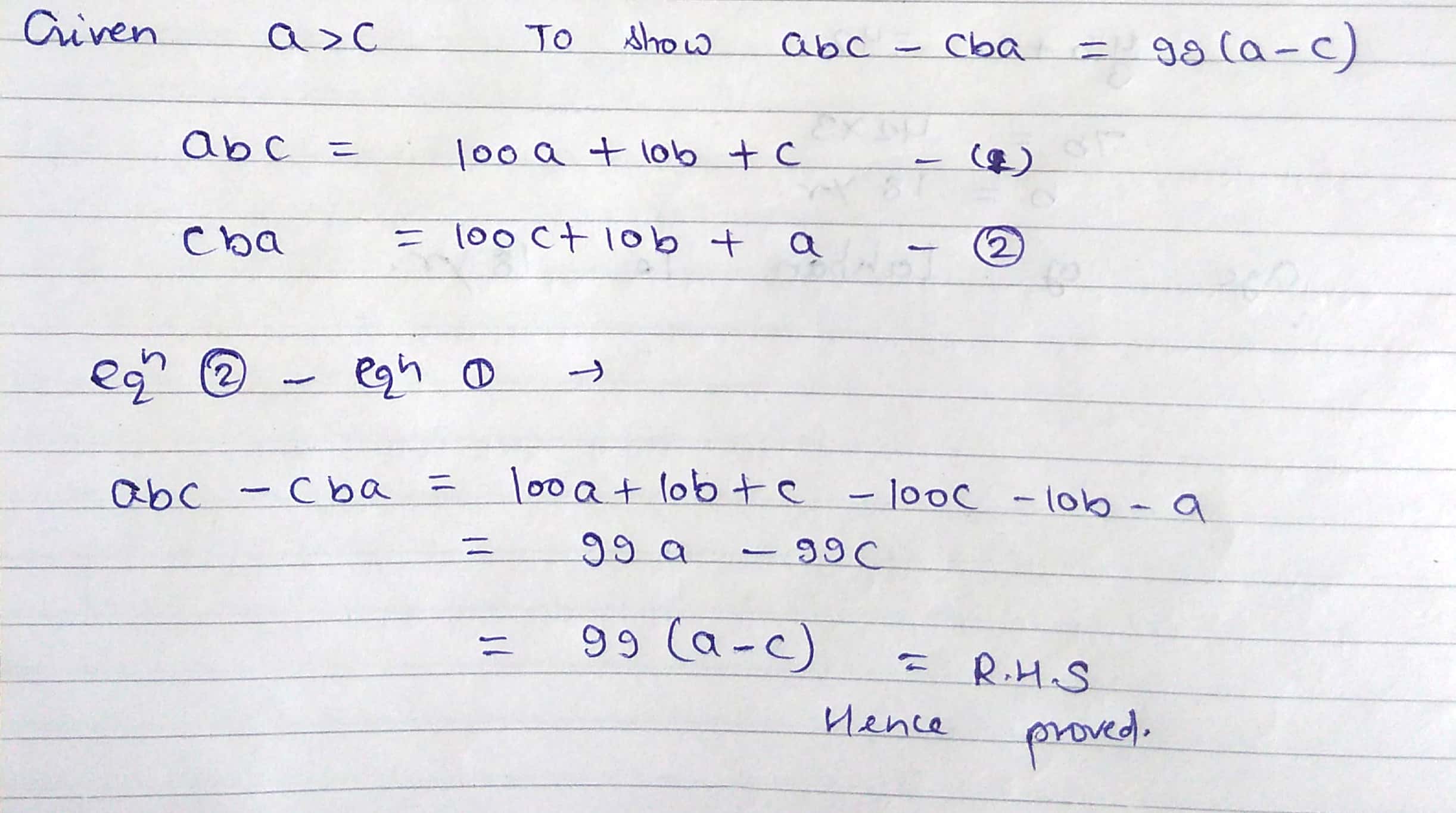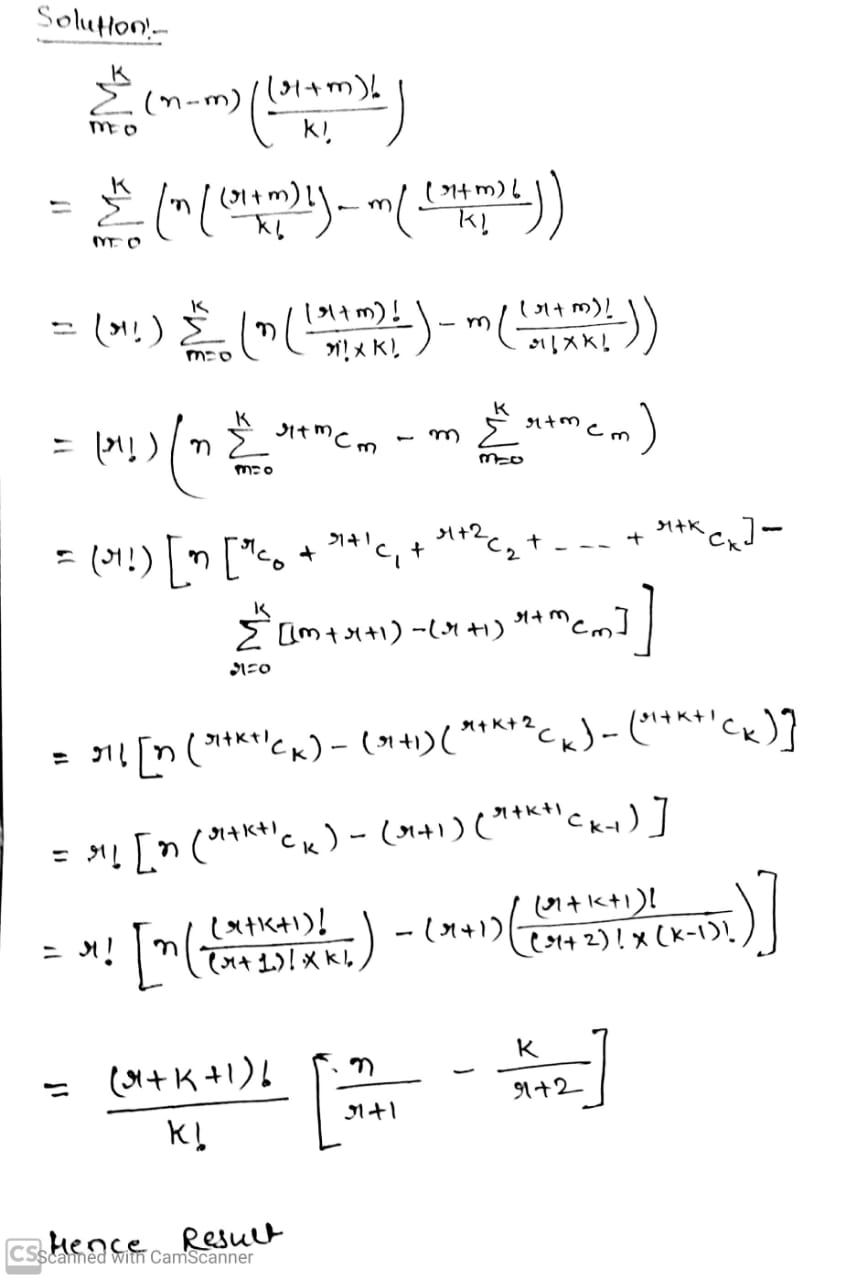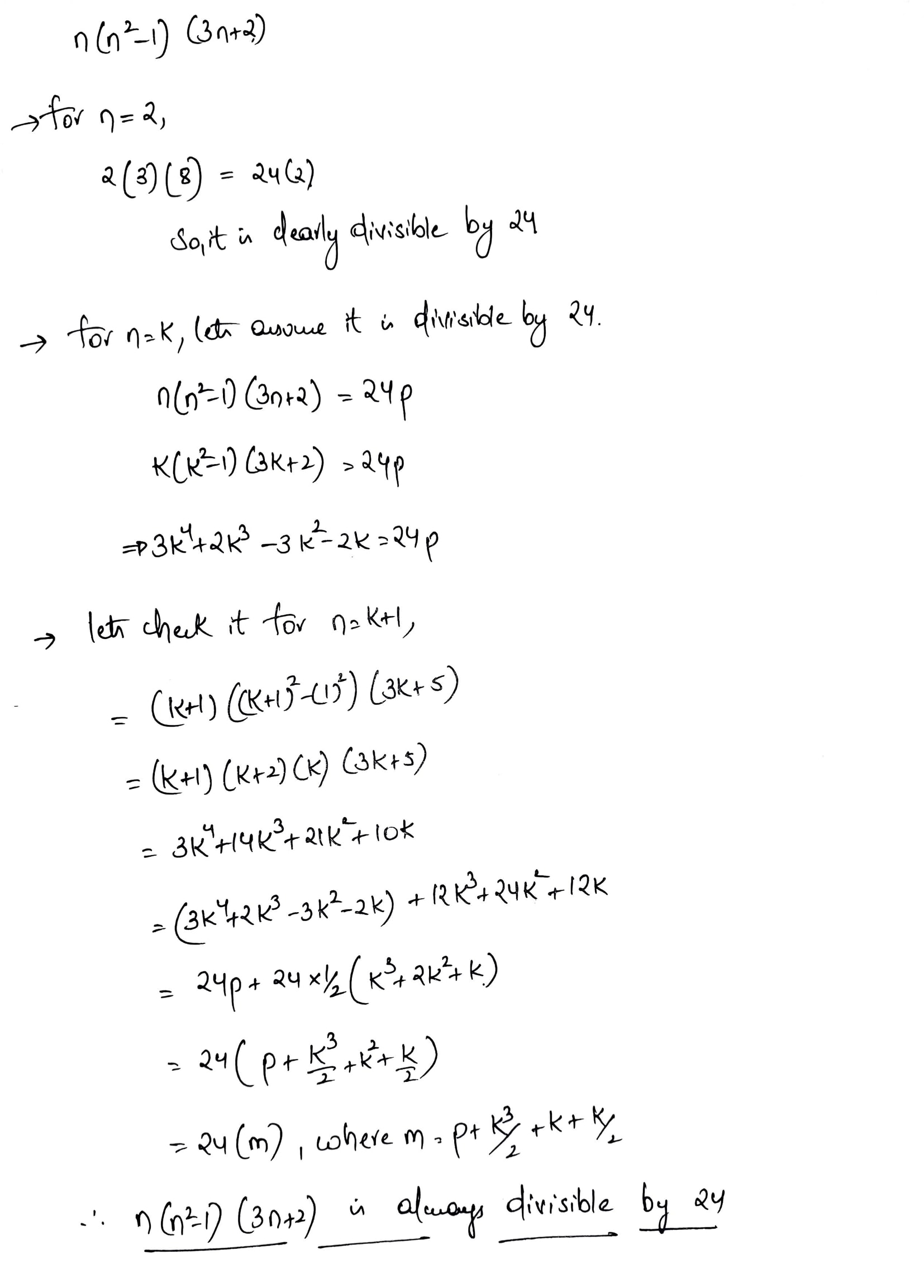Principle Of Mathematical Induction - Class 11 Engineering Maths - Extra Questions
If $$A = \left( {\begin{array}{*{20}{c}}{\cos \theta }&{i\sin \theta }\\{i\sin \theta }&{\cos \theta }\end{array}} \right)$$, where $$i = \sqrt { - 1} $$, then by the principle of Mathematics Induction prove that $${A^n} = \left( {\begin{array}{*{20}{c}}{{\mathop{\rm cosn}\nolimits} \theta }&{i{\mathop{\rm sinn}\nolimits} \theta }\\{i{\mathop{\rm sinn}\nolimits} \theta }&{{\mathop{\rm cosn}\nolimits} \theta }\end{array}} \right)$$
Using the principle mathematical induction , prove that $$\forall \, n \, \epsilon \, N$$
$$ I_n \, = \, \int_{0}^{\pi/2}cos^n \, \, x sin\, \, nx \,dx$$
$$ = \, \dfrac{1}{2^{n \, + \, 1}}\left [2 \, + \, \dfrac{2^2}{2}\, +\dfrac{2^3}{3} .... \, + \, \, \dfrac{2^n}{n} \right ]$$
Prove that $$2^n>n$$ for all positive integers $$n$$
For any natural number n , prove that inequality
|sin n x| $$\geq$$ n | sin x |
Prove that 7 is a factor of $$2^{3n}$$ - 1 for all natural numbers n.
Prove the assertions of the following problems
Prove that $$2^n > n^2$$ for any natural number $$n > 5.$$
If $$P(n)$$ is the statement $$''2^n\ge 3n"$$ and if $$P(r)$$ is true prove that $$P(r+1)$$ is true.
Using the principle of mathematical induction prove that $$2 + 4 + 6 + .... + 2n = {n^2} + n$$.
Prove that $$\left( {1 \times 2 \times 5} \right) + \left( {2 \times 3 \times 7} \right) + \left( {3 \times 4 \times 9} \right) + .....$$ is $$\dfrac{{n\left( {n + 1} \right)\left( {n + 2} \right)\left( {3n + 7} \right)}}{6}$$
Prove by mathematical induction,
$${ 1 }^{ 2 }+{ 2 }^{ 2 }+{ 3 }^{ 2 }+....+{ n }^{ 2 }=\dfrac { n\left( n+1 \right) \left( 2n+1 \right) }{ 6 } $$
Using the principle of mathematical induction, show that;
$$2+4+6+.....+2n=n^2+n$$
Using Principle of mathematical induction prove that $$6^n -1$$ divisible by $$5$$.
Using the principle of Mathematical Induction, prove the following for all $$n$$ and $$N$$
1) $${3}^{n}>{2}^{n}$$
Prove that the square of any positive integer of the form 5m+1 will leave a remainder 1 when divided by 5 for some integer m
Prove using PMI
$$\left( {1 + \frac{3}{1}} \right)\left( {1 + \frac{5}{4}} \right)\left( {1 + \frac{7}{9}} \right)...\left( {1 + \frac{{\left( {2n + 1} \right)}}{{{n^2}}}} \right) = {\left( {n + 1} \right)^2}$$
If $$P(n)$$ is the statement $$n^{2}-n+41$$ is prime, prove that $$P(1),P(2)$$ and $$P(3)$$ are true.
Prove also that $$P(41)$$ is not true.
Solve: $$(2n+7)<(n+3)^2$$
Using P.M.I. prove that
$${n^2} < {2^n}\forall n \ge 5$$
$$x = \sin t\,\,\,\,\,\,\,\,\,\,y = \cos mt$$
Prove $$\left( {1 - {x^2}} \right){y_{n + 2}} - \left( {2n - 1} \right){y_{n + 1}} - \left( {{n^2} - {m^2}} \right){y_n} = 0$$
Use the principle of mathematical induction to show that :
$$ 2 + 2^2 + ..... + 2^n = 2^{n+1} - 2 $$ for every natural number $$n.$$
Show that only one of the no $$n, n + 2$$ and $$n + 4$$ in divisible $$3$$.
Prove by method of induction, for all $$n \in $$
$$1^2 + 2^2 + 3^2 + ... + n^2 = \dfrac{n(n + 1)(2n + 1)}{6}$$.
If $${a_1},\,{a_2},\,{a_3},\,...,{a_n}$$ are in A.P. and $${a_i} > 0$$ for all i, then show that $$\dfrac{1}{{{a_1}{a_2}}} + \dfrac{1}{{{a_2}{a_3}}} + ... + \dfrac{1}{{{a_{n - 1}}{a_n}}} = \dfrac{{n - 1}}{{{a_1}{a_n}}}$$.
To prove: $$n \le 2^{n}$$ for $$n\ in\ N$$
$$P(n):n \le 2^{n}.........$$ for $$n\ in\ N$$
Can the number $$6^{n}$$, where n is a natural number, end with digit 5? Give reasons.
For every natural number $$n(>1)$$, prove that $$4^{n}+15n-1$$ is divisible by $$9$$.
Prove by method of induction; for all $$n \in N$$ $$3 + 7 + 11 + \ldots . . . +$$ to $$n$$ terms $$= n ( 2 n + 1 )$$
Prove that $$3^{n+1} > 3(n+1)$$.
"The product of three consecutive positive integers is divisible by 6". Is.this statement true or false"? Justify your answer.
Prove that $$1 + 2 + 3 + ..... + n =$$ $$\displaystyle \frac {n(n\, +\, 1)}{2}$$.
Prove that $$3^{n + 1} > 3(n + 1)$$.
Prove $$1+3+5+\cdots+(2n-1)=n^2$$
Prove $$3^{n+1}>$$$$3(n+1)$$
Prove the following using the principle of mathematical induction for all $$n\in N$$:
$$1+3+{3}^{2}+........+{3}^{n-1}=\cfrac{({3}^{n}-1)}{2}$$
Prove that $$1 + 3 + 5 + ..... + (2n - 1) = n$$ $$^2$$.
Prove the following by using principle of mathematical induction for all $$n\in N: 1.3+3.5+5.7+.......+(2n-1)(2n+1)=\cfrac{n(4{n}^{2}+6n-1)}{3}$$
Prove the following by using the principle of mathematical induction for all $$n\in N: 1.3+2.{3}^{2}+3.{3}^{3}+.....+n.{3}{^n}=\cfrac{(2n-1){3}^{n+1}+3}{4}$$
Prove the following by using the principle of mathematical induction for all $$n\in N:1.2.3+2.3.4+......+n(n+1)(n+2)=\cfrac{n(n+1)(n+2)(n+3)}{4}$$
Prove the following by using the principle of mathematical induction for all $$n \in N: \cfrac{1}{2}+\cfrac{1}{4}+\cfrac{1}{8}+.....+\cfrac{1}{{2}^{n}}=1-\cfrac{1}{{2}^{n}}$$
Prove the following by using the principle of mathematical induction for all $$n\in N:\cfrac { 1 }{ 1.2.3 } +\cfrac { 1 }{ 2.3.4 } +\cfrac { 1 }{ 3.4.5 } +.....+\cfrac { 1 }{ n(n+1)(n+2) } =\cfrac { n(n+3) }{ 4(n+1)(n+2) } $$
Prove the following by using the principle of mathematical induction for all $$n\in $$:
$$1+\cfrac{1}{(1+2)}+\cfrac{1}{(1+2+3)}+..........+\cfrac{1}{1+2+3+.....n)}=\cfrac{2n}{(n+1)}$$
Prove the following by using the principle of mathematical induction for all $$n\in N: 1.2+2.3+3.4+......+n(n+1)=\left[ \cfrac { n(n+1)(n+2) }{ 3 } \right] $$
Prove the following by using the principle of mathematical induction for all $$n\in N$$
$${ 1 }^{ 3 }+{ 2 }^{ 3 }+{ 3 }^{ 3 }+.......+{ n }^{ 3 }={ \left[ \cfrac { n(n+1) }{ 2 } \right] }^{ 2 }$$
Prove the following by using the principle of mathematical induction for all $$n\in N: 1.2+2.{2}^{2}+3.{2}^{2}+.......+n.{2}^{n}=(n-1){2}^{n+1}+2$$
Prove the following by using the principle of mathematical induction for all $$n\in N: \cfrac{1}{2.5}+\cfrac{1}{5.8}+\cfrac{1}{8.11}+......+\cfrac{1}{(3n-1)(3n+2)}=\cfrac{n}{(6n+4)}$$
Prove the following by using the principle of mathematical induction for all $$n\in N: \left( 1+\cfrac { 3 }{ 1 } \right) \left( 1+\cfrac { 5 }{ 4 } \right) \left( 1+\cfrac { 7 }{ 9 } \right) ......\left( 1+\cfrac { (2n+1) }{ { n }^{ 2 } } \right) ={ (n+1) }^{ 2 }$$
Prove the following by using the principle of mathematical induction for all $$n\in N:{10}^{2n-1}+1$$ is divisible by $$11$$
Prove the following by using the principle of mathematical induction for all $$n\in N:{x}^{2n}-{y}^{2n}$$ is divisible by $$x+y$$.
Prove the following b y using the principle of mathematical induction for all $$n\in N:1+2+3+.....+n<\cfrac{1}{8}{(2n+1)}^{2}$$
Prove the following by using principle of mathematical induction for all $$n\in N: \cfrac { 1 }{ 3.5 } +\cfrac { 1 }{ 5.7 } +\cfrac { 1 }{ 7.9 } +.....+\cfrac { 1 }{ (2n+1)(2n+3) } =\cfrac { n }{ 3(2n+3) } $$
Prove the following by using the principle of mathematical induction for all $$n\in N:\cfrac { 1 }{ 1.4 } +\cfrac { 1 }{ 4.7 } +\cfrac { 1 }{ 7.10 } +.....+\cfrac { 1 }{ (3n-2)(3n+1) } =\cfrac { n }{ (3n+1) } $$
Prove the following by using the principle of mathematical induction for all $$n\in N: P(n):a+ar+a{r}^{2}+......+a{r}^{n-1}=\cfrac{a({r}^{n}-1)}{r-1}$$
Prove the following by using the principle of mathematical induction for all $$n\in N:{ 1 }^{ 2 }+{ 3 }^{ 2 }+{ 5 }^{ 2 }+.......+({ 2n-1) }^{ 2 }=\cfrac { n(2n-1)(2n+1) }{ 3 } $$
Prove the following by using the principle of mathematical induction for all $$n\in N:n(n+1)(n+5)$$ is multiple of $$3$$.
Prove the following by using the principle of mathematical induction for all $$n\in N:\left( 1+\cfrac { 1 }{ 1 } \right) \left( 1+\cfrac { 1 }{ 2 } \right) \left( 1+\cfrac { 1 }{ 3 } \right) ......\left( 1+\cfrac { 1 }{ n } \right) =(n+1)\quad $$
Find counter examples to disprove the following statement.
A quadrilateral with all sides are equal is a square.
Using mathematical induction, prove that $$\cfrac{d}{dx}({x}^{n})=n{x}^{n-1}$$ for all positive integers $$n$$.
Prove the following by using the principle of mathematical induction for all $$n\in N:{41}^{n}-{14}^{n}$$ is a multiple of $$27$$.
Prove the following by using the principle of mathematical induction for all $$n\in N:(2n+7)< {(n+3)}^{2}$$.
Prove the following by using the principle of mathematical induction for all $$n\in N:{3}^{2n+2}-8n-9$$ is divisible by $$8$$.
Prove by induction:
$${1}^{2}+{2}^{2}+{3}^{2}+........+{n}^{2}=\cfrac{1}{6}n(n+1)(2n+1)$$
Prove by induction:
$${x}^{n}-{y}^{n}$$ is divisible by $$x+y$$ when $$n$$ is even.
Show that $${ 2 }^{ 2n }-3n-1$$ is divisible by $$9$$ for all positive integral values of $$n$$.
Prove by induction:
$$2+{2}^{2}+{2}^{3}+........+{2}^{n}=2({2}^{n}-1)$$
Prove the following by the principle of mathematical induction: $$(n\epsilon N)$$
$$1^{2} . 2 + 2^{2} . 3 + .... + n^{2} (n + 1) = \dfrac {n(n + 1)(n + 2)(3n + 1)}{12}$$.
Prove the following by the principle of Mathematical Induction.
$$(2n + 1)(2n - 1)$$ is an odd number for all $$n\epsilon N$$.
Prove by induction:
$$\cfrac{1}{1.2}+\cfrac{1}{2.3}+\cfrac{1}{3.4}+.....$$ to $$n$$ terms$$=\cfrac{n}{n+1}$$
Prove by induction:
$$1+3+5+.....+(2n-1)={n}^{2}$$
If $$p$$ and $$q$$ are any two positive integers, show that $$|\underline {pq}$$ is divisible by $$(|\underline {p})^{q} . |\underline {q}$$ and by $$(|\underline {q})^{p} . |\underline {p.}$$
$$(1 + x)^n >1 $$ + nx for n > 2 , n $$ \epsilon$$ N
x > -1 x $$\neq $$ 0
Prove by Mathematical induction that
$${ 1 }^{ 2 }+{ 3 }^{ 2 }+{ 5 }^{ 2 }...{ \left( 2n-1 \right) }^{ 2 }=\cfrac { n\left( 2n-1 \right) \left( 2n+1 \right) }{ 3 } \forall n\in N$$
Prove $$2 + 5 + 8 + 11 + ... + (3n - 1) =$$ $$\dfrac{1}{2}$$ $$n (3n + 1) n $$$$\epsilon$$ N
Prove that $$11^{n +2} + 12^{2n \, + \, 1}$$ is divisible by $$133$$ for any non-negative integral $$n$$.
Prove $$\dfrac {1}{1 \cdot 2\cdot 3 } \, + \, \dfrac {1}{2 \cdot 3\cdot 4 } \, + \, \dfrac {1}{n (n + 1)(n + 2)} \, = \, \dfrac{1(n + 3)}{4(n + 1)(n + 2)}$$
Prove the mathmatical induction that $$ \dfrac{1}{\log_x2 , \log_x4 }\, + \, \dfrac{1}{\log_x4 , \log_x8 } \, + \, ..... + \,\dfrac{1}{\log_x2^{n - 1} , \log_x4^n }$$
= $$\left (1- \dfrac{1}{n} \right ) \dfrac{1}{(\log_x2)^2} , x > 0 , \neq -1 n \epsilon N$$
$$\sqrt 2 + \sqrt 2 + \sqrt 2 + ...+ n\ terms = 2\cos \dfrac{\pi}{2^{n +1}} , n \epsilon N$$
Prove the assertions of the following problems
Prove that the expression $$n^3 \, - \, n$$ is divisible by $$24$$ for any odd $$n$$.
Let $$u_1$$ = 1, $$u_2$$ = 1 and $$u_{n \, + \, 2} \, + \, u_n \, for \, n\geq1$$.
Use mathematical induction to show that
$$u_n\, = \, \dfrac{1}{\sqrt{(5)}}\left [ \left ( \dfrac{1 \, + \, \sqrt{5}}{2} \right )^n \, - \, \left ( \dfrac{1 \, - \, \sqrt{5}}{2} \right )^n \right ]$$ for all $$n \, \geq \, 1$$
For any natural number n > 1
$$ \dfrac {1}{n \, + \, 1} \, + \, \dfrac {1}{n \, + \, 2} \, + \, ..... \, + \, \dfrac {1}{2n} > \dfrac {13}{14}$$
Given $$a_1\, = \, \dfrac{1}{2}\left ( a_0 \, + \, \dfrac{A}{a_0} \right ) \, , \,a_2\, = \, \dfrac{1}{2}\left ( a_1 \, + \, \dfrac{A}{a_1} \right )$$
and $$a_{n \, + \, 1}\, = \, \dfrac{1}{2}\left ( a_n \, + \, \dfrac{A}{a_n} \right )$$
Find $$n\geq \, 2$$ where a > 0, A > 0, prove that
$$\dfrac{a_n \, - \, \sqrt{A}}{a_n \, + \, \sqrt{(A)}}\, = \, \left (\dfrac{a_1 \, - \, \sqrt{A}}{a_1 \, + \, \sqrt{(A)}} \right )^{2^{n \, - \, 1}}$$
using mathematical induction.
Applying the principal of mathematical induction of prove that
$$ \dfrac{2 \, sin \, \theta }{cos \, \theta \, + \, 3\, cos \, \theta} \, + \, \dfrac{2 \, sin \, \theta }{cos \, \theta \, + \, 5\, cos \, \theta} \, + \, \dfrac{2 \, sin \, \theta }{cos \, \theta \, + \, cos \,(2n \, + \, 1) \theta} $$
= tan ( n + 1)$$ \theta \, - \, tan \theta$$
Prove that induction that
sin x + sin 3x + .. + sin(2n - 1) x = $$ \dfrac {sin^2 nx}{sin x} $$
Prove that mathematical induction that
$$\dfrac{1}{1 \, + \, x} \, + \, \dfrac{2}{1 \, + \, x^2} \, + \, \dfrac{4}{1 \, + \, x^4} \, + \, ... \, + \, \dfrac{2^n}{1 \, + \, x^{2^n}}$$
$$= \, \dfrac{1}{1 \, - \, }\dfrac{2^{n \, + \, i}}{1 \, + \, x^{2^{n \, + \, i}}}$$
Observing that $$1^3 \, = \, 1, \, 2^3 \, = \, 3 \, + \, 5,$$
$$3^3$$ = 7 + 9 + 11, $$4^3$$ = 13 + 15 + 17 + 19
Find a general formula for the cube of natural number n and prove it by the principle of mathematical induction
Explain the method of mathematical induction and use it to show that $$11^{n \, + \, 2} \, + \, 12^{2n \, + \, 1}$$ where n is natural number is divisible by 133
If $$x \, + \, y \, = a \, + \, b , x^2 \, + \, y^2 \, = \, a^2 \, + \, b^2 $$ then prove that the mathematical induction that $$x^n \, + \, y^n \, = \, a^n \, + \, b^n$$ for all the natural number n .
If $$y \, = \, \dfrac{log \, \, x}{x}$$ , then prove by mathematical induction
$$ y_n \, = \, \dfrac{(-1)^n \, (n!)}{x^{n \, + \,1}}\left [ log \, \, x \, - \, 1 \, -\dfrac{1}{2}\, - \, ....-\, \dfrac{1}{n} \right ]$$
If $$x^3$$ = x + 1, then show that
$$x^{3n} \, = \, a_n x \, + \, b_n \, - \, c_n x^{-1}$$
Where $$a_{n \, + \, 1} \, = \, a_n b_n :b_{n \, + \, 1} \, = \, a_n \, + \, b_n \, + \, c_n$$
and $$c_{n \, + \, 1} \, = \, a_n \, + \, c_n$$
If $$x_1x_2x_3 \, .... \, x_n \ = \, 1(x_1 \, > \, 0, i \, = \, 1,2,.....n),$$ prove that $$x_1 \, + \, x_2 \, + \, .....x_n \, \geq \, n \, (n \, \geq \, 2)$$
Prove that the mathematical induction that
$$ 1 \, + \, \dfrac{1}{2} \, + \, \dfrac{1}{3} \, + \, \dfrac{1}{4} + ...\ , \dfrac {1}{2^n} \geq 1 \, + \, \dfrac {n}{2}$$
for each no negative interger n
Prove $$^{2n} C _n \, > \, \dfrac{4^n }{n + 1}$$
Prove $$\dfrac {2n!}{(n!)^2} \, > \, \dfrac {4n}{2n \, + \, 1} $$
Prove by induction $$\forall \, n \, \epsilon \, N \, \, if y \, = \, \dfrac{x}{x^2 \, + \, a^2}$$
then $$ y_n \, = \, \dfrac{(-1)^n \, n!}{a^{n \, + \,1}}sin^{n \, + \, 1} \, \, \theta \, \, cos(n \, + \, 1) \, \, \theta$$
where $$\theta \, = \, cot^{-1} \dfrac{x}{a}$$
If 0 < $$\alpha < \, \dfrac{\pi}{4(n \, - \, 1)} $$ where n > 1 , then prove that $$\tan n$$ $$ \alpha \, > \, n \, \tan \, \alpha$$
Show by the mathematical induction that
$$ \dfrac{1}{sin 2 x } \, + \, \dfrac{1}{sin 4 x } \, + \, \dfrac{1}{sin 2^n x } \, = \, cot x \, - \, cot 2^n \, x $$
Prove that $${ 1 }^{ 2 }+{ 2 }^{ 2 }+...+{ n }^{ 2 }>\cfrac { { n }^{ 3 } }{ 3 } ,n\epsilon N$$
Prove the following by using the first principle
$$ 1+3 + 3^2 + ......+ 3^{n-1} =\frac{(3^n -1)}{2}$$.
Prove the following by PMI for all $$n$$ belong to $$N$$
$$1\times3+3\times5+5\times7 .........+(2n-1)(2n+1)=\dfrac{n(4n^2+6n-1)}{3}$$
Prove that for any positive interger $$n, n^3 -n$$ is divisible by $$6$$.
Let p$$\geq$$ 3 be an integer and $$\alpha$$ , $$\beta$$ be the roots of $$x^2$$ - (p + 1)x + 1 = 0.Using mathematical induction show that $$\alpha^n \, + \, \beta^n$$
is not divisible by p.
Prove by induction method that for all n$$\geq$$ 1
$$\int x^ne^x\, dx \, = \, n\, !\, e^x\left [ \dfrac{x^n}{n!} \, - \, \dfrac{x^{n \, - \, 1}}{(n \, - \, 1)!} \, + \, \dfrac{n^{n \, - \, 2!}}{(n \, - \, 2)!} \, + \, .....\, + \, (-1)^n \right ]$$
Let p$$\geq$$ 3 be an integer and $$\alpha$$ , $$\beta$$ be the roots of $$x^2$$ - (p + 1)x + 1 = 0.Using mathematical induction show that $$\alpha^n \, + \, \beta^n$$
is an integer
Let $$ I_m \, = \, \int_{0}^{\pi}\dfrac{1 \, - \, cos \, \, mx}{1 \, - \, cos \, \, x}dx$$
Use mathematical induction to prove that
$$I_m \, = \, m\pi \, , \, m0$$ , , 1, 2.....
By PMC, prove that inequality $$n<2^n$$ for all $$n\in N$$
Use mathematical induction to prove
$$1 + 2 + 3 + \ldots + n < \frac{1}{8}{\left( {2n + 1} \right)^2}$$
If $$c>a$$; show that $$cba-abc=99(c-a)$$.
if $$a>c$$; show that $$abc-cba=99(a-c)$$.
Using the Mathematical induction, show that for any number $$n \geq 2,$$
$$\dfrac{1}{1 + 2} + \dfrac{1}{1 + 2 + 3} + \dfrac{1}{1 + 2 + 3 + 4} + ..... +\dfrac{1}{1 + 2 + 3 + ... + n} = \dfrac{n - 1}{n + 1}$$
Let by mathematical induction, for any natural numbers n,
$$\dfrac{1}{2.5} + \dfrac{1}{5.8} + \dfrac{1}{8.11} + ..... + \dfrac{1}{(3n - 1)(3n + 2)} = \dfrac{n}{an + b}$$. Find $$a+b$$
Prove that $${2.7^n} + {3.5^n} - 5$$ is divisible by $$24$$ for all $$n \in N$$.
Prove by the principle of mathematical induction that $$2^n > n $$ for all $$n \in N.$$
Prove the following by mathematical induction $$1 + 2 + 3 + \cdots + n < \frac{1}{8}{\left( {2n + 1} \right)^2}$$
Prove that $$\displaystyle \frac{1}{{1 \cdot 3}} + \frac{1}{{3 \cdot 5}} + \frac{1}{{5 \cdot 7}} + \ldots \ldots + \frac{1}{{\left( {2n - 1} \right)\left( {2n + 1} \right)}} = \frac{n}{{2n + 1}}$$
Let $$P(n)=n(n+1)(n+2)$$ is divisible by $$12$$ then which one of the following is not true.i) $$P(3)$$ii) $$P(4)$$ii) $$P(5)$$iv) $$P(8)$$
Using PMI, prove that $${3^{2n + 2}} - 8n - 9$$ is divisible by $$64$$.
Use mathematical induction to prove:
$$\dfrac{1}{{1 \cdot 3}} + \dfrac{1}{{3 \cdot 5}} + \dfrac{1}{{5 \cdot 7}} + \ldots + \dfrac{1}{{\left( {2n - 1} \right)\left( {2n + 1} \right)}} = \dfrac{n}{{2n + 1}}$$
Prove using PMI: $$\displaystyle \frac{1}{{1.2.3}} + \frac{1}{{2.3.4}} + \frac{1}{{3.4.5}} + ... + \frac{1}{{n\left( {n + 1} \right)\left( {n + 2} \right)}} = \frac{{n\left( {n + 3} \right)}}{{4\left( {n + 1} \right)\left( {n + 2} \right)}}$$
Prove : $$1 + 2 + 3 + ... + n = \dfrac{1}{2} n (n + 1)$$
Find m if the following equation holds true $$1.2 + 2.3 + 3.4 + .. + n (n + 1) = \dfrac{1}{m} n (n + 1) (n + 2)$$
Prove that by mathematical induction $${2^{3n}} - 1$$ is divisible by $$7$$ for all natural numbers.
Find m if the following equation holds true $$2 + 4 + 6 + ... + 2n = m^2\times n (n + 1)$$
Prove that product of two consecutive natural number cannot be $$441$$.
Find m if the following equation holds true $$1.3 + 2.4 + 3.5 + ... + n (n + 2) = \dfrac{1}{m} n (n + 1)(2n + 7)$$
Prove that : $$ 1 + 3 + 3^2 + ... + 3^{n-1} = \dfrac{(3^n - 1)}{2}$$
Prove $$1.3 + 3.5 + 5.7 + ...+ (2n -1)(2n + 1) = \dfrac{n(4n^2 + 6n -1)}{3}$$
Prove that $$1^2 + 2^2 + 3^2 + .... + n^2 > \dfrac{n^2}{3}$$ for all $$n \in N$$ using principle of mathematical induction.
Prove by PMI:
$$cos \theta + cos 2\theta + ..... + cosn \theta = sin\dfrac{n\theta}{2}.cos \theta c\dfrac{\theta}{2}.cos\dfrac{(n+1)\theta}{2} $$
For any odd integer $$n\geq 1$$, Find the value of $$n^3-(n-1)^3+...........+(-1)^{n-1}1^3$$.
Prove by Induction $$a+ar+{ ar }^{ 2 }+.....$$ up to n terms =$$\cfrac { a\left( { r }^{ n }-1 \right) }{ r-1 } ,r\neq 1$$
Prove that $${25^n} - {20^n} - {8^n} + {3^n}$$ is divisible by $$5$$.
Prove that if either of $$2a+3b$$ and $$9a+5b$$ is divisible by 17 ,so is the other ,$$a,b \in N$$
Solve $$\dfrac{1}{{1.2.3}} + \dfrac{1}{{2.3.4}} + \dfrac{1}{{3.4.5}} + \cdots + \dfrac{1}{{n\left( {n + 1} \right)\left( {n + 2} \right)}} = \dfrac{{n\left( {n + 3} \right)}}{{4\left( {n + 1} \right)\left( {n + 2} \right)}}$$
Suppose $$m,n$$ are integers and $$m=n^2-n$$. Then show that $$m^2-2m$$ is divisible by $$24$$.
If $$A=\begin{bmatrix} 1 & 1 & 1 \\ 1 & 1 & 1 \\1 & 1 & 1 \end{bmatrix}$$, prove that
$$A^n=\begin{bmatrix} 3^{n-1} & 3^{n-1} & 3^{n-1} \\ 3^{n-1} & 3^{n-1} & 3^{n-1} \\ 3^{n-1} & 3^{n-1} & 3^{n-1} \end{bmatrix}, n\in N$$.
Prove that $$1.2 + 2.3 +.......n(n+1) $$=$$\frac{{n(n + 1)(n + 2)}}{3}$$ in mathematical induction.
Prove that $$2.7^{n}+3.5^{n}-5$$ is divisible by $$24$$, for all $$n\in N$$.
Prove by method of induction, for all $$n \in N$$
$$2 + 4 + 6 + .... + 2n = n\left( {n + 1} \right)$$
prove the inequalities $${\left( {n!} \right)^2} \le {n^n}\left( {n!} \right) < \left( {2n} \right)!$$ for all positive integers n .
Let $$P(n)$$ be the statement $$3^{n} > n^{n}$$. If $$P(n)$$ is true, prove that $$P(n+1)$$ is true.
Show that $$1^{2}+(1^{2}+2^{2})+(1^{2}+2^{2}+3^{2})+$$.... up to $$n$$ terms$$=\dfrac{n(n+1)^{2}}{12}$$, $$n\epsilon N$$
$${7^{2n}} + {2^{3n - 3}}{.3^{n - 1}}$$ is divisible by $$25$$ for any natural number $$n \ge 1$$. Prove that by mathematical
What must be added to $${x^4} + 2{x^3} - 2{x^2} + x - 1$$ . So that result is exactly divisible by $${x^2} + x - 2$$ ?
From principle of mathematical induction prove that
$$1+2+3+....+n=\dfrac{1}{2}n(n+1)$$
If $$33!$$ is divisible by $$2^n$$, then find the maximum value of n.
If $$A=\begin{bmatrix} \cos { \theta } & \sin { \theta } \\ -\sin { \theta } & \cos { \theta } \end{bmatrix}$$ then prove that $${ A }^{ n }=\begin{bmatrix} \cos { n\theta } & \sin { n\theta } \\ -\sin { n\theta } & \cos { n\theta } \end{bmatrix}$$, $$n\in N$$.
$$(n+1)(n+2)$$ is an even number
Show that any positive odd integers is of the form $$6q+1,6q+3$$ or $$6q+5$$, where $$q$$ is some integer.
Use the principle of mathermatical induction to prove that
$${1}^{3}+{2}^{3}+.....{n}^{3}=\cfrac{1}{4}{n}^{2}{(n+1)}^{2}$$ for every natural number $$n$$.
Given an example of a statement $$P(n)$$ which is true for all $$n\ge 4$$ but $$P(1), P(2)$$ and $$P(3)$$ are not true. Justify your answer.
Prove that $$n^{2}-n$$ in divisible by $$2$$ for any positive length $$n$$.
Prove that $$1+2+3+.....+n=\dfrac{n(n+1)}{2}$$. for $$n$$ being a natural numbers.
If $$(27)^{999}$$ is divided by 7, then the remainder is :
Prove by the principle of mathematical induction that for all $$n \in N$$:
$$1 + 4+ 7 +.... + (3n - 2) = \dfrac{1}{2}n (3n - 1)$$
Using mathematical induction prove that:$$\dfrac { 1 }{ 1.2.3 } +\dfrac { 1 }{ 2.3.4 } +\dfrac { 1 }{ 3.4.5 } +.....+\dfrac { 1 }{ n\left( n+1 \right) \left( n+2 \right) } =\dfrac { n\left( n+3 \right) }{ 4\left( n+1 \right) \left( n+2 \right) } .$$
Prove that $$n^{2}-n$$ is divisible by 2 for every positive integer.
$$1 ^ { 2 } + 2 ^ { 2 } + \ldots + n ^ { 2 } > \frac { n ^ { 3 } } { 3 } , n \in \mathbf { N }$$
For every +ve integer 'n' prove that $$7^n-3^n$$ is divisible by $$4$$.
Use the principle of mathematical induction to prove that $$a+(a+d)+(a+2d)+ .... +[a+(n-1)d]=n/2[2a+(n-1)d]$$
Show that $$n(n+1)(2n+1)$$ is multiple of $$6$$ for every natural number $$n$$.
By the principle of Mathematical induction, prove that, for $$n \geq 1.$$
$$1 ^ { 2 } + 2 ^ { 2 } + 3 ^ { 2 } + \cdots + n ^ { 2 } > \dfrac { n ^ { 3 } } { 3 }.$$
Prove for $$n\in \mathbb{N}$$.
$$1.3 + {2.3^2} + {3.3^3} + ... + n{.3^n} = \dfrac{{\left( {2n - 1} \right){3^{n + 1}} + 3}}{4}$$
Prove the following by using principle of mathematical induction for all $$n \in N$$ :
$$1+\dfrac { 1 }{ (1+2) } +\dfrac { 1 }{ (1+2+3) } +.......+\dfrac { 1 }{ (1+2+3+\dots n) } =\dfrac { 2n }{ (n+1) } .$$
Prove the following by using the principle of mathematical induction for all $$n\in N:$$
$$1+3+{ 3 }^{ 2 }+...+{ 3 }^{ n-1 }=\dfrac { \left( { 3 }^{ n }-1 \right) }{ 2 } $$
Solve:$$9\le 1-2x$$
Prove: $$\left( {2n + 7} \right) < {\left( {n + 3} \right)^2}.$$ for $$n\in\mathbb{N}$$.
Using Principle of Mathematical Induction, prove that
$$1.3 + 2.3 ^ { 2 } + 3.3 ^ { 3 } + \ldots . n .3 ^ { n } = \dfrac { ( 2 n - 1 ) 3 ^ { n + 1 } + 3 } { 4 } ,$$ where $$n \in \mathrm { N }$$
In triangle ABC, D and E are the points on the sides AB and AC. DE||BC, BD=5 cm and DE:BC=2:Find AD and the ratio of are of triangle ADE to the quadrilateral BCED.
Using principle of Mathematical induction prove that:
$$x ^ { 2 n } - y ^ { 2 n }$$ is divisible by $$x + y$$, where $$n \in N$$
Using the principle of mathematical induction, prove the following for all $$n\in N$$:
$$2+6+18+...+2.3^{n-1}=(3^n-1)$$.
Using the principle of mathematical induction, prove the following for all $$n\in N$$:
$$\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{8}+...+\dfrac{1}{2^n}=\left(1-\dfrac{1}{2^n}\right)$$.
Using the principle of mathematical induction, prove the following for all $$n\in N$$:
$$1+2+3+4+....+n=\dfrac{1}{2}n(n+1)$$.
Using the principle of mathematical induction, prove the following for all $$n\in N$$:
$$1^2+3^2+5^2+7^2+....+(2n-1)^2=\dfrac{n(2n-1)(2n+1)}{3}$$
Using the principle of mathematical induction, prove the following for all $$n\in N$$:
$$1.2+2.2^2+3.2^3+....+n.2^n=(n-1)2^{n+1}+2$$.
Using the principle of mathematical induction, prove the following for all $$n\in N$$:
$$2+4+6+8+...+2n=n(n+1)$$.
Using the principle of mathematical induction, prove the following for all $$n\in N$$:
$$\dfrac{1}{1.4}+\dfrac{1}{4.7}+\dfrac{1}{7.10}+...+\dfrac{1}{(3n-2)(3n+1)}=\dfrac{n}{(3n+1)}$$
Using the principle of mathematical induction, prove the following for all $$n\in N$$:
$$(x^{2n}-y^{2n})$$ is divisible by $$(x+y)$$.
Using the principle of mathematical induction, prove the following for all $$n\in N$$:
$$3.2^2+3^2.2^3+3^3.2^4+...+3^n.2^{n+1}=\dfrac{12}{5}(6^n-1)$$.
Using the principle of mathematical induction, prove the following for all $$n\in N$$:
$$(3^{2n+2}-8n-9)$$ is divisible by $$8$$.
Using the principle of mathematical induction, prove the following for all $$n\in N$$:
$$n(n+1)(n+2)$$ is a multiple of $$6$$.
Using the principle of mathematical induction, prove the following for all $$n\in N$$:
$$\left\{ (41)^n-(14)^n\right\}$$ is divisible by $$27$$.
Using the principle of mathematical induction, prove the following for all $$n\in N$$:
$$\left(1+\dfrac{1}{1}\right)\left(1+\dfrac{1}{2}\right)\left(1+\dfrac{1}{3}\right)......\left( 1+\dfrac{1}{n}\right)=(n+1)$$.
Using the principle of mathematical induction, prove the following for all $$n\in N$$:
$$\left(1+\dfrac{3}{1}\right)\left(1+\dfrac{5}{4}\right)\left(1+\dfrac{7}{9}\right)......\left\{ 1+\dfrac{(2n+1)}{n^2}\right\}=(n+1)^2$$.
Using the principle of mathematical induction, prove the following for all $$n\in N$$:
$$(4^n+15n-1)$$ is divisible by $$9$$.
Using the principle of mathematical induction, prove the following for all $$n\in N$$:
$$(2^{3n}-1)$$ is multiple of $$7$$.
Using the principle of mathematical induction, prove the following for all $$n\in N$$:
$$3^n \ge 2^n$$
Prove that following by using the principle of mathematical induction for all $$n\in N$$:
$$1+3+3^2+....+3^{n-1}=\dfrac{(3^n -1)}{2}$$
Prove the following by using the principle of mathematical induction for all $$n\in N$$:
$$1.2+2.2^2 +3.2^2+....+n.2^2 =(n-1)2^{n+1}+2$$
Prove that $$3^{2n}+7$$ is a multiple of 8.
Prove the following by using the principle of mathematical induction for all $$n\in N$$:
$$\dfrac {1}{1.2.3}+\dfrac {1}{2.3.4}+\dfrac {1}{3.4.5}+...+\dfrac {1}{n(n+1)(n+2)}=\dfrac {n(n+3)}{4(n+1)(n+2)}$$
Prove the following by using the principle of mathematical induction for all $$n\in N$$:
$$\left(1+\dfrac{3}{1}\right)\left(1+\dfrac{5}{4}\right)\left(1+\dfrac{7}{9}\right)......\left(1+\dfrac{(2n+1)}{n^{2}}\right)=(n+1)^{2}$$
Prove the following by using the principle of mathematical induction for all $$n\in N$$:
$$\dfrac {1}{2}+\dfrac {1}{4}+\dfrac {1}{8}+...+\dfrac {1}{2^n}=1-\dfrac {1}{2^n}$$
Prove the following by using the principle of mathematical induction for all $$n\in N$$:
$$1.3+3.5+5.7+....+(2n-1)(2n+1)=\dfrac {n(4n^2 +6n-1)}{3}$$
Prove the following by using the principle of mathematical induction for all $$n\in N$$:
$$\dfrac {1}{2.5}+\dfrac {1}{5.8}+\dfrac {1}{8.11}+...+\dfrac {1}{(3n-1)(3n+2)}=\dfrac {n}{(6n+4)}$$
Prove the following by using the principle of mathematical induction for all $$n\in N$$:
$$a+ar+ar^2+....+ar^{n-1}=\dfrac {a(r^n -1)}{r-1}$$
Using the principle of mathematical induction, prove that
$$1+3+5+7+.....+(2n-1)=n^2$$, for all $$n \in N$$
Prove that following by using the principle of mathematical induction for all $$n\in N$$:
$$1+2+3+.....+n < \dfrac{1}{8}(2n+1)^{2}$$
Prove the following by using the principle of mathematical induction for all $$n\in N$$:
$$\left(1+\dfrac{1}{1}\right)\left(1+\dfrac{1}{2}\right)\left(1+\dfrac{1}{3}\right)......\left(1+\dfrac{1}{n}\right)=(n+1)$$
Using the principle of mathematical induction, prove that
$$1^{2}+2^{2}+3^{2}+\ldots \ldots+n^{2}=\cfrac{n(n+1)(2 n+1)}{6}$$
Using the principle of mathematical induction, prove that
$$\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+....+\dfrac{1}{n(n+1)}=\dfrac{n}{n+1}$$, for all $$n\in N$$
Prove the following by using the principle of mathematical induction for all $$n\in N$$:
$$1^{2}+3^{2}+5^{2}+.....+(2n-1)^{2}=\dfrac{n(2n-1)(2n+1)}{3}$$
Using the principle of mathematical induction, prove that
$$1 \cdot 2+2 \cdot 3+\dots+n(n+1)=\cfrac{n(n+1)(n+2)}{3}$$ for all $$n \in N$$
Using the principle of mathematical induction, prove that
$$\text { (1) } 1+2+3+\cdots+n=\cfrac{n(n+1)}{2}$$, for all $$n\in N$$
Prove that following by using the principle of mathematical induction for all $$n\in N$$:
$$\dfrac{1}{1.4}+\dfrac{1}{4.7}+\dfrac{1}{7.10}+....+\dfrac{1}{(3n-2)(3n+1)}=\dfrac{n}{(3n+1)}$$
Prove the following by using the principle of mathematical induction for all $$n\in N$$:
$$\dfrac{1}{3.5}+\dfrac{1}{5.7}+\dfrac{1}{7.9}+....+\dfrac{1}{(2n+1)(2n+3)}=\dfrac{n}{3(2n+3)}$$
Prove the following by using the principle of mathematical inductions for all $$n\epsilon N$$$
$$1 + 3 + 3^{2} + ... + 3^{n - 1} = \dfrac {(3^{n} - 1)}{2}$$.
Using principle of mathematical induction, prove that
$$\cos \alpha \cos 2 \alpha \cos 4\alpha ..... \cos(2^{n-1}\alpha) = \dfrac{\sin 2^n \alpha}{2^n \sin \alpha}$$ for all $$n \in N$$.
Using the principle of mathematical induction, prove that
$$(ab)^n=a^nb^n$$ for all $$n\in N$$
Using the principle of mathematical induction, prove that
$$7^{2n}-3^{2n} $$ is divisible by $$4$$.
Using the principle of mathematical induction, prove that
$$(1+x)^n \ge (1+nx)$$ for all natural numbers $$n$$, where $$x > -I$$.
let O < A < $$\pi$$ for i = 1 , 2 , ...... n we mathematical induction to prove that
$$sinA _1 \, + \,sinA _2 \, \, + \, ....... \, + \, sinA _n \, $$
$$ \geq \, n \, sin \, \left (\dfrac{A_1 \, + \, A_2 \, + \, A_n}{n} \right )$$
where n > 1 is a merital number
p sin x + (1 - p) sin p $$\geq$$sin { px + ( 1 - p) y }
Where $$ 9 \, \geq p \, \geq \, 1$$ and $$ 0 \geq x , \, y \, \geq \pi$$
Prove that $$n^3 \, + \, 3n^2 \,+\, 5n \, + \, 3$$ is divisible by $$3$$ for any natural $$n$$.
Using the mathematical induction prove that
$$ tan^{-1} (1/3) \, + \,tan^{-1} (1/7) \, + \,tan^{-1} [1 / (n^2 \, + \, n \, + \, 10)] $$
$$= tan^{-1} [n / (\, n \, + \, 2)] $$
Show that $$49^{n}+16n-1$$ is divisible by $$64$$ for all positive integers n ?
Given $$(1 + x)^{n} \geq (1 + nx)$$, for all natural number n, where $$x > -n$$. What will be the value of $$n$$
$$1+2+3+..............n<\dfrac{1}{8}(2n+1)^2$$
Using induction method of otherwise, prove that for any non-negative integers m,n,r and k
$$\sum_{m \, = \, 0}^{k}(n \, - \, m) \, \dfrac{(r \, + \, m)!}{m!} \, = \, \dfrac{(r \, + \, k \, + \, 1)!}{k!}$$ $$\left[\dfrac{n}{r \, + \, 1} \, - \, \dfrac{k}{r \, + \, 2}\right]$$
Use Euclid's division lemma to show that any positive odd integer is of the form $$6q+1$$, or $$6q+3,\ 6q+5$$ where $$q$$ is some integers.
Using the principle of mathematical induction, prove the following for all $$n\in N$$:
$$\dfrac{1}{2.5}+\dfrac{1}{5.8}+\dfrac{1}{8.11}+...+\dfrac{1}{(3n-1)(3n+2)}=\dfrac{n}{(6n+4)}$$.
Using the principle of mathematical induction, prove the following for all $$n\in N$$:
$$\dfrac{1}{1.3}+\dfrac{1}{3.5}+\dfrac{1}{5.7}+...+\dfrac{1}{(2n-1)(2n+1)}=\dfrac{n}{(2n+1)}$$
Using the principle of mathematical induction, prove the following for all $$n\in N$$:
$$1+3+3^2+3^3+....+3^{n-1}=\dfrac{1}{2}(3^n-1)$$.
If $$A = \left[ \begin{array} { c c } { \cos \theta } & { \sin \theta } \\ { - \sin \theta } & { \cos \theta } \end{array} \right]$$ then show that for all the positive integers $$n$$ $$A ^ { n } = \left[ \begin{array} { c c } { \cos n \theta } & { \sin n \theta } \\ { - \sin n \theta } & { \cos n \theta } \end{array} \right]$$
Show that $$n(n^2-1)(3n+2)$$ is divisible by 24.
Using the principle of mathematical induction, prove the following for all $$n\in N$$:
$$(x^{2n}-1)$$ is divisible by $$(x-1)$$, where $$x\neq 1$$.
Using the principle of mathematical induction, prove the following for all $$n\in N$$:
$$1+\dfrac{1}{(1+2)}+\dfrac{1}{(1+2+3)}+....+\dfrac{1}{(1+2+3+....+n)}=\dfrac{2n}{(n+1)}$$.
Prove that $$^n$$C$$_r$$ + $$^{n - 1}$$C$$_r$$ + $$^{n - 2}$$C$$_r$$ + $$^{n - 2}$$C$$_r$$ +....................+ $$^r$$C$$_r$$ = $$^{n +1}$$C$$_{r + 1}$$
Class 11 Engineering Maths Extra Questions
- Binomial Theorem Extra Questions
- Complex Numbers And Quadratic Equations Extra Questions
- Conic Sections Extra Questions
- Introduction To Three Dimensional Geometry Extra Questions
- Limits And Derivatives Extra Questions
- Linear Inequalities Extra Questions
- Mathematical Reasoning Extra Questions
- Permutations And Combinations Extra Questions
- Principle Of Mathematical Induction Extra Questions
- Probability Extra Questions
- Relations And Functions Extra Questions
- Sequences And Series Extra Questions
- Sets Extra Questions
- Statistics Extra Questions
- Straight Lines Extra Questions
- Trigonometric Functions Extra Questions