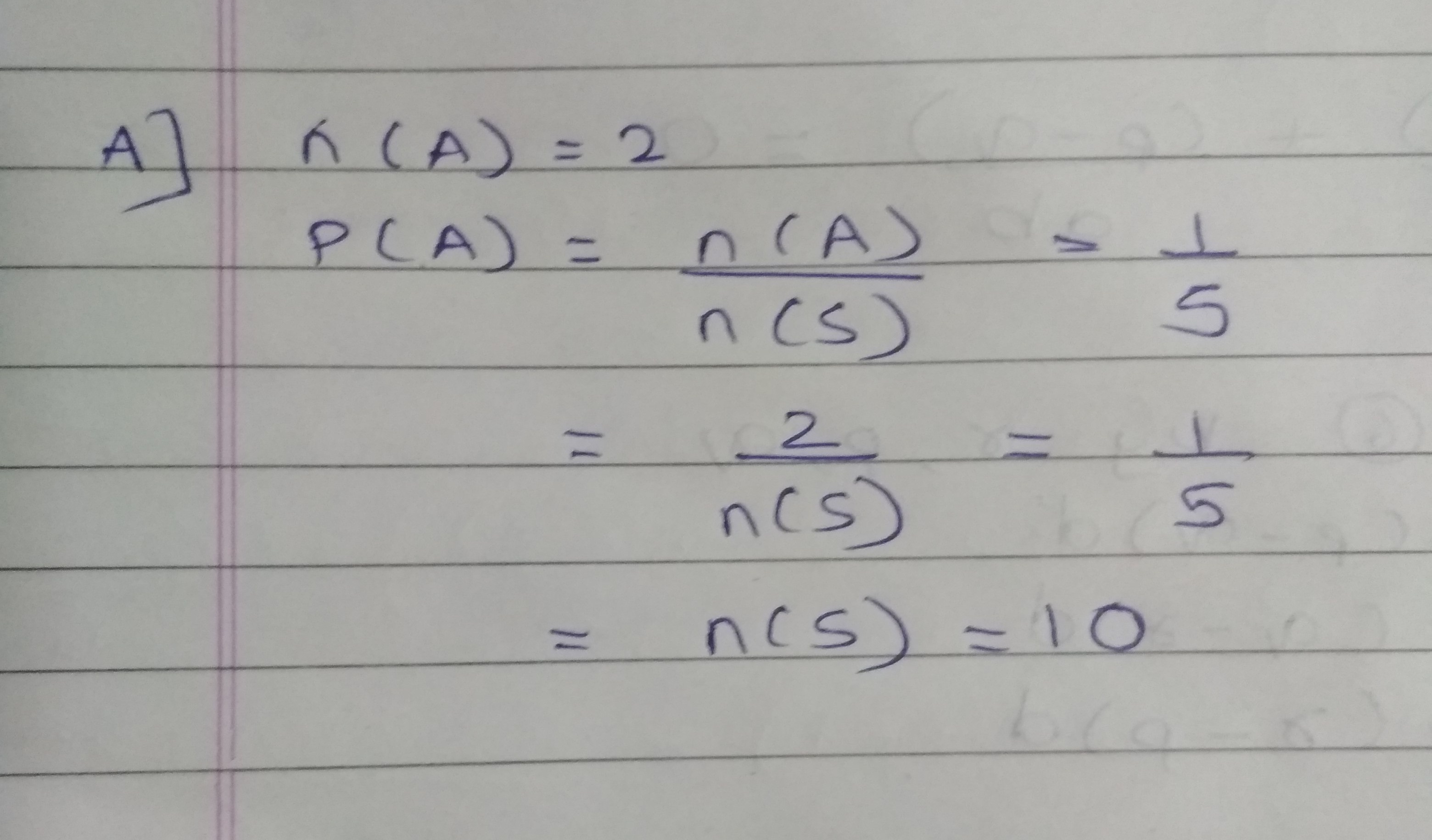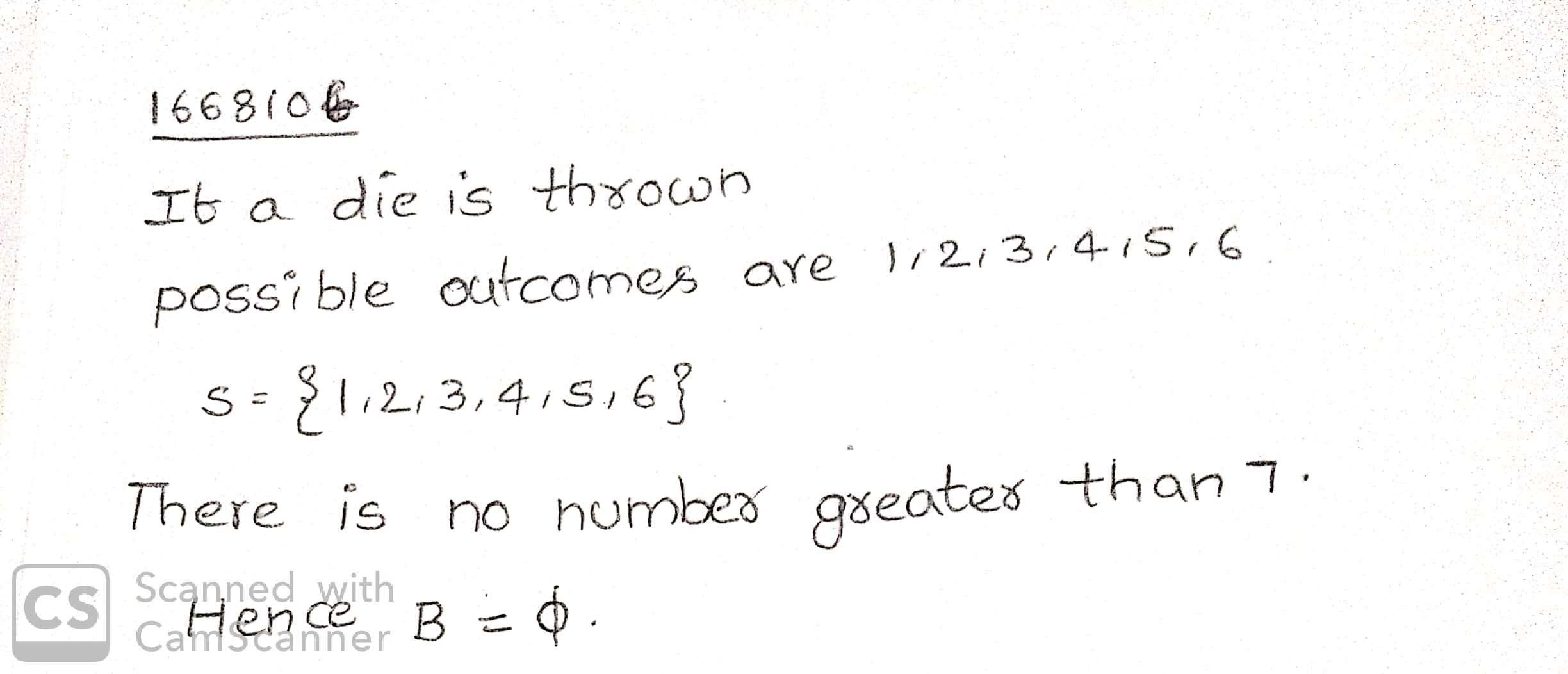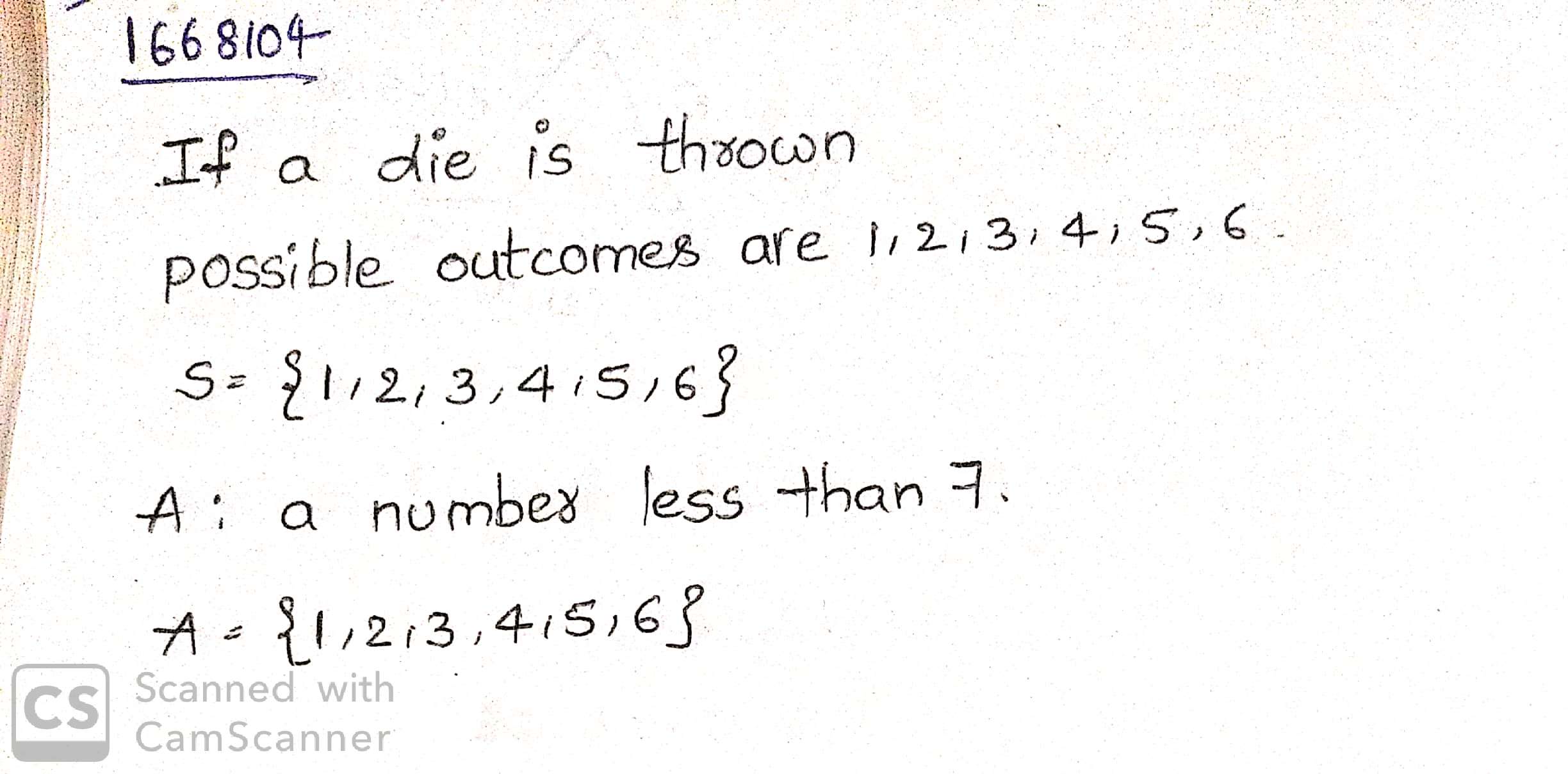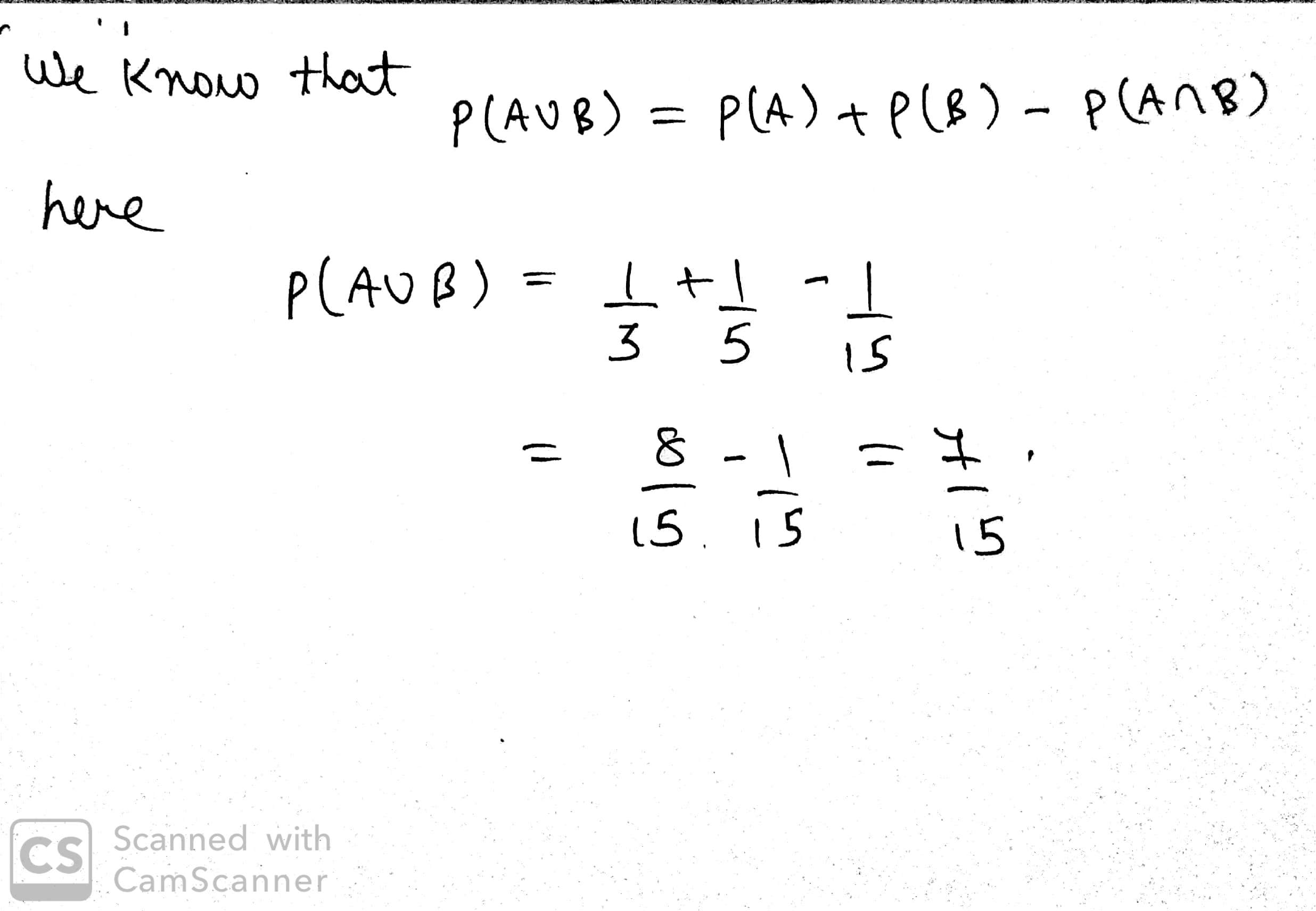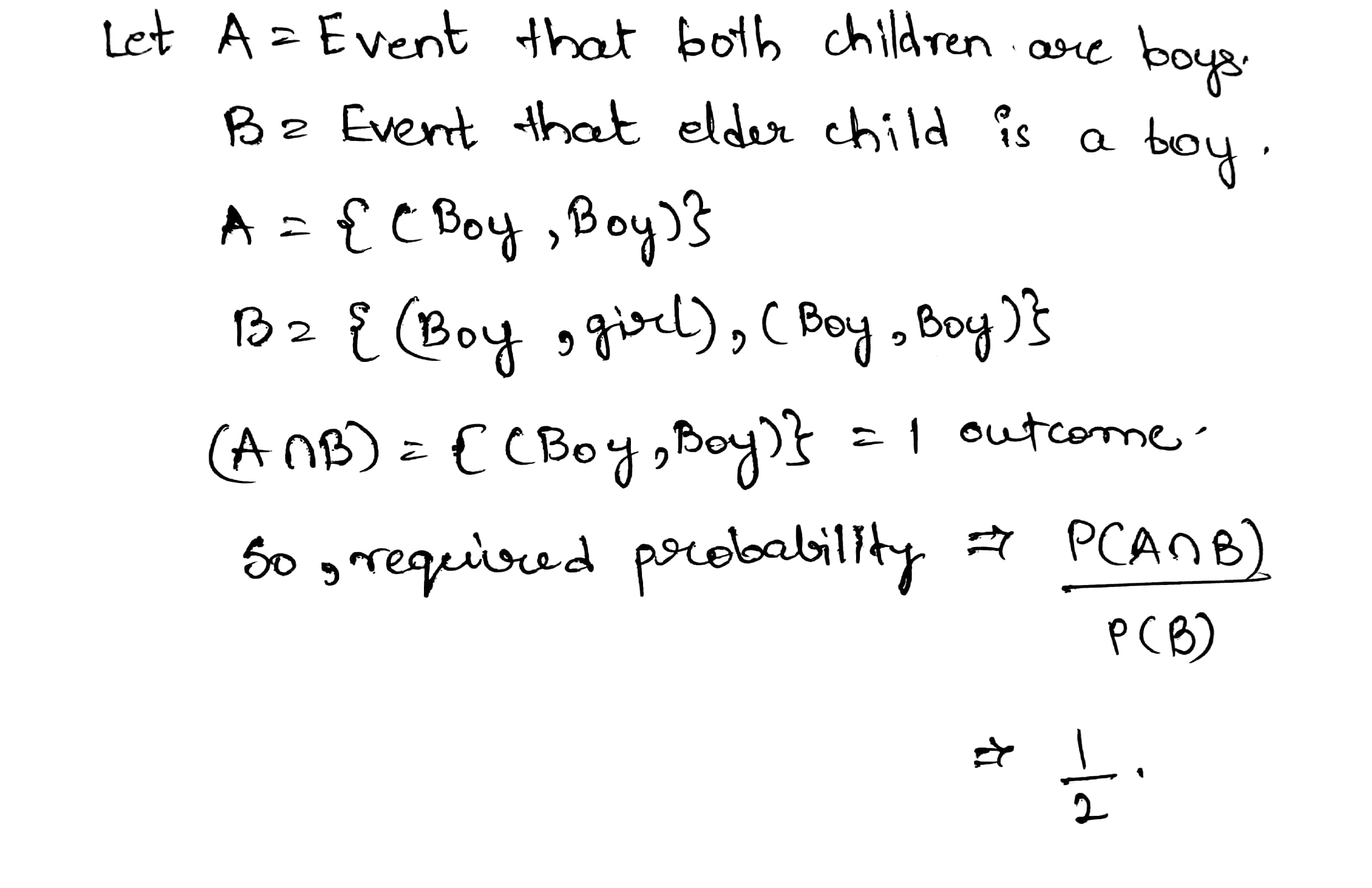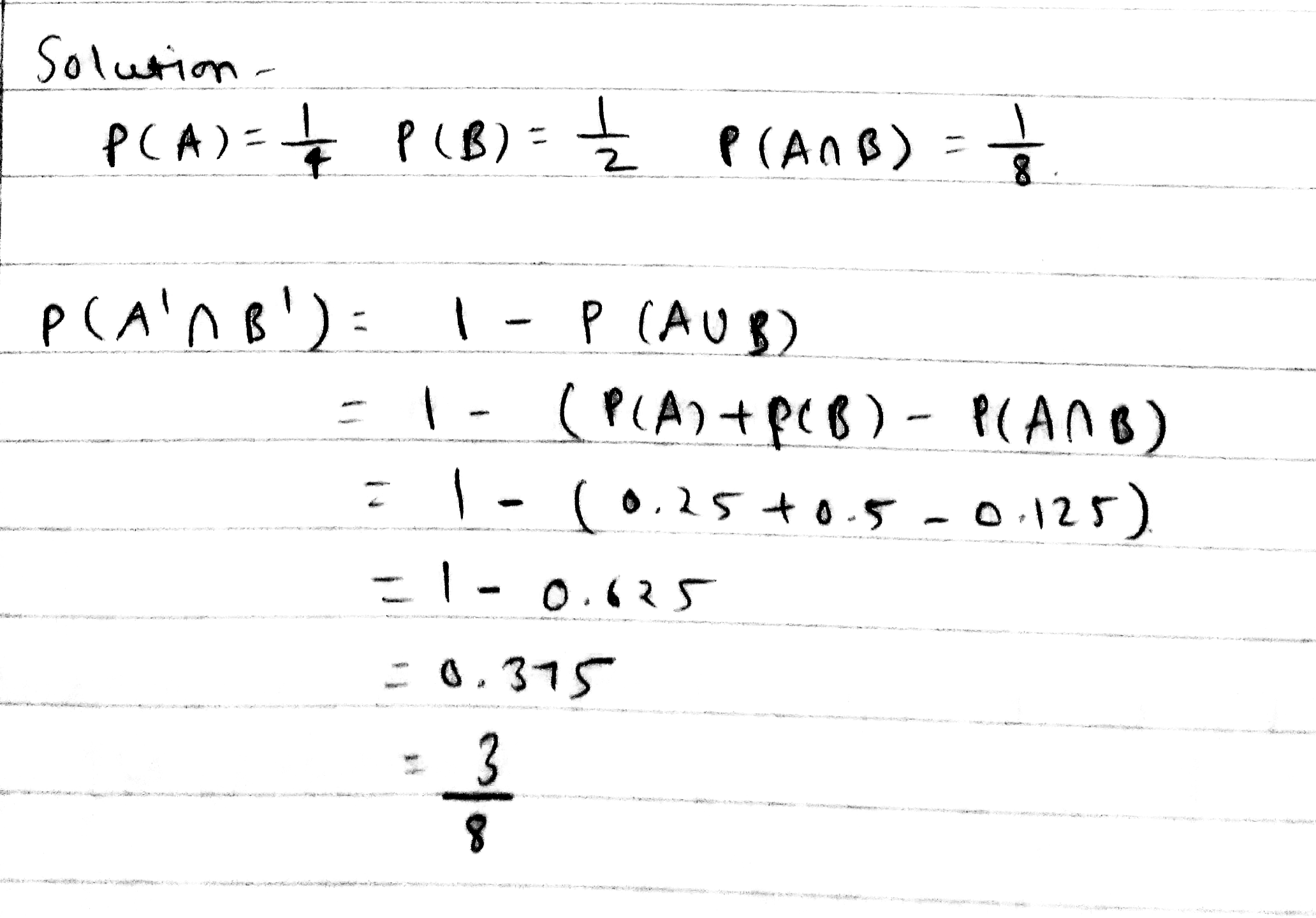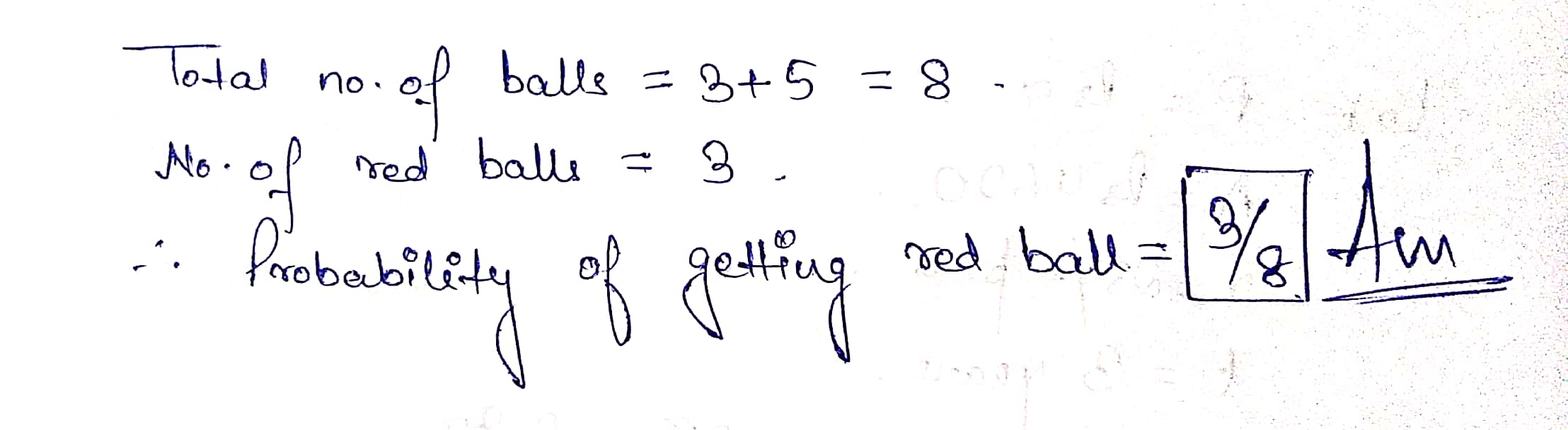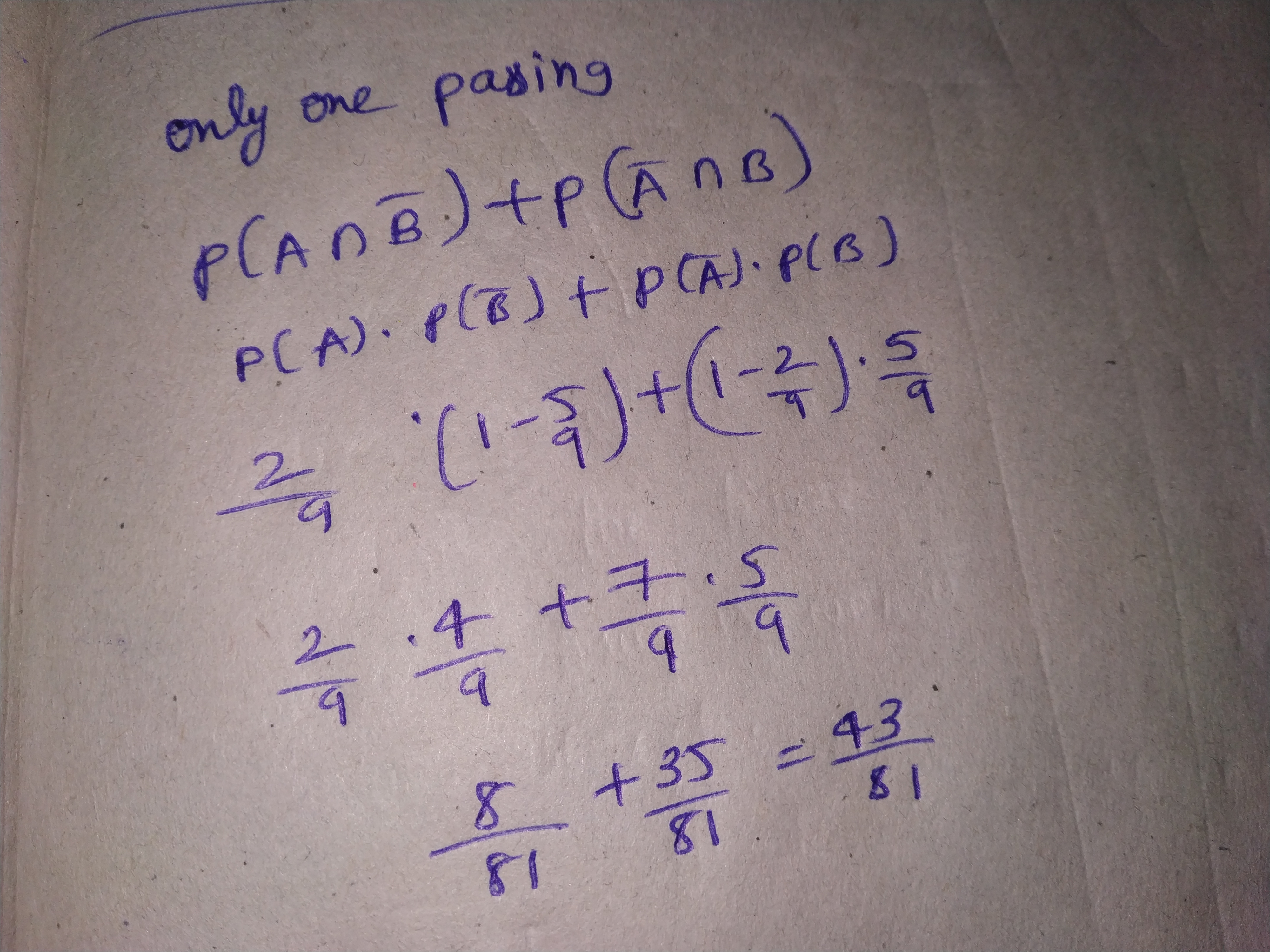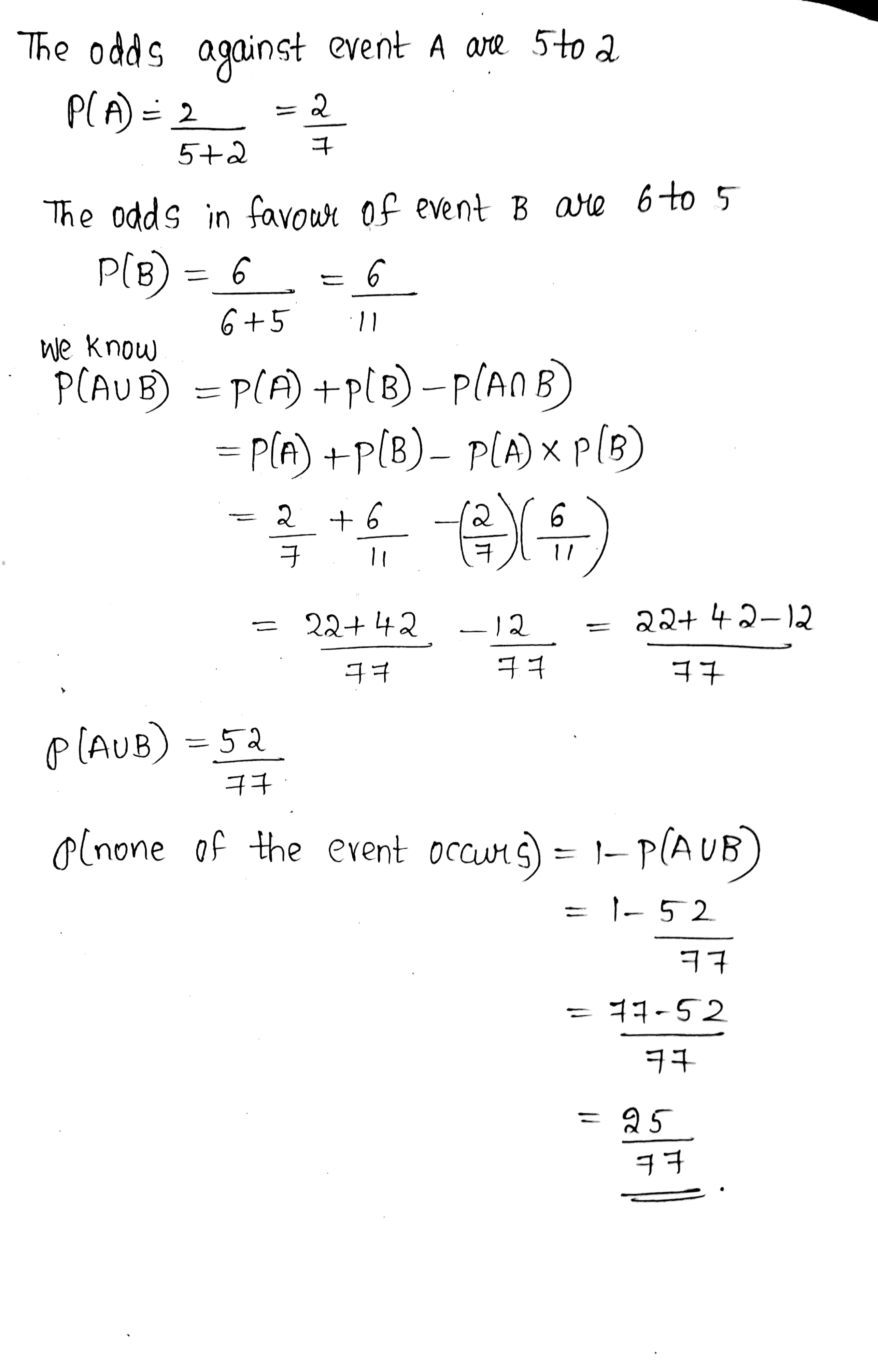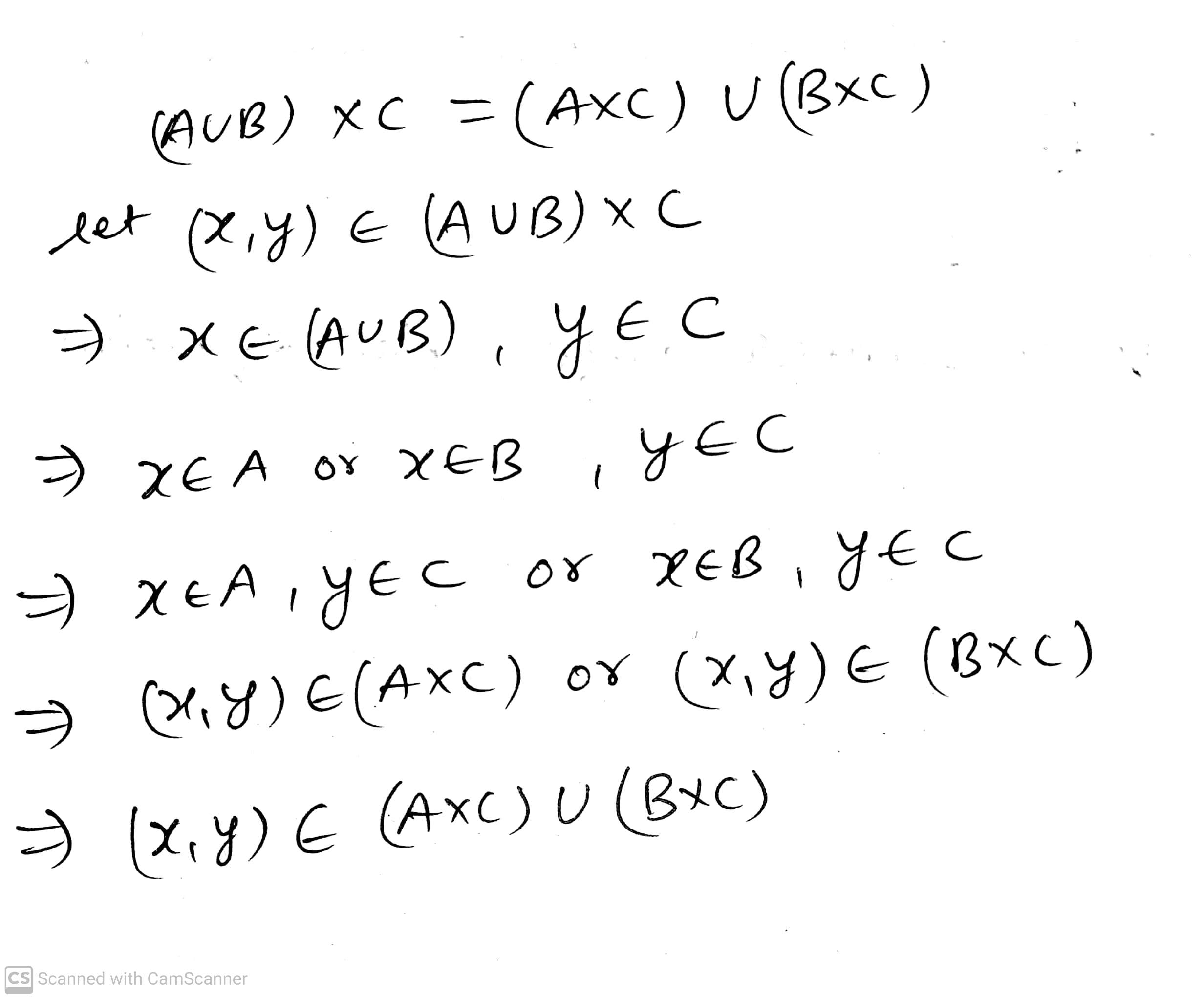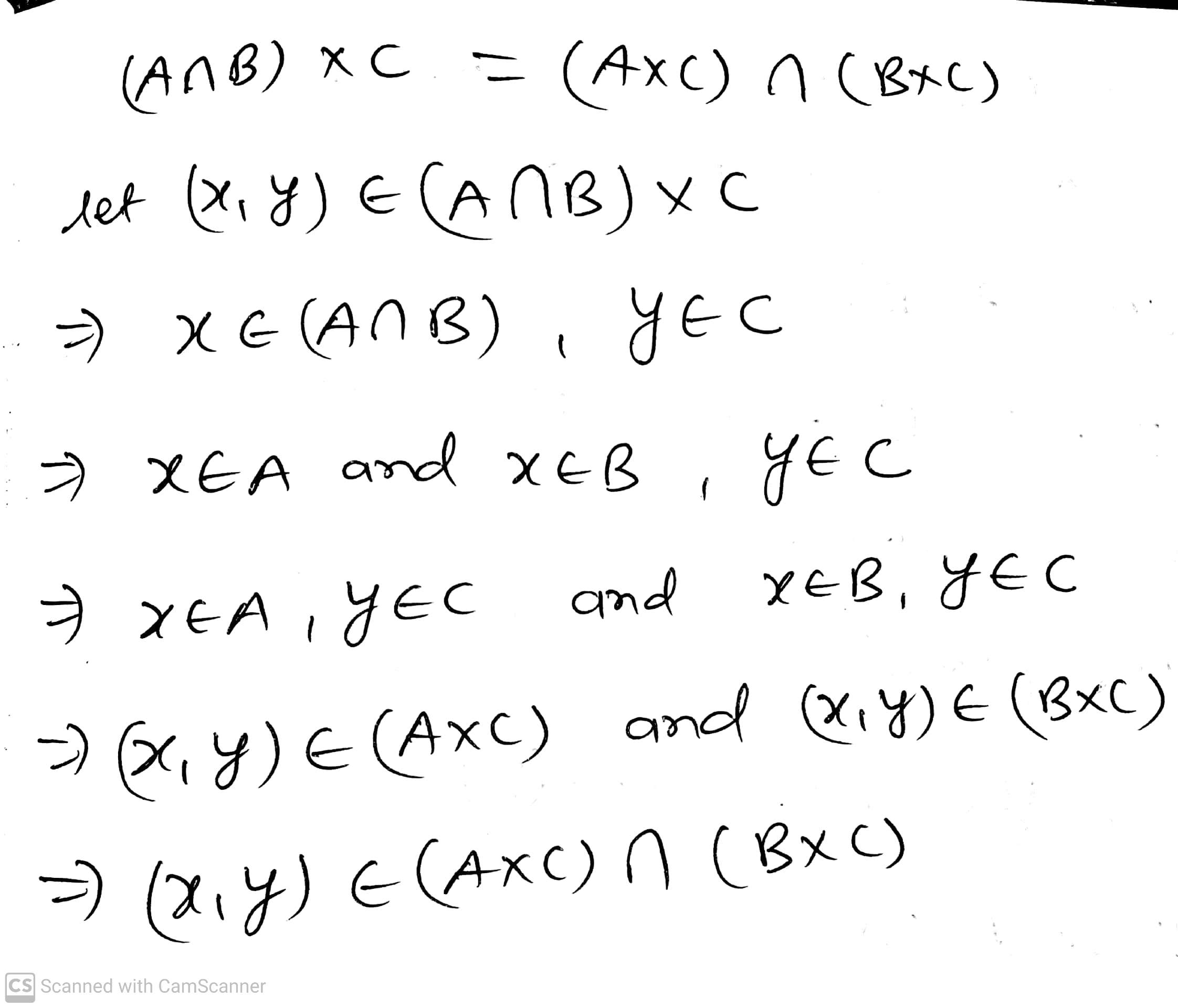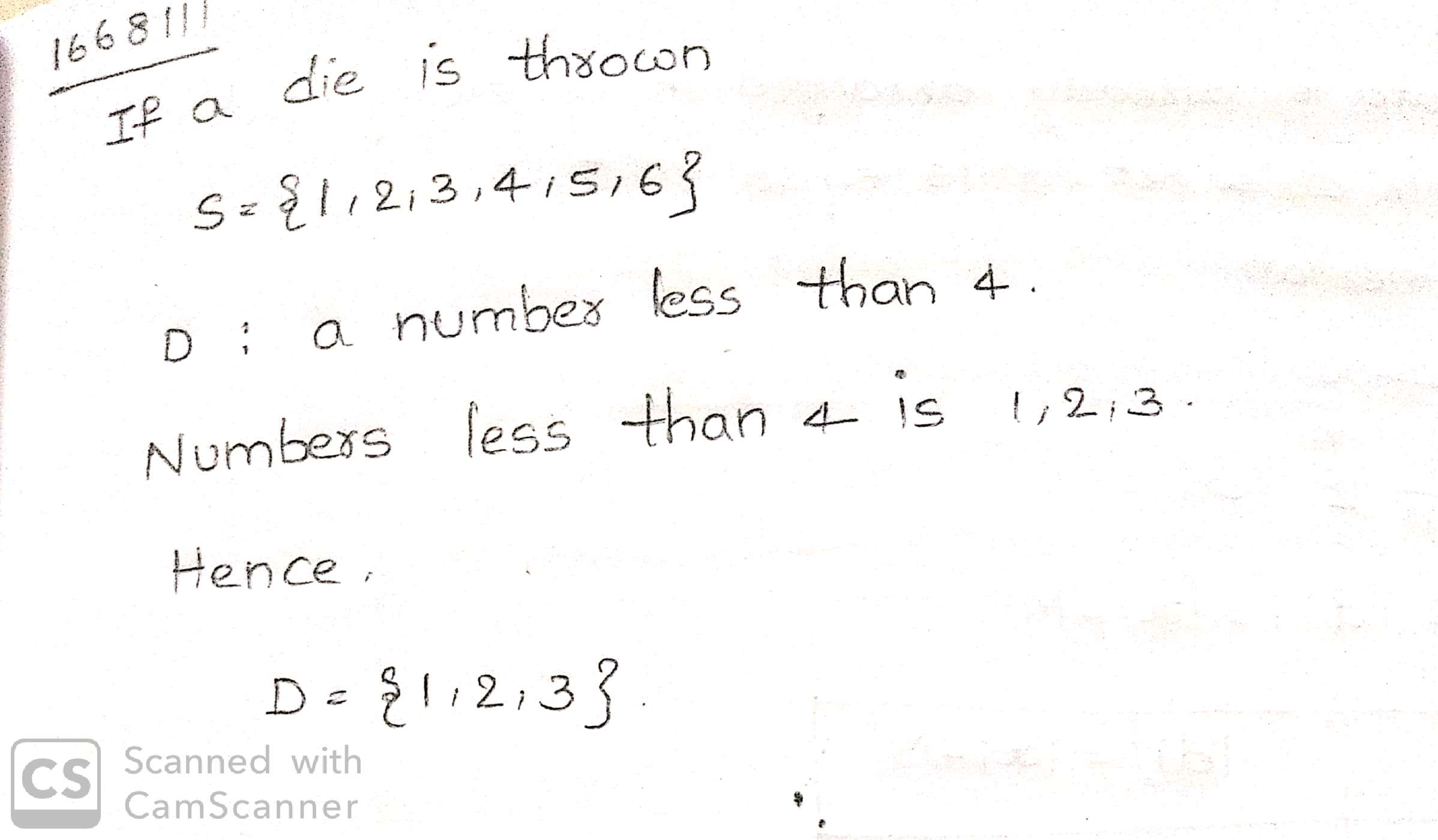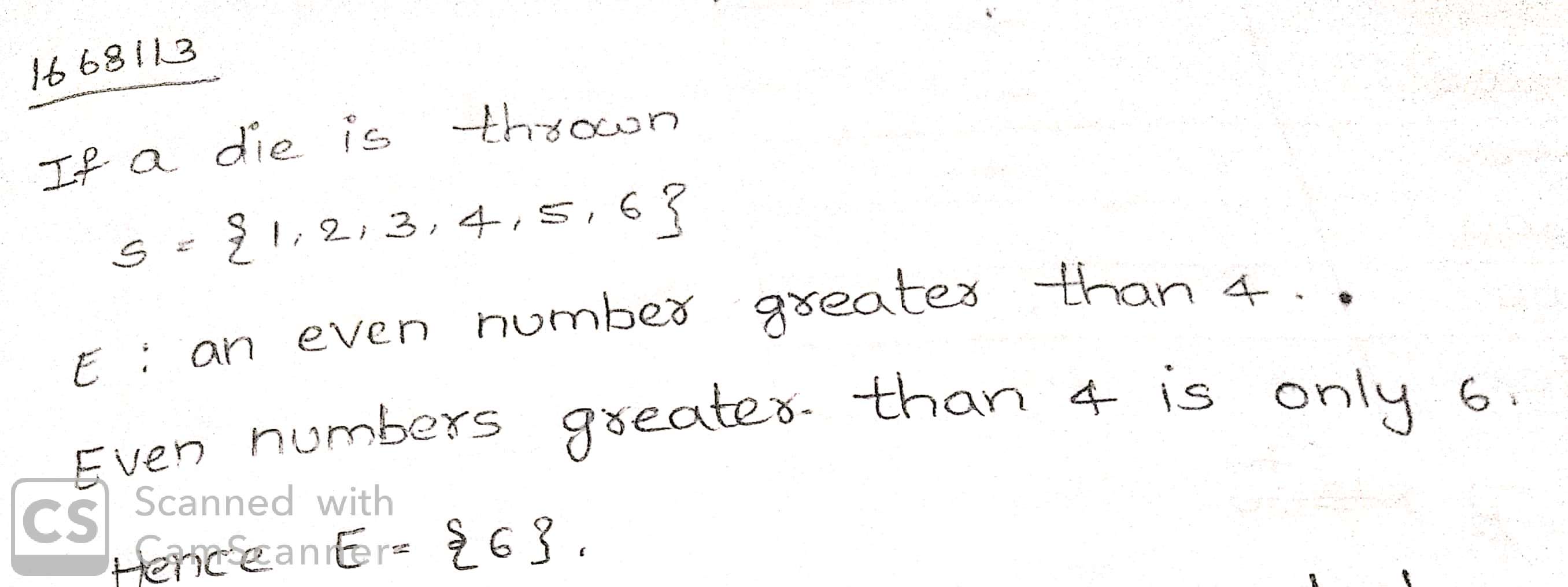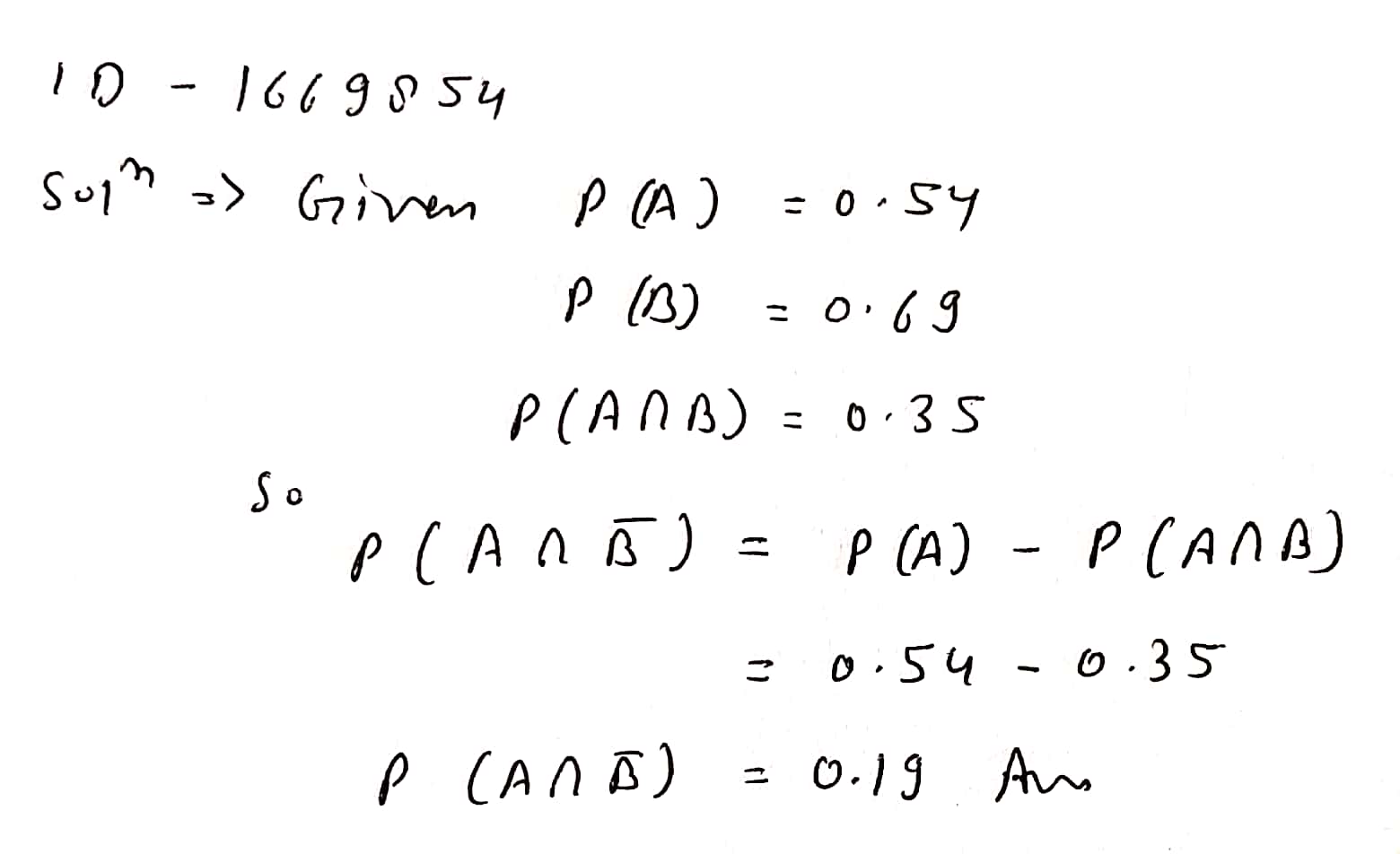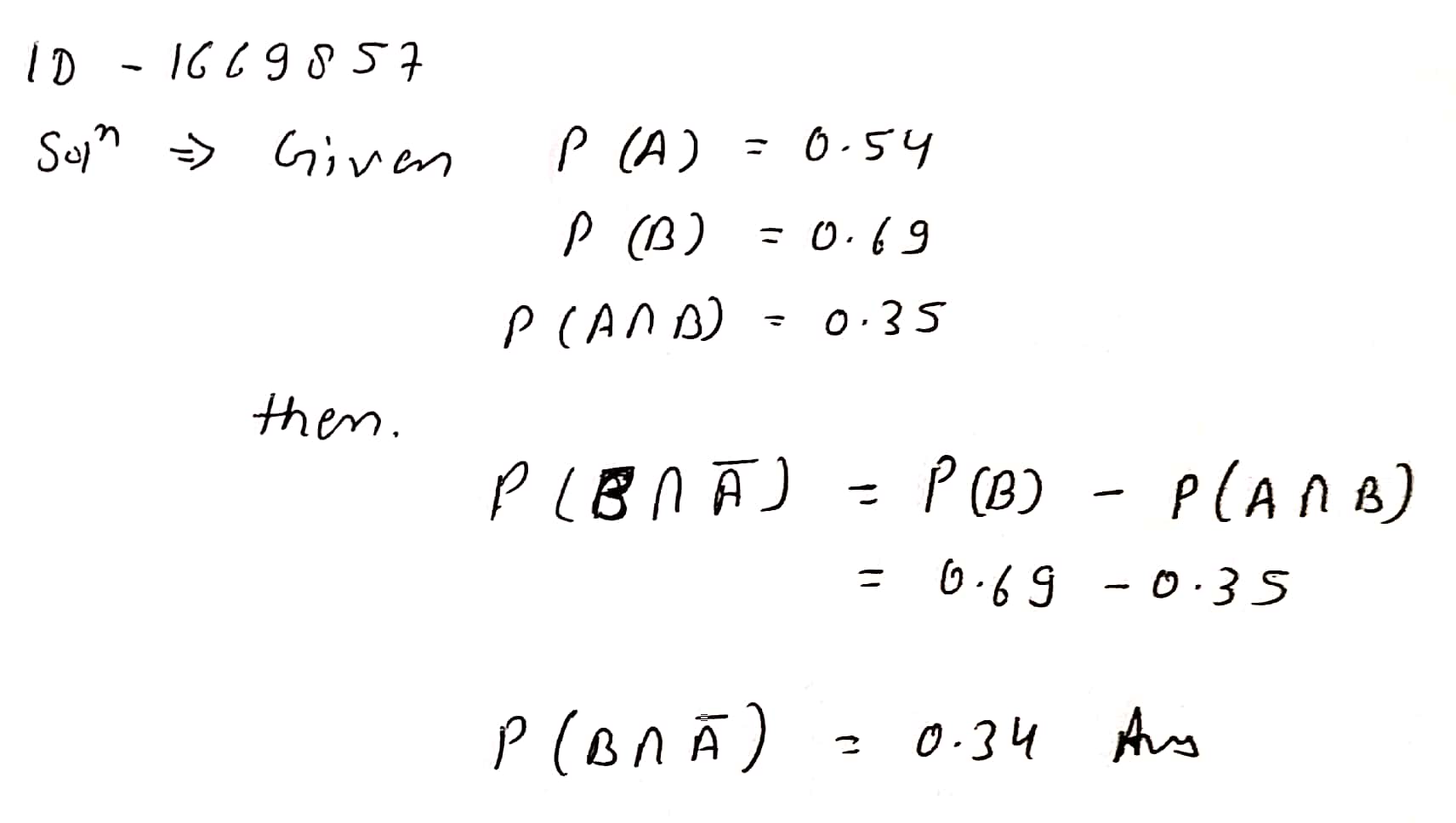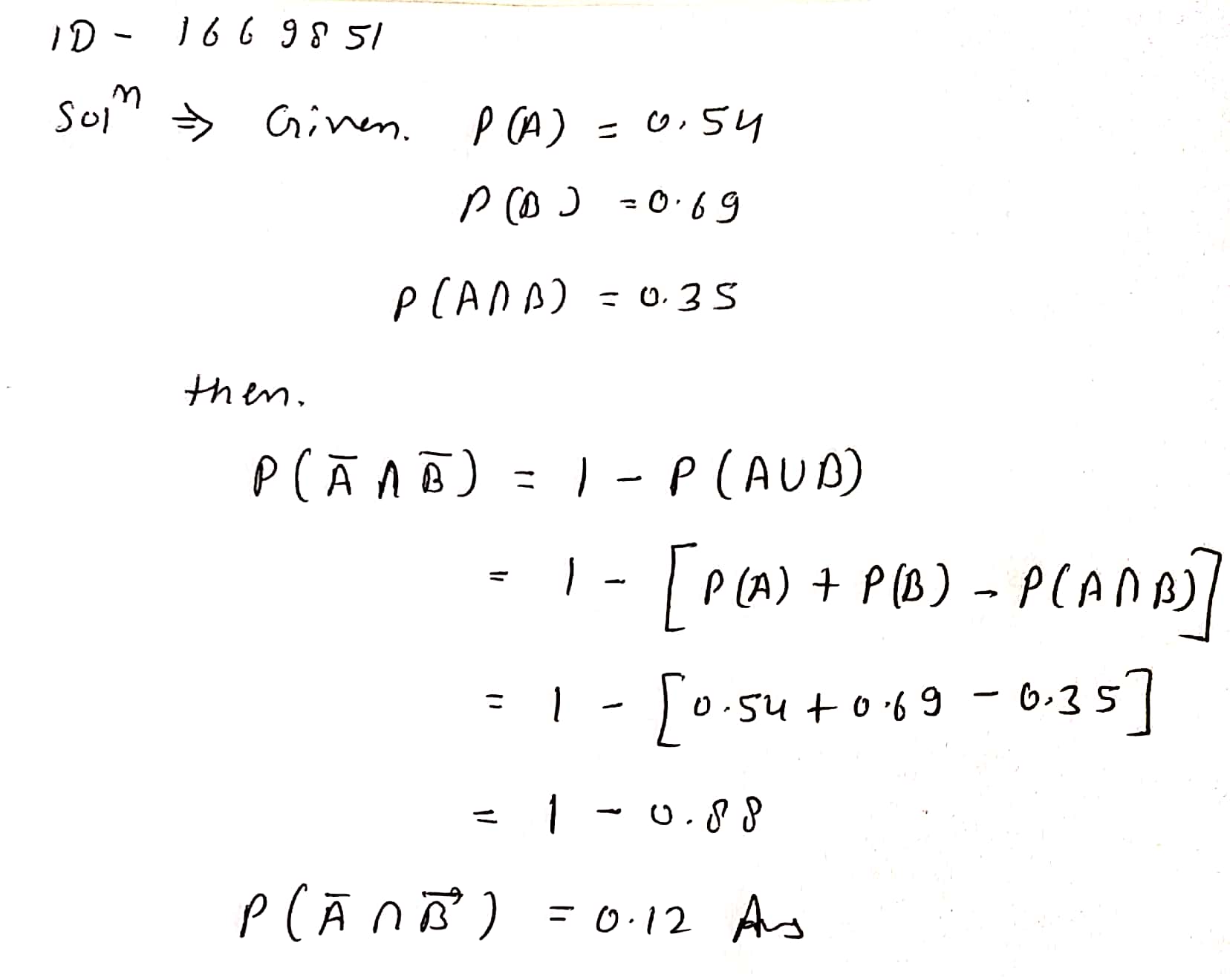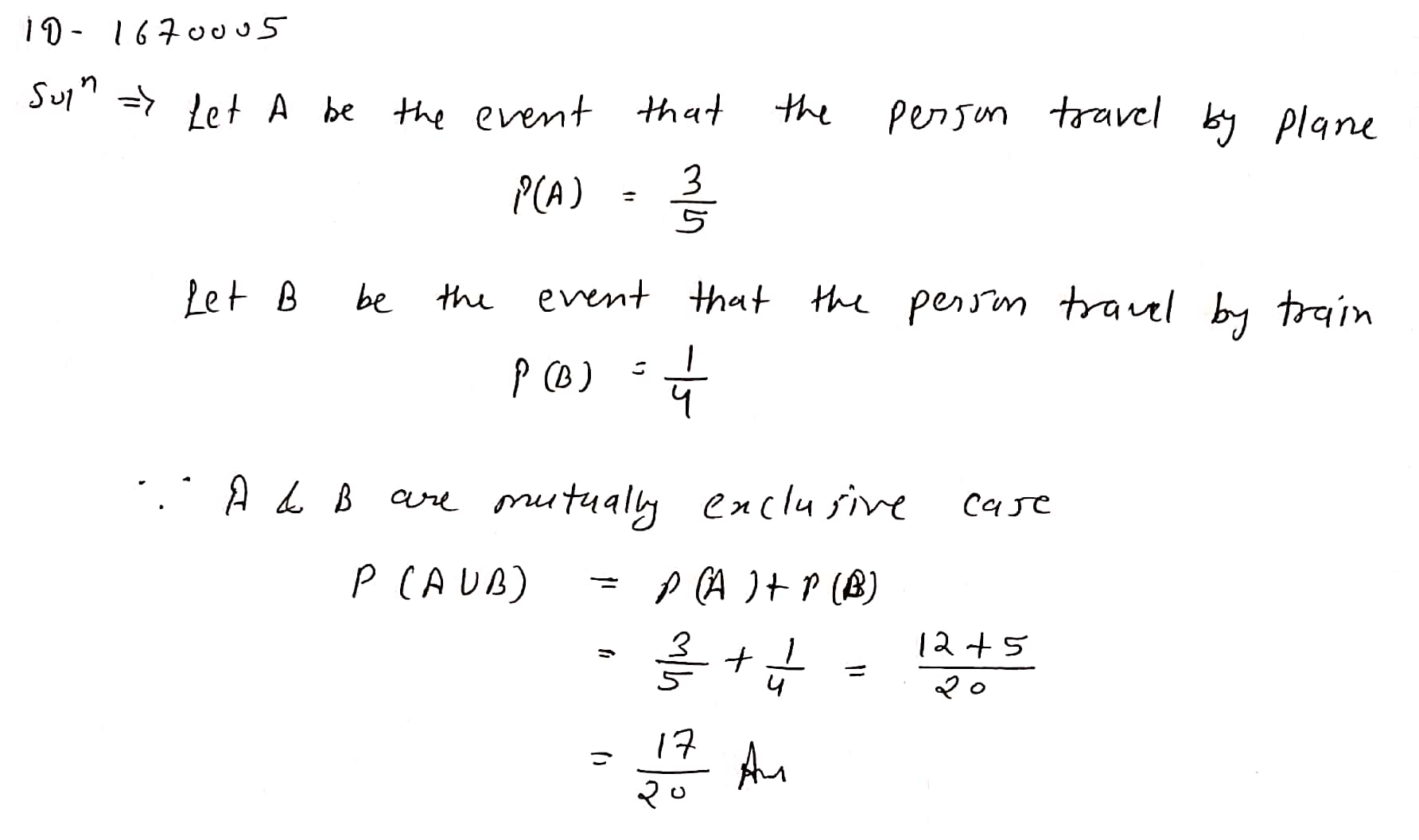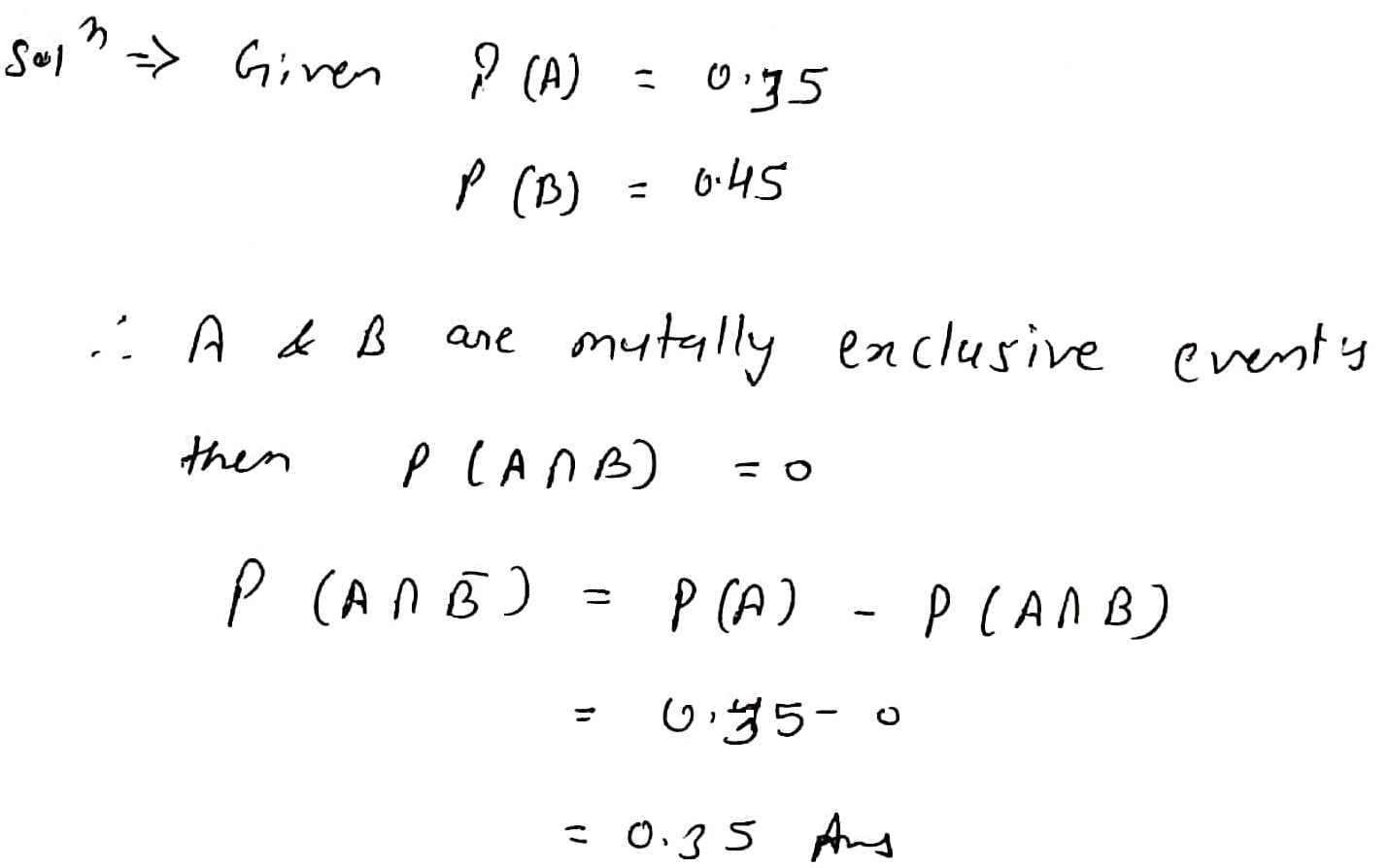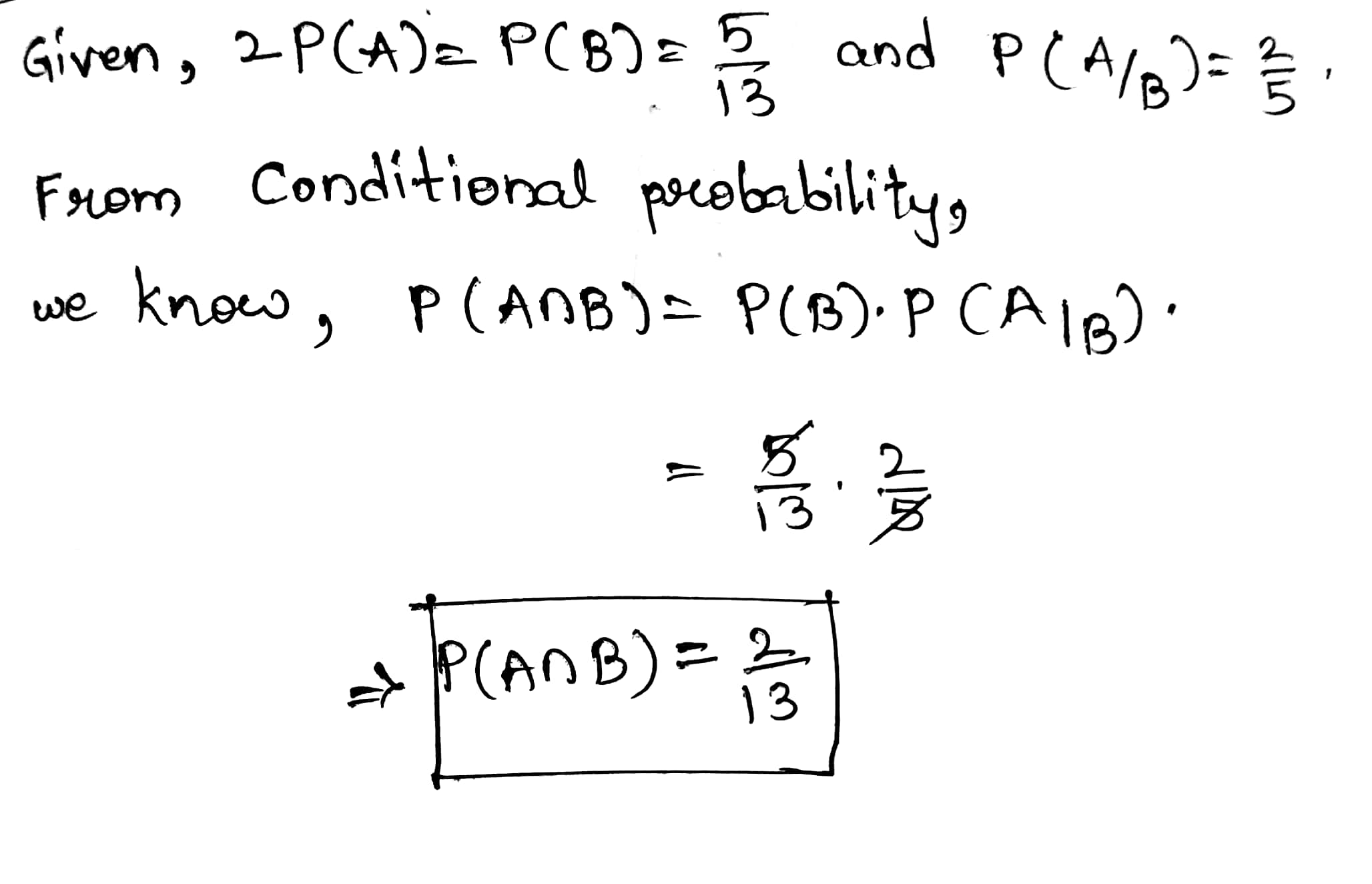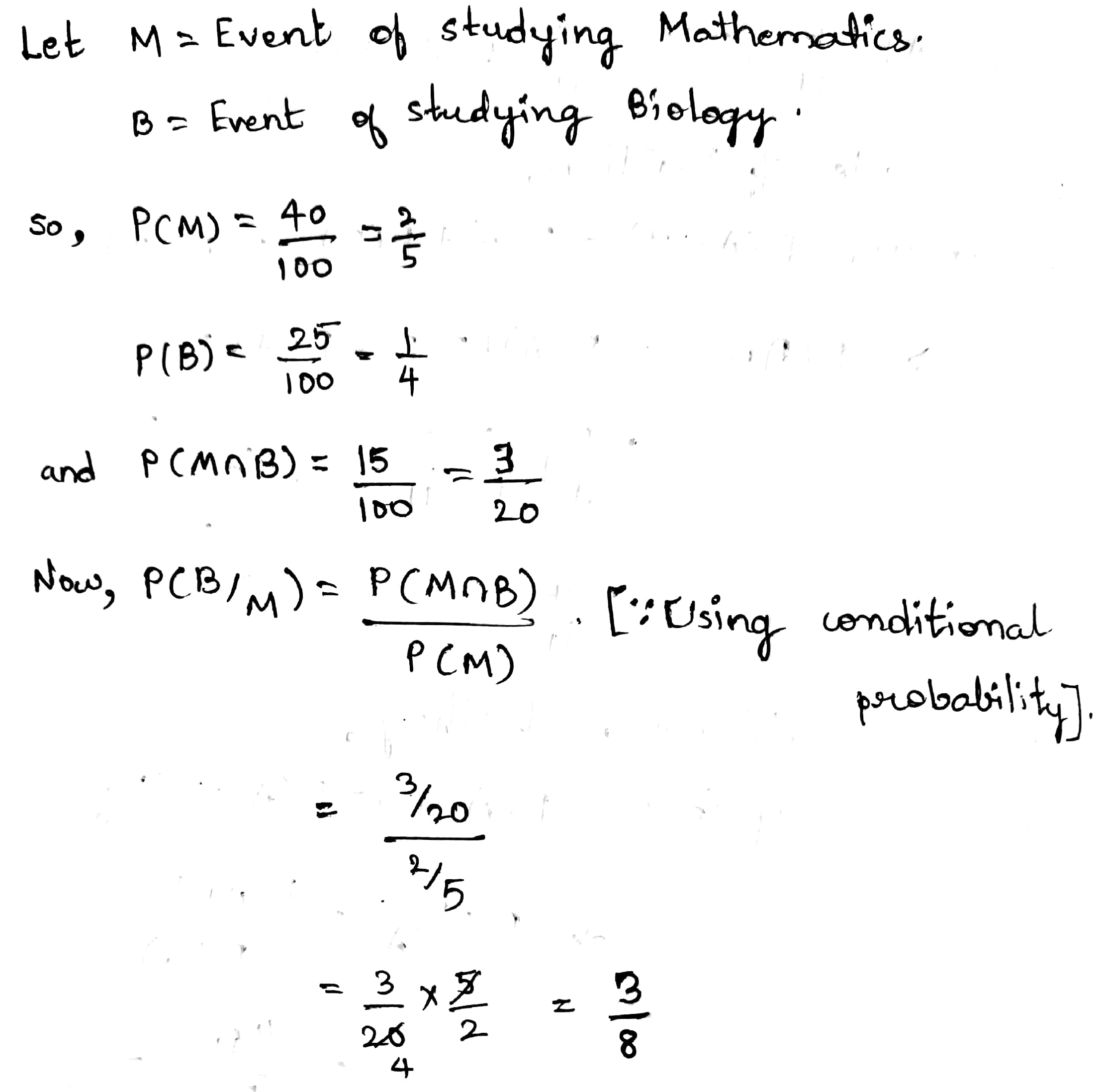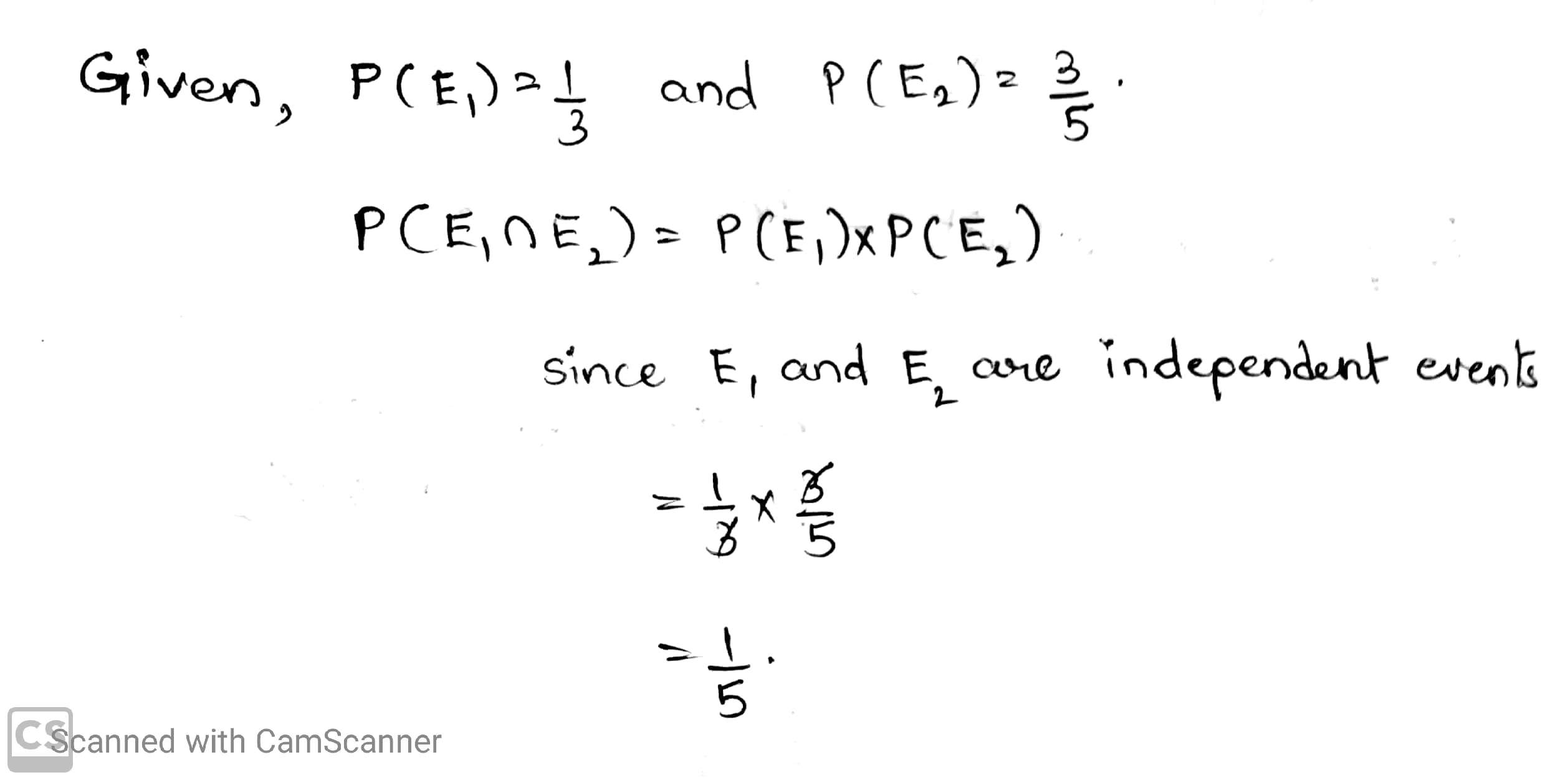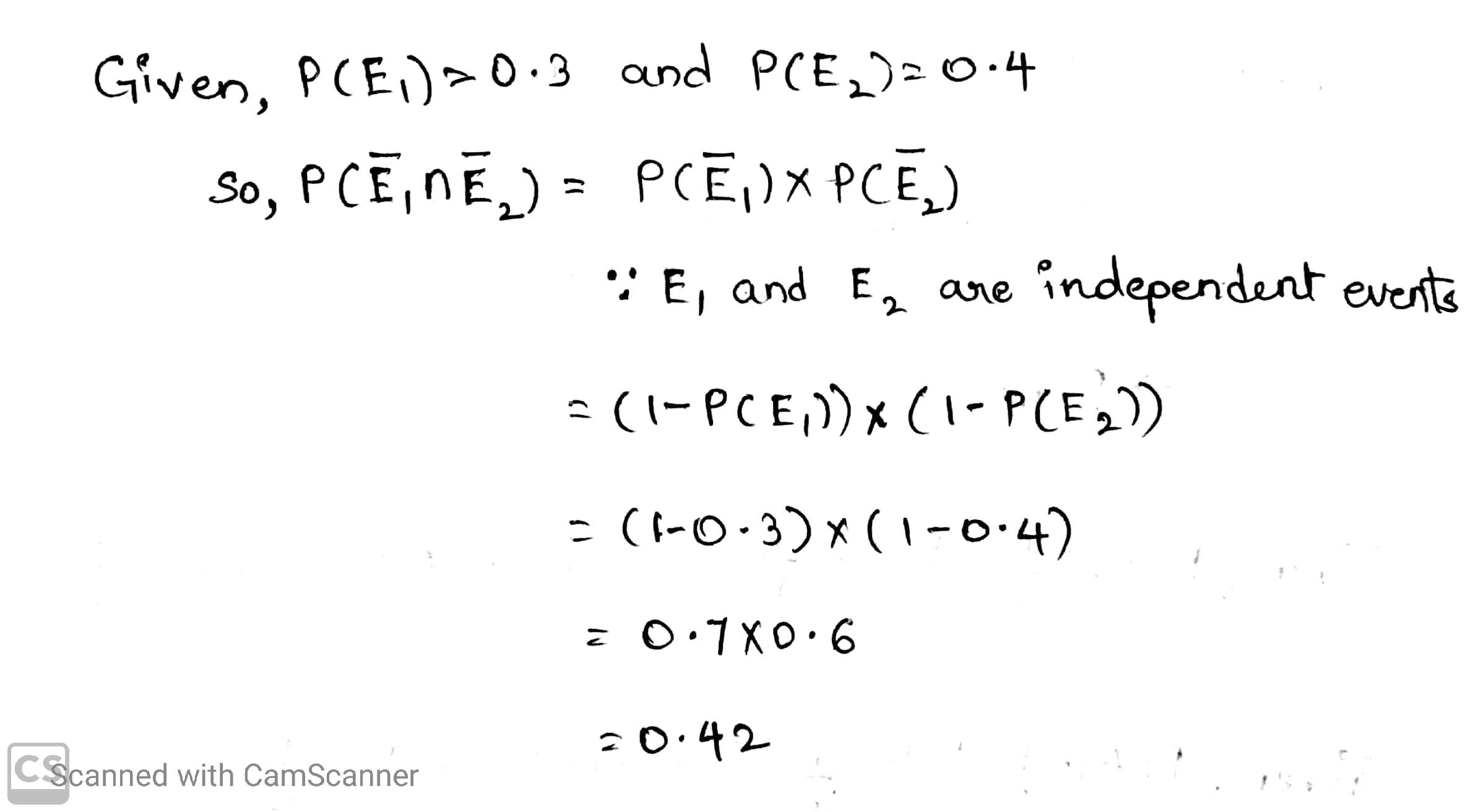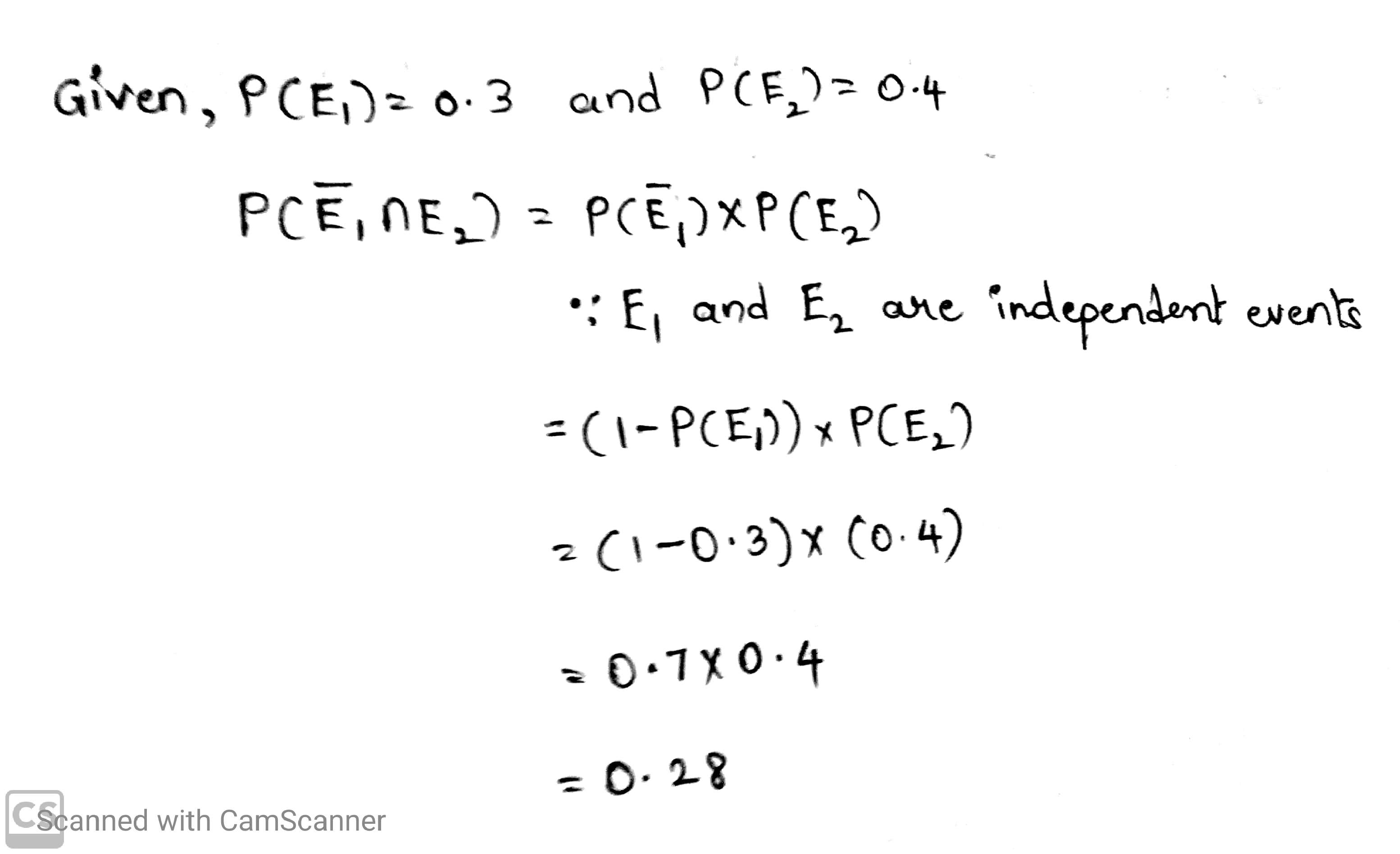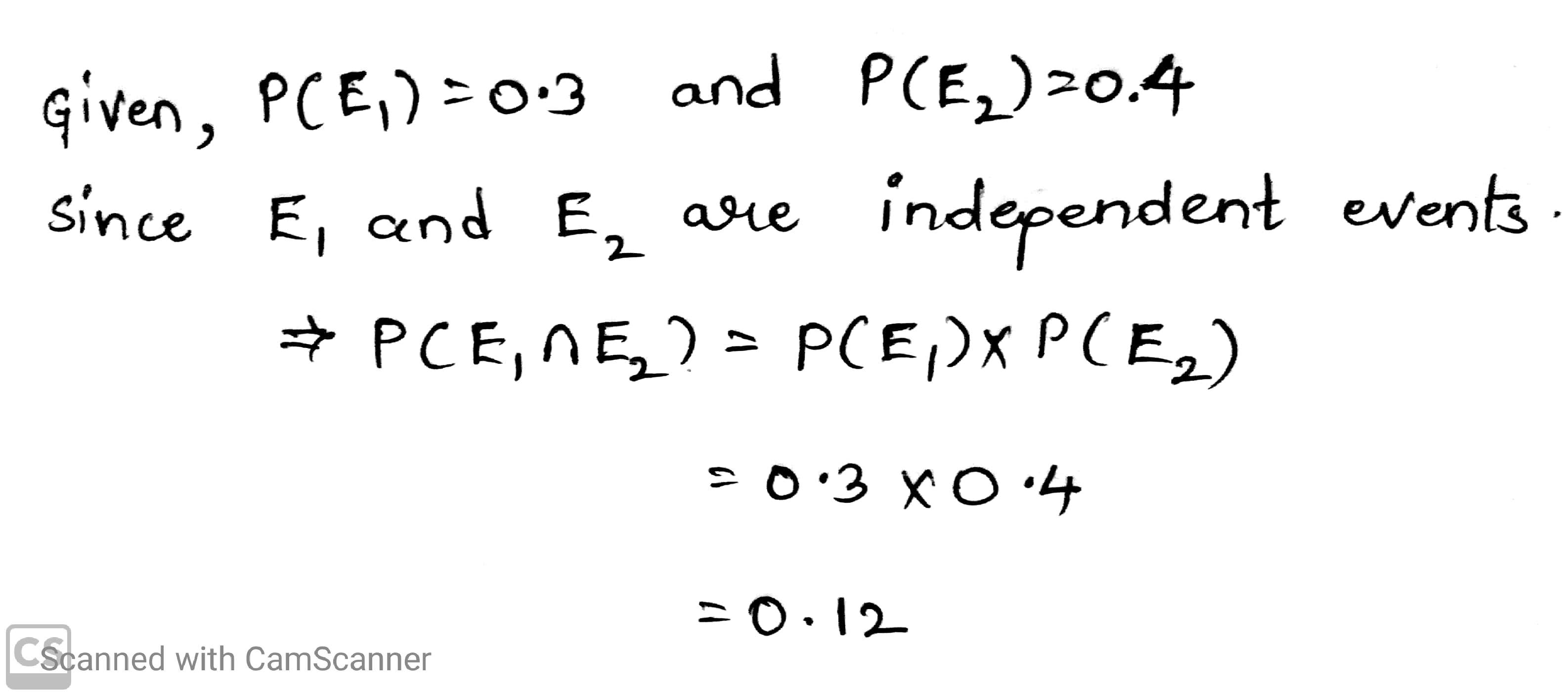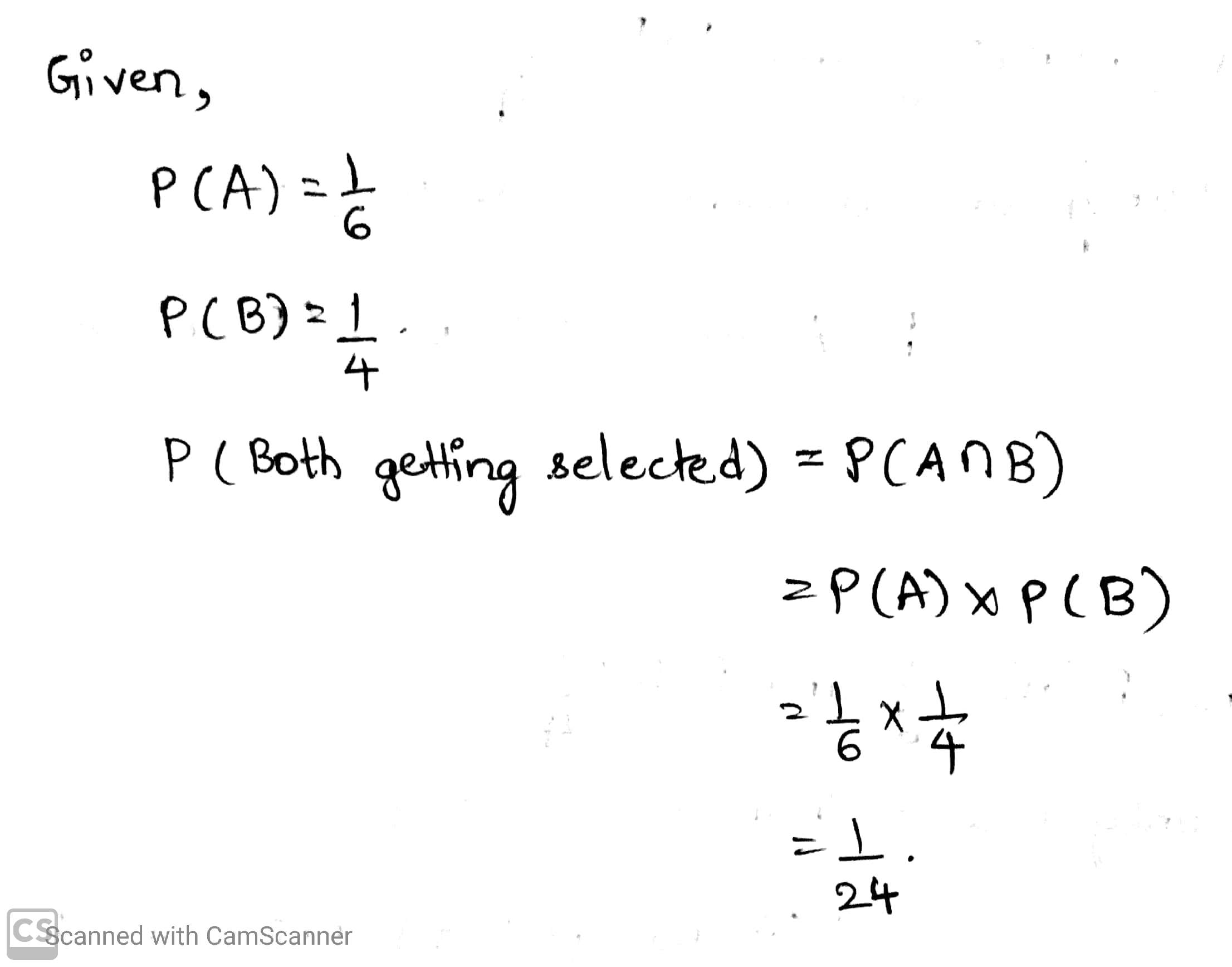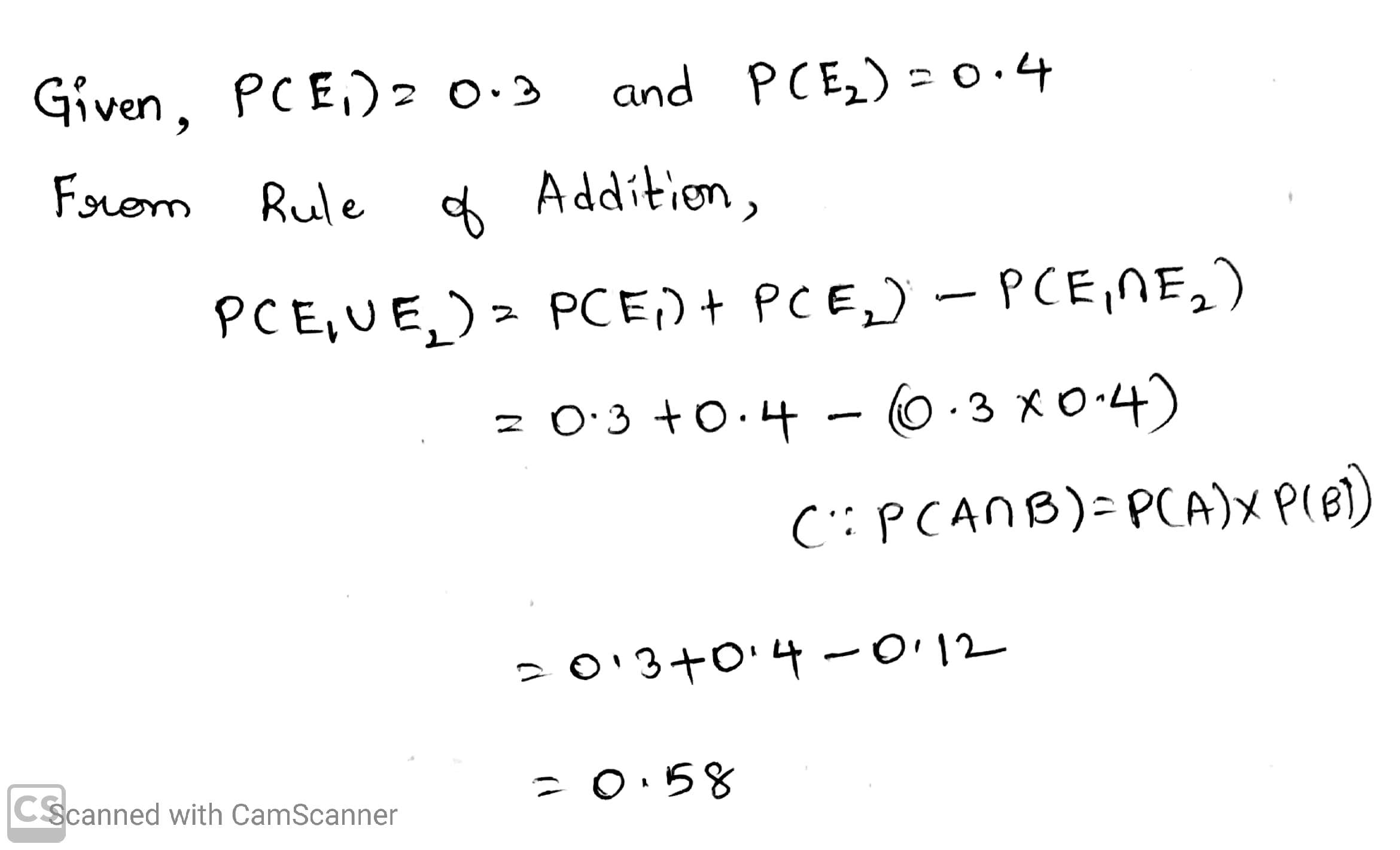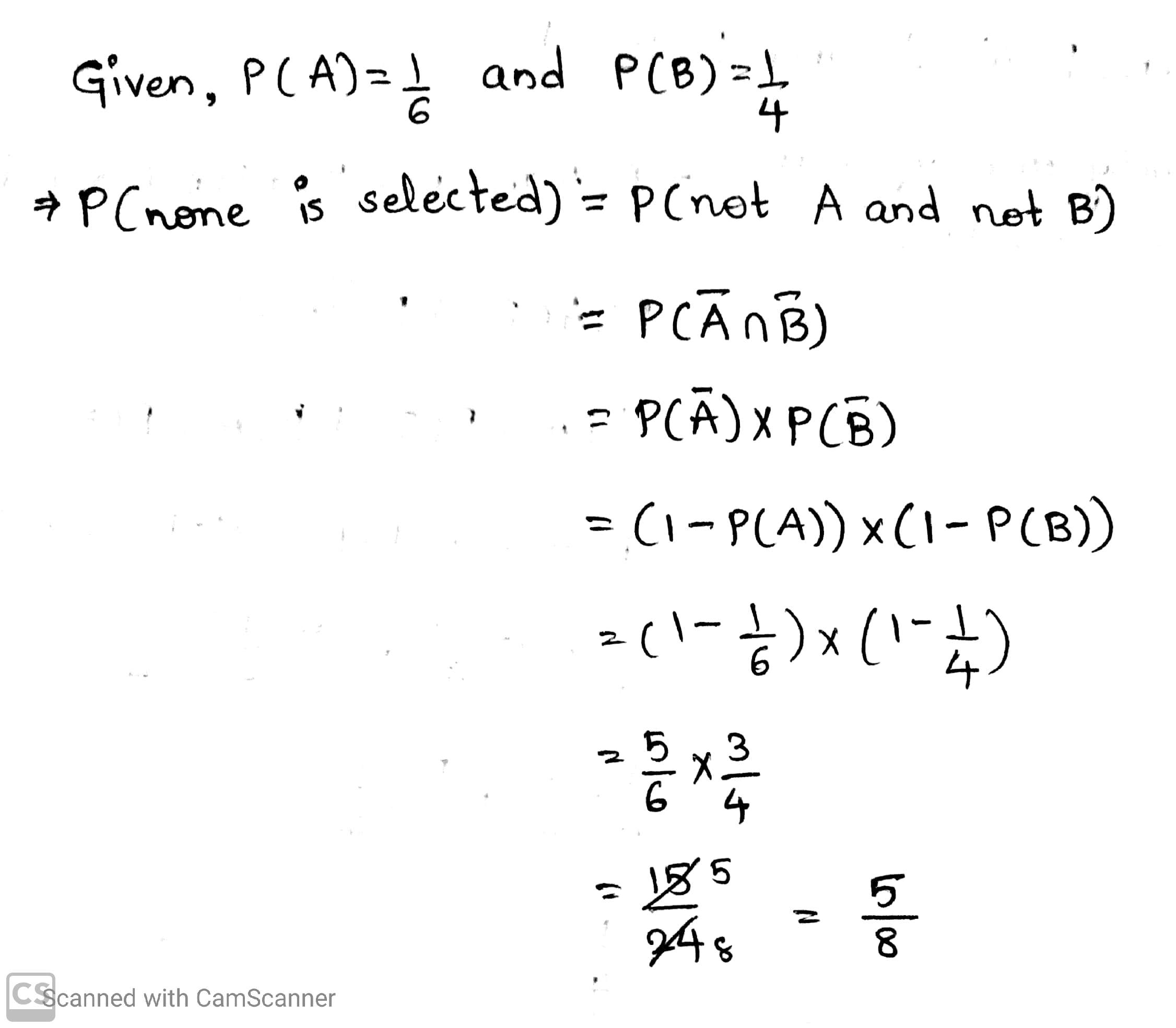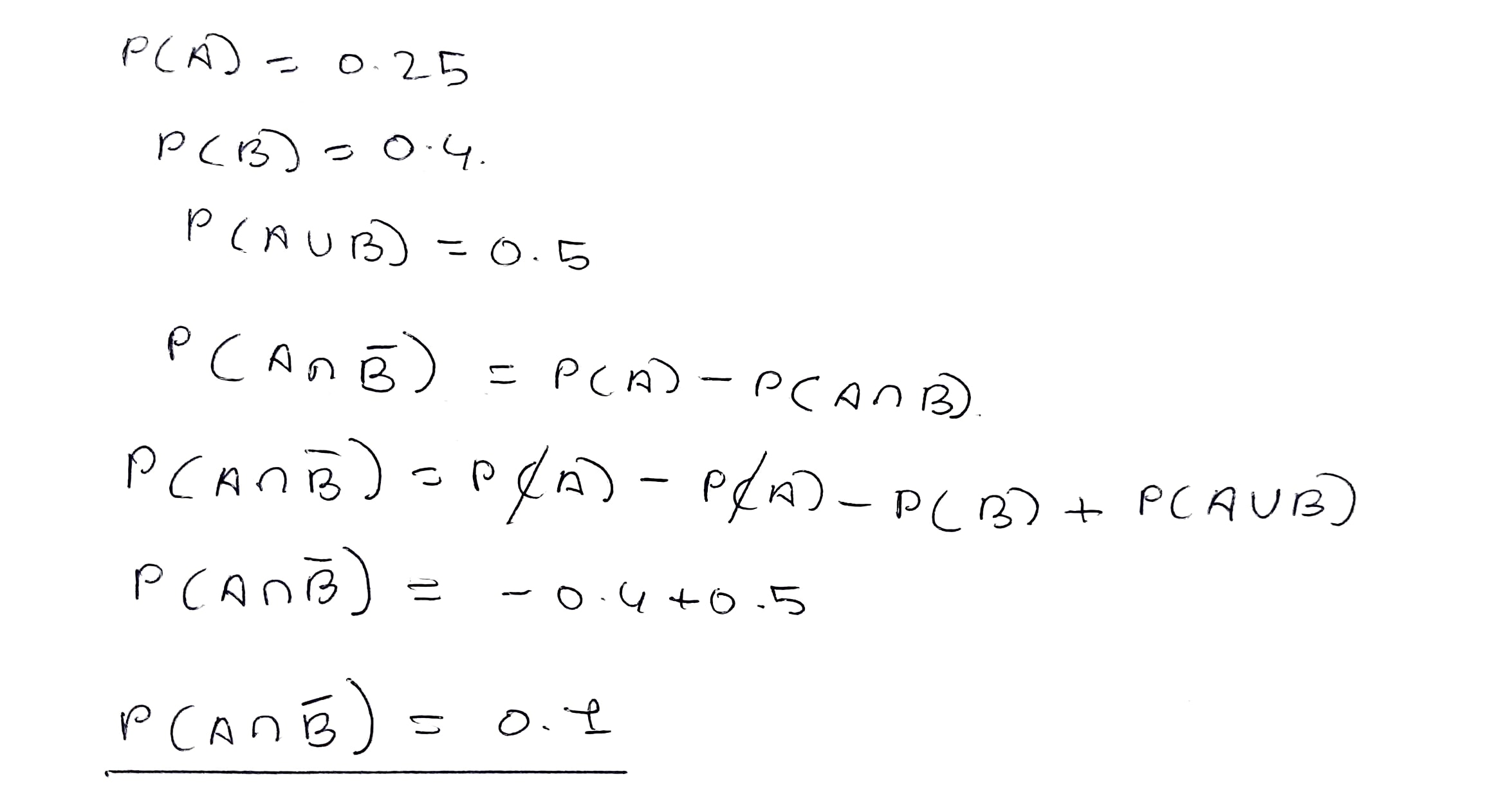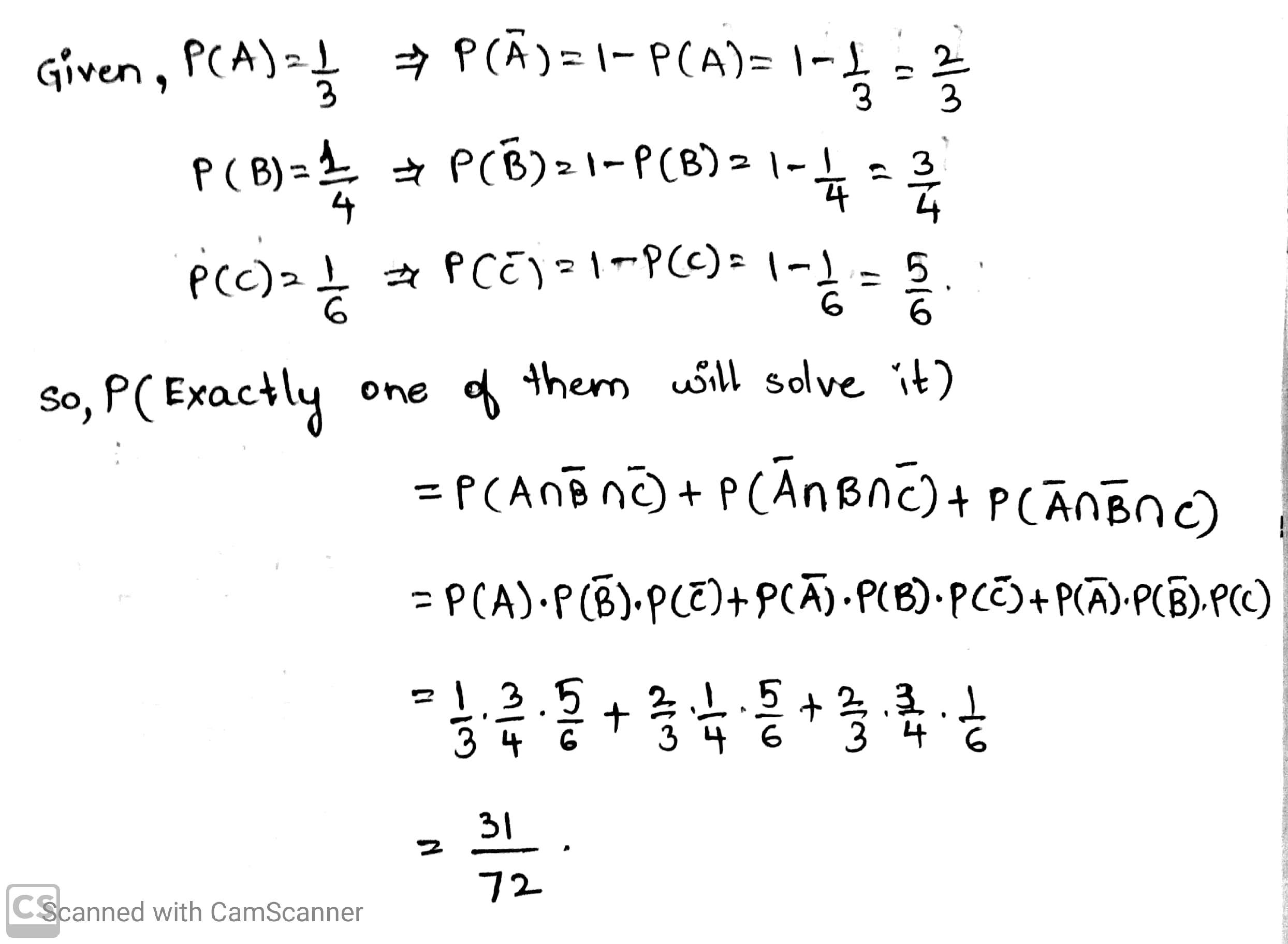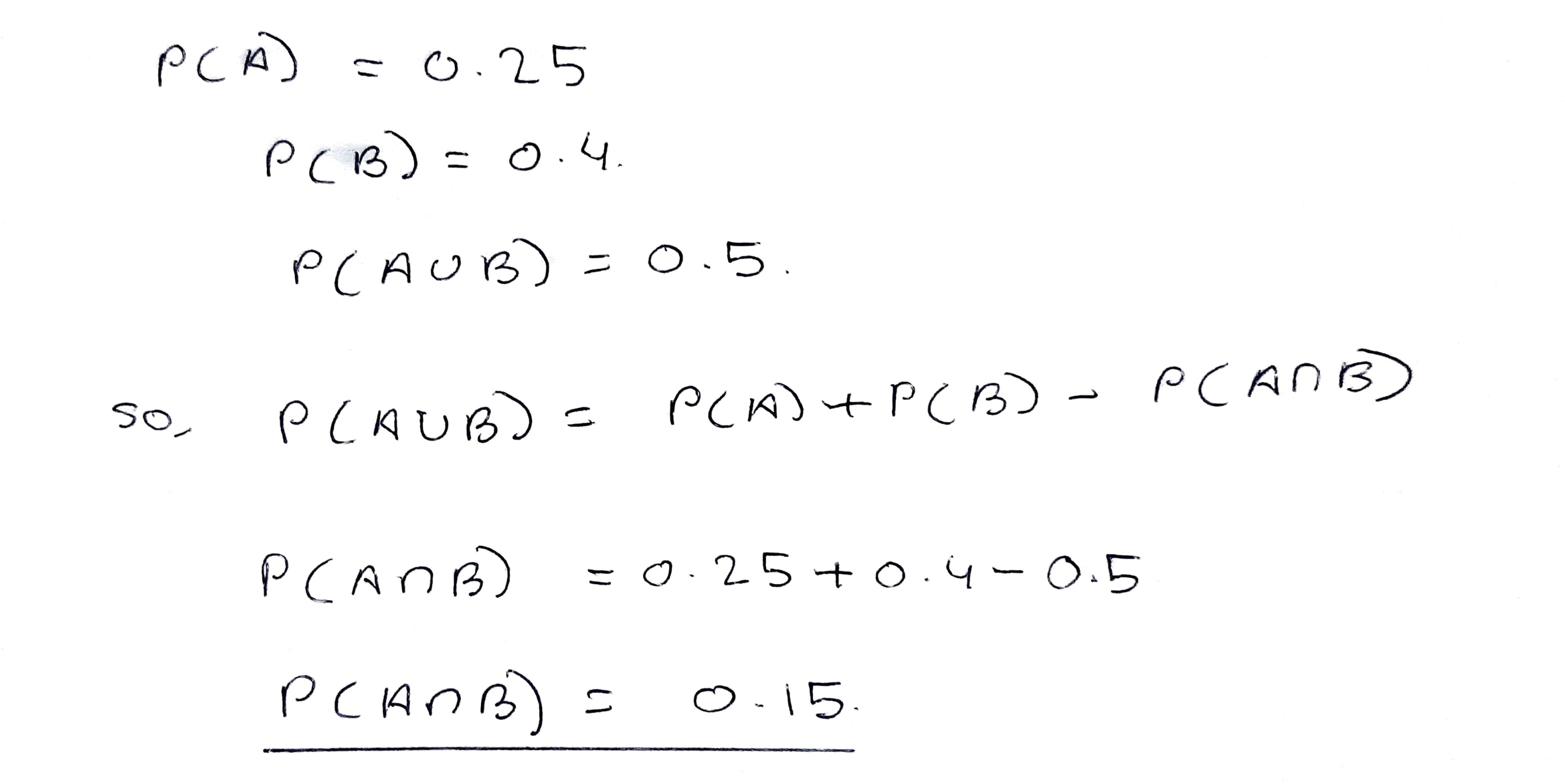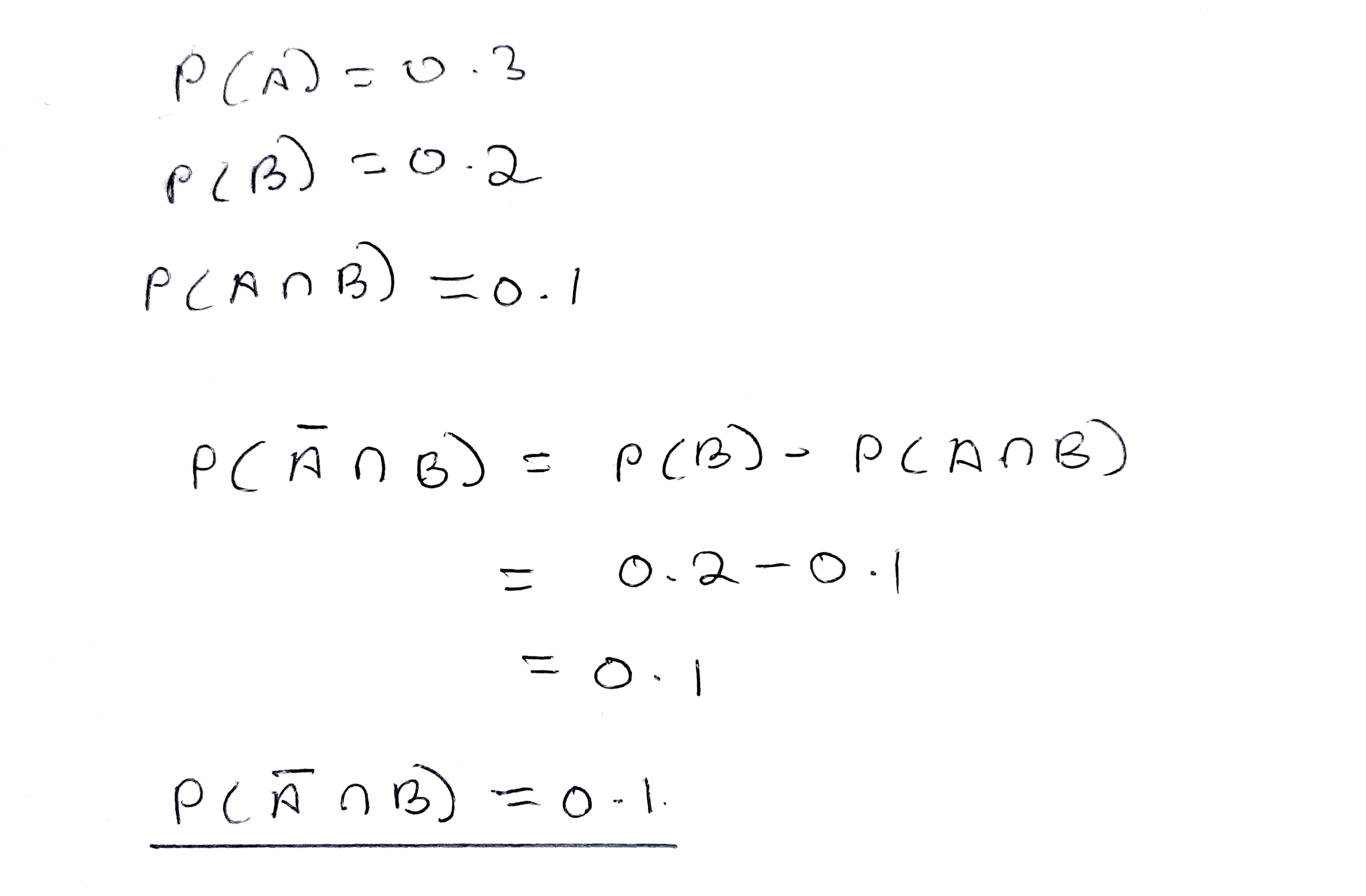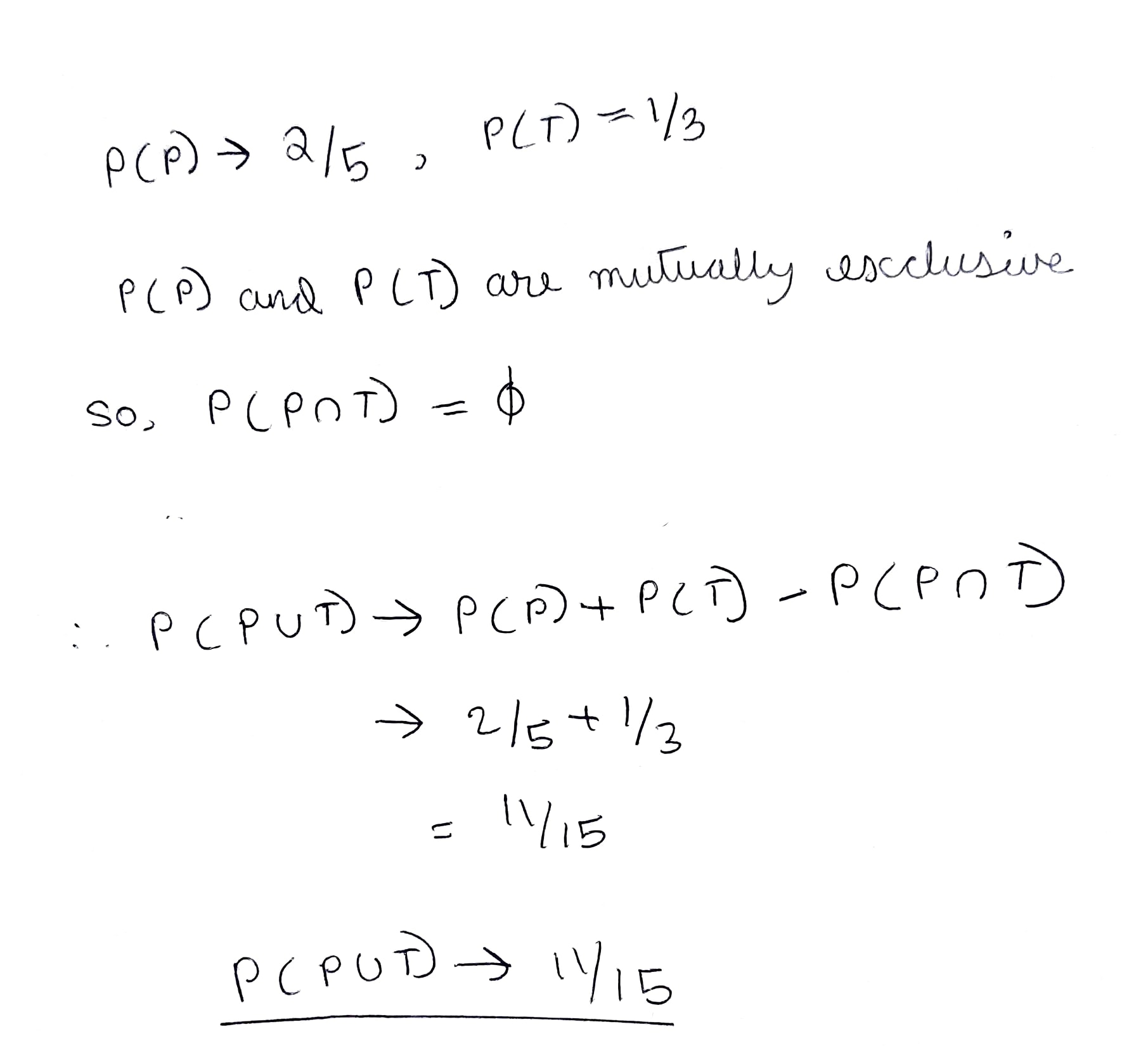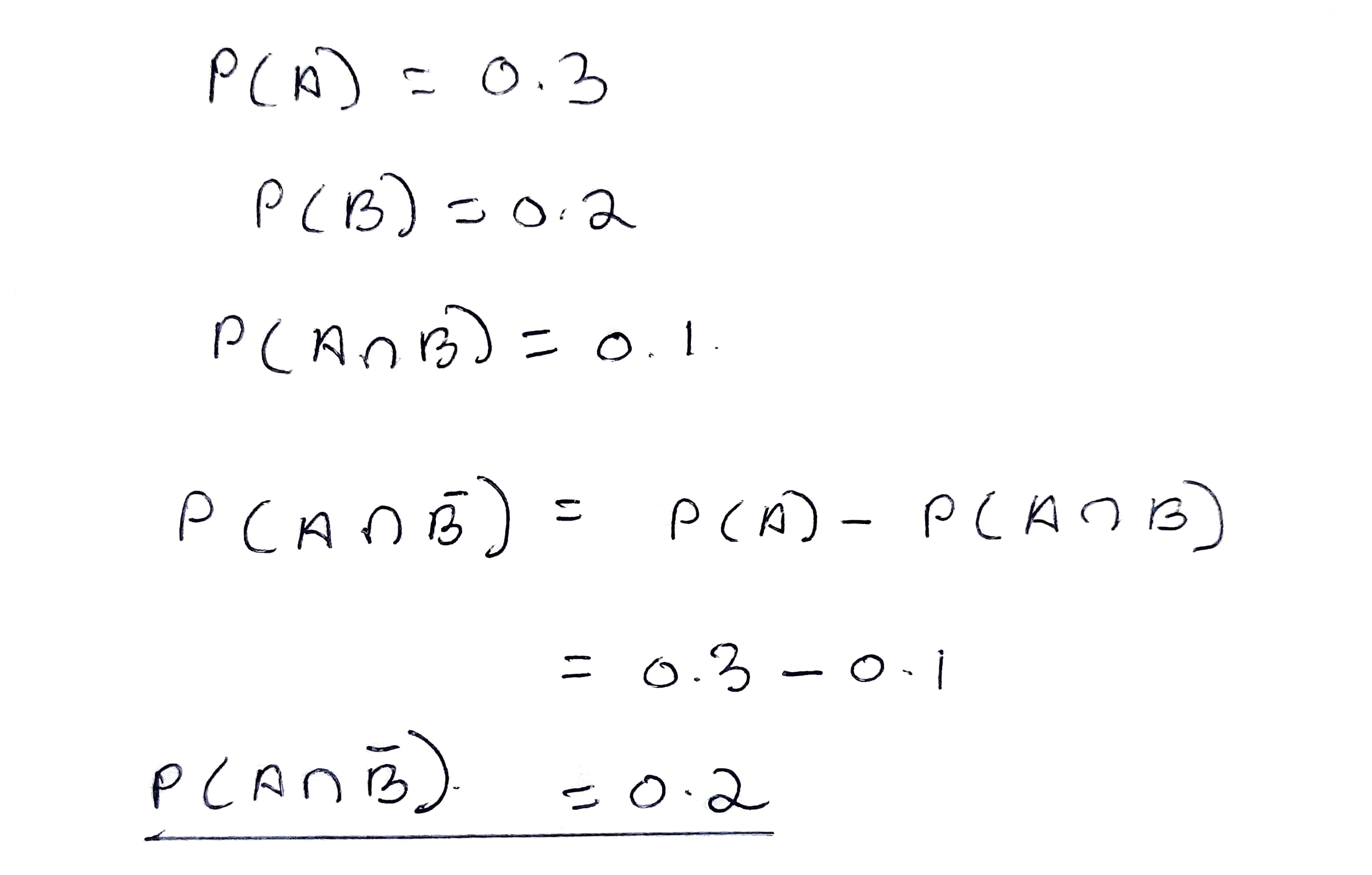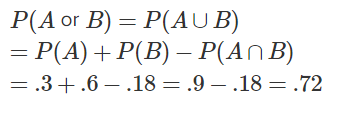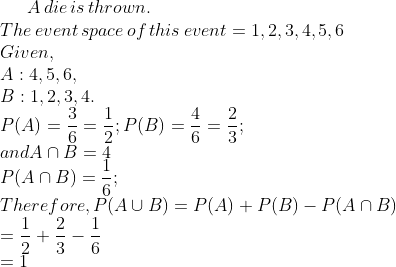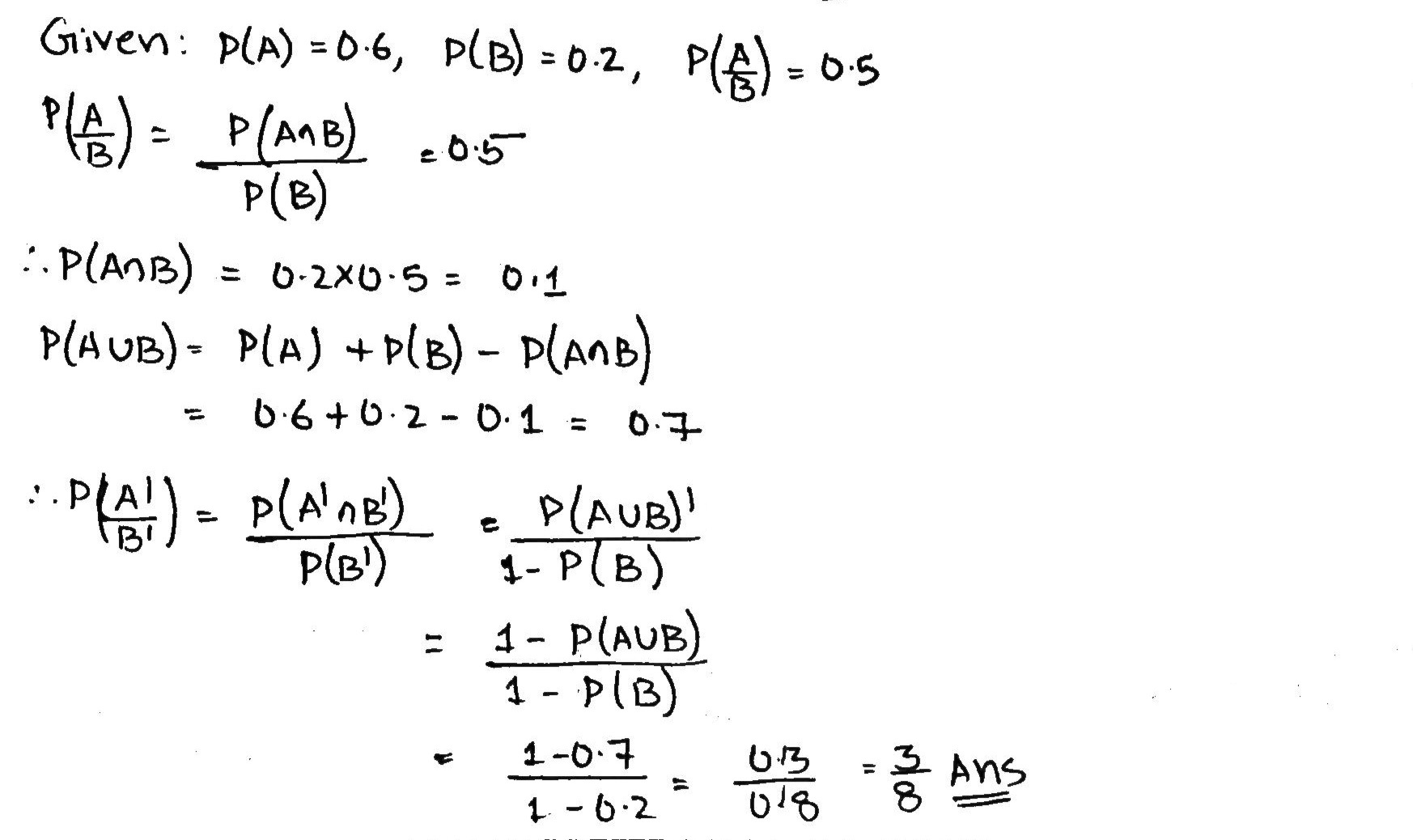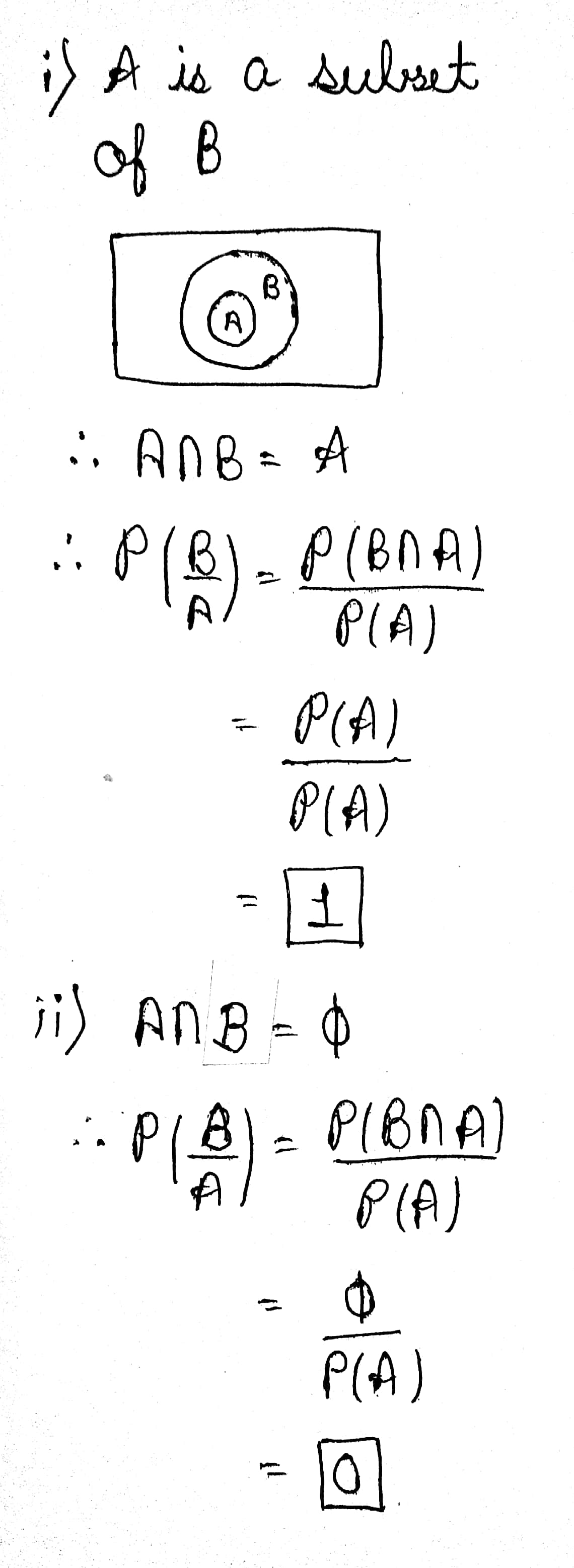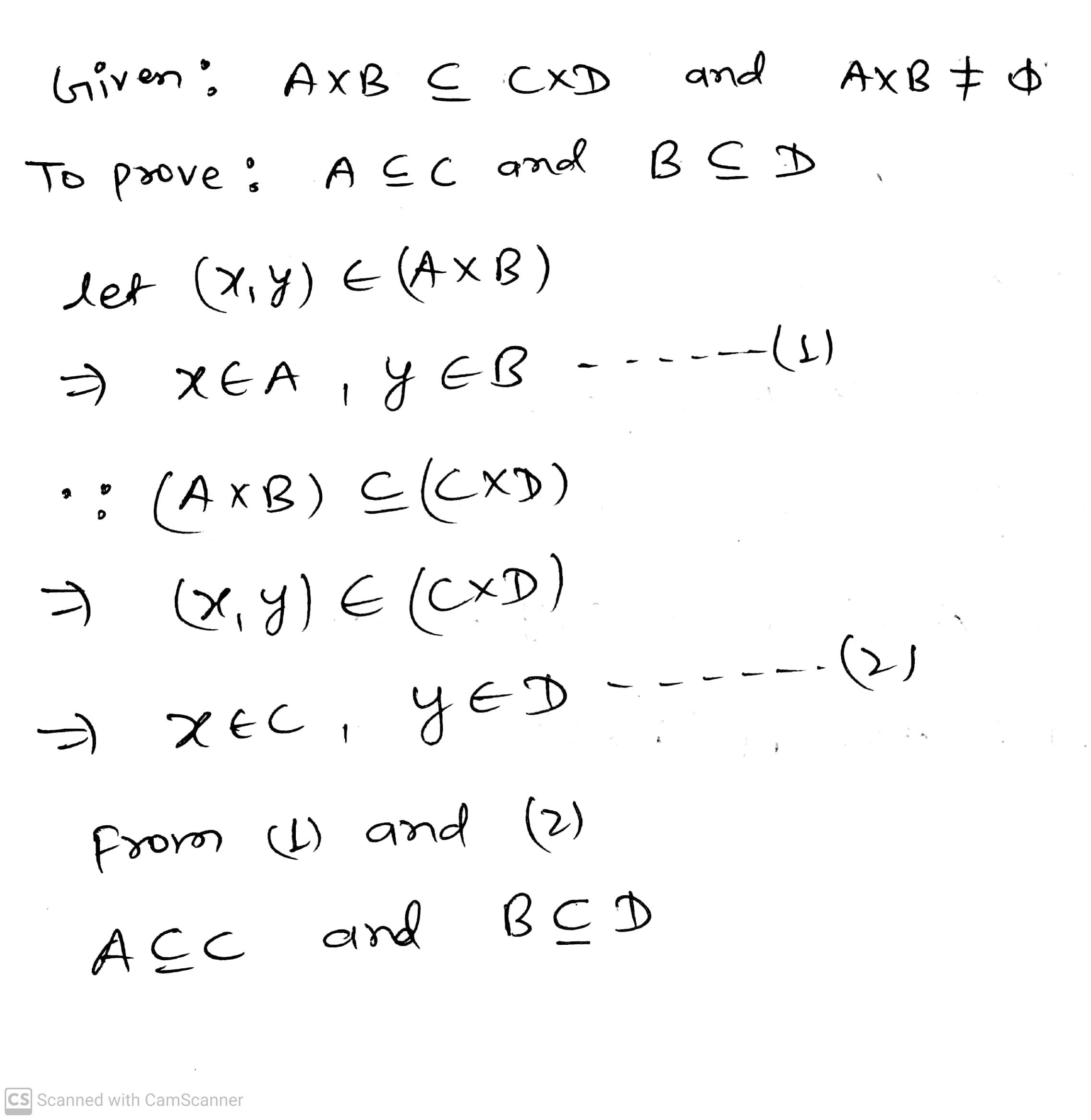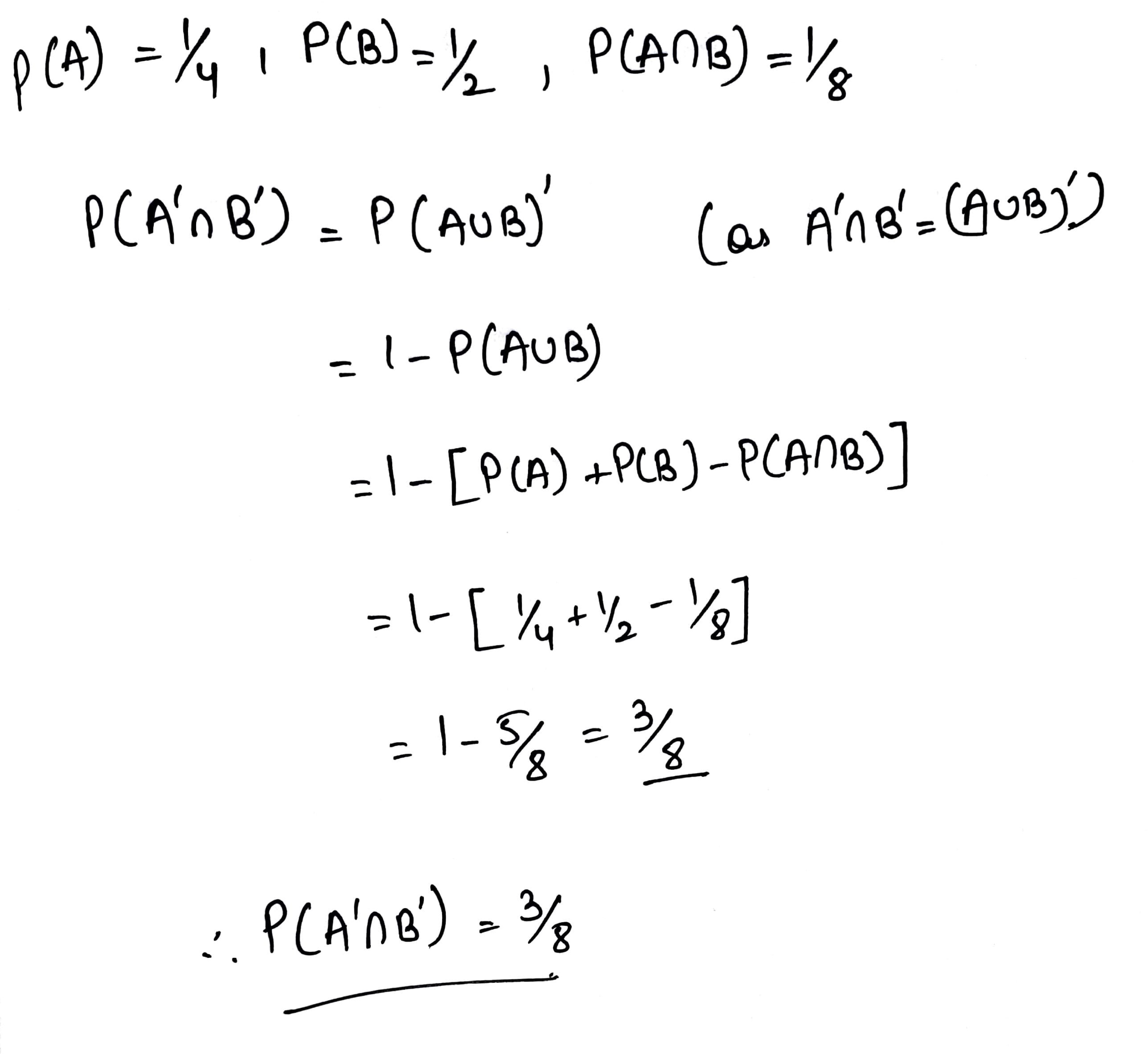Probability - Class 11 Engineering Maths - Extra Questions
A coin in tossed and if head comes up, a die is thrown. But if tail comes up, the coin is tossed again. Write the sample space of this experiment. The total no. of elements in the sample space will be
Write down all the events of the experiment 'tossing of a coin'.
$$A$$ and $$B$$
Three coins are tossed. Describe two events $$A$$ and $$B$$ which are mutually exclusive.
Three coins are tossed. Describe two events $$A$$ and $$B$$ which are not mutually exclusive.
Two unbiased coins are tossed simultaneously. Find the probability of getting
$$i.$$ two heads
$$ii.$$ one tail
$$iii.$$ at least one tail
$$iv.$$ at most one tail
$$v.$$ no tail
three events $$A, B$$ and $$C$$ which are mutually exclusive but not exhaustive.
How many play cricket only?
How many play hockey only?
How many play both the games?
Given, $$P(A) =\displaystyle \frac{3}{5}$$ and $$P(B) =\displaystyle \frac{1}{5}$$. Find $$P(A \,\text{or} \,B)$$, if $$A$$ and $$B$$ are mutually exclusive events.
If $$\displaystyle \frac{2}{11}$$ is the probability of an event. What is the probability of the event 'not $$A$$'
A box contains $$1$$ red and $$3$$ identical white balls. Two balls are drawn at random in succession without replacement. Write the sample space for this experiment
$$A$$ and $$B$$ are events such that $$P(A) = 0.42, P(B) = 0.48$$ and P(A and B) $$= 0.16$$
Determine (i) P(not A), (ii) P(not B) and (iii) P(A or B)
An experiment consists of tossing a coin and then throwing it second time if a head occurs. If a tail occurs on the first toss then a die is rolled once. Find the sample space
If $$A$$ and $$B$$ are two events such that $$P\left( A \right) = \displaystyle\frac { 1 }{ 4 } , P\left( B \right) = \displaystyle\frac { 1 }{ 2 } $$ and $$P\left( A\cap B \right) = \displaystyle\frac { 1 }{ 8 } $$, find $$8P\left( \bar A \ and\ \bar{B} \right) $$
If $$A$$ is an event of a random experiment such that $$P(A) : P(\overline {A}) = 5 : 11$$, then find $$P(A)$$ and $$P(\overline {A})$$
Find the sample space $$S$$ and number of sample points $$n(S)$$ when one die is thrown.
Write the sample space if two coins are tossed.
Write the sample space $$S$$ when two coins are tossed simultaneously.
Write the sample space when a card is drawn at random from the pack of cards bearing numbers $$1$$ to $$25$$
Three coins are tossed simultaneously, find $$S$$ and $$n(S)$$.
Write the sample space for selecting a day randomly of the week
'A coin is tossed'; write the sample space $$S$$
Write the sample space when a die is thrown.
Write the sample space $$S$$ if two coins are tossed simultaneously.
If coin is tossed, what is its sample space?
A coin is tossed once. Find the probability that it is not a tail.
A die is thrown, write a sample space $$(S)$$ and $$n(S)$$. If event $$A$$ is getting a number greater than $$4$$, write event $$A$$ and $$n(A)$$.
A coin is tossed. Write the sample space $$\left(S\right)$$.
If $$P(E)=0.05$$, what is the probability of "not $$E$$"?
$$P\left(E\right) + P\left(\text{Not}\, E\right)=$$_____.
If $$A, B$$ are two events with $$P(A\cup B) = 0.65, P(A\cap B) = 0.15$$, then find the value of $$P(A^{C}) + P(B^{C})$$
A box contains $$7$$ red marbles, $$10$$ white marbles and $$5$$ green marbles. One marble is taken out of the box at random. What is the probability that the marble taken out will be
(i) not red? (ii) white? (iii) green?
The sum of probabilities of all possible events is always
If $$U=\left\{ 1,2,3,4,5,6,7,8,9 \right\} \,A=\left\{ 1,2,3,4 \right\}$$ and $$B=\left\{ 2,4,6,8 \right\} $$. Verify that $$(A\cup B)^1=A^1 \cap B^1$$.
Equally likely events
The probability of an event A+ Probability of the event 'not A'= ____ .
Mixed/Compound/Composite event
For two events if $$A$$ and $$B$$ are independent then prove that $$A',B'$$ are also independent.
A fair coin is tossed once. Write the sample space of the Random Experiment. State whether the sample space if Finite or Infinite.
If $$A$$ and $$B$$ be two independent events then show that $$A,B'$$ are also independent.
Define a simple event.
Two coins are tossed. Find the probability, if $$P$$ is the event of getting two head
Complete the following activity.
There are 52 cards in a pack. In each pack, Total black face cards are ___. There are ___ kings of red colour. There are ____ cards which are not of diamond. In each pack total club cards are ____.
Distinguish between random sampling and non-random sampling.
The probability that a person will get an electric contract is $$\dfrac{2}{5}$$ and the probability that he will not get plumbing contract is $$\dfrac{4}{7}$$. If the probability of getting at least one contract is $$\dfrac{2}{3}$$, what is the probability that he will get both?
A coin is tossed two times, what is the probability of getting head at least once.
Three coins are tossed. Find the probability of getting atleast two head.
Given two independent events A and B such that $$P(A) = 0.3$$, $$P(B) = 0.6$$. Find
(i) P(A and not B) (ii) P(neither A nor B)
If $$n(A)=3, n(B)=5, n(A\cap B)=2$$, find $$n(A\cup B)$$.
In $$50$$ tosses of coin tail appears $$32$$ times. If a coin is tossed random, what is the probability of getting head ?
If $$P(A)=0.8$$ and $$P(B|A)=0.4$$, Find $$P(A \cap B)$$
We wish to choose one child of $$2$$ boys and $$3$$ girls. A coin is tossed. if it comes up heads, a boy is chosen otherwise a girl is chosen. Describe the sample space.
If P(E) = 0.05, what is the probability of "not E" ?
If $$n(A)=2,\ P(A)=\dfrac{1}{5}$$, then find $$n(S)$$.
Write the sample space for the experiment " a coin is tossed repeatedly three times".
In a bag there are $$3$$ balls, one black, one red and one green. Two balls are drawn one after other with replacement. State sample space and $$n(S)$$.
A coin is tossed and a die is thrown write the simple space.
Three coins are tossed together Find,
The probability of getting no tail.
An ordinary pack of $$52$$ cards is well shuffled. The top card is then turned over. What is the probability that the top card is a king card.
Check whether the probabilities $$P(A)$$ and $$P(B)$$ are consistently defined
$$P(A) = 0.5,P(B) = 0.7,P(A \cap B) = 0.6$$
The probability that Raju arrives on time at school is $$0.72$$.
Write down the probability that he will not arrive on time.
A and B are events with P(A) = $$0.5$$, P(B) = $$0.4$$ and $$P\left( {A \cap B} \right) = 0.3$$. Find the probability that:
(i) A does not occur
(ii) Neither A and nor B occurs
Given find $$P(A)=\dfrac35\ and\ P(B)= \dfrac{1}{5}$$, find $$P(A \ \text{or} \ B) $$, if $$A$$ and $$B$$ are mutually exclusive events.
Check whether the probabilities $$P(A)$$ and $$P(B)$$ are consistently defined
$$P(A) = 0.5,P(B) = 0.4,P(A \cup B) = 0.8$$
An ordinary pack of $$52$$ cards is well shuffled. The top card is then turned over. What is the probability that the top card is a red card.
Two players Neha and Shivani play a tennis match. It is known that the probability of Neha winning the match is 0.What is the probability of Shivani winning the match ?
A coin is tossed three times. Find $$P(A/B)$$ in given cases:
$$A=$$At least two heads, $$B=$$At most two heads
Given two independence events $$A$$ and $$B$$, such that $$P(A)=0.3$$ and $$P(B)=0.6$$. Find $$P(\bar A\cap \bar B)$$.
A coin is tossed three times, then find $$P(A/B)$$ in given cases:
$$A=$$Heads on third tossed, $$B=$$Heads on first two tosses.
Two coins are tossed once. Find $$P(A/B)$$ in given cases:
$$A=$$No tail appears, $$B=$$No head appears.
Given two independence events $$A$$ and $$B$$, such that $$P(A)=0.3$$ and $$P(B)=0.6$$. Find $$P(\bar {A}\cap B)$$.
Given two independent events $$A$$ and $$B$$ such that $$P(A)=0.3$$ and $$P(B)=0.6$$. Find $$P(B/A).$$
If $$P(A)=\dfrac {6}{11}, P(B)=\dfrac {5}{11}$$ and $$P(A\cup B)=\dfrac {7}{11}$$, find $$P(A|B)$$.
If $$P(A)=\dfrac {6}{11}, P(B)=\dfrac {5}{11}$$ and $$P(A\cup B)=\dfrac {7}{11}$$, then find $$P(A \cap B)$$.
Two coins are tossed once. Find $$P(A/B)$$ in given cases:
$$A=$$tail appears on one coin. $$B=$$Once shows head.
Given two independence events $$A$$ and $$B$$, such that $$P(A)=0.3$$ and $$P(B)=0.6$$. Find $$P(A\cup B)$$.
Compute $$P ( A | B ) ,$$ if $$P ( B ) = 0.25$$ and $$P ( A \cap B ) = 0.18$$
In a single throw of a die describe the following events:
$$B=$$ Getting a number greater than $$7$$
Compute $$P ( A | B ) ,$$ if $$P ( B ) = 0.25$$ and $$P ( A \cap B ) = 0.18$$
Compute $$P ( A | B ) ,$$ if $$P ( B ) = 0.25$$ and $$P ( A \cap B ) = 0.18$$
If $$P(A)=\dfrac {6}{11}, P(B)=\dfrac {5}{11}$$ and $$P(A\cup B)=\dfrac {7}{11}$$, find $$P(B/A)$$
Compute $$P ( A | B ) ,$$ if $$P ( B ) = 0.5$$ and $$P ( A \cap B ) = 0.32$$
In a single throw of a die describe the following events:
$$A=$$ Getting a number less than $$7$$
If $$P(A)=\dfrac {6}{11}, P(B)=\dfrac {5}{11}$$ and $$P(A\cup B)=\dfrac {7}{11}$$, find $$P(A \cap B).$$
If $$A$$ and $$B$$ are events such that $$P(A)=0.6, P(B)=0.3$$ and $$P(A\cap B)=0.2$$, find $$P(A/B)$$ and $$P(B/A)$$.
Given two independence events $$A$$ and $$B$$, such that $$P(A)=0.3$$ and $$P(B)=0.6$$. Find $$P(A\cap B)$$.
Fill in the blanks in the following table:
| $$P(A)$$ | $$P(B)$$ | $$P(A\cap B)$$ | $$P(A\cup B)$$ |
| $$\dfrac{1}{3}$$ | $$\dfrac{1}{5}$$ | $$\dfrac{1}{15}$$ | $$......$$ |
Complete the following statements:
The Probability of an event that cannot happen is $$\dots$$. Such an event is called $$\dots$$
Two dice were thrown and it is known that the numbers which come up were different. Find the probability that the sum of the two numbers was $$5$$.
On throwing dice once, the probability of occurence of a composite number is $$ 1 / 2 . $$
A couple has $$2$$ children. Find the probability that both are boys if it is known that
the elder child is a boy.
If $$P( event \ E)=0.47$$, then find $$P( not\ E)$$.
If $$A$$ and $$B$$ are events of the same experiments with $$P(A)=0.2,P(B)=0.5$$, then find the maximum value of $$P({ A } \cap B)$$
$$10$$% of a certain population suffer from a serious disease. A person suspected of the disease is given two independent tests. Each test makes a correct diagnosis $$90$$% of the time. The probability that the person really has the illness given that both tests are positive is $$\displaystyle \frac { k }{ 10 } $$ where $$k$$ is
$$A$$ speaks truth in $$60$$% cases, $$B$$ in $$70$$% cases. In what percentage of cases are they likely to contradict each other in stating the same fact?
If $$P(A\cup B)=P(A\cap B)\Leftrightarrow $$ then show that relation between $$P(A)$$ and $$P(B)$$ is $$P(A)=P(B)$$.
Numbers are selected at random, one at a time, from the two digit numbers $$00, 01,02,.....99$$ with replacement. An even $$E$$ occurs if and only if the product of the two digits of a selected number is $$18$$. If four numbers are selected, the probability that the event $$E$$ occurs at least $$3$$ times is $$97/{(25k)}^{4}$$. Find the value of $$k$$.
If the probability for A to fail in an examination is 0.2 and that for B is 0.3, then the probability that either A or B fails is 0.5 (T/F)
If true enter 1, else enter 0.
If the probability for $$A$$ to fail in an examination is $$0.2$$ and that for $$B$$ is $$0.3$$, then the probability that either $$A$$ or $$B$$ fails is $$0.5$$.
$$A$$ and $$B$$ alternately cut a pack of cards which is shuffled after each cut. The game is started by $$A$$ and continuous until one of the players cuts a club. The probability that $$B$$ win the game is $$k/7$$. Find $$k$$.
Out of ($$2n+1$$) tickets consecutively numbered, three are drawn at random. The chance that the numbers on them are in A.P. is $$\dfrac{30+k}{61}$$. Find the value of $$k$$.
A man takes a step forward with probability 0.4 and backward with probability 0.Suppose the man takes 11 steps and $$p_r$$ denotes the probability that the man is r steps away from his initial position, then value of
A pair of fair dice is rolled together till a sum of $$7$$ or $$11$$ is obtained. Let $$p $$ denote the probability that $$7$$ comes before $$11$$. Find the value of $$4 p$$
Let $$P(A)=0.4$$ and $$P(A\cup B)=P(A\cap B)$$, find $$5P(B)$$
A is a set containing n elements. A subset P of A is chosen at random. The set A is reconstructed by replacing the elements of the subset P. A subset Q of A is again chosen at random. The probability that
where $$|X|=$$ number of elements in X.
There are n different objects, 1, 2, 3, 4, ..., n, distributed at random in n places marked 1, 2, 3, ..., n. If p is the probability that at least three of the objects occupy places corresponding to their number, find 6p
Write the sample space of the experiment 'A coin is tossed and a die is thrown'.
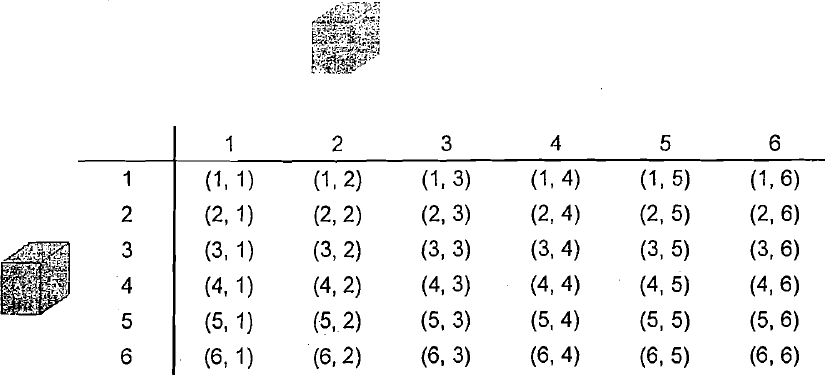
Find the sample space associated with the experiment of rolling a pair of dice (plural of die) once. Also find the number of elements of the sample space.
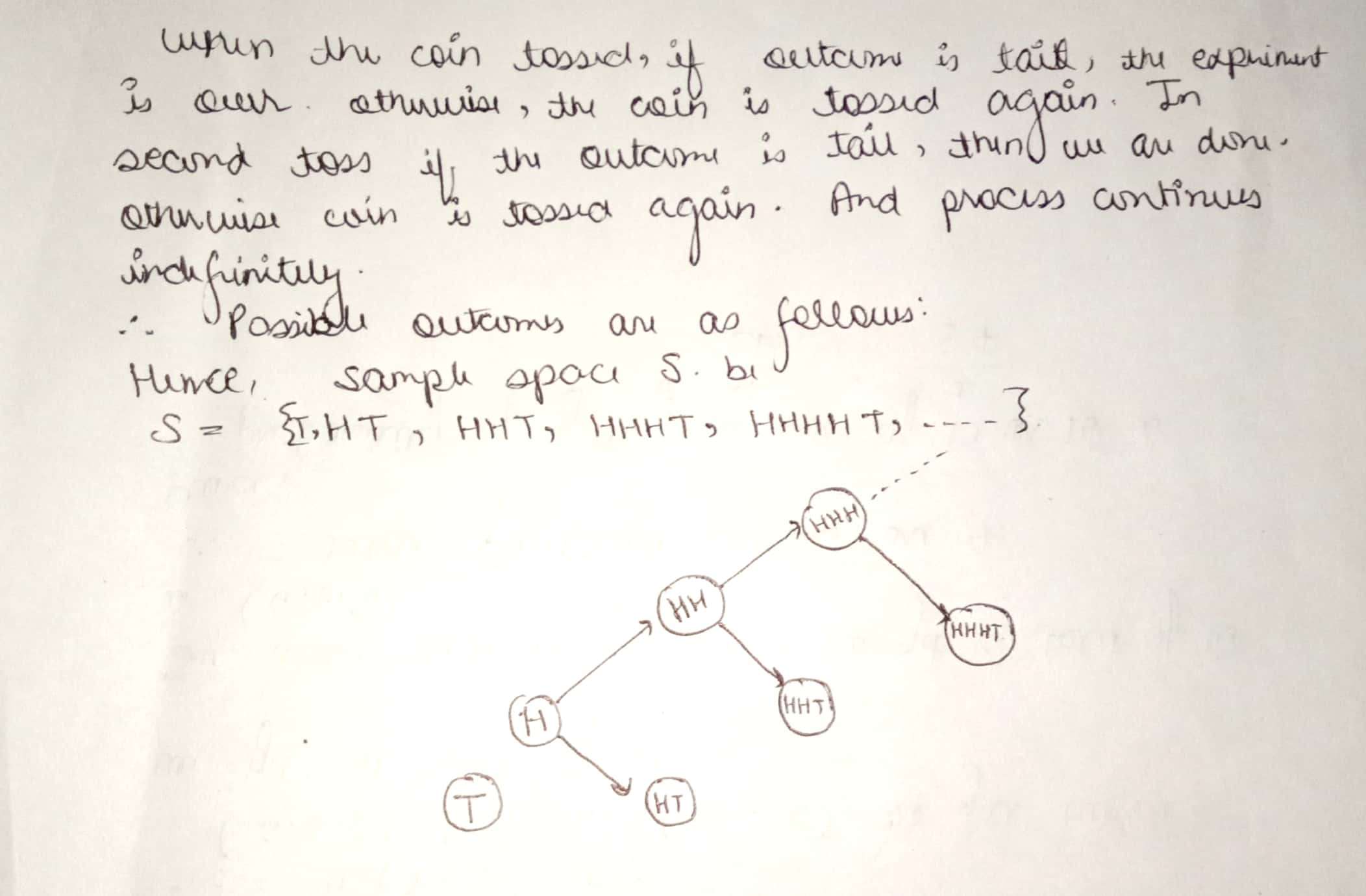
Write the sample space of the experiment 'A coin is tossed, if it shows head a coin tossed again else a die is thrown.
In a single throw of a die, the events $$\{1, 2\}$$, $$\{2, 3\}$$ are mutually exclusive. Write 1 if true and 0 if false.
If $$P\left ( A \right )=0.25, P\left ( B \right )=0.5$$ and $$P\left ( A\cap B \right )=0.14$$ find probability that neither $$'A'$$ nor $$'B'$$ occurs. Also find $$P\left ( A\cap \bar{B} \right )$$
Find $$A$$ or $$B$$
In a single toss of a coin the events {H}, {T} are mutually exclusive.
Write 1 if true and 0 if false
three events $$A, B$$ and $$C$$ which are mutually exclusive and exhaustive.
Three coins are tossed. Describe two events $$A$$ and $$B$$ which are mutually exclusive but not exhaustive.
Describe the sample space for the indicated experiment : A coin is tossed and then a die is rolled only in case a head is shown on the coin
Describe the sample space for the indicated experiment : A coin is tossed and a die is thrown
One die of red colour one of white colour and one of blue colour are placed in a bag.
One die is selected at random and rolled its colour and the number on its uppermost face is noted. Describe the sample space
A die is thrown find the probability of following events:
(i) A prime number will appear
(ii) A number greater than or equal to $$3$$ will appear
(iii) A number less than or equal to one will appear
(iv) A number more than $$6$$ will appear
(v) A number less than $$6$$ will appear
Two dice are thrown. The events $$A, B$$ and $$C$$ are as follows:
A : getting an even number on the first die
B : getting an odd number on the first die
C : getting the sum of the numbers on the dice $$\displaystyle \leq 5$$
State true or false : (give reason for your answer)
(i) $$A$$ and $$B$$ are mutually exclusive
(ii) $$A$$ and $$B$$ are mutually exclusive and exhaustive
(iii) $$A = B'$$
(iv) $$A$$ and $$C$$ are mutually exclusive
(v) $$A$$ and $$B'$$ are mutually exclusive
(vi) $$A', B', C$$ are mutually exclusive and exhaustive
Three coins are tossed describe
(i) Two events which are mutually exclusive
(ii) Three events which are mutually exclusive and exhaustive
(iii) Two events which are not mutually exclusive
(iv) Two events which are mutually exclusive but not exhaustive
(v) Three events which are mutually exclusive but not exhaustive
An experiment involves rolling a pair of dice and recording the numbers that come up describe the following events:
A : the sum is greater than $$8$$
B : $$2$$ occurs on either die
C : the sum is at least $$7$$ and a multiple of $$3$$
Which pairs of these events are mutually exclusive?
Two dice are thrown The events $$A, B$$ and $$C$$ are as follows:
A : getting an even number on the first die
B : getting an odd number on the first die
C : getting the sum of the numbers on the dice $$\displaystyle \leq 5$$
Describe the events
(i) $$A'$$
(ii) not $$B$$
(iii) $$A$$ or $$B$$
(iv) $$A$$ and $$B$$
(v) $$A$$ but not $$C$$
(vi) $$B$$ or $$C$$
(vii) $$B$$ and $$C$$
(viii) $$\displaystyle A\cap B'\cap C'$$
Three coins are tossed once. Let $$A$$ denote the event 'three heads show", $$B$$ denote the event "two heads and one tail show" $$C$$ denote the event "three tails show" and $$D$$ denote the event 'a head shows on the first coin" Which events are
(i) mutually exclusive?
(ii) simple?
(iii) compound?
A coin is tossed If it shows a tail we draw a ball from a box which contains 2 red and 3 black balls If it shows head we throw a die Find the sample space for this experiment
If $$E$$ and $$F$$ are events such that $$P(E) =$$ $$\displaystyle \frac{1}{4}$$, $$P(F) =$$ $$\displaystyle \frac{1}{2}$$ and $$P(E and F) =$$ $$\displaystyle \frac{1}{8}$$ find: (i) P(E or F) (ii) P(not E and not F)
A fair coin is tossed four times and a person win Re $$1$$ for each head and lose Rs. $$1.50$$ for each tail that turns up. Let $$p$$ be the probability of person losing Rs $$3.50$$ after $$4$$ tosses.Find $$4p$$ ?
In a class of $$60$$ students, $$30$$ opted for NCC, $$32$$ opted for NSS and $$24$$ opted for both NCC and NSS. If one of these students is selected at random, find the probability that
(i) The student opted for NCC or NSS
(ii) The student has opted neither NCC nor NSS
(iii) The student has opted NSS but not NCC
In an entrance test that is graded on the basis of two examinations the probability of a randomly chosen student passing the first examination is $$0.8$$ and the probability of passing the second examination is $$0.7$$. The probability of passing at least one of them is $$0.95$$. What is the probability of passing both?
The probability that a student will pass the final examination in both English and Hindi is $$0.5$$ and the probability of passing neither is $$0.1$$. If the probability of passing the English examination is $$0.75$$, what is the probability of passing the Hindi examination?
A speaks truth in $$75\%$$ of the cases and B in $$80\%$$ of the cases. In what percentage of cases are they likely to contradict each other in stating the same fact?
The probability of picking a non-defective item from a sample is $$\dfrac {7}{12}$$. Find the probability of picking a defective item
If A is an event of a random experiment such that $$P(A) = P(\overline {A}) = 6 : 15$$, then find $$P(A)$$
The probability that it will rain on a particular day is $$0.64$$ what is the probability that it will not rain on that day?
If A is an event of a random experiment such that $$P(A) = P(\overline {A}) = 6 : 15$$, then find $$P(\overline {A})$$
If $$A$$ is an event of a random experiment such that $$P(A) : P(\overline {A}) = 5 : 11$$, then find Verify that $$P(A) + P(\overline {A}) = 1$$
Two coins are tossed simultaneously. Find the probability that either both heads or both tails occur
Define sample space
A problem in statistics is given to solve to three students independently. Their chances of solving problem are $$\cfrac { 1 }{ 3 } ,\cfrac { 1 }{ 4 } ,\cfrac { 1 }{ 5 } $$ respectively. Find the probability that the problem is solved.
Define event
If two cubical dice are thrown simultaneously, then find the probability of getting the sum of numbers 'more than $$7$$' or 'less than $$7$$'.
There are $$15$$ tickets bearing the numbers from $$1$$ to $$15$$ in a bag and one by one ticket is drawn from this bag at random. Write the sample of (S) and n(S).
Two coins are tossed simultaneously. Write the sample space(S) of the following event A using set notation and n(A), where A is the event of getting at the most one head.
Three numbers are chosen at random without replacement from $$\{1, 2, 3, ... 14\}$$.
Let $$A=\{\text{minimum of chosen numbers is 5}\}$$
$$B=\{\text{maximum of chosen numbers is 11}\}$$ and $$P(A\cup B) = \dfrac{K+11}{91}$$, the $$K=$$ ____.
In a class of $$60$$ students, $$30$$ opted for Mathematics, $$32$$ opted for Biology and $$24$$ opted for both Mathematics and Biology. If one of these students is selected at random, find the probability that:
(i) The student opted for Mathematics or Biology.
(ii) The student has opted neither Mathematics nor Biology.
(iii) The student has opted Mathematics but not Biology.
The probability that a student selected at random from a class will pass in Mathematics is $${ 4 }/{ 5 } $$, and the probability that he/she passes in Mathematics and Computer Science is $${ 1 }/{ 2 } $$. What is the probability that he/she will pass in Computer Science if it is known that he has passed in Mathematics?
A, B, C are aiming to shoot a ballon, A will succeed $$4$$ times out of $$5$$ attempts. The chance of B to shoot the ballon is $$3$$ out of $$4$$ and that of C is $$2$$ out of $$3$$. If the three aim the ballon simultaneously, then find the probability that atleast two of them hit the balloon.
A bag contains cards which are numbered from $$2$$ to $$90$$. A card is drawn at random from the bag. Find the probability that it bears
(i) a two digit number (ii) a number which is a perfect square
A bag contains $$3$$ red balls and $$5$$ black balls. A ball is drawn at random from the bag. What is the probability that the ball drawn is (i) red (ii) not red.
In a school, there are $$20$$ teachers who teach mathematics or physics. Of these, $$12$$ teach mathematics and $$4$$ teach both physics and Mathematics. How many teach physics?
If the probability of winning a game is $$0.3$$, what is the probability of loosing it?
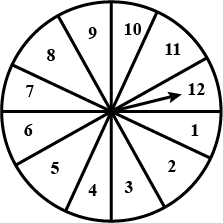
A game of chance consists of spinning an arrow which is equally likely to come to rest pointing to one of the number $$1,2,3,.....12$$ as shown in Fig. What is the probability that it will point to:
(i) $$10$$ (ii) an odd number (iii) a number which is a multiple of $$3$$ (iv) an even number.
The probability of selecting a green marble at random from a jar that contains only green, white and yellow marbles is $$0.25$$. The probability of selecting a white marble at random from the same jar is $$\dfrac{1}{3}$$. If this jar contains $$10$$ yellow marbles. What is the total number of marbles in the jar?
(i) A lot of $$20$$ bulbs contain $$4$$ defective ones. One bulb is drawn at random from the lot. What is the probability that this bulb is defective?
(ii) Suppose the bulb drawn in (i) is not defective and not replaced. Now bulb is drawn at random from the rest. What is the probability that thisbulb is not defective?
Let $$A$$ and $$B$$ be two independent event then show that $$P(A\cap B)=1-P(A')P(B')$$.
A piggy bank contains a hundred $$50$$ paise coins, fifty Rs. $$1$$ coins, twenty Rs. $$2$$ coins and ten Rs. $$5$$ coins. If it is equally likely that one of the coins will fall out when the bank is turned upside down, find the probability that the coin which fell
(i) will be a $$50$$ paise win (ii) will be of value more than Rs. $$1$$ (iii) will be of value less than Rs. $$5$$ (iv) will be Rs. $$1$$ or Rs. $$2$$ coin
A balloon vendor has 2 red,3 blue and 4 green balloons. He wants to choose one of them at random to give it to Pranali . What is the probability of the event that Pranali gets:
(i) a red balloon
(ii) a blue balloon
(iii) a green balloon.
$$12$$ defective pens are accidentally mixed with $$132$$ good ones. It is not possible to just look at pen and tell whether or not it is defective. One pen is taken out at random from this lot. Determine the probability that the pen taken out is good one.
In a building programme the event that all the materials will be delivered at the correct time is M, and the event that the building programme will be completed on time is F. Given that $$P(M)=0.8$$ and $$P\left( M\bigcap { F } \right) =0.65$$. If $$P(F)=0.7$$, find the probability that the building programme will be completed on time if all the materials are not delivered at the correct time.
A lot consists of $$144$$ ball pens of which $$20$$ are defective and others are good. Nuri will buy if it is defective. The shopkeeper draws one pen at random and gives it to her. What is the probability that
(i) She will buy it (ii) She will not buy it.
Show that $$A \cup B = A \cap B$$ implies $$A = B$$
Let $$A$$ and $$B$$ be events such that $$P(A)-\dfrac{1}{6}, P(B)=\dfrac{1}{4}$$ and $$P\left( A\cap B \right) =\dfrac { 1 }{ 12 } $$. Find $$P(B/A).P(A/B)$$.
$$A={x/x}$$ is a two digit number, which divisible by $$2$$ (or) $$3$$ and $$x\le { 50}$$,$$B={x/x}$$ is a two digit number, which divisible by $$6$$ and $$x\le { 50}$$.Find- $$n(A\cup B)=$$?
- $$n(A\cap B)=$$?
- $$n(A\cup B)=$$?
- $$n(A\cap B)=$$?
Probability of solving specific problem independently by A and B are $$\dfrac{1}{2}$$ and $$\dfrac{1}{3}$$, respectively. If both try to solve the problem independently, find the probability that
(i) the problem is solved
(ii) exactly one of them solves the problem
A coin is tossed and a dice is rolled simultenuesously. Write the sample space S and n(S)
The probabilities that student will receive $$A, B, C$$ or $$D$$ grade are $$0.40, 0.35, 0.15$$ and $$0.10$$ respectively. Find the probability that a student will recive
i) not an A grade
ii) B or C grade
iii) at most C grade
Assume that $$P(A)=P(B)$$. Show that $$A=B$$Is it true that for any sets $$A$$ and $$B,P(A)\cup P(B)=P(A \cup B)$$? Justify.
Probability of an event is $$0.3$$ then what is the probability that even will not occur?
A bag $$A$$ contains $$10$$ white and $$3$$ black balls. Another bag $$B$$ contains $$3$$ white and $$5$$ black balls. Two balls are transferred from bag $$A$$ and put in the bag $$B$$ and a ball is drawn from bag $$B$$. Find the probability that the ball drawn is white ball.
If A and B are two events such that $$P\left( A \right) = \frac{1}{4},P\left( B \right) = \frac{1}{2}$$ and $$P\left( {A \cap B} \right) = \frac{1}{8}$$ find P$$A \cup B$$.
Given two independent events $$A,\ B$$ such that $$P(A)=0.3,\ P(B)=0.6$$. Determine
$$P(A\ and\ B)$$
Given two independent events $$A,\ B$$ such that $$P(A)=0.3,\ P(B)=0.6$$. Determine
$$P(not\ A\ and\ B)$$
Given two independent events $$A,\ B$$ such that $$P(A)=0.3,\ P(B)=0.6$$. Determine
$$P(A\ and\ not\ B)$$
Let $$A$$ & $$B$$ be two independent events such that $$P(A)=1/3$$ & $$P(B)=1/4$$ match the entries from the following two column
It is known that a box of $$550\ bulbs$$ contains $$22$$ defective bulbs. One blubs is taken out at random from the box. Find the probability of getting
(1) defective bulb
(2) good blub
In a hostel, 60% of the students read Hindi newspaper, 40%read English newspaper and 20% read both Hindi and English newspapers. A student is selected at random:
(i) Find the probability that she reads neither Hindi or English newspaper.
(ii) If she reads Hindi newspaper, find the probability that she reads English newspaper.
(iii) If she reads English newspaper. Find the probability that she reads Hindi newspaper.
In a throw of 4 dice, find the probability that at least one die shows up 4 .
$$A$$ and $$B$$ are two independent events of an experiment .if $$P\left( {not\ B} \right) = 0.65,\ P\left( {A \cup B} \right) = 0.85$$ ,find $$P(A)$$.
A market research group conducted a survey of $$2,000$$ consumers and reported that $$1720$$ consumers liked product $$P_{1}$$ and $$1,4500$$ consumers liked product $$P_{2}$$. What is the least number that must have liked both the products.
If A and B are two events such that P(A)=$$\frac{1}{4},P\left( B \right) = \frac{1}{2}$$ and $$P\left( {A \cap B} \right) = \frac{1}{8}$$ , find p (not A and not B)
Three fair coins are tossed.If both heads and tails appear , determine the probability that exactly one head appears.
If $$A$$ and $$B$$ are two events, such that $$P(A) = 0.3, P(B) = 0.6$$ and $$P(B/A) = 0.5$$, then $$P(A \cup B) = $$
If A and B are independent events such that P(A)= $$0.3$$ and P(B)= $$0.4$$, then find :
(i) P(A and B)
(ii) P(A or B)
The probability that a student entering a university will graduate is $$0.4$$. Find the following probabilities out of $$3$$ students of the university:none will graduate
2. only one will graduate3. all will graduate.
If $$A,\ B,\ C$$ are three events show that
$$ P(A\cup B\cup C)=P(A)+P(B)+P(C)-P(A\cap B)-P(b\cap C)-P(C\cap A)+P(A\cap B\cap C)$$
Two dice are thrown together. Find the probability that the product of the numbers on the top of the dice is:
(a) $$6$$ (b) $$12$$ (c) $$7$$
In a survey of $$600$$ students in a school,
(i) $$160$$ students were found to be taking Tea $$215$$ taking Coffee, $$150$$ were taking both Tea and Coffee.
(ii) $$150$$ students were found to be taking tea and $$225$$ taking coffee, $$100$$ were taking both Tea and Coffee.Find how many students were taking neither tea nor coffee ?
Rahim takes out all the hearts from the cards. What is the probability of
Picking out a card that is not a heart.
A bag contains $$3$$ red and $$3$$ green balls. Write the sample space S and n(S) for the experiment of 'drawing two balls at random simultaneously from the bag'.
Ar a selection, the probability of selection of $$A$$ is $$\frac { 1 } { 7 }$$ and that of $$8$$ is $$\frac { 1 } { 5 }$$ . If A and $$B$$ are independent events, then the probability that neither of them would be selected is ?
Rahim takes out all the hearts from the cards. What is the probability of
Picking out an ace from the remaining pack.
Cards marked with numbers $$4$$ to $$99$$ are placed in a box and mixed thoughtly. One card is drawn from this box. Find the probability that the number on the card is a perfect square between $$91$$ and $$99$$.
A box contains $$20$$ identical balls of which $$5$$ are white and $$15$$ black. The balls are drawn at random from the box one at a time with replacement. The probability that a white ball is drawn fro the $$3^{rd}$$ time on $$6^{th}$$ drawn is
An unbiased die bearing the integers $$-2$$ to $$3$$ is thrown once
find the probability that the number drawn is,
A perfect square
$$15$$ cards numbered $$1,2,3,4,...,14,15$$ are put in a box and mixed thoroughly. A man draws a card at random form the box. Find the probability that the number on the card is divisible by $$3$$
The probability that a leap year not to contain $$53$$ Sundays is.
A card is drawn at random from a pack of $$52$$ cards. Find the probability that the card drawn is a black king.
$$15$$ cards numbered $$1,2,3,4,...,14,15$$ are put in a box and mixed thoroughly. A man draws a card at random form the box. Find the probability that the number on the card is a prime number.
Cards marked with numbers $$4$$ to $$99$$ are placed in a box and mixed thoughtly. One card is drawn from this box. Find the probability that the number on the card is a prime number less than $$30$$.
Define sure event.
If two coins are tossed. Then find the probability of the following events
Getting no head
A bag contains 18 balls out of which x balls are red. If one ball is drawn at random from the bag, what is the probability that it is not red ?
Write the sample space $$(S)$$ for the experiment of tossing two coins. Write $$n(S)$$ also.
A coin is biased so that heads is three times as likely to appear as tails. Find $$P\left(H\right)$$ and $$P\left(T\right)$$. If such a coin is tossed twice find the probability that head occurs at least once.
The probability of guessing the correct answer to a certain questions is $$\dfrac { x }{ 2 } .$$ If the probability of not guessing the correct answer is$$\dfrac { 3x }{ 2 } ,$$ then find the value of x.
A pair of dice is thrown. Find the probability of getting a sum of numbers which is perfect cube and divisible by $$3$$.
If the probability of winning a game is 9/11, what is the probability of its losing ?
State and prove Addition theorem on probability.
A coin is tossed repeatedly until a tail comes up for the first time. write the sample space for this experiment.
A die is thrown $$100$$ times with frequency for the outcomes $$1,2,3,4,5$$ and $$6$$ as given this following table
Find the probability of getting
Number greater than $$5$$ as an outcome.

| Marks | No. of students |
| $$1-20$$ | $$8$$ |
| $$21-40$$ | $$12$$ |
| $$41-50$$ | $$15$$ |
| $$51-60$$ | $$20$$ |
| $$61-70$$ | $$13$$ |
| $$71-80$$ | $$17$$ |
| $$81-90$$ | $$5$$ |
If $$A$$ and $$B$$ are independent events such that $$P(A\cup B)=0.6, P(A)=0.2$$, find P(B).
In a race of $$12$$ cars, the probability that car $$A$$ will win is $$\dfrac{1}{5}$$ and of car $$B$$ is $$\dfrac{1}{6}$$ and that of car $$C$$ is $$\dfrac{1}{3}$$. Find the probability that only one of them won the race.
A pair of dice is rolled. If the outcome is doubiet a cone is tossed. Determine the total number of elementary events associated to this experiment.
A typical PIN (personal identification number) is a sequence of any four symbols chosen from the 26 letters the alphabet and the ten digits.If all PINs are equally likely, what is the probability that a randomly chosen PIN contain repeated symbol?
The number $$1,2,3,4$$ are written separately on four slips of paper. The slips are put in a box and mixed thoroughly. A person draws two slips from the box, one after the other, without replacement. Desrcibe the sample space for the experiment.
Two persons appear for an interview.Probability of their selection are $$\dfrac {1}{4}$$ and $$\dfrac {1}{6}$$ respectively. Find the probability that none of them gets selected.
Given two independence events $$A$$ and $$B$$ such that $$P(A)=0.3$$ and $$P(B)=0.6$$. Find $$P(\bar {A}\cap \bar B)$$.
If A and B are two events such that $$P(A)=\frac{1}{4}P(B)=\frac{1}{2}$$ and $$P(A\cap B)=\frac{1}{8}$$ find the P ( not A and not B)
If $$P(E)=0.23$$, find $$P(\overline{ E})$$.
A bag contains $$3$$ red balls and $$5$$ black balls. A ball is drawn at random from the bag. What is the probability that the ball drawn is red?
If $$A$$ and $$B$$ are two events such that $$P(A\cap B)=0.32$$ and $$P(B)=0.5$$, find $$P(A/B)$$.
If $$A$$ and $$B$$ are two events such that $$2P(A)=P(B)=\dfrac {5}{13}$$ and $$P(A/B)=\dfrac {2}{5}$$, find $$P(A\cup B)$$.
If $$A$$ and $$B$$ are two event such that,
$$P(A)=\dfrac {6}{11},\ P(B)=\dfrac {5}{11}$$ and $$P(A\cup B)=\dfrac {7}{11}$$, find $$P(A\cap B), \ P(A/B),\ P(B/A)$$.
A coin is tossed three times. Find $$P(A/B)$$ in given cases:
$$A=$$At most two tails, $$B=$$At least one tail.
A die is thrown three times. Find $$P(A/B)$$ and $$P(B/A)$$, if
$$A=4$$ appear on the third toss, $$B=6$$ and $$5$$ appear respectively on first two tosses.
If $$P(A)=\dfrac {6}{11}, P(B)=\dfrac {5}{11}$$ and $$P(A\cup B)=\dfrac {7}{11}$$, find $$P(B|A)$$.
Given two independent events $$A$$ and $$B$$ such that $$P(A)=0.3$$ and $$P(B)=0.6$$. Find $$P(A\cup B)$$.
If $$A$$ and $$B$$ are two event such that,
$$P(A)=\dfrac {1}{3},\ P(B)=\dfrac {1}{4}$$ and $$P(A\cap B)=\dfrac {1}{12}$$, then find $$P(A/B)$$ and $$P(B/A)$$.
Given two independence events $$A$$ and $$B$$ such that $$P(A)=0.3$$ and $$P(B)=0.6$$. Find $$P(\bar {A}\cap B)$$.
If $$A$$ and $$B$$ are events such that $$P(A)=0.6, P(B)=0.3$$ and $$P(A\cap B)=0.2$$, find $$P(A/B)$$ and $$P(B/A)$$.
Given two independence events $$A$$ and $$B$$ such that $$P(A)=0.3$$ and $$P(B)=0.6$$. Find $$P( B/A)$$
Two coins are tossed once. Find $$P(A/B)$$ in given cases:
$$A=$$No tail appears, $$B=$$No head appears.
$$A=$$No tail appears, $$B=$$No head appears.
Given two independent events $$A$$ and $$B$$, such that $$P(A)=0.3$$ and $$P(B)=0.6$$. Find $$P(A^{\prime}\cap B^{\prime})$$.
A card is thrown from a pack of $$52$$ cards so that each cards equally likely to be selected. In which of the following cases are the events $$A$$ and $$B$$ independent?
$$A=$$the card drawn is spade, $$B=$$the card drawn in an ace.
Two coins are tossed once. Find $$P(A/B)$$ in given cases:
$$A=$$tail appears on one coin. $$B=$$Once shows head.
Given two independent events $$A$$ and $$B$$, such that $$P(A)=0.3$$ and $$P(B)=0.6$$. Find $$P(A\cap \bar {B})$$.
Given two independent events $$A$$ and $$B$$ such that $$P(A)=0.3$$ and $$P(B)=0.6$$. Find $$P(A/ B).$$
Given two independence events $$A$$ and $$B$$ such that $$P(A)=0.3$$ and $$P(B)=0.6$$. Find $$P(A/ B).$$
If $$A$$ and $$B$$ be two events such that $$P(A)=\dfrac{1}{4}, P(B)=\dfrac{1}{3}$$ and $$P(A\cup B)=\dfrac{1}{2}$$ then show that $$A$$ and $$B$$ are independent events.
A die is thrown three times. Find $$P(A/B)$$ and $$P(B/A)$$, if
$$A=4$$ appear on the third toss, $$B=6$$ and $$5$$ appear respectively on first two tosses.
Kamal and Monika appeared for an interview for two vacancies. The probability of Kamal's selection is $$\dfrac13$$ and that of Monika's selection is $$\dfrac15$$. Find the probability that none of them will be selected
Kamal and Vimal appeared for an interview for two vacancies. The probability of Kamal's selection is $$\dfrac13$$ and that of Vimal's selection is $$\dfrac15$$. Find the probability that only one of them will be selected.
If $$A$$ and $$B$$ be two events such that $$P(A)=\dfrac{1}{4}, P(B)=\dfrac13$$ and $$P(A\cup B)=\dfrac12$$ then show that $$A$$ and $$B$$ are independence events.
Kamal and Monika appeared for an interview for two vacancies. The probability of Kamal's selection is $$\dfrac13$$ and that of Monika's selection is $$\dfrac15$$. Find the probability that both of them will be selected.
The odds against a certain event are $$5$$ to $$2$$ and the odds in a fvour of another event independent to the former are $$6$$ to $$5$$. Find the probability that none of the events will occur.
The odds against a certain event are $$5$$ to $$2$$ and the odds in a favor of another event independent to the former are $$6$$ to $$5$$. Find the probability that at least one of the events will occur.
Kamal and Monika appeared for an interview for two vacancies. The probability of Kamal's selection is $$\dfrac13$$ and that of Monika's selection is $$\dfrac15$$. Find the probability that at least one of them will be selected
Kamal and Monika appeared for an interview for two vacancies. The probability of Kamal's selection is $$\dfrac13$$ and that of Monika's selection is $$\dfrac15$$. Find the probability that none of them will be selected.
Kamal and Monika appeared for an interview for two vacancies. The probability of Kamal's selection is $$\dfrac13$$ and that of Monika's selection is $$\dfrac15$$. Find the probability that at least one of them will be selected.
The probability that $$A$$ hits a target is $$\dfrac13$$ and the probability that $$B$$ hits it, is $$\dfrac25$$. What is the probability that the target will be hit, if each one of $$A$$ and $$B$$ shoots at the target?
The probability of student $$A$$ passing an examination is $$\dfrac29$$ and of students, $$B$$ passing is $$\dfrac59$$. Assuming the two events: $$A$$ passes'. $$B$$ passes' as independent, find the probability of only one of them passing the examination
Given the probability that $$A$$ can solve a problem is $$\dfrac23$$ and the probability that $$B$$ can solve the same problem is $$\dfrac35$$. Find the probability that none of the two will be able to solve the problem.
The probability of student $$A$$ passing an examination is $$\dfrac29$$ and of students, $$B$$ passing is $$\dfrac59$$. Assuming the two events: $$A$$ passes'. $$B$$ passes' as independent, find the probability of only $$A$$ passing the examination
The odds against a certain event are $$5$$ to $$2$$ and the odds in a favor of another event independent to the former are $$6$$ to $$5$$. Find the probability that none of the events will occur.
The odds against a certain event are $$5$$ to $$2$$ and the odds in a favor of another event independent to the former are $$6$$ to $$5$$. Find the probability that at least one of the events will occur.
The probability of student $$A$$ passing an examination is $$\dfrac29$$ and of students, $$B$$ passing is $$\dfrac59$$. Assuming the two events: $$A$$ passes'. $$B$$ passes' as independent, find the probability of
only $$A$$ passing the examination
Two balls are drawn at random with replacement from a box containing $$10$$ black and $$8$$ red balls. Find the probability that one of them is black and other is red.
If $$A$$ and $$B$$ are mutually exclusive such that $$P(A)=0.35$$ and $$P(B)=0.45$$, find
$$P(A\cap \bar{B})$$
$$P(A\cap \bar{B})$$
Compute $$P ( A | B ) ,$$ if $$P ( B ) = 0.5$$ and $$P ( A \cap B ) = 0.32$$
$$P ( B ) = 0.5$$
If $$A$$ and $$B$$ are two event such that
$$P(A)=\dfrac {6}{11},\ P(B)=\dfrac {5}{11}$$ and $$P(A\cup B)=\dfrac {7}{11}$$, find $$P(A\cap B), \ P(A/B),\ P(B/A)$$.
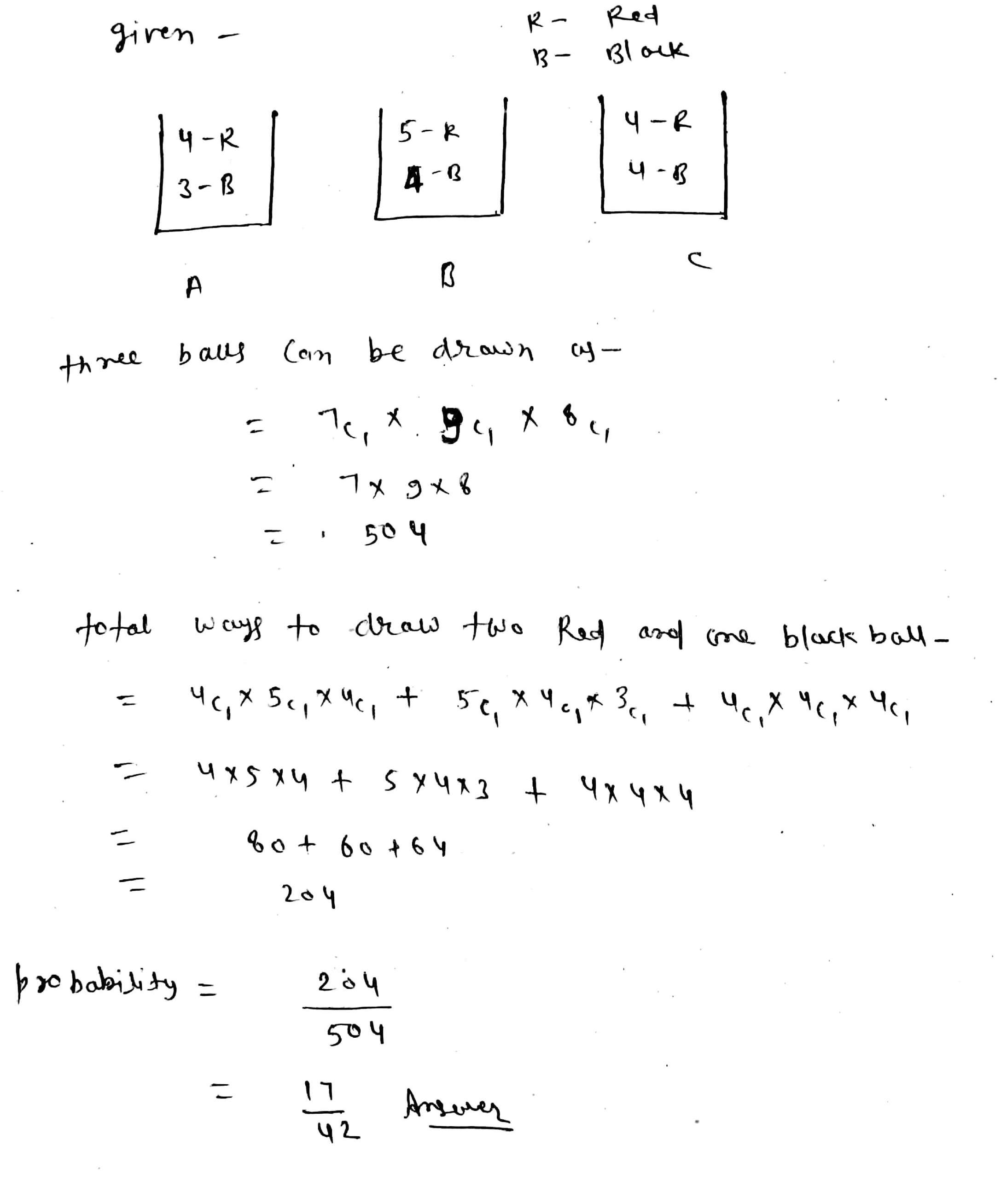
There are three urn $$A, B$$ and $$C$$. Urn $$A$$ contains $$4$$ red balls and $$3$$ black balls. Urn $$B$$contain $$5$$ red balls and $$4$$ black balls. Urn contain $$C$$ contains $$4$$ red and $$4$$ black balls. One ball is draw from each of these urns. What is the probability that $$3$$ balls drawn consist of $$2$$ red ball and a black ball?
If $$P(A)=\dfrac {6}{11}, P(B)=\dfrac {5}{11}$$ and $$P(A\cup B)=\dfrac {7}{11}$$, find $$P(A/B).$$
If $$A$$ and $$B$$ are two events such that $$P(A\cap B)=0.32$$ and $$P(B)=0.5$$, find $$P(A/B)$$
If $$A$$ and $$B$$ are mutually exclusive such that $$P(A)=0.35$$ and $$P(B)=0.45$$, find $$P(A\cap B)$$
$$\begin{array} { l } { \text { Given that the two numbers appearing on throwing two dice are different. Find } } \\ { \text { the probability of the event 'the sum of numbers on the dice is } 4 \text { '. } } \end{array}$$
If $$A$$ and $$B$$ are two event such that, $$P(A)=\dfrac {1}{3},\ P(B)=\dfrac {1}{4}$$ and $$P(A\cap B)=\dfrac {1}{12}$$, find $$P(A/B)$$ and $$P(B/A)$$.
If $$P(A)=0.4, P(B)=0.3$$ and $$P(B/A)=0.5$$, find $$P(A\cap B)$$ and $$P(A/B)$$.
Compute $$P ( A | B ) ,$$ if $$P ( B ) = 0.25$$ and $$P ( A \cap B ) = 0.18$$$$P ( B ) = 0.25$$
Given two independence events $$A$$ and $$B$$ such that $$P(A)=0.3$$ and $$P(B)=0.6$$. Find$$P(A\cap B)$$
If $$A$$ and $$B$$ are mutually exclusive such that $$P(A)=0.35$$ and $$P(B)=0.45$$, find $$P(A\cup B)$$
If $$A$$ and $$B$$ are mutually exclusive such that $$P(A)=0.35$$ and $$P(B)=0.45$$, find $$P(\bar{A}\cap \bar{B})$$
Prove that $$(A\cup B)\times C=(A\times C)\cup (B\times C)$$.
Prove that $$(A\cap B)\times C=(A\times C)\cap (B\times C)$$.
Given two independence events $$A$$ and $$B$$ such that $$P(A)=0.3$$ and $$P(B)=0.6$$. Find$$P(A\cap \bar B)$$
If $$A$$ and $$B$$ are mutually exclusive such that $$P(A)=0.35$$ and $$P(B)=0.45$$, find $$P(\bar{A}\cap \bar{B})$$
If $$A$$ and $$B$$ are mutually exclusive such that $$P(A)=0.35$$ and $$P(B)=0.45$$, find
$$P(A\cap B)$$
Compute $$P ( A | B ) ,$$ if $$P ( B ) = 0.5$$ and $$P ( A \cap B ) = 0.32$$$$P ( B ) = 0.5$$
Given two independence events $$A$$ and $$B$$ such that $$P(A)=0.3$$ and $$P(B)=0.6$$. Find$$P(A\cup B)$$
Compute $$P ( A | B ) ,$$ if $$P ( B ) = 0.25$$ and $$P ( A \cap B ) = 0.18$$
$$P ( B ) = 0.25$$
Given two independence events $$A$$ and $$B$$ such that $$P(A)=0.3$$ and $$P(B)=0.6$$. Find
$$P(A\cap B)$$
Given two independence events $$A$$ and $$B$$ such that $$P(A)=0.3$$ and $$P(B)=0.6$$. Find$$P(\bar {A}\cap \bar B)$$
Given two independence events $$A$$ and $$B$$ such that $$P(A)=0.3$$ and $$P(B)=0.6$$. Find $$P(A/ B)$$
The contents of three bags $$I, II$$ and $$III$$ are as follows:Bag $$I:1$$ white, $$2$$ black $$3$$ red ballsBag $$II:2$$ white, $$1$$ black $$1$$ red ballsBag $$III:4$$ white, $$5$$ black $$3$$ red ballsA bag is chosen at random and two balls are drawn. What is the probability that the balls are white and red?
Given two independence events $$A$$ and $$B$$ such that $$P(A)=0.3$$ and $$P(B)=0.6$$. Find
$$P(\bar {A}\cap B)$$
Given two independence events $$A$$ and $$B$$ such that $$P(A)=0.3$$ and $$P(B)=0.6$$. Find
$$P(\bar {A}\cap \bar B)$$
Given two independence events $$A$$ and $$B$$ such that $$P(A)=0.3$$ and $$P(B)=0.6$$. Find
$$P(A\cup B)$$
A coin is tossed and then a die is thrown. Describe the sample space for this experiment.
If a coin is tossed two times, describe the sample space associated to this experiment.
Write the sample space for the experiment of tossing a coin four times.
A coin is tossed once. Write its sample space
Two dice are thrown. Describe the sample space of this experiment.
If a coin is tossed three times (or three coins are tossed together), then describe the sample space for this experiment.
Given two independence events $$A$$ and $$B$$ such that $$P(A)=0.3$$ and $$P(B)=0.6$$. Find$$P(\bar {A}\cap B)$$
An experiment consists of boys-girl composition of families with $$2$$ children.
What is the sample space if we are interest in knowing whether is a boy or girl in the order of their births
In a random sampling three items are selected from a lot. Each item is tested and classified as defective $$(D)$$ or non-defective $$(N)$$. Write the sample space of this experiment.
A coin is tossed and then a die is rolled only in case a head is shown on the coin. Describe the sample space for this experiment.
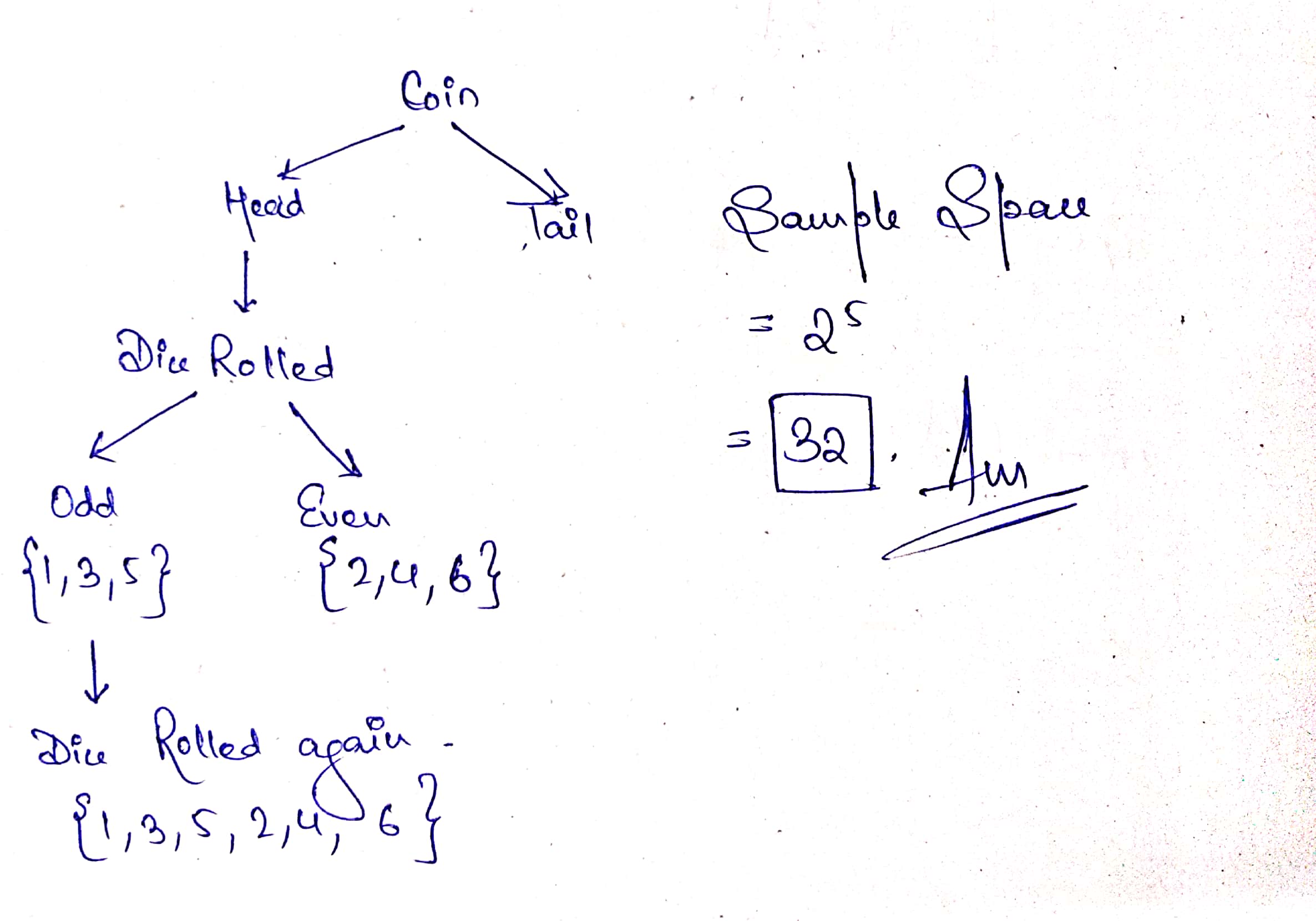
An experiment consists of tossing a coin and then tossing it second time if head occurs. If a tail occurs on the first toss, then a die is tossed once. Find the sample space.
Given two independence events $$A$$ and $$B$$ such that $$P(A)=0.3$$ and $$P(B)=0.6$$. Find$$P(\bar {A}\cap B).$$
A coin is tossed twice. If the second throw result in a tail, a die is thrown. Describe the sample space for this experiment.
A coin is tossed twice. If the second drawn result in a head, a die is rolled, Write the sample space for this experiment.
A coin is tossed. If it shows tail, we drawn a ball from a box which contains $$2$$ red $$3$$ black balls; if it shows head, we throw a die. Find the sample space of this experiment.
A bag contains one white and one red ball. A ball is drawn from the bag . If the ball drawn is white it is replaced in the bag and again a ball is drawn. Otherwise, a die is tossed. Write the sample space for this experiment.
In a single throw of a die describe the following event:
$$D=$$ Getting a number less than $$4$$
There are three coloured dice of red, white and black. these dice are placed in a bag.
One die is drawn at random from the bag and rolled, its colour and the number on its uppermost face is noted. Describe the sample space for this experiment.
Three coins are tossed. Describe three events $$A, B$$ and $$C$$ which are mutually exclusive and exhaustive.
In a single throw of a die describe the following event:
$$F=$$ Getting a number not less than $$3$$
Three coins are tossed once. Describe the following events associated with this random experiment.
$$A=$$ Getting three heads, $$B=$$ Getting two heads and one tail,
$$C=$$ Getting three tails, $$D=$$ Getting a head on the first coin.
Which events are compound events
Three coins are tossed. Describe
two events $$A$$ and $$B$$ which are mutually exclusive.
An experiment consists of the boys-girl composition of families with $$2$$ children.
What is the sample space if we are interested in the number of boys in a family
In a single throw of a die describe the following event:
$$E=$$ Getting an even number greater than $$4$$
In a single throw of a die describe the following event:
$$C=$$ Getting a multiple of $$3$$
A card is picked up form a deck of $$52$$ playing cards
What is the sample space of the experiment.
The numbers $$1,2,3$$ and $$4$$ are written separately on four slips of paper. The slips are then put in a box and mixed thoroughly. A person draws two slips from the box, one after the other without replacement. Describe the following events:$$A=$$ The number on the first slip is larger than the one on the second slip. $$B=$$ The number on the second slip is greater than $$2$$ $$C=$$ The sum of the numbers on the two slip is $$6$$ or $$7$$ $$D=$$ The number on the second slips is twice that on the first slip. Which pair (s) of events is (are) mutually exclusive
Three coins are tossed. Describe
two events $$A$$ and $$B$$ which are mutually exclusive but not exhaustive.
If $$A$$ and $$B$$ mutually exclusive events associated with a random experiment such that $$P(A)=0.4$$ and $$P(B)=0.5$$, then find $$P(\bar{A}\cap B)$$
Two dice are thrown. The events $$A,B,C,D,E$$ and $$F$$ are described as follows:
$$A=$$ Getting an even number on the first die.
$$B=$$ Getting an odd number on the first die.
$$C=$$ Getting at most $$5$$ as sum of the number on the two dice.
$$D=$$ Getting the sum of the numbers on the dice greater than $$5$$ but less than $$10$$.
$$E=$$ Getting at least $$10$$ as the sum of the numbers on the dice.
$$F=$$ Getting an odd number on one of the dice.
Describe the following events: $$A$$ and $$B, B$$ or $$C, B$$ and $$C, A$$ and $$E, A$$ or $$F, A$$ and $$F$$
A die is thrown twice. Each time the number appearing on it is recorded. Describe the following events :$$A=$$ Both numbers are odd.$$B=$$ Both numbers are even.
$$C=$$ Sum of the numbers is less than $$6$$Also, Find $$A\cup B, A\cap B, A\cup C, A\cap C$$. Which pairs of events are mutually exclusive
$$B=$$ Both numbers are even.
$$C=$$ Sum of the numbers is less than $$6$$
Also, Find $$A\cup B, A\cap B, A\cup C, A\cap C$$. Which pairs of events are mutually exclusive
$$A$$ and $$B$$ are two events such that $$P(A)=0.54, P(B)=0.69$$ and $$P(A\cap B)=0.35$$.Find
$$P(A\cap \bar{B})$$
$$A$$ and $$B$$ are two events such that $$P(A)=0.54, P(B)=0.69$$ and $$P(A\cap B)=0.35$$.Find
$$P(B\cap \bar{A})$$
If $$A$$ and $$B$$ mutually exclusive events associated with a random experiment such that $$P(A)=0.4$$ and $$P(B)=0.5$$, then find $$P(A\cap\bar{B})$$
If $$A$$ and $$B$$ are two events associated with a random experiment such that $$P(A)=0.3, P(B)=0.4$$ and $$P(A\cup B)=0.5$$, find $$P(A\cap B)$$.
If $$A$$ and $$B$$ are two events associated with a random experiment such that $$P(A)=0.5, P(B)=0.3$$ and $$P(A\cap B)=0.2$$, find $$P(A\cup B)$$.
There are three events $$A, B, C$$ one of which must and only one can happen, the odds are $$8$$ to $$3$$ against $$A, 5$$ to $$2$$ against $$B$$.Find the odds against $$C$$.
$$A$$ and $$B$$ are two events such that $$P(A)=0.54, P(B)=0.69$$ and $$P(A\cap B)=0.35$$.Find
$$P(\bar{A}\cap \bar{B})$$
If $$A$$ and $$B$$ are two events such that $$P(A)=0.54, P(B)=0.69$$ and $$P(A\cap B)=0.35$$.Find $$P(A\cup B)$$
One of the two events must happen. Given that the chance of one is two-third of the other, find the odds in favour of the other.
Fill in the blanks in the following table:
| $$P(A)$$ | $$P(B)$$ | $$P(A\cap B)$$ | $$P(A\cup B)$$ |
| $$0.5$$ | $$0.35$$ | $$.....$$ | $$0.7$$ |
If $$A$$ and $$B$$ are mutually exclusive such that $$P(A)=0.35$$ and $$P(B)=0.45$$, find
$$P(\bar{A}\cap \bar{B})$$
A sample space consists of $$9$$ elementary events $$E_{1}, E_{2}, E_{3}, ....., E_{8}, E_{9}$$ whose probabilities are $$P(E_{1})=P(E_{2})=0.08, P(E_{4})=0.1, (E_{6}=P(E_{7})=0.2, P(E_{8})=P(E_{9})=0.07$$
Suppose $$A=\left\{E_{1}, E_{5}, E_{8}\right\}, P(B)\left\{E_{2}, E_{5}, E_{8}, E_{9}\right\}$$
Using the addition law of probability, find $$P(A\cup B)$$
If $$A$$ and $$B$$ are mutually exclusive such that $$P(A)=0.35$$ and $$P(B)=0.45$$, find
$$P(A\cap B)$$
The probability that a person will travel by plane is $$\dfrac{3}{5}$$ and that he will travel by train is $$\dfrac{1}{4}$$. What is the probability that he (she) will travel by plane or train?
If $$A$$ and $$B$$ are mutually exclusive such that $$P(A)=0.35$$ and $$P(B)=0.45$$, find
$$P(A\cup B)$$
A fair coins is tossed $$8$$ times. Find the probability that:
(i) it shows no head
(ii) it shows head at least once.
When two dice are rolled :
List the outcomes for the event that total is less than $$5$$.
If $$A$$ and $$B$$ are mutually exclusive such that $$P(A)=0.35$$ and $$P(B)=0.45$$, find
$$P(A\cap \bar{B})$$
A couple has $$2$$ children. Find the probability that both are boys if it is known that
one of the children is a boy
The probability that a student select a coat is $$\dfrac {4}{5}$$ and the probability that he will buy a shirt given that buys a coat is $$0.4$$. Find the probability that he will buy both a shirt and a coat.
A coin is tossed and then a die is thrown. Find the probability or obtaining a $$6$$ given that a head came up.
A die is thrown once. What is the probability of getting a number less than 3 ?
In a hostel $$60\%$$ of the students read Hindi newspaper, $$40\%$$ read English newspaper and $$20\%$$ read Hindi and English newspapers. A student is selected at random.
Find the probability that he reads neither Hindi nor English newspaper.
Let $$A$$ and $$B$$ be the events such that $$2P(A)=P(B)=\dfrac {5}{13}$$ and $$P(A/B)=\dfrac {2}{5}$$.
Find $$P(A\cap B)$$
In a case, $$40\%$$ students study mathematics; $$25\%$$ study biology and $$15\%$$ study both mathematics and biology. One student is selected at random.
Find the probability that he studies biology if it is known that he studies mathematics.
Let $$A$$ and $$B$$ be the events such that $$P(A)=\dfrac {7}{13}, P(B)=\dfrac {9}{13}$$ and $$P(A \cap B)=\dfrac {4}{13}$$.
Find $$P(A\cup B)$$
The probability that a certain person will buy a shirt is $$0.2$$, the probability that he will buy a coat is $$0.3$$ and the probability that he will buy a shirt given that he buys a coat is $$0.4$$. Find the probability that he will buy both a shirt and a coat.
In a case, $$40\%$$ students study mathematics; $$25\%$$ study biology and $$15\%$$ study both mathematics and biology. One student is selected at random.
Find the probability that
he studies mathematics if it is known that he studies biology
Let $$E_1$$ and $$E_2$$ be the events such that $$P(E_1)=\dfrac {1}{3}$$ and $$P(E_2)=\dfrac {3}{5}$$
Find $$P(E_1 \cap E_2)$$, when $$E_1$$and $$E_2$$ are independent,
A bag contains $$17$$ tickets, numbered from $$1$$ to $$17$$. A ticket is drawn and then another ticket is drawn without replacing the first one. Find the probability that both the tickets may show even numbers.
If $$E_1$$ and $$E_2$$ are independent events such that $$P(E_1)=0.3$$ and $$P(E_2)=0.4$$, find $$P(\bar E_1 \cap \bar E_2)$$
Two integers are selected at random from integers $$1$$ through $$11$$. If the sum is even, find the probability that both the numbers selected are odd.
If $$E_1$$ and $$E_2$$ are independent events such that $$P(E_1)=0.3$$ and $$P(E_2)=0.4$$, find $$P(\bar E_1 \cap E_2)$$.
If $$E_1$$ and $$E_2$$ are independent events such that $$P(E_1)=0.3$$ and $$P(E_2)=0.4$$, find $$P(E_1 \cap E_2)$$.
$$A$$ and $$B$$ appear for an interview for two vacancies in the same post. The probability of $$A's$$ selection is $$\dfrac 16$$ and that of $$B's$$ selection is $$\dfrac 14$$. Find the probability that both of them are selected
If $$E_1$$ and $$E_2$$ are independent events such that $$P(E_1)=0.3$$ and $$P(E_2)=0.4$$, find $$P(E_1 \cap E_2)$$
Arun and Ved appeared for an interview for two vacancies. The probability of Arun's section is $$1/4$$ and that of Ved's rejection is $$2/3$$. Find the probability that at least one of them will be selected.
$$A$$ and $$B$$ appear for an interview for two vacancies in the same post. The probability of $$A's$$ selection is $$\dfrac 16$$ and that of $$B's$$ selection is $$\dfrac 14$$. Find the probability that
only one of them is selected
$$A$$ and $$B$$ appear for an interview for two vacancies in the same post. The probability of $$A's$$ selection is $$1/6$$ and that of $$B's$$ selection is $$1/4$$. Find the probability that none is selected.
If A and B are two events associated with random experiment such that $$P(A)=0.25$$, $$P(B)=0.4$$ and $$P(A$$ or $$B)=0.5$$, find the values of $$P(A$$ and $$\bar{B})$$.
The probabilities of $$A, B, C$$ solving a problem are $$\dfrac 13, \dfrac 14$$ and $$\dfrac 16$$ respectively. If the three try to solve the problems simultaneously, find the probability that exactly one of them will solve it.
Given the probability that $$A$$ can solve a problem is $$\dfrac 23$$ and the probability that $$B$$ can solve the same problems is $$\dfrac 35$$, find the probability that none of the two will solve the problem .
A combination lock on a suitcase has $$3$$ wheels, each labelled with nine digits from $$1$$ to $$9$$. If an opening combination is a particular sequence of three digits with no repeats, what is the probability of a person guessing the right combination?
A town has two fire-extinguishing engines, functioning independently. The probability of availability of each engine when needed is $$0.95$$. What is the probability that an engine is available when needed?
If A and B are two events associated with a random experiment such that $$P(A)=0.25$$, $$P(B)=0.4$$ and $$P(A$$ or $$B)=0.5$$, find the value of $$P(A$$ and $$B)$$.
If A and B are two events associated with a random experiment for which $$P(A)=0.60, P(A$$ or $$B)=0.85$$ and $$P(A$$ and $$B)=0.42$$, find $$P(B)$$.
If A and B be two events associated with a random experiment such that $$P(A)=0.3, P(B)=0.2$$ and $$P(A\cap B)=0.1$$, find $$P(\bar{A}\cap B)$$.
Two coins are tossed simultaneously. Find the probability of getting at least $$1$$ head.
Two coins are tossed simultaneously. Find the probability of getting
exactly $$1$$ head
The probability that a company executive will travel by plane is $$(2/5)$$ and that he will travel by train is $$(1/3)$$. Find the probability of his travelling by plane or train.
If A and B are two mutually exlcusive events such that $$P(A)=(1/2)$$ and $$P(B)=(1/3)$$, find $$P(A$$ or $$B)$$.
A die is thrown twice. What is the probability that at least one of the two throws comes up with the number $$4$$?
If A and B be two events associated with a random experiment such that $$P(A)=0.3, P(B)=0.2$$ and $$P(A\cap B)=0.1$$, find $$P(A\cap \bar{B})$$.
Two coins are tossed simultaneously. Find the probability of getting
at most $$1$$ head
From a well-shuffled pack of $$52$$ cards, a card is drawn at random. Find the probability of its being a king or a queen.
In a class, $$30\%$$ of the students offered mathematics, $$20\%$$ offered chemistry and $$10\%$$ offered both. If a student is selected at random, find the probability that he has offered mathematics or chemistry.
Given that $$ P(\bar{A}) = 0.4 , P(B) = 0.2 $$ and $$ P \left (\dfrac{A}{B} \right ) = 0.5 $$ . Find $$ P ( A \cup B ) $$ .
An experiment consists of rolling a die and then tossing a coin if the number on the die is
even. If the number on the die is odd, the coin is tossed twice. Write the sample space for this
experiment
If $$ A $$ and $$ B $$ are two events such that $$ P(A)=\dfrac{1}{2}, P(B)=\dfrac{1}{3} $$ and $$ P(A \cap B)=\dfrac{1}{4} . $$ Find:
(ii) $$ \mathbf{P}(\mathbf{B} \mid \mathbf{A}) $$
The probability that at least one of the two events A and B occurs is $$0.6$$. If A and B occur simultaneously with probability $$ 0.3, $$ evaluate $$ \mathrm{P}(\overline{\mathrm{A}})+\mathrm{P}(\overline{\mathrm{B}}) $$
If $$ A $$ and $$ B $$ are two events such that $$ P(A)=\dfrac{1}{2}, P(B)=\dfrac{1}{3} $$ and $$ P(A \cap B)=\dfrac{1}{4} . $$ Find:
(i) $$ \mathbf{P}(\mathrm{A} \mid \mathbf{B}) $$
Let $$ A $$ and $$ B $$ be two events . If $$ P(A) = 0.2 , P(B) = 0.4 , P(A \cup B) = 0.6 $$ then find $$ P(A / B) $$.
If $$ A $$ and $$ B $$ are two events such that $$ P(A)=\dfrac{1}{2}, P(B)=\dfrac{1}{3} $$ and $$ P(A \cap B)=\dfrac{1}{4} . $$ Find:
(iii) $$ \mathrm{P}\left(\mathrm{A}^{\prime} \mid \mathrm{B}\right) $$
Three events $$ A $$, B and $$ C $$ have probabilities $$ \dfrac{2}{5}, \dfrac{1}{3}$$ and $$\dfrac{1}{2} $$ respectively. Given that $$ P(A \cap B)=\dfrac{1}{5} $$ and $$ P(B \cap C)=\dfrac{1}{4}, $$ find the value of $$ P(C \mid B) $$ and $$ P\left(A^{\prime} \cap C^{\prime}\right) $$
Let $$ E_{1} $$ and $$ E_{2} $$ be two independent events such that $$ P\left(E_{1}\right)=p_{1} $$ and $$ P\left(E_{2}\right)=P_{2} $$Describe in words of the events whose probabilities are:
(i) $$ P_{1} P_{2} $$
Let $$ E_{1} $$ and $$ E_{2} $$ be two independent events such that $$ P\left(E_{1}\right)=p_{1} $$ and $$ P\left(E_{2}\right)=P_{2} $$Describe in words of the events whose probabilities are:
(ii) $$ \left(1-p_{1}\right) p_{2} $$
If $$ A $$ and $$ B $$ are two events such that $$ P(A)=\dfrac{1}{2}, P(B)=\dfrac{1}{3} $$ and $$ P(A \cap B)=\dfrac{1}{4} . $$ Find:
(iv) $$ \mathrm{P}\left(\mathrm{A}^{\prime} \mid \mathrm{B}^{\prime}\right) $$
Let $$ E_{1} $$ and $$ E_{2} $$ be two independent events such that $$ P\left(E_{1}\right)=p_{1} $$ and $$ P\left(E_{2}\right)=P_{2} $$Describe in words of the events whose probabilities are:
(iii) $$ 1-\left(1-p_{1}\right)\left(1-p_{2}\right) $$
Form a 'Road safety commitee' of two, from 2 boys ( $$ \mathrm{B}_{1}, \mathrm{B}_{2} $$ ) and 2 girls $$ \left(\mathrm{G}_{1}, \mathrm{G}_{2}\right) $$.
Complete the following activity to write the sample space.
(a) Committee of 2 boys $$ =\square $$
(b) Committee of 2 girls $$ =\square $$
(c) Committee of one boy and one girl
$$= \begin{array}{|l|}\hline \\ B_1,G_1 \\ \hline \end{array}:\square:\square:\square$$
$$ \therefore $$ Sample space $$ =\{\ldots, \ldots, \ldots, \ldots, \ldots, \ldots\} $$
Suppose S is the event that will snow tomorrow and $$P(S) = 0.03.$$
Find $$P(S')$$
Five Students A, B, C, D and E are competing in a long distance race. Each students probability of winning the race is given below:
$$A \rightarrow 20\%, B \rightarrow 22\%, C \rightarrow 7\%, D \rightarrow 15\%$$ and $$E \rightarrow 36\%$$
(i)who is most likely to win the race ?
(ii) Who is least likely to win the race ?
(iii) Find the sum of probabilities given.
(iv) Find the probability that either A or D will win the race.
(v) Let S be the event that B will win the race.
(a) Find $$P(S)$$
(b) State in words, the complementary event S'.
(c) Find $$P(S')$$
If A and B are two events such that
$$P(A/B) = p, P(A) = p, P(B) = \frac{1} {3}$$ and $$P(A \cup B) = \frac{5} {9}$$, then p = ______.
For the following experiment write sample space $$' \mathrm{S}' $$ and number of sample points $$ \mathrm{n}(\mathrm{S}) $$.
One coin and one die are thrown simultaneously.
Write sample space ' $$ \mathrm{S}^{\prime} $$ and number of sample point $$ \mathrm{n}(\mathrm{S}) $$ for the following experiment. Also write events $$ \mathrm{A},\mathrm{B},\mathrm{C} $$, in the set form and write $$ \mathrm{n}(\mathrm{A}), \mathrm{n}(\mathrm{B}), \mathrm{n}(\mathrm{C}) $$
Three coins are tossed simultaneously.
Condition for event $$ \mathrm{A}: $$ To get at least two heads.
Condition for event $$ \mathrm{B}: $$ To get no head.
Condition for event $$ C: $$ To get head on the second coin.
Write sample space ' $$ \mathrm{S} $$ ' and number of sample point $$ \mathrm{n}(\mathrm{S}) $$ for the following experiment. Also write events $$ \mathrm{A},\mathrm{B},\mathrm{C} $$,in the set form and write $$ \mathrm{n}(\mathrm{A}), \mathrm{n}(\mathrm{B}), \mathrm{n}(\mathrm{C}) $$.
From three men and two women, the environment committee of two persons is to be formed.
Condition for event $$ \mathrm{A}: $$ There must be at least one woman member.
Condition for event $$ \mathrm{B}: $$ One man, one woman committee to be formed.
Condition for event $$ C: $$ There should not be a woman member.
Do the following activity
Activity II: Decide the sample space yourself and fill in the following boxes.
Given two independent events $$A$$ and $$B$$ such that $$P(A)=0.3, P(B)=0.6$$. Find
$$P(A$$ and not $$B)$$
If $$2P\left( A \right) =P\left( B \right) =\cfrac{5}{13}$$ and $$P\left( \cfrac { A }{ B } \right) =\cfrac{2}{5}$$, then find $$P\left( A\cup B \right) $$
Given two independent events $$A$$ and $$B$$ such that $$P(A)=0.3, P(B)=0.6$$. Find
$$P(A$$ and $$B)$$
Given two independent events $$A$$ and $$B$$ such that $$P(A)=0.3, P(B)=0.6$$. Find
$$P(A$$ or $$B)$$
Let $$A$$ and $$B$$ be independent events with $$P(A)=0.3$$ and $$P(B)=0.4$$. Find
$$P(A \cap B)$$
A die is thrown. Let $$A$$ be the events that the number obtained: is greater than $$3$$. $$B$$ be the event that the number obtained is less than $$5$$. Find $$P(A \cup B)$$
If $$P(A)=0.8, \ p(B)=0.5$$ and $$P(B|A)=0.4$$ Find
$$P(A \cup B)$$
Complete the following statements:
The probability of an event is greater than or equal to $$\dots$$ and less than or equal to $$\dots$$
Complete the following statements:
The probability of an event that is certain to happen is $$\dots$$. Such an event is called $$\dots$$
If $$A$$ and $$B$$ are independent events and $$P(A)=0.3$$, $$P(B)=0.4$$, then find:
(i) $$P\left( A\cap B \right) $$
(ii) $$P\left( A\cup B \right) $$
(iii) $$P\left( \cfrac { A }{ B } \right) $$
(iv) $$P\left( \cfrac { B }{ A } \right) $$
Two dice and thrown then,
What is the sample space for pair ?
A and B two events in which $$ P(A) = \dfrac{1}{3} . P(B) = \dfrac{1}{4} and P(AB) = \dfrac{1}{12} $$ then find $$ P(\dfrac{B}{A}) $$
If $$A$$ are independent events, where $$P(A)=0.3$$, $$P(B)=0.6$$, then find:
(i) $$P\left( A\cap B \right) $$
(ii) $$P\left( A\cup \overline { B } \right) $$
(iii) $$P\left( A\cup B \right) $$
(iv) $$P\left( \overline { A } \cap \overline { B } \right) $$
From a cartoon of bulbs , 3 bulbs are drawn randomly . Test bulb and classified into damage (D) and not damage (N). Find the sample space if this test.
Two dice and thrown then,
What is the sample space for sum of digits appear is 8 ?
If a bag contains 4 balls of different colours Red (R), Blue (B), Yellow (Y) and White (W). If two balls drawn at random, what is its sample?
If P(A) - 0.4, P(B) = 0 . 8 P(B/A ) = 0.6 , then find P(A/B) and $$ P (A\cup B)$$
There are three events $$A,B,C$$ one which must and only one can happen; the odds are $$8$$ to $$3$$ against $$A$$, $$5$$ to $$2$$ against $$B$$. The odds against $$C$$ is $$43:17k$$. Find the value of $$k$$ ?
In a class of $$55$$ students, the number of students studying in different subject are, $$23$$ in Mathematics, $$24$$ in physics, $$19$$ in Chemistry, $$12$$ in Mathematics and Physics, $$9$$ in Mathematics and Chemistry, $$7$$ in Physics and Chemistry and $$4$$ in all the three subjects. Find the number of students who have taken exactly one subject.
A sum of money is rounded off to the nearest rupee. The probability that the round off error is at least ten paisa is $$\dfrac { 9k }{ 100 } $$.The value of $$k$$ is
An unbiased coin is tossed. If the result is a head, a pair of unbiased dice is rolled and the number obtained by adding the numbers on the two faces is noted. If the result is a tail, a card from a well shuffled pack of eleven cards numbered $$2,3,4,......12$$ is picked and the number on the card is noted. The probability that the noted number is either $$7$$ and $$8$$ is $$1k3/792$$,where $$k$$ is ten's place of the number $$1k3$$. F ind the value of $$k$$. {$$1k3$$ =$$100$$+$$10\times k$$+$$3$$}
An urn contains $$2$$ white and $$2$$ black balls. A ball is drawn at random. If it is white it is not replaced into the urn. Otherwise it is replaced along with another ball of same colour. The process is repeated. The probability that the third ball drawn is black is$$1-\dfrac { k }{ 30 } $$.Find the value of $$k$$ ?
Urn $$A$$ contains $$6$$ red and $$4$$ black balls and urn $$B$$ contains $$4$$ red and $$6$$ black balls. One ball is drawn at random from urn $$A$$ and placed in urn $$B$$. Then one ball is drawn at random from urn $$B$$ and placed in urn $$A$$. If one ball is now drawn at random from urn $$A$$, the probability that it is found to be red is $$4k/55$$.Find the value of $$k$$
A pair of fair dice is rolled together till a sum a either 5 or 7 is obtained. If p denoted the probability that 7 comes before 5, find 15p
A baised coin with probability $$p(0 < p < 1)$$ of heads is tossed until a head appears for the first time. If the probability that the number of tosses required is even is $$\dfrac25$$, find $$3p$$.
A coin has probability $$p$$ of showing head when tossed. It is tossed $$n$$ times. Let $$p_n$$ denote the probability that no two (or more) consecutive heads occur, then
If $$A, B, C$$ are three independent events of an experiment such that, $$P(A\cap B^{C} \cap C^{C}) =\dfrac {1}{4}, P(A^{C} \cap B\cap C^{C}) = \dfrac {1}{8}, P(A^{C} \cap B^{C} \cap C^{C}) = \dfrac {1}{4}$$, then find $$P(A), P(B), P(C)$$
If $$A$$ and $$B$$ are two independent events such that $$P(\overline{A} \cap B) = \dfrac{2}{15}$$ and $$P(A \cap \overline{B}) = \dfrac{1}{6},$$ then find $$P(A)$$ and $$P(B).$$
Let A, B, C be three events such that $$P(A) = 0.3 ,\ P(B) = 0.4 ,\ P(C) = 0.8,\ P(A \cap B) = 0.08,\ P(A \cap C) = 0.28,$$ $$\ P(A \cap B \cap C) = 0.09$$. If $$P(A \cup B \cup C) \ge 0.75$$. Show that $$P(B \cap C)$$ lies in the interval $$[0.23,\ 0.48]$$.
If $$A$$ and $$B$$ are independent events with $$P(A)=0.2,P(B)=0.5$$. then find $$P(A/B)$$
Two customers are visiting a particular shop in the same week (Monday to Saturday). Each is equally likely to visit the shop on any one day as on another. What is the probability that both will visit the shop on:
(i) the same day (ii) different days (iii) consecutive days
$$A$$ and $$B$$ are seeking admission into $$IIT$$. If the probability for $$A$$ to be selected is $$0.5$$ and that both to be selected is $$0.3$$, them is it possible that, the probability of $$B$$ to be selected is $$0.9 $$?
$$A$$ and $$B$$ are events with $$P(A)=0.6,P(B)=0.7$$ then compute $$P(A \cap B)$$.
$$A$$ and $$B$$ are events with $$P(A)=0.5,P(B)=0.4$$ and $$P(A \cap B)=0.3$$. Find the probability that
neither $$A$$ and $$B$$ occurs.
Five statements $${ S }_{ 1 }, { S }_{ 2 }, { S }_{ 3 }, { S }_{ 4 }, { S }_{ 5 }$$ are allotted specific seats $${ P }_{ 1 }, { P }_{ 2 }, { P }_{ 3 }, { P }_{ 4 }, { P }_{ 5 }$$ to sit in the class. On the examination day they are allotted seats randomly. Let event $${ E }_{ i }$$ be that $${ S }_{ i }$$ and $${ S }_{ i+1 }$$ are not adjacent then find the value of $$P\left( { E }_{ 1 }\cap { E }_{ 2 }\cap { E }_{ 3 }\cap { E }_{ 4 } \right) $$.
A class consists of $$100$$ students, $$25$$ of them are girls and $$75$$ boys, $$20$$ of them are rich and remaining poor, $$40$$ of them are fair complexioned. The Probability of selecting a fair complexioned rich girl is
For any sets $$A$$ and $$B ,$$ show that $$P ( A \cap B ) = P ( A ) \cap P ( B ).$$
Let $$A$$ and $$B$$ be two events such that $$P(A) =0.6, P(B)=0.2$$ and $$P(A/B)=0.5,$$ then find $$P\left( { A }^{ \backprime }/{ B }^{ \backprime } \right) .$$
A coin is thrown, if coin shows head, a dice is rolled. If dice shows an odd number then the dice is rolled again. Find the sample space.
A and b are events such that P(A)$$\neq$$0.Find $$p(\frac{B}{A})$$ if
(i) A is a subset of B
(ii) $$A\cap B=\emptyset $$
If $$A\times B\subseteq C\times D$$ and $$A\times B\neq \phi$$, prove that $$A\subseteq C$$ and $$B\subseteq D$$.
The probability that Hemant passes in English is $$(2/3)$$ and the probability that he passes in Hindi is $$(5/9)$$. If the probability of his passing both the subjects is $$(2/5)$$, find the probability that he will pass in at least one of these subjects.
If $$A$$ and $$B$$ be two events such that $$P(A)=\cfrac{1}{4}$$, $$P(B)=\cfrac{1}{2}$$ and $$P\left( A\cap B \right) =\cfrac{1}{8}$$, then find $$P\left( \overline { A } \cap \overline { B } \right) $$
$$\left[ 1-P\left( A \right) \right] =P(B)P\left( \overline { A } \right) =P\left( \overline { A } \right) P(B)$$
Class 11 Engineering Maths Extra Questions
- Binomial Theorem Extra Questions
- Complex Numbers And Quadratic Equations Extra Questions
- Conic Sections Extra Questions
- Introduction To Three Dimensional Geometry Extra Questions
- Limits And Derivatives Extra Questions
- Linear Inequalities Extra Questions
- Mathematical Reasoning Extra Questions
- Permutations And Combinations Extra Questions
- Principle Of Mathematical Induction Extra Questions
- Probability Extra Questions
- Relations And Functions Extra Questions
- Sequences And Series Extra Questions
- Sets Extra Questions
- Statistics Extra Questions
- Straight Lines Extra Questions
- Trigonometric Functions Extra Questions