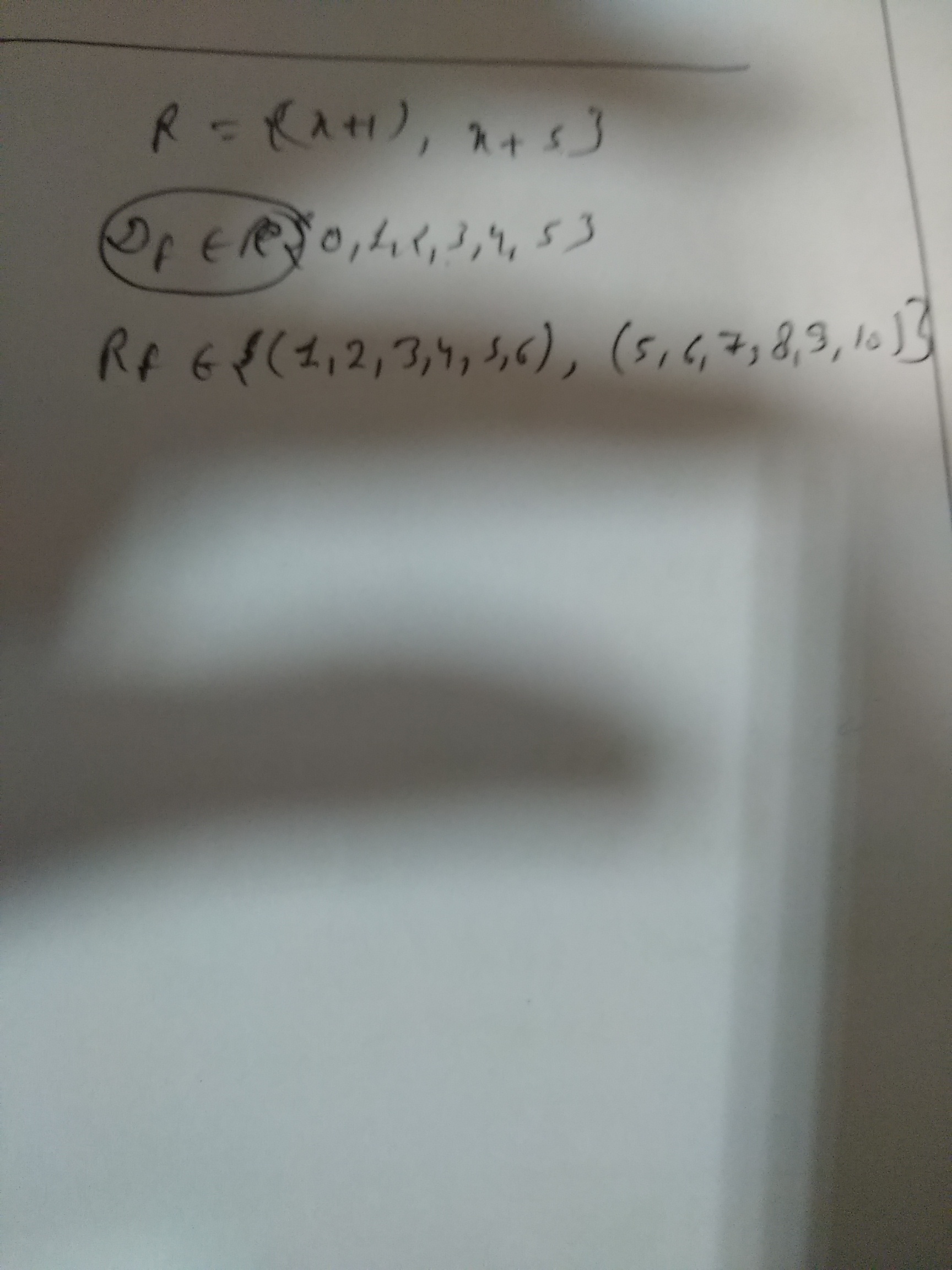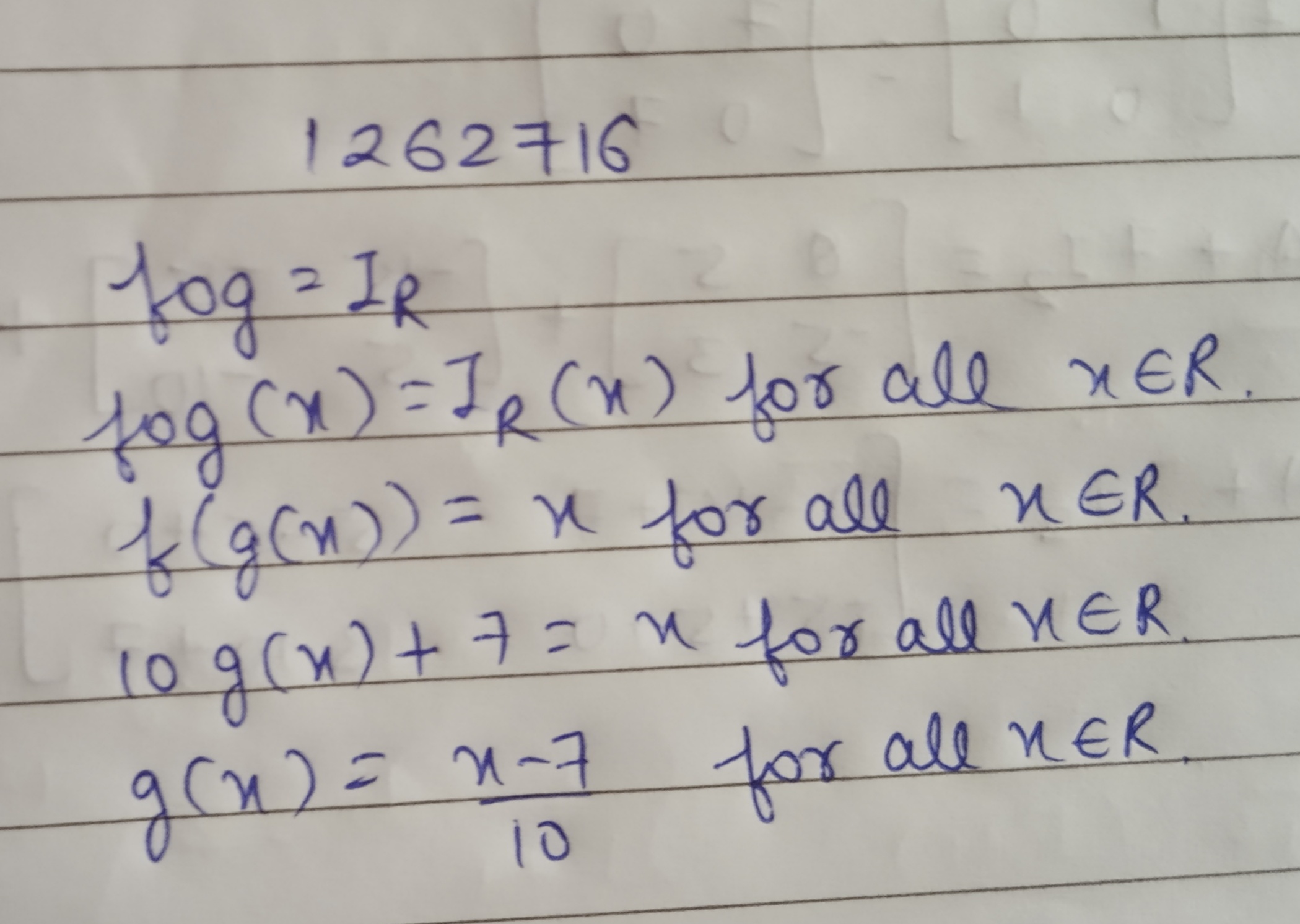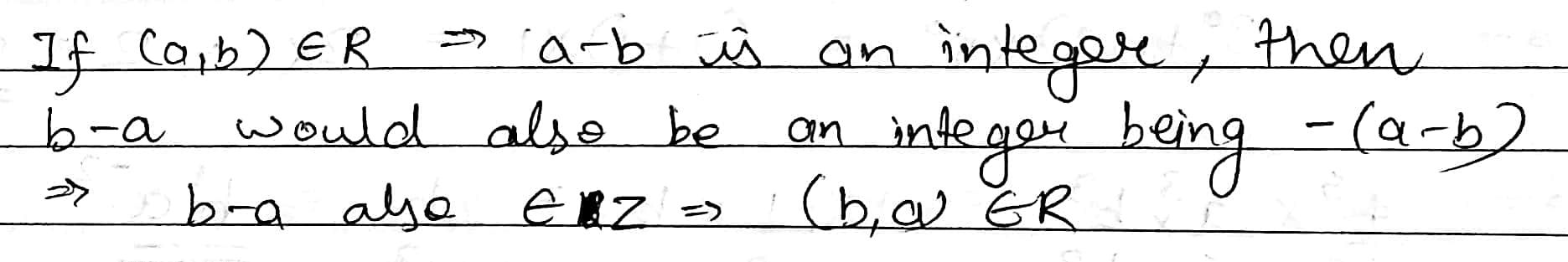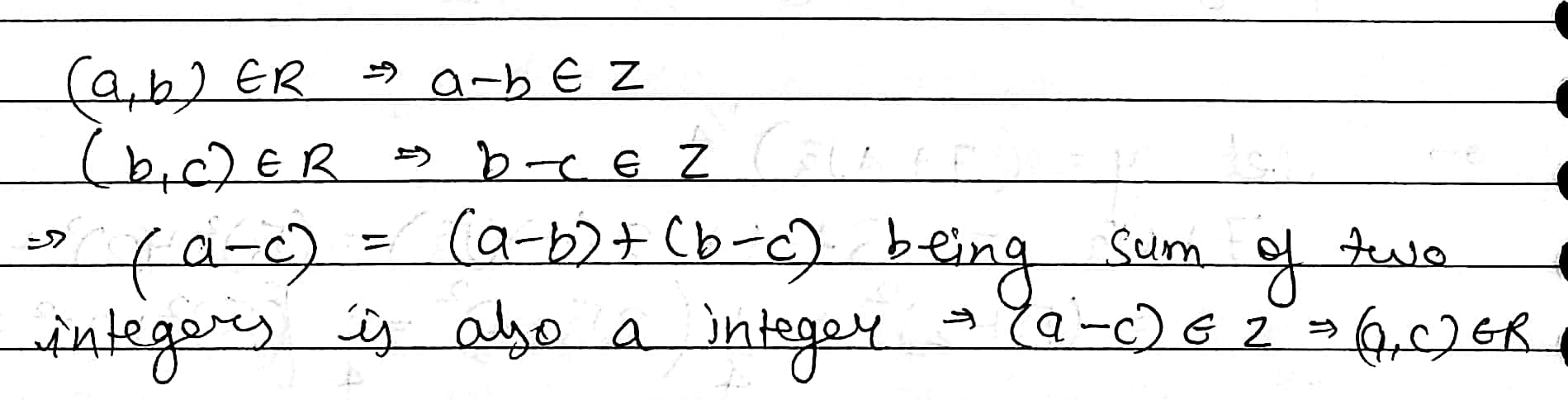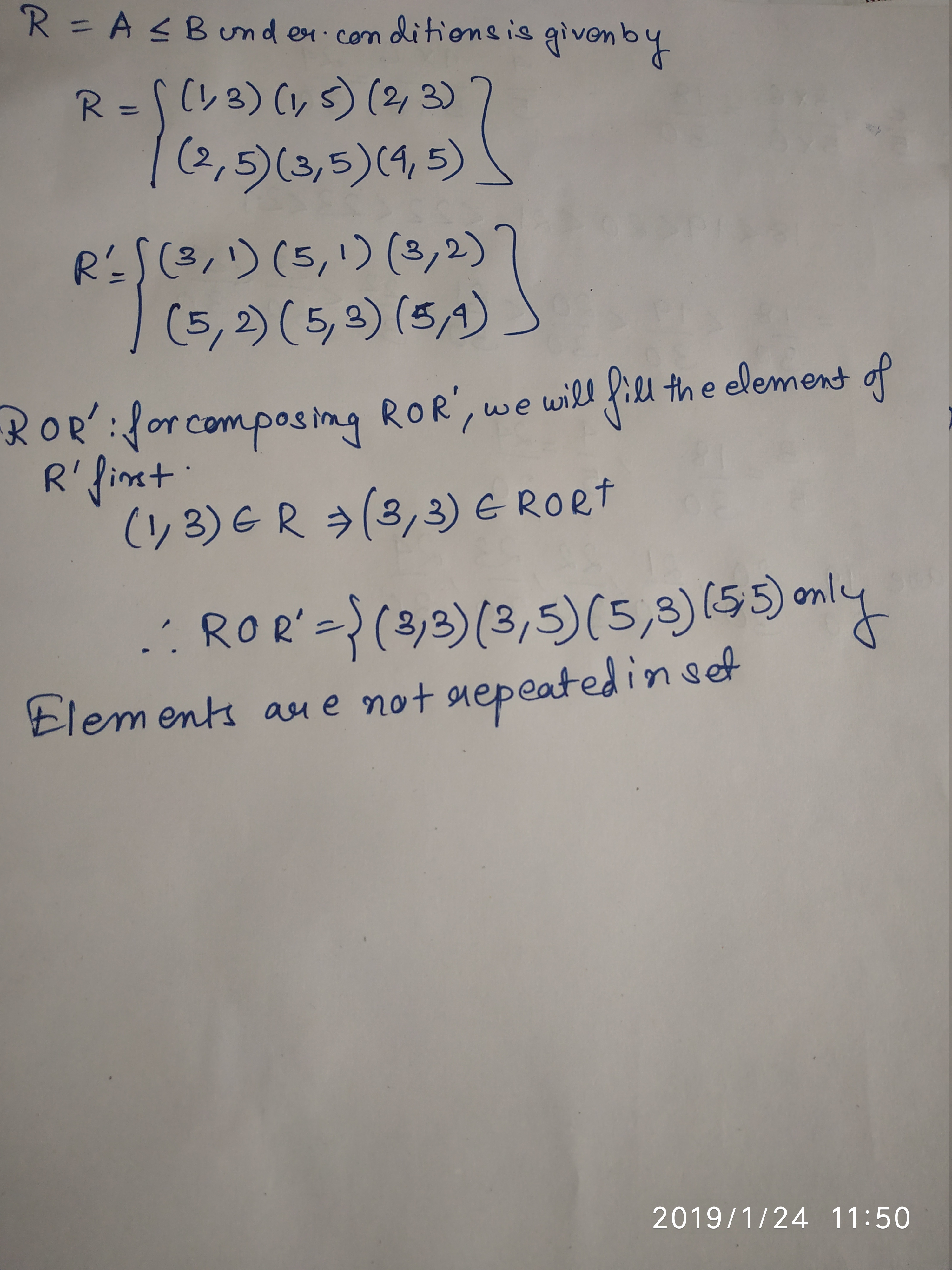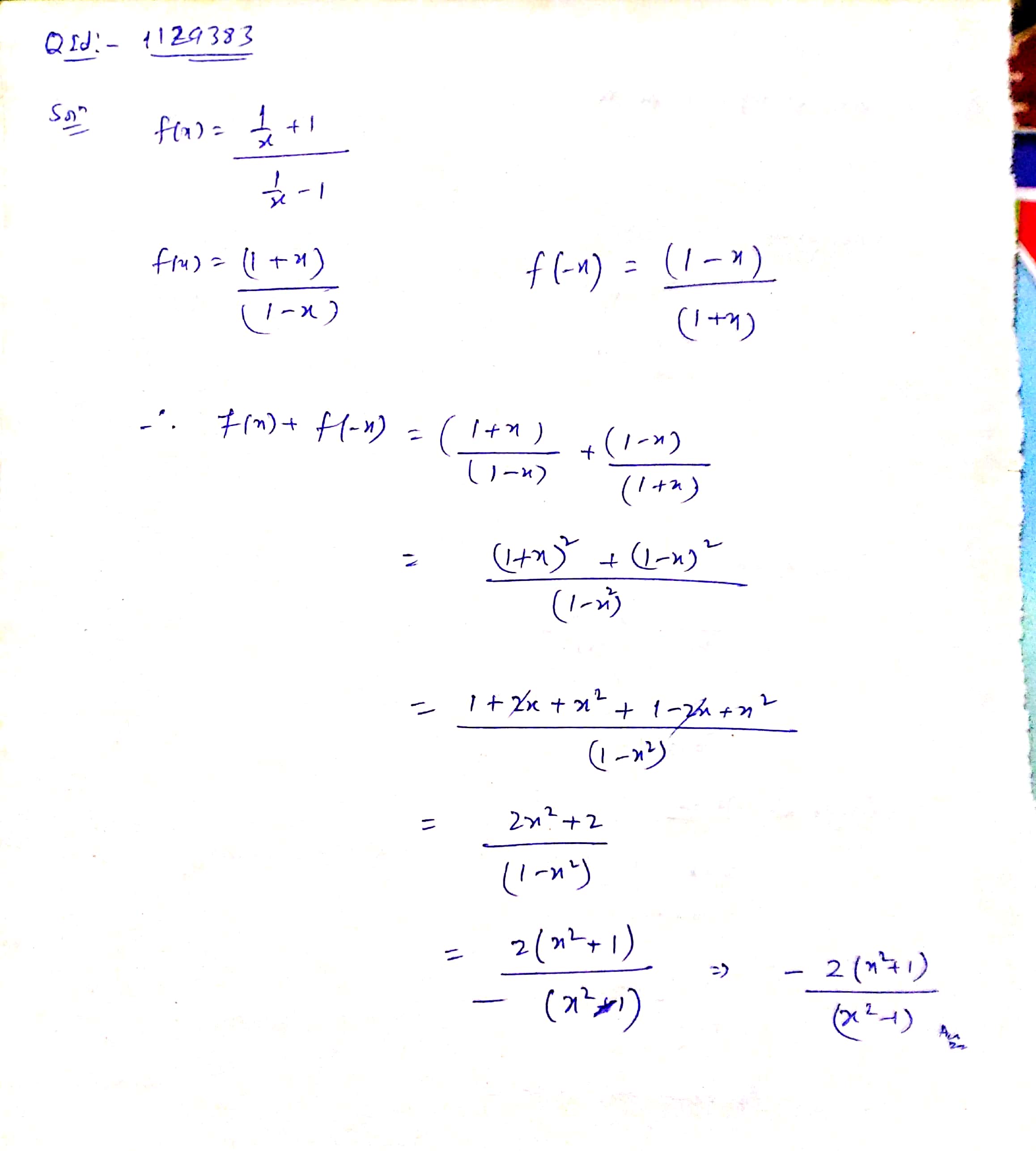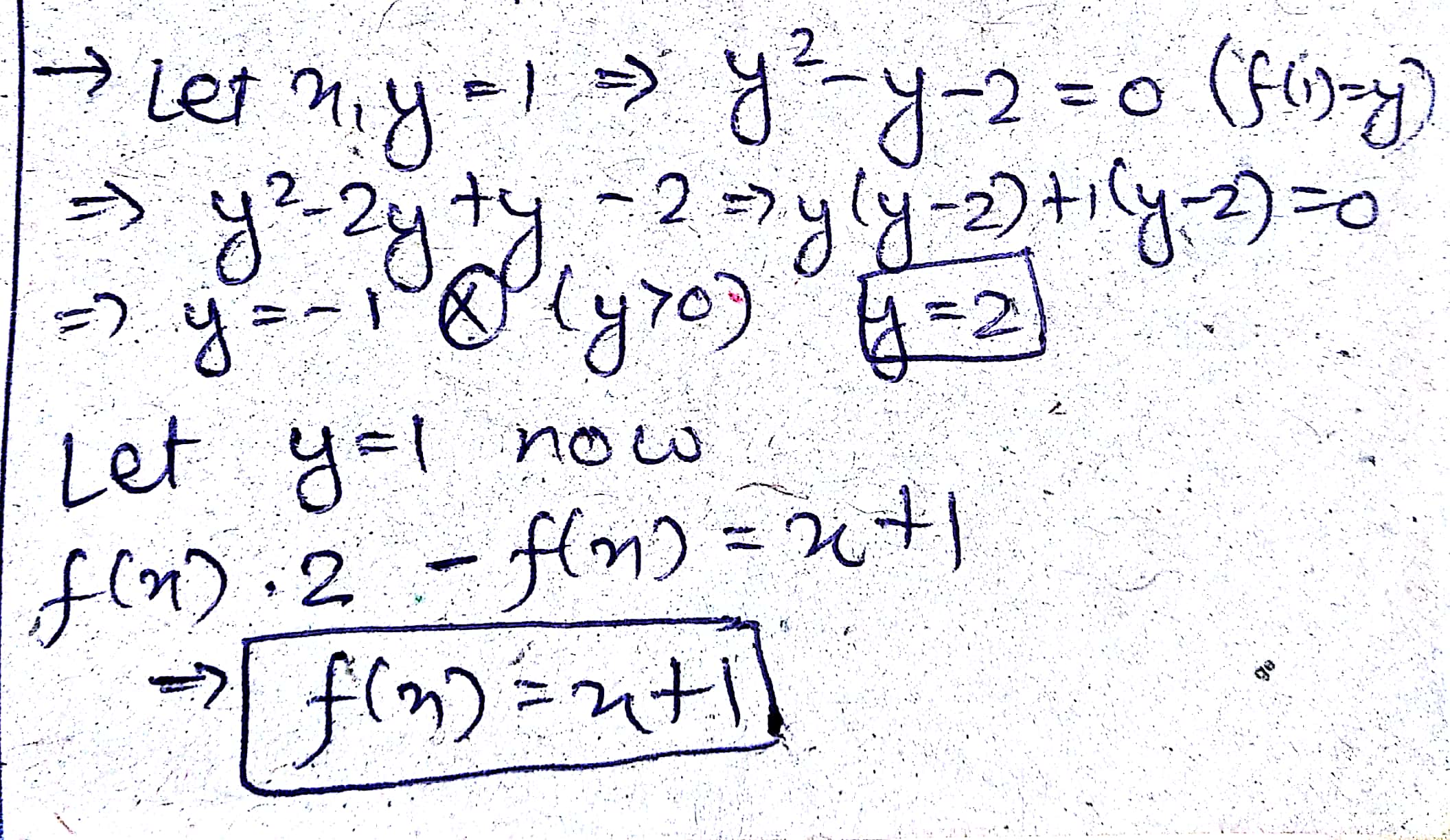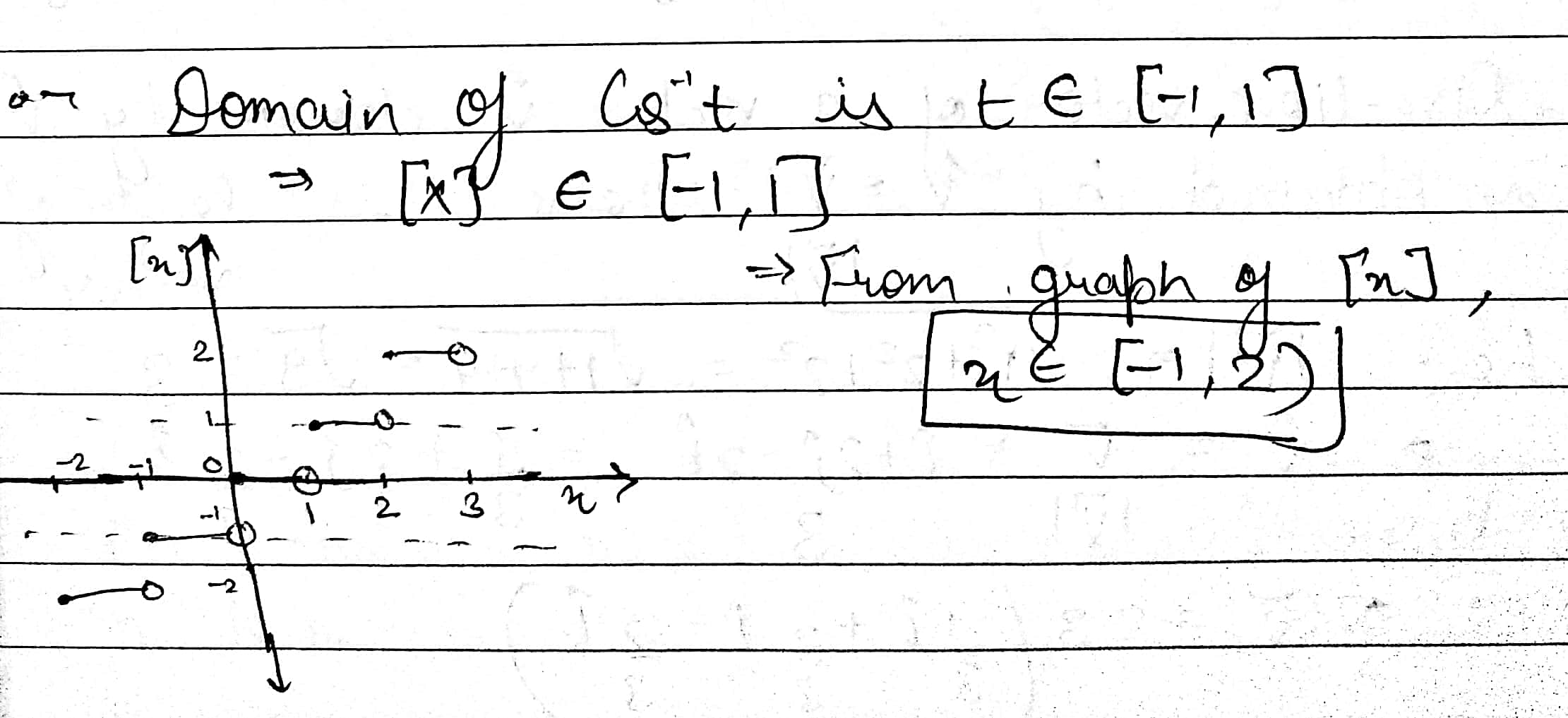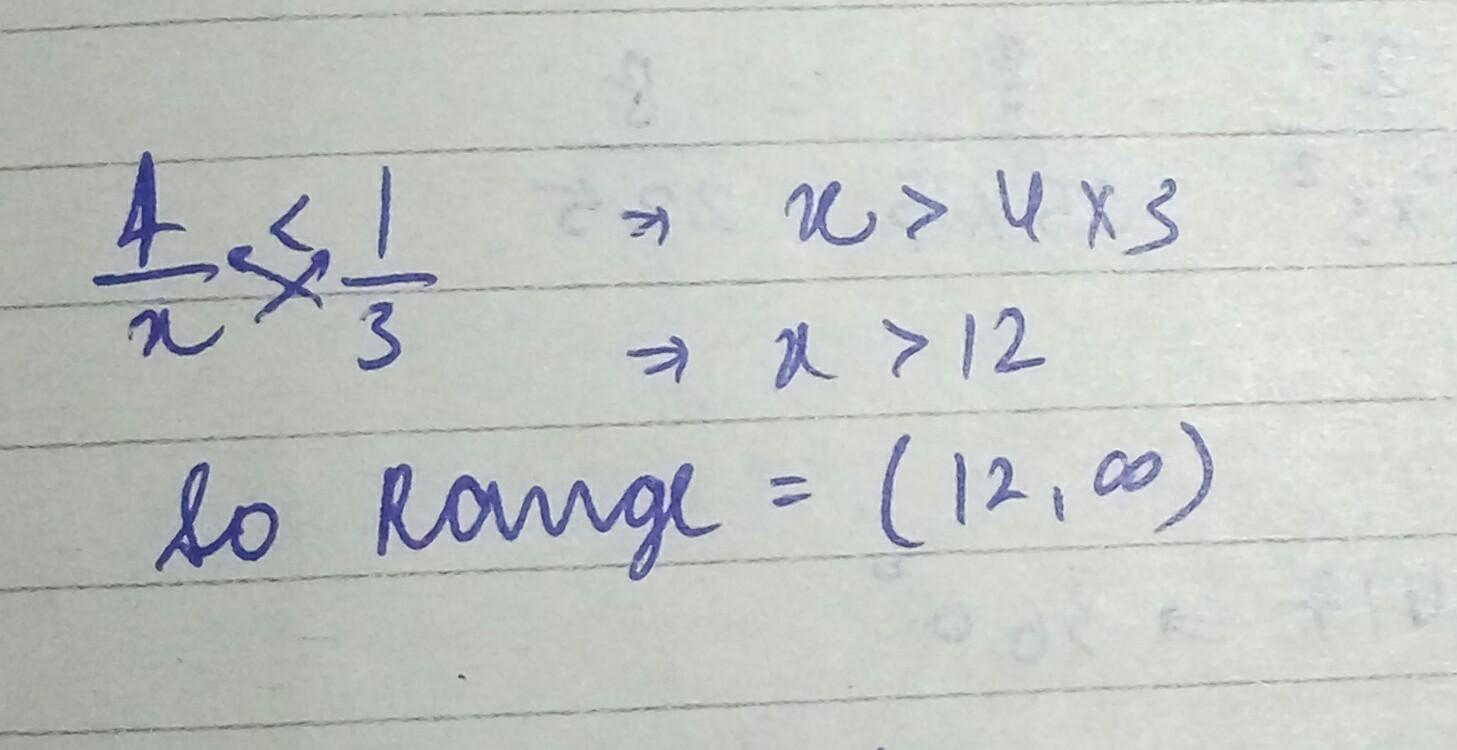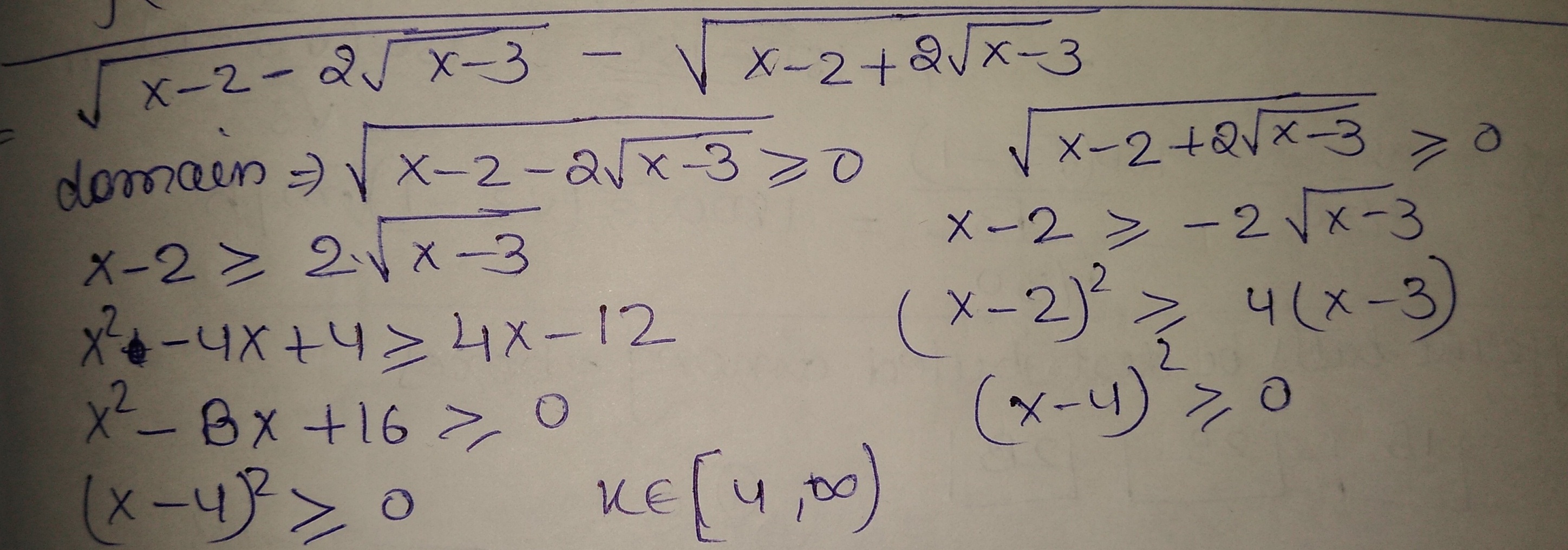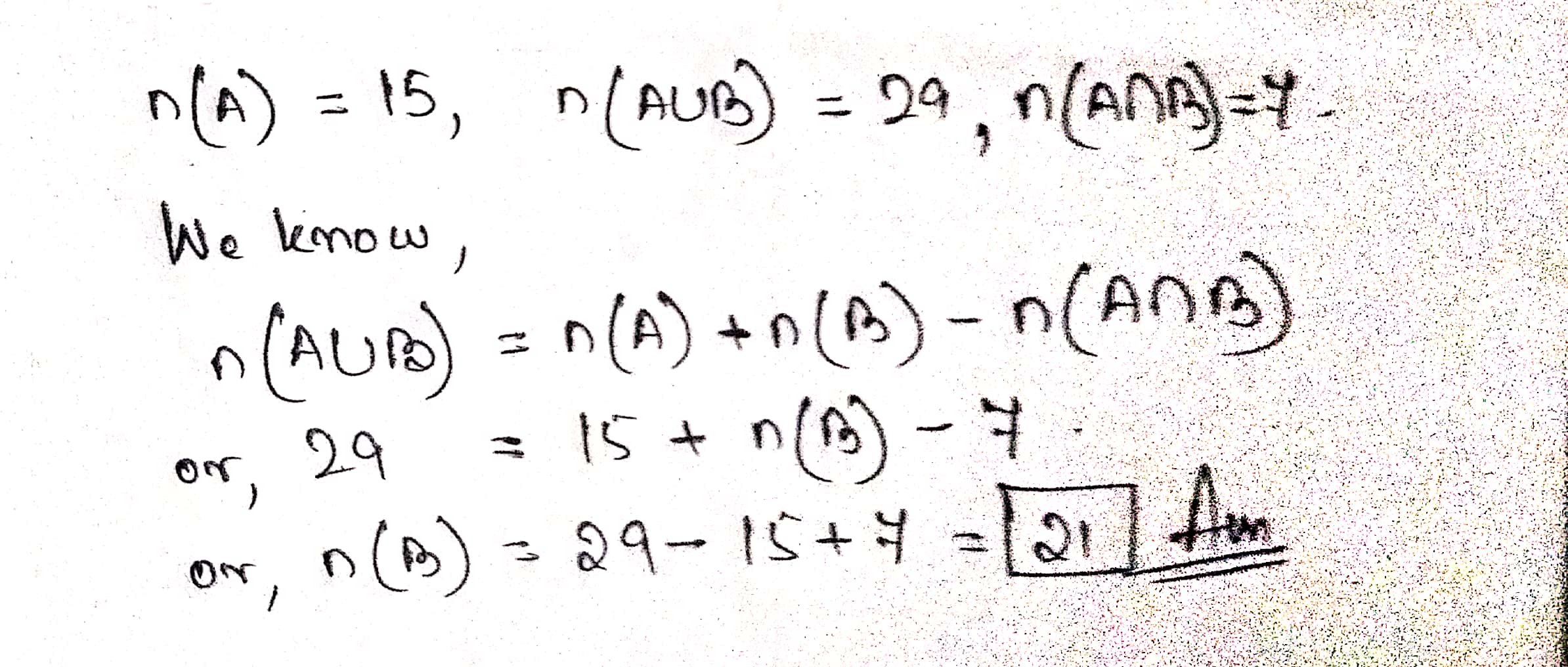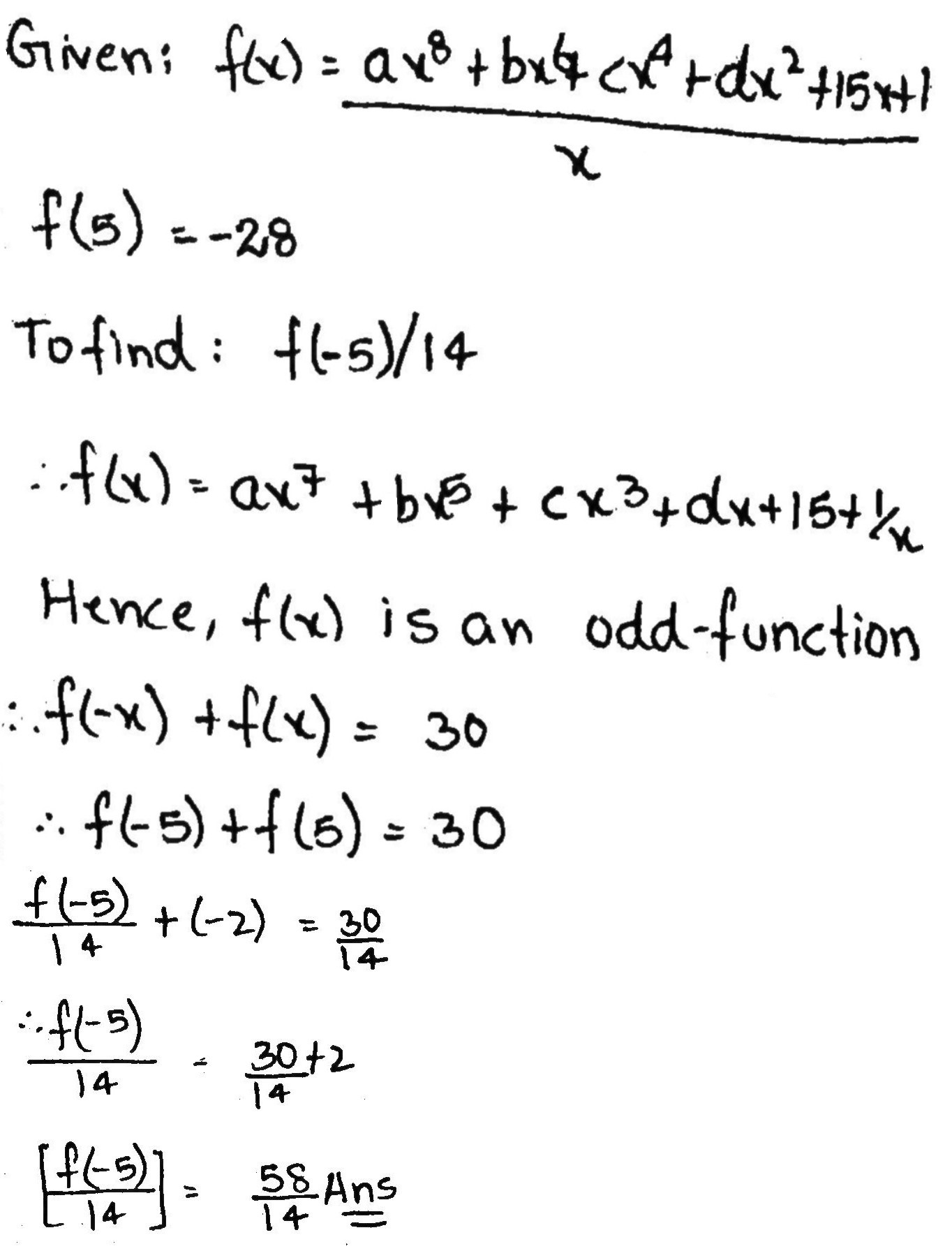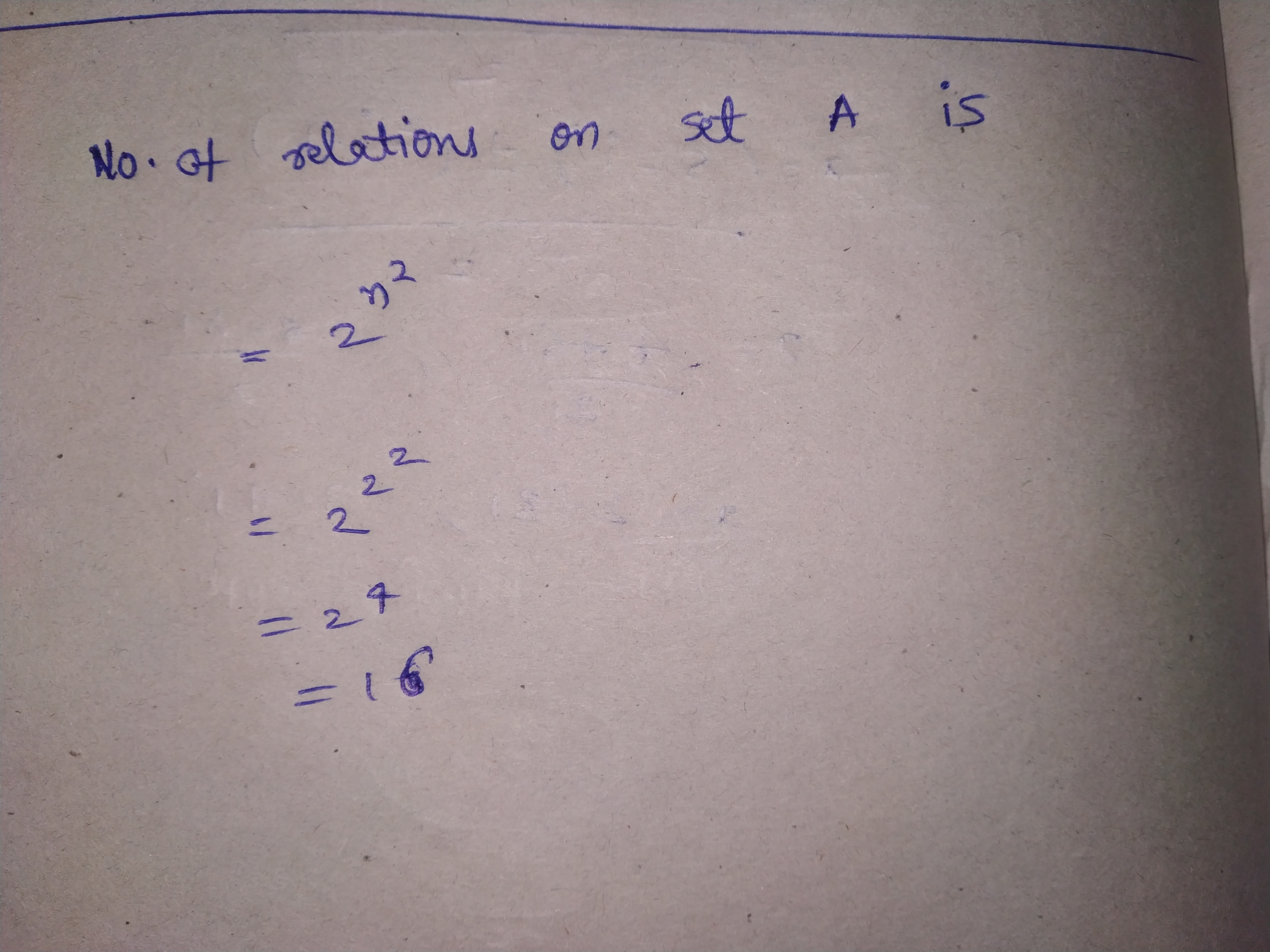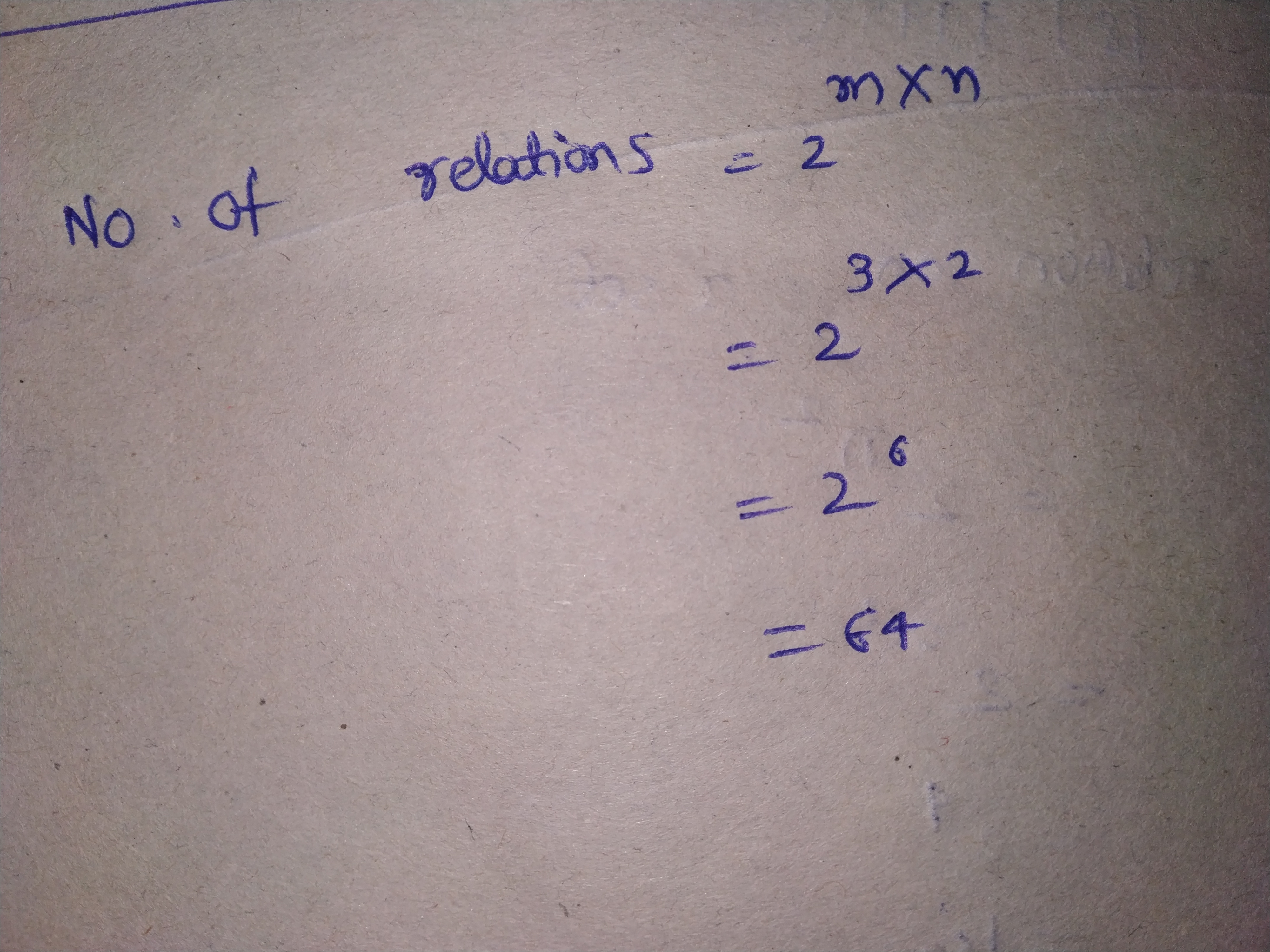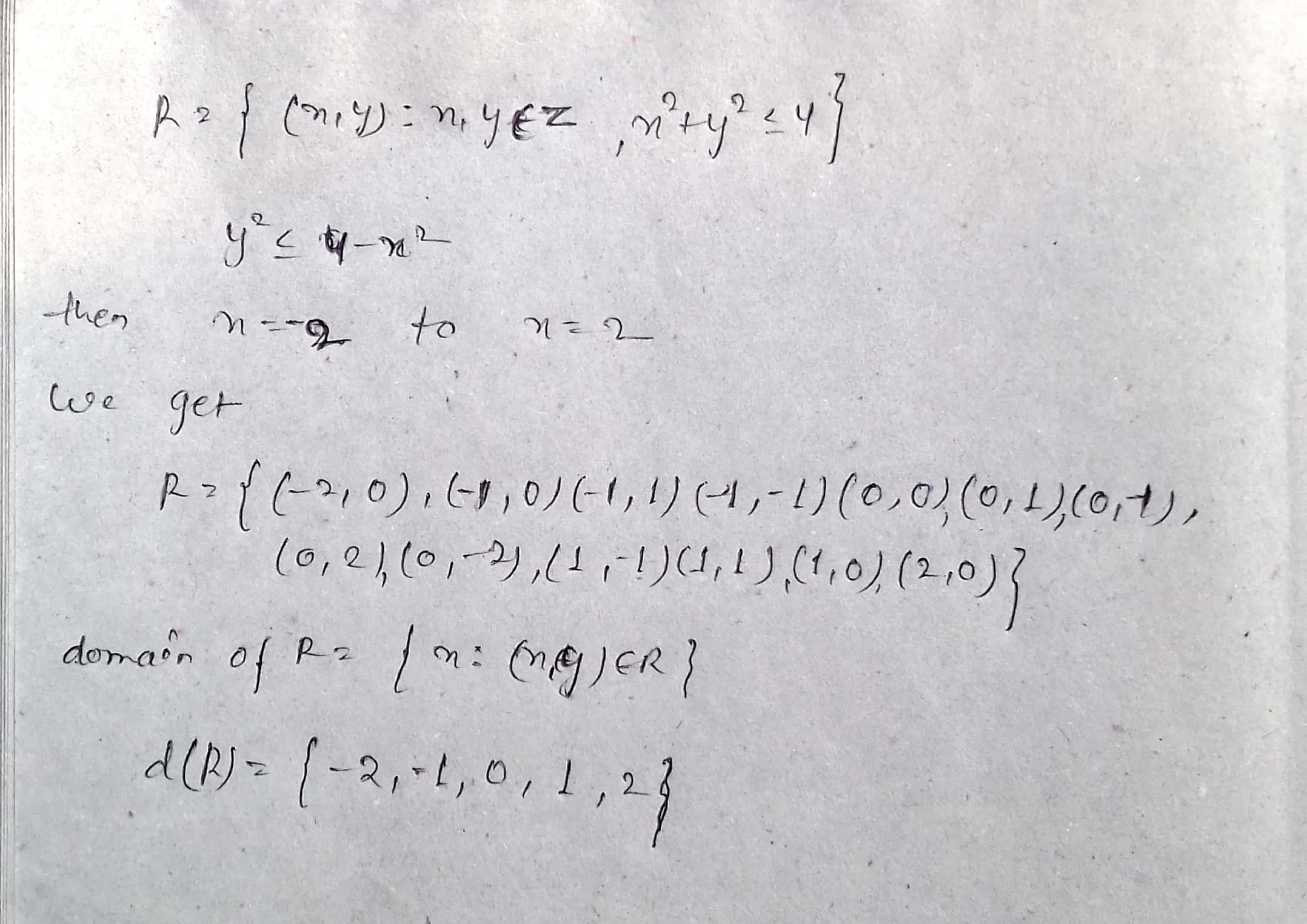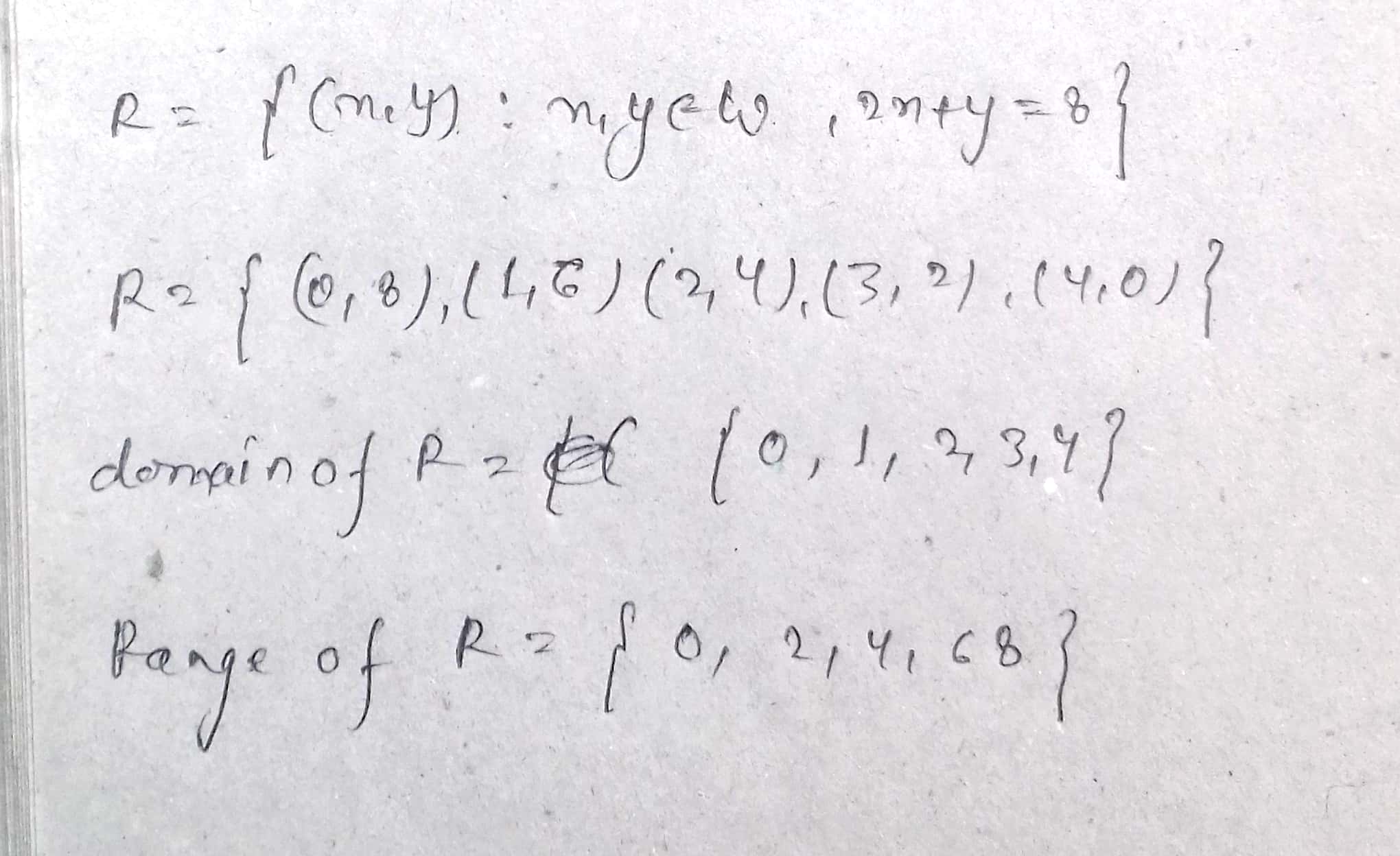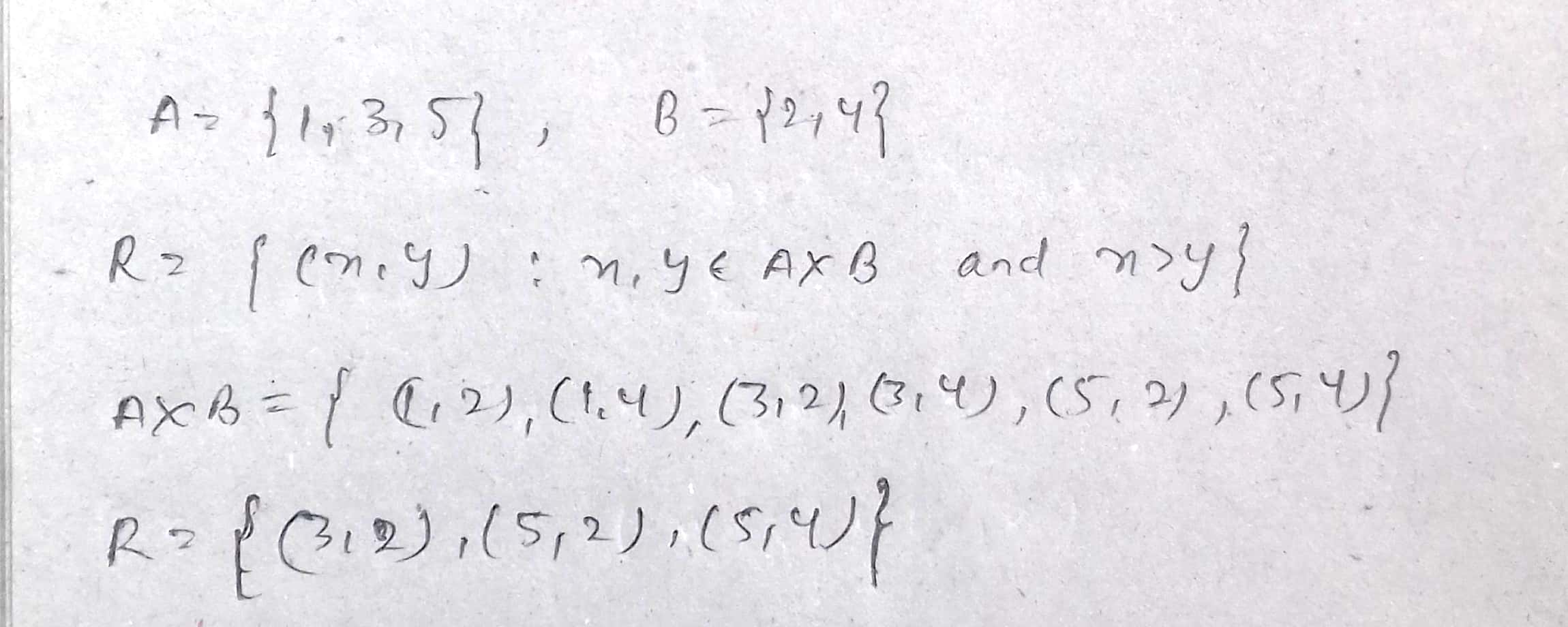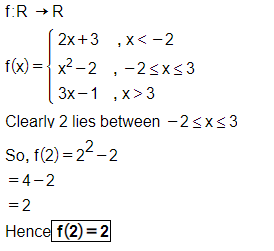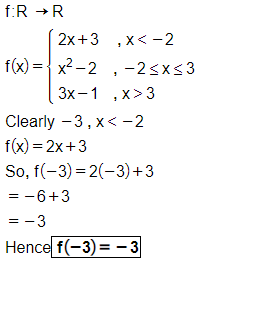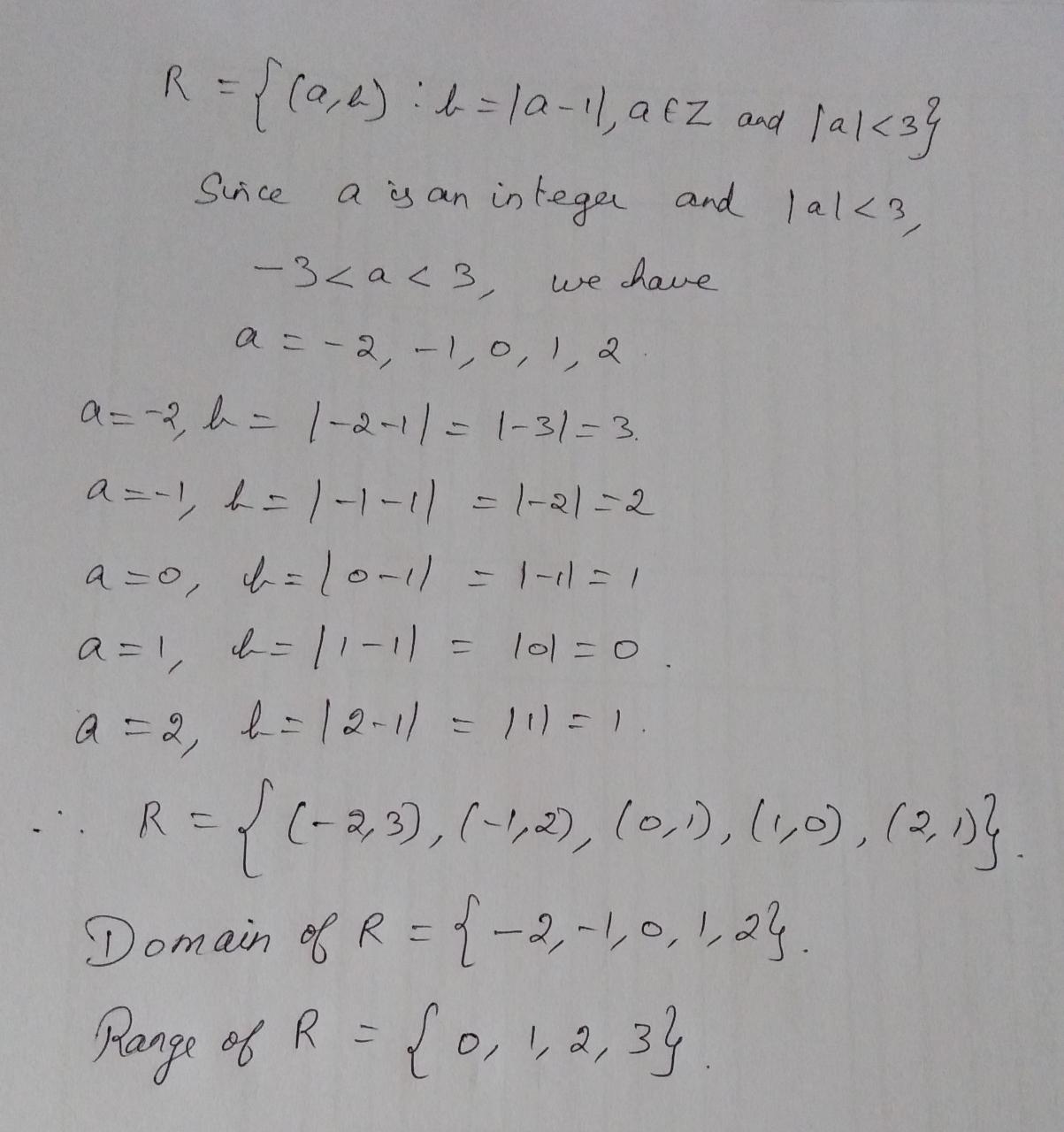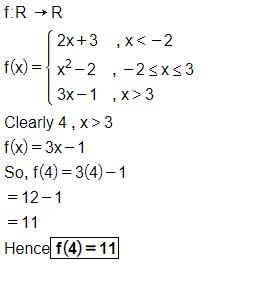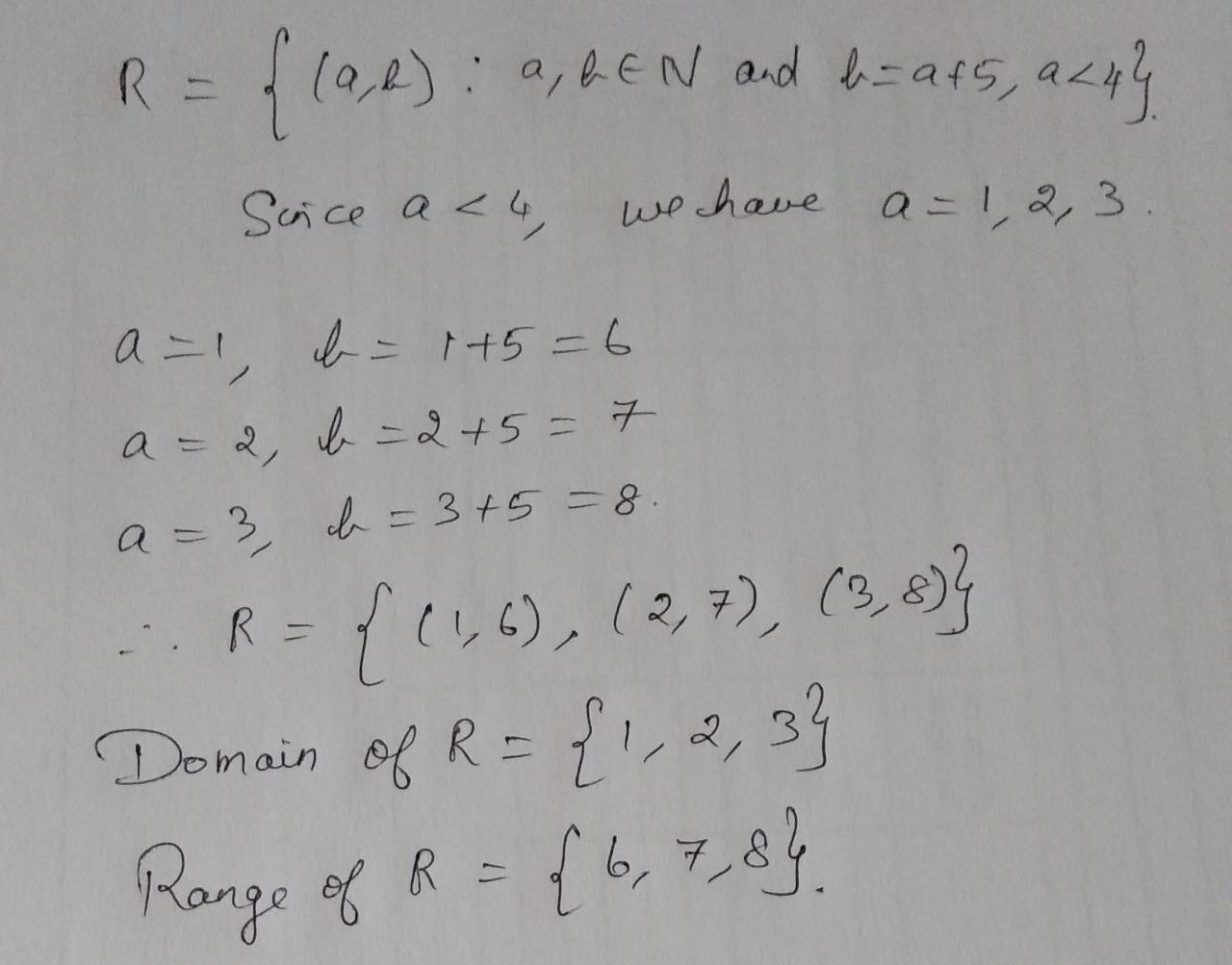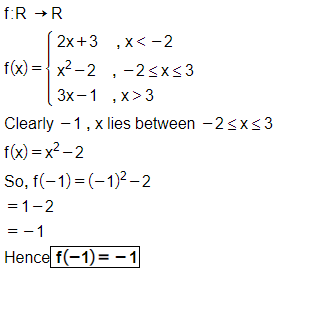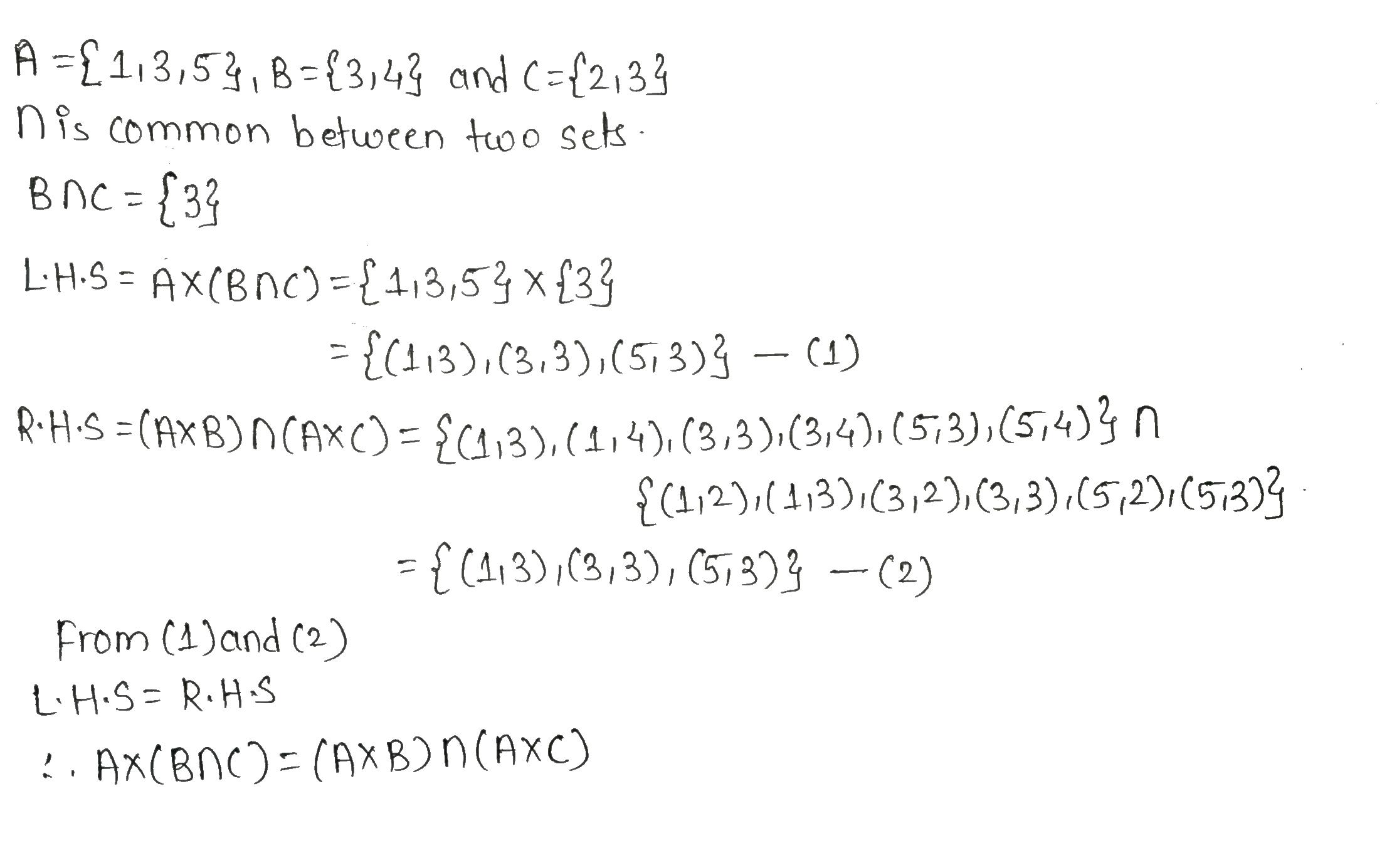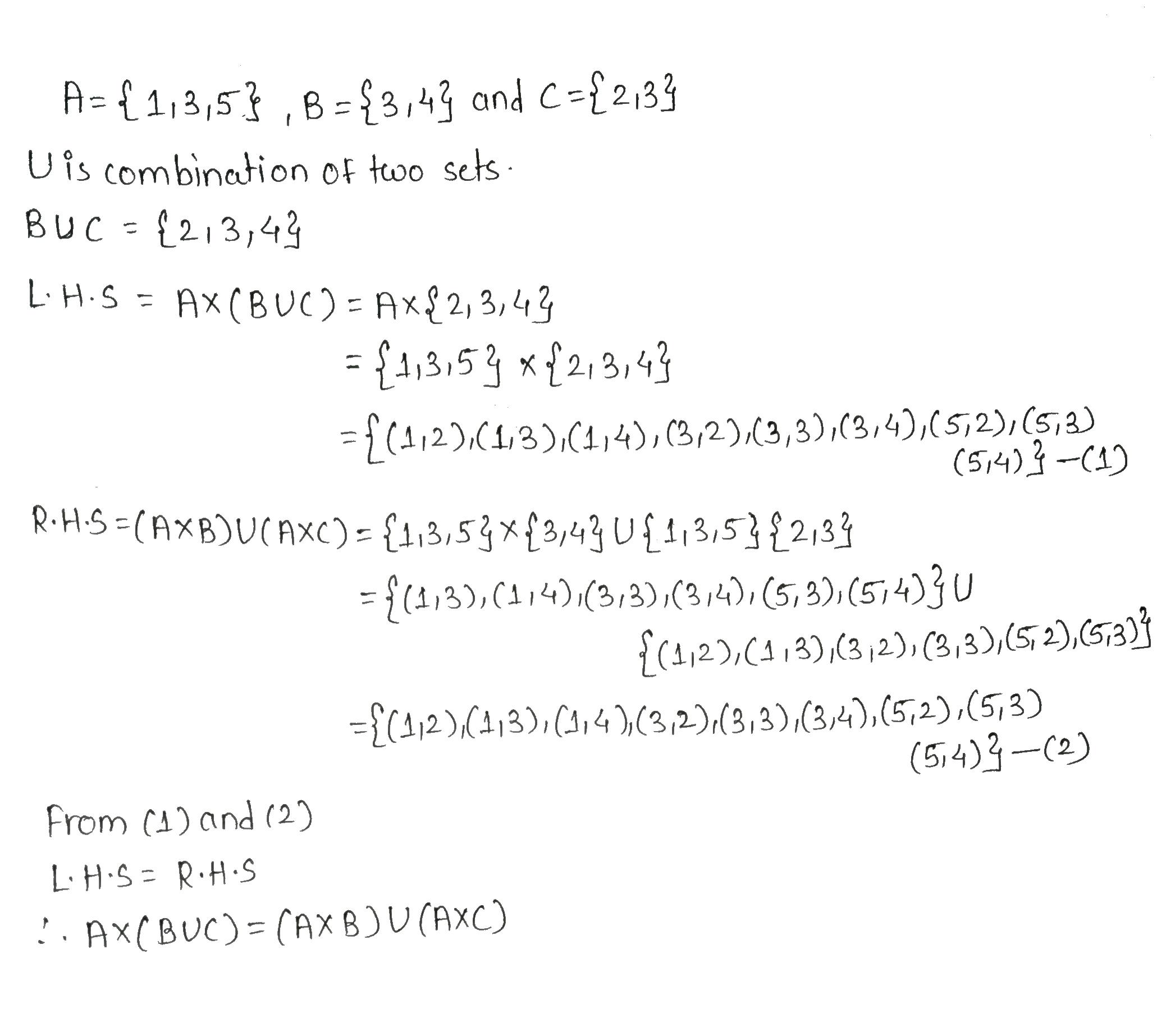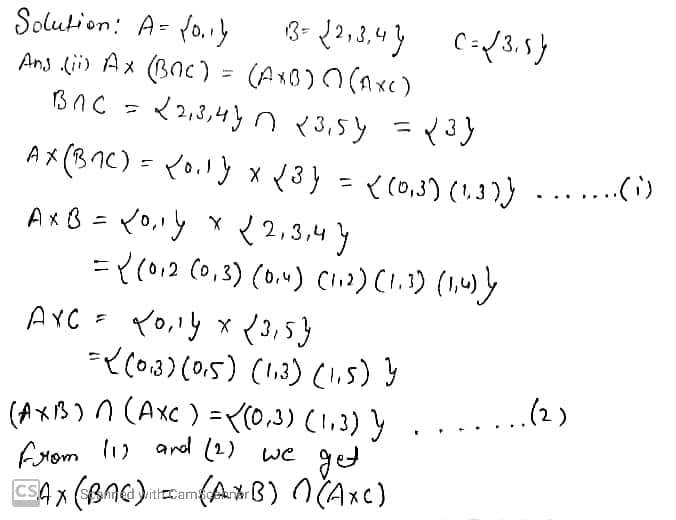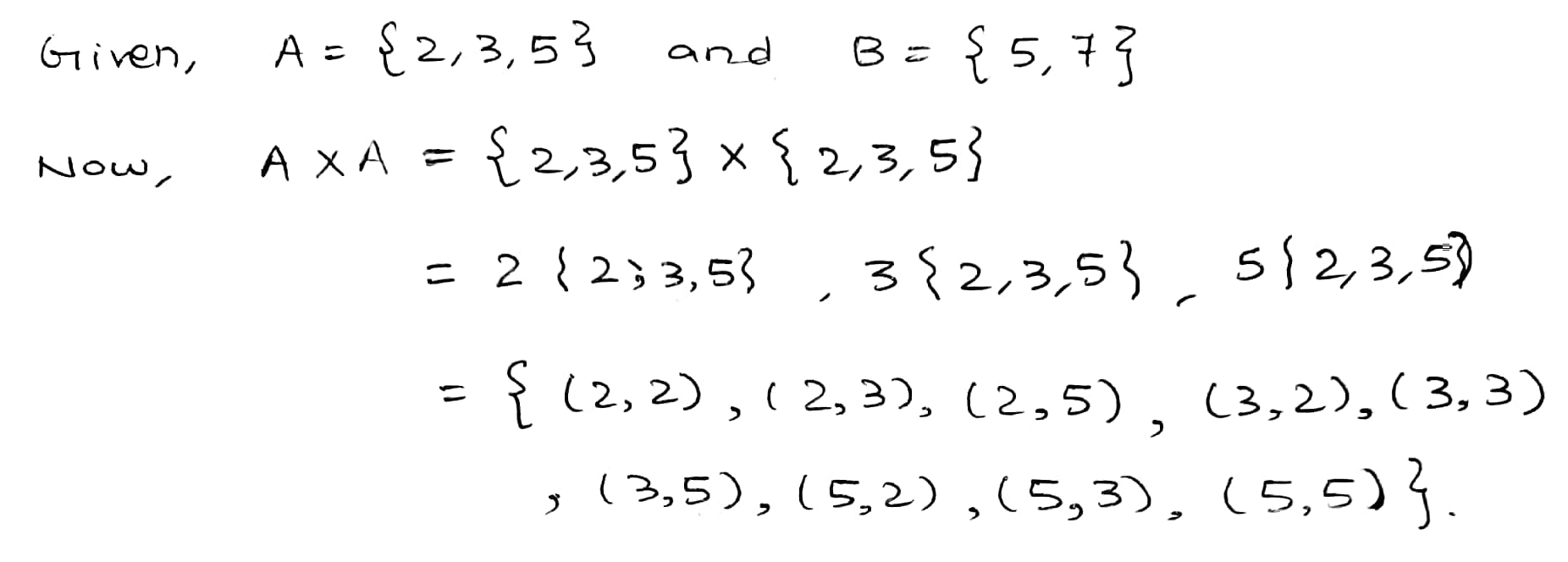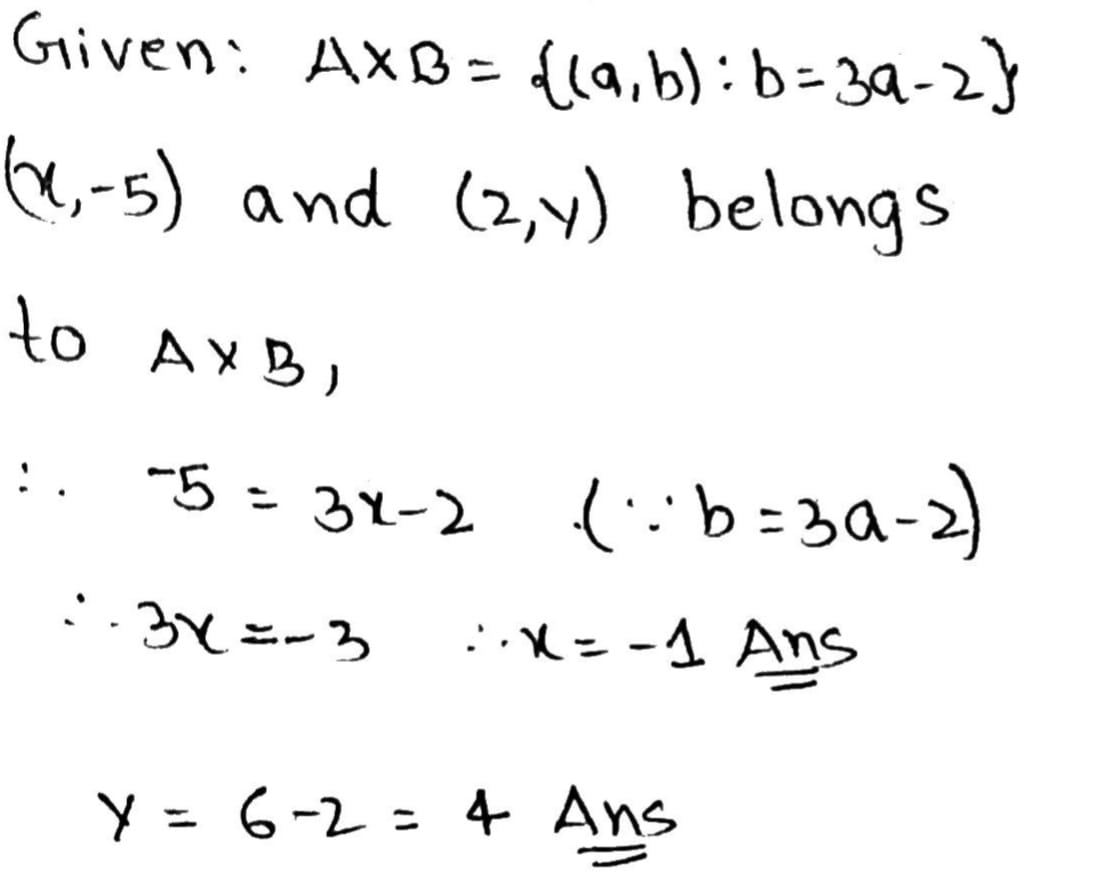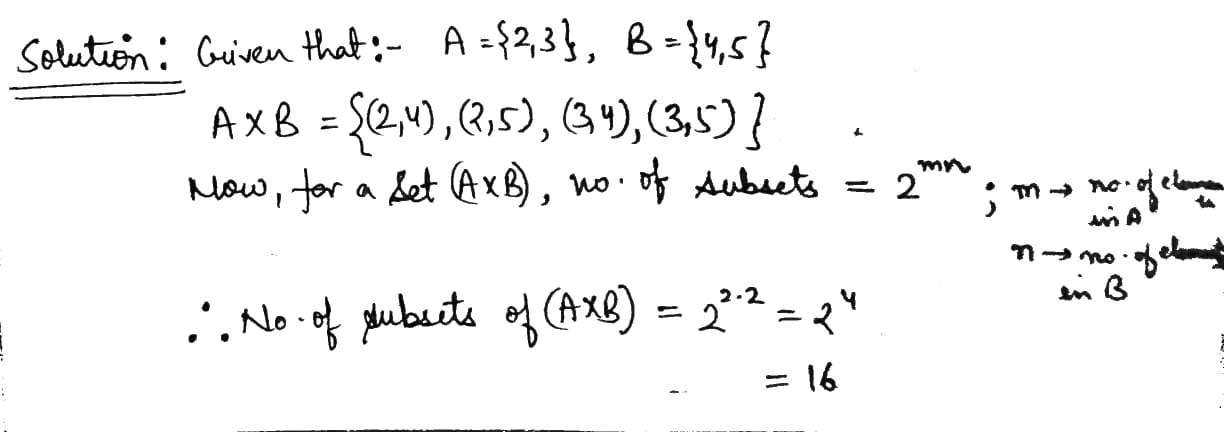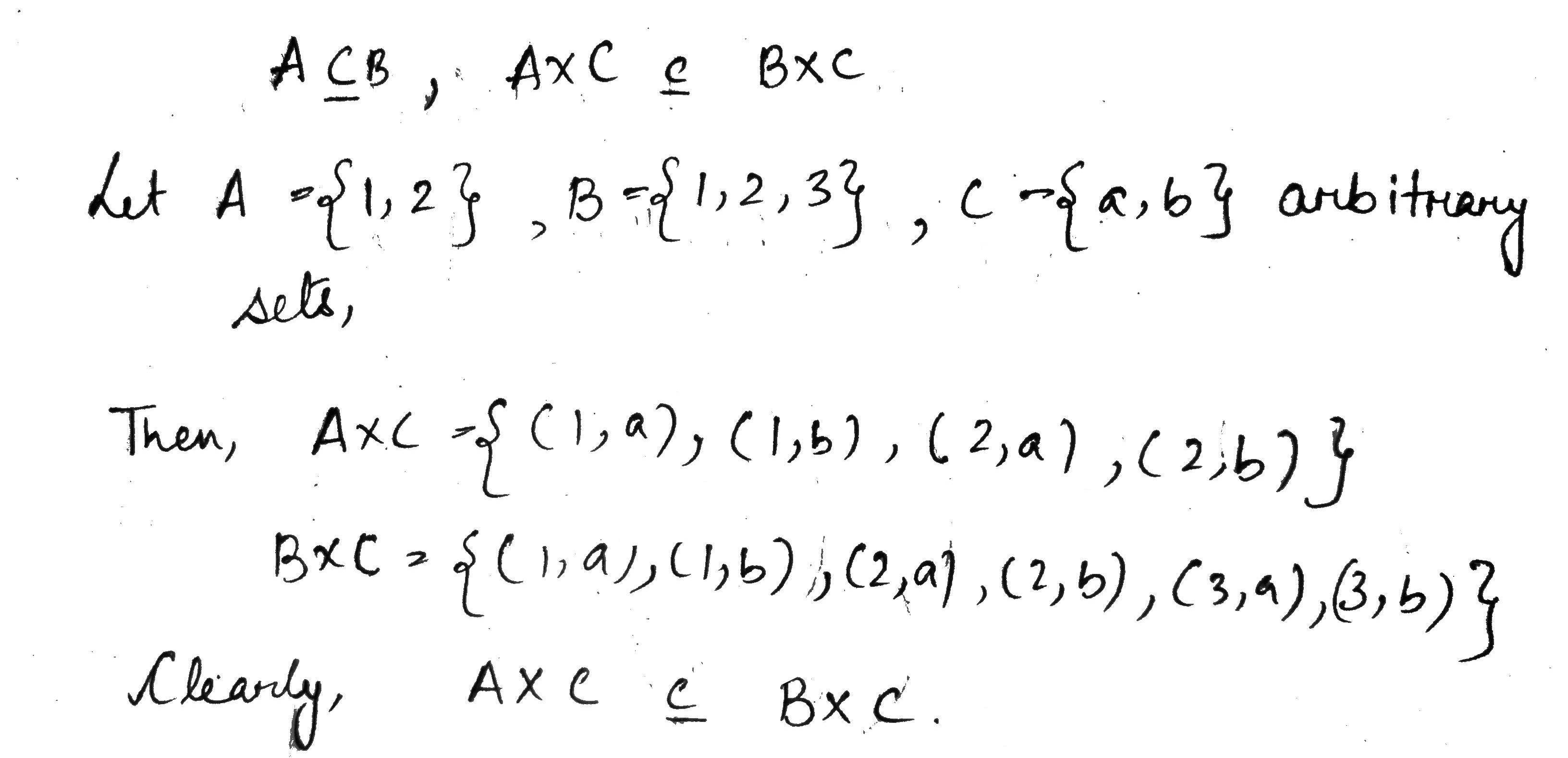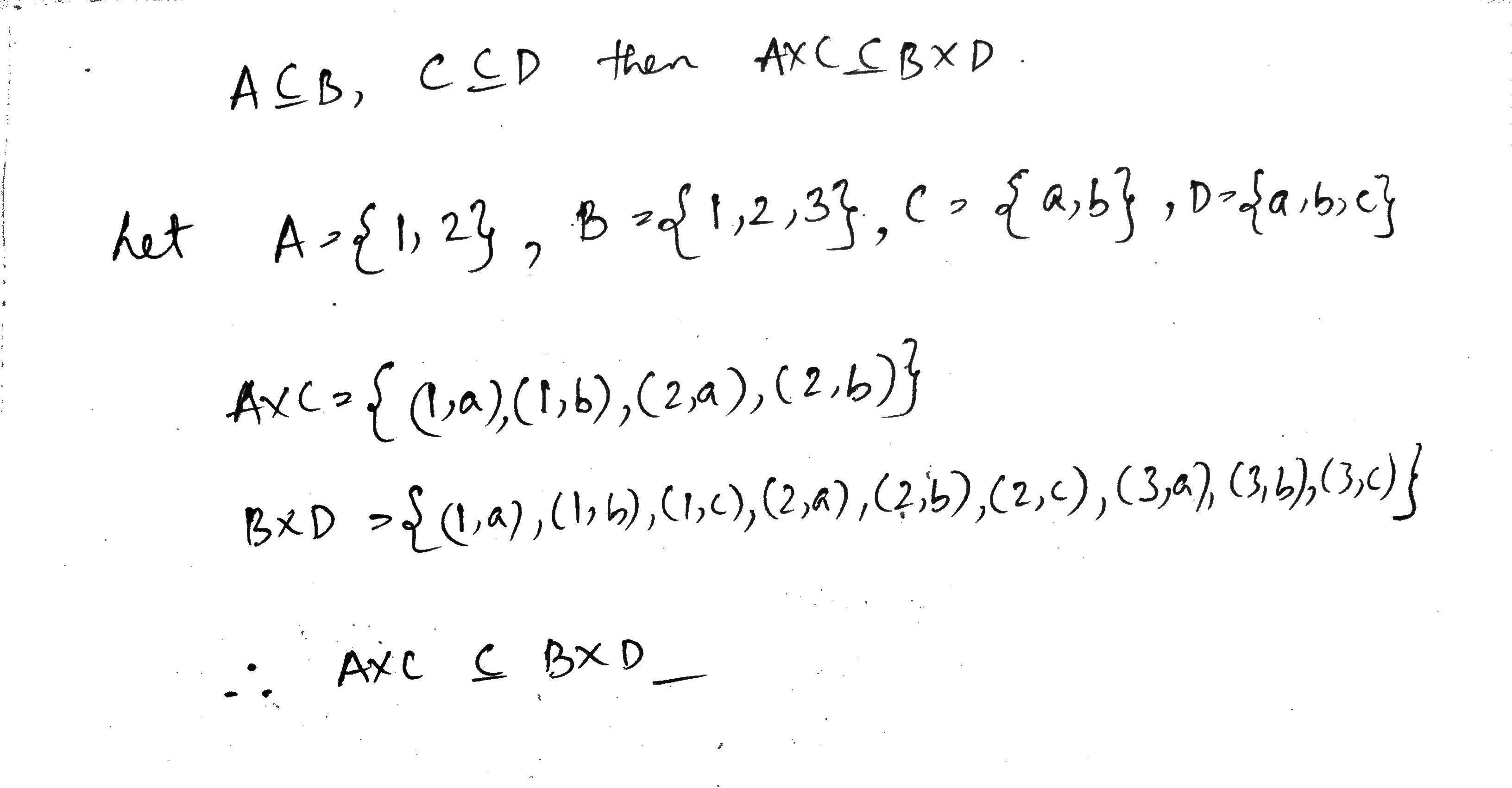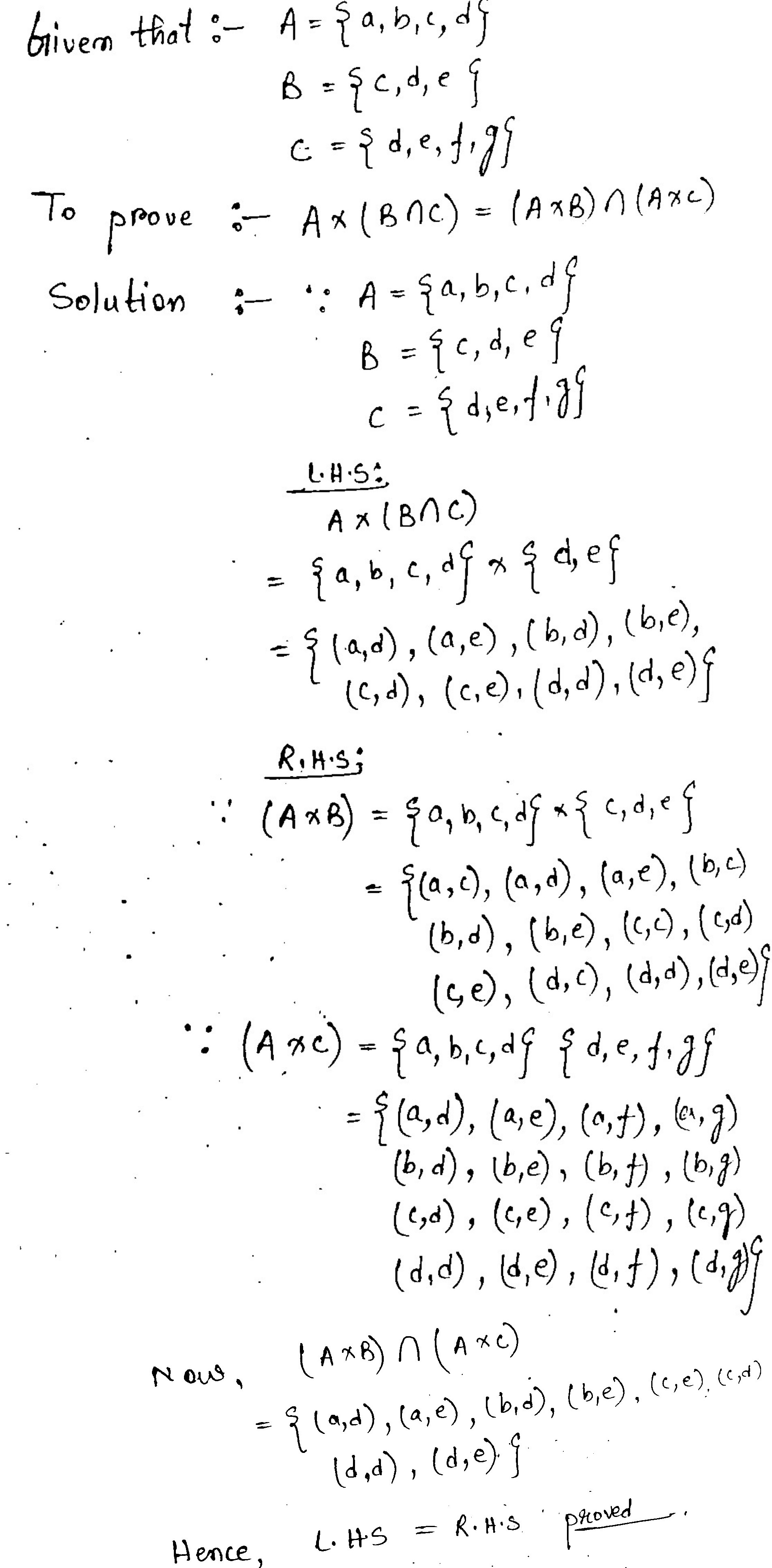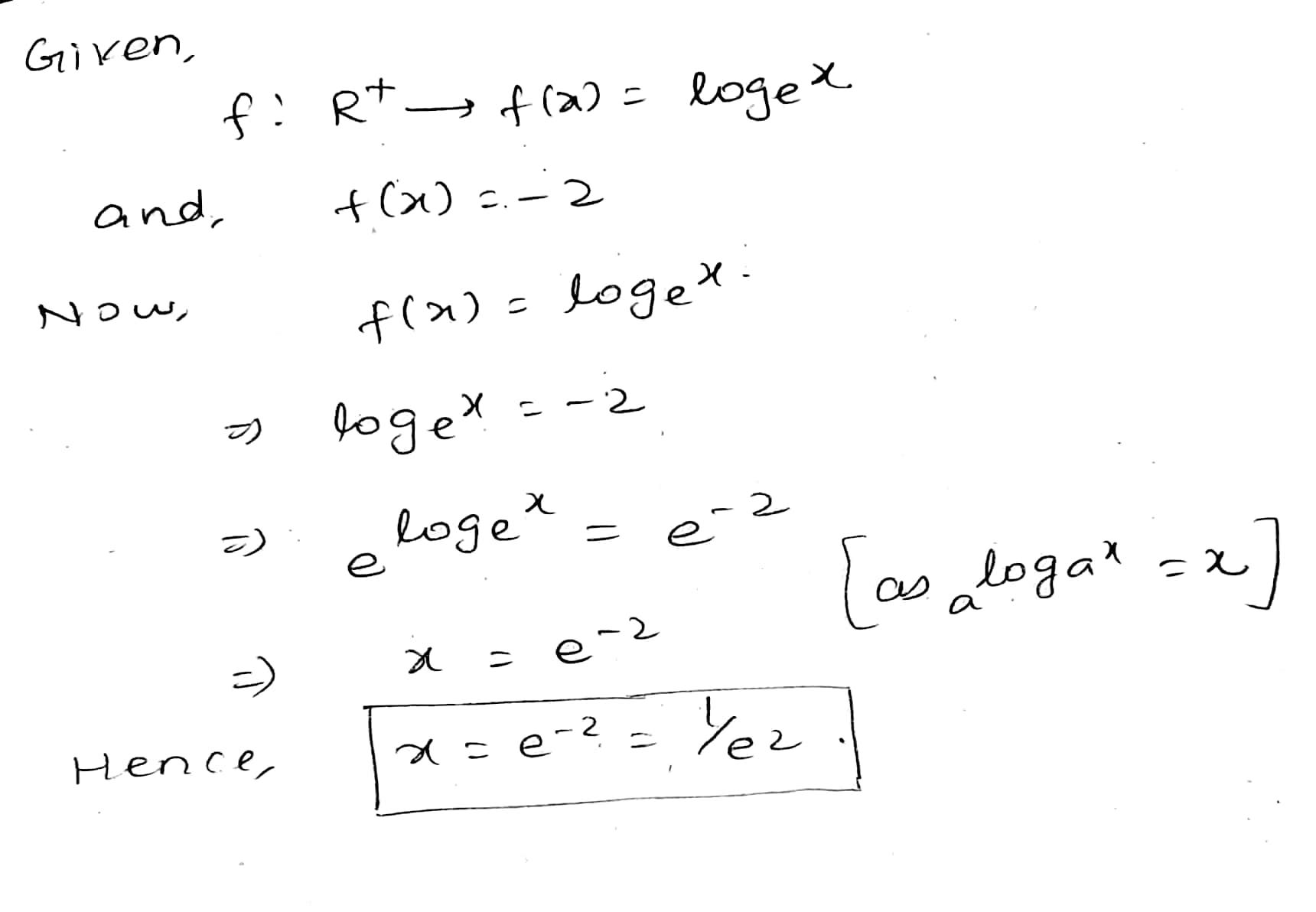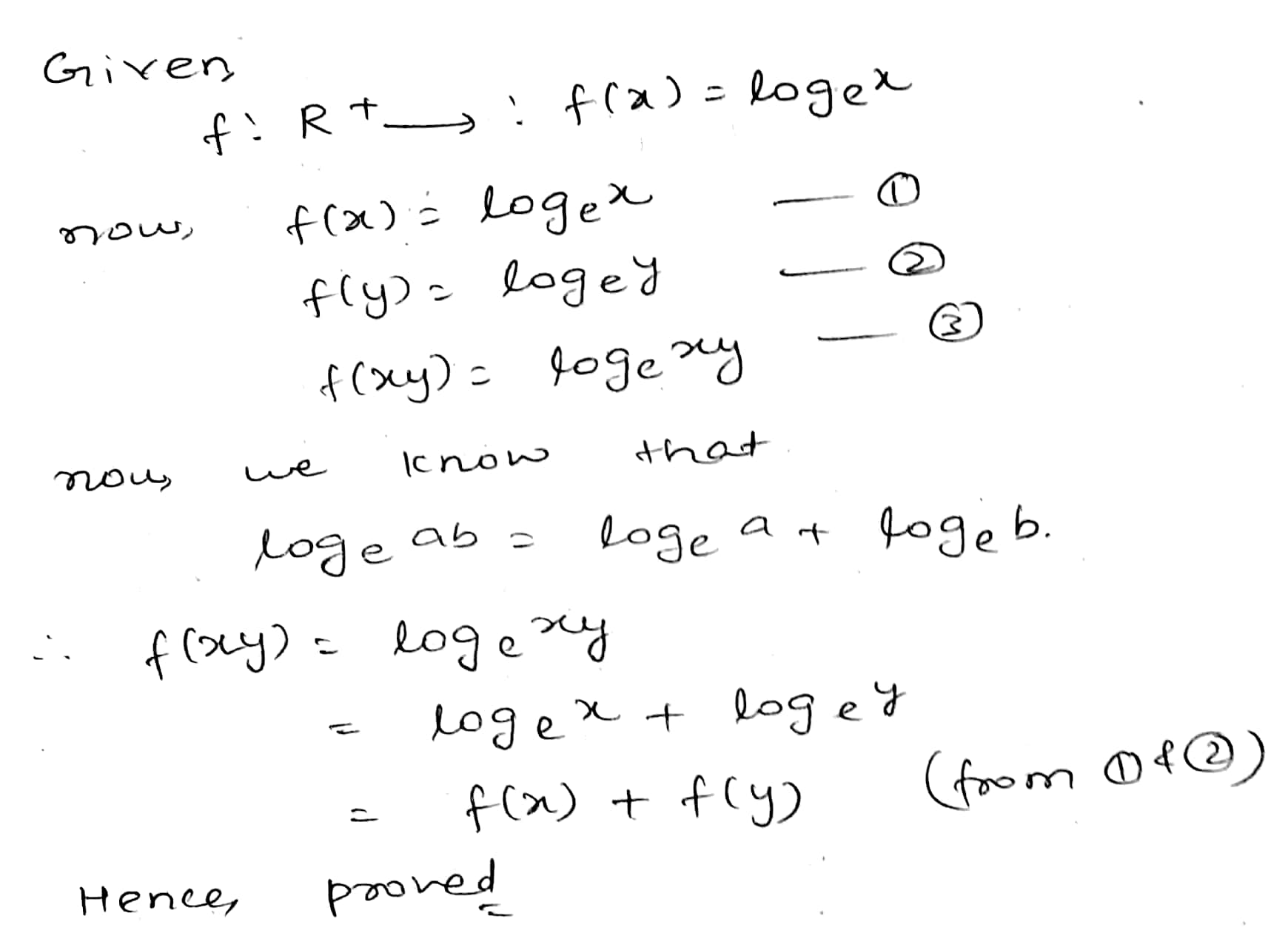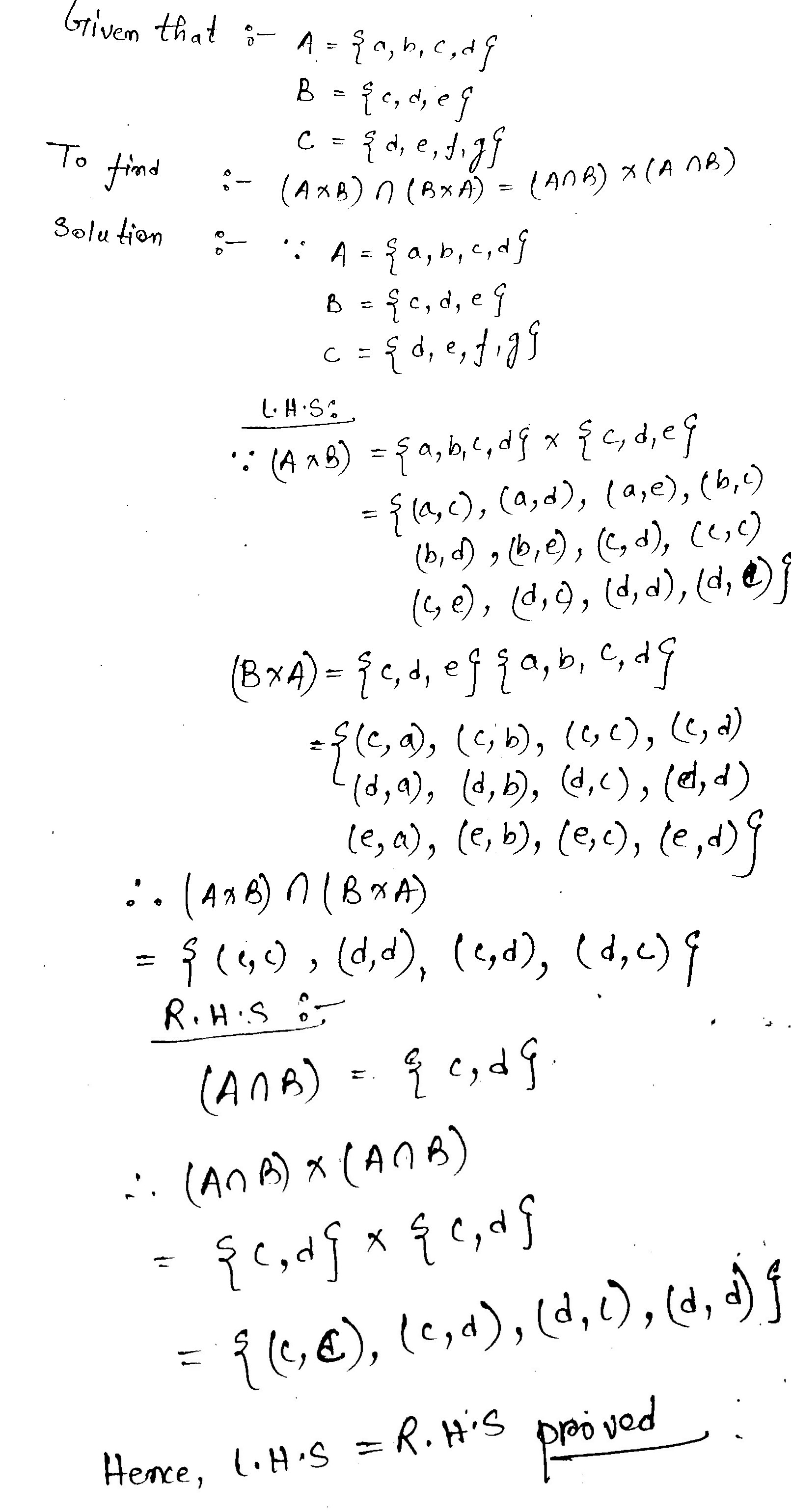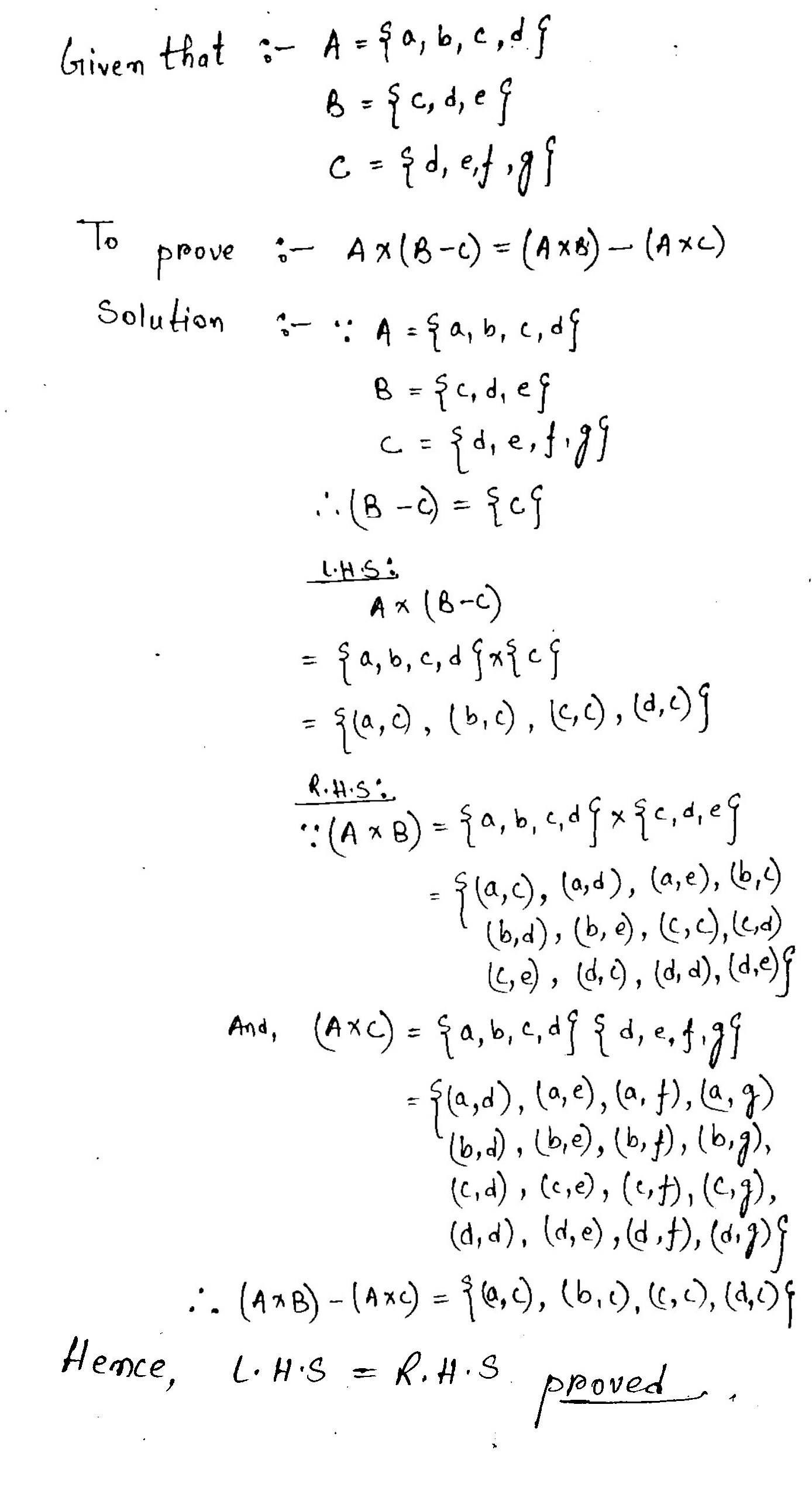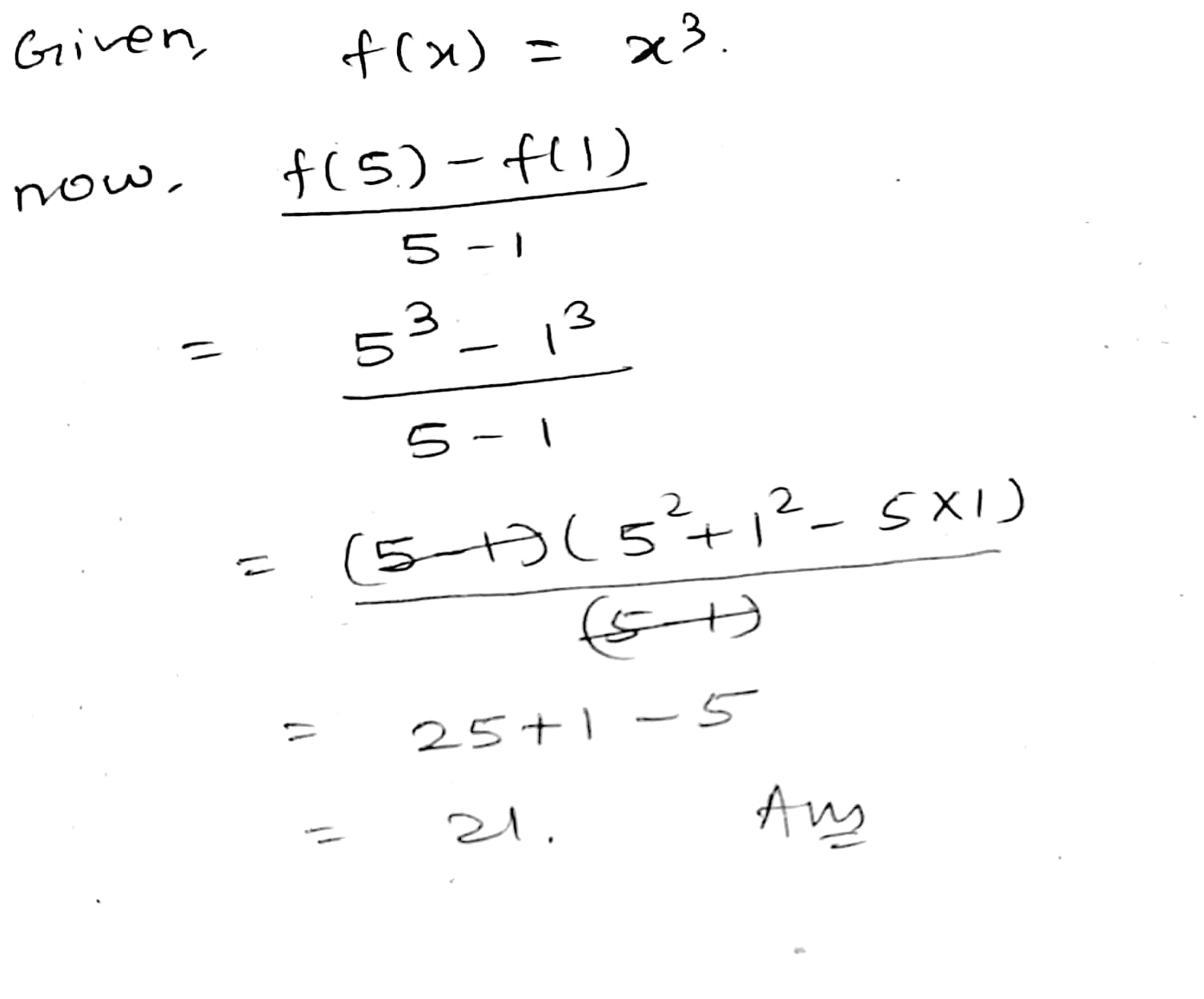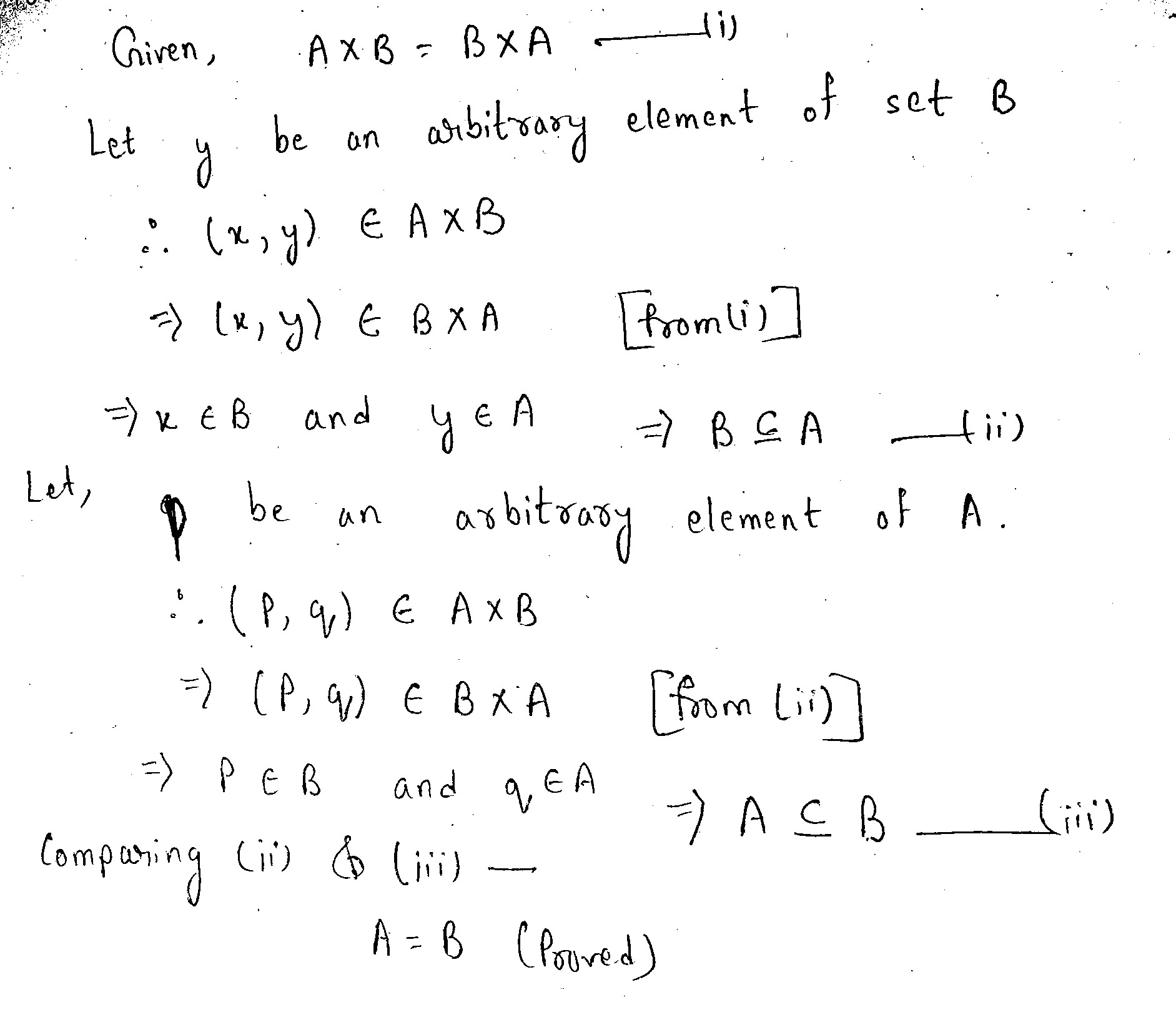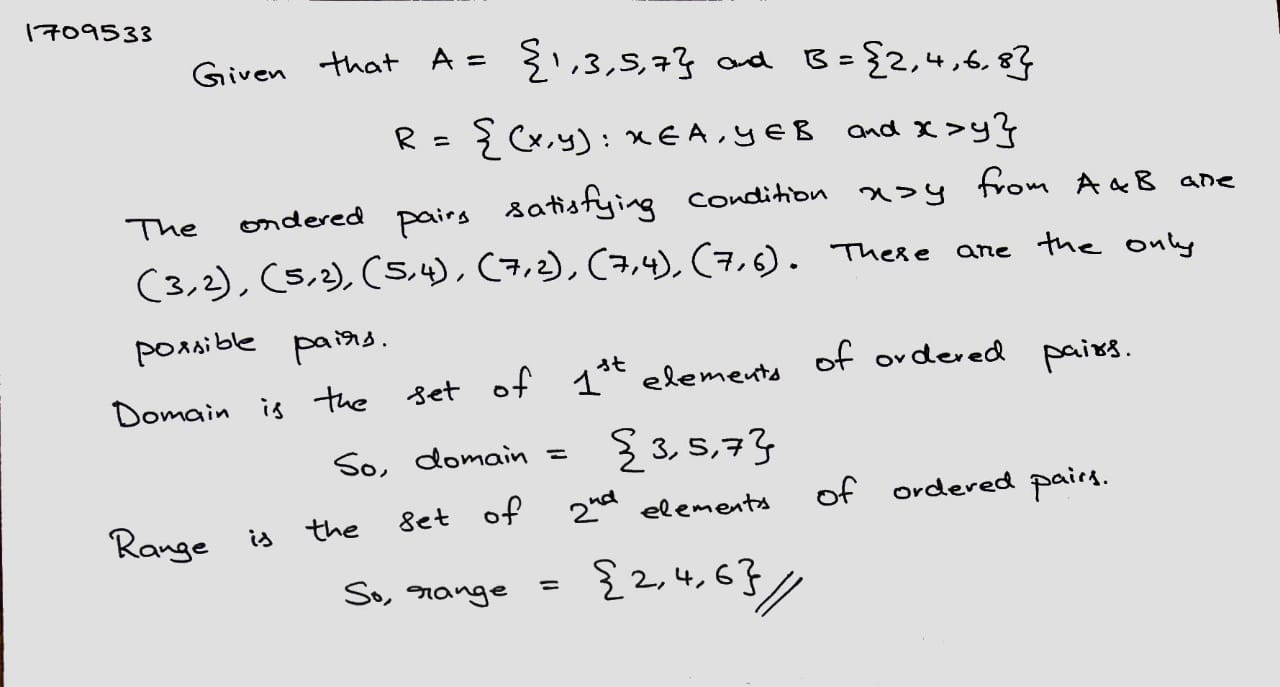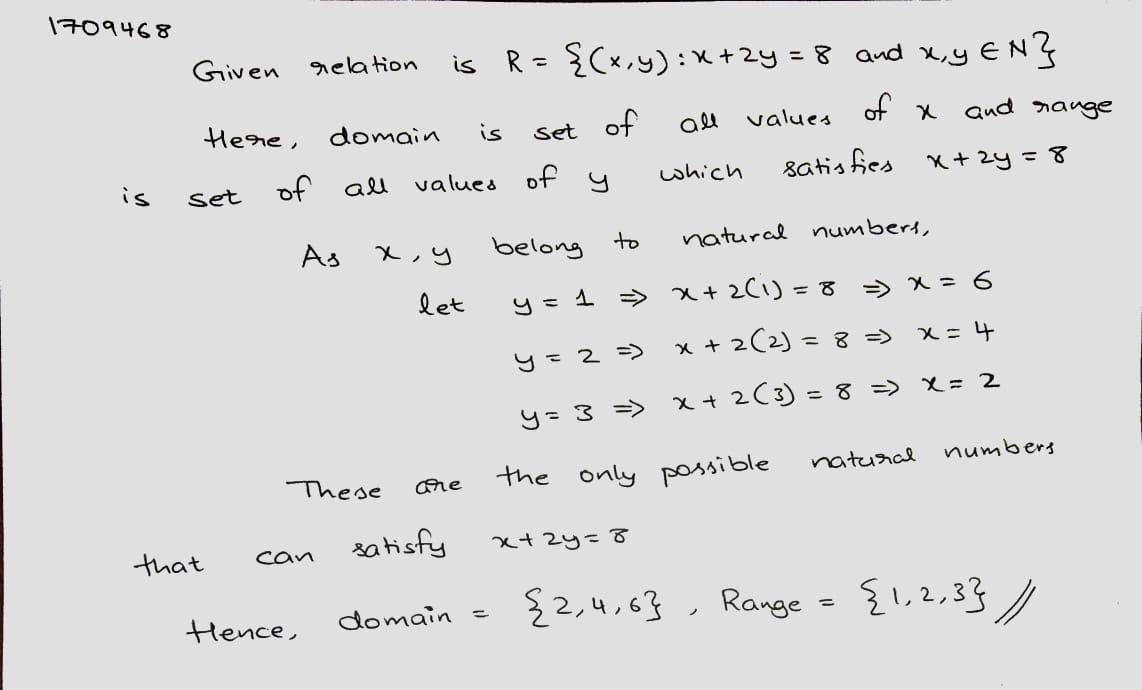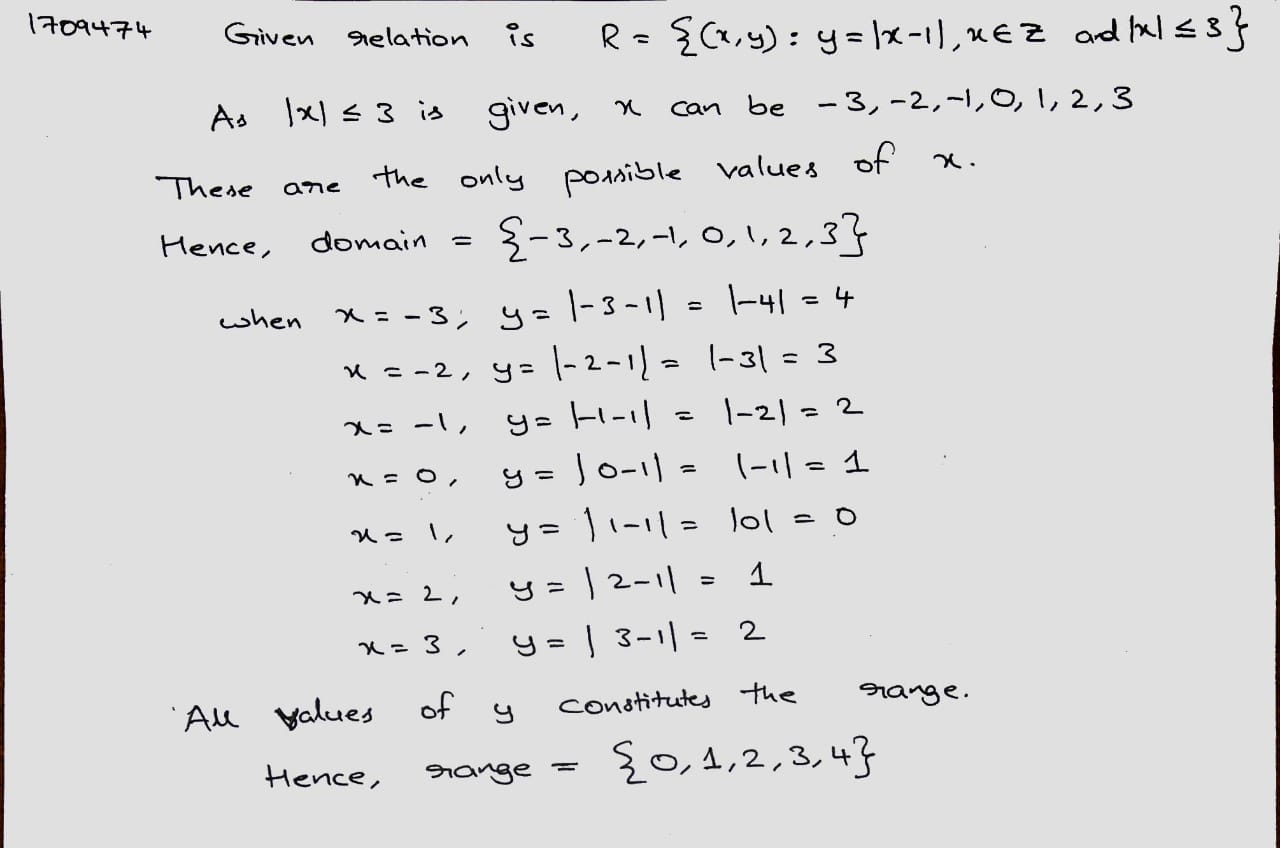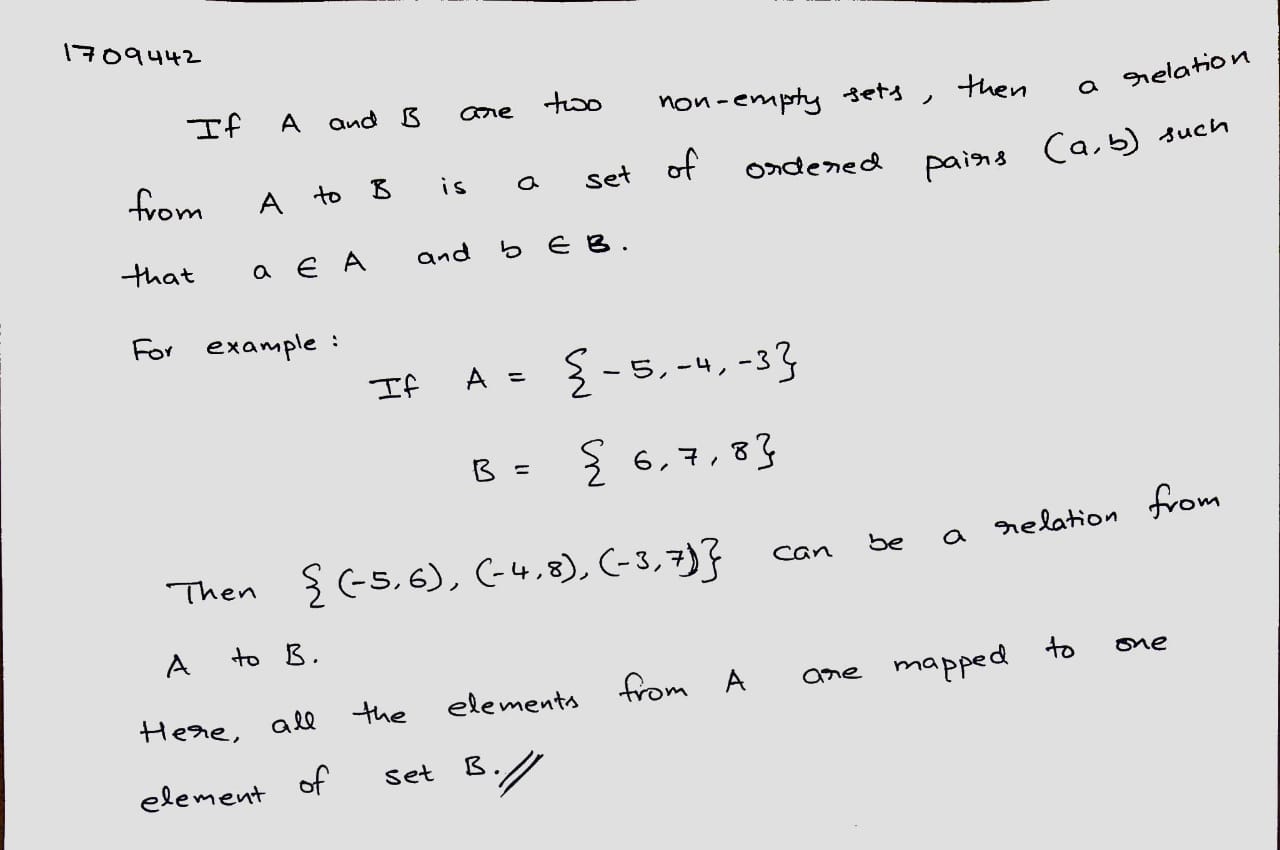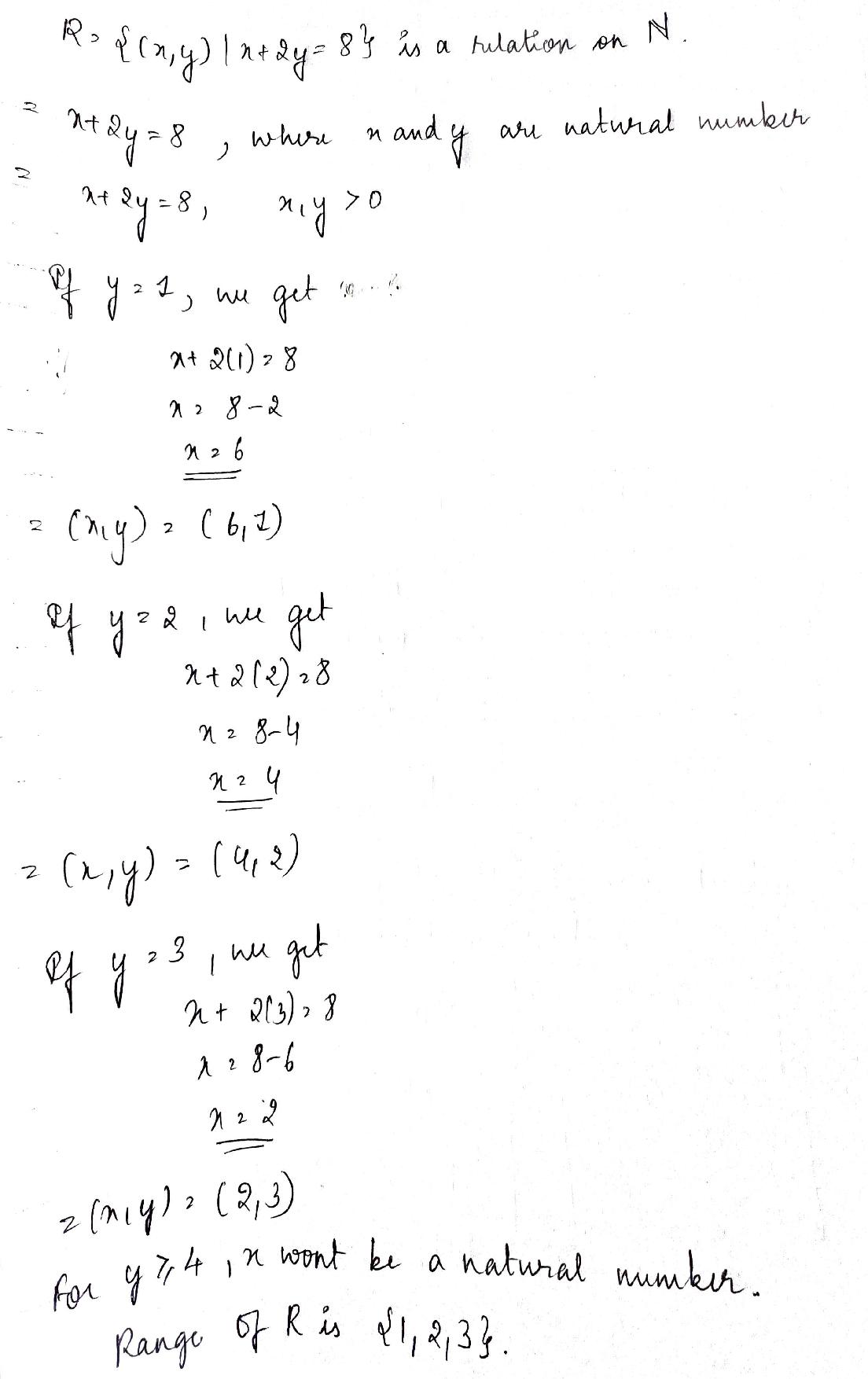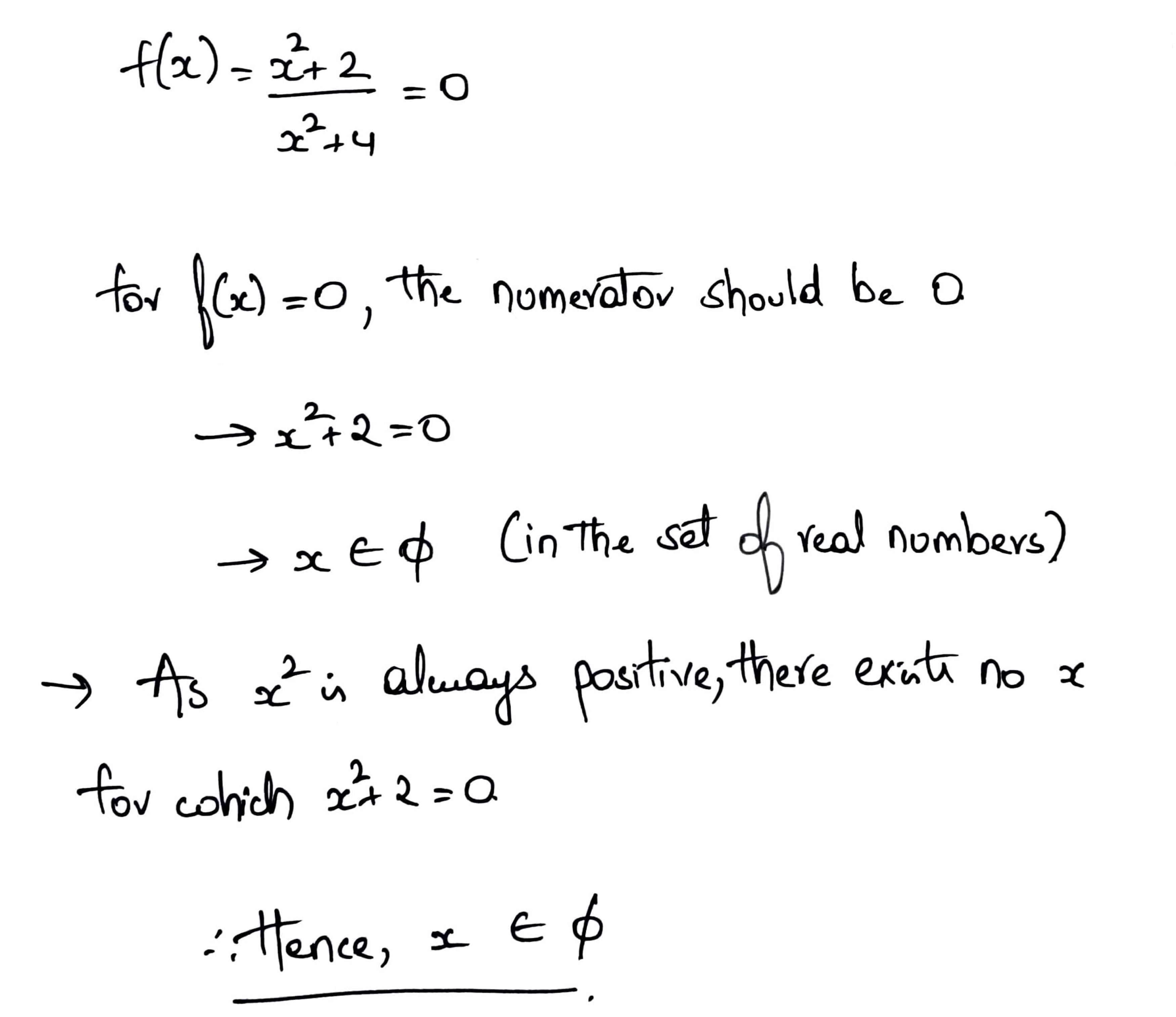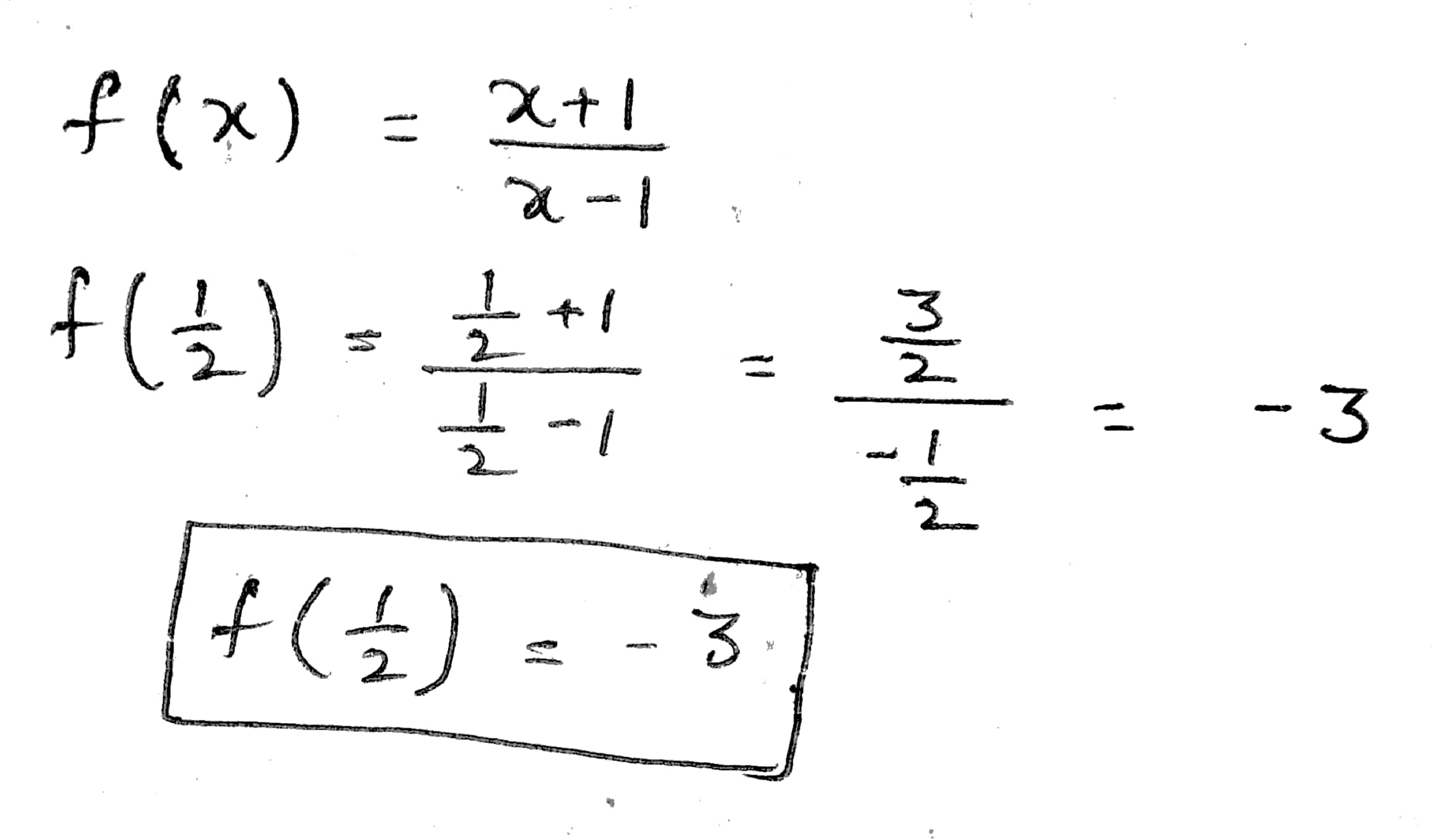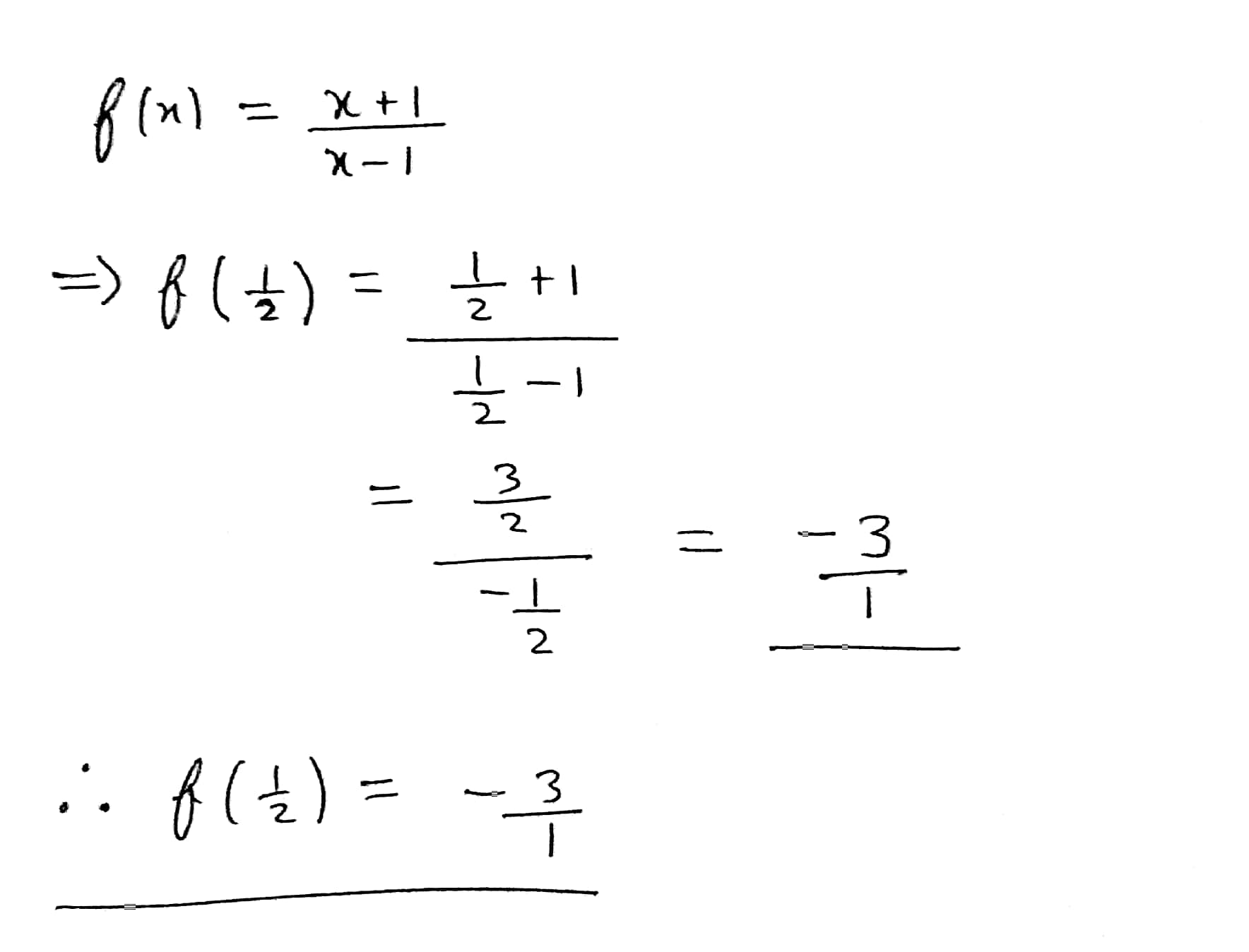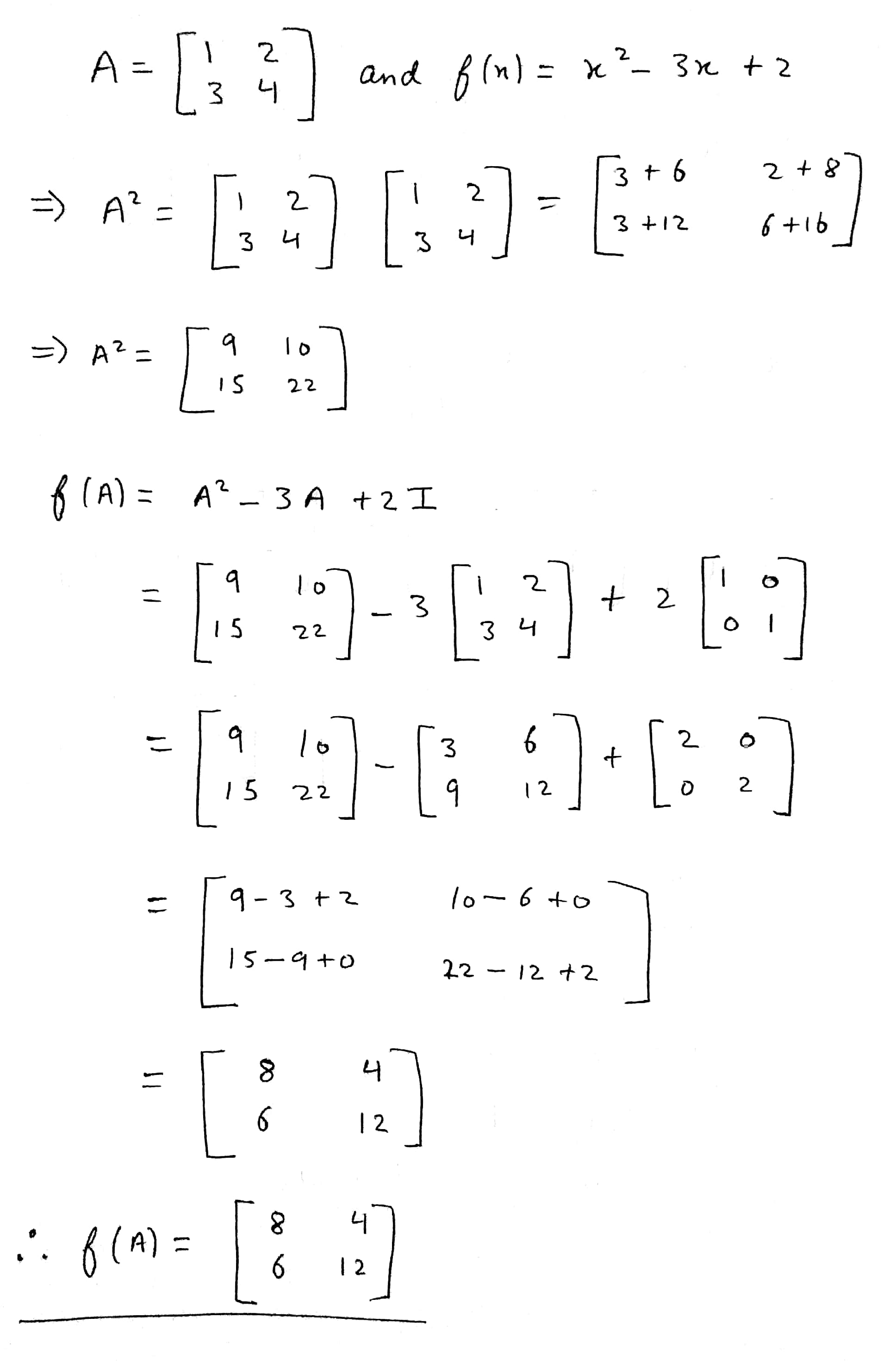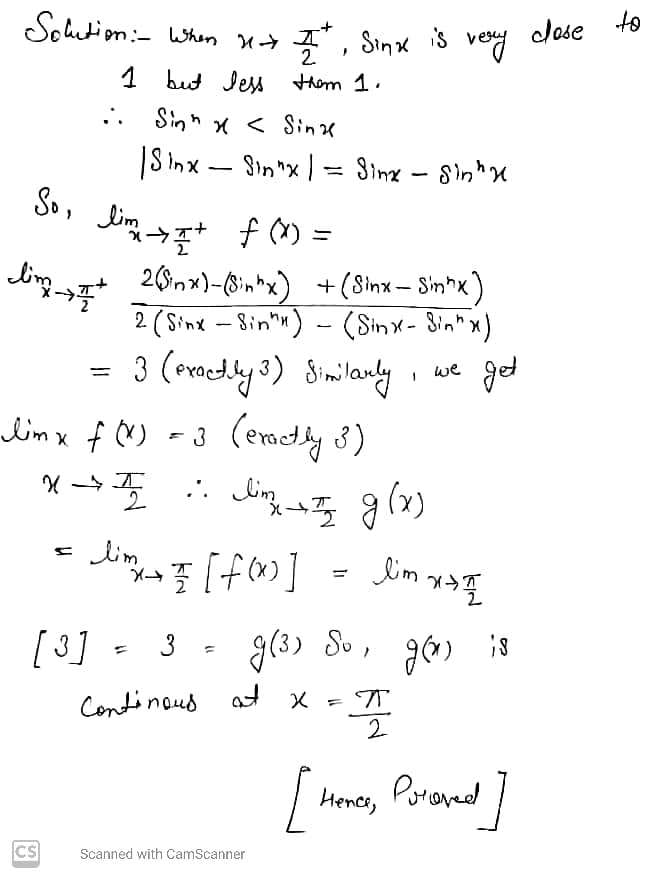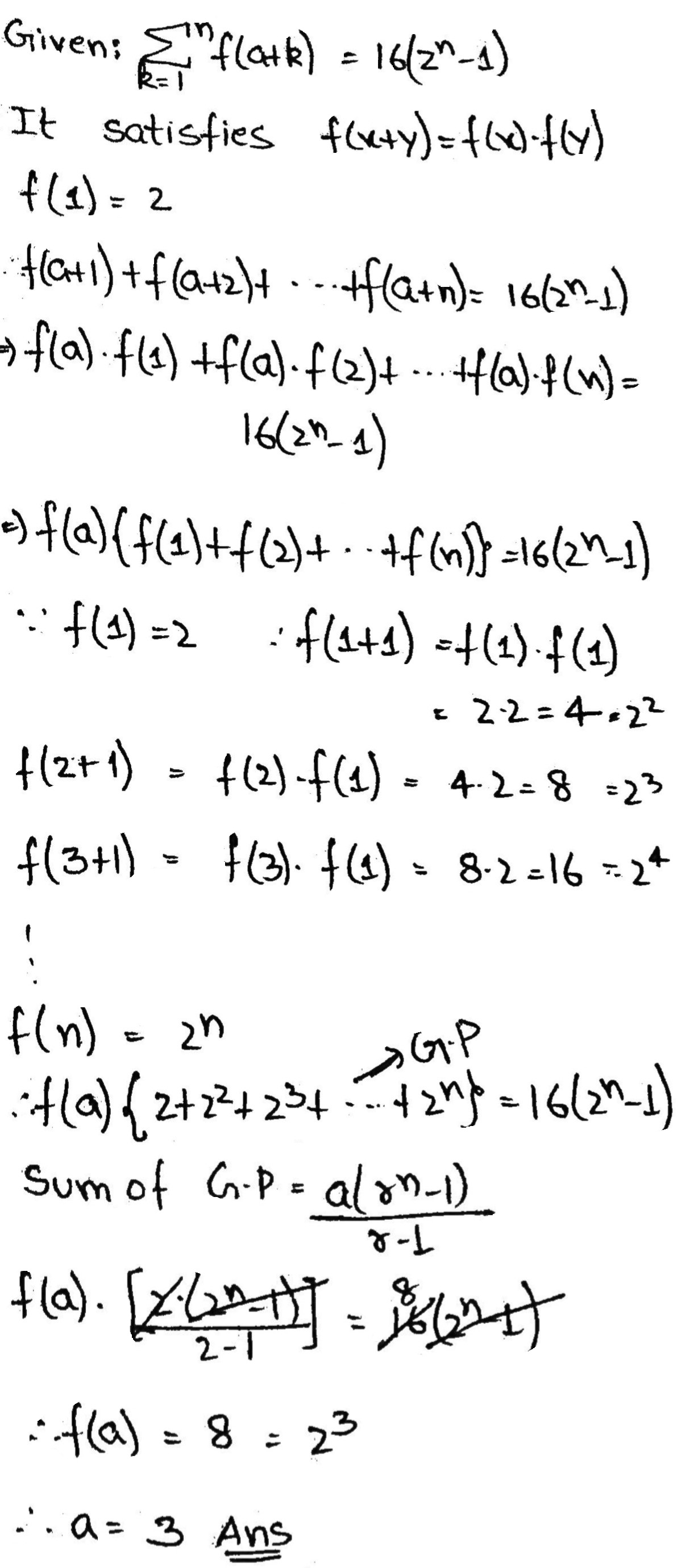Relations And Functions - Class 11 Engineering Maths - Extra Questions
$$\displaystyle f\left ( x \right )=1 $$ and $$ \phi \left ( x \right )=\sin ^{2}x+\cos ^{2}x.$$
Show that both functions are equal?
State whether the given statement is true or false. If true enter $$1$$ or else enter $$0$$.
$$(x, y)$$ is an ordered pair, whose first component is $$x$$ and the second component is $$y$$.
The cartesian product $$A\times A$$ has $$9$$ elements among which are found $$(-1, 0)$$ and $$(0, 1)$$. Find the set $$A$$ and the remaining elements of $$A\times A$$.
If $$x$$ is real, then find the solution set of $$\sqrt{x+1}+\sqrt{x-1}=1$$.
Use the elements of set A ={x, y, z} to form all possible ordered pairs. Find the number of elements in the ordered pair.
Given below are some points, with their co-ordinates.
$$P(4, 3), Q(-3, 2), R(5, 1), S(0, -4)$$ What is the $$y-$$coordinate of point $$R$$ ?
State whether each of the following statements are true or false. If the statement is false rewrite the given statement correctly
(i) If $$P = \{m, n\}$$ and $$Q = \{n, m\}$$ then $$\displaystyle P\times Q = \{(m, n), (n, m)\}$$
(ii) If $$A$$ and $$B$$ are non-empty sets then $$\displaystyle A\times B$$ is a non-empty set of ordered pairs $$(x, y)$$ such that $$\displaystyle x\in A$$ and $$\displaystyle y\in B$$
(iii) If $$A = \{1, 2\}, B = \{3, 4\}$$ then $$\displaystyle A\times \left ( B\cap \phi \right )=\phi $$
If $$\displaystyle \left ( \frac{x}{3}+1,y-\frac{2}{3} \right )=\left ( \frac{5}{3},\frac{1}{3} \right )$$ find the values of x and y
Find the number of ordered pairs in $$R o R$$ ?
$$A = \{1, 2, 3, 5\}$$ and $$B = \{4, 6, 9\}$$. Define a relation $$R$$ from $$A$$ to $$B$$ by $$R = \{(x, y):$$ the difference between $$x$$ and $$y$$ is odd $$\displaystyle x\in A, y\in B\}$$. Write $$R$$ in roster form
Let $$A = \{1, 2, 3, 4, 6\}$$ and $$R$$ be the relation on $$A$$ defined by $$\{(a, b): a, \displaystyle b\in A\ , b$$ is exactly divisible by $$a\}$$
(i) Write $$R$$ in roster form
(ii) Find the domain of $$R$$
(iii) Find the range of $$R$$
State whether the given statement is true or false. If true enter $$1$$ or else enter $$0$$. $$(x, y)$$ is an ordered pair whose components are $$x$$ and $$y$$.
Let $$A$$ and $$B$$ be two sets such that $$n(A) = 3$$ and $$n(B) = 2$$. If $$(x, 1), (y, 2), (z, 1)$$ are in $$\displaystyle A\times B$$ find $$A$$ and $$B$$ where $$x, y$$ and $$z$$ are distinct elements
Suppose $$3$$ bulbs are selected at random from a lot. Each bulb is tested and classified as defective $$(D)$$ or non-defective $$(N)$$. Write the sample space of this experiment?
Let $$A =\{x, y, z\}$$ and $$B = \{1, 2\}$$. Find the number of relations from $$A$$ to $$B$$.
Determine the domain and range of the relation $$R$$ defined by $$R = \{(x, x + 5) : \displaystyle x\in \{0, 1, 2, 3, 4, 5\}\}$$
Write the relation $$R = \{(x,\displaystyle x^{3}): x\mbox{ is a prime number less than 10}\}$$ in roster form
For the given function F= { (1, 3), (2, 5), (4, 7), (5, 9), (3, 1) }, write the domain and range.
If $$k$$ is given a real constant $$f(x)$$ is a real quadratic in '$$x$$ such that $$f(x + k) = f(-x)$$. The coefficient of $$x^2$$ is $$1$$. Find $$f(x)$$.
A function $$f : [-3, 7) \rightarrow R$$ is defined as follows
$$f(x)=\left\{\begin{matrix}4x^2-1; & -3 \leq x < 2 \\ 3x-2; & 2\leq x\leq 4 \\ 2x-3; & 4 < x < 7 \end{matrix}\right.$$
(i) $$f(5)+f(6)$$
(ii) $$ f(1)-f(3)$$
(iii) $$ f(-2)-f(-4)$$
(iv) $$\dfrac{f(3)+f(1)}{2f(6)-f(1)}$$
Let R be a relation from A = {1,2,3,4} to B = {1,3,5} i.e. (a,b) $$\epsilon$$ R if a < b then find R o $$R^{-1}$$
If $$G=\left\{ 7,8 \right\} $$ and $$H=\left\{ 5,4,2 \right\} $$, find $$H\times G$$.
Let $$S=\{1,2,3\}$$ and a relation $$R$$ is defined by $$aRb$$ iff $$a=b$$ then find $$R$$.
If $$f(x)=\log_e\sec x$$ and $$\phi(x)=\log_e\tan x$$ then prove that $$e^{2f(x)}-e^{2\phi(x)}=1$$.
Find the domain of definations of the following functions:
$$f(x)=\sqrt {1-\sqrt {1-x^{2}}}$$
Let $$A = \left\{ {1,2,3,4} \right\}$$ and $$R$$ is a relation on $$A$$ such that $$R = \left\{ {\left( {a,b} \right):a = 2b} \right\}$$
If $$A = \{a, b, c\}$$ , $$B = \{1, 2\}$$ , then find $$A \times B , \, B \times A \, and \, A \times A$$
If the relation $$R: A \rightarrow B$$ where $$A = \{1, 2, 3, 4\}, B = \{1, 3, 5\}$$ is defined by $$R = \{(x, y): x < y, x \in A, y \in B\}$$ then find $$R$$ and $$R^{-1}$$.
If $$P = \{a , b\}$$ and $$Q = \{x, y, z\}$$, show that $$P \times Q \neq Q \times P.$$
Let $$A=\{1,-1\}$$. Then find $$A\times A$$.
Given $$R = \{(x, y): x, y \in W, x^2 + y^2 = 25\}$$, where $$W$$ is the set of all whole numbers. Find the domain and range of $$R$$.
If $$R = \{(x, y)|y = 2x + 7|$$, where $$x \in R$$ and $$-5 \le x \le 5\}$$ is relation, find the domain of $$R$$.
If $$f(x) = x + (1/x)$$, show that $$\{f(x)\}^3 = f(x^3) + 3f(1/x)$$
If $$A = \{0, 1\}$$ and $$B = \{1, 2, 3\}$$, show that $$A \times B \neq B \times A$$
Let $$A = \{1, 2, 3\}$$. Find the number of relations from $$A$$ to $$A.$$
The Cartesian product $$P\times P$$ has $$16$$ elements among which two elements are $$(a,b)$$ and $$(c,d)$$. Find the set $$P$$ and the remaining elements of $$P\times P$$
If $$\dfrac{1}{{\left| a \right|}} > \dfrac{1}{b}$$, then $$\left| a \right| < b$$, where a & b are non-zero real numbers.
Let A = {1,2} and B = {3,4}. Find the number of relations from A to B.
Find the domain and range of the following real functions:
i) $$f(x) = -|x|$$
ii) $$f(x) = \sqrt{9 - x^2}$$
If $$f\left( x \right) = {x^3} - \frac{1}{{{x^3}}}$$, prove that $$f\left( x \right) + f\left( {\frac{1}{x}} \right) = 0$$
Find domain and range of
$$R = \{ (a, b) / a \in N, \, \, \, a < 5 \, \, \text{ and} \, \, b = 2\}$$
If $$A=\left\{ 3,4 \right\} \quad and\quad B=\left\{ 1,2 \right\} $$ then of $$A\times B$$ is .
Determine the domain and the range of the relation $$R$$ defined by $$R=\{ \left( x+1,\quad x+5 \right) :x\in \{ 0,\quad 1,\quad 2,\quad 3,\quad 4,\quad 5\}\}$$
$$R=\{(x+1), x+5\}$$
$$D_f\in R\{0, 1, 2, 3, 4, 5\}$$
$$R_f\in \{(1, 2, 3, 4, 5, 6), (5, 6, 7, 8, 9, 10)\}$$.
Show that the relation $$R$$ in the set $$Z$$ of integers given by
$$R=\left\{(a,b):2\ divides\ a-b\right\}$$
$$2\left \{ (a,b)=2 divides a=b \right \}$$
where R is in set 2 of integers
a-a=0
2 divides a-a
$$\Rightarrow (a,a)\epsilon R$$ $$\therefore R$$ is reflexive
Let $$(a,a)\epsilon R$$
$$\therefore 2$$ divides $$a-b\Rightarrow a-b=2n$$
for same $$n\epsilon z\Rightarrow b-a=2(-n)$$
$$\Rightarrow $$ 2 divides $$b-a=(b,a)\epsilon R$$
R is symmetric
Let (a,b) & $$(b,c)\epsilon R$$
2 divides a-b & b-c
$$\therefore a-b=2n$$ & $$b-c=2n_{2}$$
for same $$n_{1},n_{2}\epsilon 2$$
$$=2n_{1}+2n_{2}=a-c=2(n_{1}+n_{2})$$
$$\therefore 2$$ divides a-c
$$(a,c)\epsilon R$$
$$\therefore (a,b)(b,c)\epsilon R\Rightarrow (a,c)\epsilon R$$
$$\therefore R$$ is transitive
So, R is an equivalence relation
If $$ p(x)=ix^2+5x+8$$, then $$p{(-1)}$$=
The value of $$x$$ satisfying the equation $$-3(x+6)=24$$ ?
Let $$f:R\rightarrow R$$ be defined as $$f(x)=10x+7$$. Find the function $$g:R\rightarrow R$$ such that $$gof=fog=I_{R}$$.
If $$f(x)=\cfrac{\sin{([x]\pi)}}{{x}^{2}+x+1}$$, where $$[x]$$ denotes the integral part of $$x$$. Show that $$f(x)$$ is a constant function.
If $$A=\left\{1,2\right\}$$, form the set $$A\times A\times A$$.
If $$A = \left\{ {1,2} \right\},B = \left\{ {x:x \in N\,\,and\,\,{x^2} - 9 = 0} \right\},$$ Find $$A \times B.$$
If $$A\times B=\left\{\left(a,1\right),\left(b,3\right),\left(a,3\right),\left(b,1\right),\left(a,2\right),\left(b,2\right)\right\}$$.Find $$A$$ and $$B$$
Find $$x$$ and $$y$$ if $$\left(x+3,5\right)=\left(6,2x+y\right)$$
Let $$R$$ be relation from $$Q$$ to $$Q$$ defined by $$R=\left\{(a,b):a,b\ \in \ Q\ and\ a-b\ \in \ Z\right\}$$.
Show that :
$$(a,b)\ \in \ R$$ implies that $$(b,a)\ \in \ R$$.
If $$(a, b)\in R$$
$$\Rightarrow a-b$$ is an integer, then $$b-a$$ would also be an integer being $$-(a-b)$$
$$\Rightarrow b-a$$ also $$\in Z\Rightarrow (b, a)\in R$$.
Find the relations between $$a$$ and $$b$$, so tat the function $$f$$ defined by:
$$f\left( x \right)=\begin{cases} ax+1, \\ bx+3, \end{cases}\begin{matrix} if\ x\le 3 \\ if\ x>3 \end{matrix}$$
is continuous at $$x=3$$.
If $$A=\left\{a,b\right\}$$ and $$B=\left\{1,2,3\right\}$$ find $$\left(A\times B\right)\cap\left(B\times\,A\right)$$
The cartesian product $$A\times A$$ has $$9$$ elements among which are found $$\left(-1,0\right)$$ and $$\left(0,1\right)$$.Find the set $$A$$ and the remaining elements of $$A\times A$$
If $$A=\left\{1,3,5,6\right\}$$ and $$B=\left\{2,4\right\}$$.Find $$A\times\,B$$ and $$B\times \,A$$
Let $$R$$ be relation from $$Q$$ to $$Q$$ defined by $$R=\left\{(a,b):a,b\ \in \ Q\ and\ a-b\ \in \ Z\right\}$$.
Show that :
$$(a,b)\ \in \ R$$ and $$(b,c)\ \in R$$ implies that $$(a,c)\ \in \ R$$.
$$(a, b)\in R\Rightarrow a-b\in Z$$
$$(b, c)\in R\Rightarrow b-c\in Z$$
$$\Rightarrow (a-c)=(a-b)+(b-c)$$ being sum of two integers is also a integer
$$\Rightarrow (a-c)\in z\Rightarrow (a, c)\in R$$.
Find the values of $$a$$ and $$b$$ if $$\left(3a-2,b+3\right)=\left(2a-1,3\right)$$
If $$A=\left\{a,b\right\}$$ and $$B=\left\{1,2,3\right\}$$ find $$A\times A$$ and $$B\times\,B$$
List the relation R defined by $$R=\left \{ (a,b):a\leq b^{3} \right \}$$ in Roaster form. $$a,b \in N$$
If $$A=\left\{a,b\right\}$$ and $$B=\left\{1,2,3\right\}$$ find $$A\times B$$ and $$B\times\,A$$
Let $$R=\left\{ \left( a,{ a }^{ 3 } \right) :\text{a is a prime number less than }\ 5 \right\} $$ be a relation. Find the range of $$R$$.
Write the domain of the relation $$R$$ defined on the set $$\mathbb{Z}$$ of integers as follows:
$$(a,b)\in R\Leftrightarrow {a}^{2}+{b}^{2}=25$$
If $$R=\left\{ (x,y):x+2y=8 \right\} $$ is a relation on $$N$$, then write the range of $$R$$.
If $$R=\left\{ (x,y):{ x }^{ 2 }+{ y }^{ 2 }\le 4;x,y\in \mathbb{Z} \right\} $$ is a relation on $$\mathbb{Z}$$, write the domain of $$R$$.
Write the identity relation on set $$A=\left\{ a,b,c \right\} $$.
Find the domain and range of each of the following real value functions:
$$f(x)= |x-1|$$
There are four men and six women on the city councils. If one council number is selected for a committee at random, how likely that it is a woman
Enter 1 if it is true else enter 0.For the relation $$\displaystyle R = \{ (-1, 1), (1, 1), (-2, 4), (2, 4), (3, 9)\}$$ is dom $$\displaystyle (R) = \{-2, -1, 1, 2, 3\}$$ and range $$\displaystyle (R) = \{1, 4,9\}$$.
Let the relation $$R$$ be defined in $$N$$ by $$aRb$$ if $$2a+3b=30$$. Then $$R=$$ ....
Let the relation $$R$$ be defined on the set $$A=\left\{ 1,2,3,4,5 \right\} $$ by $$R={(a,b):a^2b^2 < 8}.$$ Then $$R$$ is given by ______.
For the set $$A=\left\{1,2,3\right\}$$, define a relation $$R$$ in the set $$A$$ as follows:
$$R=\left\{(1,1),(2,2),(3,3),(1,3)\right\}$$
Write the ordered pairs to be added to $$R$$ to make it the smallest equivalence relation.
Let $$R$$ relation defined on the set of natural number $$N$$ as follows:
$$R=\left\{(x,y): x\in \ N, y\in \ N, 2x+y=41\right\}$$. Find the domain and rang of the relation $$R$$. Also verify $$R$$ is reflexive, symmetric and transitive.
If $$R$$ be a relation $$<$$ from $$A=\{1,2,3,4\}$$ to $$B=\{1,3,5\}$$ i.e., $$(a,b) \in$$ R if $$a<b$$, then find $$ROR^{-1}$$
Let $$A=\left \{ 1, 2, 3, 4 \right \}$$ and $$B=\left \{ x, y, z \right \}$$. Consider the subset $$R=\left \{ (1, x),(1,y),(2,z),(3,x) \right \}$$of $$A\times B.$$ Is R, a relation from A to B? If yes, find domain and range of R. Draw arrow diagram of R and represent R in a tabular form.
If $$f: R\rightarrow R$$ defined by $$f(x)=x^2+1$$, then the values of $$f^{-1}(17)$$ are a and b, then a+b =?
For each set of ordered pairs below, state whether it is a function or not give reasons(i){(3, 2), (4, 2), (5, 2)}
if a function enter 1 else 0
if a function enter 1 else 0
If $$x, y\in \left [ 0, 2\pi \right ]$$, then find the total number of ordered pairs $$\left ( x, y \right )$$ satisfying the equation $$\sin x\cos y=1$$
Let a relation R be defined by
$$\displaystyle R= \left \{ \left ( 4,5 \right ), \left ( 1,4 \right ), \left ( 4,6 \right ), \left ( 7,6 \right ), \left ( 3,7 \right ) \right \}$$ then find $$\displaystyle R o R$$
Given a relation $$\displaystyle R=\left \{ \left ( 1,2 \right ),\left ( 2,3 \right ) \right \}$$ on the set of natural numbers,Find the minimum number of ordered pairs should be added so that the enlarged relation is symmetric,transitive and reflexive.
Use elements of set P = {2 , 3} to find the number of all possible ordered pairs.
Let $$A$$ and $$B$$ be two sets such that $$\displaystyle A\times B$$ Consists of $$6$$ elements. If three elements of $$\displaystyle A\times B$$ are $$\displaystyle \left ( 1,4 \right ),\left ( 2,6 \right ),\left ( 3,6 \right )$$ then $$\:B\times A$$. is $$=\left \{ \left ( a,1 \right ),\left ( 6,1 \right ),\left ( 4,d \right ),\left ( c,2 \right ) ,\left ( 4,3 \right )\left ( b,3 \right )\right \}$$. Find $$a+b+c+d$$
Given $$A = \{5, 6, 7\}$$ and $$B = \{3, 4\}$$. Form all possible ordered pairs and write the total number of ordered pairs formed so that both the components are from B.
Let $$A = \{1, 2\}$$ and $$B = \{2, 3, 4\}$$.If $$ B \times B= \{(2,2), (2,3),(2, 4), (3,2), (3,3), (3,4) , (4,2), (4,3), (4,4)\}$$. Please enter $$1$$ or else $$0$$.
Please enter $$1$$ or else $$0$$.
Let $$A = \{1, 2\}$$ and $$B = \{2, 3, 4\}$$, then $$B \times A=\{(2,1),(2,2), (3,1), (3,2),(4,1),(4,2)\}$$. If true enter $$1$$, or else enter $$0$$.
Let $$A = \{1, 2\}$$ and $$B = \{2, 3, 4\}$$, then $$ A \times A = \{ (1,1), (1,2),(2,1), (2,2)\}$$. If true enter $$1$$, or else enter $$0$$.
Let $$A = \{1, 2\}$$ and $$B = \{2, 3, 4\}$$, then $$ A \times B = \{ (1,2), (1,3),(1, 4), (2,2), (2,3), (2,4) \}$$. If true enter $$1$$, or else enter $$0$$.
Given $$A = \{5, 6, 7\}$$ and $$B = \{3, 4\}$$. Form all possible ordered pairs and write the total number of ordered pairs formed. So that :
Both the components are from AFind the total number of such pairs.
If $$A = \{x, y\}$$ and $$B = \{y, x\}$$ ; then $$A \times B = ?$$ What are the number of elements of such set?
If $$A =$$ {$$x$$ : $$x \,\,\in\,\, W$$, $$3 \leq x < 6$$}, $$B = \{3, 5, 7\}$$ and $$C = \{2, 4\}$$; find : $$(A - B) \times C$$
If P = {a, b, c} and Q = {b, c, d} ; find number of elements in $$(P \cap Q) \times P$$
Given $$A = \{ x \in W : 7 \le x \leq 10 \}, $$ find $$ A \times A.$$
If $$M=\{x : x \,\,\epsilon\,\, N, 1 < x \leq 4\}$$ and $$N = \{y : y\,\,\epsilon\,\,W, y < 3\}$$; Find: $$n(N$$ $$\times$$ $$N$$).
Given $$M = (0, 1, 2)$$ and $$N = (1, 2, 3)$$. Find $$(M \cup N)\times (M - N)$$
If $$M=\{x : x \,\,\epsilon\,\, N, 1 < x \leq 4\}$$ and $$N = \{y : y\,\,\epsilon\,\,W, y < 3\}$$; find M $$\times$$ N :Also find the number of such ordered pairs.
$$\displaystyle R_{4}= \left \{ \left ( 1,3 \right ), \left ( 2,5 \right ), \left ( 4,7 \right ), \left ( 5,9 \right ), \left ( 3,1 \right ) \right \}$$
Is it a mapping?
If it is true enter 1, else enter 0.
Given ordered pairs : (5, 4), (5, 5), (5, 6), (6, 4), (6, 5), (6, 6), (6, 7), (8, 4), (8, 5), (8, 6), (8,8).Use these ordered pairs to find the following relation :$$R_4$$ = "is greater than"
Given ordered pairs : (5, 4), (5, 5), (5, 6), (6, 4), (6, 5), (6, 6), (6, 7), (8, 4), (8, 5), (8, 6), (8,8).
Use these ordered pairs to find the following relation :
Given ordered pairs : (5, 4), (5, 5), (5, 6), (6, 4), (6, 5), (6, 6), (6, 7), (8, 4), (8, 5), (8, 6), (8,8).Find the ordered pair(s) from above given list which satisfies the following relation.$$R_3$$ = "is one less than"
Given ordered pairs : (5, 4), (5, 5), (5, 6), (6, 4), (6, 5), (6, 6), (6, 7), (8, 4), (8, 5), (8, 6), (8,8).
Find the ordered pair(s) from above given list which satisfies the following relation.
Given A = {8, 9, 10, 12}, B = {2, 3, 4, 5} and the relation R from A to B means : "is multiple of" :
Write the domain range of relation R.
Let $$\displaystyle A=\left \{ 1,2,3,4,5 \right \},B=\left \{ 1,3,5,7,9,10,17,26,30 \right \}$$ Which of the following sets of ordered pairs are (i) relations (ii) functions (iii) neither,from A to B
(a)$$\displaystyle R_{1}=\left \{ \left ( 1,3 \right ),\left ( 3,3 \right ),\left ( 5,17 \right ) ,\left ( 1,2 \right )\right \}$$
(b) $$\displaystyle R_{2}=\left \{ \left ( 3,7 \right ),\left ( 4,5 \right ),\left ( 5,30 \right ) \right \}$$
(c) $$\displaystyle R_{3}=\left \{ \left ( x,y \right ):x \epsilon A,y \epsilon B,x+y=8 \right \}$$
(d) $$\displaystyle R_{4}=\left \{ \left ( x,y \right ):x \epsilon A,y\epsilon B,y=x^{2}+1 \right \}$$ (e)$$\displaystyle R_{5}=\left \{ \left ( x,y \right ):x\epsilon A,y\epsilon B,y=2x-1 \right \}$$
Find the number of ordered pairs in $$\displaystyle R^{-1} o R.$$
Write the relation, represented by the arrow diagram given below, in roster form. Also, write the domain and range of the relation.
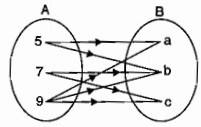
Given ordered pairs : (5, 4), (5, 5), (5, 6), (6, 4), (6, 5), (6, 6), (6, 7), (8, 4), (8, 5), (8, 6), (8,8).Use these ordered pairs to find the following relation :$$R_2$$ = "is equal to"
Given ordered pairs : (5, 4), (5, 5), (5, 6), (6, 4), (6, 5), (6, 6), (6, 7), (8, 4), (8, 5), (8, 6), (8,8).
Use these ordered pairs to find the following relation :
Given ordered pairs : (5, 4), (5, 5), (5, 6), (6, 4), (6, 5), (6, 6), (6, 7), (8, 4), (8, 5), (8, 6), (8,8).Use these ordered pairs to find the following relation :$$R_1$$ = "is less than"
Given ordered pairs : (5, 4), (5, 5), (5, 6), (6, 4), (6, 5), (6, 6), (6, 7), (8, 4), (8, 5), (8, 6), (8,8).
Use these ordered pairs to find the following relation :
Let $$f$$ be a function from the set of positive integers to the set of real number such that
(i) $$f(1)=1$$
(ii) $$\displaystyle \sum_{r=1}^{n} rf(r) =n(n+1)f(n),\forall n\geq 2$$
then find the value of $$2126 f(1063)$$
Let $$\displaystyle f\left ( x \right )=\frac{9^{x}}{9^{x}+3}$$. Show $$f(x)+f(1-x)=1$$, and hence evaluate $$\displaystyle f\left ( \frac{1}{1996} \right )+f\left ( \frac{2}{1996} \right )+f\left ( \frac{3}{1996} \right )+...+f\left ( \frac{1995}{1996} \right )$$.
Which of the following are identity relations of set $$A = \{1, 2, 3\}$$
1.$$\displaystyle R_{1}=\left \{ (1,1),(2,2) \right \}$$2.$$R_{2}=\left \{ (1,1),(2,2)(3,3),(1,3) \right \}$$3.$$R_{3}=\left \{ (1,1),(2,2),(3,3) \right \}$$
Let $$A=\{1, 3, 5, 7\}$$ and $$B = \{2, 4, 6, 8\}$$ be two sets $$R$$ be a relation from $$A$$ to $$B$$ defined by the phrase $$\displaystyle “(x,y)\in R\Rightarrow x>y".$$ Find relation $$R$$ and its domain and range.
Define a sequence $$\left<f_0(x),\,f_1(x),\,f_2(x),\dots\right>$$ of functions by $$f_0(x)=1,\;f_1(x)=x,\; \ \ \begin{pmatrix}f_n(x)\end{pmatrix}^2-1=f_{n+1}(x)f_{n-1}(x)$$, for $$n\,\ge\,1$$. Prove that each $$f_n(x)$$ is a polynomial with integer coefficients.
Solve the
$$2\dfrac{1}{5}-\dfrac{-1}{3}$$
The cartesian product $$\displaystyle A\times A$$ has $$9$$ elements among which are found $$(-1, 0)$$ and $$(0, 1)$$. Find the set $$A$$ and the remaining elements of $$\displaystyle A\times A$$
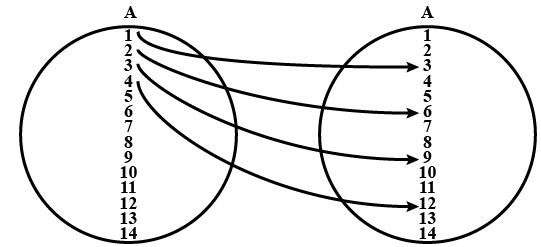
Let $$A = \{1, 2, 3, .... , 14\}$$. Define a relation $$R$$ from $$A$$ to $$A$$ by $$R = \{(x, y): 3x - y = 0$$ where $$x, y \displaystyle \in A\}$$. Write down its domain, co-domain and range.
If $$G = \{7, 8\}$$ and $$H = \{5, 4, 2\}$$, find $$\displaystyle G\times H $$ and $$\displaystyle H\times G $$.
Define a relation $$R$$ on the set $$N$$ of natural numbers by $$R = \{(x, y): y = x + 5, x$$ is a natural number less than $$4; x, \displaystyle y\in N\}$$. Depict this relationship using roster form. Write down the domain and the range.
Let $$f, g$$ : $$\displaystyle R\rightarrow R$$ be defined respectively by $$f(x) = x + 1, g(x) = 2x - 3$$. Find $$f + g, f - g$$ and $$\displaystyle \frac{f}{g}$$
Let $$R$$ be the relation on $$Z$$ defined by $$R =$$ $$\{(a, b): a, b \in Z, a -b$$ is an integer$$\}$$. Find the domain and range of $$R.$$
The figure shows a relationship between the sets $$P$$ and $$Q$$. Write this relation in
(i) in set-builder form (ii) roster form
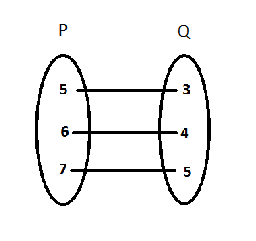
If $$A = \{2, 4, 6, \}$$, $$B = \{5, 7, 1, 9\}$$.
Let R be the relation ‘is less than’ from A to B. Find Domain (R) and Range (R).
If $$R = \left \{(x, y) : x + 2y = 8\right \}$$ is a relation on $$N,$$ write the range of $$R.$$
If $$f(x)=4-3x$$, find $$f(-5)$$ and $$f(13)$$
In the problem below, $$f(x)={x}^{2}$$ and $$g(x)=4x-2$$
Find the following function:
$$(f\times g)(x)$$
Find the following function:
A function $$f : (-3, 7)\rightarrow R$$ is defined as follows:
$$f(x) = \left\{\begin{matrix} 4x^{2} -1;& -3 \leq x < 2\\ 3x - 2; & 2\leq x \leq 4\\ 2x - 3; & 4 < x \leq 6\end{matrix}\right.$$
Find:
$$f(1) - f(-3)$$
A function $$f : (-3, 7)\rightarrow R$$ is defined as follows:
$$f(x) = \left\{\begin{matrix} 4x^{2} -1;& -3 \leq x < 2\\ 3x - 2; & 2\leq x \leq 4\\ 2x - 3; & 4 < x \leq 6\end{matrix}\right.$$
Find:
$$\dfrac {f(3) + f(-1)}{2f(6) - f(1)}$$
A function $$f : [-7, 6) \rightarrow R$$ is defined as follows
$$f(x)=\left\{\begin{matrix}x^2+2x+1; &-7 \leq x < -5 \\ x+5;& -5\leq x\leq 2 \\ x-1;& 2 < x < 6 \end{matrix}\right.$$
(iii) $$ 2f(-4)+3f(2)$$
(ii) $$f(-7)-f(-3)$$
(iv) $$\dfrac{4f(-3)+2f(4)}{f(-6)-3f(1)}$$
A function $$f : (-3, 7)\rightarrow R$$ is defined as follows:
$$f(x) = \left\{\begin{matrix} 4x^{2} -1;& -3 \leq x < 2\\ 3x - 2; & 2\leq x \leq 4\\ 2x - 3; & 4 < x \leq 6\end{matrix}\right.$$
Find:
$$f(-2) - f(4)$$
Let $$ f(x)=\sqrt{x+\sqrt{0+\sqrt{x+\sqrt{0+\sqrt{x+......}}}}}$$.If $$f(a)=4$$ and$$ f(a)=\dfrac{p}{q}$$ where p and q are relatively prime natural numbers then $$ (a > 0)(p+q)$$ is equal to
Let $$\quad f(x)=\sqrt { \cfrac { { x }^{ 2 }+ax+4 }{ { x }^{ 2 }+bx+16 } } $$ is defined for all real $$x$$, then find the number of possible ordered pairs $$(a,b)$$ (where $$a,b\in I$$)
$$ f(x) = \sqrt{\dfrac{x^{2}+ax+4}{x^{2}+bx+16}} $$ to be defined for all real a,
$$ x^{2}+ax+4\geqslant 0 $$ & $$ x^{2}+bx+16> 0...(1) $$
$$ x^{2}+ax+4< 0 $$ & $$ x^{2}+bx+16< 0 $$ (both simultaneously)...(2)
$$ (2)\rightarrow $$ [Not Possible as Positive coefficient]
for (1) to be true Discriminant $$ \Rightarrow B^{2}-4AC = D $$
for $$ x^{2}+ax+4\geq 0\rightarrow D\leqslant 0 $$
$$ x^{2}+bx+16> 0 \rightarrow D< 0 $$
$$ a^{2}-4\times 4\times 1 \leqslant 0 $$ $$ b^{2}-4\times 16\times 1< 0 $$
$$ a^{2}\leqslant 16 $$ $$ b^{2}-64< 0\rightarrow b^{2}< 64 $$
$$ a\epsilon [-4,4] $$ $$ b\epsilon (-8,8) $$
Ordered Pair, $$ (-4,-7)(-4,-6)(-4,-5)(-4,-4)(-4,-3)....(-4,7) $$
$$ (-3,-7)(-3-6).......(-3,7) $$
.
.
.
$$ (3,-7)(3,-6)....(3,7) $$
$$ (4,-7)(4,-6)(4,-5)...(4,0).....(4,7) $$
Which term of the A.P. $$3,10,17,......$$ wil be $$84$$ more than its $$13$$th term?
Find the intervals of monotocity of the function $$f(x)=2x^2-\log |x|, x\neq 0$$.
A function $$f(x)$$ is defined as $$f(x) = x^{2} + 3$$. Find $$f(0), f(1), f(x^{2}), f(x + 1)$$ and $$f(f(1))$$.
If A = {a, b, c, d}, B={1, 2, 3}, find whether or not the following sets of ordered pairs are relations from A to B or not
(a) $$R_1$$ ={(a, 1), (a, 3)}
(b) $$R_2$$ = { (b, 1), (c, 2), (d, 1)}
(c) $$R_3$$ = {(a, 1), (b, 2),( 3, c)}
N is the set of positive integers and ~ be a relation on $$N\times N $$ defined (a, b) ~ (c, d) iff ad = bc.Is it equivalence relation.
A class has $$175$$ students. The following table shows the number of students studying one or more of the following subjects in this class :
| Subject | Number of students |
| Mathematics | $$100$$ |
| Physics | $$70$$ |
| Chemistry | $$46$$ |
| Mathematics and Physics | $$30$$ |
| Mathematics and Chemistry | $$28$$ |
| Physics and Chemistry | $$23$$ |
| Mathematics, Physics and Chemistry | $$18$$ |
Suppose $$f$$ is the collection of all ordered pairs of real numbers and x = 6 is the first element of some ordered pair in $$f$$. Suppose the vertical line through x = 6 intersects the graph of $$f$$ twice. Is $$f$$ a function? Why or why not?
If $$X= \{1, 2, 3, 4, 5\}$$ and $$Y = \{ 1, 3, 5, 7,9\}$$ determine which of the following sets are (i) mappings (ii) relations (ii) neither of X to Y.
(a) $$R_1 = { (x, y): y = x + 2 , x \in X, y \in Y}$$
(b) $$R_2$$ $$= \{ (1, 1), ( 2, 1), (3, 3), (4, 3), ( 5, 5)\}$$
(c) $$R_3$$ $$= \{ (1, 1), (1, 3), (3, 5), (3, 7), (5, 7)\}$$
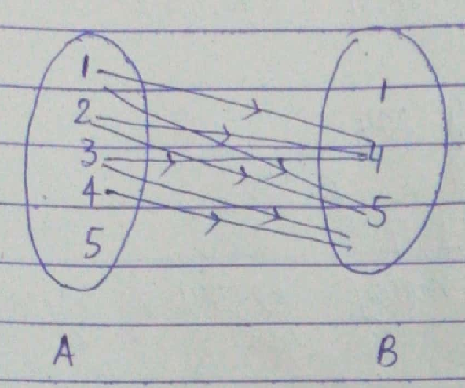
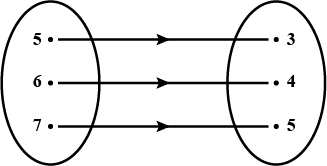
(d) $$R_4$$ $$= \{ (1, 3), (2, 5), (4, 7), (5, 9), (3, 1)\}$$
Let a relation R be defined by
R = {(4, 5), ( 1, 4), ( 4, 6), (7, 6), (3, 7)}.
Find (i) R o R (ii) $$R^{-1}$$ o R.
Let $$A= {1, 2, 3, 4, 5}$$, $$B = { 1, 3, 5, 7, 9, 10, 17, 26, 30}.$$ Which of the following sets of ordered pairs are (i) relations (ii) functions (iii) neither, from A to B
(a) $$R_1$$= {(1, 3), (3, 3), (5, 17), (1, 2)}
(b) $$R_2$$ = {(3, 7), (4, 5), ( 5, 30)}
(c) $$R_3 = {(x, y): x \in A, y \in B, x+y =8}$$
(d) $$R_4 = {(x, y): x \in A, y \in B, y=x^2+1}$$
(e) $$R_5 = {(x, y): x \in A, y \in B, y=2x-1}$$
The following relation is defined on the set of real numbers. $$aRb$$ if $$|a - b| > 0$$.
Let, $$f(x+1)=2x^2-3x-1$$, then find the value of $$f(0)$$ and $$f(x+2)$$.
If $$f(x) = x+7 $$ and $$g(x) = x-7$$, $$x \in R $$, find $$(fog)(7)$$. function $$f:R \rightarrow R$$ defined by $$f(x) = \frac{3x+5}{2}$$ is an invertible function, find $$f^{-1}$$
$$f:[0,2] \rightarrow R $$ is defined as $$ f(x) = \sqrt{x^3 +2 - 2\sqrt{x^3 + 1}} + \sqrt{x^3 +10 - 6\sqrt{x^3 + 1}} $$ and $$g(x) = \int f(x) dx.$$ if $$ g(1) = 3$$ then $$g(\frac{1}{3}) = $$
Let $$f(x)=\cos(\log x)$$ the prove that $$f(x).f(y)=\dfrac{1}{2}\left[f\left(\dfrac{y}{x}\right)+f(xy)\right]$$.
If $$(2.3)^{x} = (0.23)^{y} =1000$$ then find the value of $$\dfrac{1}{x} -\dfrac{1}{y}$$
Let $$R$$ be a relation $$ < $$ from $$A={1,2,3,4}$$ to $$B={1,3,5},i.e.,(a,b) \in R \Leftrightarrow a < b$$ , then $$R o R^{-1}$$ is:
a) {$$(1,3),(1,5),(2,3),(2,5),(3,5),(4,5)$$}
b) {$$(3,1),(5,1),(3,2),(5,2),(5,3),(5,4)$$}
Let $$A = \{1, 2\}$$ and $$B = \{3, 4\}$$. Find the number of relations from $$A$$ to $$B$$.
Verify$$A=\{1,2\}$$
$$B=\{1,2,3,4\}$$$$C=\{5,6\}$$$$D=\{5,6,7,8\}$$. Prove $$A\times (B \cap C)=(A\times B) \cap (A\times C)$$
A relation R is defined on the set $$z$$ of integers as follows. $$(x, y)\in R\Leftrightarrow x^2+y^2=25$$. Express $$R$$ and $${R}^{-1}$$ as the set of ordered pairs and hence find their respective domains.
Let $$A=\left\{x,y,z\right\}$$ and $$B=\left\{1,2\right\}$$. Find the number of relations from $$A$$ to $$B$$.
If $$A =\left\{2, 4, 6, 9\right\}, B = \left\{4, 6, 18, 27, 54\right\}$$ and a relation $$R$$ from $$A$$ to $$B$$ is defined by $$R = \{(a, b) : a \, \in \, A, \, b \, \in \, B, \,\,\, a \, \,\text{is a factor of b and }\ a < b\}$$
If $$f(x)=\dfrac{1}{1-x}$$, show that $$f[f\{f(x)\}]=x$$.
Let $$R$$ be a relation in $$N$$ defined as $$R = \{(x, y) \in \, N \times N : \, x + 2y = 39\}$$ Find the domain, co-domain and range of $$R$$. Also write $$R^{-1}$$ in roster form.
Let $$A=\{1,2,3\}$$ and $$B=\{3,4\}$$ then find $$A\cap B$$ and then find $$A\times (A\cap B)$$.
If $$f(x)=2x-5$$, then what is the value of $$f(2)+f(5)$$?
If $$f(x) = x^2- 3x +4$$, then find the value of x satisfying $$f(x) = f( 2x+1).$$
If $$A = {2,3,4,5,6,7,8,9}$$ given by $$R = \left\{ \left( x,y \right) :x\in A,y\in A\ and \ divides\ y \right\}$$ then find the domain and range of $$R$$.
If $$f\ {(x)}= \dfrac { \dfrac { 1 }{ x } +1 }{ \dfrac { 1 }{ x } -1 } $$ then the value of $$f\ {(x)}+f\ {(-x)}$$ is
If $$R=\{ (1,-1),(2,-2),(3,-1)\} $$ is relation, then find the range of R.
If $$f(x) = \dfrac{(x - 1)}{(x + 1)}$$ then prove that $$f(2x) = \dfrac{3f(x) + 1}{f(x) + 3}$$
Find the value$$ \left| 7 \right|\times\left| -4\right|\times \left|4-9 \right|\times \left|7 \right|\times \left| -4 \right|\times \left|4-9 \right|$$
Let $$'*'$$ be a binary operation on set Q of rational number defined as $$a*b=\dfrac{ab}{5}$$. Write the identity for $$'*'$$, if any.
Find range & domain of following $$\sqrt {4 - {x^2}} $$
If $$f\left( x \right) = x + \dfrac{1}{x}$$, prove that $${\left( {f\left( x \right)} \right)^3} = f\left( {{x^3}} \right) + 3f\left( {\dfrac{1}{x}} \right)$$
If $${e^{f\left( x \right)}} = \dfrac{{10 + x}}{{10 - x}},x \in \left( { - 10,0} \right)$$ and $$f\left( x \right) = k.f\left( {\dfrac{{200x}}{{100 + {x^2}}}} \right)$$ then $$k$$ =
Let $$A=\{-1,1\}$$ then find $$A\times A$$.
If $$A=\left\{1,2,3\right\}$$ and $$B=\left\{3,4\right\}$$ and $$C=\left\{1,3,5\right\}$$.Find $$\left(A\times\,B\right)\cap\left(A\times\,C\right)$$
The simplified form of $$\left ({\dfrac {x(x - 5y)} {{x^2} - 6xy + 5{y^2}} } \times {\dfrac {(x + y)(x - y)} {{x^2} + xy}}\right )$$ is
The number of relations from $$A = \{ 2,6 \}$$ to $$B = \{ 1,3,5,6,7 \}$$ that are not functions from A to $$B$$ is
$$y=\dfrac{x-2}{2x+3}$$Express in the form $$f(x,y) = 0$$
Let $$A=\left\{1, 2, 3, 4, 5\right\}$$ and $$B=\left\{1, 4, 5\right\}$$. Let $$R$$ be a relation 'is less than' from $$A$$ to $$B$$. Find the domain, co domain and range of $$R$$.
$$A=\{ 1,2,3,4,5\} \quad \quad B=\{ 1,4,5\} $$
$$R\rightarrow A$$ is less than $$B$$
Domain is $$\{ 1,2,3,4\} $$
Co-domain is $$\{ 1,4,5\} $$
range is $$\{ 4,5\} $$
A function $$f\::\:R\rightarrow R$$ satisfy the equation $$f\left(x\right)f\left(y\right)-f\left(xy\right)=x+y$$ for all $$x,y\in R$$ and $$f\left(y\right)>0$$, then ?
Let $$x, y=1$$
$$\Rightarrow y^2-y-2=0$$ $$(f(1)=y)$$
$$\Rightarrow y^2-2y+y-2$$
$$\Rightarrow y(y-2)+1(y-2)=0$$
$$\Rightarrow y=-1$$ (y > 0)$$ $$y=2$$
Let $$y=1$$ now
$$f(x).2-f(x)=x+1$$
$$\Rightarrow f(x)=x+1$$.
If the function $$f(x)$$ given by $$f(x)=\begin{cases}3ax+b & if \, x > 1 \\ 11 & if\, x=1 \\5ax-2b & if \, x < 1\end{cases}$$ is continuous at x=1, then find the values of a and b.
For x $$\in$$ R, the range of the given expression $$\dfrac{x^2 + 34x - 71}{x^2 + 2x - 7}$$ is
R.E.F image
let $$ y = \frac{x^{2}+34x-71}{x^{2}+2x-7} \Rightarrow x^{2}(y-1)+x(2y-34)-7y+71=0$$
As $$ x \epsilon R, \Rightarrow D \geqslant 0$$
$$ \Rightarrow (2y - 34)^{2} + 4(y-1)(7y-71) \geqslant 0$$
$$ \Rightarrow (y-17)^{2}+(7y^{2}-78y+71)\geqslant 0 $$
$$ \Rightarrow 8y^{2}-112y+306\geqslant 0$$
$$ \Rightarrow 4y^{2}-56y+153\geqslant 0$$
$$ D=(56)^{2}-16(153)=688 > 0 \Rightarrow Roots \Rightarrow y = \frac{56\pm \sqrt{688}}{8}$$
$$ \Rightarrow $$ Range $$= y \,\epsilon (-\infty , \alpha ]\cup [\beta ,\infty )$$
Number of solutions satisfying $$| x | + | x - 2 | \leq 2$$ for $$x \in R$$ is
Let $$f:$$ $$R \rightarrow R$$ be given by $$f ( x ) = x ^ { 2 } + 3 .$$ Find ( a ) $$\{ x : f ( x ) = 28 \}$$ ( b ) the pre-images of $$39$$ and $$2$$ under $$f.$$
We have function R $$ \rightarrow $$ R defined by f(x) $$ = x^{2}+3$$
i.e its domain & range are real no.
1) f(x) = 28 = $$ x^{2}+3$$
$$ x^{2} = 25 \Rightarrow x = \pm 5$$
Therefore , for range 28 Pre - image is 5 & -5
2) f(x) = 39.
$$ x^{2}+3 = 39$$
$$ x^{2} = 36 \Rightarrow x = \pm 6 $$
Now f(x) = 2
$$ x^{2} + 3 = 2$$
$$ x^{2} = -1$$
$$ x = \pm i$$ But the value of x is not are
value, both i & -i are complex no.
therefore, 2 is not an image under f.
Find the range
$$f(x)=\dfrac{1}{\sqrt{x-5}}$$
Find the domain of $$\cos^{-1}[X]$$ where $$[X]$$ is the greatest integer functions.
Domain of $$\cos^{-1}t$$ is $$t\in [-1, 1]$$
$$\Rightarrow [x]\in [-1, 1]$$
$$\Rightarrow$$ From graph of $$[x]$$, $$x\in [-1, 2)$$.
Find the domain and range of the following real functions :
$$f ( x ) = - | x |$$
If $$A=\left\{1,2,3\right\}$$ and $$B=\left\{3,4\right\}$$ and $$C=\left\{1,3,5\right\}$$.Find $$A\times\left(B\cup\,C\right)$$
$$n ( A ) + n ( B ) - n ( A \cap B ) =$$
Is $$a\leq a^2$$, $$a\in R$$ true? Why or why not?
If $$a,b,c\in{R}^{+}$$ such that $$a+b+c=18$$, then the maximum value of $${a}^{2}{b}^{3}{c}^{4}$$ is
If $$f ( x ) = \frac { a ^ { x } + a ^ { - x } } { 2 }$$ then $$f ( x + y ) f ( x - y )$$ is equal to:
A relation $$R$$ is defined from a set $$A=[2,3,4,5]$$ to a set $$B=[3,6,7,10]$$ as follows:
$$(x,y)\in R\Leftrightarrow x$$ is relatively prime to $$y$$.Express R as a set of ordered pairs and determine its domain and range.
If $$A=\left\{1, 2, 4,5\right\} $$ and $$B=\left\{a,b\right\}$$ Find the total number of relations from $$A$$ to $$B$$.
Write the relations as sets of ordered pairs $$\left\{\left(x,y\right) : y = 3x, x\in \left\{1,2,3\right\}, y\in \left\{3,6,9,12\right\}\right\} $$
If $$A={1, 2, 4} $$ and $$B={a, b}$$ Find the total number of relations from A to B.
If f = {(4, 5), (5, 6), (6, -4) and g = {(4, -4), (6, 5),(8, 5)} then find$$ A)f+g\ \ \ \ B)f-g\ \ \ \ C)2f+4g\ \ \ \ D)f+4\ \ \ \ E)fg\ \ \ \ F)f/g\ \ \ \ G)|f| \ \ \ \ H)\sqrt{f}\ \ \ \ I)f^2\ \ \ \ G)f^3$$
If $$f:A\rightarrow A$$, then range of $$f$$ where $$A=\left\{1,2,3,4\right\}$$ and $$f\left(x\right)={x}^{2}+x+2$$
If $$f\left(x\right)={x}^{2}+2x+3,$$ then find $$\dfrac{f\left(x+h\right)-f\left(x-h\right)}{h},\,\,h\neq 0$$
Let $$X=\left\{1,2,3,4,5\right\}$$.If the relation $$g=\left\{\left(1,2\right),\left(2,3\right),\left(3,4\right),\left(4,5\right),\left(5,1\right)\right\}$$ on $$X$$ is a function from $$X$$ to $$X$$.then find $$g\left(g\left(g\left(2\right)\right)\right)$$
If $$f\left(x\right)+f\left(\dfrac{1}{x}\right)=f\left(x\right)f\left(\dfrac{1}{x}\right)$$ and $$f\left(3\right)=28$$ find $$f\left(\dfrac{1}{3}\right)$$
If $$A \times B = \left\{ {\left( {p,q} \right),\left( {p,r} \right),\left( {m,q} \right),\left( {m,r} \right)} \right\}$$
Find A and B
If $$f\left(x\right)=\dfrac{x+1}{x-1}$$ the show that $$f\left(x\right)+f\left(\dfrac{1}{x}\right)=0$$
Find whether $$f\left(x\right)=\dfrac{{a}^{x}+1}{{a}^{x}-1}$$ is even, odd or neither odd nor even.
If $$\dfrac { 4 }{ x } <\dfrac { 1 }{ 3 },$$ what is the possible range of value for $$x$$?
$$\dfrac{4}{x} < \dfrac{1}{3}$$
$$\Rightarrow x > 4\times 3$$
$$\Rightarrow x > 12$$
So Range $$=(12, \infty)$$.
Let $$X=\left\{1,2,3,4,5\right\}$$.If the relation $$g=\left\{\left(1,2\right),\left(2,3\right),\left(3,4\right),\left(4,5\right),\left(5,1\right),\right\}$$ on $$X$$ is a function from $$X$$ to $$X$$.then find $$g\left(g\left(g\left(4\right)\right)\right)$$
Let $$f(x)=\left\{\begin{matrix} x^3+x^2+10x, & x < 0\\ x^2e^x, & x\geq 0\end{matrix}\right.$$. Investigate the behaviour of the function for $$x\in R$$.
The domain of $$f(x)=\sqrt { x-2-2\sqrt { x-3 } } -\sqrt { x-2+2\sqrt { x-3 } } $$
$$\sqrt{x-2-2\sqrt{x-3}}-\sqrt{x-2+2\sqrt{x-3}}$$
domain $$\Rightarrow \sqrt{x-2-2\sqrt{x-3}}\geq 0$$ $$\sqrt{x-2+2\sqrt{x-3}}\geq 0$$
$$x-2 \geq 2\sqrt{x-3}$$ $$x-2 \geq -2\sqrt{x-3}$$
$$x^{2}-4x+x\geq 4x-12$$ $$(x-2)^{2}\geq 4(x-3)$$
$$x^{2}-Bx+16\geq 0$$ $$(x-4)^{2}\geq 0$$
$$(x-y)^{2}\geq 0$$ $$x\epsilon [4,\infty )$$
Find the range of $$\ln{\left[{\left\{x\right\}}^{2}+3\left\{x\right\}+2\right]}$$ where $$\left\{x\right\}$$ is a fractional function.
Find the range of $$f\left(x\right)=\dfrac{\left\{x\right\}}{\left\{x\right\}+1}$$
Let $$f:R\rightarrow R$$ be defined by $$f\left(x\right)=\dfrac{x+1}{{x}^{2}+2},\,x\in \,R$$.Find $$f\left(4\right)$$
Let $$f:R\rightarrow R$$ be defined by $$f\left(x\right)=\dfrac{x+1}{{x}^{2}+2},\,x\in \,R$$.Find $$f\left(0\right)$$
If $$n(A)=15, n(A\cup B)=29, n(A\cap B)=7$$ then $$n(B)=$$?
Let $$A$$ and $$B$$ be two sets such that $$n\left(A\right)=5$$ and $$n\left(B\right)=2$$.If $$a,b,c,d,e$$ are distinct and $$\left(a,2\right),\left(b,3\right),\left(c,2\right),\left(d,3\right),\left(e,2\right)$$ are in $$A\times B$$,find $$A$$ and $$B$$
Express $$A=\left\{\left(a,b\right):2a+b=5,a,b\in\,W\right\}$$ as the set of ordered pairs.
Suppose that f(x) is a function of the form f(x)= $$\frac{ax^{8}+bx^{6}+cx^{4}+dx^{2}+15x+1}{x}(x\neq 0)$$ If f(5)=-28 then the value of f(-5) /14 is equal to
$$f=\{(4,3),(6,7)\}\ \ \ g=\{(4,9),(6,5)\}$$ find $$f+g$$
If $$f(x+y)=f(x).f(y)$$ then prove that $$f\left( x \right) ={ \left[ f\left( 1 \right) \right] }^{ x }$$
If $$f(x+y)=f(x)+f(y)$$. Then prove that $$f(x)=x.f(1)$$
Let $$|X|$$ denote the number of elements in a set $$X$$.let $$S=\{1,2,3,4,5,6\}$$ be a sample space ,where each elements is equally likely to occur.If A and B are independent events associated with $$S$$, then the number of ordered pairs $$(A,B)$$ such that $$1\le |B|<|A|$$ equals.
Let $$f:R^+ \to R$$, where $$R^+$$ is the set of all positive real numbers, be such that $$f(x)=\log_e x$$.
Determine
whether $$f(xy)=f(x)+f(y)$$ holds.
Find the domain and range of each of the following real value functions:
$$f(x)= -|x|$$
Which one of the given relations on $$A=\left\{ 1,2,3 \right\} $$ is a function?
$$f=\left\{ \left( 1,3 \right) ,\left( 2,3 \right) ,\left( 3,2 \right) \right\} $$, $$g=\left\{ \left( 1,2 \right) ,\left( 1,3 \right) ,\left( 3,1 \right) \right\} $$
$$f=\{(1,3),(2,3),(3,2)\}$$
$$\Rightarrow$$ As we can see, in $$f$$, each element of the domain set has unique image.$$\therefore$$ $$f$$ is a function.
$$g=\{(1,2),(1,3),(3,1)\}$$
$$\Rightarrow$$ In $$g$$, the element $$1$$ of the domain set has two images $$2$$ and $$3$$ of the range set.
$$\therefore$$ $$g$$ is not a function.
what is the fundamental difference between a relation and a function? Is every relation a function?
Find the domain and range of each of the following real value functions:
$$f(x)=\sqrt {x-1}$$
Find the domain of each of the following real valued functions of real variable:
$$f(x)=\dfrac {x^2+2x+1}{x^2-8x+12}$$
Determine the domain and range of the relation R defined by $$R=\{(x, x+5):x\in \{0, 1, 2, 3, 4, 5\}\}$$.
Let $$f:(0, \infty)\to R$$ and $$g:R\to R$$ be defined by $$f(x)=\sqrt x$$ and $$g(x)=x$$. Find $$f+g, f-g, fg$$ and $$\dfrac {f}{g}$$.
Determine the domain and range of the relation R defined by $$R=\{(x, x^3):x$$ is a prime number less than $$10\}$$.
Let $$A=\{1, 2\}$$ and $$B=\{3, 4\}$$. Find the total number of relations from A into B.
A relation R is defined from a set $$A=\{2, 3, 4, 5\}$$ to a set $$B=\{3, 6, 7, 10\}$$ as follows:
$$(x, y)\in R\Leftrightarrow x$$ is relatively prime to y.
Express R as a set of ordered pairs
Write the following relation as the sets of ordered pairs.
A relation R on the set $$\{1, 2, 3, 4, 5, 6, 7\}$$ defined by $$(x, y)\in R\Leftrightarrow x$$ is $$\{1, 2, 3, 4, 5, 6, 7\}$$ defined by $$(x, y)\in R\Leftrightarrow x$$ is relatively prime to y.
$$R=\left\{\begin{matrix}(2, 3), (2, 5), (2, 7), (3, 2), (3, 4), (3, 5), (3, 7), (4, 3), (4, 5), (4, 7), (5, 2), (5, 3), (5, 4), (5, 6), (5, 7), (6, 5), \end{matrix}\right.$$
$$ \left.\begin{matrix}(6, 7), (7, 2), (7, 3), (7, 4), (7, 5), (7, 6), (7, 7)\end{matrix}\right\}$$.
Let $$A=\{1, 2\}$$ and $$B=\{3, 4\}$$. Find the total number of relations from A into B.
Determine the domain and range of the following relations.
$$S=\{(a, b): b=|a-1|, a\in Z$$ and $$|a|\leq 3\}$$.
Determine the domain and range of the relation R defined by $$R=\{(x, x+5):x\in \{0, 1, 2, 3, 4, 5\}\}$$.
Determine the domain and range of the following relation.
$$R=\{(a, b):a\in N, a < 5, b=4\}$$.
Determine the domain and range of the following relation.
$$R=\{(a, b):a\in N, a < 5, b=4\}$$.
Let $$A=\{a, b\}$$. List all relations on A and find their number.
Determine the domain and range of the following relations.
$$S=\{(a, b): b=|a-1|, a\in Z$$ and $$|a|\leq 3\}$$.
Let $$A=\{x, y, z\}$$ and $$B=\{a, b\}$$. Find the total number of relations from A into B.
Let R be the relation on Z defined by $$R=\{(a, b):a, b\in Z, a-b$$ is an integer$$\}$$. Find the domain and range of R.
Let $$A=\{1, 2, 3, 4, 5, 6\}$$. Let R be a relation on A defined by $$R=\{(a, b):a, b\in A, b$$ is exactly divisible by a$$\}$$ Find the range of R.
Let $$A=\{1, 2, 3,....., 14\}$$. Define a relation on a set A by $$R=\{(x, y): 3x-y=0$$, where $$x, y\in A\}$$.
Depict this relationship using an arrow diagram. Write down its domain, co-domain and range.
$$R=\{(x,y):3x-y=0,$$ where $$x,y\in A\}$$
Or,
$$R=\{(x,y):2x=y,\,$$ where $$x,y\in A\}$$
As
$$3\times 1=3$$
$$3\times 2=6$$
$$3\times 3=9$$
$$3\times 4=12$$
Or
$$R=\{(1,3),(2,6),(3,9),(4,12)\}$$
Domain $$(R)=\{1,2,3,4\}$$
Range $$(R)=\{3,6,9,12\}$$
Co-domain $$(R)=A$$
Answer the following question in one word or one sentence or as per the exact requirement of the question. If $$R=\{(x, y):x, y\in Z, x^2+y^2\leq 4\}$$ is a relation defined on the set Z of integers, then write domain of R.
Let $$A=\{1, 2, 3, 4, 5, 6\}$$. Let R be a relation on A defined by $$R=\{(a, b):a, b\in A$$, b is exactly divisible by a$$\}$$. Find the domain of R.
$$A=\{1, 2, 3, 5\}$$ and $$B=\{4, 6, 9\}$$. Define a relation R from A to B by $$R=\{(x, y):$$ the difference between x and y is odd, $$x\in A, y\in B\}$$. Write R in Roster form.
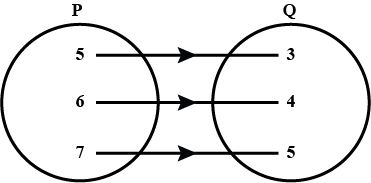
Define a relation R on the set N of natural numbers by $$R=\{(x, y):y=x+5$$, x is a natural number less than $$4, x, y\in N\}$$.
Depict this relationship using (i) roster form (ii) an arrow diagram. Write down the domain and range or R.
(i)We have,
$$R=\{(x, y) :y=x+5$$,
(ii) Domain $$(R)=[1, 2, 3]$$,
$$R=\{(x, y) :y=x+5$$,
x is a natural number less than $$4, x, y\in N$$
$$R=\{(1, 6), (2, 7), (3, 8)\}$$
(ii) Domain $$(R)=[1, 2, 3]$$,
Range $$(R)=\{6, 7, 8\}$$.
Answer the following question in one word or one sentence or as per exact requirement of the question.
If $$R=\{(x, y): x, y\in W, 2x+y=8\}$$, then write the domain and range of R.
Determine the domain and range of the relation R defined by $$R=\{(x, x^3):x$$ is a prime number less than $$10\}$$.
Determine the domain and range of the following relations.$$S=\{(a, b): b=|a-1|, a\in Z$$ and $$|a|\leq 3\}$$.
If $$f(x)+f(x+4)=f(x+2)+f(x+6)$$ then find the period of $$f(x)$$.
Answer the following question in one word or one sentence or as per exact requirement of the question.
If $$A=\{1, 3, 5\}$$ and $$B=\{2, 4\}$$, list the elements of R, if $$R=\{(x, y):x, y\in A\times B$$ and $$x > y\}$$.
Let $$R=\{(x, y):x+2y=8\}$$ be a relation on N. Write the range of R.
Find the domain and range of the relation
$$R=\{(-1, 1), (1, 1), (-2, 4), (2, 4)\}$$.
Let $$R=\{(a, a^3):a$$ is a prime number less than $$10\}$$. Find dom(R).
Let $$R=\{(a, a^3):a$$ is a prime number less than $$10\}$$. Find R.
Let $$R=\{(a, a^3):a$$ is a prime number less than $$10\}$$. Find range (R).
Let $$R=\{(a, a^3):a$$ is a prime number less than $$5\}$$. Find the range of R.
Let $$f: R\rightarrow R: f(x)=3x+2$$, find $$f\{f(x)\}$$.
Let $$f: R\rightarrow R$$ be defined by
$$f(x)=\left\{\begin{matrix} 2x+3, & when & x < -2\\ x^2-2, & when & -2\leq x\leq 3\\ 3x-1, & when & x > 3\end{matrix}\right.$$
Find $$f(2)$$.
Let $$R=\{\left(a, \dfrac{1}{a}\right):a\in N$$ and $$1 < a < 5\}$$. Find the doman and range of R.
Let $$f: R\rightarrow R$$ be defined by
$$f(x)=\left\{\begin{matrix} 2x+3, & when & x < -2\\ x^2-2, & when & -2\leq x \leq 3\\ 3x-1, & when & x >3\end{matrix}\right.$$
Find $$f(-3)$$.
Let $$R=\{(a, b):b=|a-1|, a\in Z$$ and $$|a| < 3\}$$. Find the domain and range of R.
Let $$f: R\rightarrow R$$ be defined by
$$f(x)=\left\{\begin{matrix} 2x+3, & when & x < -2\\ x^2-2, & when & -2\leq x \leq 3\\ 3x-1, & when & x > 3\end{matrix}\right.$$
Find $$f(4)$$.
Let $$R=\{(a, b):a, b\in N$$ and $$a+3b=12\}$$. Find the domain and range of R.
Let $$R=\{(a, b):a, b\in N$$ and $$b=a+5, a < 4\}$$. Find the domain and range of R.
For any sets $$\displaystyle A, B$$ and $$\displaystyle C$$, prove that:
$$\displaystyle A \times (B \cup C) = (A \times B)\cup (A \times C)$$
Let $$f:R\rightarrow R$$ be defined by
$$f(x)=\left\{\begin{matrix} 2x+3, & when & x < -2\\ x^2-2, & when & -2\leq x \leq 3\\ 3x-1, & when & x > 3\end{matrix}\right.$$
Find $$f(-1)$$.
If $$\displaystyle A = \{1, 3, 5\}, B = \{3, 4\}$$ and $$\displaystyle C = \{2, 3\}$$, verify that
$$\displaystyle A \times (B \cap C) = ( A \times B) \cap (A \times C)$$
If $$\displaystyle A = \{1, 3, 5\}, B = \{3, 4\}$$ and $$\displaystyle C = \{2, 3\}$$, verify that
$$\displaystyle A \times (B \cup C) = ( A \times B) \cup (A \times C)$$
Let $$\displaystyle A = \{ x \in W : x < 2 \}, B = x \in N : 1 < x \leq 4\}$$ and $$\displaystyle C = \{3, 5\}$$. Verify that :
$$\displaystyle A \times (B \cap C) = (A \times B) \cap (A \times C)$$
If $$\displaystyle A = \{2, 3, 5\}$$ and $$\displaystyle B = \{5, 7\}$$, find $$A \times A$$ and enter the number of elements of it.
The number of elements are 9
Let $$\displaystyle A \times B = \{ (a, b) : b = 3a - 2\}.$$ If $$\displaystyle (x, -5)$$ and $$\displaystyle (2, y)$$ belong to $$\displaystyle A \times B $$, find the values of $$\displaystyle x $$ and $$\displaystyle y$$.
If the answer is $$\displaystyle x = -1, y = 4$$ then $$1,$$ else $$0$$
Let $$\displaystyle A = \{2, 3 \}$$ and $$\displaystyle b = \{ 4, 5\}$$. Find $$\displaystyle (A \times B)$$. How many subsets will $$\displaystyle (A \times B)$$ have?
Enter 1 if it is true else enter 0.If $$\displaystyle A = \{2, 3, 5\}$$ and $$\displaystyle B = \{5, 7\}$$, then $$\displaystyle A \times B = \{(2, 5), (2, 7), (3, 5), (3, 7), (5, 5), (5, 7)\}$$
Enter 1 if it is true else enter 0.
If $$\displaystyle A = \{2, 3, 5\}$$ and $$\displaystyle B = \{5, 7\}$$, find $$B \times B$$ and enter the value of no of pair which contain the same element.
If $$\displaystyle A = \{2, 3, 5\}$$ and $$\displaystyle B = \{5, 7\}$$, find:
$$B \times A$$
Let $$\displaystyle A = \{ x \in W : x < 2 \}, B = x \in N : 1 < x \leq 4\}$$ and $$\displaystyle C = \{3, 5\}$$. Verify that :
$$\displaystyle A \times (B \cup C) = (A \times B) \cup (A \times C)$$
Let $$\displaystyle A = \{-3, -1\}, B = \{1, 3\}$$ and $$\displaystyle C = \{3, 5\}$$. Find $$\displaystyle A \times B$$, and enter the value of number of elements of it.
If $$\displaystyle A$$ and $$\displaystyle B$$ are nonempty sets, prove that
$$\displaystyle A \times B = B \times A \iff A = B$$.
If $$\displaystyle A = \{5, 7\}$$, find $$\displaystyle A \times A$$ and enter the value of number of elements of it.
If $$\displaystyle A \subseteq B$$, prove that $$\displaystyle A \times C \subseteq B \times C$$ for any set $$\displaystyle C$$.
For any sets $$\displaystyle A, B$$ and $$\displaystyle C$$, prove that:
$$\displaystyle A \times (B - C) = (A \times B)- (A \times C)$$
If $$\displaystyle A \subseteq B$$ and $$\displaystyle C \subseteq D$$ then prove that $$\displaystyle A \times C \subseteq B \times D$$.
Let $$\displaystyle A = \{-3, -1\}, B = \{1, 3\}$$ and $$\displaystyle C = \{3, 5\}$$. Find $$\displaystyle A \times (B \times C)$$ and enter the value of number of elements of it.
For any sets $$\displaystyle A, B$$ and $$\displaystyle C$$, prove that:
$$\displaystyle A \times (B \cap C) = (A \times B)\cap (A \times C)$$
Let $$\displaystyle A = \{-3, -1\}, B = \{1, 3\}$$ and $$\displaystyle C = \{3, 5\}$$. Find $$\displaystyle B \times C$$ and enter the value of number of elements of it.
Lets $$\displaystyle A = \{1, 2\}$$ and $$\displaystyle B = \{2, 3\}$$. Then, write down the no. of all possible subsets of $$\displaystyle A\times B$$.
Let $$\displaystyle A = \{a, b, c, d\}, B = \{c, d, e\}$$ and $$\displaystyle C = \{d, e, f, g \}$$. Then verify each of the following identities:
$$\displaystyle A \times (B \cap C) = ( A \times B ) \cap (A \times C)$$
Let $$ R^+ $$ be the set all positive real numbers.
Let $$ f : R^+ \rightarrow : f(x) = log_ex $$
Find $$ \{x:x \epsilon R^+ and f(x) = -2 \}$$
Let $$ R^+ $$ be the set all positive real numbers.
Let $$ f : R^+ \rightarrow : f(x) = log_ex $$
Find out whether $$f(xy) = f(x) +f (y)$$ for all $$ x, y \epsilon R^+ $$
Let $$\displaystyle A = \{2, 3, 5\}$$ and $$\displaystyle R = \{(2, 3), (2, 5), (3, 3), (3, 5)\}$$.
Show that $$\displaystyle R$$ is a binary relation on $$\displaystyle A$$. Which element is common between domain and range of $$R$$.
The correct answer is 3
Let $$\displaystyle A = \{a, b, c, d\}, B = \{c, d, e\}$$ and $$\displaystyle C = \{d, e, f, g \}$$. Then verify each of the following identities:
$$\displaystyle (A \times B) \cap ( B \times A) = ( A \cap B) \times ( A \cap B)$$
Let $$\displaystyle A = \{0, 1, 2, 3, 4, 5, 6, 7, 8 \}$$ and let $$\displaystyle R = \{(a, b): a, b \in A$$ and $$2a + 3b = 12\}$$.
Express $$\displaystyle R$$ as a set of ordered pairs. Show that $$\displaystyle R$$ is a binary relation on $$\displaystyle A$$.
Which element is common between domain and range.
Let $$\displaystyle A = \{a, b, c, d\}, B = \{c, d, e\}$$ and $$\displaystyle C = \{d, e, f, g \}$$. Then verify each of the following identities:
$$\displaystyle A \times (B - C) = (A \times B ) - ( A \times C )$$
If $$ f(x) = x^3 $$, find the value of $$ \frac{ {f(5) - f(1) } }{ (5-1)} .$$
If $$ f(x) = \dfrac {x+1}{x-1} $$ then show that $$ f[\left\{ f(x) \right\} ]=x$$
Let $$\displaystyle R $$ be a relation on $$\displaystyle Z $$, defined by $$\displaystyle (x, y) \in R \iff x^2 + y^2 = 9$$. Then, write $$\displaystyle R $$ as set of ordered pairs. How many elements are there in its domain?
If $$ f(x) = \frac {x-1}{x+ 1} $$ then show that $$ f( \frac {1}{x}) = - f(x) $$
If $$ f(x) = x^3 - \frac {1}{x^3} $$ then show that $$ f(x) + f( \frac {1}{x}) = 0 $$
Find the domain and range of $$ f(x) = \dfrac {1}{x} $$.
If $$ f (x) =x^2 - 3x + 4 $$ and $$ f(x) = f(2x+ 1) $$, find the values of $$x $$.
If $$ f(x) = \frac {1}{(1-x)} $$ then show that $$ f[f\left\{ f(x) \right\} ]=x$$
If $$ f(x) = \dfrac {x-1}{x+ 1} $$ then show that $$ f ( \frac {-1}{x} ) = \frac {-1}{f(x)} $$
If $$ f(x) = \frac {1}{(2x+ 1)} and x \neq \frac {-1}{2} $$ then prove that $$ f\left\{ f(x) \right\} = \frac {2x+ 1}{2x+ 3} $$, when it is given that $$ x \neq \frac {-3}{2} $$
If $$\displaystyle A = \{5 \}$$ and $$\displaystyle B = \{5, 6\}$$, write down all possible subsets of $$\displaystyle A \times B$$.
Prove that $$\displaystyle A \times B = B \times A \implies A = B$$.
Let $$\displaystyle A = \{ a, b\}$$. List all relations on $$\displaystyle A$$ and find their number.
Find the domain and range of $$ f(x) = \dfrac {1}{2 -sin x} $$
Let $$\displaystyle R = \{( x, x^2) : x $$ is a prime number less than $$\displaystyle 10 \}$$.
Find dom $$\displaystyle (R)$$ and range $$\displaystyle (R)$$.
Find the domain and range of $$ f(x) = \dfrac {x-3}{2-x} $$.
Let $$\displaystyle A = \{1, 2, 3\}$$ and $$\displaystyle B = \{4\}$$.
How many relations can be defined from $$\displaystyle A $$ to $$\displaystyle B$$?
Find the domain and range of $$ f(x) = \dfrac {x^2 -16}{x -4} $$.
Find the domain and range of $$ f(x) = \dfrac {x^2 -9}{x- 3}$$
Let $$\displaystyle A$$ and $$\displaystyle B$$ be two nonempty sets.
What do you mean by the domain and range of a relation?
Number of positive integers $$ x $$ for which $$ f(x)=x^{3}-8 x^{2}+20 x-13 $$ is a prime number is.
Let $$\displaystyle A = \{ 1, 3, 5, 7\}$$ and $$\displaystyle B = \{2, 4, 6, 8\}$$.
Let $$\displaystyle R = \{(x, y) : x \in A, y \in B \ and \ x > y \}$$.
Find dom $$\displaystyle (R)$$ and range $$\displaystyle (R)$$.
Find the domain and range of each of the relations given below:
$$\displaystyle R = \{ (x, y) : x + 2y = 8$$ and $$\displaystyle x, y \in N\}$$.
Find the domain and range of each of the relations given below:
$$\displaystyle R = \{ (x, y) : y = |x - 1|, x \in Z$$ and $$\displaystyle |x|\leq 3\}$$.
Define a relation $$\displaystyle R$$ from $$\displaystyle Z $$ to $$\displaystyle Z $$, given by
$$\displaystyle R = \{ (a, b) : a, b \in Z $$ and $$\displaystyle (a - b)$$ is an integer $$\displaystyle \}$$.
Find dom $$\displaystyle (R)$$ and range $$\displaystyle (R)$$
Let $$\displaystyle A = \{ 2, 4, 5\}$$ and $$\displaystyle B = \{1, 2, 3, 4, 6, 8\}$$.
Let $$\displaystyle R = \{(x, y) : x \in A, y \in B \ and \ x$$ divides $$\displaystyle y \}$$.
How many common elements are there between dom $$\displaystyle (R)$$ and range $$\displaystyle (R)$$.
Let $$\displaystyle A$$ and $$\displaystyle B$$ be two nonempty sets.
What do you mean by a relation from $$\displaystyle A$$ to $$\displaystyle B$$?
Let $$f : R \rightarrow R f(x^2 + x + 3) + 2f(x^2 - 3x + 5) = 6x^2 - 10x + 17 \space \forall \space x \epsilon \space R$$, then the value of f(5) is
If $$R=\left \{ \left ( x,y \right ):x+2y=8 \right \}$$ is a relation on $$N$$, write the range of $$R$$.
Let $$A=\left\{a,b,c \right\}$$ and the relation $$R$$ be define on $$A$$ as follows:
$$R=\left\{(a,a),(b,c),(a,b)\right\}$$.
Then, write the minimum number of ordered pairs to be added in $$R$$ to make $$R$$ reflexive and transitive.
If $$f:R \rightarrow R$$ is defined by $$f(x)=x^2-3x+2$$, find $$f(f(x))$$
Let R be a relation from N to N defined by R = {(a, b) : a, b $$\epsilon$$ N and a = $$b^2$$}. Are the following true?
(ii) (a, b) $$\epsilon$$ R, implies (b, a) $$\epsilon$$ R
Let A = {1, 2, 3...14}. Define a relation R from A to A by R = {(x, y) : 3x - y = 0}, where x, y $$\epsilon$$ A. Write down its domain, codomain and range.
Show that the relation $$R$$ in the set
$$A=\left\{ x \in Z :0 \le x \le 12 \right\}$$, given by
$$R=\left\{ (a, b): | a-b| \ is\ a\ multiple\ of\ 4 \right\}$$
Is $$g=\left\{(1,1),(2,3),(3,5),(4,7) \right\}$$ a function? If $$g$$ is described by $$g(x)=\alpha x +\beta$$, then what value should be assigned to $$\alpha$$ and $$\beta$$.
The given figure shows a relationship between the sets P and Q. Write this relation
(i) in set-builder for.
(ii) in roster form.
What is its domain and range?
If $$f: R\to R$$ is defined by $$f(x)=x^2 -3x+2$$, write $$f(f(x))$$.
Let R be a relation from N to N defined by R = {(a, b) : a, b $$\epsilon$$ N and a = $$b^2$$}. Are the following true?
(i) (a,a) $$\epsilon$$ R, for all a $$\epsilon$$ N
Let R be a relation from N to N defined by R = {(a, b) : a, b $$\epsilon$$ N and a = $$b^2$$}. Are the following true?
(iii) (a, b) $$\epsilon$$ R, (b, c) $$\epsilon$$ R implies (a, c) $$\epsilon$$ R.
Justify your answer in each case.
If $$A=\left\{1,2,3 \right\}$$ and $$f, g$$ are relation corrosponding to the subset of $$A\times A$$ indicated against them, which of $$f, g$$ is a function? Why?
$$f=\left\{(1,3),(2,3),(3,2)\right\}$$
$$g=\left\{(1,2),(1,3),(3,1)\right\}$$
If $$R$$ is the set of all real numbers, what do the Cartesian products $$R \times R$$ and $$R \times R \times R$$ represent?
Let $$A=\left\{ 1, 2, 3, 4, 5, 6\right\}$$. Define a relation $$R$$ from $$A$$ to $$A$$ by $$R =\left\{(x, Y): y=x+1\right\}$$
Write down the domain, condomain and range of $$R$$
If $$(x+1, y-2)=(3, 1)$$, find the values of $$x$$
Let $$A=\left\{ 1, 2, 3,.......14\right\}$$. Define a relation $$R$$ from $$A$$ to $$A$$ by $$R =\left\{ (x, y):3x-y=0, x, y \in A\right\}$$. Write down its domain, co-domain and range.
Define range of a relation.
If $$P=\left\{ a, b, c \right\}$$ and $$Q=\left\{ r \right\}$$, from $$P \times Q$$ and $$Q \times P$$. Are these two products equal?
Define ordered pair.
Define domain of a relation.
If $$\left( \dfrac x3+1, y-\dfrac 23 \right)=\left( \dfrac 53, \dfrac 13 \right)$$ find x and y
Let $$A=\left\{ 1, 2, 3, 4, 6 \right\}$$. Let $$R$$ be the relation on $$A$$ defined by $$\left\{(a, b): a, b \in A, b\right.$$ is exactly divisible by $$a\left. \right\}$$,
Find the domain of $$R$$
Let $$R$$ be a relation from $$Q$$ to $$Q$$ defined by $$R=\left\{(a, b)\ a, b\in Q\right.$$ and $$\left.a-b \in Z \right\}$$. Show that $$(a, a)gR$$, for all $$a \in Q$$
If A = {1 , 2 , 3} B = { 4 , 5 , 6} , then which of the following is relation from A to B ? Justify your answer also.
$$ {( 1 , 6) , (2 , 6) ( 3 , 6) } $$
Let $$A=\left\{ \right.1, 2, 3, 4), B=\left\{1, 5, 9, 11, 15, 16\right\}$$ and $$f=\left\{ (1, 5), (2, 9), (3, 1), (4, 5), (2, 11)))\right.$$.
Is the following true?
$$f$$ is a relation from $$A$$ to $$B$$
Justify your answer.
If A = {1 , 2 , 3} B = { 4 , 5 , 6} , then which of the following is relation from A to B ? Justify your answer also.
$$ ( 1 , 4), (3 , 5), (3 , 6 )$$
Let $$N$$ be the set of natural numbers and the relation $$R$$ be defined on $$N$$ such that $$R=\left\{ (x, y):y=2x, x, y\in N \right\}$$. What is the domain, co-domain and range of $$R$$?
Is this relation a function?
If A = {1 , 2 , 3} B = { 4 , 5 , 6} , then which of the following is relation from A to B ? Justify your answer also.
$$ { (1 , 5), ( 3 , 4) ( 5 , 1), (3 ,6)} $$
Let $$A=\left\{ 1, 2, 3, 4, 6 \right\}$$. Let $$R$$ be the relation on $$A$$ defined by $$\left\{(a, b): a, b \in A, b\right.$$ is exactly divisible by $$a\left. \right\}$$,
Find the range of $$R$$
Express the following relation in the rules from defined in N:
$$ {(2 , 3) , ( 4 , 2) , (6 , 1) , } $$
If a relation $$ \phi$$ RR from set C of complex numbers to a set R of real numbers is so defined that $$ x \phi y \Leftrightarrow |x| = y $$
$$ ( 1 + i) \phi 3 $$
Express the following relation in the rules from defined in N:
$$ {(1 , 3) , ( 2 , 5) , (3 , 7) , (4 , 9).........} $$
In in a set of integers Z , a relation R is defined in such a way that $$ x Ry \Leftrightarrow x^{2} + y^{2} = 25 $$ , then write R and $$ R^{-1}$$ in the from of a set order pairs and also write their domain .
If a relation $$ \phi $$ RR from set C of complex numbers to a set R of real numbers is so defined that $$ x \phi y \Leftrightarrow |x| = y $$
$$ 3 \phi (-3) $$
If a relation $$ \phi $$ RR from set C of complex numbers to a set R of real numbers is so defined that $$ x \phi y \Leftrightarrow |x| = y $$
$$ ( 2 + 3i) \phi 13 $$
If A = {1 , 2 , 3} B = { 4 , 5 , 6} , then which of the following is relation from A to B ? Justify your answer also.
$$ {( 2 , 4), (2 , 6)( 3 , 6)( 4 , 2)}$$
A relation R from set A = { 2 , 3 , 4 , 5) to set B = { 3 , 6 , 7 , 10 } is defined in such a way that $$ xRY \Leftrightarrow x $$ is a prime number related to y . Write relation R in the set from order pairs and also fined domain and range of if.
If A = {1 , 2 , 3} B = { 4 , 5 , 6} , then which of the following is relation from A to B ? Justify your answer also.
$$ A \times B $$
Express the following relation in the rules from defined in N:
$$ {(2 , 1) , ( 3 , 2) , (4 , 3) ,( 5 , 4)....... }$$
Express the following relations in the from of sets or orders pairs :
$$ R_{2} $$ is relation from set A = {8 ,9 , 10 , 11 } to set B = (5 , 6 , 7 8} such that " y = x - 2
If $$f : R \rightarrow R , f (x) = x^{2} ,$$ then find
$$\{ x | f (x) = 4 \}$$
If f : R \rightarrow R , f (x) = x^{2} ,$$ then find
{ y | f (y) = - 1 }
Any relation P is defined in set R0 of non zero real numbers by following ways :
$$ xPy \Leftrightarrow x^{2} + y^{2} = 1 $$
If a relation $$ \phi $$ RR from set C of complex numbers to a set R of real numbers is so defined that $$ x \phi y \Leftrightarrow |x| = y $$
$$ ( 1 + i) \phi 1 $$
Express the following relations in the from of sets or orders pairs :
$$ R_{1} $$ is relation from set A = { 1 , 2 , 3 , 4 , 5 , 6 } to set B = (1 , 2 , 3} such that "x = 2y "
Express the following relations in the from of sets or orders pairs :
$$ R_{3} $$ is relation from set A = {0 , 1 , 2......10} defined by 2x + 3y = 12.
Any relation P is defined in set R0 of non zero real numbers by following ways :
$$ xPy \Leftrightarrow + xy = 1 $$
Any relation P is defined in set $$R_o$$ of non zero real numbers by following ways :
$$ xPy \Leftrightarrow ( x + y) $$ is a rational number.
Express the following relations in the from of sets or orders pairs :
$$ R_{3} $$ is relation from set A = {5 , 6 , 7 ,8} to set B = { 10 , 12 , 15 , 16 , 18} is defined such that "x is divisor of y''
If A = { 1 ,2} , then write all non - zero relations defined in A.
Find the domain and range of the following relations
$$ R_{1} = \left \{ ( x ,y) : x , y \in N , x + y = 10\right \} $$
In the set of real numbers R , two relations $$R_{1} and R_{2}$$ can be defines as
$$ aR_{1}b \Leftrightarrow a - b >0 $$
In the set of real numbers R , two relations $$R_{1} and R_{2}$$ can be defines as
$$ aR_{2}b \Leftrightarrow |a| \leq b $$
In the set of real numbers R two , relations $$ R_{1} and R_{2}$$ are defined as
$$ aR_{1}b \Leftrightarrow |a| = |b| $$
Find the domain and range of the relaton R
$$ R = { ( x + 1, x + 5)} : x \in { 0 , 1 , 2 , 3 , 4 , 5} $$
Solve :
$$f(x) = 5 - 3x $$
Find $$f(16)$$.
In the set of real numbers R two , relations $$ R_{1} and R_{2}$$ are defined as
$$ aR_{1}b \Leftrightarrow |a| \leq |b| $$
If statement is $$P(n): (n+ 3) < 2^{n+3}$$ then write $$P(4)$$.
Given $$A = \{5, 6, 7\}$$ and $$B = \{6, 8, 10\}$$, then : $$(A \cup B)\times B$$Find the number of elements in the above set obtained.
If $$A = \{5, 6, 7, 8\}$$ and $$B =\{6, 8, 10\}$$ find total elements in $$(A \cup B) \times (A \cap B)$$.
If the ordered pairs $$(a - 3, a + 2b)$$ and $$(3a - 1, 3)$$ are equal, find the value of $$a+b$$.
Given $$A = \{2, 3, 5\}$$ and $$B = \{6, 10, 14, 18\}$$ ; find the number of elements in relation $$R$$ such that $$R=\{(x, y) \,\,\epsilon\,\, A \times B,x < y \text{ and }\displaystyle \frac{y}{x} \,\,\epsilon \,\,N \}$$
If $$M=\{x : x \,\,\epsilon\,\, N, 1 < x \leq 4\}$$ and $$N = \{y : y\,\,\epsilon\,\,W, y < 3\}$$; find : N $$\times$$ MAlso find the number of such ordered pairs.
Let $$f:R-\left\{ 1 \right\} \rightarrow R$$ be defined $$f(x)=\cfrac { x+1 }{ x-1 } $$, show that $$f(x)+f\left( \cfrac { 1 }{ x } \right) =0$$ for $$\left( x\neq 0 \right) $$.
If $$f(x) = 2e^{x} - c\ ln\ x$$ monotonically increases for every $$x\epsilon (0, \infty)$$, then the true set of values of $$c$$ is ?
If $$f\left( x \right) = \cos \left( {\log x} \right)$$, than show that $$f\left( {\frac{1}{x}} \right).f\left( {\frac{1}{y}} \right) - \frac{1}{2}\left[ {f\left( {\frac{x}{y}} \right) + \left( {xy} \right)} \right]$$
Solve : $$f(x) = \dfrac{x^2 +2}{x^2 + 4}$$
If $$f\left(x\right)=x+2,\,g\left(x\right)={x}^{2}-x-2,$$ then find $$\dfrac{g\left(1\right)+g\left(2\right)+g\left(3\right)}{f\left(-4\right)+f\left(-2\right)+f\left(2\right)}$$
Find the range of $$f\left(x\right)={\sin}^{-1}{\left(\ln{\left[x\right]}\right)}+\ln{\left({\sin}^{-1}{\left[x\right]}\right)},$$ where $$\left[x\right]$$ is the greatest function.
If f(x) = $$\frac{x + 1}{x - 1}$$; then f($$\frac{1}{2}$$)
If f(x) = $$\frac{x + 1}{x - 1}$$; then f($$\frac{1}{2}$$)=
Let $$f : R-\{2\} \rightarrow R$$ be defined by $$f(x)=\dfrac{x^{2}-4}{x-2}$$and $$g: R \rightarrow R$$ be defined by $$g(x)=x+2$$ . Find whether $$f \equiv g$$ or not.
Let f(x)=$$\frac{ax+b}{cx+d}$$.Then fof(x)=x provided that.
What do you mean by a binary relation on a set $$\displaystyle A$$?
Define the domain and range of a relation on $$\displaystyle A$$.
For any sets $$\displaystyle A$$ and $$\displaystyle B$$, prove that:
$$\displaystyle (A \times B) \cap ( B \times A) = (A \cap B) \times (B \cap A)$$.
Let $$\displaystyle A = \{ 2, 3, 4, 5\}$$ and $$\displaystyle B = \{3, 6, 7, 10\}$$.
Let $$\displaystyle R = \{(x, y) : x \in A, y \in B $$ and $$\displaystyle x $$ divides $$\displaystyle y \}$$.
Which element is common between the domain and range?
If $$ A = \left( \begin{array} { l l } { 1 } & { 2 } \\ { 3 } & { 4 } \end{array} \right) \& f ( x ) = x ^ { 2 } - 3 x + 2 . $$ find f ( A )
Let $$\displaystyle A = \{ 1, 2, 3, 4, 6\}$$ and let $$\displaystyle R = \{(a, b) : a, b \in A $$ and $$\displaystyle a $$ divides $$\displaystyle b \}$$.
Enter 1 if both dom $$\displaystyle (R)$$ and range $$\displaystyle (R)$$ are same else enter 0
Let $$\displaystyle A = \{2, 3 \}$$ and $$\displaystyle B = \{ 3, 5 \}$$.
How many relations can be defined from $$\displaystyle A $$ to $$\displaystyle B $$?
Let $$\displaystyle A = \{ 1, 2, 3, 5, 6\}$$
Define a relation $$\displaystyle R $$ from $$\displaystyle A $$ to $$\displaystyle A $$ by $$\displaystyle R = \{ (x, y) : y = x + 1 \}$$. How many common elements are there in between dom $$\displaystyle (R)$$ and range $$\displaystyle (R)$$.
Let $$\displaystyle R = \{ (x, y): x, y \in Z$$ and $$\displaystyle x^2 + y^2 \leq 4 \}$$.
Enter 1 if dom $$\displaystyle (R) $$ and range $$\displaystyle (R)$$ are same else enter 0
Domain and range are same.
Let $$ fx=\begin{cases} x^{ 2 }-4x+3,\quad x<3 \\ x-4,\quad x\geq 3 \end{cases}\quad and\quad g(x)=\begin{cases} x-3,\quad x<4 \\ x^{ 2 }+2x+2,\quad x\geq 4 \end{cases}$$
Describe the function $$ f / g $$ and find its domain.
Let f(x) be a function satisfying the condition f(-x)=f(x) for all real x. if f(0)exists ,find its value
Let $$\displaystyle R = \{(x, x + 5) : x \in \{0,1, 2, 3, 4, 5\} \}$$
Find dom $$\displaystyle (R)$$ and range $$\displaystyle (R)$$. And enter the common element between them.
If $$g(x) = \left\{\begin{matrix} [f(x)], & x \in (0, \pi/2) \cup (\pi / 2, \pi) \\ 3, & x=\pi/2 \end{matrix}\right.$$
and $$f(x) = \dfrac{2(\sin x - \sin^n x) + |\sin x - \sin^n x|}{2(\sin x - \sin^n x) - |\sin x - \sin^n x|}, n \in N$$
Where $$[\cdot]$$ denotes the greatest integer function. Prove that $$g(x)$$ is continuous at $$ x=\pi /2$$ when $$n>1$$.
Consider the set $$A=(1,2,3)$$ and $$R$$ be the smallest equivalence relation on $$A$$, then $$R=$$ ______
Let $$Z$$ be the set of integers and $$R$$ be the relation defined in $$Z$$ such that $$aRb$$ if $$a-b$$ is divisible by $$3$$. Then $$R$$ partitions the set $$Z$$ into ______ pairwise disjoint subsets.
Solve :
$$f(x) = 5 - 3x $$
Find $$ff(x)$$, in its simplest form.
Define a Cartesian product of two sets.
Solve :
$$f(x) = 5 - 3x $$
Find $$ f (x + 2) $$.
If f is a function satisfying
$$f(x + y) = f(x) f(y) \forall x, y \epsilon N$$ such that $$f(1) 3$$ and $$\sum_{x}^{n} = 1 f(x) = 120$$ find the value of n.
Find the natural number a for which $$\sum_{k=1}^{n}f(a + k) = 16(2^n -1)$$, where the function f satisfies the relation f(x+y) = f(x) f(y) for all natural numbers x, y and further f(1) = 2.
Class 11 Engineering Maths Extra Questions
- Binomial Theorem Extra Questions
- Complex Numbers And Quadratic Equations Extra Questions
- Conic Sections Extra Questions
- Introduction To Three Dimensional Geometry Extra Questions
- Limits And Derivatives Extra Questions
- Linear Inequalities Extra Questions
- Mathematical Reasoning Extra Questions
- Permutations And Combinations Extra Questions
- Principle Of Mathematical Induction Extra Questions
- Probability Extra Questions
- Relations And Functions Extra Questions
- Sequences And Series Extra Questions
- Sets Extra Questions
- Statistics Extra Questions
- Straight Lines Extra Questions
- Trigonometric Functions Extra Questions