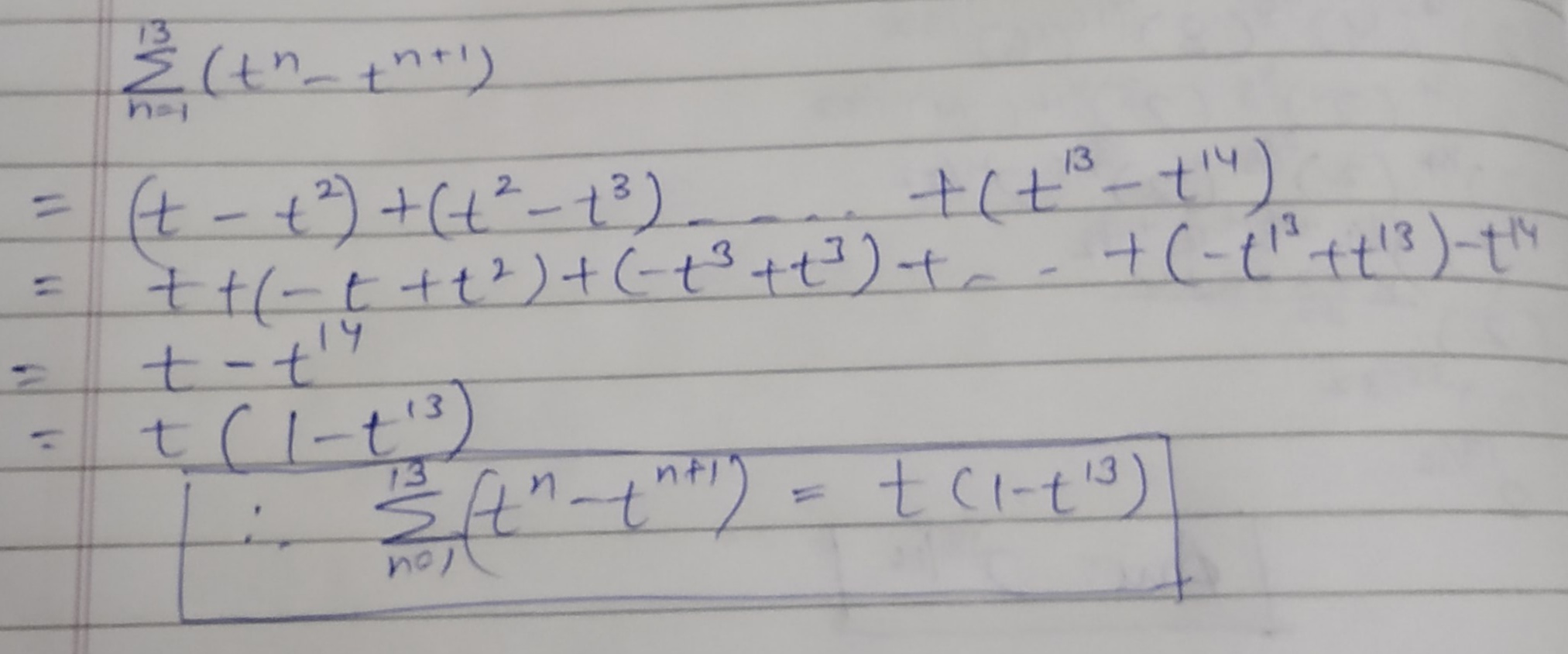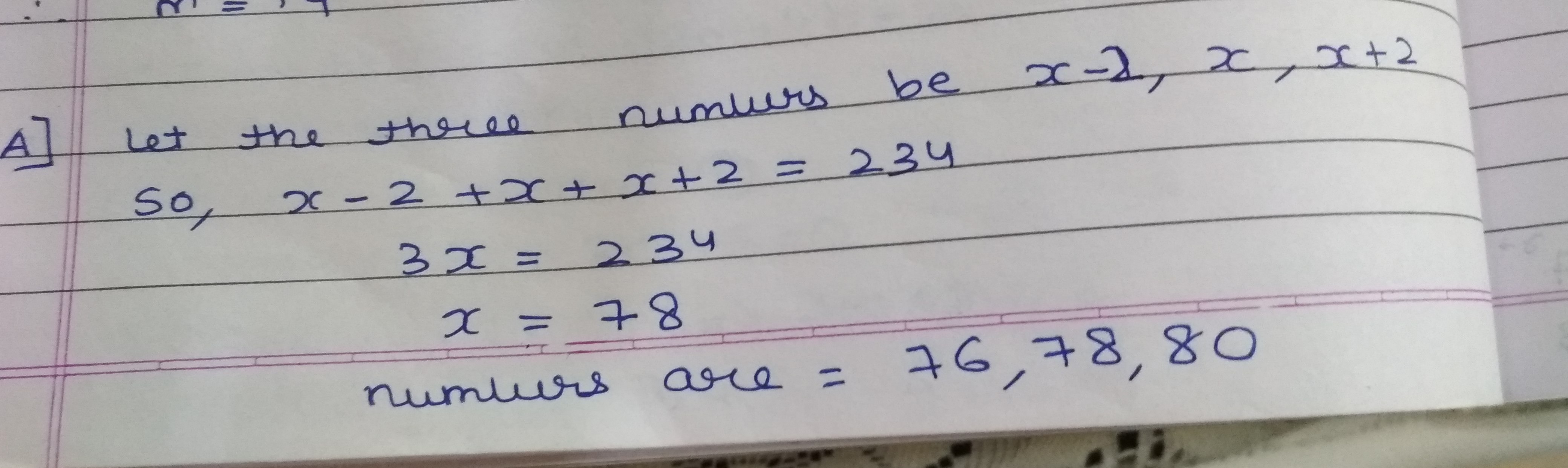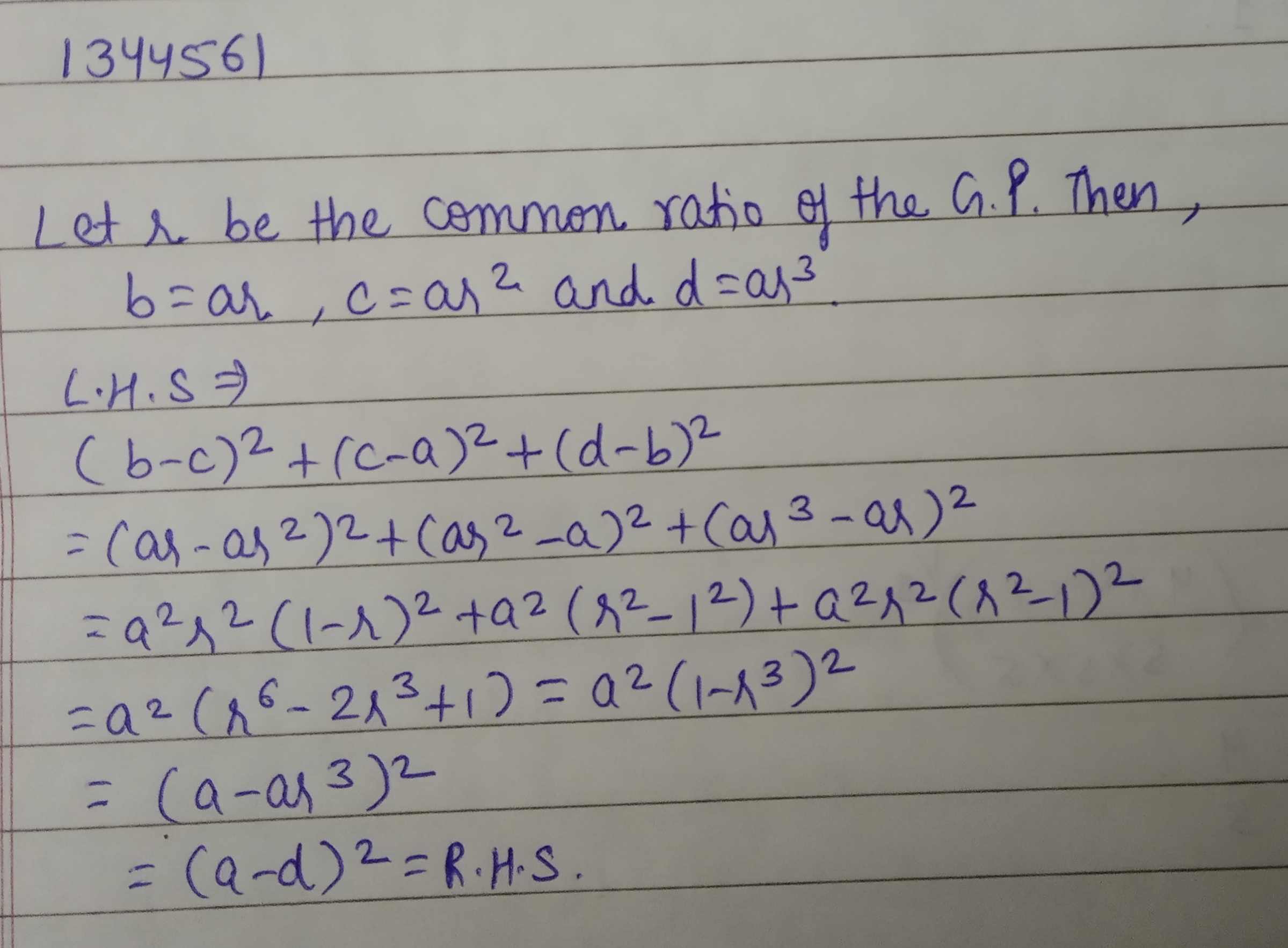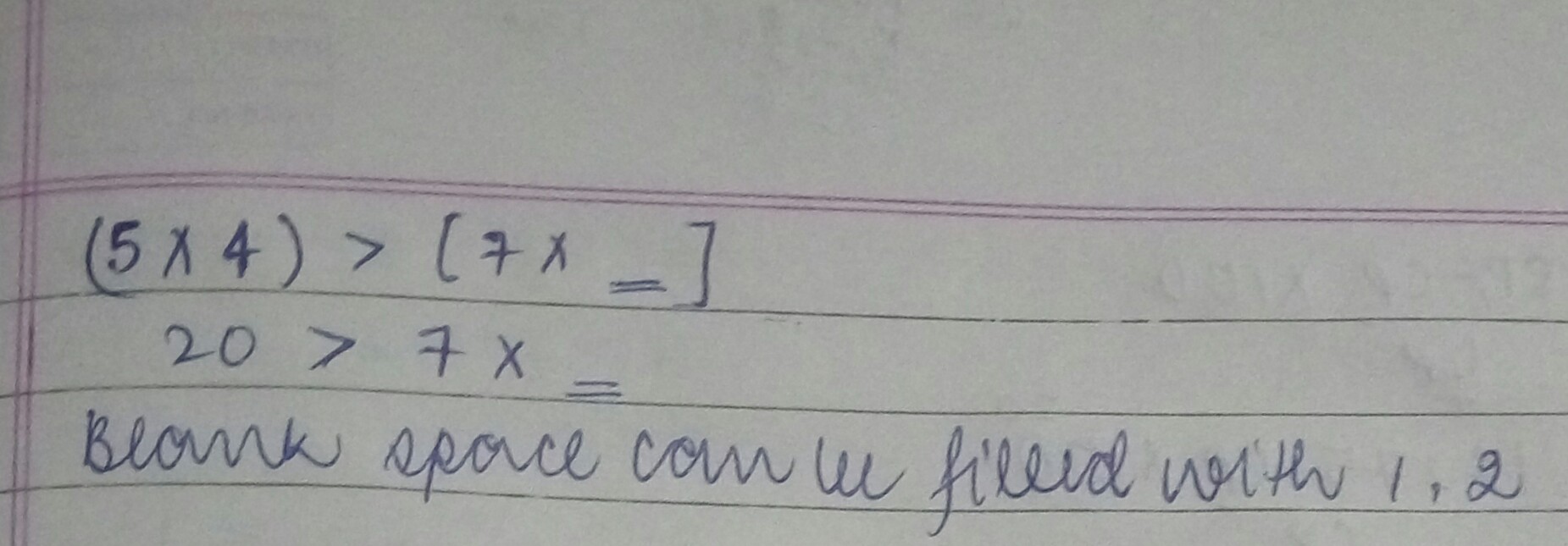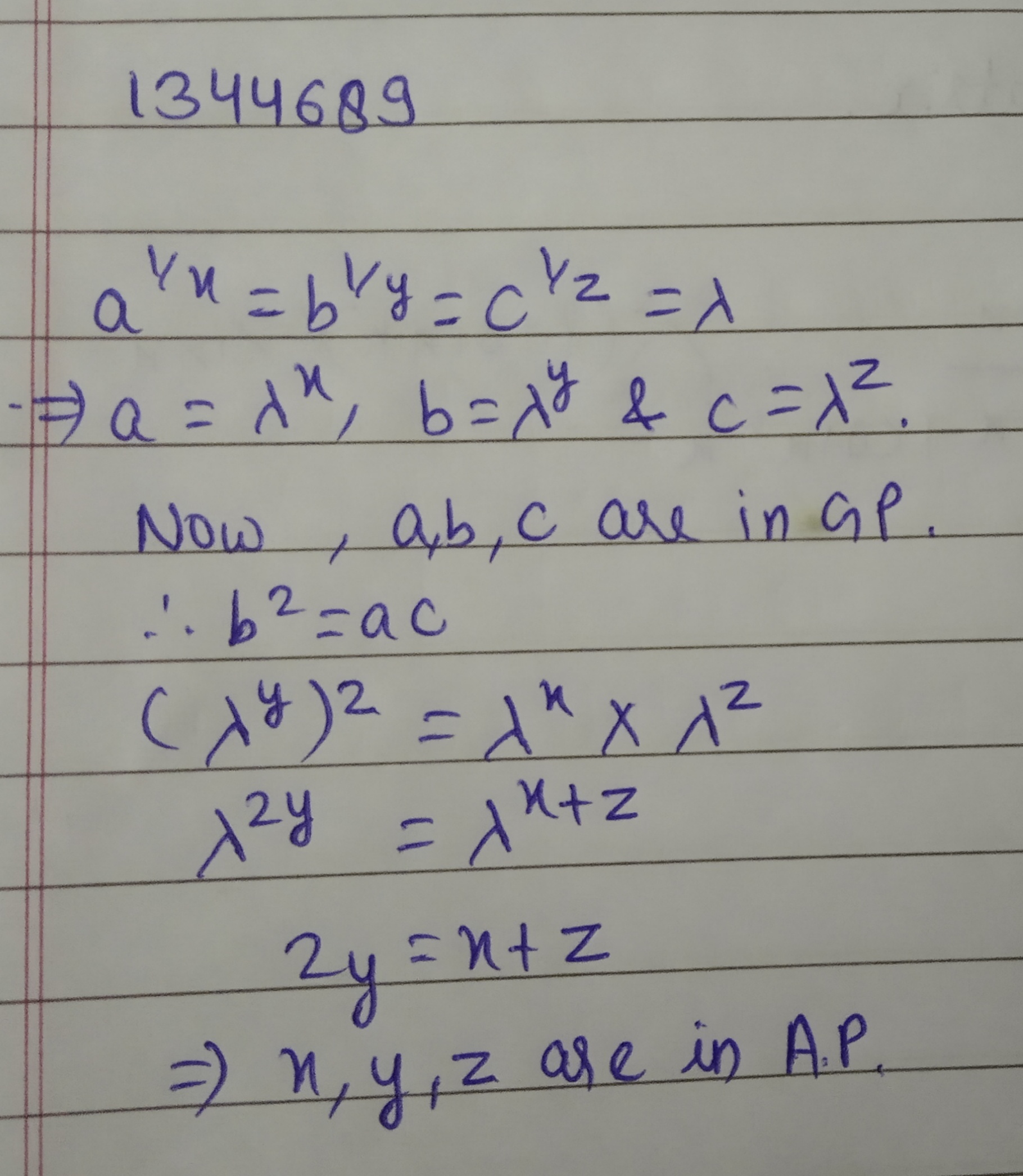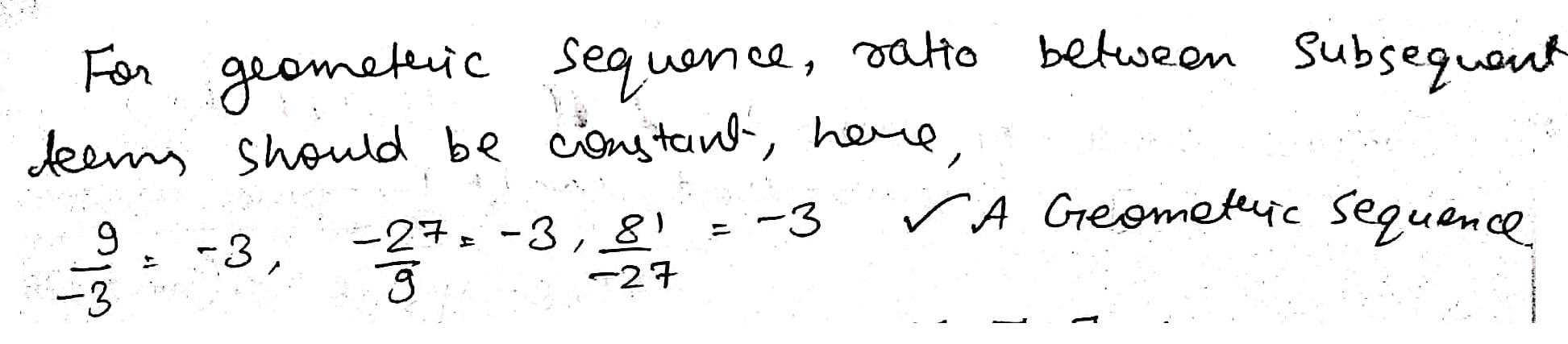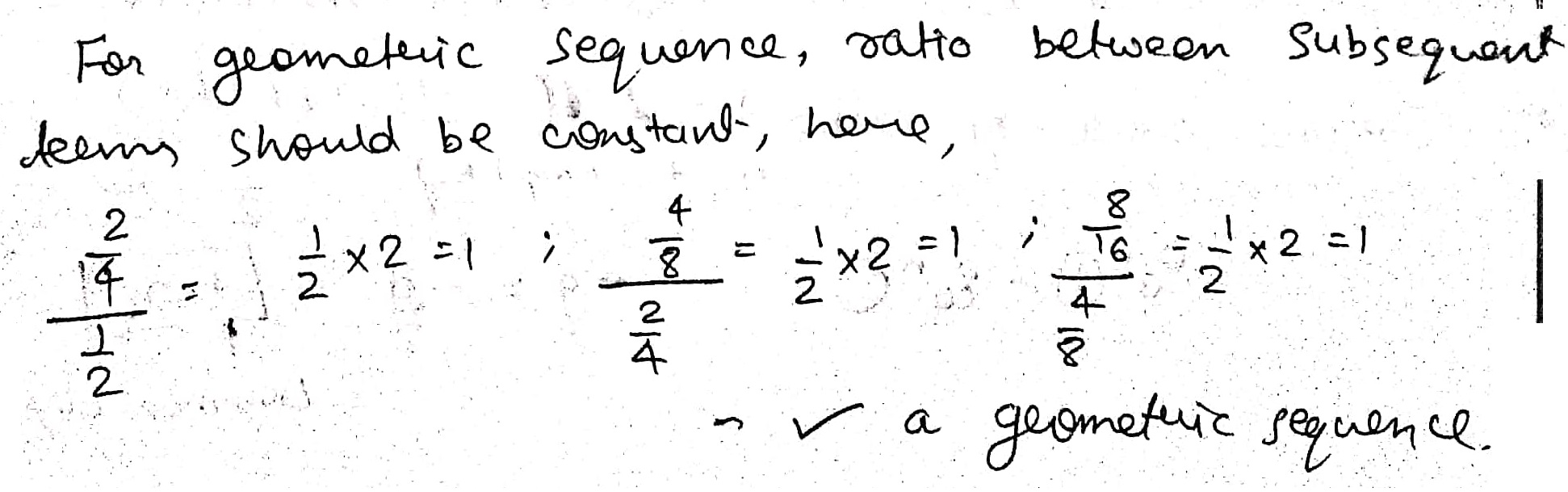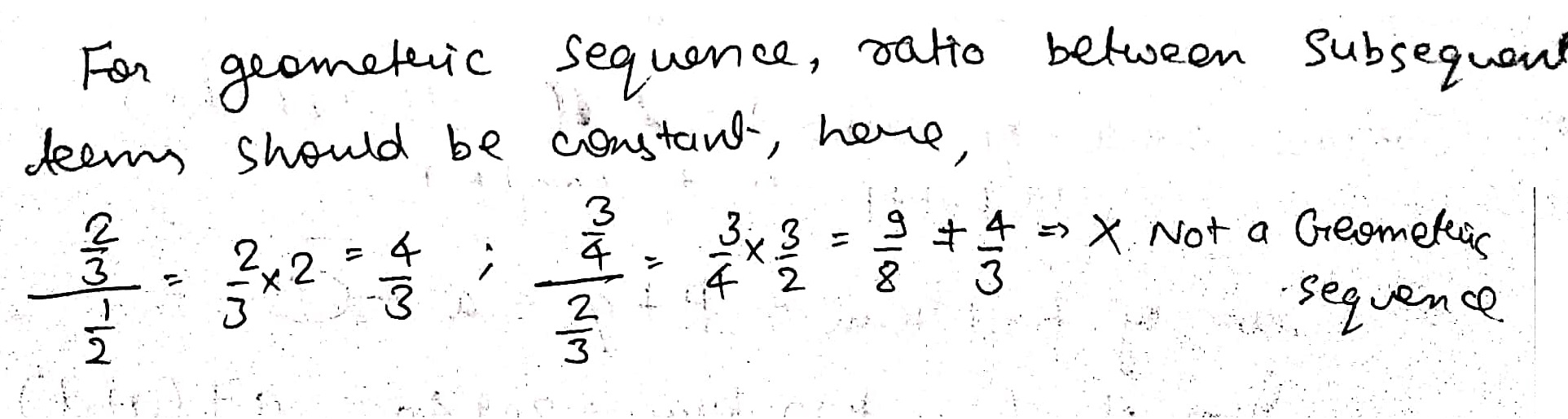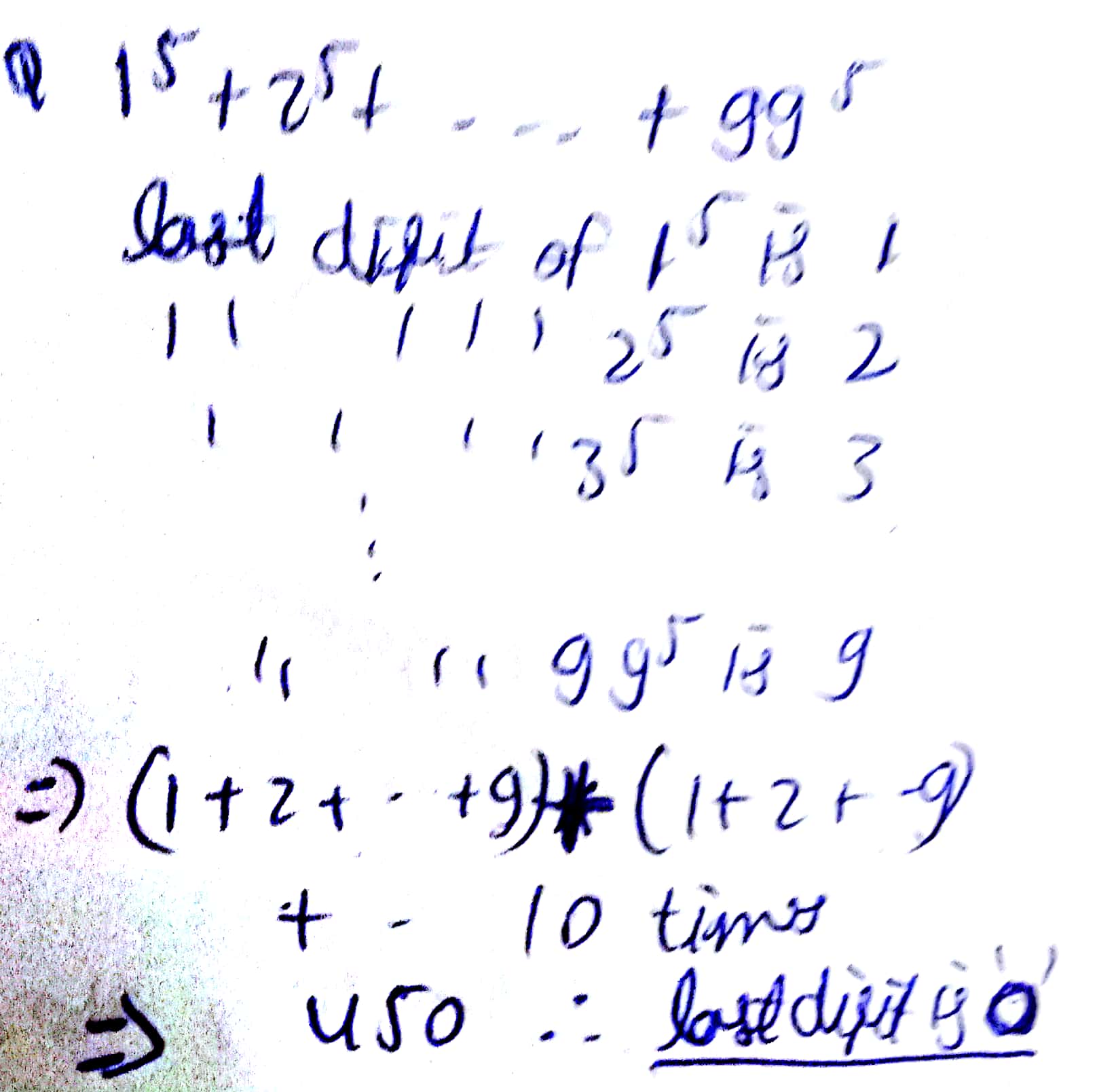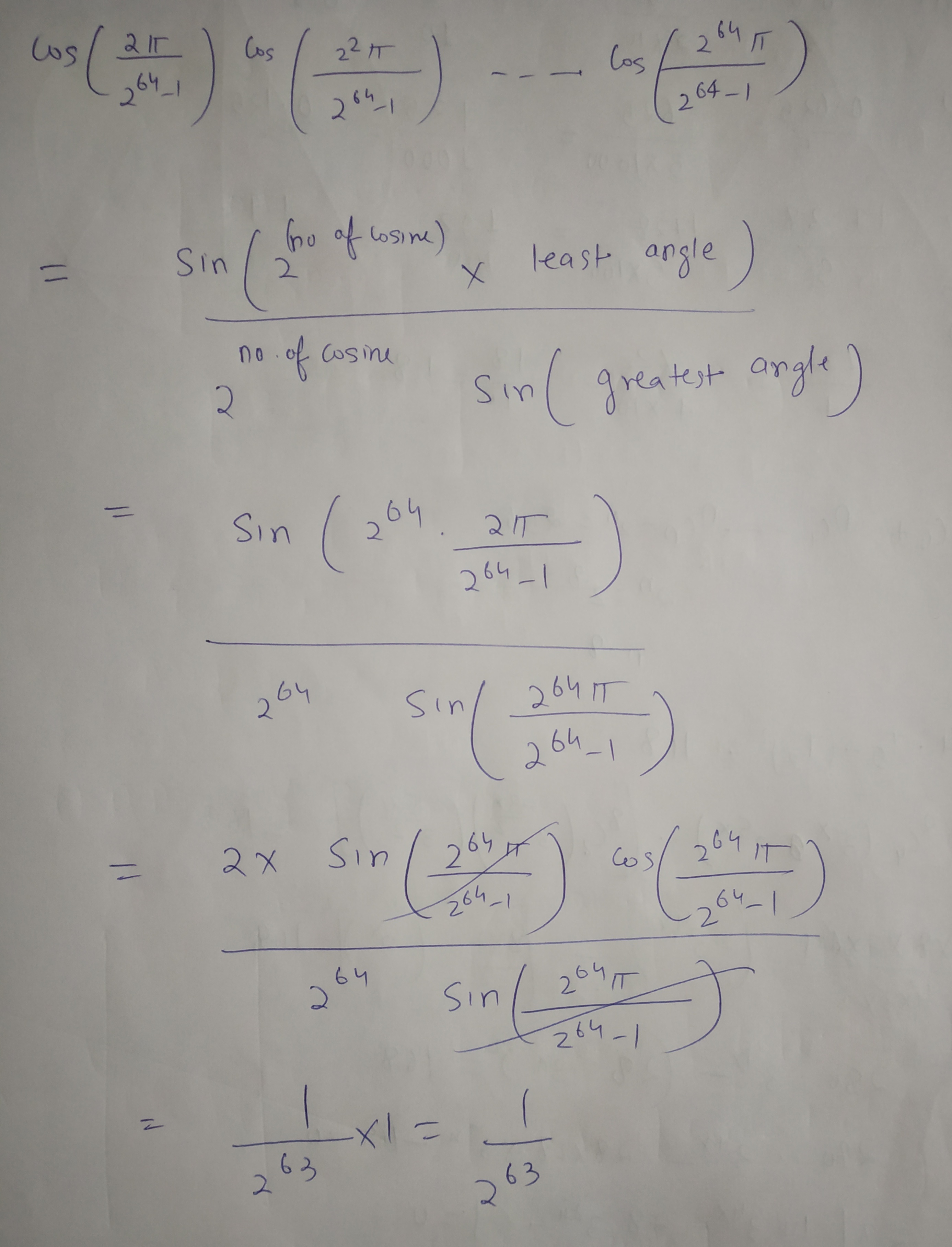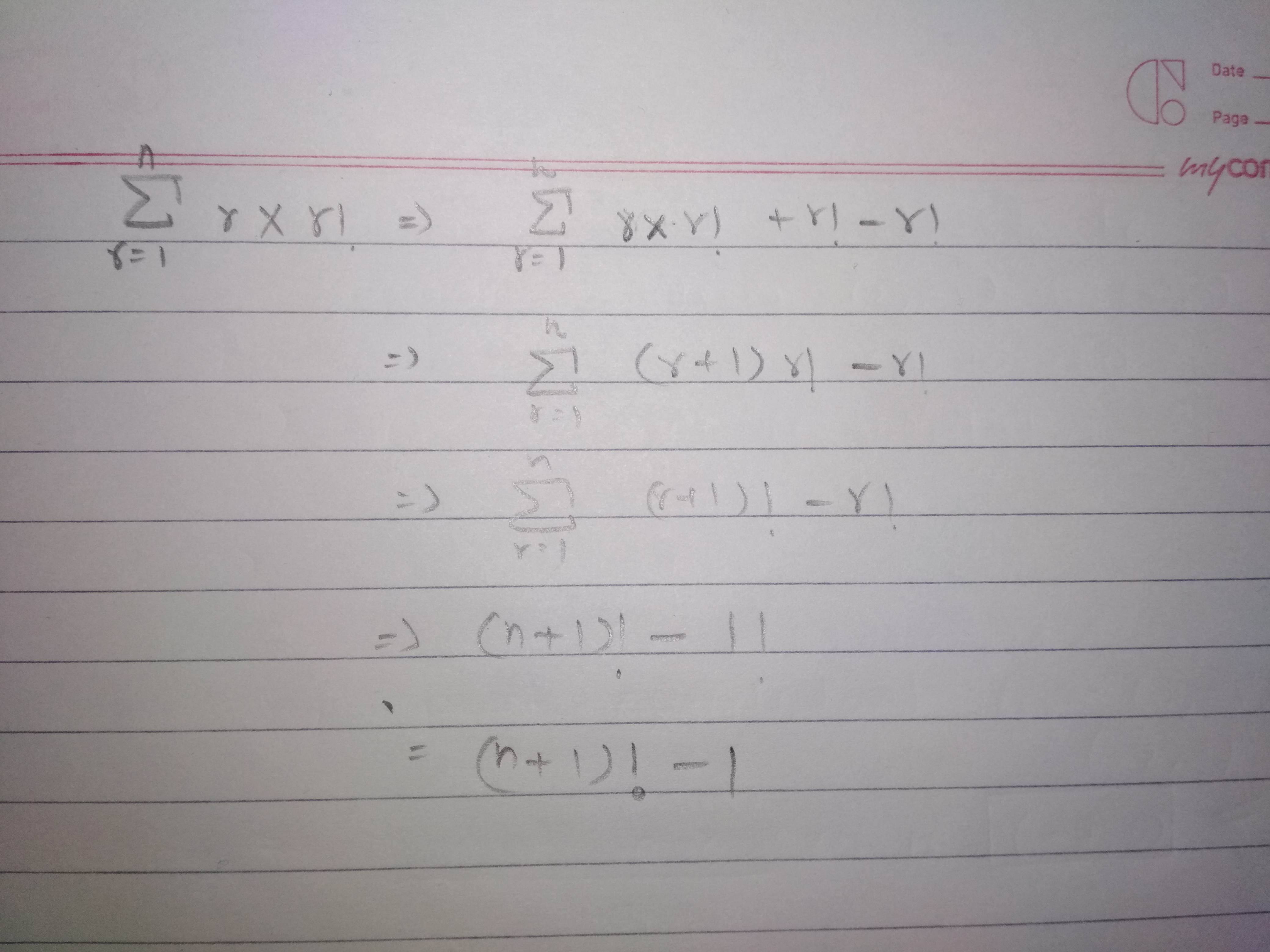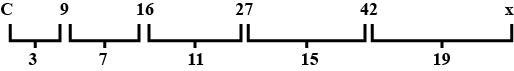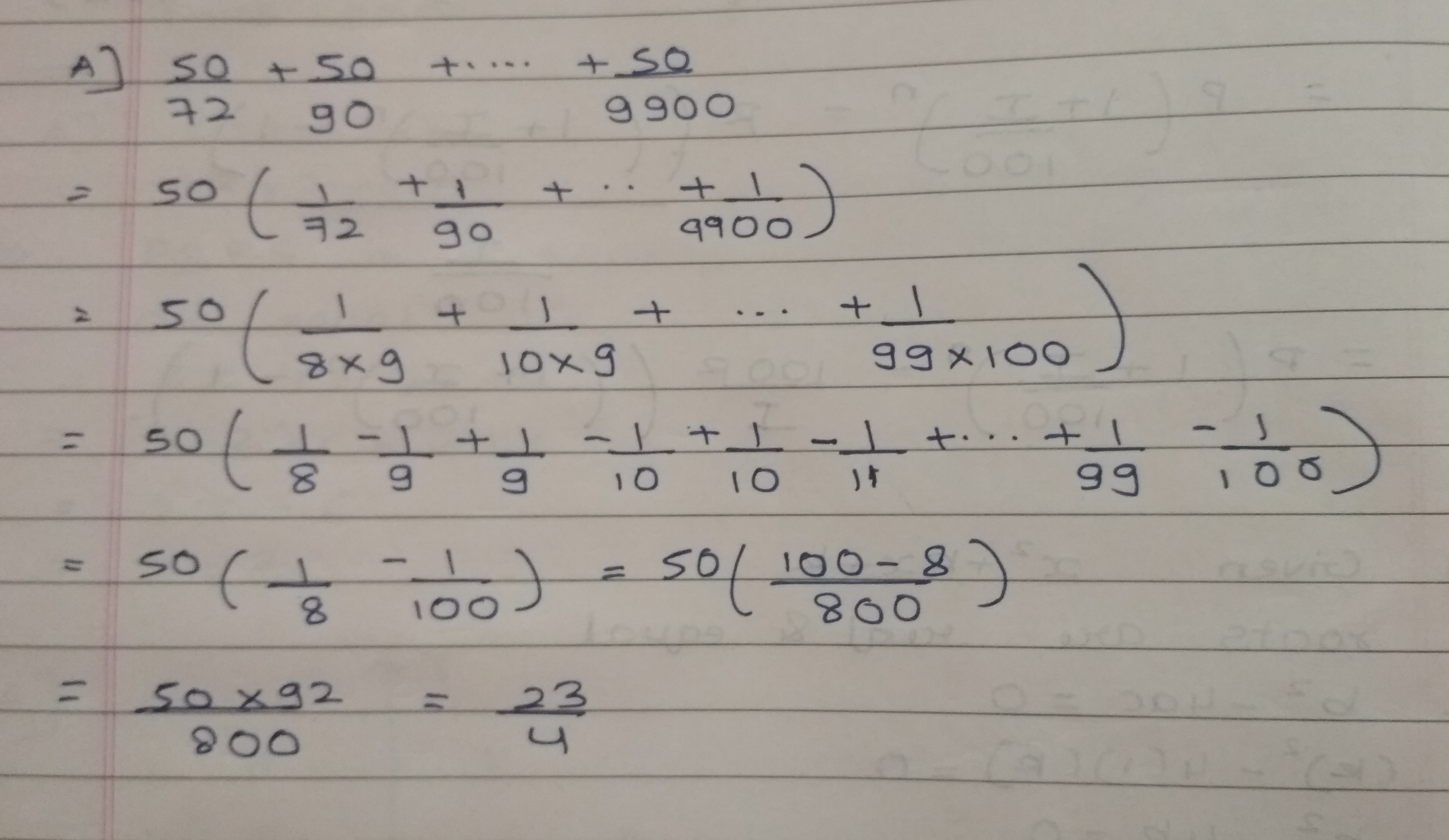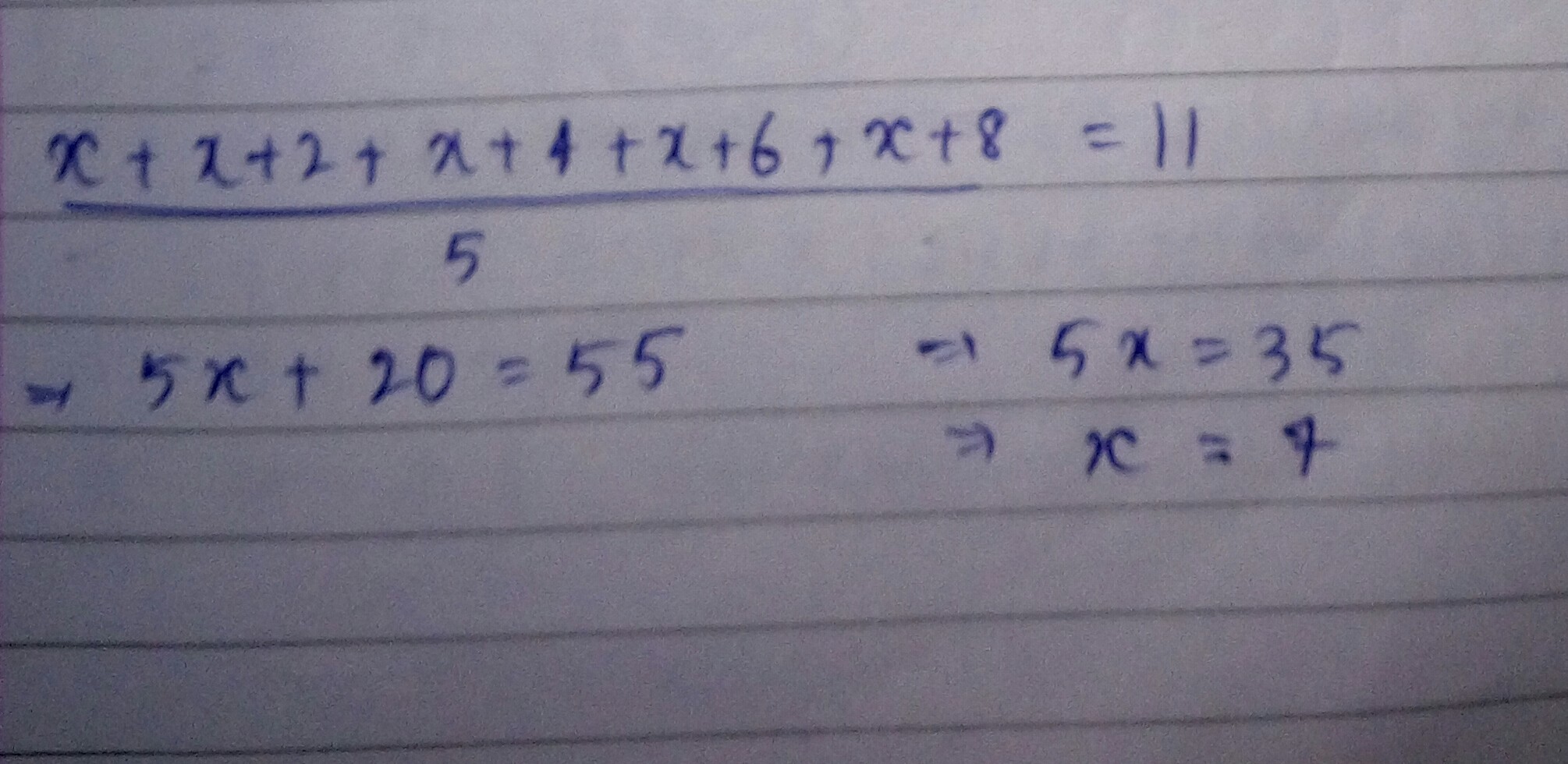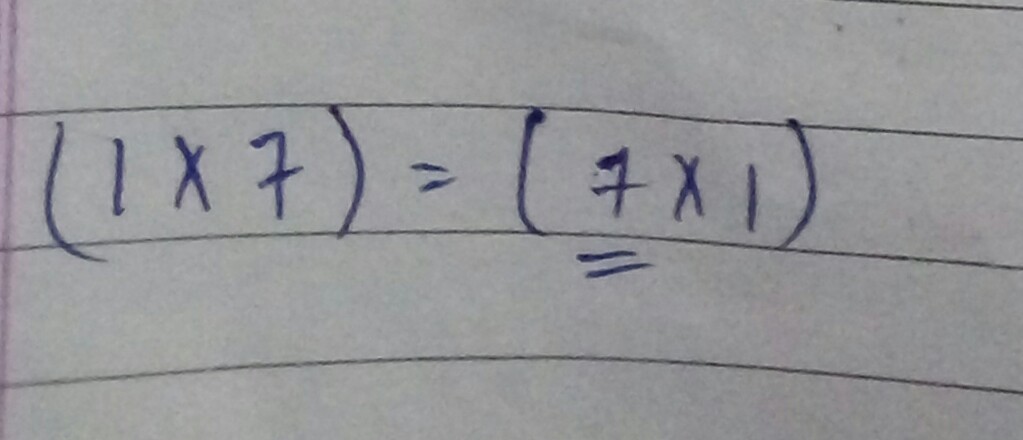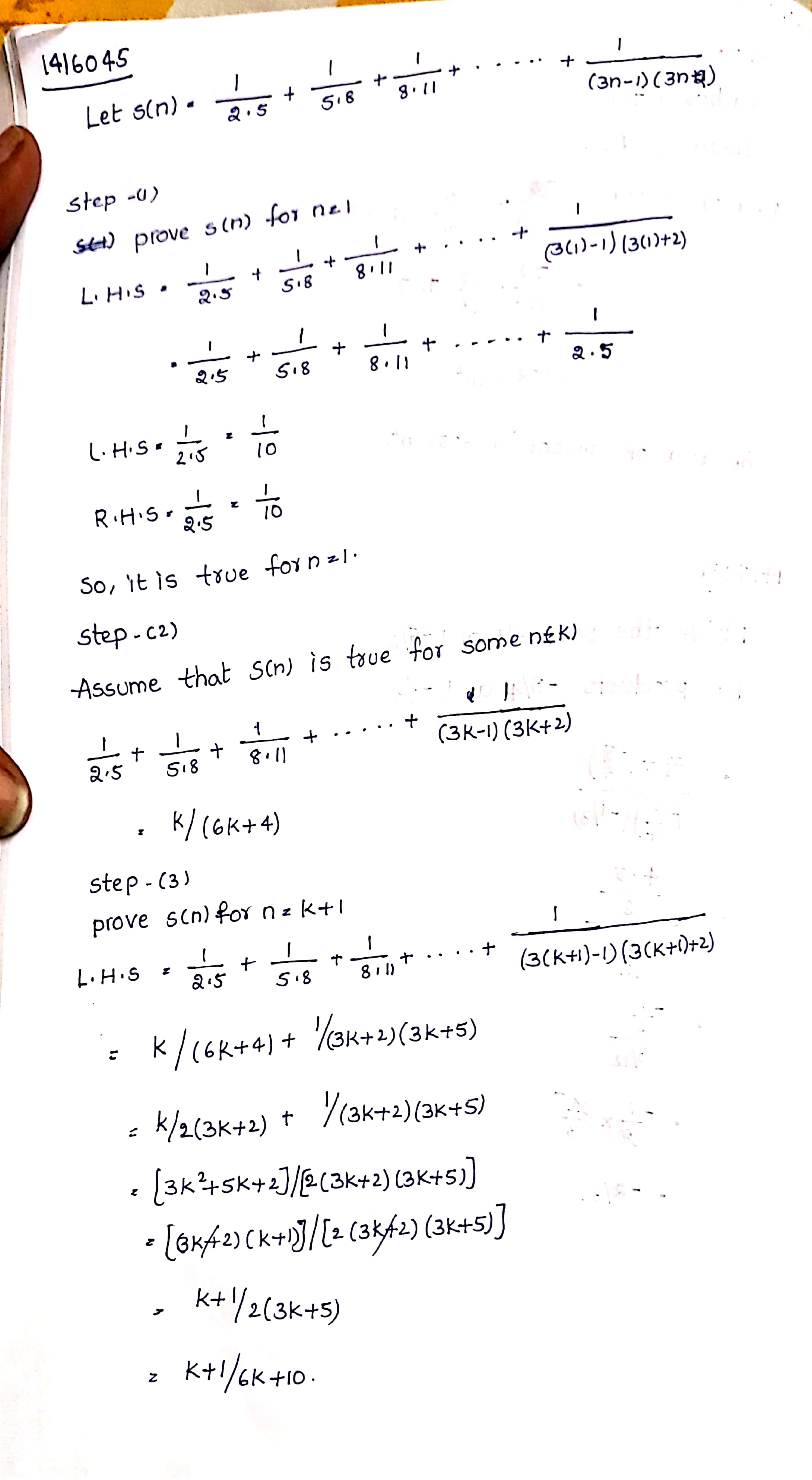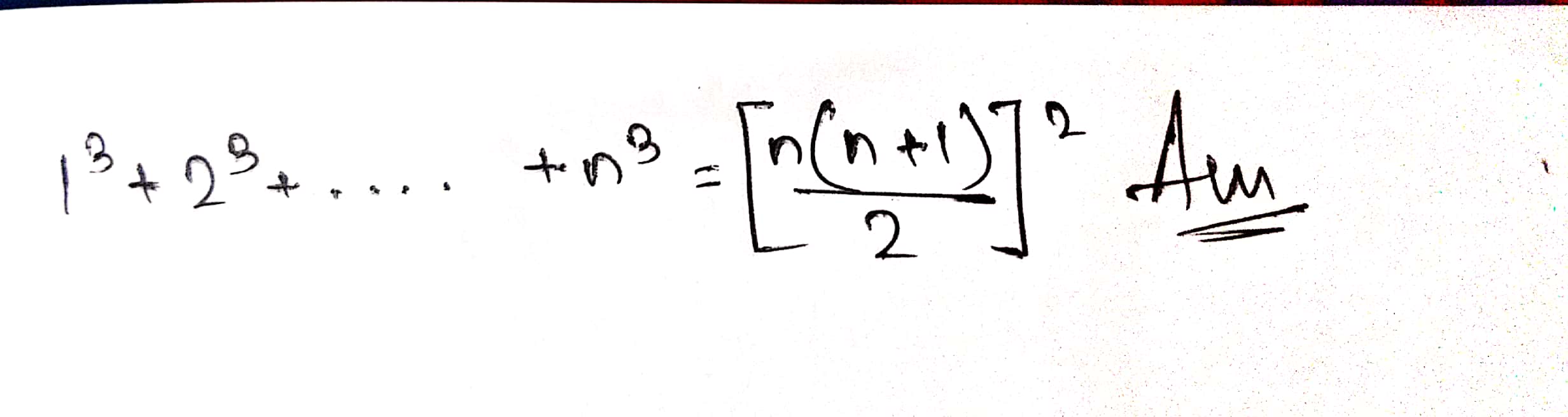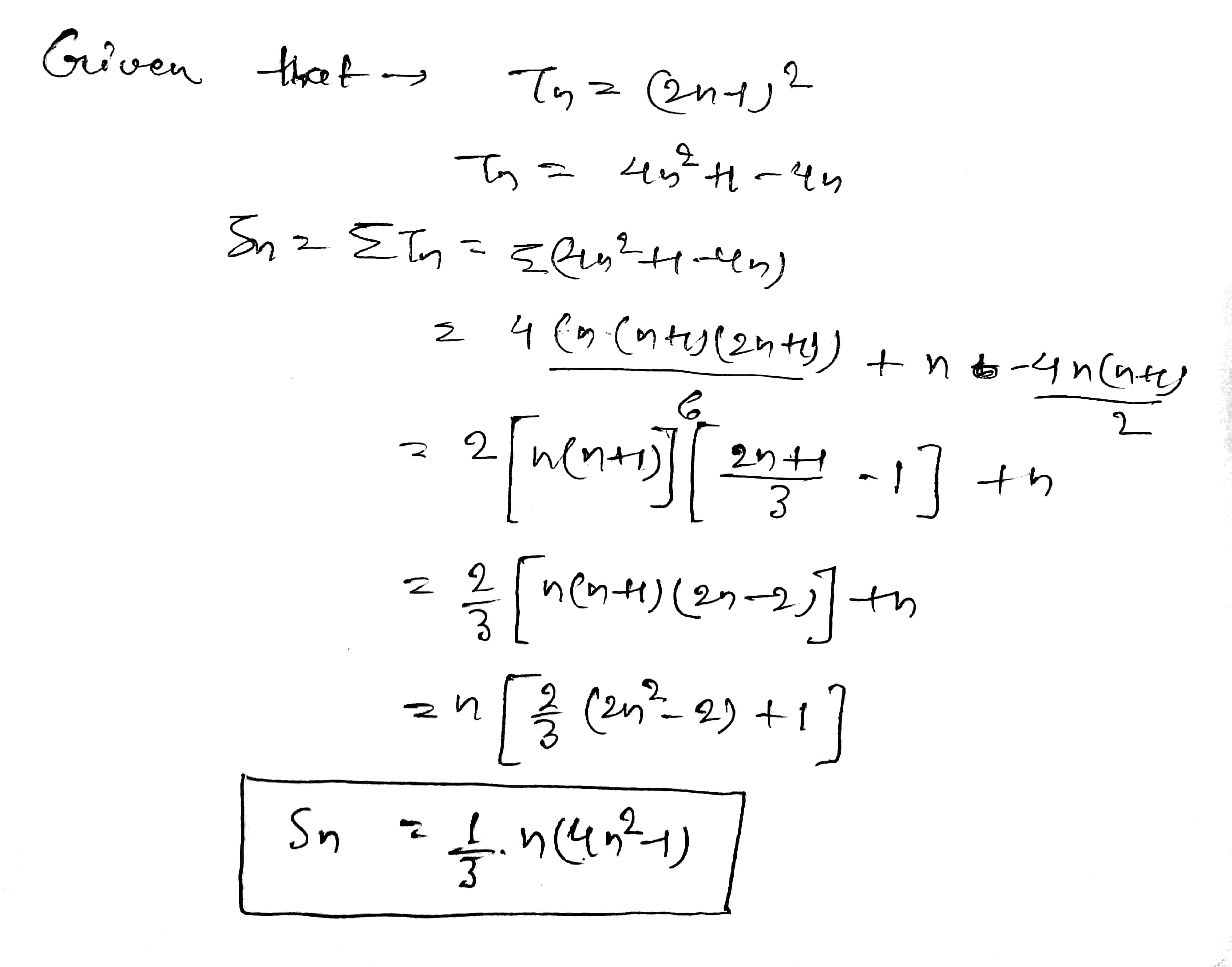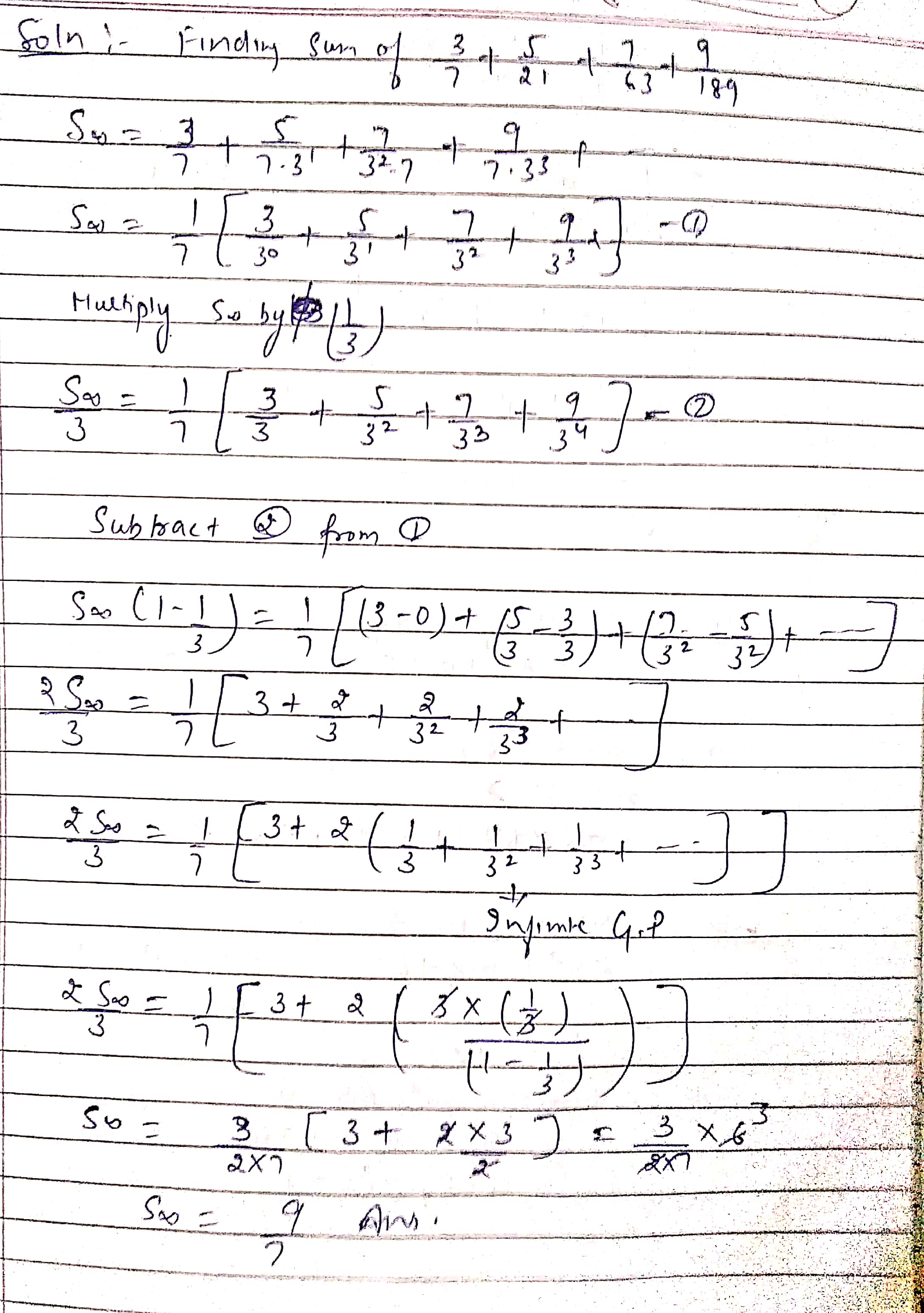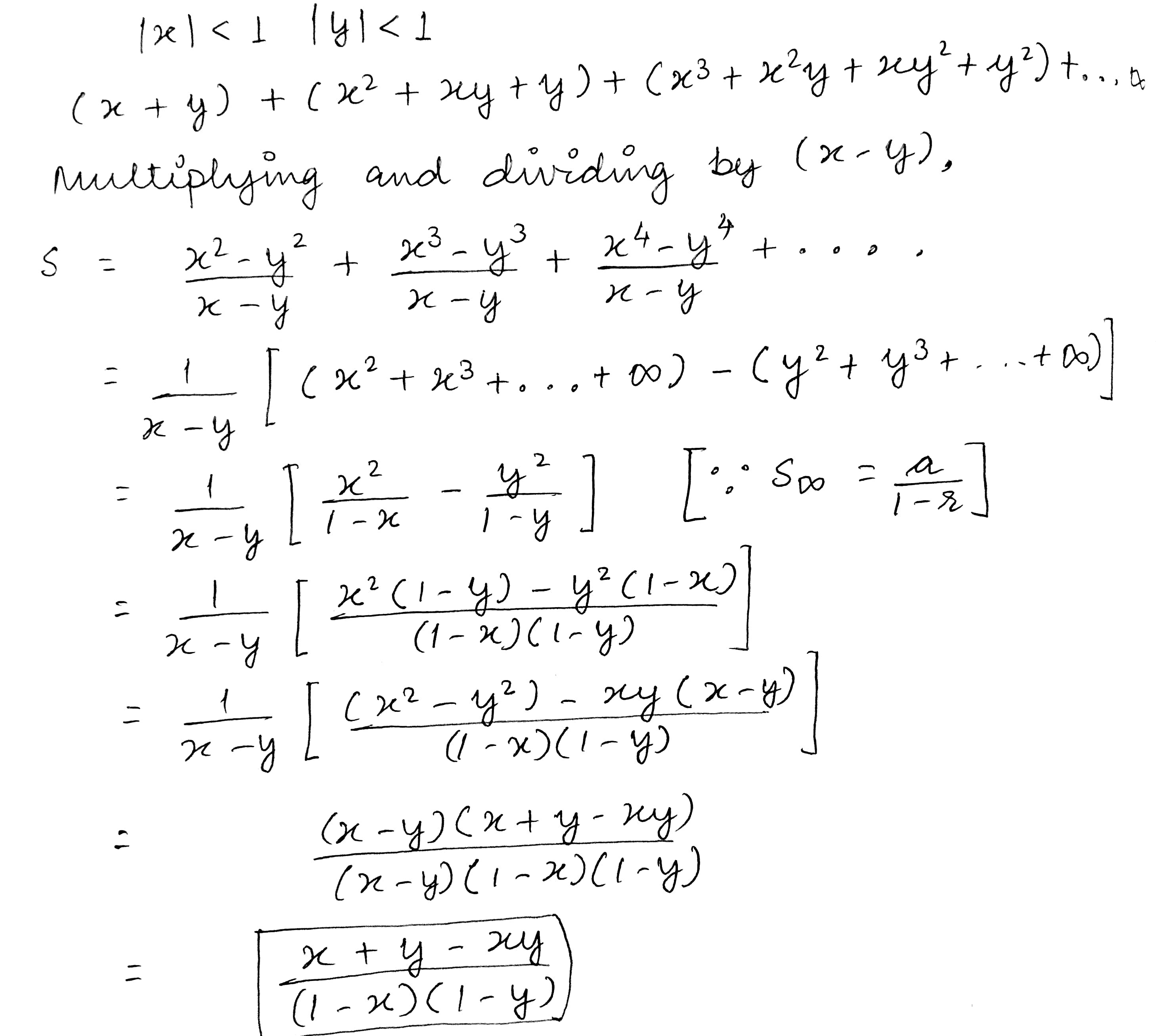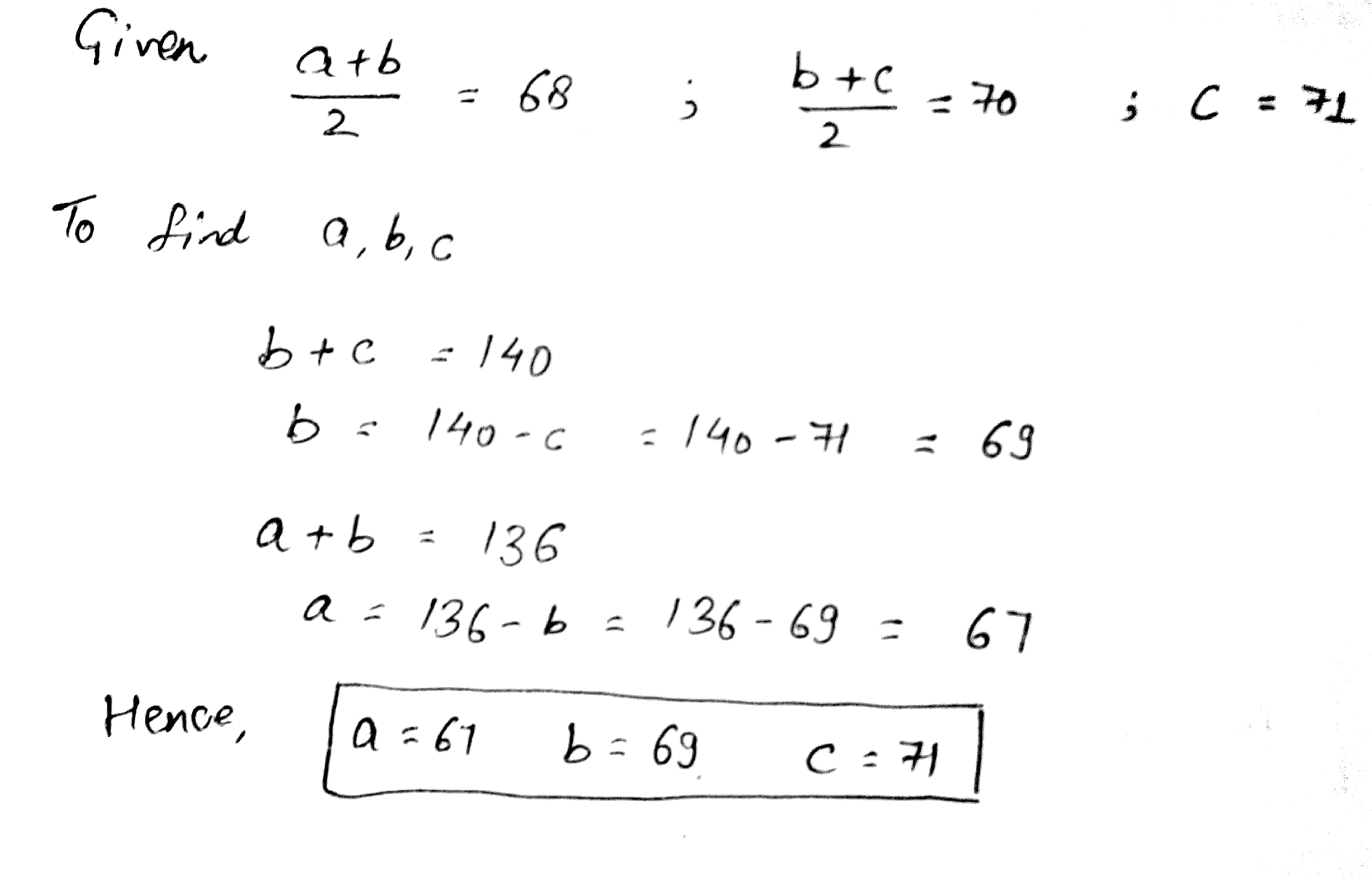Class 11 Engineering Maths - Sequences And Series

The sum of the infinite series $$\displaystyle{1+\frac{1+2}{2!} + \frac{1+2+2^2}{3!} + \frac{1+2+2^2+2^3}{4!}+ \,...}$$ is $$\displaystyle{e^y-e^x}$$ Find $$x+y^2$$

$$\displaystyle S={ 1+\frac { 1+2 }{ 2! } +\frac { 1+2+2^{ 2 } }{ 3! } +\frac { 1+2+2^{ 2 }+2^{ 3 } }{ 4! } +\, ... }$$
Now, $$\displaystyle { t }_{ n }=\frac { { 2 }^{ n }-1 }{ n! } $$
$$\displaystyle S=\sum _{ n=0 }^{ \infty }{ { t }_{ n } } =\sum _{ n=0 }^{ \infty }{ \frac { { 2 }^{ n } }{ n! } } -\sum _{ n=0 }^{ \infty }{ \frac { 1 }{ n! } } ={ e }^{ 2 }-e$$

Therefore, $$x+y^2=5$$

Ans: 5

Write four more numbers in the following pattern-
$$ \displaystyle \frac{-1}{3} $$, $$ \displaystyle \frac{-2}{6} $$, $$ \displaystyle \frac{-3}{9} $$, $$ \displaystyle \frac{-4}{12} $$..........

We have
$$ \displaystyle \frac{-2}{6} $$=  $$ \displaystyle \frac{-1\times 2}{3\times 2} $$
$$ \displaystyle \frac{-3}{9} $$= $$ \displaystyle \frac{-1\times 3}{3\times 3} $$
$$ \displaystyle \frac{-4}{12} $$=$$ \displaystyle \frac{-1\times 4}{3\times 4}$$
or $$ \displaystyle \frac{-1\times 1}{3\times1}$$ =  $$ \displaystyle \frac{-1}{3} $$
$$ \displaystyle \frac{-1\times 2}{3\times2}$$ =  $$ \displaystyle \frac{-2}{6} $$
$$ \displaystyle \frac{-1\times 3}{3\times3}$$ =  $$ \displaystyle \frac{-3}{9} $$
$$ \displaystyle \frac{-1\times 4}{3\times 4}$$ =  $$ \displaystyle \frac{-4}{12} $$
Thus we observe a pattern in these numbers
The other numbers would be $$ \displaystyle \frac{-1\times 5}{3\times 5}$$ =  $$ \displaystyle \frac{-5}{15} $$,
$$ \displaystyle \frac{-1\times 6}{3\times61}$$ =  $$ \displaystyle \frac{-6}{18} $$,$$ \displaystyle \frac{-1\times 1}{3\times7}$$ =  $$ \displaystyle \frac{-7}{21} $$

Find the first $$3$$ terms of a G.P. if $$a = 4$$ and $$r = 2$$.

$$T_1 = a = 4 \ \ T_2 = ar = 4 \times 2 = 8 \ \ T_3 = ar^2 = 4 \times 2^2 = 16$$
$$\therefore $$ The first three terms of the G.P. are $$4, 8, 16$$.

Find the sum of all natural numbers from $$1$$ to $$200$$ which are divisible by $$4$$.

We have to find sum $$4+8+12+...+200$$
Clearly, it is arithmetic progression.
Here, $$a=4, d=4$$
Let there are n terms and 200 is nth term. Then,
$$a+(n-1)d=200$$
$$\Rightarrow 4+(n-1)4=200$$
$$\Rightarrow (n-1)4=196$$
$$\Rightarrow (n-1)=49$$
$$\Rightarrow n=50$$
Therefore,
$$S_{50}=\frac{50}2[4+200]$$
$$\Rightarrow S_{50}=25\times204=5100$$

Find the arithmetic mean of 4 and 6.

Given that, $$a=4, \ b=6$$
$$\therefore n=2$$

We know that,

$$\text{mean}= \cfrac{\displaystyle \sum_{i=1}^{n} a_i}{n}$$

$$\Rightarrow \cfrac{a+b}2 = \cfrac{4+6}2 = 5$$.

Hence, the arithmetic mean of $$4$$ and $$6$$ is $$5$$.

Find the common ratio and the general term of the following geometric sequences.
$$0.02, 0.006, 0.0018, .....$$

We are given that the sequence is a G.P.

The common ratio is, $$r=\dfrac {0.006}{0.02}=0.3$$

The first term of the G.P. is $$a=0.02$$

The general term of the sequence is, $${t}_{n}=0.02{(0.3)}^{n-1}$$

A.M. of $$a-2$$, $$a$$, $$a+2$$ is ____.

Arithmetic mean $$= \dfrac{\text{Sum of all observations}}{\text{No. of observations}}$$

$$\Rightarrow$$ A.M $$=\cfrac { a-2+a+a+2 }{ 3 } = \cfrac {3a}3$$

$$\Rightarrow$$ A.M $$=a $$

A water tank has steps inside it. A monkey is sitting on the top most step. (ie, the first step) The water level is at the ninth step.
(a) He jumps $$3$$ steps down and then jumps back $$2$$ step up. In how many jumps will he reach the water level?
(b) After drinking water, he wants to go back. For this, he jumps $$4$$ steps up and then jumps back $$2$$ steps down in every move. In how many jumps will he reach back the top step?

$$(a)$$ Monkey Jumps $$3$$ steps down and $$2$$ steps up so, in total he jumped $$1$$ step down.Therefore , Now he is at $$second$$ step and water level is at the $$ninth$$ step.
Now, he will reach water level in $$9-2=7$$ jumps.

$$(b)$$ He jumps 4 steps up and 2 steps down ,so totally he climbs 2 steps up in 6 Jumps,Similarly we can divide 9 steps as follows
$$\Rightarrow9=2+2+2+3$$
After reaching the third Step, As he jumps up $$3$$ more Steps He will reach the top step and till then there will be no more steps to climb.(Means after $$3$$ more Jumps he will reach the top step)

Now, the number of jumps he made to reach the top $$=2\times 6+2\times 6+2\times 6+3=12+12+12+3=39$$

A.M. of $$1, 2, x, 3$$ is $$0$$, then $$x=$$ _____.

Arithmetic mean $$= \dfrac{\text{Sum of all observations}}{\text{No. of observations}}$$

$$\Rightarrow 0=\cfrac { 1+2+x+3 }{ 4 } \\ \Rightarrow 0=6+x\\ \Rightarrow x=-6 $$

Complete the following patterns:
(i) $$40, 35, 30$$, , ,
(ii) $$0, 2, 4$$, _ , _ , _ .
(iii) $$84, 77, 70$$, _ , _ , _ .
(iv) $$4.4, 5.5, 6.6$$, _ , _ , _ .
(v) $$1, 3, 6, 10$$, _ , _ , _ .
(vi) $$1, 1, 2, 3, 5, 8, 13, 21$$, _ , _ , _ . (This sequence is called FIBONACCI SEQUENCE)
(vii) $$1, 8, 27, 64$$, _ , _ , ___ .

$$(i)$$ $$40,35,30,25,20$$

Here the series is decreased with difference $$=5$$ between each number.

$$(ii)$$ $$0,2,4,6,8,10$$

Here the Series is increased with increment $$=2$$

$$(iii)$$ $$84,77,70,63,56,49$$

Here the Series is decreased with difference $$=7$$

$$(iv)$$ $$4.4,5.5,6.6,7.7,8.8,9.9$$

Here the Series is increased with increment $$=1.1$$

$$(v)$$ $$1,3,6,10,15,21,28$$

Here the Series is increased with increasing increment i.e. $$3-1=2,6-=3,10-6=4,15-10=5,21-15=6,28-21=7$$

$$(vi)$$ $$1,1,2,3,5,8,13,21,34,55,89$$

Here first 2 numbers add with each other to form next number

Similarly, second and Third number add together and result is the fourth Number and so on.

$$(vii)$$ $$1,8,27,64,125,216,343$$

This Series is the Series of Cubes as $$1^3,2^3,3^3,4^3,5^3,6^3,7^3$$

A geometric series consists of four terms and has a positive common ratio. The sum of the first two terms is 8 and the sum of the last two terms is $$72$$. Find the series

Let the sum of the four terms of the geometric series be $$a + ar + ar^{2} + ar^{3}$$ and $$r > 0$$
Given that $$a + ar = 8$$ and $$ar^{2} + ar^{3} = 72$$
Now, $$ar^{2} + ar^{3} = r^{2}(a + ar) = 72$$
$$\Rightarrow r^{2}(8) = 72 \therefore r = \pm 3$$
Since $$r > 0$$, we have $$r = 3$$.
Now, $$a + ar = 8\Rightarrow a = 2$$
Thus, the geometric series is $$2 + 6 + 18 + 54$$.

Find the sum of n terms of the series $$\left(4-\displaystyle\frac{1}{n}\right)+\displaystyle \left(4-\frac{2}{n}\right)+\displaystyle \left(4-\frac{3}{n}\right)+$$........

$$\Rightarrow (4+4+4+......n times) +\left (\dfrac {1}{n}+\dfrac {2}{n}+\dfrac {3}{n}+......+\dfrac {n} {n} \right) $$

$$\Rightarrow 4n+\dfrac {1}{n}(1+2+3+....+n)$$

$$\Rightarrow 4n+\dfrac {1}{n}\dfrac {n(n+1)} {2}$$

$$\Rightarrow 4n+\dfrac {n+1}{2}$$

$$\Rightarrow \dfrac {9n+1}{2}$$

Write the smallest $$7-$$digits largest and smallest number having three different digits.

Let the $$9$$ is greatest decimal digit, the greatest $$7-$$ digit number would begin with as many nines as possible.

Since there must be $$3$$ different digits in the $$7-$$ digits number,

Let begin with five nines and fill the last two places with $$8$$ and $$7$$.

The smallest seven digit number is $$1000000$$

But we need three different digits it will be $$1000002$$

Now,

Let find their sum $$=9999987+1000002=10999989$$.

$$\dfrac{1}{{1.2.3}} + \dfrac{1}{{2.3.4}} + \dfrac{1}{{3.4.5}} + \,..... + \dfrac{1}{{n\left( {n + 1} \right)\left( {n + 2} \right)}} = \dfrac{{n\left( {n + 3} \right)}}{{4\left( {n + 1} \right)\left( {n + 2} \right)}}$$

$${S_n} = {1 \over {1.2.3}} + {1 \over {2.3.4}} + ... + {1 \over {n\left( {n + 1} \right)\left( {n + 2} \right)}}$$

$$ = {1 \over 2}\left[ {{{3 - 1} \over {1.2.3}} + {{4 - 2} \over {2.3.4}} + ... + {{n + 2 - n} \over {n\left( {n + 1} \right)\left( {n + 2} \right)}}} \right]$$

$$ = {1 \over 2}\left[ {{1 \over {1.2}} - {1 \over {2.3}} + {1 \over {2.3}} - {1 \over {3.4}} + ... + {1 \over {n\left( {n + 1} \right)}} - {1 \over {\left( {n + 1} \right)\left( {n + 2} \right)}}} \right]$$4

$$ = {1 \over 2}\left[ {{1 \over {1.2}} - {1 \over {\left( {n + 1} \right)\left( {n + 2} \right)}}} \right]$$

$$ = {1 \over 2}\left[ {{{\left( {n + 1} \right)\left( {n + 2} \right) - 2} \over {2\left( {n + 1} \right)\left( {n + 2} \right)}}} \right]$$

$$ = {1 \over 2}\left[ {{{{n^2} + 3n} \over {2\left( {n + 1} \right)\left( {n + 2} \right)}}} \right]$$

$$ = {{n\left( {n + 3} \right)} \over {4\left( {n + 1} \right)\left( {n + 2} \right)}}$$

Solve: $$\displaystyle \sum_{n = 1}^{13}(t^n - t^{n + 1}) =$$

$$ \displaystyle \sum_{n=1}^{13} (t^{n}-t^{n+1}) $$

$$ \displaystyle = (t-t^{2})+(t^{2}-t^{3})...+(t^{13-t^{14}}) $$

$$ \displaystyle = t+(-t+t^{2})+(-t^{3}+t^{3})+...+(-t^{13}+t^{13})-t^{14} $$

$$ \displaystyle = t-t^{14} $$

$$ \displaystyle = t(1-t^{13}) $$

$$ \displaystyle \therefore \sum_{n=1}^{13}(t^{n}-t^{n+1}) = t(1-t^{13}) $$

1143812_1106557_ans_6c75a0e9069641cda24e932d83c0837b.jpg

If $$\alpha ,\,\beta \,,\gamma $$ are in A.P. show that $$\cot\,\beta = \dfrac{{\sin \alpha - \sin \gamma }}{{\cos \gamma - cos\alpha }}.$$

We have,

$$\alpha ,\beta ,\gamma $$ are in A.P.

So,

$$2\beta =\alpha +\gamma $$ ……… (1)

R.H.S

$$ =\dfrac{\sin \alpha -\sin \gamma }{\cos \gamma -\cos \alpha } $$

$$ =\dfrac{2\cos \left( \dfrac{\alpha +\gamma }{2} \right)\sin \left( \dfrac{\alpha -\gamma }{2} \right)}{2\sin \left( \dfrac{\gamma +\alpha }{2} \right)\sin \left( \dfrac{\alpha -\gamma }{2} \right)} $$

$$ =\dfrac{\cos \left( \dfrac{\alpha +\gamma }{2} \right)}{\sin \left( \dfrac{\alpha +\gamma }{2} \right)} $$

$$ =\cot \beta $$

Hence, proved.

complete the table . what do you notice about the numbers in the orange band ?
1 7 13
2 8 14
3 9 15
4 10 16
5 11 17
6 12

We consider given table ,

1. if we consider row of table then we find that ,

Difference between $${{1}^{st}}$$ and $${{2}^{nd}}$$ number is $$=6$$

And difference between $${{2}^{nd}}$$ and $${{3}^{rd}}$$ number also =6

From this calculation required number is $$=18$$

2. if we consider column then we notice that number are start to $$13$$ and going up to 17

That means 13,14,15,16,17….

Difference is $$=1$$

Hence required number is $$18$$

Ans $$18$$

$${ a }_{ 1 }=5;{ a }_{ 4 }=9\dfrac { 1 }{ 2 }$$ find $${ a }_{ 2 },{ a }_{ 3 }$$

$${a_1} = 5$$

$${a_4} = 9\frac{1}{2}$$

$$a + 3d = \frac{{19}}{2}$$

$$5 + 3d = \frac{{19}}{3}$$

$$3d = \frac{{19}}{2} - 5$$

$$3d = \frac{9}{2}$$

$$d = \frac{3}{2}$$

$$so,\,{a_2} = a + d = 5 + \frac{3}{2} = \frac{{13}}{2} = 6\frac{1}{2}$$

$${a_3} = a + 2d = 5 + 2 \times \frac{3}{2} = 5 + 3 = 8$$

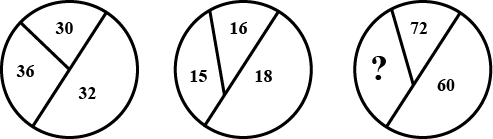
If,
$$ 1, 5, 8=76$$
$$ 2, 7, 3=25$$
$$ 3, 4, 9=89$$
$$ 4, 5, 7=69$$
THEN
$$5, 3, 8$$=?

We have,

$$ 8\times 10-\left( 5-1 \right)=76 $$

$$ 3\times 10-\left( 7-2 \right)=25 $$

$$ 9\times 10-\left( 4-3 \right)=89 $$

$$ 7\times 10-\left( 5-4 \right)=69 $$

Then,

$$8\times 10-\left( 3-5 \right)=82$$

Hence, this is the answer.

If the mean of $$20,\,14,\,16,\,19,\,p$$ and $$21$$ is $$27$$ then find the value of $$'p'$$

Given numbers.

$$20,14,16,19,p,21$$

And mean of these numbers is $$27$$.

Since, total number $$=6$$.

Therefore,

$$Mean=\dfrac{sum\,of\,total\,numbers}{total\,numbers}$$

$$ \dfrac{20+14+16+19+p+21}{6}=27 $$

$$ 90+p=162 $$

$$ p=72 $$

Hence, the value of $$p$$ is $$72$$.

The first term of a GP isThe sum of the third and fifth term isFind the common ratio of GP.

$${\textbf{Step - 1: Framing equations using the given conditions}}{\text{.}}$$

$${\text{We are given with the first term to be }}1{\text{,}}a = 1.$$

$${\text{Also we know the sum of third and fifth term of the GP}}{\text{.}}$$

$${\text{So we know that }}{n^{th}}{\text{term of a GP is }}a{r^{n - 1}}.$$

$$\therefore {\text{third term = }}a{r^2}{\text{, fifth term}} = a{r^4}.$$

$${\text{As per the given condition, }}a{r^2} + a{r^4} = 90$$

$${\text{Substituting }}a = 1,{\text{we can write}}$$

$${r^2}(1 + {r^2}) = 90.$$

$${\textbf{Step - 2: Solving the above equation to find the common ratio}}{\text{.}}$$

$${\text{Let }}{r^2}{\text{ be }}x,{\text{so we can write,}}$$

$${x^2} + x - 90 = 0$$

$${x^2} + 10x - 9x - 90 = 0$$

$$x(x + 10) - 9(x + 10) = 0$$

$${\text{On factorizing we get,}}(x + 10)(x - 9) = 0$$

$$\therefore x = - 10,x = 9$$

$${r^2} = - 10,{r^2} = 9.$$

$${\text{So discarding the negative value we get, }}{r^2} = 9 \Rightarrow r = 3.$$

$${\textbf{Therefore, the common ratio of the GP = 3}}{\text{.}}$$

$$13,25,14,23,15,21,16,?,?$$
1) $$14,11$$
2) $$19,17$$

$$1, 3, 25, 14, 23, 15, 21, 16, ?, ?$$

(odd terms) alternate numbers increased by $$1$$

Even terms decreased by $$2$$

$$\therefore$$ Answer is $$(19, 17)$$.

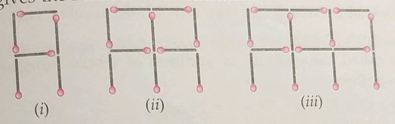
Look at the following matchstick pattern of letter $$A$$, the $$A's$$ are not separate. Two neighbouring $$A's$$ have two common matchsticks. Observe the pattern and find the rule that gives the number of matchsticks.

in 1st it has 6 matchsticks in 2nd it has 10 matchsticks then it has 14 matchsticks

i.e. in nth figure it has 6+4(n-1) matchsticks

i.e. 2+4n

If $$a,b,c$$ are in AP and $$b,c,d$$ are in GP and $$\dfrac{1}{c},\dfrac{1}{d}, \dfrac{1}{e}$$ are in AP, prove that $$a,c,e$$ are in GP.

$$a,b,c$$ are in AP.

$$b-a=c-b$$ .......(1)

$$b,c,d$$ are in GP.

$$c^2=bd$$ ......(2)

Also, $$\dfrac{1}{c}, \dfrac{1}{d}, \dfrac{1}{e}$$ are in AP.

$$\dfrac{1}{d}-\dfrac{1}{c}=\dfrac{1}{e}-\dfrac{1}{d}$$

$$\dfrac{2}{d}=\dfrac{1}{c}+\dfrac{1}{e}$$ .......(3)

To prove : $$a,c,e$$ are in GP $$\implies c^2=ae$$.

From 1,

$$b=\dfrac{a+c}{2}$$

From 2, $$d=\dfrac{c^2}{b}$$

Substituting these values in 3, we get,

$$\dfrac{2b}{c^2}=\dfrac{1}{c}+\dfrac{1}{e}$$

$$\dfrac{2(a+c)}{2c^2}=\dfrac{1}{c}+\dfrac{1}{e}$$

$$\dfrac{a+c}{c^2}=\dfrac{e+c}{ce}$$

$$\dfrac{a+c}{c}=\dfrac{e+c}{e}$$

$$ae+ce=ec+c^2$$

$$c^2=ae$$

Thus, $$a,c,e$$ are in GP.

Find the sum of series $$1+2+3+4+5+6+...+n$$.

The given series is in AP with $$a=1,d=1$$

Sum of series is given as

$$S_n =\dfrac n2[2a+(n-1)d]$$

$$=\dfrac n2(2+n-1)$$

$$=\dfrac{n(n+1)}2$$

Calculate the sum of the series $$1+3+5+7+....2n-1$$.

$$1+3+5+7+....2n-1$$

The given series is in AP

$$a=1,d=2$$

The sum of series is

$$S_n=\dfrac n2[2a+(n-1)d]$$

$$=\dfrac n2[2+(n-1)2]$$

$$=\dfrac n2(2n)=n^2$$

Find the $${15^{th}}$$ term of the series $$3,9,15,21,27,33,....$$

The given series is $$3,9,15,21,27,33,....$$

The given series is in $$AP$$ with$$a=3,d=9-3=6$$

The $$15^{th}$$ term is given as $$a_{15}=a+14d\\3+14(6)\\3+84=87$$

Find the sum to $$n$$ terms of the series
$$5+11+19+29+......$$

Given,

$$5+11+19+29+......+n$$

$$11-5=6,19-11=8,29-19=10,.....$$

Therefore the series reduces to,

$$6+8+10+....+n$$

Sum of this series is given by,

$$S_n=2n+6$$

when $$n=0\rightarrow 2(0)+6=6$$

when $$n=1\rightarrow 2(1)+6=8$$

when $$n=2\rightarrow 2(2)+6=10$$

when $$n=n\rightarrow 2(n)+6=2n+6$$

Find the sum of terms of the sequence till n terms : $$6+9+16+27+42+....+n$$ $$ terms$$.

$$ S=6+9+16+27+42+....... n$$ terms

$$ S=6+9+16+27+.............$$

$$O=6+(3+7+11+15+...n+\ terms)$$- $$T_{n}$$

$$T_{n}=6+\dfrac{n-1}{2}(2.3+(n-2)4)$$

$$T_{n}=6+\dfrac{(n-1)(4n-2}{2}$$

$$T_{n}=6+(n-1)(2n-1)$$

$$T_{n}=2n^{2}-3n+7$$

$$ S\displaystyle\sum_{r=1}^{n}T_{r}=2\displaystyle\sum_{r=1}^{n}r^{2}+7\displaystyle\sum_{r=1}^{n}1-3\displaystyle\sum_{r=1}^{n}r$$

$$=\dfrac{2(n)(n+1)(2n+1)}{6}+7n\dfrac{3n(n+1)}{2}$$

$$=\dfrac{2n(n+1)(2n+1)+42n-9n(n+1)}{6}$$

$$=\dfrac{4n^{3}+2n^{2}+4n^{2}+2n+42n-9n^{2}-9n}{6}$$

$$=\dfrac{4n^{2}-3n^{2}+35n}{6}$$

Find the average of the first five multiples of $$10$$.

Average of first $$5$$ multiples of $$10 = \dfrac{10+20+30+40+50}{5} = \dfrac{150}{5} = 30$$

Find the missing number in the series :
40 , 54 , 82 , ? , 180 , 250

1112238_1190558_ans_c8ddbc75a10541bdb882d8ee4141581d.jpeg

Write opposites of the following :
$$30\ km$$ north

$$30\ km$$ South

If $$18, a, b, -3$$ are in $$AP$$ then find $$a+b$$.

Let $$p$$, be the first term i.e; $$18$$

And, $$d$$, be the common difference,

From given series,

$$4th$$ term $$=p+3d=-3$$

$$\implies 18+3d=-3$$

Hence, $$d=-7$$

So, $$a=p+d=18-7=11$$

And, $$b=p+2d=18-14=4$$

Therefore,

$$a+b=11+4=15$$

Solve: $$2-\dfrac{3}{5}.$$

Given

$$2-\dfrac{3}{5}$$

$$=\dfrac{10-3}{5}$$

$$=\dfrac{7}{5}$$

Find the term of the series $$25, 22\dfrac{3}{4}, 20\dfrac{1}{2},18\dfrac{1}{4}.....$$ which is numerically smallest.

The given series is an A.P., i.e., $$a=25,d=-9/4.$$
$$T_n=a+(n-1)d=(25+\dfrac{9}{4})-\dfrac{9}{4}n$$
or $$T-n=\dfrac{109}{4}-\dfrac{9}{4}n$$
Now $$T_n$$ will be negative if $$\dfrac{109}{4}-\dfrac{9}{4} n<0$$ or $$n > 12 \dfrac{1}{9}$$.
Above shows that $$T_{13}$$ will be the first negative term and hence $$T_{12}$$ will be the smallest positive terms. $$T_{13}=-2,T{12}=\dfrac{1}{4}$$ is numerically smallest.

Solve for a.
$$\frac{3a-2}{7}-\frac{a-2}{4}=2,$$

To solve $$\rightarrow \frac{3a-2}{7}-\frac{a-2}{4}= 2$$

Take 2 cm of 7 and 4

$$=\frac{12a-8-7a+14}{28}=2$$

$$= 12a-7a+14-8 =56$$

$$= 5a+6=56$$

$$=5a=50$$

$$a=10$$

1115637_1201949_ans_3df07b5f4eba4b10b9f389202bee7486.jpg

If $${ 1 }^{ 2 }+{ 2 }^{ 3 }+{ 3 }^{ 2 }+.....+\left( 2003 \right) ^{ 2 }=\left( 2003 \right) \left( 4007 \right) \left( 334 \right) $$ and$$\left( 1 \right) \left( 2003 \right) +\left( 2 \right) \left( 2002 \right) +\left( 3 \right) \left( 2001 \right) =\left( 2003 \right) \left( 334 \right) \left( x \right) ,$$ then x equals

1209285_1269611_ans_91eb2df895d349ceb753b65a67b7fb00.jpeg

The mean of first 10 whole numbers is

1304731_1262813_ans_c2e16708d9bf46cc9009bcdedfeff85e.JPG

Find three consecutive odd numbers whose sum is $$147$$.

A] let 3 consecutive add numbers be

x-2,x, x+2

As, x-2+x+x+2=147

$$\Rightarrow $$ 3x=147

$$\Rightarrow $$x=49

$$\therefore $$ 3 numbers are 47,49,51

1192453_1294776_ans_9cda3a6975454cfaaef79738aeaaa668.jpg

Find three consecutive even number whose sum is $$234$$.

A] Let the three numbers be x-2, x, x+2

so, x - 2 + x + x + 2 = 234

3x = 234

x = 78

numbers are = 76, 78, 80

1182373_1292778_ans_a13e9ac0374b4b25833add39ea7e89ef.jpg

$$5,10,15,20,..$$.

1905279_1306714_ans_b5d9cc2b148445239663ced093348a9a.jpg

Prove that $$\sum\limits_{n=1}^{\infty}\dfrac{1}{n!}=e-1$$.

We've,

$$e^x=1+\dfrac{x}{1!}+\dfrac{x^2}{2!}+..........$$ for $$x\in \mathbb{R}$$.

Now,

$$e=1+\dfrac{1}{1!}+\dfrac{1}{2!}+........$$

or, $$e-1$$$$=\sum\limits_{n=1}^{\infty}\dfrac{1}{n!}$$.

Hence proved.

Fill in the blanks:
$$\dfrac {2}{8} \times 3 = \dfrac {2}{8} + -+-+- $$

$$\dfrac {2}{8}\times 3 =\dfrac {2}{8}+\dfrac{2}{8}+\dfrac {2}{8}$$

[multiplication is repeated addition]

Ia, b, c are is G.P and a - b, c - a and b - a are in H.P, then a + 4b + c is equal to

H.P condition,

$$\dfrac{1}{a-b}+\dfrac{1}{b-c}=\dfrac{2}{c-a}$$

$$\Rightarrow a^2-2b^2+c^2+2ab+2bc-4ac=0$$

$$\Rightarrow (a+b+c)^2=a^2+b^2+c^2+2ab+2bc+2ca=0+3b^2+6ac=9b^2$$

$$\therefore a+b+c=3b$$ or $$a+b+c=-3b$$

$$\Rightarrow a+b+3b+c=0$$

$$\therefore a+4b+c=0$$

Write the solution set of $$\left|x+\dfrac{1}{x}\right|>2$$.

We have,

$$\left| x+\dfrac{1}{x} \right|>2$$

Now,

$$ {{x}^{2}}+1>2x $$

$$ \Rightarrow {{x}^{2}}+1-2x>0 $$

$$ \Rightarrow {{\left( x-1 \right)}^{2}}>0 $$

$$ \Rightarrow x-1>0 $$

$$ \Rightarrow x>1 $$

Hence, this is the answer.

Find three consecutive odd numbers whose sum is $$234$$.

A] Let the three numbers be x-2, x, x+2

so, x-2 + x + x + 2 = 234

3 x = 234

x = 78

numbers area = 76, 78, 80

1192454_1294779_ans_e3f9cb7ddfbd4657aaf31212a576fc2f.jpg

$$1,2,4,8,16,...$$.

1906843_1306596_ans_d15731462ce14e168689e873aee22953.jpg

If $$a,b,c,d$$ are in GP, show that
$$(b-c)^2+(c-a)^2+(d-b)^2=(a-d)^2$$

1340008_1344561_ans_90141c56bf7f4738b0c775f11028214d.jpg

Fill in the blanks in the expressions with the proper numbers.
$$(5\ \times 4) > (7\times \Box )$$

$$ (5\times 4)> [7\times _{=}]$$

$$ 20> 7\times _{=}$$

Blanks space can be field with 1,2

1189184_1354042_ans_12eaabdfe8874429b0bbe301db1318e3.jpg

If $$a,b,c$$ are in GP and $$a^{1/x}=b^{1/y}=c^{1/z}$$, prove that $$x,y,z$$ are in AP.

1340007_1344689_ans_aa82e608c9174142b8d536ff639b23b9.jpg

The sum of the first 20 terms of the series $$1+\dfrac{3}{2}+\dfrac{7}{4}+\dfrac{15}{8}+\dfrac{31}{16}+....,$$ is

Given,

$$n=20$$

$$a=1$$

$$d=\dfrac{3}{2}-1=\dfrac{1}{2}$$

Formula:

$$S_n=\dfrac{n}{2}[2a+(n-1)d]$$

Therefore,

$$=\dfrac{20}{2}\left [ 2(1)+(20-1)\dfrac{1}{2} \right ]$$

$$=10\left [ 2+\dfrac{19}{2} \right ]$$

$$=115$$

Hence, this is the answer.

$$x = 1 + a + a ^ { 2 } + \ldots \infty , y = 1 + b + b ^ { 2 } + \ldots \infty$$ then $$1 + a b + a ^ { 2 } b ^ { 2 } + \ldots \infty =$$

$$\begin{array}{l} We\, have \\ x=1+a+{ a^{ 2 } }+......=\dfrac { 1 }{ { 1-a } } \\ y=1+b+{ b^{ 2 } }+.......=\dfrac { 1 }{ { 1-b } } \\ 1+ab+{ a^{ 2 } }{ b^{ 2 } }+.......=\dfrac { 1 }{ { 1-ab } } \\ =\dfrac { 1 }{ { 1-\left( { 1-\dfrac { 1 }{ x } } \right) \left( { 1-\dfrac { 1 }{ y } } \right) } } \\ =\dfrac { 1 }{ { 1-\left( { 1-\dfrac { 1 }{ x } -\dfrac { 1 }{ y } +\dfrac { 1 }{ { xy } } } \right) } } \\ =\dfrac { 1 }{ { \dfrac { 1 }{ x } +\dfrac { 1 }{ y } -\dfrac { 1 }{ { xy } } } } \\ =\dfrac { { xy } }{ { y+x-1 } } \\ \end{array}$$

Hence, this is the answer.

P and Q are brothers, X and Y are sisters, son of P is the brother of Y. How is Q related to X ?

On the basis of statements, we conclude that Q is the brother of P and P's son is the brother of Y, so Y is the daughter of P. Thus, Q is the uncle of X.

The Fibonacci sequence is defined by $$1=a_{1}=a_{2}$$ and $$a_{n}=a_{n-1}+a_{n-1},n > 2$$.
Find $$\dfrac {a_{n}}{a_{n}+1}$$ for $$n=1,2,3,4$$.

$$a_{1}=a_{2}=1$$

$$a_{n}=a_{n-1}+a_{n-1}$$

find $$\dfrac{a_{n}}{a_{n}+1}$$

a) $$n=1 \Rightarrow \dfrac{a_{1}}{a_{1}+1}=\dfrac{1}{1+1}=\dfrac{1}{2}$$

b) $$n=2 \Rightarrow \dfrac{a_{2}}{a_{2}+1}=\dfrac{1}{1+1}=\dfrac{1}{2}$$

c) $$n=3 \Rightarrow \dfrac{a_{3}}{a_{3}+1}=\dfrac{2}{2+1}=\dfrac{2}{3}$$

d) $$n=4 \Rightarrow \dfrac{a_{4}}{a_{4}+1}=\dfrac{3}{3+1}=\dfrac{3}{4}$$.

1215278_1352810_ans_989d0263c3b7403cb8faa14bebbcf032.jpg

Identify whether the following sequence is a geometric sequence or not.
$$-3,9,-27,81$$

For geometric sequence, ratio between subsequent terms should be constant, here,

$$=\dfrac{9}{-3}=-3$$,

$$\dfrac{-27}{9}=-3$$,

$$\dfrac{81}{-27}=-3$$

A Geometric sequence.

1214421_1395919_ans_9b5d2becadff48779877f305eb283d61.jpg

Identify whether the following sequence is a geometric sequence or not.
$$2,6,18,54$$

For geometric sequence, ratio between subsequent terms should be constant, here,

$$\dfrac{6}{2}=3$$, $$\dfrac{18}{6}=3$$, $$\dfrac{54}{18}=3$$

A Geometric sequence.

1214416_1395900_ans_d854a76fe7f64544942bf8e38dfe9958.jpg

If the heights of 5 persons are 144 cm, 152 cm, 151 cm, 158 cm, and 155 cm respectively. Find the mean height.

Mean Height = $$\dfrac{144+152+151+158+155}{5}=\dfrac{760}{5}=152$$ $$cm$$

Fill the squares with all the numbers from 46 to 54

rule:- total of each line should be 150.
49
46
52 47

$$a=53$$	$$b=48$$	$$49$$
$$46$$	$$c=50$$	$$d=54$$
$$e=51$$	$$52$$	$$47$$

Working:

$$49+d+47=150$$

$$\Rightarrow d=150-49-47=54$$

$$46+c+d=150$$

$$\Rightarrow c=150-46-d=104-d=104-54=50$$

$$b+c+52=150$$

$$\Rightarrow b+50+52=150$$

$$\Rightarrow b=150-102=48$$

$$a+48+49=150$$

$$\Rightarrow a=150-97=53$$

$$53+46+e=150$$

$$\Rightarrow e=150-99=51$$

The mean of $$45,84,75,87,47$$ is

The given data is $$45,84,75,87,47$$

The no .of observations are $$5$$

The sum of observations $$45+48+75+87+47=302$$

The mean of observations is given as $$\dfrac{302}{5}=60.4$$

Identify whether the following sequence is a geometric sequence or not.
$$1,4,9,16$$

For geometric sequence, ratio between subsequent terms should be constant, here,

$$\dfrac{4}{1}=4, \dfrac{9}{4}\neq 4$$

$$\Rightarrow x$$ Not a geometric sequence.

1214419_1395913_ans_01700b013638494ca62d09e95cc41b93.jpg

Identify whether the following sequence is a geometric sequence or not.
$$\dfrac{1}{2},\dfrac{2}{4},\dfrac{4}{8},\dfrac{8}{16}$$

For geometric sequence, ratio between Subsequent terms should be constant, here,

$$\dfrac{\dfrac{2}{4}}{\dfrac{1}{2}}=\dfrac{1}{2}\times 2=1$$;

$$\dfrac{\dfrac{4}{8}}{\dfrac{2}{4}}=\dfrac{1}{2}\times 2=1; \dfrac{\dfrac{8}{16}}{\dfrac{4}{8}}=\dfrac{1}{2}\times 2=1$$.

1214425_1395929_ans_6985f0f149fb4b9991b34c7c0617c10f.jpg

Identify whether the following sequence is a geometric sequence or not.
$$\dfrac{1}{2},\dfrac{2}{3},\dfrac{3}{4},\dfrac{4}{5}$$

For geometric sequence, ratio between subsequent terms should be constant, here,

$$\dfrac{\dfrac{2}{3}}{\dfrac{1}{2}}=\dfrac{2}{3}\times 2=\dfrac{4}{3}; \dfrac{\dfrac{3}{4}}{\dfrac{2}{3}}=\dfrac{3}{4}\times \dfrac{3}{2}=\dfrac{9}{8}+\dfrac{4}{3}$$

$$\Rightarrow x$$ Not a Geometric sequence.

1214424_1395925_ans_5a821b0c90184aa2aff607a5709c0622.jpg

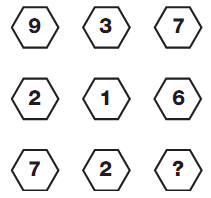
Find the value of question mark .

Working in columns, start with the top numbers, and subtract the number in the centre, to give the result in the bottom row.

Thus, required value = $$7-6=1$$

Identify whether the following sequence is a geometric sequence or not.
$$25,5,1,\dfrac{1}{5}$$

1214418_1395909_ans_65d786a1cc0149cab245db8f8e30eea5.jpg

The fourth term of a G.P. is 8 and the 7th term is 64, find the G.P.

Let the series be $$a,ar,ar^2\cdots $$

$$\implies ar^3=8\cdots (1)$$

$$\implies ar^6=64 \cdots (2)$$

$$(2)\div (1)$$

$$\dfrac{ar^6}{ar^3}=\dfrac{64}{8}$$

$$r^3=8$$

$$\implies r=\sqrt[3]{8}$$

$$r=2$$

$$\implies a=1$$

So the series is

$$1, 1 \times 2, 1\times 2^2, .....\implies1,2,4,.....$$

Find the mean of 43, 51, 50, 57 and 54.

The numbers given are 43, 51, 50, 57 and 54.
The mean of the given numbers will be.
$$= \frac{43 + 51 + 50 + 57 + 54}{5}$$
$$= \frac{225}{5}$$
$$= 51$$

Find the sum of the following series:
$$ 0.6+0.66+0.666+...$$ to n terms.

Let $$ S_n = 0.6+0.66+0.666+...$$ to n terms.

Then,

$$ S_n = 0.6+0.66+0.666+...$$ to n terms

$$ \Rightarrow S_n = \dfrac{6}{9} ( 0.1+0.11+0.111+...$$ to n terms )

$$ \Rightarrow S_n = \dfrac{6}{9}\left \{ 0.9+0.99+0.999+... to \, n \, terms \right \}$$

$$ \Rightarrow S_n = \dfrac{6}{9} \left \{ \left ( 1-\dfrac{1}{10} \right )+\left (1- \dfrac{1}{10^2} \right )+\left ( 1 -\dfrac{1}{10^3}\right )+...+\left ( 1-\dfrac{1}{10^n} \right ) \right \}$$

$$ \Rightarrow S_n = \dfrac{6}{9}\left \{ n-\left ( \dfrac{1}{10}+\dfrac{1}{10^2}+\dfrac{1}{10^3}+...+\dfrac{1}{10^n} \right ) \right \}$$

$$ \Rightarrow S_n = \dfrac{6}{9}\left \{ n-\dfrac{1}{10}\dfrac{\left ( 1-\left ( \dfrac{1}{10} \right )^{n} \right )}{1-\dfrac{1}{10}} \right \} = \dfrac{6}{9}\left \{ n-\dfrac{1}{9}\left ( 1-\dfrac{1}{10^{n}} \right ) \right \}$$

Increased by 3

Given that the mean of 15 observations is 32
resulting mean increased by 3
= 32 + 3
= 35

The sum of the following series to infinity $$\displaystyle \frac{1}{1.3.5} +\frac{1}{3.5.7} +\frac{1}{5.7.9} +\,...\,\infty is $$ $$\dfrac{1}{3c}$$ .Find $$c$$

$$\displaystyle \frac{1}{1.3.5} +\frac{1}{3.5.7} +\frac{1}{5.7.9} +\,...\,\infty $$

$$=\displaystyle \frac { 1 }{ 4 } \left( \frac { 4 }{ 1.3.5 } +\frac { 4 }{ 3.5.7 } +\frac { 4 }{ 5.7.9 } +\, ...\, \infty \right) $$

We can write,
$$\displaystyle \frac { 4 }{ 1.3.5 } =\frac { 1 }{ 1.3 } -\frac { 1 }{ 3.5 } $$

$$\displaystyle \frac { 4 }{ 3.5.7 } =\frac { 1 }{ 3.5 } -\frac { 1 }{ 5.7 } $$

Similarly, $$\displaystyle \frac { 4 }{ 5.7.9 } =\frac { 1 }{ 5.7 } -\frac { 1 }{ 7.9 } $$

So, the series can be written as
$$\displaystyle =\frac { 1 }{ 4 } \left( \frac { 1 }{ 1.3 } -\frac { 1 }{ 3.5 } +\frac { 1 }{ 3.5 } -\frac { 1 }{ 5.7 } +\frac { 1 }{ 5.7 } -\frac { 1 }{ 7.9 } +.....\infty \right) $$

$$=\dfrac{1}{4} \dfrac{1}{3}$$

$$=\dfrac{1}{12}$$

Comparing with the given value ,
$$c=4$$

The sum of the series $$\displaystyle \frac2{3!}+\frac4{5!}+\frac6 {7!}+...$$ to $$\infty$$ = $$\displaystyle \frac{a}{e}$$. Find $$(a+3)^2$$.

$$\displaystyle S=\frac { 2 }{ 3! } +\frac { 4 }{ 5! } +\frac { 6 }{ 7! } +...$$

$$\displaystyle { t }_{ n }=\frac { 2n }{ \left( 2n+1 \right) ! } =\frac { 1 }{ 2n! } -\frac { 1 }{ \left( 2n+1 \right) ! } $$

We know, $$\dfrac { { e }^{ x }+{ e }^{ -x } }{ 2 } $$= $$\displaystyle \sum_{n=0}^{\infty}\frac{x^{2n}}{(2n)!}$$ and $$\dfrac { { e }^{ x }+{ e }^{ -x } }{ 2 } $$= $$\displaystyle \sum_{n=0}^{\infty}\frac{x^{2n}}{(2n)!}$$

$$\therefore \displaystyle S=\sum _{ n=0 }^{ \infty }{ { t }_{ n } } =\sum _{ r=0 }^{ \infty }{ \frac { 1 }{ 2n! } } -\sum _{ r=0 }^{ \infty }{ \frac { 1 }{ \left( 2n+1 \right) ! } } =\frac { 1 }{ 2 } \left( e+\frac { 1 }{ e } \right) -\frac { 1 }{ 2 } \left( e-\frac { 1 }{ e } \right) =\frac { 1 }{ e } $$

Therefore, $$(a+3)^2=16$$.... a=1

Ans: 16

If $$A_{n}= (n, n + 1)$$ then $$10(A_{10}A_{11})^{2}+11(A_{11}+A_{12})^{2}+......+20(A_{20}A_{21})^{2}$$ is equal to

As $${ \left( { A }_{ n }{ A }_{ n+1 } \right) }^{ 2 }={ \left( \left( n,\left( n+1 \right) \left( \left( n+1 \right) ,\left( n+2 \right) \right) \right) \right) }^{ 2 }=2$$
then
$$10(A_{ 10 }A_{ 11 })^{ 2 }+11(A_{ 11 }+A_{ 12 })^{ 2 }+......+20(A_{ 20 }A_{ 21 })^{ 2 }\\ =2\left( 10+11+12+...+20 \right) =530$$

Sum of the series $$\displaystyle 1+\left ( 1+2 \right )+\left ( 1+2+3 \right )+\left ( 1+2+3+4 \right )+... $$ to n terms be $$\displaystyle \frac{1}{m}n\left ( n+1 \right )\left [ \frac{2n+1}{k}+1 \right ]$$ .Find the value of k+m.

$$T_{ n }=\left( 1+2+3.....n \right) =\dfrac { n\left( n+1 \right)

}{ 2 } =\dfrac { 1 }{ 2 } \left( n^{ 2 }+n \right) $$

Putting $$n=1,2,3.......n$$ on adding, we get

$$S_{ n }=\dfrac { 1 }{ 2 } \left( \Sigma n^{ 2 }+\Sigma n \right) $$

$$S_{ n }=\dfrac { 1 }{ 2 } \left[ \dfrac { n\left( n+1 \right) \left(2n+1 \right) }{ 6 } +\dfrac { n\left( n+1 \right) }{ 2 } \right] $$

$$S_{ n }=\dfrac { 1 }{ 4 } n\left( n+1 \right) \left[ \dfrac { 2n+1 }{ 3} +1 \right] =\dfrac { n\left( n+1 \right) \left( n+2 \right) }{ 6 } $$

$$m=4 , k=3 \quad \quad So , \space m+k=7$$

Considre the sequence $$\displaystyle \left ( a_{n} \right )n\geq 0 $$ given by the following relation:$$\displaystyle a_{0}=4,a_{1}=22,$$ and for all $$\displaystyle n\geq 2,$$ $$\displaystyle a_{n}=6a_{n-1}-a_{n-2}.$$ Prove that there exist sequences of positive integers $$\displaystyle \left ( x_{n} \right )n\geq 0,\left ( y_{n} \right )n\geq 0 $$ such that$$\displaystyle a_{n}=\frac{y^{2}_{n}+7}{x_{n}-y_{n}},$$ for all $$\displaystyle n\geq 0.$$

Observe that $$\displaystyle a_{n} $$ is an even positive integer for all n and that the sequence $$\displaystyle \left ( a_{n} \right )n\geq 0 $$ is increasing. The last asssertion follows inductively if we write the recursive relation under the form $$\displaystyle a_{n}-a_{n-1}=5\left ( a_{n-1}-a_{n-2} \right )+4a_{n-2}.$$ Define $$\displaystyle x_{n}=\frac{a_{n}+a_{n-1}}{2},y_{n}=\frac{a_{n}-a_{n-1}}{2}$$ whith x0 = 3, y0 = 1. Observe that $$\displaystyle x_{n}=3x_{n-1}+4y_{n-1}$$ and $$\displaystyle y_{n}=2x_{n-1}+3y_{n-1}. $$ We have $$\displaystyle a_{n}=x_{n}+y_{n},$$ hence it is sufficient to prove that$$\displaystyle x_{n}+y_{n}=\frac{y^{2}_{n}+7}{x_{n}-y_{n}} $$ or $$\displaystyle x^{2}_{n}=2y^{2}_{n}+7 $$ for all n. We use induction. The equality is true for n = 0. Suppose that $$\displaystyle x^{2}_{n-1}=2y^{2}_{n-1}+7. $$ Then $$\displaystyle x^{2}_{n}-2y^{2}_{n}-7=\left ( 3x_{n-1}+4y_{n-1} \right )^{2}-2\left ( 2x_{n-1+3y_{n-1}} \right )^{2}-7 $$ $$\displaystyle =x^{2}_{n-1}-2y^{2}_{n-1}-7=0, $$ which proves our claim. Try your hand at the following problems.

If the set natural numbers, is partitioned into subsets $$\displaystyle S_{1}= \left \{ 1 \right \},S_{2}= \left \{ 4,5,6 \right \},S_{4}= \left \{ 7,8,9,10 \right \}$$ The last terms of these groups is $$1,1+2,1+2+3,1+2+3+4 .....$$. Find the sum of the elements in the subset $$S_{50}$$.

$$\displaystyle = 1+2+3+...n = \frac{n\left ( n+1 \right )}{2}$$ The terms in nth group will be n and in A.P. of common difference-1 and first term being

$$\displaystyle \frac{n\left ( n+1 \right )}{2}$$ [ i.e. last term as first term and d= -1 intead of+1 ]

$$ \displaystyle S_{2}= \frac{n}{2}\left [ 2.\frac{n\left ( n+1 \right )}{2}+\left ( n-1 \right )\left ( -1 \right ) \right ]= \frac{n}{2}\left ( n^{2}+1 \right )$$

$$\displaystyle \therefore S_{50}= 25\times \left ( 2501 \right )= 62525 $$

sum the series $$1+2+...…….+100$$

Series sum : - $$1+2+.........+100$$

sum of natural numbers upto $$100$$

We known,

$$S_n=\dfrac{n(n+1)}{2}$$

$$\therefore S_{100}=100\times \dfrac{101}{2}$$

$$=101\times 50$$

$$\boxed{S_{100}=5050}$$

sum of the series is $$1+3+6+10+15+... $$ to n terms $$\displaystyle \frac{n\left ( n+m \right )\left ( n+p \right )}{k}$$.Find $$k-m-p$$ ?

$$S=1+3+6+10+15+.....$$

$$S= 1+3+ 6+10+......$$

$${ a }_{ n }=1+2+3+4+5+.........$$

$${ a }_{ n }=\dfrac { n(n+1) }{ 2 } $$

$$S=\dfrac { \sum { { n }^{ 2 }+ } \sum { n } }{ 2 } =\dfrac { \dfrac{ n(n+1)(2n+1) }{ 6 } +\dfrac { n(n+1) }{ 2 } }{ 2 } $$

$$S=\dfrac { n(n+1) }{ 4 } (\dfrac { 2n+1 }{ 3 } +1)$$

$$S=\dfrac { n(n+1)(2n+4) }{ 12 } $$

$$S=\dfrac { n(n+1)(n+2) }{ 6 } $$

$$k=6,m=1,n=2$$

So $$k-m-n=3$$

Sum of the series $$4+6+9+13+18+...$$ to $$n$$ terms be $$\displaystyle =\frac{n}{k}\left ( n^{2}+3n+m \right )$$.Find $$m-k$$ ?

$$S_{ n }=4+6+9+13+18.......+T_{ n }$$

$$S_{ n }=0+4+6+9+... +T_{ n-1 }+T_{ n } $$

Subtracting Both we get

$$T_{ n }=4+2+3+4+....... $$

$$T_{ n }-4=(2+3+4+..... ) (n-1 \space Terms)$$

$$T_{ n }-4=\dfrac { n-1 }{ 2 } (2\times 2+(n-2))$$

$$T_{ n }-4=\dfrac { (n-1)(n+2) }{ 2 } $$

$$T_{ n }=\dfrac { 1 }{ 2 } \left( n^{ 2 }+n+6 \right) $$

$$T_{ n }=\dfrac { 1 }{ 2 } n\left( n+1 \right) +3$$

$$S_{ n }=\dfrac { 1 }{ 2 } (\dfrac { n(n+1)(2n+1) }{ 6 } +\dfrac { n(n+1)}{ 2 } )+3n$$

$$S_{ n }=\dfrac { n }{ 6 } \left( n^{ 2 }+3n+20 \right) $$

$$m=20 \space and \space k=6 .\quad \quad So, \space m-k=14$$.

Find the sum of 2n terms of the series $$\displaystyle 5^{3}+4.6^{3}+7^{3}+7^{3}+4.8^{3}+9^{3}+4.10^{3}+....$$

$$\displaystyle S_{2n}=( n$$ odd terms $$)+( n$$ even terms $$)$$
$$\displaystyle =\left ( 5^{3}+7^{3}+9^{3}+....n\:terms \right )+4\left ( 6^{3}+8^{3}+10^{3}+....n\:terms \right )$$
$$\displaystyle =\sum_{r=1}^{n}\left ( 2r+3 \right )^{3}+4\Sigma \left ( 2r+4 \right )^{3}$$
$$\displaystyle =\sum_{r=1}^{n}\left [ 8r^{3}+36r^{2}+54r+27 \right ]+48\left [ r^{3}+2r^{2}+4r+8 \right ]$$
$$\displaystyle =\sum_{r=1}^{n}\left [ 40r^{3}+228r^{2}+438r+283 \right ]$$
Now put $$r=1, 2, 3, .....n$$ add and use the formula for $$\displaystyle \Sigma n,\Sigma n^{2},\Sigma n^{3}$$

$$=n\left[ 10n^{ 3 }+96n^{ 2 }+363n+540 \right] $$

If $$\displaystyle s_{n}=1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+...\frac{1}{n},\left ( n\: \epsilon \: N \right )$$, then $$\displaystyle s_{1}+s_{2}+s_{3}+s_{4}+...s_{n}=\left ( n+\lambda \right )s_{n+1}-\left ( n+1 \right )$$. Find the value of $$\displaystyle \lambda $$

$$\displaystyle P=\frac{a+b}{2a-b}+\frac{c+b}{2c-b}$$

$$\displaystyle =\dfrac{a+\dfrac{2ac}{a+c}}{2a-\dfrac{2ac}{a+c}}+\dfrac{c+\dfrac{2ac}{a+c}}{2c-\dfrac{2ac}{a+c}}\, as\, b=\dfrac{2ac}{a+c}$$

$$\displaystyle = \dfrac{a+3c}{2a}+\dfrac{3a+c}{2c}=1+\dfrac{3}{2}\left ( \dfrac{c}{a}+\dfrac{a}{c} \right )\geq 4$$
So, $$\displaystyle \sqrt{\lambda \sqrt{\lambda \sqrt{\lambda ........\infty }}}=\lambda ^{\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{b}}+.....\infty =\lambda ^{\frac{1/2}{1-1/2}}=\lambda $$
$$\Rightarrow \displaystyle \lambda =4$$

Find the sum to $$n$$ terms of the sequence $$8, 88, 888, 8888, ....$$ .

The given sequence is $$8, 88, 888, 8888 ....$$

This sequence is not a G.P. However,it can be changed to G.P. by writing the term as

$$\displaystyle{

S }_{ n }=8+88+888+8888+......+n\quad terms$$

$$ =\dfrac { 8 }{ 9 } \left[

9+99+999+9999+....to\quad n\quad terms\quad \right] $$

$$ =\dfrac { 8 }{ 9 }

\left[ (10-1)+({ 10 }^{ 2 }-1+({ 10 }^{ 3 }-1)+({ 10 }^{ 4

}-1+....\quad to\quad n\quad terms \right] $$

$$ =\dfrac { 8 }{ 9 } \left[

(10+{ 10 }^{ 2 }+......\quad n\quad terms)-(1+1+1+...\quad n\quad terms)

\right] $$

$$ =\dfrac { 8 }{ 9 } \left[ \dfrac { 10({ 10 }^{ n }-1) }{ 10-1 }

-n \right] $$ [Sum of GP$$=\cfrac { a({ r }^{ n }-1) }{ r-1 }$$ when $$\quad r>1$$]

$$ =\dfrac { 8 }{ 9 } \left[ \dfrac { 10({ 10 }^{ n }-1) }{ 9 }

-n \right] $$

$$ =\dfrac { 80 }{ 81 } ({ 10 }^{ n }-1)-\dfrac { 8 }{ 9 } n$$

If $$a,b,c$$ and $$d$$ are in $$G.P.$$ show that $$\displaystyle ({ a }^{ 2 }+{ b }^{ 2 }+{ c }^{ 2 })({ b }^{ 2 }+{ c }^{ 2 }+{ d }^{ 2 })={ (ab+bc+cd) }^{ 2 }$$.

$$a, b, c, d$$ are in G.P.
Therefore,
$$\displaystyle bc=ad\quad

\quad \quad ...(1)\\ { b }^{ 2 }=ac\quad \quad \quad ...(2)\\ { c }^{ 2

}=bd\quad \quad \quad ...(3)$$
Now $$R.H.S ={ (ab+bc+cd

})^{ 2 }\\ ={ (ab+ad+cd })^{ 2 }\quad \left[ \text{Using (1) }\right] \\ {

={ \left[ { ab+d(a+c) } \right] }^{ 2 } }\\ ={ a }^{ 2 }{ b }^{ 2

}+2abd(a+c)+{ d }^{ 2 }{ (a+c) }^{ 2 }\\ ={ a }^{ 2 }{ b }^{ 2 }+2{ a

}^{ 2 }bd+2abcd+{ d }^{ 2 }{ ({ a }^{ 2 }+2ac+{ c }^{ 2 }) }\\ ={ a }^{ 2

}{ b }^{ 2 }+2{ a }^{ 2 }{ c }^{ 2 }+{ 2b }^{ 2 }{ c }^{ 2 }+{ d }^{ 2

}{ a }^{ 2 }+2{ d }^{ 2 }{ b }^{ 2 }+{ d }^{ 2 }{ { c }^{ 2 }\left[

\text{Using (1) and (2) } \right] }\\ ={ a }^{ 2 }{ b }^{ 2 }+{ a

}^{ 2 }{ c }^{ 2 }+{ a }^{ 2 }{ c }^{ 2 }+{ b }^{ 2 }{ c }^{ 2 }+{ b

}^{ 2 }{ c }^{ 2 }+{ d }^{ 2 }{ { a }^{ 2 }+ }{ d }^{ 2 }{ b }^{ 2 }+{ d

}^{ 2 }{ b }^{ 2 }+{ d }^{ 2 }{ c }^{ 2 }\\ ={ a }^{ 2 }{ b }^{ 2 }+{ a

}^{ 2 }{ c }^{ 2 }+{ a }^{ 2 }{ d }^{ 2 }+{ b }^{ 2 }\times { b }^{ 2

}+{ b }^{ 2 }{ c }^{ 2 }+{ b }^{ 2 }{ { d }^{ 2 }+ }{ c }^{ 2 }{ b }^{ 2

}+{ c }^{ 2 }\times { c }^{ 2 }+{ c }^{ 2 }{ d }^{ 2 }\\ ={ a

}^{ 2 }({ b }^{ 2 }+{ c }^{ 2 }+{ d }^{ 2 })+{ b }^{ 2 }({ b }^{ 2 }+{ c

}^{ 2 }+{ d }^{ 2 })+{ c }^{ 2 }({ b }^{ 2 }+{ c }^{ 2 }+{ d }^{ 2 })\\

=({ a }^{ 2 }+{ b }^{ 2 }+{ c }^{ 2 })({ b }^{ 2 }+{ c }^{ 2 }+{ d }^{ 2

})\\ =L.H.S.$$
$$\therefore ({ a

}^{ 2 }+{ b }^{ 2 }+{ c }^{ 2 })({ b }^{ 2 }+{ c }^{ 2 }+{ d }^{ 2 })={

(ab+bc+cd) }^{ 2 }$$

If $${S}_{n}={(4)}^{n}+3$$, what is the units digit of $${S}_{100}$$?

Begin by listing the first few terms of the sequence in order to find the pattern:
$${S}_{1}={4}^{1}+3=4+3=7$$
$${S}_{2}={4}^{2}+3=16+3=19$$
$${S}_{3}={4}^{3}+3=64+3=67$$
$${S}_{4}={4}^{4}+3=256+3=259$$
The units digit of all odd-numbered terms is $$7$$.

The units digit of all even-numbered terms is $$9$$.

Because $${S}_{100}$$ is an even-numbered term, its units digit will be $$9$$.

Rahul's father wants to deposit some amount of money every year on the day of Rahul's birthday. On his $$1st$$ birth day $$Rs.100$$, on his $$2nd$$ birth day $$Rs.300$$, on his $$3rd$$ birth day $$Rs.600$$, on his $$4th$$ birthday $$Rs.1000$$ and so on.
What is the amount deposited by his father on Rahul's $$15th$$ birthday.

Let $$T_n$$ be the $$n^{th}$$ term of the series, then

$$S = 100[1 + 3 + 6 + 10 + 15 ........ T(n-1) + T(n)]$$

$$S = 100 [1 + 3 + 6 + 10.....................+ T(n-1) + T(n)]$$

Subtract both equations :

$$0 =100[ 1 + ( 2 + 3 + 4 + 5 ....... T(n) - T(n-1)) - T(n)]$$

$$T(n) =100 [1 + 2 + 3 + 4 + 5 ......... n]$$ (This is the series of the difference between yearly deposits]

It can be seen that the difference between the year's amounts are

$$2nd-1st=300-100=200$$

$$3rd-2nd=600-300=300$$

$$4th-3rd=1000-600=400$$)

$$T(n) = 100\left[\dfrac{n(n+1)}{2}\right]$$

Now we can tell by this formula of T(n),The amount deposited on $$15th$$ Birthday as follows

$$T(15)=100\times\dfrac{15\times16}{2}=12000$$

Therefore on his $$15th$$ birthday his father will deposit $$12000$$.

The product of two numbers is $$119$$ and their AM is $$12$$. Find the numbers.

We know that the arithmetic mean between two numbers $$a$$ and $$b$$ is $$AM=\frac { a+b }{ 2 }$$.

Here, it is given that $$AM=12$$, therefore,

$$AM=\frac { a+b }{ 2 } \\ \Rightarrow 12=\frac { a+b }{ 2 } \\ \Rightarrow a+b=12\times 2\\ \Rightarrow a+b=24\quad ....(1)$$

It is also given that the product of two numbers $$a$$ and $$b$$ is $$119$$, thus,

$$ab=119.....(2)$$

Now using equations 1 and 2, consider,

$$(a-b)^2=(a+b)^2-4ab=(24)^2-(4\times 119)=576-476=100$$ implies that

$$a-b=10.....(3)$$

Adding equations 1 and 3, we have

$$(a+a)+(b-b)=24+10\\ \Rightarrow 2a=34\\ \Rightarrow a=\frac { 34 }{ 2 } =17$$

Substitute the value of $$a$$ in equation 1 as follows:

$$17+b=24$$

$$b=24-17=7$$

Hence, the numbers are $$17$$ and $$7$$.

Find $$x$$, if the given numbers are in A.P. $$5$$, $$(x - 1)$$, $$0$$

We know that the arithmetic mean between two numbers $$a$$ and $$b$$ is $$AM=\frac { a+b }{ 2 }$$.

Here, it is given that $$AM=(x-1)$$, $$a=5$$ and $$b=0$$, therefore,

$$AM=\frac { a+b }{ 2 } \\ \Rightarrow x-1=\frac { 5+0 }{ 2 } \\ \Rightarrow x-1=\frac { 5 }{ 2 } \\ \Rightarrow 2(x-1)=5\\ \Rightarrow 2x-2=5\\ \Rightarrow 2x=5+2\\ \Rightarrow 2x=7\\ \Rightarrow x=\frac { 7 }{ 2 }$$

Hence, $$x=\frac { 7 }{ 2 }$$

Find the last digit of $$1^5 + 2^5 + ..... + 99^5$$.

$$ 1^{5}+2^{5}+....+99^{5} $$

last digest of $$ 1^{5} $$ is $$1$$

last digest of $$ 2^{5} $$ is $$2$$

last digest of $$ 3^{5} $$ is $$3$$

$$.$$

last digest of $$ 99^{5} $$ is 9

$$ \Rightarrow (1+2+...+9)+(1+2+9) $$

$$ +...10 $$ times

$$ \Rightarrow 450 \therefore $$ last digit is $$'0'$$

1106159_513689_ans_0e04a66917eb4e70ab4409616d6b96df.jpg

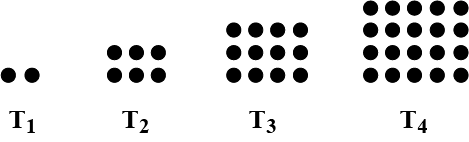
The following geometric arrays suggest a sequence of numbers.
(a) Find the next two terms.
(b) Find the $$100^{th}$$ term.
(c) Find the $$n^{th}$$ term.

So, $$T_5=T_4+10=20+10=30=5\times 6$$
$$T_6=T_5+12=30+12=42=6\times 7....$$
$$T_{100}=100\times 101=10, 100$$
$$T_n=n\times (n+1)=n^2+n$$.
1111003_569390_ans_db363d5ae7bf4dc78f9ffa7749c9a29b.png

1111003_569390_ans_db363d5ae7bf4dc78f9ffa7749c9a29b.png

Find the sum of all the digits of the result of the subtraction $$10^{99} - 99$$.

$$10^{99}$$ has ninety nine $$0$$ and one $$1$$

On subtracting $$99$$ , we'll get a number with ninety seven $$9$$ and ending with $$01$$

$$10^{99}- 99 = \underset{97\text{ times}}{\underbrace{99...99}}01$$

Sum of all digits of this number $$= (97\times 9) + (1\times 0) + (1\times 1) = 874$$

The sum of the first $$n$$ terms of a sequence is $$\dfrac {7^{n} - 6^{n}}{6^{n}}$$, Find its $$n^{th}$$ term. Determine whether the sequence is A.P. or G.P

$$S_{n} = \dfrac {7^{n} - 6^{n}}{6^{n}}$$
$$= \dfrac {7^{n}}{6^{n}} - \dfrac {6^{n}}{6^{n}} = \left [\dfrac {7}{6}\right ]^{n} - 1$$
$$S_{n - 1} = \left [\dfrac {7}{6}\right ]^{n - 1} - 1$$
$$t_{n} = S_{n} - S_{n - 1}$$
$$= \left [\dfrac {7}{6}\right ]^{n} - 1 - \left [\left (\dfrac {7}{6}\right )^{n - 1} - 1\right ]$$
$$= \left [\dfrac {7}{6}\right ]^{n} - \left [\dfrac {7}{6}\right ]^{n - 1}$$
$$= \left [\dfrac {7}{6}\right ]^{n - 1} \left [\dfrac {7}{6} - 1\right ]$$
$$\therefore t_{n} = \dfrac {1}{6} \left [\dfrac {7}{6}\right ]^{n - 1}$$
Now, $$\dfrac {t_{n + 1}}{t_{n}} = \dfrac {\dfrac {1}{6}\left [\dfrac {7}{6}\right ]^{n}}{\dfrac {1}{6} \left [\dfrac {7}{6}\right ]^{n - 1}}$$
$$= \left [\dfrac {7}{6}\right ]^{n - (n - 1)} = \dfrac {7}{6}$$
$$\therefore \dfrac {7}{6}$$ is constant.
$$\therefore$$ The given sequence is a G.P.
$$\therefore$$ The given sequence is a G.P., $$t_{n} = \dfrac {1}{6}\left [\dfrac {7}{6}\right ]^{n - 1}$$

Find the sum to infinite terms of the series
$$\dfrac {7}{5} \left (1 + \dfrac {1}{10^{2}} + \dfrac {1.3}{1.2} \cdot \dfrac {1}{10^{4}} + \dfrac {1.3.5}{1.2.3} \cdot \dfrac {1}{10^{6}} + ......\right )$$

$$\dfrac { 7 }{ 5 } \left( 1+{ \left( \dfrac { 1 }{ { 10 }^{ 2 } } \right) }^{ 1 }+\dfrac { 1.3 }{ 1.2 } \times { \left( \dfrac { 1 }{ { 10 }^{ 2 } } \right) }^{ 2 }+... \right) $$

$$\dfrac { 7 }{ 5 } \left( 1+\dfrac { \dfrac { 1 }{ 2 } }{ 1! } \times { 2 }^{ 1 }.{ \left( \dfrac { 1 }{ { 10 }^{ 2 } } \right) }^{ 1 }+\dfrac { \dfrac { 1 }{ 2 } .\dfrac { 3 }{ 2 } }{ 2! } \times { 2 }^{ 2 }.{ \left( \dfrac { 1 }{ { 10 }^{ 2 } } \right) }^{ 2 }+\dfrac { \dfrac { 1 }{ 2 } .\dfrac { 3 }{ 2 } .\dfrac { 5 }{ 2 } }{ 3! } \times { 2 }^{ 3 }.{ \left( \dfrac { 1 }{ { 10 }^{ 2 } } \right) }^{ 3 }... \right) $$

$$=\dfrac { 7 }{ 5 } \left( 1+\dfrac { \dfrac { 1 }{ 2 } }{ 1! } \times { \left( \dfrac { 2 }{ { 10 }^{ 2 } } \right) }^{ 1 }+\dfrac { \dfrac { 1 }{ 2 } .\left( \dfrac { 1 }{ 2 } +1 \right) }{ 2! } \times { \left( \dfrac { 2 }{ { 10 }^{ 2 } } \right) }^{ 2 }+\dfrac { \dfrac { 1 }{ 2 } .\left( \dfrac { 1 }{ 2 } +1 \right) .\left( \dfrac { 1 }{ 2 } +2 \right) }{ 3! } \times { \left( \dfrac { 2 }{ { 10 }^{ 2 } } \right) }^{ 3 }... \right) $$

$$=\dfrac { 7 }{ 5 } { \left( 1-\dfrac { 2 }{ { 10 }^{ 2 } } \right) }^{ \dfrac { -1 }{ 2 } }$$ $$\left[ \because { \left( 1-x \right) }^{ -n }=1+\dfrac { nx }{ 1! } +\dfrac { n(n+1) }{ 2! } { x }^{ 2 }+... \right] $$

$$=\dfrac { 7 }{ 5 } { \left( \dfrac { 98 }{ { 10 }0 } \right) }^{ \dfrac { -1 }{ 2 } }$$

$$=\dfrac { 7 }{ 5 } \times \dfrac { 10 }{ 7\sqrt { 2 } } $$

$$=\sqrt { 2 } $$

If the sum of the first $$n$$ natural numbers is $${S}_{1}$$ and that of their squares is $${S}_{2}$$ and cubes is $${S}_{3}$$, then show that $$9{ S }_{ 2 }^{ 2 }={ S }_{ 3 }(1+8{ S }_{ 1 })$$.

Sum of first $$n$$ natural numbers is $$\dfrac { n(n+1) }{ 2 } $$

Sum of squares of first $$n$$ natural numbers is $$\dfrac { n(n+1)(2n+1) }{ 6 } $$

Sum of cubes of first $$n$$ natural numbers is $${ \left( \dfrac { n(n+1) }{ 2 } \right) }^{ 2 }$$

RHS:

$$=S_3(1+8S_1)$$

$$={ \left( \cfrac { n(n+1) }{ 2 } \right) }^{ 2 }\times \left( 1+8\times { \left( \cfrac { n(n+1) }{ 2 } \right) } \right) \\ ={ \left( \cfrac { n(n+1) }{ 2 } \right) }^{ 2 }\times \left( 4{ n }^{ 2 }+4n+1 \right) \\ ={ \left( \cfrac { n(n+1) }{ 2 } \right) }^{ 2 }\times { \left( 2n+1 \right) }^{ 2 }\\ = \left(\cfrac{n(n+1)(2n+1)}{2}\right)^2\\ =9\times { \left( \cfrac { n(n+1)(2n+1) }{ 6 } \right) }^{ 2 }\\ =9{ { S }_{ 2 } }^{ 2 }$$

Hence proved

The sum of first $$n$$ terms of a sequence is $$\cfrac { { 6 }^{ n }-{ 5 }^{ n } }{ { 5 }^{ n } } $$
Find its $$n^{th}$$ term and examine whether the sequence is an A.P of G.P.

Sum of $$n$$ terms $$=S_{n}=\dfrac{6^{n}-5^{n}}{5^{n}}=\left ( \dfrac{6}{5} \right) ^{n}-1$$

Sum of $$(n-1)$$ terms $$=S_{n-1}=\left(\dfrac{6}{5}\right)^{n-1}-1$$

So, $$n^{th}$$ term $$=S_{n}-S_{n-1}=\left(\dfrac{6}{5}\right)^{n}-\left(\dfrac{6}{5}\right)^{n-1}=\dfrac{1}{6}\left(\dfrac{6}{5}\right)^{n}$$

So, this sequence is a G.P with common ratio $$=\dfrac{6}{5}$$

Find the sum of the series $$1\cdot 2+2\cdot 3+3\cdot 4+\cdots +n\left( n+1 \right) $$.

Assume that
$$1\cdot 2+2\cdot 3+3\cdot 4+\cdots +n\left( n+1 \right) =A+Bn+C{ n }^{ 2 }+D{ n }^{ 3 }+E{ n }^{ 4 }+\cdots$$,
where $$ A, B, C, D, E, \cdots$$ are quantities independent of $$n$$, whose values have to be determined.
Change $$n$$ into $$n+1$$; then
$$1\cdot 2+2\cdot 3+\cdots +n\left( n+1 \right) +\left( n+1 \right) \left( n+2 \right) =A+B\left( n+1 \right) +C{ \left( n+1 \right) }^{ 2 }+D{ \left( n+1 \right) }^{ 3 }+E{ \left( n+1 \right) }^{ 4 }+\cdots $$
By subtraction,
$$\left( n+1 \right) \left( n+2 \right) =B+C\left( 2n+1 \right) +D\left( 3{ n }^{ 2 }+3n+1 \right) +E\left( 4{ n }^{ 3 }+6{ n }^{ 2 }+4n+1 \right) +\cdots$$.
This equation being true for all integral values of $$n$$, the coefficients of the respective powers of $$n$$ on each side must be equal; thus $$E$$ and all succeeding coefficients must be equal to zero, and
$$3D=1$$; $$3D+2C=3$$; $$D+C+B=2$$;
whence $$D=\dfrac { 1 }{ 3 } ,C=1, B=\dfrac { 2 }{ 3 } $$.
Hence the sum $$=A+\dfrac { 2n }{ 3 } +{ n }^{ 2 }+\dfrac { 1 }{ 3 } { n }^{ 3 }$$.
To find $$A$$, put $$n=1$$; the series then reduces to its first term, and
$$2=A+2$$, or $$A=0$$.
Hence $$1\cdot 2+2\cdot 3+3\cdot 4+\cdots +n\left( n+1 \right) =\dfrac { 1 }{ 3 } n\left( n+1 \right) \left( n+2 \right) $$.

Find the $${ n }^{ th }$$ convergent to $$\dfrac { 6 }{ 5- } \dfrac { 6 }{ 5- } \dfrac { 6 }{ 5- } \cdots $$.

We have $${ p }_{ n }=5{ p }_{ n-1 }-6{ p }_{ n-2 }$$; hence the numerators form a recurring series any three consecutive terms of which are connected by the relation
$${ p }_{ n }-5{ p }_{ n-1 }+6{ p }_{ n-2 }$$.
Let $$S={ p }_{ 1 }+{ p }_{ 2 }x+{ p }_{ 3 }{ x }^{ 2 }+\cdots +{ p }_{ n }{ x }^{ n-1 }+\cdots $$;
then, we have $$S=\dfrac { { p }_{ 1 }+\left( { p }_{ 2 }-5{ p }_{ 1 } \right) x }{ 1-5x+6{ x }^{ 2 } } $$.
But the first two convergents are $$\dfrac { 6 }{ 5 }$$, $$\dfrac { 30 }{ 19 }$$;
$$\therefore S=\dfrac { 6 }{ 1-5x+6{ x }^{ 2 } } =\dfrac { 18 }{ 1-3x } -\dfrac { 12 }{ 1-2x } $$;
whence $${ p }_{ n }=18\cdot { 3 }^{ n-1 }-12\cdot { 2 }^{ n-1 }=6\left( { 3 }^{ n }-{ 2 }^{ n } \right) $$.
Similarly if $${ S }^{ ' }={ q }_{ 1 }+{ q }_{ 2 }x+{ q }_{ 3 }{ x }^{ 2 }+\cdots +{ q }_{ n }{ x }^{ n-1 }+\cdots $$,
we find $${ S }^{ ' }=\dfrac { 5-6x }{ 1-5x+6{ x }^{ 2 } } =\dfrac { 9 }{ 1-3x } -\dfrac { 4 }{ 1-2x } $$;
whence $${ q }_{ n }=9\cdot { 3 }^{ n-1 }-4\cdot { 2 }^{ n-1 }={ 3 }^{ n+1 }-{ 2 }^{ n+1 }$$.
$$\therefore \dfrac { { p }_{ n } }{ { q }_{ n } } =\dfrac { 6\left( { 3 }^{ n }-{ 2 }^{ n } \right) }{ { 3 }^{ n+1 }-{ 2 }^{ n+1 } } $$.

If n is a multiple of $$6$$, show that each of the series $$\displaystyle n-\frac{n(n-1)(n-2)}{\left\lfloor 3\right.}\cdot 3+\frac{n(n-1)(n-2)(n-3)(n-4)}{\left\lfloor 5\right.}\cdot 3^2-.....,$$ $$\displaystyle n-\frac{n(n-1)(n-2)}{\left\lfloor 3\right.}\cdot \frac{1}{3}+\frac{n(n-1)(n-2)(n-3)(n-4)}{\left\lfloor 5\right.}\cdot\frac{1}{3^2}-.....,$$ is equal to zero.

$$\Rightarrow $$ Let $${ \left( 1+x \right) }^{ n }=1+{ c }_{ 1 }x+{ c }_{ 2 }{ x }^{ 2 }+...$$

$${ \left( 1+ix \right) }^{ n }=1+i{ c }_{ 1 }x-{ c }_{ 2 }{ x }^{ 2 }+i{ c }_{ 3 }{ x }^{ 3 }+{ c }_{ 4 }{ x }^{ 4 }+i{ c }_{ 5 }{ x }^{ 5 }-....$$

$${ \left( 1-ix \right) }^{ n }=1-i{ c }_{ 1 }x-{ c }_{ 2 }{ x }^{ 2 }+i{ c }_{ 3 }{ x }^{ 3 }+{ c }_{ 4 }{ x }^{ 4 }-i{ c }_{ 5 }{ x }^{ 5 }-....$$

$$\therefore 2ix\left( { c }_{ 1 }-{ c }_{ 3 }{ x }^{ 2 }+i{ c }_{ 5 }{ x }^{ 4 }-.... \right) ={ \left( 1+ix \right) }^{ n }-{ \left( 1-ix \right) }^{ n }$$

Put $${ x }^{ 2 }=3$$, so that $$x=\sqrt { 3 } $$, and let $${ S }_{ 1 }$$ denote the value of the first series;also as usual

Let $$w,{ w }^{ 2 }$$ be the imaginary cube roots of unity;

so that $$w=\cfrac { -1+\sqrt { -3 } }{ 2 } ;{ w }^{ 2 }=\cfrac { -1-\sqrt { -3 } }{ 2 } $$

We have

$$2i\sqrt { 3 } { S }_{ 1 }={ \left( 1+\sqrt { -3 } \right) }^{ n }-{ \left( 1-\sqrt { -3 } \right) }^{ n }$$

$$={ \left( -2{ w }^{ 2 } \right) }^{ n }-{ \left( -2w \right) }^{ n }$$

$$={ 2 }^{ n }-{ 2 }^{ n }=0$$

when n is a multiple of $$6$$, for then

$${ \left( -w \right) }^{ n }=1,{ \left( -{ w }^{ 2 } \right) }^{ n }=1$$

Put $${ x }^{ 2 }=\cfrac { 1 }{ 3 } $$ and let $${ S }_{ 2 }$$denote the sum of the series, them;-

$$\cfrac { 2i }{ \sqrt { 3 } } { S }_{ 2 }={ \left( 1+\cfrac { \sqrt { -1 } }{ \sqrt { 3 } } \right) }^{ n }-{ \left( 1-\cfrac { \sqrt { -1 } }{ \sqrt { 3 } } \right) }^{ n }$$

$$={ \left( \cfrac { \sqrt { -3 } -1 }{ \sqrt { -3 } } \right) }^{ n }-{ \left( \cfrac { \sqrt { -3 } +1 }{ \sqrt { -3 } } \right) }^{ n }$$

$$={ \left( \cfrac { 2w }{ \sqrt { -3 } } \right) }^{ n }-{ \left( \cfrac { -2{ w }^{ 2 } }{ \sqrt { -3 } } \right) }^{ n }$$

$$=0$$

if n is a multiple of $$6$$

The $$4^{th}$$ term of a geometric sequence is $$\dfrac {2}{3}$$ and the seventh term is $$\dfrac {16}{81}$$. Find the geometric sequence

Given that $$t_{4} = \dfrac {2}{3}$$ and $$t_{7} = \dfrac {16}{81}$$.
Using the formula $$t_{n} = ar^{n - 1}, n = 1, 2, 3, ....$$ for the general term we have,
$$t_{4} = ar^{3} = \dfrac {2}{3}$$ and $$t_{7} = ar^{6} = \dfrac {16}{81}$$.
Note that in order to find the geometric sequence, we need to find $$a$$ and $$r$$.
By dividing $$t_{7}$$ by $$t_{4}$$ we obtain,
$$\dfrac {t_{7}}{t_{4}} = \dfrac {ar^{6}}{ar^{3}} = \dfrac {\dfrac {16}{81}}{\dfrac {2}{3}} = \dfrac {8}{27}$$.
Thus, $$r^{3} = \dfrac {8}{27} = \left (\dfrac {2}{3}\right )^{3}$$ which implies $$r = \dfrac {2}{3}$$.
Now, $$t_{4} = \dfrac {2}{3}\Rightarrow ar^{3} = \left (\dfrac {2}{3}\right )$$.
$$\Rightarrow a \left (\dfrac {8}{27}\right ) = \dfrac {2}{3}$$

$$\Rightarrow a = \dfrac {9}{4}$$
Hence, the required geometric sequence is $$a, ar, ar^{2}, ar^{3}, ..., ar^{n - 1}, ar^{n}, ....$$
That is, $$\dfrac {9}{4}, \dfrac {9}{4}\left (\dfrac {2}{3}\right ),\dfrac {9}{4}\left (\dfrac {2}{3}\right )^{2}, .....$$

Express $$\sqrt{19}$$ as a continued fraction, and find a series of fractions approximating to its value.

$$\sqrt{19}=4+(\sqrt{19}-4)=4+\displaystyle\frac{3}{\sqrt{19}+4};$$
$$\displaystyle \frac{\sqrt{19}+4}{3}=2+\frac{\sqrt{19}-2}{3}=2+\frac{5}{\sqrt{19}+2};$$
$$\displaystyle\frac{\sqrt{19}+2}{5}=1+\frac{\sqrt{19}-3}{5}=1+\frac{2}{\sqrt{19}-3};$$
$$\displaystyle\frac{\sqrt{19}+3}{2}=3+\frac{\sqrt{19}-3}{5}=3+\frac{5}{\sqrt{19}+3};$$
$$\displaystyle\frac{\sqrt{19}+3}{5}=1+\frac{\sqrt{19}-2}{5}=1+\frac{3}{\sqrt{19}+2};$$
$$\displaystyle\frac{\sqrt{19}+2}{3}=2+\frac{\sqrt{19}-4}{3}=2+\frac{1}{\sqrt{19}+4};$$
$$\sqrt{19}+4=8+(\sqrt{19}-4)=8+......$$
after this the quotients $$2, 1, 3, 1, 2, 8$$ recur$$;$$ hence
$$\displaystyle \sqrt{19}=4+\frac{1}{2+\frac{1}{1+\frac{1}{3+\frac{1}{1+..}}}}$$

Show that $$1+\dfrac { 1 }{ 3\cdot { 2 }^{ 2 } } +\dfrac { 1 }{{ 2 }^{ 4 } } +\dfrac { 1 }{ 7.{ 2 }^{ 6 } } +....=\log _{ e }{ 3 } $$.

We know from expansions

$$\log { (1+x) } =x-\dfrac { { x }^{ 2 } }{ 2 } +\dfrac { { x }^{ 3 } }{ 3 } -\dfrac { { x }^{ 4 } }{ 4 } +.....$$

$$\log { (1-x) } =-x-\dfrac { { x }^{ 2 } }{ 2 } +\dfrac { { x }^{ 3 } }{ 3 } -\dfrac { { x }^{ 4 } }{ 4 } +.....$$

So $$\log { (1+x) } +\log { (1-x) } =2(x+\dfrac { { x }^{ 3 } }{ 3 } +\dfrac { { x }^{ 5 } }{ 5 } +.....)$$

For $$x=\dfrac { 1 }{ 2 } $$

$$\log { (\dfrac { 3 }{ 2 } ) } -\log { (\dfrac { 1 }{ 2 } ) } =2(\dfrac { 1 }{ 2 } +\dfrac { { (\dfrac { 1 }{ 2 } ) }^{ 3 } }{ 3 } +\dfrac { { (\dfrac { 1 }{ 2 } ) }^{ 5 } }{ 5 } +.....)$$

$$\log { \left (\dfrac { \dfrac { 3 }{ 2 } }{ \dfrac { 1 }{ 2 } } \right ) } =1+\dfrac { { (\dfrac { 1 }{ 2 } ) }^{ 2 } }{ 3 } +\dfrac { { (\dfrac { 1 }{ 2 } ) }^{ 4 } }{ 5 } +.....)$$

$$\log { (3) } =1+\dfrac { 1 }{ 3\cdot { 2 }^{ 2 } } +\dfrac { 1 }{ 5\cdot { 2 }^{ 4 } } +\dfrac { 1 }{ 7\cdot { 2 }^{ 6 } } +.....)$$

If $${ u }_{ 1 }=\dfrac { a }{ b } ,{ u }_{ 2 }=\dfrac { b }{ a+b } ,{ u }_{ 3 }=\dfrac { a+b }{ a+2b } ,\cdots $$, each successive fraction being formed by taking the denominator and the sum of the numerator and denominator of the preceding fraction for its numerator and denominator respectively, show that $${ u }_{ \infty }=\dfrac { \sqrt { 5 } -1 }{ 2 } $$.

Here, $${ u_1 }=\cfrac { { p }_{ 1 } }{ { q }_{ 1 } } ,{ u }_{ 2 }=\cfrac { { p }_{ 2 } }{ { q }_{ 2 } } ,{ u }_{ 3 }=\cfrac { { p }_{ 3 } }{ { q }_{ 3 } } ,.....$$

Where, $${ p }_{ n }={ q }_{ n-1 }$$ and $${ q }_{ n }={ q }_{ n-1 }+{ p }_{ n-1 }$$

$${ q }_{ n }={ q }_{ n-1 }+{ q }_{ n-2 }$$

Hence,, $${ q }_{ 1 }+{ q }_{ 2 }x+{ q }_{ 3 }{ x }^{ 2 }+....$$ is a recurring series in which the scale of relation is $$1-x-{ x }^{ 2 }$$

$${ q }_{ 1 }=b,{ q }_{ 2 }=a+b$$

$${ q }_{ 1 }+{ q }_{ 2 }x+{ q }_{ 3 }{ x }^{ 2 }+....=\cfrac { { q }_{ 1 }+({ q }_{ 2 }-{ q }_{ 1 })x }{ 1-x-{ x }^{ 2 } } $$

$$=\cfrac { b+ax }{ 1-x-{ x }^{ 2 } } $$

Let $$\cfrac { b+ax }{ 1-x-{ x }^{ 2 } } =\cfrac { A }{ 1-\alpha x } +\cfrac { B }{ 1-\beta x } ;$$

Then $${ q }_{ n }=A{ \alpha }^{ n-1 }+B{ \beta }^{ n-1 };{ p }_{ n }={ q }_{ n-1 }=A{ \alpha }^{ n-2 }+B{ \beta }^{ n-2 }$$

$$\therefore \cfrac { { p }_{ n } }{ { q }_{ n } } =\cfrac { A{ \alpha }^{ n-2 }+B{ \beta }^{ n-2 } }{ A{ \alpha }^{ n-1 }+B{ \beta }^{ n-1 } } $$

Now, $$\alpha $$ and $$\beta $$ are to be found from the equations $$\alpha +\beta =1,\alpha \beta =-1$$,

Let $$\alpha $$ be the greater of the quantities; then $$\alpha =\cfrac { 1+\sqrt { 5 } }{ 2 } ;\beta =\cfrac { 1-\sqrt { 5 } }{ 2 } $$

So that $$\alpha >1,\beta <1;$$ hence the limit when $$n$$ is infinite of $${ \alpha }^{ n }$$ is infinity and $${ \beta }^{ n }$$ is $$0$$.

$$\cfrac { { p }_{ n } }{ { q }_{ n } } =\cfrac { A{ \alpha }^{ n-2 } }{ A{ \alpha }^{ n-1 } } =\cfrac { 1 }{ \alpha } =\cfrac { 2 }{ 1+\sqrt { 5 } } $$ $$=\cfrac { \sqrt { 5 } -1 }{ 2 } $$

If $$a=\underset{55}{\underbrace{111.........1}}, b=1+10+10^2+10^3+10^4$$ and $$c=1+10^5+10^{10}+....+10^{50}$$, then show following.
(i) 'a' is a not composite number
(ii) $$a\ is\ not\ equal\ bc$$

If the number of 1 repeating in the number are multiple of 3, the number is composite.

Eg: $$111=3(37) \quad 111111=3(37037)$$ etc

Since the number contains 55 ones and 55 is not a multiple of 3

Hence $$a$$ is not a composite number

$$b=1+10+{ 10 }^{ 2 }+{ 10 }^{ 3 }+{ 10 }^{ 4 }=\cfrac { (1)({ 10 }^{ 5 }-1) }{ 9 } \\ c=1+{ 10 }^{ 5 }+{ 10 }^{ 10 }+.....+{ 10 }^{ 50 }=\cfrac { (1)({ 10 }^{ 11 }-1) }{ ({ 10 }^{ 5 }-1) } \\ a=1+10+{ 10 }^{ 2 }+....+{ 10 }^{ 55 }=\cfrac { ({ 10 }^{ 56 }-1) }{ 9 } \\ \Rightarrow a\neq bc$$

If $$ \sum_{r=0}^{n} \dfrac { (-1)^r \cdot C_r}{(r+1)(r+2)(r+3) } = \dfrac {1}{a(n+b) } , $$ then $$a+b$$ is :

Let $$ X= \sum_{r=0}^{n} \dfrac { (-1)^r \cdot C_r}{(r+1)(r+2)(r+3) } = \sum_{r=0}^{n} \dfrac { (-1)^r \cdot\dfrac{n!}{r!(n-r)!}}{(r+1)(r+2)(r+3)} $$

We know that $$ C_r = \dfrac{n!}{r!(n-r)!} $$

Moreover, we know that $$ (r+1)\times r!= (r+1)! $$

Multiply by $$(n+1)(n+2)(n+3)$$ in both numerator and denominator in $$X$$. We get :

$$ X= \sum_{r=0}^{n} \dfrac { (-1)^r \cdot\dfrac{(n+3)!}{(r+3)!(n-r)!}}{(n+1)(n+2)(n+3)} $$

$$ X= \sum_{r=0}^{n} \dfrac { (-1)^r \cdot C^{n+3}_{r+3}}{(n+1)(n+2)(n+3) } $$

$$ \dfrac{1}{(n+1)(n+2)(n+3)} \text{will come out of summation because it is independent of r.} $$

$$ X= \dfrac{1}{(n+1)(n+2)(n+3)}\cdot \sum_{r=0}^{n} (-1)^r \cdot C^{n+3}_{r+3} $$

We know that $$ \sum_{r=0}^{n} (-1)^r \cdot C^{n}_{r} = 0 $$

Thus, $$ \sum_{r=-3}^{n} (-1)^r \cdot C^{n+3}_{r+3} =0 $$

$$ \sum_{r=0}^{n} (-1)^r \cdot C^{n+3}_{r+3} + C^{n+3}_{0} - C^{n+3}_{1} + C^{n+3}_{2} =0 $$

$$ \sum_{r=0}^{n} (-1)^r \cdot C^{n+3}_{r+3} = -( C^{n+3}_{0} - C^{n+3}_{1} + C^{n+3}_{2}) $$

$$ \sum_{r=0}^{n} (-1)^r \cdot C^{n+3}_{r+3} = -\left ( 1 - (n+3) + \dfrac{(n+3)(n+2)}{2}\right) $$

$$ \sum_{r=0}^{n} (-1)^r \cdot C^{n+3}_{r+3} = -\left (\dfrac{(n+1)(n+2)}{2}\right) $$

Using the above result in $$X$$, we get:

$$ X= \dfrac{1}{(n+1)(n+2)(n+3)}\cdot \left [-\left (\dfrac{(n+1)(n+2)}{2}\right)\right] $$

Therefore, $$ X= \dfrac{1}{(-2)(n+3)} $$

Comparing X with $$ \dfrac {1}{a(n+b)} $$ we get :

$$a= -2$$ and $$b= 3$$

Therefore, $$ a + b =-1+3= 1 $$

Study the pattern:
$$91 \times 11 \times 1 = 1001 $$
$$91 \times 11 \times 2 = 2002 $$
$$91 \times 11 \times 3 = 3003$$
Write next seven steps. Check, whether the result is correct.
Try the pattern for $$143 \times 7 \times 1, 143 \times 7 \times 2 .....$$

Pattern

$$91\times 11\times 1=1001$$

$$91\times 11\times 2=2002$$

$$91\times 11\times 3=3003$$

$$91\times 11\times 4=4004$$

$$91\times 11\times 5=5005$$

$$91\times 11\times 6=6006$$

$$91\times 11\times 7=7007$$

$$91\times 11\times 8=8008$$

$$91\times 11\times 9=9009$$

$$91\times 11\times 10=10,010$$

Another pattern for

$$143\times 7\times 1=1001$$

$$143\times 7\times 2=2002$$

Result is correct.

1168795_700585_ans_c1e29056f76a4bafbf20c85c7aa57acf.jpg

How would we multiply the numbers 13680347, 35702369 and 25692359 with 9 mentally ? What is the pattern that emerges.

To multiply a number with $$9$$ we use the following trick:- The number $$x(10-1)$$

$$13680347\times 9=(13680347)\times (10-1)=136803470-13600347$$

$$=123123123$$

$$35702369\times 9=35702369\times (10-1)=357023690-35702369$$

$$=321321321$$

$$25692359\times 9=25692359(10-1)=256923590-25692359$$

$$=231231231$$

These results repeat the digits $$1, 2$$ & $$3$$ in a cyclic pattern.

1168834_700586_ans_572f098e55de4542b21f853388a9dded.jpg

The sum of the series $$\displaystyle 1+\frac{1.3}{6}+\frac{1.3.5}{6.8}+....\infty$$ is?

Given $$1+\cfrac{1\cdot 3}{6}+\cfrac{1\cdot 3\cdot 5}{6\cdot 8}+....\infty$$

Let $$T_n$$ be the $$n^{th}$$ ter, of the Series

$$T_{ n }=\cfrac { 1\cdot 3\cdot 5\cdot 7....(2n-1) }{ 6\cdot 8\cdot 10....(2n+4) } \cfrac { [(2n+4)-(2n+1)] }{ 3 } \\ T_{ n }=\cfrac { 1 }{ 3 } \left[ \cfrac { 1\cdot 3\cdot 5\cdot 7....(2n-1) }{ 6\cdot 8\cdot 10....(2n+2) } -\cfrac { 1\cdot 3\cdot 5\cdot 7....(2n+1) }{ 6\cdot 8\cdot 10....(2n+4) } \right] \\ T_{ n }=\cfrac { 1 }{ 3 } [f(n)-f(n+1)]\\ T_{ 1 }=\cfrac { 1 }{ 3 } [f(1)-f(2)]\\ T_{ 2 }=\cfrac { 1 }{ 3 } [f(2)-f(3)]\\ T_{ 3 }=\cfrac { 1 }{ 3 } [f(3)-f(4)]\\ T_{ n }=\cfrac { 1 }{ 3 } [f(n)-f(n+1)]$$

Adding all,

$$T_{ n }=\cfrac { 1 }{ 3 } [f(1)-f(n+1)]=\cfrac { 1 }{ 3 } \left[ \cfrac { 1\cdot 3 }{ 6 } -1 \right] \\ S=1+\sum \; { T }_{ n }=1+\cfrac { 1 }{ 3 } \left[ \cfrac { 1 }{ 2 } -1 \right] =1-\cfrac { 1 }{ 6 } =\cfrac { 5 }{ 6 } $$

If $$n\epsilon N$$ and $$n$$ is even, then $$\dfrac {1}{1.(n - 1)!} + \dfrac {1}{3!(n - 3)!} + \dfrac {1}{5!(n - 5)!} + .... + \dfrac {1}{(n - 1)!1!}$$ equals.

$$S=\dfrac{1}{1(n-1)}+\dfrac{1}{3!(n-3)!}+\dfrac{1}{5!(n-5)!}+......+\dfrac{1}{(n-1)!(n-1)!}$$

$$r^{th}$$ term $$=\dfrac{1}{(2r-1)!(n-(2r-1))!}$$

$$S\times n!=^nC_1+^nC_3+^nC_5+......^nC_{n-1}$$

$$S_{even}\times n!=^nC_0+^nC_2+^nC_4+.......^nC_n.$$

$$^nC_0+^nC_1+^nC_2+^nC_3+.........^nC_n+2^n$$ ........(1)

$$^nC_0-^nC_1+^nC_2-^nC_3+........+^nC_n=0$$ ........(2)

(1)-(2)

$$2(^nC_1+^nC_3+^nC_5+........^nC_{n=1})=2^n$$

$$^nC_1+^nC_3+.......+^nC_{n-1}=2^n$$

$$s\times n!=2^n$$

$$\therefore S=\dfrac{2^n}{n!}$$

Solve the following equations.
$$\displaystyle\, 7^{x + 2} - \frac{1}{7}\cdot 7^{x + 1} - 14.7^{x - 1} + 2.7^x = 49$$

Considering the question to be:

$$7^{x+2}-\dfrac{1}{7}\cdot 7^{x+1}-14\cdot 7^{x-1}+2\cdot 7^x=49$$

$$7^{x+2}-7^{-1}\cdot 7^{x+1}-2\times 7\cdot 7^{x-1}+2\cdot 7^x=49$$

$$7^{x+2}- 7^{-1+x+1}-2\times 7^{1+x-1}+2\cdot 7^x=49$$

$$7^{x+2}- 7^{x}-2\times 7^{x}+2\cdot 7^x=49$$

$$7^{x+2}- 7^{x}=49$$

$$7^{x+2-x}=49$$

$$7^2=49$$

$$49=49$$

If $$f\left( x+y,\ x-y \right) =xy$$, then the arithmetic mean of $$f(x,y)$$ and $$f(y,x)$$ is

Given: $$f\left( x+y,x-y \right) =xy$$

Replacing $$x$$ by $$\dfrac { x+y }{ 2 } $$ and $$y$$ by $$\dfrac { x-y }{ 2 } $$

Gives $$f\left( x,y \right) =\dfrac { { x }^{ 2 }-{ y }^{ 2 } }{ 4 } $$

Now the arithmetic mean is $$\dfrac { f\left( x,y \right) +f\left( y,x \right) }{ 2 } =\dfrac { \dfrac { { x }^{ 2 }-{ y }^{ 2 } }{ 4 } +\dfrac { { y }^{ 2 }-{ x }^{ 2 } }{ 4 } }{ 2 } =0$$

If $$\alpha =\dfrac { 5 }{ 2!3 } +\dfrac { 5.7 }{ 3!{ 3 }^{ 2 } } +\dfrac { 5.7.9 }{ 4!{ 3 }^{ 3 } }$$,.... then find the value of $${ \alpha }^{ 2 }+4\alpha$$.

Let, $$\alpha=\large{\frac{5}{2!3}}+\frac{5.7}{3!3^2}+\frac{5.7.9}{4!3^3}+........$$

or, $$\alpha=\large{\frac{3.5}{2!3^2}}+\frac{3.5.7}{3!3^3}+\frac{3.5.7.9}{4!3^4}+........$$

or, $$\alpha=\large{\frac{3.(3+2)}{2!3^2}}+\frac{3.(3+2).(3+4)}{3!3^3}+\frac{3.(3+2).(3+4).(3+6)}{4!3^4}+........$$

or, $$\alpha=\left\{1+\large{\frac{\frac{3}{2}}{1!}}\left(\frac{2}{3}\right)+\large{\frac{\frac{3}{2}.\left(\frac{3}{2}+1\right)2^2}{2!3^2}}+\frac{\frac{3}{2}.\left(\frac{3}{2}+1\right).\left(\frac{3}{2}+2\right)2^3}{3!3^3}+\frac{\frac{3}{2}.\left(\frac{3}{2}+1\right).\left(\frac{3}{2}+2\right).\left(\frac{3}{2}+3\right)2^4}{4!3^4}+........\right\}-2$$

or, $$\alpha=\left\{1+\large{\frac{\frac{3}{2}}{1!}}\left(\frac{2}{3}\right)+\large{\frac{\frac{3}{2}.\left(\frac{3}{2}+1\right)}{2!}}\left(\frac{2}{3}\right)^2+\frac{\frac{3}{2}.\left(\frac{3}{2}+1\right).\left(\frac{3}{2}+2\right)}{3!}\left(\frac{2}{3}\right)^3+\frac{\frac{3}{2}.\left(\frac{3}{2}+1\right).\left(\frac{3}{2}+2\right).\left(\frac{3}{2}+3\right)}{4!}\left(\frac{2}{3}\right)^4+........\right\}-2$$

or, $$\alpha=\left(1-\large{\frac{2}{3}}\right)^{-\large{\frac{3}{2}}}-2=\large{\left(\frac{1}{3}\right)^{-\frac{3}{2}}}-2=3^{\frac{3}{2}}-2$$.

Now, $$\alpha^2+4\alpha=(3^3-4\times3\sqrt{3}+4)+4(3\sqrt{3}-2)=27-4=23$$

Prove $$1+2+3+4+5+\cdots+n=\dfrac{n(n+1)}{2}$$

The series form AP with $$a=1;d=1$$

The sum upto $$n$$ terms is $$\dfrac{n}{2}[2a+(n-1)d]\\\dfrac n 2[2(1)+n-1]\\\dfrac{n(n+1)}2$$

Find the $$n^{th}$$ term and the sum of first $$n$$ terms of the sequence $$0.3$$, $$0.33$$, $$0.333$$,$$0.3333$$,.....

$$n^{th}$$ term is $$n$$ number of $$35$$ after decimal point

sum of $$n$$ terms

$$=0.3+0.33+..........n$$ terms

$$=3(0.1+0.11+0.111............n$$ terms)

$$=\dfrac{3}{9}(0.9+0.59+........n$$ terms)

$$=\dfrac{3}{9}((1-0.1)+(1-0.1)+(1-0.001)+.......$$ n terms)

$$=\dfrac{3}{9}(n-(0.1+0.01...... $$ m terms))

$$=\dfrac{3}{9}n-\dfrac{3}{9}\times 0.1\dfrac{(1-(0.1)^{th})}{1-0.1}$$

$$=\dfrac{3}{9}n-\dfrac{3}{81}(10.1^{n})=\dfrac{n}{3}-\dfrac{1}{27}(1-0.1^{n})$$

$$=\dfrac{1}{27}(9n-1+(0.1)^{n})$$

Find the sum of the series $${1}^{2}+({1}^{2}+{2}^{2})+({1}^{2}+{2}^{2}+{3}^{2})+.....$$

$$(1^{2})+(1^{2}+2^{2}).....+(1^{2}+2^{2}.........n^{2})$$

We know that $$\displaystyle \sum_{i=1}^{n}i=\frac{n(n+1)}{2}$$

$$\displaystyle \sum_{i=1}^{n}i^2=\frac{n(n+1)(2n+1)}{6}$$

$$\displaystyle \sum_{i=1}^{n}i^3=\frac{n^{2}(n+1)^{2}}{4}$$

$$(1^{2})+(1^{2}+2^{2})..............(1^{2}+2^{2}............n^{2})$$

$$\displaystyle =\sum_{i=1}^{n}(1^{2}+2^{2}.........i^{2})$$

$$=\displaystyle \sum_{i=1}^{n}\sum_{i=1}^{i}i^{2}$$

$$=\displaystyle \sum_{i=1}^{n}\frac{i(i+1)(2i+1)}{6}=\sum_{i=1}^{n}\frac{2i^{3}+3i^{2}+i}{6}$$

$$=\displaystyle \frac{1}{3}\sum_{i=1}^{n}i^{3}+\frac{1}{2}\sum_{i=1}^{n}i^{2}+\frac{1}{6}\sum_{i=1}^{n}i$$

$$=\displaystyle \frac{1}{3}\left[n^{2}\frac{(n+1)^{2}}{4}\right]+\frac{1}{2}\left[\frac{n(n+1)(2n+1)}{6}\right]+\frac{1}{6}\left[\frac{n(n+1)}{2}\right]$$

$$\Rightarrow \dfrac{n(n+1)[n(n+1)+(2n+1)+1]}{12}$$

$$=\dfrac{n(n+1)(n^{2}+3n+2)}{12}=\dfrac{n(n+1)^{2}(n+2)}{12}$$

$$1 \, + \, \dfrac{3}{2} \, + \, \dfrac{5}{4} \, + \, \dfrac{7}{8} \, + \, ..... \, n \, terms$$

$$1,\dfrac{3}{2},\dfrac{5}{4}+.............+n$$

$$S_n=\dfrac{a}{1-r}+\dfrac{dr}{(1-r)^2}$$

$$a=1,d=2,r=\dfrac{1}{2}$$

$$S_n=\dfrac{1}{1-\frac{1}{2}}+\dfrac{(2)\frac{1}{2}}{\left ( 1-\frac{1}{2} \right )^2}$$

$$=\dfrac{1}{\frac{1}{2}}+\dfrac{1}{\frac{1}{4}}$$

$$=2+4$$

$$\therefore S_n=6$$

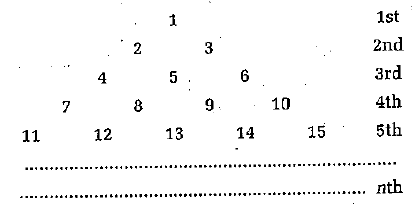
The natural numbers are written in the form of a triangle as shown below :
The sum of numbers in all the n rows .

All the numbers are natural numbers and if N be their number, then
N = 1 + 2 + 3 + 4 + .... $$ n \, = \, \dfrac{n(n \, + \, 1)}{2}$$
$$\therefore \, \, S_n \, = \, \dfrac{N(N \, + \, 1)}{2}\, = \,\dfrac{1}{2}\dfrac{n(n \, + \, 1)}{2}\left [\dfrac{n(n \, + \, 1)}{2} \, + \, 1 \right ]$$
$$ = \, \dfrac{1}{8}{n(n \, + \, 1)}(n^2 \, + \, n \, + \, 2 )$$

The sum of 'n' terms of series $$\bigg(1-\dfrac{1}{n}\bigg)+\bigg(1-\dfrac{2}{n}\bigg)+\bigg(1-\dfrac{3}{n}\bigg)+...........$$ will be

$$\left ( 1-\dfrac{1}{n}\right )+\left ( 1-\dfrac{2}{n}\right )+.........+\left ( 1-\dfrac{n}{n}\right )$$

$$a=1-\dfrac{1}{n}$$

$$d=1-\dfrac{2}{n} -1+\dfrac{1}{n} = -\dfrac{1}{n}$$

$$S_n=\dfrac{n}{2}[2a+(n-1)d]$$

$$=\dfrac{n}{2}\left [ 2\left ( 1-\dfrac{1}{n}\right )+(n-1)\left ( -\dfrac{1}{n} \right ) \right ]$$

$$=\dfrac{n}{2}\left [ 2\left ( \dfrac{n-1}{n}\right )+\left ( \dfrac{1-n}{n} \right ) \right ]$$

$$=\dfrac{n}{2}\left [ \left ( \dfrac{2n-2}{n}\right )+\left ( \dfrac{1-n}{n} \right ) \right ]$$

$$=\dfrac{n}{2}\left [ \left ( \dfrac{2n-2+1-n}{n}\right ) \right ]$$

$$=\dfrac{n}{2}\left [ \left ( \dfrac{n-1}{n}\right ) \right ]$$

$$=\dfrac{n-1}{2}$$

There are $$n$$ AM's between $$1\,\& 31$$ such that $$7th$$ mean: $${\left( {n - 1} \right)^{th}}$$ mean $$ = 5:9,$$ then find the value of $$n.$$

Let the arithmetic mean inserted be $$A1 , A2 , A3,....Am$$.

now , series is $$1,A1 , A2 , A3,....Am , 31$$

hence , $$a = 1, T_n =31 , n=n+2$$

$$T_n = a+(n-1)d$$

$$31 = 1+(n+2-1)d$$

$$30=(n+1)d$$

$$d=\dfrac{30}{n+1} $$ _______(1)

given that $$\dfrac{T_7}{T_n-1} = \dfrac{5}{9}$$

$$\dfrac{a+(7-1+1)d}{a+(n-1-1+1)d}=\dfrac{5}{9}$$

(here , $$a+(7-1+1)d$$ , +1 after 7-1 is because in the series the 1st A.M. is second in terms of series)

$$\dfrac{a+7d}{a+(n-1)d}=\dfrac{5}{9}$$

$$9a+63d = 5a+5nd-5d$$

$$4a+68d =5nd$$

$$4a= d(5n-68)$$

putting value of d frm (1)

by solving this you will get value of $$n = 14$$

If $$\displaystyle x=\sum _{ n=0 }^{ \infty }{ { a }^{ n } } ,y=\sum _{ n=0 }^{ \infty }{ { b }^{ n } } ,z=\sum _{ n=0 }^{ \infty }{ { \left( ab \right) }^{ n } } $$,
where $$a,b<1$$ then prove that $$xz+yz=xy+z$$.
Another form:
For $$0<\theta ,\phi -\cfrac { \pi }{ 2 }$$ if $$\displaystyle x=\sum _{ n=0 }^{ \infty }{ \cos ^{ 2n }{ \theta } }$$
$$\displaystyle y=\sum _{ n=0 }^{ \infty }{ \sin ^{ 2n }{ \phi } , } z=\sum _{ n=0 }^{ \infty }{ \cos ^{ 2n }{ \theta } } \sin ^{ 2n }{ \phi }$$ then prove that $$xz+yz-z=xy$$.

$$x=\dfrac { 1 }{ 1-a } $$ $$\Rightarrow\ a=\dfrac { x-1 }{ x } $$

Similarly $$b=\dfrac { y-1 }{ y } , ab=\dfrac { z-1 }{ z } $$

$$\therefore \dfrac { z-1 }{ z } =\dfrac { x-1 }{ x } =\dfrac { y-1 }{ y } $$

or $$xyz-xy=z(xy-x-y+1)$$

$$\therefore xz+yz=xy+z$$

If a , b are = ive , then from any integer n prove that
$$(a \, + \, b)^n \, < \, 2^n\, (a^n \, + \, b^n )$$

(a + b ) < 2 (a + b )
$$\therefore $$ p(1) holds goods
Assume p (m) i. e.
$$(a \, + \, b )^m \, < \, 2^m \, (a^m \, + \, b^m ) $$
We have to prove p( m + 1)
i. e. $$(a \, + \, b )^{m+ 1} \, < \, 2^{m + 1} \, (a^{m + 1}\, + \, b^{m +1} )$$
now $$(a \, + \, b )^{m+ 1} \, = \, (a \, + \, b )^{m}\, + \, (a \, + \, b ) $$
$$<2^m \, (a^m \, + \, b^m ) (a \, + \, b ) $$
$$= [a^{m + 1}\, + \, b^{m +1} \, + \, a^mb \, b^m a ]$$
$$<2^m \, [a^{m + 1}\, + \, b^{m +1} a^{m + 1}\, + \, b^{m +1} ]$$
as shown below in
$$ = 2^m [a^{m + 1}\, + \, b^{m +1} ]$$
now $$a^m b \, + \, b^m a<a^{m + 1}\, + \, b^{m +1} $$
or $$ a^m ( b \, - \, a) \, + \, b^m (a \, - \, b )< 0$$
or $$ (a^m \, - \, b^m )( b \, - \, a)\, > 0$$
or $$ (a^m \, - \, b^m )( a \, - \, b)\, > 0$$
above is true because when a and b are both +ive then either a < b or a > b
When a < b $$a^m - b^m$$ < o , a - b < 0
$$ \therefore $$ (b) holds
When a > b i. e.
$$a^m - b^m$$ < o , a - b < 0
$$ \therefore $$ (b) holds
$$ \therefore $$ p ( m + 1) holds goods hence universally true

Find the $$50_{th}$$ term of the sequence:
$$\dfrac{1}{n},\,\dfrac{n+1}{n},\,\dfrac{2n+1}{n}...................$$

$$a=\dfrac{1}{n}$$

$$d=\dfrac{2n+1}{n}-\dfrac{n+1}{n}=\dfrac{n+1}{n}-\dfrac{1}{n}=1$$

$$T_n=a+(n-1)d$$

$$T_{50}=\dfrac{1}{n}+(50-1)1$$

$$=\dfrac{1+49n}{n}$$

(a) If the roots of the equation, $$(b-c){ x }^{ 2 }+(c-a)x+(a-b)=0$$ be equal, then prove thar a,b,c are in arithmetical progression.
(b) If $$a(b-c){ x }^{ 2 }+b(c-a)x+c(a-b)=0$$ has equal roots, prove that a,b,c are in harmonical progression.

(a) $${ \left( c-a \right) }^{ 2 }-4(a-b)(b-c)=0$$
$${ c }^{ 2 }+{ a }^{ 2 }-2ca-4ab+4ac+4{ b }^{ 2 }-4bc=0$$
or $${ c }^{ 2 }+{ a }^{ 2 }-2ca+4{ b }^{ 2 }-4b(c+a)=0$$
or $${ \left( c+a \right) }^{ 2 }+{ \left( 2b \right) }^{ 2 }-2.2b(c+a)=0$$
or $${ \left[ (c+a)-2b \right] }^{ 2 }=0\therefore c+a-2b=0$$
or $$2b=a+c$$ $$\therefore $$ a,b,c arein A.P>
Alternate : $$\sum { \left( b-c \right) =0 } \therefore x=1$$ is a root since roots are equal, therefore both the roots are 1,1.
Hence their product.
$$P=1=\frac { a-b }{ b-c } \therefore 2b=a+c$$
$$\therefore $$ a,b,c are in A.P.
(b) $${ b }^{ 2 }{ \left( c-a \right) }^{ 2 }-4ac(b-c)(a-b)=0$$
or $${ b }^{ 2 }({ c }^{ 2 }+{ a }^{ 2 }-2ac)-4ac[ab-ac-{ b }^{ 2 }+bc]=0$$
or $${ b }^{ 2 }({ c }^{ 2 }+{ a }^{ 2 }-2ac+4ac)=4{ a }^{ 2 }{ c }^{ 2 }-4abc(c+a)=0$$
or $${ \left[ b(c+a) \right] }^{ 2 }+{ \left( 2ac \right) }^{ 2 }-2.2ac.b(c+a)=0$$
or $${ \left[ b(c+a)-2ac \right] }^{ 2 }=0\therefore b(c+a)=2ac$$
or $$b=\frac { 2ac }{ a+c } $$
$$\therefore $$ b is H.M. of a and c i.e. a,b,c are in H.P.
Alternate : Here $$\sum { a(b-c)=0 } $$
$$\therefore $$ $$x=1$$ is a root and since both roots are equal, they are 1,1.
$$\therefore $$ $$P=1=\dfrac { c(a-b) }{ a(b-c) } $$ or $$b=\dfrac { 2ac }{ a+c } $$
$$\therefore $$ a,b,c are in H.P.

If y = x$$^n$$ log x then
$$ y_n \, = \, n!\left [ log \, \, x \, + \, 1 \, +\dfrac{1}{2}\, +\dfrac{1}{3} .... \, + \, \, \dfrac{1}{n} \right ]$$
$$\forall \, n \, \epsilon \, N$$ and x > 0.

For p (1) we have to prove
$$y_1$$ = 1! (log x + 1)
where y = x log x for n = 1
$$y_1 \, = \, x.\dfrac{1}{x} \, + \, 1.$$ log x = (log x + 1) = 1! (log x + 1)
Thus p(1) holds good.
Now assume $$y_n \, = \, n! \, \left(log \, x \, + \, 1 \, + \, \dfrac{1}{2} \, + \, ... \, + \, \dfrac{1}{n} \right)$$
where y = $$x^n$$ log x for n = n.
p(n + 1) = $$y_{n \, + \, 1} \, of \, x^{n \, + \, 1}$$ (log x)
$$= \, y_n \, of \, \dfrac{d}{dx} \left\{x^{n \, + \, 1} \, log \, x\right\}$$
$$= \, y_n \, \left\{(n \, + \, 1) \, x^n \, log \, x \, + \, x^{n \, + \, 1} \, \dfrac{1}{x} \right \}$$
$$= \, y_n \, \left\{(n \, + \, 1) x^n \, log \, x\right\} \, + \, y_n \, (x^n)$$
= (n + 1) p (n) + n!
= (n + 1) n! $$\left[log \, x \, + \, 1 \, + \, \dfrac{1}{2} \, + \, ... \, + \, \dfrac{1}{n} \right] \, n!\dfrac{(n \, + \, 1)}{(n \, + \, 1)}$$
= (n + 1)! $$\left[log \, x \, + \, 1 \, + \, \dfrac{1}{2} \, + \, \dfrac{1}{3} \, + \, ... \, \dfrac{1}{n \, + \, 1} \right]$$
Hence p(n + 1) also holds good.

A sequence of real numbers $$a_1, a_2,$$___ $$a_n$$ is such that $$a_1=0, |a_2|=|a_1+1|, |a_3|=|a_2+1|$$, _______$$|a_n|=|a_{n-1}+1|$$. Show that A.M. of these numbers is always greater or equal to $$-1/2$$.

Squaring the given relations, we get
$$a^2_1=0$$
$$a^2_2=a^2_1+2a_1+1$$
$$a^2_3=a^2_2+2a_2+1$$
$$a^2_n=a^2_{n-1}+2a_{n-1}+1$$
and $$a^{n+1}=a^2_n+2a_n+1$$. This last relation we have written of our own to get the desired result of $$\dfrac{1}{n}\displaystyle\sum a_n$$. Adding them columns wise and cancelling, we get
$$a^2_{n+1}=2\displaystyle \sum a_n+n$$
$$\therefore 2\displaystyle\sum a_n=a^2_{n+1}-n\geq -n$$
$$\therefore \displaystyle\sum \dfrac{a_n}{n}\geq -\dfrac{1}{2}$$ or A.M.$$\geq -\dfrac{1}{2}$$.

Show that $$\dfrac{1}{a_1a_2}+\dfrac{1}{a_2a_3}+$$________$$+\dfrac{1}{a_{n-1}a_n}=\dfrac{n-1}{a_1a_n}$$.

$$\dfrac{1}{a_1}-\dfrac{1}{a_2}=\dfrac{a_2-a_1}{a_1a_2}=\dfrac{d}{a_1a_2}$$
$$\therefore d\displaystyle\sum \dfrac{1}{a_1a_2}=\displaystyle\sum \left(\dfrac{1}{a_1}-\dfrac{1}{a_2}\right)$$
The terms will cancel diagonally
$$=\dfrac{1}{a_1}-\dfrac{1}{a_n}=\dfrac{a_n-a_1}{a_1a_n}$$
$$d\displaystyle\sum \dfrac{1}{a_1a_2}=\dfrac{(n-1)d}{a_1a_n}$$
$$\therefore \displaystyle\sum \dfrac{1}{a_1a_2}=\dfrac{n-1}{a_1a_n}$$.

What is the expression of $$\tan^3x$$?

$$\tan^{3}x=3\tan x+3\tan^{2}x\tan 3{x}-\tan 3{x}$$

Find the arithmetic mean
If $$69.5$$ is the mean of $$72, 70, x, 62, 50, 71, 90, 64, 58$$ and $$82$$. Find the value of $$x.$$

$$\begin{matrix} y \\ 72 \\ 70 \\ x \\ 62 \\ 50 \\ 71 \\ 90 \\ 64 \\ 58 \\ 82 \end{matrix}\\ Arithmetic\quad mean=\sum _{ n=1 }^{ n }{ x } = \cfrac { 72+70+x+62+50+71+90+64+58+82 }{ 10 } \\ 69.5=\cfrac { 622+x }{ 10 } \\ x=73$$

Sum upto $$n$$ the series
$$6+66+666+.....$$

$$S=6+66+666+....$$
$$=\dfrac { 6 }{ 9 } \left[ 9+99+999+..... \right] $$
$$=\dfrac { 6 }{ 9 } \left[ (10-1)+({ 10 }^{ 2 }-1)+({ 10 }^{ 3 }-1)+.... \right] $$
$$=\dfrac { 6 }{ 9 } \left[ (10+{ 10 }^{ 2 }+{ 10 }^{ 3 }+.......-)\left( -1+1+1+.... \right) \right] $$
$$=\dfrac { 6 }{ 9 } \left[ 10.\dfrac { { 10 }^{ n-1 } }{ 10-1 } n \right] =\dfrac { 6 }{ 81 } [{ 10 }^{ n+1 }-9n-10]$$

Observe the following pattern:$$2^{6} = 64$$
$$2^{5} = 32$$
$$2^{4}=16$$
$$2^{3} =8$$
$$2^{2} =4$$
$$2^{1} =?$$
$$2^{0} =?$$
You can guess the value of $$2^{0}$$ by just studying the pattern!
You find that $$2^{0}$$ =1
If you start from $$3^{6} = 729$$, and proceed as shown above finding $$3^{5},3^{4},3^{3}...$$ etc, what will be $$3^{0}$$ = ?

Following the same pattern given in the question,

$$3^{6} = 729$$

$$3^{5} = 243$$

$$3^{4}=81$$

$$3^{3} =27$$

$$3^{2} =9$$

$$3^{1} =3$$

$$3^{0} =1$$. This is the answer.

Find the number of terms in the series $$20 + 19 \dfrac{1}{3} + 18 \dfrac{2}{3} + ....$$ of which the sum is $$300$$, explain the double answer.

The given series is an arithmetic series with first term $$a (= 20)$$ and the common difference $$d \left(= -\dfrac{2}{3}\right)$$.

Let the sum of $$n$$ terms be $$300$$.

Then, $$S_n = 300$$

$$\Longrightarrow \dfrac{n}{2} \{2a + (n - 1) d \} = 300$$

$$\Longrightarrow \dfrac{n}{2} \{ 2 \times 20 + (n - 1) (-2/ 3)\} = 300$$

$$\Longrightarrow n^2 - 61n + 900 = 0 \Longrightarrow (n - 25) (n - 36) = 0 \Longrightarrow n = 25$$ or $$36$$

So, sum of $$25$$ terms $$=$$ sum of $$36$$ terms $$= 300$$

Here, the common difference is negative therefore terms go on diminishing and $$31^{st}$$ term becomes zero.

All terms after $$31^{st}$$ term are negative. These negative terms when added to positive terms from $$26^{th}$$ term to $$30^{th}$$ term, they cancel out each other and the sum remains the same.

Hence, the sum of $$25$$ terms as well as that of $$36$$ terms is $$300$$.

$$2+2+4+1+8+\dfrac{1}{2}+16+......+55$$ term sum =?

1314733_1035980_ans_78cf3317ad9a447ab41d75a4449fd460.jpeg

Find the sum of series $$1+(2)(3)+(4)+(5)(6)+7+....$$ upto $$50$$ term.

Sum of $$1 + (2)(3) + 4 + (5)(6) + 7------$$ up to 50 terms.

$$1+4+7+10+13---------+73$$

$$+(2)(3)+(5)(6)+(8)(9)-----$$

$$ \Rightarrow 1+4+7+10+13----+73$$

$$ = 73 = 1 + (n-1) 3$$

$$=73 = 1 + 3n-3$$

$$=72 + 3 = 3n$$

$$n=25$$

$$=\dfrac{25}{2}(2 + (24)3)$$

$$= \dfrac{25}{2}(2+72)$$

$$=25 \times 37$$

$$= 925$$

$$\Rightarrow (2)(3)+(5)(6)+(8)(9)----+(74)(75)$$

$$ \Rightarrow \displaystyle \sum_{25}^{n=1} (3^{n}-1)(3^{n})$$

$$ \Rightarrow 3^{2n} - 3^{n} $$

$$\displaystyle \sum_{25}^{n=1} 9^{n} - 3n $$

$$ \displaystyle \sum_{25}^{n=1} 9n - \sum_{25}^{n=1} 3^{n}$$

$$ \Rightarrow \dfrac{9^{26} + 4(3^{26}) - 12 }{8 } +925 $$

Find the smallest among three consecutive odd natural numbers whose sum is $$87.$$

Let the three consecutive odd natural numbers are $$n, n+2$$ and $$n+4$$

It is given that their sum is $$87$$

So,

$$(n)+(n+2)+(n+4)=87$$

$$3n+6=87$$

$$3n=87-6=81$$

So, $$n=\dfrac { 81 }{ 3 } =27$$

Smallest no. is $$27.$$

Find the sum of series
$$0.5 + 0.55 + 0.555 + ...$$

$$S=0.5+0.55+0.55+....$$

$$\implies S=5(0.1+0.01+0.001+...)$$

The series $$0.1,0.01,0.01$$ is the G.P. with first term $$a=0.1$$ and common ratio $$r=\dfrac{0.01}{0.1}=0.1$$

We know that the sum of infinite series is $$\dfrac{a}{1-r}$$

$$\implies S=5(\dfrac{0.1}{1-0.1})$$

$$\implies S=5(\dfrac{0.1}{0.9})$$

$$\implies S=\dfrac 59$$

The sum of $$10^2+11^2+12^2+....+20^2$$ is

Formula:

$$1^2+2^2+3^2+……+n^2=\dfrac{n(n-1)(n-2)}{6}$$

$$11^2+12^2+……+20^2$$

$$=(1^2+2^2+3^2+……+20^2)- (1^2+2^2+3^2+……+10^2)$$

$$=\dfrac{20 \times 21 \times 41}{6}-\dfrac{10 \times 11 \times 21}{6}$$

$$=2870-385$$

$$=2485$$

$$\therefore 10^2+11^2+….+20^2=10^2+2485=2585$$

A plant doubled its height each yer until it reached its maximum height over the course of $$12$$ years How many years did it take for it to reach half of its maximum height?

Let the Height of the Plant be $$H$$

As it doubles every Year

height after 12 Years $$=2^{11}H$$

Half of this Height is $$2^{10}$$

which is the height in the 11th year

If $$a, b, c$$ be the respective sums of the $$n$$ terms, next $$n$$ terms and of G.P. then prove that $$a, b, c$$ are in G.P.

Let x be the first term & r be the common ratio of the G.P

$$a=\dfrac{x(1-r^n)}{1-r}$$ ………$$(1)$$

$$b=\dfrac{x(1-r^{2n})}{1-r}-a$$

$$\Rightarrow a+b=\dfrac{x(1-r^{2n})}{1-r}$$ …..$$(2)$$

$$c=\dfrac{x(1-r^{3n})}{1-r}-(a+b)$$

$$\Rightarrow a+b+c=\dfrac{x(1-r^{3n})}{1-r}$$ ……$$(3)$$

$$(2)\div (1)$$

$$\dfrac{a+b}{a}=\dfrac{1-r^{2n}}{1-r^n}$$

$$1+\dfrac{b}{a}=1+r^n$$

$$b=ar^n$$

$$(3)\div (2)$$

$$\dfrac{a+b+c}{a+b}=\dfrac{1-r^{3n}}{1-r^{2n}}$$

$$1+\dfrac{c}{a+b}=\dfrac{1+r^n+r^{2n}}{1+r^n}$$

$$\dfrac{c}{a+b}=\dfrac{r^{2n}}{1+r^n}$$

$$\dfrac{c}{a+ar^n}=\dfrac{r^{2n}}{1+r^n}$$

$$\dfrac{c}{a(1+r^n)}=\dfrac{r^{2n}}{1+r^n}$$

$$c=ar^{2n}$$

We can say that $$a, ar^n, ar^{2n}$$ are in G.P.

$$\therefore$$ a, b, c are in G.P.

If $$\displaystyle \sum _{r=1}^{n}{T_{r}=5n+2}$$ and $$\displaystyle \sum _{r=1}^{n}{T_{r}^{2}=an^{3}+bn^{2}+cn+d}$$ then the value of $$d+b+c$$

$$\sum _{ r=1 }^{ n }{ { T }_{ r } } =5n+2\\ { T }_{ 1 }=7\\ \\ \sum _{ r=1 }^{ 2 }{ { T }_{ r } } =12=>{ T }_{ 1 }+{ T }_{ 2 }=12\\ { T }_{ 2 }=5\\ Similarly\quad { T }_{ 3 }=5,{ T }_{ 4 }=5,....{ T }_{ n }=5\\ \sum _{ r=1 }^{ n }{ { T }_{ r } } ^{ 2 }={ 7 }^{ 2 }+{ 5 }^{ 2 }+{ 5 }^{ 2 }+....+{ 5 }^{ 2 }\\ a{ n }^{ 3 }+b{ n }^{ 2 }+cn+d=25n+24\\ a=0,b=0,c=25,d=24\\ $$

$$d+b+c=0+24+25=49$$

Find the next term $$3, 5, 7, 10, 11, 15, 15, 20,$$__

$$3,5,7,10,11,15,15,20$$

Alternate terms are in A.P>

$$3,7,11,15,19......->$$ all odd terms

$$5,10,15,20,25.....->$$ all even terms

$$3,5,7,10,11,15,15,20,19,25,..$$

Next term in given series is $$19$$

$$\left( 1+\dfrac { 3 }{ 1 } \right) \left( 1+\dfrac { 5 }{ 4 } \right) \left( 1+\dfrac { 7 }{ 9 } \right) ...\left( 1+\dfrac { \left( 2x+1 \right) }{ { n }^{ 2 } } \right) ={ \left( n+1 \right) }^{ 2 }.$$

$$\left( {1 + \dfrac{3}{1}} \right)\left( {1 + \dfrac{5}{4}} \right)\left( {1 + \dfrac{7}{9}} \right)...\left( {1 + \dfrac{{\left( {2n + 1} \right)}}{{{n^2}}}} \right)$$

Here $${a_n} = 1 + \dfrac{{2n + 1}}{{{n^2}}}$$

$$ = 1 + \dfrac{2}{n} + \dfrac{1}{{{n^2}}}$$

$$ = {\left( {1 + \dfrac{1}{n}} \right)^2}$$

$$ = {\left( {\dfrac{{n + 1}}{n}} \right)^2}$$

Therefore, $$\left( {1 + \dfrac{3}{1}} \right)\left( {1 + \dfrac{5}{4}} \right)\left( {1 + \dfrac{7}{9}} \right)...\left( {1 + \dfrac{{\left( {2n + 1} \right)}}{{{n^2}}}} \right)$$$$ = \prod\limits_1^n {{a_n}} $$

$$ = \prod\limits_1^n {{{\left( {\dfrac{{n + 1}}{n}} \right)}^2}} $$

$$= \prod\limits_1^n {\dfrac{{{{\left( {n + 1} \right)}^2}}}{{{n^2}}}} $$

$$ = \dfrac{{{2^2}}}{1} \times \dfrac{{{3^2}}}{{{2^2}}} \times \dfrac{{{4^2}}}{{{3^2}}} \times \dfrac{{{5^2}}}{{{4^2}}}...\dfrac{{{{\left( {n + 1} \right)}^2}}}{{{n^2}}}$$

$$ = {\left( {n + 1} \right)^2}$$

Prove $$\left( 1+\dfrac { 1 }{ 1 } \right) \left( 1+\dfrac { 1 }{ 2 } \right) \left( 1+\dfrac { 1 }{ 3 } \right) ...\left( 1+\dfrac { 1 }{ { n } } \right) ={ \left( n+1 \right) }.$$

$$\left( {1 + \dfrac{1}{1}} \right)\left( {1 + \dfrac{1}{2}} \right)\left( {1 + \dfrac{1}{3}} \right)...\left( {1 + \dfrac{1}{n}} \right)$$

Here $${a_n} = 1 + \dfrac{1}{n}$$$$ = \dfrac{{n + 1}}{n}$$

Therefore, $$\left( {1 + \dfrac{1}{1}} \right)\left( {1 + \dfrac{1}{2}} \right)\left( {1 + \dfrac{1}{3}} \right)...\left( {1 + \dfrac{1}{n}} \right)$$$$ = \prod\limits_1^n {{a_n}} $$

$$ = \prod\limits_1^n {\left( {\dfrac{{n + 1}}{n}} \right)} $$

$$ = \dfrac{2}{1} \times \dfrac{3}{2} \times \dfrac{4}{3} \times \dfrac{5}{4}...\dfrac{{\left( {n + 1} \right)}}{n}$$

$$ = \left( {n + 1} \right)$$

The arithmetic mean of the nine numbers in the given set $${\left\{9, 99, 999, 999999999 \right\}}$$ is a $$9$$ digit numbers $$N$$, all whose digits are distinct. The number $$N$$ does not contain the digit

$$A.M=\dfrac{9+99+999+999999999}{9}$$

$$=9\dfrac{1+11+111+111111111}{9}$$

$$=1+11+111+111111111$$

$$1+11=12$$

$$1+11+111=123$$

$$\therefore 1+11+111+111111111=123456789$$

$$\Rightarrow A.M.=123456789$$

Hence A.M. does not contain 0 as one of its digit.

$$\dfrac{1}{{1.2.3}} + \dfrac{1}{{2.3.4}} + \dfrac{1}{{3.4.5}} + .... + \dfrac{1}{{m\left( {n + 1} \right)\left( {n + 2} \right)}} = \dfrac{{n\left( {n + 3} \right)}}{{4\left( {n + 1} \right)\left( {n + 2} \right)}}$$

$$S=\cfrac { 1 }{ 1.2.3 } +\cfrac { 1 }{ 2.3.4 } +....+\cfrac { 1 }{ n(n+1)(n+2) } \\ S=\sum { \cfrac { 1 }{ n(n+1)(n+2) } } \\ =\sum { \cfrac { 1 }{ n+1 } \left( \cfrac { 1 }{ 2 } \left( \cfrac { 1 }{ n } -\cfrac { 1 }{ n+2 } \right) \right) } \\ =\cfrac { 1 }{ 2 } \sum { \left( \cfrac { 1 }{ n(n+1) } -\cfrac { 1 }{ (n+1)(n+2) } \right) } \\ =\cfrac { 1 }{ 2 } \sum { \left[ \left( \cfrac { 1 }{ n } -\cfrac { 1 }{ n+1 } \right) -\left( \cfrac { 1 }{ n+1 } -\cfrac { 1 }{ n+2 } \right) \right] } \\ =\cfrac { 1 }{ 2 } \sum { \left[ \left( 1-\cfrac { 1 }{ 2 } \right) -\left( \cfrac { 1 }{ 2 } -\cfrac { 1 }{ 3 } \right) +\left( \cfrac { 1 }{ 2 } -\cfrac { 1 }{ 3 } \right) -\left( \cfrac { 1 }{ 2 } -\cfrac { 1 }{ 3 } \right) +....+\left( \cfrac { 1 }{ n } -\cfrac { 1 }{ n+1 } \right) -\left( \cfrac { 1 }{ n+1 } -\cfrac { 1 }{ n+2 } \right) \right] } \\ =\cfrac { 1 }{ 2 } \left[ \cfrac { 1 }{ 2 } -\cfrac { 1 }{ (n+1)(n+2) } \right] \\ =\cfrac { 1 }{ 4 } \left[ 1-\cfrac { 2 }{ (n+1)(n+2) } \right] \\ =\cfrac { 1 }{ 4 } \cfrac { \left( { n }^{ 2 }+3n \right) }{ (n+1)(n+2) } \\ S=\cfrac { n(n+3) }{ 4(n+1)(n+2) } \\ \\ $$

Sum the series :
$$2^{1/4} \, \cdot \, 4^{1/8} \, \cdot \, 8^{1/16} \, \cdot \, 16^{1/32} \, ....$$ is equal

Consider the given series.

$$ {{2}^{1/4}}{{.4}^{1/8}}{{.8}^{1/16}}{{.16}^{1/32}}...... $$

$$ S={{2}^{1/4}}{{.2}^{2/8}}{{.2}^{3/16}}{{.2}^{4/32}}...... $$

$$ S={{2}^{\left( 1/4+2/8+3/16+4/32+....... \right)}} $$

$$ S={{2}^{1/4\left( 1+2/2+3/4+4/8+....... \right)}} $$

Let

$$T=1+\dfrac{2}{2}+\dfrac{3}{4}+\dfrac{4}{8}+.....$$ (Infinity AGP series with a=1, r=1/2, d=1)

Therefore,

$$ T=\dfrac{a}{1-r}+\dfrac{dr}{{{\left( 1-r \right)}^{2}}} $$

$$ T=\dfrac{1}{1-\dfrac{1}{2}}+\dfrac{1\times \dfrac{1}{2}}{{{\left( 1-\dfrac{1}{2} \right)}^{2}}} $$

$$ T=\dfrac{1}{\dfrac{1}{2}}+\dfrac{\dfrac{1}{2}}{{{\left( \dfrac{1}{2} \right)}^{2}}} $$

$$ T=2+2=4 $$

Therefore,

$$ S={{2}^{1/4\times 4}} $$

$$ S={{2}^{1}}=2 $$

Hence, this is the answer.

Let $$a_1, a_2, a_3, a_4, a_5$$ be a G.P. of positive real numbers such that the A.M. of $$a_2$$ and $$a_4$$ is $$117$$ and the G.M. of $$a_2$$ and $$a_4$$ is $$108$$. Then the A.M. of $$a_1$$ and $$a_5$$ is:

$${ a }_{ 1 },{ a }_{ 2 },{ a }_{ 3 },{ a }_{ 4 },{ a }_{ 5 }$$ are in G.P.

A.M. of $${ a }_{ 2 }\& { a }_{ 4 }=117$$

$${ a }_{ 2 }+{ a }_{ 4 }=234$$

G.M. of $$\quad { a }_{ 2 }\& { a }_{ 4 }=108={ a }_{ 3 }\\ { a }_{ 2 }{ a }_{ 4 }=\left( 108 \right) ^{ 2 }\\ ({ a }_{ 2 }{ -a }_{ 4 })^{ 2 }=({ a }_{ 2 }{ +a }_{ 4 })^{ 2 }-4{ a }_{ 2 }{ a }_{ 4 }\\ =\left( 234 \right) ^{ 2 }-\left( 216 \right) ^{ 2 }\\ =(450)(18)\\ { a }_{ 2 }{ -a }_{ 4 }=30\times 3=90\\ { a }_{ 2 }=162,{ a }_{ 4 }=72\\ r=\cfrac { { a }_{ 3 } }{ { a }_{ 2 } } =\cfrac { 108 }{ 162 } =\cfrac { 2 }{ 3 } \\ { a }_{ 1 }=243,{ a }_{ 5 }=\cfrac { 2 }{ 3 } (72)=48$$

A.M $$=\cfrac { { a }_{ 1 }+{ a }_{ 5 } }{ 2 } =145.5$$

In the given squences 2,5,6.....50and 3,5,7.....60
How many terms are common to both?

$$\begin{array}{l} 2,5,8,........50\\to (i) \\ \Rightarrow 3,5,7,.....60\\to (ii) \\ \Rightarrow for\, \, 1st\, \, series\, \, a=2,\, \, \\ common\, \, difference \\ { d_{ 1 } }=3\, \, and\, \, { T_{ n } }=60\rightarrow { T_{ 6 } }=2+3\left( { 60-1 } \right) =179 \\ \Rightarrow and\, \, for\, \, 2nd\, \, series\, \, \\ { a_{ 2 } }=3,\, \, { d_{ 2 } }=2,\, \, h=50\, \, term \\ \Rightarrow { T_{ 50 } }=3+{ \left( { 50-1 } \right) _{ 2 } }=101\left[ { LCm\, \, of\, \, 2\times 3=6 } \right] \\ \Rightarrow common\, \, term\, \, like\, \, 5,\, \, { 117^{ 17 } }......101 \\ \Rightarrow a=5,\, \, d=6,\, \, { t_{ n } }=101,\, \, then,\, \, { T_{ n } }=5+\left( { n-1 } \right) 6 \\ \Rightarrow 101=5+\left( { n-1 } \right) 6,\, \, n=17 \end{array}$$

A series of numbers is given as $$1, \dfrac{1}{2}, -4, 4, \dfrac{1}{8}, -16, ......$$ The next number in the series is

$$after\>-4,\>next\>term\>is\>+4,\>hence\>using\>same\>pattern\>number\>next\>to\>-16\>should\>be\>+16$$

Find the sum of place value of last 3 places in the sum of first '10' terms of : 4 + 44 + 444 + ...

$$S=4+4+4+...+444....4(10times)\\ S=4(1+11+111+....+11..1(10times)\\ S=\cfrac { 4 }{ 9 } \left( 9+99+999+....99..9(10times) \right) \\ =\cfrac { 4 }{ 9 } \left( 10+{ 10 }^{ 2 }+{ 10 }^{ 3 }+....+-10 \right) \\ \\ =\cfrac { 4 }{ 9 } \left( { 10 }^{ 2 }+{ 10 }^{ 3 }+....{ 10 }^{ 10 } \right) \\ =\cfrac { 400 }{ 9 } \left( 1+{ 10 }^{ 2 }+.....+{ 10 }^{ 8 } \right) \\ =\cfrac { 400({ 10 }^{ 9 }-1) }{ 9\times 9 } \\ =400\cfrac { 111111111 }{ 9 } =400(12345679)\\ $$

Sum of place value of last 3 places $$=600+0+0$$

$$=600$$

Find the value of $$\lim\limits_{n \to \infty}\dfrac{1}{n}\displaystyle \sum^{n}_{r=1}\sin^2 \dfrac{r\pi}{n}$$.

Now,

$$\lim\limits_{n \to \infty}\dfrac{1}{n}\displaystyle \sum^{n}_{r=1}\sin^2 \dfrac{r\pi}{n}$$

$$=\displaystyle\int\limits_{0}^{1}\sin^2 \pi x\ dx$$ [ According to the definition of definite integral]

$$=\dfrac{1}{2}\displaystyle\int\limits_{0}^{1}2\sin^2 \pi x\ dx$$

$$=\dfrac{1}{2}\displaystyle\int\limits_{0}^{1}(1-\cos 2\pi x)\ dx$$

$$=\dfrac{1}{2}\left[x-\dfrac{\sin 2\pi x}{2\pi}\right]_{0}^{1}$$

$$=\dfrac{1}{2}$$.

Sum: $$\frac{3}{1^2.2^2}+\frac{5}{2^2.3^2}+\frac{7}{3^2.4^2}+.......$$ to n terms.

$$\\(\frac{3}{1^2\cdot\>2^2})+(\frac{5}{2^2\cdot\>3^2})+(\frac{7}{3^2\cdot\>4^2})+.........(\frac{2n+1}{n^2\>(n+1)^2})\\\>now\>(\frac{3}{1^2\cdot\>2^2})=(\frac{2^2-1^2}{1^2\cdot\>2^2})=(\frac{1}{1^2})-(\frac{1}{2^2})\\(\frac{5}{2^2\cdot\>3^2})=(\frac{3^2-2^2}{2^2\cdot\>3^2})=(\frac{1}{1^2})-(\frac{1}{3^2})\\\therefore\>sum\>=((\frac{1}{1^2})-(\frac{1}{2^2})+(\frac{1}{2^2})-(\frac{1}{3^2}))+.......+[(\frac{1}{n^2})-(\frac{1}{(n+1)^2})]\\=1-(\frac{1}{(n+1)^2})\\=(\frac{n^2+2n}{(n+1)^2})$$

Vijay is planting trees. He has enough trees to plant $$6, 7$$ or $$14$$ trees in each row. What is the least number of trees Vijay could have?

We have to take $$LCM$$ of the numbers $$6, 7, 14$$ as below:

So, $$2\times 3\times 7=42$$

Vijay could have at least $$42$$ number of frees.

1424390_1065120_ans_dc264d4e5ada403491693f332dde91d4.bmp

$$1+3+5+.........+2n-1=$$

$$1+3+5+...............+2n-1\\\sum (2n-1)\\\sum 2n-\sum 1\\2\sum n-n\\2\dfrac {n(n+1)}2-n\\n^2+n-n=n^2$$

Find the $$n^{th}$$ term and sum to $$n$$ terms of the following series:
$$2 + 6 + 12 + 20 +$$____

$$2+6+12+20+.........$$

As we can see that the general term is $$r(r+1)$$

so, the $$n^{th}$$ term is $$n(n+1)$$

Sum of given series upto $$n$$ terms:

$$\Rightarrow \displaystyle\sum_{r=1}^{n}r(r+1)$$

$$=\displaystyle\sum_{r=1}^{n}r^{2}+\sum_{r=1}^{n}r$$

$$=\dfrac{n(n+1)(2n+1)}{6}+\dfrac{n(n+1)}{2}$$

$$=\dfrac{n(n+1)}{2}\left\{\dfrac{2n+1}{3}+1\right\}$$

$$=\dfrac{n(n+1)}{2}\dfrac{2n+4}{3}$$

$$=\dfrac{n(n+1)(n+2)}{3}$$

If the roots of $$x^{3}+px^{2}+qx+r=0$$ are in G.P., find the relation between $$p,q,r$$.

let the roots are $$\cfrac a t, a $$ and $$at$$

Product of the roots$$=(\cfrac a t)(a)(at)=a^3=-r$$

Sum of roots : $$a[\cfrac 1 t+1+t]=-P$$

Coefficient of $$x=$$ Sum of combinations of $$2$$ roots.

$$a(\cfrac a t)+a(at)+at(\cfrac a t)=a^2[\cfrac 1 t+t+1]=q$$

$$=>a^2(\cfrac {-p}{a})=q =>a=\cfrac {-q}{p}$$

$$a^3=\cfrac {-q^3} {p^3}=-r$$

$$=>q^3=rp^3$$

Find the $$n^{th}$$ term and sum to $$n$$ terms of the following series:
$$3 + 6 + 11 + 18 +$$____

$$S_{n}=3+6+11+18....+n^{th}$$ term

$$S_{n}=(1^{2}+2)+(2^{2}+2)+(3^{2}+2)+(4^{2}+2).......+(n^{2}+2)$$

As we can see that the general term is $$n^{2}+2$$

So, the $$n^{th}$$ term is $$n^{2}+2$$

Sum of given series upto $$n$$ terms:

$$S_{n}=(1^{2}+2^{2}+3^{2}+4^{2}......+n^{2})+2n$$

$$S_{n}=\dfrac{n(n+1)(2n+1)}{6}+2n$$

$$S_{n}n(2n^{2}+3n+13)/6$$

The value of $$\sum_\limits{i=1}^n\sum_\limits{j=1}^i\sum_\limits{k=1}^j 1=$$

$$\\\sum_{i=1}^{n}\sum_{j=1}^{i}\sum_{k=1}^{j}1\\=\sum_{i=1}^{n}\sum_{j=1}^{i}j\\=\sum_{i=1}^{n}(1+2+3+......+11i)\\= \sum_{i=1}^{n}(\frac{i(i+1)}{2})\\=\sum (\frac{(i^2)}{2})+\sum i=(\frac{n(n+1)(2n+1)}{12})+(\frac{n(n+1)}{2}) \\=(\frac{n(n+1)}{2})[(\frac{(2n+1)+6}{6})]\\=(\frac{n(n+1)(2n+7)}{12})$$

$$cos \{\frac{2\pi}{2^{64}-1}\}cos\{\frac{2^2\pi}{2^{64}-1}\}......cos\{\frac{2^{64}\pi}{2^{64}-1}\}=$$

1326011_1064810_ans_541ba33750da449d8a260a9c9398053a.jpg

find the sum : $$tan x tan 2x + tan2x tan 3x + .............+ tan nx tan(n+1)x $$.

formula:

$$\tan (a-b) = \dfrac{\tan a -\tan b}{1+\tan a \tan b}$$,

$$\Rightarrow \tan a \tan b = \dfrac{\tan a -\tan b -\tan (a-b)} {\tan (a-b)}$$

apply the same to each term, we get,

$$=\dfrac{ (\tan 2x -\tan x -\tan x + \tan 3x- \tan 2x -\tan x+ \tan 4x -\tan 3x -\tan x ......\tan (n+1)x -\tan nx -\tan x )}{\tan x}$$

$$ = \dfrac{\tan (n+1)x -(n+1)\tan x}{ \tan x}$$

If statement $$P(n)$$ is $$"3n + 1 $$ is even". Then verify that statement $$P(1)$$ is true but $$P(2)$$ is not true.

$$P(n)=3n+1$$ even

If $$n=1$$ $$P(1)=3(1)+1=4$$ $$P(1)$$ is even

if $$n=1$$ $$P(2)=3(2)+1=7$$ $$P(2)$$ is odd

$$\therefore P(1)$$ is true & $$P(2)$$ is not true.

$$7, 13, 19,...., 205$$.

The given series is $$7,13,19,...,205$$

The given series is in $$AP$$

Here $$a=7,d=6$$

So the general term is $$a_n=a+(n-1)d\\a_n=7+(n-1)6\\6n+1$$

Prove that $$\dfrac{(2n!)}{n!}=2^n (1.3.5....(2n-1))$$.

$$\dfrac{\left(2n!\right)}{n!}={2}^{n}\left(1.3.5...\left(2n-1\right)\right)$$

RHS $$ =\left(1.3.5...\left(2n-1\right)\right){2}^{n}$$

Multiply and divide by $$2.4.6...2n$$ on RHS

$$ \left[1.3.5...\left(2n-1\right)\right]{2}^{n}=\left(1.3.5...\left(2n-1\right)\right){2}^{n}\times \dfrac{2.4.6...2n}{2.4.6....2n}$$

$$ =\dfrac{\left[1.3.5...\left(2n-1\right)\right]{2}^{n}}{2.4.6....2n}$$

$$ =\dfrac{\left[\left(2n\right)\left(2n-1\right)....5.4.3.2.1\right]{2}^{n}}{2.4.6....2n}$$

$$ =\dfrac{\left(2n\right)!{2}^{n}} {2.4.6....2n}$$

$$ =\dfrac{\left(2n\right)!{2}^{n}} {{2}^{n}\left(1.2.3..n\right)}$$

$$ =\dfrac{\left(2n\right)!}{n!} = $$ LHS .proved

Find the $$n^{th}$$ term and sum to $$n$$ terms of the following series:
$$1 + 9 + 24 + 46 + 75 +$$_____

$$a_{1}=1$$

$$a_{2}=1+8=9$$

$$a_{3}=9+8+7=24$$

$$a_{4}=24+8+7+7=46$$

So, then $$k^{th}$$ term will be:

$$a_{k}=1+8(k-1)+7\dfrac{(k-1)(k-2)}{2}=\dfrac{7}{2}k^{2}-\dfrac{5}{2}k$$

Sum of first $$n$$ terms

$$=\displaystyle\sum_{k=1}^{n}\left(\dfrac{7}{2}k^{2}-\dfrac{5}{2}k\right)$$

$$=\dfrac{7}{2}\displaystyle\sum_{k=1}^{n}k^{2}-\dfrac{5}{2}\sum_{k=1}^{n}k$$

$$=\dfrac{7}{2}.\dfrac{1}{6}n(n+1)(2n+1)-\dfrac{5}{2}.\dfrac{1}{2}n(n+1)$$

$$=\dfrac{1}{12}n(n+1).(7(2n+1)-15)$$

$$=\dfrac{1}{12}n(n+1)(14n-8)$$

$$=\dfrac{1}{6}n(n+1)(7n-4)$$

Find the period of $$f\left( x \right) =\tan { \left( x+4x+9x+.......+{ n }^{ 2 }x \right) } $$

$$f\left( x \right) =\tan { \left( x+4x+9x+.......+{ n }^{ 2 }x \right) } $$

$$=\tan { \left[ x\left( 1+4+9....{ n }^{ 2 } \right) \right] } $$

$$=\tan { \left[ x\cfrac { \left( n \right) \left( n+1 \right) \left( 2n+1 \right) }{ 6 } \right] } $$

For $$\tan { \left( x \right) } $$ the period is $$\pi $$, so if we multiply $$ x$$ by some value A, the period gets divided by same value A. So, period of $$f(x)$$ will be

$$=\cfrac { 6\pi }{ n\left( n+1 \right) \left( 2n+1 \right) } $$

Prove that $${ 2 }^{ 1/4 }\cdot { 4 }^{ 1/8 }\cdot { 8 }^{ 1/16 }\cdot { 16 }^{ 1/32 }\cdot ........\cdot \infty =2$$

$${ 2 }^{ 1/4 }\cdot { 4 }^{ 1/8 }\cdot { 8 }^{ 1/16 }\cdot { 16 }^{ 1/32 }\cdot ........\cdot \infty =2$$

$${ 2 }^{ 1/4 }\cdot { 4 }^{ 1/8 }\cdot { 8 }^{ 1/16 }\cdot { 16 }^{ 1/32 }\cdot ........\cdot \infty ={ 2 }^{ 1/4 }\cdot { 2 }^{ 2/8 }\cdot { 2 }^{ 3/16 }\cdot { 2 }^{ 4/32 }\cdot ........\cdot \infty $$

$$={ 2 }^{ { 1 }/{ 4 }+{ 2 }/{ 8 }+{ 3 }/{ 16 }+{ 4 }/{ 32 }+....\infty }$$

Let $$M=\cfrac { 1 }{ 4 } +\cfrac { 2 }{ 8 } +\cfrac { 3 }{ 16 } +\cfrac { 4 }{ 32 } +....\infty $$

$$\cfrac { M }{ 2 } =\cfrac { 1 }{ 8 } +\cfrac { 2 }{ 16 } +\cfrac { 3 }{ 32 } +....\infty $$

$$M-\cfrac { M }{ 2 } =\cfrac { 1 }{ 4 } +\cfrac { 1 }{ 8 } +\cfrac { 1 }{ 16 } +\cfrac { 1 }{ 32 } +....\infty $$

$$\cfrac { M }{ 2 } =\cfrac { { 1 }/{ 4 } }{ 1-{ 1 }/{ 2 } } $$

$$\cfrac { M }{ 2 } =\cfrac { 1 }{ 2 } \Rightarrow M=1$$

$$\therefore { 2 }^{ 1/4 }\cdot { 4 }^{ 1/8 }\cdot { 8 }^{ 1/16 }\cdot { 16 }^{ 1/32 }\cdot ........\cdot \infty ={ 2 }^{ M }$$

$$=2$$

$$1+2+3+....+n < \dfrac{1}{8} (2n+1)^2$$.

$$1+2+3+....n < \dfrac {1}{8}(2n+1)^2$$

$$\Rightarrow \ \dfrac {n (n+1)}{2} < \dfrac {1}{8} (2n+1)^2$$

$$4n^2+4n < 4n^2+1+4n$$

$$0 < 1$$

Hence proved

$$5+3+2=151022$$
$$9+2+4=183652$$
$$8+6+3=482466$$
$$5+4+5=202541$$
Then . . .
$$7+2+5= ?????$$

Condition (1)

First two digit

$$ 5\times 3=15 $$

$$ 9\times 2=18 $$

$$ 8\times 6=48 $$

$$ 5\times 4=20 $$

Condition (2)

First and last digit

$$ 5\times 2=10 $$

$$ 9\times 4=36 $$

$$ 8\times 3=24 $$

$$ 5\times 5=25 $$

Condition (3)

$$ \left( IInd\,\,digit\,\,+\,\,IIIrd\,\,digit \right)\times \left( Ist\,\,digit \right)-\left( IInd\,\,digit \right)=solution $$

$$ \left( 3+2 \right)\times 5-3=22 $$

$$ \left( 2+4 \right)\times 9-2=52 $$

$$ \left( 6+3 \right)\times 8-6=66 $$

$$ \left( 4+5 \right)\times 5-4=41 $$

Then, condition (1) (2) and (3) to,

$$ 5+3+2=151022 $$

$$ 9+2+4=183652 $$

$$ 8+6+3=482466 $$

$$ 5+4+5=202541 $$

Then,

$$7+2+5=143547$$

Hence, this is the answer.

Find the total number of ways in which six $$'+'$$ and four $$'-'$$ signs can be arranged in a line such that no two $$'-'$$ signs occur together.

Let $$x_{1} $$ be the number of $$'+'$$ signs inserted before first $$'-'$$ sign

let $$x_{2},x_{3},x_{4}$$ be the number of $$'+'$$ signs inserted between $$'-'$$ signs

let $$x_{5}$$ be the number of $$'+'$$ signs inserted after last $$'-'$$ sign

$$\implies x_{1},x_{5}\geq 0,x_{2},x_{3},x_{4}\geq 1$$

and also $$x_{1}+x_{2}+x_{3}+x_{4}+x_{5}=6$$

$$x_{1}+(x_{2}-1)+(x_{3}-1)+(x_{4}-1)+x_{5}=3$$

no of ways for this is $$^{n+r-1}C_{r-1}$$ where $$n=3,r=5$$

$$=^{5+3-1}C_{5-1}=^{7}C_{4}=35$$

Find the sum to the first n terms of the series :
$$\frac{1}{{(1 - x)(1 - {x^3})}} + \frac{{{x^2}}}{{(1 - {x^3})(1 - {x^5})}} + \frac{{{x^4}}}{{(1 - {x^5})(1 - {x^7})}} + ...,x \ne 1, - 1,0$$

1121725_1094655_ans_fc6d209cb7364f12a701779e312a408a.jpg

Find the $${8^{th}}$$ term of the sequence whose first three terms are $$ 3,\, 3,\, 6$$ and each term after the second is the sum of three two terms preceding it .

Given $$3, 3, 6$$………

Now $$3, 3, 6, 9, 15, 24, 39, 63, 102$$

(It involves smaller numbers)

$$3$$

$$3+0=3$$

$$3+3=6$$

$$3+6=9$$

$$6+9=15$$

$$9+15=24$$

$$15+24=39$$

$$24+39=63$$ ($$8^{th}$$ term)

$$\therefore 63$$ is $$8^{th}$$ term.

Solve: $$\cfrac{1}{2}+\cfrac{1}{6}+\cfrac{1}{12}+\cfrac{1}{20}+.....+\cfrac{1}{1892}+\cfrac{1}{1980}=$$?

$$\dfrac{1}{2}+\dfrac{1}{6}+\dfrac{1}{12}........\dfrac{1}{1980}=S$$

$$S=\dfrac{1}{1^{2}+1}+\frac{1}{2^{2}+2}+.....\dfrac{1}{+n^{2}+n}+......\dfrac{1}{44^{2}+44}$$

now ,

$$\dfrac{1}{n^{2}+n}=\dfrac{1}{(n+1)(n)}=\dfrac{(n+1)-n}{(n)(n+1)}=\dfrac{1}{n}-\dfrac{1}{n+1}$$

$$S=\left ( 1-\dfrac{1}{2} \right )+\left ( \dfrac{1}{2}-\dfrac{1}{3} \right )+\left ( \dfrac{1}{3}-\dfrac{1}{4} \right )+......\left ( \dfrac{1}{44}-\dfrac{1}{45} \right )$$

$$=1-\dfrac{1}{45}=\dfrac{44}{45}$$

If $$a, b, c , d$$ are in G.P., show that
i) $$a^2 + b^2 , \, b^2 + c^2, \, c^2 + d^2$$ are in G.P

If $$a,b,c,d$$ are in G.P. , then

$$a=a$$

$$b=ar$$

$$c=ar^{2}$$

$$d=ar^{3}$$

where $$a$$ is the first term and $$r$$ is the common ratio.

Now,

$$a^{2}+b^{2}=a^{2}+a^{2}r^{2}=a^{2}(1+r^{2})$$

$$b^{2}+c^{2}=a^{2}r^{2}+a^{2}r^{4}=a^{2}(1+r^{2})\times r^{2}$$

$$c^{2}+d^{2}=a^{2}r^{4}+a^{2}r^{6}=a^{2}(1+r^{2})\times r^{4}$$

which are in G.P. with

first term, $$A=a^{2}(1+r^{2})$$

and common ratio, $$R=r^{2}$$

Find m if the following equation holds true: $$ 1.2 + 4.3 + 9.4 + ... n^2 (n + 1) = \dfrac{n}{m} (n + 1) (n + 2) (3n + 1)$$

$$n$$th term, $$a_{n}=n^{2}(n+1)=n^{3}+n^{2}$$

Sum of first $$n$$ terms,

$$S_{n}=\sum_{n=1}^{n}a_{n}$$

$$S_{n}=\sum_{n=1}^{n}n^{3}+\sum_{n=1}^{n}n^{2}$$

$$=\cfrac{n^{2}(n+1)^{2}}{4}+\cfrac{n(n+1)(2n+1)}{6}$$

$$=n(n+1)\left \{ \cfrac{n(n+1)}{4} +\cfrac{2n+1}{6}\right \}$$

$$=n(n+1)\left \{ \cfrac{3n^{2}+7n+2}{12} \right \}$$

$$=\cfrac{n(n+1)(n+2)(3n+1)}{12}$$

So, $$m=12$$

If $$\frac{1}{{1!9!}} + \frac{1}{{3!7!}} + \frac{1}{{5!5!}} + \frac{1}{{9!1!}} = \frac{{{2^n}}}{{10!}}$$
Then $$n = $$

Given,

$$\dfrac{1}{1!9!}+\dfrac{1}{3!7!}+\dfrac{1}{5!5!}+\dfrac{1}{7!3!}+\dfrac{1}{9!1!}=\dfrac{2^n}{10!}$$

$$\dfrac{10!}{1!\cdot 9!}+\dfrac{10!}{3!\cdot 7!}+\dfrac{10!}{5!\cdot 5!}+\dfrac{10!}{7!\cdot 3!}+\dfrac{10!}{9!\cdot 1!}=2^n$$

$$\dfrac{20}{1!}+\dfrac{1440}{3!}+\dfrac{10!}{5!\cdot 5!}=2^n$$

$$\dfrac{20}{1!}+\dfrac{1440}{3!}+\dfrac{30240}{5!}=2^n$$

$$\dfrac{20}{1}+\dfrac{1440}{6}+\dfrac{30240}{120}=2^n$$

$$\dfrac{2400+28800+30240}{120}=2^n$$

$$512=2^n$$

$$2^9=2^n$$

$$\therefore n=9$$

In a sequence of $$21$$ terms, the first $$11$$ term are in $$A.P$$ with common difference $$2$$ and the last $$11$$ terms are in $$G.P.$$ with common ratio $$2$$. If the middle term of the $$A.P.$$ is equal to the middle term of $$G.P.$$ The find the middle term of the entire sequence.

The first 11 term are in A.P with the common difference $$d=2$$ and the first term is $$a$$

Then the middle term of A.P is the $${ 6 }^{ th }$$ term i.e,

$${ a }_{ 6 }=a+(6-1)d\\ \quad =a+5.2\\ \quad =a+10$$

In case of G.P, first term is $$p$$ and the common ratio $$r=2$$.

Then the middle term of G.P is the $${ 6 }^{ th }$$ term of the G.P can be written as

$${ p }_{ 6 }=p{ r }^{ 6-1 }\\ \quad =p{ 2 }^{ 5 }$$

Acc. to Qn,

$${ a }_{ 6 }={ p }_{ 6 }\\ \Rightarrow (a+10)=p.{ 2 }^{ 5 }\longrightarrow (1)$$

also $${ 11 }^{ th }$$ term of A.P $$=$$ $${ 1 }^{ st }$$ term of G.P

so,

$${ a }_{ 11 }={ p }_{ 1 }\\ \Rightarrow a+(11-1).2=p.{ r }^{ 1-1 }\\ \Rightarrow a+20=p\longrightarrow (2)\\ $$

solving (1) and (2)

$$p=\dfrac { -10 }{ 31 } \quad and\quad a=\dfrac { -630 }{ 31 } $$

therefore middle term of the sequence is $${ 11 }^{ th }$$ of A.P or $${ 1 }^{ st }$$ term of G.P i.e, $$p=\dfrac { -10 }{ 31 } $$

Find $$n^{th} $$ term of the series
$$3\times 1^{2} , 5\times 2^{2} , 7\times 3^{2} , .....$$

$$3 + 1^{2} , 5\times 2^{2} , 7\times 3^{2},.......$$

Separate it as

$$3, 5, 7, ....$$

$$T_{n} = 3 + (n - 1)2$$

$$= 3 + 2n - 2\rightarrow (2n + 1)$$

$$1^{2}, 2^{2}, 3^{2} ....$$

$$\Rightarrow n^{2}$$

So $$n^{th}$$ term will be

$$(2n + 1)n^{2}$$.

Prove : $${1^2} + \left( {{1^2} + {2^2}} \right) + \left( {{1^2} + {2^2} + {3^2}} \right) + \ldots $$ upto $$n$$ terms $$ = \dfrac{{n{{\left( {n + 1} \right)}^2}\left( {n + 2} \right)}}{{12}}$$

Given series is $$1^2+(1^2+2^2)+(1^2+2^2+3^2)+........$$

We must find the $$n^{th}$$ term $$t_n$$ of the series

Clearly $$n^{th}$$ term of the series is,

$$1^2+2^2+3^2+............n^2=\sum n^2$$

We know that $$\sum n^2=\dfrac{n(n+1)(2n+1)}{6}$$

$$\implies t_n=\sum n^2=\dfrac{n(n+1)(2n+1)}{6}=\dfrac{1}{6}(2n^3+3n^2+n)$$

We know that sum of n terms of any series $$S_n=\sum t_n$$

$$\implies S_n=\sum t_n=\sum \dfrac{1}{6}(2n^3+3n^2+n)$$

$$=\dfrac{1}{6} \left [ \sum 2n^3+\sum 3n^2+\sum n\right ]$$

$$=\dfrac{1}{6} \left [ 2\times \dfrac{n^2(n+1)^2}{4}+3\times \dfrac{n(n+1)(2n+1)}{6}+\dfrac{n(n+1)}{2} \right ]$$

$$=\dfrac{1}{6} \left [ \dfrac{n(n+1)}{2} \times ( n(n+1)+(2n+1)+1 ) \right ]$$

$$=\dfrac{n(n+1)}{12}[n^2+3n+2]$$

$$=\dfrac{n(n+1)}{12}[(n+1)(n+2)]$$

$$=\dfrac{n(n+1)^2(n+2)}{12}$$

$$1^2+\left(\dfrac{3}{2}\right)^2+2^2+\left(\dfrac{5}{2}\right)^2+...$$ to $$40$$ terms.

Given series is $$1^{2}+\left(\dfrac{3}{2}\right)^{2} + 2^{2}+\left(\dfrac{5}{2}\right)^{2}+......+$$ to $$40$$ terms

$$1^{2}=1^{2},\left(\dfrac{3}{2}\right)^{2}= \left(1+\dfrac{1}{2}(2-1)\right)^{2}$$

$$(2)^{2}=\left(1+\dfrac{1}{2}(3-1)\right)^{2}$$......

So, the general $$n^{th}$$ term is $$t_{n}=\left(1+\dfrac{1}{2}(n-1)\right)^{2}$$

$$=\left(1+\dfrac{n}{2}-\dfrac{1}{2}\right)^{2}$$

$$=\left(\dfrac{n}{2}+\dfrac{1}{2}\right)^{2}$$

$$=\dfrac{n^{2}+2n+1}{4}$$

$$\therefore $$ Sum of n terms, $$s_{n}=\dfrac{1}{4}.\dfrac{n(n+1)(2n+1)}{6}+\dfrac{2n(n+1)}{2.4}+\dfrac{n}{4}$$

So, $$S_{40}=\dfrac{1}{4}.\dfrac{40.41.81}{6}+\dfrac{40.41}{4}+\dfrac{40}{4}$$

$$=5535+410+10$$

$$=5955$$

Find the average of first $$40$$ natural numbers?

Sum of first $$n$$ natural numbers$$=\dfrac{n\left(n+1\right)}{2}$$

So,sum of $$40$$ natural numbers$$=\dfrac{\left(40\times 41\right)}{2} = 820$$.

$$\therefore$$ the required average$$=\dfrac{820}{40}= 20.5$$

Find the sum to n terms of the series
$$ 05+11+19+29+$$......?

Given,

$$05+11+19+29+...+n$$ terms

$$11-5=6,19-11=8,29-19=10,.....n$$

Therefore the given series reduces to:

$$6+8+10+.....+n$$

$$S_n=2n+6$$

when $$n=0\rightarrow 2(0)+6=6$$

when $$n=1\rightarrow 2(1)+6=8$$

when $$n=2\rightarrow 2(2)+6=10$$

when $$n=n\rightarrow 2(n)+6=2n+6$$

Find the sum of the series $$\displaystyle\sum^n_{r=1}r\times r!$$

$$\displaystyle\sum^n_{r=1}r\times r!\Rightarrow \sum^n_{r=1}r\times r!+r!-r! $$

$$\displaystyle \Rightarrow \sum^n_{r=1}(r+1)r!-r! $$

$$\displaystyle \Rightarrow \sum^n_{r=1}(r+1)!-r! $$

$$ \Rightarrow (n+1)!-1! $$

$$ \displaystyle = (n+1)!-1 $$

1120061_1116188_ans_74e0210a0d574166921baede3ce1be9d.jpg

If sum to infinity of the series $$3-5r+7r^2-9r^3+....$$ is $$\dfrac{14}{9}$$, find r.

$$S = 3-5r+7r^2-9r^3......\infty $$

$$Sr = 3r - 5r^2+7r^3-9r^4......\infty$$

$$(1+r)S = 3-2r+2r^2-2r^3....\infty$$

$$(1+r)S = 3-2(r-r^2+r^3.....\infty)$$

$$S = \cfrac{3}{1+r} -\cfrac{2r}{(1+r)^2}$$

$$\cfrac{14}{9} = \cfrac{3+r}{(1+r)^2}$$

$$14(1+2r+r^2) = 27+9r$$

$$14r^2+19r-13 = 0$$

$$r = 0.5$$ and $$r = -1.857$$

A snail starts moving towards a point $$3$$cm away at a pace of $$1$$cm per hour. As it gets tired, it covers only half the distance compared to previous hour in each succeeding hour. In how much time will the snail reach his target?

The snail movement can be thought of that of a G.P.

$$1,0.5,0.25,....$$

$$1+0.5+0.25+... = 3$$

$$\cfrac{1-0.5^n}{1-0.5} = 3$$

$$1-0.5^n= 1.5$$

$$0.5^n = -0.5$$

which is not possible.Hence,it never reaches its target.

Find the $$nth$$ term and the sum of $$n$$ terms of the series $$1.2.4+2.3.5+3.4.6+....$$

$$1.2.4+2.3.5+3.4.6+….$$

$$\therefore n^{th} term= n\left(n+1\right)\left(n+3\right)$$

$$\therefore$$ sum $$= \displaystyle \sum_{k=1}^{n}{k\left(k+1\right) \left(k+3\right)}$$

$$= \displaystyle \sum_{k=1}^{n}\left({k}^{3}+4{k}^{2}+3k\right)$$

$$= \displaystyle \sum_{k=1}^{n}{{k}^{3}}+4\sum_{k=1}^{n}{{k}^{2}}+3\sum_{k=1}^{n}{k}$$

$${\left[\dfrac{n\left(n+1\right)}{2}\right]}^{2}+\dfrac{4n\left(n+1\right) \left(2n+1\right)}{6}+3\dfrac{n\left(n+1\right)}{2}$$

$$=\dfrac{{n}^{2}{\left(n+1\right)}^{2}}{4}+\dfrac{2n\left(n+1\right)\left(2n+1\right)}{3}+\dfrac{3}{2}n\left(n+1\right)$$

$$=n\left(n+1\right) \left[\dfrac{n\left(n+1\right)}{4}+\dfrac{n\left(2n+1\right)}{3}\dfrac{3}{2}\right]$$

$$=n\left(n+1\right)\left[\dfrac{3{n}^{2}+3n+16n+8+18}{12}\right]$$

$$=\dfrac{n\left(n+1\right)+ \left(3{n}^{2}+19n+26\right)}{12}$$ Ans

The sum of the nth term of the series 1.2.5 + 2.3.6 + 3.4.7 + .....n terms is

We have,

$$1.2.5+2.3.6+3.4.7+.......+n\ terms$$

$$1(1+1)(1+4)+2(2+1)(2+4)+3(3+1)(3+4)+............+n\ terms$$

Therefore, the general term

$$\Rightarrow n(n+1)(n+4)$$

Now, the sum of this series will be

$$\Rightarrow \displaystyle \sum_{k=1}^{n} k(k+1)(k+4)$$

$$\Rightarrow \displaystyle \sum_{k=1}^{n} (k^3+5k^2+4k)$$

Therefore,

$$\Rightarrow \dfrac{(n(n+1))^2}{4}+\dfrac{5n(n+1)(2n+1)}{6}+\dfrac{4n(n+1)}{2}$$

$$\Rightarrow \dfrac{n(n+1)}{2}\left(\dfrac{n(n+1)}{2}+\dfrac{5(2n+1)}{3}+4\right)$$

$$\Rightarrow \dfrac{n(n+1)}{2}\left(\dfrac{3n^2+23n+34}{6}\right)$$

$$\Rightarrow \dfrac{n(n+1)}{12}\left({3n^2+23n+34}\right)$$

Hence, this is the answer.

Find the sum of $$5+7+9+11+13+....$$ for $$50$$ terms.

Consider the given series.

$$5+7+9+11+13+....$$

SO, $$a=5, n=50, d=2$$

We know that the sum of the $$n$$ terms

$$S=\dfrac{n}{2}[2a+(n-1)d]$$

So,

$$S=\dfrac{50}{2}[2\times 5+(50-1)\times 2]$$

$$S=25[10+49\times 2]$$

$$S=25[10+98]$$

$$S=25[108]$$

$$S=2700$$

Hence, this is the answer.

If the roots of the equation $$x^3-12x^2+39x-28=0$$ are in A.P., then their common difference will be,

Consider the given equation.

$$x^3-12x^2+39x-28=0$$

Let the roots are $$a-d, a, a+d$$

So,

$$a-d+a+a+d=12$$

$$3a=12$$

$$a=4$$

And

$$(a-d)(a)(a+d)=28$$

$$a(a^2-d^2)=28$$

$$4(4^2-d^2)=28$$

$$(16-d^2)=7$$

$$d^2=9$$

$$d=\pm 3$$

Hence, this is the answer.

Find the sum of the given series $$6+11+16+21+......+86$$

We have,

$$6+11+16+21+27+......+86$$

$$a=6, d=5, l=86$$

We know that

$$l=6+(n-1)d$$

$$86=6+(n-1)\times 5$$

$$n=17$$

We know that

$$S_{17}=\dfrac{17}{2}[12+(17-1)\times 5]$$

$$S_{17}=\dfrac{17}{2}[12+16\times 5]$$

$$S_{17}=\dfrac{17}{2}[12+80]$$

$$S_{17}=\dfrac{17}{2}[92]$$

$$S_{17}=782$$

Hence, this is the answer.

Find:$$1^3-2^3+3^3-4^3+.....+9^3=?$$

$$1^3-2^3+3^3-4^3+........+9^3=?$$

$$\left(1^3+2^3+3^3+........+9^3\right)-2\left(2^3+4^3+6^3+8^3\right)$$

$$\left( 1^{ 3 }+2^{ 3 }+3^{ 3 }+........+9^{ 3 } \right) -2.2^3\left( 1^3+2^3+3^3+4^3 \right) $$

$$\boxed{\sum _{ r=1 }^{ n }{ n^3 } =\left(\dfrac{n\left(n+1\right)}{2}\right)^2}$$

$$\left(\dfrac{\left(9\right)\left(9+1\right)}{2}\right)^2-16\left(\dfrac{\left(4\right)\left(4+1\right)}{2}\right)^2$$

$$\left(2025-1600\right)=425$$ Ans

Sum to $$infinite$$ terms the following series:
$$1 + 4x + 7x^{2} + 10x^{3} + ..., |x| < 1$$.

$$S =1 +4x + 7x^2+ 10x^3+...$$ $$..................(1)$$

$$Sx = x+ 4x^2+ 7x^3+....$$ $$...............(2)$$

$$eq^n(1) – eq^n(2)$$, we get

$$(1 – x)S = 1 + 3x+ 3x^2+ 3x^3+…...$$ $$.........(3)$$

This is a $$G.P$$. of common ratio $$=x$$

So, using sum of $$G.P. = \dfrac{a}{ (1-r)}$$

Here, $$a = first\ term$$ and $$r = common\ ratio$$

So,

$$(1 – x)S = 1 + \dfrac{3 x}{ (1 – x)}$$

$$(1 – x)S = \dfrac{1-x+3 x}{ (1 – x)}$$

$$S = \dfrac{1+2x}{ (1 – x)^2}$$

Hence, this is the answer.

Sum to $$n$$ terms the following series:
$$1 + 2x + 3x^{2} + 4x^{3} + ...,|x| < 1$$

Consider the given series.

$$S=1+2x+3x^2+4x^3+.......+nx^{(n-1)}$$ $$...........(1)$$

On multiply by $$x$$ both sides, we get

$$Sx=x+2x^2+3x^3+4x^4+.......+nx^n$$ $$...........(2)$$

Subtract equation $$(2)$$ from equation $$(1)$$, we get

$$S-Sx=1+x+x^2+x^3+x^4+......+x^{n-1}+nx^n$$

$$S(1-x)=1+x+x^2+x^3+x^4+......+x^{n-1}+nx^n$$

So,

$$S(1-x)=\dfrac{1(1-x^n)}{1-x}+nx^n$$

$$S(1-x)=\dfrac{(1-x^n)}{1-x}+nx^n$$

$$S=\dfrac{(1-x^n)}{(1-x)^2}+\dfrac{nx^n}{1-x}$$

Hence, this is the answer.

Sum to $$n$$ terms of the following series:
$$1+\left(1+\dfrac{1}{2}\right) + \left(1 + \dfrac{1}{2} + \dfrac{1}{4}\right) + ,...$$

$$t_n = (1+\dfrac{1}{2} + \dfrac{1}{4} + .....n\, times)$$
$$=\dfrac{1\left(1-\left(\dfrac{1}{2}\right)^n\right)}{\left(1-\dfrac{1}{2}\right)} = 2\left(1-\dfrac{1}{2n}\right)$$
$$tn = \sum tn$$
$$=\sum 2 \left( 1-\dfrac{1}{2n}\right) = \sum 2 - \dfrac{2}{2n}$$
$$=2n - 2 \left(\dfrac{1}{2} + \dfrac{1}{2^2} + \dfrac{1}{263} + .... n\, times\right)$$
$$=2n-2\left(\dfrac{\dfrac{1}{2}\left(1-\dfrac{1}{2n}\right)}{\left(1-\dfrac{1}{2}\right)}\right)$$
$$=2n-n\left(1-\dfrac{1}{2n}\right)$$

Sum to $$n$$ terms the series :
$$1 \times 2+2\times 3+3\times 4+4\times 5+..$$

$$\displaystyle 1^{st} $$ term $$ 1\times 2 $$

$$\displaystyle 2^{nd} $$ term $$ 2\times 3 $$

$$\displaystyle 3^{rd} $$ term $$ 3\times 4 $$

$$\displaystyle n^{th} $$ term $$ n\times (n+1) $$

Step 1 : Find $$n^{th} $$ team (an)

Here, an $$ = n(n+1) $$

$$ = n^{n}+n $$

step $$\displaystyle 2 : S_{n} = \sum_{n = 1}^{n}an $$

$$\displaystyle = \sum_{n}^{n=1} n^{2}+n $$

$$\displaystyle = \sum_{n=1}^{n} n^{2}+\sum_{n = 1}^{n} n $$

$$\displaystyle = \frac{n(n+1)(2n+1)}{6}+\frac{n(n+1)}{2} $$

$$\displaystyle = \frac{n(n-1)}{2}(\frac{(2n+1)}{3}+1) $$

$$\displaystyle = \frac{n(n+1)}{2}(\frac{2n+1+3}{3}) $$

$$\displaystyle = \frac{n(n+1)}{2}(\frac{2n+4}{3}) $$

$$\displaystyle = \frac{2n(n+1)(n+2)}{6} = \frac{2n(n+1)(n+2)}{6} $$

1133939_1140306_ans_262f5c386a094306a58461d7970af2e5.jpeg

Let $$d$$ be the minimum value of $$f(x)=5x^2-2x+\dfrac{26}{5}$$ and $$f(x)$$ is symmetric about $$x=r$$. If $$\sum_{n=1}^{\infty}(1+(n-1)d)r^{n-1}$$ equals $$\dfrac{p}{q}$$, where $$p$$ and $$q$$ are relative prime, then find the value of $$(3q-p)$$.

Given, $$f(x)= 5x^{2}-2x+\dfrac{26}{5}$$ symmetric about $$x=r$$

$$f(x)= 5x^{2}-2x+\dfrac{1}{5}+5= 5(x-\dfrac{1}{5})^{2}+5$$

$$\Rightarrow f(x)$$ is symmetric about $$x=\dfrac{1}{5}$$ with min values, $$d=5$$

Now, $$\displaystyle S= \sum_{n=1}^{\infty }(1+(n-1)d)r^{n-1}= \sum_{n=1}^{\infty }[1+(n-1)5](\dfrac{1}{5})^{n-1}$$

$$S= 1+\dfrac{6}{5}+\dfrac{11}{5^{2}}+\dfrac{16}{5^{3}}+....$$ [A.G.P series]

$$\dfrac{1}{5}.S= \dfrac{1}{5}+\dfrac{6}{5^{2}}+\dfrac{11}{5^{3}}+...$$

_________________________

$$\dfrac{4}{5}S=1+\dfrac{5}{5}+\dfrac{5}{5^{2}}+\dfrac{5}{5^{3}}+....$$

$$= 2+(\dfrac{1}{5}+\dfrac{1}{5^{2}}+....)$$

$$= 2+\dfrac{\dfrac{1}{5}}{1-\dfrac{1}{5}}$$ [sum of infinite G.P = $$\dfrac{a}{1-r}]$$

$$\Rightarrow \dfrac{4}{5}S=2+\dfrac{1}{4}= \dfrac{9}{4}$$

$$S= \dfrac{45}{16}\Rightarrow P= 45, q=16$$

$$3q-p= 3(16)-45= 48-45=3$$

1136723_1141292_ans_20bfeabbaed447ffa7f0ae7b503155df.jpg

Sum to $$n$$ terms the series :
$$1\times 3+3\times 5+5\times 7+7\times 9+..$$

Let the $${n}^{th}$$ term be denoted by $${t}_{n}$$

$$\therefore {t}_{n}=\left( \left\{1,3,5,...\right\}\right)\times\left(\left\{3,5,7,...\right\}\right)$$

$${t}_{n}$$ of $$1,3,5,7,...$$ is $$2n-1$$

and $${t}_{n}$$ of $$3,5,7,..$$ is $$2n+1$$

$$\therefore {t}_{n}$$ of the above series is $$\left(2n-1\right)\left(2n+1\right)=4{n}^{2}-1$$

$${S}_{n}=\sum{4{n}^{2}-1}$$

$$=4\sum{{n}^{2}}-\sum{1}$$

$$=4\dfrac{n\left(n+1\right)\left(2n+1\right)}{6}-n$$

$$=\dfrac{2\left(n+1\right)\left(2n+1\right)}{3}-n$$

$$=\dfrac{2n\left(2{n}^{2}+3n+1\right)-3n}{3}$$

$$=\dfrac{n\left(4{n}^{2}+6n+2-3\right)}{3}$$

$$\therefore {S}_{n}=\dfrac{n\left(4{n}^{2}+6n-1\right)}{3}$$

A binary string of length $$N$$ is a sequence of $$0s$$ and $$1s$$. For example, $$01010$$ is a binary string of length $$5$$. For a string $$A$$ we write $$A_{i}$$ to refer to the letter at the $$i^{th}$$ position.

Let the value of $$N=6$$

$$\therefore$$ Now,

We have $$4$$ binary sequence of length $$6$$ which contain $$11011$$ as substring

They are $$011011, 111011, 110110, 110111$$

answer of $$N=6$$, is $$4$$

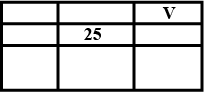
Find missing.....

The Number $$11$$ in the second circle must be replaced to $$16$$ to make a series.

From the first circle numbers are divides by $$2$$ and moves to next part in a anti clockwise sense .

$$30/2=15\\36/2=18\\32/2=16$$

From the Second circle numbers are multiplied by $$4$$ and moves to next part in a anti clockwise sense .

$$15\times 4=60\\18\times 4=72\\11\times 4=44$$

Find the sum of 1st n terms of the series 5+7+13+85+.

Consider the given function:

$$ 5+7+13+31+85+...... $$

$$ Diffrence\,\,of\,\,terms\,\,is\,\,in\,\,G.P $$

$$ \,\,\,\,\,\,\,=2,6,18...... $$

$$ Sn=5+3+13+31+85+......+{{T}_{n}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(1) $$

$$ Sn=5+7+13+31+......{{T}_{n}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(2) $$

$$ so\,\,than\,\,(1)-(2) $$

$$ Tn=5+2+6+18+......+({{T}_{n}}-{{T}_{n-1}}) $$

$$ Tn=5+2(\dfrac{{{3}^{n-1}}-1}{3-1}) $$

$$ Tn=5+({{3}^{n-1}}-1) $$

$$ Tn=4+{{3}^{n-1}} $$

$$ {{S}_{n}}=\sum\limits_{k=1}^{n}{{{T}_{k}}\,\,=\sum\limits_{k=1}^{n}{4+{{3}^{k-1}}}} $$

$$ {{S}_{n}}\,=\sum\limits_{k=1}^{n}{4+\sum\limits_{k=1}^{n}{{{3}^{k-1}}}} $$

$$ \,\,\,\,\,=(4+4+......n\,\,time\,\,)+(1+3+{{3}^{2}}+{{......3}^{n-1}}n\,\,terms $$

$$ {{S}_{n}}\,=4n+\dfrac{1.({{3}^{n}}-1)}{3-1} $$

$$ {{S}_{n}}=4n+\dfrac{{{3}^{n}}-1}{2} $$

$$ {{S}_{n}}\,\,=\dfrac{1}{2}({{3}^{n}}+8n-1) $$

Hence this is the answer.

If sum to infinity of series $$3-5r+7r^{2}-9r{3}+.$$ is $$14/9$$, find $$r$$.

$$ S = 3-5r+7r^{2}-9r^{3}+.. = \dfrac{14}{9} $$

$$ rs = 3r+5r^{2}+7r^{2}+..$$

$$ s+rs = 3-2r+2r^{2}-2r^{3}+... $$

$$ s(1+r) = 3+\dfrac{(-2r)}{1-r} $$

$$ \dfrac{14}{9}.(1+r) = 3+(\dfrac{-2r}{1-r}) $$

$$ 14+14r = 9(3(1-r))-2r\times 9 $$

$$ 14+14r = 27-27r-18r $$

$$ (14r+14)(1-r) = 27-45r $$

$$ 14r-14r^{2}+14-14r = 27-45r $$

$$ -14r^{2}+45r-13 = 0 $$

$$ 14r^{2}-45r+13 = 0 $$

value of roots of this eq$$^{n}$$

1142291_1143696_ans_d46f1ebddf8d4ef2901ac2c4b4059c8b.jpg

If a,b,c are positive real numbers in A.P and $${a^2},{b^2},{c^2}$$ are in H.P, then$$\dfrac{a}{b} + \dfrac{b}{c} + \dfrac{c}{a} = $$

Given : $$a,b,c$$ are in A.P

$$a^{2},b^{2},c^{2}$$ are in H.P

then $$2b=a+c$$ .....(1)

and $$\displaystyle \frac{2}{b^{2}}=\frac{1}{c^{2}}+\frac{1}{a^{2}}$$

i.e. $$\displaystyle \frac{1}{b^{2}}-\frac{1}{a^{2}}=\frac{1}{c^{2}}-\frac{1}{b^{2}}$$

$$\Rightarrow \displaystyle \frac{a^{2}-b^{2}}{a^{2}b^{2}}=\frac{b^{2}-c^{2}}{c^{2}b^{2}}$$

$$\Rightarrow \displaystyle \frac{(a+b)(a-b)}{a^{2}b^{2}}=\frac{(b-c)(b+c)}{c^{2}b^{2}}$$ ...(1)

Now $$\because a,b,c$$ are in A.P

$$\therefore b-a=c-a$$

$$\therefore$$ (1) becomes $$\dfrac{a+b}{a^{2}}=\dfrac{b+c}{c^{2}}$$

$$\Rightarrow ac^{2}+bc^{2}=a^{2}b+a^{2}c$$

$$bc^{2}-a^{2}b=0$$

$$\Rightarrow ac^{2}-a^{2}c=a^{2}b-bc^{2}$$

$$\Rightarrow ac(c-a)+b(c-a)(c+a)=0$$

$$\Rightarrow (c-a)[ac+bc+ca]=0$$

$$\Rightarrow c=a$$ or $$ab+bc+ca=0$$

$$\Rightarrow a=b=c$$ then $$\dfrac{a}{b}+\dfrac{b}{c}+\dfrac{c}{a}=3$$

If $$a,b,c$$ are in $$A.P$$, then show that $$10^{ax+10},10^{bx+10},10^{cx+10},x \neq 0$$ are in $$G.P$$

Given $$a,b,c$$ are in A.P.

$$\therefore b-a=c-b=d$$ (d= common difference)

$$\therefore \frac{10^{bx+10}}{10^{ax+10}}= 10^{bx+10-ax-10}$$

$$=10^{x(b-a)}$$ ______(1)

$$\therefore \frac{10^{cx+10}}{10^{bx+10}}= 10^{cx+10-bx-10}$$

$$=10^{(c-b)x}$$______(2)

$$\therefore $$ From (1), (2) & (3) we've

$$10^{ax+10}, 10^{bx+10}, 10^{cx+10}$$ are in G.P.

Sum of the series $$4+6+9+13+18+......n$$ terms , is

$$a_1=4=3+1$$

$$a_2=6=a_1+2$$

$$a_3=9=a_2+3$$

$$a_4=13=a_3+4$$

$$a_{n+1}=a_{n-2}+(n-1)$$

$$a_n=a_n+n$$

on adding all terms

$$(a_1+a_2+a_3.....a_n)=(a_1+a_2+a_3+....a_{n+1}+3+(1+2+3+.....n)$$

$$\Rightarrow a_n=3+\sum n$$

$$\Rightarrow a_n=3+\dfrac{n(n+1)}{2}$$

$$4+6+9+13+.....n\ terms\Rightarrow \sum a_n$$

$$\Rightarrow \sum_{n=1}^{n}{\left(3+\dfrac{n(n+1)}{2}\right)}$$

$$\Rightarrow 3n+\sum_{n=7}^{n} \dfrac{n^2}{2}+\sum_{n=1}^{n} \dfrac{n}{2}$$

$$\Rightarrow 3n+\dfrac{1}{2}\left[\dfrac{n(n+1)(2n+1)}{6}\right]+\dfrac{1}{2}\dfrac{n(n+1)}{2}$$

$$\Rightarrow \dfrac{36n+n(n+1)(2n+1)+3n(n+1)}{12}$$

$$4+6+9+13+....n\ terms \Rightarrow \dfrac{n}{12}[36+3n+3+2n^2+3n+1]$$

$$4+6+9+13....n\ terms \Rightarrow \dfrac{n}{6}(n^2+3n+20)$$

Find the $${10^{th}}$$ form of the series $$3 + 6 + 12 + ....$$

Consider the terms $$3,6,12,...$$

Ratio$$r=\dfrac{6}{3}=\dfrac{12}{6}=2$$

Since the common ratio's are same,the given terms are in G.P

$$\therefore\,{10}^{th}$$ term$$={T}_{10}=a{r}^{10-1}=3\times {2}^{9}=3\times 512=1536$$

The sum of the series $$1 + \frac{1}{6} + \frac{1}{{18}} + \frac{7}{{324}} + ....\infty ,$$ is

Let me try for Newton's generalised binomial theorem with $$x = 1$$

So, we have $$r y = \frac { 1 } { 6 }$$ (1) and $$\frac { r ( r - 1 ) } { 2 ! } y ^ { 2 } = \frac { 1 } { 18 }$$ (2)

Squaring ( 1$$)$$ and dividing by$$ $$( 2 )

we get $$ r = - \dfrac { 1 } { 3 }$$ and consequently $$ y = - \dfrac { 1 } { 2 }$$

which satisfies

$$\dfrac { r ( r - 1 ) ( r - 2 ) } { 3 ! } y ^ { 3 } = \dfrac { 7 } { 324 }$$

So, the sum will be

$$\left[ 1 + \left( - \dfrac { 1 } { 2 } \right) \right] ^ { - \dfrac { 1 } { 3 } }$$

$$[\dfrac { 1 } { 2 } ] ^ { - \dfrac { 1 } { 3 } }$$

$$\\ =1.2599$$

Find the average of first $$20$$ multiples of $$7$$

First 20 multiples of 7 are:- $$7\times 1,7\times 2, 7\times3, 7\times4,...........,7\times 20$$

Required average

$$=\dfrac{7\left(1+2+3+...+20\right)}{20}$$

$$=\dfrac{7\times 20\times 21}{20\times 2}$$ $$[\because $$ sum of first n numbers$$=\dfrac{n(n+1)}{2}]$$

$$=\dfrac{147}{2}=73.5$$

$${\alpha _r},{\beta _r}({\alpha _r} < {\beta _r})\;{\text{are}}\;{\text{the}}\;{\text{root}}\;{\text{of}}\;{x^2} - {r^2}\left( {r + 1} \right)x + {r^5} = 0$$ Find the value of $$\sum\limits_{r = 1}^n {\left( {3{\alpha _r} + 2{\beta _r}} \right): - } $$

Given equation : $$x^{2}-r^{2} (r+1)x+r^{5}=0$$

$$\alpha_{r}, \beta_{r}$$ are the roots of the equation

$$\Rightarrow \alpha_{r}^{2}-r^{2} (r+1) \alpha_{r}+r^{5} =0$$

$$\Rightarrow \alpha_{r}=\dfrac{r^{2} (r+1) \pm \sqrt{r^{4} (r+1)^{2} -4r^{5} }}{2}$$

$$\alpha_{r}=\dfrac{r^{3}+r^{2} \pm r^{2} \sqrt{r^{2}+2r+1-4r}}{2}$$

$$\alpha_{r}=\dfrac{r^{3}+r^{2} \pm r^{2} \sqrt{(r-1)^{2}}}{2}$$

$$\alpha_{r}= \dfrac{r^{3}+r^{2} \pm (r-1)}{2}$$

$$\alpha_{r}= \dfrac{r^{3}+r^{2}+r^{2} (r-1)}{2} , \alpha_{r}= \dfrac{ r^{3}+r^{2}-r^{2} (r-1)}{2}$$

$$\alpha_{r} = \dfrac{r^{3}+r^{2}+r^{3}-r^{2}}{2}, \alpha_{r}= \dfrac{r^{3}+r^{2}-r^{3}+r^{2}}{2}$$

$$\alpha_{r}= r^{3}, \alpha_{r}= r^{2}$$

Similarly,

$$\beta_{r}= r^{3}, \beta_{r}=r^{2}$$

$$\because \alpha_{r} < \beta_{r}$$ and $$1 \le r \le n$$

$$\Rightarrow \alpha_{r}=r^{2}, \beta_{r}= r^{3}$$

$$\sum_{r=1}^{n} (3\alpha_{r}+2\beta_{r}) :- \sum_{r=1}^{n} (3\alpha_{r}+2\beta_{r}) :- \sum_{r=1}^{n} 3r^{2}+2r^{3}$$

$$:- 3 \sum_{r=1}^{n} r^{2}+2 \sum_{r=1}^{n} r^{3}$$

$$:- 3 \dfrac{n(n+1)(2n+1)}{2}+2 \left( \dfrac{n(n+1)}{2} \right)^{2}$$

$$:- \dfrac{n(n+1)(2n+1)}{2}+\dfrac{n^{2} (n+1)^{2}}{2}$$

$$:- \dfrac{n(n+1)}{2} [2n+1+n^{2}+n]$$

$$:- \dfrac{n(n+1) (n^{2}+3n+1)}{2}$$

Find the sum to $$n$$ terms of the series, whose $$n$$th term is given by $${n}^{2}+{2}^{n}$$.

Given $$a_n=n^2+2^n$$

Now, sum of n terms is

$$S_n=\sum_{n=1}^{n}{a_n}$$

$$=\sum_{n=1}^{n}{n^2+2^n}$$

$$=\sum_{n=1}^{n}{n^2}+\sum_{n=1}^{2}{2^n}.......(1)$$

Now,

$$\sum_{n=1}^{n}{2^n}=2^1+2^2+2^3+.....+2^n$$

$$=2+4+8+....+2^n$$

This is GP with first term $$a=2$$

And common ratio $$r=\dfrac{4}{2}=2$$

We know

$$S_n=\dfrac{a(r^n-1)}{r-1}$$

$$\sum_{n=1}^{n}{2^n}=\dfrac{2(2^n-1)}{2-1}$$

$$\sum_{n=1}^{n}{2^n}=2(2^n-1)$$

We also know

$$\sum{n^2}=\dfrac{n(n+1)(2n+1)}{6}$$

Now form (1)

$$S_n=\sum_{n=1}^{n}{n^2}+\sum_{n=1}^{2}{2^n}$$

$$=\dfrac{n(n+1)(2n+1)}{6}+2(2^n-1)$$

$$2\cdot 3+3\cdot 4+4\cdot 5+.....$$ upto $$n$$ terms Find sum of $$n$$ of series.

Given series is $$2.3+3.4+4.5+......n$$terms

$$nth$$ term of the series$$=(n+1)(n+2)$$

sum upto $$n$$ terms is

$$\sum _{ n=1 }^{ n }{ (n+1)(n+2) } =\sum _{ n=1 }^{ n }{ { n }^{ 2 }+3n+2 } \\ =\sum _{ n=1 }^{ n }{ { n }^{ 2 } } +3\sum _{ n=1 }^{ n }{ n } +\sum _{ n=1 }^{ n }{ 2 } \\ =\cfrac { n(n+1)(2n+1) }{ 6 } +\cfrac { 3n(n+1) }{ 2 } +2n\\ =\cfrac { n(n+1)(2n+1)+9n(n+1)+6(2n) }{ 6 } \\ =\cfrac { n[(n+1)(2n+1)+9(n+1)+12] }{ 6 } \\ =\cfrac { n[2{ n }^{ 2 }+1+3n+9n+9+12] }{ 6 } \\ =\cfrac { n[2{ n }^{ 2 }+12n+22] }{ 6 } \\ =\cfrac { n[{ n }^{ 2 }+6n+11] }{ 3 } $$

$${1^3} - {2^3} + {3^3} - {4^3} + .... + {9^3} = $$

=$$1^3+3^3+5^3+7^3+9^3-(2^3+4^3+6^3+8^3)$$

=Sum of cubes of first 5 odd number -Sum of cubes of first 4 even number

=$$n^2(2n^2–1)-2n^2(n+1)^2$$

=1225–800

=425

Solve $$1 - \dfrac { 1 } { 2 } + \dfrac { 1 } { 3 } - \dfrac { 1 } { 4 } + \dots \infty $$

$$log(1+x)=x-(\frac{x^2}{2})+(\frac{x^3}{3})-(\frac{x^4}{4})+........ \infty\\put\>x = 1, we\>get\\log(1+1)=1-(\frac{1}{2})+(\frac{1}{3})-(\frac{1}{4})+......\infty = log2$$

Find n if the sum of the first n terms of the series $$\sqrt{3}+\sqrt{75}+\sqrt{243}+\sqrt{507}+......is435\sqrt{3}$$.

$$\sqrt {3}+\sqrt{75}+\sqrt{243}+\sqrt {507}+.......= 435\sqrt{3}$$

$$\Rightarrow \sqrt {3}+\sqrt{25\times 3}+\sqrt{81\times}+\sqrt{169\times 3}..... = 435 \sqrt{3}$$

$$ \Rightarrow \sqrt {3}+5\sqrt{3}+9\sqrt{3}+13\sqrt{3}.....= 435 \sqrt{3}$$

$$\Rightarrow \sqrt {3}[1+5+9+13+.....]= 435 \sqrt {3}$$

$$\Rightarrow 1+5+9+13 + .....=435$$

above series are in A.P

Here a=1, d=4

$$\therefore Sn = \frac {n}{2}[2a+(n-1)d]$$

$$\therefore \frac {n}{2}[2a+(n-1)d]=435$$

$$\frac {n}{2}[2\times 1+(n-1)4]=435$$

$$\therefore n[1+2n-2]=435$$

$$n(2n-1)=435$$

$$2n^2- n-435=0$$

$$n = \frac {1\pm\sqrt{1+4\times 2 \times 435}}{2.2}=\frac {1\pm 59}{4}$$

$$\therefore n=15, n = -58/4$$
$$\therefore n=15$$

Show that $$\left( 1 + 2 x + 3 x ^ { 2 } + 4 x ^ { 3 } + \ldots \ldots . \infty \right) ^ { 3 / 2 } = 1 + 3 x + 6 x ^ { 2 } + 10 x ^ { 3 } + \ldots \ldots , \infty ,$$ where $$| x | < 1$$

$$\begin{array}{l} { \left( { 1+2x+3{ x^{ 2 } }+4{ x^{ 3 } }+.......\infty } \right) ^{ 3/2 } }=1+3x+6{ x^{ 2 } }+......\infty \\ \left| x \right| <1 \\ { \left\{ { { { \left( { 1-x } \right) }^{ -2 } } } \right\} ^{ 3/2 } } \\ { \left( { 1-x } \right) ^{ -3 } }=1+3x+6{ x^{ 2 } }+.........\infty \end{array}$$

The sum of series $$\frac{1}{3\times 6}+\frac{1}{6\times 9}+\frac{1}{9\times 12}+$$...... is:

$$T_n=\cfrac{1}{3n\times 3(n+1)}=\cfrac{1}{9(n)(n+1)}=\cfrac{1}{9}\left[\cfrac{n+1-n}{n(n+1)}\right]$$

So, $$9T_n=\cfrac{1}{n}-\cfrac{1}{n+1}$$

and $$S_n=\sum T_n=T_1+T_2+\dots+T_n$$

So, $$9T_1=1-\cfrac{1}{2}\\ 9T_2=\cfrac{1}{2}-\cfrac{1}{3}\\\quad\quad \vdots\\ \quad \quad \vdots\\9T_n=\cfrac{1}{n}-\cfrac{1}{n+1}$$

on adding , we get

$$9S_n=1-\cfrac{1}{n+1}=\cfrac{n}{n+1}$$

So, $$S_n=\cfrac{n}{9(n+1)}$$

The traffic lights at three different road crossing change after every 48 seconds, 72 seconds and 108 seconds respectively.If they change simultaneously at 7 : 00 a.m, at what time will they change simultaneously again?

Consider the problem

The traffic light at three different road crossing change after every $$48seconds,72seconds$$ and $$108seconds$$ respectively

So,

$$\begin{array}{l} 48=2\times 2\times 2\times 2\times 3 \\ 72=2\times 2\times 2\times 3\times 3 \\ 108=2\times 2\times 3\times 3\times 3 \end{array}$$

Therefore, L.CM of $$48,72,108$$ is

$$\begin{array}{l} \left( { 2\times 2\times 2\times 2\times 3\times 3\times 3 } \right) \\ =432 \end{array}$$

So, time when they change again $$=432seconds$$

But we need to find time after $$ 7 am $$ So, first we convert $$432seconds$$ into minutes.

$$\begin{array}{l} Time=432\sec ond \\ =\dfrac { { 432 } }{ { 60 } } \min utes \\ \therefore \, \, Time=7\ minutes\, 12\, \ seconds \end{array}$$

Thus,

Required time $$=7am+7minutes \ 12seconds$$

$$=7:07:12am$$

satisfies the recurrence relation $$b_{n+1}=\frac{1}{3}\left ( 2b_{n}+\frac{125}{b^{2}_{n}} \right ),b_{n}\neq 0$$

$$\begin{array}{l} { b_{ n+1 } }=\frac { 1 }{ 3 } \left( { 2{ b_{ n } }+\frac { { 125 } }{ { { b_{ n } }^{ 2 } } } } \right) \\ { \lim }_{ n\to \infty }\, \, { b_{ n } }=? \\ So,\, \, let\, \, { \lim }_{ n\to \infty }\, \, { b_{ n } }={ \lim }_{ n\to \infty }\, \, { b_{ n+1 } }=t \\ If\, \, n\to \infty \, \, { b_{ n } }\to { b_{ \infty } }\, \, \& \, \, { b_{ n+1 } }\to { b_{ \infty +1 } }\cong { b_{ \infty } } \end{array}$$

Taking hint both side, we get

$$\begin{array}{l} { \lim }_{ n\to \infty }\, \, { b_{ n+1 } }=\frac { 1 }{ 3 } \left( { 2{ \lim }_{ n\to \infty }\, \, { b_{ n } }+\frac { { 125 } }{ { { \lim }_{ n\to \infty }\, \, { b_{ n } }^{ 2 } } } } \right) \\ t=\frac { 1 }{ 3 } \left[ { 2t+\frac { { 125 } }{ { { t^{ 2 } } } } } \right] \\ t=\frac { 1 }{ 3 } \left[ { \frac { { 2{ t^{ 3 } }+125 } }{ { { t^{ 2 } } } } } \right] \\ 3{ t^{ 2 } }=2{ t^{ 2 } }+125 \\ { t^{ 3 } }=125 \\ t=5 \\ So,\, \, { \lim }_{ n\to \infty }\, \, { b_{ n } }=t=5 \end{array}$$

$$\sqrt{1+3+5+7+...}$$.

$$\sqrt{1+3+5+7+...}$$

Sum of series $$1+3+5+7+...$$

$$=_{ r=1 }^{ n }{ [ (2r-1)}=\cfrac{2n(n+1)}{2}-n\\ n^2+n-n=n^2\\ \sqrt{1++5+7+...}=\sqrt{n^2}=n$$

As income is $$10\%$$ more than that of B. How much per cent is the income of B less than that of A?

Let income of $$A$$ be $$110$$.

Let income of $$B$$ be $$100$$

So, ($$\because$$ A's income is $$10\%$$ more )

So, $$\%$$ income of $$B$$ less than that of $$A= \dfrac{110-100}{110} \times 100$$

$$=\dfrac{100}{11}=9.09\%$$

An Arithmetic Series is defined as
$$f\left( n \right) = a + \left( {n - 1} \right)d,n \in N,$$ prove that A.M. of $$f\left( 1 \right)$$ and $$f\left( {2n - 1} \right)$$ is $$f\left( n \right)$$.

Solution:

Given $$f(n)=a+(n-1)d\quad ,n\in N$$

then $$f(1)=a$$

$$f(2n-1)=a+(2n-2)d=a+2(n-1)d$$

Now $$f(1)+f(2n-1)=a+a+(2n-2)d$$

$$=2[a+(n-1)d]=2f(n)$$

$$\Rightarrow \ A.M$$ of $$f(1)$$ and $$f(2n-1)$$ is $$f(n)$$.

Hence Proved

What comes next in the series?
$$2,3,6,10,17,28,?$$

1136203_1229957_ans_a1d572141b3f461c96e59b76104e2d51.jpg

Find the co-efficient of $$x ^ { 7 }$$ in the series of $$e ^ { 2 x }$$.

Expansion of $$e^x$$

$$e^x=1+\dfrac{x}{1!}+\dfrac{x^2}{2!}+\dfrac{x^3}{3!}+\dfrac{x^4}{4!}+...$$

Expansion of $$e^{2x}$$

$$e^{2x}=1+\dfrac{2x}{1!}+\dfrac{4x^2}{2!}+....\dfrac{(2x)^7}{7!}$$

Co-efficient of $$x^7=\dfrac{(2)^7}{7!}$$

$$=\dfrac{8}{315}$$

Show that : $$\dfrac{1^3}{1} + \dfrac{1^3 + 2^3}{1+3} + \dfrac{1^3 + 2^3 + 3^3}{1+3+5}$$ .........up to n terms = $$\dfrac{n}{24}[2n^2 +9n +13]$$

The given series is $$\dfrac{1^3}{1}+\dfrac{1^3+2^3}{1+3}+\dfrac{1^3+2^3+3^3}{1+3+5}+.......$$

$$x^{th}$$ term of the series $$t_r=\dfrac{1^3+2^3+3^3+....+x^3}{1+3+5+.....+(2x-1)}$$

numerator is the sum of squares of first $$n$$ natural numbers and denominator is an $$A.P$$ with $$a=1,l=2x-1,n=x$$

$$t_r=\dfrac{\dfrac{x^2(r+1)^2}{4}}{\dfrac{x}{2}(1+2x-1)}$$

$$t_r=\dfrac{x^2(r+1)^2}{4x^2}$$

$$t_r=\dfrac{(x+1)^2}{4}$$

$$t_r=\dfrac{1}{4}(x^2+2x+1)$$

Sum of $$n$$ term of the series

$$=\sum_{x=1}^{n}{t_r}$$

$$=\dfrac{1}{4}\sum_{x=1}^{n}{(x^2+2x+1)}$$

$$=\dfrac{1}{4}\sum_{x=1}^{n}{x^2}+\dfrac{1}{2}\sum_{x=1}^{n} r+\dfrac{1}{4}\sum_{x=1}^{n}{1}$$

$$=\dfrac{1}{4}n\left(\dfrac{n(n+1)(2n+1)}{6}\right)+\dfrac{1}{2}\dfrac{(n(n+1))}{2}+\dfrac{n}{4}$$

$$=\dfrac{1n}{4}\left(\dfrac{(n+1)(2n+1)}{6}+(n+1)+1\right)$$

$$=\dfrac{1}{4}n\left(\dfrac{2n^2+3n+1+6n+12}{6}\right)$$

Sum of $$n$$ terms $$=\dfrac{n(2n^2+9n+13)}{24}$$

Find the sum of $$8 + 88 + 888 + 8888 + \cdots$$

$$8 + 88 + 888 + 8888 + ....$$

$$= 8 (1 + 11 + 111 + 1111 + ...)$$

$$= \dfrac{8}{9} (9 + 99 + 999 + 9999 + ...)$$

$$= \dfrac{8}{9} (10 - 1 + 100 - 1 + 1000 - 1 + ...)$$

$$= \dfrac{8}{9} (10 + 10^2 + 10^3 + ... + 10^n - n)$$

$$= \dfrac{8}{9} \left(\dfrac{10(10^n - 1)}{10 - 1} - n \right)$$ [sum of n terms of a G.P]

$$= \dfrac{8}{9} \left(\dfrac{10(10^n - 1)}{9} - n \right)$$

Solve
$$1^{3}+\dfrac{1^{3}+2^{3}}{2}+\dfrac{1^{3}+2^{3}+3^{3}}{3}+...$$

We have,

$$1^3+\dfrac{1^3+2^3}{2}+\dfrac{1^3+2^3+3^3}{3}+........$$

let

$$T_r=\dfrac{1^3+2^3+3^3+4^3+........}{1+2+3+4.......}$$

$$=\dfrac{\left(\dfrac{r(r+1)}{2}\right)^2}{r}$$

$$S_n=\sum{T_r}=\dfrac{1}{4} r(r+1)^2$$

$$=\dfrac{1}{4}r(r^2+1^2+2r)$$

$$=\dfrac{1}{4}[r^3+r+2r^2]$$

$$=\dfrac{1}{4}[\sum r^3+\sum r+2\sum r^2]$$

$$=\dfrac{1}{4}\left[\dfrac{n^2(n+1)^2}{4}+2\dfrac{n(n+1)(2n+1)}{6}+\dfrac{n(n+1)}{2}\right]$$

$$=\dfrac{1}{4}\left[\dfrac{3n^2(n+1)^2+4n(n+1)(2n+1)+6n(n+1)}{12}\right]$$

$$=\dfrac{1}{4}\left[\dfrac{3n^2(n^2+1^2+2n)+4n[2n^2+n+2n+1]+6n^2+6n}{12}\right]$$

$$=\dfrac{1}{4}\left[\dfrac{3n^4+3n^2+6n^3+8n^3+4n^2+8n^2+4n+6n^2+6n}{12}\right]$$

$$=\dfrac{1}{48}[3n^4+14n^3+21n^2+10n]$$

Hence, this is the answer.

Find the $$A.M$$. of the series $$1, 2, 4, 8, 16, .......2^{n}$$

$$S_n=1+2+4+.....2^n$$

$$=2^0+2^1+2^2+......+2^n$$

$$=\dfrac{2^0(2^{n+1}-1)}{2-1}$$

$$=\dfrac{2^{n+1}-1}{2-1}=2^{n+1}-1$$

$$\therefore A.M=\dfrac{2^{n+1}-1}{n+1}$$

Find the sum to infinity of the series $$1 + \dfrac { 2 } { 3 } + \dfrac { 6 } { 3 ^ { 2 } } + \dfrac { 10 } { 3 ^ { 3 } } + \dfrac { 14 } { 3 ^ { 4 } } + \ldots$$

Let $$S = 1 + \dfrac{2}{3} + \dfrac{6}{3^2} + \dfrac{10}{3^3} + \dfrac{14}{3^4} + ...$$

$$S = 1 + \dfrac{2}{3} + \dfrac{6}{3^2} + \dfrac{10}{3^3} + \dfrac{14}{3^4} + ...$$

$$\dfrac{S}{3} =\quad \,\,\, \dfrac{1}{3} + \dfrac{2}{3^2} + \dfrac{6}{3^3} + \dfrac{10}{3^4} + ....$$

$$-$$ $$-$$ $$-$$ $$-$$ $$-$$

$$\overline{S- \dfrac{S}{3} = 1 + \dfrac{1}{3} + \dfrac{4}{3^2} + \dfrac{4}{3^3} + \dfrac{4}{3^4} + ...}$$

$$\dfrac{2S}{3} = 1 + \dfrac{1}{3} + \dfrac{4}{3^2} \left(1 + \dfrac{1}{3} + \dfrac{1}{3^2} + ...\right)$$

$$\dfrac{2S}{3} = \dfrac{4}{3} + \dfrac{4}{3^2} \left(\dfrac{1}{1 - \dfrac{1}{3}} \right)$$ [sum of infinite G.P]

$$= \dfrac{4}{3} + \dfrac{4}{9} \left(\dfrac{3}{2} \right) = \dfrac{4}{3} + \dfrac{2}{3} = 2$$

$$\Rightarrow S = 3$$

Evaluate $$\sum _ { k = 1 } ^ { n } \left( 2 ^ { k } + 3 ^ { k - 1 } \right)$$

$$\sum_{k=1}^{n}(2^{k}+3^{k-1})$$

$$=\sum_{k=1}^{n}2^{k}+\sum_{k=1}^{n}3^{k-1}$$

$$=2+4+8+.............+1+3+9+27$$

$$=2[\cfrac{2^{n}-1}{1}]+1[\cfrac{3^{n}-1}{2}]$$

$$=2^{n-1}-2+\cfrac{3^{n}-1}{2}$$

$$=2^{n-1}+\cfrac{3^{n}}{2}-\cfrac{5}{2}$$

$$\frac { 1 } { 1 \times 2 } + \frac { 1 } { 2 \times 3 } + \frac { 1 } { 3 \times 4 } + \ldots$$ what will be the $$n^{th}$$ term?

$$(\frac{1}{1\cdot2})+(\frac{1}{2\cdot3})+........+(\frac{1}{n(n+1)})\\=((\frac{1}{1}-(\frac{1}{2}))+((\frac{1}{2}-(\frac{1}{3}))+...........+(\frac{1}{n}-(\frac{1}{n+1})\\=1-(\frac{1}{n+1})\\=(\frac{n+1-1}{n+1})\\=(\frac{n}{n+1})$$

Sum to infinite terms of
$$1 + 3 x + 5 x ^ { 2 } + 7 x ^ { 3 } + \ldots \ldots + \infty ( \boldsymbol { H } \boldsymbol { f } | x | < 1 )$$ is

Let $$ S = 1 + 3x + 5x^{2} + 7x^{3} + ...$$

$$ xS = x + 3x^{2} + 5x^{3} + ...$$

__________________________

$$ S(1-x) = 1 + 2x + 2x^{2}+2x^{3}+...$$ [subtracting]

$$ 1+s(1-x) = 2(1+x+x^{2}+...) = \dfrac{2}{1-x}$$

$$ S(1-x)=\dfrac{2}{1-x}-1 = \dfrac{2-1+x}{1-x} = \dfrac{1+x}{1-x}$$

$$ S=\dfrac{1+x}{(1-x)^{2}}$$

Write the next term of each of the following sequences :
$$0, 2, 6, 12, 20,.....$$

We observe that,

$$0\,\,2\,\,6\,\,12\,\,20$$

$$2\,\,4\,\,6\,\,8$$

$$2\,\,2\,\,2$$

From the first difference, its easy to notice that that the next difference will be 12, which makes the next term to be 30.

$$S_{n}=an^{2}+bn+c$$

Putting $$n=1,2,3$$

$$a+b+c=0$$

$$4a+2b+c=2$$

$$9a+3b+c=6$$

Solving these, we get

$$a=1, b=-1, c=0$$

$$\therefore S_{n}=n^{2}-n$$

So, putting $$n=6$$

Next term$$=30$$

So, the series is

0,2,6,12,30,42..............so on.

The formula of the sum of first $$n$$ natural numbers is $$S = \frac { n ( n + 1 ) } { 2 }$$. If the sum of first $$n$$ natural number is $$325$$, find $$n$$.

$$S=\dfrac{n(n+1)}{2}=325$$

$$n(n+1)=650$$

$$n^2+n-650=0$$

$$\dfrac{-1\pm\sqrt{(1)^2+4(1)(650)}}{2(1)}$$

$$\dfrac{-1\pm 51}{2}$$

$$\dfrac{-1\pm 51}{2}$$ $$\dfrac{-1-51}{2}$$

$$n=25$$

$$n\neq-25$$ as $$n$$ is natural number

$$n+1=26$$

$$25$$ and $$26$$.

The decimal expansion of the rational number $$\dfrac{43}{2^{4}\times 5^{3}}$$ will terminate after how many places of decimal.

$$\dfrac{43}{(2^3\times 5^3)\times 2}=\dfrac{43}{10^3\times 2}=\dfrac{0.043}{2}=0.0125$$

$$4$$ places

$$\therefore$$ decimal expansion will terminate at $$4$$ places of decimal

Find the sum of the series : $$\dfrac{1}{3^{2}+1}+\dfrac{1}{4^{2}+2}+\dfrac{1}{5^{2}+3}+\dfrac{1}{6^{2}+4}+...\infty$$

$$\implies \sum_{n=2}^{\infty}\dfrac{1}{n^2+3n}$$

Neglecting Higher values

$$\implies \dfrac{1}{10}+\dfrac{1}{18}+\dfrac{1}{28}+\dfrac{1}{40}+\dfrac{1}{54}+\dfrac{1}{70}+\dfrac{1}{88}+\dfrac{1}{108}+\dfrac{1}{130}=0.2758$$

Write the next term of each of the following sequences :
$$6, 9, 16, 27, 42,.....$$

Difference between consecutive terms$$=4$$

So, the next term in the series $$=42+19=61$$

1380825_1265027_ans_a73556c37afa4ff587e070b66edf13ed.png

Can you find the missing numbers?

We have,

$$ 2\times 5=10 $$

$$ 5\times ?=20 $$

$$ ?\times 3=12 $$

$$ 3\times 3=9 $$

$$ 3\times 2=? $$

So,

If put first question mark$$=4$$ and second question mark$$=6$$

Then,

$$ 2\times 5=10 $$

$$ 5\times 4=20 $$

$$ 4\times 3=12 $$

$$ 3\times 3=9 $$

$$ 3\times 2=6 $$

So,

Ist question mark$$=4$$

And second question mark$$=6$$

Hence, this is the answer.

Find the sum of first $$1000$$ natural numbers and first $$1000$$ non-positive integers.

1349663_1274648_ans_e986d7a7ac3e4eb0a1770f79e28d17f2.PNG

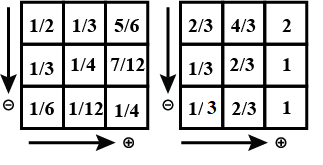
Complete the addition and subtraction box.

REF.Image

$$a)\displaystyle \frac{1}{2}+\frac{1}{3}=\frac{3+2}{6}=\frac{5}{6}$$

$$\displaystyle \frac{1}{3}+\frac{1}{4}=\frac{4+3}{12}=\frac{7}{12}$$

$$\displaystyle \frac{1}{6}+\frac{1}{12}=\frac14$$

$$\displaystyle \frac{1}{2}-\frac{1}{3}=\frac{3-2}{6}=\frac{1}{6}$$

$$\displaystyle \frac{1}{3}-\frac{1}{4}=\frac{4-3}{12}=\frac{1}{12}$$

$$\displaystyle \frac{5}{6}-\frac{7}{12}=\frac{10-7}{12}=\frac{3}{12}=\frac{1}{4}$$

REF.Image

$$b)\displaystyle \frac{2}{3}+\frac{4}{3}=\frac{6}{3}=2$$

$$\displaystyle \frac{1}{3}+\frac{2}{3}=\frac{3}{3}=1$$

$$\displaystyle \frac13+\frac23=1$$

$$\displaystyle \frac{2}{3}-\frac{1}{3}=\frac{1}{3}$$

$$\displaystyle \frac{4}{3}-\frac{2}{3}=\frac{2}{3}$$

$$2-1=1$$

1169525_1272210_ans_8533d1e548bd4ba3a0ae6ce08706dad6.png

Evaluate:
$$1 \dfrac { 1 } { 2 } + 1 \dfrac { 1 } { 3 } + 1 \frac { 1 } { 4 } + \ldots + 1 \dfrac { 1 } { 19 } =$$

$$S=\dfrac { 3 }{ 2 } +\dfrac { 4 }{ 3 } +\dfrac { 5 }{ 4 } +....\dfrac { 20 }{ 19 } $$

$${ T }_{ n }=\dfrac { n+2 }{ n+1 } =1+\dfrac { 1 }{ n+1 } $$

$$\sum { { T }_{ n } } =\sum { 1 } +\sum { \dfrac { 1 }{ n+1 } } $$

$$=n+\left( \dfrac { 1 }{ 2 } +\dfrac { 1 }{ 3 } +....\dfrac { 1 }{ 19 } \right) $$

$$=18+\int _{ 1 }^{ 18 }{ \dfrac { dx }{ x+1 } } $$

$$=18+{ \left( ln\left( x+1 \right) \right) }_{ 1 }^{ 18 }$$

$$=18+ln19-ln2$$

$$=20.25$$

Assume that $$a,b,c$$ and $$d$$are positive integers such that $$a^{5}=b^{4},c^3=d^{2}$$ and $$c-a=19$$. Determine $$d-b$$

We have,

$${{a}^{5}}={{b}^{4}}$$ and $${{c}^{3}}={{d}^{2}}$$

$$a$$ and $$c$$ are perfect squares.

As $$c-a=19$$, a is perfect $${{4}^{th}}$$ degree integer.

Only possible solutions are

$$\left( a,c \right)=\left( 81,100 \right)$$

Then,

$$ b={{\left( {{a}^{5}} \right)}^{\dfrac{1}{4}}} $$

$$ ={{\left( {{81}^{5}} \right)}^{\dfrac{1}{4}}} $$

$$ ={{\left\{ {{\left[ \left( {{3}^{4}} \right) \right]}^{5}} \right\}}^{\dfrac{1}{4}}} $$

$$ =243 $$

And

$$ d={{\left( {{c}^{3}} \right)}^{\dfrac{1}{2}}} $$

$$ ={{\left( {{100}^{3}} \right)}^{\dfrac{1}{2}}} $$

$$ =1000 $$

So,

$$ d-b=1000-243 $$

$$= 757 $$

Hence, this is the answer.

$$1+2x+3x^2+4x^3+.....\infty; |x| < 1$$.

Let $$S=1+2x+3x^{2}+3x^{2}+4x^{3}...\infty(1)$$

Multiply the above equation by x

$$Sx=x+2x^{2}+3x^{3}+4x^{4}...\infty (2)$$

subtract equation (2)form equation(1)

$$S-Sx=1+x+x^{2}+x^{3}+x^{4}+...$$

$$S(1.x)=1+x+x^{2}+x^{3}+x^{4}+...(3)$$

equation (3)forms a G.p with first term is 1, and common difference x sum of infinite terms of G.P is given by

$$\frac{a}{1-r}$$ (a=first term,r=common ratio)

Here a=1,r=x

$$S(1-x)=\frac{1}{1-x}$$

$$S=\frac{1}{(1-x)(1-x)}$$

$$\Rightarrow S=\frac{1}{(1-x)^{2}}$$

1187088_1298641_ans_651f58de4a614d71ab4c9913793027b6.jpg

Prove that
$${1}^{2}+{3}^{2}+{5}^{2}+...+{\left(2n-1\right)}^{2}=\dfrac{n}{3}\left(2n-1\right)\left(2n+1\right)$$

Let p(n)

=$$1^{2}+3^{2}+....+(2n-1)^{2}=\frac{n(2n-1)(2n+1)}{3}$$

for n=1

LHS=$$1^{2}=1$$

RHS=$$\frac{1(1)(3)}{3}=1$$

so, p(n) is true for n=1

Let p(k) be true

$$1^{2}+3^{2}+....+(2k-1)^{2}=\frac{(2k-1)(2k+1)}{3}--(1)$$

for p (k + 1)

$$1^{2}+2^{2}+...+(2(k+1)-1)^{2}=(k+1)\frac{(2(k+1)-1)}{3}(2(k+1)+1)$$

=$$1^{2}+3^{2}+...+(2k+1)^{2}=(k+1)\frac{2k+1}{3}(2k+3)--(2)$$

Form (1)

adding $$ (2k+1)^{2}$$ on both sides.

$$=1^{2}+...+(2k+1)^{2}=\frac{k(2k-1)(2k+1)}{3}+(2k+1)^{2}$$

$$=(2k+1)[\frac{k(2k-1)+3(2k+1)}{3}]$$

$$=(2k+1)[\frac{2k^{2}-k+6k+3}{3}]$$

$$=(2k+1)(\frac{2k^{2}+5k+3}{3})$$

$$=\frac{(k+1)(2k+1)(2k+3)}{3}$$

so, using mathematical induction

$$1^{2}+...(2n+1)^{2}=\frac{n(2n-1)(2n+1)}{3}$$

1206887_1296616_ans_a400fbaf8a1e492d9eac4b55aeb330f1.jpg

Find the value of $$\dfrac{50}{72}+\dfrac{50}{90}+\dfrac{50}{110}+\dfrac{50}{132}+...+\dfrac{50}{9900}$$.

$$ \frac{50}{72} + \frac{50}{90} +.... +\frac{50}{9900}$$

$$ = 50(\frac{1}{72}+\frac{1}{90}+..+\frac{1}{9900})$$

$$ = 50(\frac{1}{8\times 9}+\frac{1}{10\times 9}+ ...+\frac{1}{99\times 100})$$

$$ = 50(\frac{1}{8}-\frac{1}{9}+\frac{1}{9}-\frac{1}{10}+\frac{1}{10}-\frac{1}{11}+...+\frac{1}{99}-\frac{1}{100})$$

$$ = 50 (\frac{1}{8}-\frac{1}{100}) = 50 (\frac{100-8}{800})$$

$$ = \frac{50\times 92}{800} = \frac{23}{4}$$

1186739_1292294_ans_de34b664816a45dfab0bedaaffb51385.jpg

$$\dfrac{a}{1+i}+\dfrac{a}{(1+i)^{2}}\dfrac{a}{(1+i)^{3}}+....+\dfrac{a}{(1+i)^{n}}$$

$$\begin{array}{l} \dfrac { a }{ { 1+i } } +\dfrac { a }{ { { { \left( { 1+i } \right) }^{ 2 } } } } +\dfrac { a }{ { { { \left( { 1+i } \right) }^{ 3 } } } } +...........+\dfrac { a }{ { { { \left( { 1+i } \right) }^{ n } } } } \\ A=\left( { \dfrac { a }{ { 1+i } } } \right) \\ R=\dfrac { 1 }{ { \left( { 1+i } \right) } } \\ { S_{ n } }=\dfrac { { A\left( { { R^{ n } }-1 } \right) } }{ { R-1 } } \\ =\dfrac { { \left( { \dfrac { a }{ { 1+i } } } \right) \left\{ { { { \left( { \dfrac { 1 }{ { 1+i } } } \right) }^{ n } }-1 } \right\} } }{ { \dfrac { { 1-1-i } }{ { 1+i } } } } \\ =\dfrac { { \left( { \dfrac { a }{ { 1+i } } } \right) \left\{ { 1-{ { \left( { \dfrac { 1 }{ { 1+i } } } \right) }^{ n } } } \right\} } }{ { \left( { \dfrac { i }{ { 1+i } } } \right) } } \\ =ia\left\{ { \dfrac { { 1-{ { \left( { 1+i } \right) }^{ n } } } }{ { { { \left( { 1+i } \right) }^{ n } } } } } \right\} \end{array}$$

In the four numbers first three are in G.P. and last three are in A.P. whose common difference isIf the first and last numbers are same, then first will be

We have,

Let the four number are $$a+d,a-d,a,a+d$$

Given that common difference is $$6$$, $$d=6$$

According to given question,

The first number is same the fourth number.

Now,

The first number are $$a+d,a-d,a$$ in G.P.

We know that,

$$ {{\left( a-6 \right)}^{2}}=a\left( a+6 \right) $$

$$ \Rightarrow {{a}^{2}}-12a+36={{a}^{2}}+6a $$

$$ \Rightarrow 18a=36 $$

$$ \Rightarrow a=2 $$

Hence, the first term is $$a=2$$

Hence, this is the answer.

What will be in the '?' mark

We see that the difference between the compartments starting from $$20$$, are $$11,7,5,3,1,$$

$$\therefore$$ The question mark should be replaced with a number that is $$13$$ less than $$20$$ i.e. $$7$$

$$\therefore$$ the question mark should be replaced with number $$7$$.

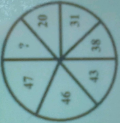
Prove that $${ 3 }^{ \frac { 1 }{ 2 } }\times { 3 }^{ \frac { 1 }{ 4 } }\times { 3 }^{ \frac { 1 }{ 8 } }.....=3$$

Given,

$$3^{\dfrac{1}{2}}\times 3^{\dfrac{1}{4}}\times 3^{\dfrac{1}{8}}\times 3^{\dfrac{1}{16}}\times ...............$$

$$=3^{\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{8}+.........}$$

$$=3^{\sum_{n=1}^{\infty }\left ( \dfrac{1}{2} \right )^n}$$

$$=3^{\dfrac{\dfrac{1}{2}}{1-\dfrac{1}{2}}}$$

$$=3^1=3$$

Hence proved.

Given that $$\left( 1 + x + x ^ { 2 } \right) ^ { n } = a _ { 0 } + a _ { 1 } x + a _ { 2 } x ^ { 2 } + \ldots + a _ { 2 n } x ^ { 2 n } ,$$ find the values of
(i) $$a _ { 0 } + a _ { 1 } + a _ { 2 } + \dots . + a _ { 2 n }$$
(ii) $$a _ { 0 } - a _ { 1 } + a _ { 2 } - a _ { 3 } \dots . . + a _ { 2 n }$$

Given,

$$\left( 1 + x + x ^ { 2 } \right) ^ { n } = a _ { 0 } + a _ { 1 } x + a _ { 2 } x ^ { 2 } + \ldots + a _ { 2 n } x ^ { 2 n } ,$$.......(1).

i) Now putting $$x=1$$ in (1) we get

$$(1+1+1)^n=a _ { 0 } + a _ { 1 } + a _ { 2 } + \dots . + a _ { 2 n }$$

or, $$3^n=a _ { 0 } + a _ { 1 } + a _ { 2 } + \dots . + a _ { 2 n }$$.
(ii) Now putting $$x=-1$$ in (1) we get,

$$(1-1+1)^n=a _ { 0 } - a _ { 1 } + a _ { 2 } - a _ { 3 } \dots . . + a _ { 2 n }$$

or, $$1=a _ { 0 } - a _ { 1 } + a _ { 2 } - a _ { 3 } \dots . . + a _ { 2 n }$$.

What is the $${1025}^{th} $$ term of the sequence $$1,2,2,4,4,4,4,8,8,8,8,8,8,8,8,?$$

Sequence is composed by powers of $$2$$ repeated $$2^n$$ times.

$$2^0=1$$ appears $$1$$ times

$$2^1=2$$ appears $$2$$ times

$$2^2=4$$ appears $$4$$ times

$$2^3=8$$ appears $$8$$ times

$$1025^{th}$$ element is $$1024$$.

1206449_1319913_ans_c6afa73f6c5648bb8ed2236091d7a28f.jpg

Find the sum of first $$n$$ terms of the series $${1^2} + \left( {{1^2} + {2^2}} \right) + \left( {{1^2} + {2^2} + {3^2}} \right) + .....$$

$$1st$$ term $$=1^2$$

$$2nd$$ term $${ = {1^2} + {2^2}}$$

$$3rd $$ term $${ = {1^2} + {2^2} + {3^2}}$$

$$nth$$ term $${ = {1^2} + {2^2} + {3^2} + ...... + {n^2}}$$

Here,

$$\begin{array}{l} { a_{ n } }={ 1^{ 2 } }+{ 2^{ 2 } }+{ 3^{ 2 } }+......+{ n^{ 2 } } \\ { a_{ n } }=\dfrac { { n\left( { n+1 } \right) \left( { 2n+1 } \right) } }{ 6 } \\ =\dfrac { { \left( { { n^{ 2 } }+n } \right) \left( { 2n+1 } \right) } }{ 6 } \\ =\dfrac { { \left( { 2{ n^{ 3 } }+{ n^{ 2 } }+2{ n^{ 2 } }+n } \right) } }{ 6 } \\ =\dfrac { { \left( { 2{ n^{ 3 } }+3{ n^{ 2 } }+n } \right) } }{ 6 } \end{array}$$

Write the seventh term of the series $$\dfrac{1}{\sqrt{2}}, -2, \dfrac{8}{\sqrt{2}},\dots \dots$$

$$\dfrac{1}{\sqrt{2}}, -2, \dfrac{8}{\sqrt{2}}…..$$ is a GP with $$a=\dfrac{1}{\sqrt{2}}$$.

Common ratio $$=\dfrac{-2}{\dfrac{1}{\sqrt{2}}}=-2\sqrt{2}=\dfrac{\dfrac{8}{\sqrt{2}}}{-2}$$

$$T_7=ar^6=\dfrac{1}{\sqrt{2}}(-2\sqrt{2})^6=\dfrac{1}{\sqrt{2}}(2^9)=256\sqrt{2}$$.

Solve:
$$2\dfrac {1}{5}+3\dfrac {1}{7}$$

We have,

$$2\dfrac { 1 }{ 5 } +3\dfrac { 1 }{ 7 } $$

$$=\dfrac { 11 }{ 5 } +\dfrac { 22 }{ 7 } =\dfrac { 77+110 }{ 35 } =\dfrac { 187 }{ 35 } =5\dfrac { 12 }{ 35 } $$

Hence, this is the answer.

Find the sum of $$1+4+7+10+.......$$ to $$22$$ terms.

$$1+4+7+10+ ..... $$ to $$22$$ terms

It is an AP with $$a = 1$$ & $$d = 3$$

$$ S_{22} = \dfrac{22}{2}[2a+21d]$$

$$= 11[2(1)+21(3)]$$

$$= 11[65] = 715 $$

Find the mean weight from the following table.
Weight $$(kg)$$ $$29$$ $$30$$ $$31$$
$$32$$ $$33$$
No.of children $$20$$ $$01$$ $$04$$ $$03$$ $$05$$

Weight $$\left( kg \right)$$ $$\left( {x}_{i} \right)$$	No. of children $$\left( {f}_{i} \right)$$	$${f}_{i} {x}_{i}$$
$$29$$	$$20$$	$$580$$
$$30$$	$$1$$	$$30$$
$$31$$	$$4$$	$$124$$
$$32$$	$$3$$	$$96$$
$$33$$	$$5$$	$$165$$
	$$\sum{{f}_{i}} = 33$$	$$\sum{{f}_{i} {x}_{i}} = 995$$

Therefore,

Mean weight $$\left( \bar{x} \right) = \cfrac{\sum{{f}_{i}{x}_{i}}}{\sum{{f}_{i}}}$$

$$\Rightarrow \bar{x} = \cfrac{995}{33} = 30.15 \; kg$$

How many terms of the geometric progression $$1+4+16+64+..........$$ must be added to get sum equal to $$5641$$?

$$GP={ 4 }^{ 0 },{ 4 }^{ 1 },{ 4 }^{ 2 },{ 4 }^{ 3 }......{ 4 }^{ n }$$ $$(n+1)$$ terms

Sum $$=5641$$

Sum of $$GP=\dfrac { a\left( { r }^{ n+1 }-1 \right) }{ r-1 } $$

$$=\dfrac { 1\left( { 4 }^{ n+1 }-1 \right) }{ 4-1 } =5641$$

$$\Rightarrow { 4 }^{ n+1 }=16924$$

$$n+1={ log }_{ 4 }16924$$

$$=7.023\approx 7$$ terms.

Sum of $$7$$ terms $$=5461$$.

Find the value of $$y$$ if $$1+4+7+10+.....+y=287$$

$$a=1,d=4-1=3,S_n=287$$

$$S_n=\dfrac{n}{2}[2a+(n-1)d]$$

$$287=\dfrac{n}{2}[2(1)+(n-1)3]$$

$$574=2n+3n^2-3n$$

$$3n^2-n-574=0$$

solving the above equation, we get,

$$\therefore n=14$$

$$S_n=\dfrac{n}{2}(a+l)$$

$$287=\dfrac{14}{2}(1+y)$$

$$287=7(1+y)$$

$$41=1+y$$

$$\therefore y=40$$

Prove that $$\dfrac{1}{1+\sqrt{2}}+\dfrac{1}{\sqrt{2}+\sqrt{3}}+\dfrac{1}{\sqrt{3}+\sqrt{4}}+ ............. +\dfrac{1}{\sqrt{8}+\sqrt{9}}$$=2

We have,

$$\dfrac{1}{1+\sqrt{2}}+\dfrac{1}{\sqrt{2}+\sqrt{3}}+\dfrac{1}{\sqrt{3}+\sqrt{4}}+ ............. +\dfrac{1}{\sqrt{8}+\sqrt{9}}$$

$$=\dfrac{1}{1+\sqrt{2}}\times{\dfrac{1-\sqrt{2}}{1-\sqrt{2}}}+\dfrac{1}{\sqrt{2}+\sqrt{3}}\times{\dfrac{\sqrt{2}-\sqrt{3}}{\sqrt{2}-\sqrt{3}}}+\dfrac{1}{\sqrt{3}+\sqrt{4}}\times{\dfrac{\sqrt{3}-\sqrt{4}}{\sqrt{3}-\sqrt{4}}}+ ............. +\dfrac{1}{\sqrt{8}+\sqrt{9}}\times{\dfrac{\sqrt{8}-\sqrt{9}}{\sqrt{8}-\sqrt{9}}}$$

$$=\dfrac{1-\sqrt{2}}{-1}+\dfrac{\sqrt{2}-\sqrt{3}}{-1}+.......................+\dfrac{\sqrt{8}-\sqrt{9}}{-1}$$

$$=\sqrt{2}$$$$-1$$$$+\sqrt{3}$$$$-\sqrt{2}$$$$+\sqrt{4}$$$$-\sqrt{3}$$$$+\sqrt{5}$$$$-\sqrt{4}$$$$+\sqrt{6}$$$$-\sqrt{5}$$$$+\sqrt{7}-\sqrt{6}+\sqrt{8}-\sqrt{7}+\sqrt{9}-\sqrt{8}$$

$$=-1+3=2$$

If a boy bats 100 times and gets 40 hits, what is his batting average ?

Batting average of boy = $$\dfrac{40}{100}$$ = $$0.4$$

Fill this square using all numbers from 21 to 29.

Let us fix $$26$$ on the topmost left-hand side box.

Taking the diagonal of the square, we have

$$26+25=51$$ and $$75-51=24$$

$$\therefore$$ put $$24$$ at the end of this diagonal.

Fix $$22$$ on the top most-right side box.

Taking the diagonal in which $$22$$ lies, we have

$$22+25=47$$ and $$75-47=28$$

$$\therefore$$ put $$28$$ at the end of this diagonal.

Clearly,

In $${1}^{st}$$ row: The required number $$=75-(26+22) =75-48=27$$

In $${1}^{st}$$ column: The required number $$= 75-(26+28) =75-54=21$$

In $${2}^{nd}$$ row: The required number $$=75- (21+25) =75-46=29$$

In $${2}^{nd}$$ column: The required number $$=75-(28+24) =75-52=27$$

$$\therefore$$ the complete magic square is as shown below:

$$26$$	$$27$$	$$22$$
$$21$$	$$25$$	$$29$$
$$28$$	$$23$$	$$24$$

look at the pattern and Solve
1 = 1X1
121 =x
12321 =x
1234321=x
_____ =11111x11111

It can be observed that the squares of the given numbers can be found by first writing the counting number up to the number of $$1$$'s and then writing the reverse counting till $$1$$.

Thus,

$$1\times 1=1$$

$$11\times 11=121$$

$$111\times 111=12321$$

$$1111\times 1111=1234321$$

$$11111\times 11111=123454321$$

If the mean of $$5$$ observations $$x,x+2,x+4,x+6$$ and $$x+8$$ is $$11$$, find the value of $$x$$.

$$ \frac{x+x+2+x+4+x+6+x+8}{5} = 11 $$

$$ \Rightarrow 5x+20=55$$ $$ \Rightarrow 5x=35 $$

$$\Rightarrow x =7 $$

1189509_1354811_ans_c2bda0a26ae440ac9564e9eafe6f13c0.jpg

In a question, 55+10 = 20 and 45+40 = 49, then 95+70 = ?

Given, 55+10 = 20 and 45+40 = 49

Means (5+5) +10 = 20 and (4+5) +40 =49

Similarly,

95+70 = (9+5)+70 = 84

Calculate the arithmetic mean, range, median and mode of the given data:
$$2,\,4,\,7,\,4,\,9,\,5,\,7,\,3,\,6,\,7$$

Arithmetic mean$$=\dfrac{sum\,\,of\,\, observations}{number\,\, of\,\, observations}$$

$$=\dfrac{2+4+7+4+9+5+7+3+6+7}{10}$$

$$=\dfrac{54}{10}=5.4$$

Median:

Arranging the data in ascending order:

$$2,\,3,\,4,\,4,\,5,\,6,\,7,\,7,\,7,\,9$$

Here the middle terms are $$5$$ and $$6$$

The average of $$5$$ and $$6=\dfrac{5+6}{2}=\dfrac{11}{2}=5.5$$

$$\therefore$$ Median$$=5.5$$

Mode:The most repeating values is $$7$$.

$$\therefore$$ Mode is $$7$$

Range$$=$$Highest observation$$-$$Lowest observation$$=9-2=7$$

Fill in the blanks in the expressions with the proper numbers.
$$(1\ \times 7)=(\Box \times 1)$$

$$ (1\times 7) = (7\times 1) $$
1189182_1354037_ans_f480ca46b0d44bb5a7c7be66d6fa66c4.jpg

Find the mean been the following:-
$$2,2,0,4,3,9,5,7$$

Mean$$=\dfrac{sum\, of \, the\, observations }{Number \, of \, observations}$$

$$=\dfrac{2+2+0+4+3+9+5+7}{8}$$

$$=\dfrac{32}{8}=4$$

$$\therefore$$ Mean$$=4$$

$$x=7$$ when $$y=5$$. Find $$y$$ when $$x=14$$.

When $$x=7\Rightarrow y=5$$

When $$x=7\times 2=14\Rightarrow y=5\times 2=10$$

$$\therefore y=10$$

if $$1 + {x^2} = \sqrt 3 x,\,\,then,\,\,\prod\limits_{n = 1}^{24} {\left( {{x^n} + \dfrac{1}{{{x^n}}}} \right)} $$ is equal to:

Given,

$$1 + {x^2} = \sqrt 3 x$$

or, $$x+\dfrac{1}{x}=\sqrt{3}$$......(1).

Now,

$$x^3+\dfrac{1}{x^3}$$

$$=\left(x+\dfrac{1}{x}\right)^3-3.x.\dfrac{1}{x}. \left(x+\dfrac{1}{x}\right)$$

$$=3\sqrt{3}-3\sqrt{3}$$ [ Using (1)]

$$=0$$.......(2).

Now,

$$\prod\limits_{n = 1}^{24} {\left( {{x^n} + \dfrac{1}{{{x^n}}}} \right)} $$

$$=\left(x+\dfrac{1}{x}\right).\left(x^2+\dfrac{1}{x^2}\right).\left(x^3+\dfrac{1}{x^3}\right)......\left(x^{24}+\dfrac{1}{x^{24}}\right)$$

$$=0$$. [ Using (2)]

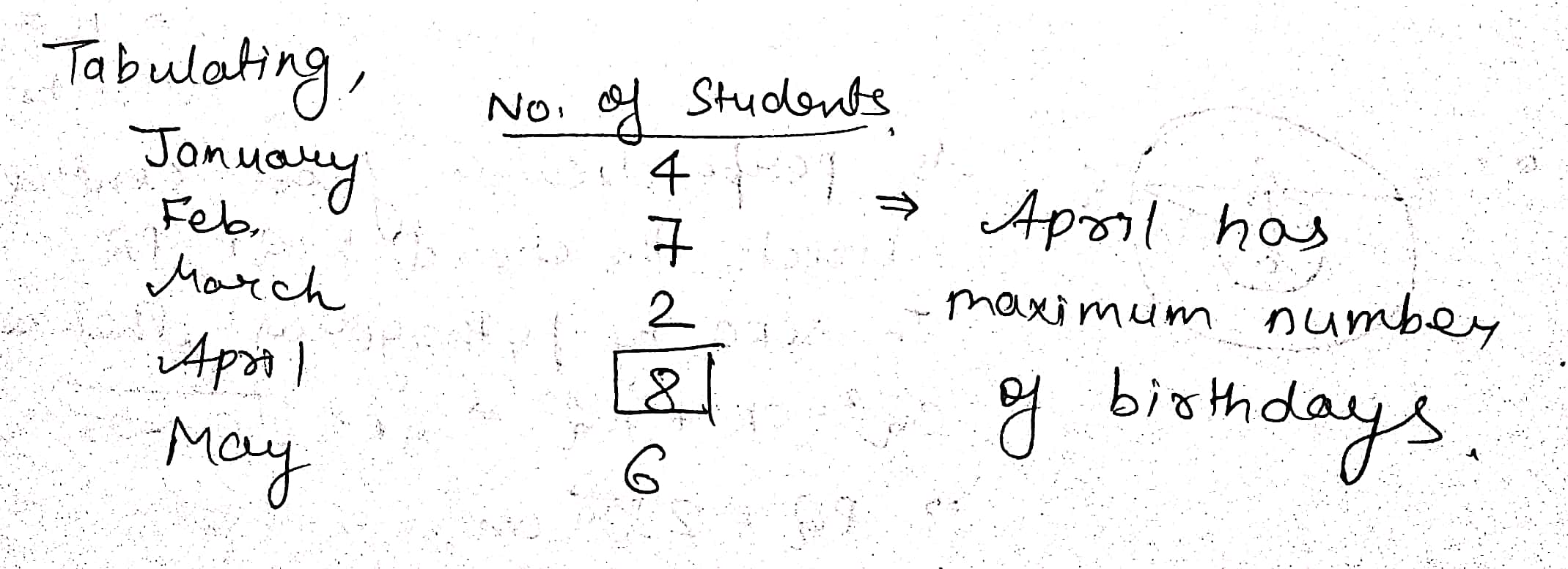
Which month has the maximum number of birthdays?_____________

Tabulating

No. of students

January $$4$$ $$\Rightarrow$$ April has maximum number of birthdays.

Feb $$7$$

March $$2$$

April $$8$$

May $$6$$

1214510_1396361_ans_5786a8309cb94a9dbb969360386ace1a.jpg

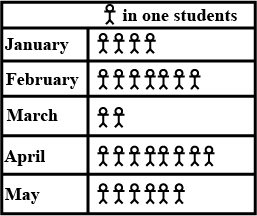
Find the mean of the following.
First seven multiples of $$6$$

The first seven multiples of $$6$$ are $$6,12,18,24,30,36,42$$

Mean of first $$7$$ multiples of $$6$$ are

$$=\dfrac{6+12+18+24+30+36+42}{7}=\dfrac{168}{7}=24$$

Find the mean of the following
First eight even natural numbers.

The first eight even natural numbers are $$2,4,6,8,10,12,14,16$$

Mean of first $$8$$ even natural numbers are

$$=\dfrac{2+4+6+8+10+12+14+16}{8}=\dfrac{72}{8}=9$$

If $${S_n}$$ denotes the sum of $$n$$ terms of an AP whose common differences is $$d$$, show that $$d = {S_n} - 2{S_{n - 1}} + {S_{n - 2}}$$

Let $$a$$ be the first term of the given $$A.P.$$

Then $$S_n=\dfrac{n}{2}\{2a+(n-1)d\}$$......(1).

Now,

$$S_n+S_{n-2}-2S_{n-1}$$

$$=\dfrac{n}{2}\{2a+(n-1)d\}$$$$+\dfrac{n-2}{2}\{2a+(n-3)d\}$$$$-2\times \dfrac{n-1}{2}\{2a+(n-2)d\}$$

$$=a\left(n+n-2-2n+2\right)+\dfrac{d}{2}\left(n^2-n+n^2-5n+6-2[n^2-3n+2 ]\right)$$

$$=\dfrac{d}{2}\times 2$$

$$=d$$.

The mean of $$12,65,84,75,a$$ is $$50$$ Find a

Given data is $$12,65,84,75,a$$

The sum of data is $$12+65+84+75+a=236+a$$

Mean is $$50$$

The sum of obseravations is given as $$50\times 5=250$$

$$\implies 236+a=250\\a=250-236=14$$

The value of p if ,the mean of $$23,25,p$$ is 24

Given data is $$23,25,p$$

Give mean is $$24$$

No. of observations is $$3$$

Sum of observations is $$24\times 3=72$$

Sum of observations is $$72=23+25+p\\p=72-48=24$$

Find the missing number:
$$ \begin{array}{|c|c|c|}\hline 5 & {6} & {12} \\ \hline 4 & {3} & {4} \\ \hline 2 & {3} & {?} \\ \hline 18 & {27} & {96} \\ \hline\end{array} $$

In the first column The numbers are $$5,4,2,18$$

Which can be given as $$(5+4)\times 2=18$$

Similarly,

In the second column The numbers are $$6,3,3,27$$

Which can be given as $$(6+3)\times 3=27$$

In the third column the numbers are $$12,4,?,96$$

Which can be given as $$(12+4)\times ?=96\implies 48\times ?=96\implies ?=2$$

So the missing number is $$2$$

Observe the given pattern
$$4\times 0+1=01$$
$$4\times 1+2=06$$
$$4\times 2+3=11$$
$$4\times3+4 =16$$ and find the $${15}^{th}$$ term.

$$4\times 0+1=01$$

$$4\times 1+2=06$$

$$4\times 2+3=11$$

$$4\times 3+4=16$$

$$4\times 4+5=21$$

$$\therefore 1,6,11,16,21,.....15$$ terms are in A.P

$$a=1, d=6-1=5$$

$$t_{15}=a+14d=1+14\times 5$$

$$=1+70=71$$

$$\therefore 15^{th} term = 71$$

1257586_1505725_ans_3a142f68daa74917bec6e58d7d88dab2.PNG

If the mean of $$x+4,5,3,6,7$$ is 5 then find x

The data $$x+4,5,3,6,7$$

Sum of observations $$x+4+5+3+6+7=25+x$$

Mean of data is $$\dfrac{25+x}{5}=5\\25+x=25\\x=0$$

Solve:
$$\frac{1}{{2.5}} + \frac{1}{{5.8}} + \frac{1}{{8.11}} + - - - + \frac{1}{{(3n - 1)(3n + 2)}}$$

Let $$S(n)=\frac{1}{2.5}+\frac{1}{5.8}+\frac{1}{8.11}+.........+\frac{1}{(3n-1)(3n-2)}$$

Step - (1)

prove s(n) for n=1

$$L.H.S = \frac{1}{2.5}+\frac{1}{5.8}+\frac{1}{8.11}+.......+\frac{1}{(3(1)-1)(3(1)+2)}$$

$$=\frac{1}{2.5}+\frac{1}{5.8}+\frac{1}{8.11}+........+\frac{1}{2.5}$$

$$L.H.S = \frac{1}{2.5}=\frac{1}{10}$$

$$R.H.S= \frac{1}{2.5}=\frac{1}{10}$$

So, it is true for n=1.

Step (2)

Assume that S(n) is true for some n(k)

$$\frac{1}{2.5}+\frac{1}{5.8}+\frac{1}{8.11}+........+\frac{1}{(3k-1)(3k+2)}$$

$$=\frac{k}{(6k+4)}$$

Step - (3)

Prove s(n) for n= k+1

$$L.H.S = \frac{1}{2.5}+\frac{1}{5.8}+\frac{1}{8.11}+......+\frac{1}{(3(k+1)-1)(3(k+1)+2)}$$

$$=\frac{k}{(6k+4)}+\frac{1}{(3k+2)(3k+5)}$$

$$=\frac{k}{2(3k+2)}+\frac{1}{(3k+2)(3k+5)}$$

$$=[3k^{2}+5k+2]/[2(3k+2)(3k+5)]$$

$$[(3k+2)(k+1)]/[2(3k+2)(3k+5)]$$

$$=\frac{k+1}{2(3k+5)}$$

$$=\frac{k+1}{6k+10}$$

1201517_1416045_ans_f1b335f0f42f4379b615702dab878bf2.jpg

A student scored marks 46 % in English, 67 % in Maths, 53 % in Hindi, 72 % in History and 58 % in Economics. As compared to other subject weightage given to Mathematics, then find weightage mean marks of students.

As per question
$$x_1 = 46, x_2 = 67, x_3 = 53, x_4 = 72, x_5 = 58$$
Let weightage of Hindi, History and Economics = x
The weightage of Maths = 2x
and of English = 3x
So, here $$w_1 = 3x, w_2 = 2x, w_3 = x, w_4 = x, w_5 = x$$
Then, weightage arithmetic mean
$$\bar{X} = \frac{\sum x_i w_i}{\sum w_i}$$
$$= \dfrac{w_1 x_1 + w_2 x_2 + w_3 x_3 + w_4 x_4 + w_5 x_5}{w_1 + w_2 + w_3 + w_4 + w_5}$$
$$= \dfrac{(46)(3x) + 67 (2x) + 53x + 72 x + 58 x}{3x + 2x + x + x + x}$$
$$= \dfrac{138x + 134x + 53x + 72x + 58x}{8x}$$
$$= \dfrac{455x}{8x} = \frac{455}{8} = 56.865$$ marks

Four terms are in $$A.P.$$ If sum of numbers is $$50$$ and largest number is four times the smaller one, then find the terms.

Let the 4 numbers are a , a + d , a + 2d , a + 3d.

Sum of 4 numbers AP = 50

a + a + d + a + 2d + a + 3d = 50

⇒ 4a + 6d = 50

⇒ 2a + 3d = 25 --------------(1)

Also given the greatest number is 4 times the least.

4(a) = a + 3d

4a - a = 3d

a = d

putting a = d in (1) , we obtain

5d = 25

d = 5

a = 5 but d = a.

∴ First four terms are 5 , 10 ,15 , 20

Find the sum of the series $$\displaystyle \frac { 1 }{ 1.2 } -\frac { 1 }{ 2.3 } +\frac { 1 }{ 3.4 } -.....\infty $$

Say $$S=\dfrac 1{1.2} + \dfrac1{2.3} + \dfrac1{3.4} +......+\dfrac1{n(n+1)}$$

Now the n-th term of the series, $$t = 1{n(n+1)}$$

or, $$t = \dfrac1n - \dfrac1{(n+1)}$$

So, $$S =$$ $$∑ t$$, as $$ n $$ runs from $$1$$ to $$n$$

or, $$S = ∑{ \dfrac1n - \dfrac1{(n+1)} }$$ , as $$n$$ runs from $$1$$ to$$n$$

or, $$S = (1 - \dfrac12) + (\dfrac12 -\dfrac13) + ..... + (\dfrac1n - \dfrac1{(n+1)})$$

or, $$S = 1 - \dfrac1{(n+1)}$$

As n tends to infinity, $$\dfrac1{(n+1)}$$ tends to $$0$$

Thus the required value of the sum is $$1$$

Simplify : $$15\times \left( -25 \right) \times \left( -4 \right) \times \left( -10 \right) $$

$$=15\times \left(-25\times -4\right)\times -10$$

$$=15\times 100\times -10$$

$$=15\times -1000$$

$$=-15000$$

$$1^{3}+2^{3}+3^{3}+.....+n^{3}$$

1311846_1588501_ans_676a1a4af6c54955b6d938a39548446c.jpg

The fourth term of a G.P. is 27 and the 7th term is 729, find the G.P.

Let the series be $$a,ar,ar^2\cdots $$

$$\implies ar^3=27\cdots (1)$$

$$\implies ar^6=729 \cdots (2)$$

$$(2)\div (1)$$

$$\dfrac{ar^6}{ar^3}=\dfrac{729}{27}$$

$$r^3=27$$

$$\implies r=\sqrt[3]{27}$$

$$r=3$$

$$\implies a=1$$

So the series is

$$1, 1 \times 3, 1 \times3^2,...... \implies1,3,9,.....$$

The seventh term of a G.P. is 8 times the fourth term and 5th term isFind the G.P.

Let the series be $$a,ar,ar^2\cdots $$

$$\implies ar^6=8ar^3$$

$$r^3=8$$

$$\implies r=\sqrt[3]8$$

$$r=2$$

$$\implies ar^4=48$$

$$a(2)^4=48$$

$$16a=48$$

$$\implies a=3$$

So the series is

$$3, 3 \times 2, 3 \times 2^2, ......\implies3,6,12,.....$$

Find AM of $$12$$ and $$14$$.

Let $$a=12$$ and $$b=14$$

AM$$=\dfrac{a+b}2$$

= $$\dfrac{12+14}2=\dfrac {26}2=13$$

Find AM of $$15$$ and $$-13$$.

Let, $$a=15$$ and $$b=-13$$

AM$$=\dfrac{a+b}2$$

=$$\dfrac{15-13}2=\dfrac {2}2=1$$

Find the sum of the series whose nth term is :
$$n^{3}-3^{n}$$

$$\sum n^3 - \sum 3^n$$

$$=\dfrac{n^2(n+1)^2}{4} - 3 . \dfrac{(3^n-1)}{(3-1)}$$

$$=\left[ \dfrac{n(n+1)}{2}\right]^2 - \dfrac{3}{2} . (3^n - 1 )$$

Find AM of $$7$$ and $$27$$.

Let $$a=7$$ and $$b=27$$

AM$$=\dfrac{a+b}2$$

= $$\dfrac{7+27}2=\dfrac {34}2=17$$

Find the sum of the series whose nth term is:
$$n(n+1)(n+4)$$

$$T_n=n(n+1)(n+4)$$

$$T_n=n^3+5n^2+4n$$

$$S_n=\sum n^3+5\sum n^2+4\sum n$$

$$=\left[\dfrac{n(n+1)}{2}\right]^2+\dfrac{5n(n+1)(2n+1)}{8}+\dfrac{4n(n+1)}{2}$$

$$=\dfrac{n(n+1)}{2}\left[\dfrac{n^2+n}{2}+\dfrac{5}{3}(2n+1)+4\right]$$

$$=\dfrac{n(n+1)}{2}\left[\dfrac{3n^2+23n+34}{6}\right]$$

$$=\dfrac{n(n+1)}{2}(3n^2+23n+34)$$.

1446963_1667348_ans_85c7a70ecf744e0f91ce6d0d81172d97.jpg

Find the arithmetic mean between $$9$$ and $$19$$.

As we know, arithmetic mean between $$a$$ & $$b$$ is $$=\dfrac{a+b}{2}$$
arithmetic mean$$=\dfrac{9+19}{2}=14$$

Find the sum of the series whose nth term is:
$$(2n-1)^{2}$$

1449552_1667350_ans_88fb7c9df952459d803beb88b3995acb.jpg

Find the sum of the series whose nth term is:
$$2n^{3}+3n^{2}-1$$

$$T_n=2n^3+3n^2-1$$

$$\because \sum T_n=S_n$$

so, $$S_n=\sum (2n^3+3n^2-1)$$

$$=2\sum n^3+3\sum n^2-\sum 1$$

$$=2\left[\dfrac{n(n+1)}{2}\right]^2+3\left[\dfrac{n(n+1)(2n+1)}{6}\right]-n$$

$$=\dfrac{n^2(n+1)^2}{2}+\dfrac{n(n+1)(2n+1)}{2}-n$$

$$=\dfrac{n(n+1)}{2}[n^2+n+2n+1[-n$$

$$=\dfrac{n(n+1)(n^2+3n+1)}{2}-n$$

$$=\dfrac{n}{2}(n^3+4n^2+4n-1)$$.

Find the sum of the following series to n terms:
$$1.2.4+2.3.7+3.4.10+...$$

Let $$T_n$$ be the terms of the given series.

Then

$$T_n (n^{th}\ term\ of\ 1,2,3...)\times (n^{th}\ term\ of\ 2,3,4...)\times (n^{th}\ term\ of\ 2,3,4...)$$

$$=[1+(n-1)\times 1].[2+(n-1)\times 1] [4+(n-1)\times 3]$$

$$=[1+n-1][2+n-1][4+3n-3]$$

$$=n (n+1)(3n+1)$$

$$=3n^3+n^2 +3n^2+n$$

$$=3n^3+4n^2 +n$$

$$T_n =3n^3+4n^2+n$$

Let $$S_n$$ denoted sum of $$n$$ terms of the given series

$$S_n =\displaystyle \sum _{n=1}^{n} T_n =\displaystyle \sum _{n=1}^{n}n^2 +\displaystyle \sum _{n=1}^{n}n$$

$$=\dfrac{3}{1} \left [\dfrac {n(n+1)}{2}\right]^2 +4\left [\dfrac {n(n+1) (2n+1)}{6}\right]+\dfrac {n(n+1)}{2}$$

$$=\dfrac {3}{4}[n(n+1)]^2+\dfrac {2n (n+1) (2n+1)}{3}+\dfrac {n(n+1)}{2}$$

$$=\dfrac {n}{12}(n+1)[9n^2 +9n+16n+8+6]$$

$$S_n =\dfrac {n}{12}(n+1)[9n^2+25n+14]$$

Find the $$20^{th}$$ term and the sum of 20 terms of the series : $$2\times 4+4\times 6+6\times 8+...$$

$$n$$th term of $$2,4,6...... $$ is

This is in AP

Here $$a=2$$

common difference $$(d)=4-2=2 $$

$$nth $$ term is $$=a+(n-1)d $$

$$=2+(n-1)2=2+2n-2=2n$$

$$n$$th term of $$4,6, 8...... $$ is

This is in AP

Here $$a=4$$

common difference $$(d)=6-4=2 $$

$$nth $$ term is $$=a+(n-1)d $$

$$=4+(n-1)2=4+2n-2=2n+2$$

$$a_n$$=nth term of $$2,4,6...... \times $$ nth term of $$4,6, 8...... $$

$$=2n(2n+2)=4n(4n+1)$$

We should find 20th term so

Put $$n=20$$

$$a_20=20 \times 4 (4 \times 20+1)=1680$$

$$S_n=\sum (4n^2+4n) $$

$$S_n=4 \sum n^2+4 \sum n$$

$$S_{20}=\dfrac{4 \times 20 \times 21 \times 41}{6}+\dfrac{4 \times 20 \times 21}{2}$$

$$S_{20}=11480+840=12320$$

Sum of the 20 terms in the series is $$12320$$

An insect is on $$0$$ point of a number line, hopping towards $$1$$. She covers half the distance from her current location to $$1$$ with each hop. So, she will be at $$1/2$$ after one hop, $$3/4$$ after two hops, and so on.
Where will the insect be after $$n$$ hops?

If we see the distance covered in each hops

Distance covered in $$1^{st}$$ hop $$\cfrac12=1-\dfrac 12$$

Distance covered in $$2^{nd}$$ hop $$\cfrac12+\cfrac14=\cfrac34=1-\dfrac 14=\cfrac{1}{2^2}$$

Similarly, Distance covered in $$3^{rd}$$ hop $$=1-\dfrac 18=1-\cfrac1{2^3}$$

observing this pattern we can say that,

Distance covered in $$n$$ hop $$=1-\left(\dfrac 12\right)^n$$

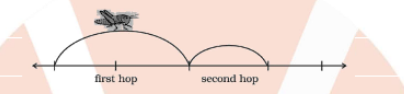
Which of the following form of an A.P.? Justify your answer.
-1, -1, -1, -1, .......

Hint:- In an A.P. common difference between each consecutive terms will always be equal.

Given:-

Sequence:- $$-1, -1, -1, -1, .......$$

Here,

Second term $$-$$ first term $$=-1-(-1)=-1+1=0$$

Third term $$-$$ second term $$=-1-(-1)=-1+1=0$$

Fourth term $$-$$ third term $$=-1-(-1)=-1+1=0$$

Since, all of the differences are equal to each other

Hence, the given sequence forms an A.P.

Justify whether it is true to say that $$-1, \dfrac{-3}{2}, -2, \dfrac{5}{2}, .....$$ forms an A.P. as $$a_2-a_1= a_3-a_2$$.

Hint:- In an A.P. common difference between each consecutive terms will always be equal.

Given:-
Sequence:- $$-1, \dfrac{-3}{2}, -2, \dfrac{5}{2}, .....$$

Here,

Second term $$-$$ first term $$=a_2-a_1=\dfrac {-3}{2}- (-1)=\dfrac {-3+2}{2}=\dfrac {-1}{2}$$

Third term $$-$$ second term $$=a_3-a_2=-2- \left (\dfrac {-3}{2} \right )=\dfrac {-4+3}{2}=\dfrac {-1}{2}$$

Fourth term $$-$$ third term $$=a_4-a_3=\dfrac {5}{2}-(-2)=\dfrac {5+4}{2}=\dfrac 92$$

Here, we can see $$a_2-a_1=a_3-a_2=\dfrac {-1}{2}$$ but $$a_4-a_3=\dfrac 92 \neq \dfrac {-1}{2} $$

Hence, the above sequence doesn't form an A.P.

The time taken by Rohan in five different races to run a distance of 500 m was 3.20 minutes, 3.37 minutes, 3.29 minutes, 3.17 minutes and 3.32 minutes. Find the average time taken by him in the races.

Total time taken by Rohan in five races

= (3.20 +3.37 +3.29 +3.17 +3.32] minutes

= 16.35 minutes

Total number of races = 5

∴ The average time taken by Rohan

= 16.35/5 minutes

= 3.27 minutes.

Find the arithmetic mean between $$15$$ and $$-7$$.

As we know, arithmetic mean between $$a$$ & $$b$$ is $$=\dfrac{a+b}{2}$$
$$mean=\dfrac{15-7}{2}=4$$

Find the arithmetic mean between $$-16$$ and $$-8$$.

As we know, arithmetic mean between $$a$$ & $$b$$ is $$=\dfrac{a+b}{2}$$
$$mean=\dfrac{-16+(-8)}{2}=-12$$

Find the geometric progression whose $$4^{\text {th }}$$ term is 54 and the $$7^{\text {th }}$$ term is 1458.

From the question it is given that,

$$4^{\text {th }}$$ term

$$a_{4}=54$$

$$7^{\text {th }}$$

term $$a_{7}=1458$$

$$a r^{3}=54$$

$$a r^{6}=1458$$

Now dividing we get,

$$a r^{6} / a r^{3}=(1458 / 54)$$

$$r^{6-3}=27$$

$$r^{3}=3^{3}$$

$$r=3$$

Then, $$a r^{3}=54$$

$$a \times 27=54$$

$$a=54 / 27$$

$$a=2$$

Therefore G.P. is $$2,6,18,54, \ldots$$

In which of the following situations do the list of numbers involved form an A.P.?
Give reasons for your answers.
The number of bacteria in a certain food item after each second, when they double in every second.

Let the number of bacteria present initially $$= x$$
Then, the number of bacteria preset after 1 sec $$= 2(x) = 2x $$
Number of bacteria present after 2 seconds $$2(2x) = 4x $$
Number of bacteria present after 3 seconds $$= 2(4x) = 8x $$
Number of bacteria present after 4 seconds $$= 2(8x) = 16x $$
So, the number of bacteria from starting to end of each second are given by $$x, 2x, 4x, 8x, 16x,....$$
Now $$d_1 = 2x-x=x,, d_2=4x-2x=2x$$
As $$d_1 \neq d_2$$, so the list of numbers does not from an A.P.

Let $$S$$ denote sum of the series $$\dfrac{3}{2^3} + \dfrac{4}{2^3} + \dfrac{5}{2^3} + \dfrac{6}{2^5} + ... \infty$$. Then the value of $$S^{-1}$$ is.

Given infinite series is,

$$\dfrac{3}{2^3} + \dfrac{4}{2^4. 3} + \dfrac{5}{2^6. 3} + \dfrac{6}{2^7. 5} + ... \infty$$.

The general term is,

$$T_r= \dfrac{r + 2}{2^{r + 1}. r. (r + 1)}$$

$$\therefore S = \displaystyle\sum_{r = 1}^{\infty} \dfrac{r + 2}{2^{r + 1}. r. (r + 1)}\\ \Rightarrow S= \displaystyle\sum_{r = 1}^{\infty} \dfrac{2(r + 1) - r}{2^{r + 1}. r. (r + 1)}\\ \Rightarrow S= \displaystyle\sum_{r = 1}^{\infty} \dfrac{1}{2^{r + 1}}\left(\dfrac{2}{r} - \dfrac{1}{r + 1}\right)\\ \Rightarrow S= \displaystyle \sum_{r = 1}^{\infty}\left(\dfrac{1}{2^r. r} - {\dfrac{1}{2^{r + 1}(r + 1)}}\right)\\ \Rightarrow S= \underset{n \rightarrow \infty}{Lim}\left[\left(\dfrac{1}{2^1. 1} - \dfrac{1}{2^2. 2}\right) + \left(\dfrac{1}{2^2.2} - \dfrac{1}{2^3. 3}\right)+ \left(\dfrac{1}{2^3. 3} - \dfrac{1}{2^4. 4}\right) + \dots + \left( \dfrac{1}{2^n} - \dfrac{1}{2^{n + 1}.(n + 1)}\right)\right]\\ \Rightarrow S= \underset{n \rightarrow \infty}{Lim} \left(\dfrac{1}{2} - \dfrac{1}{2^{n + 1} (n + 1)}\right)\\ \Rightarrow S = \dfrac{1}{2}$$

Hence, $$S^{-1} = 2$$.

The sum of first $$n$$ natural numbers is given by
$$\cfrac { 1 }{ 2 } {n}^{2}+\cfrac { 1 }{ 2 } n$$. Find
The sum of first $$5$$ natural numbers

$$\textbf{Put } n=5 \textbf{ in the given expression}$$
Sum of first n natural numbers is given by $$\cfrac { 1 }{ 2 } {n}^{2}+\cfrac { 1 }{ 2 } n$$.
Therefore, the sum of first $$5$$ natural numbers will be
$$\begin{aligned}&=\frac{1}{2} \times 5^{2}+\frac{1}{2} \times 5 \\&=\frac{25}{2}+\frac{5}{2} \\&=\frac{30}{2} \\&=15\end{aligned}$$
$$\textbf{Hence, the sum of first 5 natural numbers is 15.}$$

Fourth and seventh terms of a G.P. are $$ \dfrac{1}{18} $$ and $$ \dfrac{-1}{486} $$ respectively. Find the G.P.

Given ,
$$ t_4 = \dfrac{1}{18} $$ and $$ t_7 = \dfrac{-1}{486} $$
We know that, the general term is
$$ t_n = ar^{n - 1} $$
So ,
$$ t_4 = ar^{4 - 1} = ar^3 = \dfrac{1}{18} $$ ........... (1)
And,
$$ t_7 = ar^{7 - 1} = ar^6 = \dfrac{-1}{486} $$ .......... (2)
Dividing (2) by (1) , we have
$$ \dfrac{ar^6}{ar^3} = \dfrac{(-1/486)}{(1/18)} $$

$$ r^3 = \dfrac{-1}{27} $$

$$ r = \dfrac{-1}{3} $$

Using $$r$$ in (1) , we get
$$ a \left ( \dfrac{-1}{3} \right )^3 = \dfrac{1}{18} $$
$$ a = \dfrac{-27}{18} = \dfrac{-3}{2} $$

Hence , the G.P. is
$$ \dfrac{-3}{2} , \dfrac{-3}{2(-1/3)} , \dfrac{-3}{2 (-1/3)^2} , \dfrac{-3}{2(-1/3)^3} , $$ ...........

$$ \dfrac{-3}{2} , \dfrac{1}{2} , \dfrac{-1}{6} , \dfrac{1}{18} $$ ,...........

Define\space geometric progression.

1897433_1865437_ans_1f7b301d58e8418287ac8a013d4ef5cb.jpeg

If $$n$$ arithmetic mean are inserted in between $$1$$ and $$51$$ such that ratio of $$4th$$ and $$7th$$ arithmetic mean is $$3:5$$ then find the value of $$n$$.

$$l= a+ (n-1)d$$
$$\implies (n+1)d= 50$$

$$\implies \ d= \dfrac{50}{n+1}$$

$$A_4= \dfrac{n+201}{n+1}$$

$$A_7= \dfrac{n+ 351}{n+1}$$

According to question, $$\dfrac{A_4}{A_7}= \dfrac35$$

$$n= 24$$

Find the G.P. $$ \dfrac{1}{27} , \dfrac{1}{9} , \dfrac{1}{3} $$ , ............. $$81$$ ; find the product of fourth term from the beginning and the fourth term from the end.

$$ \dfrac{1}{27} , \dfrac{1}{9} , \dfrac{1}{3} $$ , ............. $$81$$
Here , $$ a = \dfrac{1}{27} $$ , common ratio $$ (r) = \dfrac{(1/9)}{(1/27)} = 3 $$ and $$ l = 81 $$
We know that ,
$$ l = t_n = ar^{n - 1} = 81 $$
$$ (1/27)(3)^{n - 1} = 81 $$
$$ 3^{n - 1} = 81 \times 27 = 2187 $$
$$ 3^{n - 1} = 3^7 $$
$$ n - 1 =7 $$
$$ n = 8 $$
Hence , there are $$8$$ terms in the given G.P.
Now,
$$ 4^{th} $$ term from the beginning is $$ t_4 $$ and the $$ 4^{th} $$ term from the end is $$ (8 - 4 + 1) = 5^{th} $$ term $$ (t_s) $$
Thus,
The product of $$ t_4 $$ and $$ t_5 = ar^{4 - 1} \times ar^{5 - 1} $$

$$= ar^3 \times ar^4 = a^2r^7 = (1 / 27)^2(3)^7 = 3 $$

Simplify $$1+\dfrac{1}{3}.\dfrac{1}{4}+\dfrac{1.4}{3.6}.\dfrac{1}{4^2}+...$$

On comparing the given series with the series

$$1+nx+\dfrac{n(n-1)}{2!}x^2+...$$

$$nx=\dfrac{1}{12}$$

$$\Rightarrow \dfrac{1}{n^2x^2}=144$$ ........(i)

and $$\dfrac{n(n-1)}{2!}x^2=\dfrac{1.4}{3.6}.\dfrac{1}{4^2}$$

$$\Rightarrow \dfrac{n(n-1)}{2}x^2=\dfrac{1}{72}$$ ..........(ii)

Multiplying equation (i) and (ii)

$$\dfrac{n(n-1)}{2}x^2 \times \dfrac{1}{n^2x^2}=\dfrac{1}{72} \times 144$$

$$\Rightarrow \dfrac{(n-1)}{2n}=2$$

$$\Rightarrow n-1=4n$$

$$\Rightarrow n=\dfrac{-1}{3}$$

From equation (i)

$$\Bigg(\dfrac{-1}{3}\Bigg) \times x=\dfrac{1}{12}$$

$$\Rightarrow x=\dfrac{-1}{4}$$

Hence, sum of the given series

$$=(1+x)^n=\bigg(1-\dfrac{1}{4}\bigg)^{-1/3}$$

$$=\bigg(\dfrac{4}{3}\bigg)^{1/3}$$

Find the arithmetic mean of:
$$(m + n)^2$$ and $$(m n)^2$$

Arithmetic mean of $$(m + n)^2$$ and $$(m – n)^2$$

$$=\dfrac{(m+n)^2+(m-n)^2}{2}$$

$$=\dfrac{m^2+n^2+2mn+m^2+n^2-2mn}{2}$$

$$=\dfrac{2(m^2+n^2)}{2}$$

$$=m^2+n^2$$

Write the formula to find arithmetic mean of $$3$$ numbers

Let $$3$$ nos. in an $$A.P.$$ be $$a,b,c$$

So, formula for arithmetic mean is given by:

$$AM = \dfrac{a + b + c}{3}$$

Find the arithmetic mean of:
$$3x 2y$$ and $$3x + 2y$$

Arithmetic mean of $$(3x – 3y)$$ and $$(3x + 2y) = [(3x – 3y) + (3x + 2y)]/ 2 = 6x/ 2 = 3x$$

Find the arithmetic mean of:
$$-5$$ and $$41$$

Arithmetic mean of $$-5$$ and $$41 = (-5 + 41)/ 2 = 36/3 = 18$$

the mean $$\bar{x}$$

The given numbers are $$9.8, 5.4, 3.7, 1.7, 1.8, 2.6, 2.8, 8.6, 10.5$$ and $$11.1$$;
$$\bar{x} = \frac{x1 + x2 + x3 + x5 + ..... + xn}{n}$$
$$= \frac{9.8 + 5.4 + 3.7 + 1.7 + 1.8 + 2.6 + 2.8 + 8.6 + 10.5 +11.1}{10}$$
$$= 5.8$$

Prove that :
$$\sqrt{2}=1+\dfrac{1}{2^2}+\dfrac{1.3}{2! . 2^4}+\dfrac{1.3.5}{3! . 2^6}+...$$

On comparing the given series with the series

$$1+nx+\dfrac{n(n-1)}{2!}x^2+...$$

$$nx=\dfrac{1}{4}$$

$$\Rightarrow \dfrac{1}{n^2x^2}=16$$ ........(i)

and $$\dfrac{n(n-1)}{2!}x^2=\dfrac{1.3}{2! . 2^4}$$

$$\Rightarrow \dfrac{n(n-1)}{2}x^2=\dfrac{3}{32}$$ ..........(ii)

Multiplying equation (i) and (ii)

$$\dfrac{n(n-1)}{2}x^2 \times \dfrac{1}{n^2x^2}=\dfrac{3}{32} \times 16$$

$$\Rightarrow \dfrac{(n-1)}{2n}=\dfrac{3}{2}$$

$$\Rightarrow 2n-2=6n$$

$$\Rightarrow n=\dfrac{-1}{2}$$

From equation (i)

$$\Bigg(\dfrac{-1}{2}\Bigg) \times x=\dfrac{1}{4}$$

$$\Rightarrow x=\dfrac{-1}{2}$$

Hence, the sum of the given series

$$=(1+x)^n=\bigg(1-\dfrac{1}{2}\bigg)^{-1/2}$$

$$=\sqrt{2}$$

Simplify $$1+\dfrac{1}{10}+\dfrac{1.4}{10.20}+\dfrac{1.4.7}{10.20.30}+...$$

On comparing the given series with the series

$$1+nx+\dfrac{n(n-1)}{2!}x^2+...$$

$$nx=\dfrac{1}{10}$$

$$\Rightarrow \dfrac{1}{n^2x^2}=100$$ ........(i)

and $$\dfrac{n(n-1)}{2!}x^2=\dfrac{1.4}{10.20}$$

$$\Rightarrow \dfrac{n(n-1)}{2}x^2=\dfrac{1}{50}$$ ..........(ii)

Multiplying equation (i) and (ii)

$$\dfrac{n(n-1)}{2}x^2 \times \dfrac{1}{n^2x^2}=\dfrac{1}{50} \times 100$$

$$\Rightarrow \dfrac{(n-1)}{2n}=2$$

$$\Rightarrow n-1=4n$$

$$\Rightarrow n=\dfrac{-1}{3}$$

From equation (i)

$$\Bigg(\dfrac{-1}{3}\Bigg) \times x=\dfrac{1}{10}$$

$$\Rightarrow x=\dfrac{-3}{10}$$

Hence, sum of the given series

$$=(1+x)^n=\bigg(1-\dfrac{3}{10}\bigg)^{-1/3}$$

$$=\bigg(\dfrac{10}{7}\bigg)^{1/3}$$

Prove that:
$$\dfrac{5\sqrt{2}}{7}=1+\dfrac{1}{10^2}+\dfrac{1.3}{1.2}\dfrac{1}{10^4}+...$$

On comparing the given series with the series

$$1+nx+\dfrac{n(n-1)}{2!}x^2+...$$

$$nx=\dfrac{1}{10^2}$$

$$\Rightarrow \dfrac{1}{n^2x^2}=10^4$$ ........(i)

and $$\dfrac{n(n-1)}{2!}x^2=\dfrac{1.3}{1.2}\dfrac{1}{10^4}$$

$$\Rightarrow \dfrac{n(n-1)}{2}x^2=\dfrac{3}{2 \times 10^4}$$ ..........(ii)

Multiplying equation (i) and (ii)

$$\dfrac{n(n-1)}{2}x^2 \times \dfrac{1}{n^2x^2}=\dfrac{3}{2 \times 10^4} \times 10^4$$

$$\Rightarrow \dfrac{(n-1)}{2n}=\dfrac{3}{2}$$

$$\Rightarrow 2n-2=6n$$

$$\Rightarrow n=\dfrac{-1}{2}$$

From equation (i)

$$\Bigg(\dfrac{-1}{2}\Bigg) \times x=\dfrac{1}{10^2}$$

$$\Rightarrow x=\dfrac{-1}{50}$$

Hence, the sum of the given series

$$=(1+x)^n=\bigg(1-\dfrac{1}{50}\bigg)^{-1/2}$$

$$=\dfrac{5\sqrt{2}}{7}$$

$$1+\dfrac{1}{4}+\dfrac{1.4}{4.8}+\dfrac{1.4.7}{4.8.12}+...$$

We know,

$$(1-x)^{-n}=1-n(-x)+\dfrac{-n(-n-1)x^2}{2!}...\infty

=1+nx+\dfrac{n(n+1)x^2}{2!}...\infty$$

Comparing the coefficients with that given in the question, we get.

$$\Rightarrow$$ $$nx=\dfrac{1}{4}$$ ...(i)

$$\Rightarrow$$ $$\dfrac{n(n+1)x^2}{2}=\dfrac{1}{8}$$ ...(ii)

Substituting the value of nxnx from Eq (i) in Eq (ii), we get

$$8nx^2(n+1)=2$$

$$4nx(n+1)x=1$$

$$(n+1)(x)=1$$

$$nx=1-x$$

$$\dfrac{1}{4}=1-x$$

$$x=\dfrac{3}{4}$$

Since $$nx=\dfrac{1}{4}$$

$$n=\dfrac{1}{3}$$

Substituting in the original equation, the values of n and x, we get

$$\Rightarrow(1-\dfrac{3}{4})^{\frac{-1}{3}}$$

$$=(4^{-1})^{\frac{-1}{3}}$$

$$=(4)^{\frac{1}{3}}$$

Simplify $$1-\dfrac{1}{2}.\dfrac{1}{2}+\dfrac{1.3}{2.4}\bigg(\dfrac{1}{2}\bigg)^2-\dfrac{1.3.5}{2.4.6}\bigg(\dfrac{1}{2}\bigg)^3+...$$

On comparing the given series with the series

$$1+nx+\dfrac{n(n-1)}{2!}x^2+...$$

$$nx=\dfrac{-1}{4}$$

$$\Rightarrow \dfrac{1}{n^2x^2}=16$$ ........(i)

and $$\dfrac{n(n-1)}{2!}x^2=\dfrac{1.3}{2.4}\bigg(\dfrac{1}{2}\bigg)^2$$

$$\Rightarrow \dfrac{n(n-1)}{2}x^2=\dfrac{3}{32}$$ ..........(ii)

Multiplying equation (i) and (ii)

$$\dfrac{n(n-1)}{2}x^2 \times \dfrac{1}{n^2x^2}=\dfrac{3}{32} \times 16$$

$$\Rightarrow \dfrac{(n-1)}{2n}=\dfrac{3}{2}$$

$$\Rightarrow 2n-2=6n$$

$$\Rightarrow n=\dfrac{-1}{2}$$

From equation (i)

$$\Bigg(\dfrac{-1}{2}\Bigg) \times x=\dfrac{-1}{4}$$

$$\Rightarrow x=\dfrac{1}{2}$$

Hence, the sum of the given series

$$=(1+x)^n=\bigg(1+\dfrac{1}{2}\bigg)^{-1/2}$$

$$=\sqrt{\dfrac{2}{3}}$$

Prove that:
$$\bigg(\dfrac{3}{2}\bigg)^{1/3}=1+\dfrac{1}{3^2}+\dfrac{1.4}{1.2}.\dfrac{1}{3^4}+\dfrac{1.4.7}{1.2.3}.\dfrac{1}{3^6}+...$$

On comparing the given series with the series

$$1+nx+\dfrac{n(n-1)}{2!}x^2+...$$

$$nx=\dfrac{1}{3^2}$$

$$\Rightarrow n^2x^2=\dfrac{1}{3^4}$$ ........(i)

and $$\dfrac{n(n-1)}{2!}x^2=\dfrac{1.4}{1.2}.\dfrac{1}{3^4}$$

$$\Rightarrow \dfrac{n(n-1)}{2}x^2=\dfrac{4}{2 \times 3^4}$$ ..........(ii)

Dividing equation (ii) and (i)

$$\dfrac{n(n-1)}{2}x^2 \times \dfrac{1}{n^2x^2}=\dfrac{4}{2 \times 3^4} \times 3^4$$

$$\Rightarrow \dfrac{(n-1)}{2n}=2$$

$$\Rightarrow n-1=4n$$

$$\Rightarrow n=\dfrac{-1}{3}$$

From equation (i)

$$\Bigg(\dfrac{-1}{3}\Bigg) \times x=\dfrac{1}{3^2}$$

$$\Rightarrow x=\dfrac{-1}{3}$$

Hence, the sum of the given series

$$=(1+x)^n=\bigg(1-\dfrac{1}{3}\bigg)^{-1/3}$$

$$=\dfrac{3}{2}^{1/3}$$

Prove that:
$$(1+x)^n=2^n\Bigg[1-\dfrac{n(1-x)}{(1+x)}+\dfrac{n(n+1)}{2!}\Bigg(\dfrac{1-x}{1+x}\Bigg)^2-\,...\Bigg]$$

$$R.H.S.$$

$$=2^n\Bigg[1-\dfrac{n(1-x)}{(1+x)}+\dfrac{n(n+1)}{2!}\Bigg(\dfrac{1-x}{1+x}\Bigg)^2-\,...\Bigg]$$

$$=2^n\Bigg[1+\dfrac{(1-x)}{(1+x)}\Bigg]^{-n}$$

$$\Bigg[Formula\,(1+x)^{-n}=1-nx+\dfrac{n(n+1)}{2!}x^2+\,...\Bigg]$$

$$=2^n\Bigg[\dfrac{1+x+1-x}{(1+x)}\Bigg]^{-n}=2^n\bigg(\dfrac{2}{1+x}\bigg)^{-n}$$

$$2^n\bigg(\dfrac{1+x}{2}\bigg)^{n}=2^n \times \dfrac{(1+x)^n}{2^n}$$

$$=(1+x)^n=L.H.S.$$

Evaluate $$S=1+\dfrac{4}{5}+\dfrac{7}{5^2}+\dfrac{10}{5^3}+......$$ to infinite terms. Find $$16S$$

$$S=1+\dfrac{4}{5}+\dfrac{7}{5^2}+\dfrac{10}{5^3}+......$$

Now, Dividing this equation by $$5$$

$$\dfrac S5=\dfrac15+\dfrac{4}{5^2}+\dfrac{7}{5^3}+..............$$

Subtracting the Above Equations , we get

$$S-\dfrac S5=1+\dfrac35+\dfrac{3}{5^2}+\dfrac{3}{5^3}...........\Rightarrow 4\dfrac S5=1+3(\dfrac{1}{5}+\dfrac{1}{5^2}+\dfrac{1}{5^3}.............)\\ \Rightarrow \dfrac{4S}{5}=1+3(\dfrac{1/5}{1-1/5})\\\Rightarrow \dfrac{4S}{5}=1+\dfrac{3}{4}\\\Rightarrow S=\dfrac{35}{16}\\\Rightarrow 16S=35$$

Find the sum of $$n$$ terms of $${ 1 }^{ 2 }+\left( { 1 }^{ 2 }+{ 2 }^{ 2 } \right) +\left( { 1 }^{ 2 }+{ 2 }^{ 2 }+{ 3 }^{ 2 } \right) +\left( { 1 }^{ 2 }+{ 2 }^{ 2 }+{ 3 }^{ 2 }+{ 4 }^{ 2 } \right) +...$$ from that find the sum of the first $$10$$ terms

$$1^2 + (1^2+2^2)+(1^2+2^2+3^2)+..........n$$ terms

$$=\sum_{i=1}^{n}(1^2+2^2+.....i^2)$$

$$=\sum_{i=1}^{n}\sum_{j=1}^{i}j^2$$

$$=\sum_{i=1}^{n}\dfrac{i(i+1)(2i+1)}{6}$$

$$=\sum_{i=1}^{n}\dfrac{2i^3+3i^2+i}{6}$$

$$=\sum_{i=1}^{n}\dfrac{1}{3}i^3+\sum_{j=1}^{n}\dfrac{1}{2}j^2+\sum_{k=1}^{n}\dfrac{1}{6}k$$

$$=\dfrac{1}{3}\left ( \dfrac{n^2(n+1)^2}{4} \right )+\dfrac{1}{2}\left ( \dfrac{n(n+1)(2n+1)}{6} \right )+\dfrac{1}{6}\left ( \dfrac{n(n+1)}{2} \right )$$

$$=\dfrac{n^2(n+1)^2}{12} +\dfrac{n(n+1)(2n+1)}{12} +\dfrac{n(n+1)}{12}$$

$$=\dfrac{n^2(n+1)^2+n(n+1)(2n+1)+n(n+1)}{12}$$

$$=\dfrac{n(n+1)^2(n+2)}{12}$$

$$\therefore S_{10}=\dfrac{10(10+1)^2(10+2)}{12}$$

$$=\dfrac{10(11)^2(12)}{12}$$

$$=1210$$

What is the value of ($${2^2+ 4^2+ 6^2 +... + 20^2}$$)-($${1^2 + 3^2 + 5^2+ ... + 19^2}$$)?

$$({ 2 }^{ 2 }+{ 4 }^{ 2 }+....+{ 20 }^{ 2 })-({ 1 }^{ 2 }+{ 3 }^{ 2 }+...+{ 19 }^{ 2 })\quad can\quad be\quad broken\quad as,\\ ({ 2 }^{ 2 }-{ 1 }^{ 2 })+....+({ 20 }^{ 2 }-{ 19 }^{ 2 }),\quad using\quad ({ a }^{ 2 }-{ b }^{ 2 })=(a+b)(a-b),\\ \Longrightarrow (2+1)(1)+(3+4)(1)+....+(20+19)(1),\\ \Longrightarrow 3+7+....39,\quad arithmetic\quad progression\quad with\quad 10\quad terms,\\ \Longrightarrow \dfrac {10}2(3+39)=210$$

Show that the $$3{ n }^{ th }$$ convergent to
$$\dfrac { 1 }{ 5- } \dfrac { 1 }{ 2- } \dfrac { 1 }{ 1- } \dfrac { 1 }{ 5- } \dfrac { 1 }{ 2- } \dfrac { 1 }{ 1- } \dfrac { 1 }{ 5- } \cdots $$ is $$\dfrac { n }{ 3n+1 } $$.

We have

$${ p }_{ 3n }={ p }_{ 3n-1 }-{ p }_{ 3n-2 };$$

$${ p }_{ 3n-1 }=2{ p }_{ 3n-2 }-{ p }_{ 3n-3 };$$

$${ p }_{ 3n-2 }=5{ p }_{ 3n-3 }-{ p }_{ 3n-4 };$$

$${ p }_{ 3n-3 }={ p }_{ 3n-4 }-{ p }_{ 3n-5 };$$

$${ p }_{ 3n-4 }=2{ p }_{ 3n-5 }-{ p }_{ 3n-6 }$$

From the first three equations, $${ p }_{ 3n }=4{ p }_{ 3n-3 }-{ p }_{ 3n-4 };$$

From the last two equations,

$$2{ p }_{ 3n-3 }={ p }_{ 3n-4 }-{ p }_{ 3n-6 }$$

By combining these results we have,

$${ p }_{ 3n }=2{ p }_{ 3n-3 }-{ p }_{ 3n-6 }$$

So that the scale of relation is $$1-2x+{ x }^{ 2 }$$

$${ p }_{ 3 }=1,{ q }_{ 3 }=4,{ p }_{ 6 }=2,{ q }_{ 6 }=7.....$$

$$\therefore { p }_{ 3 }+{ p }_{ 6 }x+{ p }_{ 9 }{ x }^{ 2 }+.....+{ p }_{ 3n }{ x }^{ n-1 }+....=\cfrac { { p }_{ 3 }+\left( { p }_{ 6 }-2{ p }_{ 3 } \right) x }{ 1-2x+{ x }^{ 2 } } =\cfrac { 1 }{ 1-2x+{ x }^{ 2 } } $$

Similarly, $${ q }_{ 3 }+{ q }_{ 6 }x+....+{ q }_{ 3n }{ x }^{ n-1 }+.....$$

$$=\cfrac { 4-x }{ 1-2x+{ x }^{ 2 } } $$

$$\therefore { p }_{ 3n }=n,$$

$${ q }_{ 3n }=4n-\left( n-1 \right) =3n+1$$

Find the sum of $$\displaystyle\frac{1}{(1+x)(1+ax)}+\frac{a}{(1+ax)(1+a^2x)}+\frac{a^2}{(1+a^2x)(1+a^3x)}+....$$ to $$n$$ terms.

The $$n^{th}$$ term$$=\displaystyle\frac{a^{n-1}}{(1+a^{n-1}x)(1+a^nx)}=\frac{A}{1+a^{n-1}x}+\frac{B}{1+a^nx}$$ suppose$$;$$
$$\therefore a^{n-1}=A(1+a^nx)+B(1+a^{n-1}x)$$.
Bu putting $$1+a^{n-1}x, 1+a^nx$$ equal to zero in succession, we obtain
$$A=\displaystyle\frac{a^{n-1}}{1-a}, B=-\frac{a^n}{1-a}$$.
Hence $$u_1=\displaystyle\frac{1}{1-a}\left(\displaystyle\frac{1}{1+x}-\frac{a}{1+ax}\right),$$
Similarly$$,$$ $$u_2=\displaystyle\frac{1}{1-a}\left(\displaystyle\frac{a}{1+ax}-\frac{a^2}{1+a^2x}\right),$$
________________________________________
$$u_n=\displaystyle\frac{1}{1-a}\left(\displaystyle\frac{a^{n-1}}{1+a^{n-1}x}-\frac{a^n}{1+a^nx}\right),$$
$$\therefore S_n=\displaystyle\frac{1}{1-a}\left(\displaystyle\frac{1}{1+x}-\frac{a^n}{1+a^nx}\right)$$.

If $$x=a+\displaystyle\frac{1}{b+}\frac{1}{b+}\frac{1}{a+}\frac{1}{a+}....,$$
$$y=b+\displaystyle \frac{1}{a+}\frac{1}{a+}\frac{1}{b+}\frac{1}{b+}....,$$.
Then show that $$(ab^2+a+b)x-(a^2b+a+b)y=a^2-b^2$$.

$$ x-a=\cfrac {Given, 1 }{ b+ } \cfrac { 1 }{ a+ } \cfrac { 1 }{ b+ } \cfrac { 1 }{ a+ } ....$$

$$=\cfrac { 1 }{ b+ } \cfrac { 1 }{ b+y-b } $$

$$\Rightarrow x-a=\cfrac { y }{ by+1 } $$

$$\Rightarrow byx+x-aby-a=y\longrightarrow 1$$

Similarly, $$y-b=\cfrac { 1 }{ a+ } \cfrac { 1 }{ x } =\cfrac { x }{ ax+1 } $$

$$\Rightarrow axy+y-\left( ab+1 \right) x-b=0\longrightarrow 2$$

$$\Rightarrow ax(1)-bx(2):-$$

$$\Rightarrow ax-\left( { a }^{ 2 }b+a \right) y-by+\left( a{ b }^{ 2 }+b \right) x={ a }^{ 2 }-{ b }^{ 2 }$$

$$\Rightarrow \left( a{ b }^{ 2 }+a+b \right) x-\left( { a }^{ 2 }b+a+b \right) y={ a }^{ 2 }-{ b }^{ 2 }$$

Sum the following series to n terms and to infinity $$\displaystyle\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+....$$.

General term ($${ n }^{ th }$$ term) $$=\cfrac { 1 }{ n\left( n+1 \right) } $$

We can rewrite it as $$=\cfrac { n+1-n }{ n\left( n+1 \right) } $$

$$=\cfrac { 1 }{ n } -\cfrac { 1 }{ n+1 } $$

Sum of $$n$$ terms is $$\displaystyle \sum _{ n=1 }^{ n }{ \left[ \cfrac { 1 }{ n } -\cfrac { 1 }{ n+1 } \right] } $$

$$=1+\cfrac { 1 }{ 2 } +\cfrac { 1 }{ 3 } +\cfrac { 1 }{ 4 } +\cfrac { 1 }{ n } .........-\cfrac { 1 }{ 2 } -\cfrac { 1 }{ 3 } -\cfrac { 1 }{ 4 } -\cfrac { 1 }{ n } -\cfrac { 1 }{ n+1 } $$

$$=1-\cfrac { 1 }{ n+1 } $$

Sum to infinity will get by putting $$n\rightarrow \infty $$

Then, $$1-\cfrac { 1 }{ n+1 } $$ $$=1-0=1$$ as $$n\rightarrow \infty $$

Prove that $$ \cos^3 \theta + \cos^3 \left( \theta - \dfrac {2 \pi}{n} \right) + \cos^3 \left( \theta - \dfrac {4 \pi}{n} \right) + ... $$ to $$n$$ terms $$ = 0 $$

As we know that

$$\cos { 3x } =4\cos ^{ 3 }{ x } -3\cos { x } \\ \cos ^{ 3 }{ x } =\dfrac { 3\cos { x } +\cos { 3x } }{ 4 } $$

Using that formula, we can write

$$\cos ^{ 3 }{ \theta } +\cos ^{ 3 }{ (\theta -\dfrac { 2\pi }{ n } ) } +\cos ^{ 3 }{ (\theta -\dfrac { 4\pi }{ n } ) } +...to\quad n\quad terms\\ =\frac { 3[\cos { \theta } +\cos { (\theta -\dfrac { 2\pi }{ n } ) } +\cos { (\theta -\dfrac { 4\pi }{ n } ) } +...to\quad n\quad terms]+[\cos { 3\theta } +\cos { (3\theta -\dfrac { 6\pi }{ n } ) } +\cos { (3\theta -\dfrac { 12\pi }{ n } ) } +...to\quad n\quad terms] }{ 4 } $$

As we seen from the above fromula that if $$\beta =\dfrac { 2\pi N }{ n } \quad where\quad N=1,2,3....$$

So, the sum of both of series is equal to zero.

Hence, $$\cos ^{ 3 }{ \theta } +\cos ^{ 3 }{ (\theta -\dfrac { 2\pi }{ n } ) } +\cos ^{ 3 }{ (\theta -\dfrac { 4\pi }{ n } ) } +...to\quad n\quad terms=0$$

Find Sum of Series $$ \tan^2 x \tan 2x + \dfrac {1}{2} \tan^2 2x \tan 4x + \dfrac {1}{2^2} 4x \tan 8x + ....$$ to $$n$$ terms.

$$f\left( x \right) =\cfrac { \left| x \right| }{ x } -\cfrac { { 2 }^{ { 1 }/{ x } }+1 }{ { 2 }^{ { 1 }/{ x } }-1 } $$

$$\lim _{ x\rightarrow { 0 }^{ + } }{ f\left( x \right) } =\lim _{ x\rightarrow { 0 }^{ + } }{ \left( \cfrac { \left| x \right| }{ x } -\cfrac { { 2 }^{ { 1 }/{ x } }+2-1 }{ { 2 }^{ { 1 }/{ x } }-1 } \right) } $$

$$=\lim _{ x\rightarrow { 0 }^{ + } }{ \left( \cfrac { \left| x \right| }{ x } -1+\cfrac { 2 }{ { 2 }^{ { 1 }/{ x } }-1 } \right) } $$

$$=1-1+\cfrac { 2 }{ { 2 }^{ \infty }-1 } =\cfrac { 2 }{ \infty } =0$$

As $$x\rightarrow { 0 }^{ + },\quad x>0\Rightarrow \cfrac { \left| x \right| }{ x } =1,\cfrac { 1 }{ x } \rightarrow +\infty $$

$$\lim _{ x\rightarrow { 0 }^{ - } }{ f\left( x \right) } =\lim _{ x\rightarrow { 0 }^{ - } }{ \left( \cfrac { \left| x \right| }{ x } -\cfrac { { 2 }^{ { 1 }/{ x } }+1 }{ { 2 }^{ { 1 }/{ x } }-1 } \right) } $$

$$=-1-\cfrac { { 2 }^{ -\infty }+1 }{ { 2 }^{ -\infty }-1 } =-1-\left( \cfrac { \cfrac { 1 }{ \infty } +1 }{ \cfrac { 1 }{ \infty } -1 } \right) $$

$$=-1-\left( \cfrac { 0+1 }{ 0-1 } \right) =-1+1=0$$

As $$x\rightarrow { 0 }^{ - },\quad x<0\Rightarrow \cfrac { \left| x \right| }{ x } =-1,\cfrac { 1 }{ x } \rightarrow -\infty $$

LHL$$=$$ RHL$$=0=f(0)$$ (given)

$$\rightarrow$$ It is continuous at $$x=0$$

Find the sum to infinite terms of the series $$\dfrac {x}{1 - x^{2}} + \dfrac {x^{2}}{1 - x^{4}} + \dfrac {x^{4}}{1 - x^{8}} + .....$$

We need to find value of $$\dfrac{x}{1-x^2}+\dfrac{x^2}{1-x^4}+\dfrac{x^4}{1-x^8}+.....$$

$$=\dfrac{(1+x)-1}{(1+x)(1-x)}+\dfrac{(1+x^2)-1}{(1+x^2)(1-x^2)}+\dfrac{(1+x^4)-1}{(1+x^4)(1-x^4)}+.....$$

$$=\left(\dfrac{1}{1-x}-\dfrac{1}{1-x^2}\right)+\left(\dfrac{1}{1-x^2}-\dfrac{1}{1-x^4}\right)+\left(\dfrac{1}{1-x^4}-\dfrac{1}{1-x^8}\right)+.....$$

$$=\dfrac{1}{1-x}+\left(\dfrac{1}{1-x^2}-\dfrac{1}{1-x^2}\right)+\left(\dfrac{1}{1-x^4}-\dfrac{1}{1-x^4}\right)+.....-\dfrac{1}{1-x^{\infty}}$$

$$=\dfrac{1}{1-x}-\dfrac{1}{1-x^{\infty}}$$

$$=\dfrac{1}{1-x}$$

Therefore, the sum of the given infinite series is $$\dfrac{1}{1-x}$$.

Find the sum of the following infinite series:
$$\displaystyle\sum _{ n=0 }^{ \infty }{ \cfrac { 1 }{ n! } \left[ \sum _{ k=0 }^{ n }{ \left( k+1 \right) \int _{ 0 }^{ 1 }{ { 2 }^{ -\left( k+1 \right) x }dx } } \right] }$$

$$\displaystyle \int _{ 0 }^{ 1 }{ { 2 }^{ -(k+1)x }dx=\left[ \dfrac { { 2 }^{ -(k+1)x } }{ -(k+1)\log { a } } \right] } _{ 0 }^{ 1 }=\dfrac { { 2 }^{ -(k+1) }-1 }{ -(k+1)\log { a } } $$
$$\displaystyle \therefore \sum _{ k=0 }^{ n }{ (k+1). } \left\{ \dfrac { { 2 }^{ -(k+1)x } }{ -(k+1)\log { a } } \right\} $$
$$\displaystyle=\dfrac { 1 }{ \log { a } } \sum _{ k=0 }^{ n }{ \left\{ 1-\dfrac { 1 }{ { 2 }^{ k+1 } } \right\} } $$
$$=\dfrac { 1 }{ \log { a } } \left[ (n+1)-\left\{ \dfrac { 1 }{ 2 } +\dfrac { 1 }{ { 2 }^{ 2 } } +\dfrac { 1 }{ { 2 }^{ 3 } } +...(n+1)\ terms \right\} \right] $$
$$=\dfrac { 1 }{ \log { a } } \left[ (n+1)-\dfrac { \dfrac { 1 }{ 2 } \left\{ 1-\left( \dfrac { 1 }{ 2 } \right) ^{ n+1 } \right\} }{ \left( 1-\dfrac { 1 }{ 2 } \right) } \right] $$
$$=\dfrac { 1 }{ \log { a } } \left[ (n+1)-(1-2^{ -(n+1) }) \right] $$
$$=\dfrac { 1 }{ \log { a } } \left[ n+\left( \dfrac { 1 }{ 2 } \right) ^{ n+1 } \right] $$
$$\displaystyle \therefore S=\dfrac { 1 }{ \log { a } } \sum _{ n=0 }^{ \infty }{ \left[ \dfrac { n }{ n! } +\dfrac { 1 }{ 2 } .\dfrac { \left( \dfrac { 1 }{ 2 } \right) ^{ n } }{ n! } \right] } $$
$$\displaystyle =\dfrac { 1 }{ \log { a } } \sum _{ n=0 }^{ \infty }{ \left[ \dfrac { 1 }{ (n-1)! } +\dfrac { 1 }{ 2 } .\dfrac { { x }^{ n } }{ n! } \right] }, $$
where $$x=\dfrac { 1 }{ 2 } $$
$$=\dfrac { 1 }{ \log { a } } \left[ e+\dfrac { 1 }{ 2 } { e }^{ x } \right] =\dfrac { 1 }{ \log { a } } \left( e+\dfrac { 1 }{ 2 } \sqrt { e } \right) $$

Find $$ \ \sin\theta+\ \sin({\pi}+\theta) +\ \sin(2\pi+\theta) +\ \sin(3\pi+\theta)+ \cdots $$ upto $$2021$$ terms.

$$\sin { \theta } +\sin { (\pi +\theta ) } +\sin { (2\pi +\theta )+ } ......+\sin { (2021\pi +\theta ) } \\ $$

Now

$$\sin { (\pi +\theta ) } =\sin { (3\pi +\theta ) } =.........=\sin { [(2n+1)\pi +\theta ] } =-\sin { \theta } \\ \sin { (2\pi +\theta ) } =\sin { (4\pi +\theta ) } =.........=\sin { (2n\pi +\theta ) } =\sin { \theta } \\ \therefore \sin { (2021\pi +\theta ) } +\sin { (2020\pi +\theta ) } =0\\ \sin { (2019\pi +\theta ) } +\sin { (2018\pi +\theta ) } =0\\ .\\ .\\ .\\ .\\ .\sin { (3\pi +\theta ) } +\sin { (2\pi +\theta ) } =0\\ \sin { (\pi +\theta ) } +\sin { \theta } =0\\ \therefore sum=0$$

What is value of
$$1 + x + {x^2} + {x^3} + {x^4} + .....$$
where $$x \ne 1$$

$$1+x+{x}^{2}+{x}^{3}+{x}^{4}+\dots$$

$$a=x$$

$$r=x$$

$$ 1+[\cfrac { x({ x }^{ n }-1) }{ (x-1) } ]$$ If $$x>1.$$

1.3+3.5+5.7+....+$$\left( {2n - 1} \right)\left( {2n + 1} \right) = \frac{{n\left( {4{n^2} + 6n - 1} \right)}}{3}$$

$$S=1.3+3.5+....+(2n-1)(2n+1)\\ S=\sum _{ k=1 }^{ n }{ (2k-1)(2k+1) } \\ =\sum _{ k=1 }^{ n }{ \left( { 4k }^{ 2 }-1 \right) } \\ =4\sum _{ k=1 }^{ n }{ { k }^{ 2 } } -\sum _{ k=1 }^{ n }{ 1 } \\ S\cfrac { 4n(n+1)(2n+1) }{ 6 } -n\\ =n\left( \cfrac { 2\left( { 2n }^{ 2 }+3n+1 \right) }{ 3 } -1 \right) \\ =n\left( \cfrac { \left( { 4n }^{ 2 }+6n-1 \right) }{ 3 } \right) \\ S=n\left( \cfrac { \left( { 4n }^{ 2 }+6n-1 \right) }{ 3 } \right) $$

$$\cos { \dfrac { x }{ 2 } } \times \cos { \dfrac { x }{ { 2 }^{ 2 } } } \times \cos { \dfrac { x }{ { 2 }^{ 3 } } } ..........\times \cos { \dfrac { x }{ { 2 }^{ n } } }$$$$A\rightarrow \infty$$$$\dfrac { \sin { { 2 }^{ n } } A }{ { 2 }^{ n }\sin { A } }$$

$$\begin{array}{l} \cos \frac { x }{ 2 } \cdot \left( 0 \right) \frac { x }{ { { 2^{ 2 } } } } \cdot \cos \frac { x }{ { { 2^{ 3 } } } } .......\cos \frac { x }{ { } } { 2^{ n } }n\to \frac { { \infty \sin { 2^{ n } } A } }{ { { 2^{ n } }\sin A } } & \\ now, & \\ \cos \frac { x }{ 2 } & \\ =\frac { 1 }{ 2 } \left( { \sin \frac { x }{ 2 } \cdot \cos \frac { x }{ 2 } } \right) & \frac { 1 }{ 2 } \sin \frac { x }{ 2 } =\frac { { \sin x } }{ { 2\sin \frac { x }{ 2 } } } \\ \cos \frac { x }{ { { 2^{ 2 } } } } & \\ =\frac { 1 }{ 2 } \sin \frac { x }{ { { 2^{ 2 } } } } \cos \frac { x }{ { { 2^{ 2 } } } } & \sin \frac { x }{ { { 2^{ 2 } } } } =\frac { { \sin \frac { x }{ 2 } } }{ { { 2^{ 2 } }\sin } } \\ Similarly & \\ \cos \frac { x }{ { { 2^{ n } } } } =\frac { 1 }{ 2 } \cos \frac { x }{ { { 2^{ n } } } } \sin \frac { x }{ { { 2^{ n } } } } & \sin \frac { x }{ { { 2^{ n } } } } =\frac { { \sin 2\frac { x }{ 2 } } }{ { { 2^{ n } }\sin \frac { n }{ 2 } n } } \\ \cos \frac { n }{ 2 } \cdot \cos \frac { n }{ 2 } \cos \frac { n }{ { { 2^{ 3 } } } } ...\cos \frac { n }{ { { 2^{ n } } } } A\to & \\ =\frac { { \sin { 2^{ n } } A } }{ { { 2^{ n } }\sin x } } & \end{array}$$

If $$S=\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+.............$$ to$$ \infty$$ then find $$\frac{1}{1^2}+\frac{1}{3^2}+\frac{1}{5^2}+\frac{1}{7^2}+.............$$ to$$ \infty$$ in terms of S.

$$\\S=((\frac{1}{1^2})+(\frac{1}{3^2})+(\frac{1}{5^2})+.............\infty )+((\frac{1}{2^2})+(\frac{1}{4^2})+......\infty )\\S=x+(\frac{1}{4})[(\frac{1}{1^2})+(\frac{1}{2^2})+(\frac{1}{3^2})+.......\infty ]\\S=x+(\frac{1}{4})\times s \\\therefore x=S-(\frac{S}{4})=(\frac{35}{4})$$

Find the sum of infinite terms of following series.
$$\dfrac{3}{7}+\dfrac{5}{21}+\dfrac{7}{63}+\dfrac{9}{189}+$$.....

1321139_1076997_ans_c8c02d41d0774e789408f8d9e0579dd0.jpg

Sum of infinity the following series:
$$1 + 4x^{2} + 7x^{4} + 10x^{6} + ..., |x| < 1$$.

$$S =1 +4x^2 + 7x^4+ 10x^6+...$$ $$..................(1)$$

$$Sx^2 = x^2+ 4x^4+ 7x^6+....$$ $$...............(2)$$

$$eq^n(1) – eq^n(2)$$, we get

$$(1 – x^2)S = 1 + 3x^2+ 3x^4+ 3x^6+…...$$ $$.........(3)$$

This is a $$G.P$$. of common ratio $$=x^2$$

So, using sum of $$G.P. = \dfrac{a}{ (1-r)}$$

Here, $$a = first\ term$$ and $$r = common\ ratio$$

So,

$$(1 – x^2)S = 1 + \dfrac{3 x^2}{ (1 – x^2)}$$

$$(1 – x^2)S = \dfrac{1-x^2+3 x^2}{ (1 – x^2)}$$

$$S = \dfrac{1+2x^2}{ (1 – x^2)^2}$$

Hence, this is the answer.

Find the sum to the series $$1.n+2(n-1)+3(n-2)+...+n.1$$

Given series: $$1.n+2\left(n-1\right)+3\left(n-2\right)+…..+n.1$$

$${r}^{th}$$ term $$=r\left(n-r+1\right)$$

The given series is summation of $$r\left(n-r+1\right)$$ where $$r$$ varies from $$1$$ to $$n$$.

$$\therefore Sum=\displaystyle\sum _{ r=1 }^{ n }{ \left[ \left( n+1 \right) r-{ r }^{ 2 } \right] } =\dfrac { \left( n+1 \right) \left( n \right) \left( n+1 \right) }{ 2 } -\dfrac { n\left( n+1 \right) \left( 2n+1 \right) }{ 6 }$$

$$ Sum=\dfrac { n\left( n+1 \right) }{ 2 } \left[ n+1-\dfrac { 2n+1 }{ 3 } \right]$$

Or, $$Sum=\dfrac { n\left( n+1 \right) }{ 2 } \left[ \dfrac { 3n+3-2n-1 }{ 3 } \right]$$

$$\therefore Sum=\dfrac { n\left( n+1 \right) }{ 2 } \left[ \dfrac { n+2 }{ 3 } \right] =\dfrac { n\left( n+1 \right) \left( n+2 \right) }{ 6 }$$Ans.

Sum to $$infinite$$ terms the following series:
$$1 + 5x^{2} + 9x^{4} + 13x^{6} + ...., |x| < 1$$

$$S =1 +5x^2 + 9x^4+ 13x^6+...$$ $$............(1)$$

$$Sx^2 = x^2+ 5x^4+ 9x^6+....$$ $$...............(2)$$

$$eq^n(1) – eq^n(2)$$, we get

$$(1 – x^2)S = 1 + 4x^2+ 4x^4+ 4x^6+…...$$ $$.........(3)$$

This is a $$G.P$$. of common ratio $$=x^2$$

So, using sum of $$G.P. = \dfrac{a}{ (1-r)}$$

Here, $$a = first\ term$$ and $$r = common\ ratio$$

So,

$$(1 – x^2)S = 1 + \dfrac{4 x^2}{ (1 – x^2)}$$

$$(1 – x^2)S = \dfrac{1-x^2+4 x^2}{ (1 – x^2)}$$

$$S = \dfrac{1+3x^2}{ (1 – x^2)^2}$$

Hence, this is the answer.

If $$S_n = \dfrac{3}{4} + \dfrac{5}{36} + \dfrac{7}{144} + \dfrac{9}{400} +...$$ to $$n$$ terms, then find $$\dfrac{1}{1 - S_{40}}$$.

$$a=\dfrac{3}{4}$$

$$d=\dfrac{5}{36}-\dfrac{3}{4}=\dfrac{11}{18}$$

$$S_n=\dfrac{n}{2}[2a+(n-1)d]$$

$$S_{40}=\dfrac{40}{2}\left [ 2\left ( \dfrac{3}{4} \right )+(40-1)\dfrac{11}{18} \right ]$$

$$=20\left [ \left ( \dfrac{3}{2} \right )+(39)\dfrac{11}{18} \right ]$$

$$=20\left [ \dfrac{27+39\times 11}{18} \right ]$$

$$=20\times \dfrac{76}{3}$$

$$=\dfrac{1520}{3}$$

$$\dfrac{1}{1-S_{40}}$$

$$=\dfrac{1}{1-1520}$$

$$=\dfrac{-1}{1519}$$

Sum the following series
$$\dfrac{1}{1.4.7}+\dfrac{1}{4.7.10}+\dfrac{1}{7.10.13}+....$$ to $$n$$ terms

$${T}_{n}$$ of $$1,4,7,...=1+\left(n-1\right)3=1+3n-3=3n-2$$ where $$a=1$$ and $$d=4-1=3$$

$${T}_{n}$$ of $$4,7,10...=4+\left(n-1\right)3=4+3n-3=3n+1$$ where $$a=3$$ and $$d=7-4=3$$

$${T}_{n}$$ of $$7,10,13...=7+\left(n-1\right)3=7+3n-3=3n+4$$ where $$a=7$$ and $$d=10-7=3$$

$$\therefore {T}_{n}=\dfrac{1}{6}\left[\dfrac{1}{\left(3n-2\right)\left(3n+1\right)\left(3n+4\right)}\right]$$

$${S}_{n}=\dfrac{1}{6}\dfrac{\left(3n+4\right)-\left(3n-2\right)}{\left(3n-2\right)\left(3n+1\right)\left(3n+4\right)}$$

$$=\dfrac{1}{6}\left[\dfrac{1}{\left(3n-2\right)\left(3n+1\right)}-\dfrac{1}{\left(3n+1\right)\left(3n+4\right)}\right]$$

We have $${S}_{n}=\sum{{T}_{r}}$$

$$=\dfrac{1}{6}\sum_{r=1}^{n}{\left[\dfrac{1}{\left(3n-2\right)\left(3n+1\right)}-\dfrac{1}{\left(3n+1\right)\left(3n+4\right)}\right]}$$

$$=\dfrac{1}{6}\left[\dfrac{1}{1.4}-\dfrac{1}{4.7}+\dfrac{1}{4.7}-\dfrac{1}{7.10}+....-\dfrac{1}{\left(3n+1\right)\left(3n+4\right)}\right]$$

$$\therefore {S}_{n}=\dfrac{1}{6}\left[\dfrac{1}{4}-\dfrac{1}{\left(3n+1\right)\left(3n+4\right)}\right]$$

$$=\dfrac{1}{6}\left[\dfrac{\left(3n+1\right)\left(3n+4\right)-4}{4\left(3n+1\right)\left(3n+4\right)}\right]$$

$$=\dfrac{9{n}^{2}+12n+3n+4-4}{24\left(3n+1\right)\left(3n+4\right)}$$

$$=\dfrac{9{n}^{2}+15n}{24\left(3n+1\right)\left(3n+4\right)}$$

$$=\dfrac{3n\left(3n+5\right)}{24\left(3n+1\right)\left(3n+4\right)}$$

$$=\dfrac{n\left(3n+5\right)}{8\left(3n+1\right)\left(3n+4\right)}$$

Sum to $$infinite$$ terms the following series:
$$1 + 3x + 5x^{2} + 7x^{3} + ...., |x| < 1$$.

$$S =1 +3x + 5x^2+ 7x^3+...$$ $$...........(1)$$

$$Sx = x+ 3x^2+ 5x^3+....$$ $$...............(2)$$

$$eq^n(1) – eq^n(2)$$, we get

$$(1 – x)S = 1 + 2x+ 2x^2+ 2x^3+…...$$ $$.........(3)$$

This is a $$G.P$$. of common ratio $$=x$$

So, using sum of $$G.P. = \dfrac{a}{ (1-r)}$$

Here, $$a = first\ term$$ and $$r = common\ ratio$$

So,

$$(1 – x)S = 1 + \dfrac{2x}{ (1 – x)}$$

$$(1 – x)S = \dfrac{1+x}{ (1 – x)}$$

$$S = \dfrac{1+x}{ (1 – x)^2}$$

Hence, this is the answer.

In the given diagram the circle stands for "educated", square for "lazy", triangle for "urban" and the rectangle for "honest" people. The different regions in the diagram are numbered from $$2$$ to $$13$$. Number $$4$$ will show which of the case?

Number 4 represent people who are Urban and Honest and Lazy but not educated.

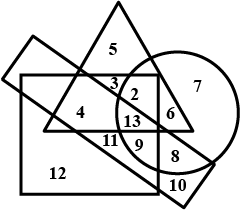
If $$\left| x \right| < 1$$ and $$\left| y \right| < 1$$, find the sum to infinity to the series

$$\left( {x + y} \right) + \left( {{x^2} + xy + y} \right)$$ + $$\left( {{x^3} + {x^2}y + x{y^2} + {y^2}} \right)$$

2042676_1196384_ans_7301f8eb7c5646d98e5626c4da8d522f.jpg

If $$a,\ b,\ c$$ are in $$A.P.$$ and $$P$$ is the $$A.M.$$ between $$a$$ and $$b$$, and $$q$$ is the $$A.M.$$ between $$b$$ and $$c$$, show that $$b$$ is the $$A.M.$$ between $$p$$ and $$q$$.

$$a,b,c$$ are in $$AP$$

$$\Rightarrow 2b=a+c\quad \longrightarrow \left( 1 \right) $$

Also given, $$P$$ is the $$AM$$ between $$a$$ and $$b$$

$$\Rightarrow P=\dfrac { a+b }{ 2 } $$ ($$\because$$ $$AM$$ of two number $$x$$ & $$y$$ is $$\dfrac { x+y }{ 2 } $$)

$$\Rightarrow 2P=a+b\quad \longrightarrow \left( 2 \right) $$

Also, $$Q$$ is the $$AM$$ between $$b$$ and $$c$$

$$\Rightarrow 2Q=b+c\quad \longrightarrow \left( 3 \right) $$

Adding $$2)$$ & $$(3)$$ we get

$$2\left( P+Q \right) =2b+a+c\quad \longrightarrow \left( 4 \right) $$

From $$(1)$$ we have $$a+c=2b$$, Using that in $$(4)$$ we get

$$2\left( P+Q \right) =2b+2b$$

$$\Rightarrow P+Q=2b\quad \longrightarrow \left( 5 \right) $$

$$\Rightarrow \dfrac { P+Q }{ 2 } =b\quad \longrightarrow \left( 6 \right) $$

Hence,

From $$(6)$$ we can conclude that $$'b'$$ is the $$AM$$ of $$P$$ & $$Q$$.

Let $$x = 111 .... 11$$ ($$20$$ digits)
$$y = 333 .... 33$$ ($$10$$ digits)
and $$z = 222 .... 22$$ ($$10$$ digits),
The value of $$\dfrac{x - y^2}{z}$$.

The d-digit integer consisting only of $$9's$$ can be written $$ 10^{d}-1 $$. set

$$ x = \dfrac{1}{9}(10^{2d}-1), y = \dfrac{1}{3}(10^{d}-1), z = \dfrac{2}{9}(10^{d}-1) $$

we claim that $$ x-z = y^{2}.$$ Indeed,

$$ x-z = \dfrac{1}{9}(10^{d}-1)((10^{d}+1)-2) = (\dfrac{1}{3}(10^{d}-1))^{2} = y^{2} .$$

Thus, for any $$ d \geq 1,(x-y^{2})/z = 1. $$ The given set of numbers corresponds to $$ d = 10.\blacksquare $$

Show that $$\cfrac { 1.2 ^{ 2 }+{ 3 }^{ 2 }+...+n }{ { 1 }^{ 2 }. 2+{ 2 }^{ 2 }. 3+...+ n } =\cfrac { 3n+5 }{ 3n+1 } $$

We have to shown that

$$\frac{{{{1.2}^2} + {{1.3}^2} + ...... + n}}{{{1^2}.2 + {2^2}.3 + ..... + n}} = \frac{{3n + 5}}{{3n + 1}}$$

Now

$$\frac{{{{1.2}^2} + {{1.3}^2} + ...... + n}}{{{1^2}.2 + {2^2}.3 + ..... + n}} = \frac{{\sum\limits_{n = 1}^n {k{{\left( {k + 1} \right)}^2}} }}{{\sum\limits_{n = 1}^k {k\left( {k + 1} \right)} }}$$

$$ = \frac{{\sum\limits_{n = 1}^n {\left( {{k^3} + 2{k^2} + k} \right)} }}{{\sum\limits_{n = 1}^k {\left( {{k^3} + {k^2}} \right)} }}$$

$$ = \frac{{\sum\limits_{n = 1}^n {{k^3} + 2\sum\limits_{n = 1}^n {{k^2}} } + \sum\limits_{n = 1}^n k }}{{\sum\limits_{n = 1}^n {{k^3}} + \sum\limits_{n = 1}^n {{k^2}} }}$$

$$ = \frac{{\frac{{{n^2}{{\left( {n + 1} \right)}^2}}}{4} + \frac{{2n\left( {n + 1} \right)\left( {2n + 1} \right)}}{6} + \frac{{n\left( {n + 1} \right)}}{2}}}{{\frac{{{n^2}{{\left( {n + 1} \right)}^2}}}{4} + \frac{{n\left( {n + 1} \right)\left( {2n + 1} \right)}}{6}}}$$

$$ = \frac{{\frac{{n\left( {n + 1} \right)}}{2}\left[ {\frac{{n + \left( {n + 1} \right)}}{2} + \frac{{2.\left( {2n + 1} \right)}}{3} + 1} \right]}}{{\frac{{n\left( {n + 1} \right)}}{2}\left[ {\frac{{n + \left( {n + 1} \right)}}{2} + \frac{{n\left( {n + 1} \right)\left( {2n + 1} \right)}}{3}} \right]}}$$

$$ = \frac{{\frac{{3n\left( {n + 1} \right) + 4\left( {2n + 1} \right) + 6}}{6}}}{{\frac{{3n\left( {n + 1} \right) + 2\left( {2n + 1} \right)}}{6}}}$$

$$ = \frac{{3{n^2} + 3n + 8n + 4 + 6}}{{3{n^2} + 3n + 4n + 2}}$$

$$ = \frac{{3{n^2} + 11n + 10}}{{3{n^2} + 7n + 2}}$$

$$ = \frac{{3{n^2} + 5n + 6n + 10}}{{3{n^2} + 3n + 4n + 2}}$$

$$ = \frac{{n\left( {3n + 5} \right)2\left( {3n + 5} \right)}}{{3n\left( {n + 2} \right) + 1\left( {n + 2} \right)}}$$

$$ = \frac{{\left( {n + 2} \right)\left( {3n + 5} \right)}}{{\left( {n + 2} \right)\left( {3n + 1} \right)}}$$

$$ = \frac{{3n + 5}}{{3n + 1}}$$

Hence, we proved the given question.

If $${\left(1+x-2{x}^{2}\right)}^{20}=\sum_{r=0}^{40}{{a}_{r}{x}^{r}}$$ then the value of $${a}_{1}+{a}_{3}+{a}_{5}+...+{a}_{39}$$

1339886_1239309_ans_c1a1cc13c9874cc398ca2c8b55c95561.PNG

What is the ninth term of the sequence whose general term $$a_{n}=(-1)^{n-1}n^{3}$$.

1183221_1224106_ans_f473cf3be13c47ffbb9d9dc6b42bd002.jpg

The sum of the infinite series $$\dfrac { 1.3 } { 2 } + \dfrac { 3.5 } { 2 ^ { 2 } } + \dfrac { 5.7 } { 2 ^ { 3 } } + \dfrac { 7.9 } { 2 ^ { 4 } } + \ldots . . . . . . . \infty.$$

$$\begin{array}{l} S=\frac { { 1.3 } }{ 2 } +\frac { { 3.5 } }{ { { 2^{ 2 } } } } +\frac { { 5.7 } }{ { { 2^{ 3 } } } } +\frac { { 7.9 } }{ { { 2^{ 4 } } } } +..... \\ \frac { S }{ 2 } =\frac { { 1.3 } }{ 2 } +\frac { { 12 } }{ { { 2^{ 2 } } } } +\frac { { 20 } }{ { { 2^{ 3 } } } } +\frac { { 28 } }{ { { 2^{ 4 } } } } +....... \\ \frac { S }{ 2 } =\frac { 3 }{ 2 } +\frac { { 12 } }{ { { 2^{ 2 } } } } +\frac { { 20 } }{ { { 2^{ 3 } } } } +\frac { { 28 } }{ { { 2^{ 4 } } } } +\frac { { 36 } }{ { { 2^{ 5 } } } } +...... \\ \\ Let\, S'=\frac { { 12 } }{ { { 2^{ 2 } } } } +\frac { { 20 } }{ { { 2^{ 3 } } } } +\frac { { 28 } }{ { { 2^{ 4 } } } } \\ S'=\frac { { 12 } }{ { { 2^{ 2 } } } } +\frac { { 20 } }{ { { 2^{ 3 } } } } +\frac { { 28 } }{ { { 2^{ 4 } } } } +\frac { { 36 } }{ { { 2^{ 5 } } } } \\ \frac { { S' } }{ 2 } =\frac { { 12 } }{ { { 2^{ 3 } } } } +\frac { { 20 } }{ { { 2^{ 4 } } } } +\frac { { 28 } }{ { { 2^{ 5 } } } } +....... \\ \frac { { S' } }{ 2 } =\frac { { 12 } }{ { { 2^{ 2 } } } } +\frac { 8 }{ { { 2^{ 3 } } } } +\frac { 8 }{ { { 2^{ 4 } } } } +\frac { 8 }{ { { 2^{ 5 } } } } +..... \\ \frac { { S' } }{ 2 } =3+8\left[ { \frac { { \frac { 1 }{ { { 2^{ 3 } } } } } }{ { 1-\frac { 1 }{ 2 } } } } \right] \\ \frac { { S' } }{ 2 } =2+8\times \frac { 1 }{ 8 } \times 2 \\ \frac { { S' } }{ 2 } =5 \\ S'=10 \\ Now, \\ \frac { S }{ 2 } =\frac { 3 }{ 2 } +10 \\ S=23 \end{array}$$

If $$\dfrac{{a}^{n}+{b}^{n}}{{a}^{n-1}+{b}^{n-1}}$$ is the A.M. between $$a$$ and $$b$$, then find the value of $$n$$

We know that arithmetic mean between $$a$$ and $$b$$ is A.M$$=\dfrac{a+b}{2}$$

Given: A.M between $$a$$ and $$b$$ is $$\dfrac{{a}^{n}+{b}^{n}}{{a}^{n-1}+{b}^{n-1}}$$

So, $$\dfrac{{a}^{n}+{b}^{n}}{{a}^{n-1}+{b}^{n-1}}=\dfrac{a+b}{2}$$

$$\Rightarrow 2\left({a}^{n}+{b}^{n}\right)=\left(a+b\right)\left({a}^{n-1}+{b}^{n-1}\right)$$

$$\Rightarrow 2{a}^{n}+2{b}^{n}=a\left({a}^{n-1}+{b}^{n-1}\right)+b\left({a}^{n-1}+{b}^{n-1}\right)$$

$$\Rightarrow 2{a}^{n}+2{b}^{n}={a}^{n}+a{b}^{n-1}+b{a}^{n-1}+{b}^{n}$$

$$\Rightarrow 2{a}^{n}+2{b}^{n}-{a}^{n}-a{b}^{n-1}-b{a}^{n-1}-{b}^{n}=0$$

$$\Rightarrow {a}^{n}-b{a}^{n-1}+{b}^{n}-a{b}^{n-1}=0$$

$$\Rightarrow {a}^{n-1}\left(a-b\right)-{b}^{n-1}\left(a-b\right)=0$$

$${a}^{n-1}-{b}^{n-1}=0$$ or $$a-b=0$$

$${a}^{n-1}={b}^{n-1}$$ or $$a=b$$ but $$a\neq b$$

$$\therefore \dfrac{{a}^{n-1}}{{b}^{n-1}}=1$$

$$\Rightarrow {\left(\dfrac{a}{b}\right)}^{n-1}={\left(\dfrac{a}{b}\right)}^{0}$$ since $${a}^{0}=1$$

Since bases are same, we can equate the powers,

$$\therefore n-1=0$$

Hence $$n=1$$

Find the sum of the series
$$\dfrac{3 \cdot 5}{5 \cdot 10} + \dfrac{3 \cdot 5 \cdot 7}{5 \cdot 10 \cdot 15} + \dfrac{3 \cdot 5 \cdot 7 \cdot 9}{ 5 \cdot 10 \cdot 15 \cdot 20} + ..... \infty$$.

$$\cfrac{3 \cdot 5}{5 \cdot 10} + \cfrac{3 \cdot 5 \cdot 7}{5 \cdot 10 \cdot 15} + \cfrac{3 \cdot 5 \cdot 7 \cdot 9}{5 \cdot 10 \cdot 15 \cdot 20} + ..... \infty$$

$${n}^{th}$$ term of the above expansion.

$${T}_{n} = \cfrac{3 \cdot 5 \cdot 7 \cdot ..... \cdot \left( 2n + 3 \right)}{{5}^{n+1} \cdot \left[ \left( n + 1 \right) ! \right]}$$

$${T}_{n} = \cfrac{\Pi_{k=1}^{n}{\left( 2k + 3 \right)}}{{5}^{n+1} \left( n + 1 \right)!}$$

$${T}_{n} = \cfrac{{2}^{n} \Pi_{k=1}^{n}{\left( k + \cfrac{3}{2} \right)}}{{5}^{n+1} \left( n + 1 \right) !}$$

$${T}_{n} = \cfrac{{2}^{n} \Pi_{k=0}^{n-1}{\left( \left( k + 1 \right) + \cfrac{3}{2} \right)}}{{5}^{n+1} \left( n + 1 \right) !}$$

$${T}_{n} = \cfrac{{2}^{n} \Pi_{k=0}^{n-1}{\left( k + \cfrac{5}{2} \right)}}{{5}^{n+1} \left( n + 1 \right) !}$$

$${T}_{n} = {\left( \cfrac{2}{5} \right)}^{n} \cfrac{ \Pi_{k=0}^{n-1}{\left( k + \cfrac{5}{2} \right)}}{5 \left( n + 1 \right) !}$$

The expansion of $${\left( 1 + t \right)}^{r}$$ is-

$${\left( 1 + t \right)}^{r} = \sum_{0}^{\infty}{{t}^{n} \cfrac{\Pi_{k=0}^{n-1}{\left( k + r \right)}}{5 \left( n + 1 \right)!}}$$

Here,

$$t = \cfrac{2}{5}$$

$$r = \cfrac{5}{2}$$

Therefore,

$$\cfrac{3 \cdot 5}{5 \cdot 10} + \cfrac{3 \cdot 5 \cdot 7}{5 \cdot 10 \cdot 15} + \cfrac{3 \cdot 5 \cdot 7 \cdot 9}{5 \cdot 10 \cdot 15 \cdot 20} + ..... \infty$$

$$= \sum_{n=1}^{\infty}{{T}_{n}}$$

$$= 1 - {\left( 1 + \cfrac{2}{5} \right)}^{\frac{2}{5}}$$

$$= 1 - {\left( \cfrac{7}{5} \right)}^{\frac{2}{5}}$$

The average of two numbers 'a' and 'b' is 68 and the average of 'b' 'c' is 70 and that and 'c' isFind the values of a, b, c.

2041227_1456457_ans_70ea797f8ee0431ebd967810e7e7f34b.jpg

Find the mean of first five prime numbers.

2045393_1570774_ans_0248f756c9024385a14b2b52ba76152b.jpg

The sum of the series $$\dfrac{1}{1 ! (n-1) ! }+\dfrac{1}{ 3! (n-3) !}+\dfrac{1}{5 ! (n-5)!}+.......+\dfrac{1}{(n-1) ! 1!}$$

2044583_1566442_ans_46118ea5a2d34c7884971b46d35eabc0.jpg

Weight $$(kg)$$	$$29$$	$$30$$	$$31$$	$$32$$	$$33$$
No.of children	$$20$$	$$01$$	$$04$$	$$03$$	$$05$$

Sequences And Series - Class 11 Engineering Maths - Extra Questions

The sum of the infinite series $$\displaystyle{1+\frac{1+2}{2!} + \frac{1+2+2^2}{3!} + \frac{1+2+2^2+2^3}{4!}+ \,...}$$ is $$\displaystyle{e^y-e^x}$$ Find $$x+y^2$$

Write four more numbers in the following pattern- $$ \displaystyle \frac{-1}{3} $$, $$ \displaystyle \frac{-2}{6} $$, $$ \displaystyle \frac{-3}{9} $$, $$ \displaystyle \frac{-4}{12} $$..........

Find the first $$3$$ terms of a G.P. if $$a = 4$$ and $$r = 2$$.

Find the sum of all natural numbers from $$1$$ to $$200$$ which are divisible by $$4$$.

Find the arithmetic mean of 4 and 6.

Find the common ratio and the general term of the following geometric sequences.$$0.02, 0.006, 0.0018, .....$$

A.M. of $$a-2$$, $$a$$, $$a+2$$ is ____.

A.M. of $$1, 2, x, 3$$ is $$0$$, then $$x=$$ _____.

A geometric series consists of four terms and has a positive common ratio. The sum of the first two terms is 8 and the sum of the last two terms is $$72$$. Find the series

Find the sum of n terms of the series $$\left(4-\displaystyle\frac{1}{n}\right)+\displaystyle \left(4-\frac{2}{n}\right)+\displaystyle \left(4-\frac{3}{n}\right)+$$........

Write the smallest $$7-$$digits largest and smallest number having three different digits.

$$\dfrac{1}{{1.2.3}} + \dfrac{1}{{2.3.4}} + \dfrac{1}{{3.4.5}} + \,..... + \dfrac{1}{{n\left( {n + 1} \right)\left( {n + 2} \right)}} = \dfrac{{n\left( {n + 3} \right)}}{{4\left( {n + 1} \right)\left( {n + 2} \right)}}$$

Solve: $$\displaystyle \sum_{n = 1}^{13}(t^n - t^{n + 1}) =$$

If $$\alpha ,\,\beta \,,\gamma $$ are in A.P. show that $$\cot\,\beta = \dfrac{{\sin \alpha - \sin \gamma }}{{\cos \gamma - cos\alpha }}.$$

complete the table . what do you notice about the numbers in the orange band ?1713281439154101651117612

$${ a }_{ 1 }=5;{ a }_{ 4 }=9\dfrac { 1 }{ 2 }$$ find $${ a }_{ 2 },{ a }_{ 3 }$$

If, $$ 1, 5, 8=76$$ $$ 2, 7, 3=25$$ $$ 3, 4, 9=89$$ $$ 4, 5, 7=69$$THEN $$5, 3, 8$$=?

If the mean of $$20,\,14,\,16,\,19,\,p$$ and $$21$$ is $$27$$ then find the value of $$'p'$$

The first term of a GP isThe sum of the third and fifth term isFind the common ratio of GP.

$$13,25,14,23,15,21,16,?,?$$1) $$14,11$$2) $$19,17$$

Look at the following matchstick pattern of letter $$A$$, the $$A's$$ are not separate. Two neighbouring $$A's$$ have two common matchsticks. Observe the pattern and find the rule that gives the number of matchsticks.

If $$a,b,c$$ are in AP and $$b,c,d$$ are in GP and $$\dfrac{1}{c},\dfrac{1}{d}, \dfrac{1}{e}$$ are in AP, prove that $$a,c,e$$ are in GP.

Find the sum of series $$1+2+3+4+5+6+...+n$$.

Calculate the sum of the series $$1+3+5+7+....2n-1$$.

Find the $${15^{th}}$$ term of the series $$3,9,15,21,27,33,....$$

Find the sum to $$n$$ terms of the series$$5+11+19+29+......$$

Find the sum of terms of the sequence till n terms : $$6+9+16+27+42+....+n$$ $$ terms$$.

Find the average of the first five multiples of $$10$$.

Find the missing number in the series : 40 , 54 , 82 , ? , 180 , 250

Write opposites of the following :$$30\ km$$ north

If $$18, a, b, -3$$ are in $$AP$$ then find $$a+b$$.

Solve: $$2-\dfrac{3}{5}.$$

Find the term of the series $$25, 22\dfrac{3}{4}, 20\dfrac{1}{2},18\dfrac{1}{4}.....$$ which is numerically smallest.

Solve for a. $$\frac{3a-2}{7}-\frac{a-2}{4}=2,$$

The mean of first 10 whole numbers is

Find three consecutive odd numbers whose sum is $$147$$.

Find three consecutive even number whose sum is $$234$$.

$$5,10,15,20,..$$.

Prove that $$\sum\limits_{n=1}^{\infty}\dfrac{1}{n!}=e-1$$.

Fill in the blanks:$$\dfrac {2}{8} \times 3 = \dfrac {2}{8} + -+-+- $$

Ia, b, c are is G.P and a - b, c - a and b - a are in H.P, then a + 4b + c is equal to

Write the solution set of $$\left|x+\dfrac{1}{x}\right|>2$$.

Find three consecutive odd numbers whose sum is $$234$$.

$$1,2,4,8,16,...$$.

If $$a,b,c,d$$ are in GP, show that$$(b-c)^2+(c-a)^2+(d-b)^2=(a-d)^2$$

Fill in the blanks in the expressions with the proper numbers.$$(5\ \times 4) > (7\times \Box )$$

If $$a,b,c$$ are in GP and $$a^{1/x}=b^{1/y}=c^{1/z}$$, prove that $$x,y,z$$ are in AP.

The sum of the first 20 terms of the series $$1+\dfrac{3}{2}+\dfrac{7}{4}+\dfrac{15}{8}+\dfrac{31}{16}+....,$$ is

$$x = 1 + a + a ^ { 2 } + \ldots \infty , y = 1 + b + b ^ { 2 } + \ldots \infty$$ then $$1 + a b + a ^ { 2 } b ^ { 2 } + \ldots \infty =$$

P and Q are brothers, X and Y are sisters, son of P is the brother of Y. How is Q related to X ?

The Fibonacci sequence is defined by $$1=a_{1}=a_{2}$$ and $$a_{n}=a_{n-1}+a_{n-1},n > 2$$.Find $$\dfrac {a_{n}}{a_{n}+1}$$ for $$n=1,2,3,4$$.

Identify whether the following sequence is a geometric sequence or not.$$-3,9,-27,81$$

Identify whether the following sequence is a geometric sequence or not.$$2,6,18,54$$

If the heights of 5 persons are 144 cm, 152 cm, 151 cm, 158 cm, and 155 cm respectively. Find the mean height.

Fill the squares with all the numbers from 46 to 54rule:- total of each line should be 150.49465247

The mean of $$45,84,75,87,47$$ is

Identify whether the following sequence is a geometric sequence or not.$$1,4,9,16$$

Identify whether the following sequence is a geometric sequence or not.$$\dfrac{1}{2},\dfrac{2}{4},\dfrac{4}{8},\dfrac{8}{16}$$

Identify whether the following sequence is a geometric sequence or not.$$\dfrac{1}{2},\dfrac{2}{3},\dfrac{3}{4},\dfrac{4}{5}$$

Find the value of question mark .

Identify whether the following sequence is a geometric sequence or not.$$25,5,1,\dfrac{1}{5}$$

The fourth term of a G.P. is 8 and the 7th term is 64, find the G.P.

Find the mean of 43, 51, 50, 57 and 54.

Find the sum of the following series:$$ 0.6+0.66+0.666+...$$ to n terms.

Increased by 3

The sum of the following series to infinity $$\displaystyle \frac{1}{1.3.5} +\frac{1}{3.5.7} +\frac{1}{5.7.9} +\,...\,\infty is $$ $$\dfrac{1}{3c}$$ .Find $$c$$

The sum of the series $$\displaystyle \frac2{3!}+\frac4{5!}+\frac6 {7!}+...$$ to $$\infty$$ = $$\displaystyle \frac{a}{e}$$. Find $$(a+3)^2$$.

If $$A_{n}= (n, n + 1)$$ then $$10(A_{10}A_{11})^{2}+11(A_{11}+A_{12})^{2}+......+20(A_{20}A_{21})^{2}$$ is equal to

Sum of the series $$\displaystyle 1+\left ( 1+2 \right )+\left ( 1+2+3 \right )+\left ( 1+2+3+4 \right )+... $$ to n terms be $$\displaystyle \frac{1}{m}n\left ( n+1 \right )\left [ \frac{2n+1}{k}+1 \right ]$$ .Find the value of k+m.

If the set natural numbers, is partitioned into subsets $$\displaystyle S_{1}= \left \{ 1 \right \},S_{2}= \left \{ 4,5,6 \right \},S_{4}= \left \{ 7,8,9,10 \right \}$$ The last terms of these groups is $$1,1+2,1+2+3,1+2+3+4 .....$$. Find the sum of the elements in the subset $$S_{50}$$.

sum the series $$1+2+...…….+100$$

sum of the series is $$1+3+6+10+15+... $$ to n terms $$\displaystyle \frac{n\left ( n+m \right )\left ( n+p \right )}{k}$$.Find $$k-m-p$$ ?

Sum of the series $$4+6+9+13+18+...$$ to $$n$$ terms be $$\displaystyle =\frac{n}{k}\left ( n^{2}+3n+m \right )$$.Find $$m-k$$ ?

Find the sum of 2n terms of the series $$\displaystyle 5^{3}+4.6^{3}+7^{3}+7^{3}+4.8^{3}+9^{3}+4.10^{3}+....$$

If $$\displaystyle s_{n}=1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+...\frac{1}{n},\left ( n\: \epsilon \: N \right )$$, then $$\displaystyle s_{1}+s_{2}+s_{3}+s_{4}+...s_{n}=\left ( n+\lambda \right )s_{n+1}-\left ( n+1 \right )$$. Find the value of $$\displaystyle \lambda $$

Find the sum to $$n$$ terms of the sequence $$8, 88, 888, 8888, ....$$ .

If $$a,b,c$$ and $$d$$ are in $$G.P.$$ show that $$\displaystyle ({ a }^{ 2 }+{ b }^{ 2 }+{ c }^{ 2 })({ b }^{ 2 }+{ c }^{ 2 }+{ d }^{ 2 })={ (ab+bc+cd) }^{ 2 }$$.

If $${S}_{n}={(4)}^{n}+3$$, what is the units digit of $${S}_{100}$$?

The product of two numbers is $$119$$ and their AM is $$12$$. Find the numbers.

Write four more numbers in the following pattern-
$$ \displaystyle \frac{-1}{3} $$, $$ \displaystyle \frac{-2}{6} $$, $$ \displaystyle \frac{-3}{9} $$, $$ \displaystyle \frac{-4}{12} $$..........

Find the common ratio and the general term of the following geometric sequences.
$$0.02, 0.006, 0.0018, .....$$

complete the table . what do you notice about the numbers in the orange band ?
1 7 13
2 8 14
3 9 15
4 10 16
5 11 17
6 12

If,
$$ 1, 5, 8=76$$
$$ 2, 7, 3=25$$
$$ 3, 4, 9=89$$
$$ 4, 5, 7=69$$
THEN
$$5, 3, 8$$=?

$$13,25,14,23,15,21,16,?,?$$
1) $$14,11$$
2) $$19,17$$

Find the sum to $$n$$ terms of the series
$$5+11+19+29+......$$

Find the missing number in the series :
40 , 54 , 82 , ? , 180 , 250

Write opposites of the following :
$$30\ km$$ north

Solve for a.
$$\frac{3a-2}{7}-\frac{a-2}{4}=2,$$

Fill in the blanks:
$$\dfrac {2}{8} \times 3 = \dfrac {2}{8} + -+-+- $$

If $$a,b,c,d$$ are in GP, show that
$$(b-c)^2+(c-a)^2+(d-b)^2=(a-d)^2$$

Fill in the blanks in the expressions with the proper numbers.
$$(5\ \times 4) > (7\times \Box )$$

The Fibonacci sequence is defined by $$1=a_{1}=a_{2}$$ and $$a_{n}=a_{n-1}+a_{n-1},n > 2$$.
Find $$\dfrac {a_{n}}{a_{n}+1}$$ for $$n=1,2,3,4$$.

Identify whether the following sequence is a geometric sequence or not.
$$-3,9,-27,81$$

Identify whether the following sequence is a geometric sequence or not.
$$2,6,18,54$$

Fill the squares with all the numbers from 46 to 54

rule:- total of each line should be 150.
49
46
52 47

Identify whether the following sequence is a geometric sequence or not.
$$1,4,9,16$$

Identify whether the following sequence is a geometric sequence or not.
$$\dfrac{1}{2},\dfrac{2}{4},\dfrac{4}{8},\dfrac{8}{16}$$

Identify whether the following sequence is a geometric sequence or not.
$$\dfrac{1}{2},\dfrac{2}{3},\dfrac{3}{4},\dfrac{4}{5}$$

Identify whether the following sequence is a geometric sequence or not.
$$25,5,1,\dfrac{1}{5}$$

Find the sum of the following series:
$$ 0.6+0.66+0.666+...$$ to n terms.

The following geometric arrays suggest a sequence of numbers.
(a) Find the next two terms.
(b) Find the $$100^{th}$$ term.
(c) Find the $$n^{th}$$ term.

Find the sum to infinite terms of the series
$$\dfrac {7}{5} \left (1 + \dfrac {1}{10^{2}} + \dfrac {1.3}{1.2} \cdot \dfrac {1}{10^{4}} + \dfrac {1.3.5}{1.2.3} \cdot \dfrac {1}{10^{6}} + ......\right )$$

The sum of first $$n$$ terms of a sequence is $$\cfrac { { 6 }^{ n }-{ 5 }^{ n } }{ { 5 }^{ n } } $$
Find its $$n^{th}$$ term and examine whether the sequence is an A.P of G.P.

If $$a=\underset{55}{\underbrace{111.........1}}, b=1+10+10^2+10^3+10^4$$ and $$c=1+10^5+10^{10}+....+10^{50}$$, then show following.
(i) 'a' is a not composite number
(ii) $$a\ is\ not\ equal\ bc$$

Study the pattern:
$$91 \times 11 \times 1 = 1001 $$
$$91 \times 11 \times 2 = 2002 $$
$$91 \times 11 \times 3 = 3003$$
Write next seven steps. Check, whether the result is correct.
Try the pattern for $$143 \times 7 \times 1, 143 \times 7 \times 2 .....$$

Solve the following equations.
$$\displaystyle\, 7^{x + 2} - \frac{1}{7}\cdot 7^{x + 1} - 14.7^{x - 1} + 2.7^x = 49$$

The natural numbers are written in the form of a triangle as shown below :
The sum of numbers in all the n rows .

If a , b are = ive , then from any integer n prove that
$$(a \, + \, b)^n \, < \, 2^n\, (a^n \, + \, b^n )$$

Find the $$50_{th}$$ term of the sequence:
$$\dfrac{1}{n},\,\dfrac{n+1}{n},\,\dfrac{2n+1}{n}...................$$

(a) If the roots of the equation, $$(b-c){ x }^{ 2 }+(c-a)x+(a-b)=0$$ be equal, then prove thar a,b,c are in arithmetical progression.
(b) If $$a(b-c){ x }^{ 2 }+b(c-a)x+c(a-b)=0$$ has equal roots, prove that a,b,c are in harmonical progression.

If y = x$$^n$$ log x then
$$ y_n \, = \, n!\left [ log \, \, x \, + \, 1 \, +\dfrac{1}{2}\, +\dfrac{1}{3} .... \, + \, \, \dfrac{1}{n} \right ]$$
$$\forall \, n \, \epsilon \, N$$ and x > 0.

Find the arithmetic mean
If $$69.5$$ is the mean of $$72, 70, x, 62, 50, 71, 90, 64, 58$$ and $$82$$. Find the value of $$x.$$

Sum upto $$n$$ the series
$$6+66+666+.....$$

Find the sum of series
$$0.5 + 0.55 + 0.555 + ...$$

Sum the series :
$$2^{1/4} \, \cdot \, 4^{1/8} \, \cdot \, 8^{1/16} \, \cdot \, 16^{1/32} \, ....$$ is equal

In the given squences 2,5,6.....50and 3,5,7.....60
How many terms are common to both?