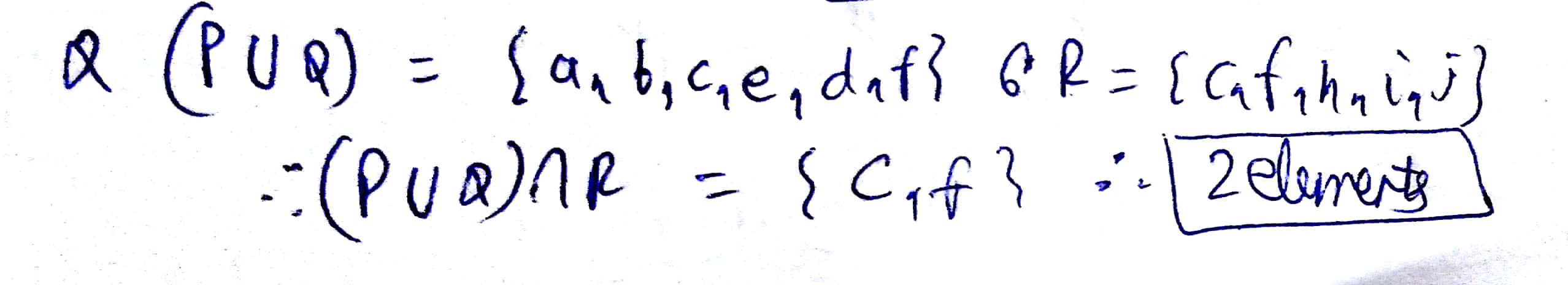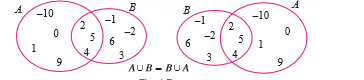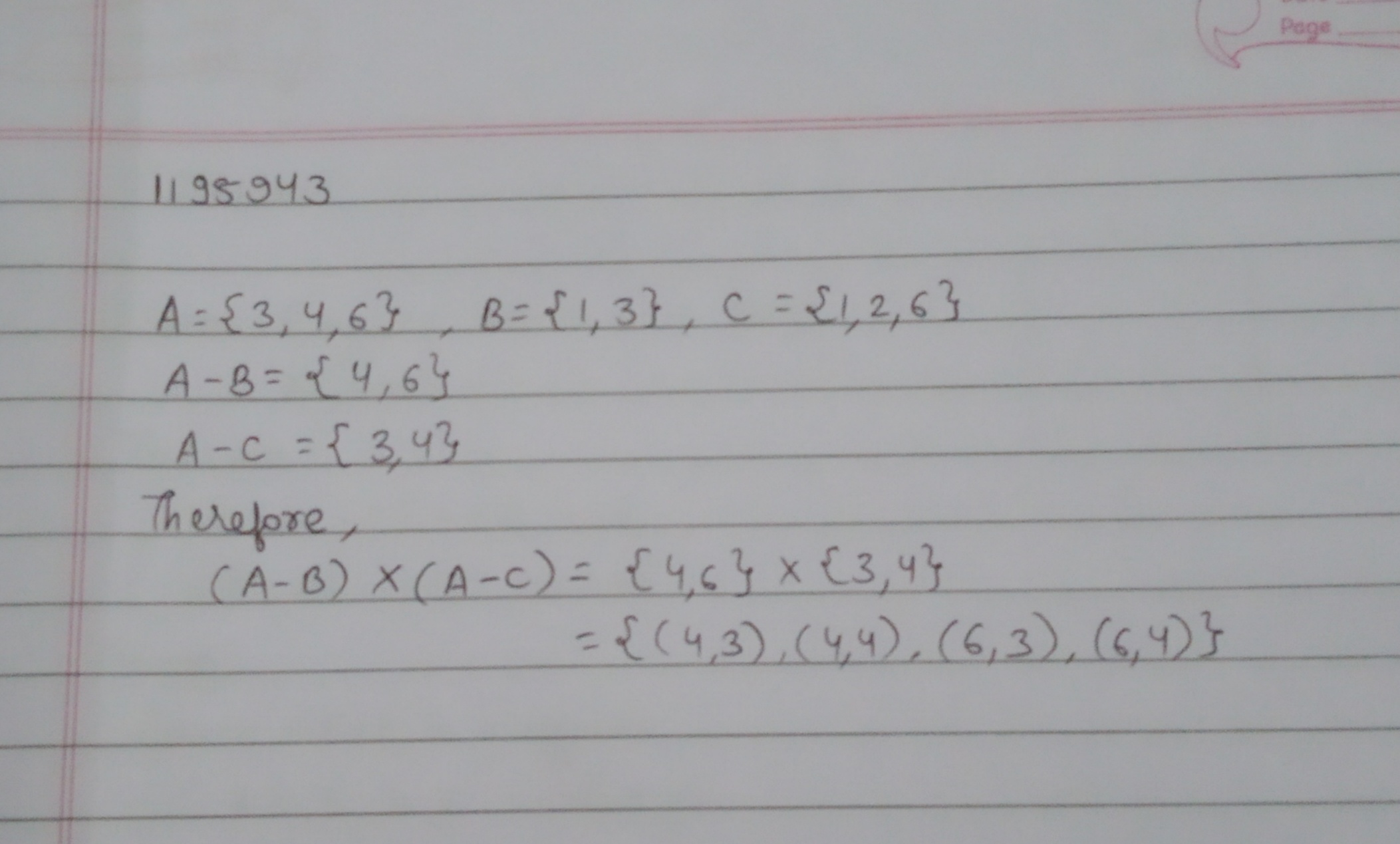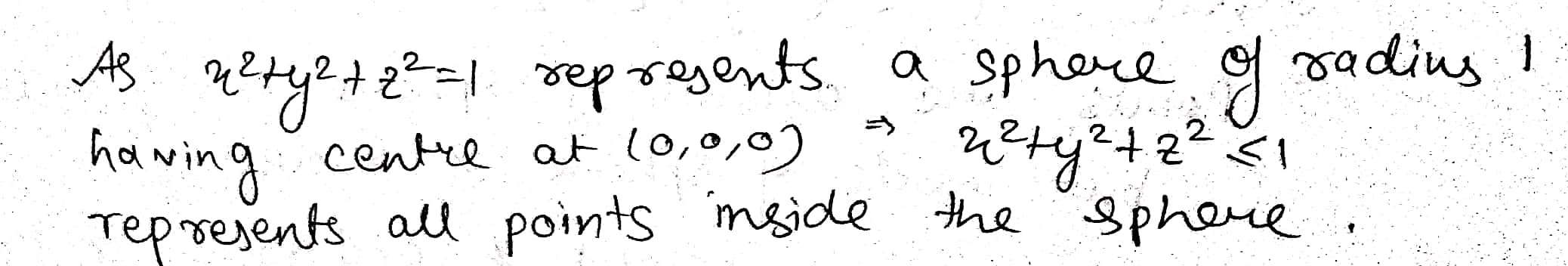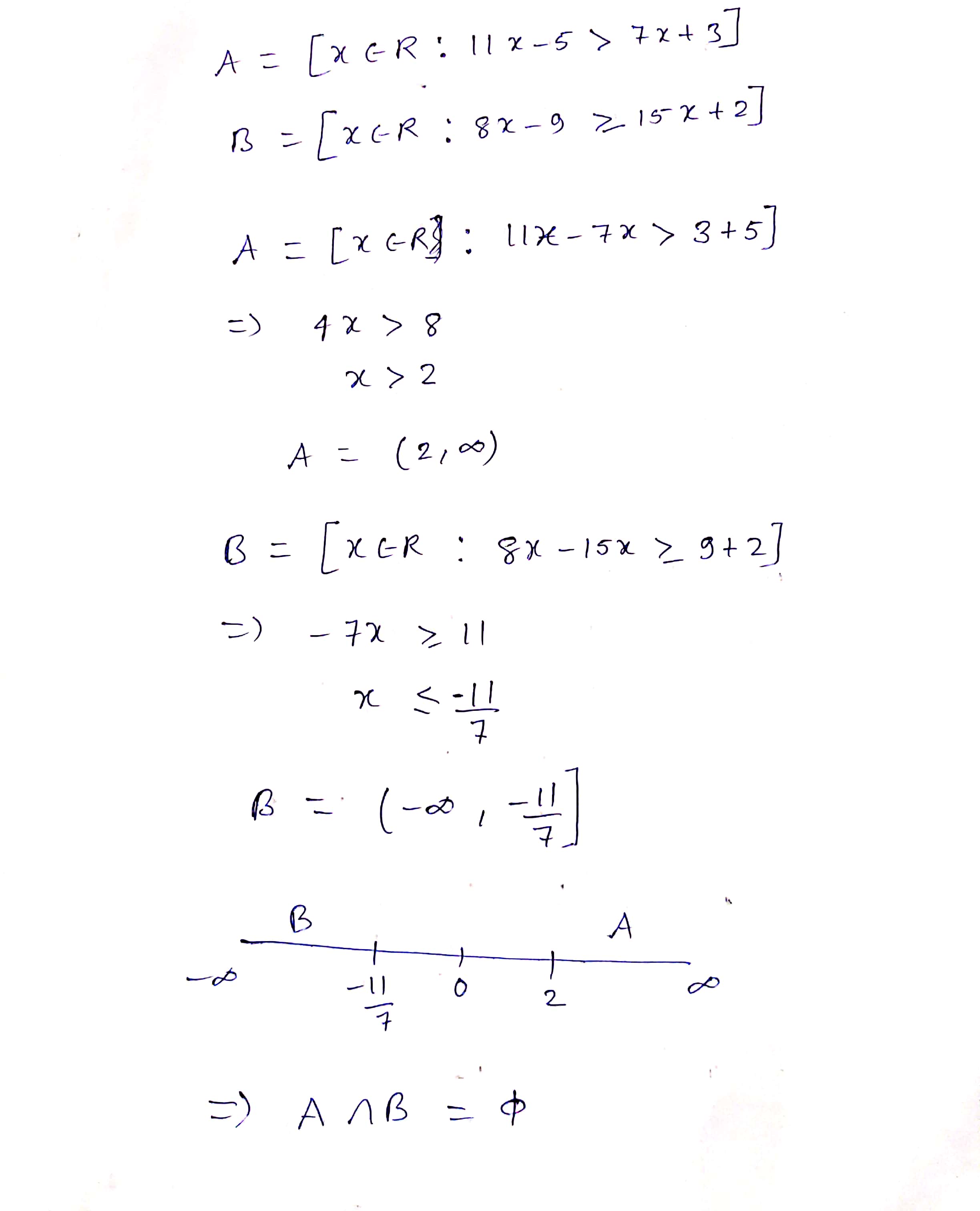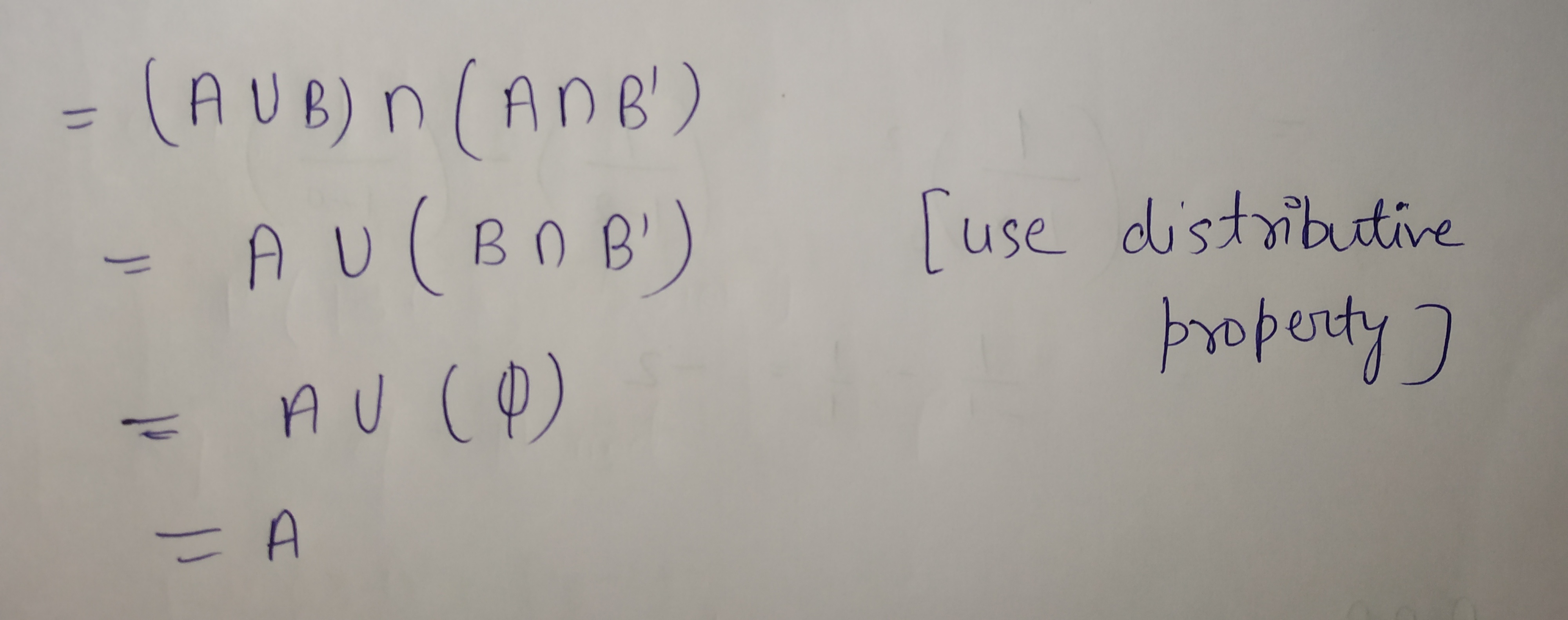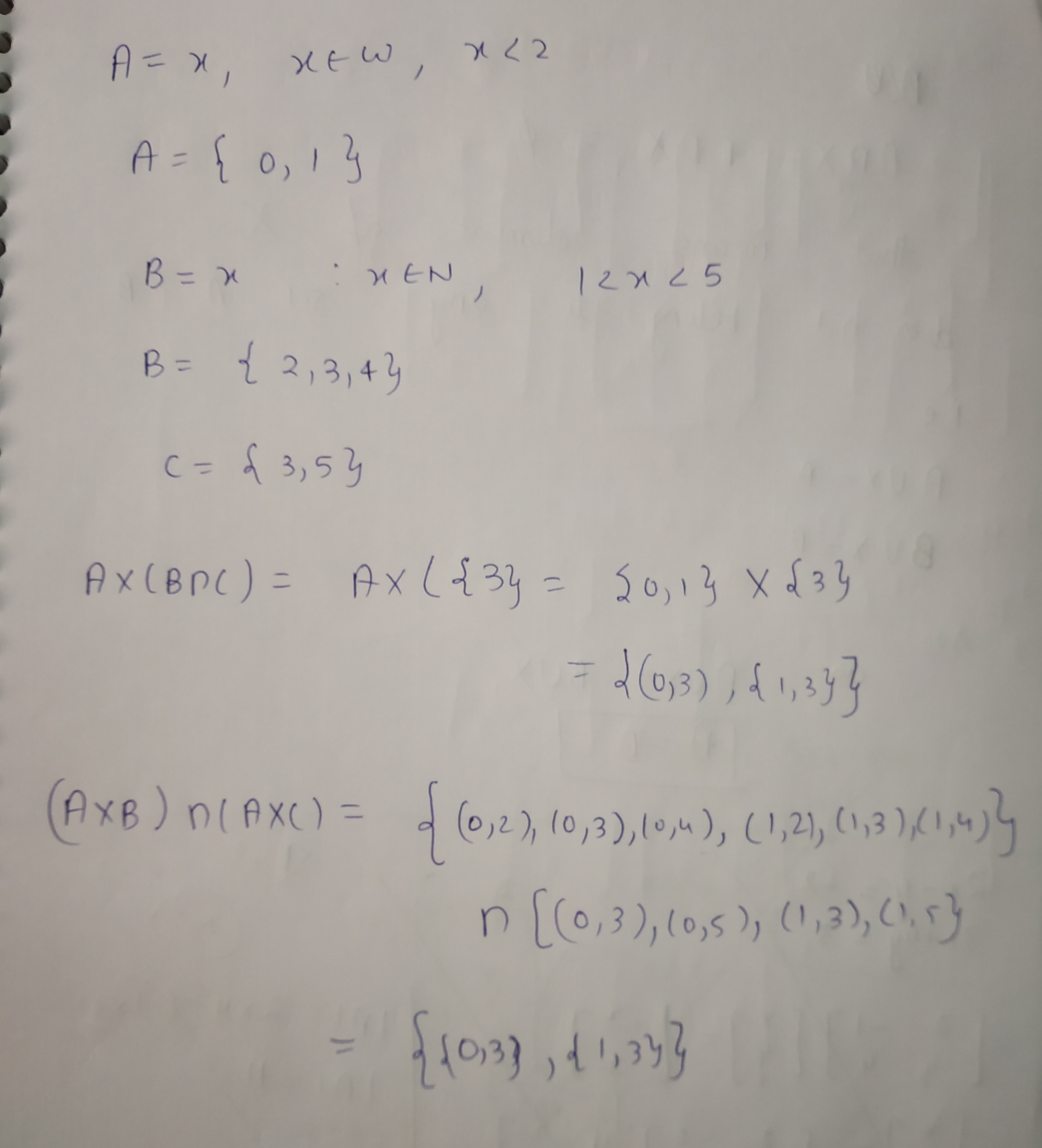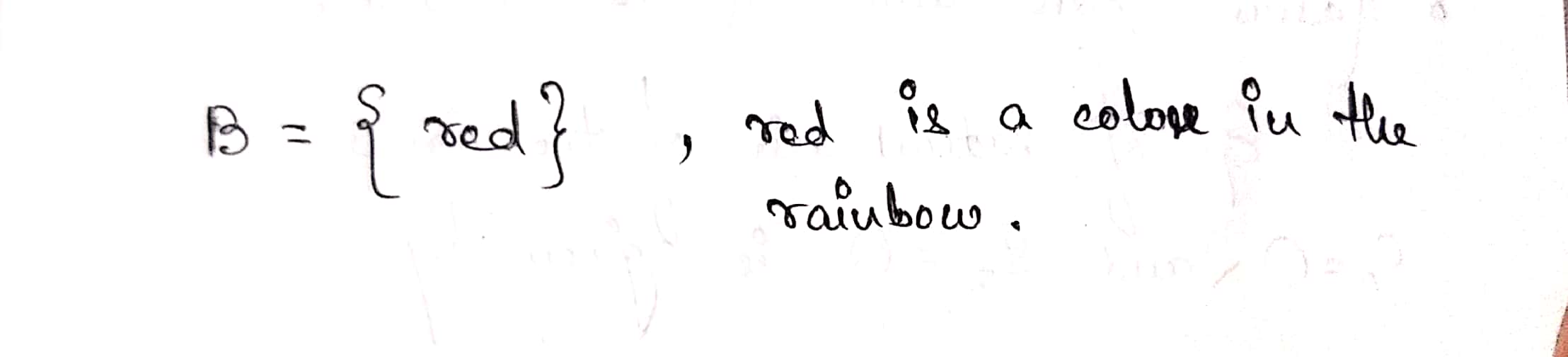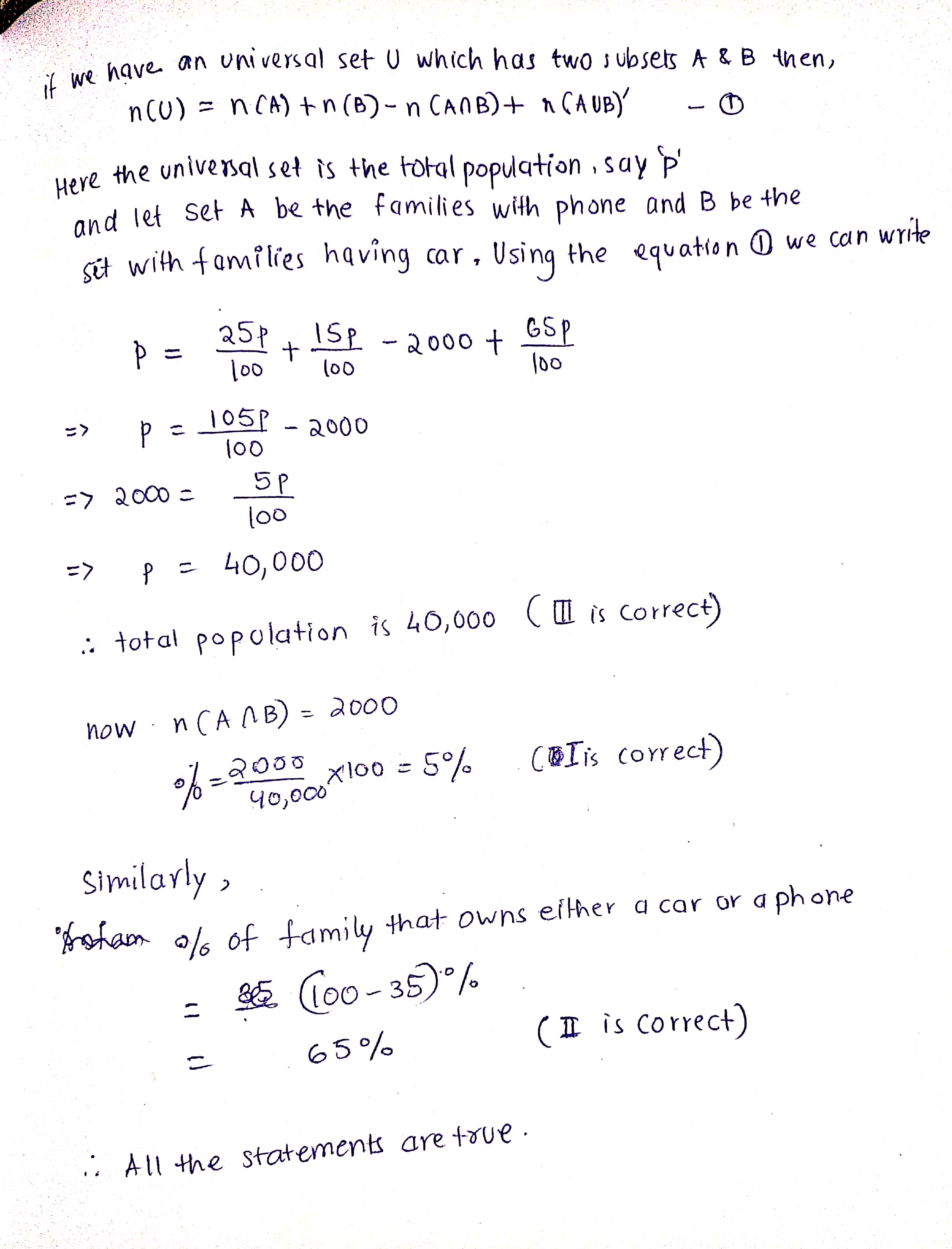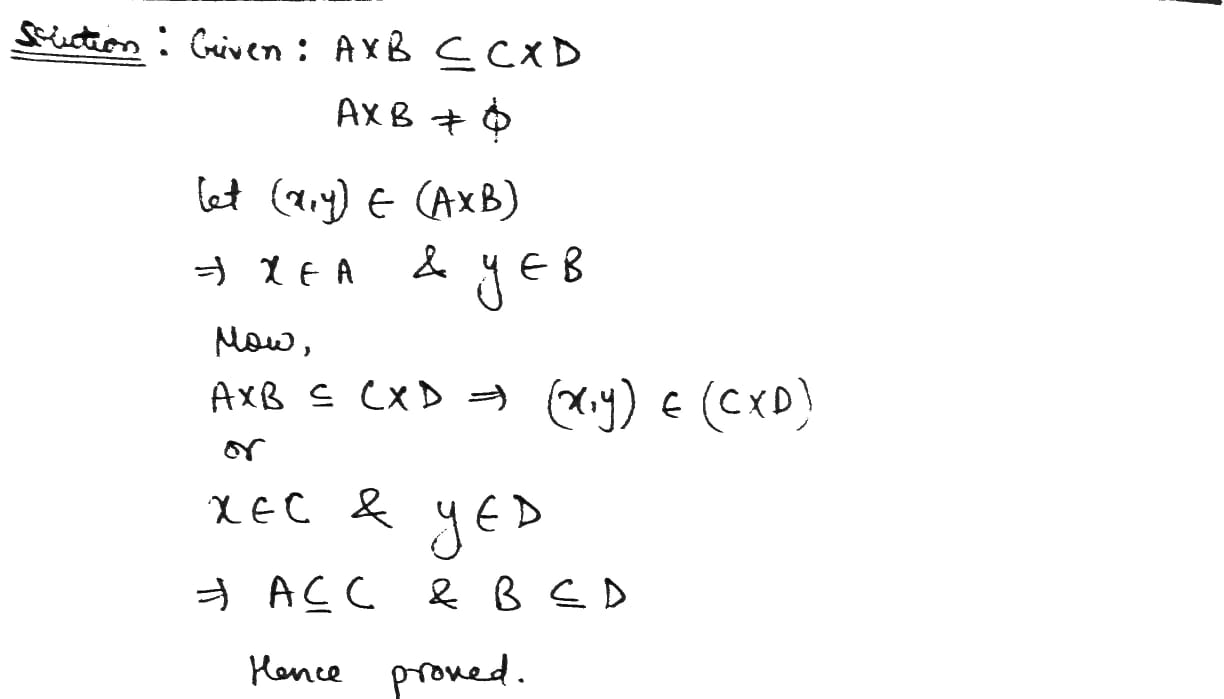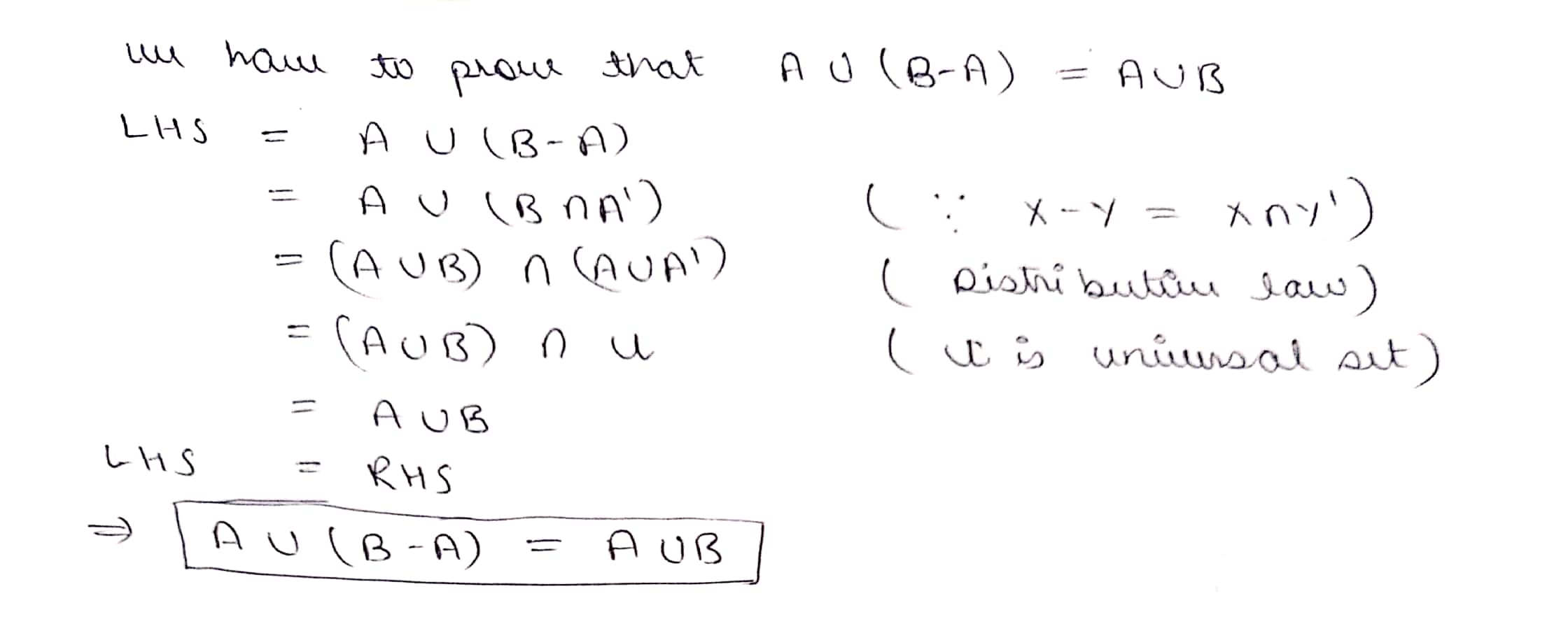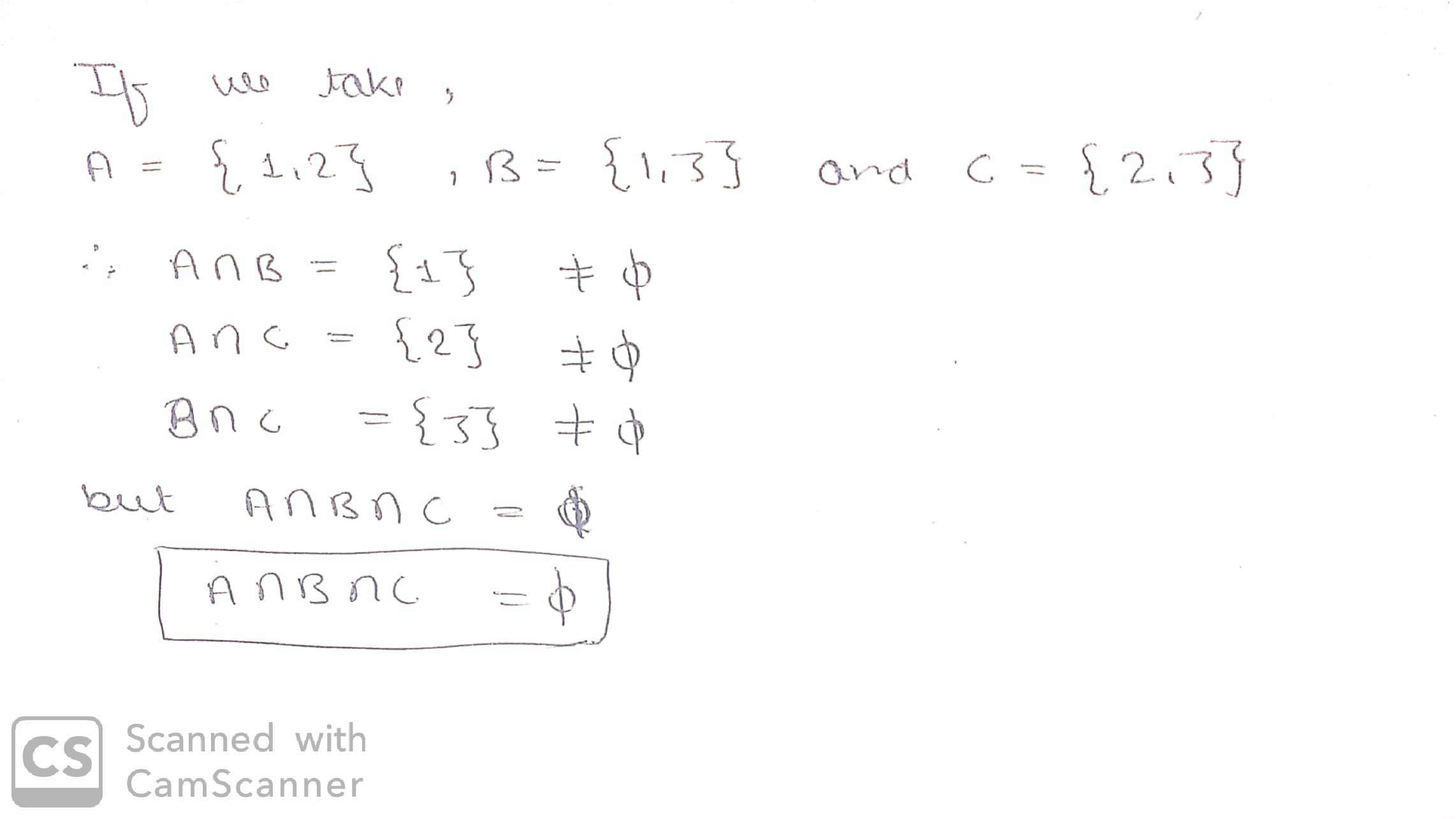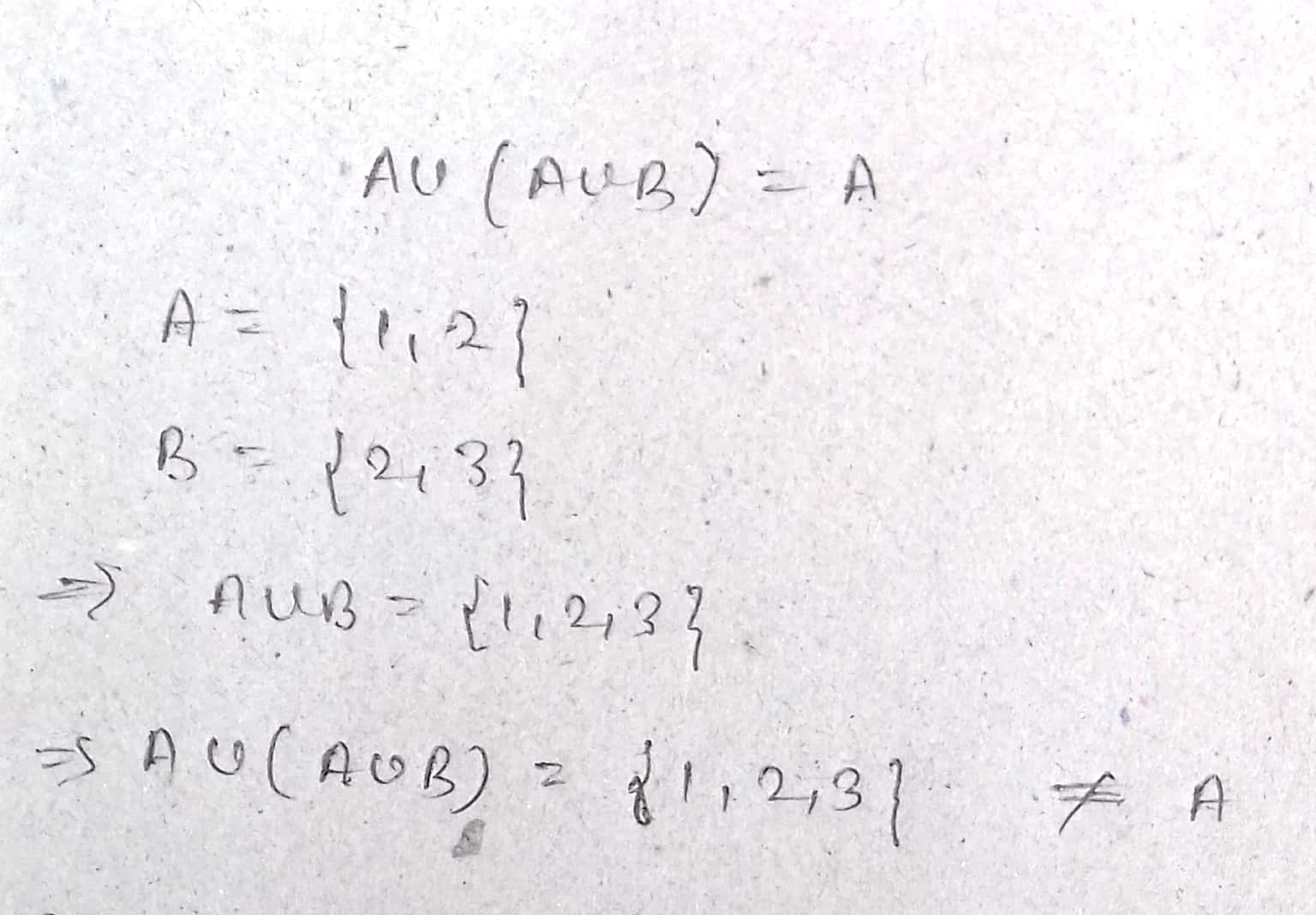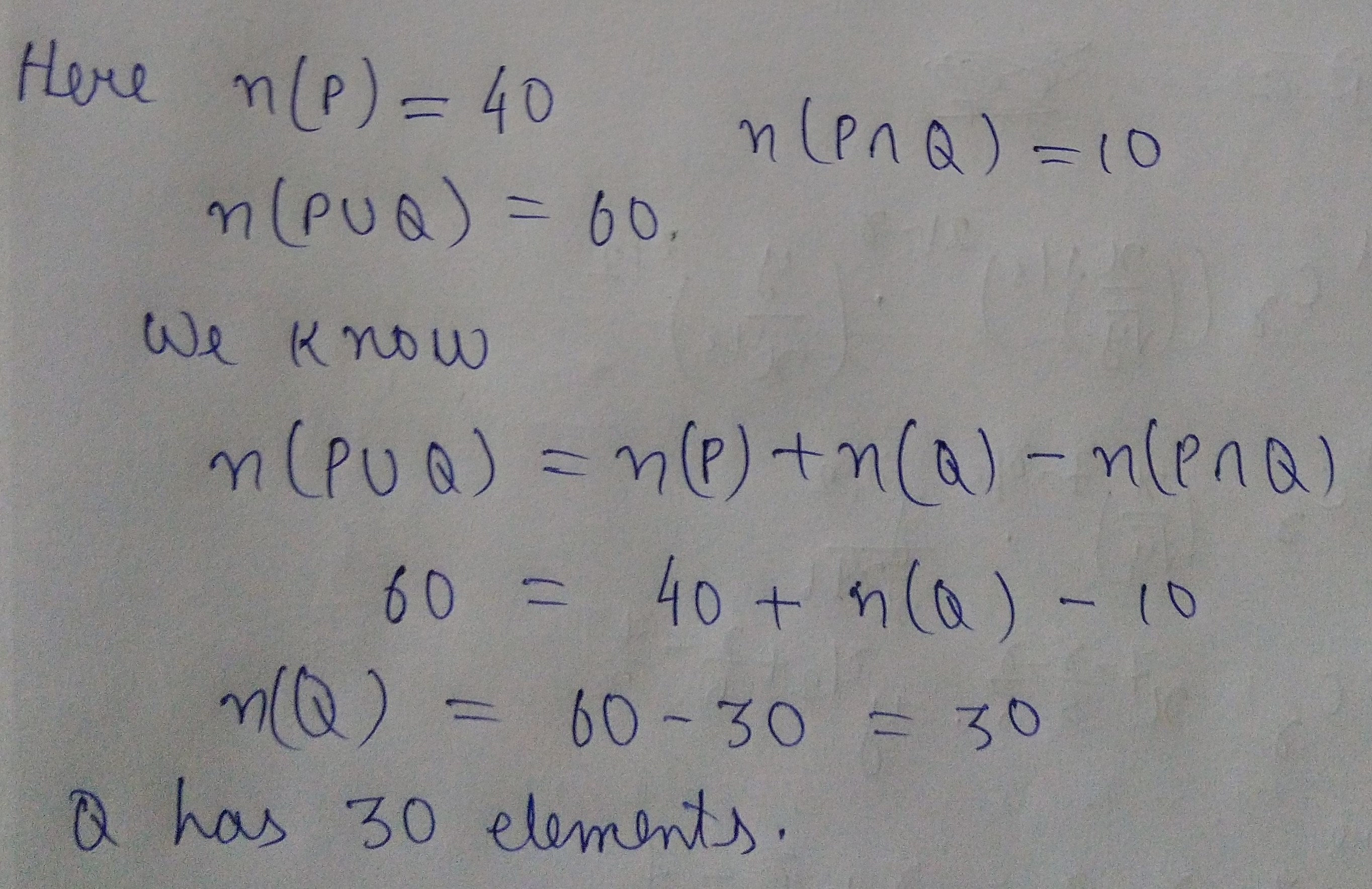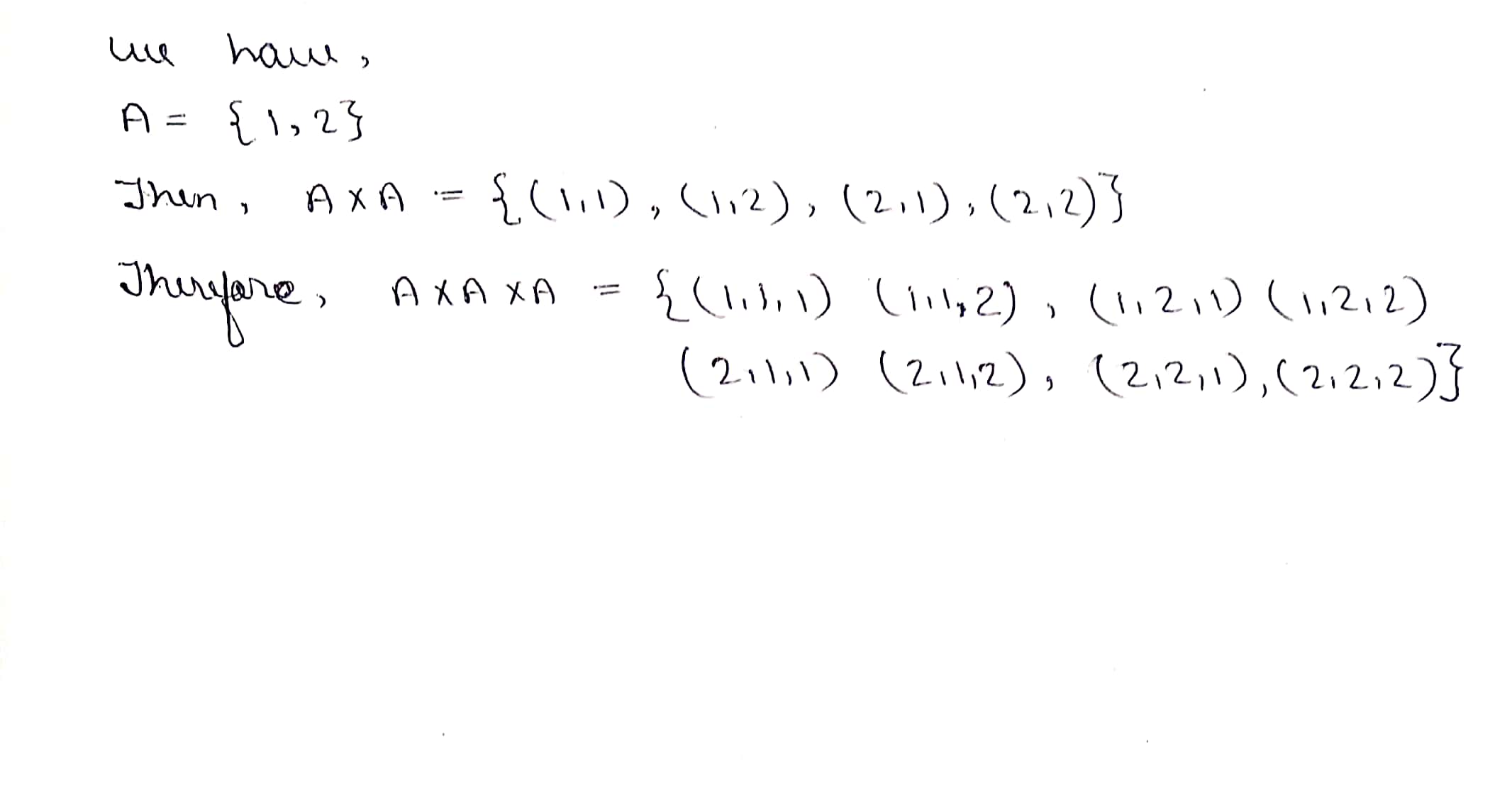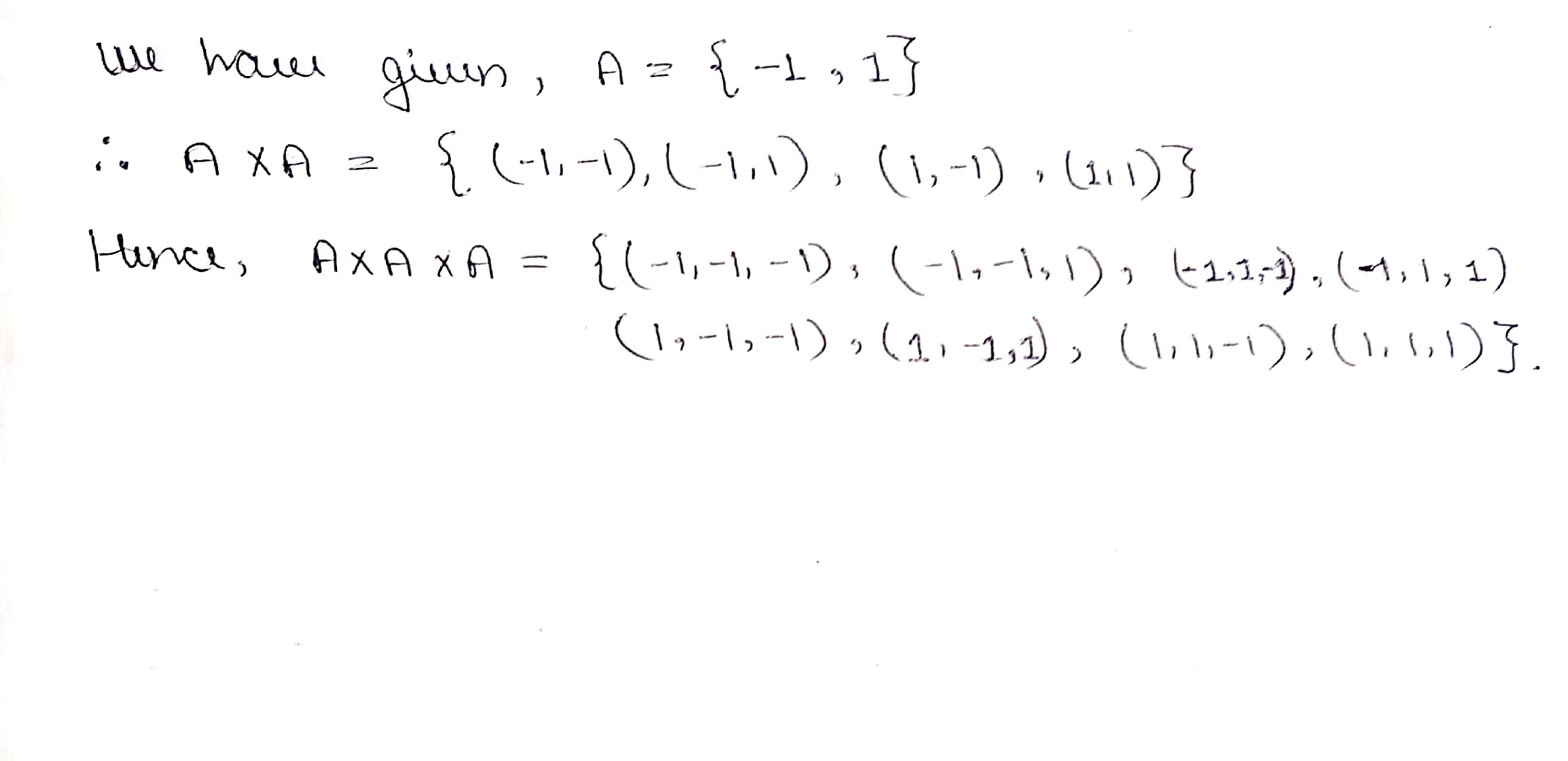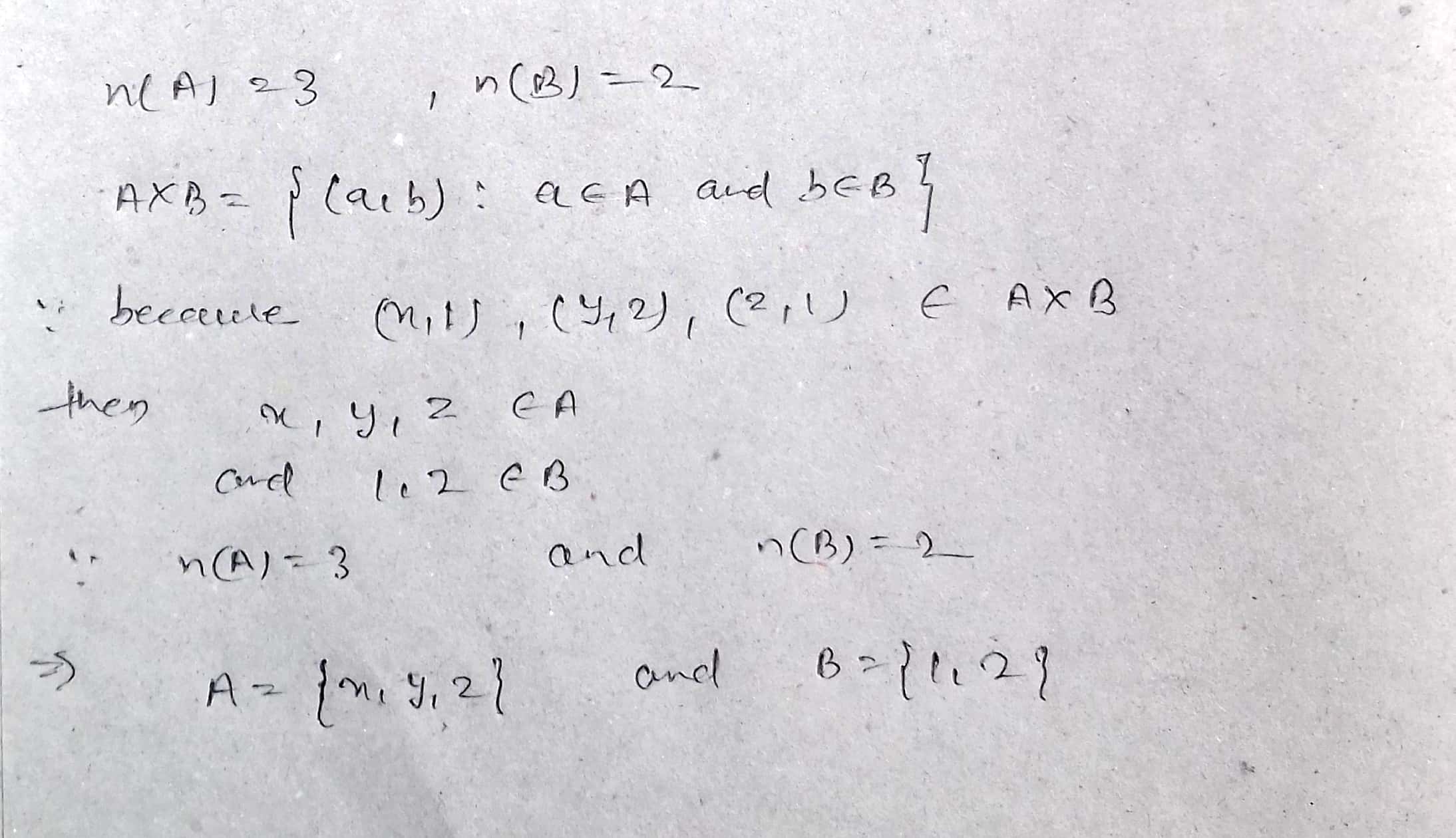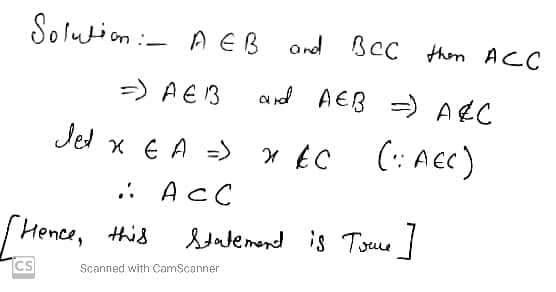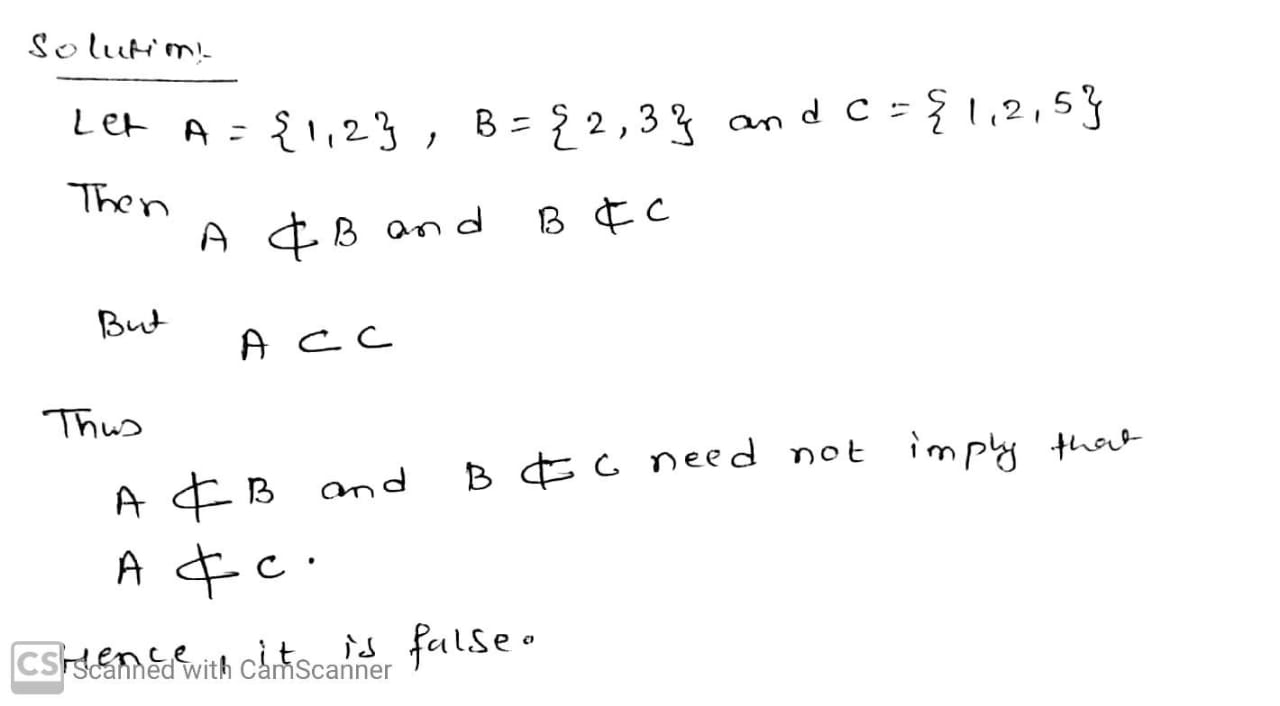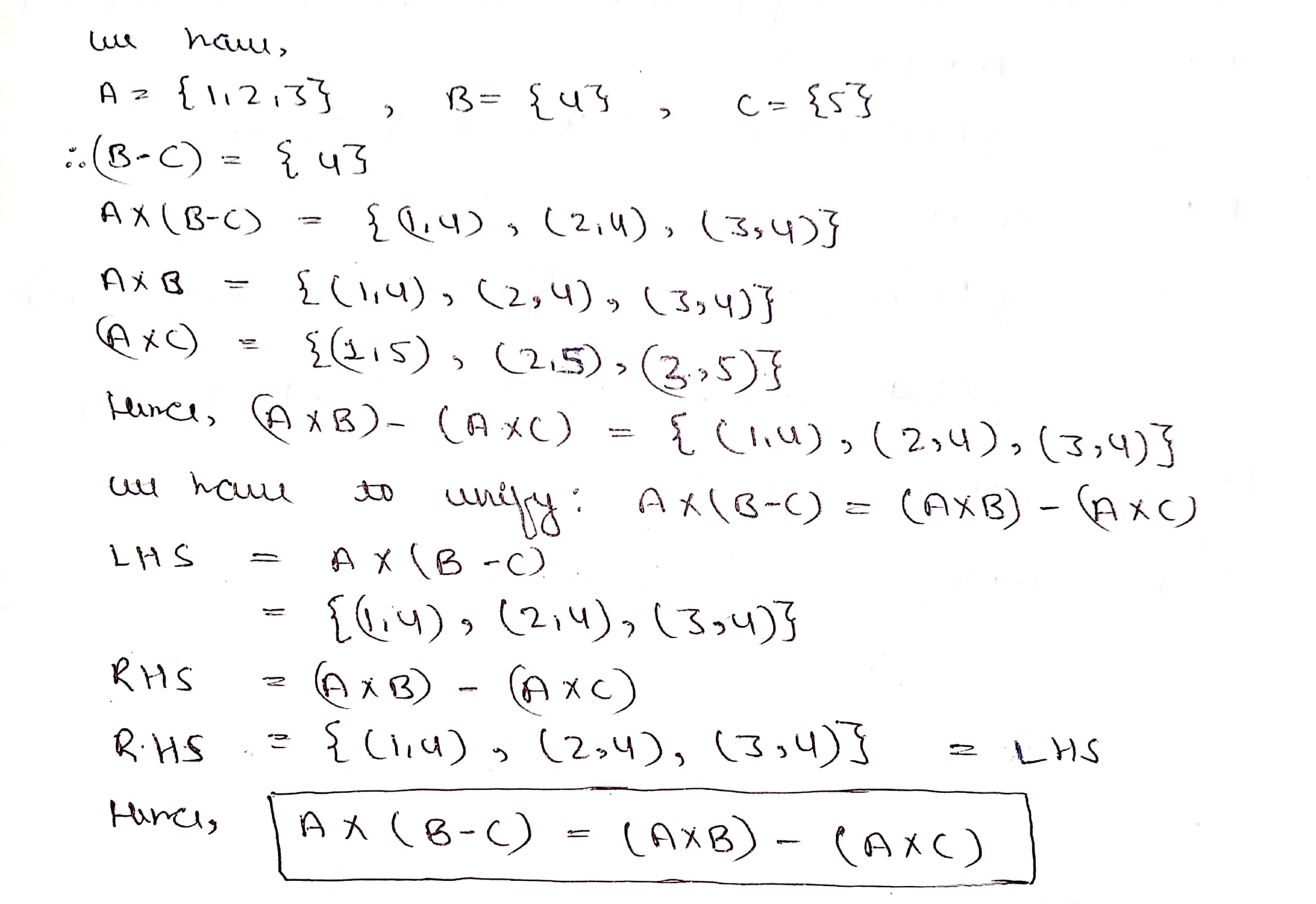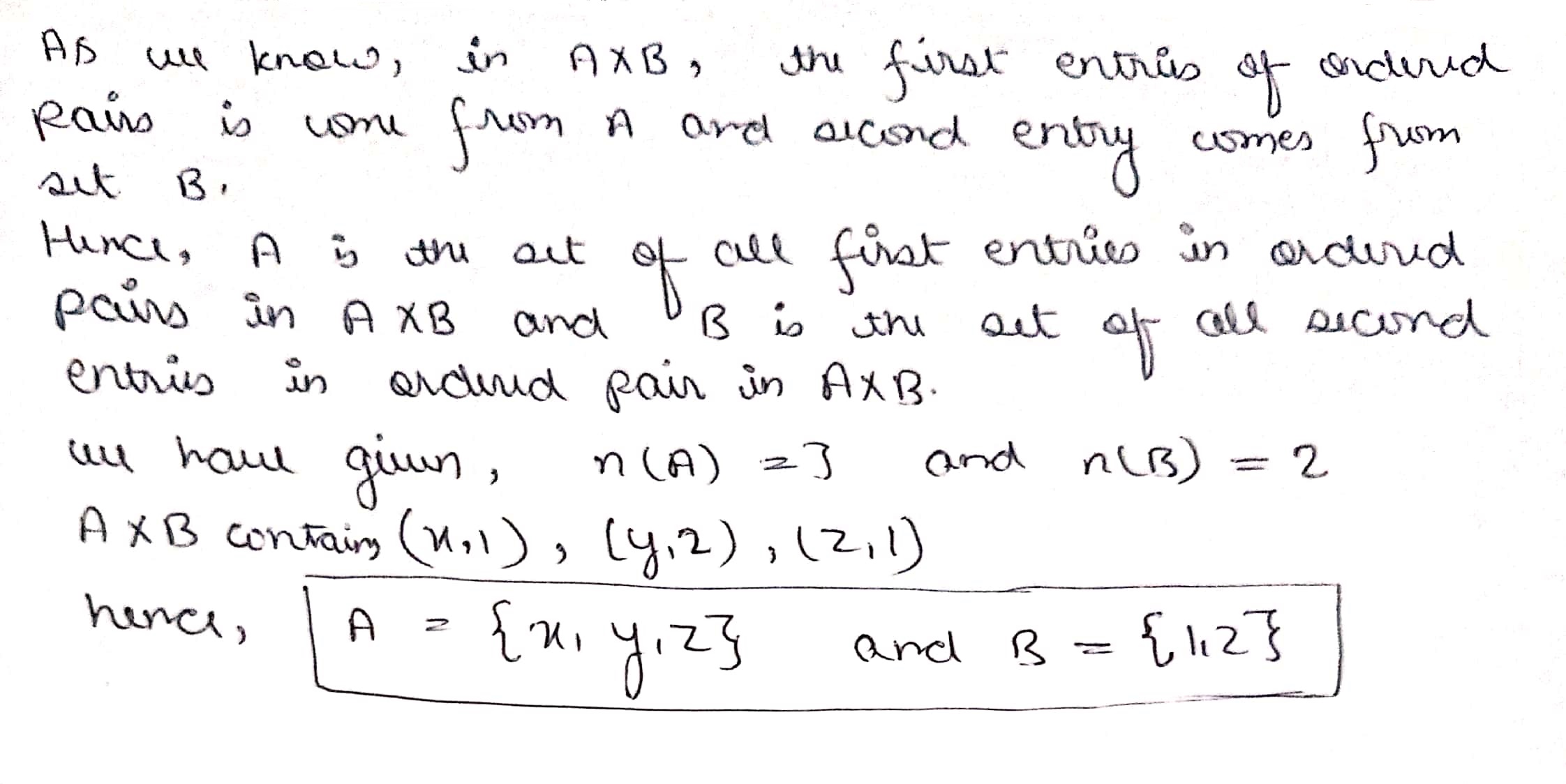Sets - Class 11 Engineering Maths - Extra Questions
Let $$A=\left \{ 1, 2, 3, 4 \right \}$$
$$S=\left \{ (a, b); a,b\in A, a\ \mbox{divides}\ b \right \}$$, write down $$S$$ explicitly
Let $$\displaystyle A=\left \{ \left ( x, y \right ):x, y \epsilon R, x^{2}y^{2}+y^{2}=1 \right \}$$ and $$\displaystyle B=\left \{ \left ( x,0 \right ):x \epsilon R, -1\leq x\leq 1 \right \}.$$ Then $$\displaystyle A\cap B= \left \{ \left ( -a, 0 \right ), \left ( 1, b \right ) \right \}$$ .Find relation between a and b
If $$S$$ and $$T$$ are two sets such that $$S$$ has $$21$$ elements. T has $$32$$ elements and $$S$$ $$\displaystyle \cap $$$$T$$ has $$11 $$ elements, then find the number of elements in $$S$$ $$\displaystyle \cup $$ $$T$$.
$$\displaystyle \left \{ a,b \right \}$$ is a subset of $$\left \{ b,c,a \right \}$$.If true enter 1 else 0.
$$\displaystyle {a,e}$$ is a subset of $$ \left \{ x:x \text{ is a vowel in the English alphabet}\right \}$$.( Enter 1 if true or 0 otherwise)
Let $$m$$ be a number in a set $$A=\displaystyle \left \{ 1,2,3 \right \} \ such \ that \ A\nsubseteq \left \{ 1,3,5 \right \}$$ and $$m\notin \{1,3,5\}$$. Then $$m$$ is:
Let $$A = \{1, 2, 3, 4, 5, 6\}$$, $$B = \{2, 4, 6, 8\}$$. Find $$A - B$$ and $$B - A$$.
Find $$n(B-C)^c$$.
If $$A=\left \{2, 3,4, 5, 6, 7\right \}$$ and $$B =\left \{3, 5, 7, 9,11, 13\right \}$$, then find $$A-B$$ and $$B -A$$
In a group of $$50$$ persons, $$14$$ drink tea but not coffee and $$30$$ drink tea. Find how many drink coffee but not tea?
$$\displaystyle n(C-T)=n(T\cup C)-n(T)=50-30=20$$
Let $$A = \{2, 4, 6, 8\}$$ and $$B = \{6, 8, 10, 12\}$$ then find $$\displaystyle A\cup B$$.
Find n$$(A\cup B)^c$$
$$\displaystyle a \epsilon \left \{ a,b,c \right \}$$, then $$\{a\}$$ is a subset of $$\{a,b,c\}$$.( Enter 1 if true or 0 otherwise)
If $$A\left \{1, 2,3\right \}$$ and $$B =\left \{1, 3, 5, 7\right \}$$, then find $$A\cup B$$
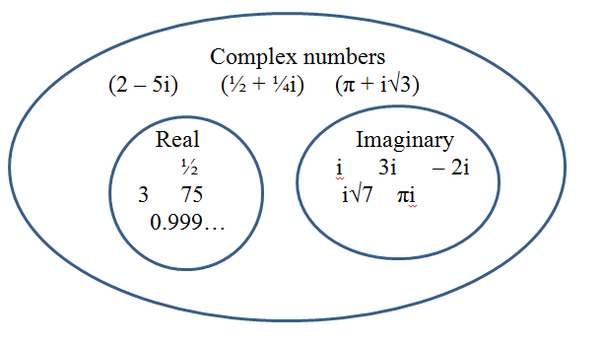
If $$R$$ is the set of real numbers and $$Q$$ is the set of rational numbers, then what is $$R-Q$$?
Let $$A = \left \{1, 2, 3, 4, 5, 6\right \}$$. Insert the appropriate symbol $$\in$$ or $$\not\in$$ in the blank spaces:
(i). .A (ii) 8 . . . A (iii). .A (iv). . A (v). .A (vi). .A
Write the following as intervals :
(i) $$\left \{x : x \: \epsilon \: R, 4 < x \leq 6\right \}$$ (ii) $$\left \{x : x \: \epsilon \: R, -12 < x < -10\right \}$$ (iii) $$\left \{x : x \: \epsilon \:R, 0 \leq x < 7\right \}$$ (iv) $$\left \{x : x \: \epsilon \:R, 3 \leq x \leq 4\right \}$$
If $$A = \{3, 6, 9, 12, 15, 18, 21\}, B = \{ 4, 8, 12, 16, 20 \},$$$$C = \{ 2, 4, 6, 8, 10, 12, 14, 16 \}, D = \{5, 10, 15, 20 \};$$ find
(i) $$A -B$$ (ii) $$A- C$$ (iii) $$A- D$$ (iv) $$B- A$$ (v) $$C- A$$ (vi) $$D- A$$ (vii) $$B- C$$ (viii) $$B- D$$ (ix) $$C- B$$ (x) $$D- B$$ (xi) $$C- D$$ (xii) $$D- C$$
(i) $$A -B$$
$$(P\cup Q)\cap R$$
$$ (P\cup Q) = \left \{ a,b,c,e,d,f \right \} $$ & $$ R = \left \{ c,f,h,i,j \right \} $$
$$ \therefore (P\cup Q)\cap R = \left \{ c,f \right \}\therefore \boxed {2\,elements} $$
Decide, among the following sets, which sets are subsets of one and another:
$$A =\{ x : x \epsilon\ \text{R and x satisfy} \ x^2- 8x + 12 = 0\},$$$$ B = \{ 2, 4, 6\}, $$$$C = \left \{ 2, 4, 6, 8, . . . \right \}, D = \left \{ 6 \right \}$$
$$A =\{ x : x \epsilon\ \text{R and x satisfy} \ x^2- 8x + 12 = 0\},$$
$$ B = \{ 2, 4, 6\}, $$
$$C = \left \{ 2, 4, 6, 8, . . . \right \}, D = \left \{ 6 \right \}$$
Which of the following sets are equivalent?
(i) $$A=\left \{ 2,4,6,8,10 \right \}, B=\left \{ 1,3,5,7,9 \right \}$$
(ii) $$X=\left \{ x:x \in \mathbb{N}, 1< x< 6 \right \}, Y=$$ { $$x:x$$ is a vowel in the English Alphabet }
(iii) $$P=$$ $$\{$$ $$x:x$$ is a prime number and $$5< x< 23$$$$\}$$
$$Q=\{x:x\in \mathbb{W},1<x<5\}$$
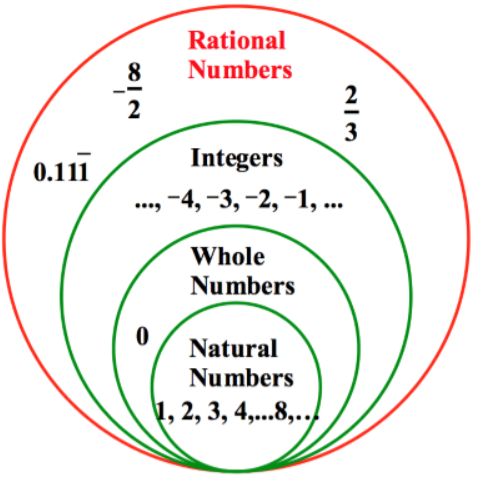
Represent the following set by using their standard notations: Set of integers
Which of the following sets are equal?
(i) $$A=\left \{ 1,2,3,4 \right \}, B=\left \{ 4,3,2,1 \right \}$$
(ii) $$A=\left \{ 4,8,12,16 \right \}, B=\left \{ 8,4,16,18 \right \}$$
(iii) $$X=\left \{ 2,4,6,8 \right \}$$
$$Y=$$ { $$x:x$$ is a positive even integer $$0< x< 10$$ }
(iv) $$P=$$ { $$x:x$$ is a multiple of $$10$$, $$x\in N$$ }
$$Q=\left \{ 10,15,20,25,30,... \right \}$$
Find out the set, which is defined as $$\{x : x - 3 < 0\}$$; x is any integer.
If $$A = \left \{3k | k \ \epsilon \mathbb {Z}\right \}$$ and $$B = \mathbb {N}$$, find $$A\triangle B$$
Write the following sets in Descriptive form
(i) $$A=\left \{ a,e,i,o,u \right \}$$
(ii) $$B=\left \{ 1,3,5,7,9,11 \right \}$$
(iii) $$C=\left \{ 1,4,9,16,25 \right \}$$
(iv) $$P=$$ { $$x:x$$ is a letter in the word 'set theory' }
(v) $$Q=$$ { $$x:x$$ is a prime number between 10 and 20 }
Find the set if it is defined as $$\{x : |x^2 - 9| = 0\}$$.
Identify the following sets as finite or infinite
(i) $$A= \left \{ 4,5,6,... \right \}$$
(ii) $$B= \left \{ 0,1,2,3,4,... 75 \right \}$$
(iii) $$X=$$ $$\{$$ $$x:x$$ is an even natural number $$\}$$
(iv) $$Y=$$ $$\{$$ $$x:x$$ is a multiple of 6 and $$x> 0$$ $$\}$$
(v) $$P=$$ The set of letters in the word 'freedom'
Let $$A=\left \{ 0,1,2,3,4,5 \right \}$$. Insert the appropriate symbol $$\in$$ or $$\notin$$ in the blank spaces
(i) $$0 ---- A$$
(ii) $$6 ---- A$$
(iii) $$3 ---- A$$
(iv) $$4 ---- A$$
(v) $$7 ---- A$$
Represent the following set by using their standard notations:Set of natural numbers
If $$n\left ( A \right )=26, n\left ( B \right )=10, n\left ( A\cup B \right )=30,n\left ( {A}' \right )=17$$, find $$n\left ( A\cap B \right )$$ and $$n\left ( \cup \right )$$.
Examine whether $$A=$$ $$\{$$ $$x:x$$ is a positive integer divisible by $$3 \}$$ is a subset of $$B=$$ $$\{$$ $$x:x$$ is a multiple of $$5$$, $$x\in N$$ $$\}$$.
Fill in the blanks with $$\subseteq $$ or $$\nsubseteq $$ to make each statement true.
(i) $$\left \{ 3 \right \}----\left \{ 0,2,4,6 \right \}$$
(ii) $$\left \{ a \right \}----\left \{ a,b,c \right \}$$
(iii) $$\left \{ 8,18 \right \}----\left \{ 18,8 \right \}$$
(iv) $$\left \{ d \right \}----\left \{ a,b,c \right \}$$
Is $$\phi =\left \{ \phi \right \}$$? Why?
If $$A$$ and $$B$$ are two sets such that $$A$$ has $$50$$ elements, $$B$$ has $$65$$ elements and $$A\cup B$$ has $$100$$ elements, how many elements does $$A\cap B$$ have?
From the sets given below, select equal sets.
$$A=\left \{ 12,14,18,22 \right \}, B=\left \{ 11,12,13,14 \right \}, C=\left \{ 14,18,22,24 \right \}, D=\left \{ 13,11,12,14 \right \},$$$$ E=\left \{ -11,11 \right \}, F=\left \{ 10,19 \right \}, G=\left \{ 11,-11 \right \}, H=\left \{ 10,11 \right \}$$.
If $$A$$ and $$B$$ are two sets containing $$13$$ and $$16$$ elements respectively, then find the minimum and maximum number of elements in $$A\cup B$$?
Let $$X=\left \{ -3,-2,-1,0,1,2 \right \}$$ and $$Y=$$ $$\{$$ $$x:x$$ is an integer and $$ -3\leq x< 2 $$$$\}$$
(i) Is $$X$$ a subset of $$Y$$?
(ii) Is $$Y$$ a subset of $$X$$?
If $$n\left ( A\cap B \right )=5, n\left ( A\cup B \right )=35, n\left ( A \right )=13, $$ find $$n\left ( B \right )$$.
Which of the sets are equal sets? State the reason.
$$\phi ,\left \{ 0 \right \},\left \{ \phi \right \}$$
If $$A=\left \{-2,-1,0,3,4 \right \}, B=\left \{-1,3,5\right \}$$, find (i) $$A-B$$
(ii) $$B-A$$
If $$A=\left \{ 3,6,9,12,15,18 \right \}, B=\left \{ 4,8,12,16,20 \right \}, C=\left \{ 2,4,6,8,10,12 \right \}$$ and $$D=\left \{ 5,10,15,20,25 \right \},$$ find
(i) $$A-B$$
(ii) $$B-C$$
(iii) $$C-D$$
(iv) $$D-A$$
(v) $$n\left ( A-C \right )$$
Let $$A$$ and $$B$$ be two finite sets such that $$n\left ( A- B \right )=30, n\left ( A\cup B \right )=180$$. Find $$n\left ( B \right )$$.
If $$n\left ( \cup \right )=38, n\left ( A \right )=16, n\left ( A\cap B \right )=12,n\left ( {B}' \right )=20$$, find $$n\left ( A\cup B \right )$$.
Given n(A)=285, n(B)=195, n(U)=500, $$n(A \cup B)=410$$, find $$n(A' \cup B')$$.
Given
the sets $$A=\left \{4,5,6,7\right \}$$ and $$B=\left \{1,3,8,9\right \}$$. Find $$
A\cap B$$
Let A = {4, 6, 8, 10 } and B = { 3, 4, 5, 6, 7 }. If $$f: A \rightarrow B$$ is defined by $$f(x)=\frac{1}{2}x+1$$ then represent f(x) by a set of ordered pairs
Given that $$U=\left \{ 3,7,9,11,15,17,18 \right \}, M=\left \{ 3,7,9,11 \right \}$$ and $$N=\left \{ 7,11,15,17 \right \}$$
Find
(i) $$M-N$$
(ii) $$N-M$$
(iii) $${N}'-M$$
(iv) $${M}'-N$$
(v) $$M\cap \left ( M-N \right )$$
(vi) $$N\cup \left ( N-M \right )$$
(vii) $$n\left ( M-N \right )$$
Given A $$= \{1, 2, 3, 4\}$$, B $$= \{3, 4, 5, 6\}$$ and C $$= \{6, 7\}$$. Verify that (A $$\cap$$ B) $$\cap$$ C = A $$\cap$$ (B $$\cap$$ C).
If A = {-1, 1}, find A $$\times$$ A $$\times$$ A.
For the given sets A= { 10, 0, 1, 9, 2, 4, 5} and B= { -1, -2, 5, 6, 2, 3, 4}, verify that set union is commutative. Also verify it by using Venn diagram.
Now, $$A\cup B$$ $$=$$ { -10, 0, 1, 9, 2, 4, 5} U $$=$$ { 1, 2, 5, 6, 2, 3, 4} $$ =$$ { -10, -2, -1,0, 1, 2, 3, 4, 5, 6, 9} .....(1)
Also, B∪AB∪A.
By Venn diagram, we have
Hence, it is verified that set union is commutative.
Also, B∪AB∪A.
By Venn diagram, we have
Hence, it is verified that set union is commutative.
Let A = {1, 2, 3}, B = {2, 4, 6, 8}, C = {3, 4, 5, 6} then prove the following :-
$$A \, \cup \, B$$ = {1, 2, 3, 4, 6, 8}
Using properties of sets, prove that $$A \cup(A \cap B)=A$$
$$A-( A-B )=$$ ...........
Given : A = {2, 3}, B = {4, 5}, C = {5, 6}, then prove the following :
$$A \, \times \, (B \, \cap \, C)$$ = {(2, 5), (3, 5)}
Given : A = {2, 3}, B = {4, 5}, C = {5, 6}, then prove the following :
$$A \, \times \, (B \, \cup \, C)$$ = {(2, 4), (2, 5), (2, 6), (3, 4), (3, 5), (3, 6)}
Verify the following identities where A = {1, 2, 3, 4, 5}, B = {2, 3, 5, 6}, C = {4, 5, 6, 7}
$$A \, \cap \, (B \, \cup \, C) \, = \, (A \, \cap \, B) \, \cup \, (A \, \cap \, C)$$
Find the smallest set a such that a union {1}={1,2,3,5,9}
Let $$A$$$$=\{1,2\},$$ and $$B$$$$=\{1,3\},$$ then prove that $$\left( A\times B \right) \cup \left( B\times A \right)=\left\{(1,3),(2,3),(3,1),(3,2),(1,1),(1,2),(2,1)\right\}$$
Given $$A ={2,3}, B = {4,5}, C ={5,6},$$ find
(i) $$A\times \left( B\cap C \right) =\ .......$$
(ii) $$\left( A\times B \right) \cup \left( B\times C \right) =\ .......$$
Comment on the following statements
$$ A-B=A\cap B'=B'-A'$$
Comment on the following statements
$$ A-\left( A-B \right) =A\cap B$$
Let $$A=\left\{1,2,3 \right\},$$ $$B=\left\{2,4,6,8 \right\},$$ $$C=\left\{2,3,5,6 \right\}$$. Then $$ A\cap \left( B\cup C \right).\ ...........$$
Set $$A=\left\{ x:x\ is\ a\ digit\ in\ the\ number\ 3591 \right\}$$
$$ B=\left\{ x:x\in N,x<10 \right\} $$. Find $$ A\cup B,A\cap B,A-B$$ and $$B-A$$.
Let A and B be two sets such that $$A\times B$$ consists of 6 elements. If three elements of $$A\times B$$ are (1,4), (2,6), (3, 6), find $$A\times B$$ and $$B\times A$$.
State whether the following statements are true or false:
i) $$1 \in \left\{ {1,2,3} \right\}$$
ii) $$a \subset \left\{ {b,c,a} \right\}$$
iii) $$\left\{ a \right\} \in \left\{ {a,b,c} \right\}$$
iv) $$\left\{ {a,b} \right\} = \left\{ {a,a,b,b,a} \right\}$$
v) The sets $$\left\{ {x:x + 8 = 8} \right\}$$ is the null set.
Write the following set in roaster form:
$$A=\{x\,:\,x$$ is an integer and $$-3\leq x\,<\,7\}$$
List all the elements of the following sets :
$$B = \left\{ {x:x = {\dfrac{1} {{2n - 1}}},1 \le n \le 5} \right\}$$
Describe the following sets in Roster form:
The sets of all letters in the word 'BETTER'.
List all the elements of the following sets :
F = { $$x$$ : $$x$$ is a letter in the word "MISSISSIPPI"}
List all the elements of the following sets :
$$A = \left\{ {x:{x^2} \le 10,x \in Z} \right\}$$
List all the elements of the following sets :
D = { $$x$$ : $$x$$ is a vowel in the word "EQUATION"}
For any two sets of A and B, prove that
$$B' \subset A' $$ if $$A \subset B$$
List all the elements of the following sets :
{$${C = x:x}$$ is an integar , $${ - {1 \over 2} < x < {9 \over 2}}$$}
In a group of $$70$$ people, $$37$$ like coffee, $$52$$ like tea and each person like at least one of the two drinks. How many people like both coffee and tea?
Let $$A$$ and $$B$$ be two sets. If $$A\cup X=B\cap X=\phi$$ and $$A\cup X=B\cup X$$ for sum set $$X$$ that $$A=B$$.
If $$A=\left\{6,9,11\right\}$$ then find $$A\cup \phi$$
Let $$U = \{1, 2, 3... 20\}$$, Let $$A, B$$ and $$C$$ be the subsets of $$U$$. Let $$A$$ be the set of all numbers, which are perfect square, $$B$$ be the set of all numbers which are multiples of $$5$$ and $$C$$ be the set of all numbers, which are divisible by $$2$$ and $$3$$?
Consider the following statements.Prove that $$A, B$$ and $$C$$ mutually exclusive.
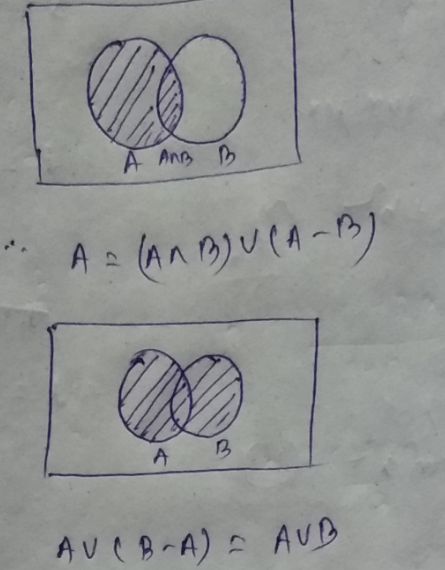
Show that for any sets A and B,A$$A=(A\cap B)\cup (A-B)$$ and $$A\cup (B-A)=A\cup B$$
If $$A=(1,2,3,4,5,6,7,8,9)$$
$$B=(1,3,5,,7,9,11,13)$$
$$C=(2,4,6,8,10,12,14)$$
$$D=(2,3,5,7,11,13,17)$$
then find $$B \cup C$$
If $$A$$ and $$B$$ are two disjoint sets $$n(A)=15$$ and $$n(B)=10$$ find $$n\left( {A \cup B} \right)$$ and $$n\left( {A \cap B} \right)$$.
Write all the elements of the set $$S = \{ 1,\{ 3\} ,\{ 5,7\} ,9,\,10\} $$.
Let $$A$$ and $$B$$ be events such that $$p\left( A \right) = \dfrac{5}{{11}},\,P\left( B \right) = \dfrac{6}{{11}}$$, and $$P\left( {A \cup B} \right) = \dfrac{7}{{11}}$$ and $$P(B/A).$$
Let A$$=\{a, e, i, o, u\}$$ and B$$=\{a, b, c, d\}$$. Is A a subset of B? No(why?). Is B a subset of A? No. (Why?)
If $$f=\left\{(4,5),(5,6),(6,-4)\right\}$$ and $$g=\left\{(4,-4),(6,5),(8,5)\right\}$$.Then $$|f-g|=?$$
find the range of the following data 18,10,8,16,9,24,12,25,13.19.
If $$A=(1,2,3,4,5,6,7,8,9)$$
$$B=(1,3,5,,7,9,11,13)$$
$$C=(2,4,6,8,10,12,14)$$
$$D=(2,3,5,7,11,13,17)$$
then find $$(A-D) \cup \left( {B - A} \right)$$
If $$A=(1,2,3,4,5,6,7,8,9)$$
$$B=(1,3,5,,7,9,11,13)$$
$$C=(2,4,6,8,10,12,14)$$
$$D=(2,3,5,7,11,13,17)$$
then find $$A-D$$
$$1800$$ boys and $$900$$ girls appeared for an examination. If $$42\%$$ of the boys and $$30\%$$ of the girls passed, find
(i) number of boys passed
(ii) number of girls passed
(iii) total number of students passed
(iv) number of students failed
(v) percentage of student failed.
Show that for any sets $$A$$ and $$B$$,
$$A=(A\cap B)\cup (A-B)$$ and $$A\cup(B-A)=(A\cup B)$$
answer is shown
If $$A=\{ 3,4,6\} , B=\{ 1,3\} $$ and $$C=\{ 1,2,6\} $$ then find $$\left( A-B \right) \times \left( A-C \right) $$
If $$A=\left\{4,5,6\right\};B=\left\{7,8\right\}$$ then show that $$A\bigcup B=B\bigcup A$$
If A={1,2,3,4,5} , B={3,4,7,8} then find $$A \cup B$$ and $$A \cap B$$ .
If $$A=\{6,9,11\}$$ and $$B=\phi$$,find $$A\cup B$$.
Let $$O=$$ Set of odd natural numbers $$=\{1,3,5,7,9,...\}$$ and $$E=$$Set of even natural numbers $$=\{2,4,6,8,10,........\}$$. Then show that $$-1 \notin E$$.
Let $$O=$$ Set of odd natural numbers $$=\{1,3,5,7,9,...\}$$ and $$E=$$Set of even natural numbers $$=\{2,4,6,8,10,........\}$$. Then show that $$3\in E$$.
Let $$O=$$ Set of odd natural numbers $$=\{1,3,5,7,9,...\}$$ and $$E=$$Set of even natural numbers $$=\{2,4,6,8,10,........\}$$. Then show that $$0.1\notin E$$.
Let $$A=\{1,2,3,4\}$$ and $$B=\{2,4,6,8\}$$. Then find $$A-B$$.
Solve
If n(A) =15 , $$n(A\cup B)=29 $$ , $$n(A \sqcap B) = 7 $$ find n(B) .
Let $$A=\left\{1, 2\right\}, B=\left\{1, 2, 3, 4\right\}$$ and $$C=\left\{5, 6\right\}$$. Verify that $$A\times (B\cap C)=(A\times B)\cap(A\times C)$$
Define subset of a set.
A subset B of a set 'A' is defined as a set in which all the elements of B are contained in A. i.e., $$B\subseteq A$$.
Let $$A , B$$ be two set such that $$n ( A ) = 4$$ and $$n ( B ) = 6$$ then the least possible number of elements in the power set of $$( A \cup B )$$ is
If $$n(A)=7, n(B)=8$$ then find the maximum and minimum number of elements of $$AUB$$.
U=$$\left\{ {1,2,3,4,5,6,7,8,9,10} \right\}$$
A=$$\left\{ {2,4,6,8,10} \right\},B = \left\{ {1,3,5,7,8,10} \right\}$$
Find $$\left( {A \cup B} \right)$$
Write all the subsets of the sets $$\left(i\right)\left\{a\right\}$$$$\left(ii\right)\phi $$.
Describe the sets of points in space whose coordinates satisfy the given inequalities or combinations of equations and inequalities.
$$x^{2}+y^{2}+z^{2}\le 1$$
As $$x^2+y^2+z^2=1$$ represents a sphere of radius having centre at $$(0, 0, 0)$$
$$\Rightarrow x^2+y^2+z^2\leq 1$$ represents all points inside the sphere.
Let $$A=\{3, 6, 12, 15, 18, 21\}, B=\{4, 8, 12, 16, 20\}, C=\{2, 4, 6, 8, 10, 12, 14, 16\}$$ and $$D=\{5, 10, 15, 20\}$$. Find $$B-D$$.
Let $$A=\{3, 6, 12, 15, 18, 21\}, B=\{4, 8, 12, 16, 20\}, C=\{2, 4, 6, 8, 10, 12, 14, 16\}$$ and $$D=\{5, 10, 15, 20\}$$. Find $$A-C$$.
Let $$A=\{3, 6, 12, 15, 18, 21\}, B=\{4, 8, 12, 16, 20\}, C=\{2, 4, 6, 8, 10, 12, 14, 16\}$$ and $$D=\{5, 10, 15, 20\}$$. Find $$C-A$$.
Let $$u=\{1, 2, 3, 4, 5, 6, 7, 8, 9\}, A=\{1, 2, 3, 4\}, B=\{2, 4, 6, 8\}$$ and $$C=\{3, 4, 5, 6\}$$. Find A'.
Let $$A=\{3, 6, 12, 15, 18, 21\}, B=\{4, 8, 12, 16, 20\}, C=\{2, 4, 6, 8, 10, 12, 14, 16\}$$ and $$D=\{5, 10, 15, 20\}$$. Find $$A-D$$.
In a group of $$50$$ persons, $$14$$ drink tea but not coffee and $$30$$ drink tea. Find how many drink coffee but not tea.
Let $$A=\{3, 6, 12, 15, 18, 21\}, B=\{4, 8, 12, 16, 20\}, C=\{2, 4, 6, 8, 10, 12, 14, 16\}$$ and $$D=\{5, 10, 15, 20\}$$. Find $$D-A$$.
Let $$A=\{3, 6, 12, 15, 18, 21\}, B=\{4, 8, 12, 16, 20\}, C=\{2, 4, 6, 8, 10, 12, 14, 16\}$$ and $$D=\{5, 10, 15, 20\}$$. Find $$B-C$$
In a group of $$950$$ persons, $$750$$ can speak Hindi and $$460$$ can speak English. Find how many can speak Hindi only.
If $$A=\{1, 2, 3, 4, 5\}, B=\{4, 5, 6, 7, 8\}, C=\{7, 8, 9, 10, 11\}$$ and $$D=\{10, 11, 12, 13, 14\}$$. Find $$B\cup C$$.
If $$A=\left\{a,b,c,d,e,f\right\}, B=\left\{c,e,g,h\right\}$$ and $$C=\left\{a,e,m,n\right\}$$, find
$$A\cup C$$
State which of the following collections are sets:
Collection of odd natural numbers less than 50.
In a group of $$50$$ persons, $$14$$ drink tea but not coffee and $$30$$ drink tea. Find how many drink tea and coffee both.
If $$A=\left\{2,3,5,7,11 \right\}$$ and $$B=\phi$$, find
$$A\cup B$$
State in the case whether $$A\subset$$ or $$A\nsubseteq B$$.
$$A=\left\{ x:x\in Z, x^2=1\right\}, B=\left\{ x:x\ in\ N, x^2=1\right\}$$
If $$A=\left\{3, \left\{ 4, 5\right\}, 6\right\}$$, State whether the following statement is true or not.$$\left\{ 4, 5\right\} \in A$$
If $$A=\{1, 2, 3, 4, 5\}, B=\{4, 5, 6, 7, 8\}, C=\{7, 8, 9, 10, 11\}$$ and $$D=\{10, 11, 12, 13, 14\}$$. Find $$B\cup D$$.
If $$A=\left\{1,2,3,4,5 \right\}, B=\left\{4,5,6,7,8 \right\}, C=\left\{7,8,9,10,11 \right\}$$ and $$D=\left\{10,11,12,13,14 \right\}$$, find :
$$A\cup B$$
State which of the given collections are sets:
Collection of all people in this world over $$50$$ year of age.
State which of the following collections are sets:
Collection of four colours of a rainbow
State which of the given collections are sets:
Collection of all countries of Asia.
State which of the given collections are sets:
Collection of all difficult problems in your maths book.
Fill in the blanks:
A collection of ......... objects is called a set.
State which of the given collections are sets:
Collection of three cities of India whose name start with the letter 'J'.
State which of the given collections are sets:
Collection of all poor people of Dhanbad.
State which of the given collections are sets:
Collection of all fools.
State which of the given collections are sets:
Collection of four countries of Asia.
State which of the following collections are sets:
Collection of all clever students of your school
State which of the following collections are sets:
Collection of some multiples of $$5$$
State which of the following collections are sets:
Collection of all rich people of Bangalore
State which of the following collections are sets:
Collection of all tall students of your class
State which of the following collections are sets:
Collection of first three days of a week
State which of the following collections are sets:
Collection of all prime numbers
State which of the following collections are sets:
Collection of all even integers which lie between $$-5$$ and $$15$$
Which of the following are sets? Justify our answer.
The collection of all boys in your class.
State whether the following pairs of sets are equal or not:
$$A = \{\text{PUPPET}\}, B = \{P, U, E, T\}$$
Given that $$A = \{2, 5, 7, 8, 10\}, B = \{5, 7, 2, x, 10\}$$ and $$A= B$$, write the value of $$x$$.
Which of the following are sets? Justify our answer.
The collection of all natural numbers less than $$100$$.
Which of the following are sets? Justify our answer.
A team of eleven best-cricket batsmen of the world
State whether the following pairs of sets are equal or not:
$$A = \{3, 5, 7, 9, 11, 13\},\quad B = \{\text{odd numbers between 2 and 14}\}$$
State which of the following collections are sets:
Collection of three healthy students of your class.
State which of the following collections are sets:
Collection of all good cricket players of India
Let $$X=\left\{1,2,3\right\}$$ and $$Y=\left\{4,5\right\}$$. Find whether the following subsets of $$X+Y$$ are function from $$X$$ to $$Y$$ or not.
$$h=\left\{(1,4),(2,5),(3,5)\right\}$$.
State which of the following collections are sets:
Collection of three youngest students of your class.
Which of the following are sets? Justify our answer.
A collection of most dangerous animals of the world.
Find the union of each of the following pairs of sets:
$$A$$ = {$$a, e, i, o, u$$} $$B$$ = {$$a, b, c$$}
Which of the following are sets? Justify our answer.
The collection of all even integers.
Which of the following are sets? Justify our answer.
A collection of novels written by the writer Munshi Prem Chand.
Find the union of each of the following pairs of sets:
$$X$$ = {$$1, 3, 5$$} $$Y$$ = {$$1, 2, 3$$}
Which of the following are sets? Justify our answer.
The collection of questions in this chapter.
Find the union of each of the following pairs of sets:
$$A$$ = {$$x: x$$ is a natural number and multiple of $$3$$}
$$B$$ = {$$x: x$$ is a natural number less than $$6$$}
Find the union of each of the following pairs of sets:
$$A$$ = {$$x: x$$ is a natural number and $$1 < x \leq 6$$}
$$B$$ = {$$x: x$$ is a natural number and $$6 < x < 10$$}
If $$A = \left \{ 1, 2, 3, 4 \right \}, B = \left \{ 3, 4, 5, 6 \right \}, C = \left \{ 5, 6, 7, 8 \right \} and D = \left \{ 7, 8, 9, 10 \right \}$$; find:
$$B C$$
If $$A = \left \{ 1, 2, 3, 4 \right \}, B = \left \{ 3, 4, 5, 6 \right \}, C = \left \{ 5, 6, 7, 8 \right \} and D = \left \{ 7, 8, 9, 10 \right \}$$; find:
$$A B C$$
Let $$A = \left \{ a,b \right \}, B = \left \{ a,b,c \right \}$$. Is $$A B$$ ? What is $$A B$$ ?
If $$A = \left \{ 1, 2, 3, 4 \right \}, B = \left \{ 3, 4, 5, 6 \right \}, C = \left \{ 5, 6, 7, 8 \right \} and D = \left \{ 7, 8, 9, 10 \right \}$$; find:
$$A B$$.
If $$A = \left \{ 1, 2, 3, 4 \right \}, B = \left \{ 3, 4, 5, 6 \right \}, C = \left \{ 5, 6, 7, 8 \right \} and D = \left \{ 7, 8, 9, 10 \right \}$$; find:
$$B D$$
If $$A = \left \{ 3, 5, 7, 9, 11 \right \}, B = \left \{ 7, 9, 11, 13 \right \}, C = \left \{ 11, 13, 15 \right \}$$ and $$D = \left \{ 15, 17 \right \}$$; find:
$$A B$$
If $$A = \left \{ 1, 2, 3, 4 \right \}, B = \left \{ 3, 4, 5, 6 \right \}, C = \left \{ 5, 6, 7, 8 \right \} and D = \left \{ 7, 8, 9, 10 \right \}$$; find:
$$A C$$
If $$A = \left \{ 1, 2, 3, 4 \right \}, B = \left \{ 3, 4, 5, 6 \right \}, C = \left \{ 5, 6, 7, 8 \right \} and D = \left \{ 7, 8, 9, 10 \right \}$$; find:
$$B C D$$
Find the union of each of the following pairs of sets:
$$A$$ = {$$1, 2, 3$$}, $$B = \phi$$
If $$A = \left \{ 1, 2, 3, 4 \right \}, B = \left \{ 3, 4, 5, 6 \right \}, C = \left \{ 5, 6, 7, 8 \right \} and D = \left \{ 7, 8, 9, 10 \right \}$$; find:
$$A B D$$
If $$A = \left \{ 3, 5, 7, 9, 11 \right \}, B = \left \{ 7, 9, 11, 13 \right \}, C = \left \{ 11, 13, 15 \right \}$$ and $$D = \left \{ 15, 17 \right \}$$; find:
$$A C D$$
If $$A = \left \{ 3, 6, 9, 12, 15, 18, 21 \right \}, B = \left \{ 4, 8, 12, 16, 20 \right \}, C = \left \{ 2, 4, 6, 8, 10, 12, 14, 16 \right \}, D $$$$= \left \{ 5, 10, 15, 20 \right \}$$; find
$$A – B$$.
If $$A = \left \{ 3, 5, 7, 9, 11 \right \}, B = \left \{ 7, 9, 11, 13 \right \}, C = \left \{ 11, 13, 15 \right \}$$ and $$D = \left \{ 15, 17 \right \}$$; find:
$$A (B C)$$
If $$A = \left \{ 3, 5, 7, 9, 11 \right \}, B = \left \{ 7, 9, 11, 13 \right \}, C = \left \{ 11, 13, 15 \right \}$$ and $$D = \left \{ 15, 17 \right \}$$; find:
$$(A B) (B C)$$
If $$A = \left \{ 3, 5, 7, 9, 11 \right \}, B = \left \{ 7, 9, 11, 13 \right \}, C = \left \{ 11, 13, 15 \right \}$$ and $$D = \left \{ 15, 17 \right \}$$; find:
$$A C$$
If $$A = \left \{ 3, 5, 7, 9, 11 \right \}, B = \left \{ 7, 9, 11, 13 \right \}, C = \left \{ 11, 13, 15 \right \}$$ and $$D = \left \{ 15, 17 \right \}$$; find:
$$(A D) (B C)$$
If $$A = \left \{ 3, 5, 7, 9, 11 \right \}, B = \left \{ 7, 9, 11, 13 \right \}, C = \left \{ 11, 13, 15 \right \}$$ and $$D = \left \{ 15, 17 \right \}$$; find:
$$B C$$
If $$A = \left \{ 3, 5, 7, 9, 11 \right \}, B = \left \{ 7, 9, 11, 13 \right \}, C = \left \{ 11, 13, 15 \right \}$$ and $$D = \left \{ 15, 17 \right \}$$; find:
$$B D$$
If $$A = \left \{ 3, 5, 7, 9, 11 \right \}, B = \left \{ 7, 9, 11, 13 \right \}, C = \left \{ 11, 13, 15 \right \}$$ and $$D = \left \{ 15, 17 \right \}$$; find:
$$A (B D)$$
If $$A = \left \{ 3, 5, 7, 9, 11 \right \}, B = \left \{ 7, 9, 11, 13 \right \}, C = \left \{ 11, 13, 15 \right \}$$ and $$D = \left \{ 15, 17 \right \}$$; find:
$$A D$$
If $$A = \left \{ 3, 6, 9, 12, 15, 18, 21 \right \}, B = \left \{ 4, 8, 12, 16, 20 \right \}, C = \left \{ 2, 4, 6, 8, 10, 12, 14, 16 \right \}, D $$$$= \left \{ 5, 10, 15, 20 \right \}$$; find
$$A – C$$
If $$A = \left \{ 3, 6, 9, 12, 15, 18, 21 \right \}, B = \left \{ 4, 8, 12, 16, 20 \right \}, C = \left \{ 2, 4, 6, 8, 10, 12, 14, 16 \right \}, D = \left \{ 5, 10, 15, 20 \right \}$$; find
$$B C$$
If $$A = \left \{ 3, 6, 9, 12, 15, 18, 21 \right \}, B = \left \{ 4, 8, 12, 16, 20 \right \}, C = \left \{ 2, 4, 6, 8, 10, 12, 14, 16 \right \}, D $$$$= \left \{ 5, 10, 15, 20 \right \}$$; find
$$D – A$$
If $$A = \left \{ 3, 6, 9, 12, 15, 18, 21 \right \}, B = \left \{ 4, 8, 12, 16, 20 \right \}, C = \left \{ 2, 4, 6, 8, 10, 12, 14, 16 \right \}, D = \left \{ 5, 10, 15, 20 \right \}$$; find
$$D B$$
If $$A = \left \{ 3, 6, 9, 12, 15, 18, 21 \right \}, B = \left \{ 4, 8, 12, 16, 20 \right \}, C = \left \{ 2, 4, 6, 8, 10, 12, 14, 16 \right \}, D $$$$= \left \{ 5, 10, 15, 20 \right \}$$; find $$C – A$$
If $$A = \left \{ 3, 6, 9, 12, 15, 18, 21 \right \}, B = \left \{ 4, 8, 12, 16, 20 \right \}, C = \left \{ 2, 4, 6, 8, 10, 12, 14, 16 \right \}, D = \left \{ 5, 10, 15, 20 \right \}$$; find
$$C D$$
If $$A = \left \{ 3, 6, 9, 12, 15, 18, 21 \right \}, B = \left \{ 4, 8, 12, 16, 20 \right \}, C = \left \{ 2, 4, 6, 8, 10, 12, 14, 16 \right \}, D = \left \{ 5, 10, 15, 20 \right \}$$; find
$$C B$$
If $$A = \left \{ 3, 6, 9, 12, 15, 18, 21 \right \}, B = \left \{ 4, 8, 12, 16, 20 \right \}, C = \left \{ 2, 4, 6, 8, 10, 12, 14, 16 \right \}, D $$$$= \left \{ 5, 10, 15, 20 \right \}$$; find
$$B – A$$
If $$A = \left \{ 3, 6, 9, 12, 15, 18, 21 \right \}, B = \left \{ 4, 8, 12, 16, 20 \right \}, C = \left \{ 2, 4, 6, 8, 10, 12, 14, 16 \right \}, D $$$$= \left \{ 5, 10, 15, 20 \right \}$$; find
$$A – D$$
If $$A = \left \{ 3, 6, 9, 12, 15, 18, 21 \right \}, B = \left \{ 4, 8, 12, 16, 20 \right \}, C = \left \{ 2, 4, 6, 8, 10, 12, 14, 16 \right \}, D = \left \{ 5, 10, 15, 20 \right \}$$; find
$$B D$$
If $$R$$ is the set of real numbers and $$Q$$ is the set of rational numbers, then what is $$R Q$$?
If $$X = \left \{ a, b, c, d \right \}$$ and $$Y = \left \{ f, b, d, g \right \}$$, find
$$Y X$$
Let $$U = \left \{ 1, 2, 3; 4, 5, 6, 7, 8, 9 \right \}, A = \left \{ 1, 2, 3, 4 \right \}, B = \left \{ 2, 4, 6, 8 \right \}$$ and $$C = \left \{ 3, 4, 5, 6 \right \}$$. Find
$$A$$
If $$ \xi=\{\text { natural numbers between } 10 \text { and } 40\} $$
$$ \mathbf{A}=\{\text { multiples of } 5\} $$ and $$ \mathrm{B}=\{\text { multiples of } 6\}, $$ then
(i) find $$ \mathrm{A} \cup \mathrm{B} $$ and $$ \mathrm{A} \cap \mathrm{B} $$
(ii) verify that $$ n(A \cup B)=n(A)+n(B)-n(A \cap B) $$
If $$A = \left \{ 3, 6, 9, 12, 15, 18, 21 \right \}, B = \left \{ 4, 8, 12, 16, 20 \right \}, C = \left \{ 2, 4, 6, 8, 10, 12, 14, 16 \right \}, D = \left \{ 5, 10, 15, 20 \right \}$$; find
$$D C$$
State which of the following collections are set:
All states of India
If $$X = \left \{ a, b, c, d \right \}$$ and $$Y = \left \{ f, b, d, g \right \}$$, find
$$X Y$$
Let $$U = \left \{ 1, 2, 3; 4, 5, 6, 7, 8, 9 \right \}, A = \left \{ 1, 2, 3, 4 \right \}, B = \left \{ 2, 4, 6, 8 \right \}$$ and $$C = \left \{ 3, 4, 5, 6 \right \}$$. Find
$$(A \cup C)$$
If $$ n(\xi)=40, n\left(A^{\prime}\right)=15, n(B)=12 $$ and $$ n\left((A \cap B)^{\prime}\right)=32, $$ find :
(i) n(A)
(ii) $$ n\left(B^{\prime}\right) $$
(iii) $$ n(A \cap B) $$
(iv) $$ n(A \cup B) $$
(v) $$ n(A-B) $$
(vi) $$ n(B-A) $$
Let $$X=\left\{Ram, Geeta, Akbar \right\}$$ be the set of students of class $$XI$$, who are in school hockey team. Let $$Y= \left\{Geeta, Divid, Ashok \right\}$$ be the set of students from Class $$XI$$ who are in school foot ball team. Find $$X \cup Y$$ and interpret the set.
Let $$A=\left\{1,2, \left\{3,4 \right\}, 5\right\}.$$ Which of the following statements are incorrect and why?
$$\left\{1,2,5 \right\} \subset A$$
If $$A =\text{{5, 7, 8, 9}}$$ then which of the following are subsets of $$A$$?
(i) $$B = \text{{5, 8}}$$
(ii) $$C = \text{{0}}$$
(iii) $$D = \text{{7, 9, 10}}$$
(iv) $$E = \text{{ }}$$
(v) $$F =\text{{8, 7, 9, 5}}$$
Let $$A=\left\{1,2, \left\{3,4 \right\}, 5\right\}.$$ Which of the following statements are incorrect and why?
$$\left\{1,2,3 \right\} \subset A$$
Define difference of sets.
If $$A=\left\{1,2,3,4 \right\}, B=\left\{3,4,5,6 \right\}, C=\left\{5,6,7,8\right\}$$ and $$D=\left\{7,8,9,10 \right\}$$; find
$$A \cup B$$
Let $$A =\left\{2,4,6,8 \right\}$$ and $$B=\left\{6,8,10,12 \right\}$$ Find $$A \cup B$$
Define union of sets.
The union of two sets $$A$$ and $$B$$ denoted by $$A \cup B$$, is the set of all those elements which arc either in $$A$$ or $$B$$ or in both $$A$$ and $$B$$
Thus, $$AB=(x:x \in A\ or\ x \in B)$$
$$\therefore x \in A \cup B \ x \in A\ or\ x \in B$$
$$x \not \in A \cup B = x \not \in A$$ and $$ z \not \in B$$
$$\bullet$$ $$A \cup B= B \cap A$$ (Commutative Law)
$$\bullet$$ $$(A \cup B)\cup C= A \cup (B \cup C)$$ (Associative law)
$$\bullet$$ $$A \cup \varphi=A$$
$$\bullet$$ $$A \cup A=A$$
$$\bullet$$ $$A \cup A=U$$
If $$A=\left\{3,6,9,12,15,18,21 \right\}, B=\left\{4,8,12,16,20 \right\}, C=\left\{2,4,6,8,10,12,14,16 \right\} , D= \left\{5,10,15,20 \right\}$$ find
$$A-D$$
If $$A=\left\{3,5,7,9,11 \right\}, B=\left\{7,9,11,13 \right\}, C=\left\{11,13,15\right\}$$ and $$D=\left\{15,17 \right\}$$; find
$$(A \cup D) \cap (B \cup C)$$
If $$A=\left\{1,2,3,4 \right\}, B=\left\{3,4,5,6 \right\}, C=\left\{5,6,7,8\right\}$$ and $$D=\left\{7,8,9,10 \right\}$$; find
$$B \cup C$$
If $$A=\left\{3,6,9,12,15,18,21 \right\}, B=\left\{4,8,12,16,20 \right\}, C=\left\{2,4,6,8,10,12,14,16 \right\} , D= \left\{5,10,15,20 \right\}$$ find
$$B-D$$
If $$A=\left\{3,5,7,9,11 \right\}, B=\left\{7,9,11,13 \right\}, C=\left\{11,13,15\right\}$$ and $$D=\left\{15,17 \right\}$$; find
$$A \cap (B \cup D) $$
If $$A=\left\{1,2,3,4 \right\}, B=\left\{3,4,5,6 \right\}, C=\left\{5,6,7,8\right\}$$ and $$D=\left\{7,8,9,10 \right\}$$; find
$$B \cup D$$
If $$A=\left\{1,2,3,4 \right\}, B=\left\{3,4,5,6 \right\}, C=\left\{5,6,7,8\right\}$$ and $$D=\left\{7,8,9,10 \right\}$$; find
$$A \cup C$$
If $$A=\left\{3,6,9,12,15,18,21 \right\}, B=\left\{4,8,12,16,20 \right\}, C=\left\{2,4,6,8,10,12,14,16 \right\} , D= \left\{5,10,15,20 \right\}$$ find
$$D-A$$
If $$A=\left\{3,6,9,12,15,18,21 \right\}, B=\left\{4,8,12,16,20 \right\}, C=\left\{2,4,6,8,10,12,14,16 \right\} , D= \left\{5,10,15,20 \right\}$$ find
$$A-C$$
If $$A=\left\{1,2,3,4 \right\}, B=\left\{3,4,5,6 \right\}, C=\left\{5,6,7,8\right\}$$ and $$D=\left\{7,8,9,10 \right\}$$; find
$$B \cup C \cup D$$
If $$A = \{11, 21, 31, 41\}, \ B = \{12,22,31,32\}$$, then fimd:
i) $$A \cup B$$
ii) $$A \cap B$$
Which of the following are sets ? Justify your answer .
Collection of even natural less than 8.
Which of the following are sets ? Justify your answer
The collection of big cities in India.
$$IV X=\left\{a,b,c,d \right\}$$ and $$Y=\left\{f,b,d,g \right\}$$ find
$$y-x$$
List the elements of the set $$P$$.
If $$A$$ and $$B$$ be two sets containing $$4$$ and $$12$$ elements respectively, what can be the minimum number of elements in $$A \cup B$$? Find also, the maximum number of elements in $$(A \cup B)$$.
None of A, B and C.
In a town of $$10,000$$ families it was found that $$40$$% families buy newspaper $$A$$, $$20$$% buy newspaper $$B$$ and $$10$$% buy newspaper $$C$$, $$5$$% families buy $$A$$ and $$B$$, $$3$$% buy $$B$$ and $$C$$ and $$4$$% buy $$A$$ and $$C$$. If $$2$$% families buy all three newspapers, find number of families which buy None of $$A, B,C$$.
Given $$\mu$$ = {x / x is an integer, $$0 \leq x \leq 10$$}
A = {x / the remainder is 1 when x is divided by 2}
B = {x / the remainder is 2 when x is divided by 3}
Find the set $$n(A \cup B)'$$
A survey was carried out to find out the types of shampoo that a group of $$150$$ women have tried. It was found that $$84$$ women have used brand $$A$$ shampoo, $$93$$ have used brand $$B$$, and $$69$$ have used brand $$C$$ of these women, $$45$$ have tried brands $$A$$ and $$B$$, $$25$$ have tried brands $$A$$ and $$C$$ and $$40$$ have tried brand $$B$$ and $$C$$. Determine the number of women who have tried only brand $$A$$.
If $$A=\left \{ a, b, p, d \right \}$$, $$B=\left \{ p, d , e \right \}$$ , $$C=\left \{ p, e, f, g \right \}$$ then verify:
(i) $$A\times (B\cap C)=(A\times B)\cap (A\times C)$$ (ii) $$A\times (B-C)=(A\times B)-(A\times C)$$
In a school with an enrolment of $$950$$ students, each student must join either the lions club or the country club or both. Given that $$646$$ students are members of the lions club and $$532$$ are members of the country club, calculate the number of students who are members of both clubs.
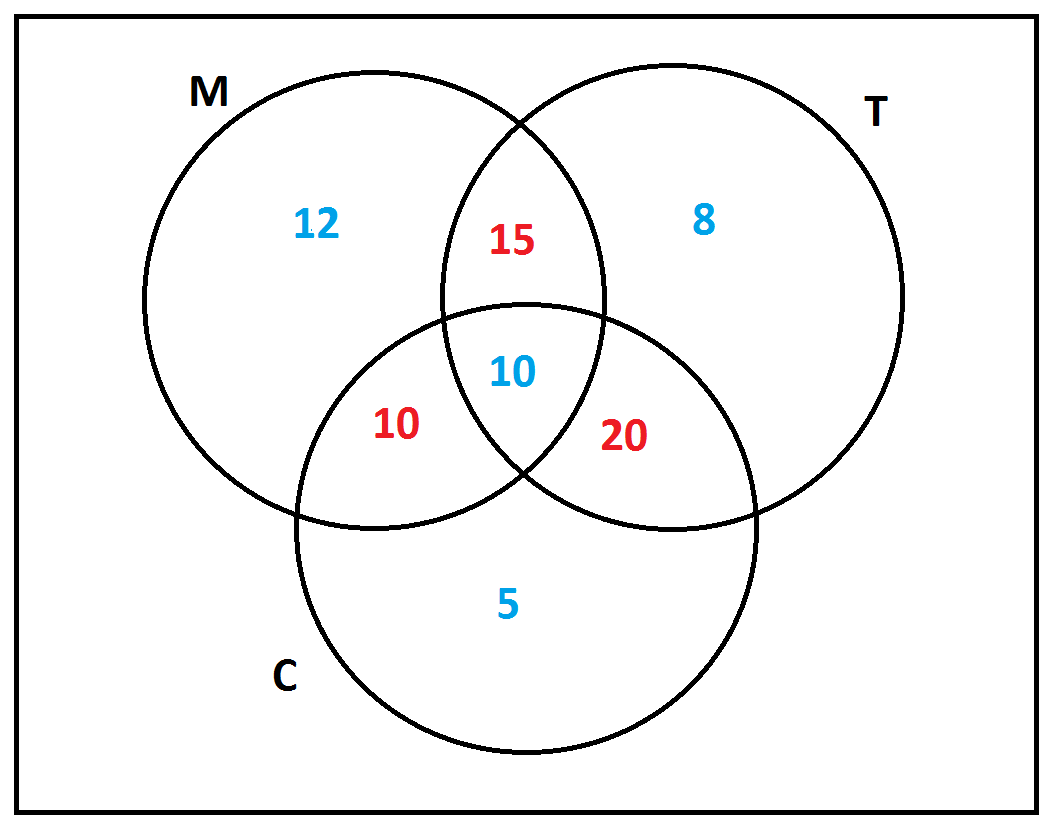
In a certain group of $$75$$ students, $$16$$ students are taking physics, geography and english; $$24$$ students are taking physics and geography, $$30$$ students are taking physics and english; and $$22$$ students are taking geography and English. However, $$7$$ students are taking only physics, $$10$$ students are taking only geography and $$5$$ students are taking only english. How many of these students are taking physics and english, but not geography?
At a certain conference of $$100$$ people there are $$29$$ Indian women and $$23$$ Indian men. Of these Indian people $$4$$ are doctors and $$24$$ are either men or doctors. There are no foreign doctors. How many foreigners are attending the conference? How many women doctors are attending the conference?
In a combined test in Maths and Chemistry; $$84\%$$ candidates passed in Maths; $$76\%$$ in Chemistry and $$8\%$$ failed in both. If $$340$$ candidates passed in the test, then how many appeared ?
In a city three daily newspaper x, y and z are published. 40% of the people of the city read x, 50% of the people read y, 30% read z, 20% read both x and y, 15% read both x and z, 10% read y and z and 24% read all of the three papers.
Can this be true ? Yes=9 No=6
In a combined test in English and Physics; $$36\%$$ candidates failed in English; $$28\%$$ failed in Physics and $$12\%$$ in both; find the total number of candidates appeared, if $$208$$ candidates have failed.
If $$\displaystyle f_{1}\left ( x \right )$$ and $$f_{_{2}}\left ( x \right )$$ are defined on domains $$\displaystyle D_{1}$$ and $$D_{2}$$ respectively, then $$\displaystyle f_{1}\left ( x \right )+f_{2}\left ( x \right )$$ is defined on $$\displaystyle D_{1}\cup D_{2}.$$ True or false?
If true enter 1 else 0.
Find total number of subsets of B = {a, b, c}
Given $$\displaystyle A=\left \{ 1, 2, 3 \right \}, B=\left \{ 3, 4 \right \},C=\left \{ 4, 5, 6 \right \}$$ .Then find $$\displaystyle \left ( A\times B \right )\cap \left ( B\times C \right )$$
Find total number of subsets of {p : p is a letter in the word 'poor'}
If $$A = \{$$$$x$$ : $$x \,\,\in\,\, W$$, $$3 \leq x < 6$$$$\}$$, $$B = \{3, 5, 7\}$$ and $$C = \{2, 4\}$$; find :
$$B - C $$
If $$A = \{x : x \,\,\epsilon\,\, W, 3 \leq x < 6\}, B = \{3, 5, 7\}$$ and $$C = \{2, 4\}$$;
find :$$n(A - B)$$.
Find the total number of subsets of each of the following set:
$$C=\{x \mid x \in W, x \leq 2\}$$
If $$C$$ is the set of letters in the word 'cooler' find number of its subsets
Find total number of subsets of A = {5, 7}
If $$T = \{ \text {x : x is a letter in the word 'TEETH'} \}$$, find all its subsets.
Given, $$A = \{$$Quadrilaterals$$\}$$, $$B = \{$$Rectangles$$\}$$, $$C = \{$$Squares$$\}$$, $$D = \{$$Rhombuses$$\}$$. State whether the following statement is correct or incorrect. Give reasons.
$$D$$ $$\subset$$ $$A$$
If $$P =$$ {factors of 36} and $$Q =$$ {factors of 48}, find $$Q - P $$
An investigator interviewed 100 students to determine their preferences for the three drinks milk coffee and tea. He reported the following, 10 students had all the three drinks, 20 had milk and coffee, 30 had coffee and tea , 25 had milk and tea, 12 had milk only. 5 had coffee only, 8 had tea only. The number of students that did not take any of the three drinks is.
According to given information, the venn diagram is below.
Now, $$n(M\cup C\cup T)=12+5+8+10+15+20+10=80$$
Now, number of people who did not took any of the drinks is $$n(M'\cap C' \cap T')= n(M\cup C \cup T)'$$
$$\Rightarrow n(M\cup C \cup T)'=N-n(M\cup C \cup T)$$
$$\Rightarrow n(M\cup C\cup T)'=100-80=20$$
Now, $$n(M\cup C\cup T)=12+5+8+10+15+20+10=80$$
Now, number of people who did not took any of the drinks is $$n(M'\cap C' \cap T')= n(M\cup C \cup T)'$$
$$\Rightarrow n(M\cup C \cup T)'=N-n(M\cup C \cup T)$$
$$\Rightarrow n(M\cup C\cup T)'=100-80=20$$
Given A = {$$x$$ : $$x \,\,\in\,\, N$$ and $$3 < x \leq 6$$} and B = {$$x$$ : $$x \,\,\in\,\, W$$ and $$x < 4$$}, then find : B - A.
Let $$\displaystyle A=\left \{ \theta :2\cos ^{2}+\theta +\sin \theta \leq 2 \right \}$$ and $$\displaystyle B= \left \{ \theta :\pi /2\leq \theta \leq 3\pi /2 \right \}.$$ Then $$\displaystyle A\cap B=\left \{ \theta :\pi /2\leq \theta \leq 5\pi /6 or \pi \leq \theta \leq 3\pi /4 \right \}$$
If true enter 1 else 0
Given, $$A = \{$$ Triangles $$\}, B = \{$$ Isosceles triangles $$\}, $$$$C =\{$$Equilateral triangles$$\}.$$ State whether the following statements are correct or incorrect. Give reasons.A $$\subset$$ B
$$C =\{$$Equilateral triangles$$\}.$$ State whether the following statements are correct or incorrect. Give reasons.
Given, $$A = \{$$ Triangles $$\}, B = \{$$ Isosceles triangles $$\}, $$$$C =\{$$Equilateral triangles$$\}.$$ State whether the following statement are correct or incorrect. Give reasons.$$C$$ $$\subset$$ $$A$$
$$C =\{$$Equilateral triangles$$\}.$$ State whether the following statement are correct or incorrect. Give reasons.
In a group of 1000 people , there are 750 who can speak Hindi and 400 who can speak Bengali. How many can speak Bengali ?
If $$A = (6, 7, 8, 9), B = (4, 6, 8, 10)$$ and $$C = \{x : x \,\,\epsilon\,\,N : 2 < x \leq 7\}$$ ; find : $$B - (A \cap C)$$ The sum of the elements in the above set is?
If total no. of elements in set A is $$a$$ and in set B is $$b$$, then $$\cfrac{a+b}{4} =$$
If universal set $$\xi = \{a, b, c, d, e, f, g, h\}, A = \{b, c, d, e, f\}, B =\{a, b, c, g, h\}$$ and $$C = \{c, d, e, f, g\}$$ find : $$ C - (B \cap A) $$Thus find the number of elements in the above set.
If $$A = (6, 7, 8, 9), B = (4, 6, 8, 10)$$ and $$C = \{x : x \,\,\epsilon\,\,N : 2 < x \leq 7\}$$ ; find : $$n(B - (A - C))$$
If $$A = (6, 7, 8, 9), B = (4, 6, 8, 10)$$ and $$C = \{x : x \,\,\epsilon\,\,N : 2 < x \leq 7\}$$ ; find : $$A - (B \cup C)$$
If $$n(\xi)$$ $$= 30, n(A) = 22, n(B) = 15$$ and $$n(A$$ $$\cup$$ $$B) = 25$$, then find : $$n(A$$$$'$$).
If $$n(A) = 40, n(B) = 27$$ and $$n(A$$ $$\cap$$ $$B) = 15 $$; find $$n(A$$ $$\cup$$ $$B)$$
Given, $$\xi$$ $$=$$ {Natural numbers between $$25$$ and $$45$$}; $$A =$$ {even numbers} and $$B$$ {multiples of $$3$$} then $$n(A) + n(B) = n(A$$ $$\cup$$$$ B) + n(A$$ $$\cap$$ $$B$$) .If true enter 1 else 0.
If $$n(\xi)$$ $$= 30, n(A) = 22, n(B) = 15$$ and $$n(A$$ $$\cup$$ $$B) = 25$$, then find : $$n(A$$ $$\cap$$ $$B$$ $$^{'}$$ $$)$$
If $$n(\xi)$$ $$= 30, n(A) = 22, n(B) = 15$$ and $$n(A$$ $$\cup$$ $$B) = 25$$, then find : $$n(B$$$$'$$$$)$$.
A and B are two overlapping sets such that n(A $$\cap$$ B) = x + 4, n(A - B) = 4x - 8 and n(B) = 3x +Find x, if n(A $$\cup$$ B) = 70.
If $$n(A) = 40, n(B) = 27$$ and $$n(A$$ $$\cap$$ $$B) = 15 $$, find $$n[(A$$ $$\cup$$ $$B) - A]$$
Given, $$n(A)=40, n(B)=27$$ and $$n(A\cup B)=15$$
From the figure, $$ (A \cup B) - A $$ is the region of " ONLY B "Hence, $$ n ((A \cup B) - A) = n (only B) $$
$$= n(B) - n(A \cap B) $$
$$= 27 - 15 $$
$$= 12 $$
If $$n(A) = 40, n(B) = 27$$ and $$n(A$$ $$\cap$$ $$B) = 15 $$; find :$$n(\mbox{only}\ A)$$
If $$n(A) = 40, n(B) = 27$$ and $$n(A$$ $$\cap$$ $$B) = 15 $$, find $$n(B - A)$$
Given, $$\xi$$ $$=$$ {Natural numbers between $$25$$ and $$45$$}; $$A =$$ {even numbers} and $$B$$ {multiples of $$3$$} then $$n(A - B)$$ = $$n(A'$$ $$\cap$$$$ B)$$ .If true enter 1 else 0.
In a community of $$175$$ persons, $$40$$ read TOI, $$50$$ read the Samachar Patrika and $$100$$ do not read any. How many persons read both the papers.
Let $$x$$ no. of people read both the newspapers. Since $$100$$ do not read any, no. of people reading both or either of newspapers$$=175-100=75$$
$$\displaystyle \therefore \left ( 40-x \right )+x+\left ( 50-x \right )=75\Rightarrow x=15$$
$$\displaystyle \therefore \left ( 40-x \right )+x+\left ( 50-x \right )=75\Rightarrow x=15$$
Let $$n$$ be a positive integer. Call a non-empty subset $$S$$ of $$\left \{1, 2, . . . , n\right \}$$ good, if the arithmetic mean of the elements of $$S$$, is also an integer. Further let $$t_n$$ denote the number of good subsets of $$\left \{1, 2, . . . , n\right \}$$. Prove that $$t_n$$ and $$n$$ are both odd or both even.
Find $$n({A\cap C}^c)$$.
In a group of $$50$$ persons, $$14$$ drink tea but not coffee and $$30$$ drink tea, then find how many drink tea and coffee both?
T : People drinking Tea
C : People drinking coffee
$$\displaystyle n(T)=n(T-C)+n(T\cap C)\Rightarrow 30=14+n(T\cap C)\Rightarrow n(T\cap C)=16$$
$$\displaystyle n(T)=n(T-C)+n(T\cap C)\Rightarrow 30=14+n(T\cap C)\Rightarrow n(T\cap C)=16$$
Let $$n$$ be a natural number and $$X =\left \{1, 2,......, n\right \}$$. For subsets $$A$$ and $$B$$ of $$X,$$ we denote $$A\Delta B$$ to be the set of all those elements of $$X$$ which belong to exactly one of $$A$$ and $$B.$$ Let $$F$$ be a collection of subsets of $$X$$ such that for any two distinct elements $$A$$ and $$B$$ in $$F$$, the set $$A\Delta B$$ has at least two elements. Show that $$F$$ has at most $$2^{n-1}$$ elements. Find all such collections $$F$$ with $$2^{n-1}$$ elements.
There are 40 students in a chemistry class and 60 students in a physics class. Find the number of students which are either in physics class or chemistry class in the following case:
The two classes meet at different hours and 20 students are enrolled in both the subjects
There are 40 students in a chemistry class and 60 students in a physics class. Find the number of students which are either in physics class or chemistry class in the following case:
The two classes meet at the same hour
Let A and B be sets, If $$A\cap X=B\cap X= \phi$$ and $$A\cup X= B \cup X$$ for some set X, prove that $$A= B$$.
Which of the following are examples of the null set?
(i) Set of odd natural numbers divisible by $$2$$
(ii) Set of even prime numbers
(iii) $$\left \{ x : x \text { is a natural numbers, $$x < 5$$ and $$x > 7}\right \}$$
(iv) $$\left \{ y : y \text { is a point common to any two parallel lines}\right \}$$
Which of the following sets are finite or infinite
(i) The set of months of a year
(ii) $$\left \{1,2,3,....\right \}$$
(iii) $$\left \{1,2,3, ....99,100\right \}$$
(iv) The set of positive integers greater than $$100$$
(v) The set of prime numbers less than $$99$$
Make correct statements by filling in the symbols $$\subset$$ or $$\not\subset$$ in blank spaces:
(i) $$\left \{2, 3, 4\right \} ...... \left \{1, 2, 3, 4,5\right \}$$
(ii) $$\left \{ a, b, c \right \} . . . \left \{ b, c, d \right \}$$
(iii) {$$x : x$$ is a student of Class XI of your school}. . .{$$x : x$$ student of your school}
(iv) {$$x : x$$ is a circle in the plane} . . .{$$x : x$$ is a circle in the same plane with radius 1 unit}
(v) {$$x : x$$ is a triangle in a plane} . . . {$$x : x$$ is a rectangle in the plane}
(vi) {$$x : x$$ is an equilateral triangle in a plane} . . . {$$x : x$$ is a triangle in the same plane}
(vii) {$$x : x$$ is an even natural number} . . . {$$x : x$$ is an integer}
Let U be the set of all triangles in a plane. If A is the set of all triangles with at least one angle different from $$60^o$$, what is A'?
List all the elements of the following sets:
(i) $$A = \left \{x : x \text { is an odd natural number}\right \}$$
(ii) $$B = \left \{x : x \text { is an integer},\frac{-1}{2} < x < \frac {9}{2}\right \}$$
(iii) $$C = \left \{x : x \text { is an integer}, x^2 \leq 4\right \}$$
(iv) $$D = \left \{x : x \text { is a letter in the word LOYAL}\right \}$$
(v) $$E = \left \{x : x \text { is a month of a year not having 31 days}\right \}$$
(vi) $$F = \left \{x : x \text { is a consonant in the English alphabet which precedes k}\right \}$$
Which of the following are sets ? Justify your answer.
(i) The collection of all the months of a year beginning with the letter J.
(ii) The collection of ten most talented writers of India.
(iii) A team of eleven best-cricket batsmen of the world.
(iv) The collection of all boys in your class.
(v) The collection of all natural numbers less than $$100.$$
(vi) A collection of novels written by the writer Munshi Prem Chand.
(vii) The collection of all even integers.
(viii) The collection of questions in this Chapter.
(ix) A collection of most dangerous animals of the world
In each of the following, determine whether the statement is true or false. If it is true, prove it. If it is false, give an example.
(i) If $$x \in A$$ and $$A \in B$$, then $$x \in B$$
(ii) If $$A \subset B$$ and $$B \in C$$, then $$A \in C$$
(iii) If $$A \subset B$$ and $$B \subset C$$, then $$A C$$
(iv) If $$A \not \subset B$$ and $$B \not \subset C$$, then $$A \not \subset C$$
(v) If $$x \in A$$ and $$A \not \subset B$$, then $$x \in B$$
(vi) If $$A \subset B$$ and $$x \notin B$$, then $$x \notin A$$
Write down all the subsets of the following sets
(i) {a} (ii) {a, b} (iii) {1, 2, 3} (iv) $$\phi$$
State whether each of the following set is finite or infinite:
(i) The set of lines which are parallel to the x-axis
(ii) The set of letters in the English alphabet
(iii) The set of numbers which are multiple of $$5$$
(iv) The set of animals living on the earth
(v) The set of circles passing through the origin (0,0)
In a town of $$10,000$$ families it was found that $$40$$% families buy newspaper A, $$20$$% families buy newspaper B and $$10$$% families buy newspaper C. $$5$$% families buy A and B, $$3$$% buy B and C and $$4$$% buy A and C. If $$2$$% families buy all the three newspaper, the member of families which buy A only is ___.
If $$A, B$$ and $$C$$ are any three sets, then $$A\cap (B\triangle C) = (A\cap B)\Delta (A\cap C)$$ .If true enter 1 else 0.
$$ A\cap (B\Delta C) = A\cap \left [ (B\cup C)-(B\cap C) \right ] $$
$$ \Rightarrow A\cap (B\cup C)-A\cap (B\cap C) $$
$$ \Rightarrow (A\cap B)\cup (A\cap C)-(A\cap B)\cap (A\cap C) $$
(using distributive low)
$$ \Rightarrow \boxed {(A\cap B)\Delta (A\cap C)} $$
Write the following sets in Set - Builder form
(i) The set of all positive even numbers
(ii) The set of all whole numbers less than 20
(iii) The set of all positive integers which are multiples of 3
(iv) The set of all odd natural numbers less than 15
(v) The set of all letters in the word 'computer'
List all of the subsets of the set $$\left\{ a,b,c,d \right\} $$
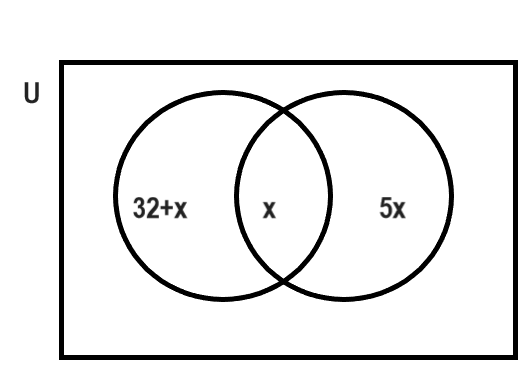
$$A$$ and $$B$$ are two sets such that $$n\left ( A-B \right )=32+x, n\left ( B-A \right )=5x$$ and $$n\left (A\cap B \right )=x$$ Illustrate the information by means of a Venn diagram. Given that $$n\left ( A \right )=n\left ( B \right )$$.
Calculate (i) The value of $$x$$ (ii) $$n\left ( A\cup B \right )$$.
$$n(A-B)=32+x $$
$$n(B-A)=5x $$
$$n(A\cap B)=x$$
$$n(A)=n(B) $$
$$(1) n(A)=n(B)$$
$$32+x+x=5x+x$$
$$32+2x=6x$$
$$6x-2x=32$$
$$4x=32$$
$$x=8$$
$$(2)n(A)=32+x+x $$
$$=32+2x$$
$$=32+2\times 8 $$
$$x=48$$
$$n(B) = 5x+x $$
$$=6x $$
$$=6\times 8$$
$$=48$$
$$n(A\cup B) = n(A)+n(B)-n(A\cap B)$$
$$=48+48-8$$
$$=96-8$$
$$=88$$
so, the value of $$x=8$$ and $$n(A\cup B) =88 $$
Let $$A=$$ { $$x:x$$ is a natural number $$< 11$$ }
$$B=$$ { $$x:x$$ is an even number and $$1< x< 21$$ }
$$C=$$ { $$x:x$$ is an integer and $$15\leq x\leq 25$$ }
(i) List the element of $$A, B, C$$
(ii) Find $$n(A), n(B), n(C)$$.
(iii) State whether the following are True (T) or False (F)
(a) $$7\in B$$
(b) $$16\notin A$$
(c) $$\left \{ 15,20,25 \right \}\subset C$$
(d) $$\left \{ 10,12 \right \}\subset B$$
Let A={-5, -3, -2, -1}, B={-2, -1, 0} and C={-6, -4, -2}. Find A ( B \ C) and (A \ B) \ C. What can we conclude about set difference operation?
For A={5,10,15,20}; B={6,10,12,18,24} and C={7,10,12,14,21,28}, verify whether $$A$$\$$ (B$$ \ $$C)$$$$=(A$$\ $$B)$$ \ $$C$$. Justify your answer
Find
i)$$A\cap B$$ if (i) $$A=\left \{10,11,12,13\right \}, B= \left \{12,13,14,15 \right \}$$
ii) $$A= \left \{5,9,11\right \} ,B=\varnothing$$
Find the union of the following sets.
(i) $$A=\left \{1,2,3,5,6\right \} $$ and $$B=\left \{4,5,6,7,8\right \}$$
(ii) $$X =\left \{3,4,5 \right \} $$ and $$Y =\varnothing$$
If $$U=\left \{ x:1 \leq x\leq 10, x\in \mathbb{N} \right \}, A=\left \{ 1,3,5,7,9 \right \}$$ and $$B=\left \{ 2,3,5,9,10 \right \}$$
Find
(i) $${A}'$$
(ii) $${B}'$$
(iii) $${A}'\cup {B}'$$
(iv) $${A}'\cap {B}'$$
If $$A={4, 6, 7, 8, 9}, B={2, 4, 6}$$ and $$C={1, 2, 3, 4, 5, 6}$$, then find
(i) $$A\cup (B\cap C)$$ (ii) $$A\cap (B\cup C)$$ (iii) $$A\setminus (C\setminus B)$$
Let A = \{a, b, c, d, e, f, g, x, y, z \}, B = \{ 1, 2, c, d, e\} and C = \{ d, e, f, g, 2, y\}.
Verify $$A\setminus (B \cup C)=(A \setminus B)\cap (A \setminus C)$$.
For $$A=\left \{ x| -3 \leq x< 4, x\in R \right \}, B=\left \{ x|x < 5, x\ on\ \mathbb{N} \right \}$$ and C= { 5, 3, 1, 0, 1, 3}, show that $$A \cap (B \cap C)= (A \cap B)\cup (A \cap C)$$.
First note that the set A contains all the real numbers (not just integers) that are greater than or equal to -3 and less than 4.
On the other hand the set B contains all the positive integers that are less than 5. So,
$$A=\left \{ x| -3 \leq x< 4, x\in R \right \}, B=\left \{ x|x < 5, x \in \mathbb{N} \right \}$$; that is, A consists of all real numbers from -3 upto 4 but 4 is not included.
Also, $$B=\left \{ x|x < 5, x\in \mathbb{N} \right \}$$ $$={1, 2, 3, 4}$$. Now, we find
$$B \cup C$$$$={1, 2, 3, 4}$$$$\cup$$ $${-5, -3, -1, 0, 1, 3}$$
$$= { 1, 2, 3, 4, -5, -3, -1, 0}$$; thus
$$A \cup (B \cup C)$$= A $$\cap $$$$ {1, 2, 3, 4, -5, -3, -1, 0}$$
$$={-3, -1, 0, 1, 2, 3}$$ (1)
Next, to find $$(A \cap B)\cup (A \cap C)$$, we consider
$$A \cap B =\left \{ x| -3 \leq x< 4, x\in R \right \} \cap $$$$ \{1, 2, 3, 4\}=\{1, 2, 3\}$$
$$A \cap C =\left \{ x| -3 \leq x< 4, x\in R \right \} \cap $$ $$\{-5, -3, -1, 0, 1, 3\}$$
$$=\{-3, -1, 0, 1, 2, 3\}$$
Hence, $$(A \cap B)\cup (A \cap C)$$ $$= {1, 2, 3}$$ $$\cup $$ $$\{-3, -1, 0, 1, 3\}$$
$$= \{ -3, -1, 0, 1, 2, 3\}.$$
Now (1) and (2) imply $$A \cap (B \cup C)=(A \cap B)\cup (A \cap C)$$
On the other hand the set B contains all the positive integers that are less than 5. So,
$$A=\left \{ x| -3 \leq x< 4, x\in R \right \}, B=\left \{ x|x < 5, x \in \mathbb{N} \right \}$$; that is, A consists of all real numbers from -3 upto 4 but 4 is not included.
Also, $$B=\left \{ x|x < 5, x\in \mathbb{N} \right \}$$ $$={1, 2, 3, 4}$$. Now, we find
$$B \cup C$$$$={1, 2, 3, 4}$$$$\cup$$ $${-5, -3, -1, 0, 1, 3}$$
$$= { 1, 2, 3, 4, -5, -3, -1, 0}$$; thus
$$A \cup (B \cup C)$$= A $$\cap $$$$ {1, 2, 3, 4, -5, -3, -1, 0}$$
$$={-3, -1, 0, 1, 2, 3}$$ (1)
Next, to find $$(A \cap B)\cup (A \cap C)$$, we consider
$$A \cap B =\left \{ x| -3 \leq x< 4, x\in R \right \} \cap $$$$ \{1, 2, 3, 4\}=\{1, 2, 3\}$$
$$A \cap C =\left \{ x| -3 \leq x< 4, x\in R \right \} \cap $$ $$\{-5, -3, -1, 0, 1, 3\}$$
$$=\{-3, -1, 0, 1, 2, 3\}$$
Hence, $$(A \cap B)\cup (A \cap C)$$ $$= {1, 2, 3}$$ $$\cup $$ $$\{-3, -1, 0, 1, 3\}$$
$$= \{ -3, -1, 0, 1, 2, 3\}.$$
Now (1) and (2) imply $$A \cap (B \cup C)=(A \cap B)\cup (A \cap C)$$
Let A = {10, 15, 20, 25, 30, 35, 40, 45 } 50 , B = { 1, 5,10,15, 20, 30} and C = { 1, 5,15, 20, 35, 45, }. Verify $$A\setminus (B\cap C)=(A\setminus B)\cup (A\setminus C)$$.
If A and B be two finite sets such that the total number of subsets of A is $$960$$ more than the total number of subsets of B, then $$n(A)-n(B)$$ (where n(x) denotes the number of elements in set x) is equal to?
Show that the relation R defined by $$\left( a,b \right) R \left( c,d \right)$$ such that $$a+d=b+c$$ on AXA, where $$A=\left\{ 1,2,....10 \right\}$$ is an equivalence relation. Hence write the equivalence class $$\left[ 3,4 \right] ;a,b,c,d\in A.$$
$$ A-\left( B\cup C\cup D \right) =\left( A-B \right) \cap\ ........ \cap\ ........$$
If $$A = \{2, 3, 4, 8, 10\}, B = \{3, 4, 5, 10, 12\}$$ and $$C = \{4, 5, 6, 12, 14\}$$
Find :$$n (A \cup \,B) \, \cap \, (A \ \cup \, C)$$
$$ \left( A\cup B \right) -C=\left( A-C \right) \cup$$ ........
Let $$ A=\left\{ \left( x,y \right) :x,y\ \in\ R, { x }^{ 2 }{ +y }^{ 2 }=1 \right\}$$
and $$ B=\left\{ \left( x,0 \right) :x\ \in\ R, -1\le x\le 1 \right\}$$, then $$ A\cap B=$$ ...........
If A = {1, 2} and B = {1, 3} prove that $$(A \, \times \, B) \, \cup \, (B \, \times \, A)$$ = {(1, 3), (2, 3), (3, 1), (3, 2), (1, 1), (1, 2), (2, 1)}
In a pollution study of $$1500$$ Indian rivers the following data were reported. $$520$$ were polluted by sulphur compounds, $$335$$ polluted by phosphate, $$425$$ were polluted by crude oil, $$100$$ were polluted by both crude oil and sulphur compounds, $$180$$ were polluted by both sulphur compounds and phosphates, $$150$$ were polluted by both phosphates and crude oil and $$28$$ were polluted by sulphur compounds, phosphates, and crude oil. How many of the rivers were polluted by at least one of the three impurities ? How many of the rivers were polluted by exactly one of the three impurities ?
Set $$U={1,2,3,4,5,6,7,8,9}$$
$$ A=\left\{ x:x\ \in N,30\le { x }^{ 2 }\le 70 \right\} $$
$$B=\left\{x:x\ is\ a\ prime\ number\ <10\ \right\}$$
Find $$ A',B'\left( A\cup B \right) ,A'\cap B',\left( A-B \right) '$$
Let $$U=R$$ (the set of all real numbers)
If $$ A=\left\{ x:x\in R,0<x<2 \right\},$$
$$ B=\left\{ x:x\in R,1<x\le 3 \right\},$$
Find $$ A',B',A\cup B,A\cap B,A-B.$$
We have
$$A\prime =R-A=\{ x:x\in R\ and\ x\in A\}$$
$$=\{ x:(x\in R\ and\ x\ge 2)$$
or $$(x\in R\ and\ x\le 0\}$$ [See the diagram also]
$$=\{ x:x\in R\ and\ x\ge 2\} \cup \{ x:x\in R\ and\ x\le 0\}$$
$$ B\prime =\{ x:x \in R\ and\ x \le 2\}$$ $$\cup \left\{ x:x\in R\ and\ x>3 \right\} $$
Similarly $$A\cup B=\{ x:x\in R\ and\ 0<x\le 3\}$$
$$A\cap B=\{ x:x\in R\ and\ 1<x<2\}$$
$$A-B=\{ x:x\in R\ and\ 0<x\le 1\}$$
Note : In such problems use of real number line is useful.
Given $$A ={1,2,3}, B ={3,4}, C ={4,5,6},$$
then show that $$A\cup \left( B\cup C \right) =\{ 1,2,3,4,5,6\}$$
and $$\left( A\times B \right) \cap \left( B\times C \right) =\{ 3,4\}$$
Show that $$ \left( A-B \right) \cup \left( B-A \right) =\left( A\cup B \right) \cap \left( A'\cup B' \right)$$
(i) $$ A-\left( B-C \right) =\left( A-B \right) \cup \left( A\cap C \right)$$
(ii) $$ A-B=\left( A\cup B \right) -B=A-\left( A\cap B \right)$$
Verify these equalities if
$$A=\left\{ 1,2,3,4,5,6,7 \right\} , B=\left\{ 3,5,6,7,9,11 \right\} $$
and $$C=\left\{ 2,5,6,9,20 \right\} $$
Let $$U$$ be the set of all people and $$M$$ = {Males}, $$S$$ = { College students } , $$T$$ = { Teenagers } , $$W$$ = { People having heights more than five feet }. Express each of the following in the notation of set theory.
(i) College students having heights more than five feet.
(ii) People who are not teenagers and have their heights less than five feet.
(iii) All people who are neither males nor teenagers nor college students
There are $$240$$ students in class XI of a school, $$130$$ play cricket, $$100$$ play football, $$75$$ play volleyball, $$30$$ of these play cricket and football. $$25$$ play volleyball and cricket, $$15$$ play football and volleyball. Also catch students play atleast one of the three games. How many students play all the three games?
Let $$A = [x \in R:11x - 5\rangle 7x + 3]$$ and $$B = [x \in R:8x - 9 \ge 15x + 2]$$
Find $$A \cap B$$ and represent it on the number line
Let A and B be two sets with a finite number of elements. Assume that there is injective mapping from A to B and that there is an injective mapping from B to A. Prove that there is a bijective mapping from A to B.
Find a, b if, $$\left[ 7,-\sqrt { 35 } \right]\bigcup {\left[ {5,\sqrt {35} } \right]} =[a, b]$$
For a non-empty set $$X$$, if operation $$*:P(X) \times P(X) \Rightarrow P(X)$$ is defined as $$A*B=(A-B)\cup(B-A),\forall A,B \in P(X)$$ then show that empty set $$\phi$$ is the identity for $$*,$$ and all elements $$A$$ of $$P(X)$$ are invertible with $$A^{-1}=A$$
If $$A ={ 1, 3, 5, ..........17}$$ and $$B= { 2, 4, 6, ......18}$$ and $$N$$ ( the set of natural numbers) is the universal set, then show that $$A' \cup ((A\cup B )\cap B')=N$$.
Which of the following statements are false and why?
(a) $$a\subset \{ a, b, c\}$$
(b) $$\varnothing \in \{c, d\}$$.
Prove: $$A-B= A-(A\cup B)$$
$$A=\left\{1,2,3,4\right\}$$
$$B=\left \{3,4,5,6\right\}$$
$$x=\left\{1,2,3,..10\right\}$$
$$(A\cup B)'=A'\cap B'$$
If $$A,B$$ are any two sets and $$C\subset\ A\bigcup B$$. Then is it true that $$C\subseteq A$$ or $$C\subseteq B$$?
If $$A \cup B = A \cup C$$ and $$A \cap B = A \cap C$$, then prove that $$B=C$$.
For any two sets, prove that: $$A\cup (A\cap B)=$$$$A\cap (A\cup B)=A$$
Using properties of sets, show that for any two sets A and B,$$ (A\cup B)\cap (A\cup B')=A$$
In a group of 50 students, the number of student studying French, English, Sanskrit were found to be as follows:French = 17, English = 13, Sanskrit = 15French and English = 9, English and Sanskrit = 4French and Sanskrit = 5, English, French and Sanskrit =Find the number of students who study(i) French only(ii) English only(iii) Sanskrit only(iv) English and Sanskrit but not French(v) French and Sanskrit but no English(vi) French and English but no Sanskrit(vii) at least one of the three languages(viii) none of the three language
If $$A={x:x\in W, x<2} , \quad B={x:x\in N, 1<x<5},\quad c={3, 5}$$: then verify that:$$A\times (B\cap C)=(A\times B)\cap (A\times C)$$
If $$A$$ and $$B$$ are two sets such that $$A\subset B$$ then what is $$A\cup B$$?
If $$n(A)=15,\ n(A\cup B)=29,\ n(A\cap B)=7$$ then find $$n(B)$$.
A is the set of real zeroes of the polynomial $$x^2+16$$. Is A an empty set? Give reasons?
If A = {1, 2, 3, 4} B = {3,4,5,6}, C = {4,5,6,7,8} and
Universal set n = {1,2,3,4,5,6,7,8,9,10}.
verify demorgans law.
Given, $$A = \left\{ {x: - 2 < x \le 5,x \in R} \right\}$$ and $$\left\{ {x: - 5 \le x < 3,x \in R} \right\}$$$$U=\{x:-5\le x\le 5\}$$
i) $$A \cap B$$
ii) $$A' \cap B$$ on different number lines.
i) $$A \cap B$$
ii) $$A' \cap B$$ on different number lines.
If $$U=\left\{1,2,3,4,5,6,7,8,9\right\},A=\left\{2,4,6,8\right\} $$ and $$B=\left\{2,3,5,7\right\}$$ verify that
$$(A \cup B)'=A' \cap B'$$
Prove that: $$1.P\left( {1,1} \right) + 2.P\left( {2,2} \right) + 3.P\left( {3,3} \right) + ... + n.P\left( {n,n} \right) = P\left( {n + 1,n + 1} \right) - 1$$
If $$U=\left\{1,2,3,4,5,6,7,8,9\right\},A=\left\{2,4,6,8\right\} $$ and $$B=\left\{2,3,5,7\right\}$$ verfy that
$$(A \cap B)'=A' \cup B'$$
If $$S$$ is any set, then the family of all the subsets of $$S$$ is called the power set of $$S$$ and it is denoted by $$P(S)$$. Power set of a given set is always non-empty. If $$A$$ has n elements, then $$P(A)$$ has ?
If $$A'\cup B=U$$, then show that $$A\subset B$$
$$A' \cup B = U$$
we have $$A' \cup B = U'$$
$$(A' \cup B)' = U'$$
$$A \cap B' = \phi$$
It means no elements is common in $$A$$ & $$B$$ which would only possible if $$A$$ & $$B$$ are disjoint sets hence for that $$A \subset B$$. It is true.
$$\mathop {\lim }\limits_{x \to 0} \cfrac{{1 - \cos (1 - \cos 2x)}}{{{x^4}}}$$
Write the following set by roaster method : The set of all natural numbers $$'x'$$ such that $$4x+9<5$$.
Prove that $$A\cup B=A\cap B$$, if $$A=B$$.
Prove that : $$A-\left( B\cup C \right) =\left( A-B \right) \cap \left( A-C \right) $$ without using venn diagram.
A and b are two sets such that $$n(A)=3$$ and $$n(B)=6$$.
Find (i) minimum value of $$n\left( A\cup B \right) $$
(ii) maximum value of $$n\left( A\cup B \right) $$
Describe the following set by set property method $${0, 3, 8, 15, 24, 35}$$
If $$A=\{x:x $$ is a factor of $$72\}$$, $$B=\{x:x$$ is a multiple of $$4<41\}$$ .Find $$(A-B)\cup(B-A)$$ ?
Prove by using venn diagram
$$A-\left( B\cup C \right) =\left( A-B \right) \cap \left( A-C \right) $$
$$A-(B\cup B)=(A-B)\cap (A-C)$$
Decide which of the following are equal sets and which are not? Justify your answer.
$$A=\left\{ x|3x-1=2 \right\} $$
$$B=\left\{ x|x\quad is\quad a\quad natural\quad number\quad but\quad x\quad is\quad neither\quad prime\quad nor\quad composite \right\} $$
$$C=\left\{ x|x\in N,x<2 \right\} $$
Find the number of three element sets of positive integers {a,b,c} such that $$a \times b \times c = 2310$$
Let $$A=\left\{a, e, i, o, u\right\}$$ and $$B=\left\{a, b, c, d\right\}$$. Is $$A$$ a subset of $$B$$? No. (Why?). Is $$B$$ a subset of $$A$$? No. (Why?)
$$(A\cap B')'\cup (B\cap C)=?$$
If $$A{a,b,c}$$ then the number of equivalence relations on $$A$$ is ?
A and B are two sets having $$3$$ elements in common.If $$n ( \mathrm { A } ) = 5 , n ( \mathrm { B } ) = 4$$ then Find $$n\left( {A \times B} \right)\,and\,n\left[ {\left( {A \times B} \right) \cap \left( {B \times A} \right)} \right]$$
Write the following set in the roster method: $$B=\{y|y$$ is a colour in the rainbow$$\}$$.
Of the members of three athletic team s in a school $$21$$ are in cricket team, $$26$$ are in hockey team and $$29$$ are in the football team. Among them, $$14$$ play hockey and cricket, $$15$$ play hockey and football, and $$12$$ play football and cricket. Eight play all the three games. Find the total number of members in the three athletic team.
Let
C= Set of members of cricket team
H= Set of members of Hockey team
F= Set of members of Football team
$$n(C)=21,n(H)=26,n(F)=23$$
$$n(H\cap C)=14,n(H\cap F)=15,n(F\cap C)=12$$
$$n(C\cap H\cap F)=8$$
Total number of members = $$n(C\cap H\cap F)$$
$$=n(C)+n(H)+n(F)-n(C\cap H)-n(H\cap F)-n(C\cap F)+n(C\cap H\cap F)$$
$$=21+26+29-14-15-12+8=43$$
Let $$A,B$$ and $$C$$ be the sets such that $$A \cup B = A \cup C$$ and $$A \cap B = A \cap C.$$ Show that $$B=C$$
In certain town, 25% of the families own a phone and 15% own a car; 65% families own neither a phone nor a car and 2000 families own both a car and a phone. Then find the correct statement among the following;
(a) 5% families own both a car and a phone.
(b) 35% families own either a car and a phone.
(c) 40,000 families live in the town.
For two sets if $$n(A)=4$$ and $$n(B)=3$$ then find the number of elements if $$A\Delta B$$.
Let $$A=\{1,2,3,4\}$$ and $$B=\{2,4,6,8\}$$. Then find $$A\cup B$$.
Let $$A=\{1,2,3,4\}$$ and $$B=\{2,4,6,8\}$$. Then find $$A\Delta B$$.
Let $$O=$$ Set of odd natural numbers $$=\{1,3,5,7,9,...\}$$ and $$E=$$Set of even natural numbers $$=\{2,4,6,8,10,........\}$$. Show that $$2\in E$$.
Let, $$A=\{1,2,3,4\}$$ and $$B=\{2,4,6,8\}$$. Then find $$B-A$$.
If $$P=\left\{x\ |\ 24 < x < 30\right\}$$ and $$Q=\left\{x\ |\ 25 < x < 32\right\}$$, prove that $$P-Q\neq Q-P$$
Let $$O=$$ Set of odd natural numbers $$={1,3,5,7,9,...}$$ and $$E=$$Set of even natural numbers $$={2,4,6,8,10,........}$$.
Fill in the blank using symbol $$\in $$ or $$\notin $$.
$$1 __ O$$
Find the union and intersection of the following pair of sets
$$A=\left\{ 2,\ 3,\ 5,\ 6,\ 7 \right\} ;\ B=\left\{ 4,\ 5,\ 7,\ 8 \right\} $$
If $$f\left(x\right)=x^ {2}+1$$, find $$f'\left(2\right)$$ from the first principle.
If $$A \times B \subseteq C\times D$$ and $$A \times B\neq \phi,$$ prove that $$A \subseteq C$$ and $$B \subseteq D$$.
Out of $$100$$ students $$15$$ passed in English $$12$$ passed in Mathematics, $$8$$ Science, $$4$$ in English and Science in all the three. Find how many passed in English and Mathematics but not in Science
Given n(u)=100
$$n\left( E \right) = 15,$$
$$n\left( M \right) = 12,$$
$$n\left( S \right) = 8$$
$$n\left( {E \cap M} \right) = 6,n\left( {M \cap S} \right) = 7,$$
$$n\left( {E \cap S} \right)....4,\,and\,n\left( {E \cap M \cap S} \right) = 4$$
$$a = n\left( {E \cap M \cap S} \right) = 4$$
$$a + d = n\left( {M \cap S} \right) = 7$$
$$\therefore \,$$ $$\,\,d = 3$$
$$a + b = n\left( {M \cap E} \right) = 6$$
$$\therefore \,\,\,\,\,b = 2$$
$$a+c=n\left( { S\cap E } \right) =4$$
$$\therefore \,\,\,\,c = 0$$
$$\,\,\,\,\,\,\,a + b + d + e = n(M) = 12$$
$$\therefore \,\,\,4 + 2 + 3 + e = 12$$
$$\therefore \,e = 3$$
$$\,\,\,\,a + b + c + g = 15$$
$$\therefore \,4 + 2 + 0 + g = n(E) = 15$$
$$\therefore \,g = 9$$
$$\,\,a + c + d + f = n(S) = 8$$
$$\therefore \,4 + 0 + 3 + f = 8$$
$$\therefore \,f = 1$$
The number of students passed in English and Mathematics but not in science $$b=2$$
Suppose $$A_{ 1 }, A_{ 2 },A_{ 30 }$$ are thirty sets each with five elements and $$B_{ 1 }, B_{ 2 },., B_{ n }$$ are in sets each with three elements. Let $$ \overset { 30 }{ \underset { i=1 }{ \cup } } Ai=\overset { n }{ \underset { j=1 }{ \cup } } { B }_{ j }=S$$. Assume the each element of $$S$$ belongs to exactly ten of the $$A_{ i }$$ and exactly $$9$$ of $$B_{ j }s $$. Find n.
If $$A=\left\{1,2,3,4\right\},\,\,B=\left\{3,4,5,6\right\}$$ and $$C=\left\{1,2,4,6,7\right\}$$ then find $$A\cap\left(B\cap \,C\right)$$
If $$A=\left\{1,2,3,4\right\},\,\,B=\left\{3,4,5,6\right\}$$ and $$C=\left\{1,2,4,6,7\right\}$$ then find $$A\cap\left(B\cup \,C\right)$$
Let $$A=\left\{a,c,i,o,u\right\}$$ & $$B=\left\{a,i,u\right\}$$ show that $$A \cup B=A$$.
Let $$A=\{1,2,3,4,5\}$$ and $$B=\{2,4,6\}$$ then find $$A\cup B$$ and $$A\cap B$$.
If $$A=\left\{a,b\right\},\,\,B=\left\{x,y\right\}$$ and $$C=\left\{a,c,y\right\}$$, then verify that $$A\times\left(B\cup \,C\right)=\left(A\times B\right)\cup\left(A\times C\right)$$
Verify whether $$A\subset B$$ for the sets $$A=\left\{\left\{a,b,c\right\}\right\}, B=\left\{1,\{a,b,c\},2\right\}$$
Fill in the blanks
A _______ is a collection of numbers gathered to give some meaningful information.
Which of the following are sets? Justify the answer. Justify your answer
The collection of all even integers.
Which of the following are sets? Justify the answer.
The collection of ten most talented writers of India.
In a survey of $$400$$ students in a school, $$100$$ were listed as taking apple juice. $$150$$ as taking orange juice and $$75$$ were listed as taking both apple as well as orange juice. Find how many students were taking neither apple nor orange juice.
Write down all possible subsets of the following set.
$$\{a\}$$.
From the diagram, relation between A and B.......
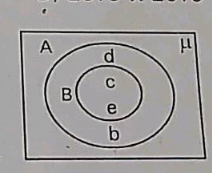
Write down all possible subsets of the following set.
$$\{a, b, c\}$$.
From the diagram, relation between A and B............
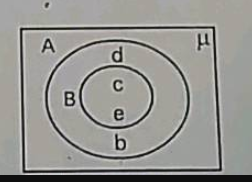
Write down all possible subsets of the following set.
$$\{1, \{1\}\}$$.
Decide among the following sets, which are subsets of which:
$$A=\{x : x$$ satisfies $$x^2-8x+12=0\}$$,
$$B=\{2, 4, 6\}$$,
$$C=\{2, 4, 6, 8,.....\}$$,
$$D=\{6\}$$.
Write down all possible subsets of the following set.
$$\{0, 1\}$$.
Let $$A=\{3, 6, 12, 15, 18, 21\}, B=\{4, 8, 12, 16, 20\}, C=\{2, 4, 6, 8, 10, 12, 14, 16\}$$ and $$D=\{5, 10, 15, 20\}$$. Find $$A-D$$.
Let $$u=\{1, 2, 3, 4, 5, 6, 7, 8, 9\}, A=\{1, 2, 3, 4\}, B=\{2, 4, 6, 8\}$$ and $$C=\{3, 4, 5, 6\}$$. Find B'.
Write down all possible subsets of the following set.
$$\{\phi\}$$.
Let $$A=\{3, 6, 12, 15, 18, 21\}, B=\{4, 8, 12, 16, 20\}, C=\{2, 4, 6, 8, 10, 12, 14, 16\}$$ and $$D=\{5, 10, 15, 20\}$$. Find $$C-A$$.
Let $$A=\{3, 6, 12, 15, 18, 21\}, B=\{4, 8, 12, 16, 20\}, C=\{2, 4, 6, 8, 10, 12, 14, 16\}$$ and $$D=\{5, 10, 15, 20\}$$. Find $$B-A$$.
Let $$A=\{3, 6, 12, 15, 18, 21\}, B=\{4, 8, 12, 16, 20\}, C=\{2, 4, 6, 8, 10, 12, 14, 16\}$$ and $$D=\{5, 10, 15, 20\}$$. Find $$B-D$$.
Let $$u=\{1, 2, 3, 4, 5, 6, 7, 8, 9\}, A=\{1, 2, 3, 4\}, B=\{2, 4, 6, 8\}$$ and $$C=\{3, 4, 5, 6\}$$. Find $$(A')'$$.
Let $$A=\{3, 6, 12, 15, 18, 21\}, B=\{4, 8, 12, 16, 20\}, C=\{2, 4, 6, 8, 10, 12, 14, 16\}$$ and $$D=\{5, 10, 15, 20\}$$. Find $$D-A$$.
Let $$A=\{3, 6, 12, 15, 18, 21\}, B=\{4, 8, 12, 16, 20\}, C=\{2, 4, 6, 8, 10, 12, 14, 16\}$$ and $$D=\{5, 10, 15, 20\}$$. Find $$A-C$$.
Let $$A=\{3, 6, 12, 15, 18, 21\}, B=\{4, 8, 12, 16, 20\}, C=\{2, 4, 6, 8, 10, 12, 14, 16\}$$ and $$D=\{5, 10, 15, 20\}$$. Find $$B-C$$.
Let $$u=\{1, 2, 3, 4, 5, 6, 7, 8, 9\}, A=\{1, 2, 3, 4\}, B=\{2, 4, 6, 8\}$$ and $$C=\{3, 4, 5, 6\}$$. Find $$(B-C)'$$.
Let $$A=\{1, 2, 4, 5\}, B=\{2, 3, 5, 6\}, C=\{4, 5, 6, 7\}$$. Verify the following identity.
$$A\cap (B-C)=(A\cap B)-(A\cap C)$$.
Let $$A=\{1, 2, 4, 5\}, B=\{2, 3, 5, 6\}, C=\{4, 5, 6, 7\}$$. Verify the following identity.
$$A\cap(B\cup C)=(A\cap B)\cup(A\cap C)$$.
Let $$A=\{1, 2, 4, 5\}, B=\{2, 3, 5, 6\}, C=\{4, 5, 6, 7\}$$. Verify the following identity.
$$A\cap (B\triangle C)=(A\cap B)\triangle(A\cap C)$$.
Let $$A=\{1, 2, 4, 5\}, B=\{2, 3, 5, 6\}, C=\{4, 5, 6, 7\}$$. Verify the following identity.
$$A-(B\cup C)=(A-B)\cap (A-C)$$.
Let $$A=\{1, 2, 4, 5\}, B=\{2, 3, 5, 6\}, C=\{4, 5, 6, 7\}$$. Verify the following identity.
$$A-(B\cap C)=(A-B)\cup (A-C)$$.
If $$u=\{2, 3, 5, 7, 9\}$$ is the universal set and $$A=\{3, 7\}, B=\{2, 5, 7, 9\}$$, then prove that $$(A\cap B)'=A'\cup B'$$.
Let $$A=\{1, 2, 4, 5\}, B=\{2, 3, 5, 6\}, C=\{4, 5, 6, 7\}$$. Verify the following identity.
$$A\cup(B\cap C)=(A\cup B)\cap (A\cup C)$$.
Let $$u=\{1, 2, 3, 4, 5, 6, 7, 8, 9\}, A=\{2, 4, 6, 8\}$$ and $$B=\{2, 3, 5, 7\}$$. Verify that $$(A\cup B)'=A'\cap B'$$.
For any two sets A and B, prove that $$A\cup (B-A)=A\cup B$$.
For any two sets A and B, prove that $$A-(A-B)=A\cap B$$.
For any two sets A and B, prove that $$A\cap B\subset A$$.
For any two sets A and B, prove that $$A-(A\cap B)=A-B$$.
For any two sets A and B, prove that $$(A-B)\cup(A\cap B)=A$$.
For any two sets A and B, prove that $$A\subset B\Rightarrow A\cap B=A$$.
Find sets A, B and C such that $$A\cap B, A\cap C$$ and $$B\cap C$$ are non-empty sets and $$A\cap B\cap C=\phi$$.
For any two sets, check whether $$A\cup (A\cup B)=A$$.
For three sets A, B and C, show that $$A\subset B\Rightarrow C-B\subset C-A$$.
For any two sets A and B, show that the following statements are equivalent.
(i) $$A\subset B$$
(ii) $$A-B=\phi$$
(iii) $$A\cup B=B$$
(iv) $$A\cap B=A$$.
If P and Q are two sets such that P has $$40$$ elements, $$P\cup Q$$ has $$60$$ elements and $$P\cap Q$$ has $$10$$ elements, how many elements does Q have?
Let $$A=\{1, 2\}, B=\{1, 2, 3, 4\}, C=\{5, 6\}$$ and $$D=\{5, 6, 7, 8\}$$. Verify that $$A\times C\subset B\times D$$.
A survey shows that $$76\%$$ of the Indians like oranges, whereas $$62\%$$ like bananas. What percentage of the Indians like both oranges and bananas?
If $$A=\{1, 2\}$$, form the set $$A\times A\times A$$.
Answer the following question in one word or one sentence or as per exact requirement of the question.
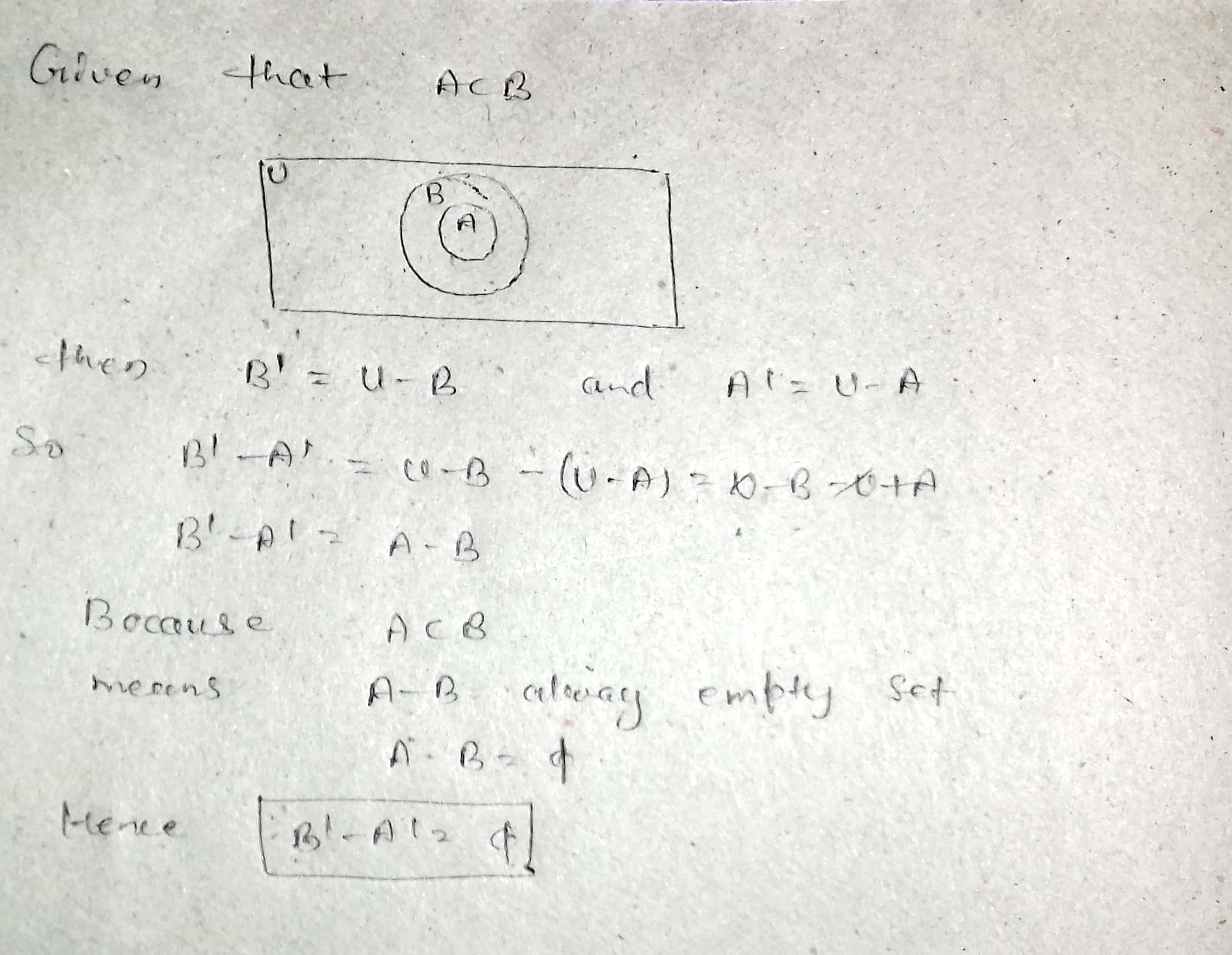
If A and B are two sets such that $$A\subset B$$, then write $$B'-A'$$ in terms of A and B.
If $$A=\{-1, 1\}$$, find $$A\times A\times A$$.
If A and B are sets, then prove that $$A-B, A\cap B$$ and $$B-A$$ are pair wise disjoint.
If $$A=\{1, 2, 3, 4, 5\}, B=\{4, 5, 6, 7, 8\}, C=\{7, 8, 9, 10, 11\}$$ and $$D=\{10, 11, 12, 13, 14\}$$. Find $$A\cup B$$.
For three sets A, B and C, show that $$A\cap B=A\cap C$$ need not imply $$B=C$$.
Using properties of sets, show that for any two sets A and B, $$(A\cup B)\cap (A\cup B')=A$$.
For three sets A, B and C, show that $$A\subset B\Rightarrow C-B\subset C-A$$.
Answer the following question in one word or one sentence or as per exact requirement of the question.
Let A and B be two sets such that $$n(A)=3$$ and $$n(B)=2$$. If $$(x, 1), (y, 2), (z, 1)$$ are in $$A\times B$$, write A and B.
If $$A=\{1, 2, 3, 4, 5\}, B=\{4, 5, 6, 7, 8\}, C=\{7, 8, 9, 10, 11\}$$ and $$D=\{10, 11, 12, 13, 14\}$$. Find $$A\cup C$$.
For any two sets, prove that $$A\cup (A\cup B)=A$$.
If $$A=\{1, 2, 3, 4, 5\}, B=\{4, 5, 6, 7, 8\}, C=\{7, 8, 9, 10, 11\}$$ and $$D=\{10, 11, 12, 13, 14\}$$. Find $$A\cup B\cup C$$.
If $$A=\{1, 2, 3, 4, 5\}, B=\{4, 5, 6, 7, 8\}, C=\{7, 8, 9, 10, 11\}$$ and $$D=\{10, 11, 12, 13, 14\}$$. Find $$A\cup B\cup D$$.
If $$A=\{2, 3\}, B=\{4, 5\}, C=\{5, 6\}$$, find $$A\times (B\cup C), A\times (B\cap C), (A\times B)\cup (A\times C)$$.
Let A and B be two sets such that: $$n(A)=20, n(A\cup B)=42$$ and $$n(A\cap B)=4$$. Find $$n(A-B)$$.
Is the following represent a set? justify your answer.
The collection of good hockey players in India.
Which of the following are sets? justify your answer.
The collection of all whole numbers less than $$10$$
If $$A=\{1, 2, 3, 4, 5\}, B=\{4, 5, 6, 7, 8\}, C=\{7, 8, 9, 10, 11\}$$ and $$D=\{10, 11, 12, 13, 14\}$$. Find $$B\cup C\cup D$$.
Let $$X = \{n \in N : 1 \le n \le 50\}.$$ If $$A = \{n \in X : n$$ is a multiple of $$2\}$$ and $$B = \{n \in X : n$$ is a multiple of $$7\}$$, then the number of elements in the smallest subset of X containing both A and B is _____.
If $$A=\{1, 2, 3, 4, 5\}, B=\{4, 5, 6, 7, 8\}, C=\{7, 8, 9, 10, 11\}$$ and $$D=\{10, 11, 12, 13, 14\}$$. Find $$A\cap(B\cup C)$$.
For any two sets of A and B, prove that $$B'\subset A'\Rightarrow A\subset B$$.
Let A and B be two sets such that: $$n(A)=20, n(A\cup B)=42$$ and $$n(A\cap B)=4$$. Find $$n(B)$$.
Let A and B be two sets such that: $$n(A)=20, n(A\cup B)=42$$ and $$n(A\cap B)=4$$. Find $$n(B-A)$$.
Is the following represent a set? justify your answer.A team of $$11$$ best cricket players of India.
Is the following represent a set? justify your answer.The collection of all question in this chapter.
Which of the following are sets? justify your answer.
The collection of all persona of Kolkata whose assessed annual incomes exceed (say) $$Rs\ 20\ lakh$$ in the financial year $$2016-17$$
Is the following represent a set? justify your answer.The collection of all the months of the year whose names begin with the letter $$M$$.
Which of the following are sets? justify your answer.
The collection of all interesting books.
Which of the following are sets? justify your answer.
The collection of all rich persons of Kolkata
Is the following represent a set? justify your answer.A collection of Hindi novels written by Munshi Prem Chand.
Which of the following are sets? justify your answer.
The collection of all those students of your class whose ages exceed $$15$$ years.
Is the following represent a set? justify your answer.The collection of all difficult chapters in this book.
Which of the following are sets? justify your answer.
The collection of all short boys of your class.
State in the case whether $$A\subset B$$ or $$A\nsubseteq B$$.
$$A=\left\{ x:x\ is\ an\ even\ natural\ number\right\}, B=\left\{ x:x\ is\ an\ integer\right\}$$
If $$A=\left\{a,b,c,d,e,f\right\}, B=\left\{c,e,g,h\right\}$$ and $$C=\left\{a,e,m,n\right\}$$, find
$$B\cup C$$
State in the case whether $$A\subset$$ or $$A\nsubseteq B$$.
$$A=\left\{ x:x\ is\ a\ real\ number\right\}, B=\left\{x:x\ is\ a\ complex\ number\right\}$$
We may write a real number $$x$$ as $$x+0i$$. So, every real number is a complex number.
As also can be explained from the above image that each Real number is a Complex number.
$$\therefore A \subset B$$
As also can be explained from the above image that each Real number is a Complex number.
$$\therefore A \subset B$$
State in the case whether $$A\subset$$ or $$A\nsubseteq B$$.
$$A=\left\{ 0, 1, 2, 3\right\}, B=\left\{ 1, 2, 3, 4, 5\right\}$$
If $$A=\left\{a,b,c,d,e,f\right\}, B=\left\{c,e,g,h\right\}$$ and $$C=\left\{a,e,m,n\right\}$$, find
$$A\cup B$$
Which of the following are sets? justify your answer.
The collection of all interesting dramas written by Shakespeare.
State in the case whether $$A\subset$$ or $$A\nsubseteq B$$.
$$A=\left\{ x:x\ is\ an\ integer\right\}, B=\left\{ x:x\ is\ a\ rational\ number\right\}$$
The symbol $$⊆$$ means is a subset of. The symbol $$⊂$$ means is a proper subset of.
Since, every integer is a rational number.
So, in
$$A=\{x:x$$ is an integer $$\},$$ $$B=\{x:x$$ is a rational number $$\}$$
So,
$$A \subset B$$
State in the case whether $$A\subset$$ or $$A\nsubseteq B$$.
$$A=\phi, B=\{0\}$$
State in the case whether $$A\subset$$ or $$A\nsubseteq B$$.
$$A=\{1, 2, 3\}, B=\{1, 2, 4\}$$
State in the case whether $$A\subset$$ or $$A\nsubseteq B$$.
$$A=\left\{ x:x\ is\ an\ isosceles\ triangle\ in\ a\ plane\right\}$$, $$B=\left\{ x:x\ is\ an\ equilateral\ triangle\ in\ the\ same\ plane\right\}$$
State in the case whether $$A\subset$$ or $$A\nsubseteq B$$.
$$A=\left\{ x:x\ is\ a\ square\ in\ a\ plane\right\}, B=\left\{ x:x\ is\ a\ rectangle\ in\ the\ same\ plane\right\}$$
If $$A=\left\{1,2,3,4,5 \right\}, B=\left\{4,5,6,7,8 \right\}, C=\left\{7,8,9,10,11 \right\}$$ and $$D=\left\{10,11,12,13,14 \right\}$$, find :
$$A\cup C$$
If $$A=\left\{1,2,3,4,5 \right\}, B=\left\{4,5,6,7,8 \right\}, C=\left\{7,8,9,10,11 \right\}$$ and $$D=\left\{10,11,12,13,14 \right\}$$, find :
$$B\cup D$$
Examine whether the following statements is true or false:
$$\left\{ a, b\right\} \nsubseteq \left\{ b, c,a\right\}$$
State in the case whether $$A\subset$$ or $$A\nsubseteq B$$.
$$A=\left\{x:x\ is\ a\ square\ in\ a \ plane\right\}, B=\left\{x:x\ is\ a\ rectangle\ in\ the\ same\ plane\right\}$$
Examine whether the following statements are true or false:
$$\left\{ a\right\} \in \left\{ a, b,c\right\}$$
Examine whether the following statements are true or false:
$$\left\{ \phi \right\} \subset \left\{ a, b,c\right\}$$
If $$A=\left\{1,2,3,4,5 \right\}, B=\left\{4,5,6,7,8 \right\}, C=\left\{7,8,9,10,11 \right\}$$ and $$D=\left\{10,11,12,13,14 \right\}$$, find :
$$(A\cup B) \cup C$$
State in the case whether $$A\subset$$ or $$A\nsubseteq B$$.
$$A=\left\{x:x\ is\ an\ even\ natural\ number\ less\ than\ 8\right\}, B=\left\{ x:x\ is\ a \ natural\ number\ which\ divides\ 32\right\}$$
If $$A=\left\{1,2,3,4,5 \right\}, B=\left\{4,5,6,7,8 \right\}, C=\left\{7,8,9,10,11 \right\}$$ and $$D=\left\{10,11,12,13,14 \right\}$$, find :
$$B\cup C$$
If $$A$$ and $$B$$ are two sets such that $$A\subseteq B$$ then find :
$$A\cup B$$
Examine whether the following statements are true or false:
$$A=$$ set of all circles of unit radius in a plane and $$B=$$ set of all circles in the same plane then $$A\subset B$$.
If $$A=\left\{2x : x \in N\ and\ 1 \le x < 4 \right\}, B=\left\{(x+2): x \in N\ and\ 2\le x < 5 \right\}$$ and $$C=\left\{x : x \in N\ and\ 4 < x < 8 \right\}$$, find
$$A\cup B$$
Examine whether the following statements are true or false:
$$\left\{ a, e\right\} \subset \left\{ x:x\ is\ a\ vowel\ in\ the\ English\ alphabet \right\}$$
If $$A=\left\{3, \left\{ 4, 5\right\}, 6\right\}$$.State whether the following statement is true or not.
$$\left\{ \left\{ 4, 5\right\} \right\} \subseteq A$$
$$\left\{ \left\{ 4, 5\right\} \right\} \subseteq A$$
If $$A=\left\{3, \left\{ 4, 5\right\}, 6\right\}$$, State whether the following statement is true or not.
$$\left\{4, 5\right\}\subseteq A$$
If $$A=\left\{2,4,6,8,10,12 \right\}$$ and $$B=\left\{3,4,5,6,7,8,10 \right\}$$, find
$$(A-B)\cup (B-A)$$
State whether the given statement is true or false:
If $$A\subset B$$ and $$x\notin B$$ then $$x\notin A$$.
If $$A=\left\{a,b,c,d,e\right\},B=\left\{a,c,e,g\right\}$$ and $$C=\left\{b,c,f,g\right\}$$, verify that:
$$B\cup C=C\cup B$$
Prove that $$A\subseteq B, B\subseteq C$$ and $$C\subseteq A\Rightarrow A=C$$.
If $$U$$ is the universal set and $$A\subset U$$ then fill in the blanks :
$$\phi ' \cup A =......$$
If $$A=\left\{3, \left\{ 4, 5\right\}, 6\right\}$$,State whether the following statement is true or not
$$\left\{ 3, 4, 5\right\} \subseteq A$$
If $$A=\left\{3, \left\{ 4, 5\right\}, 6\right\}$$, State whether the following statement is true or not.
$$\left\{ 3, 6\right\} \subseteq A$$
If $$A=\left\{3, \left\{ 4, 5\right\}, 6\right\}$$, State whether the following statement is true or not.
$$\phi \subseteq A$$
If $$U$$ is the universal set and $$A\subset U$$ then fill in the blanks :
$$A\cup A' =......$$
If $$A=\left\{3, \left\{ 4, 5\right\}, 6\right\}$$, State whether the following statement is true or not.$$\left\{ \phi \right\} \subseteq A$$
For any sets $$A$$ and $$B$$. prove that:
$$A\cap B'=\phi\Rightarrow A\subset B$$
State whether the given statement is true or false:
If $$A, B$$ and $$C$$ are three sets such that $$A\in B$$ and $$B\subset C$$ then $$A\subset C$$.
State whether the following pairs of sets are equal or not:
$$A =\{2, 4, 6, 8,10\},\quad B = \{\text{even natural numbers}\}$$
For any sets $$A$$ and $$B$$. prove that:
$$A'\cup B=U\Rightarrow A\subset B$$
State whether the following pairs of sets are equal or not:
$$A = \{x|x\text{ is a letter in the word SOPHIA}\}$$
$$B = \{x|x\text{ is a letter in the word MUMTAZ}\}$$
State whether the given statement is true or false:
If $$A\subseteq \phi$$ then $$A=\phi$$.
If $$A\subset B$$, show that $$(B' -A')=\phi$$
State whether the given statement is true or false:If $$A, B$$ and $$C$$ are three sets such that $$A\nsubseteq B$$ and $$B\nsubseteq C$$ then $$A\nsubseteq C$$.
State whether the given statement is true or false:
If $$A, B$$ and $$C$$ are three sets such that $$A\subset B$$ and $$B\in C$$ then $$A\in C$$.
If $$A\subset B$$, prove that $$B' \subset A'$$.
Let $$A= (1, 2, (3, 4), 5)$$. Which of the following statements are incorrect and why?
(i) $$(3, 4) A$$
(ii) $$(3, 4)\epsilon A$$
(iii) $$((3, 4)) A$$
(iv) $$1 A$$
(v) $$1 A$$
(vi) $$(1, 2, 5) A$$
(vii) $$(1, 2, 5) A$$
(viii) $$(1, 2, 3) A$$
(ix) $$\not{\bigcirc} A$$
(x) $$\not{\bigcirc} A$$
(xi) $$(\not{\bigcirc}) A$$
If $$A$$ and $$B$$ are two sets such that $$A \subset B$$, then what is $$A ∪ B$$ ?
Which of the following are sets? Justify our answer:
The collection of all months of a year beginning with the letter $$J$$
If $$A$$ = {$$x: x$$ is a natural number}, $$B$$ ={$$x: x$$ is an even natural number}, $$C$$ = {$$x: x$$ is an odd natural number} and $$D$$ = {$$x: x$$ is a prime number}, find
$$A B$$
State whether the following pairs of sets are equal or not:
$$A = \{\text{kids 5 metres tall}\}, B = \{x : x \in N \text{ and }\,2x = 3\}$$
Which of the following are sets? Justify our answer.
The collection of ten most talented writers of India.
Let $$U = \left \{ 1, 2, 3; 4, 5, 6, 7, 8, 9 \right \}, A = \left \{ 1, 2, 3, 4 \right \}, B = \left \{ 2, 4, 6, 8 \right \}$$ and $$C = \left \{ 3, 4, 5, 6 \right \}$$. Find
$$(B C)$$
If $$A$$ = {$$x: x$$ is a natural number}, $$B$$ ={$$x: x$$ is an even natural number}, $$C$$ = {$$x: x$$ is an odd natural number} and $$D$$ = {$$x: x$$ is a prime number}, find
$$A D$$
If $$A$$ = {$$x: x$$ is a natural number}, $$B$$ ={$$x: x$$ is an even natural number}, $$C$$ = {$$x: x$$ is an odd natural number} and $$D$$ = {$$x: x$$ is a prime number}, find
$$B C$$
If $$A$$ = {$$x: x$$ is a natural number}, $$B$$ ={$$x: x$$ is an even natural number}, $$C$$ = {$$x: x$$ is an odd natural number} and $$D$$ = {$$x: x$$ is a prime number}, find
$$C D$$
If $$A$$ = {$$x: x$$ is a natural number}, $$B$$ ={$$x: x$$ is an even natural number}, $$C$$ = {$$x: x$$ is an odd natural number} and $$D$$ = {$$x: x$$ is a prime number}, find
$$A C$$
Let $$U = \left \{ 1, 2, 3; 4, 5, 6, 7, 8, 9 \right \}, A = \left \{ 1, 2, 3, 4 \right \}, B = \left \{ 2, 4, 6, 8 \right \}$$ and $$C = \left \{ 3, 4, 5, 6 \right \}$$. Find
$$B$$
If $$U = \left \{ 1, 2, 3, 4, 5,6,7,8, 9 \right \}, A = \left \{ 2, 4, 6, 8 \right \}$$ and $$B = \left \{ 2, 3, 5, 7 \right \}$$. Verify that
$$(A \cup B)’ = A’ ∩ B’$$
Let $$U = \left \{ 1, 2, 3; 4, 5, 6, 7, 8, 9 \right \}, A = \left \{ 1, 2, 3, 4 \right \}, B = \left \{ 2, 4, 6, 8 \right \}$$ and $$C = \left \{ 3, 4, 5, 6 \right \}$$. Find
$$(A \cup B)$$
Let $$U = \left \{ 1, 2, 3, 4, 5, 6, 7, 8, 9 \right \}, A = \left \{ 1, 2, 3, 4 \right \}, B = \left \{ 2, 4, 6, 8 \right \}$$ and $$C = \left \{ 3, 4, 5, 6 \right \}$$. Find
$$(A’)’$$
If $$A$$ = {$$x: x$$ is a natural number}, $$B$$ ={$$x: x$$ is an even natural number}, $$C$$ = {$$x: x$$ is an odd natural number} and $$D$$ = {$$x: x$$ is a prime number}, find
$$B D$$
Show that if $$A B$$, then $$C B C A$$.
State which of the following collections are set:
All the beautiful flowers.
State which of the following collections are set:
Four colours of a rainbow.
State which of the following collections are set:
All clever people of Lucknow.
If $$X$$ and $$Y$$ are two sets such that $$X\cup Y$$ has $$18$$ elements, $$X$$ has $$8$$ elements and $$Y$$ has $$15$$ elements; how many elements does $$X Y$$ have?
State which of the following collections are set:
All tall students of your school.
State which of the following collections are set:
Four cities of India having more than one lakh population.
Fill in the blanks to make each of the following a true statement:
$$A \cup A = .$$.
If $$ \xi=\{1,2,3, \ldots .9\}, A=\{1,2,3,4,6,7,8\} $$ and $$ B=\{4,6,8\}, $$ then find.
(i) $$ A^{\prime} $$
(ii) $$ B^{\prime} $$
(iii) $$ A \cup B $$
(iv) $$ \mathrm{A} \cap \mathrm{B} $$
(v) $$ A-B $$
(vi) $$ B-A $$
(vii) $$ (A \cap B)^{\prime} $$
(viii) $$ A^{\prime} \cup B^{\prime} $$
Also verify that:
(a) $$ (A \cap B)^{\prime}=A^{\prime} \cup B^{\prime} $$
(b) $$ n(A)+n\left(A^{\prime}\right)=n(\xi) $$
(c) $$ n(A \cap B)+n\left((A \cap B)^{\prime}\right)=n(\xi) $$
(d) $$ n(A-B)+n(B-A)+n(A \cap B)=n(A \cup B) $$
If $$ \mathrm{A}\{\mathrm{x}: \mathrm{x} \in \mathrm{N} \text { and } 3<\mathrm{x}<7\} $$ and $$ \mathrm{B}=\{\mathrm{x}: \mathrm{x} \in \mathrm{W} \text { and } \mathrm{x} \leq 4\}, $$ find
$$ \mathrm{B}-\mathrm{A} $$
State which of the following collections are set:
All months of a year having at least 30 days.
If $$ \xi=\{x: x \in W, x \leq 10\}, A .=\{x: x \geq 5\} $$ and $$ B=\{x: 3 \leq x<8\}, $$ then verify that:
$$ B-A=B \cap A^{\prime} $$
If $$ \mathrm{A}\{\mathrm{x}: \mathrm{x} \in \mathrm{N} \text { and } 3<\mathrm{x}<7\} $$ and $$ \mathrm{B}=\{\mathrm{x}: \mathrm{x} \in \mathrm{W} \text { and } \mathrm{x} \leq 4\}, $$ find
$$ \mathrm{A} \cup \mathrm{B} $$
State which of the following collections are set:
Last three days of a week.
If $$ \xi=\{x: x \in W, x \leq 10\}, A .=\{x: x \geq 5\} $$ and $$ B=\{x: 3 \leq x<8\}, $$ then verify that:
$$ A-B=A \cap B^{\prime} $$
If $$ \mathrm{A}\{\mathrm{x}: \mathrm{x} \in \mathrm{N} \text { and } 3<\mathrm{x}<7\} $$ and $$ \mathrm{B}=\{\mathrm{x}: \mathrm{x} \in \mathrm{W} \text { and } \mathrm{x} \leq 4\}, $$ find
$$ A-B $$
If $$ n(\xi)=32, n(A)=20, n(B)=16 $$ and $$ n\left((A \cup B)^{\prime}\right)=4, $$ find :
$$ n(A-B) $$
Let set A = $$\text{{6, 8, 10, 12}}$$ and set B = $$\text{{3, 9, 15, 18}}.$$
Insert the symbol $$\in$$ or $$\notin$$ to make each of the following true :
$$(i) 6 . A$$
$$(ii) 10 . B$$
$$(iii) 18 . B$$
$$(iv) (6 + 3) . B$$
$$(v) (15 9) . B$$
$$(vi) 12 . A$$
$$(vii) (6 + 8) . A$$
$$(viii) 6$$ and $$8 . A$$
State whether true or false:
(i) Set $$\text{{4, 5, 8}}$$ is same as the set $$\text{{5, 4, 8}}$$ and the set $$\text{{8, 4, 5}}$$
(ii) Sets $$\text{{a, b, m, n}}$$ and $$\text{{a, a, m, b, n, n}}$$ are same.
(iii) Set of letters in the word $$suchismita$$ is $$\text{{s, u, c, h, i, m, t, a}}$$
(iv) Set of letters in the word $$MAHMOOD$$ is $$\text{{M, A, H, O, D}}$$.
$$M = \{x : x \,is \,a \,natural \,number \,between \,0 \,and \,8)$$ and $$N = \{x : x \,is \,a \,natural \,number \,from \,5 \,to \,10\}$$. Find:
(i)$$M-N$$ and $$n(M-N)$$
(ii)$$N-M$$ and $$n(N-M)$$
If $$ n(A-B)=12, n(B-A)=16 $$ and $$ n(A \cap B)=5, $$ find:
(i) $$ n(A) $$
(ii) $$ n(B) $$
(iii) $$ n(A \cup B) $$
Find, whether or not, each of the following collections represent a set:
(i) The collection of good students in your school.
(ii) The collection of the numbers between 30 and 45.
(iii) The collection of fat-people in your colony.
(iv) The collection of interesting books in your school library.
(v) The collection of books in the library and are of your interest.
If $$ n(\xi)=32, n(A)=20, n(B)=16 $$ and $$ n\left((A \cup B)^{\prime}\right)=4, $$ find :
$$ n(A \cup B) $$
Given
A = {Natural numbers less than $$10$$}
B = {Letters of the word PUPPET}
C = {Squares of first four whole numbers}
D = {Odd numbers divisible by $$2$$}
Find: $$A \cap B$$ and $$(A \cup B)$$
If A = { a, b, c, d, e}, B = { c, d, e, f }, C = {b, d}, D = { a, e}
then the following statement is true or false?
$$B \ \subseteq \ A$$
If A = { a, b, c, d, e}, B = { c, d, e, f }, C = {b, d}, D = { a, e}
then the following statement is true or false?
$$D \ \subseteq \ A $$
If A = { a, b, c, d, e}, B = { c, d, e, f }, C = {b, d}, D = { a, e}
then the following statement is true or false?
$$ D \ \subseteq \ B$$
Given $$A = {a, c}, B = {p, q, r}$$ and $$C =$$ Set of digits used to form number $$1351$$.
Write all the subsets of sets $$A, B$$ and $$C.$$
If A = { a, b, c, d, e}, B = { c, d, e, f}, C = {b, d}, D = { a, e} then which of the following statement is true or false?
$$C \ \subseteq \ B$$
If A = { a, b, c, d, e}, B = { c, d, e, f }, C = {b, d}, D = { a, e}
then the following statement is true or false?
$$A \ \subseteq \ D$$
If $$A =\text{{even numbers less than 12}}$$,
$$B = \text{{2, 4}}$$,
$$C = \text{{1, 2, 3}}$$,
$$D = \text{{2, 6}}$$ and $$E = \text{{4}}$$
State which of the following statements are true :
(i)$$ B\subset A$$
(ii) $$C\subseteq A$$
(iii) $$D\subset C$$
(iv) $$D A$$
(v)$$E\supseteq B$$
(vi) $$A \supseteq B\supseteq E$$
For the universal set $$\text{{4, 5, 6, 7, 8, 9, 10, 11,12,13}}$$ ; find its subsets $$A, B, C$$ and $$D$$ such that
(i) $$A = \text{{even numbers}}$$
(ii) $$B =\text{{odd numbers greater than 8}}$$
(iii) $$C = \text{{prime numbers}}$$
(iv) $$D = \text{{even numbers less than 10}}$$
If A = { a, b, c, d, e}, B = { c, d, e, f }, C = {b, d}, D = { a, e}
then the following statement is true or false?
$$C \ \subseteq \ A$$.
Write the subset relations between the following sets.
X = set of all quadrilaterals.
Y = set of all rhombuses.
S = set of all squares.
T = set of all parallelograms.
V = set of all rectangles.
$$A= \{ 1,3,2,7 \}$$ then write any three subsets of $$A$$.
Which of the following are sets? Justify your answer.
A team of eleven best-cricket batsmen of the world.
If $$n (A) = 15, n ( A \cup B)= 29, n (A \cap B) = 7$$ then $$n (B)= $$?
Which of the following are sets? Justify your answer.A collection of most dangerous animals o fthe world.
If n(A) = 7, n(B) = 13, n(A $$\cap$$ B) = 4, then n(A $$\cup$$ B) = ?
Write the subset relation between the sets.
P is the set of all residents in Pune.
M is the set of all residents in Madhya Pradesh.
I is the set of all residents in Indore.
B is the set of all residents in India.
H is the set of all residents in Maharashtra.
Let $$A=(1, \left.2\right\}, B=[1, 2, 3, \left.4\right\}, C=\left\{5, 6\right\}$$ and $$D=( 5, 6, 7, 8 \left. \right\}$$. Verify that
$$A\times C$$ is a subset
Let $$A=\left\{1,2, \left\{3,4 \right\}, 5\right\}.$$ Which of the following statements are incorrect and why?
$$\left\{\varphi\right\} \subset A$$
Let $$A=\left\{1,2, \left\{3,4 \right\}, 5\right\}.$$ Which of the following statements are incorrect and why?
$$\left\{3,4 \right\} \subset A$$
Let $$A=\left\{1,2, \left\{3,4 \right\}, 5\right\}.$$ Which of the following statements are incorrect and why?
$$ \left\{\left\{3,4 \right\} \right\}\subset A$$
Let $$A=\left\{1, 2, 3\right\}, B =\left\{ 3, 4\right\}$$ and $$C=\left\{ 4, 5, 6\right\}$$. Find
$$(A \times B) \cup (A \times C)$$
Let $$A=\left\{1,2, \left\{3,4 \right\}, 5\right\}.$$ Which of the following statements are incorrect and why?
$$1 \subset A$$
Assume that $$P(A) P(B)$$. Show that $$A-B$$
If $$A=\left\{3,6,9,12,15,18,21 \right\}, B=\left\{4,8,12,16,20 \right\}, C=\left\{2,4,6,8,10,12,14,16 \right\} , D= \left\{5,10,15,20 \right\}$$ find
$$A-B$$
Using properties of sets, show that
$$A \cap (A \cup B)=A$$
Using properties of sets, show that
$$A \cup (A \cap B)=A$$
If $$A=\left\{1,2,3,4 \right\}, B=\left\{3,4,5,6 \right\}, C=\left\{5,6,7,8\right\}$$ and $$D=\left\{7,8,9,10 \right\}$$; find
$$A \cup B \cup D$$
Find the union and the intersection o for each of the following pairs of sets:
$$X= \left\{x : x\ is\ a\ natural\ number\ of\ and\ 1 < x \le 6 \right\}, Y=\left\{x:x\ is\ a\ natural \ numbers\ and\ 6 < x < 10\right\}$$
If $$A=\left\{3,5,7,9,11 \right\}, B=\left\{7,9,11,13 \right\}, C=\left\{11,13,15\right\}$$ and $$D=\left\{15,17 \right\}$$; find
$$(A \cap B) \cap (B \cup C)$$
If $$A=\left\{1,2,3,4 \right\}, B=\left\{3,4,5,6 \right\}, C=\left\{5,6,7,8\right\}$$ and $$D=\left\{7,8,9,10 \right\}$$; find
$$A \cup B \cup C$$
Let $$A=\left\{1,2, \left\{3,4 \right\}, 5\right\}.$$ Which of the following statements are incorrect and why?
$$\varphi \subset A$$
If $$A=\left\{3,6,9,12,15,18,21 \right\}, B=\left\{4,8,12,16,20 \right\}, C=\left\{2,4,6,8,10,12,14,16 \right\} , D= \left\{5,10,15,20 \right\}$$ find
$$B-A$$
If $$A=\left\{3,6,9,12,15,18,21 \right\}, B=\left\{4,8,12,16,20 \right\}, C=\left\{2,4,6,8,10,12,14,16 \right\} , D= \left\{5,10,15,20 \right\}$$ find
$$D-B$$
If $$A=\left\{3,6,9,12,15,18,21 \right\}, B=\left\{4,8,12,16,20 \right\}, C=\left\{2,4,6,8,10,12,14,16 \right\} , D= \left\{5,10,15,20 \right\}$$ find
$$C-B$$
If $$A=\left\{3,6,9,12,15,18,21 \right\}, B=\left\{4,8,12,16,20 \right\}, C=\left\{2,4,6,8,10,12,14,16 \right\} , D= \left\{5,10,15,20 \right\}$$ find
$$C-D$$
If $$A=\left\{3,6,9,12,15,18,21 \right\}, B=\left\{4,8,12,16,20 \right\}, C=\left\{2,4,6,8,10,12,14,16 \right\} , D= \left\{5,10,15,20 \right\}$$ find
$$D-C$$
$$IV X=\left\{a,b,c,d \right\}$$ and $$Y=\left\{f,b,d,g \right\}$$ find
$$X-Y$$
If $$A=\left\{3,6,9,12,15,18,21 \right\}, B=\left\{4,8,12,16,20 \right\}, C=\left\{2,4,6,8,10,12,14,16 \right\} , D= \left\{5,10,15,20 \right\}$$ find
$$C-A$$
If $$A=\left\{3,6,9,12,15,18,21 \right\}, B=\left\{4,8,12,16,20 \right\}, C=\left\{2,4,6,8,10,12,14,16 \right\} , D= \left\{5,10,15,20 \right\}$$ find
$$B-C$$
Fill in the blanks to make each of the following a true statement:
$$A \cup A^{'}=$$___
Which of the following are sets ? Justify your answer
The collection of Greatmen contributed to Indian culture.
Which of the following are sets ? Justify your answer
The collection of all even integers.
Which of the following are sets ? Justify your answer
The collection of various geometrical figures.
Which of the following are sets ? Justify your answer
The collection of all integers which divides 46
Which of the following are sets ? Justify your answer
The collection of the best 20 cricket batsman of the world .
If $$ A = \left \{ x : x \epsilon N , 2 \leq x \leq 9 \right \} $$ and B = { x : x is 2 digits natural numbers , sum of which digits is 8 } , then find the following sets:
$$ A-B $$
Whether following subsets of N are total ordered set for relaton " x divides y or not ".
{ 2 , 4 , 6 , 8......}
If $$ A = \left \{ x : x \epsilon N , 2 \leq x \leq 9 \right \} $$ and B = { x : x is digits natural numbers , sum of which digits is 8 } , then find the following sets:
$$ A \cup B $$
Which of the following are sets ? Justify your answer
The collection of literature written by the poet Kalidas.
If $$ A = \left \{ x : x \epsilon N , 2 \leq x \leq 9 \right \} $$ and B = { x : x is 2 digits natural numbers , sum of which digits is 8 } , then find the following sets:
$$ (A - B ) \cup (B - A ) $$
If $$ u = \left \{ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 \right \} , A = \left \{ 1, 2, 3, 4, 5, 6 \right \} B = \left \{ 2, 3, 4 \right \}$$ and $$C= \left \{ 4, 6, 8, 10 \right \}$$ then find the value of following sets:
$$( A \cap B ) \cup B $$
If $$ u = \left \{ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 \right \} , A = \left \{ 1, 2, 3, 4, 5, 6 \right \} B = \left \{ 2, 3, 4 \right \}$$ and $$C= \left \{ 4, 6, 8, 10 \right \}$$ then find the value of following sets:
$$ A' \cup B'$$
If $$ u = \left \{ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 \right \} , A = \left \{ 1, 2, 3, 4, 5, 6 \right \} B = \left \{ 2, 3, 4 \right \}$$ and $$C= \left \{ 4, 6, 8, 10 \right \}$$ then find the value of following sets:
$$( A \cup B ) \cap B $$
If $$ U = \left \{ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 \right \} , A = \left \{ 1, 2, 3, 4, 5, 6 \right \} B = \left \{ 2, 3, 4 \right \}$$ and $$C= \left \{ 4, 6, 8, 10 \right \}$$ then find the value of following sets:
$$(A \cup B')$$
P $$\cup$$ Q and P $$\cap$$ Q.
In a pollution study of 1500 Indian rivers the following data were reported.520 were polluted by sulphur compounds, 335 were polluted by phosphates, 425 were polluted by crude oil, 100 were polluted by both crude oil and sulphur compounds, 180 were polluted by both sulphur compound and phosphates, 150 were polluted by both phosphates and crude oil and 28 were polluted by sulphur compounds, phosphates and crude oil. Let "n" be the number of the rivers were polluted by at least one of the three impurities.Find sum of digits of "n" ?
Enter $$1$$ if the below relation holds true and $$0$$ if the above relation doesnot hold true: A $$\cup$$ (B$$^{'}$$$$\cup$$ A$$^{'}$$) = A $$\cup$$ (B $$\cap$$ A)$$^{'}$$
Verify that : (A $$\cup$$ B)$$^{'}$$ = A$$^{'}$$$$\cap$$ B$$^{'}$$
Given A = {$$x$$ : $$x \,\,\in\,\, N$$ and $$3 < x \leq 6$$} and B = {$$x$$ : $$x \,\,\in\,\, W$$ and $$x < 4$$}, then find : A $$\cup$$ B.
If $$A = \{x : x \,\,\epsilon\,\, W, 3 \leq x < 6\}, B = \{3, 5, 7\}$$ and $$C = \{2, 4\}$$; find : $$A \times (B - C)$$Find the number of elements in such a set.
Given A = {$$x$$ : $$x \,\,\in\,\, N$$ and $$3 < x \leq 6$$} and B = {$$x$$ : $$x \,\,\in\,\, W$$ and $$x < 4$$}, then find : A - B.
Verify $$n(A\cup B \cup C)=n(A)+n(B)+n(c)-n(A\cap B)-n(B\cap C)-n(A \cap C)+n(A \cap B\cap C)$$ for the sets given below:
(i) A={4,5,6}, B={5,6,7,8} and C={6,7,8,9}
(ii) A={a, b, c, d, e}, B={x, y, z} and C={a, e, x}
Given a non empty set X, consider $$P(X)$$ which is set of all subsets of $$X$$. Define the relation $$R$$ is $$P(X)$$ as follows:
For subsets $$A, B$$ in $$P(X), ARB$$ if and only if $$A\subset B$$. Is R an equivalence relation on $$P(X)$$? Justify your answer
If $$A=\{x:x^2-5x+6=0\}, B=\{2,3\}$$ and $$C=\{2,3,3\}$$ then prove that $$A=B=C$$.
Let $$X$$ be a non- empty set and $$*$$ be a binary operation on $$P(x)$$ defined by $$A*B = A \cap B$$ for all $$A,B \in P\left( x \right)$$. Find the identity and invertible elements
If $$^{n-1}C_3 + ^{n-1}C_4 > ^nC_3$$, then set of complete values of n is:
$$\displaystyle ^{n-1}C_{3}+^{n-1}C_{4}> ^{n}C_{3} $$
we,$$\displaystyle ^{n}C_{r}+^{n}C_{r-1} = ^{n+1}C_{r} $$
$$\displaystyle ^{n+1}C_{4}+^{n+1}C_{4-1}> ^{n}C_{3} $$
$$\displaystyle ^{n-1+1}C_{4}> ^{n}C_{3} $$
$$\displaystyle ^{n}C_{4}> ^{n}C_{3} $$
$$\displaystyle \frac{n!}{(n-4)!4!}> \frac{n!}{(n-3)!3!} $$
$$\displaystyle \frac{n!}{(n-4)!4!}> \frac{n!}{(n-3)!3!} $$
$$\displaystyle \frac{1}{4}> \frac{1}{n-3} $$
$$\displaystyle \frac{1}{n-1}-\frac{1}{4} < 0 $$
$$\displaystyle \frac{4-n+1}{4(n-1)}< 0 $$
$$\displaystyle \frac{n-3}{(n-1)}> 0 \frac{+-+}{13} $$
$$\displaystyle x\epsilon (-\infty ,1)\cup (3,\infty ) $$
If $$X=\left\{ 1,2,3,4,5,6,7,8,9,10 \right\} $$ is the universal set & $$A=\left\{ 1,2,3,4\right\},\ B=\left\{ 2,4,6,8\right\},\ C=\left\{ 3,4,5,6\right\} $$ verify the following.
a) $$A\cup \left( B\cup C \right) =\left( A\cup B \right) \cup C$$
b) $$A\cap \left( B\cup C \right) =\left( A\cap B \right) \cup \left( A\cap C \right) $$
c) $$\left( A' \right) '=A$$
If sum of all $$x$$ in $$[0,2\pi]$$ such that $$3\cot^{2}{x}+8\cot{x}+3=0$$ is $$K\pi$$ then find $$K$$.
If $$A=\left\{ x:x=4n+1,n\le 5,n\epsilon N \right\} $$ and $$B=\{ 3n:n\le 8,n\epsilon N\} $$, then find $$A-(A-B)$$.
If $$A=\left\{1,2,3\right\},\,B=\left\{1,2,3,4\right\}$$, then find the number of possible one-one functions from $$A$$ to $$B$$.
Let $$u=\{1, 2, 3, 4, 5, 6, 7, 8, 9\}, A=\{2, , 6, 8\}$$ and $$B=\{2, 3, 5, 7\}$$. Verify that $$(A\cap B)'=A'\cup B'$$.
If $$A=\{1, 2, 3\}, B=\{4\}, C=\{5\}$$, then verify that $$A\times (B-C)=(A\times B)-(A\times C)$$.
Let A and B be two sets such that $$n(A)=3$$ and $$n(B)=2$$.
If $$(x, 1), (y, 2), (z, 1)$$ are in $$A\times B$$, find A and B, where x, y, z are distinct elements.
Class 11 Engineering Maths Extra Questions
- Binomial Theorem Extra Questions
- Complex Numbers And Quadratic Equations Extra Questions
- Conic Sections Extra Questions
- Introduction To Three Dimensional Geometry Extra Questions
- Limits And Derivatives Extra Questions
- Linear Inequalities Extra Questions
- Mathematical Reasoning Extra Questions
- Permutations And Combinations Extra Questions
- Principle Of Mathematical Induction Extra Questions
- Probability Extra Questions
- Relations And Functions Extra Questions
- Sequences And Series Extra Questions
- Sets Extra Questions
- Statistics Extra Questions
- Straight Lines Extra Questions
- Trigonometric Functions Extra Questions