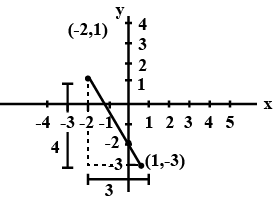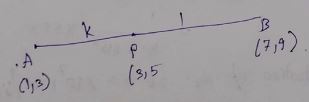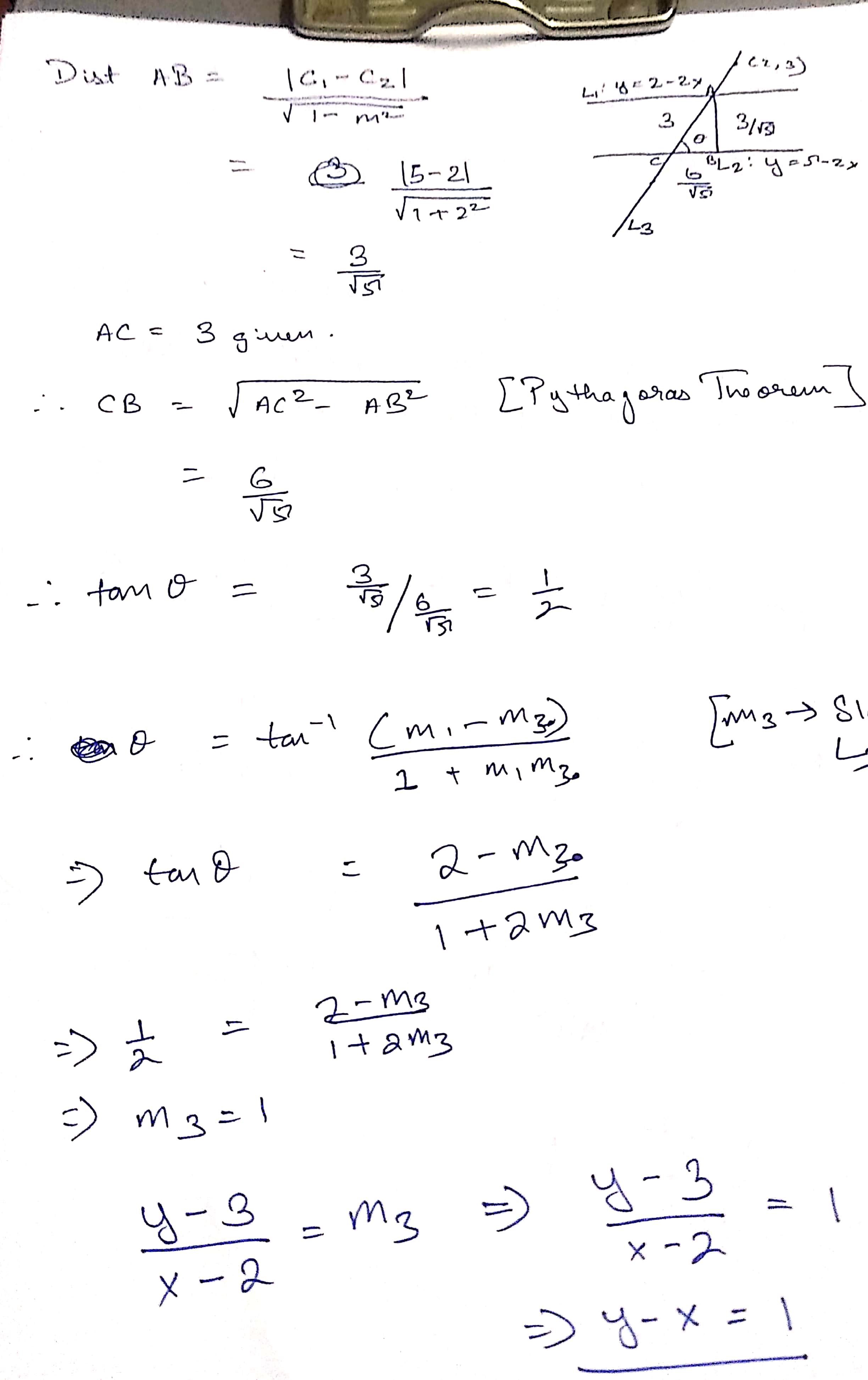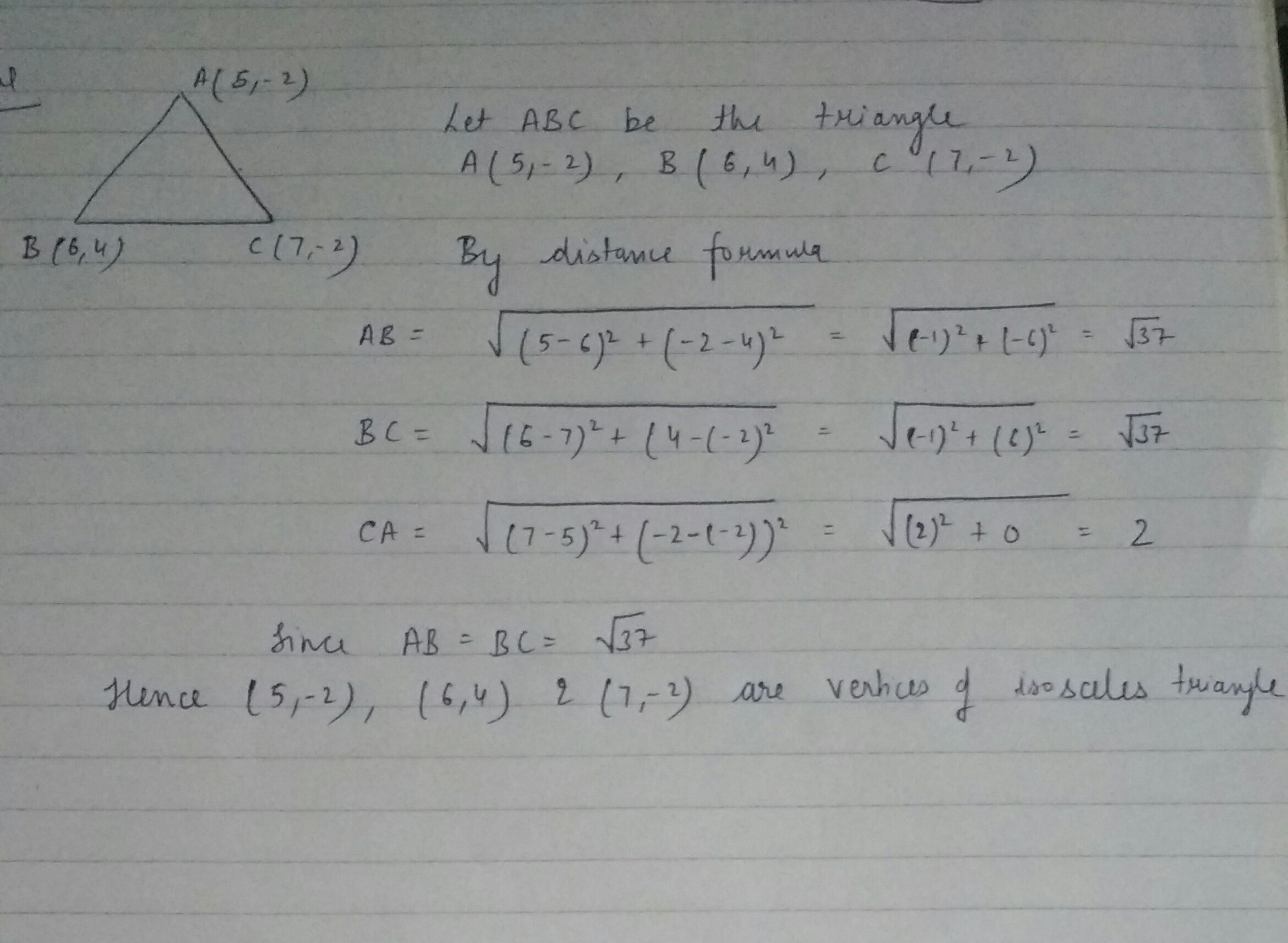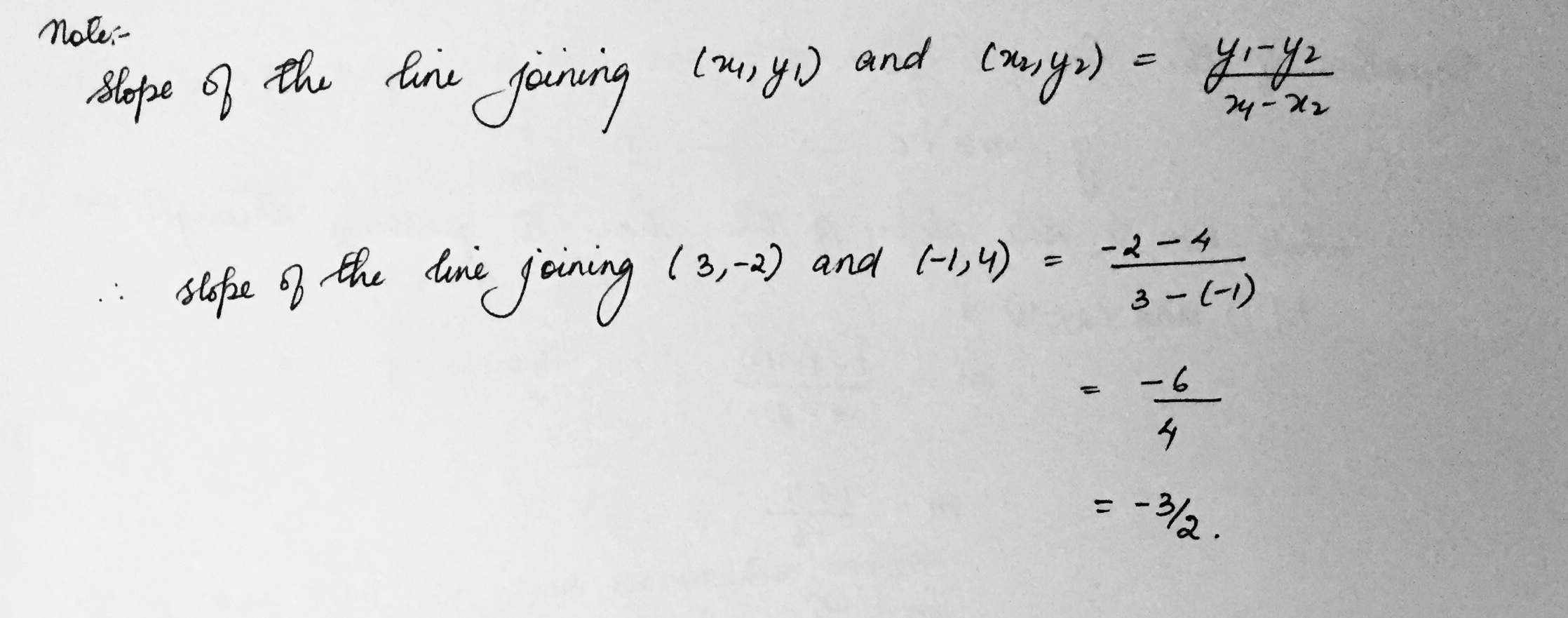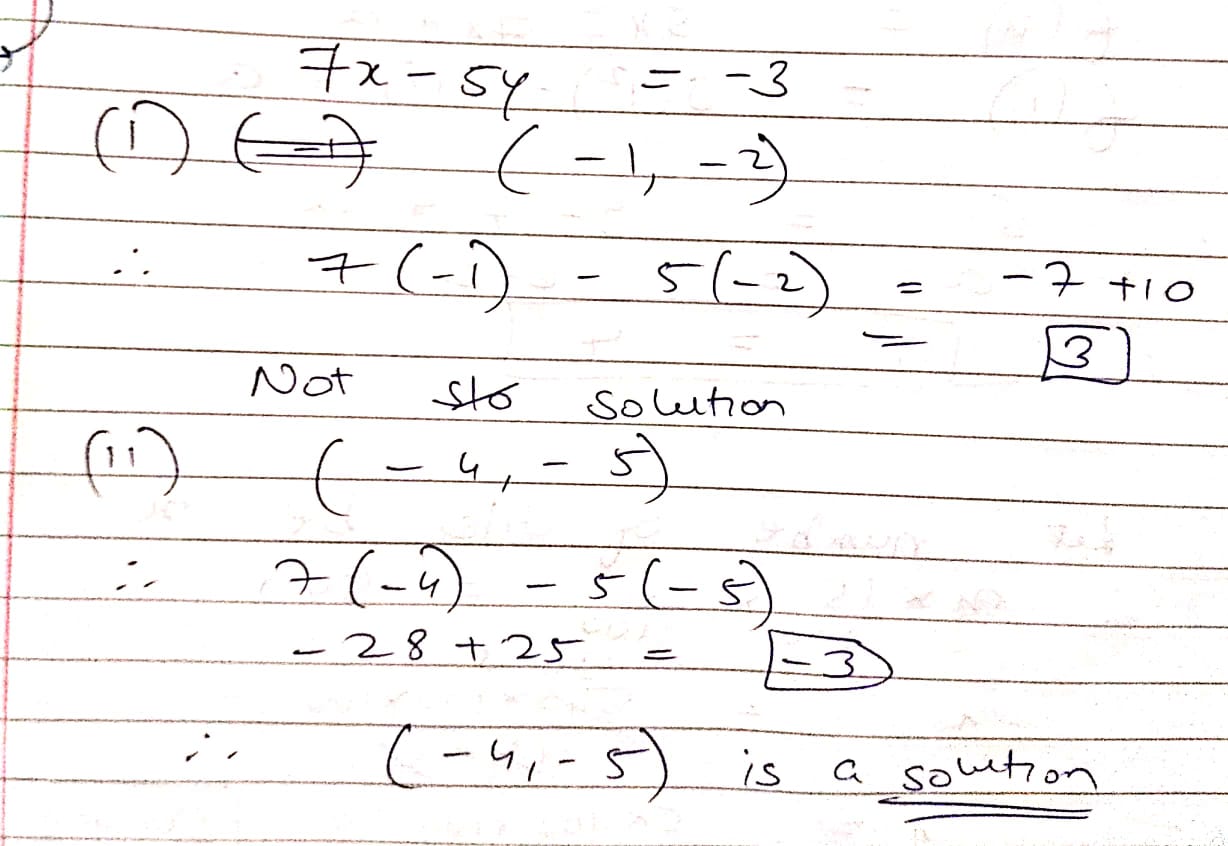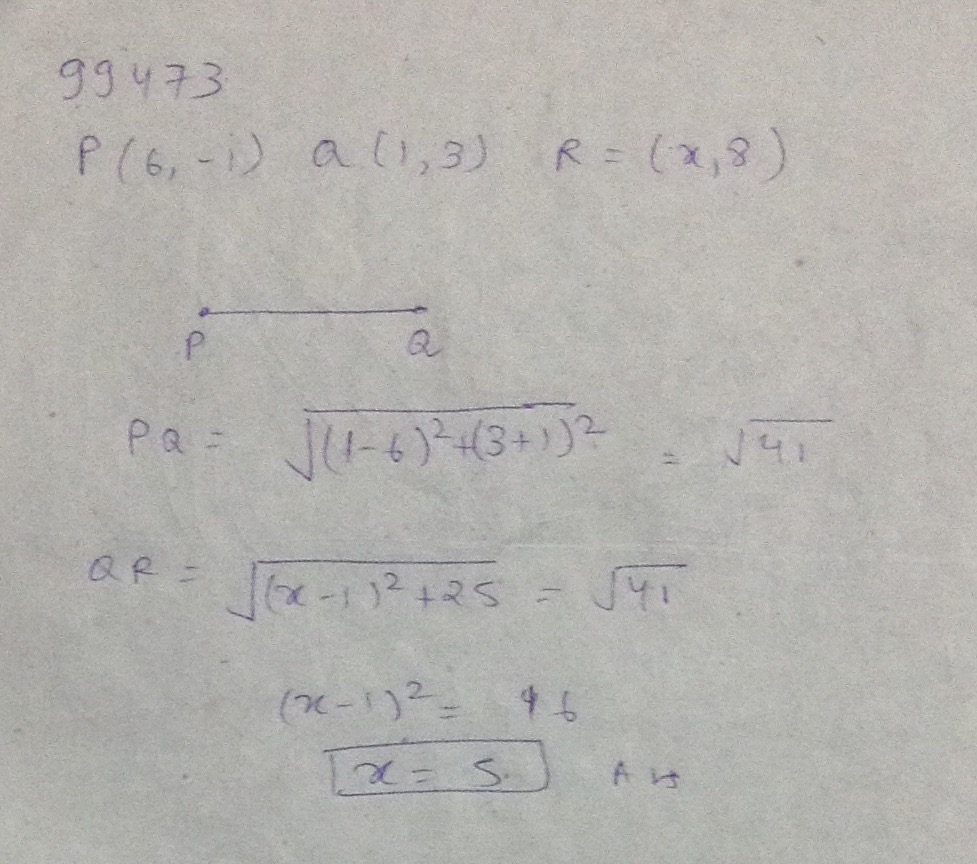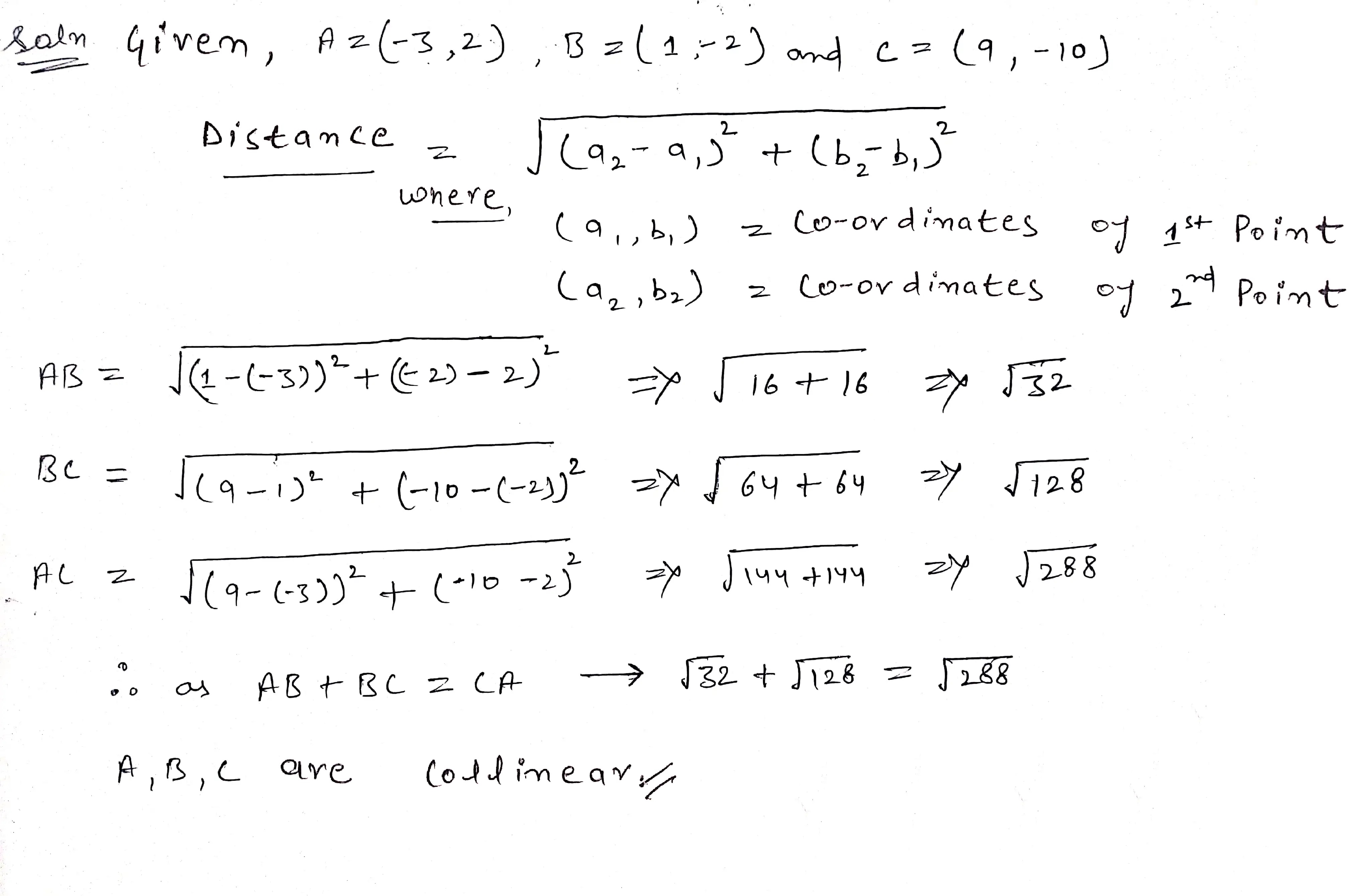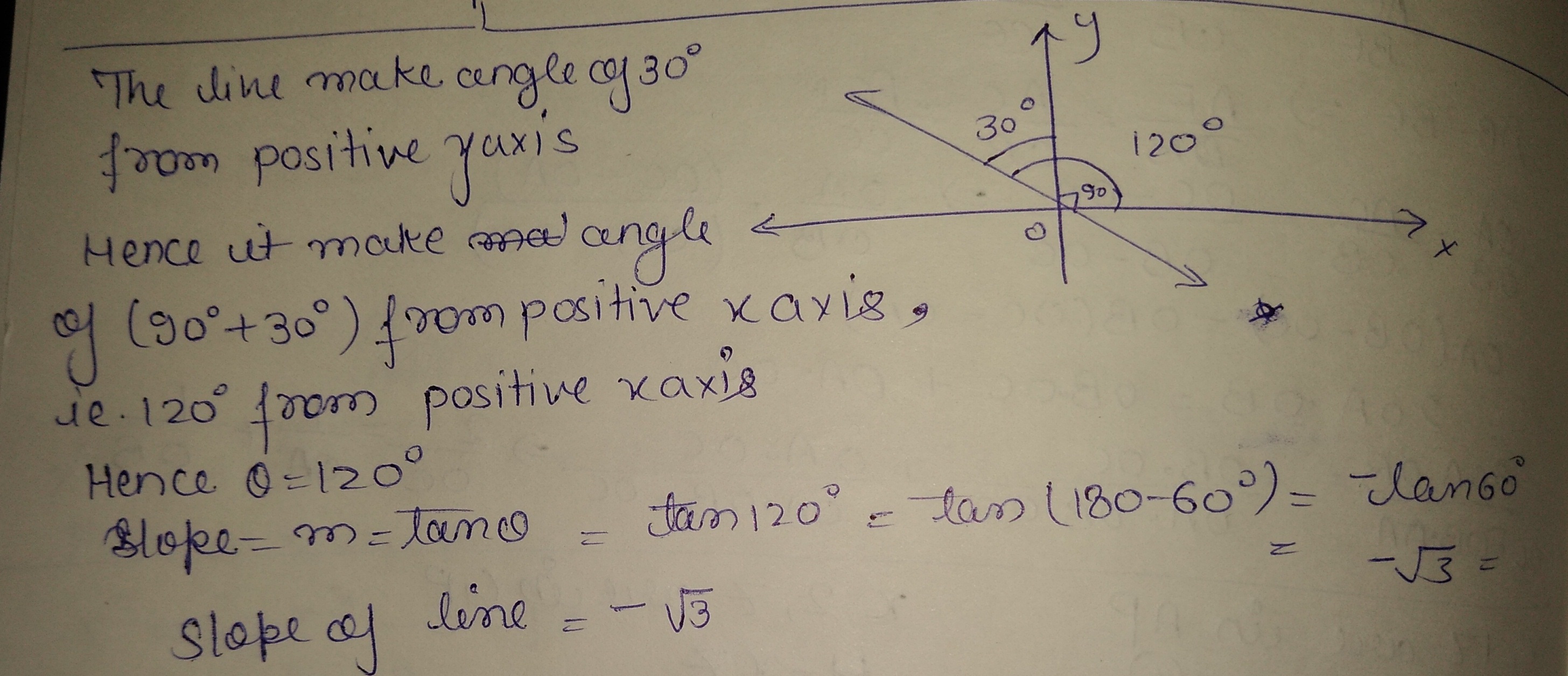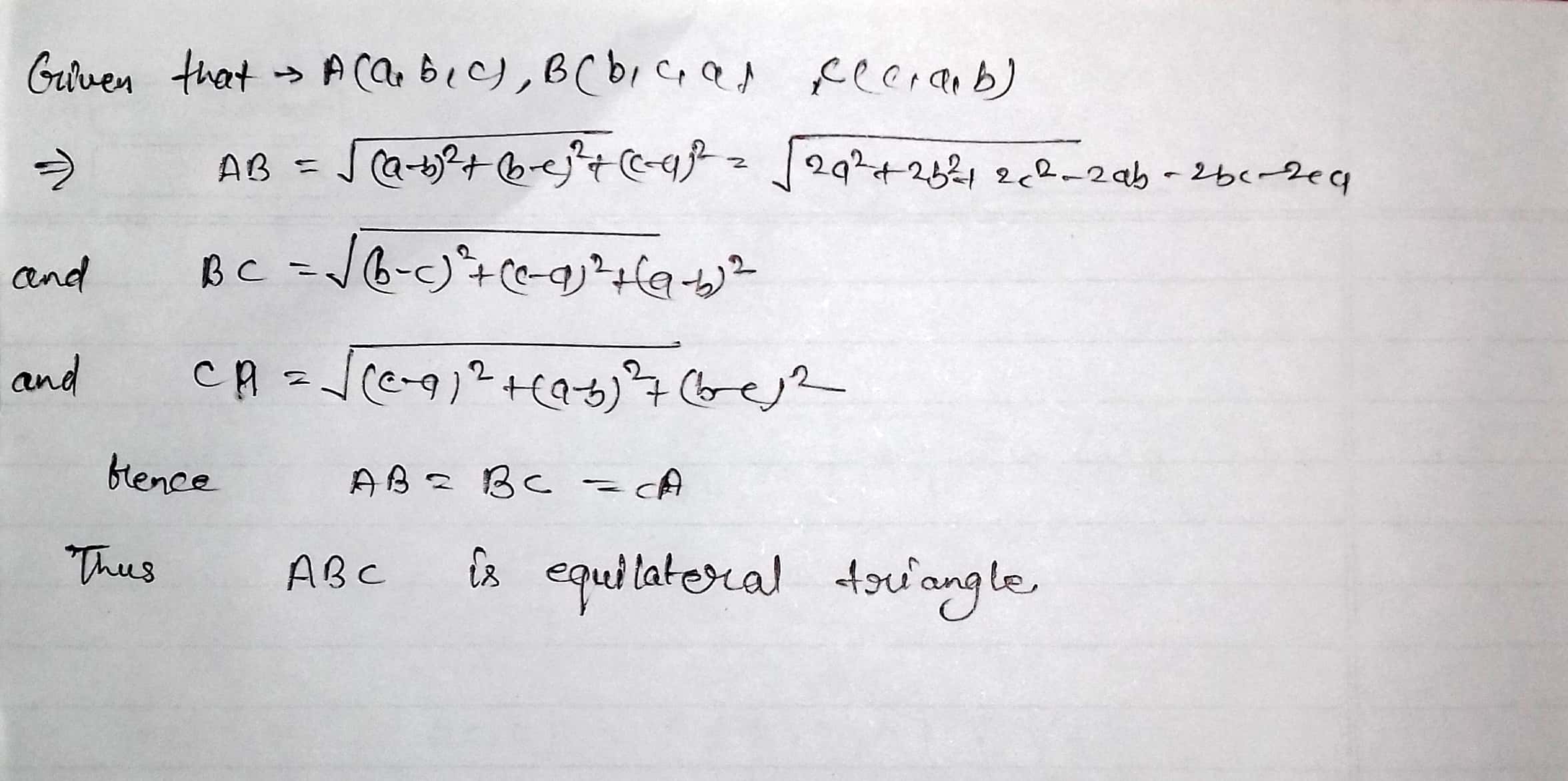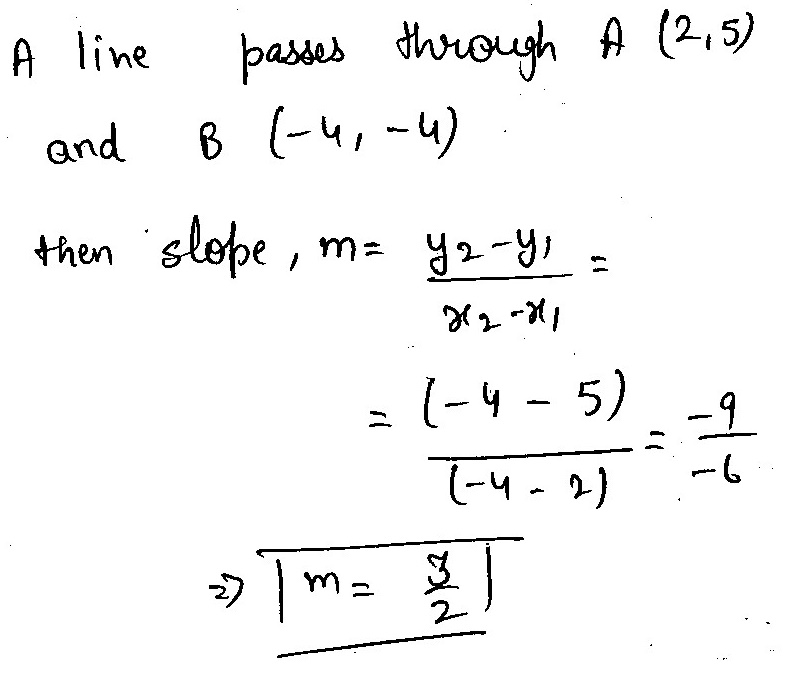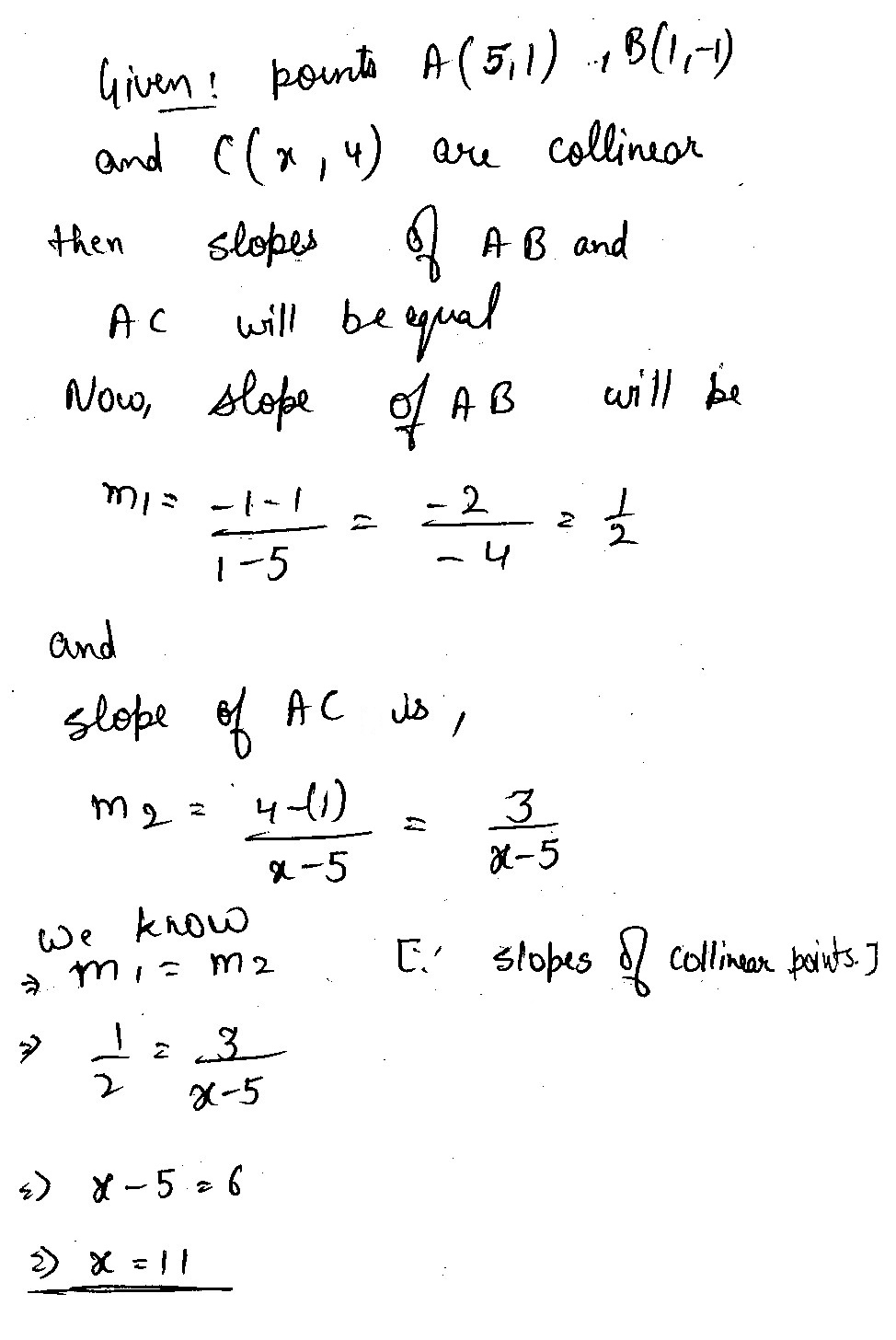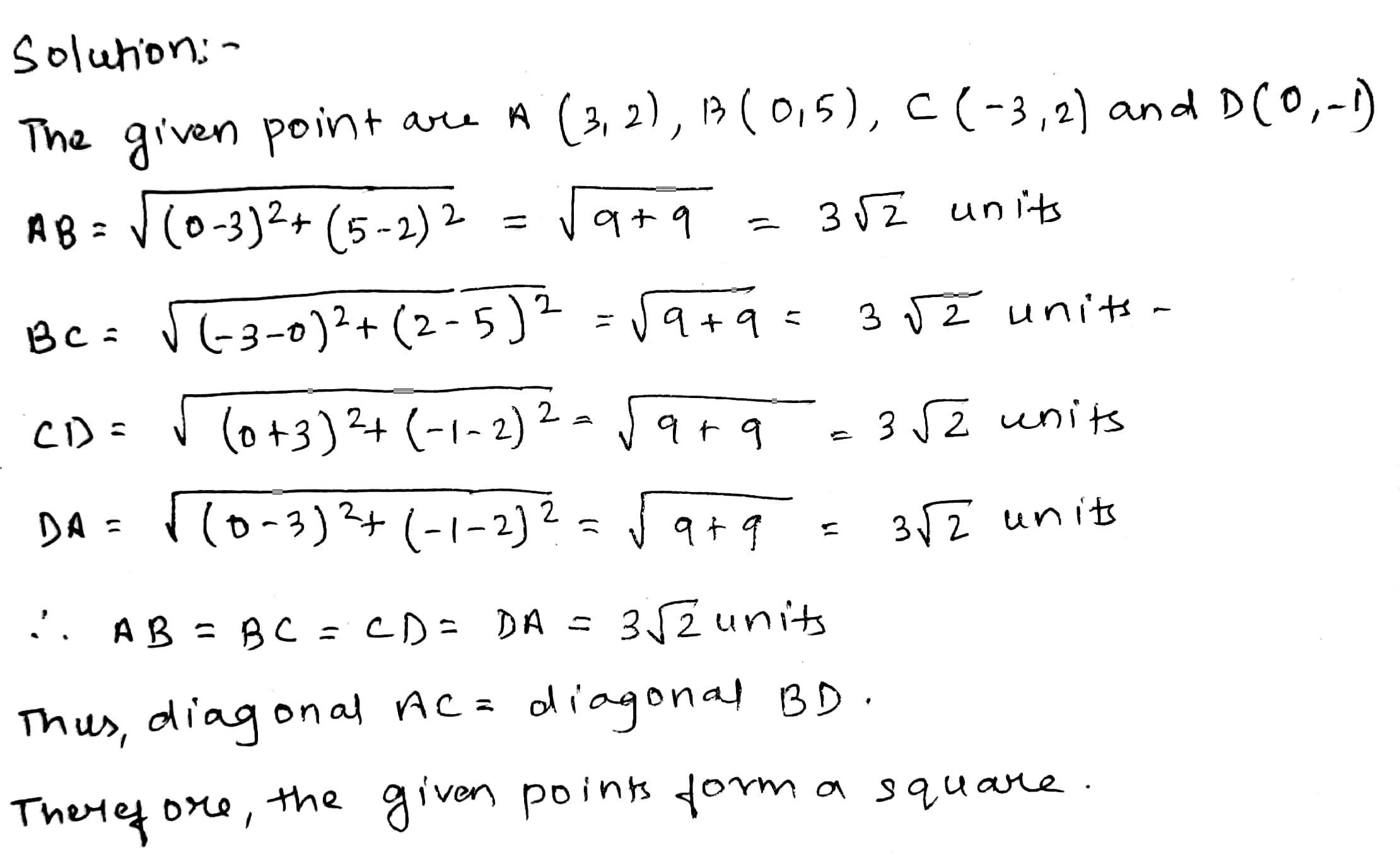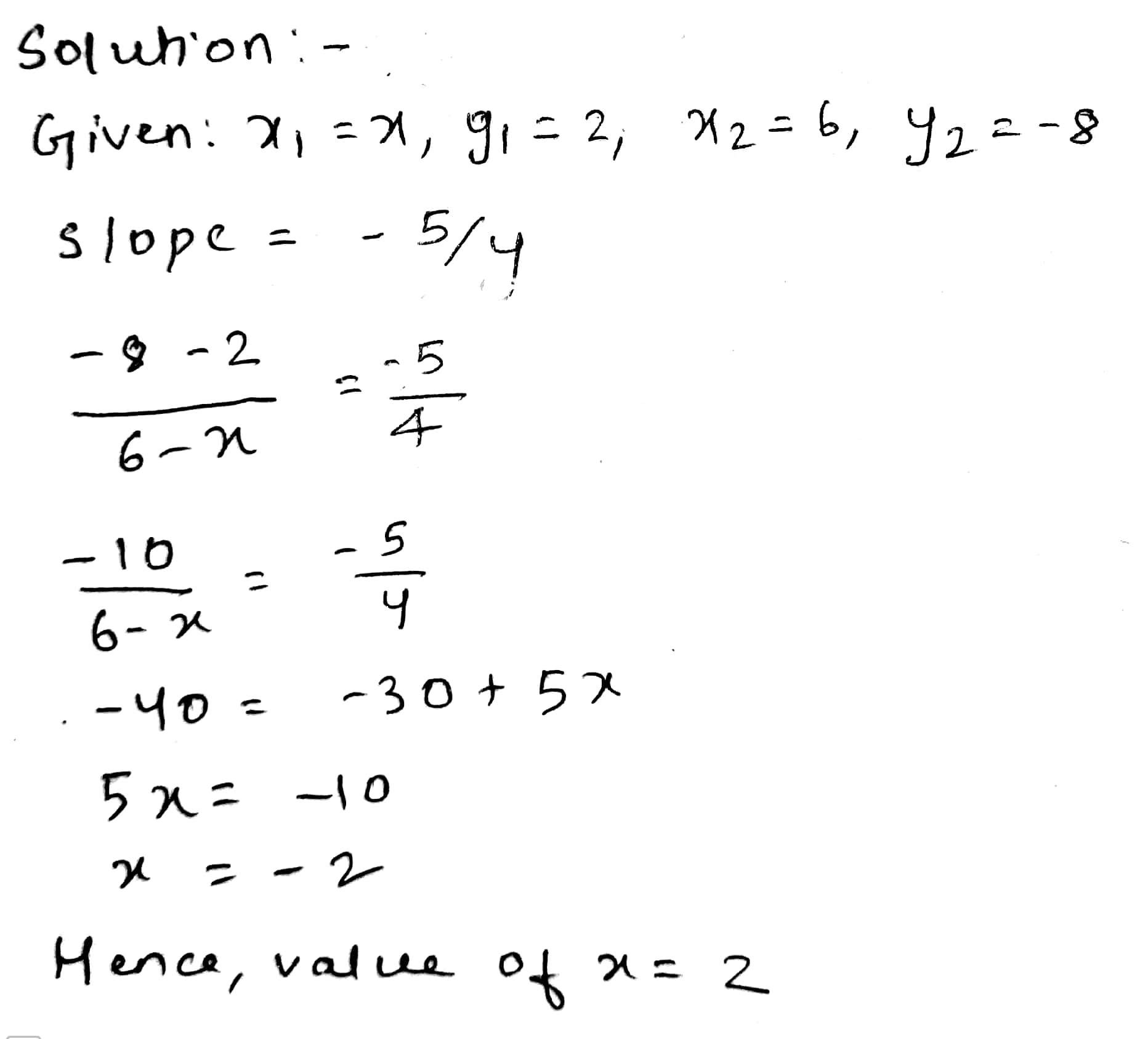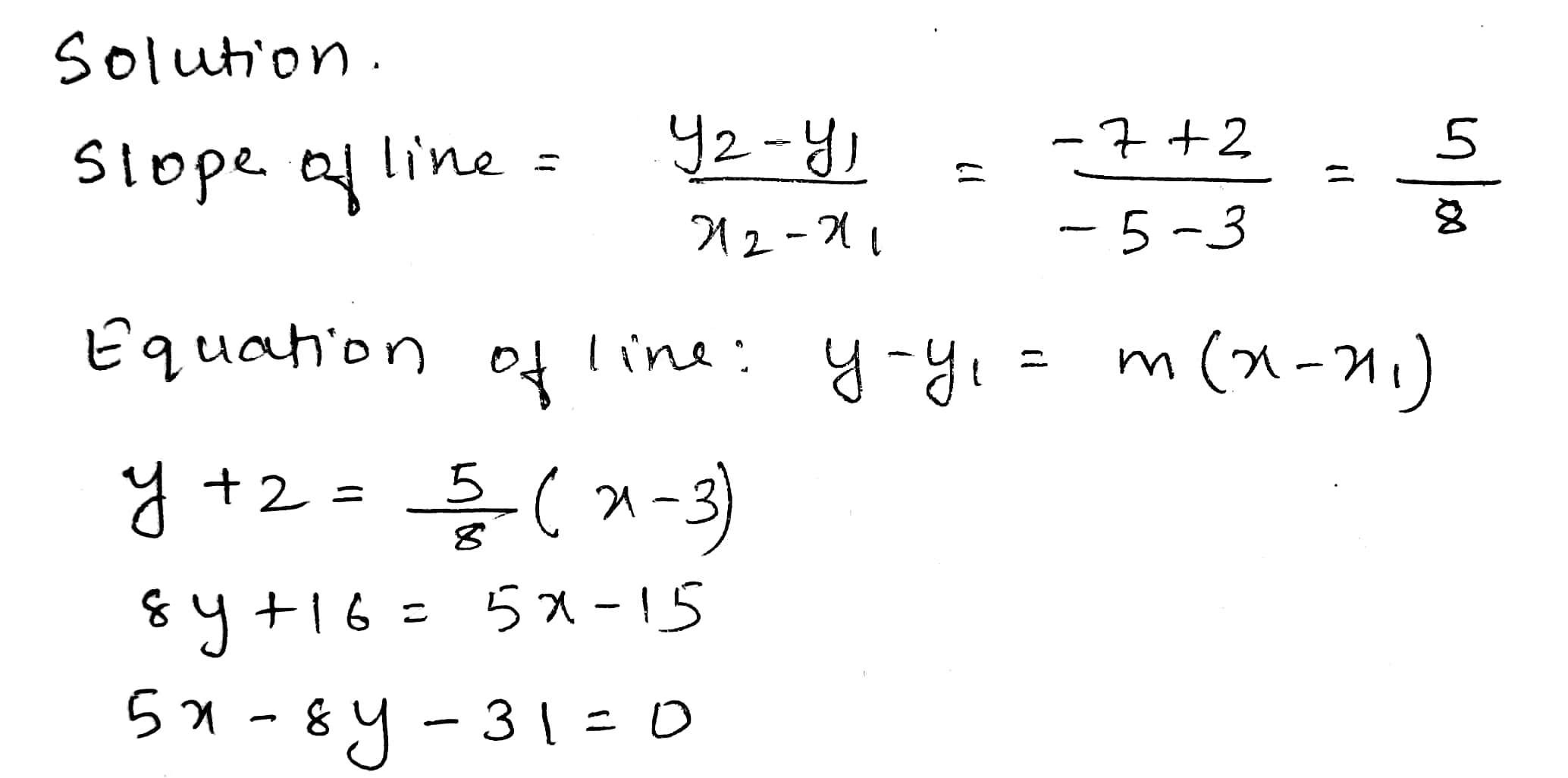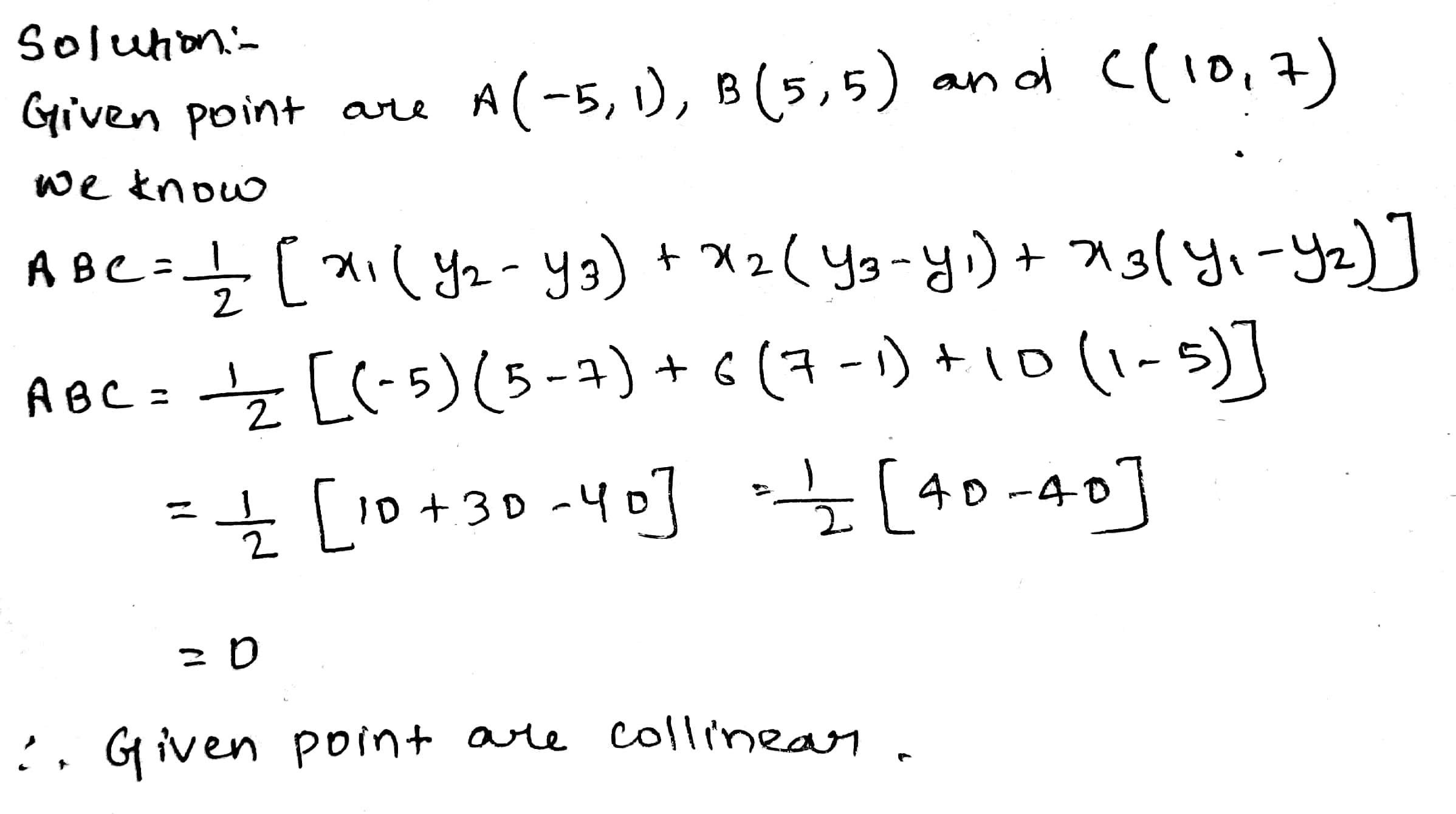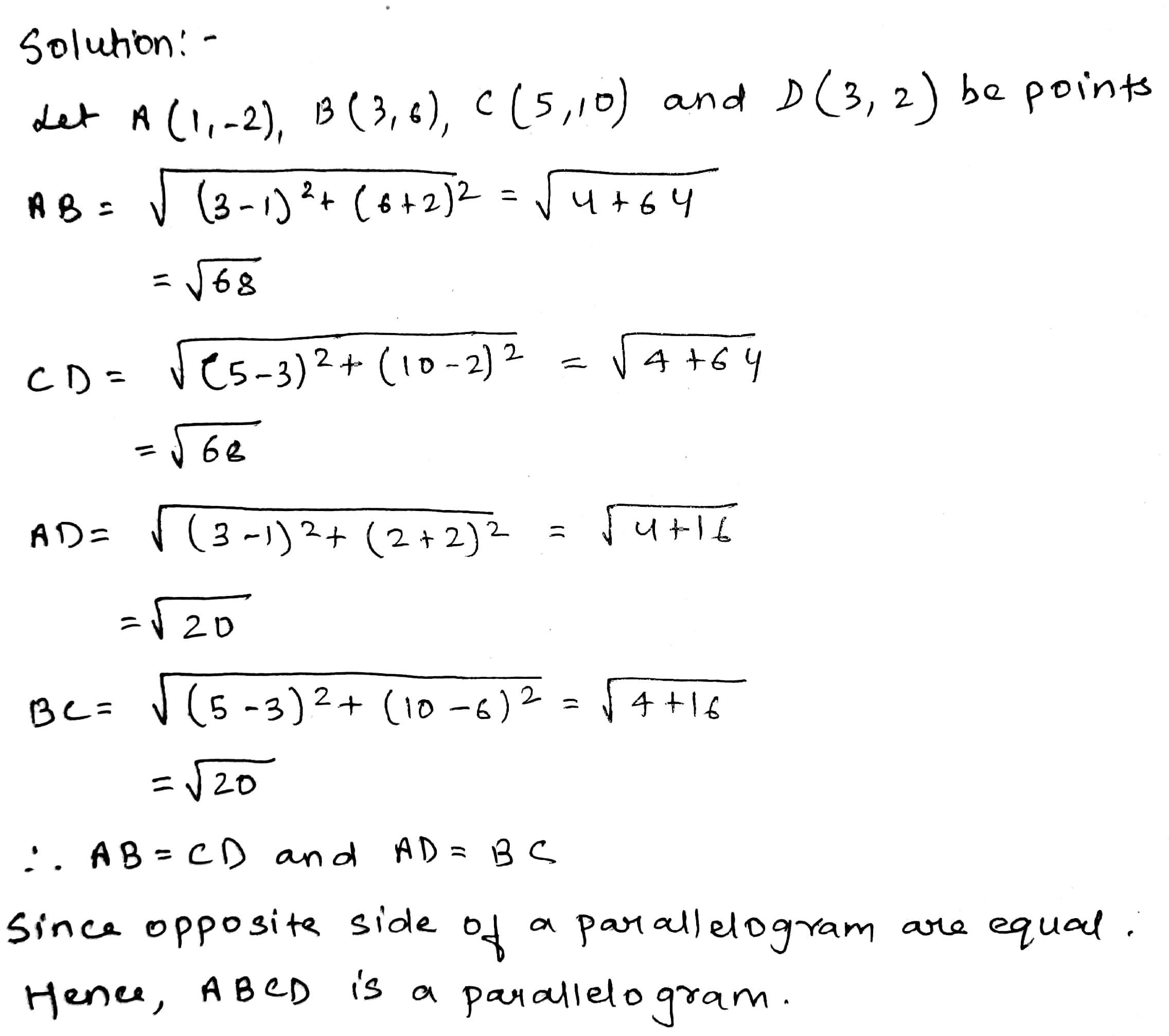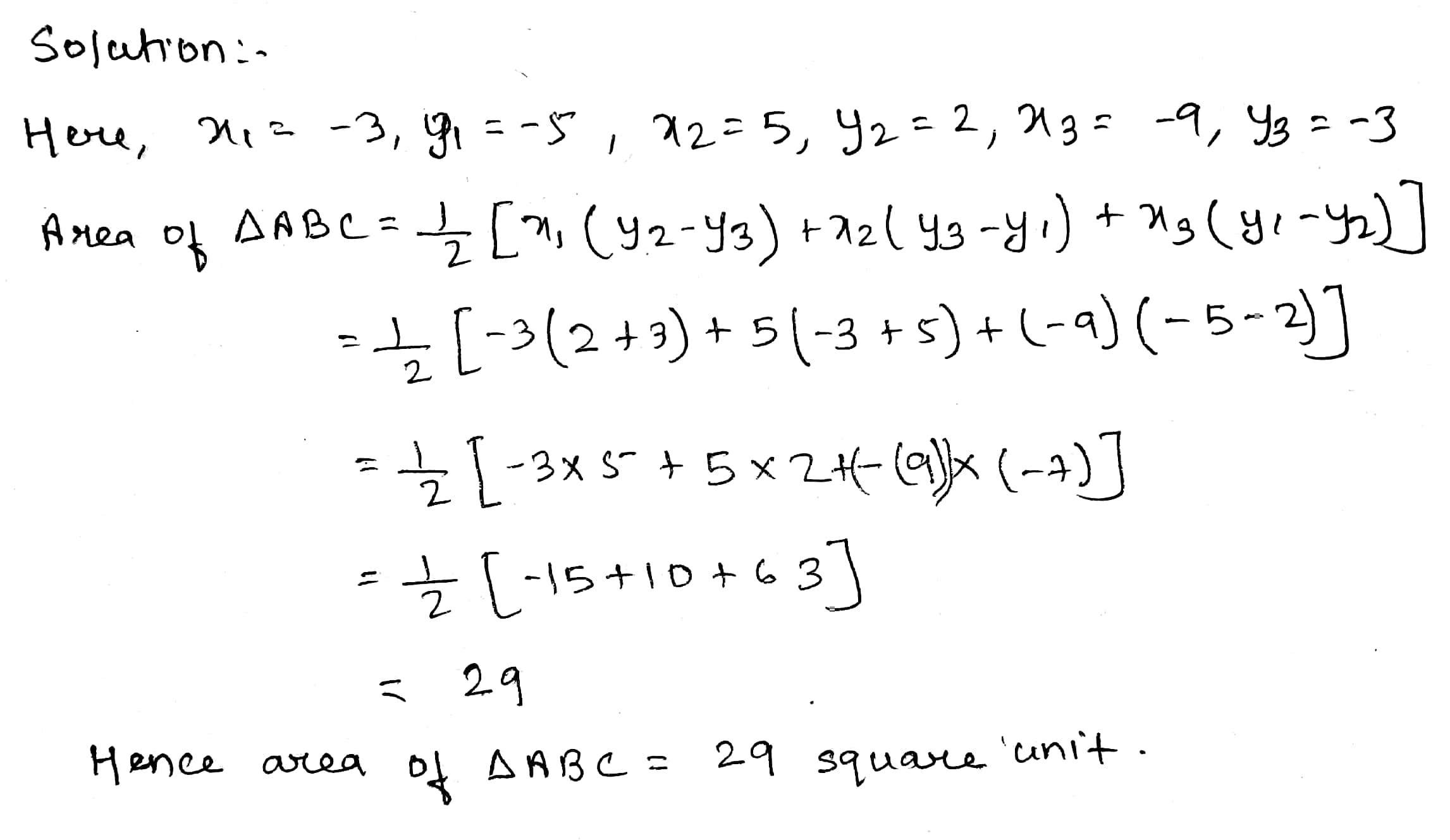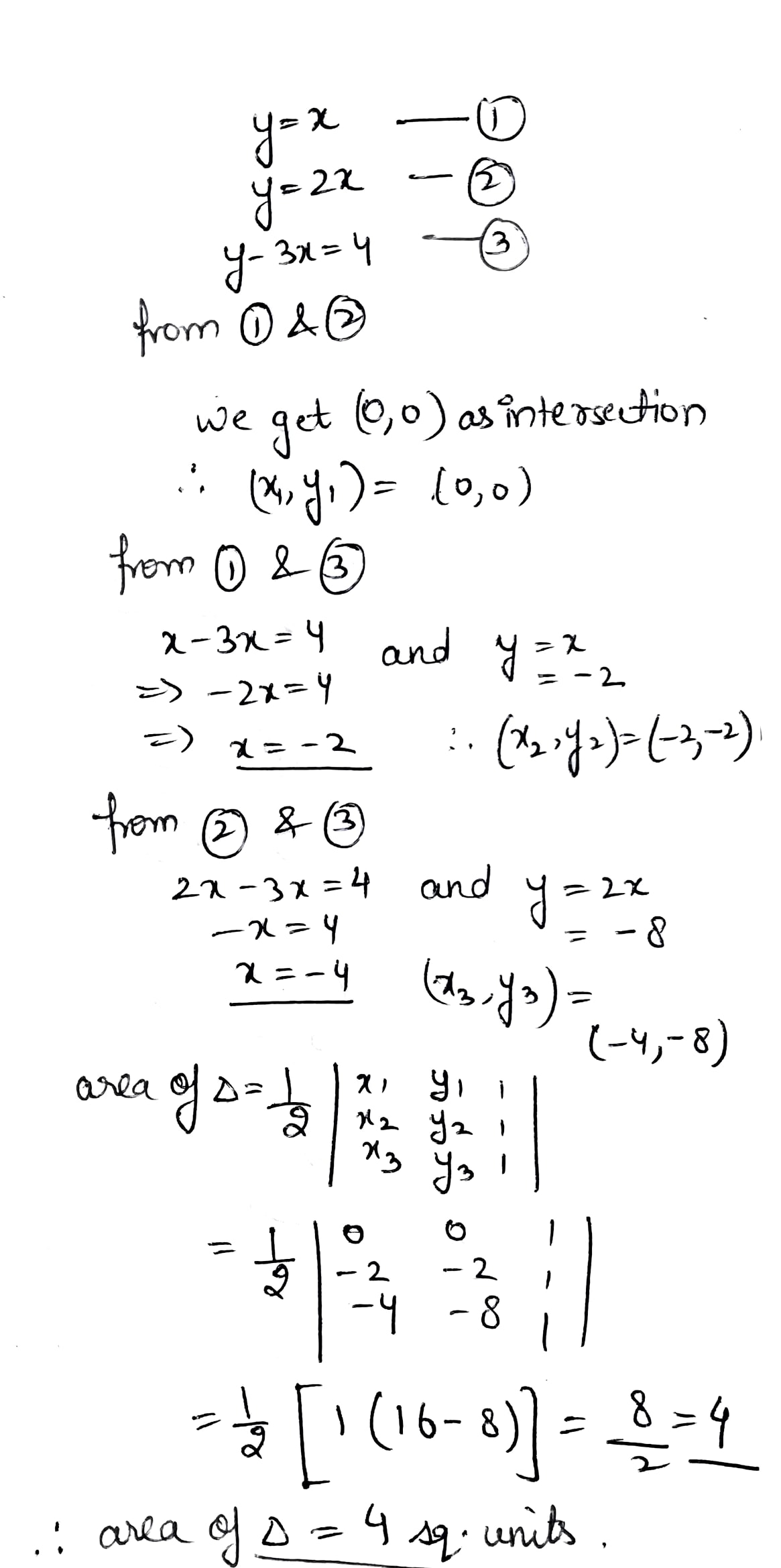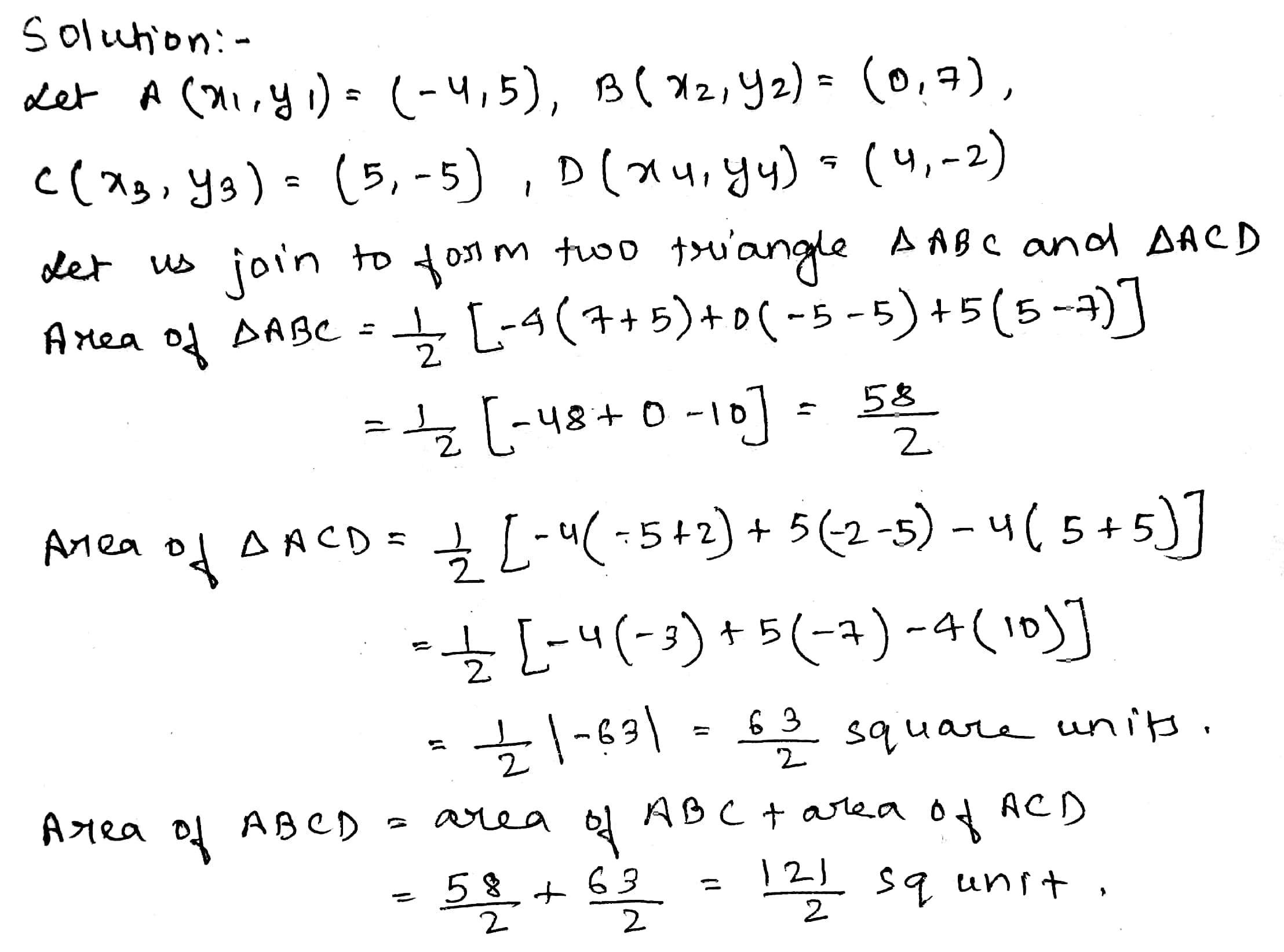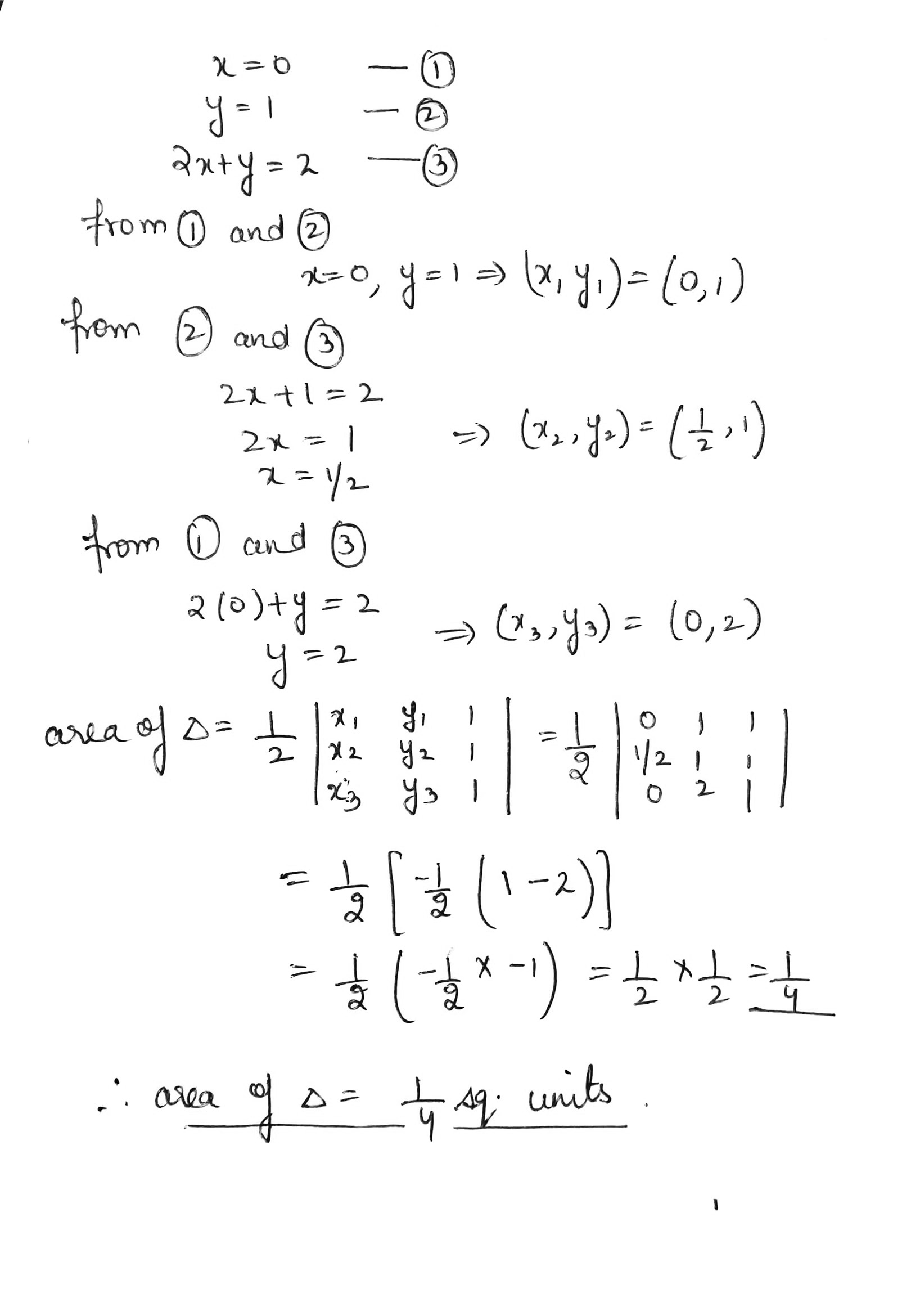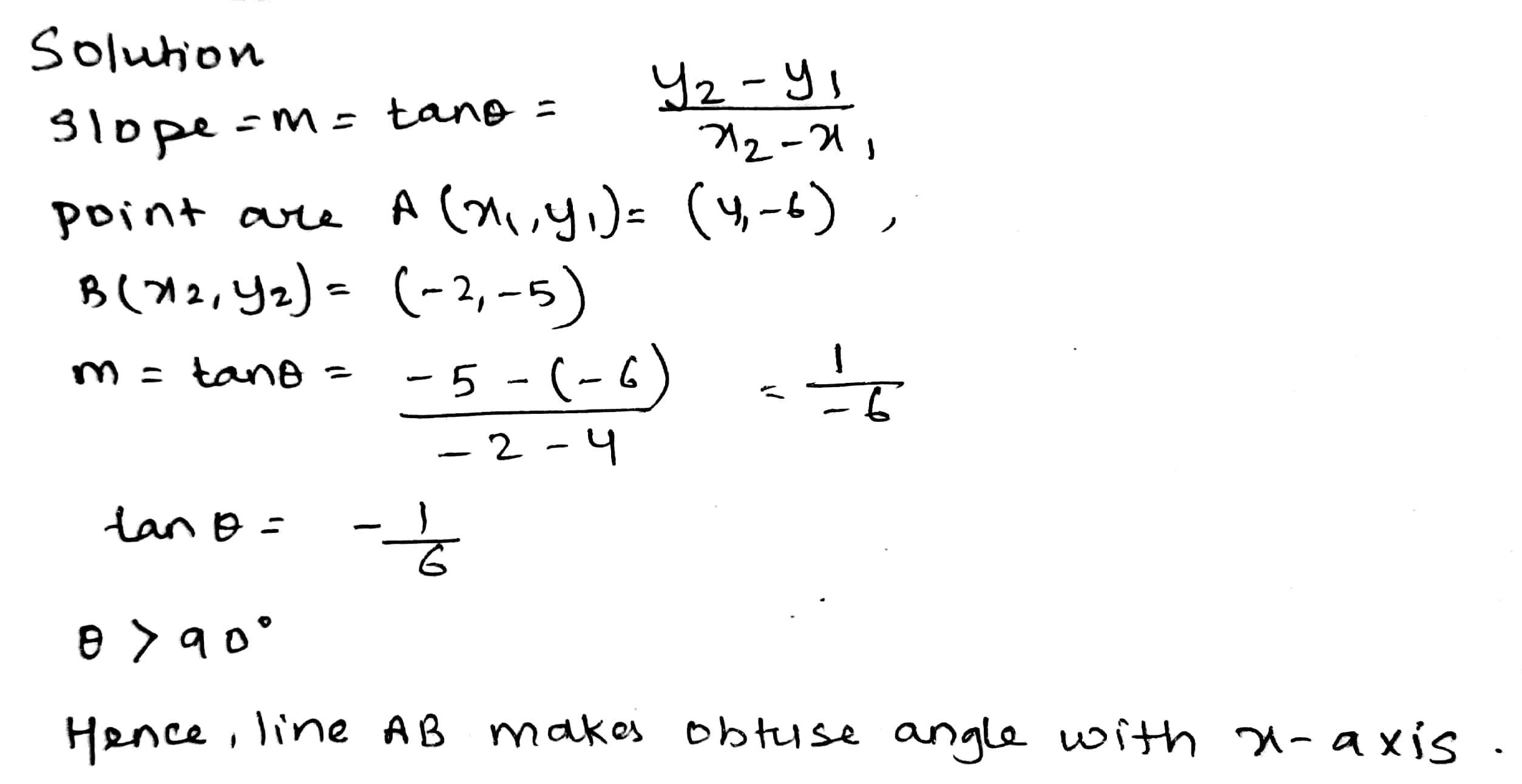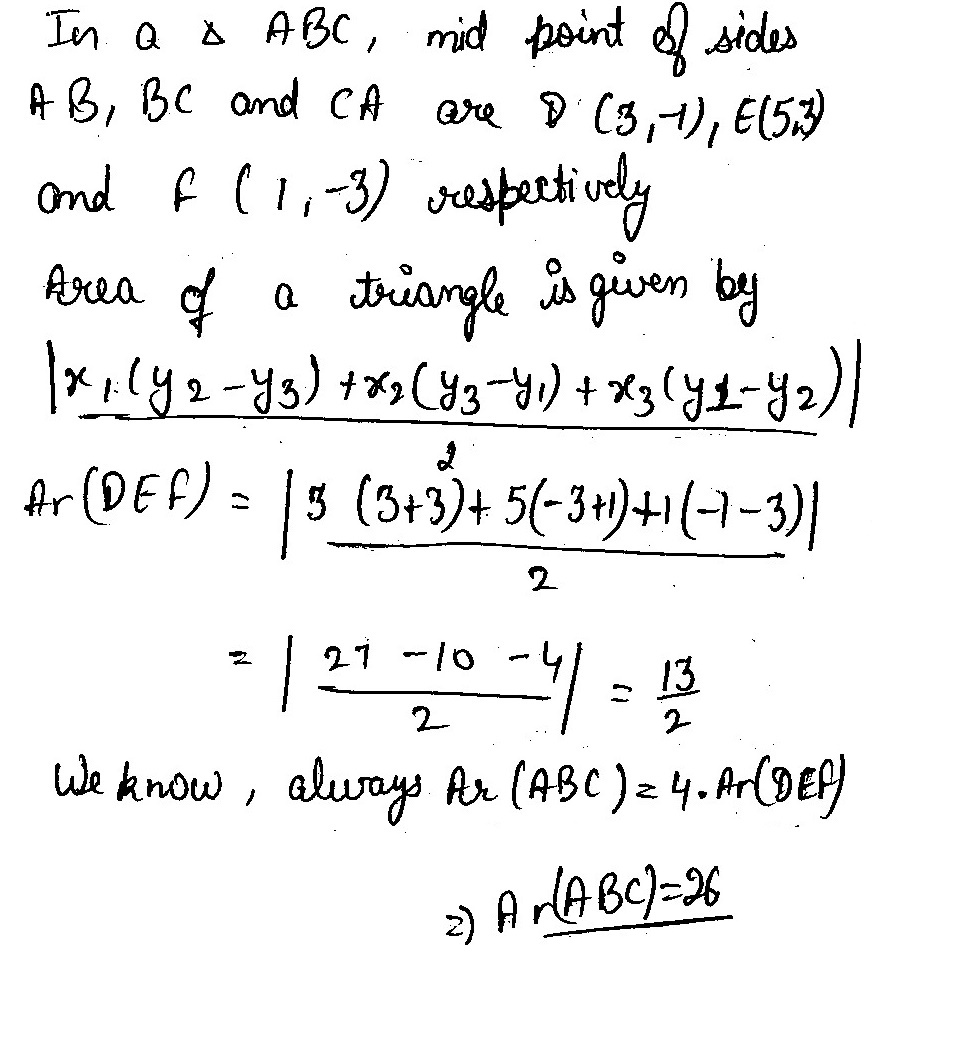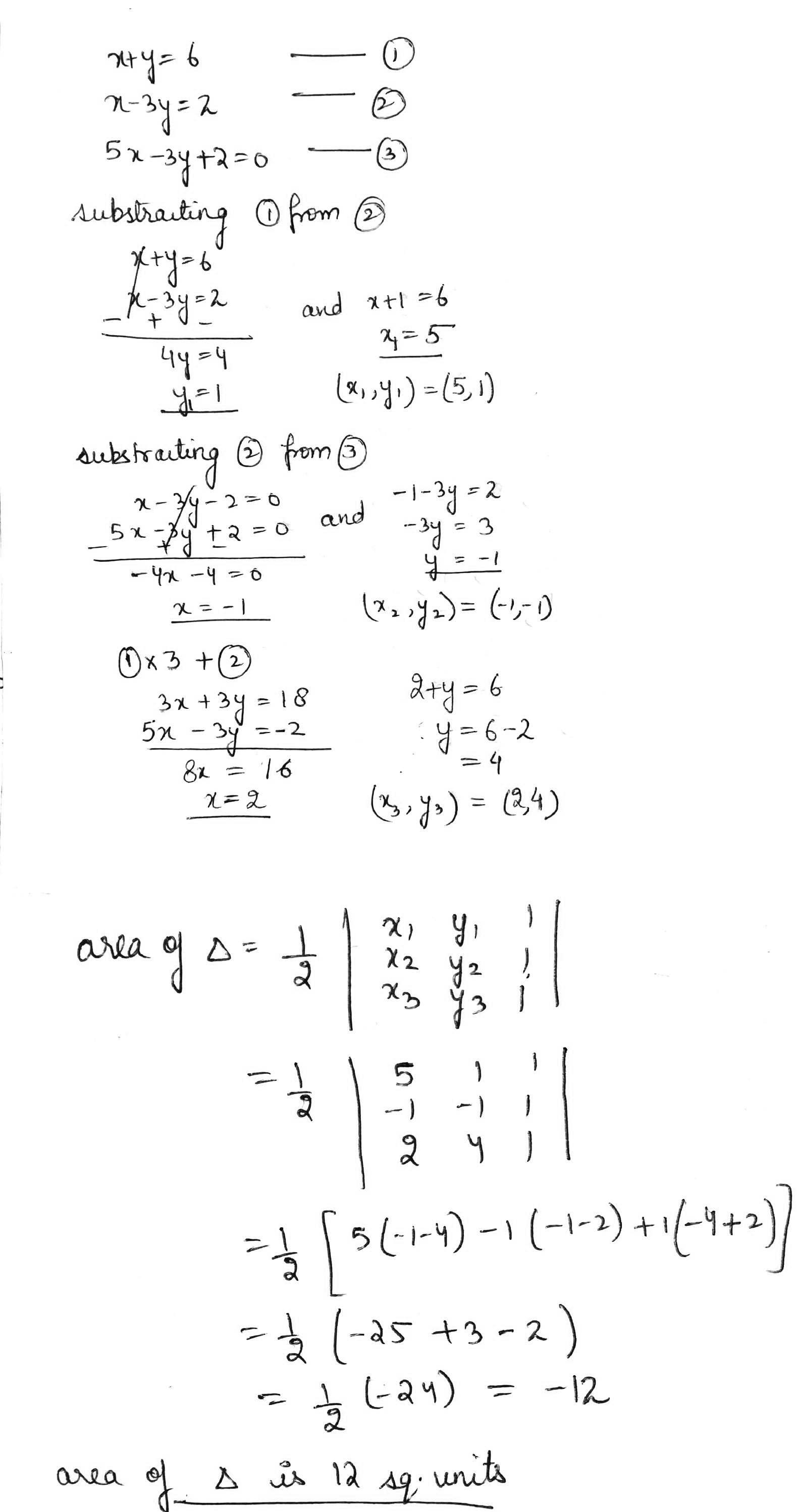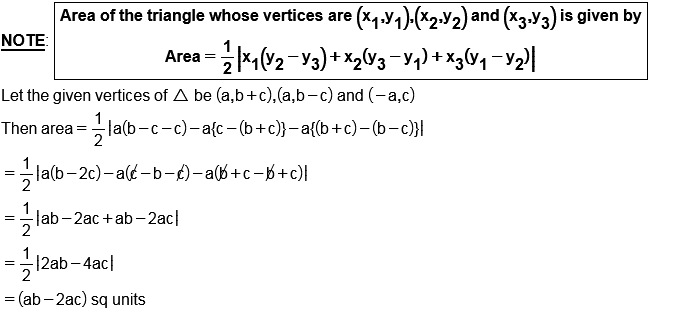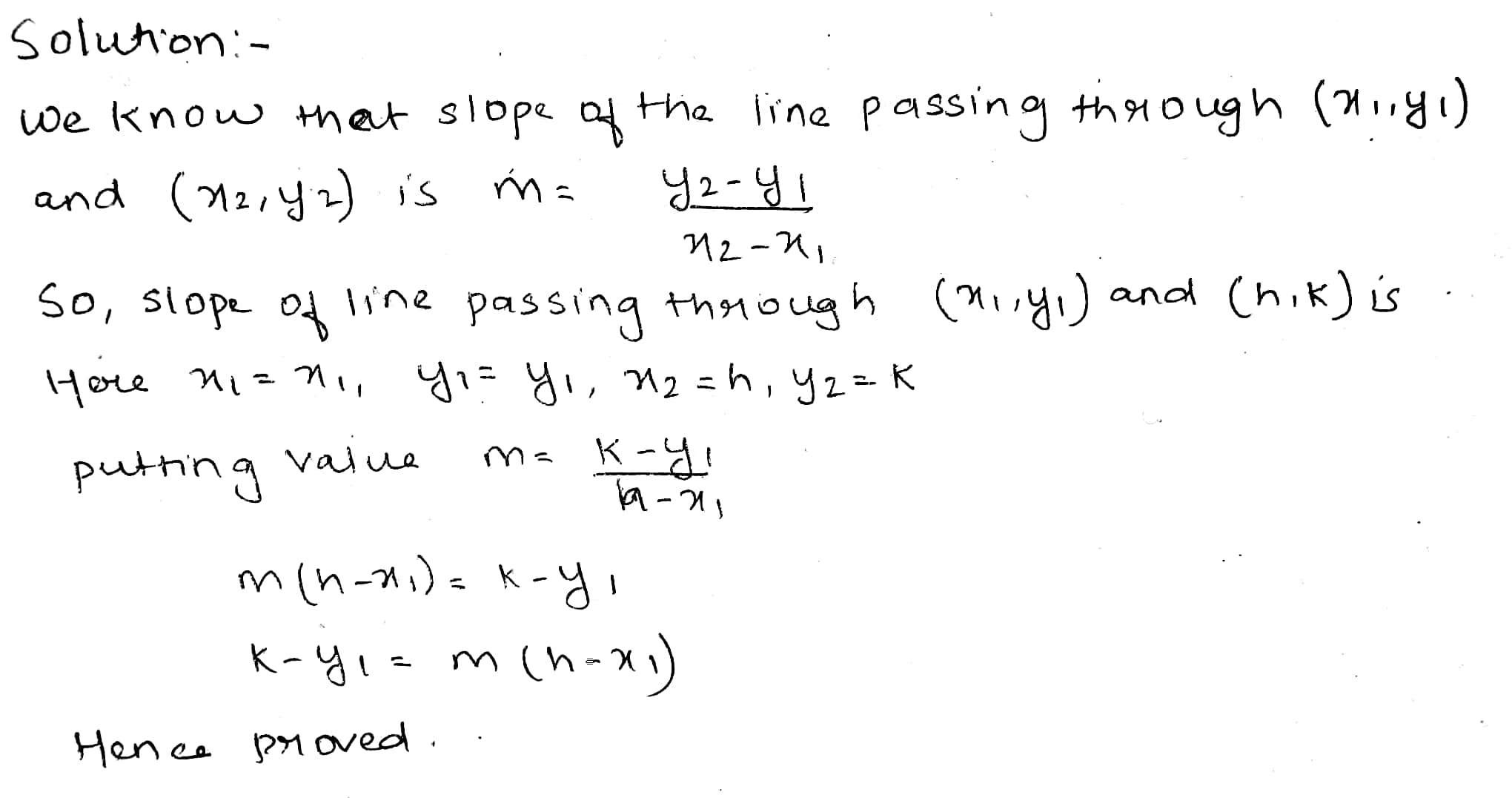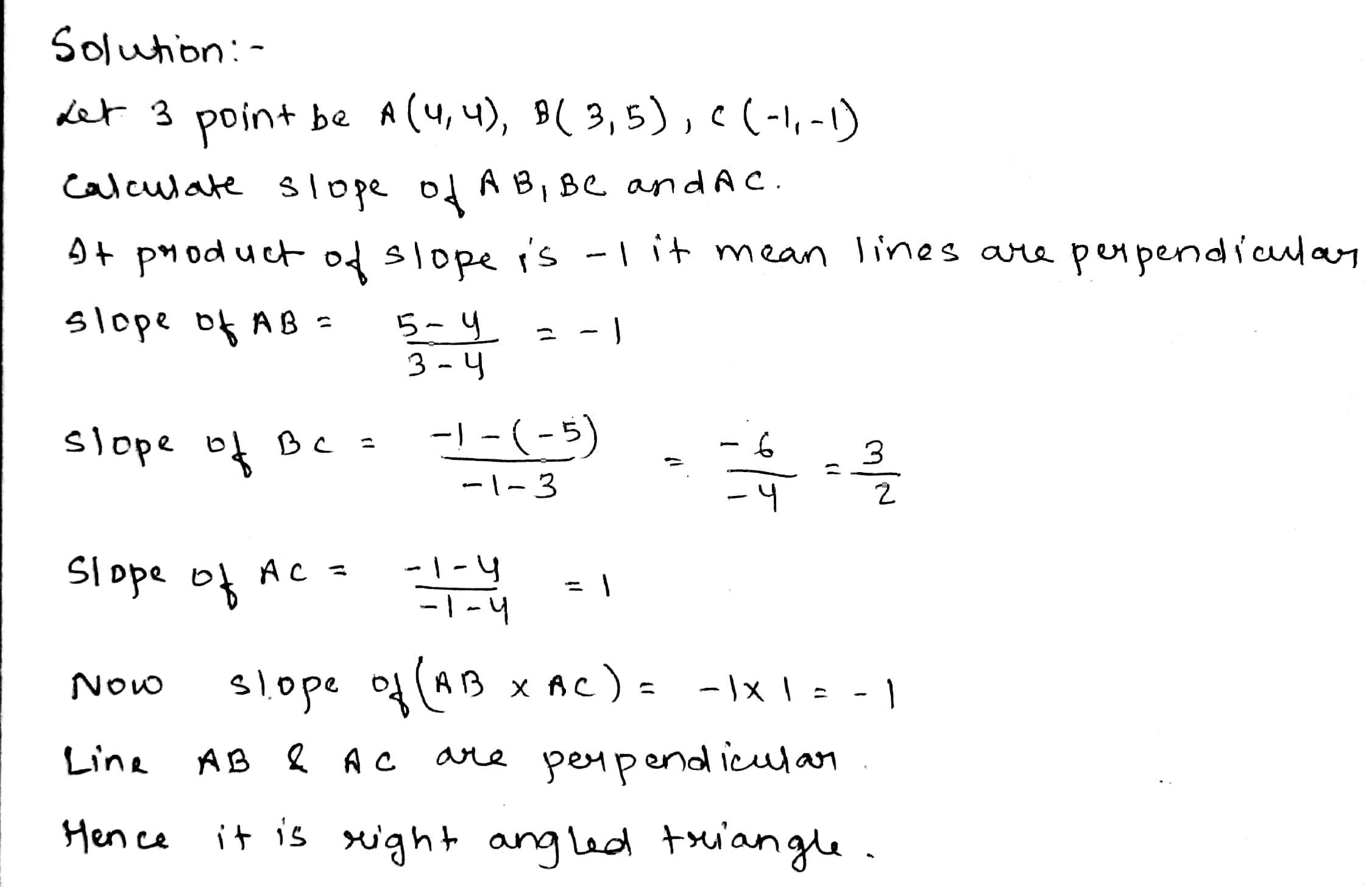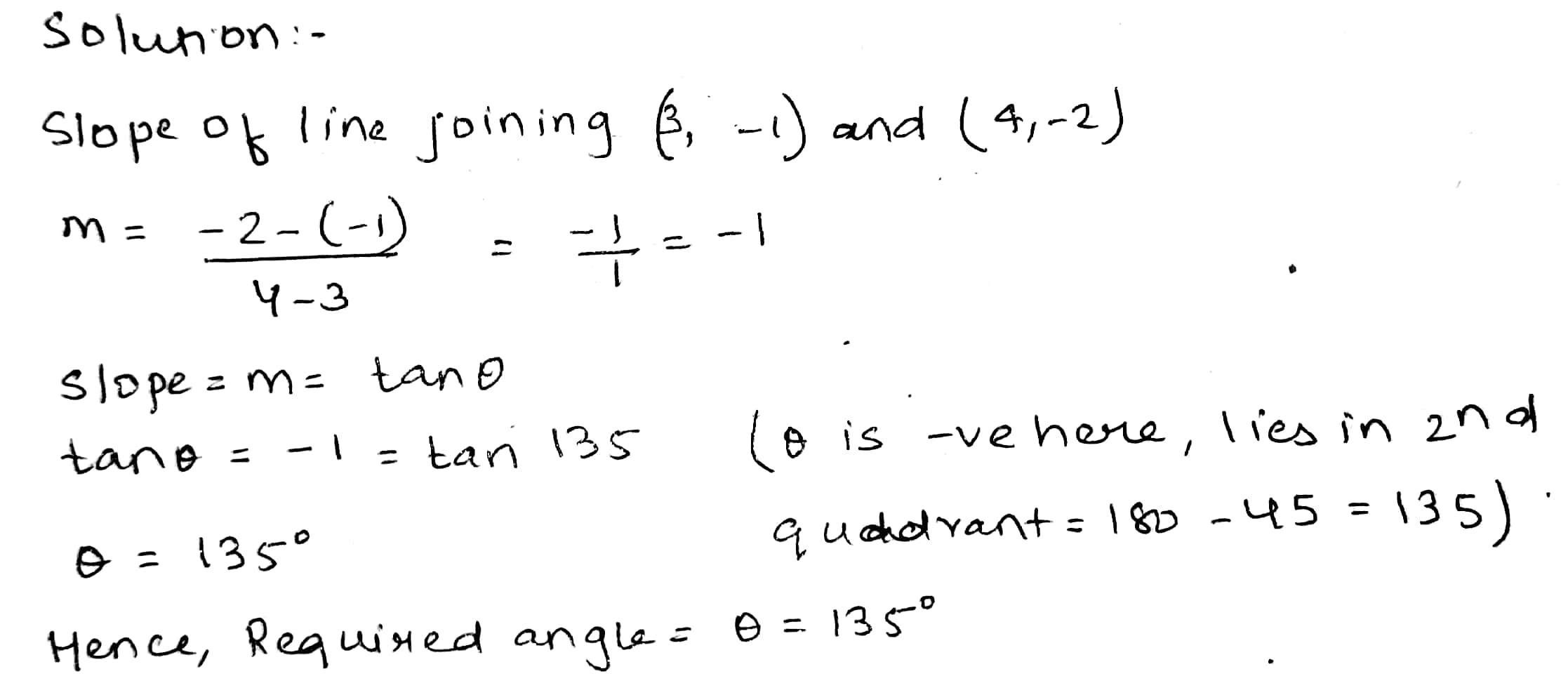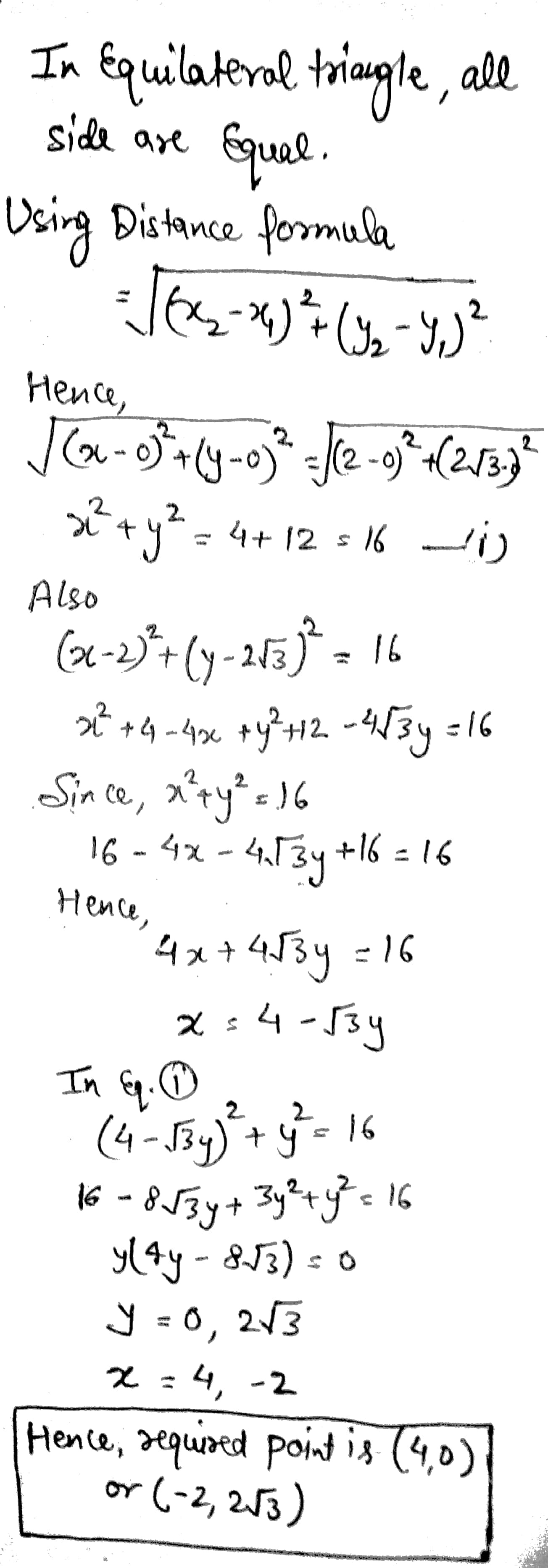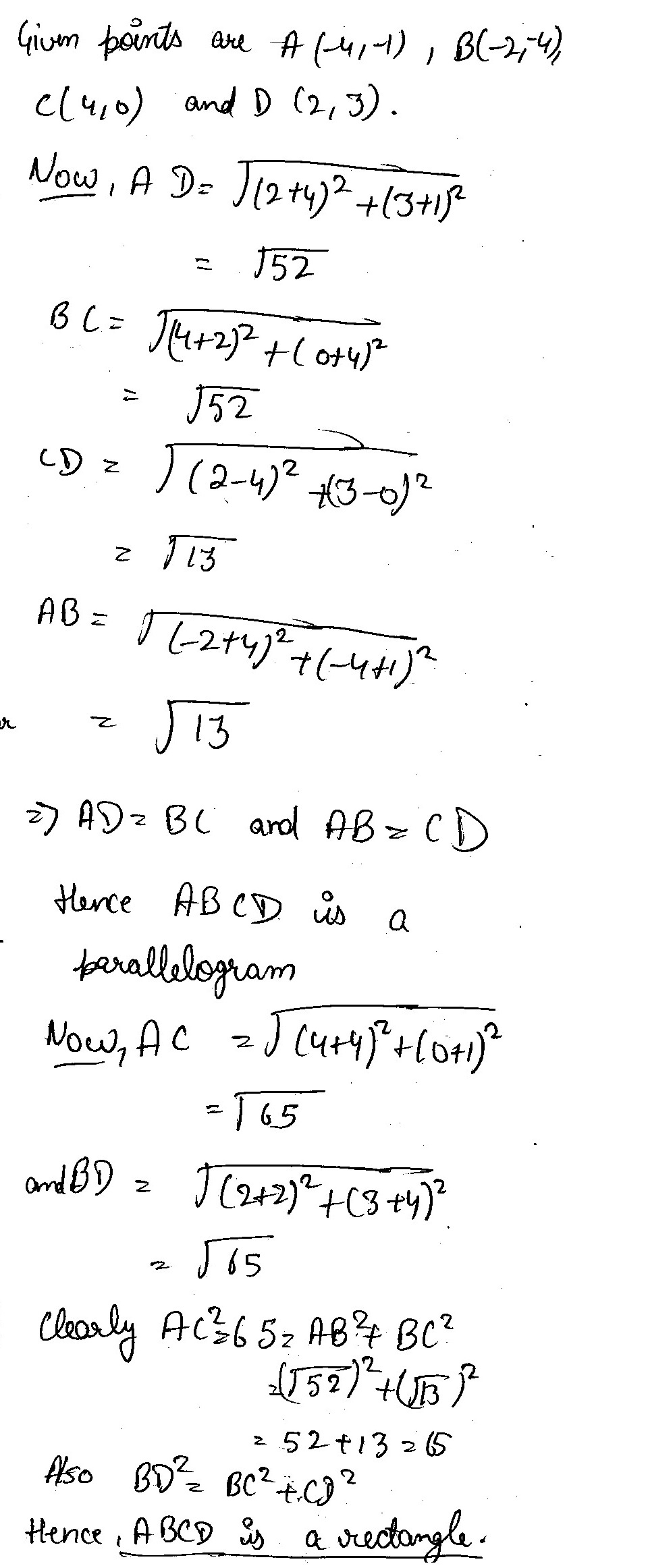Straight Lines - Class 11 Engineering Maths - Extra Questions
Find inclination (in degrees) of a line perpendicular to x-axis.
If P is the mid point of seg AB and AB $$=7$$ cm, then AP is $$3.5$$ cm
If true then enter $$1$$ and if false then enter $$0$$.
Write the slope of the line whose inclination is $$0^{\circ}$$.
Find inclination (in degrees) of a line parallel to x-axis.
Find inclination (in degrees) of a line parallel to $$y$$-axis.
Find inclination (in degrees) of a line perpendicular to y-axis.
Find the inclination of the line whose slope is 1
Find the inclination of the line whose slope is $$0$$.
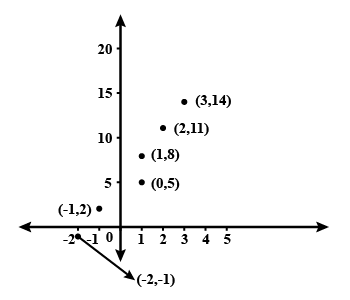
Consider the following population and year graph, find the slope of the line $$AB$$ and using it, find what will be the population in the year $$2010$$?

Find the coordinates of the foot of perpendicular from the point $$(-1, 3)$$ to the line
$$3x - 4y - 16\displaystyle = 0$$
Find the point on the X-axis which is equidistant from $$(2, -5)$$ and $$(-2, 9)$$.
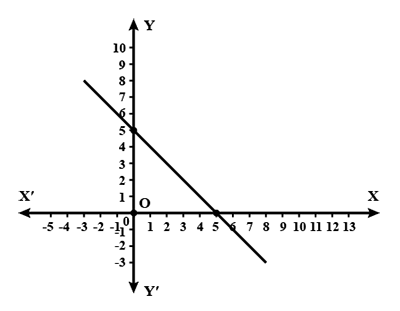
Determine the equation of the line in the given graph.
Draw the graph of $$y=3x+5$$.
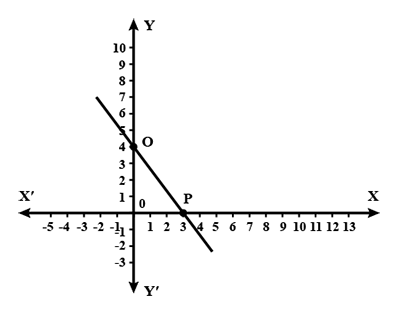
Determine the equation of the line in the given graph.
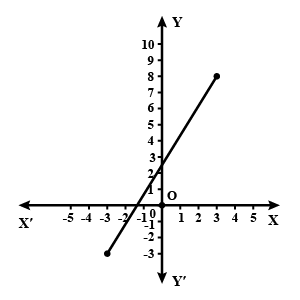
Determine the equation of the line in graph.
Find the area of a triangle whose vertices are $$A(3, 4), B(-1, 2),$$ and $$C(2, 3)$$.
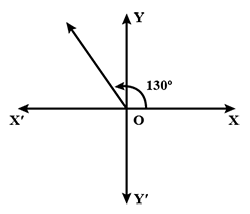
For the angle in standard position if the Initial arm rotates $$130^o$$ in anticlockwise direction, then state the quadrant in which terminal arm lies. (Draw the figure and write the answer).
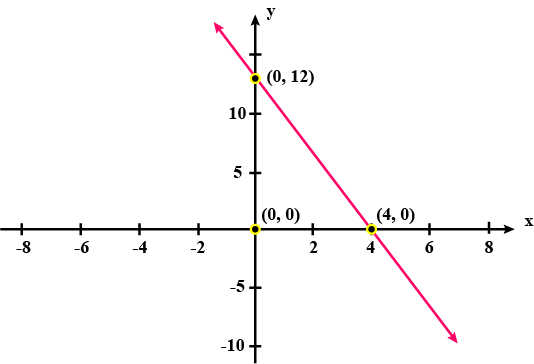
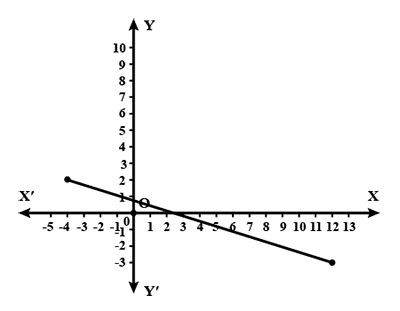
Determine the equation of the line in graph.
Find the slope of the line passing through the points $$G(-4, 5)$$ and $$H(-2, 1)$$
Find the slope of the line having its inclination $${60}^{o}$$.
Find the slope of line passing through the point $$P\left(1, -1\right)$$ and $$Q\left(-2, 5\right)$$.
Find the slope of the line passing through the points $$M(4, 0)$$ and $$N(-2, -3)$$.
Find the area of the triangle, whose vertices are $$(-5, -1), (3, -5), (5, 2).$$
Find the area of the triangle, whose vertices are $$(2, 0), (1, 2), (-1, 6)$$. What do you observe?
Find the area of the triangles (in sq. units) formed by the points $$(-2, 3), (7, 5)$$ and $$(3, -5)$$.
Show that $$S(4, 3)$$ is the circum-centre of the triangle joining the points $$A(9, 3), B(7, -1)$$ and$$ C(1, -1)$$.
Find the area of the triangle formed by joining the midpoints of the sides of a triangle whose vertices are $$(0,-1),(2,1)$$ and $$(0,3)$$.
Find the area of triangle $$\triangle ABC$$ having vertices $$A(4, 2),B(3, 9)$$ and $$C(10, 10)$$.
Find the slope of the straight line passing through the points $$(3,-2)$$ and $$(-1,4)$$.
Show that the following point taken in order form the vertices of a rhombus.
(0, 0), (3, 4), (0, 8) and (-3, 4)
Show that the three points $$(4, 2), (7, 5)\ and\ (9, 7)$$ lie on a straight line.
Find the distance between $$A(a+b,b-a)$$ and $$B(a-b,a+b)$$.
Find the angle of inclination(in degrees) of the line passing through the points $$(1,2)$$ and $$(2,3)$$
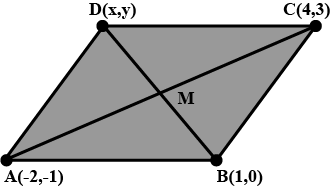
Prove that the points (-2, -1), (1, 0), (4, 3), and (1, 2) are at the vertices of a parallelogram.
A line is of length 10 and one end is at the point (2, -3); if the abscissa of the other end be 10, prove that its ordinate must be 3 or -9.
Prove (by showing that the area of the triangle formed by them is zero) that the following sets of three points are in a straight line:
$$(1,4), (3, -2),$$ and $$(-3,16)$$
Find the areas of the triangles the whose coordinates of the points are respectively.
(5, 2), (-9, -3) and (-3, -5)
Prove that the point $$\left ( -\frac{1}{14}, \frac{39}{14} \right )$$ is the centre of the circle circumscribing the triangle whose angular points are (1, 1), (2, 3), and ( - 2, 2).
Find the areas of the triangles the whose coordinates of the points are respectively.
(0, 4), (3, 6) and ( - 8, - 2)
$$(a, c + a), (a, c)$$ and $$(-a, c - a).$$
Lay down in a figure the positions of the points (1, -3) and (- 2,1), and prove that the distance between them is 5.
Find the areas of the triangles the whose coordinates of the points are respectively.(1, 3), ( - 7, 6) and (5, - 1)
Prove that the straight line x + y = 1 touches the parabola $$ y = x - x^2 . $$
Find the slope of the line joining the points $$(4, -8)$$ and $$(5, -2)$$.
Find the perpendicular distance of the point $$(-1,1)$$ from the line $$12(x+6)=5(y-2)$$.
Find the areas of the triangles the coordinates of whose angular points are $$(1, 30^o), (2, 60^o) $$ and $$(3, 90^o)$$
Find the areas of the triangles the coordinates of whose angular points are$$\left ( -a, \dfrac{\pi}{6} \right ), \left ( a, \dfrac{\pi}{2} \right )$$, and $$\left ( -2a, -\dfrac{2\pi}{2} \right )$$
Find the equation of the straight line which passes through the point $$(2,-3)$$ and the point of intersection of the lines $$x+y+4=0$$ and $$3x-y-8=0$$.
Show that the line joining the points $$A(1, -1, 2)$$ and $$B(3, 4, -2)$$ is perpendicular to the line joining the points $$C(0, 3, 2)$$ and $$D(3, 5, 6)$$.
$$(2, 30^o)$$ and $$(4, 120^o)$$
If be the origin, and if the coordinates of any two points $$P_1$$ and $$P_2$$ respectively $$(x_1, y_2)$$ and$$(x_2, y_2)$$, prove that
$$OP_1 \cdot OP_2\cdot cos P_1OP_2=x_1x_2+y_1y_2$$
Find the area of the triangle formed by the lines
$$y^{2}-9\ xy+18x^{2}=0$$ and $$y=9$$
If the point $$(x,y)$$ is equidistant from the points $$(a+b,b-a)$$ and $$(a-b,a+b),$$ prove that $$bx=ay$$
If the area of triangle formed by points $$A(x,y), B(1,2)$$ and $$C(2,1)$$ is $$68$$ units then show that $$x+y=15$$.
Find the angle which the straight line $$y = \sqrt 3 x - 4$$ makes with y-axis.
Find the area of a triangle whose vertices are (3,8), (-4,2) and (5,-1).
Find the acute angle between the lines $$2x-y+3=0$$ and $$x-3y+2=0$$.
Find the perpendicular distance of $$(0,0)$$ from $$3x+4y=12$$.
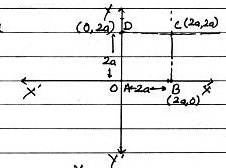
How many equilateral triangles of side 2a with one vertex at origin and side along the x-axis is possible.
$$A$$ is a point on $$x-$$axis with abscissa $$-8$$ and $$B$$ is point on $$y-$$axis with coordinate $$15$$. Find distance $$AB$$.
Find the length of sides of a triangle whose vertices are $$(1, -1), (0, 4)$$ and $$(-5, 3)$$.
Find the distance of a point P(x,y) from the origin.
Determine the ratio in which the point $$P(3, 5)$$ divides the join of $$A(1, 3)$$ & $$B(7, 9)$$.
Find the area of rhombus if its vertices are $$(3, 0), (4, 5), (-1, 4) $$ and $$ (-2, -1) $$ taken in order.
[Hint: Area of rhombus $$=\dfrac{1}{2}\times$$ product of its diagonals.]
If the point $$A(-2,1),\ B(a,b)$$ and $$C(4,-1)$$ are collinear of $$a-b=1$$. Find the value of $$a$$ of $$b$$.
The length of line PQ is 10 units and the coordinates of P are $$\left( {2, - 3} \right)$$; calculate the coordinates of point Q, if its abscissa is 10.
Find the value of a , if the distance between points $$P(a,-8,4)$$ and $$Q(-3,-5,4)$$ is 5.
If the equation of the locus of a point equidistant from the points $$\left( {{a_1},{b_1}} \right)$$ and $$\left( {{a_2},{b_2}} \right)$$ is $$\left( {{a_1} - {a_2}} \right)x + \left( {{b_1} - {b_2}} \right)y + c = 0$$, then the value of $$c$$ is
Find the equation of the line passing through the point $$(2, 3)$$ and making intercept of length $$3$$ unit between the lines $$y + 2x = 2$$ and $$y + 2x = 5$$.
If the point P(x,y) is equidistant from the points A(5,1) and B(-1,5), prove that $$3x=2y$$.
Find the values of x for which the distance between the points P(4,-5) and Q(12,x) is 10 units.
Using slopes, find the value of $$x$$ so that the points $$(6,\ -1),\ (5,\ 0)$$ and $$(x,\ 3)$$ are collinear.
The co-ordinate of the mid-points of the sides of a triangle ABC are $$D(2, 1), E(5, 3)$$ and $$F(3, 7)$$. Find the lengths and equations of its sides.
Find the angle between the lines joining the points $$(0,\ 0),\ (2,\ 3)$$ and $$(2,\ -2),\ (3,\ 5)$$.
Find the area of $$\triangle PQR$$ whose vertices are $$P(-1, 1) Q(0, 5) R(3, 2)$$
Find the point on y-axis which is equidistant from the points (5,-2) and (-3,2).
Prove that area if triangle $$ABC$$ with vertices $$A(3,2), B(11,8), C(8,12)$$ is $$25$$ square units.
Prove that the distance between the origin and the point $$(-6,\ -8)$$ is twice the distance between the points $$(4,\ 0)$$ and $$(0,\ 3)$$.
The medians AD and BE of a triangle with vertices $$A(0,b),B(0,0)$$ and $$C(a,0)$$ are perpendicular to each other, if
Find the area of the triangle formed by the point $$(0, 0) (4, 0) (0, 3)$$.
Find the equation of line equally inclined to coordinate axes and passes through $$(-5, 1, -2)$$.
Find the area (sq.units) of the triangle whose coordinates are
$$\left(2,3\right),\left(-1,0\right),\left(2,-4\right)$$.
Find a point on $$y-axis$$ which is equidistant from $$( - 5, - 2)$$ and $$( 3, 2)$$.
Find the inclination of a line whose slope is
(i) $$1$$
(ii) $$-1$$
(iii) $$\sqrt 3 $$
(iv) $$-\sqrt 3 $$
(v) $$\frac{1}{{\sqrt 3 }}$$
Find the coordinates of a point on $$x+y+3=0$$, whose distance from $$x+2y+2=0$$ is $$\sqrt{5}$$.
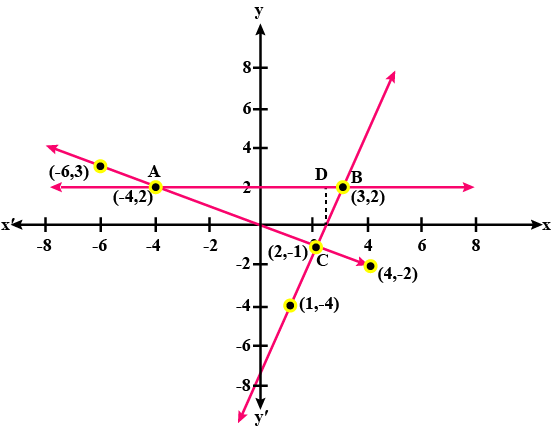
The line joining two points $$A ( 2,0 ) , B ( 3,1 )$$ is rotated about $$A$$ in anticlockwise direction through an angle of $$15 ^ { \circ } .$$ Find the equation of the line in the new position. If $$B$$ goes to $$C$$ in the new position, what will be the coordinates of $$C$$ ?
Find the slope of the line $$\dfrac{x}{3}+\dfrac{y}{2}=1$$.
Find the slope of a line, which passes through the origin, and the mid-point of the line segment joining the points $$P ( 0 , - 4 )$$ and $$B ( 8,0 )$$
Find the slope of the line whose inclination is
$$5\pi/6$$
Find the area of a triangle with sides $$3\ cm,4\ cm,5\ cm.$$
Check whether $$(5, -2)$$, $$(6, 4)$$ and $$(7, -2)$$ are the vertices of an isosceles triangles.
Find the slope of the line passing the two given points
$$( a , 0 )$$ and $$(0, b )$$
A point moves such that its distance from the point (4,0) is half that of its distance from the line $$x=16$$, find its locus.
The distance of a point $$P$$ on x-axis from $$A(11, 12)$$ is $$13$$ units. Find the co-ordinates of $$P.$$
Find the distance between the following pairs of points:-
$$(-5,7),(-1,3)$$
The distance between the points $$\left(0,0\right)$$ and $$\left(-4,3\right)$$ is
Let A(6,4) and B(2,12) be two given points. Find the slope of a line perpendicular to AB.
Find the area of the triangle formed by the mid-points of the sides of $$\triangle$$ ABC, where A(3,2), B(-5,6) and C(8,3).
Find the slope of a non-vertical line $$ax+by+c=0$$
Find the distance between the points (3,-5) and (5,-1).
Find the area of triangle formed by the points (8,-5) , (-2,-7) and (5,1) .
Show that the path of a moving point which remains at equal distance from the points $$(2, 1)$$ and $$(-3, -2)$$ is a straight line.
Find the slope of the line joining the points (3, -2)and (-1,4)
The equation of line with slope $$\dfrac 54$$ nd passing through $$(8,4)$$
Find the value k. for which the point (-1, 3) lies on the graph of the equation 2x - y + k = 0.
Find the distance between $$\left(-2,-4\right)$$ from the origin.
Find the distance of the points P (-6,8) from the origin.
Find the distance between $$\left(8,-8\right)$$ from the origin.
Find the distance between $$\left(-9,-1\right)$$ from the origin.
Find the distance between the points $$A(a,b)$$ and $$B(-a,-b)$$
Fill in the blacks.
If the area of a triangle is 0 square units then the vertices of a triangle are _____
Prove that the point $$\left( { - \dfrac{1}{{14}},\dfrac{{39}}{{14}}} \right)$$ is the centre of the circle circumscribing the triangle whose vertices are $$(1,1),(2,3),$$ and $$(-2,2)$$
If the vertices of a triangle are $$ (1,-1) , (-4,6), (-3,-5) $$ then the area of triangle is :
Find the slope of the line $$AB$$ joining $$A(a,0),B(0,b)$$?
Find the shortest distance of (3,4) from origin.
Check which at the following are solutions of the equation 7 x - 5 y = - 3i) (-1, -2) ii) (-4, -5)
Write the formula for area of triangle $$ABC$$ where A$$\left( { x }_{ 1 },{ y }_{ 1 } \right) ,B\left( { x }_{ 2 },{ y }_{ 2 } \right) $$ and $$C\left( { x }_{ 3 },{ y }_{ 3 } \right) $$
Find the locus of a point, so that the join of (-5,1) and (3,2) subtends a right angle at the moving point.
Find the area of the triangle with vertices as given below:
$$(-1,-8),(-2,-3)$$ and $$(3,2)$$
Show that the product of perpendiculars on the line $$\dfrac {x}{a}\cos \theta +\dfrac {y}{b}\sin \theta =1$$ from the points $$(\pm \sqrt {a^2 -b^2}, 0)$$ is $$b^2$$.
Find k, if R(1, -1), S (-2, k) and slope of line RS is -2.
Without using the Pythagoras theorem, show that the points (4, 4), (3, 5) and (-1, -1) are vertices of a right angles triangle.
Find the angle between the x-axis and the line joining the points (3, -1) and (4, -2)
Write the formula to find the area of triangle if the vertices is given
Fill in the blanks.
If point $$A(-3,12),B(7,6)$$ and $$C(x,9)$$ are collinear, then the value of $$x$$ is_______.
Find the slope of a line, which passes through the origin, and the mid-point of the segment joining the points P(0, -4) and B(8, 0)
A point which is equidistant from the points A (5, 4) and B (1, 6) is (3,5)
If true then enter $$1$$ and if false then enter $$0$$
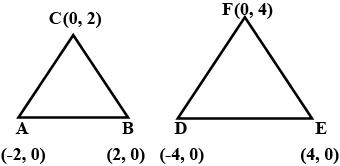
State whether the following statement is true or false.Enter $$1$$ for true and $$0$$ for false$$\triangle $$ABC with vertices A (-2, 0), B (2, 0) and C (0, 2) is similar to $$\triangle DEF$$ with vertices D (-4, 0) E (4, 0) and F (0, 4).
Find the area of the triangle whose vertices are $$(8, 4), (6, 6)$$ and $$(3, 9)$$.
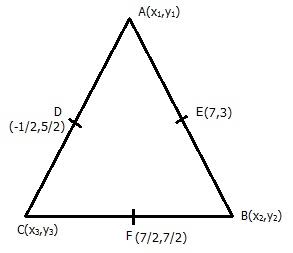
If D $$\left ( \frac{-1}{2},\frac{5}{2} \right )$$, E (7,3) and F $$\left ( \frac{7}{2},\frac{7}{2} \right )$$ are the midpoints of sides of $$\Delta$$ ABC, find the area of the $$\Delta$$ ABC.
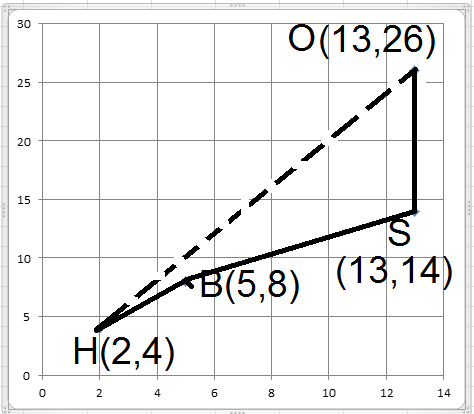
Ayush starts walking from his house to office. Instead of going to the office directly, he goes to a bank first, from there to his daughters school and then reaches the office. What is the extra distance travelled by Ayush in reaching his office? (Assume that all distances covered are in straight lines). If the house is situated at (2, 4), bank at (5, 8), school at (13, 14) and office at
(13, 26) and coordinates are in km
write answer in meter
Column II gives the area of triangles whose vertices are given in column I, match them correctly.
Find the perimeter of the triangle formed by $$(0, 0), (1, 0)$$ and $$(0, 1)$$ to nearest integer.
The points $$P(6, -1), Q(1, 3),$$ $$R = (x,8)$$ are connected such that $$PQ=QR$$ then positive value of $$x=$$
A point moves so that its distance from y-axis is half of its distance from the origin. Find the locus of the point.
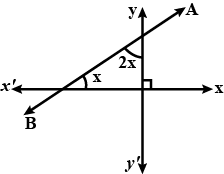
In given figure, find the inclination of line $$AB$$:
Plot the points A (1, -1), B (-1, 4) and C (-3, -1) on a graph paper to obtain the triangle ABC. Give a special name to the triangle ABC and, if possible, find its area.
If $$\Delta $$ denotes the area of the triangle with vertices $$(0, 0), (5, 0)$$ and $$\left(\dfrac56, \dfrac{25}6\right),$$ then $$\Delta$$ is equal to
If O is the origin and $$A_{n}$$ is the point with coordinates $$(n, n+1)$$ then $$(OA_{1})^{2}+(OA_{2})^{2}+ ... +(OA_{7})^{2}$$ is equal to
In the following, the coordinates of the three vertices of a rectangle ABCD are given. By plotting the given points; find, the coordinates of the fourth vertex:
A (2, 0), B (8, 0) and C (8, 4)
Claim: The co-ordinates of the fourth vertex are (2,4)
If true then enter $$1$$ and if false then enter $$0$$
Through the point P(3, 5), a line is drawn inclined at $$45^{\circ}$$ with the positive direction of x-axis. It meets the line $$x+y-6=0$$ at the point Q, O being the origin, then
$$9\left ( PQ \right )^{2}+14\left ( OP \right )^{2}+10\left ( OQ \right )^{2}$$ is equal to
If the point $$P(k - 1, 2)$$ is equidistant from the points $$A(3, k)$$ and $$B(k, 5)$$, then how many values of $$k$$ are obtained?Write $$0$$, if the value cannot be determined.
Find the value of $$x$$ so that the points $$(x, -1), (2, 1)$$ and $$(4, 5) $$ are collinear.
What is the slope of a line whose inclination with the positive direction of x axis is $$\displaystyle 120^{\circ}$$ ?
The vertices of a triangle are $$(-2, 0), (2, 3)$$ and $$(1, -3)$$.Is the triangle equilateral, isosceles or scalene?Write answer as $$'1'$$ for equilateral, $$'2'$$ for isosceles and $$'3'$$ for scalene.
The vertices of $$\displaystyle \Delta ABC$$ are (-2, 1), (5, 4) and (2, -3) respectively. Find the area of triangle.
The length of a line-segment isIf one end is at (2, -3) and the abscissa of the second end is 10, then find the number of values of ordinate the second end can take.
The distance of $$P(x, y)$$ from $$A(5, 1)$$ and $$V (-1, 5)$$ are equal then $$\dfrac xy = \dfrac pq$$. Find the value of $$p+q$$
Enter 1 if it is true else enter 0.The points $$(-3, 2), (1, -2) and (9, -10)$$ are collinear.
If the coordinates of a point on the y-axis which is equidistant from the points $$(13, 2)$$ and $$(12, -3)$$ is $$(p,q)$$, then find the value of $$p+q$$.
Find the area of the triangle formed by the midpoints of the sides of $$\Delta ABC$$, where $$A = (3, 2), B = (-5, 6)$$ and $$C = (8, 3)$$.
Find sum of values of $$a$$ for which the distance between the points $$P(11, -2)$$ and $$Q(a, 1)$$ is $$5$$ units.
Find the area of the triangle formed by the midpoints of the sides of $$\displaystyle \triangle ABC$$ where $$A=(3,2), B=(-5,6)$$ and $$C=(8,3)$$
Find the angle between the $$x$$-axis and the line joining the points $$(3,-1)$$ and $$(4,-2)$$.
If $$2p$$ is the length of perpendicular from the origin to the line whose intercepts on the axes are $$2a$$ and $$b$$, then show that $$\displaystyle {\frac{1}{p^{2}}= \frac{1}{a^{2}}+\frac{1}{b^{2}}}$$.
What are the points on the $$y$$-axis whose distance from the line $$\displaystyle \frac{x}{3}+\frac{y}{4}= 1$$ is $$4$$ units.
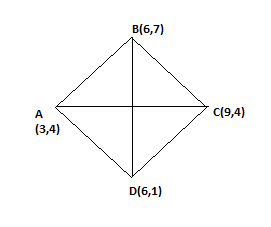
Find the area of square whose one pair of the opposite vertices are (3, 4) and (5, 6)
Find a point on the $$x$$-axis, which is equidistant from the points $$(7, 6)$$ and $$(3, 4)$$.
Find the area of the triangle formed by the lines $$\displaystyle y-x= 0,x+y= 0$$ and $$x-k= 0$$
Give the equations of two lines passing through $$\left(2, 14\right)$$. How many more such lines are there, and why?
If $$Q(0, 1)$$ is equidistant from $$P(5, -3)$$ and $$R(x, 6)$$, find the values of $$x$$. Also find the distances $$QR$$ and $$PR$$.
Find the distance between the following pairs of points :
(i) $$(2, 3), (4, 1)$$
(ii) $$( -5, 7), ( -1, 3)$$
(iii) $$(a, b), ( -a, -b)$$
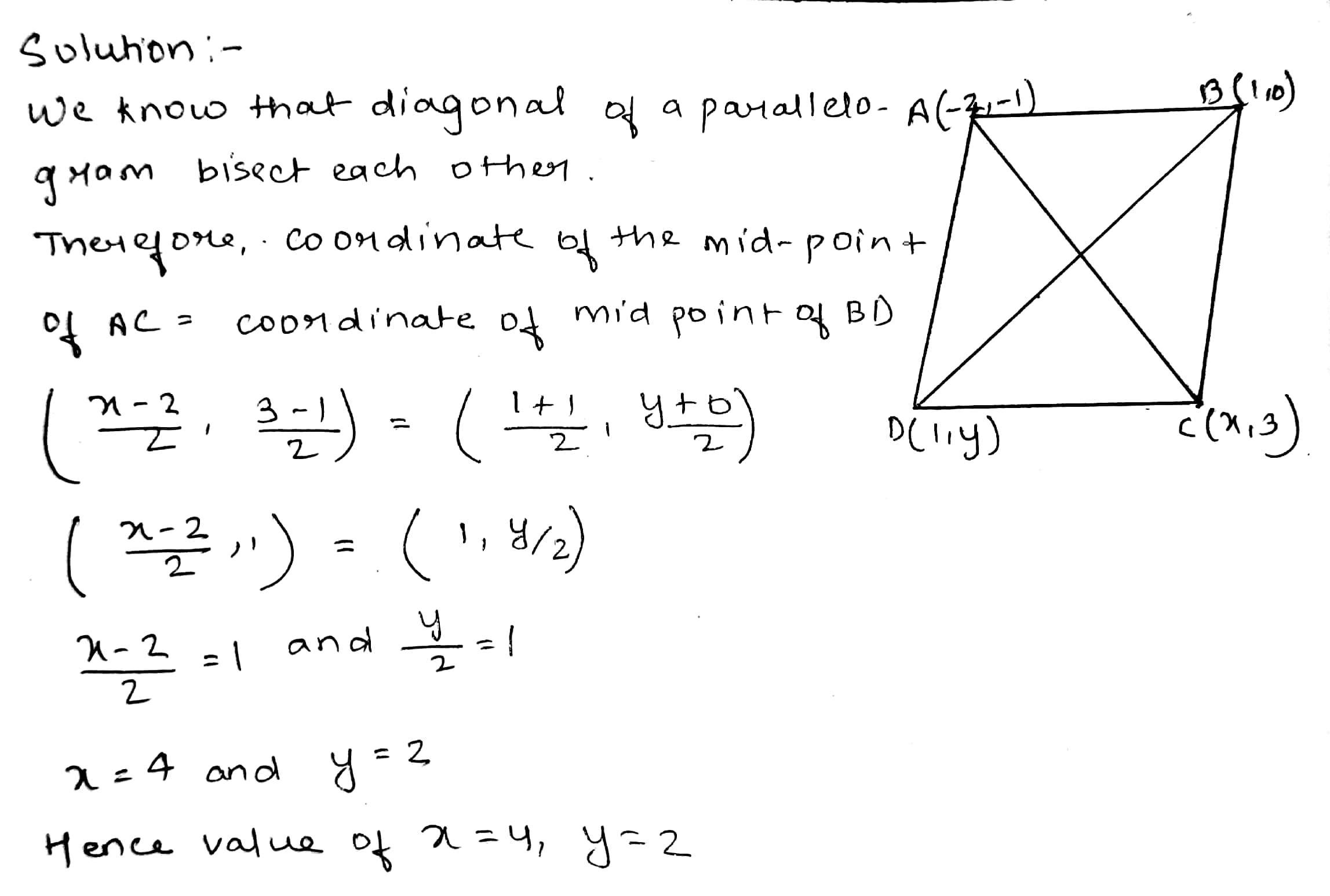
If $$(1, 2), (4, y), (x, 6)$$ and $$(3, 5)$$ are the vertices of a parallelogram taken in order, find $$x$$ and $$y$$.
Find the distance between the points $$(0, 0)$$ and $$(36, 15)$$.
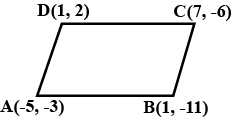
Name the type of quadrilateral formed, if any, by the following points, and give reasons for your answer:
(i) $$( -1, -2), (1, 0), ( -1, 2), ( -3, 0)$$
(ii) $$(-3, 5), (3, 1), (0, 3), (-1, -4)$$
(iii) $$(4, 5), (7, 6), (4, 3), (1, 2) $$
In each of the following find the value of $$k$$, for which the points are collinear.
(i) $$(7, -2), (5, 1), (3, k)$$
(ii) $$(8, 1), (k, -4), (2, -5)$$
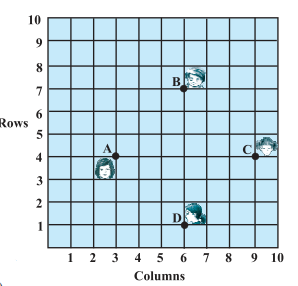
In a classroom, $$4$$ friends are seated at the points $$A$$, $$B$$, $$C$$ and $$D$$ as shown in Fig. Champa and Chameli walk into the class and after observing for a few minutes Champa asks Chameli, Dont you think $$ABCD$$ is a square? Chameli disagrees. Using distance formula, find which of them is correct. why?
Find a relation between $$x$$ and $$y$$ such that the point $$(x, y)$$ is equidistant from the point $$(3, 6)$$ and $$( -3, 4)$$.
Find the area of the triangle formed by joining the mid-points of the sides of the triangle whose vertices are $$(0, +1), (2, 1)$$ and $$(0, 3)$$. Find the ratio of this area to the area of the given triangle.
Find the area of the triangle whose vertices are :
(i) $$(2, 3), (-1, 0), (2, -4)$$
(ii) $$(-5, -1), (3, -5), (5, 2)$$
Find the centre of a circle passing through the points $$(6, -6), (3, -7)$$ and $$(3, 3)$$.
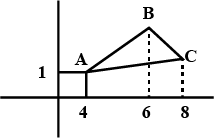
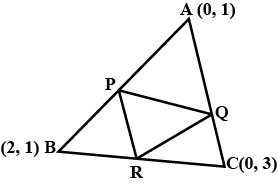
The Class $$X$$ students of a secondary school in Krishinagar have been allotted a rectangular plot of land for their gardening activity. Sapling of Gulmoharare planted on the boundary at a distance of $$ 1$$ m from each other. There is a triangular grassy lawn in the plot as shown in the Fig. The students are to sow seeds of flowering plants on the remaining area of the plot.
(i) Taking $$A$$ as origin, find the coordinates of the vertices of the triangle.
(ii) What will be the coordinates of the vertices of $$\displaystyle \Delta PQR$$ if $$C$$ is the origin?
Also calculate the areas of the triangles in these cases. What do you observe?

$$ABCD$$ is a rectangle formed by the points $$A(-1, -1)$$, $$B( -1, 4)$$, $$C(5, 4)$$ and $$D(5, -1)$$. $$P, Q,R$$ and $$S$$ are the mid-points of $$AB$$, $$BC$$, $$CD$$ and $$DA$$ respectively. Is the quadrilateral $$PQRS$$ a square? a rectangle? or a rhombus? Justify your answer.
Find, if possible, the slope of the line through the points $$(-9,4)$$ and $$(-9,-2)$$
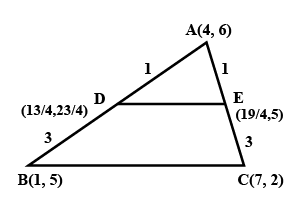
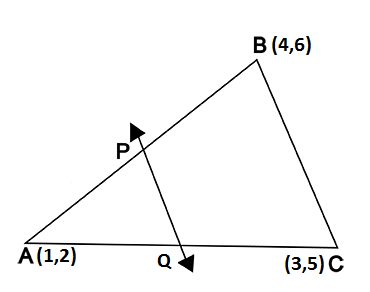
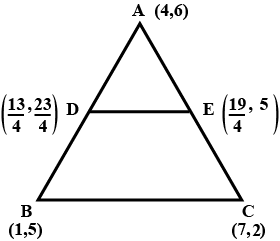
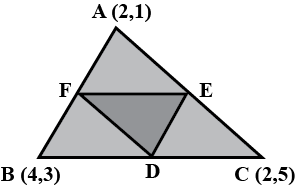
The vertices of a $$\displaystyle \Delta ABC$$ are $$A(4, 6), B(1, 5) $$and $$C(7, 2)$$. A line is drawn to intersect sides $$AB$$ and $$AC$$ at $$D$$ and $$E$$ respectively, such that $$\displaystyle \frac { AD }{ AB } =\frac { AE }{ AC } =\frac { 1 }{ 4 } $$. Calculate the area of the $$\displaystyle \Delta ADE$$ and compare it with the area of $$\displaystyle \Delta ABC$$.
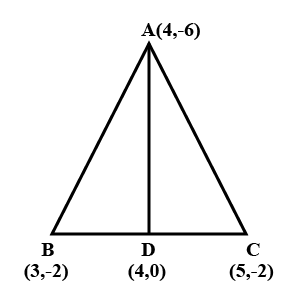
You have studied in Class IX, that a median of a triangle divides it into two triangles of equal areas. Verify this result for $$\displaystyle \Delta ABC$$ whose vertices are $$A(4, -6), B(3, -2)$$ and $$C(5, 2)$$.
Find the slope of the line that passes through the points $$(2,0)$$ and $$(2,4)$$
Find the slope of the line passing through the points $$(-1,1)$$ and $$(2,2)$$
If a point $$A(0,2)$$ is equidistant from the points $$B(3,p)$$ and $$C(p,5)$$ then find the value of $$p.$$
A $$(4, - 6$$ ), B $$(3,- 2$$ ) and C $$(5, 2)$$ are the vertices of a $$\Delta ABC $$ and AD is its median. Prove that the median AD divides $$\Delta$$ ABC into two triangles of equal areas.
If the vertices of a triangle are $$(1,-3), (4,p)$$ and $$(-9,7)$$ and its' area is $$15$$ sq. units, find the value (s) of $$p.$$
If the area of triangle $$ABC$$ formed by $$A(x, y), B(1, 2)$$ and $$C(2, 1)$$ is $$6$$ square units, then prove that $$x + y = 15$$.
Find the values of $$k$$ so that the area of the triangle with vertices $$(1,\ -1), (-4,\ 2k)$$ and $$(-k,\ -5)$$ is $$24$$ sq. units.
Mid-points of the sides $$AB$$ and $$AC$$ of $$\triangle {ABC}$$ are $$(3,5)$$ and $$(-3,-3)$$ respectively, then find the length of $$BC$$
If the points $$A(7,9), B(3,-7)$$ and $$C(-3,3)$$ are vertices of a triangle, then find the measure $$\angle{C}$$(in degrees)
Given that three points $$(1,2),(2,4),(k,6)$$ are collinear, find the value of $$k$$.
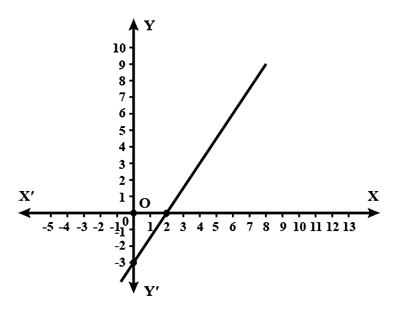
Determine the equation of the line in the given graph.
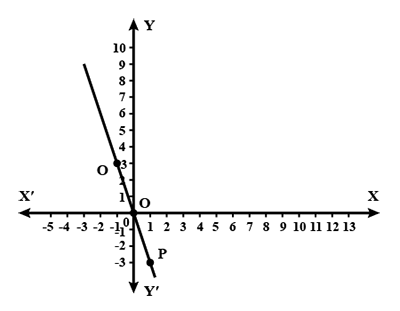
Determine the equation of the line in the given graph.
Write the equation $$4x-5y=12$$ in slope intercept form.
If $$a\ast b=ab+a+b$$, draw the graph of $$y=3\ast x+1\ast 2$$.
Find the slope of the line joining the points $$(2a, 3b)$$ and $$(a, -b)$$.
Find the slope of the line joining the points $$(0, 0)$$ and $$(\sqrt 3, 3)$$.
Find the slope of the line joining the points $$(-8)$$ and $$(5, -2)$$
Find the angle of inclination of straight line whose slope is $$\displaystyle\frac{1}{\sqrt 3}$$.
Find the slope of the line whose inclination is $$60^o$$.
Find the angle of inclination of straight line whose slope is $$0$$.
Find the angle of inclination of straight line whose slope is $$1$$.
Find the angles of inclination of straight lines whose slopes are $$\sqrt 3$$.
Find the slope of the line joining the points $$(-5, 0)$$ and $$(0, -7)$$.
Find the slope of the line joining the points $$(-4, 1)$$ and $$(-5, 2)$$
Prove that $$(-5,-3),(1,-11),(7,-6),(1,2)$$ coordinates are the vertices of parallelograms
Find the distance between the origin and the point $$(5, 12)$$.
Find the perimeter of the triangles whose vertices have the following coordinates $$(-2, 1), (4, 6), (6, -3)$$.
Find the perimeter of the triangles whose vertices have the following coordinates $$(3, 10), (5, 2), (14, 12)$$.
A point $$P(2, -1)$$ is equidistant from the points $$(a, 7)$$ and $$(-3, a)$$. Find 'a'.
Prove that the points $$A(1, -3), B(-3, 0)$$ and $$C(4, 1)$$ are the vertices of right isosceles triangle.
The distance between the points $$(3, 1)$$ and $$(0, x)$$ is $$5$$ units. Find x.
Find the radius of a circle whose centre is $$(-5, 4)$$ and which passes through the point $$(-7, 1)$$.
Find the distance between the following pairs of points $$(2, 0)$$ and $$(0, 3)$$.
Find a point on y-axis which is equidistant from the points $$(5, 2)$$ and $$(-4, 3)$$.
The coordinate of vertices of triangles are given. Identify the types of triangles $$(3, 5)(-1, 1)(6, 2)$$.
The coordinate of vertices of triangles are given. Identify the types of triangles $$(1, 6)(3, 2)(10, 8)$$.
Find the slope of the line passing through $$A (-2, 1)$$ and $$B(0, 3)$$
Prove that the set of coordinates are the vertices of parallelogram $$(4, 0), (-2, -3), (3, 2), (-3, -1)$$.
Find the distance between the following pairs of points $$(1, -3)$$ and $$(-4, 7)$$.
If the points $$A(1, 2), B(4, 6), C(3, 5)$$ are the vertices of a $$\Delta ABC$$, find the equation of the line passing through the midpoints of $$AB$$ and $$BC$$.
Prove that $$(4, 0), (-2, -3), (3, 2), (-3, -1)$$ coordinates are not the vertices of parallelogram.
The coordinate of vertices of triangles are given. Identify the types of triangles $$(3, -3)(3, 5)(11, -3)$$.
The coordinate of vertices of triangles are given. Identify the types of triangles $$(2, 1)(10, 1)(6, 9)$$.
If the middle point of two points A(-2, 5) and B(-5, y) is $$\left( \dfrac{-7}{2}, 3 \right )$$, then find the distance between points A and B.
If the area of the $$\triangle {ABC}$$ is $$68$$ sq.units and the vertices are $$A(6,7), B(-4,1)$$ and $$C(a,-9)$$ taken in order, then find the value of $$a$$.
Show that (4, 1) is equidistant from the points (-10, 6) and (9, -13)
Show that the points $$(a, a), (-a, -a)$$ and $$(-a \sqrt 3, a \sqrt 3)$$ form an equilateral triangle.
Find the area of the triangle formed by joining the mid points of the sides of the triangle, whose vertices are $$(0, 1); (2, 1)$$ and $$(0, 3)$$. Find the ratio of this area to the area of the given triangle
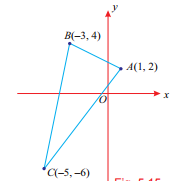
Find the area of the triangle whose vertices are $$(1,2),(-3,4)$$ and $$(-5,-6)$$
Find the area of the triangle formed by the points $$(0,0), (3,0)$$ and $$(0,4)$$.
Find the area of the triangle whose vertices are $$(-5, 7), (4, 5)$$ and $$(-4, -5).$$
If the distance of P(x,y) from A(5,1) and B(-1,5) are equal, then prove that 3x = 2y.
Find the area of the $$\triangle ABC$$, coordinates of whose vertices are $$A(4, 1), B(6, 6)$$ and $$C(8, 4)$$.
Find the areas of the triangles the whose coordinates of the points are respectively.(a, b + c), (a, b-c) and (-a, c)
If X(3, 1), Y(4, 5) and Z(-1, -1) are co-ordinates of vertices of $$\Delta$$XYZ, then find area of $$\Delta$$XYZ.
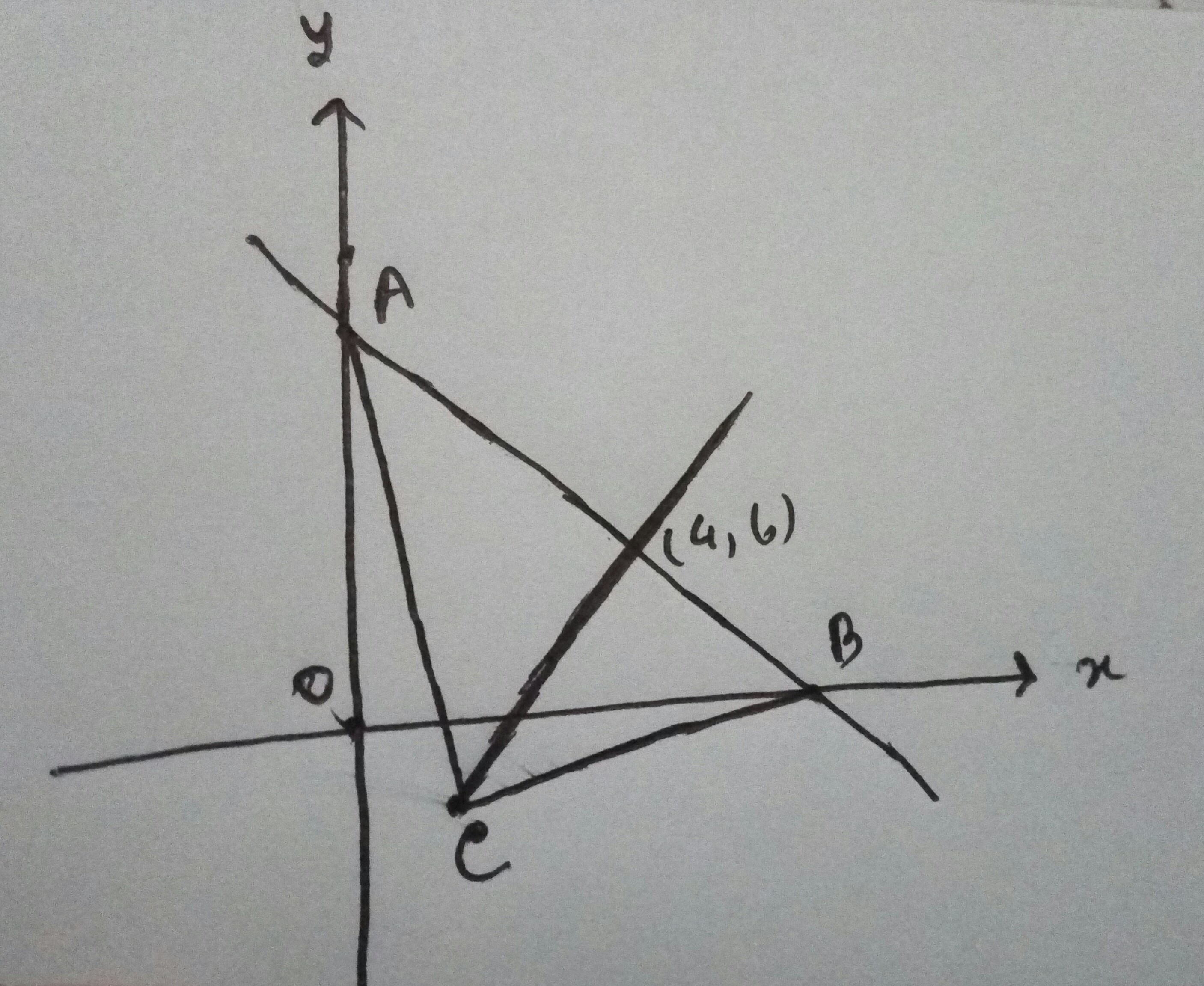
(a) What is the slope of the line joining the points $$A(2,-3)$$ and $$B(6,3)$$? Find the equation of this line.
(b) Find the co-ordinates of the point $$C$$ at which the line cuts the x-axis.
(c) Show that $$C$$ is the mid-point of the line $$AB$$.
Ayush starts walking from his house to office. Instead of going to the office directly, he goes to a bank first, from there to his daughter's school and then reaches the office What is the extra distance travelled by Ayush in reaching the office. If the house is situated at $$(2, 4)$$, bank at $$(5, 8),$$ school at $$(13, 14)$$ and office at $$(13, 26)$$ and the coordinates are in kilometers?(Assume that all distances covered are in straight lines).
$$(a\, \cos\, \phi _1, b \, \sin\, \phi _1), (a\, \cos\, \phi _2, b \, \sin\, \phi _2)$$ and $$ (a\, \cos\, \phi _3, b \, \sin\, \phi _3)$$
$$\left \{ am_1m_2, a(m_1+m_2) \right \}, \left \{ am_2m_3, a(m_2+m_3) \right \} and \left \{ am_3m_1, a(m_3+m_1) \right \}$$.
Prove that the polar coordinates $$(0, 0), \left ( 3, \dfrac{\pi}{2} \right )$$, and $$\left ( 3, \dfrac{\pi}{6} \right )$$ form an equilateral triangle.
Prove (by showing that the area of the triangle formed by them is zero) that the following set of three points are in a straight line$$(a, b + c), (b, c + a)$$ and $$(c, a + b).$$
$$ (am^2_1, 2am_1), (am^2_2, 2am_2)$$ and $$ (am^2_3, 2am_3)$$
Prove (by showing that the area of the triangle formed by them is zero) that the following set of three points are in a straight line $$ \left(-\dfrac{1}{2}, 3\right), (-5,6)$$, and $$(-8,8)$$.
$$A\left[ 3,4 \right]$$ and $$B\left[ 5,-2 \right]$$ are to given points. If $$PA=PB$$ and area of triangle $$PAB=10$$, Then $$P$$ is?
Through the point $$(3, 4)$$ are drawn two straight lines each inclined at $$45^{\circ}$$ to the straight line $$x - y = 2$$. Find their equations and also find the area of triangle bounded by the three lines.
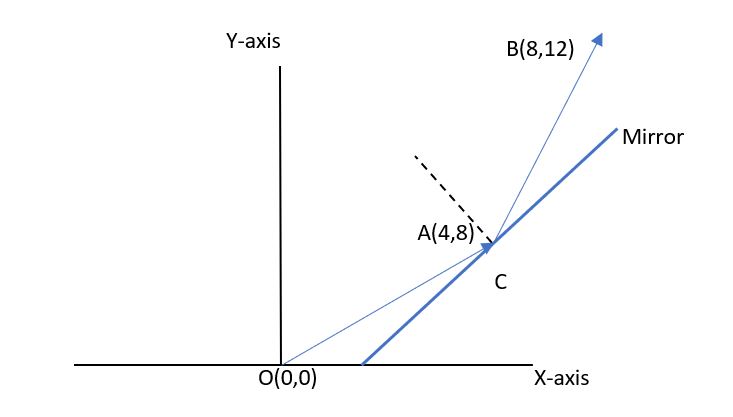
Starting at the origin, a beam of light hits a mirror(in the form of a line) at the point A$$(4, 8)$$ and reflected line passes through the point B$$(8, 12)$$. Compute the slope of the mirror.
Find perpendicular distance from the origin of the line joining the points $$(\cos \theta, \sin \theta)$$ and $$(\cos \phi, \sin \phi)$$.
Let $$ABCD$$ be a square of side $$2a$$. Find the coordinates of the vertices of this square when
(i) A coincides with the origin and $$AB$$ and $$AD$$ are along $$OX$$ and $$OY$$ respectively.
(ii) The centre of the square is at the origin and coordinate axes are parallel to the sides $$AB$$ and $$AD$$ respectivey.
If the point $$P(x,y)$$ is equidistant from the points $$A(a + b, b - a)\ \text {and}\ B(a - b, a + b)$$. Prove that $$bx = ay$$.
Find the area of the triangle whose vertices are $$(-2, 3), (3, 2)$$ and $$(-1, -8)$$ by using determinant method.
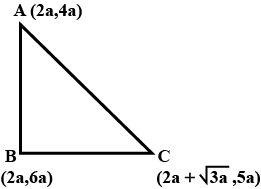
Prove that the points $$(2a,4a), (2a,6a)$$ and $$(2a+\sqrt {3}a,5a)$$ are the vertices of an equilateral triangle.
Find the circumcentre and circumradius of a triangle with vertices are $$(3,0),\ (-1,-6),\ (4,-1)$$.
If the points $$(2,1)$$ and $$(1,-2)$$ are equidistant from the point $$(x,y)$$, show that $$x+3y=0$$.
Find the values of $$x,y$$ if the distances of the point $$(x,y)$$ from $$(-3,0)$$ as well as from $$(3,0)$$ are $$4$$.
Find the angle subtended at the origin by the line segment whose end points are $$(0,100)$$ and $$(10,0)$$
Prove that $$(2,-2), (-2,1)$$ and $$(5,2)$$ are the vertices of a right angled-triangle. Find the area of the triangle and the length of the hypotenuse.
Show that the points $$(-3,2),(-5,-5),(2,-3)$$ and $$(4,4)$$ are the vertices of a rhombus. Find the area of this rhombus.
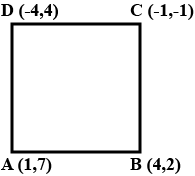
Prove that the points $$A(1,7), B(4,2), C(-1,-1)$$ and $$D(-4,4)$$ are the vertices of a square.
The length of a line segment is of $$10$$ units and the coordinates of one-end-point are $$(2,-3)$$. If the abscissa of the other end is $$10$$, find the ordinate of the other end.
Find the area of a triangle whose vertices are $$(a,c+a),(a,c)$$ and $$(-a,c-a)$$
Show that the points $$A(2,3),B(-2,2),C(-1,-2)$$ and $$D(3,-1)$$ are the vertices of a square $$ABCD$$.
Find the value of $$x$$ such that $$PQ=QR$$ where the coordinates of $$P,Q$$ and $$R$$ are $$(6,-1), (1,3)$$ and $$(x,8)$$ respectively.
The points $$A(2,0),B(9,1),C(11,6)$$ and $$D(4,4)$$ are the vertices of a quadrilateral $$ABCD$$. Determine whether $$ABCD$$ is a rhombus or not.
Three consecutive vertices of a parallelogram are $$(-2,-1), (1,0)$$ and $$(4,3)$$. Find the fourth vertex.
Prove that the points $$(4,5), (7,6), (6,3), (3,2)$$ are the vertices of a parallelogram. Is it a rectangle?
Find the area of a triangle whose vertices are
$$(6,3),(-3,5)$$ and $$(4,-2)$$
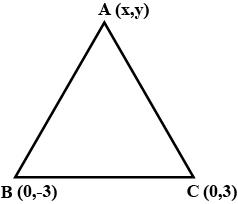
If $$(0,-3)$$ and $$(0,3)$$ are the two vertices of an equilateral triangle, find the coordinates of its third vertex.
Three vertices of a parallelogram are $$(a+b,a-b),(2a+b,2a-b)$$and $$(a-b,a+b)$$ taken in a order, the fourth vertex is $$(-b,b)$$
If true enter $$1$$ else $$0$$
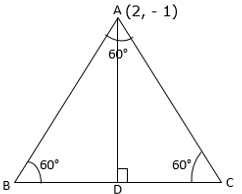
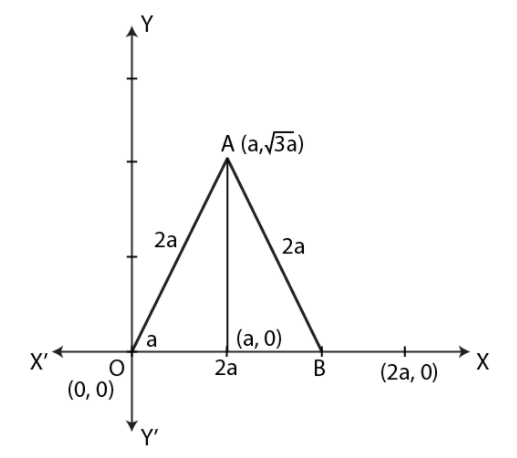
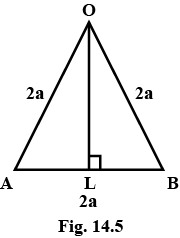
Find the coordinates of the vertices of an equilateral triangle of side 2a as shown in Fig 14.5
If $$a$$ and $$b$$ are real numbers between $$0$$ and $$1$$ such that the points $$(a,1),(1,b)$$ and $$(0,0)$$ from an equilateral triangle, then $$a=b=2-\sqrt { 3 }$$.
Find the area of the triangle $$PQR$$ if coordinates of $$Q$$ are $$(3,2)$$ and the coordinates of mid-points of the sides through $$Q$$ are $$(2,-1)$$ and $$(1,2)$$
Find the value of $$a$$ for which the area of the triangle formed by the points $$A(a,2a),B(-2,6)$$ and $$C(3,1)$$ is $$10$$ square units.
Find the area of a parallelogram $$ABCD$$ if three of its vertices are $$A(2,4),B(2+\sqrt {3},5)$$ and $$C(2,6)$$
If the vertices of a triangle are $$(1,-3),(4,p)$$ and $$(-9,7)$$ and its area is $$15$$ sq. units, find the value(s) of $$p$$.
The vertices of $$\triangle{ABC}$$ are $$(-2,1),(5,4)$$ and $$(2,-3)$$ respectively. Find the area of the triangle and the length of the altitude through $$A$$.
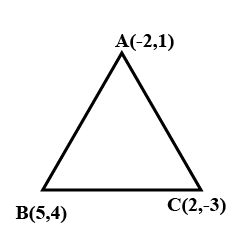
Let the opposite angular points of a square be $$(3,4)$$ and $$(1,-1)$$. Find the coordinates of the remaining angular points.
Find the fourth vertex D of a parallelogram ABCD whose three vertices are A ( -2,3 ) B (6 ,7) and C ( 8,3)
If P and Q are two points whose coordinates are $$\left( { at }^{ 2 },2at \right) $$ and $$\left( \dfrac { a }{ { t }^{ 2 } } ,\dfrac { 2a }{ t } \right) $$ respectively and S is the point (a,o). Show that $$\dfrac { 1 }{ SP } +\dfrac { 1 }{ SQ } $$ is independent of t.
Do the points $$A(3,2), B(-2,-3)$$ and $$C(2,3)$$ form a triangle? If so, name the type of triangle formed.
if A(5,2), B(2,-2) and C (-2,t) are the vertices of right angled triangle with $$\angle B={ 90 }^{ 0 },$$ then find the value of t.
Prove that $$(4, -1), (6, 0), (7, 2)$$ and $$(5, 1)$$ are the vertices of a rhombus. Is it a square?
Find the value x, if the distance between the points $$(x,-1)$$and $$(3,2)$$ is $$5$$.
Prove that the points $$(-3,0), (1,-3)$$ and $$(4,1)$$ are the vertices of an isosceles right-angled triangle. Find the area of this triangle
Show that the points (1,-1), (5,2) and (9,5) are collinear.
If two vertices of an equilateral triangle be (0,0), $$\left( 3,\sqrt { 3 } \right) $$, find the third vertex.
A line through the origin intersects $$x= 1, y=2, $$ and $$x+y =4$$, at $$A, B$$ and $$C $$respectively, such that $$OA. OB. OC = 8\sqrt2$$. Find the equation of the line is $$y=mx$$.Find the value of $$m$$
In $$\Delta ABC, A \equiv (6, 3), B \equiv (-3, 5), C \equiv (4, -2)$$. $$P$$ is any point $$(x, y)$$. Show how that $$\dfrac{\Delta(PBC)}{\Delta(ABC)} = \left|\dfrac{x + y - 2}{7}\right|$$
Find the coordinate of the point on the y axis which at a distance of $$10$$ units from the point $$\left( { - 8,4} \right)$$
Find the area of the triangle $$ABC$$ with $$A(1,-4)$$ and mid points of sides through $$A$$ being $$(2,-1)$$ and $$(0,-1)$$
A parallel line is drawn from point $$P(5, 3)$$ to $$y$$-axis, what is the distance between the line and $$y$$-axis.
If the points $$(2, 1)$$ and $$(1, -2)$$ are equidistant from the point $$(x, y)$$, show that $$x + 3y = 0$$.
Find the direction cosines of the sides of the triangle whose vertices are $$(3, 5, -4)$$ and $$(-1, 1, 2)$$ and $$( -5, -5, -2)$$. What type triangle is it?
If (-4,0) and (4,0) are two vertices of an equilateral triangle, find the coordinates of its third vertex.
Distance between parallel lines $$9x^2-6xy +y^2+18x-6y +8=0$$ is $$\dfrac{m}{\sqrt n}$$.Find $$m+n$$
Find the area of $$\triangle$$ le with coordinate of vertices $$A(-5,-1),B(3,-5)$$ and $$C(5,2)$$ resp. Find the length of median trough $$B$$.
If $$(4, 3)$$ and $$(-2, -1)$$ are positive vertex of a parallelogram and third vertex $$(1, 0)$$ then the product of co-ordinates of the four vertex?
$$\int {\dfrac{{{e^x}dx}}{{\left( {1 + {e^{2x}}} \right)}}} $$
Find the equation of a line which is equidistant from the lines $$x = -2$$ and $$x = 6$$.
Find the distance between the points:
$$\left( {\operatorname{Cos} \theta ,\operatorname{Sin} \theta } \right),\left( {\operatorname{Sin} \theta ,\operatorname-{Cos} \theta } \right)$$
Find the value of $$k$$ for which the area of the triangle with vertices $$(2,-2),(-3,3k)$$ and $$(-2,3)$$ is $$20$$sq.units.
The distances of point $$P(x,y)$$ from the points $$A(1,-3)$$ and $$B(-2,2)$$ are in the ratio $$2:3$$.
Show that :
$$5{x^2} + 5{y^2} - 34x + 70y + 58 = 0$$
Check whether $$(5, -2),(6,4)$$ and $$(7,-2)$$ are the vertices of an isosceles triangle.
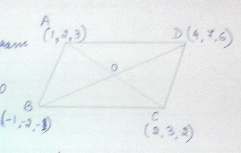
Show that the points $$A(1,2,3),B(-1,-2,-3),C(2,3,2)$$ and $$D(4,7,6)$$ are the vertices of a parallelogram.
Find the distance of the point $$(6, 8)$$ and the origin.
The points $$A(2, 9)$$, $$B(a, 5)$$, $$C(5, 5)$$ are the vertices of a triangle ABC right angled at B. find the value of $$'a'$$ and hence the area of $$\Delta ABC$$.
Find the area of triangles formed by the following points :
(3,4), (2, -1), (4, -6)
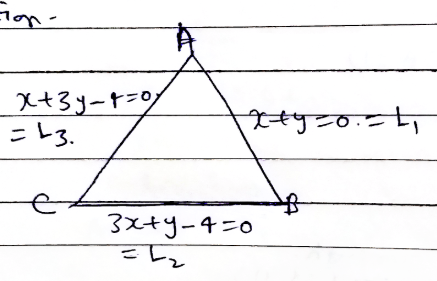
Show that straight lines $$x+y=0 , 3x+y-4=0$$ , $$x+3y-4 =0$$ form isosceles
Four points $$A(6, 3)$$, $$B)-3, 5)$$, $$C(4, -2)$$ and $$D(x, 3x)$$ are given such that $$\dfrac{\Delta DBC}{\Delta ABC}=\dfrac{1}{2}$$, find x.
Draw the graph of the equation $$\dfrac{x}{4}+\dfrac{y}{3}=1$$. Also, find the area of the triangle formed by the line and the coordinate axes.
If the vertices of a triangle have integral coordinates, prove that the triangle cannot be equilateral.
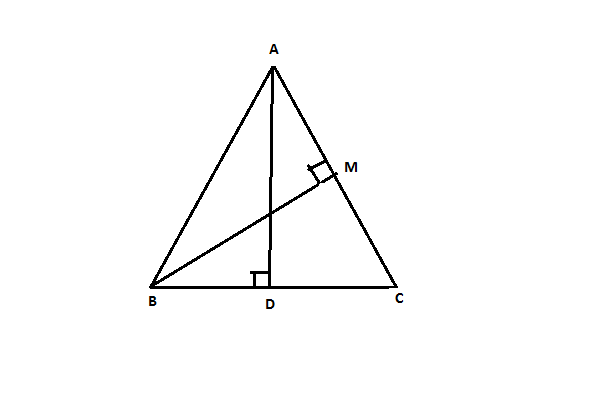
Given that $$A(5, 4), B(-3, -2)$$ and $$C(1, -8)$$ are the vertices of a $$\triangle ABC$$
Find:
i)The slope of median $$AD$$,
ii) The slope of altitude $$BM$$.
Find the area of the triangle formed by joining the mid-points of the sides whose vertices are (0, -1), (2, 1) and (0, 3). Also find the ratio of the given triangle to the newly formed triangle.
Find the acute angle between the two lines:
$$AB$$ and $$CD$$ passing through the points $$A\equiv (3,1,-2),B\equiv (4,0,-4)$$ and $$C\equiv (4,-3,3)$$, $$D\equiv (6,-2,2)$$
If a line makes angles $$90^o$$, $$60^o$$ and $$30^o$$ with the positive direction of x, y and z axis respectively find its direction cosines.
If the points $$(6, 9),(10, x)$$ and $$(-6, -7)$$ are collinear then find the value of $$x$$.
Find the value of x, if the distance between the points (x, -1) and (3, 2) is 5.
Find the relation between $$x$$ and $$y$$ if the points $$A(X,Y), B(-5,7)$$ and $$C(-4, 5) \ $$are collinear.
The line $$3x+2y=24$$ meets the y- axis at A and the x -axis at B. The perpendicular bisectors of AB meets the line through $$(0,-1)$$ parallel to x - axis at $$C$$. Find the area of the triangle ABC ?
Find the distance of the line $$4x - y = 0$$ find the point $$P(4, 1)$$ measured along the line making an angle of $$135^o$$ with the positive x-axis.
If the points $$(x, y), (-5, -2)$$ and $$(3, -5)$$ are collinear, then prove that $$3x + 8y + 31 = 0$$.
Find the perimeter of the rectangle formed by the joining the points $$A(-3,-1),B(5,-1),C(5,3)$$ and $$D(-3,3)$$ in sides.
If two vertices of an equilateral triangle are $$(3, 0)$$ and $$(6, 0)$$, find the third vertex.
Determine if the points $$(1, 5) , (2, 3)$$ and $$(-2, -11)$$ are collinear , by distance formula.
If $$D(3,-1) E(2,6) F(-5,7)$$ are the mid points of the sides of triangle $$ABC$$. find the area of $$\Delta ABC$$
Prove that the area of triangle with vertices $$(t,t-2), (t+2, t+2), (t+3, t) $$ is independent of t.
Equation of the base of an equilateral triangle is $$3x + 4y = 9$$ and its Vertex is at the point $$\left( {1,2} \right)$$ . Find the length of each side of the triangle .
Prove that the points $$(a, b), (a_{1}, b_{1}$$ and $$(a - a_{1}, b - b_{1})$$ are collinear if $$ab_{1} = a_{1}b$$.
The area of the triangle formed by points $$\left( 0,0 \right) \quad \left( { 3 }{ \quad ,\frac { \pi }{ 2 } } \right) \quad and\quad \left( { 3 }\quad ,{ \frac { \pi }{ 6 } } \right) $$ is
Find the area of whose vertices are$$A(1,1,2)$$ $$B(2,3,5)$$ and . $$C(1,5,5)$$
Find the values of $$k$$, if the area of triangle is $$35\ sq. units$$ whose vertices are $$(2, -6), (5, 4)$$ and $$(k, 4)$$.
Find the equation of locus of $$P$$, if the ratio of the distance from $$P$$ to $$(5, -4)$$ and $$(7, 6)$$ is $$2 : 3$$.
If $$(x, y)$$ be on the line joining the two points $$(1, -3)$$ and $$(-4, 2)$$, prove that $$x + y + 2 = 0$$.
If $$A\left( 5,\ 2 \right), B\left( 3,\ 4 \right), C\left( x,\ y \right)$$ are collinear and $$AB=BC$$, the find $$\left( x,\ y \right)$$.
If the points $$(4,-4),(-4,4)$$ and $$(x,y)$$ from an equilateral triangle, find $$x$$ and $$y$$.
If the points $$(1,1)(-1,-1)$$ and $$(-\sqrt {3},k)$$ are vertices of an equilateral triangle, Find the value of $$k$$
Find the value of $$k$$, if the points $$A(7, -2), B(5, 1)$$ and $$C(3, 2k)$$ are collinear.
Find the relation between $$x$$ and $$y$$ if the point $$P(x,y)$$ is equidistance from the point $$A(7,0) $$ and $$ B (0,5) $$
In PAB,PA=PB and area of PAB= sq. units. Find the coordinates of P if coordinates of A and B are (1,2) and (3,8) respectively.
If the point $$(x,y)$$ be equidistance from the point $$(a+b,b-a)$$ and $$(a-b,a+b)$$ , prove that $$bx = ay$$.
$$A(3,-4),B(5,-2),C(-1,8)$$ are the vertices of $$\triangle ABC.D,E,F$$ are the mid-points of sides $$\overline {BC},\overline {CA}$$ and $$\overline {AB}$$ respectively. Find area of $$\triangle ABC$$. Using coordinates of $$D,E,F$$, find area of $$\triangle DEF$$. Hence show that the $$ABC=4(DEF) $$
Find area of the triangle with vertices at the point given in each of the following:
$$\left (1,0\right), \left (6,0\right), \left (4,3\right)$$
$$\left (2,7\right), \left (1,1\right), \left (10,8\right)$$
$$\left (-2,-3\right), \left (3,2\right), \left (-1,-8\right)$$
Find a point which is equidistant from the points $$A\left( { - 5,4} \right)$$ and $$B\left( { - 1,6} \right)$$ .How many such points are there?
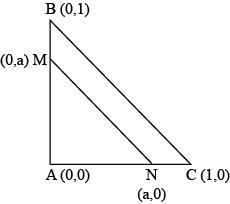
$$\triangle {ABC}$$ lies in the plane with $$A=(0,0), B(0,1)$$ and $$C(1,0)$$. Points $$M$$ and $$N$$ are chosen on $$AB$$ and $$AC$$, respectively, such that $$MN$$ is parallel to $$BC$$ and $$MN$$ divides the area of $$\triangle {ABC}$$ in half. Find the coordinates of $$M$$.
Shown that the point $$(5,-1,1),(7,-4,7),(1,-6,10)$$ and $$(-1,-3,4)$$ are the vertices of a rhombus.
Find the area of the triangle formed by joining the mid point of the triangle whose vertices are (0,-1),(2,1)and (0,3). Find the ratio of area of the triangle formed to the area of the given triangle.
Find the equation of the set of all points whose distances from $$(0, 4)$$ are $$\dfrac{2}{3}$$ of their distances from the line $$y=9$$.
The vertices of triangle ABC are A (4, 6), B (1, 5) and C (7, 2). A line is drawn to intersect sides AB and AC at D and E respectively ,such that $$\dfrac{AD}{AB}=\dfrac{AE}{AC}=\dfrac{1}{4}$$. Calculate the area of the $$\triangle ADE$$ and compare it with the area $$\triangle ABC $$ ?
Given the vertices$$A\left( {10,4} \right),B\left( { - 4,9} \right),C\left( { - 2, - 1} \right)$$ of $$\Delta $$ABC find the area of the triangle:
Solve it:-
Through the point $$(3,4)$$ are drawn two straight lines each inclined at $${45^ \circ }$$ to the straight line $$x-y=2$$ find their equations and also find the area of triangle bounded by the three lines.
Find the distance of the point $$P ( - 6,8 )$$ from the origin.
Find the area of the triangle formed by joining the mid points of the sides of the triangle
whose vertices are $$( 0 , - 1 ) , ( 2,1 )$$ and $$( 0,3 )$$ .
If $$\mathrm { A } ( 4,3 ) , \mathrm { B } ( 6 , - 2 )$$ and $$\mathrm { C } ( a , - 3 )$$ are the vertices of a triangle right angled at $$\mathrm { A } ,$$ find $$a$$ .
Find the angles between the lines
$$x-\sqrt{3}y=-1$$
Find the angles between the lines
$$x+\sqrt{3}y=1$$
Find the angles between the lines
$$x+\sqrt{3}y=5$$
Find the area of the triangle formed by joining the mid-point of the sides of the triangle whose vertices are $$(0,-1),(2,1)$$ and $$(0,3)$$. Find the ratio of this area to the area of the given triangle.
Find the linear equation between $$x$$ and $$y$$ such that $$P(x,y)$$ is equidistant from the points $$A(1,4)$$ and $$B(-1,2)$$.
Find the area of the triangle whose vertices are (-5,-1)(3,-5)(5,2)
Find a relation between $$a$$ and $$b$$ if the points $$A(-2,1), B(a,b)$$ and $$C(4,-1)$$ are collinear
Find the area of the triangle whose vertices are $$( - 5, - 1) ,(3, - 5)$$and $$(5,2)$$
If $$A = \left( {1, - 2, - 1} \right),\,B = \left( {4,0, - 3} \right),\,C = \left( {1,2, - 1} \right)$$ and $$D = \left( {2, - 4, - 5} \right)$$, find the distance between $$AB$$ and $$CD$$.
If the distance between the points $$A(4, k)$$ and $$B(1, 0)$$ is $$5 units $$, then what can be the possible values of $$k$$?
The abscissa of a point A is twice its ordinate and $$B \equiv ( 10,0 ) .$$ Find the co-ordinates of A if $$A B = 5$$ units.
The points $$A (2a,4a), B(2a,6a)$$ and $$C (2a + \sqrt 3 a,5a)$$, $$\left( {\text{when}\ a > o} \right)$$ vertices of
If the vertices of a triangle are (1, k), (4, -3), (-9, 7) and its area is 15 sq units. Find the values of k.
Find the area of the triangle formed by the line $$\dfrac{x}{a}+\dfrac{y}{b}=1$$ and the $$x-$$ axis and $$y-$$ axis.
If $$P(x, y)$$ is equidistant from $$A(a+b, b-a)$$ and $$B(a-b, a+b)$$, show that $$bx=ay$$.
Find the area of the triangle whose vertices are $$(-5,-1)(3,-5)(5,2).$$
If the point (x , y) is equivalent from the points (a + b, b - a) and (a - b, a+ b) prove that bx$$=$$ay.
Find the area of the triangle whose vertices are $$\left(10,-6\right),\left(2,5\right)$$ and $$\left(-1,3\right)$$.
If the coordinates of two points $$A,\ B$$ are $$(1,\ 2)(3,\ 8)$$ respectively, find a point $$P$$ such that$$|PA|=|PB|$$ and area of $$\triangle PAB=10$$.
The area of a triangle is $$5\ sq. unit$$. If two vertices of the triangle are $$(2,1),(3,-2)$$ and the third vertex is $$(x,y)$$ where $$y=x+3$$, then find the coordinates of the third vertex.
Find the nature of the triangle formed by the points $$A\left(4,\,0\right),\,B\left(-1,\,-1\right),C\left(3,\,5\right)$$
The point $$A\left( {0,3} \right),B\left( { - 2,a} \right)$$ and $$C\left( { - 1,4} \right)$$ are the vertices of a right angled triangle at $$A$$, find the value of $$a$$.
Find the point on the X-axis which is equidistant from A(-3,4) and B(1,-4)
Let $$P\left(-5,1\right),\,Q\left(3,\,5\right)$$ and $$A$$ divide $$PQ$$ in the ratio $$k:1$$.Find the value of $$k$$ for which the area of the triangle $$ABC$$, where $$B=\left(1,\,5\right)$$ and $$C=\left(7,-2\right)$$ is $$2$$
Find the distance of point $$(2,\ 3, -5)$$ from the plane $$x+2y-2z-9=0$$
Find a relation between x and y such that the point (x,y) is equidistant from the points (7,1) and (3,5).
If equation of line is $$\left( {y - 2\sqrt 3 } \right) = \dfrac{{\sqrt 3 + 1}}{{\sqrt 3 - 1}}\left( {x - 2} \right)$$, then find the slope.
The point $$A(2,3), B(4,-1), C(-1,2)$$ are the vertices of $$\triangle ABC$$. Find the length of perpendicular from $$C$$ on $$AB$$ and hence find area of $$\triangle ABC$$.
If the lines through the point $$(4,1,2)$$ ans $$(5,k,0)$$ is parallel to the line through $$(2,1,1)$$ and $$(3,3,-1)$$, then value of k is?
The area of a triangle whose vertices are (2, 3), (3, 5) and (7, 5) is :
What are the points on the $$y-$$axis whose distance from the line $$\dfrac{x}{3}+\dfrac{y}{4}=1$$ is $$4$$ units.
Find the joint equation of lines passing through the origin, each of which making angle of measure $$150^{o}$$ with the line $$x-y=0$$.
Show that the tangent of an angle between the lines $$\frac{x}{a}+\frac{y}{b}=1 and \frac{x}{a}-\frac{y}{b}= 1\ is \frac{2ab}{a^{2}-b^{2}}$$
Prove that the points $$\left(0,5\right), \left(0,-9\right)$$ and $$\left(3,6\right)$$ are non-collinear.
Find the foot point of $$1$$ from the point $$(-2,3)$$ to the line $$2x-y-3=0$$

Find a point on the Y - axis which is equidistant from the points A(-4,3) and B(6,5).
Find the equations of lines with slope $$-2$$ and length of perpendicular distance from origin is equal to $$\sqrt{3}$$ units.
Find a point on x-axis which is equidistant from (2, -5) and (-2, 9)
Find the points on $$x-$$axis that is equidistant from $$(2,7)$$ & $$(5,-2)$$.
If the points $$A(4,3)$$ and $$B(x,5)$$ are on the circle with centre $$O(2,3)$$, find the value of $$x$$.
Find the coordinates of points on the x-axis which are at a distance of 17 units from the point (11,-8)
The area of a trapezium is $$90$$sq.cm and its height is $$6$$cm.If one of the parallel sides is twice that of the others.Find the two parallel sides.
What are the points on the $$y-$$axis whose distance from the line $$\dfrac{x}{6}-\dfrac{y}{8}=1$$ is $$-3$$ units.
The distance between the points $$\left(8,9\right)$$ and $$\left(-7,4\right)$$ is
The points A(4,7) B(p,3) and C(7,3) are the vertices of a right triangle, right -angled at B, Find of P.
Find the distance between the points $$\left(2,1\right)$$ and $$\left(3,2\right)$$
If the three vertices of a parallelogram are $$\left(-1,3\right),\left(2,4\right)$$ and $$\left(3,5\right)$$,find the fourth vertex.
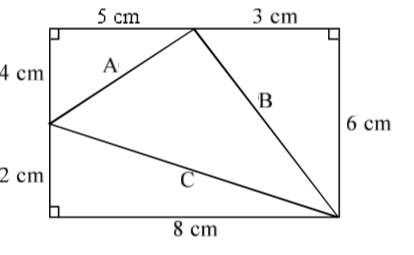
Find the area of the shaded triangle in the given figure.
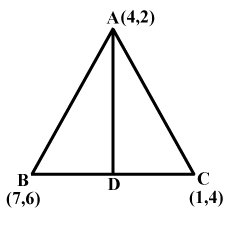
Find the co-ordinates of the incentre of the triangle whose vertices are $$\left(-2,4\right),\left(5,5\right)$$ and $$\left(4,-2\right)$$
Find the area of the triangle whose vertices are $$(2,5),(-1,0),(2,-4)$$.
Find the shortest distance between the $$x^2+y^2=9$$ and $$(6,8)$$ is
The distance between $$(4,0) $$ and $$(7,4)$$
Find the area of a triangle whose vertices are
$$(3, 6), (-1, 3), (2, -1)$$
Find the slope of the line, which makes an angle of $$30^{o}$$ with the positive direction of $$y-axis$$ measured anticlockwise.
The distance between the points $$\left(\dfrac{1}{2},\dfrac{3}{2}\right)$$ and $$\left(\dfrac{3}{2},\dfrac{-1}{2}\right)$$ is
Find the area of the triangle formed by the points $$\left(5,2\right),\,\left(-9,-3\right)$$ and $$\left(-3,-5\right)$$
If $$A(a^{2},2a)B(\frac{1}{a^{2}},\frac{-2}{a})$$ and S(1,0) then prove that $$\frac{1}{SA}+\frac{1}{SB}=1$$
A line is of length 10 units and one of its ends is (-2,3). If the ordinate of the order end is 9, prove that the abscissa of the other end is 6 or -10.
Find the distance between $$\left(3,6\right)$$ from the origin.
Find the distance between $$\left(x+3,x-3\right)$$ from the origin.
If the point $$A(2,-4)$$ is equidistance from the points $$P(3,8)$$ and $$Q(-10,y)$$ find the value of $$y$$. Also find the value of $$PQ$$.
How are the points $$(1, -1), (2, 2)$$ and $$(-1, 2)$$ situated with respect to the circle $${x}^{2}+{y}^{2}+2x–4y-5=0$$
Prove that the points $$A(0,0), B(0,2)$$ and $$C(2,0)$$ are the vertices of an equilateral triangle.
Write the perpendicular distance of point $$(-3, 2)$$ from x-axis.
Find the point on the curve $${ y=x }^{ 3 }-{ 2x }^{ 2 }-x,$$ where the tangents are parallel to $$3x-y+1=0$$.
Write the formula for area of a triangle where A$$\left( { x }_{ 1 },{ y }_{ 1 } \right) ,B\left( { x }_{ x },{ y }_{ 2 } \right) $$ and $$C\left( { x }_{ 3 },{ y }_{ 3 } \right) $$ are the vertices of a triangle $$ABC$$.
Find the area of the triangle with vertices at the points :$$(-1,-8),(-2,-3) \ and \ (3,2)$$
Find the area of the triangle with vertices at the points :$$(0,0),(6,0) \ and \ (4,3)$$
If the coordinates of the points $$A, B, C, D$$ be $$(1, 2, 3), (4, 5, 7), (-4,3, -6)$$ and $$(2, 9, 2)$$ respectively, then find the angle between the lines $$AB$$ and $$CD$$.
If the area of the triangle with vertices at the points:
$$(2,7),(1,1) \ and \ (10,8)$$
is $$\left (\dfrac {b}{2}\right )$$ sq. uts.
Then what is the value of b?
Find the area of the triangle with vertices at the points: (3,8),(-4,2) and (5,-1). If the area is $$\left ( \dfrac a2 \right )$$ sq. units, then what will be the value of $$a$$?
Find the area of the triangle with vertices as given below:
$$(0,0),(6,0)$$ and $$(4,3)$$
Show that the points $$(0,7,10),(-1,6,6)$$ and $$(-4,9,6)$$ are the vertices of an isosceles right-angled triangle.
Verify the following:
$$(0,7,10),(-1,6,6)$$ and $$(-4,9,6)$$ are vertices of a right angled traingle.
Verify the following:
$$(0,7,-10),(1,6,-6)$$ and $$(4,9,-6)$$ are vertices of an isosceles triangle.
Prove that the triangle formed by joining the three points whose coordinates are $$(1,2,3), (2,3,1)$$ and $$(3,1,2)$$ is an equilateral triangle.
Find the slope of the line which make the following angle with the positive direction of $$x-$$ axis :
$$\dfrac{2\pi}{3}$$
Find the slope of the lines which make the following angles with the positive direction of $$x-$$ axis :
$$\dfrac{\pi}{3}$$
Show that the product of perpendiculars on the line $$\dfrac {x}{a}\cos \theta +\dfrac {y}{b}\sin \theta =1$$ from the points $$(\pm \sqrt {a^2 -b^2}, 0)$$ is $$b^2$$.
Show that the points $$(a,b,c),(b,c,a)$$ and $$(c,a,b)$$ are the vertices of a equilateral triangle.
Find the inclination of a line whose slope is
$$\sqrt{3}$$
Find the slope of a line which passes through the points
$$(0, -3)$$ and $$(2, 1)$$
Find the inclination of a line whose slope is $$-1$$
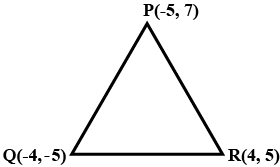
Find the area of triangle $$PQR$$ formed by the points $$P(-5, 7), Q(-4,-5)$$ and $$R(4,5)$$
Find the inclination of a line whose slope is: $$\sqrt {3}$$.
Find the slope of a line which passes through the points
$$(0, 0)$$ and $$(4, -2)$$
Find the slope of a line which passes through the points
$$(-2, 3)$$ and $$(4, -6)$$
Find the slope of a line which passes through the points
$$(2, 5)$$ and $$(-4, -4)$$
Find the equation of a line which is equidistant from the lines $$x=-2$$ and $$x=6$$
Find the equation of a line which is equidistant from the lines $$y=8$$ and $$y=-2$$.
Using slopes, show that the points $$A(6, -1), B(5, 0)$$ and $$C(2, 3)$$ are collinear.
Show that the line through the points $$(5, 6)$$ and $$(2, 3)$$ is parallel to the line through the points $$(9,-2)$$ and $$(6, -5)$$.
Show that the line through the points $$(-2, 6)$$ and $$(4, 8)$$ is perpendicular to the line through the points $$(3, -3)$$ and $$(5, -9)$$.
Using slopes, find the value of $$x$$ for which the points $$A(5, 1), B(1, -1)$$ and $$C(x, 4)$$ are collinear.
Show that the points $$A(2,-2), B(8,4), C(5,7)$$ and $$D(-1, 1)$$ are the angular points of a rectangle.
Show that $$A(3,2), B(0,5), C(-3,2)$$ and $$D(0,-1)$$ are the vertices of a square.
If $$A(2, -5), B(-2, 5), C(x, 3)$$ and $$D(1, 1)$$ be four points such that $$AB$$ and $$CD$$ are perpendicular to each other, find the value of $$x$$.
If the slope of the line joining the points $$A(x, 2)$$ and $$B(6, -8)$$ is $$\dfrac{-5}{4}$$, find the value of $$x$$.
Using slopes, prove that the points $$A(-2, -1), B(1, 0), C(4, 3)$$ and $$D(1, 2)$$ are the vertices of a parallelogram.
Find the slope and the equation of the line passing through the points:
$$(3,-2)$$ and $$(-5,-7)$$
Show that the points $$A(2,-1), B(3,4), C(-2,3)$$ and $$D(-3,-2)$$ are the vertices of rhombus.
If the points $$A(h, k), B(x_1, y_1)$$ and $$C(x_2, y_2)$$ lies on a line then show that $$(h-x_1)(y_2-y_1)=(k-y_1)(x_2-x)$$.
If the points $$A(-2,-1), B(1,0), C(x,3)$$ and $$D(1,y)$$ are the vertices of a parallelogram , find the value of $$x$$ and $$y$$.
Find the slope and the equation of the line passing through the points:
$$(a,b)$$ and $$(-a,b)$$
Show that the points $$A(-5,1), B(5,5)$$ and $$C(10,7)$$ are collinear.
Find the slope and the equation of the line passing through the points:
$$(-1,1)$$ and $$(2,-4)$$
Show that $$A(1,-2), B(3,6), C(5,10)$$ and $$D(3,2)$$ are the vertices of a parallelogram.
Find the area of $$\triangle ABC$$ whose vertices are $$A(-3,-5), B(5,2)$$ and $$C(-9,-3)$$.
Find the value of $$k$$ for which the points $$A(-2,3), B(1,2)$$ and $$C(k, 0)$$ are collinear.
Find the area of the triangle, the equation of whose sides are $$y=x, y=2x$$ and $$y-3x=4$$
Find the area of quadrilateral whose vertices are $$A(-4,5), B(0,7), C(5,-5)$$ and $$D(-4,-2)$$.
Find the area of the triangle formed by the lines $$x=0, y=1$$ and $$2x+y=2$$.
Find the area of $$\Delta ABC$$ whose vertices are $$A(1, 2), B(-2, 3)$$ and $$C(-3, -4)$$.
If the points $$A(a, 0), B(0, b)$$ and $$P(x, y)$$ are collinear, using slopes, prove that $$\dfrac{x}{a}+\dfrac{y}{b}=1$$.
A line passes through the points $$A(4, -6)$$ and $$B(-2, -5)$$. Show that the line $$AB$$ makes and obtuse angle with $$x-$$ axis.
Find the area of $$\triangle ABC$$, the midpoints of whose sides $$AB, BC$$ and $$CA$$ are $$D(3,-1), E(5,3)$$ and $$F(1,-3)$$ respectively.
Find the area of the triangle formed by the lines $$x+y=6, x-3y=2$$ and $$5x-3y+2=0$$.
Find the area of $$\Delta ABC$$ whose vertices are $$A(-5, 7), B(-4, -5)$$ and $$C(4, 5)$$.
$$A(6, 1), B(8, 2)$$ and $$C(9, 4)$$ are the vertices of a parallelogram ABCD. If E is the midpoint of DC, find the area of $$\Delta ADE$$.
If the vertices of $$\Delta$$ABC be $$A(1, -3), B(4, p)$$ and $$C(-9, 7)$$ and its area is $$15$$ square units, find the values of p.
Find the area of the triangle formed by joining the midpoints of the sides of the triangle whose vertices are $$A(2, 1), B(4, 3)$$ and $$C(2, 5)$$.
Find the area of $$\Delta ABC$$ whose vertices are $$A(3, 8), B(-4, 2)$$ and $$C(5, -1)$$.
The area of a triangle is $$5$$ sq units. Two of its vertices are $$(2, 1)$$ and $$(3, -2)$$. If the third vertex is $$(7/2, y)$$, find the value of y.
Find the area of $$\Delta ABC$$ with $$A(1, -4)$$ and midpoints of sides through A being $$(2, -1)$$ and $$(0, -1)$$.
Find the area of $$\Delta ABC$$ whose vertices are $$A(10, -6), B(2, 5)$$ and $$C(-1, 3)$$.
Find the value of k so that the area of teh triange with vertices $$A(k+1, 1), B(4, -3)$$ and $$C(7, -k)$$ is $$6$$ square units.
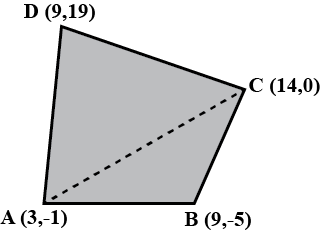
Find the area of quadrilateral ABCD whose vertices are $$A(3, -1), B(9, -5), C(14, 0)$$ and $$D(9, 19)$$.
Find the area of the triangle the coordinates of whose vertices are $$(5 , 2) , (-9 , -3)$$ and $$(-3 , -5)$$.
For what value of $$k(k > 0)$$ is the area of the triangle with vertices $$(-2, 5), (k, -4)$$ and $$(2k+1, 10)$$ equal to $$53$$ square units?
Find the area of the triangle the coordinates of whose angular points are respectively
$$(0 , 4) , (3 , 6)$$ and $$(-8 , -2)$$
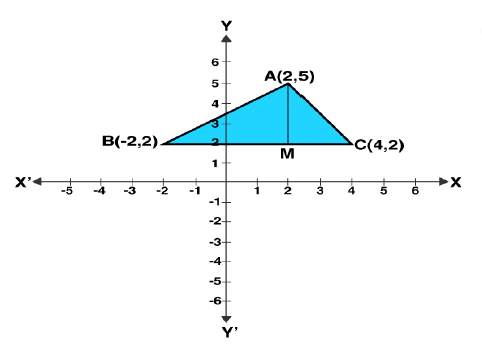
Plot the points $$\displaystyle A (2, 5), B (-2, 2)$$ and $$\displaystyle C (4, 2)$$ on a graph paper. Join $$\displaystyle AB, BC$$ and $$\displaystyle AC$$.
Calculate the area of $$\displaystyle \Delta ABC$$.
Find the area of the triangle the coordinates of whose angular points are respectively
$$(a , b + c) , (a , b - c)$$ and $$(-a , c)$$
Find the area of the triangle the coordinates of whose angular points are respectively
$$(1 , 3) , (-7 , 6)$$ and $$(5 , -1)$$
The axes being inclined at angle of $$60^{o}$$, find the inclination to the axis of $$x$$ the straight lines whose equations are
(1) $$y=2x+5$$,
And
(2) $$2y=\left(\surd3-1\right)x+7$$
Find the area of $$\Delta ABC$$ with vertices $$A(0, -1), B(2, 1)$$ and $$C(0, 3)$$. Also, find the area of the triangle formed by joining the midpoints of its sides. Show that the ratio of the areas of these two triangles is $$4:1$$.
If the point $$ P(4,-2) $$ is the one end of the focal chord $$ P Q $$ Of the $$ y^{2}=x, $$ then find the slope of the tangent at $$ Q $$.
Prove (by showing that the area of the triangle formed by them is zero) that the following sets of three points are in a straight line:
$$(1, 4), (3, -2), $$ and $$(-3, 16).$$
Find the areas of the triangles the coordinates of whose angular points are
$$(-3 , -30^\circ) , (5 , 150^\circ) , $$ and $$(7 , 210^\circ).$$
Find the areas of the triangles the coordinates of whose angular points are$$\left(-a , \dfrac {\pi}{6}\right) , \left(a , \dfrac {\pi}{2}\right) , $$ and $$\left(-2a , -\dfrac {2\pi}{3}\right).$$
A median of a triangle divides it into two triangles of equal areas. Verify this result for $$\Delta \mathrm{ABC}$$ whose vertices are $$A(4,-6), B(3,-2),$$ and $$C(5,2)$$
What is the area of the triangle formed by the points $$O(0,0), A(-3,0)$$ and $$B(5,0) ?$$
A line through the origin intersects the parabola $$ 5 y=2 x^{2} -9 x+10 $$ at two points whose $$ x $$ -coordinates add up to 17 then find the slope of the line.
The area of the $$\Delta ABC$$, coordinates of whose vertices are $$A(2,0), \ B(4,5)$$ and $$C(6,3)$$ is..........
Find the inclination of a line whose gradient is
(i)$$ \, 1$$
(ii) $$\sqrt{3}$$
(iii) $$1/\sqrt{3}$$
Prove that the area of the triangle formed by the normal's to the parabola at the points $$\left(at_{1}^{2}, 2at_{1}\right), \left(at_{2}^{2}, 2at_{2}\right)$$ and $$\left(at_{3}^{2}, 2at_{3}\right)$$ is $$\dfrac{a^{2}}{2}\left(t_{2}-t_{3}\right)\left(t_{3}-t_{1}\right)\left(t_{1}-t_{2}\right)\left(t_{1}+t_{2}+t_{3}\right)^{2}$$.
Find the area of the triangle whose vertices are $$(-8 , 4) (-6 , 6) $$ and $$(-3 , 9) $$ .
If $$A(4,2), B(7,6)$$ and $$C(1,4)$$ are the vertices of a $$\Delta A B C$$ and $$A D$$ is its median, prove that the median AD divides $$\Delta A B C$$ into two triangles of equal areas.
Find the area of the triangle whose vertices are $$(3, -4), (7, 5), (-1, 10)$$
Draw the graph of $$4x-3y+12 = 0$$ and use it to find the area of the triangle formed by the line and the co-ordinate axes. Take $$2 cm = 1$$ unit on both axes.
Find the area of the triangle whose vertices are
$$(-1.5, 3), (6, -2), (-3, 4)$$
In the given figure, $$PQR$$ is equilateral. If the coordinates of the points $$Q$$ and $$R$$ are $$(0, 2)$$ and $$(0, -2)$$ respectively, find the coordinates of the point $$P.$$
In Figure, the vertices of $$\Delta$$ ABC are $$A(4,6), B(1,5)$$ and $$C(7,2) .$$ A line segment $$DE$$ is drawn to intersect the sides $$A B$$ and $$A C$$ at $$D$$ and $$E$$ respectively such that $$\dfrac{A D}{A B}=\dfrac{A E}{A C}=\dfrac{1}{3}$$. Calculate the area of $$\Delta{ADE}$$ and compare it with area of $$\Delta{ABC}$$.
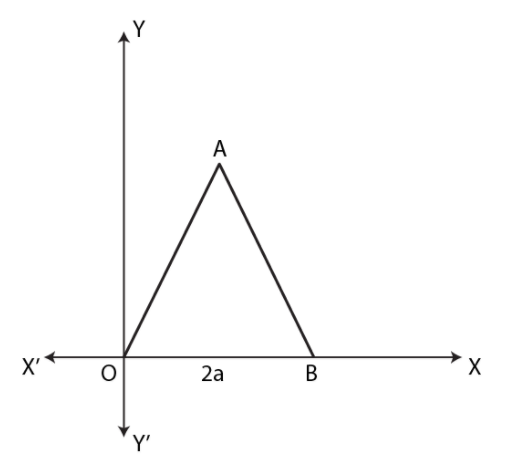
The adjoining figure shows an equilateral triangle $$OAB$$ with each side $$= 2a$$ units. Find the coordinates of the vertices.
Find the equation of the line which passes through $$\left( 2, 2\sqrt{3} \right)$$ and is inclined with the x-axis at an angle of $$75^{0}$$.
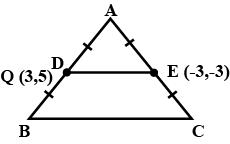
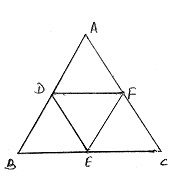
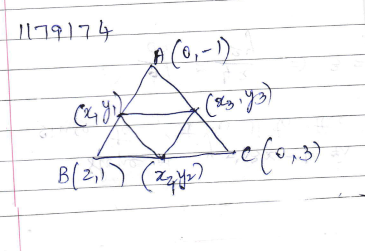
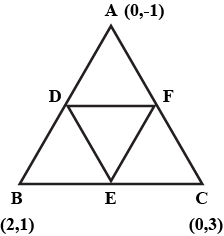
Three vertices of a triangle are $$A(1, 2), B(-3, 6)$$ and $$C(5, 4).$$ If D, E, and C, respectively, show that the area of triangle ABC is four times the area of triangle DEF.
Find the area of the quadrilateral whose vertices taken in order are $$(-4, -2), (-3, -5), (3, -2)$$ and $$(2, 3).$$
Find the area of a triangle ABC if the coordinates of the middle points of the sides of the triangle are $$(-1, -2), (6, 1)$$ and $$(3, 5).$$
Find the area of the triangle whose vertices are
$$(-5, -1), (3, -5), (5, 2)$$
Find the area of the triangle whose vertices are
$$((a + 1)(a + 2), (a + 2)), ((a + 2)(a + 3), (a + 3))$$ and $$((a, 3)(a + 4), (a + 4))$$
Find the area of the triangle whose vertices are
$$(-5, 7), (-4, -5), (4, 5)$$
Find the area of the triangle whose vertices are
$$(2, 3), (-1, 0), (2, -4)$$
Find the area of the triangle whose vertices are
$$(1, -1), (-4, 6), (-3, -5)$$
Find the area of the triangle formed by joining the mid-points of the sides of the triangles whose vertices are $$(0, -1), (2, 1)$$ and $$(0, 3).$$ Find the ratio of this area to the area of the given triangle.
The vertices of $$\Delta ABC$$ are $$A(3, 0), B(0, 6)$$ and $$(6, 9).$$ A straight line DE divides AB and AC in the ratio $$1 : 2$$ at D and E respectively, prove that $$\dfrac{\Delta ABC}{\Delta ADE} = 9$$
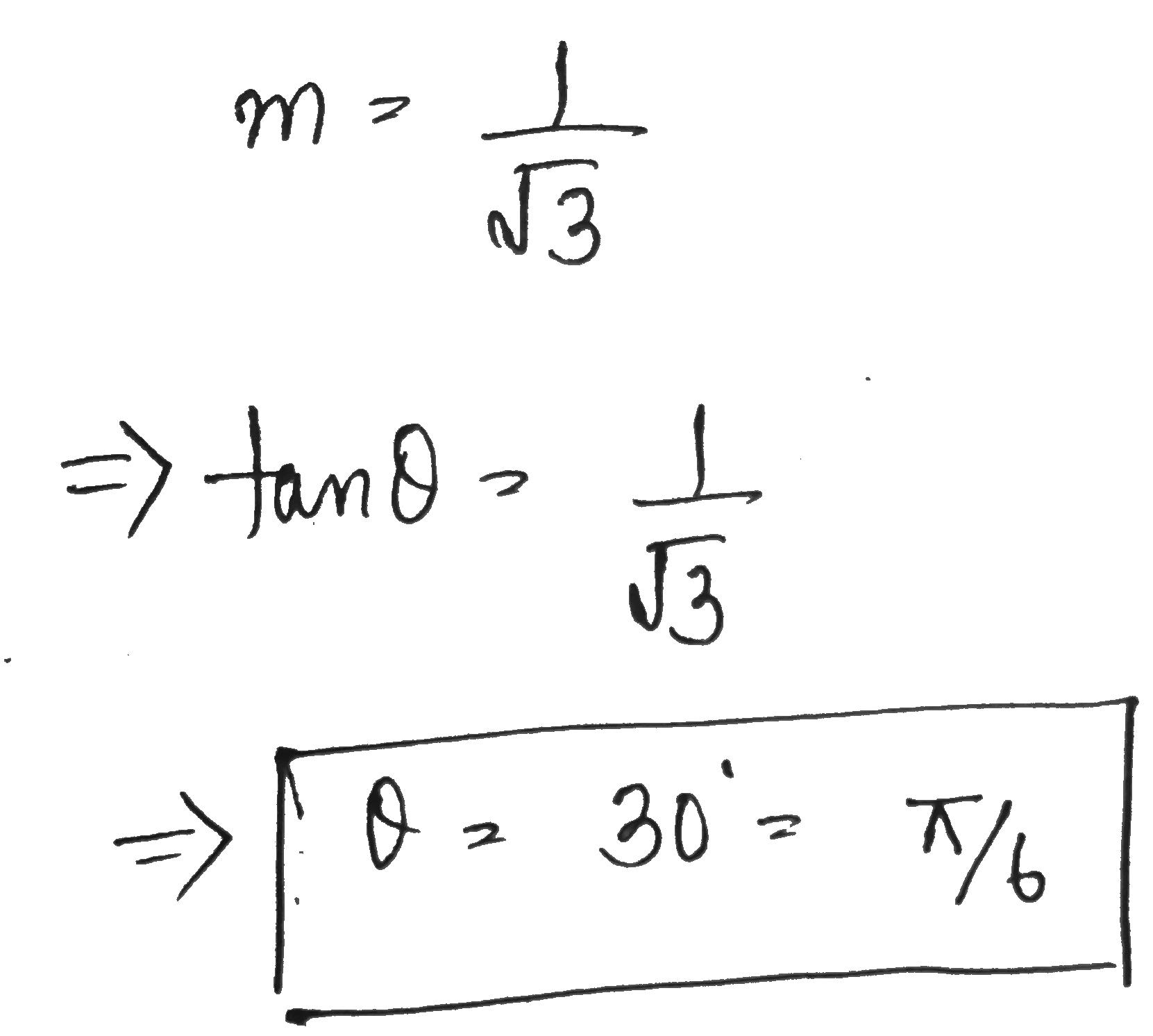
Find the inclination of the line whose slope is $$\dfrac {1}{\sqrt {3}}$$.
The sides of a triangle are given by the equations $$y - 2 = 0; y + 1 = 3(x - 2)$$ and $$x + 2y = 0$$. Find, graphically:
(i) the area of triangle;
(ii) the co-ordinates of the vertices of the triangle.
The points $$A(3,0),B(a,-2)$$ and $$C(4,-1)$$ are the vertices of triangle $$ABC$$ right angled at vertex $$A$$. Find the value $$a$$
Write the slope of the line whose inclination is $$30^{\circ}$$.
Show that points P(2, -2), Q(7, 3), R(11, -1) and S (6, -6) are vertices of a parallelogram.
Find the angle $$P$$ of the triangle whose vertices are $$P(0,-1,-2), Q(3,1,4)$$ and $$R(5,7,1)$$.
Write the slope of the line whose inclination is $$60^{\circ}$$.
Prove that the points $$A(1,-3),B(-3,0)$$ and $$C(4,1)$$ are the vertices of an isosceles right-angled triangle. Find the area of the triangle.
Verify that points P(-2, 2), Q(2, 2) and R(2, 7) are vertices of a right angled triangle.
For the linear equation, given above, draw the graph and then use the graph drawn to find the area of a triangle enclosed by the graph and the co-ordinates axes:
$$3x - (5 - y) = 7$$.
Find the slope of the lines passing through the given point. L (-2, -3) , M (-6, -8)
If A (1, -1), B (0, 4), C (-5, 3) are vertices of a triangle then find the slope of each side.
Find the slope of the lines passing through the given point. C (5, -2) , $$\triangle$$ (7, 3)
Angles made by the line with the positive direction of X-axis is given. Find the slope of these line. $$90^0$$
Show that points A(-4, -7), I3(-1, 2), C(8, 5) and D(5, -4) are vertices of a rhombus ABCD.
Find the slope of the lines passing through the given point. R(0,-3),S(0,4)
Find the slope of the lines passing through the given point. P (-3, 1) , Q (5, -2)
Angles made by the line with the positive direction of X-axis is given. Find the slope of these line. $$60^0$$
Angles made by the line with the positive direction of X-axis is given. Find the slope of these line. $$45^0$$
Find the slope of the lines passing through the given point.E(-4,-2),F(6,3)
Derive the formula for finding the angle between the lines in terms of their slopes
Show that A(-4, -7), B (-1, 2), C (8, 5) and D (5, -4) are the vertices of a parallelogram.
Show that points P(1, -2), Q(5, 2), R(3, -1), S(-1, -5) are the vertices of a parallelogram.
Find the area of $$ABC$$, where vertices are $$A(4,1)B(6,6),C(8,4)(CBSE\ 2010)$$
Find k, if PQ II RS and P(2, 4), Q (3, 6), R(3, 1), S(5, k).
The base of an equilateral triangle with side 2a lies along y -axis such that the mid- point of the base it at the origin . Find the vertices of the triangle
Find k if the line passing through points P(-12,-3) and Q(4, k) has slope $$\dfrac{1}{2}$$.
Show that the line joining the points A(4, 8) and B(5, 5) is parallel to the line joining the points C(2, 4) and DO, 7).
A line passes through $$ (x_{1} , y_{1} ) $$ and $$( h,k)$$ . If slope of the line is m , show that $$k - y_{1} = m (h -x_{1} ) $$
Find the area of the triangle whose vertices are:
$$(-5 , -1) , (3 , -5) , (5 , 2) $$
If $$(1 , 2) , (4 , y) , (x , 6) $$ and $$(3 , 5)$$ are the vertices of a parallelogram taken in order , find $$x$$ and $$y$$.
Line through the points $$(-2, 6) $$ and $$ (4,8) $$ is perpendicular to the line through the points $$(8,12)$$ and $$( x , 24 ) $$ . Find the value of x
Without using pythagoras theorem . Show that the points $$ ( 4 , 4 ) , (3,5) $$ and $$ ( -1 , 1) $$ are the vertices of a right angled triangle
Find the angle between the x-axis and the line joining the point $$(3,-1) $$ and $$ ( 4 , -2) $$
Find the area of the triangle whose vertices are:
$$(2, 3) , (-1 , 0) , (2 , -4) $$
Prove that each of the set of co-ordinates are the vertices of parallelograms.
$$(-5 , -3) , (1 , -11) , (7 , -6) , (1 , 2 )$$
Find the area of the triangle formed by joining the mid-points of the sides of the triangle whose vertices are $$(0 , -1) , (2 , 1) $$ and $$(0 , 3) $$. Find the ratio of this area to the area of the given triangle.
Check whether $$4^n+15n-1$$ is divisible by $$9$$ or not.
Find area of triangle, whose vertices are:
$$(2,5),(-2,-3)$$ and $$(6,0)$$
Find area of triangle, whose vertices are:
$$(0,0),(5,0)$$ and $$(3,4)$$
Find area of $$\triangle ABC$$, if vertices are:
$$A(2,7), B(2,2),C(10,8)$$
Show that $$ \triangle ABC $$ with vertices $$A(-2 , 0) , B(2 , 0) $$ and $$C(0 , 2)$$ is similar to $$ \triangle DEF$$ with vertices $$D(-4 , 0) , E(4 , 0) $$ and $$F(0 , 4)$$
Find area of $$\triangle ABC$$, if vertices are:
$$A(-3,5), B(3,-6),C(7,2)$$
Find area of triangle, whose vertices are:
$$(3,8),(2,7)$$ and $$(5,-1)$$
If $$A(4 , 2) , B = (7 , 6) $$ and $$C(1 , 4)$$ are the vertices of $$ \triangle ABC$$ and $$AD$$ is its median. P.T that median $$AD$$ divides $$ \triangle ABC$$ into two triangle of equal areas.
If coordinates of $$P$$ and $$Q$$ are $$(3,4)$$ and $$(12,4)$$ respectively, then find $$\angle POQ$$ where $$O$$ is origin.
The vertices of a $$\Delta ABC$$ are $$A(3, 8), B(-1, 2)$$ and $$C(6, -6)$$. Find Slope of BC.
Let the length of the sides of a triangle $$\triangle ABC$$ be integers with $$A$$ as the origin. $$(2, -1)$$ and $$(3, 6)$$ are points on the line $$AB$$ and $$AC$$ respectively (line $$AB$$ and $$AC$$ may be extended to contain these points), and lengths of exactly two sides are primes that differ by $$50$$. If $$a$$ is least possible length of the third side and $$S$$ is the least possible perimeter of the triangle, then $$aS$$ is equal to
Find the area of the figure bounded by the following curves
y = $$x^3, \, y^2$$ = x.
Find if possible, the slope of the line through the points $$(1/2,3/4)$$ and $$(-1/3,5/4)$$
Write an equation of the vertical line through the point $$(3,0)$$
A balloon moving in a straight line passes vertically above two points $$A$$ and $$B$$ on a horizontal plane $$1000\ ft.$$ When above $$A$$ it has an altitude of $${60}^{o}$$ as seen from $$B$$ and when above $$B$$, $${30}^{o}$$ as seen from $$A$$. Find the distance from $$A$$ at which it will strike the plane.
If two vertices of an equilateral triangle are $$(0,0),(3,\sqrt {3})$$, find the third vertices of the triangle.
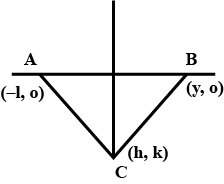
The base AB of the two equilateral triangles ABC and ABC' with side $$2a$$ lies along the X-axis such that the mid-point of AB is at the origin. Find the coordinates of the vertices C and C' of the triangles.
Find the area of a triangle :$$y=x,y=2x$$ and $$y=3x+4$$ ?
If the vertices of a triangle be $$(am_{1}^{2},2am_{1}),(am_{2}^{2},2am_{2})$$ and $$(am_{3}^{2},2am_{3})$$, then the area of the triangle is
If $$A({x}_{1},{y}_{1}),\ B({x}_{2},{y}_{2})$$ and $$ C({x}_{3},{y}_{3})$$ are vertices of an equilateral triangle whose each side is equal to $$a$$, the prove that $${ \begin{bmatrix} { x }_{ 1 } & { y }_{ 1 } & 2 \\ { x }_{ 2 } & { y }_{ 2 } & 2 \\ { x }_{ 3 } & { y }_{ 3 } & 2 \end{bmatrix} }^{ 2 }={ 3a }^{ 4 }$$.
If $$P,Q,R$$ are collinear points such that $$P(3,4),Q(7,7)$$ and $$PR=10$$, find $$R$$
The coordinate of points $$A,\ B,\ C$$ and $$D$$ are $$(-3,\ 5),\ (4,\ -2), (x,\ 3x)$$ and $$(6,\ 3)$$ respectively and $$\dfrac {\triangle ABC}{\triangle BCD}=\dfrac {2}{3}$$, find $$x$$
Find the point on the y-axis which is equidistant from the points $$(5,-2)$$ and $$(-3,2)$$
Find the distance of the line $$4x + 7y + 5 = 0$$ from the point (1, 2) along the line $$2x - y = 0$$.
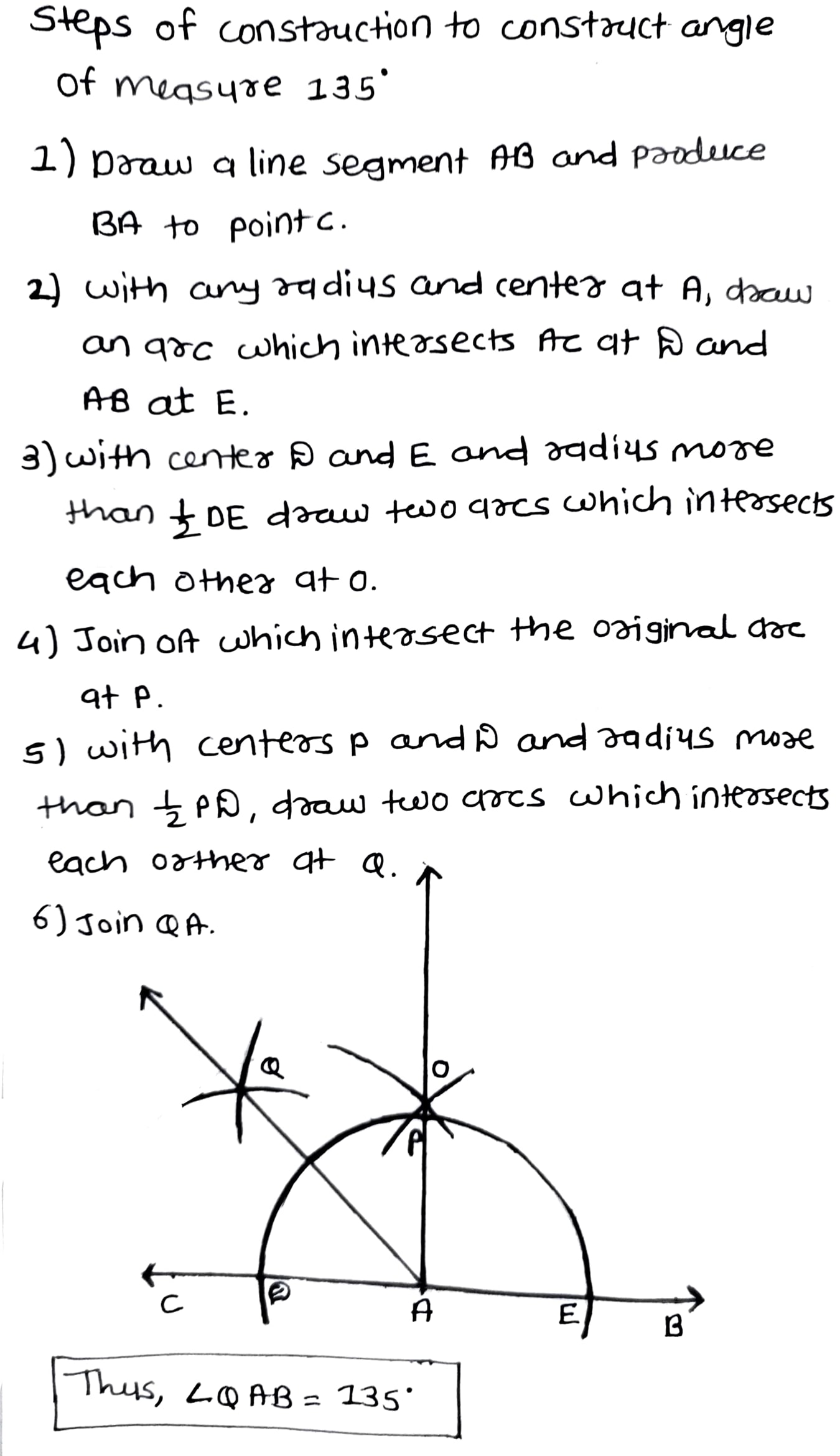
Using ruler and compasses only, construct an angle of measure $$135^{\circ}$$
If $$P,Q,R$$ are $$\left(6,-1\right),\,\left(1,3\right),\,\left(x,8\right)$$ respectively, then find the value of $$x$$ so that $$PQ=QR$$
If the equation of the locus of a point equidistant from the points $$\left({a}_{1},{b}_{1}\right)$$ and $$\left({a}_{2},{b}_{2}\right)$$ is $$\left({a}_{1}-{a}_{2}\right)x+\left({b}_{1}+{b}_{2}\right)y+c=0$$, then the value of $$c$$ is?
If (a,b) (x$$_1,y_1),(x_2, y_2) $$ are vertices of triangle . Where a, x$$_1, x_2$$, are in G . P . with common ratio 'r' and b, y$$_1, y_2$$ are in G.P with common ratio 's'. Then find area of triangle?
If the points $$A(0,0), B(2,2\sqrt 3)$$ and $$C(x,y)$$ are the vertices of an equilateral triangle, find the coordinates of point C.
If (-3,2),(1,-2) and (5,6) are the mid-point of the sides of a traingle, find the coordinates of the vertices of the traingle.
The vertices of a quadrilateral are $$A(-4, 2), B(2, 6), C(8, 5)$$ and $$D(9, -7)$$. Using slopes, show that the midpoints of the sides of the quad. $$ABCD$$ form a parallelogram.
Using slopes, show that the points $$A(-4, -1), B(-2, -4), C(4, 0)$$ and $$D(2, 3)$$ takes in order, are the vertices of a rectangle.
Find the inclination of a line whose slope is
$$\dfrac{1}{\sqrt{3}}$$
Find the slope and the equation of the line passing through the points:
$$(5,3)$$ and $$(-5,-3)$$
Find the value of $$x$$ so that the line through $$(3, x)$$ and $$(2, 7)$$ is parallel to the line through $$(-1, 4)$$ and $$(0, 6)$$.
Find the equation of a horizontal line passing through the point $$(4,-2)$$.
Class 11 Engineering Maths Extra Questions
- Binomial Theorem Extra Questions
- Complex Numbers And Quadratic Equations Extra Questions
- Conic Sections Extra Questions
- Introduction To Three Dimensional Geometry Extra Questions
- Limits And Derivatives Extra Questions
- Linear Inequalities Extra Questions
- Mathematical Reasoning Extra Questions
- Permutations And Combinations Extra Questions
- Principle Of Mathematical Induction Extra Questions
- Probability Extra Questions
- Relations And Functions Extra Questions
- Sequences And Series Extra Questions
- Sets Extra Questions
- Statistics Extra Questions
- Straight Lines Extra Questions
- Trigonometric Functions Extra Questions