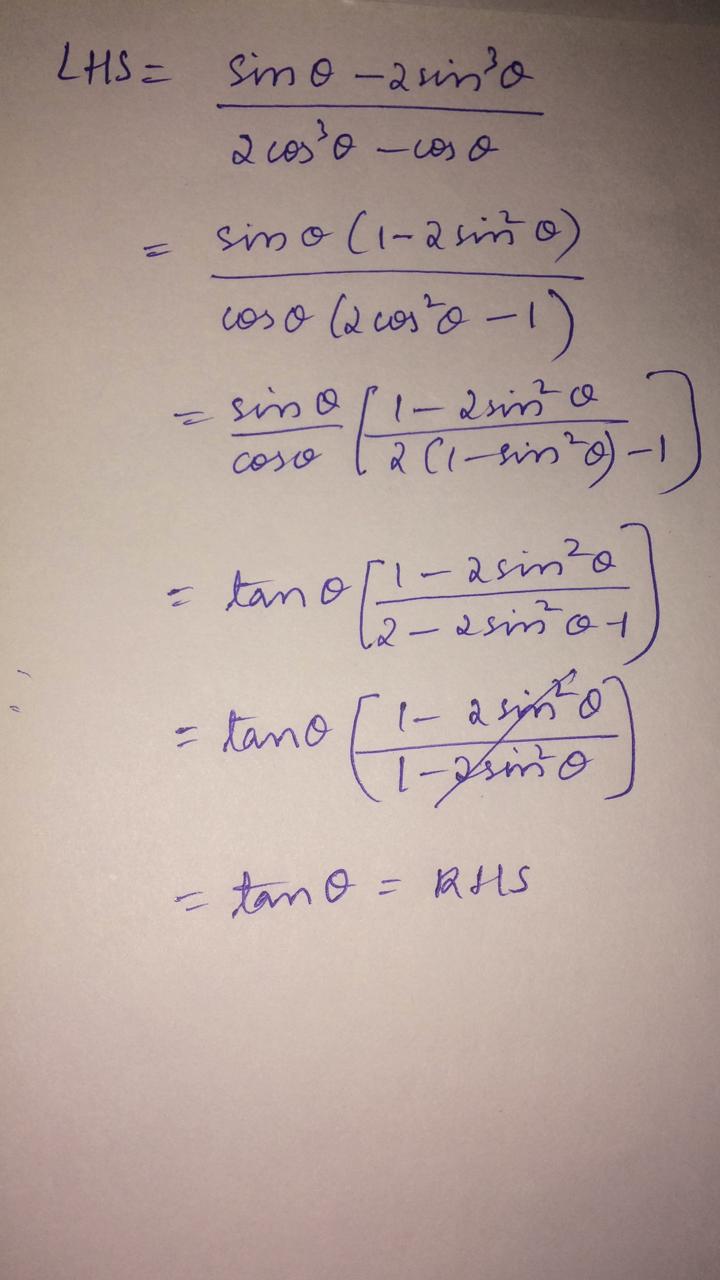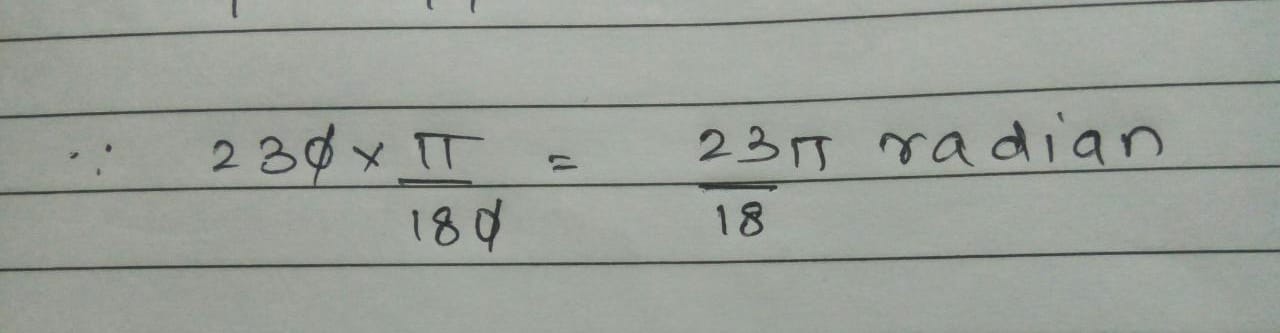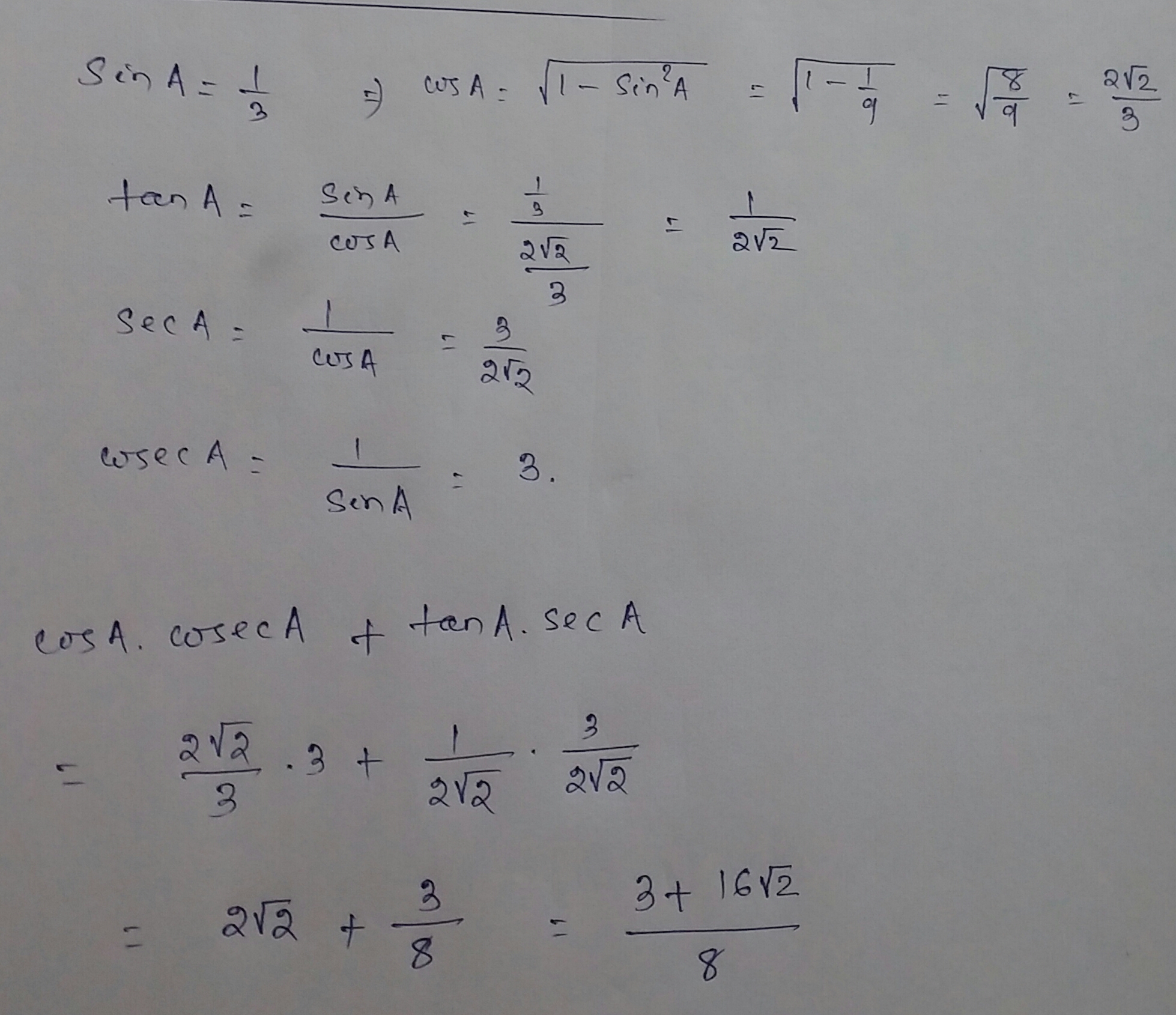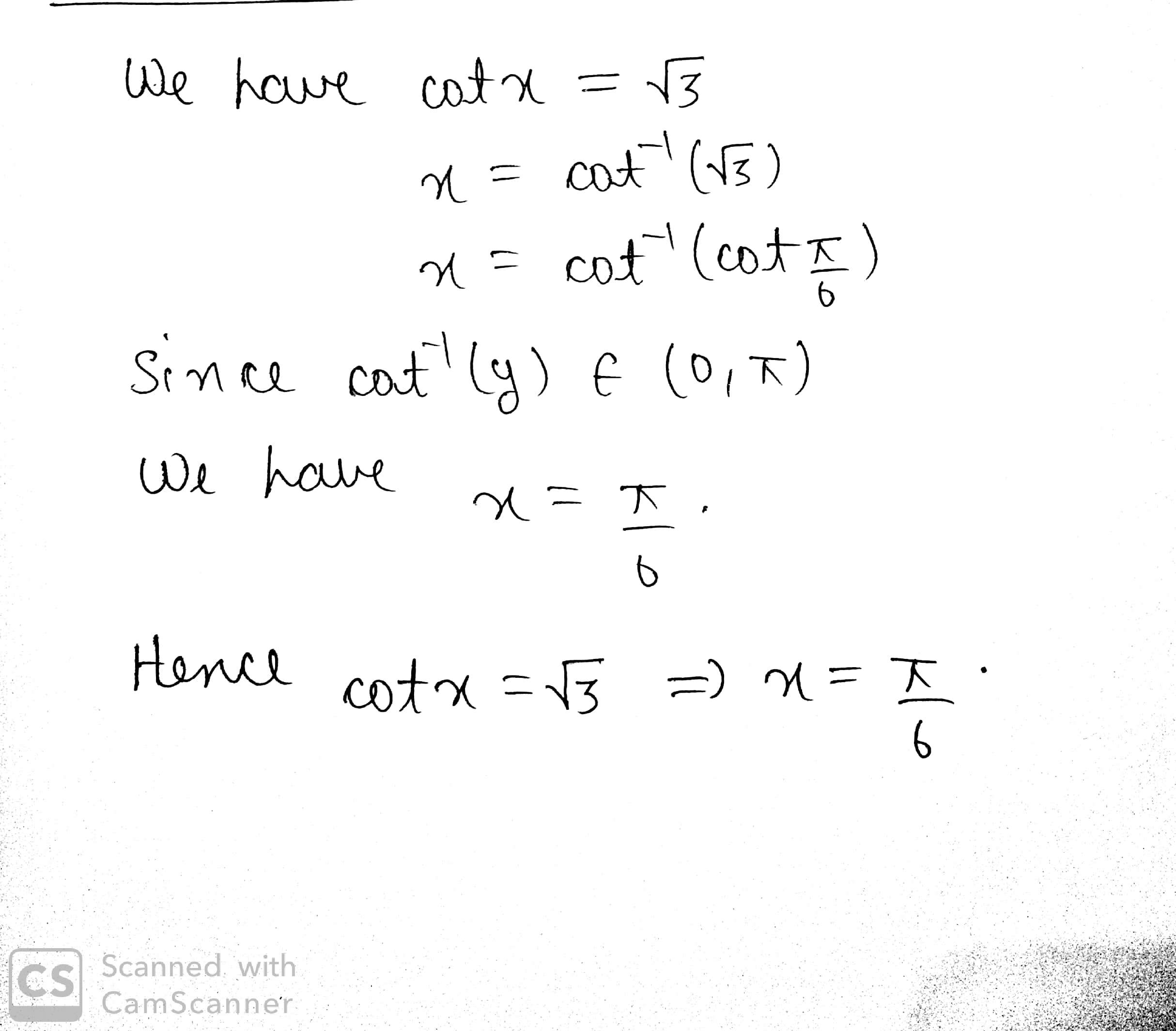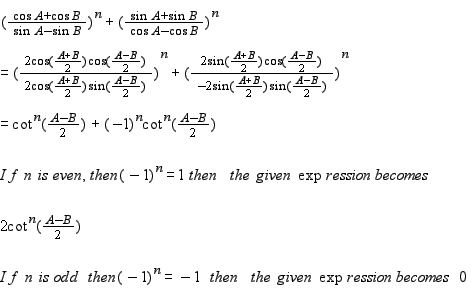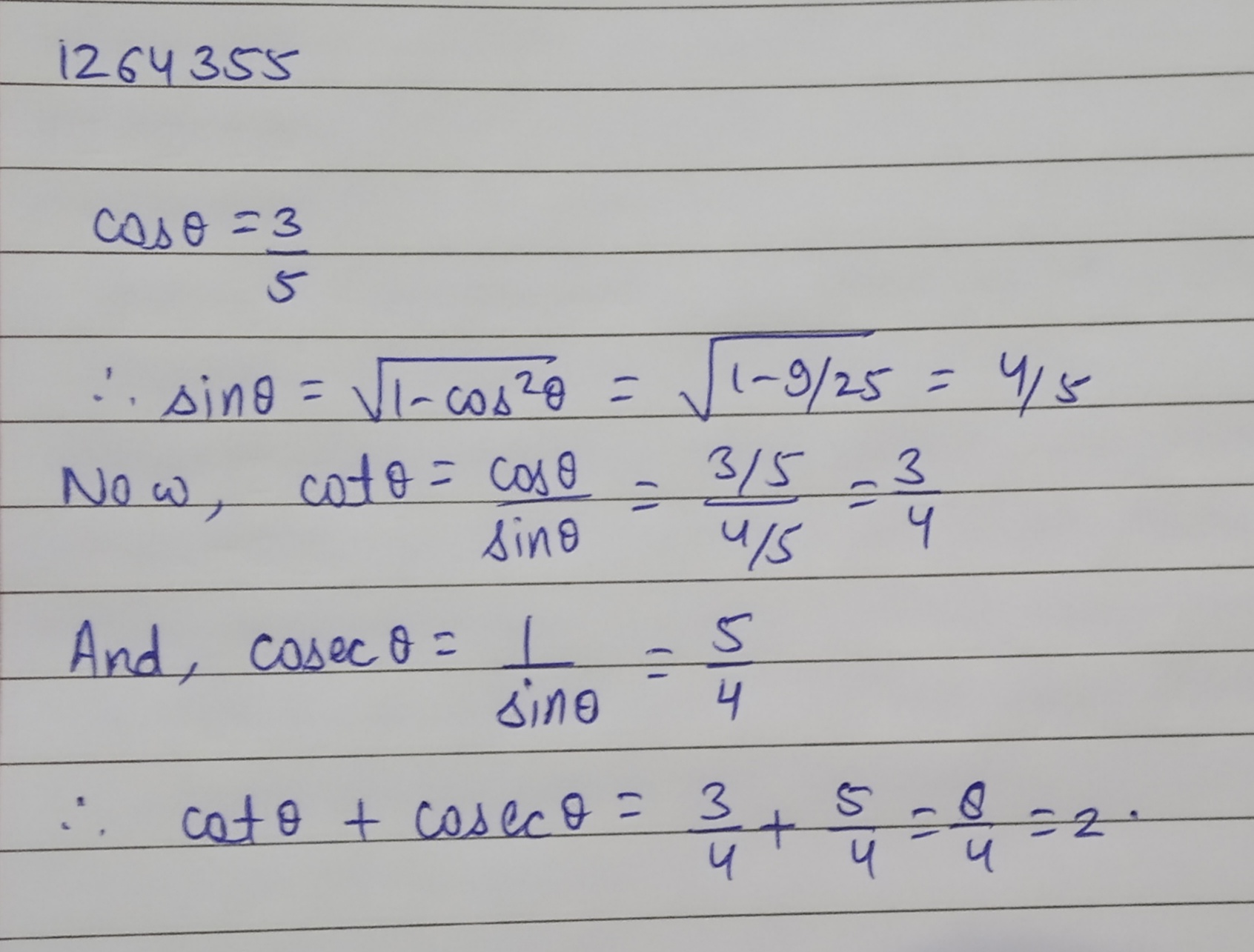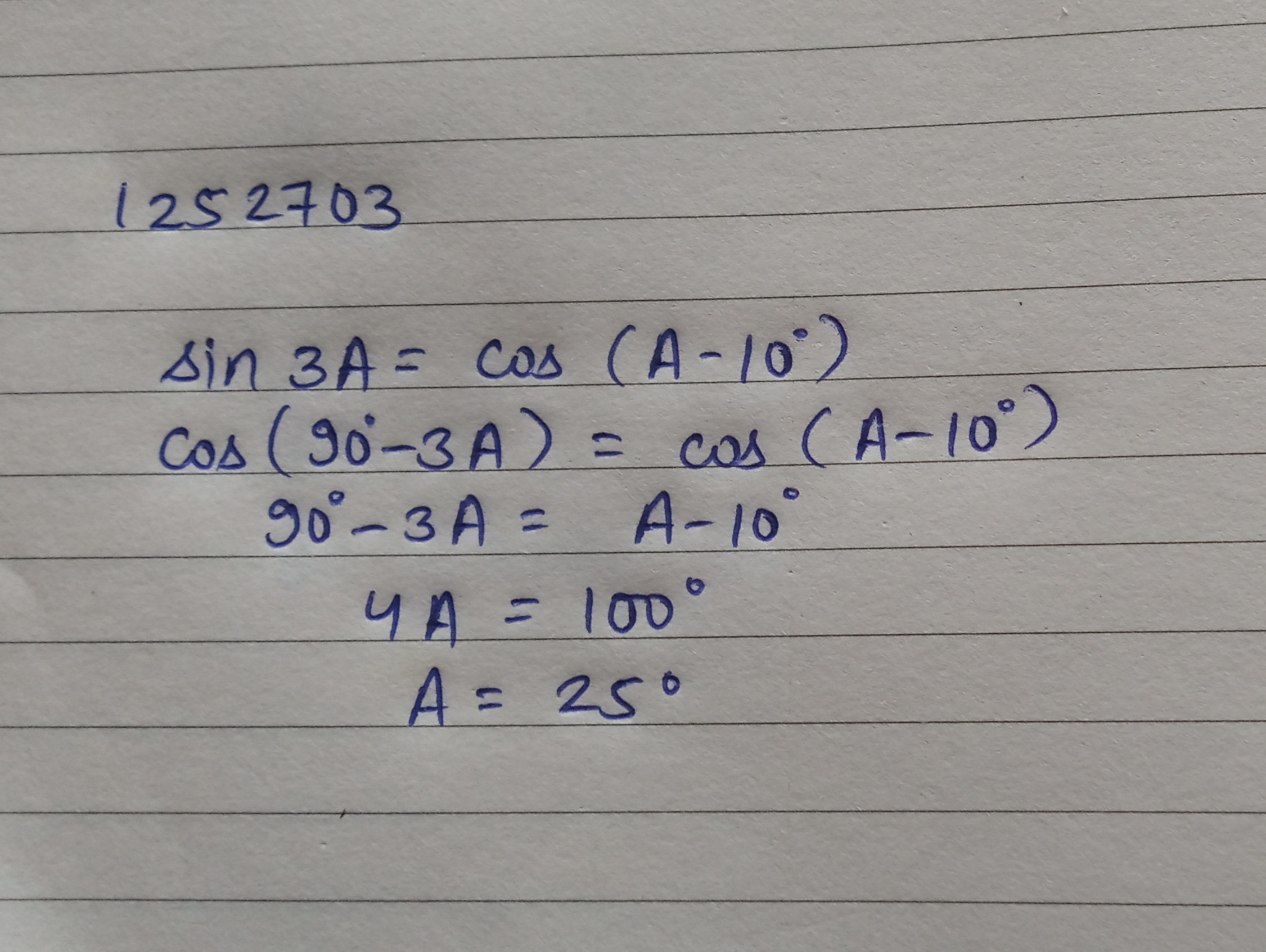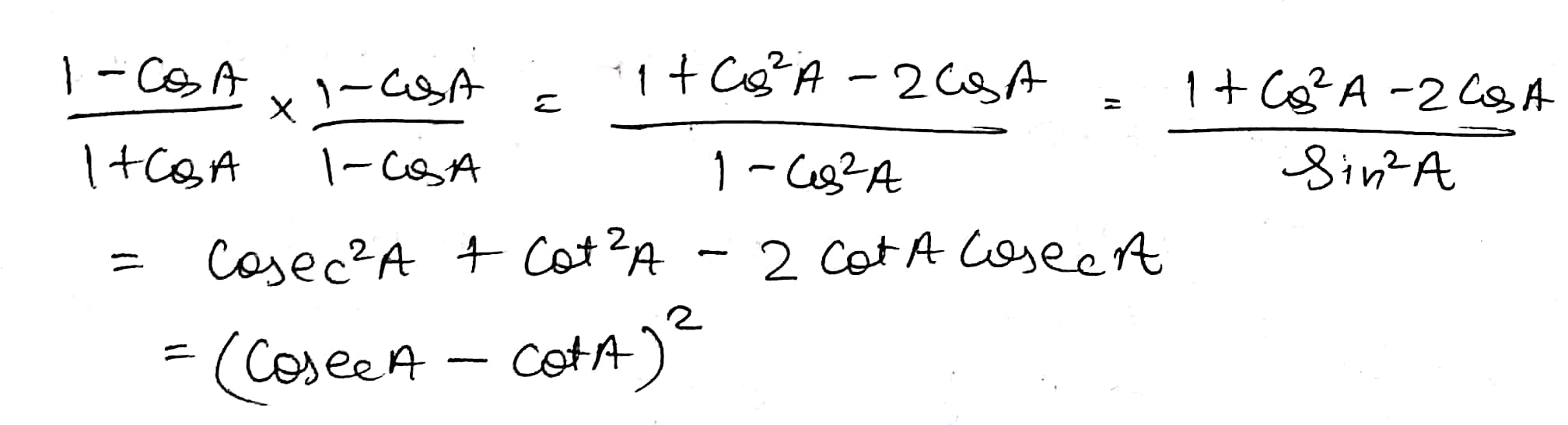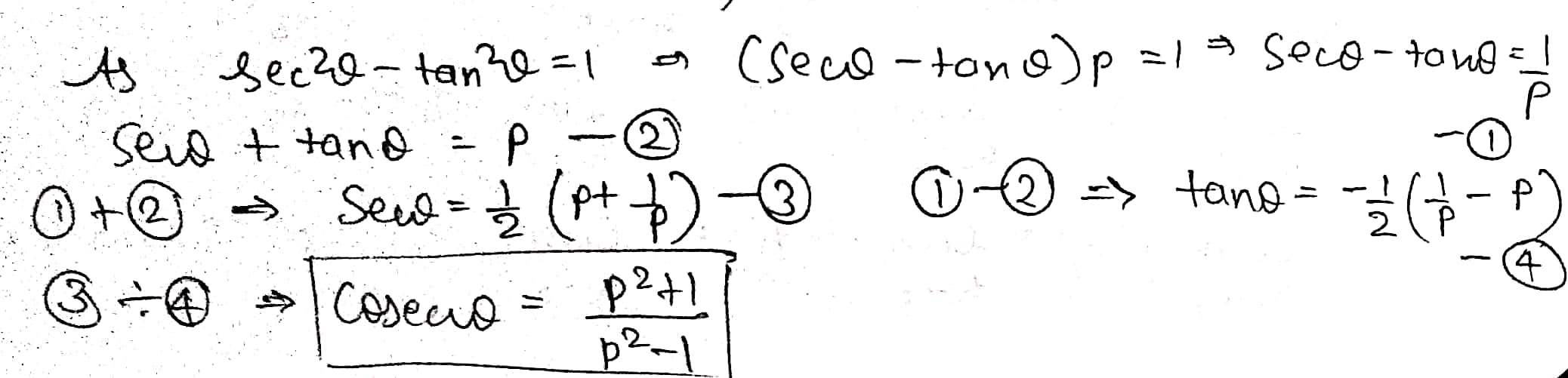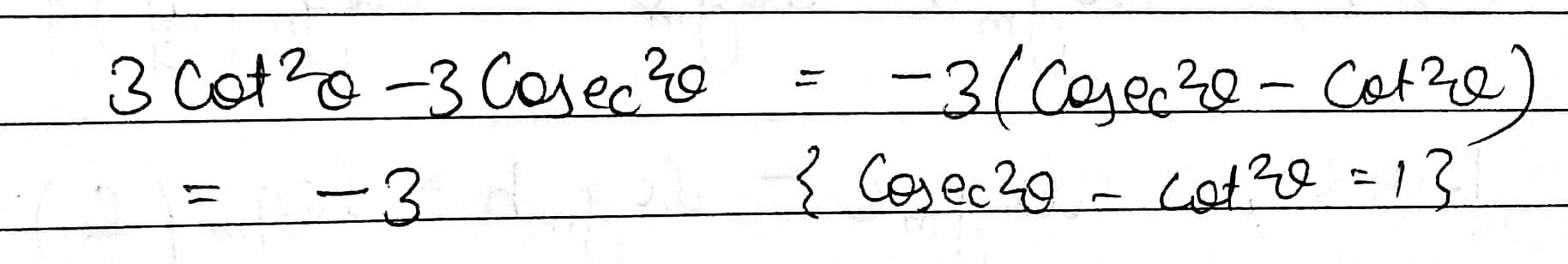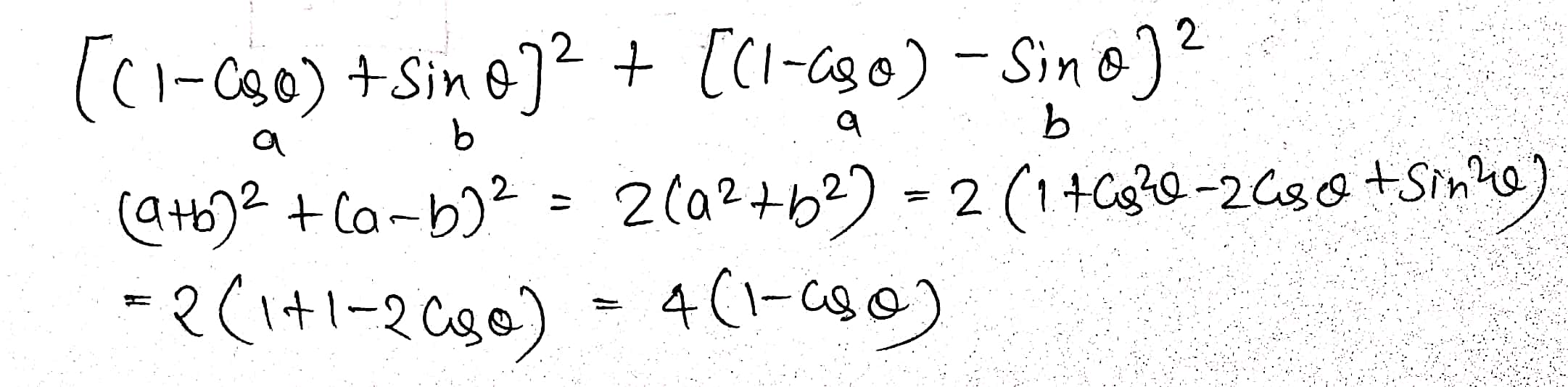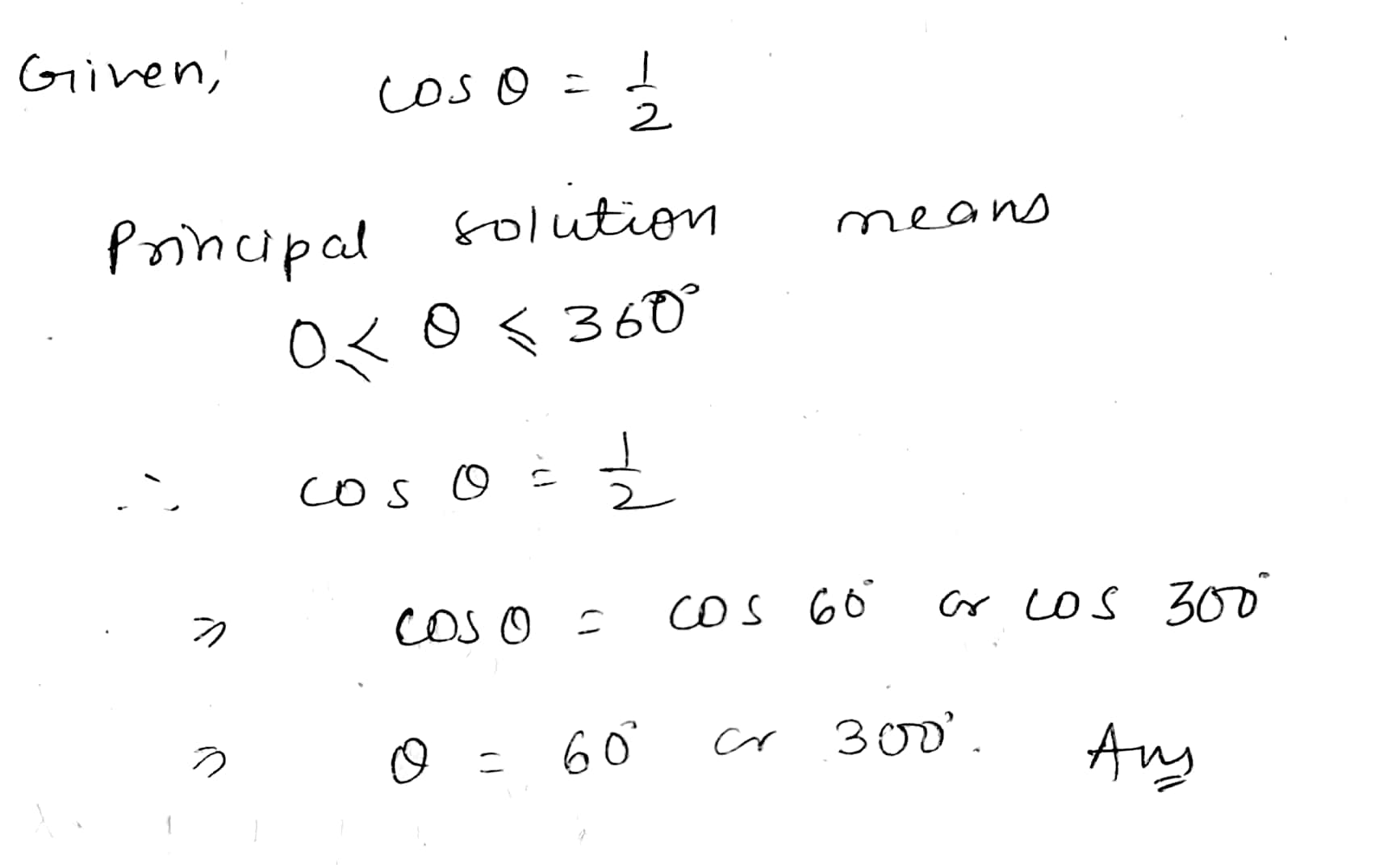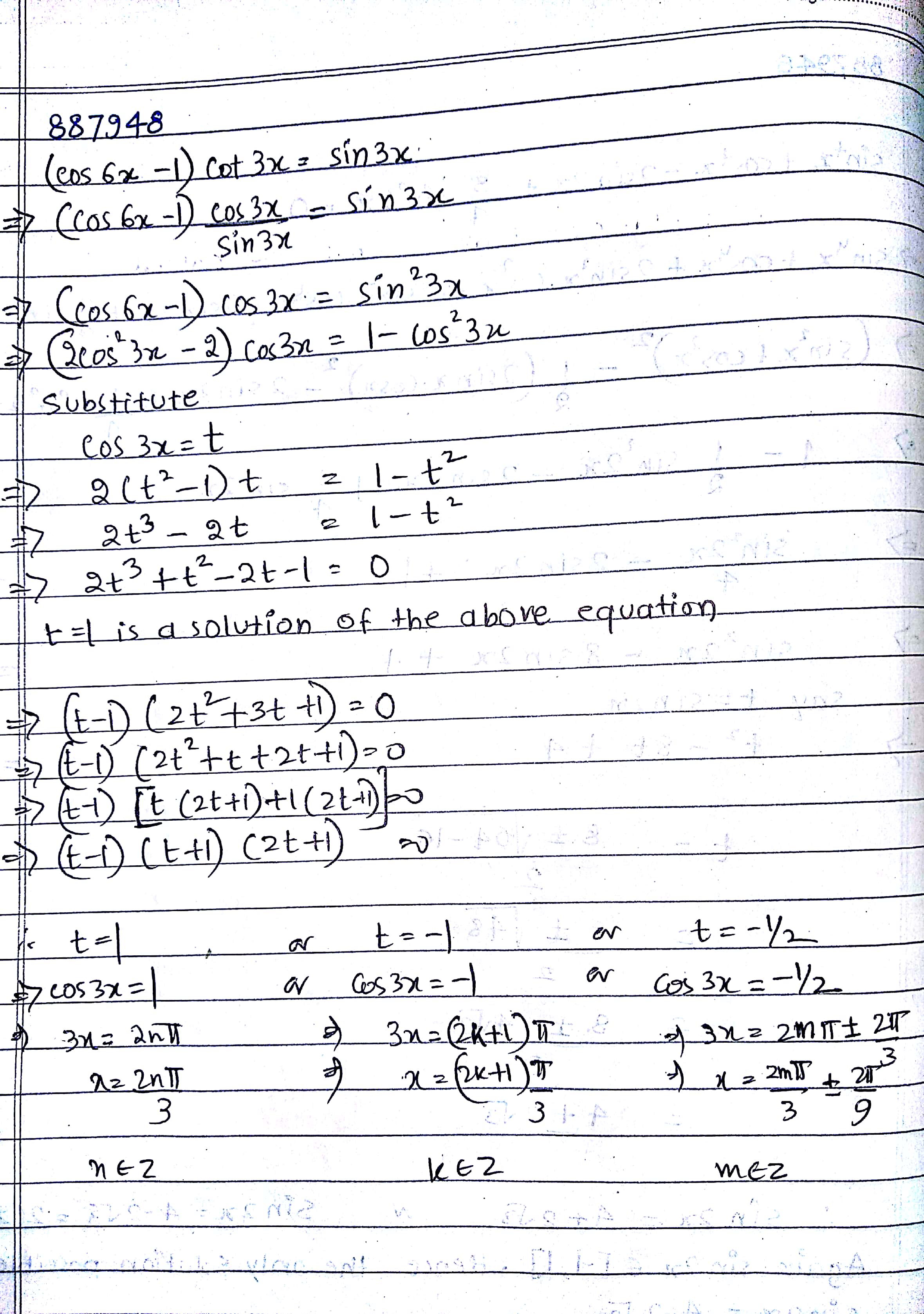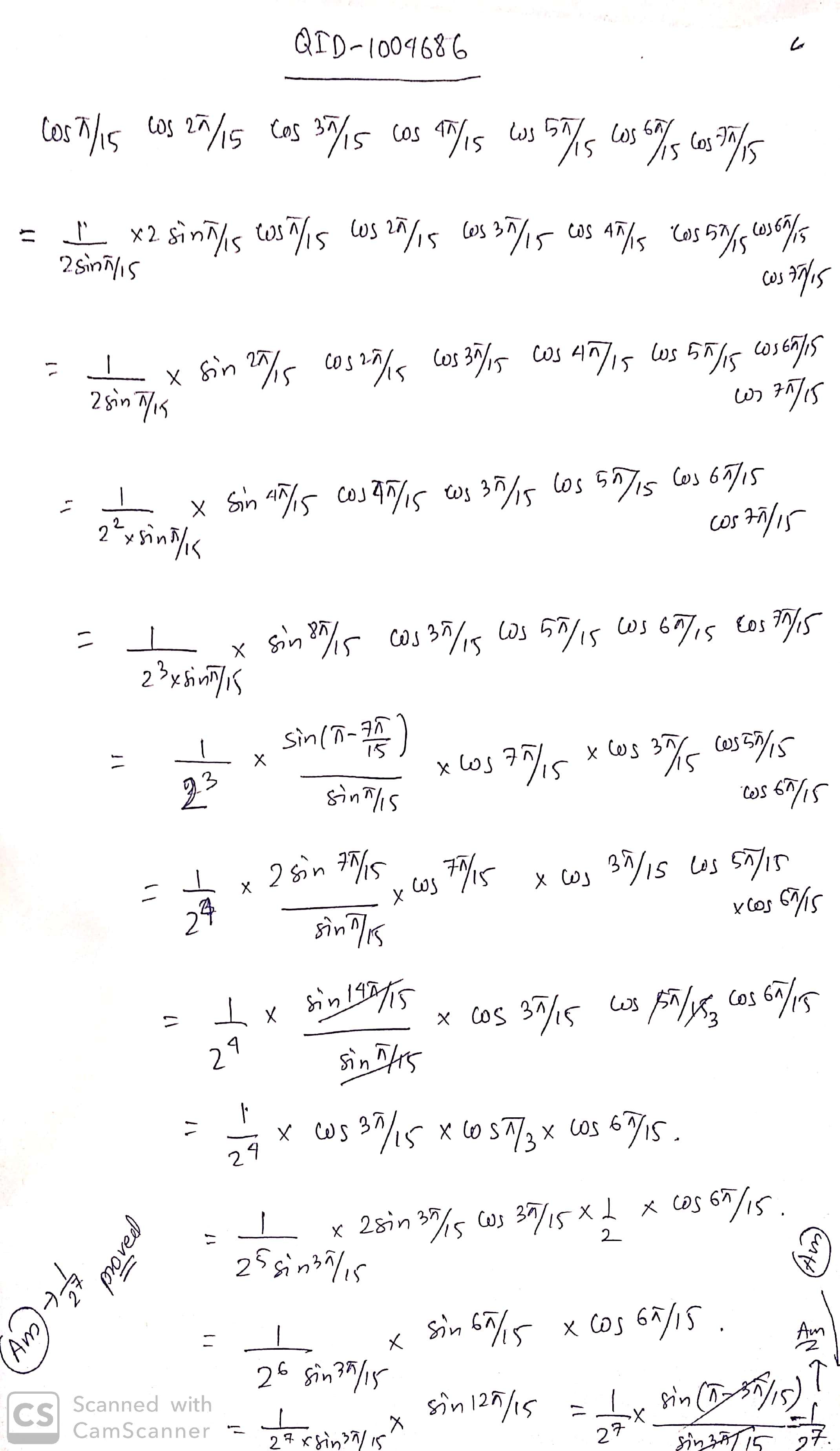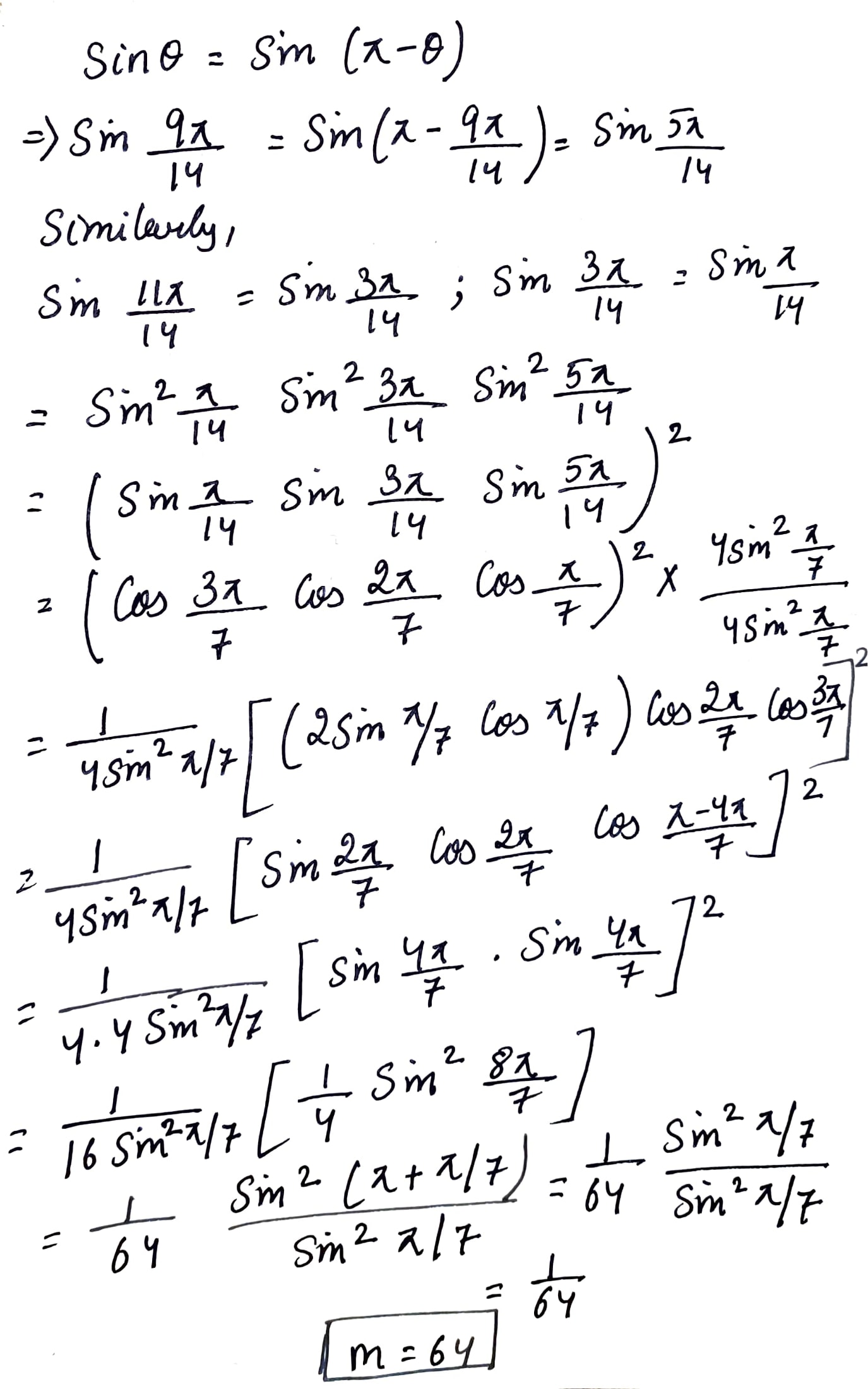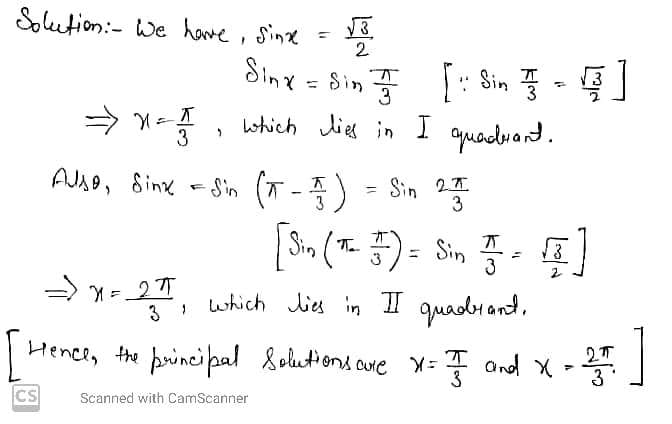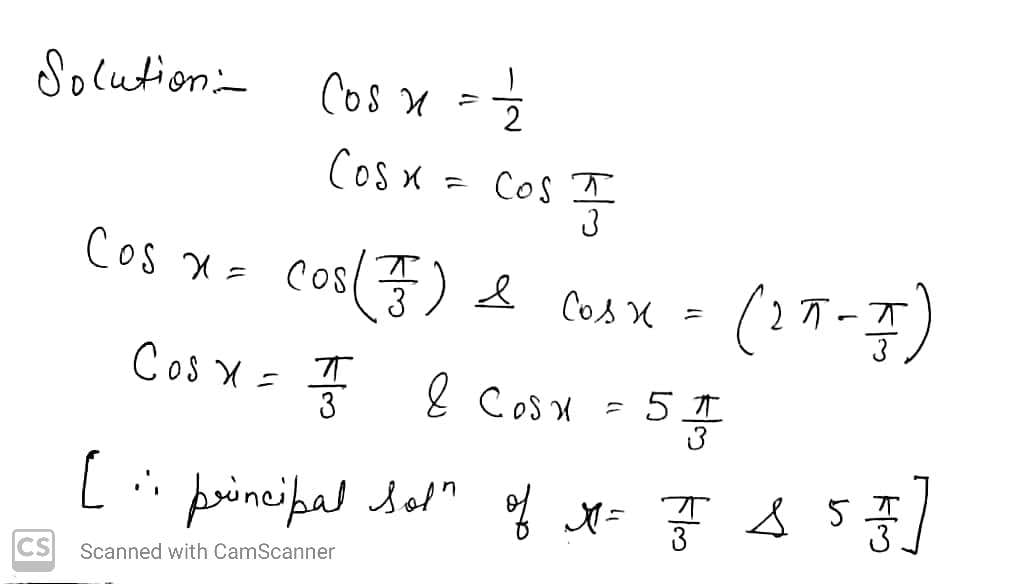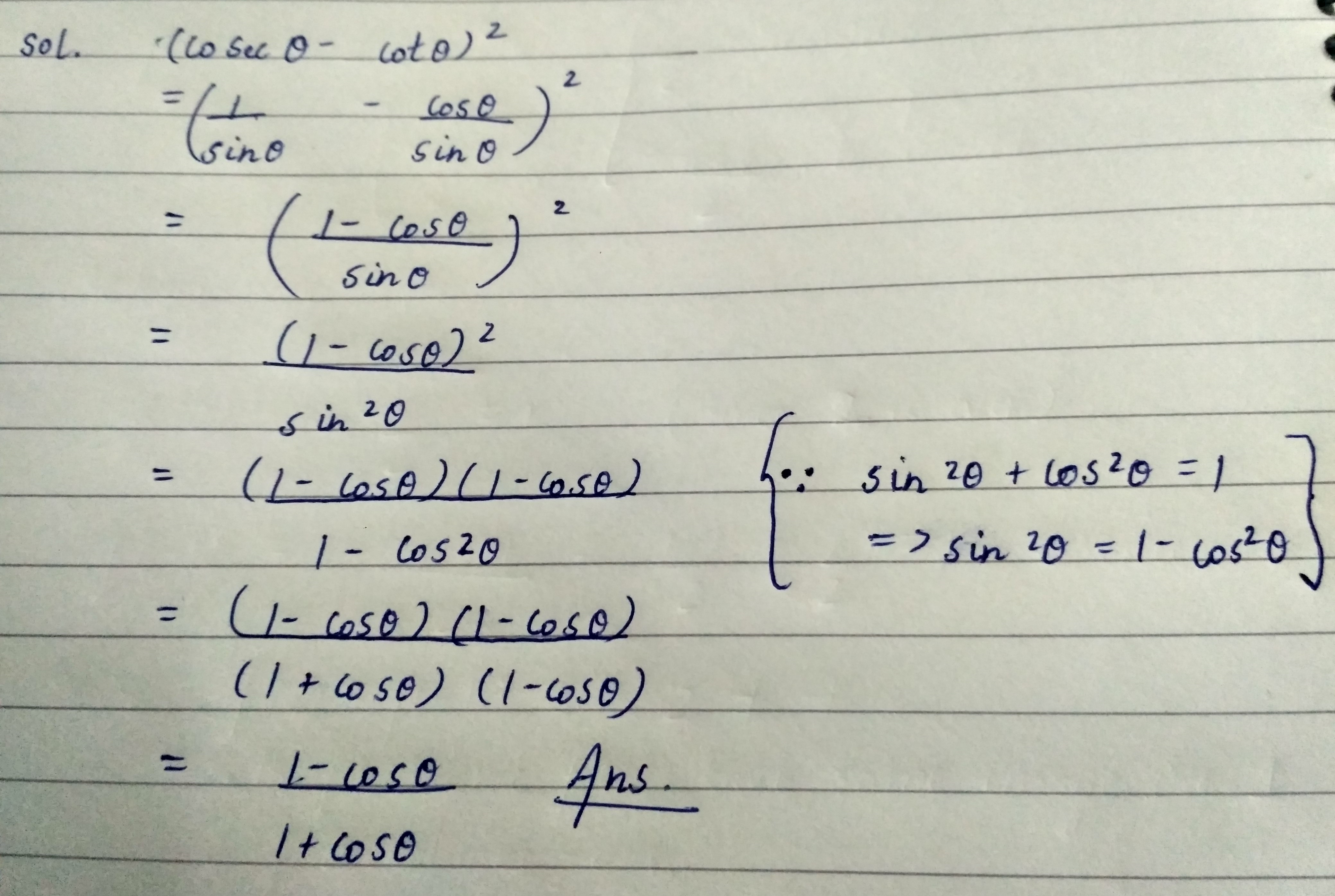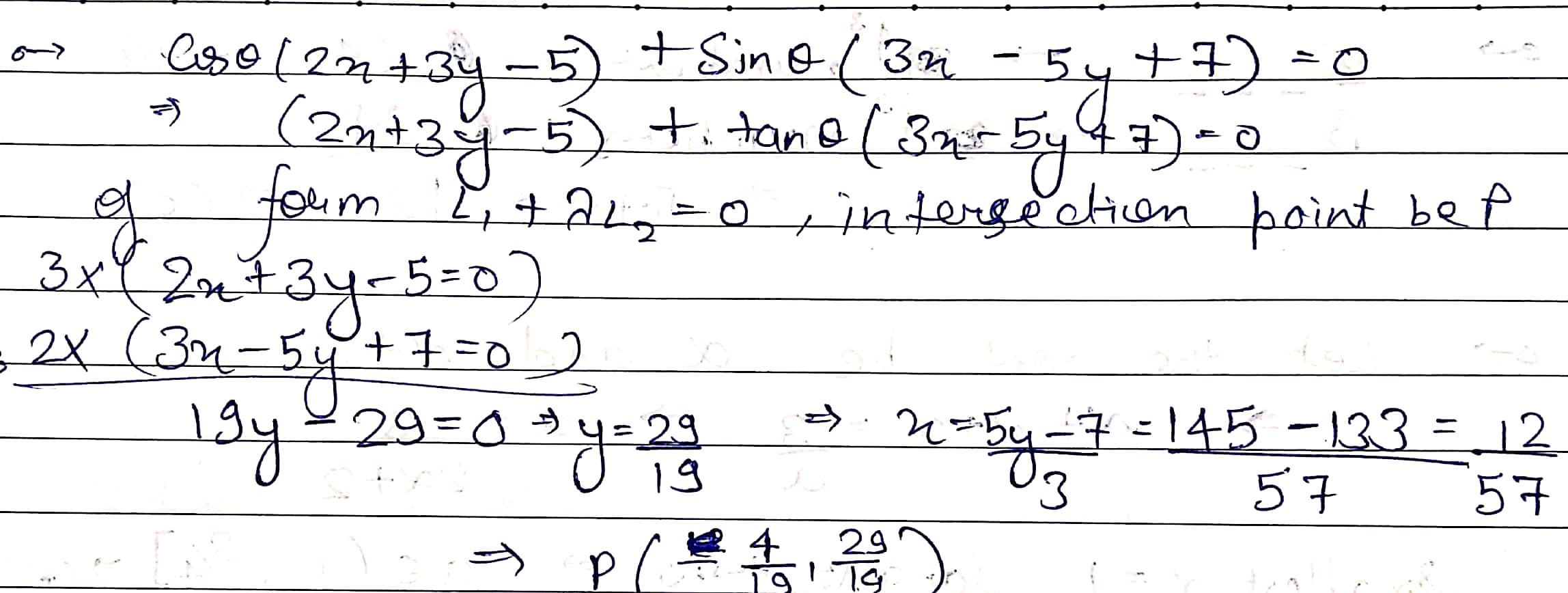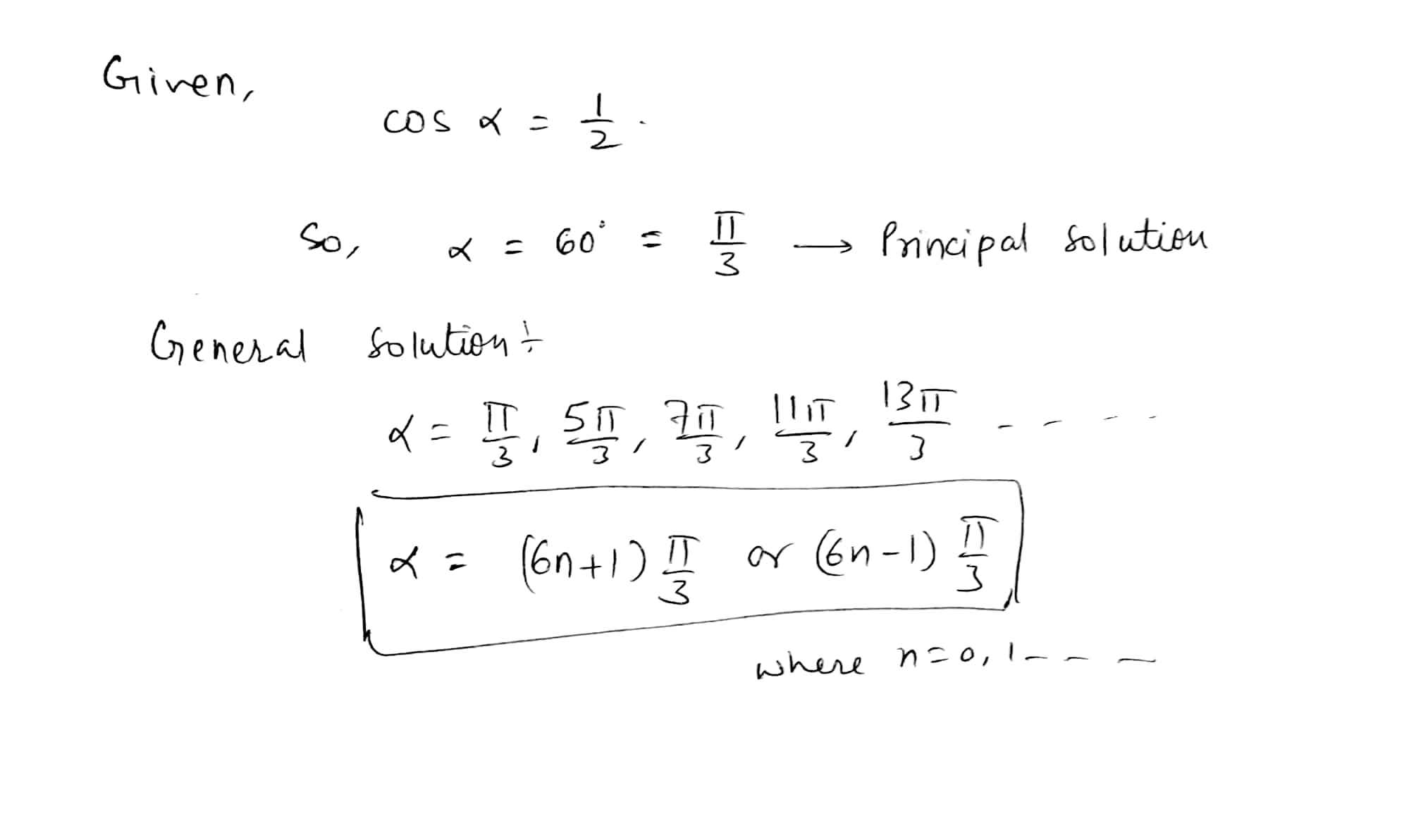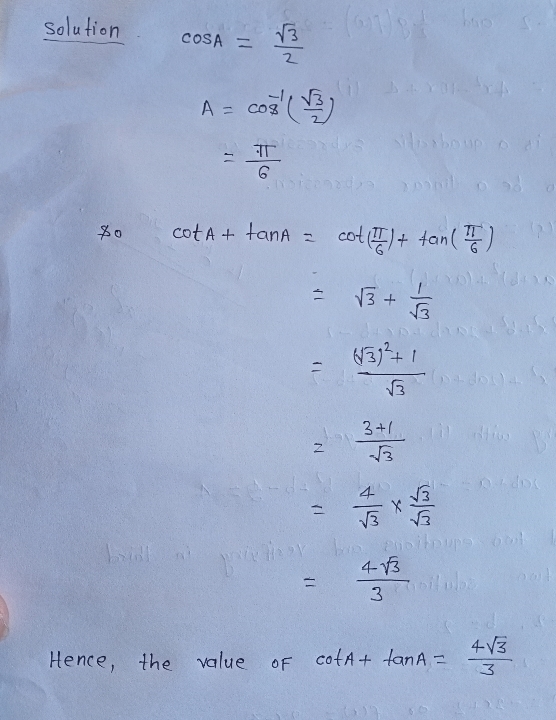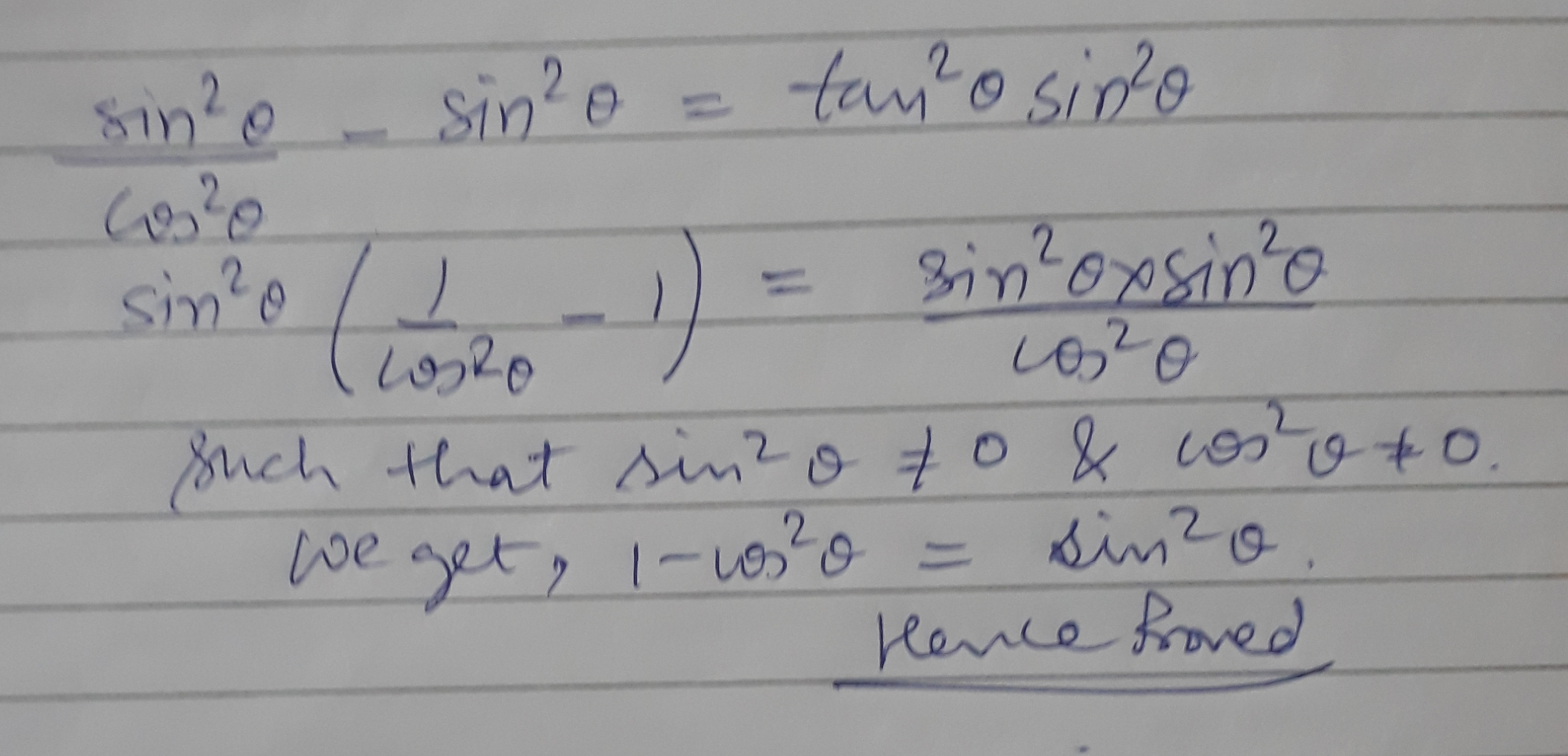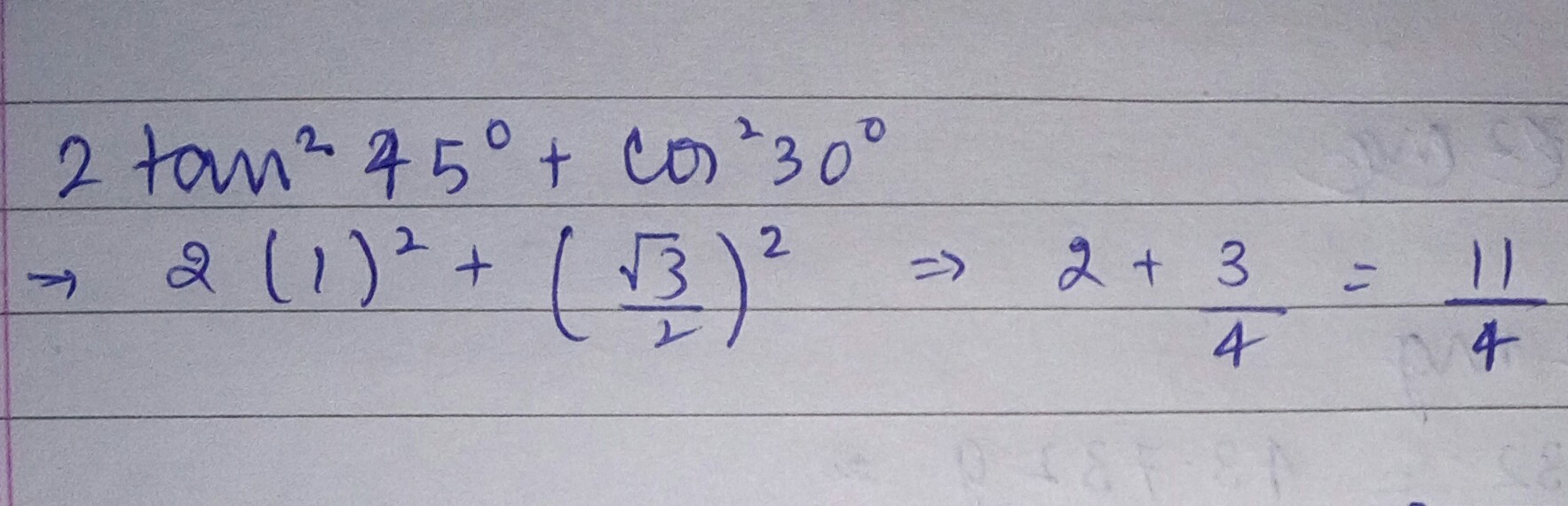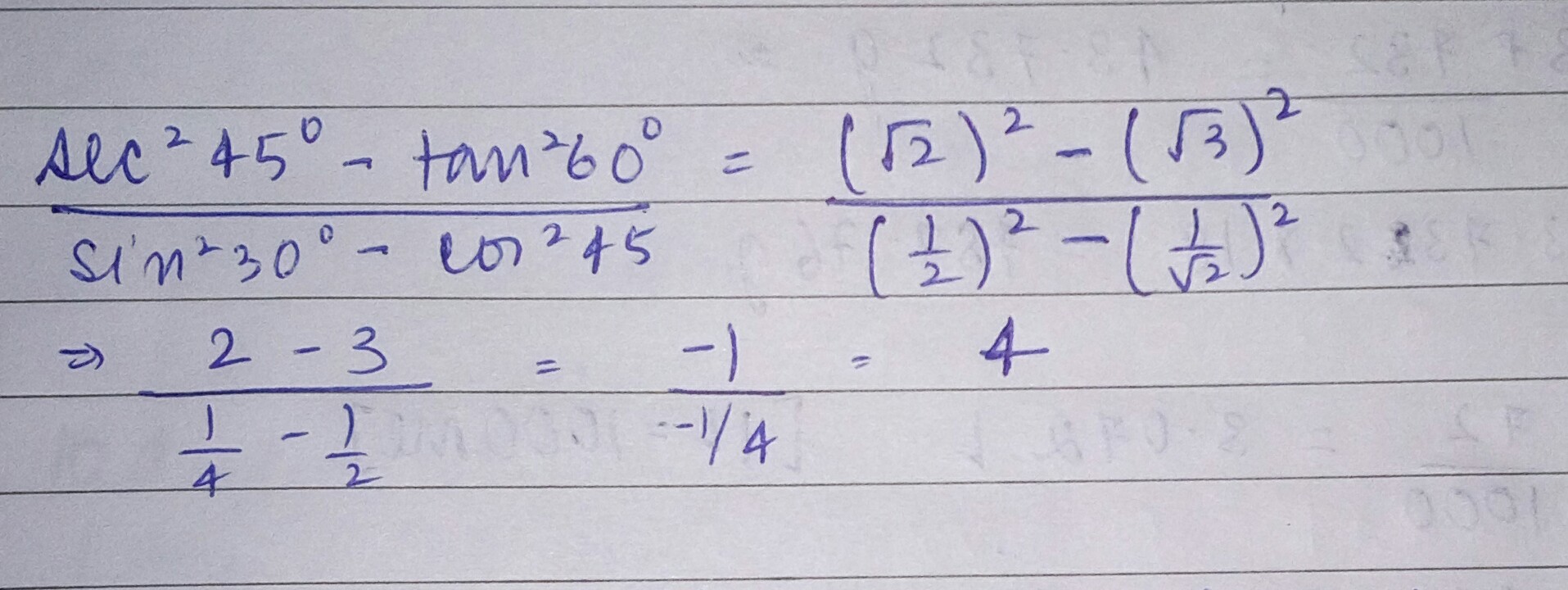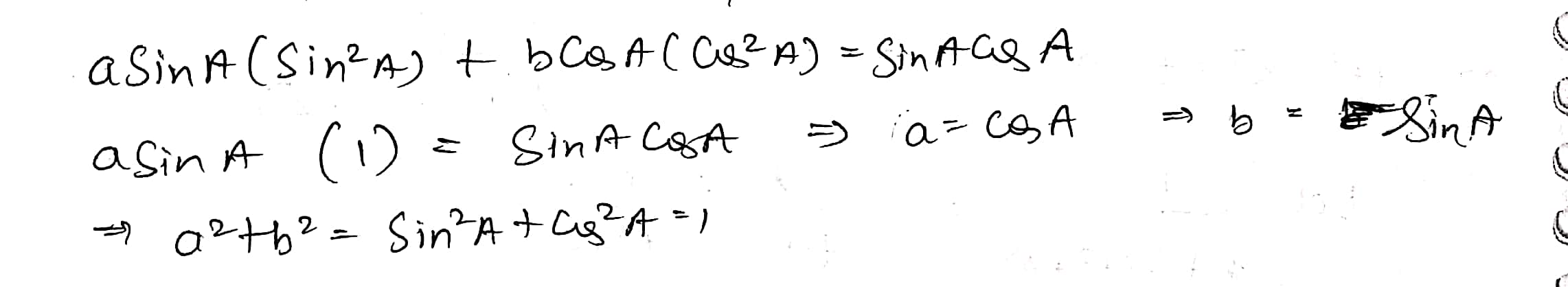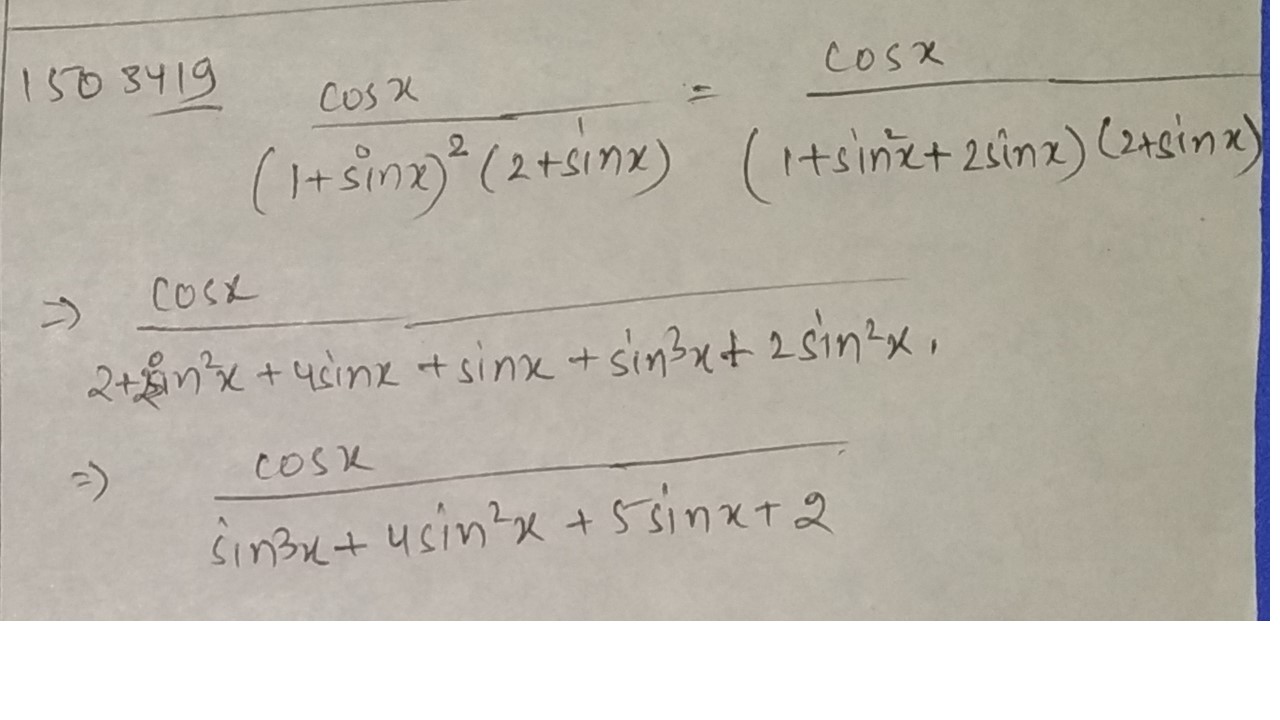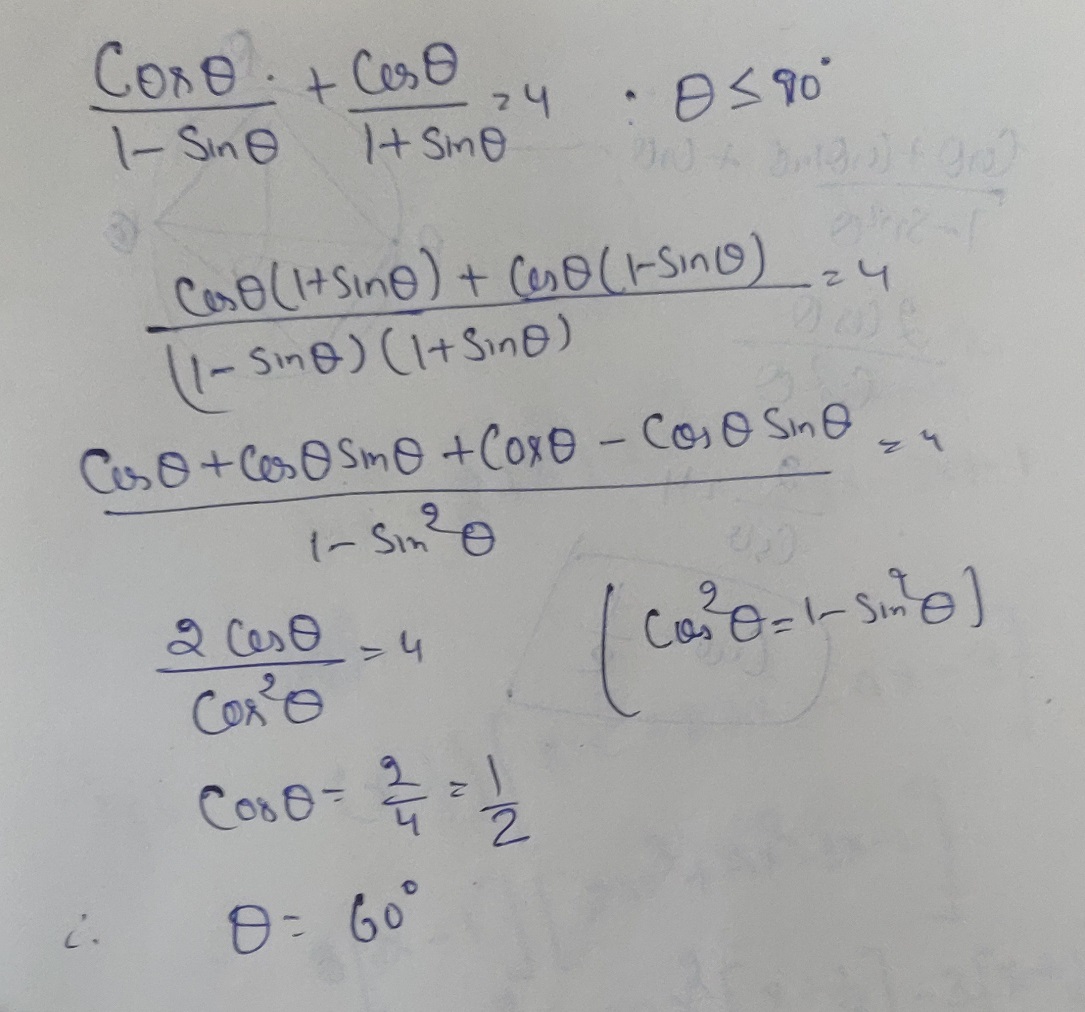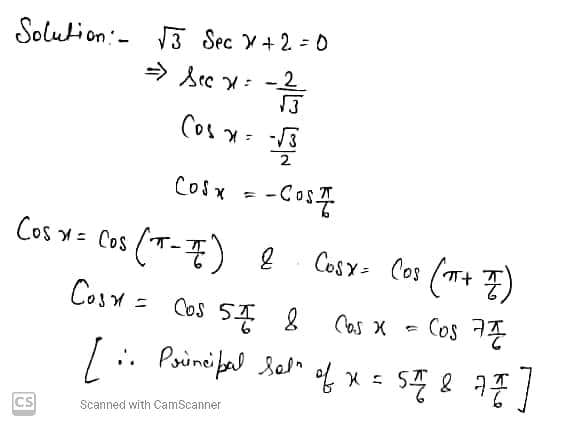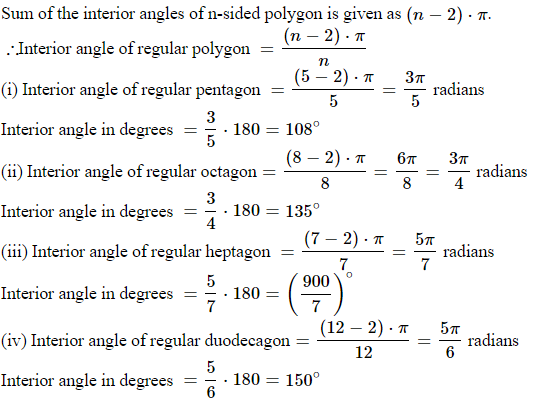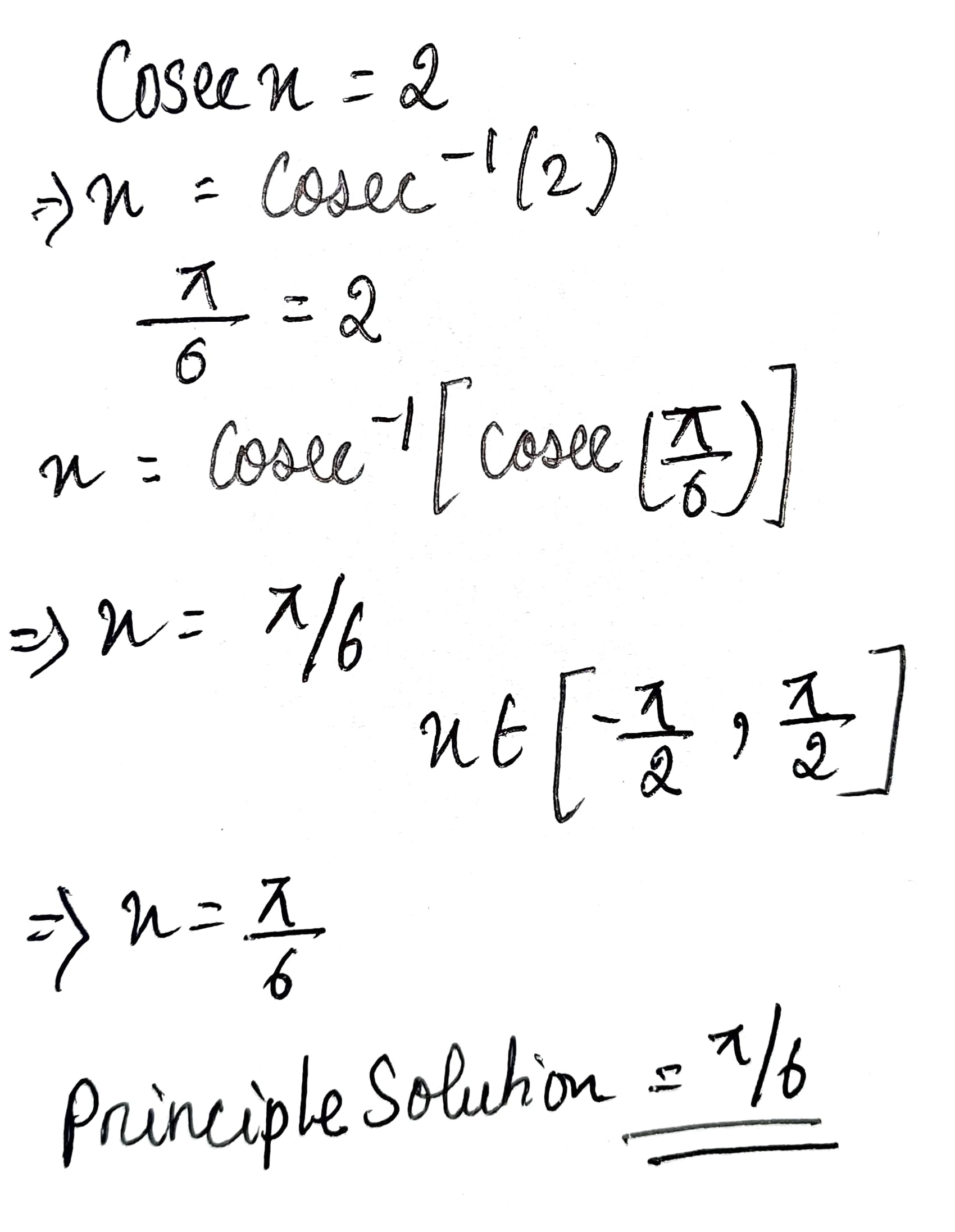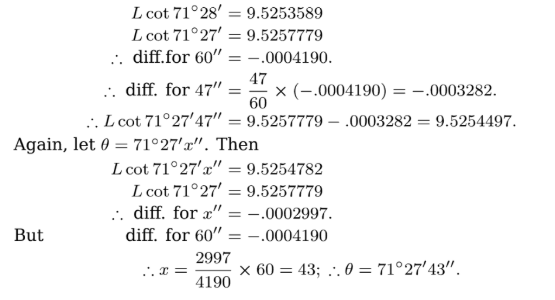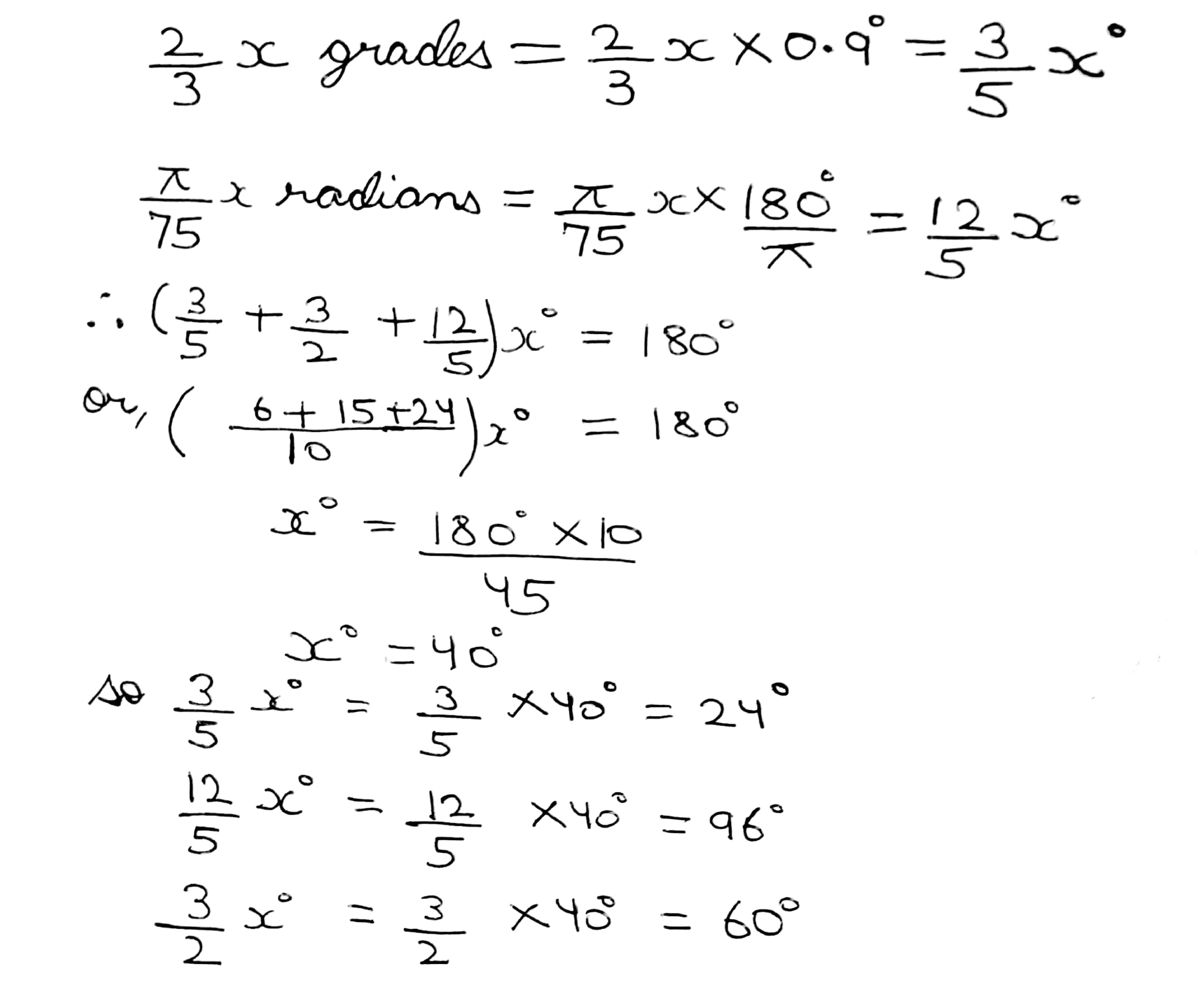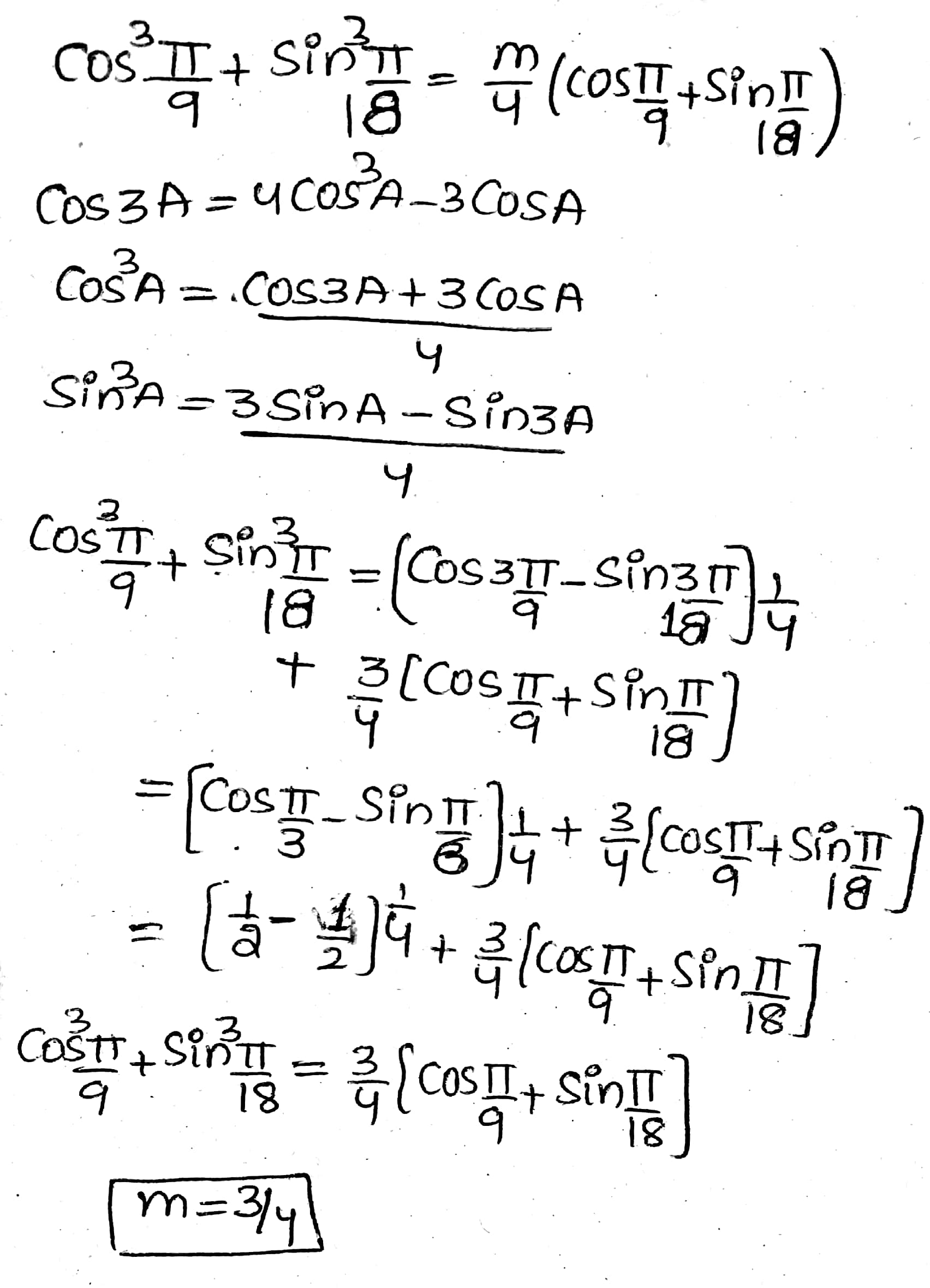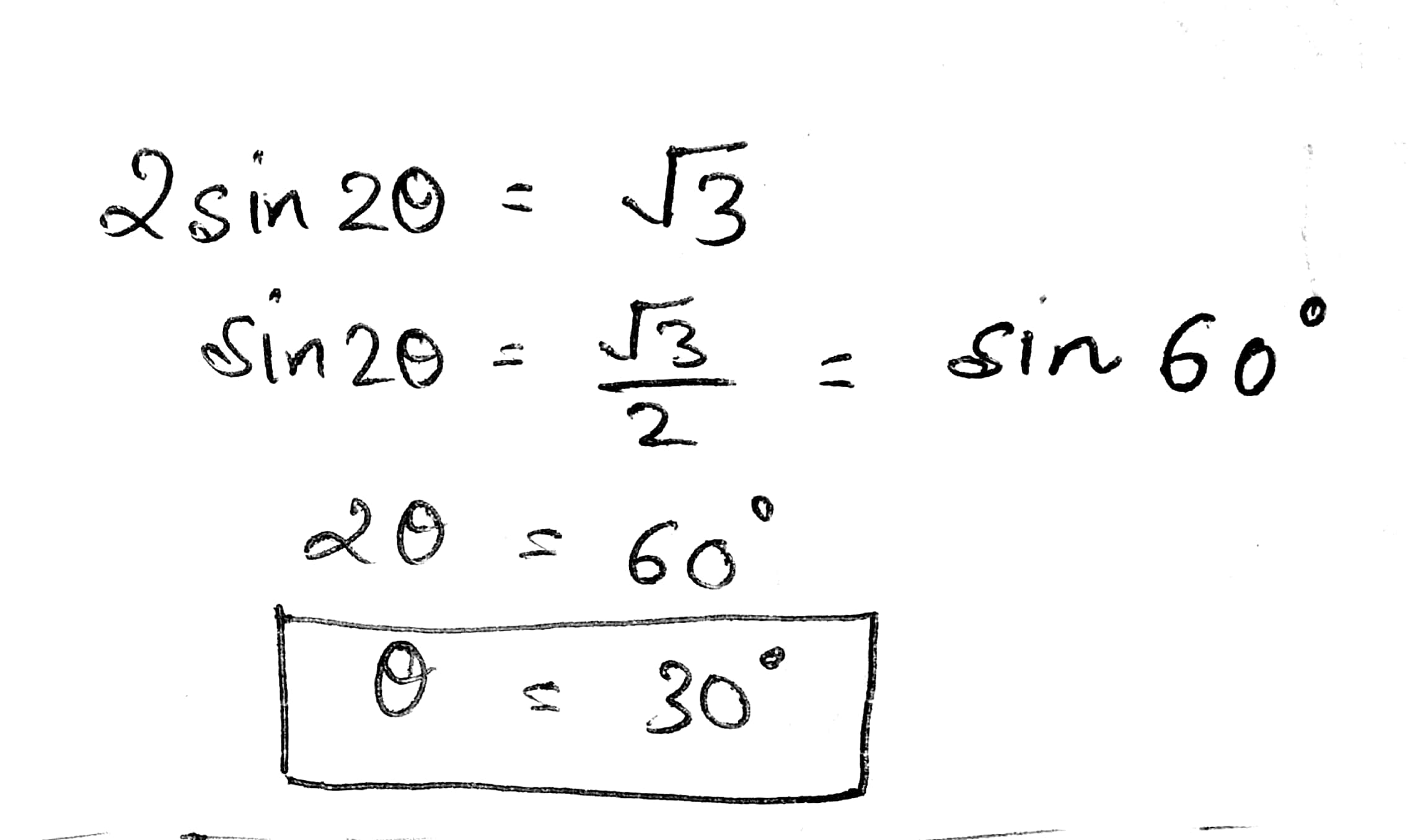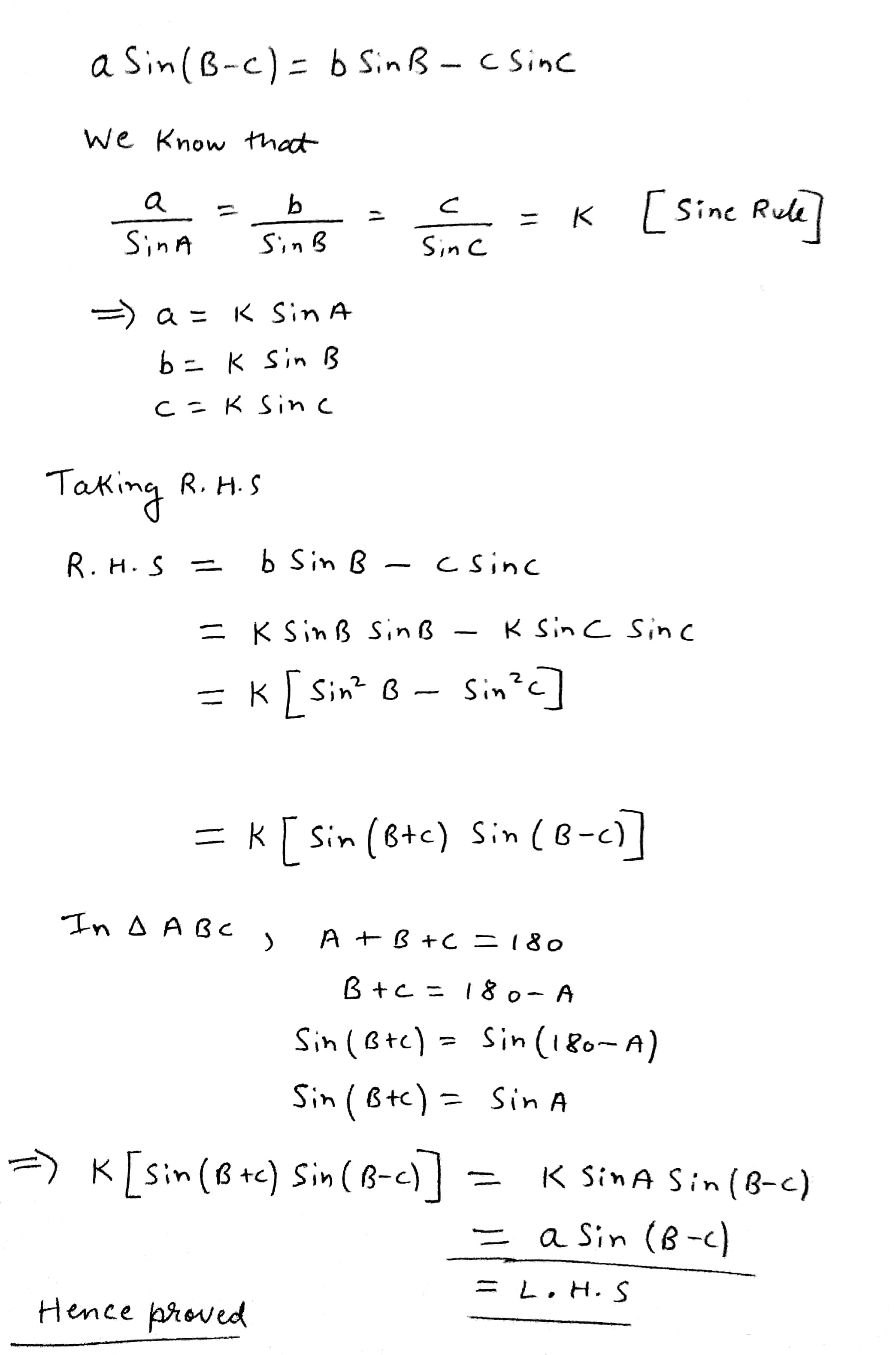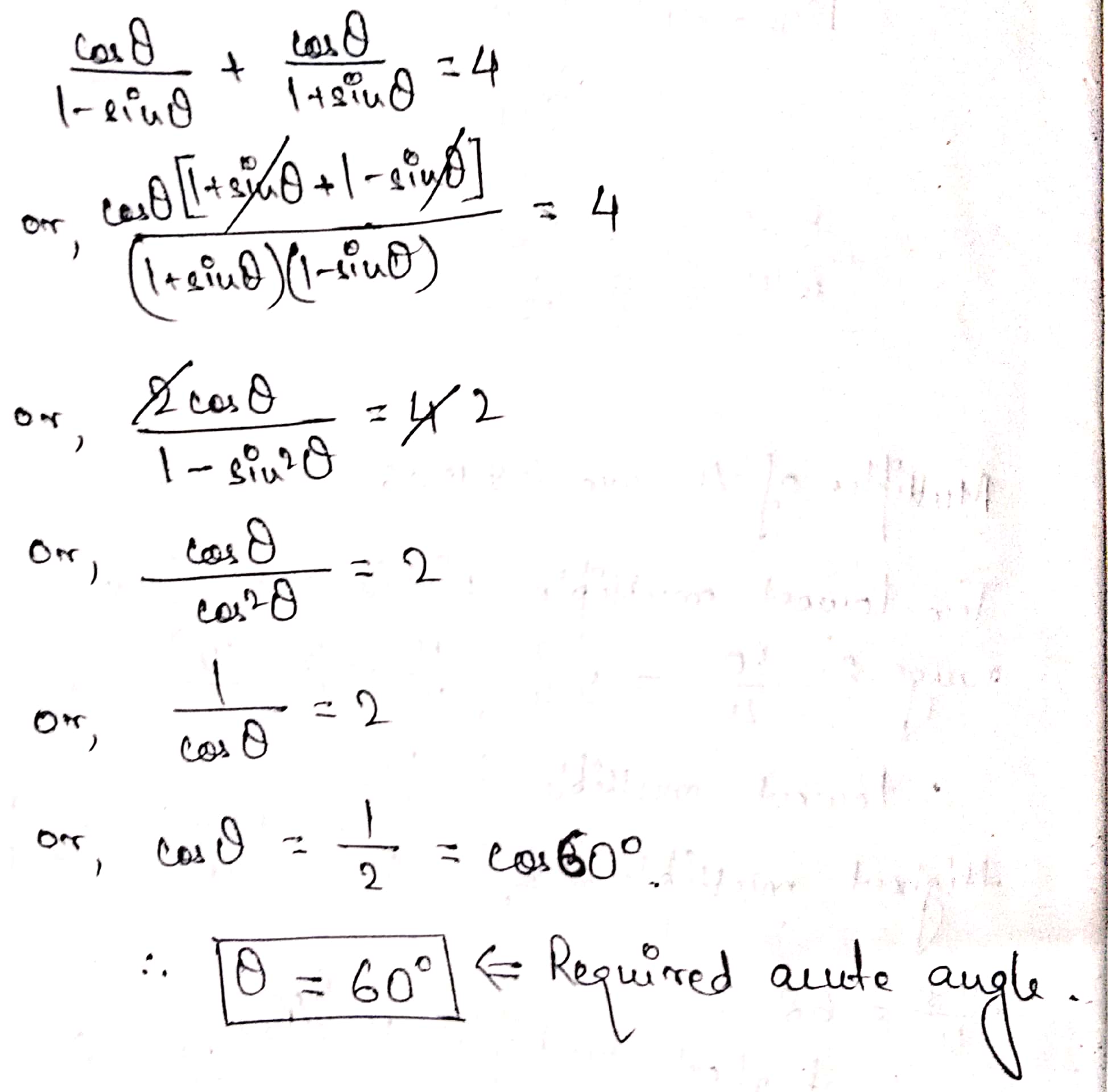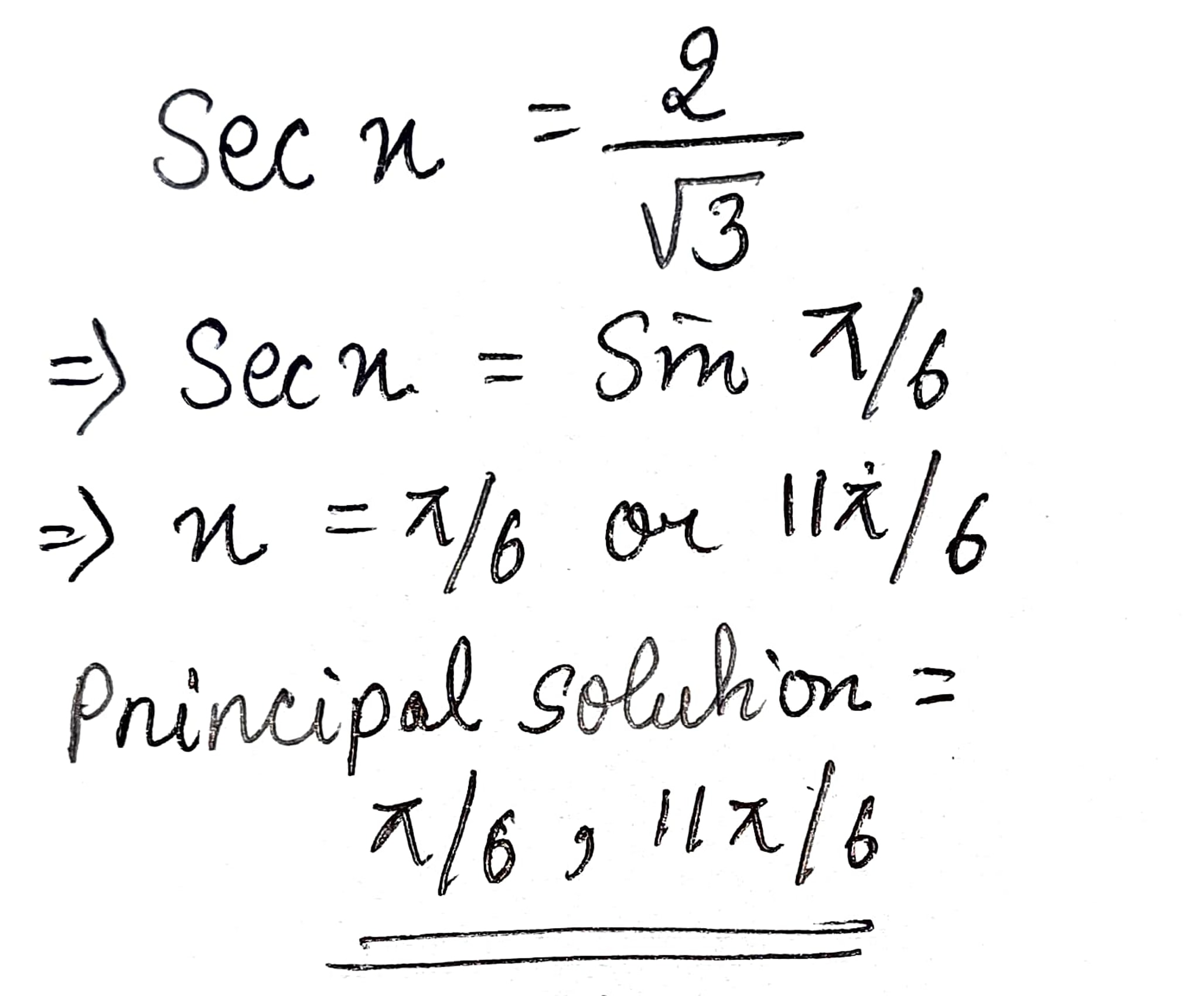Trigonometric Functions - Class 11 Engineering Maths - Extra Questions
If $$\displaystyle \alpha , \beta , \gamma \epsilon \left ( 0, \frac{\pi }{2} \right )$$, then $$\displaystyle\frac{\sin \left ( \alpha +\beta +\gamma \right )}{\sin \alpha +\sin \beta +\sin \gamma }< a$$
Find a
For any $$\theta$$, state the value of:
$$\sin ^{2}\theta+\cos ^{2} \theta$$
Prove that $$\displaystyle \frac{\cos 10^{0}+\sin 10^{0}}{\cos 10^{0}-\sin 10^{0}}=\tan a^{0}$$
Find a
Prove that:
$$\displaystyle cot^2\frac{\pi}{6}+cosec\frac{5\pi}{6}+3tan^2\frac{\pi}{6}=6$$
What is the value of $$\displaystyle \left ( \tan A+\cot A \right )\sin A\times \cos A$$ ?
What is the value of $$\displaystyle \sin ^{6 }\theta +\cos ^{6}\theta +3\sin ^{2}\theta \cos ^{2}\theta $$ ?
What is the value of $$\displaystyle \sin ^{2}25^{0}+\sin ^{2}65^{0}$$?
Prove that:
$$\displaystyle \sin^2\frac{\pi}{6}+\cos^2\frac{\pi}{3}-\tan^2\frac{\pi}{4}=-\frac{1}{2}$$
If $$\displaystyle \cos \theta =\frac{2t}{1+t^{2}}$$, then find the value of $$\displaystyle \tan \theta $$.
Write the principal value of $$\cos^{-1}[\cos (680^o)]$$.
Prove that:
$$\dfrac{sin\theta - 2sin^{3}\theta}{2cos^{3}\theta-cos\theta} =tan\theta$$
$$\dfrac{sin\theta - 2sin^{3}\theta}{2cos^{3}\theta-cos\theta} =tan\theta$$
LHS $$ = \dfrac{sin\,\theta -2\,sin^{3}\theta }{2\,cos^{3}\theta -cos\theta } $$
$$ = \dfrac{sin\,\theta (1-2\,sin^{2}\theta )}{cos\theta (2cos^{2}\theta -1)} $$
$$ = \dfrac{sin\,\theta }{cos\,\theta }\left [ \dfrac{1-2sin^{2}\theta }{2(1-sin^{2}\theta )-1} \right ] $$
$$ = tan\theta \left [ \dfrac{1-2sin^{2}\theta }{2-2sin^{2}\theta -1} \right ] $$
$$ = tan\theta \left [ \dfrac{1-2sin^{2}\theta }{1-2sin^{2}\theta } \right ] $$
$$ = tan\theta = RHS $$
Find the value of $$\cos^{2} 12^{\circ} + \cos^{2} 78^{\circ}$$
Show that $$\left( 1+\cot ^{ 2 }{ \theta } \right) \left( 1-\cos { \theta } \right) \left( 1+\cos { \theta } \right) =1\quad $$.
Prove $$\text{cosec}^{6}A - \cos^{6}A = 3\cot^{2}A \text{cosec}^{2} A + 1$$.
Simplify the following expression:
$$\displaystyle 3 \, \cos \, x \, - \, 4 \, \sin \, x \,\cos \, x \, - \, \sin^2 \, x \, - \, 1$$
Solve $$\sin\theta +\sin 5\theta =\sin 3\theta; 0\leq \theta \leq \pi$$.
Solve $$\sin x+\sqrt{3}\cos x \geq 1$$.
Prove the following identities :
$$\dfrac{1 \, - \, \cos \, \theta}{1 \, + \,\cos \, \theta} \, = \, (cosec \, \theta \, - \, \cot \, \theta)^2$$
Solve $$1-2\sin \theta -2\cos \theta +\cot \theta =0$$, $$(0 < \theta < 2\pi)$$.
Solve: $$2+7\tan^2x=3.25sec^2x$$.
Convert $$230^\circ$$ into radian.
Solve: $$4\sin^4x+\cos^4x=1$$.
Convert $$\dfrac{3\pi}{7}$$ in degrees.
$$2^{\cos 2x}=3.2^{\cos^2x}-4$$
The expression $$\dfrac{{\tan A + \sec A - 1}}{{\tan A - \sec A + 1}}$$ reduces to:
Prove that:$$\cot (\pi -\theta) = -\cot \theta$$
Prove that:$$\sec(\pi - \theta) = - \sec\theta$$
Prove that:$$\text{cosec} (\pi -\theta)= \text{cosec }\theta$$
Find the principal solution or solution of $$\sin x=\dfrac {1}{\sqrt {2}}$$.
Prove that :
$$\dfrac{1}{\sec \, \theta \, - \, \tan \, \theta} \, = \, \sec \, \theta \, + \, \tan \, \theta$$
show that $$ \sqrt { 2+\sqrt { 2+\sqrt { 2+2\cos { 8\theta } } } } =2\cos { \theta }$$, $$0<\theta<\dfrac{\pi}{8}$$
If $$\theta$$ is an acute angle and $$ sin \theta=\cos \theta$$ find $$3tan\theta$$
Find principal solution for $$\tan x =-1$$. $$x\epsilon(\dfrac{\pi}{2} ,\pi)$$
Convert $${290}^{o}$$ into radian measure
If $$a\sin \left( {\theta + \alpha } \right) = b\sin \left( {\theta + \alpha } \right)$$ show that $$\cot \theta = \dfrac{{a\cos \alpha - b\cos \alpha }}{{b\sin \alpha - a\sin \alpha }}$$.
Find the $$ particular solution$$ of $$\tan x + \tan 2x + \tan x.\tan 2x = 1$$.
$${\cos ^4}\theta + {\cos ^2}\theta = 1$$ then show that $${\sec ^4}\theta - {\sec ^2}\theta = 1$$
Prove that $$\sum a(\sin \,B - \sin C) = 0$$
Solve equation for general solution $$2(\sin \, x)^2 + (\sin \, 2x)^2 = 2$$.
Find radian measure corresponding to the degree measure $$ - {37^ \circ }30'$$
If $$\sin { A } =\cfrac { 5 }{ 13 } $$ then evaluate $$\cos { A } $$ and $$\tan { A } $$.
If $$\sin 9x = \sin x$$. Find the values of $$x$$.
Solve : $$\dfrac{1}{\text{cosec} \, \theta + \cot \, \theta} - \dfrac{1}{\sin \, \theta } = \dfrac{1}{\sin \, \theta} - \dfrac{1}{\text{cosec} \theta - \cot \theta}$$
Solve $$\sqrt { \cfrac { 1+\cos { 30 } }{ 1-\cos { 30 } } } $$
Prove $$\sin ^2\theta +\cos ^2\theta =1$$
Prove if $$sinA = sinB$$ then $$\angle A = \angle B$$.
If $$\tan { 2\theta =\cot { \left( \theta +{ 6 } \right) } } $$, where $$2\theta $$ and $$\theta +6$$ are acute angles, find the value of $$\theta $$.
Solve $$\tan x + \cot x$$
prove that:
$$1+\cot^{2} \theta = \csc^{2} \theta$$
$$ \displaystyle 1+cot^{2}\theta = cosec^{2}\theta $$
L.H.S
$$ \displaystyle 1+cot^{2}\theta = 1+\frac{cos^{2}\theta }{sin^{2}\theta } $$
$$ \displaystyle [\because cot\theta = \frac{cos\theta }{sin\theta }] = \frac{sin^{2}\theta +cos^{2}\theta }{sin^{2}\theta } $$
$$ \displaystyle [\because sin^{2}\theta +cos^{2}\theta = 1] = \frac{1}{sin^{2}\theta } $$
$$ \displaystyle [\because \frac{1}{sin\theta = cosec\theta }] = cosec^{2}\theta $$
$$ = R.H.S $$
$$ \displaystyle \therefore L.H.S = R.H.S $$
Hence proved
Solve $$\sqrt 2 \left( {\sin x + \cos x} \right) = \sqrt 3 $$
Find '$$x$$' if $$3\tan^{-1} x + \cot^{-1}x = \pi$$.
Solve $${\tan ^2}\theta + {\cot ^2}\theta = 2$$
Solve $$\tan 5\theta = \cot 2\theta $$
If $$\tan \theta=\dfrac{3}{A}$$, find $$\cos \theta \csc \theta$$.
Solve the equations
$$3(\sec^{2} \theta + \tan^{2} \theta) = 5$$.
If $$co\sec{A}=2$$, find the value of $$\cfrac{1}{\tan{A}}+\cfrac{\sin{A}}{1+\cos{A}}$$
If $$\sin{\theta}=\cfrac{1}{2}$$, show that $$(3\cos{\theta}-4{\cos}^{3}{\theta})=0$$
Write the complementary angle of $$\dfrac{1}{3}$$ of $$180^o$$.
Prove that $$\cos 4x=1-8\sin^2 x \cos^2x$$
cos $$x=\frac{1}{2}$$
Find the principle solutions.
If $$\sin A = \frac{1}{3}$$, then find the value of $${\mathop{\rm cosAcosec}\nolimits} + tanAsecA$$
$$sin A= \dfrac{1}{3}\Rightarrow cos A= \sqrt{1-sin^{2}A}= \sqrt{1-\dfrac{1}{9}}=\sqrt{\dfrac{8}{9}}=\dfrac{2\sqrt{2}}{3}$$
$$tan A= \dfrac{sin A}{cos A}= \dfrac{\dfrac{1}{3}}{\dfrac{2\sqrt{2}}{3}}= \dfrac{1}{2\sqrt{2}}$$
$$sec A= \dfrac{1}{cos A}= \dfrac{3}{2\sqrt{2}}$$
$$cosec A= \dfrac{1}{sin A}= 3$$
$$cos A. cosec A+ tan A. sec A$$
$$=\dfrac{2\sqrt{2}}{3}.3+\dfrac{1}{2\sqrt{2}}.\dfrac{3}{2\sqrt{2}}$$
$$=2\sqrt{2}+\dfrac{3}{8}=\dfrac{3+16\sqrt{2}}{8}$$
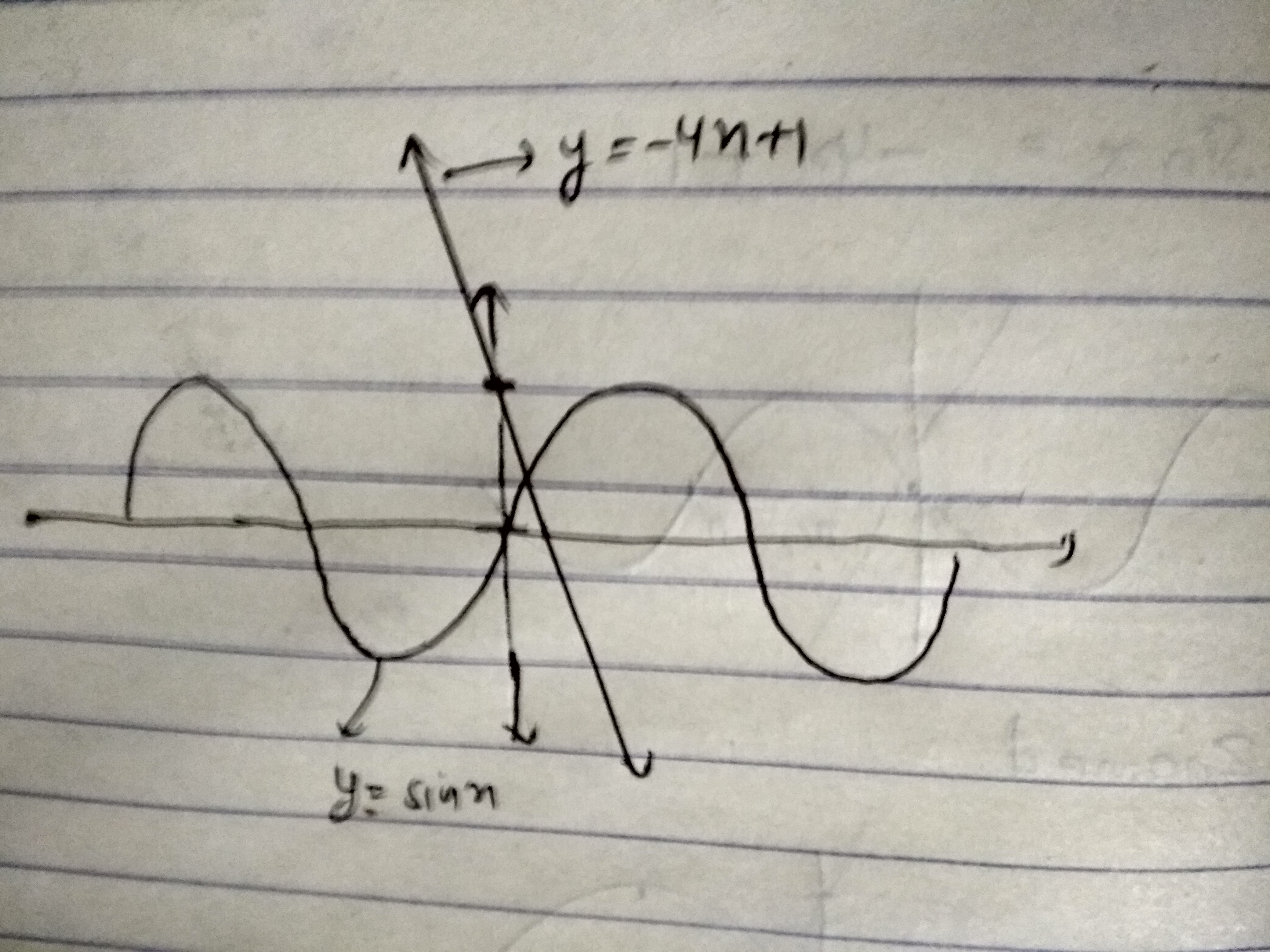
Find number of solutions of equation $$\sin x=-4x+1$$
It is clearly evident from above graph that there is only one solution for given equation .
Find the principal solution of the following equation:
$$\cot { x=\sqrt { 3 } } $$
Value of $$\sin ^ { 2 } A + \cos ^ { 2 } A = ?$$
Find the value of $${ \left( \cfrac { \cos { A } +\cos { B } }{ \sin { A } -\sin { B } } \right) }^{ n }+{ \left( \cfrac { \sin { A } +\sin { B } }{ \cos { A } -\cos { B } } \right) }^{ n }$$ (where $$n$$ is an even)
$$\displaystyle (\frac{cosA+cosB}{sinA-sinB})^{n}+(\frac{sinA+sinB}{cosA-cosB})^{n}$$
$$\displaystyle = (\frac{2cos(\frac{A+B}{2})cos(\frac{A-B}{2})}{2cos(\frac{A-B}{2})sin(\frac{A-B}{2})})^{n}+(\frac{2sin(\frac{A+B}{2})cos(\frac{A-B}{2})}{-2sin(\frac{A+B}{2})sin(\frac{A-B}{2})})^{n}$$
$$\displaystyle = cot^{n}(\frac{A-B}{2})+(-1)^{n}cot^{n}(\frac{A-B}{2})$$
if n is even, than $$(-1)^{n} = 1 $$ then the given expression becomes
$$\displaystyle 2cot^{n}(\frac{A-B}{2})$$
If n is odd then $$(-1)^{n} = -1 $$ then the given expression becomes 0
If $$0 < \theta < 90^o$$ and $$\sec \theta = \text{cosec}60^o$$ , find the value of $$2{\cos ^2}\theta - 1$$
$$ 0< \theta < 90^{\circ}$$
$$ sec\theta = cosec60$$
$$ \Rightarrow sec\theta = \frac{1}{sin60} = \frac{2}{\sqrt{3}}$$
$$ \Rightarrow \frac{1}{cos\theta } = \frac{2}{\sqrt{3}} \Rightarrow cos\theta = \frac{\sqrt{3}}{2} \Rightarrow \theta = 30^{\circ}$$
$$ 2cos^{2}\theta -1 = 2(cos30)^{2}-1$$
$$ \Rightarrow 2\times (\frac{\sqrt{3}}{2})^{2}-1$$
$$ \Rightarrow 2\times \frac{3}{4}-1\Rightarrow \frac{3}{2}-1= \frac{1}{2}$$
$$ \therefore 2cos^{2}\theta -1 = \frac{1}{2}$$
$$tan^{-1}\dfrac{1}{3}+tan^{-1}\dfrac{1}{7}+tan^{-1}\dfrac{1}{5}+tan^{-1}\dfrac{1}{8}=\dfrac{\pi }{4}.$$
$$ tan^{-1}(\frac{1}{3})+tan^{-1}(\frac{1}{7})+tan^{-1}(\frac{1}{5})+tan^{-1}(\frac{1}{8}) $$
$$ \Rightarrow tan^{-1}(\frac{10/21}{20/21})+tan^{-1}(\frac{13/40}{39/40}) $$
$$ \Rightarrow tan ^{-1}(\frac{1}{2})+tan^{-1}(\frac{1}{3}) $$
$$ \Rightarrow tan^{-1}(\frac{5/6}{5/6}) $$
$$ \Rightarrow tan^{-1}(1) $$
$$ \Rightarrow \frac{\pi }{4} $$
$$ tan^{-1}(A)+tan^{-1}B = $$
$$ tan^{-1}(\frac{A+B}{1-AB}) $$
Prove that: $$\displaystyle \frac { \sec \theta + \tan \theta - 1 } { \tan \theta - \sec \theta + 1 } = \frac { \cos \theta } { 1 - \sin \theta }$$
Solve: $$\dfrac{1+tan^2\theta}{1-tan^2\theta}=sec2\theta.$$
Prove : $$\dfrac{\cot A +\text{ cosec} A -1}{\cot A - \text{cosec} A +1} = \dfrac{1 +\cos A}{\sin A}$$
Prove $$\dfrac{1}{\sec\theta -1}-\dfrac{1}{\sec\theta +1}=2\cot^2\theta$$
Solve $$\dfrac{\cos{\theta}}{1-\sin{\theta}}+\dfrac{\cos{\theta}}{1+\sin{\theta}}=4$$ for $$\theta <90$$
solve $$ \frac{cos\theta }{1-sin\theta }+\frac{cos\theta }{1+sin\theta } = 4 $$ $$ \theta < 90$$
$$ \frac{cos\theta }{1-sin\theta }+\frac{cos\theta }{1+sin\theta } = 4 $$
$$ \frac{cos\theta (1+sin\theta )+cos\theta (1-sin\theta )}{1-sin^{2}\theta } = 4$$
$$ \frac{cos\theta +cos\theta .sin\theta +cos\theta -cos\theta sin\theta }{cos^{2}\theta } = 4 $$
$$ \therefore \frac{2cos\theta }{cos^{2}\theta } = 4 $$
$$ \therefore \frac{2}{4} = cos\theta $$
$$ \therefore cos\theta = \frac{1}{2}$$
$$ \therefore \theta = 60^{\circ}$$
If $$\cos \theta=\dfrac{3}{5}$$, find the value of $$\cot \theta +cosec \ \theta$$.
If $$\sin \theta =\dfrac{a}{\sqrt{a^2+b^2}}$$, $$0<\theta <90^o$$, find the values of $$\cos \theta$$ and $$\tan \theta$$.
The value of $$\cot^{2}C-\dfrac{1}{\sin^{2}C}$$ is
The value of $$\tan^{2}A-\sec^{2}A$$ is
Write $$\tan\theta$$ in terms of $$\sin\theta$$.
If $$\sin 3A=\cos (A-10^o)$$, then find the value of A, where 3A is an acute angle.
Prove that $$\dfrac {\cot A-\cos A}{\cot A+\cos A}=\dfrac {\text{cosec} A-1}{\text{cosec} A+1}$$
Eliminate $$\theta$$, if $$x=a\cos\theta, y=a\sin \theta$$.
Prove that :
$$(\csc A-\sin A)(\sec A-\cos A)=\dfrac {1}{\tan A+\cot A}$$
$$L.H.S = (cosec A- sin A) (sec A- cos A)$$
$$=(\frac{1}{sin A}-sin A)(\frac{1}{cos A}-cos A)=\frac{(1-sin^{2}A)(1- cos^{2}A)}{sin A cos A}$$
$$=\frac{cos^{2}A\times sin^{2}A}{sin A cos A}= sin A cos A$$
R.H.D= $$\frac{1}{tan A+ cot A}=\frac{1}{\frac{sin A}{cos A}+\frac{cos A}{sin A}}=\frac{sin A cos A}{sin^{2}A+cos^{2}A} = sin A cos A$$
$$\Rightarrow L.H.S = R.H.S$$
If $$7\csc\alpha-3\cot\alpha=7$$ prove that $$7\cot\alpha-3\csc\alpha=3$$
A] Given
$$ 7cosec \theta - 3 cot \theta = 7 $$
squaring,
$$ \Rightarrow (7 cosec \theta -3 cot \theta )^{2} = 49$$
$$ \Rightarrow 49 cosec^{2} \theta + 9 cot^{2} \theta - 2 \times 7 \times 3 cosec \theta cot \theta = 49$$
$$\Rightarrow 49 (1 + cot 2 \theta) + 9 (cosec2\theta - 1) - 42 cosec \theta cot\theta=49$$
$$\Rightarrow 49+49cot2\theta+9cosec2\theta-9 - 42 cosec \theta cot\theta=49$$
$$\Rightarrow \Rightarrow (7cot\theta)^{2} + (3cosec \theta)^{2} -2 \times 7 \times 3 cot \theta cosec \theta = 9 $$
$$\Rightarrow (7 cot\theta -3cosec\theta )^{2} = 9$$
$$ \Rightarrow 7 cot \theta - 3 cosec \theta = 3 $$
Hence proved
Prove that $$sec^{4}\theta-tan^{4}\theta=1+2 tan^{2}\theta.$$
Find the principal solution or solutions of $$\sin x = \dfrac { 1 } { \sqrt { 2 } }$$
Find the value of $$\sin (270^o)$$.
Prove $$\dfrac{1-\cos A}{1+\cos A}=(\csc A-\cot A)^2$$
$$\dfrac{1-\cos A}{1+\cos A}\times \dfrac{1-\cos A}{1-\cos A}=\dfrac{1+\cos^2A-2\cos A}{1-\cos^2A}=\dfrac{1+\cos^2A-2\cos A}{\sin^2A}$$
$$=cosec^2A+\cot^2A-2\cot A cosec A$$
$$=(cosec A-\cot A)^2$$.
If $$\sec\theta+\tan\theta=p$$, find the value of $$\csc\theta$$
As $$\sec 2\theta - \tan 2\theta = 1$$
$$(\sec \theta - \tan \theta )P = 1$$
$$\sec \theta - \tan \theta = \dfrac{1}{p}$$ ...(1)
$$\sec \theta + \tan \theta = p$$ ...(2)
eqn. (1) + (2)
$$\sec \theta = \dfrac{1}{2} \left(p + \dfrac{1}{p}\right)$$ ...(3)
eqn. (1) - (2)
$$\tan \theta = -\dfrac{1}{2} \left(\dfrac{1}{p}-p\right)$$ ...(4)
eqn. (3) $$\div$$ (4)
$$cosec \theta = \dfrac{p^2 + 1}{p^2 - 1}$$
Make the following expression a perfect square:$$1+2\sin \theta.\cos \theta$$.
Evaluate: $$3\cot^{2}\theta-3\text{cosec}^{2}\theta$$
$$3\cot^2\theta -3cosec^2\theta =-3(cosec^2\theta -\cot^2\theta)$$
$$=-3$$
$$\{cosec^2\theta -\cot^2\theta =1\}$$.
Prove that$$\frac{cosA}{1-tanA}+\frac{sinA}{1-cot A}=sinA +cosA$$
Prove
$$tan \Theta +sec\theta=\frac{1}{sec\Theta -tan\Theta }$$
$$\tan\theta +\sec\theta =\dfrac{1}{\sec\theta -\tan\theta}$$
Solving LHS$$=\tan\theta +\sec\theta$$ (on rationalising)
$$\Rightarrow \dfrac{(\tan\theta +\sec\theta)(\tan\theta -\sec\theta)}{\tan\theta -\sec\theta}=\dfrac{\tan^2\theta -\sec^2\theta}{\tan\theta -\sec\theta}$$
We know $$1+\tan^2\theta =\sec^2\theta$$
$$\Rightarrow \tan^2\theta -\sec^2\theta =-1$$
Then
$$\Rightarrow \dfrac{-1}{\tan\theta -\sec\theta}$$
$$\Rightarrow \dfrac{1}{\sec\theta -\tan\theta}=$$RHS.
The value of x fo which $$\sin(\pi x)+\cos (\pi x)=0$$
Prove that : $$(1+\sin\theta-\cos\theta)^{2}+(1-\sin\theta-\cos\theta)^{2}=4(1-\cos\theta)$$
$$[(1-\cos\theta)+\sin\theta]^2=[(1-\cos\theta)-\sin\theta)^2$$
$$(a+b)^2+(a-b)^2=2(a^2+b^2)=2(1+\cos^2\theta -2\cos\theta +\sin^2\theta)$$
$$=2(1+1-2\cos\theta)=4(1-\cos\theta)$$.
If $$\tan 9\theta=\cot \theta$$, where $$9\theta < 90^{o}$$ then find the value of $$\theta$$.
Find the degree measure of $${\dfrac{1}{4}}^{c}$$
Prove that : $$\dfrac { 1 + \sin \theta } { \cos \theta } + \dfrac { \cos \theta } { 1 + \sin \theta } = 2 \sec \theta$$
$$\frac{1+ sin\theta }{cos \theta }+\frac{cos\theta }{1+ sin\theta }=2 sec\theta $$
$$\frac{(1+sin\theta )^{2}+cos^{2}\theta }{cos \theta (1+ sin \theta )}=2 sec \theta $$
$$\frac{1+ sin^{2} \theta +2 sin \theta +cos^{2} \theta }{cos \theta (1+ sin \theta )}=2 sec \theta $$
$$sin^{2} \theta +cos^{2} \theta =1$$
$$\frac{1+1+2 sin \theta }{cos \theta (1+ sin \theta )}= 2 sec \theta $$
$$\frac{2+2 sec \theta }{cos \theta (1+ sin \theta )}= 2 sec \theta $$
$$\frac{2(1-1 sin \theta )}{cos \theta (1+ sin \theta )}= 2 sec \theta $$
$$2 sec \theta = 2 sec \theta $$ $$L.H.S=R.H.S$$
If $$\tan (A+B) =\sqrt{3}$$ and $$\tan(A-B)=\dfrac{1}{\sqrt{3}}$$ find $$A$$ and $$B$$. A and B are acute angles. Then A+B in degrees
$$sec\Theta +tan\Theta =p$$ find $$cosec\Theta $$
$$\frac { \cos { A } -\sin { A+1 } }{ \cos { A } +\sin { A-1 } } =cosecA+\cot { A } $$
Find the degree measure of $${\dfrac{\pi}{8}}^{c}$$
Express the following degrees into grades (i.e., sexagesimal system to centesimal system)
$$63^{\circ} $$
If $$\tan { \theta } +\sec { \theta } =x$$, show that $$\sin { \theta } =\cfrac { { x }^{ 2 }-1 }{ { x }^{ 2 }+1 } $$
Convert $$ \dfrac{\pi}{12} $$ radians into degree (sexagesimal system).
Find the principal solution of the following equation:
$$cos \theta=\frac{1}{2}$$
If $$A - B = C$$ and $$A + B =\frac{\pi }{2}$$ then $$\tan A = \tan B + 2\tan C$$.
State true(1) or false(0):$$\left ( \tan \theta +2 \right )\left ( 2 \tan \theta +1 \right )=5 \tan\theta +sec^{2} \theta $$
Fill in the blank$$\sec A(1-\sin A)(\sec A + \tan A)=$$ _____
The number of solutions of $$3 sec\theta-5=4 tan \theta$$ in $$[0, 4\pi]$$ be $$k$$.Find $$k$$ ?
The number of values of $$x$$ between $$0$$ and $$2\pi$$ that satisfies the equation $$\sin x+ \sin 2x+ \sin 3x=\cos x+ \cos 2x+ \cos 3x$$ must be-
$$\left ( \cos A-\cos B \right )^{2}+\left ( \sin A-\sin B \right )^{2}=c\sin ^{2}\left ( A-B \right )/2$$
Find $$2c$$
$$\sqrt{\sin ^{4}x+4\cos ^{2}x}-\sqrt{\cos ^{4}x+4\sin ^{2}x}=\cos sx$$ Find s
Solution of $$\displaystyle 3\left ( \sec ^{2}\theta+\tan^{2}\theta \right )=5$$ is $$\displaystyle \ \theta =n\pi \pm \frac { \pi }{ m } $$. Find $$m$$.
Find the maximum value of $$\sqrt{3}\sin x+\cos x$$ .
In quadrilateral $$ABCD$$ if $$\displaystyle \sin \left ( \dfrac{A+B}{2} \right )\cos \left ( \dfrac{A-B}{2} \right )+\sin \left ( \dfrac{C+D}{2} \right )\cos \left ( \dfrac{C-D}{2} \right )=2$$, then the value $$\displaystyle \sin \dfrac{A}{2}\sin \dfrac{B}{2}\sin \dfrac{C}{2}\sin \dfrac{D}{2}$$ is $$\dfrac{1}{a}$$ Find a
If $$\displaystyle 0 < x < \frac {\pi}{4}$$ and $$\displaystyle cos x + sin x = \frac {5}{4}$$, then the value of $$\displaystyle 16(cos x - sin x)^2$$ is
$$\displaystyle \frac{1+\sin 2\theta }{1-\sin 2\theta }=\left ( \frac{1+\tan \theta }{1-\tan \theta } \right )^{b}$$
.Find $$b$$
Find $$a$$ if, $$a\sin 27^{0}=\left ( 5+\sqrt{5} \right )^{1/2}-\left ( 3-\sqrt{5} \right )^{1/2}$$
If $$\sin A\, +\, cosec\: A= 2$$; find the value of $$\sin ^{2}A\, +\, cosec^{2}A$$.
If $$\displaystyle 4\cos^{2}A-3=0 $$ and $$\displaystyle 0^{\circ}\leq A \leq 90^{\circ} $$, then find $$\angle A$$ in degrees.
If $$\displaystyle f\left (x \right )= \sin \left ( \log x \right ),$$ then show that $$\displaystyle f\left (xy\right )+ f\left ( \frac{x}{y} \right )-2f\left ( x \right )\cos \left ( \log y \right )=0$$
$$\displaystyle \cos^2\ 42^{\circ}-\sin^2 48^{\circ}$$
$$\displaystyle \sin ^2 62^{\circ}-\cos ^2 28^{\circ}$$
If $$\displaystyle \sin \theta = \dfrac{45}{53}$$, find the value of $$\displaystyle cosec^2 \theta - \cot^2 \theta$$
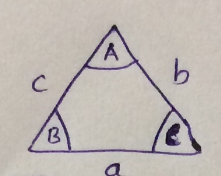
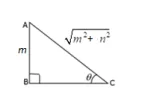
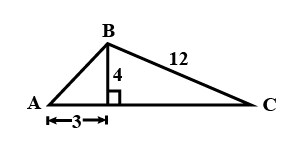
Refer to the triangle given in figure.
Find: $$\left|\cot ^{2}C\, -\displaystyle \, \frac{1}{\sin ^{2}C}\right|$$
$$\displaystyle 2\sin^2 54^{\circ}-2\cos ^2\ 36^{\circ}+4\sin^2 30^{\circ} $$
Refer to the triangle given in figure.
Find: $$|\tan ^{2}A\, -\, \sec ^{2}A|$$
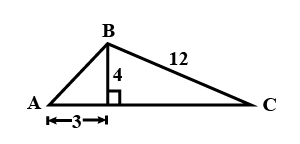
In an Isosceles triangle ABC,$$tan^{2}\, B\, -\,sec^{2}\, B\, +\, 2$$
If $$cot\, \Theta\, =\, 1$$; find the value of :
$$5\, tan^{2} \Theta\, +\, 2\, sin^{2}\, \Theta\, -\, 3$$
$$sin^{2}\, B\, +\, cos^{2}\, C$$
If sin A = cos A, find the value of $$2\, tan^{2}\, A\, -\, 2\, sec^{2}\, A\, +\, 5$$.
$$3\, -\, cot^{2}\, A\, +\, cosec^{2}\, A$$
$$(sec\, x^{\circ}\, -\, tan\, x^{\circ})\, (sec\, x^{\circ}\, +\, tan\, x^{\circ})$$
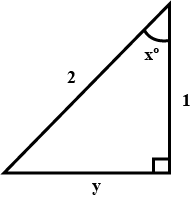
$$tan^{2}\, C\, -\, sec^{2}\, B\, +\, 2$$
Find the value of:$$\text{cosec}^{2}\,45^{\circ}\,-\,\cot^{2}\,45^{\circ}\,$$
$$\cos^{2}\, 42^{\circ}\, -\, \sin^{2}\, 48^{\circ}$$
Find the value of $$cosec^{2}\, 60^{\circ}\, -\, \tan^{2}\, 30^{\circ}$$
If $$\displaystyle \sin \theta +\cos \theta =1$$, then the value of $$\displaystyle \sin \theta \cos \theta $$ is
If $$\displaystyle \sec \theta =x+\frac{1}{4x}$$, then the value of $$\displaystyle \sec \theta +\tan \theta $$ is equal to
If $$\displaystyle A=29^{0}$$, then find the value of $$\displaystyle \sin ^{4}A+\cos ^{4}+A+2\sin ^{2}A\cos ^{2}A$$.
The value of $$\displaystyle \left ( \sin x\cos y+\cos x\sin y \right )^{2}+\left ( \cos x\cos y-\sin x\sin y \right )^{2}$$ is equal to
What is the value of $$\displaystyle \frac{\left ( \sec \theta +1 \right )^{2}+\left ( 1-\sec \theta \right )^{2}}{1+\sec ^{2}\theta }$$ ?
Prove that:
$$\displaystyle 2\, cos\frac{\pi}{13}cos\frac{9\pi}{13}+cos\frac{3\pi}{13}+cos\frac{5\pi}{13}=0$$
Prove that:
$$\displaystyle 2sin^2\frac{3\pi}{4}+2cos^2\frac{\pi}{4}+2sec^2\frac{\pi}{3}=10$$
Find the values of $$\displaystyle \theta $$ and $$p$$, if the equation $$\displaystyle x\cos \theta +y\sin \theta = p$$ is the normal form of the line $$\displaystyle \sqrt{3}x+y+2= 0.$$
Prove that:
$$\displaystyle 2sin^2\frac{\pi}{6}+cosec^2\frac{7\pi}{6}cos^2\frac{\pi}{3}=\frac{3}{2}$$
Prove the following:
$$\displaystyle \cos \left(\dfrac{3\pi}{2}+x\right) \cos(2\pi+x)\left[\cot\left(\dfrac{3\pi}{2}-x\right)+\cot (2\pi +x)\right]=1$$
(i) If A + B = $$45^o$$, prove that $$\displaystyle (cot A-1)(cotB-1)=2$$ and hence deduce that $$\displaystyle cot 22 \frac{1}{2}^o = \sqrt{2} + 1$$.
(ii) If $$\displaystyle tan(A-B) = \frac{7}{24}$$ and $$\displaystyle tan A=\frac{4}{3}$$ where A and B are acute, show that A + B = $$\displaystyle \frac{\pi}{2}$$
Express the trigonometric ratio tan A in terms of sec A.
(i) If $$\cos 3A = \sin (A - 34^0)$$, where A is an acute angle, find the value of A.
(ii) Prove the following identity, where the angles involved are acute angles for which the expression is define.
$$\dfrac{1 + \cot^2 A}{1 + \tan^2 A} = \left( \dfrac{1 - \cot A}{1 - \tan A} \right )^2$$
If $$\tan \theta + \sin \theta = m, \tan \theta - \sin \theta = n$$ and $$m\neq n$$, then show that $$m^{2} - n^{2} = 4\sqrt {mn}$$
Prove the following identity
$$\sqrt { \sec ^{ 2 }{ \theta } +cosec ^{ 2 }{ \theta } } =\tan { \theta } +\cot { \theta } $$
If $$3 \cot A = 4$$, then evaluate $$\dfrac{1 - \tan^2 A}{1 + \tan^2 A}$$
Find the value of $$\cfrac { \sec { { 15 }^{ o } } }{ co\sec { { 75 }^{ o } } } +\cfrac { \sin { { 72 }^{ o } } }{ \cos { { 18 }^{ o } } } -\cfrac { \tan { { 33 }^{ o } } }{ \cot { { 57 }^{ o } } } $$.
Prove: $$(\sin^{6}\theta + \cos^{6}\theta) = 1 - 3\sin^{2}\theta \cos^{2}\theta$$
Prove that $$\sqrt { \cfrac { 1-\sin { \theta } }{ 1+\sin { \theta } } } =\sec { \theta } -\tan { \theta } $$, (where $$\theta$$ is acute).
Prove that $${ \left( \sin { \theta } +co\sec { \theta } \right) }^{ 2 }+{ \left( \cos { \theta } +\sec { \theta } \right) }^{ 2 }=7+\tan ^{ 2 }{ \theta } +\cos ^{ 2 }{ \theta } $$
Show that $$\tan ^{ 2 }{ \theta } -\cfrac { 1 }{ \cos ^{ 2 }{ \theta } } =-1$$.
If $$(2\cos x + \sin x) = 1$$, then sum of all possible value of $$(7\cos x+ 6 \sin x)$$ is__________
Evaluate: $$\dfrac {1}{\sec A - \tan A} - \dfrac {1}{\cos A} = \dfrac {1}{\cos A} - \dfrac {1}{(\sec A + \tan A)}$$.
Prove by vector method that
$$\sin { \left( \alpha +\beta \right) } =\sin { \alpha } \cos { \beta } +\cos { \alpha } \sin { \beta } $$
Let $$OQ=OP=1$$
$$OQ$$ makes angle $$\alpha$$ and $$OP$$ makes angle $$\beta$$
with x-axis
Let $$PM$$ and $$QN$$ be perpendicular to x-axis
$$\overrightarrow { OQ }=\overrightarrow {ON } +\overrightarrow { NQ } $$
$$=|ON|\hat{i}+|NQ|\hat{j}$$
$$=(OQ\cos \alpha)\hat{i}+(OQ\sin\alpha)\hat{j}$$ $$[\because OQ=1]$$
$$=\cos\alpha\hat{i}+\sin\alpha\hat{j}$$........(1)
Similarly
$$\overrightarrow { OP } =\overrightarrow { OM } +\overrightarrow { MP } $$
$$=|OM|\hat{i}+|MP|\hat{j}$$
$$=(OP\cos\beta)\hat{i}+(OP\sin \beta)-\hat{j}$$ $$[\because OP=1]$$
$$=\cos\beta\hat{i}-\sin\beta\hat{j}$$.......(2)
$$\overrightarrow { OP} \times \overrightarrow { OQ } =(\cos\beta\hat{i}-\sin\beta\hat{j})\times (\cos\alpha\hat{i}\sin\alpha\hat{j})$$
$$\cos\beta\cos\alpha(\hat{i}\times \hat{i})+\cos\beta\sin\alpha(\hat{i}\times \hat{j})-\sin\beta\cos\alpha(\hat{j}\times \hat{i})-\sin\beta\sin\alpha(\hat{j}\times \hat{j})$$
$$=(\sin\alpha\cos\beta+\cos\alpha\sin\beta)\hat{k}$$.....(i)
$$\overrightarrow { OP } \times \overrightarrow {OQ }=|OP||OQ|\sin(\alpha+\beta)\hat{k}$$
$$=\sin(\alpha+\beta)\hat{k}$$......(iii)
By (i) and (ii)
$$\sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta$$
Prove that in a triangle with angles A,B,C and opposite sides as a,b,c $$\frac{\sin{\left(B-C\right)}}{\sin{\left(B+C\right)}} = \frac{{b}^{2}-{c}^{2}}{{a}^{2}}$$
To prove $$\to \ \dfrac {\sin (B-C)}{\sin (B+C)}\dfrac {b^2 -c^2}{a^2}$$
where $$A, B, C, \to$$ angles of $$\triangle $$
$$a, b, c\to $$ sides of $$\triangle$$
defined such that,
where $$A+B+C=\pi$$
Using Sine Rule for a $$\triangle $$
$$\dfrac {\sin A}{a}=\dfrac {\sin B}{b}=\dfrac {\sin C}{c}=b (let)$$
From here, we get
$$a=\dfrac {\sin A}{b}, b=\dfrac {\sin B}{b}, c=\dfrac {\sin C}{b}$$
$$\Rightarrow \ $$ Put values $$a, b, c$$ on $$RHS$$
$$RHS=\dfrac {b^2 -c^2}{a^2}=\dfrac {\dfrac {\sin^2 B}{b^2}-\dfrac {\sin^2 C}{b^2}}{\dfrac {\sin^2 A}{b^2}}$$
$$=\dfrac {\sin^2 B-\sin^2 C}{\sin^2 A}$$
$$[Using\ Formula \to \sin (B+C) \sin (B-C)=\sin^2 B-\sin^2C]$$
$$=\dfrac {\sin (B+C) \sin (B-C)}{\sin^2 A}\quad [As\ A+B+C=\pi \\ A=\pi -(B+C)]$$
$$=\dfrac {\sin (B+C) \sin (B-C)}{\sin^2 (\pi -(B+C))}$$
$$=\dfrac {\sin (B-C)}{\sin^2 (B+C)}$$
$$=\dfrac {\sin (B-C)}{\sin (B+C)}=LHS$$
Hence proved.
If $$f_n(\alpha)=\displaystyle\frac{\sin\alpha +\sin 3\alpha +\sin 5\alpha +.....+\sin(2n-1)\alpha}{\cos\alpha +\cos 3\alpha +\cos 5\alpha + .....+\cos(2n-1)\alpha}$$ find $$f_4(\pi /32)$$.
If $$\csc { \theta -\sin { \theta ={ a }^{ 3 } } } $$ and $$\sec { \theta } -\cos { \theta } =b^{ 3 }$$, prove that $${ a }^{ 2 }{ b }^{ 2 }\left( { a }^{ 2 }+{ b }^{ 2 } \right) =1$$
Prove that : $$\dfrac { 1 }{ 1+\sin { \theta } } +\dfrac { 1 }{ 1-\sin { \theta } } =2\sec ^{ 2 }{ \theta } $$
Prove that $$\dfrac{\sin x - \sin 3x}{\sin^{2} x - \cos^{2} x} = 2 \sin x$$
If $$\sec { \theta } =x+\dfrac { 1 }{ 4x } $$, then show that $$\tan { \theta } +\sec { \theta } =2x$$ or $$\dfrac { 1 }{ 2x } $$.
Show that $$sin^6 \theta + cos^6 \theta + 3 sin^2 \theta cos^2 \theta = 1$$
Prove $$\displaystyle \frac{\tan \, 2x \, \tan \, x}{\tan \, 2x \, - \, \tan \, x} \, = \, \sin \, 2x.$$
Prove the following identity:
$$\displaystyle \sin^2 \, (45^{\circ} \, + \, \alpha) \, - \, \sin^2 \, (30^{\circ} \, - \, \alpha) \, - \, \sin \, 15^{\circ} \, \cos \, (15^{\circ} \, + \, 2\alpha) \, = \, \sin \, 2\alpha$$
Prove the following identity:
$$\displaystyle \frac{1 \, - \, 2 \, \sin^2 \, \alpha}{1 \, + \, \sin \, 2\alpha} \, = \, \frac{1 \, - \, \tan \, \alpha}{1 \, + \, \tan \, \alpha}$$
Prove $$\displaystyle \cos^2 \, \alpha \, - \, \sin^2 \, 2\alpha \, = \, \cos^2 \, \alpha \, \cos \, 2\alpha \, - \, 2 \, \sin^2 \, \alpha \, \cos^2 \, \alpha.$$
Simplify the following expression:
$$\displaystyle \frac{1 \, + \, \sin + \, 2x}{(\sin \, x \, + \, \cos \, x)^2}$$
Prove $$\displaystyle 3 \, - \, 4 \, \cos \, 2\alpha \, + \, \cos \, 4\alpha \, = \, 8 \, \sin^4 \, \alpha.$$
Prove the following identities.
$$\displaystyle \frac{1 \, + \, \sin \, \alpha}{1 \, + \, \cos \, \alpha} \, .\frac{1 \, + \, \sec \, \alpha}{1 \, + \, \text{cosec} \, \alpha} \, = \, \tan \, \alpha.$$
Solve the following:
$$\displaystyle1 + \sec\, 20^{\circ} - \sqrt{3} \cot\, 40^{\circ}$$
Prove $$\displaystyle \frac{1}{4 \, \sin^2 \, \alpha \, \cos^2 \, \alpha} \, - \, \frac{(1 \, - \, \tan^2 \, \alpha)^2}{4 \, \tan^2 \, \alpha} \, = \, 1.$$
Prove $$\displaystyle \cot \, \alpha \, - \, \tan \, \alpha \, - \, 2 \, \tan \, 2\alpha \, - \, 4 \, \tan \, 4\alpha \, = 8 \, \cot 8 \, \alpha.$$
Solve the following equation:
$$\displaystyle \sin \, x \, - \, \sin \, 2x \,+ \, \sin \, 5x \, + \, \sin \, 8x \, = \, 0.$$
Solve the following equation:
$$\displaystyle (2 \, \sin \, x \, - \, \cos \, x) \, (1 \, + \, \cos \, x) \, = \, \sin^2 \, x.$$
Solve the following equations.
$$\displaystyle 4\sin^4 \, x \, + \cos^4 \, x=1$$
Solve the following equation:
$$\displaystyle \sin^4 \, x \, + \, \cos^4 \, x \, = \, \sin \, x \, \cos \, x.$$
Solve the following equation:
$$\displaystyle 2 \, \cos^2 \, x \, + \, 4 \, \cos \, x \, = \, 3 \,\sin^2 \, x$$
Solve the following equations.
$$\displaystyle (cos \, 6x \, - \, 1) \, cot \, 3x \, = \, sin \, 3x.$$
$$ (cos 6x-1) cot 3x = sin3x $$
$$ \Rightarrow (cos 6x- 1) \dfrac{cos3x}{sin3x} = sin3x $$
$$ \Rightarrow (cos 6x-1) cos3x = sin^{2 }3x $$
$$ \Rightarrow (2cos^2 3x-2) cos 3x = 1- cos^2 3x $$
Substitute
$$ cos 3x = t $$
$$ \Rightarrow 2(t^2 -1) t = 1-t ^2 $$
$$ \Rightarrow 2t^3 - 2t = 1-t^2 $$
$$ \Rightarrow 2t^3 + t^2 - 2t -1 = 0$$
$$ t = 1$$ is solution of the above equation
$$ \Rightarrow (t-1)(2t^2 +3t +1 ) = 0$$
$$ \Rightarrow (t-1) (2t^2 +t+2t +1) = 0$$
$$ \Rightarrow (t-1) [t (2t+1)+1(2t-1)] = 0$$
$$ \Rightarrow (t-1) (t+1) (2t+1) = 0$$
$$ \therefore t = 1 $$ or $$ t = -1 $$ or $$ t = -1/2 $$
$$ \Rightarrow cos3x =1 $$ or $$ cos 3x = -1 $$ or $$ cos 3x = -1/2 $$
$$ \Rightarrow 3x = 2n\pi \Rightarrow 3x = (2k+1)\pi \Rightarrow 3x = 2n\pi \pm \dfrac{2 \pi }{3}$$
$$ x = \dfrac{2n\pi}{3} \Rightarrow x = (2k+1) \dfrac{\pi}{3} \Rightarrow x = \dfrac{2m\pi}{3}\pm \dfrac{2\pi^3}{9}$$
$$ x \,\epsilon\, z $$ $$ k\,\epsilon\, z $$ $$m\, \epsilon\, z $$
Solve: $$\displaystyle \sin \, x \, + \, \sin \, 2x \, = \, \cos \, x \, + \, 2 \, \cos^2 \, x.$$
Solve the following equation:
$$\displaystyle 2 \, \cos^2 \, x \, - \, 1 \, = \, \sin \, 3x.$$
Solve the following equations.
$$\displaystyle 4 \, cos \, x \, - \, 2 \, cos \, 2x \, - \, cos \, 4x \, = \, 1.$$
$$ 4cos x - 2cos 2x - cos 4x =1 $$
$$ \Rightarrow 4 cos x - cos 2x - cos 4x = 1+cos 2x $$
$$ \Rightarrow 4cosx -2 cos 3x cosx = 2cos^2x $$
Say $$ cos x = t $$
$$ \Rightarrow 4t - 2t (4t^3-3t) = 2t^2 $$
$$ \Rightarrow 4t - 8t^4 + 6t^ 2 = 2t^2 $$
$$ \Rightarrow 8t^4 - 4t^2 - 4t = 0$$
$$ \Rightarrow 2t^4 - t^2 -t = 0$$
$$ \Rightarrow t (t-1) (2t^2 + 2t +1) = 0$$
$$ \therefore t = 0 $$ or $$ t = 1$$
$$ \Rightarrow cosx = 0 $$ or $$ \Rightarrow cosx = 1 $$
$$ \Rightarrow x = ( 2x+1)\pi/2 \Rightarrow x = 2 ,m\pi $$
$$ n\epsilon $$ integer $$ m\epsilon $$ integer
Solve the following equations.
$$\displaystyle 8 \, cos \, x \, cos \, 2x \, cos \, 4x \, = \, \frac{sin \, 6x}{sin \, x}.$$
$$ 8cos x \, cos 2x\, cos 4x = \dfrac{sin 6x}{sinx}$$
$$\Rightarrow 8sinx. cosx. cos2x. cos\,4x = sin 6x$$
$$ \Rightarrow 2sinx . cosx. 4cos2x . cos4x = sin6x $$
$$ \Rightarrow 4 sin 2x \, cos 2x \, cos\, 4x = sin 6x$$
$$ \Rightarrow 2(2sin2x. cos2x) cos 4x = sin6x $$
$$ \Rightarrow 2 sin 4x. cos 4x = sin6x $$
$$ \Rightarrow sin8x - sin6x = 0$$
$$ \Rightarrow 2cos\, 7x. sinx = 0$$
$$ \therefore cos 7x = 0 \,\,\, sinx = 0$$
$$ 7x = ( 2x+1) \pi/ 2 \,\,\, x = m\pi $$
$$ x = (2x+1) \pi/4 \,\,\, m\epsilon z $$
$$ x\epsilon z$$
Solve the following equation:
$$\displaystyle \cos \, 4x \, + \, 2 \, \cos^2 \, x \, = \,1.$$
Solve the following equation:
$$\displaystyle \sin^6 \, x \, + \, \cos^6 \, x \, = \, \frac{7}{16}.$$
Solve the following equation:
$$\displaystyle (1 \, - \, \tan \, x) \, (1 \, + \, \sin \, 2x) \, = \, 1 \, + \, \tan \, x$$
Solve the following equation:
$$\displaystyle \sin \, x \, + \, \sin^2 \, x \, + \, \cos^2 \, x \, = \, 0$$
Solve the following equations.
$$\displaystyle sin \, \frac{3x}{2} \, cos \, \frac{x}{2} \, = \, \frac{sin \, 2x}{2}.$$
$$\dfrac{{1 + \sin 2\theta + \cos 2\theta }}{{1 + \sin 2\theta - \cos 2\theta }} = $$
$$\dfrac{\tan A}{(1-\cot A)}+\dfrac{\cot A}{(1-\tan A)}=\sec A \cdot \text{cosec} A+1$$
If $$\sin \theta-\sqrt{6} \cos \theta=\sqrt{7} \cos \theta$$. Prove that $$\cos \theta-\sqrt{6}\sin \theta-\sqrt{7} \sin \theta=1$$.
If $$\cot \theta=\sqrt {7}$$, find the value of $$\dfrac {cosec^{2} \theta - \sec^{2}\theta}{cosec^{2} \theta + \sec^{2}\theta}$$. $$[\because \cot \theta=\dfrac{1}{ \tan \theta}]$$
Prove that : $$\tan 2x=\dfrac{2\tan x}{1-\tan^2x}$$
If $$A+B+C = \pi$$ then prove that, $$\cos 2A+\cos 2B-\cos 2C=1-4\sin A\sin B\cos C$$.
$$\cos \dfrac{\pi}{15}\cos \dfrac{2\pi}{15}\cos \dfrac{3\pi}{15}\cos \dfrac{4\pi}{15}\cos \dfrac{5\pi}{15}\cos \dfrac{6\pi}{15}\cos \dfrac{7\pi}{15}=\dfrac{1}{2^7}$$
Show that:
$$\cos^248^{\circ}-\sin^212^{\circ}=\dfrac{\sqrt{5}+1}{8}$$
The value of $$\cos^2 \, A \, + \, \cos^2 \, B \, - \, 2 \, \cos \, A \, \cos \, B \, \cos \, (A \, + \, B) \, -\, \sin^2 \, (A \, + \, B)$$
Find the real roots of the equation $$\cos ^{ 7 }{ x } +\sin ^{ 4 }{ x } =1$$ in the interval $$\left( -\pi ,\pi \right) $$ .
Prove that $$\sin^2(\dfrac{A}{2})+\sin^2(\dfrac {B}{2})+\sin^2(\dfrac {C}{2})=1-2\sin(\dfrac {A}{2})\sin\dfrac {B}{2})\sin(\dfrac {C}{2})$$.
In any triangle ABC prove the identities.
$$\sin^2A+\sin^2B-\sin^2C=2\sin A\sin B\cos C$$.
If A+B+C $$=\pi$$ Prove that: $$\dfrac{\sin 2A+\sin 2B+\sin 2C}{\sin A+\sin B+\sin C}=8\sin \bigg(\dfrac{A}{2}\bigg)\sin \bigg(\dfrac{B}{2}\bigg)\sin \bigg(\dfrac{C}{2}\bigg)$$.
In any triangle ABC prove that the identities.
$$\dfrac{\sin 2A+\sin 2B+\sin 2C}{\cos A+\cos B+\cos C-1}=8\cos(A/2)\cos (B/2)\cos (C/2)$$.
If $$A+B+C=2k$$, then prove that $$\cos^2k+\cos^2(k-A)+\cos^2(k-B)+\cos^2(k-C)=2+2\cos A\cos B\cos C$$.
Prove that: $$\sin^2A+\sin^2B+\sin^2C=2+2\cos A\cos B\cos C$$.
Express $$\sin 3A+\sin 3B+\sin 3C$$ as the product of three trigonometrical ratios where A, B, C are the angles of a triangle. If the given expression be zero, then at least one angle of the triangle is $$60^o$$
If $$A+B+C=\pi$$, prove that $$(\sin A+\sin B+\sin C)(-\sin A+\sin B+\sin C)(\sin A-\sin B+\sin C)(\sin A+\sin B-\sin C) \\ =4\sin^2A\sin^2B\sin^2C$$.
Prove that: $$\sin^2(\dfrac {A}{2})+\sin^2(\dfrac {B}{2})-\sin^2(\dfrac {C}{2})=1-2\cos(\dfrac {A}{2})\cos(\dfrac {B}{2})\sin(\dfrac{C}{2})$$.
Prove that: $$\cos^2A+\cos^2B+\cos^2C=1-2\cos A\cos B\cos C$$.
Solve $$2\sin^2x+\sqrt{3}\cos x+1=0$$.
Find m if $$\sin { A } \sin { \left( { 60 }^{ o }-A \right) } \sin { \left( { 60 }^{ o }+A \right) } =\cfrac { 1 }{ m} \sin { 3A } \quad $$
If $$x+y+z=xyz$$, prove that $$\dfrac{x+y}{1-xy}+\dfrac{y+z}{1-yz}+\dfrac{z+x}{1-zx}=\dfrac{x+y}{1-xy}\cdot \dfrac{y+z}{1-yz}\cdot \dfrac{z+x}{1-zx}$$.
If $$x+y+z=xyz$$, then prove that.
For any three angles A, B, C, $$\tan(B-C)+\tan(C-A)+\tan(A-B)=\tan(B-C)\tan(C-A)\tan(A-B)$$.
Solve: $$5\cos 2\theta +2\cos^2\left(\dfrac{1}{2}\theta \right)+1=0, -\pi < \theta < \pi$$.
Solve $$4 \cos \theta - 3 \sec \theta = 2 \tan \theta$$.
If $$x+y+z=xyz$$, prove that $$\dfrac{3x-x^3}{1-3x^2}+\dfrac{3y-y^3}{1-3y^2}+\dfrac{3z-z^3}{1-3z^2}=\dfrac{3x-x^3}{1-3x^2}\cdot \dfrac{3y-y^3}{1-3y^2}\cdot \dfrac{3z-z^3}{1-3z^2}$$.
The number of values of $$\theta$$ satisfying $$\sin \theta +\sin 3\theta +\sin 5\theta =0; 0\leq \theta \leq \dfrac{1}{2}\pi$$ is
Solve $$r\sin \theta =\sqrt{3}, r+4\sin \theta =2(\sqrt{3}+1), 0\leq \theta \leq 2\pi$$.
The smallest $$+$$ve x satisfying the equation $$log_{cos x}\sin x+\log_{\sin x}\cos x=2$$ is $$\pi /4$$.
Solve $$\sin \theta +\sin 2\theta +\sin 3\theta +\sin 4\theta =0$$.
Solve $$3\tan^2\theta -2\sin \theta =0$$.
Solve $$\cot \theta -\tan \theta =\sec \theta$$.
Solve $$\cos^{40}\theta +\sin^{58}\theta =1$$.
Solve $$sec 4\theta -sec 2\theta =2$$.
Solve $$\dfrac{\sqrt{3}}{2}\sin x-\cos x=cos^2x$$.
Solve $$\tan 3\theta +\tan \theta =2\tan 2\theta$$.
Prove that:
$$\dfrac{1}{1 \, + \, \sin \, \theta} \, + \, \dfrac{1}{1 \, - \, \sin \, \theta} \, = \, 2 \, \sec^2 \, \theta$$
Prove that :
$$\dfrac{\tan \, \theta \, + \, \sin \, \theta}{\tan \, \theta \, - \, \sin \, \theta} \, = \, \dfrac{\sec \, \theta \, + \, 1}{\sec \, \theta \, - \, 1}$$
$${\sin ^2}n\theta - {\sin ^2}(n - 1)\theta = {\sin ^2}\theta $$, where $$n$$ is constant and $$n \ne 0,1$$
Solve the equation $$\sin x+\cos x=\sin 2x-1$$.
Prove that :
$$\dfrac{tan \, \theta \, - \, cot \, \theta}{sin \, \theta \, cos \, \theta} \, = \, sec^2 \, \theta \, - \, cosec^2 \, \theta \, = \, tan^2 \, \theta \, - \, cot^2 \, \theta$$
Prove that :
$$\dfrac{(1 \, + \, cot \, A \, + \, tan \, A)(sin \, a \, - \, cos \, A)}{sec^3 \, A \, - \, cosec^3 \, A} \, = \, sin^2 \, A \, cos^2 \, A$$
Prove that:
$$\dfrac{\sin \, \theta}{1 \, + \, \cos \, \theta} \, + \, \dfrac{1 \, + \, \cos \, \theta}{\sin \, \theta} \, = \, 2 \, \text{cosec} \, \theta$$
Prove the following statements.
$$\cos^{6} A + \sin^{6}A = 1 - 3\sin^{2} A + \cos^{2} A$$.
Find the number of values of $$\theta $$ satisfying the equation $$\sin 3\theta = 4\sin \theta .\sin 2\theta .\sin 4\theta $$ in $$0 \le \theta \le 2\pi $$
Prove that :
$$\dfrac{\cos \, \theta}{1 \, - \, \sin \, \theta} \, + \, \dfrac{\cos \, \theta}{1 \, + \, \sin \, \theta} \, = \, 2 \, \sec \, \theta$$
If $$\tan \theta + \sin \theta = m $$ and $$\tan \theta - \sin \theta = n $$, show that
$$m^2-n^2 = 4 \sqrt{ mn}$$
Solve $$(sec^2 \theta - 1)(1 - cosec^2 \theta) = -1$$
Find the integrals of the function :
$$\dfrac{\sin^{2} x}{1+\cos x}$$
Prove that $$\dfrac{\sin\theta - \cos \theta +1}{\sin \theta + \cos\theta -1}=\dfrac{1}{\sec\theta - \tan \theta}, $$ using the identity $$\sec^2 \theta= 1+ \tan^2\theta.$$
Find the value of $$\sin \frac{\pi}{14}\sin\frac{3\pi}{14}\sin\frac{5\pi}{4}\sin\frac{7\pi}{14}\sin \frac{9\pi}{14} \sin\frac{11\pi}{14} \sin \frac{13\pi}{14}=\frac{1}{m}$$.Find $$m$$
Find the value of $$\dfrac{\cos A - \sin A+1}{\cos A + \sin A-1}- (\text{cosec} A + \cot A)$$
If $$\tan \theta+\dfrac {1}{\tan \theta}=2$$, find the value of $$\cot^{2}\theta+\dfrac {1}{\cot^{2}\theta}$$.
If $$\cos x+\sin x=\dfrac {1}{2}$$, Find the $$\tan x$$.
Prove the following identity:
$$\sin ^8 x - \cos^8x = (\sin^2x - \cos^2x) (1 - 2 \, \sin^2 x \cos^2 x)$$
Prove that: $$\dfrac{{1 - {\mathop{\rm sinAcosA}\nolimits} }}{{\cos A\left( {\sec A - \text{cosec}A} \right)}}.\dfrac{{{{\sin }^2}A - {{\cos }^2}A}}{{{{\sin }^3}A + {{\cos }^3}A}} = \sin A$$
If $$\sin {x} + \sin {y} + \sin {z} =3$$. Find the value of $$\cos {x} + \cos {y} + \cos {z} .$$
how to find all possible values of 2cos2x=cos02cos2x=cos0.
$$2\cos{ 2x }=\cos{ 0 }\\ \cos{ 0 }=1\\ 2\cos{ 2x }=1\\ \cos2\theta =2{ \cos }^{ 2 }\theta -1\\ 2(2{ \cos }^{ 2 }x-1)=1\\ 4{ \cos }^{ 2 }x-2=1\\ 4{ \cos }^{ 2 }x=3\\ { \cos }^{ 2 }x=\cfrac { 3 }{ 4 } \\ \cos{ x }=\pm \sqrt { \cfrac { 3 }{ 4 } } \\ \cos\cfrac { \pi }{ 6 } =\cfrac { \sqrt { 3 } }{ 2 } $$
Graph is cuttinf at four places so answer is four
Prove $$\dfrac{1}{\sec x -\tan x} -\dfrac{1}{\cos x} =\dfrac{1}{\cos x}-\dfrac{1}{\sec x+\tan x}$$
prove that $$\dfrac{{\sec \theta }}{{\sec \theta + \tan \theta }}$$=$${{\sec \theta - \tan \theta }}$$
Find $$\left( {\cos \,A + \sec A} \right){^2} + {\left( {\sin A + \text{cosec} A} \right)^2} - {\tan ^2}A - {\cot ^2}A.$$
Find $$m$$ if $$\displaystyle \sqrt {\frac{{1 - \sin \theta }}{{1 + \sin \theta }}} + \sqrt {\frac{{1 + \sin \theta }}{{1 - \sin \theta }}} = \frac{{ - m}}{{\cos \theta }},\frac{\pi }{2} < \theta < \pi $$.
If $$\tan \left( {A + B} \right) = x$$ and $${\rm{tan}}\left( {A - B} \right){\rm{ = y}}$$ find the value of $$\tan 2A$$ and $$\tan 2B$$
Prove that: $$\dfrac{1}{\text{cosec}A- \cot A}-\dfrac{1}{\sin A}=\dfrac{1}{\sin A}-\dfrac{1}{\text{cosec}A+\cot A}$$.
If $$\cos \left(\frac{3\pi}{4}+x\right)- \cos \left(\frac{3\pi}{4}-x\right)= -\sqrt m \sin x$$.Find $$m$$
Prove that $$\dfrac { 1 }{ \sec { A } -\tan { A } } -\dfrac { 1 }{ \cos { A } } =\dfrac { 1 }{ \cos { A } } =\dfrac { 1 }{ \sec { A } +\tan { A } }$$.
If $$A$$ is not an integeral multiple of $$\pi$$, find k such that $$\cos \, A . \cos \, 2A . \cos \, 4A . \cos \, 8A = \dfrac{\sin 16 A}{k \sin A}$$.
If $$\sec\phi+\tan\phi=x,$$ prove that $$\sin\phi=\dfrac{x^2-1}{x^2+1}$$.
Prove $$\dfrac{{{{\tan }^3}\theta }}{{1 + {{\tan }^2}\theta }} + \dfrac{{{{\cot }^3}\theta }}{{1 + {{\cot }^2}\theta }} = \dfrac{{1 - 2{{\sin }^2}\theta {{\cos }^2}\theta }}{{\sin \theta \cos \theta }}$$
If $$7\ \text{cosec}\alpha-3\ \cos\alpha=7$$, prove that $$7\ \cot\alpha- 3\ \text{cosec}\ \alpha=3.$$
If $$\cos^22x - \cos^26x = \sin mx \sin8x$$. Find $$m$$
Prove the following statement.
$$\sqrt {\dfrac {1 - \sin A}{1 + \sin A}} = \sec A - \tan A$$.
Show that
$$(\sec \theta-\tan \theta)^{2}=\dfrac{1-\sin \theta}{1+\sin \theta}$$
If $$3 \cot A= 4$$ check whether $$\dfrac{1-\tan^2A}{1+\tan^2A}=\cos^2A - \sin^2A$$ or not
If$$\tan A + \cot A = m \text{cosec}2A$$.Find $$m$$
Solve for $$\alpha $$$$\dfrac{\text{cosec}^2 \theta}{\text{cosec} \theta - 1} - \dfrac{\text{cosec}^2 \, \theta}{\text{cosec} \theta + 1} = \alpha \sec^2\theta$$
Prove $$\left( {1 + \,{{\tan }^2}\,\theta } \right)\,{\sin ^2}\,\theta \, = \,{\tan ^2}\,\theta $$
given $$\cot \theta=1$$Find $$\dfrac {(1+\sin \theta) (1-\sin \theta)}{ (1+\cos \theta) (1-\cos \theta)}$$
Convert $$3$$ radian into degree measure.
If $$tan\beta =2 sin\alpha sin\gamma cosec(\alpha+\gamma),$$ then $$cot\alpha, cot\beta cost\gamma$$ are in
Solve $$\cot ^{ 2 }{ x } -\tan ^{ 2 }{ x } =4\cot { 2x } \cosec { 2x } $$
Show that $$cos 2A= cos^4A - sin^4A$$
Solve $$4\cos ^{ 2 }{ x } +6\sin ^{ 2 }{ x } =5$$.
Prove that: $$\sin^2\left(\dfrac{\pi}{8}+\dfrac{A}{2}\right)-\sin^2\left(\dfrac{\pi}{8}-\dfrac{A}{2}\right)=\dfrac{1}{\sqrt{2}}\sin A$$
Find the general solution of the equation.
REF.Image.
OA = x
OB = 180 m
$$ tan\phi = 4/3 $$
$$ sin\phi = 4/5 $$
$$ sin\phi = OA/O\epsilon $$
$$ sin\phi = \dfrac{x}{180}$$
$$ 4/5 = x/180 $$
$$ x = 144$$
$$ 144 +10 = 154 m $$
$$ sin (\pi/8 + A/2) - sin^{2}(\pi/8 - \dfrac{A}{2}) = \dfrac{1}{\sqrt{2}} sinA $$
$$ sin(\pi/4) sin(A) = \dfrac{1}{\sqrt{2}}sinA $$
$$ A\epsilon (2n \pi)\epsilon R$$
Prove $$\cfrac { Sin2A }{ SinA } -\cfrac { Cos2A }{ CosA } =SecA$$
$$\cos\theta -\sin\theta= \sqrt2\sin\theta$$ show that $$ \cos\theta+ \sin\theta= \sqrt2\cos\theta$$
$$4\cos\theta -3\sec \theta =2\tan \theta$$.
simplify $$\dfrac { \sin { 2A } }{ 1+\cos { 2A } } =\tan { A } $$
Given $$\sin \phi = \dfrac{15}{17}$$, find the value of : $$\dfrac{3 - 4 \, \sin^2 \phi}{4 \, \cos^2 \phi - 3}$$
$$\sin { \cfrac { \theta }{ 2 } } \sin { \cfrac { 7\theta }{ 2 } } +\sin { \cfrac { 3\theta }{ 2 } } \sin { \cfrac { 11\theta }{ 2 } } =\sin { 2\theta } \sin { 5\theta } $$
$$\sin \theta +\cos \theta =1$$ find $$\theta $$ where $$\theta \epsilon(\dfrac{-\pi}{2}, \dfrac{\pi}{2})$$
Show that $$\dfrac{cosa+sina}{cosa-sina}=tan2a + sec 2a$$
Prove:$$\tan 3A-\tan 2A-\tan A=\tan A\tan 2A\tan 3A$$.
Prove:$$\tan 20^o+\tan 25^o+\tan 20^o\tan 25^o=1$$.
Prove : $$\sqrt{\dfrac{1 + \sin A}{1 - \sin A }} = \sec A + \tan A$$
Find m if the following equation holds true $$\dfrac{1 + \cot^2 \theta}{1 + \tan^2 \theta} = \left(\dfrac{1 + \cot \, \theta}{1 + \tan \, \theta} \right)^m$$
Prove that: $$\sec ^{ 2 }{ \theta } +\csc ^{ 2 }{ \theta } =\sec ^{ 2 }{ \theta } \csc ^{ 2 }{ \theta } $$
Prove that
$$\sec ^{ 2 }{ \theta } -\cfrac { \sin ^{ 2
}{ \theta } -2\sin { 4\theta } }{ 2\cos { 4\theta } -\cos ^{ 2 }{
\theta } } =1$$
Prove that: $$\frac{1- cos2\theta + sin2\theta}{1+ cos2\theta+ sin 2\theta}=tan\theta$$
$$Prove\quad that\quad \dfrac { \sin { \theta } -\cos { \theta } +1 }{ \sin { \theta } +\cos { \theta -1 } } =\dfrac { 1 }{ \sec { \theta } -\tan { \theta } } $$
Solve $$\cfrac { 1+\sin { A } }{ \cos { A } } +\cfrac { \cos { A } }{ 1+\sin { A } } =2\sec { A } $$
Prove $$\dfrac{\cos \, A - \sin \, A + 1}{\cos \, A + \sin \, A - 1} = \text{csc} \, A + \cot \, A$$, using the identity $$\text{csc}^2 A = 1 + \cot^2 A$$
If $$x+y+z=xyz$$, prove that $$\cfrac { 2x }{ 1-{ x }^{ 2 } } +\cfrac { 2y }{ 1-{ y }^{ 2 } } +\cfrac { 2z }{ 1-{ z }^{ 2 } } =\cfrac { 2x }{ 1-{ x }^{ 2 } } \cfrac { 2y }{ 1-{ y }^{ 2 } } \cfrac { 2z }{ 1-{ z }^{ 2 } } $$
If $$x=a+b\omega +c{ \omega }^{ 2 },y=a\omega +b{ \omega }^{ 2 }+c$$ and $$z=a{ \omega }^{ 2 }+b+c{ \omega }$$ then find the value of $$\cfrac { { x }^{ 2 } }{ yz } +\cfrac { { y }^{ 2 } }{ zx } +\cfrac { { z }^{ 2 } }{ xy } $$
If A+B+C=$$\pi$$ , then$$ \ secA \ (cosB \ cosC-sinB \ sinC)$$ is equal to__________
Prove $$\sin(60^0+\theta ) - \sin (60^0-\theta) = \sin\theta.$$
Prove $$\dfrac{\sin(A-B)}{\sin A \sin B}+\dfrac{\sin(B-C)}{\sin B \sin C}+ \dfrac{\sin(C - A)}{\sin C \sin A}= 0$$
Find the value of $$\sin{2\theta}$$ if $$\sin{\theta}=\cfrac{-3}{5}$$ and $$\pi< \theta< 3\cfrac{\pi}{2}$$
The value of sin ($$37^0$$) $$\times$$ cos ($$53^0$$) =
Prove by using vectors that $$\sin{(\alpha+\beta)}=\sin{\alpha}\cos{\beta}+\cos{\alpha}\sin{\beta}$$
Solve : $$\cos^6 A - \sin^6 A = \cos \, 2 \, A \left (1 - \dfrac{1}{4} \sin^2 \, 2 \, A\right)$$
$$tan3A - tan 2A - tan A = tan3A tan2AtanA$$.
Prove that $$\dfrac{{{{\sin }^2}A - {{\sin }^2}B}}{{\sin A\cos A - \sin B\cos B}} = \tan \left( {A + B} \right)$$
If $$m = \dfrac{\sin \, A}{\sin \,B} , n = \dfrac{\cos \, A}{\cos \, B}$$, then prove that $$(m^2 - n^2) \sin^2 B = 1 - n^2$$
Prove that : $$4 - 4 \sin^2 \left (\dfrac{x + y}{2}\right) = (\sin x - \sin y )^2 + (\cos x + \cos y)^2$$
The number of real solutions of $$ \dfrac { \pi} {2} + \cos^{-1} ( \cos x) = | \tan x | , 0 \le x \le 2 \pi$$ is ________.
Find principal and general solution of the equation, $$\cot x =-\sqrt{3}$$.
Prove that , $$\dfrac{{\sin \theta - \cos \theta + 1}}{{\sin \theta + \cos \theta - 1}} = \dfrac{1}{{\sec \theta - \tan \theta}}$$
Find the principal solutions of the following equation
$$\sin{x}=-\dfrac{1}{2}$$
If $$cosec\theta +\cot\theta =p$$, then prove that $$\cos\theta =\dfrac{p^2-1}{p^2+1}$$.
Find all solution of the equation.
$$\sin x+\sin \dfrac{\pi}{8}\sqrt{(1-\cos x)^2+\sin^2x}=0$$ in $$\left[\dfrac{5\pi}{2}, \dfrac{7\pi}{2}\right]$$.
Prove the following identity :
$$\frac{1}{sin{\theta}+cos{\theta}}+\frac{1}{sin{\theta}-cos{\theta}}=\frac{2sin{\theta}}{1-2cos^2{\theta}}$$
If $$m = \left( {\cos \theta - \sin \theta } \right)$$ and $$n = \left( {\cos \theta + \sin \theta } \right)$$ then show that $$\sqrt {{m \over n}} + \sqrt {{n \over m}} = {2 \over {\sqrt {1 - {{\tan }^2}\theta } }}$$
Evaluate : $$\cos (40^o + \theta) - \sin(50^o - \theta) + \cos 240^o + \cos 250^o \sin 240^o + \sin 250^o=?$$
If $${\tan ^{ - 1}}\alpha + {\tan ^{ - 1}}\beta = \dfrac{\pi }{4}$$, then twice write the value of $$\alpha + \beta + \alpha \beta .$$
$$ tan^{-1}(\alpha )+tan^{-1}(\beta ) = \dfrac{\pi }{4} $$
$$ \Rightarrow tan^{-1}(\dfrac{\alpha +\beta }{1-\alpha \beta }) = \dfrac{\pi }{4} $$
$$ \Rightarrow \dfrac{\alpha +\beta }{1-\alpha \beta } = tan(\dfrac{\pi }{4}) = 1 $$
$$ \Rightarrow \alpha +\beta = 1-\alpha \beta $$
$$ \Rightarrow \alpha +\beta +\alpha \beta = 1 $$
$$ \therefore \alpha +\beta +\alpha \beta = 1 $$ and $$ 2(\alpha +\beta +\alpha \beta ) = 2 $$
Find the principal solutions of the following equation
$$\tan{x}=-1$$
If $$\sqrt{3} \sin \, \theta = \cos \, \theta $$, find the value of $$\dfrac{\sin \theta \, \, \tan \theta ( 1 + \cos \, \theta)}{\sin \theta + \cos \theta}$$
Find the principal solutions of the following equation
$$\sqrt{3}\csc{x}+2=0$$
Find the principal solutions of the following equation
$$\tan{x}=-\sqrt{3}$$
If $$\cos \theta - \sin \theta = 1$$, show that $$\cos \theta + \sin \theta = 1$$
Find the principal solution of the following equation:
$$\sin{x}=\frac { \sqrt { 3 } }{ 2 } $$
Find the principal solution of the following equation:
$$\cos{x}=\frac{1}{2}$$
Evaluate
$$\cos^{4}\theta+\sin^{4}\theta=1-2\cos^{2}\theta.\sin^{2}\theta$$
If $$\cot \theta + \tan \theta = x$$ and $$\sec \theta - \cos \theta = y $$, then prove that $$x^2 y \left(\dfrac{2}{3}\right) xy^2 \left(\dfrac{2}{3}\right) = 1$$
Evaluate: $$\frac{{{{\cos }^2}\left( {{{45}^ \circ } + \theta } \right) + {{\cos }^2}\left( {{{45}^ \circ } - \theta } \right)}}{{\tan \left( {{{60}^ \circ } + \theta } \right)\tan \left( {{{30}^ \circ } - \theta } \right)}} + \cos ec\left( {{{75}^ \circ } + \theta } \right) - \sec \left( {{{15}^ \circ } - \theta } \right)$$
$$\dfrac{{\cos \,{{135}^ \circ } - \cos \,{{120}^ \circ }}}{{\cos \,{{135}^ \circ } + \cos \,{{120}^ \circ }}} = (3 - 2\sqrt 2 )$$
solve $$2|\sin x| \geqslant |\,\,x\varepsilon \,[0,4\pi ]$$
if $$\sin \theta = - \dfrac{4}{5},\,\pi < \theta < \dfrac{{3\pi }}{2},$$ then find
$$\sin 2\theta $$
$$\cos 2\theta \,$$
$$\tan 2\theta \,$$
Solution :-
Given $$sin \theta = \dfrac{-4}{5}$$ and $$\pi < \theta < \dfrac{3\pi }{2}$$
then
$$1.sin2\theta = 2sin\theta .cos\theta $$
$$cos \theta = -\dfrac{\sqrt{5^{2}-4^{2}}}{5}=-\dfrac{3}{5}$$ $$\because \pi < \theta < \dfrac{3\pi }{2}$$
$$\therefore sin 2\theta =2\times \dfrac{-4}{5}\times \dfrac{-3}{5}= \dfrac{24}{25}$$
$$2.cos 2\theta = cos^{2}\theta - sin^{2}\theta $$
$$=(\dfrac{-3}{5})^{2}-(\dfrac{-4}{5})^{2}$$
$$= \dfrac{9}{25}-\dfrac{16}{25}$$
$$= \dfrac{-7}{25}$$
$$3. tan 2\theta = \dfrac{sin2\theta }{tan 2\theta }=\dfrac{24/25}{-7/25}$$
$$=\dfrac{-24}{7}$$
Find value of $$\sin^2A{\,\,}\cot^2A +\cos^2A{\,\,}\tan^2{\,\,}A$$
If $$\cos \theta + \sin \theta = \sqrt{2} \cos \theta$$, then prove that $$\cos \theta - \sin \theta = \sqrt{2} \sin \theta$$
Prove that $$\sec^{4}\theta-\sec^{2}\theta=\tan^{4}\theta+\tan^{2}\theta$$
Solve the trigonometric equation
$$\dfrac{(\cot\ A-1+\text{cosec}\ A)^{2}}{(\cot\ A)^{2}-(1-\text{cosec}\ A)^{2}}$$
Solve:- $$\dfrac{{x\sin x}}{{1 + \cos x}}=0$$
Find the principal solution of $$\cos x = - \frac{1}{2}$$
The number of solution of the equation, $$\sin ^ { 4 } x - \cos ^ { 2 } x \cdot \sin x + 2 \sin ^ { 2 } x + \sin x = 0,0 \leq x \leq 3 \pi$$ is ..
Solve: $$\dfrac{cos7A}{secA}-\dfrac{sin7A}{cosec A}=cos 8A$$
Find the principal solutions of $$\cot{x}=-\sqrt{3}$$
The value of $$6\left( {{{\sin }^6}\theta + {{\cos }^6}\theta } \right) - 9\left( {{{\sin }^4}\theta + {{\cos }^4}\theta } \right) + 4$$ is
Solve: $$\tan 2 x-\tan 3x=0$$
Prove that $$\displaystyle \dfrac { \tan \theta } { 1 - \cot \theta } + \dfrac { \cot \theta } { 1 - \tan \theta } = 1 + \sec \theta \>cosec \theta$$
If $$\cos \theta > 0, \tan \theta+ \sin \theta=m$$ and $$\tan \theta -\sin \theta =n$$, then show that $$m^{2}-n^{2}=4\sqrt{mn}$$.
The set of angles between $$0$$& $$2\pi $$ satisfying the equation $$4{\cos ^2}\theta - 2\sqrt 2 \cos \theta - 1 = 0$$ is
Solve for $$x$$ and $$y$$:
$${ x }^{ 2 }+ 2x \sin { xy } + 1= 0$$
If $$\sum_{i=1}^{n}cos \Theta _{i}=n,$$ then the value of $$\sum_{i=1}^{n}sin\Theta _{i}$$
Find the value of sec$$\theta$$-tan$$\theta$$ if sec$$\theta$$+tan$$\theta$$=5 ,
$$\cos 2 \hat { x } + a \sin x = 2 a - 7$$ has a solution for what values of a?
Show that $$\dfrac { 1 }{ \text{cosec}\theta -\cot\theta } -\dfrac { 1 }{ \sin\theta } =\dfrac { 1 }{ \sin\theta } -\dfrac { 1 }{ \text{cosec}\theta +\cot\theta } $$
Prove the given statement :
$$\cos^{4} A - \sin^{4} A + 1 = 2\cos^{2} A$$
Simplify:-
$${\left( {\text{cos ec}\theta - \cot \theta } \right)^2}$$
Prove:
$$\cot ^{ 2 }{ A\left( \dfrac { \sec { A-1 } }{ 1+\sin { A } } \right) } +\sec ^{ 2 }{ A\left( \dfrac { \sin { A-1 } }{ 1+\sec { A } } \right) } =0 $$
Find the principle solution of the equation .
$$\sin x=-\dfrac{1}{2}$$
Prove that:
$$2 + \tan ^ { 2 } \theta + \dfrac { 1 } { \tan ^ { 2 } \theta } = \dfrac { 1 } { \sin ^ { 2 } \theta - \sin ^ { 4 } \theta }$$
If $$m\cos^2A+n\sin^2A=p$$, then $$\cot^2A=$$
$$\dfrac { { cos }^{ 2 }{ 20 }^{ \circ }+{ cos }^{ 2 }{ 70 }^{ \circ } }{ { sin }^{ 2 }{ 31 }^{ \circ + }+{ sin }^{ 2 }{ 59 }^{ \circ } } +{ sin }^{ 2 }{ 64 }^{ \circ }+cos{ 64 }^{ \circ }sin{ 26 }^{ \circ }$$
Prove the identity: $$\dfrac{{{\text{sinA}}}}{{{\text{1 + cosA}}}} = {\text{coscA}} - {\text{cotA}}$$.
If $$'\theta'$$ is the parameter, then the family of lines represented by
$$(2 cos \theta + 3 sin\theta) X + (3 cos \theta - 5 sin \theta)$$
y - $$(5cos\theta - 7 sin\theta)$$ = 0 are concurrent at the point
$$ cos\theta (2x+3y-5)+sin\theta (3x-5y+7) = 0$$
$$ \Rightarrow (2x+3y-5)+tan\theta (3x-5y+7) = 0 $$
of from $$ L_{1}+\lambda L_{2} = 0,$$ intersection point be P
$$ 3\times (2x+3y-5=0)$$
$$ 2\times (3x-5y+7=0)$$
___________________
$$19y-29 = 0\Rightarrow y = \frac{29}{19}$$ $$\Rightarrow x=\frac{5y-7}{3}=\frac{145-133}{57}=\frac{12}{57}$$
$$ \Rightarrow P(-\frac{4}{19},\frac{29}{19})$$
Prove that $$\cot \theta - \tan \theta = \dfrac{{2{{\cos }^2}\theta - 1}}{{\sin \theta \cos \theta }}$$
Prove that: $$\dfrac { \tan\theta +\sec\theta -1 }{ \tan\theta -\sec\theta -1 } =\sec\theta +\tan\theta \\ $$
Prove : $$\dfrac {\cos^{3}\theta-\sin^{3}\theta}{\cos \theta-\sin \theta}+\dfrac {\cos^{3}\theta+\sin^{3}\theta}{\cos \theta+\sin \theta}=2$$
Prove that $$\cot \theta - \tan \theta = \dfrac{{\left( {2{{\cos }^2}\theta - 1} \right)}}{{\left( {\sin \theta. \cos\theta } \right)}}$$
If $$cos\left( \alpha \right) =\dfrac { 1 }{ 2 }$$ then $$\alpha=?$$
Given that $$tan( \theta_1+ \theta_2)= \dfrac{tan \theta_1+ tan \theta_2}{1- tan \theta_1tan \theta_2} $$. Find $$ ( \theta_1+ \theta_2) $$ when $$tan \theta_1= \dfrac 12 $$ $$tan \theta_2=\dfrac 13 $$.
Evaluate: $$\tan ^ { 2 } \dfrac { \pi } { 16 } + \tan ^ { 2 } \dfrac { 2 \pi } { 16 } + \tan ^ { 2 } \dfrac { 3 \pi } { 16 } + \ldots \ldots + \tan ^ { 2 } \dfrac { 7 \pi } { 16 }$$
$$\dfrac{7\pi}{16}=\dfrac{\pi}{2}-\dfrac{\pi}{16}$$
$$\dfrac{6\pi}{16}=\dfrac{\pi}{2}-\dfrac{2\pi}{16}$$
$$\dfrac{5\pi}{16}=\dfrac{\pi}{2}-\dfrac{2\pi}{16}$$
$$\dfrac{4\pi}{16}=\dfrac{\pi}{4}$$
$$\Rightarrow \tan^2\dfrac{\pi}{16}+\tan^2\dfrac{2\pi}{16}+\tan^2\dfrac{3\pi}{16}+...…..\tan^2\dfrac{6\pi}{16}+\tan^2\dfrac{7\pi}{16}$$
$$\Rightarrow \tan^2\dfrac{\pi}{16}+\tan^2\dfrac{2\pi}{16}+\tan^2\dfrac{3\pi}{16}+...…+\tan^2\left(\dfrac{\pi}{3}-\dfrac{2\pi}{16}\right)+\tan^2\left(\dfrac{\pi}{2}-\dfrac{\pi}{16}\right)$$
$$\Rightarrow \tan^2\dfrac{\pi}{16}+\tan^2\dfrac{2\pi}{16}\tan^2\dfrac{3\pi}{16}+...…..+\cot^2\dfrac{2\pi}{16}+\cot^2\dfrac{\pi}{16}$$
$$\Rightarrow \left(\tan^2\dfrac{\pi}{16}+\cot^2\dfrac{\pi}{16}\right)+\left(\tan^2\dfrac{2\pi}{16}+\cot^2\dfrac{2\pi}{16}\right)+\left(\tan^2\dfrac{3\pi}{16}+\cot^2\dfrac{3\pi}{16}\right)+\tan^2\dfrac{4\pi}{16}$$
Solve first bracket
$$\left(\tan^2\dfrac{\pi}{16}+\cot^2\dfrac{\pi}{16}\right)=\left(\tan\dfrac{\pi}{16}+\cot\dfrac{\pi}{16}\right)^2-2\tan\dfrac{\pi}{16}\cot\dfrac{\pi}{16}$$
$$=\left(\dfrac{\sin \pi/16}{\cos \pi/16}+\dfrac{\cos \pi/16}{\sin \pi/16}\right)^2-2$$
$$=\left(\dfrac{t\times 2}{2\sin(\pi/16)\cos(\pi/16)}\right)^2-2$$
$$=\left(\dfrac{2}{\sin\pi/8}\right)^2-2$$
$$=\dfrac{4\times 2}{2\sin^2\pi/8}-2$$
$$=\dfrac{8}{(1-\cos \pi/4)}-2$$
$$=\dfrac{8}{\left(1-\dfrac{1}{\sqrt{2}}\right)}-2$$
$$=\dfrac{8\sqrt{2}}{(\sqrt{2}-1)}-2$$
$$\Rightarrow 8\sqrt{2}(\sqrt{2}+1)-2$$
Similarly $$2^{nd}$$ bracket$$=\dfrac{8}{\left(1-\cos\dfrac{\pi}{2}\right)}-2=8-2=6$$
& similarly $$3^{rd}$$ bracket$$=\dfrac{8}{(1-\cos 3\pi/4)}-2=8\sqrt{2}(\sqrt{2}-1)-2$$
Thus, equation $$(1)$$
$$\Rightarrow 8\sqrt{2}(\sqrt{2}+1)-2+6+1+8\sqrt{2}(\sqrt{2}-1-2=$$
$$\Rightarrow 16+8\sqrt{2}-2+7+8\sqrt{2}\times \sqrt{2}-8\sqrt{2}-2=$$
$$\Rightarrow 35$$.
If $$cosA=\dfrac{\sqrt{3}}{2}$$, find the value of cotA+ tanA
Prove that $$\sin^6\theta + {\cos ^6}\theta + 3\sin^2\theta \cos^2\theta = 1$$
Solve
$$\dfrac {\sin^{2}\theta}{\cos^{2}\theta}-\dfrac {\sin^{2}\theta}{1}=\tan^{2}\theta \cdot \sin^{2}\theta$$
$$\frac{sin^{2}\theta }{cos^{2}\theta }= sin^{2}\theta = tan^{2}\theta sin^{2}\theta $$
$$sin^{2}\theta (\frac{1}{cos^{2}\theta }-1)=\frac{sin^{2}\theta \times sin^{2}\theta }{cos^{2}\theta }$$
such that $$sin^{2}\theta \neq 0$$ & $$cos^{2}\theta \neq 0$$
we get , $$1-cos^{2}\theta = sin^{2}\theta $$ Hence proved.
If $$\sin\left( x-20 \right) ^{ \circ }\cos\left( 3x-10 \right) ^{ \circ }=0$$, Then find the value of x.
If $$A-B=\dfrac{\pi}{4}$$, then $$(1+\tan{A})(1-\tan{B})=$$
If $$\cot \theta =\dfrac {7}{8}$$, evaluate:
$$\dfrac {(1+\sin \theta)(1-\sin \theta)}{(1+\cos \theta)(1-\cos \theta)}$$.
If $${\tan ^{ - 1}}\sqrt 3 + {\cot ^{ - 1}}x = \frac{\pi }{2}$$ then find the value of $$x$$.
Solve:
$$(\sin \theta+\cos \theta)(\tan \theta+\cot \theta)=\csc \theta+\cot \theta$$
Prove that $$\displaystyle \frac{{\sin \theta - \cos \theta + 1}}{{\sin \theta + \cos \theta - 1}} = \frac{1}{{\sec \theta - \tan \theta }}$$, using the identity $${\sec ^2} = 1 + {\tan ^2}\theta .$$
Prove that, $${ cos20 }^{ \circ }{ cos }40^{ \circ }{ cos60 }^{ \circ }{cos80^o}=\dfrac { 1 }{ 16 } $$
Prove that, $${ sin20 }^{ \circ }{ sin }40^{ \circ }{ sin80 }^{ \circ }=\dfrac { \sqrt { 3 } }{ 8 } $$
Prove ;
$$\dfrac{\tan A}{(1+\tan^{2}A)^{2}}+\dfrac{\cot{A}}{(1+\cot^{2}A)^{2}}=\sin A \cos A$$
$$\dfrac{{\cos 5x + \cos 4x}}{{1 - 2\cos 3x}}$$ $$=$$ $$- \left( {\cos 2x + \cos x} \right)$$
Prove that : $$\dfrac { \left( 1 + \tan ^ { 2 } A \right) \cot A } { \csc ^ { 2 } A } = \tan A.$$
If $$x=a\sin\theta+b\cos\theta$$ and $$y=a\cos\theta-b\sin\theta$$, then prove that $${x}^{2}+{y}^{2}={a}^{2}+{b}^{2}$$
Evaluate the following.
$$2\tan^{2} 45^{o}+\cos^{2} 30^{o}$$
$$2\tan^245^o+\cos^230^o$$
$$\Rightarrow 2(1)^2+\left(\dfrac{\sqrt{3}}{2}\right)^2$$
$$\Rightarrow 2+\dfrac{3}{4}=\dfrac{11}{4}$$.
Evaluate the following.
$$\dfrac {\sec ^{2}60^{o}-\tan ^{2}60^{o}}{\sin ^{2}30^{o}+\cos ^{2}30^{o}}$$
$$\dfrac{\sec^245^o-\tan^260^o}{\sin^230^o-\cos^245}=\dfrac{(\sqrt{2})^2-(\sqrt{3})^2}{\left(\dfrac{1}{2}\right)^2-\left(\dfrac{1}{\sqrt{2}}\right)^2}$$
$$\Rightarrow \dfrac{2-3}{\dfrac{1}{4}-\dfrac{1}{2}}=\dfrac{-1}{-1/4}=4$$.
If sin (A+B) = 1 and sin (A-B) = $$\frac { 1 }{ \sqrt { 3 } } $$, find the value of tan A + tan B.
Prove that : $$\left( {\cos ecA - \sin A} \right)\left( {\sec A - \cos A} \right) = \dfrac{1}{{\tan A + \cot A}}$$
Give$$ (cosA-sinA)(secA-CosA)=\frac{1}{tanA+cotA}$$
L.H.S.(coscA sinA)(secA-cosA)
$$\Rightarrow L.H.S=(\frac{1}{sinA}-sinA) (\frac{1}{cosA}-cosA)$$
$$ \Rightarrow L.H.S = (\frac{1-sin^{2}A}{sinA})(\frac{1-cos^{2}A}{cosA})$$
$$\Rightarrow L.H.S=\frac{cos^{2}A.sin^{2}A}{sina.cosA}\left [ \because sin^{2}A+cos^{2}A-1 cos^{2}A-1-sin^{2}A sin^{2}A=1-cos^{2}A \right ]$$
$$\Rightarrow L.H.S=\frac{sinA.cosA}{1}$$
$$\Rightarrow L.H.S=\frac{sinA.cosA}{sin^{2}A+cos^{2}A}$$
$$\Rightarrow L.H.S=\frac{1}{\frac{sin^{2}A+cos^{2}A}{sinA.cosA}}$$
$$\Rightarrow L.H.S=\frac{1}{\frac{sin^{2}A}{sinA cosA}+\frac{cos^{2}A}{sinA.cosA}}$$
$$\Rightarrow L.H.S=\frac{1}{\frac{sinA}{cosA}+\frac{cosA}{sinA}}$$
$$\Rightarrow L.H.S=\frac{1}{tanA+cotA}$$
=R.H.S
$$\Rightarrow $$L.H.S = R.H.S
Prove that: $$\sec^{6}x-\tan^{6}x=1+3\sec^{2}x\times \tan^{2}x$$
$$\dfrac{\cos A+\sin A}{\cos A-\sin A}=0$$ find $$A$$
Solve the equation $$(\cos x-\sin x)(2\tan x+2)=0$$
Prove that:$$\dfrac{\sec A-\tan A}{\sec A+\tan A}=\left(\dfrac{\cos A}{1+\sin A}\right)^2$$.
Find the principal solution: $$2+\sqrt { 3 } sec{x}-4cosx=2\sqrt { 3 } $$
Prove the following:
$$\dfrac{(\tan\theta+\sec\theta-1)}{\tan\theta-\sec\theta+1)}=\dfrac{1+\sin\theta}{\cos\theta}$$.
Prove that : $$\left( {\sin \theta + \cos \theta } \right)\left( {\tan \theta + \cot \theta } \right) = \sec \theta + \text{cosec}\theta $$
If $$(a\sin A)=b\cos A$$ and $$a\sin^{3}A+b\cos^{3}A=\sin A\cos A$$, then prove $$a^{2}+b^{2}=1$$
$$a\sin A(\sin^2A)+b\cos A(\cos^2A)\sin A\cos A$$
$$a\sin A(1)=\sin A\cos A$$
$$\Rightarrow a=\cos A$$
$$\Rightarrow b=\sin A$$
$$\Rightarrow a^2+b^2=\sin^2A+\cos^2A=1$$.
If $$\sec \theta + \tan \theta = p$$, then find the value $$\text{cosec} \theta $$.
$$sec\theta +tan \theta =P$$ _______ (1)
$$sec^{2}\theta -tan^{2}\theta =1$$
$$(sec \theta +tan \theta )(sec \theta - tan \theta )=1$$
$$sec\theta -tan \theta = 1/P$$ _______ (2)
Subtracting (2) from (1), we get
$$2 tan \theta = P-\dfrac{1}{P}$$
$$\therefore cot \theta =\dfrac{2P}{P^{2}-1}$$
Now, $$cosec^{2}\theta -cot^{2}\theta =1$$
$$cosec^{2}\theta =1+cot^{2}\theta $$
$$\Rightarrow cosec^{2}\theta =1+(\dfrac{2P}{P^{2}-1})^{2}$$
$$\Rightarrow cosec^{2}\theta =1+\dfrac{4P^{2}}{(P^{2}-1)^{2}}$$
$$\Rightarrow cosec^{2}\theta =(P^{4}-2P^{2}+1+4P^{2})/(P^{2}-1)^{2}$$
$$\Rightarrow cosec^{2}\theta =\dfrac{P^{2}+1}{P^{2}-1}$$
If a line makes angles $$ \alpha, \beta, \gamma $$ with positive direction co-ordinate axes then prove that $$ \sin ^{2} \alpha+\sin ^{2} \beta+\sin ^{2} \gamma=2 $$
Prove that $$2{\sec ^2}\theta - {\sec ^4}\theta - 2\cos e{c^2}\theta + \cos e{c^4}\theta = {\cot ^4}\theta - {\tan ^4}\theta $$
Prove that $$\text{cosec}^6\theta = {\cot ^6}\theta + 3{\cot ^2}\theta .\text{cosec}^2\theta + 1$$
Prove that $$\displaystyle \frac{{\sin \theta }}{{1 - \cos \theta }} + \frac{{\tan \theta }}{{1 + \cos \theta }} = \cot \theta + \sec \theta .\text{cosec}\theta $$
Evaluate :
$$\dfrac { cosA-sinA+1 }{ cosA+sinA-1 } =cosecA+cotA$$.
$$\sin (A+B)=\dfrac{\surd{3}}{2}$$ and $$\cos (A-B)=\dfrac{\surd{3}}{2}$$, where $$(A+B)$$ and $$(A-B)$$ are acute angles. Find the values of $$A$$ and $$B$$ $$ A,B <90^{0}$$
Prove that $$\dfrac{{\sin \theta - 2\,{{\sin }^3}\theta }}{{2\,{{\cos }^3}\theta - \cos \,\theta }} = \tan \theta $$
Find the values of $$\theta$$,( in degrees) if $$\sin (\theta +24)=\cos \theta$$, where $$(\theta+24)^{0}$$ is an acute angle .
Prove $$\displaystyle \frac{{\tan \theta }}{{1 - \cot \theta }} + \frac{{\cot \theta }}{{1 - \tan \theta }} = 1 + cosec \theta. \sec \theta $$
If $$\sec \theta - \tan \theta = x$$, then show that $$\sec \theta + \tan \theta = \dfrac{1}{x}$$ and hence find the values of $$\cos \theta $$ and $$\sin \theta$$.
Prove $$\displaystyle \frac{{1 + \cos A}}{{\sin A}} + \frac{{\sin A}}{{1 + \cos A}} = 2\text{cosec} \ A$$
Evaluate : $$\dfrac { \cos x } { ( 1 + \sin x ) ^ { 2 } ( 2 + \sin x ) }$$
Prove that $$\displaystyle \frac{{{\mathop{\rm tanA}\nolimits} }}{{1 + \sec A}} - \frac{{\tan A}}{{1 - \sec A}} = 2\text{cosec}A$$
Prove that $$\displaystyle \frac{{\tan \theta - \cot \theta }}{{\sin \theta \cos \theta }} = {\tan ^2}\theta - {\cot ^2}\theta $$
Solve:$$\left(\cos{x}-\sin{x}\right)\left(2\tan{x}+\dfrac{1}{\cos{x}}\right)+2=0$$
Prove that $$\dfrac { \cos A+ \sin A-1 }{ \cos A-\sin A+1 } =\dfrac { 1 }{ \text{cosec}A+\cot A } $$, using the identity $$ { \text{cosec }}^{ 2 }A-{ \cot }^{ 2 }A=1.$$
Prove $$\left (\dfrac{1 + \tan^2 A}{1 + \cot^2 A}\right) = \left (\dfrac{1 - \tan A}{1 - \cot A}\right)^2$$
If $$\cos \left( {2{{\tan }^{ - 1}}x} \right) = \dfrac{1}{2},\;then\;the\;value\;of\;x\;is\;........$$
Prove that : $$\dfrac{{1 + \cos A + \sin A}}{{1 + \cos A - \sin A}} = \dfrac{{1 + {\mathop{\rm sinA}\nolimits} }}{{\cos A}}$$
Find the value of $$\theta $$,( in degrees ) if, $$\dfrac{{\cos \theta }}{{1 - \sin \theta }} + \dfrac{{\cos \theta }}{{1 + \sin \theta }} = 4;\,\,\theta \le 90^\circ $$
Prove that : $$\dfrac{{\text{cosec}\theta - 1}}{{\text{cosec}\theta + 1}} = \dfrac{{{{\cos }^2}\theta }}{{{{\left( {1 + \sin \theta } \right)}^2}}}$$
If $${ sin }^{ 2 }\theta +5{ cos }^{ 2 }\theta =4,$$ then find $$\theta $$ and hence prove that $$sec\theta +cosec\theta =2+\dfrac { 2 }{ \sqrt { 3 } } $$
Prove the following identities :
(i) $$( \sin \theta + \csc \theta ) ^ { 2 } = \sin ^ { 2 } \theta + \csc ^ { 2 } \theta + 2$$ (ii) $$\cos ^ { 4 } \theta - \sin ^ { 4 } \theta = 1 - 2 \sin ^ { 2 } \theta$$
Find the principal solution of $$\sqrt 3 \sec x + 2 = 0$$
Find the magnitude, in radians and degrees, of the interior angle of
(1) a regular pentagon,
(2) a regular heptagon,
(3) a regular octagon,
(4) a regular duodecagon,
and (5) a regular polygon of $$17$$ sides.
If $$\tan \theta + \sin \theta = m$$ and $$\tan \theta - \sin \theta = n ,$$ then
(i) $$m ^ { 2 } - n ^ { 2 } = 4 m n$$
(ii) $$m ^ { 2 } + n ^ { 2 } = 4 m n$$
(iii) $$m ^ { 2 } - n ^ { 2 } = m ^ { 2 } + n ^ { 2 }$$
(iv) $$m ^ { 2 } - n ^ { 2 } = 4 \sqrt { m n }$$
Prove that $$\dfrac{\tan A}{1+ \sec A}-\dfrac{\tan A}{1 -\sec A}=2\text{cosec}A$$
Prove that : $$sec^{4}\Theta (1-sin^{4}\Theta )-2tan^{2}\Theta =1$$
Solve the equation $$sinx+cosx=1$$
$$\frac{sinA-cosA+1}{sinA+cosA-1}=\frac{1}{secA-tanA}$$
Fin an acute angle $$\Theta $$ , when
$$\frac{cos\Theta -sin\Theta }{cos\Theta +sin\Theta }=\frac{1-{\sqrt{3}}}{1+\sqrt{3}}$$.
Find the degree measure of $${\dfrac{2\pi}{15}}^{c}$$
Solve, by factorising, the equation $$2\cos \theta\sin\theta-2\cos\theta-\sin\theta+1=0$$ for $$0\le\theta\le \pi$$
Find the principal solution of the following equation:
$$co\sec { x } =2$$
Solve the following equation:
$$2^{\sin^{2}x}+2^{\cos ^{2}x}=2\sqrt 2$$
Find the principal solution of the following equation:
$$\sqrt { 3 } co\sec { x } +2=0$$
Find the principal solution of the following equation:
$$\sqrt { 2 } \cos { x } +1=0$$
Find the principal solution of the following equation:
$$\sin { x } =\cfrac { -1 }{ 2 } $$
If $$\tan x=\dfrac {b}{a}$$, then find the value of $$\sqrt {\dfrac {a+b}{a-b}}+ \sqrt {\dfrac {a-b}{a+b}}$$
Prove that :$$\cos 2\alpha \cos 2\beta +\sin^2 (\alpha -\beta)-\sin^2 (\alpha +\beta)=\cos 2(\alpha +\beta)$$
Express in terms of a right angle the angles
$$60^{\circ}$$.
$$75^{\circ} 15'$$.
$$63^{\circ} 17'25''$$.
$$130^{\circ} 30'$$.
$$210^{\circ} 30'30''$$.
$$370^{\circ} 20'48''$$.
Mark the position of the revolving line when it has traced out the following angles:
$$\dfrac {4}{3}$$ right angle.
$$3\dfrac {1}{2}$$ right angles.
$$13\dfrac {1}{3}$$ right angles.
$$120^{\circ}$$
$$315^{\circ}$$
$$745^{\circ}$$
$$1185^{\circ}$$
$$150^{g}$$
$$420^{g}$$
$$875^{g}$$.
Express in grades, minutes, and seconds the angles
$$30^{\circ}$$
$$81^{\circ}$$
$$138^{\circ} 30'$$
$$35^{\circ} 47'15''$$
$$235^{\circ} 12'36''$$
$$475^{\circ} 13'48''$$.
Find two regular polygons such that the number of their sides may be as $$3$$ to $$2$$ and the number of degrees in an angle of the first to the number of grades in an angle of the second as $$5$$ to $$3$$.
The number of degrees in one acute angle of a right-angled triangle is equal to the number of grades in the other; express both the angles in degrees.
The circular measure of two angles of a triangle are respectively $$\dfrac {1}{2}$$ and $$\dfrac {1}{3}$$; what is the number of degrees in the third angle?
How many degrees, minutes and seconds are respectively passed over in $$11\dfrac {1}{9}$$ minutes by the hour and minute hands of a watch?
Given $$L\cot 71^o27'=9.5257779$$ and $$L\cot 71^o28'=9.5253589$$, find the value of $$L\cot 71^o27'47''$$, and solve the equation $$L\cot\theta =9.5254782$$.
With the help of the same page solve the equations
$$(1)$$ $$L\tan\theta =10.1959261$$,
$$(2)$$ $$L cosec\theta =10.0738125$$,
$$(3)$$ $$L\cos \theta =9.9259283$$, and
$$(4)$$ $$L\sin\theta =9.9241352$$.
One angle of a triangle is $$\dfrac {2}{3}x$$ grades and another is $$\dfrac {3}{2}x$$ degrees, whilst the third is $$\dfrac {\pi x}{75}$$ radians; express them all in degrees.
Prove that the number of Sexagesimal minutes in any angle is to the number of Centesimal minutes in the same angle as $$27 : 50$$.
Find the times (1) between four and five o'clock when the angle between the minute-hand and the hour-hand is $$78^{\circ}$$, (2) between seven and eight o'clock when this angle is $$54^{\circ}$$.
Find in degrees, minutes, and seconds the angle whose sine is $$.6$$, given that $$\log 6=7781513$$, $$L\sin 36^o52'=9.7781186$$, and $$L\sin 36^o53'=9.7782870$$.
Eliminate $$\theta$$ from the equations
$$\tan (\theta - \alpha) + \tan (\theta - \beta) = x$$,
and $$\cot (\theta - \alpha) + \cot (\theta - \beta) = y$$.
If $$b=14, c=11$$, and $$A=60^o$$, find B and C, given that
$$log 2=.30103$$, $$log 3=.4771213$$,
$$L\tan 11^o44'=9.3174299$$,
and $$L\tan 11^o45'=9.3180640$$.
Eliminate $$ x $$ from the equations, $$ \sin (a+x)=2 b $$ and $$ \sin (a-x)=2 c $$.
If $$b=90$$, $$c=70$$, and $$A=72^o48'30''$$, find B and C, given $$log 2=.30103$$, $$L\cot 36^o24'15''=10.1323111$$,
$$L\tan 9^o37'=9.2290071$$,
and $$L\tan 9^o38'=9.2297735$$.
The two sides of a triangle are $$540$$ and $$420$$ yards long respectively and include an angle of $$52^o6'$$. Find the remaining angles, given that
$$log 2=.30103$$, $$L\tan 26^o3'=9.6891430$$,
$$L\tan 14^o20'=9.4074189$$, and $$L\tan 14^o21'=9.4079453$$.
Find the general solution of the equation $$cos 4x = cos 2x$$
Find the general solution of the equation $$\cos 3x$$ $$+ \cos x$$ – $$\cos 2x = 0.$$
Find the general solution of $$cosec x = -2$$
Find the principal and general solutions of the question $$tan x =$$ $$\sqrt{3}$$.
Find the principal and general solutions of the equation $$cot x$$ = -$$\sqrt{3}$$
If $$\sec \theta =x+\dfrac{1}{4x'}$$, prove that $$\sec \theta +\tan \theta =2x$$ or $$\dfrac{1}{2x}$$.
Find the general solution of the equation $$sin x + sin 3x + sin 5x = 0$$
If $$x\sin^3 \theta +y \cos^3 \theta =\sin \theta \cos \theta $$ and $$\sin \theta =y \cos \theta $$, prove $$x^2 +y^2 =1$$.
If $$\tan \theta +\sin \theta =m$$ and $$\tan \theta -\sin \theta =n$$, show that $$(m^2 -n^2)=4\sqrt {mn}$$.
Find an acute angle $$\theta$$, when $$\dfrac{\cos \theta -\sin \theta }{\cos \theta +\sin \theta }=\dfrac{1-\sqrt 3}{1+\sqrt 3}$$
Define a degree measure.
Define principal solutions of trigonometric equations.
Find the principal solution of the following equations
$$\sin x=\dfrac{\sqrt{3}}{2}$$
Find the principal solution of the following equations
$$\tan x=-\dfrac{1}{\sqrt{3}}$$
Find the principal solutions of the following equation:
$$cot \theta= 0$$
Find the principal solutions of the following equation:
$$\sqrt{3} cosec \theta +2=0$$
Find he principal values of the following
$$\cot^{-1} (\sqrt{3}) $$
If $$\sin { \theta } =\cfrac{m}{\sqrt { m^{ 2 }+{ n }^{ 2 } } }$$, prove that $$m\sin { \theta } +n\cos { \theta } =\sqrt { m^{ 2 }+{ n }^{ 2 } } $$
we know that
$$\sin { \theta } =\cfrac { side\quad opposite\quad to\quad angle\quad \theta }{ hypotenuse } \quad or\quad \sin { \theta } =\cfrac { Perpendicular }{ hypotenuse } $$
$$\quad \sin { \theta } =\cfrac { m }{ \sqrt { { m }^{ 2 }+{ n }^{ 2 } } } \Rightarrow \cfrac { P }{ H } =\cfrac { m }{ \sqrt { { m }^{ 2 }+{ n }^{ 2 } } } \Rightarrow \cfrac { AB }{ BC } =\cfrac { m }{ \sqrt { { m }^{ 2 }+{ n }^{ 2 } } } $$
let
perpendicular $$=AB=m$$
hypotenuse $$=AC=\sqrt { { m }^{ 2 }+{ n }^{ 2 } } $$
where $$k$$ is positive integer
so, by pythagoras theorem
$$\Rightarrow { \left( m \right) }^{ 2 }+{ \left( BC \right) }^{ 2 }={ \left( \sqrt { { m }^{ 2 }+{ n }^{ 2 } } \right) }^{ 2 }\Rightarrow { \left( m \right) }^{ 2 }+{ \left( BC \right) }^{ 2 }={ m }^{ 2 }+{ n }^{ 2 }\Rightarrow { \left( BC \right) }^{ 2 }={ m }^{ 2 }+{ n }^{ 2 }-{ m }^{ 2 }\Rightarrow { \left( BC \right) }^{ 2 }={ n }^{ 2 }\Rightarrow BC=\sqrt { { n }^{ 2 } } =\pm n$$
but side $$BC$$ can't be negative. So, $$BC=n$$
Now we have to find the value of $$\cos { \theta } $$ and $$\tan \theta$$
we know that
$$\cos { \theta } =\cfrac { base }{ hypotenuse } $$
side adjacent to angle $$\theta$$ and base $$=BC=n$$
hypotenuse $$=AC=\sqrt { { m }^{ 2 }+{ n }^{ 2 } } $$
so, $$\cos { \theta } =\cfrac { n }{ \sqrt { { m }^{ 2 }+{ n }^{ 2 } } } $$
Now LHS=m\sin { \theta } +n\cos { \theta } =m\left( \cfrac { m }{ \sqrt { { m }^{ 2 }+{ n }^{ 2 } } } \right) +n\left( \cfrac { n }{ \sqrt { { m }^{ 2 }+{ n }^{ 2 } } } \right) =\cfrac { { m }^{ 2 }+{ n }^{ 2 } }{ \sqrt { { m }^{ 2 }+{ n }^{ 2 } } } =\sqrt { { m }^{ 2 }+{ n }^{ 2 } } =RHS\quad $$
$$\sin { \theta } =\cfrac { side\quad opposite\quad to\quad angle\quad \theta }{ hypotenuse } \quad or\quad \sin { \theta } =\cfrac { Perpendicular }{ hypotenuse } $$
$$\quad \sin { \theta } =\cfrac { m }{ \sqrt { { m }^{ 2 }+{ n }^{ 2 } } } \Rightarrow \cfrac { P }{ H } =\cfrac { m }{ \sqrt { { m }^{ 2 }+{ n }^{ 2 } } } \Rightarrow \cfrac { AB }{ BC } =\cfrac { m }{ \sqrt { { m }^{ 2 }+{ n }^{ 2 } } } $$
let
perpendicular $$=AB=m$$
hypotenuse $$=AC=\sqrt { { m }^{ 2 }+{ n }^{ 2 } } $$
where $$k$$ is positive integer
so, by pythagoras theorem
$$\Rightarrow { \left( m \right) }^{ 2 }+{ \left( BC \right) }^{ 2 }={ \left( \sqrt { { m }^{ 2 }+{ n }^{ 2 } } \right) }^{ 2 }\Rightarrow { \left( m \right) }^{ 2 }+{ \left( BC \right) }^{ 2 }={ m }^{ 2 }+{ n }^{ 2 }\Rightarrow { \left( BC \right) }^{ 2 }={ m }^{ 2 }+{ n }^{ 2 }-{ m }^{ 2 }\Rightarrow { \left( BC \right) }^{ 2 }={ n }^{ 2 }\Rightarrow BC=\sqrt { { n }^{ 2 } } =\pm n$$
but side $$BC$$ can't be negative. So, $$BC=n$$
Now we have to find the value of $$\cos { \theta } $$ and $$\tan \theta$$
we know that
$$\cos { \theta } =\cfrac { base }{ hypotenuse } $$
side adjacent to angle $$\theta$$ and base $$=BC=n$$
hypotenuse $$=AC=\sqrt { { m }^{ 2 }+{ n }^{ 2 } } $$
so, $$\cos { \theta } =\cfrac { n }{ \sqrt { { m }^{ 2 }+{ n }^{ 2 } } } $$
Now LHS=m\sin { \theta } +n\cos { \theta } =m\left( \cfrac { m }{ \sqrt { { m }^{ 2 }+{ n }^{ 2 } } } \right) +n\left( \cfrac { n }{ \sqrt { { m }^{ 2 }+{ n }^{ 2 } } } \right) =\cfrac { { m }^{ 2 }+{ n }^{ 2 } }{ \sqrt { { m }^{ 2 }+{ n }^{ 2 } } } =\sqrt { { m }^{ 2 }+{ n }^{ 2 } } =RHS\quad $$
Find the principal solution of the following equations
$$\tan x=\sqrt{3}$$
98 Find he principal values of the following
$$\cos^{2} \left ( -\dfrac{1}{\sqrt{2}} \right )$$
Solve: $$\cos x=\dfrac{1}{2}$$
Convert $$ \dfrac{3 \pi}{5} $$ radian into sexagesimal system.
Find the principal solution of the following equations
$$\sec x=2$$
Express the following angles in sexagesimal system.
$$ \dfrac{5 \pi}{6} $$
Express the following angles in sexagesimal system.
$$ \dfrac{2 \pi}{5} $$
Express the following angles in sexagesimal system.
$$ \dfrac{\pi}{2} $$
Find the principal solution of the following equations
$$\csc x=-2$$
Express the following angles in sexagesimal system.
$$ \dfrac{ \pi}{15} $$
Express the following angles in degree, minutes and seconds.
$$ \dfrac{3 \pi}{7} $$ radians
Express the following angles in degree, minutes and seconds.
$$ \dfrac{\pi}{8} $$ radians
The equations have at least one root on the interval
A root of the equation is given by $$(0 < \theta < \pi)$$
The number of distinct solutions of the equation $$\dfrac {5}{4} \cos^22x+\cos^4x+\sin^4x+\cos^6x+\sin^6x=2$$ in the interval $$[0, 2\pi]$$ is _________
If $$\displaystyle\frac{\tan\theta}{1-\cos\theta}+\frac{\cot\theta}{1-\tan\theta}=m+\sec \theta \text{cosec} \theta$$.Find $$m$$
State whether the following are true or false. Justify your answer.
(i) $$\displaystyle \sin { \left( A+B \right) =\sin { A } +\sin { B } } $$
(ii) The value of $$\displaystyle \sin { \theta } $$ increases as $$\displaystyle \theta$$ increases.
(iii) The value of $$\displaystyle \cos { \theta } $$ increases as $$\displaystyle $$ increases.
(iv) $$\displaystyle \sin { \theta } =\cos { \theta } $$ for all values of $$\displaystyle \theta $$.
(v) $$\displaystyle \cot { A } $$ is not defined for $$\displaystyle A={ 0 }^{ \circ }$$.
Prove the following identities.
$$\displaystyle\, \frac{(1 \, + \, cos \, x)(1 \, + \, cos \, 2x)}{(1 \, + \, sin \, x)(1 \, - \, cos \, 2x)} \, = \, \frac{1 \, - sin \, x}{1 \, - \, cos \, x}$$
Solve the following equations.
$$\displaystyle cos \, 3x \, tan \, 5x \, = \, sin \, 7x.$$
If in $$\triangle ABC$$, $$a \cos B \cos C + b \cos C \cos A+ c \cos A\cos B= \frac{m\triangle}{R}$$.Find $$m$$
Prove the following identities
$$\displaystyle\, \frac{sin \, 2\alpha }{1 \, + \, cos \, 2\alpha} \cdot \frac{cos \, \alpha }{1 \, + \, cos \, \alpha} \, = \, tan\frac{\alpha }{2}$$.
Find a if $$4 \cos \dfrac{2\pi}{7} \cos \dfrac{\pi}{7} -1 = a \cos \dfrac{ a\pi}{7}$$
If $$\displaystyle cosec \frac{\pi}{32} + cosec \frac{\pi}{16} +cosec \frac{\pi}{8} + cosec \frac{\pi}{4} + cosec \frac{\pi}{2} = cot \frac{\pi}{k}$$. Find k.
If $$m^2 \cos \frac{2\pi}{15} \cos \frac{4\pi}{15} \cos \frac{8\pi }{15} \cos \frac{14\pi}{15} = n^2$$, then find the value of $$\frac{m^2 - n^2}{n^2}$$.
Find m if $$\sin 12^0 \sin 18^0 \sin 42^0 \sin 48^0 \sin 72^0 \sin 78^0=\dfrac{\cos18^0}{2m}$$.
Prove $$\dfrac{\tan x}{1-\cot x}+\dfrac{\cot x}{1- \tan x}=1+ \tan x + \cot x$$
Prove $$\dfrac{{{{\tan }^3}\theta }}{{1 + {{\tan }^2}\theta }} + \,\dfrac{{{{\cot }^3}\theta }}{{1 + {{\cot }^2}\theta }} = \dfrac{{1 - 2{{\sin }^2}\theta {{\cos }^2}\theta }}{{\sin \theta \cos \theta }}$$
If $$ \cos^3\frac{\pi}{9}+ \sin^3\frac{\pi}{18} = \dfrac{m}{4} \left( \cos\frac{\pi}{9}+ \sin\frac{\pi}{18}\right)$$.Find $$m$$
Find the solution of(i) $$2 \cos ^ { 2 } \theta + 4 \sin \theta \cos \theta + 1 = 0 $$(ii) $$ { \sec } x + \tan x = 2 $$
(ii) $$ { \sec } x + \tan x = 2 $$
Prove
$$\dfrac { tan\theta }{ sec\theta -1 } =\dfrac { tan\theta +sec\theta +1 }{ tan\theta +sec\theta -1 } $$
If $$\prod _ { r = 4 } ^ { 8 } \cos \left( \dfrac { \theta } { 2 ^ { r } } \right) = \dfrac { \sin \left( \dfrac { \theta } { 2 ^ { n _ { 1 } } } \right) } { ( 2 ) ^ { n _ { 2 } } \sin \left( \dfrac { \theta } { 2 ^ { n _ { 3 } } } \right) } ,$$ then the value of $$n _ { 1 } + n _ { 3 } - n _ { 2 }$$ is
Find the value of $$\theta$$ for the equation.
$$ 2 sin 2\theta= \sqrt 3$$
If 2 sin$$\left( \theta +\dfrac { \pi }{ 3 } \right) =\cos\left( \theta -\dfrac { \pi }{ 6 } \right) ,$$ prove that $$\tan \theta +\sqrt { 3 } =0$$
Prove that
$$2\sec^{2}\theta -\sec^{4}\theta -2\csc^{2}\theta +\csc^{4}\theta =\cot^{4}\theta -\tan^{4}\theta$$
Solve $$2{ cos }^{ 2 }\theta +3sin\theta =0$$
Evaluate: $$\displaystyle \lim _{ { x\rightarrow 0 } } \dfrac { \{ \sin (\alpha +\beta )x+\sin (\alpha -\beta )x+\sin 2\alpha x\} }{ \cos ^{ { 2 } } \beta x-\cos ^{ { 2 } } \alpha x } $$
Prove that $$\frac{{\sin x - \sin 3x}}{{{{\sin }^2}x - {{\cos }^2}x}} = 2\sin x$$
In $$\Delta ABC$$, prove that:
$$asin (B-C)=bsin B-csin C$$
For what value of acute angle $$\dfrac{cos\Theta }{1-sin\Theta }+\dfrac{cos\Theta }{1+sin\Theta }=4$$ is true ?
Find the principal solution of the following equation:
$$\sec { x } =\cfrac { 2 }{ \sqrt { 3 } } $$
If $$a=21, b=11$$, and $$C=34^o42'30''$$, find A and B, given $$log 2=.30103$$,
and $$L\tan 72^o38'45''=10.50515$$.
If $$\cos { \theta } =\cfrac { q }{ \sqrt { p^{ 2 }+{ q }^{ 2 } } } $$, prove that $${ \left( \cfrac { \sqrt { p^{ 2 }+{ q }^{ 2 } } }{ p } +\cfrac { q }{ p } \right) }^{ 2 }=\cfrac { \sqrt { p^{ 2 }+{ q }^{ 2 } } +q }{ \sqrt { p^{ 2 }+{ q }^{ 2 } } -q } $$
Express in grades, minutes, and seconds the angles,
$$\dfrac {53\pi^{}}{100}$$ radians
$$\dfrac {7\pi^{}}{6}$$ radians
$$10\pi^{}$$ radians
Class 11 Engineering Maths Extra Questions
- Binomial Theorem Extra Questions
- Complex Numbers And Quadratic Equations Extra Questions
- Conic Sections Extra Questions
- Introduction To Three Dimensional Geometry Extra Questions
- Limits And Derivatives Extra Questions
- Linear Inequalities Extra Questions
- Mathematical Reasoning Extra Questions
- Permutations And Combinations Extra Questions
- Principle Of Mathematical Induction Extra Questions
- Probability Extra Questions
- Relations And Functions Extra Questions
- Sequences And Series Extra Questions
- Sets Extra Questions
- Statistics Extra Questions
- Straight Lines Extra Questions
- Trigonometric Functions Extra Questions