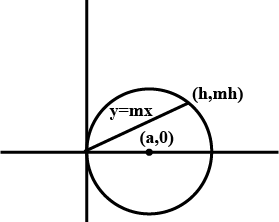Circles - Class 11 Commerce Applied Mathematics - Extra Questions

Prove that the locus of the point of intersection of the lines 
$$x \, cos \, \alpha \, + \,y \,  sin \, \alpha \, = \, a$$
and $$x \, sin \, \alpha \, - \,y \,  cos \, \alpha \, = \, b$$
is a circle whatever $$\alpha$$ may be.

In order to find the locus of the point of intersection we -have to eliminate the variable a between the lines for which we square and add.
$$\therefore \, \, \,$$ x $$^2$$ (sin $$^2$$ $$\alpha$$ + cos $$^2$$ $$\alpha$$ )+y $$^2$$ (sin $$^2$$ $$\alpha$$ + cos $$^2$$ . $$\alpha$$ ) = a $$^2$$ + b $$^2$$  
or x $$^2$$ + y $$^2$$ = a $$^2$$ + b $$^2$$ which represents a circle.

If $$y = mx$$ be the equation of a chord of a circle whose radius is $$a$$ , the origin of coordinates being one extremity of the chord and the axis of $$x$$ being a diameter of the circle, prove that the equations of a circle of which this chord is the diameter is $$(1 + m^{2})(x^{2} + y^{2}) - 2a (x + my) = 0$$ .

Equation of chord is $$y=mx$$

Let the end of chord be $$(h,mh)$$ , other end is $$(0,0)$$ .

Equation of circle is $$(x-a)^2+y^2=a^2$$ , and $$(h,mh)$$ lies on the circle

$$\therefore \ (h-a)^2+m^2h^2=a^2$$

$$\Rightarrow h^2-2ah+m^2h^2=0$$

$$\Rightarrow h-2a+m^2h=0$$

$$\Rightarrow h=\cfrac{2a}{1+m^2}$$

Equation of circle with $$(0,0)$$ and $$(h,mh)$$ diameter will be

$$(x-h)x+(y-mh)y=0$$

$$\Rightarrow x^2 -hx+y^2-mhy=0$$

$$\Rightarrow x^2+y^2=h(x+my)$$

$$(1+m^2)(x^2+y^2)=2a(x+my)$$

Find the equation of the circle whose radius 3 and which touches internally the circle  $$x^2 \, + \, y^2 \, - \, 4x \, - \, 6y \, - \, 12 \, = \, 0$$ at the point (-1, -1)

$$x^2  \, +  \, y^2$$ 4x 6y 12 = 0
Centre A is (2, 3) and radius 5 = PA, B (h, k) is the centre of the required circle of radius BP = 3 which touches the given circle internally at P (- 1, - 1)
$$\therefore$$ BA = PA PB = 5 3 = -2
Thus B divides PA in the ratio 3 : 2.
$$\therefore \, \, h \, = \, \dfrac{3.2 \, + \, 2(- 1)}{3 \, + \, 2} \, = \, \dfrac{4}{5} \, , \, k \, = \, \dfrac{3.2 \, + \, 2(- 1)}{3 \, + \, 2} \, = \, \dfrac{7}{5}$$
Hence the required circle is
(x-4/5) $$^2$$ + (y - 7/5) $$^2$$ =3 $$^2$$
Or $$5x^2 \, +  \, 5y^2$$ - 8x - 14y 32 = 0.

Find the equations of a circle which passes though the point ( 2 , 0 ) and whose center is the limit of the point of intersection of the lines 3x + 5y = 1  , (2 +  c ) x + $$5c^2$$ y  = 1  tends to 1 

Eliminating y, we get
(3c $$^2$$ 2 c - 2)x = c $$^2$$ - 1  $$\therefore  x \, = \, \dfrac{(c \, - \, 1)(c \, + \, 1)}{(c \, - \, 1)(3c \, + \, 2)} \, = \, \dfrac{c \, + \, 1}{3c \, + \, 2}$$
$$\therefore$$  limit when c $$\Rightarrow$$ 1 gives $$x = \dfrac {2}{5}$$ and hence $$y = -\dfrac {1}{25}$$ .
$$\therefore$$  Centre ( g , f) is $$\left(\dfrac {2}{5} , \dfrac {1}{25}\right)$$ . 
Circle is
$$x^2 \, + \, y^2 -\left(\dfrac {4}{5}\right)x + \left(\dfrac {2}{25}\right)y + k = 0$$
It passes through $$(2, 0)$$   $$\therefore$$ $$k = - \left(\dfrac {12}{5}\right)$$
Hence the required circle is
$$25(x^2 \, + \, y^2)-20x + 60y = 0.$$

Find the equation of circle of radius, $$3$$ , passing through the origin and having its centre on the x-axis.

center of $$x$$ axis = $$(x,0)$$  

and radius $$= 3$$ , passing through origin - 

$$\sqrt{(x-0)^{2}+(0-0)^{2}}=3$$

  $$x^{2}=9$$

  $$x = \pm  3$$

  $$\therefore$$ center $$=(3,0)$$ or $$(-3,0)$$

  $$\therefore$$ equation of circle is

  $$\left ( x-3 \right )^{2}+y^{2}=3^{2} \Rightarrow  x^{2}+y^{2}y^{2}-6x=0$$

 or 

$$(x+3)^{2}+y^{2}=3^{2}\Rightarrow x^{2}+y^{2}+6x=0$$

Find the equation of the circle whose centre is the point of intersection of the lines $$2x-3y+4=0$$ & $$3x+4y-5=0$$ and passes through the origin.

$$2x-3y+4=0$$

$$3x+4y-5=0$$

To find eqn of circle passing through $$(0,0)$$ & centre at point of intersection

$$\Rightarrow 2x-3y+4=0$$ ........ $$(i)$$  

$$3x+4y-5=0$$ ........... $$(ii)$$

Multiply $$3\times (i)$$ & $$2\times (ii)$$ & Subtract them, now we get.

$$2(3x+4y-5)=0$$

$$3(2x-3y+4)=0$$

$$6x+18-10=0$$

$$-6x-9+12=0$$

______________

$$17y-22=0$$

$$\therefore =\dfrac{22}{17}$$

on substituting $$y=\dfrac{22}{17}$$ in $$(i)$$ we get

$$2x=3y-4$$

$$=3\left(\dfrac{22}{17}\right)-4=\dfrac{66}{17}-68$$

$$\therefore x=\dfrac{-1}{17}$$

$$\therefore$$ centre of circle is at $$\left(\dfrac{-1}{17}, \dfrac{22}{17}\right)$$

Since radius of circle $$=$$ Distance from centre & origin 

$$\therefore r=\sqrt{\left(-\dfrac{1}{17}-0\right)^{2}+\left(\dfrac{22}{17}-0\right)}$$

$$r=\sqrt{\dfrac{1}{289}+\dfrac{484}{289}}$$

$$r^{2}=\dfrac{485}{289}$$

eqn of circle $$=(x-h)^{2}+(y-k)^{2}=r^{2}$$

on substituting all values we get

$$\Rightarrow \left(x+\dfrac{1}{17}\right)^{2}+\left(y-\dfrac{22}{17}\right)^{2}=\dfrac{485}{289}$$

Find the equation of the circle which passes through $$\left( 3,-2 \right)$$ , $$\left( -2,0 \right)$$ and has its centre on the line $$2x-y=3\\ $$

Given line equation be $$2x-y =3$$

Points $$(3,-2), (-2, 0)$$

Let $$(x_1,y_1)$$ be centre $$\Rightarrow 2x_1 -y_1 =3$$ ...(1)

distance from points = radius [ Radius should be equal]

$$\sqrt{(x,-3)^2+(y_1+2)^2}=\sqrt{(x+2)^2+(y+o)^2}$$

$$\Rightarrow x^2+9- 6x_1+y_1^2+4+4y_1= x_1^2+4+4x_1+y^2$$

$$\Rightarrow 10x_1- 4y_1-9=0$$ ...(2)

solving $$1$$ & $$2$$

$$\Rightarrow 10x_1- 4y_1-9y - 12= - 8x_1- 4y-12=0$$

$$= 2x_1 +3=0 \Rightarrow x_1 = \dfrac{-3}2$$

center $$=\left (-\dfrac 32, 6\right)$$

Radius $$=\sqrt{\left(3+\dfrac 32\right)^2+(-2-6)^2}=\sqrt{\left(\dfrac 92\right)^2+64}= \sqrt{\dfrac {337}{4}}$$

Circular equation is:

$$\left ( x+\dfrac {3}{2} \right )^2 +(y-6)^2=\dfrac {337}{4}$$

Obtain the differential equation of the family of circles having centre $$(0,6)$$ or centre lying on y-axis passing through the points $$(a,0)$$ and $$(-a,0)$$ .

Let family of circle be

$$(x)^2+(y-k)^2=r^2$$ (enter $$(o, k)$$ )

Passes through $$(a,o)$$

$$a^2+k^2=r^2$$

$$x^2+(y-k)^2=a^2+k^2$$

Differentiate implicitly 

$$2x+(y-k)\dfrac {dy}{dx}=0$$

$$\dfrac {dy}{dx}=\dfrac {-x}{y-k}$$

$$\dfrac {dy}{dx}+\dfrac {x}{y-k}=0$$

The equation to the circle whose radius is 4 and which touches the negative $$x$$ -axis at a distance 3 units from the origin is

$$\\\therefore\>centre(-3,4)\\\therefore\>equation\>of\>circle\\\>[x-(-3)]^2+(y-4)^2=4^2\\(x+3)^2+(y-4)^2=16\\x^2+6x+9+y^2-8y+16=16\\or\>x^2+y^2+6x-8y+9=0\\other\>case:\\the\>equation[x-(-3)]^2+[y-(-4)]^2=4^2\\(x+3)^2+(y+4)^2=16\\or\>x^2+y^2+6x+8y+9=0$$

 

Find the equation of the circle passing through the origin, having radius $$\sqrt{5}$$ and having centre on $$\overrightarrow{OX}$$ .

Since radius $$=\sqrt 5$$ , center lies on $$x-$$ axis and circle passes through center, so center will be $$(\sqrt 5,0)$$

So,equation will be 

$$(x-\sqrt 5)^2+(y-0)^2=(\sqrt 5)^2$$

$$(x-\sqrt 5)^2+(y-0)^2= 5$$

Find the equation of circle having the lines $$x^2+2xy+3x+6y=0$$ as its normal and having size just sufficient to contains the circle. $$x(x-4)+y(y-3)=0$$ .

Pair `normals are $$(x+2y)(x+3)=0$$

$$\therefore$$ Normals are $$x+2y=0$$

Point of intersection of the normal in the centre of the required circle i.e., $$C_1(-3,-3/2)$$ and centre of given xcircle $$C_2(2,3/2)$$ and radius

$$r^2=\sqrt{4+\cfrac{9}{2}}=\cfrac{5}{2}$$

Let $$r_1$$ be radius of required circle

$$r_1=|C_1+C_2|+r_2\\ \Rightarrow\sqrt{(-3-2)^2+(\cfrac{3}{2}-\cfrac{-3}{2})^2}+\cfrac{5}{2}\\=\cfrac{15}{2}$$

Hence, equation of required cicrle is 

$$x^2+y^2+6x-3y-54=0$$

The centre of a circle is $$C\left(3,5\right)$$ and one end of a diameter is $$A\left(4,3\right)$$ , find the coordinates of the other end.

Let the other end of the diameter of the given circle be $$B\left(\alpha,\beta\right)$$ whose one end is $$A\left(4,3\right)$$

Midpoint of $$AB=\left(\dfrac{\alpha+4}{2},\,\dfrac{\beta+3}{2}\right)$$

Since the centre $$C\left(5,3\right)$$ of the circle is the mid-point of $$AB$$ ,

$$\dfrac{\alpha+4}{2}=3$$ and $$\dfrac{\beta+3}{2}=5$$

$$\Rightarrow\,\alpha+4=6$$ and $$\beta+3=10$$

$$\Rightarrow\,\alpha=6-4=2$$ and $$\beta=10-3=7$$

$$\therefore\,$$ The coordinates of the other end of the diameter are $$\left(2,7\right)$$

The centre of a circle is $$C\left(5,3\right)$$ and one end of a diameter is $$A\left(4,3\right)$$ , find the coordinates of the other end.

Let the other end of the diameter of the given circle be $$B\left(\alpha,\beta\right)$$ whose one end is $$A\left(4,3\right)$$

Midpoint of $$AB=\left(\dfrac{\alpha+4}{2},\,\dfrac{\beta+3}{2}\right)$$

Since the centre $$C\left(5,3\right)$$ of the circle is the mid-point of $$AB$$ ,

$$\dfrac{\alpha+4}{2}=5$$ and $$\dfrac{\beta+3}{2}=3$$

$$\Rightarrow\,\alpha+4=8$$ and $$\beta+3=6$$

$$\Rightarrow\,\alpha=8-4=4$$ and $$\beta=6-3=3$$

$$\therefore\,$$ The coordinates of the other end of the diameter are $$\left(4,3\right)$$

If one end of a diameter of a circle is $${x}^{2}+{y}^{2}-6x-2y+4=0$$ is $$\left(-1,-2\right)$$ then find the co-ordinates of the other end of the diameter.

The given circle is $${x}^{2}+{y}^{2}-6x-2y+4=0$$     ....... $$(1)$$

is of the form $${x}^{2}+{y}^{2}+2gx+2fy+c=0$$

Its centre is $$C\left(-g,-f\right)=C\left(3,1\right)$$

Let $$A\left(-1,-2\right)$$ and $$B\left(\alpha,\beta\right)$$ be the ends of the diameter, then $$C\left(3,1\right)$$ is the midpoint of the segment $$AB$$

$$\therefore\,\dfrac{-1+\alpha}{2}=3$$ and $$\dfrac{-2+\beta}{2}=1$$

$$\Rightarrow\,-1+\alpha=6$$ and $$-2+\beta=2$$

$$\Rightarrow\,\alpha=6+1=7$$ and $$\beta=2+2=4$$

Hence, the co-ordinates of the other end of the diameter are $$\left(7,4\right)$$

If the equations of the two diameters of a circle are $$2x-y=2$$ and $$x-y=5$$ and the radius of the circle is $$6$$ , find the equation of the circle.

Here radius of the circle $$=6$$

Equations of two diameters of the circle are 

$$2x-y=2$$ .... $$(1)$$

$$x-y=5$$ .... $$(2)$$

Solving $$(1)$$ and $$(2)$$ we get

$$(2)\Rightarrow\,x=5+y$$

Substituting $$x=5+y$$ in $$(1)$$ we get

$$\Rightarrow \,2\left(5+y\right)-y=2$$

$$\Rightarrow \,10+2y-y=2$$

$$\Rightarrow\,y=2-10=-8$$  

substitute $$y=-8$$ in $$x=5+y=5-8=-3$$

Hence centre of the circle is $$\left(-3,-8\right)$$

Now the equation of the required circle is

$${\left(x+3\right)}^{2}+{\left(y+8\right)}^{2}={6}^{2}$$

$$\Rightarrow\,{x}^{2}+6x+9+{y}^{2}+16y+64-36=0$$

$$\Rightarrow\,{x}^{2}+{y}^{2}+6x+16y+37=0$$

Find the equation of the circle which passes through two  points on the x- axis which are at distances $$4$$ units from the origin and whose radius is $$5$$ units.

REF.Image

There are two circles which pass through two points A and A' on the x-axis which are at a distance of 4 units from the origin.

The center of there circles lie on the y-axis

In $$\Delta OAC, AC^{2}=OA^{2}+OC^{2}$$

$$\Rightarrow 5^{2}=4^{2}+OC^{2}\Rightarrow OC^{2}=5^{2}-4^{2}=25-16 = 9$$

$$\therefore OC=3$$ units

So, the coordinates of the centers of the required circles are C(0,3) and C'(0,-3)

Hence, the equation of the required circles are $$(x-0)^{2}+(y\pm 3)^{2}=5^{2}$$

$$\Rightarrow x^{2}+y^{2}\pm 6y-16=0$$

Find the equation of the circle which passes through $$(3, -2), (-2, 0)$$ and has its centre on the line $$2x-y=3$$ .

Equation of circle with centre $$\left(h,k\right)$$ is

$${\left(x-h\right)}^{2}+{\left(y-k\right)}^{2}={r}^{2}$$

Since the circle passes through $$\left(3,-2\right)$$

$${\left(3-h\right)}^{2}+{\left(-2-k\right)}^{2}={r}^{2}$$

$$\Rightarrow 9+{h}^{2}-6h+4+{k}^{2}+4k={r}^{2}$$

$$\Rightarrow {h}^{2}+{k}^{2}-6h+4k+13={r}^{2}$$          ........ $$(1)$$

Since the circle passes through $$\left(-2,0\right)$$

$${\left(-2-h\right)}^{2}+{\left(0-k\right)}^{2}={r}^{2}$$

$$\Rightarrow 4+{h}^{2}+4h+{k}^{2}={r}^{2}$$

$$\Rightarrow {h}^{2}+{k}^{2}+4h+4={r}^{2}$$          ........ $$(2)$$

Eqn $$\left(2\right)-$$ Eqn $$\left(1\right)$$

$$\Rightarrow {h}^{2}+{k}^{2}+4h+4-{h}^{2}-{k}^{2}+6h-4k-13={r}^{2}-{r}^{2}$$

$$\Rightarrow 10h-4k=9$$      ........ $$(3)$$

Since center $$\left(h,k\right)$$ lies on the line $$2x-y=3$$

$$2h-k=3$$         ............ $$(4)$$

Eqn $$\left(3\right)-$$ Eqn $$\left(4\right)$$

$$10h-4k-2h+k=9-3$$

$$\Rightarrow 8h-3k=6$$         ........... $$(5)$$

Solving eqn $$(4)$$ and $$(5)$$

$$8\times$$ eqn $$(4)-2\times$$ eqn $$(5)$$

$$16h-8k-16h+6k=24-12$$

$$\Rightarrow -2k=12$$ or $$k=-6$$

From $$(5)$$ we have 

$$8h=6+3k$$

$$=6-3\times 6=6-18=-12$$

$$\therefore h=\dfrac{-12}{8}=\dfrac{-3}{2}$$

Let us find the radius of the circle using eqn $$(1)$$

$${\left(3+\dfrac{3}{2}\right)}^{2}+{\left(-2+6\right)}^{2}={r}^{2}$$

$$\Rightarrow {r}^{2}=\dfrac{81}{4}+16=\dfrac{81+64}{4}=\dfrac{145}{4}$$

$$\therefore$$ equation of the circle is $${\left(x+\dfrac{3}{2}\right)}^{2}+{\left(y+6\right)}^{2}=\dfrac{145}{4}$$

or $${\left(2x+3\right)}^{2}+4{\left(y+6\right)}^{2}=145$$

Class 11 Commerce Applied Mathematics Extra Questions

• Basics Of Financial Mathematics Extra Questions
• Circles Extra Questions
• Descriptive Statistics Extra Questions
• Differentiation Extra Questions
• Functions Extra Questions
• Limits And Continuity     Extra Questions
• Logarithm And Antilogarithm Extra Questions
• Mathematical And Logical Reasoning Extra Questions
• Number Theory Extra Questions
• Numerical Applications Extra Questions
• Permutations And Combinations Extra Questions
• Probability Extra Questions
• Relations Extra Questions
• Sequences And Series Extra Questions
• Set Theory Extra Questions
• Straight Lines Extra Questions
• Tangents And Its Equations Extra Questions