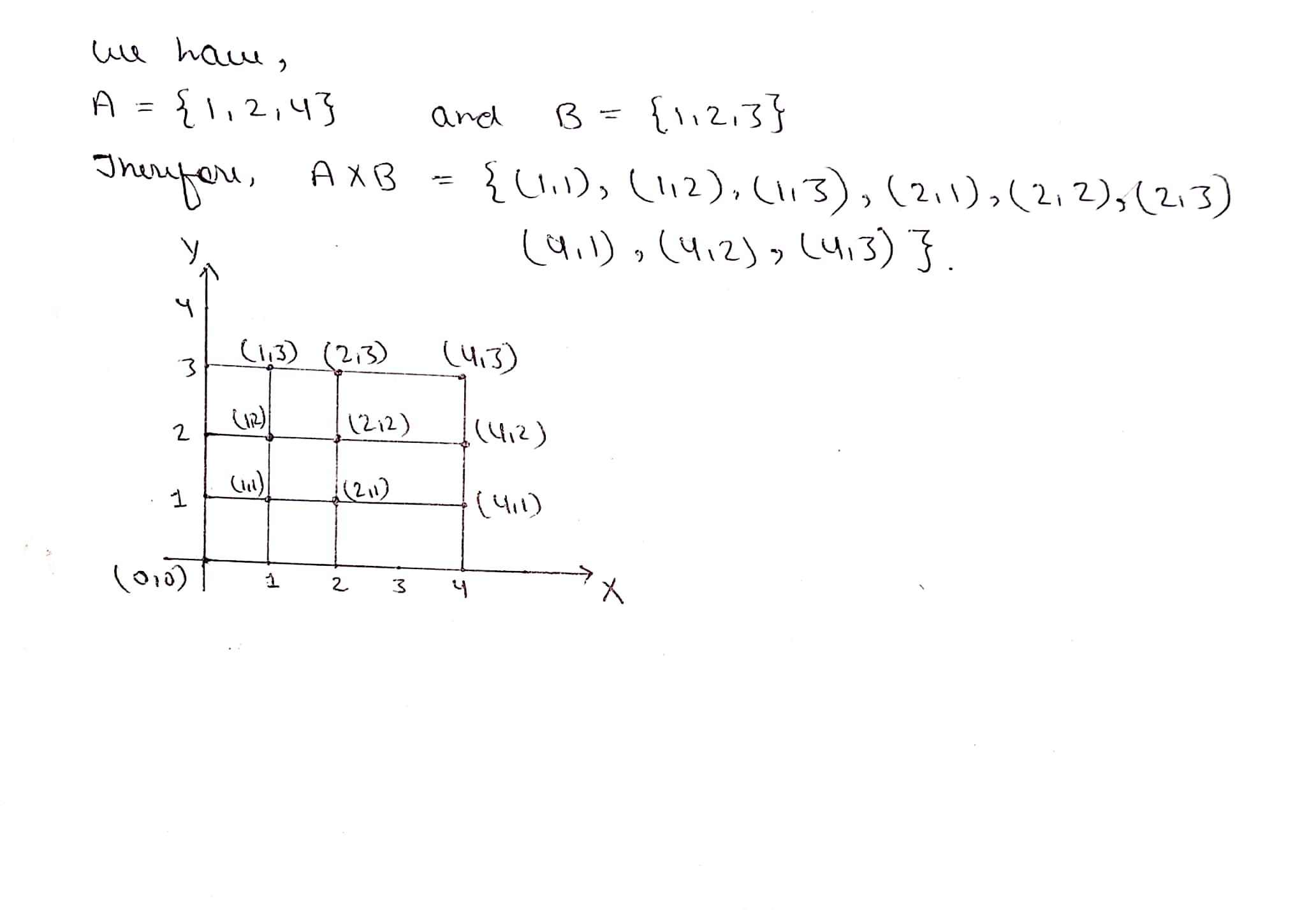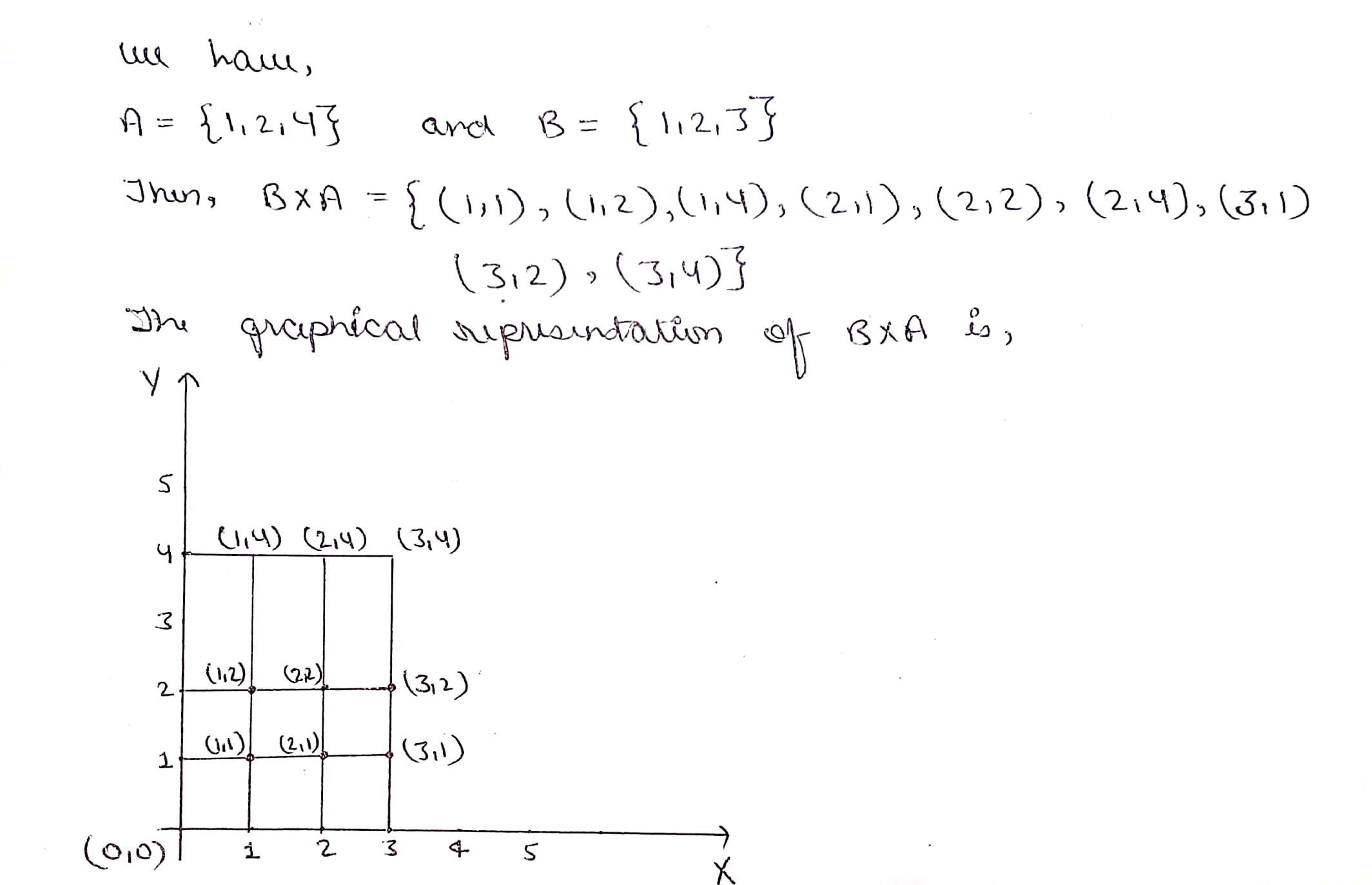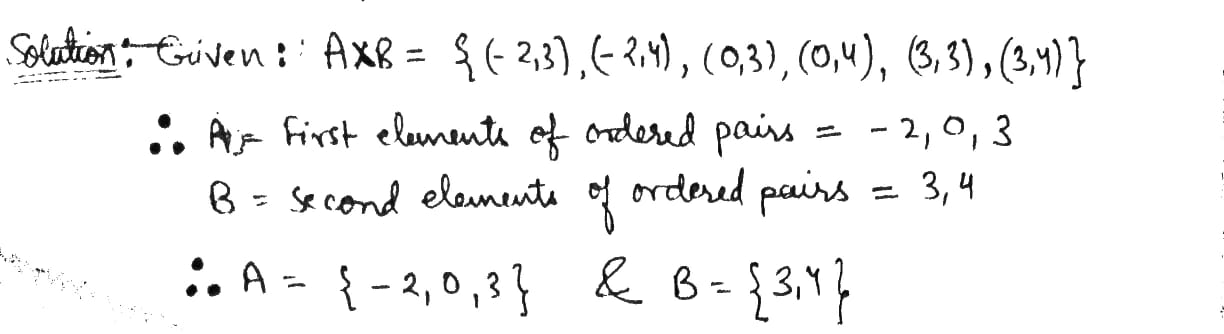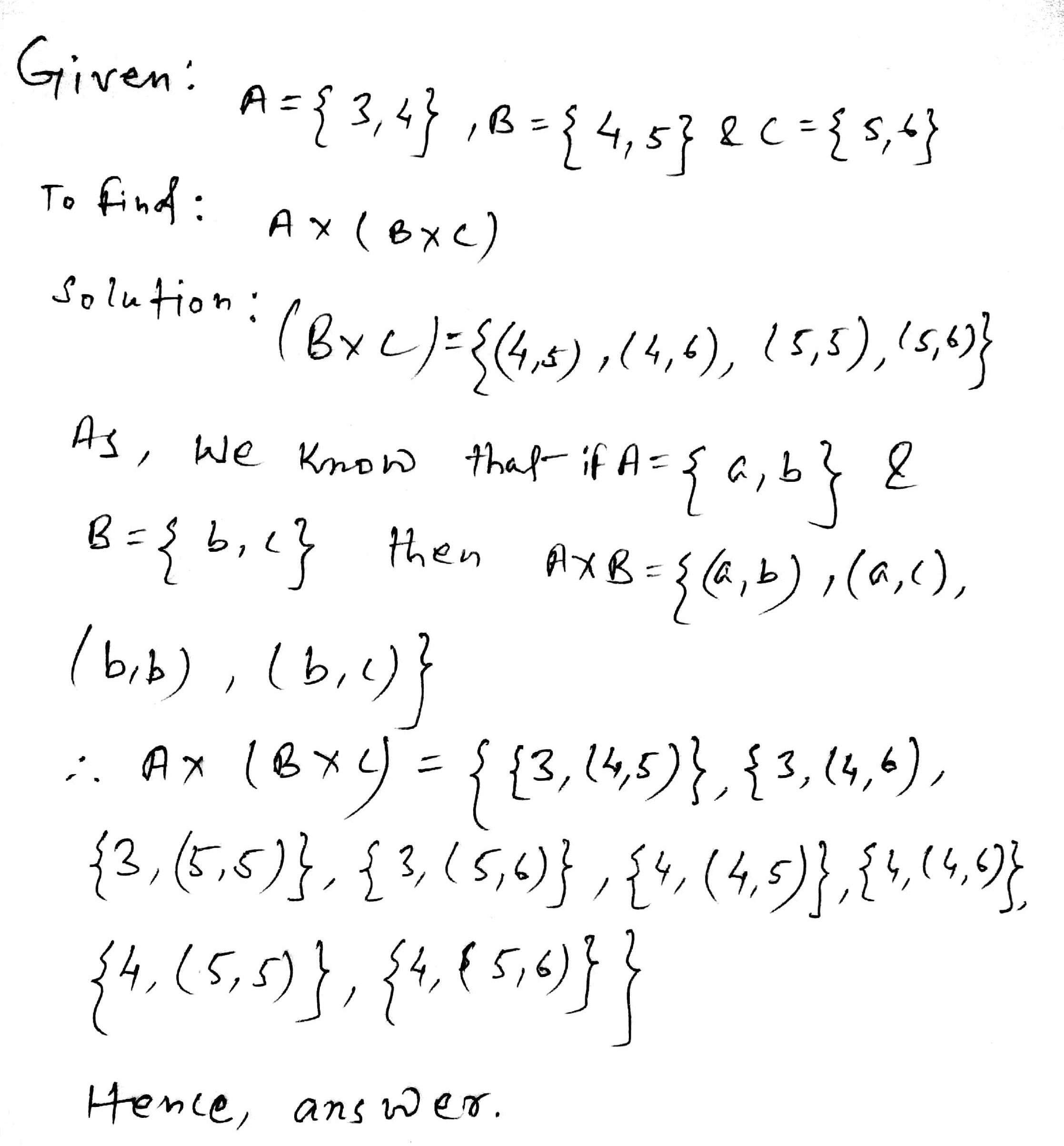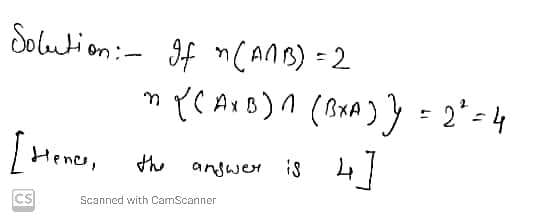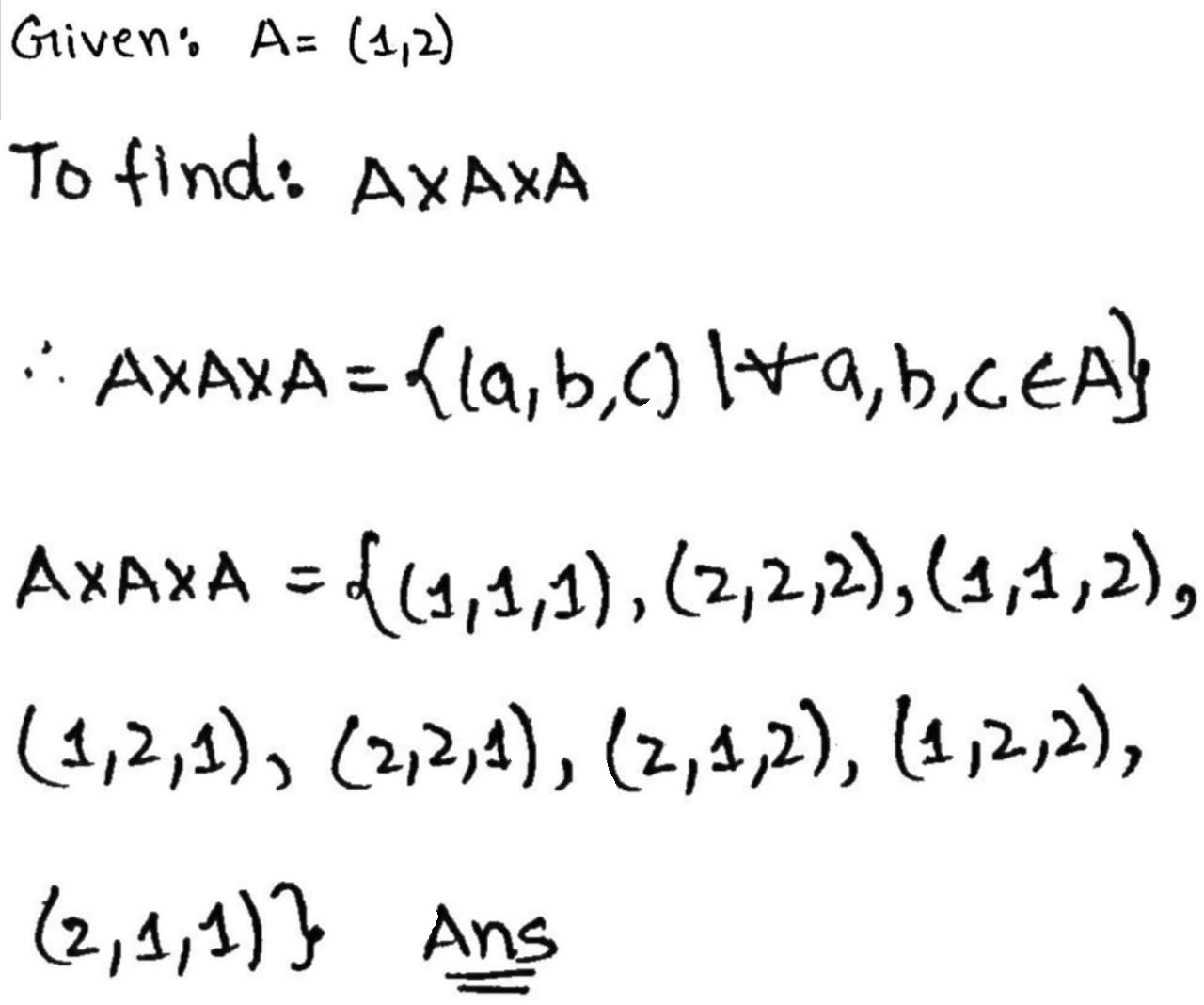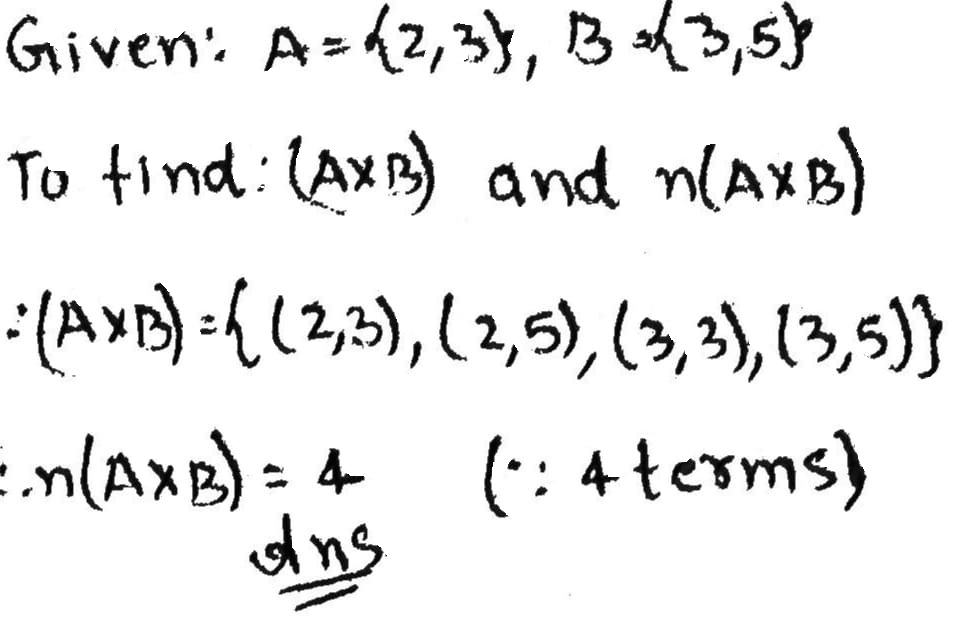Relations - Class 11 Commerce Applied Mathematics - Extra Questions

If $$A$$ has $$3$$ elements and $$B$$ has $$5$$ elements then $$A \times B$$ has ___elements.

We know if set A has $$m$$ elements and set B has $$n$$ elements, then total number of elements in set $$A\times B$$ is $$mn$$
Hence for given problem number of elements is, $$3\times 5 =15$$


Is inclusion of a subset in another, in the context of a universal set, an equivalence relation in the family of subsets of the sets? Justify your answer.

The relation in reference is not symmetric as  $$A\subset B$$  not imply  $$B\subset A.$$


Show that every relation which is symmetric and transitive need not to be  reflexive.

No. Let R={aRb in set I where both a and b are odd} Also R is symmetric and transitive.
$$\displaystyle \therefore R=\left \{ \left ( 1,3 \right ),\left ( 3,1 \right ),\left ( 1,1 \right ),.... \right \}$$
but R is not reflexive because . $$\displaystyle \left ( 2,2 \right ),\left ( 4,4 \right ) i.e.$$ all even integers belonging to I are not related to each other.


Let R be a relation on Z (the set of integers) defined as $$mRn$$, $$\:iff\:m\leq n  \forall  m,n \in Z$$ then R is anti symmetric.
If true enter 1 else enter 0

$$R$$ is anti symmetric because if $$R(m,n)$$ exist then $$R(n,m)$$ never exists .If it exists then $$m=n$$
The correct answer is $$1$$


If the set $$A$$ has $$3$$ elements and the set $$B = \{ 3, 4, 5 \}$$ then find the number of elements in $$( A \displaystyle \times  B )$$?

It is given that set $$A$$ has $$3$$ elements and the elements of set $$B$$ are $$3, 4$$ and $$5$$
$$\displaystyle \Rightarrow $$ Number of elements in set $$B = 3$$
Number of elements in $$( A \displaystyle \times  B )$$
$$=$$ (Number of elements in $$A$$) $$\displaystyle \times $$ (Number of elements in $$B$$)
$$= 3 \displaystyle \times  3 = 9$$
Thus the number of elements in $$(A \displaystyle \times  B)$$ is $$9$$


Determine which of the following are reflexive relations on set $$A= \{ 1, 2, 3\}$$.
  1. $$\displaystyle R_{1}=\{(1,1),(2,2),(3,3),(2,1)\}$$
  2. $$R_{2}=\{(1,1),(3,3),(2,1),(3,2)\}$$.
If $$R_1$$ is reflexive then answer $$1$$ and if $$R_2$$ is reflexive then answer $$2$$.

Given, $$A =\{1,2,3\}$$
Clearly, $$(1,1) (2,2), (3,3)\in R$$
Thus, $$\displaystyle R_{1} $$ is a reflexive relation on set $$A. $$
But $$\displaystyle R_{2} $$ is not a reflexive relation on $$A$$ because $$\displaystyle 2\in A$$ but $$(2,2)\notin R_{2}$$.


If $$\displaystyle A\times B = \{(a, x), (a, y), (b, x), (b, y)\}$$ Find $$A$$ and $$B$$.

It is given that $$\displaystyle A\times B = \{(a, x), (a, y), (b, x), (b, y)\}$$
We know that the Cartesian product of two non-empty sets P and Q is defined as 
$$\displaystyle P\times Q = \{(p, q) : \displaystyle p\in P,q\in Q \}$$
$$\displaystyle \therefore $$ $$A$$ is the set of all first elements of $$A\times B$$ and $$B$$ is the set of all second elements of $$A\times B$$
Thus $$A = \{a, b\}$$ and $$B = \{x, y\}$$


Let $$A = \{1, 2\}, B = \{1, 2, 3, 4\}, C = \{5, 6\}$$ and $$D = \{5, 6, 7, 8\}$$ Verify that 
(i) $$\displaystyle A\times \left ( B\cap C \right )=\left ( A\times B \right )\cap \left ( A\times C \right )$$
(ii) $$\displaystyle A\times C$$ is a subset of $$\displaystyle B\times D$$

(i) To verify : $$\displaystyle A\times \left ( B\cap C \right )=\left ( A\times B \right )\cap \left ( A\times C \right )$$
We have $$\displaystyle B\cap C=\left \{ 1,2,3,4 \right \}\cap \left \{ 5,6 \right \}=\phi $$
$$\displaystyle \therefore $$ L.H.S = $$\displaystyle A\times \left ( B\cap C \right )=A\times \phi =\phi $$

$$\displaystyle A\times B = \{(1, 1), (1, 2), (1, 3), (1, 4), (2, 1), (2, 2), (2, 3), (2, 4)\}$$
$$\displaystyle A\times C = \{(1, 5), (1, 6), (2, 5), (2, 6)\}$$
 $$\displaystyle \therefore  R.H.S. = \displaystyle \left ( A\times B \right )\cap \left ( A\times C \right )=\phi $$
$$\displaystyle \therefore  L.H.S = R.H.S$$
Hence $$\displaystyle A\times \left ( B\cap C \right )=\left ( A\times B \right )\cap \left ( A\times C \right )$$

(ii) To verify: $$\displaystyle A\times C$$ is a subset of $$\displaystyle B\times D$$
$$\displaystyle A\times C = \{(1, 5), (1, 6), (2, 5), (2, 6)\}$$
$$\displaystyle B\times D = \{(1, 5), (1, 6), (1, 7), (1, 8), (2, 5), (2, 6), (2, 7),
(2, 8), (3, 5), (3, 6), (3, 7),$$
                  $$ (3, 8), (4, 5), (4, 6), (4, 7), (4, 8)\}$$
We can observe that all the elements of set $$\displaystyle A\times C$$ are the elements of set $$\displaystyle B\times D$$ 
Therefore $$\displaystyle A\times C$$ is a subset of $$\displaystyle B\times D$$


Let $$A = \{1, 2\}$$ and $$B = \{3, 4\}$$. Write $$\displaystyle A\times B$$ and find how many subsets will $$\displaystyle A\times B$$ have? List them.

$$A = \{1, 2\}$$ and $$B = \{3, 4\}$$ 
$$\displaystyle \therefore A\times B = \{(1, 3), (1, 4), (2, 3), (2, 4)\}$$
$$\displaystyle \Rightarrow n\left ( A\times B \right )=4$$

We know that if $$n(A\times B) =r$$
Then, number of subsets of $$A\times B$$ is $$2^r$$
Therefore the set $$\displaystyle A\times B$$ has $$\displaystyle 2^{4}$$ = $$16$$ subsets.
These are
$$\phi \displaystyle \{(1, 3)\}, \{(1, 4)\}, \{(2, 3)\}, \{(2, 4)\}, \{(1, 3), (1, 4)\}, \{(1, 3), (2, 3)\},\{(1, 3), (2, 4)\},$$
$$ \{(1, 4), (2, 3)\}, \{(1, 4), (2, 4)\}, \{(2, 3), (2, 4)\}, \{(1, 3), (1, 4), (2, 3)\}, \{(1, 3), (1, 4), (2, 4)\},$$
$$ \{(1, 3), (2, 3), (2, 4)\},\{(1, 4), (2, 3), (2, 4)\}, \{(1, 3), (1, 4), (2, 3), (2, 4)\}\}$$


If $$=A \{-1, 1\}$$ then find $$\displaystyle A\times A\times A$$.

It is known that for any non-empty set $$A$$, $$\displaystyle A\times A\times A$$ is defined as 
$$\displaystyle A\times A\times A = \{(a, b, c) : a, b,  c\in A\}$$
It is given that $$A = \{-1,1\}$$
$$A\times A\times A = \{(-1, -1, -1), (-1, -1, 1), (-1, 1 ,-1), (-1, 1, 1), (1, -1, -1), (1, -1, 1),$$
                              $$ (1, 1, -1), (1, 1, 1)\}$$


Show that the relation $$R$$ in the set $$A$$ of all the books in a library of a college, given by $$R=\left\{(x, y):x\   and  \ y  have  \ same \  number  \ of \  pages \right\}$$ is an equivalence relation.

Set $$A$$ is the set of all books in the library of a college.
$$R=\left\{(x, y):\text{x  and  y  have  the  same  number  of  pages}\right\}$$
Now, $$R$$ is reflexive since $$(x, x)\in R$$ as $$x$$ and $$x$$ has the same number of pages.
Let $$(x, y)\in R\Rightarrow x$$ and $$y$$ have the same number of pages.
$$\Rightarrow y$$ and $$x$$ have the same number of pages.
$$\Rightarrow (y, x)\in R$$
$$\therefore R$$ is symmetric.
Now, let $$(x, y)\in R$$ and $$(y, z)\in R$$
$$\Rightarrow x$$ and $$y$$ and have the same number of pages and $$y$$ and $$z$$ have the same number of pages.
$$\Rightarrow x$$ and $$z$$ have the same numbers of pages.
$$\Rightarrow (x, z)\in R$$
$$\therefore R$$ is transitive.
Hence, $$R$$ is an equivalence relation.


Given an example of a relation. Which is 
(i) Symmetric but neither reflexive nor transitive.
(ii) Transitive but neither reflexive nor symmetric.
(iii) Reflexive and symmetric but not transitive.
(iv) Reflexive and transitive but not symmetric.
(v) Symmetric and transitive but not reflexive.

(i)
Let $$A=\left\{5, 6, 7\right\}$$
Define a relation $$R$$ on $$A$$ as $$R=\left\{(5, 6), (6, 5)\right\}$$
Relation $$R$$ is not reflexive as $$(5, 5), (6, 6), (7, 7)\notin R$$.
Now, as $$(5, 6)\in R$$ and also $$(6, 5)\in R$$, $$R$$ is symmetric.
$$\Rightarrow (5, 6), (6, 5)\in R$$, but $$(5, 5)\notin R$$
$$\therefore R$$ is not transitive.
Hence, relation $$R$$ is symmetric but not reflexive or transitive.

(ii)
Consider a relation $$R$$ in $$R$$ defined as
$$R=\left\{(a, b):a <b\right\}$$
For any $$a\in R$$, we have $$(a, a)\notin R$$ since $$a$$ cannot be strictly less than a itself. In fact, $$a=a$$.
$$\therefore R$$ is not reflexive.
Now, $$(1, 2)\in R(as 1< 2)$$
But, $$2$$ is not less than $$1$$.
$$\therefore (2, 1)\notin R$$
$$\therefore R$$ is not symmetric.
Now, let $$(a, b), (b, c)\in R$$.
$$\Rightarrow a< b$$ and $$b<c$$
$$\Rightarrow a<c$$
$$\Rightarrow (a, c)\in R$$
$$\therefore R$$ is transitive.
Hence, relation $$R$$ is transitive but not reflexive and symmetric.

(iii)
Let $$A=\left\{4, 6, 8\right\}$$
Define a relation $$R$$ on $$A$$ as:
$$A=\left\{(4, 4), (6, 6), (8, 8), (4, 6), (6, 4), (6, 8), (8, 6)\right\}$$
Relation $$R$$ is reflexive since for every $$\left\{a\in A, (a, a)\in R   i.e., (4, 4), (6, 6), (8, 8)\right\} \in  R$$
Relation $$R$$ is symmetric since $$(a, b)\in R\Rightarrow (b, a)\in R$$ for all $$a, b\in R$$.
Relation $$R$$ is not transitive since $$(4, 6), (6, 8)\in R$$, but $$(4, 8)\notin R$$.
Hence, relation $$R$$ is reflexive and symmetric but not transitive.

(iv)
Define a relation $$R$$ in $$R$$ as:
$$R=\left\{(a, b):a^3\geq b^3\right\}$$
Clearly $$(a, a)\in R$$ as $$a^3=a^3$$.
$$\therefore R$$ is reflexive.
Now, $$(2, 1)\in R$$ $$(\text{as}    2^3\geq 1^3)$$
But, $$(1, 2)\notin R(\text{as}    1^3 < 2^3)$$
$$\therefore R$$ is not symmetric.
Let $$(a, b), (b, c)\in R$$
$$\Rightarrow a^3\geq b^3$$ and $$b^3\geq c^3$$
$$\Rightarrow a^3\geq c^3$$
$$\Rightarrow (a, c)\in R$$
$$\therefore R$$ is transitive.
Hence, relation $$R$$ is reflexive and transitive but not symmetric. 

(v)
Let $$A=\left\{-5, -6\right\}$$.
Define a relation $$R$$ on $$A$$ as:
$$R=\left\{(-5, -6), (-6, -5), (-5, -5)\right\}$$
Relation $$R$$ is not reflexive as $$(-6, -6)\notin R$$
Relation $$R$$ is symmetric as $$(-5, -6)\in R$$ and $$(-6, -5)\in R$$
It is seen that $$(-5, -6), (-6, -5)\in R$$. 
Also, $$(-5, -5)\in R$$.
$$\therefore $$ the relation $$R$$ is transitive.
Hence, relation $$R$$ is symmetric and transitive but not reflexive.


Show that the relative $$R$$ in the set $$\left\{1, 2, 3\right\}$$ given by $$R=\left\{(1, 2), (2, 1)\right\}$$ is symmetric but neither reflexive nor transitive.

Let $$A=\left\{1, 2, 3\right\}$$
A relation $$R$$ on $$A$$ is defined as $$R=\left\{(1, 2), (2, 1)\right\}$$.
It is seen that $$(1, 1), (2, 2), (3, 3)\notin R$$.
$$\therefore R$$ is not reflexive.
Now, as $$(1, 2)\in R$$ and $$(2, 1)\in R$$, then $$R$$ is symmetric.
Now, $$(1, 2)$$ and $$(2, 1)\in R$$
However,
$$(1, 1)\notin R$$
$$\therefore R$$ is not transitive.
Hence, $$R$$ is symmetric but neither reflexive nor transitive.


Determine whether each of the following relations are reflexive, symmetric and transitive:
(i) Relation $$R$$ in the set $$A = \left\{1, 2, 3, ..., 13, 14\right\}$$ defined as
$$\ \ \ \ \ \ \ \ \ \ \ R = \left\{(x, y) : 3x - y = 0\right\}$$
(ii) Relative $$R$$ in the set $$N$$ of natural numbers defined as 
$$\ \ \ \ \ \ \ \ \ \ \ R=\left\{(x, y):y=x+5\ \text{and}  x < 4\right\}$$
(iii) Relation $$R$$ in the set $$A=\left\{1, 2, 3, 4, 5, 6\right\}$$ as 
$$\ \ \ \ \ \ \ \ \ \ \ R=\left\{(x, y):y   \text{is  divisible  by}  x\right\}$$
(iv) Relative $$R$$ in the set $$Z$$ of all integers defined as  
$$\ \ \ \ \ \ \ \ \ \ \ R=\left\{(x, y): x-y\text{ is an integer}\right\}$$
(v) Relation R in the set A of human beings in a town at a particular time given by 
$$\ \ \ \ (a) R=\left\{(x, y):x  \text{and}  y  \text{work  at  the  same  place }\right\}$$
$$\ \ \ \ (b) R=\left\{(x, y):x  \text{and}  y  \text{live  in  the  same  locality}\right\}$$
$$\ \ \ \ (c) R=\left\{(x, y):x  \text{is  exactly}  7  \text{cm  taller  than}  y\right\}$$
$$\ \ \ \ (d) R=\left\{(x, y): x  \text{is  wife  of}  y\right\}$$
$$\ \ \ \ (e) R=\left\{(x, y): x \text{ is  father  of}  y \right\}$$

(i)
$$A=\left \{ 1, 2, 3, .... 13, 14 \right\}$$
$$R=\left\{(x, y):3x-y=0\right\}$$
$$\therefore R=\left\{(1, 3), (2, 6), (3, 9), (4, 12)\right\}$$
$$R$$ is not reflexive since $$(1, 1), (2, 2) ......(14, 14)\notin R$$
Also, $$R$$ is not symmetric as $$(1, 3) \in R$$, but $$(3, 1)\notin R.$$
Also, $$R$$ is not transitive as $$(1, 3), (3, 9)\in R$$, but $$(1, 9)\notin R$$. 
Hence, $$R$$ is neither reflexive, nor symmetric, nor transitive.

(ii)
$$R=\left\{(x, y):y=x+5   \text{and}   x<4\right\}=\left\{(1, 6), (2, 7), (3, 8)\right\}$$
It is seen that $$(1, 1)\notin R\Rightarrow R$$ is not reflexive.
Also $$(1, 6)\in R$$. 
But, $$(6,1)\notin R$$. $$\therefore R$$ is not symmetric.
Now, since there is no pair in $$R$$ such that $$(x, y)$$ and $$(y, z)\in R$$, then $$(x,z )$$ cannot belong to $$R$$.
$$\therefore R$$ is not transitive.
Hence, $$R$$ is neither reflexive, nor symmetric, nor transitive. 

(iii)
$$A=\left\{1, 2, 3, 4, 5, 6\right\}$$
$$R=\left\{(x, y):\text{y  is  divisible  by  x}\right\}$$
We know that any number $$(x)$$ is divisible by itself.
$$\Rightarrow (x, x)\in R$$,
$$\therefore R$$ is reflexive.
Now, $$(2, 4)\in R$$, [ as  $$4$$  is divisible  by  $$2$$]
But,
$$(4, 2)\notin R.$$, [  as  $$2$$  is  not  divisible  by  $$4$$]
$$\therefore R$$ is not symmetric.
Let $$(x, y), (y, z)\in R$$. Then, $$y$$ is divisible by $$x$$ and $$z$$ is divisible by $$y$$.
$$\therefore z$$ is divisible by $$x$$.
$$\Rightarrow (x, z)\in R$$
$$\therefore R$$ is transitive.
Hence, $$R$$ is reflexive and transitive but not symmetric.

(iv)
$$R=\left\{(x, y):x-y  \text{is  an  integer}  \right\}$$
Now, for every $$x\in Z, (x, x)\in R$$ as $$x-x=0$$ is an integer.
$$\therefore R$$ is reflexive.
Now, for every $$x, y\in Z$$ if $$(x, y)\in R$$, then $$x-y$$ is an integer.
$$\Rightarrow -(x-y)$$ is also an integer.
$$\Rightarrow (y-x)$$ is an integer.
$$\therefore (y, x)\in R$$
$$\Rightarrow R$$ is symmetric.
Now,
Let $$(x, y)$$ and $$(y, z)\in R$$, where $$x, y, z\in Z$$.
$$\Rightarrow (x-y)$$ and $$(y-z)$$ are integers.
$$\Rightarrow x-z =(x-y)+(y-z)$$ is an integer.
$$\therefore (x, z)\in R$$
$$\therefore R$$ is transitive.
Hence, $$R$$ is reflexive, symmetric, and transitive.

(v) (a)
$$R=\left\{(x, y):x  \ and \  y  \ work \  at \  the \  same \  place\right\}$$
$$\Rightarrow (x, x)\in R$$
$$\therefore R$$ is reflexive.
If $$(x, y)\in R $$, then $$x$$ and $$y$$ work at the same place.
$$\Rightarrow y$$ and $$x$$ work at the same place.
$$\Rightarrow (y, x)\in R$$
$$\therefore R$$ is symmetric.
Now, let $$(x, y), (y, z)\in R$$
$$\Rightarrow x$$ and $$y$$ work at the same place and $$y$$ and $$z$$ work at the same place.
$$\Rightarrow x$$ and $$z$$ work at the same place.
$$\Rightarrow (x, z)\in R$$
$$\therefore R$$ is transitive.
Hence, $$R$$ is reflexive, symmetric and transitive.

(v) (b)
$$R=\left\{(x, y):\text{x  and  y  live  in  the  same  locality}\right\}$$
Clearly $$(x, y)\in R$$ as $$x$$ and $$x$$ is the same human being.
$$\therefore R$$ is reflexive.
If $$(x, y)\in R$$, then $$x$$ and $$y$$ live in the same locality.
$$\Rightarrow y $$ and $$x$$ live in the same locality.
$$\Rightarrow (y, x)\in R$$
$$\therefore R$$ is symmetric.
Now, let $$(x, y)\in R$$ and $$(y, z)\in R$$.
$$\Rightarrow $$ $$x$$ and $$y$$ live in the same locality and $$y$$ and $$z$$ live in the same locality.
$$\Rightarrow$$ $$x$$ and $$z$$ live in the same locality.
$$\Rightarrow (x, z)\in R$$
$$\therefore R$$ is transitive.
Hence, $$R$$ is reflexive, symmetric and transitive.

(v)(c)
$$R=\left\{(x, y):\text{x  is  exactly  7  cm  taller  than  y}\right\}$$
Now, 
$$(x, x)\notin R$$
Since human being $$x$$ cannot be taller than himself.
$$\therefore R$$ is not reflexive.
Now, let $$(x, y)\in R$$.
$$\Rightarrow x$$ is exactly $$7$$cm taller than $$y$$
Then, $$y$$ is not taller than $$x$$. 
$$\therefore (y, x)\notin R$$
Indeed if $$x$$ is exactly $$7$$cm taller than $$y$$, then $$y$$ is exactly $$7$$cm shorter than $$x$$.
$$\therefore R$$ is not symmetric.
Now, let $$(x, y), (y, z)\in R$$
$$\Rightarrow $$ $$x$$ is exactly $$7$$cm taller than $$y$$ and $$y$$ is exactly $$7$$cm taller than$$z$$.
$$\Rightarrow $$ $$x$$ is exactly $$14$$ taller than $$z$$.
$$\therefore (x, z)\notin R$$
$$\therefore R$$ is not transitive.
Hence, $$R$$ is neither reflexive, nor symmetric, nor transitive.

(v)(d)
$$R=\left\{(x, y):\text{x  is  the  wife  of  y}\right\}$$
Now, $$(x, x)\notin R$$
Since $$x$$ cannot be the wife of herself.
$$\therefore R$$ is not reflexive.
Now, let $$(x, y)\in R$$
$$\Rightarrow x$$ is the wife of $$y$$.
Clearly $$y$$ is not wife of $$x$$.
$$\therefore (y, x)\notin R$$
Indeed if $$x$$ is the wife of $$y$$, then $$y$$ is the husband of $$x$$.
$$\therefore R$$ is not transitive.
Let $$(x, y), (y, z)\in R$$
$$\Rightarrow $$ $$x$$ is the wife of $$y$$ and $$y$$ is the wife of $$z$$.
This case is not possible. Also, this does not imply that $$x$$ is the wife of $$z$$.
$$\therefore (x, z)\notin R$$
$$\therefore R$$ is not transitive.
Hence, $$R$$ is neither reflexive, nor symmetric, nor transitive.

(v)(e)
$$R=\left\{(x, y): \text{x  is  the  father  of  y}\right\}$$
$$(x, x)\notin R$$
As $$x$$ cannot be the father of himself.
$$\therefore R$$ is not reflexive.
Now, let $$(x, y)\in R$$
$$\Rightarrow x$$ is the father of $$y$$.
$$\Rightarrow y$$ cannot be the father of $$y$$.
Indeed, $$y$$ is the son or the daughter of $$y$$.
$$\therefore (y, x)\notin R$$
$$\therefore R$$ is not symmetric.
Now, let $$(x, y)\in R$$ and $$(y, z)\in R$$.
$$\Rightarrow x$$ is the father of $$y$$ and $$y$$ is the father of $$z$$.
$$\Rightarrow x$$ is not the father of $$z$$.
Indeed  $$x$$ is the grandfather of $$z$$.
$$\therefore (x, z)\notin R$$
$$\therefore R$$ is not transitive.
Hence, $$R$$ is neither reflexive, nor symmetric, nor transitive.


Check whether the relative $$R$$ in $$\textbf{R}$$ defined by $$R=\left\{(a, b):a\leq b^3\right\}$$ is reflexive, symmetric or transitive.

$$R=\left\{(a, b):a \leq b^3\right\}$$
It is observed that $$\left(\displaystyle\frac{1}{2}, \frac{1}{2}\right)\not \in R$$ as $$\displaystyle\frac{1}{2}>\left(\displaystyle\frac{1}{2}\right)^3=\frac{1}{8}$$.
$$\therefore R$$ is not reflexive.
Now, $$(1, 2)\in R\ (\text{as } 1<2^3=8)$$
But, $$(2, 1)\notin R(\text{as } 2>1^{3})$$
$$\therefore R$$ is not symmetric.
We have $$\left(\displaystyle 3, \frac{3}{2}\right), \left(\displaystyle\frac{3}{2}, \frac{6}{5}\right)\in R$$ as $$3 < \left(\displaystyle\frac{3}{2}\right)^3$$ and $$\displaystyle\frac{3}{2}<\left(\displaystyle\frac{6}{5}\right)^3$$.
But $$\left(3, \displaystyle\frac{6}{5}\right)\notin R$$ as $$3> \left(\displaystyle\frac{6}{5}\right)^3$$.
$$\therefore R$$ is not transitive.
Hence, $$R$$ is neither reflexive, nor symmetric, nor transitive.


Show that the relative $$R$$ in $$\textbf{R}$$ defined as $$R=\left\{(a, b):a \leq b\right\}$$, is reflexive and transitive but not symmetric.

Given, $$R=\left\{(a, b); a\leq b\right\}$$
Clearly $$(a, a)\in R$$ as $$a=a$$
$$\therefore R$$ is reflexive.
Now, $$(2, 4)\in R $$  $$ ($$ As  $$2 < 4)$$
But, $$(4, 2)\notin R$$ because $$4$$ is greater than $$2$$
$$\therefore R$$ is not symmetric.
Now, let $$(a, b), (b, c)\in R$$
Then, $$a\leq b$$ and $$b\leq c$$
$$\Rightarrow a\leq c$$
$$\Rightarrow (a, c)\in R$$
$$\therefore R$$ is transitive.
Hence,  $$R$$ is reflexive and transitive but not symmetric.


If a set contains $$m$$ elements and $$B$$ contains $$n$$ elements, then find the number of elements in $$A\times B$$.

No of elements in set $$A = m$$
No of elements in set $$B = n$$
So, no of elements in $$ A\times B $$ $$=m\times n$$
Note: $$ A\times B$$ is not equal to $$ B\times A$$ only in case $$A=B$$ they are equal.


Is it true that the every relation which is symmetric and transitive is also reflexive ? Give reasons.

Consider the set I of the integers and a relation be defined as aRb if both a and b are odd.
Clearly aRb $$\Rightarrow$$ bRa i.e. if a and b are both odd then b and a are also both odd. Similarly, aRb and bRc implies aRc and hence transitive. But this relation is not reflexive because 2 $$\epsilon$$ I but 2 is not related to 2. In general, any even number is not R-related to itself. Hence it is not reflexive.


What is the distinction between a relation and function and when do you call a relation reflexive, symmetric and transitive ?

Every mapping (function) is a relation but every relation is not a mapping.
The relation  R is said to be reflexive.
If aR a $$\forall \,\, a \, \epsilon \, A$$. (not for all)
The relation R is said to be symmetric.
If aRb then bRa. (not for all a and b).
The relation R is said to be transitive.
If aRb and bRc then aRc (not for all a, b, c)
A relation from a set A to the set B is denoted as 
R = {(x, y) :x $$\epsilon$$ A and y $$\epsilon$$ B and x R y}
$$\therefore \, R \, \subset \, A \, \times \, B$$


Given a relation $$R ={(1,2), (2, 3)}$$ on the set of natural numbers, add a minimum number of ordered pairs so that the enlarged relation is symmetric, transitive and reflexive.

For the relation R to be reflexive, it is necessary that (n, n) $$\in$$ R for every n $$\in $$ N that is, R must have all pairs (1, 1), (2, 2), (3, 3),...........
For R to be symmetric, it must contain the pair (2, 1) and (3, 2) since the pairs (1, 2) and (2, 3) are already present.
For R to be transitive, it must contain the pair (1, 3) since (1, 2) and (2, 3) are already there. We must then also include the pair (3, 1) for symmetry. Hence the relation R' obtained from R by adding a minimum number of ordered pairs to R to make it an equivalence relation is 
$$R' ={ (1, 2). (2, 1), (2, 3), (3, 2), (1, 3), (3, 1), (1, 1), (2, 2), (3, 3),.........}$$


If $$P = {(1, 2, 3)}$$ and $$Q = (4) $$find sets $$P \times Q  and Q\times P$$

$$P=\{1,2,3\}$$
$$Q=\{4\}$$
$$P\times Q =\{(1,4),(2,4),(3,4)\}$$
$$Q\times P=\{(4,1),(4,2),(4,3)\}$$


Given A = {2, 3, 4}, B = {2, 5, 6, 7}.
Construct an example of each of the following 
(i) an injective mapping from A to B.
(ii) a mapping from A to B which is not injective.
(iii) a mapping from B to A.

(i) An injective (i.e. one-one) mapping A to B may be defined as 
        $$f = {(2, 5), (3, 7), (4, 6)}$$
(ii) A mapping from A to B which is not injective may be defined as
        $$g = {(2, 2), (3, 5), (4, 2)}$$. It is many-one.
(iii) A mapping from B to A may be defined as
       $$h = {(2, 2), (5, 3), (6, 4), (7, 4)}$$.


If $$n(A)=4,n(B)=3,n(A\times B\times C)=24$$, then $$n(C)=$$

$$n(A)=4$$
$$n(B)=3$$
$$n(A\times B\times C)=24$$
$$n(C)=\cfrac { 24 }{ 4\times 3 } =2$$


Which of the following is an equivalence relation?
1)$$x<y$$
2)$$x>y$$
3)$$x-y$$ is divisible by $$5$$
4)$$x$$ divides $$y$$

$$x < y \Rightarrow y > x(false) \Rightarrow $$not symmetric
$$x > y \Rightarrow y < x(false) \Rightarrow $$not symmetric
$$x-y$$ divisible by $$5 \Rightarrow$$ reflexive
$$x-x=0$$ divisible by $$5 \Rightarrow$$ Symmetric
$$x-y$$ is divisible by $$5$$ and $$y-z$$ is divisible by $$5$$
so, $$x-z$$ is also divisible by $$5$$
$$\therefore equivalent$$


Let A = {0, 1, 2, 3 } and define a relation R as follows
R = {(0,0), (0,1), (0,3), (1,0), (1,1), (2,2), (3,0), (3,3)}.
Is R reflexive, symmetric and transitive ?

Given,
A = {0, 1, 2, 3}
(i) R is reflexive as (a,a) $$\in$$ R for every a $$\in$$ A.
(ii) R is symmetric, as (0,1) $$\in$$ R, (1,0) $$\in$$ R and (0,3) $$\in$$ R, (3,0) $$\in$$ R
(iii) R is not transitive as (3,0) (0,1) $$\in$$ R $$\implies$$ (3,1) does not exist in R.


Let $$A = \{6, 8\},$$ $$B = \{1, 3, 5\}$$ and $$R = \{(a, b): a \, \in \, A , \, b \, \in \, B , \, a - b \, is \, even\}$$.
Show that R is an empty relation from A to B.

Given, $$A=\left \{ 6,8 \right \}$$ and $$B=\left \{ 1,3,5 \right \}$$
Thus, every element $$a\in A$$ is an even number and every element  $$b\in B$$ is an odd number
So, $$(a-b)$$ will be an odd number
Thus, there is no pair $$(a,b)$$  such that  $$(a-b)$$  is even
Therefore, $$R$$  is an empty relation.


Let $$A = \{1, 2\}$$ and $$B = \{3, 4\}$$. Write $$A \times B$$. How many subsets will $$A \times B$$ have?

Given, $$A = \{1, 2\}$$ and $$B = \{3, 4\}$$. 
Now,
$$A \times B=\{(1,3),(1,4),(2,3),(2,4)\}$$.
Since $$A\times B$$ contains $$4$$ elements, so number of subsets of $$A\times B$$ is $$2^4=16$$.


If $$A=\left\{1,2\right\}$$, from the set $$A\times A\times A$$.

$$A \times A \times A = \left\{ {1,2} \right\} \times \left\{ {1,2} \right\} \times \left\{ {1,2} \right\}$$
$$=\left( {1,1,1} \right),\left( {1,1,2} \right)$$
$$=\left( {1,2,1} \right),\left( {1,2,2} \right)$$
$$=\left( {2,1,1} \right),\left( {2,1,2} \right)$$
$$=\left( {2,2,1} \right),\left( {2,2,2} \right)$$
hence,we get $$8$$ set.


what is Transitive relation?

Transitive Relation : A Binary relation
R defined on the set X is transitive
for all $$a,b,c \epsilon X$$ if aRb and bRc
then aRc.
or in symbolic form
$$\forall a,b,c\epsilon X:(aRb\wedge bRc)\Rightarrow aRc$$

1173090_1271856_ans_4d4176ad72d54e6da022a69beb4df663.jpeg


If A={1,2,3}, B={3,4}, C={4,5,6}. Find $$A\times (B\ \cap \ C)$$

$$(i)A \times \left( {B \cap C} \right)$$
$$ \cap $$  Intersection:common between two sets
$$B \cap C = \left\{ {3,4} \right\} \cap \left\{ {4,5,6} \right\} = \left\{ 4 \right\}$$
$$A \times \left( {B \cap C} \right)$$$$=$$
$$\,\left\{ {1,2,3} \right\} \times \left\{ 4 \right\}$$
$$ = \left\{ {\left( {1,4} \right),\left( {2,4} \right),\left( {3,4} \right)} \right\}$$



Let $$S$$ be a relation on the set $$R$$ of all real numbers defined by $$S=\left\{ \left( a,b \right) \in R\times R:{ a }^{ 2 }+{ b }^{ 2 }=1 \right\} $$. Prove that $$S$$ is not an equivalence relation on $$R$$.

The given relation is not reflexive as $$(1,1)\in R\times R$$ but $$(1,1)\not \in S$$ since $$1^2+1^2=2\ne 1$$.
As this relation is not reflexive so it can't be an equivalance relation.


Show that the relation $$\ge$$ on the set $$\mathbb{R}$$ of all real numbers is reflexive and transitive but not symmetric.

Let us denote the relation $$\ge$$ on the set of real numbers $$\mathbb{R}$$ be $$R=\{(a,b):a,b\in \mathbb{R} , \ a\ge b\}$$.
Then this relation $$R$$ is reflexive as $$a\ge a$$, $$\forall a\in \mathbb{R}$$.
But this relation is not symmetric as $$3\ge 2$$ but $$2\not \ge 3$$ i.e. $$(3,2)\in R$$ but $$(2,3)\not \in R$$.
Also this relation is transitive as $$a\ge b, b\ge c\Rightarrow a\ge c$$ i.e. $$(a,b)\in R, (b,c)\in R\Rightarrow (a,c)\in R$$, $$\forall a,b,c \in \mathbb{R}$$.


Let $$n$$ be a fixed positive integer. Define a relation $$R$$ on $$Z$$ as follows:
$$(a,b)\in R\Leftrightarrow $$ $$n$$ divides $$ a-b$$.
Show that $$R$$ is an equivalence relation on $$Z$$.

Let $$n$$ be a fixed positive integer.
Let the relation be $$R$$ on $$Z$$ is given by $$R=\left\{ \left( a,b \right) :n\quad \text{divides}\quad a-b \right\} $$.
We observe the following properties of relation $$R$$
Reflexivity: for any $$a\in Z$$
$$a-a=0=0\times n$$
$$\Rightarrow$$ $$n$$ divides $$a-a\Rightarrow (a,a)\in R$$
So, $$R$$ is relexive relation on $$Z$$

Symmetry: Let $$a,b\in Z$$ be such that
$$(a,b)\in R$$
$$\Rightarrow$$ $$n$$ divides $$a-b$$
$$\Rightarrow$$ $$a-b=n\lambda$$ for some $$\lambda \in Z$$
$$\Rightarrow$$ $$b-a=n(-\lambda)$$, where $$-\lambda \in Z$$
$$\Rightarrow$$ $$n$$ divides $$b-a\Rightarrow (b,a)\in R$$
Thus $$(a,b)\in R\Rightarrow (b,a)\in R$$. So, $$R$$ is a symmetric relation on $$Z$$.

Transitivity. Let $$a,b,c\in Z$$ be such that $$(a,b)\in R$$ and $$(b,c)\in R$$. Then,
$$(a,b)\in R\Rightarrow n$$ divides $$a-b\Rightarrow a-b=n\lambda$$ for some $$\lambda \in Z$$
and $$(b,c)\in R\Rightarrow n$$ divides $$b-c\Rightarrow b-c=n\mu$$ for some $$\mu \in Z$$
$$\therefore$$ $$a-b+b-c=n(\lambda +\mu)$$
$$\Rightarrow$$ $$a-c=n(\lambda +\mu)$$, where $$\lambda +\mu \in Z$$
$$\Rightarrow$$ $$n$$ divides $$a-c$$
$$\Rightarrow$$ $$(a,c)\in R$$
thus, $$(a,b)\in R$$ and $$(b,c)\in R\Rightarrow (a,c)\in R$$
So, $$R$$ is a transitive relation on $$Z$$
Hence, $$R$$ is an equivalence relation on $$Z$$.


Let $$O$$ be the origin. We define a relation between two points $$P$$ and $$Q$$ in a plane, if $$OP=OQ$$. Show that the relation, so defined is an equivalence relation.

Let us denote this relation by $$R=\{(P,Q): OP=OQ\}$$ for $$O$$ being the origin.
Now $$(P,P)\in R$$ since $$OP=OQ$$ for any  point $$P$$. So the relation is reflexive.
Again this relation is symmeric as if $$(P,Q)\in R\Rightarrow (Q,P)\in R$$ since $$OP=OP\Rightarrow OQ=OP$$ for all $$P,Q$$.
Also this relation is transitive as if  $$(P,Q)\in R, (Q,S)\in R\Rightarrow (P,S)\in R$$ since $$OP=OQ, OQ=OS\Rightarrow OP=OS$$ for all $$P, Q, S$$.
Hence the relation is reflexive, symmetric and transitive so it is an equivalance relation.


Define an equivalence relation.

A relation is said to be an equivalence relation if it is reflexive, symmetric and transitive.


Define a reflexive relation.

A relation is said to be a reflexive relation  on a given set, if each element of the set are related onto itself.
For example let $$A$$ be a set and $$R$$ is a relation defined on $$A$$. Then $$R$$ is said to be reflexive if for each $$a\in A$$, $$(a,a)\in R$$.


Define a transitive relation.

Let $$A$$ be any set. A relation $$R$$ on $$A$$ is said to be a transitive relation iff $$(a,b) \in R$$ and $$(b,c) \in R \implies (a,c) \in R$$ for all $$a,b,c \in A$$.
i.e., $$aRb$$ and $$bRc \implies aRc$$ for all $$a,b,c \in A$$.


Define a symmetric relation.

A relation R on a set A is said to be a symmetric relation iff
$$(a,b) \in R \implies (b,a) \in R$$ for all $$a,b \in A$$
i.e., $$aRb \implies bRa$$ for all $$a, \in A$$.


Write the smallest equivalence relation on the set $$A=\left\{ 1,2,3 \right\} $$.

 The smallest equivalence relation on the set $$A=\left\{ 1,2,3 \right\} $$ is $$R=\{(1,1),(2,2),(3,3)\}$$.
As it is reflexive as for all $$x\in A, (x,x)\in R$$.
Also this relation $$R$$ is symmetric as if $$(x,y)\in R\Rightarrow (y,x)\in R$$ for all $$x,y\in A$$.
Again this relation is transitive as if $$(x,y)\in R, (y,z)\in R\Rightarrow (x,z)\in R$$ for all $$x,y,z\in A$$.
Hence the relation is an equivalance relation.


Is $$*$$ defined on the set {1, 2, 3, 4, 5} by $$a*b$$ = LCM of a and b, a binary operation ? Justify your answer.

We have $$*$$ defined on the set {1, 2, 3, 4, 5} by 

$$a*b=$$ LCM of a and b

Now, $$3*4 =12$$

But $$12 $$ is not in set {1, 2, 3, 4, 5}.

Hence, $$*$$ is not a binary operation.


Find the number of reflexive relations from set $$A$$ to $$A$$, defined as $$A = {a, b, c}$$.

Given, $$A= {a, b, c}$$

Here, the number of elements in set A is 3.

We know that, if set A has $$n$$ elements, then total number of reflexive relations is $$2^{n^2-n}$$.

Here, $$n=3$$

Therefore, the total number of reflexive relations from set A to A 
$$=2^{3^2-3}=2^6=64$$


Each of the following defines a relations a relation on $$N$$:
$$x+4y=10\ x,y\ \in \ N$$
Determine which of the above relations are reflexive, symmetric and transitive,

$$x+4y=10\ x,y\ \in \ N$$
$$R=\left\{(x,y):x+4y =10,x,y\in N\right\}$$
$$R=\left\{(2,2),(6,1)\right\}$$
$$(1,1),(3,3),....\notin R$$
Thus, $$R$$ is not reflexive 
$$(6,1)\in R$$ but $$(1,6)\notin R$$
Hence, $$R$$ is not symmetric,
$$(x,y)\in R\Rightarrow x+4y=10$$ but $$(y,z)\in R$$
$$y+4x=10\Rightarrow (x,z)\in R$$
so, $$R$$ is transitive.


Each of the following defines a relations a relation on $$N$$:
$$xy$$ is square of an integer $$x,y\ \in \ N$$.
Determine which of the above relations are reflexive, symmetric and transitive,

Given $$xy$$ is square of an integer $$x,y\ \in \ N$$
$$\Rightarrow \ =\left\{(x,y):xy\ is\ a\ square\ of\ an\ integer\ x,y\ \in N \right\}$$
$$(x,x)\in R, \forall x \in N$$
As $$x^2$$ is square of an integer for any $$x\in N$$
Hence, $$R$$ is reflexive.
If $$(x,y)\in R\Rightarrow \ (y,x)\in R$$
Therefore, $$R$$ is symmetric.
If $$(x,y)\in R (y,z) \in R$$
So, $$xy$$ is square of an integer and $$yz$$ is square of an integer.
Let $$xy=m^2 $$ and $$yz=n^2$$ for some $$m,n\in Z$$
$$x=\dfrac {m^2 n^2}{y^2}$$, which is square of an integer.
so, $$R$$ is transitive.


Each of the following defines a relations a relation on $$N$$:
$$x+y=10,x,y\ \in N$$ 
Determine which of the above relations are reflexive, symmetric and transitive,

$$x+y=10, x, y\in N$$
$$R=\left\{(x,y);x+y=10x, y \in N \right\}$$
$$R=\left\{(1,9),(2,8),(3,7),(4,6),(5,5),(6,4),(7,3),(8,2),(9,1) \right\} (1,1) \in R$$
So, $$R$$ is not reflexive.
$$(x,y)\in R \Rightarrow (y,x)\in R$$
Therefore, $$R$$ is symmetric
$$(1,9)\in R (9,1)\in R\Rightarrow (1,1)\notin R$$
Hence, $$$R$$ is not transitive.


Let $$n$$ be a fixed positive integer. Define a relation $$R$$ in $$Z$$ as follows $$\forall a, b \in Z. aRb$$ if and only $$a-b$$ is divisible by $$n$$. Show that $$R$$ is an equivalence relation. 

Given that $$\forall x,b \in Z, aRb$$ if an only $$a-b$$ divisible by $$n$$
Now
Reflexive
$$aRa \Rightarrow \ (a-a)$$ divisible by $$n$$, which is true for any integer $$'a'$$ as $$0$$ divisible by $$n$$
Symmetric
$$aRb$$
$$\Rightarrow \ z-b$$ is divisible by $$n$$
$$\Rightarrow \ -b+a$$ is divisible by $$n$$
$$\Rightarrow \ -(b-s)$$ is divisible by $$n$$
$$\Rightarrow \ (b-a)$$ is divisible by $$n$$
$$\Rightarrow \ bRa$$
Hence $$R$$ is symmetric 
Transitive
Let $$aRb$$ and $$bRa$$
$$\Rightarrow \ (a-b)$$ is divisible by $$n$$ and $$(b-c)$$ is divisible by $$n$$
$$\Rightarrow \ (a-b)+(b-c)$$ is divisible by $$n$$
$$\Rightarrow \ (a-c)$$ is divisible by $$n$$
$$\Rightarrow \ aRc$$
Hence, $$R$$ is transitive.
So, $$R$$ an equivalence relation. 


If $$A=\left\{1,2,3,4 \right\}$$, define relation on $$A$$ which have properties of being.
reflexive, symmetric and transitive. 

Given that $$A=\left\{1,2,3,4 \right\}$$
Let $$R_3=\left\{(1,2),(2,1),(1,1),(2,2),(3,3),(1,3),(3,1),(2,3)\right\}$$
Hence, $$R_3$$ is reflexive, symmetric and negative.


If $$A=\left\{1,2,3,4 \right\}$$, define relation on $$A$$ which have properties of being.
symmetric but neither reflective nor transitive.

Given that $$A=\left\{1,2,3,4 \right\}$$
Let $$R_2=\left\{(1,2),(2,1)\right\}$$
Now , $$(1,2)\in R_2 (2,1)\in R_2$$
So, it is symmetric.


If $$A=\left\{1,2,3,4 \right\}$$, define relation on $$A$$ which have properties of being.
reflexive, transitive but not symmetric.

Given that $$A=\left\{1,2,3,4 \right\}$$
Let $$R_1=A=\left\{(1,1),(1,2),(2,3),(2,2),(1,3),(3,3) \right\}$$
$$R_1$$ is reflexive, since $$(1,1),(2,2),(3,3)$$ lie is $$R_1$$
Now , $$(1,2)\in R_1 (2,3)\in R_1 \Rightarrow (1,3)\in R_1$$
Hence, $$R_1$$ is also  transitive but $$(1,2),\in R_1 \Rightarrow (2,1)\in R_1$$
So, it is not symmetric.


Set A has m elements an set B has n elements. If the total number of subsets of A is $$112$$ more than total numbers of subsets of B, then the value of $$m\times n$$ is

A and B are two sets having m,n element respectively
No. of subsets of $$A=2^m$$
No. of subsets of $$B=2^n$$
$$2^m = 2^n+112$$
$$2^m - 2^n=112$$
$$2^n(2^{m- n}-1)=112$$
$$2^n(2^{m-n}-1)=2^4(2^3-1)$$
$$n=4$$
$$m-n=3$$
$$m-4=3$$
$$\Rightarrow m=7$$
$$m\times n=28$$
$$=28$$


Let $$A=\left\{1,2,3,...9\right\}$$ and $$R$$ be the relation in $$A\times A$$ defined by $$(a,b)\ R\ (c,d)$$ if $$a+b=b+c$$ for $$(a,b),(c,d)$$ in $$A\times A$$. Prove that $$R$$ is an equivalence relation and also obtain the equivalent class $$[(2,5)]$$.

Given that $$A=\left\{1,2,3,...9\right\}(a,b)\ R\ (c,d)$$ if $$a+b=b+c$$ for $$(a,b),(c,d)$$ in $$A\times A$$.
$$(c,d)\in A\times A$$ 
Let $$(a,b) R (a,b)$$
$$\Rightarrow \ a+b=b+a, \forall a, b \in A$$
which is true for any $$a, b \in A$$
Hence, $$R$$ is reflexive
Let $$(a,b)R\in (c,d)$$
$$a+d=b+c$$
$$c+b=+a\Rightarrow (c,d) R(a,b)$$
So, $$R$$ is symmetric
Let $$(a,b)R(c,d)$$ and $$(c,d)R(e,f)$$
$$a+d=b+c$$ and $$c+f=d+e$$
$$a+d=b+c$$ and $$d+e=c+f (a+d)-(d+e)=(b+c)-(c+f)$$
$$(a-e)=b-f$$
$$a+f=b+e$$
$$(a,b)R (e,f)$$
Now, equivalence class containing $$[(2,5)\ is\ \left\{(1,4),(2,5),(3,6),(4,7),(5,8),(6,9)\right\}]$$
$$\left\{(2,5)\right\}$$ is $$\left\{(1,4),(2,5),(3,6),(4,7),(5,8),(6,9)\right\}$$


Let $$R$$ be a relation on $$Z$$ (the set of integers) defined as $$mRn,iffm\le n\forall m,n\epsilon Z$$ then $$R$$ is anti symmetric.

$$R$$ is anti symmetric because if $$R(m,n)$$ exist then $$R(n,m)$$ never exists. If it exists then $$m=n$$. 
So given statement is true.


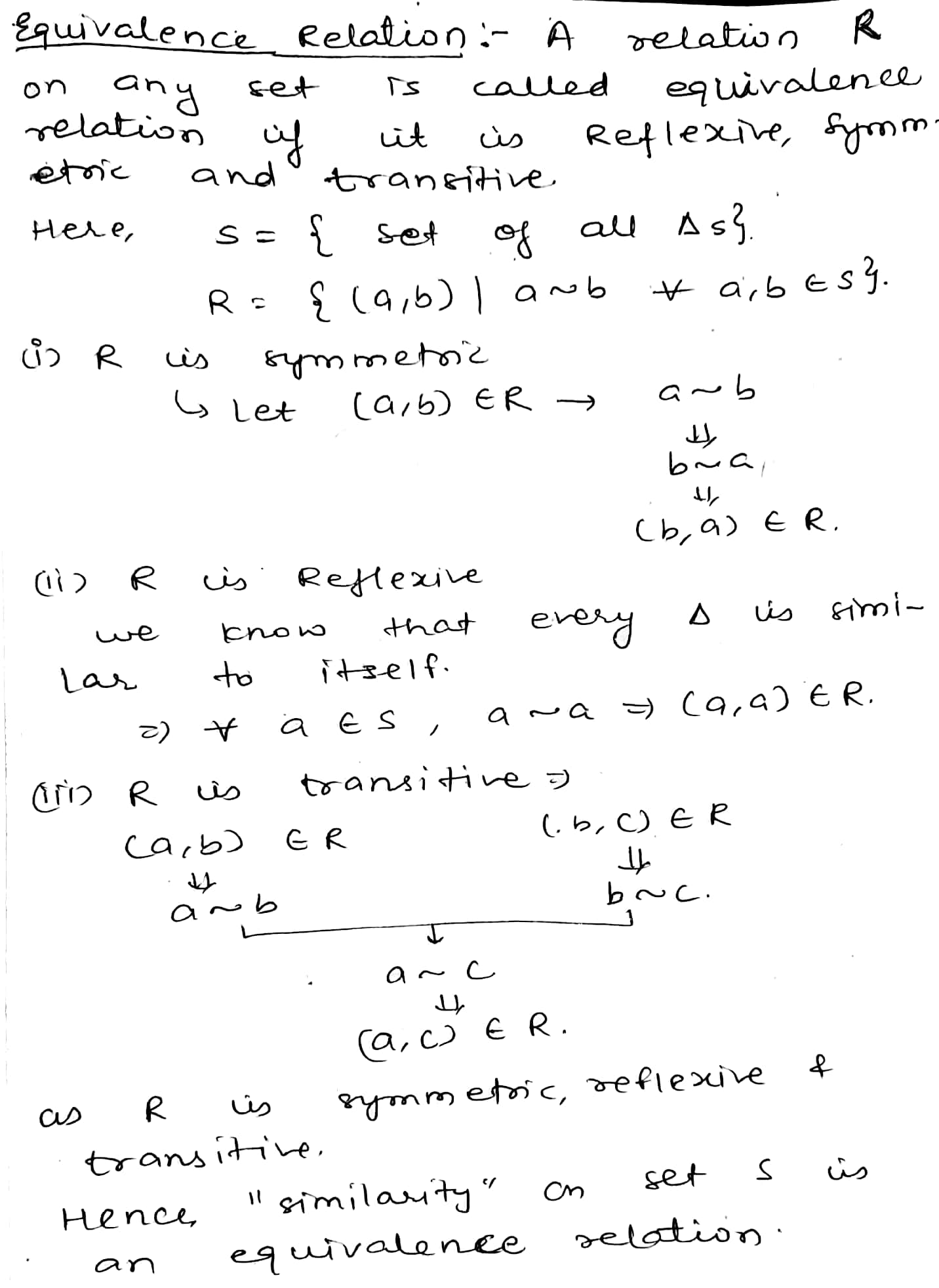
In the set of triangles in a plane the relation 'is similar to' is an equivalence relation. Prove .

Let T be the set of all triangles in a plane.
We are given that $$T_{1}\  R\   T_{2}$$
$$\Rightarrow T_{1} : T_{2}$$ for all $$T_{1}, T_{2}\in T$$
Reflexive : Let $$T_{1}\in T$$ such that $$T_{1} \ R\  T_{1}$$.
Then $$T_{1} \  R\     T\Rightarrow T_{1} : T_{1}$$ every triangle is similar to itself.
So, : is reflexive on T.
Symmetric:  Let $$T_{1}, T_{2}\in T$$ such that $$T_{1}\ R\ T_{2}$$
Then $$T_{1}\ R\ T_{2}\Rightarrow T_{1} : T_{2}\Rightarrow T_{2} : T_{1}$$
So, r is symmetric on T.
Transitive: Let $$T_{1},  T_{2}, T_{3}\in T$$ such that $$T_{1}\ R\ T_{2},T_{2}\ R\ T_{3}$$.
Then, $$T_{1}\ R\ T_{2}\Rightarrow T_{1} : T_{2}$$ and $$T_{2} : T_{3}$$ implies that $$T_{1} : T_{3}$$
So, $$R$$ is transitive on $$T$$.
Hence, $$R$$ is an equivalence relation on $$T$$.


In the set of all positive integers show that the relation '>'  is not an equivalence relation.

A relation $$R$$ is said to be in equivalence relation if it is reflexive, symmetric and transitive.
Let a relation $$R$$ in $$Z^{+} \times Z^{+}$$ defined as $$x>y \in R$$
Now, if $$(a,a) \in$$ $$Z^{+} \times Z^{+}$$
$$\implies a>a,$$ which is not true
So, $$R$$ is not reflexive
Thus, the relation '$$>$$' is not an equivalence relation on $$Z^+,$$ where $$Z^{+}$$ is set of all positive integers the set of positive integers.


Show that the relation R in $$N\times N$$ defined by $$(a, b) R (c, d)$$ if $$ad=bc$$ is an equivalence relation.

$$ad=bc$$ in an equivalence relation.
Symmetric: 
if $$(a,b) R(c,d) \in N\times N$$
$$\Rightarrow ad=bc$$
$$\\ \Rightarrow bc=ad$$
$$\\ \Rightarrow (c,d)R(a,b)$$
$$R$$ is symmetric
Reflexive:
If $$(a,b)\in \quad N\times N$$
$$\\ \Rightarrow ab=ab$$
$$\\ (a,b)\in (a,b)$$ . So $$R$$ is reflexive.
Transitive:
If $$(a,b) R(c,d)$$ and$$(c,d) R(e,f)$$
$$ \Rightarrow ad=bc$$ and $$cf=de$$
$$\Rightarrow \dfrac { a }{ b } =\dfrac { c }{ d } \quad and\quad \dfrac { c }{ d } =\dfrac { e }{ f } $$
$$\\ \Rightarrow \dfrac { a }{ b } =\dfrac { e }{ f } $$
$$af=eb$$
$$(a,b) R(e,f) \in N \times N$$
So $$R$$ is transitive
Therefore $$R$$ is in equivalence relation.


The relation  'is a subset of'  in a set of sets is not an equivalence relation. Prove.

Let A be a set.
$$A\subset A.$$ every set is a subset of itself. So, R is reflexive on A.
For any two sets A, B. If $$A\subset B$$. It is not necessary that $$B\subset A.$$ Hence not symmetric and therefore not an equivalence relation.


Show that the relation 'a R b if and only if $$a-b$$ is an even integer defined on the Z of integers is an equivalence relation.

(i) Since $$a-a=0$$ and 0 is an even integer 
$$(a, a)\in R$$
$$\therefore $$ R is reflexive.
(ii) If $$(a-b)$$ is even, then $$(b-a)$$ is also even. then, if $$(a-b)\in R, (b, a)\in R$$
$$\therefore $$ The relation is symmetric.
(iii) If $$(a, b)\in R, (b, c)\in R,$$ then $$(a-b)$$ is even, $$(b-c)$$ is even, then $$(a-b
+b-c)=a-c$$ is even.
$$\therefore $$ If $$(a, b)\in R,  (b, c)\in R$$ implies $$(a, c)\in R$$
$$\therefore $$  R is transitive.
Since R is reflexive, symmetric and transitive, it is an equivalence relation.


Let L be the set of all lines in XY-plane and R be the relation in L defined as $$R=\left \{ (L_{1}, L_{2}):L_{1} \  is \   parallel \   to\     L_{2} \right \}$$. Show that R is an equivalence relation. Find the set of all lines related to the line $$y=2x$$

Since every line $$l\in L$$ is parallel to itself, therefore $$(l, l)\in\ R\ \forall\ l\in L.$$
$$\therefore $$ R is reflexive
$$(L_{1}, L_{2})\in R\Rightarrow  L_{1} || L_{2}$$
$$\Rightarrow (L_{2}, L_{1})\in R.$$
$$\therefore R$$ is symmetric.
Next, let $$(L_{1}, L_{2})\in R$$ and also $$(L_{2}, L_{1})\in R$$
$$\Rightarrow L_{1} || L_{2} \ and\  L_{2} || L_{3}$$
$$\Rightarrow L_{1} || L_{3}  \Rightarrow   (L_{2}, L_{3})\in R$$
$$\therefore R$$ is transitive.
 Hence, R is an equivalence relation. Required set
={ 1:1  is  a  line  related  to  the  line   $$y=2x+y$$}$$ $$={ 1:1 is a line parallel to $$y=2x+4$$}
={ 1:1  is  a  line  whose  equation   is  $$y =2k+k,$$ k being any real.}


Give a non-empty set $$X$$. Consider $$P(X)$$, which is  the set of all subsets of $$X$$. Define the relation $$R$$ in $$P(X)$$ as follows:
For subsets $$A$$ and $$B$$ in $$P(X)$$, $$A R B$$ if $$A\subset B$$, is $$R$$ an equivalence relation on $$P(X)$$? 
Justify your answer.

Since $$A\subset A\forall A\in P(X),$$
$$\therefore ARA$$, $$\forall A\in P(X)$$
So, $$R$$ is reflexive.
Also for $$A, B, C\in P(X),$$ ARB and BRC
$$\Rightarrow A\subset B$$ and $$B\subset C$$
$$\Rightarrow A\subset C\Rightarrow ARC$$
$$\therefore R$$ is transitive
But, $$ARB$$ does not imply $$BRA$$.
Hence, $$R$$ is not an equivalence relation on $$P(X)$$.


An "Anti-symmetric" relation need not be reflexive relation: give an example.

The relation $$R=\left \{ (1, 1),(2, 3) \right \}$$ on the set $$A=\left \{ 1, 2, 3 \right \}$$ is an anti-symmetric relation, as the necessary condition for it is satisfied. 
But it is not reflexive as $$(2, 2),(3, 3)\notin R,$$ through $$(1, 1),(2, 2),(3, 3)\in R$$


Let R and S be two equivalence relations on set A. Prove that  $$R\cap S$$ is an equivalence relation.

Equivalence relation mean reflexive, symmetric and transitive.
Let an element $$a\in A$$. Since R and S are equivalence relations they are reflexive.
Therefore $$(a, a)\in R$$ and $$(a, a)\in S$$
So $$(a, a)\in R$$ and $$(a, a)\in S$$
So $$(a, a)\in R\cap S$$
$$\therefore R\cap S$$ is reflexive     ......(1)
Let $$(a, b)\in R\cap S$$
$$\Rightarrow (a, b)\in R$$ and $$(a, b)\in S$$
$$\Rightarrow (b, a)\in R$$ and $$(b, a)\in S$$
( Since R and S are symmetric),
$$\Rightarrow (b, a)\in R\cap S$$
$$\therefore R\cap S$$ is symmetric    ....(2)
Let $$(a, b),(b, c)\in R\cap S$$
$$\Rightarrow (a, b),(b, c)\in R\Rightarrow (a, c)\in R$$
$$\Rightarrow (a, b),(b, c)\in S\Rightarrow (a, c)\in S$$
Since R and S are transitive,
$$\Rightarrow (a, c)\in R\cap S$$
$$\Rightarrow R\cap S$$ is transitive   ....(3)
From (1), (2) and (3), $$R\cap S$$ is an equivalence relation.


If in $$N\times N$$, $$R$$ is a relation defined by the formula $$(x, y) R(p, q)$$ if and only if  $$x+q=y+p$$, show that R is an equivalence relation.

A relation R is said to be in equivalence realtion if it is reflexive,symmetric and transitive.
Reflexive:
If $$(x,y) \in N \times N$$
$$x+y=y+x$$
$$(x,y) R(x,y)$$
$$(x,y) \in N\times N$$
R is reflexive.
Symmetric:
If $$(x,y) R(p,q)$$ then,
$$x+q=p+y$$
$$p+y=x+q$$
$$(p,q) R(x,y)$$
R is symmetric.
Transitive:
If $$(x,y) R(p,q)$$ and $$(p,q) R(r,s)$$ then,
$$x+q=y+p$$
$$p+s=q+r$$
$$x+s=y+r$$
$$(x,y) R(r,s) \in N \times N$$
R is transitive
So, R is in equivalence relation 


The relation $$R$$ and $$R'$$ are symmetric in the set $$A$$, then show that $$R\cup R'$$ and $$R\cap R'$$ are symmetric.

We will prove, union of sets is symmetric  
Let $$S=R\cup R'$$
Let $$(a,b) \in S$$
$$\Rightarrow (a,b) \in R\cup R'$$
$$\Rightarrow (a,b) \in R$$ or $$(a,b) \in R'$$
$$\Rightarrow (b,a) \in R $$or $$(b,a) \in R'$$    (Since, R and R' are symmetric)
$$\Rightarrow (b,a) \in R\cup R'$$
$$\Rightarrow (b,a) \in S$$
Hence, $$S=R\cup R'$$  is symmetric.

Now, we will prove, intersection of sets is symmetric  
Let $$P=R\cap R'$$
Let $$(a,b) \in P$$
$$\Rightarrow (a,b) \in R\cap R'$$
$$\Rightarrow (a,b) \in R $$ and $$(a,b) \in R'$$
$$\Rightarrow (b,a) \in R$$ and $$(b,a) \in R'$$   (Since, R and R' are symmetric)
$$\Rightarrow (b,a) \in R\cap R'$$
$$\Rightarrow (b,a) \in P$$
Hence, $$P=R\cap R'$$  is symmetric.


Let $$A=\{1, 2, 3\}$$. Then show that the smallest equivalence relation on $$A$$ is $$\{(1, 1), (2, 2), (3, 3)\}$$

Given set $$A=\{1,2,3\}$$
Given $$R=\{(1,1),(2,2),(3,3)\}$$

Clearly, the relation $$R$$ is reflexive on $$A$$, as $$(x,x)\in R$$ for all $$x\in A$$
Since, there are no ordered pairs of the form $$(x,y)$$, so no need to check for symmetric and transitive.

Hence, the given relation is smallest equivalence relation on $$A.$$


For each set of ordered pairs below, state whether it is a function or not giving reasons
(i){(3, 2), (4, 2), (5, 2)}
if a function enter 1 else 0

A function f from X to Y is a subset of the Cartesian product X  Y subject to the following condition: every element of Xis the first component of one and only one ordered pair in the subset.In other words, for every x in X there is exactly one element y such that the ordered pair (x, y) is contained in the subset defining the function f.

Hence given ordered pair does not represent function.


Let $$\displaystyle R=\left \{ \left ( a,a \right ),\left ( b,c \right ),\left ( a,b \right ) \right \}$$ be a relation on a set $$\displaystyle A=\left \{ a,b,c \right \}.$$ Then the minimum number of ordered pairs which when added to R make it an equivalence relation are ...

$$\displaystyle \left \{ \left ( b,b \right ),\left ( c,c \right ),\left ( b,a \right ),\left ( c,b \right ),\left ( a,c \right ),\left ( c,a \right ) \right \}$$
$$\displaystyle R=\left \{ \left ( a,a \right ) ,\left ( b,c \right ),\left ( a,b \right )\right \}$$
For relexive add $$\displaystyle \left ( b,b \right ),\left ( c,c \right ).$$
$$\displaystyle \therefore R=\left \{ \left ( a,a \right ),\left ( b,c \right ),\left ( a,b \right )\left ( b,b \right ) \left ( c,c \right )\left ( c,b \right ),\left ( b,a \right )\right \}\left ( a,b \right )\epsilon R\left ( b,c \right )\epsilon R $$ so that (a,c) must belong to R.
Hence we must add (a,c) and for symmetric we must add (c,a) also.
$$\displaystyle \therefore R\left \{ \left ( a,a \right ),\left ( b,c \right ),\left ( a,b\right )\left ( b,b \right ),\left ( c,c \right ),\left ( c,b \right ),\left ( b,a \right )\left ( a,c \right ) \left ( c,a \right )\right \} $$

Ans: 6


Given $$A = \{5, 6, 7\}$$ and $$B = \{3, 4\}$$. Form all possible ordered pairs and write the total number of ordered pairs formed. So that the first component is from B and second is from A.
Find the total number of such pairs.

Possible ordered pairs with first component from Set B and second from set A are $$ (3,5), (3,6), (3,7), (4,5), (4,6), (4,7) $$
Thus, the total no. of ordered pairs formed is $$6$$.


Let $$R$$ be relation on I defined as mRn iff $$\displaystyle m\leq n.$$ Check if $$R$$ is an equivalence relation. 

Given, relation R defined on set of integer as  
$$mRn \Leftrightarrow m \le n$$

Reflexive:
R is reflexive because of the = sign in the inequality. 

Symmetric:
Let $$mRn$$
$$\Rightarrow m \le n$$
It does not implies $$n \le m$$
Hence, R is not symmetric.

Transitive:
Let $$m,n,p \in I $$ 
Let $$mRn$$, $$nRp$$
$$\Rightarrow m\le n$$ and $$n\le p$$
$$\Rightarrow m \le p$$
Hence, R is transitive.



Given $$A = \{5, 6, 7\}$$ and $$B = \{3, 4\}$$. Form all possible ordered pairs and write the total number of ordered pairs formed so that the first component is from set A and second component is from set B. 

What is the total number of such pairs?

Possible ordered pairs with first component from Set $$A$$ and second from set $$B$$ are 
$$ (5,3), (5,4), (6,3), (6,4), (7,3),(7,4) $$.
Hence, the total no. of ordered pairs formed is $$6$$.


If $$M=\{x : x \,\,\epsilon\,\, N, 1 < x \leq 4\}$$ and $$N = \{y : y\,\,\epsilon\,\,W, y < 3\}$$; 
find : $$n(M$$ $$\times$$ $$M)$$

Cartesian product of two sets is obtained by pairing each element of first set with each element of second set.
Now set  $$ M = \{2,3,4\}$$ 
and set $$ N = \{ 0,1,2 \}$$
Thus, $$M\times M=\{(2,2),(2,3),(2,4),(3,2),(3,2),(3,4),(4,2),(4,3),(4,4)\}$$ 
Hence, $$ n(M \times M)=9$$.


If $$n(A) = m$$ and $$n(B) = n$$ ; then $$n(A \times B) = mn$$.
What is the value of $$n(A \times B) = mn$$. if $$m = 6$$ and $$n = 8$$

Cartesian product of two sets is obtained by pairing each element of first set with each element of second set.

Given : $$ n(A) = m $$ and $$ n(B) = n $$

Now, $$ n(A \times B)= n(A)\times n(B)=m \times n = mn $$.
Thus when $$m=8$$ and $$n= 6$$, we have $$n(A \times B) = 48$$


The following relations are defined on the set of real numbers check them for R,S,T.
aRb iff $$\displaystyle \left | a-b \right |> 0$$

Given $$aRb  \text{iff} |a-b|>0 ; a,b\in R$$

Reflexive :
We know $$|a-a|\ngtr 0$$
Hence, $$a(\sim R)a$$
Hence, R is not reflexive.

Symmetric:
Let $$aRb$$
$$\Rightarrow |a-b|>0$$
$$\Rightarrow |b-a|>0$$
$$\Rightarrow bRa$$
Hence, R is symmetric.

Transitive:
Let $$aRb, bRc$$
$$\Rightarrow |a-b|>0 ; |b-c|>0$$
$$\Rightarrow |a-c|>0$$
R is transitive.


The following relations are defined on the set of real numbers  check them for Reflexivity,Symmetry,Transitivity.
$$\displaystyle 1+ab> 0$$

R, S both $$\displaystyle \because 1+a^{2}> 0$$ and $$\displaystyle 1+ba> 0$$ when

$$\displaystyle 1+ab> 0\neq T.$$ Consider $$\displaystyle a= 2, b= -\frac{1}{6}, c= -2.$$

aRb as $$\displaystyle 1+2\left ( -\frac{1}{6} \right )= 1-\frac{1}{3}= \frac{2}{3}> 0$$

bRc as $$\displaystyle 1+\left ( -\frac{1}{6} \right )\left ( -2 \right )= 1+\frac{1}{3}= \frac{4}{3}> 0$$

but aRc $$\displaystyle = 1+2\left ( -2 \right )= -3\ngtr 0.$$

Therefore a is not related to c and hence no transitive.


Let S be the set of all points in a plane. Let R be a relation on S such that for any two points a and b, a R b iff b is within 1 centimetre from a. Check R for reflexivity, symmetry and transitivity.

$$aRb \Leftrightarrow \text {b is within 1 cm from a} $$

Reflexivity:
R is reflexive since any point is at distance 0 from itself so that it is within 1 centimetre from itself.

Symmetry:
R is symmetric since if a point a is within 1 centimetre from another point b, then b is also within 1 centimetre from a.

Transitivity:
Let a,b,c be three points in a straight line in this order such that distance between a and b is $$\displaystyle \frac{1}{2}$$ centimetre and distance between b and c is $$\displaystyle \frac{3}{4}$$ centimetre .
Then a R b and b R c.
But $$\displaystyle a\left ( \sim R \right )$$ c since the distance between a and c is $$\displaystyle \left ( \frac{1}{2}+\frac{3}{4} \right )= \frac{5}{4}$$ centimetre which is greater than 1 centimetre.
Hence, R is not transitive. 


If $$\displaystyle \alpha ,\beta $$ be straight lines in a plane, then check $$\displaystyle R_{1}\:and\:R_{2}$$ for being reflexive, symmetric and transitive $$\displaystyle \alpha R_{1} \beta\:if\:\alpha \perp \beta\:and\:\alpha R_{2}\beta\:if\:\alpha \mid \mid \beta .$$

$$\displaystyle \alpha R_{1} \beta \:if\:\alpha \perp \beta\:$$
where $$\displaystyle \alpha ,\beta $$ are straight lines in a plane.
Let $$L$$ be set of lines in a plane

Reflexivity:
No line is perpendicular to itself.
i.e.$$\alpha $$ is not perpendicular to $$\alpha$$    $$\forall \alpha \in L$$
So, $$\alpha$$ is not related to $$\alpha$$    $$\forall \alpha \in L$$
Hence, $$R_1$$ is not reflexive.

Symmetry:
Let $$\alpha R_1 \beta$$
$$\Rightarrow \beta R_1 \alpha$$       (Two lines are mutually perpendicular to each other)
Hence, $$R_1$$ is symmetric

Transitivity:
Let $$\alpha, \beta, \gamma \in L$$
Let $$\alpha R_1 \beta$$ ; $$\beta R_1 \gamma$$
It does not implies that $$\alpha \perp \gamma$$
Hence, $$\alpha $$ not related to $$\gamma$$
Hence, $$R_1$$ is not transitive.

Given $$\alpha  R_{2} \beta \:if \:\alpha \mid \mid \beta $$
Reflexivity: 
Every line is parallel to itself.
$$\alpha R_2 \alpha $$
Hence, $$R_2$$ is reflexive.

Symmetry:
Let $$\alpha R_2 \beta$$
$$\Rightarrow \alpha \parallel \beta$$
$$\Rightarrow \beta \parallel \alpha $$ 
$$\Rightarrow \beta R_2 \alpha$$
Hence, $$R_2$$ is symmetric.

Transitivity:
Let $$\alpha R_2 \beta ,  \beta R_2 \gamma$$
$$\Rightarrow \alpha \parallel  \beta ; \beta \parallel \gamma $$     (Two lines parallel to same line are parallel to each other.)
$$\Rightarrow \alpha \parallel \gamma$$
Hence, $$R_2$$ is transitive.


reflexive, transitive but not symmetric.

We define a relation $$\displaystyle R_{1}$$ as
$$\displaystyle R_{1}= \left \{ \left ( 1,1 \right ), \left ( 2,2 \right ), \left ( 3,3 \right ), \left ( 4,4 \right ), \left ( 1,2 \right ), \left ( 2,3 \right), \left ( 1,3 \right ) \right \}$$
Then it is easy to check that
$$\displaystyle R_{1}$$ is reflexive, transitive but not symmetric.

Students are advised to write other relations of this type.


Let $$R$$ be the equivalence relation in the set $$A = {0, 1, 2, 3, 4, 5}$$ given by $$R = {(a, b) : 2\ divides (a - b)}$$. Write the equivalence class [0].  

$$A$$ = $$\left\{ 0,1,2,3,4,5 \right\} $$

$$R$$ is an equivalence relation and

$$R$$ = $$\left\{ { (a,b) : 2\quad divides\quad (a-b) } \right\}$$
The elements $$x\in A$$ satisfying $$aRx$$ constitute a subset $$A_{a}$$ of $$A$$,
called an equivalence class of $$A$$ with respect to $$R$$ determined by $$a$$.

Thus, $$[a]$$ = $$\left\{ x : x\in A\quad and\quad aRx \right\} $$

$$\therefore$$ $$[0]$$ = $$\left\{ 0,\quad 2,\quad 4 \right\}$$



Let $$T$$ be the set of all triangles in a plane with $$R$$ a relation in $$T$$ given by $$\displaystyle R=\left \{ (T_{1},T_{2}) \right \}:T_{1}$$ congruent to $$\displaystyle T_{2}$$}. Show that $$R$$ is an equivalence relation.

Since a relation $$R$$ in $$T$$ is said to be an equivalence relation if $$R$$ is reflexive, symmetric and transitive. 
(i) Since every triangle is congruent itself
$$\displaystyle \therefore $$ $$R$$ is reflexive 
 $$\displaystyle (T_{1},T_{1})\varepsilon R\Rightarrow T_{1}$$ is congruent to itself $$\displaystyle \therefore $$R$$ $$ reflexive 
(ii) $$\displaystyle (T_{1},T_{2})\epsilon R\Rightarrow T_{1}$$ is congruent to $$\displaystyle T_{2}$$
$$\displaystyle \Rightarrow T_{2}$$ is congruent to $$T_1 $$
$$\displaystyle \Rightarrow (T_{2},T_{1})\epsilon R$$
Hence $$R$$ is symmetric 
(iii) Let $$\displaystyle (T_{1},T_{2})\epsilon R$$ and $$\displaystyle (T_{2},T_{3})\epsilon R$$
Then $$T_1$$ is congruent ot $$T_2$$ and  $$\displaystyle (T_{2})$$ is congruent to $$\displaystyle (T_{3})$$
$$\displaystyle \Rightarrow T_{1}$$ is congruent to $$T_{3}$$
$$\displaystyle \Rightarrow (T_{1},T_{3})\epsilon R$$
$$\displaystyle \therefore $$ $$R$$ is transitive 
Hence $$R$$ is an equivalence relation. 


Determine whether the following relation is reflexive, symmetric and transitive

Relative $$R$$ in the set $$N$$ of natural numbers defined as $$R=\left\{(x, y):y=x+5  and  x < 4\right\}$$

enter 1-Reflexive
         2-Symmetric
         3-Transitive
         4-Equivalence
         5-None

$$R=\left\{(x, y):y=x+5   \text{and}   x<4\right\}=\left\{(1, 6), (2, 7), (3, 8)\right\}$$

It is seen that $$(1, 1)\notin R\Rightarrow R$$ is not reflexive.
Also $$(1, 6)\in R$$. 
But, $$(1, 6)\notin R$$. $$\therefore R$$ is not symmetric.

Now, since there is no pair in $$R$$ such that $$(x, y)$$ and $$(y, z)\in R$$, then $$(x,z )$$ cannot belong to $$R$$.

$$\therefore R$$ is  transitive.

Hence, $$R$$ is neither reflexive, nor symmetric, but  transitive.


Relation R in the set A of human beings in a town at a particular time given by $$R=\left\{(x, y):x \,  and \,  y \,  live \,  in \,  the \,  same \,  locality\right\}$$

enter 1-reflexive and transitive but not symmetric
         2-reflexive only
         3-Transitive only
         4-Equivalence
         5-None

$$R=\left\{(x, y):\text{x  and  y  live  in  the  same  locality}\right\}$$

Clearly $$(x, y)\in R$$ as $$x$$ and $$x$$ is the same human being.

$$\therefore R$$ is reflexive.

If $$(x, y)\in R$$, then $$x$$ and $$y$$ live in the same locality.

$$\Rightarrow y $$ and $$x$$ live in the same locality.

$$\Rightarrow (y, x)\in R$$

$$\therefore R$$ is symmetric.

Now, let $$(x, y)\in R$$ and $$(y, z)\in R$$.

$$\Rightarrow $$ $$x$$ and $$y$$ live in the same locality and $$y$$ and $$z$$ live in the same locality.

$$\Rightarrow$$ $$x$$ and $$z$$ live in the same locality.

$$\Rightarrow (x, z)\in R$$

$$\therefore R$$ is transitive.

Hence, $$R$$ is reflexive, symmetric and transitive.


Relation R in the set A of human beings in a town at a particular time given by $$R=\left\{(x, y):x  \,  is \,  exactly \,  7  \,  cm \, taller \,  than \,  y\right\}$$

enter 1-reflexive and transitive but not symmetric
         2-reflexive only
         3-Transitive only
         4-Equivalence
         5-Neither reflexive, nor symmetric, nor transitive

$$R=\left\{(x, y):\text{x  is  exactly  7  cm  taller  than  y}\right\}$$

Now, 

$$(x, x)\notin R$$

Since human being $$x$$ cannot be taller than himself.

$$\therefore R$$ is not reflexive.

Now, let $$(x, y)\in R$$.

$$\Rightarrow x$$ is exactly $$7$$cm taller than $$y$$

Then, $$y$$ is not taller than $$x$$. 

$$\therefore (y, x)\notin R$$

Indeed if $$x$$ is exactly $$7$$cm taller than $$y$$, then $$y$$ is exactly $$7$$cm shorter than $$x$$.

$$\therefore R$$ is not symmetric.

Now, let $$(x, y), (y, z)\in R$$

$$\Rightarrow $$ $$x$$ is exactly $$7$$cm taller than $$y$$ and $$y$$ is exactly $$7$$cm taller than$$z$$.

$$\Rightarrow $$ $$x$$ is exactly $$14$$ taller than $$z$$.

$$\therefore (x, z)\notin R$$

$$\therefore R$$ is not transitive.

Hence, $$R$$ is neither reflexive, nor symmetric, nor transitive.


Determine whether each of the following relations are reflexive, symmetric and transitive

Relation $$R$$ in the set $$A=\left\{1, 2, 3, 4, 5, 6\right\}$$ as $$R=\left\{(x, y):y  \,  \text{is  divisible  by}  x\right\}$$

enter 1-reflexive and transitive but not symmetric
         2-reflexive only
         3-Transitive only
         4-Equivalence
         5-None

$$A=\left\{1, 2, 3, 4, 5, 6\right\}$$

$$R=\left\{(x, y):\text{y  is  divisible  by  x}\right\}$$

We know that any number $$(x)$$ is divisible by itself.

$$\Rightarrow (x, x)\in R$$,

$$\therefore R$$ is reflexive.

Now, $$(2, 4)\in R$$, [ as  $$4$$  is divisible  by  $$2$$]

But,

$$(4, 2)\notin R.$$, [  as  $$2$$  is  not  divisible  by  $$4$$]

$$\therefore R$$ is not symmetric.

Let $$(x, y), (y, z)\in R$$. Then, $$y$$ is divisible by $$x$$ and $$z$$ is divisible by $$y$$.

$$\therefore z$$ is divisible by $$x$$.

$$\Rightarrow (x, z)\in R$$

$$\therefore R$$ is transitive.

Hence, $$R$$ is reflexive and transitive but not symmetric.


Relation $$R$$ in the set $$A$$ of human beings in a town at a particular time given by $$R=\left\{(x, y): x \,   is \,   wife \,  of \,  y\right\}$$

enter 1-reflexive and transitive but not symmetric
         2-reflexive only
         3-Transitive only
         4-Equivalence
         5-Neither reflexive, nor symmetric, nor transitive

$$R=\left\{(x, y):\text{x  is  the  wife  of  y}\right\}$$

Now, $$(x, x)\notin R$$

Since $$x$$ cannot be the wife of herself.

$$\therefore R$$ is not reflexive.

Now, let $$(x, y)\in R$$

$$\Rightarrow x$$ is the wife of $$y$$.

Clearly $$y$$ is not wife of $$x$$.

$$\therefore (y, x)\notin R$$

Indeed if $$x$$ is the wife of $$y$$, then $$y$$ is the husband of $$x$$.

$$\therefore R$$ is not transitive.

Let $$(x, y), (y, z)\in R$$

$$\Rightarrow $$ $$x$$ is the wife of $$y$$ and $$y$$ is the wife of $$z$$.

This case is not possible. Also, this does not imply that $$x$$ is the wife of $$z$$.

$$\therefore (x, z)\notin R$$

$$\therefore R$$ is not transitive.

Hence, $$R$$ is neither reflexive, nor symmetric, nor transitive.


Relation $$R$$ in the set $$Z$$ of all integers defined as  $$R=\left\{(x, y): (x-y) \,   is  \, an \,  integer\right\}$$

enter 1-reflexive and transitive but not symmetric
         2-reflexive only
         3-Transitive only
         4-Equivalence
         5-None

$$R=\left\{(x, y):x-y  \,  \text{is  an  integer}  \right\}$$

Now, for every $$x\in Z, (x, x)\in R$$ as $$x-x=0$$ is an integer.

$$\therefore R$$ is reflexive.

Now, for every $$x, y\in Z$$ if $$(x, y)\in R$$, then $$x-y$$ is an integer.

$$\Rightarrow -(x-y)$$ is also an integer.

$$\Rightarrow (y-x)$$ is an integer.

$$\therefore (y, x)\in R$$

$$\Rightarrow R$$ is symmetric.

Now,

Let $$(x, y)$$ and $$(y, z)\in R$$, where $$x, y, z\in Z$$.

$$\Rightarrow (x-y)$$ and $$(y-z)$$ are integers.

$$\Rightarrow x-z =(x-y)+(y-z)$$ is an integer.

$$\therefore (x, z)\in R$$

$$\therefore R$$ is transitive.

Hence, $$R$$ is reflexive, symmetric, and transitive.


Show that the relative $$R$$ in the set $$A=\left\{1, 2, 3, 4, 5\right\}$$ given by $$R=\left\{(a, b):|a-b| \text{ is  even}  \right\}$$, is an equivalence relation. Show that all the elements of $$\left\{1, 3, 5\right\}$$ are related to each other and all the elements of $$\left\{2, 4\right\}$$ are related to each other. But no element of $$\left\{1, 3, 5\right\}$$ is related to any element of $$\left\{2, 4\right\}$$.

$$A=\left\{1, 2, 3, 4, 5\right\}$$
$$R=\left\{(a, b):|a-b|  \text{is  even}\right\}$$
It is clear that for any element $$a\in A$$, we have $$|a-a|=0$$(which is even).
$$\therefore R$$ is reflexive.
Let $$(a, b)\in R$$
$$\Rightarrow |a-b|$$ is even.
$$\Rightarrow |-(a-b)|=|b-a|$$ is also even.
$$\Rightarrow (b, a)\in R$$
$$\therefore R$$ is symmetric.
Now, let $$(a, b)\in R$$ and $$(b, c)\in R$$.
$$\Rightarrow |a-b|$$ is even and $$|b-c|$$ is even.
$$\Rightarrow (a-c)$$ is even and $$(b-c)$$ is even.
$$\Rightarrow (a-c)=(a-b)+(b-c)$$ is even. [Sum of two even integers is even]
$$\Rightarrow |a-c|$$ is even.
$$\Rightarrow (a, c)\in R$$
$$\therefore R$$ is transitive.
Hence, $$R$$ is an equivalence relation.
Now, all elements of the set $$\left\{1, 2, 3\right\}$$ are related to each other as all the elements of this subset are odd. Thus, the modulus of the difference between any two elements will be even.
Similarly, all elements of the set $$\left\{2, 4\right\}$$ are related to each other as all the elements of this subset are even.
Also, no element of the subset $$\left\{1, 3, 5\right\}$$ can be related to any element of $$\left\{2, 4\right\}$$ as all elements of $$\left\{1, 3, 5\right\}$$ are odd and all elements of $$\left\{2, 4\right\}$$ are even. Thus, the modulus of the difference between the two elements (from each of these two subsets) will not be even.
Hence, $$R$$ is an equivalence relation.


Relation R in the set A of human beings in a town at a particular time given by $$ R=\left\{(x, y):x \,   and \,  y \,  work \,  at \,  the \,  same \,  place \right\}$$

enter 1-reflexive and transitive but not symmetric
         2-reflexive only
         3-Transitive only
         4-Equivalence
         5-None

$$R=\left\{(x, y):x \,   and \, y \, work \, at \, the \, same \, place\right\}$$

$$\Rightarrow (x, x)\in R$$

$$\therefore R$$ is reflexive.

If $$(x, y)\in R $$, then $$x$$ and $$y$$ work at the same place.

$$\Rightarrow y$$ and $$x$$ work at the same place.

$$\Rightarrow (y, x)\in R$$

$$\therefore R$$ is symmetric.

Now, let $$(x, y), (y, z)\in R$$

$$\Rightarrow x$$ and $$y$$ work at the same place and $$y$$ and $$z$$ work at the same place.

$$\Rightarrow x$$ and $$z$$ work at the same place.

$$\Rightarrow (x, z)\in R$$

$$\therefore R$$ is transitive.

Hence, $$R$$ is reflexive, symmetric and transitive.


Relation $$R$$ in the set $$A$$ of human beings in a town at a particular time given by $$R=\left\{(x, y): x \,  is \,  father \,  of \,  y \right\}$$

enter 1-reflexive and transitive but not symmetric
         2-reflexive only
         3-Transitive only
         4-Equivalence
         5-Neither reflexive, nor symmetric, nor transitive

$$R=\left\{(x, y): \text{x  is  the  father  of  y}\right\}$$

$$(x, x)\notin R$$

As $$x$$ cannot be the father of himself.

$$\therefore R$$ is not reflexive.

Now, let $$(x, y)\in R$$

$$\Rightarrow x$$ is the father of $$y$$.

$$\Rightarrow y$$ cannot be the father of $$y$$.

Indeed, $$y$$ is the son or the daughter of $$y$$.

$$\therefore (y, x)\notin R$$

$$\therefore R$$ is not symmetric.

Now, let $$(x, y)\in R$$ and $$(y, z)\in R$$.

$$\Rightarrow x$$ is the father of $$y$$ and $$y$$ is the father of $$z$$.

$$\Rightarrow x$$ is not the father of $$z$$.

Indeed  $$x$$ is the grandfather of $$z$$.

$$\therefore (x, z)\notin R$$

$$\therefore R$$ is not transitive.

Hence, $$R$$ is neither reflexive, nor symmetric, nor transitive.


Show that the relation $$R$$ in the set $$\textbf{R}$$ of real numbers, defined as $$R=\left\{(a, b):a \leq b^2\right\}$$ is neither reflexive nor symmetric nor transitive.

$$R=\left\{(a, b): a\leq b^2\right\}$$
It can be observed that $$\left(\displaystyle\frac{1}{2}, \frac{1}{2}\right)\notin R$$, since $$\displaystyle \frac{1}{2} > \left(\frac{1}{2}\right)^2=\frac{1}{4}$$.
$$\therefore R$$ is not reflexive.
Now, $$(1, 4)\in R$$ as $$1 < 4^2$$
But, $$4$$ is not less than $$1^2$$.
$$\therefore (4, 1)\notin R$$
$$\therefore R$$ is not symmetric.
Now, $$(3, 2), (2, 1.5)\in R$$
$$(\text{as}   3 < 2^2=4  \text{and}  2 < (1.5)^2=2.25)$$
But, $$3>(1.5)^2=2.25$$
$$\therefore (3, 1.5)\notin R$$
$$\therefore R$$ is not transitive.
Hence, $$R$$ is neither reflexive, nor symmetric, nor transitive.


Check whether the relation $$R$$ defined in the set $$\left\{1, 2, 3, 4, 5, 6\right\}$$ as $$R=\left\{(a, b):b=a+1\right\}$$ is reflexive, symmetric or transitive.

Let $$A=\left\{1, 2, 3, 4, 5, 6\right\}$$.
A relative $$R$$ is defined on set $$A$$ as:
$$R=\left\{(a, b):b=a+1\right\}$$
$$\therefore R=\left\{(1, 2), (2, 3), (3, 4), (4, 5), (5, 6)\right\}$$
We can find $$(a, a)\notin R$$, where $$a\in A$$.
For instance, $$(1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6)\notin R$$
$$\therefore R$$ is not reflexive.
It can be observed that $$(1, 2)\in R$$, but $$(2, 1)\notin R$$.
$$\therefore R$$ is not symmetric.
Now, $$(1, 2), (2, 3)\in R$$
But, $$(1, 3)\notin R$$
$$\therefore R$$ is not transitive.
Hence, $$R$$ is neither reflexive, nor symmetric, nor transitive.


Show that each of the relation $$R$$ in the set $$A=\left\{x\in Z: 0\leq x\leq 12\right\}$$, given by
(i) $$R=\left\{(a, b):|a-b|   \text{is  a  multiple  of  4} \right\}$$
(ii) $$R=\left\{(a, b):a=b\right\}$$
is an equivalence relation. Find the set of all elements related to $$1$$ in each case.

(i)
$$A=\left\{x\in Z:0\leq x\leq 12\right\}=\left\{0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12\right\}$$
$$R=\left\{(a, b):|a-b|   \text{is a  multiple  of  4}\right\}$$
For any element $$a\in A$$, we have $$(a, a)\in R$$ as $$|a-a|=0$$ is a multiple of $$4$$.
$$\therefore R$$ is reflexive.
Now, let $$(a, b)\in R\Rightarrow |a-b|$$ is a multiple of $$4$$.
$$\Rightarrow |-(a-b)|=|b-a|$$ is a multiple of $$4$$.
$$\Rightarrow (b, a)\in R$$
$$\therefore $$ is symmetric.
Now, let $$(a, b), (b, c)\in R$$
$$\Rightarrow |a-b|$$ is a multiple of $$4$$ and $$|b-c|$$ is a multiple of $$4$$.
$$\Rightarrow (a-b)$$ is a multiple of $$4$$ and $$(b-c)$$ is a multiple of $$4$$.
$$\Rightarrow (a-c)=(a-b)+(b-c)$$ is a multiple of $$4$$.
$$\Rightarrow |a-c|$$ is a multiple of $$4$$.
$$\Rightarrow (a, c)\in R$$.
$$\therefore R$$ is transitive.
Hence, $$R$$ is an equivalence relation.
The set of elements related to $$1$$ is $$\left\{1, 5, 9\right\}$$ since 
$$|1-1|=0$$ is a multiple of $$4$$,
$$|5-1|=4$$ is a multiple of $$4$$, and 
$$|9-1|=8$$ is a multiple of $$4$$
Hence, $$R$$ is an equivalence relation.

(ii)
$$A=\{x\in Z: 0\leq x\leq 12\}=\{0,1,2,3,4,......,11,12\}$$
$$R=\left\{(a, b):a=b\right\}=\{(0,),(1,1),(2,2),........,(11,11),(12,12)\}$$
For any element $$a\in A$$, we have $$(a, a)\in R$$, since $$a=a$$.
$$\therefore R$$ is reflexive.
Now, let $$(a, b)\in R$$.
$$\Rightarrow a=b$$
$$\Rightarrow b=a$$
$$\Rightarrow (b, a)\in R$$
$$\therefore R$$ is symmetric.
Now, let $$(a, b)\in R$$ and $$(b, c)\in R$$.
$$\Rightarrow a=b$$ and $$b=c$$
$$\Rightarrow a=c$$
$$\Rightarrow (a, c)\in R$$
$$\therefore R$$ is transitive.
Hence, $$R$$ is an equivalence relation.
The elements in $$R$$ that are related to $$1$$ will be those elements from set $$A$$ which are equal to $$1$$.
Hence, the set of elements related to $$1$$ is $$\left\{1\right\}$$.


Show that the relation $$R$$ defined in the set $$A$$ of all polygons as $$R=\{(P_1, P_2):P_1$$ and $$P_2 $$ have  same  number  of  sides$$\}$$, is an equivalence relation. What is the set of all elements in $$A$$ related to the right angle triangle $$T$$ with sides $$3, 4$$ and $$5$$?

$$R=\left\{(P_1, P_2):P_1   \text{and}  P_2  \text{have  same  the  number  of  sides}\right\}$$
$$R$$ is reflexive since $$(P_1, P_1)\in R$$ as the same polygon has the same number of sides with itself.
Let $$(P_1, P_2)\in R$$.
$$\Rightarrow P_1$$ and $$P_2$$ have the same number of sides.
$$\Rightarrow P_2$$ and $$P_1$$ have the same number of sides.
$$\Rightarrow (P_2, P_1)\in R$$
$$\therefore R$$ is symmetric.
Now,
Let $$(P_1, P_2), (P_2, P_3)\in R$$.
$$\Rightarrow P_1$$ and $$P_2$$ have the same number of sides. Also, $$P_2$$ and $$P_3$$ have the same number of sides.
$$\Rightarrow P_1$$ and $$P_3$$ have the same number of sides.
$$\Rightarrow (P_1, P_3)\in R$$
$$\therefore R$$ is transitive.
Hence, $$R$$ is an equivalence relation.
The elements in $$A$$ related to the right-angled triangle $$(T)$$ with sides $$3, 4, $$ and $$5$$ are those polygons which have $$3$$ sides (since $$T$$  is a polygon with $$3$$ sides).
Hence, the set of all elements in $$A$$ related to triangle $$T$$ is the set of all triangles.


Show that each of the relation $$R$$ in the set $$A=\left\{x\in Z: 0\leq x\leq 12\right\}$$, given by is an equivalence relation. Find the set of all elements related to $$1$$ in each case.
$$R=\left\{(a, b):a=b\right\}$$

$$A=\{x\in Z: 0\leq x\leq 12\}=\{0,1,2,3,4,......,11,12\}$$
$$R=\left\{(a, b):a=b\right\}=\{(0,0),(1,1),(2,2),........,(11,11),(12,12)\}$$
For any element $$a\in A$$, we have $$(a, a)\in R$$, since $$a=a$$.
$$\therefore R$$ is reflexive.
Now, let $$(a, b)\in R$$.
$$\Rightarrow a=b$$
$$\Rightarrow b=a$$
$$\Rightarrow (b, a)\in R$$
$$\therefore R$$ is symmetric.
Now, let $$(a, b)\in R$$ and $$(b, c)\in R$$.
$$\Rightarrow a=b$$ and $$b=c$$
$$\Rightarrow a=c$$
$$\Rightarrow (a, c)\in R$$
$$\therefore R$$ is transitive.
Hence, $$R$$ is an equivalence relation.
The elements in $$R$$ that are related to $$1$$ will be those elements from set $$A$$ which are equal to $$1$$.
Hence, the set of elements related to $$1$$ is $$\left\{1\right\}$$.


Given an example of a relation. Which is Reflexive and symmetric but not transitive.

Let $$A=\left\{4, 6, 8\right\}$$

Define a relation $$R$$ on $$A$$ as:
$$A=\left\{(4, 4), (6, 6), (8, 8), (4, 6), (6, 4), (6, 8), (8, 6)\right\}$$
Relation $$R$$ is reflexive since for every $$\left\{a\in A, (a, a)\in R   i.e., (4, 4), (6, 6), (8, 8)\right\} \in  R$$

Relation $$R$$ is symmetric since $$(a, b)\in R\Rightarrow (b, a)\in R$$ for all 
$$a, b\in R$$.

Relation $$R$$ is not transitive since $$(4, 6), (6, 8)\in R$$, but $$(4, 8)\notin R$$.

Hence, relation $$R$$ is reflexive and symmetric but not transitive.


Show that the relation $$R$$ in the set $$A$$ of points in a plane given by $$R=\left\{(P, Q): \text{distance  of  the  point  $$P$$  from  the  origin  is  same  as  the  distance  of  the  point  $$Q$$  from  the  origin}\right\}$$, is an equivalence relation. Further, show that the set of all point related to a point $$P\neq(0, 0)$$ is the circle passing through $$P$$ with origin as centre.

$$R=\left\{(P, Q): \text{distance  of  point  P from  the  origin  is  the  same  as  the  distance  of  point  Q  from  the  origin}\right\}$$
Clearly, $$(P, P)\in R$$ since the distance of point $$P$$ from the origin is always the same as the distance of the same point $$P$$ from the origin.
$$\therefore R$$ is reflexive.
Now, let $$(P, Q)\in R$$.
$$\Rightarrow$$ the distance of point $$P$$ from the origin is the same as the distance of point $$Q$$ from the origin.
$$\Rightarrow$$ The distance of point $$Q$$ from the origin is the same as the distance of point $$P$$ from the origin.
$$\Rightarrow (Q, P)\in R$$
$$\therefore R$$ is symmetric.
Now, let $$(P, Q), (Q, S)\in R$$.
$$\Rightarrow $$ The distance of points $$P$$ and $$Q$$ from the origin is the same and also, the distance of points $$Q$$ and $$S$$ from the origin is the same.
$$\Rightarrow $$ The distance of points $$P$$ and $$S$$ from the origin is the same.
$$\Rightarrow (P, S)\in R$$.
$$\therefore R$$ is  transitive.
Therefore, $$R$$ is an equivalence relation.
The set of all points related to $$P\neq (0, 0)$$ will be those points whose distance from the origin is the same as the distance of point $$P$$  from the origin.
In other words, if $$O(0, 0)$$ is the origin and $$OP=k$$, then the set of all points related to $$P$$ is at a distance of $$k$$ from the origin.
Hence, this set of points forms a circle with the centre as the origin and this  circle passes through point $$P$$.


Let $$L$$ be the set of all lines in $$XY$$ plane and $$R$$ be the relation in $$L$$ defined as $$R=\{(L_1, L_2):L_1  $$ is  parallel  to $$L_2\ \}$$. Show that $$R$$ is an equivalence relation. Find the set of all lines related to the line $$y=2x+4$$.

$$R=\left\{(L_1, L_2):L_1  \text{ is  parallel  to } L_2\right\}$$
$$R$$ is reflexive as any line $$L_1$$ is parallel to itself i.e., $$(L_1, L_1)\in R$$.
Now, let $$(L_1, L_2)\in R$$.
$$\Rightarrow L_1$$ is parallel to $$L_2$$.
$$\Rightarrow L_2$$ is parallel to $$L_1$$.
$$\Rightarrow (L_2, L_1)\in R$$
$$\therefore R$$ is symmetric.
Now, let $$(L_1, L_2), (L_2, L_3)\in R$$.
$$\Rightarrow L_1$$ is parallel to $$L_2$$. Also, $$L_2$$ is parallel to $$L_3$$.
$$\Rightarrow L_1$$ is parallel to $$L_3$$.
$$\Rightarrow R$$ is transitive.
Hence, $$R$$ is an equivalence relation.
The set of all lines related to the line $$y=2x+4$$ is the set of all lines that are parallel to the line $$y=2x+4$$.
Slope of line $$y=2x+4$$ is $$m=2$$
It is known that parallel lines have the same slopes.
The line parallel to the given line is of the form $$y=2x+c$$, where $$c\in R$$.
Hence,  the set of all lines related to the given line is  given by $$y=2x+c$$, where $$c\in R$$.


Show that the relation $$R$$ defined in the set $$A$$ of all triangles as $$R=\left\{(T_1, T_2):T_1 \text{ is  similar  to}  T_2\right\}$$, is equivalence relation. Consider three right angle triangles $$T_1$$ with sides $$3, 4, 5, T_2$$ with sides $$5, 12, 13$$ and $$T_3$$ with sides $$6, 8, 10$$. Which triangles among $$T_1, T_2$$ and $$T_3$$ are related?

$$R=\left\{ (T_1, T_2):T_1  \text{is  similar  to}  T_2\right\}$$
$$R$$ is reflexive since every triangle is similar to itself.
Further, if $$(T_1, T_2)\in R$$, then $$T_1$$ is similar to $$T_2$$.
$$\Rightarrow T_2$$ is similar to $$T_1$$.
$$\Rightarrow (T_2, T_1)\in R$$
$$\therefore R$$ is symmetric.
Now,
Let $$(T_1, T_2), (T_2, T_3)\in R$$.
$$\Rightarrow T_1$$ is similar to $$T_2$$ and $$T_2$$ is similar to $$T_3$$.
$$\Rightarrow T_1$$ is similar to $$T_3$$.
$$\Rightarrow (T_1, T_3)\in R$$
$$\therefore R$$ is transitive.
Thus, $$R$$ is an equivalence relation.
Now, we can observe that:
$$\displaystyle\frac{3}{6}=\frac{4}{8}=\frac{5}{10}\left(=\frac{1}{2}\right)$$
$$\therefore$$ The corresponding sides of triangles $$T_1$$ and $$T_3$$ are in the same ratio.
Then, triangle $$T_1$$ is similar to triangle $$T_3$$.
Hence, $$T_1$$ is related to $$T_3$$.


Let $$N$$ denote the set of all natural numbers and $$R$$ be the relation on $$N \times N$$ defined by $$(a,b)R(c,d),$$ if $$ad(b+c)=bc(a+d),$$ then show that $$R$$ is an equivalence relation.

$$(a,b)R(c,d)\Leftrightarrow ad(b+c)=bc(a+d)$$
$$ab(b+a)=ba(a+b)\Rightarrow (a,b)R(a,b)$$
Thus, the given relation is reflexive
$$(a,b)R(c,d)\Rightarrow ad(b+c)=bc(a+d)\\ ad(b+c)=bc(a+d)\Rightarrow cb(d+a)=da(c+b)\Rightarrow (c,d)R(a,b)\\ \therefore (a,b)R(c,d)\Rightarrow (c,d)R(a,b)$$
Thus, the given relation is symmetric
$$(a,b)R(c,d)\Leftrightarrow ad(b+c)=bc(a+d)\Rightarrow \dfrac { 1 }{ b } +\dfrac { 1 }{ c } =\dfrac { 1 }{ a } +\dfrac { 1 }{ d } .....(1)\\ (c,d)R(e,f)\Leftrightarrow cf(d+e)=de(c+f)\Rightarrow \dfrac { 1 }{ f } +\dfrac { 1 }{ c } =\dfrac { 1 }{ e } +\dfrac { 1 }{ d } ....(2)\\ (2)-(1)\Rightarrow \dfrac { 1 }{ f } -\dfrac { 1 }{ b } =\dfrac { 1 }{ e } -\dfrac { 1 }{ a } \Rightarrow \dfrac { 1 }{ f } +\dfrac { 1 }{ a } =\dfrac { 1 }{ e } +\dfrac { 1 }{ b } \Rightarrow af(b+e)=be(a+f)\Rightarrow (a,b)R(e,f)\\ \therefore (a,b)R(c,d)\& (c,d)R(e,f)\Rightarrow (a,b)R(e,f)$$
Thus, the given relation is transitive.
Thus, the given relation is an equivalence relation.


Prove that the relation $$R$$ defined on set $$Z$$ as $$a\ R\ b\Leftrightarrow a- b$$ is divisible by $$3$$, is an equivalence relation.

$$a\ R \ b \Leftrightarrow a-b$$ divisible by $$3$$

Reflexive:
$$a\ R \ a \Leftrightarrow a-a$$ divisible by $$3$$..... True
Therefore, the given relation $$R$$ is a reflexive relation.

Symmetric:
$$a\ R \ b \Leftrightarrow a-b$$ divisible by $$3\Rightarrow \ \ a-b = 3k$$, where $$k$$ is an integer.
Then,
$$b\ R \ a \Leftrightarrow b-a$$ divisible by $$3$$
Because $$b-a = -(a-b) = -3k$$ which is divisible by $$3$$.
Therefore, the given relation $$R$$ is a symmetric relation.

Transitive:
$$a\ R \ b \Leftrightarrow a-b$$ divisible by $$3\Rightarrow \ \ a-b = 3k$$, where $$k$$ is an integer.
$$b\ R \ c \Leftrightarrow b-c$$ divisible by $$3\Rightarrow\ \ b-c= 3p$$, where, $$p$$ is an integer
Then,
$$a\ R \ c \Leftrightarrow a-c$$ divisible by $$3$$
Because $$a -c = (a-b)+(b-c) = 3k+3p = 3 (k+p)$$ which is divisible by $$3$$.
Therefore, the given relation $$R$$ is a transitive relation.

Since, the given relation $$R$$ satisfies the reflexive, symmetric, and transitive relation properties, Therefore, it is an equivalence relation.


Let $$A=\{ x \in Z : 0 \leq x \leq 12\}$$. Show that $$R=\{(a, b) : a, b  \in A, |a-b|$$ is divisible by $$4\}$$ is an equivalence relation. Find the set of all elements related to $$1$$. Also write the equivalence class $$[2]$$.

We know that a relation $$R$$ is an equivalence relation, if it is reflexive, symmetric and transitive.

For reflexive:
$$|a-a| = 0 \Leftrightarrow (a,a) \in R, \  \forall a \in A$$

For symmetric:
$$(a,b) \in R \Leftrightarrow |a-b| = 4k = |b-a|,  \ k \in Z \Leftrightarrow (b,a) \in R, \ \forall (a,b) \in R$$

For transitive:
Let $$(a,b) \in R$$ and $$(b,c) \in R$$
Thus, we have
$$ (a,b) \in R \Leftrightarrow |a-b| = 4k_1, \ k_1 \in Z$$ and
$$(b,c) \in R \Leftrightarrow |b-c| = 4k_2, \ k_2 \in Z$$
Since $$a$$, $$b$$ and $$c$$ are integers, we have
$$|a-c| = |a-b + b-c| = |a-b|\pm|b-c| = 4(k_1\pm k_2) = 4m, \ m \in Z \Leftrightarrow (a,c) \in R$$

So, we have shown that the relation $$R$$ is reflexive, symmetric and transitive. Therefore, the relation is an equivalence relation.

Let $$x$$ be the element of $$A $$ such that $$(x,1) \in R$$  
$$|x-1|$$ is a multiple of $$4$$
$$\implies |x-1| = 0,4,8,12$$
$$x-1 = 0,4,8,12$$
$$x = 1,5,9$$ ( As $$13 \notin$$ set of A)
Set of elements related to $$1 = {1,5,9}$$

Now, let us find the elements in the equivalence class $$[2]$$.
Let $$y$$ be the element of $$A$$ such that $$(y,2) \in R$$  
$$|y-2|$$ is a multiple of $$4$$
$$\implies |y-2| = 0,4,8,12$$
$$y-2 = 0,4,8,12$$
$$y = 2,6,10$$ ( As $$14 \notin$$ set of A)
Thus, the elements in the equivalence class $$[2] = {2,6,10}$$.


Prove that intersection of equivalence relations on a set is also an equivalence relation.

We have to prove intersection of
equivalence relations on a set is equivalence
Let us suppose R and S are 2 equivalence
relations on a set A.
So set A implies $$ R\cap S $$ is also equivalence
$$ x \epsilon A \Rightarrow (x,x \epsilon R) $$ and $$ (x,x \epsilon S)$$
$$ (x,x) \epsilon  R\cap S $$
$$ \therefore R\cap S $$ is Reflexive
Now $$ (x,y) \epsilon R\cap S $$
$$ (x,y) \epsilon R $$ and $$ (x,y) \epsilon S$$
$$ (x, y)\epsilon R $$ are equivalence they are symmetric also.
$$ (y,x) \epsilon R $$ and $$ (y,x) \epsilon S.$$
$$ (y,x)\epsilon R\cap S $$
$$ \therefore  R\cap S $$ is symmetric.
finally $$ (x,y) \epsilon R\cap S $$ and $$ (y,z) \epsilon R\cap S $$
$$ (x,y) \epsilon R $$ and $$ (y,z)\epsilon R \Rightarrow (x,z) \epsilon R $$
$$ (x,y) \epsilon S $$ and $$ (y,z)\epsilon S \Rightarrow (x,z)\epsilon S $$
$$ \therefore R $$ is transitive and 's' is transitive
$$ \therefore R \cap S $$ is transitive
$$ \therefore R \cap S $$ is equivalence relation.
i.e, Intersection of equivalence relation set
is equivalence.


1116772_876419_ans_5780500bc8c9466296aae9f11cf706d0.jpg


If $$A=\left\{ 1,2,3,....,9 \right\}$$ and $$R$$ be the relation in $$A\times A$$ defined by $$\left( a,b \right) R\left( c,d \right)$$. If $$a+d=b+c$$ for $$\left( a,b \right), \left( c,d \right)$$ in $$A\times A$$. Prove that $$R$$ is an equivalence relation. Also, obtain the equivalence class $$\left[ \left( 2,5 \right)  \right]$$.

(i) Reflexive : $$ (a,b)R(c,d)$$ if $$ (a,b)(a,d)\in A\times A $$
$$ a+b = b+c $$
Consider $$ (a,b)R(a,b) \Rightarrow (a,b)\in A\times A $$
$$ \Rightarrow a+b = b+a $$ Hence $$R$$ is reflexive
(ii) Symmetric : $$(a,b)R(c,d) $$ given by $$ (a,b)(c,d)\in A\times A $$
$$ a+d = b+c \Rightarrow c+b = d+a $$
$$ \Rightarrow (c,d)R(a,b) $$ Hence $$R$$ is symmetric
(iii) equivalence relation = reflexive + symmetric + transitive
Transitive : Let $$ (a,b)R(c,d)$$ and $$ (c,d)R(c,f) $$
$$ (a,b)(c,d),(c,f)\in A\times A $$
$$ a+b = b+c $$ and $$4 c+f = d+e $$
$$ a+b = b+c $$
$$ \Rightarrow a-c = b-d...(1)$$ & $$ c+f = d+e ...(2) $$
adding (1) & (2) $$ a+f = b+e \Rightarrow (a,b)R(e,f) $$ Transitive 
So, $$R$$ is equivalence relation 
from $$ A = \left \{ 1,2,3...9 \right \} $$ are will select $$a$$ and $$b$$ such that 
$$ 2+b = 5+a $$
Let $$ b= 4 $$ and $$ a = 1 $$ Hence $$ (2+4) = (5+1) $$
and $$ [(2,5)] = \left \{ (1,4)(2,5),(3,6)(4,7)(5,8)(6,9) \right \} $$ is 
the equivalent class under relation $$R$$


Show that the relation $$R$$ in the set $$A = \left \{1, 2, 3, 4, 5\right \}$$ given by $$R = \left \{(a, b) : |a - b|\ is\ even\right \}$$, is an equivalence relation.

Given $$A = \left \{1, 2, 3, 4, 5\right \}$$ and $$R = \left \{(a, b) : |a - b|is\ even\right \}$$
To prove that it is equivalent relation we need to prove that $$R$$ is reflexive, symmetric and transitive.
(i) Reflexive:
Let $$a \epsilon A$$
then $$|a - a| = 0$$ is an even number
$$\therefore (a, a)\epsilon R, \forall a\epsilon A$$
$$\therefore R$$ is reflexive
(ii) Symmetric
Let $$a, b\epsilon A$$
$$\forall (a, b) \epsilon R\Rightarrow |a - b|$$ is even
$$\Rightarrow |-(b - a)|$$ is even
$$\Rightarrow |b - a|$$ is even
$$\Rightarrow |b - a|\epsilon R$$
or $$(b, a)\epsilon R$$
$$\therefore R$$ is symmetric
(iii) Transitive
Let $$a, b, c\epsilon A$$
$$\forall (a, b)\epsilon R$$ and $$(b, c)\epsilon R$$
we have $$|a - b|$$ is even and $$|b - c|$$ is even
$$\Rightarrow a - b$$ is even and $$b - c$$ is even
$$\Rightarrow a - b$$ is even and $$b - c$$ is even
$$\Rightarrow (a - b) + (b - c)$$ is even
$$\Rightarrow a - c$$ is even
$$\Rightarrow |a - c|$$ is even $$\Rightarrow (a, c)\epsilon R\therefore R$$ is transitive
$$\therefore R$$ is an equivalence relation.


Let $$R ={ (a, a), (b, c), (a, b)}$$ be a relation on a set $$A ={a, b, c}$$. Then the minimum number of ordered pairs which when added to make it an equivalence relation are...........

$${ (b, b), (c, c), (b, a), (c, b), ( a, c), (c, a)}$$
$$R = {( a, b), (b, c), (a, b)}$$
For reflexive add (b, b), (c, c) .
$$\therefore$$ $$R= { (a, a), ( b, c), (a, b), (b, b), (c, c)}$$
For symmetric add $$( c, b)$$ and $$( b, a) $$
$$\therefore R = {(a,a), ( b, c) ( a, b), (b, b) (c, c), (c, b), (b, a)}$$
(a, b)$$\in$$ R, (b, c)$$\in$$ R so that (a, c) must belong to R. 
Hence we must add (a, c) and for symmetric we must add (c, a) also.
$$\therefore R = {(a, a), (b, c), (a, b), (b, b), (c, c), (c, b), (b, a), (a, c), (c, a)}$$


Show that the relation $$R$$ in the set $$\mathbb{Z}$$ of integers given by $$R=\left\{(a,b): 2 \ \mbox{divides}\  (a-b)\right\}$$ is equivalence relation.

$$R=\left\{ (a,b):\ 2\ divides\ (a-b) \right\} $$
for $$R on (a,a)
$$a-a=0$$
since $$2$$ divides $$0$$,R is symmetric.
For $$(a,b)\ on\ R$$
Let $$(a-b)=2K$$
 $$(b,a)\ on\ R$$
$$(b-a)=2K$$ is divided by $$2$$
Thus $$R$$ is reflexive
For  $$(a,b)\ on\ R$$
Let $$(a-b)=2K$$
 $$(b,a)\ on\ R$$
$$(b,c)\ on\ R$$
$$(b-c)=2P$$
By solving above equations. We get,
$$(a-c)=2(K+P)$$ is divided by $$2$$.
So (a,c) satisfies $$R$$.
Thus $$R$$ is transitive.
So, $$R$$ is equivilance relation.



Let R is the equivalence relation in the set $$A = \{ 0,1,2,3,4,5\} $$ given by $$R = \{ (a,b):2$$ divides 
$$(a - b)\} $$. Write the equivalence class $$[0]$$

Set $$A = \left \{ 0,1,2,3,4,5 \right \}$$ 
$$R$$ be the equivalence relation on A.
Set $$R=\left \{ (a,b)2 \,divides \, (a-b) \right \}$$
We have to find equivalnce class $$\left [ 0 \right ]$$
To find equivalence class $$\left \{ 0 \right \}$$,put $$b=0$$
$$\Rightarrow  a-0$$ is multiple of $$2$$ . 
$$\Rightarrow $$ a is multiple of $$2 $$. 
Multiples of $$2$$ in given set are $$0,2$$ and $$4$$ . 
Hence equivalence class $$\left \{ 0 \right \}=\left \{ 0,2,4 \right \}$$


Let $$L$$ be the set of all lines in a plane and $$R$$ be the relation in $$L$$ defined as $$R = \{(L_1, L_2): L_1 \bot L_2\}$$. Show that $$R$$ is symmetric but neither reflexive nor transitive.

Given the relation $$R$$ is defined as $$R = \{(L_1, L_2): L_1 \bot L_2\}$$.
Now this relation is not reflexive as $$_{L_1}R_{ L_1}$$ does not hold as every line is not perpendicular to itself.
The relation is symmetric as $$_{L_1}R_{L_2}$$ gives $$_{L_2}R_{L_1}$$. [ As if $$L_1$$ is perpendicular to $$L_2$$ then $$L_2$$ is also perpendicular to $$L_1$$].
The relation is not transitive as $$_{L_1}R_{L_2}, _{L_2}R_{L_3}$$ does not gives $$_{L_1}R_{L_3}$$. [ As, if $$L_1$$ is perpendicular to $$L_2$$ and $$L_2$$ is perpendicular to $$L_3$$ then $$L_1$$ may of may not be perpendicular to $$L_3$$]


If $$A=[2,4,5],B=[7,8,9]$$ then $$n(A\times B)$$ is equal to?

Given $$A=[2,4,5],B=[7,8,9]$$

To find: $$n(A\times B)=?$$

$$A\times B=\{(2,7),(2,8),(2,9),(4,7),(4,8),(4,9),(5,7),(5,8),(5,9)\}$$

$$\therefore n(A\times B)=9$$


Show that the relation R on the set N of natural numbers defined as 
R = { (x, y): y - x is a multiple of 2 }
is an equivalence relation


1328544_1079788_ans_9405dddce436489a9f3eba836730f34c.jpg


If $$P = \left \{1, 2\right \}$$, Find the set $$P\times P\times P$$.

$$P \times P\times P=\left\{\left(1,1,1\right), \left(1,1,2\right),\left(1,2,1\right), \left(1,2,2\right) ,\left(2,1,1\right), \left(2,1,2\right), \left(2,2,1\right), \left(2,2,2\right)\right\}$$


State the reason why the relation $$S={(a,b)\in R \times R : a \le b^{3}}$$ on the set $$R$$ of real numbers is not transitive.

$$S = (a , b) \in R \times R ; a \le b^3$$
If $$(a, b) \in R \, \& \, (b, c) \in R$$ then $$(a, c) \in R$$
it $$a < b^3 \, \& \,b < c^3$$ then $$a < c^3$$
$$\begin{matrix} a & b & c & b^3 & c^3 & a <b^3 & b < c^3 & a < c^3   \\ 1 & 2 & 3 & 4 & 27 & true & True &True\\ 3 & 3/2 & 4/3 & 3.375 & 2.37 & True & True & False \end{matrix}$$
$$a < b^3 , b < c^3 $$ then $$a < c^3 $$ is not 
true for all real numbers.
Hence, relatipn is not transitive.


P.T on the set of natural numbers the relation R defines by x R y $$\Rightarrow x$$ <$$y$$ is transitive but not reflexive.

$$xRy \Rightarrow x < y$$
Let set of natural number be 1,2,3,4
$$\begin{array}{l} \Rightarrow \left( { 1,2 } \right) ,\left( { 2,3 } \right) ,\left( { 3,4 } \right) ,\left( { 4,5 } \right) ,\left( { 5,6 } \right)  \\ \Rightarrow \begin{array} { *{ 20 }{ c } }{ 1<2 } \\ { 1\, \, R\, \, 2 } \end{array},\begin{array} { *{ 20 }{ c } }{ 2<3 } \\ { 2\, \, R\, \, 3 } \end{array} \\ \therefore \begin{array} { *{ 20 }{ c } }{ 1<3 } \\ { 1\, \, R\, \, 3 } \end{array},hence\, \, it\, \, is\, \, transitive \end{array}$$
$$ \Rightarrow$$ if a R b, b R c, and c R a then it is transitive
$$ \Rightarrow 1\measuredangle 1,\,\,2\measuredangle 2$$
Hence, it is not reflexive.


How many equivalence relations on the set {1,2,3} containing (1,2) and (2,1) are there in all? Justify your answer.

Total possible pairs $$=\{(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2),(3,3)\}$$
$$Reflexive$$ means (a,a) should be in relation.
So, $$(1,1),(2,2),(3,3)$$ should be in relation.
$$Symmetric$$ means if (a,b) is in relation, then (b,a) should be in relation.
So, since$$(1,2)$$ is in relation, $$(2,1)$$ should also be in relation
$$Transitive$$ means if (a,b) is in relation and (b,c) is in relation, then (a,c) is in relation.
So, if $$(1,2)$$ is in relation and $$(2,1)$$ is in relation, then $$(1,1)$$ should be in relation.
Relation $$R_1=\{(1,2),(2,1),(1,1),(2,2),(3,3)\}$$
Total possible pairs $$=\{(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2),(3,3)\}$$
So, smallest relation is $$R_1=\{(1,2),(2,1),(1,1),(2,2),(3,3)\}$$
If we add $$(2,3)$$
then we have to add $$(3,2)$$ also, as it is symmetric
but, as $$(1,2)\ \&\ (3,2)$$ are there, we need to add $$(1,3)$$ also, as it is transitive
As we are adding $$(1,3)$$ we should add $$(3,1)$$ also, as it is symmetric
Relation $$R_2=\{(1,2),(2,1),(1,1),(2,2),(3,3),(2,3),(3,2),(1,3),(3,1)\}$$
Hence, only two possible relation are there which are equivalence.


If A and B have n elements in common,then the number of elements common to $$A \times B\,and\,B \times A\,$$ is:

Let A and B be two non-empty sets heaving n elements in common, then we have 
$$ (A\times B)\cap (C\times D) = (A\cap C)\times (B\cap  D) $$

It is given that $$ n(A\cap B) = n $$ elements 

Now $$ n[(A\cap B)\times (B\cap A)] = n.n = n^{2} $$ elements

Hence, $$ A\times B $$ and $$ B\times A $$ have $$ n^{2} $$ elements in common .


Total number of equivalence relations defined in the set $$S = \{ a , b , c \}$$ is ?

Step 1.
  • Consider the relation R1 = { (a,a) }
it is reflexive ,symmetric and transitive
  • similarly R2= {(b,b)} , R3= {(c,c)} are reflexive ,symmetric and transitive
Step 2.
  • Also R4 = {  (a,a) ,(b,b),(c,c), (a,b),(b,a)}
it is reflexive as(x,x)∈R(a,a)∈R for all x∈a,b,ca∈1,2,3
it is symmetric as (x,y)∈R=>(y,x)∈R(a,b)∈R=>(b,a)∈R for all  x,y∈a,b,ca∈1,2,3
also it is transitive as (a,b)∈R,(b,a)∈R=>(a,a)∈R(1,2)∈R,(2,1)∈R=>(1,1)∈R
Step. 3
  •  The relation defined by R = {(a,a), (b,b) , (c,c) , (a,b), (a,c),(b,a),(b,c), (c,a),(c,b)}
is reflexive symmetric and transitive
 
  • Thus Maximum number of equivalance relation on set 
A={a,b,c}A={1,2,3} is 5


For real numbers $$x$$ and $$y$$ we write $$_x R_y$$ iff $$x-y+\sqrt{ 2 } $$ is an irrational numbers. Then relation $$R$$ is reflexive and symmetric also. 

For every value of x belongs to R, $$x-x+\sqrt{2}$$
i.e., $$\sqrt{2}$$ is an irrational number.
Therefore, it is reflexive.
Now Let's say $$x=\sqrt{2}$$ and $$y=2$$ then $$x-y+\sqrt{2}=2\sqrt{2}-2$$ which is irrational 
but when $$y=\sqrt{2}$$ and $$x=2$$,
$$x-y+\sqrt{2}$$ is not irrational;
$$\therefore$$ it is not symmetric.



Given that $$R=\left\{(a, b)|3\ divides a-b\right\}$$ is an equivalence relation in steel in the set of integers $$Z$$. What is the number of partitions of $$Z$$?

Given that:

$$R=\left\{ (a,\ b)\ :\ 3\ divides\ a-b \right\}$$


Case I : Reflexive

Since,  $$a-a=0$$

And                                              

$$ 3\ \ divides\ \ 0,\ \ \ \therefore \ \ \dfrac{0}{2}=0 $$

$$ \Rightarrow 2\ divides\ \ a-a $$

$$ \therefore (a,\ 0)\ \in \ R. $$

$$ \therefore R\ \text{is}\ \text{reflexive} $$


Case II : - Symmetric

$$ \text{If}\ \text{3 divides a - b,} $$

$$ \text{then, 3 divides - (a - b) i}\text{.e}\text{. b - a} $$

 $$ \text{Hence, If ( a , b) }\in \text{R, Then ( b , a) }\in R $$

 $$ \therefore R\ \text{is}\ \text{symmetric}\text{.} $$


 $$ \text{Case}\ \text{III}\text{. Transitive}\text{.} $$

 $$ \text{If 3 divides ( a - b) and 3 divides ( b - c)} $$

 $$ \text{So, 2 divides ( a - b) + ( b - c)} $$

 $$ \text{also,} $$

 $$ \text{2 divides ( a - c)} $$


 $$ \therefore If ( a , b)\ \in R\ \text{and}\ ( b ,\ c)\ \in R $$

 $$ then, $$

 $$ ( a ,\ c)\ \in R $$

 $$ \text{Thus, R is an equivalence relation in z}\text{.} $$


Hence, this is the answer.



State true or false:
A relation $$R $$ in a set $$A$$ is called symmetric if $$(a,b) \in R $$ implies that $$(b,a) \in R ,\forall a,b \in A  $$.

We know that a relation $$R $$ in a set $$A$$ is called symmetric if $$(a,b) \in R $$ implies that $$(b,a) \in R ,\forall a,b \in A  $$.
Thus, the given statement is true.


Prove that if $$R$$ is an equivalence relation then $$R^{-1}$$ is also.

R be an equilence relation 
$$a\quad { R^{ -1 } }b=b\, \, R\, a$$
R is an equilance relation 
$$aRa\, \, a{ R^{ -1 } }a\, \, \, \, { R^{ -1 } }$$ is reflexive
$$\begin{array}{l} a{ R^{ -1 } }b\, \, \, \, \, bRa \\ aRb\, \,  \end{array}$$ systematic
$$a{ R^{ -1 } }b\, \, \, \, b{ R^{ -1 } }c$$
R is transitive
$$cRa\, \, \, \, a{ R^{ -1 } }c$$
$${ R^{ -1 } }$$ is transitive
combining we say $${ R^{ -1 } }$$ is equivalence


If the set $$A$$ has $$3$$ elements and the set $$B=(3,4,5)$$ find the number of elements in $$(A\times B)$$?

$$\begin{matrix} Number\, \, of\, \, elements\, \, in\, \, A=3 \\ Number\, \, of\, \, elements\, \, in\, \, B=3 \\ Number\, \, of\, \, elements\, \, in\, \left( { A\times B } \right)  \\ =3\times 3\, \, \, =9 \\  \end{matrix}$$


Let $$A$$ and $$B$$ be two sets such that $$A\times\,B$$ consists of $$6$$ elements.If three elements of $$A\times B$$ are $$\left\{\left(1,4\right),\left(2,6\right),\left(3,6\right)\right\}$$.Find $$A\times B$$ and $$B\times A$$

Since $$\left\{\left(1,4\right),\left(2,6\right),\left(3,6\right)\right\}$$ are the elements of $$A\times B$$.
It follows that the elements of set $$A=\left\{1,2,3\right\}$$ and $$B=\left\{4,6\right\}$$
Hence $$A\times B=\left\{\left(1,4\right),\left(1,6\right),\left(2,4\right),\left(2,6\right),\left(3,4\right),\left(3,6\right)\right\}$$
$$B\times A=\left\{\left(4,1\right),\left(4,2\right),\left(4,3\right),\left(6,1\right),\left(6,2\right),\left(6,3\right)\right\}$$



If A= $$\left\{ x:{ x }^{ 2 }+5x+6=0,x\quad \epsilon \quad N \right\} $$ then $$n\left( A  \right) =..........$$

$${x}^{2}+5x+6=0$$

$${x}^{2}+3x+2x+6=0$$

$$x\left(x+3\right)+2\left(x+3\right)=0$$

$$\left(x+3\right)\left(x+2\right)=0$$

$$x=\left\{-2,-3\right\}\notin N$$

$$\therefore n\left(A\right)=0$$


Give an example of a relation. which is reflexive and symmetric and Transitive

$$\textbf{Step -1: Define a set and relation.}$$
                 $$\text{Let set }A = \text{{1, 2, 3}}$$A=1,2,3
                 $$\text{And relation }R = (1, 1), (1, 3), (3, 1), (2, 2), (2, 3), (3, 3)$$
$$\textbf{Step -2: Check for reflexive.}$$
R=(1,1),(1,3),(3,1),(2,2),(3,3)                 $$\text{Relation is reflexive if, }(a, a) \in R \text{ for every }a\in A$$
                 $$\text{Since, }(1, 1), (2, 2), (3, 3)\in R\text{ and }(1, 2, 3)\in A$$
                 $$\therefore \text{R is reflexive.}$$
$$\textbf{Step -3: Check for symmetric.}$$
                 $$\text{Relation is symmetric if, }(a, b) \in R \text{ and }(b, a) \in R\text{ for every }(a, b)\in A$$
                 $$\text{Since, }(1, 3)\in R\text{ and } (3, 1)\in R \text{ and }(1, 3)\in A$$
                 $$\therefore \text{R is symmetric.}$$
$$\textbf{Step -3: Check for transitive.}$$
                 $$\text{Relation is transitive if, }(a, b) \in R \text{ and }(b, c) \in R \text{ then }(a, c)\in R \text{ for every }(a, b, c)\in A$$
                 $$\text{Since, }(1, 2)\in R\text{ and } (2, 3)\in R \text{ and }(1, 3)\in R \text{ also {1, 2, 3}}\in A$$
                 $$\therefore \text{R is transitive.}$$
$$\textbf{Here R is reflexive, symmetric and transitive.}$$


$$R=\left\{(a,b):a,b \epsilon N,a \neq b\ and\ a\ divided\ b\right\}$$ is $$R$$ reflexive. Give reason

$$R = \left\{ \left( a, b \right) : a, b \; \in \; N, \; a \ne b \text{ and a divided by b} \right\}$$

Since $$a \ne b$$.

Therefore,

$$\left\{ \left( a, a \right), \left( b, b \right) \right\} \notin R$$

Hence $$R$$ is not reflexive.


If $$A=\left\{1,2\right\}$$.Find $$A\times A\times A$$

We have $$A=\left\{1,2\right\}$$
$$A\times A=\left\{1,2\right\}\times\left\{1,2\right\}$$
$$=\left\{\left(1,1\right),\left(1,2\right),\left(2,1\right),\left(2,2\right)\right\}$$
$$A\times A\times A=\left\{\left(1,1\right),\left(1,2\right),\left(2,1\right),\left(2,2\right)\right\}\times\left\{1,2\right\}$$
$$=\left\{(\left(1,1\right),1),\left((1,2),1\right),\left((2,1),1\right),\left((2,2),1\right),\left((1,1),2\right),\left((1,2),2\right),\left((2,1),2\right),\left((2,2),2\right)\right\}$$


Prove that every identity relation on a set is reflexive, but the converse is not necessarily true.

Let $$A=\left \{a,b,c\right \}$$
Let $$I_A$$ is an identity relation of $$A$$.
Then, $$I_A=\left \{(a,a),a\epsilon A\right \}$$
So, identity relation will be reflexive.
Let $$R$$ be reflexive relation such that
$$R=\left \{(a,a),(b,b),(c,c),(a,b),(b,c)\right \}$$
$$R$$ contains $$(a,b)$$ and $$(b,c)$$ which are not elements of an identity relation.
So, it is not necessary that a reflexive relation is always an identity relation.


Show that the relation $$R$$ on the set $$Z$$ of all integer, given by $$R = \{(a, b) : 2$$ divides $$(a - b)\}$$ is an equivalence relation.

$$2$$ divides $$(a-b)\implies a-b=2{k}$$
$$(a,a)\implies a-a=0$$ 
As $$2$$ divides $$0$$  So $$R$$ is reflexive
Let  $$R$$ contains $$(a,b)\implies a-b=2{k}\implies b-a=-2{k}$$ 
As $$b-a=-2{k}\implies (b,a)$$ satisfies $$R$$
So $$R$$ is symmetric
Let $$(a,b),(b,c)$$ satisfies $$R\implies a-b=2 k_1,b-c=2{k_2}\implies a-c=2(k_1+k_2)$$
So $$(a,c)$$ also satisfies $$R$$
So $$R$$ is transitive 
Since $$R$$  is Reflexive ,Symmetric and transitive So $$R$$ is an equivalence relation 


Let $$A=\left\{ 1,2,3 \right\} $$ and $$R=\left\{ \left( 1,2 \right) ,\left( 1,1 \right) ,\left( 2,3 \right)  \right\} $$ be a relation on $$A$$. What minimum number of ordered pairs may be added to $$R$$, so that it may become a transitive relation on $$A$$?

Given, $$A=\left\{ 1,2,3 \right\} $$ and $$R=\left\{ \left( 1,2 \right) ,\left( 1,1 \right) ,\left( 2,3 \right)  \right\} $$.
Now this relation is not transitive as $$(1,2)\in R, (2,3)\in R$$ but $$(1,3)\not \in R$$.
So to make $$R$$ transitive we are to add this order pair.
Then the relation will be $$R=\{(1,2), (1,1), (2,3),(1,3)\}$$.
This relation $$R$$ is transitive.
So minimum one pair is to be added to make $$R$$ symmetric.


Let $$R$$ be the relation defined on the set $$A=\left\{ 1,2,3,4,5,6,7 \right\} $$ by $$R=\left\{ \left( a,b \right) :\ \text{both a and b are either odd or even} \right\} $$. Show that $$R$$ is an equivalence relation. Further, show that all the elements of the subset $$\left\{ 1,3,5,7 \right\} $$ are related to each other similarly all the elements of the subset $$\left\{ 2,4,6 \right\} $$ too.

The relation $$R$$ on set $$A=\left\{ 1,2,3,4,5,6,7 \right\} $$ is defined by 

$$R=\left\{ \left( a,b \right) :\ \text{both a and b are either odd or even} \right\} $$

We observe the following properties of $$R$$ on $$A$$

Reflexivity: Clearly, $$(1,1), (2,2), (3,3), (4,4), (5,5), (6,6), (7,7)\in R$$. So, $$R$$ is a reflexive relation in $$A$$

Symmetric: Let $$a,b\in A$$ be such that $$(a,b)\in R$$. 

Then, $$(a,b)\in R$$

Both $$a$$ and $$b$$ are either odd or even

Both $$b$$ and $$a$$ are either odd or even

$$\Rightarrow$$ $$(b,a)\in R$$

Thus, $$(a,b)\in R\Rightarrow (b,a)\in R$$ for all $$a,b\in A$$

So, $$R$$ is a symmetric relation on $$A$$

Transitivity: Let $$a, b, c\in Z$$ be such that $$(a,b)\in R,(b,c)\in R$$. 

Then, $$(a,b)\in R\Rightarrow$$ Both $$a$$ and $$b$$ are either odd or even

$$(b,c)\in R\Rightarrow$$ Both $$b$$ and $$c$$ are either odd or even

If both $$a$$ and $$b$$ are even, then

$$(b,c)\in R\Rightarrow$$ Both $$b$$ and $$c$$ are even

If both $$a$$ and $$b$$ are odd, then

$$(b,c)\in R\Rightarrow$$ Both $$b$$ and $$c$$ are odd

$$\therefore$$ Both $$a$$ and $$c$$ are even or odd. Therefore $$(a,c)\in R$$

So, $$(a,b)\in R$$ and $$(b,c)\in R\Rightarrow (a,c)\in R$$

Consequently, $$R$$ is a transitive relation on $$A$$

Hence, $$R$$ is an equivalence relation on $$A$$

We observe that two numbers in $$A$$ are related if both are odd or both are even.

 Since $$\left\{ 1,3,5,7 \right\} $$ has all odd numbers of $$A$$. So, all the numbers of $$\left\{ 1,3,5,7 \right\} $$ are related to each other.

 Similarly, all the numbers of $$\left\{ 2,4,6 \right\} $$ are related to each other as it contains all even numbers of set $$A$$.

 An even ,odd number in $$A$$ is related to an even ,odd number in $$A$$ respectively. 

So, no number of the subset $$\left\{ 1,3,5,7 \right\} $$ is related to any number of the subset $$\left\{ 2,4,6 \right\} $$


Show that the relation $$R$$ defined by $$R=\left\{ \left( a,b \right) :3\  \text{divides}\ a-b\ \text{for} \  a,b\in Z \right\} $$ is an equivalence relation.

The relation is $$R$$ on $$Z$$ is given by $$R=\left\{ \left( a,b \right) :3\  \text{divides}\ a-b\ \text{for} \  a,b\in Z \right\} $$ .
We observe the following properties of relation $$R$$
Reflexivity: for any $$a\in Z$$
$$a-a=0=0\times 3$$
$$\Rightarrow$$ $$3$$ divides $$a-a\Rightarrow (a,a)\in R$$
So, $$R$$ is relexive relation on $$Z$$
Symmetry: Let $$a,b\in Z$$ be such that
$$(a,b)\in R$$
$$\Rightarrow$$ $$3$$ divides $$a-b$$
$$\Rightarrow$$ $$a-b=3\lambda$$ for some $$\lambda \in Z$$
$$\Rightarrow$$ $$b-a=3(-\lambda)$$, where $$-\lambda \in Z$$
$$\Rightarrow$$ $$3$$ divides $$b-a\Rightarrow (b,a)\in R$$
Thus $$(a,b)\in R\Rightarrow (b,a)\in R$$. So, $$R$$ is a symmetric relation on $$Z$$.
Transitivity. Let $$a,b,c\in Z$$ be such that $$(a,b)\in R$$ and $$(b,c)\in R$$. Then,
$$(a,b)\in R\Rightarrow 3$$ divides $$a-b\Rightarrow a-b=3\lambda$$ for some $$\lambda \in Z$$
and $$(b,c)\in R\Rightarrow 3$$ divides $$b-c\Rightarrow b-c=3\mu$$ for some $$\mu \in Z$$
$$\therefore$$ $$a-b+b-c=3(\lambda +\mu)$$
$$\Rightarrow$$ $$a-c=3(\lambda +\mu)$$, where $$\lambda +\mu \in Z$$
$$\Rightarrow$$ $$3$$ divides $$a-c$$
$$\Rightarrow$$ $$(a,c)\in R$$
thus, $$(a,b)\in R$$ and $$(b,c)\in R\Rightarrow (a,c)\in R$$
So, $$R$$ is a transitive relation on $$Z$$
Hence, $$R$$ is an equivalence relation on $$Z$$


Show that the relation $$R$$ on the set $$A=\left\{ x\in Z;0\le x\le 12 \right\} $$, given by $$R=\left\{ \left( a,b \right) :a=b \right\} $$, is an equivalence relation.

The given relation $$R$$ is reflexive as $$(a,a)\in R$$ since $$a=a$$ for all $$a\in A$$.
Again the relation is symmetric as if $$(a,b)\in R$$ this gives $$(b,a)\in R$$ since $$a=b\Rightarrow b=a$$ for all $$a,b \in A$$.
Also the relation is transitive as if $$(a,b)\in R,(b,c)\in R$$ this gives $$(a,c)\in R$$ since $$a=b,b=c\Rightarrow a=c$$ for all $$a,b,c\in A$$.
Hence the given relation is reflexive, symmertic and transitive so it's a equivalance relation.


Let $$R$$ be a relation on the set $$A$$ of ordered pairs of non-zero integers defined by $$(x,y)R(u,v)$$. If $$xv=yu$$, then show that $$R$$ is an equivalence relation.

The relation $$R$$ on $$Z\times Z$$ is defined by
$$(x,y)R(u,v)\Leftrightarrow xv=yu$$ for all $$(x,y),(u,v)\in Z\times Z$$
We observe the following properties of $$R$$ on $$Z\times Z$$

Reflexivity: For any $$(x,y)\in Z\times Z$$
$$xy=yx$$
$$\Rightarrow$$ $$(x,y)R(x,y)$$
Thus, $$(x,y)R(x,y)$$ for all $$(x,y)\in Z\times Z$$
So, $$R$$ is a reflexive relation on $$Z\times Z$$

Symmetry: Let $$(x,y), (u,v)\in Z\times Z$$ such that $$(x,y)R(u,v)$$. Then, $$(x,y)R(u,v)\Rightarrow xv=yu\Rightarrow uy=vx\Rightarrow(u,v)R(x,y)$$
Thus, $$(x,y)R(u,v)\Rightarrow (u,v)R(x,y)$$ for all $$(x,y), (u,v)\in Z\times Z$$
So, $$R$$ is a symmetric relation on $$Z$$

Transitivity: Let $$(x,y),(u,v),(a,b)\in Z\times Z$$ be such that $$(x,y)R(u,v)$$ and $$(u,v)R(a,b)$$
Then,
$$(x,y)R(u,v)\Rightarrow xv=yu$$
and $$(u,v)R(a,b)\Rightarrow ub=va$$
$$\Rightarrow$$ $$(xv)(ub)=(yu)(va)\Rightarrow xb=ya\Rightarrow (x,y)R(a,b)$$
So, $$R$$ is a transitive relation on $$Z\times Z$$
Hence, $$R$$ is an equivalence relation on $$Z\times Z$$


Prove that the relation $$R$$ on $$Z$$ defined by $$\left( a,b \right) \in R\Leftrightarrow$$ $$5 $$ divides $$ a-b$$, is an equivalence relation on $$Z$$.

Let the relation be $$R$$ on $$Z$$ is given by $$R=\left\{ \left( a,b \right) :5\quad \text{divides}\quad a-b \right\} $$.
We observe the following properties of relation $$R$$
Reflexivity: for any $$a\in Z$$
$$a-a=0=0\times 5$$
$$\Rightarrow$$ $$5$$ divides $$a-a\Rightarrow (a,a)\in R$$
So, $$R$$ is relexive relation on $$Z$$
Symmetry: Let $$a,b\in Z$$ be such that
$$(a,b)\in R$$
$$\Rightarrow$$ $$5$$ divides $$a-b$$
$$\Rightarrow$$ $$a-b=5\lambda$$ for some $$\lambda \in Z$$
$$\Rightarrow$$ $$b-a=5(-\lambda)$$, where $$-\lambda \in Z$$
$$\Rightarrow$$ $$5$$ divides $$b-a\Rightarrow (b,a)\in R$$
Thus $$(a,b)\in R\Rightarrow (b,a)\in R$$. So, $$R$$ is a symmetric relation on $$Z$$.
Transitivity. Let $$a,b,c\in Z$$ be such that $$(a,b)\in R$$ and $$(b,c)\in R$$. Then,
$$(a,b)\in R\Rightarrow 5$$ divides $$a-b\Rightarrow a-b=5\lambda$$ for some $$\lambda \in Z$$
and $$(b,c)\in R\Rightarrow 5$$ divides $$b-c\Rightarrow b-c=5\mu$$ for some $$\mu \in Z$$
$$\therefore$$ $$a-b+b-c=5(\lambda +\mu)$$
$$\Rightarrow$$ $$a-c=5(\lambda +\mu)$$, where $$\lambda +\mu \in Z$$
$$\Rightarrow$$ $$5$$ divides $$a-c$$
$$\Rightarrow$$ $$(a,c)\in R$$
thus, $$(a,b)\in R$$ and $$(b,c)\in R\Rightarrow (a,c)\in R$$
So, $$R$$ is a transitive relation on $$Z$$
Hence, $$R$$ is an equivalence relation on $$Z$$.


Show that the relation $$R$$ on the set $$Z$$ of integers, given by $$R=\left\{ \left( a,b \right) :2\ \text{divides}\  a-b \right\} $$ is an equivalence relation.

The relation $$R$$ on $$Z$$ is given by $$R=\left\{ \left( a,b \right) :2\quad \text{divides}\quad a-b \right\} $$
We observe the following properties of relation $$R$$

Reflexivity: for any $$a\in Z$$
$$a-a=0=0\times 2$$
$$\Rightarrow$$ $$2$$ divides $$a-a\Rightarrow (a,a)\in R$$
So, $$R$$ is relexive relation on $$Z$$

Symmetry: Let $$a,b\in Z$$ be such that
$$(a,b)\in R$$
$$\Rightarrow$$ $$2$$ divides $$a-b$$
$$\Rightarrow$$ $$a-b=2\lambda$$ for some $$\lambda \in Z$$
$$\Rightarrow$$ $$b-a=2(-\lambda)$$, where $$-\lambda \in Z$$
$$\Rightarrow$$ $$2$$ divides $$b-a\Rightarrow (b,a)\in R$$
Thus $$(a,b)\in R\Rightarrow (b,a)\in R$$. So, $$R$$ is a symmetric relation on $$Z$$.

Transitivity. Let $$a,b,c\in Z$$ be such that $$(a,b)\in R$$ and $$(b,c)\in R$$. Then,
$$(a,b)\in R\Rightarrow 2$$ divides $$a-b\Rightarrow a-b=2\lambda$$ for some $$\lambda \in Z$$
and $$(b,c)\in R\Rightarrow 2$$ divides $$b-c\Rightarrow b-c=2\mu$$ for some $$\mu \in Z$$
$$\therefore$$ $$a-b+b-c=2(\lambda +\mu)$$
$$\Rightarrow$$ $$a-c=2(\lambda +\mu)$$, where $$\lambda +\mu \in Z$$
$$\Rightarrow$$ $$2$$ divides $$a-c$$
$$\Rightarrow$$ $$(a,c)\in R$$
thus, $$(a,b)\in R$$ and $$(b,c)\in R\Rightarrow (a,c)\in R$$
So, $$R$$ is a transitive relation on $$Z$$
Hence, $$R$$ is an equivalence relation on $$Z$$


$$m$$ is said to be related to $$n$$, if $$m$$ and $$n$$ are integers and $$m-n$$ is divisible by $$13$$. Does this define an equivalence relation?

Let us denote this relation by $$R$$.
Now this relation is reflexive as $$(x,x)\in R$$ as $$x-x=0$$ is always divisible by $$13$$ for all $$x$$.
Similarly the relation is also symmetric as if $$(x,y)\in R$$ this gives $$(y,x)\in R$$ as if $$x-y$$ is divisible by $$13$$ then $$y-x$$ is also divisible by $$13$$ for all $$x,y$$.
Again this relation $$R$$ is also transitive as if $$(x,y)\in R, (y,z)\in R$$ this gives $$(x,z)\in R$$ as $$x-y=13k_1$$....(1) [ Since $$x-y$$ is divisible by $$13$$] and $$y-z=13k_2$$....(2) [ Since $$y-z$$ is also divisible by $$13$$]
Now adding (1) and (2) we get, 
$$x-z=13(k_1+k_2)$$. [ For $$k_1 $$ and $$k_2$$ integers]
This gives $$x-z$$ is also divisible by $$13$$.
So the relation is also transitive.
Hence the relation is reflexive, transitive and symmetric so it is an equivalance relation.


Show that the relation $$R$$, defined on the set $$A$$ of all polygons as 
$$R=\left\{ \left( { P }_{ 1 },{ P }_{ 2 } \right) :{ P }_{ 1 } \ \text{and}\  { P }_{ 2 }\ \text{ have same number of sides}\ \right\} $$ is an equivalence relation. What is the set of  elements in $$A$$ related to the right angle triangle $$T$$ with sides $$3,4$$ and $$5$$?

The relation $$R$$ on the set of $$A$$ of all polygons is defined as 

$$R=\left\{ \left( { P }_{ 1 },{ P }_{ 2 } \right) :{ P }_{ 1 }\ \text{ and}\ { P }_{ 2 }\ \text{ have same number of sides} \right\} $$

We observe the following properties of $$R$$ on $$A$$

Reflexivity: Let $$P$$ be any polygon in $$A$$. 

Then, $$P$$ and $$P$$ have same number of sides
$$\Rightarrow$$ $$(P,P)\in R$$

Thus $$(P,P)\in R$$ for all $$P\in A$$. So, $$R$$ is a reflexive relation on $$A$$Symmetry: Let $${P}_{1},{P}_{2}$$ be two polygons in $$A$$ such that $$({P}_{1},{P}_{2})\in R$$. 

Then,
$$({P}_{1},{P}_{2})\in R$$

$$\Rightarrow$$ $${P}_{1}$$ and $${P}_{2}$$ have same number of sides

$$\Rightarrow$$ $${P}_{2}$$ and $${P}_{1}$$ have same number of sides

$$\Rightarrow$$ $$({P}_{2},{P}_{1})\in R$$

So, $$R$$ is symmetric on $$A$$Transitivity: Let $${P}_{1},{P}_{2},{P}_{3}$$ be three polygons in $$A$$ such that $$({P}_{1},{P}_{2})\in R$$ and $$({P}_{2},{P}_{3})\in R$$

Then
$$({P}_{1},{P}_{2})\in R\Rightarrow {P}_{1}$$ and $${P}_{2}$$ have same number of sides

and $$({P}_{2},{P}_{3})\in R\Rightarrow {P}_{2}$$ and $${P}_{3}$$ have same number of sides

$${P}_{1}$$ and $${P}_{3}$$ have same number of sides.

$$\Rightarrow$$ $$({P}_{1},{P}_{3})\in R$$

Thus, $$({P}_{1},{P}_{2})\in R$$ and $$({P}_{2},{P}_{3})\in R\Rightarrow ({P}_{1},{P}_{3})\in R$$

So, $$R$$ is a transitive relation on $$A$$

Hence, $$R$$ is an equivalence relation on $$A$$Let $$P$$ be polygon in $$A$$ such that $$(P,T)\in R$$, where $$T$$ is a right angled triangle with sides $$3, 4$$ and $$5$$. 

Then, $$(P,T)\in R$$

Polygon $$P$$ and triangle $$T$$ have same number of sides

$$P$$ is any triangle in $$A$$

Hence, the set of all elements in $$A$$ related to $$T$$ so $$T$$ is the set of all triangles in $$A$$.


Let $$Z$$ be the set of integers. Show that the relation $$R=\left\{ \left( a,b \right) :a,b\in Z\ \text{and a+b is even }\right\} $$ is an equivalence relation on $$Z$$.

The given relation $$R$$ on the set of integers $$Z$$ is reflexive as $$(x,x)\in R$$ as $$2x$$ is even for all $$x\in Z$$.
Again the relation is symmetric as if $$(x,y)\in R\Rightarrow (y,x)\in R$$ since $$x+y$$ is even gives $$y+x$$ is also even for all $$x, y\in Z$$.
Again this relation $$R$$ is transitive as if $$(x,y)\in R$$ and $$(y,z)\in R$$ this gives $$(x,z)\in R$$ as $$x+y=2k_1$$.....(1) [ Since $$x+y$$ is even ] and $$y+z=2k_2$$.....(2) [ Since $$y+z$$ is even] [ For $$k_1$$ and $$k_2$$ being integers]
Now adding (1) and (2) we get 
$$x+2y+z=2(k_1+k_2)$$
or, $$x+z=2(k_1+k_2-y)$$
This gives $$x+z$$ is even.
Hence this relation is also transitive.
So the relation is equivalance relation.


Let $$F$$ be the set of all human beings in town in a particular time. Then check whether the relation is as equivalence relation.
$$R=\{(x,y): x \text{ is  mother of } \ y\}$$.

The relation is not reflexive as $$(x,x)\not \in R$$ for any $$x\in F$$ since $$x$$ can't be its own mother.
Similarly the relation is not symmetric as if $$(x,y)\in R$$ this does not give $$(y,x)\in R$$ since if $$x$$ is mother of $$y$$ this does not mean that $$y$$ is also mother of $$x$$ for any $$x,y\in F$$.
Again this relation $$R$$ is not transitive as if $$(x,y)\in R, (y,z)\in R$$ this does not give $$(x,z)\in R$$ for any $$x,y,z\in F$$.
So this relation is not equivalance.


Let $$R$$ be the equivalence relation on the set $$Z$$ of integers given by $$R=\left\{ \left( a,b \right) :2\ \text{ divides}\ a-b \right\} $$. Write the equivalence class $$[0]$$.

$$[0]=\left\{ 0,\pm 2,\pm 4,\pm 6 \right\} $$
We have
 $$R=\left\{ \left( a,b \right) :2\ \text{ divides}\ a-b \right\} $$
For any $$a\in Z$$
$$[a]=\left\{ x:\left( x,a \right) \in R \right\} =\left\{ x:2\ \text{ divides}\ x-a \right\} $$
$$[0]=\left\{ x\in Z:2\ \text{ divides}\ x-0 \right\} =\left\{ x\in Z:2\ \text{divides}\ x \right\} =\left\{ 0,\pm 2,\pm 4,\pm 6,... \right\} $$


If $$R$$ and $$S$$ are transitive relations on a set $$A$$, then prove that $$R\cup S$$ may not be transitive relation on $$A$$.

Let $$A=\left\{a,b,c\right\}$$
then $$R=\left\{\left(a,a\right),\left(a,b\right),\left(b,a\right),\left(b,b\right)\right\}$$
and $$S=\left\{\left(b,b\right),\left(b,c\right),\left(c,b\right),\left(c,c\right)\right\}$$ be transitive
Now, $$\left(a,b\right)\in R\cup S$$
Also,$$\left(b,c\right)\in R\cup S$$
But $$\left(a,c\right)\notin S\cup S$$
$$\therefore\,R\cup S$$ is not transitive.


If $$R$$ is a symmetric relation on a set $$A=\{1,2,3\}$$, then write the  relation between $$R$$ and $${R}^{-1}$$.

Here $$R$$ and $$R^{-1}$$ will be same.
As $$R$$ is symmetric relation on $$A$$ then $$R$$ can be written as
$$R=\{(a,b),(b,a)\}$$ for all $$a,b\in A$$.
Then $$R^{-1}=\{(b,a),(a,b)\}$$ for all $$a,b\in A$$.
So $$R=R^{-1}$$. 


Let $$C$$ be the set of all complex numbers and $${C}_{0}$$ be the set of all non-zero complex numbers. Let a relation $$R$$ on $${C}_{0}$$ be defined as
$${z}_{1}R{z}_{2}\Leftrightarrow \cfrac{{z}_{1}-{z}_{2}}{{z}_{1}-{z}_{2}}$$ is real for all $${z}_{1},{z}_{2}\in {C}_{0}$$. 
Show that $$R$$ is an equivalence relation.

$$(i)$$Test for reflexivity:
Since ,$$\dfrac{{z}_{1}-{z}_{1}}{{z}_{1}+{z}_{1}}=0,$$ which is a real number.
So,$$\left({z}_{1},{z}_{1}\right)\in R$$
Hence,$$R$$ is a reflexive relation.
$$(ii)$$Test for symmetric:
Let $$\left({z}_{1},{z}_{2}\right)\in R$$
$$\Rightarrow\,\dfrac{{z}_{1}-{z}_{2}}{{z}_{1}+{z}_{2}}=x$$, where $$x$$ is real
$$\Rightarrow\,-\dfrac{{z}_{1}-{z}_{2}}{{z}_{1}+{z}_{2}}=-x$$
$$\Rightarrow\,\dfrac{{z}_{2}-{z}_{1}}{{z}_{2}+{z}_{1}}=-x$$ is also a real number.
So,$$\left({z}_{2},{z}_{1}\right)\in R$$
Hence,$$R$$ is symmetric relation.
$$(iii)$$Test for transitivity:
Let $$\left({z}_{1},{z}_{2}\right)\in R$$ and $$\left({z}_{2},{z}_{3}\right)\in R$$
Then $$\dfrac{{z}_{1}-{z}_{2}}{{z}_{1}+{z}_{2}}=x$$
$$\Rightarrow\,{z}_{1}-{z}_{2}=x{z}_{1}+x{z}_{2}$$
$$\Rightarrow\,{z}_{1}\left(1-x\right)={z}_{2}\left(1+x\right)$$
$$\Rightarrow\,\dfrac{{z}_{1}}{{z}_{2}}=\dfrac{1+x}{1-x}$$         .......$$(1)$$
Also,$$\dfrac{{z}_{2}-{z}_{3}}{{z}_{2}+{z}_{3}}=y$$
$$\Rightarrow\,{z}_{2}-{z}_{3}=y{z}_{2}+y{z}_{3}$$
$$\Rightarrow\,{z}_{2}\left(1-y\right)={z}_{3}\left(1+y\right)$$
$$\Rightarrow\,\dfrac{{z}_{2}}{{z}_{3}}=\dfrac{1+y}{1-y}$$         .......$$(2)$$ 
Dividing $$(1)$$ and $$(2)$$, we get
$$\dfrac{{z}_{1}}{{z}_{3}}=\dfrac{1+x}{1-x}\times\dfrac{1-y}{1+y}=z$$ where $$z$$ is a real number.
$$\dfrac{{z}_{1}-{z}_{3}}{{z}_{1}+{z}_{3}}=\dfrac{z-1}{z+1},$$ which is real.
$$\Rightarrow\,\left({z}_{1},{z}_{3}\right)\in R$$             .......$$(3)$$
From $$(1),(2)$$ and $$(3)$$ we have as $$R$$ is an equivalence relation.


Let $$Z$$ be the set of all integers and $${Z}_{0}$$ be the set of all non-zero integers. Let a relation $$R$$ on $$Z\times {Z}_{0}$$ be defined as follows:
$$(a,b)R(c,d)\Leftrightarrow ad=bc$$ for all $$(a,b),(c,d)\in Z\times {Z}_{0}$$
Prove that $$R$$ is an equivalence relation on $$Z\times {Z}_{0}$$.

We observe the following properties of $$R$$
Reflexivity:
Let $$\left(a,b\right)\in Z\times{Z}_{0}$$
$$\Rightarrow\,a,b\in\,Z,{Z}_{0}$$
$$\Rightarrow\,ab=ba$$
$$\Rightarrow\,\left(a,b\right)\in\,R$$ for all $$\left(a,b\right)\in Z\times{Z}_{0}$$
So,$$R$$ is reflexive on $$Z\times{Z}_{0}$$
Symmetry:
Let $$\left(a,b\right),\left(c,d\right)\in Z\times{Z}_{0}$$ such that $$\left(a,b\right)R\left(c,d\right)$$
$$\Rightarrow\,ad=bc$$
$$\Rightarrow\,cb=da$$
$$\Rightarrow\,\left(c,d\right)R\left(a,b\right)$$
Thus, $$\left(a,b\right)R\left(c,d\right)\Rightarrow\,\left(c,d\right)R\left(a,b\right)$$ for all $$\left(a,b\right),\left(c,d\right)\in Z\times{Z}_{0}$$
So,$$R$$ is symmetric on $$Z\times{Z}_{0}$$
Transitivity:
Let $$\left(a,b\right),\left(c,d\right),\left(e,f\right)\in N\times{N}_{0}$$ such that $$\left(a,b\right)R\left(c,d\right)$$ and $$\left(c,d\right)R\left(e,f\right)$$
Then,$$\left(a,b\right)R\left(c,d\right)\Rightarrow\,ad=bc$$
$$\left(c,d\right)R\left(e,f\right)\Rightarrow\,cf=de$$
$$\Rightarrow\,\left(ad\right)\left(cf\right)=\left(bc\right)\left(de\right)$$
$$\Rightarrow\,af=be$$
$$\Rightarrow\,\left(a,b\right)R\left(e,f\right)$$ for all values of $$\left(a,b\right),\left(c,d\right),\left(e,f\right)\in N\times{N}_{0}$$
So, $$R$$ is transitive on $$N\times{N}_{0}$$
Hence the given relation is an equivalence relation.


Write the smallest reflexive relation on set $$\left\{ 1,2,3,4 \right\} $$.

Let $$A=\{1,2,3,4\}$$.
The smallest reflexive relation on set $$\left\{ 1,2,3,4 \right\} $$ is $$\left\{ \left( 1,1 \right) ,\left( 2,2 \right) ,\left( 3,3 \right) ,\left( 4,4 \right)  \right\} $$. [ Since for each $$a\in$$ A, $$(a,a)\in$$ the relation.]


State the reason for the relation $$R$$ on the set $$\left\{ 1,2,3 \right\} $$ given by $$R=\left\{ \left( 1,2 \right) ,\left( 2,1 \right)  \right\} $$ not to be transitive.

$$(1,2)\in R$$ and $$(2,1)\in R$$ but $$(1,1)\notin R$$
We observe that $$(1,2)\in R$$ and $$(2,1)\in R$$ but $$(1,1)\notin  R$$. hence R is not transitive.


For the set $$A=\left\{ 1,2,3 \right\} $$, define a relation $$R$$ on the set $$A$$ as follows:
$$R=\left\{ \left( 1,1 \right) ,\left( 2,2 \right) ,\left( 3,3 \right) ,\left( 1,3 \right)  \right\} $$
Write the ordered pairs to added to $$R$$ to make the smallest equivalence relation.

It is clearly evident that R is a reflexive relation and also a transitive relation ,
but it is not symmetric as (1,3) is present in R but (3,1) is not present in R .

So, To make R an equivalence relation we can simply add (3,1) to R which will also not disturb transitivity and reflexivity .



If $$A=\{1, 2, 4\}$$ and $$B=\{1, 2, 3\}$$, represent following set graphically.
$$A\times B$$.


1421667_1666230_ans_547d205830274d628adf07e184b0133e.jpg


Let $$A=\{3, 5\}$$ and $$B=\{7, 11\}$$. Let $$R=\{(a, b):a\in A, b\in B, a-b$$ is odd$$\}$$. Show that R is an empty relation from A into B.

$$A=\{3,5\}$$ and $$B=\{7,11\}$$
Also, 
$$R=\{(a,b):a\in A,\,b\in B,\,a-b$$ is odd $$\}$$
$$a$$ are the elements of $$A$$ and $$b$$ are the elements of $$B.$$
$$\therefore$$  $$a-b=3-7,\,3-11,\,5-7,\,5-11$$
$$\Rightarrow$$  $$a-b=-4,-8,-2,-6$$
Here, $$a-b$$ is always an even number.
So, $$R$$ is an empty relation from $$A$$ to $$B.$$


If $$A=\{1, 2, 4\}$$ and $$B=\{1, 2, 3\}$$, represent following set graphically.
$$B\times A$$.


1421668_1666232_ans_ec1fd71420864351a5ffda1d689124af.jpg


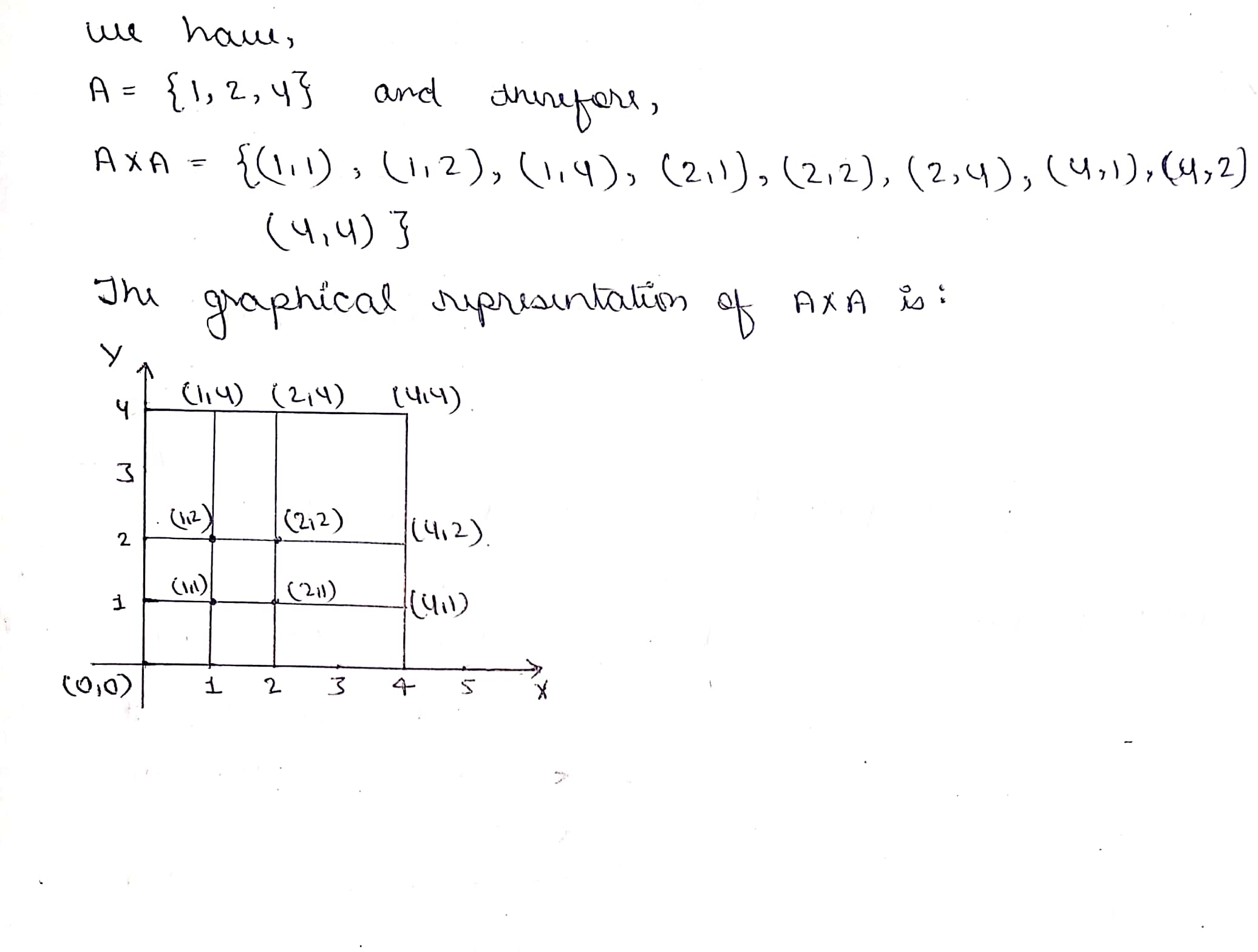
If $$A=\{1, 2, 4\}$$ and  represent following set graphically.
$$A\times A$$.


1421669_1666233_ans_5654773620ff4d35a0cf510c92af2945.jpg


Check if the relation $$R$$ in the set $$R$$ of real numbers defined as
$$R = \{(a,b) : a < b\}$$ is 
(i) symmetric;
(ii) transitive

$$R=\{(a,b): a < b\}$$
(i) Checking for symmetric,
if $$(a,b)\in R$$ such that $$a<b$$
then,
$$(b,a)\in R$$ not possible
example,
$$(2,3)\in R$$
but, $$(3,2)\in R$$
$$\therefore$$ Relation $$R$$ is not symmetric

(ii) Checking for transitive,
if $$(a,b)\in R$$ and $$(b,c)\in R$$
such that $$a<b$$ and $$b<c$$
then clearly, $$a<c$$
i.e $$(a,c)\in R$$
$$\therefore$$ Relation $$R$$ is transitive.


Show that the relation R on $$N\times N$$, defined by $$(a, b) R (c, d)\Leftrightarrow a+d=b+c$$ is an equivalent relation.


1672269_1705098_ans_4f15fec51a90463f84a05c3871837971.jpeg


Let $$R=\{(a, b):a, b\in Z$$ and $$(a+b)$$ is even $$\}$$.
Show that R is an equivalence relation on Z.

(i) Let $$a\in Z$$. Then, $$a+a=2a$$, which is even. So, $$a$$ R $$a.$$
(ii) Let $$a$$ R $$b.$$ Then,
$$a R b\Rightarrow a+b$$ is even
$$\Rightarrow b+a$$ is even
$$\Rightarrow b\  R \  a$$.
(iii) Let $$a$$ R $$b$$ and $$b$$ R $$c.$$ Then,
a R b and b R c $$\Rightarrow (a+b)$$ is even and $$(b+c)$$ is even.
$$\therefore (a+c)=\{(a+c)+2b\}-2b$$
$$=\{(a+b)+(b+c)-2b\}$$, which is even
$$\Rightarrow a \  R \ c[\because$$ each of $$(a+b), (b+c)$$ and $$2b$$ is even$$]$$.


Let A be the set of all triangles in a plane. Show that the relation $$R=\{(\Delta_1, \Delta_2):\Delta_1\sim \Delta_2\}$$ is an equivalence relation on A.


1546211_1705094_ans_d49f900dd03e4472bb79d2954c2a5c73.jpg


Show that the relation R defined on the set $$A=\{1, 2, 3, 4, 5\}$$, given by $$R=\{(a, b):|a-b|$$ is even$$\}$$ is an equivalence relation.

(i)$$|a−a|=0$$, which is even, So, $$a R a.$$

(ii) $$a R b\Rightarrow |a−b|$$ is even

$$\Rightarrow |−(a−b)|$$ is even

$$\Rightarrow |b−a|$$ is even

$$\Rightarrow bRa.$$

$$(iii) aRb,bRc\Rightarrow |a−b|$$ is even and $$|b−c|$$ is even

$$\Rightarrow (a−b)$$ is even and $$(b−c)$$ is even

$$\Rightarrow {(a−b)+(b−c)}$$ is even

$$\Rightarrow (a−c)$$ is even

$$\Rightarrow |a−c|$$ is even

$$\Rightarrow aRc.$$


Let $$R=\{(a, b):a, b\in Z$$ and $$(a-b)$$ is divisible by $$5\}$$.
Show that R is an equivalence relation on Z.

Given:

R={(a,b):a,b∈Z and (a−b) is divisible by 5}.

$$R = (a,b)$$

$$(a-b)$$ is divisible by $$5$$

Reflexive

$$(a,a) \Rightarrow (a-a)$$ is divisible by $$5$$

Symmetric

$$(a, b)\Leftrightarrow (b, a)$$

$$(a-b)$$ is divisible by $$5$$

$$(b-a)$$ is divisible by $$5$$

Transitive

$$(a,b), (b,c)\Leftrightarrow (a,c)$$

$$(a-b)$$ is divisible by $$5$$

$$(b-c)$$ is divisible by $$5$$

$$(a-c)$$ is divisible by $$5$$

R is an equivalent relation on Z


Let S be the set of all sets and let $$R=\{(A, B):A\subset B)\}$$, i.e., A is a proper subset of B. Show that R is not symmetric.

Given,

$$R=\left \{ (A,B):A⊂B) \right \}$$

A is a proper subset of B

$$(A⊂B  \ and \ B⊂C)\Rightarrow (A⊂C)$$. 

So, R is transitive.

If $$A⊂B$$ then $$B⊂C$$ is not true. So, R is not symmetric.


Let S be the set of all sets and let $$R=\{(A, B) : A\subset B)\}$$, i.e., A is a proper subset of B. Show that R is transitive.

Given,

$$R=\left \{ (A,B):A⊂B) \right \}$$

A is a proper subset of B

$$(A⊂B  \ and \ B⊂C)\Rightarrow (A⊂C)$$. 

So, R is transitive.


On the set S of all real numbers, define a relaiton $$R=\{(a, b): a\leq b\}$$. Show that R is transitive.

Given,

$$R=\left \{ (a,b):a \leq b \right \}$$

Reflexive Property

The Reflexive Property states that for every real number x, $$x = x$$.

Symmetric Property

The Symmetric Property states that for all real numbers x  and  y,

if  $$ x=y$$, then $$y=x$$.

Transitive Property

The Transitive Property states that for all real numbers x ,y,  and  z,

if  $$ x=y$$ and $$y=z$$ , then $$x=z$$

when, $$a=1,b=1,2$$

So, $$(1,2), (2,3)$$ is possible, and $$(1,3)$$ is also possible as $$1 \le 3$$.

Therefore, R is transitive.


Let A be the set of all points in a plane and let O be the origin. Show that the relation $$R=\{(P, Q): P, Q\in A$$ and $$OP=OQ\}$$ is an equivalence relation.

Let $$O$$ be the origin and 

let $$P, Q, X$$ be any three points in a plane.

Then, 

(i) $$OP=OP$$ is always true. So, R is reflexive.

(ii) $$OP=OQ\Rightarrow OQ=OP$$. So, R is symmetric.

(iii) $$(OP=OQ \ and \ OQ=OX)\Rightarrow (OP=OX)$$. So, R transitive.

Hence, R is an equivalence relation.


On the set S of all real numbers, define a relation $$R=\{(a, b):a\leq b\}$$. Show that R is reflexive.

Given,

$$R=\left \{ (a,b):a \leq b \right \}$$

Reflexive Property

The Reflexive Property states that for every real number x, $$x = x$$.

when, $$a=1,b=1,2$$

So, $$(1,2)$$ is possible, and $$(1,1), (2,2)$$ is also possible as $$1 \le 1$$. and $$2 \le 2$$. 

Symmetric Property

The Symmetric Property states that for all real numbers x  and  y,

if  $$ x=y$$, then $$y=x$$.

Transitive Property

The Transitive Property states that for all real numbers x ,y,  and  z,

if  $$ x=y$$ and $$y=z$$ , then $$x=z$$

Therefore, R is reflexive


Let S be the set of all sets and let $$R=\{(A, B):A\subset B)\}$$, i.e., A is a proper subset of B. Show that R is not reflexive.


1546234_1705180_ans_78cd39ba7ec4428ba13ce598548e8f8c.JPG


Let $$A=\{1, 2, 3, 4, 5, 6\}$$ and let $$R=\{(a, b): a, b\in A$$ and $$b=a+1\}$$. Show that R is not reflexive.

Given,

$$A=\left \{ 1,2,3,4,5,6 \right \}$$

$$R=\left \{ (a,b):a,b\in A \ and \ b=a+1 \right \}$$

Reflexive Property

The Reflexive Property states that for every real number x, $$x = x$$.

when $$a=1,b=1+1=2$$

so, we get, $$(1,2)$$ is possible, but $$(1,1)$$ is not possible, as $$b=a+1$$  and $$1 \ne 2+1$$

Symmetric Property

The Symmetric Property states that for all real numbers x  and  y,

if  $$ x=y$$, then $$y=x$$.

Transitive Property

The Transitive Property states that for all real numbers x ,y,  and  z,

if  $$ x=y$$ and $$y=z$$ , then $$x=z$$

Therefore, R is not reflexive.


On the set S of all real numbers, define a relation $$R=\{(a, b):a\leq b\}$$. Show that R is not symmetric.

Given,

$$R=\left \{ (a,b):a \leq b \right \}$$

Reflexive Property

The Reflexive Property states that for every real number x, $$x = x$$.

Symmetric Property

The Symmetric Property states that for all real numbers x  and  y,

if  $$ x=y$$, then $$y=x$$.

when, $$a=1,b=1,2$$

So, $$(1,2)$$ is possible, but $$(2,1)$$ is not possible, as $$2\le 1$$

Transitive Property

The Transitive Property states that for all real numbers x ,y,  and  z,

if  $$ x=y$$ and $$y=z$$ , then $$x=z$$

Therefore, R is not symmetric.


Let $$A=\{1, 2, 3, 4, 5, 6\}$$ and let $$R=\{(a, b): a, b\in A$$ and $$b=a+1\}$$. Show that R is not symmetric.

Given,

$$A=\left \{ 1,2,3,4,5,6 \right \}$$

$$R=\left \{ (a,b):a,b\in A \ and \ b=a+1 \right \}$$

Reflexive Property

The Reflexive Property states that for every real number x, $$x = x$$.

Symmetric Property

The Symmetric Property states that for all real numbers x  and  y,

if  $$ x=y$$, then $$y=x$$.

when $$a=1,b=1+1=2$$

so, $$(1,2)$$ is possible, but $$(2,1)$$ is not possible, as $$b=a+1$$  and $$1 \ne 2+1$$

Transitive Property

The Transitive Property states that for all real numbers x ,y,  and  z,

if  $$ x=y$$ and $$y=z$$ , then $$x=z$$

Therefore, R is not symmetric.


Let $$A=\{1, 2, 3, 4, 5, 6\}$$ and let $$R=\{(a, b):a, b\in A$$ and $$b=a+1\}$$. Show that R is not transitive.

Given,

$$A=\left \{ 1,2,3,4,5,6 \right \}$$

$$R=\left \{ (a,b):a,b\in A \ and \ b=a+1 \right \}$$

Reflexive Property

The Reflexive Property states that for every real number x, $$x = x$$.

Symmetric Property

The Symmetric Property states that for all real numbers x  and  y,

if  $$ x=y$$, then $$y=x$$.

Transitive Property

The Transitive Property states that for all real numbers x ,y,  and  z,

if  $$ x=y$$ and $$y=z$$ , then $$x=z$$

when $$a=1,b=1+1=2$$

when $$a=2,b=2+1=3$$

so, $$(1,2), (2,3)$$ is possible, but $$(1,3)$$ is not possible, as $$b=a+1$$  and $$3 \ne 1+1$$

Therefore, R is not transitive.


Let S be the set of all real numbers and let $$R=\{(a, b):a, b\in S$$ and $$a=\pm b\}$$. Show that R is an equivalence relation on S.


1557286_1705201_ans_3abbc004be5348da9dcca3631398d4b5.jpg


If $$\displaystyle A = \{5, 7\}$$, find $$\displaystyle A \times A \times A$$,  and enter the value of number of elements of it.

$$A=\{5,7\}$$
$$A\times A=\{5,7\}\times \{5,7\}$$
$$\Rightarrow$$  $$A\times A=\{(5,5),(5,7),(7,5),(7,7)\}$$
Now,
$$(A\times A)\times A=\{(5,5),(5,7),(7,5),(7,7)\}\times \{5,7\}$$
                        $$=\{(5,5,5),(5,7,5),(7,5,5),(7,7,5),(5,5,7),(5,7,7),(7,5,7),(7,7,7)\}$$
$$\therefore$$  $$A\times A\times A=\{(5,5,5),(5,7,5),(7,5,5),(7,7,5),(5,5,7),(5,7,7),(7,5,7),(7,7,7)\}$$


If $$\displaystyle A \times B = \{(-2, 3), (-2, 4), (0, 3), (0, 4), (3, 3), (3, 4)\}$$, Find $$n(A)+n(B)$$.


1848329_1708158_ans_39e95b30e5bc46b486fe629fd6ef0eed.jpeg


If $$\displaystyle A$$ and $$\displaystyle B$$ be two sets such that $$\displaystyle n(A) = 3, n(B) = 4$$ and $$\displaystyle n(A \cap B) = 2$$ then find:$$\displaystyle n(B \times A)$$

$$\displaystyle n(B \times A) = n(B) \times n(A)=12$$.


If $$\displaystyle A$$ and $$\displaystyle B$$ be two sets such that $$\displaystyle n(A) = 3, n(B) = 4$$ and $$\displaystyle n(A \cap B) = 2$$ then find:
$$\displaystyle n(A \times B)$$

We know that $$n(A \times B) = n(A) \times n(B)=12$$. 


Let $$\displaystyle A = \{-3, -1\}, B = \{1, 3\}$$ and $$\displaystyle C = \{3, 5\}$$. Find $$\displaystyle (A \times B) \times C$$ and enter the value of number of elements of it.

$$A=\{-3,-1\},\,B=\{1,3\}$$ and $$C=\{3,5\}$$
$$\Rightarrow$$  $$A\times B=\{-3,-1\}\times \{1,3\}$$
$$\Rightarrow$$  $$A\times B=\{(-3,1),(-3,3),(-1,1),(-1,3)\}$$
Now,
$$\Rightarrow$$  $$(A\times B)\times C=\{(-3,1),(-3,3),(-1,1),(-1,3)\}\times \{3,5\}$$
                              $$=\{(-3,1,-3),(-3,3,3),(-1,1,3),(-1,3,3),(-3,1,5),(-3,3,5),(-1,1,5),(-1,3,5)\}$$


For any two sets $$\displaystyle A $$ and $$\displaystyle B $$, show that $$\displaystyle A \times B$$ and $$\displaystyle B \times A$$ have an element in common if and only if $$\displaystyle A$$ and $$\displaystyle B$$ have an element in common.


2016091_1708344_ans_0c59f1feed8243c9a7741375f6317ae9.png


Let $$\displaystyle R = \{(a, b) : a, b \in Z$$ and $$(a - b)$$ is even$$\}$$.
Then, show that $$\displaystyle R$$ is an equivalence relation on $$\displaystyle Z$$.


1858711_1708577_ans_f497f89d58834f48b62bfab8fedd4459.jpeg


What is an equivalence relation?
Show that the relation of 'similarity' on the set $$\displaystyle S$$ of all triangles in a plane is an equivalence relation.


1858802_1708570_ans_103c2eda76c14ef1826075f0a7d36386.jpeg


If $$\displaystyle A$$ and $$\displaystyle B$$ be two sets such that $$\displaystyle n(A) = 3, n(B) = 4$$ and $$\displaystyle n(A \cap B) = 2$$ then find:
$$\displaystyle n\{(A \times B) \cap (B \times A)\}$$

Since$$\displaystyle A$$ and $$\displaystyle B$$ have $$\displaystyle 2$$ elements in common, so $$\displaystyle (A \times B)$$ and $$\displaystyle (B \times A)$$ will have $$2^2 = 4$$ elements in common. 


If $$\displaystyle A = \{ 3, 4\}, B = \{4, 5\}$$ and $$\displaystyle C = \{5, 6\}$$, find $$\displaystyle A \times (B \times C)$$.

Is the answer: $$\displaystyle \{ (3, 4, 5), (3, 4, 6), (3, 5, 5), (3, 5, 6), (4, 4, 5), (4, 4, 6), (4, 5, 5), (4, 5, 6)\}$$

If yes then enter $$1$$ else $$0$$


1849972_1708735_ans_03c8e0d7ab234e4690109fe6648aa21c.jpg


Let $$\displaystyle A $$ and $$\displaystyle B $$ be two sets such that  $$\displaystyle n(A) = 5, n(B)=3$$ and $$\displaystyle n(A \cap B)=2$$.
$$\displaystyle n\{(A \times B) \cap (B \times A)\}$$


1972890_1708721_ans_032b0f3b9ed74b15b7fa0f59e8f13a33.jpeg


Let $$\displaystyle A $$ and $$\displaystyle B $$ be two sets such that  $$\displaystyle n(A) = 5, n(B)=3$$ and $$\displaystyle n(A \cap B)=2$$.
$$\displaystyle n (A \times B )$$

$$\displaystyle n ( A \times B) = n(A). n(B)=5 \times 3=15$$.


If $$\displaystyle A \subseteq B$$, prove that $$\displaystyle A \times C =  B \times C$$.


1847751_1708737_ans_8089e057e83e45dda1f93ad4aa16033e.jpg


In the set of natural numbers. $$N$$ define a relation $$R$$ as follows: $$\forall\  n, m \in N, nRm$$ if on division by $$5$$ each of the integers $$n$$ and $$m$$ leaves the remainder less than $$5$$, i,e,, one of the numbers $$0,1,2,3$$ and $$4$$. Show that $$R$$ is equivalence relation. Also, obtain the pairwise disjoint subsets determined by $$R$$.

$$R$$ is reflexive since for each a $$\in N, aRa$$, 
$$R$$ is symmetric since if $$aRb$$, then $$bRa$$ for $$a, b\ \in N$$.
Also $$R$$ is transitive since for $$a,b,c\ \in N$$, if $$aRb$$ and $$bRa$$, then $$aRc$$
Hence $$R$$ is an equivalence relation in $$N$$ which will partition the set $$N$$ into the pairwise disjoint subsets. 
The equivalent classes are as mentioned below:
$$A_0=\{5,10,15,20,...\}$$
$$A_1=\{1,6,11,16,21,...\}$$
$$A_2=\{2,7,12,17,22,...\}$$
$$A_3=\{3,8,13,18,23,...\}$$
$$A_4=\{4,9,14,19,24,...\}$$
It is evident that the above five sets are pairwise disjoint and
$$A_0 \cup A_1 \cup A_2 \cup A_3 \cup A_4 =\bigcup\limits_{i=0}^4 A_i=N$$. 


Each of the following defines a relations a relation on $$N$$:
$$x$$ is greater than $$y, x, y\ \in \ N$$.
Determine which of the above relations are reflexive, symmetric and transitive,

$$x$$ is greater than $$y, x, y\ \in \ N$$.
$$(x,x)\in R$$
For $$xRx x > x$$ is not true for any $$x\in N$$
Therefore, $$R$$ is not reflexive
Let $$(x,y)\in R\Rightarrow xRy$$
$$x > y$$
but $$y > x$$ is not true for any $$x, y \in N$$
Thus, $$R$$ is not symmetric
Thus, $$R$$ is not symmetric
Let $$xRt$$ and $$yRz$$
$$x > y$$ and $$y> z\Rightarrow x > z$$
$$\Rightarrow \ xRz$$
So, $$R$$ is transitive.


Let $$R$$ be the equivalence relation in the set $$Z$$ of integer given by $$R=\left\{(a,b) : 2 \text{ divides}\  a-b\right\}$$. Show that relation $$R$$ is transitive. Write the equivalence class $$[0]$$ .

$$R=\{(a,b):2\ \text{divides}\ a-b\}$$

Transitive:
If $$2$$ divides $$(a,-b)$$, and $$2$$ divides $$(b-c),$$
So, $$2$$ divides $$(a-b)+(b-c)$$ also
So, $$2$$ divides $$(a-c)$$

$$\therefore (a-b) \in R$$ and $$(b-c) \in R$$, then $$(a-c)\in R$$

Therefore, $$R$$ is transitive.

Now, Equivalence class $$[0]$$:
 This means that one element is $$0$$, we need to find other elements which satisfy $$R$$

So, $$(a,0)\in R$$ where $$a\in Z$$
Because given that $$R$$ is in set $$Z$$, so both $$a$$ and $$b$$ belong to set $$Z$$

Now,
If $$(a,0)\in R$$
$$2$$ divides $$a-$$
i.e $$2$$ divides $$a$$
 
So, Possible values of $$a$$ are $$0, \pm 2, \pm 4, \pm 6, \pm 8, ....$$
i.e all even numbers and $$0$$

We use $$\pm$$ because $$2$$ can divide $$2$$ and $$-2$$
So, Equivalence class $$[0] =\{0, \pm 2, \pm 4, \pm 6, .... \}$$


Let $$A=\left\{0,1,2,3\right\}$$ and define a relation $$R$$ on $$A$$ as follows:
$$R=\left\{(0,0),(0,1),(0,3),(1,0),(1,1),(2,2),(3,0),(3,3)\right\}$$ 
Is $$R$$ reflexive? symmetric tranxitive?

$$R$$ is reflexive symmetric, but not transitive since for $$(1,0)\ \in R$$ and $$(0,3)\ \in R$$  where $$(1,3)\ \notin R$$.


Show that the relation $$R$$ in the set 
$$A=\left\{ x \in Z :0 \le x \le 12 \right\}$$, given by 
$$R=\left\{ (a, b): a=b \right\}$$ is an equivalence relation. Find the set of all elements related to $$1$$ in each case.

$$a\ R\ a \Rightarrow a=a\forall a \in A$$
hence $$R$$ is reflexive 
$$a\ R\ b\Rightarrow a=b$$
$$\Rightarrow b=a \Rightarrow b\ R\ a$$, hence $$R$$ is symmetric $$a\ R\ b$$ and $$b\ R\ c$$
$$\Rightarrow  a=b$$ and $$b=c$$
$$\Rightarrow  a=c, =a\ R\ c$$
hence $$R$$ is transitive 
Therefore $$R$$ is an equivalence Relation,
$$a\ R\ 1 \Rightarrow a=1$$
Therefore the elements related to $$1$$ is $$\left\{ 1 \right\}$$


Show that the relation $$R$$ defined in the set $$A$$ of all polygons as $$R=\left\{ (P_1, P_2 ):P_3\ and\ P_2\ have\ same\ number\ of\ sides \right\}$$, is an equivalence relation. What is the set of all elements in $$A$$ related to the right angle triangle $$T$$ with sides $$3, 4$$ and $$5$$?

$$(P, P)\in R$$ as $$P$$ and $$P$$ have sane number of sides hence $$R$$ is reflexive.
$$(P, Q) \in R \Rightarrow P$$ and $$Q$$ have same number of sides 
$$\Rightarrow Q$$ and $$P$$ have same number of sides 
$$\Rightarrow (Q, P) \in R$$
hence $$R$$ is symmetric 
$$(P, Q) \in R$$ and $$(Q, R) \in R$$
$$\Rightarrow P$$ and $$Q$$ have number of sides, $$Q$$ and $$R$$ have same number of sides. $$P$$ and $$R$$ have same number of sides 
$$\Rightarrow (P, R) \in R$$
hence $$R$$ is transitive 
$$\therefore R$$ is an equivalence Relation 
$$T$$ is a Triangle 
$$( P, T)\in R$$
$$\Rightarrow P$$ and $$T$$ have same number of sides 
$$\Rightarrow P$$ is also a triangle 
$$\therefore$$ set of all elements related as $$T$$ is the set of all triangle in $$A$$.


N is a set of natural numbers. If a relation R is defined in set $$ N \times N $$ such that $$( a , b ) R ( c , d )\Leftrightarrow  ad = bc \forall (a ,b)(c , d) \in N \times N$$, then prove that R is an equivalence relation.

Set N = {1 , 2 , 3 , 4......} = Set of natural numbers
A relation R in $$ N \times N $$ is defined as
Here, to prove R is equivalence relation , we have to show that R is reflexive , symmetric and transitive.
Reflexivity : Let
$$ ( a , b) \in N \times N $$
$$ ( a , b ) \in N \times N $$
$$ \Rightarrow a .b  =  ba$$(Commulative law of multiplication)
$$ \Rightarrow ( a ,b) R ( a ,b) \forall  ( a ,b) \in N \times N $$ 
R is reflexive relation.
Symmetricity : Let $$ ( a ,b)(c ,d) \in N \times N $$ is in this way$$ ( a , b)R(c , d)( a , b)( c, d)$$
$$ \Rightarrow ad =  bc $$
$$ \Rightarrow bc = ad $$
$$ \Rightarrow cd = da $$
$$ \Rightarrow (c, d) R ( a ,b) $$


A  relation R is defined in a set $$Q_{0}$$ set of non  zero rational numbers such that $$ aRb \Leftrightarrow  a = 1 / b , \forall  a , b \in Q_{0}$$ Is R is equivalence relations.

Given: Set $$Q(0)$$ = Set of non zero rational numbers.
A relation  in $$Q_{0}$$ is defined as
$$ aRb \Leftrightarrow  a = 1 / b , \forall  a , b \in Q_{0}$$ 
If R is reflexive , symmetric and transitive than R is an equivalence relation.
Reflexivity :Let $$ a \in Q_{0}$$
$$ ( a, a) \notin  R \forall  a \notin  Q_{0}$$
So, R is not reflexive relation.
R is also not equivalence relation.


Let $$ {(a ,b) | a , b \in R }$$ where I is set of integers . Relations $$ R_{1}$$ on x is defined in the following way $$ ( a ,b)R_{1} ( c ,d) \Rightarrow  b - d  =  a - c$$ Prove that $$ R_{1}$$ is an equivalence relation.

Given : Set $$ X = {(a , b) : a , b \in I }$$
Where I is the set of intergers
A relation R in X is defined as :
$$ ( a ,b)R_{1} ( c ,d) \Rightarrow  b - d  =  a - c \forall  ( a, b) ( c , d) \in X $$
To prove that R is equivalence relation , we have to prove  that R is reflexive , symmetric and transitive.
Reflexivity : Let $$ (a ,b) \in X $$
$$ \Rightarrow  b - b =  a  - a  = 0 $$ 
R is reflexive relation.


A relation R in a set $$ C_{0} $$ of non zero complex numbers is defines as :
$$ z_{1}R{z_{2}} \Leftrightarrow  \dfrac{z_{1} - z_{2}}{z_{1} + z_{2}} $$ a real number.Prove that R is an equivalence relation.

Given : Set $$ C_{0} $$ = set of the non - zero complex number a relation R in defined as :
$$ z_{1}R_{z_{2}} \Leftrightarrow  \dfrac{z_{1} - z_{2}}{z_{1} + z_{2}} $$is real $$ \forall  z_{1} , z_{2} \in C_{0}$$
$$ z  \in C_{0} \Leftrightarrow  \dfrac{z - z}{z + z} = 0 $$ is a real number.
$$ \Rightarrow zRz$$
$$ \Rightarrow ( z , z) \in R \forall  z \in C_{0}$$
$$ \Rightarrow \dfrac{z_{2} - z_{1}}{z_{2} + z_{1}} = - \left ( \dfrac{z_{1} - z_{2}}{z_{1} + z_{2}} \right ) $$
$$ \Rightarrow (z_{2} , z_{1}) \in R $$ 
So , $$ (z_{1}, z_{2}) \in R \Rightarrow  (z_{2}, z_{1}) \in R $$


A relation R is defined in a set T of triangles situated in a plane such that $$ xRY \Leftrightarrow x $$ is similar to y . Prove that R is an equivalence relation.

Given : Set T = { Set of similar triangles }
A relation R in T is defined as:
$$ xRY \Leftrightarrow x $$ is similar to $$ y \forall  x , y \in T $$
To prove R is an equivalence relation , we have to prove that R is reflexive , symmetric and transitive.
Symmetricity : Let $$ x \in T $$
$$ x \in f \Rightarrow  x $$ is similar to x.
$$  \Rightarrow  ( x , x ) \in R \forall  x \in T $$
R is a reflexive relation.


Let $$A = \left \{1, 2, 3, .... 9\right \}$$ and $$R$$ be relation in $$A\times A$$ defined by $$(a, b)R (c, d)$$ if $$a + d = b + c$$ for $$(a, b), (c, d)$$ in $$A\times A$$. Prove that $$R$$ is an equivalence relation. Also obtain the equivalence class $$[(2, 5)].$$

$$A =\{1, 2, 3...9\}$$
$$R$$ in $$A \times A$$
$$(a, b)$$ $$R$$ $$(c, d)$$ if $$(a, b)(c, d)$$ $$\in$$ $$A \in A$$
$$a +b = b + c$$
Consider $$(a, b)$$ $$R$$ $$(a, b)$$  $$(a, b)\in A\times A$$
$$a + b = b + a$$
Hence, $$R$$ is reflexive.
Consider $$(a, b)$$ $$R$$ $$(c, d)$$ given by $$(a, b)$$ $$(c, d)$$ $$\in$$ $$A \times A$$
$$a + d = b + c => c + b = d + a$$
$$\Rightarrow (c, d)R(a, b)$$
Hence $$R$$ is symmetric.
Let $$(a, b)$$ $$R$$ $$(c, d)$$ and $$(c, d)$$ $$R$$ $$(e, f)$$
$$(a,b),(c,d),(e,f),\in A\times A$$
$$a + b = b + c$$ and $$c + f = d + e$$
$$a + b = b + c$$
$$\Rightarrow a -c =b-d$$-- (1)
$$c+f=d+e$$-- (2)
Adding (1) and (2)
$$a-c+c+f=b-d+d+e$$
$$a+f=b+e$$
$$(a,b)R(e,f)$$
$$R$$ is transitive.
$$R$$ is an equivalence relation.
We select from set $$A = \{1, 2, 3,....9\}$$
$$a$$ and $$b$$ such that $$2 + b = 5 + a$$
so $$b=a+3$$
Consider $$(1,4)$$ 
$$(2,5)$$ $$R$$ $$(1,4)\Rightarrow 2+4=5+1$$
$$[(2, 5)={(1,4)(2,5),(3,6),(4,7),(5,8),(6,9)}] $$ is the equivalent class under relation $$R.$$


Let $$R$$ be the equivalence relation on the set $$Z$$ of integers given by $$R=\left\{ \left( a,b \right) :\ 2\ \text{divides}\ a-b \right\} $$. Write the equivalence class {0}.

R = (a,b) : 2 divides (a-b)
$$  \Rightarrow (a-b) $$ is a multiple of 2.
To find equivalence class $${0} ,$$ put $$ b = 0$$
So, $$ (a-0) $$ is a multiple of 2
$$ \Rightarrow $$ a is a multiple of 2
So, In set z of integers, all the multiple
of 2 will come in equivalence
class $$ \left \{ 0 \right \} $$
Hence, equivalence class $$ \left \{ 0 \right \} = \left \{ 2x \right \} $$
where x = integer (z)

1180095_876247_ans_57bef52a0a5b4c02b0963b668727f6db.JPG


Check whether the relation $$R$$ in $$R$$ defined by $$R=\left\{\left(a,\,b\right):a\le {b}^{3}\right\}$$ is reflexive, symmetric or transitive.

$$R=\left\{\left(a,\,b\right):a\le {b}^{3}\right\}$$
Here $$R$$ is set of real numbers
Hence both $$a$$ and $$b$$ are real numbers.
$$1.$$If the relation is reflexive, then $$\left(a,\,a\right)\in R$$
i.e.,$$a\le {a}^{3}$$
For $$a=1,\,\,{a}^{3}\le 1\Rightarrow 1\le 1$$
For $$a=2,\,\,{a}^{3}\le 8\Rightarrow 2\le 8$$
For $$a=\dfrac{1}{2},\,\,{a}^{3}\ge \dfrac{1}{8}$$
Hence $$a\le {a}^{3}$$ is not true for all values of $$a$$
So, the given relation is not relexive.
To check whether symmetric or not:
If $$\left(a,\,b\right)\in R$$ then $$\left(b,\,a\right)\in R$$
If $$a\le {b}^{3}$$ then $$b\le {a}^{3}$$
For $$a=2,\,b=3,\,2<{2}^{3},\,\,3<{2}^{3}$$
For $$a=2,\,b=9,\,2<{9}^{3},\,\,9>{2}^{3}$$
Since $$b\le {a}^{3}$$ is not true for all values of $$a$$ and $$b$$
Hence the given relation is not symmetric.
To check whether transitive or not:
If $$\left(a,\,b\right)\in R$$ and $$\left(b,\,c\right)\in R$$ then $$\left(a,\,c\right)\in R$$
If $$a\le {b}^{3}$$ and $$b\le {c}^{3}$$ then $$a\le {c}^{3}$$
For $$a=1,\,b=2,\,c=3,\,{b}^{3}=8,\,{c}^{3}=27\Rightarrow a\le {b}^{3},\,b\le {c}^{3}$$ and $$a\le {c}^{3}$$
For $$a=3,\,b=\dfrac{3}{2},\,c=\dfrac{4}{3},\,{b}^{3}={\left(\dfrac{3}{2}\right)}^{3}=3.375,\,{c}^{3}={\left(\dfrac{4}{3}\right)}^{3}=2.37\Rightarrow a\le {b}^{3},\,b\le {c}^{3}$$ and $$a\ge {c}^{3}$$
Since if $$a\le {b}^{3},\,b\le {c}^{3}$$ and $$a\le {c}^{3}$$ is not true for all values of $$a,\,b,\,c$$.
Hence, the given relation is not transitive.
$$\therefore$$ the given relation is neither reflexive, symmetric or transitive.


Show that the relation R on the set N of natural numbers defined as 
R = { (x, y): y - x is a multiple of 2 } is equivalance


2041680_1079671_ans_cf89dd88cc8a4c5e963e038a242582a8.jpg


A relation R on the set of complex numbers is defined by $$z_1$$ R$$z_2$$ if and only if $$(z_1- z_2) / (z_1+ z_2)$$ is real. Show that R is an equivalence relation.

Here $$z_1$$ R $$z_2$$ for all complex number $$z_1$$.
For we have $$\frac{z_1 - z_1}{z_1+ z_2} =0$$ is real, then $$\frac{z_1 - z_1}{z_1 +z_2}$$ is real, then $$\frac{z_2 - z_1}{z_2+z_1}$$ is also real.
Hence $$z_1Rz_2\rightarrow z_2 Rz_1$$.
We now show that R is transitive.
Let $$z_1= x_1+iy_1 , z_2 = x_2+iy_2 $$ and $$z_3 = x_3 +iy_3$$ be three complex numbers such that $$z_1Rz_2$$ and $$z_2Rz_3$$. 
Now $$z_1Rz_2 \Rightarrow \frac{z_1 - z_2}{z_1 + z_2}$$ is real 
$$\Rightarrow \frac{(x_1 -x_2)+ i( y_1- y_2)}{(x_1+ x_2) + i(y_1+ y_2)}$$ is real
$$\Rightarrow \frac{[(x_1 - x_2) +i(y_1-y_2)][(x_1+ x_2)-i(y_1-y_2)]}{(x_1+x_2)^2+ (y + y_2)^2]}$$ is real
$$\Rightarrow (y_1 -y_2) (x_1+x_2)- ( x_1 -x_2)- ( y_1 +y_2)= 0$$
$$\Rightarrow 2x_2y_1 - 2 y_2x_1 = 0\Rightarrow (x_1/ y_1)= (x_2/y_2)$$ ........(1)
Similarlly $$z_2Rz_3 =\frac{x_2}{y_2}= \frac{x_3}{y_3}$$       ...(2)
From (1) and (2), we have $$\frac{x_1}{y_1} = \frac{x_3}{y_3}$$
Hence $$z_1Rz_3$$.
Thus $$z_1Rz_2$$ and $$z_2Rz_3\Rightarrow z_1Rz_3$$.
Hence R is transitive. It follows that R is an equivalence relation.
Note: If we consider R is a relation on the set of all complex number but 0(~R)0 for we have $$\frac{0-0}{0+0}=\frac{0}{0}$$ which is indeterminate. Hence in order that R may be an equivalence relation the set on which R is defined must be non-zero complex numbers.


Let $$R$$ be arelation on the set $$A$$, then $$R$$ is symmetric. Prove that $${R}^{-1}$$ is symmetric.

$$R$$ is a relation on $$A$$ and is symmetric.
Let $$R$$ be $$\left\{(a,a),(b,b),(c,c)\right\}$$
$$R^{-1}=\left\{(a,a),(b,b),(c,c)\right\}$$ is clearly symmetric.

1031740_1039159_ans_14346058b70e48ae8d223c07c094b13f.JPG


If $$\displaystyle A = \{1, 2 \}$$, find $$\displaystyle A \times A \times A$$ and enter the value of elements of it.


1859803_1708727_ans_6b4924a7931e48b7b744eda2698be80a.jpeg


Let $$\displaystyle A = \{2, 3 \}$$ and $$\displaystyle B = \{ 3, 5 \}$$.
Find $$\displaystyle ( A \times B ) $$ and then $$\displaystyle n(A \times B )$$.

The answer is 4
1854996_1709613_ans_011f9abe028e4ff5a9f21596b9a7e643.jpeg


Let $$N$$ be the set of natural numbers and $$R$$ be the relation on $$ N \times N $$ defined by $$(a , b)\ R\ (c , d) $$ iff $$ad = bc $$ for all $$a , b , c , d \in N $$. Show that $$R$$ is an equivalence relation. 

We know that a relation $$R$$ is an equivalence relation if it is reflexive, symmetric and transitive.
For reflexive:
For any $$(a,b)\in\,N \, \times \,N;$$ $$ab=ba$$
$$\Rightarrow (a,b)R(a,b)$$ 
Thus, $$R$$ is reflexive.

For symmetric:
Let $$(a,b)R(c,d)$$ for any $$a,b,c,d,\in N$$
$$\therefore ad=bc$$
$$\Rightarrow cb=da$$
$$\Rightarrow (c,d)R(a,b)$$
$$\therefore R$$ is symmetric.

For transitive:
Let $$(a,b)R(c,d)$$ and $$(c,d)R(e,f)$$ for $$a,b,c,d,e,f\in N$$
Then $$ad=bc$$ and $$ef=de$$
$$\Rightarrow a\,d\,c\,f=bcde$$ 
$$\Rightarrow af=be$$
$$\Rightarrow (a,b)R(e,f)$$
Thus, $$ R$$ is transitive.

Hence,  $$R$$ is an equivalence relation.


Show that relation  $$R$$  in the set  $$N*N$$  defined by  $$\left ( a,b \right )R\left ( c,d \right )$$  if  $$a^{2}+d^{2}=b^{2}+c^{2}\forall a,b,c,d\epsilon N$$, is an equivalence relation.


1961177_1781990_ans_90fb894ffcda4ffd80cfa08b0d7195df.jpg


Class 11 Commerce Applied Mathematics Extra Questions