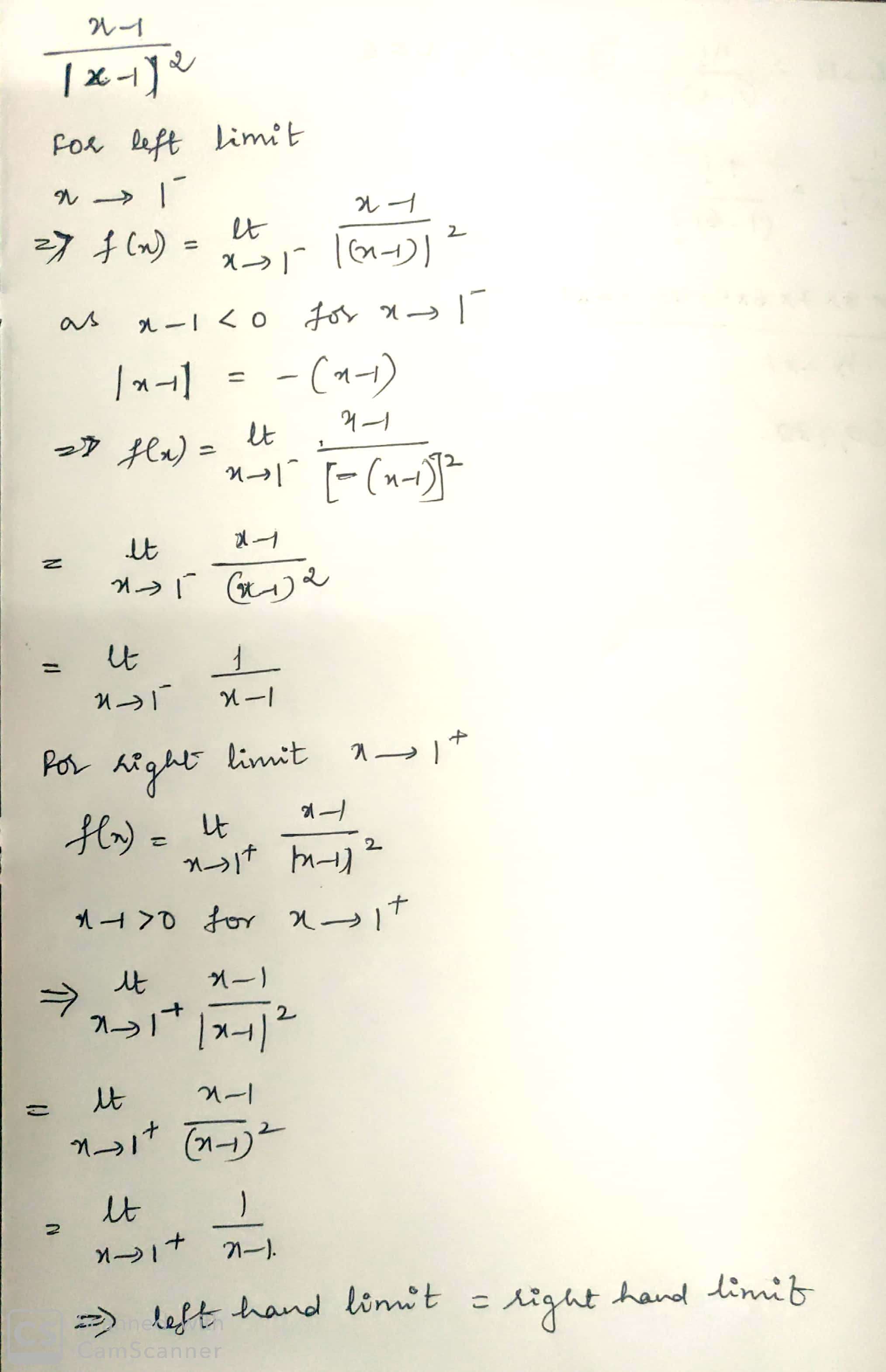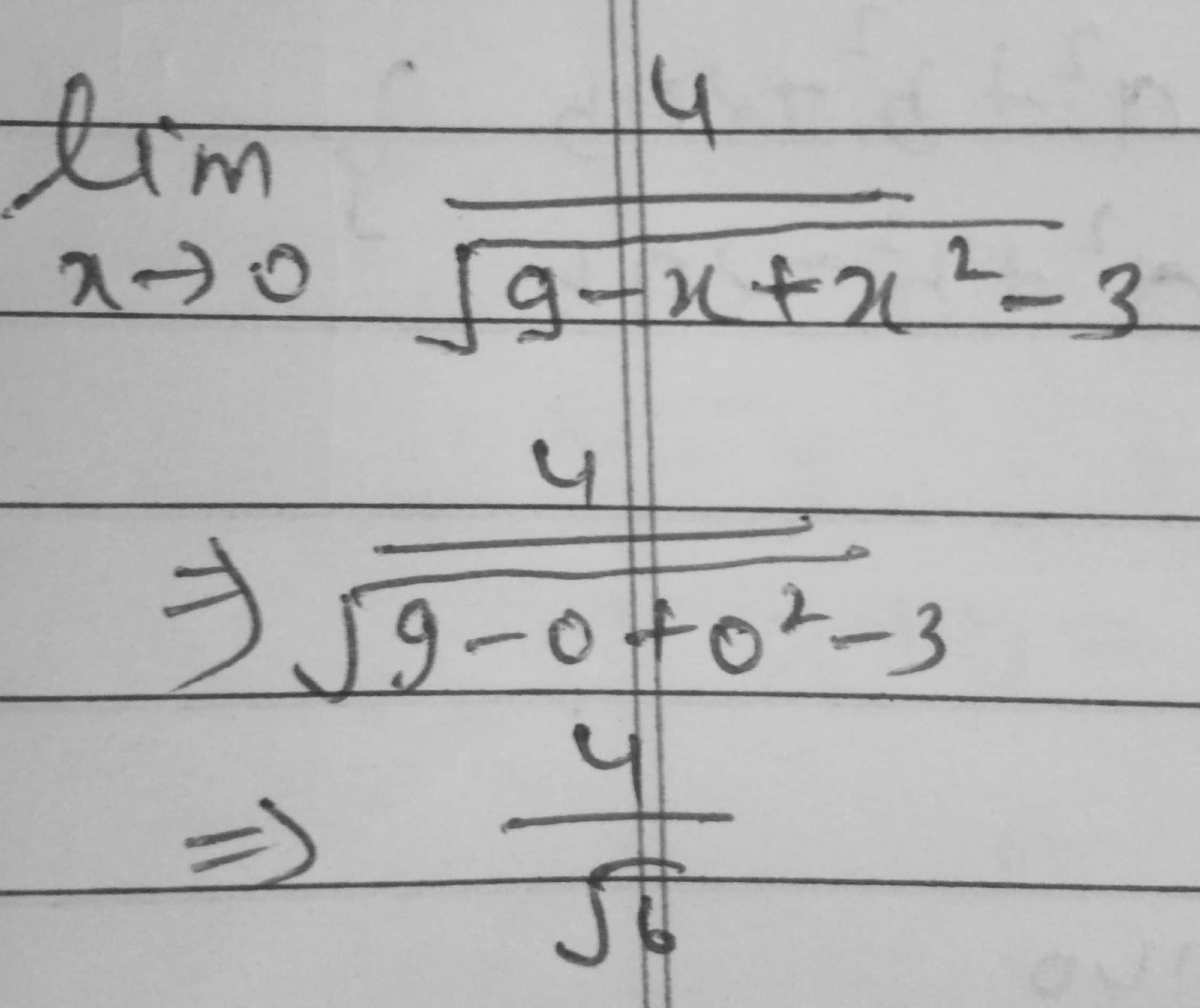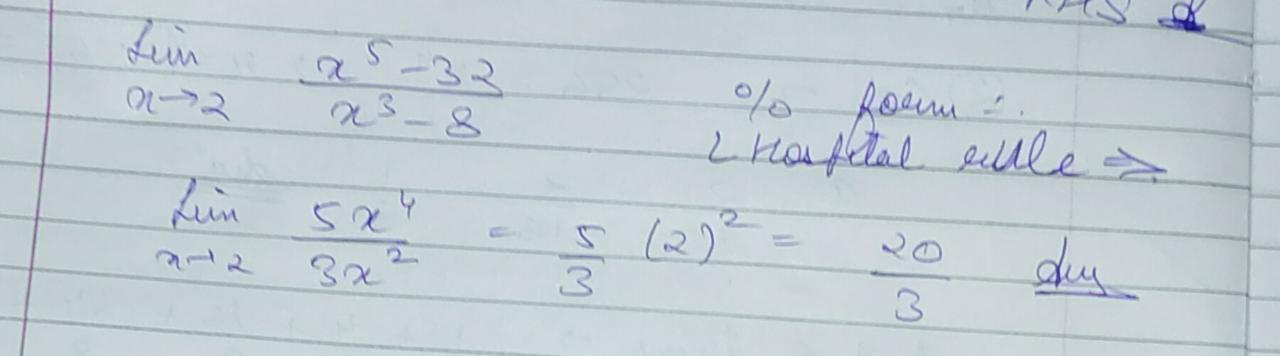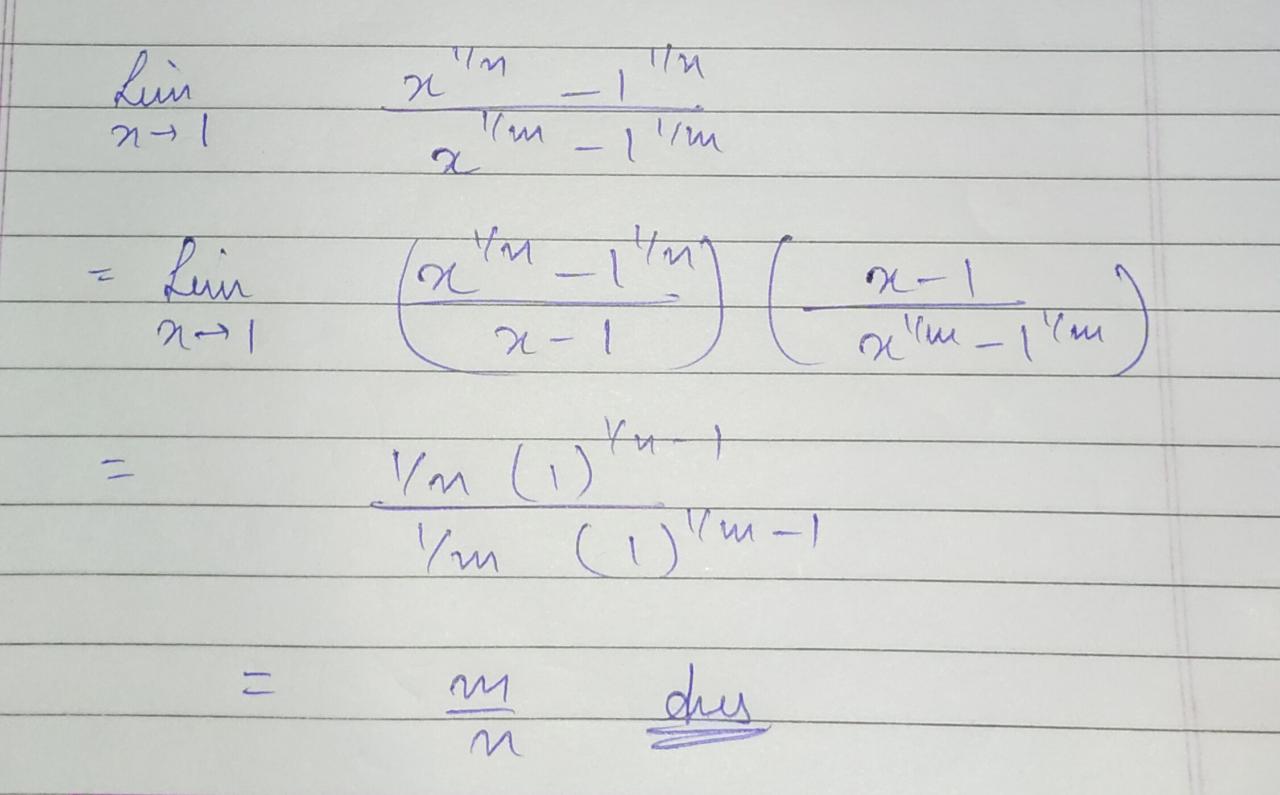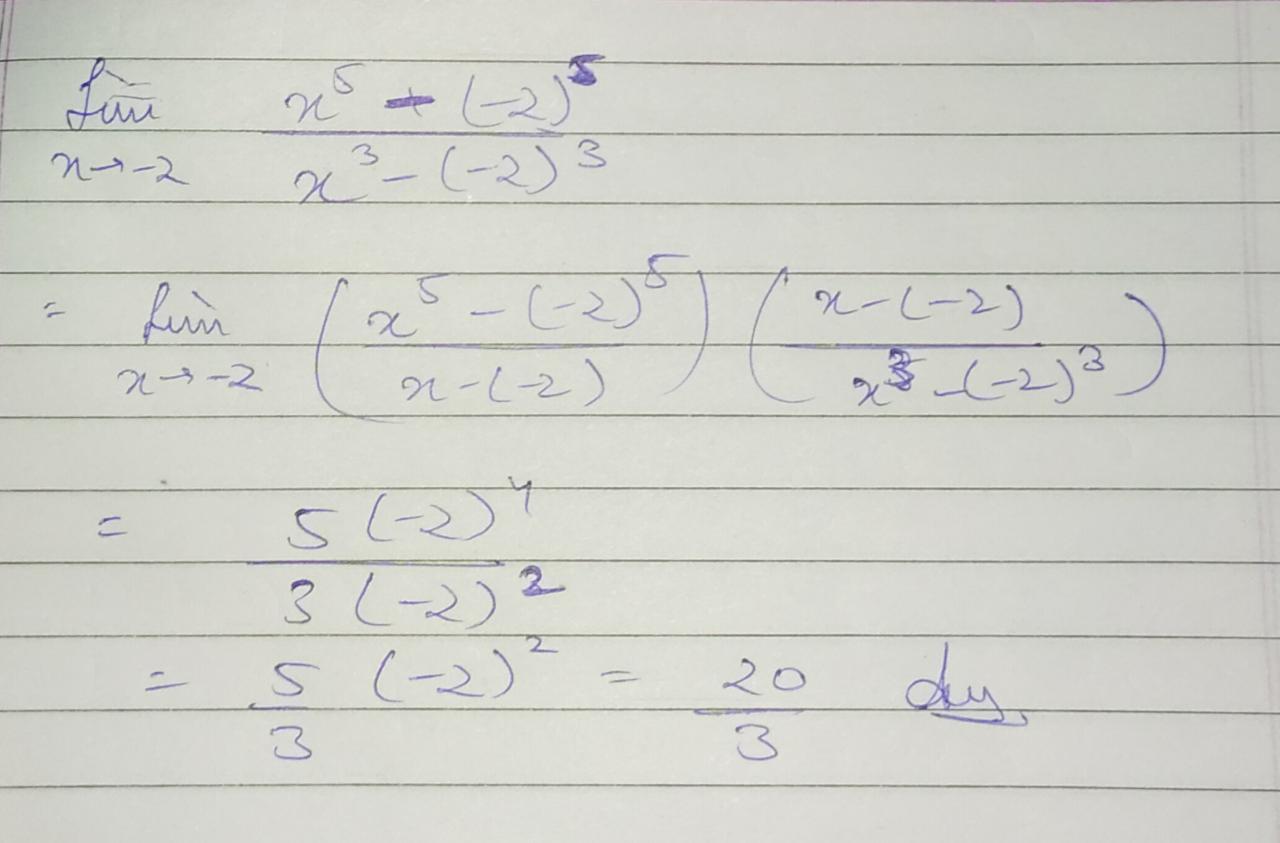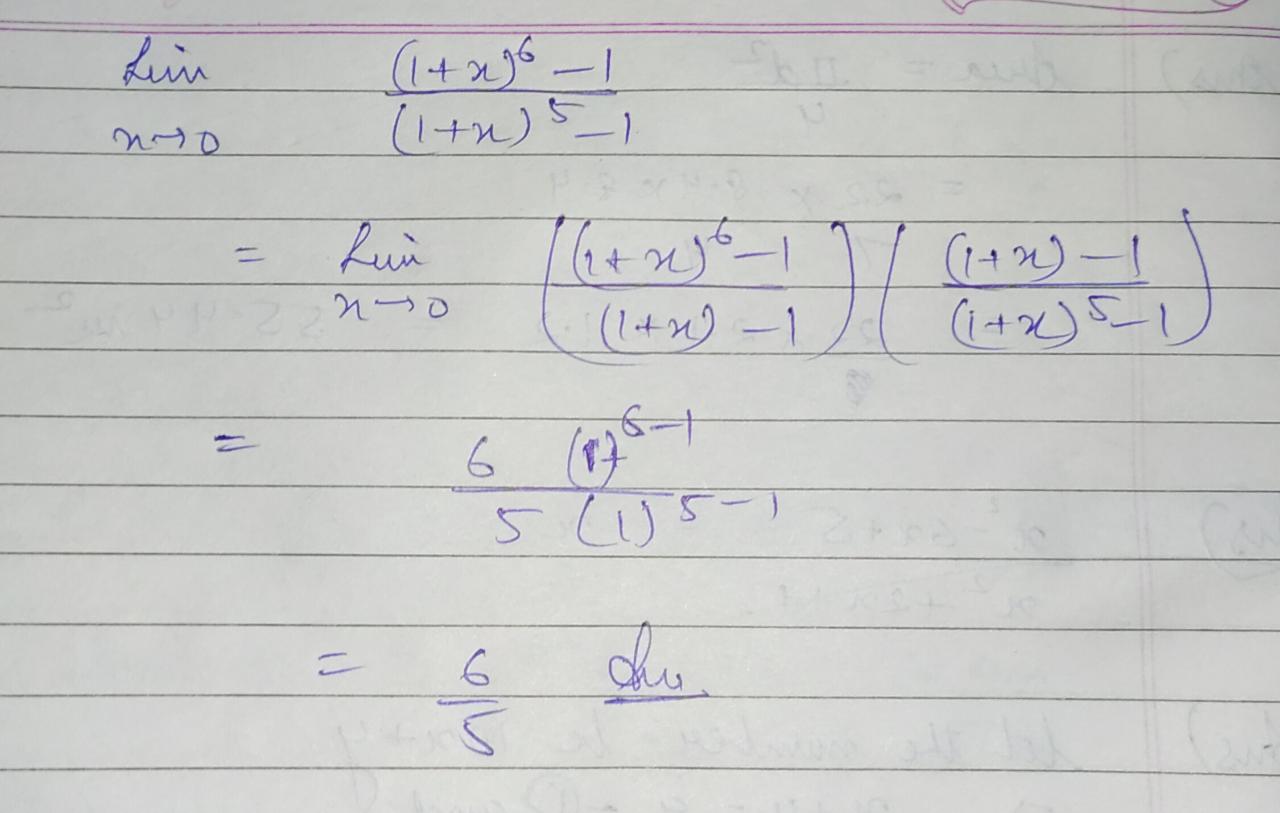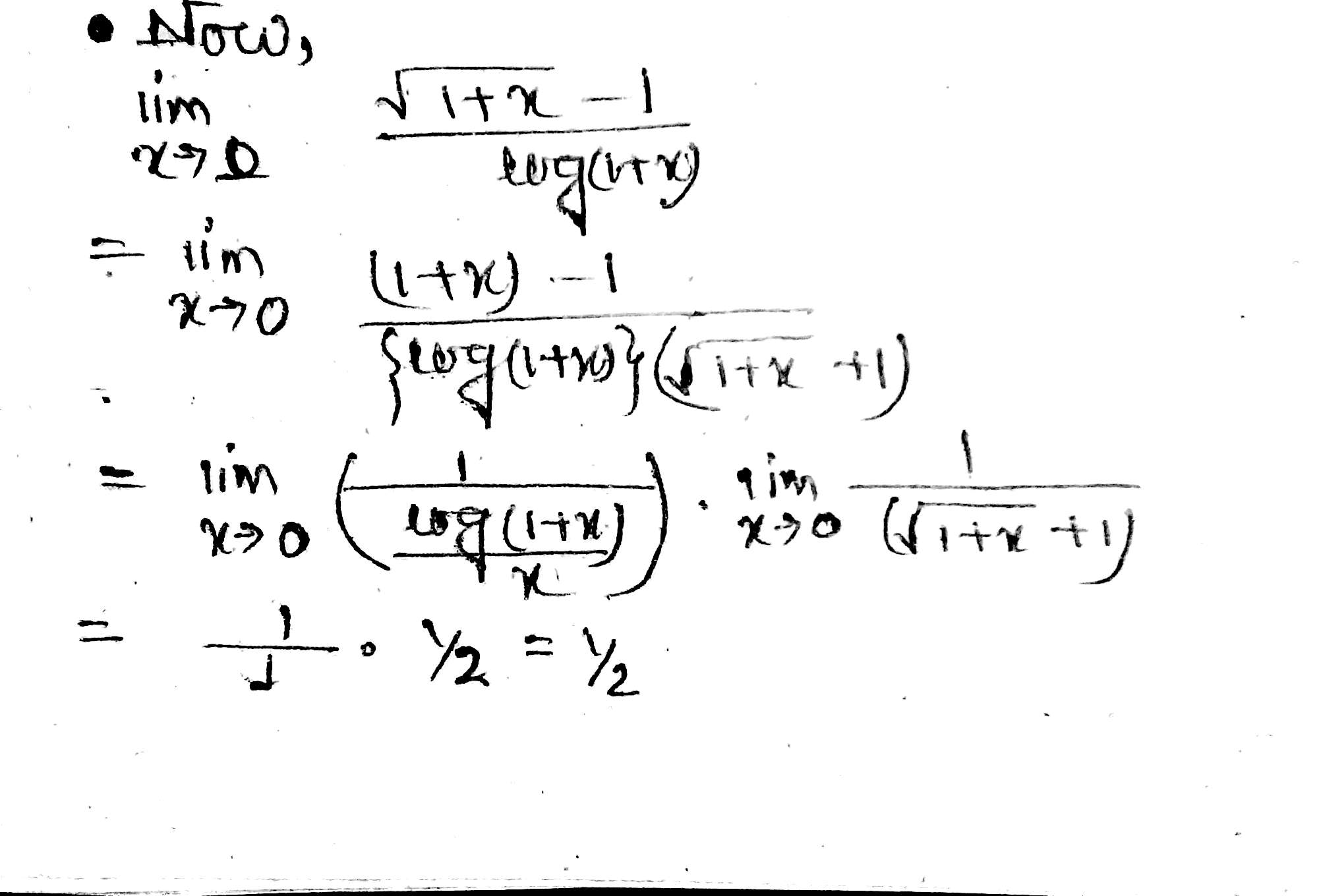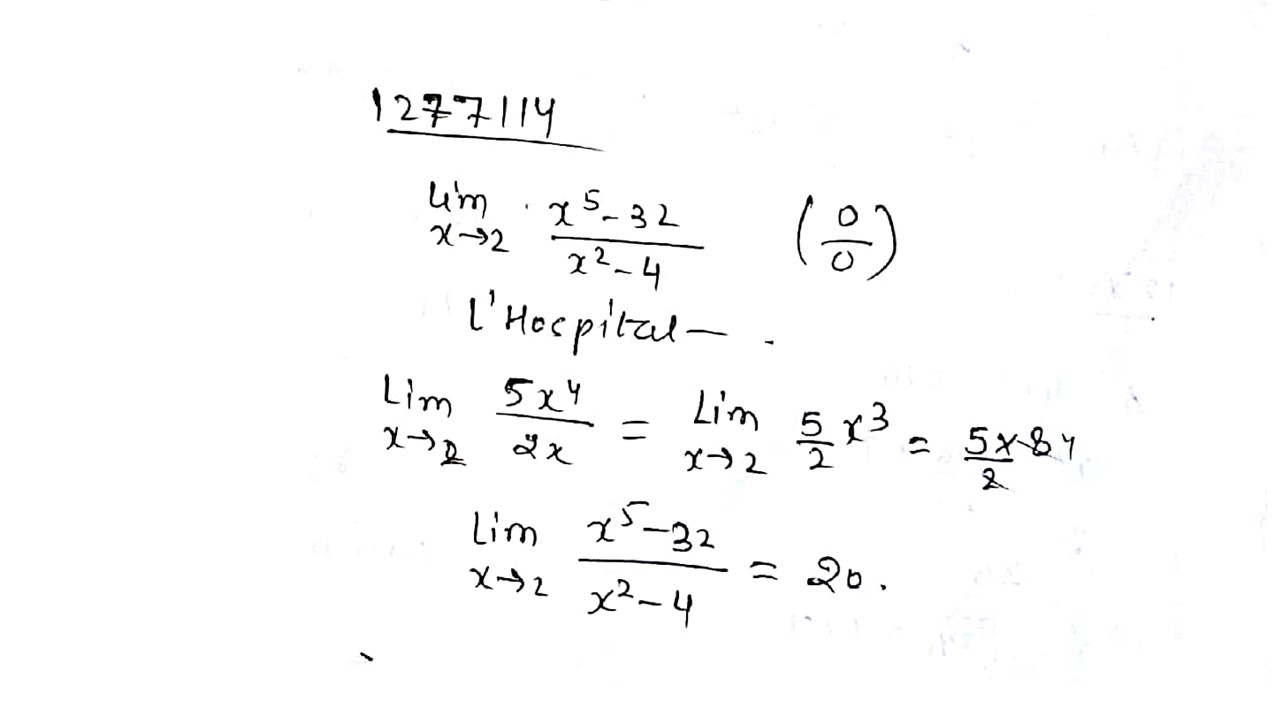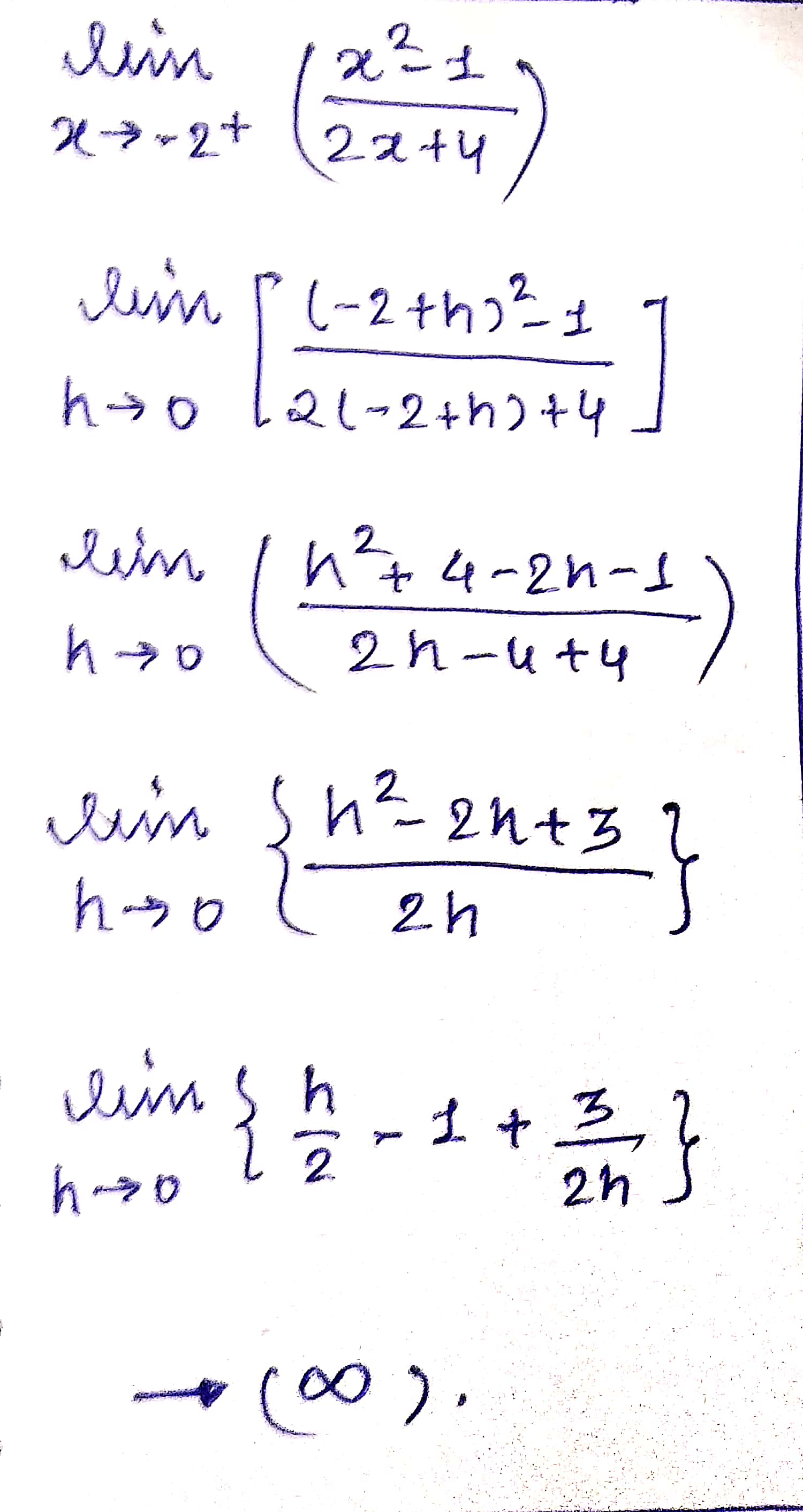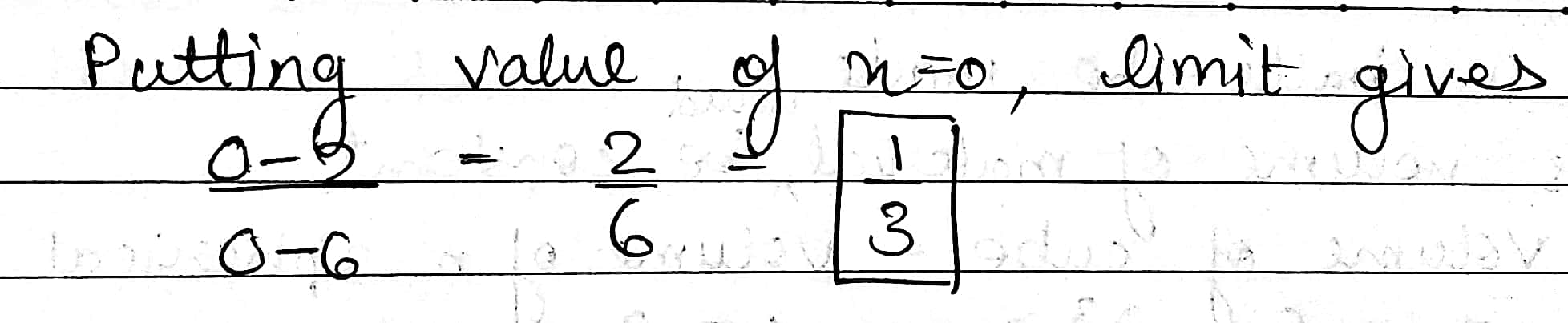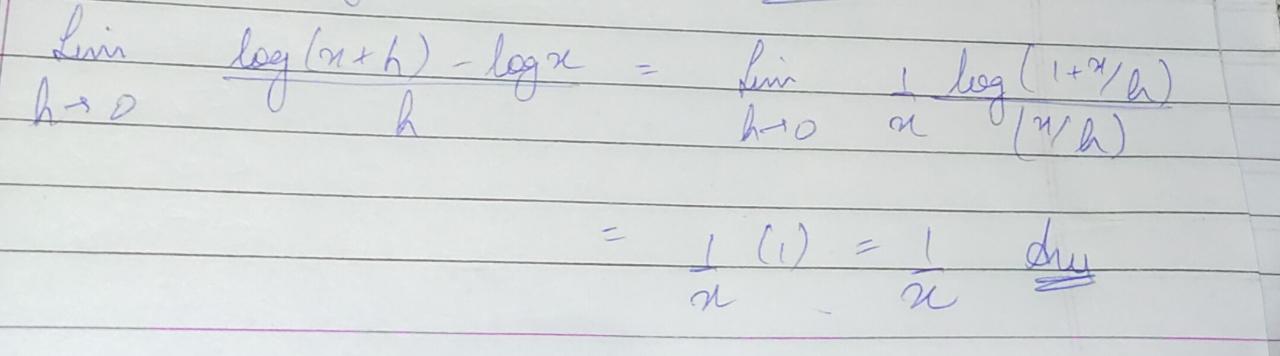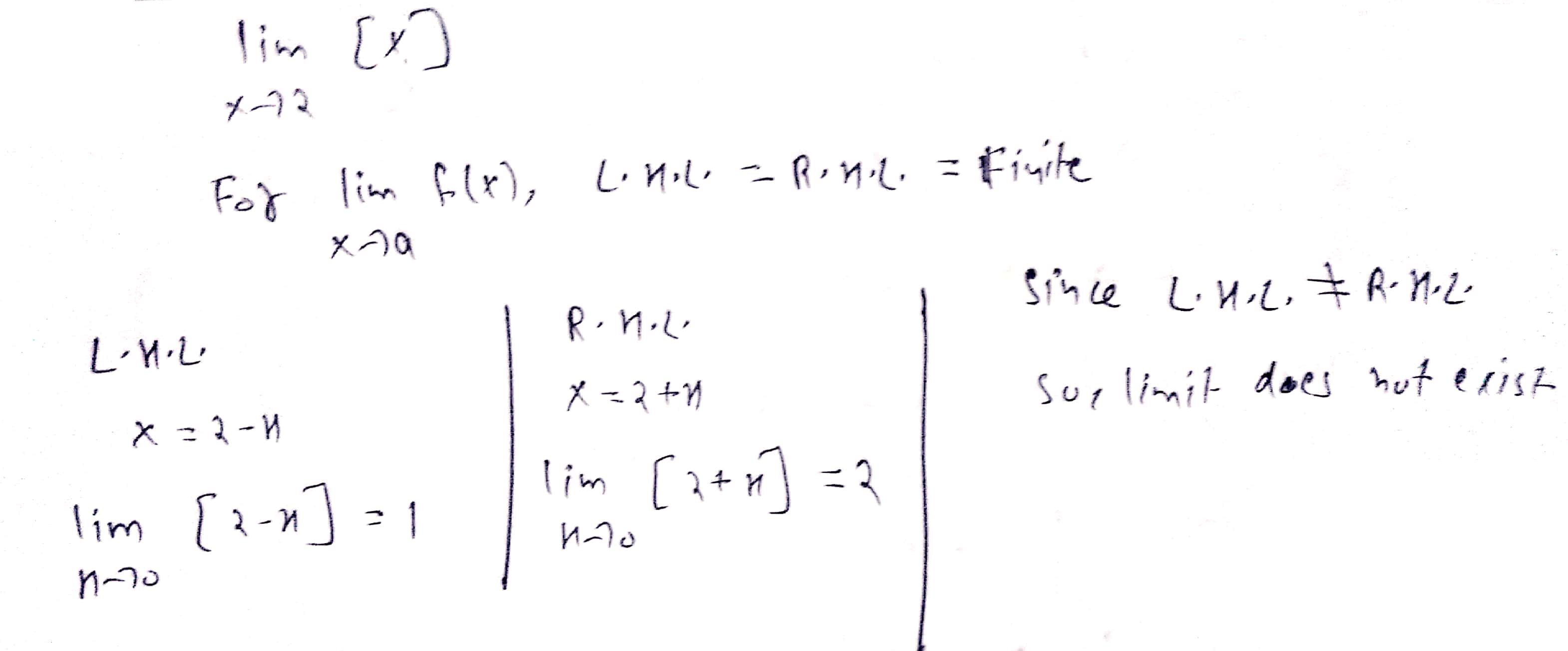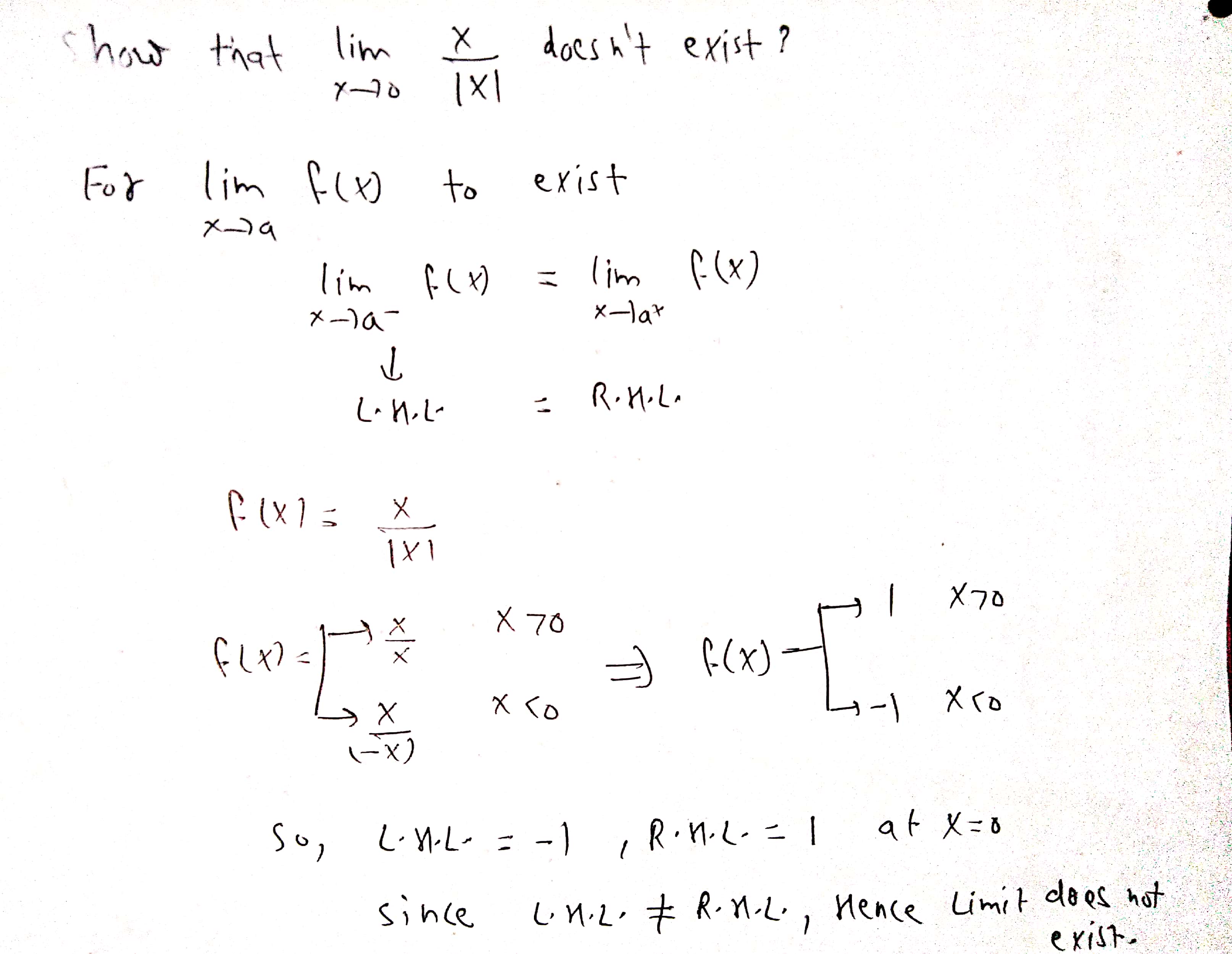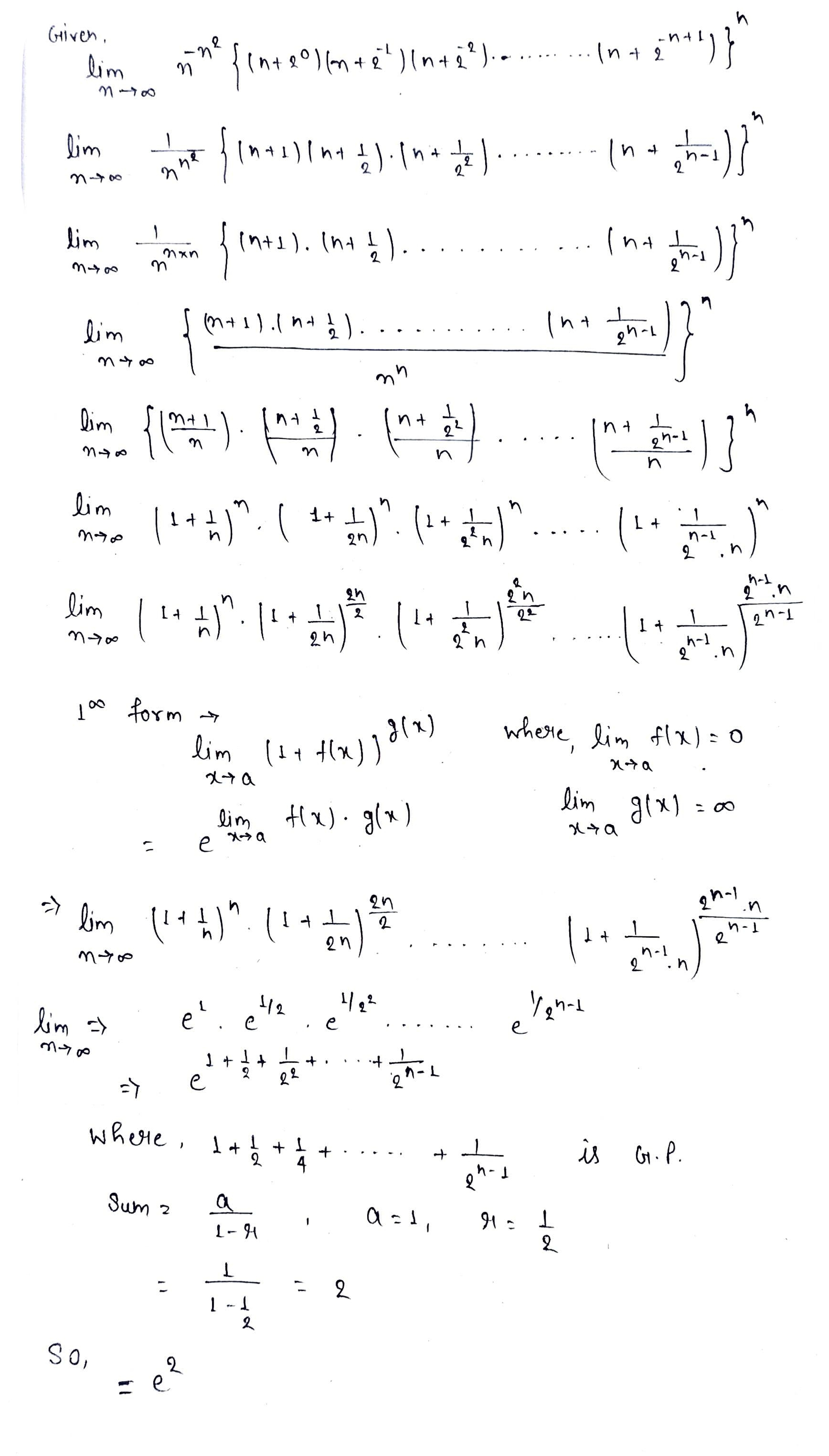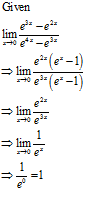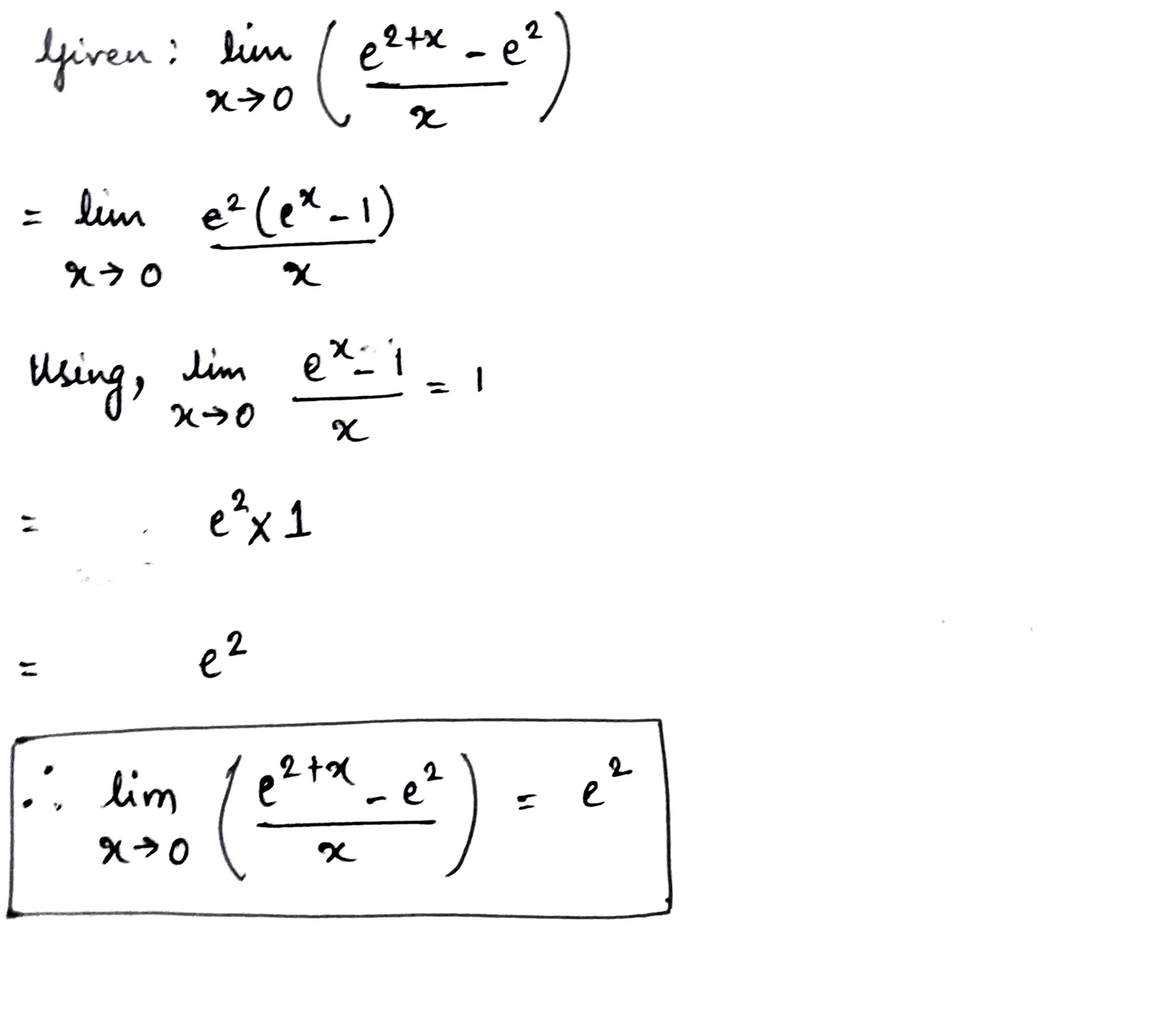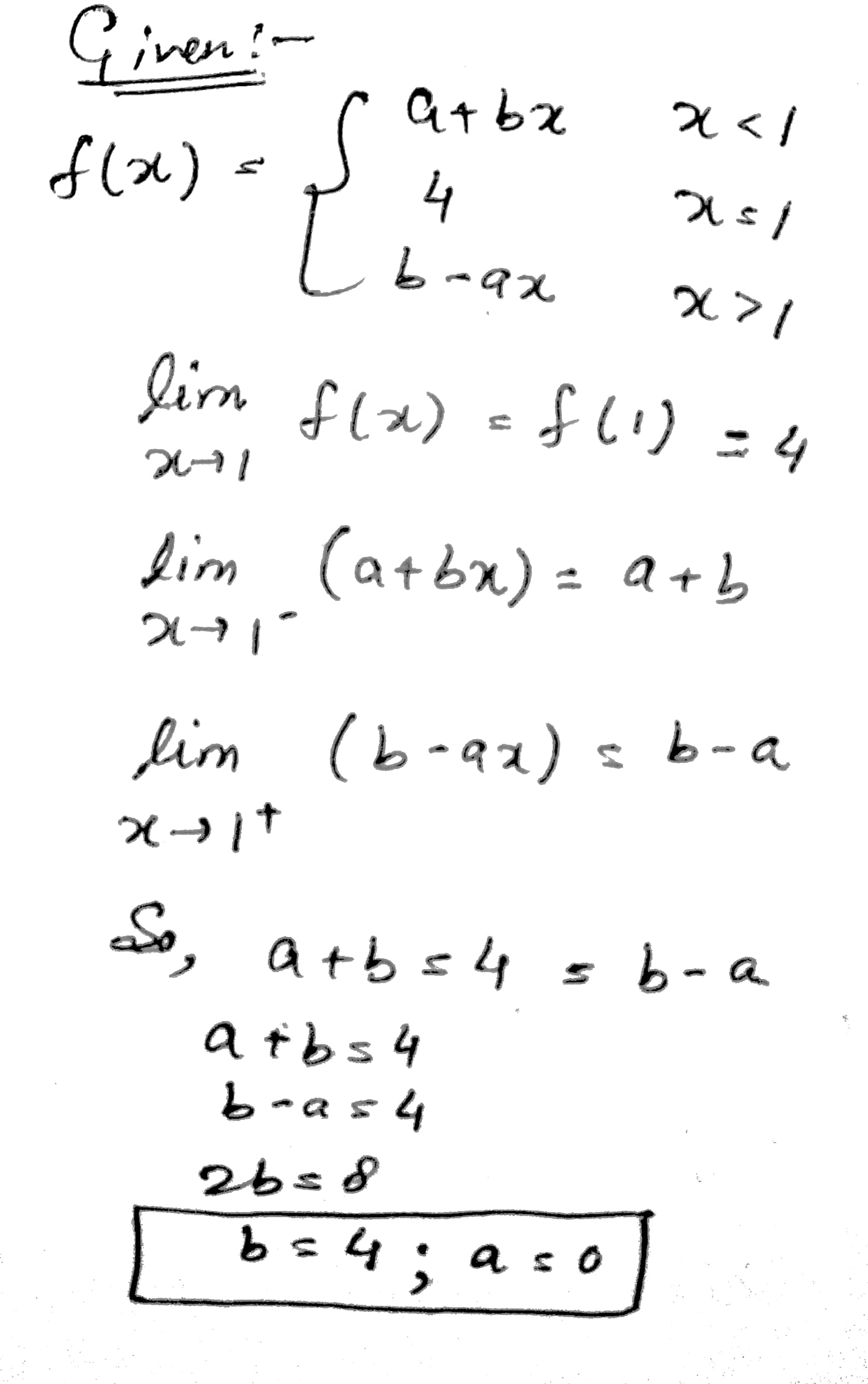Limits And Continuity     - Class 11 Commerce Applied Mathematics - Extra Questions

Evaluate the given limit: $$\displaystyle \lim_{x\rightarrow 0}x\,\sec x$$

The value of $$\displaystyle \lim_{x\rightarrow 0}x\,\sec x$$
$$=\lim_{x\rightarrow 0}\dfrac{x}{\cos \,x}$$
$$=\dfrac{0}{\cos \,0}$$
$$=\dfrac{0}{1}=0$$


$$\lim_{x\rightarrow 0^-} \dfrac{|x|}{x} = -1$$

$$L=\lim _{ x\rightarrow { 0 }^{ + } }{ \dfrac { |x| }{ x }  } $$
$$|x|=-x$$ for $$(x<0)$$
$$\therefore L=\lim _{ x\rightarrow { 0 }^{ + } }{ \dfrac { -x }{ x }  } \\ \Rightarrow L=-1$$


Show that $$\lim_{x \rightarrow 0^+} \dfrac{|x|}{x} = 1$$

Let $$L=\lim _{ x\rightarrow { 0 }^{ + } }{ \dfrac { |x| }{ x }  } $$
$$|x|=x$$ for $$(x>0)$$
Therefore, $$ L=\lim _{ x\rightarrow { 0 }^{ + } }{ \dfrac { x }{ x }  } $$
$$ \Rightarrow L=1$$
Hence, shown.


$$f(x)=\dfrac{x-1}{|x-1|^2}$$
Find both right and left hand limit of limit is exist at x=1


1314585_1065199_ans_ea7fc585fb0e4cf2a777fc347a9ba162.jpg


$$\underset {x \rightarrow \infty}{lim}\left(\dfrac{1+2x}{1+3x}\right)^x$$

$$\lim _{ x\rightarrow \infty  }{ { \left( \dfrac { 1+2x }{ 1+3x }  \right)  }^{ x } } \\ \\ =\lim _{ x\rightarrow \infty  }{ { \left( \dfrac { \dfrac { 1 }{ x } +2 }{ \dfrac { 1 }{ x } +3 }  \right)  }^{ x } } \\ =\lim _{ x\rightarrow \infty  }{ { \left( \dfrac { 2 }{ 3 }  \right)  }^{ x } } \\ =0$$


$$\lim\limits_{x\to 0}\dfrac{e^{2x}-1}{\sin 3x}=$$

Now,
$$\displaystyle\lim_{x\rightarrow 0}\dfrac{(e^{2x}-1)}{(\sin 3x)}$$

$$=\displaystyle\lim_{x\rightarrow 0}\dfrac{\dfrac{(e^{2x}-1)}{2x}\times 2}{\dfrac{\sin 3x}{3x}\times 3}$$

$$=\dfrac{2}{3}\times \dfrac{\displaystyle\lim_{2x\rightarrow 0}\dfrac{(e^{2x}-1)}{2x}}{\displaystyle\lim_{3x\rightarrow 0}\dfrac{\sin 3x}{3x}}$$

$$=\dfrac{2}{3}\times \dfrac{1}{1}=\dfrac{2}{3}$$.


If 
$$f\left( x \right) = \dfrac{{\tan x}}{{x - \pi }}$$, then
$$\underset{x\to \pi }{\mathop{\lim }}\,f\left( x \right)=?$$

We have,

$$f\left( x \right)=\dfrac{\tan x}{x-\pi }$$

 

Since, $$\underset{x\to \pi }{\mathop{\lim }}\,f\left( x \right)$$

 

Now,

$$\underset{x\to \pi }{\mathop{\lim }}\,\left( \dfrac{\tan x}{x-\pi } \right)$$

 

This is the $$\dfrac{0}{0}$$ form.

 

So, apply L-Hospital rule,

$$ \underset{x\to \pi }{\mathop{\lim }}\,\left( \dfrac{{{\sec }^{2}}x}{1-0} \right) $$

$$ \underset{x\to \pi }{\mathop{\lim }}\,\left( {{\sec }^{2}}x \right) $$

$$ \underset{x\to \pi }{\mathop{\lim }}\,{{\left( \sec x \right)}^{2}} $$

$$ ={{\left( \sec \pi  \right)}^{2}} $$

$$ ={{\left( -1 \right)}^{2}} $$

$$ =1 $$

 

Hence, this is the answer.



$$\mathop {\lim }\limits_{x \to \infty} {\left( {1 + \frac{1}{x}} \right)^{2x}}$$

We have,

$$\displaystyle {{\left( \underset{x\to \infty }{\mathop{\lim }}\,{{\left( 1+\dfrac{1}{x} \right)}^{x}} \right)}^{2}}$$ 

We know that

$$\displaystyle \underset{x\to \infty }{\mathop{\lim }}\,{{\left( 1+\dfrac{1}{x} \right)}^{x}}=e$$

 Therefore,

$$={{e}^{2}}$$

Hence, this is the answer.



$$Lt _ { x \rightarrow 0 } \dfrac { x } { \sqrt { 1 + x } - 1 }$$

$$\lim_{x\rightarrow 0}\dfrac{x}{\sqrt{1+x}-1}$$ Apply L Hospital's Rule

$$\lim_{x\rightarrow 0}\dfrac{1}{\dfrac{1}{2\sqrt{1+x}}}=2$$


Evaluate $$\lim_{x \rightarrow 0 }\dfrac{\log x+\log\dfrac{1+x}{x}}{x}$$

We have,
$$\lim_{x\to\ 0}\dfrac{log\ x+log\ \dfrac{1+x}{x}}{x}$$
$$\lim_{x\to\ 0}\dfrac{log\ x+log\ (1+x)-log\ x}{x}$$
$$\lim_{x\to\ 0}\dfrac{log\ (1+x)}{x}$$

Apply L-hospital rule
$$\lim_{x\to\ 0}\dfrac{\dfrac{1}{(1+x)}\times 1}{1}$$
$$\lim_{x\to\ 0}\dfrac{1}{(1+x)}$$
$$=\dfrac{1}{(1+0)}$$
$$=1$$

Hence, this is the answer.


$$\mathop {\lim }\limits_{x \to 0} \frac{4}{{\sqrt {9 - x + {x^2} - 3} }}$$

$$\displaystyle\lim_{x\rightarrow 0}\dfrac{4}{\sqrt{9-x+x^2-3}}$$
$$\Rightarrow \dfrac{4}{\sqrt{9-0+0^2-3}}$$
$$\Rightarrow \dfrac{4}{\sqrt{6}}$$.

1193276_1260004_ans_12ebe57c980c4f10994784a7d1f7f22f.jpg


$$\displaystyle \lim _{ x\rightarrow 0 }{ \dfrac { \log{(3+x)}-\log{(3-x)} }{ x }  } $$

We have,
$$\mathop {\lim }\limits_{x \to 0} \dfrac{{\log \left( {3 + x} \right) - \log \left( {3 - x} \right)}}{x}$$

Now,
$$\begin{array}{l} ={ \lim   }_{ x\to 0 }\dfrac { { \log  \left( { 3\left( { 1+\dfrac { x }{ 3 }  } \right)  } \right) -\log  \left( { 3\left( { 1-\dfrac { x }{ 3 }  } \right)  } \right)  } }{ x }  \\ ={ \lim   }_{ x\to 0 }\dfrac { { \log  \left( { 1+\dfrac { x }{ 3 }  } \right) -\log  \left( { 1-\dfrac { x }{ 3 }  } \right)  } }{ x }  \\ ={ \lim   }_{ x\to 0 }\dfrac { { \log  \left( { 1+\dfrac { x }{ 3 }  } \right)  } }{ { \dfrac { x }{ 3 } \times 3 } } +\dfrac { { \log  \left( { 1-\dfrac { x }{ 3 }  } \right)  } }{ { \dfrac { { -x } }{ 3 } \times 3 } }  \\ =\dfrac { 2 }{ 3 }  \end{array}$$

Hence, this is the answer.


Solve:
$$\displaystyle \lim_{x\rightarrow 0}\dfrac{3\sin^{2}x-2\sin x^{2}}{3x^{2}}$$

We have,
$$\mathop {\lim }\limits_{x \to 0} \,\,\dfrac{{3{{\sin }^2}x - 2\sin {x^2}}}{{3{x^2}}}$$

This is the $$\dfrac{0}{0}$$ form.
So, apply L-hospital rule,
$$ \mathop {\lim }\limits_{x \to 0} \,\,\dfrac{{6\sin x.\cos x - 2\cos{x^2}.2x}}{{6x}}$$
$$ \mathop {\lim }\limits_{x \to 0} \,\,\dfrac{\sin x.\cos x}{x} - \dfrac{4x\cos{x^2}}{{6x}}$$
$$ \mathop {\lim }\limits_{x \to 0} \,\,\dfrac{\sin x.\cos x}{x} - \dfrac{2\cos{x^2}}{{3}}$$
$$ = 1-\dfrac{{ 2}}{3}$$
$$ = \dfrac{{ 1}}{3}$$

Hence, this is the answer.


$$\underset { x\rightarrow a }{ \lim } { \left( \dfrac { x+1 }{ 2x+1 }  \right)  }^{ { x }^{ 2 } }=$$

We have,

$$\underset{x\to a}{\mathop{\lim }}\,{{\left( \dfrac{x+1}{2x+1} \right)}^{{{x}^{2}}}}$$


Taking limit and we get,

$$ \Rightarrow \underset{x\to a}{\mathop{\lim }}\,{{\left( \dfrac{x+1}{2x+1} \right)}^{{{x}^{2}}}} $$

$$ \Rightarrow {{\left( \dfrac{a+1}{2a+1} \right)}^{{{a}^{2}}}} $$


Hence, this is the answer.


$$\mathop {\lim }\limits_{x \to 3} \cfrac{{{x^2} - x - 6}}{{{x^3} - 3{x^2} + x - 3}}$$

We have,
$$\mathop {\lim }\limits_{x \to 3} \cfrac{{{x^2} - x - 6}}{{{x^3} - 3{x^2} + x - 3}}$$

$$\mathop {\lim }\limits_{x \to 3} \cfrac{{{x^2} - 3x+2x - 6}}{{x^2(x - 3) + 1(x - 3)}}$$

$$\mathop {\lim }\limits_{x \to 3} \cfrac{{x(x - 3)+2(x - 3)}}{{x^2(x - 3) + 1(x - 3)}}$$

$$\mathop {\lim }\limits_{x \to 3} \cfrac{{(x - 3)(x +2)}}{{(x^2+1)(x - 3)}}$$

$$\mathop {\lim }\limits_{x \to 3} \cfrac{{(x +2)}}{{(x^2+1)}}$$

$$=\cfrac{{(3 +2)}}{{(3^2+1)}}$$

$$=\cfrac{5}{10}$$

$$=\cfrac{1}{2}$$

Hence, this is the answer.


The value of $$\displaystyle x\xrightarrow { lim }\infty\, x\sin\frac{\pi}{4x}\,\cos\frac{\pi}{4x} $$

$$\lim _{ x\rightarrow \infty  }{ x\sin { (\cfrac { \pi  }{ 4x } ) } \cos { (\cfrac { \pi  }{ 4x } ) }  } \\ \lim _{ x\rightarrow \infty  }{ \cfrac { \sin { (\cfrac { \pi  }{ 4x } ) } \cos { (\cfrac { \pi  }{ 4x } ) }  }{ \cfrac { 1 }{ x }  }  } $$
Let $$\cfrac { 1 }{ x } =t$$ then as $$x\rightarrow \infty ,t\rightarrow 0$$
$$\therefore \lim _{ t\rightarrow 0 }{ \cfrac { 2\sin { (\cfrac { \pi t }{ 4 } ) } .\cos { (\cfrac { \pi t }{ 4 } ) }  }{ 2t }  } \\ \lim _{ t\rightarrow 0 }{ \cfrac { \sin { \cfrac { \pi t }{ 2 }  }  }{ 2t }  } $$
We know that 
$$\lim _{ x\rightarrow 0 }{ \cfrac { \sin { x }  }{ x }  } =1$$
Using this ,
$$\lim _{ t\rightarrow 0 }{ \cfrac { \sin { (\cfrac { \pi  }{ 2 } )t }  }{ 2t }  } =\lim _{ t\rightarrow 0 }{ \cfrac { \sin { (\cfrac { \pi  }{ 2 } )t }  }{ 2(\cfrac { \pi  }{ 2 } t).(\cfrac { 2 }{ \pi  } ) }  } \\ =\cfrac { \pi  }{ 4 } \lim _{ t\rightarrow 0 }{ \cfrac { \sin { (\cfrac { \pi  }{ 2 } t) }  }{ \cfrac { \pi t }{ 2 }  }  } \\ =\cfrac { \pi  }{ 4 } $$


Evaluate $$\lim _ { x \rightarrow 2 } \dfrac { x ^ { 5 } - 32 } { x ^ { 3 } - 8 }$$


1309870_1533316_ans_252896f9935341bdb56f8936888a4559.jpeg


$$\mathop {\lim }\limits_{x \to 1} {{\root n \of x  - 1} \over {\root m \of x  - 1}}$$ ( m and n integers) is equal to 


1327970_1567013_ans_37639e96025344b2affe025c742a1d43.jpeg


Evaluate: $$\mathop {\lim }\limits_{x \to  - 2} {{{x^5} + 32} \over {{x^3} + 8}}$$


1327926_1566479_ans_d1f8902d82694b10902eb223e9860093.jpeg


$$\lim _{ x\rightarrow a }{ \dfrac { { x }^{ 7 }-{ a }^{ 7 } }{ { x }^{  }-{ a }^{  } }  }$$

$$\lim _{ x\rightarrow a }{ \dfrac { { x }^{ 7 }-{ a }^{ 7 } }{ { x }^{  }-{ a }^{  } }  }$$

Using L hospitals Rule

$$\lim _{ x\rightarrow a } 7x^6=7a^6$$



Evaluate: $$\lim _ { x \rightarrow 0 } \dfrac { ( 1 + x ) ^ { 6 } - 1 } { ( 1 + x ) ^ { 5 } - 1 }$$


1326020_1565923_ans_d72ef66b614944f7b961248aa9f2384b.jpeg


Evaluate $$ \underset {x \rightarrow -2 } {\lim} \dfrac{tan \, \pi x}{x + 2} $$ 

$$ \underset {x \rightarrow -2 } {\lim} \dfrac{tan \, \pi x}{x + 2} $$   ($$ 0/0 $$ form) 

Applying L'Hospital's Rule we get : 

$$ \underset {x \rightarrow -2 } {\lim} \dfrac{\dfrac{d(tan\, \pi x)}{dx}}{\dfrac{d(x + 2)}{dx}} $$ 

 $$ \underset {x \rightarrow -2 } {\lim} \dfrac{\pi (sec^2 \pi x)}{1} $$ 

Applying limit we get 
$$ = \pi ( \because \, sec^2 (-2 \pi) = 1) $$


Prove that $$ \underset {x \rightarrow 0 } {\lim} \left  ( \dfrac{e^x - 1}{x}  \right  ) = 1 $$ 

We have 
$$ \underset {x \rightarrow 0} {\lim} \dfrac{e^x - 1}{x} $$ 

$$ \underset {x \rightarrow 0} {\lim} \left \{ \dfrac{ \left [ 1 + x + \dfrac{x^2}{2^1} + \dfrac{x^3}{3^1} + ----- \right ] - 1}{x} \right \} $$   $$ \left [\because \, e^x = 1 + x + \dfrac{x^2}{2^1} + ----  \right ] $$ 

$$ \underset {x \rightarrow 0} {\lim} \left \{ \dfrac{x + \dfrac{x^2}{2^1} + \dfrac{x^3}{3^1} + -----}{x} \right \} $$ 

$$ \underset {x \rightarrow 0} {\lim} x \left \{ \dfrac{1 + \dfrac{x}{2^1} + \dfrac{x^2}{3^1} + -----}{x}  \right \} $$ 

$$ = 1 + 0 = 1 $$


Evaluate $$ \underset {x \rightarrow 0 } {\lim}\dfrac{x \, tan \, 4x}{1 - cos \, 4x} $$ 

$$ \underset {x \rightarrow 0 } {\lim}\dfrac{x \, tan \, 4x}{1 - cos \, 4x} $$ 

$$ = \underset {x \rightarrow 0 } {\lim}\dfrac{x \, sin \, 4x}{cos\,4x[2\,sin^22x]} $$ 

$$ =  \underset {x \rightarrow 0 } {\lim}\dfrac{2x\,sin\, 2s \, cos\, 2x}{cos \, 4x(2\,sin^22x)} $$ 

$$ = \underset {x \rightarrow 0 } {\lim} \left  ( \dfrac{cos\,2x}{cos\,4x} \dfrac{2x}{sin\,2x} \times \dfrac{1}{2}  \right  ) $$ 

$$ = \dfrac{1}{2} \dfrac{\underset {2x \rightarrow 0} {\lim} cos\,2x}{\underset {4x \rightarrow 0} {\lim} cos\,4x} \times \underset {2x \rightarrow 0} {\lim} \left  ( \dfrac{2x}{sin\,2x}  \right  ) = \dfrac{1}{2} \times 1 = \dfrac{1}{2} $$


The value of $$ \underset {h \rightarrow 0 } {\lim} \dfrac{e^{2h} - 1}{h} $$ 

$$ \underset {2h \rightarrow 0 } {\lim} \dfrac{e^{2h} - 1}{2h} \times 2 $$ 

$$ = 1 \times 2 = 2 $$


$$\displaystyle \underset{x\rightarrow \infty }{lt}\frac{e^{x^{2}}-1}{e^{x^{2}}+1}= $$

$$\displaystyle \underset{x\rightarrow \infty }{Lt}\dfrac{e^{x^{2}}-1}{e^{x^{2}}+1}$$
$$=\displaystyle \underset{x\rightarrow \infty }{Lt}\dfrac{1-\left (

\dfrac{1}{e} \right )^{x^{2}}}{1+\left ( \dfrac{1}{e} \right )^{x^{2}}}=

\dfrac{1-0}{1+0}= 1.$$
$$\because \displaystyle e> 1 \therefore

\dfrac{1}{e}< 1$$ and $$\displaystyle \left ( \dfrac{1}{e} \right

)^{x^{2}}\rightarrow 0$$ as $$\displaystyle x\rightarrow \infty $$


$$\displaystyle \lim_{x\rightarrow \pi /3}\frac{3\:\tan x-\tan ^{3}x}{\cos (x+\dfrac{\pi}{6})}$$ is equal to

Reqd. limit is equal to
$$=\displaystyle \lim_{x\rightarrow \pi

/3}\frac{\tan x(\sqrt{3}-\tan x)(\tan x+\sqrt{3})}{\left

(\frac{1}{2}\cos x\left ( \sqrt{3}-\tan x \right )  \right )}$$

$$=\displaystyle \lim_{x\rightarrow \pi /3}\frac{2\tan x(\tan x+\sqrt{3})}{\cos x}$$

$$=\displaystyle \frac{2(\sqrt{3})(\sqrt{3}+\sqrt{3})}{1/2}=24$$


 The value $$\displaystyle \lim_{x\rightarrow \tan^{-1}3}\frac{\tan ^{6}x-2\tan ^{5}x-3\tan ^{4}x}{\tan ^{2}x-4\tan x+3}$$ is

$$\displaystyle \lim_{x\rightarrow \tan^{-1}3}\tan ^{4}x\frac{\tan ^{2}x-2\tan x-3}{\tan ^{2}x-4\tan x+3}$$

$$=\displaystyle \lim_{x\rightarrow \tan^{-1}3}\tan ^{4}x\frac{(\tan x-3)(\tan x+1)}{(\tan x-3)(\tan x-1)}$$

$$=\displaystyle \lim_{x\rightarrow \tan^{-1}3}\tan ^{4}x\frac{(\tan x+1)}{(\tan x-1)}=3^{4}\left(\frac{3+1}{3-1}\right)=162$$


Prove that the derivative of an odd function is always an even function.

Since f is differentiable, so by definition we have
$$\displaystyle f'\left( x \right) =\lim _{ h\rightarrow 0 }{ \frac { f\left( x+h \right) -f\left( x \right)  }{ h }  } $$
$$\displaystyle \Rightarrow f'\left( -x \right) =\lim _{ h\rightarrow 0 }{ \frac { f\left( -x+h \right) -f\left( -x \right)  }{ h }  } =\lim _{ h\rightarrow 0 }{ \frac { f\left( -\left( x-h \right)  \right) -f\left( -x \right)  }{ h }  } $$

If $$f\left( x \right)$$ is odd, then $$f\left( -x \right) =-f\left( x \right)$$

$$\displaystyle \therefore f'\left( -x \right) =\lim _{ h\rightarrow 0 }{ \frac { -f\left( x-h \right) +f\left( x \right)  }{ h }  } =-\lim _{ h\rightarrow 0 }{ \frac { f\left( x-h \right) -f\left( x \right)  }{ h }  } $$
$$\displaystyle =\lim _{ h\rightarrow 0 }{ \frac { f\left( x-h \right) -f\left( x \right)  }{ -h }  } =f'\left( x \right) $$

Hence, $$f'(-x)=f'(x)$$
Hence, derivative of an odd function is even


Evaluate the Given limit: $$\displaystyle \lim_{x\rightarrow 0}\frac{\sin \,ax}{\sin \,bx},a\,,b\neq 0$$

$$\displaystyle

\lim_{x\rightarrow 0}\frac{\sin \,ax}{\sin \,bx}=\lim_{x\rightarrow

0}\frac{\left ( \frac{\sin \,ax}{ax} \right )\times ax}{\left (

\frac{\sin \,bx}{bx} \right )\times bx}$$

$$=\displaystyle \left (

\frac{a}{b} \right )\times \frac{\lim_{x\rightarrow 0}\left (

\frac{\sin \,ax}{ax} \right )}{\lim_{x\rightarrow 0}\left ( \frac{\sin

\,bx}{bx} \right )}$$  

$$= \displaystyle \left ( \frac{a}{b}

\right )\times \frac{1}{1} =  \frac{a}{b}$$


Evaluate the given limit: $$\displaystyle \lim_{x\rightarrow 0}\frac{\cos \,2x-1}{\cos \,x -1}$$

$$\displaystyle \lim_{x\rightarrow 0}\frac{\cos \,2x-1}{\cos \,x -1}$$
$$=\displaystyle

\lim_{x\rightarrow 0}\frac{\cos \,2x-1}{\cos \,x -1}=\lim_{x\rightarrow

0}\frac{1-2\sin ^{2}x-1}{1-2\sin ^{2}\frac{x}{2}-1},$$   

Using $$\displaystyle \left [ \cos \,x=1-2\sin ^{2}\frac{x}{2} \right ]$$
$$= \displaystyle

\lim_{x\rightarrow 0}\frac{\sin ^{2}x}{\sin

^{2}\frac{x}{2}}=\lim_{x\rightarrow 0}\frac{\left ( \frac{\sin

^{2}x}{x^{2}} \right )\times x^{2}}{\left ( \frac{\sin

^{2}\frac{x}{2}}{\left ( \frac{x}{2} \right )^{2}} \right )\times

\frac{x^{2}}{4}}$$
$$= 4\cdot \displaystyle \frac{\lim_{x\rightarrow

0}\left ( \frac{\sin ^{2}x}{x^{2}} \right )}{\lim_{x\rightarrow 0}\left (

\frac{\sin ^{2}\frac{x}{2}}{\left ( \frac{x}{2} \right )^{2}} \right

)}=4$$


Find the value of $$\displaystyle \lim_{x\rightarrow \frac{\pi }{2}}\frac{\tan 2x}{x-\frac{\pi }{2}}$$

$$\displaystyle \lim_{x\rightarrow \frac{\pi }{2}}\frac{\tan 2x}{x-\frac{\pi }{2}}$$
Put $$\displaystyle x-\frac{\pi }{2}=y$$ so that $$\displaystyle x\rightarrow \frac{\pi }{2},\,y\rightarrow 0$$
$$\displaystyle

\therefore \lim_{x\rightarrow \frac{\pi }{2}}\frac{\tan

\,2x}{x-\frac{\pi }{2}}=\lim_{y\rightarrow 0}\frac{\tan 2\left (

y+\frac{\pi }{2} \right )}{y}$$
$$=\displaystyle \lim_{y\rightarrow 0}\frac{\tan \left ( \pi +2y \right )}{y}$$
$$=\displaystyle

\lim_{y\rightarrow 0}\frac{\tan \,2y}{y}$$    
$$=\displaystyle \lim_{y\rightarrow 0}\frac{\tan \,2y}{2y}\cdot 2 =(1)\cdot 2=2$$


Evaluate the given limit: $$\displaystyle \lim_{x\rightarrow 0}\frac{ax+x\,\cos \,x}{b\,\sin \,x}$$

$$\displaystyle

\lim_{x\rightarrow 0}\frac{ax+x\,\cos \,x}{b\,\sin

\,x}=\frac{1}{b}\lim_{x\rightarrow 0}\frac{x\left ( a+\cos \,x \right

)}{\sin \,x}$$
$$=\displaystyle \frac{1}{b}\lim_{x\rightarrow

0}\left ( \frac{x}{\sin \,x} \right )\times \lim_{x\rightarrow 0}\left (

a+\cos \,x \right )$$
$$\displaystyle = \frac{1}{b}\times

\frac{1}{\left ( \lim_{x\rightarrow 0}\frac{\sin x}{x} \right )}\times

\lim_{x\rightarrow 0}\left ( a+\cos x \right )$$
= $$\displaystyle

\frac{1}{b}\times \left ( a+\cos \,0 \right )= \frac{a+1}{b}$$


$$\lim_{x \rightarrow a} \dfrac{x cos a - a cos x}{x - a}$$

$${\lim}_{x\rightarrow a}{\dfrac{x\cos{a}-a\cos{x}}{x-a}}$$
$$={\lim}_{x\rightarrow a}{\dfrac{x\cos{a}-a\cos{a}+a\cos{a}-a\cos{x}}{x-a}}$$
$$={\lim}_{x\rightarrow a}{\dfrac{\left(x-1\right)\cos{a}+a\left(\cos{a}-\cos{x}\right)}{x-a}}$$
$$={\lim}_{x\rightarrow a}{\cos{a}+\dfrac{-2a\sin{\left(\dfrac{x+a}{2}\right)}\sin{\left(\dfrac{x-a}{2}\right)}}{x-a}}$$
$$={\lim}_{x\rightarrow a}{\cos{a}+\dfrac{-2a\sin{\left(\dfrac{x+a}{2}\right)}\sin{\left(\dfrac{x-a}{2}\right)}}{2\times\dfrac{x+a}{2}\dfrac{x-a}{2}}}\times\dfrac{x+a}{2}$$ since $${\lim}_{\theta}{\rightarrow 0}\dfrac{\sin{\theta}}{\theta}=1$$
$$=\cos{a}-a\left(\dfrac{a+a}{2}\right)=\cos{a}-{a}^{2}$$


Find: $$\displaystyle\lim_{n\rightarrow \infty}\displaystyle\sum^{n}_{r=1}=\frac{1}{16r^2+8r-3}$$.

$$\displaystyle \lim_{n \rightarrow \infty} \sum_{n=1}^{\infty} \dfrac{1}{16r^{2}+8r-3}$$
$$\displaystyle \lim_{n \rightarrow \infty} \sum_{n=1}^{\infty} \dfrac{1}{(4r-1)(4r+3)}$$
$$\displaystyle \lim_{n \rightarrow \infty} \sum_{n=1}^{\infty} \dfrac{1}{4} \left[ \dfrac{1}{4r-1}- \dfrac{1}{4r+3} \right]$$
$$\displaystyle \lim_{n \rightarrow \infty} \dfrac{1}{4} \left[ \dfrac{1}{3}- \dfrac{1}{7}+ \dfrac{1}{7}- \dfrac{1}{11} + \dfrac{1}{11} - \dfrac{1}{15}+ \dfrac{1}{15}..... \right]$$
$$\dfrac{1}{4} \left[ \dfrac{1}{3}- \dfrac{1}{\infty} \right]$$
$$\dfrac{1}{12}$$.


Calculate the following limits.
$$\displaystyle \lim_{x \, \rightarrow \, 0} \, \frac{sin \, 3x}{2x}.$$

$$\lim\limits_{x\to0}\dfrac{\sin3x}{2x}$$

$$=\lim\limits_{x\to0}\dfrac{\sin3x}{3x}\dfrac{3x}{2x}$$

$$=\dfrac{3}{2}$$


Find the following limit.
$$\displaystyle \lim_{x \, \rightarrow \, 0 } \, \frac{\cos \, (x/2) \, - \, \sin \, (x/2)}{\cos \, x}.$$

$$= \displaystyle \lim_{x\rightarrow 0} \dfrac {\cos \dfrac {x}{2} - \sin \dfrac {x}{2}}{\cos x}$$

at $$x = 0$$
$$= \dfrac {\cos \dfrac {0}{2} - \sin \dfrac {0}{2}}{\cos 0}$$ [here $$\cos 0 = 1\ \sin 0 = 0]$$

$$= \dfrac {1 - 0}{1}$$

$$= \dfrac {1}{1}$$.


Solve $$\lim _{ x\rightarrow 2 }{ (\dfrac { { x }^{ 5 }-32 }{ { x }^{ 3 }-8 } ) }$$

Formula:
$$lim_{x \rightarrow a} \dfrac{x^m - a^m}{x^n - a^n} = \dfrac{m}{n} (a)^{m - n}$$

$$lim_{x \rightarrow 2} \dfrac{x^5 - 32}{x^3 - 8}$$

$$ = lim_{x \rightarrow 2} \dfrac{x^5 - 2^5}{x^3 - 2^3}$$

$$= \dfrac{5}{3} (2)^{5 - 3} $$

$$= \dfrac{5}{3}\times 4$$

$$ = \dfrac{20}{3}$$




Solve $$\lim _{ x\rightarrow 0 }{ \dfrac { \cos { x } -\cot { x }  }{ x }  }$$

$$\mathop {\lim }\limits_{x \to 0} $$ $$\dfrac { { \cos  x-\cot  x } }{ x } $$

$$ = \mathop {\lim }\limits_{x \to 0} $$ $$\dfrac { { \cos  x-\dfrac { { \cos  x } }{ { \sin  x } }  } }{ x } $$

$$ = \mathop {\lim }\limits_{x \to 0} $$ $$\dfrac { { \sin  x\cos  x-\cos  x } }{ { x\sin  x } } $$

$$ = \mathop {\lim }\limits_{x \to 0} $$ $$\dfrac{{\cos x\left( {\sin x - 1} \right)}}{{x\sin x}}$$

Now , 

$$\mathop {\lim }\limits_{x \to {0^ - }} $$ $$\dfrac { { \cos  x\left( { \sin  x-1 } \right)  } }{ { x\sin  x } } $$

$$\, = \,\,\mathop {\lim }\limits_{h \to 0} $$ $$\dfrac { { \cos  \left( { 0-h } \right) \left( { \sin  \left( { 0-h } \right) -1 } \right)  } }{ { \left( { 0-h } \right) \sin  \left( { 0-h } \right)  } } $$

$$= \,\mathop {\lim }\limits_{h \to 0} $$ $$\dfrac{{\cosh \left( { - \sinh  - 1} \right)}}{{ - h \times  - \sinh }}$$

$$ = \,\,\mathop {\lim }\limits_{h \to 0} $$ $$\dfrac { { -\cosh  \left( { \sinh  +1 } \right)  } }{ { h\sinh   } } $$

$$=-\infty $$

$$\mathop {\lim }\limits_{x \to {0^ + }} $$ $$\dfrac { { \cos  x\left( { \sin  x-1 } \right)  } }{ { x\sin  x } } $$

$$ = \,\,\mathop {\lim }\limits_{h \to 0} $$ $$\dfrac { { \cos  \left( { 0+h } \right) \left( { \sin  \left( { 0+h } \right) -1 } \right)  } }{ { \left( { 0+h } \right) \sin  \left( { 0+h } \right)  } } $$

$$ = \,\mathop {\lim }\limits_{h \to 0} $$ $$\dfrac { { \cosh  \left( { \sinh  -1 } \right)  } }{ { h\sinh   } } $$

$$\,\,\,\,\, = \dfrac{{1 \times  - 1}}{0}$$

$$=-\infty $$

So ,$$\mathop {\lim }\limits_{x \to 0} $$ $$\dfrac { { \cos  x-\cot  x } }{ x } \, =\, -\infty $$



Apply the lmitsto given expression $$\displaystyle\lim_{x\rightarrow 0}\left(\left((x+1)(x+2)(x+3)(x+4)\right)^{\dfrac{1}{4}}-x\right)$$.

$${\lim}_{x\rightarrow 0}{\left({\left(x+1\right)\left(x+2\right)\left(x+3\right)\left(x+4\right)}^{\frac{1}{4}}-x\right)}$$
$$=\left({\left(0+1\right)\left(0+2\right)\left(0+3\right)\left(0+4\right)}^{\frac{1}{4}}-0\right)$$
$$={24}^{\frac{1}{4}}$$
$$={\left(\sqrt{24}\right)}^{\frac{1}{2}}$$
$$=\sqrt{\left(2\sqrt{6}\right)}$$


Solve:  $$\displaystyle \lim_{ n\rightarrow\infty}$$ $$\dfrac{\Sigma n^2 \, \Sigma n^3}{\Sigma n^6} =$$? If your answer is in the form $$\dfrac{p}{q}$$ ,then find $$|p-q|$$.

$$\dfrac{\displaystyle \sum n^2\displaystyle\sum n^3}{\displaystyle\sum n^6}$$

$$=\dfrac{\left(\dfrac{1}{3}n^3+\dfrac{1}{2}n^2+\dfrac{1}{6}n\right)\left(\dfrac{1}{4}n^4+\dfrac{1}{2}n^3+\dfrac{1}{4}n^2\right)}{\dfrac{1}{7}n^7+\dfrac{1}{2}n^6+\dfrac{1}{2}n^5-\dfrac{1}{6}n^3+\dfrac{1}{42}n}$$

$$=\dfrac{n^2\left(\dfrac{1}{3}+\dfrac{1}{2n}+\dfrac{1}{6n^2}\right)n^4\left(\dfrac{1}{4}+\dfrac{1}{2n}+\dfrac{1}{4n^2}\right)}{n^7\left(\dfrac{1}{7}+\dfrac{1}{2n}+\dfrac{1}{2n^2}-\dfrac{1}{6n^4}+\dfrac{1}{42n^6}\right)}$$

$$=\dfrac{\dfrac{1}{3}\times \dfrac{1}{4}}{\dfrac{1}{7}}=\dfrac{7}{12}$$ 

$$\left(\dfrac{p}{q}\right)\Rightarrow |p-q|=|7-12|=5$$

Taking limit n $$\rightarrow$$ $$\infty$$,
anything by infinity equals zero,
so remaining terms including n vanishes, only constants remain. 


$$\displaystyle\lim_{x\rightarrow 0}\dfrac{x\tan 2x-2x\tan x}{(1-\cos 2x)^2}$$ equals?

$$ \displaystyle \lim_{x\rightarrow 0}\frac{x\,tan2x-2x tanx}{(1-cos\, 2x)^{2}}$$
$$ 1-cos\, 2x = 2 sin^{2}x $$
$$ \displaystyle \lim_{x\rightarrow 0}\dfrac{x(tan 2x- 2tanx)}{(2sin^{2}x)}$$
$$ \left [ \Rightarrow tanx = \dfrac{2tanx}{1-tan^{2}x} \right ]$$
$$ \displaystyle \lim_{x\rightarrow 0} \dfrac{x\left ( \dfrac{2tanx}{1-tan^{2}x}-2tanx \right )}{(2sin^{2}x)^{2}}$$
$$ \displaystyle \lim_{x\rightarrow 0} \dfrac{x(2tanx-2tanx + 2tan^{3}x)}{(2sin^{2}x)^{2}(1-tan^{2}x)}$$
$$ \displaystyle \lim_{x\rightarrow 0}\dfrac{x\, 2tan^{3}x}{(1-tan^{2}x)(4 sin^{2}x)}$$
$$ \displaystyle \lim_{x\rightarrow 0}\dfrac{x2 sin^{2}x}{tan^{2}x (1-tan^{2}x)(1/2 sin^{2}x)}$$
divide numerator and denominator by x
$$ \displaystyle \lim_{x\rightarrow 0} \dfrac{1}{2 cos^{3}x \left(1-tan^{2}x\right)\left(\dfrac{sinx}{x}\right)}$$
$$ \displaystyle \lim_{x\rightarrow 0}\dfrac{sinx}{x} = 1 , cos(0) = 1 , tan0 = 0 $$
Applying limit $$ x \rightarrow 0$$
$$ \displaystyle \lim_{x\rightarrow 0}\dfrac{1}{2(1)(1-0)1}$$
$$ = \boxed{1/2}$$

1178733_1069118_ans_bf45618e232c4aff90f0d8c5c2e33a48.jpg


Evaluate: $$\mathop {\lim }\limits_{x \to 3} \left[ {\dfrac{1}{{x - 3}} + \dfrac{{9x}}{{27 - {x^3}}}} \right]$$

$$\begin{array}{l} { \lim  }_{ x\to 3 }\left[\dfrac { 1 }{ { x-3 } } +\dfrac { { 9x } }{ { 27-{ x^{ 3 } } } }\right]  \\ ={ \lim   }_{ x\to 3 }\left[ { \dfrac { 1 }{ { x-3 } } -\dfrac { { 9x } }{ { { x^{ 3 } }-27 } }  } \right]  \\ ={ \lim   }_{ x\to 3 }\dfrac { { { x^{ 2 } }+3x+9-9x } }{ { \left( { x-3 } \right) \left( { { x^{ 2 } }+3x+9 } \right)  } }  \\ ={ \lim   }_{ x\to 3 }\dfrac { { { x^{ 2 } }-6x+9 } }{ { \left( { x-3 } \right) \left( { { x^{ 2 } }+3x+9 } \right)  } }  \\ ={ \lim   }_{ x\to 3 }\dfrac { { { { \left( { x-3 } \right)  }^{ 2 } } } }{ { \left( { x-3 } \right) \left( { { x^{ 2 } }+3x+9 } \right)  } } \end{array}$$
$$=\lim\limits_{x\to 3}\dfrac{x-3}{x^3+3x+9}$$
$$=0$$.


The value of $$\displaystyle \underset{x\to \infty }{\mathop{\lim }}\,\left( x\sin \left( \dfrac{3}{x} \right) \right)$$

We have,

$$\displaystyle \underset{x\to \infty }{\mathop{\lim }}\,\left( x\sin \left( \dfrac{3}{x} \right) \right)$$

$$\displaystyle \underset{x\to \infty }{\mathop{\lim }}\,\left( 3\dfrac{\sin \left( \dfrac{3}{x} \right)}{\left( \dfrac{3}{x} \right)} \right)$$

Let $$h=\dfrac{3}{x}$$

Therefore,

$$ \displaystyle \underset{h\to 0}{\mathop{\lim }}\,\left( 3\dfrac{\sinh }{h} \right) $$

$$ \displaystyle 3\underset{h\to 0}{\mathop{\lim }}\,\left( \dfrac{\sinh }{h} \right) $$

$$ =3\times 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left[ \,\because \underset{x\to 0}{\mathop{\lim }}\,\left( \dfrac{\sin x}{x} \right) \right] $$

$$ =3 $$

Hence, this is the answer.



If $$\displaystyle \lim_{x\rightarrow 0} \dfrac {\sin \sqrt {x}}{\sqrt [4]{x}}$$.


1351885_1130567_ans_fde757f55a9242d6ba1abf3283d4c6c4.jpg


Evaluate $$\lim_{x\rightarrow 1}\frac{x^{15}-1}{x^{10}-1}$$

Consider the given function:

  $$ f\left( x \right)=\dfrac{{{x}^{15}}-1}{{{x}^{10}}-1} $$

 $$ =\dfrac{{{\left( {{x}^{5}} \right)}^{3}}-{{\left( 1 \right)}^{3}}}{{{\left( x \right)}^{2}}-{{\left( 1 \right)}^{2}}} $$

 $$ =\dfrac{\left( {{x}^{5}}-1 \right)\left( {{x}^{10}}+1+{{x}^{5}} \right)}{\left( {{x}^{5}}-1 \right)\left( {{x}^{5}}+1 \right)} $$

 $$ =\dfrac{{{x}^{10}}+{{x}^{5}}+1}{\left( {{x}^{5}}+1 \right)} $$

 $$ =1 $$

Hence this is the answer.



Solve: $$\underset{x \rightarrow 2}{\lim} \dfrac{a^{\tan x} - a^{\sin x}}{\tan x - \sin x}, a > 0$$

$$\displaystyle\lim_{x\rightarrow 2}\dfrac{a^{\tan x}-a^{\sin x}}{\tan x-\sin x}$$
$$=\left(\displaystyle\lim_{x\rightarrow 2} a^{\tan x}-\displaystyle\lim_{x\rightarrow 2}a^{\sin x}\right)\times \dfrac{1}{\displaystyle\lim_{x\rightarrow 2}\tan x-\displaystyle\lim_{x\rightarrow 2}\sin x}$$
$$=\dfrac{a^{\tan 2}-a^{\sin 2}}{\tan 2-\sin 2}$$
$$\therefore \displaystyle\lim_{x\rightarrow 2}\dfrac{a^{\tan x}-a^{\sin x}}{\tan x-\sin x}=\dfrac{a^{\tan 2}-a^{\sin 2}}{\tan 2-\sin 2}$$.


Evaluate:$$\mathop {\lim }\limits_{x \to 0} \left( {{{\left( {x + 1} \right)}^{\frac{2}{3}}} - {{\left( {x - 1} \right)}^{\frac{2}{3}}}} \right)$$

$$\displaystyle \lim_{x\rightarrow 0}((x+1)^{\frac{2}{3}}-(x-1)^{\frac{2}{3}})$$

this is not at form $$\dfrac{0}{0}$$

So just put the values 

$$(1)^{\frac{2}{3}}-(-1)^{\frac{2}{3}}$$

cube root of $$-1$$  is $$-1$$

then square of $$1$$ is $$1$$

$$=1-1$$

$$=0$$


Solve $$\mathop {\lim }\limits_{x \to \frac{\pi }{4}} \dfrac{{f\left( x \right) - f\left( {\dfrac{\pi }{4}} \right)}}{{x - \dfrac{\pi }{4}}}$$, where $$f\left( x \right) = \sin 2x$$

$$f(\dfrac \pi4)=\sin\dfrac\pi2=1$$

$$\mathop {\lim }\limits_{x \to \frac{\pi }{4}} \dfrac{{f\left( x \right) - f\left( {\dfrac{\pi }{4}} \right)}}{{x - \dfrac{\pi }{4}}}=\mathop {\lim }\limits_{x \to \frac{\pi }{4}} \dfrac{{\sin2x - 1}}{{x - \dfrac{\pi }{4}}}$$

It is of the form $$\dfrac00$$

So we will apply L Hospital Rule 

$$\mathop {\lim }\limits_{x \to \dfrac{\pi }{4}} \dfrac{\dfrac{d}{dx}({\sin2x - 1})}{\dfrac{d}{dx}{(x - \dfrac{\pi }{4})}}=\dfrac{2\cos2x}{1}=2\cos\dfrac\pi2=0$$



Evaluate the limit
$$\mathop {\lim }\limits_{x \to \frac{\pi }{6}} \frac{{{{\cot }^2}x - 3}}{{\cos ecx - 2}}$$

$${\lim _{x \to \frac\pi6}}\frac{{\cot^2 x - 3}}{{{cosecx-2}}}$$

it is of the form $$\dfrac00$$

So, we will apply L Hospital rule until we will get determinate form

Differentiating numerator and denominator we will get,
$${\lim _{x \to \frac\pi6}}\frac{{-2\cot x cosec^2x}}{{{-\cot xcosecx}}}={\lim _{x \to \frac\pi6}}2cosecx=2\times2=4$$ 



Evaluate: 
$$\mathop {\lim }\limits_{x \to 0} \frac{{\sqrt {1 + \sin x}  - \sqrt {1 - \sin x} }}{x}$$

$$\mathop {\lim }\limits_{x \to 0} \dfrac{{\sqrt {1 + \sin x}  - \sqrt {1 - \sin x} }}{x}$$
it is of the form of $$\dfrac00$$

So, we will apply L Hospital rule 
$$ \lim_{x \to 0}\dfrac{\dfrac{d}{dx}({\sqrt {1 + \sin x}  - \sqrt {1 - \sin x} )}}{\dfrac{d}{dx}x}=\lim_{x \to 0}\dfrac{\dfrac{\cos x}{2\sqrt{1+\sin x}}+\dfrac{\cos x}{2\sqrt{1-\sin x}}}{1}=\dfrac{\dfrac12+\dfrac12}{1}=1$$


Evaluate:
$$\lim\limits_{x\to 0}\dfrac{\sqrt{1+x}-1}{\log(1+x)}$$

Now,
$$\displaystyle\lim_{x\rightarrow 0}\dfrac{\sqrt{1+x}-1}{log(1+x)}$$
$$=\displaystyle\lim_{x\rightarrow 0}\dfrac{(1+x)-1}{\{log (1+x)\}(\sqrt{1+x}+1)}$$
$$=\displaystyle\lim_{x\rightarrow 0}\left(\dfrac{1}{\dfrac{log(1+x)}{x}}\right)\cdot \displaystyle\lim_{x\rightarrow 0}\dfrac{1}{(\sqrt{1+x}+1)}$$
$$=\dfrac{1}{2}\cdot \dfrac{1}{2}=\dfrac{1}{2}$$.

1181601_1196314_ans_cc995859cf3344fe850ca677a1503149.jpg


Prove that
$$L = \lim _ { n \rightarrow \infty } \left( 1 + \frac { 4 } { n } \right) ^ { 3 n }$$ = $$12$$

$$\underset{n \rightarrow \infty}{lim} \left(1 + \dfrac{4}{n} \right)^{3n}$$
Apply exponent rule
$$4a^x = e^{ln (a^x)} = e^{x ln a}$$
$$\left(1 + \dfrac{4}{n} \right)^{3n} = e^{3n \, ln \, \left(1 + \frac{4}{n} \right)} $$
$$\underset{x \rightarrow \infty}{lim} (e^{3n \, ln \left(1 + \frac{4}{n} \right)})$$
$$\rightarrow $$ Apply limit chain rule
$$g (n) = 3n \, ln \left(1 + \dfrac{4}{n} \right) \,\, f(4) = e^4$$
$$\rightarrow \underset{n \rightarrow \infty}{lim} 3n \, ln (1 + \dfrac{4}{n}) = 3 \, \underset{n \rightarrow \infty}{lim} 3n \, ln (1 + \dfrac{4}{n})^n$$
$$\rightarrow 3 \underset{n \rightarrow \infty}{lim} \dfrac{ln (1 + 4/n)}{1/n}$$
Applying L hospital Rule as undetermined form is there
we get
$$\rightarrow  3 \underset{n \rightarrow \infty}{lim} \left(\dfrac{4n}{n + 4} \right) = 12$$
$$\left(\dfrac{4n}{n + 4} = \dfrac{4}{1 + 4/n} \right)$$
$$\underset{n \rightarrow \infty}{lim} \dfrac{4}{n} = 0$$
Now 
$$\underset{n \rightarrow 12}{lim} e^4 = e^{12}$$


Evaluate: $$\lim _ { x \rightarrow 1 } \frac { ( \ln ( 1 + x ) - \ln 2 ) \left( 3.4 ^ { x - 1 } - 3 x \right) } { \left[ ( 7 + x ) ^ { \frac { 1 } { 3 } } - ( 1 + 3 x ) ^ { \frac { 1 } { 2 } } \right] \cdot \sin ( x - 1 ) }$$

$$\displaystyle \lim_{x\rightarrow 1} \dfrac {(ln (1 + x) - ln 2)(3 . 4^{x - 1} - 3x)}{[(7 + x)^{\dfrac {1}{3}} - (1 + 3x)^{\dfrac {1}{2}}] \sin (x - 1)}$$

$$\displaystyle \lim_{h\rightarrow 0} \dfrac {ln \left (\dfrac {1 + 1 + h}{2}\right ) 3[4^{h + 1 - 1} - (1 + h]}{[(7 + 1 + h)^{\dfrac {1}{3}} - (1 + 3 + 3h)^{\dfrac {1}{2}} . \sin (1 + h -1)}$$

$$\underset{h\rightarrow 0}{lim}\dfrac{ln(h/2)3[4^h-(1+h)]}{[(8+h)^{1/3}-(4+3h)^{1/2}].\sin(h)}$$

$$\displaystyle \lim_{h \rightarrow 0} \dfrac {\dfrac {ln(1 + h/2)}{2(h/2)} . 3. [4^{h} - (1 + h)]}{2\left \{\left [1 + \dfrac {h}{8} \times \dfrac {1}{3} + .....\right ] - \left [1 + \dfrac {3h}{4} \times \dfrac {1}{2} + ....\right ]\right \}}$$

$$\displaystyle \lim_{h\rightarrow 0} \dfrac {\dfrac {3}{4} \left [\dfrac {4^{h} - 1}{h} - 1\right ]}{\dfrac {1}{h} \left [\dfrac {h}{24} - \dfrac {3h}{8}\right ]}$$

$$= -\dfrac {9}{4} ln (4/e)$$.


Evaluate $$\displaystyle \lim_{x\rightarrow \pi/2} \dfrac {1 + \cos 2x}{(\pi - 2x)^{2}}$$.

$$\displaystyle \lim_{x\rightarrow \pi/2} \dfrac {1 + \cos 2x}{(\pi - 2x)^{2}}$$
(Putting $$x = \dfrac {\pi}{2} + h$$, when $$x\rightarrow \dfrac {\pi}{2}, h\rightarrow 0)$$

$$= \lim_{h\rightarrow 0} \dfrac {1 + \cos 2\left (\dfrac {\pi}{2} + h\right )}{\left \{\pi - 2\left (\dfrac {\pi}{2} + h\right )\right \}^{2}}$$

$$= \displaystyle \lim_{h\rightarrow 0} \dfrac {1 + \cos (\pi + 2h)}{(4h^{2})}$$

$$= \displaystyle \lim_{h\rightarrow 0} \dfrac {1 - \cos 2h}{4h^{2}}$$

$$= \displaystyle \lim_{h\rightarrow 0} \dfrac {2\sin^{2} h}{4h^{2}}$$

$$= \dfrac {1}{2} \displaystyle \lim_{h\rightarrow 0} \left (\dfrac {\sin h}{h}\right )^{2}$$

$$= \dfrac {1}{2} \times 1 = \dfrac {1}{2}$$.


$$\mathop {\lim }\limits_{x \to \tfrac{\pi }{2}} (secx - tanx)$$

$$ \lim_{x\rightarrow\dfrac  \pi2}\,(sec\,x-tan\,x)$$

$$ \Rightarrow \lim_{x\rightarrow \dfrac{\pi}{2}} \left [ \dfrac{1}{cos\,x} - \dfrac{sin\,x}{cos\,x} \right ]$$

$$  \Rightarrow \lim_{x\rightarrow \dfrac{\pi}{2}} \left [ \dfrac{1 - sin\,x}{cos\,x} \right ] $$

$$  \Rightarrow \lim_{x\rightarrow \pi/2} \dfrac{(cos\,x \dfrac{x}{2} - sin\,\dfrac x2)^{2}}{cos^{2}\dfrac{x}{2} - sin^{2} \dfrac x2}$$

$$ \left \{ \therefore 1 = sin^{2} dfrac x2 + cos^{2} x/2 ,  sin\,x = 2\,sin x/2 cos x/2 ,cos\,x = cos^{2} \dfrac{x}{2} - sin^{2} \dfrac{x}{2}\right \}$$

$$  \Rightarrow \lim_{x\rightarrow \dfrac{\pi}{2}} \dfrac{(cos \,x/2 - sin\, x/2)^{2}}{(cos x/2 - sin\, x/2)(cos \,x/2 + sin \,x/2)}$$

$$  \Rightarrow \lim_{x\rightarrow \dfrac \pi2} \dfrac{cos\, x/2 - sin\, x/2}{cos\, x/2 + sin \,x/2}$$

$$ \Rightarrow 0 $$


Solve:
 $$\underset{x \rightarrow 2}{lim} \dfrac{x^5 - 32}{x^2 - 4}$$.

$$ \lim_{x\rightarrow 2} \frac{x^{5}-32}{x^{2}-4}$$ $$ (\frac{0}{0})$$
L' Hospital-
$$ \lim_{x\rightarrow 2} \frac{5x^{4}}{2x} = \lim_{x\rightarrow 2} \frac{5}{2}x^{3} = \frac{5\times 8}{2}$$
$$ \lim_{x\rightarrow 2}\frac{x^{5}-32}{x^{2}-4} = 20. $$

1117382_1277114_ans_2b85ecd0536746fda8a01107d6cd9040.JPG


If $$\underset { x\rightarrow a }{ lim } \frac { 2x-\sqrt { { x }^{ 2 }+{ 3a }^{ 2 } }  }{ \sqrt { x+a } -\sqrt { 2a }  } =\sqrt { 2 } $$ (where $$a\in { R }^{ + })$$ then a is equal to

$${ \lim   }_{ x\to a }\cfrac { { 2x-\sqrt { { x^{ 2 } }+3{ a^{ 2 } } }  } }{ { \sqrt { x+a } -\sqrt { 2a }  } } =\sqrt { 2 }$$

$$  \\ The\, objective\, is\, to\, find\, a=? \\ { \lim   }_{ x\to a }\cfrac { { \left[ { 4{ x^{ 2 } }-\left( { { x^{ 2 } }+3{ a^{ 2 } } } \right)  } \right] \left[ { \sqrt { x+a } +\sqrt { 2a }  } \right]  } }{ { \sqrt { x+a } -\sqrt { 2a }  } } =\sqrt { 2 }  \\ { \lim   }_{ x\to a }\left[ { \cfrac { { 3\left( { x-a } \right) \left( { x+a } \right)  } }{ { \left( { x+a } \right)  } }  } \right] \left( { \cfrac { { 2\sqrt { 2a }  } }{ { 4a } }  } \right) =\sqrt { 2 }  \\ \cfrac { { 6a\times 2\sqrt { 2a }  } }{ { 4a } } =\sqrt { 2 }  \\ 3\sqrt { 2a } =\sqrt { 2 }  \\ 3\sqrt { a } =1 \\ a=\cfrac { 1 }{ 9 }$$

Hence, this is the answer.


Solve
$$\lim_{x \rightarrow \infty} \dfrac{1}{(1-x)^{2}}$$

Given,

$$\lim _{x\to \infty \:}\left(\dfrac{1}{\left(1-x\right)^2}\right)$$

$$=\dfrac{\lim _{x\to \infty \:}\left(1\right)}{\lim _{x\to \infty \:}\left(\left(1-x\right)^2\right)}$$

$$=\dfrac{1}{\infty \:}$$

$$=0$$


$$\mathop {\lim }\limits_{x \to 0} \dfrac{{\cos x}}{{\pi  - x}}$$

We have,
$$\lim_{x\to 0}\dfrac{\cos x}{\pi-x}$$
$$=\dfrac{\cos 0}{\pi-0}$$
$$=\dfrac{1}{\pi}$$

Hence, this is the answer.


$$\lim _{ x\rightarrow 2 }{ \frac { { x }^{ 7 }-128 }{ { x }^{ 5 }-32 }  } $$

$$\lim _{ x\longrightarrow 2 }{ \cfrac { { x }^{ 7 }-128 }{ { x }^{ 5 }-32 }  } \\ =\lim _{ x\longrightarrow 2 }{ \cfrac { { x }^{ 7 }-{ 2 }^{ 7 } }{ { x }^{ 5 }-{ 2 }^{ 5 } }  } =\lim _{ x\longrightarrow 2 }{ \cfrac { \cfrac { { x }^{ 7 }-{ 2 }^{ 7 } }{ x-2 }  }{ \cfrac { { x }^{ 5 }-{ 2 }^{ 5 } }{ x-2 }  }  } \\ =\cfrac { \lim _{ x\longrightarrow 2 }{ \cfrac { { x }^{ 7 }-{ 2 }^{ 7 } }{ { x }-2 }  }  }{ \lim _{ x\longrightarrow 2 }{ \cfrac { { x }^{ 5 }-{ 2 }^{ 5 } }{ { x }-2 }  }  } \\ =\cfrac { 7.{ 2 }^{ 6 } }{ 5.{ 2 }^{ 4 } } \\ =\cfrac { 7 }{ 5 } \times { 2 }^{ 2 }=\cfrac { 7 }{ 5 } \times 4=\cfrac { 28 }{ 5 } $$


Prove that every rational function is a continuous. 

Every rational number is of form $$=\dfrac{P}{2}$$
where $$q\neq 0$$ & p, q are polynomial function.
Let $$f(x)=\dfrac{P(x)}{q(x)}, q(x)\neq 0$$
where $$p(x)$$ & $$q(x)$$ are polynomials
Since $$p(x)$$ & $$q(x)$$ are polynomials are we know that every polynomial function is continuous.
$$p(x), q(x)$$ are continuous functions if p, q are continuous then $$\dfrac{p}{q}$$ is continuous. Thus $$f(x)=\dfrac{p(x)}{q(x)}$$ is continuous except at $$q(x)=0$$.

1190595_1326495_ans_514e3a14551a40dc874697b0cb5e3354.jpeg


$$\lim\limits_{x-\infty }\dfrac{\cos x+\sin^{2}x}{x+1}$$       

$$\cos x$$ at $$x\rightarrow \infty$$ lies between $$-1$$ to $$1.$$
$$\sin^2x$$ at $$x\rightarrow \infty$$ lies between $$0$$ to $$1.$$
Hence, $$\underset { x\rightarrow \infty  }{ Lt } \dfrac { \cos x+\sin^2x }{ x+1 } =0$$
Hence, the answer is $$\underset { x\rightarrow \infty  }{ Lt } \dfrac { \cos x+\sin^2x }{ x+1 } =0.$$



Evaluate $$\displaystyle \lim_{x \rightarrow -2^{+}}\dfrac{x^{2}-1}{2x+4}$$.

$$\lim_{x \rightarrow -2^{+}}  (\frac{x^{2}-1}{2x+4})$$

$$\lim_{h\rightarrow 0} [\frac{(-2+h)^{2}-1}{2(-2+h)}+4]$$

$$\lim_{h\rightarrow 0} (\frac{h^{2}+4-2h-1}{2h-4+4})$$

$$\lim_{h\rightarrow 0} \left \{ \frac{h^{2}-2h+3}{2h} \right \}$$

$$ \lim_{h\rightarrow 0} \left \{ \frac{h}{2}-1+\frac{3}{2h} \right \}$$

$$ \rightarrow (\infty ).$$


1175705_1348150_ans_3f0eb1f1b33e4286aa40b1665c47e2a0.jpg


$$\displaystyle \lim _{ x\rightarrow 0 } \dfrac{x^{3}+3x^{2}-9x-2}{x^{3}-x-6}$$

Putting value of x=0,limit gives
$$\frac{0-2}{0-6}=\frac{2}{6}={\frac{1}{3}}$$

1188261_1343611_ans_f2bcb3e5ba16499aa4b1d4135c056426.jpg


$$\underset { x\rightarrow 0 }{ lim } \frac { sin(2+x)-sin(2-x) }{ x } $$

$$\lim_{x\rightarrow 0}\dfrac{\sin{\left(2+x\right)}-\sin{\left(2-x\right)}}{x}$$
$$=\lim_{x\rightarrow 0}\dfrac{2\sin{\left(\dfrac{2+x-2+x}{2}\right)}\cos{\left(\dfrac{2+x+2-x}{2}\right)}}{x}$$
$$=\lim_{x\rightarrow 0}\dfrac{2\sin{\left(\dfrac{2x}{2}\right)}\cos{\left(\dfrac{4}{2}\right)}}{x}$$
$$=\lim_{x\rightarrow 0}\dfrac{2\sin{x}\cos{2}}{x}$$
$$=2\times 1\times\cos{2}$$
$$=2\cos{2}$$


Evaluate
$$\underset { h\rightarrow 0 }{ lim } \dfrac { \left( a+h \right) ^{ 2 }sin(a+h)-{ a }^{ 2 }sina }{ h } $$


1896576_1439677_ans_5ba3b6138bd44b8b90493c25f4778406.jpg


Solve:
$$\lim_{x\rightarrow 0}\cfrac{(1-\cos 3x)}{x\sin 2x}$$

We have,
$$\lim_{x\rightarrow 0}\cfrac{(1-\cos 3x)}{x\sin 2x}$$

Apply L-hospital rule,
$$\lim_{x\rightarrow 0}\cfrac{(0+3\sin 3x)}{\sin 2x+2x\cos 2x}$$
$$\lim_{x\rightarrow 0}\cfrac{(3\sin 3x)}{\sin 2x+2x\cos 2x}$$
$$\lim_{x\rightarrow 0}\cfrac{9x\left(\dfrac{\sin 3x}{3x}\right)}{2x\times \dfrac{\sin 2x}{2x}+2x\cos 2x}$$
$$\lim_{x\rightarrow 0}\cfrac{9\left(\dfrac{\sin 3x}{3x}\right)}{2\times \dfrac{\sin 2x}{2x}+2x\cos 2x}$$
$$=\dfrac{9}{2}$$

Hence, this is the answer.


Evaluate:$$\displaystyle {\lim}_{x\rightarrow 0}{\dfrac{{\sin}^{2}{2x}}{{\sin}^{2}{4x}}}$$

$$={\lim}_{x\rightarrow 0}{\dfrac{\dfrac{{\sin}^{2}{2x}}{{\left(2x\right)}^{2}}\times4{x}^{2}}{\dfrac{{\sin}^{2}{4x}}{{\left(4x\right)}^{2}}\times 16{x}^{2}}}$$

$$=\lim_{x\rightarrow 0}\dfrac{4{x}^{2}}{16{x}^{2}}=\dfrac{1}{4}$$


Evaluate $$\displaystyle\lim_{x\to 3} \left(\dfrac{x^4-81}{2x^2-5x-3}\right)$$

$$\displaystyle\lim_{x\to 3} \left(\dfrac{x^4-81}{2x^2-5x-3}\right)$$

The expression takes the form $$\dfrac 00$$ 

Using Lhospital~s Rule 

$$\displaystyle\lim_{x \to 3}\dfrac {4x^3}{4x-5}$$

$$\dfrac{4(3)^3}{4(3)-5}$$

$$\dfrac {4\times 27}{12-5}=\dfrac {108}7$$


Evaluate:$$\displaystyle \lim_{x\rightarrow 0}\cos x \cot 2x$$

$$\lim_{x\rightarrow 0} cos x cot 2x$$
=$$\lim_{x\rightarrow 0}\frac{cos x. cos 2x}{sin 2x}$$
=$$\lim_{x\rightarrow 0}\frac{cos x. cos 2x}{2 sin x cos x}$$
$$=\frac{1}{2}\lim_{x\rightarrow 0}\frac{cos 2x}{cos x}$$
$$= \frac{1}{2}\frac{cos 0}{cos 0}=\frac{1}{2}$$

1243357_1525794_ans_dff11c78b8954c488b7499a0c27bf8a3.PNG


Using the $$\in -\delta $$ definition prove that $$\underset { x\rightarrow 3 }{ lim } \left( { x }^{ 2 }+2x-8 \right) =7$$

Suppose $$f(x)=x^2+2x-8$$
$$\displaystyle\lim_{x\rightarrow 3}f(x)=7$$
For any value of $$f > 0$$ s.t $$0 < |x-7| < 0$$
We need to find a value ef s.t
$$0 < |f(x)-7| < ef$$
$$|x^2+2x-8-7| < ef$$
$$\Rightarrow |x^2+2x-15| < ef$$
$$\Rightarrow |(x+5)(x-3)| < ef$$
$$\Rightarrow |x+5||x-3| < ef$$
Since we are interest in the domain where $$x\rightarrow 3$$, we have a limit $$x\in(1, 4)$$ and this area $$|x+5|=x+5 < 7$$
So, $$|f(x)-7|=|x+5|\cdot |x-3| < 7|x-3|$$
We know that $$|x-3| < f$$
So $$|f(x)-7| < f/7$$
Pick $$ef=f/7\Rightarrow |f(x)-7| < ef$$ provided
$$0 < f < |x-3|$$.

1237246_1500365_ans_68680540bf7943fbb5e9ea84f76f500d.PNG


Using the $$\in -\delta $$ definition prove that $$\underset { x\rightarrow -2 }{ lim } \left( 3x+8 \right) =2$$

The function $$f(x)=3x+8$$ is a polynomial and as such it is continuous every $$x\in R$$. Then $$\displaystyle\lim_{x\rightarrow 2}f(x)=f(-2)=3\times 2+8=-6+8=2$$
To prove it by using the definition of limit,
$$|f(x)-2|=|3x+8-2|=|3x+6|=3|x+2|$$
For $$x\in (2-f, 2+f)$$ with $$f > 0$$, we have $$|f(x)-2|=3|x+1| < 3f$$
Given any $$e > 0$$, chose $$f_e < e/3$$ s.t
$$x\in (-2-f_e, -2+f_e)\Rightarrow |f(x)-(-2)| < 3f_e < \in$$
which proves the result.

1237247_1500356_ans_4b7845973b474d7cb26826e0cf86096c.PNG


Evaluate : $$\underset { h\rightarrow 0 }{ lim } \dfrac { { log }_{ a }(x+h)-{ log }_{ a }x }{ h } $$


1318186_1538939_ans_b5e30733b57d4774b3e9f9649d0f7ee1.jpeg


Find $$\displaystyle\lim_{x\rightarrow 1^+}\dfrac{1}{x-1}$$.

We have to compute $$\displaystyle\lim_{x\rightarrow 1^+}\dfrac{1}{x-1}$$

Put $$x=1+h$$
Now as $$x\rightarrow1^+$$ $$h\rightarrow 0$$
So,
$$\Rightarrow \displaystyle\lim_{h\rightarrow 0}\dfrac{1}{1+h-1}$$

$$\Rightarrow \displaystyle\lim_{h\rightarrow 0}\dfrac{1}{h}\rightarrow \infty$$.


Find $$\displaystyle\lim_{x\rightarrow 2}[x]$$.


1410439_1667564_ans_81a81253e7c747ca95d45aea9c8f8200.jpg


Find $$\displaystyle\lim_{x\rightarrow 1}[x]$$.


1411160_1667567_ans_31eec23eb30b4ed39c529d5b3b246a0e.jpg


Show that $$\displaystyle\lim_{x\rightarrow 0}\dfrac{1}{x}$$ does not exist.

We have,
$$L.H.L  :\ \  \displaystyle\lim_{x\rightarrow 0^-}f(x)=\displaystyle\lim_{h\rightarrow 0}f(0-h)=\displaystyle\lim_{h\rightarrow 0}\dfrac{1}{-h}\rightarrow -\infty$$

$$R.H.L:\ \ \displaystyle\lim_{x\rightarrow 0^+}f(x)=\displaystyle\lim_{h\rightarrow 0}(0+h)=\displaystyle\lim_{h\rightarrow 0}\dfrac{1}{h}\rightarrow \infty$$

Since, $$\displaystyle\lim_{x\rightarrow 0^-}f(x)\neq \displaystyle\lim_{x\rightarrow 0^+}f(x)$$.

Hence, $$\displaystyle\lim_{x\rightarrow 0}f(x)$$ does not exist.


If $$\displaystyle\lim_{x\rightarrow 0^+}\dfrac{2}{x^{1/5}}=a$$ then $$\dfrac1a$$ is equal to____.

Given,
$$\displaystyle \lim_{x\to 0^+}\dfrac {2}{x^{1/5}}=a$$

$$a=\displaystyle \lim_{x\to 0^+}\dfrac {2}{x^{1/5}}=+\infty$$

$$\therefore \dfrac1a=0$$


If $$\displaystyle\lim_{x\rightarrow 0^+}\dfrac{1}{3x}=a$$ then $$\dfrac {1} a$$ is equal to____.

Given,
$$\displaystyle \lim_{x\rightarrow 0^+}{\dfrac{1}{3x}}=a$$

Put $$x=h$$

$$a=\displaystyle \lim_{h\rightarrow 0^+}{\dfrac{1}{3h}}=\infty$$

$$\therefore \dfrac1a=0$$


If $$\displaystyle\lim_{x\rightarrow -8^+}\dfrac{2x}{x+8}=a$$ then $$\dfrac1a$$ is equal to____.

Given,
$$\displaystyle \lim_{x\to -8^+}\dfrac {2x}{x+8}=a$$

$$x=-8+H$$

$$a=\displaystyle \lim_{H\to 0^+}\dfrac {2(-8+H)}{(-8+H)+8}$$

$$a=\displaystyle \lim_{H\to 0^+}\dfrac {-16+2H}{H}=\infty$$

$$\therefore \dfrac1a=0$$


Show that $$\displaystyle\lim_{x\rightarrow 0}\dfrac{x}{|x|}$$ does not exist.


1410403_1667516_ans_e4b8392253204c55a0db807d1f901005.jpg


Solve: $$\displaystyle\lim_{h\rightarrow 0}\dfrac{\sqrt{x+h}-\sqrt{x}}{h}, x\neq 0$$.

$$\displaystyle\lim_{h\rightarrow 0}\dfrac{\sqrt{x+h}-\sqrt{x}}{h}, x\neq 0$$.

Rationalizing..

Multiplying and Dividing by $$\dfrac{\sqrt {x+h}+\sqrt x}{\sqrt {x+h}+\sqrt x}$$ 

$$\displaystyle \lim _{h \to 0} \dfrac{\sqrt {x+h}-\sqrt x}{h}\times \dfrac{\sqrt {x+h}+\sqrt x}{\sqrt {x+h}+\sqrt x}$$

$$\displaystyle \lim _{h \to 0} \dfrac{x+h-x}{h(\sqrt{x+h}+\sqrt x)}$$

$$\displaystyle \lim _{h \to 0} \dfrac{1}{(\sqrt{x+h}+\sqrt x)}$$

Substituting the value

$$\Rightarrow\dfrac {1}{\sqrt {x} +\sqrt x}=\dfrac 1{2\sqrt x}$$



Find $$\displaystyle\lim_{x\rightarrow \tfrac{5}{2}}[x]$$.

$$\displaystyle \lim_{x\to \dfrac {5}{2}} [x]$$

For $$\displaystyle \lim_{x \to 9} 1-[x]\quad $$ exist $$L.H.S=R.H.S=$$ Finite

$$L.H.L$$

$$x=\dfrac {5}{2}-h$$

$$\displaystyle \lim_{h\to 0} \left [\dfrac {5}{2}-h\right]=2$$

$$R.H.L$$

$$x=\dfrac {5}{2}+h$$

$$\displaystyle \lim_{h\to 0} \left [\dfrac {5}{2}+h\right]=2$$


Show that $$\displaystyle\lim_{x\rightarrow 2^-}\dfrac{x}{[x]}\neq \displaystyle\lim_{x\rightarrow 2^+}\dfrac{x}{[x]}$$.


1414788_1667570_ans_627a94bd88354c8abe00cb34e31e2700.jpg


Evaluate the following limits.
$$\displaystyle\lim_{x\rightarrow 1}\dfrac{x^2+1}{x+1}$$.

$$\underset{x \rightarrow 1}{\lim} \dfrac{x^2 + 1}{x + 1}$$

if $$x \rightarrow 1$$, then expression $$\rightarrow \dfrac{2}{2} \rightarrow$$ not indeterminate form

so, limit can be found, by simple putting the value 

$$\underset{x \rightarrow 1}{\lim} \dfrac{x^2 + 1}{x + 1} = \dfrac{2}{2} = 1$$


State Yes or No.
$$\displaystyle\lim_{x\rightarrow 3^+}\dfrac{x}{[x]}$$ is equal to $$\displaystyle\lim_{x\rightarrow 3^-}\dfrac{x}{[x]}$$.

Let us consider
$$L_1=\displaystyle \lim_{x\to 3^+} \dfrac {x}{[x]}$$

$$x=3+h$$

$$L_1=\displaystyle \lim_{h\to 0} \dfrac {3+h}{[3+h]}=1$$

Now,
$$L_2=\displaystyle \lim_{x\to 3^-} \dfrac {x}{[x]}$$

$$x=3-h$$

$$\displaystyle \lim_{h\to 0} \dfrac {3-h}{[3-h]}=\dfrac {3}{2}$$

$$L_1 \neq L_2$$

$$\displaystyle \lim_{x\to 3^+} \dfrac {x}{[x]}$$, is not equal to $$\displaystyle \lim_{x\to 3^-} \dfrac {x}{[x]}$$

The answer is No.


Find $$\displaystyle\lim_{x\rightarrow -5/2}[x]$$.

$$\displaystyle \lim_{x\rightarrow \tfrac{-5}{2}}[x]$$

For $$\displaystyle \lim_{x\rightarrow a}f(x)$$ to exist, L.H.L=R.H.L= finite

L.H.L
$$x=\dfrac{-5}{2}-x$$

$$\displaystyle \lim_{x\rightarrow 0}\left[-\dfrac{5}{2}-x\right]=-3$$

R.H.L.
$$x=\dfrac{-5}{2}+x$$

$$\displaystyle \lim_{x\rightarrow 0}\left[-\dfrac{5}{2}+x\right]=-3$$

Since, L.H.L=R.H.L=finite,

Hence, Limit exists.

And is equal to $$-3$$


Evaluate the following limit.
$$\displaystyle\lim_{n\rightarrow 4}\left(n^2\sqrt n\right)$$.

$$\displaystyle\lim_{n\rightarrow 4}\left(n^2\sqrt n\right)$$.

Substituting the value of $$n$$ 

$$= 4^2\sqrt 4$$

$$=(16)(2)=32$$



Evaluate the following limits.
$$\displaystyle\lim_{n\rightarrow 2}\sqrt {x+2}\sqrt x$$


$$\displaystyle\lim_{x\rightarrow 2}\sqrt {x+2}\sqrt x$$

Substituting the value of $$x$$ 

$$\implies \sqrt {2+2}\sqrt 2=\sqrt 4\sqrt 2=2\sqrt 2$$



Evaluate the following limits :
$$\displaystyle \lim_{x\to 2}\left(\dfrac {3^x +3^{3-x}-12}{3^{3-x}-3^{x/2}}\right)$$

Given limit 
$$\displaystyle \lim_{x\to 2}\left(\dfrac {3^x +3^{3-x}-12}{3^{3-x}-3^{x/2}}\right)$$
$$=\displaystyle \lim _{ x\rightarrow 2 }{ \left\{ \dfrac { { 3 }^{ x }+\dfrac { { 3 }^{ 3 } }{ { 3 }^{ x } } -12 }{ \dfrac { { 3 }^{ 3 } }{ { 3 }^{ x } } -{ 3 }^{ x/2 } }  \right\}  } \\=\displaystyle \lim _{ x\rightarrow 2 }{ \left\{ \dfrac { { t }^{ x }+\dfrac { 27 }{ t^{ x } } -12 }{ \dfrac { 27 }{ t^{ x } } -t }  \right\}  } \quad [put\ { 3 }^{ x/2 }=t]$$
$$=\displaystyle \lim _{ t\rightarrow 3 }{ \left( \dfrac { { t }^{ 4 }-12{ t }^{ 2 }+27 }{ 27-{ t }^{ 3 } }  \right)  } \\=\displaystyle \lim _{ t\rightarrow 3 }{ \dfrac { \left( { t }^{ 2 }-3 \right) \left( t+3 \right) \left( t-6 \right)  }{ \left( 3-t \right) \left( 9+3t+{ t }^{ 2 } \right)  }  } $$
$$=\displaystyle \lim _{ t\rightarrow 3 }{ \dfrac { \left( { t }^{ 2 }-3 \right) +\left( t+3 \right)  }{ -\left( 9+3t-{ t }^{ 2 } \right)  }  } \\=\dfrac { \left( 9-3 \right) \left( 3+3 \right)  }{ -\left( 9+9+9 \right)  } =\dfrac { -36 }{ 27 } =\dfrac { -4 }{ 3 } $$


Evaluate the following limits :
$$\displaystyle \lim_{x\to 0}\left(\dfrac {a^x - b^x}{x}\right)$$

Given limit 
$$=\displaystyle \lim _{ x\rightarrow 0 }{ \left\{ \dfrac { \left( { a }^{ x }-1 \right) -\left( { b }^{ x }-1 \right)  }{ x }  \right\}  } \\ \displaystyle=\lim _{ x\rightarrow 0 }{ \left( \dfrac { { a }^{ x }-1 }{ x }  \right)  } -\lim _{ x\rightarrow 0 }{ \left( \dfrac { { b }^{ x }-1 }{ x }  \right)  }\\ =\left( \log { a } -\log { b }  \right) .$$


Evaluate the following limits :
$$\displaystyle \lim_{x\to 0}\left(\dfrac {a^x -a^{-x}}{x}\right)$$

Given limit 
$$=\displaystyle\lim _{ x\rightarrow 0 }{ \left\{ \left( \dfrac { { a }^{ 2x }-1 }{ 2x }  \right) \times \dfrac { 2 }{ { a }^{ x } }  \right\}  } \\=\left[ \left( \log { a }  \right) \times \dfrac { 2 }{ 1 }  \right] \\=2\log { a } $$


Evaluate the following limits :
$$\displaystyle \lim_{x\to 0}\left(\dfrac {e^x -x-1}{x}\right)$$

Given limit 
$$\displaystyle \lim_{x\to 0}\left(\dfrac {e^x -x-1}{x}\right)$$
$$=\displaystyle \lim _{ x\rightarrow 0 }{ \left\{ \left( \dfrac { ({ e }^{ x }-1) }{ x }  \right) -1 \right\}  } \\=\lim _{ x\rightarrow 0 }{ \left( \dfrac { { e }^{ x }-1 }{ x }  \right)  } -1=(1-1)=0$$


Evaluate the following limits :
$$\displaystyle \lim_{x\to 0}\left(\dfrac {e^{bx}-e^{ax}}{x}\right), 0 < a < b$$

Given limit 
$$=\displaystyle \lim _{ x\rightarrow 0 }{ \left\{ \dfrac { \left( { e }^{ bx }-1 \right) -\left( { e }^{ ax }-1 \right)  }{ x }  \right\}  } \\ \displaystyle=\lim _{ bx\rightarrow 0 }{ \left\{ \left( \dfrac { { e }^{ bx }-1 }{ bx }  \right) .b \right\}  } -\lim _{ ax\rightarrow 0 }{ \left\{ \left( \dfrac { { e }^{ ax }-1 }{ ax }  \right) .a \right\}  } $$
$$=(1\times b)-(1\times a)\\=(b-a)$$


Evaluate the following limits :
$$\displaystyle \lim_{x\to 4}\left(\dfrac {e^x -e^4}{x-4}\right)$$

$$\displaystyle \lim_{x\to 4}\left(\dfrac {e^x -e^4}{x-4}\right)$$
Put $$(x-4)=y$$, so that when $$x\to 4$$ then $$y\to 0$$.
$$\therefore \ $$ given limit 
$$=\displaystyle \lim_{y\to 0}\left(\dfrac {e^{y+4}-e^4}{y}\right)\\=e^4 .\displaystyle \lim_{y\to 0}\left(\dfrac {e^{y}-1}{y}\right)\\=(e^4 \times 1)=e^4$$


Evaluate the following limits :
$$\displaystyle \lim_{x\to 0}\left(\dfrac {e^{3x}-e^{2x}}{x}\right)$$

Given limit 
$$=\displaystyle \lim_{x\to 0}\dfrac {(e^{3x}-1)-(e^{2x}-1)}{x}$$
$$=\displaystyle \lim_{x\to 0}\dfrac {(e^{3x}-1)}{x}- \displaystyle \lim_{x\to 0}\left(\dfrac {e^{2x}-1}{x}\right)$$
$$=\displaystyle \lim_{x\to 0}\left\{3\left(\dfrac {e^{3x}-1}{3x}\right) \right\}- \displaystyle \lim_{x\to 0}\left\{2\left(\dfrac {e^{2x}-1}{3x}\right) \right\}$$
$$=(3\times 1)-(2\times 1)=(3-2)=1$$


Evaluate $$lim_{ n \to \infty} n ^{-n^2}\left\{( n + 2^{o})(n + 2^{-1})(n + 2^{-2})....(n + 2^{-n + 1})\right\}^n$$


1881519_1752241_ans_14faed90236e4c378ac4670fcd8d5c99.jpg


Evaluate the following limits :
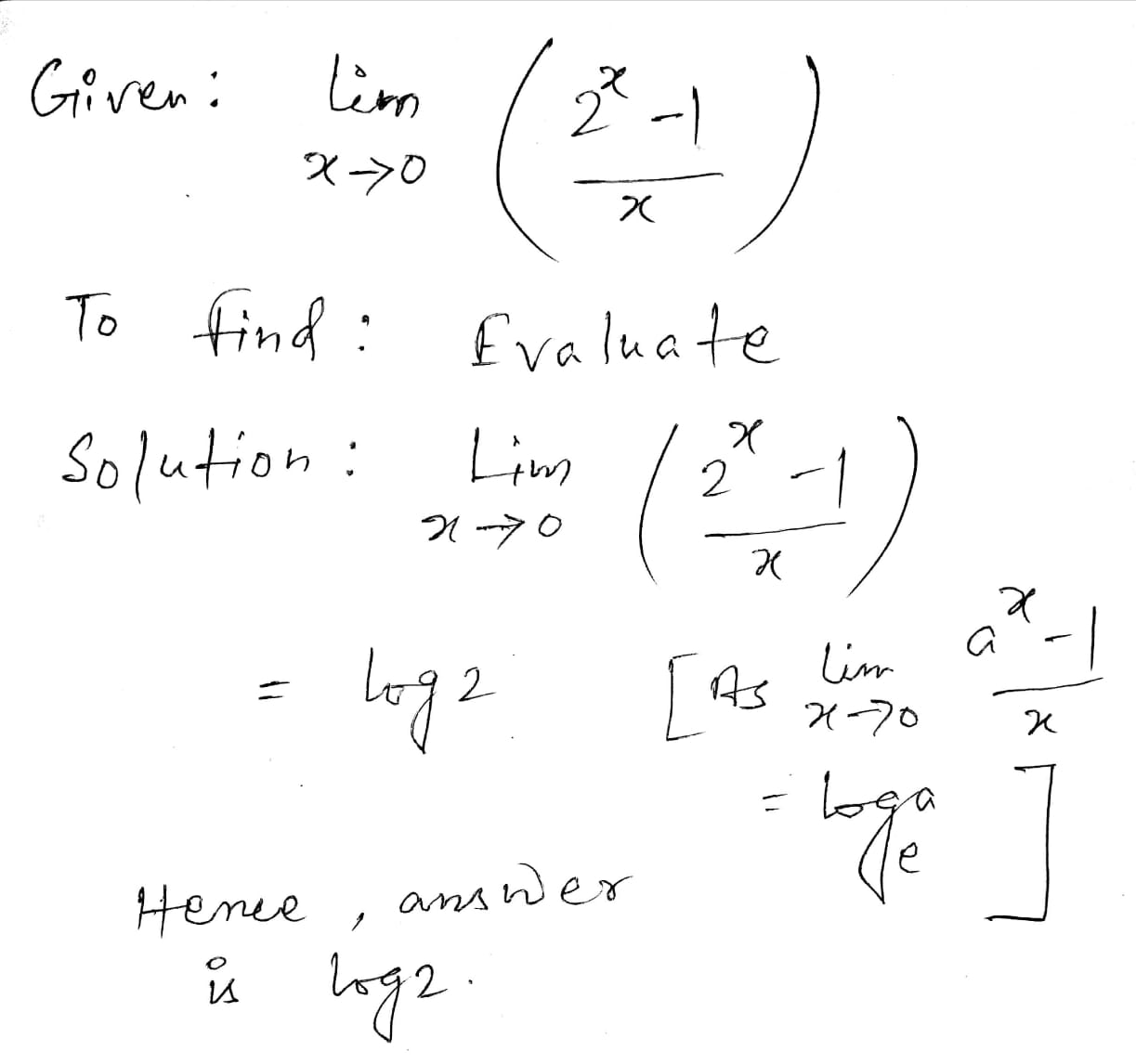
$$\displaystyle \lim_{x\to 0}\left(\dfrac {2^x -1}{x}\right)$$


1878153_1710497_ans_1a87e8b751154e9d95bfadd35c84190b.jpeg


Find the limits of 
$$ \dfrac{ 1 -x + \log x}{1 - \sqrt{2x - x^2}} , $$ when $$ x = 1 $$ .

Let L = $$ \dfrac{ 1 -x + \log x}{1 - \sqrt{2x - x^2}}$$
Putting $$ x = 1 + h $$
If $$ x \rightarrow 1 \\ 1 + h \rightarrow 1 \\ \therefore h \rightarrow 0 $$
$$ \lim_{x\rightarrow 1} L = \lim_{h \rightarrow 0} \dfrac{ 1 - ( 1 + h) + \log(1+h)}{1 -  \sqrt{2 (1+h) - ( 1-h)^2 } } $$
$$ \lim_{x\rightarrow 1} L = \lim_{h \rightarrow 0} \dfrac{ 1 -  1 - h + \log(1+h)}{1 -  \sqrt{2 + 2h - ( 1+ h^2 + 2h) } } $$
$$ \lim_{x\rightarrow 1} L = \lim_{h \rightarrow 0} \dfrac{ - h + \log(1+h)}{1 -  \sqrt{2 + 2h -  1- h^2 - 2h } } $$
$$ \lim_{x\rightarrow 1} L = \lim_{h \rightarrow 0} \dfrac{ - h + \log(1+h)}{1 -  \sqrt{  1- h^2  } } $$
$$ \lim_{x\rightarrow 1} L = \dfrac{ 0 + \log(1+0)}{1 -  \sqrt{  1- 0^2  } } $$
$$ \lim_{x\rightarrow 1} L = \dfrac{ 0 + 0}{1 -  1 } $$
$$ \lim_{x\rightarrow 1} L = 0 $$


$$ \displaystyle \lim _{x \rightarrow 0}\left(\dfrac{1+5 x^{2}}{1+3 x^{2}}\right)^{1 / x^{2}}= $$  ___________

$$\displaystyle \lim _{x \rightarrow 0}\left(\dfrac{1+5 x^{2}}{1+3 x^{2}}\right)^{1 / x^{2}}$$
$$=\dfrac{\displaystyle \lim _{x \rightarrow 0}\left(1+5 x^{2}\right)^{1 / x^{2}}}{\lim \left(1+3 x^{2}\right)^{1 / x^2}}$$
$$\dfrac{\displaystyle \lim _{x \rightarrow 0}\left\{\left(1+5 x^{2}\right)^{\dfrac{1}{5 x^{2}}}\right\}^{5}}{\displaystyle \lim _{x \rightarrow 0}\left\{\left(1+3 x^{2}\right)^{\dfrac{1}{3 x^{2}}}\right\}^{3}}$$
$$= e^{5-3}=e^{2}  $$


The value of $$ \displaystyle \lim _{x \rightarrow \infty} \dfrac{\log _{e}\left(\log _{e} x\right)}{e^{\sqrt{x}}} $$ is

$$\operatorname{Let} L= \displaystyle lim_{x \rightarrow \infty} \dfrac{\log _{e}\left(\log _{e} x\right)}{e^{\sqrt{x}}}=\left(\dfrac{\infty}{\infty} \text { form }\right) $$
$$ =\displaystyle \lim _{x \rightarrow \infty} \dfrac{\dfrac{1}{x \log _{e} x}}{e^{\sqrt{x}} \dfrac{1}{2 \sqrt{x}}} $$
$$ =\displaystyle \lim _{x \rightarrow \infty} \dfrac{2 \sqrt{x}}{e^{\sqrt{x}} x \log _{e} x} $$
$$ =\displaystyle \lim _{x \rightarrow \infty} \dfrac{2}{e^{\sqrt{x}} \sqrt{x} \log _{e} x} $$
$$ =0 $$


Let $$\displaystyle \lim_{T\infty} \dfrac{1}{T} \displaystyle \int_{0}^{T} (sinx + sin ax)^2dx=L ,$$then

(A) For a=0, $$I=\displaystyle \int_{0}^{T}sin^2xdx= I=\displaystyle \int_{0}^{T} \dfrac{1-cos2x}{2}dx$$
$$=\left[\dfrac{x}{2}-\dfrac{1}{4}sin2x\right]_{0}^{T} =\dfrac{T}{2}-\dfrac{1}{4}sin2T$$
$$\left[x-\dfrac{1}{4}sin2x-\dfrac{1}{4a}sin2ax\dfrac{sin(a-1)x}{a-1}-dfrac{sin(a+1)x}{a+1}\right]_{0}^{T}$$
$$\therefore L=\dfrac{1}{2}-\left[\dfrac{1}{4}-\displaystyle \lim_{T→∞}\dfrac{1}{4}\dfrac{sin2T}{T}\right]=\dfrac{1}{2}$$

(B) For a=1,$$ \displaystyle \int_{0}^{T}4sin^2xdx \Rightarrow L=2$$

(C) For a=-1, $$\displaystyle \int_{0}^{T} 0dx=0 \Rightarrow L=0 $$

(D) For $$a\neq 0,-1,1,$$
$$ I=\displaystyle \int_{0}^{T}(sin^2x+sin^2ax +2sinx.sinax)dx$$
$$ = \displaystyle \int_{0}^{T} \left( \dfrac{1-cos2x}{2}+\dfrac{1-cos2ax}{2}+cos(a-1)x-cos(a+1)x\right)dx $$
$$=\left[ x-\dfrac{1}{4}sin2x-\dfrac{1}{4a}sin2ax\dfrac{sin(a-1)x}{a-1}-\dfrac{sin(a+1)x}{a+1}\right]_{0}^{T} $$
$$\therefore L=\displaystyle \lim_{T→∞}\dfrac{T}{T}-\lim_{T→∞}\dfrac{1}{T}$$
$$\left[\dfrac{1}{4}sin2x-\dfrac{1}{4a}sin2ax+\dfrac{sin(a-1)x}{a-1}-\dfrac{sin(a+1)x}{a+1}\right]_{0}^{T}$$
$$\Rightarrow L=1$$


$$\displaystyle \lim_{x \to -\infty} \left[\dfrac{x^4 \sin \left(\dfrac{1}{x}\right)+x^2}{\left(1+|x|^3\right)}\right]=$$_____________

$$ \displaystyle \lim _{x \rightarrow-\infty}\left[\dfrac{x^{4} \sin \left(\dfrac{1}{x}\right)+x^{2}}{\left(1+|x|^{3}\right)}\right]$$
$$=\displaystyle \lim _{x \rightarrow-\infty}\left[\dfrac{x \sin \left(\dfrac{1}{x}\right)+\dfrac{1}{x}}{\dfrac{1}{x^{3}}-1}\right]$$
$$=\displaystyle \lim _{x \rightarrow-\infty}\left[\dfrac{\dfrac{\sin \left(\dfrac{1}{x}\right)}{\dfrac{1}{x}}+\dfrac{1}{x}}{\dfrac{1}{x^{3}}-1}\right]=\dfrac{1+0}{0-1}=-1$$


Evaluate $$\displaystyle \lim_{x\rightarrow \infty} 2^{x} \sin \left (\dfrac {a}{2^{x}}\right )$$.

$$\displaystyle \lim_{x\rightarrow \infty} 2^{x} \sin \left (\dfrac {a}{2^{x}}\right )$$
$$= \displaystyle \lim_{x\rightarrow \infty} \dfrac {a\times \sin \left (\dfrac {a}{2^{x}}\right )}{a} \times 2^{x}$$
$$= \displaystyle \lim_{x\rightarrow \infty} \dfrac {a\sin \left (\dfrac {a}{2^{x}}\right )}{\left (\dfrac {a}{2^{x}}\right )}$$
$$= a\times \displaystyle \lim_{x\rightarrow \infty} \dfrac {\sin \left (\dfrac {a}{2^{x}}\right )}{\left (\dfrac {a}{2^{x}}\right )}$$
$$= a \times 1 = a$$.


Evaluate $$\displaystyle \lim_{x\rightarrow 1}\dfrac {e^{x} - e^{-x}}{e^{x} + e^{-x}}$$.

$$\displaystyle \lim_{x\rightarrow 1}\dfrac {e^{x} - e^{-x}}{e^{x} + e^{-x}}$$
$$= \displaystyle \lim_{x\rightarrow 1} e^{-x} \left [\dfrac {e^{x}}{e^{-x}} - 1\right ] / e^{-x} \left [\dfrac {e^{x}}{e^{-x}} + 1\right ]$$
$$= \displaystyle \lim_{x\rightarrow 1} \dfrac {e^{x + x} - 1}{e^{x + x} + 1}$$
$$= \displaystyle \lim_{x\rightarrow 1} \dfrac {e^{2x} - 1}{e^{2x} + 1}$$
$$= \dfrac {e^{2(1)} - 1}{e^{2(1)} + 1} = \dfrac {e^{2} - 1}{e^{2} + 1}$$.


$$\displaystyle \lim_{x\rightarrow 0}\dfrac {ae^{x} - b\cos x + ce^{-x}}{x\sin x} = 2$$, then find the value of $$a, b$$ and $$c$$.

$$\displaystyle \lim_{x\rightarrow 0} \dfrac {ae^{x} - b \cos x + ce^{-x}}{x\sin x} = 2 .... (i)$$
$$\Rightarrow \displaystyle \lim_{x\rightarrow 0} \dfrac {ae^{x} + b\sin x - ce^{-x}}{x\cos x + \sin x} = 2$$
$$\Rightarrow \displaystyle \lim_{x\rightarrow 0} \dfrac {ae^{x} + b\cos x + ce^{-x}}{-x\sin x + \cos x + \cos x} = 2$$
$$\Rightarrow \dfrac {ae^{0} + b\cos 0 + ce^{0}}{0 + \cos 0 + \cos 0} = 2$$
$$\Rightarrow \dfrac {a + b + c}{2} = 2 .... (ii)$$
From equation (i),
$$\displaystyle \lim_{x\rightarrow 0} \dfrac {a \left (1 + x + \dfrac {x^{2}}{2!} + ...\right ) - b \left (1 - \dfrac {x^{2}}{2!} + \dfrac {x^{4}}{4!} - ... \right ) + c\left (1 - x + \dfrac {x^{2}}{2!} - ...\right )}{x\left (x - \dfrac {x^{3}}{3!} + \dfrac {x^{5}}{5!} - ...\right )} = 2$$
$$\Rightarrow \displaystyle \lim_{x\rightarrow 0} \dfrac {(a - b + c) + x(a - c) + x^{2} \left (\dfrac {a}{2} + \dfrac {b}{2} + \dfrac {c}{2}\right ) + ...}{x^{2} \left (1 - \dfrac {x^{2}}{3!} + ...\right )} = 2$$
$$a = c, c - b + c = 0, a + b + c = 4$$
$$\Rightarrow 2a - b = 0$$,
$$\Rightarrow b = 2a \Rightarrow a = 1 = c, b = 2$$
Hence, $$a = 1, b = 2, c = 1$$.


$$\lim_{x \rightarrow a} \frac{\sqrt[m]{x}-\sqrt[m]{a}}{x-a}$$




The value of $$\mathrm{f}(0)$$ such $$\displaystyle \mathrm{f}(\mathrm{x})=\frac{1-\cos^{2}\mathrm{x}+\sin^{2}\mathrm{x}}{\sqrt{\mathrm{x}^{2}+1}-1}(\mathrm{x}\neq 0)$$ is continuous at $$\mathrm{x}=0$$ is

Given $$\displaystyle { f }({ x })=\frac { 1-\cos ^{ 2 }{ x } +\sin ^{ 2 }{ x }  }{ \sqrt { { x }^{ 2 }+1 } -1 } ({ x }\neq 0)$$
Since, $$f(x)$$ is continuous at $$x=0$$
$$\lim _{ x\rightarrow 0 }{ f(x)=f(0) } $$

$$\lim_{x\rightarrow 0}\displaystyle \frac{1-cos^{2}x+sin^{2}x}{\sqrt{x^{2}+1}-1}$$

$$\displaystyle =\lim_{x\rightarrow 0}\frac{2sin^{2}x}{x^{2}}(\sqrt{x^{2}+1}+1)$$

$$=2\lim_{x\rightarrow 0}\left (\displaystyle  \frac{sin\, x}{x} \right )^2\lim_{x\rightarrow 0}(\sqrt{x^{2}+1}+1)$$
$$=2 \times 1 \times 2=4$$
$$\therefore f(0)=4$$ 


If $$f(x) =\displaystyle \frac{a\sin x -bx +cx^2+ x^3}{2x^2 \ell n(1+ x)- 2x^3+ x^4}$$, when $$x\neq 0$$ and $$f(x)$$ is continuous at $$x = 0$$, find value of $$200\times f(0)$$

$$\displaystyle \lim_{x\rightarrow 0}\frac{a\left [
x-\displaystyle \frac{x^3}{6}+\frac{x^5}{120}-....... \right ]-bx +cx^2+
x^3}{2x^2\left [x-\displaystyle \frac{x^2}{2}+\frac{x^3}{3}.........  \right
]-2x^3+x^4}$$
$$=\lim_{x\rightarrow 0}\displaystyle \frac{(a- b) x +cx^2+\left [
1-\displaystyle \frac{a}{6} \right
]x^3+\displaystyle \frac{ax^5}{120}+.....}{\displaystyle \frac{2x^5}{3}-\displaystyle \frac{x^6}{2}+......}$$
for this limit to be exist, $$a- b = 0, c = 0$$, & $$1-\displaystyle \frac{a}{6} =0$$
$$\Rightarrow a = b = 6$$ & $$c = 0$$.
then $$f(0) =\displaystyle \frac{6}{120}.\frac{3}{2}=\frac{3}{40}  \Rightarrow   200\: f(0) = 15$$


$$\displaystyle \Delta (x)=\begin{vmatrix} \tan x & \tan (x+h) & \tan (x+2h) \\ \tan (x+2h) & \tan x & \tan (x+h) \\ \tan (x+h) & \tan (x+2h) & \tan x \end{vmatrix}$$
Find the value of $$\displaystyle \lim_{h\rightarrow 0}\frac{\sqrt{3}\Delta (\pi /3)}{h^{2}}$$

Using $$C_{3}\rightarrow C_{3}-C_{2}$$ and $$C_{2}\rightarrow C_{2}-C_{1}$$, we can write
$$\displaystyle

\frac{\Delta }{h^{2}}=\begin{vmatrix} \tan x & [\tan (x+h)-\tan

x]/h & [\tan (x+2h)-\tan (x+h)]/h \\ \tan (x+2h) & [\tan x-\tan

(x+2h)]/h & [\tan (x+h)-\tan x]/h  \\ \tan (x+h) & [\tan

(x+2h)-\tan (x+h)]/h & [\tan x-\tan (x+2h)]/h \end{vmatrix}$$
But 
$$\displaystyle \lim_{h\rightarrow 0}\frac{\tan (x+h)-\tan x}{h}$$
$$=\displaystyle \lim_{h\rightarrow 0}\frac{1}{h}\frac{\sin (x+h)\cos x-\cos (x+h)\sin x}{\cos (x+h)\cos x}$$
$$=\displaystyle

\lim_{h\rightarrow 0}\frac{1}{h}\frac{\sin h}{\cos (x+h)\cos x}=\sec

^{2}x$$ or (use $$\frac{\mathrm{d} }{\mathrm{d} x}(\tan x)=\sec ^{2}x$$)
Similarly, $$=\displaystyle \lim_{h\rightarrow 0}\frac{\tan (x+2h)-\tan (x+h)}{h}=\sec ^{2}x$$
and $$=\displaystyle \lim_{h\rightarrow 0}\frac{\tan x-\tan (x+2h)}{h}=-2\sec ^{2}x$$
Thus,

$$\displaystyle \frac{\Delta (x)}{h^{2}}=\begin{vmatrix} \tan x  &

\sec ^{2}x  & \sec ^{2}x \\ \tan x & -\sec ^{2}x & \sec

^{2}x  \\ \tan x & \sec ^{2}x  & -2\sec ^{2}x

\end{vmatrix}$$ $$=\displaystyle \begin{vmatrix} \tan x  & \sec

^{2}x  & \sec ^{2}x \\ 0 & -3\sec ^{2}x & 0  \\ 0 & 0

 & -3\sec ^
{2}x \end{vmatrix}$$
$$=\displaystyle 9\:\tan x\:\sec ^{4}x $$ [Using $$R_{2}\rightarrow R_{2}-R_{1}$$  and $$R_{3}\rightarrow R_{3}-R_{1}$$]
So $$\displaystyle \lim_{h\rightarrow 0}\frac{\sqrt{3}\Delta (\pi /3)}{h^{2}}=9\times 3\times 2^{4}=216$$


Match the entries in Column I with entries in Column II


1118859_254766_ans_6d089593f21f4d2e89d33fbb01a3f293.jpg


Calculate the following limits.
$$\displaystyle \lim_{n \, \rightarrow \, \infty} \, \frac{5^{n \, + \, 1} \, + \, 3^n \, - \, 2^{2n}}{5^n \, + \, 2^n \, + \, 3^{n \, + \, 2}}, \, n \, \epsilon \, N.$$

$$\displaystyle\lim\limits_{n\to\infty} \dfrac{5^{n+1}+3^n-2^{2n}}{5^n+2^n+3^{n+2}}$$

Dividing both numerator and denominator by $$5^n$$:-

$$=\displaystyle\lim\limits_{n\to\infty} \dfrac{5+\dfrac{3^n}{5^n}-\dfrac{4^{n}}{5^n}}{1+\dfrac{2^n}{5^n}+9\dfrac{3^{n}}{5^n}}$$

Since  $$\dfrac{2}{5}<\dfrac{3}{5}<1$$

$$\implies \lim\limits_{n\to\infty}\dfrac{2^n}{5^n}=\lim\limits_{n\to\infty}\dfrac{3^n}{5^n}=0$$

Hence-


$$=\displaystyle\lim\limits_{n\to\infty} \dfrac{5+\dfrac{3^n}{5^n}-\dfrac{4^{n}}{5^n}}{1+\dfrac{2^n}{5^n}+9\dfrac{3^{n}}{5^n}}$$

$$=\dfrac{5+0-0}{1+0+0}$$

$$=5$$


Calculate the following limits.
$$\displaystyle \lim_{x \, \rightarrow \, 0} \, \frac{\cos \, 4x \, - \, cos \, 6x}{\sin^2 \, 5x}.$$

$$\displaystyle\lim\limits_{x\to 0} \dfrac{\cos 4x-\cos 6x}{\sin^25x}$$

$$=\displaystyle\lim\limits_{x\to 0} \dfrac{2\sin 5x\sin x}{\sin^25x}$$

$$=\displaystyle\lim\limits_{x\to 0} \dfrac{2\sin x}{\sin 5x}$$

$$=\displaystyle\lim\limits_{x\to 0} \dfrac{2\sin x}{x}\dfrac{5x}{\sin 5x}\dfrac{1}{5}$$

$$=\dfrac{2}{5}$$


Solve:
$$\lim_{x\rightarrow 0}\dfrac{x\sqrt{y^2-(y-x)^2}}{\left \{ \sqrt{(8xy-4x^2)}+\sqrt{8xy} \right \}^3}$$

$${\lim}_{x\rightarrow\,0}{\dfrac{x\sqrt{{y}^{2}-{\left(y-x\right)}^{2}}}{{\left(\sqrt{8xy-4{x}^{2}}+\sqrt{8xy}\right)}^{3}}}$$

$$={\lim}_{x\rightarrow\,0}{\dfrac{x\sqrt{\left(y-y+x\right)\left(y+y-x\right)}}{{\left(2\sqrt{x\left(2y-x\right)}+2\sqrt{2y}\sqrt{x}\right)}^{3}}}$$

$$={\lim}_{x\rightarrow\,0}{\dfrac{x\sqrt{x\left(2y-x\right)}}{8x\sqrt{x}{\left(\sqrt{2y-x}+\sqrt{2y}\right)}^{3}}}$$

$$={\lim}_{x\rightarrow\,0}{\dfrac{\sqrt{\left(2y-x\right)}}{8{\left(\sqrt{2y-x}+\sqrt{2y}\right)}^{3}}}$$

$$={\dfrac{\sqrt{\left(2y-0\right)}}{8{\left(\sqrt{2y-0}+\sqrt{2y}\right)}^{3}}}$$

$$={\dfrac{\sqrt{2y}}{8{\left(2\sqrt{2y}\right)}^{3}}}$$

$$={\dfrac{\sqrt{2y}}{8\times 8\times 2y\sqrt{2y}}}$$

$$=\dfrac{1}{128y}$$


evaluate
$$\underset { x\rightarrow 0 }{ lim } \dfrac { x\tan x }{ \left( 1-\cos x \right)  } $$


2039658_1322718_ans_c855159c8dd44c3e955be554e0b040dc.jpg


Evaluate:$$\lim_{x\rightarrow 0}\dfrac{e^{3x}-e^{2x}}{e^{4x}-e^{3x}}$$

Given
$$\lim_{x\rightarrow 0}\frac{e^{3x}-e^{2x}}{e^{4x}-e^{2x}}$$
$$\Rightarrow \lim_{x\rightarrow 0}\frac{e^{2x}(e^{x}-1)}{e^{2x}(e^{x}-1)}$$
$$\Rightarrow \lim_{x\rightarrow 0}\frac{e^{2x}}{e^{3x}}$$
$$\Rightarrow \lim_{x\rightarrow 0}\frac{1}{e^{x}}$$
$$\Rightarrow \frac{1}{e^{x}}=1$$

1212582_1505773_ans_5d3bb26f514b4752aea2d88f62ea1a53.png


Evaluate the following limits :
$$\displaystyle \lim_{x\to 0}\left(\dfrac {3^{2+x}-9}{x}\right)$$


1878255_1710499_ans_616b94a0308b4ad7b3be91bd6765a71c.jpeg


Find absolute maximum and minimum values of a function f given by $$f(x)=12x^{4/3}-6x^{1/3}, x\in [-1, 1]$$.

$$f(x)=12x^{4/3}-6x^{1/3}x\in [-1, 1]$$

$$f'(x)=16x^{1/3}-2x^{-2/3}$$

$$=\dfrac{2(8x-1)}{x^{2/3}}$$

For critical points, $$f'(x)=0$$

$$\therefore f'(x)=0$$

$$\Rightarrow \dfrac{2(8x-1)}{x^{2/3}}=0$$

$$\Rightarrow x=\dfrac{1}{8}$$

$$f(-1)=12+6=18$$

$$f(1)=6$$

$$f(1/8)=-9/4$$

Absolute maximum $$=18$$ at $$x=-1$$
Absolute minimum $$=-9/4$$ at $$x=1/8$$.


Evaluate the following limits :
$$\displaystyle \lim_{x\to 0}\left(\dfrac {e^{2+x}-e^2}{x}\right)$$


1982522_1710481_ans_437c28402d6a4340b8488af82c9b4459.jpg


Evaluate the following limits :
$$\displaystyle \lim_{x\to 0}\left(\dfrac {e^{4x}-1}{x}\right)$$


1982520_1710479_ans_b23f6ab3d3894283af8b3ce928cd9fe6.jpg


Suppose $$F ( x ) \left\{ \begin{array} { c l } { a + b x , } & { x _ { c 1 } } \\ { 4 , } & { x = 1 } \\ { b - a x , } & { x > 1 } \end{array} \right.$$ and $$\lim f ( x ) \cdot f ( x )$$ What are the possible values of a and b?


2044439_1564797_ans_6dd860b040bc464bb4e852d075b4ffde.jpg


Class 11 Commerce Applied Mathematics Extra Questions