Correlation - Class 11 Commerce Economics - Extra Questions

Define the positive co-relation.

A positive correlation is a relationship between two variables such that their values increase or decrease together .

Examples of positively correlated variables include:

  • Hours spent studying and grade point averages.
  • Education and income levels.
  • Poverty and crime levels.
  • Evaluated stress levels and blood pressure readings.
  • Smoking and lung disease.


For the given lines of regression, $$3x - 2y = 5$$ and $$x - 4y = 7$$, find:
coefficient of correlation $$r(x, y)$$

The two regression lines are
$$3x - 2y = 5 ....(1)$$
$$x - 4y = 7 .... (2)$$
From equation $$(1)\ 3x - 2y = 5$$
$$3x = 2y + 5$$
$$x = \dfrac {2}{3}y + \dfrac {5}{3}$$
$$\therefore b_{xy} = \dfrac {2}{3}$$ (Regression of $$x$$ on $$y$$)
From equation $$(2)\ x - 4y = 7$$
$$4y = x - 7$$
$$y = \dfrac {x}{4} - \dfrac {7}{4}$$
$$\therefore b_{yx} = \dfrac {1}{4}$$ (Regression of $$y$$ and $$x$$)

The two regression lines are
Coefficient of correlation $$= |r|$$
$$= \sqrt {b_{xy}\cdot b_{yx}}$$
$$= \sqrt {\dfrac {1}{4}\times \dfrac {2}{3}}$$
$$= \sqrt {\dfrac {1}{6}} = \dfrac {\sqrt {6}}{6}$$


From the equation of the two regression lines, $$4x + 3y + 7 = 0$$ and $$3x + 4y + 8 = 0$$, find: Coefficient of correlation.

Coefficient of correlation $$|r| = \sqrt{b_{yx} . b_{xy}} = \sqrt{\dfrac{-3}{4} \times \dfrac{-3}{4}}$$
$$\Rightarrow r = \pm \dfrac{3}{4}$$
But r has the same sign as regression coefficients.
$$\therefore r = \dfrac{-3}{4}$$


Prove that coefficient of correlation lies between $$-1$$ and $$1$$.

$$p=\cfrac { \sum { \left( x.\overline { x }  \right) \left( y-\overline { y }  \right)  }  }{ \sqrt { \sum { { \left( x.\overline { x }  \right)  }^{ 2 } } \sum { { \left( y-\overline { y }  \right)  }^{ 2 } }  }  } $$
$$=\cfrac { \sum { XY }  }{ \sqrt { \sum { { X }^{ 2 } } \sum { { Y }^{ 2 } }  }  } $$
Where $$(X=\left( x.\overline { x }  \right) ;Y=\left( y-\overline { y }  \right) $$
$$\therefore$$ by Swchwarz's inequality
$$(S{X}^{2}{Y}^{2})\le \sum { { X }^{ 2 } } \sum { { Y }^{ 2 } } $$
$$\cfrac { { \left( \sum { XY }  \right)  }^{ 2 } }{ \sum { { X }^{ 2 } } \sum { { Y }^{ 2 } }  } \le 1$$
$${ p }^{ 2 }\le 1$$
$$\Rightarrow$$ $$-1\le p\le 1$$
Hence value of correlation coefficient lies between $$-1$$ and $$1$$


Find the coefficient of correlation from the following data.
$$x$$$$2$$$$3$$$$5$$$$7$$$$3$$
$$y$$$$15$$$$17$$$$4$$$$5$$$$4$$

$$n=5$$
$$x$$$$y$$$$x-\bar{x}$$            $$y-\bar{y}$$           $$(x-\bar{x})(y-\bar{y})$$            $$(x-\bar{x})^2$$         $$(y-\bar{y})^2$$
$$2$$$$15$$$$-2$$$$6$$$$-12$$$$4$$$$36$$
$$3$$$$17$$$$-1$$$$8$$$$-8$$$$1$$$$64$$
$$5$$$$4$$$$1$$$$-5$$$$-5$$$$1$$$$25$$
$$7$$$$5$$$$3$$$$-4$$$$-12$$$$9$$$$16$$
$$3$$$$4$$$$-1$$$$-5$$$$5$$$$1$$$$25$$
$$\sum x=20$$         $$\sum y=45$$         $$\sum(x-\bar{x})(y-\bar{y})=-32$$       $$\sum(x-\bar{x})^2=16$$     $$\sum(y-\bar{y})^2=166$$
$$\bar{x}=\displaystyle\frac{\sum x}{n}=\frac{20}{5}=4$$
$$\bar{y}=\displaystyle\frac{\sum y}{n}=\frac{45}{5}=9$$
Coefficient of correlation $$r=\displaystyle\frac{\sum (x-\bar{x})(y-\bar{y})}{\sqrt{\sum(x-\bar{x})^2}\sqrt{\sum(y-\bar{y})^2}}$$
$$=\displaystyle\frac{-32}{\sqrt{16}\sqrt{166}}$$
$$=\displaystyle\frac{-32}{4\times 12.8841}$$
$$=\displaystyle\frac{-32}{51.5364}$$
$$=-0.64$$.


Calculate coefficient of correlation from the following data: 
$$x$$$$y$$
$$3$$$$15$$
$$10$$$$17$$
$$8$$$$4$$
$$6$$$$5$$
$$8$$$$4$$

$$x$$          $$y$$          $$x-\bar{x}$$        $$(y-\bar{y})$$        $$(x-\bar{x})(y-\bar{y})$$       $$(x-\bar{x})^2$$$$(y-\bar{y})^2$$
$$3$$$$15$$$$-4$$$$6$$$$-24$$$$16$$$$36$$
$$10$$$$17$$$$3$$$$8$$$$24$$$$9$$$$64$$
$$8$$$$4$$$$1$$$$-5$$$$-5$$$$1$$$$25$$
$$6$$$$5$$$$-1$$$$-4$$$$4$$$$1$$$$16$$
$$8$$$$4$$$$1$$$$-5$$$$-5$$$$1$$$$25$$

$$\sum (x-\bar{x})(y-\bar{y})=-6, \sum(x-\bar{x})^2=28$$
$$\sum x=35, \sum y=45$$
$$\sum(y-\bar{y})^2=166$$
$$\bar{x}=7, \bar{y}=9$$
$$r_{xy}=\displaystyle\frac{\sum(x-\bar{x})(y-\bar{y})}{\sqrt{\sum (x-\bar{x})^2}\sqrt{\sum (y-\bar{y})^2}}$$
$$=\displaystyle\frac{-6}{\sqrt{28}\cdot\sqrt{166}}$$
$$=\displaystyle\frac{-6}{5.29\times 12.88}$$
$$=\displaystyle\frac{-6}{68.13}$$
$$=-0.088$$ Approx.


Calculate the correlation coefficient between $$x$$ and $$y$$ for the following data:
$$x$$$$5$$$$9$$$$13$$$$17$$$$21$$
$$y$$$$12$$$$20$$$$25$$$$33$$$$35$$

$${ x }_{ i }$$$${ y }_{ i }$$$${ u }_{ i }$$$${ v }_{ i }$$$${ u }_{ i }^{ 2 }$$$${ v }_{ i }^{ 2 }$$$${ u }_{ i }{ v }_{ i }$$
512-8-1364169104
920-4-5162520
132500000000
173348166432
21358106410080
$$\sum { { x }_{ i } } =65$$$$\sum { { y }_{ i } } =125$$$$\sum { { u }_{ i } } =0$$$$\sum { { v }_{ i } } =0$$$$\sum { { u }_{ i }^{ 2 } } =160$$$$\sum { { v }_{ i }^{ 2 } } =358$$$$\sum { { u }_{ i }{ v }_{ i } } =236$$
$$\overline { x } =\cfrac { 1 }{ n } \sum { { x }_{ i } } =\cfrac { 1 }{ 5 } \times 65=13$$
$$\overline { y } =\cfrac { 1 }{ n } \sum { { y }_{ i } } =\cfrac { 1 }{ 5 } \times 125=25$$
$$\rho (x,y)=\rho (u,v)=\cfrac { n\sum { { u }_{ i }{ v }_{ i } } -\sum { { u }_{ i } } \sum { { v }_{ i } }  }{ \sqrt { n\sum { { u }_{ i }^{ 2 } } -{ (\sum { { u }_{ i }^{ 2 } } ) }^{ 2 } } \sqrt { n\sum { { v }_{ i }^{ 2 } } -{ (\sum { { v }_{ i }^{ 2 } } ) }^{ 2 } }  } $$
$$=\cfrac { 5\times 236-0\times 0 }{ \sqrt { 5\times 160-{ 0 }^{ 2 } } \sqrt { 5\times 358-{ 0 }^{ 2 } }  } =\cfrac { 236 }{ 239.33 } $$
$$=0.98$$


If "$$r$$" is a coefficient of correlation of two variables $$x$$ and $$y$$, then prove that:
$$r = \dfrac {\sigma_{x}^{2} + \sigma_{y}^{2} - \sigma_{x - y}^{2}}{2\sigma_{x}.\sigma_{y}}$$ Where $$\sigma_{x}^{2}, \sigma_{y}^{2}$$ and $$\sigma_{x - y}^{2}$$ are the variance of $$x, y$$ and $$x - y$$ respectively.

Coefficient of correlation of $$x$$ and $$y$$ is $$r$$ and
$$\sigma_{x}^{2}, \sigma_{y}^{2}$$ and $$\sigma_{x - y}^{2}$$ are varience of $$x, y$$ and $$x - y$$
$$\sigma_{x - y}^{2} = \dfrac {1}{n}[(x - y) - (\overline {x} - \overline {y})]^{2}$$
$$\sigma_{x - y}^{2} = \dfrac {1}{n}[(x - y) - (\overline {x}) + (\overline {y})]^{2}$$
$$\sigma_{x - y}^{2} = \dfrac {1}{n} [(x - \overline {x}) - (y - \overline {y})]^{2}$$
$$\sigma_{x - y}^{2} = \dfrac {1}{n} [(x - \overline {x})^{2} + (y - \overline {y})^{2} - 2(x - \overline {x})(y - \overline {y})]$$
$$\sigma_{x - y}^{2} = \dfrac {1}{n} [(x - \overline {x})^{2}] + \dfrac {1}{n} [(y - \overline {y})^{2}] - 2\dfrac {1}{n}(x - \overline {x})(y - \overline {y})$$
$$\sigma_{(x - y)}^{2} = \sigma_{x}^{2} + \sigma_{y}^{2} - 2r\sigma_{x}\sigma_{y}$$
$$2r\sigma_{x}\sigma_{y} = \sigma_{x}^{2} + \sigma_{y}^{2} - \sigma_{(x - y)}^{2}$$
$$\therefore r = \dfrac {\sigma_{x}^{2} + \sigma_{y}^{2} - \sigma_{(x - y)}^{2}}{2\sigma_{x}\sigma_{y}}$$.


Find the coefficient of correlation from the following data.
$$x$$$$-10$$$$-5$$$$0$$$$5$$$$10$$
$$y$$$$5$$$$9$$$$7$$$$11$$$$13$$

$$n=5$$
$$x$$$$y$$$$x-\bar{x}$$          $$y-\bar{y}$$        $$(x-\bar{x})(y-\bar{y})$$             $$(x-\bar{x})^2$$     $$(y-\bar{y})^2$$
$$-10$$$$5$$$$-10$$$$-4$$$$40$$$$100$$$$16$$
$$-5$$$$9$$$$-5$$$$0$$$$0$$$$25$$$$0$$
$$0$$$$7$$$$0$$$$-2$$$$0$$$$0$$$$4$$
$$5$$$$11$$$$5$$$$2$$$$10$$$$25$$$$4$$
$$10$$$$13$$$$10$$$$4$$$$40$$$$100$$$$16$$
$$\sum x=0$$     $$\sum y=45$$$$\sum(x-\bar{x})(y-\bar{y})=90$$      $$\sum(x-\bar{x})^2=250$$      $$\sum(y-\bar{y})^2=40$$
$$\bar{x}=\displaystyle\frac{\sum x}{n}=\frac{0}{5}=0$$
$$\bar{y}=\displaystyle\frac{\sum y}{n}=\frac{45}{5}=9$$
Coefficient of correlation $$r=\displaystyle\frac{\sum(x-\bar{x})(y-\bar{y})}{\sqrt{\sum(x-\bar{x})^2}\sqrt{\sum(y-\bar{y})^2}}$$
$$=\displaystyle\frac{\sqrt{90}}{\sqrt{250}\sqrt{40}}$$
$$=\sqrt{\displaystyle\frac{90}{10000}}$$
$$=\displaystyle\frac{90}{100}$$
$$=0.9$$


Calculate the Spearman's ranks correlation coefficient for the following data and interpret the result:
$$X$$35548095737335918381
$$Y$$40607590707538957570

 $$X$$ $$Y$$ Rank $$X$$ Rank $$Y$$ $$d$$ $${ d }^{ 2 }$$
 $$35$$ $$40$$ $$1$$ $$2$$ $$1$$ $$1$$
 $$54$$ $$60$$ $$2$$ $$3$$ $$1$$ $$1$$
 $$80$$ $$75$$ $$4$$ $$5$$ $$1$$ $$1$$
 $$95$$ $$90$$ $$8$$ $$6$$ $$2$$ $$4$$
 $$73$$ $$70$$ $$3$$ $$4$$ $$1$$ $$1$$
 $$73$$ $$75$$ $$3$$ $$5$$ $$2$$ $$4$$
 $$35$$ $$38$$ $$1$$ $$1$$ $$0$$ $$0$$
 $$91$$ $$95$$ $$7$$ $$7$$ $$0$$ $$0$$
 $$83$$ $$75$$ $$6$$ $$5$$ $$1$$ $$1$$
 $$81$$ $$70$$ $$5$$ $$4$$ $$1$$ $$1$$
$$\sum { { d }^{ 2 } } =14$$
Sperman rank correlation  coefficient $$=r=1-\dfrac { 6\sum { { d }^{ 2 } }  }{ n({ n }^{ 2 }-1) } $$
$$r=1-\dfrac { 6(14) }{ 10(100-1) } \\ r=1-\dfrac { 84 }{ 990 } =1-.084=.915$$


For a bivariate data $$b_{YX} = -1.2$$ and $$b_{XY} = -0.3$$, find the correlation coefficient between $$x$$ and $$y$$.

We know, correlation co efficient
$$r=\sqrt { { b }_{ XY }\times { b }_{ YX } } $$
$$\therefore r=\sqrt { -1.2\times -0.3 } $$
$$r=\sqrt { 0.36 } $$
$$r=-0.6$$ (as $${ b }_{ XY }, { b }_{ YX }$$ negative)
$$\therefore $$X and Y are negatively correlated with $$r=-0.6$$


If Cov(x,y)= 1125, Ox= 47.5, and Oy= 39.Find r.

Cov / Ox * Oy = 1125 / (47.8*39.6)

= 0.59



Calculate the coefficient of correlation between $$X$$ and $$Y$$ series from the following data:
$$n = 15, \overline {x} = 25, \overline {y} = 18, \sigma_{X} = 3.01, \sigma_{Y} = 3.03, \sum (x_{i} - \overline {x})(y_{i} - \overline {y}) = 122$$.

Correlation $$= \rho = \dfrac{Cov(X, Y)}{\sigma_x \sigma_y}$$

$$\displaystyle Cov(x, y) = \sum^{n}_{i = 1} \frac{(X_i - \bar{X})(Y_i - \bar{Y})}{n - 1}$$

$$Cov (X, Y) = \dfrac{122}{14} = \dfrac{61}{7}$$

$$\rho = \dfrac{61}{7(3.01)(3.01)} = 0.955$$


If $$\displaystyle \sum d_i^2 = 25$$, $$n = 6$$ find rank correlation coefficient where $$d_i$$ is the difference between the ranks of $$i^{th}$$ values.

Given that:
$$\sum di^2=25$$, $$n=6$$

The rank coefficient is given by
$$r=1-\dfrac{6\sum di^2}{n(n^2-1)}$$
$$r=1-\dfrac{6\times 25}{6(6^2-1)}$$
$$r=1-\dfrac{5}{7}$$
$$r=\dfrac{2}{7}.$$

This is the required solution.


If the rank correlation coefficient is $$0.6$$ and the sum of squares of difference of ranks is $$66$$, then find the number pairs of observations.

$$P = 1 - 6 \dfrac{\sum di^2}{n(n^2 - 1)}$$
$$0.6 = 1 - \dfrac{6 \times 66}{n(n^2 - 1)}$$
$$\dfrac{6 \times 66}{n(n^2 - 1)} = 0.4 $$
$$n(n^2 -1) = \dfrac{3}{2} \times 66 \times 10 = 990$$
$$n = 10 $$
$$10(10^2 - 1) = 10 (99) = 990$$



Find out Spearman's rank correlation:

X

Y

20

60

11

63

72

26

65

35

43

43

29

51

50

37



Interpretate the value of coefficient of correlation (r) lies between -1 to 1.

Interpretation of degree of correlation:
1. Perfect: If the value is near ± 1, then it said to be a perfect correlation: as one variable increases, the other variable tends to also increase (if positive) or decrease (if negative).
2. High degree: If the coefficient value lies between ± 0.50 and ± 1, then it is said to be a strong correlation.
3. Moderate degree: If the value lies between ± 0.30 and ± 0.49, then it is said to be a medium correlation.
4. Low degree: When the value lies below + .29, then it is said to be a small correlation.
5. No correlation: When the value is zero.



Find the value of correlation from the following information:

Price (Rs.)

PPE kit (supply)

500

25

700

35

800

40

1000

50

1100

55

1200

60

1400

70

1500

75

1800

90

2000

100



The two lines of regressions are $$x+2y-5=0$$ and $$2x+3y-8=0$$ and the variance of $$x$$ is $$12$$. Find the variance of $$y$$ and the coefficient of correlation.

The given equation of the lines of regression are
$$x+2y-5=0.......(i)$$
and $$2x+3y-8=0.....(ii)$$

Rewriting the equations $$(i)$$ and $$(ii)$$, we have
From equation $$(i)$$
$$y=\cfrac{-x}{2}+\cfrac{5}{2}$$
$$y=-0.5x+2.5$$ *regression line of $$y$$ on $$x$$)
$${ b }_{ yx }=r\cfrac { { \sigma  }_{ y } }{ { \sigma  }_{ x } } =-0.5....(iii)$$

From eqution $$(ii)$$,
$$x=\cfrac{-3}{2}y+\cfrac{8}{2}$$
$$x=-1.5y+4$$( regression line of $$x$$ on $$y$$)
$${ b }_{ xy }=r\cfrac { { \sigma  }_{ x } }{ { \sigma  }_{ y } } $$
$$\therefore { r }^{ 2 }={ b }_{ yx }\times { b }_{ xy }=(-0.5)\times (-1.5)=0.75$$
$$\therefore$$ $$r=\sqrt{0.75}=\pm 0.866$$

But $${b}_{xy}$$ and $${b}_{yx}$$ being both $$-$$ve therefore, $$r$$ is also $$-$$ve.

Correlation coefficient $$(r)=-0.866$$

Varianceof $$x$$ i.e., $${ \sigma  }_{ x }^{ 2 }=12$$
$$\therefore$$ $${\sigma}_{x}=\sqrt{12}$$

From equation $$(iii)$$
$$r\cfrac { { \sigma  }_{ y } }{ { \sigma  }_{ x } } =-0.5$$
$$-0.866.\cfrac{{\sigma}_{x}}{\sqrt { 12 } }=-0.5$$
$${ \sigma  }_{ y }=\cfrac { 0.5\times \sqrt { 12 }  }{ 0.866 } =2$$
$$\therefore$$ Variance of $$y$$ i.e., $${ \sigma  }_{ y }^{ 2 }=4$$


In a contest the competitors are awarded marks out of $$20$$ by two judges. The scores of the $$10$$ competitors are given below. Calculate Spearman's rank correlation.
Competitors$$A$$$$B$$$$C$$$$D$$$$E$$$$F$$$$G$$$$H$$$$I$$$$J$$
Judge $$A$$$$2$$$$11$$$$11$$$$18$$$$6$$$$5$$$$8$$$$16$$$$13$$$$15$$
Judge $$B$$$$6$$$$11$$$$16$$$$9$$$$14$$$$2$$$$4$$$$3$$$$13$$$$17$$

Competitors       Judge $$A$$ Score        $$R_1$$          Judge $$B$$ Score              $$R_2$$            Difference $$d=R_1-R_2$$           $$d^2$$
$$A$$$$2$$$$10$$$$6$$$$8$$$$2$$$$4$$
$$B$$$$11$$$$5.5$$$$11$$$$6$$$$-0.5$$$$0.25$$
$$C$$$$11$$$$5.5$$$$16$$$$3$$$$2.5$$$$6.25$$
$$D$$$$18$$$$1$$$$9$$$$7$$$$-6$$$$36$$
$$E$$$$6$$$$8$$$$14$$$$4$$$$4$$$$16$$
$$F$$$$5$$$$9$$$$20$$$$1$$$$8$$$$64$$
$$G$$$$8$$$$7$$$$4$$$$9$$$$-2$$$$4$$
$$H$$$$16$$$$2$$$$3$$$$10$$$$-8$$$$64$$
$$I$$$$13$$$$4$$$$13$$$$5$$$$-1$$$$1$$
$$J$$$$15$$$$3$$$$17$$$$2$$$$1$$$$1$$
$$\sum d^2=196.5$$
As $$B$$ and $$C$$ has same job rating of $$5$$, their average rank is $$\dfrac{5+6}{2}=5.5$$.
As there is one tie in ranks $$R_1$$ of 2 items, there is one correction in Spearman's rank correlation.
$$r=1-\dfrac{6\begin{bmatrix}\sum d^2+\dfrac{1}{12}(m^3-m)\end{bmatrix}}{n(n^2-1)}$$

$$=1-\dfrac{6[196.5+\dfrac{1}{12}(2^3-2)]}{10(10^2-1)}$$

$$=1-\dfrac{6[196.5+\dfrac{1}{12}(8-2)]}{10(100-1)}$$

$$=1-\dfrac{6(196.5+0.5)}{990}$$

$$=1-\dfrac{6(197)}{990}=1-\dfrac{1182}{990}$$

$$=1-1.193=-0.1939$$
$$= -0.194$$


The two lines of regressions are $$4x+2y-3 = 0$$ and $$3x+6y+5 = 0$$. Find the correlation coefficient between $$x$$ and $$y$$.

Let $$4x+2y-3=0$$ be the regression equation of $$y$$ on $$x$$ and 
$$3x+6y+5=0$$ the regression equation of $$x$$ on $$y$$ then

$$2y=-4x+3$$
$$y=-2x+\dfrac{3}{2}$$
$$\therefore         b_{yx}=-2$$
and,              
$$3x=-6y-5$$
$$x =-\dfrac{6}{3}y-\dfrac{5}{3}$$
$$x =-2y-\dfrac{5}{3}$$
$$\therefore          b_{xy} = -2$$

$$r^2 = b_{yx}\times b_{xy}$$
$$=-2\times -2=4>1$$ which is impossible.

So regression equation of $$y$$ on $$x$$ is
$$3x+6y+5=0$$                ..........(i)

and regression equation of $$x$$ on $$y$$ is
$$4x+2y-3=0$$                 ...........(ii)

From (i), we get
$$6y=-3x-5$$
$$y=-\dfrac{1}{2}x-\dfrac{5}{6}$$
$$\therefore b_{yx}=-\dfrac{1}{2}$$

From (ii), we get
$$4x=-2y+3$$
$$x=-\dfrac{1}{2}y+\dfrac{3}{4}$$
$$\therefore b_{xy}=-\dfrac{1}{2}$$

$$\therefore$$ Correlation coefficient is given by
$$|r|=\sqrt{b_{yx}.b_{xy}}$$

$$=\sqrt{-\dfrac{1}{2}\times -\dfrac{1}{2}} = \dfrac{1}{2}$$
$$\Rightarrow r = \pm \dfrac{1}{2}$$

But $$r$$ has the same sign as regression coefficient
$$\therefore r =-\dfrac{1}{2}$$.


A psychologist selected a random sample of $$22$$ students. He grouped them in $$11$$ pairs so that the students in each pair have nearly equal scores in an intelligence test. In each pair, one student was taught by method $$A$$ and the other by method $$B$$ and examined after the course. The marks obtained by them after the course are as follows:
Pairs$$1$$$$2$$$$3$$$$4$$$$5$$$$6$$$$7$$$$8$$$$9$$$$10$$$$11$$
Method $$A$$$$24$$$$29$$$$19$$$$14$$$$30$$$$19$$$$27$$$$30$$$$20$$$$28$$$$11$$
Method $$B$$$$37$$$$35$$$$16$$$$26$$$$23$$$$27$$$$19$$$$20$$$$16$$$$11$$$$21$$
Calculate Spearman's Rank correlation

PairsMethod $$A (X)$$     $$R_{X}$$Method           $$B(Y)$$$$R_{Y}$$$$(R_{X} - R_{Y})^{2} = d^{2}$$
$$1$$$$24$$$$6$$$$37$$$$1$$$$(5)^{2} = 25$$
$$2$$$$29$$$$3$$$$35$$$$2$$$$(1)^{2} = 1$$
$$3$$$$19$$$$8.5$$$$16$$$$9.5$$$$(-1)^{2} = 1$$
$$4$$$$14$$$$10$$$$26$$$$4$$$$(6)^{2} = 36$$
$$5$$$$30$$$$1.5$$$$23$$$$5$$$$(-3.5)^{2} = 12.25$$
$$6$$$$19$$$$8.5$$$$27$$$$3$$$$(5.5)^{2} = 30.25$$
$$7$$$$27$$$$5$$$$19$$$$8$$$$(-3)^{2} = 9$$
$$8$$$$30$$$$1.5$$$$20$$$$7$$$$(-5.5)^{2} = 30.25$$
$$9$$$$20$$$$7$$$$16$$$$9.5$$$$(-2.5)^{2} = 6.25$$
$$10$$$$28$$$$4$$$$11$$$$11$$$$(-7)^{2} = 49$$
$$11$$$$11$$$$11$$$$21$$$$6$$$$(5)^{2} = 25$$
$$N = 11$$$$\sum d^{2} = 225$$
Spearman's Rank correlation:
$$R = 1 - \dfrac {6\left [\sum d^{2} + \dfrac {1}{12} ((2^{3} - 2) + (2^{3} - 2) + (2^{3} - 2))\right ]}{n^{3} - n}$$
$$= 1 - \dfrac {6\left [225 + \dfrac {1}{12} (18)\right ]}{(11)^{3} - 11}$$
$$= 1 - \dfrac {6[225 + 1.5}{1331 - 11} = 1 - \dfrac {6[226.5]}{1320}$$
$$= 1 - \dfrac {1359}{1320} = 1 - 1.0296 = -0.0296$$


The following results were obtained with respect to two variable x and y:
$$\sum x = 30, \sum  y = 42, \sum xy = 199, \sum x^2 = 184, \sum y^2 = 318, n = 6.$$ Find the correlation coefficient between x and y.

$$b_{yx} = \dfrac{\sum xy - \dfrac{1}{n} \sum x. \sum y}{\sum x^2 - \dfrac{1}{n} (\sum x)^2}$$
$$= \dfrac{199 - \dfrac{1}{6} (30)(42)}{184 - \dfrac{1}{6} (30)^2}$$
$$= \dfrac{199 - 210}{184 - 150} = \dfrac{-11}{34} = - 0.323$$
$$b_{xy} = \dfrac{\sum x y - \dfrac{1}{n} \sum x \sum y}{\sum y^2 - \dfrac{1}{n} (\sum y)^2}$$
$$= \dfrac{199 - \dfrac{1}{6} (30)(42)}{318 - \dfrac{1}{6}(42)^2}$$
$$= \dfrac{199 - 210}{318 - 294} = \dfrac{-11}{24} = -0.458$$

Correlation coefficient between x and y.
$$r^2 = b_{yx} . b_{xy}$$
$$= (-0.323) \times (- 0.458)$$
$$= 0.1479$$
$$\therefore r = \sqrt{0.1479} = -0.384$$
Since $$b_{xy}$$ and $$b_{yx}$$ have the same sign, that is why we have used negative sign with r.


For $$10$$ pairs of observation on two variables $$x$$ and $$y$$, the following data are available.
$$\sum (x - 2) = 30, \sum (y - 5) = 40, \sum (x - 2)^{2} = 900$$.
$$\sum (y - 5)^{2} = 800, \sum (x - 2)(y - 5) = 480$$.
Find the correlation coefficient between $$x$$ and $$y$$

Let $$x = x_{i}$$ and $$y = y_{i}$$
Let $$u_{i} = x_{i} - 2$$ and $$v_{i} = y_{i} - 5$$
Then it is given that,
$$n= 10, \sum u_{i} = 30, \sum v_{i} = 40, \sum u_{i}^{2} = 900, \sum v_{i}^{2} = 800, \sum u_{i}v_{i} = 480$$
$$\therefore \overline {u} = \dfrac {\sum u_{i}}{n} = \dfrac {30}{10} = 3$$
$$\overline {v} = \dfrac {\sum vi}{n} = \dfrac {40}{10} = 4$$
Since the correlation coefficient is independent of change of origin and scale, correlation coefficient between $$x$$ and $$y$$ is
$$r(x, y) = r(u, v)$$
$$= \dfrac {\dfrac {1}{n}\sum u_{i} v_{i} - \overline {u}\overline {v}}{\sqrt {\dfrac {1}{n}\sum u_{i}^{2} - (\overline {u})^{2}} \cdot \sqrt {\dfrac {1}{n} \sum v_{i}^{2} - (\overline {v^{2}})}}$$
$$= \dfrac {\dfrac {480}{10} - 3\times 4}{\sqrt {\dfrac {900}{10} - (3)^{2}}\cdot \sqrt {\dfrac {800}{10} - (4)^{2}}}$$
$$= \dfrac {48 - 12}{\sqrt {81}\cdot \sqrt {64}} = \dfrac {36}{9\times 8} = \dfrac {4}{8} = 0.5$$


The following table shows the mean and standard deviation of the marks of Mathematics and Physics scored by the students in a school
MathematicsPhysics
Mean$$84$$$$81$$
Standard Deviation$$7$$$$4$$
The correlation coefficient between the given marks is $$0.86$$. Estimate the likely marks in Physics if the marks in Mathematics are $$92$$.

$$\overline x = 84,    \overline y = 81$$
$$\sigma_x = 7,      \sigma_y = 4$$
$$r = 0.86$$
$$\therefore b_{yx} = r . \dfrac{\sigma_y}{\sigma_x}$$
$$= 0.86 \times \dfrac{4}{7} = 0.49$$

$$\therefore$$ Regression equation of y on x

$$y - \overline y = b_{yx} (x - \overline x)$$
$$y - 81 = 0.49 (x - 84)$$
$$y - 81 = 0.49 x - 41.16$$
$$\Rightarrow y = 0.49 x + 39.84$$

Putting $$x = 92,$$
$$y = 45.08 + 39.84 = 84.92$$

Hence, the likely marks in Physics are $$84.92.$$


For $$10$$ points of observations on two variables $$X$$ and $$Y$$, the following data are available:
$$\sum (x - 2) = 30, \sum y - 5 = 40, \sum (x - 2)^{2} = 900$$
$$\sum (y - 5)^{2} = 800, \sum (x - 2)(y - 5) = 480$$.
Find the correlation coefficient between $$X$$ and $$Y$$.

The basic formula for calculating correlation coefficient 
$$\text{corr}(X,Y)=\dfrac{n\sum xy - \sum x\sum y }{\sqrt{(n\sum x^2 - (\sum x)^2)(n\sum y^2-(\sum y)^2)}}$$     .....(1)
where $$n$$ $$=$$ no. of observations and $$n=10$$ in our case.


We need to find out each of the terms in equation (1).
From the given data,
$$\sum (x-2)=30 $$
$$\implies \sum x - 2\sum 1 = 30$$
$$\implies \sum x -2n = 30$$
$$\implies \sum x -20 = 30$$

$$\therefore \sum x =10$$      ....(2)


$$\sum y - 5 = 40$$
$$\therefore \sum y =45$$ .....(3)


$$\sum(x-2)^2 = 900$$
$$\implies \sum (x^2-4x-4) = 900$$
$$\implies \sum x^2 -4\sum x - 4\sum 1 = 900$$
$$\implies \sum x^2 -4\times 10 + 4\times 10 = 900$$.... from $$(2)$$
$$\therefore \sum x^2 =900$$ ------ $$(4)$$


$$\sum (y-5)^2 = 800$$
$$\implies \sum (y^2-10y+25) = 800$$
$$\implies \sum y^2 -10\sum y+25\sum 1 =800$$
$$\implies \sum y^2 -10\times 45+25\times 10 = 800$$..... from $$(3)$$
$$\therefore \sum y^2 = 1000$$ --------$$(5)$$

$$\sum (x-2)(y-5) = 480$$
$$\implies \sum (xy - 5x -2y+10) =480$$
$$\implies \sum xy - 5\sum x -2\sum y+10\sum 1=480$$
$$\implies \sum xy-5\times 10-2\times 45+10\times 10=480$$.....from $$(2) \& (3)$$
$$\therefore \sum xy = 520$$---------$$(6)$$

Substituting $$(2),(3),(4),(5),(6)$$ in $$(1)$$ gives us
$$corr(X,Y) = \dfrac{10\times 520 - 10\times 45}{\sqrt{(10\times 900-10^2)(10\times 1000-45^2)}}$$
$$corr(X,Y)=0.564$$


The equations of the two regression line are $$2x+3y-6=0$$ and $$5x+7y-12=0$$
Find
$$(a)$$ Correlation coefficient
$$(b)$$  $$\dfrac{\sigma_x}{\sigma_y}$$

Let $$2{x}+3{y}-6=0$$ be $$x$$ on $$y$$ and $$5{x}+7{y}-12=0$$ be $$y$$ on $$x$$
$$2{x}+3{y}-6=0\implies x=-\dfrac{3}{2}y+3\implies bxy=-\dfrac{3}{2}$$
$$5{x}+7{y}-12=0\implies y=-\dfrac{5}{7}x+\dfrac{12}{7}\implies byx=-\dfrac{5}{7}$$
$$r=\sqrt{bxy byx}=\sqrt{\dfrac{15}{14}}$$
$$byx=\dfrac{r \sigma _y}{\sigma_x}=-\dfrac{5}{7},bxy=\dfrac{r\sigma_x}{\sigma_y}=-\dfrac{3}{2}\implies \dfrac{\sigma_x^2}{\sigma_y^2}=\dfrac{\dfrac{3}{2}}{\dfrac{5}{7}}=\dfrac{21}{10}\implies \dfrac{\sigma_x}{\sigma_y}=\sqrt{\dfrac{21}{10}}$$


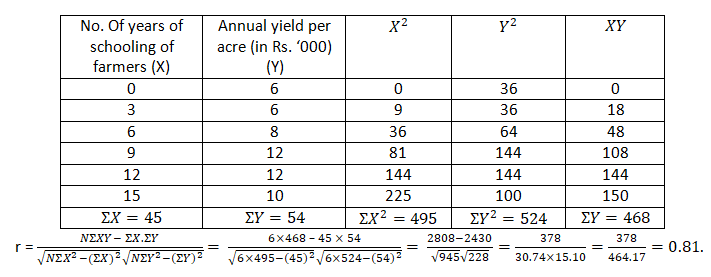
Calculate coefficient of correlation from the following data and interpret the result.
Number of Years of Schooling of Farmers03691215
Annual Yield per Acre (in '000)668121210

The solution is as follows:
Interpretation: Since r = 0.81, there is fairly high degree of positive correlation between between number of years of schooling of farmers and annual yield per acre.
2149574_2027378_ans_51f4bab311264a8b90e7db617257e412.PNG


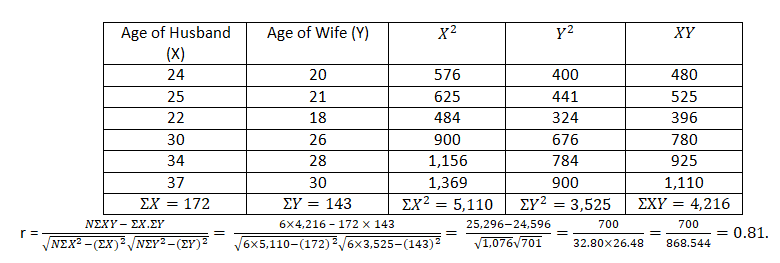
Calculate coefficient of correlation for the ages of husband and wife.
Age of Husband (X)242522303437
Age of Wife (Y)202118262830

Solution is as follows:
2150268_2027698_ans_eca7f6388d5f4245a41b5fc930fb8fdb.PNG


Class 11 Commerce Economics Extra Questions