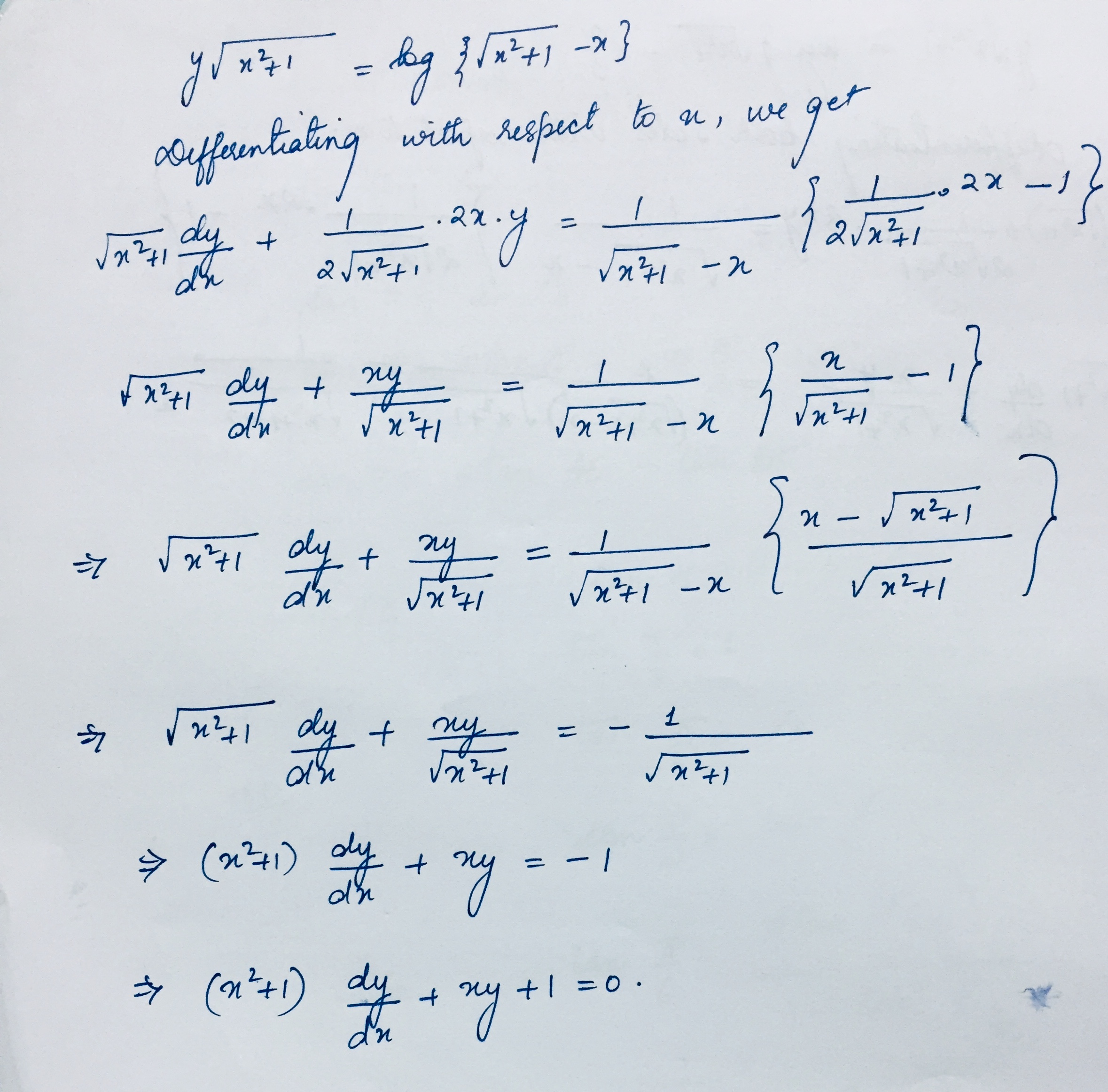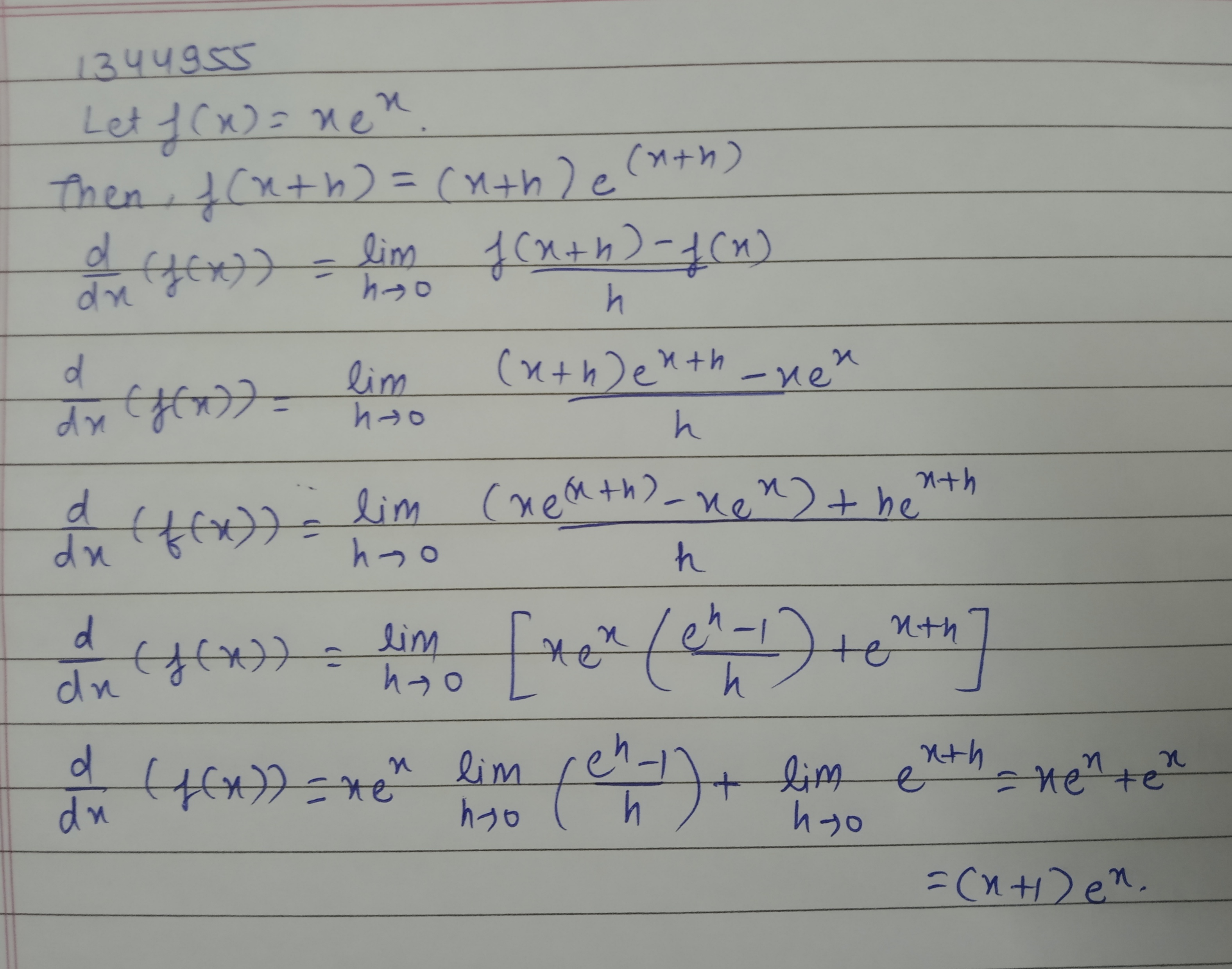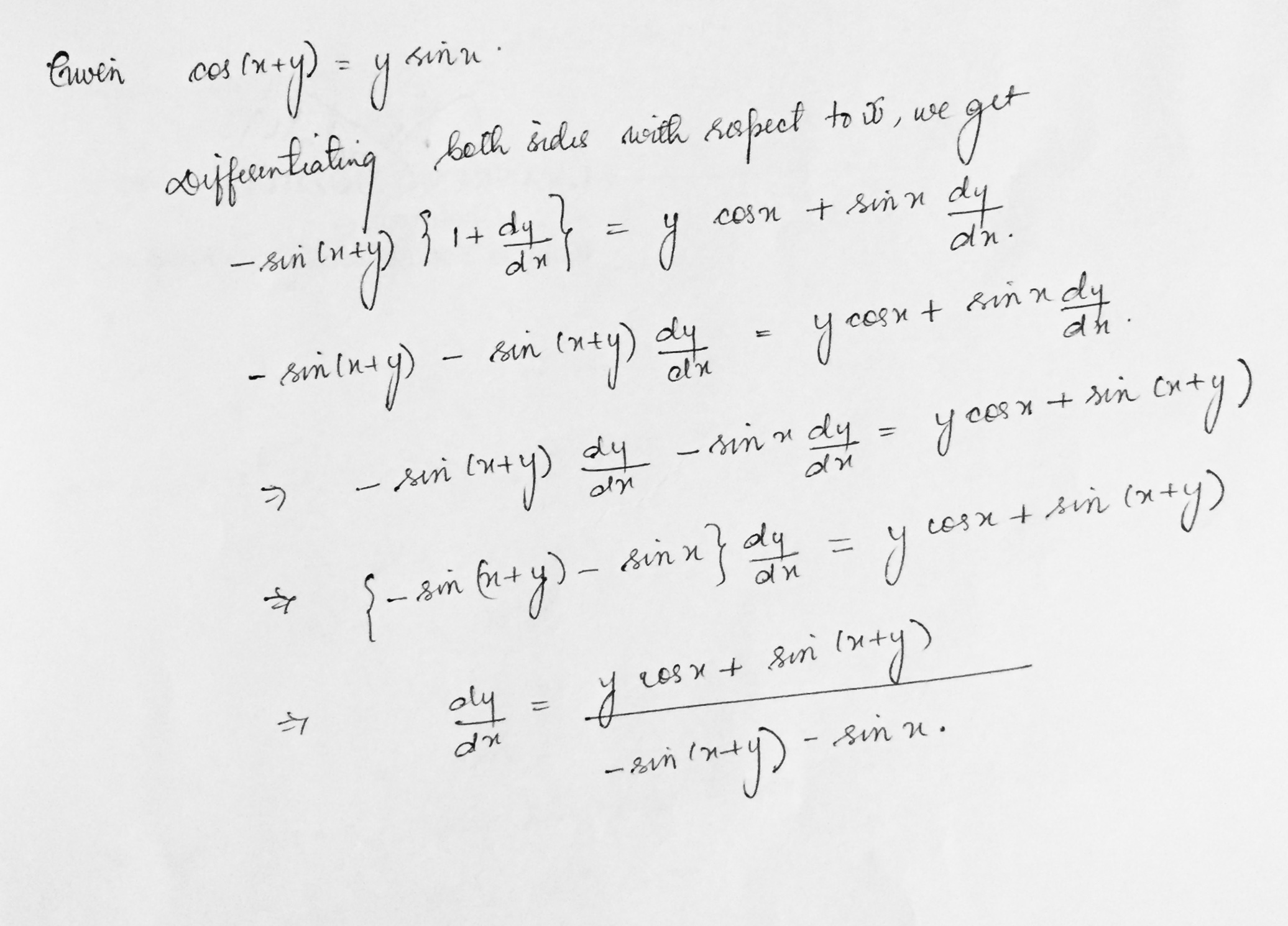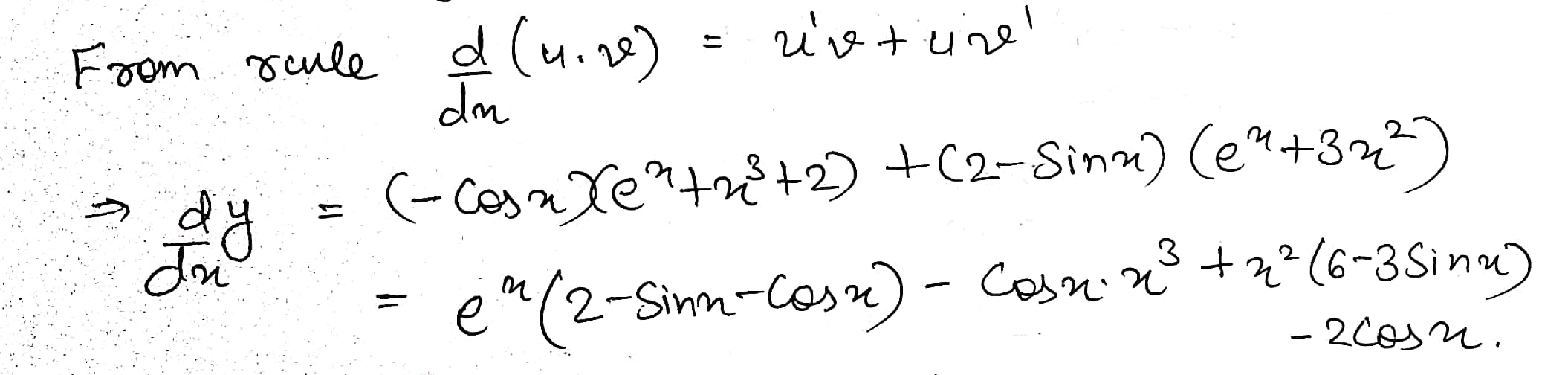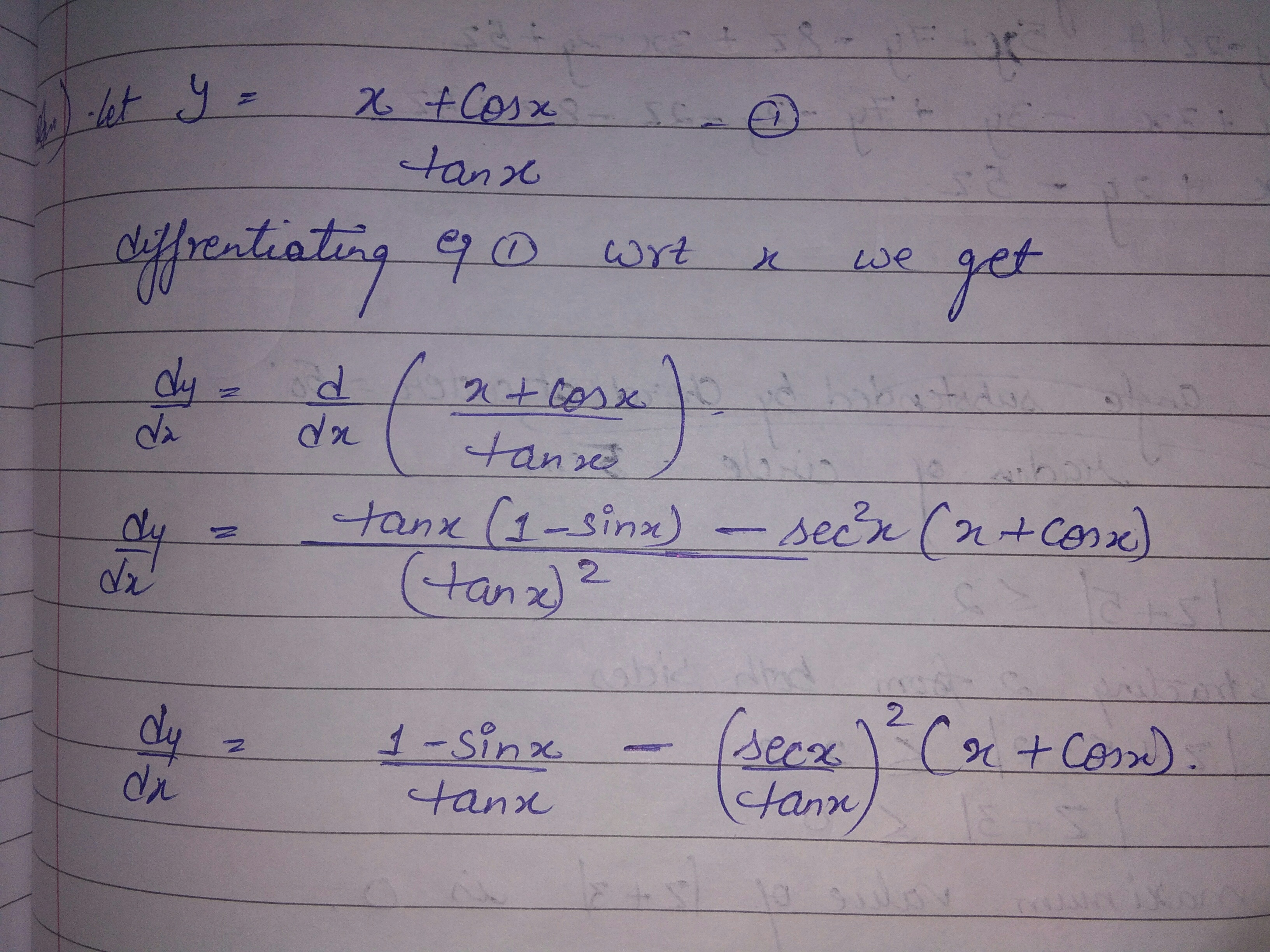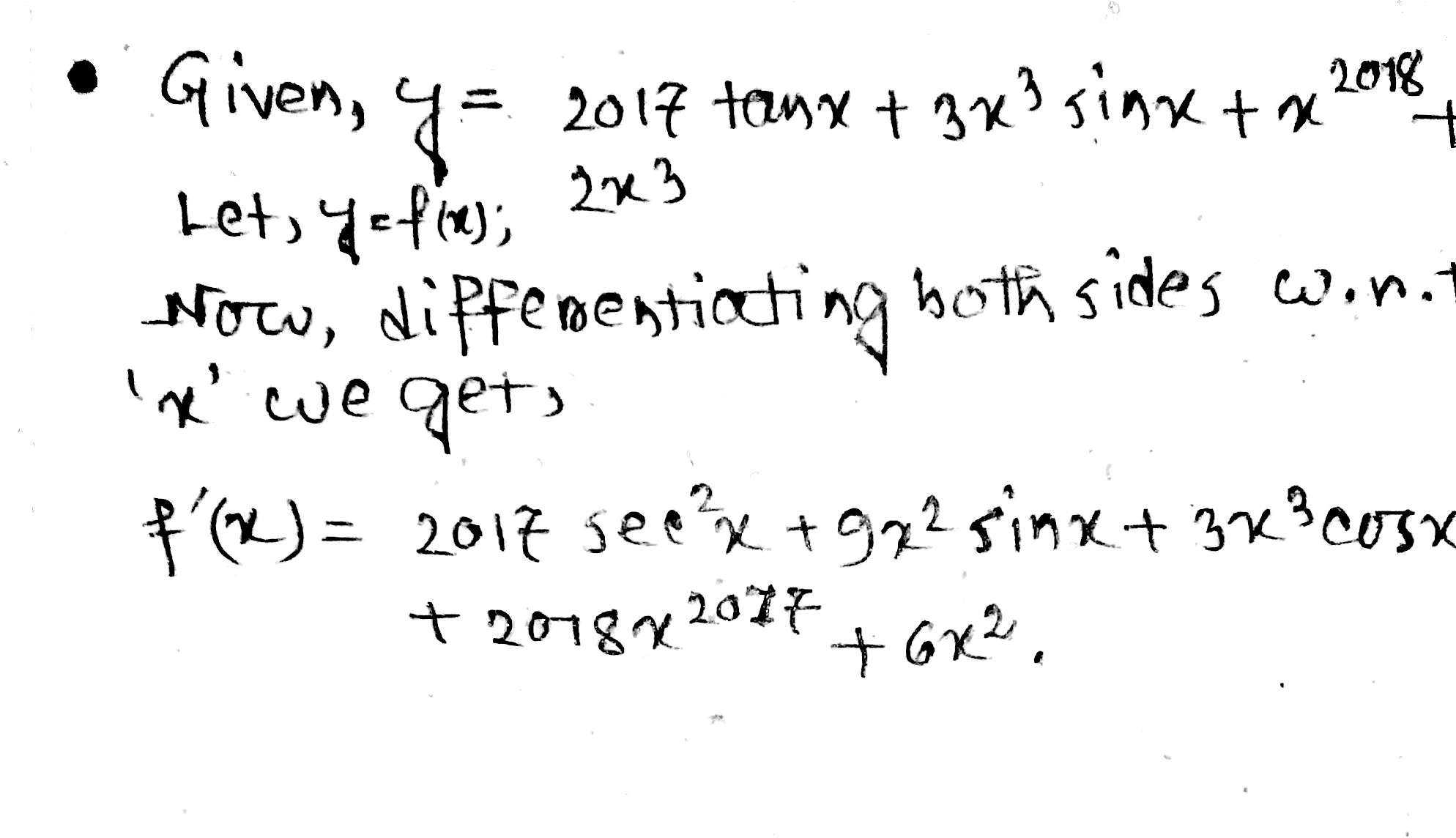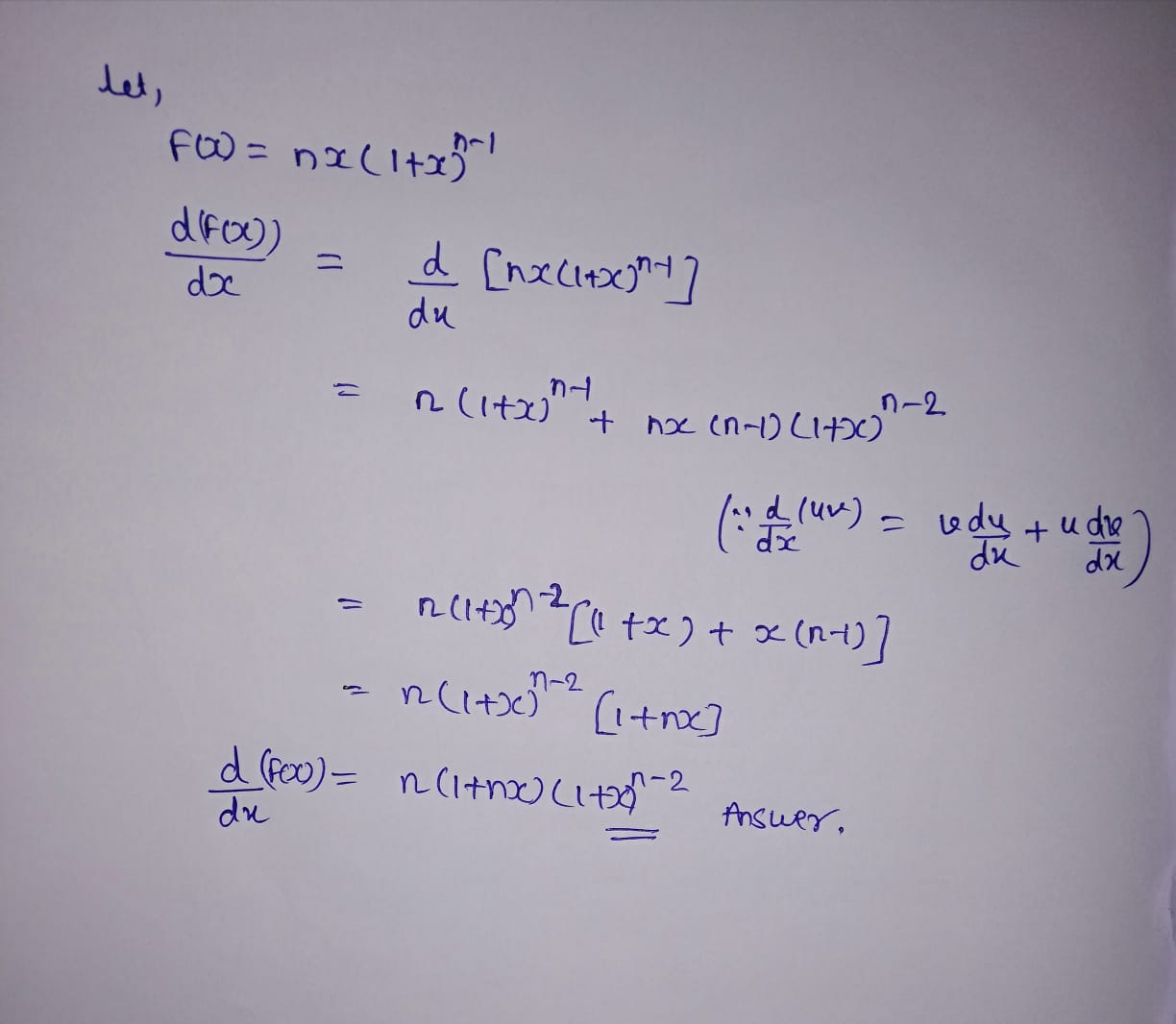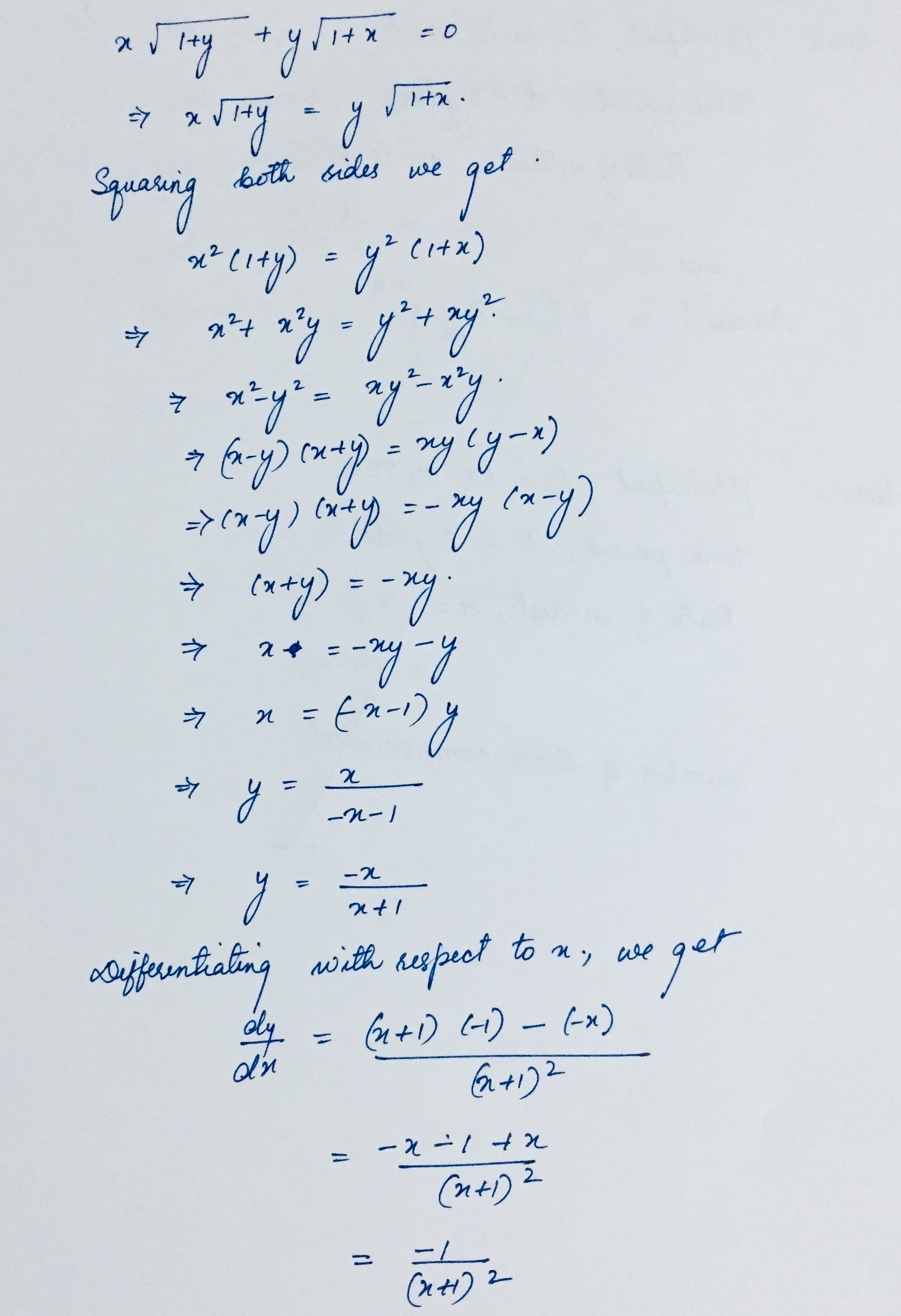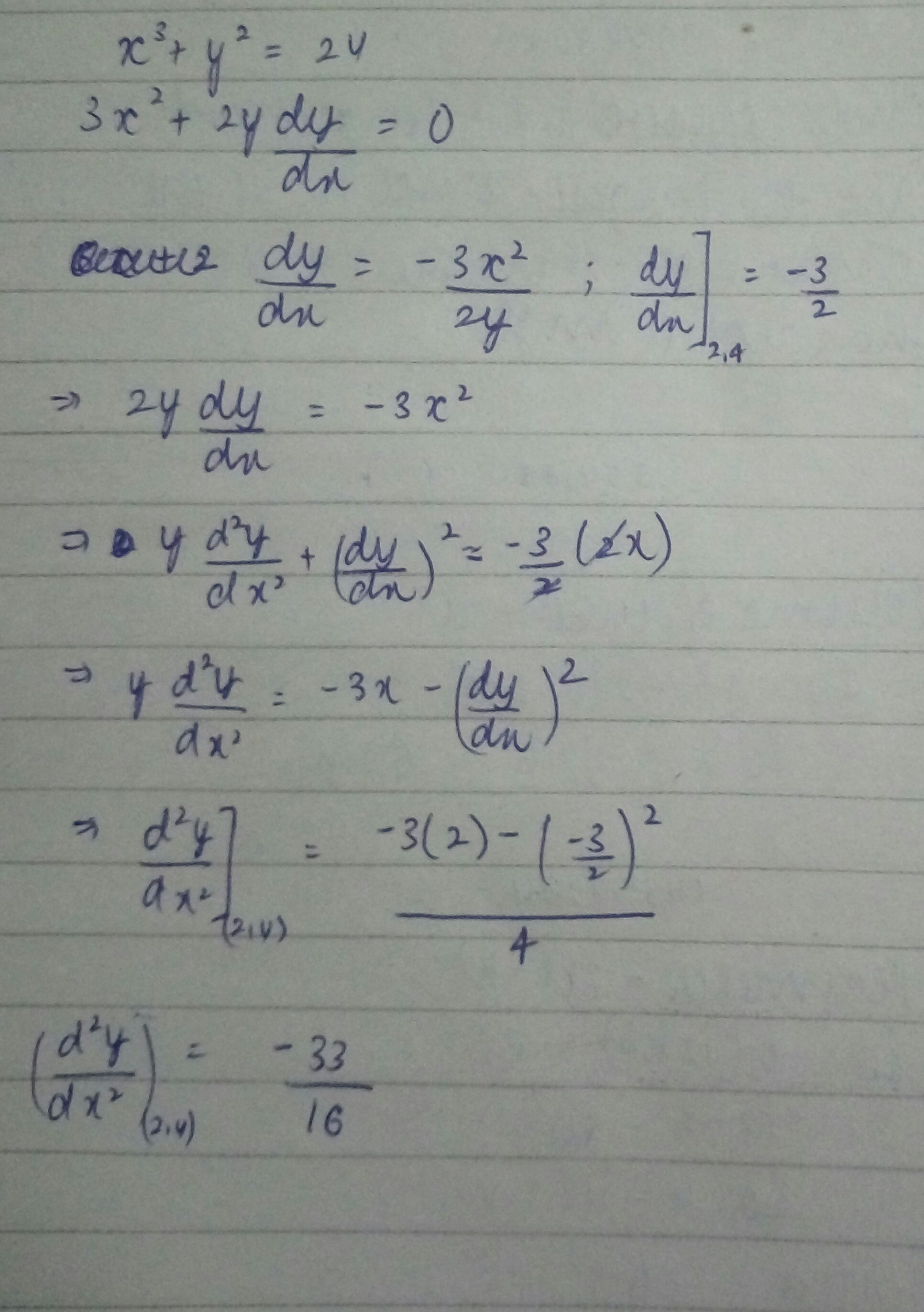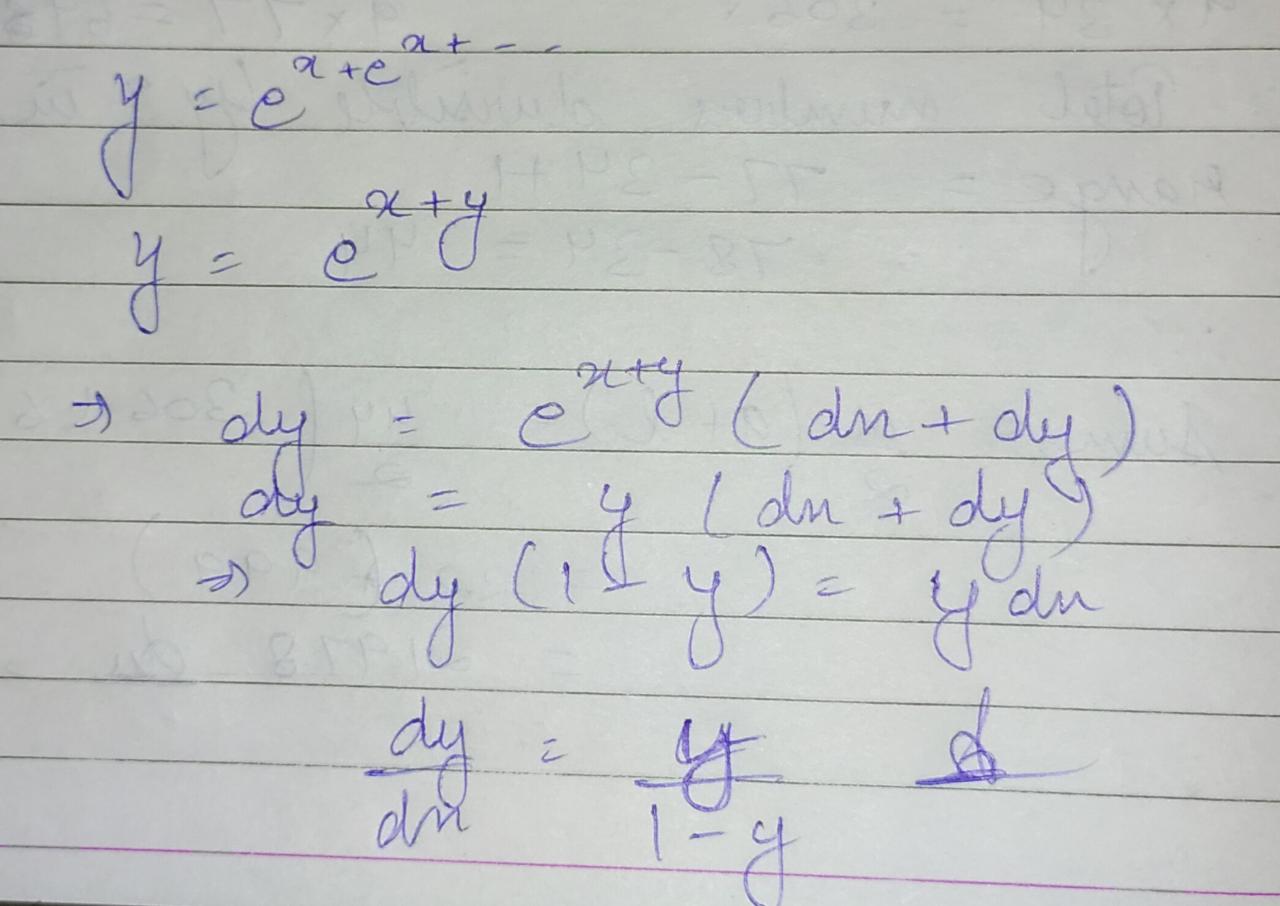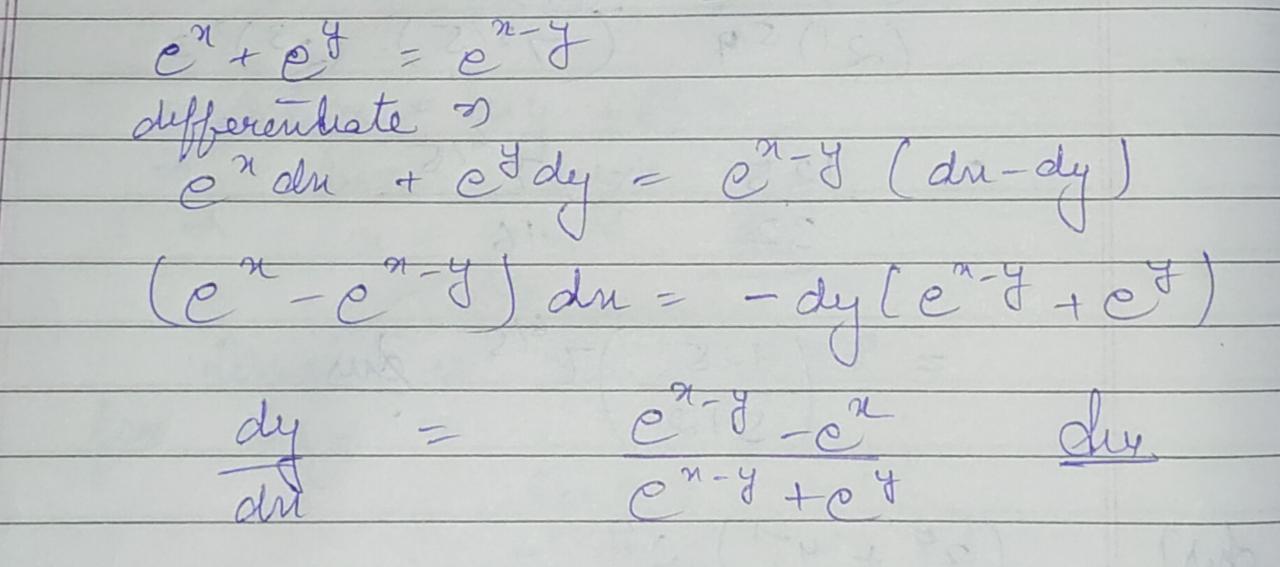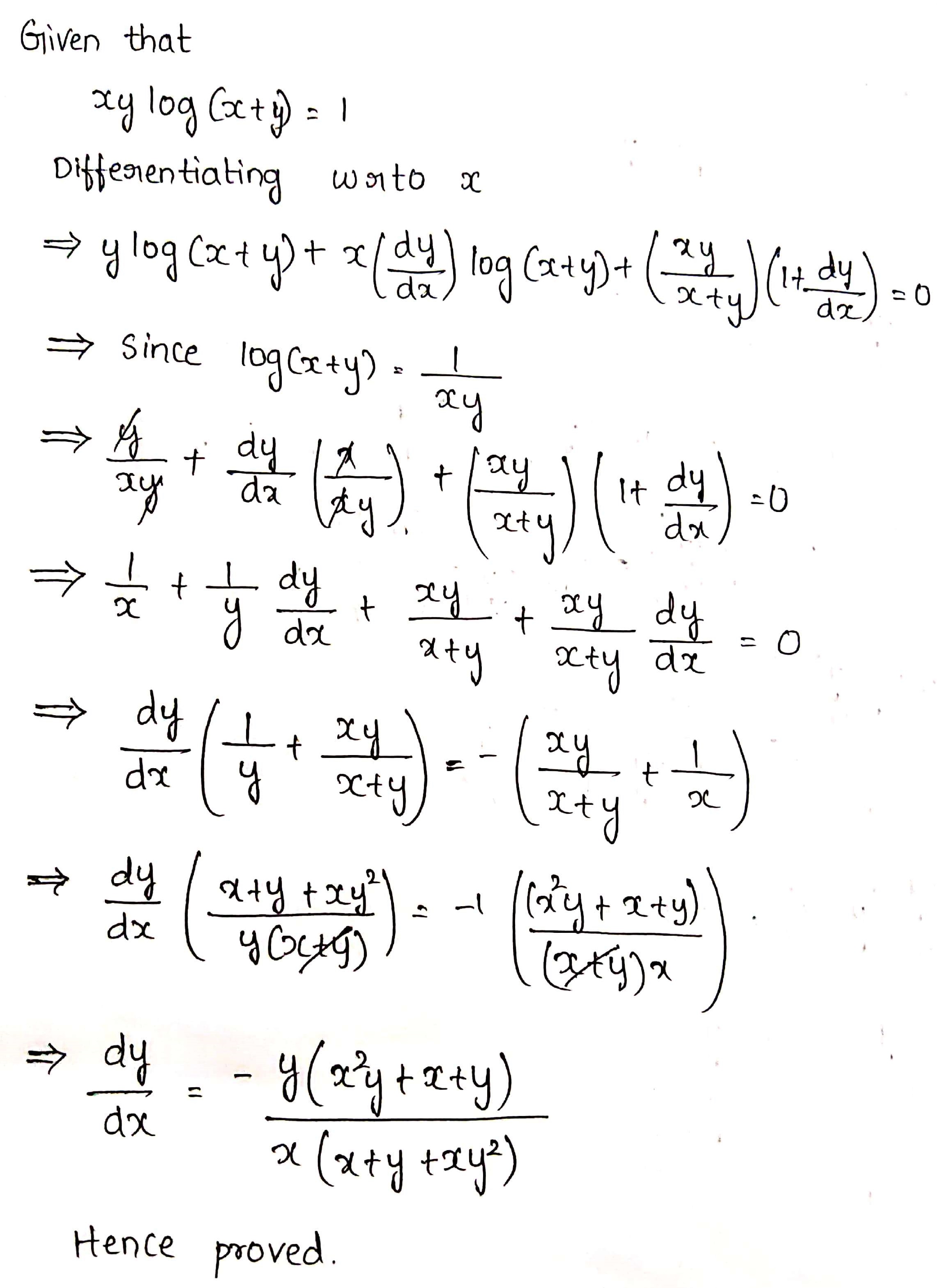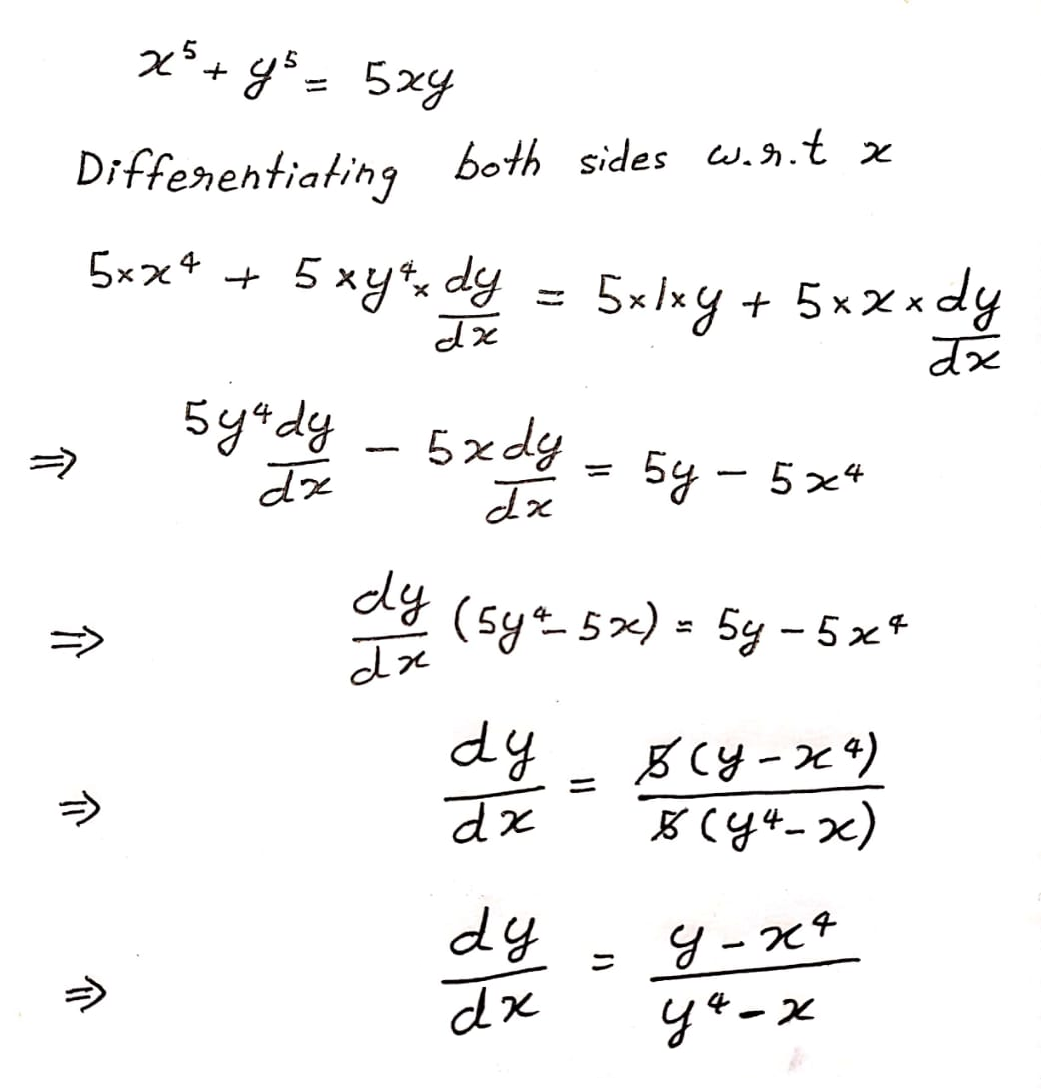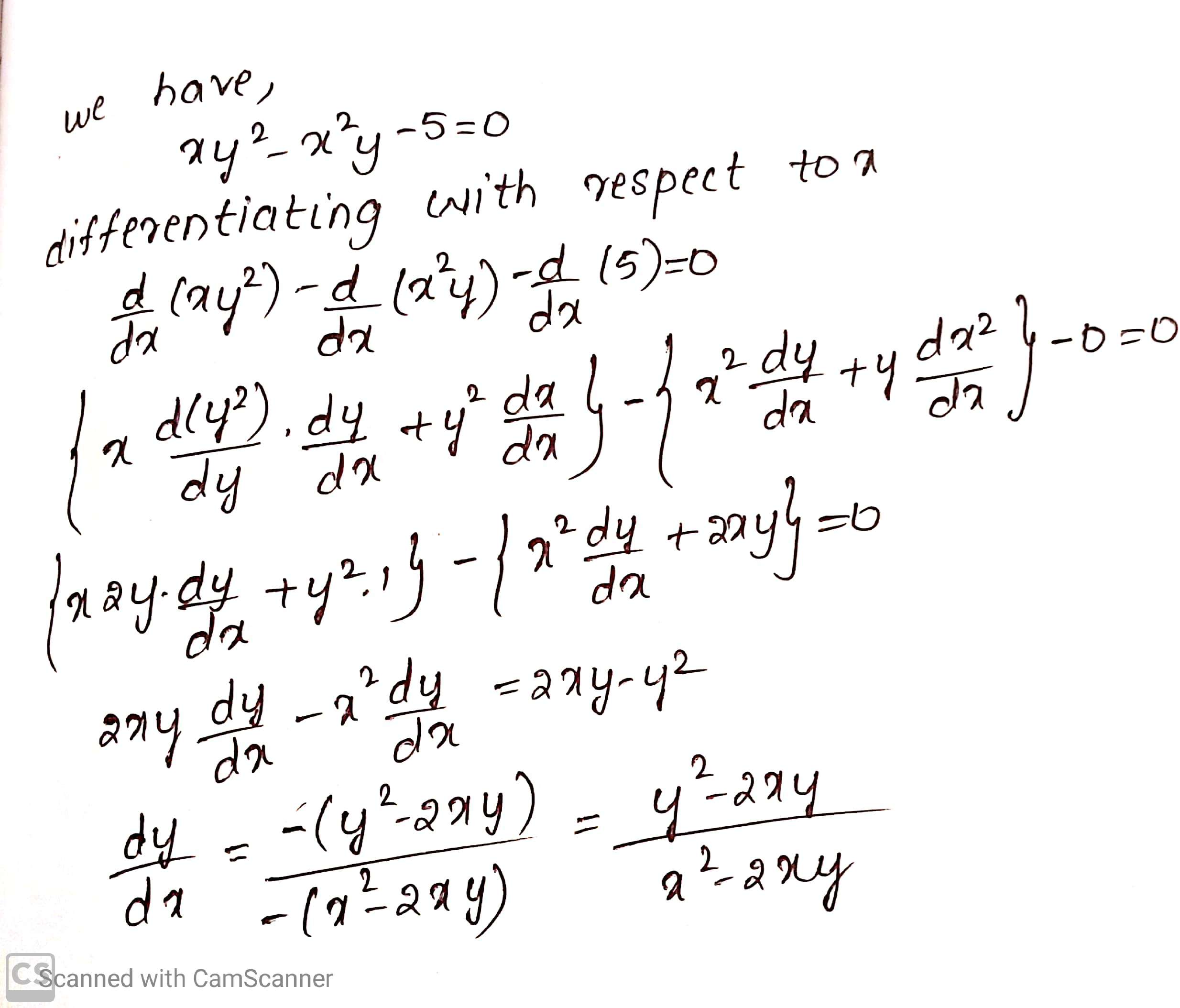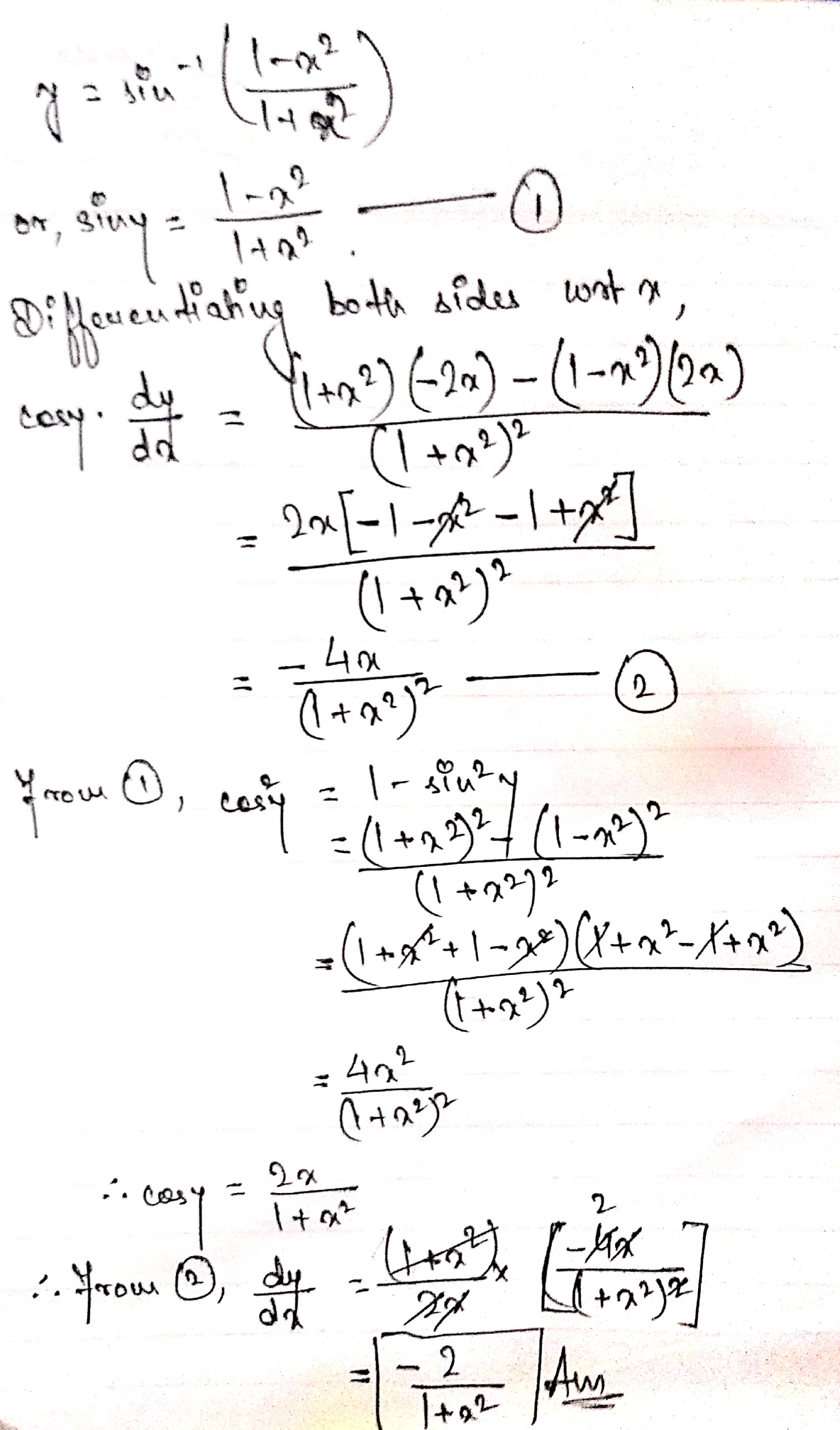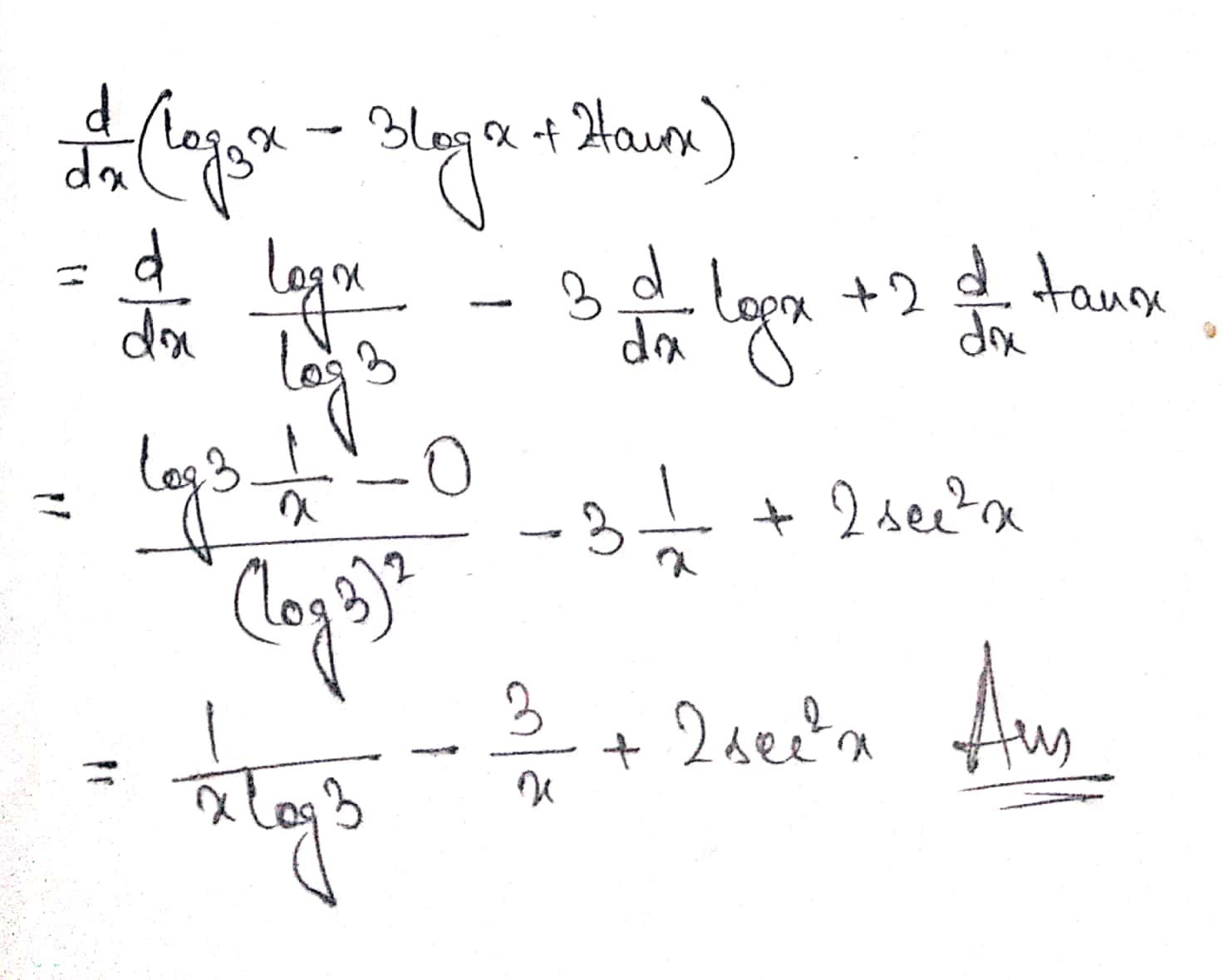Differentiation - Class 11 Commerce Applied Mathematics - Extra Questions
Find $$ \displaystyle \frac{dy}{dx} $$ of $$ax + by^2 = \cos y$$
Find the derivative of the following functions: $$\displaystyle \sin x \cos x $$
Find $$ \displaystyle \frac{dy}{dx} $$ of $$2x + 3y = \sin y$$
Find $$ \displaystyle \frac{dy}{dx} $$ of $$xy + y^2 = \tan x + y$$
Find the derivative of the function given by $$f(x) = (1 + x) (1 + x^2) (1 + x^4) (1 + x^8)$$ and hence find $$f'(1).$$
Find derivative of the following functions (it is to be understood that $$a, b, c, d, p, q, r$$ and $$s$$ are fixed non-zero constants and $$m$$ and $$n$$ are integers) : $$\displaystyle \left ( x^{2}+ 1 \right )\cos \, x$$
Differentiate the given function w.r.t. $$x$$:
$$\sin^3x + \cos^6 x$$
If $$y = x^{x}$$, then find $$\dfrac {dy}{dx}$$
Find the derivative of the following functions (it is to be understood that $$a, b, c, d, p, q, r $$ and $$s$$ are fixed non-zero constants and $$m$$ and $$n$$ are integers) : $$(ax + b)\displaystyle ^{n} (cx + d)\displaystyle ^{m}$$
If $$f(x)=\tan { 2x } \tan { 3x } \tan { 5x } $$, then prove that $$f'(x)=5\sec ^{ 2 }{ 5x } -3\sec ^{ 2 }{ 3x } -2\sec ^{ 2 }{ 2x } $$
Find the $$\dfrac{dy}{dx}$$ by implicit differentiation. $$x^2 - 8xy + y^2 = 8$$
Find $$\cfrac { dy }{ dx } $$ where $$ { x }^{ 3 }+{ y }^{ 3 }+3xy=7$$.
Differentiable $$\log_7(log x)$$ with respect to $$x$$.
Find the value of $$f'(e)$$ where $$f(x)=\log_e(\log_ex)$$.
$$y = \sqrt{log \,x+\sqrt{log \,x + \sqrt{log \,x}}} +$$_____ $$\infty$$ show that $$\dfrac{dy}{dx} = \dfrac{1}{x(2y - 1)}$$.
If $$\sqrt{x}+\sqrt{y}=4$$ then find $$\dfrac{dy}{dx}$$ at $$x=1$$.
Find $$\dfrac{dy}{dx}$$ :
$$x+y^2=\log y + x^2$$
If $$f(x)= \left| x-2 \right| +\left| x-5 \right|$$ then find $$f'(4)$$.
If $$y=3x^{2}$$,Find $$\dfrac {dy}{dx}=?$$
If $$e^{y}+xy=e$$, find $$y''(0)$$
Find $$\dfrac{dy}{dx}$$ when $$x^2 + y^2 = c^2$$.
$$\dfrac{{dy}}{{dx}}\, + \,\dfrac{y}{x}\,\,{\rm I}n\,y\, = \,\dfrac{y}{{{x^2}}}{\left( {{\rm I}n\,y} \right)^2}$$
Differentiate: $$ \sqrt { \dfrac { \left( x-3 \right) \left( { x }^{ 2 }+4 \right) }{ { 3 }x^{ 2 }+4x+5 } }$$
If $$\sin y = x\sin (a + y)$$ , then show
$$ \dfrac{dy}{dx}=\dfrac{\sin \left( a+y \right)}{\cos y-x.\cos \left( a+y \right)} $$
Find $$ \dfrac{{dy}}{{dx}},x = a\left( {\cos t + \log \tan \frac{t}{2}}
\right),y = a\sin t$$
If $$e^x + e^y = e^{x+y}$$, find $$\dfrac{dy}{dx} $$.
Find $$\dfrac{dy}{dx}$$ for $$y=e^{\sqrt{x}}$$.
Differentiate $${\tan ^{ - 1}}\left( {\frac{{\sqrt {1 + {x^2}} - 1}}{x}} \right)$$ with respect to $${\sin ^{ - 1}}x$$
Differentiate with respect to $$x$$.
$$y = x\tan x$$
Differentiate the following w.r.t.x:
$$5^x\cdot \sec^{-1}2x$$
Differentiate $$x = \tan (e^{-y})$$
Find $$\dfrac {dy}{dx}$$$$\dfrac{{dx}}{{dt}} = ap\cos pt,\dfrac{{dy}}{{dt}} = - bp\sin pt$$
Differentiate the following w.r.t.x:
$$\sin^{-1}x+\cos^{-1}x$$
If $$y = {3^{2\log x + 7}}$$ then $$\dfrac{{dy}}{{dx}}$$
Differentiate the following function:
$${x}^{\log{x}}+{(\log{x})}^{x}$$
$$y=x^{\log x}+(\log x)^x$$
$$u=x^{\log x}\Rightarrow \log u+=(\log x)^2$$
$$\Rightarrow \dfrac{1}{u}\dfrac{du}{dx}=\dfrac{2\log (x)}{x}$$
$$\Rightarrow \dfrac{du}{dx}=\dfrac{2(\log x)x}{x}$$
$$v=(\log x)^x\Rightarrow \log v=x \log (\log x)$$
$$\Rightarrow \dfrac{1}{v}\dfrac{dv}{dx}=\dfrac{x}{x\log x}+\log (\log x)$$
$$\Rightarrow \dfrac{dy}{dx}=\left(\log x)^x\left(\dfrac{1}{\log x}+\log(\log x\right)\right)$$
$$\therefore \dfrac{dy}{dx}=\dfrac{dv}{dx}+\dfrac{du}{dx}$$
$$=\dfrac{2(\log x)^{\log x}}{x}+(\log x)^x\left(\dfrac{1}{\log x}+\log (\log x)\right)$$
If $$y=\sin {\sqrt {1-x^{2}}}$$, then find $$\dfrac{dy}{dx}$$.
Find:
$$\dfrac{d}{{dx}}\left\{ {\dfrac{{5 + 4x}}{{x + 3}}} \right\}$$
If $$y = {a^{\dfrac{1}{2}{{\log }_a}\cos x}}.$$ Find $$\dfrac{{dy}}{{dx}}$$
Find the derivative of $$f\left ( x \right )=1+x+x^{2}+--+x^{50}atx=1$$.
Find the derivate of $$\ {e^{\sqrt {2x + 1} }}$$ with respect to $$x$$ at $$x=12$$
If $$y = \sqrt x + \dfrac{1}{{\sqrt x }},$$ then show that $$2x\dfrac{{dy}}{{dx}} + y = 2\sqrt x $$
$$ y = \sqrt{x}+\dfrac{1}{\sqrt{x}}$$
$$ \dfrac{dy}{dx} = \dfrac{1}{2\sqrt{x}}+ \dfrac{\dfrac{-1}{2\sqrt{x}}}{x}$$
$$ = \dfrac{1}{2\sqrt{x}}-\dfrac{1}{2x\sqrt{x}}$$
$$ 2x\dfrac{dy}{dx} = 2x(\dfrac{1}{2\sqrt{x}}-\dfrac{1}{2x\sqrt{x}})$$
$$ = 2(\dfrac{\sqrt{x}}{2}-\dfrac{1}{2\sqrt{x}}) = \sqrt{x} -\dfrac{1}{\sqrt{x}}$$
$$ \therefore 2x\dfrac{dy}{dx}+y = \sqrt{x}-\dfrac{1}{\sqrt{x}}+\sqrt{x}+\dfrac{1}{\sqrt{x}}$$
$$ = 2\sqrt{x}$$
$$ \therefore \boxed{2x\dfrac{dy}{dx}+y = 2\sqrt{x}.}$$
Find the derivative of $$sin^{2}x$$ with respect to x using product rule.
Let $$y=\log(\sin x)$$ find $$\dfrac{d^2y}{dx^2}$$.
Find $$\dfrac{dy}{dx} $$, if $$x\ \sin\ y+y\ \sin\ x=0$$.
$$y=x^3-x^2-x+7$$ find x =? when $$\dfrac{dy}{dx}=0$$
Differentiate $$\log(sin\ x)(log\ x)$$
Differentiate: $${\sin}^{2}{3x}.{\tan}^{3}{2x}$$
Find $$\dfrac {dy}{dx}$$ for $$y= \left( \sin 20x+{{a}^{2x}}+10 \right) \\$$
If $$x\sqrt { 1-{ y }^{ 2 } } +y\sqrt { 1-{ x }^{ 2 } } =1$$, prove that $$\dfrac { dy }{ dx } =-\sqrt { \frac { { 1-y }^{ 2 } }{ { 1-x }^{ 2 } } . } $$
$$x\sqrt{1-y^2}+y\sqrt{1-x^2}=1$$
Differentiating throughout with respect to x we get
$$x\dfrac{1}{2\sqrt{1-y^2}}\cdot (-2y)\dfrac{dy}{dx}+\sqrt{1-y^2}+y\dfrac{1}{2\sqrt{1-x^2}}\cdot (-2x)+\sqrt{1-x^2}\dfrac{dy}{dx}=0$$
$$\Rightarrow \dfrac{-xy}{\sqrt{1-y^2}}\dfrac{dy}{dx}+\sqrt{1-y^2}+\dfrac{(-xy)}{\sqrt{1-x^2}}+\sqrt{1-x^2}\dfrac{dy}{dx}=0$$
$$\Rightarrow \left(\dfrac{-xy}{\sqrt{1-y^2}}+\sqrt{1-x^2}\right)\dfrac{dy}{dx}=\dfrac{dy}{\sqrt{1-x^2}}-\sqrt{1-y^2}$$
$$\Rightarrow \left(\dfrac{-xy+\sqrt{(1-x^2)(1-y^2)}}{\sqrt{1-y^2}}\right)\dfrac{dy}{dx}=\left(\dfrac{xy-\sqrt{(1-x^2)(1-y^2)}}{\sqrt{1-x^2}}\right)$$
$$\Rightarrow \dfrac{-(xy-\sqrt{(1-x^2)(1-y^2)})}{\sqrt{1-y^2}}$$ $$\dfrac{dy}{dx}$$ $$=\dfrac{(xy-\sqrt{(1-x^2)(1-y^2)})}{\sqrt{1-x^2}}$$
$$\Rightarrow \dfrac{dy}{dx}=-\dfrac{\sqrt{1-y^2}}{\sqrt{1-x^2}}$$
Hence $$\dfrac{dy}{dx}=-\sqrt{\dfrac{1-y^2}{1-x^2}}$$.
$$y=x^{3}-3x+2$$ Find $$\frac{dy}{dx}$$ if the given function is continuous.
If $${x^y} + {y^x} = {a^b}$$ then show that $$\dfrac{{dy}}{{dx}} = - \left[ {\dfrac{{y{x^{y - 1}} + {y^x}\log y}}{{{x^y}\log x + x{y^{x - 1}}}}} \right]$$
Find $$\dfrac{dy}{dx}$$ if $$xy=e^{x-y}$$
$${\left( {{x^2} + {y^2}} \right)^2} = xy,$$ then $$\dfrac{dy}{dx}$$
Find derivative of $$f(x)=x \cos x$$
If $$y\sqrt { { x }^{ 2 }+1 } =log\{ \sqrt { { x }^{ 2 }+1 } -x\} ,$$ show that $${ (x }^{ 2 }+1)\dfrac { dy }{ dx } +xy+1=0.$$
$$\sqrt{x^{2}+1}= log \left \{ \sqrt{x^{2}+1}-x \right \}$$
Differentiating with reset to be x we get
$$\sqrt{x^{2}+1}\frac{dy}{dx}+\frac{1}{2\sqrt{x^{2}+1}}.2x.y=\frac{1}{\sqrt{x^{2}+1}-x}\left \{ \frac{1}{2\sqrt{x^{2}+1}}2x-1 \right \}$$
$$\sqrt{x^{2}}\frac{dy}{dx}+\frac{xy}{\sqrt{x^{2}+1}}=\frac{1}{\sqrt{x^{2}+1}-x}\left \{ \frac{x}{\sqrt{x^{2}+1}-1} \right \}$$
$$\Rightarrow \sqrt{x^{2}+1}\frac{dy}{dx}+\frac{xy}{\sqrt{x^{2}+1}}=\frac{1}{\sqrt{x^{2}+1}-x}\left \{ \frac{x-\sqrt{x^{2}+1}}{\sqrt{x^{2}+1}} \right \}$$
$$\Rightarrow \sqrt{x^{2}+1}\frac{dy}{dx}+\frac{xy}{\sqrt{x^{2}+1}}=\frac{-1}{\sqrt{x^{2}+1}}$$
$$\Rightarrow (x^{2}+1)\frac{dy}{dx}+xy=-1$$
$$\Rightarrow (x^{2}+1)\frac{dy}{dx}+xy+1=0.$$
Find f'(-3) using definition if $$f\left( x \right) =\frac { 2x }{ x-3 } $$
Find $$\dfrac { d }{ dx } { \sin }^{ 3 }4x{ \cos }^{ 8 }5x$$
$$\dfrac{d}{dx}(\sin^34x\cos^85x)$$
Let $$u=\sin^34x$$ and $$v=\cos^85x$$
$$\therefore \dfrac{d}{dx}(\sin^34x\cos^85x)=\dfrac{d}{dx}(uv)=u\dfrac{dv}{dx}+v\dfrac{du}{dx}$$
$$=\sin^34x\cdot \dfrac{d}{dx}(\cos^85x)+\cos^85x\dfrac{d}{dx}(\sin^34x)$$ …..$$(1)$$
Here $$\dfrac{d}{dx}(\cos^85x)=\dfrac{d}{d(\cos 5x)}\{(\cos 5x)^8\}\cdot \dfrac{d(\cos 5x)}{dx}$$
$$=8(\cos 5x)^7\cdot \dfrac{d}{d(5x)}(\cos (5x))=\dfrac{d(5x)}{dx}$$
$$=8\cos^{-1}5x\cdot (-\sin 5x)\cdot 5\dfrac{dx}{dx}$$ $$[\because \dfrac{d(\cos x)}{dx}=-\sin x]$$
$$=-40\sin 5x\cos^75x$$.
and $$\dfrac{d}{dx}(\sin^34x)=\dfrac{d}{d(\sin 4x)}\{(\sin 4x)^3\}.\dfrac{d(\sin 4x)}{dx}$$
$$=3\sin^24x\cdot \dfrac{d(\sin 4x)}{d(4x)}\cdot \dfrac{d(4x)}{dx}$$
$$=3\sin^24x\cos 4x 4\dfrac{dx}{dx}$$ $$[\because \dfrac{d}{dx}(\sin x)=\cos x]$$
$$=12\sin^24x\cos 4x$$
From $$(1)$$,
$$\dfrac{d}{dx}\sin^34x\cos^85x=\sin^34x.(-40\sin 5x\cos^75x)+\cos^85x(12\sin^24x\cos 4x)$$
$$=-40\sin^34x\sin 5x\cos^75x+12\cos^85x\sin^24x\cos 4x$$
$$=4(-10\sin^34x\sin 5x\cos^75x+3\sin^24x\cos 4x\cos^85x)$$
$$=4\cos^75x\cdot \sin^24x(3\cos 4x\cos 5x-10\sin 4x\sin 5x)$$
$$=4\cos^75x\sin^24x\left(\dfrac{3\cos (4x+5x)+\cos(4x-5x)}{2}-10\times \dfrac{\cos (4x-5x)-\cos (4x+5x)}{2}\right)$$
$$=4\cos^75x\sin^24x\left(\dfrac{3\cos 9x+3\cos (-x)-10\cos (-x)+\cos 9x}{2}\right)$$
$$=2\cos^75x\sin^24x(4\cos 9x-7\cos x)$$ $$[\because \cos (-x)=\cos x]$$
$$\therefore \dfrac{d}{dx}(\sin^34x\cos^85x)=2\cos^75x\sin^24x(4\cos 9x-7\cos x)$$.
Differentiate $$xe^x$$ from first principles.
If $$\cos (x+y)=y \sin x$$, then find $$\dfrac { dy }{ dx } .$$
Given
$$\cos(x+y)=y\sin x$$
Differentiating both sides with respect to x, we get
$$-\sin(x+y)\left\{1+\dfrac{dy}{dx}\right\}=y\cos x+\sin x\dfrac{dy}{dx}$$
$$-\sin(x+y)-\sin(x+y)\dfrac{dy}{dx}=y\cos x+\sin x\dfrac{dy}{dx}$$
$$\Rightarrow -\sin(x+y)\dfrac{dy}{dx}-\sin x\dfrac{dy}{dx}=y\cos x+\sin(x+y)$$
$$\Rightarrow \left\{-\sin (x+y)-\sin x\right\}\dfrac{dy}{dx}=y\cos x+\sin(x+y)$$
$$\Rightarrow \dfrac{dy}{dx}=\dfrac{y\cos x+\sin(x+y)}{\sin(x+y)-\sin x}$$.
Differentiate the following $$w.r.t.x$$.
$$\sqrt{x}.cotx$$
Find $$\dfrac{dy}{dx}$$ :
$$\sin x +\cos y = 5x+4$$
Differentiate of the function $$x^{3}+y^{3}+3x^{2}y=a^{3}$$ with respect to $$x$$.
Find $$\dfrac{dy}{dx}$$ :
$$\sin x - 3x = 5y$$
If $$x^py^q=(x+y)^{p+q}$$ then prove that $$\dfrac{dy}{dx}=\dfrac{y}{x}$$.
If $$f(x)=x+\log x$$ find $$f^{\prime}(x)$$
Find drivative of $$y=(2-\sin x)(e^{x}+x^{3}+2)$$ with respect to $$x$$.
From rule $$\dfrac{d}{dx} (u.x) = u'v + uv'$$
$$\Rightarrow \dfrac{dy}{dx} = (-\cos x)(e^x + x^3 + 2) + (2-\sin x)(e^x + 3x^2)$$
$$=e^x(2-\sin x - \cos x) - \cos x.x^3 + x^2 (6 - 3 \sin x) - 2\cos x$$.
Find $$\dfrac{dy}{dx}$$ if $$3x+4y=9$$
Find the derivative of $$\dfrac{x+\cos x}{\tan x}$$
Let $$y=\dfrac{x+\cos x}{\tan x}$$ ………….$$(1)$$
differentiating equation $$(1)$$ wrt x we get
$$\dfrac{dy}{dx}=\dfrac{d}{dx}\left(\dfrac{x+\cos x}{\tan x}\right)$$
$$\dfrac{dy}{dx}=\dfrac{\tan x(1-\sin x)-\sec^2x(x+\cos x)}{(\tan x)^2}$$
$$\dfrac{dy}{dx}=\dfrac{1-\sin x}{\tan x}-\left(\dfrac{\sec x}{\tan x}\right)^2(x+\cos x)$$.
Differentiate $$\sin^{2} x$$ wrt $$x$$
Find $$\dfrac{dy}{dx}$$
$$y=\sin x.\ \cos x$$
$$f((x)=\log x+\sin x$$ find $$f^{\prime }(x)$$
Differentiate with respect to $$x$$:
$$\ e^{-3x} \log (1+x)$$
If $$\sin\theta + 2\cos\theta =1$$ then prove that $$2\sin\theta -\cos\theta=0$$.
Differentiate with respect to $$x$$:
$$e^x \log \sin 2x$$
Find $$\dfrac{dy}{dx}$$ in the following:
$$4x+3y=\log(4x-3y)$$
Differentiate the following w.r.t. x:$$\cos x .e^{4x+5}$$
Let $$y=\log(1+\sin x)$$ for $$0\le x\le \dfrac{\pi}{2}$$, find $$\dfrac{dy}{dx}$$.
Differentiate with respect to $$x$$:
$$e^x\tan x$$
Differentiate $$x^{2}$$ with respected to $$x^{3}$$.
Differentiate $$e^x \tan x $$ with respect to $$x$$.
Differentiate the following functions with respect to $$x$$:
If $$y=\tan^{-1}\left (\dfrac {2x}{1-x^2}\right), x > 0$$, prove that $$\dfrac {dy}{dx} =\dfrac {4}{1+x^2}$$
If $$y=\log \sin x +e^x \tan x$$, then find $$\dfrac{dy}{dx}$$.
Differentiate w.r.t. $$x$$:$$\sin 5x \cos 3x$$
Find $$\dfrac{dy}{dx}$$, if $$y=e^x 5^x$$.
Differentiate w.r.t $$x $$:$$y=x^2 \sin 2x$$
Differentiate w.r.t. $$x $$:$$y=e^{3x-2} \sin 3x$$
Find $$\dfrac{dy}{dx}$$, if $$y=(3x+2)^x$$.
Find $$\dfrac{dy}{dx}$$, if $$2x+3y=\sin x$$.
If $$y=x\sin (a+y),$$ then prove that $$\dfrac {dy}{dx}=\dfrac {\sin^2 (a+y)}{\sin (a+y)-y \cos (a+y)}$$.
Differentiate w.r.t. $$x$$:$$\dfrac{x}{y^3}=1$$
Differentiate w.r.t. $$x$$:$$y=e^{3x} \sin 4x$$
Differentiate w.r.t. $$x$$:$$y=\sin x \sin 2x$$
If $$y=x^2 \tan x$$, find $$\dfrac{dy}{dx}$$.
Find $$\dfrac{dy}{dx}$$, if $$ax + by^2 =\cos y$$.
Differentiate w.r.t. $$x $$:$$y=(\cos x)(1-\sin^2 x)$$
If $$y=e^x+\sin x -4x^3$$, find $$\dfrac{dy}{dx}$$.
Solve the following differential equation.
$$\dfrac{dy}{dx}=3x$$
If $$x^3+y^3=3axy$$, find $$\dfrac{dy}{dx}$$.
If $$x^2+2xy+y^3=42$$, find $$\dfrac{dy}{dx}$$.
If $$x^2+y^2=t-\dfrac{1}{t}$$ and $$x^4+y^4=t^ 2+\dfrac{1}{t^2}$$, then prove that $$\dfrac{dy}{dx}=\dfrac{1}{x^3y}$$.
If $$y=x\sin y$$, then prove that $$\dfrac {dy}{dx}=\dfrac {y}{x(1-x\cos y)}$$.
Is every differentiable function continuous? is every continuous function differentiable?
Find absolute value of $$dy/dx$$ at $$x=1$$ if $$\displaystyle y^{x}.x^{y}=1$$
If $$f(x)$$ is differentiable everywhere, then $${ \left| f(x) \right| }^{ 2 }$$ is differentiable everywhere.( Enter 1 if true or 0
otherwise)
Given a function g which has derivative $${g}'\left ( x \right )$$ for all x satisfying $${g}'\left ( 0 \right )=2$$ and $$g\left ( x+y \right )=e^{y}g\left ( x \right )+e^{x}g\left ( y \right )$$ for all $$x, y\epsilon R$$,$$ g(5)=32.$$ The value of $$\dfrac{{g}'\left ( 5 \right )-2e^{5}}{16}$$ is
Differentiate the function with respect to $$x$$
$$\cos x^3 . \sin^2 (x^5)$$
Find the derivative of the following:
$$(5x^{3} + 3x - 1)(x - 1)$$.
Find the derivative of the following:
$$x^{-4} (3 - 4x^{-5})$$.
Find $$ \displaystyle \frac{dy}{dx} $$ of $$\sin^2 x + \cos^2 y = 1$$
Find $$ \displaystyle \frac{dy}{dx} $$ of $$x^3 + x^2 y + xy^2 + y^3 = 81$$
Find the derivative of the following functions (it is to be understood that $$a, b, c, d, p, q, r$$ and $$s$$ are fixed non-zero constants and $$m$$ and $$n$$ are integers) : $$(ax + b) (cx + d)^{2}$$
Find the derivative of $$\displaystyle x^{-3}\left ( 5+3x \right )$$
Find $$ \displaystyle \frac{dy}{dx} $$ of $$\sin^2 y + \cos xy = k$$
Find $$ \displaystyle \frac{dy}{dx} $$ of $$x^2 + xy + y^2 = 100$$
Find the derivative of the following:
$$x^{5} (3 - 6x^{-9})$$.
Find the derivative of the following functions (it is to be understood that $$a, b, c, d, p, q, r$$ and $$s$$ are fixed non-zero constants and $$m$$ and $$n$$ are integers) : $$(px + q)\displaystyle \left ( \frac{r}{x}+s \right )$$
Find the derivative of the following functions (it is to be understood that $$a, b, c, d, p, q, r $$ and $$s$$ are fixed non-zero constants and $$m$$ and $$n$$ are integers) : $$\displaystyle \cos ec\, x\,\cot \,x$$
Find the derivative of the following functions (it is to be understood that $$a, b, c, d, p, q, r$$ and $$s$$ are fixed non-zero constants and $$m$$ and $$n$$ are integers) : $$\displaystyle \left ( ax^{2}+\sin \,x \right )\left ( p + q \,\cos
\,x \right )$$
Differentiate the given function w.r.t. $$x$$.
$$y=\displaystyle e^x + e^{x^2} + ... + e^{x^5}$$
Find $$ \displaystyle \frac{dy}{dx} $$ of $$\displaystyle y = \sin^{-1} ( 2 x \sqrt{1 - x^2} ) , -\frac{1}{\sqrt{2}} < x < \frac{1}{\sqrt{2}}$$
Differentiate the function w.r.t. $$x$$.
$$\displaystyle \sqrt{ \frac{(x - 1)(x - 2)}{(x - 3)(x - 4) (x - 5)} }$$
Find the derivative of the following functions (it is to be understood that $$a, b, c, d, p, q, r, s$$ and $$s$$ are fixed non-zero constants and $$m$$ and $$n$$ are integers) : $$\displaystyle x^{4}\left ( 5\,\sin \,x-3\,\cos \,x \right )$$
Find the derivative of the following functions (it is to be understood that $$a, b, c, d, p, q, r$$ and $$s$$ are fixed non-zero constants and $$m$$ and $$n$$ are integers) : $$\displaystyle \left ( x+\cos \,x \right )\left ( x-\tan \,x \right )$$
Differentiate the function w.r.t. $$x$$.
$$(x + 3)^2 . (x + 4)^3 . (x + 5)^4$$
Find the derivative of the following functions (it is to be understood that $$a, b, c, d, p, q, r$$ and $$s$$ are fixed non-zero constants and $$m$$ and $$n$$ are fixed integers) : $$\displaystyle \left ( x+\sec \,x \right )\left ( x-\tan \,x \right )$$
Differentiate $$(x^2 - 5x + 8)(x^3 + 7x + 9)$$ in three ways mentioned below,
(i) By using product rule
(ii) By expanding the product to obtain a single polynomial
(iii) By logarithmic differentiation
Do they all give the same answer?
Find $$\dfrac{dy}{dx}$$ of the function
$$x^y + y^x = 1$$
Find $$\displaystyle \frac{dy}{dx}$$ of $$y^x = x^y$$
If $$x\sqrt {1+y}+y\sqrt{1+x}=0$$, for $$-1< x< 1$$, prove that $$\cfrac{dy}{dx}=\cfrac { 1 }{ { \left( 1+x \right) }^{ 2 } } $$
If $$\sin y = x \sin (a + y)$$, then prove that $$\dfrac{dy}{dx} = \dfrac{\sin^2 (a+y)}{\sin a}$$.
If $$x^y + y^x = a^b$$, then find $$\dfrac{dy}{dx}$$.
Find $$\cfrac { dy }{ dx } $$ where $$y=\log { \left( \sec { x } \right) \ \ } 0\le x\le \cfrac { \pi }{ 2 } $$
If $$x^y = a^x$$, prove that $$\dfrac{dy}{dx}=\dfrac{x\log_ea-y}{x\log_ex}$$.
Solve: $$\dfrac {dy}{dx} = \cos (x + y)$$
If $$y=f(x)$$ is a differentiable function of $$x$$, then show that
$$\cfrac { { d }^{ 2 }x }{ d{ y }^{ 2 } } =-{ \left( \cfrac { dy }{ dx } \right) }^{ -3 }.\cfrac { { d }^{ 2 }y }{ d{ x }^{ 2 } } $$
Solution of differential equation $$x^2=1+(\dfrac{x}{y})^{-1}\, \dfrac{dy}{dx}+\dfrac{(\dfrac{x}{y})^{-2}\, (\dfrac{dy}{dx})^2}{2!}+\dfrac{(\dfrac{x}{y})^{-3}\,(\dfrac{dy}{dx})^3}{3!}+....$$ is
If $$(x^2+y^2)^2=xy$$, find $$\displaystyle\frac{dy}{dx}$$.
Differentiate the following functions w.r.t.$$x$$.
$$\sqrt{x+\displaystyle\frac{1}{x}}$$.
If $$y=1+x.{e}^{y}$$, show that $$\dfrac { dy }{ dx } =\dfrac { { e }^{ y } }{ 2-y } $$
Find the equation of the tangent to the curve $$y=\dfrac { x-y }{ \left( x-2 \right) \left( x-3 \right) }$$ at the point where it cuts the x-axis.
If $$u$$ and $$v$$ are differentiable functions of $$x$$ and if $$y=u+v$$ then $$\cfrac { dy }{ dx } =\cfrac { du }{ dx } +\cfrac { dv }{ dx } $$
Calculate $$\displaystyle\, f\, (x) + f'\, (x) + 2$$, if $$f\, (x) = x\, \sin\, 2x$$
Prove the following identities
$$\displaystyle\, 2f'\, \left ( x +\tfrac{\pi }{3} \right )\, f'\, \left ( x -\tfrac{\pi }{6} \right )\, = f'\, (0)\, -\, f\, \left ( 2x +\tfrac{\pi }{6} \right )$$, where $$f\, (x) = \cos\, x$$
If $$y=(x^2+1)^5\sin 4x$$, find $$\dfrac{dy}{dx}$$.
Find the derivative of $$\displaystyle\, y \, =\, x\sqrt{1 \, +\, x^2}$$
If $$ y=x^4+4^x+\log x-1$$, find $$\cfrac{dy}{dx}$$.
If $$x^3-y^3+\tan (xy)= \log (x+y)$$, find $$\cfrac{dy}{dx}$$
Find the derivative of the following
(i) $$x^{x^n}+x^{n^x}$$(ii)$$\ log{\sqrt{x^2+1}}$$
If $$x = at^{4}, y = bt^{3}$$, then find $$\dfrac {dy}{dx}$$.
If $$y = 4x^{4} + 2x^{3} + \dfrac {5}{x} + 9$$, then find $$dy/dx$$.
If $${1 \over 2}\left( {{e^y} - {e^{ - y}}} \right) = x$$ , prove that
$$ \cfrac { dy }{ dx } =\cfrac { 1 }{ \sqrt { { x }^{ 2 }+1 } } $$
$$y={ e }^{ \left\{ \sin ^{ 2 }{ x } +\sin ^{ 4 }{ x } +\sin ^{ 6 }{ x } +... \right\} }$$, then $$\cfrac { dy }{ dx } =$$
Differentiate the following
$${ x }^{ 2 }{ (3x-2) }^{ 4 } \cos x$$
Differentiate$$f\left( x \right) = \ln \left( {1 + {x^2}} \right)$$
Let $$x^2y^3=(x+y)^5$$ then find $$\dfrac{dy}{dx}$$
If $$x^2+y^2+ 2gx + 2fy + 2hxy +c =0 $$ find $$\frac{dy}{dx}$$
If $$y = \log \left[ {\dfrac{{x + \sqrt {{x^2} + 25} }}{{\sqrt {{x^2} + 25 - x} }}} \right]$$ , find $$\dfrac{{dy}}{{dx}}$$
If $$y = sin^2(\log (2x + 3))$$, find $$\dfrac{dy}{dx}$$.
If $${\left( {{x^2} + {y^2}} \right)^2} = xy,$$ then $$ \left (\cfrac{dy}{dx} \right )$$ is,
Let $$y=xe^x$$ then prove that $$x\dfrac{dy}{dx}=(1+x)e^x$$.
Find $$\dfrac{{dy}}{{dx}}\,,\,if\,\,{x^{\dfrac{2}{3}}}\, + \,{y^{\dfrac{2}{3}\,}}\, = \,{a^{\dfrac{2}{3}}}.$$
$$\sqrt{\dfrac{x}{y}}+\sqrt{\dfrac{y}{x}}=4$$, Then $$\dfrac{dy}{dx}=$$
If $$\sin(x+y)=\log(x+y)$$, then: $$\dfrac{dy}{dx}$$=
Find $$f'(x)$$
$$f\left( x \right) = \sqrt {{4^x} - {{\left( {44} \right)}^x}} + \frac{3}{{{{\log }_4}\left( {1 - x} \right)}}$$
Differentiate the following w.r.t. x:
$$e^{x^3}$$.
Let $$xy=x+y$$ then prove that $$\dfrac{dy}{dx}+\dfrac{1}{(x-1)^2}=0$$.
Find $$\dfrac{dy}{dx}$$ for $$y=\log\left(\dfrac{1-x^2}{1+x^2}\right)$$.
If $$y = \dfrac{{{{\sin }^{ - 1}}x}}{{\sqrt {1 - {x^2}} }}$$, prove that $$\left( {1 - {x^2}} \right)\dfrac{{dy}}{{dx}} - xy = 1$$
If $$y={(2x+3)}^{(3x-5)},$$ find $$\dfrac{dy}{dx}$$.
Let $$f:\left[ {1,\infty } \right] \to \left[ {2,\infty } \right]$$ if $$f\left( 1 \right) = 2.$$ be differentiable function such that $$6\int_1^x {f\left( t \right)dt = 3xf\left( x \right) - {x^3}} $$ then the value of $$f\left( 2 \right)$$ is....
If $$y={y}^{\sqrt{x}}+{x}^{\sqrt{e}}$$, find $$\cfrac{dy}{dx}$$
If $$y+\sin { y } =\cos { x } $$, find $$\cfrac { dy }{ dx } $$
Find $$\dfrac {dy}{dx}$$ if $$y=\cos^{-1}(e^{x})+\sqrt {\sqrt {e^{\sqrt {x}}}}$$
If $${ x }^{ y }={ a }^{ x }.Prove \ that\ \cfrac { dy }{ dx } =\cfrac { x\log _{ e }{ a-y } }{ x\log _{ e }{ x } } $$
Solve: $$\dfrac{d}{dx}x\sin^2 x$$
Differentiate w.r.t $$x$$ :
$$\dfrac { 3 }{ 4 } \log { { x }^{ 2 } }$$
If $$y = \dfrac{1}{{\sqrt {{a^2} - {x^2}} }}$$, find $$\dfrac{{dy}}{{dx}}$$
If y=tan x.log{sin x} then $$y'$$ at $$x=\dfrac{\pi}{4}$$ is?
If $$\sqrt{x}+\sqrt{y}=\sqrt{a}$$ prove that $$\dfrac{dy}{dx}=-\sqrt{\dfrac{y}{x}}$$.
If $$y=\log _{ 5 }{ \left( \log _{ 7 }{ x } \right) } $$, find $$\dfrac {dy}{dx}$$
Find $$\dfrac {dy}{dx}$$ at $$x=1,y=\dfrac {\pi}{4}$$ if $$\sin^{2}y+\cos xy=k$$.
Differentiate the following w.r.t.x:
$$\sqrt{x} \cdot cosec^{-1}\left(\dfrac{1}{4x}\right)$$
If $$ y^{2}=(x-c)^{3} $$, then find $$\dfrac{dy}{dx}$$.
If $$y=\dfrac{\sin^2x}{1+\cot x}+\dfrac{\cos^2x}{1+\tan x}$$ then $$y^{'}$$ is equal to?
Find derivative of $$(ax + b)^n (cx + d)^n$$
If $$ x^y - y^x= 1 $$ , then the value of $$ \dfrac {dy}{dx} $$ is :
Differentiate $$f(x) = \dfrac{{\log \left( {1 + 3x} \right) - \log x}}{{\left( {1 - 2x} \right)}}$$
If $$x=at^2$$ and $$y=2at$$, then find $$\dfrac{d^2y}{dx^2}$$.
$${\text{if}}\;{\text{y = }}{{\text{e}}^{\text{x}}}{\text{ cos x,prove}}\;{\text{that}}\;$$$$\dfrac{{dy}}{{dx}} = \sqrt 2 {e^x}\cos \left( {x + \dfrac{\pi }{4}} \right)$$
Differentiate $$\sin^{2}\ 3x. \tan^{3}\ 2x$$
If $$y=sin^{-1}\left[2tan^{-1}\sqrt{\dfrac{1-x}{1+x}}\right]$$ then find $$\dfrac{dy}{dx}$$.
$$y = 6{x^4} - 5{x^3} - 4{x^2}$$
Diff. with respect to $$x$$
Find $$\dfrac{{dy}}{{dx}}$$ if $$y = {\left( {x + \dfrac{1}{x}} \right)^x}$$
If $$y = \dfrac{{{x^{\sin x}}}}{{1 + x + {x^2}}}$$, Find the $$\dfrac{{dy}}{{dx}}$$
$${y^x} = {x^y}$$
If $$y=\dfrac{{\sin 4x}}{{{x^2} + 16}}$$, then find $$\dfrac {dy}{dx}$$
If $$y=\log (\dfrac{x}{a+bx})^x$$, prove that $$x^3\dfrac{d^2y}{dx^2}=(x\dfrac{dy}{dx}-y)^2$$
Find $$\cfrac{dy}{dx}$$, if $$y={ e }^{ \sin ^{ 2 }{ x } }\left\{ 2\tan ^{ -1 }{ \sqrt { \cfrac { 1+x }{ 1-x } } } \right\} $$.
The degree and order of differential equation $$\left(\dfrac{d^2y}{dx^2} \right)^2 =\left(y + \dfrac{dy}{dx} \right)^{\frac{1}{2}}$$ is which of the following?
Find $$\dfrac{dy}{dx}$$ for $$y = {e^x}\left( {a\cos x + b\sin x} \right)$$.
Compute the derivative of $$6x^{100}-x^{55}+x$$.
Find the derivative of $$\sin 2 x \cos 3 x$$
Find $$\dfrac{dy}{dx}$$ for $$y=\dfrac{\tan x}{x}\log x^x$$.
If $$f (x) = 2017 \times tan x + 3x^{3}sinx+x^{2018}+2x^{3}$$ then find $$f'(x)$$.
Given, $$y=2017\tan x+3x^3\sin x+x^{2018}+2x^3$$
Let, $$y=f(x)$$;
Now, differentiation both sides w.r.t. 'x', we get,
$$f'(x)=2017\sec^2x+9x^2\sin x+3x^3\cos x+2018x^{2077}+6x^2$$.
Differentiate $$\dfrac{{e}^{x}-tan{x}}{cot{x}-{x}^{n}}$$ w.r.t $$x$$.
Find $$\cfrac{dy}{dx}$$, if $${x}^{2}+xy+{y}^{2}=100$$.
Find $$\dfrac{dy}{dx}$$ of the following implicit functions :$$y^{3}-3y^{2}x=x^{3}+3x^{2}y$$
If $$y=\dfrac{\sin x+\cos x}{\sin x-\cos x}$$ find $$\dfrac{dy}{dx}$$.
If $$\sqrt { x } + \sqrt { y } = \sqrt { a } ,$$ prove that $$\frac { d y } { d x } = - \sqrt { \frac { y } { x } }$$
If sin$$^2$$ x + cos$$^2$$ y = 1 find $$\dfrac{dy}{dx}$$
Differentiate the following:
(i) $$x ^ { 2 } \sin x$$(ii) $$x ^ { 2 } e ^ { x }$$
(iii) $$e ^ { \sqrt { a x + b } }$$
Differentiate w.r.t $$x$$ in $$nx (1 + x)^{n - 1}$$.
If $$(x^2+y^2)^2=xy$$, then $$\dfrac {dy}{dx}$$.
Find $$\dfrac{dy}{dx}$$ for $$y=\tan\sqrt{\sin x}$$.
If $$\cos y=x\cos\left(a+y\right)$$, with $$\cos a\neq\pm1$$, prove that $$\dfrac{dy}{dx}=\dfrac{\cos^{2}\left(a+y\right)}{\sin a}$$.
Solve
$$ \int \dfrac{x^{3}}{x^{3}+1}dx$$
If $${ 3x }^{ 2 }+4xy-{ 7y }^{ 2 }=0$$ Find $$(a)\dfrac { dy }{ dx }$$ and $$(b)\dfrac { { d }^{ 2 }y }{ { dx }^{ 2 } }$$
$$x\sqrt{1+y}+y\sqrt{1+x} = 0 $$ Show that: $$\dfrac{dy}{dx} = \dfrac{-1}{(1+x)^{2}}$$
Find $$\dfrac{dy}{dx}$$ if $$y = \left(x + \dfrac{1}{x}\right)^x + {x}^{\left(x + \frac{1}{x}\right)}$$
$$y=\left(x+\dfrac{1}{x}\right)^x+x^{x+\dfrac{1}{x}}$$
Let $$u=\left(x+\dfrac{1}{x}\right)^x$$
$$\Rightarrow log x=x log\left(x+\dfrac{1}{x}\right)$$
$$\Rightarrow \dfrac{1}{u}\dfrac{dy}{dx}=\dfrac{x}{\left(x+\dfrac{1}{x}\right)}\left(1-\dfrac{1}{x^2}\right)+log\left(x+\dfrac{1}{x}\right)$$
$$\Rightarrow \dfrac{1}{u}\dfrac{dy}{dx}=\dfrac{\left(x-\dfrac{1}{x}\right)}{\left(x+\dfrac{1}{x}\right)}+log\left(x+\dfrac{1}{x}\right)$$
$$\Rightarrow \dfrac{dy}{dx}=u\left[\dfrac{\left(x-\dfrac{1}{x}\right)}{\left(x+\dfrac{1}{x}\right)}+log \left(x+\dfrac{1}{x}\right)\right]$$
Let $$v=x^{x+\dfrac{1}{x}}$$
$$log v=\left(x+\dfrac{1}{x}\right)log x$$
$$\Rightarrow \dfrac{1}{v}\dfrac{dv}{dx}=\left(1-\dfrac{1}{x^2}\right)log x+\left(x+\dfrac{1}{x}\right)\dfrac{1}{x}$$
$$\Rightarrow\dfrac{dv}{dx}=v\left[\left(1-\dfrac{1}{x^2}\right)log x+\left(1+\dfrac{1}{x^2}\right)\right]$$
$$\dfrac{dy}{dx}=\dfrac{du}{dx}+\dfrac{dv}{dx}$$
$$=u\left[\dfrac{x-\dfrac{1}{x}}{x+\dfrac{1}{x}}+log \left(x+\dfrac{1}{x}\right)\right]+v\left[\left(1-\dfrac{1}{x^2}\right)log x+\left(1+\dfrac{1}{x^2}\right)\right]$$
$$\left(x+\dfrac{1}{x^2}\right)^x\left[\dfrac{x-\dfrac{1}{x}}{x+\dfrac{1}{x}}+log\left(x+\dfrac{1}{x}\right)\right]+x^{x+\dfrac{1}{x}}\left[\left(1-\dfrac{1}{x^2}\right) log x+x^{x+\dfrac{1}{x}}\left(1+\dfrac{1}{x^2}\right)\right]$$.
If $$y=\tan(2x+3)$$ find $$\dfrac { dy }{ dx } $$
If $$x\sqrt { 1+y } +y\sqrt { 1+x } =0,$$ prove that $$\dfrac { dy }{ dx } =\dfrac { -1 }{ { (1+x) }^{ 2 } } .$$
$$x\sqrt{1+y}+y\sqrt{1+x}=0$$
$$\Rightarrow x\sqrt{1+y}=y\sqrt{1+x}$$
Squaring both sides we get
$$x^2(1+y)=y^2(1+x)$$
$$\Rightarrow x^2+x^2y=y^2+xy^2$$
$$\Rightarrow x^2-y^2=xy^2-x^2y$$
$$\Rightarrow (x-y)(x+y)=xy(y-x)$$
$$\Rightarrow (x-y)(x+y)=-xy(x-y)$$
$$\Rightarrow (x+y)=-xy$$
$$\Rightarrow x=-xy-y$$
$$\Rightarrow x=(-x-1)y$$
$$\Rightarrow y=\dfrac{x}{-x-1}$$
$$\Rightarrow y=\dfrac{-x}{x+1}$$
Differentiating with respect to x, we get
$$\dfrac{dy}{dx}=\dfrac{(x+1)(-1)-(-x)}{(x+1)^2}$$
$$=\dfrac{-x-1+x}{(x+1)^2}$$
$$=\dfrac{-1}{(x+1)^2}$$.
Differentiate
$$x^{x\cos x}+\dfrac{x^{2}+1}{x^{2}-1}$$ w.r.t.x.
Differentiate $$\log (x+\sqrt{a^{2}+x^{2}})$$
Let $$x^{3}+y^{2}=24$$. What is the value of $$\dfrac{d^{2}y}{dx^{2}}$$ at the point $$(2,4)$$?
$$ x^{2}+y^{2}=2y$$
$$3x^{2}+2y \frac{dy}{dx} = 0 $$
$$\frac{dy}{dx} = \frac{-3x^{2}}{2y}; \frac{dy}{dx}]_{2,4} =\frac{-3}{2} $$
$$ \Rightarrow 2y \frac{dy}{dx}= -3x^{2}$$
$$ \Rightarrow y \frac{d^{2}y}{dx^{2}}+(\frac{dy}{dx})^{2} = \frac{-3}{2}(2x)$$
$$ \Rightarrow y \frac{d^{2}y}{ax^{2}}] $$ $$ =-3x-(\frac{dy}{dx})^{2} $$
$$ \Rightarrow \frac{d^{2}y}{dx^{2}}]_{2,y} = \frac{-3(2)-(\frac{-3}{2})^{2}}{4}$$
$$ (\frac{d^{2}y}{dx^{2}})_{2,4} =\frac{-33}{16}$$
Find $$\dfrac{d}{dx} (x^{3} \log_{e}x)$$
Find $$\dfrac{dy}{dx}$$$$8x^{2}+9y=6x+2$$
Find $$\dfrac{dy}{dx}$$ : $$4x^{2}-\log x =y^{2}+\sin x -\cos x$$
Find $$\frac{dy}{dx}, if x^{y}=e^{x-y}$$
If $$x=y\sqrt {1-y^{2}}$$, then $$\dfrac {dy}{dx}$$ equals to?
Differentiate:$$y=k{x}^{n}$$
Find $$\dfrac{dy}{dx}$$ : $$\sin x +7x^{2}+y^{2}=5$$
If $$ \sqrt{1-x^{2}}+\sqrt{1-y^{2} }=a$$ find $$ \dfrac{d y}{d x}$$
If $$y=3x^2-4x$$ find $$\dfrac{dy}{dx}$$
Solve $$\frac{dy}{dx}=\dfrac{1}{cos (x+y)}$$
differentiate
$$y=log\left( { 3x }^{ 2 }+2x+1 \right) $$
Find derivative of f(x) $$f(x)=x\sin x$$
Find $$\dfrac{dy}{dx}$$, if $${x}^{3}+8xy+{y}^{3}=64$$.
If $$x^3y^5 = (x + y)^8$$, then show that $$\dfrac{dy}{dx} = \dfrac{y}{x}$$
Find $$\dfrac{dy}{dx}$$, if $$x^3 + y^2 + xy = 10$$
If $${ xy }^{ 2 }=1$$, then prove that $$2\dfrac { dy }{ dx } +{ y }^{ 3 }=0$$.
If $$y={ e }^{ { x+e }^{ { x+e }^{ { x+e }^{ x+...\infty } } } }$$, then prove that $$\dfrac { dy }{ dx } =\dfrac { y }{ 1-y } $$.
If $$y = {e^x}\cos x,$$ then prove that $$\dfrac{{dy}}{{dx}} = \sqrt 2 {e^x}\cos \left( {x + \dfrac{\pi }{4}} \right)$$.
Find $$\dfrac { dy }{ dx } $$, if $$y=\sqrt { 1+\sin 2x } $$.
If $$f(x) = 1 + x + x^{2} + ..... + x^{100}$$ then find $$f'(1)$$.
If $$y=\frac{a-x}{a+x}(x\neq -a)$$, find $$\frac{dy}{dx}$$
Find $$\dfrac{{dy}}{{dx}}$$ ,if $${e^x} + {e^y} = {e^{x - y}}$$.
Differentiate the following functions with respect to $$x$$:
$$\dfrac {\sqrt {x^2+1}+\sqrt {x^2-1}}{\sqrt {x^2+1}-\sqrt {x^2-1}}$$
If $$xy=1,$$ prove that $$\dfrac{dy}{dx}+y^{2}=0$$.
If $$xy \log(x+y)=1,$$ prove that $$\dfrac{dy}{dx}=-\dfrac{y(x^{2}y+x+y)}{x(xy^{2}+x+y)}$$.
Find $$\dfrac{dy}{dx}$$ in the following:
$$x^{5}+y^{5}=5\ xy$$
If $$y= x \sin (a+y),$$ prove that $$ \dfrac{dy}{dx}= \dfrac{\sin^{2}(a+y)}{\sin (a+y) -y \cos(a+y)}$$.
If $$\sin (xy)+\dfrac{y}{x}=x^{2}-y^{2},$$ find $$\dfrac{dy}{dx}$$.
A circular disc of radius 3 cm is being heated. Due to expansion, its radius increases at the rate of 0.05 cm/sec. Find the rate at which its area is increasing when radius is 3.2 cm.
Find $$\dfrac{dy}{dx}$$, if $$2x+3y=\sin y$$.
Find $$\dfrac {dy}{dx},$$ when
$$x=a\left(1-\cos {\theta}\right)$$ and $$y=a \left(\theta + \sin {\theta} \right)$$ at $$\theta =\dfrac {\pi}{2}$$
Differentiate the following function with respect to x.
$$x^3\sin x$$.
Differentiate the following function with respect to x.
$$(1+x^2)\cos x$$.
Differentiate the following function with respect to x.
For the function $$f(x)=\dfrac{x^{100}}{100}+\dfrac{x^{99}}{99}+.....+\dfrac{x^2}{2}+x+1$$. Prove that $$f'(1)=100f'(0)$$.
Differentiate the following function with respect to x.
$$\dfrac{a+b\sin x}{c+d\cos x}$$.
Find $$\dfrac {dy}{dx}$$, where $$xy^2-x^2y-5=0$$.
Differentiate the following function :
$$(2x+3)(3x-5)$$
Find $$\dfrac {dy}{dx}$$, where $$(x^2 +y^2)^2 =xy$$
Differentiate the following function :
$$ax^3+bx^2+cx+d$$, where $$a, b, c, d$$ are constant.
Differentiate the following function :
$$x(1+x)^3$$
Differentiate the following function :
$$\left (x-\dfrac {1}{x}\right)^2$$
Differentiate the following function with respect to x.
$$x^4(5\sin x-3\cos x)$$.
Let f(x) = ( x - 1) (x - 2) ( x - 3)..........( x - n), $$n \space \epsilon \space N$$ and $$f'(n) = 5040$$, then the value of n is
Differentiate the following with respect to $$x$$:
$$e^{3x}\cos 2x$$
If $$ x^{2}+y^{2}=R^{2}(\text { where } R>0) $$ and $$ k=\dfrac{y^{\prime \prime}}{\sqrt{\left(1+y^{\prime 2}\right)^{3}}} $$
then find $$ k $$ in terms of $$ R $$ alone.
Let $$f(x)=x+\dfrac{1}{2x+\dfrac{1}{2x+ \dfrac{1}{2x + \cdots \infty}}}$$
Compute the value of $$ f(50) . f^{\prime}(50) $$
If $$f$$ is a real function such that $$f(x) > 0, f'(x)$$ is continuous for all real $$x$$ and $$ax \ge 2 \sqrt {f(x)}-2a\ f(x), (ax\neq 2)$$ show that $$\sqrt {f(x)}\ge \dfrac {\sqrt {f(1)}}{x}, x\ge 1$$.
Use the function $$f(x)=x^{1/x}, x > 0$$, to determine the bigger of the two number $$e^{\pi}$$ and $$\pi^{e}$$
Differentiate the following w.r.t.x: $$ \log \left[\tan ^{3} x \cdot \sin ^{4} x \cdot\left(x^{2}+7\right)^{7}\right] $$
If u, v and w are function of x , then show that
Undefined control /cfrac
in two ways - first by repeated aplication of product rule , second by logarithmic differentiation .
If $$ax^{2}+\dfrac{b}{x}\ge c$$ for all positive $$x$$ where $$a > 0$$ and $$b > 0$$, show that $$27ab^{2}\ge 4c^{3}$$
If $$y=y(x)$$ and it follows the relation $$2e^{xy^{2}}+y \cos (x^{2})=4,$$ then $$|y '(0)|$$ is equal to
Let $$ \displaystyle \left ( a-b\cos y \right )\left ( a+b\cos x \right )=a^{2}-b^{2}$$ and $$\displaystyle \frac{dy}{dx}=\frac{\sin xf\left ( y ) \right )}{\left ( a+b\cos x \right )^{2}}$$. If $$a^{2}-b^{2}=192, then f\left ( \pi /2 \right ). $$
If $$ \displaystyle y=\left ( x^{2}+1 \right )\sin x $$ then $$\left ( \dfrac{\pi}2 \right )^{2}-y_{20}\left ( \dfrac{\pi}2 \right ) $$ is equal to
Differentiate the following function with respect to $$x$$:
$$(\log x)^x + x^{\log x}$$.
If $$y = f(u)$$ is a differentiable function of $$u$$ and $$u = g(x)$$ is a differentiable function of $$x$$, then prove that $$y = f(g(x))$$ is a differentiable function of $$x$$ and $$\dfrac {dy}{dx} = \dfrac {dy}{du}\times \dfrac {dy}{dx}$$
If $$x^x + x^y + y^x = a^b$$, then find $$\dfrac {dy}{dx}$$.
If $$y = \tan^{2} (\log x^{3})$$, find $$\dfrac {dy}{dx}$$.
Find $$\dfrac {dy}{dx}$$ if $$x\sin y + y\sin x = 0$$
Find the derivative of $$\displaystyle\, y = (x \, +\, 1)(x \, +\, 2)^2$$
Find the derivative of $$\displaystyle\, y = e^x(x^2 \, -\, 2x \, +\, 2)$$
Find the sum of $$\dfrac {1}{1 + x} + \dfrac {2x}{1 + x^{2}} + \dfrac {4x^{3}}{1 + x^{4}} + .... + \dfrac {2^{n} x^{2^{n} - 1}}{1 + x^{2^{n}}}$$.
If y = $$x^x$$ + $$(sinx)^{cotx}$$ . find $$\frac{dy}{dx}$$
If $$y = {\tan ^{ - 1}}\left( {\dfrac{a}{x}} \right) + \log \sqrt {\dfrac{{x - a}}{{x + a}}} \,$$ , prove that $$\dfrac{{dy}}{{dx}} = \dfrac{{2{a^3}}}{{{x^4} - {a^4}}}$$
Differentiate $$x^{\sin x}, x > 0$$ with respect to $$x$$.
Differentiate the function with respect to x:
$$x^{\sin x} + (\sin x)^{\cos x}$$
If $$y=x^x+x^7+7^x+7^7$$, then $$\dfrac{dy}{dx}=?$$
Establish the following
If $$\sqrt{1-{x}^{2}}+\sqrt{1-{y}^{2}}=a(x-y)$$ then $$\cfrac{dy}{dx}=\sqrt { \cfrac { 1-{ y }^{ 2 } }{ 1-{ x }^{ 2 } } } $$
$$x \cos (a + y) = \cos y$$
then prove that
$$\dfrac { dy }{ dx } =\dfrac { { \cos }^{ 2 }(a+y) }{ { \sin }_{ a } }$$
If $$y=xlog\left(\dfrac{x}{a+bx}\right)$$ prove that $$x^3y_2=(xy_1-y)^2$$.
Evaluate:$$x^x-2^{\sin x}$$.
If $$x\sqrt {1+y}+y\sqrt {1+x}=0$$ and $$x \neq y$$, show that $$\dfrac {dy}{dx}=\dfrac {-1}{(1+x)^{2}}$$
Differentiate:
$${ xy + y}^{ 2 } = \tan x + y$$ ?
Differentiate $$y=\dfrac { 4\sin { \theta } }{ 2+\cos { \theta } } $$ than $$\dfrac { dy }{ dx }= $$ ?
$$f(x) = \sqrt {\log_{1/2}\left (\dfrac {5x - x^{2}}{4}\right )}$$.
$$f(x)=\sqrt{\log_{1/2}(\dfrac{5x-x^2}{4})}$$
$$\log_{\dfrac{1}{2}}(\dfrac{5x-x^2}{4})\ge 0$$
$$\dfrac{5x-x^2}{4} \le (\dfrac{1}{2})^0$$ $$ \because{\begin{bmatrix}b<a\\a>1\\b>a\end{bmatrix}}{}$$
$$\dfrac{5x-x^2}{4} \le 1$$
$$5x-x^2 \le 4$$
$$x^2-5x \le -4$$
$$x^2-5x+4 \ge 0$$
$$x^2-4x-x+4 \ge 0$$
$$x(x-4)-1(x-4) \ge 0$$
$$(x-1)(x-4) \ge 0$$
$$x=(-\infty,1)\cup (4,\infty)$$ Refer image(1)
another condition
$$\dfrac{5x-x^2}{4} >0 \Rightarrow 5x-x^2 >0\Rightarrow x^2-5c < 0$$
$$x(x-5) < 0$$ Refer image.2
They value of $$x$$
$$x\in (0,1)\cup (4,5)$$
Implict function $$ { x }^{ 3 }+{ y }^{ 3 }=3axy$$
If, $$\sin ( x y ) + \frac { y } { x } = x ^ { 2 } - y ^ { 2 }$$.
Find $$\dfrac { d y } { d x }$$.
Differentiate w.r.t $$x$$ :$$x^y +y^x =1$$
Differentiate wrt to x. $${ tan }^{ -1 }( \sqrt { \frac { 1-sin 4x }{ 1+sin 4x }}) $$ = $$\dfrac {psin8x}{1-sin4x}$$ then p=
If $$x$$ = $$\dfrac{ t^2}{1 + t^2}$$ , $$y$$ = $$\dfrac{2at}{1 + t^2}$$ then $$\dfrac{dy}{dx}$$ =
Find $$\dfrac {dy}{dx}$$ while:
$$x^{y}+y^{x}=a^{b}$$
If $$l^{2}+m^{2}=1$$, then find the maximum value of $$l+m$$.
$$y=\sin^{-1}\left(\dfrac{1-x^2}{1+x^2}\right), 0 < x < 1$$.$$Find\ \dfrac{dy}{dx}$$
$$\frac{d}{dx}(log_{3}x-3 log_{e}x+2 tan x)$$
If $$\log \sqrt{x^{2}+y^{2}}= \tan^{-1} \left(\dfrac{y}{x}\right),$$ then prove that $$\dfrac{dy}{dx} = \dfrac{x+y}{x-y}$$.
Differentiate the following with respect to $$x$$:
$$e^{-5x}\cot 4x$$
undefined
Find $$\dfrac{dy}{dx}$$ in the following:
$$\tan^{-1}(x^{2}+y^{2})=a$$
$$\tan^{-1}(x^{2}+y^{2})=a$$
If $$x \sqrt{1+y}+y \sqrt{1+x}=0,$$ then prove that $$(1+x^{2}) \dfrac{dy}{dx}+1=0.$$
Find the derivative of the function given by
Differentiate $$ ( x^{2} - 5x + 8) (x^{3} + 7x + 9) $$ in three ways mentioned below :
by loagarithmic differentiation
Do they all give the same answer.
If $$\displaystyle y = \frac{ax^{2}} {\left (x-a\right )\left (x-b\right )\left (x-c\right )} + \frac{bx} {\left (x-b\right )\left (x-c\right )} + \frac{c} {x-c} + 1$$
prove that $$\displaystyle \frac{y^{'}} {y} = \frac{1} {x} \left (\frac{a} {a-x} + \frac{b} {b-x} + \frac{c} {c-x} \right )$$ (IIT-JEE, 1998)
Class 11 Commerce Applied Mathematics Extra Questions
- Basics Of Financial Mathematics Extra Questions
- Circles Extra Questions
- Descriptive Statistics Extra Questions
- Differentiation Extra Questions
- Functions Extra Questions
- Limits And Continuity Extra Questions
- Logarithm And Antilogarithm Extra Questions
- Mathematical And Logical Reasoning Extra Questions
- Number Theory Extra Questions
- Numerical Applications Extra Questions
- Permutations And Combinations Extra Questions
- Probability Extra Questions
- Relations Extra Questions
- Sequences And Series Extra Questions
- Set Theory Extra Questions
- Straight Lines Extra Questions
- Tangents And Its Equations Extra Questions