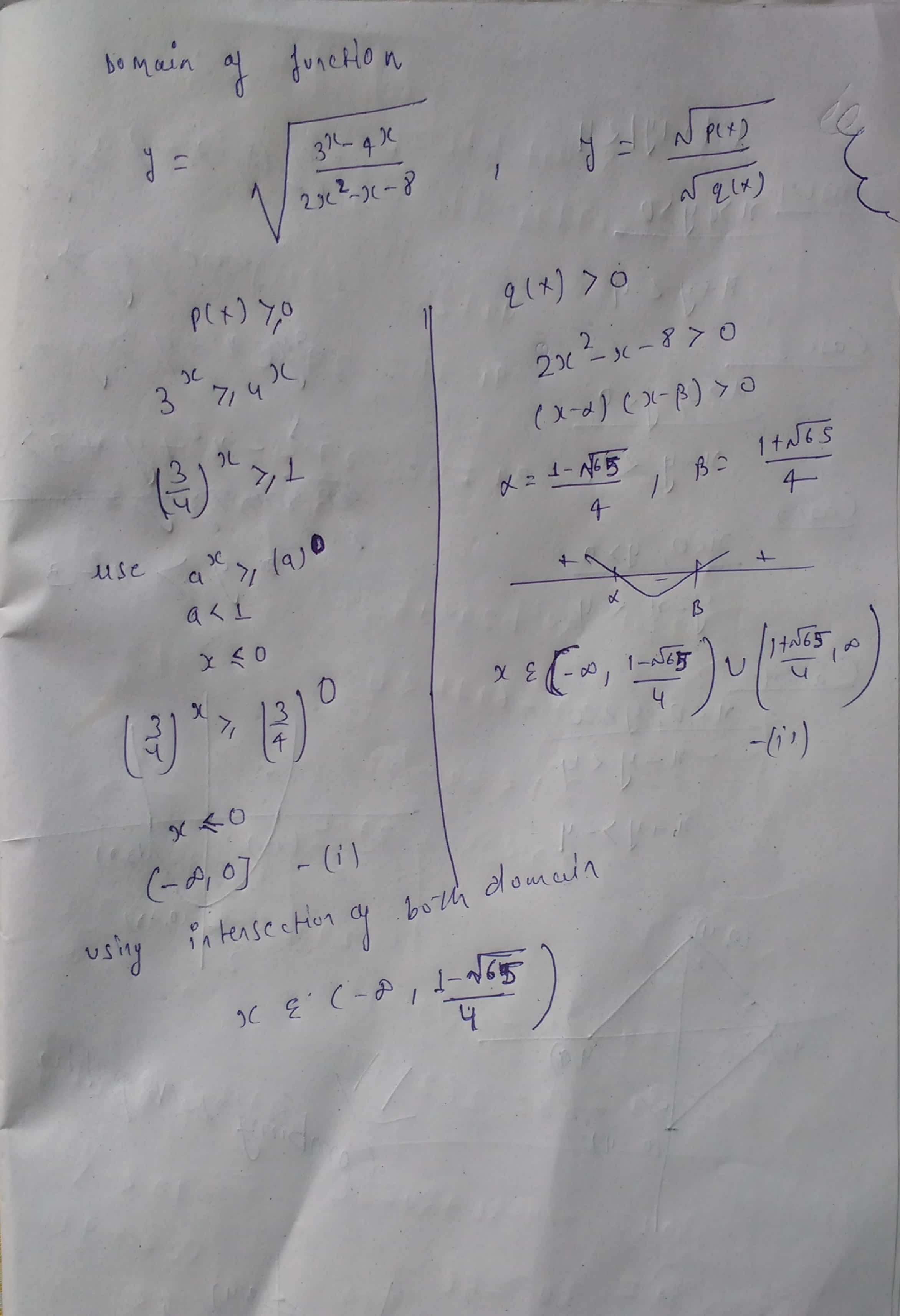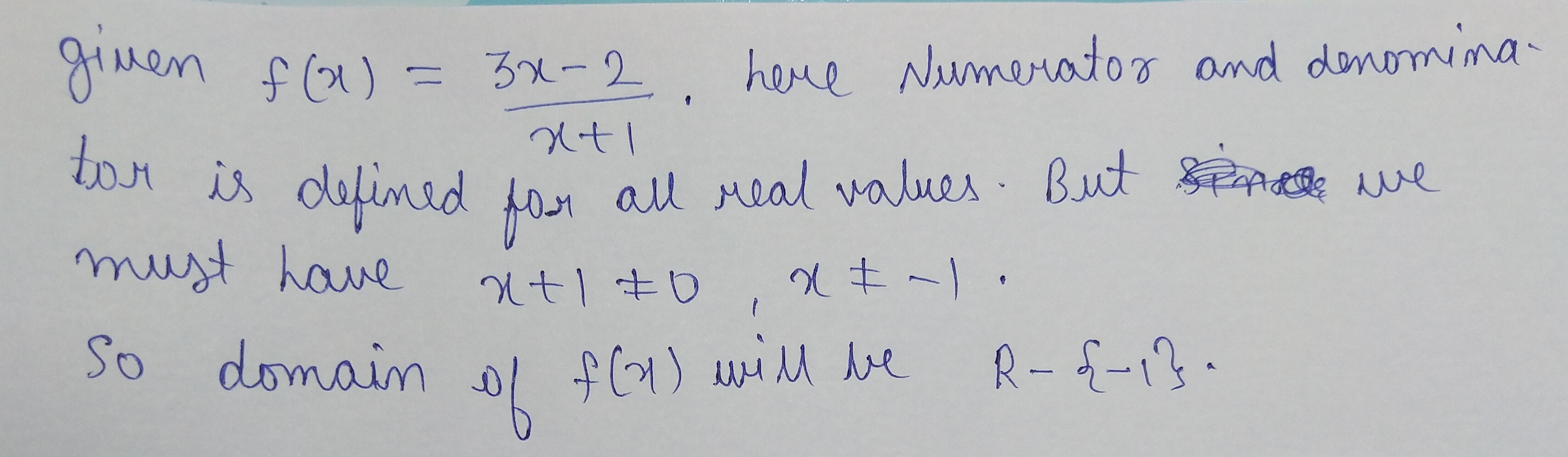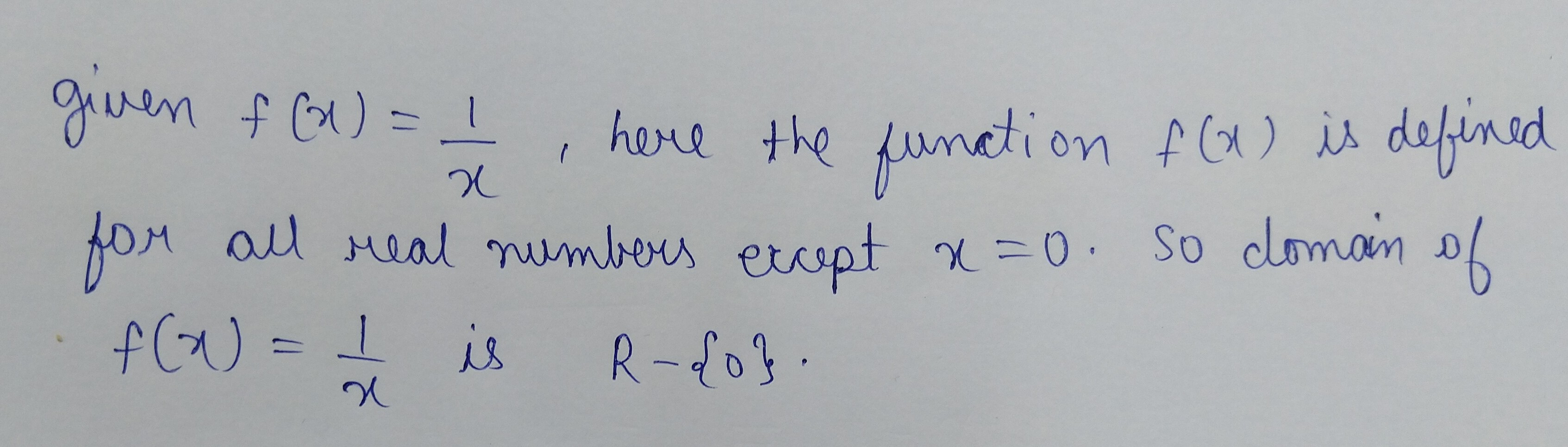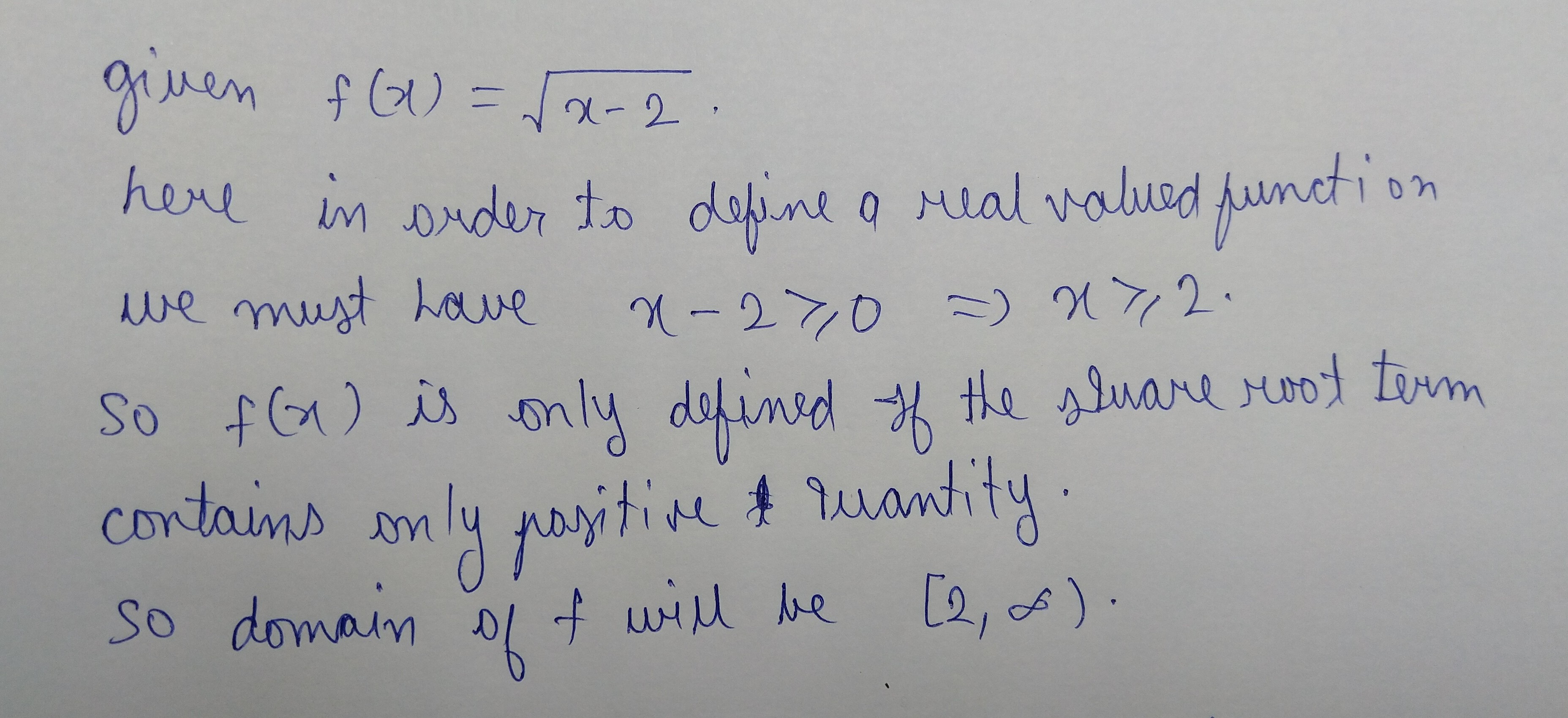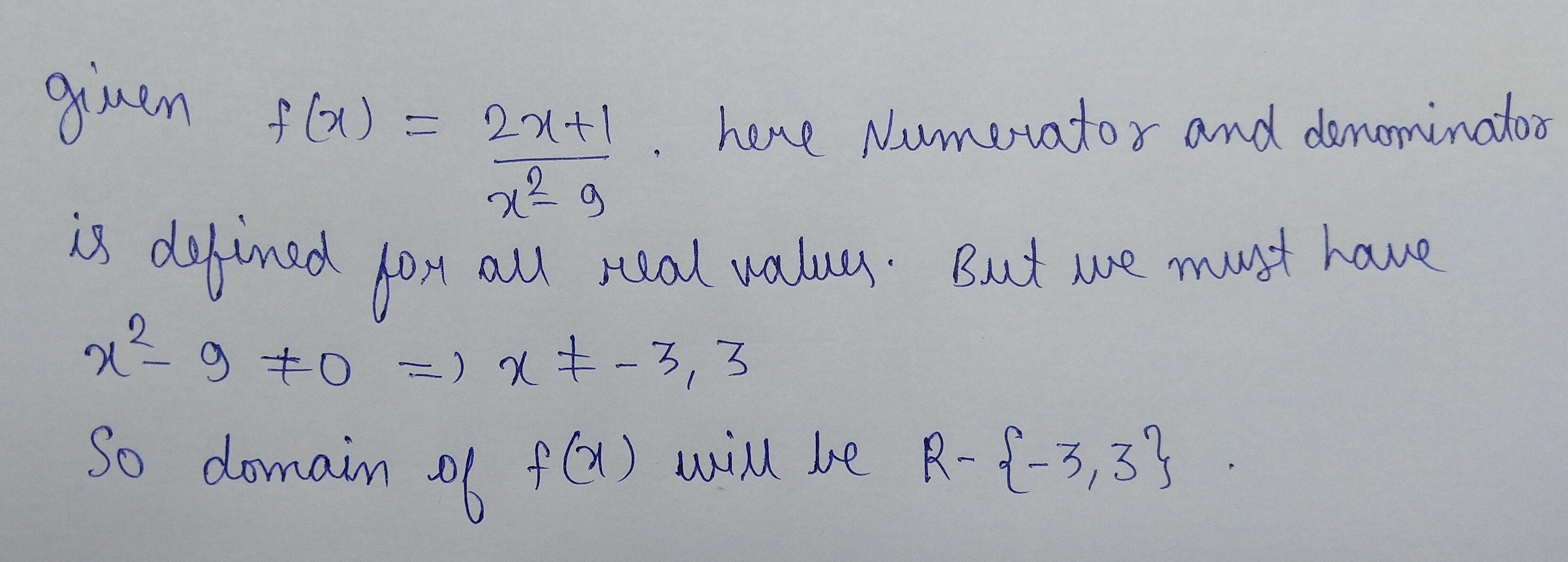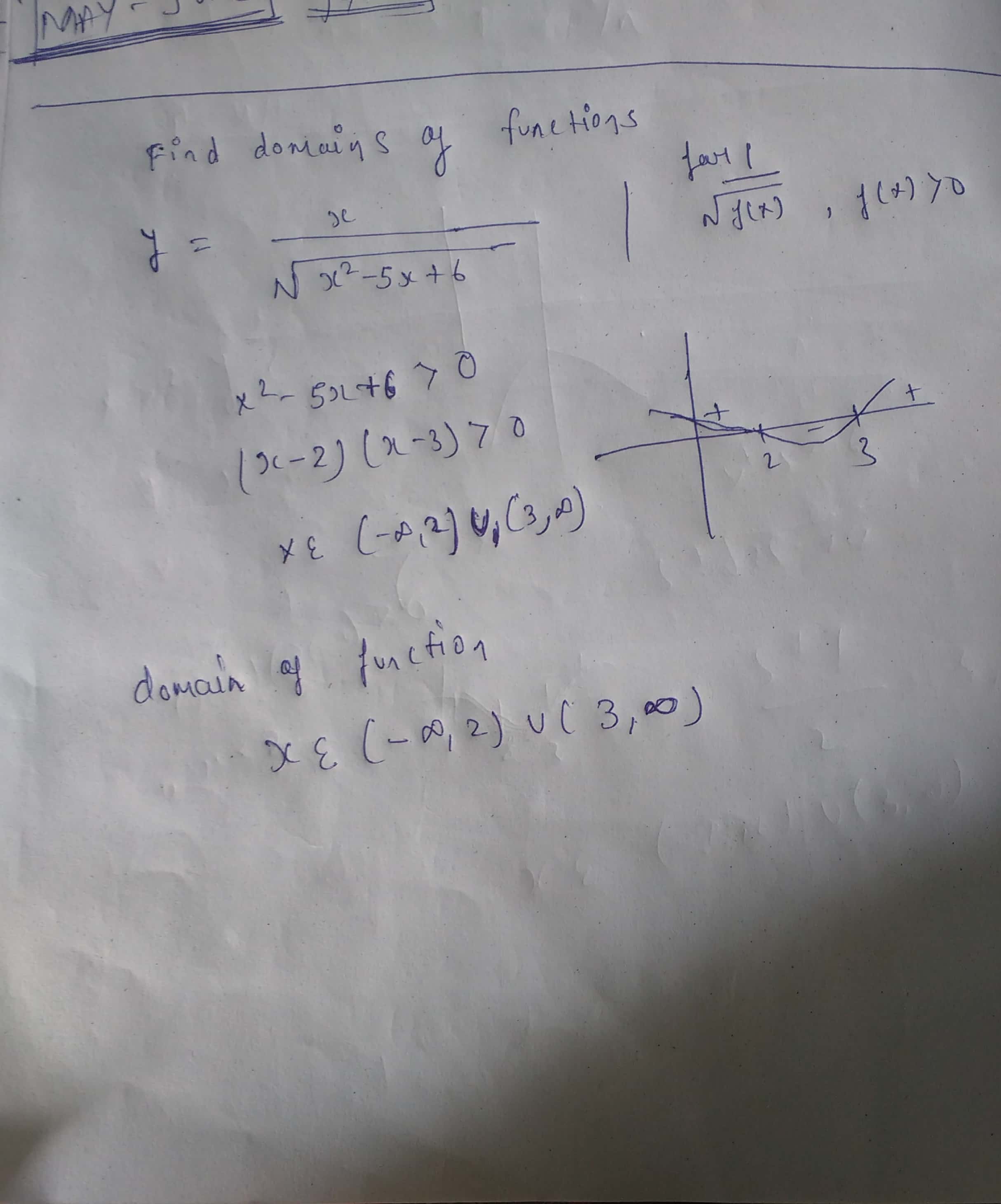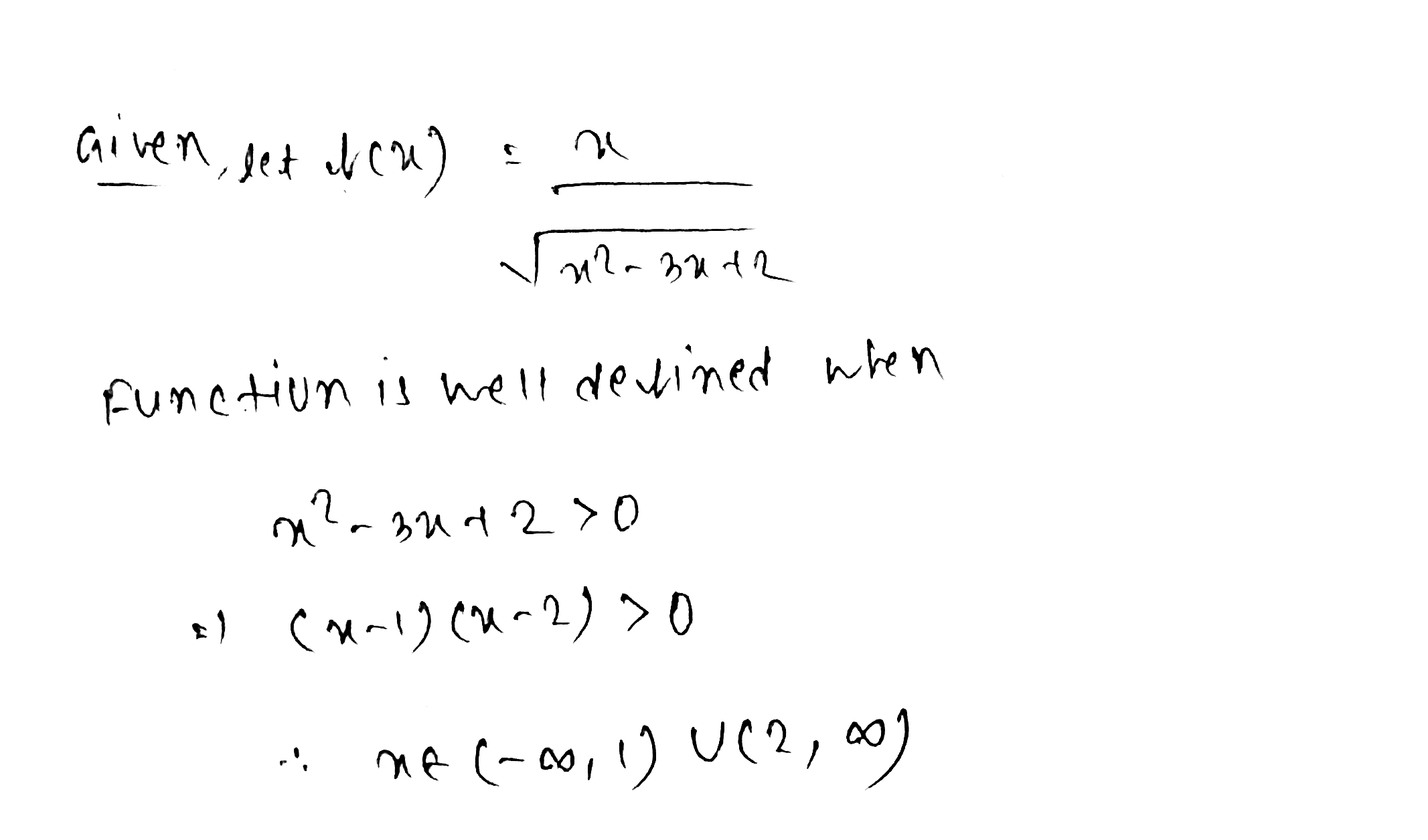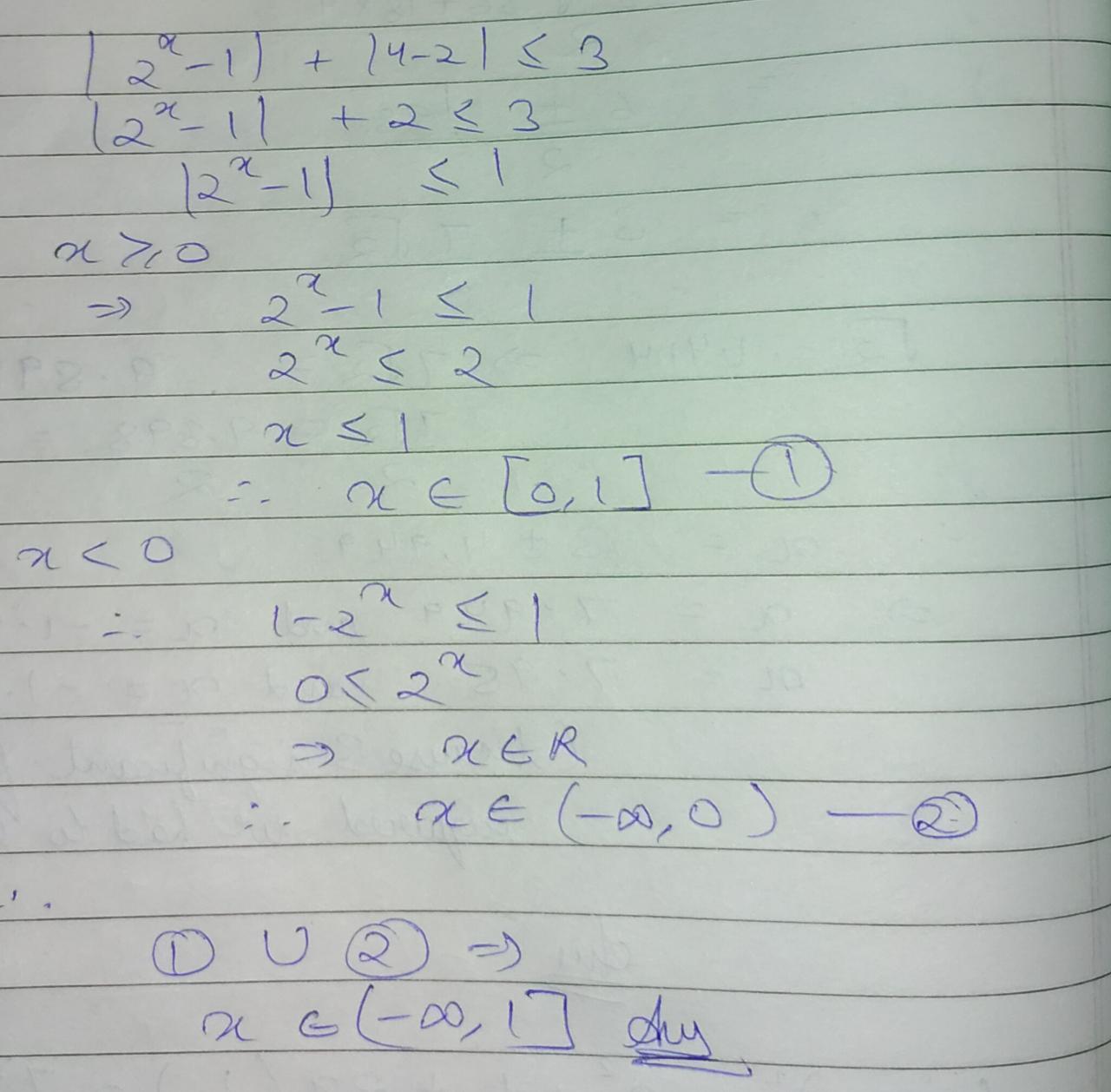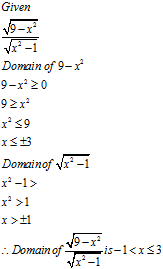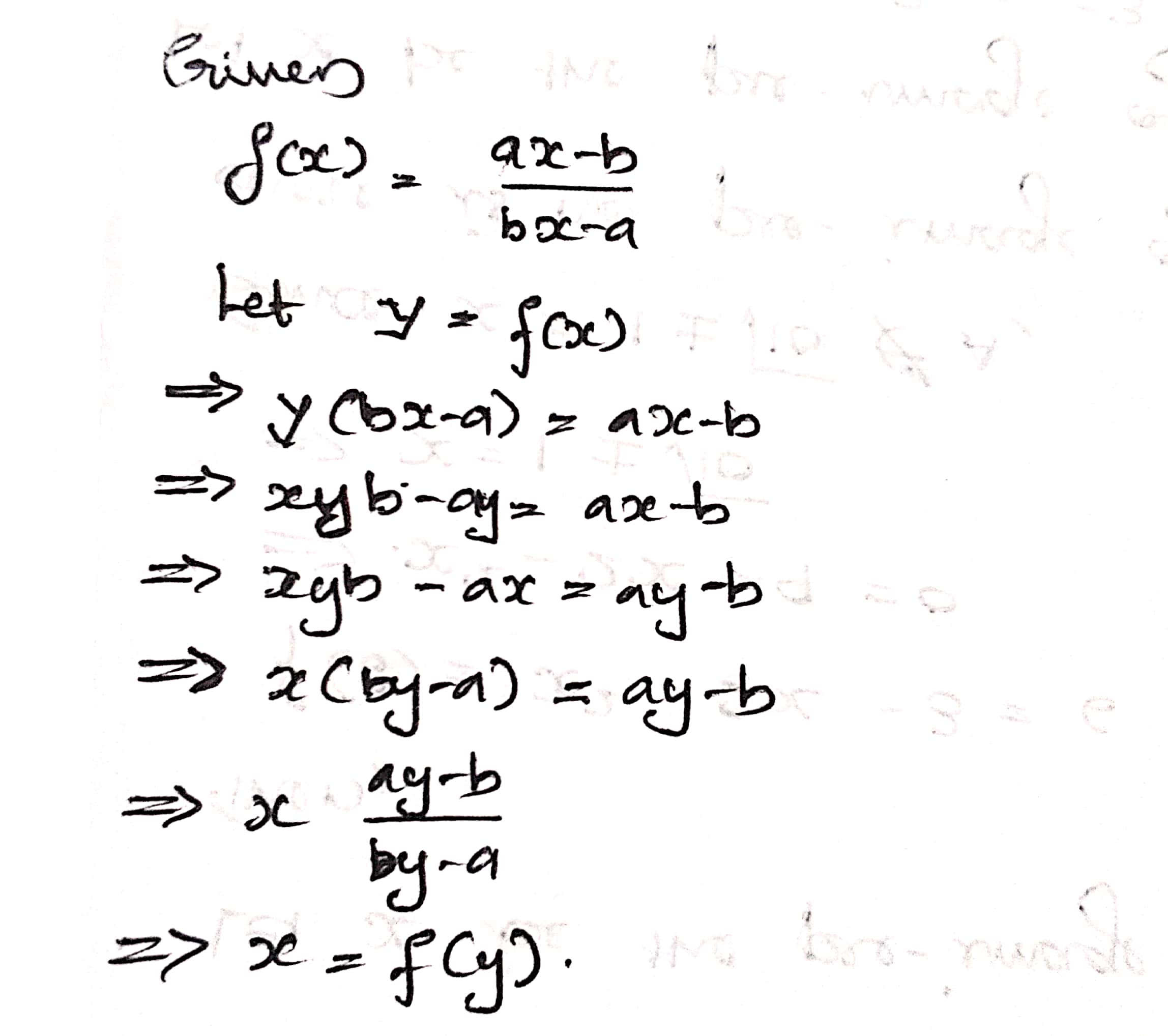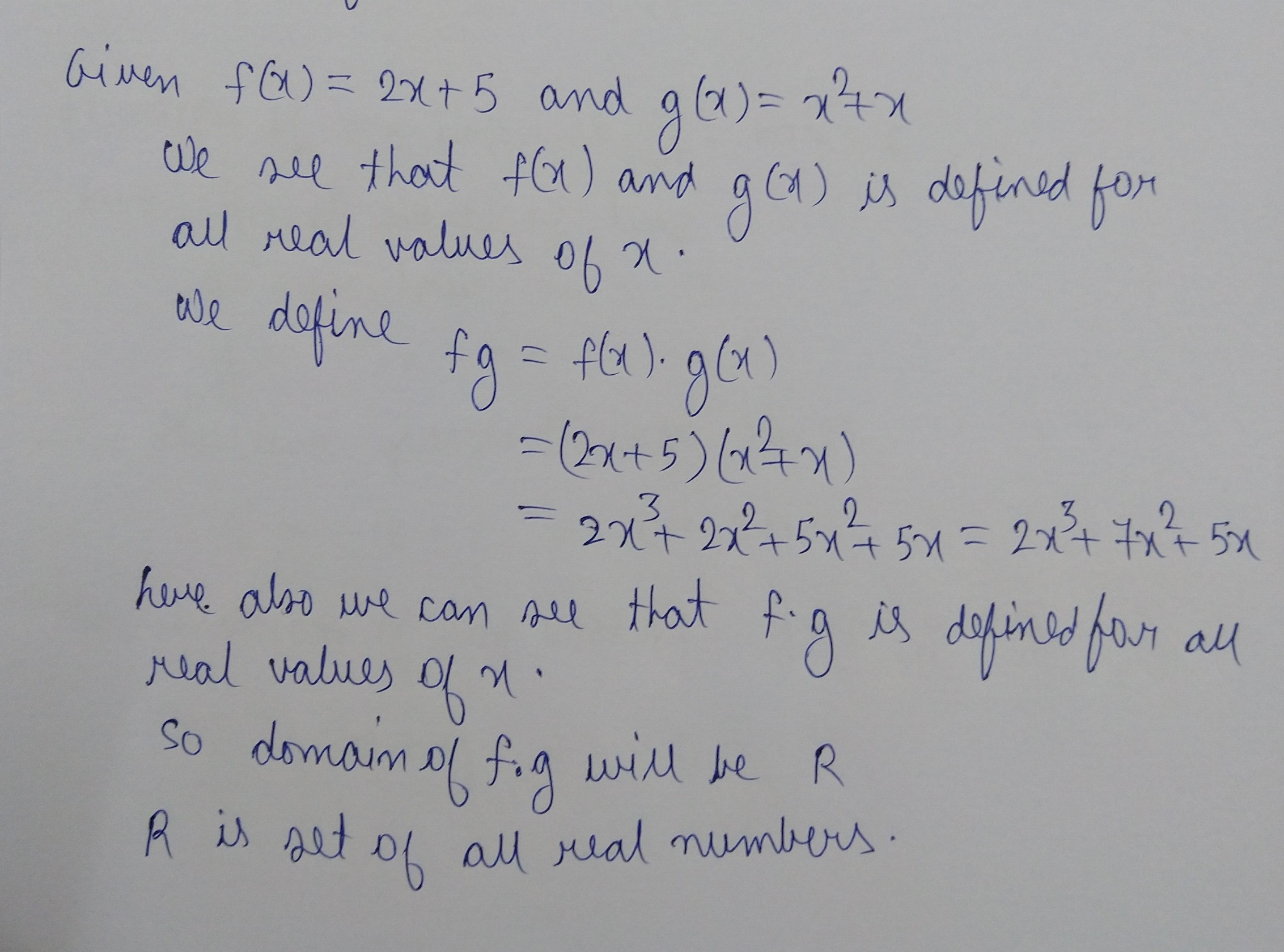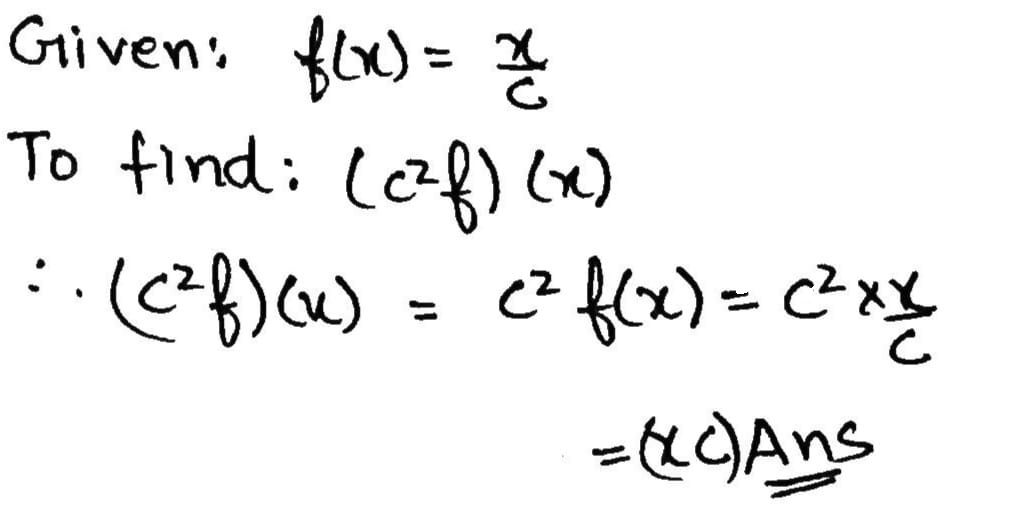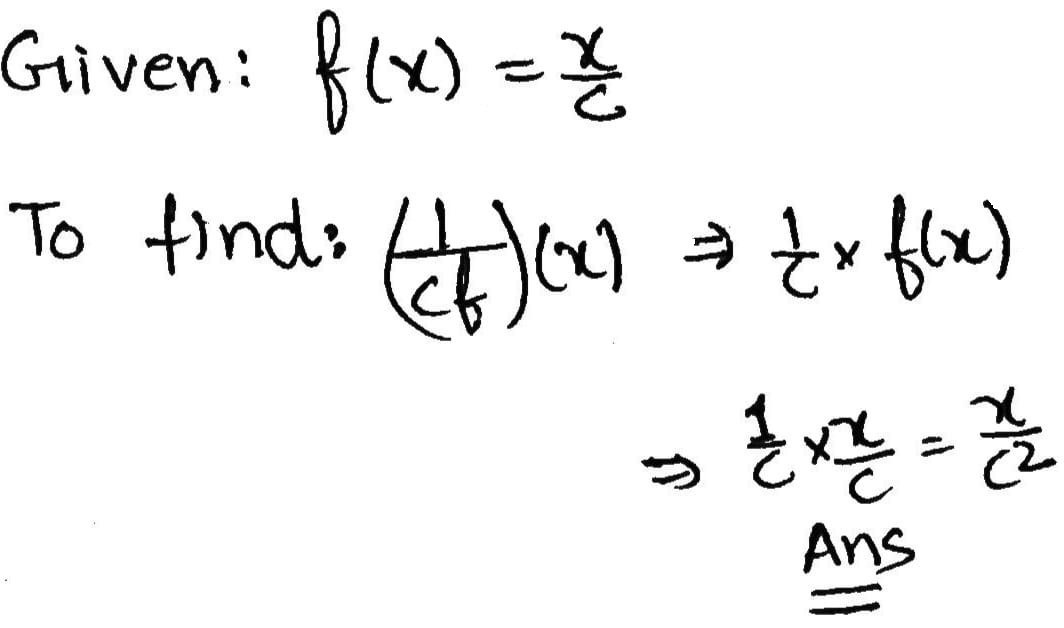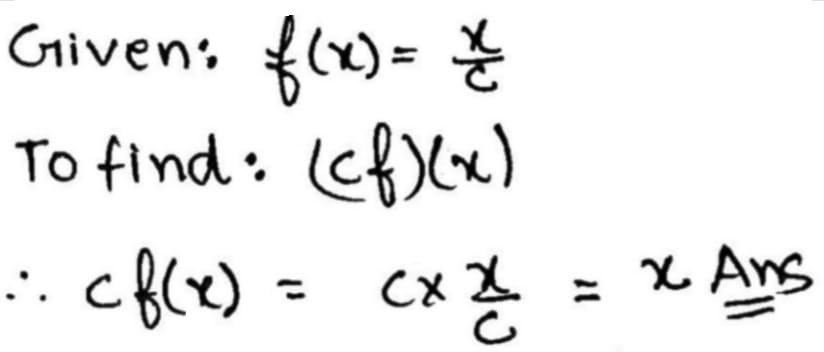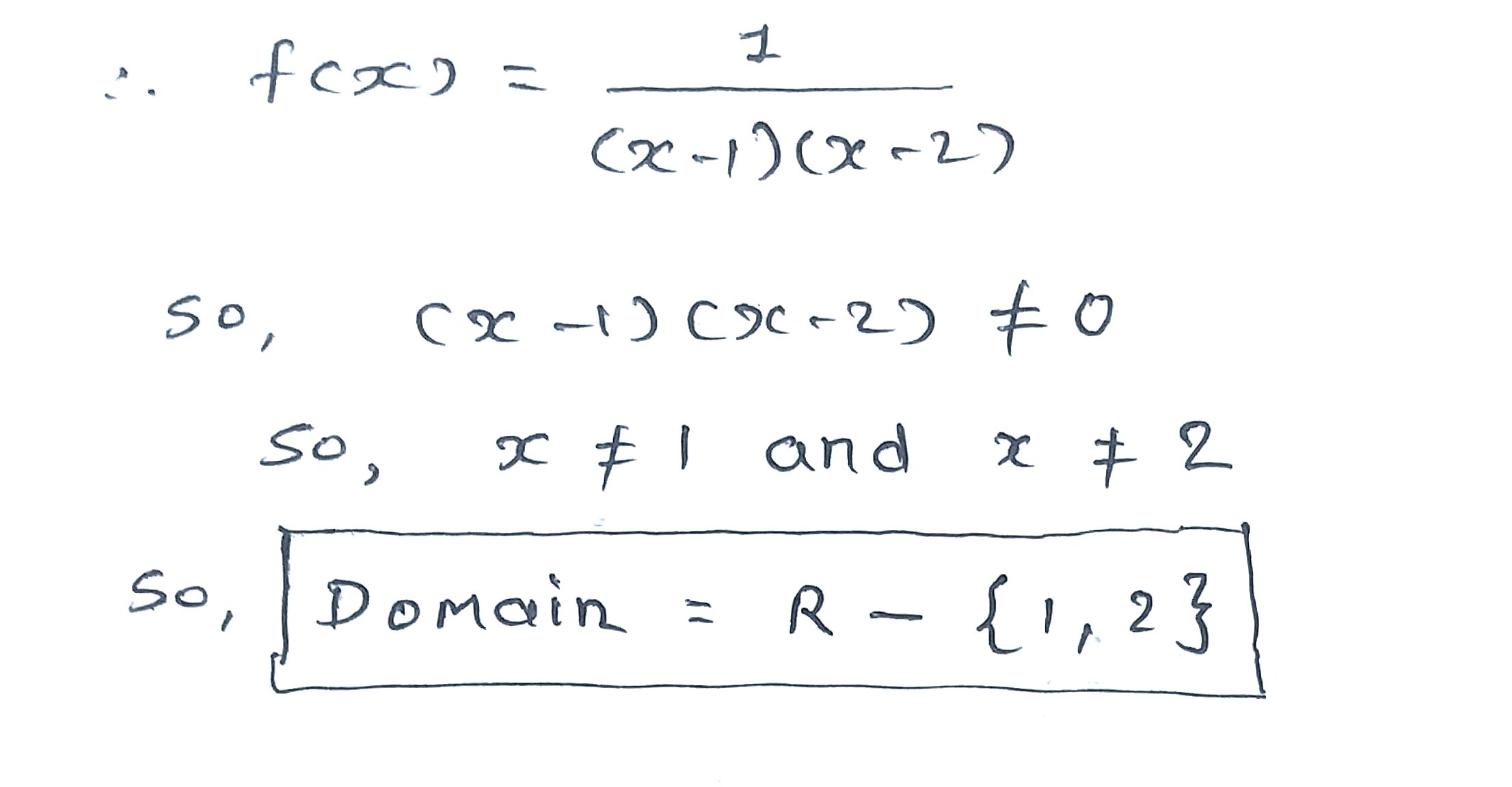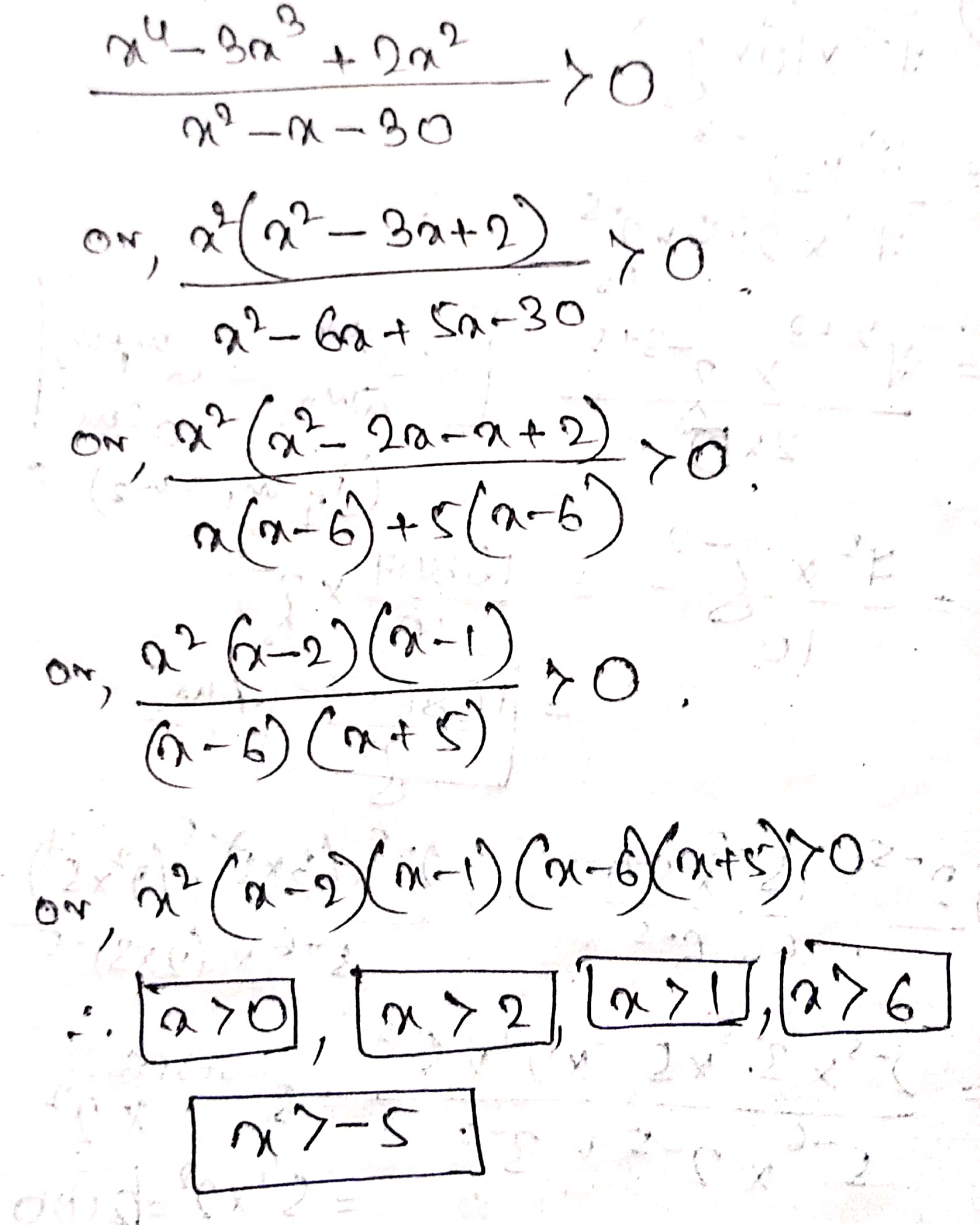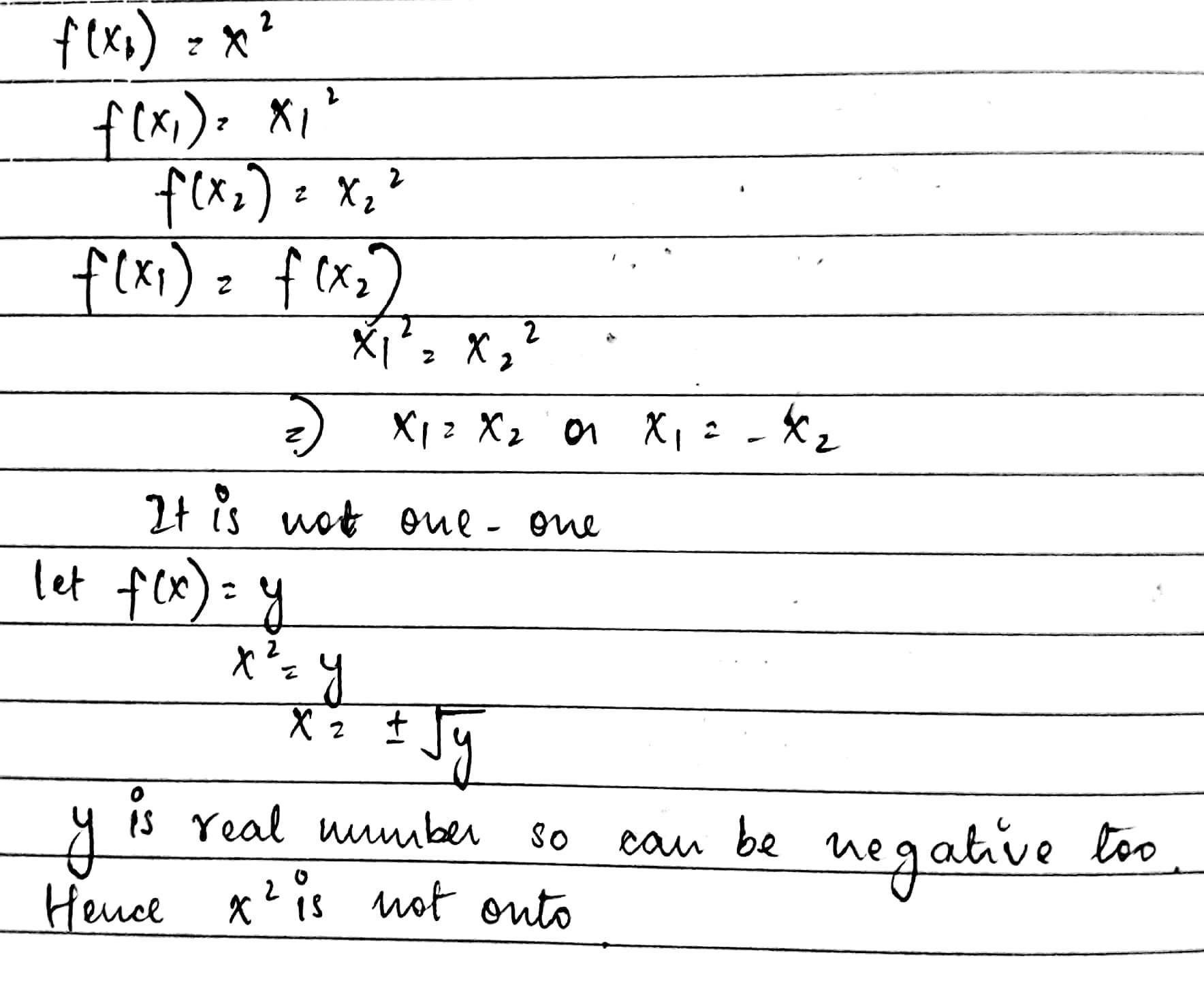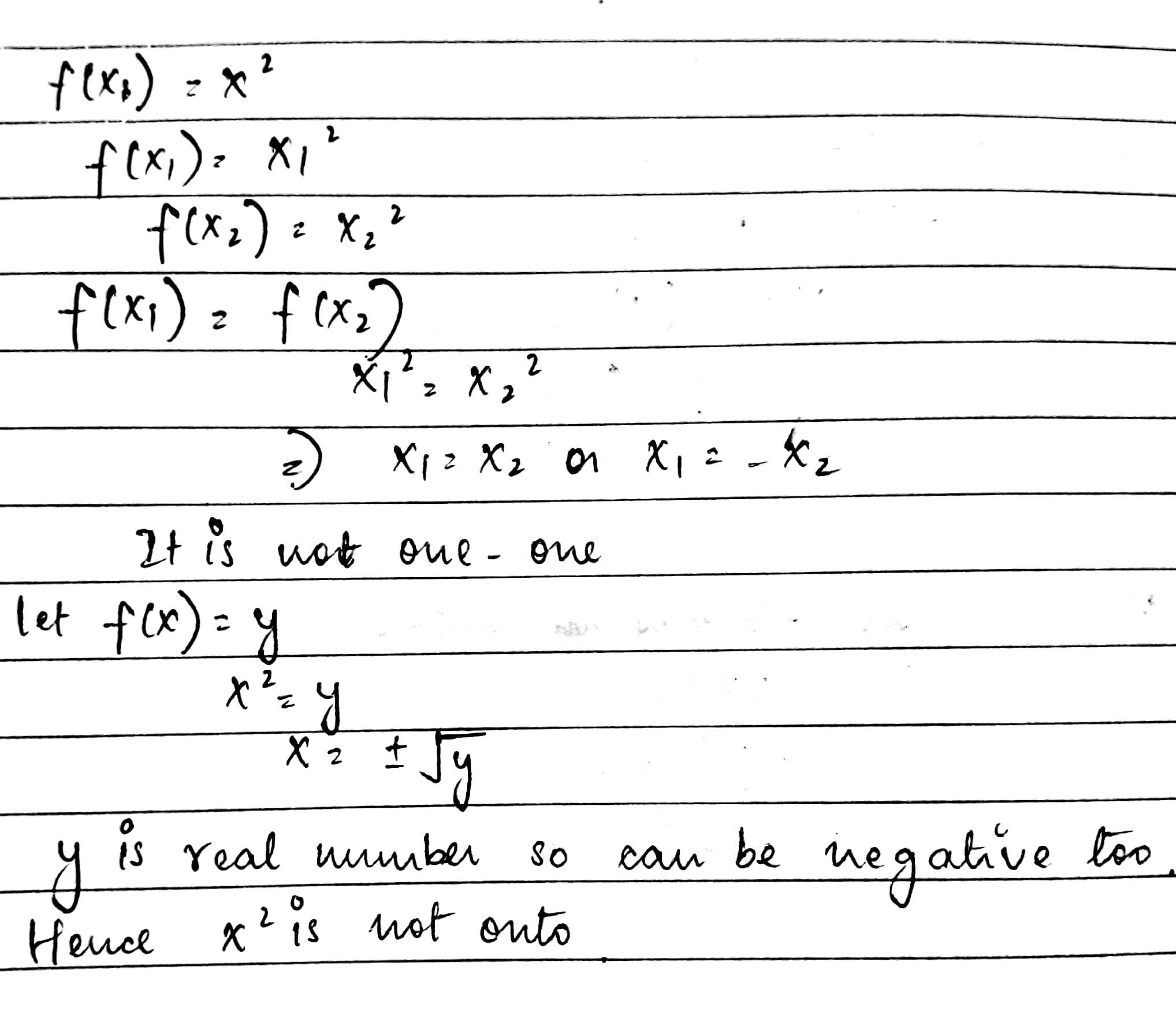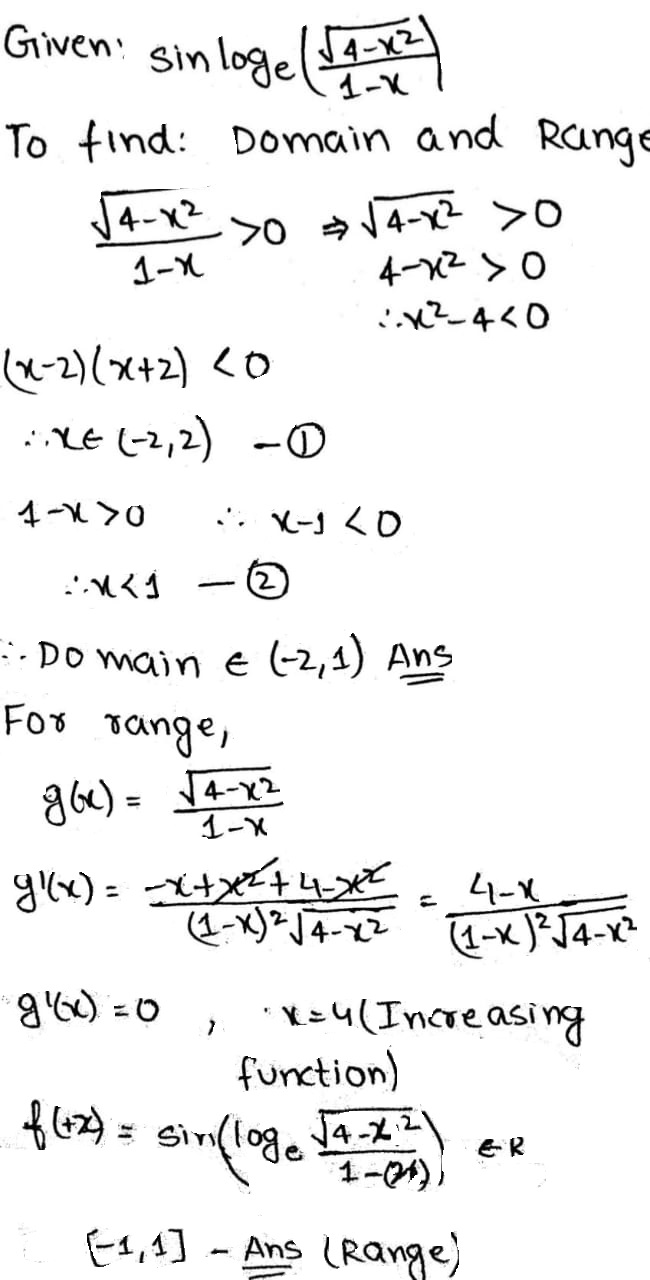Functions - Class 11 Commerce Applied Mathematics - Extra Questions
If $$f(x)=\sqrt{x+2}+\dfrac{1}{\log_{10} (1-x)}$$. Find the domain of definition of $$f(x)$$.
Find the domains of definition of the following functions.
$$\displaystyle y \, = \, \frac{\sqrt{6x \, - \, x^2 \, - \, 5}}{5^{x \, - \, 2} \, - \, 1}.$$
Let $$f(x)=\sqrt{x+2}+\dfrac{1}{\log_{10}(1-x)}$$. Then find the domain of $$f(x)$$.
Find the domains of definition of the following functions.
$$\displaystyle y \, = \, \sqrt{\frac{3^x \, - \, 4^x}{2x^2 \, - \, x \, - \, 8}}.$$
If $$f(x)=\dfrac {2x+3}{3x-2}$$
Prove that $$fof$$ is an identity function
Find the domain and range of :-
(i) $$\sqrt x - 1$$
(ii) $$(x-1)$$
A relation R is defined on the set Z of integers as follows: (x, y)$$\in R' x^2+y^2= 25$$
Express R and $$R^{-1}$$ as the sets of ordered pairs and hence find their respective domains.
Find the domain and range of $$f(x) = \sqrt{x - 5}$$
The domain of $$f(x)=\sqrt{\sin ^{-1}(\log _{2}x)}$$ is
Find the domain of the function:$$f(x)=\dfrac{1}{\sqrt{x^2-4x}}$$.
Find the domain of the function $$f(x)=\dfrac{x^2}{\sqrt{(a-x)(x-b)}}$$, $$b>a$$.
Solve:
$$x\sqrt {1 + {x^2}} + \log \left( {x + \sqrt {{x^2} + 1} } \right).$$
Find the domain of the following
(i)$$f\left( x \right) = \sqrt {\left[ {{x^2}} \right] - 1} + \sqrt {3 - \left[ {{x^2}} \right]} $$
Find the domain of function $$\sqrt{25-x^2}$$
Find the domain of the following real functions :
(i)$$f\left( x \right)=\sqrt{16-x^2}$$
The domain of Function $$\sqrt{9-x^2}$$
The value of $$f(3) $$ if $$f(x)=\dfrac1{x^2-x}$$
Find the Domain of the following function:
$$y=\dfrac{x}{\sqrt{1+x}}$$
Find the domain for the following functions :
(a)$$y=1-\log _{ 10 }{ x } $$ (b)$$y=\frac { 1 }{ \sqrt { { x }^{ 2 }-4x } } $$
Find the domain of $$y=\dfrac{\sqrt{x-25}} {x+5}$$
Find the domain of the function $$f(x)=\dfrac{1}{\sqrt{2x^2+5x+2}}$$.
Find the domain and range of the real function $$f(x)=\frac{1}{1-x^{2}}$$
Find the domain of
$$f(x)=\sqrt { 4 - 9 x ^ { 2 } }$$
Find the domain and the inverse of the following functions:
$$f(x)=\dfrac{1}{1-x^{2}}$$
Find the domain of $$ f(x)=\sqrt{9-x^{2}} $$
Find $$f(5)$$ if $$f(x)=x^2+3x+2$$
Find the domain and the range of the following function:
$$f(x) =\dfrac{x-3}{2x+1}$$
The domain of function $$\sqrt{x^2-4}$$ is
Find the domain and the inverse of the following functions:
$$f(x)=\dfrac{x^{2}}{1+x^{2}}$$
Find the domain & range of the following function.
$$f\left(x\right)=\dfrac{{x}^{2}-3x+2}{{x}^{2}+x-6}$$
Find the domain of each of the following real value functions real variable:
$$f(x)=\dfrac {1}{\sqrt {x^2 -1}}$$
Find the domain of each of the following real valued functions of real variable:
$$f(x)=\dfrac {3x-2}{x+1}$$
Find the domain of each of the following real valued functions of real variable:
$$f(x)=\dfrac {1}{x}$$
Find the domain of each of the following real value functions real variable:
$$f(x)=\sqrt {x-2}$$
Find the domain of:
$$\sec^{-1} x - \tan^{-1} x$$.
Find the domain of each of the following real valued functions of real variable:
$$f(x)=\dfrac {2x+1}{x^2 -9}$$
Find the domain of each of the following real valued functions of real variable:
$$f(x)=\dfrac {1}{x-7}$$
Given $$A=\left\{2,3,4 \right\}, B=\left\{2,5,6,7 \right\}$$. Construct an example of each of the following.
a mapping from $$A$$ to $$B$$ which is not injective.
Given $$A=\left\{2,3,4 \right\}, B=\left\{2,5,6,7 \right\}$$. Construct an example of each of the following.
a mapping from $$A$$ to $$B$$.
If the mappings, $$f$$ and $$g$$ are given by $$f=\left\{(1,2),(3,5),(4,1)\right\}$$ and $$g=\left\{(2,3),(5,1),(1,3)\right\}$$.
Give an example of a map
which is not one-one but onto.
Give an example of a map
which is one-one but not onto.
Give an example of a map
which is neither one-one but nor onto.
Given $$A=\left\{2,3,4 \right\}, B=\left\{2,5,6,7 \right\}$$. Construct an example of each of the following.
an injective mapping from $$A$$ to $$B$$.
If domain for $$y=\cos^{-1}\left (\dfrac {1-2|x|}{3}\right )+\log_{|x-1|}x$$ is $$x\in (a, b)\cup (c, d)$$. Find $$a+b+c+d$$
Let $$\displaystyle y= \sqrt{\frac{\left ( x+1 \right )\left ( x-3 \right )}{x-2}}.$$
Find all the real values of x for which y takes real values.
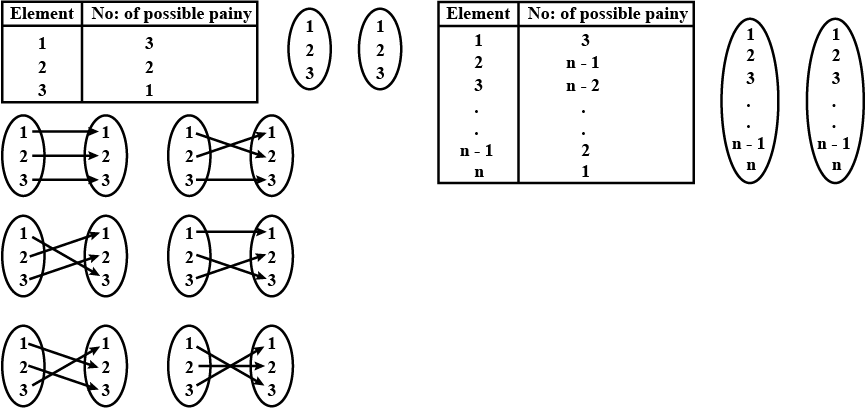
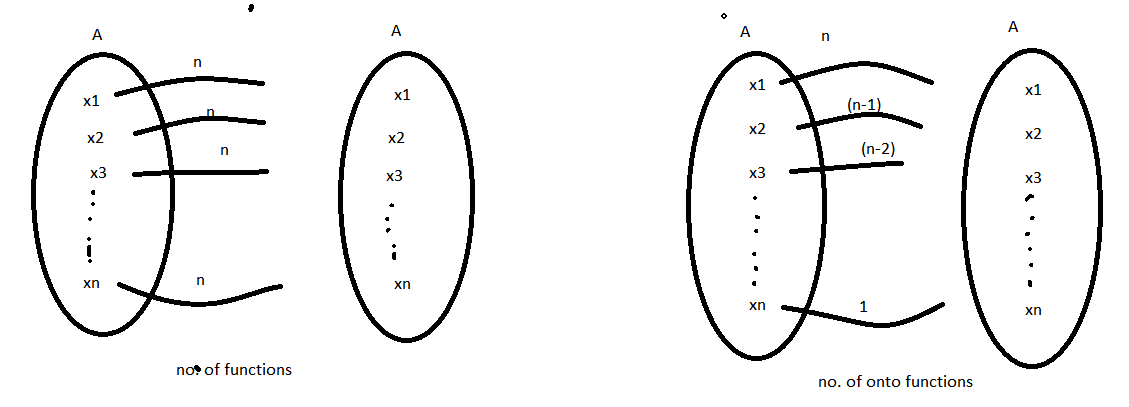
Find the number of all onto functions from the set $$\left \{1, 2, 3, ...., n\right \}$$ to itself
Find the domain of the real valued square root function $$f$$ given below
$$f(x)=\sqrt{(2x)}$$
If the domain of the real valued function $$f$$ given below
$$f(x)=\sqrt{\dfrac{-x+1}{x+3}}$$ is $$(-\infty,-x)\cup(-x,1]$$.Find $$x$$
Find the domain of the real valued rational function $$f$$ given below
$$f(x)=1/({x}^{3}+{x}^{2}-2x)$$
If the domain of $$f(x)=\sqrt{2x+1}$$ is $$\Big[ \dfrac{-1}{m},\infty\Big) $$.Find $$m$$
The domain of the real valued sine function $$f(x)=2\sin{(x-1)}$$ is $$(-\infty,\infty)$$. If true enter 1 else0.
Find the domain of the real valued exponential function $$f$$ given below
$$f(x)={e}^{(x-4)}$$
Show that, if $$f : R - \left \{ \dfrac{7}{5} \right \}\rightarrow R -\left \{ \dfrac{3}{5} \right \}$$ is defined by f (x) = $$\dfrac{3x + 4}{5x - 7}$$ and $$g : R -\left \{ \dfrac{3}{5} \right \}\rightarrow R -\left \{ \dfrac{7}{5} \right \}$$ is defined by g(x) = $$\dfrac{7x + 4}{5x - 3}$$,
then log = $$l_A$$ and gof = $$l_B$$, where $$l_A$$ and $$l_B$$ are called identity functions on sets A and B.
Find the domains of definition of the following functions.
$$\displaystyle y \, = \, \sqrt{\sin \, x} \, + \, \sqrt{16 \, - \, x^2}.$$
Let $$A$$ be a set of $$n$$ distinct elements. Then, the total number of distinct functions from $$A$$ to $$A$$ is .... and out of these .... are onto functions.
Let $$f:D\rightarrow R$$, where $$D$$ is the domain of $$f$$. Find the inverse of $$f$$, if it exists
$$f\left( x \right) ={ 1-2 }^{ -x }$$
$$f\left( x \right) ={ \left( 4-{ \left( x-7 \right) }^{ 3 } \right) }^{ 1/5 }$$
$$f\left( x \right) ={ \ell n\left( x+\sqrt { { 1+x }^{ 2 } } \right) }$$
Find the domains of definition of the following functions.
$$\displaystyle y \, = \, \frac{x}{\sqrt{x^2 \, - \, 5x \, + \, 6}}.$$
Let $$f:\mathbb{N}\to \mathbb{N}$$ be defined by $$f(n)=\begin{cases}\dfrac{n+1}{2}, &\mbox{if}\ n\ \mbox{is odd}\\ \dfrac{n}{2}, &\mbox{if}\ n\ \mbox{is even}\end{cases}$$.$$n\in \mathbb{N}$$
State whether the function $$f$$ is bijective. Justify your answer.
If $$:R\rightarrow R$$ defined by $$f(x)=1+{ x }^{ 2 }$$, then show that $$f$$ is neither $$1-1$$ nor onto
Find the domain of $$f\left( x \right) = \sqrt {\left( {\left[ x \right] - 1} \right)} + \sqrt {\left( {4 - \left[ x \right]} \right)} $$
(where[] represents the greater integer function)
show that $$ f : A \rightarrow B$$ and $$ g : B \rightarrow C $$ are onto, then $$gof : A \rightarrow$$ is also onto:
Let $$f: [ \alpha, \infty) \rightarrow [x, \infty), f(x) = x^2 -6x +5 $$ then find three possible value of $$'\alpha'$$ if $$f(x) $$ is onto.
Let $$f(x) = \sqrt{2 -x -x^{2}}$$ and $$g(x) = cos x$$. Check given statement is true or not?
I. Domain of $$f((g(x))^{2})$$ = Domain of $$f(g(x))$$
Find the domain of $$f(x)=\sqrt{\sin x}+\sqrt{16-x^2}$$.
Find the domain of $$f(x) = \log_{10}\log_{2}\log_{\pi/2}(\tan^{-1}x)^{-1}$$
Let $$f: N \rightarrow Y$$ be a function defined by $$f(x) = 4x^2+ 12x+15$$, where $$Y=$$ range of $$f.$$ Show that$$ f $$ is invertible and find the inverse of $$f$$.
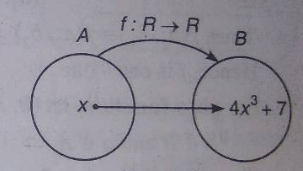
If $$f: R\rightarrow R $$ be the function defined by $$f(x) = 4x^3+7$$, then show that $$f$$ is a bijection.
Find the domain for which the function $$f(x)=3{x}^{2}-2x$$ and $$g(x)=9x-6$$ are equal.
Evaluate:$$\displaystyle \int \sin^2 x \cos^2 x dx $$
Simplify $$\dfrac{1}{1+a^{m-n}}+\dfrac{1}{1+a^{n-m}}$$
Find the domain of
$$f\left( x \right) = \sqrt {\left( {\left[ x \right] - 1} \right)} + \sqrt {\left( {4 - \left[ x \right]} \right)} $$
(where [ ] represents the greatest integer function).
Find the domain of $$f(x) = \sqrt{x + 2} + {log_{10}}(1 - x)$$
The domain of definition of the function $$y(x)$$ given by $$2^x+2^y=2$$ is
If $$f:R\rightarrow S,defined\ by\ f\left( x \right) =\sin { x } -\sqrt { 3 } \cos { x } +1$$, is onto, then find the set $$S$$ ?
Domain of $$f\left( x \right) = \dfrac{{{x^2} + 3x + 5}}{{{x^2} - 5x + 4}}$$ is
Show that $$f: N→N$$ = $$x-1$$, if $$x$$ is even is both one-one and onto
Let $$f:R \to R$$ be defined by i) $$f\left( x \right) = x + 1$$ ii) $$f\left( x \right) = x + \left| x \right|$$. Determine whether or not $$f$$ is onto.
The domain of $$\frac{1}{\sqrt{x-x^{2}}}+\sqrt{3x-1-2x^{2}}$$ is:
The domain of the function $$\dfrac{x}{\sqrt{x^2-3x+2}}$$ is
If $$f(x + y) = f(xy) \forall x, y\epsilon R$$ then prove that $$f$$ is a constant function.
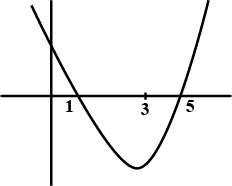
The domain of the function$$\sqrt{x^{2}-5x+6}+\sqrt{2x+8-x^{2}}$$is
The domain of $$f(x)=\dfrac{x^2-8}{x-2}$$
f(x) and g(x) are linear function such that for all x, f(g(x)) and g(f(x)) are Identity functions. If f(0) = 4 and g(5) = 17, compute f(2006)
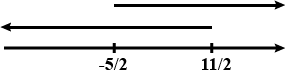
Solve: $$\dfrac { \left| x-1 \right| }{ x+2 } <1$$
Find the domain of $$f(x)=\sqrt { \cos\left(\sin{x}\right) } $$
Find the domain $$\dfrac { { x }^{ 3 }-5x+3 }{ { x }^{ 2 }-1 } $$
Find domain of the function $$f\left( x \right) =\sqrt { 4-\sqrt { 5+2x } } $$.
Find the solution of the inequation $$ \left| 2 ^ { x } - 1 \right| + | 4 - 2 | \leq 3 $$
Find the largest possible domain for the real valued function given by $$f\left( x \right) = \dfrac{{\sqrt {9 - {x^2}} }}{{\sqrt {{x^2} - 1} }}.$$
Find the largest possible domain for the real-valued function given by$$f(x)=\dfrac{\sqrt{9-x^2}}{\sqrt{x^2-1}}$$
Write the domain of the real function $$f(x)=\sqrt{\left[ x \right] -x}$$.
Write the domain of the real function $$f(x)=\sqrt{x-\left[ x \right] }$$.
If $$f:A\rightarrow B$$ and $$g:B\rightarrow C$$ are onto functions, then show that $$g\circ f$$ is an onto function.
Write the domain of the real function $$f(x)=\cfrac{1}{\sqrt{\left[ x \right] -x}}$$.
Write the domain of the real function $$f$$ defined by $$f(x)=\sqrt{25-{x}^{2}}$$.
Find the domain of each of the following real value functions real variable:
$$f(x)=\sqrt {9-x^2}$$
Find the domain and range of each of the following real value functions:
$$f(x)=\dfrac {ax-b}{cx-d}$$
Find the domain and range of each of the following real value functions:
$$f(x)=\dfrac {ax-b}{bx-a}$$
Find $$f(g(x)). f(x) = 5x^2 - 2x + 3\ and\ g(x) = 4x^2 + 7x - 5.$$
Let $$f(x)=2x+5$$ and $$g(x)=x^2+x$$. Describe $$f-g$$
Find the domain in each case.
Let $$f(x)=2x+5$$ and $$g(x)=x^2+x$$. Describe $$fg$$
Find the domain in each case.
Find the domain and range of each of the following real value functions:
$$f(x)=\sqrt {x-3}$$
Let $$f(x)=2x+5$$ and $$g(x)=x^2+x$$. Describe $$f/g$$
Find the domain in each case.
Let $$f(x)=2x+5$$ and $$g(x)=x^2+x$$. Describe $$f+g$$
Find the domain in each case.
Give an example of a function which is onto but not one-one.
Let $$f =\{ (0, -5),(1,-2),(2,1),(3,4),(4,7) \}$$ be linear function from $$Z$$ into $$Z$$. Write an expression for $$f. $$
Let $$ f: R \rightarrow R : f(x) = \dfrac {x}{c} , $$where c is constant.
Find $$ (c^2 f)(x) $$
Let $$ f: R \rightarrow R : f(x) = \dfrac {x}{c} , $$where $$c$$ is constant.
Find $$ \left( \dfrac {1}{cf}\right)(x) $$
Let $$ f: R \rightarrow R : f(x) = \dfrac {x}{c} , $$where $$c$$ is constant.
Find $$(cf)(x)$$.
Are the following set of ordered pairs function? If so, examine whether the mapping is injective or surjective.
$$\left\{(x,y):x \text{ is a person },y\text{ is the mother of } x \right\}$$.
Are the following set of ordered pairs function? If so, examine whether the mapping is injective or surjective.
$$\left\{(a,b):a \text{ is a person } ,b \text{ is an ancestor of } a \right\}$$.
The function 't' which maps temperature in degree Celsius into temperature in degree Fahrenheit is defined by $$ t (c) = \frac{9C}{5} + 32$$. Find
(i) t (0)
The function 't' which maps temperature in degree Celsius into temperature in degree Fahrenheit is defined by $$ t (c) = \frac{9C}{5} + 32$$. Find
(ii) t (28)
The function 't' which maps temperature in degree Celsius into temperature in degree Fahrenheit is defined by $$ t (c) = \frac{9C}{5} + 32$$. Find
(iii) t (-10)
The function $$'t'$$ which maps temperature in degree Celsius into temperature in degree Fahrenheit is defined by $$ t (c) = \dfrac{9C}{5} + 32$$. Find the value of $$C$$, when $$t (C) = 212.$$
Is the function $$\sin (\sin^{-1}n)$$ bijective? Which is defined on $$[-1,1]$$ to $$[-1,1]$$
Write the domain and range of the function $$f(x)=x^{3}+1$$
Examine which of the following is / are functions :
{( 1 ,a)(2 , b)( 1 ,b)(2 ,a)}
Find the domain and range of the following real function:
$$f(x)=|x-1|$$
Define an identity function and draw its graph also find its domain and range.
Examine which of the following is / are functions :
{(a , 0)(b ,0), (c ,1)( d , 1)}
Examine which of the following is / are functions :
{(1 ,2),(2 ,3),(3 , 4), ( 2 , 1)}
Define a constant function and draw its graph also find its domain and range.
Examine which of the following is / are functions :
{( a ,a)(b , b)( c ,c)}
Examine which of the following is / are functions :
{( a ,b)}
Examine which of the following is / are functions :
$$ \left \{ ( x ,y): x , y \in R , y^{2} = x \right \} $$
Examine which of the following is / are functions :
$$ \left \{ (x , y) : x , y \in R , x = y^{3} \right \} $$
Examine which of the following is / are functions :
{( 4 , 1)(4,2),(4 , 3), ( 4 , 4)}
Examine which of the following is / are functions :
{( 1, 4)(2 , 4),(3 , 4), ( 4 , 4 )}
Examine which of the following is / are functions :
$$ \left \{ ( x , y) : x , y \in R , x^{2} = y \right \} $$
A function $$R\rightarrow R$$ is defined by $$\displaystyle f\left ( x \right )=\frac{\alpha x^{2}+6x-8}{\alpha +6x-8x^{2}}$$. If $$f$$ is an onto function for $$\alpha \in [P, Q]$$ then $$P + Q$$ is
Find the domain of the real valued linear function $$f$$ given below
$$f(x)=x+1$$
Find the domain of the real valued linear function $$f$$ given as below:
$$f(x)=\dfrac{(x-1)}{(x-3)}$$
Find the domain of the real valued logarithmic function $$f$$ given below
$$f(x)=\ln({x}^{2}-9)$$
Indicate the domain of definition of the function and simplify the given expression.
$$\displaystyle\, y = x\frac{1 + 2(x + 4)^{-0.5}}{2 - (x + 4)^{0.5}} + (x + 4)^{0.5} + 4(x + 4)^{-0.5}$$
Let $$f=\left\{(1,1),(2,3),(0,-1),(-1,3)\right\}$$ be a linear function from $$z$$ to $$z$$ , find $$f(x)$$ where $$x$$ is the set of integers.
Find the domain of $$\sqrt[3]{5x-3}$$
Find the domain of $$\cfrac{1}{((x-1)(x-2)}$$.
The domain of the real-valued function $$f\left( x \right) =\log_{10}{\sqrt{\cfrac{(3-x)(x+2)}{(x+1)(x-4)}}}$$ does not contain the intervals $$(-\infty,-5)$$ and $$(5,6)$$.
find the domain of x$$\dfrac{x^4-3x^3+2x^2}{x^2-x-30} > 0$$.
Give an example of a function which is neither one-one nor onto.
Show that the function $$f:R\rightarrow R:f(x)=x^2$$ is neither one-one nor onto.
Show that the function $$f: R\rightarrow R:f(x)=\sin x$$ is neither one-one nor onto.
Let $$X = \{ 1, 2, 3 ,4\}, Y = \{1,5,9, 11, 15 , 16 \}$$ and $$f = \{ (1,5) , (2,9), ( 3,1), (4,5), 92, 11)\}$$. Are the following true?
(i) $$f$$ is a relation from $$X$$ to $$Y$$.
(ii) $$f$$ is function from $$X$$ to $$Y$$. Justify your answer in each case.
Number of integers in the domain of function, satisfying $$f(x) + f(x^{-1}) = \dfrac{x^3 + 1}{x}$$, is
If $$ f ( x + \frac {1}{x} ) = (x^2 +\frac {1}{x^2} ) $$ for all $$ x \epsilon R - \left\{0 \right\} $$ then write an expression for $$ f(x) $$.
If $$f(x) =$$ sin log$$_e \left ( \frac{\sqrt{4 - x^2}}{1 - x} \right )$$, then the domain of $$f(x)$$ is_________ and its range is _______________. (IIT-JEE, 1985)
Class 11 Commerce Applied Mathematics Extra Questions
- Basics Of Financial Mathematics Extra Questions
- Circles Extra Questions
- Descriptive Statistics Extra Questions
- Differentiation Extra Questions
- Functions Extra Questions
- Limits And Continuity Extra Questions
- Logarithm And Antilogarithm Extra Questions
- Mathematical And Logical Reasoning Extra Questions
- Number Theory Extra Questions
- Numerical Applications Extra Questions
- Permutations And Combinations Extra Questions
- Probability Extra Questions
- Relations Extra Questions
- Sequences And Series Extra Questions
- Set Theory Extra Questions
- Straight Lines Extra Questions
- Tangents And Its Equations Extra Questions