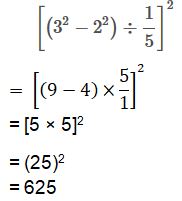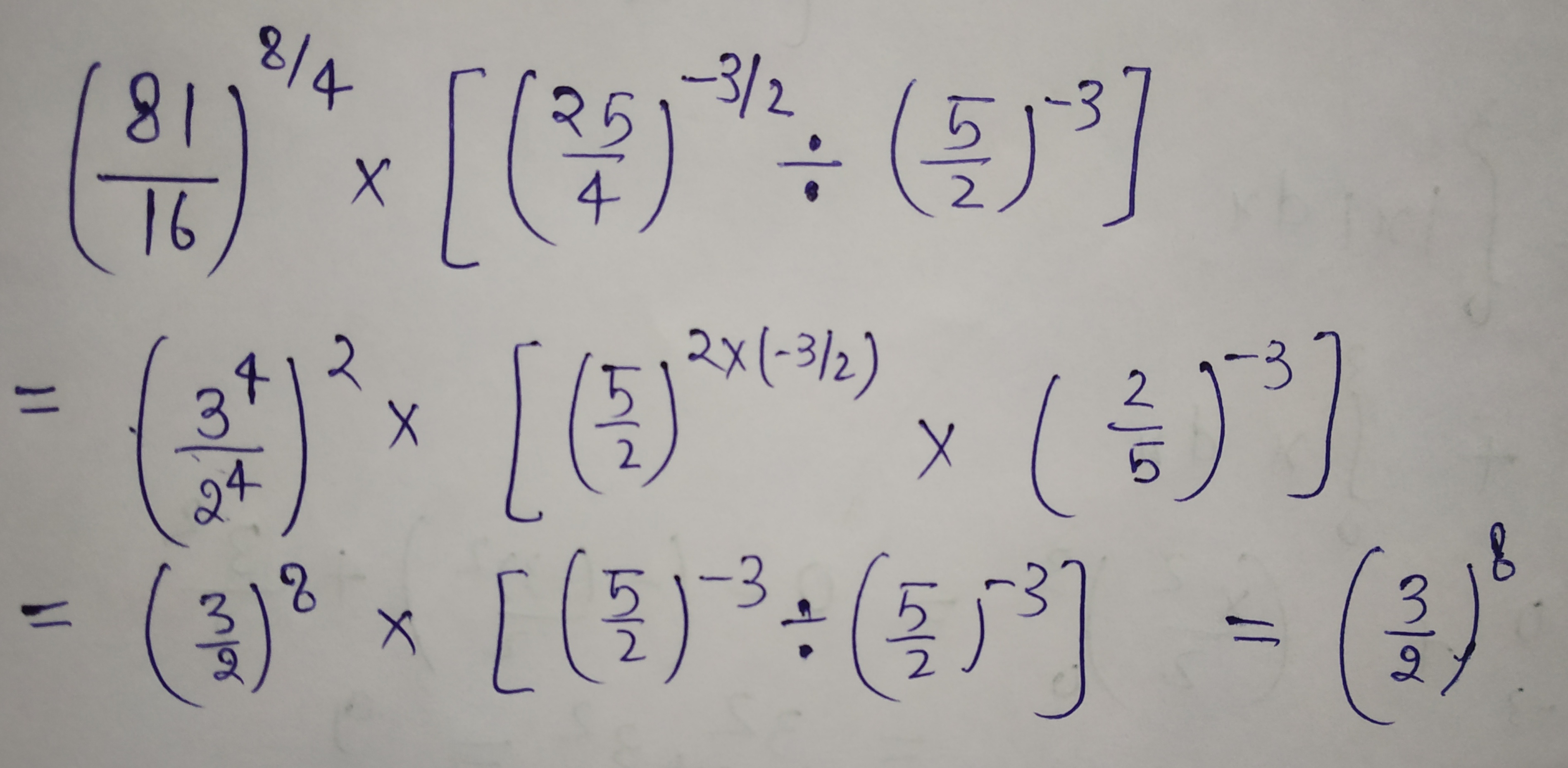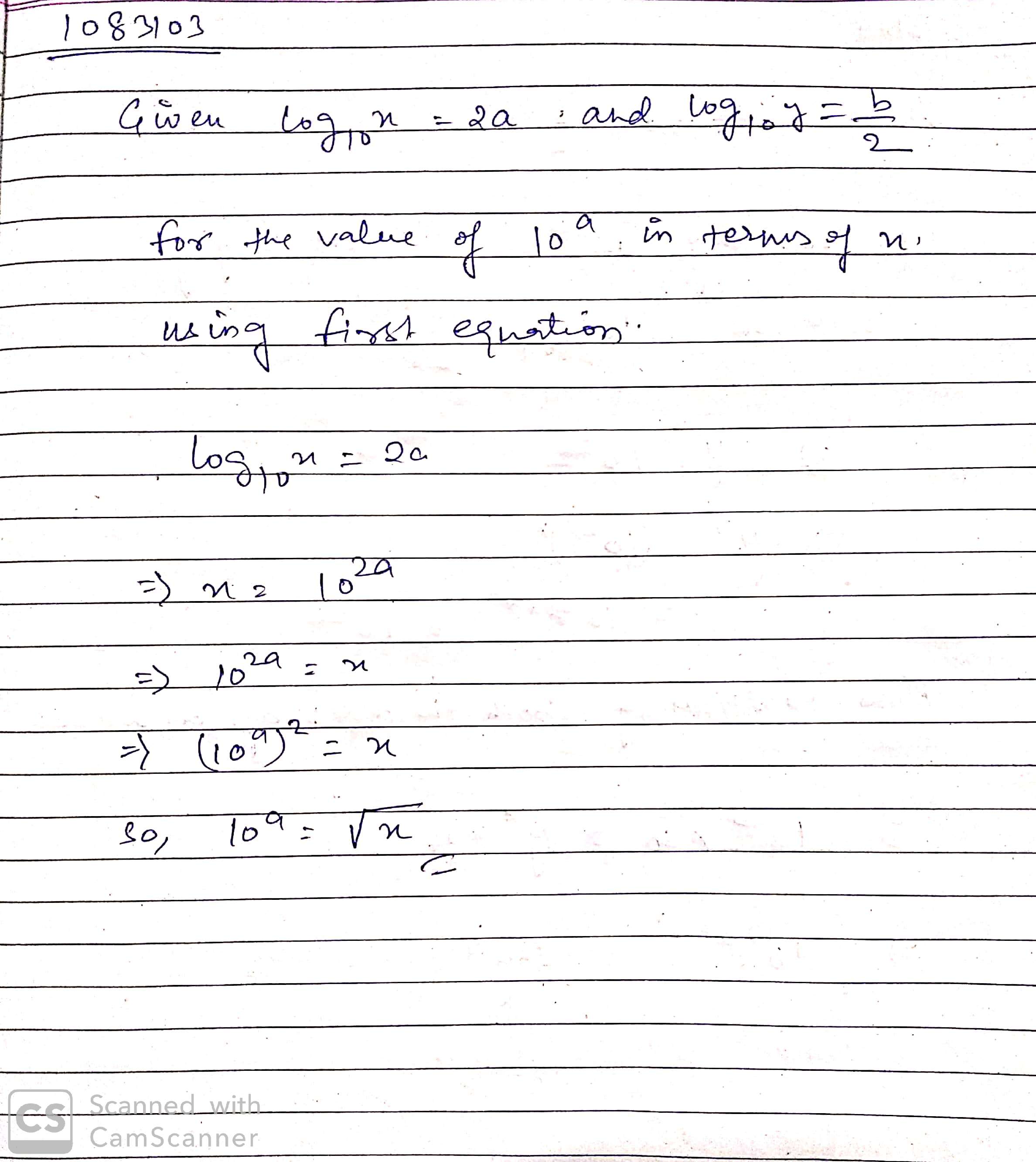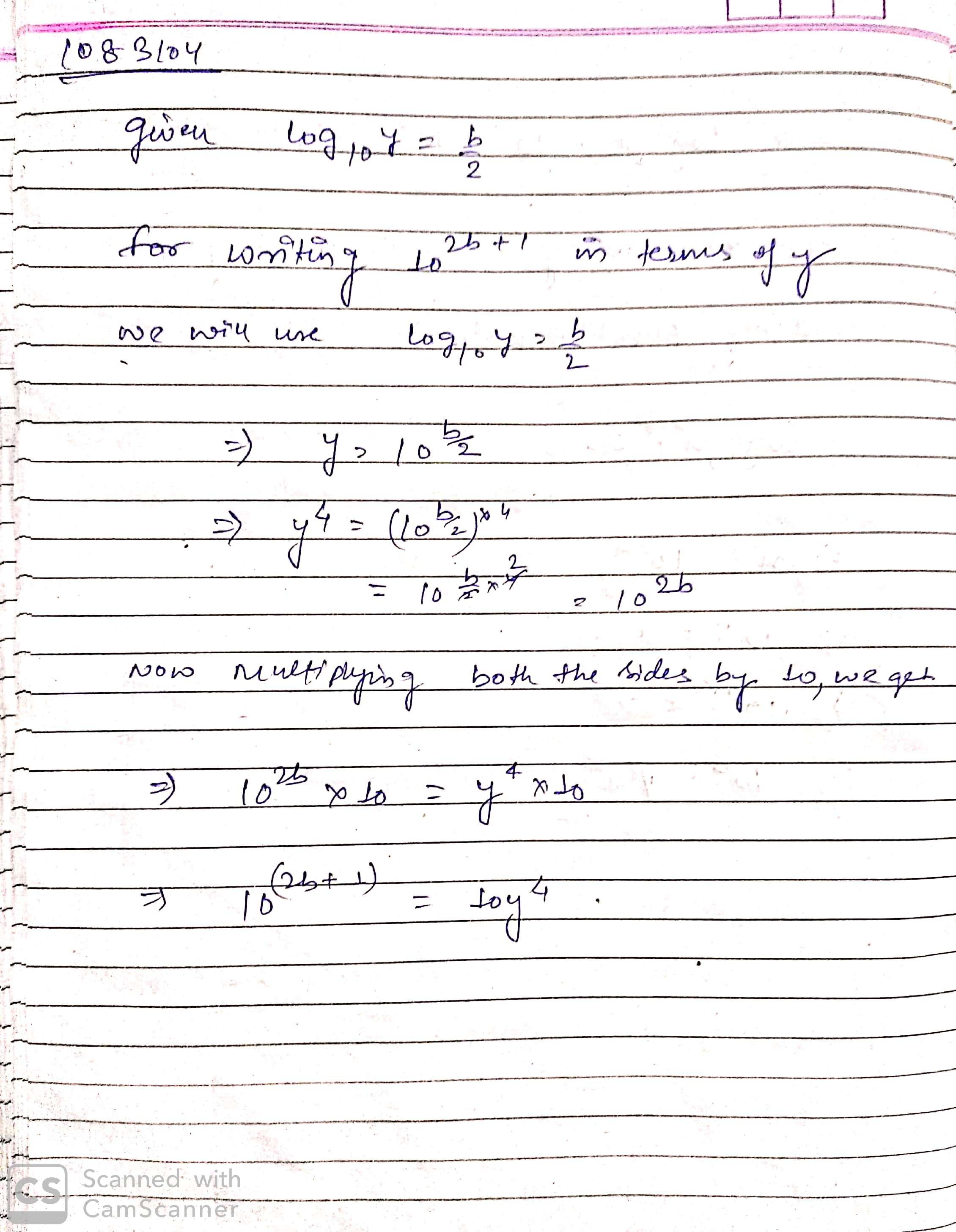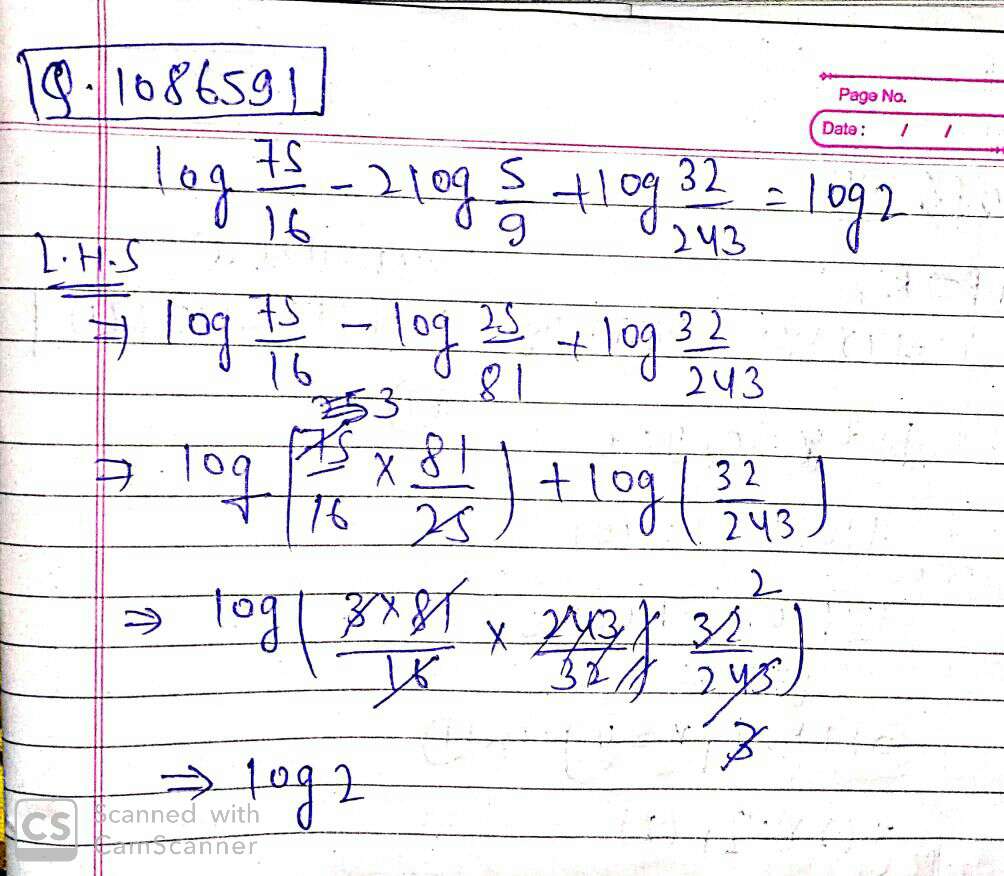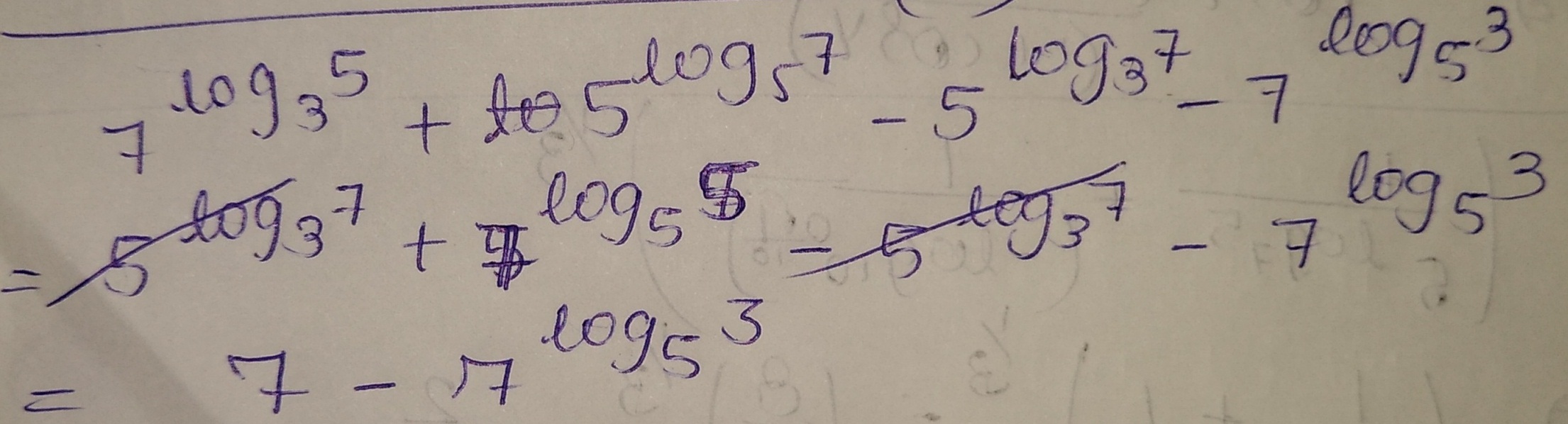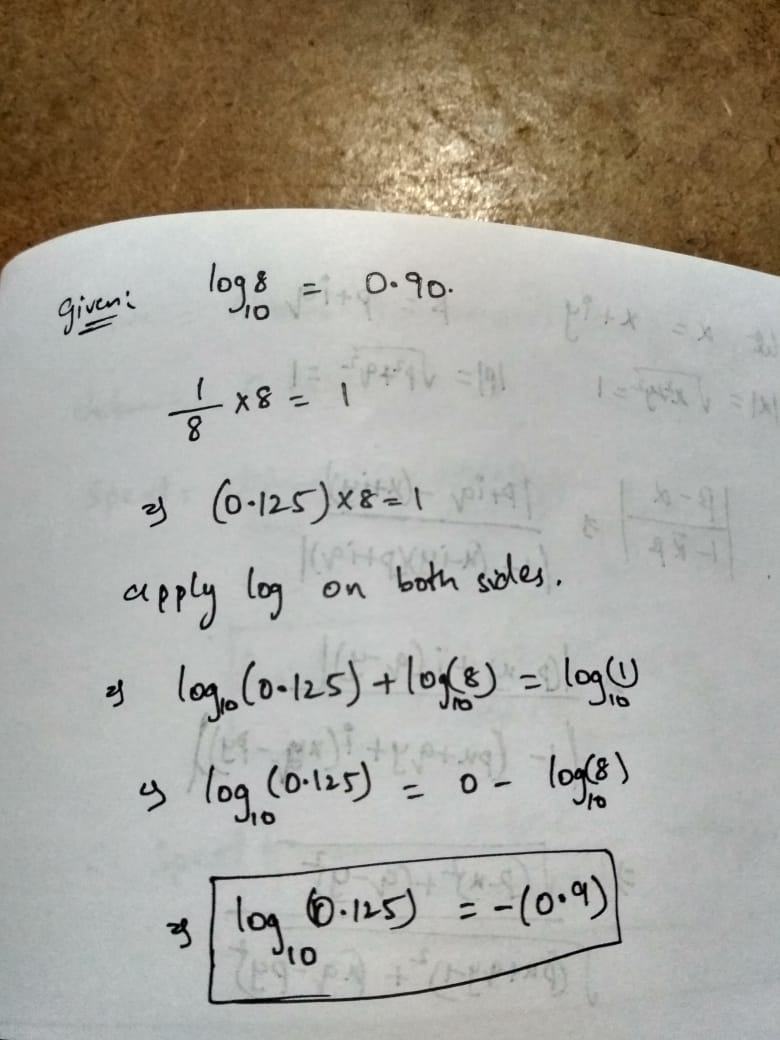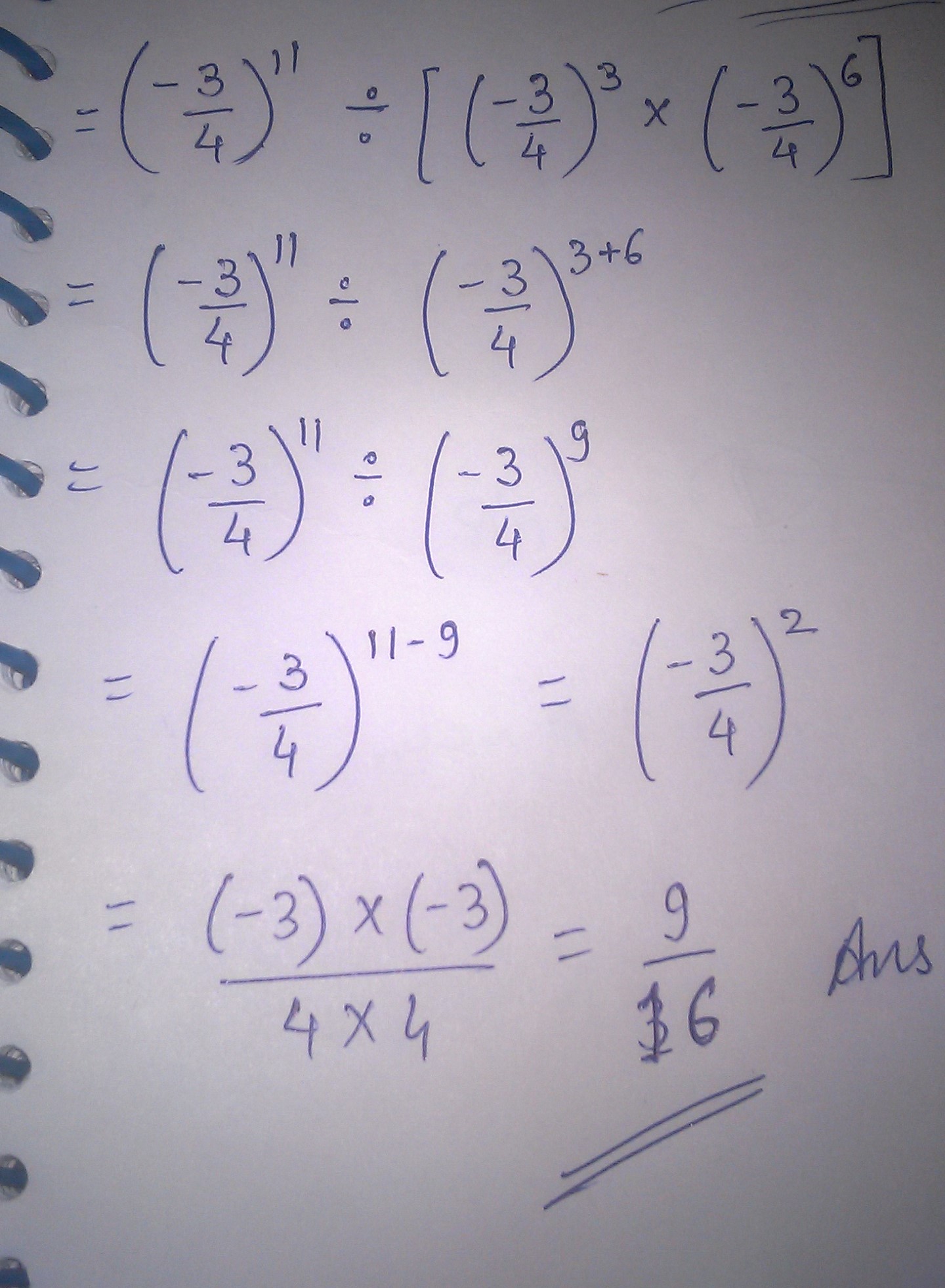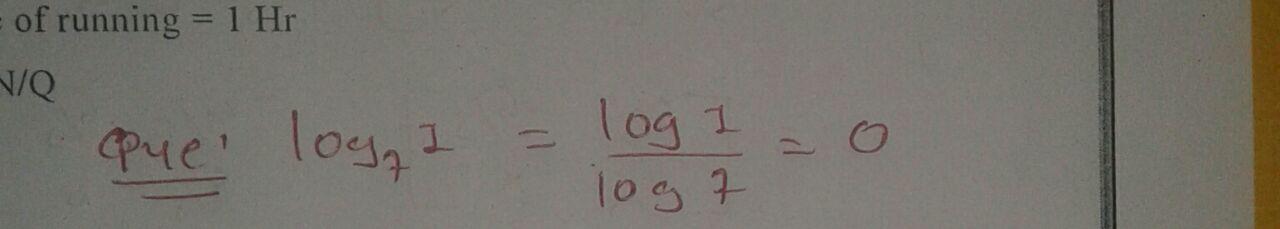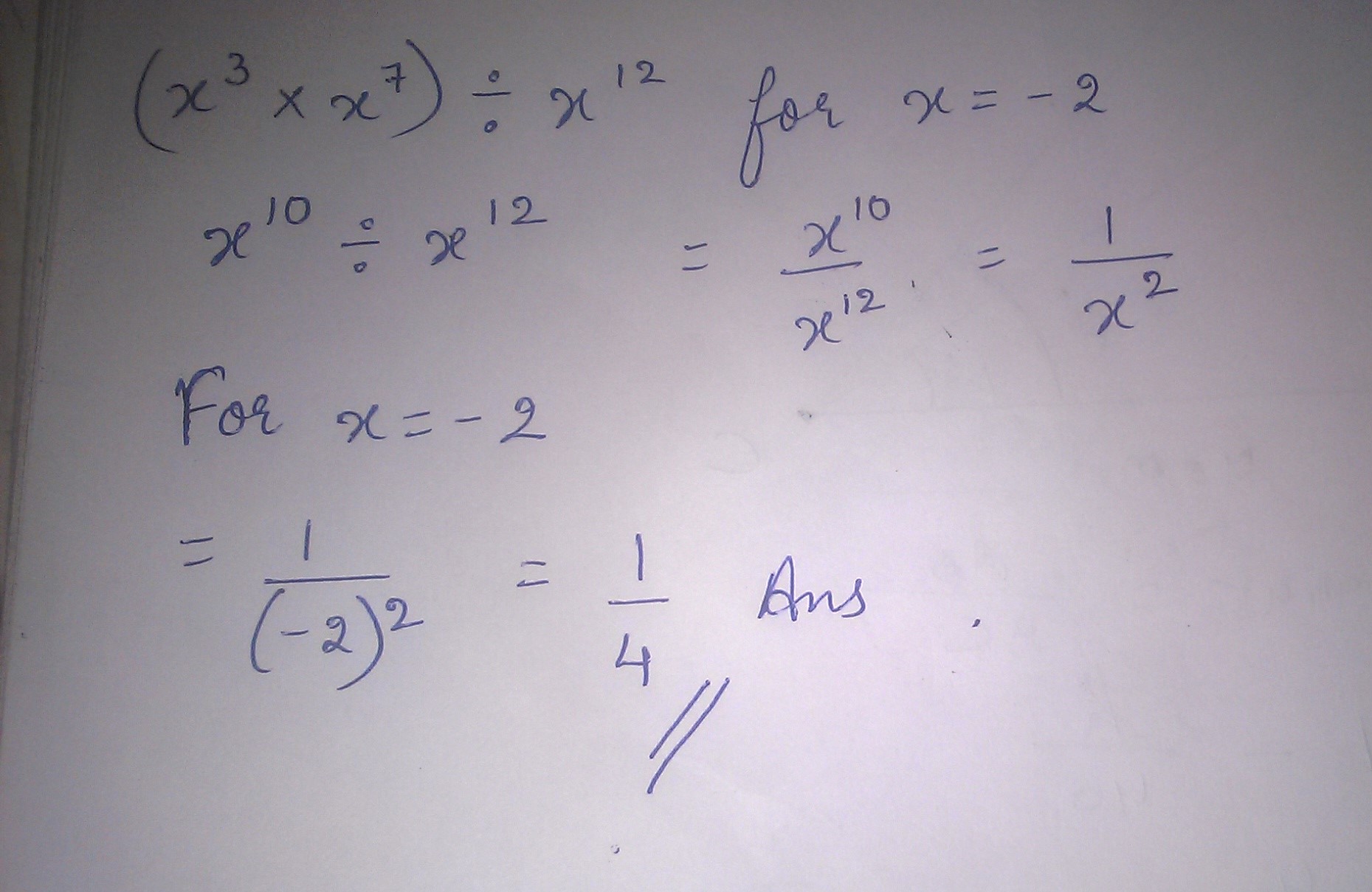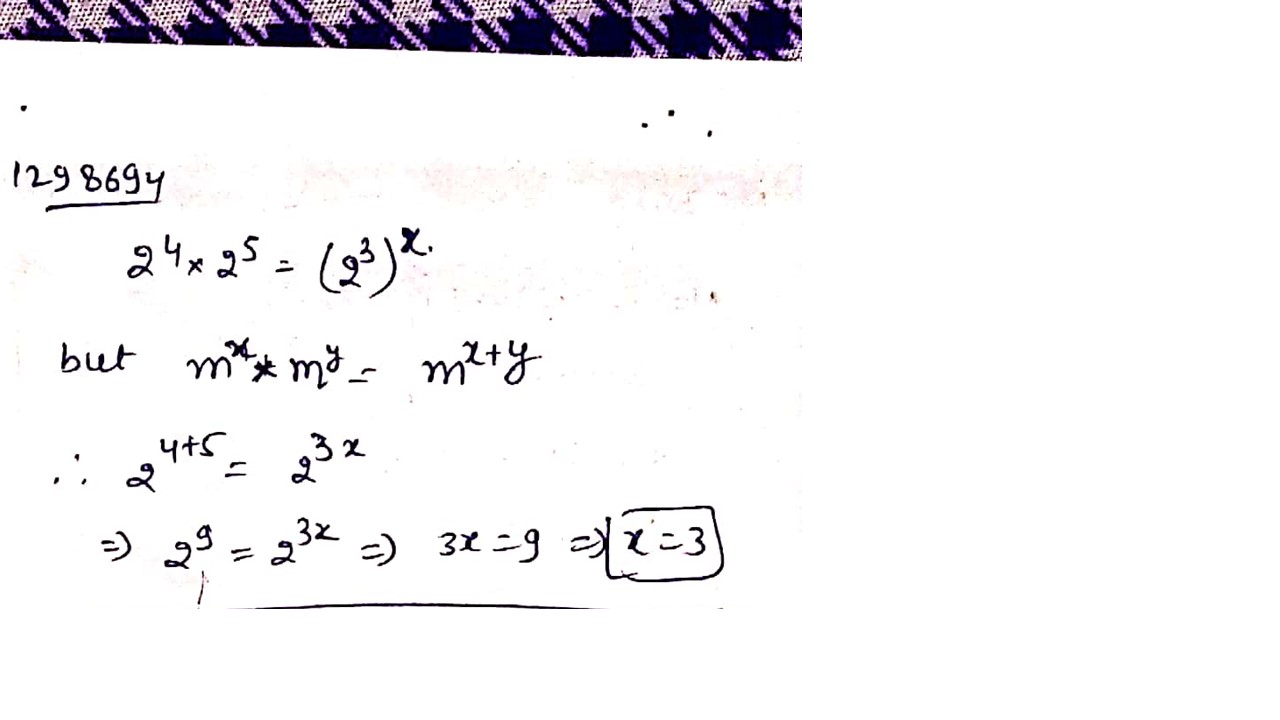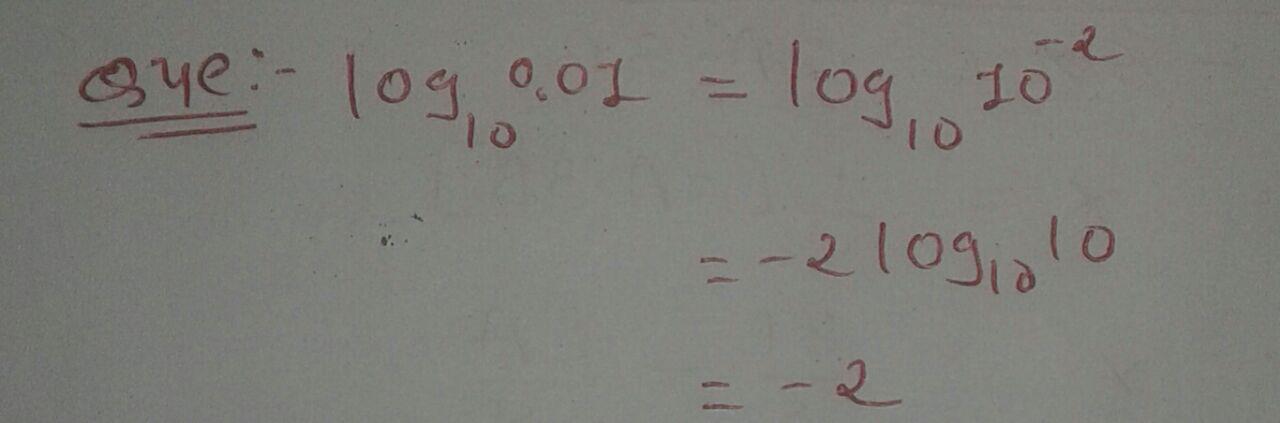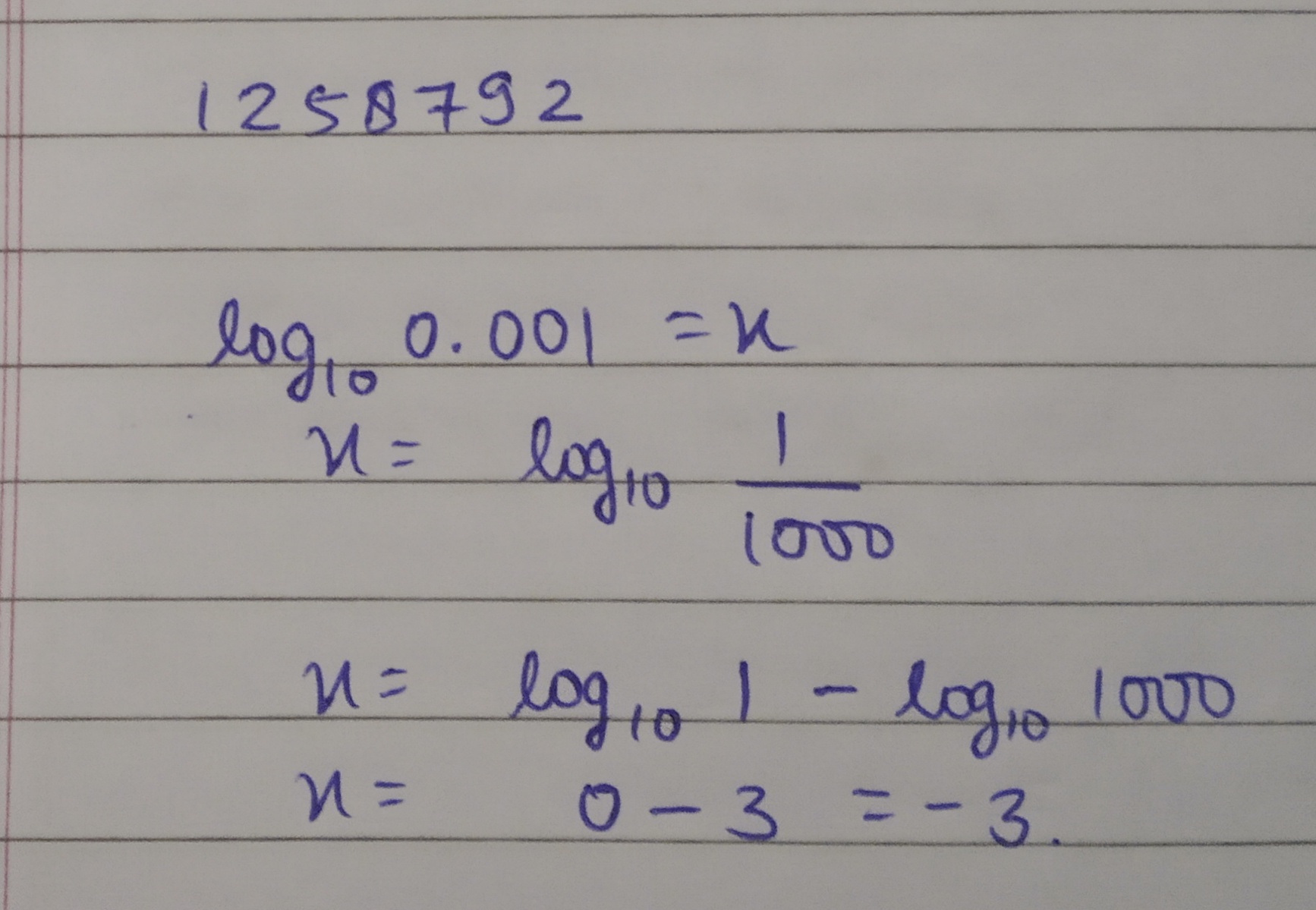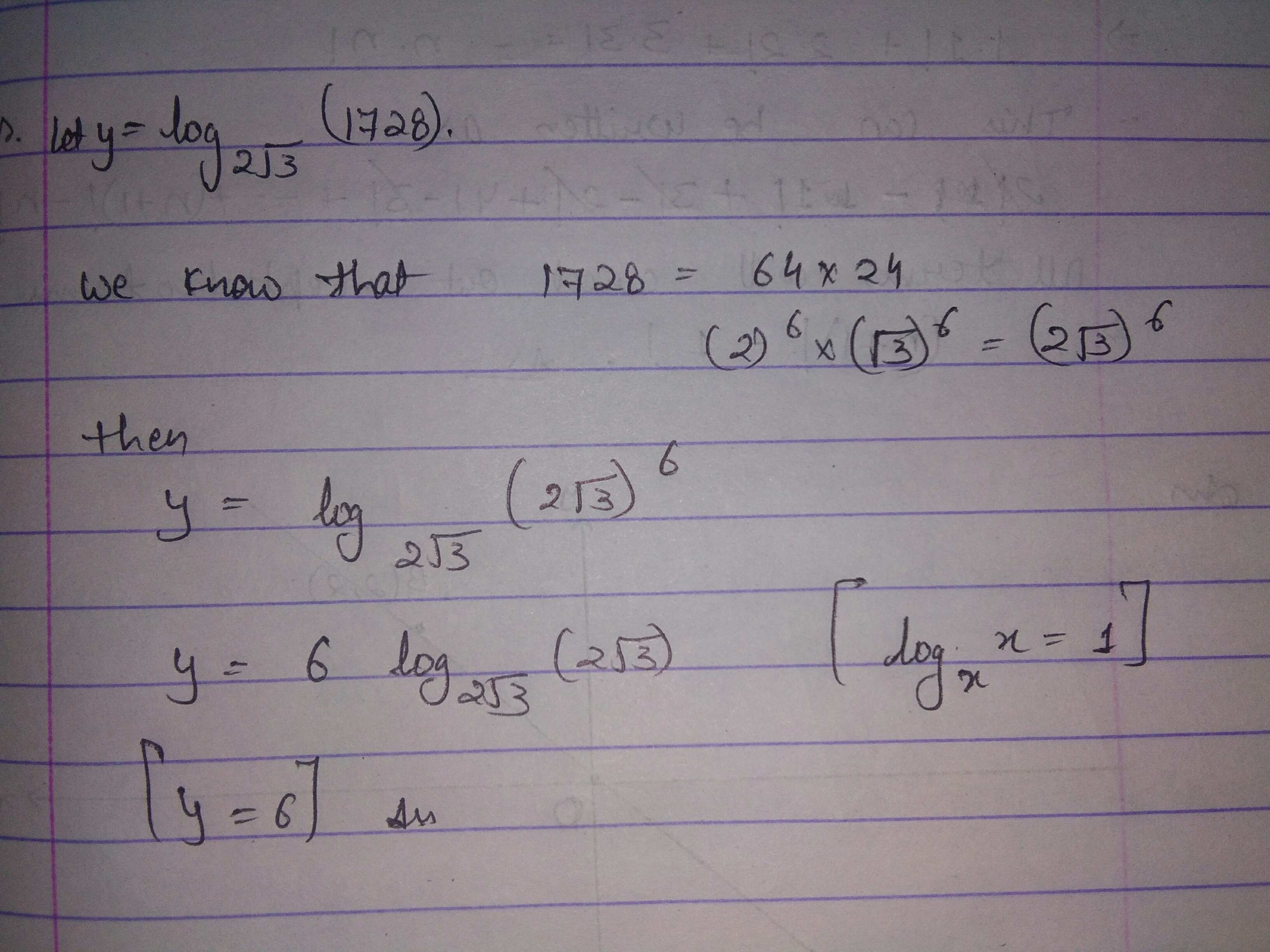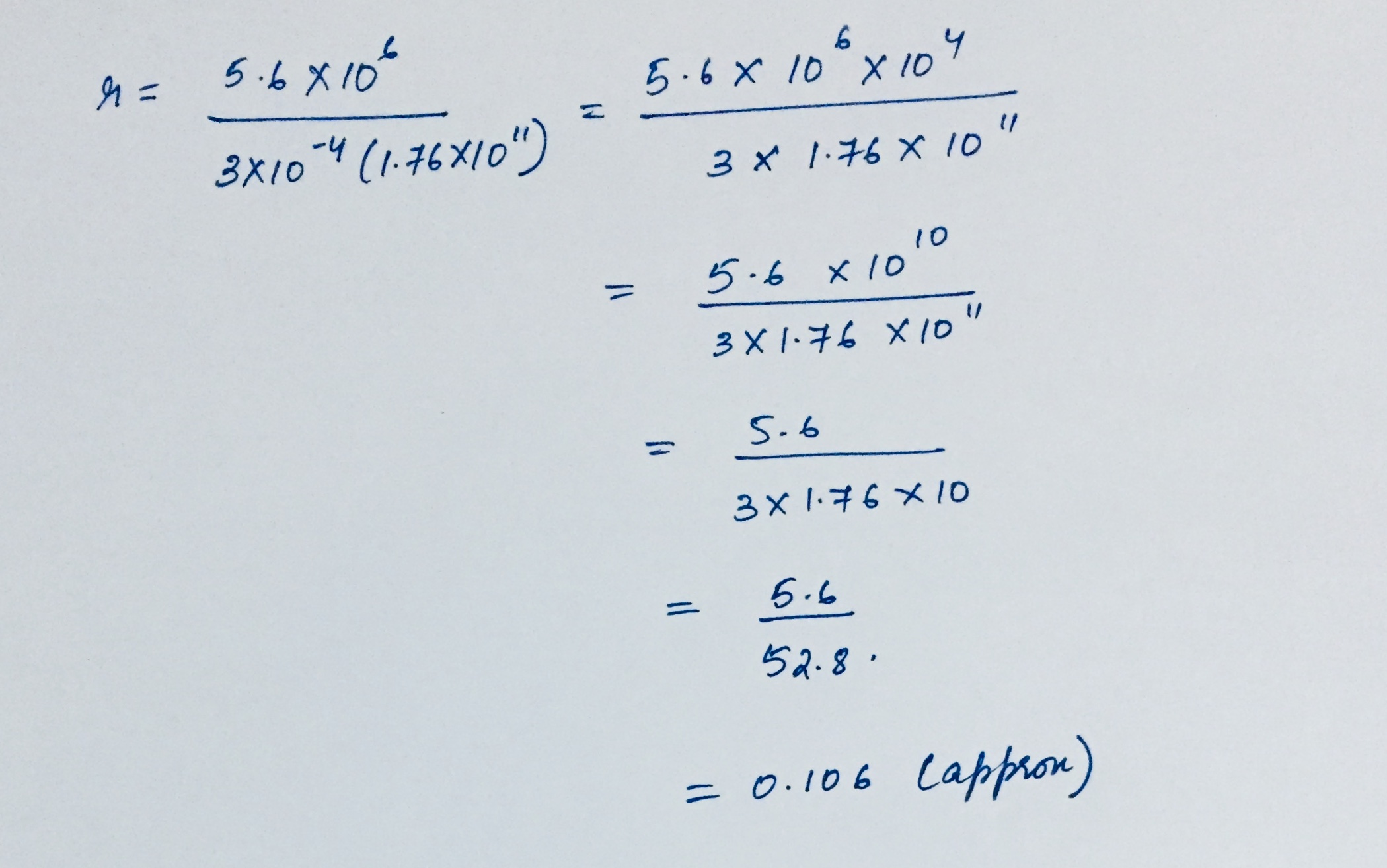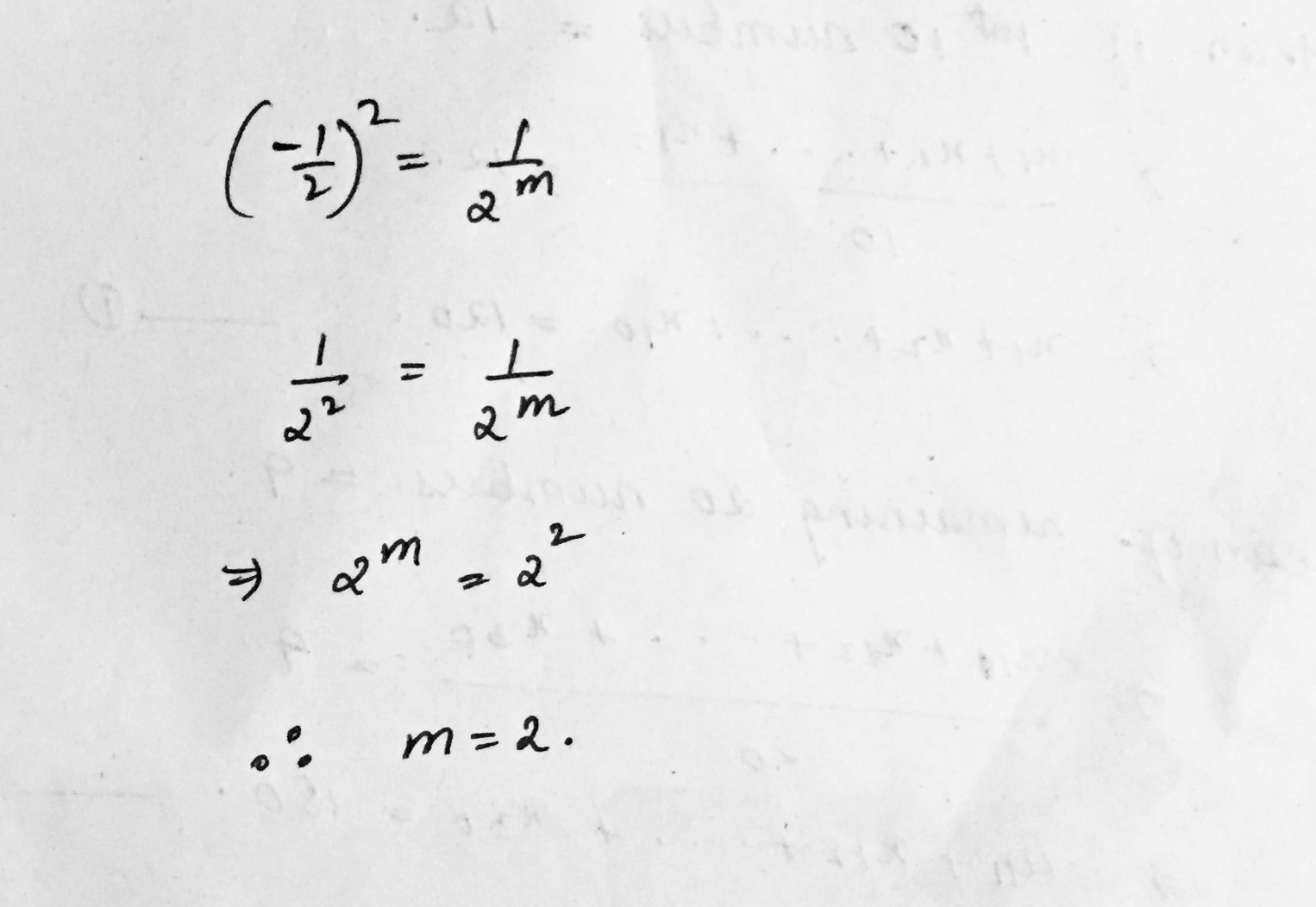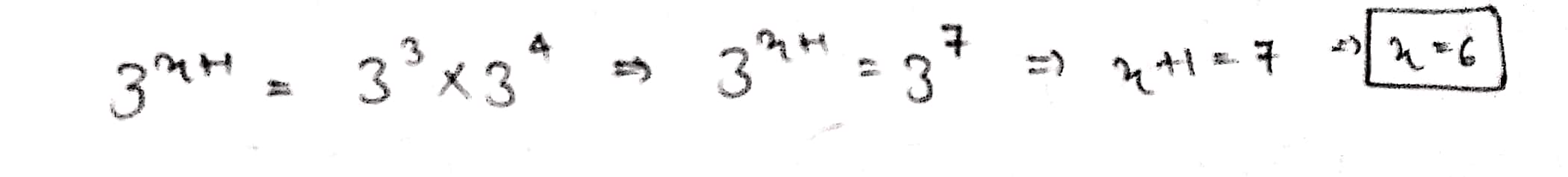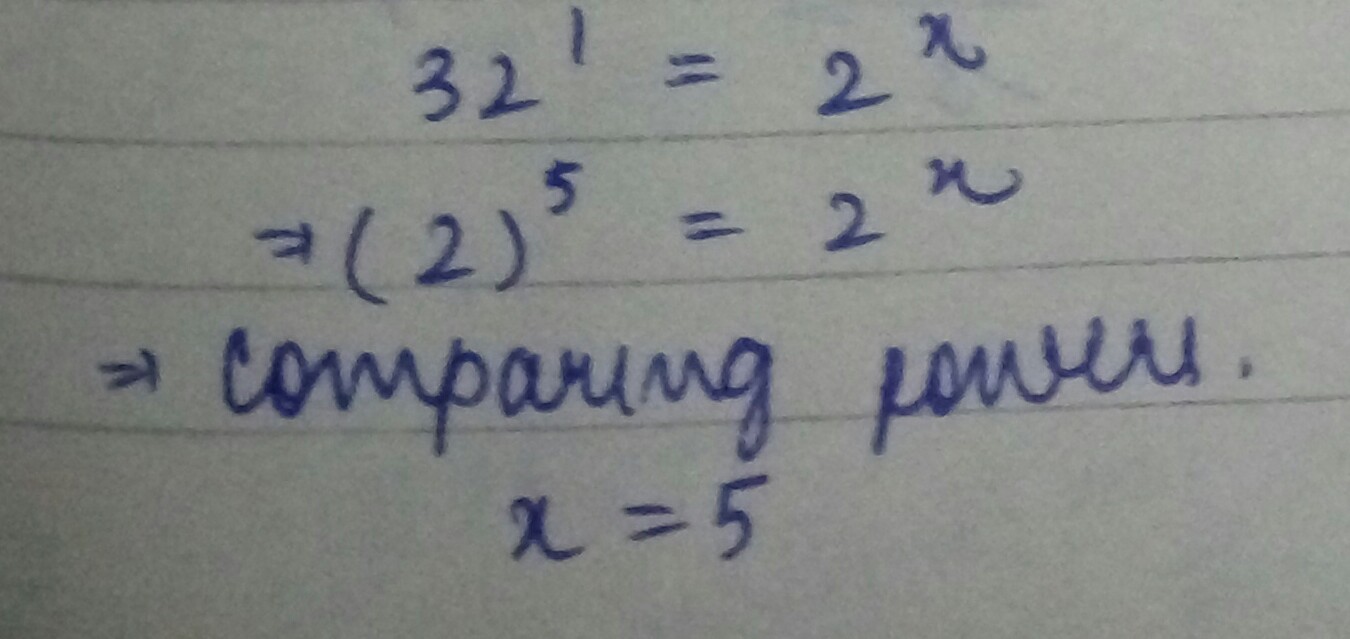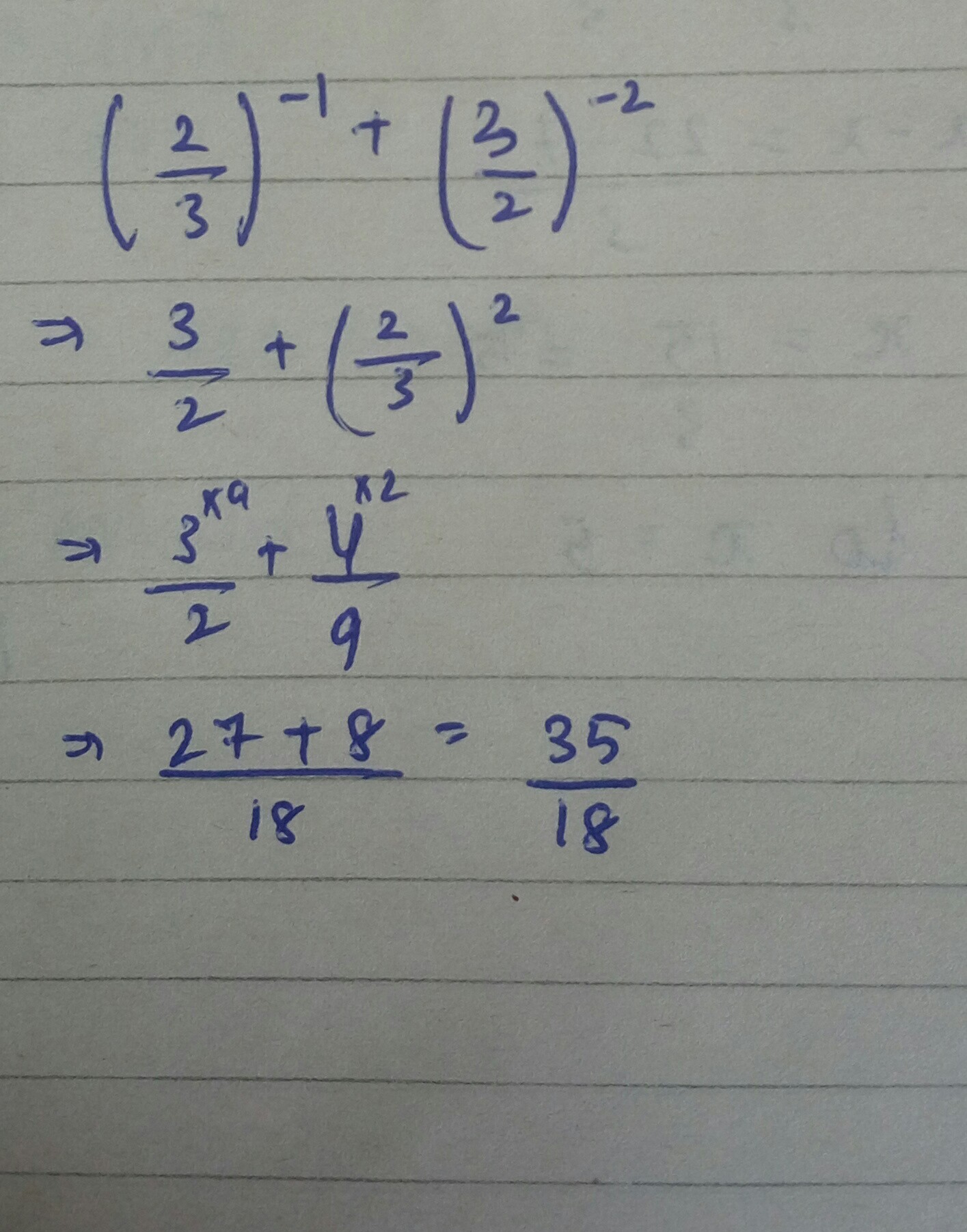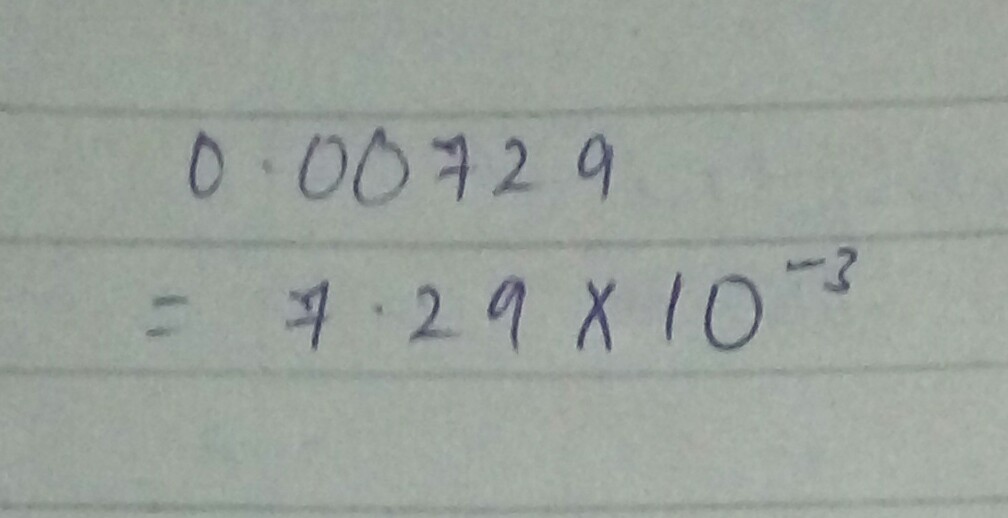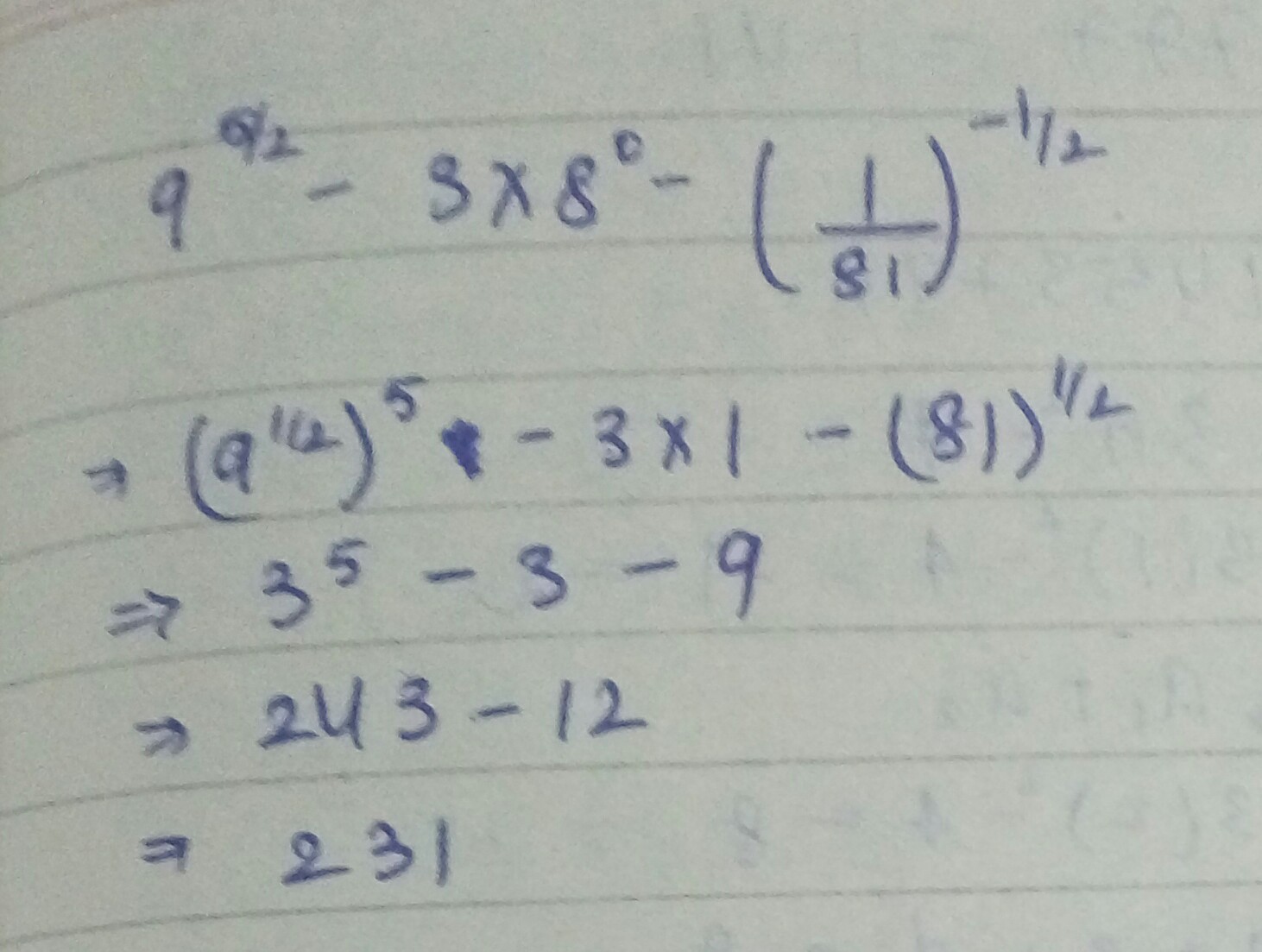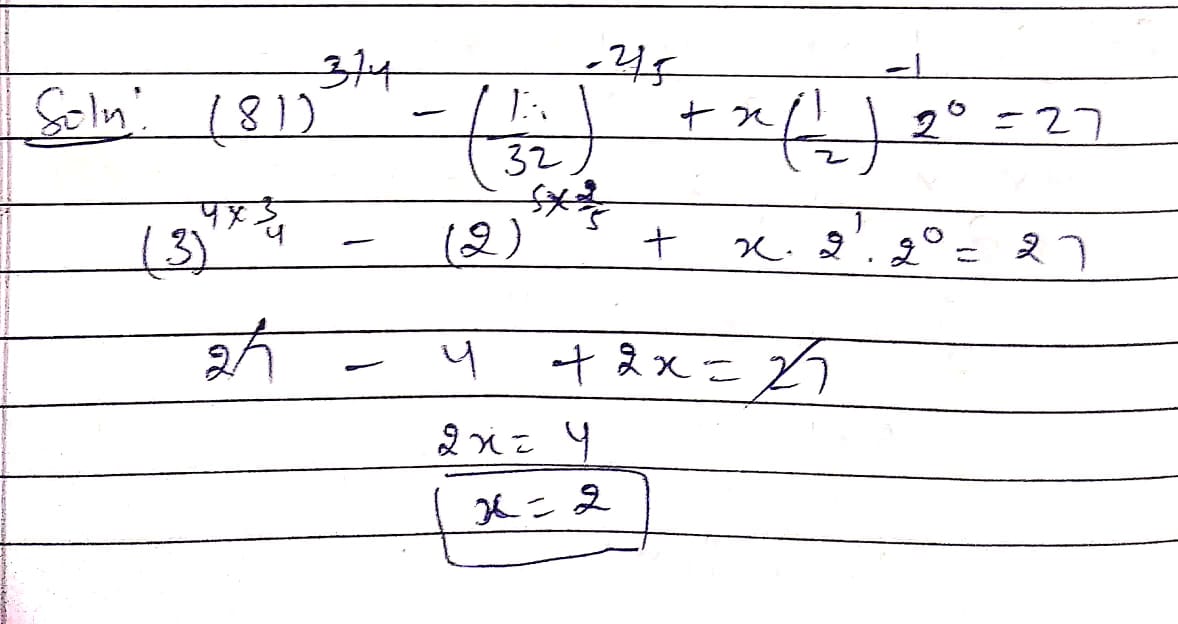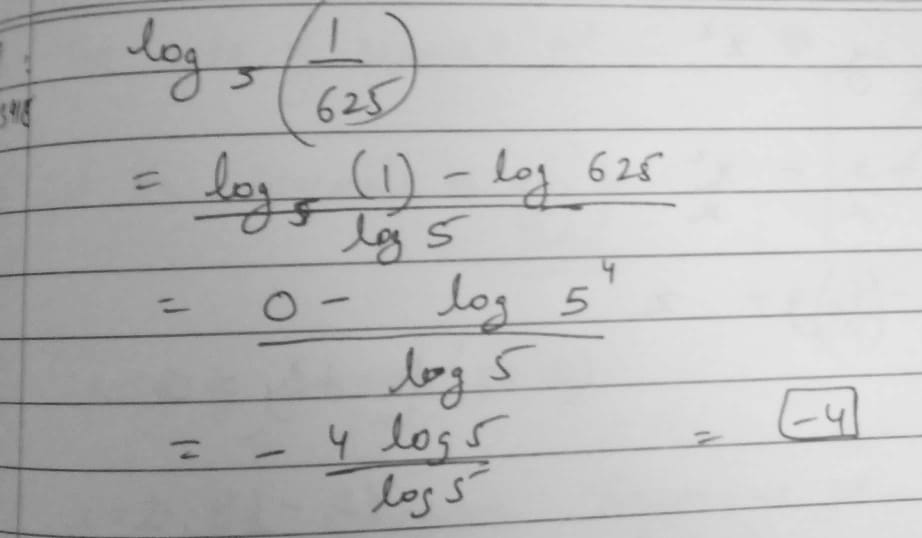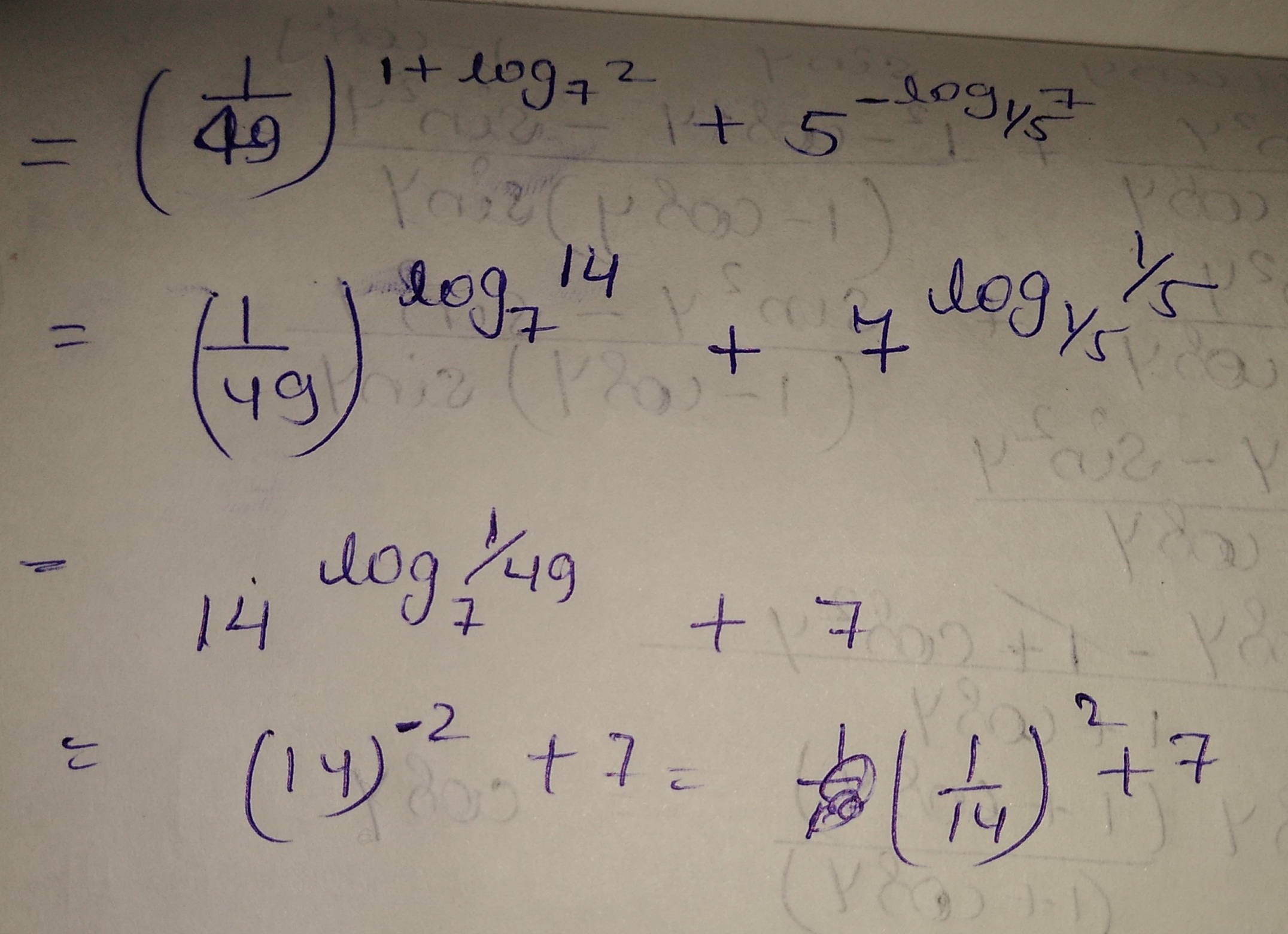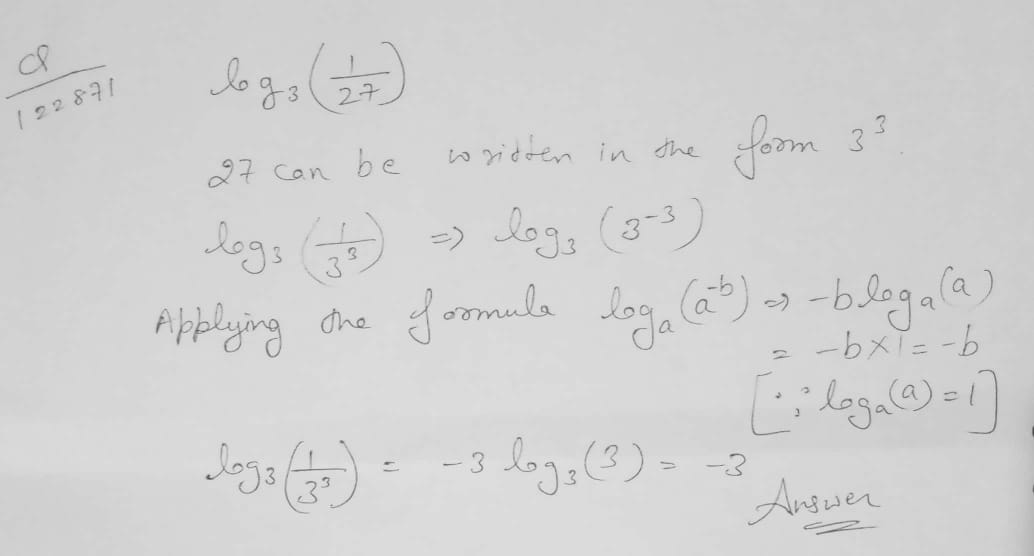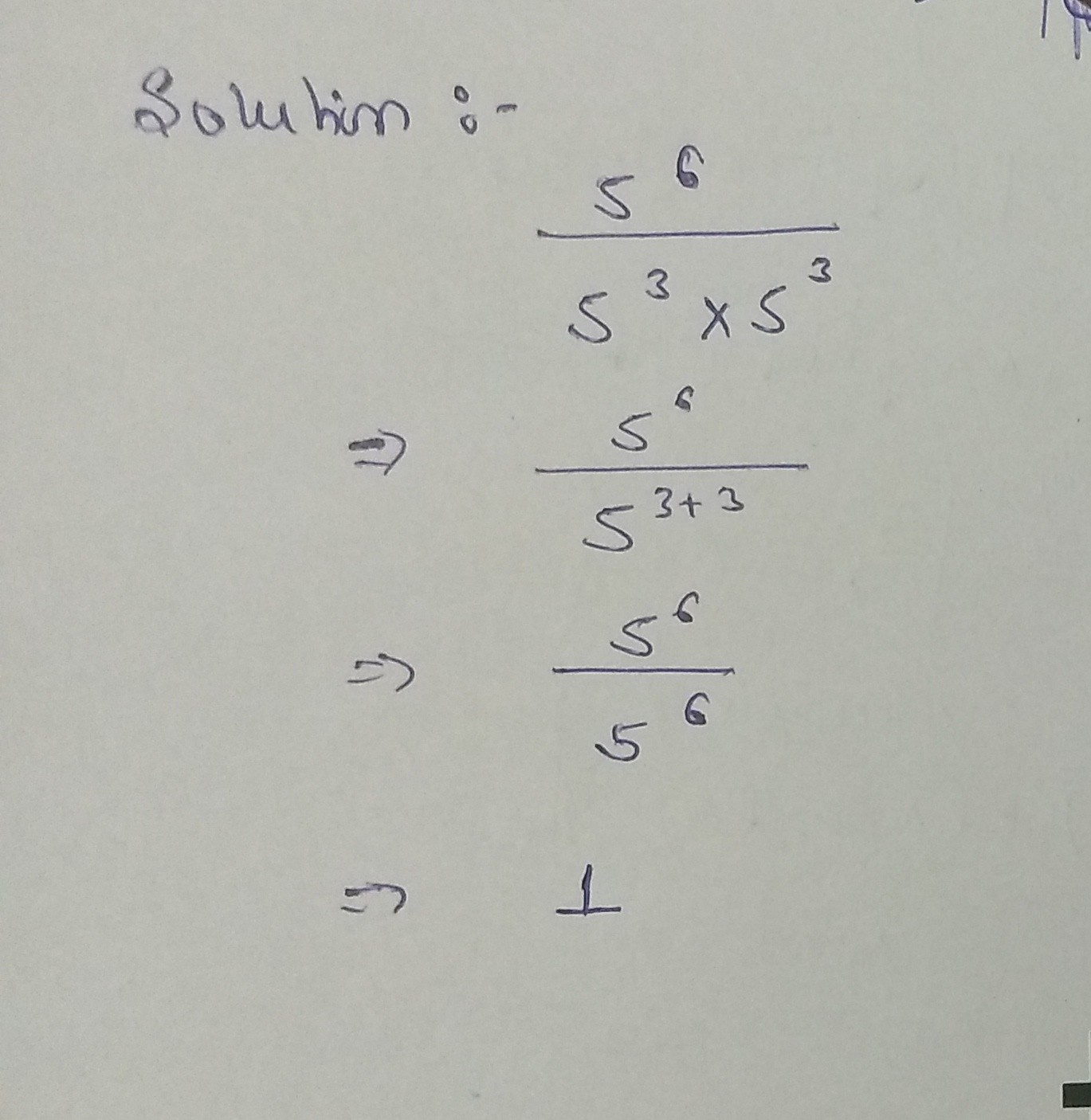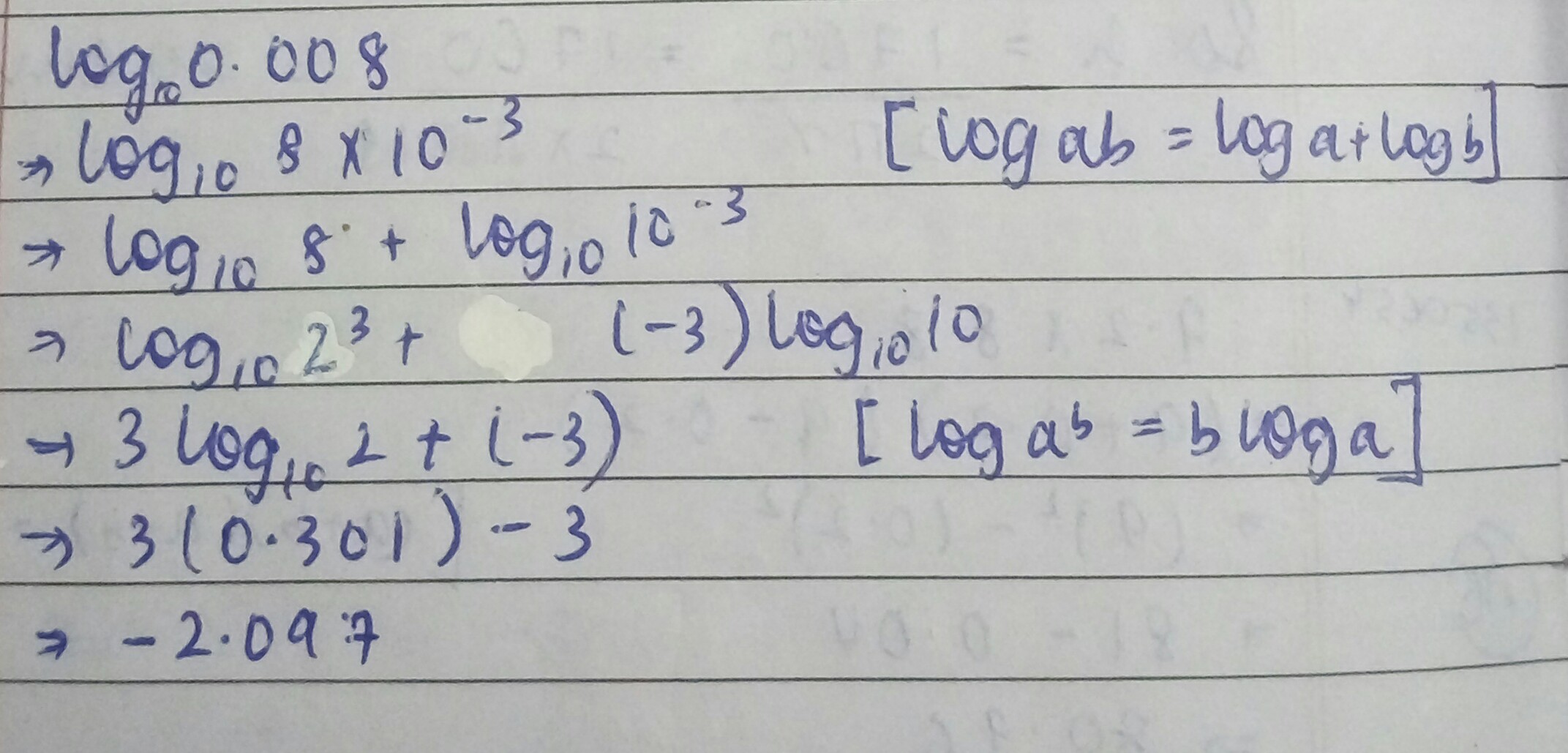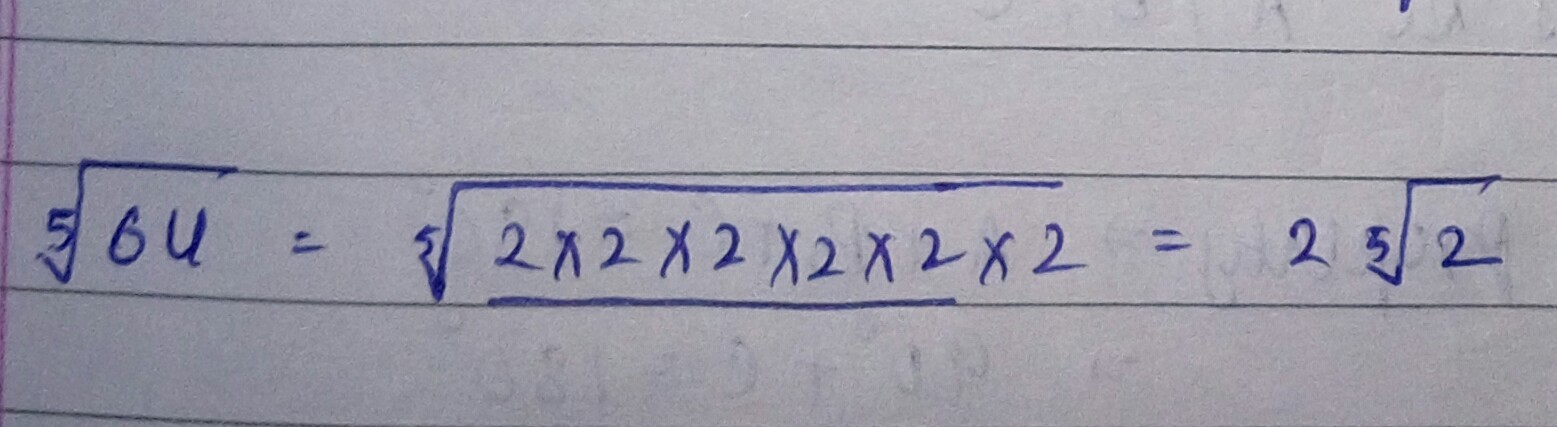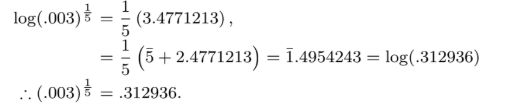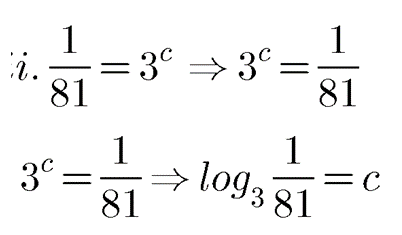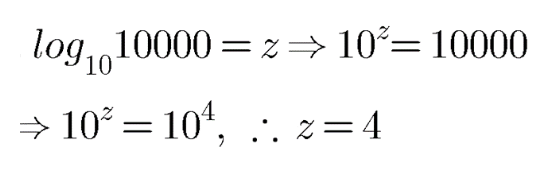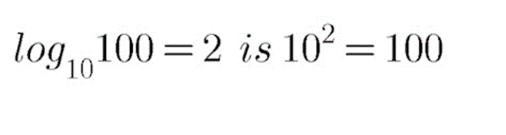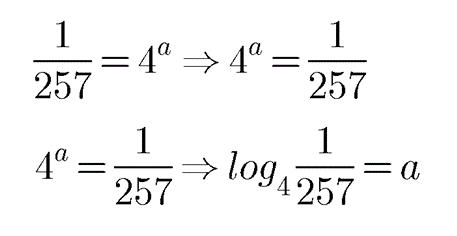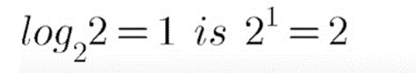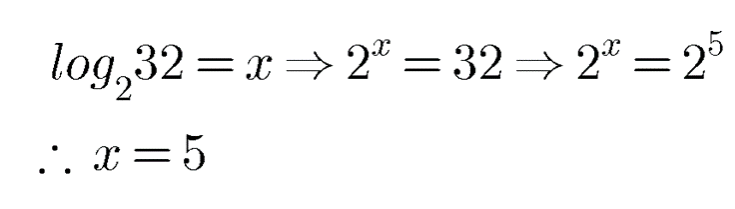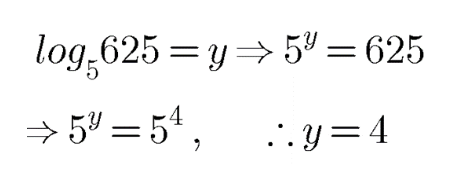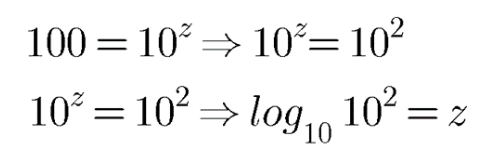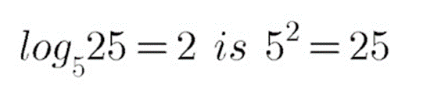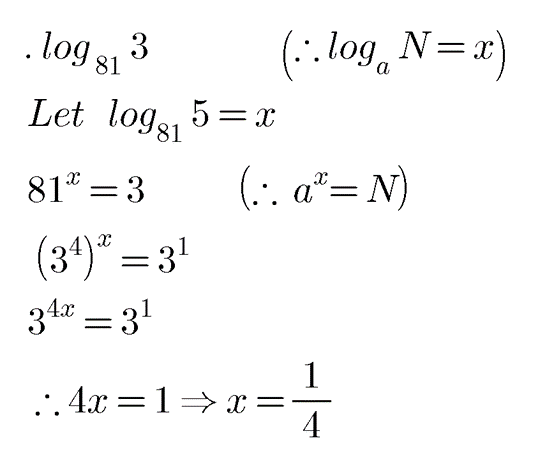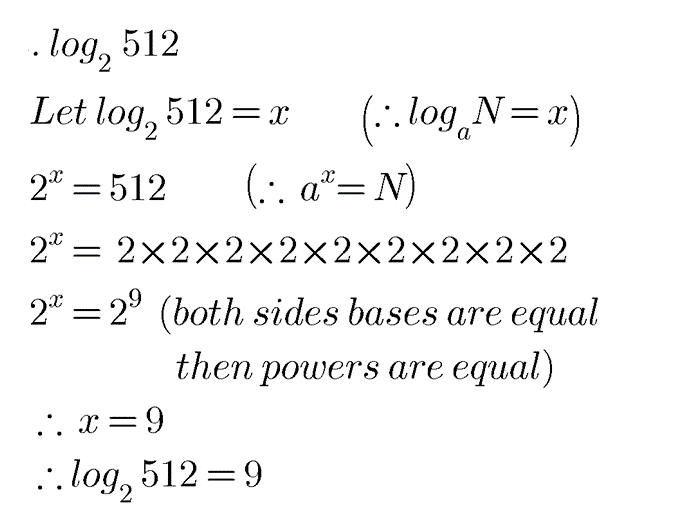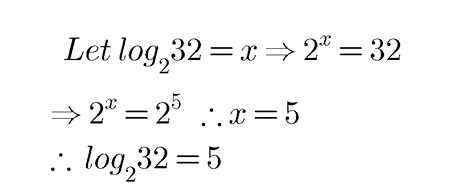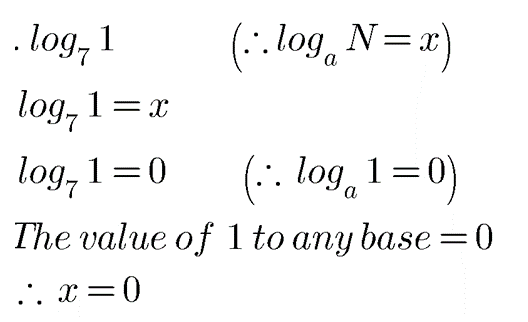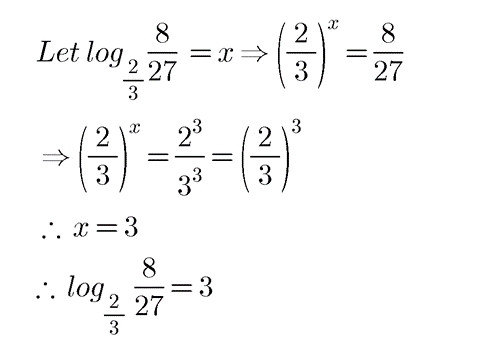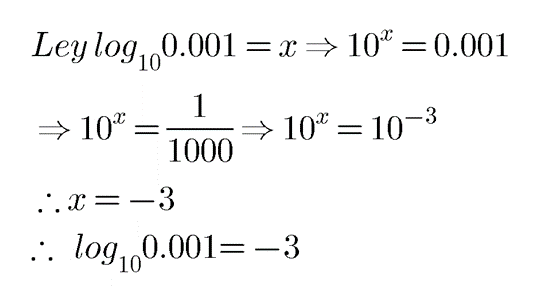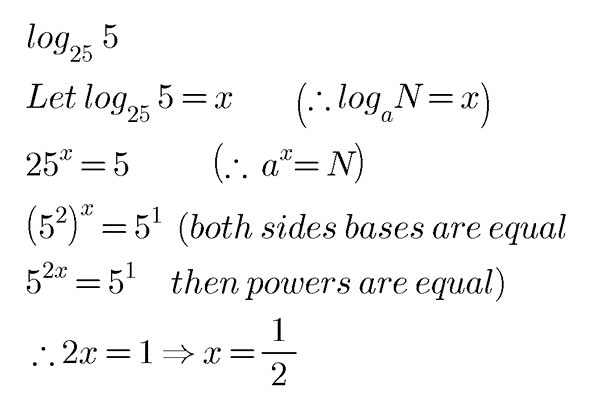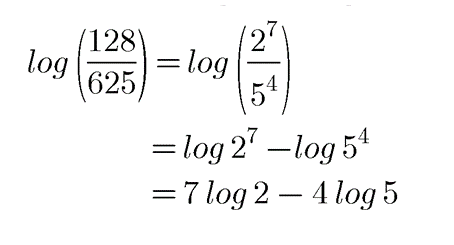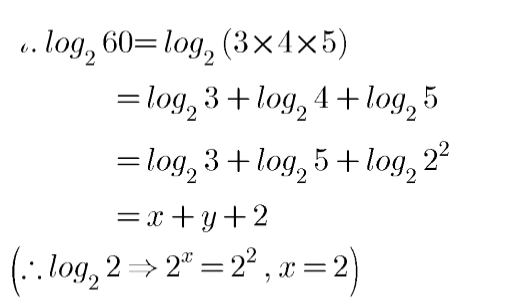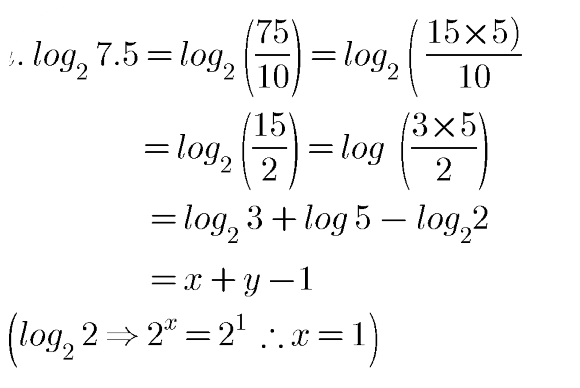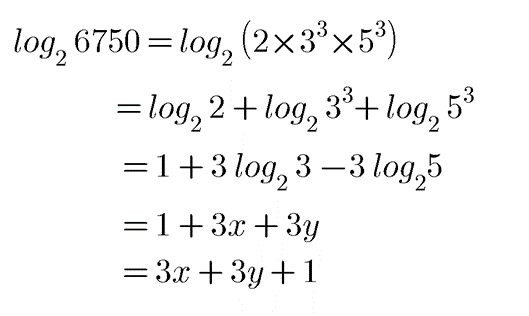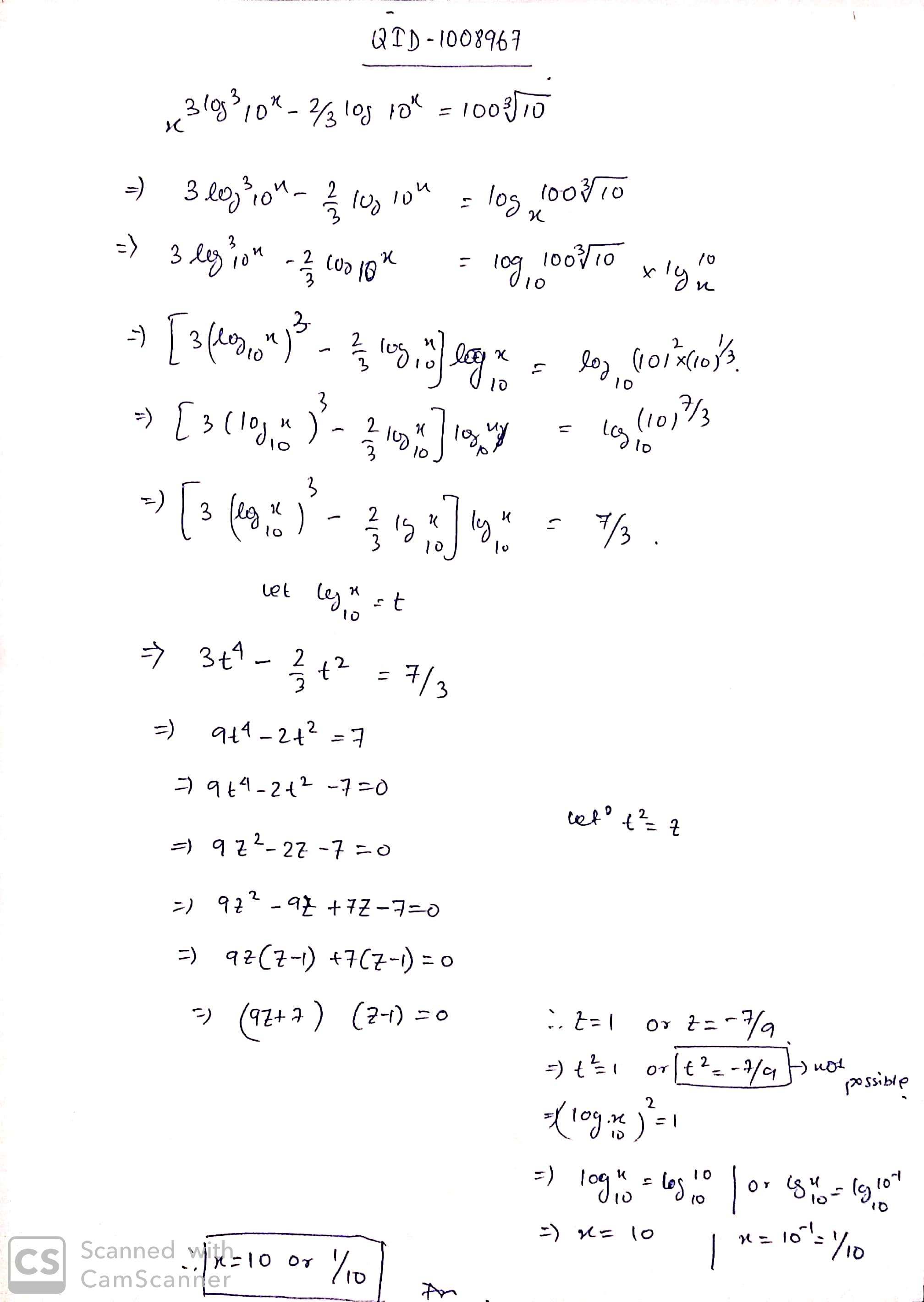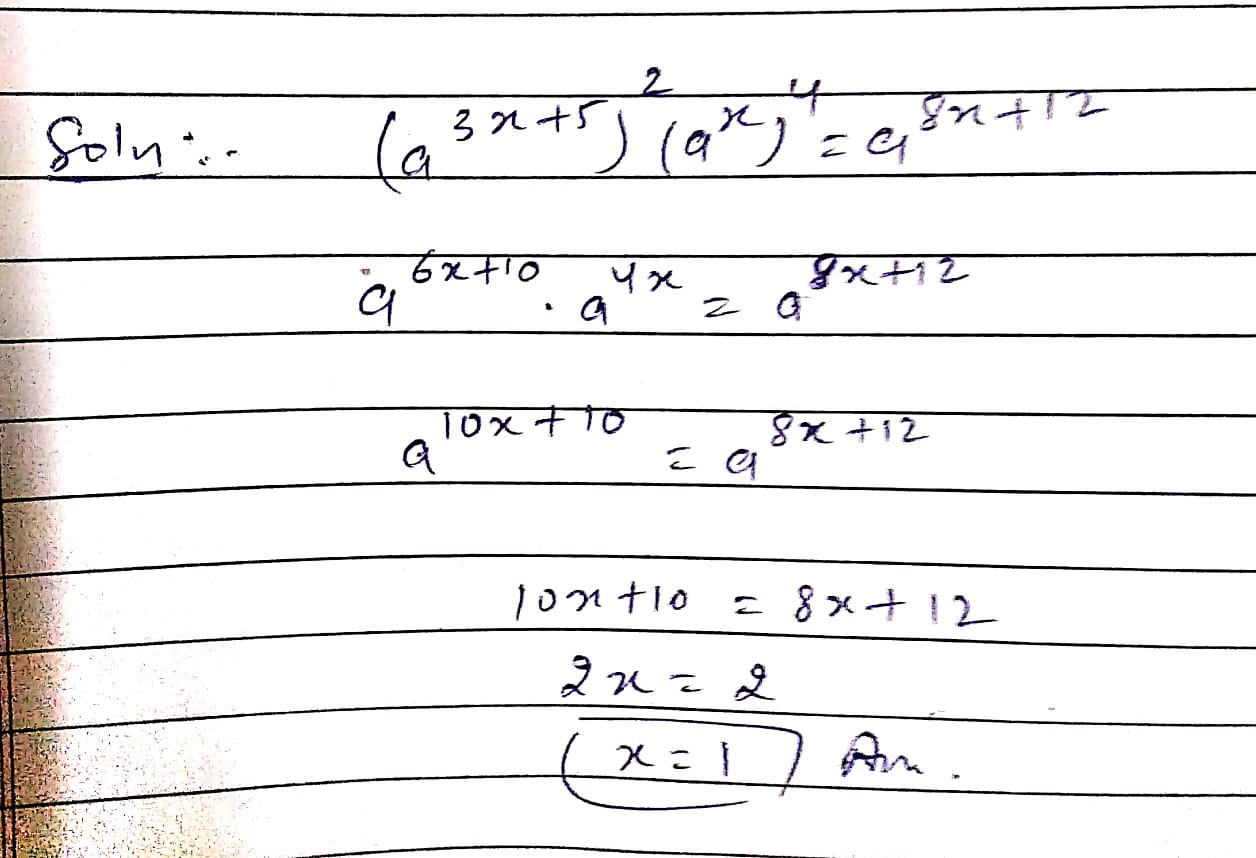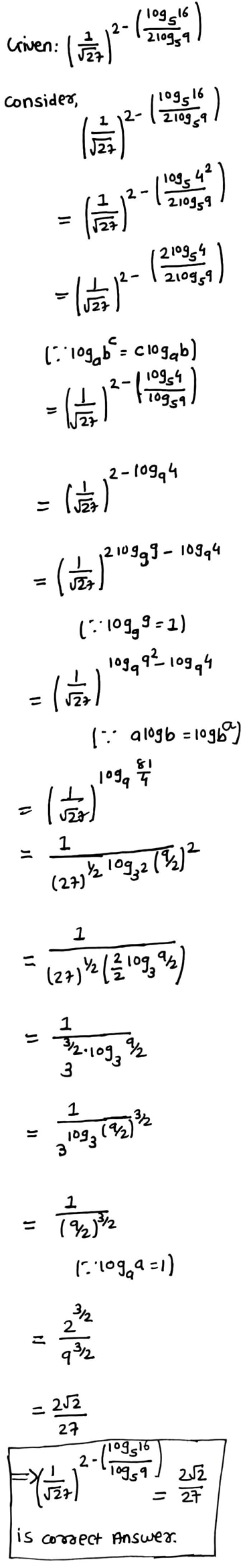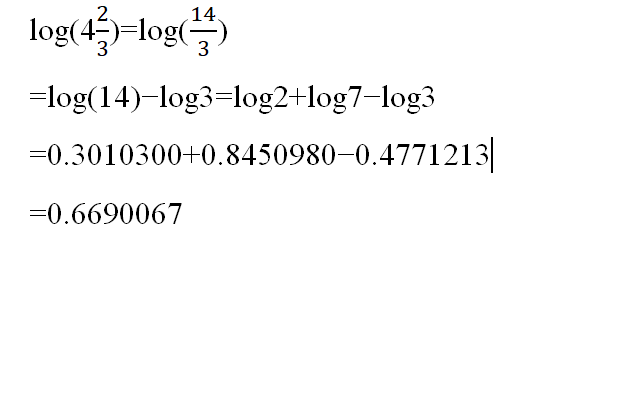Logarithm And Antilogarithm - Class 11 Commerce Applied Mathematics - Extra Questions
Write the characteristic of 1235.3 by using their standard forms:
Simplify:
$$\dfrac{8^{-1} \times 5 ^{3}}{2^{-4}}$$
If $$\displaystyle \log_{10} .001 = a$$, then $$-a$$=
Compute:
$$(4^7)^2\times (4^{-3})^4$$
Compute:
$$(\dfrac{56}{28})^0 \div (\dfrac{2}{5})^3 \times \dfrac{16}{25} $$
Compute:
$$(2^{-9}\div 2^{-11})^4 $$
Find the characteristic of the logarithm of the number $$5395.$$
$$(12)^{-2} \times 3^2 $$ is equal to $$\dfrac{1}{16} $$.
If true then enter $$1$$ and if false then enter $$0$$
Compute the absolute value of:
$$(-5)^4 \times (-5)^6 \div (-5)^{9} $$
Compute:
$$(9^0 \times 4^{1}) $$
The value of x,if $$\log_{10} x = -2$$ is $$k$$.then $$100x$$=?
Show that $$\displaystyle \left ( 2\sqrt{2} \right )^{-2/3}= \frac{1}{2}.$$ can be written as $$\displaystyle \log _{2\sqrt{2}} 2= -\frac{2}{3}$$
$$\displaystyle \log _{3}\frac{1}{243}= -5.$$
Show that $$\displaystyle 5^{0}= 1$$ can be written as $$\displaystyle \log _{25}1= 0$$
Express $$\displaystyle \log _{100}0.1= -\frac{1}{2}$$ in exponential form:
$$\displaystyle 4^{3/2}= 8$$
If $$3^{-2}$$ is $$\cfrac{1}{m}$$, then the value of $$m$$ is
If $$(-4)^{-2}$$ is $$\cfrac{1}{m}$$, then the value of $$m$$ is
Find the value of: $$(3^0 + 4^{-1}) \times 2^2$$
Evaluate $$\displaystyle \left ( \frac{5}{8} \right )^{-7} \times \left ( \frac{8}{5} \right )^{-4}$$ is $$ \frac { 512 }{m } $$
Value of $$m$$ is
Evaluate $$(5^{-1} \times 2^{-1}) \times 6^{-1}$$ is $$\frac{1}{m}$$
Value of $$m$$ is
Evaluate $$\displaystyle \frac{8^{-1} \times 5^3}{2^{-4}}$$
Find the value of $$m$$ for which $$5^m \div 5^{-3} = 5^5$$
Evaluate: $$-\displaystyle \left \{ \left ( \frac{1}{3} \right )^{-1} - \left ( \frac{1}{4} \right )^{-1} \right \}^{-1}$$
Find $$x$$, if $$(4^{-1} + 8 ^{-1} ) \times (3^{-1} - 9^{-1}) \div \displaystyle \frac{1}{12} = 5^x$$
By what number should $$\displaystyle \left ( \frac{-2}{3} \right )^{-3}$$ be divided so that the quotient may be $$\displaystyle \left ( \frac{4}{27} \right )^{-2}$$
Simplify: $$\left(\cfrac{3}{2} \right)^{0} \times \left(\cfrac{4}{5}\right)^{-2}$$
Simplify : $$\displaystyle \frac{25 \times t^{-4}}{5^{-3} \times 10 \times t^{-8}} (t \neq 0)$$
Simplify: $$3^0 +2^{-2}$$
Simplify $$\displaystyle \left [ \left ( \frac{2}{3} \right )^{-1} \times \left ( \frac{3}{4} \right )^{-1} \right ]^{-1}$$
Find the value $$\displaystyle 27^{\cfrac{1}{3} } \times 16^{\cfrac{-1}{4} }$$
By what number should $$\displaystyle \left ( \frac{3}{4} \right )^{-3}$$ be divided so that the quotient becomes $$128$$ ?
Find the value $$(512)^{\frac{-2}{9}} $$
For what negative values of $$x$$, will $$x^{18}$$ be equal to $$x^{20}$$?
For what positive values of $$x$$, will $$x^{18}$$ be greater than $$x^{20}$$?
For what negative values of $$x$$, will $$x^{20}$$ be greater than $$x^{18}$$?
If $$\displaystyle \log_{3}a=4$$, then find the value of $$a$$.
Find the value of x if $$x^3 = \displaystyle \left ( \frac{6}{5} \right )^{-3} \times \left ( \frac{6}{5} \right )^6.$$
$${ 3 }^{ 3 }\times { 3 }^{ 6 }\times { 3 }^{ 7 }=$$?
Suppose $$m$$ and $$n$$ are distinct integers. Can $$\cfrac { { 3 }^{ m }\times { 2 }^{ n } }{ { 2 }^{ m }\times { 3 }^{ n } } $$ be an integer? Give reasons.
$${ 2 }^{ 5 }\times { 5 }^{ 2 }\times { 2 }^{ 3 }\times 5=$$?
$$ { 2 }^{ 5 }\times { 2 }^{ 6 }=2^?$$
Simplify:
$${ 3 }^{ 1 }\times { 3 }^{ 2 }\times { 3 }^{ 3 }\times { 3 }^{ 4 }\times { 3 }^{ 5 }\times { 3 }^{ 6 }$$
Simplify:
$${2}^{2}\times {3}^{3}\times {2}^{4}\times {3}^{5}\times {3}^{6}$$
Simplify and give reasons:
$${ \left[ \left( { 3 }^{ 2 }-{ 2 }^{ 2 } \right) \div \cfrac { 1 }{ 5 } \right] }^{ 2 }$$
Rakesh solved some problems of exponents in the following way. Do you agree with the solutions? If not why? Justify your argument.
$${ x }^{ -3 }\times { x }^{ -2 }={ x }^{ -6 }$$
Find the value of '$$n$$' in the following:
$${ \left( \cfrac { 2 }{ 3 } \right) }^{ 3 }\times { \left( \cfrac { 2 }{ 3 } \right) }^{ 5 }={ \left( \cfrac { 2 }{ 3 } \right) }^{ n-2 }\quad $$
If $$\log_{2}x = 3$$, then $$x =$$ ______
Find the value of '$$x$$' such that
$$\cfrac{1}{49}\times {7}^{2x}={7}^{8}$$
Using logarithmic table find the value of the following.
(i) $$\log { 23.17 }$$
(ii) $$ \log { 9.321 }$$
(iii) $$ \log { 329.5 } $$
(iv) $$\log { 0.001364 } $$
(v) $$\log { 0.9876 }$$
(vi) $$ \log { 6576 } $$
Find, by inspection, the characteristics of the logarithms of $$21735, 23.8, 350, .035, .2, .87, .875$$.
Given $$\log 2 = .3010300, \log 3 = .4771213, \log 7 = .8450980$$, find the value of $$\log \sqrt [3]{12}$$.
Given $$\log 2 = .3010300, \log 3 = .4771213, \log 7 = .8450980$$, find the value of $$\log 14.4$$.
Given $$\log2 = {^{.}3010300}, \log3 = {^{.}4771213}, \log7 = {^{.}8450980},$$ find the value of
$$\log 84$$.
Given $$\log 2 = .3010300, \log 3 = .4771213, \log 7 = .8450980$$, find the value of $$\log 4\dfrac{3}{2}$$.
Given $$\log2 = {^{.}3010300}, \log3 = {^{.}4771213}, \log7 = {^{.}8450980},$$ find the value of
$$\log {^{.}128}.$$
Given $$\log2 = {^{.}3010300}, \log3 = {^{.}4771213}, \log7 = {^{.}8450980},$$ find the value of
$$\log 64$$.
Give the position of the first significant figure in the numbers whose logarithms are
$$\bar{2} {^{.}7781513}, {^{.}6910815}, \bar{5} {^{.}4871384}.$$
How many digits are there in the integral part of the numbers whose logarithms are respectively
$$4{^{.}30103}, 1{^{.}4771213}, 3{^{.}69897}, {^{.}56515}?$$
Given $$\log2 = {^{.}3010300}, \log3 = {^{.}4771213}, \log7 = {^{.}8450980},$$ find the value of
$$\log {^{.}0125}.$$
Given $$\log2 = {^{.}3010300}, \log3 = {^{.}4771213}, \log7 = {^{.}8450980},$$ find the value of
$$\log \sqrt[4]{^{.}0105}.$$
Find the product of $$37.203, 3.7203, .037203, 372030$$, having given that
$$\log 37.203 = 1.5705780$$, and $$\log 1915631 = 6.2823120$$.
Evaluate : $$2^5\times 2^8\div 2^6$$
Given $$\log2 = {^{.}3010300}, \log3 = {^{.}4771213}, \log7 = {^{.}8450980},$$ find the value of
$$\log \sqrt{\dfrac{35}{27}}.$$
Solve the following equations.
$$\displaystyle log_2 \, (4^x \, + \, 4) \, - \, log_2 \, (2{x \, + \, 1} \, - \, 3) \, = \, 0.$$
Write value of $$\sqrt [ 3 ]{ 2 } \times \sqrt [ 4 ]{ 2 } \times \sqrt [ 12 ]{ 32 } $$
Solve the following equation:
$$\displaystyle\, 5^{x - 1} = 10^x\cdot 2^{-x}\cdot 5^{x + 1}$$
Rewrite the following equation in the logarithm from :
$$5^0 \, = \, 1$$
Rewrite the following equation in the logarithm from :
$$(2\sqrt{2})^{-2/3} \, = \, \dfrac{1}{2}.$$
Rewrite the following equation in the exponential form.
$$log_{5\sqrt{5}} \, 5 \, = \, \dfrac{2}{3}$$
Rewrite the following equation in the exponential form.
$$log_{100} \, 0.1 \, = \, -\dfrac{1}{2}$$
Solve $$x^{\sqrt{x}} \, = \, (\sqrt {x})^x$$
Find the value of $${(23.17)^{{1 \over {5.76}}}}$$ using log table.
Rewrite the following equation in the exponential form.
$$\log_3 \, \frac{1}{243} \, = \, -5.$$
Evaluate : $${2^{{{\log }_3}5}} - {5^{{{\log }_3}2}}$$
$${ \left[ { \left( \dfrac { 15 }{ 12 } \right) }^{ 3 } \right] }^{ 4 }$$
If $$x=243$$, then find the value of $${x^{\frac{1}{5}}} \times {x^{ - \frac{1}{5}}}$$
Solve: $$\log (3x + 2) + \log (3x - 2) = \log5$$
Convert the following to logarithmic form:
$$5^{2} =25$$
If $$X^\cfrac{a}{b} =1, $$ then find the value of $$'a'$$.
Find the value of x for which
$${\left( {{3 \over 4}} \right)^6} \times {\left( {{{16} \over 9}} \right)^5} = {\left( {{4 \over 3}} \right)^{x + 2}}$$
Simplify:
$$\log_{10}5 + 2\log_{10}4$$
Find the value of $$x$$ for which $${ \left( \dfrac { 5 }{ 3 } \right) }^{ -4 }\times { \left( \dfrac { 5 }{ 3 } \right) }^{ -5 }={ \left( \dfrac { 5 }{ 3 } \right) }^{ 3x }$$
$$[(64)^{-2}]^{-3} \div [{(-8)^{2}}^{3}]^{2}$$
Simplify :
$$\left[ \left( \dfrac { 1 }{ 2 } \right) ^{ -3 }+\left( \dfrac { 1 }{ 3 } \right) ^{ -3 }+\left( \dfrac { 1 }{ 4 } \right) ^{ -3 } \right]$$
If $$\log_{10}4=0.6021$$ and $$\log_{10}5=0.6990$$, then find the value of $$\log_{10}1600$$.
Express $$\log_{10}\sqrt[5]{108}$$ in terms of $$\log_{10}2$$ and $$\log_{10}3$$.
Using log tables, calculate $$\frac{{24.18 \times 0.004592}}{{0.09588 \times 3.7619}}$$
Find the value of $$x$$ for which $$\left\{ \left( \dfrac { -2 }{ 7 } \right) ^{ 2 } \right\} ^{ x } \times \left( \dfrac { -7 }{ 2 } \right) ^{ 2 } = \dfrac{-8}{343}$$.
Evaluate $${a^6} \div {a^4}$$
Find $$x$$ if $${4^{2x}} = \dfrac{1}{{32}}$$
Show that $$\log_{b^3}a\times \log_{a^3}b\times\log_{a^3}c=\dfrac{1}{27}$$.
Simplify
$${\left( {\frac{{81}}{{16}}} \right)^{\frac{8}{4}}} \times \left[ {{{\left( {\frac{{25}}{4}} \right)}^{ - \frac{3}{2}}} \div {{\left( {\frac{5}{2}} \right)}^{ - 3}}} \right]$$
Simplify : $${\left[ {5{{\left( {{8^{\frac{1}{3}}} + {{27}^{\frac{1}{3}}}} \right)}^3}} \right]^{\frac{1}{4}}}$$
Solve $${\left( {\sqrt[3]{{\dfrac{2}{3}}}} \right)^{x - 1}}\, = \dfrac{{27}}{8}$$
Simplify :
$$\dfrac{{{8^{3a}} \times {2^5} \times {2^{2a}}}}{{4 \times {2^{11a}} \times {2^{ - 2a}}}}$$
Find the value of $$log_7343$$.
Let factorise 343. we get
So,$$ 343 = 7 \times 7 \times 7 $$
$$ 343 = 7^{3}$$
So, $$log_{7}343 = log_{7}7^{3}$$
now, as we know, $$ log_{a}b^{n} = n log a^{b}$$
& If $$ log_{a}^{a}$$ is given, then
$$ log_{a}^{a} = 1 $$
So, $$ log_{7}343 = log_{7}7^{3} = 3 log_{7}7 $$
therefore, $$\boxed{log_{7}343 = 3} $$
Find the value of $${ \log }_{ 10 }\dfrac { 76 }{ 3.8 } $$
Evaluate:-
$${\left( {\frac{2}{7}} \right)^2}\, \times \,{\left( {\frac{7}{2}} \right)^{ - 3}}\, \div \,\,{\left\{ {{{\left( {\frac{7}{5}} \right)}^{ - 2}}} \right\}^{ - 4}}$$
Solve: $$(64)^{\dfrac{2}{3}} + 9^{\dfrac{3}{2}}$$.
$${\left( {\frac{4}{5}} \right)^2}\, \times \,{5^4}\, \times \,{\left( {\frac{2}{5}} \right)^{ - 2}}\, \div \,{\left( {\frac{5}{2}} \right)^{ - 3}}$$
Using laws of exponents, simplify and write the answer in exponential form:
(i) $$3^2 \times 3^4 \times 3^8$$ (ii) $$\dfrac{6^{15}}{6^{10}}$$
Solve
$$\log_{\frac{1}{3}}(x^2 + 8) = -2$$
Solution of $$3^{3x-5}=\frac{1}{9^x}$$ is
If $$log_2 x=a$$ and $$log_5y=a$$, write $$100^{2a-1}$$ in terms of x and y.
Determine the value of $${3^2} -\{ {\log}3\}^6$$
Simplify:$$\left[(64)^{-3}\times (81)^{-\frac{9}{4}}\right]^{-\frac{1}{9}}$$
Simplify:
$$\dfrac{{3 \times {7^2} \times {{11}^8}}}{{21 \times {{11}^3}}}$$
Simplify: $$a^3 \times a^3 \times 5a^4$$.
$${5^{x - 3}}\,\,\, \times \,{3^{2x - 8}} = 225$$
Solve $${\left( { - \frac{3}{5}} \right)^{ - 3}}$$
Simplify $$\log c\sqrt c $$
Find the zeroes of the polynomial $$p\left( x \right) = x - \log _2{16}$$.
Solve: $$\dfrac{{{3^5}\times{{10}^5}\times25}}{{{5^7}\times{6^5}}}$$
Given $$log_{10}x=2a$$ and $$log_{10}y=\dfrac{b}{2}$$. Write $$10^a$$ in terms of x.
Given $$log_{10}x=2a$$ and $$log_{10}y=\dfrac{b}{2}$$, write $$10^{2b+1}$$ in terms of y.
$$log\dfrac{75}{16}-2log\dfrac{5}{9}+log\dfrac{32}{243}=log 2$$.
Find $$\log _{ 7 }{ 1 } $$
Express the following in exponential form.
$$\dfrac{5}{6}\times \dfrac{5}{6}\rightarrow \left(\dfrac{5}{6}\right)^2$$.
Solve:
$$\displaystyle {\left\{ {{{\left( {\frac{1}{3}} \right)}^{ - 1}} - {{\left( {\frac{1}{4}} \right)}^{ - 1}}} \right\}^{ - 1}}$$
Simplify : $$4\sqrt{16} - 6\sqrt[3]{343} + 18 \sqrt[5]{243} - \sqrt{196}$$
value of ln10?
Solve $${(3.968)^{\frac{3}{2}}}$$
Solve :
$$\log M = \log {\left( {0.9} \right)^{20}}$$
If $${\left( {2.381} \right)^x} = {\left( {0.2381} \right)^y} = {10^z}$$ , then find the value of $$\frac{1}{y} + \frac{1}{z} - \frac{1}{x}$$
What will be the value of $$log_2 \ (log_3 \ 81)$$?
Find the value of $$\log_{2}{32}$$.
$$log_{\dfrac12}8=?$$
If $$log_{10}8=0.90$$ find the value of :
(i) $$log_{10}4$$
(ii) $$log\sqrt{32}$$
(iii) $$log \ 0.125$$
Compute the following
$$7^{\log_{3}5}+5^{\log_{5}7}-5^{\log_{3}7}-7^{\log_{5}3}$$
$$7^{log_3^5}+5^{log_5^7}-5^{log_3^7}-7^{log_5^3}$$
$$=5^{log_3^7}+7^{log_5^5}-5^{log_3^7}-7^{log_5^3}$$
$$=7-7^{log_5^3}$$.
Using laws of exponents, simplify and write the answer in exponential form:
(i) $${7}^{x}\times {7}^{2}$$
(ii) $${2}^{5}\times {5}^{5}$$
(iii) $${a}^{4}\times {b}^{4}$$
Using laws of exponents, simplify and write the answer in exponential form:
(i) $${3}^{2}\times {3}^{4}\times {3}^{8}$$
(ii) $${6}^{15}\div {6}^{10}$$
(iii) $${a}^{3}\times {a}^{2}$$
Evaluate the following
$$\dfrac {\left(\dfrac {12}{13}\right)^{5}\times \left(\dfrac {-1}{3}\right)}{\dfrac {1}{81}\times \left(\dfrac {12}{13}\right)^{3}}$$
Find the value of
$$log5.4$$
simplify :
$${\left( {{3^4}} \right)^3}$$
Solve: $$\dfrac{3^2 \times 3^2 \times 2^2}{3^2 \times 6}$$
Simplify the following using laws of exponents.
$${9^2} \times {9^{18}} \times {9^{10}}$$
Simplify the following using laws of exponents.
$$({3^2}) \times {({3^2})^4}$$
Apply laws of exponents and simplify.
$$(3^{0}\times2^{5})+5^{0}$$
simplify:
$$\left( {\frac{{{2^{20}}}}{{{2^{15}}}}} \right) \times {2^3}$$
Simplify the following using laws of exponents.
$${2^{10}} \times {2^4}$$
Solve :$$\dfrac{(3^5)^2\times 7^3}{(3^3)^3 \times 7^2}$$
If $$\log _{ 10 }{ 2 } =0.3010$$, then $$\log _{ 10 }{ 50 } $$ is
Find the value of $$\log_{\sqrt{3}}81$$.
$$log^{(81)}_{(\sqrt{3})}$$
$$=log^{3^4}_{(\sqrt{3})}$$
$$=log^{(\sqrt{3})^8}_{\sqrt{3}}$$
$$=8 log^{\sqrt{3}}_{\sqrt{3}}$$
$$=8[\because log^a_a=1$$ for $$a > 1]$$.
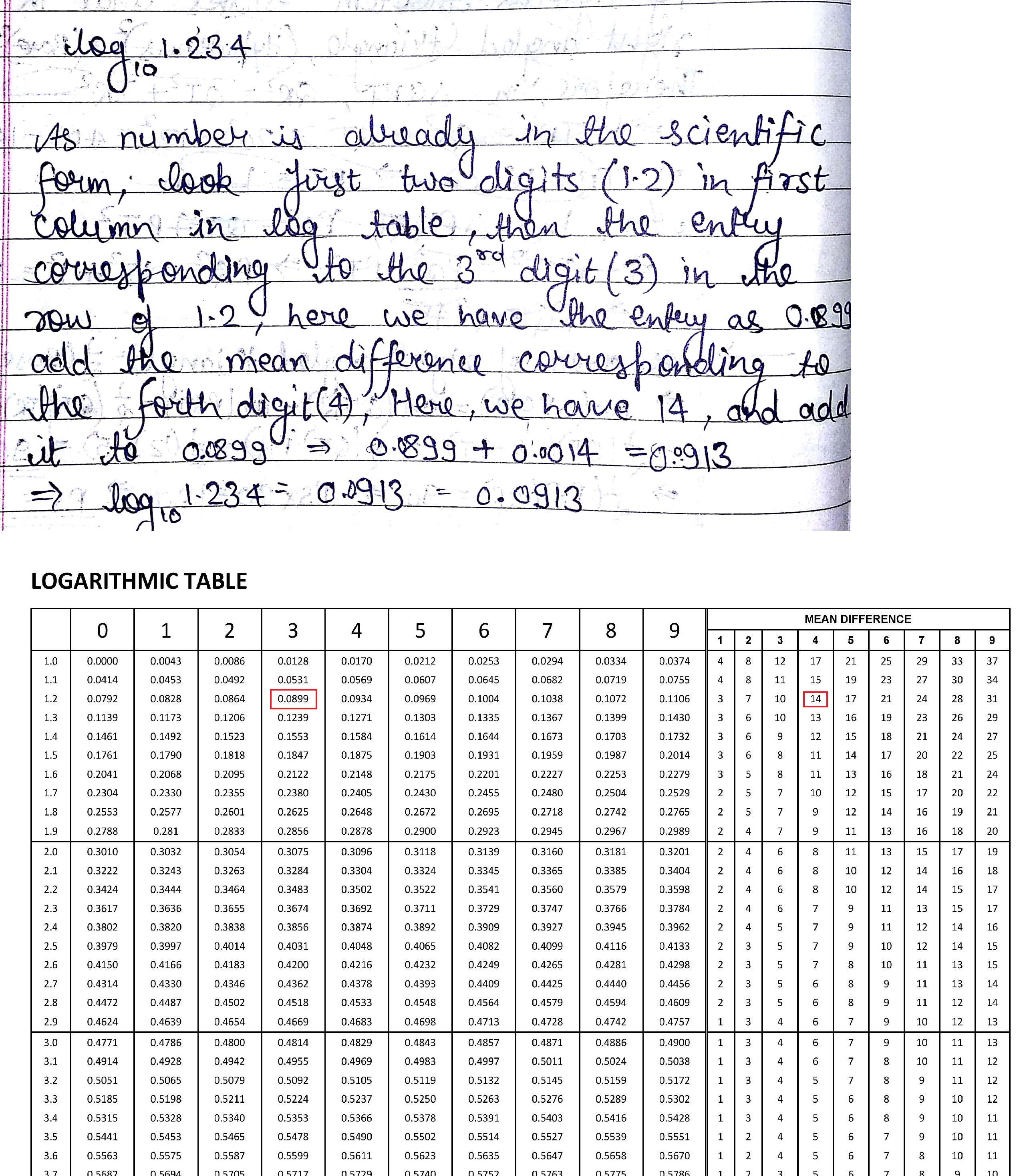
Using the log table find the value of $$1.234$$.
$$log_{10}1.234$$
As number is already in the scientific form, look first two digits $$(1.2)$$ in first column in log table, then the entry corresponding to the $$3^{rd}$$ digit $$(3)$$ in the row of $$1.2$$, here we have the entry as $$0.899$$ add the mean difference corresponding to the forth digit $$(4)$$, Here, we have $$14$$, and add it to $$0.899\Rightarrow 0.899+0.0014=0.0913$$
$$\Rightarrow log_{10}1.234=0.0913=0.0913$$.
Solve $$\left( 3 ^ { - 7 } \div 3 ^ { - 10 } \right) \times 3 ^ { - 5 }$$
Find the value of $$[\{(a^3)^{-3}\}^0]^{100}$$.
If $${\log _{10}}8 = 0.90$$
find $$\log 0.125$$
Given : $$ log_{10}8 = 0.90.$$
$$ \frac{1}{8}\times 8 = 1$$
$$ \Rightarrow (0.25) \times 8 = 1$$
apply log on both sides.
$$ \Rightarrow log_{10}(0.125)+log_{10}(8) = log_{10}(1)$$
$$ \Rightarrow log_{10}(0.125) = 0-log_{10}(8)$$
$$ \Rightarrow log_{10}(0.125) = -(0.9)$$
If $${\log _{10}}8 = 0.90;$$ find the value of :a)$${\log _{10}}4$$b)$$\log \sqrt {32} $$c)$$\log 0.125$$
$$a^{m}.a^{n}=$$
Find the value of the following.
$$4^{4}$$
Solve the exponent
$${17^2} \cdot {17^{ - 5}}$$
By what number should $$( - 6 ) ^ { - 2 }$$ be multiplied so that the product would be equal to $$( 9 ) - 1 .$$ ?
$$(-\dfrac{3}{4})^{11}\div [ (-\dfrac{3}{4})^{3}\times (-\dfrac{3}{4}^{6}) ] $$
$$=\left(-\dfrac{3}{4}\right)^{11}\div \left[\left(-\dfrac{3}{4}\right)^3\times \left(-\dfrac{3}{4}\right)^6\right]$$
$$=\left(-\dfrac{3}{4}\right)^{11}\div \left(-\dfrac{3}{4}\right)^{3+6}$$
$$=\left(-\dfrac{3}{4}\right)^{11}\div \left(-\dfrac{3}{4}\right)^{9}$$
$$=\left(-\dfrac{3}{4}\right)^{11-9}=\left(-\dfrac{3}{4}\right)^2$$
$$=\dfrac{(-3)\times (-3)}{4\times 4}=\dfrac{9}{16}$$.
Given:$$\log{2}=0.3010$$ and $$\log{3}=0.4771$$, find the value of $$\log{12}$$.
Find the value of y if : $$(100)^2\times(10)^5=(1000)^y$$
Find the value of $$m$$ if :
$$\left( \dfrac { 2 }{ 9 } \right)^3 \times \left( \dfrac { 2 }{ 9 } \right)^{-6} =\left( \dfrac { 2 }{ 9 } \right)^{2m-1}$$
Simplify the following using laws of expressions
$$(2x)^{4}\div (2x)^{2}$$
Determine the value of the following
$$\log_{7}{1}$$
$$ log_{7}1= \frac{log1}{log7} = 0$$
Express as a power of $$3$$ in $$729$$ and $$343$$.
Find the value of $$(x^{3}\times x^{7})\div x^{12}$$ for x = (-2).
$$(x^3+x^7)\div x^{12}$$ for $$x=-2$$
$$x^{10}\div x^{12}=\dfrac{x^{10}}{x^{12}}=\dfrac{1}{x^2}$$
For $$x=-2$$
$$=\dfrac{1}{(-2)^2}=\dfrac{1}{4}$$.
Find the value $$x$$ if $${2^4}*{2^5} = {({2^3})^x}$$
$$2^{4}\times 2^{5}=(2^{3})^{x}$$
but $$ m^{x}\times m^{y}=m^{x+y}$$
$$\therefore 2^{4+5}=2^{3x}$$
$$\Rightarrow 2^{9}=2^{3x} {\Rightarrow }3x=9\Rightarrow x=3$$
Determine the value of the following
$$\log_{10}{0.01}$$
$$ log_{10}0.01 = log_{10}10^{-2}$$
$$ = -2 log^{10}10 $$
$$ = -2 $$
If $$log_{10}0.001 =x$$, then find $$x$$.
If $$x ^ { 2 } + y ^ { 2 } = 47 x y$$ then show that $$\log \left( \dfrac { x + y } { 7 } \right) = \dfrac { 1 } { 2 } ( \log x + \log y ).$$
Find the value of $$log_{2\sqrt{3}}1728$$
Let $$y =log _{2\sqrt{3}}(1728)$$.
we know that $$1728= 64\times 24$$
$$(2)^{6}\times (\sqrt{3})^{6}=(2\sqrt{3})^{6}$$
then
$$y = log _{2\sqrt{3}}$$ $$(2\sqrt{3})^6$$
$$y=6 log_{2\sqrt{3}}$$ $$(2\sqrt{3})$$ $$ [log _{x }x=1]$$
$$[y=6]$$.
Solve : $$\left( 6 ^ { - 1 } - 8 ^ { - 1 } \right) ^ { - 1 } + \left( 2 ^ { - 1 } - 3 ^ { - 1 } \right) ^ { - 1 }$$
Solve $$\dfrac { 5.6\times { 10 }^{ 6 } }{ { 3\times 10 }^{ -4 }(1.76\times { 10 }^{ 11 }) } $$
$$r =\frac{5.6\times10^{6}}{3\times 10^{-4}(1.76\times10^{11})}$$
$$=\frac{5.6\times10^{6}\times10^{4}}{3\times1.76\times10^{11}}$$
$$=\frac{5.6\times10^{10}}{3\times1.76\times10^{11}}$$
$$=\frac{5.6}{3\times 1.76\times 10}$$
$$=\frac{5.6}{52.8}$$
=0.106(approx)
Find the product: $$a^{2} \times 2a^{22} \times 4a^{26}$$.
Solve : $$\sqrt { \dfrac { 256 a ^ { 4 } b ^ { 4 } } { 625 a ^ { 6 } b ^ { 2 } } } = ?$$
Using laws of exponents, simplify and write the answer in exponential form: $$\left( { 3 }^{ 4 } \right) ^{ 3 }$$
Find the product : $$\left( \dfrac { 1 } { 2 } p ^ { 3 } q ^ { 6 } \right) \left( - \dfrac { 2 } { 3 } p ^ { 4 } q \right) \left( p q ^ { 2 } \right).$$
If $${ (0.2) }^{ x }=2$$ and $${ \log }_{ 10 }2=0.3010$$, then what is the value of $$x$$
$$y={ log }_{ 10}x$$ then $$x=$$
Evaluate $$\log_2 128+\log _3 243$$
Evaluate:\log_{\frac{1}{100}}{\dfrac{1}{10000}}
$${ \left( \frac { -1 }{ 2 } \right) }^{ 2 }=\frac { 1 }{ { 2 }^{ m } } $$
$$(-\frac{1}{2})^{2}=\frac{1}{2^{m}}$$
$$\frac{1}{2^{2}}=\frac{1}{2^{m}}$$
$$\Rightarrow 2^{m}=2^{2}$$
$$\therefore m=2$$
Evaluate:$$\log_{49}{343}$$
Show that $$\log{\left(\dfrac{243}{343}\right)}=5\log{3}-3\log{7}$$
Solve:
$$3^{x+1}=27\times 3^{4}$$
Solve: $$\dfrac{25\times t^{-4}}{5^{-3}\times 10\times t^{-8}}$$
Simplify
$${ 32 }^{ 1 }={ 2 }^{ x }$$
$$32^1=2^x$$
$$\Rightarrow (2)^5=2^x$$
$$\Rightarrow$$ Comparing powers
$$x=5$$.
Simplify $$\sqrt [3]{4}\times \sqrt [3]{16}$$
Simplify : $$\dfrac{2^3 .3^4. 4}{3 .32}$$
Express each of the following exponential expressions as a rational number. $${ \left( \dfrac { 2 }{ 3 } \right) }^{ \left( -1 \right) }+{ \left( \dfrac { 3 }{ 2 } \right) }^{ \left( -2 \right) }$$
$$\left(\dfrac{2}{3}\right)^{-1}+\left(\dfrac{3}{2}\right)^{-2}$$
$$\Rightarrow \dfrac{3}{2}+\left(\dfrac{2}{3}\right)^2$$
$$\Rightarrow \dfrac{3}{2}+\dfrac{4}{9}$$
$$\Rightarrow \dfrac{27+8}{18}=\dfrac{35}{18}$$.
For $$a=27, b=8, m=\dfrac{1}{3}$$ verify $$(ab)^{m}=a^{m}b^{m}$$
Write each of the following number in the form $$k \times { 10 }^{ n }$$ where $$1\le k\ 10$$ and n is an integer.
$$(v)\ 0.00729$$
$$0.00729$$
$$=7.29\times 10^{-3}$$.
Solve : $${ 9 }^{ \dfrac { 5 }{ 2 } }-3\times { 8 }^{ \circ }-\left( \dfrac { 1 }{ 81 } \right) ^{ -\dfrac { 1 }{ 2 } }$$
$$9^{\dfrac{5}{2}}-3\times 8^o-\left(\dfrac{1}{81}\right)^{\dfrac{-1}{2}}$$
$$\Rightarrow (9^{1/2})^5-3\times 1-(81)^{1/2}$$
$$\Rightarrow 3^5-3-9$$
$$\Rightarrow 243-12$$
$$\Rightarrow 231$$.
$$\dfrac { log\sqrt { 8 } }{ log8 } $$ is equal to.
Multiply $${a^2}$$ with $$\left( {{a^3} + 3{a^2}b + {b^3} + 3a{b^2}} \right)$$.
The value of $$p^3$$ if $$13p=69$$
Find the value of $$\log 4.5$$.
Simplify:
$${ \left( \dfrac { 1 }{ 2 } \right) }^{ 5 }{ -\left( \dfrac { 3 }{ 2 } \right) }^{ 3 }$$
If $$ a = 3 $$ and $$ b = -2 $$, find the value of :
$$ (a+b)^{ab} $$
If $$ a = 3 $$ and $$ b = -2 $$, find the value of :
$$a^{b}+b^{a} $$
Simplify:
$${2}^{3}\times 5$$
Simplify:
$$0\times{10}^{2}$$
Convert the following to logarithmic form:
$$2^{6} = 64$$
Convert the following to logarithmic form:
$$7^{x} = 100$$
Convert the following to logarithmic form:
$$(81)^{3/4} = 27$$
Convert the following to logarithmic form:
$$9^{0} = 1$$
Convert the following to logarithmic form:
$$3^{-2} = 1/9$$
Convert the following to logarithmic form:
$$6^{1} = 6$$
Convert the following to logarithmic form:
$$10^{-2} = 0.01$$
Convert the following to logarithmic form:
$$5^{2} = 25$$
Convert the following into exponential form:
$$\log _{8} 4 = 2/3$$
Evaluate the following:
$$2\log 5 + \log 8 - 1/2 \log 4 $$
Convert the following into exponential form:
$$\log _{10} (0.001) = -3$$
Evaluate the following:
$$ 2 \log 5+ \log3 + 3 \log 2 -1/2 \log 36 - 2 \log 10 $$
Convert the following into exponential form:
$$\log _{2} 32 = 5$$
Convert the following into exponential form:
$$\log _{8} 32 = 5/3$$
Convert the following into exponential form:
$$\log _{2} 0.25 = -2$$
Convert the following into exponential form:
$$\log _{3} 81 = 4$$
Convert the following into exponential form:
$$\log _{a} (1/a) = -1$$
Convert the following into exponential form:
$$\log _{3} 1/3 = -1$$
Given $$ 3 \left ( \log 5 - \log3 \right ) - \left ( \log 5 -2\log 6 \right ) = 2 -\log n, $$ Find n .
Evaluate the following :
$$ \log 2 + 16 \log 16/15 +12 \log 25/24 + 7 \log 81/80 $$
Express each of the following as a single logarithm:
$$1/2 \log 36 +2 \log 8 - \log 1.5 $$
Express the following as a single logarithm:
$$ 2 \log _{10} 5-\log_{10} 2 + 3 \log _{10} 4 + 1$$
Evaluate the following :
$$ 2 \log _{10} 5 + \log_{10}8 -1/2 \log_{10} 4 $$
Solve for $$x:$$
$$ \log x + \log 5=2 \log 3 $$
Express each of the following as a single logarithm:
$$ 1/2 \log 25-2 \log 3+1 $$
Express each of the following as a single logarithm:
$$ 2 \log 3 - 1/2 \log 16 + \log 12 $$
Prove the following :
$$ \log 4\div \log_{10} 2= \log_{3} 9 $$
Prove the following :
$$ \log_{10} 25 + \log_{10} 4 = \log_{5} 25 $$
Solve for $$x$$:
$$ x = \log 125/ \log 25 $$
Solve the following equations :
$$ \log \left ( 3x +2 \right )+ \log\left ( 3x - 2 \right ) = 5 \log 2 $$
Prove the following :
$$ 27 ^{\log 2 } = 8^{\log 3} $$
Solve for x:
$$ \log_{3}x- \log_{3} 2=1 $$
If $$ \log x /\log 5 = \log y^{2} / \log 9/ \log \left ( 1/3 \right ), $$ find $$x$$ and $$y$$ .
Given $$ 2 \log _{10} x+1 = \log _{10} 250,$$ find $$x$$
Prove the following :
$$ 3 ^{\log 4 } = 4^{\log 3} $$
Solve for $$x:$$
$$ \left ( \log 8/\log 2 \right ) \times \left ( \log 3/\log \sqrt{3} \right ) = 2 \log x $$
Solve the following equations :
$$ \log_{10}\left ( x +2 \right ) + \log_{10}\left ( x-2 \right ) = \log_{10}3+3 \log_{10}4$$
Given $$ 2 \log _{10} x+1 = \log _{10} 250,$$ find
$$ \log _{10} 2 x $$
Show that :
$$ 1 / \log_{2} 42 + 1 / \log_{3} 42+ 1 / \log_{7} 42 = 1 $$
Find out the value of $$log(8621).$$
Solve for x:
$$ \log_{2}x+ \log_{8}x+ \log_{32} x = 23/15 $$
Use logarithm table to find the logarithm of the following numbers:
$$25795$$
Using logarithm, find the value of $$6.45\times 981.4$$
Given that $$\displaystyle \log_a A = x$$ is similar to $$\displaystyle a^x = A$$.
If true then write 1 and if false then write 0
If $$\log 2 = 0.3010$$ and $$\log 3 = 0.4771$$, then the value of $$\log 3.6$$ is $$0.55a2$$. where a is 3rd digit of the given value,then $$a=?$$
If $$\displaystyle \log_3 m = x$$ and $$\displaystyle \log_3 n = y$$, then $$\displaystyle 3^{1 - 2y + 3x}$$ can be expressed in terms of $$m$$ and $$n$$ as $$\displaystyle \frac {3m^3}{n^2}$$.If true then write 1 and if false then write 0.
If $$\displaystyle \log_{10} x = 2a$$ and $$\displaystyle \log_{10} y = \tfrac {b}{2}$$, then $$\displaystyle 10^a$$ in terms of $$x$$ is $$\displaystyle \sqrt x$$.
If true then write 1 and if false then write 0.
If true then write 1 and if false then write 0.
$$\displaystyle \log _{2}32= 5$$
Evaluate: $${ \left( 6.32 \right) }^{ 2 }\times \sqrt [ 4 ]{ 83.94 } $$[Hint: Use logarithm tables]
Evaluate: $$\dfrac { { \left( 17.42 \right) }^{ \frac { 2 }{ 3 } }\times 18.42 }{ \sqrt { 126.37 } } $$If the answer is not an whole number then write the whole number just smaller than the answer.[Hint: Use logarithm tables]
Find the value of '$$x$$' such that
$$25\times {5}^{x}={5}^{8}$$
Find the value of $$\log_{81}3$$
Simplify:
$${ 10 }^{ -1 }\times { 10 }^{ 2 }\times {10}^{-3} \times { 10 }^{ 4 }\times { 10 }^{ -5 }\times { 10 }^{ 6 }$$
Simplify $$(2^{3})^{-2} \times (3^{2})^{2}$$
Obtain the equivalent logarithmic form of the following.
(i) $${ 2 }^{ 4 }=16$$
(ii) $${ 3 }^{ 5 }=243$$
(iii) $${ 10 }^{ -1 }=0.1$$
(iv) $${ 8 }^{ -\frac { 2 }{ 3 } }=\dfrac { 1 }{ 4 }$$
(v) $${ 25 }^{ \frac { 1 }{ 2 } }=5$$
(vi) $${ 12 }^{ -2 }=\dfrac { 1 }{ 144 } $$
Simplify $$\dfrac {(2^{2})^{3}}{(3^{2})^{2}}$$
If $$2^{p} = 32$$, find the value of $$p \ .$$
Given: $$2^{p} = 32$$
$$2^{p} =2\times2\times2\times2\times2= 2^{5}$$
$$2^{p} =2\times2\times2\times2\times2= 2^{5}$$
$$\Rightarrow 2^{p} = 2^{5}$$
Hence, the value of $$p$$ is $$5.$$
Find the value of the following:
$$\left (\dfrac {3}{8}\right )^{5} \times \left (\dfrac {3}{8}\right )^{4}\div \left (\dfrac {3}{8}\right )^{9}$$
Find the value of the following:
$$3^{4} \times 3^{-3}$$
Change the following from exponential form to logarithmic form.
(i) $${ 3 }^{ 4 }=81$$
(ii) $${ 6 }^{ -4 }=\dfrac { 1 }{ 1296 } $$
(iii) $${ \left( \dfrac { 1 }{ 81 } \right) }^{ \frac { 3 }{ 4 } }=\dfrac { 1 }{ 27 } $$
(iv) $${ \left( 216 \right) }^{ \frac { 1 }{ 3 } }=6$$
(v) $${ \left( 13 \right) }^{ -1 }=\frac { 1 }{ 13 } $$
Simplify: $$2^{5}\times 2^{3}$$
Find (i) $$\log { 86.76 }$$
(ii) $$\log { 730.391 }$$
(iii) $$\log { 0.00421526 } $$
If $$Kx = |\ln (x)|$$ has $$3$$ solutions find out the limiting values of $$K$$ for which this is possible.
We have to draw the graphs of both the functions.
L is $$y=k'x $$ ; where $$k'$$ is the limiting value of $$k$$. Below $$k'$$ ; the equations will have 3 solutions for all $$x$$.
Let $$y=k'x $$ touch $$y=\left | \ln(x) \right |$$ at $$x=x_{o}$$
$$\therefore \:$$ Slope of $$\left | \ln(x) \right |$$ at $$x=x_{o}$$ will be $$\dfrac{1}{x_{o}}$$
and, Slope of $$(k'x)$$ at $$x=x_{o}=k'$$
Also, $$k'x_{o}=\ln(x_{o})\:\Rightarrow \: k'=\dfrac{\ln(x_{o})}{x_{o}}$$
and, $$k'=\dfrac{1}{x_{o}}$$
$$\Rightarrow \: \dfrac{\ln(x_{o})}{x_{o}}=\dfrac{1}{x_{o}}\:\:\Rightarrow \:\: \dfrac{1}{x_{o}}\left ( \ln(x_{o})-1 \right )=0$$
$$\Rightarrow \: x_{o}=e$$
Hence, the limiting values of $$k$$ for which equation will have 3 solutions will be,
$$k\:\epsilon \: (0,\dfrac{1}{e})$$
Given $$\log_{10} 2 = {^{.}30103},$$ find $$\log_{25}200.$$
Write the characteristic of each of the following
(i) $$\log { 4576 } $$
(ii) $$\log { 24.56 } $$
(iii) $$\log { 0.00257 } $$
(iv) $$\log { 0.0756 } $$
(v) $$\log { 0.2798 } $$
(vi) $$\log { 6.453 } $$
Write the characteristic of the following.
(i) $$\log { 27.91 }$$
(ii) $$\log { 0.02871 }$$
(iii) $$\log { 0.000987 }$$
(iv) $$\log { 2475 } $$
Given that $$\log { 4586 } =3.6615$$, find
(i) $$\log { 45.86 } $$
(ii) $$\log { 45860 }$$
(iii) $$\log { 0.4586 } $$
(iv) $$\log { 0.004586 }$$
(v) $$\log { 0.04586 }$$
(vi) $$\log { 4.586 } $$
Determine the value of x for which the 6th term in $$\left ( 2^{log_2(\sqrt{g^{x-y}+7})}+\frac{1}{2^{\frac{1}{5}log_2(3^{x-1}+1)}} \right )$$ is 84.
Solve the following equation:
$$\displaystyle\, \frac{3}{2^{\log x}} = \frac{1}{64}$$
Solve the following equations.
$$\displaystyle (6.25)^{2 \, - \, x} = \, \frac{1}{2^{x \, + \, 3}}.$$
Solve the following equations.
$$\displaystyle 6.9^{0.5x \, - \, 2} \, + \, 2.3^{x \, - \, 6} \, = \, 56.$$
Find the value of $$x$$ if $${2^4} \times {2^5} = {\left( {{2^3}} \right)^x}.$$
Represent the following mixed infinite decimal periodic fractions as common fractions:
$$\displaystyle\, log_{1/2} (log_3\, cos(\pi /6) - log_3\, sin (\pi /6))$$
simplify: $${\left\{ {5\left( {{{16}^{\dfrac{1}{4}}} + {{27}^{\dfrac{1}{3}}}} \right)} \right\}^{\dfrac{1}{4}}}$$
Solve$$\log {10^4}\left( {1 + {1 \over {2x}}} \right)-\log {10^3} = \log 10\left( {\root \of (0.75x-0.5) + 2} \right)$$
Solve $$log_{10} tan1^\circ \, + \, log_{10} tan2^\circ \, + \, ........ \, + \, log_{10} tan89^\circ$$
Solve the equations:$$3^x \, 5^y \, = \, 75 $$ $$ 3^y 5^x \, = \, 45 $$
$$ 3^y 5^x \, = \, 45 $$
Prove the following identities :
If $$a^2 \, + \, b^2 \, = \, 7ab$$ , prove that $$\log\dfrac{1}{3}(a \, + \, b) \, = \dfrac{1}{2}[\log a +\log b]$$
Substituting the values, find $$n$$
$$\cfrac{0.1}{0.2}=\left( \cfrac{10}{80} \right)^{1/n}$$ or $$\left( \cfrac{1}{2} \right)^{1}=\left( \cfrac{1}{2} \right)^{3/n}$$
$$Express\quad in\quad logarithmic\quad form:\\ { 5 }^{ 3 }=125$$
The value of x satisfying the equation $${4^{{{\log }_9}^3}} + {9^{{{\log }_2}^4}} = {10^{{{\log }_c}^{83}}}$$ is
If $${4^{{{\log }_2}2x}} = 36$$ , then find x.
Solve the equation $$\dfrac{3}{2}\log_4(x+2)^2+3=\log_4(4-x)^3+\log_4(6+x)^3$$.
Find $$x$$ : $$3(2^{x} + 1) -2^{x+2} + 5 =0$$
Solve : $$\log_3(\sqrt{x}+|\sqrt{x}-1|)=\log_9(4\sqrt{x}-3+4|\sqrt{x}-1|)$$
Prove that $$x^{\log y-\log z}.x^{\log z-\log x}.x^{\log x-\log y}=1$$.
The simplified value of $$\sqrt {72} + \sqrt {800} - \sqrt {18} $$ is
Prove that:$$\log(1+2+3)=\log 1+\log 2+\log 3$$.
Find the value of $${49^{\left( {1 - {{\log }_7}2} \right)}} + {5^{ - {{\log }_5}4}}.$$
Solve:
$$( \dfrac{2 \times 3.0 \times 10^{-25}}{9.1 \times
10^{-31}})^{}$$
If $$\left(\dfrac{21}{19}\right)^4\times \left(\dfrac{19}{7}\right)^4=b^4$$.Find $$b$$
Simplify the following.
$${ 3 }^{ 2 }\div { 3 }^{ 4 }$$
Simplify the following.
$${ a }^{ x }\div { a }^{ y }$$
$${\log _{2\sqrt 3 }}1728$$
If $$2^{x+1} = 3^{1-x}$$ then find the value of x.
Simplify the following.
$${ x }^{ 3 }\div { x }^{ 7 }$$
using log tables, calculate $${\left[ {\frac{{5.3 \times 2.843}}{{0.80341}}} \right]^{\frac{1}{3}}}$$
Using Log tables calculate $${\frac{{{{\left( {4.63} \right)}^2} \times {{\left( {0.08341} \right)}^{\frac{2}{5}}}}}{{{{\left( {0.006743} \right)}^{\frac{1}{4}}}}}}$$
Simplify the following. $${ 3 }^{ 4 }\times { 4 }^{ 4 }$$
Simplify the following.
$${ 5 }^{ 7 }\div { 5 }^{ 3 }$$
Simplify: $$\dfrac{{16 \times {2^{n + 1}} - 4 \times {2^n}}}{{16 \times {2^{n + 2}} - 2 \times {2^{n + 2}}}}$$
How to find $$\log$$ of any number?
Solve:$$x=(a^{2/3})^3 \div a^{3/2} \times a^{-3}$$ If $$a=\dfrac{1}{4}$$. Find $$x^{-1}$$
Find $$x$$ if
a) $${2^x} = 22$$
b) $${3^x} = 243$$
Find out the value of n if $${ 3 }^{ n }={ 4 }^{ n-1 }$$
Simplify
$${8^{\frac{2}{3}}} - \sqrt 9 \times 10 + \left( {\frac{1}{{144}}} \right)$$
The value of $$2^{\log_{4}{25}}$$ is ____
Solve for $$x$$
$$\displaystyle {(81)^{\frac{3}{4}}} - {\left( {\frac{1}{{32}}} \right)^{\frac{{ - 2}}{5}}}+ x{\left( {\frac{1}{2}} \right)^{ - 1}}{\times 2^0} = 27$$
Solve for $$x$$
$${2^{3x + 3}} = {2^{3x + 1}} + 48.$$
$$\log_{e}(101)$$ gives $$\log_{e}10=2.3026$$
If $$\log{x}=0$$ then $$x=?$$
$$\log\dfrac {20}{10}=?$$
Evaluate:$$\dfrac{\left(\dfrac{-3}{5}\right)^3\times \left(\dfrac{9}{25}\right)^2\times \left(\dfrac{-18}{125}\right)^0}{\dfrac{-27}{125}\times \left(\dfrac{-3}{5}\right)}$$.
Solve: $$\log_{x^2-1}(x+1)<1$$
$$\log_{e}(4.04)$$ given $$\log_{10}4=0.6021,\log_{10}e=0.4343$$
$$\log_{e}(9.01)$$ gives $$\log_{e}3=1.0986$$
Find the value of:
$$2(6(\sqrt{3})^{5})(\sqrt{3})+20\times (\sqrt{3})^{3}(\sqrt{2})^{3}+6(\sqrt{3})(\sqrt{2})^{5}$$
If we multiply m with $${ \left( \dfrac { 256 }{ 6561 } \right) }^{ -\dfrac { 5 }{ 8 } }$$ we get $$1$$, then $$m =$$
The value of $$\log_{5}\left(\dfrac{1}{625}\right)$$ is
$$ log_5(\dfrac{1}{625})$$
$$ = \dfrac{log_5(1)-log625}{log5}$$
$$ = \dfrac{0-log 5^4}{log^{5}}$$
$$ = \dfrac{-4log5}{log5} = \boxed{-4} $$
Compute the following
$$\left(\dfrac {1}{49}\right)^{1+\log_{7}2}+5^{-\log_{1/5}7}$$
$$=\left(\dfrac{1}{49}\right)^{1+log_7^2}+5^{-log_{1/5}^7}$$
$$=\left(\dfrac{1}{49}\right)^{log_7^{14}}+7^{log_{1/5}^{1/5}}$$
$$=14^{log_7^{1/49}}+7$$
$$=(14)^{-2}+7$$
$$=\left(\dfrac{1}{14}\right)^2+7$$.
Solve : $$2^{3x + 1} + 2^7 = (-4)^4$$
If $$\dfrac{{{9^b} \times {3^2} \times {{\left( {{3^{\dfrac{{ - b}}{2}}}} \right)}^{ - 2}} - {{\left( {27} \right)}^b}}}{{{3^{3a}} \times {2^3}}} = \dfrac{1}{{27}}$$, then prove that $$a - b = 1$$.
$$-9\log_{3}^{(b + 2)} = ?$$.
Find the value of
$$\log_{2} { 5^{ \frac{1}{3} } }$$
Expand $$\dfrac{5x^2+4x+7}{\left(2x+3\right)^{\frac{3}{2}}}$$
Solve:
$$8x^7+x^7+x=?$$
if $$x=7$$
For any base show that
log (1+2+3)= log 1+ log 2+ log3.
Note that , in general,
log (a+b+c)$$\neq $$ log a+ log b +log c.
Solve the following:-
$$\left(\dfrac{2^6 \times 3^4}{6^3}\right)^2\times \left(\dfrac{3^3 \times 2^5}{3 \times 8}\right)^3$$
$$log_x\ a\ +- log_{ax}a\ +\ 3log_{a^{2}x}\ a\ =\ 0$$
Solve and write the answer in one term.
$$\log 2 + 1$$.
If $$\log 2=0.3010,\log 3=0.4771,\log 7=0.8451$$ and $$\log 11=1.0414$$, then find the value of the following :
$$\log \left(\dfrac {11}{7}\right)^{5}$$
If $$log _{2\sqrt 3} 1728=x$$ then find x
Solve:
$$\log_{3}{\left(\dfrac{1}{27}\right)}=-3$$
Evaluate $$\log _ { 3 } \left( \log _ { 9 } x + \frac { 1 } { 2 } + 9 ^ { x } \right) = 2 x$$
Solve:
$$\left(-\dfrac {1}{2}\right)^{3}\times \left(-\dfrac {1}{2}\right)^{4}$$
Find the value of $$2[(2^{-1}\times 4^{-1})\div 2^{-2}]$$.
If $$\log 2=0.3010,\log 3=0.4771,\log 7=0.8451$$ and $$\log 11=1.0414$$, then find the value of the following :
$$\log 36$$
$${(x \div y)^{ - 1}} = {x^{ - 1}} \div {y^{ - 1}}$$ by taking $$x = \frac{7}{{11}}$$
If $$\log 2=0.3010,\log 3=0.4771,\log 7=0.8451$$ and $$\log 11=1.0414$$, then find the value of the following :
$$\log \dfrac {42}{11}$$
Solve :- $${{{5^6}} \over {{5^3} \times {5^3}}}$$
If $$\log 2=0.3010,\log 3=0.4771,\log 7=0.8451$$ and $$\log 11=1.0414$$, then find the value of the following :
$$\log 5^{1/3}$$
If $$\log 2=0.3010,\log 3=0.4771,\log 7=0.8451$$ and $$\log 11=1.0414$$, then find the value of the following :
$$\log 70$$
$${\log _2}x + \frac{1}{2}{\log _2}(x + 2) = 2$$
$$\log2^x+1/2 \log_{2}(x+2)=2$$
$$\log _{ 2 }{ x } +\log _{ 2 }{ \left( x+2 \right)^{ { y }_{ 2 }} } =\log _{ 2 }{ { 2 }^{ 2 } } $$
$$\log_{2}[x(x+2)^{y_{2}}]=\log_{2}4$$
$$x(x+2)^{y_{2}}=4$$
$$(x+2)^{y_{2}}=4/x$$ [sequencing both sides]
$$x+2=\dfrac {16}{x^2}$$
$$x^{2}(x+2)=16$$
$$x^{3}+2x^{2}-16=0$$
$$(x-2)(x^{2}+4x+8)=0$$
$$x=2$$
Find the value of $$x $$ if $$\displaystyle 14 \times {10^{ - 4}} = \log {{500} \over x}$$
$$4^{3.5} : 2 ^5$$ is the same as
If $$\log 2=0.3010,\log 3=0.4771,\log 7=0.8451$$ and $$\log 11=1.0414$$ then find the value of the following
$$\log \dfrac {121}{120}$$
$${2}^{9}\times{2}^{5}$$
Find the value of $$\log 7$$ using series expansion.
Find the value of $$\log_2 2^{2^2}$$.
The value of a for which $$\log _ { a } ( 1 \times 2 ) - \log _ { a } ( 2 \times 3 ) + \log _ { a } ( 3 \times 4 ) - \log _ { a } ( 4 \times 5 ) + \log _ { a } ( 5 \times 6 ) = \log _ { e } 36$$ is ...
Simplify the following using laws of exponent
$$(\dfrac{3x^2y^2}{axy^4})^2$$
Simplify the following using laws of exponent
$$[7^8 \times 12^8]\div [14^8 \times 6^8]$$
Using $$\log{2}=0.3010$$ and $$\log{3}=0.4771$$ and $$\log{7}=0.8451$$ find the value of $$\log{6}^{50}$$
Find $$n$$
$$\dfrac {9^{n+1}+4^{n+1}}{9^{n}+4^{n}}=6$$
Simplify and express:
$$\displaystyle \frac{2^{3}\times 3^{4}\times 4}{3\times 32}$$
Solve:
$$2^{5}\times 2^{4}\div 2^{3}$$
Prove that
$$\dfrac { 1 }{ { log }_{ ab }(abc) } +\dfrac { 1 }{ { log }_{ bc }(abc) } +\dfrac { 1 }{ { log }_{ ca }(abc) } =2$$
If $${ a }^{ 2 }+{ b }^{ 2 }=3ab,$$ show that $$\log\left( \dfrac { a+b }{ \sqrt { 5 } } \right) =\dfrac { 1 }{ 2 } \left( \log a+\log b \right) $$
$$32^{1/5}$$ is equal to ___.
solve : $$\left[ \left\{ \left( \dfrac { - 1 } { 3 } \right) ^ { 2 } \right\} ^ { - 2 } \right] ^ { - 1 }$$
Find the value of $$x$$ if $${25}^{x}\sqrt[x]{{5}^{x-1}}=1$$
$${ \left[ { \left( \dfrac { 5 }{ 7 } \right) }^{ 2 } \right] }^{ 3 }\times { 7 }^{ 6 }\div { \left( { 5 }^{ 3 } \right) }^{ 2 }$$ is equal to ____.
$${ log }_{ 10 }2+{ 16log }_{ 10 }(\frac { 16 }{ 15 } )+{ 12log }_{ 10 }(\frac { 25 }{ 24 } )+{ 7log }_{ 10 }(\frac { 81 }{ 80 } )$$
Express $$\log _{ 10 }{ 2 } +1\quad in\quad the\quad from\quad of\quad \log _{ 10 }{ x. } $$
Find the value of :
(i) $$\log_{1/2}{8}$$
(ii) $$\log_5{0.008}$$
(iii) $$\log_5{3125}$$
(iv) $$\log_7{\sqrt[3]{7}}$$
The value of $$log\, 0.008........$$
$$log_{10}0.008$$
$$\Rightarrow log_{10}8\times 10^{-3}$$ [ log ab = log a+ log b]
$$\Rightarrow log_{10}8+log_{10}10^{-3}$$
$$\Rightarrow log_{10}2^{3}+(-3) log_{10}10$$
$$\Rightarrow 3log_{10}2+(-3)$$ [ log ab = b log a]
$$\Rightarrow 3(0.301)-3$$
$$\Rightarrow -2.097$$
Simplify: $$\sqrt [5] {64}$$
$$\sqrt[5]{64}=\sqrt[5]{2\times 2\times 2\times 2\times 2\times 2}=\sqrt[25]{2}$$.
Find the approximate value of
(i) $${ log }_{ e }101$$, given that $${ log }_{ e }10=2.3026$$
(ii) $${ 3 }^{ 2.04 }$$ given that $${ log }_{ e }3=1.0986$$.
If $$a=log_{24}12, b=log_{36}24, c=log_{48}36$$. Prove that $$1+abc=2bc$$.
$$\log _33+\log _416$$
Write $${2}^{10}=1024$$ in logarithmic form.
$$\log _6216+\log _7343$$
Find the value of $$\log_{\sqrt{2}} 16$$.
Write $${3}^{5}=243$$ in logarithmic form.
Find the value of i) $${ 2 }^{ 6 }$$ii) $${ 9 }^{ 3 }$$iii) $${ 11 }^{ 2 }$$
Simplify: $$\dfrac {a^{m}\times a^{n}}{a^{m-n}}$$
find the value of $$\dfrac { \log _{ 4 }{ 7 } }{ \log _{ 4 }{ 5 } } -\dfrac { \log _{ 9 }{ 5 } }{ \log _{ 9 }{ 7 } } $$
Show that $$\log{\left(\dfrac{108}{605}\right)}=2\log{2}+3\log{3}-\log{5}-2\log{11}$$
Write $${6}^{3}=216$$ in logarithmic form.
Find the value of $$x$$ if $$\log \sin \sqrt x=0$$
Evaluate: $$\log_{4}\log_{3}\log_{2}{x}=0$$
If $$\log_{x}\dfrac 18=\dfrac{-3}{2}$$ then x is equal to
If $$\log_4x=12$$, then $$\log_2 \dfrac x4$$ is equal to
Simplify:$${a}^{\frac{\log_{b}{\left(\log_{b}{N}\right)}}{\log_{b}{a}}}$$
Solve:$$\log_{e}\log_{5}\left[\sqrt{2x-2}+3\right]=0$$
Find the value of $$\log _8512+\log _28$$
Solve:$$\log{\left(\log{x}\right)}+\log{\left(\log{{x}^{3}}-2\right)}=0$$
Solve for $$x:\,\,\dfrac{\log_{10}{\left(x-3\right)}}{\log_{10}{\left({x}^{2}-21\right)}}=\dfrac{1}{2}$$
Find $${x}^{\log{x}+4}=32$$ where base of logarithm is $$2$$
NTR says that the degree of $$(x^5-5)(x^2+3)$$ isDo you agree with him?How?
Simplify: $$\displaystyle \frac { 2\sqrt { 30 } }{ \sqrt { 6 } } -\frac { 3\sqrt { 140 } }{ \sqrt { 28 } } +\frac { \sqrt { 275 } }{ \sqrt{55} } $$
log 5- log 7 =?
If $$a^x=b, b^y=a$$ then show that $$xy=1$$.
In exponential form $$729=3^a$$, what is the value of $$a$$?
The exponential form of $$625$$ is $$5^k$$ then value of $$k$$ is ___.
Write the given expression in exponential form.
$$4a^3\times 6ab^2\times c^2$$.
Write the following in exponential form.
(i) $$log_{10}100=2$$
(ii) $$log_{5}25=2$$
(iii) $$log_{2}2=1$$
Simplify:$$\log_{\frac{1}{3}}{\sqrt[4]{729\sqrt[3]{{9}^{-1}{27}^{\frac{-4}{3}}}}}$$
The exponential form of $$512$$ is $$2^k$$ then value of $$k$$ is ___.
Solve:$${9}^{1+\log{x}}-{3}^{1+\log{x}}-210=0$$ where base of $$\log$$ is $$3$$
If $$\log_{10}{\left({x}^{2}-12x+36\right)}=2$$
Find the $$5$$th root of $$.003$$, having given $$log 3=.4771213$$ and $$log 312936=5.4954243$$.
Given $$log 11=1.0413927$$ and $$log 13=1.1139434$$, find the values of
$$(1)$$ $$log 1.43$$, $$(2)$$ $$log 133.1$$, $$(3)$$ $$log \sqrt[4]{143}$$, and $$(4)$$ $$log \sqrt[3]{.00169}$$.
Given $$log 4=.60206$$ and $$log 3=.4771213$$, find the logarithms of $$.8, .003, .0108$$, and $$(.00018)^{\dfrac{1}{7}}$$.
Given $$\log2 = {^{.}3010300}, \log3 = {^{.}4771213}, \log7 = {^{.}8450980},$$ find the value of
$$\log \sqrt[3]{12}.$$
Find the value of $$(1)$$ $$7^{\dfrac{1}{7}}$$, $$(2)$$ $$(84)^{\dfrac{2}{5}}$$, and $$(3)$$ $$(.021)^{\dfrac{1}{5}}$$, having given
$$log 2=.30103$$, $$log 3=.4771213$$,
$$log 7=.8450980, log 132057=5.1207283$$,
$$log 588453=5.7697117$$, and $$log 461791=5.6644438$$.
Find the numerical value of the logarithms of $$7, 11$$ and $$13$$; given $$\mu=\cdot 43429448, \log 2=\cdot 30103000$$.
Solve
$$\dfrac{16\times 10^2\times 64}{2^4\times 4^2}$$
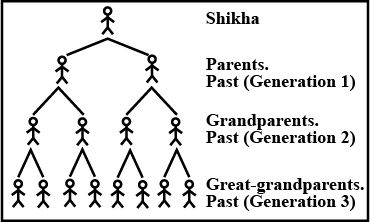
While studying her family's history. Shikha discovers records of ancestors she has had in the past $$12$$ generations. She started to make a diagram to help her figure this out. The diagram soon become very complex.
Make a graph showing the number of ancestors in each of the $$12$$ generations.
Two machines can be hooked together. When something is sent through this hook up, the output from the first machine becomes the input for the second.
When two machines hooked together do the same work as $$(\times 10^2)$$ machine does? Is there more than one arrangement of two machines that will work?
For the following repeater machines, how many times the base is applied and how much the total stretch is ?
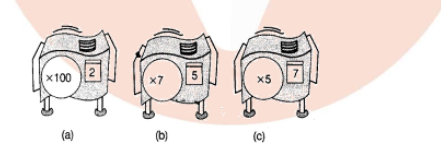
Find a single repeater machine that will do the same work as the hook -up.
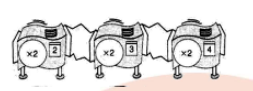
Find a single machine that will do the same job as the given hook-up.
$$A(\times 2^3)$$ machine followed by $$(\times 2^{-2})$$ machine.
Find a single machine that will do the same job as the given hook-up.
$$A(\times 5^{99})$$ machine followed by $$(5^{-100})$$ machine.
Shikha has an order from a golf course designer to put palm trees through $$a(\times 2^3)$$ machine and then through $$(\times 3^3)$$ machine. She thinks she can do the job with a single repeater machine. What single repeater machine should she use?
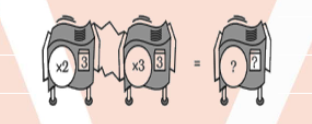
Find a single repeater machine that will do the same work as the hook -up.
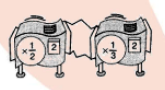
For the hook-up, determine whether there is a single repeater machine that will do the same work. If so, describe or draw it.
A machine $$(\times x^y)$$ with input $$a$$ will give an output $$ax^y$$
When, multiple such machines are hooked up their stretching powers are multiplied.
Machine $$1$$ is $$(\times 7^3)$$
Machine $$2$$ is $$(\times 7^2)$$
As per the law of exponent- $$a^m \times a^n =a^{m+n}$$
So,
The work that can be performed by the repeater machine is equal to $$7^3 \times 7^2=7^{5}$$.
So, Yes, $$(\times 7^{5})$$ is a single machine the can perform the same amount of work as given hooked up machines.
It is described in diagram with $$7$$ as base and $$5$$ as power.
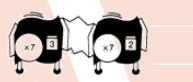
For the hook-up, determine whether there is a single repeater machine that will do the same work. If so, describe or draw it.
A machine $$(\times x^y)$$ with input $$a$$ will give an output $$ax^y$$
When, multiple such machines are hooked up their stretching powers are multiplied.
Machine $$1$$ is $$(\times 0.5^2)$$
Machine $$2$$ is $$(\times 0.5^3)$$
As per the law of exponent- $$a^m \times a^n =a^{m+n}$$
So,
The work that can be performed by the repeater machine is equal to $$0.5^2 \times 0.5^3=0.5^{5}$$.
It is described in a figure with $$0.5$$ as base and $$5$$ as power.
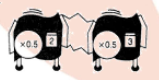
Find a single repeater machine that will do the same work as the hook -up.
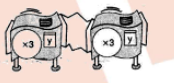
Find the value of:
$$(-3)^{2} \times 5^2$$
The diameter of the Sun is $$1.4\times 10^9\ m$$ and the diameter of the Earth is $$1.2756\times 10^7\ m$$. Compare their diameters by division.
Simplify and write in exponential form:
$$\dfrac{9^8 \times (x^2)^5}{(27)^4 \times (x^3)^2}$$
Simplify:
$$\dfrac{7^3 \times 11^4 \times 13^0 }{7^2 \times 11^2}$$
Find $$x$$.
$$\left( \dfrac 25\right)^{2x+6}\times \left( \dfrac 25\right)^{3}=\left( \dfrac 25\right)^{x+2}$$
Simplify:
$$\dfrac{[(-5)^3]^4 \times 8^2}{4^3 \times (25)^5}$$
Simplify and write in exponential form:
$$\dfrac{(-3)^5\times 8^3 \times 2^5}{3^2 \times 4^4}$$
Simplify:
$$\dfrac{(-2)^3 \times (3x)^2 \times (-xy^3)}{3x^2y}$$
The left column of the chart lists the lengths of input chains of gold. Repeater machines are listed across the top. The other entries are the outputs you get when you send the input chain from that row the repeater machine from that column. Copy and complete the chart.
| Input Length | Repeater Machine | ||
| $$x\ 2^3$$ | |||
| $$40$$ | $$125$$ | ||
| $$2$$ | $$162$$ | ||
| $$81$$ |
Simplify:
$$\left( \dfrac{4}{13}\right)^{4}\times \left( \dfrac{13}{7}\right)^{2}\times \left( \dfrac{7}{4}\right)^{3}$$
Evalute
$$2^3 \times 5^2$$
Evaluate
$$2^3 \times 4^2$$
Simplify and write in exponential form:
$$\dfrac{3^2 \times 7^8 \times 13^6}{21^2 \times 91^3}$$
Elaluate
$$2^2 \times 3^3$$
Simplify and write in exponential form:
$$(-3)^6 \times (-5)^6$$
Simplify and write in exponential form:
$$\bigg(\dfrac{3}{10}\bigg)^5 \times \bigg(\dfrac{2}{15}\bigg)^5$$
If $$(9^n \times 3^5 \times 27^3)(3\times 81^4)=27 $$, find $$n$$.
Evaluate
$$3^3 \times 5^2$$
Write the following in logarithmic form:
$$\frac{1}{81}=3^{c}$$.
Write the following in logarithmic form:
$$10=5^{b}$$.
Elaluate
$$3^2 \times 4^2$$
Evaluate
$$(2 / 3)^3 \times (3/4)^2$$
Elaluate
$$(4 \times 3)^3$$
Evaluate
$$(3 / 5)^2 \times (-2 / 3)^3$$
Elaluate
$$5^3 \times 2^4$$
Write the following in logarithmic form:
$$7=2^{x}$$
Elaluate
$$(5 \times 4)^2$$
Evaluate
$$(-3 / 4)^3 \times (2 / 3)^4$$
Solve the following:
$$\log _{10}100000=z$$
Write the following in exponential form:
$$\log _{10}100=2$$
We have $$\log _{2}32$$. Show that we get the same result by writing $$32=2^{5}$$ and then using power rules. Verify the answer.
Write the following in logarithmic form:
$$\dfrac{1}{257}=4^{a}$$
Write the following in exponential form:
$$\log _{2}2=1$$
Solve the following:
$$\log _{2}16=2$$ $$\therefore x^{2}=16\Rightarrow x=\pm 4$$
Is it correct or not?
Solve the following:
$$\log _{2}32=x$$
Solve the following:
$$\log _{5}625=y$$
Write the following in logarithmic form:
$$100=10^{z}$$
Write the following in exponential form:
$$\log _{5}25=2$$
Determine the value of the following:
$$\log _{81}3$$
Determine the value of the following:
$$\log _{2}\left ( \frac{1}{16} \right )$$.
Determine the value of the following:
$$\log _{2}512$$.
Determine the value of the following:
$$\log _{10}0.01$$.
Find the value of:
$$\log _{2}32$$
Determine the value of the following:
$$\log _{7}1$$.
Find the value of:
$$\log _{\dfrac{2}{3}}\dfrac{8}{27}$$.
Determine the value of the following:
$$\log _{\frac{2}{3}}\left ( \frac{8}{27} \right )$$.
Find the value of:
$$\log _{10}0.001$$
Determine the value of the following:
$$\log _{25}5$$
Express each of the following in logarithmic form:
$$10^{-3}=0.001$$
Express each of the following in logarithmic form:
$$5^{3}=125$$
Expand the following:
$$\log \left ( \dfrac{128}{625} \right )$$.
Evaluate the following in terms of $$x$$ and $$y$$, if it is given that $$x=\log _{2}3$$ and $$y=\log _{2}5$$.
$$\log _{2}60$$.
Evaluate the following in terms of $$x$$ and $$y$$, if it is given that $$x=\log _{2}3$$ and $$y=\log _{2}5$$.
$$\log _{2}7.5$$.
Evaluate the following in terms of $$x$$ and $$y$$, if it is given that $$x=\log _{2}3$$ and $$y=\log _{2}5$$.
$$\log _{2}6750$$.
Evaluate the following in terms of $$x$$ and $$y$$, if it is given that $$x=\log _{2}3$$ and $$y=\log _{2}5$$.
$$\log _{2}15$$.
Determine the value of the following:
$$2^{2+\log _{2}3}$$.
Find the logarithm of :
100 to the base 10
Express the each of following in exponential form:
$$\log _{a}A = x$$
Express the each of following in exponential form:
$$log_{10}0.01=-2$$
Find the logarithm of :
0.01 to the base 10
Find the logarithm of :
32 to the base 4
Solve for x :
$$\log_{10} x = -2$$
Express the each of following in exponential form:
$$\log _{10}1 = 0$$
Express each of the following in logarithmic form:
$$3^{-2}=\dfrac{1}{9}$$
Express the each of following in exponential form:
$$\log_{8}0.125=-1$$
Find the logarithm of :
0.001 to the base 10
Evaluate :
$$log_{2}\dfrac{1}{8}$$
Find x if :
$$\log_{9}243=x$$
Find the logarithm
27 to the base 4
Evaluate :
$$\log_{10}0.01$$
Find x if :
$$\log_{4}32=x-4$$
Find the logarithm of :
0.125 to the base 2
Find the logarithm
$$\dfrac{1}{81}$$ to the base 27
Find the logarithm
$$\dfrac{1}{16}$$ to the base 4
Evaluate :
$$log_{5}1$$
State , true or false :
$$\log_{2}8=3 $$ and $$\log _{8}2=\dfrac{1}{3}$$
If $$\log_{10}2=a $$ and $$\log_{10}3=b;$$ Express each of the following in terms of 'a' and 'b'
$$\log 2.25$$
Prove that :
$$2 \log\dfrac{15}{18}-\log\dfrac{25}{162}+\log\dfrac{4}{9}=\log2$$
Evaluate :
$$\log_{16}8=x$$
State , true or false
$$\dfrac{\log25}{\log5}=\log x$$
Evaluate :
$$\log_{5}125=x$$
Solve for x :
$$\dfrac{\log128}{\log32}=x$$
If $$\log_{10}2=a $$ and $$\log_{10}3=b;$$ Express each of the following in terms of 'a' and 'b'
$$\log2\dfrac{1}{4}$$
If $$\log_{10}2=a $$ and $$\log_{10}3=b;$$ Express each of the following in terms of 'a' and 'b'
$$\log 60$$
Solve for x :
$$\dfrac{\log81}{\log27}=x$$
Evaluate :
$$log_{0.5}16=X$$
If $$\log 2 = 0.3010$$ and $$\log 3=0.4771;$$ find the value of :
$$\log 25$$
If $$ x = \log 0.6; y = \log 1.25 $$ and $$z = \log 3-2 \log 2$$ , find the values of :
$$5^{x+y-z}$$
If log 2 = 0.3010 and 0.4771; find the value of :
log 1.2
If $$\log_{10}8=0.90;$$ find the value of :
$$\log 0.125$$
If $$\log_{10}8=0.90;$$ find the value of :
$$\log\sqrt{32}$$
If $$\log 2 = 0.3010$$ and $$\log 3=0.4771;$$ find the value of :
$$\log 3.6$$
If $$\log 2 = 0.3010$$ and $$\log 3=0.4771;$$ find the value of :
$$\log 15$$
Given : $$2 \log_{10}x+1=\log_{10}250,$$
Find:
$$\log_{10}2x$$
Find x , if :
$$\log_{x}625=-4$$
If $$ x = \log 0.6; y = \log 1.25 $$ and $$z = \log 3-2 \log 2$$ , find the values of :
$$x+y-z$$
Write the following in logarithm form:
$$10^{4} = 10000$$
Write the following in logarithm form:
$$2^{10} = 1024$$
If $$\log_{\sqrt{27}}x=2\dfrac{2}{3}$$, find $$x.$$
Write the following in the power form :
$$\log_{5} 25 = 2$$
Solve for x
$$\log_{x}15\sqrt{5}=2-\log_{x}3\sqrt{5}$$
Write the following in logarithm form:
$$4^{3/2} = 8$$
Solve for x , if
$$\log_{x}49-\log_{x}7+\log_{x}\dfrac{1}{343}=2$$
Evaluate :
$$\dfrac{\log_{5}8}{\log_{25}16\times \log_{10}10}$$
Write the following in logarithm form:
$$10^{-3} = 0.001$$
Write the following in logarithm form:
$$5^{-2} =\frac{1}{25}$$
If $$\log_{125} P =\frac{1}{6}$$ then find the value of $$P$$.
Write the following in the power form :
$$\log_{10} 0.1 = 1$$
Prove that:
$$\log 630 = \log 2 + 2 \log 3 + \log 5 + \log 7$$.
Write the following in the power form :
$$log_{3} (\frac{1}{27} ) = -3$$
Write the following in the power form :
$$\log_{\sqrt{2}} 4 = 4$$
If $$\log_{81} x =\frac{3}{2}$$, then find the value of $$x$$.
If $$\log_{4} m = 1.5$$, then find the value of $$m$$.
Prove that :
$$\log_{4} [\log_{2}(\log_{2} (\log_{3} 81))] = 0$$
Write the following in the power form :
$$\log_{10} 0.001 = 3$$
Write the following in the power form :
$$\log_{3} 729 = 6$$
Prove that:
$$\log\frac{9}{14}+\log\frac{35}{24}-\log\frac{15}{16}=0$$
If $$\log 2 = 0.3010, \log 3 = 0.4771, \log 7 = 0.8451$$ and $$\log 11 = 1.0414$$, then find the value of the following :
$$\log\left ( \frac{11}{7} \right )^{5}$$
If $$\log 2 = 0.3010, \log 3 = 0.4771, \log 7 = 0.8451$$ and $$\log 11 = 1.0414$$, then find the value of the following :
$$\log70$$
If $$\log 2 = 0.3010, \log 3 = 0.4771, \log 7 = 0.8451$$ and $$\log 11 = 1.0414$$, then find the value of the following :
$$\log36$$
Find the value of $$3^{2}-\log_{3}^{4}$$
If $$\log 2 = 0.3010, \log 3 = 0.4771, \log 7 = 0.8451$$ and $$\log 11 = 1.0414$$, then find the value of the following :
$$\log\frac{42}{11}$$
If $$\log 2 = 0.3010, \log 3 = 0.4771, \log 7 = 0.8451$$ and $$\log 11 = 1.0414$$, then find the value of the following :
$$\log5^{1/3}$$
Prove that:
$$\log 10 + \log 100 + \log 1000 + \log 10000 = 10$$
If $$\log 2 = 0.3010, \log 3 = 0.4771, \log 7 = 0.8451$$ and $$\log 11 = 1.0414$$, then find the value of the following :
$$\log\frac{121}{120}$$
Prove that:
$$\log_{5} 3 . \log_{3} 4 . \log_{2} 5 = 2$$
Find the logarithm of the following numbers by using log table :
$$2813$$
Find the characteristic of logarithm of following numbers :
$$1270$$
Find the logarithm of the following numbers by using log table :
$$27.28$$
Find the logarithm of the following numbers by using log table :
$$0.678$$
Find the logarithm of the following numbers by using log table :
$$400$$
Give the solution of following questions in one term :
$$\log 2 + 1$$
Find the characteristic of logarithm of following numbers :
$$20.125$$
Find the logarithm of the following numbers by using log table :
$$9$$
Find the characteristic of logarithm of following numbers :
$$70$$
Find the value of $$x$$ in the following :
$$\log x = 0.452$$
Find the logarithm of the following numbers by using log table :
$$0.08403$$
Find the logarithm of the following numbers by using log table :
$$0.00003258$$
Find the logarithm of the following numbers by using log table :
$$0.000287$$
Find the value of $$x$$ in the following :
$$\log x = \bar{2}.6727$$
Find the logarithm of the following numbers by using log table :
$$0.00003208$$
Find the logarithm of the following numbers by using log table :
$$0.000125$$
Find the logarithm of the following numbers by using log table :
$$1.234$$
Find the logarithm of the following numbers by using log table :
$$0.0035$$
If $$\frac{\log144}{\log12}=\log x$$, then find the value of $$x$$.
Find the value of $$\log 0.001$$.
Prove that:
$$\log_{3} 4 . \log_{4} 5 . \log_{5} 6 . \log_{6} 7 . \log_{7}\log_{8} 9 = 2$$
If $$\log 52.04 = 1.7163, \log 80.65 = 1.9066$$ and $$\log 9.753 = 0.9891$$, then find the value of
$$\log\frac{52.04*80.65}{9.753}$$
Prove that:
$$\log_{10} \tan 1^{0}. \log_{10} \tan 2^{0}. \log_{10} \tan 89^{0} = 0$$
If $$\log 7 = 0.8451$$ and $$\log 3 = 0.4771$$, then find $$\log (21)^{5}$$.
If $$\log 2 = 0.3010$$, then find the value of $$\log 200$$.
$$\log 2 = 0.3010$$ and $$\log 3 = 0.4771$$, then find the value of $$\log (0.06)^{6}$$
If $$\log 32.9= 1.5172, \log 568.1 = 2.7544$$ and $$\log 13.28 = 1.1232$$, then find the value of
$$\log\frac{(13.28)^{3}}{32.9*568.1}$$
By using logarithm, find the value of
$$\frac{520.4*8.065}{97.53}$$
$$\log_{10} 3= 0.4771$$, then find $$\log_{10} 0.027$$.
If $$5^{-p} = 4^{-q} = 20^r$$; show that:
$$\displaystyle \frac{1}{p} + \frac{1}{q} + \frac{1}{r} = 0$$
$$\log_x (\log_9 (3^x - 9)) < 1$$
If $$\dfrac {241}{4000}=\dfrac {241}{{2}^{m}{5}^{n}}$$, find $$m$$ and $$n$$ values?
Evaluate =$$\sqrt[100]{10^{10^{10}}}$$
Simplify the following expressions.
(a) $$\displaystyle\, 5^{log \, 5/log \, 25}$$
(b) $$\displaystyle\, log_2 \, log \, 100$$
Simplify the following expressions.
$$\displaystyle\, 0.(1 \, + \, 9^{log_3 \, 8})^{log_5 \, 5}$$
Calculate $$\displaystyle \log_5 9.8$$ in terms of $$a$$ and $$b$$, if $$\log 2 = a$$ and $$\log 7 = b$$.
$${x^{3{{\log }^3}{{10}^x} - {2 \over 3}\log {{10}^x} = 100\root 3 \of {10} }}$$
Solve the following equations.
$$\displaystyle log_3 \, log_4 \, log_2 \, x \, = \, 0.$$
Solve the following equation.
$$\displaystyle\, \log^2_{1/2}\, (4x) + \log_2 \left ( \frac{x^2}{8} \right ) = 8$$
Solve $$\sqrt{\log_2\ x^{4}}+4\log_4\sqrt{\dfrac{2}{x}}=2$$
$$\log _{ x }{ y } =10\log _{ 2 }{ y } =100$$ then $$y=$$
Find approximate value of $${\log _e}(4.04)\,\ \ if \ \ \,{\log _{10}}4\, = \,0.6021\,and\,{\log _{10}}e = 0.4343$$
Solve for $$x$$
$${({a^{3x + 5}})^2}\times {({a^x})^4} = {a^{8x + 12}}$$
Prove that :$$\dfrac{2^{30} + 2^{29}+ 2^{28} }{2^{31} + 2^{30}- 2^{29}}=\dfrac{7}{10}$$
Given: $$2 \log _ { 10 ^ { x } } + 1 = \log _ { 10 } 250$$. Find $$x$$ and $$\log _ { 10 } 2 x$$
Find the value of $$\log { _{ 5 } }$$ $$0.008$$
log 6 + 2 log 5 + log 4 - log 3 - log 2
Solve:
$$\dfrac{1}{1+a^{n-m}}+\dfrac{1}{1+a^{m-n}}$$
Express in terms of bases to the power of exponenets
$$8.9^{2}$$
Evaluate : $$\left( \dfrac { 5 } { 3 } \right) ^ { x } \cdot \left( \dfrac { 9 } { 25 } \right) ^ { x ^ { 2 } + 2 x - 11 } = \left( \dfrac { 5 } { 3 } \right) ^ { 9 }$$
Solve:
$$(-48p^{4})\div(-9p^{2})$$
the value $$\left( \frac { 1 }{ \sqrt { 27 } } \right) ^{ 2-\left( { log }_{ 5 }{ 16/2log }_{ 5 }9 \right) } =$$
Find the appropriate value of $$\log_{10}$$ $$(1016)$$, given $$\log_{10}e=0.4343$$
$$|x-1|^A = (x-1)^7$$, where $$A=log_3x^2 -2log_x9.$$
Given $$\log2 = {^{.}3010300}, \log3 = {^{.}4771213}, \log7 = {^{.}8450980},$$ find the value of
$$\log 14{^{.}4}.$$
From the tables find the seventh root of $$.000026751$$. Making use of the tables, find the approximate values.
Evaluate: $$\log_{3}{2}\log_{4}{3}\log_{5}{4}...\log_{64}{63}$$
$$log_2(4^x-5.2^x+2) > 2$$.
$$=4^x-5.2^x+2 >2^2$$
$$=(2^x)^2-5.2^x+2>4$$
Let $$2^x=t$$
$$t^2-5t-2>0$$
$$t=\cfrac {5\pm\sqrt {25+8}}{2}=\cfrac {5\pm\sqrt {33}}{2}$$
$$=\left(t-\left(\cfrac {5+\sqrt {33}}{2}\right)\right)\left(t-\left(\cfrac {5-\sqrt {33}}{2}\right)\right) >0$$
(Refer to Image)
$$\therefore$$ $$2^x\epsilon \underset {negative}{\left(-\infty,\cfrac {51-\sqrt {33}}{2}\right)}t\left(\cfrac {5+\sqrt {33}}{2},\infty\right)$$
$$\log$$ is not defined
$$\therefore$$ $$x\epsilon \left(\log_2\cfrac {5+\sqrt {33}}{2},\log_2\infty\right)$$ .
Find, by inspection the characteristic of the logarithms of $$21735, 23 ^{.}8, 350, {^{.}035}, {^{.}2}, {^{.}87}, {^{.}875}.$$
$$\log 2 ^ { 3 } + \log 3 + \log 5 = ?$$
Which is greater $$x=\log _{ 3 }{ 5 } \quad or\quad y=\log _{ 17 }{ 25 } $$?
Show that :
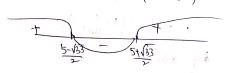
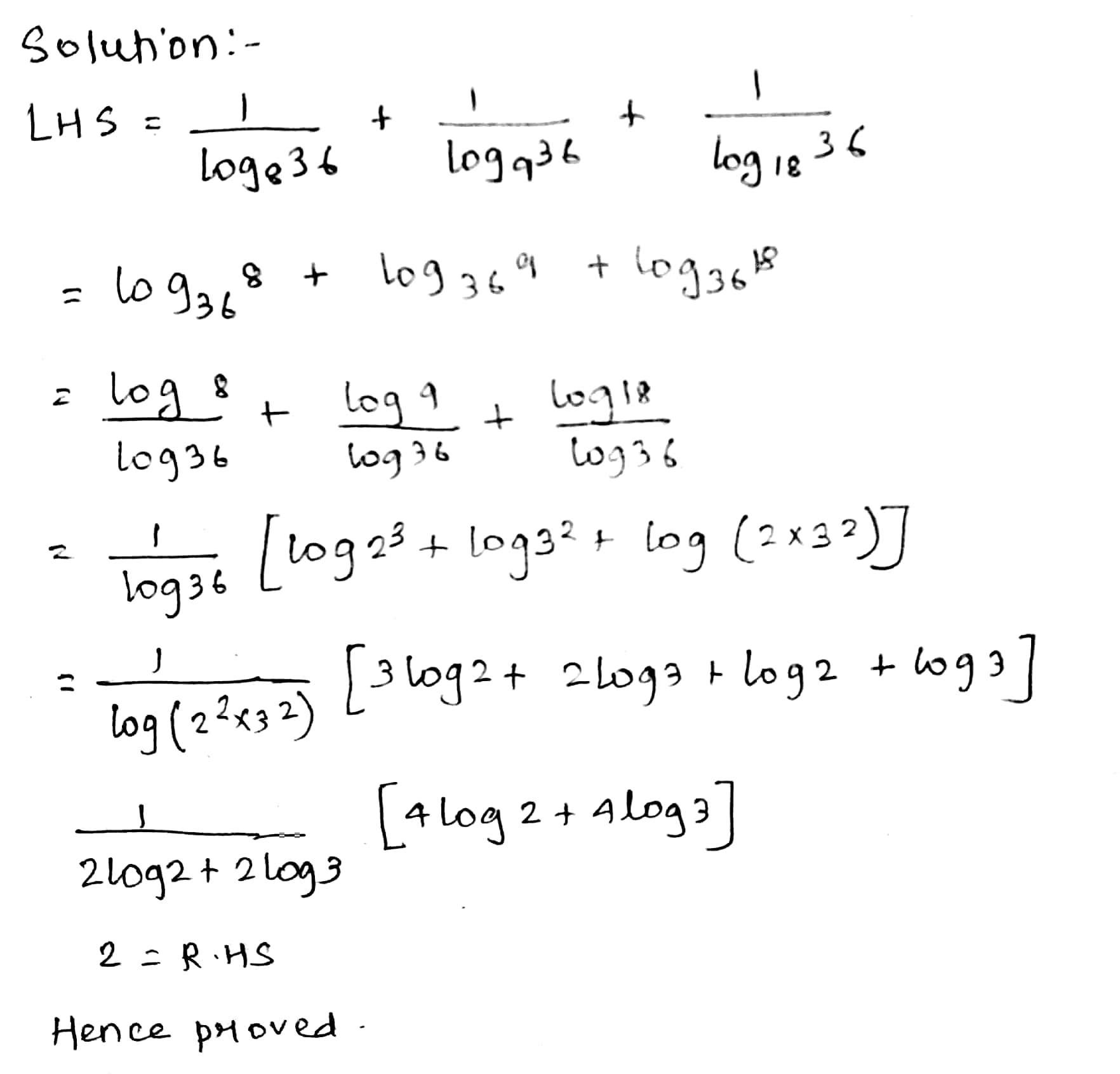
$$ 1/ \log_{8} 36 + 1 / \log_{9} 36+ 1 / \log_{18} 36=2 $$
Given $$\log2 = {^{.}3010300}, \log3 = {^{.}4771213}, \log7 = {^{.}8450980},$$ find the value of
$$\log 4\dfrac{2}{3}.$$
Find the value of $$\log 6 + 2 \log 5 + \log 4 \log 3 \log 2$$.
Class 11 Commerce Applied Mathematics Extra Questions
- Basics Of Financial Mathematics Extra Questions
- Circles Extra Questions
- Descriptive Statistics Extra Questions
- Differentiation Extra Questions
- Functions Extra Questions
- Limits And Continuity Extra Questions
- Logarithm And Antilogarithm Extra Questions
- Mathematical And Logical Reasoning Extra Questions
- Number Theory Extra Questions
- Numerical Applications Extra Questions
- Permutations And Combinations Extra Questions
- Probability Extra Questions
- Relations Extra Questions
- Sequences And Series Extra Questions
- Set Theory Extra Questions
- Straight Lines Extra Questions
- Tangents And Its Equations Extra Questions