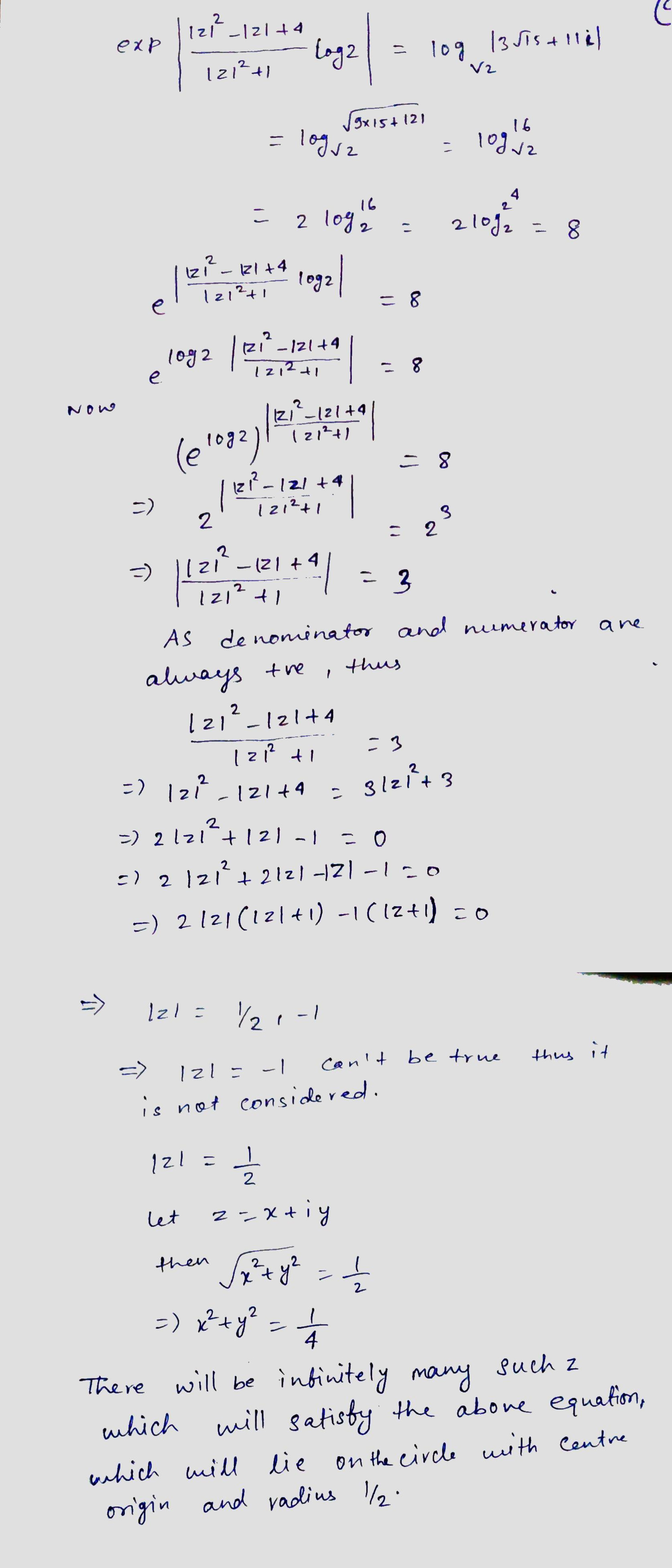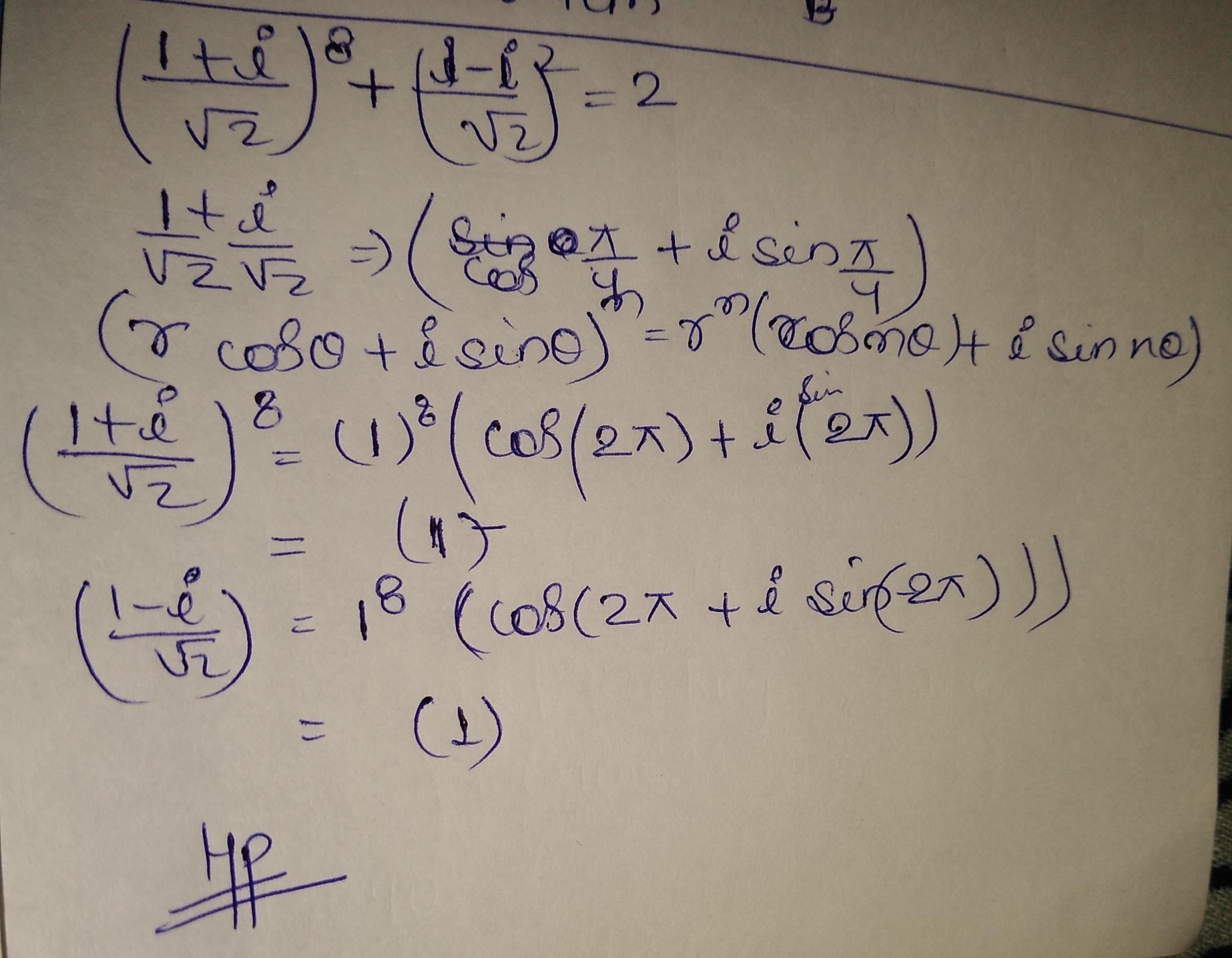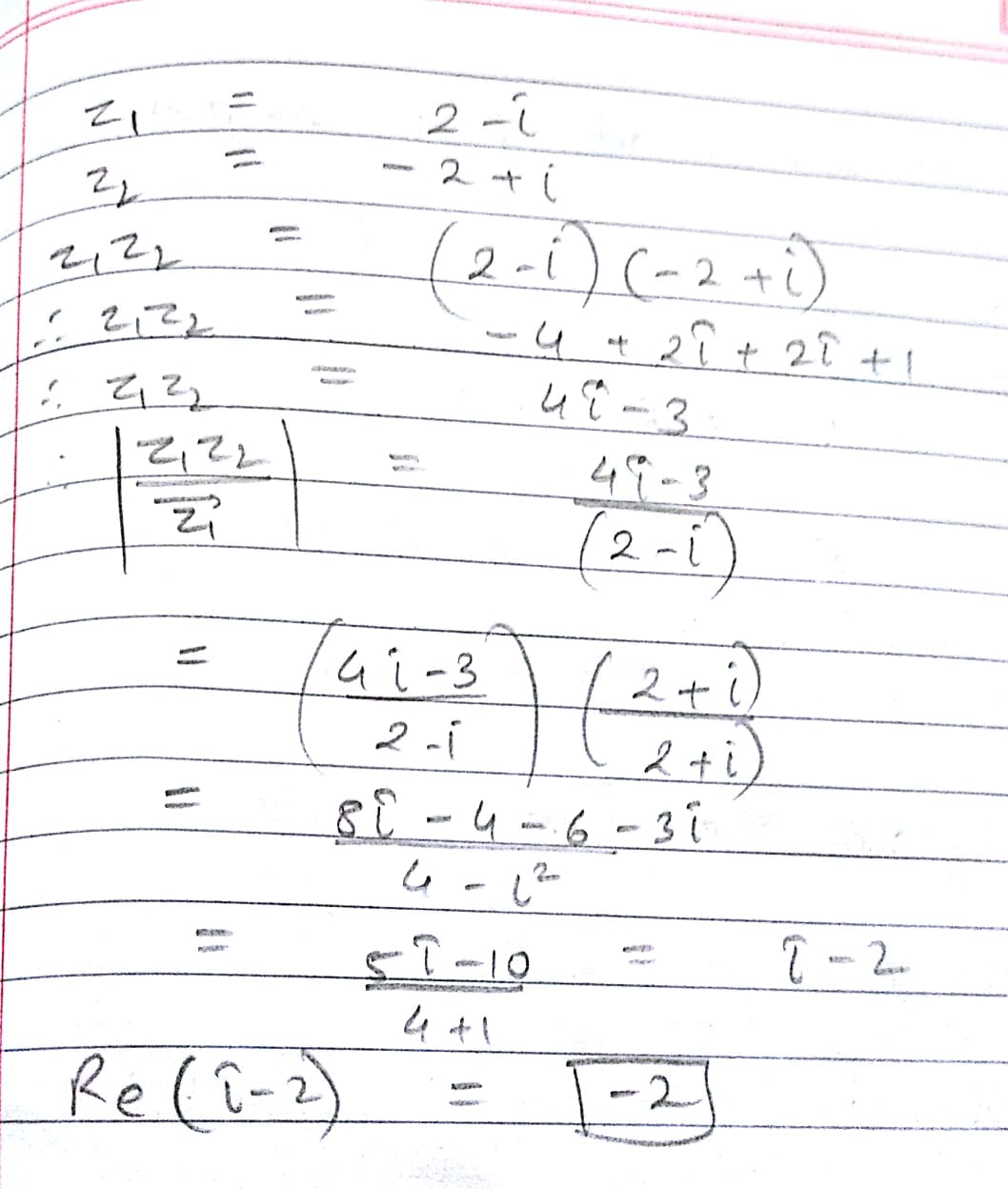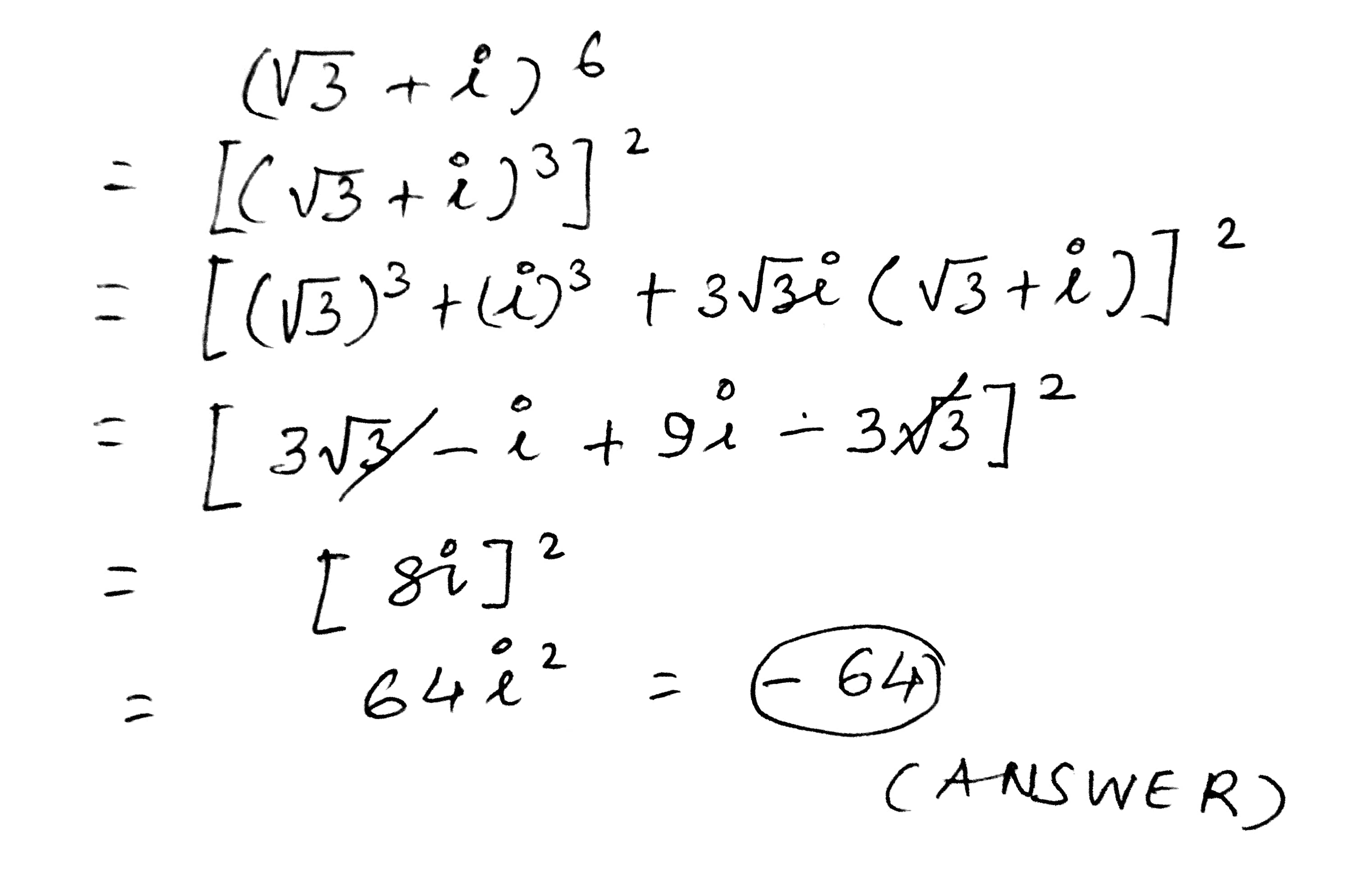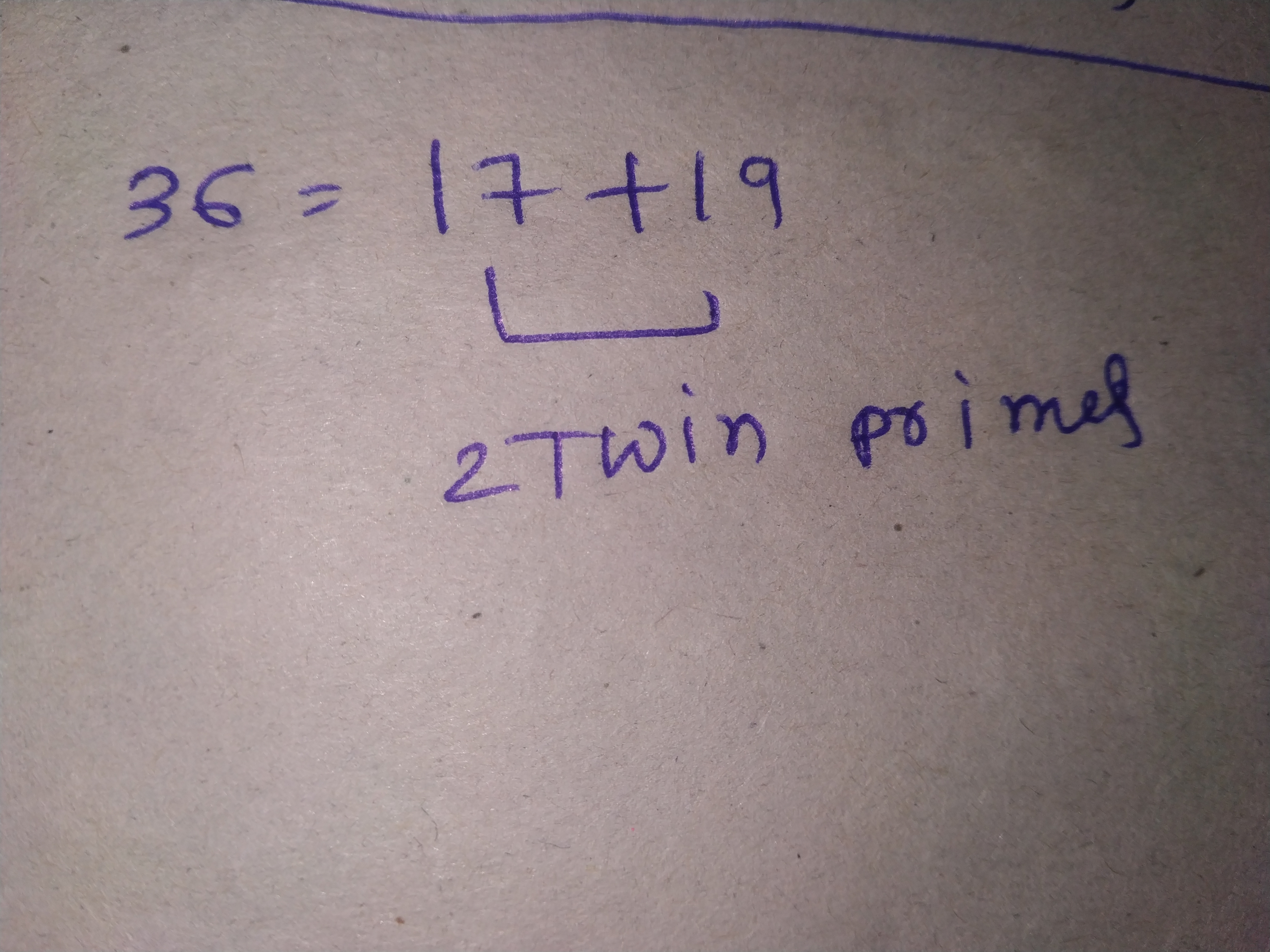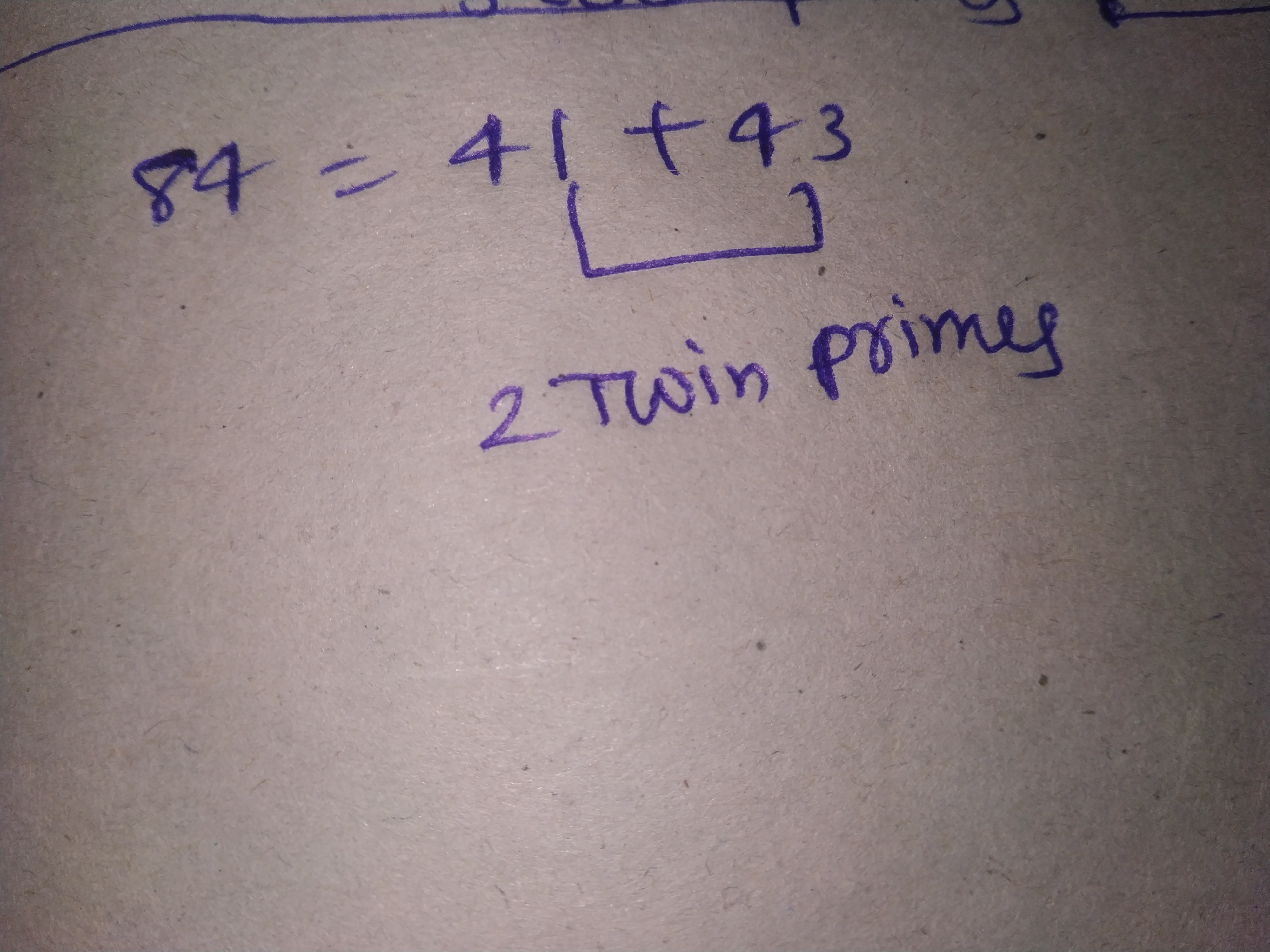Number Theory - Class 11 Commerce Applied Mathematics - Extra Questions

If $$Z_{1}$$ and $$Z_{2}$$ are two complex numbers and $$c> 0,$$ then prove that
$$\left | z_{1}+z_{2} \right |^{2}\leq \left ( 1+c \right )\left | z_{1} \right |^{2}+\left ( 1+c^{-1} \right )\left | z_{2} \right |^{2}$$

We have to prove:
$$\left | z_{1}+z_{2} \right |^{2}\leq \left ( 1+c \right )\left | z_{1} \right |^{2}+\left ( 1+c^{-1} \right )\left | z_{2} \right |^{2}$$
i.e. $$\left | z_{1} \right |^{2}+\left | z_{2} \right |^{2}+z_{1}\bar{z}_{2}+\bar{z}_{1}z_{2}\leq \left ( 1+c \right )\left | z_{1} \right |^{2}+\left ( 1+c^{-1} \right )\left | z_{2} \right |^{3}$$
or $$z_{1}\bar{z}_{2}+\bar{z}_{1}z_{2}\leq c\left | z_{1} \right |^{2}+c^{-1}\left | z_{2} \right |^{2}$$
or $$\displaystyle c\left | z_{1} \right |^{2}+\frac{1}{c}\left | z_{2} \right |^{2}-z_{1}\bar{z}_{2}-\bar{z}_{1}z_{2}\geq 0$$ (using Re$$\left ( z_{1}\bar{z}_{2} \right )\leq \left | z_{1}\bar{z}_{2} \right |$$)
or $$\displaystyle \left ( \sqrt{c}\left | z_{1} \right |-\frac{1}{\sqrt{c}}\left | z_{2} \right | \right )^{2}\geq 0$$ which is always true.


Let $$z_{1}$$ and $$z_{2}$$ be complex numbers such that $$z_{1}\neq z_{2}$$ and $$\left | z_{1} \right |=\left | z_{2} \right |.$$ If $$z_{1}$$ has positive real part and $$z_{2}$$ has negative imaginary part, then show that $$\displaystyle \frac{z_{1}+z_{2}}{z_{1}-z_{2}}$$ is purely imaginary.

$$\displaystyle z_{1}=r\left ( \cos \theta +i\sin \theta  \right ), -\frac{\pi }{2}< \theta < \frac{\pi }{2}$$
$$z_{2}=r\left ( \cos \phi +i\sin \phi  \right ), -\pi < \phi < 0$$
$$\Rightarrow $$ $$\displaystyle \frac{z_{1}+z_{2}}{z_{1}-z_{2}}=-i\cot \left ( \frac{0-\phi }{2} \right ), -\frac{\pi }{4}< \frac{\theta -\phi }{2}< \frac{3\pi }{4}$$
Hence purely imaginary


Multiply $$3\sqrt { -7 } -5\sqrt { -2 } $$ by $$3\sqrt { -7 } +5\sqrt { -2 } $$

$$(3\sqrt{-7}-5\sqrt{-2})\times(3\sqrt{-7}+5\sqrt{-2})$$
$$=(3\sqrt{7}\text i-5\sqrt{2}\text i)\times(3\sqrt{7}\text i+5\sqrt{2}\text i)$$
$$=-(3\sqrt{7}-5\sqrt{2})\times(3\sqrt{7}+5\sqrt{2})$$
$$=-(63+15\sqrt{14}-15\sqrt{14}-50)$$
$$=-13$$


Find the modulus of complex number $$-2+2\sqrt{3}i$$.

Let $$z=-2+2\sqrt{3}i$$
Then, modulus of z = $$|z|=\sqrt{(-2)^2+(2\sqrt{3})^2}=\sqrt{16}=4$$.


Compute :
$$(1 \, + \, i)^{-1}$$

$$(1 \, + \, i)^{-1} \, = \, \dfrac{1}{1 \, + \, i} \, = \, \dfrac{1 \, - \, i}{1 \, - \, i^2} \ = \, \dfrac{1 \, - \, i}{2}$$


Locate the points representing the complex number for which $${ \log }_{ 1/2 }\dfrac { \left| z-1 \right| +4 }{ \left| z-1 \right| -2 } >1$$

Put $$\left| z-1 \right| =t=+ive$$
Since its base is less than $$1$$, the given inequality 
implies that $$\dfrac { t+4 }{ t-2 } <{ \left( \dfrac { 1 }{ 2 }  \right) 
 }^{ 1 }=\dfrac { 1 }{ 2 }$$
or $$\dfrac { 2t+8 }{ t-2 } <1$$ or $$\dfrac { 2t+8 }{ t-2 } -1<0$$
or $$\dfrac { t+10 }{ t-2 } <0$$ where $$t$$ is $$+ive$$
We cannot multiply by $$t-2$$ as we do not know whether it is $$
+ive$$ or $$-ive$$.
$$\therefore t-2<0$$ or $$t<2$$
Again $${ \log }_{ 1/2 }\left( \dfrac { t+4 }{ t-2 }  \right) >1$$ (given)
Now order relation occurs only in real numbers and we know that 
$$\log \ x$$ is real only when $$x$$ is $$+ive$$ $$i.e.,>0$$
$$\therefore \dfrac { t+4 }{ t-2 }$$ is $$+ive\Rightarrow t>2$$
Since results $$(1)$$ and $$(2)$$ cannot hold together and hence 
no such $$z$$ exists which satisfies the given inequality.


compute.
$$[ (cos \theta \, + \, i \, sin \, \theta )  (\, cos \theta \, - \, i sin \theta  ) ] = ?$$

$$[(cos \, \theta \, + \, i \, sin \, \theta) (cos \, \theta \, - \, i \, sin \, \theta)]$$
$$= \, (cos^2 \, \theta \, - \, i^2 \, sin^2 \, \theta)$$
$$= \, (cos^2 \, \theta \, + \, sin^2 \, \theta)\, = \, 1.$$


Prove the identity,$$|1+z_1\bar{z_2}|^2+|z_1-z_2|^2=(1+|z_1|^2)(1+|z_2|^2)$$

Given,

$$|1-z_1\bar{z}_2|^2-|z_1-z_2|^2$$

$$=(1+z_1 ^2z_2 ^2-2 z_1 z_2)-(z_1 ^2+z_2^2-2z_1z_2)$$

$$=1+z_1^2z_2^2-2z_1z_2-z_1^2-z_2^2+2z_1z_2$$

$$=1+z_1^2z_2^2-z_1^2-z_2^2$$.......(1)

$$(1-|z_1|^2)(1-|z_2|^2)$$

$$=1-|z_2|^2-|z_1|^2+|z_1|^2|z_2|^2$$.......(2)

Comparing (1) and (2), it's clear that,

$$|1-z_1\bar{z}_2|^2-|z_1-z_2|^2=(1-|z_1|^2)(1-|z_2|^2)$$


Solve $$\left(\dfrac{1+i}{1-i}\right)^{24}$$

$$\displaystyle{{ \left( \frac { 1+i }{ 1-i }  \right)  }^{ 24 }\\ { \left( \frac { 1+i }{ 1-i } \times \frac { 1+i }{ 1+i }  \right)  }^{ 24 }\\ { \left( \frac { { (i+i) }^{ 2 } }{ 1-{ i }^{ 2 } }  \right)  }^{ 24 }\\ { \left( \frac { 1+{ i }^{ 2 }+2i }{ 2 }  \right)  }^{ 24 }\\ { \left( \frac { 1-1+2i }{ 2 }  \right)  }^{ 24 }\\ { i }^{ 24 }\\ { { (i }^{ 2 }) }^{ 12 }\\ 1}$$


Prove the identity $$|1-z_1{z_2}|^2-|z_1-z_2|^2=(1-|z_1|^2)(1-|z_2|^2)$$

Given,

$$|1-z_1\bar{z}_2|^2-|z_1-z_2|^2$$

$$=(1+z_1 ^2z_2 ^2-2 z_1 z_2)-(z_1 ^2+z_2^2-2z_1z_2)$$

$$=1+z_1^2z_2^2-2z_1z_2-z_1^2-z_2^2+2z_1z_2$$

$$=1+z_1^2z_2^2-z_1^2-z_2^2$$.......(1)

$$(1-|z_1|^2)(1-|z_2|^2)$$

$$=1-|z_2|^2-|z_1|^2+|z_1|^2|z_2|^2$$.......(2)

Comparing (1) and (2), it's clear that,

$$|1-z_1\bar{z}_2|^2-|z_1-z_2|^2=(1-|z_1|^2)(1-|z_2|^2)$$


The HCF of two or more prime numbers is always __________ 

 HCF of two or more prime number is always One. 


If $$\left( {a + ib} \right)\left( {c + id} \right) = A + iB$$, then show that $$\left( {{a^2} + {b^2}} \right)\left( {{c^2} + {d^2}} \right) = {A^2} + {B^2}$$.


$$\left( {a + ib} \right)\left( {c + id} \right) = A + iB\,\,\,\,\,\left( 1 \right)$$

$$\left( {a - ib} \right)\left( {c - id} \right) = A - iB\,\,\,\,\,\left( 2 \right)$$

$$Multiply.$$

$$\left( {a + ib} \right)\left( {a - ib} \right)\left( {c + id} \right)(c-id) = \left( {A + iB} \right)\left( {A - iB} \right)$$

$$\left( {{a^2} + {b^2}} \right)\left( {{c^2} + {d^2}} \right) = {A^2} + {B^2}$$



If $$(a+ib)(c+id)=A+iB$$, then show that $$({a^2} + {b^2})({c^2} + {d^2}) = {A^2} + {B^2}$$

$$\left( {a + ib} \right)\left( {c + id} \right) = A + iB{\text{   }} \to {\text{ }}\left( 1 \right)$$
$${\text{   Replace i by  - i,}}$$
$${\text{A  =  iB  =  }}\left( {a - ib} \right)\left( {c - id} \right)\,{\text{  }} \to \left( 2 \right)$$
$$\left( {A + iB} \right)\left( {A - iB} \right) = \left( {a + ib} \right)\left( {c + id} \right)\left( {a - ib} \right)\left( {c - id} \right)$$
$${\text{  =  (a - ib)}}\left( {a + ib} \right)\left( {c + id} \right)\left( {c - id} \right)$$
$${\text{ =  }}\left( {{a^2} - {{\left( {ib} \right)}^2}} \right)\left( {{c^2} - {{\left( {id} \right)}^2}} \right)$$
$${\text{  =  }}\left( {{a^2} + {b^2}} \right)\left( {{c^2} + {d^2}} \right)$$
    $${\text{ (}}\because {i^2} =  - 1)$$


Define and Give one example of each :
a) Parallel lines
b) Intersecting lines
c) Perpendicular line
d) Prime Number
e) Twin Prime
f) Even Number

(a) Parallel lines are two lines that are always the same distance apart and never touch each other. 
Ex : $$3x+2y=10,\;3x+2y=4$$
(b) Intersecting lines are two lines that meet exactly at  one point 
Ex : $$3x+2y=10,\;4x+5y=6$$ 
(c) Perpendicular lines are two lines that  intersect each other at right angle.
Ex : $$3x-2y=10,\;2x+3y=-5$$ 
(d) The numbers which are divisible only by $$144 or itself are called prime numbers.
Ex : $$3,7,11,....$$ 
(e) Twin prime numbers are those which have difference of $$2$$
Ex : $$11,13$$
(f) A prime number which is also an even number is called even prime number.
Ex : $$2$$.


Find the values of the following:
$$(1+i\sqrt {3})^{3}$$

$${(1 + i\sqrt 3 )^3}$$
$$=(1)^3+(i\sqrt3)^3+3(1)^2i\sqrt3+3(1)(i\sqrt3)^2$$
$$=1-3\sqrt3i+3\sqrt3i-9=-8$$


Find the value of $${(-1+\sqrt{-3})}^{2}+{(-1-\sqrt{-3})}^{2}$$.

$$\begin{array}{l} { \left( { -1+\sqrt { -3 }  } \right) ^{ 2 } }+{ \left( { -1-\sqrt { -3 }  } \right) ^{ 2 } } \\ ={ \left( { -1 } \right) ^{ 2 } }+{ \left( { \sqrt { 3 }  } \right) ^{ 2 } }+2\left( { -1 } \right) \left( { \sqrt { 3 }  } \right) +{ \left( { -1 } \right) ^{ 2 } }+{ \left( { -\sqrt { 3 }  } \right) ^{ 2 } } \\ =1-3-2\sqrt { 3 } +1-3+2\sqrt { -3 }  \\ =2-6 \\ =-4 \end{array}$$


Find the modules and the argument of the complex no $$Z=1+i$$

Given,

$$z=1+i$$

$$z=1+i$$

modulus: $$|z|=\sqrt{(1)^2+(1)^2}=\sqrt{2}$$

$$\theta =\tan^{1}\left ( \dfrac{1}{1} \right )=\tan^{1}(1)$$

argument: $$\therefore \theta =\dfrac{\pi}{4}$$


If $$a = \frac{{ - 1 + \sqrt {3i} }}{2}$$ , $$b = \frac{{ - 1 - \sqrt {3i} }}{2}$$ then show that $$\,\,{a^2} = b$$ and $$\,\,{b^2} = a$$.

Given,

$$a=\dfrac{-1+\sqrt{3}i}{2}$$

$$a^2=\left(\dfrac{-1+\sqrt{3}i}{2}\right)^2$$

$$=\dfrac{-2-2\sqrt{3}i}{2^2}$$

$$=-\dfrac{2\left(1+\sqrt{3}i\right)}{2^2}$$

$$=\dfrac{-1-\sqrt{3}i}{2}$$

$$=b$$

----------------------------------

$$b=\dfrac{-1-\sqrt{3}i}{2}$$

$$b^2=\left(\dfrac{-1-\sqrt{3}i}{2}\right)^2$$

$$=\dfrac{-2+2\sqrt{3}i}{2^2}$$

$$=-\dfrac{2\left(-1+\sqrt{3}i\right)}{2^2}$$

$$=\dfrac{-1+\sqrt{3}i}{2}$$

$$=a$$


$$z=2+3i$$ find $$|z|$$

$$z=2+3i$$ 
$$|z|=\sqrt {x^2+y^2}\\|z|=\sqrt {2^2+3^2}=\sqrt {4+9}=\sqrt {13}$$


Find the principal arguments of the following Complex Number
(i) $$5 + 5i$$

Given,

$$z=5+5i=a+ib$$

Principle argument,

$$\theta =\tan ^{-1}\left (\dfrac{b}{a}  \right )=\tan ^{-1}\left (\dfrac{5}{5}  \right )=\tan ^{-1}(1)$$

$$\therefore \theta =\dfrac{\pi}{4}$$


If $${z_1},{z_2} \in C,$$ then $$\left| {\dfrac{{{z_1}}}{{{z_2}}}} \right|$$.

Let $$z_{1}=x_{1}+iy_{1}, z_{2}=x_{2}+iy_{2}$$

where $$x_{1},x_{2},y_{1},y_{2}\in R$$

$$\left | \dfrac{z_{1}}{z_{2}} \right |=\dfrac{\left | z_{1} \right |}{\left | z_{2} \right |}$$ $$(z_{2}\neq 0)$$

$$=\dfrac{\sqrt{x_{1}^{2}+y_{1}^{2}}}{\sqrt{x_{2}^{2}+y_{2}^{2}}}$$


Let $$Z = x + iy$$ and $$\omega = \dfrac {1 - iZ}{Z - i}$$. If $$|\omega| = 1$$, show that $$Z$$ is purely real.

$$|w|=1$$
$$|\dfrac{1-iz}{z-i}|=1$$

$$|1-iz|=|z-i|$$
$$|1-i(x+iy)|=|x+i(y-1)|$$, where $$z=x+iy$$.
$$\sqrt{(1+y)^2+(-x)^2}=\sqrt{x^2+(y-1)^2}$$
$$(1+y)^2+x^2=x^2+(y-1)^2$$
$$y=0$$
$$z=x+i0=x$$, which is purely real.


Find the modulus of $$\frac{{1 + i}}{{1 - i}} - \frac{{1 - i}}{{1 + i}}$$

$$\\z= (\dfrac{1+i}{1-i})-(\dfrac{1-i}{1+i})$$

$$\\=(\dfrac{(1+i)^2-(1-i)^2}{(1-i)(1+i)})$$

$$\\=(\dfrac{1^2+i^2+2i-1^2-i^2+2i}{1^2-i^2})$$

$$\\=(\dfrac{4i}{2})$$

$$\\=2i$$

$$\\\therefore |z|=|2i|=2$$



Solve: $$x^2 - (3\sqrt{2} - 2i)x - \sqrt{2}i = 0$$

Given,

$$x^2-\left(3\sqrt{2}-2i\right)x-\sqrt{2}i=0$$

$$\left(a+bi\right)^2-\left(3\sqrt{2}-2i\right)\left(a+bi\right)-\sqrt{2}i=0$$

$$\left(a^2-b^2-3\sqrt{2}a-2b\right)+i\left(-\sqrt{2}+2a+2ab-3\sqrt{2}b\right)=0+0i$$

$$\begin{bmatrix}a^2-b^2-3\sqrt{2}a-2b=0\\ -\sqrt{2}+2a+2ab-3\sqrt{2}b=0\end{bmatrix}$$

solving the above 2 equations, we get,

$$\begin{pmatrix}a=\dfrac{3\sqrt{2}-4}{2},&b=-\dfrac{-\sqrt{2}+2}{2}\\ a=\dfrac{3\sqrt{2}+4}{2},&b=-\dfrac{2+\sqrt{2}}{2}\end{pmatrix}$$

$$x=\dfrac{3\sqrt{2}-4}{2}-\dfrac{-\sqrt{2}+2}{2}i,\dfrac{3\sqrt{2}+4}{2}-\dfrac{2+\sqrt{2}}{2}i$$


State whether the given statement is true or false $$\overline{(z^{-1})} \, = \, (\bar{z})^{-1}$$

We have,
$$\overline {(z^{-1}})=(\overline z)^{-1}$$

$$\overline {\left |z^{-1}\right|}=|\overline z|^{-1}$$

$$\overline {\left |\dfrac{1}{z}\right|}=\dfrac{1}{|\overline z|}$$

$$\dfrac{1}{|\overline {z}|}=\dfrac{1}{|\overline z|}$$


Hence, this is the answer.


Express $$\dfrac{{5 + i\sqrt 2 }}{{2i}}$$ in the form of $$x + iy$$.

$$\dfrac{5+i\sqrt{2}}{2i}=x+iy$$

$$\dfrac{5}{2i}+\dfrac{i\sqrt{2}}{2i}=x+iy$$

$$\dfrac{5i}{2{i}^{2}}+\dfrac{\sqrt{2}}{2}=x+iy$$

$$\dfrac{5i}{-2}+\dfrac{\sqrt{2}}{2}=x+iy$$ since $${i}^{2}=-1$$

$$\dfrac{\sqrt{2}}{2}-i\dfrac{5}{2}=x+iy$$

Comparing both the sides, we have

$$x=\dfrac{\sqrt{2}}{2}$$ and $$y=-\dfrac{5}{2}$$

$$\therefore\,x+iy=\dfrac{\sqrt{2}}{2}+i\left(-\dfrac{5}{2}\right)$$


If $$\dfrac{{{{\left( {1 + i} \right)}^2}}}{{2 - i}} = x - iy,$$ then find the value of $$x + y$$.

$$\dfrac{(1+i)^{2}}{2-i}=x-iy$$

$$=\dfrac{1+i^{2}+2i}{2-i}$$

$$=\left ( \dfrac{2i(2+i)}{2-i(2+i)} \right )$$

$$=\dfrac{4i-2}{4+1}$$

$$=\dfrac{4i}{5}-\dfrac{2}{5}$$

$$x=\dfrac{-2}{5},y=\dfrac{-4}{5}$$

$$x+y=\dfrac{-6}{5}$$


Find the real and imaginary parts of the complex number z=$$\dfrac{3i^{20}-i^{19}}{2i-1}$$

$$z=\dfrac{3i^{20}-i^{19}}{2i-1}=\dfrac{3(1)-(-i)))}{2i-1} $$=$$\dfrac{3+i}{-1+2i} $$

$$=\dfrac{3+i}{-1+2i}\times \dfrac{-1-2i}{-1-2i} $$

$$=\dfrac{-3-6i-i-2i^{2}}{(-1^{2})+2^{2}} $$

$$=\dfrac{-1-7i}{5} =\dfrac{-1}{5}-\dfrac{7}{5}i $$
$$Re(z)=-\dfrac{1}{5} $$ and $$Im(z)=\dfrac{-7}{5} $$


If $${\left( {\frac{{1 + i}}{{1 - i}}} \right)^3} - {\left( {\frac{{1 - i}}{{1 + i}}} \right)^3} = x + iy$$, then find $$(x,\,y)$$,

$$ \left ( \dfrac{1+i}{1-i} \right )^{3} - \left ( \dfrac{1-i}{1+i} \right )^{3} = x+iy$$

Rationalizing, we get, 

$$ \left ( \dfrac{(1+i)^{2}}{2} \right )^{3} - \left ( \dfrac{(1-i)^{2}}{2} \right )^{3} = x + iy$$

$$ \left ( \dfrac{1+2i-1}{2} \right )^{3}-\left ( \dfrac{1-2i-1}{2} \right )^{3}=x+iy$$

$$ (i)^{3} - (-i)^{3} = x + iy $$

$$ -i - (+i) = x + iy$$

$$- 2i = x + iy$$

so, $$y = - 2$$
 
$$x = 0$$



For the complex number$$\sqrt { 37 } + \sqrt { - 19 }$$.
Real part is $$\sqrt 37$$ and imaginary is $$\sqrt 19$$
Enter 1 if true or 0 for false

$$\\\sqrt{37}+\sqrt{-19}\\=\sqrt{37}+\sqrt{-1}\sqrt{19}$$

$$\\=\sqrt{37}+\sqrt{19}i$$

$$\therefore$$ Real Part = $$\sqrt{37}$$ 
& Imaginary Part = $$\sqrt{19}$$


What are twin-primes ?

Pair of prime numbers whose difference is $$2$$ called twin-primes. For example, $$(3,5), (5,7)$$ etc.


Express the following in the form of a = ib, a,b$$\epsilon$$R $$i = \sqrt{-1}$$. State the values of a and b.
 $$(1 + 2i)(-2 + i)$$

 $$(1 + 2i)(-2 + i)\\-2+i-4i-2\\-4-3i\\a=-4,b=-3$$


If ABC are angles of a triangle such that x = cis A, y = cis B, z = cis C, then find value of xyz

Given:- 
$$x = cis{A}$$
$$y = cis{B}$$
$$z = cis{C}$$
To find:- $$xyz = ?$$
Solution:-
Since $$A, B$$ and $$C$$ are angles of a triangle.
Therefore,
$$A + B + C = 180°$$
$$xyz$$
$$= cis{A} \cdot cis{B} \cdot cis{C}$$
$$= cis{\left( A + B + C \right)}$$
$$= cis{180°}$$
$$= \cos{180°} + i \sin{180°}$$
$$= -1 + i \left( 0 \right) = -1$$
Hence the value of $$xyz$$ is $$-1$$.


Give three pairs of prime numbers whose difference is $$2$$. [Remark: Two prime numbers whose difference is $$2$$ are called twin primes].

As we know,
Two prime numbers whose difference is 22 are called twin primes.
examples are as:
$$3, 5$$
$$41, 43$$
$$71, 73$$.


If $$z \neq 0$$ is a complex number,then prove that $$Re(z) = 0 \Longrightarrow  Im(z^2)=0$$.

If $$z \neq 0$$, let $$z = x + iy$$.
Then, $$z^2=(x+iy)(x+iy)$$
$$\Rightarrow z^2= x^2-y^2+i(2xy)$$
$$\because Re(z)= 0$$
$$ \Longrightarrow x=0$$
$$\Longrightarrow Im(z^2)=2xy=0$$


If $$(a + ib) (c + id) (e + if)(g +ih) = A + iB$$, then prove that $$(a^2 + b^2) (c^2 + d^2)(e^2 + f^2)(g^2 + h^2) = A^2 + B^2$$. 

$$(a + ib) (c + id) (e + if)(g +ih) = A + iB$$
$$\therefore \left|(a + ib) (c + id) (e + if)(g +ih)\right| = \left|A + iB\right|$$
or $$\left|(a + ib)\right| \times \left|(c + id)\right| \times \left|(e + if)\right| \times \left|(g +ih)\right| = \left|A + iB\right|$$
or $$\sqrt{a^2 + b^2} \times \sqrt{c^2 + d^2} \times \sqrt{e^2 + f^2} \times \sqrt{g^2 + h^2} = \sqrt{A^2 + B^2}$$
On squaring both sides, we get
$$(a^2 + b^2) (c^2 + d^2)(e^2 + f^2)(g^2 + h^2) = A^2 + B^2$$


If $$z = x + iy$$ and $$w = \dfrac{(1 - iz)}{(z - i)}$$ and $$\left|w\right| = 1$$, then prove that $$z$$ is purely real.

We have, 
$$\left|w\right| = 1
\Longrightarrow \left|\dfrac{1 - iz}{z - i}\right| = 1$$
or $$\dfrac{\left|1 - iz\right|}{\left|z - i\right|} =1$$
or $$\left|1 - iz\right| = \left|z - i\right|$$       (1)
or $$\left|1 - i (x + iy) \right| = \left|x + iy - i\right|$$, where $$ z = x + iy$$
or $$\left|1 + y - ix\right| = \left|x + i(y - 1)\right|$$
or $$\sqrt{(1+y)^2 + (-x)^2} = \sqrt{x^2 + (y - 1)^1}$$
or $$(1 + y)^2 + x^2 = x^2 + (y-1)^2$$
or $$y = 0$$
$$\Longrightarrow z = x + i0 = x,$$ which is purely real.

Ans: 1


If $$(x+iy)^3=u+iv$$, then prove that $$\displaystyle \frac{u}{x}+\frac{v}{y} =4(x^2 - y^2)$$. 

Given, $$(x+iy)^3=u+iv$$
$$x^3+(iy)^3 + 3. x. iy(x+iy) = u+iv$$
$$x^3+i^3y^3+3x^2yi+3xy^2 i^2=u+iv$$
$$x^3-iy^3+3x^2yi-3xy^2=u+iv$$
$$(x^3-3xy^2)=i(3x^2y-y^3)=u+iv$$
On equating real and imaginary parts, we get
$$u=x^3-3xy^2, v=3x^2y-y^3$$
$$\displaystyle \therefore \frac{u}{x}+\frac{v}{y}
=\frac{x^3-3xy^2}{x}+\frac{3x^2y-y^3}{y}
$$
$$\displaystyle=\frac{x(x^2-3y^2)}{x}+\frac{y(3x^2-y^2)}{y}
$$
$$=x^2-3y^2+3x^2-y^2
=4x^2-4y^2
=4(x^2-y^2)$$


If $$z_1$$ and $$z_2$$ are complex numbers and $$u = \sqrt{z_1z_2}$$, then prove that 
$$\left|z_1\right| + \left|z_2\right| = \left|\displaystyle \frac{z_1 + z_2}{2}+u\right| + \left|\displaystyle \frac{z_1 + z_2}{2}-u\right|$$.

$$\left|\dfrac{z_1 + z_2}{2}+u\right| + \left|\dfrac{z_1 + z_2}{2}-u\right|$$
$$=\left|\dfrac{z_1 + z_2}{2}+\sqrt{z_1z_2}\right| + \left|\dfrac{z_1 + z_2}{2}-\sqrt{z_1z_2}\right|$$
$$= \left|\dfrac{(\sqrt{z_1} + \sqrt{z_2})^2}{2}\right| + \left|\dfrac{(\sqrt{z_1} - \sqrt{z_2})^2}{2}\right|$$
$$= \left|\dfrac{(p+q)^2}{2}\right| + \left|\frac{(p-q)^2}{2}\right|$$ (where $$p = \sqrt{z_1}$$ and $$q = \sqrt{z_2}$$)  
$$= \dfrac{1}{2}\left[\left|p+q\right|^2 + \left|p-q\right|^2\right]$$
$$= \dfrac{1}{2}\left[2\left|p\right|^2 +2\left|q\right|^2 \right]$$
$$= \left|p\right|^2 + \left|q\right|^2$$
$$= \left|p^2\right| + \left|q^2\right|$$
$$= \left|z_1\right| + \left|z_2\right|$$

Ans: 1


If $$ \left|z_1 + z_2\right| = \left|z_1\right| + \left|z_2\right|$$, then show that $$arg(z_1) = arg(z_2)$$. 

$$\left|z_1 + z_2\right| =$$ $$\left|z_1\right| + \left|z_2\right|$$
or $$\left|z_1 + z_2\right|^2 = \left|z_1\right|^2 + \left|z_2\right|^2 + 2\left|z_1\right| \left|z_2\right|$$
or $$\left|z_1\right|^2 + \left|z_2\right|^2 + 2Re(z_1\overline{z}_2) = \left|z_1\right|^2 + \left|z_2\right|^2 + 2\left|z_1\right| \left|z_2\right|$$
or $$2Re(z_1\overline{z}_2) = 2\left|z_1\right| \left|z_2\right|$$
$$\Longrightarrow cos (\theta_1 - \theta_2) = 1$$
$$\Longrightarrow \theta_1 - \theta_2 = 0$$
$$\Longrightarrow arg(z_1) = arg(z_2)$$

Ans: 1


If $$\left|z_1 - z_2\right| = \left|z_1\right| + \left|z_2\right|$$, then prove that $$arg(z_1) - arg (z_2) = \pi$$ . I

$$\left|z_1 - z_2\right| = \left|z_1\right| + \left|z_2\right|$$
or $$\left|z_1 - z_2\right|^2 = \left|z_1\right|^2 + \left|z_2\right|^2 + 2\left|z_1\right| \left|z_2\right|$$
or $$\left|z_1\right|^2 + \left|z_2\right|^2 - 2Re(z_1\overline{z}_2) = \left|z_1\right|^2 + \left|z_2\right|^2 + 2\left|z_1\right| \left|z_2\right|$$
or $$-2Re(z_1\overline{z}_2) = 2\left|z_1\right| \left|z_2\right|$$
$$\Longrightarrow cos (\theta_1 - \theta_2) = -1$$
$$\Longrightarrow \theta_1 - \theta_2 = \pi$$ 

Ans: 1


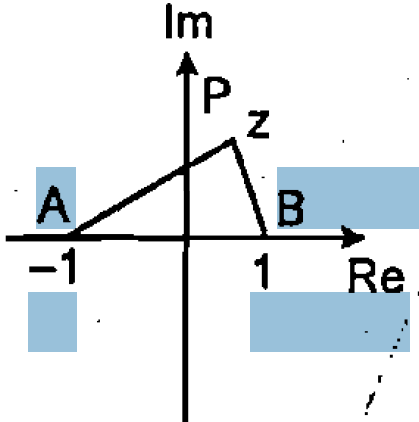
Find the minimum value of $$\left | 1+z \right |+\left | 1-z \right |.$$

$$\left | 1+z \right |+\left | 1-z \right |\geq \left | 1+z+1-z \right |$$ (triangle inequality)
$$\Rightarrow $$ $$\left | 1+z \right |+\left | 1-z \right |\geq 2$$
$$\therefore $$ minimum value of $$\left ( \left | 1+z \right |+\left | 1-z \right | \right )=2$$
Geometrically $$\left | z+1 \right |+\left | 1-z \right |=\left | z+1 \right |+\left | z-1 \right |$$
which represents sum of distances of $$z$$ from $$1$$ and $$-1$$
it can be seen easily that minimum $$\left ( PA+PB \right )=AB=2$$
1032289_332835_ans_372ec579868a4122a5e9dc36ef764fd3.png


$$2^{i}=e^{i(lnx)}$$.

$$2^{i}=e^{i\ln 2}=\left [ \cos \left ( \ln 2 \right )+i\sin \left ( \ln 2 \right ) \right ]$$
$$\cos \left ( \ln 2 \right )+i\sin \left ( \ln 2 \right )=e^{i\left ( \ln 2 \right )}$$


Compute the modulus of complex number $$z=\sqrt5-2i$$

$$|z|=\sqrt{\sqrt5^2+2^2}=\sqrt{9}=3$$.


If $$\displaystyle a+ib=\dfrac { { \left( x+i \right)  }^{ 2 } }{ { 2x }^{ 2 }+1 } $$, prove that $$\displaystyle { a }^{ 2 }+{ b }^{ 2 }=\dfrac { { \left( { x }^{ 2 }+1 \right)  }^{ 2 } }{ { \left( 2x^2+1 \right)  }^{ 2 } } $$.

$$\displaystyle a+ib=\frac { { \left( x+i \right)  }^{ 2 } }{ { 2x }^{ 2 }+1 } $$

$$\displaystyle =\frac { { x }^{ 2 }+{ i }^{ 2 }+2xi }{ 2{ x }^{ 2 }+1 } $$

$$\displaystyle =\frac { { x }^{ 2 }-1+2xi }{ 2{ x }^{ 2 }+1 } $$

$$\displaystyle =\frac { { x }^{ 2 }-1 }{ 2{ x }^{ 2 }+1 } +i\left( \frac { 2x }{ 2{ x }^{ 2 }+1 }  \right) $$

On comparing real and imaginary parts, we obtain

$$\displaystyle a=\frac { { x }^{ 2 }-1 }{ 2{ x }^{ 2 }+1 } and\quad b=\frac { 2x }{ 2{ x }^{ 2 }+1 } $$

$$\displaystyle

\therefore \quad { a }^{ 2 }+{ b }^{ 2 }={ \left( \frac { { x }^{ 2 }-1

}{ 2{ x }^{ 2 }+1 }  \right)  }^{ 2 }+{ \left( \frac { 2x }{ 2{ x }^{ 2

}+1 }  \right)  }^{ 2 }$$

$$\displaystyle =\frac { { x }^{ 4 }+1-{ 2x }^{ 2 }+4{ x }^{ 2 } }{ { \left( 2{ x }^{ 2 }+1 \right)  }^{ 2 } } $$

$$\displaystyle =\frac { { x }^{ 4 }+1+{ 2x }^{ 2 } }{ { \left( 2{ x }^{ 2 }+1 \right)  }^{ 2 } } $$

$$\displaystyle =\frac { { \left( { x }^{ 2 }+1 \right)  }^{ 2 } }{ { \left( 2{ x }^{ 2 }+1 \right)  }^{ 2 } } $$

$$\displaystyle

\therefore \quad { a }^{ 2 }+{ b }^{ 2 }=\frac { { \left( { x }^{ 2 }+1

\right)  }^{ 2 } }{ { \left( 2{ x }^{ 2 }+1 \right)  }^{ 2 } } $$
Hence, proved.


Express $$\cfrac{2+i}{(1+i)(1-2i)}$$ in the form of $$a+ib$$. Find its modulus and argument.

Here $$\cfrac{2+i}{(1+i)(1-2i)}=\cfrac{2+i}{1+i-2i-2{i}^{2}}=\cfrac{2+i}{3-i}$$

$$=\cfrac { 2+i }{ 3-i } \times \cfrac { 3+i }{ 3+i } =\cfrac { 6+3i+2i+{ i }^{ 2 } }{ 9+1 } $$

$$=\cfrac { 5+5i }{ 10 } =\cfrac{1}{2}+\cfrac{1}{2}i=\left( \cfrac { 1 }{ 2 } ,\cfrac { 1 }{ 2 }  \right) $$

$$\therefore$$ Modulus $$=\displaystyle \sqrt { { \left( \cfrac { 1 }{ 2 }  \right)  }^{ 2 }+{ \left( \cfrac { 1 }{ 2 }  \right)  }^{ 2 } } =\cfrac { 1 }{ \sqrt { 2 }  } $$
Since $$\left( \cfrac { 1 }{ 2 } ,\cfrac { 1 }{ 2 }  \right) $$ lies in the first quadrant
$$\therefore$$ Argument ($$\alpha$$)$$=\tan ^{ -1 }{ \left| \cfrac { 1/2 }{ 1/2 }  \right|  } =\tan ^{ -1 }{ (-1) } =\cfrac { \pi  }{ 4 } $$


Find the real and imaginary parts of the complex number $$\dfrac {a + ib}{a - ib}$$

$$=\dfrac {a + ib}{a - ib}\cdot \dfrac{a+ib}{a+ib}$$, [rationalize the denominator]

$$=\dfrac{(a+ib)^2}{a^2-i^2b^2}=\dfrac{a^2+i^2b^2+2iab}{a^2+b^2}$$

$$=\dfrac{a^2-b^2+(2ab)i}{a^2+b^2}$$

$$=\dfrac{a^2-b^2}{a^2+b^2}+\dfrac{2ab}{a^2+b^2}i$$

Hence real part is  $$\dfrac{a^2-b^2}{a^2+b^2}$$ and imaginary part is $$\dfrac{2ab}{a^2+b^2}$$


Find the number of integral solution of $$(1-i)^x=2^x$$.

Let first find the value of $$|1-i|$$
$$1-i$$ is the complex no in the form of $$x+i y=0$$
where $$x=1$$ and $$y=-1$$
$$|1-i|=\sqrt2$$
Given $$|1-i|^x=2^x$$
$$\Rightarrow (\sqrt2)^x=2^x$$
$$\Rightarrow (\sqrt2)^x=(\sqrt2)^{2x}$$
compair power
$$\Rightarrow x=2x$$
$$\Rightarrow x=0$$
So the answer is $$0$$
Hence, there is only $$1$$ integral solution.


If $$z$$ and $$\alpha$$ complex numbers such that $$|z| = |\alpha| = r, r > 0$$ and $$\omega = \dfrac {z - \overline {\alpha}}{r^{2} + z\overline {\alpha}}$$, find $$Re(\omega)$$.

$$|z=|\alpha|=r$$
$$z=a_1 +ib_1 \ \Rightarrow z=\sqrt {a_1^2 +b_1^2}=r \Rightarrow a_1^2 +b_1^2 =a_2^2 +b_2^2$$
$$x=a_2+ib_2 \Rightarrow \ x=\sqrt {a_2^2 +b_2^2} =r \ a_1^2 -a_2^2 =b_2^2 -b_1^2$$
$$w=\dfrac {a_1 +ib_1 -a_2 -ib_2}{r^2 +a_1 a_2 -b_1 b_2} \Rightarrow \dfrac {a_1 -a_2 +ib_1 -ib_2}{r^2 +a_1 a_2 -b_1 b_2}$$
$$Re(w)=\dfrac {a_1 -a_2}{r^2 +a_1 a_2 -b_1 b_2}$$
$$a_1^2 +b_1^2 $$ or $$a_2^2 +b_2^2$$


If the ratio $$\left (\dfrac {1 - z}{1 + z}\right )$$ is purely imaginary, then find value of $$|z|$$.

$$z=x+cy\\ \Rightarrow\dfrac{1-z}{1+z}=\left[ \cfrac { 1-x-cy }{ 1+x+cy }  \right] \\ =\cfrac { \left( 1-x-cy \right) \left( 1+x-cy \right)  }{ \left( 1+x+cy \right) \left( 1+x-cy \right)  } \\ =\cfrac { 1+x-cy-x-{ x }^{ 2 }+cxy-cy-cxy+{ x }^{ 2 }{ y }^{ 2 } }{ { \left( 1+x \right)  }^{ 2 }+{ y }^{ 2 } } \\ =\cfrac { 1-{ x }^{ 2 }-{ y }^{ 2 }-2xy }{ { \left( 1+x \right)  }^{ 2 }+{ y }^{ 2 } } \\ $$ 

So, $$=\cfrac { 1-{ x }^{ 2 }-{ y }^{ 2 } }{ { \left( 1+x \right)  }^{ 2 }+{ y }^{ 2 } } =0\\ 1-{ x }^{ 2 }-{ y }^{ 2 }=0\\ { x }^{ 2 }+{ y }^{ 2 }=1\\ \left| z \right| =\sqrt { { x }^{ 2 }+{ y }^{ 2 } } =\sqrt { 1 } =1$$

 



If $$a=\cfrac { 1+i }{ \sqrt { 2 }  } $$, find the value of $${ a }^{ 6 }+{ a }^{ 4 }+{ a }^{ 2 }+1$$

$${ a }^{ 6 }+{ a }^{ 4 }+{ a }^{ 2 }+1={ a }^{ 4 }\left( { a }^{ 2 }+1 \right) +1\left( { a }^{ 2 }+1 \right) \\ =\quad \left( { a }^{ 2 }+1 \right) \left( { a }^{ 4 }+1 \right) \quad ..............eq\quad \left( 1 \right) \\ Here,\\ \quad \quad \quad a=\cfrac { 1+i }{ \sqrt { 2 }  } \\ \Rightarrow \quad \sqrt { 2a } =1+i\\ Squaring\quad both\quad sides,\\ { \left( \sqrt { 2 } a \right)  }^{ 2 }={ \left( 1+i \right)  }^{ 2 }\\ \Rightarrow 2{ a }^{ 2 }=1+2i+i^{ 2 }\quad \left( { i }^{ 2 }=-1 \right) \\ \Rightarrow 2{ a }^{ 2 }=2i\\ \quad { a }^{ 4 }=-1\\ \left( { a }^{ 2 }+1 \right) \left( { a }^{ 4 }+1 \right) =\left( 1+1 \right) \left( -1+1 \right) =0$$



If $$\left| { z }_{ 1 } \right| =2,\left| { z }_{ 2 } \right| =3,\left| { z }_{ 3 } \right| =4$$ and $$\left| 2{ z }_{ 1 }+3{ z }_{ 2 }+4{ z }_{ 3 } \right| =10$$, then absolute value $$8{ z }_{ 2 }{ z }_{ 3 }+27{ z }_{ 3 }{ z }_{ 1 }+64{ z }_{ 1 }{ z }_{ 2 }$$ must be equal to-

$$|z_1|=2,z_1\bar{z_1}=4$$

$$|z_2|=3,z_2\bar{z_2}=9$$

$$|z_3|=4,z_3\bar{z_3}=16$$

$$|8z_2z_3+27z_3z_1+64z_1z_2|$$

$$\implies|2z_1\bar{z_1}z_2z_3+3z_2\bar{z_2}z_3z_1+4z_3\bar{z_3}z_1z_2|$$

$$\implies|z_1z_2z_3||2\bar{z_1}+3\bar{z_2}+4\bar{z_3}|$$

$$\implies 2\times 3\times 4|2{z_1}+3{z_2}+4{z_3}|$$

$$\implies 24\times 10=240$$



Find the points of the plane which satisfy the following equations.
$$\displaystyle \left | \, \frac{z \, - \, 2}{z \, + \, 3} \, \right | \, = \, 1.$$


1148852_889382_ans_df2109de7ef7424db5aeb8ae9e7e415d.jpg


Find the points of the plane which satisfy the following equations.
$$\displaystyle \left | \, \frac{z \, + \, i}{z \, - \, 3i} \, \right | \, = \, 1.$$


1148847_889386_ans_088cb905849a48bdb195466f369c37b2.pdf


Simplify the following :
$$\dfrac{(1 \, - \, i)^3}{1 \, - \, i^3}$$

$$\dfrac{(1 \, - \, i)^3}{1 \, - \, i^3}$$ $$ = \, \dfrac{(1 \, - \, i)^2}{1 \, + \, i^2 \, + \, i} \, = \, \dfrac{-2i}{i} \, = \, -2 \, $$


Express the following  in the form A + iB :
$$\dfrac{1}{1 \, - \, \cos \theta \, + \, 2i \, \sin \theta}$$

$$\dfrac{1}{1 \, - \, cos \theta \, + \, 2i \, sin \theta} \, = \, \dfrac{1}{2 \, sin^2 \dfrac{\theta}{2} \, + \, 4i \, sin \dfrac{\theta}{2} \, cos \dfrac{\theta}{2}}$$
$$= \, \dfrac{1}{2sin (\theta / 2)} \, \cdot \, \dfrac{1}{[sin(\theta / 2) \, + \, 2i \, cos \, (\theta / 2)]}$$
$$= \, \dfrac{1}{2sin (\theta / 2)} \, \cdot \, \dfrac{sin(\theta / 2) \, - \, 2i \, cos \, (\theta / 2)}{sin^2(\theta / 2) \, + \, 4 \, cos^2 \, (\theta / 2)}$$
$$=\,\dfrac{1 \, - \, 2i \, cot \, (\theta /2)}{2sin^2(\theta / 2) \, + \, 4[ 2cos^2 \, (\theta / 2)]}$$
Change the double angle.
$$= \,\dfrac{1 \, - \, 2i \, cot \, (\theta /2)}{5 \, + \, 3 \, cos \theta}$$


Put the following in the form A + iB :
$$\dfrac{(a \, + \, ib)^2}{(a \, - \, ib)} \, - \, \dfrac{(a \, - \, ib)^2}{(a \, + \, ib)}$$

$$\dfrac{(a \, + \, ib)^2}{(a \, - \, ib)} \, - \, \dfrac{(a \, - \, ib)^2}{(a \, + \, ib)} \, = \, \dfrac{(a \, + \, ib)^3 \, - \, (a \, - \, ib)^3}{(a \, - \, ib)(a \, + \, ib)}$$  
$$= \, \dfrac{2(3a^2 \, . \, ib \, + \, i^3b^3)}{a^2 \, + \, b^2} \, = \, \dfrac{2(3a^2b \, - \, b^3)}{a^2 \, + \, b^2}i$$
$$= \, \dfrac{2b(3a^2 \, - \, b^2)}{a^2 \, + \, b^2}i$$


If $$Z_r \, = \, \left ( \cos\dfrac{r\pi }{10} \, + \, i \, \sin \dfrac{r\pi }{10}\right ).$$ Then,  find the value of $$Z_1 \cdot Z_2 \cdot Z_3 \cdot Z_4 $$

$$Z_1 \, = \, \cos\dfrac{\pi }{10} \, + \, i \, \sin \dfrac{\pi }{10}=e^{i\pi/10}.$$

$$Z_2 \, = \, \cos\dfrac{2\pi }{10} \, + \, i \, \sin \dfrac{2\pi }{10}=e^{i2\pi/10}.$$

$$Z_3 \, = \, \cos\dfrac{3\pi }{10} \, + \, i \, \sin \dfrac{3\pi }{10}=e^{i3\pi/10}.$$

$$Z_4 \, = \, \cos\dfrac{4\pi }{10} \, + \, i \, \sin \dfrac{4\pi }{10}=e^{i4\pi/10}.$$

So, 

$$Z_1 \cdot Z_2 \cdot Z_3 \cdot Z_4$$

$$=e^{\dfrac {\pi}{10}}e^{\dfrac {2\pi}{10}}e^{\dfrac {3\pi}{10}}e^{\dfrac{4\pi}{10}}$$

$$=e^{ {\dfrac{\pi} {10}} \cdot (1+2+3+4)}$$

$$=e^{i\pi}=cos\pi+isin\pi=-1$$


If $$i{ z }^{ 3 }+{ z }^{ 2 }-z+i=0$$, then show that $$\left| z \right| =1$$.

Dividing throughout by $$i$$ and knowing that $$ \cfrac { 1 }{ i } =-i$$ 
we get
$$ { z }^{ 3 }-i{ z }^{ 2 }+iz+1=0$$
or $$ { z }^{ 2 }\left( z-i \right) +i\left( z-i \right) =0 \qquad as\ 1=-{ i }^{ 2 }$$ 
or $$ \left( z-i \right) \left( { z }^{ 2 }+i \right) =0$$
$$ \therefore z=i$$ or $${ z }^{ 2 }=-i$$
$$ \therefore \left| z \right| =\left| i \right| =1$$
$$ \left| { z }^{ 2 } \right| ={ \left| z \right|  }^{ 2 }=\left| -i \right| =1$$
$$ \therefore \left| z \right| =1$$
Hence in either case $$ \left| z \right| =1$$.


$$The\quad complex\quad number\quad \cfrac { { 2 }^{ n } }{ { (1+i) }^{ 2n } } +\cfrac { { (1+i) }^{ 2n } }{ { 2 }^{ n } } ,\quad n\quad \in Z,\quad is\quad equal\quad to\quad $$

$$\cfrac { { 2 }^{ n } }{ { (1+i) }^{ 2n } } +\cfrac { { (1+i) }^{ 2n } }{ { 2 }^{ n } } ,\quad n\quad \in I\\ { (1+p) }^{ 2 }=1-1+2i=2i\\ \cfrac { { 2 }^{ n } }{ { (2i) }^{ n } } +\cfrac { { (2i) }^{ n } }{ { 2 }^{ n } } =\quad \cfrac { { 2 }^{ n } }{ i^{ n }x{ 2 }^{ n } } +\cfrac { i^{ n }x{ 2 }^{ n } }{ { 2 }^{ n } } \\ =\cfrac { 1 }{ 4 } +{ i }^{ n }\\ =\cfrac { 1+{ 2 }^{ n } }{ { i }^{ n } } \\ =\cfrac { 1+{ (-1) }^{ n } }{ { i }^{ n } } \\ if\quad n\quad is\quad even\quad { (-1) }^{ n }=1=\cfrac { 2 }{ { i }^{ n } } \\ n\quad is\quad odd\quad { (-1) }^{ n }=-1=0$$


Find all the values of $$z$$ which satisfy the equation
exp$$\left| \dfrac { { \left| z \right|  }^{ 2 }-\left| z \right| +4 }{ { \left| z \right|  }^{ 2 }+1 } \log2 \right| ={ \log }_{ \sqrt { 2 }  }\left| 3\sqrt { 15 } +11i \right| $$


1317004_1001092_ans_b7a910b38c994aefa8a1257d359c45fb.jpg


Find the modulus and argument of the complex number:
$$\dfrac{1}{1+i}$$

Consider,
$$z=\dfrac{1}{1+i}$$

$$z=\dfrac{1}{1+i}\ \times\ \dfrac{1-i}{1-i}$$

$$z=\dfrac{1-i}{(1+i)(1-i)}$$

$$z=\dfrac{1-i}{1^2-i^2}$$

$$z=\dfrac{1-i}{1-(-1)}$$ -------- We know that $$i^2=-1$$

$$z=\dfrac{1-i}{2}$$

$$z=\dfrac{1}{2}-\dfrac{1}{2}i$$

This is the complex number of the form $$z=x+iy$$

$$x=\dfrac{1}{2}$$ and $$y=-\dfrac{1}{2}$$

We know that, $$Modulus=\sqrt{x^2+y^2}$$

$$=\sqrt{\dfrac{1}{4}+\dfrac{1}{4}}$$

$$=\sqrt{\dfrac{2}{4}}$$

$$=\dfrac{1}{\sqrt{2}}$$

Argument:

$$\dfrac{1}{2}+\left(-\dfrac{1}{2}\right)i=r\cos \theta+i\ r\sin \theta$$

Equating the real parts,

$$\dfrac{1}{2}=r\cos \theta$$

$$\dfrac{1}{2}=\dfrac{1}{\sqrt{2}}\cos \theta$$ ------ Above, $$modulus=r=\dfrac{1}{\sqrt{2}}$$

$$\cos \theta=\dfrac{1}{\sqrt{2}}$$

Similarly, equating the imaginary parts we get,

$$-\dfrac{1}{2}=r\sin \theta$$

$$\implies \sin \theta=-\dfrac{1}{\sqrt{2}}$$

Here, $$\sin \theta$$ is $$-ve$$ and $$\cos \theta$$ is $$+ve$$. Hence, $$\theta$$ is in 4th quadrant.

So, $$Argument=-45^\circ=-\dfrac{\pi}{4}\ radians$$


For any two complex number $$z_1$$ and $$z_2$$ prove that $$Re(z_1z_2)= Rez_1Rez_2-I mz_1Imz_1$$

Let $${ z }_{ 1 }=a+ib,{ z }_{ 2 }=x+iy$$
$${ z }_{ 1 }{ z }_{ 2 }=\left( a+ib \right) \left( x+iy \right) =ax+aiy+ibx+{ i }^{ 2 }by$$
$$Re\left( { z }_{ 1 }{ z }_{ 2 } \right) =ax-by$$
$$Re\left( { z }_{ 1 }{ z }_{ 2 } \right) =Re\left( { z }_{ 1 } \right) Re\left( { z }_{ 2 } \right) -Im({ z }_{ 1 })Im({ z }_{ 2 })$$
Hence proved


let $$z_1$$ and $$z_2$$ be two complex number such that $$|1-{z_1}z_2|^2-|z_1-z_2|^2=k\left(1-|z_1|^2\right)\left(1-|z_2|^2\right)$$  find the value of $$k$$

Given,

$$|1-\bar{z}_1{z}_2|^2-|z_1-z_2|^2$$

$$=(1+z_1 ^2z_2 ^2-2 z_1 z_2)-(z_1 ^2+z_2^2-2z_1z_2)$$

$$=1+z_1^2z_2^2-2z_1z_2-z_1^2-z_2^2+2z_1z_2$$

$$=1+z_1^2z_2^2-z_1^2-z_2^2$$.......(1)

$$(1-|z_1|^2)(1-|z_2|^2)$$

$$=1-|z_2|^2-|z_1|^2+|z_1|^2|z_2|^2$$.......(2)

Comparing (1) and (2), it's clear that,

$$|1-z_1\bar{z}_2|^2-|z_1-z_2|^2=(1-|z_1|^2)(1-|z_2|^2)$$

$$\therefore k=1$$


If $$\left( {a + ib} \right) = \frac{{1 + i}}{{1 - i}}$$ , then prove that $$\left( {{a^2} + {b^2}} \right) = 1$$

According to question,

$$a+ib=\dfrac{1+i}{1-i}$$

On taking modulus on both side we get,

$$|a+ib|=\dfrac{|1+i|}{|1-i|}$$

=>  $$\sqrt{a^2+b^2}=\dfrac{1}{1}$$

=>  $$a^2+b^2=1$$

Hence proved


How solve and what is its meaning
$$z_{1}=2+3i$$
$$z_{2}=3+4i$$
$$\left|z_{1}+z_{2}\right|=?$$

$$z_1 = 2+3i$$
$$z_2 = 3+4i$$

$$\implies z_1 + z_2 = 5+7i$$

$$\therefore |z_1 + z_2| = \sqrt{5^2 + 7^2} = \sqrt{25 + 49} = \sqrt{74}$$

It is modulus of a complex number


Let $$\dfrac{1}{a+ib}=c+id$$ for non-zero $$a,b$$, then find $$c,d$$.

Given,
$$\dfrac{1}{a+ib}=c+id$$
or, $$\dfrac{a-ib}{a^2+b^2}=c+id$$
or, $$\dfrac{a}{a^2+b^2}+i\dfrac{-b}{a^2+b^2}=c+id$$
Comparing the real and imaginary part both sides we get,
$$c=\dfrac{a}{a^2+b^2},d=\dfrac{-b}{a^2+b^2}$$.


Find the modulus and the arguments of each of the complex numbers is $$z=-\sqrt{3}+i$$

$$z =  - \sqrt 3  + i$$
$$\left| z \right| = \sqrt {{{\left( { - \sqrt 3 } \right)}^2} + {1^2}}  = \sqrt {3 + 1}  = 2$$
$$\tan \phi  = \left| {\dfrac{y}{x}} \right| = \left| { - \dfrac{1}{{\sqrt 3 }}} \right| = \dfrac{1}{{\sqrt 3 }}$$
$$ = \phi  = \dfrac{\pi }{6}$$
Since $$z$$ lies in second quadrant so, argument of $$z$$=$$z = \pi  - \phi $$
$$ = \pi  - \dfrac{\pi }{6}$$
$$ = \dfrac{{5\pi }}{6}$$



Find real values of $$\theta $$ for which$$\left( {\dfrac{{4 + 3i\;\sin \theta }}{{1 - 2i\;\sin \theta }}} \right)$$ is purely real.  

Given: 
$$\Rightarrow\dfrac{4+3i \sin(\theta)}{1-2i\sin{\theta}}$$    .......(i)

As the function is purely real, the imaginary part of eqn.(i) would be 0
rationalizing eqn.(i) we get,

$$\Rightarrow\dfrac{4+3i \sin(\theta)}{1-2i\sin{\theta}} \times \dfrac{1+2i\sin{\theta}}{1+2i\sin{\theta}}$$

$$\Rightarrow\dfrac{(4+3i \sin(\theta))\times (1+2i\sin(\theta))}{1^2-(2i\sin{\theta})^2}$$

.......{$$since,(a+b)(a-b) = a^2 - b^2$$ }

$$\Rightarrow\dfrac{4+8i\sin\theta+3i\sin\theta+6i^2\sin^2\theta}{1-4i^2\sin^2\theta}$$

$$\Rightarrow\dfrac{4+11i\sin\theta-6\sin^2\theta}{1+4\sin^2\theta}$$

.......{$$since, i^2=-1$$ }

$$\Rightarrow \dfrac{1}{1+4\sin\theta} \times [(4-6\sin^2\theta)+ i (11\sin\theta)]$$

the imainary part is equal to zero for eqn. (i) to be purely real.
$$\therefore$$ 
$$\Rightarrow\dfrac{11\sin\theta}{1+4\sin^2\theta} = 0$$

$$\Rightarrow\sin\theta = 0$$

the general solution for $$ \sin\theta = 0$$ is $$\theta \in n\pi \quad where,n \in Z$$

Hence, for $$\theta \in n\pi \quad where,n \in Z$$

$$\Rightarrow\dfrac{4+3i \sin(\theta)}{1-2i\sin{\theta}}$$ is purely real.


Prove that $${\left( {1 + i} \right)^4}{\left( {1 + \dfrac{1}{i}} \right)^4} = 16$$

 $$ LHS $$

 $$ {{\left( 1+i \right)}^{4}}{{\left( 1+\dfrac{1}{i} \right)}^{4}} $$

 $$ ={{\left( 1+i \right)}^{2}}{{\left( 1+\dfrac{1}{i} \right)}^{2}}{{\left( 1+i \right)}^{^{2}}}{{\left( 1+\dfrac{1}{i} \right)}^{2}} $$

 $$ ={{\left( 1+i \right)}^{2}}{{\left( 1+i \right)}^{^{2}}}{{\left( 1+\dfrac{1}{i} \right)}^{2}}{{\left( 1+\dfrac{1}{i} \right)}^{2}} $$

 $$ =\left( {{1}^{2}}+{{i}^{2}}+2i \right)\left( {{1}^{2}}+{{i}^{2}}+2i \right)\left( {{1}^{2}}+\dfrac{1}{{{i}^{2}}}+\dfrac{2}{i} \right)\left( {{1}^{2}}+\dfrac{1}{{{i}^{2}}}+\dfrac{2}{i} \right) $$

 $$ =\left( 1-1+2i \right)\left( 1-1+2i \right)\left( {{1}^{2}}+\dfrac{1}{-1}+\dfrac{2}{i} \right)\left( {{1}^{2}}+\dfrac{1}{-1}+\dfrac{2}{i} \right) $$

 $$ =2i\times 2i\times \dfrac{2}{i}\times \dfrac{2}{i} $$

 $$ =16 $$

 $$ RHS $$


Hence, proved.


$$\dfrac{4+3i}{(2+3i)(4-3i)}$$.

$$\cfrac{4+3i}{(2+3i)(4-3i)}$$
$$\cfrac{(4+3i)(4+3i)}{25(2+3i)}$$
$$\cfrac{7+24i}{25(2+3i)}$$
$$\cfrac{(7+24i)(2-3i)}{25 \times 13}$$
$$\cfrac{14-21i+48i+72}{325}$$
$$\cfrac{86+27i}{325}$$


For any two complex numbers $$z_1,z_2$$ and any two real numbers a and b,
$$|az_1-bz_2|^2+|bz_1+az_2|^2=.....$$  .

$$|az_1-bz_2|^2+|bz_1+az_2|^2$$
$$=|az_1|^2|+|bz_2|^2-2|abz_1z_2|+|bz_1|^2+|az_2|^2+2|az_1bz_2|$$
$$=a^2|z_1|^2+b^2|z_2|^2+b^2|z_1|^2+a^2(|z_2|)^2$$
$$=a^2(|z_1|^2+|z_2|^2)+b^2(|z_1|^2+|z_2|^2)$$
$$=(a^2+b^2)(|z_1|^2+|z_2|^2)$$.


Among the complex numbers $$Z$$ satisfying the condition $$|z+3-\sqrt{3}i| = \sqrt{3}$$, find the number having the least positive argument.


1360189_1133996_ans_70c21869723a47d590bbd8257bd57be8.jpg


Show that:
$$\left(\dfrac{1+i}{\sqrt{2}}\right)^{8}+\left(\dfrac{1-i}{\sqrt{2}}\right)^{8}=2$$

$$\left(\dfrac{1+i}{\sqrt{2}}\right)^8+\left(\dfrac{1-i}{\sqrt{2}}\right)^2=2$$
$$\dfrac{1}{\sqrt{2}}+\dfrac{i}{\sqrt{2}}$$
$$\Rightarrow \left(\cos \dfrac{\pi}{4}+i\sin\dfrac{\pi}{4}\right)$$
$$(r\cos \theta +i\sin\theta)^n=r^n(\cos n\theta)+i\sin n\theta)$$
$$\left(\dfrac{1+i}{\sqrt{2}}\right)^8=(1)^8(\cos(2\pi)+i\sin (2\pi))$$
$$=(1)$$
$$\left(\dfrac{1-i}{\sqrt{2}}\right)=1^8(\cos(2\pi +ii\sin(2\pi)))$$
$$=(1)$$.

1198036_1158330_ans_c356a9d748da4b17bb1b5133adaa00b1.jpg


Find the value of $${ x }^{ 3 }+2{ x }^{ 2 }-3x+21$$ if $$x=1+2i$$

$$x^3+2x^2-3x+21$$ if $$x=1+2i$$
$$(x-1)^2=(2i)^2$$
$$x^2-2x+1=-4$$
$$x^2-2x+5=0$$
$$\therefore x^3+2x^2-3x+21$$
$$=x(x^2-2x+5)+4x^2-8x+21$$
$$=0+4x^2-8x+21$$
$$=4(x^2-2x+5)+1$$
$$=0+1$$
$$=1$$
Value is $$1$$.


Let $$z_{1}=2-i,z_{2}=-2+i$$. Find $$Re\left(\dfrac {z_{1} z_{2}}{ \vec {z_{1}}}\right)$$


1118068_1163939_ans_35ede8965a19452e8350e7c9978d94dd.jpeg


Find the expanded form when $$z$$ is divided by $$z-0.5$$


1050648_1177652_ans_6de383a760154f10a4537949f7654bf1.png


Show that if $$\left| \dfrac { z - 3 i } { z + 3 i } \right| = 1 ,$$ then $$z$$ is a real number.

$$|(\dfrac{z-3i}{z+3i})|=1\\|z-3i|=|z+3i|\\|x+iy-3i|=|x+iy+3i|\\|x+i(y-3)|=|x+i(y+3)|\\\sqrt{x^2+(y-3)^2}=\sqrt{x^2+(y+3)^2}\\x^2+(y-3)^2=x^2+(y+3)^2\\(y-3)^2=(y+3)^2\\y-3=\pm (y+3)\\\therefore y-3 = y+3 or -3 = 3 \>which \>is\> not\> possible\\then\>y-3 = -(y+3)or \>y =0\\so\>z = x+iy = x+0 = x\\\ $$ 

z is real number.



If $$|z-1|+|z-3| \le 8$$, then find the range of $$|z-4|$$.

Given :$$|z+1|+|z-3| \le 8$$ 

To find : Range of $$|z-4|$$

Triangle Inequality : $$|z_1 + z_2| \le |z_1| + |z_2|$$

$$\to |z +1 + 2 -3| \le 8$$

$$\to |2z - 2| \le 8$$

$$\to |z  -1| \le 4$$

$$\to |z| \le 3$$

Now,

$$\to ||z| - 4| \le |z - 4| \le ||z| + 4|$$

$$\to 1 \le |z - 4| \le 7$$

$$\therefore |z-4| \in [1,7]$$


 Express the following in the form of a = ib, a,b$$\epsilon$$R $$i = \sqrt{-1}$$. State the values of a and b.
 $$(1+i)(1-i)^{-1}$$

$$(1+i)(1-i)^{-1}\\\dfrac{1+i}{1-i}\\\dfrac{(1+i)^2}{1-i^2}\\\dfrac{1-1+2i}2=i\\a=0,b=1$$


Show that $$(-1 + \sqrt 3 i)^3$$ is a real number.

$$\Rightarrow (\displaystyle -1+\sqrt 3 i)^3$$

$$\Rightarrow -1+3\sqrt 3i-3(-3)-3\sqrt 3i$$      $$[\because (a-b)^3=a^3-b^3-3ab(a-b)]$$

$$\Rightarrow-1+9=8$$

It is a real number.


Express $$(5-3i)^{3}$$ in the form $$a+ib$$.

$$\textbf{Use} \mathbf{(a-b)^3}\ \textbf{expansion}$$

$$(5-3i)^3=5^3-3\times5^2\times3i+3\times5\times(3i)^2-(3i)^3$$   $$[\because (a-b)^3=a^3-3a^2b+3ab^2-b^3]$$
              $$=125-3\times25\times3i+3\times5\times9i^2-27i^3$$
               $$=125-225i-135+27i$$              $$[\because i^2=-1]$$
               $$=-10-198i$$

$$\textbf{Hence,} \mathbf{(5-3i)^3}\ \textbf{in}\ \mathbf{(a+ib)}\ \textbf{form is}\ \mathbf{-10-198i}$$


Simplify: $$\left( -\sqrt { 3 } +\sqrt { -2 }  \right) \left( 2\sqrt { 3 } -i \right) $$=(a + ib)$$\left( -\sqrt { 3 } +\sqrt { -2 }  \right) $$. Find value of a and b.

$$\left( -\sqrt { 3 } +\sqrt { -2 }  \right) \left( 2\sqrt { 3 } -i \right) =\left( a+ib \right) \left( -\sqrt { 3 } +\sqrt { -2 }  \right) $$

$$\Rightarrow \left( -\sqrt { 3 } +i\sqrt { 2 }  \right) \left( 2\sqrt { 3 } -i \right) =\left( a+ib \right) \left( -\sqrt { 3 } +i\sqrt { 2 }  \right) $$

$$\Rightarrow \left( 2\sqrt { 3 } -i \right) =\left( a+ib \right) $$

$$\Rightarrow a=2\sqrt { 3 } ,\quad b=-1$$


Simplify and express the result in the form of $$a+ib$$ 
$$(\sqrt{3}+i)^6$$


2042820_1534994_ans_94566cd3c27148a5affcbadad03d4f90.jpg


Find the possible missing twins for the following number so that they become twin primes.
$$89$$.

Twin primes: Two prime numbers are said to be twin primes if there is only one composite number between them.
So, twin prime number can be obtained by adding or subtracting 2 to the given number.
$$89 + 2=91$$, or $$89−2=87$$
but $$87$$ is not a prime number.
$$∴89,91$$ -Twin primes 


Express the following number as the sum of twin primes.
$$36$$.


1504807_1658867_ans_0fb7167f97ba41a1bc56ed0cdab5fcbe.jpg


Find the possible missing twins for the following number so that they become twin primes.
$$101$$.

Twin primes: Two prime numbers are said to be twin primes if there is only one composite number between them.
So, twin prime number can be obtained by adding or subtracting 2 to the given number.
$$101 + 2=103$$, or $$101−2=99$$
but $$99$$ is not a prime number.
$$∴101,103$$ -Twin primes 


Find the possible missing twins for the following number so that they become twin primes.
$$29$$.

Twin primes: Two prime numbers are said to be twin primes if there is only one composite number between them.
So, twin prime number can be obtained by adding or subtracting 2 to the given number.
$$29 + 2=31$$ or $$29-2=27$$
but $$27$$ is not a prime number.
$$\therefore29, 31$$ -Twin primes 


Evaluate $$(\sqrt {-36}\times \sqrt{-25})$$.

$$(\sqrt{-36}\times \sqrt{-25})$$
$$\Rightarrow \sqrt{36} \ . \sqrt{-1} \ \times \sqrt{25} \ . \sqrt{-1}$$
$$\Rightarrow(6i\times 5i)=30i^{2}=-30$$


Define twin prime numbers.

$$A \space pair\space of\space prime\space numbers\space is\space said\space to\space be\space twin\space primes\space it\space they\space differ\space by \space$$$$2$$. $$Eg:$$ $$(3,5)$$ & $$(11,13)$$


Given the output of the following,
when num1 = 4, num2 = 3, num3 = 2
1. num1 + = num2 + num3
    print (num1)
2. num1 = num1 * (num2 + num3)
    print (numl)
3. num1 = num2* (num2 + num 3)
    print(num1)
4. num1 = '5' + '5'
    print (numl)

undefined
1985814_1940777_ans_f57c5ad14e9b476cbe5def461827586e.jpg


Prove that if $$\displaystyle x \, + \,\frac{1}{x} \, = \, 2 \, cos \, \alpha, \, then \, x^n \, + \, \frac{1}{x^n} \, = \, 2 \, cos \, n\alpha.$$

$$x+\cfrac{1}{x}=2\cos\alpha$$ (Given)
To Prove:
$$x^{n}+\cfrac{1}{2^:{n}}=2\cos n\alpha$$
Proof:
$$x^{2}+1=2x\cos\alpha$$-----------------(1)
then,
$$x^{2n}+1=2x^{k}\cos(n\theta)$$----------------------(2)
By Induction:
$$n=1: x^{2}+1=2\cos\theta$$--------------------------This is just Equation 1 is so true.
From Pythagoras and trigonometric relations, this also means:
$$\sqrt{4x^{2}-(x^{2}+1)^{2}}=2x\sin\theta=(x^{2}+1)\tan\theta$$

Assume that, $$n=k:\,\,\,x^{2k}+1=2x^{k}\cos(k\theta)$$ is true.
Then,
$$n=k+1:\,\,x^{2k+1}\cos(k\theta+\theta)$$
Now, $$x=\cos\theta+i\sin\theta$$
$$x^{n}+x^{-n}=\cos n\theta+i\sin n\theta+\cos n\theta-i\sin n\theta=2\cos n\theta$$
$$\therefore\,\,x^{n}+\cfrac{1}{x^{n}}=2\cos n\alpha$$


Given: $${ z }_{ 1 }+{ z }_{ 2 }+{ z }_{ 3 }=A;{ z }_{ 1 }+{ z }_{ 2 }w+{ z }_{ 3 }{ w }^{ 2 }=B;{ z }_{ 1 }+{ z }_{ 2 }{ w }^{ 2 }+{ z }_{ 3 }{ w }^{  }=C$$ where $$w$$ is cube rott of unity
Prove: $${ \left| A \right|  }^{ 2 }+{ \left| B \right|  }^{ 2 }+{ \left| C \right|  }^{ 2 }=3\left( { \left| { z }_{ 1 } \right|  }^{ 2 }+{ \left| { z }_{ 2 } \right|  }^{ 2 }+{ \left| { z }_{ 3 } \right|  }^{ 2 } \right) $$

We
$${ \left| A \right|  }^{ 2 }+{ \left| B \right|  }^{ 2 }+{ \left| C \right|  }^{ 2 }=A\overline { A } +B\overline { B } +C\overline { C } ....(1)$$
$$A\overline { A } =\left( { z }_{ 1 }+{ z }_{ 2 }+{ z }_{ 3 } \right) \left( \overline { { z }_{ 1 } } +\overline { { z }_{ 2 } } +\overline { { z }_{ 3 } }  \right) ={ z }_{ 1 }{ z }_{ 1 }+{ z }_{ 2 }{ z }_{ 2 }+{ z }_{ 3 }{ z }_{ 3 }+\overline { { z }_{ 1 } } \left( { z }_{ 2 }+{ z }_{ 3 } \right) +\overline { { z }_{ 2 } } \left( { z }_{ 3 }+{ z }_{ 1 } \right) +\overline { { z }_{ 3 } } \left( { z }_{ 1 }+{ z }_{ 2 } \right) ....$$
$$B\overline { B } =\left( { z }_{ 1 }+{ z }_{ 2 }\omega +{ z }_{ 3 }{ \omega  }^{ 2 } \right) \left( \overline { { z }_{ 1 } } +\overline { { z }_{ 2 }\omega  } +\overline { { z }_{ 3 }{ \omega  }^{ 2 } }  \right) =\left( { z }_{ 1 }+{ z }_{ 2 }\omega +{ z }_{ 3 }{ \omega  }^{ 2 } \right) \left( \overline { { z }_{ 1 } } +\overline { { z }_{ 2 } } { \omega  }^{ 2 }+\overline { { z }_{ 3 } } \omega  \right) \quad \left[ \because \overline { \omega  } ={ \omega  }^{ 2 };\left( \overline { { \omega  }^{ 2 } }  \right) =\omega  \right] $$
$$={ z }_{ 1 }\overline { { z }_{ 1 } } +{ z }_{ 2 }\overline { { z }_{ 2 } } { \omega  }^{ 3 }+{ z }_{ 3 }\overline { { z }_{ 3 } } { \omega  }^{ 3 }+\overline { { z }_{ 1 } } \left( { z }_{ 2 }\omega +{ z }_{ 3 }{ \omega  }^{ 2 } \right) +\overline { { z }_{ 2 } } \left( { z }_{ 3 }{ \omega  }^{ 4 }+{ z }_{ 1 }{ \omega  }^{ 2 } \right) +\overline { { z }_{ 3 } } \left( { z }_{ 1 }\omega +{ z }_{ 2 }{ \omega  }^{ 2 } \right) ={ \left| { z }_{ 1 } \right|  }^{ 2 }+{ \left| { z }_{ 2 } \right|  }^{ 2 }+{ \left| { z }_{ 3 } \right|  }^{ 2 }+\overline { { z }_{ 1 } } \left( { z }_{ 2 }\omega +{ z }_{ 3 }{ \omega  }^{ 2 } \right) +\overline { { z }_{ 2 } } \left( { z }_{ 3 }{ \omega  }^{ 4 }+{ z }_{ 1 }{ \omega  }^{ 2 } \right) +\overline { { z }_{ 3 } } \left( { z }_{ 1 }\omega +{ z }_{ 2 }{ \omega  }^{ 2 } \right) ....(2)\quad $$
Similarly
$$C\overline { C } ={ \left| { z }_{ 1 } \right|  }^{ 2 }+{ \left| { z }_{ 2 } \right|  }^{ 2 }+{ \left| { z }_{ 3 } \right|  }^{ 2 }+\overline { { z }_{ 1 } } \left( { { z }_{ 2 }{ \omega  }^{ 2 }+z }_{ 3 }\omega  \right) +\overline { { z }_{ 2 } } \left( { z }_{ 3 }{ \omega  }^{ 2 }+{ z }_{ 1 }{ \omega  }^{ \quad  } \right) +\overline { { z }_{ 3 } } \left( { z }_{ 1 }{ \omega  }^{ 2 }+{ z }_{ 2 }{ \omega  }^{  } \right) ....(3)$$
Adding (1), (2) and (3), we get
$$A\overline { A } +B\overline { B } +C\overline { C } =3\left[ { \left| { z }_{ 1 } \right|  }^{ 2 }+{ \left| { z }_{ 2 } \right|  }^{ 2 }+{ \left| { z }_{ 3 } \right|  }^{ 2 } \right] +\overline { { z }_{ 1 } } \left[ { z }_{ 2 }\left( 1+\omega +{ \omega  }^{ 2 } \right) +{ z }_{ 3 }\left( 1+{ \omega  }^{ 2 }+\omega  \right)  \right] +\overline { { z }_{ 2 } } \left[ { z }_{ 2 }\left( 1+\omega +{ \omega  }^{ 2 } \right) +{ z }_{ 1 }\left( 1+{ \omega  }^{ 2 }+\omega  \right)  \right] +\overline { { z }_{ 3 } } \left[ { z }_{ 2 }\left( 1+\omega +{ \omega  }^{ 2 } \right) +{ z }_{ 2 }\left( 1+{ \omega  }^{ 2 }+\omega  \right)  \right] $$
From (1) and (2) we conclude
$${ \left| A \right|  }^{ 2 }+{ \left| B \right|  }^{ 2 }+{ \left| C \right|  }^{ 2 }=3\left[ { \left| { z }_{ 1 } \right|  }^{ 2 }+{ \left| { z }_{ 2 } \right|  }^{ 2 }+{ \left| { z }_{ 3 } \right|  }^{ 2 } \right] $$


Perform the indicated operations.
$$\displaystyle (- \, 1 \, + \, \sqrt{3i})^3.$$

$$(a+b)^{3}=a^{3}+b^{3}+3a^{2}b+3ab^{2}$$
$$(-1+\sqrt{3i})^{3}=(-1)^{3}+(\sqrt{3i})+(\sqrt{3i})+(\sqrt{3i})+3(-1)^{2}(\sqrt{3i})+3(-1)(\sqrt{3i})^{2}$$
$$=-1+3i\sqrt{3i}+3\sqrt{3i}-3\times 3i$$
$$=-1+3i\sqrt{3i}+3\sqrt{3i}-9i$$


Solve $$\left(\dfrac {1}{1-4i}-\dfrac {2}{1+i}\right)\left(\dfrac {3-4i}{5+i}\right)$$

$$\left( {\dfrac{1}{{1 - 4i}} - \dfrac{2}{{1 + i}}} \right)\left( {\dfrac{{3 - 4i}}{{5 + i}}} \right)$$

$$ = \left( {\dfrac{{1 + i - 2 + 8i}}{{1 + i - 4i + 4}}} \right)\left( {\dfrac{{3 - 4i}}{{5 + i}}} \right)$$

$$ = \left( {\dfrac{{ - 1 + 9i}}{{5 - 3i}}} \right)\left( {\dfrac{{3 - 4i}}{{5 + i}}} \right)$$

$$ = \left( {\dfrac{{ - 3 + 4i + 27i + 36}}{{25 + 5i - 15i + 3}}} \right)$$

$$ = \left( {\dfrac{{33 + 31i}}{{28 - 10i}}} \right)$$



Solve $$\dfrac {1}{1+i}$$

Rationalizing $$\dfrac{1}{{1 + i}}$$.


$$\dfrac{1}{{1 + i}} = \dfrac{1}{{1 + i}} \times \dfrac{{1 - i}}{{1 - i}}$$


$$ = \dfrac{{1 - i}}{{\left( {{1^2}} \right) - \left( {{i^2}} \right)}}$$


$$ = \dfrac{{1 - i}}{{1 + 1}}$$


$$ = \dfrac{{1 - i}}{2}$$



Express the following number given in the form $$a+ib$$.
$$(5i)\left(-\dfrac{3}{5}i\right)$$.

$$\left( 5i \right) \left( -\cfrac { 3i }{ 5 }  \right) \\ =-3{ i }^{ 2 }\\ =-3\left( -1 \right) \qquad \left[ \because { i }^{ 2 }=-1 \right] \\ =3\\ =3+i\left( 0 \right) $$
Comparing with a+ib,
$$a=3,b=0$$
Therefore, $$3+i(0)$$


If $$|z + 1| = z + 2 (1 + i)$$, then find $$z$$.

$$\left | z+1 \right |=z+2(1+i)$$

Let  $$z=x+iy$$

$$\left | x+iy+1 \right |=x+iy+2(1+i)$$

$$\sqrt{(x+1)^{2}+y^{2}}=x+iy+2+2i$$

$$\sqrt{(x+1)^{2}+y^{2}}+0i=(x+2)+i(y+2)$$

$$\Rightarrow y+2=0$$

$$y=-2$$

And,
$$x+2=\sqrt{(x+1)^{2}+y^{2}}$$

$$x+2=\sqrt{(x+1)^{2}+(-2)^{2}}$$

Squaring both sides,
$$(x+2)^{2}=(x+1)^{2}+4$$

$$x^{2}+4+4x=x^{2}+1+2x+4$$

$$2x=1$$

$$x=\cfrac{1}{2}$$

Therefore, $$z=\cfrac{1}{2}-2i$$


Define twin primes.Determine twin primes between $$ 50 $$ and $$ 1000 $$


2039359_1269195_ans_77bb1d51ed6f447b81c1722dd71ae5f2.jpg


What are twin-primes? Write all pairs of twin-primes between $$50$$ and $$100$$.

Twin primes are pair of prime numbers which differ by 2
So, all the pairs of twin primes between 50 and 100 are - (59,61) and (71,73)


Express the following number as the sum of twin primes.
$$120$$.

The twin prime numbers are pair of prime numbers whose difference is equal to 2
Now, for 120, first divide 120 by 2 , we get 60 and then by adding 1 and subtracting 1 , we get two numbers 
60-1=59
60+1=61
Here, 59 and 61 are prime numbers which have a difference of 2 and add up to form 120
59+61=120



Express the following number as the sum of twin primes.
$$84$$.


1504809_1658868_ans_c1eb8f52e51a4e188aa6f9869c2b27f4.jpg


Class 11 Commerce Applied Mathematics Extra Questions