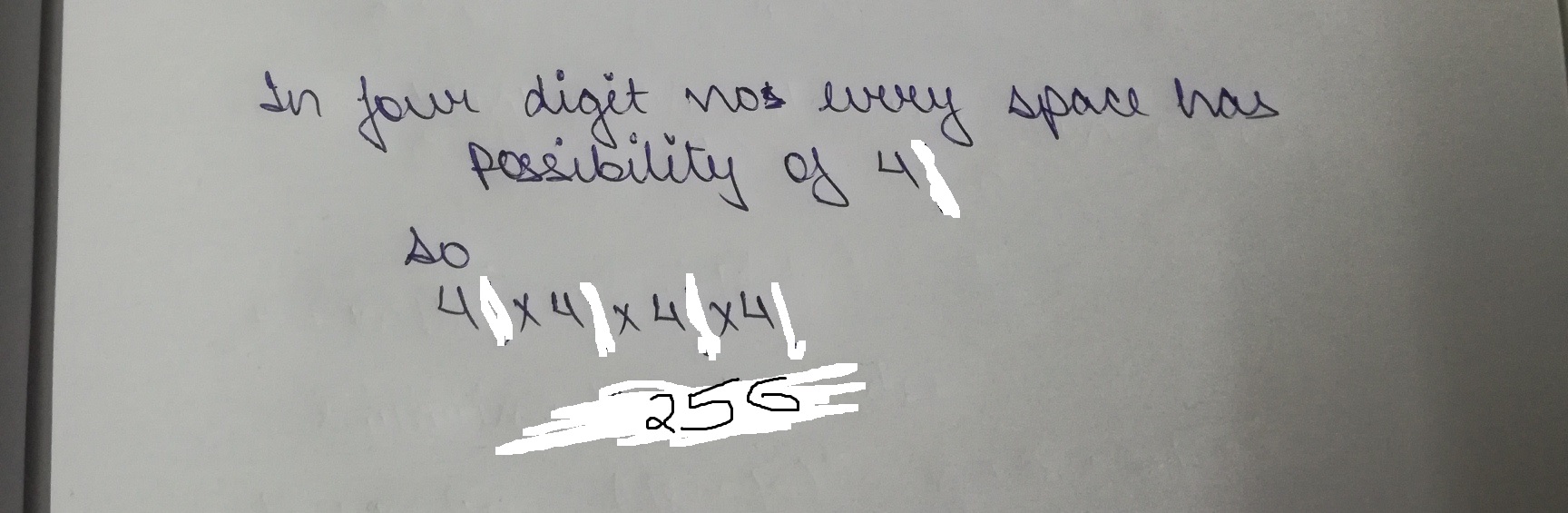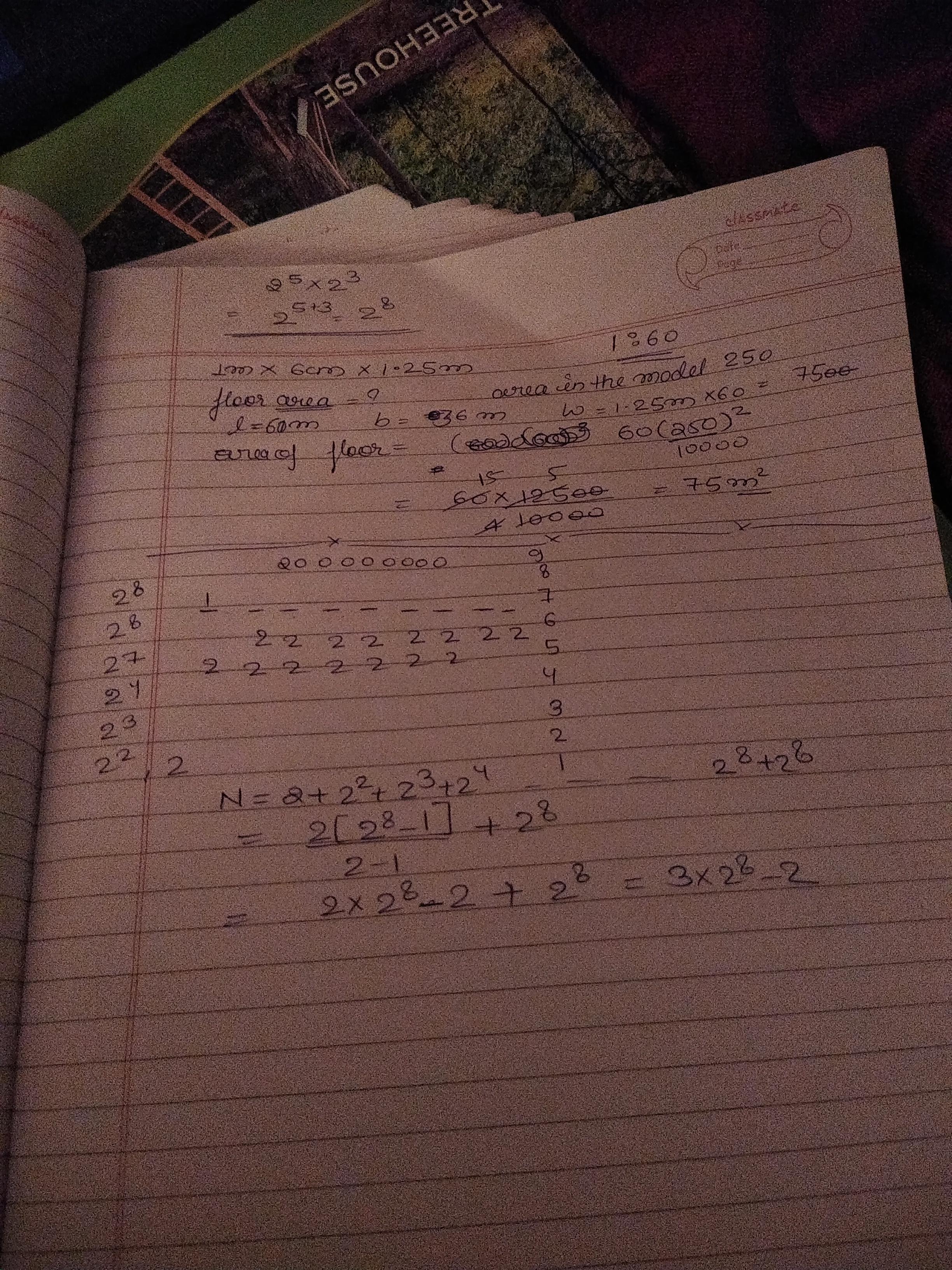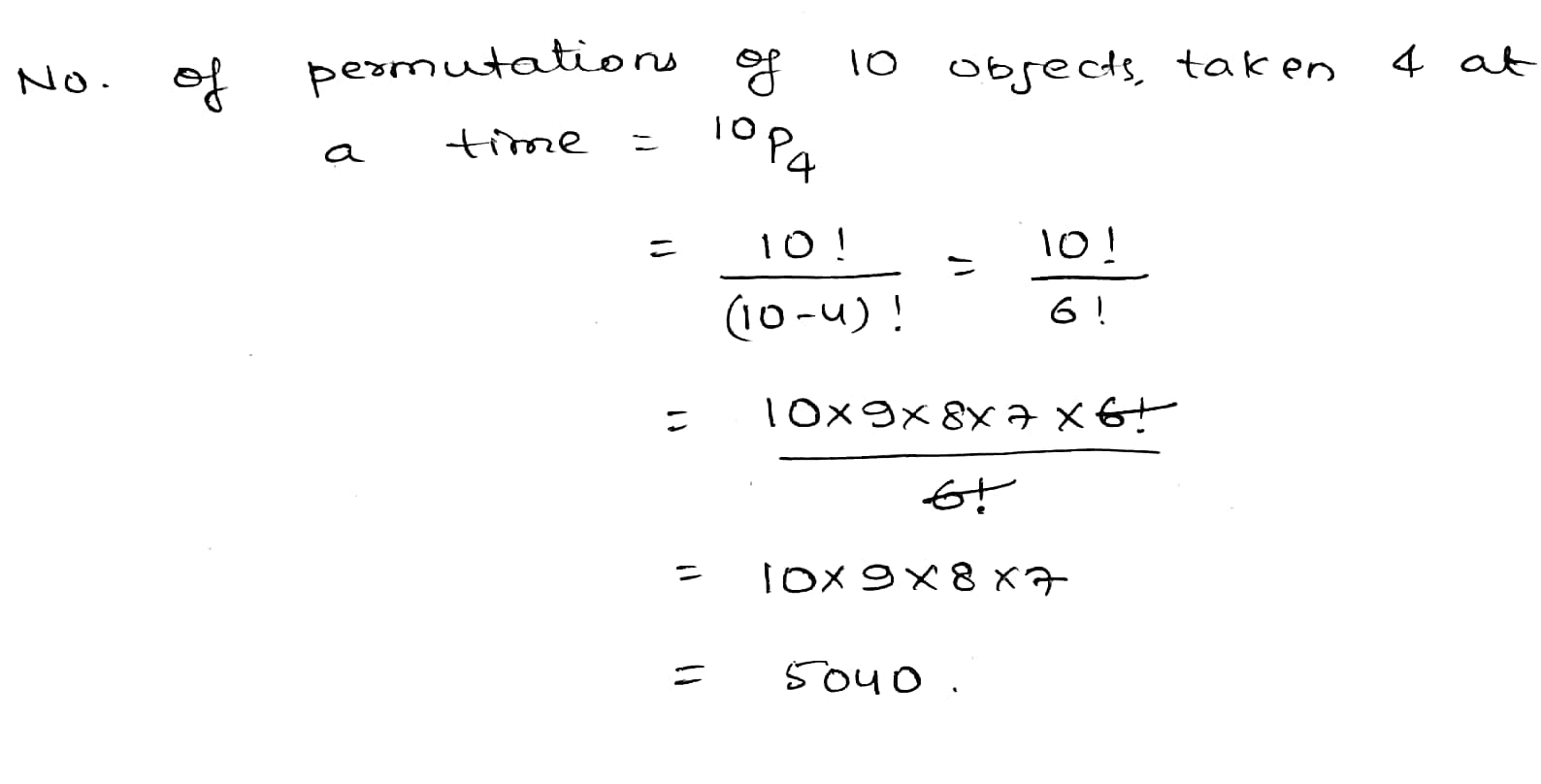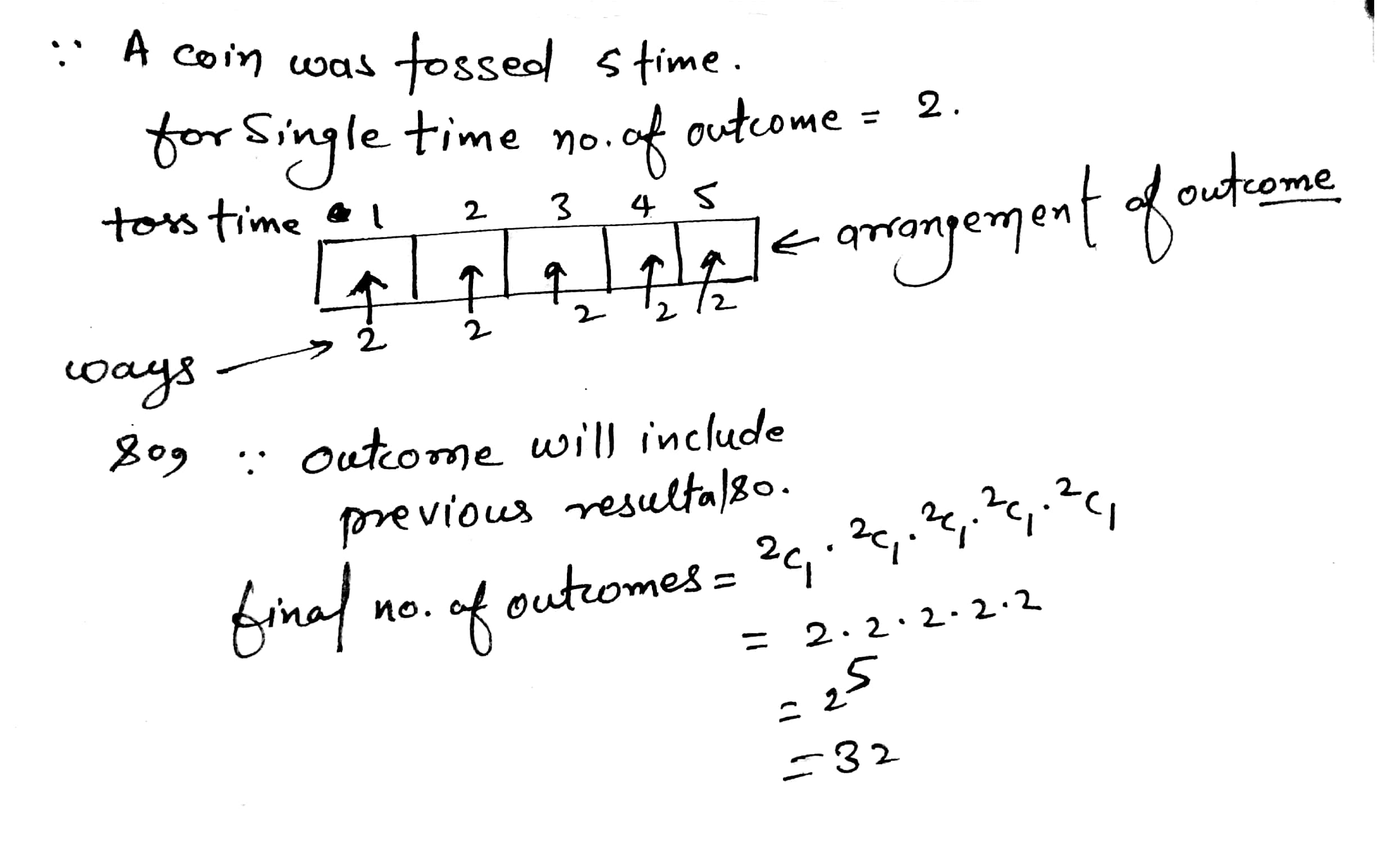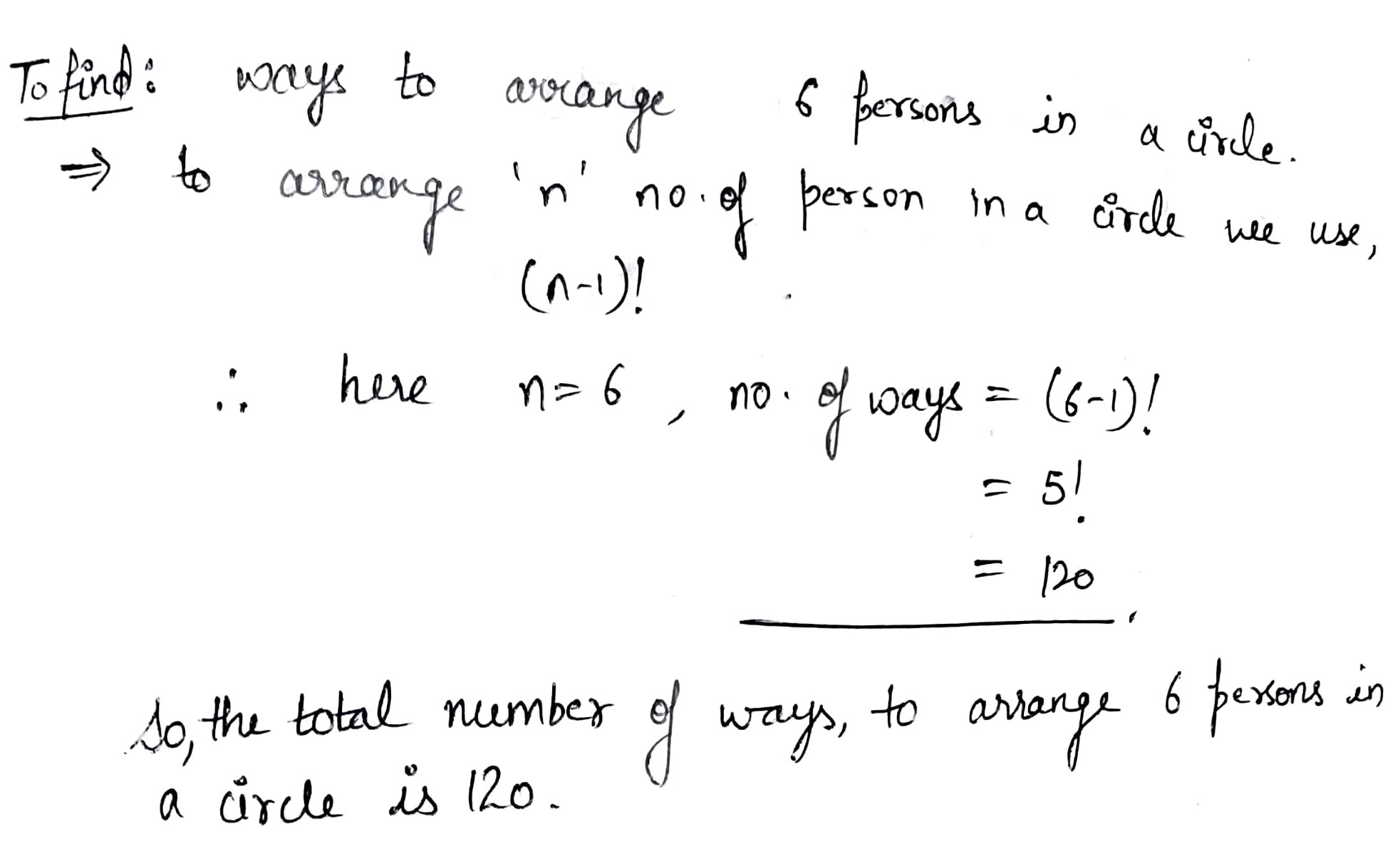Permutations And Combinations - Class 11 Commerce Applied Mathematics - Extra Questions

In how many different ways can the letters of the word ' KURUKSHETRA' be arranged?


Number of letters in the word 'KURUKSHETRA' is $$11$$ of which $$2$$ are $$K$$'s, $$2$$ are $$U$$'s, $$2$$ are $$R$$'s and remaining are different.
Thus required number of permutations
$$=\dfrac{11!}{2!2!2!}$$
$$=4989600$$


In how many different ways can the letters of the word `KURUKSHETRA' be arranged?

no. of letter in word $$ = 11 $$
$$ \Rightarrow $$ letters which are repeated 
are $$ K,U,R $$ (all 2 times)
So, no. of ways, letters 
can be arranged are:-
$$ \dfrac{11!}{2!2!2!} = 4989600 $$.


Prove that the number of ways in which $$8$$ different flowers can be strung to form a garland so that $$4$$ particular flowers are never separated is $$\dfrac{1}{2}4!4!$$

Tie 4 flowers so that we have now in all five (4 different and- one bunch). These five can be arranged in a garland in $$\dfrac{1}{2}$$ i.e. (n - 1)! i.e. $$\dfrac{1}{2}$$ (4!) ways. The bunch can be arranged in 4! ways. Hence by fundamental theorem total is $$\dfrac{1}{2}(4!.4!)$$


Determine the number of rectangles that can be formed on a chess-board.

We know that ,

The no. of rows and columns in a chase board  $$8\times 8$$

Number of ways to select $$1$$ grid from a column $$=8$$

Now, I can select $$1,2,3,4,5,6,7$$and $$8$$ adjacent grid from the row to from a square $$8\times 8$$.

Hence, number of ways selecting this way $$=8\left( 1+2+3+4+5+6+7+8 \right)$$.

Then,

Total number of ways $$=8\left( 1+2+3+......8 \right)+7\left( 1+2+3+.....8 \right)+6\left( 1+2+3+.....8 \right)+...............+1\left( 1+2+3+.....8 \right)$$

$$ =\left( 1+2+3+4+5+6+7+8 \right)\left( 1+2+3+4+5+6+7+8 \right) $$

$$ =36\times 36 $$

$$ =1296 $$

Hence, this is the required number of ways.


There are p intermediate stations on a railway line from Delhi to Amritsar. In how many way can a super-fast train stop at three of these intermediate stations if no two of them are to be consecutive?

$$(p -3) $$non-stopping. There will be $$(p - 3) + 1 = p - 2$$ gaps where three stopping stations could be located. 
$$\therefore \, ^{p \, - \, 2}C_3$$ ways.


How many different words can be formed from the letters of the word GANESHPURI when:
The letter $$G$$ always occupies the first place.

GANESHPURI: No. of letters $$= 10$$ vevels are AEUI i.e. 4 and consonants 6.
Having fixed up $$G$$ at first place we are left with the permutation of remaining $$9$$ letters which can be arranged in $$9$$!ways.


How many different words can be formed from the letters of the word GANESHPURI when:
All the letters are taken.

GANESHPURI: No. of letters $$= 10$$ vevels are AEUI i.e. 4 and consonants 6.
When all the letters are taken, then they can be arranged in $$^{10}P_{10}$$ i.e. $$10$$ ways.


How many $$2$$ digits numbers can be formed form the digits $$0,2,4,5,7$$ if the repetition o fthe digits (a)is not allowed (b)is allowed

$$\left( a \right)\,4 \times 4 = 16$$
$$\left( b \right)\,4 \times 5 = 20$$


In how many ways $$5$$ persons can sit at a round table, if two of the person do not sit together?

Suppose The $$5$$ persons are $$A,B,C,D,E$$
Total number of ways that $$5$$ persons can sit at a round table $$(m)=\dfrac{^5p_5}{5}=24.$$

There’s $$1$$ way to sit $$A$$ because all seats look alike at an empty table. Then, there are $$2$$ ways to seat $$B$$, $$3$$ ways to seat $$C$$, $$2$$ ways to seat $$D$$, and one empty seat for $$E$$,
Say total ways so that two of the person do not sit together $$(n)=1\times 2\times 3\times 2\times 1=12$$

Hence, the resultant $$=m-n=24-12=12.$$
In $$12$$ ways, $$5$$ persons can sit at a round table, if two of the person do not sit together.


Find the number of $$5$$ lettered palindromes which can be formed using the letters from the English alphabets.

For 5 lettered palindrome, we can fill the first 3 letters randomly and then the last 2 letters will become fixed.

there are 26 letters.

therefore the number of ways $$=26 \times 26\times 26= 26^3=17,576$$


Find the number of different words formed with the letters of the word HARYANA.

Total numbe of letters in $$HARYANA=7$$
Among which $$A$$ is recurring $$=3$$

The total no. of different words that can be formed from the letters of the word $$Haryana=\dfrac{7!}{3!}=7\times\ 6\times\ 5\times 4=840$$



Find the number of words each containing of $$3$$ consonants and $$3$$ vowels that can be formed from letters of the word Circumference. In how many of these all c's will be together.

Given Word - Circumference
Consonants - {c,c,c},{r,r},m,n,f
Vowels - i,u,{e,e,e}

Total no. of ways of selecting and arranging 3 consonants = {3 Alike}+{2 Alike + 1 Distinct}+{3 Distinct}
=1+$$^{2}C_{1}\times ^{4}C_{1}\times \dfrac{3!}{2!}+^{5}C_{3}\times 3!$$=85

Total no. of ways of selecting and arranging 3 vowels = {3 Alike }+{2 Alike 1 Distinct}+{3 Distinct }
=1+$$1\times ^{2}C_{1}\times \dfrac{3!}{2!}$$+$$^{3}C_{3}\times 3!$$=13

Total no. of ways of arranging them together i.e total no. of words that can be formed = $$^{6}C_{3}\times85\times 13=20\times 85\times 13=22100$$

Let's see the case of all c's together now ,
Total no. of ways of selecting consonants = 1
Total no. of ways of selecting and arranging vowels =13

Total no. of words = $$^{4}C_{1}\times 13=52$$









Find the number of ways in which 410 different diamonds can be arranged to make a necklace.

$$410$$ diamond have to be arranged in a circular shape 

no of ways $$=\dfrac{(410-1)!}2 \Rightarrow\dfrac{ (409)!}2$$

$$\therefore 410$$ different diamonds can be  arranged to make a round necklace in $$\dfrac{(409)!}2$$ ways


No. of different 4 digit nos that can be formed with the digits 2,3,4,7 with repetition

In four digit nos every space has 
possibility of 4 
So 
$$ 4\times 4\times 4\times 4 $$ 
$$ 256 $$ 

1112185_1200610_ans_64a1afe4f97b43ab931e93c5433d6a37.jpg


Find the number of natural numbers which are less than $$2\times 10^{8}$$ and which can be written by means of the digit $$1$$ and $$2$$.


1142447_1204364_ans_4361ffd6bb104504b844d567cf1c52e0.jpg


Show that a number of the form $$14^{n}$$, where $$n$$ is a natural number can never end with digit zero.

Consider the series of $$14^n$$
Which is $$14,196,2744,38416...$$
If we observe the units digit has only $$2$$ repeated numbers $$4,6$$
For zero to occupy units place either $$10$$ or both $$2,5$$ should be multiplied which doesn't take place here 
So zero cannot be the units digit of the series $$14^n$$



If $$\dfrac {^{ 56 }{ P }_{ r+6 }}{^{ 54 }{ P }_{ r+3 }}=30800:1$$, Find $$r$$.

Given,
$$\dfrac {^{ 56 }{ P }_{ r+6 }}{^{ 54 }{ P }_{ r+3 }}=30800$$
$$\dfrac{\dfrac{56!}{(56-r-6)!}}{\dfrac{54!}{(54-r-3)!}}=30800$$
$$\dfrac{56\times 55\times 54!}{(56-r-6)!}\times \dfrac{(54-r-3)!}{54!}=30800$$
$$\dfrac{(51-r)!}{(50-r)!}=\dfrac{30800}{56\times 55}$$
$$51-r=10$$

$$\therefore r=41$$

Hence, this is the answer.


If there are two jobs such that they can be performed independently in m and n ways respectively, then either of the two jobs can be performed in ....... ways.

There are $$2$$ jobs that can be performed in $$m$$ and $$n$$ ways respectively.
$$\therefore$$ By fundamental principle of multiplication either of the jobs can be done in $$(m$$ + $$n)$$ ways.
 


The circular permutations of $$6$$ different things taken all at a time is .....

The number of circular permutations of $$n$$ things taken $$r$$ at a time is $$=\dfrac{^nP_r}{r}$$
Here we are taking all the $$n$$ things at a time.
$$\therefore$$ No. of permutations $$=\dfrac{^nP_r}{n}=\dfrac{n!}{n}$$
                                      $$=(n-1)!$$
In circular permutation, the first thing or the first place doesn't matter. So we place any of the $$n$$ things in any $$1$$ place and arrange the other $$(6-1)$$ things in $$(6-1)!$$ ways = $$5! = 120$$ ways.


How many different words can be formed with the letters of the word HARYANA ?

There are 7 letters in the word 'HARYANA' of which 3 are A:s and remaining all are each of its own kind.
So, total number of words $$\displaystyle=\frac {7!} {3!1!1!1!} = \frac {7!}{3!}=840.$$


Number of words formed, with or without meaning, using all the letters of the word EQUATION, using each letter exactly once is x!.Find the value of x.

There are eight letters in the word 'EQUATION' . So, the total number of words is equal to the number of arrangement of these letters, taken all at a time. The number of such arrangement is $$ ^8P_8= 8!.$$ Hence, the total number of words $$= 8!.$$


In how many ways can the letter of the word $$PERMUTATIONS$$ can be arranged so that all the vowels come together

There are total $$12$$ letters in the word $$PERMUTATIONS$$, with $$T$$ repeated twice.
Number of vowels in the given word are $$5$$.
Since vowels have to always occur together, so they are considered as a single object . This single object (letter) together with the remaining $$7$$ letters will give us $$8$$ objects (letters).  
These $$8$$ objects in which there are $$2$$ $$T's$$ can be arranged in $$\cfrac{8!}{2!}$$ ways .Corresponding to each of these arrangements, the $$5$$ different vowels can be arranged in $$5!$$ ways.
Therefore, by multiplication principle, required number of arrangements in this case $$=\cfrac {8!}{2!} \times 5!= 2419200$$



In how many ways can $$8$$ athletes finish a race for Gold Silver and Bronze medals?

This is the number of permutations of 8 distinct objects taken three at a time without repetition (here it means same person cannot get both silver and bronze) Thus $$\displaystyle ^{8}P_{3}=8\times 7\times 6=336$$ ways


How many 3 letter code can be formed by using the five vowels without repetitions? 

$$A , E , I , O , U$$
No repetition
$$3$$ Letter code 
Selecting and Averaging $$3$$
$$\\ \Rightarrow ^{ 5 }{ P }_{ 3 }\\ \Rightarrow \dfrac { 5! }{ 2! } \\ \Rightarrow 5\times 4\times 3\\ \Rightarrow 60 $$
Hence the correct answer is $$60$$ Ways are possible.


It is required to seat 5 men and 4 women in a row so that the women occupy the even places. How many such arrangements are possible? 

$${\textbf{Step 1: Find the arrangement using given condition}}$$ 

                $${\text{Total number of people }}$$ $$=9$$ , 

                $${\text{Now according to question women’s occupy the even places such as}}$$ $${(2,4,6,8)}$$ 

                $${\text{and rest will be by men’s.}}$$

                $$\text{So Let’s denote men with – M and women’s with – W, }$$         

                $$\text{then the sitting arrangement will be given as,}$$

                $${\text{M W M W M W M W M}}$$

                $${\text{Arrangement of}}$$ $$4$$ $${\text{women’s can be given as}}$$

                $${\text{Total Number of ways}}$$ $$={}^{4}{{P}_{4}}$$

                $${\text{Total Number of ways}}$$ $$=4!$$

                $${\text{Total Number of ways}}$$ $$=4\times 3\times 2\times 1$$

                $${\text{Total Number of ways}}$$ $$=24$$

                $${\text{Arrangement of}}$$ $$5$$ $${\text{men's can be given as}}$$

                $${\text{Total Number of ways}}$$ $$={}^{5}{{P}_{5}}$$

                $${\text{Total Number of ways}}$$ $$=5!$$

                $${\text{Total Number of ways}}$$ $$=5\times 4\times 3\times 2\times 1$$

                $${\text{Total Number of ways}}$$ $$=120$$

                $${\text{Total number of arrangement}}$$ $$=24\times 120$$

                $${\text{Total number of arrangement}}$$ $$=2880$$

$${\textbf{Hence, Total number of possible arrangement will be}}$$ $${\mathbf{2880.}}$$



If the letters of the word $$MASTER$$ are permuted in all possible ways and the words thus formed are arranged in dictionary order, then find the rank of the word $$MASTER$$.

Let us arrange the word $$MASTER$$ in alphabetic order
$$AEMRST$$
Thus as per dictionary rank it is the first word.
Now keeping $$A$$ fixed, the rest of the $$5$$ words can be re-arranged in $$5!$$ ways.
$$=120$$.
Thus the rank of the word starting with $$E$$ will be greater than $$120$$.
Now keeping $$E$$ as the first letter, the rest of the words can be re-arranged in $$5!$$ ways or $$120$$ ways.
Now, let us fix $$M$$ as the first letter. Rearranging the next letters in alphabetic order gives
$$MAERST$$. Keeping $$E$$ as the third letter, $$RST$$ can be permuted in $$3!$$ or $$6$$ ways.
The next letter to occupy third position is $$R$$
$$MAREST$$. Again $$3!=6$$ ways. The next letter to occupy the third position is $$S$$, $$MASERT$$. Let $$E$$ be the fourth letter, the remaining letters can be permuted in $$2$$ ways. Then comes, $$MASRET$$, again $$2$$ ways. 
Then comes $$MASTER$$.
Hence the rank is $$120+120+6+6+2+2+1=257$$.


In how many ways $$4$$-digits numbers can be formed using the digits $$1,2,3,7,8,9$$ without repetition? How many of these are even numbers?

P_Total there are $$6$$ digits, from which we have to form $$4$$ digits number.
We need to choose $$4$$ digits randomly and form a number without repeating any digit.
In this process, we need to determine the number of possibilities where order does not matter.
So, we use the permutation formula and that is
$$_{ }^{n}P_{r}=\dfrac{n!}{(n-r)!},$$ where n is the total number of objects and $$r$$ is the number of objects taken at a time.
Given, $$n=6$$ and $$r=4$$
$$\therefore$$  $$_{ }^{6}{P}_{4}=\dfrac{6!}{(6-4)!}$$
            $$=\dfrac{6!}{2!}$$ 
            $$=\dfrac{6\times 5\times 4\times 3\times 2!}{2!}$$
            $$=6\times 5\times 4\times 3$$
            $$=360$$
$$\therefore$$  $$_{ }^{6}P_{4}=360$$
$$\therefore$$  In $$360$$ ways the $$4$$-digits numbers can be form using the digits $$1,2,3,7,8,9$$.

From these, the even numbers must contain the last digit as $$2$$ or $$8$$.
If we fix $$2$$ or $$8$$ at $$4^{th}$$ place, then there are $${ }^5P_{3}$$ ways for each.
$$\therefore$$ Total number of even numbers $$=2\times { }^5P_{3}$$
                                                        $$=2\times \dfrac{5!}{(5-3)!}$$
                                                        $$=2\times \dfrac{5!}{2!}$$

                                                        $$=2\times \dfrac{5\times 4\times 3\times 2\times1}{2\times 1}$$
                                                        $$=120$$
$$\therefore$$ there are total $$120$$ even numbers.


What is fundamental counting principle? What is the meaning of $$^{ n }{ P }_{ r }$$?

Solution:
Fundamental principle of counting:
(i) Multiplication Principle: If an operation can be performed in $$'m'$$ different ways; following which a second operation can be performed in $$'n'$$ different ways, then the two operations in succession can be performed in $$m\times n$$ ways. This can be extended to any finite number of operations.
(ii) Addition Principle:If an operation can be performed in $$'m'$$ different ways and another operation, which is independent of the first operation, can be performed in $$'n'$$ different ways. Then either of the two operations can be performed in $$(m+n)$$ ways. This can be extended to any finite number of mutually exclusive operations.
Meaning of $${}^nP_r:$$
The number of permutations of $$n$$ different things, taking $$r$$ at a time is denoted by $${}^nP_r.$$


How many different ways can the letters of word CONSTITUTION be arranged? How many of these will have the letter $$N$$, both at the beginning and at the end?

$$CONSTITUITION$$
$$O\times2  I\times2\\T\times3 N\times2\\C\times1 S\times1\\U\times1$$
The total ways it can be
arrange$$=\cfrac{12!}{2!2!3!2!}$$
If $$N$$ is first and last place
$$=2\times \cfrac{10!}{2!2!3!}\\=\cfrac{10!}{2!3!}$$


Find the number of seven digited palindromes that can be formed using 0, 1, 2, 3, 4.

The number should be of the form $$ABCDCBA$$
Number of ways of selecting $$A$$ are $$4$$ as the possible digits are $$1,2,3,4$$.
Number of ways of selecting $$B$$ are $$5$$ as $$0$$ is also a possibility.
Similarly
Number of ways of selecting $$C$$ is $$5$$ 
Number of ways of selecting $$D$$ is $$5$$ 
Hence the number of ways $$=4\times 5\times 5\times 5=500$$


In how many ways can the letters of the word 'PERMUTATIONS' be arranged if the
(i) words start with $$P$$ and ends with $$S$$ and 
(ii) Vowels are all together.

$$(i)$$ Words start with $$P$$ and end with $$S:$$  
When we fix $$P$$ at the left end and $$S$$ at the right end, then we are left with $$10$$ letters.  
Hence, required no. of ways $$=\dfrac{10!}{2!}=1814400$$
$$(ii)$$ Vowels are all together: 
There are $$5$$ vowels in the given word, $$1 E, 1 U, 1 A, 1 I$$, and $$1 O$$. 
Since these vowels are occurring together, so consider them as one letter, and when this letter is combined with the remaining $$7$$ letters, then we have $$8$$ letters in all, which can be arranged in $$\dfrac{8!}{2!}$$ ways. 
Corresponding to the arrangements, the $$5$$ vowels can be arranged in $$5!$$ ways.  
Hence, required no. of ways $$=\dfrac{8!}{2!}\times 5! = 20160 \times 5! = 24,19,200$$


There are 12 balls of which 4 are red, 3 black and 5 white: In how many ways can you arrange the balls so that no two white balls may occupy consecutive positions if balls of the same colour are identical?

Balls of the same colour identical.
 Let us arrange 4 red and 3 black balls in a row in$$\dfrac{7!}{3! 4!} \, = \, 35$$
Now there will be 8 gaps in which 5 identical white balls can be arranged in $$\dfrac{1}{5!}   \, \, ^8P_5$$ or in
$$ ^8C_5 \, \cdot \, \dfrac{5!}{5!}  \, = \, \dfrac{8!}{3! 5!} \, = \, 42 $$
Hence by fundamental theorem $$35\times 42 = 1960$$ ways.


How many different words can be formed from the letters of the word GANESHPURI when:
The letter $$P$$ and $$I$$ respectively occupy the first and last places.

GANESHPURI: No. of letters $$= 10$$ vevels are AEUI i.e. 4 and consonants 6.
$$P$$ occupies $$1^{st}$$ and $$I$$ occupies the last place and so we have to arrange the remaining $$8$$ letters which can be done in $$8$$! ways.


A candidate is required to answer 6 out of 10 questions which are divided into two groups each containing 5 questions and he is not permitted to attempt more than 4 from each group. In how many ways can he make up his choice?

Group A 5, Group B 5. Questions to be attempted 6 but not more than 4 from any group (4A,2B), (3A,3B), (2A, 4B).
$$^{5}C_{4}$$ x $$^{5}C_{2}$$ + $$^{5}C_{3}$$ x $$^{5}C_{3}$$ x $$^{5}C_{2}$$ x $$^{5}C_{4}$$
= 50 + 100 + 50 = 200.


A businessman hosts a dinner to $$21$$ guests. He is having $$2$$ round tables which can accommodate $$15$$ and $$6$$ persons each. In how many ways can he arrange the guests?

Out of $$21,$$ we can choose $$15$$ for one table in $${}^{21}C_{15}$$ ways 
And for each selection we are left with $$6$$ guests for the second table having $$6$$ seats. 
This can be chosen in $${}^{6}C_{6}$$ ways. 
Now $$15$$ for round table $$A$$ can be arranged in $$(14)!$$ ways and $$6$$ for round table B can be arranged in $$5!$$ ways. 
Hence the total number is $$^{21}C_{15}\times {}^{6}C_{6} \times 14! \times 5!$$.


Prove that at any time, the total number of persons on the earth who shake hands an odd number of times is even.

To prove the assertion, we first  assign to each hand shake a number in natural order. Then our assertion is equivalent to the following : "For every n, after a handshake with number n, the number of people who have made an odd number of handshake is even." This statement depend on n and will be prove by induction. For convenience, we we call the people who have made an odd number of handshake type A and rest type B, that is, type B are those people who had made an even number of handshakes.
 After the handshake with number 1, we have two people of type A, an even number. After a mth handshake, let let the number of people of type A be even and let the handshake number m + 1 take place. Three cases arise : the handshake number  m + 1 will occur between (a) two people of type A (b) two people of type B, (c) a person of type A and type B.
In case (a), two person of type A add one handshake to their odd number handshakes and becomes of type B; in case (b) two person of type B become of type A and in case (c) a person of type A becomes of type B and person of type B is changed into type A. Thus the number of people of type A either decrease by two or increase by two or remains unchanged. In any case the number remains even and the proof is complete


A person invites a party of $$10$$ friends at dinner and place them $$5$$ at one round table, $$5$$ at the other round table.$$4$$ at one round table and $$6$$ at other round table.The find the ratio, of number of circular permutations in case (i) to case (ii).~

In first case the no of permutation is $$\displaystyle ^{10}C_5\times4!\times4!$$
in second case the no of permutation is $$\displaystyle ^{10}C_4\times3!\times5!$$
Ratio$$=\dfrac{^{10}C_5\times4!\times4!}{^{10}C_4\times3!\times5!}=\dfrac{4\times6}{5\times5}=\dfrac{24}{25}$$


How many four digit natural numbers not exceeding the number $$4321$$ can be formed using the digits $$1,\ 2,\ 3,\ 4,$$ if repetition is allowed?

The total numbers starting with $$1$$ is $$4\times 4\times 4=64$$
Starting with $$2$$ is $$4\times 4\times 4=64$$
Starting with $$3$$ is $$4\times 4\times 4=64$$
Starting with $$44$$ is $$4\times 4=16$$
Now number with $$43..$$ given as
$$4344$$ - $$(1)$$
$$4343$$ - $$(2)$$
$$4333$$ - $$(3)$$
$$4334$$ - $$(4)$$
$$4323$$ - $$(5)$$
$$4322$$ - $$(6)$$
$$4321$$ - $$(7)$$
$$\therefore$$ Total numbers $$=64+64+64+16+7$$
$$=215$$.


Find the total number of permutation of $$k$$ different things in a row taken not more than $$r$$ at a time (each thing may be repeated any number of times ) 

When we arrange one thing at a time, the number of possible permutations is $$k$$
When we arrange them two at a time the number of possible permutations are $$k\times k={k}^{2}$$ and so on.Thus the total number of permutations are
$$k+{k}^{2}+{k}^{3}+...+{k}^{r}=\dfrac{k\left({k}^{r}-1\right)}{k-1}$$ for $$n>1$$


In how many ways four men and three women may sit around a round table if all the women
i) always sit tohether
ii) never sit together

Case 1: If all three women always sit together

We can club the 3 women in one group and the number of arrangements of this group will be $$3!$$

Now, 4 men and 1 group of women can be arranged arround a round table $$=(5-1)!$$

Hence, Total arrangements $$=4!3!=144.$$


Now, case 2: If all three women never sit together

Total arrangements without any constraints $$=6!$$

From case 1, we know the arrangements if women always sit together.

Hence, Total arrangements $$=6!-144=720-144=576$$=6!−4!3!=576




Find the distinct permutations of the letters of the word MISSISSIPPI?

MISSISSIPPI $$=\left\{{M}^{1},{I}^{4},{S}^{4},{P}^{2}\right\}$$
Total no.of distinct permutations $$ =\dfrac{\left(1+4+4+2\right)!}{1!4!4!2!}$$
$$ =\dfrac{11!}{1!4!4!2!}= 34650$$


In how many ways a child can select $$5$$ balls from $$4$$ black, $$3$$ white $$ ,2$$ green and $$1$$ yellow balls? (Assume balls of same color are identical)

Since  the total number of ball is 10 and we  have select 5 balls.
1156611_1103065_ans_e8750662e20943ed9bb1f32a7519d182.jpg


The number of times the digit $$5$$ will be written while listing the integers from $$1$$ to $$1000$$ is $$xyz$$ then the value of $$(x + y + z)$$ is equal to 

$$1+9+8+1+9\times 9+8\times 9+9+9+8+1$$
$$\Rightarrow 271\,times$$
$$\therefore xyz=271$$
$$\therefore x=2;y=7;z=1$$
$$\therefore x+y+z=2+7+1$$
$$\boxed{x+y+z=10}$$

1351872_1130366_ans_1376ec90b00a445884f90a070f4b813c.png


Find the number of ways in which $$12$$ different flowers can be arranged in a garland so that.

Number of ways arranging in garden = $$^{12}{C_{12}}$$
$$ = 12! = \,479,001,600\,ways$$


How many six-digit odd numbers, greater than $$6,00,000$$, can be formed from the digits $$5, 6, 7, 8, 9$$ and $$0$$ if repetition of digits is allowed.

For a odd number, we must have unit place as a odd number.
And for greater than $$6,00,000$$ we must have the lakh place as either 6,7,8 or 9
Hence,
Lakh place can be selected in $$4$$ ways.
ten thousand place can be selected in $$6$$ ways.
and so on till unit place which can be selected in $$3$$ ways.
Hence, total = $$4.6^4.3$$ ways


How many 4  letter words can be formed using the letters of the word PROPORTION.

Given word is PROPORTION
we have $$2 P's , 2 R's, 3 o's $$ and 1 T, 1 and N 

1. word with four  distinct letters
Total letters (distinct) $$= 6$$
$$\therefore \, ^6 P_4 \times 4! = 360$$ ways

2. Words with exactly a letter repeated twice $$^3P_1 = 3$$ way
The other two letters can be selected in $$5P_2 = 10$$ ways
Now each combination can be arranged in $$4! \times 2! = 12$$ ways
Total no. = $$3 \times 10 \times 12 = 360$$

3. Words with exactly  two distinct letters repeated twice 
Two letters out of $$3$$ repeating = $$^3P_2$$ ways
Now each combination can be arranged in $$4! \times 2! \times 2!= 6$$ ways
Total = $$3 \times 6 = 18$$

4. Words with exactly a letter repeated 
We have only $$O, $$

$$\therefore ^5P_1 = 5$$

each combination can be arranged in $$4!/3! = 4$$
Total = $$1 \times 5 \times 4 = 20$$

$$\therefore$$ Total arrangement $$= 360 + 360 + 18 + 20 $$
                                   $$= 758 $$ ways


In how many ways can $$8$$ persons be seated on two round tables of capacity $$5$$ & $$3$$.

Step 1:  We have select $$5$$ out of $$8$$ members to be seated on big table 
 no of ways =$$^{8}C_{5}=\dfrac{8!}{5!3!}=\dfrac{8\times 7\times 6}{6}=56$$

Step 2: we arrange $$5$$ selected members around big table 
No of ways $$=(5-1)!=4!$$

Step 3: we arrange $$3$$ remaining members around small table 
No of ways $$=(3-1)!=2!$$
\therefore  Total no ways $$=\dfrac{8}{5}\times 4!\times 2!$$
$$=56\times 24\times 2$$
$$=56\times 48$$
$$=2688$$
$$8$$ person can be seated around $$2$$ different table in $$2688$$ ways


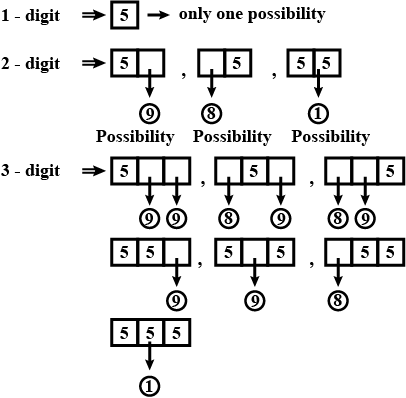
How many numbers of five digits can be made with the digits $$1,2,3$$ each of which can be used at most thrice in a number?

The five digit number can be of the format of aaabc or aabbc
where a,b,c are the digits

$$Case -1 \ (aaabc):$$

The number which is repeated thrice can be chosen in 3 ways {from 1, 2, and 3}
The number $$aaabc$$ can be rearranged in $$\dfrac{5!}{3!} =\dfrac{ 120}{6} = 20$$ ways.
There can be $$3\times20 = 60$$ such numbers.

$$Case -2\  (aabbc):$$

The number which is not repeated can be chosen in 3 ways {from 1, 2, and 3}
The number $$aabbc$$ can be rearranged in $$\dfrac{5!}{2!\times2!} = \dfrac{120}{4} = 30$$ ways
There can be $$3\times30 = 90$$ such numbers.

Number of 5-digit numbers that follow the given restrictions $$= 60 + 90 = 150$$


Find the number of ways in which 5 men and 4 women can be seated on a round table, so that no two women are together.

No. of men $$=5$$
No. of women$$=4$$
$$(5 - 2)!4!$$
$$ \Rightarrow 3! \times 4!$$
$$ = 3 \times 2 \times 1 \times 4 \times 3 \times 2 \times 1$$
$$ = 6 \times 24$$
$$ = 144$$


How many three digits numbers can be formed from the digits $$0, 1, 3, 5, 6$$ if repetition of digits
i) are allowed ii) are not allowed?


1974926_1347489_ans_f0dc82b3d3e74699b7cc3834e240ad09.jpg


In how many of the the distinct permutations of the letters in $$MISSISSIPPI$$ do the four $$I$$'s not come together?

The word MISSISSIPPI has one M, four I’s, four S’s, two P’s and a total of 11 letters.

The number of all type of arrangements possible with the given alphabets

                       

Let us first find the case when all the I’s together and so take it as one packet or unit. So now we have one M, one unit of four I’s, four S’s, two P’s and a total of 8 units.

Therefore the number of arrangements possible when all the I’s is together

                           

Hence, the distinct permutations of the letters of the word MISSISSIPPI when four I’s do not come together = 34650 – 840 = 33810.



In a group of students, $$100$$ students know Hindi, $$50$$ know English and $$25$$ know both. Each of students knows either Hindi or English. How many students are there in the group ?

$$\textbf{Step-1: Assume the sets for given languages & then apply all information's given.}$$
                 $$\text{Let E be the set of all students who know English and H be the set of all students}$$ 
                 $$\text{who know Hindi.}$$
                 $$\text{Number of students who know Hindi}$$ $$=n(H)=100$$
                 $$\text{Number or students who know English}$$ $$=n(E)=50$$
                 $$\text{Number of students who know both Hindi and English}$$ $$=n(H\cap\ E)=25$$
$$\textbf{Step-2: Use the above results & get the required unknown.}$$
                 $$\text{Since, each the students know Hindi or English}$$
                 $$\text{Number of students in group}$$
                 $$=$$ $$\text{Number of students who know Hindi or English}$$
                 $$=n(H\cup E)$$
                 $$\text{We know that}$$ $$n(H\cup E)=n(H)+n(E)-n(H\cap E)$$
                 $$=100+50-25$$
                 $$\therefore n(HUE)=125$$
$$\textbf{Hence, there are 125 students in the group.}$$


How many natural numbers less than $$1000$$ can be formed from the digits $$0, 1, 2, 3, 4, 5$$ when a digit may be repeated any number of times?

There are $$5$$ one-digit natural numbers out of the given digits.

For getting $$2-digit$$ natural numbers we cannot put $$0$$ at the ten's place. So, this place can be filled by any of the given five nonzero digits in $$5$$ ways.

The unit's digit can be filled by any of the given six digits in $$6$$ ways.
So, the number of $$2-digit$$ natural numbers $$= (5\times 6) = 30$$.

Similarly, to get a $$3-digit$$ number, we cannot put on at the hundred's place. So, this place can be filled in $$5$$ ways, each of the ten's and unit's places can be filled in $$6$$ ways.

$$\therefore$$ the number of $$3-digit$$ numbers $$= (5\times 6\times 6) = 180$$.

Required number of numbers $$= (5 + 30 + 180) = 215$$.


How many $$4-digit$$ numbers are there, when a digit may be repeated any number of times?

In a $$4-digit$$ number, $$0$$ cannot be placed at the thousand's place.

So, thousand's place can be filled by any digit from $$1$$ to $$9$$ in nine ways.

Now, each of hundred's, ten's and one's places can be filled by any of the digits from $$0$$ to $$9$$ in ten ways.

So, the required number of numbers $$= (9\times 10\times 10\times 10) = 9000$$.


What is the number of permutations of $$10$$ objects, taken $$4$$ at a time?


1846130_1709475_ans_452f0ef46c4f4554aa785277ce4e2017.jpeg


How many $$3-digit$$ numbers can be formed by using the digits $$0, 1, 3, 5, 7$$ while each digit may be repeated any number of times?

The hundred's place cannot contain $$0$$. So, it can be filled by any of the digits $$1,3, 5, 7$$.

So, there are $$4$$ ways to fill it.

Now, each of the ten's and unit's digits can be filled by any of the given five digits.

So, each can be filled in $$5$$ ways.

$$\therefore$$ the required number of numbers $$= (4\times 5\times 5) = 100$$.


How many $$3-digit$$ numbers are there when a digit may be repeated any number of times?

A $$3$$ digit number can be depicted in the following way:
____   ____   ____
   H         T          O

Where, 
$$H=hundredths \ Place$$
$$T=Tenths \ Place$$
$$O=Ones \  Place$$

As the first digit can't be a $$0$$
We may fill hundred's digit by any digit from $$1$$ to $$9$$, i.e., in $$9$$ ways. 

Each of the ten's and unit's digits may be filled in $$10$$ ways

Required number of numbers $$= (9\times 10\times 10) = 900$$.


How many $$3-digit$$ numbers above $$600$$ can be formed by using the digits $$2, 3, 4, 5, 6$$, if repetition of digits is allowed?

Given digits are $$2, 3, 4, 5, 6$$ and repetition of digits is allowed.
The hundred's place can be filled by $$6$$ in $$1$$ way only.
Each of the ten's and unit's digits can be filled by any of the given five digits in $$5$$ ways.
Required number of numbers $$= (1\times 5\times 5) = 25$$.


A child has plastic toys bearing the digits $$4, 4$$ and $$5$$. How many $$3-digit$$ numbers can he make using them?

There are $$3$$ digits out of which $$4$$ is repeated $$2$$ times and $$5$$ occurs only once.
Required number of numbers $$= \dfrac {3!}{2!} = \dfrac {3\times 2\times 1}{2} = 3$$.


How many $$4-digit$$ numbers can be formed with the digits $$0, 2, 3, 4, 5$$ when a digit may be repeated any number of times in any arrangement?

First digit can't be $$0$$, so first digit can be placed up with $$4$$ ways only
however, the next $$3$$ places may be filled by any of the numbers 
Required number of numbers $$= (4\times 5\times 5\times 5) = 500$$.


With $$17$$ consonants and $$5$$ vowels, how many words of four letters can be formed having $$2$$ different vowels in the middle and $$1$$ consonant (repeated or different) at each end?

We have to form 4 letter word
number of ways in which we can select vowels= $$^5C_2$$=10

Number of ways in which we can select consonants=$$^{17}C_1 \times ^{17}C_1$$=289

Since we can use repeated consonant at the end so 
totoal number of ways to select consonants=$$2\times 289$$=578

Hence total Number of ways in which we carried out the following operation are
                        =$$10\times 578$$
                          =5780


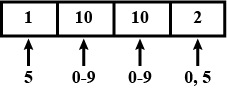
Write all possible two-digit number using the digits $$4$$ and $$0.$$ repetition of digits is allowed.

Possible two digit numbers $$= 40, 44$$


Write all possible 2-digit numbers that can be formed by using the digit $$3, 7$$ and $$9.$$ Repetition of digits is allowed.

The given digits are $$3, 7, 9$$ and repetition of digits is allowed.
Out of the given digits, the possible ways of choosing the two digits are
$$3, 7; 3, 9; 7, 9$$
Using the digits $$3$$ and $$7$$, the n numbers are
$$37, 73, 33$$ and $$77.$$
Similarly, Using the digits $$3$$ and $$9$$, the numbers are $$39, 93,$$ and $$99.$$
Using the digits $$7$$ and $$9$$, the numbers are $$79$$ and $$97.$$
Hence, all possible $$2-$$digit numbers are
$$37, 73, 33, 77, 39, 93, 99, 79, 97$$


How many $$2$$-digit even numbers can be formed from the digits $$1 , 2 , 3 , 4 , 5 $$ if the digits , can be repeated ? 

Given : $$ 1 , 2 , 3 , 4 , 5 $$ digits ($$5$$ digits)
To find : $$2$$-digit even numbers
       T           U   
      $$ \downarrow $$            $$ \downarrow $$ 
 $$5$$ ways      $$2$$ ways 
$$ \therefore $$ Required $$2$$- digits- even number 
$$ = 5 \times 2 = 10 $$ 


How many $$3$$-digit numbers can be formed from the digits $$1 , 2 , 3 , 4 $$ and $$5$$ assuming that repetition of the digits is allowed ?

Given digits are $$ 1 , 2 , 3, 4 , 5 $$.
To find: number of $$3$$-digit numbers,
Repetition of digit is allowed.
Hundred's place          Ten's place         Unit'sPlace
    $$ \downarrow $$                                       $$ \downarrow $$                         $$ \downarrow $$
   $$5$$ ways                          $$5$$ ways                  $$5$$ ways

Since repetition of digits is allowed, then each place can be filled by any of $$5$$ given digits in $$5$$ ways. Hence, three places can be filled in $$5 \times 5 \times 5 $$ ways i.e., $$125$$ ways (By fundamental principle of counting). Required number of numbers $$ = 125$$.


How many numbers can be formed using digits $$0, 1,2,....,9 $$ which is more than or equal to $$ 5000 $$ and less than $$ 6000 $$ and is divisible by $$ 5 $$ whereas any number can be repeated as many times?

The numbers which are more than or equal to $$ 5000 $$ and less than $$ 6000 $$ and is divisible by $$5 $$ has $$ 5 $$ on thousand's place and $$0 $$ or $$5 $$ on one's place and the number is $$4 $$ digits number as digits can be repeated .
hence 
total numbers = $$ 1  \times 10 \times 10 \times 2 = 200 $$ 

1880341_1873963_ans_37636c87188547b3b583f09e221c8a30.png


How many numbers each lying between $$9$$ and $$1000$$ can be formed with the digits $$0, 1, 2, 3, 7, 8$$ if repetition of the digits in a number is allowed?

List of the digits that are allowed = $$0,1,2,3,7,8$$
Repetition is allowed
Two digit number:
First digit has $$5$$ Ways $$(1,2,3,7,8)$$
Second digit has $$6$$ Ways $$(0,1,2,3,7,8)$$
Number of possible two digit number is $$30$$
Three digit number:
First digit has $$5$$ Ways $$(1,2,3,7,8)$$
Second digit has $$6$$ Ways $$(0,1,2,3,7,8)$$
Third digit has $$6$$ Ways $$(0,1,2,3,7,8)$$
Number of possible three digit number is $$180$$
Total number possible from $$9$$ to $$1000$$
$$=180+30$$
$$=210$$ Numbers


In how many different ways can $$4$$ married couples seat themselves around a circular table if (i) Spouses sit opposite each other? (ii) Men and women alternate?

$$4$$ Married couples That is $$8$$ people
Second women can be placed in $$6$$ ways and her husband in $$1$$ way.
Third women can be placed in $$4$$ ways and her husband in $$1$$ way.
Fourth women can be placed in $$2$$ ways and her husband in $$1$$ way.
Total number of ways $$6\times 4\times 2=48$$ Ways.
Arranging Men
Number of ways $$=3!=6$$ Ways
Remaining $$4$$ places $$4$$ people$$=4!=24$$ Ways
Total ways of arranging $$=24\times 6=144$$ Ways

868582_851220_ans_639b6edf9952459986eff8c3a73e85b8.PNG


Find the sum of all 4-digit numbers that can be formed using the digits 1, 2, 4, 6, 8. 

Hint : A digit can be in a place in $$4\times 3\times 2$$ ways

Solution:
For digit $$k$$ sum of it's influence in all numbers $$=(k\times { 10 }^{ 3 }+k\times { 10 }^{ 2 }+k\times { 10 }+k)4\times 3\times 2$$

$$=k\times (1111)4\times 3\times 2$$

So for $$1,3,5,7,9$$

$$=(1111)\times 4\times 3\times 2(1+3+5+7+9)$$

$$=666600$$


A coin is tossed five times and outcomes are recorded. How many possible outcomes are there?


1408944_1666413_ans_20b51ee59eb14e4b8dca10df91534114.jpg


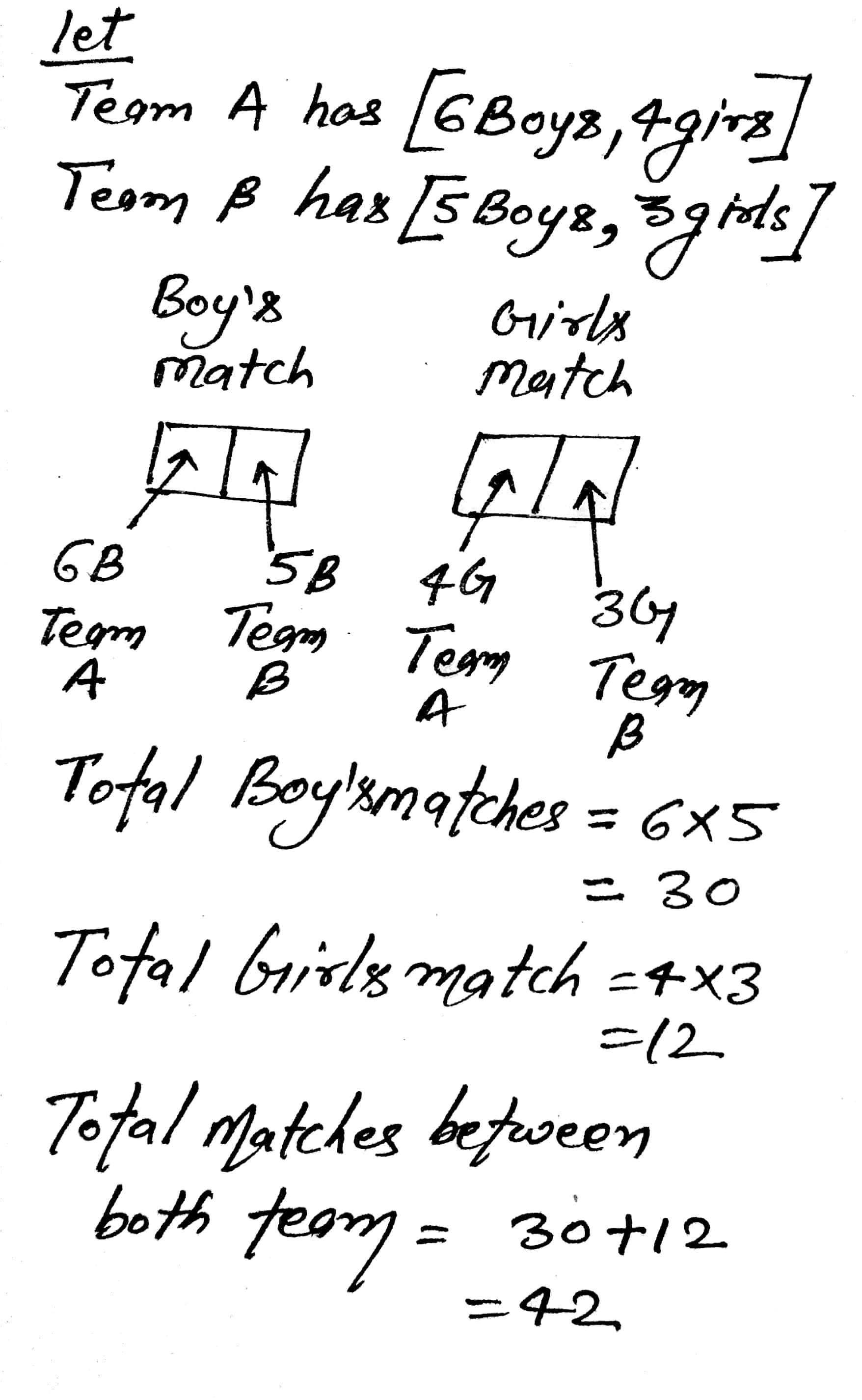
A team consist of $$6$$ boys and $$4$$ girls and other has $$5$$ boys and $$3$$ girls. How many single matches can be arranged between the two teams and a boys plays against a boys and girl plays against a girl?  


1410719_1666514_ans_c6c97784e22c4a7b80176730737411e3.jpg


In how many ways can $$6$$ persons be arranged in a circle?


1947168_1709760_ans_251f23c771c44b7b9ef12f93e75fb159.jpg


Class 11 Commerce Applied Mathematics Extra Questions