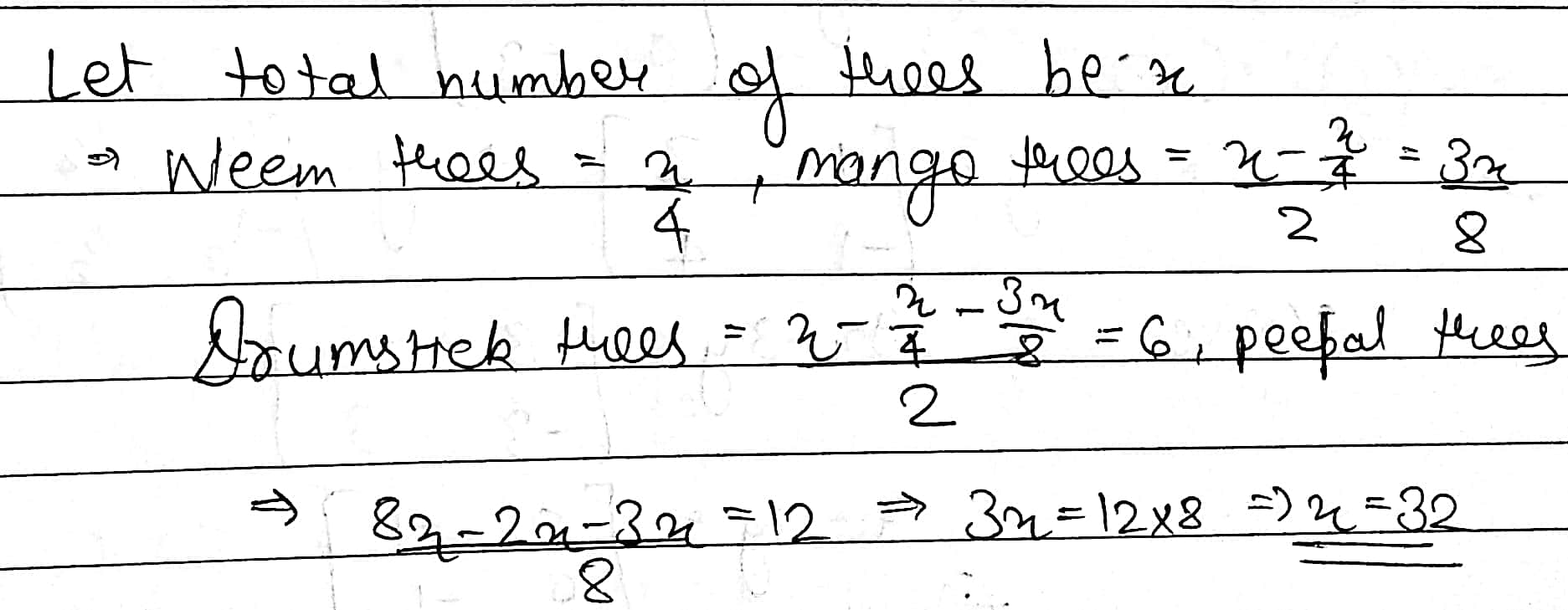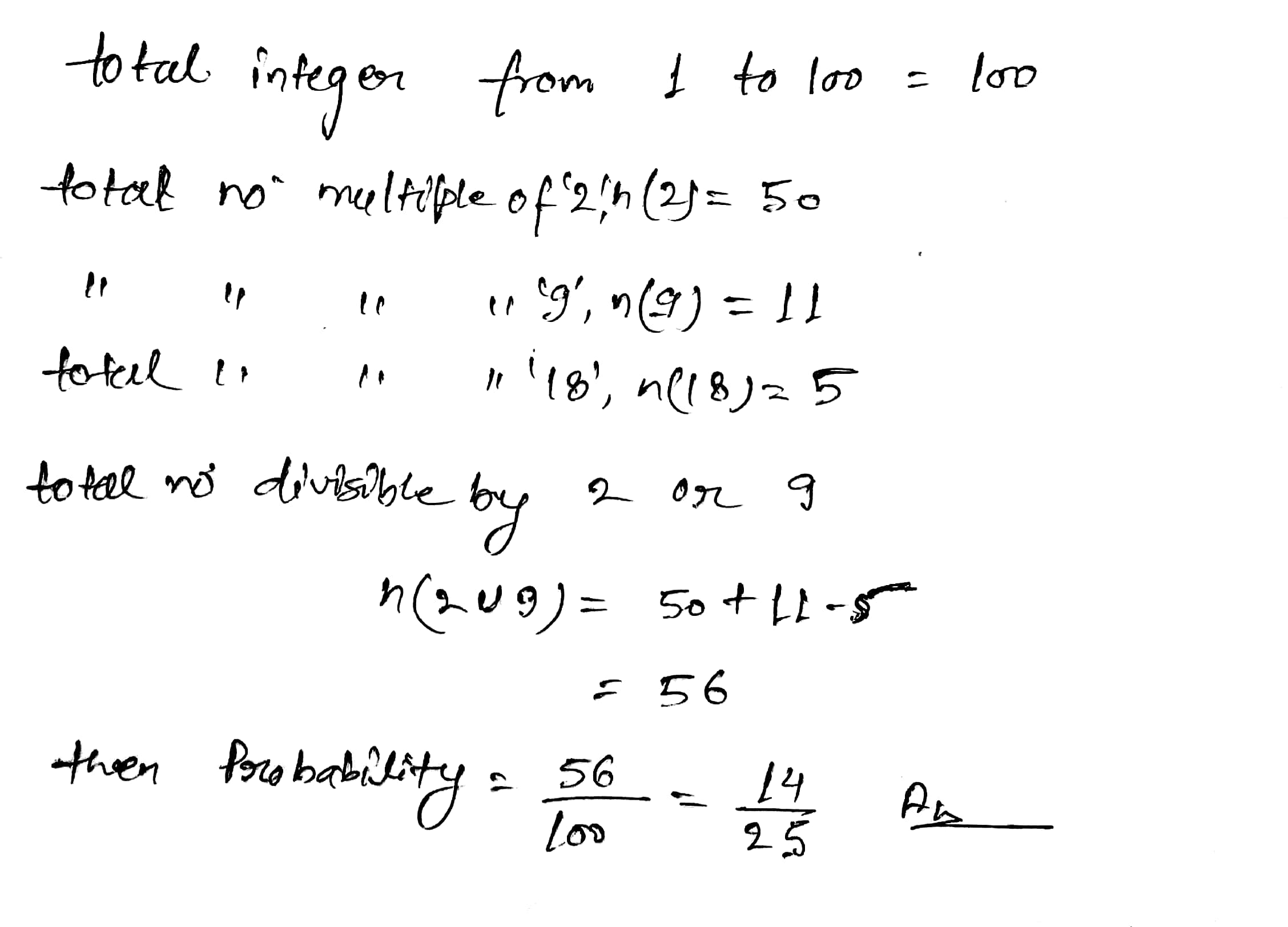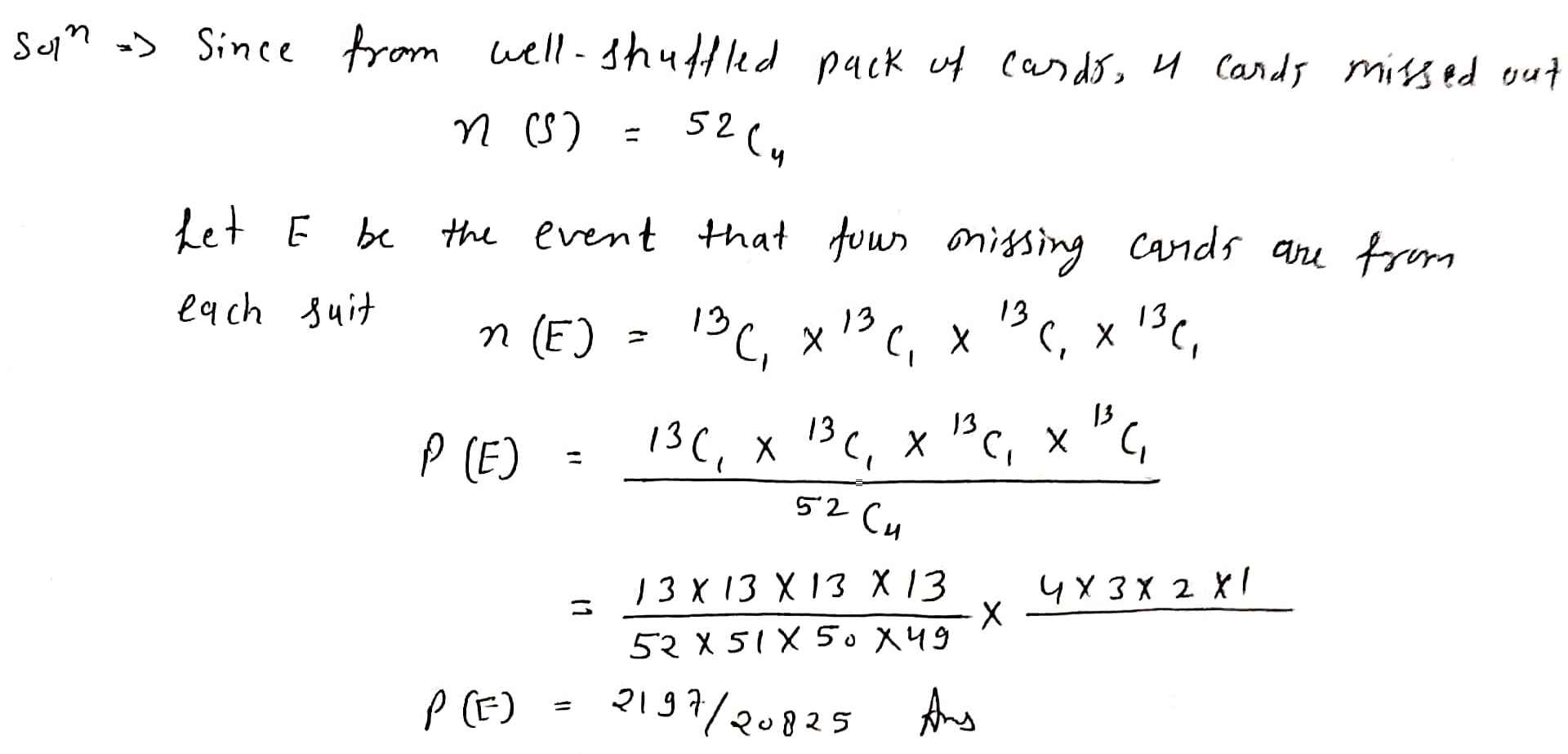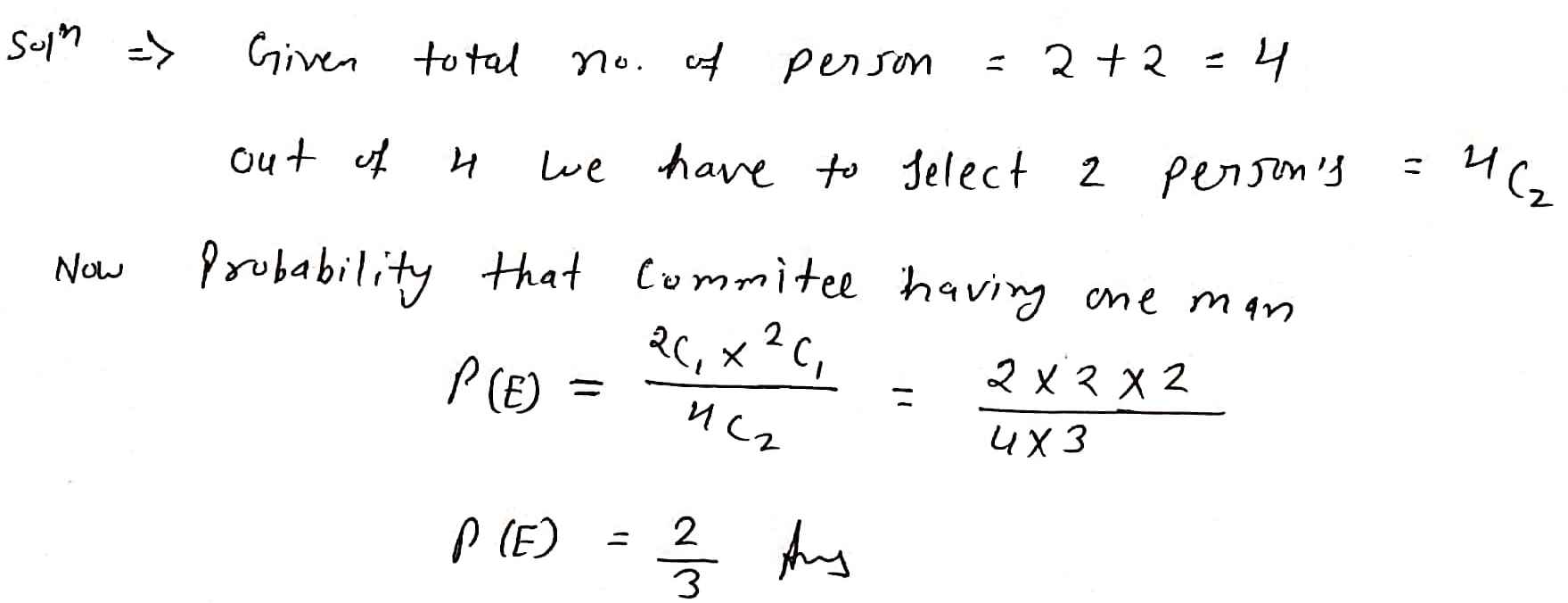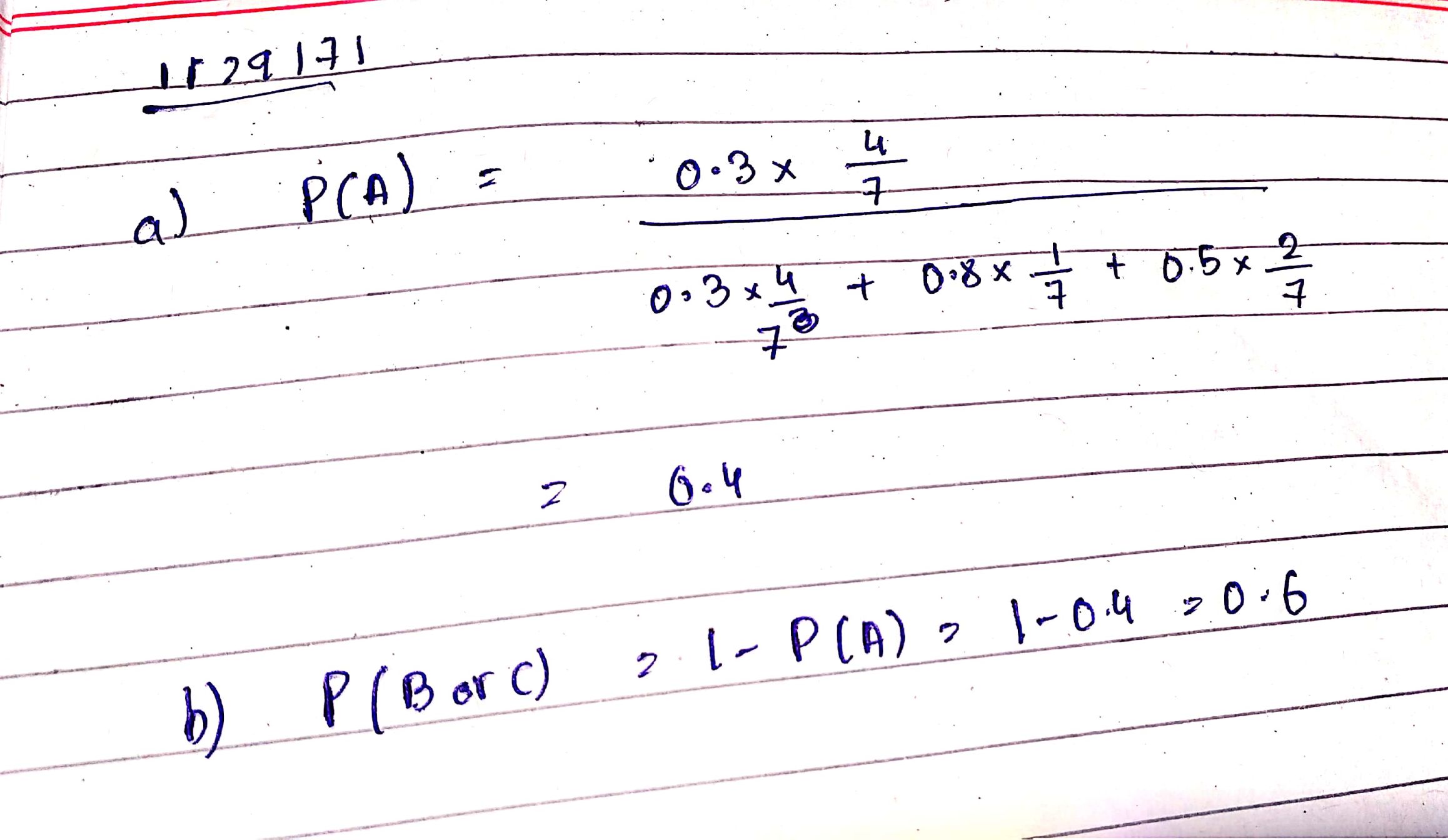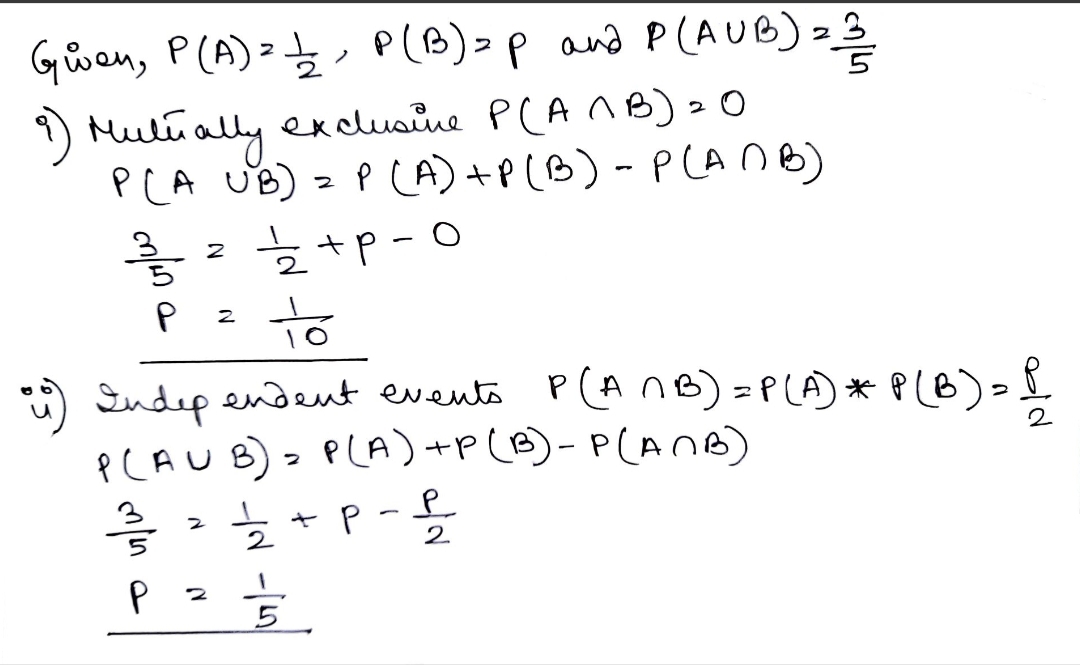Probability - Class 11 Commerce Applied Mathematics - Extra Questions
A bag contains $$7$$ white, $$5$$ black and $$4$$ red balls. Four balls are drawn without replacement. Find the probability that at least three balls are black.
A bag has $$5$$ red balls and $$7$$ yellow balls. (The balls are identical in all respects other than colour). A ball is drawn from the bag without looking into the bag. What is the probability of getting a yellow bag?
An insurance company insured 2000 scooters and 3000 motor cycles. The probability of an accident involving a scooter is 0.01 and that of a motor cycle is 0.An insured vehicle met with an accident. Find the probability that the accidented vehicle was a motor cycle.
Calculate the expected value of the sum of the two numbers obtained when two fair dice are rolled.
Define sure event .
There are $$6$$ articles in a box. Write the total numbers of article in $$10$$ such boxes.
A ball contains x white, y red, z blue balls. A ball is drawn at the random then, what is the probability of drawing blue ball.
What is a random experiment ?
What is an impossible event ?
On a busy road following data was observed about car passing through it
Find the chance that it has exactly soccupants
More than $$2$$
Less the $$5$$
| No. of occupants | No. of cars |
| $$1$$ | $$29$$ |
| $$2$$ | $$26$$ |
| $$3$$ | $$23$$ |
| $$4$$ | $$17$$ |
| $$5$$ | $$5$$ |
An ordinary pack of $$52$$ cards is well shuffled. The top card is then turned over. What is the probability that the top card is a red card.
Tell whether the following is certain to happen, possible can happen but not certain.
A die when tossed shall land up with $$8$$ on top.
For two events $$A$$ and $$B,$$ if $$\displaystyle p\left( A \right) =p\left( A|B \right) =\frac { 1 }{ 4 } $$ and $$\displaystyle p\left( B|A \right) =\frac { 1 }{ 2 } $$, then $$\displaystyle P\left( \frac { \overline { B } }{ \overline { A } } \right) =\frac { m }{ n } $$ where $$m+n=$$
Red on first draw and red on second draw
Pal's gardener is not dependable, the probability that he will forget to water the rose bush is $$\displaystyle \frac{2}{3}.$$ The rose bush is in questionable condition any how, if watered the probability of its withering is $$\displaystyle \frac{1}{2},$$ if not watered, the probability of its withering is $$\displaystyle \frac{3}{4}.$$ Pal went out of station and upon returning, he finds that the rose bush has withered, what is the probability that the gardener did not water the bush.
[Here result is known that the rose bush has withered, therefore. Bayes's theorem should be used]
Red on first draw and white on second draw
A pair of fair coins is tossed yielding the equiprobable space S={HH, HT, TH, TT}. Consider the events:
A={head on first coin}={HH, HT},
B={head on second coin}={HH, TH}
C={head on exactly one coin}={HT, TH}
Then check whether $$A, B, C$$ are independent or not.
A pack of cards is counted with face downwards. It is found that one card is missing, One card is drawn and is found to be red. Find the probability that the missing card is red.
Abag contains $$6$$ white and an unknown number of black balls $$\left ( \leq 3 \right )$$ Balls are drawn one by one with replacement from this bag twice and is found to be white on both occasion. Find the probability that the bag had exactly $$'3'$$ Black balls.
There are $$5$$ brilliant students in class $$XI$$ and $$8$$ brilliant students in class $$XII.$$ Each class has $$50$$ students, The odds in favour of choosing the class $$XI$$ are $$2:3,$$ If the class $$XI$$ is not chosen then the class $$XII$$ is chosen, A student is a chosen and is found to be brilliant, find the probability that the chosen student is from class $$XI.$$
Given that the two numbers appearing on throwing two dice are different. Find the probability of the event ' the sum of numbers on the dice is $$4$$'.
In a test an examinee either guesses or copies or knows the answer to a multiple choice question with four choices. The probability that he make, a guess is $$\dfrac{1}{3}$$ and the probability that he copies the answer is $$\dfrac{1}{6}$$. The probability that his answer is correct given that he copied it is $$\dfrac{1}{8}$$. Find the probability that he knew the answer to the question, given that he correctly answered it.
Write the probability of getting each number top face when a die was rolled in the following table and find the sum of the probabilities of all outcomes.
An insurance company insured $$2000$$ scooter drivers, $$4000$$ car drivers and $$6000$$ truck drivers. The probability of an accidents are $$0.01, 0.03$$ and $$0.15$$ respectively. One of the insured person meets with an accident. What is the probability that he is a scooter driver?
Why is tossing a coin considered to be a fair way of deciding which team should choose ends in a game of cricket?
Coloured balls are distributed in $$3$$ bags.
$${B}_{1}\rightarrow 1B, 2\ W, 3R$$
$${B}_{2}\rightarrow 2B, 4\ W, 1R$$
$${B}_{3}\rightarrow 4B, 5\ W, 5R$$
A bag is selected at random and then $$2$$ balls are drawn from the selected bag. They happen to be black and red. What is the probability that the balls come from bag $$1$$?
$$3$$ cards are given, one of them is red on both sides, one is blue on both sides & one is blue on one side red on the other side. One of them is chosen randomly & put on the table. It shows red colour on the upper side. The chance of the other side of the card being red is:
Bulbs are packed in cartons each containing $$40$$ bulbs. Seven hundred cartons were examined for defective bulbs and the results are in the following table:
| Number of defective bulbs in a carton | 0 | 1 | 2 | 3 | 4 | 5 | 6 | more than 6 |
| Frequency | 400 | 180 | 48 | 41 | 18 | 8 | 3 | 2 |
(i) No defective bulb?
(ii) Defective bulbs from $$2$$ to $$6$$?
(iii) Defective bulbs less than $$4$$?
A person writes letters to six friends and addresses the corresponding envelopes. In how many ways can the letters be placed in the envelopes so that all of them are in wrong envelope.
A person writes letters to six friends and addresses the corresponding envelopes. In how many ways can the letters be placed in the envelopes so that at least two of them are in wrong envelope.
A manufacturing firm produces steel pipes in three planet with daily production daily production of 500, 1000 and 2000 units reespectively. According to past experience, it is known that the fraction of defective output produced by the three planets are respectively 0.005,0.008,0.if a pipe is selected from a day's total production and faund to be defective, find the probability that is has come from the first plant
In a class 35% of the student are poor. 20% are meritorious and 15% are both poor and meritorious. one student is selected at random. find the probability that (i) he is poor if it is know that he meritorious.
(II) he is meritorious if it is know that he is poor.
A bag contains $$4$$ balls. Two balls are taken out without replacement and found to be white. Find the probability that all the balls of the bag are white.
A laboratory blood test is $$99\%$$ effective in detecting a certain disease when patient is infected actually by the disease. However, the test also yields a false positive result for $$0.5\%$$ of the healthy person tested if $$0.1$$ percent of the population actually has the disease, what is the probability that a person has the disease given that his test result is positive?
There are three coins, identical in appearance, one of which is ideal and other two biased with probabilities 1/3 and 2/3 respectively for a head. One coin is taken at random and tossed twice: if a head appears both times, what is the probability that the ideal coin was chosen ?
A factory has three machines $$X, Y$$ and $$Z$$ producing $$1000, 2000$$ and $$3000$$ bolts pet day respectively. The machine $$X$$ produces $$1 \%$$ defective bolts, $$Y$$ produces $$1.5 \% $$ and $$Z$$ produces $$2 \%$$ defective bolts. At the end of a day, a bolt is drawn at random and is found to be defective. What is the probability that this defective bolt has been produced by machine $$X$$?
An insurance company issued 3000 scooters, 4000 cars and 5000 trucks. The probabilities of the accident involving a scooter, a car and a truck are 0.02, 0.03 and 0.04 respectively. One of the insured vehicles meet with an accident. Find the probability that it is a (i) scooter (ii) car (iii) truck.
In answering a question on a multiple choice test, a student either knows the answer or guesses. Let $$\dfrac{3}{4}$$ be the probability that he knows the answer and $$\dfrac{1}{4}$$ be the probability that he guesses. Assuming that a student who guesses the answer will be correct with probability $$\dfrac{1}{4}$$. What is the probability that the student knows the answer given that he answered it correctly ?
Bag -I contains 3 red and 4 black balls while another Bag -II contains 5 red and 6 black b alls . One ball is drawn at random from one of the bags and it is found to be red . Find the probability that it was drawn from Bag -II.
Two dice are thrown together .What is the probability that the sum of the number on the two faces is divided by $$4$$ or $$6$$
Find p if they are mutually exclusive.
Three persons $$A, B$$ and $$C$$ apply for a job of Manager in a Private company. Chance of their selection ($$A, B$$ and $$C$$) are in the ratio $$1 : 2 : 4$$. The probability that $$A, B$$ and $$C $$can introduce changes to improve profits of company are $$0.8, 0.5$$ and $$0.3$$ respectively, if the changes does not take place, find the probability that it is due to the appointment of $$C$$.
There are four kinds of trees in an orchard. Four part of total trees are Neem trees. Half of the remaining trees are Mango trees. Half of the remaining trees are Drumstick trees and the remaining $$6$$ trees are Peepel trees. Find the total number of trees in the orchard.
8 coins are tossed simultaneously. Find the probability of getting at least 6 heads.
Suppose $$5\%$$ of men and $$0.25\%$$ of women have grey hair. A grey haired person is selected at random. What is the probability of this person being male? Assume that there are equal number of males and females.
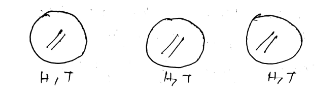
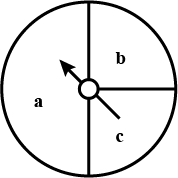
In the game of spinning arrow which comes to rest painting at regions of a or b or c (see figure), are the outcomes equally likely occur ? Give reason.
For a loaded die the probability of outcomes are given as under.
$$p\left( 1 \right) =p\left( 2 \right) =0.2,p\left( 3 \right) =p\left( 5 \right) =p\left( 6 \right) =0.1$$ and $$p\left( 4 \right) =0.3$$ The die is thrown two times. Let A and B be the events, 'same number each time' and 'a total score is 10 or more ', respectively . Determine whether or not A and B are independent.
A coin is tossed 300 times and we get head:136 times and tail:164 times.
When a coin is tossed at random, what is the probability of getting a tail?
Mother father and son line up at random for a family picture
E: son on one end
F. father in the middle Find $$P(E|F)$$
A coin is tossed $$300$$ times and we get head:$$136$$ times and tail:$$164$$ times.
When a coin is tossed at random, what is the probability of getting a head?
Tell whether the following is certain to happen, possible can happen but not certain.
Tomorrow will be a cloudy day.
If $$A$$ and $$B$$ are mutually exclusive such that $$P(A)=0.35$$ and $$P(B)=0.45$$, find $$P(A\cup B)$$
Tell whether the following is certain to happen, impossible can happen but not certain.
The next traffic light seen will be green.
A purse contains $$2$$ silver and $$4$$ copper coins. $$A$$ second purse contains $$4$$ silver and $$3$$ copper coins. If a coin is pulled at random from one of the two purses, what is the probability that it is a silver coin?
A purse contains $$2$$ silver and $$4$$ copper coins. $$A$$ second purse contains $$4$$ silver and $$3$$ copper coins. If a coin is pulled at random from one of the two purses, what is the probability that it is a silver coin
The contents of three bags $$I, II$$ and $$III$$ are as follows:
Bag $$I:1$$ white, $$2$$ black $$3$$ red balls
Bag $$II:2$$ white, $$1$$ black $$1$$ red balls
Bag $$III:4$$ white, $$5$$ black $$3$$ red balls A bag is chosen at random and two balls are drawn. What is the probability that the balls are white and red
Bag $$I:1$$ white, $$2$$ black $$3$$ red balls
Bag $$II:2$$ white, $$1$$ black $$1$$ red balls
Bag $$III:4$$ white, $$5$$ black $$3$$ red balls
A bag is chosen at random and two balls are drawn. What is the probability that the balls are white and red
In a large metropolitan area, the probabilities are $$0.87, 0.36, 0.36, 0.30$$ that a family (randomly chosen for a sample survey) owns a color television set, a black and white television set, or both kinds of sets. What is the probability that a family owns either any one or both kinds of sets
A bag contains $$4$$ red and $$5$$ black balls, a second bag contain $$3$$ red and $$7$$ black balls. One ball is drawn at random from each bag, find the probability that the
ball are of the same colour.
In an entrance test is graded on the basis of two examinations, the probability of a randomly chosen student passing the first examination is $$0.8$$ and the probability of passing the second examination is $$0.7.$$ The probability of passing at least of them is $$0.95$$. What is the probability of passing both?
An die is tossed twice. Find the probability of getting $$4,5\ or\ 6$$ on the toss and $$1,2,3\ or\ 4$$ on the second toss.
By examine the chest the chest $$X-$$ray probability that $$T.B$$ is detected when a person is actually suffering is $$0.99$$. The probability that the doctor diagnoses incorrectly that a person has $$T.B$$ on the bases of $$X-$$ray is $$0.001$$. In a certain city $$1$$ in $$1000$$ person suffers from $$T.B$$. A person is selected at random is diagnoses to have $$T.B$$. What is the chance that the actually has $$T.B$$?
$$A$$ is known to speak truth $$3$$ times out of $$5$$ times. He throws a dice and reports that it is a one. Find the probability that it is actually one.
There are four men and six women on the city councils. If one council number is selected for committee at random, how likely that it is a women?
Suppose an integer from $$1$$ through $$100$$ is chosen at random , find the probability that the integer is a multiple of $$2$$ or a multiple of $$9$$.
In a large metropolitan area, the probabilities are $$0.87, 0.36, 0.36, 0.30$$ that a family (randomly chosen for a sample survey) owns a colour television set, a black and white television set, or both kinds of sets. What is the probability that a family owns either any one or both kinds of sets?
Two balls are drawn at random with replacement from a box containing $$10$$ black and $$8$$ red balls. Find the probability that first ball is black and second is red.
Two balls are drawn at random with replacement from a box containing $$10$$ black and $$8$$ red balls. Find the probability that both balls are red.
Two balls are drawn at random with replacement from a box containing $$10$$ black and $$8$$ red balls. Find the probability that one of them is black and another is red.
Suppose an integer from $$1$$ through $$100$$ is chosen at random , find the probability that the integer is a multiple of $$2$$ or a multiple of $$9$$.
Two numbers are selected at random from integers $$1$$ through $$9$$. If the sum is even, find the probability that both the numbers are odd.
A bag contains $$5$$ white, $$7$$ red and $$3$$ black balls. If a ball is chosen at random Find the probability that it s not red.
What is the total number of elementary events associated to the random experiment of throwing three dice together
Two cards are drawn from a well shuffled pack of $$52$$ cards, one after another without replacement. find the probability that one of these is red card and the other is black.
A coin is tossed. Find the total number of elementary events and also the total number of events associated with the random experiment.
Three coins are tossed once. Describe the following events associated with this random experiment.
$$A=$$ Getting three heads, $$B=$$ Getting two heads and one tail,
$$C=$$ Getting three tails, $$D=$$ Getting a head on the first coin.
Which pairs of events are mutually exclusive
A die is thrown twice. Each time the number appearing on it is recorded. Describe the following event:
$$A=$$ Both numbers are odd.
A die is thrown twice. Each time the number appearing on it is recorded. Describe the following event:
$$B=$$ Both numbers are even.
A bag contains $$4$$ red and $$5$$ black balls, a second bag contain $$3$$ red and $$7$$ black balls. One ball is drawn at random from each bag, find the probability that the balls are of the same colour.
Two balls are drawn at random with replacement from a box containing $$10$$ black and $$8$$ red balls. Find the probability that first ball is black and second is red.
Two dice are thrown. The events $$A,B,C,D,E$$ and $$F$$ are described as follows:
$$A=$$ Getting an even number on the first die.$$B=$$ Getting an odd number on the first die.$$C=$$ Getting at most $$5$$ as sum of the number on the two dice.$$D=$$ Getting the sum of the numbers on the dice greater than $$5$$ but less than $$10$$.$$E=$$ Getting at least $$10$$ as the sum of the numbers on the dice.$$F=$$ Getting an odd number on one of the dice.
State true of false: (a)$$A$$ and $$B$$ are mutually exclusive.
(b) $$A$$ and $$B$$ are mutually exclusive and exhaustive events.
(c) $$A$$ and $$C$$ are mutually exclusive events.
(d) $$C$$ and $$D$$ are mutually exclusive and exhaustive events
(e) $$C, D$$ and $$E$$ are mutually exclusive and exhaustive events.
(f) $$A'$$ and $$B'$$ are mutually exclusive events.
(g) $$A, B, F$$ are mutually exclusive and exhaustive events.
$$A=$$ Getting an even number on the first die.
$$B=$$ Getting an odd number on the first die.
$$C=$$ Getting at most $$5$$ as sum of the number on the two dice.
$$D=$$ Getting the sum of the numbers on the dice greater than $$5$$ but less than $$10$$.
$$E=$$ Getting at least $$10$$ as the sum of the numbers on the dice.
$$F=$$ Getting an odd number on one of the dice.
(a)$$A$$ and $$B$$ are mutually exclusive.
(b) $$A$$ and $$B$$ are mutually exclusive and exhaustive events.
(c) $$A$$ and $$C$$ are mutually exclusive events.
(d) $$C$$ and $$D$$ are mutually exclusive and exhaustive events
(e) $$C, D$$ and $$E$$ are mutually exclusive and exhaustive events.
(f) $$A'$$ and $$B'$$ are mutually exclusive events.
(g) $$A, B, F$$ are mutually exclusive and exhaustive events.
(b) $$A$$ and $$B$$ are mutually exclusive and exhaustive events.
(c) $$A$$ and $$C$$ are mutually exclusive events.
(d) $$C$$ and $$D$$ are mutually exclusive and exhaustive events
(e) $$C, D$$ and $$E$$ are mutually exclusive and exhaustive events.
(f) $$A'$$ and $$B'$$ are mutually exclusive events.
(g) $$A, B, F$$ are mutually exclusive and exhaustive events.
A bag contains $$5$$ white, $$7$$ red and $$3$$ black balls. If a ball is chosen at random Find the probability that it is not red.
Two balls are drawn at random with replacement from a box containing $$10$$ black and $$8$$ red balls. Find the probability that one of them is black and another is red.
A die is thrown. Find the probability of getting:
$$2$$ or $$4$$
A bag contains $$25$$ tickets, numbered from $$1$$ to $$25$$. A ticket is drawn at random. Find the probability that the ticket will show even number.
In shuffling a pack of $$52$$ cards, four are accidently dropped; find the chance that the missing cards should be one from each suit.
A committee of two persons is selected from two men and two women. What is the probability that the committee will have one man?
There are four men and six women on the city councils. If one council number is selected for committee at random, how likely that it is a women?
In an entrance test is graded on the basis of two examinations, the probability of a randomly chosen student passing the first examination is $$0.8$$ and the probability of passing the second examination is $$0.7.$$ The probability of passing at least of them is $$0.95$$. What is the probability of passing both?
A die is thrown 100 times and outcomes are noted as given below:
| Outcome: | 1 | 2 | 3 | 4 | 5 | 6 |
| Frequency: | 21 | 9 | 14 | 23 | 18 | 15 |
Two coins are tossed simulataneously 500 times and the outcomes are noted as given below:
| Outcome: | Two heads (HH) | One head (HT or TH) | No head (TT) |
| Frequency: | 105 | 275 | 120 |
Suppose an integer from $$1$$ through $$100$$ is chosen at random , find the probability that the integer is a multiple of $$2$$ or a multiple of $$9$$.
A die is thrown 100 times and outcomes are noted as given below:
| Outcome: | 1 | 2 | 3 | 4 | 5 | 6 |
| Frequency: | 21 | 9 | 14 | 23 | 18 | 15 |
Two coins are tossed simulataneously 500 times and the outcomes are noted as given below:
| Outcome: | Two heads (HH) | One head (HT or TH) | No head (TT) |
| Frequency: | 105 | 275 | 120 |
Two coins are tossed simulataneously 500 times and the outcomes are noted as given below:
| Outcome: | Two heads (HH) | One head (HT or TH) | No head (TT) |
| Frequency: | 105 | 275 | 120 |
Let $$A$$ and $$B$$ be the events such that
$$P(A)=\dfrac {1}{2}, P(B)=\dfrac {7}{12}$$ and $$P$$ (not $$A$$ or not $$B$$)$$=\dfrac {1}{4}$$
State whether $$A$$ and $$B$$ are
mutually exclusive
Let $$ d_1 , d_2 , d_3 $$ be three mutually exclusive diseases . Let $$ S = \left \{ S_1 , S_2 , ........ S_6 \right \} $$ be the set of observable symptoms of these diseases . For example , $$ S_1 $$ is the shortness of breath , $$ S_2 $$ is the loss of weight , $$ S_3 $$ is fatigue , etc . Suppose a random sample of $$ 10000 $$ patients contains $$ 3200 $$ patients with disease $$ d_1 , 3500 $$ with disease $$ d_2 $$ and $$ 3300 $$ with diseases $$ d_3 $$ . Also , $$ 3100 $$ patients with disease $$ d_1 , 3300 $$ with disease $$ d_2 $$ and $$ 3000 $$ with disease $$ d_3 $$ show the symptoms $$ S$$ . Knowing that the patient has symptoms $$ S $$ , the doctor wishes to determine the patient's illness . On the basis of this information , what should the doctor conclude ?
Let $$E_1$$ and $$E_2$$ be the events such that $$P(E_1)=\dfrac {1}{3}$$ and $$P(E_2)=\dfrac {3}{5}$$
Find $$P(E_1 \cup E_2)$$, when $$E_1$$and $$E_2$$ are mutually exclusive.
Which of the following experiments have equally likely outcomes? Explain.
A driver attempts to start a car. The car starts or does not start.
Which of the following experiments have equally likely outcomes? Explain.
A baby is born. It is a boy or a girl.
A dice is thrown E is an event to getting 4 on dice and getting even number is event F . Are the events E and F mutually exclusive events ?
Which of the following experiments have equally likely outcomes? Explain.
A trial is made to answer a true-false question. The answer is right or wrong.
In a test, an examinee either guesses or copies or knows the answer to a multiple choice question with four choices. The probability that he makes a guess is $$\dfrac{1}{3}$$ and the probability that he copies the answer is $$\dfrac{1}{6}$$. The probability that his answer is correct given that he copied it is $$\dfrac{1}{8}$$. The probability that he knew the answer to the question given that he correctly answered it is $$\dfrac{4k}{29}$$.Find the value of $$k$$
Before a race the chances of three runners, $$A, B, C,$$ were estimated to be proportional to $$5, 3, 2$$; but during the race $$A$$ meets with an accident which reduces his chance to one-third. What are now the respective chances of $$B$$ and $$C?$$
$$P$$ makes a bet with $$Q$$ of $$8$$ pounds to $$120$$ pounds that three races will be won by the three horses $$A, B, C,$$ against which the betting is $$3$$ to $$2, 4$$ to $$1,$$ and $$2$$ to $$1$$ respectively. The first race having been a on by $$A$$, and it being known that the second race was won either by $$B$$, or by a horse $$D$$ against which the betting was $$2$$ to 1, find the value of $$P's$$ expectation.
A bag contains a coin of value $$M$$, and a number of other coins whose aggregate value is $$m$$. A person draws one at a time till he draws the coin $$M$$ : find the value of his expectation.
Total no.of outcomes in the experiment of throwing a balance die twice is_______
Given $$3$$ identical boxes $$I,II$$ and $$III$$ each containing two coins. In box $$I$$ both are gold coins, in box $$II$$ both are silver coins and in box $$III$$ one is gold and $$1$$ is silver. A coin is drawn from one of the boxes. If the coin is of gold, what is the probability that the other coin is the box is also of gold.(write answer up-to 2 decimal place)
In a knockout tournaments $$2^{n}$$ equally skilled players , $$S_{1},S_{2},......S_{2}n$$, are participating. In each round, players are divided in pair at random and winner from each pair moves in the next round. if $$S_{2}$$ reaches the semi-final, then the probability that $$S_{1}$$ wins the tournament is $$1/84$$. The value of $$n$$ equals__________.
One bag contains $$4$$ white and $$5$$ black balls. Another bag contains $$6$$ white and $$7$$ black balls. A ball is transferred from first bag to the second bag and then a ball is drawn from second bag. If the probability that the ball drawn is white $$\dfrac{29}{m}$$.Find $$m$$
For three persons $$A,B,C$$ the chances of being selected as manager of a firm are in the ratio $$4:1:2$$ respectively. The respectively probabilities for them to introduce radical changes in market strategy are $$0.3, 0.8$$ and $$0.5$$. If the changes take place, find the probability that
a) it was due to appointment of $$A$$.
b) It was due to appointment of $$B$$ or $$C$$.
A company manufacture scooters at two plants, $$A$$ and $$B$$. Plant $$A$$ produces $$80\%$$ and plant $$B$$ produces $$20\%$$ of the total product. $$85\%$$ of the scooters produced at plant $$A$$ and $$65\%$$ of the scooters produced at plant $$B$$ are of standard quality. A scooter produced by the company is selected at random and it is found to be standard quality. What is the probability that it was manufacture at plant $$A$$ ?
The members of a consulting firm rent cars from three rental agencies: $$50\%$$ from agency $$X,\ 30\%$$ from agency $$Y$$ and $$20\%$$ from agency $$Z$$.From past experience it is known that $$9\%$$ of the cars from agency $$X$$ need a service and tuning before renting , $$12\%$$ of the cars agency $$Y$$ need a service and tuning before rating and $$10\%$$ of the cars from agency $$Z$$ need a service and tuning before renting. If the rental car delivered to the firm needs service and tuning, find the probability that agency $$Z$$ is not to be blamed.
Suppose that the reliability of a HIV test is specified as follows:Of people having HIV, $$90%$$ of the test detect the disease but $$10%$$ go undetected. Of people free of HIV, $$99%$$ of the test are judged HIV-ive but $$1%$$ are diagnosed as showing HIV+ive. From a large population of which only $$0.1%$$ have HIV, one person is selected at random, given the HIV test, and the pathologist reports him/her as HIV+ive. What is the probability that the person actually has HIV?
The probability of selecting a red ball at random from a jar that contains only red, blue and orange balls is 1/4. The probability of selecting a blue ball at random from the same jar 1/3. If the jar contains 1010 orange balls, find the total number of balls in the jar.
Given that the events A and B are such that $$\text{P(A)}=\dfrac { 1 }{ 2 },\text{P(B)}=p,\text{P}(A\cup B)=\dfrac { 3 }{ 5 } $$. Find $$p$$ if $$A$$ and $$B$$ are:Mutually Exclusive EventsIndependent Events
Class 11 Commerce Applied Mathematics Extra Questions
- Basics Of Financial Mathematics Extra Questions
- Circles Extra Questions
- Descriptive Statistics Extra Questions
- Differentiation Extra Questions
- Functions Extra Questions
- Limits And Continuity Extra Questions
- Logarithm And Antilogarithm Extra Questions
- Mathematical And Logical Reasoning Extra Questions
- Number Theory Extra Questions
- Numerical Applications Extra Questions
- Permutations And Combinations Extra Questions
- Probability Extra Questions
- Relations Extra Questions
- Sequences And Series Extra Questions
- Set Theory Extra Questions
- Straight Lines Extra Questions
- Tangents And Its Equations Extra Questions