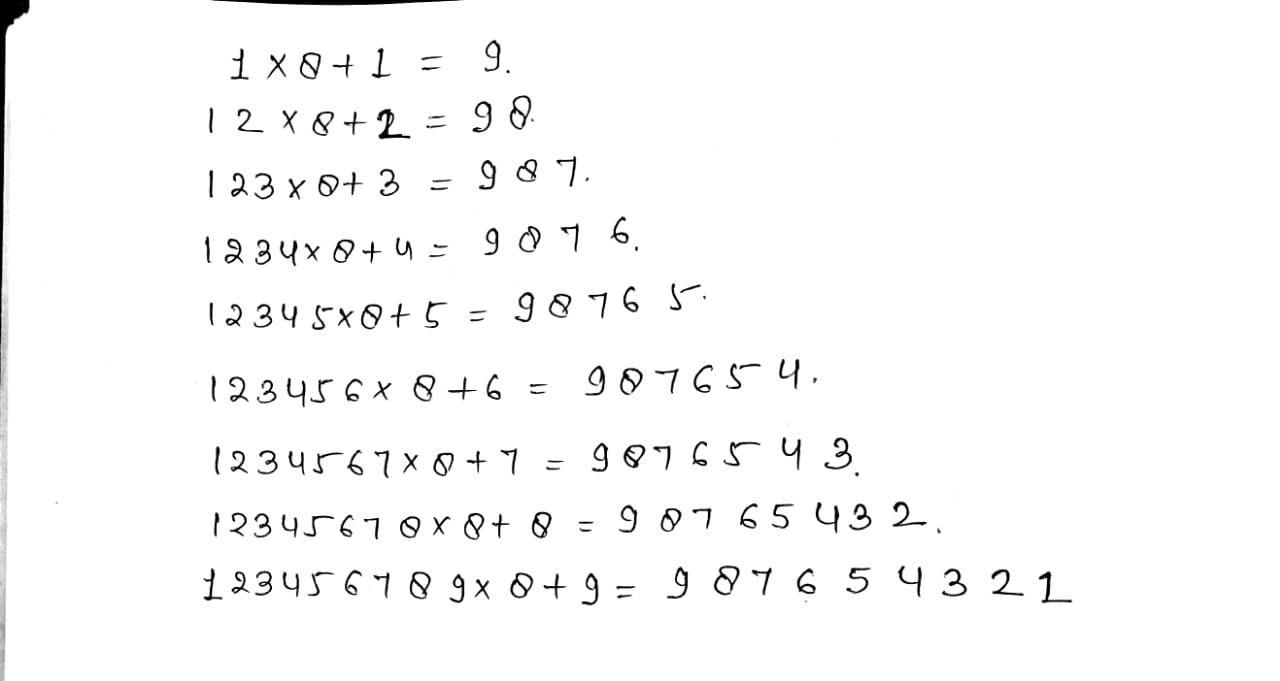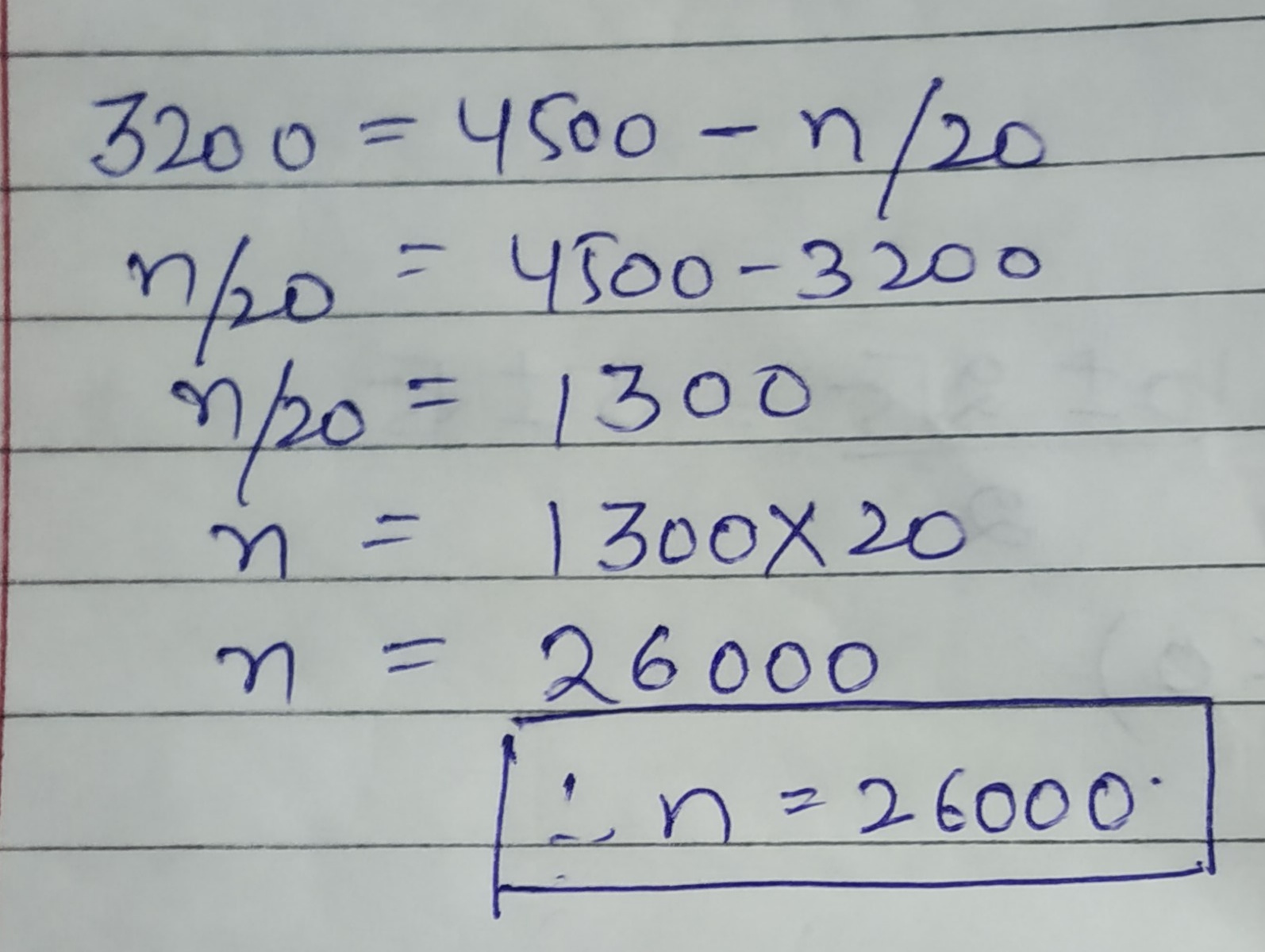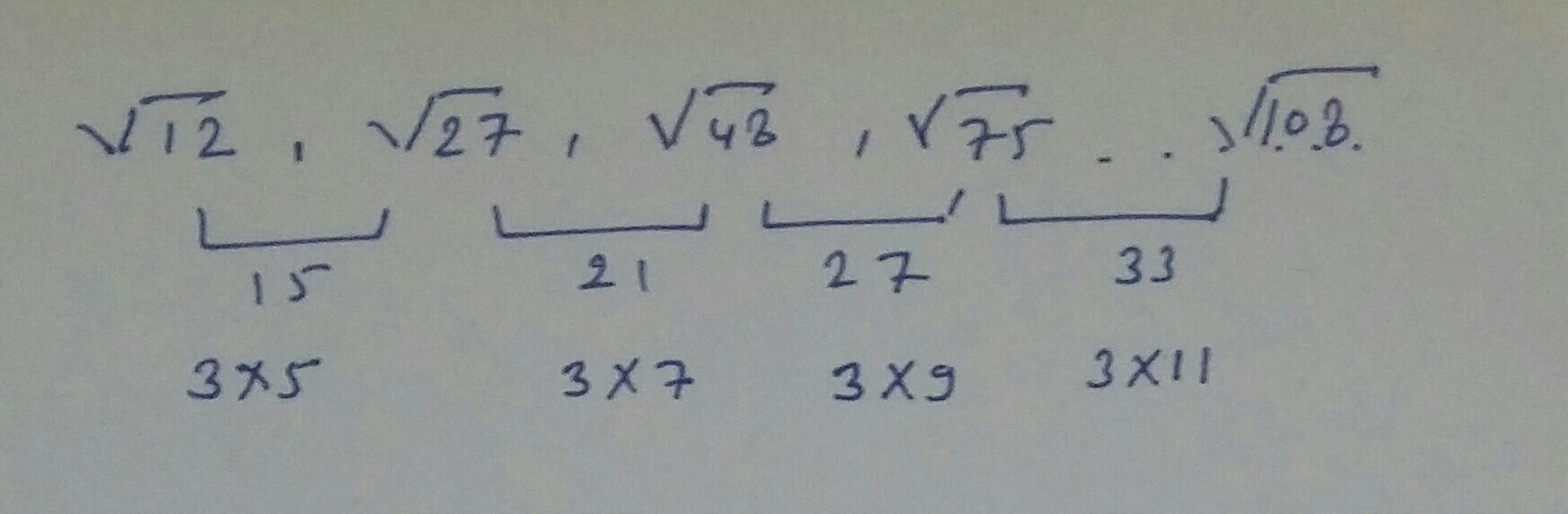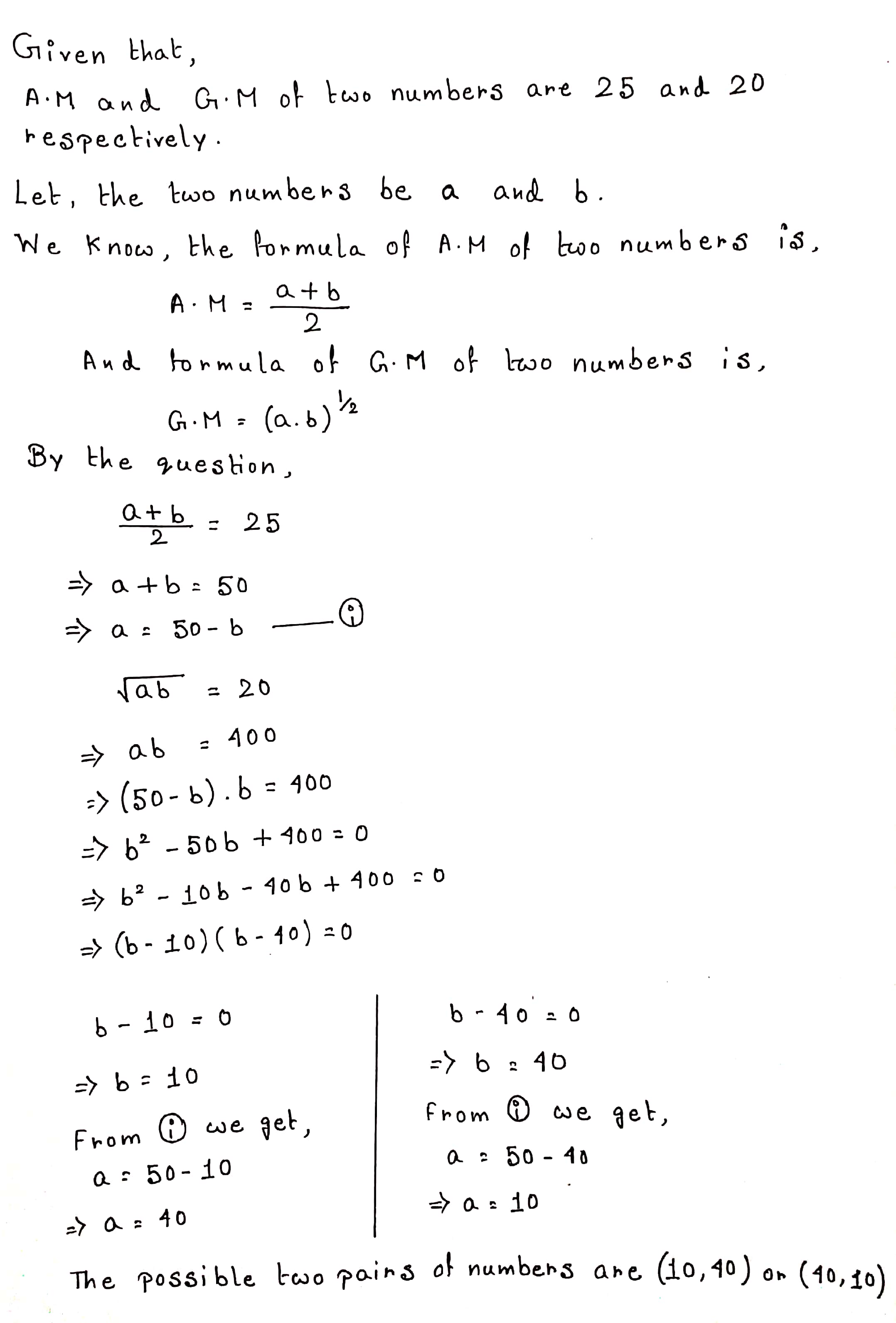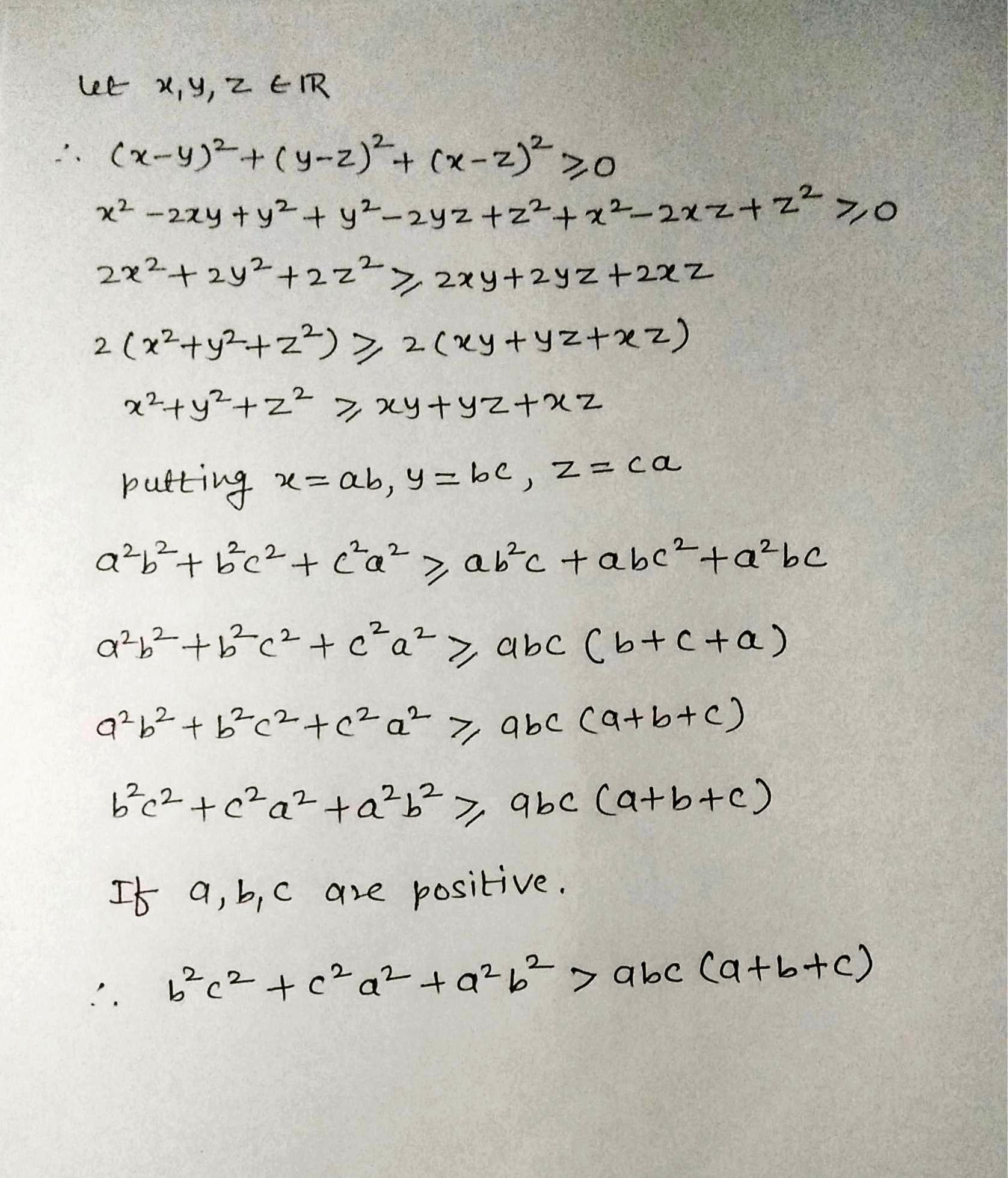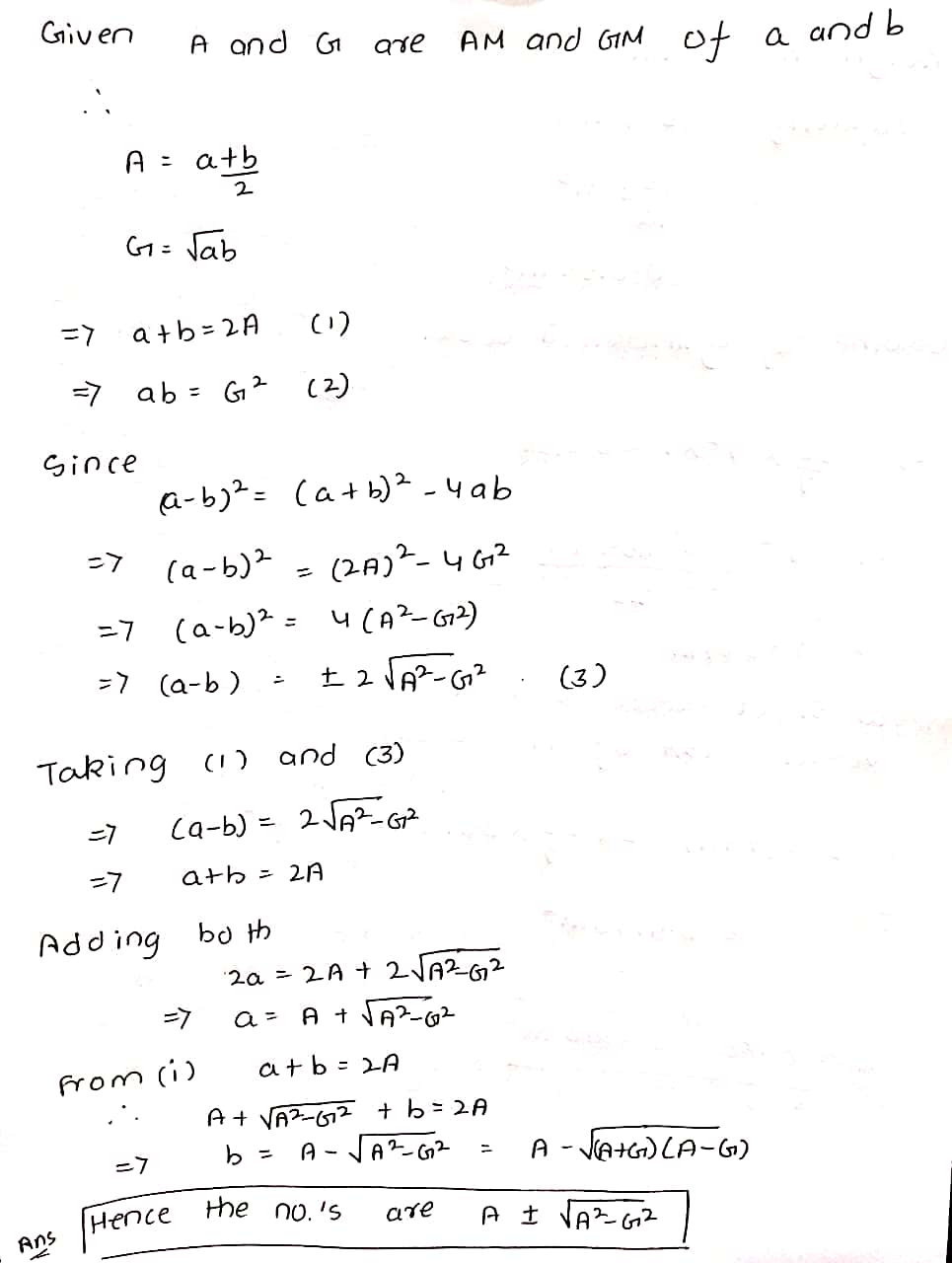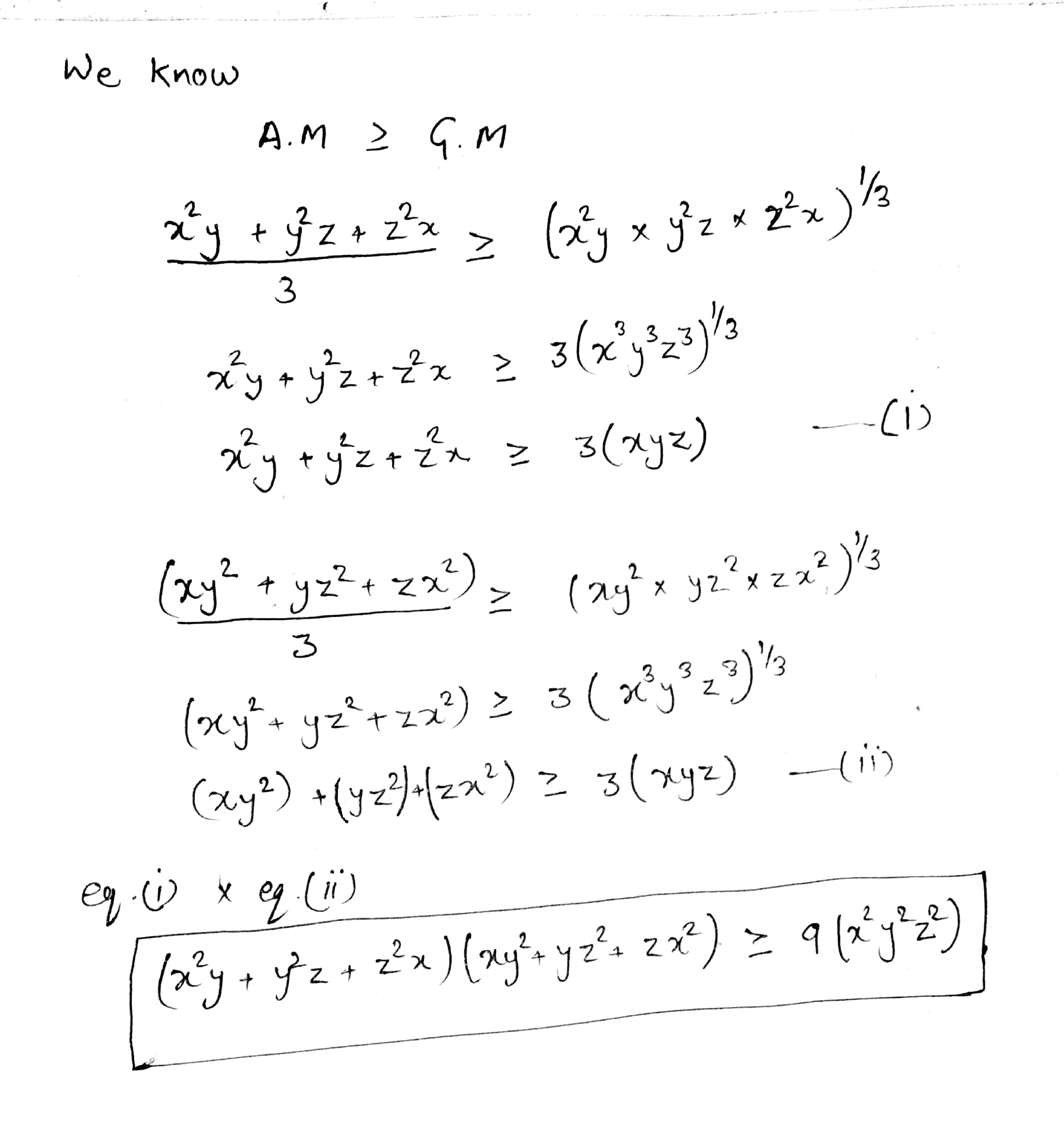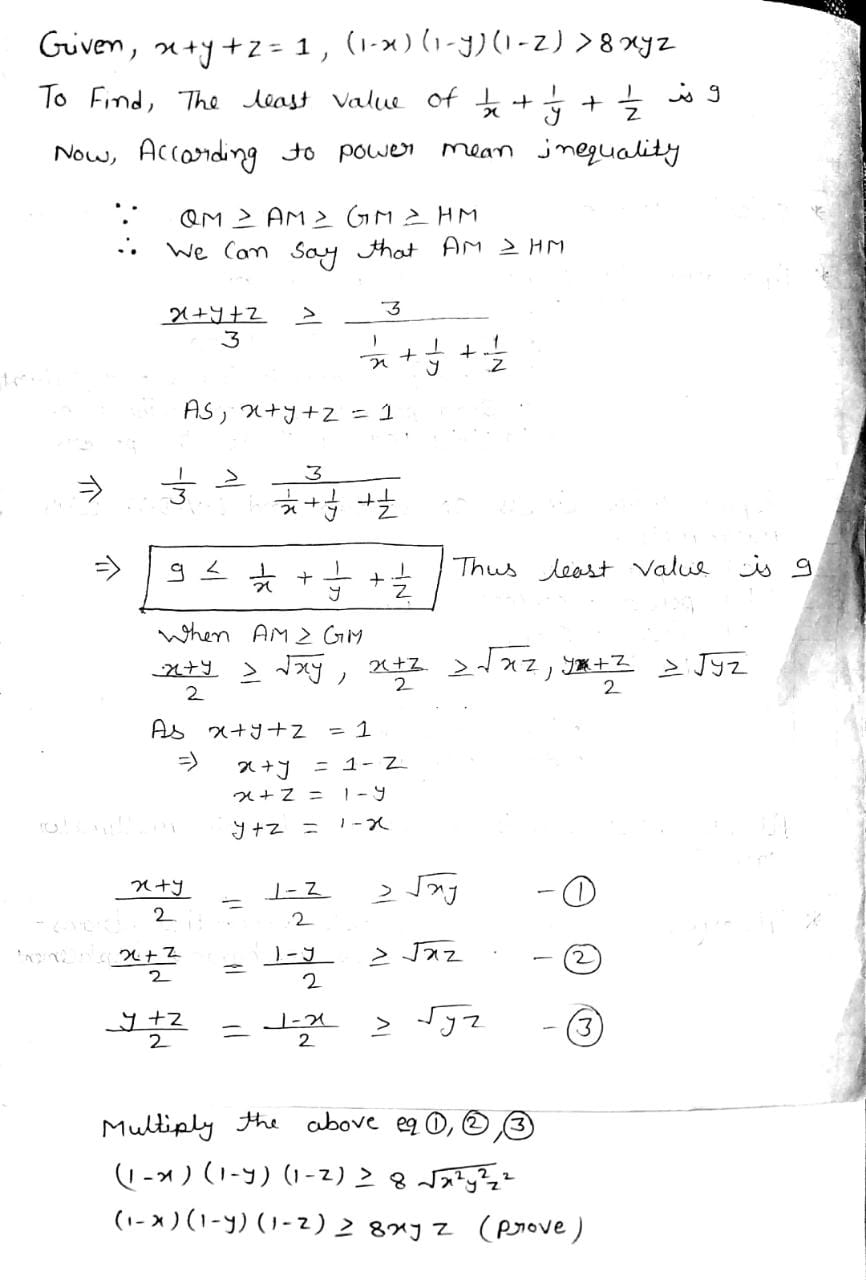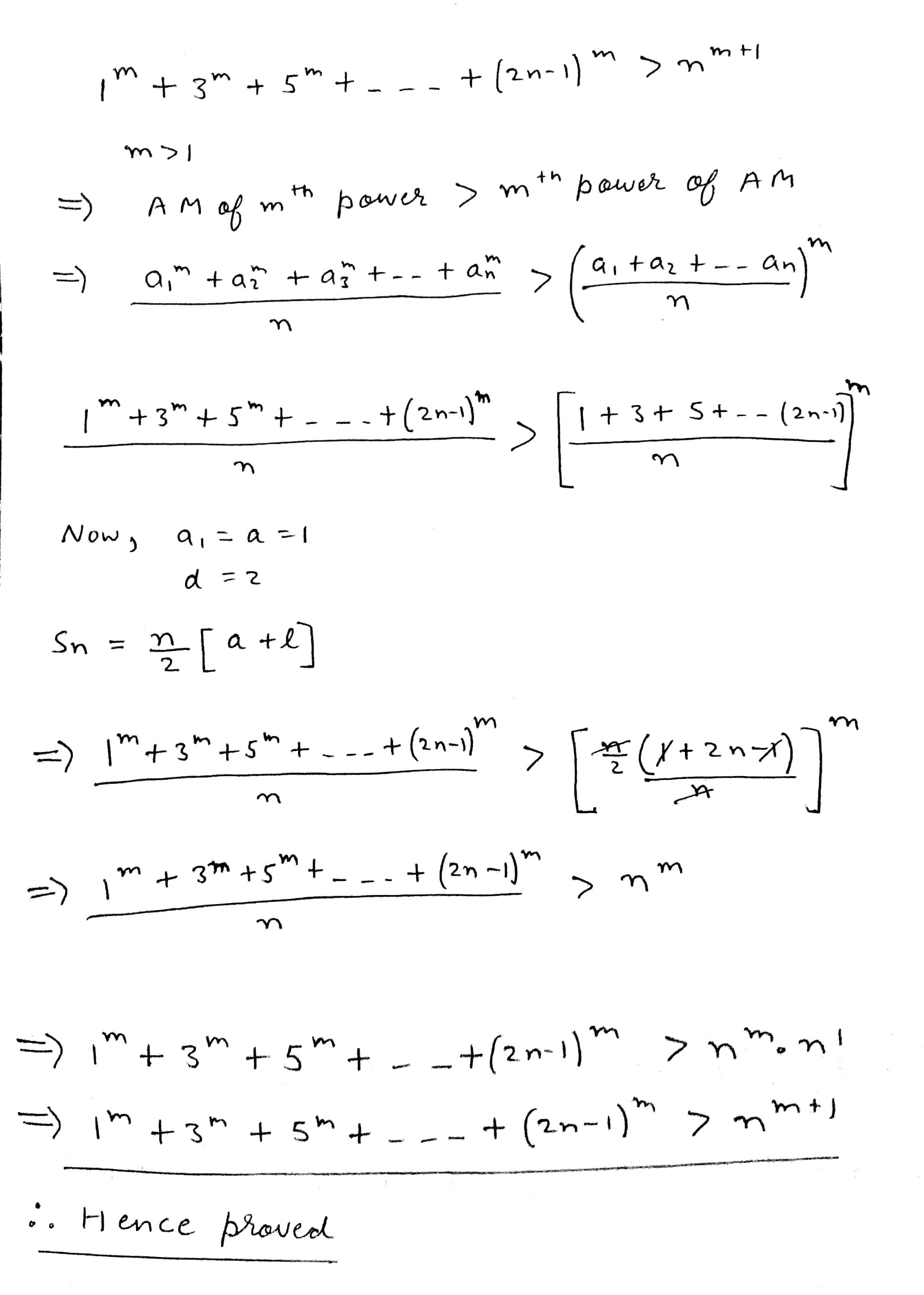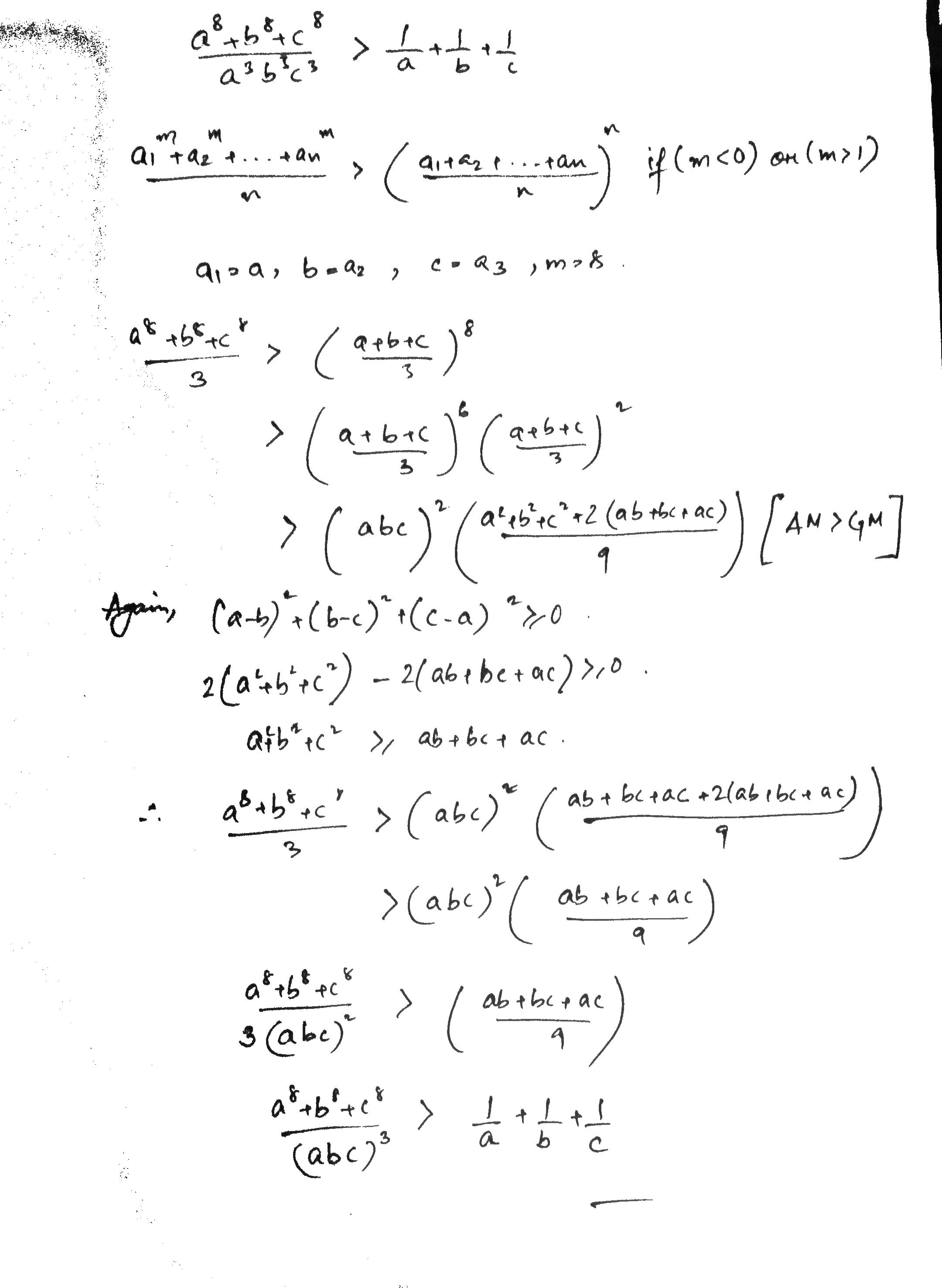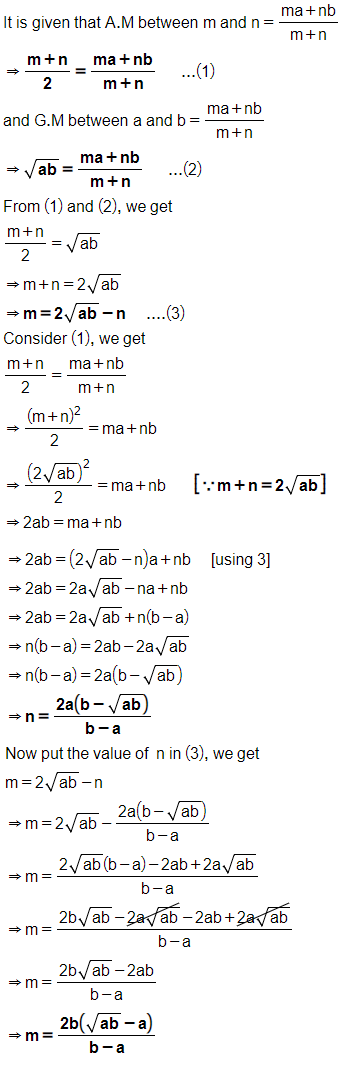Class 11 Commerce Applied Mathematics - Sequences And Series

If $$\displaystyle a_{n}=\frac{n^{2}}{3n+2}$$, find $$\displaystyle a_{5} a_1$$.

$$\displaystyle a_{1}a_{5}=\frac{1}{5}\times \frac{25}{17}=\frac{5}{17}$$

Find the value of $$n$$ so that $$\displaystyle \dfrac { { a }^{ n+1 }+{ b }^{ n+1 } }{ { a }^{ n }+{ b }^{ n } } $$ may be the geometric mean between $$a$$ and $$b$$.

We have, $$\displaystyle \frac { { a }^{ n-1

}+{ b }^{ n+1 } }{ { a }^{ n }+{ b }^{ n } } =ab$$
$$ \Rightarrow \quad { a

}^{ 2n+2 }+2{ a }^{ n+1 }b^{ n+1 }+{ b }^{ 2n+2 }=(ab)({ a }^{ 2n }+{

2a }^{ n }{ b }^{ n }+{ b }^{ 2n })$$
$$\Rightarrow \quad { a }^{ 2n+2

}+2{ a }^{ n+1 }b^{ n+1 }+{ b }^{ 2n+2 }={ a }^{ 2n+1 }b+{ 2a }^{ n+1 }{

b }^{ n+1 }+a{ b }^{ 2n+1 }$$
$$ \Rightarrow { a }^{ 2n+2 }+b^{

2n+2 }={ a }^{ 2n+1 }b+ab^{ 2n+1 }$$
$$ \Rightarrow { \quad a }^{ 2n+2

}-a^{ 2n+1 }b={ ab }^{ 2n+1 }-b^{ 2n+2 }$$
$$\Rightarrow \quad { a }^{

2n+1 }(a-b)={ b }^{ 2n+1 }(a-b)\\ \Rightarrow \left( \dfrac { a }{ b }

\right) ^{ 2n+1 }=1=\left( \dfrac { a }{ b } \right) ^{ 0 }\\

\Rightarrow 2n+1=0\\ \Rightarrow n=\dfrac { -1 }{ 2 } $$

Write the first two terms of the sequence whose $$n^{th}$$ term is $$t_{n} = 3n - 4$$

Here, $$t_{n} = 3n - 4$$
Put $$n = 1, t_{1} = 3(1) - 4 = -1$$
Put $$n = 2, t_{2} = 3(2) - 4 = 2$$
$$\therefore$$ First two terms are $$-1$$ and $$2$$.

Find the first three terms of the sequence whose $$n \ th$$ term is $$2n + 3$$.

Here, $$T_n = 2n + 3$$
To find, $$T_1$$, substitute $$n = 1$$ in $$T_n = 2n + 3$$
$$T_1 = 2(1) + 3 = 2 + 3 = 5$$
To find $$T_2$$, substitute $$n = 2$$ in $$T_n = 2n + 3$$
$$T_2 = 2(2) + 3 = 4 + 3 = 7$$
Similarly, $$T_3 = 2(3) + 3 = 6 + 3 = 9$$
$$\therefore$$ The first three terms of the sequence are $$5, 7, 9$$.

Find the next two terms in the sequence:
$$1, 2, 4, 7, 11, .....$$

The given sequence is $$1, 2, 4, 7, 11, ...$$
Here, $$t_1 = 1, t_2 = 2, t_3 = 4, t_4 = 7, t_5 = 11$$
The difference between two consecutive terms are $$1, 2, 3, 4, ...$$
$$\therefore t_6 = 11 + 5 = 16$$
$$t_7 = 16 + 6 = 22$$

Find the next two terms in the sequence: $$2, 4, 8, 16, .....$$

$$t_{1} = 2$$
$$t_{2} = 4 = 2\times 2 = t_{1} \times 2$$
$$t_{3} = 8 = 4\times 2 = t_{2} \times 2$$
$$\therefore t_{n} = 2t_{n - 1}$$
$$t_{5} = 2t_{4} = 2\times 16 = 32$$
$$t_{6} = 2t_{5} = 2\times 32 = 64$$
$$\therefore$$ The next two terms of the sequence are $$32, 64$$.

Find the first three terms of the following sequence, whose $$n^{th}$$ term is
$$t_n = 4n - 3$$

Given: $$t_n = 4n - 3$$
Put $$n = 1, t_1 = 4(1) - 3 = 1$$
Put $$n = 2, t_2 = 4 (2) - 3 = 5$$
Put $$n = 3, t_3 = 4(3) - 3 = 9$$
First three terms are $$1, 5, 9$$.

Find the first term of the sequence, where $$t_n=2n+1$$.

Here, $$t_n=2n+1$$
For n$$=1, t_1=2\times 1+1=3$$
$$\therefore$$ The first term of the sequence is $$3$$.`

If $$x$$ is the geometric mean of $$(x + 2)$$ and $$(x - 1)$$, then find the value of $$x$$.

$$G = \pm \sqrt {ab},$$ Here $$G = x$$
$$\therefore x = \pm \sqrt {(x + 2)(x - 1)}$$
$$\therefore x^{2} = (x + 2)(x - 1)$$ (Squaring on both sides)
$$\therefore x^{2} = x^{2} + x - 2$$
$$\therefore x - 2 = 0$$
$$\therefore x = 2$$.

Find the first two terms of the following sequence:
$${t}_{n}=n+2$$

Here $${t}_{n}=2$$
Put $$n=1$$, $${t}_{1}=1+2=3$$
Put $$n=2$$, $${t}_{2}=2+2=4$$
$$\therefore$$ The first terms of the sequence are $$3$$ and $$4$$.

Find the first two terms of the sequence whose $$n^{th}$$ term is
$${t}_{n}=n+2$$.

Put $$n=1$$, $${t}_{1}=1+2=3$$
put $$n=2$$, $${t}_{2}=2+2=4$$
$$\therefore$$ the first two terms are $$3$$ and $$4$$

Find the next two terms of the following sequence: $$1,3,5,7,.....$$

Given, $${t}_{1}=1,{t}_{2}=3,{t}_{3}={5},{t}_{4}=7$$
To find: $${t}_{5}$$ and $${t}_{6}$$
The difference between two consecutive terms is $$2$$.
$${t}_{5}={t}_{4}+2=7+2=9$$
$${t}_{6}={t}_{5}+2=9+2=11$$
The next two terms are $$9$$ and $$11$$

If $$t_{n} = 2n + 3$$, then find the first two terms of a given sequence

Given, $$t_{n} = 2n + 3$$
First two terms of the sequence are,
Put $$n = 1$$,
$$t_{1} = 2(1) + 3 = 5$$
Put $$n = 2$$,
$$t_{2}= 2(2) + 3 = 7$$
First two terms of the series are $$t_{1} = 5$$ and $$t_{2} = 7$$.

If $$nth$$ term of a sequence is $$t_{n} = n + 1$$, then find the first two terms of the given sequence

First two terms are given by $$t_1$$ and $$t_2$$
$$t_1=1+1=2$$
$$t_2=2+1=3$$

If $$t_n=4n$$, find $$t_1$$.

$$t_n=4n$$

For $$n=1$$,
$$\Rightarrow t_1=4(1)=4$$.

Which of the following sequences are geometric sequences
(i) $$5, 10, 15, 20, ....$$
(ii) $$0.15, 0.015, 0.0015, .....$$
(iii) $$\sqrt {7}, \sqrt {21}, 3\sqrt {7}, 3\sqrt {21},.....$$

(i) Considering the ratios of the consecutive terms, we see that $$\dfrac {10}{5}\neq \dfrac {15}{10}$$.
Thus, there is no common ratio. Hence it is not a geometric sequence.
(ii) We see that $$\dfrac {0.015}{0.15} = \dfrac {0.0015}{0.015} = ... = \dfrac {1}{10}$$.
Since the common ratio is $$\dfrac {1}{10}$$, then given sequence is a geometric sequence.
(iii) Now, $$\dfrac {\sqrt {21}}{\sqrt {7}} = \dfrac {3\sqrt {7}}{\sqrt {21}} = \dfrac {3\sqrt {21}}{3\sqrt {7}} = .... = \sqrt {3}$$. Thus, the common ratio is $$\sqrt {3}$$.
Therefore, the given sequence is a geometric sequence.

Find the sum of the following series.
(i) $$1 + 2 + 3 + .... + 45$$
(ii) $$16^{2} + 17^{2} + 18^{2} + .... + 25^{2}$$
(iii) $$2 + 4 + 6 + .... + 100$$
(iv) $$7 + 14 + 21 + .... + 490$$
(v) $$5^{2} + 7^{2} + 9^{2} + 39^{2}$$
(vi) $$16^{3} + 17^{3} + ..... + 35^{3}$$

(i) $$1+2+3.. +45$$$$=\dfrac {45(45+1)}{2}\\=1035$$

(ii) $$16^2+17^2.. +25^2$$$$=1^2+2^2+3^2... 25^2-(1^2+2^2... 15^2)\\=\dfrac {25(26)(51)}{6}-\dfrac {15(16)(31)}{6}\\=5525-1240\\=4285$$

(iii) $$2+4+6.. +100$$$$=2(1+2+3... +50)\\=2\times \dfrac {50(51)}{2}\\=2550$$

(iv) $$7+14+... +490$$$$=7(1+2+3... +70)\\=7\times \dfrac {70(71)}{2}\\=17395$$

(v) $$5^2+7^2+9^2+39^2=1676$$

(vi) $$16^3+17^3... +35^3$$$$=1^3+2^3+... 35^3-(1^3+2^3+3^3... +15^3)\\=\left (\dfrac {35(36)}{2}\right)^2-\left (\dfrac {15(16)}{2}\right)^2\\=396900-14400\\=382500$$

The sum of the first three terms of a G.P. is $$13$$ and sum of their squares is $$91$$. Determine the G.P.

Let the three terms be $$\dfrac {a}{r},a,ar$$

We are given $$\dfrac{a}{r}+a+ar=13$$ ....(i) and $${\left (\dfrac {a}{r}\right)}^2+a^2+{ar}^2=91$$ ....(ii)

Squaring equation (i) and substituting (ii), we get

$$91+2\times \dfrac {a^2}{r}+2a^2+2a^2r=169$$

$$\Rightarrow 2a^2\left (\dfrac {1}{r}+1+r\right)=78$$

Divide by equation (i)

We get $$a=3$$

Solve in (i)

We get $$r=3,\dfrac {1}{3}$$

Therefore corresponding G.P

$$1,3,9...$$ and $$9,3,1....$$

Find the common ratio and the general term of the following geometric sequences.
$$\dfrac {2}{5}, \dfrac {6}{25}, \dfrac {18}{125}, ....$$

Given sequence is a geometric sequence.
The common ratio is given by $$r = \dfrac {t_{2}}{t_{1}} = \dfrac {t_{3}}{t_{2}} = .....$$
Thus, $$r = \dfrac {\dfrac {6}{25}}{\dfrac {2}{5}} = \dfrac {3}{5}$$.
The first term of the sequence is $$\dfrac {2}{5}$$.

So, the general term of the sequence is
$$t_{n} = ar^{n - 1}, n = 1, 2, 3, ....$$
$$\Rightarrow t_{n} = \dfrac {2}{5} \left (\dfrac {3}{5}\right )^{n - 1}, n = 1, 2, 3, .....$$

If $$T_n = 2n^2 + 5$$ then find $$T_3$$

Solution:

$$T_n=2n^2+5$$

or, $$T_3=2\times 3^2+5$$

$$=2\times9+5$$

$$=18+5$$

$$=23$$

$$\therefore T_3=23.$$

The number of people who visited games village during common wealth games in New Delhi for the first four days was recorded as $$15,290, 14,181, 14,235$$ and $$10,578$$. Find the total number of people visited in these four days?

First four days number of people were $$15,290, 14,181, 14,235,$$ and $$10,578$$

Total number of people visited in these four days are $$=\left(15,290+ 14,181+14,235+10,578\right)$$

$$= 54,284$$ people

Study the pattern:
$$1 \times 8 + 1 = 9 $$
$$12 \times 8 + 2 = 98 $$
$$123 \times 8 + 3 = 987$$
$$1234 \times 8 + 4 = 9876$$
$$12345 \times 8 + 5 = 98765 $$
Write the next four steps. Can you find out how the pattern works ?

$$1\times 8+1=9$$

$$12\times 8+2=98$$

$$123\times 8+3=987$$

$$1234\times 8+4=9876$$

$$12345\times 8+5=98765$$

$$123456\times 8+6=987654$$

$$1234567\times 8+7=9876543$$

$$12345678\times 8+8=98765432$$

$$123456789\times 8+9=987654321$$.

1168781_700581_ans_833f81c680844426a5e5b6eb4d08b6d2.jpg

The arithmetic mean of the following data is $$25$$, find the value of $$k$$.
$${x}_{i}$$: $$5$$ $$15$$ $$25$$ $$35$$ $$45$$
$${f}_{i}$$: $$3$$ $$k$$ $$3$$ $$6$$ $$2$$

Arithmetic Mean =$$ \dfrac {\sum x_{i} f_{i}} {\sum f_{i}} $$

$$\Rightarrow $$ arithmetic mean =$$\dfrac {(5\times 3)+(15\times k)+(25 \times 3)+(35 \times 6)+(45 \times 2)}{3+k+3+6+2}$$

$$\Rightarrow $$arithmetic mean =$$\dfrac {15+15k+75+210+90}{3+k+3+6+2}=25$$

$$\Rightarrow 350+25k=390+15k$$

$$\Rightarrow k=4$$

Write the first five terms of each of the following sequences whose $$n^{th}$$ terms are:$${ a }_{ n }=3n+2$$

The $$n^{th}$$ term of the sequence is

$$a_{n}=3n+2 ...................eq(1)$$

1) for finding the first term of sequence $$(a_{1})$$ put n=1 in eq(1)

$$a_{1}=3\times1+2$$

$$\implies a_{1}=3+2$$

$$\implies a_{1}=5$$

2) for finding the second term of sequence $$(a_{2})$$ put n=2 in eq(1)

$$a_{2}=3\times2+2$$

$$\implies a_{2}=6+2$$

$$\implies a_{2}=8$$

3) for finding the third term of sequence $$(a_{3})$$ put n=3 in eq(1)

$$a_{3}=3\times3+2$$

$$\implies a_{3}=9+2$$

$$\implies a_{3}=11$$

4) for finding the fourth term of sequence $$(a_{4})$$ put n=4 in eq(1)

$$a_{4}=3\times4+2$$

$$\implies a_{4}=12+2$$

$$\implies a_{4}=14$$

5) for finding the fifth term of sequence $$(a_{5})$$ put n=5 in eq(1)

$$a_{5}=3\times5+2$$

$$\implies a_{5}=15+2$$

$$\implies a_{5}=17$$

Write the first five terms of each of the following sequences whose $$n$$th terms are:$${ a }_{ n }={ \left( -1 \right) }^{ n }.{ 2 }^{ n }$$

$$a_{n}=(-1)^{n}.2^{n} ...................eq(1)$$

1) To find the first term of sequence $$(a_{1})$$ put n=1 in eq(1)

$$\implies a_{1}=(-1)^{1}.2^{1}$$

$$\implies a_{1}=-1\times 2$$

$$\implies a_{1}=-2 $$

2) To find the second term of sequence $$(a_{2})$$ put n=2 in eq(1)

$$\implies a_{2}=(-1)^{2}.2^{2}$$

$$\implies a_{2}=(-1\times-1)\times (2\times 2)$$

$$\implies a_{2}=(1)\times (4) $$

$$\implies a_{2}=4 $$

3) To find the third term of sequence $$(a_{3})$$ put n=3 in eq(1)

$$\implies a_{3}=(-1)^{3}.2^{3}$$

$$\implies a_{3}=(-1\times-1\times -1)\times (2\times 2\times 2)$$

$$\implies a_{3}=(-1)\times (8) $$

$$\implies a_{3}=-8 $$

4) To find the fourth term of sequence $$(a_{4})$$ put n=4 in eq(1)

$$\implies a_{4}=(-1)^{4}.2^{4}$$

$$\implies a_{4}=(-1\times-1\times -1\times -1)\times (2\times 2\times 2\times 2)$$

$$\implies a_{4}=(1)\times (16) $$

$$\implies a_{4}=16 $$

5) To find the fifth term of sequence $$(a_{5})$$ put n=5 in eq(1)

$$\implies a_{5}=(-1)^{5}.2^{4}$$

$$\implies a_{5}=(-1\times -1\times-1\times -1\times -1)\times (2\times 2\times 2\times 2\times 2)$$

$$\implies a_{5}=(-1)\times (32) $$

$$\implies a_{5}=-32 $$

Write the first five terms of each of the following sequences whose $$n$$th terms are:$${ a }_{ n }={ n }^{ 2 }-n+1$$

$$a_{n}=n^{2}-n+1 ...................eq(1)$$

1) To find the first term of sequence $$(a_{1})$$ put n=1 in eq(1)

$$\implies a_{1}=1^{2}-1+1$$

$$\implies a_{1}=1-1+1 $$

$$\implies a_{1}=1 $$

2) To find the second term of sequence $$(a_{2})$$ put n=2 in eq(1)

$$\implies a_{2}=2^{2}-2+1$$

$$\implies a_{2}=4-2+1 $$

$$\implies a_{2}=3$$

3) To find the third term of sequence $$(a_{3})$$ put n=3 in eq(1)

$$\implies a_{3}=3^{2}-3+1$$

$$\implies a_{3}=9-3+1 $$

$$\implies a_{3}=7$$

4) To find the fourth term of sequence $$(a_{4})$$ put n=4 in eq(1)

$$\implies a_{4}=4^{2}-4+1$$

$$\implies a_{4}=16-4+1 $$

$$\implies a_{4}=13$$

5) To find the fifth term of sequence $$(a_{5})$$ put n=5 in eq(1)

$$\implies a_{5}=5^{2}-5+1$$

$$\implies a_{5}=25-5+1 $$

$$\implies a_{5}=21$$

Write the first five terms of each of the following sequences whose $$n$$th terms are:$${ a }_{ n }=\cfrac { n-2 }{ 3 } $$

$$a_{n}=\dfrac {n-2}{3} ...................eq(1)$$

1)For finding the first term of sequence $$(a_{1})$$ put n=1 in eq(1)

$$a_{1}=\dfrac {1-2}{3} $$

$$\implies a_{1}=\dfrac {-1}{3} $$

2)For finding the second term of sequence $$(a_{2})$$ put n=2 in eq(1)

$$a_{2}=\dfrac {2-2}{3} $$

$$\implies a_{2}=\dfrac {0}{3} $$

$$\implies a_{2}=0 $$

3) For finding the third term of sequence $$(a_{3})$$ put n=3 in eq(1)

$$a_{3}=\dfrac {3-2}{3} $$

$$\implies a_{3}=\dfrac {1}{3} $$

4) For finding the fourth term of sequence $$(a_{4})$$ put n=4 in eq(1)

$$a_{4}=\dfrac {4-2}{3} $$

$$\implies a_{4}=\dfrac {2}{3} $$

5) For finding the fifth term of sequence $$(a_{5})$$ put n=5 in eq(1)

$$a_{5}=\dfrac {5-2}{3} $$

$$\implies a_{5}=\dfrac {3}{3} $$

$$\implies a_{5}=1 $$

Write the first five terms of each of the following sequences whose $$n$$th terms are: $${ a }_{ n }=\cfrac { n\left( n-2 \right) }{ 2 } $$

$$a_{n}=\dfrac{n(n-2)}{2} ...................eq(1)$$

1) To find the first term of sequence $$(a_{1})$$ put n=1 in eq(1)

$$\implies a_{1}=\dfrac{1(1-2)}{2}$$

$$\implies a_{1}=\dfrac{1(-1)}{2}$$

$$\implies a_{1}=-\dfrac{1}{2} $$

2) To find the second term of sequence $$(a_{2})$$ put n=2 in eq(1)

$$\implies a_{2}=\dfrac{2(2-2)}{2}$$

$$\implies a_{2}=\dfrac{2(0)}{2}$$

$$\implies a_{2}= \dfrac{0}{2} $$

$$\implies a_{2}=0$$

3) To find the third term of sequence $$(a_{3})$$ put n=3 in eq(1)

$$\implies a_{3}=\dfrac{3(3-2)}{2}$$

$$\implies a_{3}=\dfrac{3(1)}{2}$$

$$\implies a_{3}= \dfrac{3}{2} $$

4) To find the fourth term of sequence $$(a_{4})$$ put n=4 in eq(1)

$$\implies a_{4}=\dfrac{4(4-2)}{2}$$

$$\implies a_{4}=\dfrac{4(2)}{2}$$

$$\implies a_{4}= \dfrac{8}{2} $$

$$\implies a_{4}= 4 $$

5) To find the fifth term of sequence $$(a_{5})$$ put n=5 in eq(1)

$$\implies a_{5}=\dfrac{5(5-2)}{2}$$

$$\implies a_{5}=\dfrac{5(3)}{2}$$

$$\implies a_{5}= \dfrac{15}{2} $$

Write the first five terms of each of the following sequences whose $$n$$th terms are:$${ a }_{ n }=2{ n }^{ 2 }-3n+1$$

$$a_{n}=2n^{2}-3n+1 ...................eq(1)$$

1) To find the first term of sequence $$(a_{1})$$ put n=1 in eq(1)

$$\implies a_{1}=2\times1^{2}-3\times1+1$$

$$\implies a_{1}=2-3+1 $$

$$\implies a_{1}=0$$

2) To find the second term of sequence $$(a_{2})$$ put n=2 in eq(1)

$$\implies a_{2}=2\times2^{2}-3\times2+1$$

$$\implies a_{2}=8-6+1 $$

$$\implies a_{2}=3$$

3) To find the third term of sequence $$(a_{3})$$ put n=3 in eq(1)

$$\implies a_{3}=2\times3^{2}-3\times3+1$$

$$\implies a_{3}=18-9+1 $$

$$\implies a_{3}=10$$

4) To find the fourth term of sequence $$(a_{4})$$ put n=4 in eq(1)

$$\implies a_{4}=2\times4^{2}-3\times4+1$$

$$\implies a_{4}=32-12+1 $$

$$\implies a_{4}=21$$

5) To find the fifth term of sequence $$(a_{5})$$ put n=5 in eq(1)

$$\implies a_{5}=2\times5^{2}-3\times5+1$$

$$\implies a_{5}=50-15+1 $$

$$\implies a_{5}=36$$

Write the first five terms of each of the following sequences whose $$n$$th terms are:$${ a }_{ n }=\cfrac { 2n-3 }{ 6 } $$

$$a_{n}=\dfrac{2n-3}{6} ...................eq(1)$$

1) To find the first term of sequence $$(a_{1})$$ put n=1 in eq(1)

$$\implies a_{1}=\dfrac{2\times 1-3}{6}$$

$$\implies a_{1}=\dfrac{2-3}{6} $$

$$\implies a_{1}=-\dfrac{1}{6}$$

2)To find the second term of sequence $$(a_{2})$$ put n=2 in eq(1)

$$\implies a_{2}=\dfrac{2\times 2-3}{6}$$

$$\implies a_{2}=\dfrac{4-3}{6} $$

$$\implies a_{2}=\dfrac{1}{6}$$

3) To find the third term of sequence $$(a_{3})$$ put n=3 in eq(1)

$$\implies a_{3}=\dfrac{2\times 3-3}{6}$$

$$\implies a_{3}=\dfrac{6-3}{6} $$

$$\implies a_{3}=\dfrac{3}{6}$$

$$\implies a_{3}=\dfrac{1}{2}$$

4) To find the fourth term of sequence $$(a_{4})$$ put n=4 in eq(1)

$$\implies a_{4}=\dfrac{2\times 4-3}{6}$$

$$\implies a_{4}=\dfrac{8-3}{6} $$

$$\implies a_{4}=\dfrac{5}{6}$$

5) To find the fifth term of sequence $$(a_{5})$$ put n=5 in eq(1)

$$\implies a_{5}=\dfrac{2\times 5-3}{6}$$

$$\implies a_{5}=\dfrac{10-3}{6} $$

$$\implies a_{5}=\dfrac{7}{6}$$

Write the first five terms of each of the following sequences whose $$n$$th terms are: $${ a }_{ n }=\cfrac { 3n-2 }{ 5 } $$

$$a_{n}=\dfrac{3n-2}{5} ...................eq(1)$$

1) To find the first term of sequence $$(a_{1})$$ put n=1 in eq(1)

$$\implies a_{1}=\dfrac{3\times 1-2}{5} $$

$$\implies a_{1}=\dfrac{3-2}{5} $$

$$\implies a_{1}=\dfrac{1}{5} $$

2)To find the second term of sequence $$(a_{2})$$ put n=2 in eq(1)

$$\implies a_{2}=\dfrac{3\times 2-2}{5} $$

$$\implies a_{2}=\dfrac{6-2}{5} $$

$$\implies a_{2}=\dfrac{4}{5} $$

3)To find the third term of sequence $$(a_{3})$$ put n=3 in eq(1)

$$\implies a_{3}=\dfrac{3\times 3-2}{5} $$

$$\implies a_{3}=\dfrac{9-2}{5} $$

$$\implies a_{3}=\dfrac{7}{5} $$

4) To find the fourth term of sequence $$(a_{4})$$ put n=4 in eq(1)

$$\implies a_{4}=\dfrac{3\times 4-2}{5} $$

$$\implies a_{4}=\dfrac{12-2}{5} $$

$$\implies a_{4}=\dfrac{10}{5} $$

$$\implies a_{4}=2 $$

5) To find the fifth term of sequence $$(a_{5})$$ put n=5 in eq(1)

$$\implies a_{5}=\dfrac{3\times 5-2}{5} $$

$$\implies a_{5}=\dfrac{15-2}{5} $$

$$\implies a_{5}=\dfrac{13}{5} $$

Write the first five terms of each of the following sequences whose $$n$$th terms are:$${ a }_{ n }={ 3 }^{ n }$$

The $$n^{th}$$ term of the sequence is

$$a_{n}=3^{n} ...................eq(1)$$

1) For finding the first term of sequence $$(a_{1})$$ put n=1 in eq(1)

$$a_{1}=3^{1}$$

$$\implies a_{1}=3 $$

2) For finding the second term of sequence $$(a_{2})$$ put n=2 in eq(1)

$$a_{2}=3^{2}$$

$$\implies a_{2}=3\times 3$$

$$\implies a_{2}=9$$

3) For finding the third term of sequence $$(a_{3})$$ put n=3 in eq(1)

$$a_{3}=3^{3}$$

$$\implies a_{3}=3\times 3 \times 3$$

$$\implies a_{3}=27$$

4) For finding the fourth term of sequence $$(a_{4})$$ put n=4 in eq(1)

$$a_{4}=3^{4}$$

$$\implies a_{4}=3\times 3 \times 3\times 3$$

$$\implies a_{4}=81$$

5) For finding the fifth term of sequence $$(a_{5})$$ put n=5 in eq(1)

$$a_{5}=3^{5}$$

$$\implies a_{5}=3\times3\times 3 \times 3\times 3$$

$$\implies a_{5}=243$$

The next term of the sequence $$3, 5, 7, 11, 13, 17,..$$ will be equal to:

The given sequence is a sequence of odd prime numbers $$3, 5, 7, 11, 13, 17$$. So the next term will be equal to $$19$$.

State whether the given list of numbers is a sequence or not: $$\dfrac{1}{2},\dfrac{2}{3},\dfrac{3}{4},...$$
If yes, find out the next number in the list.

Yes, the given list of numbers is a sequence because each new number in the sequence is formed using the rule $$\dfrac{n}{n+1}$$. The next number in the list is thus$$\dfrac{n}{n+1}$$ for $$4, i.e. \dfrac{4}{5}$$.

26500 were divided equally among a number of people. If the number of people is increased by 15, the number of money reduces by 30 for each person. find the number of people as well as money each person got.

Let there be "n" number of people.
$$ x_1 + x_2 ... + x_n = 26500 \rightarrow 1 \\
nx = 26500$$
equal division $$\rightarrow x_1 = x_2 = ... = x_n = x$$
Now, the number of people increased by 15 and the number of money reduces by 30
$$(x_1 - 30) + (x_2 - 30) + ... + (x_n - 30) $$

State whether the given list of numbers is a sequence or not : $$-52,53,-54,...$$ If yes, find out the next number in the list.

Yes, the given list of numbers is a sequence because each new number in the sequence is formed using the rule $$(-1)^{n}5^{n+1}$$. The next number in the list is thus $$(-1)^n 5^{n+1}$$ for $$4$$, i.e. $$5^5$$.

Choose the odd one out:
$$33,-79,42,-89,-11,35$$

42 because it is the only even number.

Rest all are odd.

Find the G.M of $$6$$ and $$24$$

$${\textbf{Step - 1: Stating how to find geometric mean of two numbers}}{\text{.}}$$

$${\text{If we two numbers }}a{\text{ and }}b,$$

$${\text{Then geometric mean of }}a,b{\text{ can be found using }}GM = \sqrt {ab} .$$

$${\textbf{Step - 2: Finding GM}}{\text{.}}$$

$${\text{We have }}a = 6,b = 24.$$

$$GM = \sqrt {6 \times 24} = \sqrt {144} = 12.$$

$${\textbf{Thus, the GM of 6 and 24 is 12}}{\text{.}}$$

The third term of the sequence whose $$n^{th}$$ term is $$\dfrac{1}{n^{2}}+1$$ is k.Find 9k

Given that:-

$${T}_{n} = \cfrac{1}{{n}^{2}} + 1$$

To find:- $${T}_{3} = ?$$

Solution:-

For $$n = 3$$, we get the $${3}^{rd}$$ term.

$$\therefore {T}_{3} = \cfrac{1}{{3}^{2}} + 1$$

$$\Rightarrow {T}_{3} = \cfrac{1}{9} + 1$$

$$\Rightarrow {T}_{3} = \cfrac{1 + 9}{9} = \cfrac{10}{9}$$.

Hence the correct answer is $$\cfrac{10}{9}$$

$$k=\dfrac {10}9$$

$$9k=10$$

If $$a,b,c$$ are three consecutive terms of A.P,Then $$b=$$____

$$ABC$$ are $$AP$$

arehmatic mean of $$A$$ and $$c$$ is $$b$$

$$b=\dfrac {A+B}{2}$$

Find the average of first twelve natural numbers.

Average of first $$n$$ natural numbers $$= \dfrac{n+1}{2}$$

So, The average of first $$12$$ natural numbers $$= \dfrac{12+1}{2} = \dfrac{13}{2} = 6.5$$

Write down the sequence if $$n$$th term is:

a) $$\dfrac{{{2^n}}}{n}$$

b) $$\dfrac{{3 + {{\left( { - 1} \right)}^n}}}{{{3^n}}}$$

$$\dfrac{2^n}{n}$$

$$=\dfrac{2^1}{1},\dfrac{2^2}{2},\dfrac{2^3}{3},\dfrac{2^4}{4},.........................,\dfrac{2^n}{n}$$

$$=2,2,\dfrac{8}{3},4,..............,\dfrac{2^n}{n}$$

$$\dfrac{3+(-1)^n}{3^n}$$

$$=\dfrac{3+(-1)^1}{3^1},\dfrac{3+(-1)^2}{3^2},\dfrac{3+(-1)^3}{3^3},\dfrac{3+(-1)^4}{3^4},.........................,\dfrac{3+(-1)^n}{3^n}$$

$$=\dfrac{2}{3},\dfrac{4}{9},\dfrac{2}{27},\dfrac{4}{81},........................,\dfrac{3+(-1)^n}{3^n}$$

The G.M. between $$1$$ and $$25$$ is ___.

$$G.M=\sqrt{a\times b}$$

$$=\sqrt{1\times 25}$$

$$=5$$

Solve: $$3200 = 4500 - \dfrac{n}{20}$$.

$$3200=4500-n/20$$

$$n/20=4500-3200$$

$$n/20=1300$$

$$n=1300\times 20$$

$$n=26000$$

$$\therefore n=26000$$.

1104390_1196621_ans_60b78843d60447c99c05b03e0803328b.jpg

Write the next term: $$\sqrt { 12 } , \sqrt { 27 } \sqrt { 48 } , \sqrt { 75 } , \dots ......$$

$$\sqrt{12}, \sqrt{27}, \sqrt{48}, \sqrt{75}, ……..\sqrt{108}$$

$$15$$ $$21$$ $$27$$ $$33$$

$$3\times 5$$ $$3\times 7$$ $$3\times 9$$ $$3\times 11$$.

1194333_1281328_ans_01556ab74836434e84978a6a56a84f77.jpg

If $$t_{n}=2n$$, find $$t_{3}$$.

We have,

$$t_n=2n$$

then, put $$n=3$$ and we get

$$t_3=2\times 3$$

$$t_3=6$$

Hence, this is the answer.

Pointing to a man in a photograph, a woman said, "His brother's father is the only son of my grandfather". How is the woman related to the man in the photograph ?

Only son of woman's grandfather means woman's father, Man's brother. So, the woman is the sister of the man.

If Mohan says that his mother is the only daughter of Shyam's mother, how is Shyam related to Mohan ?

Only daughter of Shyam's mother means that Shyam is brother of Mohan's mother . So, Shyam is uncle of Mohan.

Pointing to a photograph, a man said, " I have no brother or sister but that man's father is my father's son". Whose photograph was it ?

$$ \textbf{Step 1: Finding correct answer}$$

$$\text{ As the man has no brother or sister, the man in the photograph is none other than himself}$$

$$ \textbf{Hence, the narrator is the father of the man in the photograph, }$$ $$\textbf{so the man in the photograph is his son.} $$

If $$ a_{n}=\frac{n(n-3)}{n+4} $$ then find the $$ 18^{ th } $$ term of this sequence.

$$a_{n}=\dfrac{n(n-3)}{n+4}$$

$$18^{\mathrm{th}} $$ term is $$a_{18}=\dfrac{18\times 15}{18+4}=\dfrac{9\times 15}{11}=\dfrac{135}{11}$$

What is sequence ?

A list of numbers, arranged in a definite order according to some definite rule, is called a sequence.

Find the mean of 2 and 8

$$ {\textbf{Step 1: Find mean }} $$

$$ {\text{Given numbers are 2, 8}}{\text{.}} $$

$$ {\text{X = }}\dfrac{{{\text{2 + 8}}}}{2} $$

$$ {\text{= }}\dfrac{{10}}{5} $$

$$ {\text{= 2}} $$

$$ {\textbf{Final Answer: Hence the mean is 2}}{\text{.}} $$

The mean of data $$34,65,14,74,43$$ is

Given data is $$34,65,14,74,43$$

Sum of data $$34+65+14+74+43=230$$

Mean is $$\dfrac{430}{5}=86$$

Some equations are solved on the basis of a certain system. On the same basis, find out the correct answer for the unsolved equation
$$4\times 6\times 9=649$$
$$7\times 3\times 2=372$$
$$8\times 9\times 4=?$$

Given $$4\times 6\times 9=649$$

$$7\times 3\times 2=372$$

From the above two statements we can say that $$a\times b\times c=b a c$$

$$\implies 8\times 9\times 4=984$$

If $$ \frac{2}{3}, \mathrm{k}, \frac{5 k}{8} $$ are in A.P. then $$ \mathrm{k}= $$

Given $$\dfrac{2}{3},k,\dfrac{5 k}{8}$$ are in $$AP$$

$$\implies 2 k=\dfrac{2}{3}+\dfrac{5 k}{8}$$

$$\implies 2 k-\dfrac{5 k}{8}=\dfrac{2}{3}$$

$$\implies \dfrac{11 k}{8}=\dfrac{2}{3}$$

$$\implies k=\dfrac{16}{33}$$

If $$ \dfrac{1}{\sqrt{a}} $$ is the G.M. of 2 and $$ \dfrac{1}{4},$$ find a.

$$G_1=2$$

$$G_2=\dfrac 14$$

$$G.M.=\sqrt {G_1G_2}$$

$$G.M.=\sqrt {2\times \dfrac 14}$$

$$G.M.=\dfrac 1{\sqrt 2}$$

Comparing with $$\dfrac 1{\sqrt a}$$, we get $$a =2$$.

Find the geometric mean of the following pairs of numbers:
$$ -8 $$ and $$ -2 $$

$$x=-8$$

$$y=-2$$

$$GM=\sqrt {G_1G_2}$$

$$GM=\sqrt {(-8)(-2)}$$

$$\implies \sqrt {16}$$

$$=\pm 4$$

$$\because$$ Geometric mean lies between -8 and -2,

$$\therefore G.M. = -4$$

If AM and GM of two positive numbers a and b are 10 and 8 respectively,find the numbers

We have,

$$ \dfrac{a+b}{2} = 10 $$ and $$ \sqrt{ab} = 8 \Rightarrow a+b = 20 $$ and $$ ab = 64 $$

Clearly,$$a$$ and $$b$$ are roots of the equation

$$ x^{2}-(a+b)x+ab = 0 $$

or, $$ x^{2}-20x+64 = 0 $$

$$ \Rightarrow (x-16)(x-4) = 0 \Rightarrow x = 4,16\Rightarrow a = 4,b = 16 $$ or $$ a = 16,b = 4 $$

Divided by 2.

Mean of the given data $$= \frac{8 + 12 + 16 + 22 + 10 + 4}{6}$$

$$= \frac{72}{6} = 12$$

If $$\bar{x}$$ is the mean of n number of observations $$x_1, x_2, x_3,....,x_n,$$ then mean of $$\frac{x_1}{a}$$, $$\frac{x_2}{a}$$, $$\frac{x_3}{a}$$, $$.... ,\frac{x_n}{a}$$ is $$\frac{\bar{x}}{a}$$.

Thus, when each of the given data is divided by 2, the mean is also divided by 2.

Mean of the original data is 12.

Hence, the new mean $$= \frac{12}{2} = 6$$

Find the $${ 7 }^{ th }$$ term in the following sequence whose $${ n }^{ th }$$ terms is $${ a }_{ n }=\dfrac { { n }^{ 2 } }{ { 2 }^{ n } } $$.

Substituting $$n=7$$, we obtain
$${ a }_{ 7 }=\dfrac { 7^{ 2 } }{ { 2 }^{ 7 } } =\dfrac { 49 }{ 128 } $$

Multiplied by 3

Mean of the given data $$= \frac{8 + 12 + 16 + 22 + 10 + 4}{6}$$
$$= \frac{72}{6} = 12$$

If $$\bar{x}$$ is the mean of n number of observations $$x_1, x_2, x_3,....,x_n,$$ then mean of $$ax_1, ax_2, ax_3,....,ax_n,$$ is $$a \bar{x}$$
Thus, when each of the given data is multiplied by 3, the mean is also multiplied by 3.
Mean of the original data is 12.
Hence, the new mean = 12 x 3 = 36

Which term of the following sequences:
(a) $$ 2,2 \sqrt{2}, 4 \dots \dots$$ is $$ 128 ? $$

(a) The given sequence is $$ 2,2 \sqrt{2}, 4 \ldots \ldots $$
Here, $$ a=2 $$ and $$ r=(2 \sqrt{2}) / 2=\sqrt{2} $$
Let the $$ n^{\text {th }} $$ term of the given sequence be 128
$$ a_{n}=a r^{n-1} $$
$$ \Rightarrow(2)(\sqrt{2})^{n-1}=128 $$
$$ \Rightarrow(2)(2)^{\dfrac{n-1}{2}}=(2)^{7} $$
$$ \Rightarrow(2)^{\dfrac{n-1}{2}+1}=(2)^{7} $$
$$ \therefore \dfrac{n-1}{2}+1=7 $$
$$ \Rightarrow \dfrac{n-1}{2}=6 $$
$$ \Rightarrow n-1=12 $$
$$ \Rightarrow n=13 $$
Thus, the $$ 13^{\text {th }} $$ term of the given sequence is 128

Find the $${ 17 }^{ th }$$ and $${ 24 }^{ th }$$ term in the following sequence whose $${ n }^{ th }$$ term is $${ a }_{ n }=4n-3$$.

Substituting

Find the $${ 9 }^{ th }$$ term in the following sequence whose $${ n }^{ th }$$ terms is $${ a }_{ n }=(-1)^{ n-1 }n^{ 3 }$$

Substituting $$n=9$$, we obtain
$${ a }_{ 9 }=(-1)^{ 9-1 }(9)^{ 3 }={ 9 }^{ 3 }=729$$

Find the third term of the following sequence, whose $$n^{th}$$ term is given.
$$t_n\,=\,2n\,-\,5$$

Given, $$t_n=2n-5$$
$$\therefore t_1=2\times1-5=-3$$
$$t_2=2\times2-5=-1$$
$$t_3=2\times3-5=1$$

$$\therefore$$ $$3^{rd}$$ term of the given sequence is $$t_{3}=1$$

If $$\displaystyle a_{1},a_{2},...a_{n}$$ be an A.P. of +ive terms, then $$\displaystyle \sum_{k=1}^{n}a_{k}\geq n\sqrt{a_{1}^{2}+\left ( n-1 \right )da_{1}}$$ where d is common difference of A.P. If you think this is true write $$1$$ otherwise write $$0$$ ?

$$\displaystyle S_{n}= \frac{n}{2}\left [ a_{1}+a_{n} \right ]\geq n\sqrt{a_{1}.a_{n}} \because A.M.\geq G.M.$$
or $$\displaystyle

S_{n}\geq n\sqrt{a_{1}\left [ a_{1}+\left ( n-1 \right )d \right ]}=

n\sqrt{a_{1}^{2}+\left ( n-1 \right )da_{1}}$$

Thus answer is $$1$$.

If $$\displaystyle f\left ( x \right )=\log _{x}1/9-\log_{3}x^{2}\left ( x > 1 \right )$$, then max $$\displaystyle f\left ( x \right )$$ is equal to

Let, $$\displaystyle y=\log _{x}1/9-\log_{3}x^{2}\left ( x > 1 \right ) $$
$$=\log_x(3^{-2})-2\log_3x= -2\log_x3-2\log_3x$$
$$=-2(\log_x3+\log_3x)$$
Now since $$x>1\Rightarrow \log_3 x, \log_x3>0$$
Thus using, $$A.M\ge G.M$$
$$\Rightarrow \dfrac{\log_3x+\log_x3}{2}\ge\sqrt{\log_x3\log_3x} =1, \quad \quad \left[\because \log_ab = \dfrac{1}{\log_ba}\right] $$
Hence $$(-y)_{max} =2\times 2=2$$

$$(x-4)$$ is geometric mean of $$(x-5)$$ and $$(x-2)$$ find $$x$$.

Geometric mean of two numbers, $$ a$$ and $$ b$$ is $$ \sqrt {ab} $$
So, geometric mean of $$ (x-5), (x -2) $$ is $$ \sqrt {(x-5) \times (x-2)} =(x-4) $$

Squaring both sides,

$$ {x}^{2} - 5x - 2x + 10 = {x}^{2} - 8x + 16 $$

$$ -7x + 8x = 16 - 10 $$

$$ x = 6 $$

If $$ab = 2a +3b$$ where a > 0, b > 0, then find the minimum value of ab.

$$ab=2a+3b$$ ...(1)

Using $$AM\ge GM$$

$$\displaystyle\frac { \left( 2a+3b \right) }{ 2 } \ge { \left( 6ab \right) }^{ \frac { 1 }{ 2 } }\Rightarrow 2a+3b\ge 2{ \left( 6ab \right) }^{ \frac { 1 }{ 2 } }$$ from(1)

$$\Rightarrow \displaystyle ab\ge 2{ \left( 6ab \right) }^{ \frac { 1 }{ 2 } }\Rightarrow { \left( ab \right) }^{ \frac { 1 }{ 2 } }\ge 2{ \left( 6 \right) }^{ \frac { 1 }{ 2 } }$$

$$\Rightarrow ab\ge 24$$

If the roots of the equation $${ x }^{ 3 }-a{ x }^{ 2 }+4x-8=0$$ are real and positive, then the minimum value of $$a$$ is

Let $$\alpha ,\beta ,\gamma $$ be the roots of the given equation,

Then, $$\alpha +\beta +\gamma =a,\alpha \beta +\alpha \gamma +\beta \gamma =4,\alpha \beta \gamma =8$$

Since $$\displaystyle A.M.\ge G.M.\Rightarrow \frac { \alpha +\beta +\gamma }{ 3 } \ge \sqrt [ 3 ]{ \alpha \beta \gamma } $$

$$\displaystyle \Rightarrow \frac { a }{ 3 } \ge \sqrt [ 3 ]{ 8 } \Rightarrow a\ge 6$$

$$\therefore$$ The minimum value of $$a=6.$$

Y B T G O ?

Y B T G O ?
I series (Y T O) consist of 2nd , 7th and 12th letters from the end of alphabets.
II series (B G) consist of $$2^{nd} , 7^{th}$$ and $$12^{th}$$ letters from the beginning of the alphabets.
So, the missing letter of the second series is $$12^{th}$$ letter from the beginning i.e., L.

If $$x, y, z, u > 0$$ , then find the minimum value of $$\displaystyle \frac{x^{6}+y^{6}+2z^{3}+2u^{3}}{xyzu}$$

Using A.M $$\geq $$ G.M
$$\displaystyle \frac { { x }^{ 6 }+{ y }^{ 6 }+{ z }^{ 3 }+{ z }^{ 3

}+{ u }^{ 3 }+{ u }^{ 3 } }{ 6 } \ge { \left( { x }^{ 6 }{ y }^{ 6 }{ z

}^{ 6 } \right) }^{ { 1 }/{ 6 } }$$
$$\displaystyle \therefore \quad \frac { { x }^{ 6 }+{ y }^{ 6 }+2{ z }^{ 3 }+{ 2u }^{ 3 } }{ xyzu } \ge 6$$

Write down the sequence whose $$\displaystyle n^{th}$$ term is
(i) $$\displaystyle \frac{2^{n}}{n}$$ (ii) $$\displaystyle \frac{3+\left ( -1 \right )^{n}}{3^{n}}$$. How many terms of the sequences are are less than zero?

Let $$ t_{n}=\dfrac {2^{n}}{n}$$

Put n = 1, 2, 3, 4, ........ we get

$$ t_{1}=\dfrac {2}{1}=2$$

$$t_{2}=\dfrac {4}{2}=2$$

$$t_{3}=\dfrac {8}{3}$$

$$t_{4}=\dfrac {16}{4}=4$$

So the sequence is $$2, 2, \dfrac {8}{3}, 4, .......$$

(ii) Let $$ t_{n}=\dfrac {3+\left ( -1 \right )^{n}}{3^{n}}$$

Put n = 1, 2, 3, 4......

$$t_{1}=\dfrac {3+(-1)}{3}=\dfrac {2}{3}$$

$$t_{2}=\dfrac {3+(-1)^2}{(3)^2}=\dfrac {4}{9}$$

$$t_{3}=\dfrac {3+(-1)^3}{(3)^3}=\dfrac {2}{27}$$

$$t_{4}=\dfrac {3+(-1)^4}{(3)^4}=\dfrac {4}{81}$$

So the sequence is $$\dfrac {2}{3},\dfrac {4}{9},\dfrac {2}{27},\dfrac {4}{81},....$$

If $$\displaystyle t_{n}=\frac{1+\left ( -2 \right )^{n}}{n-1}$$, then find $$\displaystyle t_{6}-t_{5}$$.

$$\displaystyle t_{6}=\frac{1+\left ( -2 \right )^{6}}{6-1}=\frac{1+64}{5}=\frac{65}{5}=13$$
$$\displaystyle t_{5}=\frac{1+\left ( -2 \right )^{5}}{5-1}=\frac{1-32}{4}=\frac{-31}{4}$$
$$\displaystyle \therefore t_{6}-t_{5}=13-\left ( -\frac{31}{4} \right )=13+\frac{31}{4}=\frac{83}{4}=20\frac{3}{4}$$

The sum of two numbers is $$6$$ times their geometric mean show that numbers are in the ratio $$\displaystyle (3+2\sqrt { 2 } ):(3-2\sqrt { 2 } )$$

Let the two numbers are $$a$$ and $$b$$.
Thus their $$G.M=\sqrt { ab }$$
According to the given condition, $$a+b=6\sqrt { ab } \quad \quad ....(1)$$
$$\Rightarrow { (a+b) }^{ 2 }=36(ab)\quad \quad$$
Also, $${ (a-b) }^{ 2 }={ (a+b) }^{ 2 }-4ab=36ab-4ab=32ab\\ \Rightarrow a-b=\sqrt { 32 } \sqrt { ab } =4\sqrt { 2 } \sqrt { ab }$$ ........(2)
Adding (1) and (2) , we obtain $$2a=(6+4\sqrt { 2 } )\sqrt { ab }$$
$$\Rightarrow a=(3+2\sqrt { 2 } )\sqrt { ab } $$
Substituting the value of $$a$$ in (1), we obtain $$ b=6\sqrt { ab } -(3+2\sqrt { 2 } )\sqrt { ab }$$
$$\Rightarrow b=(3-2\sqrt { 2 } )\sqrt { ab } \\\Rightarrow \displaystyle \frac { a }{ b } =\frac { (3+2\sqrt { 2) } \sqrt { ab } }{ (3-2\sqrt { 2 } )\sqrt { ab } } =\frac { 3+2\sqrt { 2 } }{ 3-2\sqrt { 2 } } $$
Thus , the required ratio is $$(3+2\sqrt { 2 } ):(\quad 3-2\sqrt { 2 } )$$

If $$\displaystyle \frac { { a }^{ n }+{ b }^{ n } }{ { a }^{ n-1 }+{ b }^{ n-1 } } $$is the A.M. between $$a$$ and $$b$$, then find the value of $$n$$.

According to the given condition,

Given is the A.M between a and b, therefore,

$$\dfrac { a+b }{ 2 } =\dfrac { { a }^{ n+1 }+{ b }^{ n+1 } }{ { a }^{ n }+{ b }^{ n } } $$

$$\dfrac { a+b }{ 2 } =\dfrac { { a }^{ n }\times a+{ b }^{ n }\times b }{ { a }^{ n }+{ b }^{ n } } $$

Cross multiply.

$${ a }^{ n }\times a+{ a }^{ n }\times b+{ b }^{ n }\times a+{ b }^{ n }\times b=2{ a }^{ n }\times a+2{ b }^{ n }\times b$$

$${ a }^{ n }b+{ b }^{ n }a={ a }^{ n }a+{ b }^{ n }b$$

$${ a }^{ n }b-{ a }^{ n }a={ b }^{ n }b-{ b }^{ n }a$$

$${ a }^{ n }\left( b-a \right) ={ b }^{ n }\left( b-a \right) $$

$${ a }^{ n }={ b }^{ n }$$

a and b can only be equal if n=0. ($${ x }^{ n }=1$$)

Thus, $$n = 0.$$

Each layer of the structure below is a square. The base is made up of 100 cubes, the second layer 81 cubes and the third layer 64 cubes. If the top layer of the structure consists of 16 cubes, how many layers does the structure have in all?

Base has $$100$$ cubs = $$10^2 $$ cubs ; $$2^{nd}$$ layer has $$9^2$$ cubs 6 so on

& to p has $$16 = 4^2$$ cubs $$\therefore$$ no of layers are :-

$$\underline{10}^2, \underline{9}^2 , \underline{8}^2, \underline{7}^2, \underline{6}^2, \underline{5}^2 , \underline{4}^2 =\boxed{ 7 \,layers}$$

If the sum of $$4$$ terms of an A.P. is $$36$$, find the A.M. of these terms.

2013212_529458_ans_0937d2b37ee34d6fac54b13d75bb79c7.jpg

Find $$x$$, if the given numbers are in A.P. $$(a + b)^2 , x , (a - b)^2$$

We know that the arithmetic mean between two numbers $$a$$ and $$b$$ is $$AM=\frac { a+b }{ 2 }$$.

Here, it is given that $$AM=x$$, $$a=(a+b)^2$$ and $$b=(a-b)^2$$, therefore,

$$AM=\frac { a+b }{ 2 } \\ \Rightarrow x=\frac { (a+b)^{ 2 }+(a-b)^{ 2 } }{ 2 } \\ \Rightarrow x=\frac { (a^{ 2 }+b^{ 2 }+2ab)+(a^{ 2 }+b^{ 2 }-2ab) }{ 2 } \\ \Rightarrow x=\frac { 2a^{ 2 }+2b^{ 2 } }{ 2 } \\ \Rightarrow x=\frac { 2(a^{ 2 }+b^{ 2 }) }{ 2 } \\ \Rightarrow x=a^{ 2 }+b^{ 2 }$$

Hence, $$x=a^2+b^2$$

Find the next two terms in the sequence:
$$1,3,7,15,31,.......$$

$${ t }_{ 1 }=1,{ t }_{ 2 }=3,{ t }_{ 3 }=7,{ t }_{ 4 }=15,{ t }_{ 5 }=31$$
$${t}_{2}=3=2{t}_{1}+1$$
$${t}_{3}=2{t}_{2}+1$$
$${t}_{4}=15=2{t}_{3}+1$$
$$\therefore$$ $${t}_{n}=2{t}_{n-1}+1$$
$${t}_{6}=2{t}_{5}+1=2\times 31+1=2\times 31+1=62+1=63$$
$${t}_{7}=2{t}_{6}+1=2\times 63+1=127$$
$$\therefore$$ The next two terms of the sequence are $$63,127$$.

Find $$x$$, if $$\sqrt 2, x, \dfrac{1}{\sqrt 2}$$ are in G.P.

We know that the geometric mean between two numbers $$a$$ and $$b$$ is $$GM=\sqrt { ab }$$.

Here, it is given that $$GM=x$$, $$a=\sqrt { 2 }$$ and $$b=\frac { 1 }{ \sqrt { 2 } }$$, therefore,

$$GM=\sqrt { ab } \\ \Rightarrow x=\sqrt { \sqrt { 2 } \times \frac { 1 }{ \sqrt { 2 } } } \\ \Rightarrow x=\sqrt { 1 } \\ \Rightarrow x=1$$

Hence, $$x=1$$

Find GM between 4 and 36.

Let $$a = 4$$, $$b = 36$$
$$G = \sqrt{a \times b} = \sqrt{4 \times 36} = \sqrt{144}$$
$$G= 12$$

If $$xy=6$$, then minimum value of $$2x+3y$$ is __________.

By applying the AMGM property,

$$\dfrac{2x+3y}{2} \geq \sqrt{(2x)(3y)}$$

$$\Rightarrow 2x+3y \geq 2\sqrt{6xy}$$

$$\Rightarrow 2x+3y \geq 2\sqrt{6(6)}$$

$$\Rightarrow 2x+3y \geq 2\times 6$$

$$\Rightarrow 2x+3y \geq 12$$

Hence, minimum value of $$2x+3y$$ will be $$12$$.

If $$S_{1}, S_{2}$$ and $$S_{3}$$ are the sum of first $$n, 2n$$ and $$3n$$ terms of a geometric series respectively, then prove that $$S_{1}(S_{3} - S_{2}) = (S_{2} - S_{1})^{2}$$

Let $$a$$ be the first term of G.P. and $$r$$ be the common ratio.

$${S}_{1}=a\left (\dfrac {{r}^{n}-1}{r-1}\right)$$

$${S}_{2}=a\left (\dfrac {{r}^{2n}-1}{r-1}\right)$$

$${S}_{3}=a\left (\dfrac {{r}^{3n}-1}{r-1}\right)$$

$${ S }_{ 1 }^{ }\left( { S }_{ 3 }^{ }-{ S }_{ 2 }^{ } \right) ={ a }^{ 2 }\frac { \left( { r }^{ 4n }-2{ r }^{ 3n }+{r}^{2n} \right) }{ { \left( r-1 \right) }^{ 2 } } $$

$${ \left( { S }_{ 2 }^{ }-{ S }_{ 1 }^{ } \right) }^{ 2 }={ a }^{ 2 }\dfrac { { \left( { r }^{ 2n }-{ r }^{ n } \right) }^{ 2 } }{ { \left( r-1 \right) }^{ 2 } } ={a}^{2}\frac {\left({r}^{4n}-2{r}^{3n}+{r}^{2n}\right) }{{\left(r-1 \right) }^{2}}$$

Thus $$\text{L.H.S.}=\text{R.H.S.}$$

Hence, proved.

Shew that the highest power of $$n$$ which is contained in $$ {n^{r} - 1}$$ is equal to $$\dfrac {n^{r} - nr + r - 1}{n - 1}$$.

The highest power required is equal to the sum of the integral parts of

$$\cfrac { { n }^{ r }-1 }{ n } ,\cfrac { { n }^{ r }-1 }{ { n }^{ 2 } } ,.....,\cfrac { { n }^{ r }-1 }{ { n }^{ r-1 } } $$

$$=\left( { n }^{ r-1 }-1 \right) +\left( { n }^{ r-2 }-1 \right) +.....+\left( n-1 \right) $$

$$=\cfrac { { n }^{ r }-n }{ n-1 } -\left( r-1 \right) =\cfrac { { n }^{ r }-nr+r-1 }{ n-1 } $$

Sum of two numbers is $$6$$ times their geometric mean, show that numbers are in the ratio $$\left( 3+2\sqrt { 2 } \right) :\left( 3-2\sqrt { 2 } \right) $$.

Let the numbers be $$a$$ and $$b$$.

Geometric mean of two numbers $$a$$ and $$b$$ is $$\sqrt{ab}$$.

According to the question,

$$a+b=6\sqrt{ab}$$

$$\dfrac{a+b}{2\sqrt{ab}}=\dfrac{3}{1}$$

Apply componendo and dividendo.

$$\dfrac{a+b+2\sqrt{ab}}{a+b-2\sqrt{ab}}=\dfrac{3+1}{3-1}$$

$$\dfrac{(\sqrt{a})^2+(\sqrt{b})^2+2(\sqrt{a}\times \sqrt{b})}{(\sqrt{a})^2+(\sqrt{b})^2-2(\sqrt{a}\times \sqrt{b})}=\dfrac{4}{2}$$

$$\left ( \dfrac{\sqrt{a}+\sqrt{b}}{\sqrt{a}-\sqrt{b}} \right )^2=\dfrac{2}{1}$$

$$\dfrac{\sqrt{a}+\sqrt{b}}{\sqrt{a}-\sqrt{b}}=\dfrac{\sqrt{2}}{1}$$

Apply componendo and dividendo again.

$$\dfrac{(\sqrt{a}+\sqrt{b})+(\sqrt{a}-\sqrt{b})}{(\sqrt{a}-\sqrt{b})-(\sqrt{a}-\sqrt{b})}=\dfrac{\sqrt{2}+1}{\sqrt{2}-1}$$

$$\dfrac{\sqrt{a}+\sqrt{a}+\sqrt{b}-\sqrt{b}}{\sqrt{a}-\sqrt{a}+\sqrt{b}+\sqrt{b}}=\dfrac{\sqrt{2}+1}{\sqrt{2}-1}$$

$$\dfrac{2\sqrt{a}}{2\sqrt{b}}=\dfrac{\sqrt{2}+1}{\sqrt{2}-1}=\dfrac{\sqrt{2}+1}{\sqrt{2}-1}$$

$$\sqrt{\dfrac{a}{b}}=\dfrac{\sqrt{2}+1}{\sqrt{2}-1}$$

Square both the sides.

$$\left(\sqrt{\dfrac{a}{b}}\right)^2=\left(\dfrac{\sqrt{2}+1}{\sqrt{2}-1}\right)^2$$

$$\dfrac{a}{b}=\left(\dfrac{\sqrt{2}+1}{\sqrt{2}-1}\right)$$

$$\dfrac{a}{b}=\dfrac{3+2\sqrt{2}}{3-2\sqrt{2}}$$

Thus, $$a$$ and $$b$$ are in the ratio of $$3+2\sqrt{2}:3-2\sqrt{2}$$.

The sum of the three number is $$68$$. If the ratio of the first to second is $$3 : 2$$ and that of the second to the third is $$5 : 3$$, then the second number is

Sum of three numbers$$=68$$

Let $$x,y,z$$ be the three numbers.

Given$$:x+y+z=68$$

$$x:y=3:2\Rightarrow \dfrac{x}{y}=\dfrac{3}{2}$$

$$y:z=5:3\Rightarrow \dfrac{y}{z}=\dfrac{5}{3}$$

$$\Rightarrow 2x=3y\Rightarrow y=\dfrac{2x}{3}$$ and $$3y=5z\Rightarrow z=\dfrac{3y}{5}=\dfrac{3\times \dfrac{2x}{3}}{5}=\dfrac{2x}{5}$$

From above $$ x+y+z=68$$

$$\Rightarrow x+\dfrac{2x}{3}+\dfrac{2x}{5}=68$$

$$\Rightarrow \dfrac{15x}{15}+\dfrac{10x}{15}+\dfrac{6x}{15}=68$$

$$\Rightarrow \dfrac{15x+10x+6x}{15}=68$$

$$\Rightarrow 31x=68\times 15$$

$$\therefore x=\dfrac{68\times 15}{31}=\dfrac{1020}{31}$$

$$\therefore$$ the second number $$y=\dfrac{2x}{3}=\dfrac{2\times\dfrac{1020}{31}}{3}=\dfrac{680}{31}$$

Which is smaller? $$2$$ or $$\log _{ \pi }{ 2 } +\log _{ 2}{ \pi }$$

We know, $$AM \ge GM$$

$$\cfrac{\log_{\pi}{2}+\log_{2}{\pi}}{2} \ge \sqrt{\log_{\pi}{{2}}\times \log_{2}{\pi}}$$

$$(\log_{\pi}{2})+\log_{2}{\pi}\ge 2$$

hence, $$2$$ is less than $$\log_{\pi^2}+\log_{2}{\pi}$$

Find out if the given list of numbers $$3,8,15,24,...$$ is a sequence or not. If so, then find the $$5^{th}$$ term of the sequence.

Lets take the different between every term and the term succeeding it.

i.e. $$3-0=3,\\ 8-3=5,\\ 15-8=7,\\ 24-15=9$$

These difference from a sequence in$$A.P.$$ with $$a=3,d=2$$

$$\therefore $$ The sequence of $$3,5,7,9,11\dots$$

So, the next term is $$x-24=11,\\ x=35$$

$$six$$ term or the next term is, $$y-35=13,\\ y=48$$

The next term of the sequence $$ 1,5,25,125,.. $$ will be equal to:

$$1,5,25,125,....$$

it is an GP with multiplication factor $$5$$ therefore the next term is $$125\times5=625$$

If $$\sin { \theta } $$ is G.M of $$\sin { \phi } $$ and $$\cos { \phi } $$, then prove that $$\cos { 2\theta } =2\cos ^{ 2 }{ \left( \cfrac { \pi }{ 4 } +\phi \right) } $$

$$\sin ^{ 2 }{ \theta } =\sin { \phi } \cos { \phi } \quad \quad $$
$$2\sin ^{ 2 }{ \theta } =\sin { 2\phi } $$
$$1-\cos { 2\theta } =-\cos { \left( \pi /2+2\phi \right) } $$
$$\therefore \cos { 2\theta } =1+\cos { \left( \pi /2+2\phi \right) } $$
$$\cos { 2\theta } =2\cos ^{ 2 }{ \left( \cfrac { \pi }{ 4 } +\phi \right) } $$

In an A.P. If $$m (a_m) = n (a_n)$$. Find $$(a_{m+n} ) ^{th}$$ term

$$n$$th term of an AP is $$a+(n-1)d$$

where $$a$$ is the first term and $$d$$ is the common difference

$$a_{m}=a+(m-1)d$$

$$a_{n}=a+(n-1)d$$

It is given that

$$m(a_{m})=n(a_{n})$$

$$m\left \{a+(m-1)d \right \}=n\left \{ a+(n-1)d \right \}$$

$$ma+m(m-1)d=na+n(n-1)d$$

$$ma-na=d(n^{2}-n-m^{2}+m)$$

$$a(m-n)=d(n-m)(m+n-1)$$

$$a=-d(m+n-1)$$

Now $$(m+n)$$th term is

$$a_{m+n}=a+(m+n-1)d$$

$$=-d(m+n-1)+(m+n-1)d$$

$$=0$$

If G is the geometric mean of x and y, then
$$t\frac{1}{{{G^2} - {x^2}}} + \frac{1}{{{G^2} - {y^2}}} = \frac{1}{{{G^2}}}$$

$${ G }^{ 2 }=xy$$

$$\therefore $$LHS=

$$\cfrac { 1 }{ { G }^{ 2 }-{ x }^{ 2 } } +\cfrac { 1 }{ { G }^{ 2 }-{ y }^{ 2 } } $$

$$=\cfrac { 1 }{ xy-{ x }^{ 2 } } +\cfrac { 1 }{ xy-{ y }^{ 2 } } $$

$$=\cfrac { 1 }{ x(y-x) } -\cfrac { 1 }{ y(y-x) } $$

$$=\cfrac { 1 }{ y-x } \left[ \cfrac { 1 }{ x } -\cfrac { 1 }{ y } \right] $$

$$=\cfrac { 1 }{ y-x } \left[ \cfrac { y-x }{ xy } \right] $$

$$=\cfrac { 1 }{ xy } $$

$$=\cfrac { 1 }{ G^2 } =$$RHS

Hence, proved

Find the value of $$n$$ so that $$\dfrac{a^{n+1}+b^{n+1}}{a^{n}+b^{n}}$$ may be the geometric mean between $$a$$ and $$b$$.

Given, $$\dfrac{a^{n+1}+b^{n+1}}{a^{n}+b^{n}}$$ may be that Geometric mean between $$a$$ & $$b$$

$$GM=\sqrt{ab}$$

$$\sqrt{ab}=\dfrac{a^{n+1}+b^{n+1}}{a^{n}+b^{n}}$$

$$(ab)^{\frac{1}{2}}[a^{n}+b^{n}]=a^{n+1}+b^{n+1}$$

$$a^{(\tfrac{1}{2}+n)} \, b^{\tfrac{1}{2}}+a^{\tfrac{1}{2}}\,b^{(\tfrac{1}{2}+n)}=a^{n+1}+b^{n+1}$$

$$a^{(\tfrac{1}{2}+n)}\left[b^{\tfrac{1}{2}}-a^{\tfrac{1}{2}}\right]=b^{(n+\tfrac{1}{2})}\left[b^{\tfrac{1}{2}}-a^{\tfrac{1}{2}}\right]$$

$$a^{(\tfrac{1}{2}+n)}=\dfrac{b^{(n+\tfrac{1}{2})}\left[b^{\tfrac{1}{2}}-a^{\tfrac{1}{2}}\right]}{b^{\tfrac{1}{2}}-a^{\tfrac{1}{2}}}$$

$$a^{(\tfrac{1}{2}+n)}=b^{(n+\tfrac{1}{2})}\Rightarrow \left(\frac{a}{b}\right)^{(\tfrac{1}{2}+n)}=1$$

$$\implies\dfrac{1}{2}+n=0$$

$$\implies n=\dfrac{-1}{2}$$

1-0,1-0,...1-0

Given that,

$$ \Rightarrow 1-0,1-0,........n\,times. $$

$$ \Rightarrow 1,1,1.............n\,times. $$

$$ \Rightarrow 1\times n $$

$$ \Rightarrow n $$

Hence this is the answer.

If the distinct points on the curve $$y = 2{x^4} + 7{x^3} + 3x - 5$$ are collinear, then find the arithmatic mean of x-coordinates of the aforesaid points

Given ; Four distinct points on the curve.

$$ y = 2x^{4}+7x^{3}+3x-5$$ are collinear

Let all points are on y = mx + c (That is general from of linear equation

so,

$$ mx+c = 2x^{4}+7x^{3}+3x-5$$

$$ 2x^{4}+7x^{3}+3x-5-mx-c = 0$$

$$ 2x^{4}+7x^{3}+3x-mx-5-c = 0$$

$$ 2x^{4}+7x^{3}+(3-m)x-(5+c) = 0$$

Let that equation have four roots p,q,r & s

And we know sum of roots in bi-quadratic equation

$$ = \frac{-coff. of\, x^{2}}{coff. of \,x^{4}}$$

Then,

$$ p+q+r+s = \frac{7}{2}$$

And

Arithmetic mean $$ = \frac{-7/2}{4} = \frac{-7}{8}.$$

1118665_1200740_ans_c41c0a4fba9e4775bb3b3caf20849466.jpg

Find number of digits $$1025^{th}$$ terms of the sequence $$1,2,2,4,4,4,4,8,8,8,8,8,8,8,8,........$$ ?

The given sequence is $$1,2,2,4,4,4,4,8,8,8,8,8,8,8,8,....$$

The sequence is composed by powers of $$2$$ and repeated $${ 2 }^{ n }$$ times.

We have,

$${ 2 }^{ 0 }=1$$ and $$1$$ appears one time.

$${ 2 }^{ 1 }=2$$ and $$2$$ appears twice.

$${ 2 }^{ 2 }=4$$ and $$4$$ appears four times.

$${ 2 }^{ 3 }=8$$ and $$8$$ appears eight times.

So, the next number will be the next power of $$2$$ and it will appear $${ 2 }^{ n }$$ times.

also, the first $$1$$ is in first position, the first $$2$$ is in second position, the first $$4$$ is in fourth position and so on.

So,

there is one $$1$$, starting from position $$1$$

there are two $$2$$s, starting from position $$2$$

there are four $$4$$s, starting from position $$4$$

there are eight $$8$$s, starting from position $$8$$

$$....$$

there are one thousand and twenty four $$1024$$s, starting from position $$1024$$

So, the $${ 1025 }^{ th }$$ number is $$1024.$$

In ALFA + BETA + GAMA = DELTA, each letter stands for a unique number. Find the value of each letter.

If ALPHA +BETA+GAMA=DELTA, then the possible values of each letter would be $$(A=5,L=7,F=6,B=8,T=2,G=0,M=3,D=1,E=4)$$

and

$$(A=5,L=7,F=6,B=0,T=2,G=8,M=3,D=1,E=4)$$

There are two sections $$A$$ and $$B$$ of a class consisting of $$36$$ and $$44$$ students respectively. If the average weight of section $$A$$ is $$40$$ kg and that of section $$B$$ is $$35$$ kg, find the average weight of the whole class?

Total weight of $$80\left(36+44\right)$$ students

$$=36\times 40+44\times 35$$kg

$$=1440+1540 = 2980$$ kg.

$$\therefore$$ weight of the total class$$=\dfrac{2980}{80}$$kg $$= 37.25$$ kg

Find the next term of $$AP \sqrt{2},\sqrt{8},\sqrt{18}$$

next term of $$AP$$

$$\sqrt{2},\sqrt{8},\sqrt{18}...$$

$$d=\sqrt{2}$$

$$d=\sqrt{8}-\sqrt{2}$$

$$t_n=a+(n-1)d$$

$$t_4=a+3d=\sqrt{2}+3(\sqrt{8}-\sqrt{2})$$

$$=\sqrt{2}+3\sqrt{8}-3\sqrt{2}$$

$$=3\sqrt{8}-2\sqrt{2}$$

$$=3\sqrt{4\times 2}-2\sqrt{2}$$

$$=6\sqrt{2}-2\sqrt{2}$$

$$\boxed{t_4=4\sqrt{2}}$$

Find two numbers whose arithmetic mean is 34 and the geometric mean is 16.

Let the two numbers be $$a$$ and $$b$$ such that $$a>b$$

Then,

$$\dfrac{a+b}{2}=34$$ and $$\sqrt{ab}=16$$

$$a+b=68$$.......(1) and $$ab=256$$

$$\therefore (a-b)^2=(a+b)^2-4ab$$

$$(a-b)^2=(68)^2-4\times 256=3600$$

$$a-b=60$$.......(2)

solving eqn (1) & (2), we get,

$$a=64$$ and $$b=4$$

Hence, required numbers are $$64$$ and $$4$$.

Solve - $$234:579 ::125:?$$

$$234:579$$ $$:$$ $$:$$ $$125:x$$

$$\Rightarrow \dfrac { 234 }{ 579 } =\dfrac { 125 }{ x } $$

$$\Rightarrow x=\dfrac { 125\times 579 }{ 234 } =\dfrac { 125\times 193 }{ 78 } =309.29$$

Solve the equation for $$x$$:
$$1+4+7+10+.....+x=287$$

Given that,

$$1 + 4 + 7 + 10 + .... + x = 287$$

$${a_n} = a + \left( {n - 1} \right)d$$

$$x = 1 + \left( {n - 1} \right)\left( 3 \right) = 3n - 2$$

Also, $${S_n} = \dfrac{n}{2}\left( {a + l} \right)$$

$$287 = \dfrac{n}{2}\left( {1 + x} \right)$$

$$287 = \dfrac{n}{2}\left( {1 + 3n - 2} \right)$$

$$574 = n\left( {3n - 1} \right)$$

$$ = 3{n^2} - n - 574 = 0$$

$$ = \left( {3n + 41} \right)\left( {n - 14} \right) = 0$$

$$n = \dfrac{{ - 41}}{3},14$$

We have $$n=14$$

Therefore, $$x=3n-2=3(14)-2=40$$

If $$\dfrac { 1 }{ x+y } ,\dfrac { 1 }{ 2y } ,\dfrac { 1 }{ y+z } $$ are the three consecutive terms of an A.P. prove that x, y, z are the consecutive terms of a G.P.

We have,

$$\dfrac{1}{x+y},\dfrac{1}{2y},\dfrac{1}{y+z}$$ are the A.P.

We know that,

In terms of an A.P.

$$ {{T}_{2}}-{{T}_{1}}={{T}_{3}}-{{T}_{2}} $$

$$ \Rightarrow \dfrac{1}{2y}-\dfrac{1}{x+y}=\dfrac{1}{y+z}-\dfrac{1}{2y} $$

$$ \Rightarrow \dfrac{x+y-2y}{2y\left( x+y \right)}=\dfrac{2y-y-z}{2y\left( y+z \right)} $$

$$ \Rightarrow \dfrac{x-y}{2y\left( x+y \right)}=\dfrac{y-z}{2y\left( y+z \right)} $$

$$ \Rightarrow \dfrac{\left( x-y \right)}{\left( x+y \right)}=\dfrac{\left( y-z \right)}{\left( y+z \right)} $$

$$ \Rightarrow \left( x-y \right)\left( y+z \right)=\left( x+y \right)\left( y-z \right) $$

$$ \Rightarrow xy-{{y}^{2}}+xz-yz=xy+{{y}^{2}}-xz-yz $$

$$ \Rightarrow xz-yz+xz+yz=2{{y}^{2}} $$

$$ \Rightarrow 2xz=2{{y}^{2}} $$

$$ \Rightarrow {{y}^{2}}=xz $$

Hence, $$x,y,z$$ in G.P.

The monthly salaries in rupees of $$30$$ workers in a factory are given below:
$$5000,\ 7000,\ 3000,\ 4000,\ 4000,\ 3000,\ 3000,\ 3000,\ 8000,\ 4000,\\ 4000,\ 9000,\ 3000,\ 5000,\ 4000,\ 4000,\ 3000,\ 5000,\ 5000,\ 6000,\\ 8000,\ 3000,\ 3000,\ 6000,\ 7000,\ 7000,\ 6000,\ 6000,\ 4000,\ 8000$$.
Find the mean of monthly salary.

Total number of workers $$= 30$$

Sum of slaries of all the workers $$= \left( 8 \times 3000 \right) + \left( 7 \times 4000 \right) + \left( 4 \times 5000 \right) + \left( 4 \times 6000 \right) + \left( 3 \times 7000 \right) + \left( 3 \times 8000 \right) + 9000 \\ = 24000 + 28000 + 20000 + 24000 + 21000 + 24000 + 9000 = 15000$$

Mean of monthly salary $$= \cfrac{150000}{30} = 5000$$

Hence the mean of monthly salary is $$Rs. 5000$$.

Find the sum of the products of the corresponding terms of the sequence $$16,32$$ and $$128,32,8,2,\dfrac {1}{2}$$

Corresponding terms are $$64$$ and $$\cfrac { 1 }{ 8 } $$

Sum$$=64+\cfrac { 1 }{ 8 } =\cfrac { 5/3 }{ 8 } $$

Product$$=64\times \cfrac { 1 }{ 8 } =8$$

Introducing a woman, a man said, "Her husband is only son of my mother".How is the woman related to that man ?

Only son of man's mother means the man himself. Therefore, the man is the husband of that woman. Hence, the woman is the wife of that man.

Which term of the sequence $$24,\,23\dfrac{1}{4},\,22\dfrac{1}{2},\,21\dfrac{3}{4},...$$ is the first negative term?

$$24,\,23\dfrac{1}{4},\,22\dfrac{1}{2},\,21\dfrac{3}{4},...$$

or $$\dfrac{96}{4},\,\dfrac{93}{4},\,\dfrac{90}{4},\,\dfrac{87}{4},...$$

or $$96,\,93,\,90,\,87,...$$ are in A.P

$$a=96$$, $$d=93-96=-3$$

According to question,

$$96+\left(n-1\right)\left(-3\right)<0$$

$$\Rightarrow 99-3n<0$$

$$\Rightarrow 3n>99$$

$$\Rightarrow n>33$$

The first integer$$>33$$ is $$34$$

$$\therefore \,\,{t}_{34}$$ is the first negative term.

Find the mean of the following.
All the factors of $$48$$.

Factors of $$48$$ are $$1,2,3,4,6,8,12,16,24,48=10$$factors

Mean $$=\dfrac{1+2+3+4+6+8+12+16+24+48}{10}=\dfrac{124}{10}=\dfrac{62}{5}=12.4$$

If the mean of $$x,x+2,x+4,x+8$$ is $$20$$ find $$x$$.

Mean$$=\dfrac{x+x+2+x+4+x+8}{4}=20$$

$$\Rightarrow \dfrac{4x+14}{4}=20$$

$$\Rightarrow 4x+14=80$$

$$\Rightarrow 4x=80-14=66$$

$$\Rightarrow x=\dfrac{66}{4}=\dfrac{33}{2}=16.5$$

$$\therefore x=16.5$$

If the sides of a triangle are in Geometric Progression and the largest angle is twice the smallest angle then find the relation for $$r$$.

Let the sides of $$\Delta$$ be

$$a,\,b=ar,\,c=a{r}^{2}$$ where $$r>1$$

Here $$C=2A$$

So, $$B=\pi-A-C-\pi-3A$$

$$\Rightarrow\,\dfrac{a}{\sin{A}}=\dfrac{b}{\sin{B}}=\dfrac{c}{\sin{C}}$$

$$\Rightarrow \,\dfrac{1}{\sin{A}}=\dfrac{r}{\sin{B}}=\dfrac{{r}^{2}}{\sin{C}}$$

$$\Rightarrow \,\dfrac{1}{\sin{A}}=\dfrac{r}{\sin{3A}}=\dfrac{{r}^{2}}{\sin{2A}}$$

$$\Rightarrow \,{r}^{2}=\dfrac{\sin{2A}}{\sin{A}}=\dfrac{2\sin{A}\cos{A}}{\sin{A}}=2\cos{A}$$

and $$r=\dfrac{\sin{3A}}{\sin{A}}=\dfrac{3\sin{A}-4{\sin}^{3}{A}}{\sin{A}}=3-4{\sin}^{2}{A}$$

$$\Rightarrow\,r=3-4\left(1-{\cos}^{2}{A}\right)=4{\cos}^{2}{A}-1$$

$$\therefore\,{r}^{4}-r-1=0$$ is the required relation.

Place first nine multiples of $$6$$ in the blanks in such a manner that each row adds up to $$150$$.

1379664_1526261_ans_f689ba7f701b4ca28994497b015a1e86.png

There are $$10$$ compartments in passenger train carries on average $$15$$ passengers per compartment. If atleast $$15$$ passengers were sitting in each compartment, no any compartment has equal no of passengers , and any compartment does not exceed the number of average passengers except $${10}^{th}$$ compartment.Find how many passengers can be accommodated in $${10}^{th}$$ compartment ?

No of passengers $$= 15\times 10 = 150$$

$$15+14+13+12+11+10+9+8+7 = 99$$

$$150 -99 = 51$$

Check whether the following sequence is A.P. If it is A.P., Find the common difference.
$$0.3, 0.33, 0.333...$$

The given sequence is not an A.P. As difference between consecutive terms is not same.

Write the first five terms of the following sequence.
$$a_1=a_2=2, a_n=a_{n-1}-1, n > 2$$.

$$a_1=a_2=2\\$$

$$a_n=a_{n-1}-1$$ for $$n>2$$

So, For $$n=3$$

$$a_3=a_{3-1}-1\\$$

$$a_3=a_{2}-1\\$$

$$a_3=2-1\\$$

$$a_3=1$$

Similarly , For $$n=4$$

$$a_4=a_{4-1}-1\\$$

$$a_4=a_{3}-1\\$$

$$a_4=1-1\\$$

$$a_4=0$$

And , For $$n=5$$

$$a_5=a_{5-1}-1\\$$

$$a_5=a_{4}-1\\$$

$$a_5=0-1\\$$

$$a_5=-1$$

$$\therefore$$ $$1^{st}$$ five terms of this sequence are $$2,2,1,0,-1$$

The sum of (x+5) observations is $$(x^{4}-625)$$. Find the mean of the observations.

1869821_1582165_ans_df2f0c89c30c4f24b10e359d93aeeba1.jpg

Find the first four terms of the sequence defined by $$a_1=3$$ and $$a_n=3a_{n-1}+2$$, for all $$n > 1$$.

1407127_1666699_ans_8396cb3a4d49445c8f8c058995d18389.jpg

Write the first five terms of the following.
$$a_1=1=a_2, a_n=a_{n-1}+a_{n-2}, n > 2$$.

1407146_1666708_ans_2154991c2be4479d832c680bc1b167dc.jpg

Write the first five terms of the following sequence.
$$a_1=1, a_n=a_{n-1}+2, n > 1$$.

1407134_1666704_ans_c7e7e33620c545e094b88031b8d6d83f.jpg

Which term of the sequence $$12+8i, 11+6i, 10+4i,...$$ is purely real?

We have $$12 + 8i, 11 + 6i, \, 10 + 4i,.....$$

Let, $$n^{th}$$ term is purely real.

$$\because T_n = a + (n-1)d$$

and $$a = 12 + 8i$$

$$d = 11 + 6i - (12+8i)$$

$$= 11 + 6i - 12 -8i$$

$$= -1 -2i$$

so, $$T_n = 12 + 8i + (n-1) (-1-2i)$$

$$= 12 + 3i - n+1 - 2ni+2i$$

$$T_n = 13-n+(-2n+10)i$$

If $$T_n$$ is purely real, then $$-2n+10$$ is must be zero,

So, $$-2n + 10 = 0$$

$$n = \dfrac{10}{2} = 5$$

$$n = 5$$

Find the geometric mean of the following pairs of numbers :
$$ 2 $$ and $$ 8 .$$

$$x=8$$

$$y=2$$

$$GM=\sqrt {G_1G_2}$$

$$GM=\sqrt {(8)(2)}$$

$$\implies \sqrt {16}$$

$$=\pm 4$$

$$\because$$ Geometric mean lies between 2 and 8,

$$\therefore G.M. = 4$$

Find AM of $$5$$ and $$23$$.

Let $$a=5$$ and $$b=23$$

AM$$=\dfrac{a+b}2$$

=$$\dfrac{5+23}2=\dfrac {28}2=14$$

Which term of the sequence $$12+8i, 11+6i, 10+4i,....$$ is purely imaginary?

We have, $$12+8i, \ 11 + 6i, \ 10 + 4i$$

Let $$n^{th}$$ term is purely imaginary,

$$\because T_n = a + (n-1) d$$

and $$a = 12 + 8i$$

$$d = 11 + 6i - (12 + 8i)$$

$$= -1-2i$$

So, $$T_n = 12 + 8i + (n -1)(-1+2i)$$

$$T_n = 12+8i-n+1-2ni+2i$$

$$T_n = 13 - n +(-2n + 10)i$$

if $$T_n$$ is purely imaginary then $$13-n$$ must be zero

So, $$13-n = 0$$

$$n = 13$$

Find AM of $$2$$ and $$16$$.

$${\textbf{Step -1:}}{\textbf{ Definition of Arithmetic mean}}{\textbf{.}}$$

$${\text{It is the mean or average of the set of numbers which is computered by}}$$

$${\text{adding all the terms in the set of numbers and dividing the sum}}$$

$${\text{by total number of terms}}.$$

$${\textbf{Step -2: Write the formula and solve}}{\textbf{.}}$$

$${\text{Let }}a = 2,b = 16$$

$$a.m = \dfrac{{a + b}}{2}$$

$$ = \dfrac{{2 + 16}}{2}$$

$$ = 9$$

$${\textbf{Hence, the arithmetic mean of 2 and 16 is 9}}.$$

Find the two numbers whose A.M. is 25 and GM is 20.

1410677_1667173_ans_142f499cf16f4bcb8c6bb0396378f3d5.jpg

Find two positive numbers a and b, whose $$AM=10$$ and $$GM=8$$.

1902453_1710807_ans_a98defa6736e4eaa93ea64ec432dc0bf.jpg

Find the GM between the numbers $$5$$ and $$125$$.

The geometric mean of two numbers is the square root of their product.

GM $$= \sqrt{ab}$$

GM $$= \sqrt{( 125 \times 5 )} = \sqrt {625} = 25$$

Answer:

The geometric mean of $$125$$ and $$5$$ is $$25.$$

Find the GM between the numbers $$1$$ and $$\dfrac{9}{16}$$.

The geometric mean of two numbers is the square root of their product.

GM $$= \sqrt{ab}$$

GM $$= \sqrt{ 1 \times \dfrac{9}{16} } =\dfrac{3}{4} $$

Answer:

The geometric mean of $$1$$ and $$\dfrac{9}{16}$$ is $$\dfrac{3}{4}$$.

If a, b, c are in AP; x is the GM between a and b; y is the GM between b and c; then show that $$b^2$$ is the AM between $$x^2$$ and $$y^2$$.

Given $$a, b, c$$ are in AP.

$$\therefore (a+c)=2b, $$

Also, $$x$$ is the GM between $$a$$ and $$b; y$$ is the GM between $$b$$ and $$c$$;

$$x=\sqrt{ab}$$ and $$y=\sqrt{bc}$$

$$\Rightarrow x^2+y^2=(ab+bc)=b(a+c)=2b^2$$.

$$\implies b^2$$ is the AM between $$x^2$$ and $$y^2$$.

Find the GM between the numbers $$-8$$ and $$-2$$.

The geometric mean of two numbers is the square root of their product.

GM $$= \sqrt{ab}$$

GM $$= \sqrt{( -8 \times -2 )} = \sqrt {16} = \pm 4$$

Mean is a number which has to fall between two numbers.

Therefore we will take $$-4$$ as our answer as $$+4$$ doesn’t lie between $$-8$$ and $$-2$$

Answer:

The geometric mean of $$-8$$ and $$-2$$ is $$-4$$.

The AM between two positive numbers a and $$b(a > b)$$ is twice their GM. Prove that $$a:b=(2+\sqrt{3}):(2-\sqrt{3})$$.

Given, $$AM=2(GM)$$

$$\Rightarrow \dfrac{1}{2}(a+b)=2\sqrt{ab}\Rightarrow \dfrac{a+b}{2\sqrt{ab}}=\dfrac{2}{1}$$

$$\Rightarrow \dfrac{a+b+2\sqrt{ab}}{a+b-2\sqrt{ab}}=\dfrac{2+1}{2-1}$$

$$\Rightarrow \dfrac{(\sqrt{a}+\sqrt{b})^2}{(\sqrt{a}-\sqrt{b})^2}=\dfrac{(\sqrt{3})^2}{(1)^2}$$

$$\Rightarrow \dfrac{\sqrt{a}+\sqrt{b}}{\sqrt{a}-\sqrt{b}}=\dfrac{\sqrt{3}}{1}$$

$$\Rightarrow \dfrac{(\sqrt{a}+\sqrt{b})+(\sqrt{a}-\sqrt{b})}{(\sqrt{a}+\sqrt{b})-(\sqrt{a}-\sqrt{b})}=\dfrac{\sqrt{3}+1}{\sqrt{3}-1}$$

$$\Rightarrow \dfrac{\sqrt{a}}{\sqrt{b}}=\dfrac{\sqrt{3}+1}{\sqrt{3}-1}$$

$$\Rightarrow \dfrac{a}{b}=\dfrac{(\sqrt{3}+1)^2}{(\sqrt{3}-1)^2}=\dfrac{2+\sqrt{3}}{2-\sqrt{3}}$$.

Find the GM between the numbers $$a^3b$$ and $$ab^3$$.

The geometric mean of two numbers is the square root of their product.

GM $$= \sqrt{ab}$$

GM $$= \sqrt{( a^3b \times ab^3 )} = \sqrt {a^4b^4} = a^2b^2$$

Answer:

The geometric mean of $$a^3b$$ and $$ab^3$$ is $$a^2b^2$$.

Find the GM between the numbers $$-6.3$$ and $$-2.8$$.

The geometric mean of two numbers is the square root of their product.

GM $$= \sqrt{ab}$$

GM $$= \sqrt{( -6.3 \times -2.8 )} = \sqrt {17.64} = \pm 4.2$$

Mean is a number which has to fall between two numbers.

Therefore we will take $$-4.2$$ as our answer as $$+4.2$$ doesn’t lie between $$-6.3$$ and $$-2.8$$.

Answer:

The geometric mean of $$-6.3$$ and $$-2.8$$ is $$-4.2$$.

Find the GM between the numbers $$0.15$$ and $$0.0015$$.

The geometric mean of two numbers is the square root of their product.

GM $$= \sqrt{ab}$$

GM $$= \sqrt{ 0.15 \times 0.0015 } =\dfrac{15}{1000} =0.015$$

Answer:

The geometric mean of $$0.15$$ and $$0.0015$$ is $$0.015$$.

Write the quadratic equation, the arithmetic and geometric means of whose roots are A and G respectively.

Let the roots of the quadratic equation be $$\alpha$$ and $$\beta$$.

Then, the equation is $$(x^2-(\alpha +\beta)x+\alpha\beta =0$$

$$\therefore A=\dfrac{\alpha +\beta}{2}$$

$$\Rightarrow \alpha +\beta =2A$$

$$g=\sqrt{\alpha\beta}$$

$$\Rightarrow \alpha\beta =G^2$$.

Hence, the required equation is $$x^2-2Ax+G^2=0$$.

Find general term of series
$$\log_e(1+3x+2x^2)=3x-\dfrac{5x^2}{2}+\dfrac{9x^3}{3}-\dfrac{17x^4}{4}+..$$

$$\log_e(1+3x+2x^2)=3x-\dfrac{5x^2}{2}+\dfrac{9x^3}{3}-\dfrac{17x^4}{4}+..$$

Now,

$$1+3x+2x^2=2x^2+2x+x+1$$

$$=2x(x+1)+1(x+1)$$

$$=(2x+1)(x+1)$$

$$\log_e(1+3x+2x^2)=\log_e[(1+2x)(1+x)]$$

$$=\log_e(1+2x)+\log_e(1+x)$$

Now,

$$\log_e(1+2x)=2x-\dfrac{(2x)^2}{2}+\dfrac{(2x)^3}{3}-\dfrac{(2x)^4}{4}+....$$ --- ( 1 )

$$\log_e(1+x)=x-\dfrac{(x)^2}{2}+\dfrac{(x)^3}{3}-\dfrac{(x)^4}{4}-....$$ ---( 2 )

Adding ( 1 ) from ( 2 ) we get,

$$\log_e(1+2x)+\log_e(1+x)=\left[2x-\dfrac{(2x)^2}{2}+\dfrac{(2x)^3}{3}-\dfrac{(2x)^4}{4}+....\right]+\left[x-\dfrac{(x)^2}{2}+\dfrac{(x)^3}{3}-\dfrac{(x)^4}{4}-....\right]$$

$$\log_e(1+2x)+\log_e(1+x)=3x-\left(\dfrac{4x^2+x^2}{2}\right)+\left(\dfrac{8x^3+x^3}{3}\right)-\left(\dfrac{16x^4+x^4}{4}\right)+...$$

$$\log_e(1+2x)+\log_e(1+x)=3x-\dfrac{5x^2}{2}+\dfrac{9x^3}{3}-\dfrac{17x^4}{4}+...$$

General term of series $$=(-1)^{n-1}\left(\dfrac{2x^n+x^n}{n}\right)$$

If $$a,b,c$$ are three distinct positive real numbers in G.P., then prove that $${ c }^{ 2 }+2ab>3ac$$

Since $$a,b,c$$ are three distinct positive real numbers, so applying $$A.M> G.M$$ in $${c}^{2},ab,ab$$ we get

$$\cfrac { { c }^{ 2 }+ab+ab }{ 3 } >{ \left( { c }^{ 2 }{ b }^{ 2 }{ a }^{ 2 } \right) }^{ 1/3 }$$

$$\Rightarrow \cfrac { { c }^{ 2 }+2ab }{ 3 } >{ \left( { c }^{ 2 }ac{ a }^{ 2 } \right) }^{ 1/3 }$$

$$\Rightarrow { c }^{ 2 }+2ab>3ac\quad \quad$$ ($$b$$ is the G.M of $$a$$ and $$c$$)

Find the general term of the series
$$\log_e(1+3x)=3x-\dfrac{(3x)^2}{2}+\dfrac{(3x)^3}{3}-\dfrac{(3x)^4}{4}+....$$

$$\log_e(1+3x)=3x-\dfrac{(3x)^2}{2}+\dfrac{(3x)^3}{3}-\dfrac{(3x)^4}{4}+....$$ --- ( 1 )

$$\log_e(1-2x)=-2x-\dfrac{(2x)^2}{2}-\dfrac{(2x)^3}{3}-\dfrac{(2x)^4}{4}-....$$ ---( 2 )

Subtracting ( 2 ) from ( 1 ) we get,

$$\log_e(1+3x)-\log_e(1-2x)=\left[3x-\dfrac{(3x)^2}{2}+\dfrac{(3x)^3}{3}-\dfrac{(3x)^4}{4}+....\right]-\left[-2x-\dfrac{(2x)^2}{2}-\dfrac{(2x)^3}{3}-\dfrac{(2x)^4}{4}-....\right]$$

$$\log_e(1+3x)-\log_e(1-2x)=5x-\left(\dfrac{9x^2-4x^2}{2}\right)+\left(\dfrac{27x^3+8x^3}{3}\right)-\left(\dfrac{81x^4-16x^4}{4}\right)+...$$

$$\log_e\left(\dfrac{1+3x}{1-2x}\right)=5x-\dfrac{5x^2}{2}+\dfrac{35x^3}{3}-\dfrac{65x^4}{4}+...$$ -

General term $$=(-1)^{n-1}\left[\left(\dfrac{(3x)^n+(2x)^n}{n}\right)+\left(\dfrac{(3x)^n-(2x)^n}{n}\right)\right]$$

In how many parts an integer $$N\ge 5$$ should be dissected so that the product of the parts is maximized.

Using $$.M\ge G.M\Rightarrow \cfrac { { x }_{ 1 }+{ x }_{ 2 }+,....+{ x }_{ n } }{ n } \quad \ge { \left( { x }_{ 1 }{ x }_{ 2 },....{ x }_{ n } \right) }^{ 1/n }\Rightarrow { x }_{ 1 }{ x }_{ 2 },..{ x }_{ n }\le { \left( \cfrac { { x }_{ 1 }+{ x }_{ 2 }+,....+{ x }_{ n } }{ n } \right) }^{ n }$$

therefore maximum value of $${ x }_{ 1 }{ x }_{ 2 },....{ x }_{ n }$$ is obtained when $${ x }_{ 1 }={ x }_{ 2 }=...={ x }_{ n }\quad $$ ie., the parts are all equal

Now $${ x }_{ 1 }+{ x }_{ 2 }+,....+{ x }_{ n }=N$$

Now function to be maximised is $${ \left( \cfrac { { x }_{ 1 }+{ x }_{ 2 }+,....+{ x }_{ n } }{ n } \right) }^{ n }$$ which is a discrete function of $$n$$.

In order to arrive at some possible neighborhood we make it continuous first.

Thus changing the variable $$n$$ to $$x$$ we get

$$f(x)={ \left( \cfrac { N }{ x } \right) }^{ x }$$

for maxima, $$f'(x)=0$$ ie

$$f'(x)=f(x)\left( \ln { { \left( \cfrac { N }{ x } \right) } } -1 \right) $$

$$f'(x)=0\quad for\quad x=N/e$$

Hence the nearest integer is $$[N/e]$$ or $$[N/e]+1$$ where $$[x]$$ denoes greatest integer less than or equal to $$x$$

Calculate the greatest and least values of the function
$$f(x)=\cfrac { { x }^{ 4 } }{ { x }^{ 8 }+2{ x }^{ 6 }-4{ x }^{ 4 }+8{ x }^{ 2 }+16 } $$

$$\cfrac { 1 }{ f(x) } =\left( { x }^{ 4 }+\cfrac { 16 }{ { x }^{ 4 } } \right) +2\left( { x }^{ 2 }+\cfrac { 4 }{ { x }^{ 2 } } \right) -4\quad $$

$$A.M\ge G.M\Rightarrow { x }^{ 4 }+\cfrac { 16 }{ { x }^{ 4 } } \ge 8;{ x }^{ 2 }+\cfrac { 4 }{ { x }^{ 2 } } \ge 4\Rightarrow \cfrac { 1 }{ f(x) } \ge 12\Rightarrow f(x)\le \cfrac { 1 }{ 12 } $$

Again using $$A.M\ge G.M$$

$$\cfrac { 2{ x }^{ 6 }+8{ x }^{ 2 } }{ 2 } \ge 4{ x }^{ 4 }\Rightarrow 2{ x }^{ 6 }+8{ x }^{ 2 }-4{ x }^{ 4 }\ge 4{ x }^{ 4 }\ge 0\Rightarrow { x }^{ 8 }+2{ x }^{ 6 }-4{ x }^{ 4 }-8{ x }^{ 2 }+16\quad $$

Also

$$\quad { x }^{ 4 }\ge 0\Rightarrow \cfrac { { x }^{ 4 } }{ { x }^{ 8 }+2{ x }^{ 6 }-4{ x }^{ 4 }-8{ x }^{ 2 }+16 } \ge 0\Rightarrow f(x)\ge 0$$

Hence the greatest value is $$1/12$$ and the least value is $$0$$

Prove that $${ _{ }^{ n }{ C } }_{ 1 }{ \left( { _{ }^{ n }{ C } }_{ 2 } \right) }^{ 2 }{ \left( { _{ }^{ n }{ C } }_{ 3 } \right) }^{ 3 }....{ \left( { _{ }^{ n }{ C } }_{ n } \right) }^{ n }\le { \left( \cfrac { { 2 }^{ n } }{ n+1 } \right) }^{ { _{ }^{ n+1 }{ C } }_{ 2 } },\forall n\in N\quad $$

Consider the series $$S={ _{ }^{ n }{ C } }_{ 1 }+2{ _{ }^{ n }{ C } }_{ 2 }+3{ _{ }^{ n }{ C } }_{ 3 }+....+{ _{ }^{ n }{ C } }_{ n }\quad $$

For the series the general term is $${ T }_{ r }=r{ _{ }^{ n }{ C } }_{ r }=n\quad { _{ }^{ n-1 }{ C } }_{ r-1 }$$

$$S=\sum _{ r=1 }^{ n }{ { T }_{ r } } =\sum _{ r=1 }^{ n }{ n\quad { _{ }^{ n-1 }{ C } }_{ r-1 } } =n\times { 2 }^{ n-1 }$$

Now $$\quad A.M\ge G.M\Rightarrow \cfrac { { _{ }^{ n }{ C } }_{ 1 }+2{ _{ }^{ n }{ C } }_{ 2 }+3{ _{ }^{ n }{ C } }_{ 3 }+....+{ _{ }^{ n }{ C } }_{ n } }{ \cfrac { n(n+1) }{ 2 } } \ge { \left[ { _{ }^{ n }{ C } }_{ 1 }{ \left( { _{ }^{ n }{ C } }_{ 2 } \right) }^{ 2 }{ \left( { _{ }^{ n }{ C } }_{ 3 } \right) }^{ 3 }....{ \left( { _{ }^{ n }{ C } }_{ n } \right) }^{ n } \right] }^{ \frac { 1 }{ \dfrac { n(n+1) }{ 2 } } }$$

$$\Rightarrow \cfrac { n\times { 2 }^{ n-1 } }{ \cfrac { n(n+1) }{ 2 } } \ge { \left[ { _{ }^{ n }{ C } }_{ 1 }{ \left( { _{ }^{ n }{ C } }_{ 2 } \right) }^{ 2 }{ \left( { _{ }^{ n }{ C } }_{ 3 } \right) }^{ 3 }....{ \left( { _{ }^{ n }{ C } }_{ n } \right) }^{ n } \right] }^{ \cfrac { 2 }{ n(n+1) } }$$

$$\Rightarrow { _{ }^{ n }{ C } }_{ 1 }{ \left( { _{ }^{ n }{ C } }_{ 2 } \right) }^{ 2 }{ \left( { _{ }^{ n }{ C } }_{ 3 } \right) }^{ 3 }....{ \left( { _{ }^{ n }{ C } }_{ n } \right) }^{ n }\le { \left( \cfrac { { 2 }^{ n } }{ n+1 } \right) }^{ { _{ }^{ n+1 }{ C } }_{ 2 } }$$

Show that $$(x + y + z)^3 > 27xyz.$$

1899471_1744458_ans_971237e2f95d4497838dd868987311a3.jpg

Show that $$b^2c^2 + c^2a^2 + a^2b^2 > abc (a + b + c).$$

1899482_1744455_ans_ebf9fc3fa6a144ad884f4a212bbac377.jpg

Show that minimum value of $$ \dfrac{(x+a)(x+b) }{(x+c)}, $$ where $$ a>c, $$ $$ b>c $$ is $$ (\sqrt{a-c}+\sqrt{b-c})^{2} $$ for real values of $$ x>-c $$.

Given expression is $$ \dfrac{(x+a)(x+b) }{(x+c)}, $$.

Let $$ x+c=y $$.

Then $$\dfrac{(x+a)(x+b)}{(x+c)}=\dfrac{(y+(a-c))(y+(b-c))}{y}$$

$$ =\dfrac{y^{2}+[(a-c)+(b-c)] y+(a-c)(b-c)}{y} $$

$$=y+\dfrac{(a-c)(b-c)}{y}+(a-c)(b-c)$$

$$\left[\sqrt{y}-\sqrt{\dfrac{(a-c)(b-c)}{y}}\right]^{2}[\sqrt{a+c}\sqrt{b-c}]^{2}\ge [\sqrt{a-c}+\sqrt{b-c}]^{2}$$

$$\text{Hence, the least value is }[\sqrt{a-c}+\sqrt{b-c}]^{2}$$

If $$x,y,z$$ are positive real numbers and $$x=\cfrac { 12-yz }{ y+z } $$. The maximum value of $$(xyz)$$ equals

$$x=\cfrac { 12-yz }{ y+z } $$

$$xy+xz+yz=12$$

Consider values $$xy.yz.zx$$

Now $$A.M\ge G.M$$

$$\Rightarrow \cfrac { xy+yz+zx }{ 3 } \ge { \left( { x }^{ 2 }{ y }^{ 2 }{ z }^{ 2 } \right) }^{ 1/3 }$$

$$\Rightarrow { 4 }^{ 3/2 }\ge xyz$$

$$\Rightarrow xyz\le 8$$

The maximum value of $$xyz$$ equals $$8$$.

If $$a,b,c$$ are positive real numbers. Then prove that $${ \left( a+1 \right) }^{ 7 }{ \left( b+1 \right) }^{ 7 }{ \left( c+1 \right) }^{ 7 }>{ \left( 7 \right) }^{ 7 }{ a }^{ 4 }{ b }^{ 4 }{ c }^{ 4 }$$

Given that $$a,b,c$$ are positive real numbers. To prove that $${ \left( a+1 \right) }^{ 7 }{ \left( b+1 \right) }^{ 7 }{ \left( c+1 \right) }^{ 7 }>{ \left( 7 \right) }^{ 7 }{ a }^{ 4 }{ b }^{ 4 }{ c }^{ 4 }$$

$$LHS={ \left( a+1 \right) }^{ 7 }{ \left( b+1 \right) }^{ 7 }{ \left( c+1 \right) }^{ 7 }={ \left[ (1+a)(1+b)(1+c) \right] }^{ 7 }={ \left[ 1+a+b+c+ab+bc+ca+abc \right] }^{ 7 }...(1)$$

Now $$A.M\ge G.M$$

$$\Rightarrow \cfrac { a+b+c+ab+bc+ca+abc }{ 7 } \ge { \left( { a }^{ 4 }{ b }^{ 4 }{ c }^{ 4 } \right) }^{ 1/7 }$$

$$\Rightarrow { \left( a+b+c+ab+bc+ca+abc \right) }^{ 7 }>{ \left( 7 \right) }^{ 7 }{ a }^{ 4 }{ b }^{ 4 }{ c }^{ 4 }...(2)$$

From Eqs (1) and (2) we get

$${ \left( a+1 \right) }^{ 7 }{ \left( b+1 \right) }^{ 7 }{ \left( c+1 \right) }^{ 7 }>{ \left( 7 \right) }^{ 7 }{ a }^{ 4 }{ b }^{ 4 }{ c }^{ 4 }\quad $$

If $$x,y\in { R }^{ + }$$ satisfying $$x+y=3$$, then the maximum value of $${x}^{2}y$$ is

We have $$\cfrac { 2\left( \cfrac { x }{ 2 } \right) +y }{ 3 } \ge { \left( { \left( \cfrac { x }{ 2 } \right) }^{ 2 }y \right) }^{ 1/3 }$$ ......... $$AM\ge GM$$

$$\Rightarrow { \left( \cfrac { 3 }{ 3 } \right) }^{ 3 }\ge \cfrac { { x }^{ 2 }y }{ 4 } $$

$$\Rightarrow { x }^{ 2 }y\le 4\quad $$

Therefore, maximum value of $${x}^{2}y$$ is $$4$$.

If $$a_n = \frac{3}{4} - \big(\frac{3}{4}\big)^2 + \big(\frac{3}{4}\big)^3 + ... + (-1)^{n - 1} \big(\frac{3}{4}\big)^n$$ and $$b_n = 1 - a_n $$, then find the least natural number $$n_0$$ such that $$b_n > a_n \forall n \geq n_0$$.

$$a_n = \frac{3}{4} - \Big( \frac{3}{4}\Big)^3 + \Big( \frac{3}{4}\Big)^3 + \dots + (-1)^{n-1} \Big( \frac{3}{4}\Big)^n$$
$$ = \frac{\frac{3}{4}\Big( 1 - \Big( \frac{3}{4}\Big)^n \Big)}{1 - \Big( \frac{3}{4}\Big)}$$
$$ = \frac{3}{7} \Big( 1 - \Big( -\frac{3}{4}\Big)^n \Big)$$
Now, $$b_n = 1- a_n $$ and $$b_n > a_n $$ for $$n \geq n_0$$.
$$\therefore$$ $$ 1- a_n > a_n \Rightarrow 2a_n < 1$$
$$\Rightarrow \frac{6}{7} \Bigg[ 1 - \Big( -\frac{3}{4}\Big)^n \Bigg] < 1$$
$$\Rightarrow - \Big( -\frac{3}{4}\Big)^n < \frac{1}{6}$$
$$\Rightarrow (-3)^{n+1} < 2^{2n-1}$$
For n to be even, inequality always holds. For n to be odd, it holds for $$n \geq 7$$. Therefore, the least natural number for which it holds is 6.

If $$a,b$$ and $$c$$ are positive and $$9a+3b+c=90$$ then the maximum value of $$\left( \log { a } +\log { b } +\log { c } \right) $$ is (Base of the logarithm is $$10$$)

Given, $$9a+3b+c=90\Rightarrow 3a+b+\cfrac { c }{ 3 } =30$$

Now consider numbers $$3a,b$$ and $$\cfrac{c}{3}$$

$${ \left( 3a\times b\times \cfrac { c }{ 3 } \right) }^{ \cfrac { 1 }{ 3 } }\le \cfrac { 3a+b+\cfrac { c }{ 3 } }{ 3 } \left( GM\le AM \right) $$

$$\Rightarrow { \left( abc \right) }^{ 1/3 }\le \cfrac { 30 }{ 3 } =10$$

$$\Rightarrow abc\le 1000$$

Taking log on both side

$$\Rightarrow \log { a } +\log { b } +\log { c } \le 3\quad $$

For any $$x,y\in R,xy>0$$ then the minimum value of $$\cfrac { 2x }{ { y }^{ 3 } } +\cfrac { { x }^{ 3 }y }{ 3 } +\cfrac { 4{ y }^{ 2 } }{ 9{ x }^{ 4 } } $$ is

As $$x,y\in R$$ and $$xy> 0$$ so $$x$$ and $$y$$ will be of same sign

Therefore all the quantities $$\cfrac { 2x }{ { y }^{ 3 } } ,\cfrac { { x }^{ 3 }y }{ 3 } ,\cfrac { 4{ y }^{ 2 } }{ 9{ x }^{ 4 } } $$ are positive

Now $$A.M\ge G.M\Rightarrow \cfrac { 2x }{ { y }^{ 3 } } +\cfrac { { x }^{ 3 }y }{ 3 } +\cfrac { 4{ y }^{ 2 } }{ 9{ x }^{ 4 } } \ge 3{ \left[ \left( \cfrac { 2x }{ { y }^{ 3 } } \right) \left( \cfrac { { x }^{ 3 }y }{ 3 } \right) \left( \cfrac { 4{ y }^{ 2 } }{ 9{ x }^{ 4 } } \right) \right] }^{ 1/3 }\ge 3\times \cfrac { 2 }{ 3 } \ge 2\quad \quad $$

Minimum value is $$2$$.

Prove that $$8(a^{3}+b^{3}+c^{3})^{2}>9(a^{2}+bc)(b^{2}+ca)(c^{2}+ab)$$

1578865_1747414_ans_39c5cf68331d490fa778d5cef9224bf6.jpg

The minimum value of the sum of real numbers $${ a }^{ -5 }+{ a }^{ -4 }+3{ a }^{ -3 },1,{a}^{8}$$ and $${a}^{10}$$ with $$a> 0$$ is

Using $$A.M\ge G.M$$

$$\Rightarrow \cfrac { { a }^{ -5 }+{ a }^{ -4 }+{ a }^{ -3 }+{ a }^{ -3 }+{ a }^{ -3 }+{ a }^{ 8 }+{ a }^{ 10 }+1 }{ 8 } \ge 1$$

$$\Rightarrow { a }^{ -5 }+{ a }^{ -4 }+{ a }^{ -3 }+{ a }^{ -3 }+{ a }^{ -3 }+{ a }^{ 8 }+{ a }^{ 10 }+1\ge 8$$

$$\Rightarrow { \left( { a }^{ -5 }+{ a }^{ -4 }+{ a }^{ -3 }+{ a }^{ -3 }+{ a }^{ -3 }+{ a }^{ 8 }+{ a }^{ 10 }+1 \right) }_{ min }=8$$

Find the geometric progression whose 4th term is 54 and 7th term is 1458.

From the question it is given that,

The geometric progression whose $$4^{\text {th }}$$ term $$a_{4}=54$$

The geometric progression whose $$7^{\text {th }}$$ term

$$a_{7}=1458$$ We know that, $$a_{n}=a r^{n-1}$$

$$\begin{array}{l}a_{4}=a r^{4}-1 \\a_{4}=a r^{3}=54 \\a_{7}=a r^{6}=1458\end{array}\\$$

By dividing both we get,

$$a r^{6} / a r^{3}=1458 / 54\\$$

$$\begin{array}{l}r^{6-3}=27 \\r^{3}=3^{3} \\r=3\end{array}\\$$

To find out a, consider $$a r^{3}=54$$

$$a(3)^{3}=54\\$$

$$\begin{array}{l}a=54 / 27 \\a=2\end{array}\\$$

Therefore, $$a=2, r=3$$

$$\text { So, G.P. is } 2,6,18,54, \dots\\$$

Let $$x$$ be the arithmetic mean and $$ y, z$$ be the two geometric means between any two positive numbers. Then $$\dfrac{y^3 + z^3}{xyz}$$ = __________.

Given that $$x$$ is the A.M. between $$a$$ and $$b$$ and $$y$$, and $$z$$ are the G.M. $$s$$ between $$a$$ and $$b$$ where $$a$$ and $$b$$ are positive. Then $$a, x, b$$ are in A.P. So,

$$x = \dfrac{a + b}{2}$$

$$a, y, z, b$$ are in G.P. So,

$$y = ar$$ and $$z = ar^2$$, where $$r = {\sqrt{3}\dfrac{b}{c}}$$. Also, $$ yz = ab$$, Now,

$$\dfrac{y^3 + z^3}{xyz} = \dfrac{a^3r^3 + a^3 r^6}{ab\Big(\dfrac{a + b}{2}\Big)}$$

$$= \dfrac{a^3 \times \dfrac{b}{a} + a^3 \times \dfrac{b^2}{a^2}}{ab\Big(\dfrac{a + b}{2}\Big)}$$

$$= \dfrac{2(a^2b + ab^2)}{a^2b + ab^2}$$

$$\dfrac{y^3 + z^3}{xyz} = 2$$

Find the first negative term of sequence $$999,995,991,987,$$
$$...$$

$$AP = 999,995,991,987,...$$

Here,$$a = 999, d = 995 - 999 = -4$$

$$a_n < 0$$

$$\Rightarrow a + (n - 1)d < 0$$

$$\Rightarrow 999 + (n - 1)(-4) < 0$$

$$\Rightarrow 999 - 4n + 4 < 0$$

$$\Rightarrow 1003 - 4n < 0$$

$$\Rightarrow 1003 < 4n$$

$$\Rightarrow \dfrac{1003}{4} < n$$

$$\Rightarrow n > 250.75$$

Nearest term greater than $$250.75$$ is $$251$$

So, $$251^{st}$$ term is the first negative term

Now, we will find the $$251^{st}$$ term

$$a_n = a + (n - 1)d$$

$$\Rightarrow a_{251} = 999 + (251 - 1)(-4)$$

$$\Rightarrow a_{251} = 999 + 250 \times -4$$

$$\Rightarrow a_{251} = 999 - 1000$$

$$\Rightarrow a_{251} = -1$$

$$\therefore,-1$$ is the first negative term of the given AP.

Multiplied by 2

Given that the mean of 15 observations is 32
resulting mean multiplied by 2
= 32 x 2
= 64

The mean of 100 observation isIt is found that an observation 53 was misread asFind the correct mean.

Given the mean of 100 observations is 40.
$$\frac{\sum x}{n} = \bar{x}$$
$$\Rightarrow \frac{\sum x}{n} = 40$$
$$\Rightarrow x = 40 *
100$$
$$\Rightarrow x = 4000$$
Incorrect value of x = 4000
Correct value of x = Incorrect value of x - Incorrect observation + correct observation
= 4000 - 83 + 53
= 3970
Correct mean
$$= \frac{correct value of \sum x}{n}$$
$$= \frac{3970}{100}$$
$$= 39.7$$

Divided by 0.5

Given that the mean of 15 observations is 32
resulting mean divided by 0.5
$$= \frac{32}{0.5}$$
$$= 64$$

the value of $$\displaystyle \sum^{10}_{i = 1}(x_i - \bar{x})$$

$$\displaystyle \sum^{10}_{i = 1}(x_i - \bar{x}) = (x1 - \bar{x}) + (x2 - \bar{x}) ..... + (xn - \bar{x}) = 0$$
$$\bar{x} = 5.8$$
$$\displaystyle \sum^{10}_{i = 1}(x_i - \bar{x})$$
$$= (9.8 - 5.8) + (5.4 - 5.8) + (3.7 - 5.8) + (1.7 - 5.8) + (1.8 - 5.8) + (2.6 - 5.8) + (2.8 - 5.8) + (8.6 - 5.8) + (10.5 - 5.8) + (11.1 - 5.8)$$
$$= 4 - 4 - 2.1 - 4.1 - 4 - 3.2 - 3 + 2.8 + 4.7 + 5.3$$
$$= 0$$

Decreased by 20%

Given that the mean of 15 observations is 32
resulting mean decreased by 20%

=32−20100×32=32−20100×32

=32−6.4=32−6.4

=25.6

Increased by 60%

Given that the mean of 15 observations is 32
resulting mean increased by 60%
$$= 32 + \frac{60}{100} \times 32$$
$$= 32 + 19.2$$
$$= 51.2$$

Decreased by 7

Given that the mean of 15 observations is 32
resulting mean decreased by 7
= 32 - 7
= 25

prove that
$$2\sin^{-1} \left ( \dfrac{3}{5} \right ) = \tan^{-1} \left ( \dfrac{24}{7} \right )$$

$$\sin ^{-1} \left ( \dfrac{3}{5} \right ) = \theta \Rightarrow \sin \theta = \dfrac{3}{5} $$
$$\Rightarrow \cos\theta = \dfrac{4}{5} $$
$$\Rightarrow \tan \theta = \dfrac{3}{4} $$
$$\tan 2\theta = \dfrac{2 \tan \theta }{1 - \tan^{2} \theta } = \dfrac{2\times \dfrac{3}{4}}{1 - \dfrac{9}{16}}$$
$$= \dfrac{6 / 4}{7 / 16} = \dfrac{6}{4} \times \dfrac{16}{7}$$
$$=\left ( \dfrac{24}{7} \right ) $$
$$2\theta = \tan^{-1} \left ( \dfrac{24}{7} \right )$$
$$2\sin^{-1} \left ( \dfrac{3}{5} \right ) = \tan^{-1} \left ( \dfrac{24}{7} \right )$$

Find the value of the following :
$$\cos^{-1} \left ( \dfrac{4}{5} \right ) + \cos^{-1} \left ( \dfrac{12}{13} \right )$$

$$\cos^{-1} \left ( \dfrac{4}{5} \right ) + \cos^{-1} \left ( \dfrac{12}{13} \right ) = \cos^{-1} \left ( \dfrac{33}{65} \right )$$
$$\cos^{-1} x + \cos^{-1} y = \cos^{-1} \left [ xy - \sqrt{1 - x^{2}} \sqrt{1 - y^{2}} \right ] $$
$$\cos^{-1} \left ( \dfrac{4}{5} \right ) + \cos^{-1} \left ( \dfrac{12}{13} \right ) = $$
$$\cos^{-1}\left [ \dfrac{4}{5}\times \dfrac{12}{3} - \sqrt{1 - \dfrac{16}{25}} \sqrt{1 - \dfrac{144}{169}}\right ]$$
$$=\cos^{-1} \left [ \dfrac{48}{65} - \dfrac{3}{5} \times \dfrac{5}{13} \right ]$$
$$=\cos^{-1}\left [ \dfrac{48}{65} - \dfrac{15}{65} \right ]$$
$$=\cos^{-1} \left [ \dfrac{33}{65} \right ]$$

Find the value of the following :
$$\sin^{-1} \left ( \dfrac{8}{17} \right ) + \sin^{-1} \left ( \dfrac{3}{5} \right ) $$

$$\sin^{-1} \left ( \dfrac{8}{17} \right ) + \sin^{-1} \left ( \dfrac{3}{5} \right ) = \sin^{-1} \left ( \dfrac{77}{85} \right )$$
$$\sin^{-1} x + \sin^{-1} y = \sin^{-1} \left [ \left ( x\sqrt{1 - y^{2}} + y \sqrt{1 -x ^{2}} \right ) \right ]$$
$$=\sin^{-1}\left [ \dfrac{8}{17}\sqrt{1-\dfrac{9}{25}}+ \dfrac{3}{5} \sqrt{1 - \dfrac{64}{279}} \right ]$$
$$=\sin^{-1} \left [ \dfrac{8}{17}\times \dfrac{4}{5}\times \dfrac{3}{5}\times \dfrac{15}{17} \right ]$$
$$= \sin^{-1}\left [ \dfrac{32}{85} + \dfrac{45}{85} \right ] = \sin^{-1} \left [ \dfrac{77}{85} \right ]$$

Find the mean of 75 numbers, if the mean of 45 of them is 18 and the mean of the remaining ones is 13.

Mean of 45 numbers = 18
$$\Rightarrow$$ Sum of 45 numbers = 18 x 45 = 810
Mean of remaining (75 - 45) 30 numbers = 13
$$\Rightarrow$$ Sum of remaining 30 numbers = 13 x 30 = 390
$$\Rightarrow$$ Sum of all the 75 numbers = 810 + 390 = 1200
$$\Rightarrow$$ Mean of all the 75 numbers = $$\frac{1200}{75} = 16$$

Increased by 25%

Mean of the given data $$= \frac{8 + 12 + 16 + 22 + 10 + 4}{6}$$
$$= \frac{72}{6} = 12$$
New mean = Original mean + 25% of original mean
$$\Rightarrow$$ New mean = 12 + 25 %of 12
$$\Rightarrow$$ Mean mean = 12 + $$\frac{25}{100}$$ x 12
$$\Rightarrow$$ Mean mean = 12 + $$\frac{1}{4}$$ x 12
$$\Rightarrow$$ Mean mean = 12 + 3
$$\Rightarrow$$ Mean mean = 15

Decreased by 40%

Mean of the given data $$= \frac{8 + 12 + 16 + 22 + 10 + 4}{6}$$

$$= \frac{72}{6} = 12$$

New mean = Original mean - 40% of original mean

$$\Rightarrow$$ New mean = 12 - 40%of 12

$$\Rightarrow$$ Mean mean = 12 - $$\frac{40}{100}$$ x 12

$$\Rightarrow$$ Mean mean = 12 - $$\frac{2}{5}$$ x 12

$$\Rightarrow$$ Mean mean = 12 - 0.4 x 12

$$\Rightarrow$$ Mean mean = 12 - 4.8

$$\Rightarrow$$ Mean mean = 7.2

Multiplied by 3 and then divided by 2.

Mean of the given data $$= \frac{8 + 12 + 16 + 22 + 10 + 4}{6}$$
$$= \frac{72}{6} = 12$$
If $$\bar{x}$$ is the mean of n number of observations $$x_1, x_2, x_3,....,x_n,$$ then mean of $$\frac{a}{b} x_1, \frac{a}{b} x_2, \frac{a}{b} x_3,..., \frac{a}{b} x_n$$ is $$\frac{a}{b} \bar{x}$$.
Thus, when each of the given data is multiplied by $$\frac{3}{2}$$,
the mean is also multiplied by $$\frac{3}{2}$$
Mean of the original data is 12.
Hence, the new mean $$= \frac{3}{2} \times 12 = \frac{36}{2} = 18$$

The mean of 18, 24, 15, 2x + 1 and 12 isFind the value of x.

Mean of given data $$= \frac{18 + 24 + 15 + 2x + 1 + 12}{5}$$
$$\Rightarrow 21 = \frac{70 + 2x}{5}$$
$$\Rightarrow 5 \times 21 = 70 + 2x$$
$$\Rightarrow 105 = 70 + 2x$$
$$\Rightarrow 2x = 105 - 70$$
$$\Rightarrow 2x = 35$$
$$\Rightarrow x = \frac{35}{2}$$
$$\Rightarrow x = 17.5$$

Find the value of the following :
$$\tan^{-1} \left [ \tan\left ( \pi + \dfrac{\pi }{6} \right ) \right ]$$

$$\tan^{-1} \left [ \tan\left ( \pi + \dfrac{\pi }{6} \right ) \right ] = \tan^{1} \left [ tan \dfrac{\pi }{6} \right ]$$
$$\tan^{-1} \tan \left ( \dfrac{\pi }{6} \right )$$
$$=\dfrac{\pi }{6}\epsilon \left [ \dfrac{-\pi }{2} , \dfrac{\pi }{2} \right ]$$

Find the value of the following :
$$\cos^{-1} \left ( \cos\left ( \dfrac{13\pi }{6} \right ) \right ) $$

$$\cos^{-1} \left ( \cos\left ( 2\pi + \dfrac{\pi }{6} \right ) \right ) = \cos^{1} \cos \left ( \dfrac{\pi }{6} \right )$$
$$\dfrac{\pi }{6}\epsilon [0 , \pi ]$$

Which term of the sequence
$$ \dfrac{1}{3} , \dfrac{1}{9} , \dfrac{1}{27} ........... is \dfrac{1}{19683}? $$

Here $$ a = \dfrac{1}{3}, r = \dfrac{\dfrac{`1}{9}}{\dfrac{1}{3}} = \dfrac{1}{3} $$
Let $$ T_{n} = \dfrac{1}{19683}$$
$$ \Rightarrow ar^{n-1} = \dfrac{1}{19683} \Rightarrow \dfrac{1}{3} \left ( \dfrac{1}{3} \right )^{n-1} = \left ( \dfrac{1}{3} \right )^{9} $$

Which term of the sequence
$$ 2 , 2 \sqrt{2} , 4 , .............. is 128 ? $$

Here a = 2 , r = $$ r = \dfrac{2\sqrt{2}}{2} = \sqrt{2}$$
Let $$ T_{n} = ar^{n-1} = 128 $$ (given)
$$\Rightarrow (r)^{n-1} = 128 \Rightarrow (r)^{n-1} = \dfrac{128}{2} = 64 = (2)^{6}$$

Define sequence of numbers

Arrangement of numbers one after another , according to some rule is called a sequence of number . Or sequence is a real valued function whose domain is set of all natural numbers,
Note
The number is the sequence are called terms.
The $$ n^{th} $$ term of the sequence is denoted by $$ t_{n} or T_{n} or a{n}. $$

prove
$$\tan^{-1} \left ( \dfrac{63}{16} \right ) = \sin^{-1} \left ( \dfrac{5}{13} \right ) + \cos^{-1} \left ( \dfrac{3}{5} \right )$$

$$\tan^{-1} \left ( \dfrac{63}{16} \right ) = \sin^{-1} \left ( \dfrac{5}{13} \right ) + \cos^{-1} \left ( \dfrac{3}{5} \right )$$
$$ \sin^{-1} \left ( \dfrac{5}{13} \right ) = u \Rightarrow \sin u = \dfrac{5}{13} $$
$$\Rightarrow \cos u = \dfrac{12}{13} $$
$$\tan u = \dfrac{5}{12} $$
$$=\cos^{-1} \left ( \dfrac{3}{5} \right ) = v \Rightarrow \cos v = \dfrac{3}{5}$$
$$\sin v = \dfrac{4}{5}$$
$$\tan v = \dfrac{4}{3} $$
$$\tan (u + v ) = \dfrac{\tan u + \tan v }{1 - \tan u \tan v }$$
$$\dfrac{\dfrac{5}{12}+\dfrac{4}{3}}{1-\dfrac{5}{12}\times \frac{4}{3}} \dfrac{\left ( \dfrac{63}{36} \right )}{\left ( \dfrac{16}{36} \right )}= \left ( \dfrac{63}{16} \right )$$
$$\therefore u + v = \tan^{-1} \left ( \dfrac{63}{16} \right )$$
$$\sin^{-1} \left ( \dfrac{5}{13} \right ) + \cos ^{-1} \left ( \dfrac{3}{5} \right ) = \tan^{-1} \left ( \dfrac{63}{16} \right )$$

Find the value of the following :

$$\tan^{-1} \sqrt{x} = \dfrac{1}{2} \cos^{-1} {x}$$

put $$\sqrt{x} \tan \theta \Rightarrow \theta \tan^{-1} \sqrt{x}$$
$$RHS\dfrac{1}{2} \cos^{-1} {x}$$
$$\left ( \dfrac{1 - x}{1 + x} \right )= = \dfrac{1}{2} \cos ^{-1} $$
$$\left [ \dfrac{1- \tan^{2}\theta }{1 + \tan^{2}\theta } \right ]$$
$$=\dfrac{1}{2} \cos^{-1} [\cos 2\theta ] = \dfrac{1}{2} \times 2\theta = \theta $$
$$\tan^{-1} \sqrt{x} = LHS$$

Find the value of the following :
$$\cos^{-1} \left ( \dfrac{12}{13} \right ) + \sin^{-1} \left ( \dfrac{3}{5} \right ) $$

$$\cos^{-1} \left ( \dfrac{12}{13} \right ) + \sin^{-1} \left ( \dfrac{3}{5} \right ) = \sin^{-1}\left ( \dfrac{56}{65} \right )$$
$$\cos^{-1} \left ( \dfrac{12}{13} \right ) = \sin^{-1} \left ( \dfrac{5}{13} \right )$$
$$\sin^{-1}\left ( \dfrac{5}{13} \right ) + \sin^{-1} \left ( \dfrac{3}{5} \right )=$$
$$=\sin^{-1} \left [ \dfrac{5}{13}\times \dfrac{4}{5} + \dfrac{3}{5} \times \dfrac{12}{13} \right ] = \sin^{-1} \left ( \frac{20}{65} + \dfrac{36}{65} \right )$$
$$=\sin^{-1}\left ( \dfrac{56}{65} \right )$$

Find derivative of:
$$ y = \dfrac{\sin (ax + b)}{\cos (cx + d)} $$

$$ using \space \dfrac{u}{v} \space rule$$

$$ y = \dfrac{\sin (ax + b)}{\cos (cx + d)} $$
$$\dfrac{dy}{dx} = \dfrac{\cos (cx +d) \times \cos (ax + b)\times a - (\sin (ax + b)\times - \sin (cx + d)\times c)}{\cos^{2}(cx +d)}$$

Find the value of the following :
$$ \left [ \tan^{-1} \dfrac{1}{5} + \tan^{-1} \left ( \dfrac{1}{7} \right )\right ] + \left [ \tan^{-1} \left ( \dfrac{1}{3} \right ) + \tan^{-1} \left ( \dfrac{1}{8} \right ) \right ]$$

$$ \left [ \tan^{-1} \dfrac{1}{5} + \tan^{-1} \left ( \dfrac{1}{7} \right )\right ] + \left [ \tan^{-1} \left ( \dfrac{1}{3} \right ) + \tan^{-1} \left ( \dfrac{1}{8} \right ) \right ]$$
$$ \tan^{-1} \left [ \dfrac{\dfrac{1}{5} + \dfrac{1}{7}}{1 - \dfrac{1}{5} \times \dfrac{1}{7}} \right ] + \tan^{-1} \left [ \dfrac{\dfrac{1}{3} + \dfrac{1}{8}}{1 - \dfrac{1}{3} \times \dfrac{1}{8}} \right ]$$
$$ \tan^{-1} \left [ \dfrac{\dfrac{12}{35}}{\dfrac{34}{35}} \right ] + \tan^{-1} \left [ \dfrac{\dfrac{11}{24}}{\dfrac{23}{24}} \right ]$$
$$ \tan^{-1} \left [ \dfrac{12}{34} \right ] + \tan^{-1} \left [ \dfrac{11}{23} \right ]$$
$$= \tan^{-1} \left [ \dfrac{\dfrac{6}{17}+ \dfrac{11}{23}}{1 - \dfrac{6}{17} \times \dfrac{11}{23}} \right ] = \tan^{-1} \left [ \dfrac{\dfrac{138 + 187}{17\times 23}}{\dfrac{391-66}{17\times 23}} \right ]$$
$$= \tan^{-1}\left [ \dfrac{325}{325} \right ]$$
$$= \tan^{-1}(1)=\dfrac{\pi }{4}$$

If $$x, y, z$$ are in G.P., arithmetic mean of $$x,y$$ is $$A_1$$ and A.M. of $$y,z$$ is $$A_2$$ then prove that:

(i) $$\dfrac{1}{A_1} + \dfrac{1}{A_2} = \dfrac{2}{y}$$ (ii) $$\dfrac{x}{A_1} + \dfrac{z}{A_2} = 2$$

$$L.H.S. = \dfrac{1}{A_1} + \dfrac{1}{A_2}$$

$$= \dfrac{2}{x+ y} + \dfrac{2}{y+z}$$

$$= \dfrac{2(x+ 2y+ z)}{y(x+2y + z)}=\dfrac{2}{y}= R.H.S.$$

(ii) $$L.H.S. = \dfrac{x}{
A_1} + \dfrac{z}{A_2}$$

$$= 2 \left(\dfrac{x}{x+ y} + \dfrac{z}{y+ z} \right)$$

$$= 2$$
$$= R.H.S.$$

If $$G_1$$ and $$G_2$$ are two geometric mean between $$a$$ and $$b$$, then prove that $$G_1 G_2= ab$$.

Let $$a, G_1, G_2, b$$ are in G.P,

then $$G_1 = √(aG_2) ....(i)$$

Similarly $$G_2 = √(G_1b) ....(ii)$$

Multiplying equation (i) and (ii)

$$G_1\times G_2=\sqrt{G_1G_2}\sqrt{ab}$$

$$\sqrt{G_1G_2}=\sqrt{ab}$$

$$G_1G_2=ab$$

If AM and GM of roots of a quadratic equation are 8 and 5 respectively , then obtain the quadratic equation .

$$Let\space m\space and\space n\space be\space the\space roots\space , then\space$$
$$ \dfrac{m + n}{2} = AM = 8 \Rightarrow m + n = 16 and \sqrt{mn} = GM = 5 $$
$$Required\space quadratic\space equation\space is\space$$ $$ \Rightarrow x^{2} - $$ $$(sum\space of \space the\space roots\space) x$$$$ + \space product\space of\space the\space roots\space = 0 $$

$$ \Rightarrow x ^{2} - (m+n)x + mn = 0 $$
$$ \Rightarrow x ^{2} - 16 x + 25 = 0 $$

If $$a, b, c$$ be positive and $$ab (a+b)+bc(b+c)+ca(c+a)\geq \lambda abc$$, then value of $$\lambda $$ is

For positive quantities $$a^2b, bc^2$$,
$$A.M. \geq G.M.$$
$$\dfrac{a^2b+bc^2}{2} \geq (a^{2}b.bc^{2})^{\cfrac{1}{2}} = abc$$
$$a^2b+bc^2 \geq 2abc $$
Similarly,
$$b^2c + ca^2 \geq 2abc $$ and
$$c^2a + ab^2 \geq 2abc $$.
Adding the inequalities we get,
$$ ab(a+b) + bc(b+c) + ac (a+c) \geq 6 abc $$
Hence, $$\lambda = 6$$

Prove that the product of $$n$$ geometric mean between any two numbers is $$nth$$ power of their $$G.M$$.

Let a and b be the 2 numbers and G be the geometric mean between them.

Therefore a,b,G must be in G.P.

Common ratio $$= \dfrac{G}{a}=\dfrac{b}{G}$$

$$\Rightarrow G^2=ab\rightarrow G=\sqrt{ab}$$...(1)

Therefore,

$$a,G_1,G_2,......,G_n,b$$ form G.P.

This series has a as its first term and b as last and (n+2)th term

$$\therefore b=ar^{n+2-1}$$

$$\Rightarrow b=ar^{n+1}$$

$$r=\left (\dfrac{b}{a} \right )^{\frac{1}{n+1}}$$...(2)

Product $$=G_1G_2...G_n$$

$$=(ar)(ar^2).....(ar^n)$$

$$=a^nr^{1+2+..+n}$$

$$=a^nr^{\frac{n(n+1)}{2}}$$

From (2) we get

$$=a^n\left (\dfrac{b}{a} \right )^{\frac{n(n+1)}{2(n+1)}}$$

$$=(ab)^{\frac{n}{2}}$$

$$=(\sqrt{ab})^n$$

From (1) we get

Product $$=G^n$$

$$G_1G_2....G_n=G^n$$

If a be one A.M and $$G_1$$ and $$G_2$$ be then geometric means between b and c then $${ G }_{ 1 }^{ 3 }+{ G }_{ 2 }^{ 3 }=?$$

2039397_1279229_ans_0a6108da61b244f6b8eb21e42d76c724.jpeg

Write the next term of each of the following sequences :
$$1, 5, 14, 30, 55,.....$$

The series is as follows:-

$$1^{2}=1$$ (1st term)

$$1^{2}+2^{2}=5$$ (2nd term)

$$1^{2}+2^{2}+3^{2}=14$$

$$1^{2}+2^{2}+3^{2}+4^{2}=30$$

$$1^{2}+2^{2}+3^{2}+4^{2}+5^{2}=55$$

$$1^{2}+2^{2}+3^{2}+4^{2}+5^{2}+6^{2}=91$$......so on.

Hence, the next term in the series is 91.

If A and G be A.M. and G.M., respectively between two positive numbers, prove that the numbers are $$A\pm \sqrt {(A+G)(A-G)}$$

1961030_1429520_ans_27dff3740edf43b9a5ce27dd29ac5578.jpeg

Show that $$(x^2y + y^2z + z^2x) (xy^2 + yz^2 + zx^2) \geq 9x^2y^2z^2.$$

2037880_1744454_ans_6bf215037ca5437e871db7be0eb802f9.png

If $$x + y + z = 1,$$ show that the least value of $$\dfrac{1}{x} + \dfrac{1}{y} + \dfrac{1}{z}$$ is $$9;$$ and that $$(1 - x) (1 - y) ( 1 - z) > 8 xyz.$$

1979045_1744499_ans_323892b6e83a4a8a914e753588e460c0.jpg

Show that $$n^n > 1.3.5 .... (2n - 1).$$

2037881_1744460_ans_9525aa4f64504b659ed0e8ad5a1a725e.jpg

Find two positive numbers a and b, whose $$AM=25$$ and $$GM=20$$.

undefined

1981659_1710806_ans_33b7d06d51aa44719832a70656e313aa.jpg

If $$s$$ be the sum of $$n$$ positive unequal quantities $$a,b, c....,$$ then
$$\dfrac{s}{s-a}+\dfrac{s}{s-b}+\dfrac{s}{s-c}+.... > \dfrac{n^2}{n-1}$$.

2038096_1747020_ans_c6fba81bf5714adbb632b56363c4858e.png

If $$a$$ and $$b$$ are positive and unequal, prove that
$$a^n-b^n > n(a-b)(ab)^{\dfrac{n-1}{2}}$$.

Given , a and Positive

Let a>b

$$\to a-b>0$$

As we know that

$$ \dfrac{a^n-b^n}{a-b}=a^{n-1}+a^{n-2}b+a^{n-3}{b^2}+...+ab^{n-2}+b^{n-1}$$ $$~~~~~-(1)$$

As w eknow A.M.$$\ge$$G.M.

$$\to \dfrac{a^{n-1}+a^{n-2}b+...+ab^{n-2}+b^{n-1}}{n}\ge (a^{n-1}.a^{n-2}b..ab^{n-2}.b^{n-1})^{\dfrac{1}{n}}$$

$$\to \dfrac{a^n-b^n}{a-b}\ge n(a^{\dfrac{n-1}{2}}.b^{\dfrac{n-1}{2}})$$ ( Using 1)

$$\to a^n-b^n>n(a-b)(ab)^{\dfrac{n-1}{2}}$$

Hence proved.

If $$m$$ is negative or positive and greater than $$1$$ show that
$$1^{m}+3^{m}+5^{m}+.......+(2n-1)^{m}>n^{m+1}$$

2037899_1746956_ans_b1b3d5a03bdd4a0ebc30cdfc994776b2.jpg

Given that $$x,y,z$$ are positive reals such that $$xyz=32$$. If the minimum value of $${ x }^{ 2 }+4xy+4{ y }^{ 2 }+2{ z }^{ 2 }$$ is equal $$m$$ then the value of $$\dfrac{m}{16}$$ is

Given

xyz=32,

minimum values of $$x^2+4xy+4y^2+2z^2$$=m

To find:- value of $$\dfrac{m}{16}$$

we can write given expresssion as $$x^2+2xy+2xy+4y^2+z^2+z^2$$

As we know

Arithmetic mean$$>$$ Geometric mean

$$\dfrac{x^2+2xy+2xy+4y^2+z^2+z^2}{6}>(16x^4y^4z^4)^\dfrac{1}{6}$$

$$x^2+2xy+2xy+4y^2+z^2+z^2>6.(2xyz)^\dfrac{4}{6}$$

$$x^2+2xy+2xy+4y^2+z^2+z^2>6.(64)^\dfrac{4}{6}$$

$$x^2+2xy+2xy+4y^2+z^2+z^2>6.2^4$$

$$x^2+2xy+2xy+4y^2+z^2+z^2>96$$

so we get m=96

so value of $$\dfrac{m}{16}$$= $$\dfrac{96}{16}$$ =6

Hence the required answer is 6.

If $$\dfrac{x}{a^2-y^2}=\dfrac{y}{a^2-x^2}=\dfrac{1}{b}$$, and $$xy=c^2$$, show that when $$a$$ and $$c$$ are unequal, $$(a^2-c^2)^2-b^2c^3=0$$, or $$a^2+c^2-b^2=0$$

Given

$$\dfrac{x}{a^2-y^2}=\dfrac{y}{a^2-x^2}=\dfrac{1}{b}$$ and $$xy=c^2$$

Taking reciprocal

$$\dfrac{a^2-y^2}{x}=\dfrac{a^2-x^2}{y}=b$$

$$x=\dfrac{a^2-y^2}{b} $$and $$y=\dfrac{a^2-x^2}{b}$$

As we know that

A.M.$$\ge$$G.M.

$$\dfrac{a^2-y^2}{b}+\dfrac{a^2-x^2}{b}\ge 2\sqrt{(\dfrac{a^2-x^2)(a^2-y^2)}{b^2}}$$

$${(a^2-y^2)+(a^2-x^2)}\ge 2\sqrt{a^4-a^2(x^2+y^2)+x^2y^2)}$$

$${2a^2-(y^2+x^2)}\ge 2\sqrt{a^4-a^2(x^2+y^2)+x^2y^2)}$$

Squarring on both sides,

$$ 4a^4+(x^2+y^2)^2-4a^2(x^2+y^2)\ge 4a^4-4a^2(x^2+y^2)+4c^4$$

on comparing both the sides we get

$$2c^2=(x^2+y^2)$$

$$(x^2+y^2-2xy)=0$$

$$(x-y)^2$$=0

so x=y

Now Taking L.H.S.

$$(a^2-c^2)^2-b^2c^3$$

$$(a^2-xy)^2-(\dfrac{a^2-x^2}{y})^2(xy)^\dfrac{2}{2}$$

$$(a^2-x^2)^2-(\dfrac{a^2-x^2}{x})^2(x^2)^\dfrac{2}{2}$$ ( since x=y)

$$(a^2-x^2)^2-(a^2-x^2)^2$$

If $$a, b, c$$ are real positive quantities, show that
$$\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}< \dfrac{a^8+b^8+c^8}{a^3b^3c^3}$$.

1948261_1747134_ans_4bf7d78bd34d4a7284edc2b3a485a3a9.jpg

Show that
$$a^{2}(1+b^{2})+b^{2}(1+c^{2})+c^{2}(1+a^{2})>6abc$$

1948253_1747074_ans_c3996cb4039f423486ea6c02de29d055.jpg

The arithmetic mean between $$m$$ and $$n$$ and the geometric mean between $$a$$ and $$b$$ are each equal to $$\dfrac{ma+nb}{m+n}$$: find $$m$$ and $$n$$ in terms of $$a$$ and $$b$$.

1607947_1746434_ans_bca482c0e5c442e59211c3ad362f6900.png

Show that, if $$a, b, c, d$$ be four positive unequal quantities and $$s=a+b+c+d$$, then
$$(s-a)(s-b)(s-c)(s-d) > 81 abcd$$.

2038095_1746981_ans_edc7edab468d4550ad70d6c7027ad9c4.jpg

$${x}_{i}$$:	$$5$$	$$15$$	$$25$$	$$35$$	$$45$$
$${f}_{i}$$:	$$3$$	$$k$$	$$3$$	$$6$$	$$2$$

Sequences And Series - Class 11 Commerce Applied Mathematics - Extra Questions

If $$\displaystyle a_{n}=\frac{n^{2}}{3n+2}$$, find $$\displaystyle a_{5} a_1$$.

Find the value of $$n$$ so that $$\displaystyle \dfrac { { a }^{ n+1 }+{ b }^{ n+1 } }{ { a }^{ n }+{ b }^{ n } } $$ may be the geometric mean between $$a$$ and $$b$$.

Write the first two terms of the sequence whose $$n^{th}$$ term is $$t_{n} = 3n - 4$$

Find the first three terms of the sequence whose $$n \ th$$ term is $$2n + 3$$.

Find the next two terms in the sequence:$$1, 2, 4, 7, 11, .....$$

Find the next two terms in the sequence: $$2, 4, 8, 16, .....$$

Find the first three terms of the following sequence, whose $$n^{th}$$ term is$$t_n = 4n - 3$$

Find the first term of the sequence, where $$t_n=2n+1$$.

If $$x$$ is the geometric mean of $$(x + 2)$$ and $$(x - 1)$$, then find the value of $$x$$.

Find the first two terms of the following sequence:$${t}_{n}=n+2$$

Find the first two terms of the sequence whose $$n^{th}$$ term is$${t}_{n}=n+2$$.

Find the next two terms of the following sequence: $$1,3,5,7,.....$$

If $$t_{n} = 2n + 3$$, then find the first two terms of a given sequence

If $$nth$$ term of a sequence is $$t_{n} = n + 1$$, then find the first two terms of the given sequence

If $$t_n=4n$$, find $$t_1$$.

Which of the following sequences are geometric sequences(i) $$5, 10, 15, 20, ....$$(ii) $$0.15, 0.015, 0.0015, .....$$(iii) $$\sqrt {7}, \sqrt {21}, 3\sqrt {7}, 3\sqrt {21},.....$$

Find the sum of the following series.(i) $$1 + 2 + 3 + .... + 45$$(ii) $$16^{2} + 17^{2} + 18^{2} + .... + 25^{2}$$(iii) $$2 + 4 + 6 + .... + 100$$(iv) $$7 + 14 + 21 + .... + 490$$(v) $$5^{2} + 7^{2} + 9^{2} + 39^{2}$$(vi) $$16^{3} + 17^{3} + ..... + 35^{3}$$

The sum of the first three terms of a G.P. is $$13$$ and sum of their squares is $$91$$. Determine the G.P.

Find the common ratio and the general term of the following geometric sequences.$$\dfrac {2}{5}, \dfrac {6}{25}, \dfrac {18}{125}, ....$$

If $$T_n = 2n^2 + 5$$ then find $$T_3$$

The number of people who visited games village during common wealth games in New Delhi for the first four days was recorded as $$15,290, 14,181, 14,235$$ and $$10,578$$. Find the total number of people visited in these four days?

Study the pattern: $$1 \times 8 + 1 = 9 $$$$12 \times 8 + 2 = 98 $$$$123 \times 8 + 3 = 987$$ $$1234 \times 8 + 4 = 9876$$$$12345 \times 8 + 5 = 98765 $$Write the next four steps. Can you find out how the pattern works ?

The arithmetic mean of the following data is $$25$$, find the value of $$k$$.$${x}_{i}$$:$$5$$$$15$$$$25$$$$35$$$$45$$$${f}_{i}$$:$$3$$$$k$$$$3$$$$6$$$$2$$

Write the first five terms of each of the following sequences whose $$n^{th}$$ terms are:$${ a }_{ n }=3n+2$$

Write the first five terms of each of the following sequences whose $$n$$th terms are:$${ a }_{ n }={ \left( -1 \right) }^{ n }.{ 2 }^{ n }$$

Write the first five terms of each of the following sequences whose $$n$$th terms are:$${ a }_{ n }={ n }^{ 2 }-n+1$$

Write the first five terms of each of the following sequences whose $$n$$th terms are:$${ a }_{ n }=\cfrac { n-2 }{ 3 } $$

Write the first five terms of each of the following sequences whose $$n$$th terms are: $${ a }_{ n }=\cfrac { n\left( n-2 \right) }{ 2 } $$

Write the first five terms of each of the following sequences whose $$n$$th terms are:$${ a }_{ n }=2{ n }^{ 2 }-3n+1$$

Write the first five terms of each of the following sequences whose $$n$$th terms are:$${ a }_{ n }=\cfrac { 2n-3 }{ 6 } $$

Write the first five terms of each of the following sequences whose $$n$$th terms are: $${ a }_{ n }=\cfrac { 3n-2 }{ 5 } $$

Write the first five terms of each of the following sequences whose $$n$$th terms are:$${ a }_{ n }={ 3 }^{ n }$$

The next term of the sequence $$3, 5, 7, 11, 13, 17,..$$ will be equal to:

State whether the given list of numbers is a sequence or not: $$\dfrac{1}{2},\dfrac{2}{3},\dfrac{3}{4},...$$ If yes, find out the next number in the list.

26500 were divided equally among a number of people. If the number of people is increased by 15, the number of money reduces by 30 for each person. find the number of people as well as money each person got.

State whether the given list of numbers is a sequence or not : $$-52,53,-54,...$$ If yes, find out the next number in the list.

Choose the odd one out:$$33,-79,42,-89,-11,35$$

Find the G.M of $$6$$ and $$24$$

The third term of the sequence whose $$n^{th}$$ term is $$\dfrac{1}{n^{2}}+1$$ is k.Find 9k

If $$a,b,c$$ are three consecutive terms of A.P,Then $$b=$$____

Find the average of first twelve natural numbers.

Write down the sequence if $$n$$th term is:a) $$\dfrac{{{2^n}}}{n}$$b) $$\dfrac{{3 + {{\left( { - 1} \right)}^n}}}{{{3^n}}}$$

The G.M. between $$1$$ and $$25$$ is ___.

Solve: $$3200 = 4500 - \dfrac{n}{20}$$.

Write the next term: $$\sqrt { 12 } , \sqrt { 27 } \sqrt { 48 } , \sqrt { 75 } , \dots ......$$

If $$t_{n}=2n$$, find $$t_{3}$$.

Pointing to a man in a photograph, a woman said, "His brother's father is the only son of my grandfather". How is the woman related to the man in the photograph ?

If Mohan says that his mother is the only daughter of Shyam's mother, how is Shyam related to Mohan ?

Pointing to a photograph, a man said, " I have no brother or sister but that man's father is my father's son". Whose photograph was it ?

If $$ a_{n}=\frac{n(n-3)}{n+4} $$ then find the $$ 18^{ th } $$ term of this sequence.

What is sequence ?

Find the mean of 2 and 8

The mean of data $$34,65,14,74,43$$ is

Some equations are solved on the basis of a certain system. On the same basis, find out the correct answer for the unsolved equation$$4\times 6\times 9=649$$$$7\times 3\times 2=372$$$$8\times 9\times 4=?$$

If $$ \frac{2}{3}, \mathrm{k}, \frac{5 k}{8} $$ are in A.P. then $$ \mathrm{k}= $$

If $$ \dfrac{1}{\sqrt{a}} $$ is the G.M. of 2 and $$ \dfrac{1}{4},$$ find a.

Find the geometric mean of the following pairs of numbers:$$ -8 $$ and $$ -2 $$

If AM and GM of two positive numbers a and b are 10 and 8 respectively,find the numbers

Divided by 2.

Find the $${ 7 }^{ th }$$ term in the following sequence whose $${ n }^{ th }$$ terms is $${ a }_{ n }=\dfrac { { n }^{ 2 } }{ { 2 }^{ n } } $$.

Multiplied by 3

Which term of the following sequences:(a) $$ 2,2 \sqrt{2}, 4 \dots \dots$$ is $$ 128 ? $$

Find the $${ 17 }^{ th }$$ and $${ 24 }^{ th }$$ term in the following sequence whose $${ n }^{ th }$$ term is $${ a }_{ n }=4n-3$$.

Find the $${ 9 }^{ th }$$ term in the following sequence whose $${ n }^{ th }$$ terms is $${ a }_{ n }=(-1)^{ n-1 }n^{ 3 }$$

Find the third term of the following sequence, whose $$n^{th}$$ term is given.$$t_n\,=\,2n\,-\,5$$

If $$\displaystyle a_{1},a_{2},...a_{n}$$ be an A.P. of +ive terms, then $$\displaystyle \sum_{k=1}^{n}a_{k}\geq n\sqrt{a_{1}^{2}+\left ( n-1 \right )da_{1}}$$ where d is common difference of A.P. If you think this is true write $$1$$ otherwise write $$0$$ ?

If $$\displaystyle f\left ( x \right )=\log _{x}1/9-\log_{3}x^{2}\left ( x > 1 \right )$$, then max $$\displaystyle f\left ( x \right )$$ is equal to

$$(x-4)$$ is geometric mean of $$(x-5)$$ and $$(x-2)$$ find $$x$$.

If $$ab = 2a +3b$$ where a > 0, b > 0, then find the minimum value of ab.

If the roots of the equation $${ x }^{ 3 }-a{ x }^{ 2 }+4x-8=0$$ are real and positive, then the minimum value of $$a$$ is

Y B T G O ?

If $$x, y, z, u > 0$$ , then find the minimum value of $$\displaystyle \frac{x^{6}+y^{6}+2z^{3}+2u^{3}}{xyzu}$$

Write down the sequence whose $$\displaystyle n^{th}$$ term is(i) $$\displaystyle \frac{2^{n}}{n}$$ (ii) $$\displaystyle \frac{3+\left ( -1 \right )^{n}}{3^{n}}$$. How many terms of the sequences are are less than zero?

If $$\displaystyle t_{n}=\frac{1+\left ( -2 \right )^{n}}{n-1}$$, then find $$\displaystyle t_{6}-t_{5}$$.

The sum of two numbers is $$6$$ times their geometric mean show that numbers are in the ratio $$\displaystyle (3+2\sqrt { 2 } ):(3-2\sqrt { 2 } )$$

If $$\displaystyle \frac { { a }^{ n }+{ b }^{ n } }{ { a }^{ n-1 }+{ b }^{ n-1 } } $$is the A.M. between $$a$$ and $$b$$, then find the value of $$n$$.

Each layer of the structure below is a square. The base is made up of 100 cubes, the second layer 81 cubes and the third layer 64 cubes. If the top layer of the structure consists of 16 cubes, how many layers does the structure have in all?

If the sum of $$4$$ terms of an A.P. is $$36$$, find the A.M. of these terms.

Find $$x$$, if the given numbers are in A.P. $$(a + b)^2 , x , (a - b)^2$$

Find the next two terms in the sequence:
$$1, 2, 4, 7, 11, .....$$

Find the first three terms of the following sequence, whose $$n^{th}$$ term is
$$t_n = 4n - 3$$

Find the first two terms of the following sequence:
$${t}_{n}=n+2$$

Find the first two terms of the sequence whose $$n^{th}$$ term is
$${t}_{n}=n+2$$.

Which of the following sequences are geometric sequences
(i) $$5, 10, 15, 20, ....$$
(ii) $$0.15, 0.015, 0.0015, .....$$
(iii) $$\sqrt {7}, \sqrt {21}, 3\sqrt {7}, 3\sqrt {21},.....$$

Find the sum of the following series.
(i) $$1 + 2 + 3 + .... + 45$$
(ii) $$16^{2} + 17^{2} + 18^{2} + .... + 25^{2}$$
(iii) $$2 + 4 + 6 + .... + 100$$
(iv) $$7 + 14 + 21 + .... + 490$$
(v) $$5^{2} + 7^{2} + 9^{2} + 39^{2}$$
(vi) $$16^{3} + 17^{3} + ..... + 35^{3}$$

Find the common ratio and the general term of the following geometric sequences.
$$\dfrac {2}{5}, \dfrac {6}{25}, \dfrac {18}{125}, ....$$

Study the pattern:
$$1 \times 8 + 1 = 9 $$
$$12 \times 8 + 2 = 98 $$
$$123 \times 8 + 3 = 987$$
$$1234 \times 8 + 4 = 9876$$
$$12345 \times 8 + 5 = 98765 $$
Write the next four steps. Can you find out how the pattern works ?

The arithmetic mean of the following data is $$25$$, find the value of $$k$$.
$${x}_{i}$$: $$5$$ $$15$$ $$25$$ $$35$$ $$45$$
$${f}_{i}$$: $$3$$ $$k$$ $$3$$ $$6$$ $$2$$

State whether the given list of numbers is a sequence or not: $$\dfrac{1}{2},\dfrac{2}{3},\dfrac{3}{4},...$$
If yes, find out the next number in the list.

Choose the odd one out:
$$33,-79,42,-89,-11,35$$

Write down the sequence if $$n$$th term is:

a) $$\dfrac{{{2^n}}}{n}$$

b) $$\dfrac{{3 + {{\left( { - 1} \right)}^n}}}{{{3^n}}}$$

Some equations are solved on the basis of a certain system. On the same basis, find out the correct answer for the unsolved equation
$$4\times 6\times 9=649$$
$$7\times 3\times 2=372$$
$$8\times 9\times 4=?$$

Find the geometric mean of the following pairs of numbers:
$$ -8 $$ and $$ -2 $$

Which term of the following sequences:
(a) $$ 2,2 \sqrt{2}, 4 \dots \dots$$ is $$ 128 ? $$

Find the third term of the following sequence, whose $$n^{th}$$ term is given.
$$t_n\,=\,2n\,-\,5$$

Write down the sequence whose $$\displaystyle n^{th}$$ term is
(i) $$\displaystyle \frac{2^{n}}{n}$$ (ii) $$\displaystyle \frac{3+\left ( -1 \right )^{n}}{3^{n}}$$. How many terms of the sequences are are less than zero?

Find the next two terms in the sequence:
$$1,3,7,15,31,.......$$

If G is the geometric mean of x and y, then
$$t\frac{1}{{{G^2} - {x^2}}} + \frac{1}{{{G^2} - {y^2}}} = \frac{1}{{{G^2}}}$$

Solve the equation for $$x$$:
$$1+4+7+10+.....+x=287$$

Find the mean of the following.
All the factors of $$48$$.

Check whether the following sequence is A.P. If it is A.P., Find the common difference.
$$0.3, 0.33, 0.333...$$

Write the first five terms of the following sequence.
$$a_1=a_2=2, a_n=a_{n-1}-1, n > 2$$.

Write the first five terms of the following.
$$a_1=1=a_2, a_n=a_{n-1}+a_{n-2}, n > 2$$.

Write the first five terms of the following sequence.
$$a_1=1, a_n=a_{n-1}+2, n > 1$$.

Find the geometric mean of the following pairs of numbers :
$$ 2 $$ and $$ 8 .$$

Find general term of series
$$\log_e(1+3x+2x^2)=3x-\dfrac{5x^2}{2}+\dfrac{9x^3}{3}-\dfrac{17x^4}{4}+..$$

Find the general term of the series
$$\log_e(1+3x)=3x-\dfrac{(3x)^2}{2}+\dfrac{(3x)^3}{3}-\dfrac{(3x)^4}{4}+....$$

Calculate the greatest and least values of the function
$$f(x)=\cfrac { { x }^{ 4 } }{ { x }^{ 8 }+2{ x }^{ 6 }-4{ x }^{ 4 }+8{ x }^{ 2 }+16 } $$