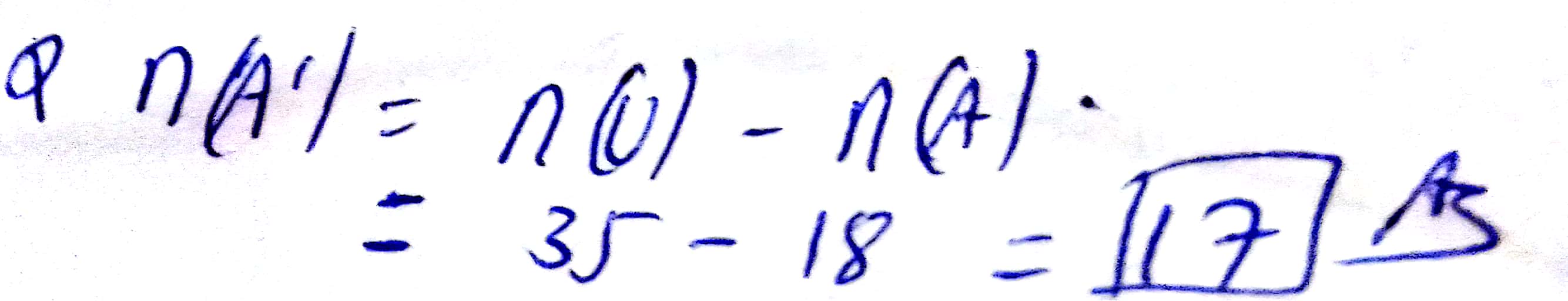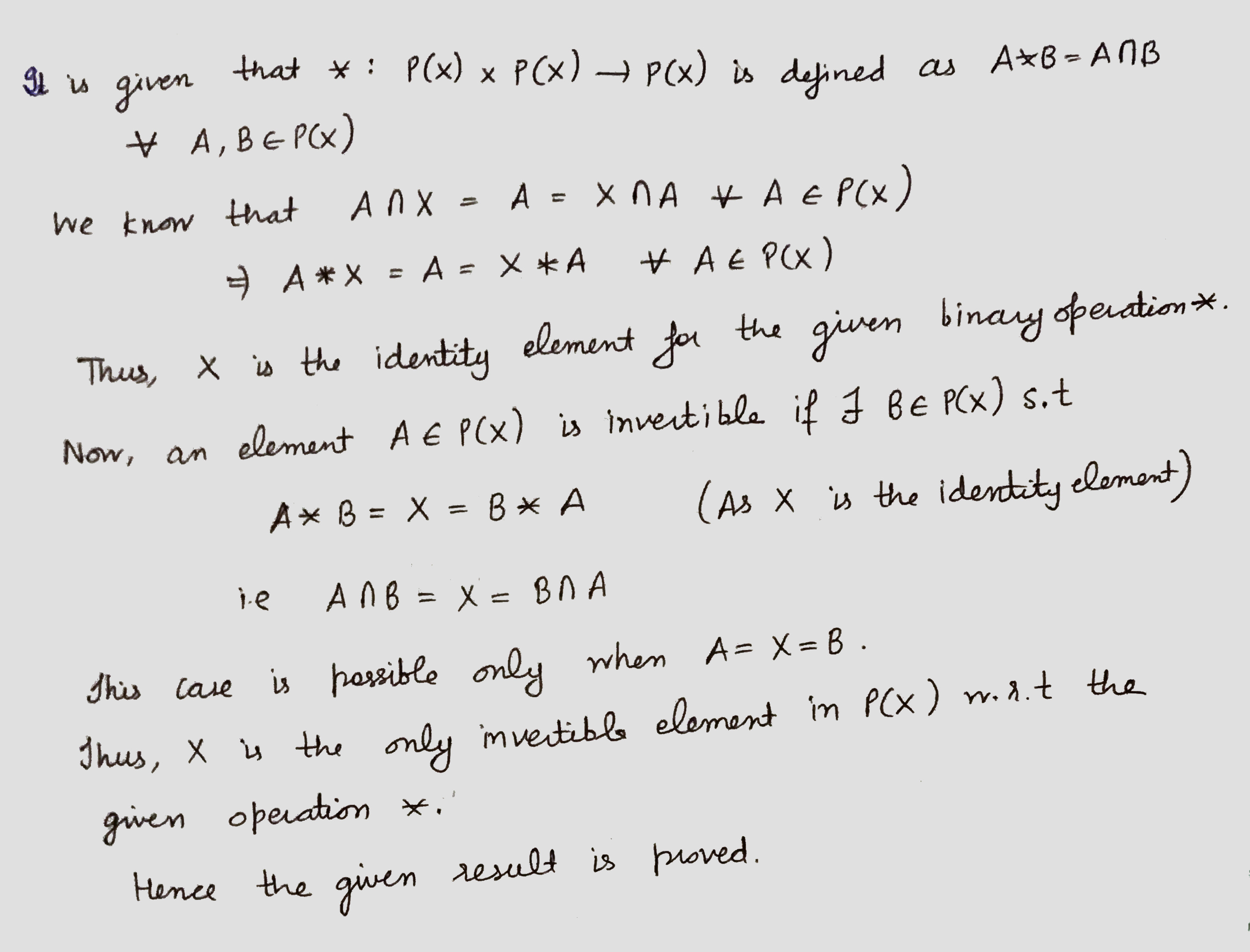Set Theory - Class 11 Commerce Applied Mathematics - Extra Questions

Is $$\{1 , 2, 4, 16, 64\} =\{x : x \text{ is a factor of }32\}$$ ? Give reason.

Factors of $$ 32  = 1, 2, 4, 8, 16, 32 $$


Since the given set has $$ 64 $$ and does not have $$ 8 $$, the given set is not equal to {$$  x: x $$ is a factor of $$ 32 $$ }


Write the set $$A= \left \{1,4,9, 16,........\right \}$$ in set builder form.

Consider the given set.

$$A=\left\{ 1,4,9,16,25,...... \right\}$$

 

We know that,

$$1, 2, 3, 4, 5,……,$$ are the natural numbers.

And $$1, 4, 9, 16, 25,…..,$$ are the squares of this numbers.

 

Therefore,

$$A=\left\{ x:x={{n}^{2}},where\,n\in N \right\}$$

 

Hence, this is the set of $$A$$.



If $$A = \left \{1 ,2,3\right \}, B =\left \{2,4,5,6\right \}$$ and $$C =\left \{1 ,3,5,7\right \}$$, then find the universal set

As we know $$U = A \cup B \cup C$$
 $$U = \left \{1, 2, 3, 4, 5, 6, 7\right \}$$ can be taken as the universal set.


Are the following sets equal ?
$$A = \left \{x: x \text {is a letter in the word reap}\right \}$$
$$B = \left \{ x : x \text {is a letter in the word paper}\right \}$$

$$A=\left \{r,e,a,p\right \}$$
$$B= \left \{p, a,e, r\right \}$$
So, A and B are equal sets.


If $$U = \{ a, b, c, d, e, f, g, h\}$$, find the complements of the following sets:
(i) $$A = \{a, b, c\}$$ 
(ii) $$B = \{d, e, f, g\}$$ 
(iii) $$C = \{a, c, e, g\}$$ 
(iv) $$D = \{ f, g, h, a\}$$

We know that complement of set $$A$$ is 
$$A'=U-A$$

Given $$U=\left \{a,b,c,d,e,f,g,h\right \}$$

(i) $$A=\left \{a,b,c\right \}$$
$$A'=\left \{d,e,f,g,h\right \}$$

(ii) $$B=\left \{d,e,f,g\right \}$$
$$\therefore B'=\left \{a,b,c,h\right \}$$

(iii) $$C=\left \{a,c,e,g\right \}$$
$$\therefore C'=\left \{b,d,f,h\right \}$$

(iv) $$D=\left \{f,g,h,a\right \}$$
$$\therefore D'=\left \{b,c,d,e\right \}$$


$$\mu$$ represents the set of students in class $$8$$ and $$n(\mu) = 35$$. 
A is the set of students in the class $$8$$ who have to wear spectacles and $$n(A) = 18$$. 
Find $$n(A')$$.

$$ n(A^{1}) = n(u)-n(A) $$
$$ = 35-18 = \boxed {17} $$ 

1103195_514572_ans_7ebcab783676419db5419bfcdbc25de4.jpg


If $$U=\left\{ 2,4,6,8,10,12,14,16,18,20 \right\} ,\quad W=\left\{ 2,6,12,18 \right\} $$, find $$W'$$

$$W'=\left\{ 4,8,10,14,16,20 \right\} $$


If a set A is defined as $$A = \{ x : x^2 - 9 \neq 0, \forall x \epsilon $$ integers}, calculate, the elements of set A.

Since,
$$x^2 - 9 \neq 0$$
$$x^2 \neq 9$$
$$x^2 \neq \pm 3$$
$$\therefore A = \{ 0, \pm1, \pm 2, \pm 4, \pm 5 ........\}$$


Represent the following set by using their standard notations: Set of rational numbers

set of rational number $$=Q$$.


Represent the following set by using their standard notations: Set of real numbers

Set of real numbers  $$=R$$.


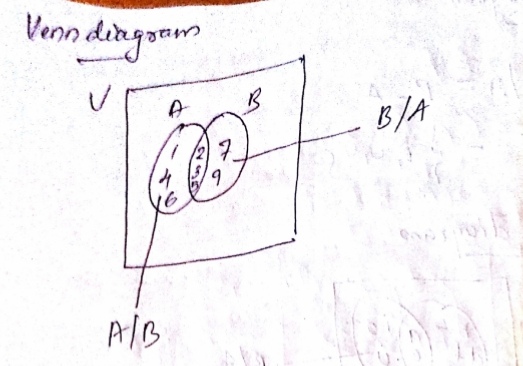
Let $$A$$ and $$B$$ be subsets of a set $$U$$. Identify  if  the given statement is right or wrong:
$$A/B = B/ A$$

$$A$$ and $$B$$ are subsets  of $$U$$.
$$A/B = B/A$$
$$A-B \neq B-A $$
The given statement is wrong


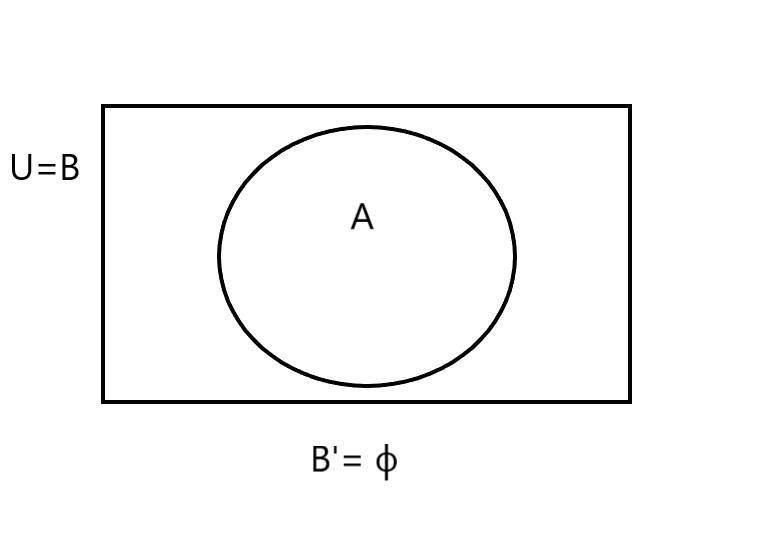
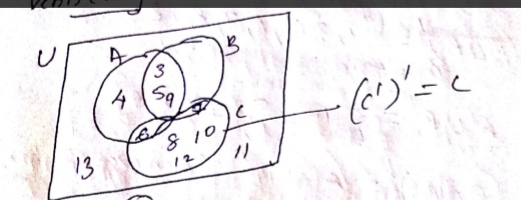
Let $$A$$ and $$B$$ be subsets of a set $$U$$. Identify if the given statement is the wrong statement:
$$(A')' = A$$

$$A$$ and $$B$$ are subsets of set $$U$$.
$$((A'))' = A$$
The given statement is not wrong .
$$(A')' = A $$  (Law of double component).


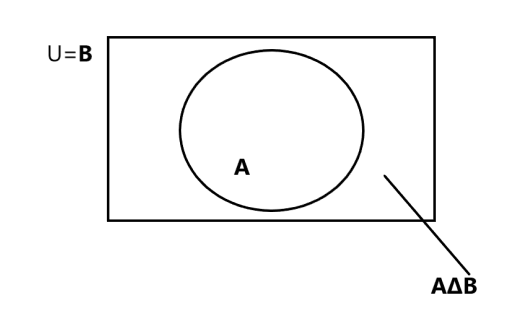
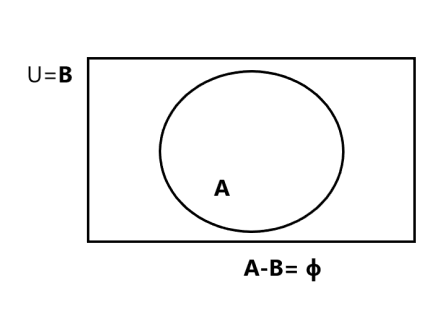
If $$U = \left \{x|x \leq 25, x\epsilon \mathbb {N}\right \}, A = \left \{x|x\epsilon U, x\leq 15\right \}$$ and $$B = \left \{x|x \epsilon U, 0 < x \leq 25\right \}$$, list the elements of the following set and draw Venn diagram:
$$A\triangle B$$

$$U=\{1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25\}$$
$$A=\{1,2,3,4,5,6,7,8,9,10,11,12,13,14,15\}$$
$$B=U$$
$$A\Delta B =\{16,17,18,19,20,21,22,23,24,25\}$$
Elements in $$A$$ and $$B$$ excluding elements both $$A$$ and $$B$$.

941713_559248_ans_b2aa65d43f4c40e18c13301dca411cd5.png


If $$U = \left \{x|x \leq 25, x\epsilon \mathbb {N}\right \}, A = \left \{x|x\epsilon U, x\leq 15\right \}$$ and $$B = \left \{x|x \epsilon U, 0 < x \leq 25\right \}$$, list the elements of the following set and draw Venn diagram:
$$A$$ \ $$B$$

$$U=\{1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25\}$$
$$A=\{1,2,3,4,5,6,7,8,9,10,11,12,13,14,15\}$$
$$B=U$$
$$A$$\$$B$$
$$=\phi $$
$$A$$ is a subset of $$B$$.

941700_559247_ans_fa6e33d68ad54d1794c4cf7b61f2cf4d.png


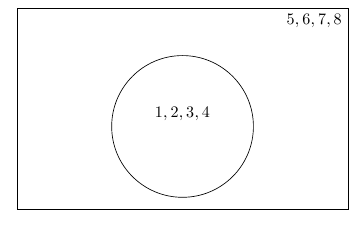
If $$A = \left \{1, 2, 3, 4\right \}, U = \left \{1, 2, 3, 4, 5, 6, 7, 8\right \}$$, find $$A'$$ in $$U$$ and draw Venn diagram

$$A=\{1,2,3,4\}$$
$$U=\{1,2,3,4,5,6,7,8\}$$
$$A'=\{5,6,7,8\}$$

1158039_559243_ans_7c94e001e17f44ba920825cb9bae3d22.png


Represent the following set by using their standard notations: Set of positive integers

Set of positive integer $$= Z^+$$


Let $$A$$ be the set of all even natural numbers. What is the complement of $$A$$ in $$\mathbb {N}$$?

If we remove all even natural numbers from $$\mathbb {N}$$, we are left with all odd natural numbers. Hence
$$A' = \left \{x |x\epsilon \mathbb {N}\text {and x is odd}\right \}$$.
Observe $$A\cup A' = \mathbb {N}$$.


Let $$A$$ and $$B$$ be subsets of a set $$U$$. Identify if the given statement is right or wrong  
$$A\cup A' = U$$

$$A$$ and $$B$$ are subset of $$U$$.
$$A\cup A' = A\cup (U-A) $$(bacause $$A'=U-A$$)
$$A\cup A' = U $$(Complement law)


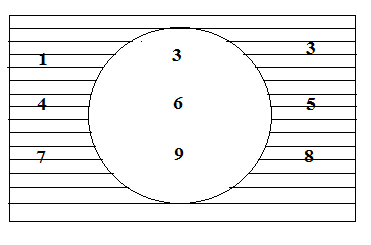
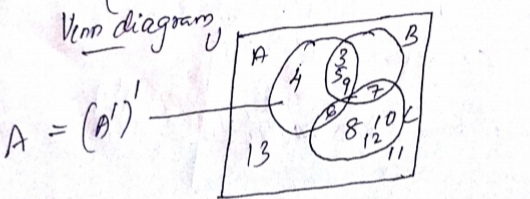
Suppose $$U = \left \{1, 2, 3, 4, 5, 6, 7, 8, 9\right \}, A = \left \{1, 2, 3, 4\right \}$$ and $$B = \left \{2, 4, 6, 8\right \}$$. Write down the following sets:
$$A'$$. How $$(A\cup B)'$$ is related to $$A'$$ and $$B'$$? What relation you see between $$(A\cap B)'$$ and $$A'$$ and $$B'$$?

$$U=\{1,2,3,4,5,6,7,8,9\}$$
$$A=\{1,2,3,4\}$$
$$B=\{2,4,6,8\}$$
$$A\cup B =\{1,2,3,4,6,8\}$$
$$(A\cup B)'=\{5,7,9\}$$
$$A'=\{5,6,7,8,9\}$$
$$B'=\{1,3,5,7,9\}$$
$$A'\cap B'=\{5,7,9\}$$
$$(A\cup B)'=A'\cap B'$$(De Morgans law)
$$A\cap B=\{2,4\}$$
$$(A\cap B)'=\{1,3,5,6,7,8,9\}$$
$$A'\cup B' =\{1,2,3,4,5,6,7,8,9\}$$
$$(A\cap B)'=A'\cup B'$$(De Morgans law)



Let $$U = \left \{1, 2, 3, 4, 5, 6, 7, 8, 9\right \}$$ and $$A$$ be the set of all multiples of $$3$$ in $$U$$. Find $$A'$$ and $$U$$

Given : $$U=\{1,2,3,4,5,6,7,8,9\}$$
Let $$A$$ be the set af all multiples of $$3$$ in $$U$$.
We observe $$A = \left \{3, 6, 9\right \}$$. 
If we remove these from $$U$$, the remaining elements are $$1, 2, 4, 5, 7,8$$. 
In the figure, the shaded portion shows $$A'$$
Hence $$A' = \left \{1, 2, 4, 5, 7, 8\right \}$$.


611120_559287_ans_1dda552d9902447b93f0915cbe2356f7.png


If $$U = \left \{1, 2, 3, 4, 5\right \}$$ and $$A = \left \{2, 4, 5\right \}$$ then find $$A'$$.

$$U= \left \{1, 2, 3, 4, 5\right \}$$
$$A=\left \{2, 4, 5\right \}$$

$$A' = U - A$$
$$A' = \left \{1, 2, 3, 4, 5\right \} - \left \{2, 4, 5\right \}$$
$$\therefore A' = \left \{1, 3\right \}$$


Suppose $$U = \left \{3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13\right \}, A = \left \{3, 4, 5, 6, 9\right \}, B = \left \{3, 7, 9, 5\right \}$$ and $$C = \left \{6, 8, 10, 12, 7\right \}$$. Write down the following set and draw Venn diagram for :
$$C'$$

$$U=\{3,4,5,6,7,8,9,10,11,12,13\}$$
$$A=\{3,4,5,6,9\}$$
$$B=\{3,7,9,5\}$$
$$C=\{6,8,10,12,7\}$$
$$C'=\{3,4,5,9,11,13\}$$

945548_559256_ans_a3137f1f84c64cc984294141e45389c3.jpg


If U = {1, 2, 3, 4, 5, 6, 7, 8, 9} and A = {1, 2, 3, 4}, B = {2, 4, 6, 8}, C = {3, 4, 5, 6} then prove the following :
A' = {5, 6, 7, 8, 9}

$$A = \{ 1, 2, 3, 4\}$$
$$U = \{ 1, 2, 3, 4, 5, 6, 7, 8, 9\}$$
$$A' = U - A =\{ 5, 6, 7, 8, 9\}$$
Hence proved.


Given : A = {2, 3}, B = {4, 5}, C = {5, 6}, then prove the following :
$$(A  \times \, B) \, \cup \, (B \, \times \, C)$$ = {(2, 4), (2, 5), (3, 4), (3, 5)} $$\cup$$ {(4, 5), (4, 6), (5, 5), (5, 6)} = All the ordered pairs as they are disjoint.

$$A = \{ 2,3\};$$         $$B = \{ 4,5\};$$           $$C = \{ 5,6\}$$ 
$$(A\times B) = \{(2,4), (2,5), (3, 4) , (3,5)\}$$
$$(B\times C) = \{(4,5), (4,6), (5, 5) , (5,6)\}$$
$$(A\times B)\cup (B\times C) = \{(2,4), (2,5), (3, 4) , (3,5), $$$$(4,5), (4,6), (5, 5) , (5,6)\}$$
Hence all the ordered pairs are disjoint.


Set $$ A=\left\{ x:x\ \in\ I,{ x }^{ 4 }-{ x }^{ 3 }-{ 2x }^{ 2 }+2x=0 \right\}$$
      $$ B=\left\{ x:x\ \in\ N,{ 2x }^{ 2 }-1<7 \right\}$$
Are $$A$$ and $$B$$ comparable?

Yes.
In fact $$A=\left\{ -\surd  { 2 } ,0,1\surd  { 2 }  \right\}$$
and $$B=\left\{1\right\}$$ so that $$B\subset A$$.


List out the element :
$$A =$$ set of odd numbers between $$50$$ and $$75$$ 
$$B =$$ the first ten squares of natural numbers
$$C =$$ $$ \{x : x \in z, \, -5 < n < + 6\}$$

$$A=\left \{ 51,53,55,57,59,61,63,65,67,69,71,73 \right \}$$

$$B=\left \{ 1,4,9,16,25,36,49,64,81,100 \right \}$$

$$C=\left \{ -4,-3,-2,-1,0,1,2,3,4,5 \right \}$$


If $$U = \{ 1,2,3,4,5,6,7,8,9,10\} $$                                                      
                        $$A = \{ 1,2,6,7\} $$
                        $$B = \{ 3,4,5,1\} $$
                        $$C = \{ 6,7,8,4\} $$
Find
(i)$${\left( {A \cup B} \right)^\prime } \cap {\left( {A \cup C} \right)^\prime }$$
(ii)$$(C' - A) - \left( {A - C} \right)$$
(iii)$$\left( {B \cap C} \right) \cup \left( {A \cap C} \right)$$
(iv)$${\left( {A \cup B \cup C} \right)^\prime }$$

$$1. A\cup B = \{1,2,3,4,5,6,7\}$$
$$\implies (A \cup B)^{'} = \{8,9,10\}$$
$$A \cup C =\{1,2,4,6,7,8\}$$
$$(A \cup C)^{'} = \{3,5,9,10\}$$
$$\implies (A \cup B)^{'} \cap (A \cup C)^{'} = \{9,10\}$$
$$2. C^{'} = \{1,2,3,5,9,10\}$$
$$C^{'}-A = \{3,5,9,10\}$$
$$A-C = \{1,2\}$$
$$(C^{'}-A) - (A-C) = \{3,5,9,10\}$$
$$3. B \cap C = \{4\}$$
$$A \cap C = \{6,7\}$$
$$(B \cap C) \cup (A \cap C) = \{4,6,7\}$$
$$4. A\cup B\cup C = \{1,2,3,4,5,6,7,8\}$$
$$(A\cup B \cup C)^{'} = \{9,10\}$$


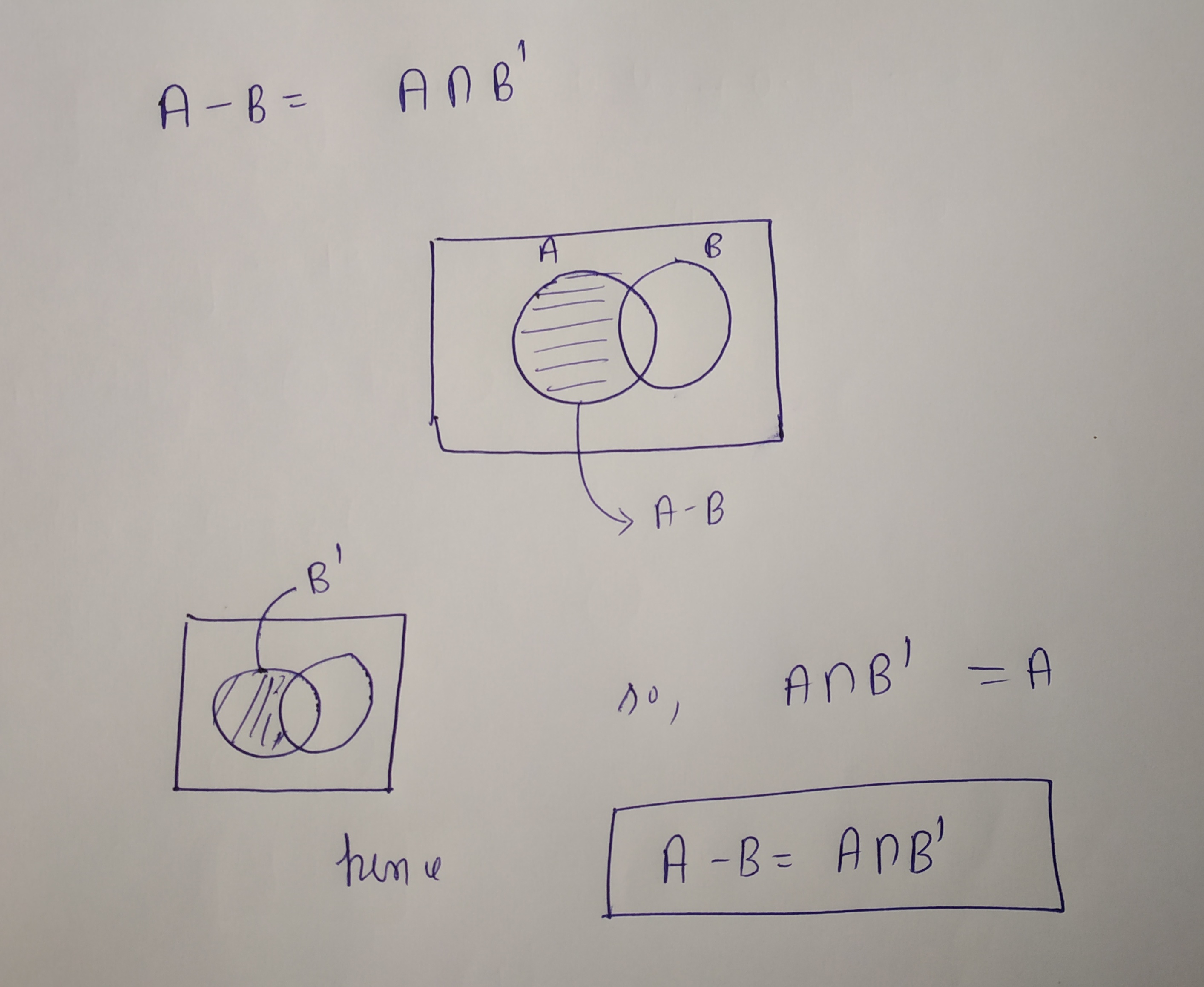
$$A-B=A\cap \bar{B}$$


1326516_1063423_ans_1b460acfee3043a1825e9baa395573b9.jpg


List the elements of the following sets.
(i)G={all the factors of 20}
(ii)F={the multiple of 4 between 17 and 61 which are divisible by 7}
(iii)S={x:x is a letter in the word 'MADAM'}
(iv)P={x:x is a whole number between 3.5 and 6.7}

(i) G={1,2,4,5,10,20}
(ii) F={28,56}
(iii) S={A,D,M}
(iv) P={4,5,6}


Fill in the blanks to make each of the following a true statement:
$$A A = $$.

$$A ∩ A’ = \phi$$


Find sets $$A, B$$ and $$C$$ such that $$A B, B C$$ and $$A C$$ are non-empty sets and $$A B C = \phi$$.

Let, $$A = \left \{ 0,1 \right \}$$
$$B = \left \{ 1,2 \right \}$$
And, $$C = \left \{ 2,0 \right \}$$
Accordingly,
$$A ∩ B = \left \{ 1 \right \}$$
$$B ∩ C = \left \{ 2 \right \}$$
And, $$A ∩ C = \left \{ 0 \right \}$$
$$\therefore A ∩ B, B ∩ C$$ and $$A ∩ C$$ are not empty sets.
However, $$A ∩ B ∩ C = \phi$$.


Taking the sets of natural numbers as the universal set, write down the complements of the following sets
$$\left\{x:x\ is\ a\ perfect\ square \right\}$$

{x:x∈Nx:x∈N and is not perfect square }


$$\mu$$  = {a, b, c, d, e, f, g, h, i, j}
P = {a, b, c, e}.
Q = {b, c, d, f} and
R = {c, f, h, i, j}
Number of elements of the set $$(P \cap Q)' \cup R$$ is:

$$P \cap Q =  \{b, c\}$$
$$(P \cap Q)' = \{a, d, e, f, g, h, i, j\}$$
$$(P \cap Q)' \cup R = \{a, c, d, e, f, g, h, i, j\}$$
$$\Rightarrow n((P \cap Q)' \cup R) = 9$$


$$A$$ is a set containing $$n$$ elements. A subset $$P$$ of $$A$$ is chosen. The set $$A$$ is reconstructed by replacing the elements of $$P$$. A subset $$Q$$ of $$A$$ is again chosen. Let $$\space ^nC_2\times k^{n-2}$$  be the number of ways of choosing $$P$$ and $$Q$$ so that $$P\cap Q$$ contains exactly two elements.Find $$k$$ ?

Let $$A = \left\{a_1, a_2, a_3, ... , a_n\right\}$$
The two elements $$P$$ and $$Q$$ such that $$P\cap Q$$ can be chosen out of $$n$$ is $$\space ^nC_2$$ ways a general element of $$A$$ must satisfy one of the following possibilities : (here general element be $$a_i(1\le i\le n)$$)
$$(i) \space a_i\in P$$ and $$a_i \in Q $$
$$(ii)\space a_i \in P$$ and $$a_i \notin Q$$
$$(iii)\space a_i\notin P$$ and $$a_i \in Q$$
$$(iv)\space a_i \notin P$$ and $$a_i \notin Q$$
Let $$a_1, a_2 \in P\cap Q$$
there is only one choice each of them (i.e. (i) choice) and three choices (ii), (iii) and (iv) for each of remaining $$(n-2)$$ elements.
$$\therefore\quad$$ No. of ways of remaining elements $$= 3^{n-2}$$
Hence, the no. of ways in which $$P\cap Q$$ contains exactly two elements $$= \space ^n{C}_{2} \times 3^{n-2}$$


Consider the non-empty set consisting of children in a family. 

$$(\alpha)$$ x is a brother of y.
The above relation is symmetric & transitive
If true enter 1 else 0 

Given xRy ⇒ x is brother of y.

(i) xRx ⇒ x is brother of x [not possible]
∴R is not reflexive.

(ii) xRy ⇒ x is brother of y 
then, we can say y is brother/sister of x 
$$\therefore y\not Rx$$
∴R is not symmetric.

(iii) if xRy & yRz ⇒ x is brother of y & y is brother of z
then, we can say x is brother of z i.e, xRz
∴ if xRy & yRz ⇒ xRz
∴R is transitive.


The set of all x for which $$\displaystyle \log \left ( 1+x\right )\leq x$$ is equal to $$\displaystyle \left ( -1,\infty  \right ).$$
True or False ? true=5 False=8

Given inequality $$\log(1+x)\leq x$$
For above inequality to be defined,
$$1+x\geq 0$$ 
$$\Rightarrow x \ge -1$$

Since $$\log x\leq 0$$ for all $$x\epsilon (0,1)$$ and $$\log x\leq x$$ for all $$x\epsilon (1,\infty)$$

Hence,$$x\geq -1$$.
The solution set is $$(-1,\infty)$$.


Rewrite $$\displaystyle \left | x-1 \right |< 3$$ in the form $$\displaystyle a\leq x\leq b.$$,
b-a=?

$$\displaystyle \pm \left ( x-1 \right )< 3\Rightarrow x-1< 3\Rightarrow x< 4$$ and $$\displaystyle -\left ( x-1 \right )< 3 \Rightarrow -2< x$$ $$\displaystyle \therefore \left | x-1 \right |< 3 \Rightarrow -2< x< 4.$$


The set S and E are defined as given below: $$\displaystyle S=\left \{ \left ( x, y \right ):\left | x-3 \right |< 1 and \left | y-3 \right |< 1 \right \}$$ $$\displaystyle E=\left \{ \left ( x, y \right ):4x^{2}+9y^{2}-32x-54y+109\leq 0 \right \}$$ then $$\displaystyle S\subset E$$ 
If true enter 0 else enter 1.

In $$E,4{x^{2}}+9{y^{2}}-32{x}-54{y}+109\leq 0$$
$$\implies \dfrac{(x-4)^{2}}{9}+\dfrac{(y-3)^{2}}{4}\leq 1$$
$$\implies (x,y)$$ are points on or inside the ellipse
$$\implies x-3\in [-2,4],|y-3|\in [0,2]$$
$$\implies S \subset E$$
The correct answer is $$0$$


Alternately:-
Ans. $$True$$.
We first observe that $$|x-3|<1$$
$$\Rightarrow -1<x-3<1$$
$$\Rightarrow 2<x<4$$
Similarly $$|y-3|<1\rightarrow2<y<4$$.
Thus $$S$$ consists of all points inside the square bounded by the lines $$x=2$$, $$x=4$$, $$y=2$$ and $$y=4$$.
This square region is shown in the figure by vertical lines.
Again $$4x^{ 2 }+9y^{ 2 }-32x-54y+109$$
$$=4(x^{ 2 }-8x+16)+9(y^{ 2 }-6y+9)-36$$
$$=4(x-4)^{ 2 }+9(y-3)^{ 2 }-36$$.
Hence $$4x^{ 2 }+ 9y^{ 2 }-32x-54y+109\le0$$ 
$$\Rightarrow 4(x-4)^{ 2 }+9(y-3)^{ 2 }-36\le0$$
$$\Rightarrow \dfrac { \left( x-4 \right) ^{ 2 } }{ 9 } +\dfrac { \left( y-3 \right) ^{ 2 } }{ 4 } \le 1$$.
Thus the set $$E$$ consists of all points within and on the ellipse whose centre is $$(4,3)$$ and semi major and minor axes are $$3$$ and $$2$$ respectively. This region is shown by dots in the diagram.
We now show that $$S\subset E$$.


$$A'$$

Universal Set $$ =\{x:x\epsilon N, 10\le x\le 35\} $$
$$\therefore$$ {$$ 10,11,12,1314,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35 $$ }

And  $$ A=\{x\epsilon N, x\le 16\} $$
$$\therefore A = \{ 1,2,3,4,5,6,7,8,9,10,11,12,1314,15,16 \}$$

So, $$ {A}' =U- A =  $$ { $$ 17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35 $$ } $$ = \left\{ x:x\epsilon N:17\le x \le 35 \right\} $$


$$B'$$

Universal Set $$ =\{x:x\epsilon N, 10\le x\le 35\} $$
 { $$ 10,11,12,1314,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35 $$ }

And $$B=\{30,31,32,33,34,35 \}$$

So, $$ {B}' =U- B =\{10,11,12,1314,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29\}$$
$$ = \left\{ x:x\epsilon N: 10\le x \le29 \right\} $$


If $$\xi$$ = {$$a, b, c, d, e, f,  g, h$$}, $$A = $$ {$$b, c, d, e, f$$}, $$B =$$ {$$a, b, c, g, h$$} and $$C =$$ {$$c, d, e, f, g$$} ,
then find $$C$$$$'$$$$ - B$$$$'$$.

$$\xi $$ $$= \{a,b,c,d,e,f,g,h\}$$

$$A = \{b,c,d,e,f\}$$

$$B = \{a,b,c,g,h\}$$

$$C = \{c,d,e,f,g\}$$

$${ C' }$$ $$= \{a,b,h\}$$

$${ B'}$$ $$= \{d,e,f\}$$

$${ C' }$$ - $${ B' }$$ $$= \{a,b,h\} - \{d,e,f\}$$

               $$= \{a,b,h\}$$


$$N'$$

Universal Set $$ =\{x\epsilon Z: -6< x\le 6\} $$
$$\therefore U =\{ -5,-4,-3,-3,-2,-1,0,1,2,3,4,5,6 \}$$

And N $$ = \{0,1,2,3,4,5, 6......... \}$$

So, $$ {N}'=U- N =  \{ -5,-4,-3,-2,-1 \}$$.


Taking the set of natural numbers as the universal set, write down the complements of the following sets:
(i) {$$x : x$$ is an even natural number} 
(ii) {$$x : x$$ is an odd natural number} 
(iii) {$$x : x$$ is a positive multiple of $$3$$} 
(iv) { $$x : x$$ is a prime number }
(v) {$$x : x$$ is a natural number divisible by $$3$$ and $$5$$}
(vi) {$$ x : x$$ is a perfect square } 
(vii) { $$x : x$$ is a perfect cube}
(viii) $$\left \{x : x + 5 = 8 \right \}$$ 
(ix) $$\left \{x : 2x + 5 = 9\right \}$$ 
(x) $$\left \{x : x \geq 7\right \}$$ 
(xi) $$\left \{x : x \epsilon N \ and \ 2x + 1 > 10 \right \}$$

U= N: Set of natural numbers
(i) $$\{x:x \text {is an even natural number}\}' = \{x:x \text{ is an odd natural number}\}$$
(ii) $$\{x:x \text {is an odd natural number}\}' = \{x:x \text {is an even natural number}\}$$
(iii) $$\{x:x \text{ is a positive multiple of 3}\}' = \{x:x \in N \text{ and x is not a multiple of 3}\}$$
(iv) $$\{x:x \text {is a prime number}\}' = \{x:x \text {is a positive composite number and x=1}\}$$
(v) $$\{x:x \text{is a natural number divisible by 3 and 5}\}' $$
$$= \{x:x \text{is a natural number that is not divisible by 3 or 5}\}$$
(vi) $$\{x:x \text {is a perfect square}\}' = \{x:x \in N \text {and x is not a perfect square}\}$$
(vii) $$\{x:x \text{is a perfect cube}\}' = \{x:x \in N \text {and x is not a perfect cube}\}$$
(viii) $$\left \{x:x+5=8\right \}' = \left \{x:x \in N \text {and } x\neq 3\right \}$$
(ix) $$\left \{x:2x+5=9\right \}' = \left \{x:x \in N \text {and} x\neq 2\right \}$$
(x) $$\left \{x:x\geq 7\right \}' = \left \{x:x\in N \text {and} x < 7\right \}$$
(xi) $$\left \{x:x \epsilon N \text{and} 2x+1>10\right \}' = \left \{x:x\in N and x\leq \frac{9}{2}\right \}$$


If $$U = \left \{x|x \leq 25, x\epsilon \mathbb {N}\right \}, A = \left \{x|x\epsilon U, x\leq 15\right \}$$ and $$B = \left \{x|x \epsilon U, 0 < x \leq 25\right \}$$, list the elements of the following set and draw Venn diagram:
$$A'$$ and $$U$$

$$U=\{1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25\}$$
$$A=\{1,2,3,4,5,6,7,8,9,10,11,12,13,14,15\}$$
$$B=U$$
$$A'=\{16,17,18,19,20,21,22,23,24,25\}$$

941680_559245_ans_2c70dfcaf4a542149b8e32af24320a7e.png


Write the following set in set builder form:
$$\left \{1, 4, 7, 10, 13, 16, ...\right \}$$

$$\{1,4,7,10,13,16......\}$$
$$\{x:x\in N\quad and\quad3x+1\}$$
$$N$$ is the set of all natural numbers.


If $$U = \left \{x|x \leq 25, x\epsilon \mathbb {N}\right \}, A = \left \{x|x\epsilon U, x\leq 15\right \}$$ and $$B = \left \{x|x \epsilon U, 0 < x \leq 25\right \}$$, list the elements of the following sets and draw Venn diagram:
$$B'$$ in $$U$$

$$U=\{1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25\}$$
$$A=\{1,2,3,4,5,6,7,8,9,10,11,12,13,14,15\}$$
$$B=\{1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25\}$$
$$B=U$$
$$B'=\phi$$

941694_559246_ans_3274b19f3db5457689dc8141a01f2a28.png


Suppose $$U = \left \{1, 2, 3, 4, 5, 6, 7, 8, 9\right \}, A = \left \{1, 2, 3, 4\right \}$$ and $$B = \left \{2, 4, 6, 8\right \}$$. How $$(A\cup B)'$$ is related to $$A'$$ and $$B'$$? What relation you see between $$(A\cap B)'$$ and $$A'$$ and $$B'$$?

$$U=\left\{ 1,2,3,4,5,6,7,8,9, \right\} $$
$$ A=\left\{ 1,2,3,4 \right\}$$
$$ B=\left\{ 2,4,6,8 \right\}$$
$$  A\cup B=\left\{ 1,2,3,4,6,8 \right\}$$
$${ \left( A\cup B \right)  }^{ ' }=\left\{ 5,7,9 \right\}$$
$$ { A }^{ ' }=\left\{ 5,6,7,8,9 \right\}$$
$$  { B }^{ ' }=\{ 1,3,5,7,9\} $$
$$ { A }^{ ' }\cap { B }^{ ' }=\left\{ 5,7,9 \right\} $$
$$ { \left( A\cup B \right)  }^{ ' }={ A }^{ ' }\cap { B }^{ ' }$$
$$A\cap B=\{ 2,4\}$$
$$ \\ { \left( A\cap B \right)  }^{ ' }=\left\{ 1,3,5,6,7,8,9 \right\} $$
$$ { A }^{ ' }\cup { B }^{ ' }={ \left( A\cap B \right)  }^{ ' }$$


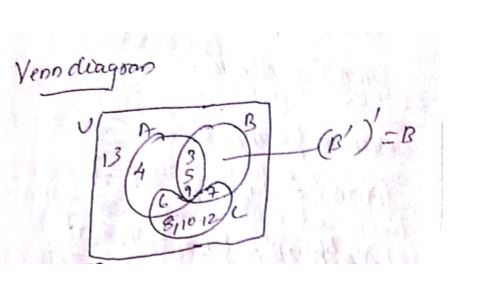
Suppose $$U = \left \{3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13\right \}, A = \left \{3, 4, 5, 6, 9\right \}, B = \left \{3, 7, 9, 5\right \}$$ and $$C = \left \{6, 8, 10, 12, 7\right \}$$. Write down the following sets and draw Venn diagram for each:
$$(B')'$$

 $$\left( B' \right)^{'}=B$$
 $$\left( B' \right) =\left\{ 3,7,9,5 \right\}$$

1174486_559258_ans_93393ad927e84384bdf3163a81bf3006.JPG


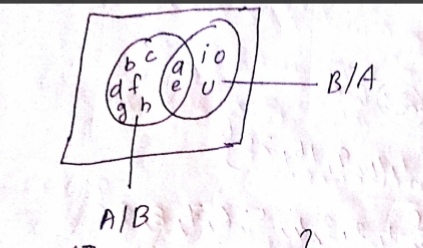
Find $$(A\setminus B)$$ and $$(B\setminus A)$$ for the following sets and draw Venn diagram:
$$A = \left \{a, b, c, d, e, f, g, h\right \}$$ and $$B = \left \{a, e, i, o, u\right \}$$

$$A=\{a,b,c,d,e,f,g,h\}$$
$$B=\{a,e,i,o,u\}$$
$$A/B=A-B$$
$$=\{b,c,d,f,g,h\}$$
$$B/A=B-A$$
$$=\{i,o,u\}$$

945561_559266_ans_af97cabebdf74aa9b5ff0f52753dc18b.jpg


Let $$A$$ and $$B$$ be subsets of a set $$U$$. Identify the given statement is right or wrong:
$$A\triangle B = B\triangle A$$

  • $$A$$  and $$B$$ subset of $$U$$.
$$A\Delta B =(A\cup B)-(A\cap B)$$
$$B\Delta A=(B\cup A)-(B\cap A)$$
$$A\cup B=B\cup A$$
$$A\cap B = B\cap A$$
So,$$A\Delta B = B\Delta A$$
The given statement is right.


Suppose $$U = \left \{3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13\right \}, A = \left \{3, 4, 5, 6, 9\right \}, B = \left \{3, 7, 9, 5\right \}$$ and $$C = \left \{6, 8, 10, 12, 7\right \}$$. Write down the following set and draw Venn diagram for :
$$(A')'$$

$$U=\{3,4,5,6,7,8,9,10,11,12,13\}$$
$$A=\{3,4,5,6,9\}$$
$$B=\{3,7,9,5\}$$
$$C=\{6,8,10,12,7\}$$
$$(A')'=A$$(law of complement)

945552_559257_ans_b9845343d5fa43b9987affb8a121fdc8.jpg


Let $$A$$ and $$B$$ be subsets of a set $$U$$. Identify the given statement is right or wrong:
$$(A/B)' = A'/B'$$

  • $$A$$ and $$B$$ Subset of set $$U$$.
$$(A/B)'=(A-B)'$$
$$=U-(A-B)$$
$$=U-A+B$$
$$A'/B' = U-A-(U-B)$$
$$=U-A+B$$
So,$$(A/B)'=A'/B'$$


Find $$(A\setminus B)$$ and $$(B\setminus A)$$ for the following sets and draw Venn diagram:
$$A = \left \{1, 2, 3, 4, 5, 6\right \}$$ and $$B = \left \{2, 3, 5, 7, 9\right \}$$

$$A=\{1,2,3,4,5,6\}$$
$$B=\{2,3,5,7,9\}$$
$$A/B=\{1,4,6\}$$
$$B/A=\{7,9\}$$

945563_559267_ans_d6f810290bb8465594219e459e182e09.jpg


Suppose $$U = \left \{3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13\right \}, A = \left \{3, 4, 5, 6, 9\right \}, B = \left \{3, 7, 9, 5\right \}$$ and $$C = \left \{6, 8, 10, 12, 7\right \}$$. Write down the following sets and draw Venn diagram for each:
$$(C')'$$

$$U=\{3,4,5,6,7,8,9,10,11,12,13\}$$
$$A=\{3,4,5,6,9\}$$
$$B=\{3,5,7,9\}$$
$$C=\{6,8,10,12,7\}$$
$$(C')'=C$$

945553_559259_ans_fbc8f02a5434464e946ba4d0902abecf.jpg


In a class, there are $$100$$ students out of which $$45$$ study mathematics, $$48$$ study physics, $$40$$ study chemistry, $$12$$ study both mathematics and physics, $$11$$ study both physics and chemistry, $$15$$ study both mathematics  and chemistry and $$5$$ study all three subjects. A student is selected at random, then find the probability that the selected student studies $$- (a)$$ only one subject  $$(b)$$ neither physics nor chemistry

Total students $$= 100$$
$$N(M)=45$$              N(M) represents number of students studying maths
$$N(P)=48$$
$$N(C)=40$$
$$N(M \ and \ P) = 12,\,  (M \ and \ C) = 15, N(P \ and \ C) = 11$$
$$N(M\ and \ P \ and \ C) = 5$$
student studying only maths
$$= N(M)-N(M \ and \ P)- N(M \ and \ C)+N(M\ \&\ P\ \& \ C)$$
$$= 45-12-15+5$$
$$= 23$$
student studying only physics
$$= N(P)-N(P \ and \ M)-N(P \ and \ C)+N(P\ \& \ M\ \& \ C)$$
$$= 48-12-11+5=30$$
students studying only chem 
$$=N(C)-N(C\ and\ P)-N (C\ and \ M)+N(P\ and\ C\ \& \ M)$$
$$=40-11-15+5=19$$
a) probability that student studies only one subject 
$$=\dfrac{19+30+23}{100}=0.72$$ 
b) probability that student studies neither physics nor chemistry 
$$=$$ probability that student studies only Maths $$=\dfrac{23}{100}=0.23$$

1061729_793355_ans_f7ec424d2ce34ad4bc33c8ff6a17777e.PNG


If $$S=\{ 2, 4, 6, 8, 10, 12\}$$ and $$A=\{ 4, 8, 12\}$$, find A'.

$$S=$$$$(2,4,6,8,10,12)$$
$$A=(4,8,12)$$
$$A$$ is a subset of $$S$$ as set $$S$$ contains all the elements of set $$A$$.
$$A'$$ contains all the elements that are in set $$S$$ but not in set $$A$$.
Hence, $$A'=$$$$\{2,6,10\}$$


In a group of 1000 people three are 750 who can speak Hindi and 400 who can speak Bengali. How many can speak both Hindi and Bengali  ? 

$$\textbf{Step -1: Stating the given values}$$
                  $$\text{Let H and B be the set of people who can speak Hindi and bengali respectively.}$$
                  $$\text{Given, }n(H\cup B)=1000$$
                                $$n(H) = 750$$
                                $$n(B) = 400$$
                                $$n(H\cap B) = ?$$
$$\textbf{Step -2: Using General addition rule of sets.}$$
                  $$n(H\cup B) = n(H) + n(B) - n(H\cap B)$$
                  $$1000 = 750 + 400 - n(H\cap B)$$
                  $$n(H\cap B)= 150$$
                  $$\text{Hence 150 people can speak both Hindi and Bengali.}$$

$$\textbf{Hence, 150 people can speak both Hindi and Bengali.}$$


If $$x^2+6x-5=\bar{A}+ A$$ where A represents a set. Find x.

$$A+\bar A=1$$
$$x^{2}+6{x}-5=\bar A+A$$
$$\implies x^{2}+6{x}-5=1$$
$$x^{2}+6{x}-6=0\implies x=\dfrac{-6\pm\sqrt{36+24}}{2}=-3\pm\sqrt{15}$$


If U = {0,1,2,3,4,5,6,7,8,9,10}, A = {1,2,3,4,5}, B = {2,4,6,8,10}, find (A-B)'.

$$U=\left \{ 0,1,2,3,4........10 \right \}$$ 
$$A=\left \{ 1,2,3,4,5 \right \}$$ 
$$B=\left \{ 2,4,6,8,10 \right \}$$ 
$$A\cup B=\left \{ 2,4 \right \}$$ 
$$(A-B)=\left \{ 1,3,5 \right \}$$ 
$$(A-B)'=\left \{ 0,2,4,6,8,10 \right \}$$


if $$(1,3),(2,5)$$ and $$(3,3)$$ are three-element of $$A \times B$$ and the total number of element in $$A \times B$$ is $$6$$ then the remaining element of $$A \times B$$ are

$$A\times B=6$$
$$3$$ elements of $$A$$ are $$\left\{1, 2, 3\right\}$$
$$2$$ elements of $$B$$ are $$\left\{3, 5\right\}$$
Total elements in $$A\times B=3\times 2=6$$
Remaining elements of $$A\times B$$ are
$$(1, 5),\ (2, 3),\ (3, 5)$$


Given, universal set = $$\left \{ x\epsilon Z:-6< \times \leq6 \right \}$$ N={n:n is a non-negative number} and
P={x:x is a non-positive number}. Find 
(i)N' ,
(ii)P.

Consider the given function,

$$ U=\left\{ x\in Z:-6<x\le 6 \right\} $$

$$ N=\left\{ n:n\,\text{is}\,\text{a}\,\text{non}\,\text{negative}\,\text{number} \right\} $$

$$ P=\left\{ x:x\text{is}\,\text{a}\,\text{non}\,\text{positive}\,\text{number} \right\} $$

Then,

$$ U=\left\{ -5,-4,-3,-2,-1,0,1,2,3,4,5 \right\} $$

$$ N=\left\{ 0,1,2,3,4,5 \right\} $$

$$ P=\left\{ -5,-4,-3,-2,-1,0 \right\} $$

$$ (i).N'=U-N $$

$$ =N'=\left\{ 1,2,3,4,5 \right\} $$

$$\left( ii \right).P=\left\{ -5,-4,-3,-2,-1,0 \right\}$$

Hence, this is the answer.


Match the roster form with set builder form.

1). $$ \left \{ x \,is\, prime\, number\, and\, a\, divisor\, of\, 6 \right \} $$

Prime number $$ = 2,3,5,7 $$

Divisor of $$ 6 = 1,2,3,6 $$

Numbers which are both prime and divisor of 6 

$$ = \left \{ 2,3 \right \} $$

2). $$ \left \{ x:x \,is\, an\, odd \,natural\, number \,smaller\, then\, 10\, \right \} $$

The natural number starts from $$1$$ onwards.

Numbers which are both odd and natural 

which are less then $$ 10 = \left \{ 1,3,5,7,9 \right \} $$

3). $$ \left \{ x:x\, is\, a\, natural\, number\, and \,divisor\, of \,6\,  \right \} $$

Natural starts from 1 onwards 

Divisors of $$ 6 = 1,2,3,6 $$

Numbers which are both natural numbers 

and divisor of $$ 6 = \left \{ 1,2,3,6 \right \} $$

4). $$ \left \{ x:x\, is\, a\, letter\, of \,the\, word\, MATHEMATICS \right \} $$

Repetitions are not considered and 

solution set consists of letters only once 

solution set $$ = \left \{ M,A,T,H,E,I,C,S \right \} $$

A] $$ \left \{ 1,2,3,6 \right \} = 3] \left \{ x:x \,is \,a \,natural\, number\, and\, \,divisors\, of\, 6 \,\right \} $$

B] $$\left \{ 2,3 \right \} = 1]\left \{ x:x \,is\, a\, prime \,number\, and \,divisor\, of\, \,6 \right \} $$

C]$$ \left \{ M,A,T,H,E,I,C,S \right \} = 4 \left \{ x:x\, is \,a \,letter\, of\, word\, \,MATHEMATICS \right \} $$

D]$$ \left \{ 1,3,5,7,9 \right \} = 2]\left \{ x:x\, is\, an\, odd \,natural\, number\, \,smaller\, then \,10 \right \} $$ 


Classify the following as a finite or infinite set:
(i) $$A=\{ x\epsilon N:\quad (x-1)(x-2)=0\} $$
(ii) $$B=\{ x\epsilon N:\quad x\quad is\quad odd\} $$

(i) $$A=\left\{ x\in N:(x-1)(x-2)=0 \right\} $$
finite
(ii) $$B=\left\{ x\in N:x\quad is\quad odd \right\} $$
infinite


If $$A$$ and $$B$$ be two sets containing $$6$$ and $$3$$ elements respectively, what can be the minimum number of elements in $$A\cup B$$. Also, find the maximum number of elements in $$A\cup B$$

$${\textbf{Step -1: Find maximum number of elements.}}$$
                  $${\text{Given,}}$$
                  $$n(A) =6$$
                  $$n(B) =3$$
                  $${\text{Minimum number of elements in}}$$ $$A\cup B=6.$$
                  $${\text{A is subset of B.}}$$
                  $${\text{Maximum number of elements in}}$$ $$A\cup B=6+3=9.$$
                  $${\textbf{[All element taken in both set A and B and elements in both sets are different.]}}$$
$${\textbf{Hence , maximum number of elements in}}$$ $$\mathbf{(A \cup B) =9.}$$


In an exam, $$27\%$$ students failed in Maths, $$24\%$$ students failed in English and $$20\%$$ students failed in both the subjects.
i) Find the percentage of students who failed in any of the subjects.
ii) Find the percentage of students who passed in both the subjects.
iii) If $$414$$ students passed in both the subjects, find the total number of students.

$$n\left( A \right) =27,n\left( B \right) =24,n\left( A\bigcap { B }  \right) =20$$
i) $$n\left( A\bigcup { B }  \right) =27+24-20$$
$$=31$$%
ii) $$n\left( \bar { A\bigcup { B }  }  \right) =100-31=69$$%
iii) $$69$$% of x$$=414$$
$$\Rightarrow \cfrac { 69 }{ 100 } \times x=414\Rightarrow x=\cfrac { 414\times 100 }{ 69 } $$
$$=600$$


Given $$\phi , A = \{ 1,3 \} , B = \{ 1,5,9 \} , C = \{ 1,3,5,7,9 \}$$ , write $$\subset$$ or $$\not\subset$$ in the following   

(i) $$\phi....... \dot B$$
(ii) $$A.......\dot C$$
(iii) $$A.......\dot B$$
(iv) $$B.......\dot C$$
(v) $$\dot C$$.......$$\dot C$$

$$(i) \phi \subset \dot{B}$$

$$(ii) A \not\subset\dot{C}$$

$$(iii) A \not\subset\dot{B}$$

$$(iv) B \not\subset\dot{C}$$

$$(v) \dot{C} \subset \dot{C}$$


Write the following set in roster form :

(i)  $$A =$$ {  $$x : x$$  is an integer and  $$- 3 < x < 7$$ }

$$A={x;x\quad is \quad an\quad integer\quad and\quad -3<x<7}$$
In roster form
$$A{-2,-1,0,1,2,3,4,5,6}$$


Let, $$A=\{1,2,3,4\}$$ and $$U=\{1,2,3,4,5,6,7,8,9,10\}$$. Then find $$A'$$.

Now,

$$A=\{1,2,3,4\}$$ and $$U=\{1,2,3,4,5,6,7,8,9,10\}$$

Then 

$$A'=U-A$$

$$A'=\{5,6,7,8,9,10\}$$.


Let $$B=\{2,4,6,8\}$$ and $$U=\{1,2,3,4,5,6,7,8,9,10\}$$. Then find $$B'$$.

Now,
$$B=\{2,4,6,8\}$$  and $$U=\{1,2,3,4,5,6,7,8,9,10\}$$
Then 
$$B'$$
$$=U-B$$
$$=\{1,3,5,7,9,10\}$$.


Out of $$100$$ students $$15$$ passed in English $$12$$ passed in Mathematics, $$8$$ Science, $$4$$ in English and Science in all the three. Find how many passed in more than one subject only?

Given$$n\left(  \cup  \right) = 100$$
$$n\left( E \right) = 15,$$
$$n\left( M \right) = 12,$$
$$n\left( S \right) = 8$$
$$n\left( {E \cap M} \right) = 6,n\left( {M \cap S} \right) = 7,$$
$$n\left( {E \cap S} \right)....4,\,and\,n\left( {E \cap M \cap S} \right) = 4$$
$$a = n\left( {E \cap M \cap S} \right) = 4$$
$$a + d = n\left( {M \cap S} \right) = 7$$
$$\therefore \,\,\,\,\,\,\,\,d = 3$$
$$a + b = n\left( {M \cap E} \right) = 6$$
$$\therefore \,\,\,\,\,b = 2$$
$$a + c = n\left( {S \cap E} \right) = 4$$
$$\therefore \,\,\,\,c = 0$$
$$\,\,\,\,\,\,\,\,a + b + d + e = n(M) = 12$$
$$\therefore \,\,\,4 + 2 + 3 + e = 12$$
$$\therefore \,e = 3$$
$$\,\,\,\,\,\,a + b + c + g = 15$$
$$\therefore \,4 + 2 + 0 + g = n(E) = 15$$
$$\therefore \,g = 9$$
$$\,\,\,a + c + d + f = n(S) = 8$$
$$\therefore \,4 + 0 + 3 + f = 8$$
$$\therefore \,f = 1$$
The number of students pass in more than one subject  $$ = a + b + c + d = 4 + 2 + 0 + 3 = 9$$

1239746_1329459_ans_3e9d33da5ccd4fee80b5758d71b6ca79.JPG


Without using truth table, show that $$p\wedge (q\vee \sim p)\equiv p\wedge q$$.

$$P\cap  (q\vee \sim p)$$  
$$(P\cap q)\vee  (q\wedge \sim p)$$  
$$=(p\cap q)\vee I$$
$$=(P\cap q)$$


Let $$U=\{ 1,2,3,4,5,6\} ,A=\{ 2,3\} andB=\{ 3,4,5\} .Find\quad A',B',A'\cap B',A\cup B$$ and hence show that $$(A\cup B)=A'\cap B'.$$

A′=U−A={1,4,5,6}A′=U−A={1,4,5,6}
B′=U−B={1,2,6}B′=U−B={1,2,6}
A′∩B′={1,6}A′∩B′={1,6}
A∩B={2,3,4,5}A∩B={2,3,4,5}
∴(A∪B)′={1,6}=A′∩B′


Let $$A=\{3, 6, 12, 15, 18, 21\}, B=\{4, 8, 12, 16, 20\}, C=\{2, 4, 6, 8, 10, 12, 14, 16\}$$ and $$D=\{5, 10, 15, 20\}$$. Find $$A-B$$.

The given sets are:

$$A=\left\{3,6,12,15,18,21\right\},\quad B=\left\{4,8,12,16,20\right\}$$

$$C=\left\{2,4,6,8,10,12,14,16\right\},\ D=\left\{5,10,15,20\right\}$$

Therefore $$A- B=\left\{x:x\in A\ and\ x\notin B\right\}=\left\{3,6,15,18,21\right\}$$

$$\boxed {Hence, A-B=\left\{3,6,15,18,21\right\}}$$


If $$A=\{x\in C: x^2=1\}$$ and $$B=\{x\in C :x^4=1\}$$, then write $$A-B$$ and $$B-A$$.

given $$A=\left\{x\in c: x^2=1\right\}$$

               $$=\left\{x\in c: x=\pm 1\right\}$$

               $$=\left\{1, -1\right\}$$

so $$A=\left\{1, -1\right\}$$

similarly we get  $$B=\left\{1, -1, i, -i \right\}$$

$$A-B=\left\{1, -1\right\}-\left\{1, -1, i, -i\right\}$$

$$=\left\{\phi \right\}$$

$$B-A=\left\{1, -1, i, -i\right\}-\left\{1, -1\right\}$$

$$=\left\{i, -i\right\}$$


For any two sets of A and B, prove that $$A'\cup B=u\Rightarrow A\subset B$$.


Let $$x\in A$$. Then,

$$x\in A\Rightarrow x\in u\Rightarrow x\in A\cup B\Rightarrow x\in B$$           

   $$[\because x\not{\in}A']$$

$$\therefore A\subset B$$.



If $$U=\left\{1,2,3,4,5,6,7,8,9 \right\}, A=\left\{1,2,3,4 \right\}, B=\left\{2,4,6,8 \right\}$$ and $$C=\left\{1,4,5,6 \right\}$$, find :
$$C'$$

$$U=\left\{1,2,3,4,5,6,7,8,9 \right\}, A=\left\{1,2,3,4 \right\}, B=\left\{2,4,6,8 \right\}$$ and $$C=\left\{1,4,5,6 \right\}$$

$$C'=U-C=\left\{1,2,3,4,5,6,7,8,9 \right\}-\left\{1,4,5,6 \right\}$$$$=\left\{2,3,7,8,9 \right\}$$


If $$U=\left\{1,2,3,4,5,6,7,8,9 \right\}, A=\left\{1,2,3,4 \right\}, B=\left\{2,4,6,8 \right\}$$ and $$C=\left\{1,4,5,6 \right\}$$, find :
$$A'$$

$$A'=U-A=\left\{1,2,3,4,5,6,7,8,9 \right\}-\left\{1,2,3,4 \right\}$$
$$A'=\left\{5,6,7,8,9 \right\}$$


If $$U=\left\{1,2,3,4,5,6,7,8,9 \right\}, A=\left\{1,2,3,4 \right\}, B=\left\{2,4,6,8 \right\}$$ and $$C=\left\{1,4,5,6 \right\}$$, find :
$$(B')'$$

$$U=\left\{1,2,3,4,5,6,7,8,9 \right\}, A=\left\{1,2,3,4 \right\}, B=\left\{2,4,6,8 \right\}$$ and $$C=\left\{1,4,5,6 \right\}$$

$$B'=U-B=\left\{1,2,3,4,5,6,7,8,9 \right\}-\left\{2,4,6,8 \right\}$$$$=\left\{1,3,5,7,9 \right\}$$

$$(B')'=U-B'=\left\{1,2,3,4,5,6,7,8,9 \right\}-\left\{1,3,5,7,9 \right\}$$$$=\left\{2,4,6,8 \right\}$$


If $$U=\left\{1,2,3,4,5,6,7,8,9 \right\}, A=\left\{1,2,3,4 \right\}, B=\left\{2,4,6,8 \right\}$$ and $$C=\left\{1,4,5,6 \right\}$$, find :
$$B'$$

$$U=\left\{1,2,3,4,5,6,7,8,9 \right\}, A=\left\{1,2,3,4 \right\}, B=\left\{2,4,6,8 \right\}$$ and $$C=\left\{1,4,5,6 \right\}$$

$$B'=U-B=\left\{1,2,3,4,5,6,7,8,9 \right\}-\left\{2,4,6,8 \right\}$$$$=\left\{1,3,5,7,9 \right\}$$


If $$A=\left\{a,b,c,d,e\right\},B=\left\{a,c,e,g\right\}$$ and $$C=\left\{b,c,f,g\right\}$$, verify that:
$$A\cap B=B\cap A$$

Given $$A=\left\{ a,b,c,d,e \right\} $$ and $$B=\left\{ a,c,e,g \right\} $$

1) $$A\cap B=\left\{ a,c,e \right\} $$          Equation (1)

2) $$B\cap A=\left\{ a,c,e \right\} $$         Equation (2)

Thus, from equation (1) and (2),
$$A\cap B=B\cap A$$


If $$A=\left\{a,b,c,d,e\right\},B=\left\{a,c,e,g\right\}$$ and $$C=\left\{b,c,f,g\right\}$$, verify that:
$$B\cap C=C\cap B$$

Given $$B=\left\{ a,c,e,g \right\} $$ and $$C=\left\{ b,c,f,g \right\} $$

$$B\cap C=\left\{ x:x\in B\quad and\quad x\in C\quad  \right\} $$
$$\therefore B\cap C=\left\{ c,g \right\} $$        Equation (1)

$$C\cap B=\left\{ x:x\in C\quad and\quad x\in B\quad  \right\} $$
$$\therefore C\cap B=\left\{ c,g \right\} $$          Equation (2)

From equation (1) and (2), 
$$B\cap C=C\cap B$$


If $$A=\left\{a,b,c,d,e\right\},B=\left\{a,c,e,g\right\}$$ and $$C=\left\{b,c,f,g\right\}$$, verify that:
$$A\cap C=C\cap A$$

Given $$A=\left\{ a,b,c,d,e \right\} $$ and $$C=\left\{ b,c,f,g \right\} $$

1) $$A\cap C=\left\{ x:x\in A\quad and\quad x\in C \right\} $$
$$\therefore A\cap C=\left\{ b,c \right\} $$         Equation (1)

2) $$C\cap A=\left\{ x:x\in C\quad and\quad x\in A \right\} $$
$$\therefore C\cap A=\left\{ b,c \right\} $$         Equation (2)

From equation (1) and (2),
$$A\cap C=C\cap A$$


Let $$A=\left\{a,b,c\right\}, B=\left\{b,c,d,e\right\}$$ and $$C=\left\{c,d,e,f\right\}$$ be subsets of $$U=\left\{a,b,c,d,e,f\right\}$$. Then verify that:
$$(A')'=A$$


1861146_1708301_ans_14363fcdcd1b41a6be900de4ff6d4e0a.jpeg


If $$U = \left \{ a, b, c, d, e, f, g, h \right \}$$, find the complements of the following sets:
$$C = \left \{ a, c, e, g \right \}$$

$$C = \left \{ a, c, e, g \right \}$$
$$\therefore C’ = \left \{ b, d, f, h \right \}$$


Taking the set of natural numbers as the universal set, write down the complements of the following sets:
{$$x: x$$ is an odd natural number}

We know that
$$U = N$$ Set of natural numbers
$$\{x: x\ is\ an\ odd\ natural\ number\}´ = \{x: x\ is\ an\ even\ natural\ number\}$$


Taking the set of natural numbers as the universal set, write down the complements of the following sets:
{$$x: x$$ is an even natural number}

We know that
$$U = N$$ Set of natural numbers
$$\{x: x\ is\ an\ even\ natural\ number\}´ = \{x: x\ is\ an\ odd\ natural\ number\}$$


If $$U = \left \{ a, b, c, d, e, f, g, h \right \}$$, find the complements of the following sets:
$$B = \left \{ d, e, f, g \right \}$$

$$B = \left \{ d, e, f, g \right \}$$
$$\therefore B’ = \left \{ a, b, c, h \right \}$$


If $$U = \left \{ a, b, c, d, e, f, g, h \right \}$$, find the complements of the following sets:
$$A = \left \{ a, b, c \right \}$$

$$A = \left \{ a, b, c \right \}$$
$$A’ = \left \{ d, e, f, g, h \right \}$$


If $$U = \left \{ a, b, c, d, e, f, g, h \right \}$$, find the complements of the following sets:
$$D = \left \{ f, g, h, a \right \}$$

$$D = \left \{ f, g, h, a \right \}$$
$$\therefore D’ = \left \{ b, c, d, e \right \}$$


Taking the set of natural numbers as the universal set, write down the complements of the following sets:
{$$x: x \geq 7$$}

We know that
$$U = N$$ Set of natural numbers
{$$x: x \geq 7$$}´ = {$$x: x ∈ N$$ and $$x < 7$$}


Taking the set of natural numbers as the universal set, write down the complements of the following sets:
{$$x: 2x + 5 = 9$$}

We know that
$$U = N$$ Set of natural numbers
{$$x: 2x + 5 = 9$$}´ = {$$x: x ∈ N$$ and $$x ≠ 2$$}


Taking the set of natural numbers as the universal set, write down the complements of the following sets:
{$$x: x + 5 = 8$$}

We know that
$$U = N$$ Set of natural numbers
{$$x: x + 5 = 8$$}´ = {$$x: x ∈ N$$ and $$x ≠ 3$$}


Taking the set of natural numbers as the universal set, write down the complements of the following sets:
{$$x: x N$$ and $$2x + 1 > 10$$}

We know that
$$U = N$$ Set of natural numbers
{$$x: x ∈ N$$ and $$2x + 1 > 10$$}´ = {$$x: x ∈ N$$ and $$x \leq 9/2$$}


Taking the set of natural numbers as the universal set, write down the complements of the following sets:
{$$x: x$$ is perfect cube}

We know that
$$U = N$$ Set of natural numbers
$$\{x: x$$ is a perfect cube$$\}´ = \{x: x ∈ N$$ and $$x$$ is not a perfect cube$$\}$$


Taking the set of natural numbers as the universal set, write down the complements of the following sets:
{$$x: x$$ is a positive multiple of 3}

We know that
$$U = N$$ Set of natural numbers
{$$x: x$$ is a positive multiple of $$3$$}´ = {$$x: x ∈ N$$ and $$x$$ is not a multiple of $$3$$}


Taking the set of natural numbers as the universal set, write down the complements of the following sets:
{$$x: x$$ is a perfect square}

We know that
$$U = N$$ Set of natural numbers
{$$x: x$$ is a perfect square}´ = {$$x: x ∈ N$$ and $$x$$ is not a perfect square}


Taking the set of natural numbers as the universal set, write down the complements of the following sets:
{$$x: x$$ is a prime number}

We know that
$$U = N$$ Set of natural numbers
{$$x: x$$ is a prime number}´ ={$$x: x$$ is a positive composite number and $$x = 1$$}


Taking the set of natural numbers as the universal set, write down the complements of the following sets:
{$$x: x$$ is a natural number divisible by 3 and 5}

We know that
$$U = N$$ Set of natural numbers
{$$x: x$$ is a natural number divisible by $$3$$ and $$5$$}´ = {$$x: x$$ is a natural number that is not divisible by $$3$$ and $$5$$}


Fill in the blanks to make each of the following a true statement:
$$(U ∩ A)' = ……$$.

$$(U ∩ A)' =( A)' = A'$$
$$\therefore (U ∩ A)' = A'$$


Fill in the blanks to make each of the following a true statement:
$$U A = $$.

$$(U ∩ A')' = (A')' =A$$
$$\therefore (U ∩ A')' = A$$


If $$X$$ and $$Y$$ are two sets such that $$X$$ has $$40$$ elements, $$X\cup Y$$ has $$60$$ elements and $$X Y$$ has $$10$$ elements, how many elements does $$Y$$ have?

It is given that,
$$n(X) = 40$$
$$n(X ∪ Y) = 60$$
$$n(X ∩ Y) = 10$$
We know that
$$n(X ∪ Y) = n(X) + n(Y) – n(X ∩ Y)$$
$$\therefore 60 = 40 + n(Y) – 10$$
$$\therefore n(Y) = 60 – (40 – 10) = 30$$
Thus, the set $$Y$$ has $$30$$ elements.


If $$U = \left \{ 1, 2, 3, 4, 5,6,7,8, 9 \right \}, A = \left \{ 2, 4, 6, 8 \right \}$$ and $$B = \left \{ 2, 3, 5, 7 \right \}$$. Verify that
$$(A B) = A \cup B$$

It is given that
$$U = \left \{ 1, 2, 3, 4, 5,6,7,8, 9 \right \}$$
$$A = \left \{ 2, 4, 6, 8 \right \}$$
$$B = \left \{ 2, 3, 5, 7 \right \}$$
$$(A ∩ B)’ = \left \{ 2 \right \}’ = \left \{ 1, 3, 4, 5, 6, 7, 8, 9 \right \}$$
$$A’ \cup  B’ = \left \{ 1, 3, 5, 7, 9 \right \} U \left \{ 1, 4, 6, 8, 9 \right \} = \left \{ 1, 3, 4, 5, 6, 7, 8, 9 \right \}$$
Therefore, $$(A ∩ B)’ = A’ \cup B’$$.


Fill in the blanks to make each of the following a true statement:
$$U’ ∩ A' = ……$$.

$$U’ ∩ A' = \phi ∩ A' = \phi$$
$$\therefore U’ ∩ A' = \phi$$


If $$S$$ and $$T$$ are two sets such that $$S$$ has $$21$$ elements, $$T$$ has $$32$$ elements, and $$S T$$ has $$11$$ elements, how many elements does $$S T$$ have?

It is given that
$$n(S) = 21$$
$$n(T) = 32$$
$$n(S ∩ T) = 11$$
We know that
$$n (S ∪ T) = n (S) + n (T) – n (S ∩ T)$$
$$\therefore n (S ∪ T) = 21 + 32 – 11=42$$
Thus, the set $$(S ∪ T)$$ has $$42$$ elements.


If A = {x : x=2n, n<5}, then find A when
$$\xi=N$$

Natural numbers less than $$5$$ are $$1,2,3,4.$$
Given $$x=2n$$, putting $$n=1,2,3,4$$ ,we get,
$$x=2\times1,2\times2,2\times3,2\times4$$
$$=2,4,6,8.$$
The given set i.e.,A can be written as {$$2,4,6,8$$}
(Every set is a subset of universal set i.e., A $$\subset \xi$$)


If $$U=\{0,1,2,3,4\}$$ and $$ A=\{1,4\},B=\{1,3\}$$ show that $$(A \cup B)'=A' \cap B'$$

Given if  $${U=0,1,2,3,4,}$$ and $$A=\{1,4\} \ B=\{1,3\}$$

From de-morgan's laws we can say,
$$(A\cup B)=A'\cap B'$$

$$(A\cup B)'=U-A\cup B$$
$$={0,1,2,3,4}-[\{1,4\} \cup \{1,3\}]$$
$$=\{0,1,2,3,4\}-\{1,3,4\}$$
$$(A\cup B)=\{0,2\}................(1)$$

$$A'\cap B'=\{U-A\} \cap \{U-B\}$$

$$=[\{0,1,2,3,4\}-\{1,4\}]\cap [\{0,1,2,3,4\}-\{1,3\}]$$
$$=\{0,2,3\}\cap\{0,2,4\}$$
$$=\{0,2\}$$......................(2)

So,
$$(1)=(2)$$
$$(A \cup B)'=(A' \cap B')$$


If A = {x : x=2n, n<5}, then find A when
$$\xi=I$$

Integers less than 5 are ......,$$-4,-3,-2,-1,0,1,2,3,4$$
Given 2n i.e .......,$$2\times -2,2\times -1,2\times 0,2\times 1,2\times 2,2\times 3,2\times 4,$$
i.e ...... $$-4,-2,0,2,4,6.8.$$
The given set i.e.,A can be written as {$$...,-4,-2,0,2,4,6,8$$}
(Every set is a subset of universal set i.e., A $$\subset \xi$$)


If A = {x : x=2n, n<5}, then find A when
$$\xi=W$$

Whole numbers less than $$5$$ are $$0,1,2,3,4.$$
Given 2n i.e., $$2\times0,2\times1,2\times2,2\times3,2\times4,$$ i.e., $$0,2,4,6,8.$$
The given set i.e.,A can be written as {$$0,2,4,6,8$$}
(Every set is a subset of universal set i.e., A $$\subset \xi$$)


Let all the students of a class is an Universal set. Let set A be the students who secure 50% or more marks in Maths. Then write the complement of set A.

All the students of a class is a Universal set i.e.
U = set of all the students of a class and
A = set of the students who secure 50% or more marks in Maths
So, the complement of set A, A' = U- A = set of the students who secure less than 50% marks in Maths.


If $$A \subset B$$ then show that $$C-B \subset C-A$$


$${\textbf{Step -1:}}{\textbf{ Find a variable for the set}}{\textbf{.}}$$
                 $${\text{Let x}} \in {\text{C}} - {\text{B}}$$
$${\textbf{Step -2: Solve the set to show C}} - {\textbf{B}} \subset {\textbf{C}} - {\textbf{A}}{\textbf{.}}$$
                 $$ \Rightarrow {\text{x}} \in {\text{C and x}} \notin {\text{B}}$$
                 $$ \Rightarrow {\text{x}} \in {\text{C and x}} \notin {\text{A }} \boldsymbol{\left(\because {{\text{A}} \subset {\text{B}}} \right)}$$
                 $$ \Rightarrow {\text{x}} \in {\text{C}} - {\text{A}}$$
$${\textbf{Hence, it is proved that C}} - {\textbf{B}} \subset {\textbf{C}} - {\textbf{A}}{\textbf{.}}$$



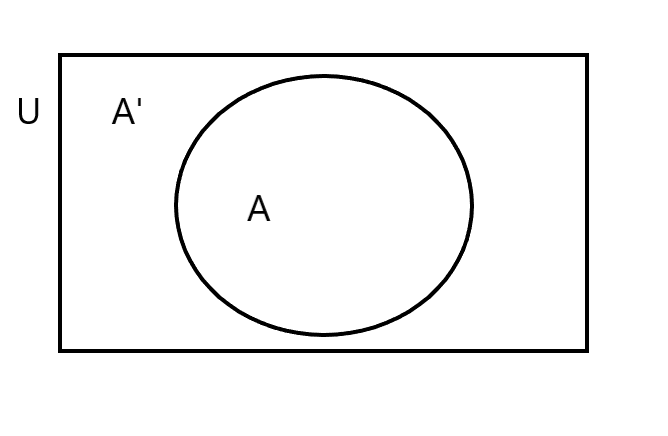
Define complement of a set

Let UU be the universal set and AA a subset of UU. Then the complement of AA is the set of all elements of UU which are not the elements of AA and is denoted by A′A′
Properties:
∙ A∪A′∙ A∪A′
∙ A∩A′=φ∙ A∩A′=φ
∙ (A′)′=A∙ (A′)′=A
∙ (A∪B)′=A′∩B′∙ (A∪B)′=A′∩B′
∙ (A∩B)′=A′∪B′


Taking the sets of natural numbers as the universal set, write down the complements of the following sets
$$\left\{x:x\ \in N\ and\ 2x+1 > 10 \right\}$$

{x:x∈Nx:x∈N and 2x+1≤102x+1≤10 } ={1,2,3,4}


Taking the sets of natural numbers as the universal set, write down the complements of the following sets
$$\left\{x:x\ > 7 \right\}$$

{1,2,3,4,5,6}


Let $$U =\left\{1,2,3,4,5,6,7,8,9,10 \right\}$$ and $$A=\left\{1,3,5,7,9 \right\}$$ Find $$A^{'}$$

A′=U−A={2,4,6,8,10}


If $$U=\left\{1,2,3,4,5,6,7,8,9 \right\}, A^{'}= \left\{2,4,6,8 \right\}$$ and $$B^{'}=\left\{2,3,5,7 \right\}$$ Verify that
$$(A \cap B)^{'}=A^{'} \cup B^{'}$$

A′={1,3,5,7,9}A′={1,3,5,7,9} B′={1,4,6,8,9}B′={1,4,6,8,9}
A′∪B′={1,3,4,5,6,7,8,9}A′∪B′={1,3,4,5,6,7,8,9}
A∩B={2}A∩B={2}
∴(A∩B)′={13,4,5,6,7,8,9}∴(A∩B)′={13,4,5,6,7,8,9}
∴(A∩B)′=A′∪B′


If $$\xi$$ = {$$x$$ : $$x \leq 10$$, $$x \,\,\epsilon\,\,N$$}, A = {$$x$$ : $$x \geq  4$$}, and B = {$$x$$ : $$2 < x < 7$$} ; find number of elements in $$(A \cup B)^{'}$$

$$ \xi = $$ { $$ 1,2,3,4,5, 6, 7, 8, 9, 10 $$ } as $$ x $$ is a natural number less than or equal to $$ 10 $$. 
$$ A = $$ { $$ 4,5, 6, 7, 8, 9, 10 $$ } as $$ x $$ is a number greater than or equal to $$ 4 $$  and the universal set is already defined as $$ \xi $$.
And, $$ B = $$ { $$ 3, 4, 5, 6 $$ } as $$ x $$ is a natural number less than $$  7 $$ and more than $$ 2 $$.
Union of two sets has the elements of both the sets.
So, $$ A \cup B = $$ { $$ 3, 4, 5, 6, 7, 8, 9, 10 $$ }. 
And $$ { (A \cup B)}^{'} = \xi - (A \cup B) =  $$  {$$ 1, 2 $$ }  (Since,  $$ \xi - (A \cup B) $$ will have the elements of $$ \xi $$ which are not in $$ (A \cup B) $$ ).


$$(A\cap B)'$$

The sets will be
$$ U = $$ {$$ 1, 2, 4, 8, 16, 32,64,128 $$ }
$$ A = $$ {$$ 1, 4, 16, 64 $$ }
$$ B = $$ {$$ 1, 8, 64 $$ }

$$ (A\cap B) = $$ { $$ 1, 64$$ }
Now, $$ {(A \cap B)}^{ \prime} = U - (A \cap B) =$$  { $$ 2, 4, 8, 16, 32,128 $$}


From the set of all solution of the equation  $$ { 2 }^{ \left| y \right|  }-\left| { 2 }^{ y-1 }-1 \right| ={ 2 }^{ y-1 }+1$$,find the square of the least integer satisfying the equation ?

Given, $${ 2 }^{ \left| y \right|  }-\left| { 2 }^{ y-1 }-1 \right| ={ 2 }^{ y-1 }+1$$ 
Case I: When $$y\in (-\infty ,0]$$
$$\therefore { 2 }^{ -y }+\left( { 2 }^{ y-1 }-1 \right) ={ 2 }^{ y-1 }+1 \Rightarrow { 2 }^{ -y }=2\Rightarrow y=-1\in (-\infty ,0]$$   ...(i)
Case II: When $$ (0,1] $$
$$\therefore { 2 }^{ y }+\left( { 2 }^{ y-1 }-1 \right) ={ 2 }^{ y-1 }+1 \Rightarrow { 2 }^{ y }-{ 2 }^{ y }=0 $$
$$\Rightarrow { 2 }^{ y }=2\Rightarrow y=1\in (0,1]$$   ...(ii)
Case III: When $$y\in \left( 1,\infty  \right) $$
$$\therefore { 2 }^{ y }-{ 2 }^{ y-1 }+1={ 2 }^{ y-1 }+1$$   
$$\Rightarrow { 2 }^{ y }-2.{ 2 }^{ y-1 }=0\Rightarrow { 2 }^{ y }-{ 2 }^{ y }=0$$ true for all $$y>1$$      ...(iii)
$$ \therefore $$ From Equations (i),(ii),and (iii), we get $$ y\in \left\{ -1 \right\} \cup [1,\infty )$$


$$(A\cup B)'$$

The sets will be
$$ U = $$ {$$ 1, 2, 4, 8, 16, 32,64,128 $$ }
$$ A = $$ {$$ 1, 4, 16, 64 $$ }
$$ B = $$ {$$ 1, 8, 64 $$ }

$$ (A\cup B) = $$ { $$ 1,4,8,16,64$$ }
Now, $$ {(A \cup B)}^{ \prime} = U - (A \cup B) =$$  { $$ 2,32,128 $$}


In a survey of population of 450 people, it is found that 205 can speak English (E), 210 can speak Hindi (H) and 120 people can speak Tamil, If 100 people can speak both E and H, 80 can speak both E and T, 5 can speak both H and T, and 20 can speak all the three languages, find the number of people who can speak E but not H or T. Find also the number of people who can speak neither E nor H nor T.

$$\displaystyle n\left ( U \right )= 450, n\left ( E \right )= 205, n\left ( H \right )= 210, n\left ( T \right )= 120$$
$$\displaystyle n\left ( E\cap H \right )= 100, n\left ( E\cap T \right )= 80, n\left ( H\cap T \right )= 35$$
$$\displaystyle n\left ( E\cap H\cap T \right )= 20.$$

Number of people who can speak E but not H and T is 
$$\displaystyle n\left ( E\cap {H}'\cap {T}' \right )= n\left ( E\cap \left ( H\cup T \right )' \right )$$
$$\displaystyle = n\left ( E \right )-n\left ( E\cap \left ( H\cup T \right ) \right )$$ 
$$\displaystyle = n\left ( E \right )-n\left \{ \left ( E\cap H \right )\cup \left ( E\cap T \right ) \right \}$$
$$\displaystyle = n\left ( E \right )-\left [ n\left ( E\cap H \right )+n\left ( E\cap T \right )-n\left \{ \left ( E\cap H \right )\cap \left ( E\cap T \right ) \right \} \right ]$$
$$\displaystyle = n\left ( E \right )-n\left ( E\cap H \right )-n\left ( E\cap T \right )+n\left ( E\cap H\cap T \right )$$
$$\displaystyle = 205-100-80+20$$
$$\displaystyle \Rightarrow n(E\cap H'\cap T')= 225-180= 45$$

Next, we have to find number of people who cannot speak E,H and T
$$\displaystyle n\left ( {E}'\cap {H}'\cap {T}' \right )= n\left ( E\cup H\cup T \right )'$$
$$\displaystyle = n\left ( U \right )-n\left ( E\cup H\cup T \right )$$   ....(1)

$$\displaystyle n\left ( E\cup H\cup T \right )= n(E)+n(H)+n(T)-n(E\cap H)-n(H\cap T)-n(E\cap T)+n(E\cap H\cap T)$$
$$\displaystyle \Rightarrow n(E\cup H\cup T)= \left ( 205+210+120 \right )-\left ( 100+80+35 \right )+20 =340$$

Hence from (1)
$$\displaystyle n\left ( {E}'\cap {H}'\cap {T}' \right )= 450-340= 110$$



Given a non-empty set X, consider the binary operation *: $$ P(X) \times P(X)\rightarrow P(X)$$ given by$$ A*B =A \cap B \forall A, B $$ in P(X) , where P(X) is the power set of X. Show that X is the identity element for this operation and X is the only invertible element in P(X) with respect to the operation *.


1444658_708672_ans_459430b3f25540e99f519e49c4b1d22c.jpeg


Find $$P\cap Q$$ and represent on the number line 
$$P=\left\{x : 8x-1 > 5x+2,x\in N\right\}$$ and $$Q=\left\{x:7 x \ge 3(x+6), x\in N\right\}$$

$$\begin{array}{l} P=x:8x-1>5x+2,x\in N\, \, and\, \, Q=x:7x>3x+18 \\ \Rightarrow 8x-1>5x+2\, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \Rightarrow 7x>3x+18 \\ \Rightarrow 3x>3\, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \Rightarrow 4x>18 \\ \, \, \, \, \, \, \, x>1\, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, x>\frac { 9 }{ 2 }  \\ \therefore P\cup Q=\left( { \frac { 9 }{ 2 } ,\propto  } \right) \, \, \,  \end{array}$$


Class 11 Commerce Applied Mathematics Extra Questions