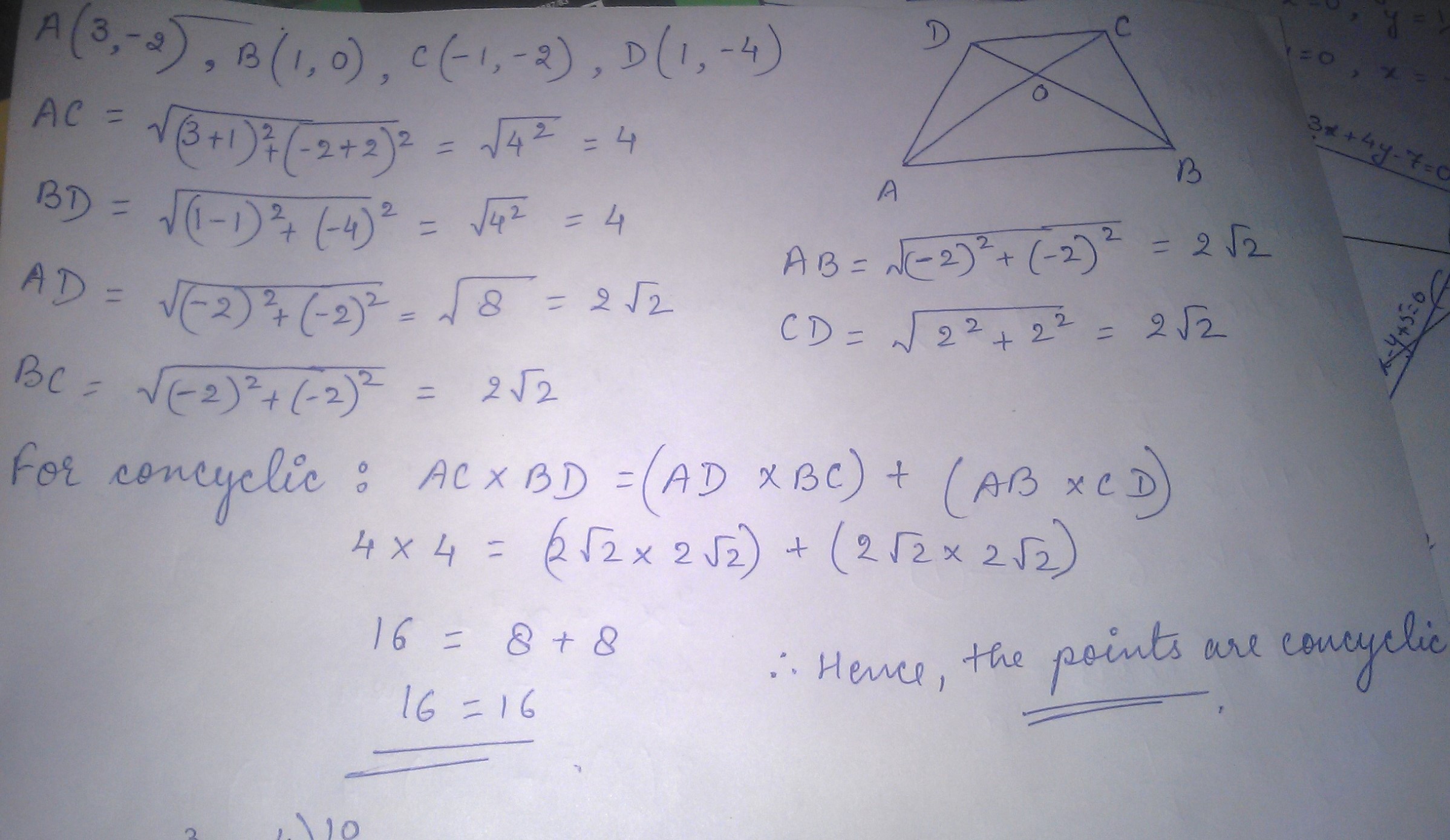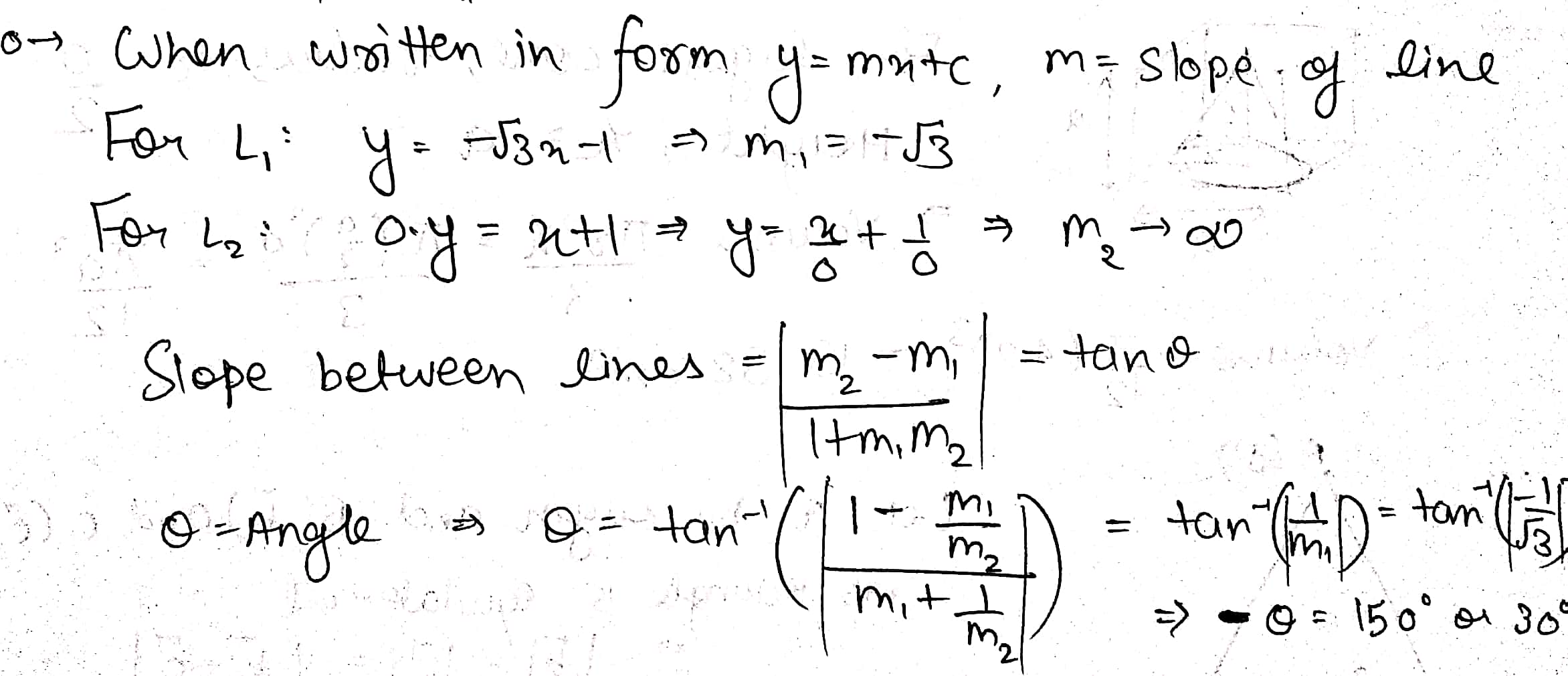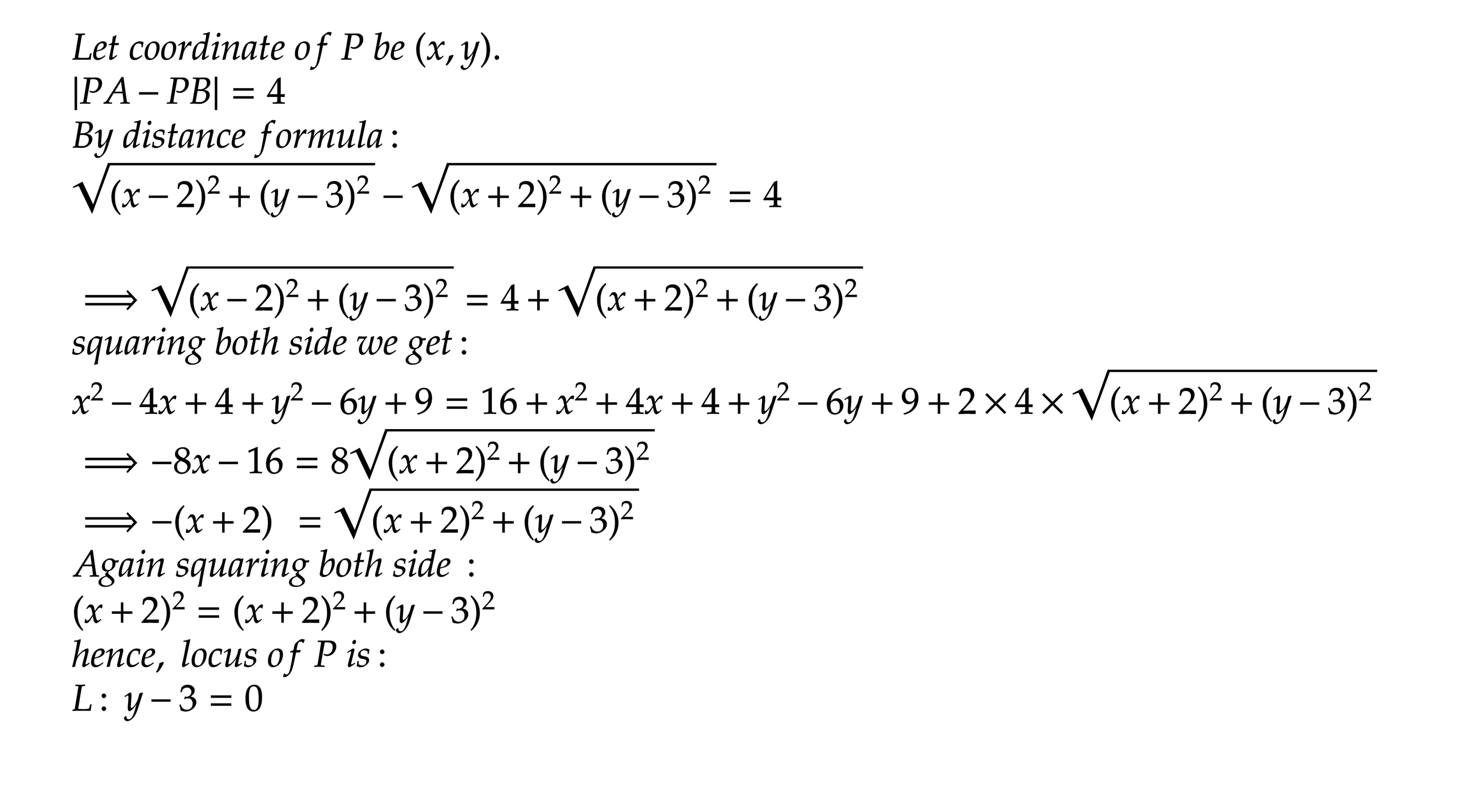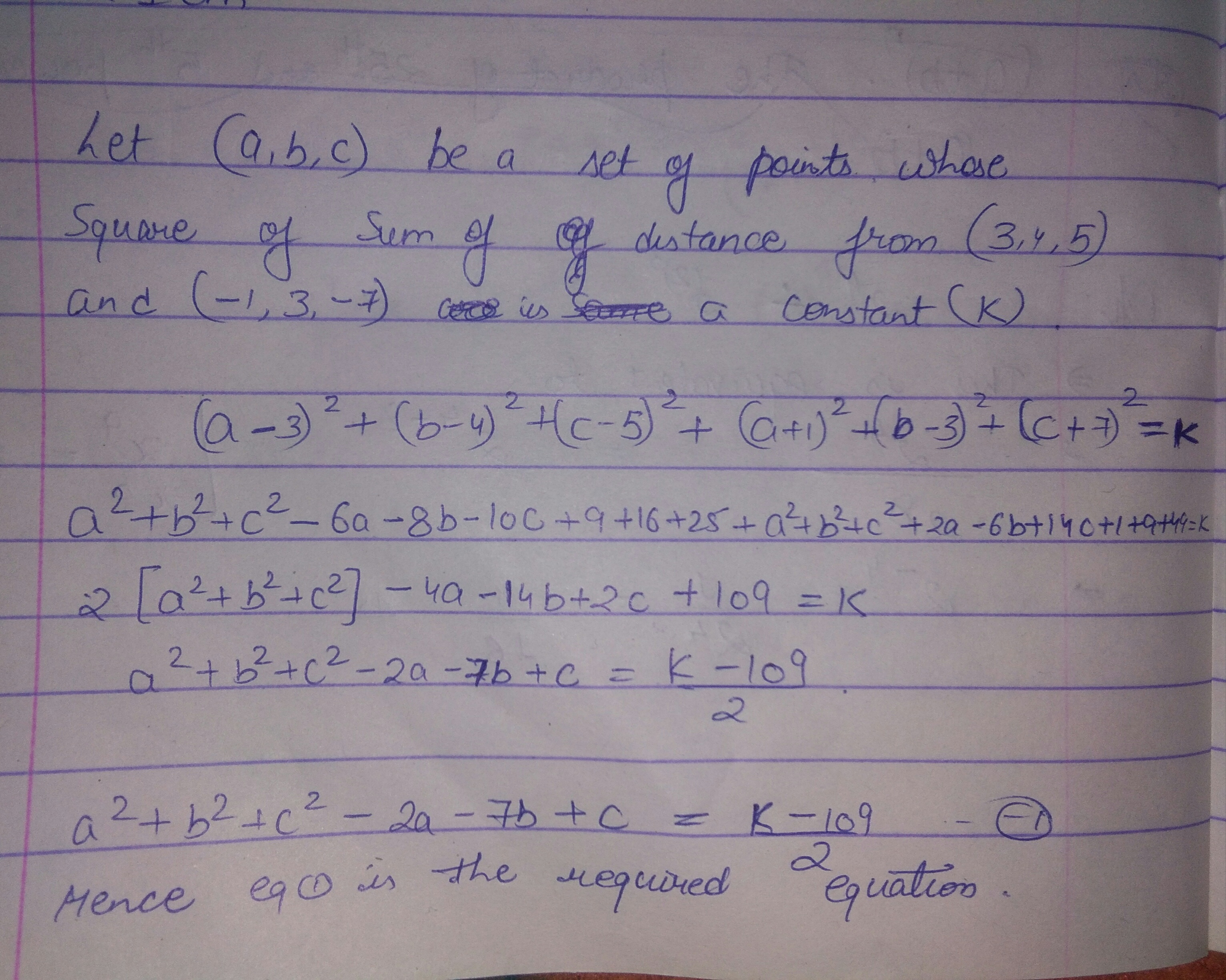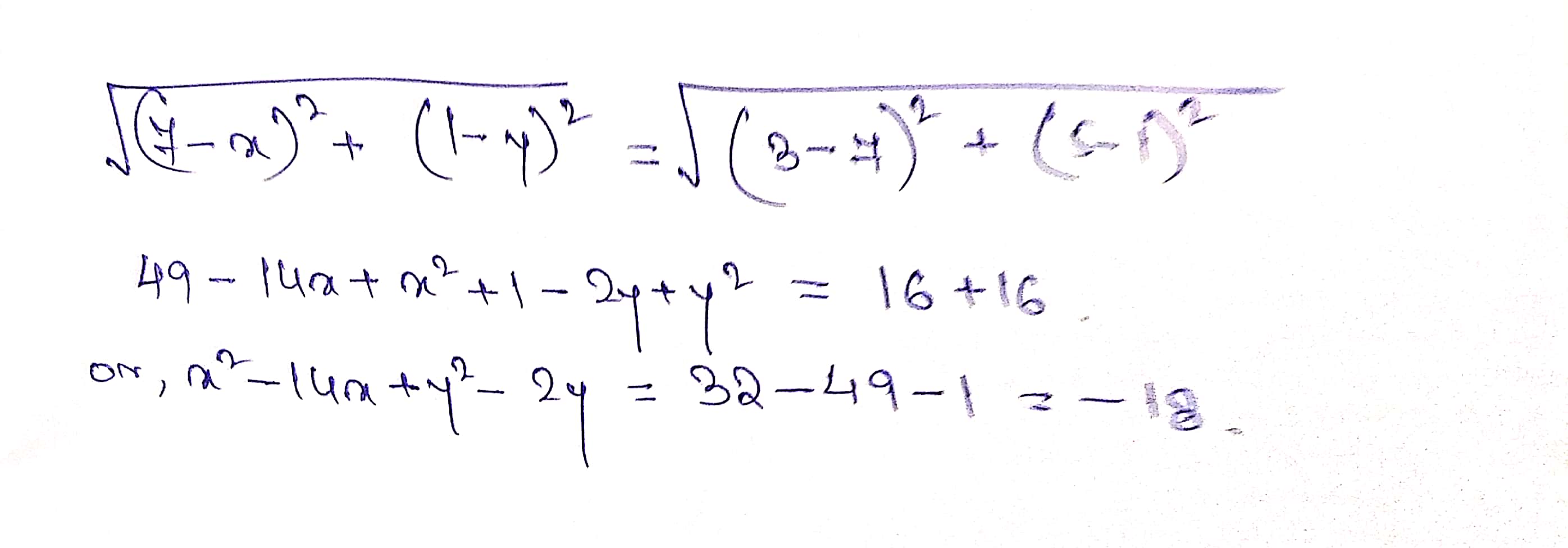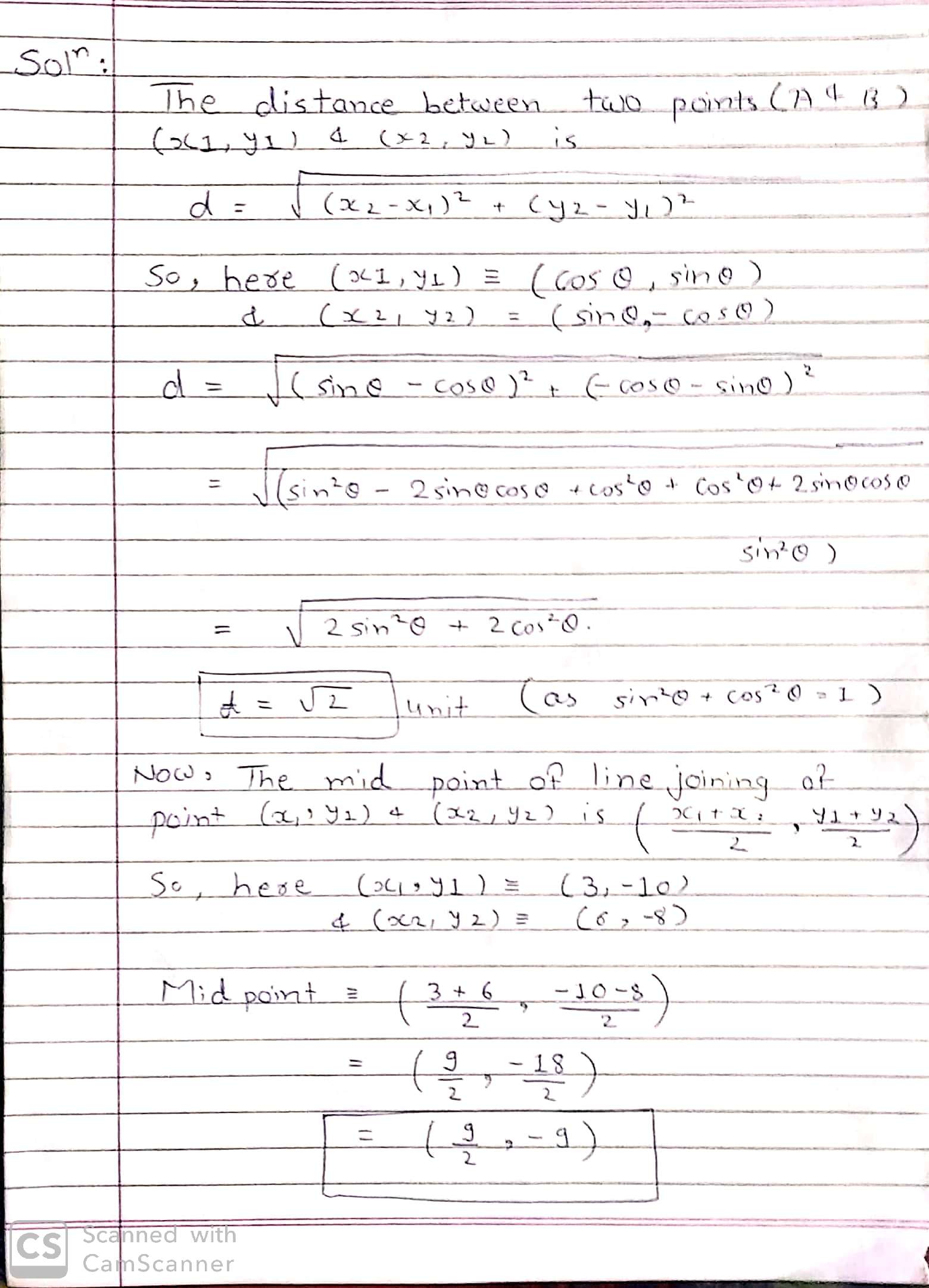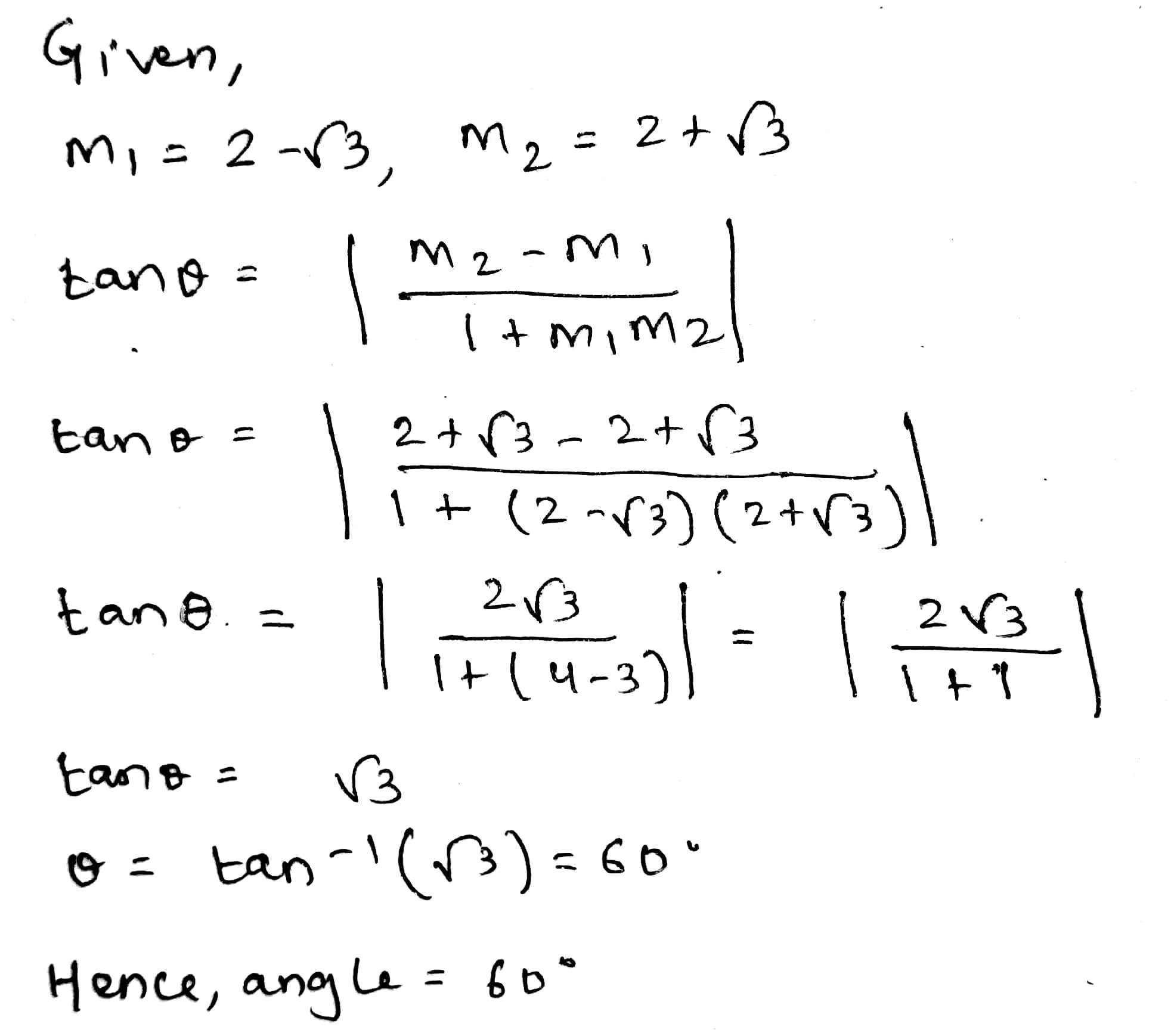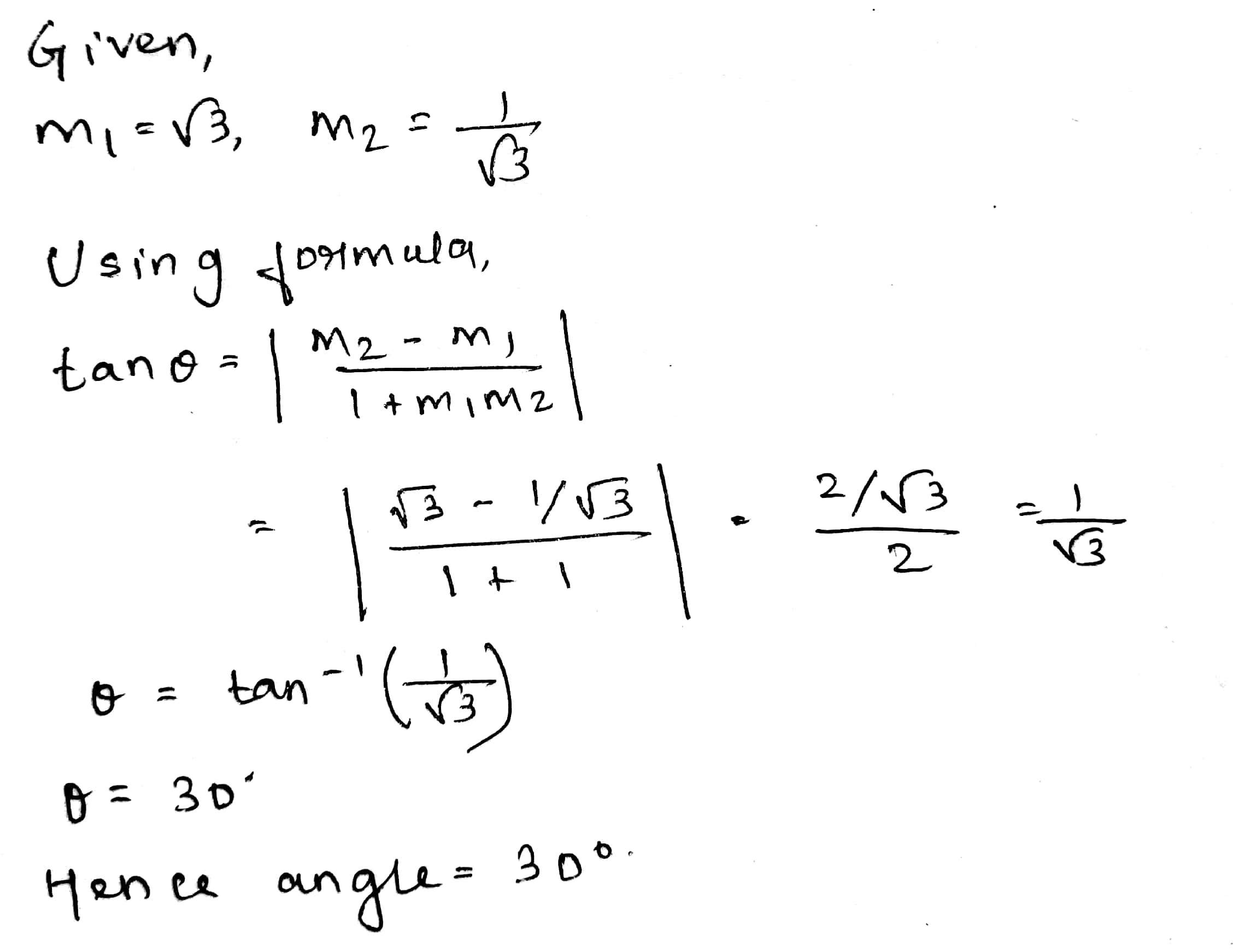Straight Lines - Class 11 Commerce Applied Mathematics - Extra Questions
How many points are there on the x-axis which are at a distance of $$ 2 \sqrt{5}$$ from the point $$(7, 4)$$?
Determine whether the points are vertices of a right triangle $$A(-3, -4)$$, $$B(2, 6)$$ and $$C(-6, 10)$$
The point on the y-axis equidistant from $$(-5, 2)$$ and $$(9, -2)$$ is $$(0,-m)$$, them $$m$$
Find the perimeter of a triangle whose vertices have the coordinates $$(3,10),(5,2)$$ and $$(14,12)$$.
Show that the two parabolas $$ x^2 + 4a (y - 2b - a ) = 0 $$ and $$ y^2 = 4b (x - 2a + b) $$ intersect at right angles at a common end of the latus rectum of each.
Which point on x-axis is equidistant from $$(5,9)$$ and $$(-4,6)$$?
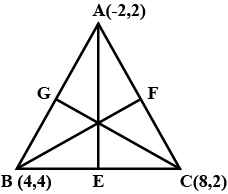
The vertices of a triangle are $$A\left( { - 2,\,2} \right),\,B\left( {4,\,4} \right)\,and\,C\left( {8,\,2} \right).$$ Find the length of the medians to the sides
$${\text{let}}{\mkern 1mu} AE,BF,CG{\mkern 1mu} \;{\text{are}}{\mkern 1mu} \;{\text{Medians}}{\mkern 1mu} \;E{\mkern 1mu} \;{\text{is}}{\mkern 1mu} \;{\text{mid}}{\mkern 1mu} \;{\text{point}}{\mkern 1mu} \;{\text{of}}{\mkern 1mu} BC$$
$$\therefore E = \left( {6,3} \right)$$
Similarly, $$F = \left( {3,2} \right)$$
$$G = \left( {1,3} \right)$$
$$AE = \sqrt {{{\left( {6 + 2} \right)}^2} + {{\left( {3 - 2} \right)}^2}} $$
$$\sqrt {64 + 1} = \sqrt {65} \,unit$$
$$BF = \sqrt {{{\left( 1 \right)}^2} + {2^2}} = \sqrt {1 + 4} = \sqrt {5\,} unit$$
$$CG= \sqrt {{7^2} + {{\left( { - 1} \right)}^2}} = \sqrt {50} unit$$
Find the slope of the line passing through the points $$(3, -2)$$ & $$(7, -2)$$
Find the value of $$x$$ for which the distance between $$p(2, -3)$$ and $$q(x, 5)$$ is $$10$$ units.
Find a point on $$x-axis$$ which is equidistant from $$A(2, -5)$$ and $$(-2, 9)$$.
Find the slope of line which passes through the point (7,11) and (9,15) .
Show that the points $$(3, -2), (1, 0), (-1, -2)$$ and $$(1, -4)$$ are concyclic
REF.Image
$$A(3,-2), B(1,0), C(-1,-2), D(1,-4)$$
$$AC = \sqrt{(3+1)^{2}+(-2+2)^{2}}= \sqrt{4^{2}}=4$$
$$BD= \sqrt{(1-1)^{2}+(-4)^{2}}= \sqrt{4^{2}}=4$$
$$AD= \sqrt{(-2)^{2}+(-2)^{2}}= \sqrt{8}= 2\sqrt{2}$$
$$AB= \sqrt{(-2)^{2}+(-2)^{2}}= 2\sqrt{2}$$
$$CD= \sqrt{2^{2}+2^{2}}= 2\sqrt{2}$$
$$BC= \sqrt{(-2)^{2}+(-2)^{2}}= 2\sqrt{2}$$
For concyclic : $$AC\times BD= (AD\times BC)+ (AB \times CD)$$
$$4 \times 4= (2\sqrt{2}\times 2\sqrt{2})+(2\sqrt{2}\times 2\sqrt{2})$$
$$16= 8+8$$
$$16=16$$
$$\therefore $$ Hence, the points are concyclic
Find the point on x-axis which is equidistant from the points (2,-5) and (-2,9).
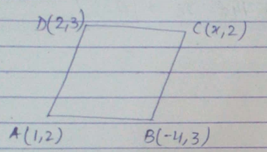
If the points $$A(1,2), B(-4,3), C(x,2)$$ and $$D(2,3)$$ form parallelogram find the value of $$x$$.
In a parallelogram
$$AB=CD$$
$$\Rightarrow \sqrt { { (1+4) }^{ 2 }+{ (2-3) }^{ 2 } } =\sqrt { { (2-x) }^{ 2 }+{ (3-2) }^{ 2 } } \\ \Rightarrow 25+1={ (2-x) }^{ 2 }+1\\ \Rightarrow { (2-x) }^{ 2 }=25\\ \Rightarrow 2-x=\pm 5$$
if$$\quad 2-x=-5\quad \Rightarrow x=7$$
if$$\quad 2-x=5\quad \Rightarrow x=-3$$
If the point $$A(a,2)$$ is equidistant from the points $$B(8,-2)$$ and $$C(2,-2)$$, the value of $$a$$.
If $$(a,b)$$ is the mid-point of the line segment joining the points $$A\left( {10, - 6} \right),B\left( {k,4} \right)$$ and $$a-2b=18$$,find the value of $$k$$ and the distance AB.
Solution -
$$a=\frac{10+K}{2}$$ $$b=\frac{-6+4}{2}=-1$$
$$a= 18-2=16$$ $$[\because a-26=18]$$
$$16=\frac{10+k}{2}$$
$$k=22$$
Distance $$AB = \sqrt{(22-10)^{2}+(4+6)^{2}}$$
$$=\sqrt{144+100}$$
$$=\sqrt{244}$$
$$=2\sqrt{61}$$
A point P on X-axis is at distance 13 from A(11,12). Find the coordinates of P.
If $$P ( 2 , P )$$ is the mid point of the line segment joining the the points. $$A ( 6 , - 5 )$$ and $$B ( - 2,11 )$$ find the value of $$P .$$
Find the slope of the line whose inclination is $$30^{o}$$
21 - 3(b - 7) = b + 20
equation $$\Rightarrow $$
$$ 21-3(b-7) = b+20$$
$$ 21-3b-3(-7) = b+20$$
$$ 21 -3b+21=b+20$$
$$ 42-3b=b+20$$
$$ 22 = 4b$$
$$ b = \frac{22}{4}$$
$$ b = \frac{11}{2}$$
Given line $$ 5x-y = 1$$
slope of line $$ = \frac{-5}{-1} = 5$$
we have to take a line perpendicular
to this line
Find the inclination of a line whose slope is
(i) $$1$$
(ii) $$-1$$
(iii) $$\sqrt 3 $$
(iv) $$-\sqrt 3 $$
(v) $$\frac{1}{{\sqrt 3 }}$$
(i) $$ tan\theta =1 \Rightarrow \theta 45^{\circ}$$ ACW from $$tan^{x}- axis$$.
(ii) $$-1 =tan\theta \Rightarrow \theta = 135^{\circ}$$ ACW.
(iii) $$ tan \theta =\sqrt{3}\Rightarrow \theta =60^{\circ}$$ ACW.
(iv) $$ tan\theta =-\sqrt{3}\Rightarrow \theta = 120^{\circ}$$ ACW.
(v) $$ tan\theta =\frac{1}{\sqrt{3}}\Rightarrow \theta =30^{\circ}$$ ACW.
Find the slope of the line perpendicular to $$AB$$ if $$A=(0,-5)$$ and $$B=(-2,4)$$.
Find the distance between the following pairs of points:-
$$(2,3),(4,1)$$
Find the angle between the line $$\sqrt {3}x+y+1=0$$ and $$x+1=0$$.
When written in form $$y=mx+c$$, $$m=$$ slope of line
For $$L_1:$$ $$y=-\sqrt{3}x-1=m_1=-\sqrt{3}$$
For $$L_2: o.y=x+1\Rightarrow y=\dfrac{x}{0}+\dfrac{1}{0}\Rightarrow m_2\rightarrow \infty$$
Slope between lines $$=\left|\dfrac{m_2-m_1}{1+m_1m_2}\right|=\tan\theta$$
$$\theta =$$Angle $$\Rightarrow \theta =\tan^{-1}\left(\left|\dfrac{1-\dfrac{m_1}{m_2}}{m_1+\dfrac{1}{m_2}}\right|\right)=\tan^{-1}\left(\left|\dfrac{1}{m_1}\right|\right)=\tan^{-1}\left(\left|\dfrac{1}{\sqrt{3}}\right|\right)$$
$$\Rightarrow -\theta =150^o$$ or $$30^o$$.
If point $$(x,y)$$ is equidistant from point $$(3,k)$$ and $$(k,3)$$ then find the value of $$k$$ when $$x\neq y$$
if (x,y)is equidistant form point (3,k)& (k,3).
then
$$\sqrt{(x-3)^{2}+(y-k)^{2}=(x-k)^{2}+(y-3)^{2}}$$
on both sides=
$$ (x-3)^{2}+(y-k)^{2}=(x-k)^{2}+(y-3)^{2}$$
$$ x^{2}+9-6x+y^{2}+k^{2}-2ky=y^{2}+x^{2}-2kx+9+6y+k^{2}$$
(2k-6)x=(2k-6)y
(2k-6)(x-y)=0[x+y]then
then 2k-6=0
[k=3]
Show that the point A(-2,3,5), B(1,2,3) and C(7,0,-1) are collinear .
Find the distance of the point $$P(-6,8)$$ from the origin.
Let $$A (6,4)$$ and $$B(2,12)$$ be two given points. Find the slope of a line perpendicular to $$AB$$.
$$A ( 0,2 ) , B ( 0,5 )$$ be any two points, then the distance between them is _________.
The distance between the two points is $$5.$$ One of them is $$(3, 2)$$ and the ordinate of the second is $$-1$$ , then find sum of its x-coordinate.
Mid-points of the sides AB and AC of $$\Delta ABC$$ are $$(3, 5)$$ and $$(-3, -3)$$, respectively, then find the length of BC.
The vertices of a triangle are A $$(2, 2)$$, B $$(-4, -4)$$, C $$(5, -8)$$. Then, if the length of the median through C is $$\sqrt m$$.Find $$m$$
If P$$(x, y)$$ is a point in the coordinate plane such that locus of P is
Find the angles between the lines $$\displaystyle \sqrt{3}x+y= 1$$ and $$x+\sqrt{3}y= 1$$
Find the slope of a line passing through the points with coordinates $$(-1, 0)$$ and $$(1, 3)$$.
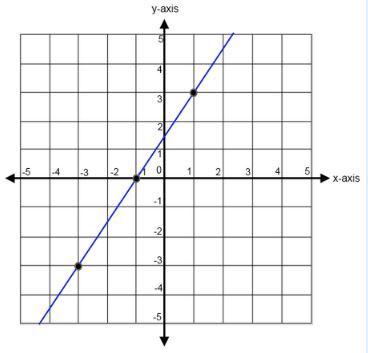
Find the equation of the line that passes through the points $$(-1,0)$$ and $$(-2,4)$$
The distance between A(1, 3) and B(x, 7) isCalculate the possible values of x
A chair is $$5$$ feet from one wall of a room and $$7$$ feet from the wall at a right angle to it. How far is the chair from the intersection of the two walls?
Find the slope of the line with inclination $$60^\circ$$
Prove that the equations to the straight lines passing through the origin which make an angle $$\alpha$$ with the straight line $$ y + x = 0 $$ are given by the equation
$$ x^2 + 2xy \sec 2 \alpha + y^2 = 0 . $$
Prove that the angle between the straight lines joining the origin to the intersection of the straight line $$y = 3x + 2$$ with the curve $$ x^2 + 2xy + 3y^2 + 4x + 8y - 11 = 0 $$ is $$ \tan^{-1} \dfrac {2 \sqrt2}{3}$$
Prove that the points $$(3, 0) (6, 4)$$ and $$(-1, 3)$$ are the vertices of a right angled isosceles triangle.
R.E.F image
We can safely assume that AB and BC are the isosceles sides.
By distance formula, $$AB=\sqrt{(-1-3)^{2}+(3-0)^{2}}=\sqrt{16+9}=5$$
$$BC=\sqrt{(3-6)^{2}+(0-4)^{2}}=\sqrt{9+16}=5$$
Since AB=BC, the $$\Delta ABC$$ is isosceles.
For proving $$\angle ABC$$ is right, we use the relation $$m_{1}\times m_{2}=-1$$
where $$m_{1}$$ is slope of line AB and $$m_{2}$$ of BC :
$$m_{1}=\dfrac{3-0}{-1-4}=\dfrac{3}{-4}$$ $$m_{2}=\dfrac{4-0}{6-3}=\dfrac{4}{3}$$
$$m_{1}\times m_{2}=\dfrac{-3}{4}\times \dfrac{4}{3}=-1$$
Hence proved, $$\Delta ABC$$ is right angled isosceles.
Find the value of $$k$$ if the angle between St. lines $$4x - y + 7 = 0, kx - 5y - 9 = 0$$ is $$45^{\circ}$$.
Prove that the product of the lengths of the perpendiculars drawn from the points $$(\sqrt{a^2-b^2}, 0)$$ and$$ (-\sqrt{a^2-b^2}, 0)$$ to the line $$\dfrac{x}{a} cos\theta+\dfrac{y}{b}sin\theta= 1$$ is $$b^2$$.
Perpendicular Length from Point to line $$P(x_{1},y_{1}) $$
$$ ax+by+c = 0 $$
$$ d = \dfrac{|ax_{1}+by_{1}+c|}{\sqrt{a^{2}+b^{2}}} $$
given line $$ \dfrac{x}{a}cos\theta +\dfrac{y}{b}sin\theta = 1 $$
given Point $$ (-\sqrt{a^{2}-b^{2}},0)$$ and $$ (\sqrt{a^{2}-b^{2}},0) $$
Product of Perpendicular distance from
both Point to line
$$ = \dfrac{\left|-\dfrac{\sqrt{a^{2}-b^{2}}}{a}cos\theta +0-1\right|}{\sqrt{\dfrac{cos^{2}\theta }{a^{2}}+\dfrac{sin^{2}\theta }{b^{2}}}}\times \dfrac{\left | \sqrt{\dfrac{a^2-b^2}{a}}cos \theta + 0 -1 \right |}{\sqrt{\dfrac{cos^2\, \theta}{a^2} + \dfrac{sin^2}{b^2}}}$$
$$ = \dfrac{\dfrac{-cos^{2}\theta }{a^{2}}(a^{2}-b^{2})+1}{\dfrac{cos^{2}\theta }{a^{2}}+\dfrac{sin^{2}\theta }{b^{2}}} = \dfrac{(-cos^{2}\theta +\dfrac{b^{2}}{a^{2}}cos^{2}\theta+1)a^{2}b^{2}}{(b^{2}cos^{2}\theta +a^{2}sin^{2}\theta )} $$
$$ = \dfrac{\dfrac{(a^{2}sin^{2}\theta +b^{2}cos^{2}\theta )a^{2}b^{2}}{a^{2}}}{(a^{2}sin^{2}\theta +b^{2}cos^{2}\theta )} = b^{2} $$
Show that the quadrilateral whose vertices are $$(2,-1),(3,4),(-2,3)$$ and $$(-3,-2)$$ is a rhombus.
Which point on y-axis is equidistant from $$(2,3)$$ and $$(-4,1)$$?
Two vertices of an isosceles triangle are $$(2,0)$$ and $$(2,5)$$. Find the third vertex if the length of the equal sides is $$3$$.
Let $$\Delta$$ABC be the isosceles triangle, the third vertex be C(a,b).
and A(2,0) and B(2,5)
Let AC and BC be equal sides of the triangle
By distance formula we have,
$$D=\sqrt{(x_2-x_1)+(y_2-y_1)}$$
$$\therefore AB=\sqrt{(2-2)^2+(5-0)^2}=\sqrt{25}=5$$
Now,
$$AC=3$$ [length of equal sides=3 ]
$$AC^2=3^2=9$$..........(a)
but by distance formula,
$$AC^2=\sqrt{(a-2)^2+b^2}$$...........(b)
Combining (a) and (b)
$$\Rightarrow (a-2)^2+b^2=9$$
$$\Rightarrow a^2+4-4a+b^2=9$$
$$\Rightarrow a^2+b^2-4a=5$$ ---------- (1)
Consider BC
$$BC^2=\sqrt{(a-2)^2+(b-5)^2}$$
but BC=3
$$\therefore (a-2)^2+(b-5)^2=9$$
$$\Rightarrow a^2+4-4a+b^2+25-10b=9$$
$$\Rightarrow a^2+b^2-4a-10b+20=0$$ ------- (2)
$$\Rightarrow -10b+20+5=0$$ ---------(from 1 )
$$\Rightarrow 10b=25$$
$$\Rightarrow b=\dfrac{25}{10}=\dfrac{5}{2}$$
Now, $$a^2+\dfrac{25}{4}-4a=5$$
$$\Rightarrow a^2-4a=\dfrac{-5}{4}$$
$$\Rightarrow a^2-4a+\dfrac{5}{4}=0$$
$$\Rightarrow a=\dfrac{4\pm\sqrt{16-4*1*\dfrac{5}{4}}}{2}$$
$$=\dfrac{4\pm\sqrt{11}}{2}$$
$$=\dfrac{2+\sqrt{11}}{2},\dfrac{2-\sqrt{11}}{2}$$
$$\therefore$$ Coordinate of third vertex (a,b) = $$(\dfrac{2+\sqrt{11}}{2},\dfrac{5}{2})$$ and $$(\dfrac{2-\sqrt{11}}{2},\dfrac{5}{2})$$
Find the centre of the circle passing through $$(6,-6),(3,-7)$$ and $$(3,3)$$
Name the quadrilateral formed, if any, by the following points and give reasons for your answers:
$$A(-1,-2),B(1,0),C(-1,2),D(-3,0)$$
Prove that the points $$(3,0),(4,5),(-1,4)$$ and $$(-2,-1)$$, form a rhombus. Also, find its area.
If the point $$P(x,y)$$ is equidistant from the points $$A(5,1)$$ and $$B(1,5)$$ prove that $$x=y$$.
Prove that the points $$(3,-2), (4,0), (6,-3)$$ and $$(5,-5)$$ are the vertices of a parallelogram.
If $$A=(2,3)$$, $$B=(-2,3)$$ and $$P$$ moves such that $$|PA-PB|=4$$, then find the locus of $$P$$.
If $$(-4,0)$$ and $$(4,0)$$ are two vertices of an equilateral triangle, find the coordinates of its third vertex.
If $$P(2,-1), Q(3,4), R(-2,3)$$ and $$S(-3,-2)$$ be four points in a plane, show that PQRS is a rhombus but not a square. Find the area of the rhombus.
Prove that the points $$(-2, -1), (1, 0), (4,3)\ and\ (1,2)$$ are the vertices of a parallelo-gram. Is it a rectangle?
If coordinate of two points $$A$$ and $$B$$ are $$(3,4)$$ and $$(5,-2)$$ find coordinates of $$P$$ if $$PA$$=$$PB$$ and area of $$\triangle PAB=10$$
Find the angle between the x-axis and the line joining the point $$(3,-1)$$ and $$(4,-2)$$.
Find the points on the X-axis which are at a distance of $$2\sqrt{5}$$ from the point $$(7,-4)$$. How many such points are there?
If $$R(x, y)$$ is a point on the line segment joining the points $$P(a, b)$$ and $$Q(b, a)$$, the prove that $$x + y = a + b$$.
Show that $$O(0,0),C(a,0),B(a,b),C(0,b)$$ are the vertices of a rectangle. If $$P(x,y) $$ is a point in the coordinates plane, then prove using formula that $$PQ^{2}+PB^{2}=PA^{2}+PC^{2}$$.
$$O(o, o), A(o,o), B(a,b), c(a,b)$$
$$OA=BC, OC=AB$$
$$OA=2, BC=a$$
$$OC=b, AB=b$$
$$\therefore OA=BC$$ & $$OC=AB$$
eqn of $$OC, x=0$$
$$OA\Rightarrow y=0$$
$$AB\Rightarrow x=a$$
$$BC\Rightarrow y=b$$
Let $$P(x,y)$$ be in co-ordinates plane
To prove
$$PO^{2}+PB^{2}=PA^{2}+PC^{2}$$
$$PO=\sqrt{(x-0)^{2}+(y-0)^{2}}$$
$$=\sqrt{x^{2}+y^{2}}$$ .......... $$(1)$$
$$PB=\sqrt{(x-0)^{2}+(y-0)^{2}}$$ ......... $$(2)$$
$$PA=\sqrt{(x-a)^{2}+(y-0)^{2}}$$
$$=\sqrt{(x-a)^{2}+y^{2}}$$ ........... $$(3)$$
$$PC=\sqrt{(x-0)^{2}+(y-0)^{2}}$$
$$=\sqrt{x^{2}+(y-b)^{2}}$$ .......... $$(4)$$
$$PO^{2}+PB^{2}=x^{2}+y^{2}+(x-a)^{2}+(y-b)^{2}$$
$$PA^{2}+PC^{2}=(x-a)^{2}+y^{2}+x^{2}+(y-b)^{2}$$
$$\therefore PO^{2}+PB^{2}=PA^{2}+PC^{2}$$
Hence proved
In each of the following find the value of $$'k'$$, for which the points are collinear.
$$(7, -2), (5, 1), (3, k)$$.
If the distance between points $$(x,0)$$ and $$(0,3)$$ is $$5$$, what are the values of $$x$$?
Find the point on Y-axis which is equidistant from $$(-6,4)$$ and $$(2,-8)$$.
Prove that the points $$A(-5,4),B(-1,-2)$$ and $$(5,2)$$ the vertices of an isosceles right-angled triangle. Find the coordinates of D, so that ABCD is a square.
$$A(-5, 4)\ B(-1, -2)\ C(5, 2)$$.
$$AB=\sqrt{4^2+6^2}=\sqrt{52}$$
$$BC=\sqrt{6^2+4^2}=\sqrt{52}$$
$$AC=\sqrt{10^2+2^2}=\sqrt{104}$$
It is isosceles triangle.
with $$AB=BC$$
For making square
$$BD=AC=\sqrt{104}$$
$$\sqrt{(x+1)^2+(y+2)^2}=\sqrt{104}$$------(1)
Also, slope of $$AC$$ is $$\dfrac{-1}{slope\ of\ BD}$$
Slope of $$BD=\dfrac{y+2}{x+1}=\dfrac{-1}{\dfrac{-2}{10}}$$
$$\dfrac{y+2}{x+1}=5$$------(2)
from (1) & (2)
$$x=1\ y=8$$
$$D(1, 8)$$ is new vertex of square.
If the image of the point $$(2, 1)$$ with respect to a line mirror be $$(5, 2)$$, find the equation of the mirror.
We have
$$y-\dfrac{3}{2}=-3\left(x-\dfrac{7}{2}\right)$$
$$2y-3=-3(2x-7)$$
$$2y-3=-6x+21$$
$$6x+2y=24$$
$$3x+y=12$$
Hence this is the centre
If the points $$(1,1), (-1,-1)$$ and $$(-\sqrt{3},k)$$ are vertices of an equilateral triangle find the value of $$k$$.
Find the point on the x-axis which is equidistant from the points $$(2,-5)$$ and $$(-2,9)$$.
Find the ordinate of point whose abscissa is $$10$$ and which is at a distance of $$10$$ units from the point $$P(2,-3)$$.
Find all possible values of $$a$$ for which the distance between the points $$A(a,-1)$$ and $$B(5,3)$$ is $$5$$ units.
Prove that the points $$A(-2, -1), B(1, 0), C(4, 3)$$ and $$D(1, 2)$$ are the vertices of a parallelogram $$ABCD$$.
Find a point on the x-axis which is equidistant from the points $$(7,6)$$ and $$(3,4)$$.
Find that point on y axis which as equidistant from point $$(6,5)$$ and $$(-4,3)$$
Find the co-ordinates of the point equidistant from the points $$A( - 2, - 3),B( - 1,0)$$ and $$C(7, - 6)$$
Find the cosine of the angle $$A$$ of the triangle with vertices $$A(1, -1), B(6, 11)$$ and $$C(1, 2)$$.
Find the distance between the points A (a,b) and B(b,a) if a-b=4.
If point (x,y) is equidistant from points (7,1) and (3,5) show that y =x-2
$$ \rightarrow $$ using distance formula
$$ \rightarrow \sqrt{(x-7)^{2}+(y-1)^{2}} = \sqrt{(x-3)^{2}+(y-5)^{2}}$$
$$ \Rightarrow -14x+49-2y+1 = -6x+9-10y+25$$
$$ \Rightarrow 8x-8y = 16 $$
$$ \Rightarrow x - y = 2 \Rightarrow y = x-2 $$
Find a point on $$Y$$-axis which is equidistant from $$P(-6,4)$$ and $$Q(2,-8)$$.
Find the equation of a straight line:
with slope $$-1/3$$ and $$y-intercept$$ $$-4$$.
Prove that the points $$(0,\,-1).(2,\,1).(0,\,3)$$ and $$(-2,\,1).$$ are the vertices of square?
Show that the points (12 , 8),(-2 , 6) and (6 , 0), are the vertices of a right angled triangle.
Find the coordinates of point P which divides the line segment joining $$A(-2,-7)$$ and $$ B(6,1)$$ in the ratio $$5:3$$
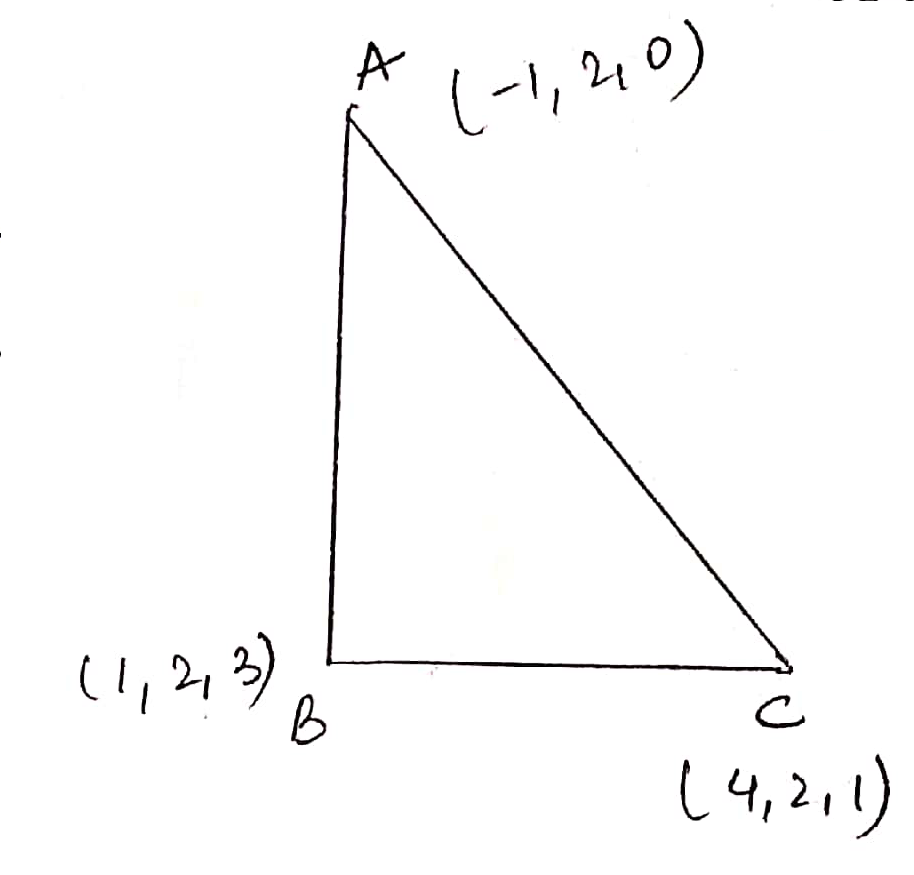
If $$A$$ is $$( - 1,2,0 ) , B$$ is $$( 1,2,3 )$$ and $$C$$ is $$( 4,2,1 ) ,$$ then prove that $$\Delta A B C$$ is an isosceles right triangle.
Distance formula $$\sqrt{\left( x_2-x_1\right)^2+\left( y_2-y_1\right)^2+\left(z_2-z_1\right)^2}$$
$$\Rightarrow AB=\sqrt{\left( 1+1\right)^2+\left( 2-2\right)^2+\left( 3-0\right)^2}$$
$$=\sqrt{4+9}$$
$$=\sqrt{13}$$
$$\Rightarrow BC=\sqrt{\left( 4-1\right)^2+\left(2-2\right)^2+\left( 1-3\right)^2}$$
$$=\sqrt{9+4}$$
$$=\sqrt{13}$$
$$\Rightarrow AC=\sqrt{\left( 4+1\right)^2+\left( 2-2\right)^2+\left(1-0\right)^2}$$
$$=\sqrt{25+1}$$
$$=\sqrt{26}$$
Since $$AB=BC$$
$$\therefore ABC$$ is an isosceles triangle
$$\Rightarrow AB^2+BC^2=\left( \sqrt{13}\right)^2+\left( \sqrt{13}\right)^2$$
$$=13+13$$
$$=26$$
$$=\left(AC\right)^2$$
$$\therefore AB^2+BC^2=AC^2$$
$$\therefore \angle B=90$$
$$\Rightarrow \triangle ABC$$ is an isosceles right angled triangle.
Hence, proved.
How many points are there on the $$x-$$axis whose distance from the point $$(2,3)$$ is less than $$3$$ units ?
Given point (2, 3)
Let point be (x, 0)
$$\sqrt{(x-2)^{2}+(3-0)^{2}} < 3$$
$$=\sqrt{(x-2)^{2}+9} < 3$$
$$=(x-2)^{2}+9 < 9$$
$$=x^{2}+4-4x+9 <9$$
$$=x^{2}-4x+4 < 0 $$
$$= (x-2)^{2} < 0$$
Thus there are infinite points.
If the distances of $${ P }({ x },{ y })$$ from $${ A }(5,1)$$ and $${ B }(-1,5)$$ are equal then, prove that $$3{ x }=2{ y }.$$
If the point $$P(1,2)$$ lies on line segment joining the points $$A(2,4)$$ and $$B(4,8)$$ then find $$\dfrac{{AP}}{{AB}}$$.
Find the angle between the curves given below :
$$y^{2}=4x,\ x^{2}+y^{2}=5$$
evaluate:
$$3x-5y=16;x-3y=8$$
If the slope of a line joining $$A(2,x)B(-3,7)$$ is $$1$$ then find $$x$$.
Find the equation of the set of points such that the sum of the square of its distance from the points (3,4,5) and (-1, 3, -7) is a constant.
Let (a,b,c) be a set of points whose square of sum of distance from (3,4,5) and (-1,3,-7) is a constant (k)
$$(a-3)^{2}+(b-4)^{2}+(c-5)^{2}+(a+1)^{2}+(b-3)^{2}+(c+7)^{2}=k$$
$$a^{2}+b^{2}+c^{2}-6a-8b-10c+9+16+25+a^{2}+b^{2}+c^{2}+2a-6b+140+1+9+44=k$$
$$2[a^{2}+b^{2}+c^{2}]-4a-14b+2c+109=k$$
$$a^{2}+b^{2}+c^{2}-2a-7b+c=\frac{k-109}{2}$$
$$a^{2}+b^{2}+c^{2}-2a-7b+c=\frac{k-109}{2}$$ _______ (1)
Hence equation (1) is the required equation.
Are the points given below collinear? If, state which point lies between the other two $$d(P,Q)=11, d(Q,R)=6.5, d(P,R)=4.5$$
If $$\left(1,x\right)$$ is at $$\sqrt{10}$$ units from $$\left(0,0\right)$$ then find the values of $$x$$
If the points $$A\left(2,0,0\right),\,B\left(4,p,q\right)$$ and $$C\left(1,5,2\right)$$ are collinear,find the values of $$p$$ and $$q$$
If the points $$A\left(1,0,-2\right),\,B\left(2,p,q\right)$$ and $$C\left(-1,5,2\right)$$ are collinear,find the values of $$p$$ and $$q$$
If the points $$A\left(-1,-2,1\right),\,B\left(-2,p,q\right)$$ and $$C\left(1,-2,-1\right)$$ are collinear,find the values of $$p$$ and $$q$$.
If the points $$A\left(4,2,2\right),\,B\left(4,p,q\right)$$ and $$C\left(2,3,3\right)$$ are collinear,find the values of $$p$$ and $$q$$
Find the relation between x and y such that the point (x,y) is equidistnat from the points (7,1) and (3,5)
Given $$A=(3,1)$$ and $$B(0,y-1)$$. Find $$y$$ if $$AB=5$$.
find the distance between A(cos $$\theta $$,Sin$$\theta $$) and B (sin$$\theta $$,-Cos$$\theta $$) using distance formula.find the co-ordinates of the mid point of the line joining the points (3,-10 ) and (6,-8).
If $$A(1, 2), B(-3, 2)$$ and $$C(3, -2)$$ be the vertices of a $$\triangle ABC$$, show that
$$\tan A=2$$
If $$A(1, 2), B(-3, 2)$$ and $$C(3, -2)$$ be the vertices of a $$\triangle ABC$$, show that
$$\tan B=\dfrac{2}{3}$$
A line is of length $$10$$ and one end is at the point $$(2, -3);$$ if the abscissa of the other end be $$10$$, prove that its ordinate must be $$3$$ or $$-9$$.
$$ A $$ is a point on the parabola $$ y^{2}=4 a x . $$The normal at $$ A $$ cuts the parabola again at point $$ B $$.If $$ A B $$ subtends a right angle at the vertex of the parabola. find the slope of $$ A B $$
Find the slope of the line passing through the following pairs of points:
$$(a, -b)$$ and $$(b, -a)$$
Find the slope of the line whose inclination is:
$$72^\circ 30'$$
We know that, the slope of a line is given by the tan of its inclination.
Slope $$= tan 72^\circ 30' = 3.1716$$ (Refer table)
Find the slope of the line passing through the following pairs of points:
$$(-2, -3)$$ and $$(1, 2)$$
Find the slope of the line whose inclination is:
$$46^\circ$$
We know that, the slope of a line is given by the tan of its inclination.
Slope $$= tan 46^\circ = 1.0355$$ (Refer table)
Find the slope of the line passing through the following pairs of points:
$$(-4, 0)$$ and origin
Find the inclination of the line whose slope is:
$$1.0875$$
Slope $$= tan\theta = 1.0875$$
$$\Rightarrow \theta = 47^\circ 24'$$ (Refer table)
Find the inclination of the line whose slope is:
$$0.7646$$
Slope $$= tan \theta = 0.7646$$
$$\Rightarrow \theta = 37^\circ 24'$$ (Refer table)
Without using the distance formula, show that the points $$A (4, 5), B (1, 2), C (4, 3) $$and $$D (7, 6)$$ are the vertices of a parallelogram.
Find the slope of the line parallel to AB if:
$$A = (0, -3)$$ and $$B = (-2, 5)$$
Without using the distance formula, show that the points $$A (4, -2), B (-4, 4)$$ and $$C (10, 6)$$ are the vertices of a right-angled triangle.
Find the slope of the line perpendicular to $$AB$$ if:
$$A = (0, -5)$$ and $$B = (-2, 4)$$
Find the slope of the line parallel to AB if:
$$A = (-2, 4)$$ and $$B = (0, 6)$$
The line passing through $$(0, 2)$$ and $$(-3, -1)$$ is parallel to the line passing through $$(-1, 5)$$ and $$(4, a)$$. Find $$a.$$
Find the slope of the line perpendicular to AB if:
$$A = (3, -2)$$ and $$B = (-1, 2)$$
$$(-2, 4), (4, 8), (10, 7)$$ and $$(11, -5)$$ are the vertices of a quadrilateral. Show that the quadrilateral, obtained on joining the mid-points of its sides, is a parallelogram.
The line passing through $$(-4, -2)$$ and $$(2, -3)$$ is perpendicular to the line passing through $$(a, 5)$$ and $$(2, -1)$$. Find $$a.$$
Determine $$x$$ so that the slope of the line through $$(1, 4)$$ and $$(x, 2)$$ is $$2.$$
Coordinates of $$A$$ are $$(1,1)$$ and of $$A_{n}$$ are $$(n, 2n + 1)$$, $$O$$ is the origin, then match the columns :
$$ A_{1}, A_{2},....A_{n} $$ are points on the line $$y=x$$ lying in the positive quadrant such that $$ OA_{n}=n O \ A_{n-1}, O $$ being the origin . If $$ OA_{1}=1$$ then the coordinates of $$A_{8}$$ are $$ (3a \sqrt 2, 3a \sqrt 2) $$ where $$a$$ is equal to
Find the value of $$x$$ for which the distance between the points $$P(2x,-5)$$ and $$Q(3x,-2)$$ is 5 units.
The x-coordinate of point P is twice its y-coordinate. If P is equidistant from $$Q(2, -3)$$ and $$R(-3, 6)$$ then find the coordinate of P.
Let $$ABC$$,be a triangle such that the coordinates of the vertex $$A$$ are $$(-3,1)$$.Equation of the median through $$B$$ is $$ 2x+y-3=0$$ and equation of the angular bisector of $$C$$ is $$7x-4y-1=0$$.Find the slope of line $$BC$$.
Prove that the points $$(at^2_1, 2at_1)$$, $$(at^2_2, 2at_2)$$ and $$(0, a)$$ will be collinear, if $$t_1t_2=-1$$.
Show that $$A(2, 3), B(4, 5)$$ and $$C(3, 2)$$ can be the vertices of a rectangle. Find the coordinates of the fourth vertex.
Given: $$A=\left( 2,3 \right) ;B=\left( 4,5 \right) ;C=\left( 3,2 \right) $$
Slope of $$AB=\cfrac { 5-3 }{ 4-2 } =1$$
Slope of $$BC=\cfrac { 2-5 }{ 3-4 } =\cfrac { -3 }{ -1 } =3$$
Slope of $$AC=\cfrac { 2-3 }{ 3-2 } =-1$$
Slope of $$AB\times $$ Slope of $$AC=-1$$
$$\therefore AB\bot AC$$
Let $$D=(x,y)$$
Slope of AC=Slope of BD
$$\therefore \cfrac { 3-2 }{ 2-3 } =\cfrac { 5-y }{ 4-x } $$
$$\Rightarrow 5-y=x-4\Rightarrow x+y-9=0$$
Also, Slope of $$BD\times $$ Slope of $$DC=-1$$
$$\Rightarrow \cfrac { 5-y }{ 4-x } \times \cfrac { y-2 }{ x-3 } =-1$$
$$\Rightarrow \left( 5-y \right) \left( y-2 \right) =\left( 3-x \right) \left( 4-x \right) $$
$$\Rightarrow 5y-10-{ y }^{ 2 }+2y=12-3x-4x+{ x }^{ 2 }$$
$$\Rightarrow { y }^{ 2 }-7y+10=-{ x }^{ 2 }+7x-12$$
Puttig $$y=9-x$$
$${ \left( 9-x \right) }^{ 2 }-7\left( 9-x \right) +10+{ x }^{ 2 }-7x+12=0$$
$$\Rightarrow 81+{ x }^{ 2 }-18x-63+7x+10+{ x }^{ 2 }-7x+10=0$$
$$\Rightarrow 2{ x }^{ 2 }-18x+40=0$$
$${ x }^{ 2 }-9x+20=0\Rightarrow x=5$$ or $$x=4$$
If $$x=5,y=4$$
If $$x=4,\quad y=5$$
$$\left( 4,5 \right) $$ is already a vertex (B)
$$\therefore D=(5,4)$$
$$\therefore $$Four vertices are $$A(2,3);B(4,5);C(3,2);D(5,4)$$
Find the points on the x-axis, whose distance from the line $$\dfrac{x}{3}+\dfrac{y}{4}=1$$ are $$4$$ units.
Find the angle between the lines whose slopes are $$(2-\sqrt 3)$$ and $$(2+\sqrt 3)$$.
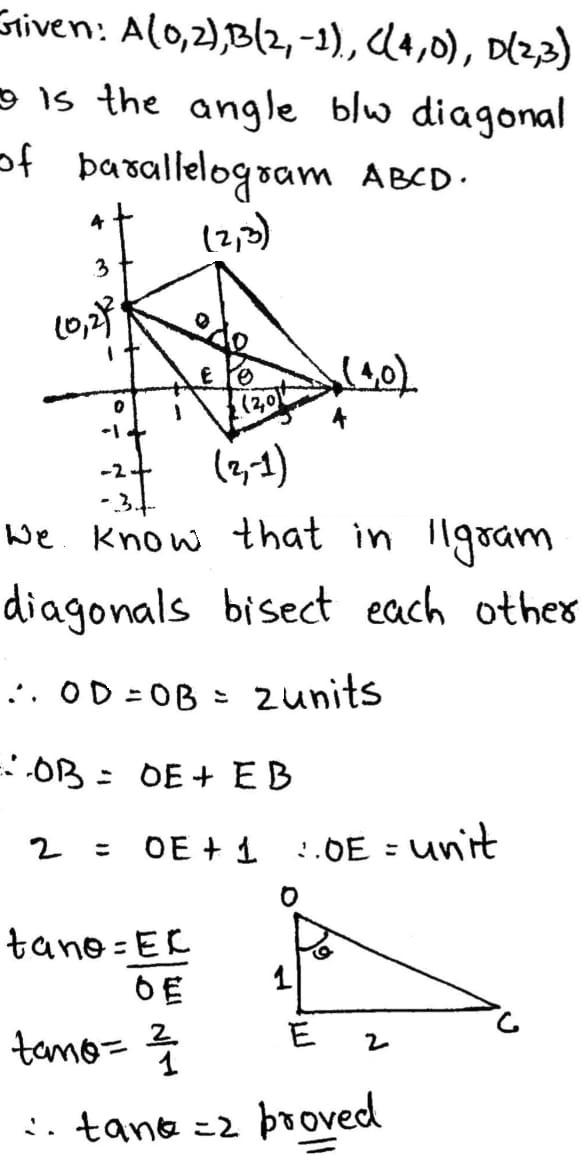
If $$\theta$$ us the angle between the diagonals of a parallelogram $$ABCD$$ whose vertices are $$A(0, 2), B(2, -1), C(4, 0)$$ and $$D(2, 3)$$. Show that $$\tan \theta=2$$.
If $$\theta$$ is the angle between the lines joining the points $$A(0, 0)$$ and $$B(2, 3)$$, and the points $$C(2, -2)$$ and $$D(3, 5)$$, show that $$\tan \theta=\dfrac{11}{23}$$.
If $$A(1, 2), B(-3, 2)$$ and $$C(3, -2)$$ be the vertices of a $$\triangle ABC$$, show that
$$\tan C=\dfrac{4}{7}$$
Find the angle between the lines whose slopes are $$\sqrt 3$$ and $$\dfrac{1}{\sqrt 3}$$.
Class 11 Commerce Applied Mathematics Extra Questions
- Basics Of Financial Mathematics Extra Questions
- Circles Extra Questions
- Descriptive Statistics Extra Questions
- Differentiation Extra Questions
- Functions Extra Questions
- Limits And Continuity Extra Questions
- Logarithm And Antilogarithm Extra Questions
- Mathematical And Logical Reasoning Extra Questions
- Number Theory Extra Questions
- Numerical Applications Extra Questions
- Permutations And Combinations Extra Questions
- Probability Extra Questions
- Relations Extra Questions
- Sequences And Series Extra Questions
- Set Theory Extra Questions
- Straight Lines Extra Questions
- Tangents And Its Equations Extra Questions