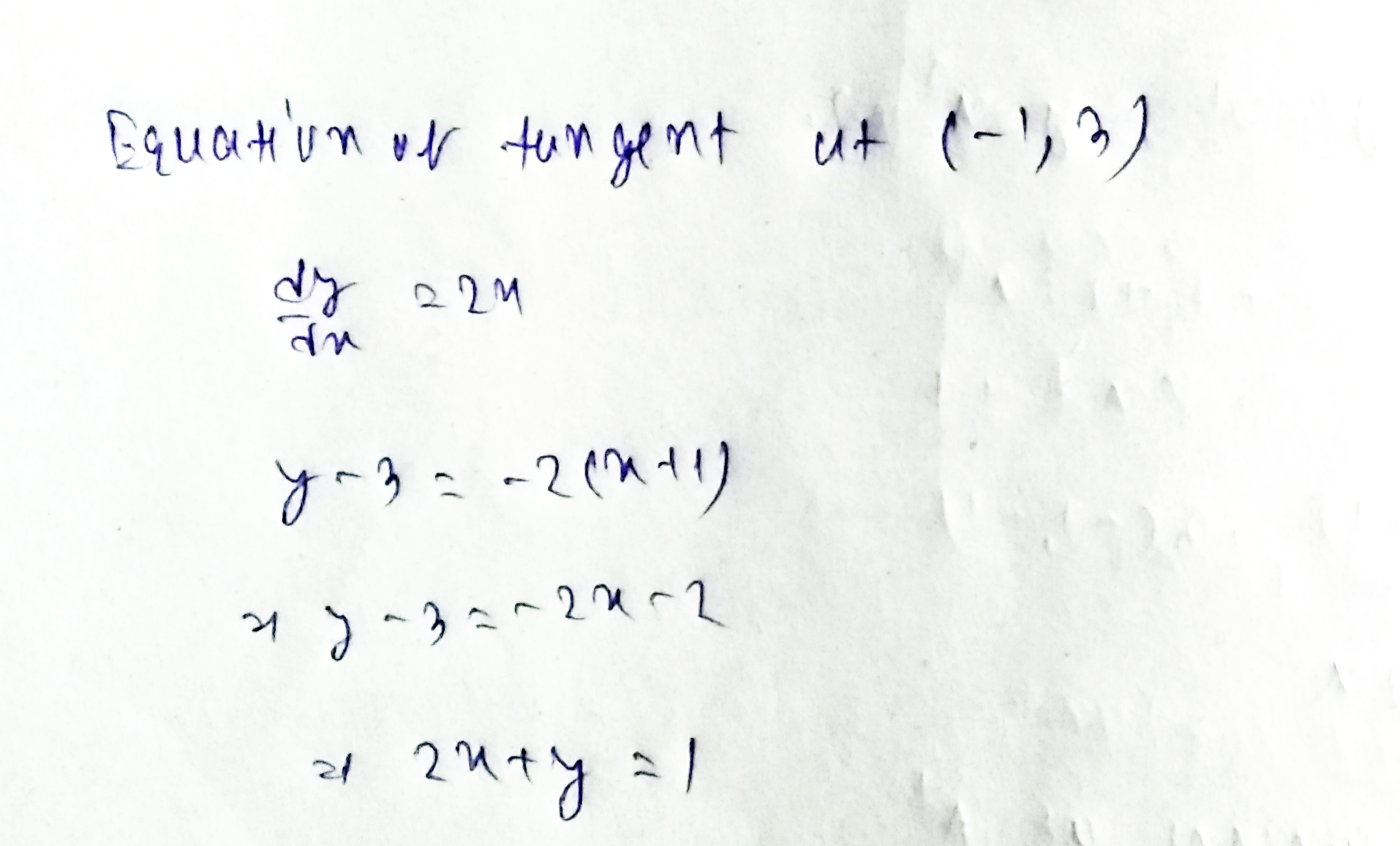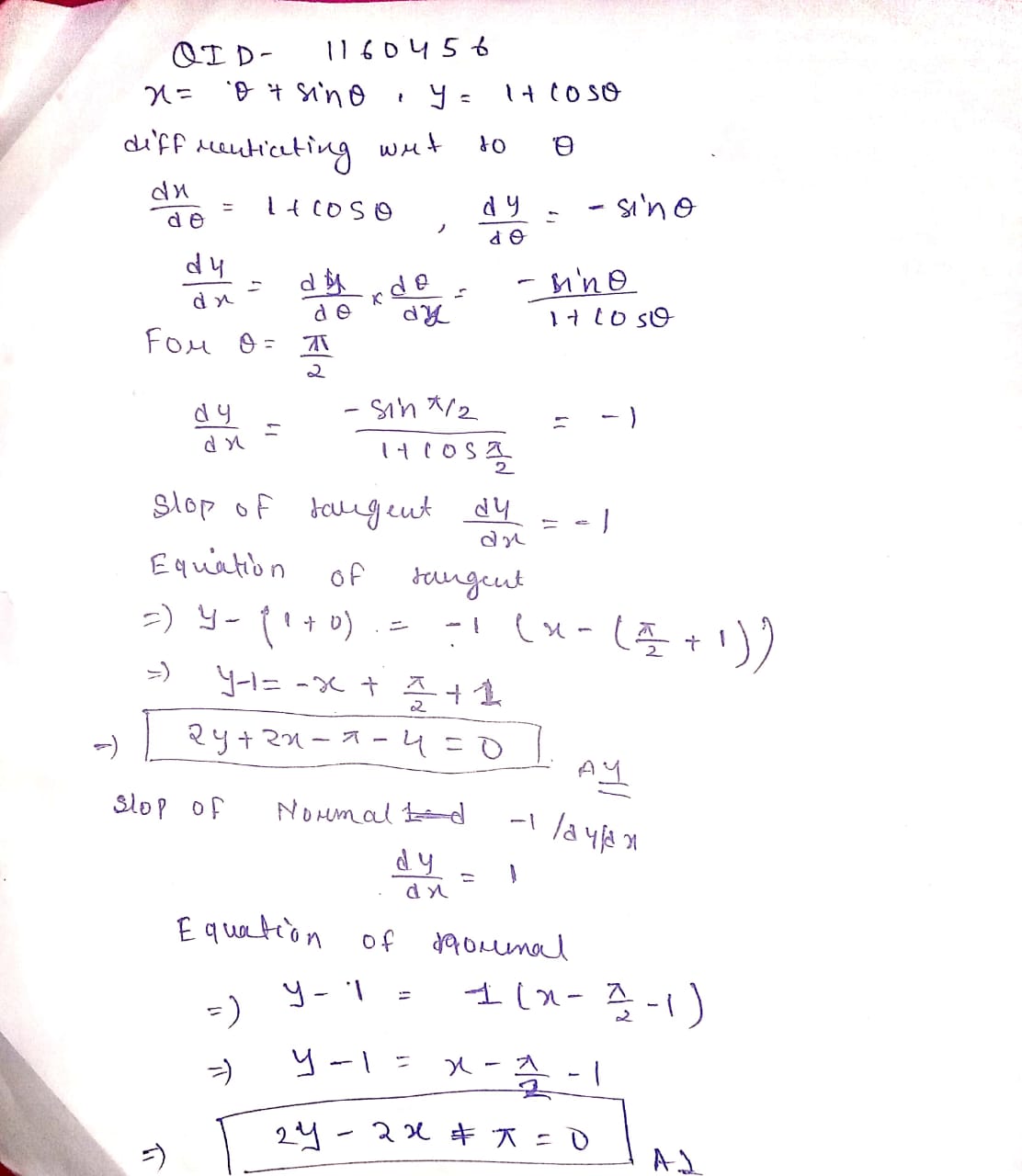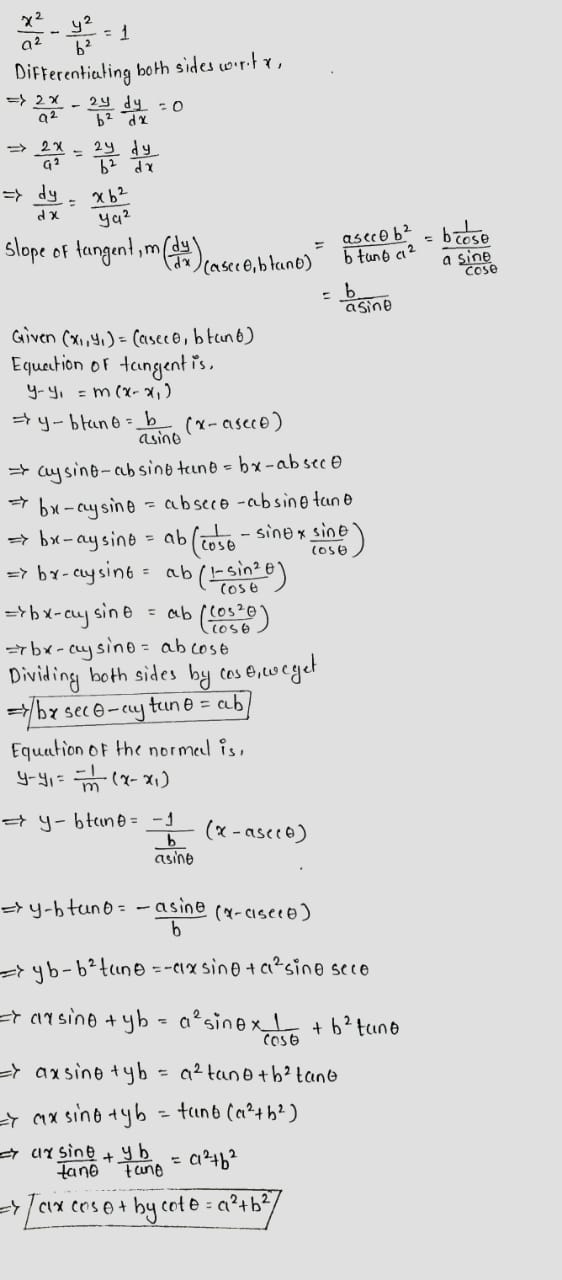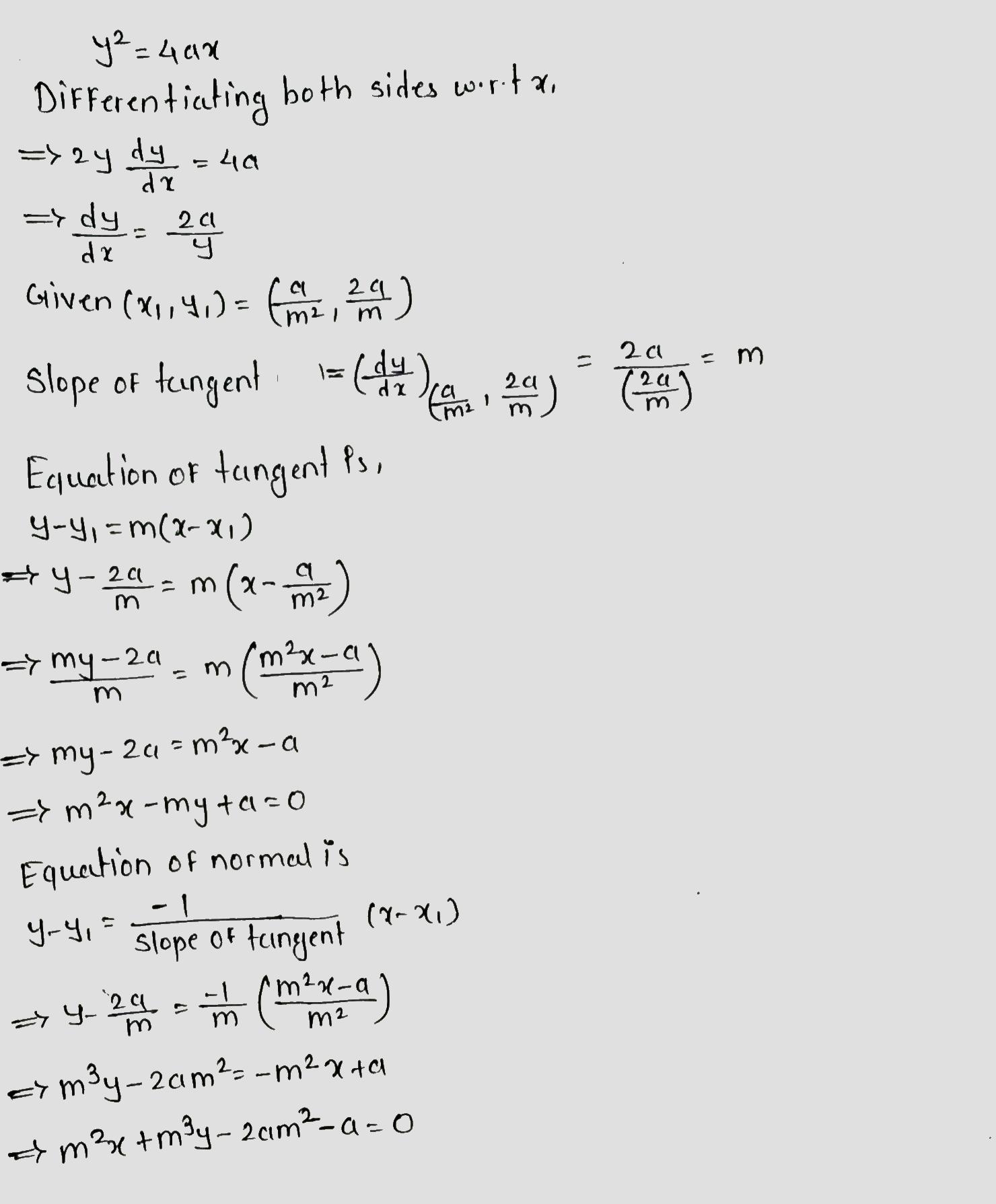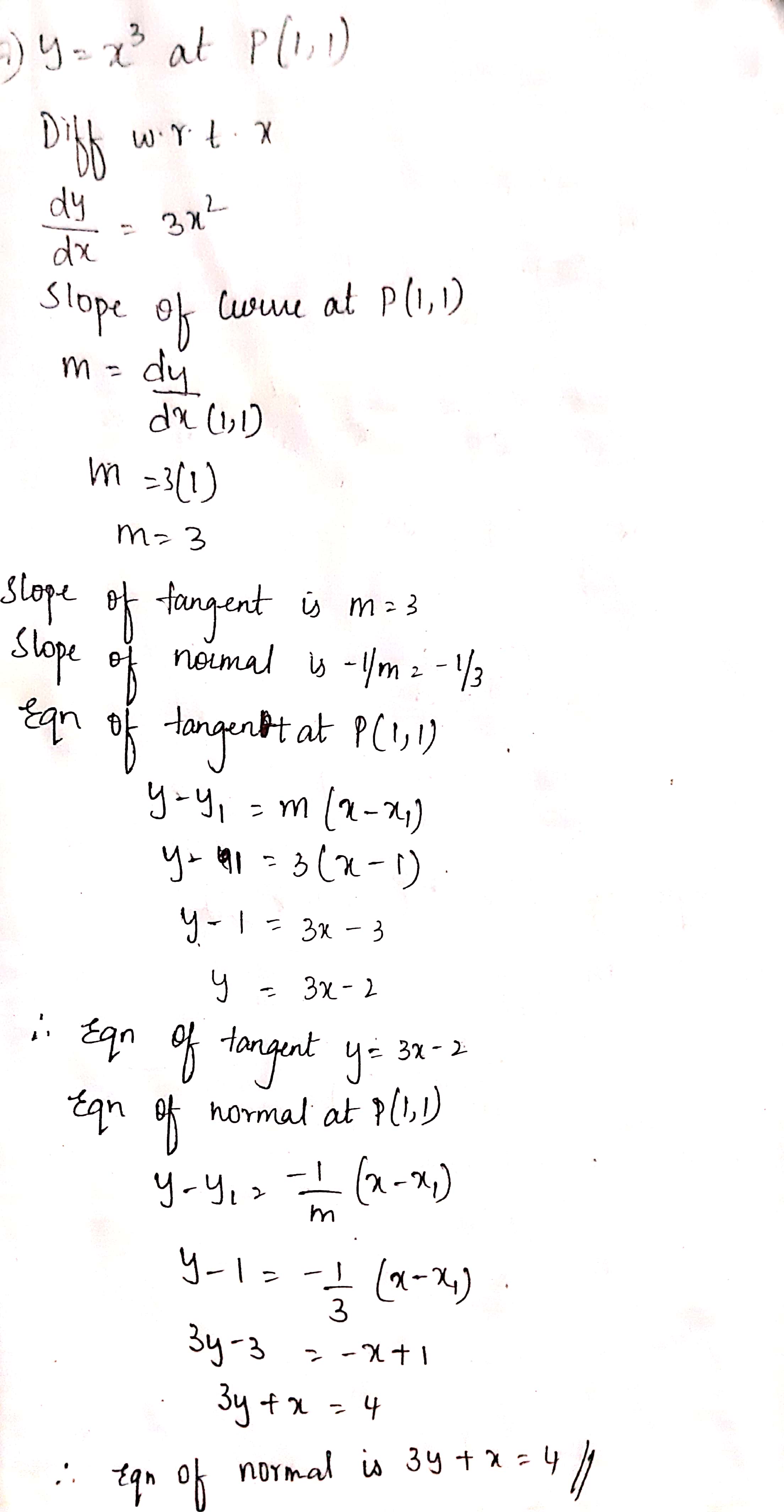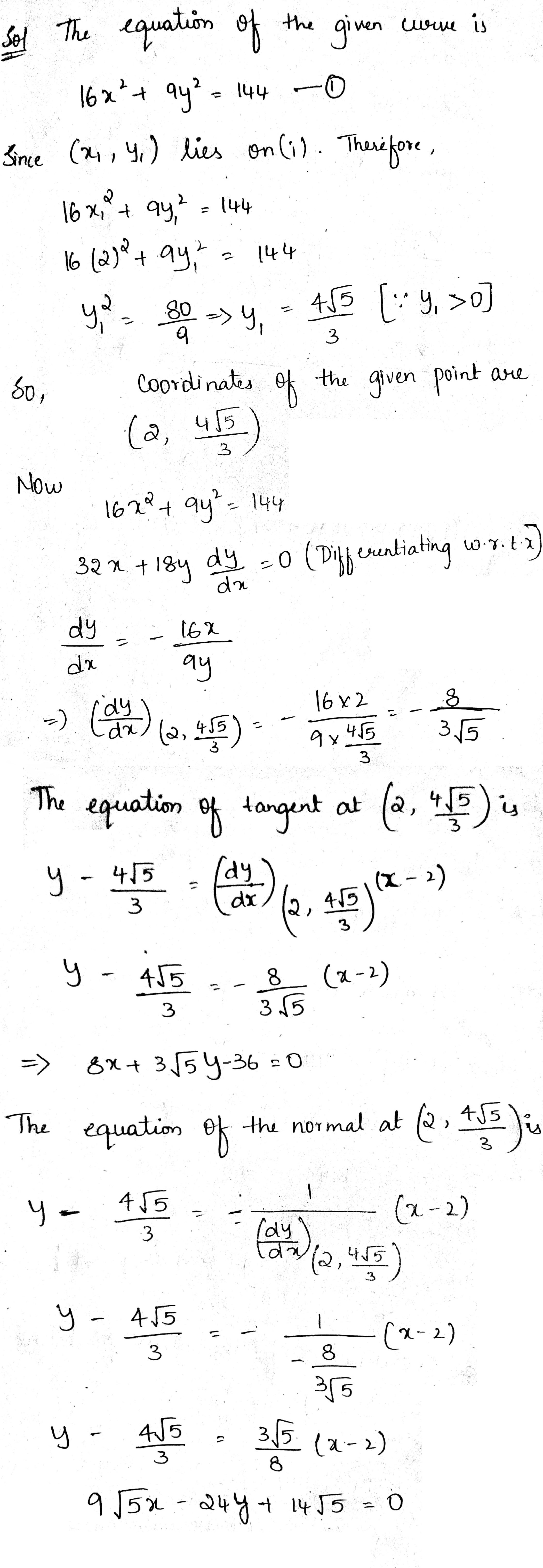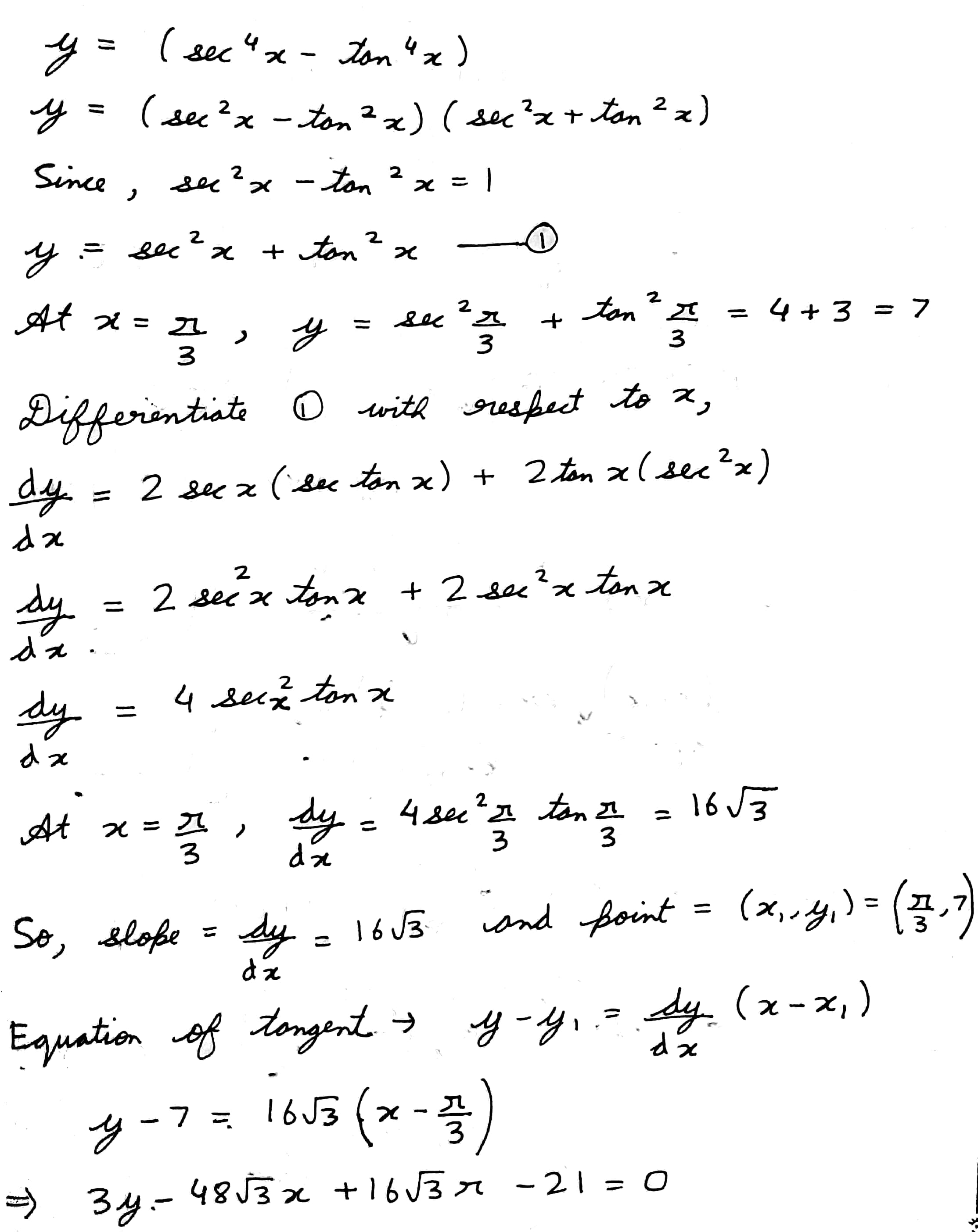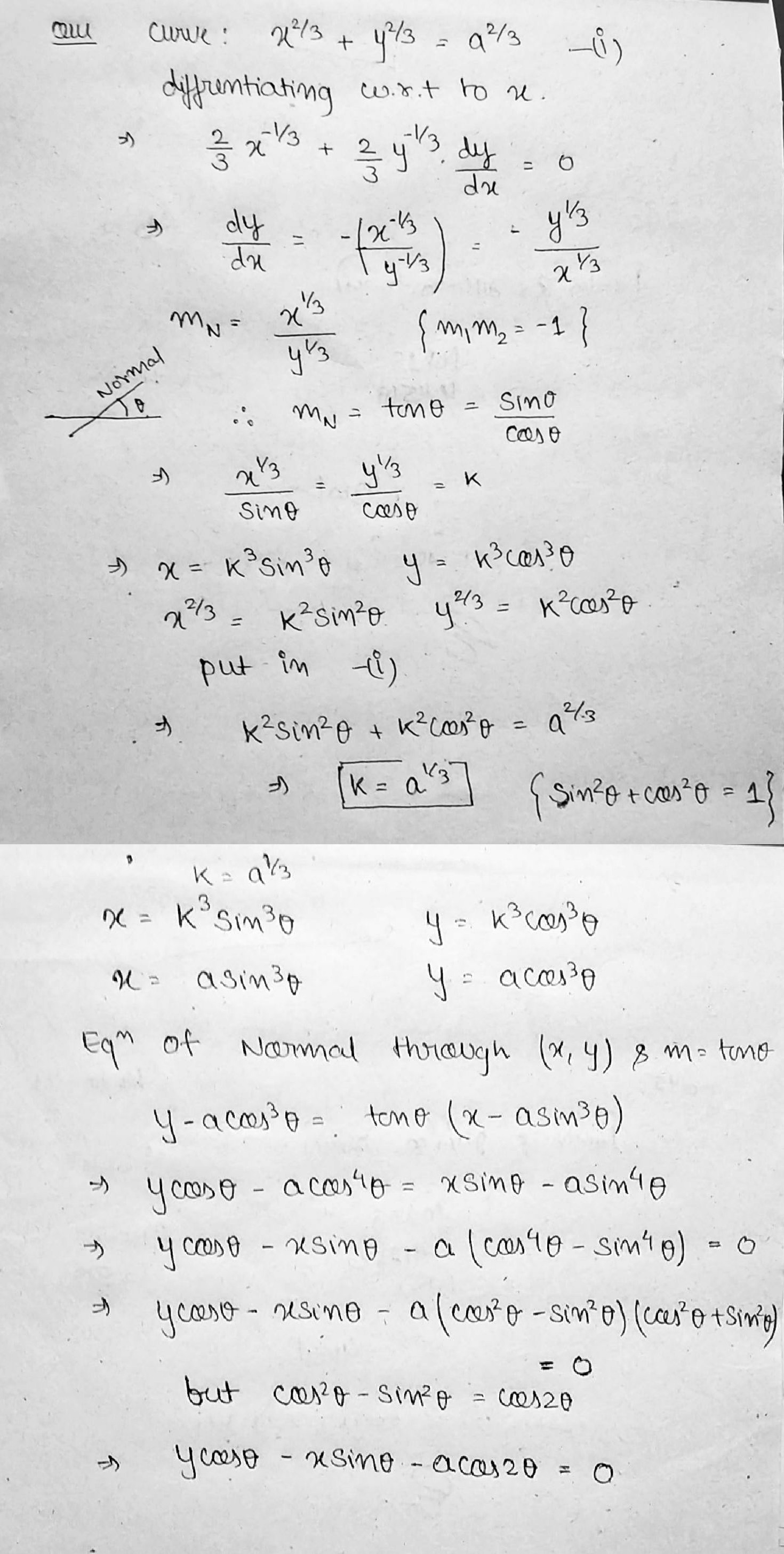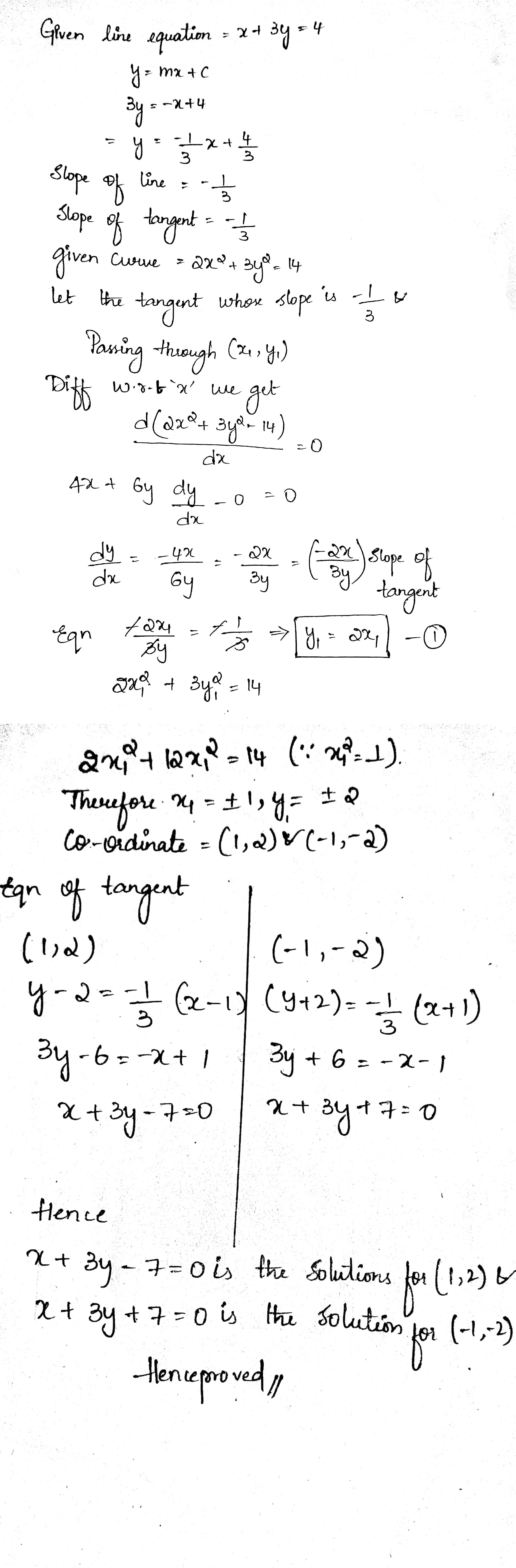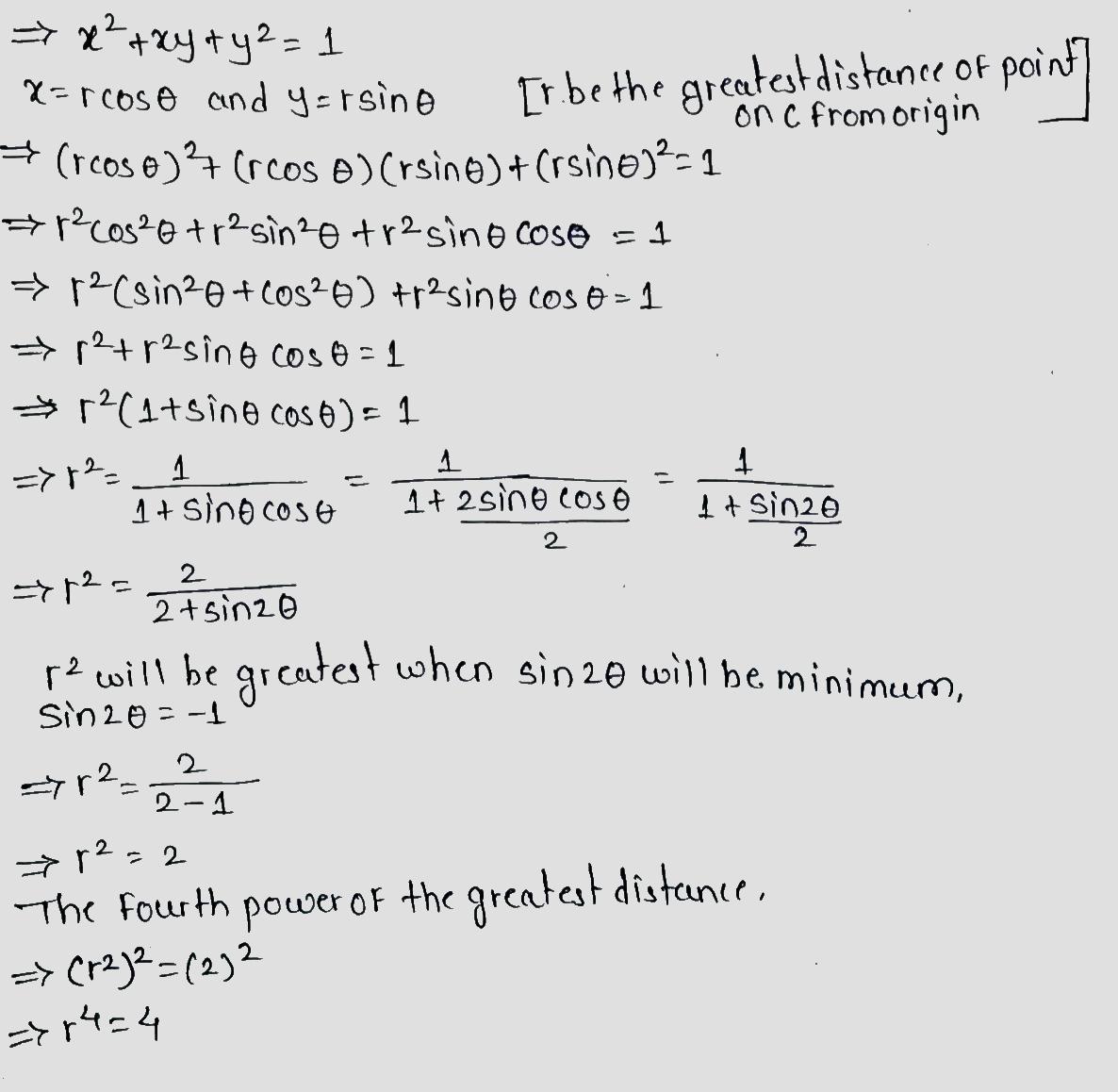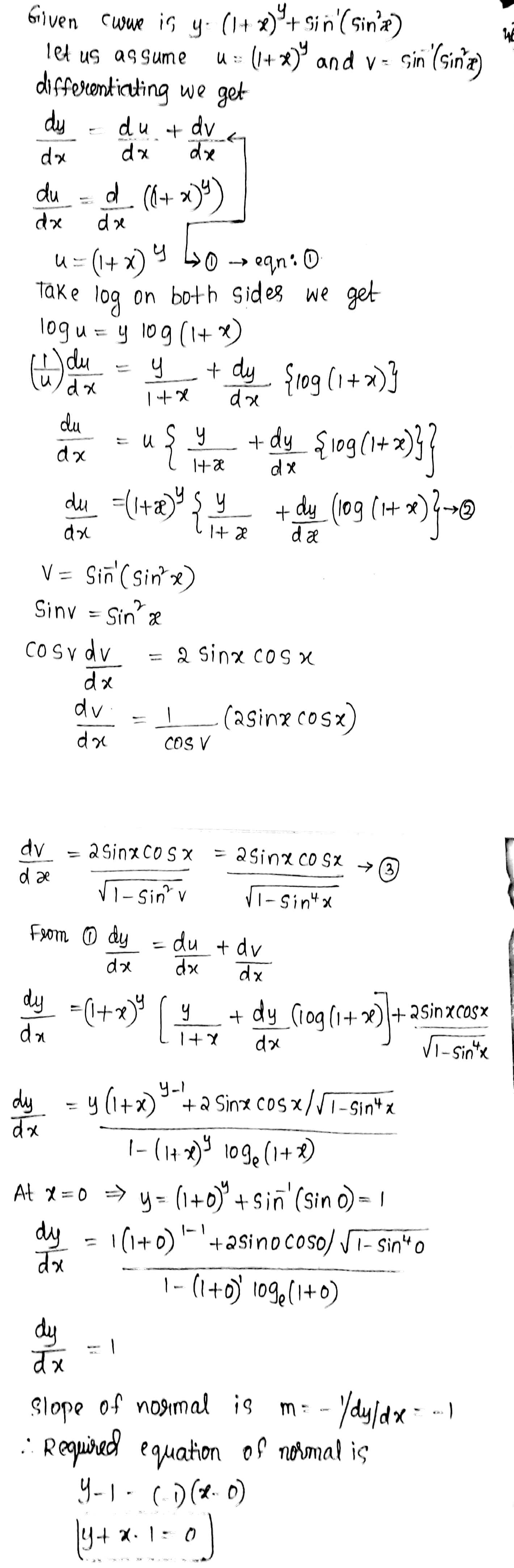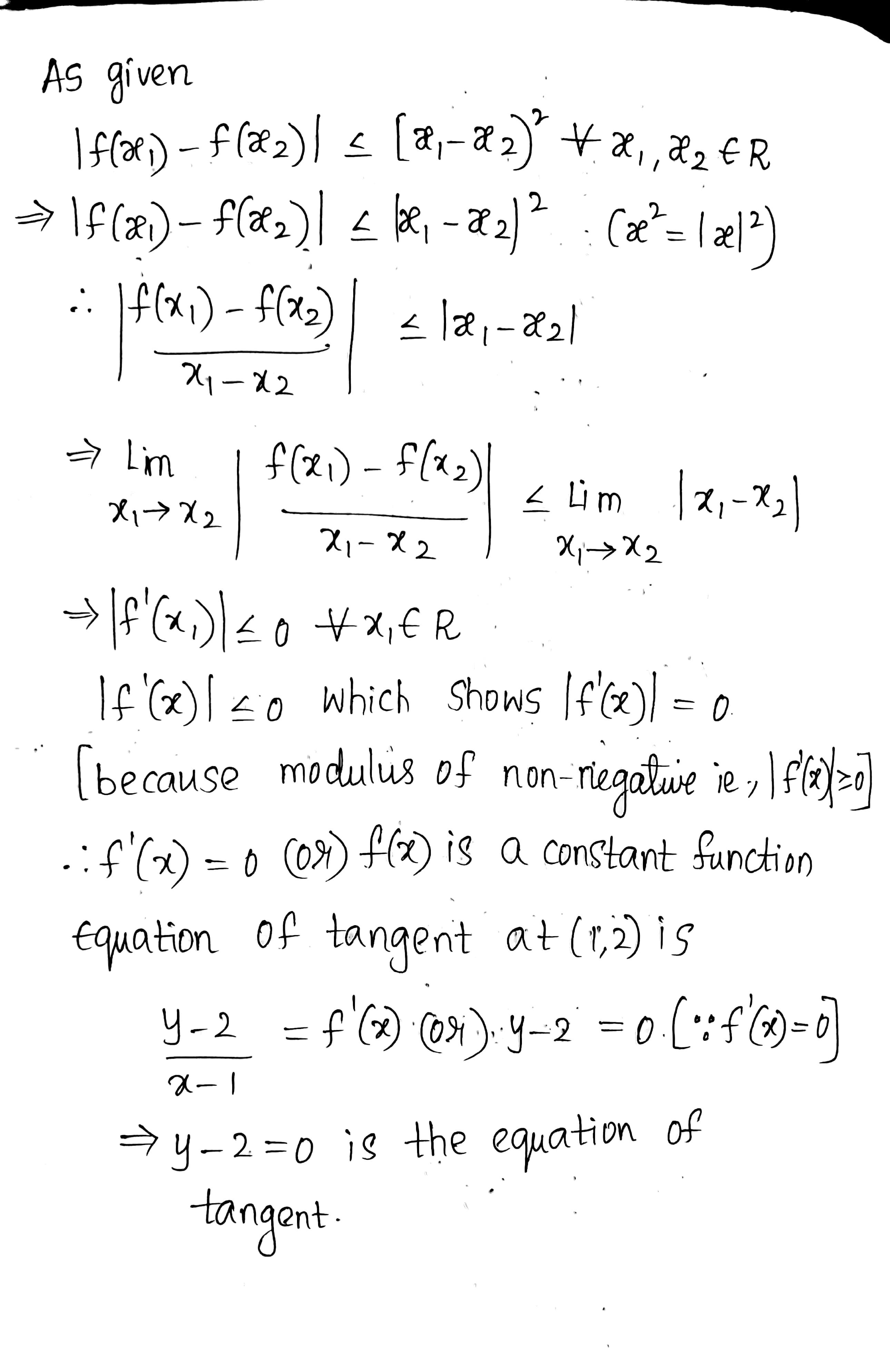Tangents And Its Equations - Class 11 Commerce Applied Mathematics - Extra Questions

Find the equation of the normal to the parabola $$y^{2} = 4x$$, which is
(i) parallel to the line $$y = 2x - 5$$,
(ii) perpendicular to the line $$x + 3y + 1 = 0$$.

Slope of tangent to parabola is $$2y\dfrac{dy}{dx}=4$$
$$\Rightarrow \dfrac{dy}{dx}=\dfrac{2}{y}$$
$$\therefore$$ Slope of normal $$m=-\dfrac{1}{\dfrac{dy}{dx}}=-\dfrac{y}{2}$$
$$(i)$$ parallel to the line $$ y=2x-5$$
$$\therefore m=2$$ ... ($$\because$$ Slope will be same)
$$m=-\dfrac{y}{2}=2\rightarrow y=-4$$
Putting value of $$y$$ in equation of parabola we get $$x=4$$. 
So point on parabola for the normal is $$(4,-4)$$
$$\therefore$$ equation is $$y-(-4)=2(x-4)$$
$$2x-y=12$$
$$(ii)$$ perpendicular to the line $$ x+3y+1=0$$
$$\therefore m=3$$ ....... $$(\because $$ Slope will be= -$$\dfrac{1}{Slope\space of\space perpendicular\space line}$$)
$$m=-\dfrac{y}{2}=3\rightarrow y=-6$$
Putting value of $$y$$ in equation of parabola we get $$x=9$$. 
So point on parabola for the normal is $$(9,-6)$$
$$\therefore$$ equation is $$y-(-6)=3(x-9)$$
$$3x-y=33$$


Find the equation of tangents to the curve $$y = \cos x ,x \in \left[ { - 2\pi ,2\pi } \right]$$   , which passes through $$(0,1)$$ 

The equation of curve $$y=\cos x$$
The slope of tangent is $$\dfrac {dy}{dx}=\dfrac d{dx}\cos x\\\dfrac {dy}{dx}=-\sin x\\\left.\dfrac {dy}{dx}\right|_{(0,1)}=-\sin 0=0$$
it passes through $$(0,1)$$
$$\implies y-1=0(x-0)\\y=1$$
It is the equation of tangent


The perpendicular from the origin to then line $$y=mx+c$$ meets it at the point $$(-1, 2)$$. Find the values of m & c.


1225255_1227171_ans_911207abd34e4fe3a09174dd48acd72e.jpg


Find the equations of the tangent and the normal to the following curves. 
$$x^2 + y^2 + xy = 3 \, at \, P (1, 1)$$

$$x^{2}+y^{2}+xy=3$$

Differentiating w.r.t. $$x$$ , we get

$$2x+2y\cfrac{\mathrm{d} y}{\mathrm{d} x}+x\cfrac{\mathrm{d} y}{\mathrm{d} x}+y=0$$

$$(2y+x)\cfrac{\mathrm{d} y}{\mathrm{d} x}=-2x-y$$

$$\cfrac{\mathrm{d} y}{\mathrm{d} x}=\cfrac{-2x-y}{2y+x}$$

Slope of the tangent at $$(1,1)$$ is $$m=\left ( \cfrac{\mathrm{d} y}{\mathrm{d} x} \right )_{(1,1)}=\cfrac{-3}{3}=-1$$

So, the equation of the tangent is

$$y-1=m(x-1)$$

$$y-1=-x+1$$

$$y+x=2$$

Slope of the normal at $$(1,1)$$ is $$=-\cfrac{1}{m}=1$$

So, the equation of the normal is

$$y-1=1(x-1)$$

$$y=x$$


Find the equation of the normal to the curve $$y=4x^3-3x+5$$ which are perpendicular to the line $$9x-y+5=0$$.

$$y=4{x^3}-3{x}+5\implies \dfrac{d y}{d x}=12{x^2}-3$$
Given tangent is parallel to $$9{x}-y+5=0$$
$$\implies 12{x^2}-3=9\implies x=\pm 1\implies y=6,4$$
Equation of normal is $$y-6=-\dfrac{1}{9}(x-1)\implies x+9{y}=55$$ or $$y-4=-\dfrac{1}{9}(x+1)\implies x+9{y}=35$$


Find the equation of tangent to the curve $$y = x^2 + 4x + 1$$ at $$(-1, -2)$$.

Consider the given curve.
$$y=x^2+4x+1$$

On differentiating w.r.t $$x$$, we get
$$\dfrac{dy}{dx}=2x+4$$

At point $$(-1, -2)$$
$$\dfrac{dy}{dx}|_{(-1, -2)}=2(-1)+4$$
$$\dfrac{dy}{dx}|_{(-1, -2)}=-2+4=2$$

Therefore, the equation of tangent
$$y+2=2(x+1)$$
$$y=2x$$

Hence, this is the answer.


$$x^2 = 4y$$ : Find the equation of tangent passing through (-1,2)

$$x^2=4y$$
Slope of tangent at any point is given by $$\dfrac{dy}{dx}$$
Differentiating w.r.t x
$$2x=4\dfrac{dy}{dx}\\\dfrac{dy}{dx}=\dfrac{x}{2}$$
At point $$(-1,2)$$
$$\left.\dfrac{dy}{dx}\right|_{(-1,2)}=\dfrac{-1}{2}$$
Equation of tangent passing through $$(-1,2)$$

$$y-2=\dfrac{-1}{2}(x+1)\\2y-4=-x-1\\x+2y-3=0$$


Find the equation of the tangent and the normal to the following curve at the indicated point.
$$y^2=4ax$$ at $$(x_1, y_1)$$.

$$y^2=4ax$$
Differentiating both sides w.r.t. $$x,$$
$$\Rightarrow$$  $$2y\dfrac{dy}{dx}=4a$$

$$\Rightarrow$$  $$\dfrac{dy}{dx}=\dfrac{2a}{y}$$

Slope of tangent at $$(x_1,y_1)=\left(\dfrac{dy}{dx}\right)_{(x_1,y_2)}=\dfrac{2a}{y_1}=m$$
Equation of tangent is,
$$y-y_1=m(x-x_1)$$
$$\Rightarrow$$  $$y-y_1=\dfrac{2a(x-x_1)}{y_1}$$
$$\Rightarrow$$  $$yy_1-y_1^2=2ax-2ax_1$$
$$\Rightarrow$$  $$yy_1-4ax_1=2ax-2ax_1$$
$$\Rightarrow$$  $$yy_1=2ax+2ax_1$$
$$\Rightarrow$$  $$yy_1=2a(x+x_1)$$
Equation of normal is,
$$y-y_1=\dfrac{1}{Slope\,of\,tangent}(x-x_1)$$

$$\Rightarrow$$  $$y-y_1=\dfrac{-1}{m}(x-x_1)$$

$$\Rightarrow$$  $$y-y_1=\dfrac{-y_1}{2a}(x-x_1)$$
$$\therefore$$  Equation of tangent is $$yy_1=2a(x+x_1)$$
$$\therefore$$  Equation of normal is $$y-y_1=\dfrac{-y_1}{2a}(x-x_1)$$


Find the equation of the tangent and the normal to the following curve at the indicated point.
$$x=at^2$$, $$y=2at$$ at $$t=1$$.

$$x=at^2$$ and $$y=2at$$
Differentiate w.r.t $$t,$$ we get,
$$\Rightarrow$$  $$\dfrac{dx}{dt}=2at$$ and $$\dfrac{dy}{dt}=2a$$
$$\Rightarrow$$  $$\dfrac{dy}{dx}=\dfrac{\dfrac{dy}{dt}}{\dfrac{dx}{dt}}=\dfrac{2a}{2at}=\dfrac{1}{t}$$

Slope of tangent, $$m=\left(\dfrac{dy}{dx}\right)_{t=1}=\dfrac{1}{1}=1$$
Now, $$(x_1,y_1)=(a,2a)$$
Equation of tangent is,
$$y-y_1=m(x-x_1)$$
$$\Rightarrow$$  $$y-2a=1(x-a)$$
$$\Rightarrow$$  $$x-y=x-a$$
$$\Rightarrow$$  $$x-y+a=0$$
Equation of normal,
$$y-y_1=\dfrac{-1}{m}(x-x_1)$$
$$\Rightarrow$$  $$y-2a=-1(x-a)$$
$$\Rightarrow$$  $$y-2a=-x+a$$
$$\Rightarrow$$  $$x+y=3a$$
$$\therefore$$  Equation of tangent is  $$x-y+a=0$$
$$\therefore$$  Equation of normal is $$x+y=3a$$



Find the equation of the tangent to the curve $$\sqrt{x}+\sqrt{y}=a$$ at the point $$\left (\dfrac {a^2}{4}, \dfrac {a^2}{4}\right)$$.

$$\sqrt{x}+\sqrt{y}=a$$
Differentiate both sides w.r.t $$x,$$
$$\Rightarrow$$  $$\dfrac{1}{2\sqrt{x}}+\dfrac{1}{2\sqrt{y}}\dfrac{dy}{dx}=0$$

$$\Rightarrow$$  $$\dfrac{dy}{dx}=\dfrac{-\sqrt{y}}{\sqrt{x}}$$

$$(x_1,y_1)=\left(\dfrac{a^2}{4},\dfrac{a^2}{4}\right)$$

Slop of tangent , $$m=\left(\dfrac{dy}{dx}\right)_{\left(\dfrac{a^2}{4},\dfrac{a^2}{4}\right)}=\dfrac{-\sqrt{\dfrac{a^2}{4}}}{\sqrt{\dfrac{a^2}{4}}}=-1$$
Equation of tangent,
$$y-y_1=m(x-x_1)$$
$$\Rightarrow$$  $$y-\dfrac{a^2}{4}=-1\left(x-\dfrac{a^2}{4}\right)$$

$$\Rightarrow$$  $$y-\dfrac{a^2}{4}=-x+\dfrac{a^2}{4}$$

$$\Rightarrow$$  $$x+y=\dfrac{a^2}{2}$$


Find the equation of the tangent and the normal to the following curve at the indicated point.
$$xy=c^2$$ at $$\left (ct, \dfrac {c}{t}\right)$$.

$$xy=c^2$$
Differentiating both sides w.r.t. $$x,$$
$$\Rightarrow$$  $$x\dfrac{dy}{dx}+y=0$$
$$\Rightarrow$$  $$\dfrac{dy}{dx}=\dfrac{-y}{x}$$
$$\Rightarrow$$  $$(x_1,y_1)=\left(ct,\dfrac{c}{t}\right)$$
Slope of tangent, $$m=\left(\dfrac{dy}{dx}\right)_{\left(ct,\dfrac{c}{t}\right)}=\dfrac{\dfrac{-c}{t}}{ct}=\dfrac{-1}{t^2}$$
Equation of tangent is,
$$y-y_1=m(x-x_1)$$
$$\Rightarrow$$  $$y-\dfrac{c}{t}=\dfrac{-1}{t^2}(x-ct)$$

$$\Rightarrow$$  $$\dfrac{yt-c}{t}=\dfrac{-1}{t^2}(x-ct)$$

$$\Rightarrow$$  $$yt^2-ct=-x+ct$$
$$\Rightarrow$$  $$x+yt^2=2ct$$
Equation of normal is,
$$y-y_1=\dfrac{-1}{m}(x-x_1)$$
$$\Rightarrow$$  $$y-\dfrac{c}{t}=t^2(x-ct)$$
$$\Rightarrow$$  $$yt-c=t^3x-ct^4$$
$$\Rightarrow$$  $$xt^3-yt=ct^4-c$$
$$\therefore$$  Equation of tangent is $$x+yt^2=2ct$$.
$$\therefore$$  Equation of normal is $$xt^3-yt=ct^4-c$$


Find the equation of the tangent and the normal to the following curve at the indicated point.
$$y=x^2$$ at $$(0, 0)$$.

The equation of curve is $$y=x^2$$

Differentiate w.r.t. x we get
$$\left(\dfrac{dy}{dx}\right)_{x_1,y_1}=2x_1$$

$$\left(\dfrac{dy}{dx}\right)_{0, 0}=0$$

So, the tangent at $$(0, 0)$$ is $$||$$ to x-axis
$$\therefore y=0$$

the normal at $$(0, 0)$$ is $$||$$ to y-axis
$$\therefore x=0$$.


Find the equation of the normal to $$y=2x^3-x^2+3$$ at $$(1, 4)$$.

$$y=2x^3-x^2+3$$
Differentiate both sides w.r.t. $$x,$$
$$\Rightarrow$$  $$\dfrac{dy}{dx}=6x^2-2x$$
$$\Rightarrow$$  Slop of tangent $$=\left(\dfrac{dy}{dx}\right)_{(1,4)}=6(1)^2-2(1)=6-2=4$$

$$\Rightarrow$$  Slop of normal $$=\dfrac{-1}{Slop\,of\,tangent}=\dfrac{-1}{4}$$

$$\Rightarrow$$  $$(x_1,y_1)=(1,4)$$                [ Given ]
Equation of normal is,
$$y-y_1=m(x-x_1)$$
$$\Rightarrow$$  $$y-4=\dfrac{-1}{4}(x-1)$$

$$\Rightarrow$$  $$4y-16=-x+1$$
$$\Rightarrow$$  $$x+4y=17$$


Find the equation of the tangent and the normal to the following curve at the indicated point.
$$\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1$$ at $$(\sqrt{2}a, b)$$.

The equation of the given curve is $$\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1$$
Differentiating w.r.t $$x,$$ we get,
$$\Rightarrow$$  $$\dfrac{dy}{dx}=\dfrac{b^2}{a^2}\dfrac{x}{y}$$

$$\Rightarrow$$  $$\left(\dfrac{dy}{dx}\right)_{(\sqrt{2}a,b)}=\dfrac{b^2\sqrt{2}a}{a^2b}=\dfrac{\sqrt{2}b}{a}$$ 
Slope of the tangent $$=m=\dfrac{\sqrt{2}b}{a}$$
Here, $$(x_1,y_1)=(\sqrt{2}a,b)$$
Thus, the equation of the tangent is
$$y-y_1=m(x-x_1)$$
$$\Rightarrow$$  $$y-b=\dfrac{\sqrt{2}b}{a}(x-\sqrt{2}a)$$
$$\Rightarrow$$  $$ay-ab=\sqrt{2}bx-2ab$$
$$\Rightarrow$$  $$\sqrt{2}bx-ay-ab=0$$
Equation of the normal is 
$$y-y_1=\dfrac{-1}{m}(x-x_1)$$
$$\Rightarrow$$  $$y-b=\dfrac{-a}{\sqrt{2}b}(x-\sqrt{2}a)$$
$$\Rightarrow$$  $$\sqrt{2}by-\sqrt{2}b^2=-ax+\sqrt{2}a^2$$
$$\Rightarrow$$  $$ax+\sqrt{2}by-\sqrt{2}(a^2+b^2)=0$$
$$\therefore$$  The equation of the tangent is $$\sqrt{2}bx-ay-ab=0$$
$$\therefore$$  The equation of the normal is $$ax+\sqrt{2}by-\sqrt{2}(a^2+b^2)=0$$


If the tangent to a curve at a point $$(x, y)$$ is equally inclined to the coordinate axes, then write the value of $$\dfrac{dy}{dx}$$.

Since tangent is equally inclined, it must be making $$45^o$$ with x-axis .
So, $$\dfrac{dy}{dx}=tan(45^o)=1$$


Find the equation of the tangent and the normal to the following curve at the indicated point.
$$x=a\sec t, y=b\tan t$$ at $$t$$.

$$x=a\sec t$$ and $$y=b\tan t$$
Differentiating w.r.t $$t,$$ we get,
$$\Rightarrow$$  $$\dfrac{dx}{dt}=a\sec t\tan t$$ and $$\dfrac{dy}{dt}=b\sec^2t$$
Slope of tangent, $$m=\left(\dfrac{dy}{dx}\right)_{(t=t)}=\dfrac{b}{a} cosec\, t$$
Now, $$(x_1,y_1)=(a\sec t, b\tan t)$$

The equation of tangent :
$$y-y_1=m(x-x_1)$$
$$\Rightarrow$$  $$y-b\tan t=\dfrac{b}{a}cosec t(x-a\sec t)$$
$$\Rightarrow$$  $$y-\dfrac{b\sin t}{\cos t}=\dfrac{b}{a\sin t}\left(x-\dfrac{a}{\cos t}\right)$$

$$\Rightarrow$$  $$\dfrac{y\cos t-b\sin t}{\cos t}=\dfrac{b}{a\sin t}\left(\dfrac{x\cos t-a}{\cos t}\right)$$

$$\Rightarrow$$  $$y\cos t-b\sin t=\dfrac{b}{a\sin t}(x\cos t-a)$$
$$\Rightarrow$$  $$ay\sin t\cos t-ab\sin^2t=bx\cos t-ab$$
$$\Rightarrow$$  $$bx \cos t-ay\sin t \cos t-ab(1-\sin ^2t)=0$$
$$\Rightarrow$$  $$bx \cos t-ay\sin t\cos t=ab \cos ^2t$$
Dividing both sides by $$\cos^2t,$$
$$\Rightarrow$$  $$bx\sec t-ay\tan t=ab$$

Equation of normal is,
$$y-y_1=m(x-x_1)$$
$$\Rightarrow$$  $$y-b\tan t=\dfrac{-a}{b}\sin t(x-a\sec t)$$
$$\Rightarrow$$  $$\dfrac{y\cos t-b\sin t}{\cos t}=\dfrac{-a}{b}\sin t\left(\dfrac{x\cos t-a}{\cos t}\right)$$
$$\Rightarrow$$  $$y\cos t-b\sin t=\dfrac{-a}{b}\sin t(x\cos t-a)$$
$$\Rightarrow$$  $$by\cos t-b^2\sin t=-ax\sin t\cos t+a^2\sin ^2t$$
$$\Rightarrow$$  $$ax\sin t\cos t+by\cos t=(a^2+b^2)\sin t$$
Dividing both sides by $$\sin t,$$
$$\Rightarrow$$  $$ax\cos t+by\cot t=a^2+b^2$$
$$\therefore$$  The equation of tangent is $$bx\sec t-ay\tan t=ab$$.
$$\therefore$$  The equation of normal is $$ax\cos t+by\cot t=a^2+b^2$$





Find the equation of the tangent to the curve $$y=-5x^2+6x+7$$ at the point $$\left (\dfrac {1}{2}, \dfrac {35}{4}\right)$$.

The equation of the given curve is 
$$y=-5x^2+6x+7$$

$$\dfrac{dy}{dx}=-10x +6$$

$$\left(\dfrac{dy}{dx}\right)_{\left(1/2, 35/4\right)}=-\dfrac{10}{2}+6=1$$

The required equation of the tangent at $$\left(1/2, 35/4\right)$$ is 

$$y-\dfrac{35}{4}=\left(\dfrac{dy}{dx}\right)_{\left(1/2, 35/4\right)}\left(x-\dfrac{1}{2}\right)$$

$$y-\dfrac{35}{4}=1\left(x-\dfrac{1}{2}\right)$$

$$y=x+\dfrac{33}{4}$$


Find the equation of the normal to the curve $$y=2x^2+3 \sin x $$ at $$x=0$$.

The equation of the given curve is 

$$y=2x^2+3\sin x$$         ........(1)

Putting $$x=0$$ in 1, we get, $$y=0$$.

So, the point of contact is $$(0,0)$$.

Now, $$y=2x^2+3\sin x$$

$$\dfrac{dy}{dx}=4x+3\cos x$$

$$\left(\dfrac{dy}{dx}\right)_{(0,0)}=4\times 0 +3\cos 0=3$$

So, the equation of the normal at $$(0,0)$$ is :

$$y-0=-\dfrac{1}{3}(x-0)$$

$$x+3y=0$$


Find the equation of the tangent and the normal to the given curve at the indicated point:
$$y=\cot^{2}x-2\cot x+2  \ \ at \ \ x=\dfrac{\pi}{4}$$


1546223_1706839_ans_0218706a23f149ed90a4c3088cd96090.jpg


Find the equation of all lines having slope -1 that are tangents to the curve  $$y=\dfrac{1}{x-1}, x\neq 1$$.

The equation of the given curve is $$y=\dfrac{1}{x-1}, x\neq 1$$.

The slope of the tangents to the given curve at any point $$(x, y)$$ is given by, 

$$\dfrac{dy}{dx}=\dfrac{-1}{(x-1)^2}$$

If the slope of the tangent is $$-1$$, then we have: 

$$\dfrac{-1}{(x-1)^2}=-1$$

$$\Rightarrow (x-1)^2=1$$

$$\Rightarrow x-1=\pm 1$$

$$\Rightarrow x=2, 0$$

When $$x = 0$$, $$y = -1$$ and when $$x = 2, y = 1.$$

Thus, there are two tangents to the given curve with the slope $$-1$$. These are passing through the points $$(0,-1)$$ and $$(2, 1).$$

$$\therefore$$ The equation of the tangent through $$(0,-1)$$ is given by,

$$y-(-1)=-1(x-0)\Rightarrow x+y+1=0$$

And equation of the tangent through $$(2, 1)$$ is given by, 

$$y- 1 = -1 (x- 2)$$  

$$\Rightarrow y + x - 3 = 0 $$

Hence, the equations of the required lines are $$y + x + 1 = 0$$ and $$y+x-3=0$$


Find the equations of all lines having slope $$0$$ which are tangent to the curve $$y=\cfrac{1}{x^2-2x+3}$$.

The equation of the given curve is  $$y=\cfrac{1}{x^2-2x+3}$$.
The slope of the tangent to the given curve at any point $$(x, y)$$ is given by, 
$$\displaystyle \frac{dy}{dx}=\frac{-(2x-2)}{(x^2-2x+3)^3}=\frac{-2(x-1)}{(x^2-2x+3)^3}$$
If the slope of the tangent is $$0$$, then we have:
 $$\cfrac{-2(x-1)}{(x^2-2x+3)^3}=0$$
When $$x = 1, \displaystyle y=\frac{1}{1-2+3}=\frac{1}{2}$$
$$\therefore $$ the equation of the tangent through $$\left ( 1, \cfrac{1}{2} \right )$$ is given by, 
$$y-\cfrac{1}{2}=0(x-1)\Rightarrow y = \cfrac{1}{2}$$


Find the equation of all lines having slope $$2$$ which are tangents to the curve $$y=\cfrac{1}{x-3}, x\neq 3$$.

The equation of the given curve is $$y=\cfrac{1}{x-3}, x\neq 3$$.
The slope of the tangent to the given curve at any point $$(x, y)$$ is given by, 
$$\cfrac{dy}{dx}=\cfrac{-1}{(x-3)^2}$$
If the slope of the tangent is $$2$$, then we have: 
$$\cfrac{-1}{(x-3)^2}=2$$
$$\Rightarrow 2(x-3)^2=-1$$
$$\Rightarrow (x-3)^2=\cfrac{-1}{2}$$
This is not possible since the L.H.S. is positive while the R.H.S is negative.
Hence, there is no tangent to the given curve having slope $$2$$. 


Find the equations of the tangent and normal to the given curves at the indicated points:
(i) $$y = x^4 - 6x^3 + 13x^2 -10x + 5$$  at $$(0, 5)$$.
(ii) $$y = x^4- 6x^3 + 13x^2- 10x + 5$$ at $$(1, 3)$$
(iii) $$y = x^3$$ at $$(1, 1)$$
(iv) $$y = x^2$$ at $$(0, 0)$$
(v) $$x=\cos t, y=\sin t$$ at $$t=\dfrac{\pi}4$$

(i)
We have
$$y = x^4 - 6x^3 + 13x^2 -10x + 5$$
$$\Rightarrow \cfrac{dy}{dx} =4x^3-18x^2+26x-10$$
$$\therefore \displaystyle \left(\frac{dy}{dx} \right)_{(0,5)}=-10$$
Thus, the slope of the tangent at $$(0, 5)$$ is $$-10$$. Ergo equation of the tangent is given as,
$$(y-5)=-10(x-0)\Rightarrow 10x+y-5=0$$
The slope of the normal at $$(0, 5)$$ is $$\cfrac{-1}{\text{Slope of the tangent at}   (0, 5)}=\cfrac{1}{10}$$.
Therefore, the equation of the normal at $$(0, 5)$$ is given as,
$$(y-5)=\cfrac{1}{10}(x-0)\Rightarrow 10y-50=x\Rightarrow x-10y+50=0$$

(ii)
We have 
$$y = x^4 - 6x^3 + 13x^2 -10x + 5$$
$$\Rightarrow \cfrac{dy}{dx} =4x^3-18x^2+26x-10$$
$$\therefore \displaystyle \left(\frac{dy}{dx} \right)_{(1,3)}=4-18+26-10=2$$
Thus, the slope of the tangent at $$(1, 3)$$ is $$2$$. Ergo equation of the tangent is given as,
$$(y-3)=2(x-1)\Rightarrow 2x-y+1=0$$
The slope of the normal at $$(1, 3)$$ is $$\cfrac{-1}{\text{Slope of the tangent at}   (1, 3)}=-\cfrac{1}{2}$$.
Therefore, the equation of the normal at $$(1, 3)$$ is given as,
$$(y-3)=-\cfrac{1}{2}(x-1)\Rightarrow x+2y-7=0$$

(iii)
On differentiating with respect to $$x$$, we get:
 $$\cfrac{dy}{dx}=3x^2$$
$$\displaystyle \left(\frac{dy}{dx}\right)_{(1,1)} =3(1)^2=3$$
Thus, the slope of the tangent at $$(1, 1)$$ is $$3$$ and the equation of the tangent is given as,
$$y-1=3(x-1)\Rightarrow y=3x-2$$
The slope of the normal at $$(1, 1)$$ is $$\displaystyle \frac{-1}{\text{Slope of the tangent at} (1, 1)}=\frac{-1}{3}$$.
Therefore, the equation of the normal at $$(1, 1)$$ is given as, 
$$\displaystyle y-1=-\frac{1}{3}(x-1) \Rightarrow x+3y-4=0$$

(iv)
We have 
$$y = x^2$$
$$\Rightarrow \cfrac{dy}{dx} =2x$$
$$\therefore \displaystyle \left(\frac{dy}{dx} \right)_{(0,0)}=0$$
Thus, the slope of the tangent at $$(0, 0)$$ is $$0$$. Ergo equation of the tangent is given as,
$$(y-0)=0(x-0)\Rightarrow y=0$$
The slope of the normal at $$(0, 0)$$ is $$\cfrac{-1}{\text{Slope of the tangent at}   (0, 0)}=-\infty$$.
Therefore, the equation of the normal at $$(0, 0)$$ is given as,
$$(y-0)=-\infty(x-0)\Rightarrow x=0$$


Find the equations of the tangent and normal to the given curve at the indicated point:
$$y = x^4- 6x^3 + 13x^2- 10x + 5$$ at $$(1, 3)$$

We have
$$y = x^4 - 6x^3 + 13x^2 -10x + 5$$

$$\Rightarrow \cfrac{dy}{dx} =4x^3-18x^2+26x-10$$

$$\therefore \displaystyle \left(\frac{dy}{dx} \right)_{(1,3)}=4-18+26-10=2$$

Thus, the slope of the tangent at $$(1, 3)$$ is $$2$$. 

So, equation of the tangent is given as,

$$(y-3)=2(x-1)\Rightarrow 2x-y+1=0$$

The slope of the normal at $$(1, 3)$$ is $$\cfrac{-1}{\text{Slope of the tangent at}   (1, 3)}=-\cfrac{1}{2}$$.

Therefore, the equation of the normal at $$(1, 3)$$ is given as,
$$(y-3)=-\cfrac{1}{2}(x-1)\Rightarrow x+2y-7=0$$


Find the equation of the tangent line to the curve $$y = x^2 - 2x +7$$ which is.
(a) parallel to the line $$2x - y + 9 = 0$$.
(b) perpendicular to the line $$5y- 15x = 13.$$

(a)
The equation of the given curve is  $$y = x^2 - 2x +7$$.
On differentiating with respect to $$x$$, we get: 
$$\cfrac{dy}{dx}=2x-2$$
The equation of the line is $$2x -y + 9 = 0.\Rightarrow y = 2x + 9 $$
This is of the form $$y = mx + c. $$
Slope of the line $$= 2 $$
If a tangent is parallel to the line $$2x- y + 9 = 0$$, then the slope of the tangent is equal to the slope of the line.
Therefore, we have: $$2=2x-2$$
$$\Rightarrow 2x=4\Rightarrow x=2$$
Now, at $$x = 2 $$
$$\Rightarrow y = 2^2-2\times 2 + 7 = 7 $$
Thus, the equation of the tangent passing through $$(2, 7)$$ is given by, 
$$y-7=2(x-2)$$
$$\Rightarrow y -2x-3=0 $$
Hence, the equation of the tangent line to the given curve (which is parallel to line $$(2x - y + 9 = 0)$$ is $$y-2x-3=0.$$

(b)
The equation of the line is $$5y -15x = 13. $$
Slope of the line $$= 3  $$
If a tangent is perpendicular to the line $$5y- 15x = 13$$, 
then the slope of the tangent is $$\dfrac{-1}{\text{Slope of the line}}=\dfrac{-1}{3}$$.
$$\Rightarrow \dfrac{dy}{dx}= 2x-2=\dfrac{-1}{3}$$
$$\Rightarrow 2x =\dfrac{-1}{3}+2$$
$$\Rightarrow 2x=\dfrac{5}{3}$$
$$\Rightarrow x=\dfrac{5}{6}$$
Now, at  $$x=\dfrac{5}{6}$$
$$\Rightarrow y=\dfrac{25}{36}-\dfrac{10}{6}+7=\dfrac{25-60+252}{36}=\dfrac{217}{36}$$
Thus, the equation of the tangent passing through $$\left ( \dfrac{5}{6}, \dfrac{217}{36} \right )$$ is given by, 
$$\left(y-\dfrac{217}{36} \right )=-\dfrac{1}{3}\left ( x-\dfrac{5}{6} \right )$$
$$\Rightarrow =\dfrac{36y-217}{36}-\dfrac{1}{18}(6x-5)$$   
$$\Rightarrow 36y-217=-2(6x-5)$$
$$\Rightarrow 36y-217=-12x+10$$
$$\Rightarrow 36y+12x-227=0$$  
Hence, the equation of the tangent line to the given curve 
(which is perpendicular to line $$5y-15x = 13)$$ is $$36y+12x-227=0$$


Find the equation of the tangent to the curve $$y=\sqrt {3x-2}$$ which is parallel to the line $$4x-2y+5=0$$

Slope of line $$4x-2y+5=0$$ is $$2$$; which means slope of required tangent is also $$2$$.
Curve: $${y}^{2}=(3x-2)$$; which is a parabola
Equation of a tangent to parabola with slope $$m$$ is given by $$(y-{y}_{1})=m(x-{x}_{1})+\dfrac{a}{m}$$; here $$({x}_{1}, {y}_{1})$$ is  the vertex of parabola.
Given: $${y}_{1}=0; {x}_{1}=\dfrac{2}{3}$$ and $$a =\dfrac{3}{8}$$
So equation of tangent to the curve is $$y=2\left (x-\dfrac{2}{3}\right)+\dfrac{3}{8}$$


Find the equation of the normal to the curve $$ y = x^3

+ 2x + 6 $$ which are parallel to the line $$x + 14y + 4 = 0$$. 

Given equation of curve is 
$$y=x^3+2x+6$$        .....(1)
Differentiating w.r.t $$x$$, we get
$$\cfrac{dy}{dx}=3x^2+2$$

Let $$P(x_1,y_1)$$ be any point on the curve.
Slope of the tangent to the given curve at $$P(x_1,y_1)$$ is 
 $$\left(\cfrac{dy}{dx}\right)_{(x_1,y_1)}=3x_1^2+2$$

 Slope of the normal to the given curve at point $$P(x_1,y_1)$$ is 
 $$\cfrac{-1}{\text{Slope of the tangent at the point} (x_1, y_1)}$$
$$=\cfrac{-1}{3x^2+2}$$

The equation of the given line is $$x + 14y + 4 = 0$$ which can be written as 
$$y=-\cfrac{1}{14}x-\cfrac{4}{14}$$ (which is of the form $$y = mx + c$$)
So,  Slope of this line = $$-\cfrac{1}{14}$$

Since, the normal is parallel to this line.
So, slope of normal = slope of the given line.
$$\therefore \cfrac{-1}{3x_1^2+2}=\cfrac {-1}{14}$$
$$\Rightarrow 3x_1^2+2=14$$
$$\Rightarrow 3x_1^2=12$$
$$x_1^2=4$$
$$x_1=\pm 2$$
Since, $$P(x_1,y_1)$$ lies on the curve 
$$y_1=x_1^3+2x_1+6$$    (by (1))
When $$x_1 = 2$$,
$$\Rightarrow  y_1 = 8 + 4 + 6 = 18$$     
 
When $$x_1 =- 2$$, 
$$\Rightarrow y_1 = -8 -4 + 6 =- 6$$      
Therefore, there are two normals to the given curve with slope $$\cfrac{-1}{14}$$ and passing through the points $$(2, 18)$$ and $$(-2, -6)$$.
Thus, the equation of the normal through $$(2, 18)$$ is given by, 
$$y-18=\cfrac{-1}{14}(x-2)$$
$$\Rightarrow 14y-252=-x+2$$
$$\Rightarrow x+14y-254=0$$
And, the equation of the normal through $$(-2, -6)$$ is given by, 
$$y-(-6)=\cfrac{-1}{14}[x-(-2)]$$
$$\Rightarrow y+6=\dfrac{-1}{14}(x+2)$$
$$\Rightarrow 14y+84=-x-2$$
$$\Rightarrow x+14y+86=0$$
Hence, the equations of the normals to the given curve (which are parallel to the given line) are$$ x+14y-254=0$$ and $$x+14y+86=0$$.


Find the equation of the tangent line to the curve $$y = x^2 - 2x +7$$ which is perpendicular to the line $$5y- 15x = 13.$$

The equation of the line is $$5y -15x = 13. $$

Slope of the line $$= 3  $$

If a tangent is perpendicular to the line $$5y- 15x = 13$$, 

then the slope of the tangent is $$\dfrac{-1}{\text{Slope of the line}}=\dfrac{-1}{3}$$.

$$\Rightarrow \dfrac{dy}{dx}= 2x-2=\dfrac{-1}{3}$$

$$\Rightarrow 2x =\dfrac{-1}{3}+2$$

$$\Rightarrow 2x=\dfrac{5}{3}$$

$$\Rightarrow x=\dfrac{5}{6}$$

Now, at  $$x=\dfrac{5}{6}$$

$$\Rightarrow y=\dfrac{25}{36}-\dfrac{10}{6}+7=\dfrac{25-60+252}{36}=\dfrac{217}{36}$$

Thus, the equation of the tangent passing through $$\left ( \dfrac{5}{6}, \dfrac{217}{36} \right )$$ is given by, 

$$\left(y-\dfrac{217}{36} \right )=-\dfrac{1}{3}\left ( x-\dfrac{5}{6} \right )$$

$$\Rightarrow =\dfrac{36y-217}{36}-\dfrac{1}{18}(6x-5)$$   

$$\Rightarrow 36y-217=-2(6x-5)$$

$$\Rightarrow 36y-217=-12x+10$$

$$\Rightarrow 36y+12x-227=0$$  

Hence, the equation of the tangent line to the given curve
(which is perpendicular to line $$5y -15x = 13)$$ is $$36y+12x-227=0$$


Find the equations of the tangent and normal to the given curve at the indicated point:
$$y = x^2$$ at $$(0, 0)$$.

We have
$$y = x^2$$

$$\Rightarrow \cfrac{dy}{dx} =2x$$

$$\therefore \displaystyle \left(\frac{dy}{dx} \right)_{(0,0)}=0$$

Thus, the slope of the tangent at $$(0, 0)$$ is $$0$$. Ergo equation of the tangent is given as,

$$(y-0)=0(x-0)\Rightarrow y=0$$

The slope of the normal at $$(0, 0)$$ is $$\cfrac{-1}{\text{Slope of the tangent at}   (0, 0)}=-\infty$$.

Therefore, the equation of the normal at $$(0, 0)$$ is given as,
$$(y-0)=-\infty(x-0)\Rightarrow x=0$$


Find the equation of the normal at the point ($$am^2

, am^3$$ ) for the curve $$ay^2

= x^3$$ .

Given equation of curve is 
$$ay^2=x^3$$
 Differentiating w.r.t.  $$x$$, we get
$$2ay \cfrac{dy}{dx}=3x^2$$
$$\Rightarrow \cfrac{dy}{dx}=\cfrac{3x^2}{2ay}$$

Slope of the tangent to the curve at $$(am^{ 2 },am^{ 3 })$$ is 
$$ \displaystyle \left( \begin{matrix} \frac { dy }{ dx }  \end{matrix} \right) _{ (am^{ 2 },am^{ 3 }) }=\frac { 3(am^{ 2 })^{ 2 } }{ 2a(am^{ 3 }) } =\frac { 3a^{ 2 }m^{ 4 } }{ 2a^{ 2 }m^{ 3 } } =\frac { 3m }{ 2 } $$

Slope of normal at $$(am^{ 2 },am^{ 3 })$$
$$ =\cfrac{-1}{\text{slope of the tangent at} (am^2, am^3)}=\cfrac{-2}{3m}$$

 Equation of the normal at $$(am^{ 2 },am^{ 3 })$$ is 
$$y-am^3=\cfrac{-2}{3m}(x-am^2)$$
$$\Rightarrow 3my-3am^4=-2x+2am^2$$
$$\Rightarrow 2x+3my-am^2(2+3m^2)=0$$ 


Find the points on the curve $$y=x^3-2x^2-x$$ at which the tangent lines are parallel to the line $$y=3x-2$$.

$$y={x}^{3}-2{x}^{2}-x$$.
$${ y }^{ 1 }={ 3x }^{ 2 }-4x-1$$
when this is parallel to $$y=3x-2$$, then slopes are equal
$$\Rightarrow { 3x }^{ 2 }-4x-1=3$$
$$\Rightarrow { 3x }^{ 2 }-6x+2x-4=0\quad \Rightarrow \left( 3x+2 \right) \left( x-2 \right) =0$$
$$x=\dfrac { -2 }{ 3 } ,2$$
$$y=\dfrac { -14 }{ 27 } ,-2$$


Find a point on the curve $$y = {x^3} - 3x$$ where the tangent is parallel to the chord joining $$(1,-2)$$ and $$(2,2)$$.

$$y = {x^3} - 3x........(1)$$
$${m_1} = \left( {\cfrac{{dy}}{{dx}}} \right) = 3{x^2} - 3$$
$${m_2}$$ by point $$(1, - 2),(2,2)$$
$${m_2} = \cfrac{{2 + 2}}{{2 - 1}} = 4$$
parallel
$$\begin{array}{l}3{x^2} - 3 = 4\\x =  \pm \sqrt {\cfrac{7}{3}} \end{array}$$
Put in eq$$(1)$$
$$y = {\left( {\sqrt {\cfrac{7}{3}} } \right)^3} - 3\left( {\sqrt {\cfrac{7}{3}} } \right)$$
$$y = {\left( {-\sqrt {\cfrac{7}{3}} } \right)^3} + 3\left( {\sqrt {\cfrac{7}{3}} } \right)$$


Find the pair of tangents from the origin to the circle $${x^2} + {y^2} + 2gx + 2fy + c = 0$$ and hence condition for these tangents to be perpendicular.

Equation is: $$S{S_1} = {T^2}$$
$$ \Rightarrow ({x^2} + {y^2} + 2gx + 2fy + c)c = {(x \times 0 + y \times 0 + gx + fy + c)^2}$$
$$ \Rightarrow (x + y + 2gx + 2fy + c)c = {(gx + fy + c)^2}$$
These are pair of tangents.


Find the equation of tangent and normal to the curve $$x=sin3t$$, $$y=cos2t$$ at $$t = \frac{\pi }{4}$$.

$$\begin{array}{l}\frac{{dy}}{{dx}} = \frac{{\frac{{dy}}{{dt}}}}{{\frac{{dx}}{{dt}}}} = \frac{{ - 2\sinh 2t}}{{3\cos 3t}}\\t = \frac{\pi }{4}\\ = \frac{{ - 2}}{3} \times \frac{1}{{ - 1/\sqrt 3 }} = \frac{{ + 2\sqrt 2 }}{3}\end{array}$$
Point $$x = \frac{1}{{\sqrt 2 }},y = 0$$
Tangent
$$\begin{array}{l}y - {y_1} = \frac{{dy}}{{dx}}(x - {x_1})\\ = y - 0 = \frac{{2\sqrt 2 }}{3}\left( {x - \frac{1}{{\sqrt 2 }}} \right)\end{array}$$
Normal
$$\begin{array}{l}y - {y_1} =  - \frac{{dy}}{{dx}}(x - {x_1})\\ = y - 0 = \frac{-3}{{2\sqrt 2 }}\left( {x - \frac{1}{{\sqrt 2 }}} \right)\end{array}$$


Find the equation of normals to the curve
$$y={x}^{3}+2x+6$$ which are parallel to the line $$x+14y+4=0$$

Slop of normal $$=-\dfrac{dx}{dy}=\dfrac{-1}{14}$$
$$\Rightarrow \dfrac{dy}{dx}=14$$
$$3x^2+2=14$$
$$x^2=4\Rightarrow x=\pm 2$$
$$\therefore (2,18) and (-2,-6)$$
the required equation of normal are 
$$\dfrac{y-18}{x-2}=\dfrac{-1}{14}$$ and $$\dfrac{y+6}{x+2}=\dfrac{-1}{14}$$

1069091_1094923_ans_91d72e23e13b4a328837442cb852e9b0.png


The line to the normal of the curve $$xy=1$$ is ?

ax+by+c=0

slope of line m1 =-a/b

now for curve

xy=1

differentiate

xdy/dx +y=0

dy/dx =-y/x

 dy/dx =-1/x2

this is the slope of tangent

then slope of normal at any point is m =x2

so -a/b =x2

a and b should be apposite sign



Find the equation of tangents to the curve $$y =\cos  x $$, that are parallel to the line $$x+2y=0$$

$$y=\cos x$$

The slope of equation is given as $$\dfrac {dy}{dx}=\dfrac d{dx} \cos x\\\dfrac {dy}{dx}=\sin x$$

The slope of tangent parallel to $$x+2y=0$$ is $$\dfrac {-1}2$$

$$\implies \sin x=\dfrac {-1}2\\\sin x=\sin -\dfrac \pi 6\\x=-\dfrac \pi 6$$

$$\implies y=\cos -(\dfrac \pi 6)=\dfrac {\sqrt 3}2$$

The equation of tangent is 

$$y-\dfrac {\sqrt 3}2=\dfrac {-1}{2}\left(x+\dfrac \pi 6\right)\\2y-\sqrt 3+x+\dfrac \pi 6=0\\6x+12y-6\sqrt 3+\pi=0$$


Find the equation of the normal to the curve $${y}^{2}={ax}^{3}\ at\left (a,a\right)$$ 

Slop of normal = $$-1/dy/dx$$
As $${y}^{2}=a{x}^{2}$$
$$\Rightarrow\quad 2y\dfrac{dy}{dx}=3a{x}^{2}$$
$$\Rightarrow \quad \dfrac{dy}{dx}=\dfrac{3a{x}^{2}}{2y}$$ at $$a,a=\dfrac{3{a}^{2}}{2a}=\dfrac{3}{2}{a}^{2}$$
$$\Rightarrow\quad -1/\left(\dfrac{dy}{dx}\right)= \dfrac{-2}{3a^{2}}$$
$$\Rightarrow\quad $$Equation of normal
$$y-a=\dfrac{-2}{3{a}^{2}}\left(x-a\right)$$
$$3{a}^{2}y-3{a}^{3}=-2x+2a$$
At$$\left(a,a\right)\quad {a}^{2}={a}^{4}\quad \Rightarrow\quad m=\dfrac{-2}{3{a}^{2}}$$
$$\Rightarrow\quad $$Equation $$3y-3=-2x+2 $$ or $$3y+3=-2x-2$$



Find the equation of the tangent to the curve $$y = 3 x ^ { 2 } - x + 1 \text { at } P ( 1,3 )$$.

Given curve$$y=3{x}^{2}-x+1$$

$$\dfrac{dy}{dx}=6x-1$$

$$\left[\dfrac{dy}{dx}\right]_{\left(1,3\right)}=6\times 1-1=6-1=5$$

Equation of tangent at $$P\left(1,3\right)$$ is

$$y-3=5\left(x-1\right)$$

$$y-3=5x-5$$

or $$5x-y-2=0$$ is  the equation of the tangent to the given curve.


Find the equation of the tangent(s) to the following graphs at the points(s) whose $$x$$ or $$y$$- coordinates is given:
$$y={x}^{2}-2$$, where $$y=-2$$

$$y=x^2-2\quad \Rightarrow \ \dfrac {dy}{dx}=2x$$
when $$y=-2,\ -2=x^2-2\ \Rightarrow \ x^2=0\ \Rightarrow \ x=0$$
$$\Rightarrow \ \dfrac {dy}{dx}=0$$
$$\Rightarrow \ $$ Tangent is passing through $$(0,\ -2)$$ and has slope $$=0$$
$$\Rightarrow \ $$ equation : $$y+2=0\ \Rightarrow \ y=-2$$



Find the equation of the normal to the curve $$y = 4{x^3} - 3x + 5$$ which are perpendicular to the line $$9x - y + 5 = 0$$


1121444_1180221_ans_aa4cdb26f4514f4e83c5066c3f07c44a.jpg


Find the equation of the tangent(s) to the following graphs at the points(s) whose $$x$$ or $$y$$- coordinates is given
$$y={x}^{2}$$ where $$x=2$$

$$y=x^{2},x=2$$
$$y=4$$
Equation of tangent at $$A(2,4)$$
$$\dfrac {dy}{dx}=2x$$
$$y-4=4(x-2)$$
$$\Rightarrow \quad  \quad y-4=4x-8$$
$$\Rightarrow \quad  \quad 4x-y=4$$


Find the equation of the normal to the circle $$x ^ { 2 } + y ^ { 2 } = 5$$  at the point $$(1, 2)$$. 

Since the tangent is perpendicular to the radius 
of the circle at the point (1,2) the normal, which is 
$$\perp $$ lag to the tangent must be $$ \parallel $$ el to the radius 
So we need gradient, since we have given fixed point 
(1,2) with center (0,0) 
gradient (slope of the normal is ) $$ = \frac{1-0}{2-0} = \frac{1}{2} $$
equation of normal $$ \Rightarrow y-y_{1} = m(x-x_{1}) $$
$$ (y-1) = \frac{1}{2}(x-2) $$
$$ 2y-2 = x-2 $$
$$ 2y = x $$
$$ y = \frac{1}{2}x $$ 

1211643_1183336_ans_ef2dbaf899084370805653b5ac00d117.jpg


Find the equation of tangent & normal to curve $$2x^{3}+2y^{3}-9xy=0$$ at the point $$(2,1)$$

$$2{ x }^{ 3 }+2{ y }^{ 3 }-9xy=0$$
$$6{ x }^{ 2 }+6{ y }^{ 2 }\cfrac { dy }{ dx } -9y-9x\cfrac { dy }{ dx } =0$$
$$\Rightarrow \left( 6{ x }^{ 2 }-9y \right) +\left( 6{ y }^{ 2 }-9x \right) \cfrac { dy }{ dx } =0$$
$$\Rightarrow \cfrac { dy }{ dx } =\cfrac { 9y-6{ x }^{ 2 } }{ 6{ y }^{ 2 }-9x } $$
At $$(2,1)\cfrac { dy }{ dx } =\cfrac { 9-24 }{ 6-18 } =\cfrac { 15 }{ 12 } =\cfrac { 5 }{ 4 } $$
Equation of tangent$$=(y-1)=\cfrac { 5 }{ 4 } \left( x-2 \right) $$
$$\Rightarrow 5x-4y-2=0$$
Equation of normal$$\Rightarrow (y-1)=\cfrac { -4 }{ 5 } \left( x-2 \right) $$
$$\Rightarrow 5y+4x-13=0$$


Find the equation of the tangent(s) to the following graphs at the points(s) whose $$x$$ or $$y$$- coordinates is given:
$$y={x}^{2}+2$$ where $$x=-1$$


1092333_1192014_ans_db95d653aefa492b8cf1bbc2c049fc51.png


Find the equation of the tangent to the curve
$$y={x}^{2}-2$$ at $$y=-1$$

Given $$y=-1,y=x^{2}-2$$
$$=-1+2=x^{2}$$
$$= x=\pm 1$$
$$\therefore  A(1,-1),B(-1,-1)$$
$$\dfrac {dy}{dx}=2x$$
Equation of tangent at $$‘A‘$$
$$y+1=2(x-1)$$
Equation of tangent at $$‘B‘$$
$$y+1=-2(x+1)$$


Find the equation of the normal to the curve $$y=\sqrt{6x+3}$$ at the point for which $$x=13$$.

$$\dfrac{dy}{dx}=\dfrac{6}{2\sqrt{6x+3}}=\dfrac{3}{\sqrt{6x+3}}$$ at $$x=13, \dfrac{dy}{dx}=\dfrac{3}{\sqrt{81}}=\dfrac{1}{3}$$
As slope of normal $$=\dfrac{-1}{dy/dx}=-3$$
and at $$x=13, y=\sqrt{81}=9$$
$$\Rightarrow $$ Normal passes through $$(13, 9)$$ and slope $$=-3$$
$$\Rightarrow$$ its equation : $$y-9=-3(x-13)$$
$$\Rightarrow y=-3x+48$$


A curve has equation $$y=x(x-a)(x+a)$$,where $$a$$ is a constant. Find the equations of the tangents to the graph at the points where it crosses the x-axis.

$$y=x(x-a)(x+a)=x({x}^{2}-{a}^{2})={x}^{3}-{a}^{2}{x}^{2}$$
At x-axus, $$y=0$$
$$\therefore$$ $$x=0,x=0,x=-a$$
$$(0,0)$$, $$(a,0)$$, $$(-a,0)$$
$$\cfrac{dy}{dx}=3{x}^{2}-2a{x}^{2}$$
$$y-0=0(x-0)$$;  $$y-0={a}^{2}(x-a)$$
$$y=0....(i)$$ ;   $$y={a}^{2}x-{a}^{3}....(ii)$$
$$y-0=5{a}^{2}(x+a)$$
$$\Rightarrow$$ $$y=5{a}^{2}x+5{a}^{3}....(iii)$$


Equation of the normal line to $$y = \log x$$ at the point at which the curve crosses $$x-axis$$ is

$$y=\log x$$ cuts $$x$$ axis at $$x=1$$
Slope of tangent at $$x=1$$ is $$y=\log x$$
$$\cfrac{dy}{dx}=\cfrac{1}{x}$$
Slope$$=1$$
Slope of normal at $$x=1$$ is $$-1$$
Equation of normal point $$(0,1)$$ $$m=-1$$
$$y-0=-1(x-1)$$
$$\implies y=-x+1$$
$$\implies x+y=1$$


Show that the equation of normal at any point on the curve $$x = 3\cos t  - {\cos ^3}t $$,  $$y = 3\sin t  - {\sin ^3}t$$ is $$4\left( {y\,{{\cos }^3}t  - x{{\sin }^3}t } \right) = 3\sin 4t $$.



1133428_1215207_ans_377fe58631634eb3bd07bb58c4f9ab12.jpg


If the line joining the points $$( 0,3 )$$ and $$( 5 , - 2 )$$ is a tangent to the curve $$y = \frac { c } { x + 1 } ,$$ then the value of $$c$$ is ?

Given the points
$$(0,3)(5, - 2)$$
tangant the curve 
$$y = \frac{c}{{x + 1}}$$
We know that 
$$(y - {y_1}) = \frac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}(x - {x_1})$$
$${x_1} = 0,{y_1} = 3,{x_2} = 5,{y_2} = 2$$
$$(y - 3) = \frac{{ - 2 - 3}}{{5 - 0}}(x - 5)$$
$$y - 3 = \frac{{ - 5}}{5}(x - 5)$$  
$$y - 3 =  - x + 5$$
$$x + y = 5 + 3 \Rightarrow x + y = 8$$
$$y(x + 1) = c$$
$$xy + y = c\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_(i)$$
$$x + y = 8\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_(ii)$$
Compair  both equation and than
$${c = 8}$$


Find the equation of the normal to the curve $${x}^{2}=4y$$ which passes through the point $$\left(1,2\right)$$

Curve is $${x}^{2}=4y$$
$$\Rightarrow 2x\dfrac{dx}{dx}=4\dfrac{dy}{dx}$$
$$\Rightarrow \dfrac{dy}{dx}=\dfrac{2x}{4}=\dfrac{x}{2}$$
Slope of the normal$$=\dfrac{-1}{\dfrac{dy}{dx}}=\dfrac{-1}{\dfrac{x}{2}}=\dfrac{-2}{x}$$
Let $$\left(h,k\right)$$ be the point where normal and curve intersect.
$$\therefore$$ Slope of normal at $$\left(h,k\right)$$ is $$=\dfrac{-2}{h}$$
Equation of normal passing through $$\left(h,k\right)$$ with slope $$\dfrac{-2}{h}$$
is $$y-{y}_{1}=m\left(x-{x}_{1}\right)$$
$$y-k=\dfrac{-2}{h}\left(x-h\right)$$
Since normal passes through $$\left(1,2\right)$$, it will satisfy its equation
$$2-k=\dfrac{-2}{h}\left(1-h\right)$$
$$\Rightarrow k=2+\dfrac{2}{h}\left(1-h\right)$$       ........$$(1)$$
Since $$\left(h,k\right)$$ lies on the curve $${x}^{2}=4y$$
$${h}^{2}=4k$$ or $$k=\dfrac{{h}^{2}}{4}$$           ........$$(2)$$
Using $$(1)$$ and $$(2)$$ 
$$2+\dfrac{2}{h}\left(1-h\right)=\dfrac{{h}^{2}}{4}$$
$$\Rightarrow 2+\dfrac{2}{h}-2=\dfrac{{h}^{2}}{4}$$
$$\Rightarrow \dfrac{2}{h}=\dfrac{{h}^{2}}{4}$$
$$\Rightarrow {h}^{3}=8$$
$$\Rightarrow h={8}^{\frac{1}{3}}$$
Put $$h=2$$ in eqn$$(2)$$ we get
$$k=\dfrac{{h}^{2}}{4}=\dfrac{{2}^{2}}{4}=1$$
Hence $$h=2,k=1$$
Put $$h=2$$ and $$k=1$$ in equation of normal we get
$$y-1=\dfrac{-2}{2}\left(x-2\right)$$
$$\Rightarrow y-1=-x+2$$
$$\therefore x+y=3$$


Find the equations of tangent and normal to the curves at the indicated points on it.
(i) $$\quad y = x ^ { 2 } + 4 x + 1$$  at  $$( - 1 , - 2 )$$
(ii) $$2 x ^ { 2 } + 3 y ^ { 2 } - 5 = 0$$  at  $$( 1,1 )$$
(iii)$$ \quad x = a \cos ^ { 3 } \theta , y = a \sin ^ { 3 } \theta$$  at  $$\theta = \dfrac { \pi } { 4 }$$

i) $$\dfrac{dy}{dx}=2x+4$$ at $$(-1,-2)\implies m=2$$
 Equation of tangent $$y+2=2(x+1)\implies 2x-y=0$$
 Equation of normal $$y+2=\dfrac{-1}{2}(x+1)\implies x+2y+5=0$$
ii)$$\dfrac{dy}{dx}=\dfrac{5-4x}{6y}$$ at $$(1,1)\implies m=\dfrac{-1}{6}$$
Equation of tangent $$(y-1)=\dfrac{-1}{6}(x-1)\implies x+6y-7=0$$
Equation of normal $$(y-1)=6(x-1)\implies 6x-y-5=0$$
iii)$$\dfrac{dy}{dx}=-\tan\theta$$ at $$\theta=\dfrac{\pi}{4}\implies m=-1$$
Equation of tangent $$(y-\dfrac{a}{2\sqrt2})=-1(x-\dfrac{a}{2\sqrt2})\implies \sqrt2(x+y)=a$$
Equation of normal $$y-\dfrac{a}{2\sqrt 2}=x-\dfrac{a}{2\sqrt2}\implies x-y=0$$


The equation of tangent at $$(5,3)$$ for the curve $$ x^2-y^2=16$$

Given point $$(5,3)$$
Given equation of curve $$x^2-y^2=16$$
Slope of tangent is given as $$2x-2y\dfrac {dy}{dx}=0\\\dfrac{dy}{dx}=\dfrac xy\\\left.\dfrac {dy}{dx}\right|_{(5,3)}=\dfrac 53$$
Slope of tangent is $$(y-3)=\dfrac 53(x-5)\\3y-9=5x-25\\5x-3y-16=0$$


The tangent at $$(4,6)$$ to the curve $$y^2=9x$$

$$y^2=9x\\2y\dfrac {dy}{dx}=9\\\dfrac {dy}{dx}=\dfrac 9{2y}\\\left.\dfrac {dy}{dx}\right|_{(4,6)}=\dfrac 34$$
Equation of tangent $$y-6=\dfrac 32(x-4)\\2y-12=3x-12\\3x-2y=0$$


The equation of tangent at $$(1,2)$$ on the curve $$x^2=2y$$

Given point $$(1,2)$$
Given equation is $$x^2=2y$$
Slope of tangent at given point is given as $$2x=2\dfrac{dy}{dx}\\\dfrac{dy}{dx}=x\\\left.\dfrac{dy}{dx}\right|_{(1,2)}=1$$
The equation of tangent is given as $$(y-2)=1(x-1)\\x-y+1=0$$


Show that the equation of normal at any point on the curve $$x = 3\cos \theta  - {\cos ^3}\theta ,$$ $$y = 3\sin \theta  - {\sin ^3}\theta $$ is $$4(y{\cos ^3}\theta  - x{\sin ^3}\theta ) = 3\sin 4\theta $$.

We have $$ x = 3 cos  \theta  - cos^3 \theta $$
therefore $$  \frac {dx}{d \theta } = - 3 sin  \theta  + 3 cos^2 \theta sin \theta  = -3 sin  \theta  ( 1- cos^2 \theta) = - 3 sin^3 \theta $$
$$ \frac {dy}{d \theta  } = 3 cos  \theta - 3sin^2 \theta cos \theta  = 3 cos \theta  ( 1 -sin^2 \theta ) - 3 cos^2 \theta $$
$$ \frac {dy}{dx} = - \frac { cos^3 \theta}{ sin^3 \theta } $$   therefore , slope of normal $$ = + \frac { sin^3 \theta }{ cos^3 \theta} $$
hence the equation of normal is 
$$ y -( 3 sin \theta  - sin^3 \theta ) - \frac { sin^3 \theta }{ cos^3 \theta} [ x - (3 cos  \theta  - cos^3 \theta ) ] $$
$$ \Rightarrow y cos^2 \theta  - 3 sin \theta cos^3 \theta  + sin^3 \theta cos^3 \theta = x sin^3 \theta  - 3 sin^3 \theta cos \theta  + sin^3 \theta  cos^3 \theta $$
$$ \Rightarrow y cos ^3 \theta  - x sin^3 \theta = 3 sin \theta  cos \theta ( cos^2 \theta  - sin^2 \theta) $$

$$ \Rightarrow y cos ^3 \theta  - x sin^3 \theta= \frac {3}{2} sin 2 \theta . cos  2 \theta $$

$$ \Rightarrow y cos ^3 \theta  - x sin^3 \theta= \frac {3}{4} sin 4 \theta $$

or $$ 4(y cos^3 \theta - x sin^3 \theta)= 3 sin  4 \theta $$


Find the equations of the tangent and the normal to the curve $$y = \dfrac{x - 7}{(x - 2) ( x - 3)}$$ at the point where it cuts the x-axis.

The equation cuts $$\text{x-axis}$$ at $$(7,0)$$

$$\dfrac{dy}{dx}=\dfrac{(x^2-5x+6)-(x-7)(2x-5)}{(x^2-5x+6)^2}$$

At $$(7,0)$$
 Slope at tangent is $$20$$
Equation is $$y=20(x-7)\implies 20x-y-140=0$$
 Slope at Normal is $$\dfrac{-1}{20}$$
Equation is $$y=\dfrac{-1}{20}(x-7)\implies x+20y-7=0$$


Find the points on the curve $$\dfrac{x^2}{4}+\dfrac{y^2}{25}=1$$ at which the tangents are parallel to the y-axis.

$$(2, 0), (-2, 0)$$.
Let $$P(x_1, y_1)$$ be a point on the curve $$\dfrac{x^2}{4}+\dfrac{y^2}{25}=1$$. Then,
$$\dfrac{x^2_1}{4}+\dfrac{y^2_1}{25}=1$$
Now, $$\dfrac{x^2}{4}+\dfrac{y^2}{25}=1$$
$$\Rightarrow \dfrac{x}{2}+\dfrac{2y}{25}\dfrac{dy}{dx}=0$$
$$\Rightarrow \dfrac{dy}{dx}=-\dfrac{25}{4}\dfrac{x}{y}$$
$$\Rightarrow \left(\dfrac{dy}{dx}\right)_P=-\dfrac{25}{4}\dfrac{x_1}{y_1}$$
If the tangent at P is parallel to y-axis, then
$$\dfrac{1}{\left(\dfrac{dy}{dx}\right)_P}=0$$
$$\Rightarrow -\dfrac{4}{25}\dfrac{y_1}{x_1}=0$$
$$\Rightarrow y_1=0$$
Putting $$y_1=0$$ in (i), we get
$$\dfrac{x^2_1}{4}=1$$
$$\Rightarrow x_1=\pm 2$$
Hence, required points are $$(\pm 2, 0)$$.


Find the equation of the tangent and the normal to the following curve at the indicated point.
$$y^2=\dfrac{x^3}{4-x}$$ at $$(2, -2)$$.

$$y^2=\dfrac{x^3}{4-x}$$                       [ Given ]

Differentiating both sides w.r.t. $$x,$$

$$\Rightarrow$$  $$2y\dfrac{dy}{dx}=\dfrac{(4-x)(3x^2)-x^3(-1)}{(4-x)^2}$$

$$\Rightarrow$$  $$2y\dfrac{dy}{dx}=\dfrac{12x^2-3x^3+x^3}{(4-x)^2}$$

$$\Rightarrow$$  $$2y\dfrac{dy}{dx}=\dfrac{12x^2-2x^3}{(4-x)^2}$$

$$\Rightarrow$$  $$\dfrac{dy}{dx}=\dfrac{12x^2-2x^3}{2y(4-x)^2}$$

$$(x_1,y_1)=(2,-2)$$                       [ Given ]


Slope of tangent, $$m=\left(\dfrac{dy}{dx}\right)_{(2,-2)}=\dfrac{12(2)^2-2(2)^3}{2(-2)(4-2)^2}$$

                                                              $$=\dfrac{48-16}{-16}$$

                                                              $$=-2$$

Equation of tangent :

$$y-y_1=m(x-x_1)$$

$$\Rightarrow$$  $$y+2=-2(x-2)$$

$$\Rightarrow$$  $$y+2=-2x+4$$

$$\Rightarrow$$  $$2x+y-2=0$$

Equation of normal is,

$$y-y_1=\dfrac{-1}{m}(x-x_1)$$

$$\Rightarrow$$  $$y+2=\dfrac{1}{2}(x-2)$$

$$\Rightarrow$$  $$2y+4=x-2$$

$$\Rightarrow$$  $$x-2y-6=0$$


Find the equation of the tangent and the normal to the following curve at the indicated point.
$$y=2x^2-3x-1$$ at $$(1, -2)$$.

$$y=2x^2-3x-1$$                  [ Given ]
Differentiate both sides w.r.t $$x,$$
$$\Rightarrow$$  $$(x_1,y_1)=(1,-2)$$
Slop of tangent, $$m=\left(\dfrac{dy}{dx}\right)_{(1,-2)}=4-3=1$$
Equation of tangent is,
$$y-y-1=m(x-x_1)$$
$$\Rightarrow$$  $$y+2=1(x-1)$$
$$\Rightarrow$$  $$y+2=x-1$$
$$\Rightarrow$$  $$x-y-3=0$$
Equation of normal is,
$$y-y_1=\dfrac{-1}{m}(x-x_1)$$
$$\Rightarrow$$  $$y+2=-1(x-1)$$
$$\Rightarrow$$  $$y+2=-x+1$$
$$\Rightarrow$$  $$x+y+1=0$$
$$\therefore$$  Equation of tangent is $$x-y-3=0$$
$$\therefore$$  Equation of normal is $$x+y+1=0$$


Find the equation of the tangent and the normal to the following curve at the indicated point.
$$c^2(x^2+y^2)=x^2y^2$$ at $$\left(\dfrac{x}{\cos\theta}, \dfrac{c}{\sin\theta}\right)$$.

The given curve is,
$${ c }^{ 2 }\left( { x }^{ 2 }+{ y }^{ 2 } \right) ={ x }^{ 2 }{ y }^{ 2 }$$

The above equation can  be rewritten  as,

$${ y }^{ 2 }=\frac { { c }^{ 2 }{ x }^{ 2 } }{ { x }^{ 2 }-{ c }^{ 2 } } $$

To get the slope at any point , differentiate with respect to  x.

$$\displaystyle 2y\frac { dy }{ dx } =\frac { \left( { x }^{ 2 }-{ c }^{ 2 } \right) \cdot { c }^{ 2 }2x-{ c }^{ 2 }{ x }^{ 2 }2x }{ { \left( { x }^{ 2 }-{ c }^{ 2 } \right)  }^{ 2 } } =-\frac { 2{ c }^{ 4 }x }{ { \left( { x }^{ 2 }-{ c }^{ 2 } \right)  }^{ 2 } } $$

or

$$\displaystyle y\frac { dy }{ dx } =-\frac { { c }^{ 4 }x }{ { \left( { x }^{ 2 }-{ c }^{ 2 } \right)  }^{ 2 } } $$

Put the co-ordinates of the point i.e.$$\left( \frac { c }{ cos\theta  } ,\frac { c }{ sin\theta  }  \right) $$ in the above equation.

Thus,
$$\displaystyle \frac { dy }{ dx } =\frac { -\frac { c }{ cos\theta  } \cdot { c }^{ 4 } }{ \frac { c }{ sin\theta  } { \left( \frac { { c }^{ 2 } }{ { cos }^{ 2 }\theta  } -{ c }^{ 2 } \right)  }^{ 2 } } $$

 or

$$\displaystyle \frac { dy }{ dx } =\frac { -\frac { c }{ cos\theta  } \cdot { c }^{ 4 } }{ \frac { c }{ sin\theta  } { \left( \frac { { c }^{ 2 } }{ { cos }^{ 2 }\theta  } -{ c }^{ 2 } \right)  }^{ 2 } } =-{ cot }^{ 3 }\theta $$

Using point slope form the equation of the  tangent is,

$$\displaystyle y-\frac { c }{ sin\theta  } =-{ cot }^{ 3 }\theta \left( x-\frac { c }{ cos\theta  }  \right) \\ y=x{ cot }^{ 3 }\theta +c{ \cdot cot }^{ 3 }\theta \cdot sec\theta +c\cdot cosec\theta \\ y=x{ cot }^{ 3 }\theta +c\cdot { cosec }^{ 3 }\theta $$

(answer)

The  slope of  the normal is,

$${ m }_{ normal }=-\dfrac { 1 }{ { m }_{ tangent } } ={ tan }^{ 3 }\theta $$

Use the  point slope form,

$$\displaystyle y-\frac { c }{ sin\theta  } ={ tan }^{ 3 }\theta \cdot \left( x-\frac { c }{ cos\theta  }  \right) $$

$$ y={ tan }^{ 3 }\theta \cdot x+\frac { c }{ sin\theta  } -\dfrac { c\cdot { tan }^{ 3 }\theta  }{ cos\theta  } $$

$$ y={ tan }^{ 3 }\theta x+\dfrac { c\cdot cos2\theta  }{ sin\theta \cdot { cos }^{ 4 }\theta  } $$

(answer)


Find the equation of the tangent and the normal to the following curve at the indicated point.
$$\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1$$ at $$(x_0, y_0)$$.

$$\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1$$
Differentiating both sides w.r.t. $$x,$$

$$\dfrac{2x}{a^2}-\dfrac{2y}{b^2}\dfrac{dy}{dx}=0$$

$$\Rightarrow$$  $$\dfrac{2y}{b^2}\dfrac{dy}{dx}=\dfrac{2x}{a^2}$$

$$\Rightarrow$$  $$\dfrac{dy}{dx}=\dfrac{xb^2}{ya^2}$$

Slope of tangent, $$m=\left(\dfrac{dy}{dx}\right)_{(x_0,y_0)}=\dfrac{x_0b^2}{y_0a^2}$$

Equation of tangent :
$$y-y_1=m(x-x_1)$$

$$\Rightarrow$$  $$y-y_0=\dfrac{x_0b^2}{y_0a^2}(x-x_0)$$

$$\Rightarrow$$  $$yy_0a^2-y_0^2a^2=xx_0b^2-x_0^2b^2$$

$$\Rightarrow$$  $$xx_0b^2yy_0a^2=x_0^2b^2-y_0^2a^2$$            ----- ( 1 )

Since $$(x_0,y_0)$$ lies on the given curve,

$$\Rightarrow$$  $$\dfrac{x_0^2}{a^2}-\dfrac{y_0^2}{b^2}=1$$

$$\Rightarrow$$  $$x_0^2b^2-y_0^2a^2=a^2b^2$$

 Substituting this in ( 1 ), we get
$$\Rightarrow$$  $$xx_0b^2-yy_0a^2=a^2b^2$$

Dividing both sides by $$a^2b^2,$$

$$\Rightarrow$$  $$\dfrac{xx_0}{a^2}-\dfrac{yy_0}{b^2}=1$$

Equation of normal :
$$y-y_1=\dfrac{-1}{m}(x-x_1)$$

$$\Rightarrow$$  $$y-y_0=\dfrac{-y_0a^2}{x_0b^2}(x-x_0)$$

$$\Rightarrow$$  $$yx_0b^2-x_0y_0b^2=-xy_0a^2+x_0y_0a^2$$

$$\Rightarrow$$  $$xy_0a^2+yx_0b^2=x_0y_0a^2+x_0y_0b^2$$

$$\Rightarrow$$  $$xy_0a^2+yx_0b^2=x_0y_0(a^2+b^2)$$

Dividing both sides by $$x_0y_0$$

$$\Rightarrow$$  $$\dfrac{a^2x}{x_0}+\dfrac{b^2y}{y_0}=a^2+b^2$$




Find the equation of the tangent and the normal to the following curve at the indicated point.
$$y=x^2+4x+1$$ at $$x=3$$.

$$y=x^2+4x+1$$                                 ----- ( 1 )

Differentiating both sides w.r.t. $$x,$$

$$\Rightarrow$$  $$\dfrac{dy}{dx}=2x+4$$

Slope of tangent, $$m=\left(\dfrac{dy}{dx}\right)_{x=3}=2(3)+4$$
                                                           $$=10$$

Substituting $$x=3$$ in equation ( 1 ) we get

 $$y=(3)^2+4(3)+1$$

$$\Rightarrow$$  $$y=9+12+1$$

$$\Rightarrow$$  $$y=22$$

So, $$(x_1,y_1)=(3,22)$$

Equation of tangent :

$$\Rightarrow$$  $$y-y_1=m(x-x_1)$$

$$\Rightarrow$$  $$y-22=10(x-3)$$

$$\Rightarrow$$  $$y-22=10x-30$$

$$\Rightarrow$$  $$10x-y-8=0$$

Equation of normal:

$$y-y_1=\dfrac{-1}{m}(x-x_1)$$

$$\Rightarrow$$  $$y-22=\dfrac{-1}{10}(x-3)$$

$$\Rightarrow$$  $$10y-220=-x+3$$

$$\Rightarrow$$  $$x+10y-223=0$$



Find the equation of the tangent and the normal to the following curve at the indicated point.
$$y^2=4ax$$ at $$\left (\dfrac {a}{m^2}, \dfrac {2a}{m}\right)$$

$$y^2=4ax$$                      [ Given ]

Differentiating both sides w.r.t. $$x,$$

$$\Rightarrow$$  $$2y\dfrac{dy}{dx}=4a$$

$$\Rightarrow$$  $$\dfrac{dy}{dx}=\dfrac{2a}{y}$$

$$(x_1,y_1)=\left(\dfrac{a}{m^2},\dfrac{2a}{m}\right)$$

Slope of tangent $$\displaystyle =\left(\dfrac{dy}{dx}\right)_{\left(\frac{a}{m^2},\frac{2a}{m}\right)}=\dfrac{2a}{\dfrac{2a}{m}}=m$$

Equation of tangent :

$$y-y_1=m(x-x_1)$$

$$\Rightarrow$$  $$y-\dfrac{2a}{m}=m\left(x-\dfrac{a}{m^2}\right)$$

$$\Rightarrow$$  $$\dfrac{my-2a}{m}=m\left(\dfrac{m^2x-a}{m^2}\right)$$

$$\Rightarrow$$  $$my-2a=m^2x-a$$

$$\Rightarrow$$  $$m^2x-my+a=0$$

Equation of normal :
$$y-y_1=\dfrac{-1}{m}(x-x_1)$$

$$\Rightarrow$$  $$y-\dfrac{2a}{m}=\dfrac{-1}{m}\left(x-\dfrac{a}{m^2}\right)$$

$$\Rightarrow$$  $$\dfrac{my-2a}{m}=\dfrac{-1}{m}\left(\dfrac{m^2x-a}{m^2}\right)$$

$$\Rightarrow$$  $$m^3y-2am^2=-m^2x+a$$

$$\Rightarrow$$  $$m^2x+m^3y-2am^2-a=0$$


Determine the equation(s) of tangent(s) line to the curve $$y=4x^3-3x+5$$ which are perpendicular to the line $$9y+x+3=0$$.

Given line $$=9y+x+3=0$$
$$\Rightarrow x+3=-9y$$
$$\Rightarrow y=\dfrac{-x}{9}-\dfrac{1}{3}$$
$$\therefore$$ Slope $$m_1=\dfrac{-1}{9}$$
We know $$m_1m_2=-1$$
$$\dfrac{-1}{9}\times m_2=-1$$
$$m_2=9$$
Given equation of curve is $$y=4x^3-3x+5$$
$$\therefore$$ Slope $$\dfrac{dy}{dx}=12x^2-3$$
which is $$m_2$$
$$\therefore$$ equating the slopes $$m_2$$, we have
$$12x^2-3=9$$
or, $$12x^2=12$$
or, $$x^2=1$$
$$\Rightarrow x_a=\pm 1$$
at $$x_1=1$$
$$y_1=4(1)^3-3(1)+5$$
$$y_1=6$$
at $$x_2=-1$$
$$y_2=4(-1)^3-3(-1)+5$$
$$=-4+3+5$$
$$y_2=4$$
also
Therefore, required equation are
$$y-y_1=m(x-x_1)$$ and $$y-y_2=m(x-x_2)$$
i.e., $$y-6=9(x-1)$$ and $$y-4=9(x+1)$$
$$y=9x-3$$ and $$y=9x+13$$.


Find the equation of the tangent line to the curve $$y=x^2+4x-16$$ which is parallel to the line $$3x-y+1=0$$.

$$3x-y+1=0$$
$$\dfrac{d}{dx}(3x)-\dfrac{dy}{dx}+\dfrac{d}{dx}(1)=0$$
$$\dfrac{dy}{dx}=3$$
$$y={x}^2+4x-16$$
$$\dfrac{dy}{dx}=2x+4$$
Hence
$$2x+4=3$$
$$x=\dfrac{3-4}{2}=\dfrac{-1}{2}$$
at $$x=\dfrac{-1}{2}$$ $$y=\left(-\dfrac{1}{2}\right)^2+4\left(-\dfrac{1}{2}\right)-16=\dfrac{1}{4}-2-16$$
$$y=\dfrac{-71}{4}$$
so the point $$p\left(-\dfrac{1}{2}, \dfrac{-71}{4}\right)$$
equtaion of tangent
$$y-\left(-\dfrac{71}{4}\right)=3\left(x-\left(-\dfrac{1}{2}\right)\right)$$
$$y+\dfrac{71}{4}=3\left(x+\dfrac{1}{2}\right)$$
$$3x-y=\dfrac{71}{4}-\dfrac{3}{2}=\dfrac{71-6}{4}=\dfrac{65}{4}$$
$$12x-4y=65$$.


Find the equation of the tangent and the normal to the following curve at the indicated point.
$$x=\dfrac{2at^2}{1+t^2}, y=\dfrac{2at^3}{1+t^2}$$ at $$t=1/2$$.

$$x=\dfrac{2at^2}{1+t^2}, y=\dfrac{2at^3}{1+t^2}$$
at $$t=1/2$$
$$\dfrac{dx}{dt}=\dfrac{(1+t^2)4at-2at^2(2t)}{(1+t^2)^2}=\dfrac{4at}{(1+t^2)^2}$$

$$\dfrac{dy}{dt}=\dfrac{(1+t^2)6at^2-2at^3(2t)}{(1+t^2)^2}=\dfrac{6at^2+2at^4}{(1+t^2)^2}$$

$$\dfrac{dy}{dt}\times \dfrac{dt}{dx}=\dfrac{6at^2+2at^4}{(1+t^2)^2}\times \dfrac{(1+t^2)^2}{4at}$$

$$\dfrac{dy}{dx}=\dfrac{3t+t^3}{2}$$
at point $$t=\dfrac{1}{2}$$
$$\dfrac{dy}{dx}=\dfrac{13}{16}$$
Slope of tangent $$=\dfrac{13}{16}$$
Equation of tangent
$$y-y_1=m(x-x_1)$$
$$\Rightarrow y_1=\dfrac{2a(1/2)^3}{1+\left(\dfrac{1}{2}\right)^2}=\dfrac{a}{5}, x_1=\dfrac{2a\left(\dfrac{1}{2}\right)^2}{1+\left(\dfrac{1}{2}\right)^2}=\dfrac{2a}{5}$$

$$\Rightarrow y-\dfrac{a}{5}=\dfrac{13}{16}\left(x-\dfrac{2a}{5}\right)$$
Slope of normal$$=\dfrac{-16}{13}$$
Equation of normal
$$y-\dfrac{a}{5}=\dfrac{-16}{13}\left(x-\dfrac{2a}{5}\right)$$.

1394921_1660457_ans_46f20fa85e4b471fb54663cc416ae38e.jpg


Find the equation of the tangent and the normal to the following curve at the indicated point.
$$x^2=4y$$ at $$(2, 1)$$.

$$x^2=4y$$                  [ Given ]

Differentiate both sides w.r.t. $$x,$$

$$\Rightarrow$$  $$2x=4\dfrac{dy}{dx}$$

$$\Rightarrow$$  $$\dfrac{dy}{dx}=\dfrac{x}{2}$$

Slope of the tangent, $$m=\left(\dfrac{dy}{dx}\right)_{(2,1)}=\dfrac{2}{2}=1$$

$$(x_1,y_1)=(2,1)$$                     [ Given ]

Equation of tangent :

$$y-y_1=m(x-x_1)$$

$$\Rightarrow$$  $$y-1=1(x-2)$$

$$\Rightarrow$$  $$y-1=x-2$$

$$\Rightarrow$$  $$x-y-1=0$$

Equation of normal :

$$y-y_1=\dfrac{-1}{m}(x-x_1)$$

$$\Rightarrow$$  $$y-1=-1(x-2)$$

$$\Rightarrow$$  $$y-1=-x+2$$

$$\Rightarrow$$  $$x+y-3=0$$



Find the equation of the tangent and the normal to the following curve at the indicated point.
$$x=3\cos\theta -\cos^3\theta, y=3\sin\theta -\sin^3\theta$$.

$$x=2\cos \theta-\cos^3\theta$$
Differentiating w.r.t. $$\theta,$$ we get,
$$\Rightarrow$$  $$\dfrac{dx}{d\theta}=-3\sin\theta+3\cos^2\theta\sin\theta$$
$$y=3\sin\theta-\sin^3\theta$$
Differentiating w.r.t. $$\theta,$$ we get,
$$\Rightarrow$$  $$\dfrac{dy}{d\theta}=3\cos\theta-3\sin^2\theta\cos\theta$$

$$\Rightarrow$$  $$\dfrac{dy}{dx}=\dfrac{\dfrac{dy}{d\theta}}{\dfrac{dx}{d\theta}}=\dfrac{3\cos\theta-3\sin^2\theta\cos\theta}{-3\sin\theta+3\cos^2\theta\sin\theta}$$
                            $$=\dfrac{\cos\theta(1-\sin^2\theta)}{-\sin\theta(1-\cos^2\theta)}$$

                            $$=\dfrac{\cos^3\theta}{-\sin^3\theta}$$

                            $$=-\cot^3\theta$$
$$\therefore$$  Slope of the tangent, $$m=\dfrac{dy}{dx}=-\cot^3\theta$$
The equation of the tangent is
$$y-y_1=m(x-x_1)$$
$$\Rightarrow$$  $$y-3\sin\theta+\sin^3\theta=-\cot^3\theta(x-3\cos\theta+\cos^3\theta)$$
$$\Rightarrow$$  $$y-3\sin\theta+\sin^3\theta=-\dfrac{\cos^3\theta}{\sin^3\theta}(x-3\cos\theta+\cos^3\theta)$$

$$\Rightarrow$$  $$y\sin^3\theta-3\sin^4\theta+\sin^6\theta=-x\cos^3\theta+3\cos^4\theta-cos^6\theta$$
$$\Rightarrow$$  $$y\sin^3\theta+x\cos^3\theta+\sin^6\theta+\cos^6\theta=3\cos^4\theta+3\sin^4\theta$$
$$\Rightarrow$$  $$x\cos^3\theta+y\sin^3\theta+1=3$$
$$\therefore$$  $$x\cos^3\theta+y\sin^3\theta=2$$

The equation of the normal is
$$y-y_1=\dfrac{-1}{m}(x-x_1)$$
$$\Rightarrow$$  $$y-3\sin\theta+\sin^3\theta=\dfrac{1}{\cot^3\theta}(x-3\cos\theta+\cos^3\theta)$$

$$\Rightarrow$$  $$y-3\sin\theta+\sin^3\theta=\dfrac{\sin^3\theta}{\cos^3\theta}(x-3\cos\theta+\cos^3\theta)$$

$$\Rightarrow$$  $$y\cos^3\theta-3\sin\theta\cos^3\theta+\sin^3\theta\cos^3\theta=x\sin^3\theta-3\cos\theta\sin^3\theta+\sin^3\theta\cos^3\theta$$
$$\Rightarrow$$  $$x\sin^3\theta-y\cos^3\theta=-3\sin\theta\cos^3\theta+3\cos\theta\sin^3\theta$$


Find the equation of the tangent and the normal to the following curve at the indicated point.
$$4x^2+9y^2=36$$ at $$(3\cos\theta, 2\sin\theta)$$.

The given equation is,
$$4x^{ 2 }+9{ y }^{ 2 }=36$$
or
$${ y }^{ 2 }=\dfrac { \left( 36-4{ x }^{ 2 } \right)  }{ 9 } $$

Differentiate to get slope of tangent,

$$\displaystyle 2y\frac { dy }{ dx } =-\frac { 4 }{ 9 } 2x$$

$$\Rightarrow  \dfrac { dy }{ dx } =-\dfrac { 4x }{ 9y } $$

Thus the slope of tangent at $$\left( 3cos\theta ,2sin\theta  \right) $$,

$$\displaystyle \frac { dy }{ dx } =-\frac { 4\cdot 3cos\theta  }{ 9\cdot 2sin\theta  } =-\frac { 2cot\theta  }{ 3 } $$

Apply point-slope form to get the equation of tangent.

$$\displaystyle y-2sin\theta =-\frac { 2 }{ 3 } cot\theta \left( x-3cos\theta  \right) $$

$$ y=-\dfrac { 2 }{ 3 } cot\theta \cdot x+2\dfrac { { cos }^{ 2 }\theta  }{ sin\theta  } +2sin\theta $$

$$ y=-\dfrac { 2 }{ 3 } cot\theta \cdot x+2cosec\theta $$


For finding the equation of the normal.

$${ m }_{ normal }=-\dfrac { 1 }{ { m }_{ tangent } } =\dfrac { 3 }{ 2 } tan\theta $$

Hence,
Apply point-slope form to get the equation of normal.

$$y-2sin\theta =\dfrac { 3 }{ 2 } tan\theta \left( x-3cos\theta  \right) $$

$$ y=\dfrac { 3 }{ 2 } tan\theta \cdot x-\dfrac { 9 }{ 2 } sin\theta +2sin\theta $$

$$ y=\dfrac { 3 }{ 2 } tan\theta \cdot x-\dfrac { 5 }{ 2 } sin\theta $$

(answer)




Find the equation of the tangent and the normal to the following curve at the indicated point.
$$x=a(\theta +\sin\theta), y=a(1-\cos\theta)$$ at $$\theta$$.


1428474_1660460_ans_032ae30e014f4809bccd45d228237775.jpg


Find an equation of normal line to the curve $$y=x^3+2x+6$$ which is parallel to the line $$x+14y+4=0$$.

The given equation of curve $$y = x^3 + 2x + 6$$ which is parallel to line $$x + 14 y + 4 = 0$$

Now   $$x + 14y + 4 = 0$$

or $$14 y \therefore x + 4$$

or , $$y = \dfrac{-1}{14} x + \left(\dfrac{4}{-14} \right)$$

$$\therefore \dfrac{dy}{dx} = -\dfrac{1}{14} \rightarrow $$ slope of normal
curve equation $$y = x^3 + 2x + 6$$

Slope, $$\dfrac{dy}{dx} = 3x^2 + 2$$

$$\therefore $$ from $$m_1 m_2 = -1$$     [$$\because$$ curves & lines are $$\bot$$ to each other]

$$\left(\dfrac{-1}{14} \right) (3x^2 + 2) = -1$$   [$$m_1 , m_2 \rightarrow$$ slopes]

$$3x^2 + 2 = 14$$

$$3x^2 = 12$$

$$x = \pm 2$$

at $$x = 2$$                   at $$x = -2$$

$$y = 8 + 4 + 6$$        $$y = -8-4+ 6$$

$$y = 18$$                    $$y = -6$$

$$\therefore $$ points are $$(2, 18) \, \& \, (-2, -6)$$

$$\therefore$$ equation of normal lines at given points are

$$y - 18 = \dfrac{-1}{14} (x - 2)$$             and   $$y + 6 = \dfrac{-1}{14} (x + 2)$$

$$\Rightarrow 14y - 252 = -x + 2$$       and   $$14y + 84 = -x - 2$$

$$x + 14y = 254$$                       and $$x + 14y = -86$$


Find the equation of the normal to the curve $$ay^2=x^3$$ at the point $$(\text{am}^2, \text{am}^3)$$.

$$ay^2=x^3$$
Slope of tangent is $$\dfrac{dy}{dx}$$
$$ay^2=x^3$$
differentiating wrt x
$$\dfrac{d(ay^2)}{dx}=\dfrac{d}{dx}(x^3)$$
$$2ay\cdot \dfrac{dy}{dx}=3x^2$$
$$\dfrac{dy}{dx}=\dfrac{3x^2}{2ay}$$
$$\left[\dfrac{dy}{dx}\right]_{(am^2, am^3)}=\dfrac{3(am^2)^2}{2a\cdot (am^3)}=\dfrac{3}{2}m$$

we know that
slope of tangent$$\times$$slope of normal$$=-1$$
Slope of normal$$=\dfrac{-1}{\dfrac{3m}{2}}=\dfrac{-2}{3m}$$
Equation of normal at $$(am^2, am^3)$$ & having slope$$-\dfrac{2}{3m}$$
$$(y-am^3)=\dfrac{-2}{3m}(x-am^2)$$

$$3m(y-am^3)=-2(x-am^2)$$

$$2x+3my-am^2(3m^2+2)=0$$
Required equation
$$2x+3my-am^2(3m^2+2)=0$$.


Find the equation of the tangent and the normal to the following curve at the indicated point.
$$x=\theta +\sin\theta, y=1+\cos\theta$$ at $$\theta =\dfrac {\pi}{2}$$.

$$x=\theta +\sin\theta$$, $$y=1+\cos\theta$$
Differentiating wrt so $$\theta$$
$$\dfrac{dx}{d\theta}=1+\cos\theta$$, $$\dfrac{dy}{d\theta}=-\sin\theta$$
$$\dfrac{dy}{dx}=\dfrac{dy}{d\theta}\times \dfrac{d\theta}{dy}=\dfrac{-\sin\theta}{1+\cos\theta}$$
For $$\theta =\dfrac{\pi}{2}$$
$$\dfrac{dy}{dx}=\dfrac{-\sin \pi/2}{1+\cos\dfrac{\pi}{2}}=-1$$
Slope of tangent $$\dfrac{dy}{dx}=-1$$
Equation of tangent
$$\Rightarrow y-(1+0)=-1\left(x-\left(\dfrac{\pi}{2}+1\right)\right)$$
$$\Rightarrow y-1=-x+\dfrac{\pi}{2}+1$$
$$\Rightarrow 2y+2x-\pi -4=0$$
Slope of normal $$-1/dy/dx$$
$$\dfrac{dy}{dx}=1$$
Equation of normal
$$\Rightarrow y-1=1\left(x-\dfrac{\pi}{2}-1\right)$$
$$\Rightarrow y-1=x-\dfrac{\pi}{2}-1$$
$$\Rightarrow 2y-2x+ \pi =0$$.

1394911_1660456_ans_829bb23d31404b4aa870baaae7d24711.jpg


Find the equation of the tangent line to the curve $$y=x^2-2x+7$$ which is perpendicular to the line $$5y-15x=13$$.

$$y=x^2-2x+7$$                             [ Given ]

Differentiating both sides w.r.t. $$x,$$ we get

$$\Rightarrow$$  $$\dfrac{dy}{dx}=2x-2$$

The equation of line is $$5y-15x=13$$

$$5y-15x=13$$

$$\Rightarrow$$  $$5y=15x+13$$

$$\Rightarrow$$  $$y=3x+\dfrac{13}{5}$$                [ Dividing both sides by $$5$$ ]

This is of the form $$y=mx+c$$

$$\therefore$$   Slope of the line $$=3$$

If a tangent is perpendicular to the line $$5y-15x=13,$$ then slope of the tangent is $$\dfrac{-1}{slope\,of\,the\,line}=\dfrac{-1}{3}$$

$$\Rightarrow$$  $$2x-2=\dfrac{-1}{3}$$

$$\Rightarrow$$  $$2x=\dfrac{-1}{3}+2$$

$$\Rightarrow$$  $$2x=\dfrac{-1+6}{3}$$

$$\Rightarrow$$  $$2x=\dfrac{5}{3}$$

$$\Rightarrow$$  $$x=\dfrac{5}{6}$$

$$\Rightarrow$$  $$y=x^2-2x+7$$

$$\Rightarrow$$  $$y=\left(\dfrac{5}{6}\right)^2-2\left(\dfrac{5}{6}\right)+7$$

$$\Rightarrow$$  $$y=\dfrac{25}{36}-\dfrac{10}{6}+7$$

$$\Rightarrow$$  $$y=\dfrac{25}{36}-\dfrac{60}{36}+\dfrac{252}{36}$$

$$\Rightarrow$$  $$y=\dfrac{25-60+252}{36}$$

$$\Rightarrow$$  $$y=\dfrac{217}{36}$$
$$\therefore$$  The equation of the tangent passing through $$\left(\dfrac{5}{6},\dfrac{217}{36}\right).$$
$$y-y_1=m(x-x_1)$$

$$\Rightarrow$$  $$y-\dfrac{217}{36}=-\dfrac{1}{3}\left(x-\dfrac{5}{6}\right)$$

$$\Rightarrow$$  $$\dfrac{36y-217}{36}=\dfrac{-1}{18}(6x-5)$$

$$\Rightarrow$$  $$36y-217=-2(6x-5)$$

$$\Rightarrow$$  $$36y-217=-12x+10$$

$$\Rightarrow$$  $$36y+12x-217-10=0$$

$$\Rightarrow$$  $$36y+12x-227=0$$

$$\therefore$$  The equation of the tangent line to the given curve is $$36y+12x-227=0$$


Find the equation of the tangent to the curve $$y=\sqrt{3x-2}$$ which is parallel to the line $$4x-2y+5=0$$.

$$48x-24y=23$$.
Let $$(x_1, y_1)$$ be the point of contact of tangent to the curve $$y=\sqrt{3x-2}$$ which is parallel to the line $$4x-2y+5=0$$. Then,
$$\left(\dfrac{dy}{dx}\right)_{(x_1, y_1)}=$$(slope of the line $$4x-2y+5=0$$)
$$\Rightarrow \left(\dfrac{dy}{dx}\right)_{(x_1, y_1)}=2$$ ……..(i)
Now, $$y=\sqrt{3x-2}\Rightarrow \dfrac{dy}{dx}=\dfrac{3}{2\sqrt{3x-2}}\Rightarrow \left(\dfrac{dy}{dx}\right)_{(x_1, y_1)}=\dfrac{3}{2\sqrt{3x_1-2}}$$ ……..(ii)
From (i) and (ii), we get
$$\dfrac{3}{2\sqrt{3x_1-2}}=2\Rightarrow 9=16(3x_1-2)\Rightarrow x_1=\dfrac{41}{48}$$
Since $$(x_1, y_1)$$ lies on $$y=\sqrt{3x-2}$$. Therefore,
$$y_1=\sqrt{3x_1-2}$$
$$\Rightarrow y_1=\sqrt{\dfrac{41}{16}-2}=\dfrac{3}{4}$$
So, the point of contact is $$\left(\dfrac{41}{48}, \dfrac{3}{4}\right)$$
The equation of tangent at $$\left(\dfrac{41}{48}, \dfrac{3}{4}\right)$$ is
$$y-\dfrac{3}{4}=2\left(x-\dfrac{41}{48}\right)$$ or, $$48x-24y=23$$.


At what points will be tangents to the curve $$y=2x^3-15x^2+36x-21$$ be parallel to $$x$$-axis? Also, find the equations of the tangents to the curve at these points.

$$y=2x^3-15x^2+36x-21$$
$$\dfrac{dy}{dx}=6x^2-30x+36$$
Now, $$\dfrac{dy}{dx}=0$$
or, $$6x^2-30x+36=0$$
or, $$x^2-5x+6=0$$
or, $$x^2-3x-2x+6=0$$
or, $$x(x-3)-2(x-3)=0$$
$$x=2, x=3$$
when $$x=2$$
$$(y)_{x=2}=2.2^3-15.2^2+36.2-21=16-60+72-21=7$$
$$(\dfrac{dy}{dx})_{x=2}=6.2^2-30.2+36=24-60+36=0$$
$$(y)_{x=3}=2.3^3-15.3^2+36.3-21=6$$
Points are $$(2, 7), (3, 6)$$
The equation of tangent at $$(2, 7)$$ parallel to x-axis $$y-7=0(x-2)$$ $$y-7=0$$
The equation of tangent at $$(3, 6)$$ parallel to x-axis is $$y-6=0(x-3)$$ or $$y-6=0$$.


Find the equation of the tangent to the curve $$x=\sin 3t, y=\cos 2t$$ at $$t=\dfrac{\pi}{4}$$.

$$x=\sin 3t$$ $$y=\cos 2t$$ at $$t=\dfrac{\pi}{4}$$
$$\dfrac{dy}{dt}=-2\sin 2t$$
$$\dfrac{dx}{dt}=3\cos 3t$$
$$\dfrac{\dfrac{dy}{dt}}{\dfrac{dx}{dt}}=\dfrac{-2\sin 2t}{3\cos 3t}$$
$$\left[\dfrac{dy}{dx}\right]_{t=\dfrac{\pi}{4}}=\dfrac{-2\sin 2\cdot \dfrac{\pi}{4}}{3\cos 3\times \dfrac{\pi}{4}}=\dfrac{-2\sin\dfrac{\pi}{2}}{3\cos \dfrac{3\pi}{4}}=\dfrac{2\sqrt{2}}{3}$$
$$x=\sin 3t=\sin \dfrac{3\pi}{4}=\dfrac{1}{\sqrt{2}}$$
$$y=\cos 2t=\cos \dfrac{\pi}{2}=0$$
The equation of the tangent
$$y-0=\dfrac{dy}{dx}\left(x-\dfrac{1}{\sqrt{2}}\right)$$
$$y=\dfrac{2\sqrt{2}}{3}\left(x-\dfrac{1}{\sqrt{2}}\right)$$
$$2\sqrt{2}x-3y=2$$.


Find the equation of the tangents to the curve $$3x^2-y^2=8$$, which passes through the point $$\left (\dfrac {4}{3}, 0\right)$$.

$$3x^2-y^2=8$$

diff w.r.t 'x'
$$6x-2y\dfrac{dy}{dx}=0$$
$$\dfrac{dy}{dx}=\dfrac{3x}{y}$$
$$\left(\dfrac{dy}{dx}\right)_{(x_1, y_1)}=\dfrac{3x_1}{y_1}$$

The equation of tangent at $$(x_1, y_1)$$ is
$$y-y_1=\dfrac{3x_1}{y_1}(x-x_1)$$

Tangent passes through the point $$(4/3, 0)$$
$$0-y_1=\dfrac{3x_1}{y_1}\left(\dfrac{4}{3}-x_1\right)$$
$$-y^2_1=4x_1-3x^2_1$$

using equation (i) $$8-3x^2_1=4x_1-3x_1^2$$
$$x_1=2$$
$$3.(2)^2-y^2_1=8$$
$$y^2_1=-8+12=4$$
$$y_1=\pm 2$$
$$\therefore$$ The points are $$(2, 2)$$ and $$(2, -2)$$

The equation of tangent $$(2, 2)$$ is
$$y-2=3(x-2)$$
$$y=3x-4$$

The equation of tangent $$(2, -2)$$ is
$$y+2=-3(x-2)$$
$$y=-3x+4$$
$$3x+y=4$$.


Find the equation of the tangent to the curve $$x^2+3y-3=0$$, which is parallel to the line $$y=4x-5$$.

$$C:x^2+3y-3=0$$
diff  wrt x, we have
$$\Rightarrow 2x+3\dfrac{dy}{dx}=0$$
$$\Rightarrow m=-\dfrac{2}{3}x$$
Tangent is $$||$$ to $$y =4x-5$$
$$\therefore$$ slope $$=4$$
$$-\dfrac{2}{3}x=4$$
$$x=-6$$
$$\therefore (-6)^2+3y-3=0$$
$$3y=3-36$$
$$y=-11$$
$$(y-(-11))=4(x-(-6))$$
$$y+11=4x+24$$
$$4x-y+13=0$$.


Write the equation of the tangent drawn to the curve $$y=\sin x$$ at the point $$(0, 0)$$.

Given: curve: $$y=\sin x$$

To find: Eq of tangent drawn to curve at $$(0, 0)$$
solution: $$y=\sin x$$

$$\dfrac{dy}{dx}=\cos x$$

$$\left.\dfrac{dy}{dx}\right]_{(0, 0)}=\cos 0=1$$

Equation of tangent at $$(0, 0)$$ $$y-0=1(x-0)$$
$$\Rightarrow y=x$$
$$\therefore y=x$$ is required equation.


Write the equation of the normal to the curve $$y=\cos x$$ at $$(0, 1)$$.

$$y=\cos x$$ at $$(0, 1)$$

To find normal we have to find slope of that normal at $$(0, 1)$$
$$y'=-\sin x$$

$$m_{normal}=\left.\dfrac{1}{\sin x}\right|_{x=0}=\infty$$

$$\therefore$$ Equation of normal

$$\Rightarrow (y-1)=m_{normal}(x-0)$$

Since $$m_{normal}$$ is infinity.

Equation of normal is $$x=0$$.


Write the equation of the normal to the curve $$y=x+\sin x\cos x$$ at $$x=\dfrac{\pi}{2}$$.

$$y=x+\sin x\cos x$$

Differentiating both side with respect to x.
$$\dfrac{dy}{dx}=1+\cos^2x-\sin^2x$$

Slope of tangent$$=\left(\dfrac{dy}{dx}\right)_{x=\dfrac{\pi}{2}}=0$$

Slope of normal $$=-\dfrac{1}{0}$$

if $$x=\dfrac{\pi}{2}$$ then $$y=\dfrac{\pi}{2}+\sin\dfrac{\pi}{2}\cos\dfrac{\pi}{2}=\dfrac{\pi}{2}$$

So the point $$\left(\dfrac{\pi}{2}, \dfrac{\pi}{2}\right)$$

Equation of the normal
$$y-y_1=m(x-x_1)\Rightarrow y-\dfrac{\pi}{2}=\dfrac{-1}{0}\left(x-\dfrac{\pi}{2}\right)$$
$$\Rightarrow x=\dfrac{\pi}{2}$$ or $$2x=\pi$$.


Write the equation of the tangent to the curve $$y=x^2-x+2$$ at the point where it crosses the $$y$$-axis.

$$y=x^2-x+2$$ curve which crosses y-axis that means $$x=0$$

Now, $$y=x^2-x+2$$

$$\dfrac{dy}{dx}=2x-1$$

$$\left[\dfrac{dy}{dx}\right]_{x=0}=-1$$

Hence tangent at $$x=0$$

Now when $$x=0$$, $$y=2$$
$$y=\left(\dfrac{dy}{dx}\right) x+c=-x+c$$

so, $$2=-0+c$$ or $$c=2$$

so the equation of the tangent

$$y=-x+2$$

or $$x+y-2=0$$.


Find the points on the curve $$y=x^{3}-3x$$, where the tangent to the curve is parallel to the chord joining $$(1, -2)$$ and $$(2,2)$$.

Let $$(x_1,y_1)$$ be the required point.

Slope of the chord $$=\dfrac{y_2-y_1}{x_2-x_1}$$

                                $$=\dfrac{2+2}{2-1}$$                [ Here, $$x_1=1,y_1=-2$$ and $$x_2=2,y_2=2$$ ]

                                $$=4$$
Given,
$$y=x^3-3x$$

Differentiate both sides w.r.t. $$x,$$

$$\Rightarrow$$  $$\dfrac{dy}{dx}=3x^2-3$$             ----- ( 1 )

Slope of the tangent $$(m)=\left(\dfrac{dy}{dx}\right)_{(x_1,y_1)}$$

                                            $$=3x_1^2-3$$
It is given that the tangent and the chord are parallel.

$$\therefore$$  Slope of the tangent $$=$$ Slope of the chord

$$\Rightarrow$$  $$3x_1^2-3=4$$

$$\Rightarrow$$  $$3x_1^2=7$$

$$\Rightarrow$$  $$x_1^2=\dfrac{7}{3}$$

$$\Rightarrow$$  $$x=\pm\sqrt{\dfrac{7}{3}}$$

$$Case\,I:$$
When $$x_1=\sqrt{\dfrac{7}{3}}$$

On substituting value of $$x_1$$ in equation ( 1 ), we get

$$y_1=\left(\sqrt{\dfrac{7}{3}}\right)^2-3\left(\sqrt{\dfrac{7}{3}}\right)$$

$$y_1=\dfrac{7}{3}\sqrt{\dfrac{7}{3}}-3\sqrt{\dfrac{7}{3}}$$

$$y_1=\dfrac{-2}{3}\sqrt{\dfrac{7}{3}}$$

$$\therefore$$  $$(x_1,y_1)=\left(\sqrt{\dfrac{7}{3}},\,\dfrac{-2}{3}\sqrt{\dfrac{7}{3}}\right)$$

$$Case\,II:$$
When $$x_1=-\sqrt{\dfrac{7}{3}}$$
On substituting this in equation ( 1 ), we get
$$y_1=\left(-\sqrt{\dfrac{7}{3}}\right)^3-3\left(-\sqrt{\dfrac{7}{3}}\right)$$

     $$=\dfrac{-7}{3}\sqrt{\dfrac{7}{3}}+3\sqrt{\dfrac{7}{3}}$$

     $$=\dfrac{2}{3}\sqrt{\dfrac{7}{3}}$$

$$\therefore$$  $$(x_1,y_1)=\left(-\sqrt{\dfrac{7}{3}},\dfrac{2}{3}\sqrt{\dfrac{7}{3}}\right)$$




Find the equation of the tangent and the normal to the given curve at the indicated point:
$$\dfrac{x^{2}}{a^{2}}-\dfrac{y^{2}}{b^{2}}=1$$ at $$(a\sec\theta, b\tan\theta)$$


1671710_1706805_ans_9a38bfbf393645bdbb695f055a82cdad.jpeg


Find the equation of the tangent and the normal to the given curve at the indicated point:
$$y^{2}=4ax$$ at $$\left(\dfrac{a}{m^{2}},\dfrac{2a}{m}\right)$$


1671723_1706790_ans_0a3f3d5d238b440389b8448db37316c7.jpeg


Find the equation of the tangent and the normal to the given curve at the indicated point:
$$y^{2}=4ax$$ at $$(at^{2},2at)$$


1546219_1706823_ans_60567df999ab409cbf2e8385e0ff1105.JPG


Find the equation of the tangent and the normal to the given curve at the indicated point:
$$y=x^{2}-2x+7$$ at $$(1,6)$$

 Given curve is  $$ y={{x}^{2}}-2x+7 $$
 $$ \dfrac{dy}{dx}=2x-2 $$
 $$ m=\dfrac{dy}{dx}_{\left( 1,6 \right)}^{{}}=2\left( 1 \right)-2 $$
 $$ \,\,\,\,\,\,\,\,\,\,\,\,=0 $$
 $$ Equation\,of\text{ tangent at}\left( 1,6 \right) $$
 $$ y-y_{1}^{{}}=m\left( x-x_{1}^{{}} \right) $$
 $$ y-6=0\left( x-1 \right) $$
 $$ \Rightarrow y=6 $$
 $$ Slope\,of\,normal=\frac{-1}{m} $$
 $$ Equation\,of\,normal\,at\left( 1,6 \right) $$
 $$ y-y_{1}^{{}}=m\left( x-x_{1}^{{}} \right) $$
 $$ y-6=\frac{-1}{0}\left( x-1 \right) $$
 $$ \Rightarrow x-1=0 $$
 $$ \Rightarrow x=1 $$


Find the equation of the tangent and the normal to the given curve at the indicated point:
$$y=x^{3}$$ at $$P(1,1)$$


1546186_1706812_ans_ea4d1739070747dd8f6e45c4ca2688b6.jpg


Find the equation of the tangent and the normal to the given curve at the indicated point:
$$\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1$$ at $$(a\cos\theta, b\sin\theta)$$


1570190_1706798_ans_f564f293b16046769557df036e3ebac2.png


Find the equation of the tangent and the normal to the given curve at the indicated point:
$$16x^{2}+9y^{2}=144$$ at $$(2,y_{1})$$, where $$y_{1}>0$$


1546235_1706842_ans_c3798a1876e446f09f9a7986537cc710.jpg


Find the equation of the normal to the curve $$y=(\sin 2x+\cot x+2)^{2}$$ at $$x=\dfrac{\pi}{2}$$

Given equation of curve is $$y=(\sin 2 x+\cot x+2)^2$$

$$\implies \dfrac{d y}{d x}=2(\sin 2 x+\cot x+2)(\cos 2 x\times 2-\text{cosec}^2 x)$$

At $$x=\dfrac{\pi}{2},y=\left(\sin 2\times \dfrac{\pi}{2}+\cot \dfrac{\pi}{2}+2\right)^2=\left(0+0+2\right)^2=4$$

At $$x=\dfrac{\pi}{2},\dfrac{d y}{d x}=2\left(\sin 2\times \dfrac{\pi}{2}+\cot \dfrac{\pi}{2}+2\right)\left(\left(2\cos 2 \times \dfrac{\pi}{2}\right)-\text{cosec}^2 \dfrac{\pi}{2}\right)=2(0+0+2)(-2-1)=-12$$

So the slope of the tangent at $$\bigg(\dfrac{\pi}{2},4\bigg)$$ is $$m=-12$$

As we know that

If the slope of tangent is $$m$$ then the slope of the normal is $$\dfrac{-1}{m}$$

Hence the slope of the normal is $$\dfrac{-1}{-12}=\dfrac{1}{12}$$

Also we know that

The equation line passing through $$(x_1,y_1)$$ with slope $$m$$ is $$y-y_1=m(x-x_1)$$

Here $$x_1=\dfrac{\pi}{2},y_1=4,m=\dfrac{1}{12}$$

Equation of normal is $$y-4=\dfrac{1}{12}\left(x-\dfrac{\pi}{2}\right)$$

$$\implies y-4=\dfrac{1}{24}\left(2 x-\pi\right)$$

$$\implies 24 y-96=2 x-\pi$$

$$\implies 24 y-2 x+\pi-96=0$$

Hence the equation of normal to the curve at $$x=\dfrac{\pi}{2}$$ is    $$24 y-2 x+\pi-96=0$$


Find the equation of the tangent to the curve $$\sqrt{x}+\sqrt{y}=a$$ at $$\left(\dfrac{a^{2}}{4}, \dfrac{a^{2}}{4}\right)$$


1671944_1706844_ans_2303f4b0c05f4015bfffebee38d3bea9.jpeg


Find the equation of the tangent to the curve $$y=(\sec^{4}x-\tan^{4}x)$$ at $$x=\dfrac{\pi}{3}$$


1564674_1706850_ans_b961dc25b49e437d939126b0a35c4004.jpg


Find the equation of the tangent to the curve $$x^{2}+3y=3$$, which is parallel to the line $$y-4x+5=0$$.,

Given,
$$x^{2}+3y=3\Rightarrow 2x+3\dfrac{dy}{dx}=0$$

$$\therefore slope\Rightarrow \dfrac{dy}{dx}=\dfrac{-2x}{3}=m$$

Since the tangent is parallel to  $$y-4x+5=0 \Rightarrow y=4x-5$$
$$\therefore $$ on comparing with $$y=mx+c$$
we get $$m=4$$

$$\therefore$$ the slope of the tangent $$=4$$.

So, $$\dfrac{-2x}{3}=4\Rightarrow x=-6$$.

$$x^{2}+3y=3$$.
on putting $$x=-6$$ in above equation
$$(-6)^2+3y=3 \Rightarrow y=-11$$

The equation of the tangent at $$(-6,-11)$$ with slope $$-4$$ is $$y+11=4(x+6)$$.


Show that the tangent to the curve $$y=2x^{3}-4$$ at the points $$x=2$$ and $$x=-2$$ are parallel.

Given,
$$y=2x^{3}-4$$

$$x_1=2\Rightarrow y_1=(2\times 8-4)=12$$

$$x_2=-2\Rightarrow y_2=2\times (-8)-4=20$$

now, differentiating $$y$$, we get

$$\dfrac{dy}{dx}=6x^{2}$$

$$\Rightarrow m_1= \left(\dfrac{dy}{dx}\right)_{(2,12)}=24$$

$$\Rightarrow m_2=\left(\dfrac{dy}{dx}\right)_{(-2,20)}=24$$

$$\therefore m_{1}=m_{2}$$

So, the tangents at the respective two points are parallel


Show that the equation of the tangent to the hyperbola $$\dfrac{x^{2}}{a^{2}}-\dfrac{y^{2}}{b^{2}}=1$$ at $$(x_{1}, y_{1})$$ is $$\dfrac{xx_{1}}{a^{2}}-\dfrac{yy_{1}}{b^{2}}=1$$


1546255_1706846_ans_800fadf0cefd491bafb3e0caae87006c.jpg


Find the equation of the tangent to the curve $$x^2+2y=8$$, which is perpendicular to the line $$x-2y+1=0$$


1570194_1706878_ans_00426ef3727b47da8019ac19b49e9d96.png


Find the equation of the tangent at $$t=\dfrac{\pi}{4}$$ for the curve $$x=\sin 3t, y=\cos 2t$$

Given equation of curve is $$x=\sin 3 t,y=\cos 2 t$$

$$\implies \dfrac{d x}{d t}=3\cos 3 t,\dfrac{d y}{d t}=-2\sin 2 t$$

$$\implies \dfrac{d y}{d x}=\dfrac{\left(\dfrac{d y}{d t}\right)}{\left(\dfrac{d x}{d t}\right)}=\dfrac{-2\sin 2 t}{3\cos 3 t}$$

At $$t=\dfrac{\pi}{4},x=\sin 3\times \dfrac{\pi}{4}=\sin \dfrac{3\pi}{4}=\dfrac{1}{\sqrt{2}},y=\cos 2 \times \dfrac{\pi}{4}=\cos \dfrac{\pi}{2}=0$$

At $$t=\dfrac{\pi}{4},\dfrac{d y}{d x}=\dfrac{-2\times \sin 2\times \dfrac{\pi}{4}}{3\cos 3\times \dfrac{\pi}{4}}=\dfrac{-2\sin \dfrac{\pi}{2}}{3\cos \dfrac{3\pi}{4}}=\dfrac{2\sqrt{2}}{3}$$

So the slope of the tangent at $$\bigg(\dfrac{1}{\sqrt{2}},0\bigg)$$ is $$m=\dfrac{2\sqrt{2}}{3}$$

Also we know that

The equation line passing through $$(x_1,y_1)$$ with slope $$m$$ is $$y-y_1=m(x-x_1)$$

Here $$x_1=\dfrac{1}{\sqrt{2}},y_1=0,m=\dfrac{2\sqrt{2}}{3}$$

Equation of tangent is $$y-0=\dfrac{2\sqrt{2}}{3}\left(x-\dfrac{1}{\sqrt{2}}\right)$$

$$\implies y=\dfrac{2}{3}\left(\sqrt{2} x-1\right)$$

$$\implies 3 y=2\sqrt{2}  x-2$$

$$\implies 2\sqrt{2} x-3 y-2=0$$

Hence the equation of tangent to the curve at $$t=\dfrac{\pi}{4}$$ is    $$2\sqrt{2} x-3 y-2=0$$



Prove that the equation of the normal to $$x^{2/3}+y^{2/3}=a^{2/3}$$ is $$y\cos \theta-x\sin \theta= a\cos 2\theta$$,where $$\theta$$ is the angle which the normal makes with axis of $$x$$.


1765677_1757283_ans_a0074abe4aa44d75a9f1e87be3d22ed7.jpg


Find the equation of the tangent to the curve $$2x^{2}+3y^{2}=14$$, parallel to the line $$x+3y=4$$.


1546725_1706870_ans_788c6973750549e29e79069f074facd9.jpg


Find the equation of tangent to the curve $$x=(\theta+\sin\theta), y=(1+\cos\theta)$$ at $$\theta=\dfrac{\pi}{4}$$

$$x=(\theta+\sin\theta)\Rightarrow \dfrac{dx}{d\theta}=(1+\cos\theta)$$.

$$y=(1+\cos\theta)\Rightarrow \dfrac{dy}{d\theta}=-\sin\theta$$.

$$\therefore \dfrac{dy}{dx}=\dfrac{dy/d\theta}{dx/d\theta}=\dfrac{-\sin\theta}{(1+\cos\theta)}$$.

$$\left(\dfrac{dy}{dx}\right)$$ at $$\theta=\dfrac{\pi}{4}=\dfrac{-\sin\left(\dfrac{\pi}{4}\right)}{\left(1+\cos\dfrac{\pi}{4}\right)}=\dfrac{1}{\sqrt{2}}.\dfrac{1}{\left(1+\dfrac{1}{\sqrt{2}}\right)}$$

$$=\dfrac{-1}{(\sqrt{2}+1)}\times \dfrac{(\sqrt{2}-1)}{(\sqrt{2}-1)}=(1-\sqrt{2})$$.

At $$\theta=\dfrac{\pi}{4}$$, we have $$x=\left(\dfrac{\pi}{4}+\sin\dfrac{\pi}{4}\right)=\left(\dfrac{\pi}{4}+\dfrac{1}{\sqrt{2}}\right)$$, and 
$$y=\left(1+\cos\dfrac{\pi}{4}\right)=\left(1+\dfrac{1}{\sqrt{2}}\right)$$.

Required equation of tangent is
$$\dfrac{y-\left(1+\dfrac{1}{\sqrt{2}}\right)}{x-\left(\dfrac{\pi}{4}+\dfrac{1}{\sqrt{2}}\right)}=(1-\sqrt{2})$$.

$$\Rightarrow{y-\left(1+\dfrac{1}{\sqrt{2}}\right)}=(1-\sqrt{2})\left ({x-\dfrac{\pi}{4}-\dfrac{1}{\sqrt{2}}}\right)$$


If the curve C in the xy place has the equation $$x^{2}+xy+y^{2} = 1$$, then the fourth power of the greatest distance of a point on C from the origin, is


1776289_1758753_ans_15d372964e28436a8ecd92ad37450390.jpeg


Find the equation of the normal to the curve $$y = (1+x)^{y}+\sin ^{-1}(\sin ^{2}x)$$ at x=0.


1794382_1758822_ans_906fd4dc419a4697a5ad0e7ea12fdafb.jpg


Find the equation of tangent to the curve $$y=\sqrt{3x-2},$$ which is parallel to the line $$4x-2y+5=0.$$

Given, curve $$y=\sqrt{3x-2}$$    $$\implies\, y^{2}= 3x-2$$            ....(i)

To get the equation of tangent to the curve $$y^{2}= 3x-2$$, which is a parabola, first we have to find the coordinates of point from where tangent line passes.

Let the coordinates of the point on parabola be (a,b), then this coordinate will satisfy the equation (i).
Therefore, from (i), we have $$b^{2}= 3a-2$$                 .....(ii)

Now differentiating the equation (i) with respect to x, we get 
$$ 2y\dfrac{dy}{dx}=3$$
$$\implies\,   (\dfrac{dy}{dx})= \dfrac{3}{2y}$$

Now slope of the required tangent line 
$$m_{1}= (\dfrac{dy}{dx})_{a,b}= \dfrac{3}{2b}$$

As it is given that required tangent line is parallel to the given line $$4x-2y+5=0$$, so, the slopes of lines are equal.
Therefore, 
$$\dfrac{3}{2b}= \dfrac{-4}{-2}$$
$$\implies\, 4b=3$$
$$\implies\, b=\dfrac{3}{4}$$

Substituting this value $$b=\dfrac{3}{4}$$ in equation (ii), we get 
$$(\dfrac{3}{4})^{2}+ 2= 3a$$
$$\implies\, 3a = \dfrac{41}{16}$$     $$\implies\,a=\dfrac{41}{48}$$

Now the coordinates of the point on tangent are $$\dfrac{41}{48}, \dfrac{3}{4}$$ and slope is 2. 
Hence, equation of tangent is obtained by $$y-b = m(x-a)$$
$$\implies\,   y- \dfrac{3}{4}= 2(x - \dfrac{41}{48})$$
$$\implies\, \dfrac{4y-3}{4}= \dfrac{2(48x-41)}{48}$$
$$\implies\, (4y-3)= \dfrac{48x - 41}{6}$$
$$\implies\, 24y- 18= 48x- 41$$
$$\implies\, 48x - 24y= 41- 18$$        
$$\implies\, 48x- 24y-23=0$$ is the required equation of tangent.


Find the equation of the normal at the point $$(am^{2}, am^{3})$$ for the curve $$ay^{2}= x^{3}.$$

Given curve          $$ay^{2}= x^{3}$$
On differentiating, we get 
$$2ay\dfrac{dy}{dx}= 3x^{2}$$
$$\implies\, \dfrac{dy}{dx}= \dfrac{3x^{2}}{2ay}$$
$$\implies\,      \dfrac{dy}{dx}\, at\, (am^{2}, am^{3})= \dfrac{3 \times a^{2}m^{4}}{2a \times am^{3}}= \dfrac{3m}{2}$$
$$\therefore$$ Slope of normal =$$\dfrac{-1}{slope\, of\, tangent}$$    
                             =$$-\dfrac{1}{\dfrac{3m}{2}}= -\dfrac{2}{3m}$$
Equation of normal at the point $$(am^{2}, am^{3})$$ is given by 
$$\dfrac{y- am^{3}}{x- am^{2}}=-\dfrac{2}{3m}$$
$$\implies\, 3my- 3am^{4}=-2x + 2am^{2}$$
$$\implies\, 2x+ 3my - am^{2}(2 + 3m^{2})=0$$
Hence, equation of normal is $$2x+ 3my- am^{2}( 2+ 3m^{2})=0$$


Find the equation of all the tangents to the curve $$ y=cos(x+y), -2 \pi \le x \le 2 \pi $$ that are parallel to the line $$ x+2y=0 $$.

Given that $$ y = cos  ( x + y ) \Rightarrow \frac {dy}{dx} = - sin ( x + y) [   1 + \frac {dy}{dx} ] .....(i) $$
or $$ \frac {dy}{dx} = - \frac { sin ( x +y) }{ 1+ sin ( x+ y) } $$
Since tangent is parallel to $$ x + 2y = 0 $$therefore solpe of tangent $$ = - \frac {1}{2} $$
therefore , $$ - \frac { sin (x+y) }{  1 + sin ( x+y) }= - \frac {1}{2} \Rightarrow  cos^2 ( x+y) + sin^2 ( x+y) = y^2 + 1 $$
$$ \Rightarrow 1 = y^2 + 1 $$ or $$ y = 0 $$
Therefore , $$ cos x = 0 $$
therefore , $$ x = ( 2n +1)  \frac  { \pi}{2} , n = 0 , \pm 1, \pm  2 ..... $$
Thus , $$ x = \pm \frac { \pi}{2} , \pm \frac { 3 \pi}{2} $$ but $$ x = \frac { \pi}{2} , x = \frac { -3 \pi}{2} $$ satisfy equations (ii) 
hence the points are $$ ( \frac { \pi}{2}, 0),( \frac { -3 \pi }{2} , 0 )  $$
Therefore , equation of tangent at $$ (  \frac { \pi}{2}, 0 ) $$ is $$ y = - \frac {1}{2}  ( x - \frac  { \pi}{2} ) $$ or $$ 2x +4y - \pi = 0 $$ and equation of tangent at $$ (  \frac  { -3 \pi}{2} , 0 ) $$ is $$ y  = - \frac {1}{2} ( x + \frac { 3 \pi}{2}) $$ or $$ 2x +4y + 3 \pi = 0 $$


Find the equations of tangents to the curve $$3x^{2}- y^{2}=8$$, which pass through the point $$(\dfrac{4}{3}, 0)$$

Let the point of contact be $$(x_{0}, y_{0})$$

Now given curve is $$3x^{2}- y^{2}=8$$

Differentiating w.r.t x we get , $$6x- 2y.\dfrac{dy}{dx}=0$$
$$\implies\, \dfrac{dy}{dx}= \dfrac{6x}{2y}= \dfrac{3x}{y}$$       $$\implies\, [\dfrac{dy}{dx}]_{x_{0}, y_{0}}= \dfrac{3x_{0}}{y_{0}}$$

Now equation of required tangent is 
$$(y- y_{0})= \dfrac{3x_{0}}{y_{0}}(x- x_{0})$$         ...(i)

$$\because$$        (i) passes through $$(\dfrac{4}{3},0)$$

$$\therefore (0- y_{0})= \dfrac{3x_{0}}{y_{0}}(\dfrac{4}{3}- x_{0})$$          
$$\implies\, -y_{0}^{2}= 4x_{0}- 3x_{0}^{2}$$

Also, $$\because (x_{0}, y_{0})$$ lie on given curve $$3x^{2}- y^{2}=8$$

$$\implies\,  3x_{0}^{2}- y_{0}^{2}=8$$        $$\implies\,y_{0}^{2}= 3x_{0}^{2}-8$$

Putting $$y_{0}^{2}$$ in (ii) we get 
$$-(3x_{0}^{2}-8)= 4 x_{0}- 3x_{0}^{2}$$        $$\implies\, 4x_{0}=8$$       $$\implies\, x_{0}=2$$

$$\therefore\, y_{0}= \sqrt{3 \times 2^{2}-8}= \sqrt{4}= \pm 2 $$

Therefore, equations of required tangents are 
$$(y-2)= \dfrac{3 \times 2}{2}(x-2)\, and\, (y+2)= \dfrac{3 \times 2}{-2}(x-2)$$
$$\implies\, y-2= 3x-6\, and \, y+2= -3x+6$$
$$\implies\, 3x-y-4=0\, and \, 3x+y-4=0$$


Find the equation of tangent to the curve 
$$x= sin 3t, y= cos 2t$$ at t=$$\dfrac{\pi}{4}.$$

Here,    $$y= cos 2t$$        $$\therefore \dfrac{dy}{dt}= -2 sin 2t$$

Also,    $$x= sin 3t$$        $$\therefore \dfrac{dx}{dt}= 3 cos 3t$$

$$\implies\,   \dfrac{dy}{dx}=\dfrac{\dfrac{dy}{dt}}{\dfrac{dx}{dt}}= \dfrac{-2 sin 2t}{3 cos 3t}$$

$$\therefore (\dfrac{dy}{dx})_{t=\dfrac{\pi}{4}}= \dfrac{-2 sin {\pi}{2}}{3 cos \dfrac{3 \pi}{4}}$$

=$$\dfrac{-2 \times 1}{3 \times (-\dfrac{1}{\sqrt{2}})}= \dfrac{ 2 \sqrt{2}}{3}$$

If t=$$\dfrac{\pi}{4}$$ then 

x=$$sin \dfrac{3 \pi}{4}= \dfrac{1}{\sqrt{2}},$$

y= cos $$\dfrac{2 \pi}{4}= cos \dfrac{\pi}{2}=0$$

Therefore, equation of tangent at t=$$\dfrac{\pi}{4} i.e,\, at (\dfrac{1}{\sqrt{2}},0)$$ is given by 

$$y-0=\dfrac{dy}{dx}(x- \dfrac{1}{\sqrt{2}})$$

$$implies\,   y-0=\dfrac{2 \sqrt{2}}{4}(x- \dfrac{1}{\sqrt{2}})$$

$$implies\,     3y= 2 \sqrt{2x}-2 $$




Find the equation of tangent and normals to the following curves at the indicated points on them : $$y=x^2+2e^x2$$ at $$(0,4)$$

$$y=x^2+2e^x2$$
$$\therefore \dfrac{dy}{dx}=\dfrac{d}{dx}(x^2+2e^x+2)$$
$$=2x+2x e^x+0$$
$$=2x+2e^x$$
$$\therefore \left(\dfrac{dy}{dx}\right)_{at\ (0,4)}=2(0)+2e^o=2$$
$$=$$ slope of the tangent at $$(0,4)$$ is
$$y-4=2(x-0)$$
$$\therefore y-4=2x$$
$$\therefore 2x-y+4=0$$
The slope of the normal at $$(0,4)$$
$$=\dfrac{-1}{\left(\dfrac{dy}{dx}\right)_{at\ (0,4)}}=-\dfrac{1}{2}$$
$$\therefore$$ the equation oof the normal at $$(0,4)$$ is
$$y-4=-\dfrac{1}{2}(x-0)$$
$$\therefore 2y-8=-x$$
$$\therefore x+2y-8=00$$
Hence, the equation of tangent and normal are
$$2x-y+4=0$$ and $$x+2y-8=0$$ respectively.


The equation of normal to the curve $$ y=tan \quad x \quad at (0,0) $$ is _______.

The eqution of normal to the curve $$ y=tan x $$ at $$ (0,0) is x+y=0 $$
$$ \because y=tan x \Rightarrow \frac{dy}{dx}=sec^2x $$
$$ \Rightarrow \left( \dfrac { dy }{ dx }  \right) _{ (0,0) }=sec^20=1 $$ and 
$$ -\frac{1}{\left( \dfrac { dy }{ dx }  \right) }=-\dfrac{1}{1} =-1$$
$$ \therefore $$ Equation of normal to the curve $$ y=tan x\ \ at (0,0) $$ is 
$$ y-0=-1(x-0) $$
$$ \Rightarrow y+x=0 $$


Find the equation of tangent and normals to the following curves at the indicated points on them : $$x \sin 2y=y \cos 2x$$ at $$\left(\dfrac{\pi}{4},\dfrac{\pi}{2}\right)$$

$$x \sin 2y=y \cos 2x$$
Differentiating both side w.r.t. $$x$$, we get
$$x \dfrac{d}{dx}(\sin 2y)+\sin 2y\dfrac{d}{dx} (x)=y.\dfrac{d}{dx}(\cos 2x)+ \cos 2x.\dfrac{dy}{dx}$$
$$=x. \cos 2y.\dfrac{d}{dx} (2y)+ \sin 2y \times 1=y.(- \sin 2x)\dfrac{d}{dx} (2x)+ \cos 2x \dfrac{dy}{dx}$$
$$\therefore x \cos 2y \times 2 \dfrac{dy}{dx}+ \sin 2y=- y \sin 2x \times 2+ \cos 2x \dfrac{dy}{dx}$$
$$\therefore (2x \cos 2y- \cos 2x) \dfrac{dy}{dx}=- 2y \sin 2x - \sin 2y$$
$$\therefore \dfrac{dy}{dx} =\dfrac{-2 y \sin 2x- \sin 2y}{2x \cos 2y- \cos 2x}$$
$$\therefore \left(\dfrac{dy}{dx}\right)_{at\ \left(\dfrac{\pi}{4},\dfrac{\pi}{2}\right)}==\dfrac{-2 \left(\dfrac{\pi}{2}\right) \sin \dfrac{\pi}{2}- \sin \pi}{2\left(\dfrac{\pi}{4}\right) \cos \pi- \cos \dfrac{\pi}{2}}$$
$$\dfrac{-\pi (1)-0}{\dfrac{\pi}{2}(-1)-0}$$
$$=\dfrac{-\pi}{\left(-\dfrac{\pi}{2}\right)}$$
$$=2$$
$$=$$slope of the tangent at $$\left(\dfrac{\pi}{4},\dfrac{\pi}{2}\right)$$ 
$$\therefore$$ the equation of the tangent at $$\left(\dfrac{\pi}{4},\dfrac{\pi}{2} \right)$$ is
$$\therefore y -\dfrac{\pi}{2}=2 \left(x-\dfrac{\pi}{4} \right)$$
$$\therefore y-\dfrac{\pi}{2}=2x-\dfrac{\pi}{2}$$
$$\therefore 2x-y=0$$
The Slope of normal at $$\left(\dfrac{\pi}{4},\dfrac{\pi}{2} \right)$$
$$=\dfrac{-1}{\left(\dfrac{dy}{dx}\right)_{at\ \left(\dfrac{\pi}
{4},\dfrac{\pi}
{2}\right)}}$$ 
$$=\dfrac{-1}{2}$$
$$\therefore$$ the equation of te noral at $$\left(\dfrac{\pi}
{4},\dfrac{\pi}
{2}\right)$$ is
$$y-\dfrac{\pi}{2}=-\dfrac{1}{2} \left(x- \dfrac{\pi}{2}\right)$$
$$\therefore 2y- \pi=-x+ \dfrac{\pi}{4}$$
$$\therefore 8y-4 \pi =-4 x+ \pi$$
$$\therefore 4x+8y-5 \pi=0$$
hence, the equation of tangent and normal are
$$z-y=0$$ and $$4x+8y-5 \pi=0$$ respectively.


Find the equation of tangent and normals to the following curves at the indicated points on them : $$2xy+\pi \sin y=2 \pi $$ at $$\left(1, \dfrac{\pi}{2}\right)$$

$$2xy+\pi \sin y=2 \pi $$
Differentiating both side w.r.t. $$x$$, we get
$$2 \left[ x \dfrac{dy}{dx}+y.\dfrac{d}{dx}(x)\right]=\pi \cos y \dfrac{dy}{dx}=0$$
$$\therefore 2x\dfrac{d}{dx}+2y \times 1+ \pi \cos y \dfrac{d}{dx}=0$$
$$\therefore \dfrac{d}{dx}=\dfrac{-2}{2x+ \pi \cos y}$$
$$\left(\dfrac{d}{dx}\right)_{at 1, \left(1, \dfrac{\pi}{2}\right)}=\dfrac{-2 \left(\dfrac{\pi}{2} \right)}{2(1)+ \pi \cos \dfrac{\pi}{2} }$$
$$=\dfrac{-\pi}{2+ \pi (0)}$$
$$-\dfrac{\pi}{2}$$
$$=$$slope of the tangent at $$\left(1,\dfrac{\pi}{2}\right)$$ 
$$\therefore$$ the equation of the tangent at $$\left(1,\dfrac{\pi}{2}\right)$$ is
$$y-\dfrac{\pi}{2}=-\dfrac{\pi}{2}(x-1)$$
$$\therefore 2y- \pi=- \pi x+ \pi$$
$$\therefore \pi x+2y-2 \pi=0$$
The Slope of normal at $$\left(1,\dfrac{\pi}{2}\right)$$
$$=\dfrac{-1}{\left(\dfrac{dy}{dx}\right)_{at\ \left(1,\dfrac{\pi}{2}\right)}}$$ 
$$=\dfrac{1-}{\left(\dfrac{\pi}{2}\right)}$$
$$=\dfrac{2}{\pi}$$
$$\therefore$$ the equation of the normal at $$\left(1,\dfrac{\pi}{2}\right)$$ is
$$y-\dfrac{\pi}{2}=\dfrac{2}{\pi}(x-1)$$
$$\therefore \pi y-\dfrac{\pi^2}{2}=2x-2$$
$$\therefore 2 \pi y- \pi^2=4x-4$$
$$\therefore 4x-2 \pi y+ \pi^2-4=0$$
hence, the equation of tangent and normal are
$$\pi x+2y-2 \pi=0$$ and $$4x-2 \pi y + \pi^2-4=0$$ respectively.


Find the equation of tangent and normals to the following curves at the indicated points on them : $$x^2-\sqrt{3xy}+2y^2=5\ \ at (\sqrt{3,2})$$

$$x^2-\sqrt{3xy}+2y^2=5$$
Differentiating both side w.r.t. $$x$$, we get
$$2x-\sqrt 3 \left[ x \dfrac{dy}{dx}+y.\dfrac{d}{dx}(x)\right]=+2 \times \dfrac{dy}{dx}=0$$
$$\therefore 2x=\sqrt {3x}\dfrac{dy}{dx}=\sqrt{3y} \times 1+4y \dfrac{dy}{dx}=0$$
$$\therefore (4y-\sqrt{3x})\dfrac{dy}{dx}=\sqrt{3y}-2x$$
$$\therefore \dfrac{dy}{dx}=\dfrac{\sqrt {3y}-2x}{4y-\sqrt{3x}}$$
$$=\dfrac{2x-\sqrt{3x}}{\sqrt{3x}-4y}$$
$$\therefore \left(\dfrac{dy}{dx}\right)_{at(\sqrt 3,2)}=\dfrac{2 \sqrt 3- \sqrt 3(2)}{\sqrt 3 (\sqrt 3)-4 (2)}=0$$
$$=$$slope of the tangent at $$(\sqrt 3,2)$$ 
$$\therefore$$ the equation of the tangent at $$(\sqrt 3,2)$$ is
$$y-2=0 (x-\sqrt 3)$$
$$\therefore y-2=0$$
$$=\therefore y=2$$
The slope of normal at $$(\sqrt 3,2)$$
$$=\dfrac{-1}{\left(\dfrac{dy}{dx}\right)_{at\ (\sqrt 3,2)}}$$ where $$\left(\dfrac{dy}{dx}\right)_{at\ (\sqrt 3,2)}=0$$
$$\therefore$$ the slope normal at $$(\sqrt 3,2)$$does not exist.
$$\therefore$$ normal is parallel to $$Y-$$axis
$$\therefore$$ equation of normal is of the form $$x=k$$
Since, it passes the point $$(\sqrt 3,2),k=\sqrt 3$$
$$\therefore$$ equation of the normal is $$x=\sqrt 3$$
hence, the equation of tangent and normal are
$$y=2$$ and $$x=\sqrt 3$$ respectively.


Find the equation of tangent and normals to the following curves at the indicated points on them : $$x^3+y^3-9xy=0$$ at $$(2,4)$$

$$x^3+y^3-9xy=0$$
Differentiating both side w.r.t. $$x$$, we get
$$3x^2+3y^2 \dfrac{dy}{dx}-9 \left[ x \dfrac{dy}{dx}+y.\dfrac{d}{dx}(x)\right]=0$$
$$\therefore 3x^2+3y^2 \dfrac{dy}{dx}-9x\dfrac{dy}{dx}-9yx1=0$$
$$\therefore (3y^2-9x) \dfrac{dy}{dx}=9y-3x^2$$
$$\therefore \dfrac{dy}{dx}=\dfrac{9y-3x^2}{3y^2-9x}$$
$$\therefore \left(\dfrac{dy}{dx}\right)_{at\ (2,4)}=\dfrac{9(4)-3(2)^2}{3(4)^2-9(2)}$$
$$=\dfrac{36-12}{48-18}$$
$$=\dfrac{24}{30}$$
$$=\dfrac{4}{5}$$
$$=$$slope of the tangent at $$(2,4)$$ 
$$\therefore$$ the equation of the tangent at $$(2,4)$$ is
$$y-4=\dfrac{4}{5}(x-2)$$
$$\therefore 5y-20=4x-8$$
$$\therefore 4x-5y+12=0$$
The slope of normal at $$(2,4)$$
$$=\dfrac{-1}{\left(\dfrac{dy}{dx}\right)_{at\ (2,4)}}=-\dfrac{5}
{4}$$
$$\therefore $$ the equation of the tangent at $$(2,4)$$ is
$$y-4=\dfrac{4}{5}(x-2)$$
$$\therefore 4y-16=-5x+10$$
$$\therefore 5x+4y-26=0$$
hence, the equation of tangent and normal are
$$4x-5y+12=0$$ and $$5x+4y-26=0$$ respectively.


Find the equation of tangent to the curve $$x^2+y^2-2x-4y+1-0$$ which a parallel to the $$X-$$axis.

Let $$P(x_1,y_1)$$ be the point on the curve $$x^2+y^2-2x-4y+1=0$$ where the tangent is parallel to $$X-$$axis
Differentiating $$x^2+y^2-2x-4y+1=0$$ w.r.t $$x$$ we get
$$2x+2y\dfrac{dy}{dx}2 \times 1-4\dfrac{dy}{dx}+0=0$$
$$\therefore (2y-4)\dfrac{dy}{dx}=2-2x$$
$$\therefore \dfrac{d}{dx}=\dfrac{2-2x}{2y-4} =\dfrac{1-x}{y-2}$$
$$=\therefore \left(\dfrac{dy}{dx}\right)_{at\ x_1,y_1}$$
$$=\dfrac{1-x_1}{y_1-2}$$
$$=$$ slope of the tangent at $$(x_1, y_1)$$
Since, the tangent is parallel to $$X-$$ axis,
slope of the tangent $$0$$
$$\therefore \dfrac{1-x_1}{y_1-2}=0$$
$$\therefore 1-x_1=0$$
$$\therefore x_1=1$$
Since, $$(x_1, y_1)$$ lies on $$x^2+y^2-2x-4y+1=0$$
$$x_1^2+y_1^2-2x_1-4y_1+1=0$$
When $$x_1=1,\ (1)^2+y_1^2-2(1)-4y_1+1=0$$
$$\therefore 1+y_1^2-2-4y_1+1=0$$
$$\therefore y_1^2-y_1=0$$
$$\therefore  y_1(y_1-4)=0$$
$$\therefore y_1=0$$or $$y_1=4$$
$$\therefore $$ the coordinates of the points are $$(1,0)$$ or $$(1,4)$$
Since , the tangents aare parallel to $$X-$$axis their equation are of the from $$y=k$$
If it passes through the point $$(1,0),k=0$$ and it passes through the point $$(1,4),k=4$$
Hence, the equation of the tanganes are $$y=0$$ and $$y=4$$


Find the equation of tangent and normals to the following curves at the indicated points on them : $$x=\sin \theta$$ and $$y=\cos 2 \theta$$ at $$\theta=\dfrac{\pi}{6}$$

When $$\theta=\dfrac{\pi}{6},\ x= \sin \dfrac{\pi}{6}$$ and $$y=\cos \dfrac{\pi}{3}$$
$$\therefore =\dfrac{1}{2}$$ and $$y=\dfrac{1}{2}$$
Hence, the point at which we want too find the equation of tangent and normal is $$\left(\dfrac{1}{2},\dfrac{1}{2} \right)$$.
Now, $$x=\sin \theta,\ t= \cos 2 \theta$$
Differentiating both side w.r.t. $$\theta$$, we get
$$\dfrac{dx}{d \theta}=\dfrac{d}{d \theta}(\sin\theta)=\cos \theta$$
and
$$\dfrac{dx}{d \theta}=\dfrac{d}{d \theta} (\cos 2 \theta)=- \sin 2 \theta \dfrac{d}{d \theta}(2 \theta)$$
$$=-\sin 2 \theta \times 2$$
$$=-2 \sin 2 \theta$$
$$\therefore \dfrac{dx}{d y}=\dfrac{\left(\dfrac{dy}{d \theta}\right)}{\left(\dfrac{dx}{d \theta}\right)}$$
$$=\dfrac{-2 \sin 2 \theta}{\cos \theta}$$
$$\therefore \left(\dfrac{dy}{d \theta}\right)_{at\ \theta=\dfrac{\pi}{6}}=\dfrac{-2 \sin \dfrac{\pi}{3}}{\cos \dfrac{\pi}{6}}$$
$$=\dfrac{-2 \left(\dfrac{\sqrt 3}{2} \right)}{\left(\dfrac{\sqrt 3}{2} \right)}$$
$$-2$$
$$=$$slope of the tangent at $$\theta=\dfrac{\pi}{6}$$ 
$$\therefore$$ the equation of the tangent at $$\theta=\dfrac{\pi}{6}$$ i.e. at $$\left(\dfrac{1}{2},\dfrac{1}{2}\right)$$
$$y-\dfrac{1}{2}=-2 \left(x-\dfrac{1}{2} \right)$$
$$\therefore y-\dfrac{1}{2}=-2x+1$$
$$\therefore 2y-1=-4x+2$$
$$\therefore 4x+2y-3=0$$
The slope of normal at $$\theta=\dfrac{\pi}{6}$$
$$=-\dfrac{1}{\left(\dfrac{dy}{dx}\right)}_{at\ \dfrac{\pi}{6}}$$
$$=\dfrac{-1}{-2}=\dfrac{1}{2}$$
$$\therefore$$ equation of the normal at $$\theta =-\dfrac{\pi}{2}$$,at $$\left(\dfrac{1}{2},\dfrac{1}{2}\right)$$ is
$$y-\dfrac{1}{2}-\dfrac{1}{2} \left(x-\dfrac{1}{2} \right)$$
$$\therefore 2y-1=x-\dfrac{1}{2}$$
$$\therefore 4y-2=2x-1$$
$$\therefore 2x-4y+1==$$
hence, the equation of tangent and normal are
$$4x+2y-3=0$$ and $$22-4y+1=0$$ respectively.


Find the equation of tangent and normals to the following curves at the indicated points on them : $$x=\sqrt t, y=t-\dfrac{1}{\sqrt t}$$ at $$=4$$

When $$t=4,\ x= \sqrt 4$$ and $$y=4-\dfrac{1}{\sqrt 4}$$
$$\therefore x=2$$ and $$y=4-\dfrac{1}{2}=\dfrac{7}{2}$$
Hence, the 
point at which we want to find the equation of tangent and normal is $$\left(2,\dfrac{7}{2} \right)$$.
Now, $$x=\sqrt t,\ y=t-\dfrac{1}{\sqrt t}$$
Differentiating both side w.r.t. $$x$$, we get
$$\dfrac{dx}{d t}=\dfrac{1}{2 \sqrt t}$$
and $$\dfrac{dy}{dx}=\dfrac{d}{d t} \left(t-\dfrac{1}{\sqrt t}\right)$$
$$=\dfrac{1}{-\dfrac{1}{2}}t^{-\dfrac{3}{2}}$$
$$1+\dfrac{1}{2t^{\dfrac{3}{2}}}$$
$$=\dfrac{2t^{\dfrac{3}{2}}+1}{2t^{\dfrac{3}{2}}}$$
$$\therefore \dfrac{dy}{dx}=\dfrac{\left(\dfrac{dy}{dx}\right)}{\left(\dfrac{dy}{dx}\right)}$$
$$=\dfrac{\left(\dfrac{2t^{\dfrac{3}{2}+1}}{2t^{\dfrac{3}{2}}}\right)}{\left(\dfrac{1}{2 \sqrt t}\right)}$$

$$=\dfrac{2t^{\dfrac{3}{2}+1}}{2t^{\dfrac{3}{2}}}
\times 2 \sqrt t$$
$$=\dfrac{2t^{\dfrac{3}{2}+1}}{t}$$
$$\therefore \left(\dfrac{dy}{dx}\right)_{at\ t=4}$$$$=\dfrac{2(4)^{\dfrac{3}{2}}+1}{4}$$
$$=\dfrac{2 \times 8+1}{4}$$
$$=\dfrac{17}{4}$$
$$=$$slope of the tangent at $$t=4$$ 
$$\therefore$$ the equation of the tangent at $$t=4$$ i.e at $$\left(2, \dfrac{7}{2} \right)$$ is
$$y-\dfrac{7}{2}=\dfrac{17}{4}(x-2)$$
$$\therefore 4y-14=71x-34$$
$$\therefore 17x-4y-20=0$$
The slope of normal at $$t=4$$
$$=\dfrac{-1}{\left(\dfrac{dy}{dx}\right)}_{at\ t=4}$$
$$=\dfrac{-1}{\left(\dfrac{17}{4}\right)}$$
$$=-\dfrac{4}{17}$$
$$\therefore$$ the equation of the normal at $$t=4$$ i.e at $$\left(2, \dfrac{7}{2}\right)$$ is
$$y-\dfrac{7}{2}=-\dfrac{4}{17}(x-2)$$
$$\therefore 34y-119=-8+16$$
$$\therefore 8x+34y-135=0$$
hence, the equation of tangent and normal are
$$17x-4y-20=0$$ and $$8x+34y-135=0-$$ respectively.


Solve the following: Find the equation of the tangent and normal drawn to the curve $$y^{4}-4x^{2}-6xy=0$$ at the point $$M(1,2)$$.

$$y^{4}-4x^{4}-6xy=0$$
Differentiating both sides w.r.t\ x, we get
$$4y^{2}\dfrac{dy}{d}-4\times 4x^{3}-6\left[x\dfrac{dy}{dx}+y.\dfrac{d}{dx}(x)\right]=0$$
$$\therefore 4y^{3}\dfrac{dy}{dx}-16x^{3}-6x\dfrac{dy}{dx}-6y\times 1=0$$
$$\therefore (4y^{3}-6x)\dfrac{dy}{dx}=16x^{3}+6y$$
$$\therefore \dfrac{dy}{dx}=\dfrac{16x^{3}+6y}{4y^{2}-6x}$$
$$=\dfrac{8x^{3}+3y}{2y^{3}-3x}$$
$$\therefore \left(\dfrac{dy}{dx}\right)_{at\ (1,2)}=\dfrac{8(1)^{3}+3(2)}{2(2)^{3}-3(1)}$$
$$=\dfrac{8+6}{16-3}$$
$$=\dfrac{14}{13}$$
= slope of the tangent at $$(1,2)$$
$$\therefore$$ the equation of the tangent at $$M(1,2)$$ is
$$y-2=\dfrac{14}{13}(x-1)$$
$$\therefore 13y-26=14x-14$$
$$\therefore 14x-13y+12=0$$
The slope of normal at $$(1,2)$$
$$=\dfrac{-1}{\left(\dfrac{dy}{dx}\right)_{at\ (1,2)}}$$
$$=\dfrac{-1}{\left(\dfrac{14}{13}\right)}$$
$$=-\dfrac{13}{14}$$
$$\therefore$$ the equation of normal at $$M(1,2)$$ is
$$y-2=\dfrac{13}{14}(x-1)$$
$$\therefore 14y-28=13x-13$$
$$\therefore 13x+14y-41=0$$
Hence, the equation of tangent and normal are
$$14x-13y+12=0$$ and $$13x+14y-41=0$$ respectively.


Find the equation of all lines having slope -1 that are tangents o the curve $$ y = \dfrac{1}{x-1} , x \neq 3$$

Given, $$ y = \dfrac{1}{x-1} , $$
$$\dfrac{dy}{dx} = \dfrac{-1}{(x-1)^2} ,$$ but given slope $$=-1$$
$$\dfrac{-1}{(x-1)^{2}}  = -1 \Rightarrow  (x-1) ^{2} = 1$$
$$x - 1 = \pm  1 \Rightarrow $$
$$x = 2 , x =  0 $$ 
when $$ x= 2 , y = 1 $$ 
when $$x = 0 , y = -1 $$ 
The points are $$ (2, 1) $$
equation of the through  having slope $$=-1$$ 
is $$ y - 1 = -1  ( x - 2) \Rightarrow  y + x = 3 $$ 
or $$x + y - 3 = 0 $$ and equations of the line through $$ ( 0 , -1)$$
$$ y + 1 = -1 (x - 0)$$
$$ \therefore  y + x + 1 = 0$$


Find the equal of the normal to curve $$y^{2} = 4x$$ which passes through the point $$(1, 2)$$.

Given, $$y^{2} = 4x$$
$$2y \times \dfrac{dy}{dx} = 4 \Rightarrow \dfrac{dy}{dx} = \dfrac{4}{2y} = 2/y$$
slope of tangent $$= \dfrac{2}{2} = 1 ..... \left ( \dfrac{dy}{dx} \right )$$
hence slope of normal = $$^{-1}/dy/_{dx} = -1$$
$$\therefore $$ equation of normal $$y - 2 = -(x - 1)$$
$$y + x - 3 = 0$$


Find the equations of the tangent line to the curve $$y = x ^{2} - 2x + 7 $$ which is 
parallel to the line $$ 2x - y + 9 = 0 $$

Given, $$y = x ^{2} - 2x + 7 $$ 
$$\dfrac{dy}{dx} = 2x - 2 $$ and slope $$ = 2 $$
$$2 x -2 = 2 \Rightarrow  2 x = 4 \Rightarrow  x = 2 $$ 
when $$x = 2 , y = (2)^{2} - 2 (2) + 7 = 7 $$
$$\therefore $$ equation of tangent is 
$$ y - 7 = 2 ( x - 2)\\ 2x - y + 3 = 0\\ \Rightarrow 2x - y + 3 = 0 $$


Find the equations of all lines having slope $$0$$ which are tangent to the curve 
$$ y = \dfrac{1}{x^{2} - 2x + 3}$$

Given, $$ y = \dfrac{1}{x^{2} - 2x + 3}$$
$$\dfrac{dy}{dx} = \dfrac{-1}{(x^{2} - 2x + 3^{2})} \times  (2x - 2)\\$$
$$\therefore \dfrac{-(2x - 2)}{(x^{2} - 2x + 3)^{2}} = 0 \Rightarrow  x = 1 $$ 
When $$x = 1 , y = \dfrac{1}{2}$$
$$\therefore $$ equation the line $$ y - \dfrac{1}{2} = 0 (x - 1)$$
$$ y = \dfrac{1}{2} \Rightarrow  2y = 1 $$or $$2y - 1 = 0$$


Find the equations of the tangents and normal to the given curves at the indicated points :
$$ y = x ^{3} $$ at $$ (1,1) $$

Given, $$ y = x ^{3} $$ 
$$\dfrac{dy}{dx} = 3x^{2}$$
$$\therefore $$ Slope of the tangents at $$x = 1 = 3 $$
$$\therefore $$ Equation of tangents is $$ y - 1 = 3 ( x -1)$$
$$ 3x - y - 2 = 0 $$
$$\therefore $$ slope of normal $$= \dfrac{-1}{3}$$
$$\therefore $$ equation of normal is $$y - 1 = \dfrac{-1}{3} (x - 1) $$
$$3y - 3 = - (x -1) $$
$$x + 3y - 4 = 0 $$


Find the equations of the tangents and normal to the given curves at the indicated points :
$$ y = x ^{4} - 6 x ^{3} +  13 x^{2} - 10x + 5 $$at $$(1,3)$$

$$y=x^4-6x^3+13x^2-10x+5$$
$$\dfrac{dy}{dx} = 4x^{3} - 18x^{2}  + 26x - 10$$ 
$$Slope\space of\space the\space tangent\space at$$ $$x = 1 $$
$$\dfrac{dy}{dx}|_{x=1}=\space 4-18+26-10$$
$$\dfrac{dy}{dx}|_{x=1}=2$$
$$Equation \space of \space tangent: \space y-3=2(x-1)$$
$$Equation \space of \space tangent:y=2x+1$$
$$Since \space of \space tangent\space is \space 2 \space then\space slope \space of \space normal= \space \dfrac{-1}{2}$$
$$Equation \space of \space normal \space:y-3=\dfrac{-1}{2}(x-1)$$
$$Equation \space of \space normal \space:2y-6=-x+1$$
$$$$Equation \space of \space normal \space:2y+x=7$$


Find the equations of the tangents and normal to the given curves at the indicated points :
$$ y = x ^{4} - 6 x ^{3} +  13 x^{2} - 10x + 5 $$at $$(0,5)$$

Given, $$ y = x ^{4} - 6 x ^{3} +  13 x^{2} - 10x + 5 $$ 
$$\dfrac{dy}{dx}  = 4x^{3} - 18x^{2} + 26x - 10  $$ 
slope at $$(0,5) = -10 $$
$$\therefore $$ Equation of tangents at $$(0,5) $$ is $$ 
y - 5 = 10 (x - 0) $$
$$y - 5 = -10 x$$
$$ 10 x + y - 5 = 0 $$ 
slope of the normal at $$  (0,5) = \dfrac{-1}{-10} = \dfrac{1}{10}$$
$$\therefore $$ equation of normal is 
$$ y - 5 = \dfrac{-1}{-10}(x - 0) = 10 y - 50 = x $$
$$x - 10 y + 50 = 0 $$


Find the equations of the tangents and normal to the given curves at the indicated points :
$$ y = x ^{2} $$ at $$ (0,0)$$

Given, $$ y = x ^{2} $$
$$\dfrac{dy}{dx} = 2x$$
$$\therefore $$ slope at $$x = 0 $$ is  $$0 $$
$$\therefore $$ Equation of tangents is $$ y - 0 = 0 (x - 0) \Rightarrow  = 0 $$ 
slope  of the normal $$ = -1 / (0)$$
$$\therefore $$ equations of normal $$ y - 0 = \dfrac{-1}{0} (x - 0)\Rightarrow  x = 0 $$


Find the equation of the tangents and normal to the parallel $$ y^{2} = 4ax$$at the point $$ ( at ^{2} , 2at)$$

Given, $$ y ^{2} = 4ax $$
$$2y \times  \dfrac{dy}{dx} = 4a\times  1 \Rightarrow   \dfrac{dy}{dx} =  \dfrac{2a}{y}$$
$$ \dfrac{dy}{dx}|_{x = at^{2}, y = 2at} =  \dfrac{2a}{2at} = 1/ t $$ 
slope of tangent  $$1/t$$ 
and  slope of  normal = $$-1/dy/dx = -t $$
$$\therefore $$ equation of tangent is 
$$ y - 2at = t (x - at^{2}) \Rightarrow  xt + y - 2at at^{3} = 0$$


Find the equation of the normal at the point $$ (am^{2} , am ^{3}) $$ for the curve $$ay^{2} = x^{3}$$

Given, $$ay^{2} = x^{3}$$
$$a \times  2 y \times \dfrac{dy}{dx} = 3x^{2} \Rightarrow   \dfrac{dy}{dx} =  \dfrac{3x^{2}}{2ay}$$
$$ \dfrac{dy}{dx}|_{am^{2} , am^{3}} =  \dfrac{3a^{2}m^{4}}{2a\times am^{3}} =  \dfrac{3}{2} m $$
$$\therefore $$ slope of the normal $$= -1/ \dfrac{dy}{dx} =  \dfrac{-2}{3m}$$
$$\therefore $$ equation of normal  is 
$$ y - am ^{3} = \dfrac{-2}{3m} (x - am^{2})$$
$$\therefore  2x + 3my - am ^{2}(3m^{2}+2) = 0$$


Find the equation of the normal to the curve $$ y = x^{3} + 2x + 6 $$ which are parallel to the line $$x + 14 y + 4 = 0 $$

$$ y = x^{3} + 2x + 6 $$
$$\dfrac{dy}{dx}= 3x^{2} + 2 $$
slope of the normal $$= -1/\dfrac{dy}{dx} = -1/3x^{2}+ 2 $$
slope of the parallel line $$\dfrac{-1}{14}$$
$$\therefore \dfrac{-1}{3x^{2} + 2} = \dfrac{-1}{14} = 3a^{2} + 2 = 14 $$
$$3a^{2} = 12 , a^{2} = 4 , a = \neq 2 $$
Since ( a, b)  is on the curve $$ b = a^{3} + 2a + 6 $$
when a = 2 , b = 8 + 4  + 6 = 18 , $$
when $$a = -2 , b = -8 - 4 + 6 = -6 $$
points are $$ (2,18) $$ and $$ ( -2 , -6) $$
$$\therefore $$
There are two normal lines
$$ 14 y - 14\times  18 = -x + 2 \Rightarrow  x + 14 y = 254 $$ and $$ y + 16 = \frac{-1}{14} (x +2)$$
$$14 y + 84 = -x -2 \therefore  x + 14 y + 86 = 0 $$


Find the equations of the tangent line to the curve $$y = x ^{2} - 2x + 7 $$ which is 
parallel to the line $$ 5y - 15x = 13 $$

Slope $$ = 3 \therefore $$ slope of any line $$\perp = -1/3$$ slope of the curve $$ = 2x - 2 $$
$$\therefore 3 \times  (2x - 2) = 6 -1 \Rightarrow  6x - 6 = -1 $$
$$\Rightarrow 6x = 5 \Rightarrow x = 5/6$$
$$ y - \dfrac{217}{36} = \dfrac{-1}{3} x + \dfrac{5}{18}$$
$$12x + 36 y - 227 = 0 $$


Find the equations of the tangents and normal to the hyperbola $$\dfrac{x^{2}}{a^{2}} - \dfrac{y^{2}}{b^{2}} = 1 $$ at the point (x_{0},y_{0})$$

$$\dfrac{1}{a^{2}} (2x) - \dfrac{1}{b^{2}} \left ( \dfrac{dy}{dx} \right )=0$$
$$\dfrac{2y}{b^{2}} \dfrac{dy}{dx} = \dfrac{2x}{a^{2}} \Rightarrow  \dfrac{dy}{dx} = \dfrac{xb^{2}}{ya^{2}} =\dfrac{b^{2}}{a^{2}} (\dfrac{x}{y})$$
$$\dfrac{dx}{dy}]_{(x_{0},y_{0})} =\dfrac{b^{2}}{a^{2}} \times \left ( \dfrac{x_{0}}{y_{0}} \right )$$


Find the equation of the tangents to the curve $$y = \sqrt{3x-2}$$ which is parallel to the line $$ 4 x - 2y + 5 = 0 $$

$$y  = \sqrt{3x-2}$$
$$\dfrac{dy}{dx} = \dfrac{1}{2\sqrt{3x-2}} = \dfrac{3}{2\sqrt{3x-2}}$$
$$\therefore \dfrac{dy}{dx}]_{(a,b)} = \dfrac{3}{2\sqrt{3a-2}}$$


Find the equation of all lines having slope 2 which are tangents to the curve
$$y = \dfrac{1}{x - 3}, x \neq 3$$


1897918_1860314_ans_ccdf102b6f7844458a6c8e7da47252b8.jpeg


For curves $$ y= sin^2 X$$, find equation of normal at 
$$\left ( \frac{\pi }{3}, \frac{3}{4} \right )$$.

Given curve, $$y = sin^2 x$$ Diff. w.r.t. $$x,$$
$$\Rightarrow \frac{dy}{dx} = 2 sin x cos x$$
at $$\left ( \frac{\pi }{3}, \frac{3}{4} \right )$$
$$\left ( \frac{dy}{dx} \right )_{\left ( \frac{\pi }{3}, \frac{3}{4} \right )} = 2 sin \frac{\pi }{3} cos \frac{\pi }{3}$$
$$ = 2.\frac{\sqrt{3}}{2}. \frac{1}{2} = \frac{\sqrt{3}}{2}$$
$$\therefore$$ At $$\left ( \frac{\pi }{3}, \frac{3}{4} \right )$$, slope of tangent $$ = \frac{\sqrt{3}}{2}$$
So, at $$(\frac{\pi }{3}, \frac{3}{4})$$ slope of normal 
$$ = - \frac{1}{dy / dx}$$
$$ = - \frac{1}{\sqrt{3}/2} = \frac{-2}{\sqrt{3}}$$
$$\therefore$$ At $$(\frac{\pi }{3}, \frac{3}{4})$$ equation of normal
$$ y - \frac{3}{4} = - \frac{2}{\sqrt{3}} (x - \frac{\pi }{3})$$.
$$\Rightarrow \sqrt{3} y - \frac{3}{4} \sqrt{3} = -2x + \frac{2\pi }{3}$$
$$\Rightarrow 2x + \sqrt{3}y - \frac{3\sqrt{3}}{4} = \frac{2\pi }{3}$$
Hence, required equation of normal is 
$$ 2x + \sqrt{3}y = \frac{2\pi }{3} + \frac{3\sqrt{3}}{4}$$


Find equation of tangent and normal following curves, at given points.
(c) $$ xy = a^2$$, at $$ \left ( at, \frac{a}{t} \right )$$

Given curve, $$ xy = a^2$$
Diff. w.r.t. $$x$$,
$$ x \frac{dy}{dx} + y = 0$$
$$\Rightarrow \frac{dy}{dx} = - \frac{y}{x}$$
At point $$(at, \frac{a}{t}), (\frac{dy}{dx})_{(at, \frac{a}{t})} = - \frac{a/t}{at}$$
$$\Rightarrow (\frac{dy}{dx})_{(at, \frac{a}{t})} = - \frac{1}{t^2}$$
At point $$(at, \frac{a}{t})$$ equation of tangent
$$ y - \frac{a}{t} = - \frac{1}{t^2} (x - at)$$
$$\Rightarrow t^2y - at = - x + at$$
$$\Rightarrow x + t^2y = 2at$$
Hence, equation of tangent is $$ x + t^2y = 2at$$.
Again at point $$ (at, \frac{a}{t})$$ equation of normal,
$$ y - \frac{a}{t} = + t^2 (x - at)$$
$$\Rightarrow yt - a = t^3 (x - at)$$
$$\Rightarrow yt - a = t^3 x - at^4$$
$$\Rightarrow t^3x - yt = at^4 - a$$
$$\Rightarrow t^3x - yt = a (t^4 - 1)$$
Hence, eq. of normal is $$ t^3x - yt = a (t^4 - 1)$$.



Find equation of tangent and normal following curves, at given points.
(b) $$y^2 = 4ax$$, at $$ x = a$$

(b) Given curve, $$y^2 = 4ax$$ ...(i)
Putting at $$ x =a$$ in equation (i)
$$ y^2 = 4a^2$$
$$\Rightarrow y^2 = 4a^2$$
$$\Rightarrow y = \pm 2a$$
Hence, points of contact are $$(a, 2a)$$ and $$(a, -2a)$$.
DifF. (i) w.r.t. x,
$$ 2y. \frac{dy}{dx} = 4a$$
$$\Rightarrow \frac{dy}{dx} = \frac{2a}{y}$$
At paoint $$ (a, 2a)$$
$$\Rightarrow (\frac{dy}{dx})_{(a, 2a)} = \frac{2a}{2a} = 1$$
$$\Rightarrow (\frac{dy}{dx})_{(a, 2a)} = 1$$
At point $$(a, 2a)$$ equation of tangent,
$$ y - 2a = 1 (x - a)$$
$$ x - y + a = 0$$
Again, at $$(a 2a)$$ equation of normal
$$ y - 2a = - 1(x - a)$$
$$\Rightarrow x + y - 3a = 0$$
Hence, at $$ (a, 2a)$$ equation of tangent is $$ x - y + a = 0$$ and equation of normal is $$ x + y - 3a = 0$$


Find equation of tangent and normal following curves, at given points.
(f) $$ y = 2x^2 - 3x - 1$$, at $$(1, -2)$$

Given curve, $$ y = 2x^2 - 3x - 1$$ ...(i)
Diff w.r.t. $$'x'$$
$$\frac{dy}{dx} = 4x -3 $$
At point $$(1, -2)$$
$$(\frac{dy}{dx})_{(1, -2)} = 4 \times 1 - 3 = 1$$
So $$(\frac{dy}{dx})_{(1, -2)} = 1$$
At point $$(1, -2)$$ equation of tangent.
$$ y + 2 = 1 (x - 1)$$
$$\Rightarrow x - y = 3$$
Hence, equation of tangent $$ x - y = 3$$.
Again, at point $$(1, -2)$$ equation of normal
$$ y + 2 = -1 (x - 1)$$
$$\Rightarrow x + y + 1 = 0$$
Hence equation of normal $$ x + y + 1 = 0$$.


Find all equations of lines which are tangent to the curve $$ y + \frac{2}{x - 3} = 0$$ and slope of those is $$2$$.

Give curve, $$ y + \frac{2}{x - 3} = 0$$
$$ y = - \frac{2}{x - 3}$$ ...(i)
Diff. w.r.t. x,
$$\frac{dy}{dx} = \frac{2}{(x - 2)^2}$$
Given, slope $$ = 2$$
then, $$ \frac{2}{(x - 3)^2} = 2$$
$$\Rightarrow (x - 3)^2 = 1$$
$$\Rightarrow x - 3 = \pm 1$$
$$\Rightarrow x = \pm 1 + 3$$
$$\Rightarrow x = 4, 2$$
Putting $$ x = 4$$ in eq. (i)
$$ y = \frac{-2}{4 - 3} = -2$$
Then, point $$ = (4, -2)$$
Again putting, $$ x = 2$$ in eq. (i)
$$ y = \frac{-2}{2 - 3} = 2$$
Then, point $$ = (2, 2)$$
Now, tangent at point $$(4, -2)$$,
$$ y - (-2) = 2 (x - 4)$$
$$\Rightarrow y + 2 = 2x - 8$$
$$\Rightarrow 2x - y - 10 = 0$$
Again, tangent at point $$(2, 2)$$
$$y - 2 = 2 (x - 2)$$
$$\Rightarrow y - 2 = 2x - 4$$
$$\Rightarrow 2x - y - 2 = 0$$
Hence, required equations are $$ 2x - y - 10 = 0$$ and $$ 2x - y - 2 = 0$$.



Find equation of tangent and normal following curves, at given points.
(a) $$y = x^2 + 4x + 1$$, at $$ x = 3$$

(a) Given curve, $$ y = x^2 + 4x + 1$$          .........(i)
Putting $$x = 3$$ in equation (i),
$$ y = (3)^2 + 4 (3) + 1$$
$$ y = 22$$
So, point of contact $$ = (3, 22)$$
DifF. (i) w.r.t. x,
$$ \frac{dy}{dx} = 2x + 4$$
$$ \Rightarrow (\frac{dy}{dx})_{(3, 22)} = 2 \times 3 + 4$$
$$\Rightarrow (\frac{dy}{dx})_{(3, 22)} = 10$$
So, at point $$(3, 22)$$ equation of tangent
$$ y - 22 = 10 ( x - 3)$$
$$\Rightarrow y - 22 = 10x - 30$$
$$\Rightarrow 10x - y = 8$$
So, equation of tangent, $$10x - y = 8$$.
Again, at $$(3, 22)$$, equation of normal,
$$ y - 22 = - \frac{1}{10} (x - 3)$$
$$\Rightarrow 10y - 220 = - x +3$$
$$\Rightarrow x + 10 y = 223$$
So, equation of normal $$ x + 10y = 223$$



Find equation of tangent and normal following curves, at given points.
(d) $$ y^2 = 4ax$$, at $$ \left ( \frac{a}{m^2}, \frac{2a}{m} \right )$$

Given curve, $$ y^2 = 4ax$$
Diff w.r.t. $$x,$$
$$ 2y \frac{dy}{dx} = 4a$$
$$\Rightarrow \frac{dy}{dx} = \frac{2a}{y}$$
At point $$\left ( \frac{a}{m^2}, \frac{2a}{m} \right )$$
$$\Rightarrow (\frac{dy}{dx})_{(\frac{a}{m^2}, \frac{2a}{m})} = \frac{2a}{2a/m}$$
$$ (\frac{dy}{dx})_{(\frac{a}{m^2}, \frac{2a}{m})} = m$$
At point$$ (\frac{a}{m^2}, \frac{2a}{m})$$ equation of tangent
$$ y - \frac{2a}{m} = m \left ( x - \frac{a}{m^2} \right )$$
$$\Rightarrow my - 2a = m^2 \left ( x - \frac{a}{m^2} \right )$$
$$\Rightarrow my - 2a = m^2 x - a$$
$$\Rightarrow m^2x - my + a = 0$$
Hence, equation of tangent.
$$m^2x - my + a = 0$$.
Again, at point $$\left ( \frac{a}{m^2}, \frac{2a}{m} \right )$$ equation of normal
$$ y - \frac{2a}{m} = - \frac{1}{m}\left ( x - \frac{a}{m^2} \right )$$
$$\Rightarrow \frac{my - 2a}{m} = - \frac{1}{m} \left ( \frac{m^2 x - a}{m^2} \right )$$
$$\Rightarrow m^2 (my - 2d) = - (m^2 x - a)$$
$$\Rightarrow m^3y - 2am^2 = - m^2x + a$$
$$\Rightarrow m^x + m^3y = a (2m^2 + 1)$$
Hence, equation of normal
$$M62x + m^3y = a (2m^2 + 1)$$



Find equation of tangent and normal following curves, at given points.
(g) $$ x = at^2, y = 2 at, t = 1$$

Given $$ x = at^2, y = 2at$$ ...(i)
Diff. w.r.t. $$'t'$$
$$\frac{dx}{dt} = 2at, \frac{dy}{dt} = 2a$$
$$\because \frac{dy}{dx} = \frac{dy / dt}{dx/dt} = \frac{2a}{2at}$$
$$\Rightarrow \frac{dy}{dx} = \frac{1}{t}$$
At$$ t = 1$$
$$(\frac{dy}{dx})_{t = 1} = \frac{1}{1} = 1$$
So $$ (\frac{dy}{dx})_{t = 1} = 1$$
Equation of tangent
$$ y - 2at = 1 (x - at^2)$$
At $$ t = 1$$
$$ y - 2a = x - a$$
$$\Rightarrow x - y + a = 0$$
Hence equation of tangent $$ x - y + a = 0$$
Again, equation of normal
$$y - 2at = - 1 (x - a t^2)$$
At $$ t = 1$$
$$ y - 2a = - (x - a)$$
$$\Rightarrow x + y - 3a = 0$$
Hence, equation of normal $$ x + y - 3a = 0$$



For curve $$x - a sin^3t, y = b cos^3t $$ find equation n of tangent at $$ t = \frac{\pi }{2}$$

Diff. given curve w.r.t. $$'t'$$
$$\frac{dx}{dt} = 3a sin^2 t cos t $$ and $$\frac{dy}{dt} = -3b cos^2 t sin t $$
So, $$\frac{dy}{dx} = \frac{dy / dt}{dx / dt}$$
$$ = \frac{-3 b cos^2 t sin t}{3a^2sin^2 t cos t}$$
$$ = - \frac{b cos t}{a sin t}$$
When $$ t = \frac{\pi }{2}$$, then
$$\left ( \frac{dy}{dx} \right )_{t = \frac{\pi }{2}} = - \frac{b cos \frac{\pi }{2}}{a sin \frac{\pi }{2}} = 0$$
So, at $$ t = \frac{\pi }{2}$$ then $$ x = a$$ and $$ y = 0$$
So, at $$ t = \frac{\pi }{2}$$ or at $$(a, 0)$$, equation of tangent of given curve
$$ y - 0 = 0 (x - a)$$
or $$ y = 0$$



Find equation of tangent and normal following curves, at given points.
(h) $$ x = \theta + sin \theta, y - 1 - cos\theta $$ at $$ 0 = \frac{\pi }{2}$$

Given,
$$ x = \theta + sin \theta, y - 1 - cos\theta $$
Diff. w.r.t. $$\theta$$,
$$\frac{dx}{d\theta } = 1 + cos\theta, \frac{dy}{d\theta } = sin \theta $$
$$\therefore \frac{dy}{dx} = \frac{dy/d\theta }{dx/d\theta } = \frac{sin \theta }{1 + cos\theta }$$
At $$ \theta = \frac{\pi }{2}$$
$$(\frac{dy}{dx})_{\theta = \frac{\pi }{2}} = \frac{sin \pi/2}{1 + cos\pi/2} = \frac{1}{1 + 0}$$
So, $$(\frac{dy}{dx})_{\theta \frac{\pi }{2}} = 1$$
Equation of tangent,
$$ y - (1 - cos \theta ) = 1 [x - (\theta + sin \theta )]$$
At $$ \theta = \frac{\pi }{2}$$
$$ y - \left ( 1 - cos\frac{\pi }{2} \right ) = [ x - (\frac{\pi }{2} + sin \frac{\pi }{2})]$$
$$\Rightarrow y - (1 - 0) = [x - (\frac{\pi }{2} + 1)]$$
$$ y - 1 = x - \frac{\pi }{2} - 1$$
$$\Rightarrow x - y = \frac{\pi }{2}$$
Hence, equation of tangent $$ x - y = \frac{\pi }{2}$$
Again, equation of normal
$$ y - (1 - cos \theta ) = -1 [x - (\theta + sin \theta )]$$
At $$ \theta = \frac{\pi }{2}$$
$$ y - \left ( 1 - cos \frac{\pi }{2} \right ) = - [x - \left ( \frac{\pi }{2} + sin \frac{\pi }{2} \right )]$$
$$\Rightarrow y - 1 + 0 = - x + \frac{\pi }{2} + 1$$
$$\Rightarrow x + y = 2 + \frac{\pi }{2}$$
Hence, equation of normal $$x + y = 2 + \frac{\pi }{2}$$.


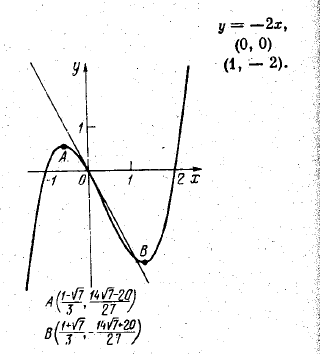
For the curve $$y = 4x^3-  2x^5$$, find all the points at which the tangents passes through the origin.

The equation of the given curve is $$y = 4x^3 - 2x^ 5 $$.
Differentiating w.r.t. $$x$$, we get
$$\displaystyle \Rightarrow  \frac{dy}{dx}=12x^2-10x^4$$

Let $$P(x_1,y_1)$$ be the point on the curve  at which tangent passes through the orgin.
Slope of the tangent at  $$P(x_{ 1 },y_{ 1 })$$ is $$\left( \cfrac { dy }{ dx }  \right) _{ x_{ 1 },y_{ 1 } }=12{ x_{ 1 } }^{ 2 }-10{ x_{ 1 } }^{ 4 }$$.

Equation of the tangent at $$(x_1, y_1)$$ is given by,  
$$y-y_1=(12x_1^2-10x_1^4)(x-x_1)$$               ....(1)
Since, the tangent passes through the origin (0, 0)
So, equation (1) becomes
$$-y_1=(12x_1^2-10x_1^4)(-x_1)$$
$$y_1=12x_1^3-10x_1^5$$          .....(2)

Since, $$P(x_1,y_1)$$ lies on the curve
So ,$$y_1=4x_1^3-2x_1^5$$          ......(3)
From eqn (2) and (3), we get
$$ 12x_1^3-10x_1^5=4x_1^3-2x_1^5$$
$$\Rightarrow 8x_1^5-8x_1^3=0$$
$$\Rightarrow x_1^5-x_1^3=0$$
$$\Rightarrow x_1^3(x_1^2-1)$$
$$\Rightarrow x_1=0, \pm 1$$
When $$x_1 = 0, y_1 = 4 (0)^3 - 2 (0)^5= 0$$. 
When $$x_1 = 1, y_1 = 4 (1)^3 - 2(1)^5= 2$$. 
When $$x_1 = -1, y_1 = 4 (-1)^3 - 2(-1)^5= -2$$.
Hence, the required points are $$(0, 0), (1, 2)$$ and $$(-1, -2)$$. 


Let tangent at a point P on the curve $$\displaystyle x^{2m}y^{\frac{n}{2}}=a^{\frac{4m+n}{2}}$$ meets the x-axis and y-axis at A and B respectively if AP : PB is $$\displaystyle \dfrac{n}{\lambda m}$$ where P lies between A and B then find the value of $$\displaystyle \lambda $$.

$$\displaystyle x^{2m}y^{\dfrac{n}{2}}=a^{^{\dfrac{4m+n}{2}}}$$

$$\Rightarrow \displaystyle 2m\varphi nx+\frac{n}{2}\varphi ny=\frac{4m+n}{2}\varphi na$$

$$\Rightarrow \displaystyle \frac{2m}{x}+(\frac{n}{2})\frac{1}{y}\frac{dy}{dx}=0$$

$$\Rightarrow \displaystyle \frac{dy}{dx}=\left ( \frac{-2m}{x} \right )\frac{2y}{n}$$

Let P be the point $$\displaystyle (x_{1},y_{1})$$
So equation of tangent is $$\displaystyle y-y_{1}=\left ( \dfrac{4m}{n},\dfrac{y_{1}}{x_{1}} \right )(x-x_{1})$$
Let tangent meet the axes the axes at A and B respectively 
$$\displaystyle A=\left ( \dfrac{4m+m}{4m}x_{0},0 \right )$$         $$\displaystyle B=\left (0, \dfrac{4m+n}{n}.y_{1} \right )$$
Let P divides AB in ratio $$\displaystyle \mu :1$$
$$\displaystyle \therefore x_{1}=\dfrac{\mu 0.+1.\left ( \dfrac{4m+n}{4m} \right )x_{1}}{\mu +1}\therefore 4m+n=4m(\mu +1)$$
Also $$\displaystyle \mu (4m+n)=n(\mu +1)\therefore \mu =\dfrac{n}{4m}$$
$$\displaystyle \therefore \lambda =4$$


Construct the graph of the function y = $$(x^2$$ + x) (x - 2). Write the equation of the tangent to the graph at the point with abscissa $$x_0$$ =Find the coordinates of the points of intersection of the tangent and the graph of the function.


1116746_890125_ans_4f6a6fe28aff4870a3167f8176893148.png


Find the equations of the tangent and normal to the curve $$x = a \sin^{3} \theta$$ and $$y = a\cos^{3}\theta$$  at $$\theta = \dfrac {\pi}{4}.$$

Let $$x = asin^3\theta, y = acos^3\theta$$
$$\dfrac{dx}{d\theta}=3asin^2\theta cos\theta$$
$$\dfrac{dy}{d\theta}=-3acos^2\theta sin\theta$$
$$\dfrac{dy}{dx}=\dfrac{-3acos^2\theta sin\theta}{3asin^2\theta cos\theta}=-cot\theta$$
$$\left.\begin{matrix}\dfrac{dy}{dx}\end{matrix}\right|_{\theta=\dfrac{\pi}{4}}=-1$$
Equation of tangent at $$\theta=\dfrac{\pi}{4}$$
$$y-acos^3\dfrac{\pi}{4}=-1(x-asin^3\dfrac{\pi}{4})$$
$$y+x=\dfrac{2a}{2\sqrt{2}}\Rightarrow y+x=\dfrac{a}{\sqrt{2}}$$
Equation of normal at $$\theta=\dfrac{\pi}{4}$$
$$y-\dfrac{a}{2\sqrt{2}}=1\left ( x-\dfrac{a}{2\sqrt{2}} \right )$$
Therefore, $$y-x =0.$$


Find the equation of the tangent and normal to the parabola $$ x^2-4x-8y+12=0$$ at $$\left( {4,\dfrac{3}{2}} \right)$$.

$${x}^{2}-4x-8y+12=0$$
Differentiating w.r.t $$x$$  we get
$$2x-4-8\dfrac{dy}{dx}+0=0$$
$$\Rightarrow 8\dfrac{dy}{dx}=2x-4$$
$$\Rightarrow \dfrac{dy}{dx}=\dfrac{2x-4}{8}=\dfrac{x-2}{4}$$
$$\Rightarrow \left[\dfrac{dy}{dx}\right]_{\left(4,\dfrac{3}{2}\right)}=\dfrac{4-2}{4}=\dfrac{2}{4}=\dfrac{1}{2}$$
$$\therefore$$ Slope $$\,\,m=\dfrac{1}{2}$$
Equation of the tangent is $$y-{y}_{1}=m\left(x-{x}_{1}\right)$$
$$y-\dfrac{3}{2}=\dfrac{1}{2}\left(x-4\right)$$
$$\Rightarrow \dfrac{2y-3}{2}=\dfrac{x-4}{2}$$
$$\Rightarrow 2y-3=x-4$$
or $$x-2y-1=0$$ is the equation of the tangent.
Equation of the normal is $$y-{y}_{1}=\dfrac{-1}{m}\left(x-{x}_{1}\right)$$
$$y-\dfrac{3}{2}=\dfrac{-1}{\dfrac{1}{2}}\left(x-4\right)$$
$$\Rightarrow \dfrac{2y-3}{2}=-2x+8$$
$$\Rightarrow 2y-3=-4x+16$$
or $$2y-3+4x-16=0$$ 
or $$4x+2y-19=0$$ is  the equation of the normal.


Find the equation of the normal to the curve $$y=(1+x)+(\sin^2x)$$ at $$x=0$$.

$$y=\left(1+x\right)+{\sin}^{1}x$$
$$\dfrac{dy}{dx}=1+2\sin{x}\cos{x}$$ at $$x=0$$
$$\dfrac{dy}{dx}=1$$ slope of round $$=-1$$
At $$x=0=1 y=1$$
$$\therefore y-1=-1\left(x-0\right)=x+y=1$$


To find the equation of tangent and normal to the circle $$x^2+y^2-3x+4y-31=0$$ at the point $$(2, 3)$$.

$${ x^{ 2 } }+{ y^{ 2 } }-3x+4y-31=0 \\ differentiate\, \, w.r\, \, to\, \, x \\ \Rightarrow 2x+2ydy/dx-3+4dy/dx=0 \\ \Rightarrow dy/dx\left( { 2y+4 } \right) +2x-3=0 \\ \therefore dy/dx=\frac { { 3-2x } }{ { \left( { 2y+4 } \right)  } }  \\ \Rightarrow { \left( { dy/dx } \right) _{ 2/3 } }=\frac { { 3-4 } }{ { 6+4 } } =\frac { { -1 } }{ { 10 } }  \\ \frac { { dx } }{ { dy } } =-10 \\ \therefore equation\, \, of\, \, \tan  gent= \\ \Rightarrow \left( { y-3 } \right) =dy/dx\left( { x-2 } \right)  \\ \Rightarrow y-3=\frac { { -1 } }{ { 10 } } \left( { x-2 } \right) , \\ 10y-30=x+2, \\ x+10y=32 \\ equation\, \, of\, \, normal \\ \Rightarrow \left( { y-3 } \right) =\frac { { dx } }{ { dy } } \left( { x-2 } \right) ,\, \, y-3=+10\left( { x-2 } \right)  \\ \Rightarrow 10x-y=17$$


Find the equation of tangent and normal to the curve at the indicated points on it $$y={ x }^{ 2 }+4x+1$$ at $$\left( -1,-2 \right) $$

$$y=x^2+4x+1$$      Points $$(-1, -2)$$
Step $$1$$:- $$y'=2x+4$$
$$\dfrac{dy}{dx}(x=-1)=2\times (-1)+4$$
$$=2$$
$$m=2$$
Step $$2$$:- Equation of tangent:
$$y-y'=m(x-x_1)$$
$$y-(-2)=2(x-(-1))$$
$$y+2=2(x+1)$$
$$y+2=2x+2$$
$$y+2-2x-2=0$$
$$-2x+y=0$$
$$2x-y=0$$
Step $$3$$:- $$m_1m_2=7$$
$$m_1m_2=-7$$
$$2\times m_2=-7$$
$$m_2=-\dfrac{7}{2}$$
Step $$4$$:- $$y-(-2)=-\dfrac{1}{2}(x-(-1))$$
$$y+2=-\dfrac{1}{2}(x+1)$$ $$\therefore$$ Equation of tangent is $$2x-y=0$$
$$2y+4=-x=1$$ $$\therefore$$ Equation of normal is $$x+2y+5=0$$
$$2y+4+x+1=0$$
$$x+2y+5=0$$.

1231713_1502176_ans_9aa2e7c466ef4967a5752346c17356c3.jpg


If the tangent at $$(x_{1}y_{1})$$ to the curve $$x^{3}+y^{3}=a^{3}$$ meets the curve again in $$(x^{2},y^{2})$$, then prove that $$\dfrac{x_{2}}{x_{1}}+\dfrac{y_{2}}{y_{1}}=-1$$ .


1975533_1757309_ans_400ce2f1c3f343f4ad18bb28d941ef5d.jpg


The point $$A(2,2)$$ lies on the curve $$y = x^2 - 2x + 2$$. The normal to the curve at $$A$$ intersects the curve again at $$B$$. Find the coordinate of $$B$$.


1415796_1649030_ans_5ccaf099eb8d4c80a37c45f155121537.jpg


If $$\left | f(x_{1})-f(x_{2}) \right |< (x_{1}-x_{2})^{2}$$ for all $$x_{1},x_{2} \epsilon R.$$ Find the equation of tangent of tangent to the curve y= f(x) at the point(1, 2)


1795779_1758862_ans_2c18f711dfa54508baf7df19fc5a0e5c.jpg


Find equation of tangent and normal following curves, at given points.
(e) $$  \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1$$, at (a sec 0, b tan 0)


1960837_1873548_ans_088ff2458ad348c19d409d0542039d5a.JPG


Class 11 Commerce Applied Mathematics Extra Questions