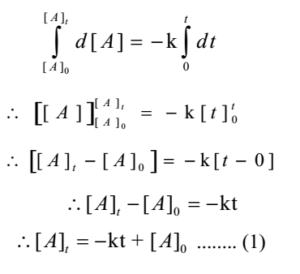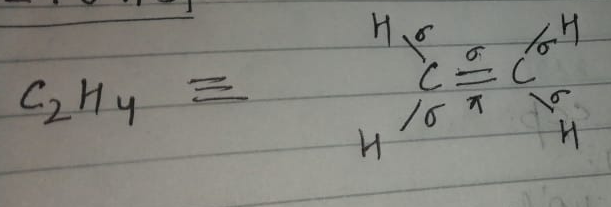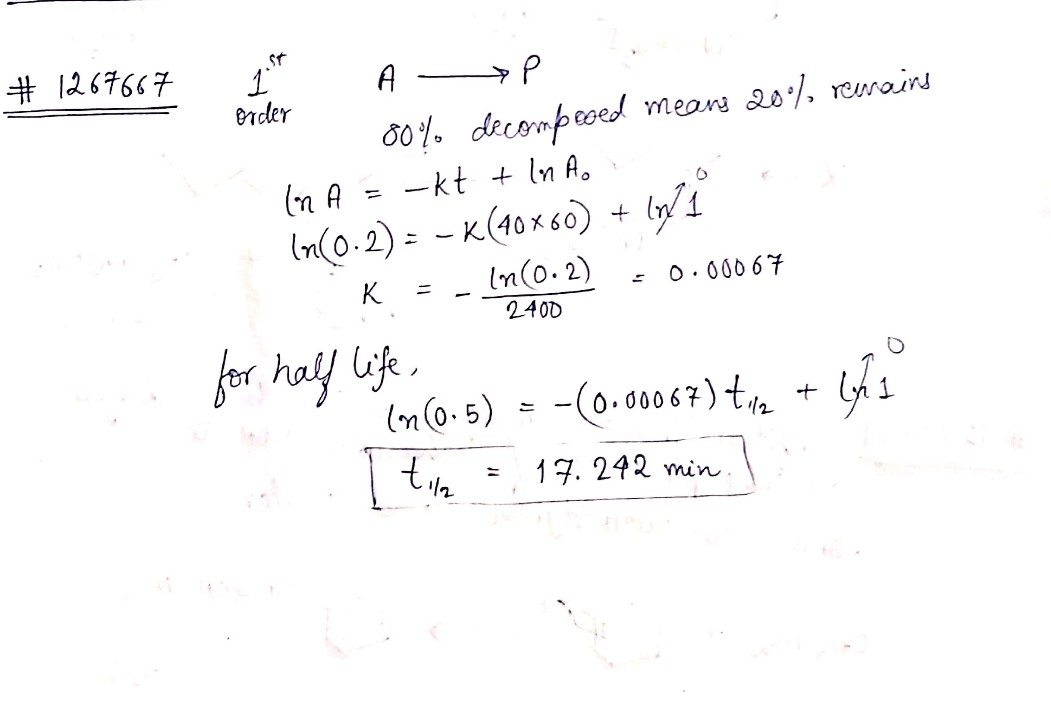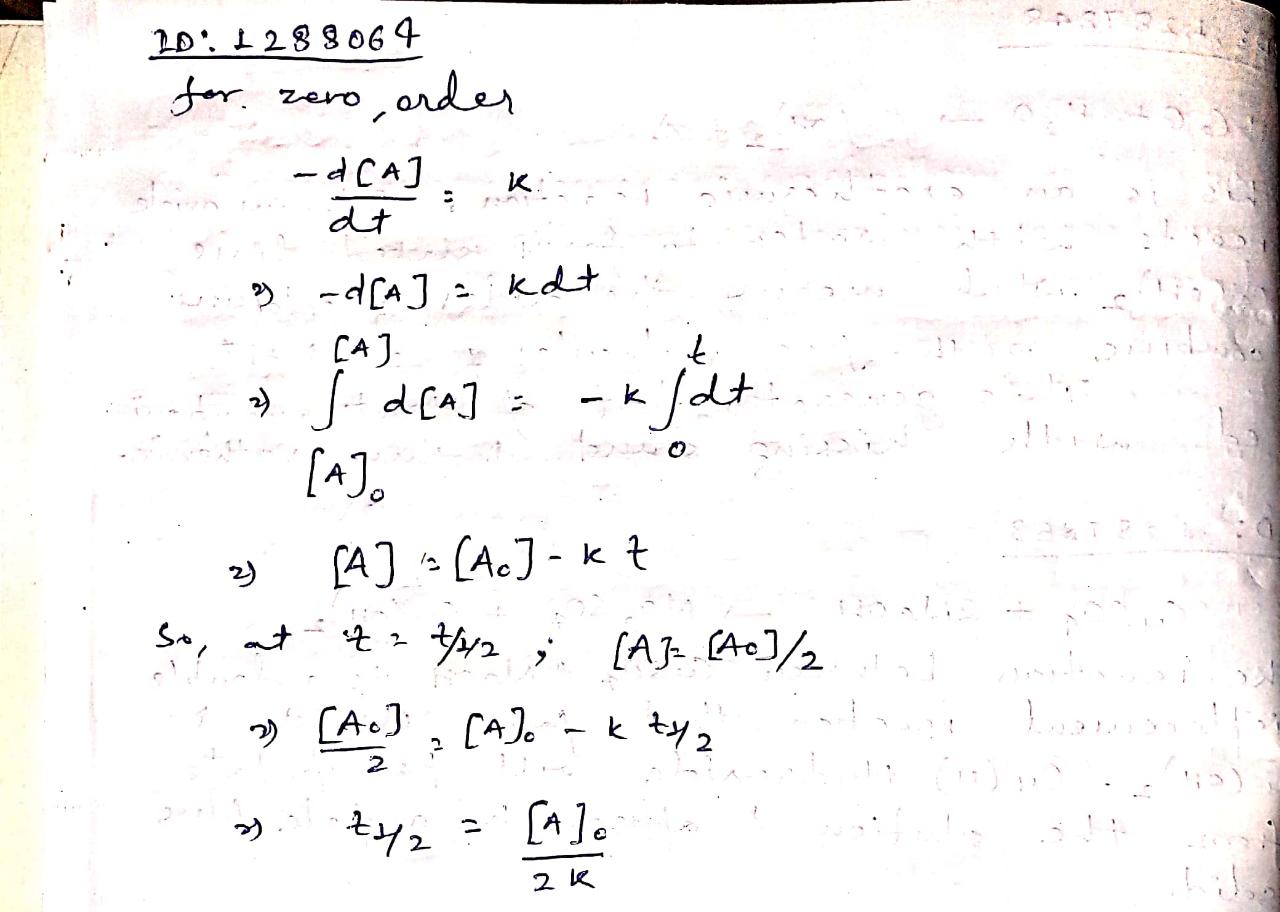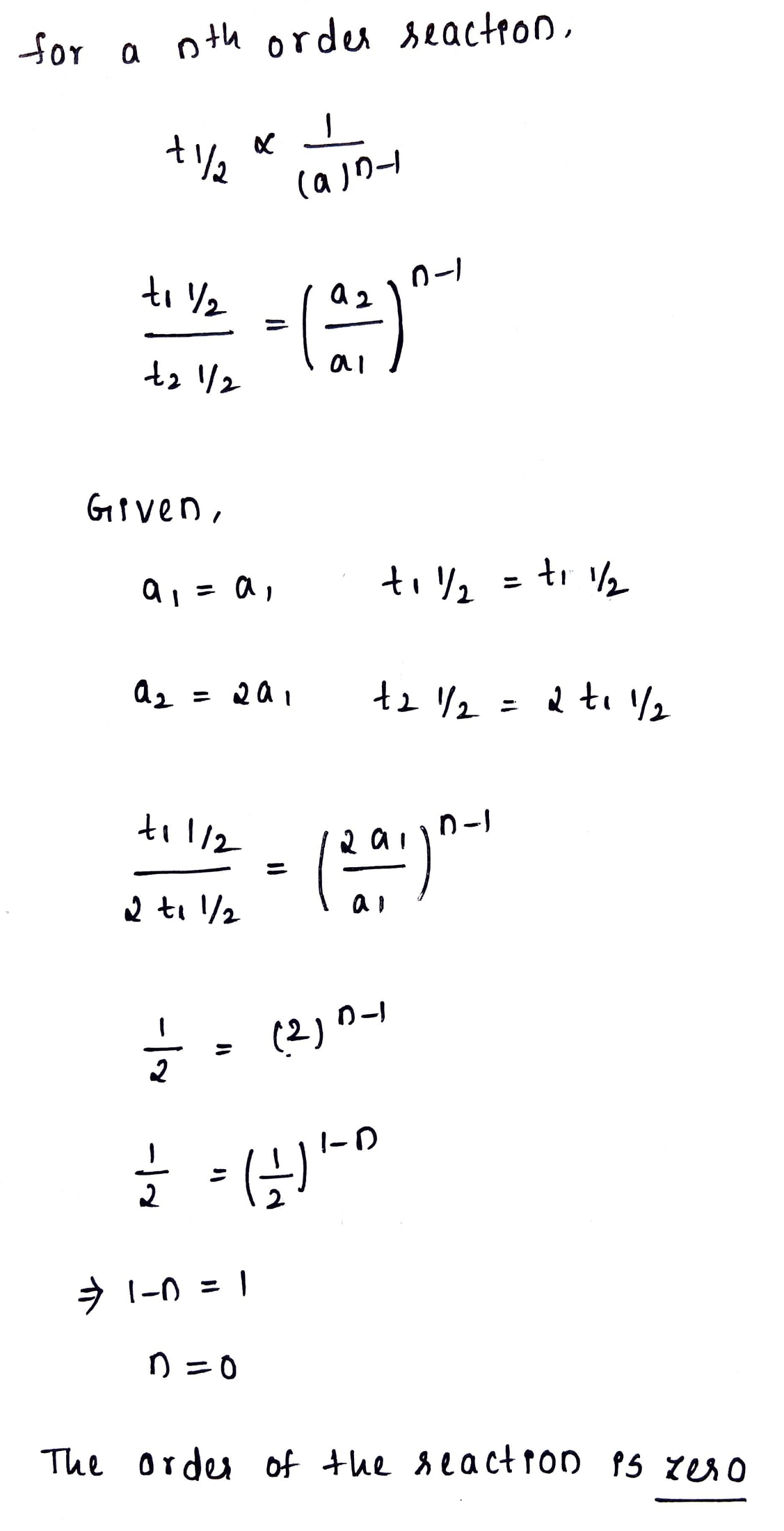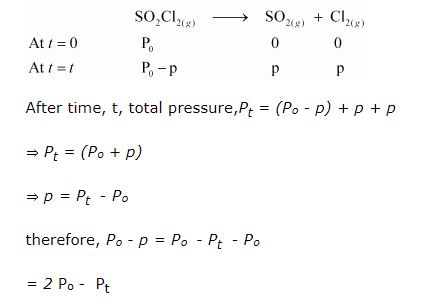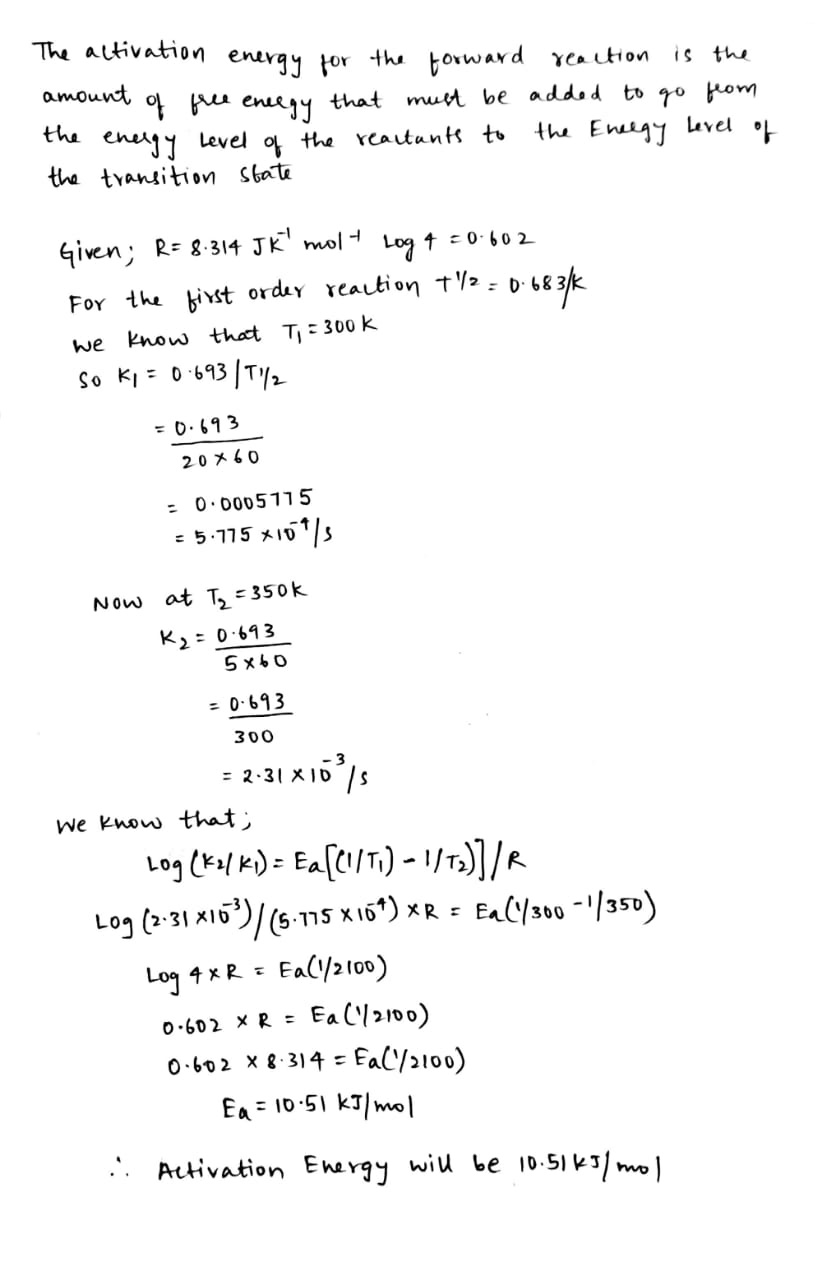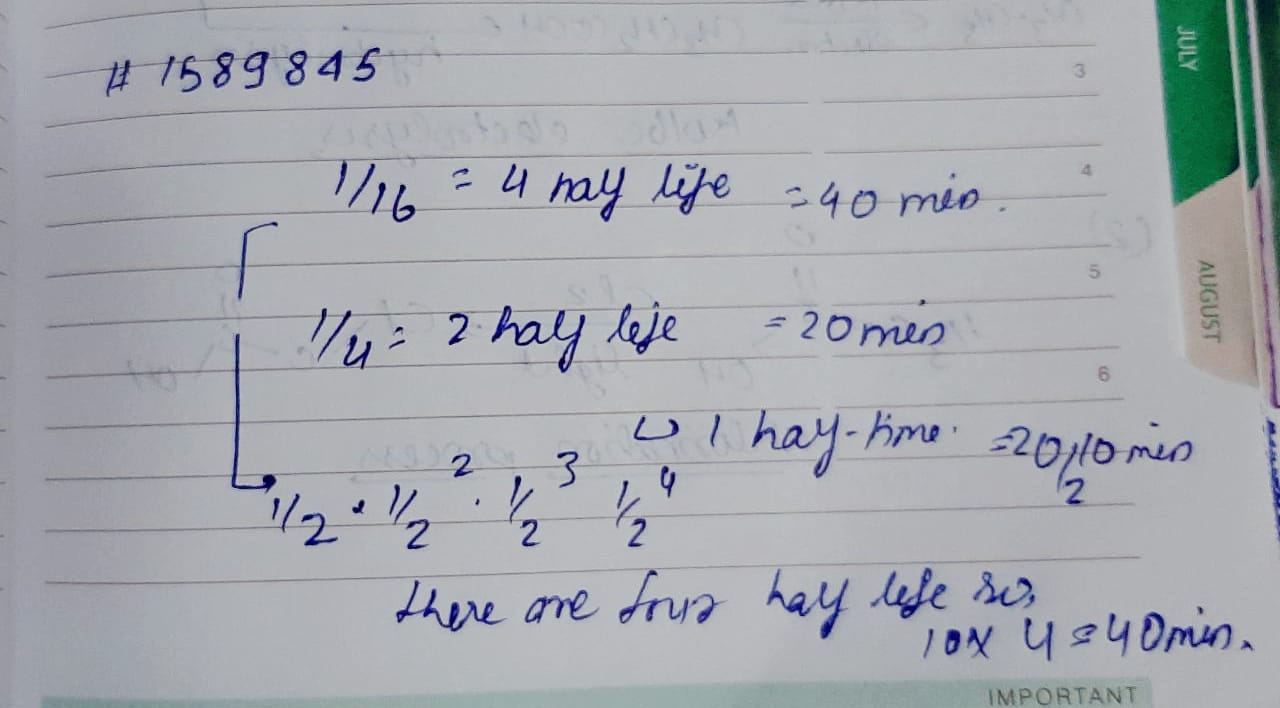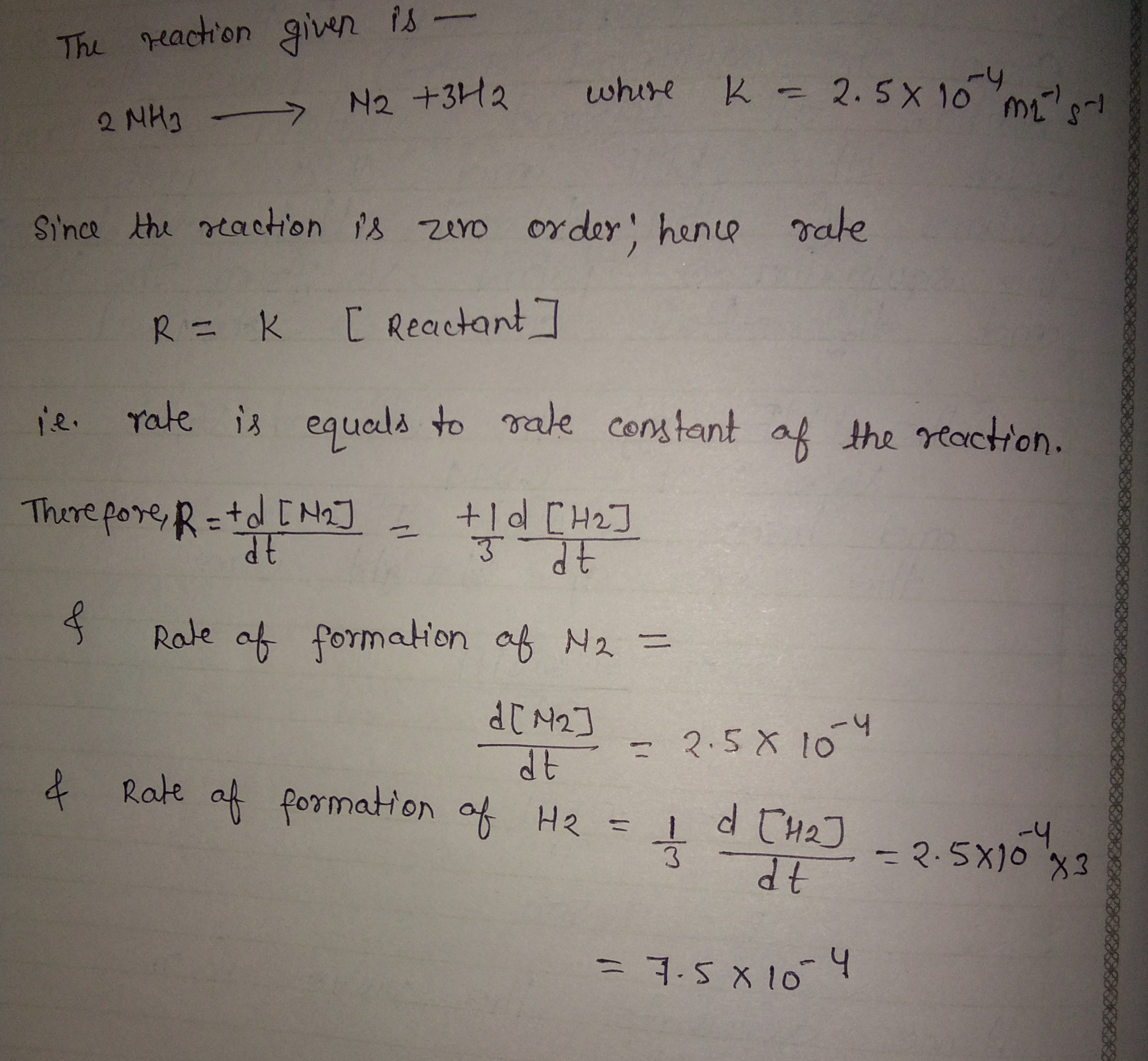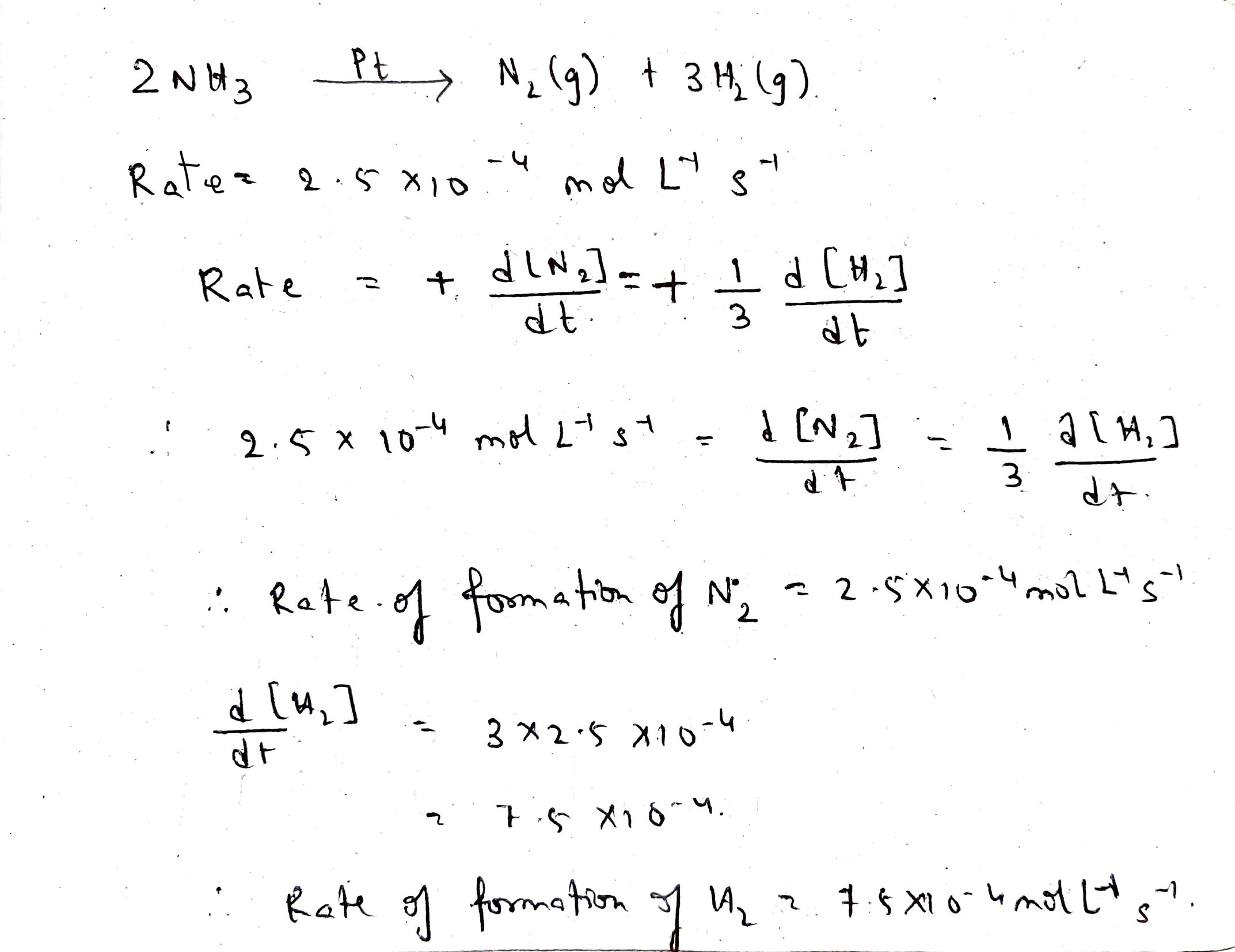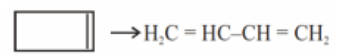Chemical Kinetics - Class 12 Engineering Chemistry - Extra Questions
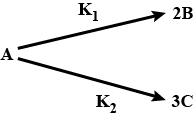
For the two parallel reactions $$\displaystyle A\overset{k_{1}}{\rightarrow}B$$ and $$\displaystyle A\overset{k_{2}}{\rightarrow}C,$$ show that the activation E' for the disappearance of A is given in terms of activation energies $$\displaystyle E_{1}$$ and $$\displaystyle E_{2}$$ for the two paths by $$\displaystyle E'=\frac{k_{1}E_{1}+k_{2}E_{2}}{k_{1}+k_{2}}$$
What is threshold energy?
A radioactive isotope is being produced at a constant rate $$x$$. Half life of the radioactive substance is '$$y$$'. After sometime, the number of radioactive nuclei becomes constant the value of this constant is ________
The gaseous reaction $${A_2} \to {\rm{ }}2A$$ is first order in $$A_2$$. After $$12.3$$ minutes $$65\%$$ of $$A_2$$ remains undecompensed. How long will it take to decompose $$90\%$$ of $$A_2$$? What is the half life of the reaction?
For a zero order reaction at $$200K$$ reaction complete in 5 minutes while at $$300 K$$, same reaction, completes in $$2.5$$ minutes. What will be the activation energy in calorie? $$(R = 2 Cal/(mol.K); \ ln 2 = 0.7)$$
At $$300 \,K, 50%$$ of molecule collide with energy grater than or equal to $$E_a$$. At what temperature, $$25%$$ molecule will have energy greater than or equal to $$E_a$$.
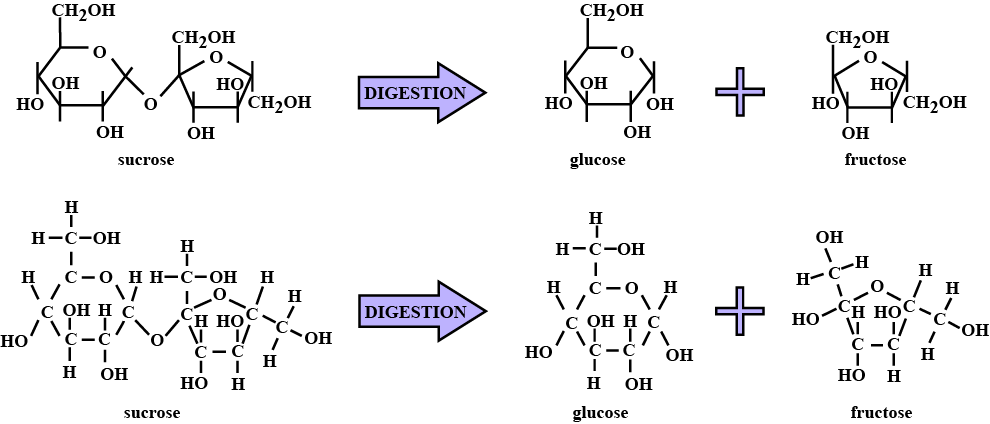
Inversion of cane sugar is pseudo first order reaction. Give reason.
Define (i) Rate Constant
(ii) Energy of Activation of a reaction
What is activation energy?
After five half-life periods for a first order reaction, what fraction of reactant remains?
Explain why?Rate of reaction is change in concentration in a given time interval. The change in concentration is (final concentration - initial concentration). As the reaction progresses the change in concentration of reactants decreases and that of products increases. D C gets a negative sign in case of reactants and
positive sign in case of products.
Calculate the rate of reaction for the change $$2A \rightarrow Products$$, when rate constant of the reaction is $$2.1 \times 10^{-5} time^{-1}$$ and $$[A]^{0} = 0.2\ M$$.
The time required for a first-order reaction for $$99$$% completion is $$x$$ times for the time required for $$90$$% completion. $$x$$ is:
The rate of reaction is fast when the activation energy is _______ (small/large).
A reaction is said to be of zero if the rate is entirely independent of the concentration of the reactants.
If true enter 1, if false enter 0.
Collision frequency depends upon concentration and temperature.
If true enter 1, if false enter 0.
Molecules must collide before they react.
If true enter 1, if false enter 0.
State whether the statement is True or False:
Two molecules can react only if they have a correct relative orientation.
______ (Kinetics/Ionic equilibrium) studies of reactions involve molecular reactions.
Initial pressure of $$A$$ in mm is___________.
Ethylene is produced by, $$C_4H_8\xrightarrow {\Delta} 2C_2H_4$$. The constant is $$2.48\times 10^{-4} sec^{-1}$$. Time in hours (nearest integer) in which the molar ratio of the ethylene to cyclobutane in reaction mixture will attain the value of 100 is___________.
A first order reaction is $$20\%$$complete in 10 min. The specific rate constant of the reaction is_________ ($$in\:\: min^{-1}$$).
Derive the relation between half-life period and rate constant for first order reaction
Half life period of a _________ order reaction is ________ of the concentration of the reactant.
Sucrose decomposes in acid solution into glucose and fructose according to the first order rate law with $$t_{1/2}=3$$hours. What fraction of the sample of sucrose remains after $$8$$hours?
What is half-life of a reaction? Derive formula for finding out half-life from first order rate reaction.
Write the characteristics of first order reaction.
Derive the integrated rate equation for the rate constant of a zero order reaction.
Derive an expression for the rate constant for a first order reaction.
Show that for a first order reaction, the time required for 99.9% completion of the reaction is 10 times that required for 50% completion.
What happens to the half life period for a first order reaction, if the intial concentration of the reactants is increased?
Give a detailed account of the collision theory of reaction mils of Bimolecular gaseous reactions.
Give two examples of gaseous first-order reactions.
Define collision frequency. Give an example for Pseudo-first order reaction.
Write short notes on:
(a) Threshold Energy, (b) Energy of Activation.
For a zero order reaction $$t_{1/2}$$ is proportional to what?
The half life of $$^{212}Pb$$ is $$10.6\ hour$$. It undergoes decay to its daughter (unstable) element $$^{212}Bi$$ of half life $$60.5$$ minute. Calculate the time at which the daughter element will have maximum activity.
$$^{ 131 }{ I }$$ has half life period $$133$$ hour. After $$79.8$$ hour, what fraction of $$^{ 131 }{ I }$$ will remain?
$$^{ 90 }{ Sr }$$ shows $$\beta$$-activity and its half life period is $$28$$ years. What is the activity of a sample containing $$1 g$$ of $$^{ 90 }{ Sr }$$?
A chemist prepares $$1.00 g$$ of pure $$_{ 6 }^{ 11 }{ C }$$. This isotope has half life of $$21$$ minutes, decaying by the equation:
$$_{ 6 }^{ 11 }{ C } \rightarrow _{ 5 }^{ 11 }{ B } + _{ 1 }^{ 0 }{ e }$$
(a) What is the rate of disintegration per second (dps) at start?
(b) What are the activity and specific activity of $$_{ 6 }^{ 11 }{ C }$$ at start?
(c) How much of this isotope $$_{ 6 }^{ 11 }{ C }$$ is left after $$24$$ hours of its preparation?
Binding energy per nucleon of $$_{ 1 }^{ 2 }{ H }$$ and $$_{ 2 }^{ 4 }{ He }$$ are $$1.1 MeV$$ and $$7 MeV$$ respectively. Calculate the amount of energy released in the following process:
$$_{ 1 }^{ 2 }{ H }+_{ 1 }^{ 2 }{ H }\longrightarrow $$ $$_{ 2 }^{ 4 }{ He }$$
For the dissociation of gaseous $$HI$$, the energy of activation is $$44.3kcal$$. Calculate the energy of activation for the reverse reaction. Given, $$\Delta H$$ for the formation of $$1$$ mole of $$HI$$ from $${H}_{2}$$ and $${I}_{2}$$ is $$-1.35kcal$$.
Thermal decomposition of a compound is of first order. If $$50\%$$ sample of the compound is decomposed in $$120$$ minute, how long will it take for $$90\%$$ of the compound to decompose?
A drop of solution (volume $$0.05\ mL$$) contains $$3\times { 10 }^{ -6 }\ mole$$ $${ H }^{ + }$$ ions. If the rate of disappearance of the $${ H }^{ + }$$ ions is $$1\times { 10 }^{ 7 }$$ $$mol$$ $${ litre }^{ -1 }$$ $${ sec }^{ -1 }$$, how long would it take for $${ H }^{ + }$$ ions in the drop to disappear?
For a reaction $$X\rightarrow Y)$$, heat of reaction is $$+83.68kJ$$, energy of reactant $$X$$ is $$167.36kJ$$ and energy of activation is $$209.20kJ$$. Calculate (i) threshold energy (ii) energy of product $$Y$$ and (iii) energy activation of the reverse reaction $$(Y\rightarrow X)$$.
Sucrose decomposes in acid solution into glucose and fructose according to first order rate law with $$t_{ {1}/{2}} = 3\ Hrs$$. What fraction of the sample of sucrose remains after $$8$$ hours.
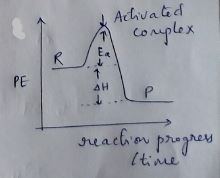
Give the definition of $$(X)$$ denoted in graph:
For the decomposition of ethylene oxide into $$CH_4$$ and CO, the variation of total pressure (P) of the reaction mixture with time is as given below:
t/s 0 300 600 900
P/mm 120 127.2 134.0 140.3
Show that the reaction is a first order reaction.
The half-life of a first order reaction is $$900$$ min at $$820\ K$$. Estimate its half-life at $$720$$K if the energy of activation of the reaction is $$250\ kJ\ mol^{-1}$$.
Calculate the activation energy for a reaction of which rate constants becomes 4 times when temperature changes from $$30^0C$$ to $$50^0C$$ [R= 8.314 $$J mol^{-1}K^{-1}$$]
Write the two steps involved in the mechanism of the enzyme-catalyzed reaction.
Derive an integrated rate equation for rate constant of a zero order reaction.
For a first order reaction $$A\to P$$, the temperature $$(T)$$ and dependent rate constant $$(k)$$, was found to follow the equation $$\log k = -(2000)\dfrac{1}{T} + 6.0$$. What is activation energy?
A first-order reaction is $$40\%$$ complete in $$50$$ min. How long(minutes) will it take to $$80\%$$ completion?
Sucrose decomposes in solution into glucose and fructose according to the first order rate law. With $$t^{1/2} 3$$ Hr. What fraction of sample of sucrose remains after $$8$$ hour?
For a first order reaction, time required for $$99.0$$% completion is $$x$$ times for the first time required for the completion of $$90$$% of the reaction $$x$$ is:
Derive an expression for the rate constant of a First order reaction.
For the zero order reaction $$A\rightarrow 2B$$, the rate constant is $$2\times {10}^{-6}M$$ $${min}^{-1}$$. The reaction is started with $$10M$$ $$A$$.
(i) What will be the concentration of A after 2 days (ii) What is the initial half-life of the reaction
(iii) In what time, the reaction will complete?
How can the rate of the chemical reaction, namely, decomposition of hydrogen peroxide be increased?
For a homogeneous gaseous reaction, $$A \longrightarrow B+C+D$$, the initial pressure was $$P_{0}$$ while pressure at time $$t$$ was $$P$$. Derive an expression for rate constant $$K$$ in terms of $$P_{0},P$$ and $$t$$. [Assume first-order reaction]
A reaction occurs in 3 steps having rate constant $${ K }_{ 1 },{ K }_{ 2 },{ K }_{ 3 }$$ the overall rate constant of the reaction $$1\triangle $$
$$K=\frac { { K }_{ 1 }{ K }_{ 2 } }{ { K }_{ 3 } } $$The $${ E }_{ a }$$ energies of first, second and third steps are 30, 60, 40$$kJ{ mol }^{ -1 }$$ respectively. Determine activation energy of the reaction.
A and B are two different chemical species undergoing 1st order decomposition with half lives equal to $$5$$ sec. and $$7.5$$ sec. respectively. If the initial concentration of A and B are in the ratio $$3:2$$, calculate $$\cfrac{{C}_{A}}{{C}_{B}}$$, after three half lives of A. Report your answer after multiplying it with $$100$$.
The rate of most of the reaction double when their temperature is raised from $$298 \ K$$ to $$308 \ K$$. Calculate the activation energy of such a reaction.
In gaseous reaction important for understanding the upper atmosphere, $$H_2O$$ and $$O$$ react bimolecularly to form two $$OH$$ radicals. $$\Delta H$$ for this reaction is $$72 \,J$$ at $$500 \,K$$ and $$E_a = 77 \,kj \,mol^{-1}$$, then calculate $$E_a$$ for the bimolecular recombination of $$2OH$$ radicals to form $$H_2O$$ and $$O$$ at $$500 \,K$$.
Given that the temperature coefficient for the saponification of ethyl acetate by $$NaOH$$ is $$1.75$$. Calculate activation energy for the saponification of ethyl acetate.
A first order reaction takes $$69.3$$ minutes for $$50\%$$ completion. How much time will be needed for $$80\%$$ completion?
The rate constant for decomposition of $$COCl_2(g)$$ according to following reaction $$COCl_2(g) \rightarrow CO(g) + Cl_2 (g); \Delta H = 19 \,kcal/mol$$, expressed as $$ln \,k = 15 - \dfrac{5000}{T}$$
Calculate activation energy for given reaction. $$(in \,\,K cal/mol)$$.
Calculate the age of a vegetarian beverage whose tritium content is only $$15\%$$ of the level in living plants. Given $$t_{\frac{1}{2}}$$ for $$_{1}H^{3} = 12.3$$ years. ($$log 2 = 0.3, log3 = 0.48$$)
In gaseous reaction important for the understanding of the upper atmosphere $${ H }_{ 2 }O$$ and $$O$$ react bimolecularly to form two $$OH$$ radicals. $$ \Delta H$$ for this reaction is 72 kJ at 500 K and $${ E }_{ a }$$ is 77 kJ $${ mol }^{ -1 }$$ $${ E }_{ a }$$ for the bimolecular recombination of two OH radicals to form $${H}_{2}O$$ and $$O$$ is: (in kJ $${ mol }^{ -1 }$$)
The reaction is:
$$H_2O+O\longrightarrow 2OH$$ , $$\Delta H= -72 kJ$$; $$E_a=77kJ/mol$$
$$2OH\longrightarrow H_2O+O$$ , $$E_a=?$$ (Refer to Image)
$$E_a$$ for the reverse reaction
$$=(E_a)_{forward}+\Delta H$$
$$=77+(-72)=5kJ$$
For a zero order chemical reaction,
$$2N{ H }_{ 3 }(g)\rightarrow { N }_{ 2 }(g)+3{ H }_{ 2 }(g)$$
rate of reaction $$=0.1$$ atm/sec. Initially only $$N{ H }_{ 3 }$$ is present and its pressure $$=3$$ atm. Calculate total pressure at $$t=10$$ sec.
Calculate the fraction of molecules of reactants having energy equal to or greater than activation energy?
The rate of the reaction quadruples when the temperature changes from $$293K$$ to $$313K$$ .Calculate the energy of activation?
A first order reaction is 75% completed in 72 min. How long time will it take for
(i) 50% completion (ii) 87.5% completion
For a zero order chemical reaction,
$$2NH_{3}(g)\rightarrow N_{2}(g) + 3H_{2}(g) $$
rate of reaction = 0.1 atm /sec. Initially only $$NH_{3}$$ is present and its pressure = 3atm. Calculate total pressure at t = 10 sec.
The rate of r$$\times$$n becomes $$ 4 $$ times when temp. changes from $$ 293 K $$ to $$ 313 K $$ Calculate energy of activation (Ea) of the rxn assuming that it does not change with temp. $$ (R= 8.3/4 JK^-mol^{-1} ) $$
The $$t_{1/2}$$ of first order reaction is $$60$$ minutes. What percentage will be left after $$240$$ minutes?
Which reaction will have the greater temperature dependence tor the rate constant - one with a small value of energy of activation (E) or one with a large value of activation energy(E)?
What is zero order reaction?
Write two applications of integrated rate equation.
$$3/4^{th}$$ of a first-order reaction is completed in 32 min. Calculate the time required to complete $$15/16^{th}$$ part of the reaction.
If A $$\rightarrow$$ products is a first order reaction then, write the integrated law equation.
Derive the integrated rate equation for expressing the rate constant of a first order :
$$R\rightarrow P$$
In this type of reaction, the sum of the powers of concentrations of reactants in rate law is equal to 1, that is the rate of the reaction is proportional to the first power of the concentration of the reactant. Consider the reaction $$R \rightarrow P$$ again. Therefore, the rate law for this reaction is,
Rate is directly proportional to [R]
We know that $$[R] = -kt + [R]_0 $$ ( from equation II). Taking log of both sides, we get
$$ln[R] = -kt + ln[R]_0$$ ………………………….(IV)
$$ ln[R]/[R]_0 = -kt$$ …………………………….(V)
$$k = (1/t) ln [R]_0 /[R] $$………………………(VI)
Now, consider equation II again. At time t1 and time t2, the equation II will be [R]1 = -kt1 + [R]0 and [R]2 = -kt2 + [R]0 respectively, where [R]1 and [R]2 are concentrations of the reactants at time t1 and t2 respectively. Subtracting second equation from first one, we get
$$ln [R]_1– ln[R]_2 = -kt_1 – (- kt_2 )$$
$$ ln[R]_1 /[R]_2 = k (t_2 – t_1)$$
$$k = [1/(t_2 – t_1)] ln[R]_1 /[R]_2$$
Now, taking antilog of both sides of equation V, we get $$[R] = [R]_0e^{-kt}$$
Comparing this equation with equation of a straight line y = mx + c, if we plot ln [R] against t, we get a straight line with slope = -k and intercept $$ = ln[R]_0$$
On removing natural logarithm from equation VI, the first-order reaction can also be written as,
$$k = 2.303/t log[R]_0 /[R]$$ …………..(VII)
If we plot a graph of $$log[R]_0 /[R]$$ against t, we get slope = k/2.303
A certain reaction is $$50\%$$ complete in $$20\ minutes$$ at $$300k$$; the reaction is $$50\%$$ complete in $$5$$ minutes at $$350k$$ calculate the activeity energy, of it is a first order reaction.
Activation energy of a reaction is 100 kJ/mol. By using a catalyst $$E_a$$ decreases by 75%. What will be the effect on rate of reaction at $$20^0C$$? Consider all other things are equal.
A rain in $$50\%$$ completed om shown and $$75\%$$ in d$$4$$ hours. Find the order of reaction :
In the equation $$K$$=$$A.e^ {\dfrac{-Ea}{RT}}$$, what does the term 'A' represent?
The solution of $${ H }_{ 2 }{ O }_{ 2 }$$ of normality 0.73 is catalytically decomposed. What will be the concentration at the end of 45mins, assuming the decompostion to follow first order rate law if half life is 15 minute?
Derive an expression for integrated rate law for a zero order reaction.
That's the expression for integrated rate law for zero order reaction.
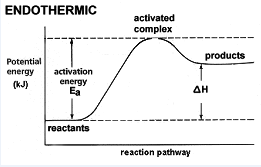
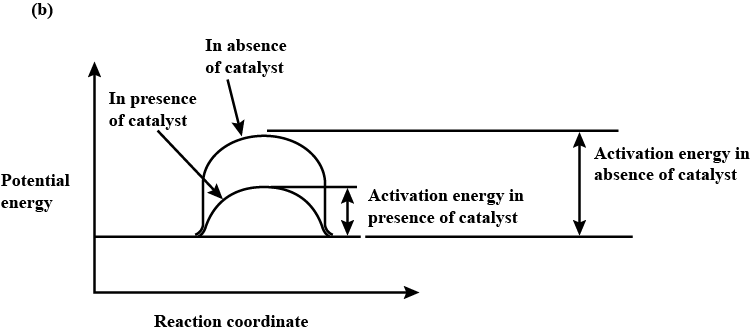
Draw energy profile diagram of potential energy with reaction progress. Show that position for the following in the diagram.
(a) Activated complex
(b) Energy of activition
For a substitution reaction, rate constant increases by factor $$10.6$$ when temperature changes from $${25}^{o}C$$ to $${35}^{o}C$$. Calculate energy of activation of the reaction.
The activation energy for the reaction, 2 $$HI(g) \rightarrow H_2 + I_2 (g)$$ is $$209.5 k J mol^{-1}$$ at 581 K. Calculate the fraction of molecules of reactants having energy equal to or greater than activation energy ?
For a first order reaction, $$A\longrightarrow$$ Product, the temperature dependent rate constant (k) was found to follow the equation $$logk=-\frac { 2000 }{ T } +6$$ calculate the pre-exponential factor (A) and activation energy for the reaction.
The rate of the chemical reaction doubles for an increase of 10 K in absolute temperature from 298 K. Calculate $${ E }_{ a }$$.
Derive the relation between half life and rate constant for a first order reaction.
In a reaction $$A\longrightarrow B+C$$, The following data were obtained:
t in seconds 0 900 1800
conc. of A 50.8 19.7 7.62
Prove that it is a first order reaction.
Sucrose is converted to glucose and fructose of acidic solution which is first order reaction.
Its a $$1$$st Order Reaction.
The activation energy for the reaction $${ 2HI }_{ (g) }\rightarrow { H }_{ 2 }{ I }_{ 2(g) }$$ is 209.5 $$209.5\quad { mol }^{ -1 }$$ at 581 K. Calculate the fraction of molecules of reactants having energy equal to or greater than activation energy.
The rate constant of a reaction is $${ 1.5\times }10^{ 7 }{ S }^{ -1 }{ at\quad 50 }^{ o }$$ and $${ 4.5\times }10^{ 7 }{ S }^{ -1 }{ at\quad 100 }^{ o }$$, calculate value of activation energy (Ea) for the reaction. $${ 8.314\quad JK }^{ -1 }{ mol }^{ -1 }$$
The rate constants of a reaction at 500 K and 700 K are $${ 0.02s }^{ -1 } and { 0.07 }s^{ -1 }$$ respectively. Calculate the values of Ea and A.
What is the hybridisation of $${{\text{C}}_2}{{\text{H}}_4}$$. Draw its structure also.
hybridisation of $$C$$ is $$s{p^2}$$
In the $$1^{st}$$ order reaction $$A \longrightarrow$$ products $$80\%$$ of given sample of compound decomposes in $$40\ mins $$. What is half life period of reaction ?
Derive the relationship between half life period and rate constant of a zero order reaction.
For a chemical reaction, what is the effect of a catalyst on the following?
(i) Activation energy of the reaction
(ii) Rate of the reaction.
One mole of an organic compound(A) with molecular formula $$C_{3}H_{8}O$$ reacts completely with two moles of hydroiodic acid at high temperature to form 'x' & 'y'. Identify 'A', 'X' & 'Y' in the reaction.
According to collision theory, write name of two factors which increases the rate of reaction as temperature increase.
Write any two characteristics of first order reaction.
Show that, in a first order reaction, time required for completion of $$99.9 \%$$ is $$10$$ times of half life. $$(log 10 =1)$$
A drug is known to be ineffective after it has decomposed $$30\%$$. The original concentration of one sample was $$500\ units/mL$$. When analysed $$20$$ months later, the concentration was found to be $$420\ units/mL$$. Assuming that decomposition is of $$1$$ order, what will be the expiration time of the drug. What is the half life of drug.
Define activation energy of a reaction .
The equation $$ A + B \rightarrow C $$ has zero order . What is the rate equation?
Can a reaction have zero Activation Energy ?
For the reaction $$A \rightarrow $$ products, the following data is given for a particular run.
time(min): 0 5 15 35
$$\dfrac {1}{[A]}(M^{-1}) :$$ 1 2 4 8
Determine the order of the reaction.
For the assumed reaction $$ X_2 + 3Y_2 \rightarrow 2XY_3 $$ , write the rate of equation in terms of rate of disappearance of $$ Y_2 $$ .
For an elementary reaction $$ 2A + B \rightarrow 3C $$ the rate of appearance of $$ C $$ at time 't' is $$ 1.3 \times 10^{-4} \, mol \, L^{-1} \,s^{-1} $$ .
Calculate at this time rate of the reaction .
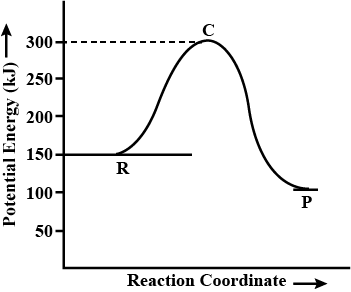
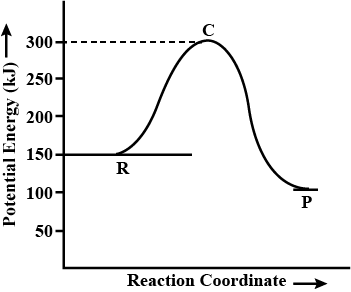
From the graph, What is the activation energy for forward reaction ?
The decomposition of $$NH_{3}$$ on platinum surface
$$2NH_{3}(g) \overset{Dt}{\rightarrow} N_{2}(g) + 3H_{2}(9)$$
is zero order with $$k = 2.5 \times 10^{-4} mol L^{-1} S^{-1}$$ What are the rates of production of $$N_{2}$$ and $$H_{2}$$
Write the rate law for a first order reaction . Justify the statement that half life for a first order reaction is independent of the initial concentration of the reactant .
The rate law for a reaction is expressed as : rate $$ = k[Cl_2][NO]^2 $$
Find out the orders of the reaction with respect to $$ Cl_2 $$ and with respect to $$ NO $$ and also the overall order of the reaction .
Define Rate equation with example.
Define Threshold Energy of a Reaction.
Write the rate equation for the reaction $$ A_2 + 3B_2 \rightarrow 2C $$ , if the overall order of the reaction is zero .
Explain why $$ H_2 $$ and $$ O_2 $$ do not react at room temperature .
| Observation No. | Time (in minute) | $$P_x$$ (in mm of Hg) |
| 1 | 0 | 800 |
| 2 | 100 | 400 |
| 3 | 200 | 200 |
(i) Find the rate constant.
(ii) Find the time for 75% completion of the reaction.
(iii) Find total pressure when pressure of $$X$$ is 700 mm of Hg.
In case of unimolecular reaction, the time required for 99.9% of the reaction to take place is x times that required for half of the reaction. The value of x is_________.
The specific rate constant of the decomposition of $$N_2O_5$$ is $$0.008 min^{-1}$$. The volume of $$O_2$$ collected after 20 minute is 16 mL. The volume in ml that would be collected at the end of reaction. $$NO_2$$ formed is dissolved in $$CCl_4$$ is
The acid catalysed hydrolysis of an organic A at $$30^oC$$ has a half-life of 100 minutes when carried out in a buffer solution of $$pH=5$$ and 10 minutes when carried out at $$pH=4$$. Both the times the half-life are independent of the initial concentration of A. If the rate of reaction is given by $$rate=K[A]^m[H^+]^n$$, $$m+n$$ is ___________.
Dimethyl ether gaseous phase decomposition is: $$CH_3OCH_3\rightarrow CH_4+H_2+CO$$ at 750 K having rate constant $$6.72\times 10^{-3} min^{-1}$$. The time in which initial pressure of 400 mm in closed container becomes 750 mm in hours (to the nearest integer) is________.
A reaction $$2A\rightarrow Products$$, has a rate constant $$3.5\times 10^{-4} mol^{-1} litre^{-1} sec^{-1}$$. If the time required for the concentration of A to change from 0.260 M to 0.011 M $$x\times 10^5 sec$$ then $$x$$ is___________.(to the nearest integer)
An organic compound undergoes first-order decomposition. The time taken for its decomposition to 1/8 and 1/10 of its initial concentration are $$t_{1/8}$$ and $$t_{1/10}$$ respectively. The value of $$\frac {[t_{1/8}]}{[t_{1/10}]}\times 10$$ is ______ (take $$log_{10}2 = 0.3$$)
The gas phase decomposition of dimethyl ether follows first order kinetics,
$$CH_3OCH_3(g)\rightarrow CH_4(g)+H_2(g)+CO(g)$$
The reaction is carried out in a constant volume container at $$500^oC$$ and has a half-life of 14.5 minute. Initially only dimethyl ether is present at a pressure of 0.40 atmosphere. The total pressure of the system after 12 minutes assuming ideal gas behaviour in atm is__________. (write answer as the first integer after decimal, e.g., if answer is $$2.56$$ then answer should be $$5$$)
$$CH_3OCH_3(g)\rightarrow CH_4(g)+H_2(g)+CO(g)$$
The reaction is carried out in a constant volume container at $$500^oC$$ and has a half-life of 14.5 minute. Initially only dimethyl ether is present at a pressure of 0.40 atmosphere. The total pressure of the system after 12 minutes assuming ideal gas behaviour in atm is__________. (write answer as the first integer after decimal, e.g., if answer is $$2.56$$ then answer should be $$5$$)
If the percentage decompostion in $$100$$ minutes at the same temperature but at an initial pressure of $$600$$ mm is $$(70+x)$$ find the value of $$x$$__________.
Half-life period of reation in minutes is:
(Give answer to the nearest integer)
If pressure of $$Cl_2O_7$$ after $$100$$ sec in atm is $$x$$, then $$1000x$$ is__________.
For a gaseous reaction $$A\, \rightarrow\, B\, +\, 2C$$ at $$250^\circ$$C, following data were observed. The partial pressure of the gases at 100th min will be (in 100x mm)
| Time (min) | 0 | 20 | 40 | 60 |
| Total pressure (mm Hg) | 400 | 500 | 587.6 | 664 |
The decomposition of a compound is found to follow a first-order rate law. If it takes 15 min for 20% of the original material to react, the specific rate constant is ________. ($$in \:\:min^{-1}$$ )
[If the answer is X, write the value of 1000X in nearest integer value possible]
Catalytic decomposition of nitrous oxide by gold at $$900^{0}C$$ at an initial pressure of 200 mm was 50 % in 53 min and 73 % in 100 min. The amount that will compose in 100 min at the same temperature but at an initial pressure of 600 mm is (multiply the answer by 100) :
If the initial concentration of reactants in a certain reaction is doubled, the half-life period of the reaction doubles. The order of the reaction is:
Reaction $$A+B\longrightarrow C+D$$ follow's following rate law rate $$=k={ \left[ A \right] }^{ \frac { 1 }{ 2 } }{ \left[ B \right] }^{ \frac { 1 }{ 2 } }$$. Starting with initial conc. of one mole of A and B each, what is the time taken for amount of A of become 0.25 mole. Given $$k = 2.31\times 10^{-3} sec^{-1}$$. (in sec). (Answer in the form of 100X)
The rate for the decomposition of $$NH_{3}$$ on platinum surface is zero order. What are the rate of production of $$N_{2}$$ and $$H_{2}$$ if $$K = 2.5 \times 10^{-4} mol\ litre^{-1} s^{-1}$$.
The recombination of methyl radicals has no activation barrier. The activation energy values for the first step in the thermal thermal decomposition of acetaldehyde given and $$E_{photochemical}$$ are $$309.32\;kJ\;mol^{-1}$$ and $$41.8\;kJ\;mol^{-1}$$ respectively.
Calculate the overall activation energy for the thermal decomposition of acetaldehyde.
The rate constant for a first order reaction is $$60\ s^{-1}$$. How much time will it take to reduce the initial concentration of the reactant to its $$1/16^{th}$$ value?
For the decomposition of azo-isopropane to hexane and nitrogen at $$543 K$$, the following data are obtained.
| $$t (sec)$$ | $$P$$(mm of $$Hg$$) |
| $$0$$ | $$35.0$$ |
| $$360$$ | $$54.0$$ |
| $$720$$ | $$63.0$$ |
The following data were obtained during the first order thermal decomposition of $$SO_{2}Cl_{2}$$ at a constant volume.
$$SO_{2}Cl_{2}(g)\rightarrow SO_{2}(g) + Cl_{2} (g)$$
| Experiment | $$Time/s^{-1}$$ | Total pressure/ atm |
| $$1$$ | $$0$$ | $$0.5$$ |
| $$2$$ | $$100$$ | $$0.6$$ |
For a first order reaction, we have:
$$\displaystyle k = \dfrac {2.303}{100} log \dfrac {0.5}{2 \times 0.5 - 0.6}$$
$$\displaystyle k = 2.23 \times 10^{-23} /s$$
Rate $$\displaystyle = kP_{SO_2Cl_2}$$
The total pressure is $$0.65$$ atm.
$$\displaystyle P_{SO_2Cl_2} = 2p_o-p_t = 2 \times 0.5 - 0.65 = 0.35 \: atm$$
Hence, rate $$\displaystyle = 2.23 \times 10^{-3} \times 0.35 $$
Rate $$\displaystyle = 7.805 \times 10^{-4} \: atm/s$$
$$\displaystyle k = \dfrac {2.303}{t} log \dfrac {P_o}{2P_o-P_t}$$
$$\displaystyle k = \dfrac {2.303}{100} log \dfrac {0.5}{2 \times 0.5 - 0.6}$$
$$\displaystyle k = 2.23 \times 10^{-23} /s$$
Rate $$\displaystyle = kP_{SO_2Cl_2}$$
The total pressure is $$0.65$$ atm.
$$\displaystyle P_{SO_2Cl_2} = 2p_o-p_t = 2 \times 0.5 - 0.65 = 0.35 \: atm$$
Hence, rate $$\displaystyle = 2.23 \times 10^{-3} \times 0.35 $$
Rate $$\displaystyle = 7.805 \times 10^{-4} \: atm/s$$
Consider a certain reaction $$A\rightarrow$$ Products with, $$k = 2.0 \times 10^{-2}s^{-1}$$. Calculate the concentration of A remaining after $$100$$ s, if the initial concentration of A is $$1.0 mol L^{-1}$$.
$$10\ g$$ atoms of an $$\alpha$$-active radioisotope are disintegrating in a sealed container. In one hour, the helium gas collected at STP is $$11.2{ cm }^{ 3 }$$. Calculate the half-life of the radioisotope.
In hydrogenation reaction at $${ 25 }^{ o }C$$, it is observed that hydrogen gas pressure falls from $$2$$ $$atm$$ to $$1.2$$ $$atm$$ in $$50$$ $$min$$. Calculate the rate of reaction in molarity per $$sec$$. $$\left( R=0.0821\ litre\cdot atm\ { K}^{ -1 }\ { mol }^{ -1 } \right) $$
The first order reaction is 20% complete in 20 minutes. Calculate the time it will take the reaction to complete 80%.
The reaction
$$2{ N }_{ 2 }{ O }_{ 5 }\left( g \right) \rightarrow 4N{ O }_{ 2 }\left( g \right) +{ O }_{ 2 }\left( g \right)$$
Follows first order kinetics. The pressure of a vessel containing only $${ N }_{ 2 }{ O }_{ 5 }$$ was found to increase from 50 mm Hg to 87.5 mm Hg in 30 min. The pressure exerted by the gases after 60 min. will be :(Assume temperature remains constant)
For a first order reversible reaction $$A\underset {K_{b}}{\xleftarrow {K_{f}}}B$$, the initial concentration of $$A$$ and $$B$$ are $$[A]_{0}$$ and zero respectively. If concentrations at equilibrium are $$[A]_{eq.}$$ and $$[B]_{eq.}$$, derive an expression for the time taken by $$B$$ to attain concentration equal to $$[B]_{eq/2}$$.
$$A$$ and $$B$$ are two different chemical species undergoing 1st order decomposition with half lives equal to $$5$$ sec and $$7.5$$ sec respectively. If the initial concentration of $$A$$ and $$B$$ are in the ratio $$3:2$$. Calculate $$\cfrac { { C }_{ { A }_{ 1 } } }{ { C }_{ { B }_{ 1 } } } $$ after three half lives of $$A$$. Report your answer after multiplying it with $$100$$.
In a zero order reaction, the time taken to reduce the concentration of reactant from 50% to 25% is 30 minutes.What is the time required to reduce the concentration from 25% to 12.5% ?
The activation energy of the reaction is $$75kJ/mol$$ in absence of a catalyst and it lowers to $$50.14kJ/mol$$ with a catalyst. How many times will the rate of reaction grow in presence of a catalyst if the reaction proceeds at $$25^\circ C$$?
For a chemical reaction the specific rate constant at 600K is $$1.60\times { 10 }^{ 6 }{ s }^{ -1 }$$, calculate the rate constant for the reaction at 700K, if energy of activation for the reaction is $$2.209\ KJ\ { mol }^{ -1 }$$.
A first-order reaction is $$50\%$$ completed in $$40$$ minutes at $$300\ K$$ and in $$20$$ minutes at $$320\ K$$ . Calculate the activation energy of the reaction.
[Given: log $$2=0.3010$$, log $$4=0.6021$$, R=$$8.314$$ $$JK^{-1}$$ $$mol^{-1}$$]
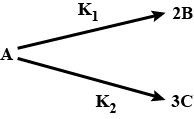
For a first order reaction
Percentage of $$B$$ in the product is $$30$$%. Calculate the value of $$k_{1}$$ and $$k_{2}. (t_{1/2})_{over\ all} = 100\ hr$$.
$$[B] = 2[A_0] \, e^{-k_1 t}$$
$$[C] = 3[A_0] \, e^{-k_2 t}$$
$$[A] = [A_0] \, e^{-(k_1 + k_2) t}$$
% of $$[B] = \dfrac{2[A_0] e^{-k_1 t} \times 100}{2[A_0] e^{-k_1 t} + 3[A_0] e^{-k_2t}}$$
$$\dfrac{30}{100} = \dfrac{2e^{-k_1 t}}{2e^{-k_1 t} + 3e^{-k_2 t}}$$
$$\dfrac{3}{10} = \dfrac{1}{1 + \dfrac{3}{2} e^{(k_2 - k_1) t}}$$
$$3 + \dfrac{9}{2} e^{-(k_2 - k_1)t} = 10$$
$$e^{-(k_2 - k_1)t} . \dfrac{14}{9}$$
$$k_1 - k_2 = ln \dfrac{14}{9}$$
at $$t = 100 hr$$
$$k_1 - k_2 = 0.4418 \times 10^{-2}$$
$$\dfrac{ln^2}{k_1 + k_2} = 100 hr$$
$$k_1 + k_2 = 0.693 \times 10^{-2}$$
by solving $$k_1 = 0.5674 \,\, k_2 = 0.1256$$
The reaction $$A(aq) \rightarrow B(aq) + C (aq)$$ is monitored by measuring optical rotation of reaction mixture at different time interval. The species $$A,\ B$$ and $$C$$ are optically active with specific rotations $$20^0, 30^0$$ and $$-40^0$$ respectively. Starting with pure $$A$$ if the value of optical rotation was found to be $$2.5^0$$ after $$6.93$$ minutes and optical rotation was $$-5^0$$ after infinite time. Find the rate constant for first order conversion of $$A$$ into $$B$$ and $$C$$.
a) Derive an integrated rate equation for rate constant of a first order reaction.
b) Draw a graph of potential energy V/S reaction co-ordinates showing the effect of catalyst on activation energy $$(E_a)$$ of a reaction.
a) Consider a general first order reaction
R $$\rightarrow$$ P
The differential rate equation for given reaction can be written as
Rate$$=-\dfrac{d[R]}{dt}=K[R]^1$$
Rearrange above equation.
$$ \dfrac{d[R]}{[R]}=-K\times dt$$
Integrating on both sides of the given equation
$$\displaystyle\int\dfrac{d[R]}{[R]}=-k\displaystyle\int dt$$
ln[R]$$=-Kt+I$$ ..$$(1)$$
Where I is Integration constant
At $$t=0$$ the concentration of reactant [R]$$=[R]_0$$ where $$[R]_0$$ is initial concentration of reactant
Substituting in equation $$(1)$$ we get
ln $$[R]_0=(-K\times 0)+I$$
ln $$[R]_0=I$$ $$(2)$$
Substitute I value in equation $$(1)$$
ln $$[R]=-Kt+ln [R]_0$$
$$Kt=ln[R]_0-ln R$$
$$Kt =ln\dfrac{[R]_o}{[R]}$$
or $$K=\dfrac{1}{t}ln\dfrac{[R]_0}{[R]}$$.
or $$K=\dfrac{2.303}{t}log\dfrac{[R]_0}{[R]}$$.
R $$\rightarrow$$ P
The differential rate equation for given reaction can be written as
Rate$$=-\dfrac{d[R]}{dt}=K[R]^1$$
Rearrange above equation.
$$ \dfrac{d[R]}{[R]}=-K\times dt$$
Integrating on both sides of the given equation
$$\displaystyle\int\dfrac{d[R]}{[R]}=-k\displaystyle\int dt$$
ln[R]$$=-Kt+I$$ ..$$(1)$$
Where I is Integration constant
At $$t=0$$ the concentration of reactant [R]$$=[R]_0$$ where $$[R]_0$$ is initial concentration of reactant
Substituting in equation $$(1)$$ we get
ln $$[R]_0=(-K\times 0)+I$$
ln $$[R]_0=I$$ $$(2)$$
Substitute I value in equation $$(1)$$
ln $$[R]=-Kt+ln [R]_0$$
$$Kt=ln[R]_0-ln R$$
$$Kt =ln\dfrac{[R]_o}{[R]}$$
or $$K=\dfrac{1}{t}ln\dfrac{[R]_0}{[R]}$$.
or $$K=\dfrac{2.303}{t}log\dfrac{[R]_0}{[R]}$$.
In a first order reaction, $$x$$ is converted into $$y$$. $$40\%$$ of the sample decomposes in $$112$$ min. What is the half life of this reaction?
The rate constants of a reaction at $$500K$$ and $$700K$$ are $$0.02{s}^{-1}$$ and $$0.07{s}^{-1}$$ respectively. Calculate the values of $$Ea$$ and $$A$$:
What is zero order reaction? Explain with suitable example.
The half life for the reaction, $${ N }_{ 2 }{ O }_{ 5 }\rightleftharpoons 2{ NO }_{ 2 }+\frac { 1 }{ 2 } { O }_{ 2 }$$ in 24 hour at $${ 30 }^{ 0 }C$$ starting with 10g of $$N_{ 2 }{ O }_{ 5 }$$ how many grams of $$N_{ 2 }{ O }_{ 5 }$$ will remain after a period of 96 hours.
A hydrogenation reaction is carried out at 5000 k. If the same reaction is carried out in the presence of a catalyst at the same rate, the temperature required is $$400 K$ $. What would be the value of the activation energy of the reaction if the catalyst lowers the activation barrier by $$20 kJ { mol\quad L }^{ -1}$$?
A first order reaction is 90% completed in 25 seconds. Find the rate constant and half-life period.
The rate of reaction becomes four times when the temperature changes from $$300 \ K$$ to $$320 \ K$$ Calculate the energy of activation of the reaction, assuming that it does not change with temperature.
A first Order reaction has a rate constant value of $$0.00510\, min^{-1}$$. If we begin with $$0.10M$$ Concentration of the reactant , how much of the reactant will remain after $$300h$$?
The temperature coefficient for the saponification of ethyl acetate by $$NaOH$$ is $$1.75$$. Calculate the activation energy.
A certain reaction is 50% complete in 20 minutes at 300K and the same reaction is again 50% complete minutes at 350K. Calculate the activation energy if it is a first order reaction. $$[R = 8.314\,J{K^{ - 1}}\,\,mo{l^{ - 1}},\log \,\,4 = 0.602 ]$$
The rates of most reactions double when their temperature is raised from $$298\ K$$ to $$308\ K$$. Calculate their activation energy.
Calculate the energy of activation of a reaction for which rate constant becomes doubles by Increase of 10$$\mathrm { K }$$ temperature from 298$$\mathrm { K }$$
It is given that T1 = 298 K
∴T2 = (298 + 10) K
= 308 K
We also know that the rate of the reaction doubles when temperature is increased by 10°.
Therefore, let us take the value of k1 = k and that of k2 = 2k
Also, R = 8.314 J K - 1 mol - 1
Now, substituting these values in the equation:
= 52897.78 J mol - 1
= 52.9 kJ mol - 1
Let the most probable velocity of hydrogen molecules at a temp. 1 degree c is Vsuppose all the molecules dissociate into atoms when temperature is raised to (2t+273) degree c then the new rms velocity is
The reaction $$A\rightarrow B$$ follows first order kinetics. The time taken for 0.8 mole of A to produce 0.6 mole B is 1 hour. What is the time taken for conversion, 0.9 mole of A to produce 0.675 mole of B?
For the first order reaction the time taken to reduce the initial concentration by a factor of 1/4 is 20 minutes The time required to reduce initial concentration by a factor of 1/16 is
(a) 20 min
(b) 10 min
(c) 80 min
(d) 40 min
(e) 5 min
The half life period of a first order reaction is $$6.0h$$. Calculate the rate constant.
Show that the time required for the completion of three-fourth of a twice first-order reaction time required for the completion of half-reaction.
A certain physiologically important first-order reaction has an activation energy equal to $$45.0\ kJ/ mol$$ at normal body temperature $$(37^oC)$$. Without a catalyst the rate constant for the reaction is $$5.0\times 10^{-4}s^{-1}$$. To be effective in the human body, where the reaction is catalysed by an enzyme, the rate constant must be at least $$2.0\times 10^{-2}s^{-1}$$. If the activation energy is the only factor affected by the presence of the enzyme, by how much must the enzyme lower the activation energy of the reaction to achieve the desired rate?
For the reaction $$A\to B+C$$ the following data were obtained:
| $$t(s)$$ | $$0$$ | $$900$$ | $$1800$$ |
| $$[A]$$ | $$50.8$$ | $$19.7$$ | $$8.62$$ |
A drop $$(0.05\ mL)$$ of a solution contains $$3.0\times 10^{-6}$$ mole of $$H^+$$ ions. If the rate constant of disappearance of $$H^+$$ is $$1.0\times 10^7\ mol/L /s$$, how long would it take for $$H^+$$ ions in drop to disappear?
The rate constant of the first order reaction, that is, decomposition of ethylene oxide into $$CH_4$$ and $$CO$$, may be described by the following equation
$$\log k(s^{-1})=14.34-\dfrac {1.25\times 10^4}{T}K$$.
Find energy of activation and rate constant at $$397^oC$$.
What will be the time taken to decrease the reactant concentration from $$2\times 10^{-2}$$ mol $$lit^{-1}$$ to $$1\times 10^{-2}$$ mole $$lit^{-1}$$ ?
From the following data for the reaction between A and B:
$$[A]$$, mol $$L^{-1}$$ $$[B]$$, mol $$L^{-1}$$ Initial rate, mol $$L^{-1}s^{-1}$$ at Initial rate, mole $$L^{-1}s^{-1}$$, at $$300$$K $$320$$K $$2.5\times 10^{-4}$$ $$3.0\times 10^{-5}$$ $$5.0\times 10^{-4}$$ $$2.0\times 10^{-3}$$ $$5.0\times 10^{-4}$$ $$6.0\times 10^{-5}$$ $$4.0\times 10^{-3}$$ - $$1.0\times 10^{-3}$$ $$6.0\times 10^{-5}$$ $$1.6\times 10^{-2}$$ -
Calculate the energy of activation.
| $$[A]$$, mol $$L^{-1}$$ | $$[B]$$, mol $$L^{-1}$$ | Initial rate, mol $$L^{-1}s^{-1}$$ at | Initial rate, mole $$L^{-1}s^{-1}$$, at |
| $$300$$K | $$320$$K | ||
| $$2.5\times 10^{-4}$$ | $$3.0\times 10^{-5}$$ | $$5.0\times 10^{-4}$$ | $$2.0\times 10^{-3}$$ |
| $$5.0\times 10^{-4}$$ | $$6.0\times 10^{-5}$$ | $$4.0\times 10^{-3}$$ | - |
| $$1.0\times 10^{-3}$$ | $$6.0\times 10^{-5}$$ | $$1.6\times 10^{-2}$$ | - |
Calculate the energy of activation.
What is the energy of activation for this reaction?
How long does it take for reactant concentration to decrease from $$4\times 10^{-4}$$ mole $$lit^{-1}$$ to $$2\times 10^{-4}$$ mole $$lit^{-1}$$?
Shw that in case of a first-factor reaction, the time required for $$93.75\%$$ of the reaction to take place is four times that required for half of the reaction.
The decomposition of $$N_2O$$ into $$N_2$$ and O in the presence of gaseous argon follows second-order kinetics, with
$$k=(5.0\times 10^{11}L mol^{-1}s^{1-})e^{-29000k/T}$$
What is the energy of activation of this reaction?
A given sample of milk turns sour at room temperature $$20^{\circ}C)$$ in $$64\ hour$$. In a refrigerator at $$3^{\circ}C$$, milk can be stored three times as long before it sours. Estimate
(a) The activation energy for souring of milk,
(b) How long it take milk to sour at $$40^{\circ}C$$?
Calculate the rate constant and half life period for first order reaction having activation energy $$39.3\ kcal\ mol^{-1}$$ at $$300^{\circ}C$$ and the frequency constant $$1.11 \times 10^{11} \sec^{-1}$$.
For a reversible first order reaction, $$A\underset {K_{2}}{\overset {K_{1}}{\rightleftharpoons}} B; K_{f} = 10^{-2} s^{-1}$$ and $$\dfrac {B_{eq.}}{A_{eq.}} = 4$$; If $$A_{0} = 0.01\ ML^{-1}$$ and $$B_{0} = 0$$, what will be concentration of $$B$$ after $$30\sec$$.
The oxidation of certain metal is found to obey the equation $$A = \alpha t + \beta$$, where $$A$$ is the thickness of the oxide film at time $$t, \alpha$$ and $$\beta$$ are constants. What is the order of this reaction.
Match order of the reaction (in List -I) with the corresponding rate constant (in List -II) :
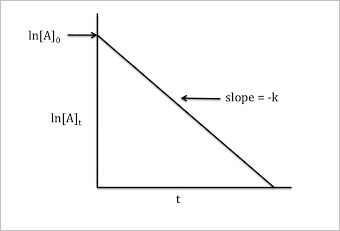
A graph between ln K and $$ \dfrac{1}{T} $$ for a reaction is given . Here k is rate constant and $$ T $$ is temperature in Kelvin .
If $$ OA = a $$ and $$ OB = b $$ , answer the following :
What is the activation energy $$ (E_a) $$ of the reaction ?
From the graph, What is the activation energy for backward reaction?
The decomposition of $$ NH_{3} $$ on platinum surface is zero order reaction.
What are the rates of production $$ N_{2} $$ and $$ H_{2} $$ If $$ K = 2.5 \times10 ^{-4} mol L^{-1}s^{-1} $$
The rate constant of a first order reaction increases from $$ 2 \times 10^{-2} $$ to $$ 4 \times 10^{-2} $$ when the temperature changes from $$ 300 \,K $$ to $$ 310\,K $$ . Calculate the activation energy $$ (E_a) $$ .
$$ (log \, 2 = 0.301 \ , \ log \, 3 = 0.4771 \ , \ log \, 4 = 0.6021 ) $$
Define half-life of a reaction. Write the expression of half-life for :i. zero-order reaction
ii. first-order reaction.
ii. first-order reaction.
The decomposition of $$NH_{3}$$ on a platinum surface takes place as follows:
$$2NH_{3}(g) \overset{Pt}{\rightarrow} N_{2}(g) + 3H_{2}(g)$$
The reaction is of zero order with $$k = 2.5 \times 10^{-4} mol\ L^{-1}\ s^{-1}$$. What are the rates of production of $$N_{2}$$ and $$H_{2}$$?
$$2NH_{3}(g) \overset{Pt}{\rightarrow} N_{2}(g) + 3H_{2}(g)$$
Give an example of a pseudo first order reaction.
For an elementary reaction $$ 2A + B \rightarrow 3C $$ the rate of appearance of $$ C $$ at time 't' is $$ 1.3 \times 10^{-4} \, mol \, L^{-1} \,s^{-1} $$ .
Calculate at this time rate of disappearance of A .
The rate of a reaction quadruples when the temperature changes from 293 K to 313 K. Calculate the energy of activation of the reaction assuming that is does not change with temperature.
All energetically effective collisions do not result in a chemical change. Explain with the help of an example.
All energetically effective collisions do not result in a chemical change. For example, formation of methanol from bromoethane depends upon the orientation of reactant molecules as shown below:
$$\mathrm{CH}_{3} \mathrm{Br}+\overline{0} \mathrm{H} \rightarrow \mathrm{CH}_{3} \mathrm{OH}+\mathrm{Br}^{-}$$
The proper orientation of reactant molecules leads to bond formation whereas improper orientation makes them simply bounce back and no products are formed.
The activation energy for the acid-catalyzed hydrolysis of sucrose is $$6.22\ kJ\ mol^{-1}$$, while the activation energy is only $$2.15\ kJ\ mol^{-1}$$ when hydrolysis catalyzed by the enzyme sucrase. Explain.
The activation energy for the reaction $$2HI_{(g)}\rightarrow H_2{(g)}+I_2{(g)}$$ is $$209.5 kJmol^{-1}$$ at 581 K . Calculate the fraction of molecules of reactants having energy equal to or greater than activation energy.
The decomposition of A into products has value of k as $$4.5 \times 10^{3} s^{-1}$$ at $$10^{\circ} C$$ and energy of activation is $$60$$ kJ $$mol^{-1}$$. At what temperature (in kelvin) would k be $$15 \times 10^{3} s^{-1}$$?
The rate of a particular reaction quadruples on increasing temperature from $$293$$ K to $$313$$ K. For this reaction, Calculate activation energy.
Gaseous cyclobutene isomerizes to butadiene in a first order process which has 'k' value of $$3.3 \times 10^{-4} s^{-1} $$ at $$153^{\circ} C $$. The time in minutes it takes for the isomerization to proceed $$40\%$$ to completion at this temperature is __________.
(Rounded off to the nearest integer)
Integrated rate law for $$1^{st}$$ order reaction,
$$3.3 \times 10^{-4} \times t = \ln \left (\dfrac{100}{60} \right ) $$
$$t = 1547.956$$ sec
$$t = 25.799$$ min
$$t= 26$$ min
The decomposition of $$NH_3$$ on plantinum surface is a zero order reaction. if rate constant (k) is $$4\times 10^{-3}Ms^{-1}$$. how long will it take to reduce the initial concentration of $$NH_3$$ from $$0.1M$$ to $$0.064M$$.
Class 12 Engineering Chemistry Extra Questions
- Alcohols,Phenols And Ethers Extra Questions
- Aldehydes,Ketones And Carboxylic Acids Extra Questions
- Amines Extra Questions
- Biomolecules Extra Questions
- Chemical Kinetics Extra Questions
- Chemistry In Everyday Life Extra Questions
- Coordination Compounds Extra Questions
- Electrochemistry Extra Questions
- General Principles And Processes Of Isolation Of Elements Extra Questions
- Haloalkanes And Haloarenes Extra Questions
- Polymers Extra Questions
- Solutions Extra Questions
- Surface Chemistry Extra Questions
- The D-And F-Block Elements Extra Questions
- The P-Block Elements Extra Questions
- The Solid State Extra Questions