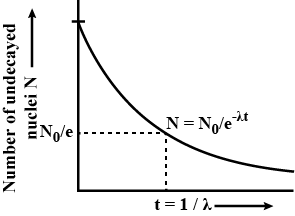
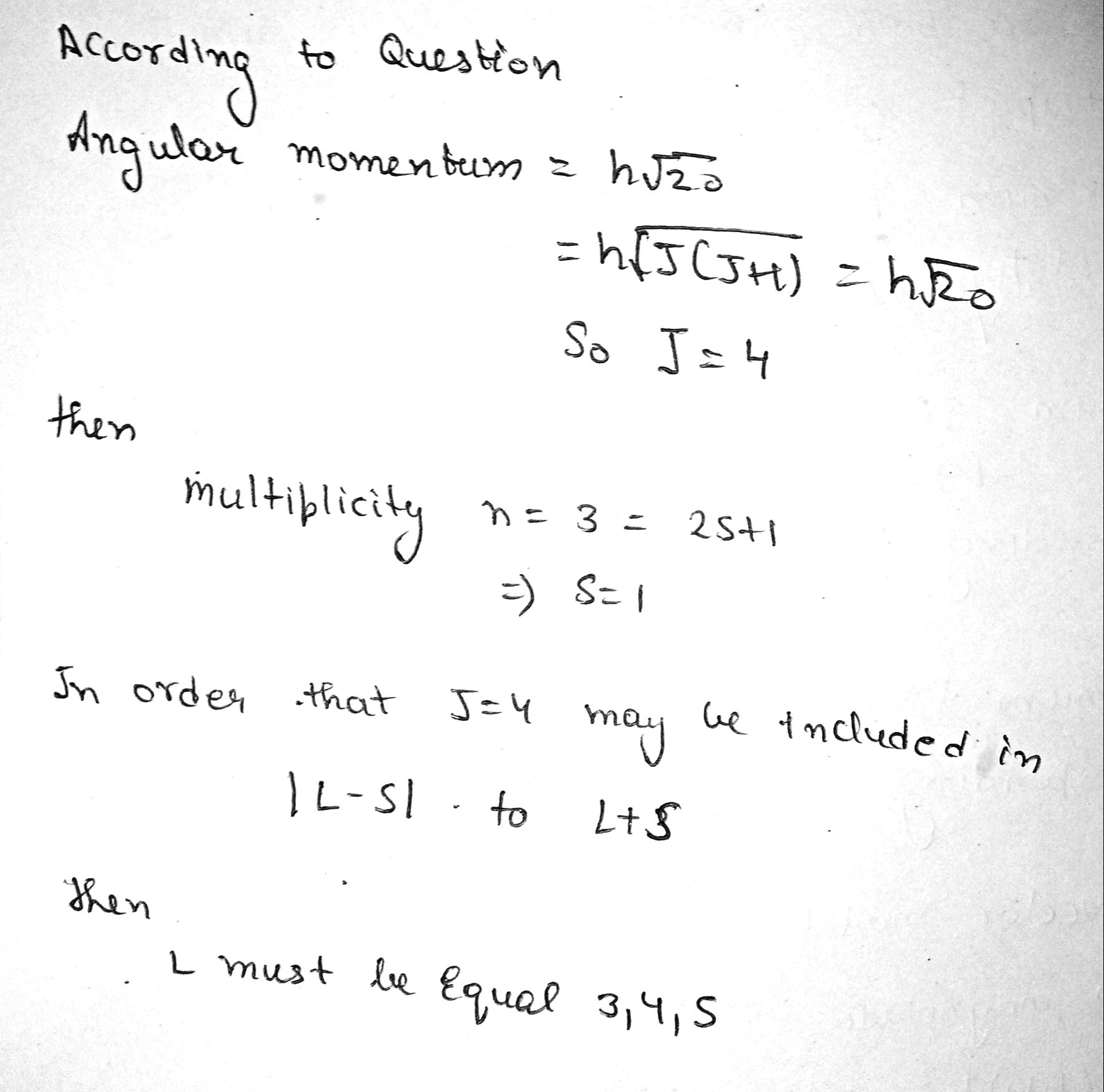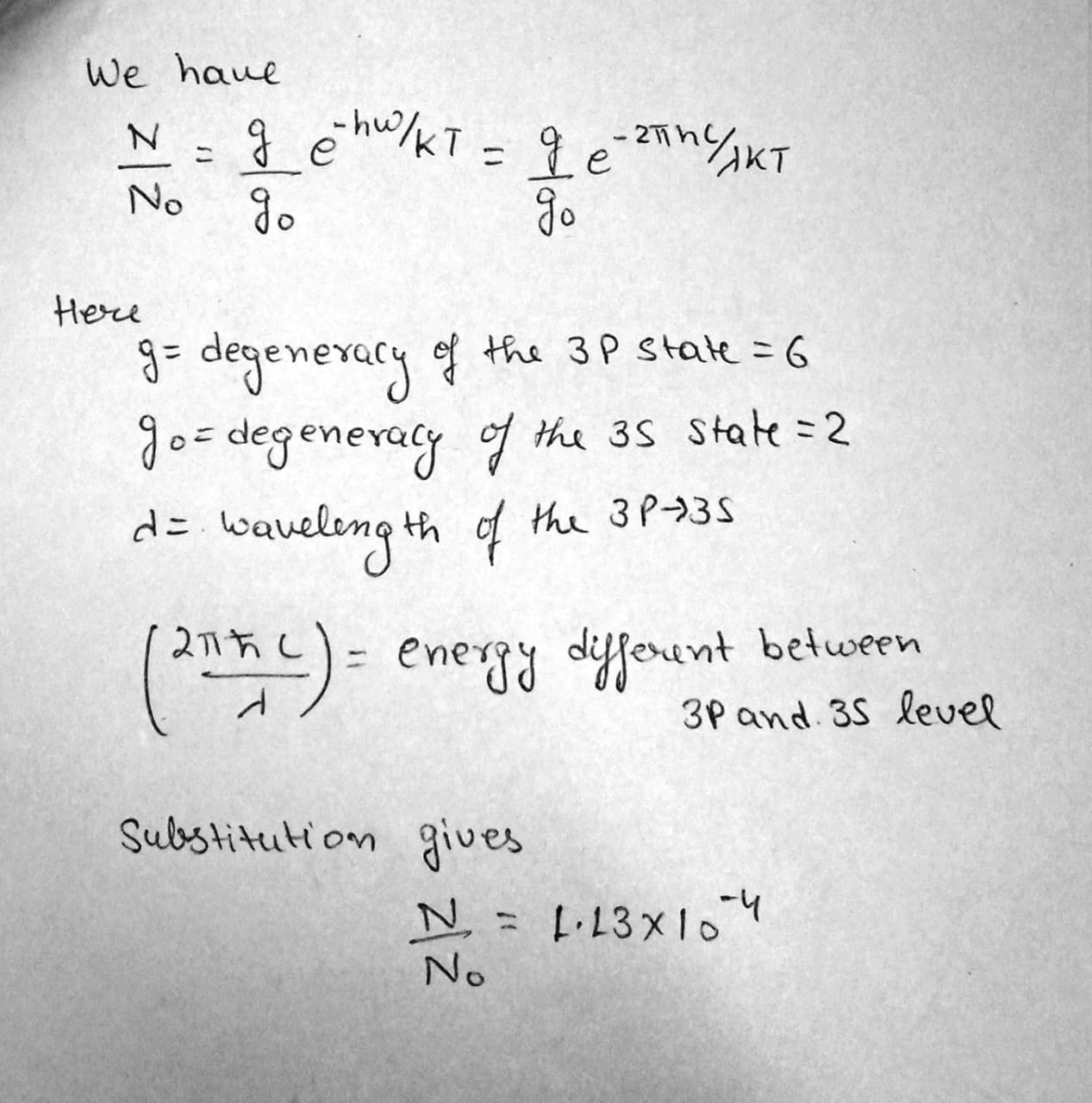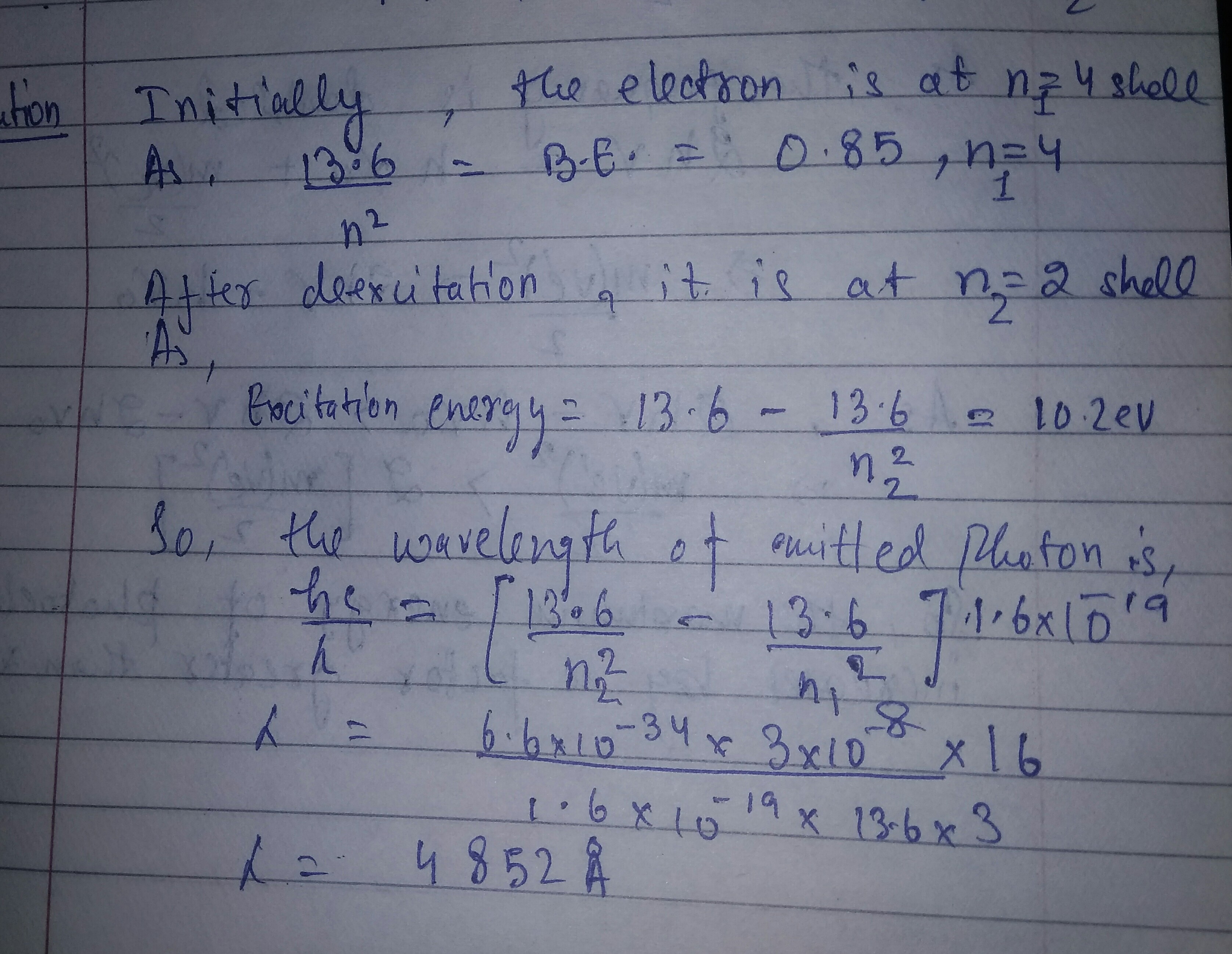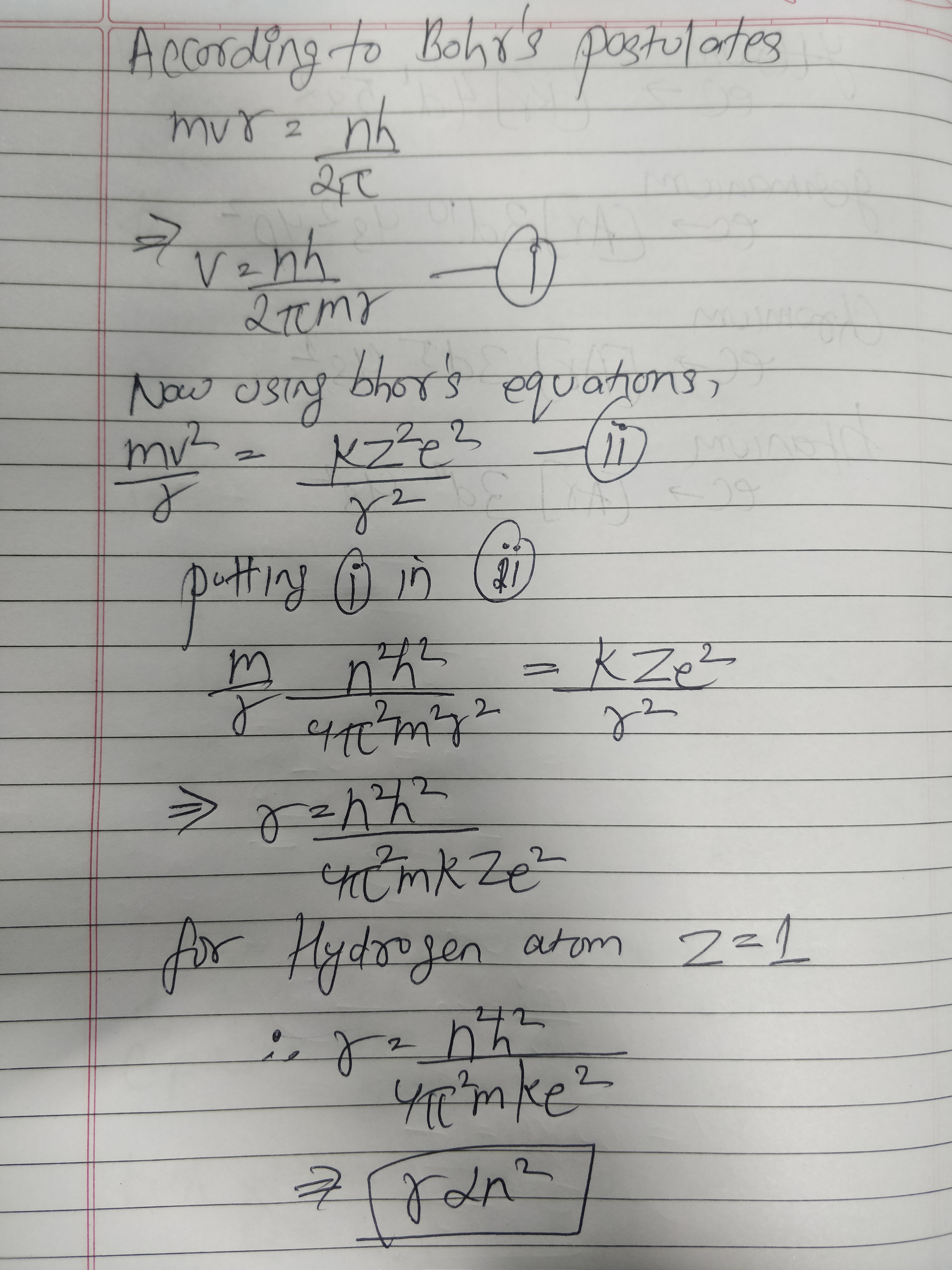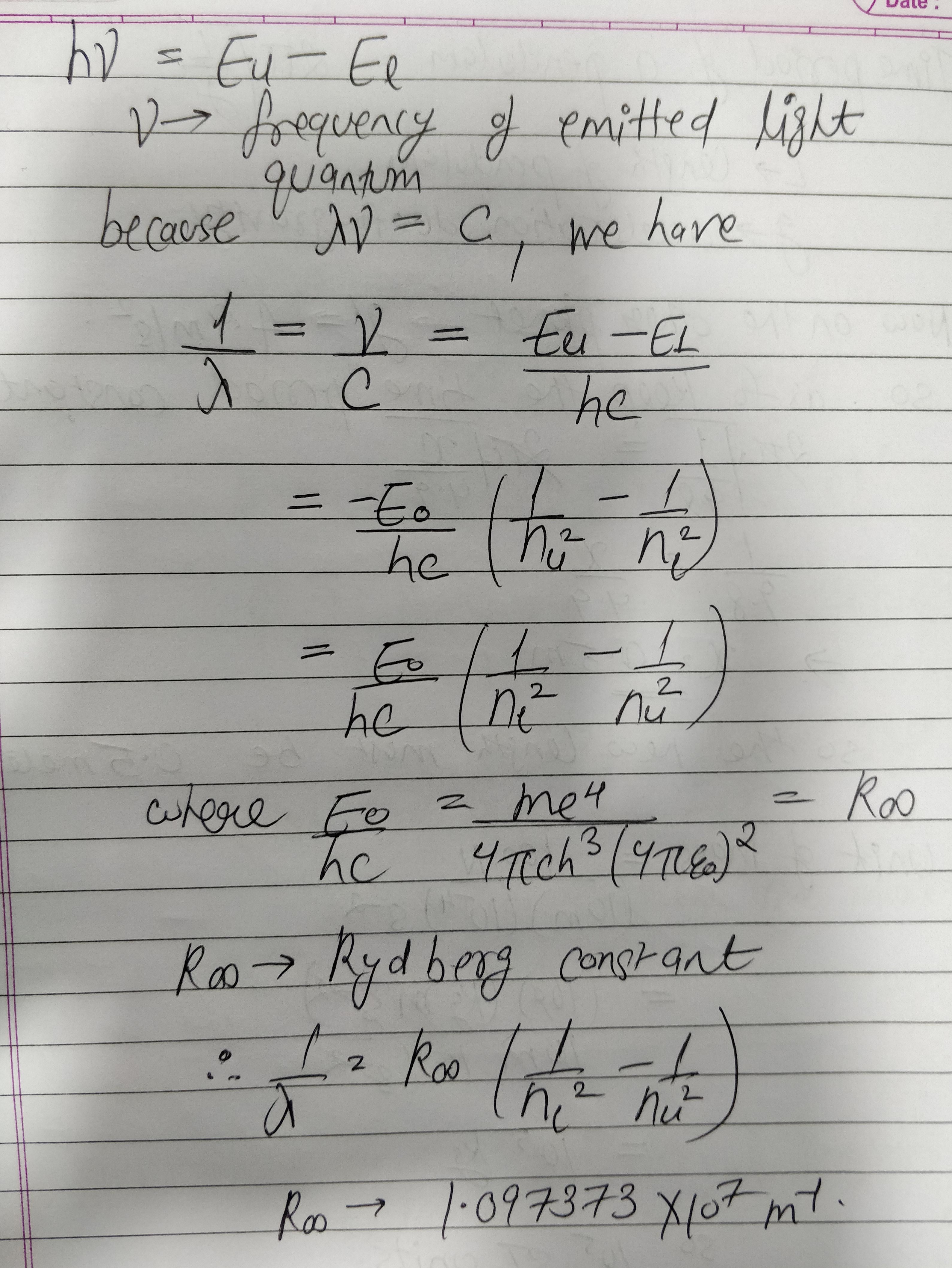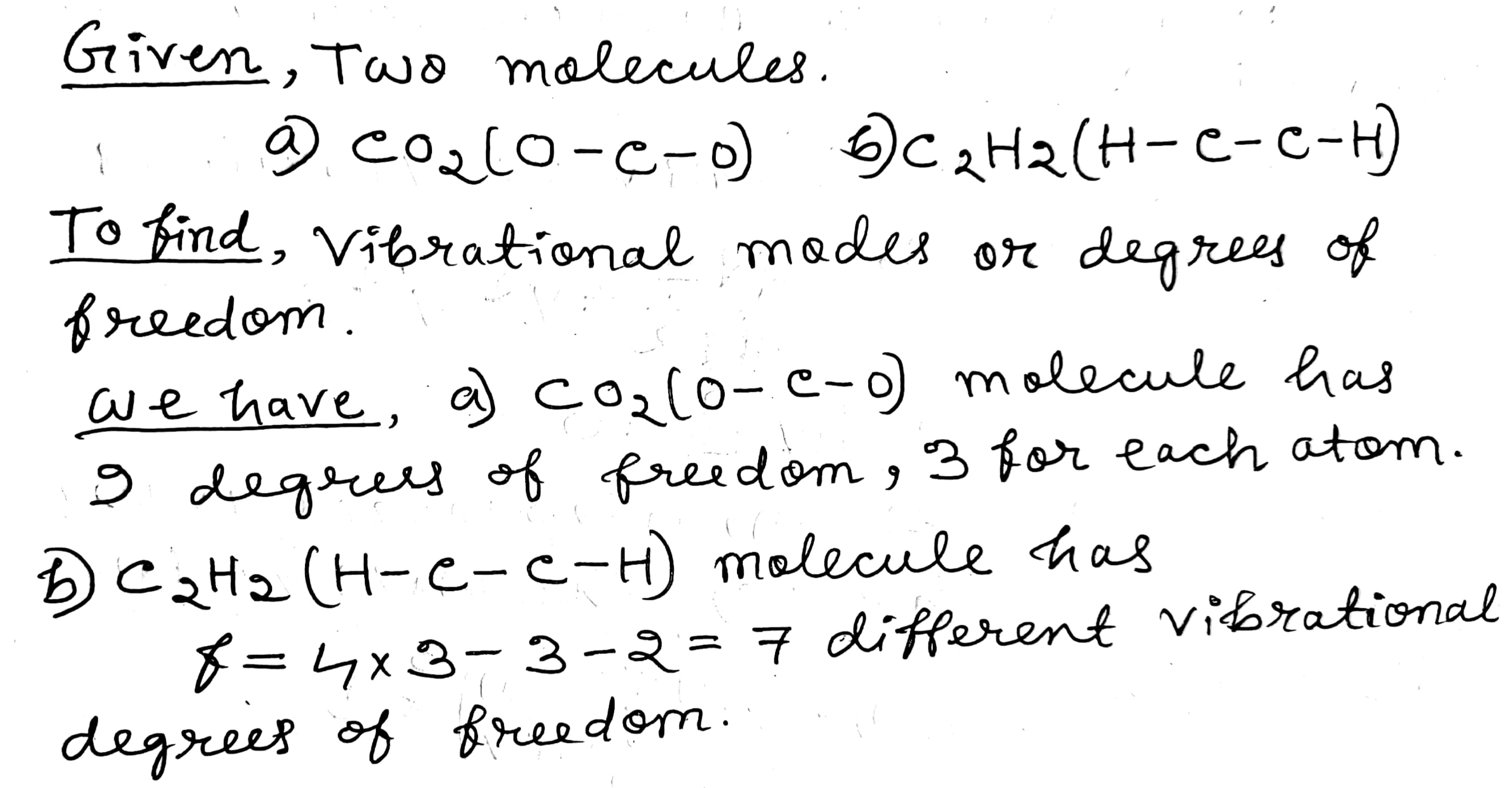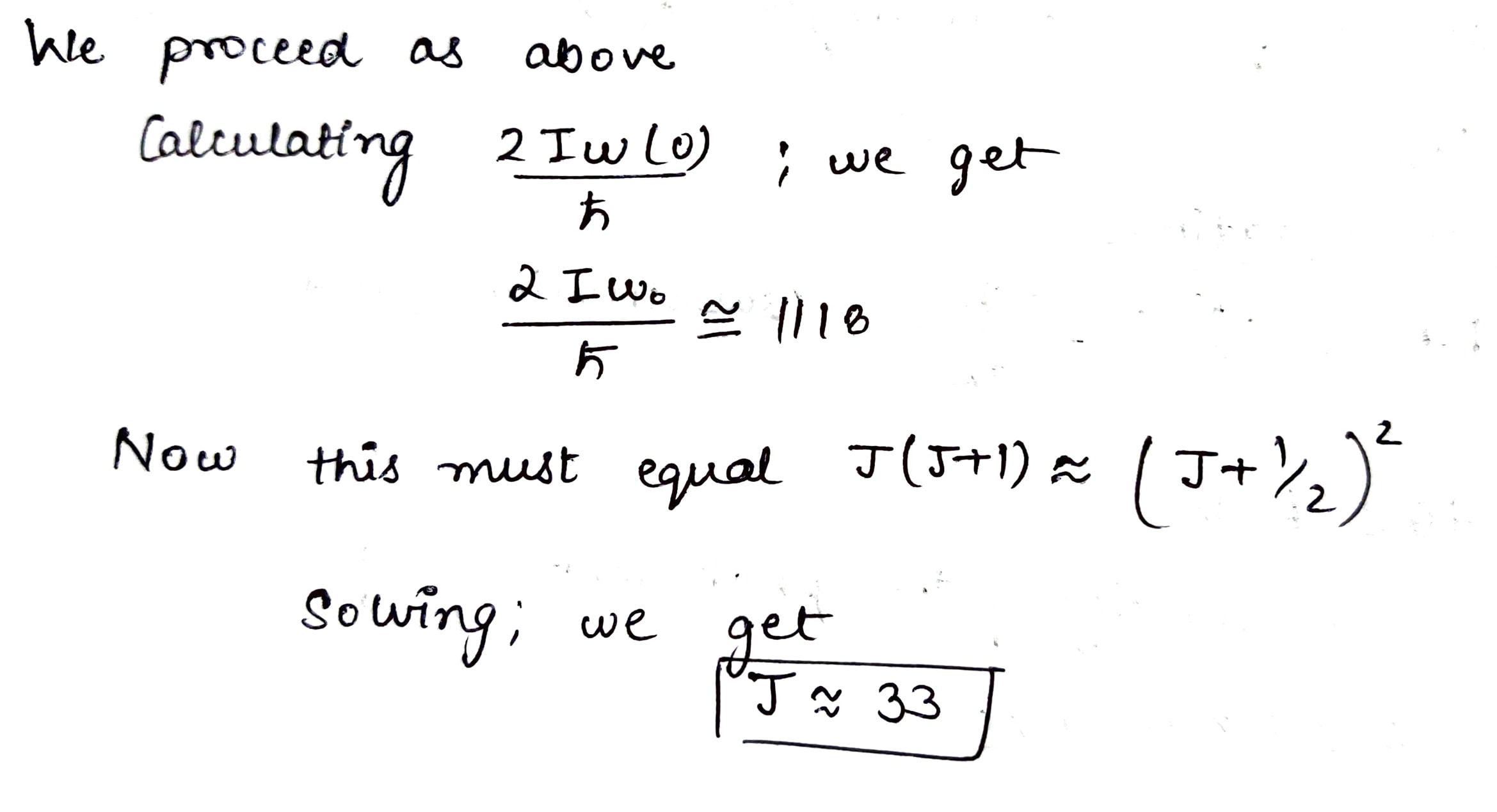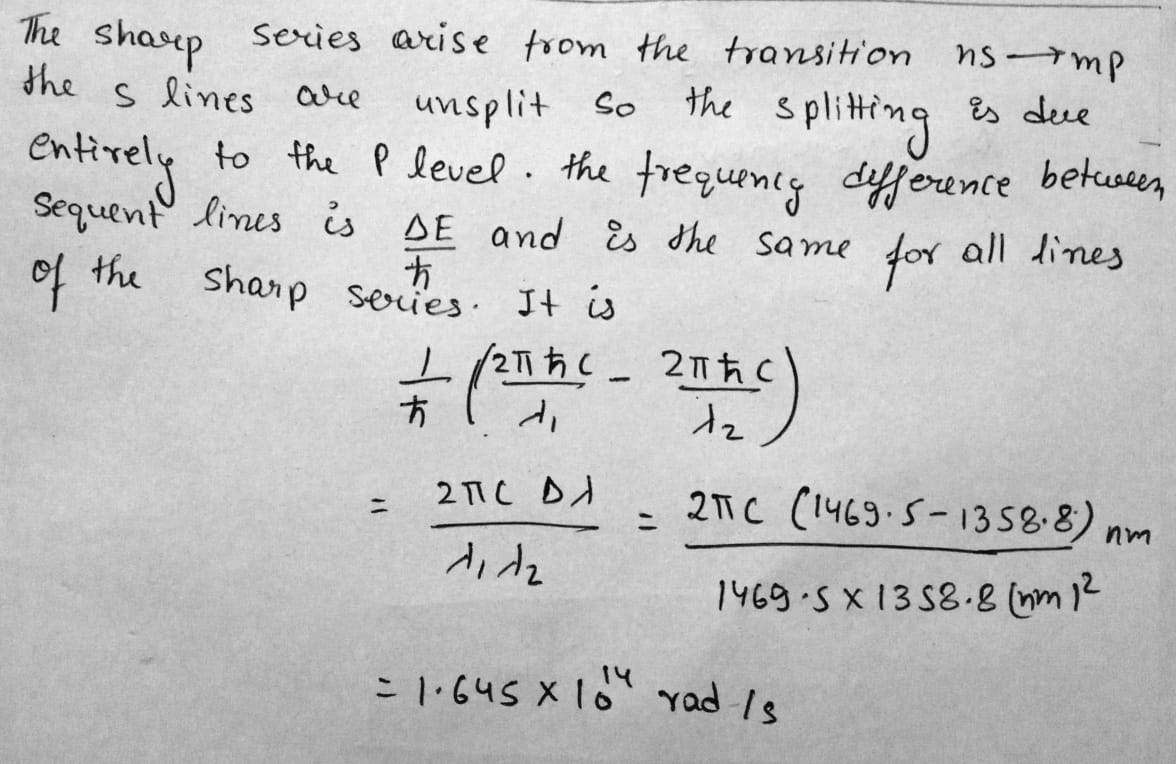Atoms - Class 12 Medical Physics - Extra Questions
A narrow beam of protons with kinetic energy $$T = 1.4 \, MeV$$ falls normally on a brass foil whose mass thickness $$ \rho d = 1.5 \, mg/cm^2 $$. The weight ratio of copper and zinc in the foil is equal to $$ 7 : 3 $$ respectively. Find the fraction of the protons scattered through the angles exceeding $$ \theta_{0} = 30^{\circ} $$.
A uniform magnetic field B exists in a region. An electron projected perpendicular to the field goes in a circle. Assuming Bohr's quantization rule, calculate the radius of $$n$$th orbit and the minimum possible speed of electron.
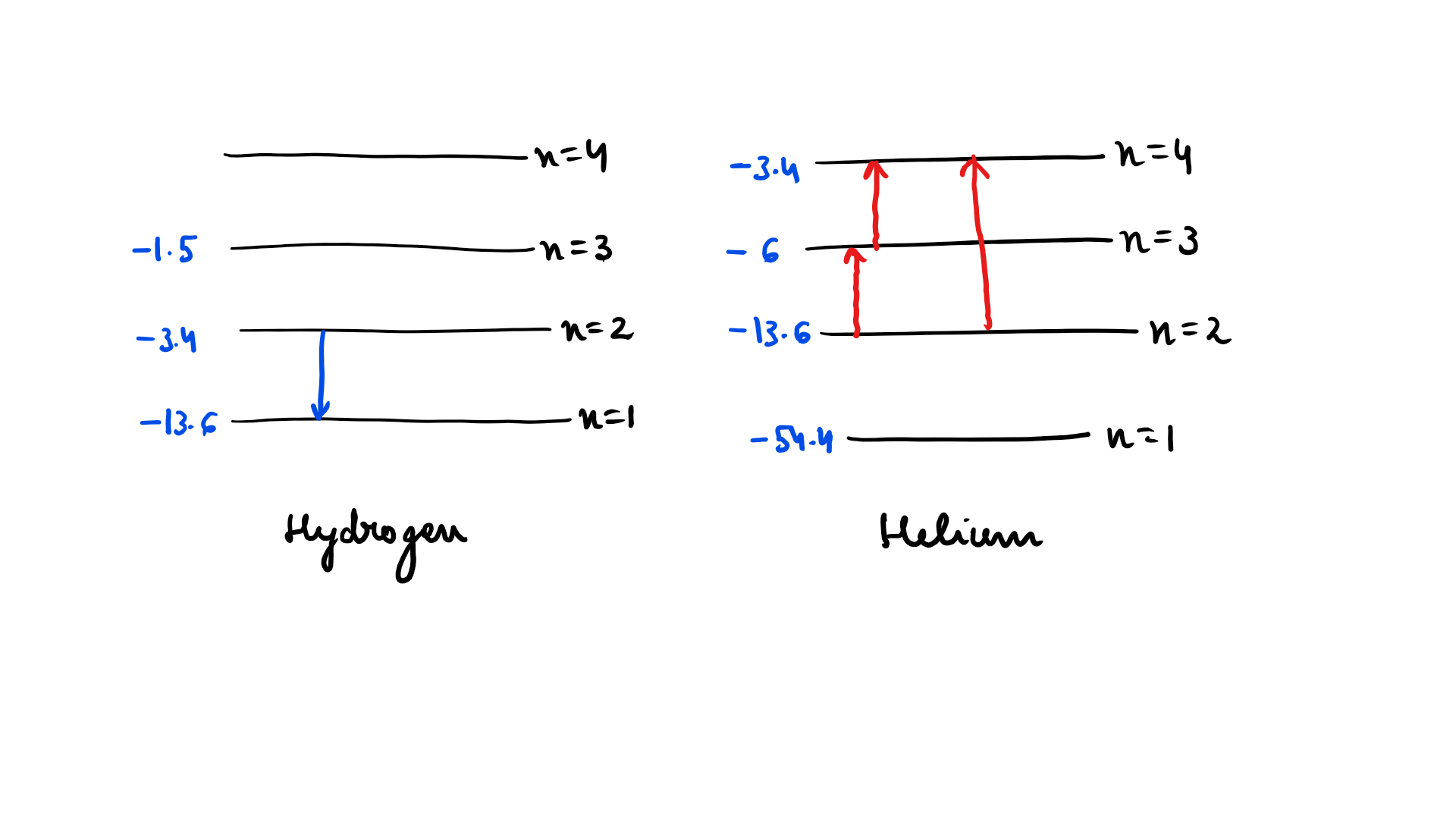
A $$100\space eV$$ electron collides with a stationary helium ion $$(He^+)$$ in its ground state and excites to a higher level. After the collision, $$He^+$$ ion emits two photons in succession with wavelengths $$1085\mathring{A}$$ and $$304\mathring{A}$$. Find the principal quantum number of the excited state. Also, calculate the energy of the electron after the collision. Given $$h = 6.63\times10^{-34}J\space s$$.
The electron in a hydrogen atom makes a transition $$n_1\rightarrow n_2$$, where $$n_1$$ and $$n_2$$ are the principal quantum numbers of the two energy states. Assume Bohr's model to be valid. The time period of the electron in the initial state is eight times that in the final state. What are the possible values of $$n_1$$ and $$n_2$$?
During Rutherford's experiment, generally, the thin foil of heavy atoms like gold was used and bombarded by the $$\alpha$$-particles. If the thin foil of light atoms like aluminium etc. is used, what difference would have been observed?
Using Bohr's postulates derive the expression for the frequency of radiation submitted when electron in hydrogen atom undergoes transition from higher energy state (quantum number $$n_{i}$$) to the lower state, $$(n_{f})$$
when electron in hydrogen atom jumps from energy state $$n_i=4 \;to\; n_f=3,2,1$$. Identify the special series to which the emission lines holding belong.
State the postulates of Bohr atom model. Obtain an expression for the radius of the $$n$$th orbit of hydrogen atom.
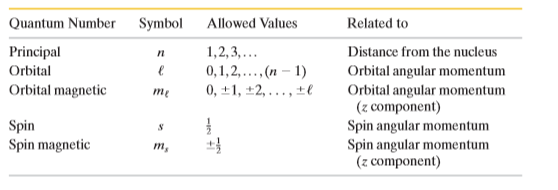
(a) How many sub-shells are associated with n = 4 ?
(b) How many electrons will be present in the sub-shells having $$m_s$$ value of -1/2 for n = 4 ?
State two ways of providing energy to a metal to emit electrons from its surface.
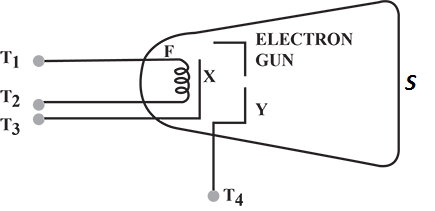
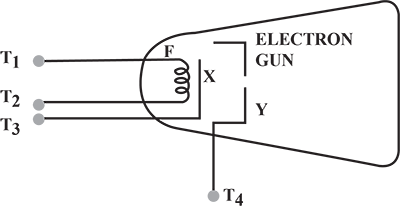
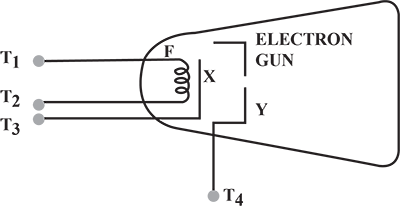
Diagram shows an electron gun inside a cathode ray tube. Label the screen with the letter S.
How is a cathode ray tube used to convert an electric signal into a visual signal ?
State two uses of a cathode ray tube.
Name one device in which the cathode ray tube is used.
What is the effect on the thermion beam in a cathode ray tube if the anode voltage value is reduced but remains above zero?
Can we use a screen coated with barium platinocyanide in a cathode ray tube? If so what effects do we observe on the screen?
Name spectral series of hydrogen which lies in the ultraviolet region of electromagnetic spectrum.
Name a common device where a hot cathode ray tube is used.
Draw a simplified labelled diagram of a hot cathode ray tube.
(i) In a cathode ray tube what is the function of anode?
(ii) State the energy conversion taking place in a cathode ray tube.
(iii) Write one use of cathode ray tube.
Name the three main parts of a Cathode Ray Tube.
Name a material which exhibits fluorescence when cathode rays fall on it.
Answer the following question based on a hot cathode ray tube. Name the charged particles.
Define Bohr's orbit or stationary orbit.
Explain different types of spectral lines?
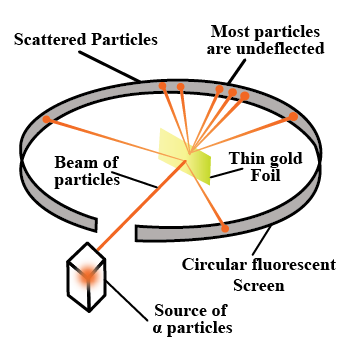
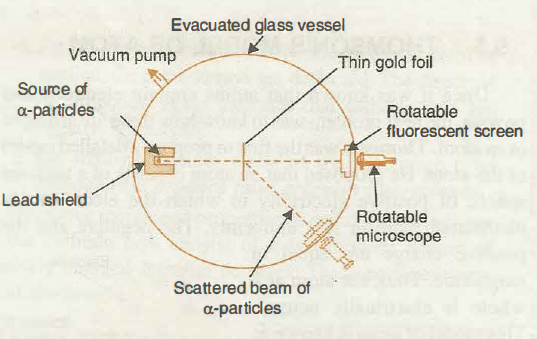
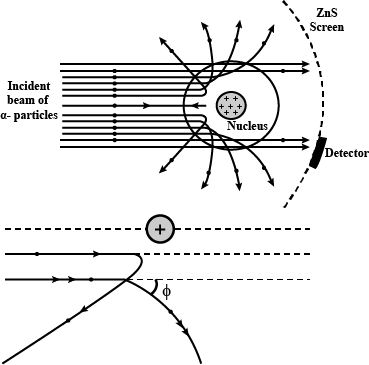
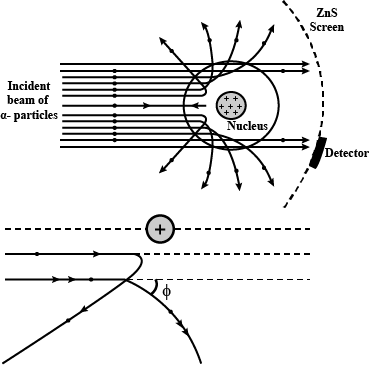
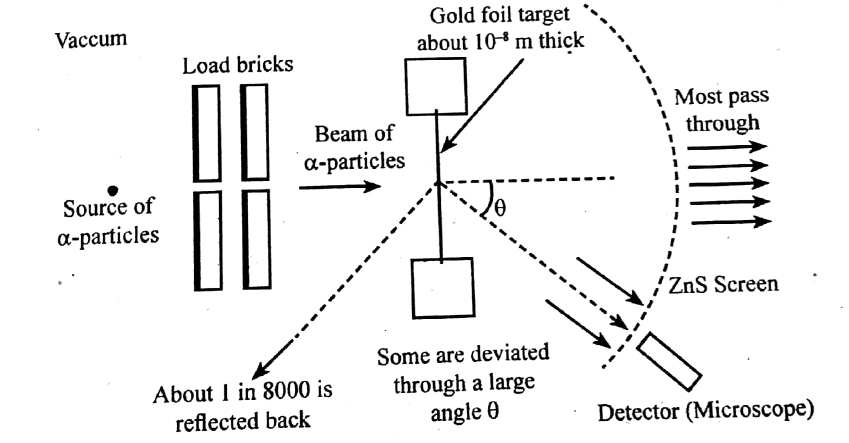
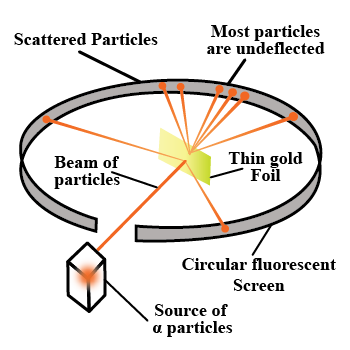
With the help of neat diagram, describe the Geiger-Marsden experiment.
What is photon?
In a cathode ray tube, why is the filament made of tungsten?
Diagram shows an electron gun inside a cathode ray tube. You have two batteries one of 6 V and other of 1000 V. Show on the diagram how to connect these batteries between the terminals $$T_1,\, T_2,\, T_3,\, and\, T_4$$ in order to produce an electron beam from the gun.
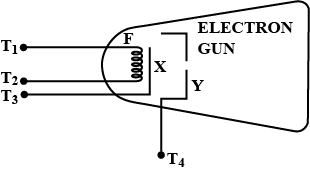
In a cathode ray tube, why is the cathode coated with thorium and carbon?
An electron in $$nth$$ excited state in a hydrogen atom comes down to first excited state by emitting ten different wavelengths. Find the value of $$n$$ (an integer).
Diagram shows an electron gun inside a cathode ray tube. Draw a pair of plates $$P_1\, and\, P_2$$ to apply the electric field in the diagram and show the deflection of the particles emitted by X in between the plates $$P_1\, and P_2$$.
Draw a neat and well labelled diagram of Rutherford's $$\alpha-$$ particle scattering experiment.
The radius of the innermost electron orbit of a hydrogen atom is $$5.3 \times 10^{-11}$$ m. Calculate the radius of n = 3 orbit of the same atom.
Obtain the first Bohrs radius and the ground state energy of a muonic hydrogen atom [i.e., an atom in which a negatively charged muon $$(\mu ^-)$$ of mass about $$207m_e$$ orbits around a proton].
Suppose you are given a chance to repeat the alpha-particle scattering experiment using a thin sheet of solid hydrogen in place of the gold foil. (Hydrogen is a solid at temperatures below 14 K.) What results do you expect?
In the study of Geiger-Marsdon experiment on scattering of $$\alpha-particles$$ by a this foil of gold, draw the trajectory of $$\alpha-particles$$ in the coulomb field of target nucleus. Explain briefly how one gets the information on the size of the nucleus from this study:
From the relation $$R = R_{0}A^{1/3}$$, where $$R_{0}$$ is constant and A is the mass number of the nucleus, show that nuclear matter density is independently of A
With the help of a neat labelled diagram, describe the Geiger- Marsden experiment. What is mass defect ?
The photoelectric work function for a metal surface is 2.3 eV. If the light of wavelength $$ 6800\ A^\circ$$ is incident on the surface of metal find threshold frequency and incident frequency. Will there be an emission of photoelectrons or not ?
[Velocity of light c = $$3 \times 10^8 m/s$$, Planck's constant, $$h=6\cdot 63 \times 10^{-34 }Js$$]
When the sun is directly overhead, the surface of the earth receives $$1.4\times {10}^{3}W$$ $${m}^{-2}$$ of sunlight. Assume that the light is monochromatic with average wavelength $$500nm$$ and that no light is absorbed in between the sun and the earth's surface. The distance between the sun and the earth is $$1.5\times {10}^{11}m$$ (a) Calculate the number of photons falling per second on each square metre of earth's surface directly below the sun (b) How many photons are there in each cubic metre near the earth's surface at any instant? (c) How many photons does the sun emit per second?
The earth revolves around the sun due to gravitational attraction. Suppose that the sun and the earth are point particles with their existing masses and that Bohr's quantization rule for angular momentum is valid in the case of gravitation. (a) Calculate the minimum radius the earth can have for its orbit. (b) What is the value of the principal quantum number n for the present?
Using Bohr's atomic model, derive an equation for radius of orbit of an electron.
In a process a neutron which is initially at rest, decays into a proton, an electron and an antineutrino. The ejected electron has a momentum of $$ p_1 = 2.4 \times 10^{-26} kg m/s $$ and the antineutrino has $$ p_2 = 7.0 \times 10^{-27} kg m/s $$ . Find the recoil speed of the proton if the electron and the antineutrino are ejected (a) along the same direction (b) in mutually perpendicular directions (Mass of the proton $$m_p = 1.67 \times 10^{-27} $$ )
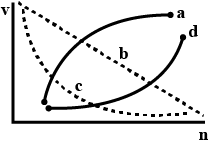
Which of the following curves may represent the speed of the electron in a hydrogen atom as a function of the principal quantum number n?
In an experiment on $$\alpha$$-particle scattering by a thin foil of gold, draw a plot showing the number of particles scattered versus the scattering angle $$\theta$$. Why is it that a very small fraction of the particles are scattered at $$\theta > 90^\circ$$?
Describe the Geiger-Marsden experiment. What are Its observations and conclusions?
Show that if the 63 electrons in an atom of europium were assigned to shells according to the logical sequence of quantum numbers, this element would be chemically similar to sodium.
(A correspondence principle problem.) Estimate (a) the quantum number $$l$$ for the orbital motion of Earth around the Sun and (b) the number of allowed orientations of the plane of Earths orbit. (c) Find $$ \theta_{min}$$ the half-angle of the smallest cone that can be swept out by a perpendicular to Earths orbit as Earth revolves around the Sun.
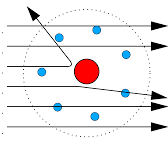
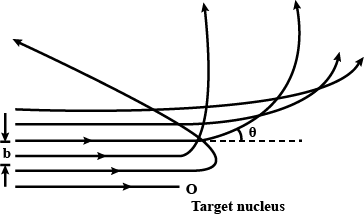
The trajectories, traced by different $$\alpha$$-particles, in the Geiger-Marsden experiment were observed as shown in the figure.
(i) What names are given to the symbols b and $$\theta$$ shown here?
(ii) What can we say about the values of b for (i) $$\theta = 0^\circ$$ (ii) $$\theta = 0^\circ$$ = p radians?
The spectrum of a star in the visible and the ultraviolet region was observed and the wavelength of some of the lines that could be identified was found to be:
$$824\, \overset{\circ}{A}, 970\, \overset{\circ}{A}, 1120\, \overset{\circ}{A}, 2504\, \overset{\circ}{A}, 5173\, \overset{\circ}{A}, 6100\, \overset{\circ}{A}$$
Which of these lines cannot belong to the hydrogen atom spectrum? (Given Rydbergconstant $$R = 1.03 \times 10^7\,m^{-1}$$ and $$\dfrac{1}{R}= 970 \,\overset{\circ}{A}$$. Support your answer with suitable calculations.
Answer the following question, which help you understand the difference between Thomson's model and Rutherford's model better.
In which model is it completely wrong to ignore multiple scattering for the calculation of a average angle of scattering of a particles by a thin foil?
Answer the following question, which help you understand the difference between Thomson's model and Rutherford's model better.
Keeping other factors fixed, it is found experimentally that for small thickness $$t$$, the number of $$\alpha$$-particles scattered at moderate angles is proportional to $$t$$. What clue does this linear dependence on $$t$$ provide?
Describe Rutherford's experiment on scattering of $$\alpha$$-particles. How do it help in discovery of nucleus ?
The only partially filled subshell of a certain atom contains three electrons, the basic term of the atom having $$L = 3$$. Using the Hund rules, write the spectral symbol of the ground state of the given atom.
How many and which values of the quantum number J can an atom possess in the state with quantum numbers S and L equal respectively to
(a) $$2$$ and $$3$$; (b) $$3$$ and $$3$$; (c) $$5/2$$ and $$2$$?
Write the spectral designation of the term whose degeneracy is equal to seven and the quantum numbers L and S are interrelated as $$L = 3S$$.
Write the spectral symbols for the terms of a two-electron system consisting of one p electron and one d electron.
Write the spectral designations of the terms of the hydrogen atom whose electron is in the state with principal quantum number $$n = 3$$.
An atom is in the state whose multiplicity is three and the total angular momentum is $$ h\sqrt{20} $$. What can the corresponding quantum number L be equal to ?
An atom possessing the total angular momentum $$h\sqrt{6} $$ is in the state with spin quantum number $$S = 1$$. In the corresponding vector model the angle between the spin momentum and the total angular momentum is $$ \theta = 73.2^{\circ} $$. Write the spectral symbol for the term of that state.
For an HF molecule find the number of rotational levels located between the zeroth and first excited vibrational levels assuming rotational states to be independent of vibrational ones. The natural vibration frequency of this molecule is equal to $$7.79\times 10^{14}$$ rad/s, and the distance between the nuclei is $$91.7\,pm$$.
A system comprises an atom in $$^{2}P_{3/2} $$ state and a d electron. Find the possible spectral terms of that system.
Find the ratio of the number of atoms of gaseous sodium in the state $$3P$$ to that in the ground state $$3S$$ at a temperature $$ T=2400\,K$$. The spectral line corresponding to the transition $$ 3P \rightarrow 3S$$ is known to have the wavelength $$ \lambda = 589\,nm$$.
(i) State bohr's quantization condition for defining stationary orbits. How does de broglie hypothesis explain the stationary orbits?
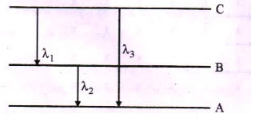
(ii) Find the relation between the three wavelengths $${ \lambda }_{ 1 }$$,$${ \lambda }_{ 2 }$$ and $${ \lambda }_{ 3 }$$ from the energy level diagram shown below.
Show that the radius of the orbit in hydrogen atoms varies as $$\displaystyle { n }^{ 2 }$$, where n is the principal quantum number of the atom.
(a) Using Bohr's second postulate of quantization of orbital angular momentum show that the circumference of the electron in the $$n^{th}$$ orbital state in hydrogen atom is n times the de Broglie wavelength associated with it.
(b) The electron in hydrogen atom in initially in the third excited state.What is the maximum number of spectral lines which can be emitted.When it finally moves to the ground state?
Passing down to the ground state, excited $$Ag^{109}$$ nuclei emit either gamma quanta with energy $$87\,keV$$ or K conversion electrons whose binding energy is $$26\,keV$$. Find the velocity of these electrons.
On the basis of Bohr's theory, derive an expression for the radius of the of the $$n^{th}$$ orbit of an electron of hydrogen atom.
Obtain an expression for the radius of Bohr orbit for $$H$$-atom.
Calculate the radius of second Bohr orbit in hydrogen atom from the given data.
Mass of electron= $$9.1\times { 10 }^{ -31 }Kg$$
Charge on the electron$$=1.6\times { 10 }^{ -19 }C$$
Planck's constant=$$6.63\times { 10 }^{ -34 }J-s$$
Permitivitty of free space = $$\quad 8.85\times { 10 }^{ -12 }{ C }^{ 2 }/N{ m }^{ 2 }\quad $$
Find the value of energy of electron in eV in the third Bohr orbit of hydrogen atom.
(Rydberg's constant $$\left(R\right)=1.097 \times {10}^{7}{m}^{-1}$$
Planck's constant $$\left(h\right)=6.63 \times {10}^{-34}J-s$$,
Velocity of light in air $$\left(c\right)=3 \times {10}^{8}{m}/{s}$$).
What conclusion was drawn by Rutherford based on Geiger-Marsden's experiment on scattering of alpha particles?
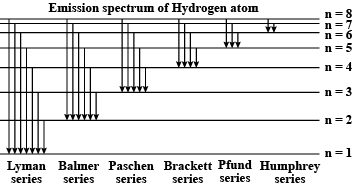
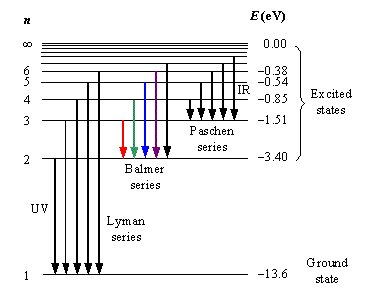
Explain the spectral series of hydrogen atom (diagram not necessary).
When a vapour is excited at low pressure by passing an electric current through it, a spectrum is obtained.
a) Draw a spectral series of emission lines in hydrogen.
b) Name the different series of hydrogen atom.
c) In which region Lyman series is located.
Answer the following question based on a hot cathode ray tube. State the approximate voltage used to heat the filament.
The electron in the hydrogen atom is moving with a speed of $$2.3 \times 10^6 m/s$$ in an orbit of radius $$0.53 \mathring{A}$$. Calculate the period of revolution of electron. ($$\pi = 3.142$$)
Draw the diagram representing the schematic arrangement of the Geiger-Marsdon experimental setup tor the alpha particle scattering.
(a) Write the $$\beta-decay$$ of tritium in symbolic from.
(b) Why is it experimentally found difficult to detect neutrinos in this process?
Radiation coming from transitions $$n=2$$ to $$n=1$$ of hydrogen atoms falls on helium ions in $$n=1$$ and $$n=2$$ states. What are the possible transition of helium ions as they absorb energy from the radiation ?
In a mixture of H - $$He^+ $$ gas ($$He^+$$ is singly ionized He atom). H atoms and $$He^+$$ ions are excited to their respective first excited states. Subsequently, H atoms transfer their total excitation energy to $$He^+$$ ions (by collisions ). Assume that the Bohr model of is atom exactly valid.
A radiation of wavelength $$\lambda$$ is incident on a metal surface having $$ 620 nm$$ threshold wavelength. The stopping potential of the electron emitted is $$4.9 V$$. What is the value of $$\lambda$$ (in nm)?
Describe Rutherford's atomic model.
A proton and an alpha particle having the same kinetic energy are allowed to pass through a uniform magnetic field perpendicular to the direction of their motion. Compare the radii of the paths of proton and alpha particle.
What is the wavelength of light emitted when the electron in hydrogen atom undergoes transition from an energy level with n=4 to an energy level with n=2 ? What is the colour of the radiation ?
The energy of a photon is equal to $$3$$ kilo $$eV$$. Calculate its linear momentum.
which an electron in hydrogen atom jumps from the third excited state to the ground state
A beam of light having wavelengths distributed uniformly between 450 nm to 550 nm passes through a sample of hydrogen gas. Which wavelength will have the least intensity in the transmitted beam?
What is the effective mass of photon having wavelength $$\lambda$$?
The wavelength of $$H_\alpha$$ line Balmer's series of hydrogen spectrum is $$6563 \ \mathring{A}$$. Find the:
(i) Wavelength of $$H_ \gamma$$ (gamma) line of Balmer series.
(ii) Shortest wavelength of Bracket series.
A hydrogen atom in a state having a binding energy of $$0.85\ eV$$ makes transition to a state with excitation energy $$10.2\ eV$$
Identify the quantum numbers $$n$$ of the upper and the lower energy states involved in the transition.
The transition from the state $$n=4$$ to $$n=3$$ in hydrogen-like atom results in ultraviolet radiation. Infrared radiation will be obtained in the transition from?
A photon collides with a stationary hydrogen atom in the ground state inelastically. The energy of the colliding photon is $$10.2$$ eV. After a time interval of the order of a microsecond, another photon collides with same hydrogen atom with an energy of $$15$$ eV. What will be observed by the detector?
Show that angular speed of electron in $${n}^{th}$$ Bohr's orbit is equal to :
$$ =\dfrac { \pi { me }^{ 4 } }{ { 2 }\epsilon _{ 0 }^{ 2 }{ h }^{ 3 }{ n }^{ 3 } }$$ or frequency of revolution, $$f=\dfrac { \pi { me }^{ 4 } }{ { 2 }\epsilon _{ 0 }^{ 2 }{ h }^{ 3 }{ n }^{ 3 } }$$
Obtain the expression for radius of $${n}^{th}$$ Bohr orbit and show that the radius is proportion to square of the principal quantum number.
Using expression for energy of electron, obtain the Bohr's formula for hydrogen spectral line.
In a sample of hydrogen-like atoms all of which are in the ground state, a photon beam containing photons of various energies is passed. In the absorption spectrum, five dark lines are observed. The number of bright lines in the emission spectrum will be (Assume that all transitions take place)
Using postulates of Bohr's theory of hydrogen atom, show that radii of orbits increases as $$n^2$$.
The angular speed of electron in the nth orbit of hydrogen atom is
Describe the drawback of Rutherford's model of atom.
Find the radius of a $$He^+$$ ion in the state $$n=1$$.
How many times does the electron go round the first orbit in a second?
Find the approximate number of molecules contained in a vessel of volume 7 liters at $$0^{\circ}C$$ at
If the atom $$_{100}Fm^{215}$$ follows Bohr's model and the radius of the 5th orbit of this atom is p times the Bohr radius, then the value of p is :
Find the ratio of diameter of electron in 1st Bohr orbit to that in 4th bohr orbit
Write three conclusions made by Rutherford based on the alpha particle scattering experiment.
What conclusion was drawn by Rutherford from his $$\alpha$$ -particle scattering experiment?
The Bohr's radius is given by $$a_{0}=\dfrac{\varepsilon_{0}h^{2}}{\pi me^{2}}$$. Verify that the RHS has dimensions of length.
What do you think would be the observation if the $$\alpha$$ particle scattering experiment is carried out using a foil of a metal other than gold?
What is the Rutherford's atomic model?
Enlist the conclusions drawn by Rutherford from his $$\alpha$$ ray scattering experiment.
Explain emission and absorption spectra
What will happen if instead of goldfoil, aluminium foil is used in the experiment of Rutherford's experiment of $$\alpha $$ scattering particle?
A hydrogen atom emits ultraviolet radiation of wavelength $$102.5 n m.$$ What are the quantum numbers of the states involved in the transition ?
Explain the conclusions of Rutherford's model of Atom.
Find the maximum Coulomb force that can act on the electron due to the nucleus in a hydrogen atom.
Find the radius and energy of a $$He^+$$ ion in the states (a) n = 1, (b) n = 4 and (c) n = 10.
(a) How many l values are associated with $$n =3$$ ? (b) How many $$m_l$$ values are associated with $$ l= 1$$?
An electron, trapped in a one-dimensional infinite potential
well $$250\ pm$$ wide, is in its ground state. How much energy must it
absorb if it is so jump up to the state with $$n=4?$$
A hydrogen atom is excited from its ground state to the state with $$n=4$$;
what are the highest
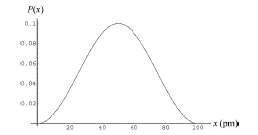
An electron is trapped in a one dimensional infinite potential well that is $$100\ pm$$ wide; the electron is in its ground state. What is the probability that you can detect the electron in an interval of width $$\Delta x=5.0\ pm$$ centered at $$x=$$
$$25\ pm$$
A one dimensional infinite well of length $$200\ pm$$ contains an electron in its third excited state. We position an electron detector probe of width $$2.00\ pm$$ so that it is centered on a point of maximum probability density.
What is the probability of detection by the probe?
Which scientist concluded that the size of the nucleus is very small as compared to the size of an atom?
How many electron states are there in the following shells: $$(a) n ! 4, (b) n ! 1, (c) n ! 3, (d) n ! 2$$?
A hydrogen atom is excited from its ground state to the state with $$n=4$$
How many different energies are possible
What are the frequency range of the Lyman series?
How many electron states are in these subshells:$$ (a) n = 4, l = 3; (b) n = 3, l = 1 ; (c) n = 4, l = 1 ; (d) n = 2, l =0$$ ?
An electron in a multielectron atom has $$m_l = +4$$ . For this electron, what are (a) the value of l , (b) the smallest possible value of n, and (c) the number of possible values of $$m_s$$?
State Bohrs quantization condition for defining stationary orbits.
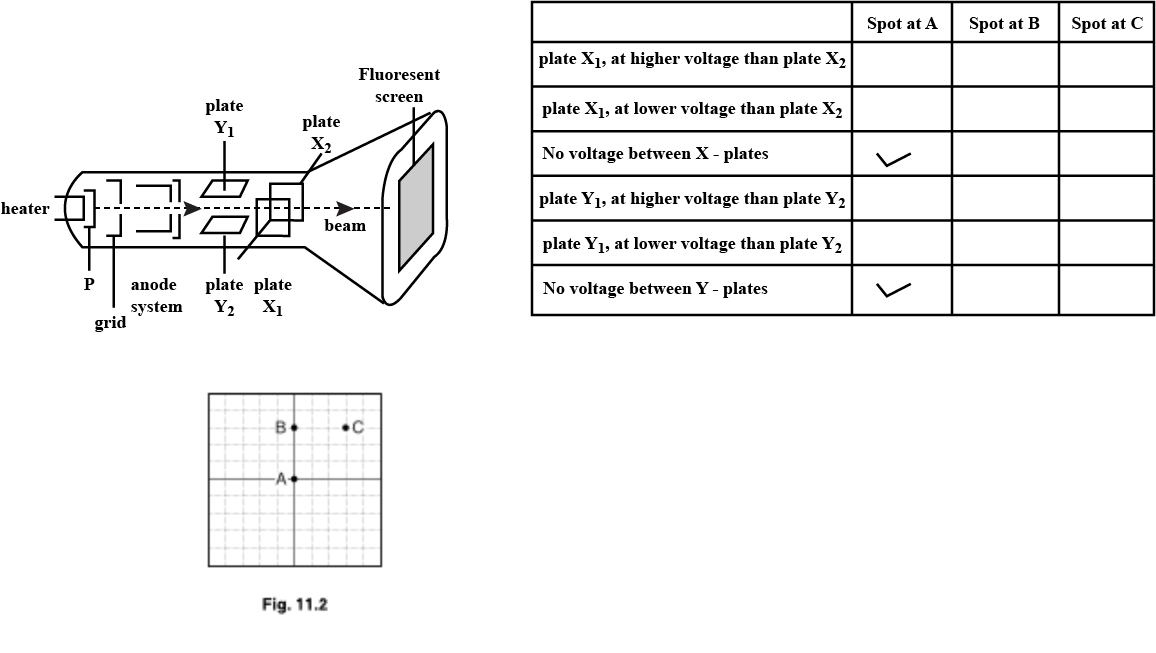
Figure shows the main components of a cathode-ray oscilloscope.
(a) (i) State the function of component P.
(ii) Tick one box to complete the sentence correctly.
A cathode-ray oscilloscope contains
$$\square$$ air at about five times normal atmospheric pressure.
$$\square$$ air at about normal atmospheric pressure.
$$\square$$ air at about one fifth of normal atmospheric pressure.
$$\square$$ a vacuum.
$$\square$$ neon gas.
(b) Fig. $$11.2$$ shows the front view of the screen of the cathode-ray oscilloscope.
With no voltage applied between the X-plates or between the Y-plates, the spot is at A.
(i) Places two ticks in each of the each of the table to describe the voltage across the plates when the spot is at points B and C. the column for the spot at A has been completed as an example.
(iii) Explain your answers for the spot at point B.
An electron is in a state with $$ n = 3$$. What are (a) the number of possible values of l , (b) the number of possible values of $$m_l$$, (c) the number of possible values of $$m_s$$, (d) the number of states in the $$n = 3$$ shell, and (e) the number of subshells in the $$ n = 3$$ shell?
In the subshell $$ l = 3$$ , (a) what is the greatest (most positive) $$m_l $$ value, (b) how many states are available with the greatest $$ m_l $$ value, and (c) what is the total number of states available in the subshell?
What is the ratio of radii of the orbits corresponding to the first excited state and ground state in a hydrogen atom?
Write the expression for Bohr's radius in the hydrogen atom.
The radius of the innermost electron orbit of a hydrogen atom is $$5.1 \times 10^{-11} m$$.What is the radius of the orbit in the second excited state?
Which part of atom was discovered by Rutherford.
Electric Potential and Potential Energy Due to Point Charges(35)
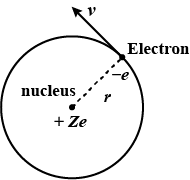
In 1911, Ernest Rutherford and his assistants Geigerand Marsden conducted an experiment in which they scattered alpha particles (nuclei of helium atoms) from thin sheets of gold. An alpha particle, having charge $$+2_e$$ and mass $$6.64 \times 10^{-27} \,kg$$, is a product of certain radio active decays. The results of the experiment led Rutherford to the idea that most of an atoms mass is in a very small nucleus, with electrons in orbit around it. (This is the planetary model of the atom, which well study in Chapter 42.) Assume an alpha particle, initially very far from a stationary gold nucleus, is fired with a velocity of $$2.00 \times 10^7 \,m/s$$ directly toward the nucleus $$(charge +79_e)$$. What is the smallest distance between the alpha particle and the nucleus before the alpha particle reverses direction? Assume the gold nucleus remains stationary.
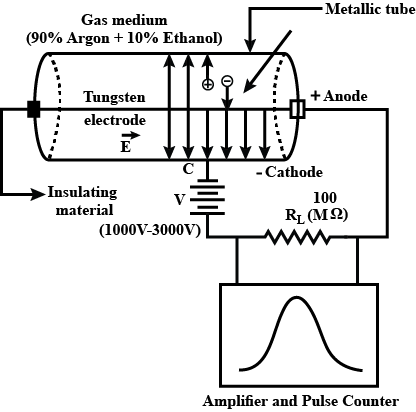
Explain the construction and working of a Geiger-Muller Counter.
How was it shown that atom has empty space?
Explain Rutherford-Soddy law.
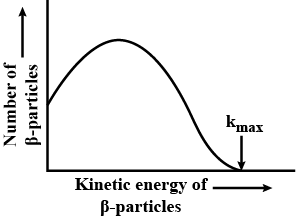
Out of which, $$\alpha$$ and $$\beta$$ rays, has wide spectrum?
Out of which, $$\alpha$$ and $$\beta$$ rays, has wide spectrum ?
What does it mean when we say that $$\beta$$-ray spectrum is a continuous energy spectrum ?
Choose the correct alternatives from the clues given at the end of the each statement:
The positively charged part of the atom possess most of the mass in ..................
(Rutherford's model / both the models)
The radius of $$1^{st}$$ electron orbit of hydrogen atom is $$5.3\times 10^{-11}m$$. What is the radius of $$2^{nd}$$ orbit?
What is the ratio of radii of the orbits corresponding to first excited state and ground state of hydrogen atom?
Suppose you are given a chance to repeat the alpha-particle scattering experiment using a thin sheet of solid hydrogen in place of the gold foil. (Hydrogen is a solid at temperatures below $$14K$$.) What results do you expect?
In accordance with the Bohr's model, find the quantum number that characteristics the earth's revolution around the sun in an orbit of radius $$1.5\times 10^{11}m$$ with orbital speed $$3\times10^{4}m/s$$. (Mass of earth = $$6.0\times10^{24}$$).
Choose the correct alternatives from the clues given at the end of the each statement:
An atom has a nearly continuous mass distribution in a ............. but has a highly non-uniform mass distribution in.
(Thomson's model / Rutherford's model)
When a beryllium metal is bombarded with an alpha particle, a new element carbon is produced. But when a gold plate is bombarded with an alpha particle, no new element is produced. Why?
Why the atomic spectrum of an element is called the finger print of that element?
Based on Rutherford’s model of an atom, which sub-atomic particles are present in the nucleus of an atom?
Consider the possible vibrations modes in the following linear molecules:
(a) $$CO_2 (O - C - O) $$; (b) $$C_2H_2 (H - C - C - H) $$
Is it possible for a hydrogen $$(_1^1 H)$$ nucleus to emit an alpha particle? Give a reason for your answer.
Calculate for a hydrogen atom and a $$He^+$$ ion:
(a) the radius of the first Bohr orbit and the velocity of an electron moving along it;
(b) the kinetic energy and the binding energy of an electron in the ground state;
(c) the ionization potential, the first excitation potential and the wavelength of the resonance line $$(n' = 2 \rightarrow n = 1) $$.
Evaluate how many lines there are in a true rotational spectrum of CO molecules whose natural vibration frequency is $$ \omega = 4.09 \times 10^{14}\,s^{-1}$$ and moment of inertia $$I = 1.44 \times 10^{-39} \, g\cdot cm^{2}$$.
The difference between $$(n+2)^{th}$$ Bohr radius and $$n^{th}$$ Bohr radius is equal to the $$(n-2)^{th}$$ Bohr radius. The value of $$n$$ is:
The difference between $$\left ( n+2 \right )^{th}$$ Bohr radius and $$n^{th}$$ Bohr radius is equal to the $$\left ( n-2 \right )^{th}$$ Bhor radius. The value of $$n$$ is ?
(a) Using Bohr's postulates, obtain the expression for total energy of the electron in the $${n}^{th}$$ orbit of hydrogen atom.
(b) What is the significance of negative sign in the expression for the energy?
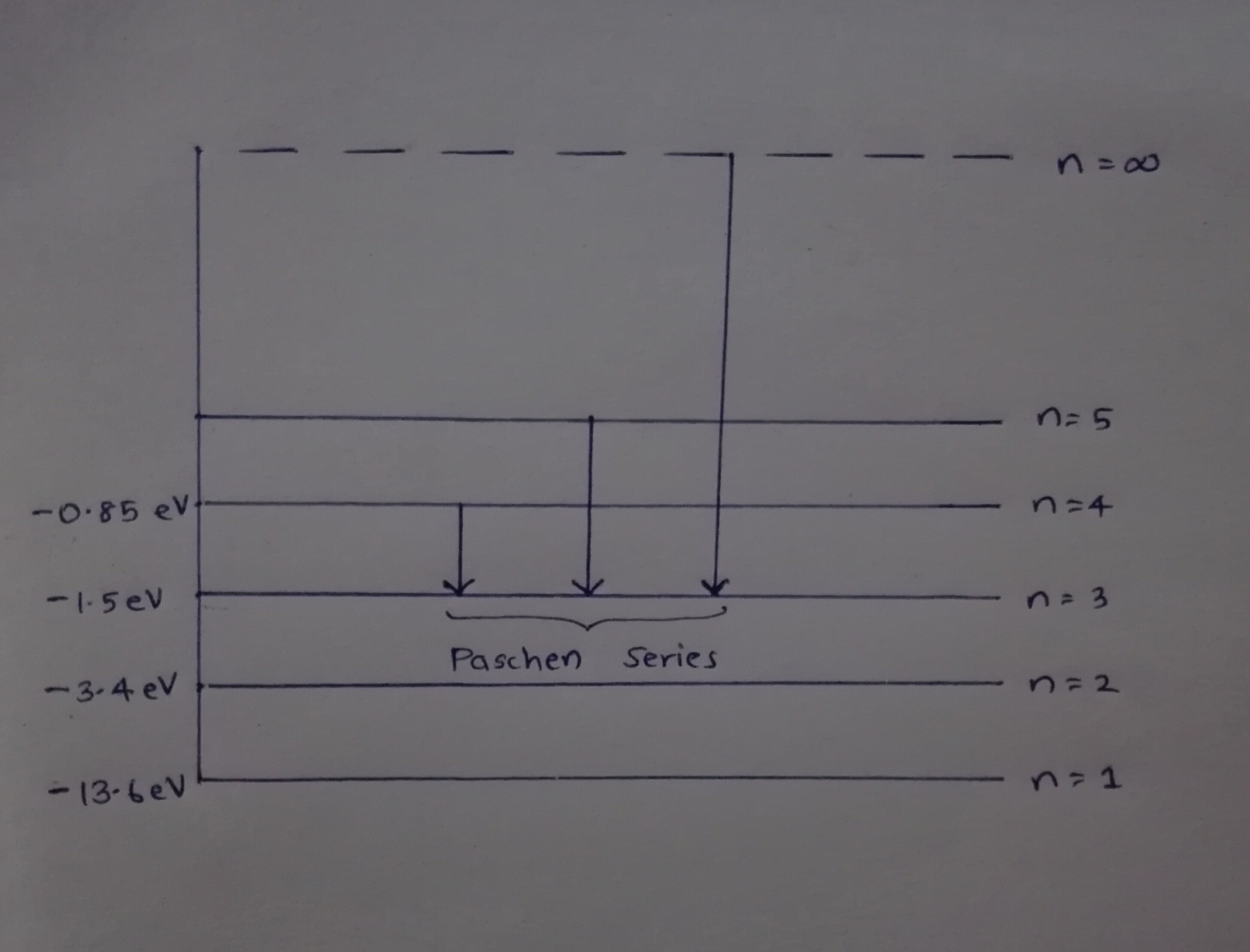
(c) Draw the energy level diagram showing how the line spectra corresponding to Paschen series occur due to transition between energy levels.
The fraction occupied by nucleus in an atom is _________.
Define intensity of radiation on the basis of photon picture of light. Write its S.I. unit.
Using Bohr's postulates of the atomic model, derive the expression for radius of n$$^{th}$$ electron orbit. Hence obtain the expression for Bohr's radius.
Rutherford's experiment of scattering of $$\alpha-$$particles showed for the first time that the atom has ________.
True or False
Rutherford's atomic model was successful in explaining stability of the atom.
In Rutherford's $$\alpha$$-ray scattering experiment method:(1) Some rays were completely deflected back. (2) Most of the rays passed straight. Give reasons for the above observations.
(2) Most of the rays passed straight.
Give reasons for the above observations.
In a cathode ray tube, state:
(i) the purpose of covering cathode by thorium and carbon.(ii) the purpose of the fluorescent screen.(iii) how is it possible to increase the rate of emission of electrons.
$$(i)$$ Why is a cathode ray tube evacuated to a low pressure?
$$(ii)$$ What happens if the negative potential is changed on a grid?
Wavelengths of the first lines of the Lyman series, Paschen series and Balmer series in hydrogen spectrum are denoted by $$\lambda _L ,\lambda _P \,\, and \,\,\lambda _B$$ respectively. Arrange these wavelength in increasing order.
Explain emission and absorption spectra.
Explain the different types of spectral series in a hydrogen atom.
The short wavelength limit for the Lyman series of the hydrogen spectrum is $$913.4\overset{o}{A}$$. Calculate the short wavelength limit for Balmer series of the hydrogen spectrum.
Calculate the shortest and longest wavelengths of Balmer series of hydrogen atom. Given $$R=1.097\times 10^7m^{-1}$$.
Write the different types of Hydrogen Spectral series. The Lyman series of Hydrogen spectrum lies in the ultraviolet region. Why?
Name the phenomenon which shows the quantum nature of electromagnetic radiation.
What is the nuclear radius of $$_{ 4 }^{ }{ { Be }^{ 8 } }$$ nucleus?
By assuming Bohr's postulates derive an expression for radius of $$n^{th}$$ orbit of electron, revolving round the nucleus of hydrogen atom.
If the Bohr model of hydrogen atom, the electron is treated as a particle going in a circle with the centre at the proton. The proton itself is assumed to be fixed in an inertial frame. The centripetal force is provided by the Coloumb attraction. In the ground state, the electron goes round the proton in a circle of radius $$5.3 \times 10^{-11} m $$ . Find the speed of the electron in the ground state. Mass of the electron $$ = 9.1 \times 10^{-31} kg $$ and charge of the electron $$ = 1.6 \times 10^{-19} C $$
The terminology of different parts of the electromagnetic spectrum is given in the text. Use the formula $$E=hv$$ (for energy of a quantum of radiation photon) and obtain the photon energy in units of $$eV$$ for different parts of the electromagnetic spectrum. In what ways are the different scales of photon energies that you obtain related to the sources of electromagnetic radiation.?
Find the shortest wavelength in Paschen series if, the longest wavelength in Balmer series is 6563 $$A^0$$
Explain Rutherford's $$\alpha$$-ray scattering experiment with a neat diagram.
Explain the significance of quantum number?
What are the postulates of Rutherford? What are his drawbacks ?
Using Bohr's postulates, derive the expression for the total energy of the electron revolving in nth orbit of hydrogen atom. Find the wavelength of $$ H_{\alpha} $$ line, given the value of Rybderg constant, $$ R = 1.1 \times 10^7m^{-1} $$
A hydrogen atom in a state having a binding energy of $$0.85\ eV$$ makes transition to a state with excitation energy $$10.2\ eV$$
Find the wavelength of the emitted radiation.
An electron in hydrogen atom stays in 2nd orbit for $$10 ^ { - 8 }$$ . How many, revolutions will it make till it jumps to the ground state ?
An electron in a multielectron atom is known to have the quantum number $$l = 3$$. What are its possible $$n, m_l, and m_s $$ quantum numbers?
For a helium atom in its ground state, what are quantum numbers $$ ( n,\ l,\ m_l,\ $$ and $$m_s ) $$ for the (a) spin-up electron and (b) spin-down electron?
A recently named element is darmstadtium (Ds), which has 110 electrons. Assume that you can put the 110 electrons into the atomic shells one by one and can neglect any electron electron interaction. With the atom in ground state, what is the spectroscopic notation for the quantum number l for the last electron?
An electron is trapped in a one-dimensional infinite well
and is in its first excited state. Fig. indicates the five longest
wavelengths of light that the electron could absorb in transitions
from this initial state via a single photon absorption: $$\lambda_a=80.78\ nm,\lambda_b=33.66\ nm, \lambda_c=19.23\ nm, \lambda_d=12.62\ nm, $$ and $$\lambda_e=8.98\ nm$$.
What is the width of the potential well?

Two of the three electrons in a lithium atom have quantum numbers $$ (n, l, m_l, m_s )$$ of $$(1,0,0, \frac {+1}{2})$$and $$(1,0,0, \frac {-1}{2}) $$. What quantum numbers are possible for the third electron if the atom is (a) in the ground state and (b) in the first excited state?
Show that the number of states with the same quantum number n is $$2n^2$$.
How many electron State are there in a shell defined by the quantum number $$n= 5$$?
A narrow beam of alpha particles with kinetic energy $$1.0\ MeV $$ falls normally on a platinum foil $$1.0\ \mu m $$ thick. The scattered particles are observed at an angle of $$60^{\circ}$$ to the incident beam direction by means of a counter with a circular inlet area $$1.0\ cm^2 $$ located at the distance $$10\ cm$$ from the scattering section of the foil. What fraction of scattered alpha particles reaches the counter inlet ?
The gravitational attraction between electron and proton in a hydrogen atom is weaker than the coulomb attraction by a factor of about $$10^{-10}$$. An alternative way of looking at this fact is to estimate the radius of the first Bohr orbit of a hydrogen atom if the electron and proton were bound by gravitational attraction. You will find the answer interesting.
Answer the following question, which help you understand the difference between Thomson's model and Rutherford's model better.
Is the probability of backward scattering (i.e, scattering of $$\alpha$$-particles at angles greater than $$90^{0}$$) predicted by Thomson's model much less, about the same, or much greater than that predicted by Rutherford's model?
The first line of the sharp series of atomic cesium is a doublet with wavelengths $$1358.8$$ and $$1469.5\,nm$$. Find the frequency intervals (in rad/s units) between the components of the sequent lines of that series.
Find the effective cross section of a uranium nucleus corresponding to the scattering of alpha particles with kinetic energy $$T = 1.5\ MeV$$ through the angles exceeding $$ \theta_{0} = 60^{\circ} $$.
A narrow beam of alpha particles with kinetic energy $$T = 0.50\ MeV $$ falls normally on a golden foil whose mass thickness is $$ \rho d = 1.5 mg/cm2$$. The beam intensity is $$I_{0} = 5.0 \times 10^{5} $$ particles per second. Find the number of alpha particles scattered by the foil during a time interval $$ \tau = 30\ min$$ into the angular interval
(a) $$59-61^{\circ} $$ ; (b) over $$ \theta_{0} = 60^{\circ} $$.
A narrow beam of alpha particles with kinetic energy $$T = 0.50\ MeV$$ and intensity $$I = 5.0 \times 10^5 $$ particles per second falls normally on a golden foil. Find the thickness of the foil if at a distance $$r = 15\ cm $$ from a scattering section of that foil the flux density of scattered particles at the angle $$\theta = 60^{\circ} $$ to the incident beam is equal to $$J = 40$$ particles/$$(cm^2 \cdot s)$$.
A narrow beam of protons with velocity $$ \nu = 6 \times 10^{6} m/s $$ falls normally on a silver foil of thickness $$ d = 1.0\, \mu m $$. Find the probability of the protons to be scattered into the rear hemisphere $$ (\theta > 90^{\circ}) $$
The effective cross section of a gold nucleus corresponding to the scattering of monoenergetic alpha particles within the angular interval from $$ 90^{\circ} $$ to $$180^{\circ} $$ is equal to $$ \Delta \sigma= 0.50\ kb$$. Find:
(a) the energy of alpha particles;
(b) the differential cross section of scattering $$ d \sigma / d \Omega $$ (kb/sr) corresponding to the angle $$ \theta = 60^{\circ} $$.
A narrow beam of alpha particle with kinetic energy $$ T = 900\, keV$$ falls normally on a golden foil incorporating $$ n = 1.1 \times 10^{19} $$ nuclei / $$cm^2$$. Find the fraction of alpha particles scattered through the angles $$ \theta < \theta_{0} = 20^{\circ} $$.
A particle of mass $$m$$ moves along a circular orbit in a centro-symmetrical potential field $$ U(r) = \dfrac{kr^2}{2}$$. Using the Bohr quantization condition, find the permissible orbital radii and energy levels of that particle.
Class 12 Medical Physics Extra Questions
- Alternating Current Extra Questions
- Atoms Extra Questions
- Current Electricity Extra Questions
- Dual Nature Of Radiation And Matter Extra Questions
- Electric Charges And Fields Extra Questions
- Electromagnetic Induction Extra Questions
- Electromagnetic Waves Extra Questions
- Electrostatic Potential And Capacitance Extra Questions
- Magnetism And Matter Extra Questions
- Moving Charges And Magnetism Extra Questions
- Nuclei Extra Questions
- Ray Optics And Optical Instruments Extra Questions
- Semiconductor Electronics: Materials, Devices And Simple Circuits Extra Questions
- Wave Optics Extra Questions