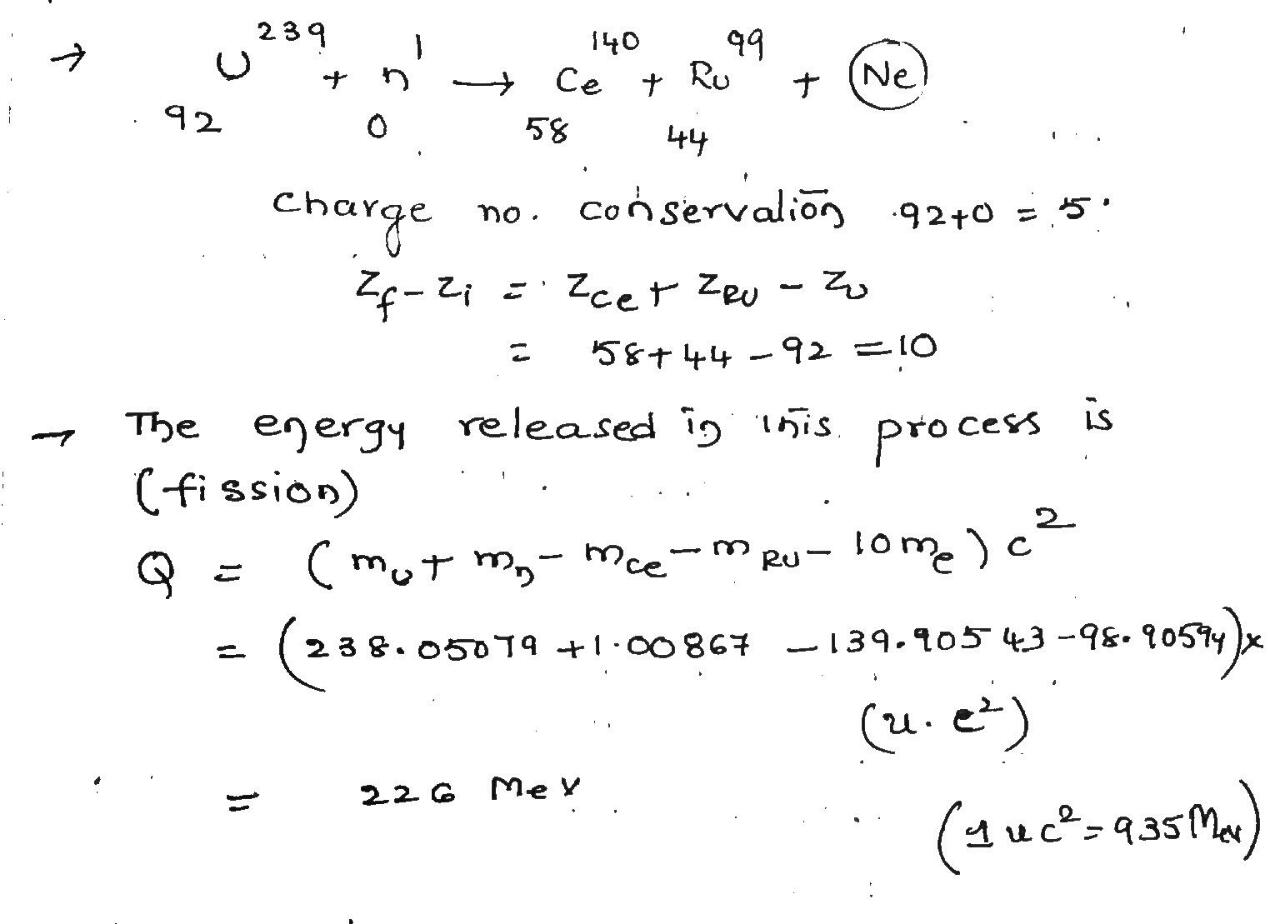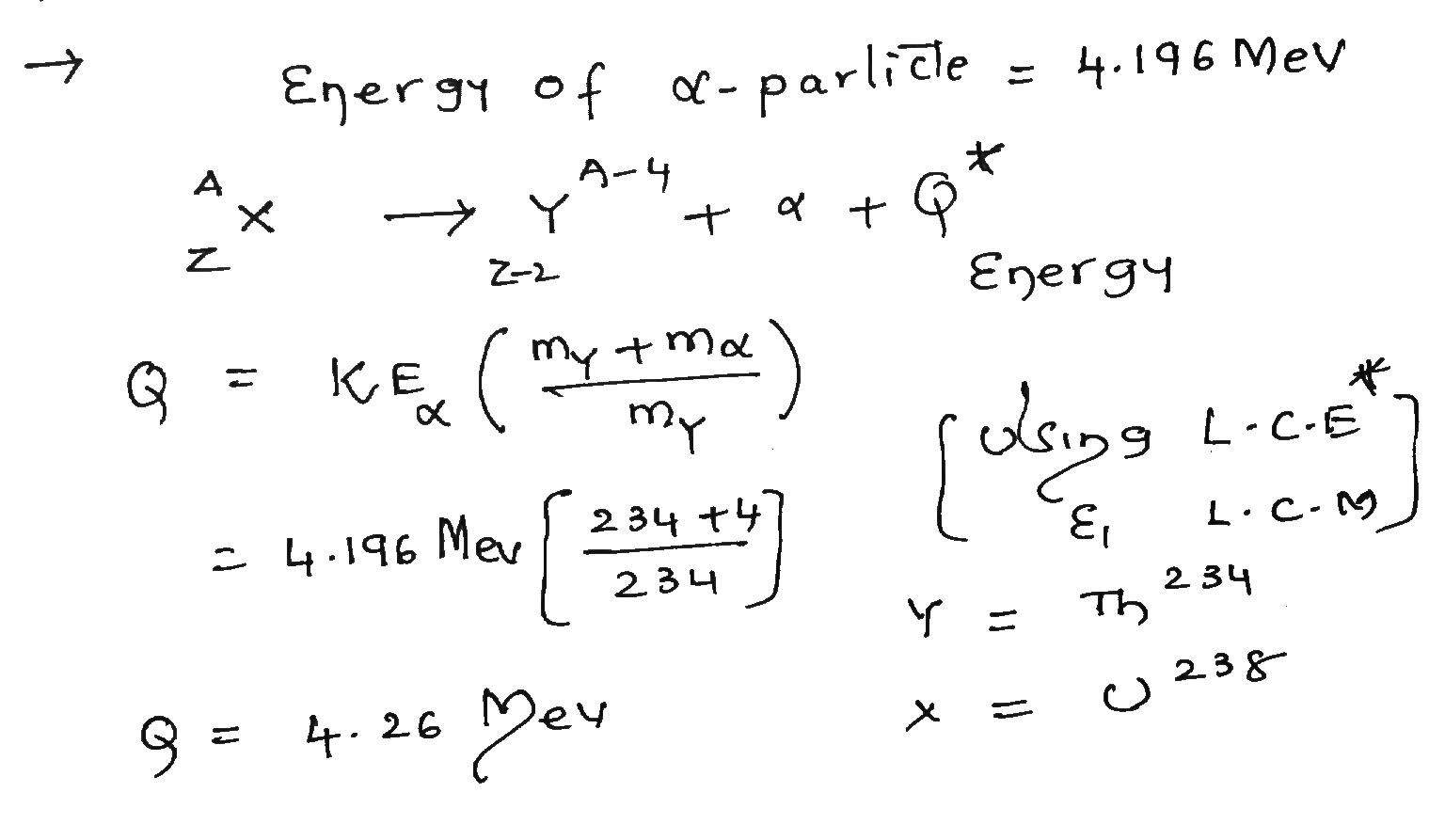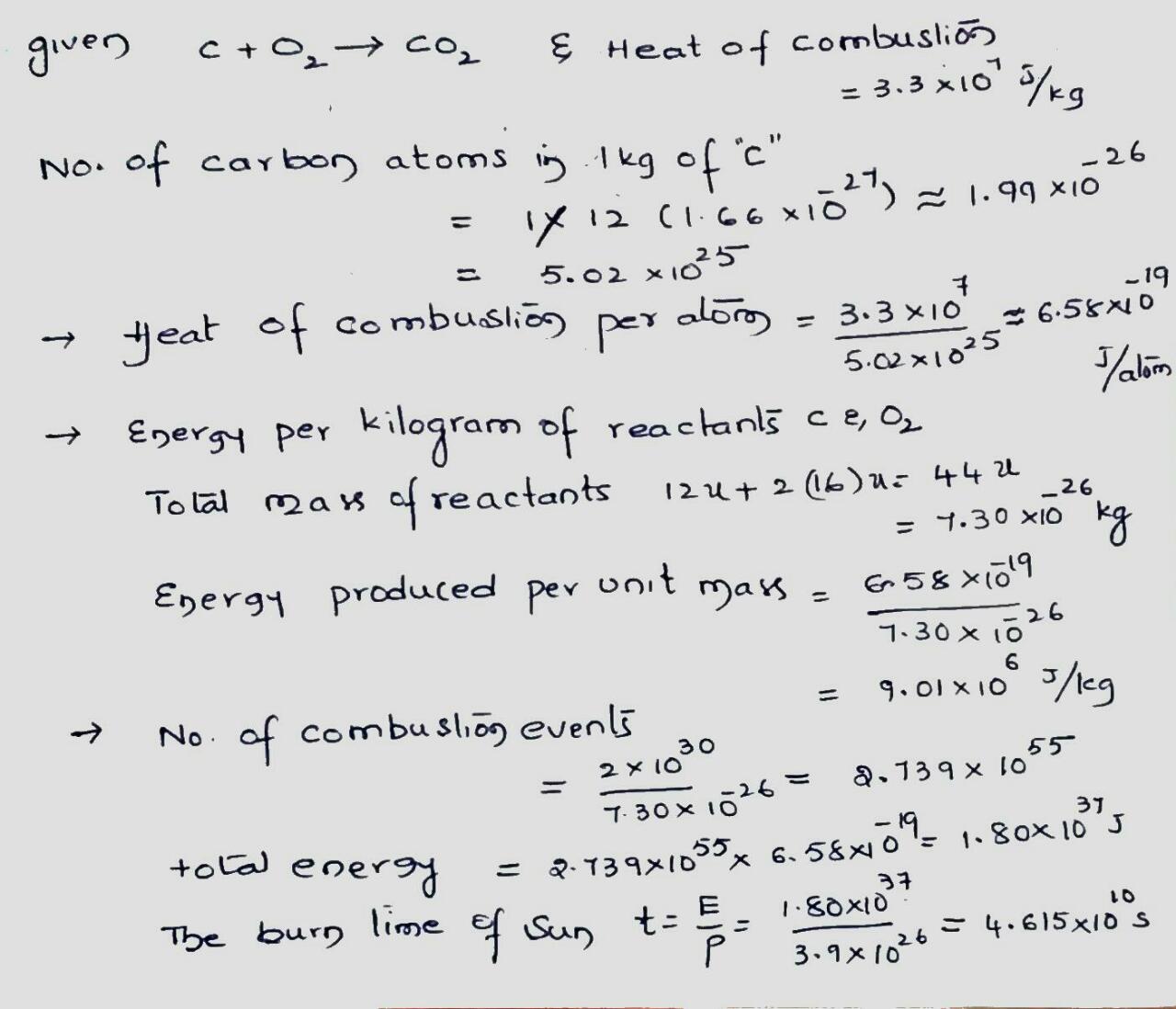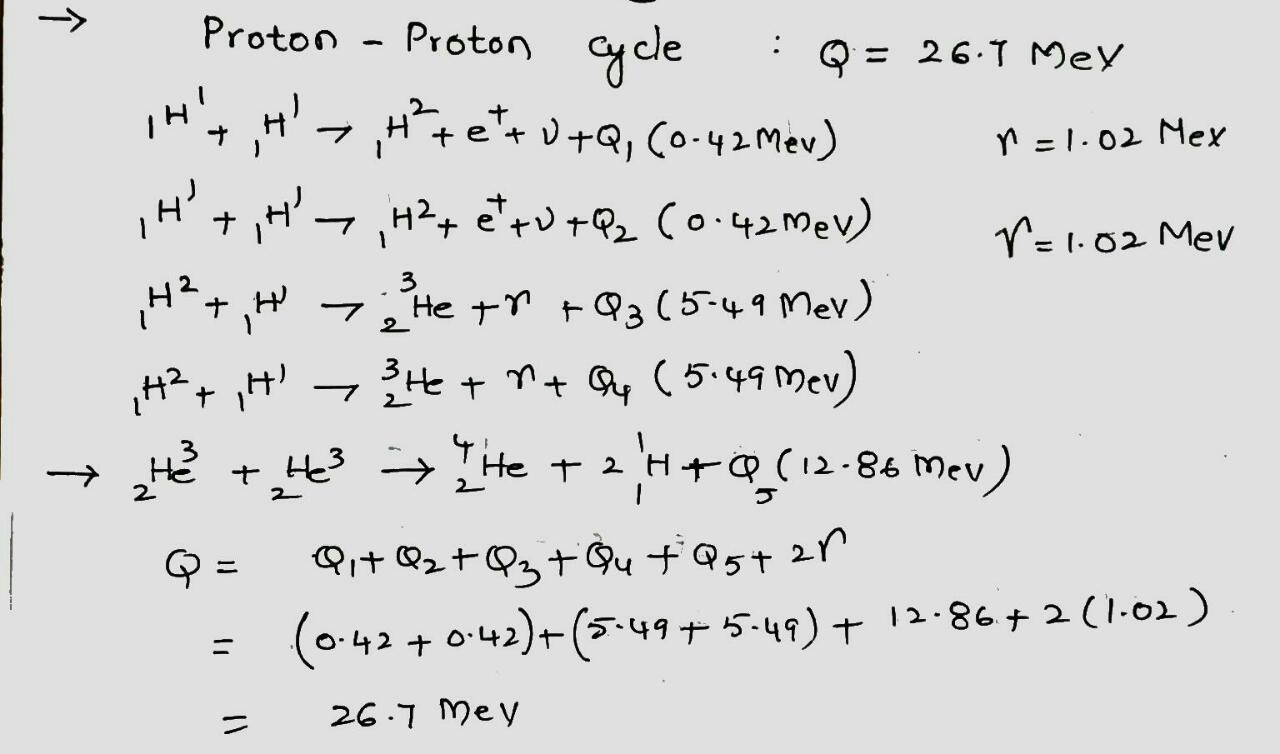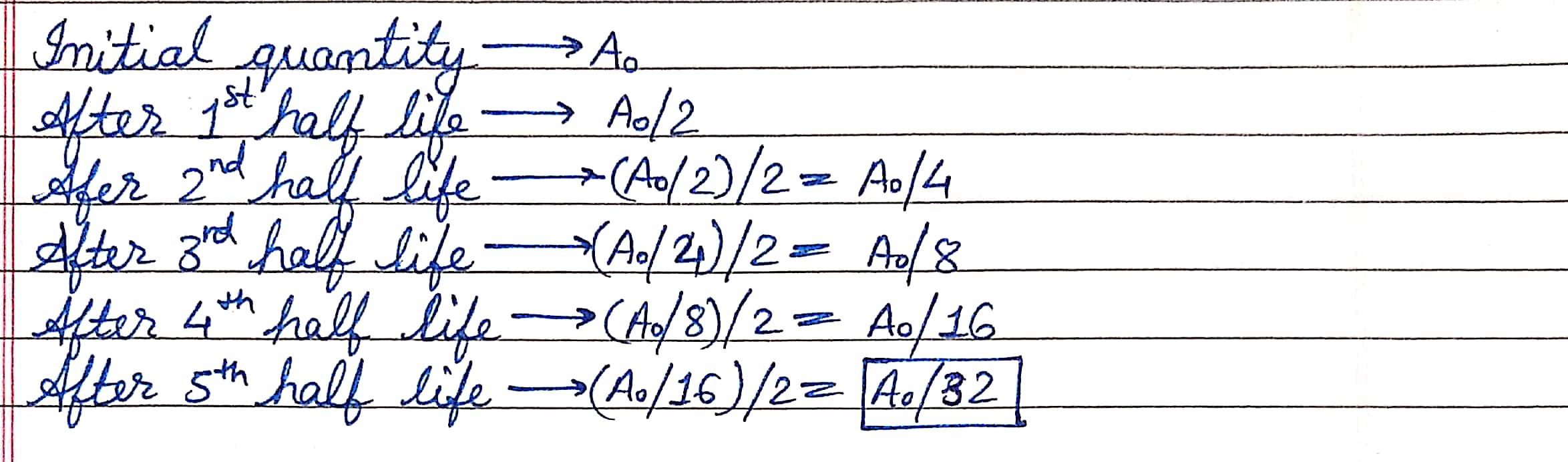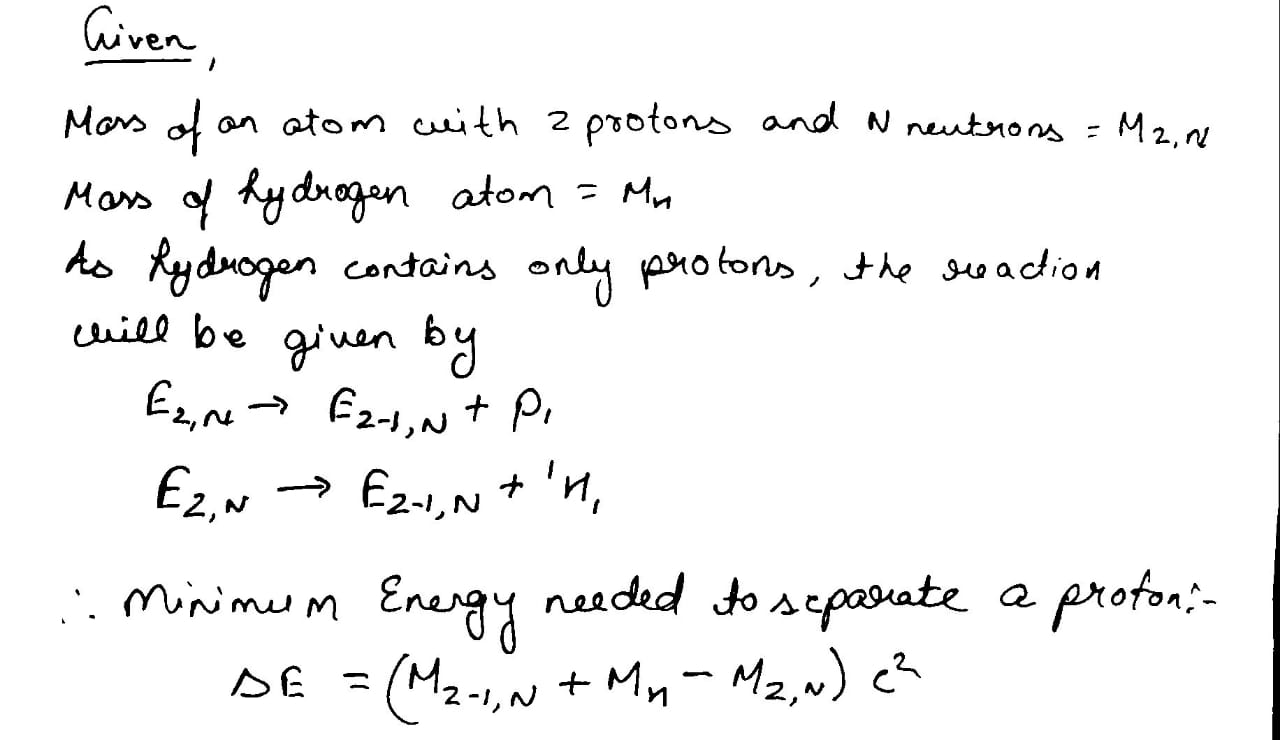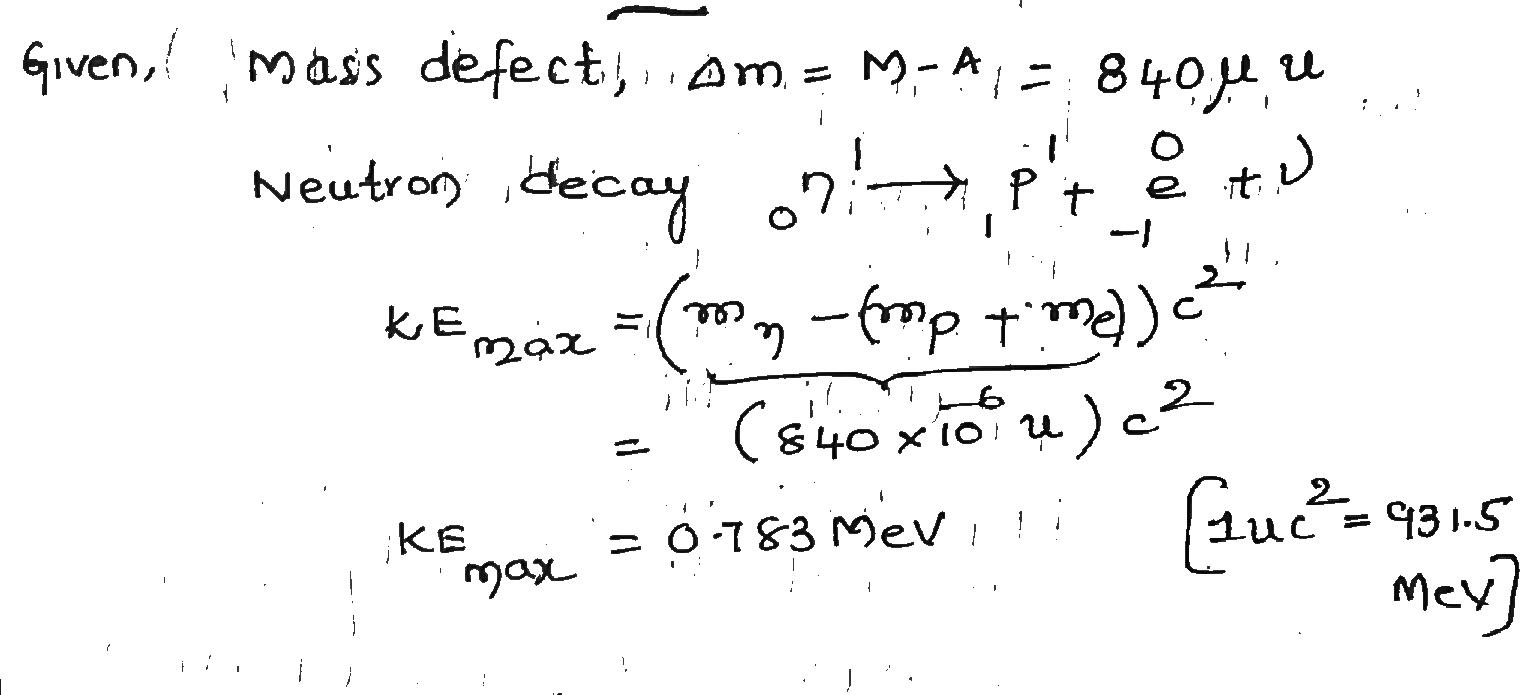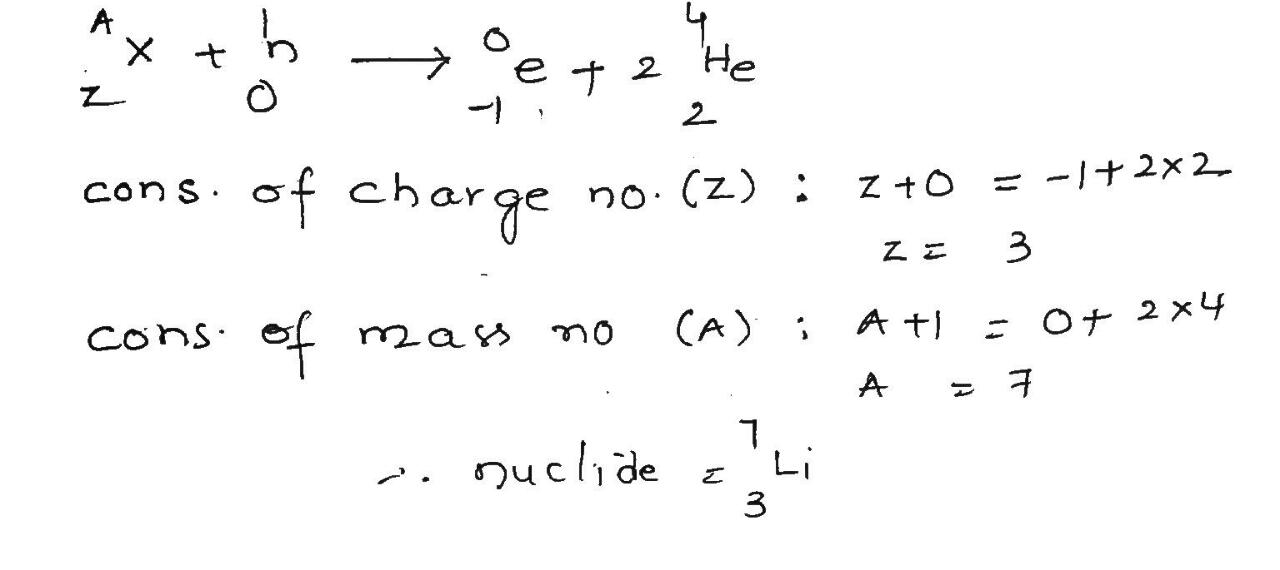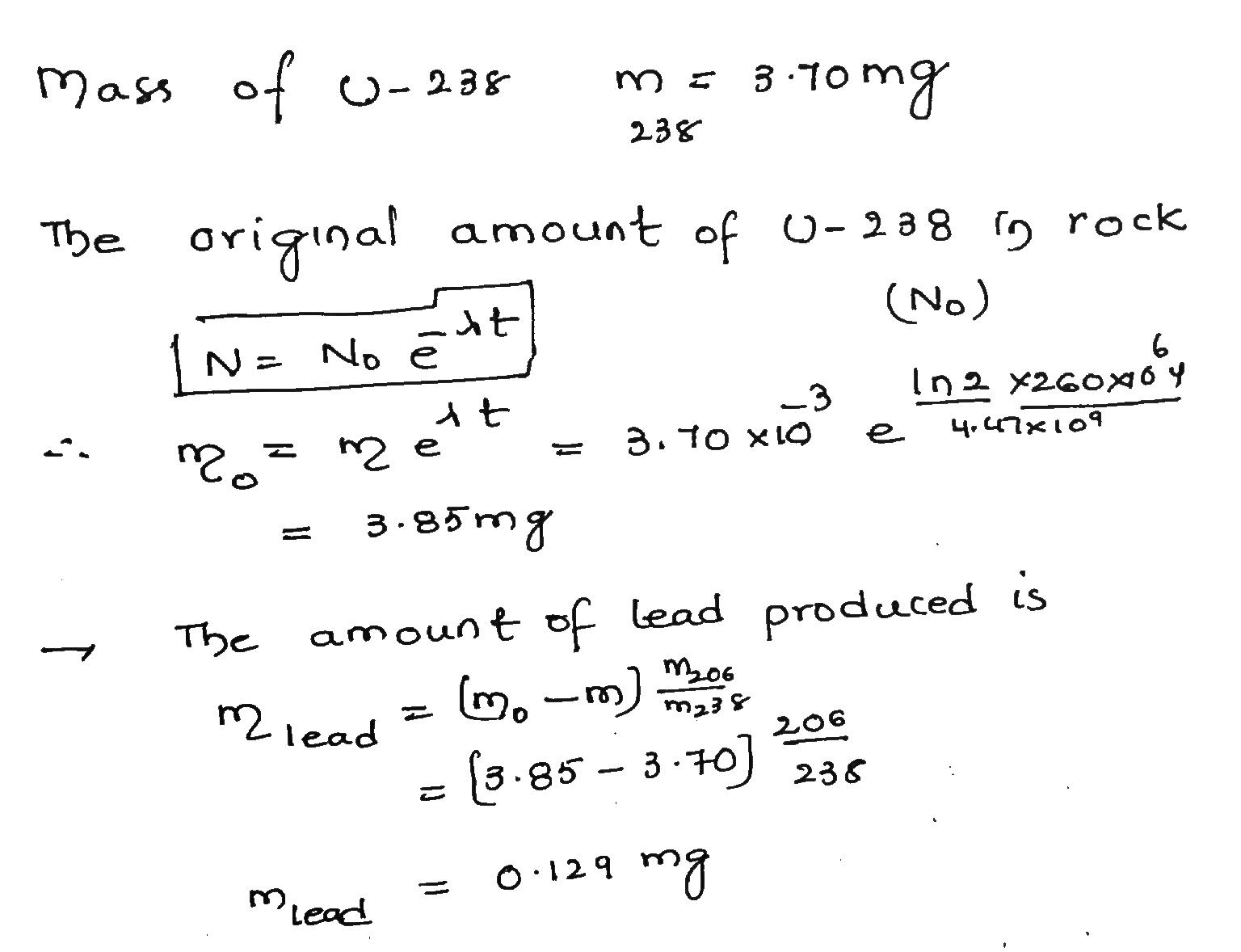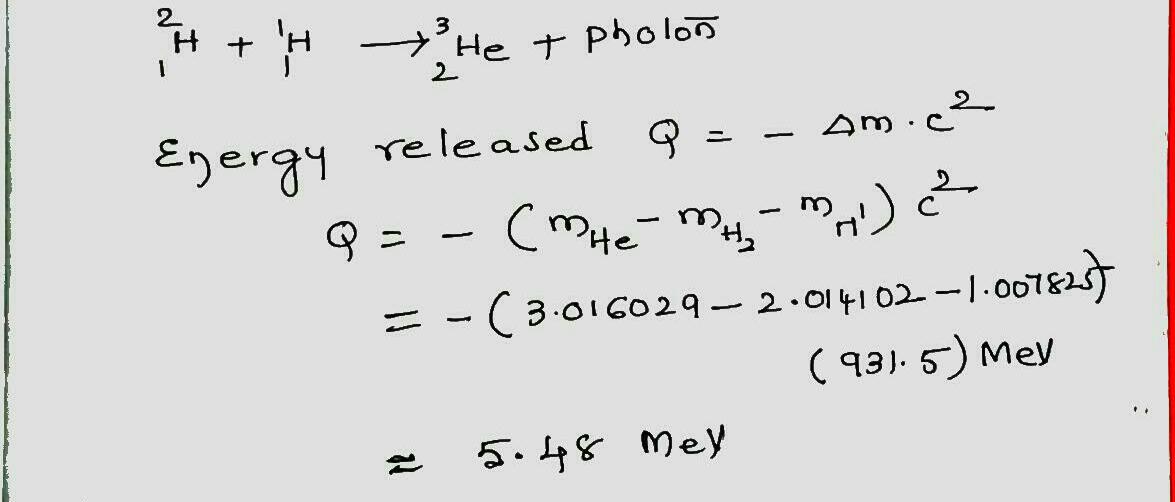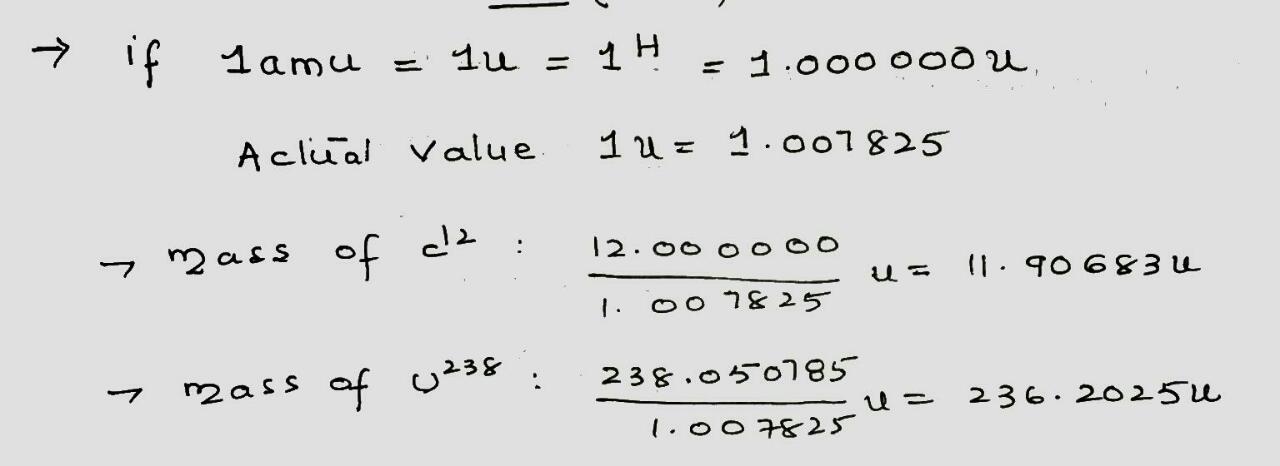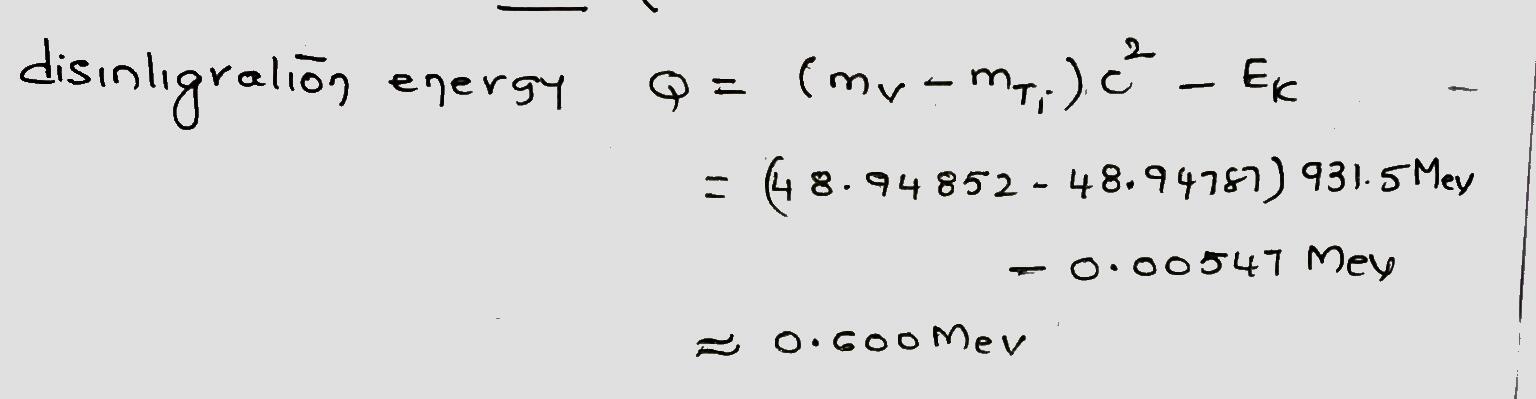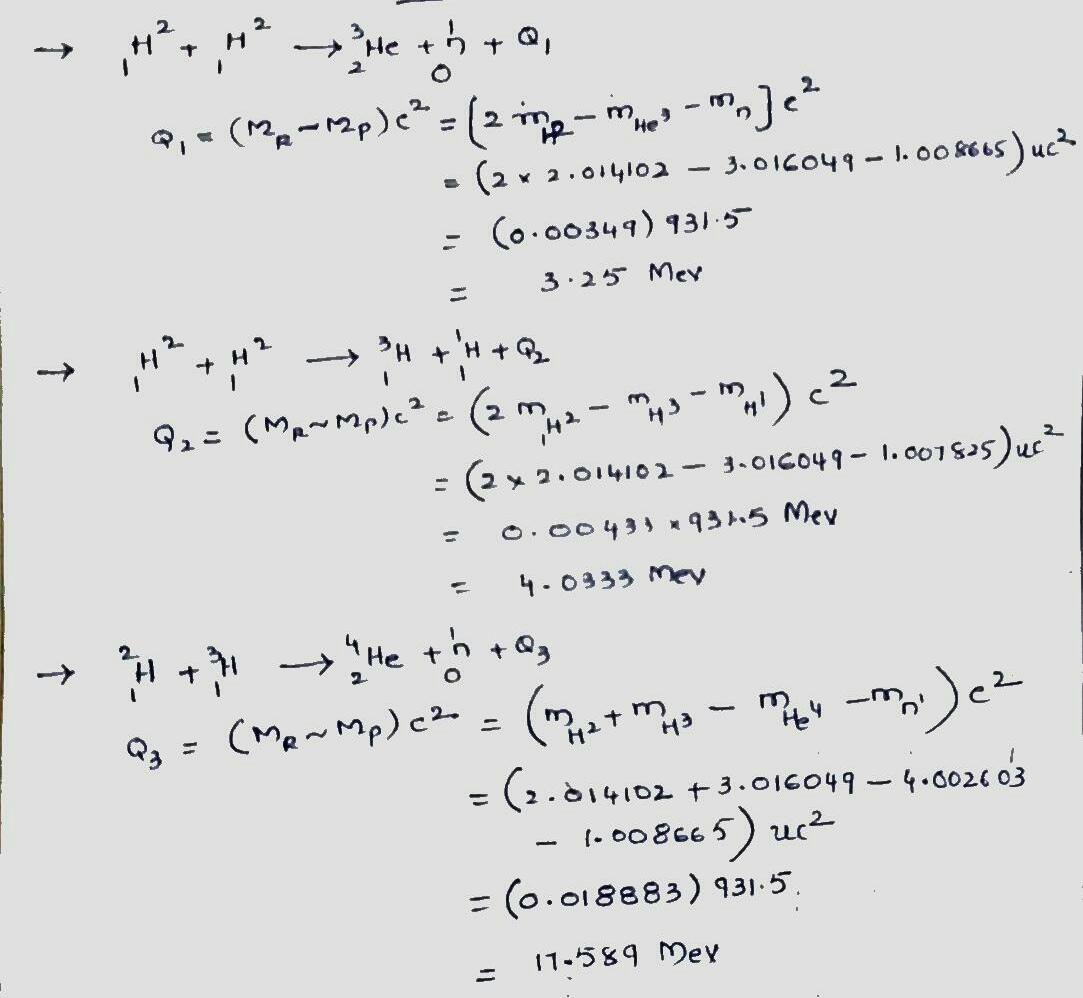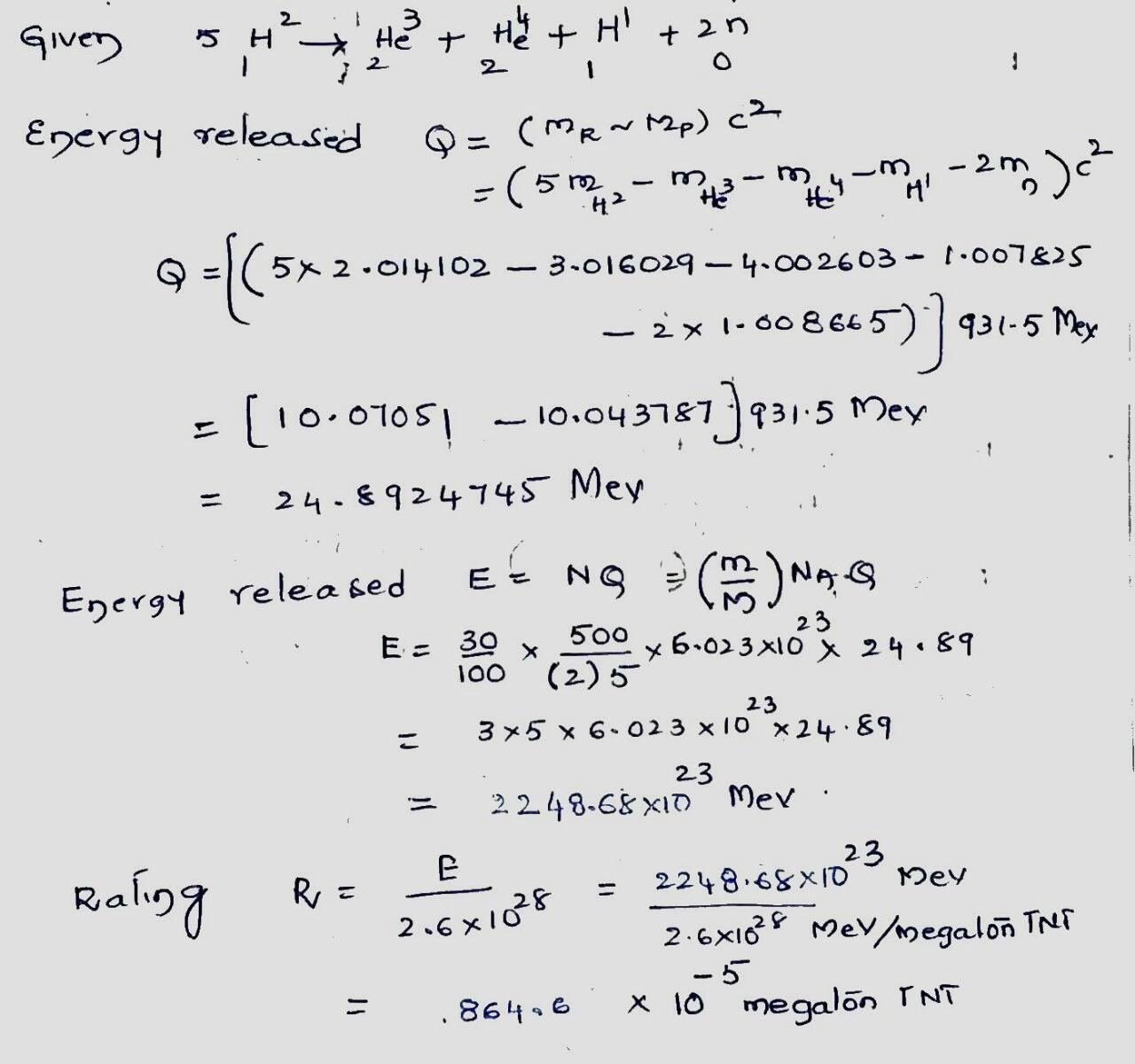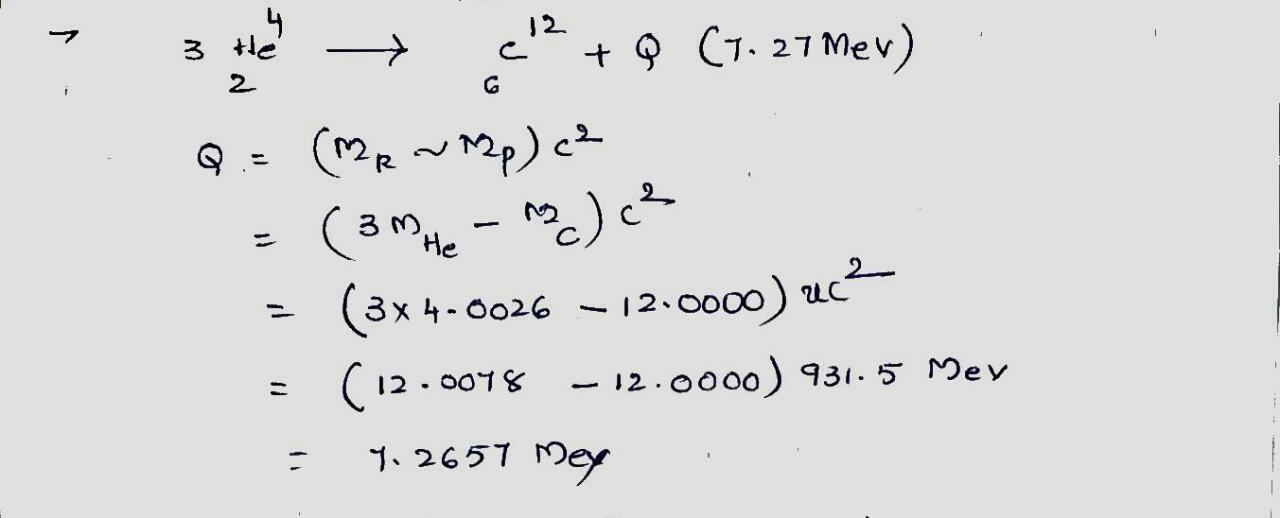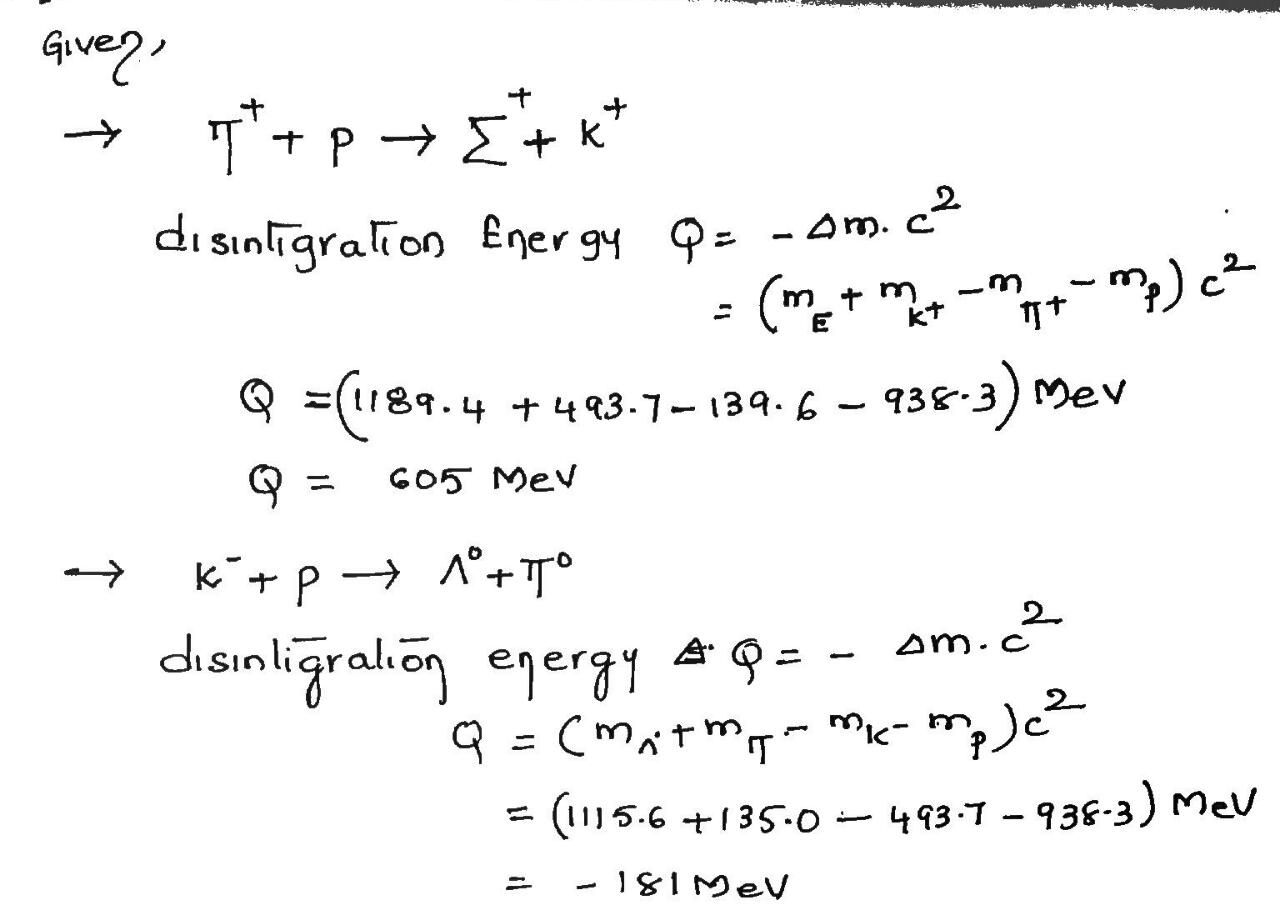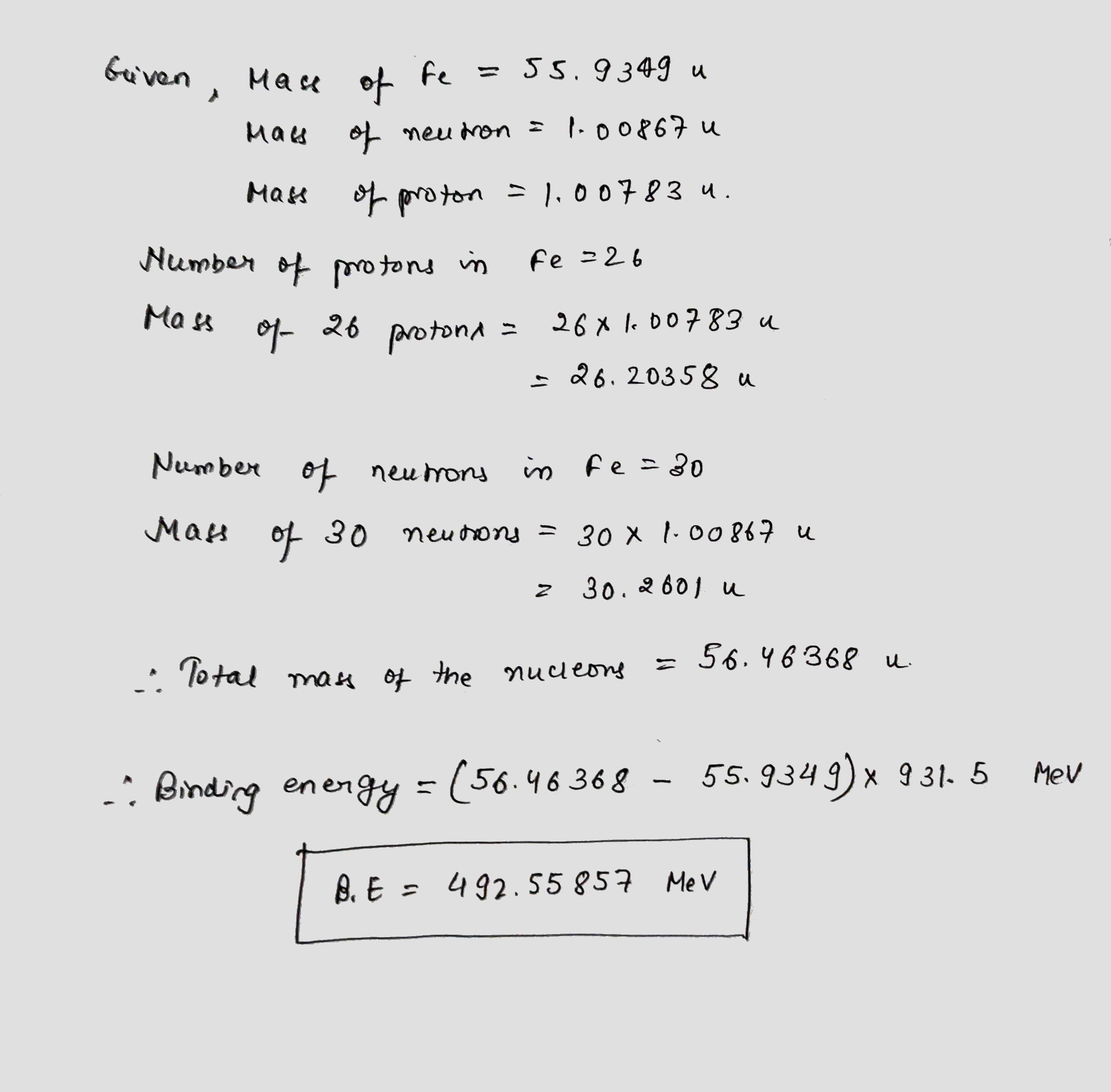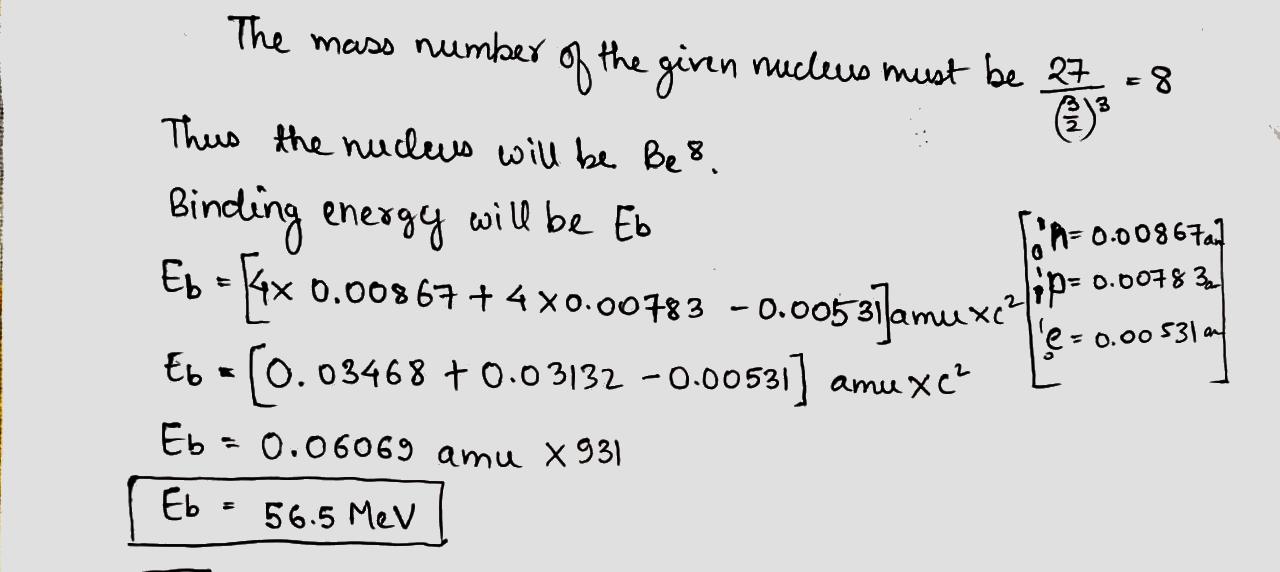Nuclei - Class 12 Medical Physics - Extra Questions
Find the binding energy of an $$\alpha$$-particle from the following data:
Mass of helium nucleus$$=4.001265$$ a.m.u; mass of proton $$=1.007277$$ a.m.u. Mass of neutron $$=1.00866$$ a.m.u (take $$1$$ a.m.u$$=931.5$$ MeV)
The binding energies per nucleon for deutron $$(_{1}H^{2})$$ and helium $$(_{2}He^{4})$$ are $$1.1$$ MeV and $$7.0$$ MeV respectively. Calculate the energy released, when two deutrons fuse to form a helium nucleus $$(_{2}He^{4})$$.
The binding energy per nucleon for $$_{6}C^{12}$$ nucleons is $$7.68$$MeV and that for $$_{6}C^{13}$$ is $$7.47$$ MeV. Calculate the energy required to remove a neutron from $$_{6}C^{13}$$ nucleons.
What is (a) mass defect, and (b) binding energy in Oxygen $$^{16}_{8}{O}$$, whose nuclear mass is $$15.995$$ amu. $$(m_p=1.0078$$amu$$;$$ $$m_n=1.0087$$amu$$)$$.
A neutron breaks into a proton and an electron. Calculate the energy produced in this reaction in MeV. Mass of an electron $$=9\times {10}^{-31}kg$$, mass of proton $$=1.6725\times {10}^{-27}kg$$, mass of neutron $$=1.6747\times {10}^{-27}kg$$ and speed of light $$=3\times {10}^{8}m{s}^{-1}$$
Calculate the energy released if $$U^{238}$$-nucleus emits an $$\alpha-$$particle.
OR
Calculate the energy released in MeV in the following nuclear reaction
$$^{238}_{92}U \rightarrow ^{234}_{90}Th + ^{4}_{2}He + Q$$
Given Atomic mass of $$^{238}U = 238.05079 \,u$$
Atomic mass of $$^{234}Th = 234.04363 \,u$$
Atomic mass of alpha particle $$= 4.00260 \,u$$
$$1 \,u = 931.5 \,MeV / c^2$$
Is the decay spontaneous ? Give reasons.
What are the different types of nuclear reactions?
Answer the following question:
Identify the nature of the radioactive radiations emitted in each step of the decay process given below:
$$^{A}_{Z}X \rightarrow ^{A-4}_{Z-1}W$$
Answer the following question:
A heavy nucleus splits into two lighter nuclei. Which one of the two-parent nucleus or the daughter nuclei has more binding energy per nucleon ?
Give reason for the release of $$21.6\ MeV$$ energy in the fusion of deuterium reaction.
Write one nuclear fusion reaction.
Why is a very high temperature required for the process of nuclear fusion? State the approximate temperature required.
Which of the isotope of Uranium is easily fissionable? Give reason.
The isotope $$_{ 5 }^{ 12 }{ B }$$ having a mass 12.014 u undergoes $$\beta $$ -decay to $$_{ 6}^{ 12 }{ C }$$ , $$_{ 6 }^{ 12 }{ C }$$ has an excited state of the nucleus ($$_{ 5 }^{ 12 }{ C^* }$$ ) at 4.041 MeV above its ground state. If $$_{ 5 }^{ 12 }{ B }$$ decays to $$_{ 6 }^{ 12 }{ C^* }$$, the maximum kinetic energy of the $$\beta $$-particle in units of MeV is
(1 u = 931.5 MeV/$${ c }^{ 2 }$$, where c is the speed of light in vacuum).
The binding energy of $$_{ 17 }^{ }{ { Cl }^{ 35 } }$$ nucleus is $$298$$ MeV. Find its atomic mass. The mass of hydrogen atom $$\left( _{ 1 }^{}{ { H }^{ 1 } } \right)$$ is $$1.008143$$ a.m.u. Given $$1$$ a.m.u. $$=931$$ MeV.
(a) Show that the mass M of an atom is given approximately by $$M_{app}$$ = $$Am_p$$ ,where A is the mass number and $$m_p$$ is the proton mass. For (b) $$^1 H$$, (c) $$^{31} P$$, (d) $$^{120} Sn$$, (e) $$^{197}Au$$, and (f) $$^{239} Pu$$, use Table 42-1 to find the percentage deviation between $$M_{app}$$ and M:
Percentage deviation = $$ \frac {M_{app}M}{M}100$$
(g) Is a value of $$M_{app}$$ accurate enough to be used in a calculation ofa nuclear binding energy?
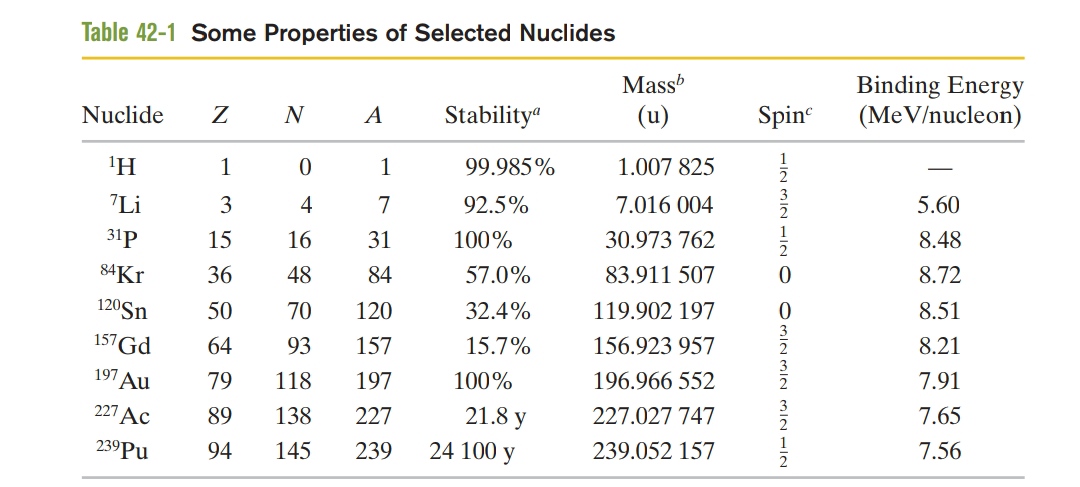
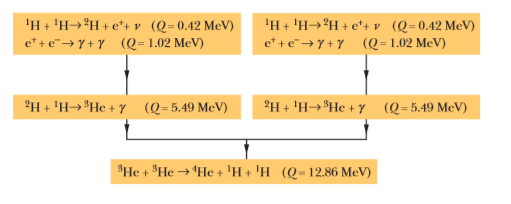
Consider the fission of $$^{238}U$$ by fast neutrons. In one fission event, no neutrons are emitted and the final stable end products,after the beta decay of the primary fission fragments,are $$^{140}Ce$$ and $$^{99}Ru$$.
(a) What is the total of the beta-decay events in the two beta-decay chains?
(b) Calculate $$Q$$ for this fission process. The relevant atomic and particle masses are
| $$^{238}U$$ | $$ 238.05079 \ u $$ | $$^{140}Ce$$ | $$ 139.90543 \ u $$ |
| $$n$$ | $$ 1.00866 \ u $$ | $$^{99}Ru$$ | $$ 98.90594 \ u $$ |
A $$^{238}U$$ nucleus emits a 4.196 MeV alpha particle. Calculate the disintegration energy Q for this process, taking the recoil energy of the residual $$^{234}Th$$ nucleus into account.
(a) Calculate the disintegration energy $$Q$$ for the fission of the molybdenum isotope $$^{98}Mo$$ into two equal parts. The masses you will need are $$97.905 41 \ u$$ for $$^{98}Mo$$ and $$48.950 02 \ u$$ for $$^{49}Sc$$.(b) If $$Q$$ turns out to be positive, discuss why this process does not occur spontaneously.
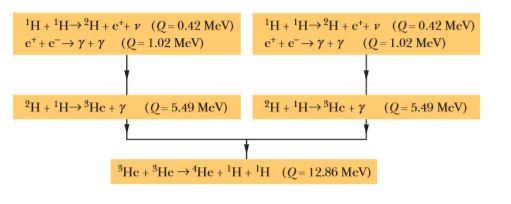
Verify the three $$Q$$ values reported for the reactions given in the above figure. The needed atomic and particle masses are
| $$^1H$$ | $$1.007 825 \ u$$ | $$^4He$$ | $$4.002 603 \ u$$ |
| $$^2H$$ | $$2.014 102 \ u$$ | $$e^{\pm}$$ | $$0.000 548 6 \ u$$ |
| $$^3He$$ | $$3.016 029 \ u$$ |
(Hint: Distinguish carefully between atomic and nuclear masses, and take the positrons properly into account.)
Coal burns according to the reaction $$C + O_2 \rightarrow CO_2 $$. The heat of combustion is $$3.3 \times 10^7 \ J/kg$$ of atomic carbon consumed.
(a) Express this in terms of energy per carbon atom.
(b) Express it in terms of energy per kilogram of the initial reactants, carbon and oxygen.
(c) Suppose that the Sun (mass $$= 2.0 \times 10^{30} \ kg$$) were made of carbon and oxygen in combustible proportions and that it continued to radiate energy at its present rate of $$3.9 \times 10^{26} \ W$$. How long would the Sun last?
We have seen that $$Q$$ for the overall proton-proton fusion cycle is $$26.7 \ MeV$$. How can you relate this number to the $$Q$$ values for the reactions that make up this cycle, as displayed in the above figure?
Calculate the Q values f the fusion reaction $$ ^4He +^4 He = ^8Be $$
In such a fusion energetically favourable? the atomic mass of $$ ^8 Be $$ is 8.0053 u and that of $$ ^4He $$ is 4.0026 u.
Lithium (Z = 3) has two stable isotopes $$^6Li$$ and $$^7Li$$. When neutrons are bombarded on lithium sample, electrons and $$\alpha$$ - particles are ejected. Write down the nuclear processes taking place.
Find the energy liberated in the reaction
$$ ^{223}Ra \rightarrow ^{209}Pb + ^{14}C $$
the atomic masses needed are as follows
$$ ^{223}Ra \quad ^{209}Pb \quad ^{14}C $$
$$ 22.018u \quad 208.981 u \quad 14.003 u $$
Potassium -40 can decay in three modes. it can decay by $$ \beta^- $$emission $$ \beta^+ $$ emission or electron capture .(a) write the equations showing the end products.(b) Find the Q-values in each of the three cases. Atomic masses of $$ ^{40}_{18}Ar, \ ^{40}_{19}K$$ and $$^{40}_{20}Ca $$ are 39.9624 u , 39.9640 u and 39.9626 u respectively.
How much quantity of radioactive substance will remain in decayed after 5 half-lives period ?
Initial quantity $$\rightarrow A_o$$
After $$1^{st}$$ half life $$\rightarrow A_o/2$$
After $$2^{nd}$$ half life $$\rightarrow (A_o/2)/2=A_o/4$$
After $$3^{rd}$$ half life $$\rightarrow (A_o/4)2=A_o/8$$
After $$4^{th}$$ half life $$\rightarrow (A_o/8)/2=A_o/16$$
After $$5^{th}$$ half life $$\rightarrow (A_o/16)/2=A_o/32$$.
Hydrogen bomb is based on the principle of
The mass defect for the nucleus of $$_{2}He^{4}$$ is $$0.0303 a.m.u$$. The approximate value of binding energy per nucleon in $$MeV$$ will be $$(1 \mathrm{a}.\mathrm{m}.\mathrm{u}=931\mathrm{M}\mathrm{e}\vee)$$
In plants and animals, the ratio of C$$^{14}$$ to C$$^{12}$$ is _______.
The energy released during a nuclear reaction is called _______ energy
When an $$\alpha$$-particle is ejected, the atomic number of the atom decreases by ___________ .
If the binding energy per nucleon for $$_3$$Li$$^7$$ is 5.6 MeV, the total binding energy of a lithium nucleus is _______ MeV.
The mass of $$_{2}He^{4}$$ nnucleus is $$0.03$$ amu less than the sum of the masses of $$2$$ protons and $$2$$ neutrons. What is the binding energy per nucleon?
Find out the binding energy per nucleon of an $$\alpha$$-particle in MeV. It is given that the masses of $$\alpha$$-particle, proton and neutron are respectively $$4.00150$$ a.m.u., $$1.00728$$ a.m.u. and $$1.00867$$ a.m.u.
Calculate the binding energy of an alpha-particle. Given mass of proton $$=1.0073$$ a.m.u., mass of neutron $$=1.0087$$ a.m.u., mass of $$\alpha$$-particle$$=4.0015$$a.m.u.
The total energy of an electron in the first excited state of the hydrogen atom is $$-3.4$$eV. Find the out its (i) kinetic energy and (ii) potential energy in this state.
$$\alpha$$-particle is emitted from a $$_{88}^{226}Re$$ nucleus. If the energy of $$\alpha$$-particle is 4.662 MeV, then what is the total free energy in this decay?
The masses pf $$ ^{11}C and ^{11}B $$ are respectively $$11.0114 u and 11.0093 u $$. find the maximum energy a positron can have in the $$ \beta^+ $$ decay of $$ ^{11}C to ^{11} B $$
How much energy is released in the following reaction :
$$ ^7Li + p \rightarrow \alpha + \alpha $$ tomic mass of $$^Li = 7.0160 u $$ and that of $$ ^He = 4.0026 i=u $$
In the reaction $$\mathrm{p}+^{19} \mathrm{F} \rightarrow \alpha+^{16} \mathrm{O},$$ the masses are
$$\begin{array}{ll}m(\mathrm{p})=1.007825 \mathrm{u}, & m(\alpha)=4.002603 \mathrm{u} \\m(\mathrm{F})=18.998405 \mathrm{u}, & m(\mathrm{O})=15.994915 \mathrm{u}\end{array}\\$$
Calculate the $$Q$$ of the reaction from these data.
Which one of the following cannot emit radiation and why ? Excited nucleus, excited electron.
The nuclide $$ ^{14} C$$ contains (a) how many protons and (b) how many neutrons?
What is the binding energy per nucleon of the europium isotope $$^{152}_{63} Eu$$? Here are some atomic masses and the neutron mass.
$$^{152} _{63}Eu$$ 151.921 742 u $$^1H$$ 1.007 825 u
n 1.008 665 u
In the reactions given below:
(a) $$^{11}_{6}C \rightarrow ^{z}_{y}B + x + v$$
(b) $$^{12}_{6}C + ^{12}_{6}C \rightarrow ^{20}_{a}Ne + ^{c}_{b}He$$
Find the values of x, y, z and a, b, c.
A nucleus of mass number A, has a mass defect $$\Delta m.$$ Give the formula, for the binding energy per nucleon, of this nucleus.
The mass of H atom is less than sum of the masses of a proton and electron. Why is this?
Distinguish between isotopes and isobars. Give one example for each of the species.
What other name is given to nuclear fusion? Give reason.
Write the nuclear equations for:
$${\beta}^{+}$$- decay of $$_{ 43 }^{ 97 }{ Tc }$$
Write the nuclear equations for:
$$\alpha$$- decay of $$_{ 88 }^{ 226 }{ Ra }$$
Write the nuclear equations for:
$${\beta}^{-}$$- decay of $$_{ 83 }^{ 210 }{ Bi }$$
What is radioactivity?
Fill in the blanks.
The equation $$E=mc^2$$ is derived by the scientist _________.
Define binding energy of electron.
Four physical quantities are given in Column I and their order the values in Column II. Match the options appropriately :
When the number of nucleons in nucleus increase, the binding energy per nucleon first _________ and then _________ with increase of mass number.
The mass defect per nucleon is called ___________.
For greater stability, a nucleus should have greater value of binding energy per nucleon. Why?
State any two differences between chemical reactions and nuclear reactions.
Fill in the Blanks
In nuclear reactions we have the conservation of ___________.
Define specific binding energy.
A $$\mu-meson$$ (charge $$-e$$, mass $$=207m$$, where $$m$$ is the mass of the electron) can be captured by a proton to form a hydrogen-like "mesic" atom. Calculate the radius of the first Bohr orbit, the binding energy, and the wavelength of the line in the Lyman series for such an atom. The mass of the proton is $$1836$$ times the mass of the electron. The radius of the first Bohr orbit and the binding energy of Hydrogen are $$0.529\mathring{A}$$ and $$13.6\space eV$$, respectively. Take $$R = 109678\space cm^{-1}$$
In Column I consider each process just before and just after it occurs. Initial system is isolated from all other bodies. Consider all product particles (even those having rest mass zero) in the system. Match the system in Column I with the result they produce in Column II
Match column I with column II
In Column I some of the nuclear reactions are given. Match this with the energy involved in these reactions in Column II :
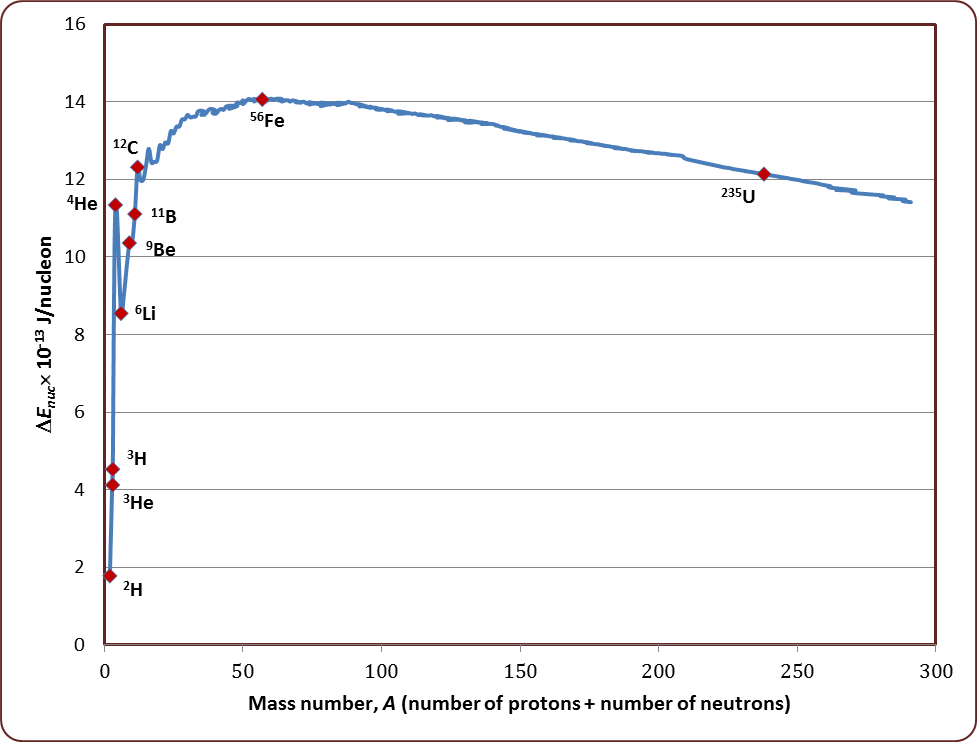
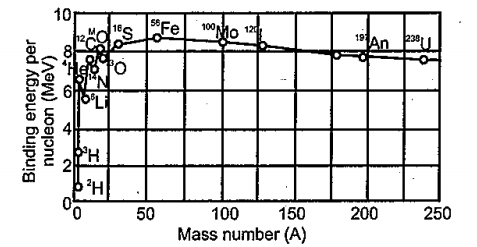
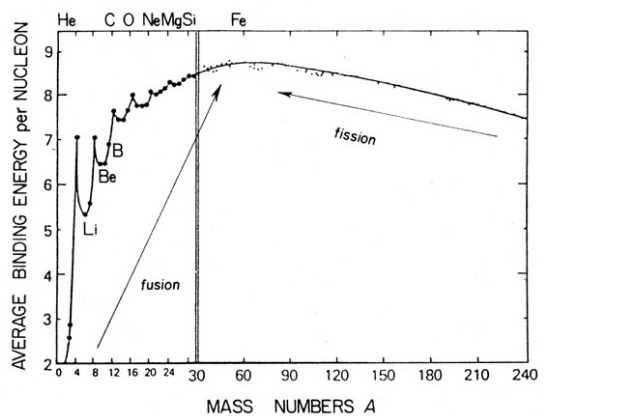
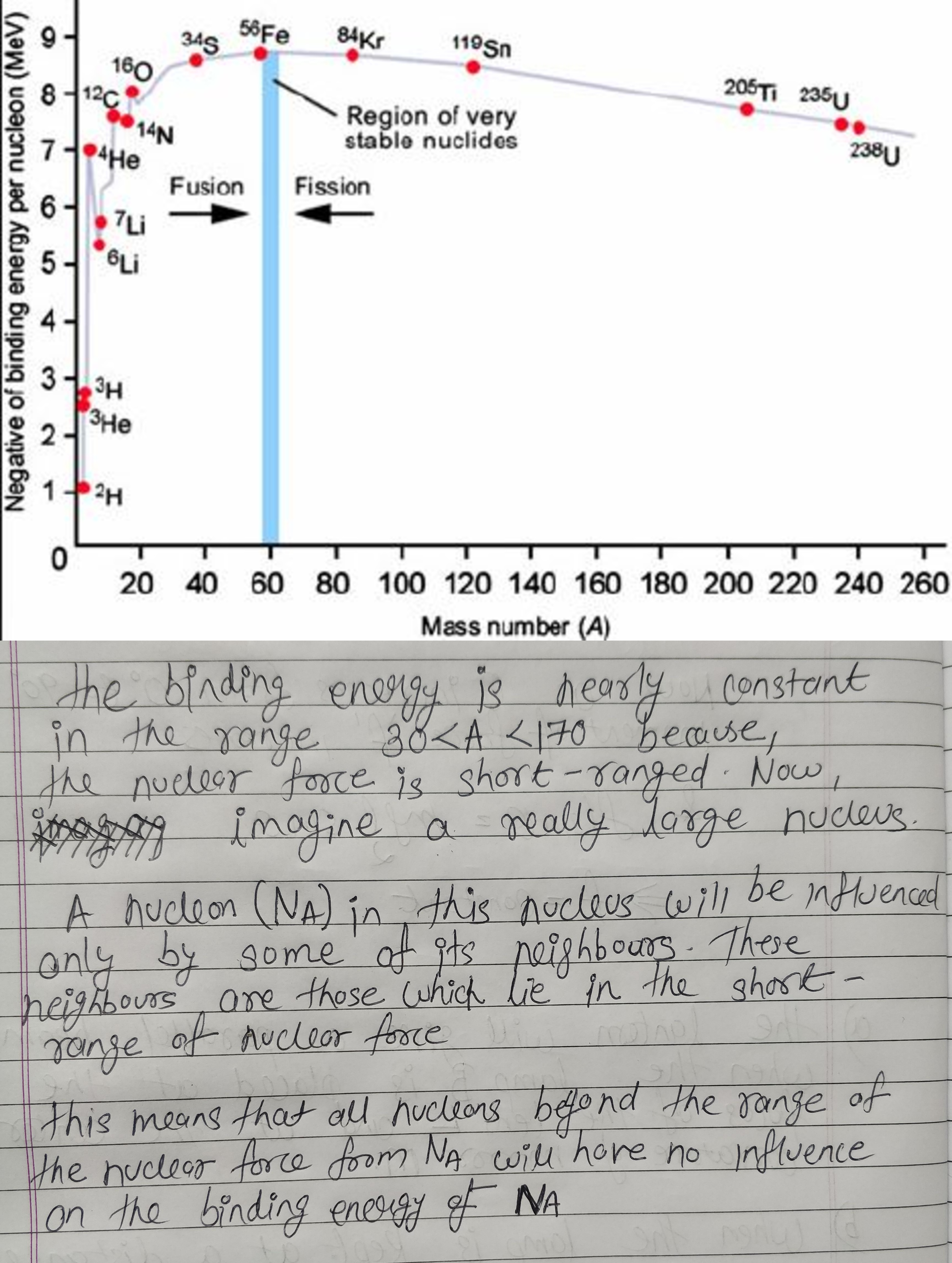
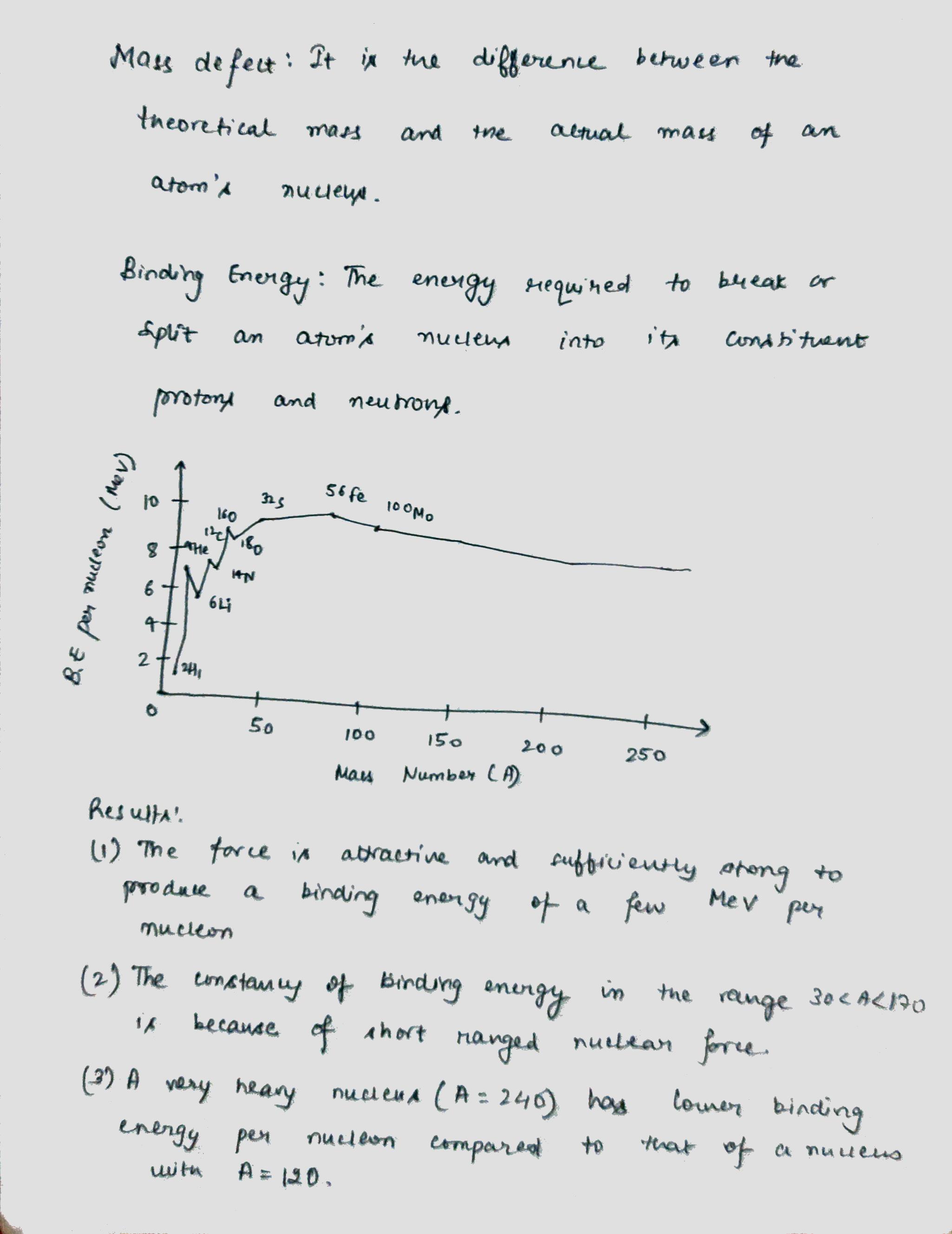
Draw a plot of BE/A versus mass number A for 2 $$\leq$$ A $$\leq$$ Use this graph to explain the release of energy in the process of nuclear fusion of two light nuclei.
From the plot, it can be clearly seen that after an atomic mass of nearly 56, which corresponds to Iron, the binding energy starts decreasing (i.e. Iron is the most tightly bound nucleus). Before Iron the binding energy is rapidly increasing mostly. Thus in general we can say that if two light nuclei fuse to form a heavy nuclei, they will release energy and hence will reach a more stable state.
Write the relation for binding energy (B.E) (in MeV) of a nucleus of mass $$\displaystyle _{Z}^{A}{M}$$, atomic number (Z) and mass number (A) in terms of the masses of its constituents - neutrons and protons.
The fission properties of $$^{239}_{94}Pu$$ are very similar to those of $$^{235}_{92}U$$. The average energy released per fission is 180 MeV. How much energy, in MeV, is released if all the atoms in 1 kg of pure $$^{239}_{94}Pu$$ undergo fission?
How long can an electric lamp of 100 W be kept glowing by fusion of 2.0 kg of deuterium? Take the fusion reaction as :
$$^2_1H\, +\, ^2_1\, \rightarrow\, ^3_2He\, +\, n\, +\, 3.27\, MeV$$.
(i) What characteristic property of nuclear force explains the constancy of binding energy per nucleon $$\left({BE}/{A}\right)$$ in the range of mass number $$'A'$$ lying $$30 < A < 170$$?
(ii) Show that the density of nucleus over a wide range of nuclei is constant-independent of mass number $$A$$.
Write symbolically the nuclear $$\beta^+$$ decay process of $$_{6}^{11}C$$. Is the decayed product X an isotope or isobar of ($$_{6}^{11}C$$)? Given the mass values m ($$_{6}^{11}C$$) = 11.011434 u and m (X) = 11.009305 u. Estimate the Q-value in this process.
The mass of deutron $$(_1H^2)$$ nucleus is $$2.013553$$ a.m.u. If the masses of proton and neutron are $$1.007275$$ a.m.u. and $$1.008665$$ a.m.u. respectively. Calculate the mass defect, the packing fraction, binding energy and binding energy per nucleon.
Obtain the binding energy of the nuclei $$_{26}Fe^{56}$$ and $$_{83}Bi^{209}$$ in units of MeV from the following data: mass of hydrogen atom $$=1.007825$$ a.m.u., mass of neutron $$=1.08665$$ a.m.u.; mass of $$_{26}Fe^{56}$$ atom $$=55.934939$$ a.m.u. and mass of $$_{83}Bi^{209}$$ atom $$=208.980388$$a.m.u. Also calculate binding energy per nucleon in the two cases.
Find out the binding energy per nucleon of an $$\alpha$$-particle in MeV. It is given that the masses of $$\alpha$$-particles, proton and neutron are respectively $$4.00150$$ a.m.u., $$1.00728$$a.m.u. and $$1.00867$$ a.m.u.
(a) Draw the plot of blinding energy per nucleon (BE/A)
as a function of mass number. Write two important conclusion that can be drawn regarding the nature of nuclear source.
(b) Use this graph to explain the release of energy in both the process of nuclear fusion and fission.
(c) Write the basic nuclear process of neutron undergoing $$\beta $$-decay. why is the detection of neutrinos found very difficult?
(a)Conclusions drawn from the graph:
(i) The nuclear force is very attractive and strong to produce binding energy of the order of MeV per nucleon.
(ii)The nuclear force is a short range force which can be shown by its value being constant in the range 30<A<170.
(b)In nuclear fission a heavier nucleus breaks into lighter nuclei to release high binding energy per nucleon. In nuclear fusion, the binding energy of the fused heavier nucleon is more than the binding energy of the lighter nuclei which combined to form the heavier nuclei. Energy is also released in nuclear fusion.
(c)the basic nuclear process of neutron undergoing $$\beta$$ decay is:
$$n\rightarrow p+\vec e+\vec \nu$$
Neutrinos have high penetrating power which makes their detection difficult.
The binding energy per nucleon of $$_{2}He^{4}$$ is $$7.075$$ MeV. What is its total binding energy?
_____________ is the energy released during nuclear reactions.
The mass of $$_{3}Li^{7}$$ nucleus is $$0.042$$ a.m.u. less than the sum of masses of its nucleons. Find the binding energy per nucleon.
Calculate the (i) mass defect, (ii) binding energy and (iii) the binding energy per nucleon for a $$_{6}C^{12}$$ nucleus. Nuclear mass of $$_6C^{12}=12.000000$$ a.m.u., mass of hydrogen nucleus $$=1.007825$$ a.m.u. and mass of neutron $$=1.008665$$ a.m.u.
The binding energy per nucleon for $$C^{12}$$ is $$7.68$$ MeV and that for $$C^{13}$$ is $$7.47$$ MeV. What is the energy required to remove a neutron from $$C^{13}$$?
With the help of one example, explain how the neutron to proton ratio changes during alpha decay of a nucleus.
Explain nuclear fusion with an equation.
The mass of deutron $$(_1H^2)$$ nucleus is $$2.013553$$ a.m.u. If the masses of proton and neutron are $$1.007275$$ a.m.u. and $$1.008665$$ a.m.u. respectively, calculate the mass defect, the packing fraction , binding energy and binding energu per nucleon.
Obtain the binding energy of a nitrogen nucleus $$(_7N^{14})$$ from the following data: $$m_H=1.00783$$ a.m.u., $$m_n=1.0087$$ a.m.u.; $$m_N=14.00307$$ a.m.u.
What is the significance of binding energy per nucleon of a nucleus?
In our Nature, where is the nuclear fusion reaction taking place continuously?
What is the signeficance of binding energy per nucleon of a nucleus of a radioactive element?
Write one balanced reaction representing nuclear fusion.
Which reaction is responsible for solar energy? Name the major component of solar energy that reaches us.
Define mass defect of a nucleus. Binding energy of $${ _{ 8 }^{ }{ O } }^{ 16 }$$ is $$127.5MeV$$. Write the value of its 'binding energy per nucleon'. Write the value of $$1eV$$ energy in joule.
The atomic mass of Uranium $$^{238}_{92}U$$ is 238-0508 u, while that of Thorium $$^{234}_{90}Th$$ is 234.0436 u, and that of Helium $$^4_2He$$ is 4.0026 u. Alpha decay converts $$^{238}_{92}U$$ into $$^{234}_{90}Th$$ as shown below:
$$^{238}_{92}U \rightarrow ^{234}_{90}Th + ^4_2He + energy$$
Determine the energy released in this reaction.
In a certain star, three alpha particles undergo fusion in a single reaction to form $$^{12}_{6}C$$ nucleus. Calculate the energy released in this reaction in $$MeV$$.
Given: $$m(^{4}_{2}He) = 4.002604\ u$$ and $$m(^{12}_{6}C) = 12.000000\ u$$
(a) What do you mean by $$Q$$ value of a nuclear reaction?
(b) Write down the expression for $$Q$$ value in the class of $$\alpha$$ decay.
What are isotopes and isobars?
Write any five differences between Nuclear Fission and Nuclear Fusion.
Calculate the binding energy and binding energy per nucleon (in MeV) of a nitrogen nucleus $$(^{14}_7N)$$ from the following data :
Mass of proton = 1.00783 u
Mass of neutron = 1.00867 u
Mass of nitrogen nucleus = 14.00307 u
Calculate mass defect and binding energy per nucleon of $$^{20}_{10}Ne,$$ given
Mass of $$^{20}_{10}Ne=19.992397$$u
Mass of $$^1_1H=1.007825$$u
Mass of $$^1_0n=1.008665$$u.
What is the name given to the atoms whose nuclei contain the same number of proton but different number of neutrons?
If speed of light is doubled then how much binding energy of nucleus will become?
The three stable isotopes of neon: $$_{ 10 }^{ 20 }{ Ne },_{ 10 }^{ 21 }{ Ne }$$ and $$_{ 10 }^{ 22 }{ Ne }$$ have respective abundances of $$90.51$$%, $$0.27$$% and $$9.22$$%. The atomic masses of the three isotopes are $$19.99u,20.99u$$ and $$21.99u$$ respectively. Obtain the average atomic mass of neon.
What is meant by binding energy? If the masses of proton, neutron and alpha $$(\alpha)$$ particles are $$1.00728\ amu, 1.00867\ amu$$ and $$4.00150\ amu$$ respectively, then find the binding energy per nucleon of alpha particle. $$[1\ amu = 931\ MeV]$$.
The binding energies per nucleon for deuterium and helium are $$1.1$$ MeV and $$7.0$$ MeV respectively. How much amount energy, in joules, will be liberated when $$10^6$$ deuterons take part in the reaction.
(a) Explain the processes of nuclear fission and nuclear fusion by using the plot of binding energy per nucleon (BE/A) versus the mass number $$A$$.
(b) A radioactive isotope has a half-life of $$10$$ years. How long will it take for the activity to reduce to $$3.125$$%?
A. The value of binding energy per nucleon gives a measure of the stability of that nucleus greater is the binding energy per nucleon of a nucleus , more stable is the nucleus.
The above graph shown, binding energy per nucleon drawn against mass number A.
The saturation effect of nuclear forces is the property responsible for the approximate constancy of binding energy in range 30<A<17030<A<170
It is clear from the curve that binding energy per nucleon of the fused nucle is more than there of the light nuclei taking part nuclear fusion .
Hence energy gets released in the process.
In a nuclear fission , the sum of the masses of the final products is less than the sum of the masses of the reactant component
B. $$N = N_{o} e ^{- \lambda t}$$ But $$ N = \dfrac{N_{o}}{32}$$
$$\dfrac{N_{o}}{32} = N_{o} e^{-\lambda t}$$
$$2^{-5} = e^{-\lambda t}$$
5 ln2 = \lambda t$$
but given half life so $$\lambda = \dfrac{ln2}{10}$$
so t = 50 Years
Four nuclei of an element undergo fusion to form a heavier nucleus, with release of energy. Which of the two - the parent or the daughter nucleus - would have higher binding energy per nucleon?
What is meant by the terms half-life of a radioactive substance and binding energy of a nucleus?
The binding energy per nucleon for $$_{6}C^{12}$$ is $$7.68\ MeV$$ and that for $$_{6}C_{13}$$ is $$7.47\ MeV$$. Calculate the energy required to remove a neutron from $$_{6}C_{13}$$.
Write one balanced equation each to show.
(i) Nuclear fission
(ii) Nuclear fusion
(iii) Emission of $$\beta^-$$(i.e., a negative beta particle).
Name the isotope of Uranium which is easily fissionable.
Write a nuclear reaction when Uranium $$238$$ emits an alpha particle to form a Thorium(Th) nucleus.
Differentiate between half life and average life of a radioactive substance.
Write the nuclear equations for:
$$\alpha$$- decay of $$_{ 92 }^{ 242 }{ Pu }$$
The kinetic energy of an $$\alpha - $$particle which flies out of the nucleus of a $$Ra^{226}$$ atom in radioactive disintegration is $$4.78\ M\ ev$$. Find the total energy evolved during the escape of the $$\alpha - $$particle.
The figure indicates the potential energy curve of a diatomic molecule. What will be the value of binding energy?
How much energy will be released when $$10\ kg$$ of $$U^{235}$$ is completely converts into energy :
In a old rock, ratio of nuclei of uranium and lead is $$1:1$$. Half life of uranium is $$4.5 \times 10^n$$ yrs. Let initially it contains only uranium nuclei. How old is the rock?
When a $$U^{238}$$ nucleus originally at rest, decay by emitting an alpha particle having a speed $$1.5\times 10^{7}\ m^{-1}$$. Then calculate the kinetic energy of the residual nucleus.
Calculate the energy released in $$meV$$ in the following nuclear reaction:
$$_{ 92 }^{ 298 }{ U\longrightarrow _{ 90 }^{ 234 }{ TH }+_{ 2 }^{ 4 }{ He }+Q }$$
[Mass of $$_{ 92 }^{ 298 }U=238.05079\ u$$ Mass of $$_{ 90 }^{ 234 }{ TH }=234.043630\ u]$$
[Mass of $$_{ 92 }^{ 298 }U=238.05079\ u$$ Mass of $$_{ 90 }^{ 234 }{ TH }=234.043630\ u]$$
Draw a plot of the binding energy per nucleon as a function of mass number for a large number of nuclei, $$2\ \leq \ A\ \leq 240$$. How do you explain the constancy fo biding energy per nucleon in the range $$30\ \leq \ A\ \leq 170$$ using the property that nuclear force is short-ranged?
Find the binding of the nucleus of lithium isotope $$_3Li^7$$ and hence find the binding energy per nucleon in it $$(M_{_3Li^7} = 7.014353 \ \text{amu}, M_{_1H^1} = 1.007826$$, mass of neutron = $$1.00867 \ u$$)
Find the binding energy of the nucleus of lithium isotope $$_{3}{Li}^{7}$$ and hence find the binding energy per nucleon in it.\left({ M }_{ _{ 3 }{ Li }^{ 7 } }=7.014353amu, { M }_{ _{ 1 }{ H }^{ 1 } }=1.007826, mass of netron=1.00867\ u\right)
Which process is responsible in Hydrogen bomb ?
If 20 N force is applied on a wall which doesn't move the wall than work done by wall is............
Nuclear fusion is responsible in Hydrogen Bomb involving joining of hydrogen nuclei to form Helium and releasing destructive amount of energy.
As there is no displacement of wall, work done(dot product of force and displacement) by the wall is $$0$$(zero).
matter is neither created nor destroyed a chemical reaction More simply the mass of products is equal to the mass of the reaction in a chemical reaction.
Obtain the binding energy (in $$MeV$$) of a nitrogen nucleus $$(^{14}_{7}N)$$, given $$m(^{14}_{7}N)=14.00307\ u$$
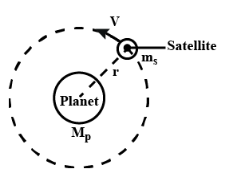
Define binding energy of a satellite. Obtain an expression for the binding energy of a satellite revolving around the earth at a certain altitude.
Explain binding energy curve.Write its importance .What is gamma decay? Explain with example.
Find the binding energy of a H-atom in the state n=2
The mass of the nucleus $$_7N^{14}$$ is $$14.00000amu$$. Calculate the binding energy per nucleon of $$_7N^{14}$$ in MeV. Mass of proton$$=1.00759amu$$, mass of neutron$$=1.00898amu$$ and $$1 amu=931 MeV.$$
A sample has $$1000$$ nuclear samples find after how much time will they remain $$250$$.
Explain why, in a nuclear reactor, the chain reaction stops if the control rods are fully inserted into the graphite.
Assume that the mass of a nucleus is approximately given by $$M = Am_p$$, where $$A$$ is the mass number. Estimate the density of matter in $$kgm^{-3}$$ inside a nucleus. What is the specific gravity of nuclear matter?
What are isotopes?
Define binding energy and obtain an expression for binding energy of a satellite revolving in a circular orbit round the earth.
Binding Energy can be defined as the minimum energy required to be supplied to it order to free the satellite from the gravitational influence of the planet. (i.e; in order to take the satellite from the orbit to as point if infinity.)
Consider a satellite revolving around a planet with speed V at a distance r.
$$KE=\dfrac{1}{2} m_sV^2$$
$$P.E= \dfrac{GM_pm_s}{r}$$
$$E=\dfrac{GM_pm_s}{r^2}$$=$$\dfrac{msV^2}{r}$$$$\Rightarrow m_3V^2$$=$$\dfrac{4M_pm_s}{r}$$
$$KE=\dfrac{1}{2} $$$$ \dfrac{Gm_sM_p}{r}$$
$$T.E=K.E+P.E=\dfrac{1}{2}$$$$\dfrac{GM_pm_s}{r}-\dfrac{GM_pm_s}{r}$$
$$T.E=\dfrac{-GM_pm_s}{2r}$$
$$B.E+T.E=0$$(at infinite $$TE=0$$)
$$B.E=\dfrac{GP_pm_s}{2r}=0$$
$$B.E=\dfrac{GM_pm_s}{2r}$$
Hence Binding energy of satellite G of man $$m_s$$ revolving around a planet of man $$M_p$$ in a radius r
is$$=\dfrac{GM_pm_s}{2r}$$
Consider a satellite revolving around a planet with speed V at a distance r.
$$KE=\dfrac{1}{2} m_sV^2$$
$$P.E= \dfrac{GM_pm_s}{r}$$
$$E=\dfrac{GM_pm_s}{r^2}$$=$$\dfrac{msV^2}{r}$$$$\Rightarrow m_3V^2$$=$$\dfrac{4M_pm_s}{r}$$
$$KE=\dfrac{1}{2} $$$$ \dfrac{Gm_sM_p}{r}$$
$$T.E=K.E+P.E=\dfrac{1}{2}$$$$\dfrac{GM_pm_s}{r}-\dfrac{GM_pm_s}{r}$$
$$T.E=\dfrac{-GM_pm_s}{2r}$$
$$B.E+T.E=0$$(at infinite $$TE=0$$)
$$B.E=\dfrac{GP_pm_s}{2r}=0$$
$$B.E=\dfrac{GM_pm_s}{2r}$$
Hence Binding energy of satellite G of man $$m_s$$ revolving around a planet of man $$M_p$$ in a radius r
is$$=\dfrac{GM_pm_s}{2r}$$
If the nucleon of a nucleous are separated far aprat from each others the sum of mass of all these nucleons is larger than the mass of nucleus where does this mass difference come.
Write the nuclear equations for:
$${\beta}^{+}$$- decay of $$_{ 6 }^{ 11 }{ C }$$
Write nuclear reaction equations for
Electron capture of $$_{ 54 }^{ 120 }{ Xe }$$
Find whether alpha decay or any of the beta decay are allowed for $$_{ 89 }^{ 236 }{ Ac }$$.
Given masses are $$M(_{ 89 }^{ 236 }{ Ac })=226.028356$$ a.m.u; $$M(_{ 87 }^{ 222 }{ Fr })=222.017415$$a.m.u; $$M(_{ 90 }^{ 236 }{ Th }) =226.017388$$a.m.u; $$M(_{ 88 }^{ 226 }{ Ra })=226.025406$$ a.m.u; $$M(_{ 2 }^{ 4 }{ He })=4.002603$$ a.m.u
$${ _{ 92 }^{ }{ U } }^{ 238 }$$ changes to $${ _{ 85 }^{ }{ At } }^{ 210 }$$ by a series of $$\alpha$$ and $$\beta$$ decays. Find number of $$\alpha$$- decays undergone (an integer)
Identify $$X$$ in the following nuclear reactions:
$$\ ^{1}H+\ ^{0}Be\rightarrow X+n$$
What is the minimum energy that is required to break a nucleus of $$^{12} \mathrm{C}$$ ( of mass $$11.99671 \mathrm{u}$$ ) into three nuclei of $$^{4} \mathrm{He}$$ (of mass $$4.00151 \mathrm{u} \text { each }) ?$$
Draw the graph showing the variation of binding energy per nucleon with mass numbers. Give the reason for the decrease of binding energy per nucleon for nuclei with higher mass number.
What is the binding energy per nucleon of $$^{262} Bh$$? The mass of the atom is 262.1231 u.
What is the binding energy per nucleon of the rutherfordium isotope$$^{259} _{104}Rf$$? Here are some atomic masses and the neutron mass.
$$^{259}_{104}Rf$$ 259.105 63 u $$^1H$$ 1.007 825 u
n 1.008 665 u
The first of the following two reactions can occur, but
the second cannot.
Explain.
$$K^0_S \rightarrow \pi^+ + \pi^-$$ (can occur)
$$\wedge^0 \rightarrow \pi^+ + \pi^-$$ (cannot occur)
Compare and contrast the nature of $$\alpha-, \beta-$$ and $$\gamma-$$ radiations.
Answer the following question
In the following nuclear reaction
$$n + ^{235}_{92}U \rightarrow ^{144}_{Z}Ba + ^{A}_{36}X + 3n,$$
Assign the values of Z and A.
Calculate the binding energy per $$^{40}_{20}CA$$ nucleon nucleus.
[Given: $$m\left ( ^{40}_{20}Ca \right ) = 39.962589 \,u$$
$$m_n$$ (mass of a neutron) $$= 1.008665 \,u$$
$$m_p$$ (mass of a proton) $$= 1.007825 \,u$$
$$1 \,u = 931 \,MeV / c^2]$$
Give one example of Isotopes.
Name the constituents of the nucleus of an atom.
Nucleus consists of protons and neutrons.
A radioactive source emits three type of radiations. Name the radiation of zero mass.
Before the neutrino hypothesis, the beta decay process was thought to be the transition $$n\rightarrow p+{e}^{-}$$. If this was true, show that if the neutron was at rest, the proton and electron would emerge with fixed energies and calculate them. Experimentally, the electron energy was found to have a large range.
A radioactive source emits three types of radiations. Name the radiation which travels with the speed of light.
A radioactive source emits three types of radiations. Name the radiation which is most penetrating.
A nuclide 1 is said to be the mirror isobar of nuclide 2 if $${Z}_{1}={N}_{2}$$ and $${Z}_{2}={N}_{1}$$
Which nuclide out of the two mirror isobars have greater binding energy and why?
The mass of a H - atom is less than the sum of the masses of a proton and electron. Why is this ?
State what is meant by the term isotopes. Use the terms proton number and nucleon number in your explanation.
What happens to the atomic number of the nucleus when an $$\alpha$$ particle is emitted?
When an $$\alpha$$ particle captures one electron, what does it change to?
When an $$\alpha$$ particle captures two electrons, what does it change to?
A radioactive source emits three type of radiations. Name the radiation which has the lowest penetrating power.
A certain nucleus $$A$$ (mass number $$238$$ and atomic number $$92$$) is radioactive and becomes a nucleus $$B$$ (mass number $$234$$ and atomic number $$90$$) by the emission of a particle. Name the particle emitted.
What happens to the position of an element in the periodic table when its nucleus emits an $$\alpha$$ particle? Give reason for your answer.
What happens to the mass number of the nucleus when an $$\alpha$$ particle is emitted?
A certain nucleus $$A$$ (mass number $$238$$ and atomic number $$92$$) is radioactive and becomes a nucleus $$B$$ (mass number $$234$$ and atomic number $$90$$) by the emission of a particle. State the change in the form of a reaction.
What changes occur in a nucleus of a radioactive element when it emits an alpha particle? Give one example in support of your answer.
The diagram in figure shows a radioactive source $$S$$ placed in a thick lead walled container. The radiations given out are allowed to pass through a magnetic field. The magnetic field (shown as $$x$$) acts perpendicular to the plane of paper inwards. Arrows shows the paths of the radiation $$A$$, $$B$$ and $$C$$. Explain clearly how you arrive at naming the radiations labelled $$A$$, $$B$$ and $$C$$.
Name two isotopes of uranium which are fissionable.
State one similarity in the process of nuclear fission and fusion
Why is a nuclear fusion reaction called a thermo nuclear reaction?
What is meant by binding energy per nucleon ? How is it related with the stability of nucleus ?
A student says that a heavy form (isotope) of hydrogen decomposes by $$\alpha$$-decay. How would you react ?
Explain nuclear mass defect.
Calculate Q-value for the reaction
$$^{235}_{92}U + ^{1}_{0}n \rightarrow ^{140}_{54} Xe + ^{94}_{34}Sr + 2^{1}_{0}n + Q$$
Given: Mass of $$^{235}_{92}U = 235.0435\,u$$
Mass of $$^{140}_{54}Xe = 139.9054 \,u$$
Mass of $$^{94}_{34}Sr = 93.9063 \,u$$
Mass of $$^{1}_{0}n = 1.00867 \,u$$
Which out of iron or lead, is easier to take out an nucleon from ?
If the nucleons of a nucleus are divided, then total mass increases. Where does this mass come from ?
What is meant by critical mass in nuclear chain reaction ?
Calculate the binding energy of an alpha particle given its mass to be 4.00151 u.
Two stable isotopes of lithium $$_{ 3 }^{ 6 }{ Li }$$ and $$_{ 3 }^{ 7 }{ Li }$$ have respective abundance of $$7.5$$% and $$92.5$$%. These isotopes have masses $$6.01512u$$ and $$7.01600u$$ respectively. Find the atomic mass of lithium.
What is $$\alpha-$$ decay? What type energy spectrum do $$\alpha-$$ particles have?
Calculate binding energy for $$_{26}^{56}Fe$$ nucleus [Given: mass of $$_{26}^{56}Fe=55.9349 u,$$ mass of neutron $$=1.00867u,$$ mass of proton $$=1.00783u$$ and $$1\ u=931MeV/c^2$$]
If the nucleuns of a nucleus are divided, then total mass increases. Where does this mass come from?
Write the nuclear equations for:
$${\beta}^{-}$$- decay of $$_{ 15 }^{ 32 }{ P }$$
$$C^{14}$$ disintegrates by $$\beta-emission$$ with a reaction energy (Q value) of 0.155 MeV. A $$\beta-particle$$ with an energy of 0.025 MeV is emitted in a direction at $$135^o$$ to the direction of motion of the recoil nucleus. Determine the momenta of the three particles $$(\beta^-=\overline v, ^{14}N)$$ involve in this disintegration in MeV/c units (where c is speed of light in vacuum). $$(M_0=0.511 MeV/c^2)$$
A nuclear reaction is given as
$$p+^{15}N\rightarrow _Z^AX+n$$
Find, A, Z and identify the nucleus X.
Find the Q value of the reaction
$$N^{14}+\alpha \rightarrow O^{17}+p$$
The masses of $$N^{14}, He^4, p,$$ and $$O^{17}$$ are, respectively, 14.00307 u, 4.00260 u, 1.00783 u, and 16.99913 u. Find the total kinetic energy of the products if the striking $$\alpha-$$ particle has the minimum kinetic energy required to initiate the reaction:
Find whether $$\alpha$$- decay or any of the $$\beta-$$ decay are allowed for $$_{89}^{226}Ac$$. Given masses are: $$M(_{89}^{226}Ac)=226.028356 amu$$$$M(_{87}^{222}Fr)=222.017415 amu$$$$M(_{90}^{226}Th)=226.017388 amu$$$$M(_{88}^{226}Ra)=226.025406 amu$$$$M(_2^4He)=4.002603 amu$$
The nuclear reaction $$n+_5^{10}B\rightarrow _3^7Li+_2^4He$$ is observed to occur even when very slow-moving neutrons $$(M_n=1.0087 amu)$$ strike a boron atom at rest. For a particular reaction in which $$K_n=0$$, the helium $$(M_{He}=4.0026 amu)$$ is observed to have a speed of $$9.30\times 10^6 ms^{-1}$$. Determine (a) the kinetic energy of the lithium $$(M_{Li}=7.0160 amu)$$ and (b) the Q value of the reaction.
A nuclear reaction is given as
$$p+^{15}N\rightarrow _Z^AX+n$$
Find the Q value of the reaction
Calculate the ground state Q value of the induced fission reaction in the equation
$$n+_{92}^{235}U\rightarrow _{92}^{236}U^*\rightarrow _{40}^{99}Ze+_{52}^{134}Te+3n$$
if the neutron is thermal. A thermal neutron is in the thermal equilibrium with its environment; it has an average kinetic energy given by (3/2) kT. Given: $$m(n)=1.0087 amu, M(^{235}U)=235.0439 amu, M(^{99}Zr)=98.916 amu M(^{134}Te)=133.9115 amu$$
The binding energy of $$_{17}^{35}Cl$$ nucleus is 298 MeV. Find its atomic mass. Given, mass of a proton $$(m_p)=1.007825 amu$$, mass of neutron $$(m_n)=1.008665 amu$$
What is meant by binding energy of nucleus? Determine the binding energy per nucleon of an $$\alpha$$ particle if the masses of proton, neutron and $$\alpha$$- particle are $$1.00728amu$$, $$1.00867amu$$ and $$4.00150amu$$ respectively.
(Given: $$1amu=931MeV$$)
Calculate the binding energy per nucleon for $$_{10}^{20}Ne, _{26}^{56}Fe$$ and $$_{92}^{238}U$$. Given that mass of neutron is 1.008665 amu, mass of proton is 1.007825 amu, mass of $$_{10}^{20}Ne$$ is 19.9924 amu, mass of $$_{26}^{56}Fe$$ is 55.93492 amu, $$_{92}^{238}U$$ is 238.050783 amu
Find the binding energy of an $$\alpha-$$ particle from the following data.
Mass of the helium nucleus $$=4.001265 amu$$
Mass of proton $$=1.007277 amu$$
Mass of neutron $$=1.00866 amu$$
(take $$1 amu=931.4813 MeV)$$
Find whether $$\alpha-decay$$ or any of the $$\beta-decay$$ are allowed for $$_{89}^{226}Ac$$
Write the decay equations and expressions for the disintegration energy Q of the following decay: $$\beta^-$$ decay, $$\beta^+$$ decay, electron capture
What is the minimum photon energy required to remove the least bound neutron of $$_{20}^{40}Ca$$ and $$_{18}^{40}Ar$$. The necessary atomic masses (in u) are given below:
$$M(^{40}Ca)=39.062591 u$$
$$M(^{39}Ca)=38.970719 u$$
$$M(^{40}Ca)=39.962383 u$$
$$M(^{39}Ar)=38.964314 u$$
$$m_n=1.008665 u$$
The neutron separation energy is defined as the energy required to remove a neutron from the nucleus. Obtain the neutron separation energy of the nuclei $$^{27}_{13}Al$$ from the following data:
$$m(^{26}_{13}Al)\, =\, 25.986895\, u$$
$$m(^{27}_{13}Al)\, =\, 26.981541\, u$$
The radio nuclide $$^{11}C$$ decays according to
$$^{11}_{6}C\, \rightarrow\, ^{11}_5B\, +\, e^+\, +\, \nu $$: $$T_{1/2}$$ $$= 20.3\ min$$
The maximum energy of the emitted positron is $$0.960\ MeV$$.
Given the mass values:
$$m\, (^{11}_{6}C)\, =\, 11.011434\, u$$ and $$m\, (^{11}_{6}B)\, =\, 11.009305\, u$$
Calculate $$Q$$ and compare it with the maximum energy of the positron emitted.
Find the Q-value and the kinetic energy of the emitted $$\alpha$$- Particle in the $$\alpha$$-decay of (a) $$^{220}_{86}Rn$$ and (b) $$^{226}_{88}Ra$$.Given:
$$m\, (^{226}_{88}Ra)\, =\, 226.02540\, u$$,
$$m\, (^{222}_{86}Rn)\, =\, 222.01750\, u$$,
$$m\, (^{216}_{84}Po)\, =\, 216.00189\, u$$
$$m\, (^{226}_{88}Ra)\, =\, 226.02540\, u$$,
$$m\, (^{222}_{86}Rn)\, =\, 222.01750\, u$$,
$$m\, (^{216}_{84}Po)\, =\, 216.00189\, u$$
Consider the fission of $$^{238}_{92}U$$ by fast neutrons. In one fission event, no neutrons are emitted and the final end products, after the beta decay of the primary fragments, are $$^{140}_{58}Ce$$ and $$^{99}_{44}Ru$$. Calculate Q for this fission process. The relevant atomic and particle masses are:
$$m(^{238}_{92}U) = 238.05079 u$$
$$m(^{140}_{58}Ce )\, =\,139.90543\, u$$
$$m(^{99}_{44}U) =98.90594 u$$.
Under certain circumstances, a nucleus can decay by emitting a particle more massive than an $$\alpha$$-particle. Consider the following decay processes:
$$^{223}_{88}Ra\, \rightarrow\, ^{209}_{82}Pb\, +\, ^{14}_6C$$
$$^{223}_{88}Ra\, \rightarrow\, ^{219}_{86}Rn\, +\, ^{4}_2He$$
Calculate the Q-values for these decays and determine that both are energetically allowed.
For the $$\beta^+$$ (positron) emission from a nucleus, there is another competing process known as electron capture (electron from an inner orbit, say, the K shell, is captured by the nucleus and a neutrino is emitted).
$$e^+\, +\, ^A_ZX\, \rightarrow\, ^A_{Z - 1}Y\, +\, v$$
Show that if $$\beta^+$$ emission is energetically allowed, electron capture is necessarily allowed but not vice versa.
Assume that there is no repulsive force between the electrons in an atom but the force between positive and negative charges is given by Coulomb's law as usual. Under such circumstance. calculate the ground state energy of a $$He-$$atom
A neutron with kinetic energy $$K=10\ MeV$$ activates a nuclear reaction
$$n+^{ 12 }{ C }\quad \rightarrow {^{ 9 } Be+\alpha }$$
whose threshold $${ E }_{ th }=6.17\ MeV$$. Find the kinetic energy of the alpha particles outgoing at right angles to the direction of the incoming neutron.
[Take $$u=931.1\ MeV$$]
Conservation of energy gives,
$${ m }_{ 1 }{ c }^{ 2 }+{ m }_{ 2 }{ c }^{ 2 }+{ K }_{ 1 }={ m }_{ 3 }{ c }^{ 2 }+{ m }_{ 4 }{ c }^{ 2 }+{ K }_{ 3 }+{ K }_{ 4 }$$
or $$Q+{ K }_{ 1 }={ K }_{ 3 }+{ K }_{ 4 }$$ ... ($$1$$)
Momentum conservation along $$x-$$axis.
$$\sqrt { 2{ m }_{ 1 }{ K }_{ 1 } } =\sqrt { 2{ m }_{ 4 }{ K }_{ 4 } } \cos { \theta }$$
or, $${ m }_{ 1 }{ K }_{ 1 }={ m }_{ 4 }{ K }_{ 4 }\cos ^{ 2 }{ \theta }$$...($$2$$)
Along $$y-$$axis
$$\sqrt { 2{ m }_{ 3 }{ K }_{ 3 } } =\sqrt { 2{ m }_{ 4 }{ K }_{ 4 } } \sin { \theta }$$
or, $${ m }_{ 3 }{ K }_{ 3 }={ m }_{ 4 }{ K }_{ 4 }\sin ^{ 2 }{ \theta }$$ ($$3$$)
Adding ($$2$$) and ($$3$$)
$${ m }_{ 1 }{ K }_{ 1 }+{ m }_{ 3 }{ K }_{ 3 }={ m }_{ 4 }{ K }_{ 4 }$$
or, $${ K }_{ 4 }=\dfrac { { m }_{ 1 } }{ { m }_{ 4 } } { K }_{ 1 }+\dfrac { { m }_{ 3 } }{ { m }_{ 4 } } { K }_{ 3 }$$
Substituting the value of $${ K }_{ 4 }$$ in equation($$1$$), we get
$$Q+\left( 1-\dfrac { { m }_{ 1 } }{ { m }_{ 4 } } \right) { K }_{ 1 }=\left( 1+\dfrac { { m }_{ 3 } }{ { m }_{ 4 } } \right) { K }_{ 3 }$$
Here, $$Q=\dfrac { { -E }_{ th } }{ \left( 1+\dfrac { { m }_{ 1 } }{ { m }_{ 2 } } \right) } =\dfrac { -6.17 }{ \left( 1+\dfrac { 1 }{ 12 } \right) } =-6.17\left( \dfrac { 12 }{ 13 } \right) =-5.69\ MeV$$
Thus $$\left( 1+\dfrac { 4 }{ 9 } \right) { K }_{ 3 }=-5.69+\left( 1-\dfrac { 1 }{ 9 } \right) \left( 10 \right)$$
$${ K }_{ 3 }=\dfrac { 9 }{ 13 } \left[ -5.69+8.89 \right] =2.21\ MeV$$
$${ m }_{ 1 }{ c }^{ 2 }+{ m }_{ 2 }{ c }^{ 2 }+{ K }_{ 1 }={ m }_{ 3 }{ c }^{ 2 }+{ m }_{ 4 }{ c }^{ 2 }+{ K }_{ 3 }+{ K }_{ 4 }$$
or $$Q+{ K }_{ 1 }={ K }_{ 3 }+{ K }_{ 4 }$$ ... ($$1$$)
Momentum conservation along $$x-$$axis.
$$\sqrt { 2{ m }_{ 1 }{ K }_{ 1 } } =\sqrt { 2{ m }_{ 4 }{ K }_{ 4 } } \cos { \theta }$$
or, $${ m }_{ 1 }{ K }_{ 1 }={ m }_{ 4 }{ K }_{ 4 }\cos ^{ 2 }{ \theta }$$...($$2$$)
Along $$y-$$axis
$$\sqrt { 2{ m }_{ 3 }{ K }_{ 3 } } =\sqrt { 2{ m }_{ 4 }{ K }_{ 4 } } \sin { \theta }$$
or, $${ m }_{ 3 }{ K }_{ 3 }={ m }_{ 4 }{ K }_{ 4 }\sin ^{ 2 }{ \theta }$$ ($$3$$)
Adding ($$2$$) and ($$3$$)
$${ m }_{ 1 }{ K }_{ 1 }+{ m }_{ 3 }{ K }_{ 3 }={ m }_{ 4 }{ K }_{ 4 }$$
or, $${ K }_{ 4 }=\dfrac { { m }_{ 1 } }{ { m }_{ 4 } } { K }_{ 1 }+\dfrac { { m }_{ 3 } }{ { m }_{ 4 } } { K }_{ 3 }$$
Substituting the value of $${ K }_{ 4 }$$ in equation($$1$$), we get
$$Q+\left( 1-\dfrac { { m }_{ 1 } }{ { m }_{ 4 } } \right) { K }_{ 1 }=\left( 1+\dfrac { { m }_{ 3 } }{ { m }_{ 4 } } \right) { K }_{ 3 }$$
Here, $$Q=\dfrac { { -E }_{ th } }{ \left( 1+\dfrac { { m }_{ 1 } }{ { m }_{ 2 } } \right) } =\dfrac { -6.17 }{ \left( 1+\dfrac { 1 }{ 12 } \right) } =-6.17\left( \dfrac { 12 }{ 13 } \right) =-5.69\ MeV$$
Thus $$\left( 1+\dfrac { 4 }{ 9 } \right) { K }_{ 3 }=-5.69+\left( 1-\dfrac { 1 }{ 9 } \right) \left( 10 \right)$$
$${ K }_{ 3 }=\dfrac { 9 }{ 13 } \left[ -5.69+8.89 \right] =2.21\ MeV$$
A radio nuclide $$A_1$$ with decay constant $$\lambda_1$$ transforms into a radio nuclide $$A_2$$ with decay constant $$\lambda_2$$. Assuming that at the initial moment, the preparation contained only the radio nuclide $$A_1$$
(a) Find the equation describing accumulation of radio nuclide $$A_2$$ with time.
(b) Find the time interval after which the activity of radio nuclide $$A_2$$ reaches its maximum value.
A stationary $$Pb^{200}$$ nucleus emits an $$\alpha -$$particle with a $$K.E.$$, $$K=5.77\ MeV$$. Find the recoil velocity of daughter nucleus. What fraction of the total energy liberated in this decay is accounted for by the daughter nucleus?
Show that the minimum energy needed to separate a proton from a nucleus with $$Z$$ protons and $$N$$ neutrons is
$$\triangle E = (M_{Z - 1, N} + M_{H} - M_{Z, N})C^{2}$$
where $$M_{Z, N} =$$ mass of an atom with $$Z$$ protons and $$N$$ neutrons in the nucleus and $$M_{H} =$$ mass of a hydrogen atom. This energy is known as proton - separation energy.
Suppose the potential energy between electron and proton at a distance $$r$$ is given by $$U=-ke$$ in (r), where $$k$$ is a positive constant. Use Bohr's theory to obtain the energy of $$n^{th}$$ energy level for such an atom.
In the fusion reaction,
$$_{1}^{2}H + _{1}^{2}H \rightarrow _{2}^{3}He + _{0}^{1}n$$
The masses of deuteron, helium and neutron are $$2.015u, 0.017u$$ and $$1.009u$$ respectively. If $$1\ kg$$ of deuteron completely undergoes fusion, then calculate free energy.
$$[1u = 9.31\ MeV/c^{2}]$$.
The mass defect for the nucleus of lithium is $$0.058135$$ $$amu$$. What is the binding energy(to the nearest integer) per nucleon for lithium in $$MeV$$ will be_______.
In a nuclear reactor, fission is produced in $$1g$$ of $$_{ }^{ 235 }{ U }(235.0349a.m.u)$$. In assuming that $$_{ 53 }^{ 92 }{ Kr }(91.8673a.m.u)$$ and $$_{ 36 }^{ 141 }{ Ba }(140.9139a.m.u)$$ are produced in all reactions and no energy is lost, write the complete reaction and calculate the total energy produced in kilowatt hour. Given: $$(1 a.m.u=931MeV)$$
The nuclear reaction$$n+_{ 5 }^{ 10 }{ B }\rightarrow _{ 3 }^{ 7 }{ Li }+_{ 2 }^{ 4 }{ He }$$is observed to occur even when very slow-moving neutrons $$({M}_{n}=1.0087a.m.u)$$ strike a boron atom at rest. For a particular reaction in which $${K}_{n}=0$$, the helium $$({M}_{He}=4.0026a.m.u)$$ is observed to have a speed of $$9.30\times {10}^{6}m{s}^{-1}$$. Determine (a) the kinetic energy of the lithium $$({M}_{Li}=7.0160a.m.u)$$ and (b) the $$Q$$ value of the reaction.
is observed to occur even when very slow-moving neutrons $$({M}_{n}=1.0087a.m.u)$$ strike a boron atom at rest. For a particular reaction in which $${K}_{n}=0$$, the helium $$({M}_{He}=4.0026a.m.u)$$ is observed to have a speed of $$9.30\times {10}^{6}m{s}^{-1}$$. Determine (a) the kinetic energy of the lithium $$({M}_{Li}=7.0160a.m.u)$$ and (b) the $$Q$$ value of the reaction.
Calculate the ground state $$Q$$ value of the induced fission reaction in the equation$$n+_{ 92 }^{ 235 }{ U }\rightarrow _{ 92 }^{ 235 }{ U }^{\ast}\rightarrow _{ 52 }^{ 134 }{ Te }+3n$$if the neutron is thermal. A thermal neutron is in thermal equilibrium with its environment; it has an average kinetic energy given by $$(3/2)kT$$.
Given $$m(n)=1.0087a.m.u$$, $$M(_{ }^{ 235 }{ U })=235.0439a.m.u$$; $$M(^{ 99 }{ Zr })=98.916a.m.u$$;
$$M(_{ }^{ 134 }{ Te })=133.9115a.m.u$$
if the neutron is thermal. A thermal neutron is in thermal equilibrium with its environment; it has an average kinetic energy given by $$(3/2)kT$$.
Given $$m(n)=1.0087a.m.u$$, $$M(_{ }^{ 235 }{ U })=235.0439a.m.u$$; $$M(^{ 99 }{ Zr })=98.916a.m.u$$;
$$M(_{ }^{ 134 }{ Te })=133.9115a.m.u$$
$$M(_{ }^{ 134 }{ Te })=133.9115a.m.u$$
In the fission of $$_{ 94 }^{ 239 }{ Pu }$$ by a thermal neutron, two fission fragments of equal masses and sizes are produced and four neutrons are emitted. Find the force between the two fission fragments at the moment they are produced. Given $${R}_{0}=1.1fermi$$
A nuclear reaction is given as
$$p+_{ }^{ 15 }{ N }\rightarrow _{ Z }^{ A }{ X }+n$$
(a) Find $$A,Z$$ and identify the nucleus $$X$$
(b) Find the $$Q$$ value of the reaction
(c) If the proton were to collide with the $$_{ }^{ 15 }{ N }$$ at rest, find the minimum KE needed by the proton to initiate the above reaction.
(d) If the proton has twice the energy in (c) and the outgoing neutron emerges at an angle of $${90}^{o}$$ with the direction of the incident proton, find the momentum of the nucleus $$X$$
[Given, $$m(p)=1.007825u,m(_{ }^{ 15 }{ C })=15.0106u$$
$$m(_{ }^{ 16 }{ N })=16.0061u,m(_{ }^{ 15 }{ N })=15.000u$$
$$m(_{ }^{ 16 }{ O })=15.9949u,m(n)=1.008665u$$,
$$m(_{ }^{ 15 }{ O })=15.0031u\quad and\quad 1u=931.5MeV$$]
(a) Find $$A,Z$$ and identify the nucleus $$X$$
(b) Find the $$Q$$ value of the reaction
(c) If the proton were to collide with the $$_{ }^{ 15 }{ N }$$ at rest, find the minimum KE needed by the proton to initiate the above reaction.
(d) If the proton has twice the energy in (c) and the outgoing neutron emerges at an angle of $${90}^{o}$$ with the direction of the incident proton, find the momentum of the nucleus $$X$$
[Given, $$m(p)=1.007825u,m(_{ }^{ 15 }{ C })=15.0106u$$
$$m(_{ }^{ 16 }{ N })=16.0061u,m(_{ }^{ 15 }{ N })=15.000u$$
$$m(_{ }^{ 16 }{ O })=15.9949u,m(n)=1.008665u$$,
$$m(_{ }^{ 15 }{ O })=15.0031u\quad and\quad 1u=931.5MeV$$]
(a) How many atoms are contained in $$1.0 \ kg$$ of pure $$^{235}U$$?
(b) How much energy,in joules,is released by the complete fissioning of $$1.0 \ kg$$ of $$^{235}U$$? Assume $$Q = 200 \ MeV$$.
(c) For how long would this energy light a $$100 \ W$$ lamp?
The radioactive nuclide $$^{99}Tc$$ can be injected into a patients bloodstream in order to monitor the blood flow, measure the blood volume, or find a tumor, among other goals. The nuclide is produced in a hospital by a cow containing $$^{99}Mo$$, a radioactive nuclide that decays to $$^{99} Tc$$ with a half-life of 67 h. Once a day, the cow is milked for its $$^{99}Tc$$, which is produced in an excited state by the $$^{99}Mo$$; the $$^{99} Tc$$ de-excites to its lowest energy state by emitting a gamma-ray photon, which is recorded by detectors placed around the patient. The de-excitation has a half-life of 6.0 h. (a) By what process does $$^{99} Mo$$ decay to $$^{99}Tc$$? (b) If a patient is injected with an $$8.2 \times 10^7 Bq $$ sample of $$^{99}Tc$$, how many gamma-ray photons are initially produced within the patient each second? (c) If the emission rate of gamma-ray photons from a small tumor that has collected $$^{99}Tc$$ is 38 per second at a certain time, how many excitedstate $$^{99}Tc$$ are located in the tumor at that time?
Calculate the disintegration energy $$Q$$ for the fission of $$^{52}Cr$$ into two equal fragments. The masses you will need are
| $$^{52}Cr$$ | $$51.94051 \ u$$ | ^{26}Mg | $$25.98259 \ u$$ |
A typical chest x-ray radiation dose is 250 $$\mu Sv$$, delivered by x-rays with an RBE factor of 0.Assuming that the mass of the exposed tissue is one-half the patients mass of 88 kg, calculate the energy absorbed in joules.
Some uranium samples from the natural reactor site were found to be slightly enriched in $$^{235}U$$, rather than depleted.Account for this in terms of neutron absorption by the abundant isotope $$^{238}U$$ and the subsequent beta and alpha decay of its products.
A 75 kg person receives a whole-body radiation dose of $$ 2.4 \times 10^{-4} Gy$$, delivered by alpha particles for which the RBE fac-tor isCalculate (a) the absorbed energy in joules and the dosee in (b) sieverts and (c) rem.
A free neutron decays according to Eq. $$(\triangle = M-A)$$ . If the neutronhydrogen atom mass difference is $$840 \mu u$$, what is the maximum kinetic energy $$K_{max}$$ possible for the electron producedin a neutron decay?
A certain stable nuclide, after absorbing a neutron, emits an electron and the new nuclide splits spontaneously into two alpha particles. Identify the nuclide.
A particular rock is thought to be 260 million years old. If it contain 3.70 mg of $$^{238}U$$, how much $$^{206}Pb$$ should it contain? SeeProblem 61.
What is the $$Q$$ of the following fusion process?
$$ ^2 H_1 + ^1 H_1 \rightarrow ^3 He_2 + photon $$
Here are some atomic masses.
| $$^2 H_1$$ | $$2.014 102 \ u$$ |
| $$^1 H_1$$ | $$1.007 825 \ u$$ |
| $$^3 He_2$$ | $$3.016 029 \ u$$ |
What mass of phosphorus is needed to dope $$1.0
g$$ of silicon so that the number density of conduction electrons in the silicon is increased by a multiply factor of $$10^6$$ from the $$10^{16} m^3$$ in pure silicon.
The thermal energy generated when radiation from radionuclides is absorbed in matter can serve as the basis for a small power source for use in satellites, remote weather stations, and other isolated locations. Among the many fission products that may be extracted chemically from the spent fuel of a nuclear reactor is $$^{90}Sr \ (T_{1/2} = 29 \ y)$$. This isotope is produced intypical large reactors at the rate of about $$18 \ kg/y$$. By its radioactivity,the isotope generates thermal energy at the rate of $$0.93 \ W/g$$. (a) Calculate the effective disintegration energy $$Q_{eff}$$ associated with the decay of a $$^{90}Sr$$ nucleus. (This energy $$Q_{eff}$$ includes contributions from the decay of the $$^{90}Sr$$ daughter products in its decay chain but not from neutrinos, which escape totally from the sample.) (b) It is desired to construct a power source generating $$150 \ W$$ (electric power) to use in operating electronic equipment in an underwater acoustic beacon. If the power source is based on the thermal energy generated by 90Sr and if the efficiency of the thermalelectric conversion process is $$5.0 \%$$, how much $$^{90}Sr$$ is needed?
Calculate the Q value for the (a) first and (b) second decay and determine that both are energetically possible. (c) The Coulomb barrier height for alpha-particle emission is 30.0 MeV. What is the barrier height for $$14C$$ emission? (Be careful about the nuclear radii.) The needed atomic masses are
$$223{Ra} \rightarrow 209{pb} + 14C and 223{Ra} \rightarrow 219{Rn} + 4{He} $$
Calculate the Q value for the (a) first and (b) second decay and determine that both are energetically possible. (c) The Coulomb barrier height for alpha-particle emission is 30.0 MeV. What is the barrier height for $$^{14} C$$ emission? (Be careful about the nuclear radii.) The needed atomic masses are
$$^{223}Ra$$ 223.018 50 u $$^{14}C$$ 14.003 24 u
$$^{209}Pb$$ 208.981 07 u $$^4He$$ 4.002 60 u
$$^{219}Rn$$ 219.009 48 u
If the unit for atomic mass were defined so that the mass of $$^ 1H$$ were exactly 1.000 000 u, what would be the mass of (a) $$^{12}C$$ (actual mass 12.000 000 u) and (b) $$^{238}U $$ (actual mass 238.050 785 u)?
Find the disintegration energy Q for the decay of $$^{49}V$$ by K-electron capture . The needed data are $$ m_V = 48.948 52 u ,$$ m_Ti = 48.947 87 u $$, and $$ E_K = 5.47 keV$$.
Verify the $$Q$$ values reported in equations,
$$^2H + \ ^2H \rightarrow \ ^3He + n$$ $$ (Q=+3.27 \ MeV) $$,
$$^2H + \ ^2H \rightarrow \ ^3H + \ ^1H$$ $$ (Q=+4.03 \ MeV) $$, and
$$^2H + \ ^3H \rightarrow \ ^4He + n$$ $$ (Q=+17.59 \ MeV) $$,
The needed masses are
| $$^1H$$ | $$1.007825 \ u$$ | $$^4He$$ | $$4.002603 \ u$$ |
| $$^2H$$ | $$2.014102 \ u$$ | $$n$$ | $$1.008665 \ u$$ |
| $$^3H$$ | $$3.016049 \ u$$ |
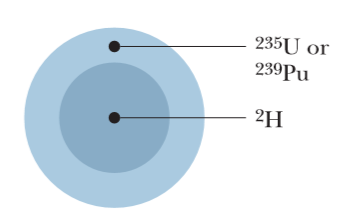
The above figure shows an early proposal for a hydrogen bomb. The fusion fuel is deuterium, $$^2H$$. The high temperature and particle density needed for fusion are provided by an atomic bomb trigger" that involves a $$^{235}U$$ or $$^{239}Pu$$ fission fuel arranged to impress an imploding, compressive shock wave on the deuterium. The fusion reaction is
$$5 \ ^2H \rightarrow ^3He + ^4H + ^1H + 2n$$
(a) Calculate $$Q$$ for the fusion reaction. The following table is given for needed atomic masses.
| $$^1H$$ | $$1.007 825 \ u$$ | $$^4He$$ | $$4.002 603 \ u$$ |
| $$^2H$$ | $$2.014 102 \ u$$ | $$e^{\pm}$$ | $$0.000 548 6 \ u$$ |
| $$^3He$$ | $$3.016 029 \ u$$ |
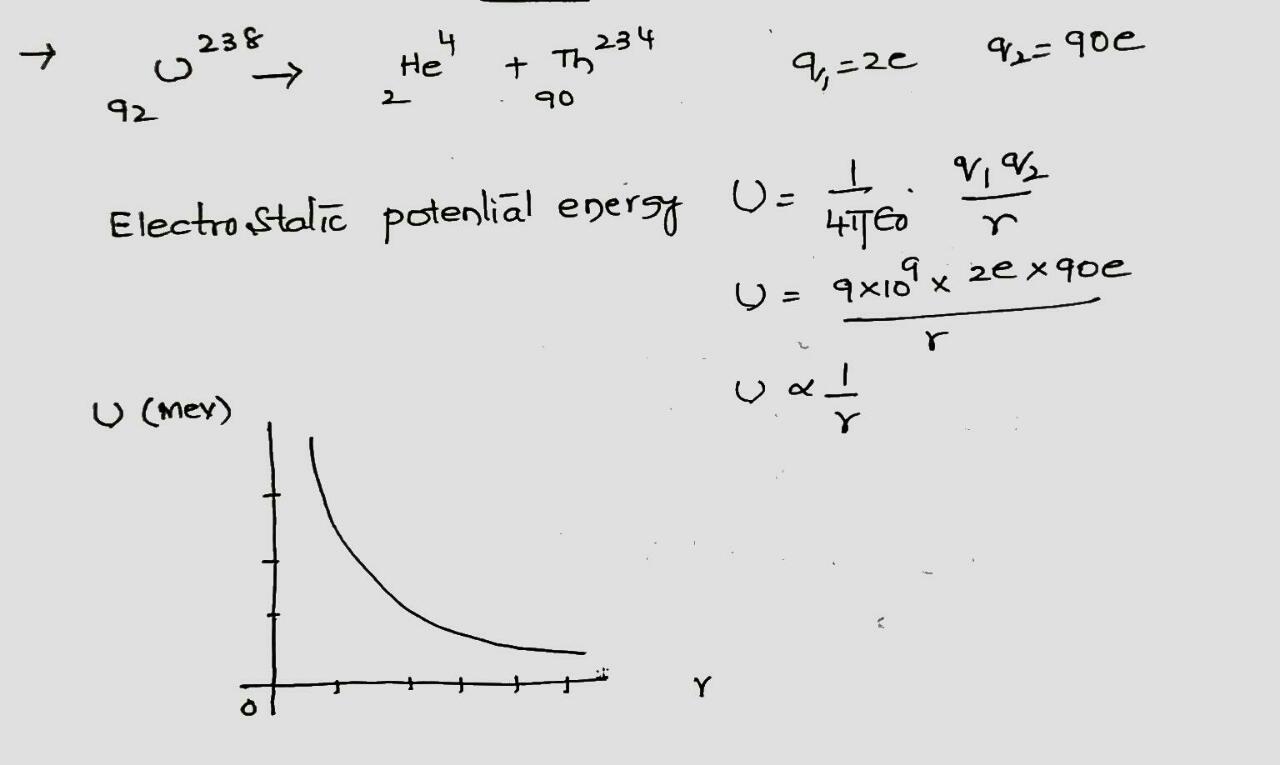
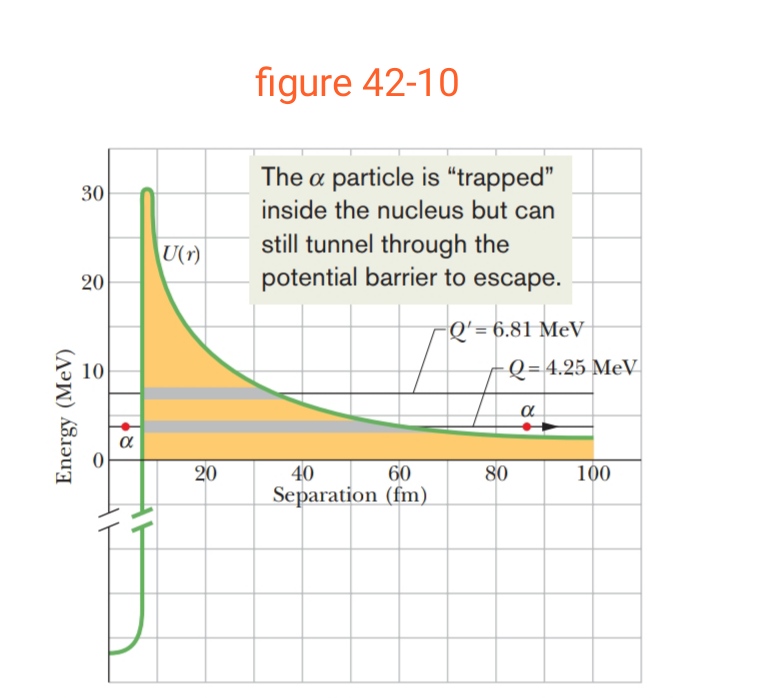
Consider a $$^{238}U$$ nucleus to be made up of an alpha particle$$(^4He)$$ and a residual nucleus $$(^{234}Th)$$. Plot the electrostatic potential energy U(r), where r is the distance between these particles. Coverthe approximate range $$10 fm < r <100 fm $$ and compare your plotwith that of Fig. 42-10.
In certain stars the carbon cycle is more effective than the proton-proton cycle in generating energy. This carbon cycle is
$$ ^{12}C + ^1H \rightarrow ^{13}N + \gamma $$ $$Q_1 = 1.95 \ MeV$$,
$$ ^{1}N \rightarrow ^{13}C + e^+ + v $$ $$Q_2 = 1.19$$,
$$ ^{13}C + ^1H \rightarrow ^{14}N + \gamma $$ $$Q_3 = 7.55$$,
$$ ^{14}N + ^1H \rightarrow ^{15}O + \gamma $$ $$Q_4 = 7.30$$,
$$ ^{15}O \rightarrow ^{15}N + e^+ + v $$ $$Q5 = 1.73$$, $$ ^{15}N + ^1H \rightarrow ^{12}C + ^4He $$ $$Q_6 = 4.97$$.
(a) Show that this cycle is exactly equivalent in its overall effects to the proton-proton cycle of the above figure. (b) Verify that the two cycles,as expected,have the same $$Q$$ value.
Show that the energy released when three alpha particles fuse to form $$^{12}C$$ is $$7.27 \ MeV$$. The atomic mass of $$^4He$$ is $$4.0026 \ u$$, and that of $$^{12}C$$ is $$12.0000 \ u$$.
Nuclei with magic no. of proton $$Z=2,8,20,28,50,52$$ and magic no. of neutrons $$N=2,8,20,28,50,82$$ and $$126$$ are found to be very stable
(i) Verify this by calculting the proton separation energy $${S}_{p}$$ for $${ _{ 50 }^{ }{ Sn } }^{ 120 }\left( Z=50 \right) $$ and $${ _{ 51 }^{ }{ Sb } }^{ 121 }\left( Z=51 \right) $$. The protn separation energy for a nuclide is the minimum energy required to separate the least tightly bound proton from a nucleus of that nuclide. It is given by
$${S}_{p}=[M{Z}_{-1,n}+{M}_{{H}^{-}}-{M}_{ZN}]{c}^{2}$$
Given $$_{ }^{ 119 }{ In }=118.9058u,_{ }^{ 120 }{ Sn }=119.902199u,_{ }^{ 121 }{ Sb }=120.903842u,_{ }^{ 1 }{ H }=1.0078252u$$
(ii) What does the existence of magic number indicate?
Consider the decay $$\Lambda^{o} \rightarrow p | \pi^{-}$$ with the $$\Lambda^{o}$$ at rest.
(a) Calculate the disintegration energy. What is the kinetic energy of (b) the proton and (c) the pion?
Calculate the disintegration energy of the reactions
(a) $$\pi^{+} + p \rightarrow \sum^{+} + K^{+}$$ and (b) $$K^{-} + p \rightarrow \Lambda^{o} + \pi^{o}$$.
What Is the longest wavelength of a photon that can ionize a hydrogen atom in its ground state? Specify the type of radiation.
A radioactive source emits three type of radiations. From which part of the atom do these radiations come?
Draw the graph showing the variation of binding energy per nucleon with the mass number for a large number of nuclei $$2 < A < 240.$$ What are the main inferences from the graph ? How do you explain the constancy of binding energy in the range $$30 < A < 170$$ using the property that the nuclear force is short-ranged ? Explain with the help of this plot the release of energy in the processes of nuclear fission and fusion.
The variation of binding energy per nucleon versus mass number is shown in figure. Inferences from graph
(1) The nuclei having mass number below $$20$$ and above $$180$$ have relatively small binding energy and hence they are unstable.
(2) The nuclei having mass number $$56$$ and about $$56$$ have maximum binding energy - $$5.8 \,MeV$$ and so they are most stable.
(3) Some nuclei have peaks, e.g.,$$^{4}_{2}He, ^{12}_{6}C, ^{12}_{6}O;$$ this indicates that these nuclei are relatively more stable than their neightbours.
(i) Explanation of constancy of binding energy: Nuclear force is short ranged, so every nucleon interacts with its neighbours only, therefore binding energy per nucleon remains constant.
(ii) Explanation of nuclear fission: When a heavy nucleus $$(A \geq 235 \,say)$$ breaks into two lighter nuclei (nuclear fission), the binding energy per nucleon increases i.e, nucleons get more tightly bound. This implies that energy would be released in nuclear fission.
(iii) Explanation of nuclear fusion: When two very nuclei $$(A \leq 10)$$ join to form a heavy nucleus, the binding is energy per nucleon of fused heavier nucleus more than the binding energy per nucleon of lighter nuclei, so again energy would be released in nuclear fusion.
(1) The nuclei having mass number below $$20$$ and above $$180$$ have relatively small binding energy and hence they are unstable.
(2) The nuclei having mass number $$56$$ and about $$56$$ have maximum binding energy - $$5.8 \,MeV$$ and so they are most stable.
(3) Some nuclei have peaks, e.g.,$$^{4}_{2}He, ^{12}_{6}C, ^{12}_{6}O;$$ this indicates that these nuclei are relatively more stable than their neightbours.
(i) Explanation of constancy of binding energy: Nuclear force is short ranged, so every nucleon interacts with its neighbours only, therefore binding energy per nucleon remains constant.
(ii) Explanation of nuclear fission: When a heavy nucleus $$(A \geq 235 \,say)$$ breaks into two lighter nuclei (nuclear fission), the binding energy per nucleon increases i.e, nucleons get more tightly bound. This implies that energy would be released in nuclear fission.
(iii) Explanation of nuclear fusion: When two very nuclei $$(A \leq 10)$$ join to form a heavy nucleus, the binding is energy per nucleon of fused heavier nucleus more than the binding energy per nucleon of lighter nuclei, so again energy would be released in nuclear fusion.
'Radioactivity is a nuclear phenomenon'. Comment on this statement.
Explain mass defect and binding energy. Explain the main results obtained from the graph between binding energy per nucleon and mass number.
Find the Q-value and the kinetic energy of the emitted $$\alpha$$- particle in the $$\alpha$$- decay of (a) $$_{ 88 }^{ 226 }{ Ra }$$ (b) $$_{ 86 }^{ 222 }{ Rn }$$
Given
$$m\left( _{ 88 }^{ 226 }{ Ra } \right) =226.02540u;\quad m\left( _{ 86 }^{ 222 }{ Rn } \right) =222.01750u;\quad m\left( _{ 86 }^{ 222 }{ Rn } \right) =220.01137u;\quad m\left( _{ 84 }^{ 216 }{ Po } \right) =216.00189u$$
The Q value of a nuclear reaction $$A+b\rightarrow C+d$$ is defined by $$Q=({m}_{A}+{m}_{B}-{m}_{c}-{m}_{d})$$ where the masses refer to the respective nuclei. Determine from the given data the Q-value of the following reactions and state whether the reactions are exothermic or endothermic.
(i) $$_{ 1 }^{ 1 }{ H }+_{ 1 }^{ 3 }{ H }\rightarrow _{ 1 }^{ 2 }{ H }+_{ 1 }^{ 2 }{ H }$$
(ii) $$_{ 6 }^{ 12 }{ C }+_{ 6 }^{ 12 }{ C }\rightarrow _{ 10 }^{ 20 }{ Ne }+_{ 2 }^{ 4 }{ He }$$
Atomic masses are given to be
$$m\left( _{ 1 }^{ 2 }{ H } \right) =2.014102u;\quad m\left( _{ 1 }^{ 3 }{ H } \right) =3.016049;\quad m\left( _{ 6 }^{ 12 }{ C } \right) =12.00000u;\quad m\left( _{ 10 }^{ 20 }{ Ne } \right) =19.992439u$$
What is $$\alpha$$-decay ? What type of energy spectrum do $$\alpha$$-particles have ?
Calculate binding energy for $$^{56}_{26}Fe$$ nucleus [ Given: mass of $$^{56}_{26}Fe = 55.9349 \,u,$$ mass of neutron $$= 1.00867 \,u,$$ mass of proton $$= 1.00783 \,u$$ and $$1 \,u = 931 \,MeV/c^2$$].
Describe $$\alpha$$-decay in a radioactive nucleus. Explain that the energy spectrum of $$\alpha$$-particles obtained from the decay is wide spectrum of group of energies.
Find the energy Q liberated in $$ \beta^{-} $$ and $$\beta^{+} $$ -decays and in K- capture if the masses of the parent atom $$M_{p}$$, the daughter atom $$M_{d}$$ and an electron $$m$$ are known.
Under certain circumstances, a nucleus can decay by emitting $$a$$- particle more massive than an $$a$$- particle. Consider the following decay processes:
$$\quad _{ 88 }^{ 223 }{ Ra }\rightarrow _{ 82 }^{ 209 }{ Pb }+_{ 6 }^{ 14 }{ C }$$
$$\quad _{ 88 }^{ 223 }{ Ra }\rightarrow _{ 86 }^{ 219 }{ Rn }+_{ 2 }^{ 4 }{ He }$$
Calculate the Q-values for these decays and determine that both are energetically allowed.
Determine the spectral symbol of an atomic singlet term if the total splitting of that term in a weak magnetic field of induction $$ B = 3.0\,kG$$ amounts to $$ \Delta E = 104 \mu eV$$.
Taking into account the motion of the nucleus of a hydrogen atom, find the expressions for the electron's binding energy in the ground state and for the Rydberg constant. How much (in per cent) do the binding energy and the Rydberg constant, obtained without taking into account the motion of the nucleus, differ from the more accurate corresponding values of these quantities ?
Calculate the binding energy of a K electron in vanadium whose L absorption edge has the wavelength $$ \lambda_{L} = 2.4\,nm $$
Find the binding energy of an L electron in titanium if the wavelength difference between the first line of the K series and its short-wave cut-off is $$ \Delta \lambda = 26\,pm$$.
The neutron separation energy is defined as the energy required to remove a neutron from the nucleus. Obtain the neutron separation energies of the nuclei $$_{ 20 }^{ 41 }{ Ca }$$ $$_{ 13 }^{ 27 }{ Al }$$ from the following data
$$m\left( _{ 20 }^{ 40 }{ Ca } \right) =39.962591u;\quad m\left( _{ 20 }^{ 41 }{ Ca } \right) =40.962278u;\quad m\left( _{ 13 }^{ 26 }{ Al } \right) =25.986895u;\quad m\left( _{ 13 }^{ 27 }{ Al } \right) =26.981541u$$
A stationary $$Pb^{200}$$ nucleus emits an alpha-particle with kinetic energy $$T_{\alpha} = 5.77 \,MeV$$. Find the recoil velocity of a daughter nucleus. What fraction of the total energy liberated in this decay is accounted for by the recoil energy of the daughter nucleus ?
For atoms of light and heavy hydrogen (H and D) find the difference
(a) between the binding energies of their electrons in the ground state;
(b) between the wavelengths of first lines of the Lyman series.
Find the difference in binding energies of a neutron and a proton in a $$B^{11}$$ nucleus. Explain why there is the difference.
Making use of the tables of atomic masses, determine the energies of the following reactions:
(a) $$Li^{7} (p , n) Be^{7}$$;
(b) $$Be^{9} (n , \gamma ) Be^{10}$$;
(c) $$Li^{7} (\alpha , n ) B^{10} $$;
(d) $$O^{16} (d , \alpha) N^{14} $$
Calculate in atomic mass units the mass of
(a) a $$Li^{8}$$ atom whose nucleus has the binding energy $$41.3\,MeV$$;
(b) a $$C^{10}$$ nucleus whose binding energy per nucleon is equal to $$6.04\,MeV$$.
To activate the reaction $$(n, \alpha)$$ with stationary $$B^{11}$$ nuclei, neutrons must have the threshold kinetic energy $$T_{th} = 4.0\,MeV$$. Find the energy of this reaction.
What kinetic energy must a proton possess to split a deuteron $$H^2$$ whose binding energy is $$E_{b} = 2.2\,MeV$$ ?
Find the energy required for separation of a $$Ne^{20} $$ nucleus into two alpha-particles and a $$C^{12}$$ nucleus if it known that the binding energies per one nucleon in $$Ne^{20} , He^{4} $$ , and $$C^{12}$$ nuclei are equal to $$8.03 , 7.07 $$ and $$7.68\,MeV $$ respectively.
Making use of the tables of atomic masses, find:
(a) the mean binding energy per one nucleon in $$O^{16}$$ nucleus;
(b) the binding energy of a neutron and an alpha-particle in a $$B^{11} $$ nucleus.
(c) the energy required for separation of an $$O^{16}$$ nucleus into four identical particles.
Find the binding energy of a nucleus consisting of equal numbers of protons and neutrons and having the radius one and a half times smaller than that of $$Al^{27} $$ nucleus.
Assuming that the splitting of a $$U^{235}$$ nucleus liberates the energy of $$200\,MeV$$, find:
(a) the energy liberated in the fission of one kilogram of $$U^{235}$$ isotope, and the mass of coal with calorific value of $$30\,kJ/g$$ which is equivalent to that for one kg of $$U^{235}$$;
(b) the mass of $$U^{235}$$ isotope split during the explosion of the atomic bomb with $$30\,kt$$ trotyl equivalent if the calorific value of trotyl is $$4.1\,kJ/g$$.
A negative pion with kinetic energy $$ T = 50\,MeV$$ disintegrated during its flight into a muon and a neutrino. Find the energy of the neutrino outgoing at right angles to the pion's motion direction.
See the diagram. By conservation of energy
$$ \sqrt{m^{2}_{\pi} c^{4} + c^{2} p^{2}_{\pi}} = c p_{\nu} + \sqrt{m^{2}_{\mu} c^{4} + p^{2}_{\pi} c^{4} + p^{2}_{\mu} c^{4} + p^{2}_{\pi} c^{2} + c^{2} p^{2}_{\nu}} $$
or $$ \left (\sqrt{m^{2}_{\pi} c^{4} + c^{2} p^{2}_{\pi}} - cp_{\nu} \right )^{2} = m^{2}_{\mu} c^{4} + c^{2}p^{2}_{\pi} + c^{2} p^{2}_{\nu} $$
or $$m^{2}_{\pi} c^{4} - 2 c\ p_{\nu} \sqrt{m^{2}_{\pi} c^{4} + c^{2}p^{2}_{\pi}} = m^{2}_{\mu} c^{4} $$
Hence the energy of the neutrino is
$$E_{\nu} = c\ p_{\nu} = \dfrac{m^{2}_{\pi}c^{4} - m^{2}_{\mu} c^{4}}{2 (m_{\pi} c^{2} + T)} $$
on writing $$ \sqrt{m^{2}_{\pi} c^{4} + c^{2} p^{2}_{\pi} + c^{2} p^{2}_{\pi}} = m_{\pi} c^{2} + T $$
Substitution gives $$E_{\nu} = 21.93\,MeV$$
$$ \sqrt{m^{2}_{\pi} c^{4} + c^{2} p^{2}_{\pi}} = c p_{\nu} + \sqrt{m^{2}_{\mu} c^{4} + p^{2}_{\pi} c^{4} + p^{2}_{\mu} c^{4} + p^{2}_{\pi} c^{2} + c^{2} p^{2}_{\nu}} $$
or $$ \left (\sqrt{m^{2}_{\pi} c^{4} + c^{2} p^{2}_{\pi}} - cp_{\nu} \right )^{2} = m^{2}_{\mu} c^{4} + c^{2}p^{2}_{\pi} + c^{2} p^{2}_{\nu} $$
or $$m^{2}_{\pi} c^{4} - 2 c\ p_{\nu} \sqrt{m^{2}_{\pi} c^{4} + c^{2}p^{2}_{\pi}} = m^{2}_{\mu} c^{4} $$
Hence the energy of the neutrino is
$$E_{\nu} = c\ p_{\nu} = \dfrac{m^{2}_{\pi}c^{4} - m^{2}_{\mu} c^{4}}{2 (m_{\pi} c^{2} + T)} $$
on writing $$ \sqrt{m^{2}_{\pi} c^{4} + c^{2} p^{2}_{\pi} + c^{2} p^{2}_{\pi}} = m_{\pi} c^{2} + T $$
Substitution gives $$E_{\nu} = 21.93\,MeV$$
A nuclear reaction is given as
$$p+ \ ^{15}N\rightarrow \ _Z^AX+n$$
a) Find $$A, Z$$ and identify the nucleus $$X$$.
b) Find the $$Q$$ value of the reaction.
c) If the proton were to collide with the $$^{15}N$$ at rest, find the minimum $$KE$$ needed by the proton to initiate the above reaction
Class 12 Medical Physics Extra Questions
- Alternating Current Extra Questions
- Atoms Extra Questions
- Current Electricity Extra Questions
- Dual Nature Of Radiation And Matter Extra Questions
- Electric Charges And Fields Extra Questions
- Electromagnetic Induction Extra Questions
- Electromagnetic Waves Extra Questions
- Electrostatic Potential And Capacitance Extra Questions
- Magnetism And Matter Extra Questions
- Moving Charges And Magnetism Extra Questions
- Nuclei Extra Questions
- Ray Optics And Optical Instruments Extra Questions
- Semiconductor Electronics: Materials, Devices And Simple Circuits Extra Questions
- Wave Optics Extra Questions