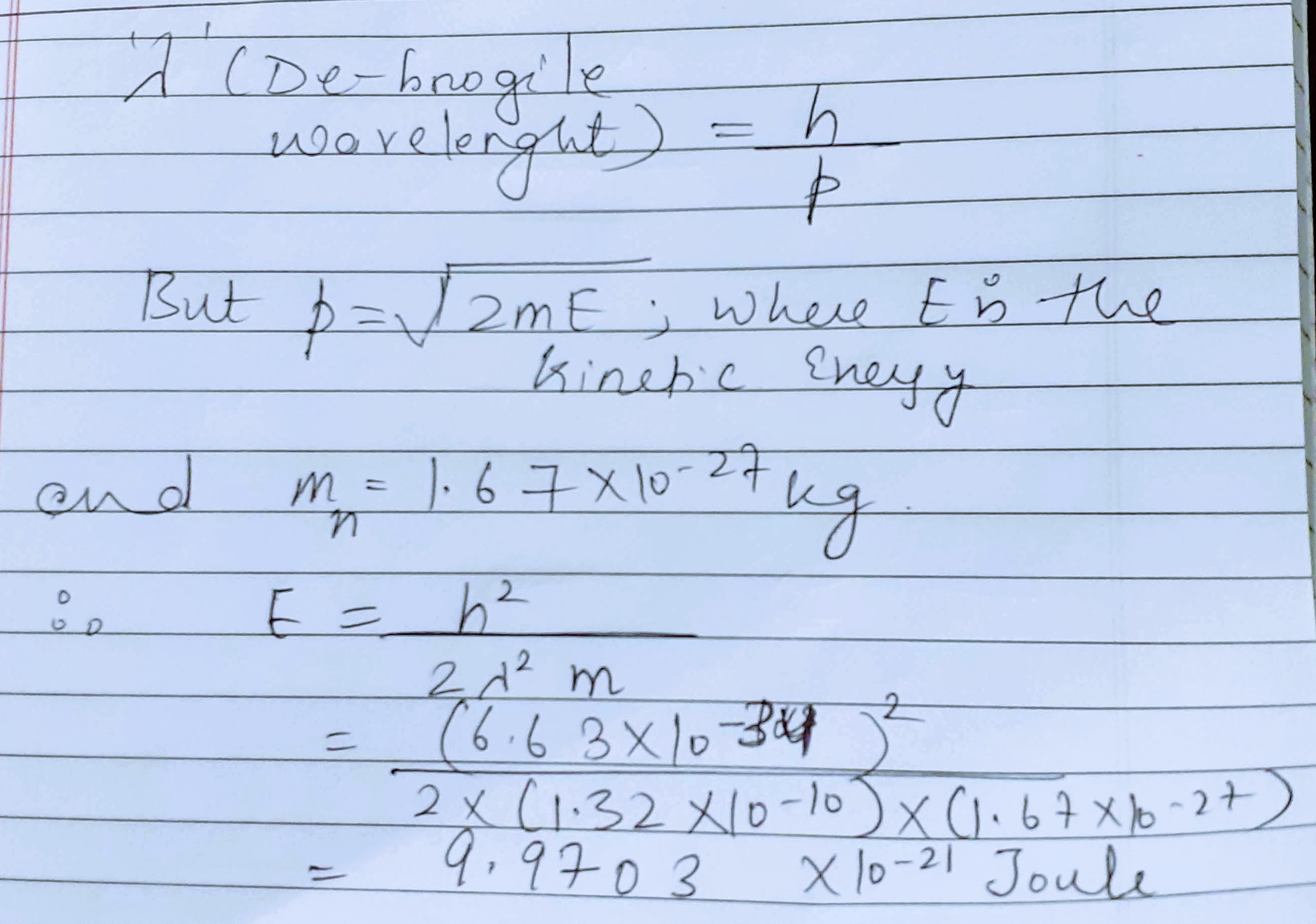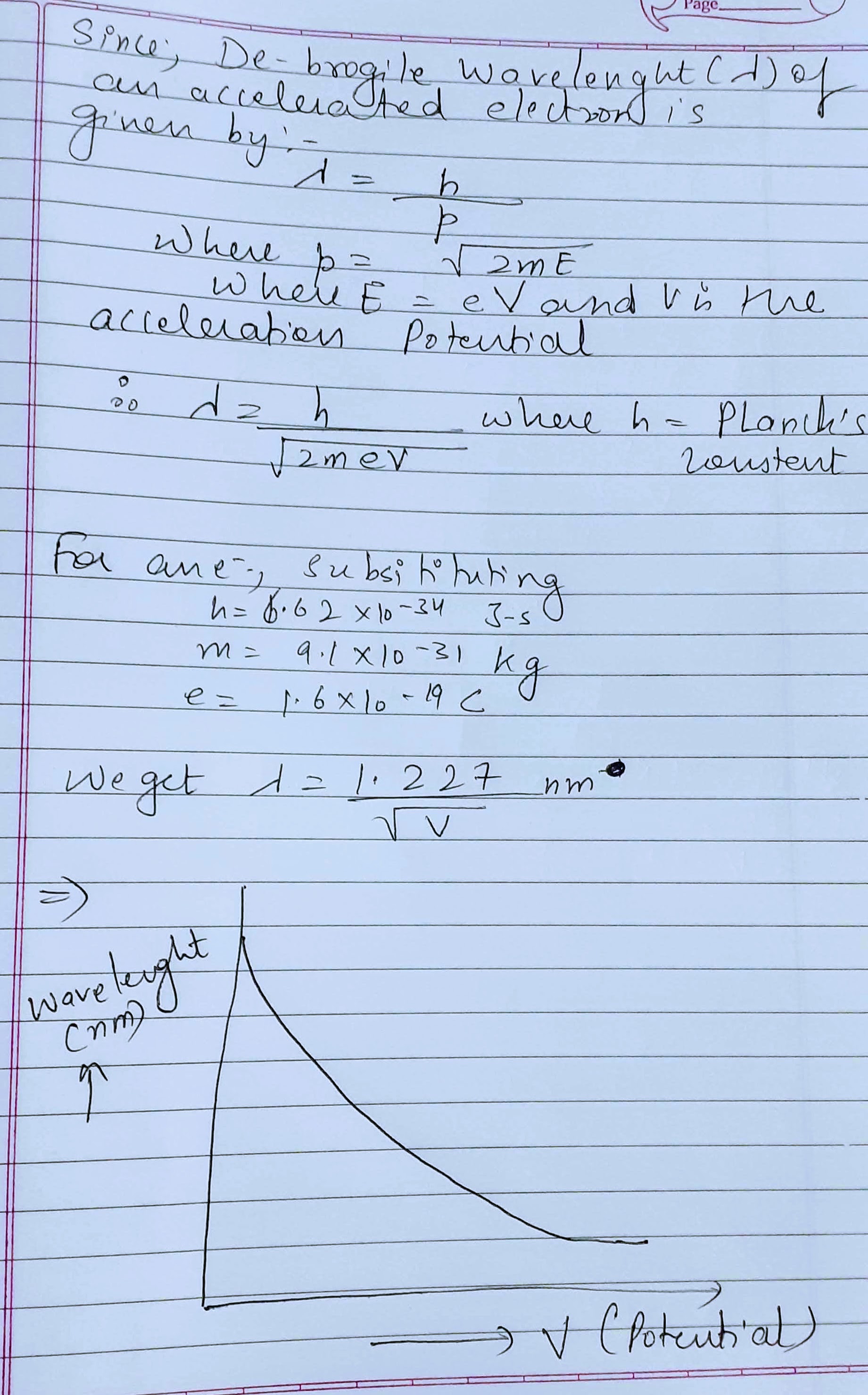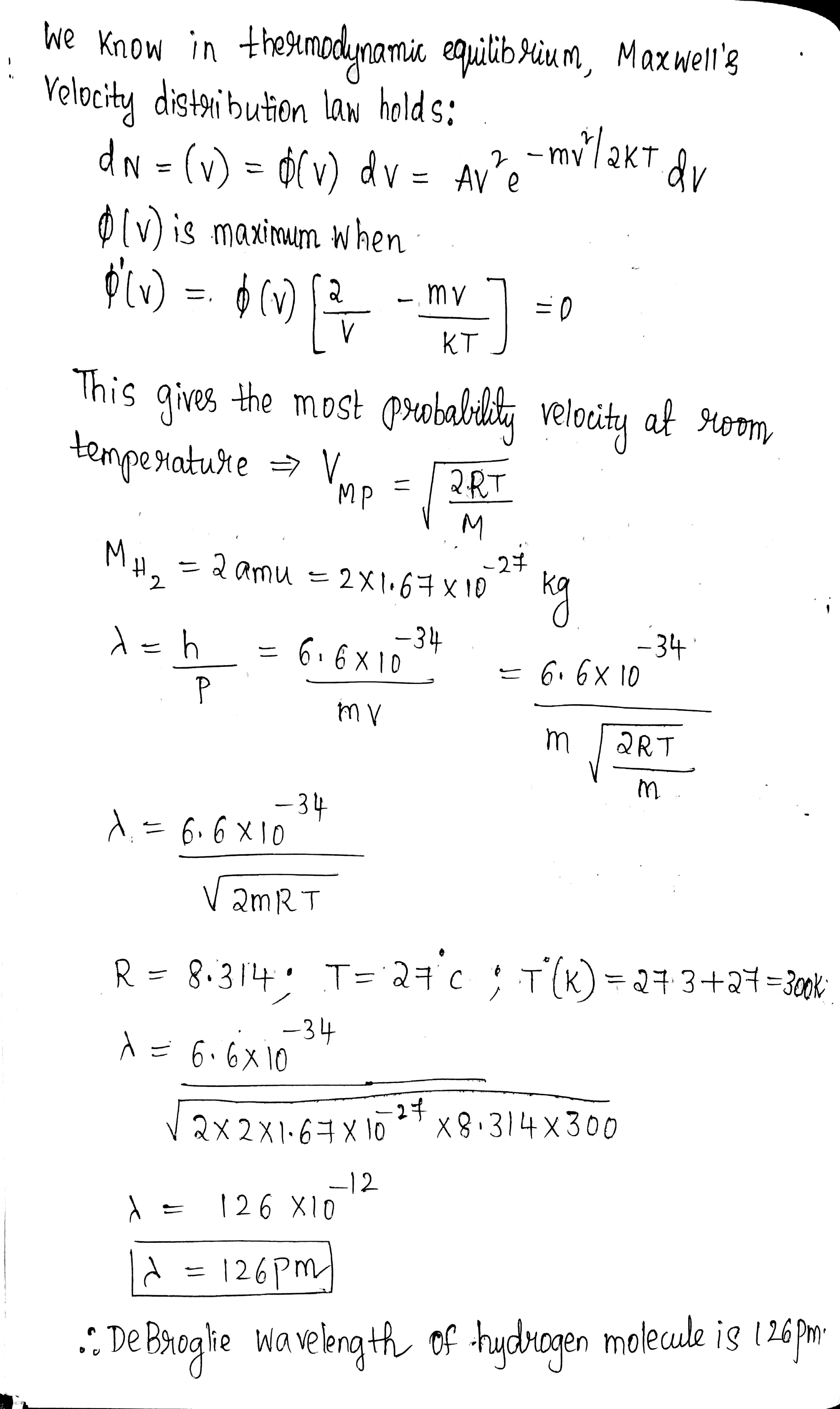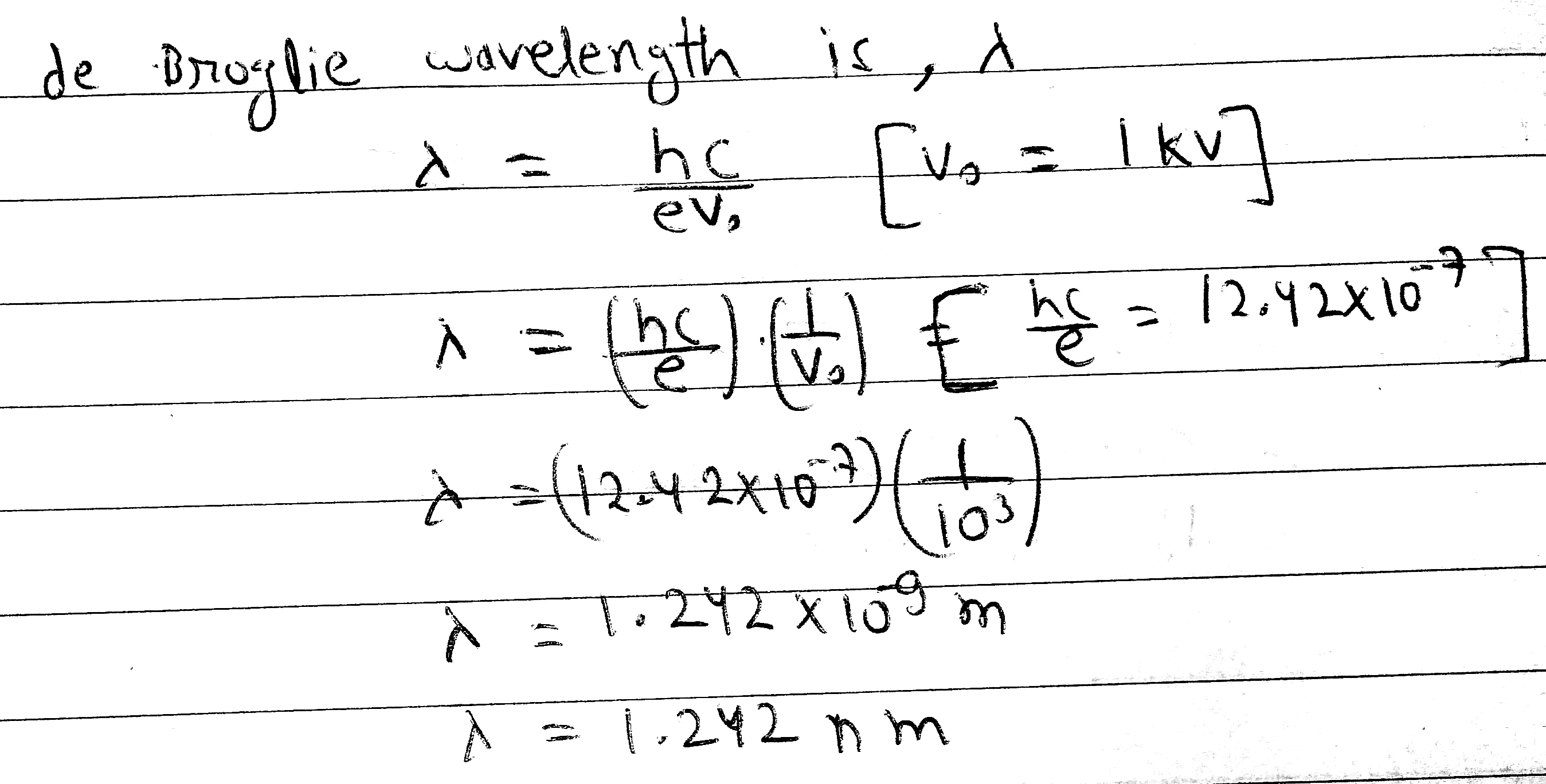Class 12 Medical Physics - Dual Nature Of Radiation And Matter

An electron in an atom absorbs radiation of wavelength 392.n.m and later on it emits energy in the from of photons of two different wavelengths. If one of the wavelength is 712 n.m. Calculate the other.

Given,

Energy, $$E=\dfrac{hc}{\lambda }$$ (where, $$\lambda $$ is wavelength)

Energy absorbed wavelength,$$\lambda =392\,nm$$

One wave length is $$\lambda '=712\,nm$$

From conservation of energy.

Energy absorbed by electron = Energy emitted in first wave + Energy emitted in second wave

$$ \dfrac{hc}{\lambda }=\dfrac{hc}{\lambda '}+\dfrac{hc}{\lambda ''} $$

$$ \lambda ''=\dfrac{\lambda '\times \lambda }{\lambda '-\lambda }=\dfrac{712\times 392}{712-392}=872.2\,nm $$

Hence, second wavelength is $$872.2\,nm$$

The energy of the photons causing the photoelectrons emission

1483094_1153941_ans_63f271a2ba594e7d9a98bb6bd10c8278.jpg

How many photons are emitted per second by $$a\ 5\ mW$$ laser source operating at $$632.8\ nm$$?

Wavelength $$=632.8\ nm$$

$$=6328\ A^o$$

Power $$=5\ mW$$

$$\therefore \ E=\dfrac {hc}{\lambda}$$

$$=\dfrac {12375}{\lambda (A^o)}$$

$$\therefore \ $$ Energy $$=\dfrac {12375}{6328}$$

$$=1.955\ eV$$

$$\therefore \ $$ Energy of photon in eV $$=1.955\times 1.6\times 10^{-19}$$

$$=3.12895\times 10^{-19}$$eV

Let no. of photons emitted in one second $$=n$$

$$\therefore \ $$ No. of photons emitted per second

$$n=\dfrac {Power }{Energy\ of\ photon}$$

$$=\dfrac {5\times 10^{-3}}{3.1289\times 10^{-19}}$$

$$=1.597\times 10^{16}$$

If the kinetic energy of the particle is increased to $$16$$ times previous the percentage change in the deBrogille wavelength of the particle is

$$\lambda =\dfrac { h }{ \sqrt { 2mh } } $$

$${ \lambda }^{ 1 }=\dfrac { h }{ \sqrt { 2m\times 16h } } $$ [Increase by $$16$$ times]

$$\lambda =\dfrac { \lambda }{ 4 } $$

Percentage change in de-Broglie wavelength

$$\dfrac { \lambda -{ \lambda }^{ 1 } }{ \lambda } \times 100=\left( 1-\dfrac { { \lambda }^{ 1 } }{ \lambda } \right) \times 100$$

$$=\left( 1-\dfrac { 1 }{ 4 } \right) \times 100$$

$$=75$$%

The electron with The electron with de Broglie wavelength $$\lambda $$ is bombarded on a metal target. Found that photons are emitted through de Broglie wavelength.

Let $$E_k$$ be the K.E of incident electrons, its linear momentum $$P=\sqrt{2mE_k}$$

De-Broglie wavelength relates to electron is

$$\lambda =\dfrac{h}{p}=\dfrac{h}{\sqrt{2mE_k}}$$

$$E_k=\dfrac{n^2}{2m\lambda}$$

The cut-off wavelength of the emitted x-ray is related to K.E of incident electron.

$$\dfrac{hc}{\lambda_o}=E_k=\dfrac{h^2}{2m\lambda}$$

$$\Rightarrow \lambda =\dfrac{2mc\lambda^2}{h}$$.

1211928_1264809_ans_bc0f1c85b85746a8a3c9a2a98b9d68ac.JPG

The stopping potential in an experiment of photon is 2eV. What is the maximum kinetic energy of photoelectrons emitted ?

Stopping potential, $$V_{o}=2eV$$

Maximum kinetic energy, $$K_{max}=eV_{o}$$

$$K_{max}=1.6\times 10^{-19} \times 2=3.2\times 10^{-19}$$ Joules

Electrons with de Broglie wavelength $$\lambda$$ are bombarded on a metal target. It is found that photons are emitted from the metal target. The minimum wavelength of emitted photons is [m = mass of eletron]

Let $$E_x$$ be the K.E of the incident electron,

it's linear momentum ,$$P = \sqrt {2mEx} $$

Now,

de-Brogli wavelength related to electron is

$$\lambda = \frac{h}{P} = \frac{h}{{\sqrt {2mEx} }}$$

$$or,\,Ex = \frac{{{h^2}}}{{2m{\lambda ^2}}}$$

The minimum wavelength ,$${\lambda _ \circ }$$

$$\frac{{hc}}{{{\lambda _ \circ }}} = Ex = \frac{{{h^2}}}{{2m{\lambda ^2}}}$$

or, we get $${\lambda _ \circ } = \frac{{2mc{\lambda ^2}}}{h}$$

A nucleus $$X$$ is in the higher energy state where its energy is $$450 \mathrm { keV }$$ . If it comes to ground state (assuming ground state energy to be zero), what is the wavelength of the photon emitted?

Given that :-

Energy $$= E = 450 keV$$

Ground state energy $$= 0$$

$$\therefore $$ Energy of photon released $$= E - 0 = 450 - 0$$

$$(\Delta E)$$

$$\Delta E = 450 KeV = 450 \times 10^3 eV = 450 \times 10^3 \times 1.6 \times 10^{-19} J$$

$$\Delta E = 450 \times 1.6 \times 10^{-16} J$$

$$\Delta E = \dfrac{hC}{\lambda}$$

$$\lambda =$$ wavelength $$= \dfrac{hc}{\Delta E} = \dfrac{6.62 \times 10^{-34} \times 3 \times 10^8}{450 \times 1.6 \times 10^{-16}}$$

$$\lambda = 2.76 \times 10^{-12} m = 2.76 pm$$

Wavelength of photon emitted $$= \lambda = 2.76 pm$$

Visible light has wavelengths in the range of $$400\, nm$$ to $$780\, nm$$. Calculate the range of energy of the photons of visible light.

$$\lambda_1=400nm$$ to $$\lambda_2=780nm$$
$$h=6.63\times10^{-34}j-s,$$ $$c=3\times10^8m/s,$$

The energy is given as:

$$E=hv=\dfrac{hc}{\lambda}$$

$${ E }_{ 1 }=\dfrac { 6.63\times { 10 }^{ -34 }\times 3\times { 10 }^{ 8 } }{ 400\times { 10 }^{ -9 } } =\dfrac { 6.63\times 3 }{ 4 } \times { 10 }^{ -19 }=5\times { 10 }^{ -19 }J$$

$${ E }_{ 2 }=\dfrac { 6.63\times 3 }{ 7.8 } \times { 10 }^{ -19 }=2.55\times { 10 }^{ -19 }J$$

So, the range is $$5\times10^{-19}J$$ to $$2.55\times10^{-19}J.$$

Two neutral particles are kept 1 m apart. Suppose by some mechanism some charge is transferred from one particle to the other and the electric potential energy lost is completely converted into a photon. Calculate the longest and the next smaller wavelength of the photon possible.

r = 1 m
Energy = $$\dfrac { { kq }^{ 2 } }{ R } =\dfrac { { kq }^{ 2 } }{ 1 } $$

Now, $$\dfrac { { kq }^{ 2 } }{ 1 } =\dfrac { hc }{ \lambda } $$

or $$\lambda=\dfrac { hc }{ { kq }^{ 2 } } $$

For max $$'\lambda '$$,=$$q$$ should be min,
For minimum 'e' = $$1.6\times10^{-19}C$$

Max $$\lambda=\dfrac { hc }{ { kq }^{ 2 } } =0.863\times10^3=863m.$$

For next smaller wavelength = $$\dfrac { 6.63\times 3\times 10^{ -34 }\times { 10 }^{ 8 } }{ 9\times { 10 }^{ 9 }\times { \left( 1.6\times 2 \right) }^{ 2 }\times { 10 }^{ -38 } } =\dfrac { 863 }{ 4 } =215.74m$$

A 100 W light bulb is placed at the center of a spherical chamber of radius 20 cm. Assume that 60% of the energy supplied to the bulb is converted into light and that the surface of the chamber is perfectly absorbing. Find the pressure exerted by the light on the surface of the chamber.

Power = 100 W
Radius = 20 cm
60% is converted to light = 60 w

Now, Force = $$\dfrac { power }{ velocity } =\dfrac { 60 }{ 3\times { 10 }^{ 8 } } =2\times { 10 }^{ -7 }N.$$

Pressure = $$\dfrac { force }{ area } =\dfrac { 2\times { 10 }^{ -7 } }{ 4\times 3.14\times { (0.2) }^{ 2 } } =\dfrac { 1 }{ 8\times 3.14 } \times { 10 }^{ -5 }$$

$$=0.039\times 10^{-5}=3.9\times10^{-7}=4\times10^{-7}$$ $$N/m^2$$

Find the maximum magnitude of the linear momentum of a photoelectron emitted when light of wavelength 400 nm falls on a metal having work function 2.5eV.

Energy of photoelectron

$$\Rightarrow 1/2$$ $$mv^2$$ $$=$$ $$\dfrac{hc}{\lambda}$$ $$- $$ $$ hv_0$$

$$=$$ $$\dfrac{4.14\times10^{-15} 3\times10^8}{4\times10^{-7}}$$ $$-2.5ev=0.605$$ $$ev.$$

We know KE = $$\dfrac{P^2}{2m}$$

$$\Rightarrow P^2 = 2m\times KE.$$

$$P^2=2\times9.1\times10^{-31}\times0.605\times1.6\times10^{-19}$$

$$P=4.197\times10^{-25}kg-m/s$$

In a photoelectric experiment, the collector plate is at 2.0 V with respect to the emitter plate made of copper $$(\varphi =4.5eV)$$. The emitter is illuminated by a source of monochromatic light of wavelength 200nm. Find the minimum and maximum kinectic energy of the photoelectrons reaching the collector.

$$\phi =4.5$$ eV,$$\lambda =200$$ nm
Stopping potential or energy = $$E-\phi =\dfrac { hc }{ \lambda } -\phi $$

$$\dfrac{1240}{200}-4.5$$

$$6.21-4.5=1.7eV$$
Minimum 1.7 V is necessary to stop the electron

The minimum kinetic energy is

$$K.E=2eV$$
[Since the electric potential of 2 V is reqd. to accelerate the electron to reach the plates]

the maximum kinetic energy will be

$$K.E=(2+1.7)eV$$ $$= 3.7 eV$$

Calculate de Broglie wavelength for an average helium atom in a furnace at $$400\,K$$. Given the mass of helium $$= 4.002\,amu$$.

As we know,

de Broglie wavelength,$$\lambda=\dfrac{h}{p}$$

Mean K.E of helium atom $$=\dfrac{3kT}{2}$$

or $$E=\dfrac{3\times (1.38\times10^{-38})\times400}{2}$$

In terms of momentum, the energy is given by

$$p=\sqrt{2mE}$$

$$p=\sqrt{2\times(4.004\times1.66\times10^{-27})\times 3\times(1.38\times10^{-23})\times200}$$

Now, $$\lambda=\dfrac{6.625\times10^{-34}}{p}$$

Substituting the value of p and solving it, we get

$$\lambda=0.63\times10^{-10}m$$

At what rate does the Sun emit photons? For simplicity, assume that the Sun's entire emission at the rate of $$3.9 \times 10^{26} \mathrm{W}$$ is at the single wavelength of $$550 \mathrm{nm}$$

Let $$R$$ be the rate of photon emission (number of photons emitted per unit time) of the Sun and let $$E$$ be the energy of a single photon. Then the power output of the Sun is given by $$P=R E .$$

Now

$$E=h f=h d \lambda\\$$

where $$h=6.626 \times 10^{-34} \mathrm{J}$$.s is the Planck constant, $$f$$ is the frequency of the light emitted, and $$\lambda$$ is the wavelength. Thus $$P=R h c / \lambda$$ and

$$R=\dfrac{\lambda P}{h c}=\dfrac{(550 \mathrm{nm})\left(3.9 \times 10^{26} \mathrm{W}\right)}{\left(6.63 \times 10^{-34} \mathrm{J} \cdot \mathrm{s}\right)\left(2.998 \times 10^{8} \mathrm{m} / \mathrm{s}\right)}=1.0 \times 10^{45} \mathrm{photons} / \mathrm{s}\\$$

Light of wavelength $$2.40 \mathrm{pm}$$ is directed onto a target containing free electrons. (a) Find the wavelength of light scattered at $$30.0^{\circ}$$ from the incident direction. (b) Do the same for a scattering angle of $$120^{\circ}$$

(a) When a photon scatters from an electron initially at rest, the change in wavelength is given by

$$\Delta \lambda=(h / m c)(1-\cos \phi)\\$$

where $$m$$ is the mass of an electron and $$\phi$$ is the scattering angle.

Now, $$h / m c=2.43 \times 10^{-12} , \mathrm{m}=2.43 \mathrm{pm}, \mathrm{so}\\$$

$$\Delta \lambda=(h / m c)(1-\cos \phi)=(2.43 \mathrm{pm})\left(1-\cos 30^{\circ}\right)=0.326 \mathrm{pm}\\$$

The final wavelength is

$$\lambda^{\prime}=\lambda+\Delta \lambda=2.4 \mathrm{pm}+0.326 \mathrm{pm}=2.73 \mathrm{pm}\\$$

(b) $$\mathrm{Now}, \Delta \lambda=(2.43 \mathrm{pm})\left(1-\cos 120^{\circ}\right)=3.645 \mathrm{pm}$$ and

$$\lambda^{\prime}=2.4 \mathrm{pm}+3.645 \mathrm{pm}=6.05 \mathrm{pm}\\$$

What percentage increase in wavelength leads to a $$75 \%$$ loss of photon energy in a photon-free electron collision?

If $$E$$ is the original energy of the photon and $$E^{\prime}$$ is the energy after scattering, then the dfractional energy loss is

$$\dfrac{\Delta E}{E}=\dfrac{E-E^{\prime}}{E}=\dfrac{\Delta \lambda}{\lambda+\Delta \lambda}\\$$

using the result from Sample Problem - "Compton scattering of light by electrons."

Thus

$$\dfrac{\Delta \lambda}{\lambda}=\dfrac{\Delta E / E}{1-\Delta E / E}=\dfrac{0.75}{1-0.75}=3=300 \%\\$$

A $$300 \%$$ increase in the wavelength leads to a $$75 \%$$ decrease in the energy of the photon.

The PE of a particle of mass m is given by $$V_{(x)} = \left\{\begin{matrix}E_0 \\0 \end{matrix}\right.$$ $$\begin{matrix}0 \le x \le 1 \\ x > 1 \end{matrix}$$

$$\lambda_1$$ and $$\lambda_2$$ are the de-Broglie wavelengths of the particle, when $$0 \le x \le 1$$ and $$x > 1$$ respectively. The total energy of the particle is $$42E_0$$. If the ratio $$\dfrac{\lambda_1}{\lambda_2}$$ is $$\sqrt{x} $$, find $$x$$.

Kinetic Energy, $$KE = 2E_0 - E_0 = E_0$$ for $$0 \le x \le 1$$

Wavelength, $$\lambda_1 = \displaystyle \frac{h}{\sqrt{2mE_0}}$$

$$KE = 2E_0$$ for $$x > 1 \therefore \displaystyle \lambda_2 = \frac{h}{\sqrt{4mE_0}}$$

$$\therefore \displaystyle \frac{\lambda_1}{\lambda_2} = \sqrt{2}$$.

What amount of energy should be added to an electron to reduce its de Broglie wavelength from 100 to 50 pm?

Momentum of the particle $$p = \dfrac{h}{\lambda}$$
Initial momentum $$p_i = \dfrac{6.63\times 10^{-34}}{100\times 10^{-12}} = 6.63\times 10^{-24} \ kg.m/s$$
Initial energy $$E_i = \dfrac{p_i^2}{2m } = \dfrac{(6.63\times 10^{-24})^2}{2\times 9.1\times 10^{-31}} = 2.4\times 10^{-17} \ J$$
Final momentum $$p_f = \dfrac{6.63\times 10^{-34}}{50\times 10^{-12}} = 13.26\times 10^{-24} \ kg.m/s$$
Final energy $$E_f = \dfrac{p_f^2}{2m } = \dfrac{(13.26\times 10^{-24})^2}{2\times 9.1\times 10^{-31}} = 9.7\times 10^{-17} \ J$$
Thus energy added $$\Delta E = E_f-E_i = (9.7 - 2.4)\times 10^{-17} = 7.3\times 10^{-17} \ J$$
$$\implies \ \Delta E = \dfrac{7.3\times 10^{-17}}{1.6\times 10^{-19}} \ eV = 450 \ eV$$

The radius of an $$\alpha$$-particle moving in a circle in a constant magnetic field is half of the radius of an electron moving in circular path in the same field. The de Broglie wavelength of $$\alpha$$-particle is $$x$$ times that of the electrons. Find $$x$$ (an integer).

Radius of a charged particle in a magnetic field is given by : $$R = \dfrac{mV}{qB}$$

$$\therefore$$ momentum = $$p = mV = RqB$$

It is given that radius of alpha particle is half of electron.
We know that the charge of an alpha particle is twice of that of an electron.
Therefore momentum remains same for both electron and alpha particle .

de Broglie wavelength = $$\dfrac{h}{p}$$

Since momentum is same, ratio of wavelengths is $$1$$ .

An $$\alpha$$-particle and a proton are accelerated from rest by a potential difference of $$100\ V$$. After this, their de Broglie wavelengths are $$\lambda_{\alpha}$$ and $$\lambda_p$$, respectively. The ratio $$\lambda_p/\lambda_{\alpha}$$, to the nearest integer, is:

Kinetic energy = K.E = $$ qV $$

De Broglie wavelength = $$\dfrac{h}{\sqrt{2mK.E}}$$ = $$\dfrac{h}{\sqrt{2mqV}}$$

Therefore ratio $$\dfrac{\lambda_p}{\lambda_{\alpha}}$$ = $$\dfrac{\sqrt{m_{\alpha}q_\alpha}}{\sqrt{m_pq_p}}$$

Alpha particle has 4 times the mass and twice the charge of a proton .

$$\dfrac{\lambda_p}{\lambda_{\alpha}}$$ = $$\sqrt{8}$$ $$\approx$$ 3

A proton is fired from very far away towards a nucleus with charge $$Q=120e$$, where $$e$$ is the electronic charge. It makes a closest approach of $$10 fm$$ to the nucleus. The de-Broglie wavelength (in unit of $$fm$$) of the proton at its start is:
(take the proton mass, $$m_p=(5/3)\times 10^{-27} kg; h/e=4.2\times 10^{-15}Js/C; $$
$$\dfrac {1}{4\pi \epsilon_0}=9\times 10^9m/F; 1fm=10^{-15} m)$$

On conserving energy of the proton we get :

$$\dfrac{1}{2}mv^2$$ = K$$\dfrac{q_1q_2}{R}$$

So, $$v =$$ $$\sqrt{\dfrac{2Kq_1q_2}{mR}}$$

$$\lambda$$ = $$\dfrac{h}{mv}$$ = $$\dfrac{h\sqrt{R}}{\sqrt{2mKq_1q_2}}$$ = $$\dfrac{h\sqrt{10\times10^{-15}}}{\sqrt{2\times\dfrac{5}{3}\times10^{-27}\times9\times10^9\times120\times e^2}}$$

$$=\dfrac{\dfrac{h}{e}\times10^{-7}}{6\times10^{-8}}$$ $$=\dfrac{4.2\times10^{-15}\times10^{-7}}{6\times10^{-8}}$$ $$=7\times10^{-15}\ m = 7\ fm$$

Calculate the (a) smaller and (b) larger value of the semiclassical angle between the electron spin angular momentum vector and the magnetic field in a SternGerlach experiment. Bear in
mind that the orbital angular momentum of the valence electron in the silver atom is zero.

The magnitude of the spin angular momentum is
$$ S= \sqrt{s{(s+1)\hbar} } = (\sqrt3/{2} )\hbar $$
where $$s = \frac {1}{2}$$ is used. The z component is either $$S_z = \frac { \hbar}{ 2}$$ or $$\frac {-\hbar}{2}$$.
(a) If $$S_z = \frac {+\hbar}{2}$$ the angle $$ \theta $$ between the spin angular momentum vector and the positive z axis is
$$ \theta = cos^{-1} \frac {S_z}{ S} = cos^{-1} \frac {1}{\sqrt3} =54.7°$$
(b) If $$S_z = \frac {-\hbar}{2} $$ the angle is $$ \theta = 180°– 54.7 $$= 125.3° ≈125°.

An electron and photon have same energy 100 eV. Which has greater associated wavelength?

de Broglie wavelength associated with electron
$$\lambda_e=\dfrac{h}{\sqrt{2mE_\alpha}}=E_e=\dfrac{h^2}{2m\lambda_e^2}...(i)$$

Also wavelength of photon of energy $$E_ph$$is

$$E_ph=\dfrac{hc}{\lambda_{ph}}\Rightarrow E_{ph}^2=\dfrac{h^2c^2}{\lambda_{ph}^2}...(ii)$$

Given $$E_e=E_{ph}=E(say)=100eV...(iii)$$

Dividing (ii) by (i) and using (iii), we get

$$E=\dfrac{h^2c^2/\lambda_{ph}^2}{h^2/2m\lambda_e^2}$$or

$$E=\dfrac{2mc^2\lambda_e^2}{\lambda_{ph}^2}$$

$$\therefore \dfrac{\lambda}{\lambda_{ph}}=\sqrt{\dfrac{E}{2mc^2}}$$

As E=100eV $$2mc^2\cong 1 MeV$$

$$\therefore E<<2mc^2\Rightarrow \lambda_e<\lambda_{ph}$$

That is, wavelength associated with photon is greater as compared to electron of same energy.

If an electron has a wavelength does it also have a colour?

1329311_1150846_ans_49daa90382594999a9f168148f6bdfc7.jpg

What is the momentum of a photon if the wavelength of X-rays is 1 angstrom?

Given that,

Wave length$$\lambda =1\,\overset{\circ }{\mathop{A}}\,$$

We know that,

$$ \lambda =\dfrac{h}{p} $$

$$ p=\dfrac{6.26\times {{10}^{-34}}}{{{10}^{-10}}} $$

$$ p=6.26\times {{10}^{-24}}\,kgm/s $$

Hence, this is the required solution

A parallel beam of monochromatic light of wavelength $$500\ nm$$ is incident normally on a perfectly absorbing surface. The power through any cross-section of the beam is $$10 W$$.
The number of photons absorbed per second by the surface is $$k\times 10^{19}$$. what is a value of k?

Energy of each photon :-

(a) $$E=hc$$

$$=1242/500$$

$$=2.48eV$$

In $$1$$ second $$10J$$ energy passes through any cross - section of the beam,

Thus, the no. of photons $$\Rightarrow n=10J/2.48eV$$

$$n=2.52\times { 10 }^{ 19 }$$

(b) Total moment of all the protons

$$p=nh/c=10J/3\times { 10 }^{ 8 }$$

$$p=3.33\times { 10 }^{ -8 }Nsec.$$

De Broglie wavelength for an average helium atom in a furnace at 400 K is $$k\times 10^{-10} m$$. Find the value of k. Here, Given the mass of helium $$=4.002 amu$$

Given : $$T = 400 \ K$$             $$m = 4.002 \ amu = 4.002\times 1.67\times 10^{-27} \ kg$$
Velocity of He atom   $$v = \sqrt{\dfrac{3kT}{m}} $$
$$v= \sqrt{\dfrac{3\times 1.38\times 10^{-23}\times 400}{4.002\times 1.67\times 10^{-27}}} = 1574 \ m/s$$
de-Broglie wavelength   $$\lambda = \dfrac{h}{mv}$$
$$\implies \ \lambda = \dfrac{6.63\times 10^{-34}}{4.002\times 1.67\times 10^{-27}\times 1574} = 0.63\times 10^{-10} \ m$$

If the wavelength of electromagnetic radiation is doubled, what happens to the energy of photon?

The energy of photon, $$E=h\nu=\dfrac{hc}{\lambda}$$ where $$h=$$ Plank's constant, $$c=$$ velocity of light and $$\lambda=$$ wavelength.

Thus, $$E \propto \dfrac{1}{\lambda}$$

Hence, if the wavelength is doubled, the energy of photon will be half.

Give an example where energy is converted into matter

Nuclear Fission of Light Elements:

The fission of two nuclei heavier than iron or nickel generally absorbs energy and thus converts energy to mass, while the fission of nuclei lighter than iron or nickel releases energy. In nuclear fusion, the reverse obtains.

Why we do not observe de Broglie wave in daily life?

de Broglie wavelength for a particle is given as,

$$\lambda = \dfrac{planck's\ constant}{momentum\ of\ particle}$$

For daily-life macroscopic objects, this value is very very low, hence those objects don't appear to be performing any noticeable wave-like behavior.

An insulated metal plate yields photoelectrons when first illumminated by ultraviolet light but then after some time photoelectron emission stops. Explain

After some time, the metal plate acquire sufficient positive charge and thus positive electric potential to hold-on to the electrons which tend to emit under influence of incident UV light.

Explain the concept of de Broglie waves (matter wave).

1310884_1139257_ans_7c8affb4925e4c10bf7a70c4b0a05595.jpg

Answer the following questions:

(a) Quarks inside protons and neutrons are thought to carry fractional charges $$[(+2/3)e ; (1/3)e]$$. Why do they not show up in Millikan's oil-drop experiment ?

(b) What is so special about the combination e/m? Why do we not simply talk of e and m separately?

(c) Why should gases be insulators at ordinary pressures and start conducting at very low pressures?

(d) Every metal has a definite work function. Why do all photoelectrons not come out with the same energy if incident radiation is monochromatic? Why is there an energy distribution of photoelectrons?

(e) The energy and momentum of an electron are related to the frequency and wavelength of the associated matter wave by the relations: $$E = h \nu$$, p = $$\displaystyle\frac{h}{\lambda }$$.
But while the value of $$\displaystyle\lambda$$ is physically significant, the value of $$\nu$$ (and therefore, the value of the phase speed n $$\displaystyle\lambda)$$ has no physical significance. Why?

(a) Quarks are considered to be confined within a proton or neutron by forces that grow stronger as one tries to pull them apart. It, therefore, seems that though fractional charges may exist in nature, observable charges are still integral multiples of e.

(b) Both the basic relations, $$e \,V = (1/2) m \,v^2$$ or $$e \,E = m\, a$$ and $$e \,B \,v =m \,v^2/r$$, for electric and magnetic fields, respectively, show that the dynamics of electrons is determined not by e, and m separately but by the combination e/m .

(c) At low pressures, ions have a chance to reach their respective electrodes and constitute a current. At ordinary pressures, ions have no chance to do so because of collisions with gas molecule and recombination.

(d) Work function merely indicates the minimum energy required for the electron in the highest level of the conduction band to get out of the metal. Not all electrons in the metal belong to this level. They occupy a continuous band of levels. Consequently, for the same incident radiation, electrons knocked off from different levels come out with different energies.

(e) The absolute value of energy E (but not momentum p) of any particle is arbitrary to within an additive constant. Hence, while is physically significant, absolute value of of a matter wave of an electron has no direct physical meaning. The phase speed is likewise not physically significant. The group speed given by $$\displaystyle\frac{dv}{d(1/\lambda )} = \frac{dE}{dp}\, \left (\frac{p^2}{2m} \right ) = \frac{p}{m}$$, is physically meaningful.

(a) An X-ray tube produces a continuous spectrum of radiation with its short wavelength end at 0.45 . What is the maximum energy of a photon in the radiation?
(b) From your answer to (a), guess what order of accelerating voltage(for electrons) is required in such a tube?

(a) $$\lambda=0.45\times10^{-10}m$$

maximum energy is $$E=hc/\lambda=27.6\times10^3eV=27.6keV$$

(b) Accelerating voltage provides energy to the electrons for producing X-rays. To get a X-rays of 27.6 keV, the incident electrons must possess at least $$27.6 keV$$ of kinetic electric energy. Hence, an accelerating voltage of the order of 30 keV is required for producing X-rays.

Fill in the blanks with suitable answer
The energy of a photon is given by the formula _____________

$$ E = h\nu $$ where

$$ h = $$ Planck's Constant $$ = 6.626 \times 10 ^{-34} $$

$$ \nu = \text{frequency of incoming radiation} $$

$$ E = \dfrac{hc}{\lambda} $$ where

$$ c = \text{velocity of light} = 3 \times 10^8 $$

$$ \lambda = \text{wavelength of incoming radiation} $$

You might have seen mercury street lamps. The light blue glow given by these lamps has a wavelength of = 436nm. What is its frequency?

$$ \lambda = 436 \, nm $$

$$ \nu = ? $$

$$ \nu = \dfrac{c}{\lambda}$$

$$ \nu = \dfrac{3 \times 10^8 \, m s^{-1}}{436 \times 10^{-9} \, m} $$

$$ \boxed{\nu = 6.88 \times 10^{14} Hz}$$

State how de-Broglie wavelength $$(\lambda )$$ of moving particles varies with their linear momentum (p).

$$\lambda =\dfrac{h}{p}$$

$$\implies \lambda \propto \dfrac{1}{p}$$
From the above equation it is clear that wavelength is inversely proportional to momentum.

Derive an expression for de Broglie wavelength of matter waves.

de Broglie equated the energy equations of Planck (wave) and Einstein (particle).

$$E=hv$$ (planck's relation)

$$E=m{ c }^{ 2 }$$ (Einstein's mass - energy relation)

$$hv=m{ c }^{ 2 }$$

$$\dfrac { hc }{ \lambda } =m{ c }^{ 2 }$$ (or)

$$\lambda =\dfrac { h }{ mc }$$

For a particle moving with a velocity $$V$$,

$$\lambda =\dfrac { h }{ mV } =\dfrac { h }{ p }$$

where $$p=mV$$ is the momentum of the particle.

A ball of mass 0.12 kg is moving with a speed 20 m/s. Calculate the de Broglie wavelength. (Planck constant $$h = 6.62 \times 10^{-34} J.s$$)

The de-broglie wavelength of a moving object is of mass $$m$$ with speed $$v$$ is given as

$$\lambda=\dfrac{h}{mv}$$

$$=\dfrac{6.62\times 10^{-34}J.s}{0.12kg\times 20m/s}$$

$$=2.7583\times 10^{-34}m$$

Show with the help of a labelled graph how their wavelength $$(\lambda)$$ varies with their linear momentum (p).

The above graph shows the variation of wavelength($$\lambda$$) with linear momentum($$p$$).

($$\lambda = \dfrac{h}{p}$$)

Find the de Broglie wavelength of electrons moving with a speed of $$7\times 10^6ms^{-1}$$.

Velocity of electron $$v = 7\times 10^6 \ m/s$$

de Broglie wavelength $$\lambda = \dfrac{h}{mv}$$

$$\therefore$$ $$\lambda = \dfrac{6.6\times 10^{-34}}{(9.1\times 10^{-31})(7\times 10^6)} = 0.104 \times 10^{-9} \ m = 1.04 $$ Angstrome

Calculate the momentum of a photo of energy $$6\times 10^{-19}$$J.

Energy of the given photon $$E = 6\times 10^{-19} J$$

Momentum of the photon $$p = \dfrac{E}{c}$$

where $$c$$ is the speed of light.

$$\therefore$$ $$p = \dfrac{6\times 10^{-19}}{3\times 10^8} = 2\times 10^{-27}$$ $$m/s$$

Assume that a 100 W sodium vapour lamp rediates its energy uniformly in all directions in the form of photons with an associated wavelength of 589 nm.
At what rate are photons emitted from the lamp?

Energy of single photon is given as,

$$E = \dfrac{hc}{\lambda}$$

Let $$N$$ be the number of photons emitting per second.

Thus, power $$P = \dfrac{Nhc}{\lambda}\implies N = \dfrac{P\lambda}{hc}$$

$$\implies N = \dfrac{100\times589\times10^{-9}}{6.63\times10^{-34}\times3\times10^8} = 2.96\times10^{20} photons/second$$

S is isotropic monochromatic source of constant power P. r is very large and v is frequency of radiation .The number of photons crossing per unit time the given surface is in $$n=\dfrac{P\Delta S cos \theta}{k \pi vr^2h}$$ .Find k if $$\Delta S$$ is the area of small section.

The radiant power at the given surface would be,

$$P_1 = \dfrac{P\Delta Scos\theta}{4\pi r^2}$$

So number of photons crossing per unit time is, $$n=\dfrac{P_1}{h\nu}=\dfrac{P\Delta Scos\theta}{4\pi\nu r^2h}$$

Comparing with the given expression, $$k=4$$.

Assume that a 100 W sodium vapour lamp rediates its energy uniformly in all directions in the form of photons with an associated wavelength of 589 nm.
At what distance from the lamp will the average flux of photons be 1.00 photons /$$(cm^2s)$$ ?

Energy of single photon is given as,

$$E = \dfrac{hc}{\lambda}$$

Let $$N$$ be the number of photons emitting per second.

Thus, power $$P = \dfrac{Nhc}{\lambda}\implies N = \dfrac{P\lambda}{hc}$$

Thus, at distance $$d$$ from the light source, the average flux of photons will be, $$\dfrac{P\lambda}{hc\times4\pi d^2}$$

So, $$\dfrac{100\times589\times10^{-9}}{6.63\times10^{-34}\times3\times10^8\times4\pi\times d^2} = 1.00\ photons/(cm^2s)\implies d=4.85\times10^9 cm$$

An electron, an alpha $$(\alpha)$$ particle and a proton have same kinetic energies. Which one of these particles has largest de Broglie wavelength?

Debroglie wavelength is defined as:

$$\lambda = \cfrac{h}{p}$$

Also, kinetic energy of a particle is:

$$KE = \cfrac{p^2}{2m}$$

$$\implies \lambda = \cfrac{h}{\sqrt{2m KE}}$$

Since kinetic energy is same,

$$\lambda \propto \cfrac{1}{\sqrt m}$$

Since an electron has very low mass, it will have largest debroglie wavelength.

A light beam of wavelength $$400\ nm$$ is incident on a metal plate of work function $$2.2 \ eV$$. A particular electron absorbs a photon and makes some collisions before coming out of the metal. Assuming that $$10\%$$ of the instantaneous energy is lost to the metal in each collision, find the minimum number of collisions the electron can suffer before it becomes unable to come out of metal. (Use $$hc=12400 \ eV \ \dot{A}$$)

Energy of a photon of 400nm will be $$E=\dfrac{1240eVnm}{400nm}=3.1eV$$

Energy after first collision $$0.9E$$

energy after second collision $$09\times 0.9E=0.81E$$

energy after $$n^{th} $$ collision will be $$(0.9)^nE$$

Electron will not be able to come out if $$(0.9)^nE $$ becomes less than $$2.2eV$$ so $$n=4$$ will be minimum required collision to stop it from ejection.

An $$\alpha$$ particle moves in circular path of radius $$0.83cm$$. In the presence of a magnetic field of $$0.25Wb/{m}^{2}$$. Find the De Broglie wavelength associated with the particle

radius of path $$ r= \dfrac{mv}{qB} = \dfrac{p}{qB} $$
$$p$$ is momentum of the charged particle.
For $$\alpha$$ particle $$q= 3.2\times 10^{-19} C$$ .
$$ B $$ is given as $$0.25$$ all in SI units
so momentum $$p= rqB$$
put $$r=.0083 meter $$ we get De Broglie wavelength $$\lambda = \dfrac{h}{p} = 9.939\times 10^{-13} meter $$
where $$h$$ is Planck constant whose value is $$ 6.6 \times 10^{-34} Joule-second$$

Find the energy of photon in each of the following:
A. Microwaves of wavelength $$1.5\ cm$$
B. Red light of wavelength $$660\ nm$$
C. Radiowaves of frequency $$96\ MHz$$
D. $$X-$$rays of wavelength $$0.17\ nm$$

(a) Energy of photon is given by the following relation

$$E=\dfrac{hc}{\lambda }$$

It is given that wavelength of microwave is

$$ \lambda =1.5\,\,cm=0.015\,\,m $$

$$ E=\dfrac{6.62\times {{10}^{-34}}\times 3\times {{10}^{8}}}{0.015} $$

$$ E=1324\times {{10}^{-26}}\,J $$

(b) Red light of wavelength 660 nm

$$ \lambda =660\times {{10}^{-9}}\,m $$

$$ =\dfrac{6.62\times {{10}^{-34}}\times 3\times {{10}^{8}}}{660\times {{10}^{-9}}} $$

$$ =0.03\times {{10}^{-17}}\,J $$

$$ \nu =96\times {{10}^{6}}\,Hz $$

$$ \lambda =\dfrac{1}{96\times {{10}^{6}}} $$

$$ \lambda =0.0104\times {{10}^{-6}}\,m $$

$$ E=\dfrac{6.62\times {{10}^{-34}}\times 3\times {{10}^{8}}}{0.0104\times {{10}^{-6}}\,} $$

$$ E=1909.6\times {{10}^{-20}}\,J $$

(d) X− rays of wavelength 0.17 nm

$$ \lambda =0.17\times {{10}^{-9}}\,m $$

$$ E=\dfrac{6.62\times {{10}^{-34}}\times 3\times {{10}^{8}}}{0.17\times {{10}^{-9}}} $$

$$ E=116.82\times {{10}^{-17}}\,J $$

When light of frequency $$2.2\times 10^{15}Hz$$ is incident on a metal surface, photoelectrons emitted can be stopped by a retarding potential of $$6.6\ V$$. For light of frequency $$4.6\times 10^{15}Hz$$, the reverse potential is $$16.5\ V$$. Find $$h$$

We know that-

$$eV=h\nu-\phi$$

$$\implies e(V_2-V_1)=h(\nu_1-\nu_2)$$

$$\implies h=\dfrac{e(V_2-V_1)}{\nu_2-\nu_1}$$

$$\implies h=\dfrac{1.6\times 10^{-19}\times 9.9}{2.4\times 10^{15}}$$

$$\implies h=6.6\times 10^{-34}Js$$

The energy and momentum of an electron are related to the frequency and wavelength of the associated matter wave by the relations:
$$E = h v, p = \dfrac{h}{\lambda}$$
But while the value of $$\lambda$$ is physically significant, the value of $$v$$ (and therefore, the value of the phase speed $$v$$ $$\lambda$$) has no physical significations. Why?

The absolute value of energy E (but not momentum p) of any particle is arbitrary to within an additive constant. Hence, while is physically significant, the absolute value of a matter-wave of an electron has no direct physical meaning. The phase speed is likewise not physically significant. The group speed given by $$\displaystyle\frac{dv}{d(1/\lambda )} = \dfrac{dE}{dp}\, \left (\dfrac{p^2}{2m} \right ) = \dfrac{p}{m}$$, is physically meaningful.

In an experiment of photoelectric effect, the slope of the cut-off voltage versus frequency of incident light is found to be $$4.2\times 10^{-15} V s$$. Calculate the value of Plank's constant.

Formula,

$$hv=eV$$

$$h=e\times \dfrac{V}{v}$$

$$\Rightarrow h=1.6\times 10^{-19}\times 4.2\times 10^{-15}$$

$$\therefore h=6.72\times 10^{-34}\ J-s$$

Hence, this is the answer.

What kinetic energy of a neuron will be associated by the de-broglie wavelength $$1.32 \times 10^{-10}m$$?

1328460_1087780_ans_23f5282c116b43a1bffd15827a0a79fd.jpg

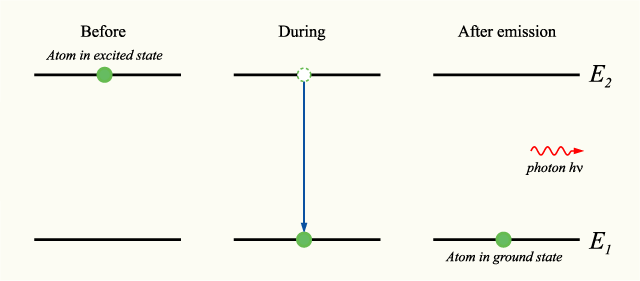
An atom absorbs a photon of wavelength $$500 nm $$ emits another photon of wavelength $$700nm$$ find the net energy absorbed by the atom in the process

$${\lambda _1} = 500\,nm = 500 \times {10^{ - 9}}\,m$$

$${\lambda _2} = 700\,nm = 700 \times {10^{ - 9}}\,m$$

$${E_1} - {E_2}$$ = Energy absorbed by the atom in the process $$=hc\left[ {1/{\lambda _1} - 1/{\lambda _2}} \right]$$

$$ = 6.63 \times 3\left[ {1/5 - 1/7} \right] \times {10^{ - 9}} = 1.136 \times {10^{ - 19}}J$$

We get, $$1.136 \times {10^{ - 19}}J.$$

What is photoelectric effect? State and explain its characteristics.

1327123_1119720_ans_ba523540df3b4a86a8f9123d993ec45e.jpeg

Find the frequency of 1 MeV photon. Given wavelength of a 1 keV photon is $$1.24 \times {10^{ - 9}}m$$

Hint: $$E = h\nu $$

We know that $$E = \dfrac{hc}{\lambda}$$

$$E_1 \lambda_1 = E_2 \lambda_2$$

Putting values

$$ 1 \times 10^3 ev \times 1.24 \times 10^{-9}= 1 \times 10^{6} ev \times \lambda_2$$

$$\lambda_2 = 1.24 \times 10^{-12} m$$

now, $$C = f \lambda$$

$$ f = \dfrac{c}{\lambda}$$

so $$f = 2.419 \times 10^{20}$$

The energy of a photo is equal to the kinetic energy of proton. Let $$ \lambda_1 $$ be the de-Broglie wavelength of the photon and $$ \lambda_2 $$ be the wavelength of the radiation and the de-Broglie wavelength of a photon of that radiation?

We know that,

The de- Broglie wave length is

$$\lambda =\dfrac{h}{p}$$

Now, photon energy

$$E=h\nu $$

So, the de- Broglie wave length of photon is

$$ {{\lambda }_{1}}=\dfrac{h}{p} $$

$$ {{\lambda }_{1}}=\dfrac{h}{\sqrt{2mE}}....(I) $$

Now, the de- Broglie wave length of radiation is

$$ E=h{{\nu }_{2}} $$

$$ E=\dfrac{hc}{{{\lambda }_{2}}} $$

$$ {{\lambda }_{2}}=\dfrac{hc}{E}....(II) $$

Now, from equation (I) and (II)

$$ \dfrac{{{\lambda }_{1}}}{{{\lambda }_{2}}}=\dfrac{h}{\sqrt{2mE}}\times \dfrac{E}{hc} $$

$$ \dfrac{{{\lambda }_{1}}}{{{\lambda }_{2}}}\sim \dfrac{E}{\sqrt{E}} $$

$$ \dfrac{{{\lambda }_{1}}}{{{\lambda }_{2}}}=\sqrt{E} $$

Hence, the de-Broglie wavelength of a photon of that radiation is $${\sqrt{E}}$$

A $$1\ MeV$$ positron and a $$1\ MeV$$ electron meet each moving in opposite directions. They annihilate each other by emitting two photons. If the rest mass energy of an electron is $$0.51\ MeV$$, the wavelength of each photon is ?

1329308_1139795_ans_d7e970046c3d448a9140defeca7b21ce.jpg

What is the de-Broglie wavelength of an electron beam accelerated through a potential difference of $$25 \,V$$?

e-Broglie wavelength of an electron $$\lambda = \dfrac{12.27}{\sqrt{V}} \ A^o$$

$$\implies \ \lambda = \dfrac{12.27}{\sqrt{25} } = 2.45 \ A^o$$

Find the de-Broglie wave length related to an election accelerated by $$10^4$$ volt

$$\lambda = \dfrac{12.3}{\sqrt V} \mathring { A }; $$ $$\lambda = \dfrac{12.3}{\sqrt 10^4} \mathring { A }; $$ $$\lambda = \dfrac{12.3}{\sqrt 10^2} \mathring { A }=.123 \mathring{A} $$

Find the typical de-Broglie wavelength of an electron in a metal at $${27}^{o}C$$ and compare it with the mean separation between two electrons in a metal which is given to be about $$2\times{10}^{-10}m$$

It cap be obtained that de-Broglie wavelength of the electron,
$$\lambda = 62.3 \times 10^{-10}\,m = 62.3\,A$$
Mean separation between two electrons in the metal,

$$d=2\overset{\circ}{A}$$

$$\therefore \dfrac{\lambda}{d}=\dfrac{62.3}{2}=31$$

i.e de-Broglie wavelength of the electron is much larger than the separation between two electrons in the metal.

The radius of two bohr radius of a hydrogen like atom are $$r_1$$ and $$r_2$$. Find the wave length of photon when electron jumps from $$r_2$$ to $$r_1$$.

$$E_2=\dfrac{-Ke^2}{2r_2}$$
$$E_1=\dfrac{-Ke^2}{2r_1}$$
$$DE=E_2-E_1=\dfrac{Ke^2}{2}[\dfrac{1}{r_1}-\dfrac{1}{r_2}]=\dfrac{Ke^2(r_2-r_1)}{2r_1r_2}=\dfrac{hc}{\lambda}$$
$$\lambda=\dfrac{2ch\,\,r_1r_2}{Ke^2(r_2-r_1)}$$

An electron and a proton have the same kinetic energy. Which one of the two has the larger de Broglie wavelength and why?

An electron has the larger wavelength.
Reason: de-Broglie wavelength in terms of kinetic energy is $$\lambda=\dfrac{h}{\sqrt{2mE_k}}\propto \dfrac{1}{\sqrt{m}}$$ for the same kinetic energy.
As an electron has a smaller mass than a proton, an electron has larger de Broglie wavelength than a proton for the same kinetic energy.

What will be the energy of each photon in monochromatic light of frequency $$5\times10^{14}Hz$$?

We can use Einstein's formula for the energy,

$$E=hf$$

Where,

$$h=6.63\times10^{-34}J$$ is Planck's constant.

$$f=5\times10^{14}Hz$$ is the frequency.

$$E=6.63\times10^{-34}\times5\times10^{14}$$

$$=3.31\times10^{-19}J$$

$$=2.07eV$$.

Find out the ratio between de-Broglie wavelength of proton and a-particle of equal energy.

$$ K = \dfrac{1}{2} mv^2 = \dfrac{1}{2} \dfrac{(mv)^2}{m} = \dfrac{p^2}{2m} $$

$$ \therefore $$ $$ p = \sqrt{2mK} $$

$$ \lambda = \dfrac{h}{p} = \dfrac{h}{\sqrt{2mK}} $$

For same energy $$ \lambda \propto \dfrac{1}{\sqrt{m}} $$

$$ \therefore $$ $$ \dfrac{\lambda_p}{\lambda_{\alpha}} = \sqrt{\dfrac{m_{\alpha}}{m_p}} = \sqrt{\dfrac{4m_p}{m_p}} = \dfrac{2}{1} $$

$$ \therefore $$ $$ \lambda_{p} : \lambda_{\alpha} $$

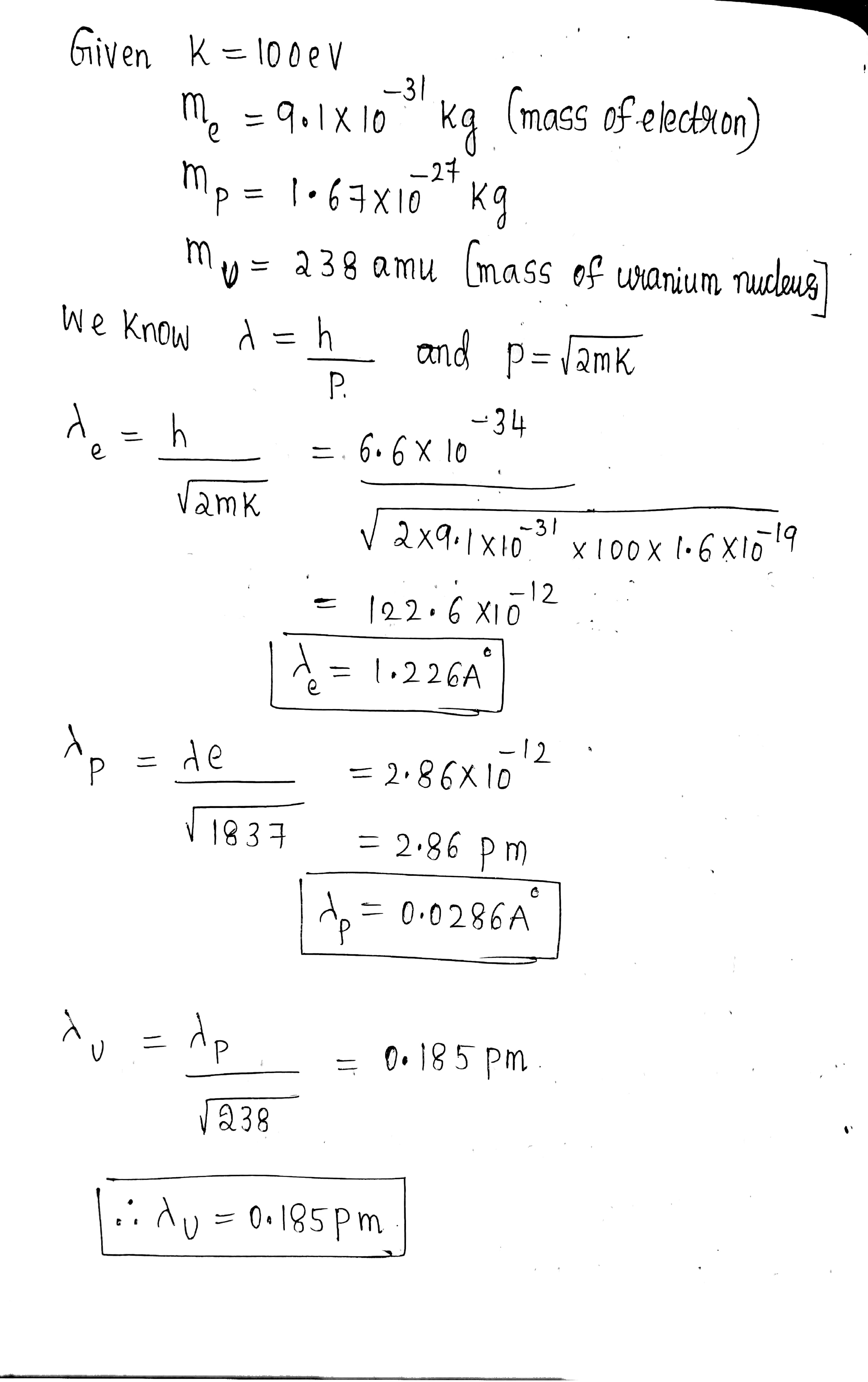
Calculate the de Broglie wavelengths of an electron, proton, and uranium atom, all having the same kinetic energy $$100\ eV $$.

1881062_1854511_ans_6fbc642c005543d8a1f7880e0a84f103.jpg

At room temperature $$ (T = 300\,K)$$ neutron are in thermal equilibrium. Calculate its de-Broglie wavelength.

Temperature $$ (T) = 300\,K $$

$$ \lambda = \dfrac{3.08}{\sqrt{T}} \mathring A $$

$$ = \dfrac{30.8}{\sqrt{300}} \mathring A = \dfrac{30.8}{17.32} \mathring A = 1.78 \mathring A $$

According to de-Broglie hypothesis, write formula of wavelength of matter waves.

$$ \lambda = \dfrac{h}{p} $$

Where , h = Planck's constant

p = momentum.

Derive the expression for a de Broglie wavelength $$ \lambda $$ of a relativistic particle moving with kinetic energy T. At what values of T does the error in determining $$ \lambda $$ using the non-relativistic formula not exceed $$1\% $$ for an electron and a proton ?

1881070_1854519_ans_95d026bcbb3a40729f23d2b1385fdbff.jpg

The potential energy of a particle varies as
$$V(x)=E_{o} ; 0\leq x \leq 1$$
$$=0; x >1$$
For $$0\leq x \leq 1$$, de Broglie wavelength is $$\gamma_{1}$$ and for $$x >1$$ the de Broglie wavelength is $$\gamma_{2}$$.
Total energy of the particle is $$2E_{o}$$. If $$\gamma_{1}/\gamma_{2}=\sqrt x$$. Find $$x$$

For $$0\leq x\leq 1$$, Kinetic energy $$E_1=E_0=\dfrac{p_1^2}{2m} \Rightarrow p_1=\sqrt{2mE_0}$$
For $$x> 1$$, $$E_2=2E_0=\dfrac{p_2^2}{2m} \Rightarrow p_2=\sqrt{4mE_0}$$
now, $$\gamma_1=\dfrac{h}{p_1}=\dfrac{h}{\sqrt{2mE_0}} $$ and $$\gamma_2=\dfrac{h}{p_2}=\dfrac{h}{\sqrt{4mE_0}} $$
$$\therefore \dfrac{\gamma_1}{\gamma_2}=\dfrac{2}{\sqrt 2}=\sqrt 2$$

Give reasons for the following
Laser is used in cutting metals.

Because laser beams are parallel, coherent , monochromatic and polarized in 1 direction, these are using in cutting metals.

In metal cutting through lasers, the process works by directing the laser beam through a nozzle to a workpiece. A combination of heat and pressure creates beam, vapourises or is blown away by a jet of gas leaving an edge with high quality surface finish.

State the factors on which the following depend
i) Kinetic energy of photo electrons.
ii) Number of photo electrons.

K.E of photoelectron depends on frequency of incident light

No. of photoelectron depends on intensity of incident radiation provided frequency is greater than threshold frequency.

Distinguish between ordinary light and laser light.

The main difference between ordinary light(i.e the light comes from incandescent lamp) and laser light is :

1. Coherence : Ordinary light diverges in all directions whereas the light from laser does not diverge.

2. Monochromaticity: Laser beams are monochromatic (i.e. of single wavelength only) whereas ordinary light is non-monochromataic ( i.e. mixed wavelength is mixture of different colors).

Give reasons for the following
Ordinary key chain laser light should not be directly viewed.

Ordinary key chain lasers should not be directly viewed because laser is a light source that can be dangerous to people exposed to it. These are hazardous to a persons's eyesight. The coherence and lower divergence of these laser light means that it can be focussed by the eye into an extremely small spot on retina, resulting in localised burning and permanent damage in seconds.

The de Broglie wavelength of an electron moving with a velocity of $$1.5\times 10^8 ms^{-1}$$ is equal to that of a photon. Find the ratio of the kinetic energy of the photon to that of the electron.

The de Broglie wavelength for electron = $$\lambda = h/p = c/\nu$$

Given $$\lambda_e = \lambda_p$$

KE of electron = $$1/2 \times m \times v^2 = 1/2 \times p \times v_e$$

Substituting for p in the above equation, we get

K.E of electron : $$\dfrac{hv_e}{2\lambda_e}$$

$$\therefore \lambda_e = \cfrac{h \times v_e}{2 \times KE_e}$$

The K.E of photon is given by : $$\dfrac{hc}{\lambda_p}$$

$$\therefore \lambda_p = \cfrac{h \times c}{ KE_p}$$

Given that the wavelengths are equal .

Taking ratio we get : $$\dfrac{v_e}{2 \times KE_e}$$ = $$\dfrac{c}{KE_p}$$

Then,

$$\dfrac{KE_p}{KE_e} = \dfrac {2 \times c}{v_e} = $$ $$\dfrac{2 \times 3 \times 10 ^8}{1.5 \times 10^8} = 4$$

A monochromatic source of light operating at 200 W emits $$4\times 10^{20}$$ photons per second. Find the wavelength of the light $$(in \times 10^{-7}m)$$

We know that , Power = (Number of photons per second ) $$\times$$ $$\dfrac{hC}{\lambda}$$

200 = $$4\times10^{20}\times \dfrac{2\times10^{-25}}{\lambda}$$

$$\therefore \lambda$$ = 4$$\times10^{-7}$$ m

A parallel beam of monochromatic light of wavelength 663 nm is incident on a totally reflecting plane mirror. The angle of incident is $$60^o$$ and the number of photons striking the mirror per second is $$1.0\times 10^{19}$$. If the force exerted by light beam on the mirror is $$Y\times10^{-8}N$$. Find Y.

momentum $$ p = \frac{h}{\lambda}$$ = $$10^{-27} Kg m/s$$

Force exerted by 1 photon = change in momentum = $$2* p Cos i = p$$

Force exerted by $$ 10^{19}$$ photons =$$10^{-27} * 10^{19} = 10^{-8} N$$

So force extered in $$10^{-8} N$$ is 1

The potential energy of a particle of mass m is given by $$\displaystyle V\left( x \right) =\left\{ \begin{matrix} { E }_{ 0 } \\ 0 \end{matrix}\begin{matrix} 0\le x\le 1 \\ x>1 \end{matrix} \right\} $$
$$\displaystyle { \lambda }_{ 1 }$$ and $$\displaystyle { \lambda }_{ 2 }$$ are the de-Broglie wavelengths of the particle, when $$\displaystyle 0\le x\le 1$$ and $$\displaystyle x>1$$ respectively.
If the total energy of particle is $$\displaystyle { 2E }_{ 0 }$$, find $$\displaystyle \left( { { \lambda }_{ 1 } }/{ { \lambda }_{ 2 } } \right) $$.

Total energy , $$E=T+V$$ where T=Kinetic energy and V=potential energy.

When $$0\leq x\leq 1$$, $$2E_0=T+E_0 \Rightarrow T=E_0$$

de-Broglie wavelength, $$\lambda_1=\dfrac{h}{\sqrt{2mT}}=\dfrac{h}{\sqrt{2mE_0}}$$

When $$x>1, 2E_0=T+0 $$ or $$T=2E_0$$

now, $$\lambda_2=\dfrac{h}{\sqrt{2mT}}=\dfrac{h}{\sqrt{2m2E_0}}$$

Thus, $$\dfrac{\lambda_1}{\lambda_2}=\sqrt 2$$

The ratio of energy of photon of $$\lambda$$ = 2000 A$$^{o}$$ to that of $$\lambda$$ = 4000 A$$^{o}$$

$$E_1 = hv_1 = h$$$$\displaystyle\dfrac{c}{\lambda_1}$$ $$= \displaystyle\dfrac{hc}{2000}$$

$$E_2$$ $$= hv_2 = h$$$$\displaystyle\dfrac{c}{\lambda_2}$$ $$= \displaystyle\dfrac{hc}{4000}$$

$$\displaystyle\dfrac{E_1}{E_2}$$ = $$\displaystyle\dfrac{hc \times 4000}{2000 \times hc}=2$$

The ratio of the energy of a photon of 2000 nm wavelength radiation to that of 4000 nm radiation is :

As we know,
E = hv
So,
$$E_1/E_2 = \lambda_2 /\lambda_1 = 4000/2000 = 2$$

Find the typical de Broglie wavelength associated with a He atom in helium gas at room temperature ($$27 °C$$) and 1 atm pressure; and compare it with the mean separation between two atoms under these conditions.

Mass of $$He$$ atoms,

$$m = \dfrac{{Atomic\,mass\,of\,He}}{{Avogadro's\,number}}$$

$$\begin{array}{l} =\dfrac { 4 }{ { 6\times { { 10 }^{ 23 } } } } g \\ \Rightarrow m=6.67\times { 10^{ -27 } }kg \end{array}$$

De-broblie wavelength,

$$\lambda = \dfrac{h}{p} = \dfrac{h}{{\sqrt {3mkT} }}m$$

$$ = \dfrac{{6.63 \times {{10}^{ - 34}}}}{{\sqrt {3 \times 6.67 \times {{10}^{ - 27}} \times 1.38 \times {{10}^{ - 23}} \times 300} }}m$$

$$\lambda = 7.3 \times {10^{ - 11}}m$$

Now using the kinetic gas equation for one mole of a gas

$$\begin{array}{l} PV=RT=kNT \\ \Rightarrow \dfrac { V }{ N } =\dfrac { { kT } }{ P } \end{array}$$

Mean Separation,

$$\begin{array}{l} { r_{ 0 } }={ \left( { \dfrac { { Molar\, volume } }{ { Avogardo's\, number } } } \right) ^{ \dfrac { 1 }{ 3 } } } \\ ={ \left( { \dfrac { V }{ N } } \right) ^{ \dfrac { 1 }{ 3 } } } \\ ={ \left( { \dfrac { { kT } }{ P } } \right) ^{ \dfrac { 1 }{ 3 } } } \\ \Rightarrow { r_{ 0 } }={ \left( { \dfrac { { 1.38\times { { 10 }^{ -23 } }\times 300 } }{ { 1.01\times { { 10 }^{ 5 } } } } } \right) ^{ \dfrac { 1 }{ 3 } } }m \\ { r_{ 0 } }=3.4\times { 10^{ -9 } }m \end{array}$$

So, from the above calculation we say that the mean separation between two atoms is much larger than the de-Broglie wave length.

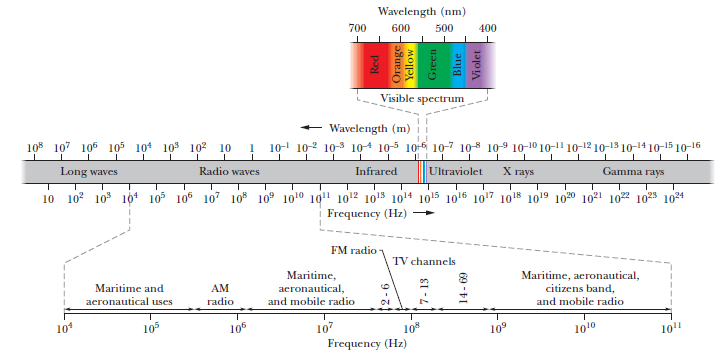
The terminology of different parts of the electromagnetic spectrum is given in the text. Use the formula $$E = h\nu$$ (for energy of a quantum of radiation: photon) and obtain the photon energy in units of eV for different parts of the electromagnetic spectrum. In what way are the different scales of photon energies that you obtain related to the sources of electromagnetic radiation?

Photon energy $$(For\, \lambda \, =\, 1\, m)$$
$$=\displaystyle \frac{6.63\, \times\, 10^{-34}\, \times\, 3\, \times10^8}{1.6\, \times\, 10^{-19}}\, eV\, =\, 1.24\, \times\, 10^{-6}\, eV$$
Photon energy for other wavelengths in the figure for electromagnetic spectrum can be obtained by multiplying approximate powers often. Energy of a photon that a source produces indicates the spacings of the relevant energy levels of the source. For example, $$\lambda \, =\, 10^{-12}$$ corresponds to photon energy $$=\, 1.24\, \times\, 10^6\, eV\, =\, 1.24\, MeV$$ This indicates that nuclear energy levels (transition between which causes $$\gamma$$-ray emission) are typically spaced by 1 MeV or so. Similarly, a visible wavelength $$\lambda \, =\, 5\, \times\, 10^{-7}\, m$$, corresponds to photon energy= 2.5 eV. This implies that energy levels (transition between which gives visible radiation) are typically spaced by a few eV.

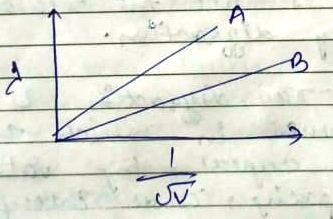
Plot a graph showing variation of de-broglie wavelength $$\lambda $$ versus $$\frac { 1 }{ \sqrt { V } } $$ where v is acclerating potential for two particles A and B carrying same charge but of masses $${ m }_{ 1 },{ m }_{ 2 }({ m }_{ 1 }>{ m }_{ 2 })$$. Which one of the two represents a particle of smaller mass and why?

The de-Broglie wavelength is given by

$$ \lambda = \dfrac{h}{\sqrt{2mqV}} $$

The graph of $$ \lambda $$ vs $$ \dfrac{1}{\sqrt{V}} $$ is a straight line with slope $$ \dfrac{h}{\sqrt{2mq}}$$

Since charge $$ q $$ of A and B is same , slope is $$ \dfrac{1}{\sqrt{m}}$$

Since, $$ m1 > m2 $$

$$ \text{Slope of B} < \text{Slope of A}$$

More is the slope, less is the mass, since slope of A is larger .So plot A represents smaller mass $$ m2 $$

(a) Why photoelectric effect cannot be explained on the basis of wave nature of light? Give reasons.
(b) Write the basic features of photon picture of electromagnetic radiation on which Einstein's photoelectric equation is based.

$$a)$$ According to Photoelectric effect experiments, there exist a threshold frequency below which, no electrons are emitted.

According to the wave picture of light the free electrons at the surface of the metal (over which the beam of radiation falls) absorb the radiant energy continuously. the greater the intensity of radiation. the greater are the amplitude of electric and magnetic fields consequently. the greater the intensity. the greater should be the energy absorbed by each electron in this picture the maximum kinetic energy of the photo electrons on the surface is then expected to increase with increase in intensity. Also no matter what the frequency of radiation is a sufficiently intense beam of radiation(over sufficient time) should be able to impart enough energy to the electrons, so that they exceeds the minimum energy needed to escape from the metal surface.A threshold frequency therefore should not exist.

Further we should note that in the wave picture, the absorption of energy by electron takes place continuously over the entire wave front of the radiation. since a large number of electrons absorb energy. the energy absorbed per electron per unit time turns out to be small. explicit calculation estimate that it can take hours or more for single electron to pick up sufficient energy to overcome the work function and come out of the metal. this conclusion is again in streaking contrast to observation that the photoelectric emission is instantaneous. in short, the wave picture is unable to explain the most basic features of photoelectric emission.

$$b)$$The basic features of photon picture of light are:-

$$1)$$ In interaction of radiation with matter radiation behaves as if it is made up of particles called photons.

$$2)$$Each Photon has energy $$E$$$$(h\upsilon )$$and Momentum $$p$$($${ h\upsilon }/{ c })$$and speed $$c$$ the speed of light.

$$3)$$All photons of light of a particular frequency $$ \upsilon$$, or wavelength$$\lambda$$, have the same energy$$E=(h\upsilon ={ hc }/{ \lambda })$$ and momentum$$p=({ h\upsilon }/{ c }={ h }/{ \lambda }) $$whatever the intensity of radiation maybe by increasing the intensity of light of given wavelength, there is only an increase in the number of photons per second crossing a given area, with each Photon having the same energy thus, Photon energy is independent of intensity of radiation.

$$4)$$Photons are electrically natural and are not defected by electric and magnetic field.

$$5)$$In a photon particle collision (such as Photon-electron collision). the total energy and total momentum are conserved. however, the number of photons may not be conserved in a collision. the photon may be observed on a new Photon may be created.

Given the ground state energy $$E_0 = - 13.6 \,eV$$ and Bohr radius $$a_0 = 0.53 \, \overset{o}{A}$$ . Find out how the de Broglie wavelength associated with the electron orbiting in the ground state would change when it jumps into the first excited state.

$${ r }_{ n }={ a }_{ 0 }\frac { { n }^{ 2 } }{ Z } \\ { r }_{ n }={ 0.53 }\frac { { n }^{ 2 } }{ Z } \\ $$

when the electron is in its ground state:

$${ r }_{ 1 }=0.53\frac { 1 }{ Z } =0.53\quad \\ (Z=1\quad for\quad hydrogen\quad atom\quad for\quad wish\quad { E }_{ \circ }=-13.6e\\ $$

$${ r }_{ 2 }=0.53\times { \left( 2 \right) }^{ 2 }=0.53\times 4\\ From\quad de-Broglie's\quad relation:\\ 2\pi { r }_{ n }=n\lambda \\ \lambda =\frac { 2\pi { r }_{ n } }{ { n }_{ 1 } } =\frac { 2\pi \times 0.53 }{ 1 } =2\pi \times 0.53\\ { \lambda }^{ ' }=\frac { 2\pi { r }_{ 2 } }{ { n }_{ 2 } } =\frac { 2\pi \times 0.53\times 4 }{ 2 } \\ =2\pi \times 0.53\times 2\\ =2\lambda \\$$

$$\therefore$$ Wavelength would get doubled.

Yellow colours seen in fireworks are due to the emission of light with wavelength around 588 nm when sodium salts are burned. Calculate the frequency of yellow light of wave length 588 nm.

$$ \lambda = 588 \, nm $$

$$ \nu\lambda = c $$

$$ \nu = \dfrac{3 \times 10^8 \, m \, s^{-1}}{588 \times 10^9 \, m} $$

$$ = 5.1 \times 10^{14} \, s^{-1} $$

$$ = 5.1 \times 10^{14} \, Hz $$

What is photoelectric effect? Give Einsteins explanation of the phenomenon.

Photoelectric Effect:

The phenomenon of emission of electrons from metal surface when exposed to light energy of a suitable frequency is known as photoelectric effect.

Einstein’s Explanation:

As per Einstein, an incident photon having energy $$ h\nu $$ ejects electron from a metal having work function $$W = h\nu_0 $$ and imparts kinetic energy K.E. $$ = \dfrac{1}{2}mv^2 $$ to it.

Einstein proposed a theory in 1905 to explain photoelectric effect.

When a photon of energy $$ h\nu $$ falls on a metal surface , its energy is used in 2 ways.

1.A part of energy is used to liberate electron from the metal surface. This is called $$ W $$ workfunction.

2.The remaining energy is used to impart kinetic energy of electron.

$$ h\nu = W + \dfrac{1}{2}mv^2 $$

When $$ \nu = \nu_0 $$ ,K.E = 0;

Then eq. will become $$ h\nu_0 = W $$

Substituting,

$$ h\nu - h\nu_0 = \dfrac{1}{2}mv^2 $$

This is Einstein’s photoelectric equation.

List any three applications of laser.

Lasers in medicine:

· Used for bloodless surgery.

· Used to destroy kidney stones

· Used in cancer diagnosis and therapy

· Used to remove tumours

Lasers in communication:

· Used in optical fibre communication to send information over large distance with less loss

· Used in underwater communication network

· Used in space communication radar and satellites

Lasers in Industries:

· Used to cut glass and quartz

· Used in electronic industries for IC’s

· Used for heat treatment in automobile industry

· Used in reading bar codes.

Draw a neat diagram of Helium -Neon gas laser tube.

1155155_560766_ans_2fc43a2273aa475c9952dca64b4e345d.png

Derive an expression for de-Brogile wavelength of matter waves.

de Broglie's wavelength of matter waves: de Broglie equated the energy equations of Planck(wave) and Einstein(particle).
For a wave of frequency $$\nu $$, the energy associated with each photon is given by Planck's relation,

$$E=h\nu$$ ...............$$(1)$$
Where $$h$$ is Planck's constant.
According to Einstein's mass energy relation, a mass m is equivalent to energy,
$$E=mc^2$$ ............$$(2)$$
where $$c$$ is the velocity of light.
If, $$h\nu=mc^2$$
$$\therefore \displaystyle\frac{hc}{\lambda}=mc^2$$ (or) $$\lambda=\displaystyle\frac{h}{mc}$$ ...........$$(3)$$
(since $$\nu=\displaystyle \frac{c}{\lambda}$$)
For a particle moving with a velocity $$v$$, if $$c=v$$ from equation $$(3)$$
$$\lambda =\displaystyle\frac{h}{mv}=\dfrac{h}{p}$$
Where $$p=mv$$, the momentum of the particle. These hypothetical matter waves will have appreciable wavelength only for very light particles.

Write down de Broglie's relation and explain the terms therein.

De-Broglie relation relates a body's momentum with its wavelength.

It is given as

$$\lambda=\dfrac{h}{p}$$

where $$\lambda$$ is its de-broglie wavelength

$$h$$ is the plank's constant

$$p$$ is the moving body's momentum.

All photo electrons are not emitted with the same energy as the incident photons. Why?

An electron is bounded with the nucleus of the metal atom with coulombic interaction. When a photon is incident on the metal surface, some of the energy of the photon is used up to overcome the coulombic interaction, which is knows as work function of the metal, and the remaining energy of the photon becomes the kinetic energy of the emitted photo electrons.

Maximum kinetic energy of the photo electrons $$K.E_{max} = h\nu - \phi$$

where $$h\nu$$ is the energy of photon and $$\phi$$ is the work function of metal.

$$\implies$$ $$K.E_{max}< h\nu$$

Hence photo electrons are not emitted with the same energy as the incident photons.

Determine De-Broglie Wave equation.

De-Broglie Wave: The waves which are associated with matter are called matter waves or de Broglie waves.
Wave equation: According to quantum theory, the energy of a photon is given by the formula:
$$E = hv$$ .....(i)
where, $$h =$$ Planck constant and $$v =$$ Frequency of light.
Suppose the mass of photon is $$m$$.
$$\therefore$$ By Einstein's mass energy relation,
$$E = m{c}^{2}$$ ......(ii)
where, $$c =$$ velocity of light.
Now, from equation (i) and (ii), we get
$$m{c}^{2} = hv \Rightarrow m = \dfrac{hv}{{c}^{2}}$$
But, $$v = \dfrac{c}{\lambda}$$ $$\therefore m = \dfrac{hc}{\lambda c}$$
$$m = \dfrac{h}{\lambda c}$$ .....(iii)
If the momentum of photon be $$p$$, then
$$p = mc$$
or $$p = \dfrac{hc}{\lambda c}$$ [from equation (iii)]
or $$p = \dfrac{h}{\lambda} \Rightarrow \lambda = \dfrac{h}{p}$$
Which is called De-Broglie wave equation.
Again, if the velocity of mass $$m$$ is $$v$$, then
$$p = mv$$ and $$\lambda = \dfrac{h}{mv}$$
which is De-Broglie relation.

What is deBroglie's hypothesis? Write the expression for the wavelength associated with a moving particle.

De Broglie hypothesis says that all matter has both particle and wave nature.
The wave nature of a particle is quantified by de Broglie wavelength defined as, $$\lambda = \dfrac{h}{mv}$$
where $$h$$ is Plank's constant, $$m$$ is mass of the particle and $$v$$ is velocity of the particle.

Find energy of photon of wavelength $$4000\overset{o}{A}$$.

Given, $$\lambda =4000\overset{o}{A}$$
$$=4000\times 10^{-10}$$m
$$=4\times 10^{-7}$$m
We know that,
$$E=hv$$
But, $$c=v=v=\displaystyle\frac{c}{\lambda}$$
$$\therefore E=\displaystyle\frac{c}{\lambda}$$ $$[\therefore h=6.6\times 10^{-34}]$$
$$E=\displaystyle\frac{6.6\times 10^{-34}\times 3\times 10^8}{4\times 10^{-7}}$$J and C$$=3\times 10^{4}$$
E$$=4.95\times 10^{-19}$$J
The energy of photon is $$4.95 \times 10^{-19}$$J.

What are basic processes involved in the working of a LASER?

LASER is an acronym for Light Amplification by Stimulated Emission of Radiation. The working of LASER is as follows:

A laser is created when the electrons in atoms in special glasses, crystals, or gases absorb energy from an electrical current or another laser and become excited.
These excited electrons move from a lower-energy orbit to a higher-energy orbit around the atom’s nucleus. When they return to their normal or “ground” state, the electrons emit photons (particles of light).
These photons are all at the same wavelength and are coherent. In contrast with ordinary visible light which comprises of multiple wavelengths and is not coherent.

An electron, an $$\alpha$$ particle and a proton have the same kinetic energy. Which of these particles has the shortest de Broglie wavelength?

Kinetic energy is given by $$E=\dfrac{1}{2}mv^2$$

Same kinetic energy implies that electron has highest velocity (as mass is lowest).

Assume mass of electron as 1 unit. Now, mass of proton approx 1836 and mass of alpha particle is 4 times that is 7344.

Now calculate velocity in each case

For electron $$v=\sqrt{2E}$$, proton $$v=\sqrt{\dfrac{2E}{1836}}$$ and alpha particle $$v=\sqrt{\dfrac{2E}{7344}}$$

Also de-Broglie wavelength is given by $$\lambda=\dfrac{h}{mv}$$

Now calculate momentum in each case

For electron $$mv=\sqrt{2E} \times 1$$ proton $$mv=\sqrt{\dfrac{2E}{1836}} \times 1836$$ and alpha particle $$mv=\sqrt{\dfrac{2E}{7344}} \times 7344$$

Clearly electron has least momentum. Hence it has largest de-Broglie wavelength. And Alpha particle has least wavelength

Write the formula for de Broglie wavelength. An electron is moving with speed of $$0.5\times { 10 }^{ 3 }m/s$$. Find the de Broglie wavelength associated with it.

Mass of electron$$=m_e=9.11\times 10^{-31}Kg$$

speed of electron$$=V_e=0.5\times 10^{3}m/s$$

Planck constant$$=h=6.626\times 10^{-34}m^2Kg/s$$

De Broglie wavelength associated with electron $$=\lambda$$

Momentum of the electron is given by,

Momentum of the electron$$=P=m_eV_e=\dfrac{h}{\lambda}$$

putting the values we get,

$$P=9.11\times 10^{-31}\times 0.5\times 10^{3}=\dfrac{6.626\times 10^{-34}}{\lambda}$$

$$\therefore \lambda=\dfrac{6.626\times 10^{-34}}{9.11\times 10^{-31}\times 0.5\times 10^{3}}$$

$$\therefore \lambda=1.46\times 10^{-6}m=$$ De Broglie wavelength

Find the initial momentum of electron if the momentum of electron is changed by $$Pm$$ and the de Broglie wavelegth associated with it changes by $$0.50$$%.

By De-Broglie equation,

$$\lambda=h/mv=h/P_m$$..(1)

$$P$$ is the initial momentum of electron and $$P_m$$ be the decrease in momentum of electron, when wavelength of electron change by $$0.50$$%

$$\lambda+0.5\lambda/100=h/(P-P_m)$$

$$100.5\lambda/100=h/(P-P_m)$$..(2)

By eq (1) and (2),

$$P=1.99P_m$$

$$\therefore $$ Initial momentumof electron is $$1.99P_m$$

The work function for the surface of aluminium is 4.2 eV. How much potential difference will be required to stop the emission of maximum energy electrons emitted by light of 2000 $$\dot{A}$$ wavelength? What will be the wavelength of that incident light for which stopping potential will be $$0$$ ?

Given, Work function$$4.2eV$$

$$\lambda=$$ wavelength $$=200\mathring { A } $$

When stopping potential will be $$0$$

the wavelength$$=?$$

Work function of the metal $$Q_0=4.2eV\\ \quad=4.2\times1.6\times10^{-19}J\\ \quad=6.72\times10^{-14}J$$

wavelength of incident radiation

$$\lambda=200\mathring{A}\\ \quad=2000\times10^{-10}m$$

Now, using the formula for energy of a photon,

$$E=\cfrac{hc}{\lambda}\\ E=\cfrac{6.62\times10^{-34}\times3\times10^8}{2000\times10^{-10}}\\ \quad=9.93\times10^{-19}J$$

As energy of incident photon

$$E>Q_0$$ hence photoelectric emission will take place.

A beam of light has three wavelengths 4121 A, 4972 A and 6216 A with a total intensity of $$3.6 \times 10^{-3} \, Wm^{-2}$$ equally distributed amongst the three wavelengths .The beam falls normally on an area $$ 1.0 cm^2$$ of a clean metallic surface of work function 2.3 eV .Assume that there is no loss of lighy by reflection and that each energetically oapable photon eject one electron .Calculate the number of photoelectrons liberated in two seconds

The maximum wavelength capable of emitting photo-electron is,

$$\lambda_m = \dfrac{hc}{\phi_o}=\dfrac{6.63\times10^{-34}\times3\times10^8}{2.3\times1.6\times10^{-19}}=5404A$$

So photons with wavelength of $$4121A\ and\ 4972A$$ would be able to eject photo-electrons.

So Intensity of photons of both the wavelengths is, $$I=1.2\times10^{-3}Wm^{-2}$$

Power, $$P=1.2\times10^{-3}\times10^{-4}m^2=1.2\times10^{-7}W$$

Number of photo-electrons ejected per second by $$4121A$$ wavelength is, $$N_1=\dfrac{P\lambda}{hc} = \dfrac{1.2\times10^{-7}\times4121\times10^{-10}}{6.626\times10^{-34}\times3\times10^8}=249\times10^9$$

Similarly, Number of photo-electrons ejected per second by $$4972A$$ wavelength is, $$N_2=\dfrac{P\lambda}{hc} = \dfrac{1.2\times10^{-7}\times4972\times10^{-10}}{6.626\times10^{-34}\times3\times10^8}=300\times10^9$$

So total number of photo-electrons emitted per second is, $$N=N_1+N_2=549\times10^9$$

total number of photo-electrons emitted in two second is, $$1098\times10^9$$

Give an expression for de-Broglie's wavelength of matter waves?

Expression for de-Broglie's wavelength of matter waves.:
$$ \displaystyle \lambda = \dfrac {h}{P}= \dfrac {h}{mV}$$
$$ \displaystyle \lambda =$$ de-Broglie's wavelength
$$ \displaystyle h=$$ Planck's constant
$$ \displaystyle P=$$ momentum
$$ \displaystyle m=$$ mass
$$ \displaystyle V=$$ velocity

Calculate the de-Broglie wavelength of an electron moving with one fifth of the speed of light. Neglect relativistic effects. ($$h = 6.63 \times 10^{-34}\ J.s., c = 3 \times 10^8\ m/s$$, mass of electron $$= 9 \times 10^{-31}\ kg$$)

By de-Broglie's theory, the wavelength of any particle $$\lambda=\cfrac hp$$ and $$p=m_V$$ $$\therefore \lambda=\cfrac h{m_V}$$

$$_V=\cfrac c5=\cfrac{3\times10^8}5$$

$$\therefore\lambda=\cfrac{6.63\times10^{-34}\times5}{9\times10^{-31}\times3\times10^8}=1.23\times10^{-11}m$$

Answer:- $$1.23\times10^{-11}metres$$

State de Broglie hypothesis.

Louis de Broglie, in 1924, stated that a wave is associated with a moving particle (i.e. matter) and so named these waves as matter waves. He proposed that just like light has dual nature, electrons also have wave like properties.
Wavelength of a moving particle is given by $$\lambda = \dfrac{h}{p}$$
where $$h$$ is the Planck's constant and $$p$$ is the momentum of moving particle.

How does one explain the emission of electrons from a photosensitive surface with the help of Einstein's photoelectric equation?

In photoelectric effect, an electron from a photosensitive surface, absorbs a quantum of electromagnetic radiation energy$$\left( h\upsilon \right) $$. If this energy absorbed exceeds the minimum energy needed for the electron to escape from the photosensitive surface( Work function$${ \phi }_{ o }$$ ) ,the electron are emitted with maximum kinetic energy ($${ k }_{ max } $$) ;

$${ k }_{ max }=\quad h\upsilon -{ \phi }_{ o }$$

This is Einstein's photoelectric equation.

Intensity of a LASER beam $$(\lambda =6600\overset{o}{A})$$ is $$6$$ mW. Calculate no. of photons passing along path of beam in per second.

Wavelength of laser beam $$\lambda = 6600\times 10^{-10} \ m = 6.6\times 10^{-7} \ m$$
Energy of one photon $$E = \dfrac{hc}{\lambda} = \dfrac{(6.6\times 10^{-34})\times (3\times 10^8)}{6.6\times 10^{-7}} = 3\times 10^{-19}\ J$$
Power $$P =6mW = 6\times 10^{-3} \ W$$
So, number of photons per second $$N = \dfrac{P}{E}$$
$$\implies \ N= \dfrac{6\times 10^{-3}}{3\times 10^{-19}} = 2\times 10^{16}$$ Photons per second

Write any three experimental observations of photoelectric effect.

$$Existence\ of\ threshold\ frequency:$$

For a given metal, no photoelectrons are emitted if the frequency of the incident light is lower than a certain frequency. If the light frequency is below this threshold frequency for that metal, no photoelectrons can be emitted, no matter the intensity of the incident radiation is or for how long it falls on the surface of the metal.

$$Emission\ is\ instantaneous:$$

Emission of photoelectrons takes place almost instantaneously after the light shines on the metal, with no detectable time delay. It does not depend on the intensity of the incident radiation.

$$Maximum\ Kinetic\ Energy\ of\ the\ photoelectron\ is\ independent\ of\ the\ intensity\ of\ incident\ E.M.\ radiation:$$

Photoelectrons emitted from a metal have a range of velocities from zero up to a maximum $$V_{max}$$. The maximum kinetic energy $$\dfrac{1}{2}mV^2_{max}$$ was found to depend linearly on the frequency of the radiation and is independent of its intensity.

An electron, in a hydrogen-like atom, is in an excited state. It has a total energy of $$-3.4\ eV$$. Calculate the kinetic energy.(in ev)

As given,

$$En=3.4eV$$

The kinetic energy is equal to the magnitude of total energy in this case

$$\therefore$$ $${ K }_{ E }=3.4eV$$

Write the expression for the de-Broglie wavelength of a particle.

The de-Broglie wavelength of a particle is an attribute associated to the particle's velocity. It is manifested in all the particles in quantum mechanics, according to wave-particle duality, and it determines the probability density of finding the object at a given point of the configuration space.

The de Broglie wavelength is inversely proportional to the particle momentum.

de-Broglie wavelength $$\lambda = \dfrac{h}{p}$$
where $$h$$ is the Planck's constant and $$p$$ is the linear momentum of the particle.

Find the maximum kinetic energy of photo-electron liberated from the surface of lithium ($$\phi =2.39eV$$) by electromagnetic radiation whose electric component varies with time as $$F=a(1+\cos \omega t) \cos \omega_{o}t$$, where $$'a'$$ is a constant, $$\omega=6\times 10^{14}\ rad/sec$$
and $$\omega_{o}=3.60\times 10^{15}\ rad/s$$.

$$E=a(1+\cos \omega t)\cos \omega _{o}t+ a \cos \omega_{o}t \cos \omega_{o} t$$
$$\Rightarrow \quad E=a \cos \omega_{o}t+\dfrac{1}{2}a \cos (\omega + \omega_{o})t+\dfrac{1}{2} a \cos(\omega - \omega_{o})t$$
This is a complex vibration consisting of harmonic components of frequencies $$\omega_{o},(\omega + \omega_{o})$$ and $$(\omega - \omega_{o})$$. The highest angular frequency is $$(\omega + \omega_{o})$$.
Now, $$hv=\phi+k_{max}$$
So, $$k_{max}=\dfrac{h}{2\pi}(\omega + \omega_{o})-\phi$$
$$=\dfrac{6.6\times 10^{-34}}{2\pi}(6\times 10^{14}+3.6\times 10^{15})-2.39\times 1.6\times 10^{-19}$$
$$=4.41\times 10^{-19}-3.82\times 10^{-19}$$
$$=0.59\times 10^{-19}J$$
$$=0.37\ eV$$

A sample of monoatomic hydrogen gas contains n atoms all the third excited state. Find the minimum value of n so that on subsequent de-excitation all possible different energy photons are emitted.

Initial state, $${ n }_{ i }=3\\ final\quad possible\quad states,\quad { n }_{ f }=2,1\\$$

$$ \therefore$$ position transitions: $$3\rightarrow 2\\ 3\rightarrow 1\\ 2\rightarrow 1$$

Show that it is not possible for a photon to be completely absorbed by a free electron.

If the i undergoes an elastic collision with a photon. Then applying energy conservation to this collision. We get $$hC/\lambda +m_0c^2=mc^2$$
and applying conservation of momentum $$h/\lambda=mv$$
Mass of $$e = m = \dfrac { { m }_{ 0 } }{ \sqrt { 1-{ v }^{ 2 }/{ c }^{ 2 } } } $$
from the above equation it can be easily shown that $$V=C$$ or $$V=0$$
both of these results have no physical meaning hence it is not possible for a photon to be completely absorbed by a free electron.

An electron microscope uses eletrons accelerated by a voltage of $$50kV$$. Determine the deBroglie wavelength associated with the electrons. If other factors (such as numerical aperture, etc) are taken to be roughly the same, how does the resolving power of an electron microscope compare with that of an optical microscope which uses yellow light?

Consider the question

$$v = 50kV = 50 \times {10^3}volt$$

K.E of electron $$E=50\times { 10^{ 3 } }eV$$

$$\begin{array}{l} 50\times { 10^{ 3 } }\times 1.6\times { 10^{ -19 } } \\ 50\times 1.6\times { 10^{ -16 } }J \\ de-Broglie\, wave\, length\, of\, electron\, is\, \lambda =\dfrac { h }{ { \sqrt { 2mE } } } \\ =\dfrac { { 6.63\times { { 10 }^{ -34 } } } }{ { \sqrt { 2\times 9.11\times { { 10 }^{ -31 } }\times 50\times 1.6\times { { 10 }^{ -16 } } } } } \\ =5.5\times { 10^{ -12 } }m \\ \end{array}$$

For yellow light , wave length $$\lambda = 5.9 \times {10^{ - 7}}m$$ since the revolving power is inversely proportional to wave length ,an electron microscope is about $${10^5}$$ times that of optical microscope.

A TV station is operated at $$100MW$$ with a signal frequency of $$10MHz$$. Calculate the number of photons radiated per second by its antenna.

We know that,

$$P=nh\nu$$

where,

$$P$$=power

$$n$$=number of photon

$$h$$=plank constant

$$\nu$$=frequency

So,

$$n=\dfrac{P}{h\nu}$$

$$n=\dfrac{100}{6.6\times 10^{-34}\times 10} $$

$$n=1.5\times 10^{34} photon/s$$

A hydrogen atom in a state having a binding energy 0.85eV makes a transiton to a state of excitation energy 10.2eV.The wave length of emitted photon is _____________nm.

Initially, the electron is at $$n=4$$ shell

As. $$\dfrac{13.6}{n^{2}}=B.E.=0.85, n_{1}=4$$

After deexcitation, it is at $$n-[2]=2$$ shell

As,

Excitation energy $$=13.6-\dfrac{13.6}{n_{2}^{2}}=10.2\ eV$$

So, the wavelength of emitted photon is

$$\dfrac{he}{\lambda}=\left[\dfrac{13.6}{n_{2}^{2}}-\dfrac{13.6}{n_{1}^{2}}\right]1.6.\times 10^{-19}$$

$$\lambda =\dfrac{6.6\times 10^{-34}\times 3\times 10^{-8}\times 16}{1.6\times 10^{-19}\times 136\times 3}$$

$$\lambda=4852\ \overset { o }{ A } $$

A particle moving with velocity that is three times that of velocity of electron. If ratio of de-Brogile wave length of particle to that of the electron is $$1.8 \times 10^{-4}$$. Find mass of particle ($$m_e = 9.1 \times 10^{-31}$$ kg )

We use De broglie expression

$$\lambda=\dfrac{h}{mv}$$

So we can write,

$$\lambda_e=\dfrac{h}{m_ev_e}$$ (1)

$$\lambda_p=\dfrac{h}{m_pv_p}$$ (2)

$$v_p=3v_e$$ (3)

Substituting (3) in (2)

$$\lambda_p=\dfrac{h}{m_p3v_e}$$ (4)

Dividing (4) by (3)

$$\frac{\lambda_p}{\lambda_e}=\dfrac{h}{m_p3v_e}.\dfrac{m_ev_e}{h}=1.8\times10^{-4}$$

$$\therefore \dfrac{m_e}{3m_p}=1.8\times10^{-4}$$

$$\therefore \dfrac{m_e}{m_p}=5.4\times10^{-4}$$

$$m_p=\dfrac{9.1\times10^{-31}}{5.4\times10^{-4}}$$

$$m_p=1.685\times10^{-27}kg$$

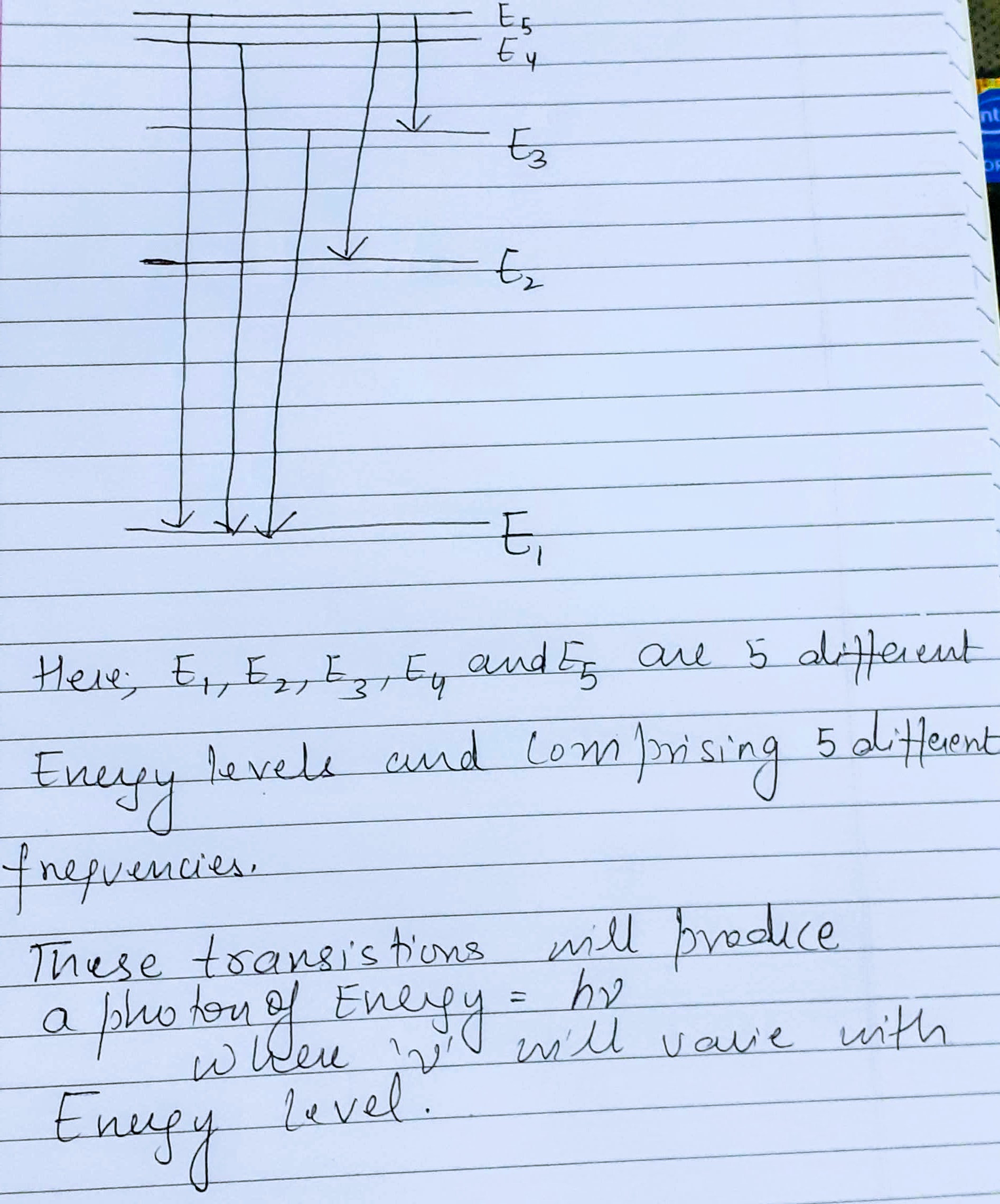
Show five energy levels of an atom, one being much lower than the other four. Five transitions between the levels are indicated, each of which produces a photon of definite energy and frequency.

1322311_1065329_ans_35c23eca800d42538f1d1275e9f51d29.jpg

Find out velocity of electron so that its momentum is equal to that of photon with a wavelength $$\lambda = 52000 \mathring{A}$$

Using $$\lambda = \dfrac{h}{mv}$$

Or $$52000\times 10^{-10} = \dfrac{6.6\times 10^{-34}}{9.1\times 10^{-31}\times v}$$

$$\implies \ v = 139 \ m/s$$

How many photons per second enter one eye if you look directly at a 100 W light bulb 2.00 m away? Assume a pupil diameter of 4.00 mm and a wavelength of 600 nm. How many photons per second enter your eye if a 1.00 m W laser beam is directed into your eye? $$ \lambda = 633 nm ) $$

Given,
Wavelength of light $$\lambda =600nm=600\times {{10}^{-9}}m$$

Power $$P=100\,W$$

Diameter of pupil $${{D}_{p}}=4mm=4\times {{10}^{-3\,}}m$$

Energy of one photon $${{E}_{\lambda }}=\dfrac{hc}{\lambda }=\dfrac{6.626\times {{10}^{-34}}\times 3\times {{10}^{8}}}{600\times {{10}^{-9}}}=3.3\times {{10}^{-19}}\,J$$

Area of sphere (2m radius) $${{A}_{2m}}=4\pi {{r}^{2}}=4\pi \times {{2}^{2}}=16\pi \,{{m}^{2}}$$

Area of pupil $${{A}_{p}}=\dfrac{\pi {{D}_{p}}^{2}}{4}=\dfrac{\pi (4\times {{10}^{-3}})}{4}=\pi {{10}^{-3}}\,{{m}^{2}}$$

Intensity at 2m from source $${{I}_{2m}}=\dfrac{P}{{{A}_{2m}}}=\dfrac{100}{16\pi }$$

Power fall on pupil $${{P}_{p}}={{I}_{2m}}\times {{A}_{p}}=\dfrac{100}{16\pi }\times \pi {{10}^{-3}}=6.25\times {{10}^{-3}}\,W$$

Number of photons $$N=\dfrac{{{P}_{p}}}{{{E}_{\lambda }}}=\dfrac{6.25\times {{10}^{-3}}}{3.3\times {{10}^{-19}}}=1.89\,\times {{10}^{16}}\,photons$$

(b)

Given,

Laser wavelength $$\lambda =633nm$$

Energy fall on eye $$P=1\,m\,W={{10}^{-3}}\,\,W$$

Energy in one photon $${{E}_{\lambda }}=\dfrac{hc}{\lambda }=\dfrac{hc}{\lambda }=\dfrac{6.626\times {{10}^{-34}}\times 3\times {{10}^{8}}}{633\times {{10}^{-9}}}=3.14\times {{10}^{-19}}\,J$$

Number of photons $$N=\dfrac{P}{{{E}_{\lambda }}}=\dfrac{{{10}^{-3}}}{3.14\times {{10}^{-19}}}=3.14\times {{10}^{16}}\,photons$$

If the velocity of a particle is increased three times then the percentage decreases in its de Broglie wavelength will be

$$\lambda=\dfrac{1}{\sqrt{KE}}=\dfrac{1}{\sqrt{\dfrac{1}{2}mv^{2}}}\propto\dfrac{1}{v}$$

Given $$v_{2}=3v_{1}$$

$$\Rightarrow \lambda_{1}v_{1}=\lambda_{2}v_{2}$$

$$\Rightarrow \lambda_{1}v_{1}=\lambda_2\times (3v_{1})$$

$$\Rightarrow \lambda_{1}v_{1}=3\lambda_{2}v_{1}$$

$$\Rightarrow \lambda_{1}=3\lambda_{2}$$

$$\Rightarrow \lambda_{2}=\dfrac{1}{3}\lambda_{1}$$

Percent $$\Rightarrow \dfrac{1}{3}\times 100=33.33$$%

Show graphically, the variation of the de Broglie wavelength $$\left( \lambda \right)$$ with the potential $$\left( V \right)$$ through which an electron is accelerated from rest.

1322250_1054367_ans_f6047cfef4f049ce866eaf13061550cf.jpg

An electron, an $$\alpha-particle$$ and a proton have the same de Broglie wavelength. Which of these particles has (i) the minimum kinetic energy (ii) the maximum kinetic energy and why? Is what why has the wave nature of electron been exploited in electron microscope?

1322303_1064420_ans_be24ec3023e042aca61e2c070dd1cd8c.jpg

An electron and alpha particle have the same de Broglie wavelength associated with them. How are their kinetic energies related to each other?

de Broglie wavelength is given by:

$$\lambda=\dfrac{h}{p}=\dfrac{h}{\sqrt{2mK}}$$

Given $$\lambda_{\alpha}=\lambda_e$$ (de Broglie's wavelength of $$\alpha$$ particle= de Broglie's wavelength of $$e$$ )

$$\dfrac{h}{\sqrt{2m_{\alpha}K_{\alpha}}}=\dfrac{h}{\sqrt{2m_eK_e}}$$ $$m_{\alpha}=6.64\times 10^{-27}kg$$

$$m_e=9.1\times 10^{-31}kg$$

$$\sqrt{\dfrac{K_{\alpha}}{K_e}}=\sqrt{\dfrac{m_e}{m_{\alpha}}}$$

$$\dfrac{K_{\alpha}}{K_e}=\dfrac{m_e}{m_{\alpha}}$$

$$\dfrac{K_e}{K_{\alpha}}=\dfrac{m_{\alpha}}{m_e}=7294\Rightarrow K_e=7294K_{\alpha}$$

A hydrogen atom initially in ground level absorbs a photon,which excites it to the n=4 level.Determine the wavelength and frequency of the photon.

For ground state $$n_{1}=1$$ and $$n_{2}=4$$

Energy of photon absorbed $$E=E_{2}-E_{1}$$

$$\displaystyle =13.6\left(\frac{1}{1^{2}}-\frac{1}{4^{2}}\right)$$

$$=13.6\times \dfrac{15}{16}ev$$

$$=\dfrac{13.6\times 15}{16}\times 1.6\times 19^{-9}$$

$$E=2.04\times 10^{-18}J$$

$$\displaystyle \lambda =\frac{hc}{E}=\frac{6.6\times 10^{-34}\times 3\times 10^{8}}{2.04\times 10^{-18}}$$

$$\lambda =9.7\times 10^{-8}m$$

$$\gamma =\dfrac{c}{\lambda }$$

$$=\dfrac{3\times 10^{8}}{9.7\times 10^{-8}}$$

$$=3.1\times 10^{-15}$$

A photon and electron have got the same de Broglie wavelength. Explain which has greater total energy.

We know that,

For electron

$$E=m{{c}^{2}}.....(I)$$

Also,

$$ \lambda =\dfrac{h}{mv} $$

$$ m=\dfrac{h}{\lambda v} $$

Now, put the value of m in equation (I)

$$ E=\dfrac{h}{\lambda v}\times {{c}^{2}} $$

$$ E=\dfrac{h{{c}^{2}}}{\lambda v} $$

Now, for photon

$$E'=h\nu =h\dfrac{c}{\lambda }...(II)$$

Now, dividing equation (I) by (II)

$$ \dfrac{E}{E'}=\dfrac{h{{c}^{2}}\lambda }{hc\times \lambda v} $$

$$ \dfrac{E}{E'}=\dfrac{c}{v} $$

Now,

$$ \dfrac{E}{E'}=\frac{c}{v} $$

$$ c>v\dfrac{E}{E'}>1 $$

$$ E>E' $$

The total energy of an electron is greater than the total energy of a photon

Hence, this is the required solution

Why is the de Broglie wavelength associated with macroscopic objects (cricket ball, car etc) is not served in daily life?

The concept of De Broglie wavelength does not form a part of classical mechanics.You may take it as a rule of thumb that such concepts can only be applied to microscopic particles to get practical results. Even though these properties are present in macroscopic particles also, it is not humanely possible to observe them.

Coming to the exact reason,

De Broglie wavelenghth of a moving particle= Planck’s constant/Momentum of the particle= Planck’s constant/(Mass of the particle x velocity of the particle)

So, as you can see, for particles which macroscopic(i.e., relatively massive) the De Broglie wavelength is very less and the wave like characteristics are diminished to a certain extent(that is, not observable).

Monochromatic light of frequency $$6 \times 10^{14}$$ Hz is produced by a laser. The power emitted is $$2 \times 10^{-3}$$ W
(i) What is the energy of the photon in the light beam?
(ii) How many photons per second, on an average are emitted by the source ?

$$\rightarrow $$ dual nature of radiation and matter.

givern. $$V=6\times 10^{+14} Hz$$

power emitted by light $$p=2\times 10^{-3}w$$

energy of one photon is given by

energy $$=hv\rightarrow i$$

Number of photons emitted per second $$=\dfrac {power}{enwrgy\ of\ one\ photon}$$

$$=\dfrac {2\times 10^{-3}}{6.63\times 10^{-34}\times 6\times 10^{14}}$$

$$\Rightarrow \ 5.03\times 10^{15}\ \rightarrow \ ii$$

A particle of mass M at rest decay into two particles of masses $$ m_1$$ and $$m_2 $$ having velocities $$ v_1$$ and $$v_2 $$ respectively. Find the ratio of de-Broglie wavelength of the two particles.

Let $${{m}_{1}}\,$$ and $${{m}_{2}}$$ are the masses of two particles. They have $${{v}_{1}}$$ and $${{v}_{2}}$$ as velocities.

According to conservation of momentum

$$ {{m}_{1}}{{v}_{1}}+{{m}_{2}}{{v}_{2}}=0 $$

$$ \dfrac{{{v}_{1}}}{{{v}_{2}}}=\dfrac{{{m}_{2}}}{{{m}_{1}}} $$

De Broglie wavelength is

$$ \lambda =\dfrac{h}{mv} $$

$$ so, $$

$$ \dfrac{{{\lambda }_{1}}}{{{\lambda }_{2}}}=\dfrac{{{m}_{2}}{{v}_{2}}}{{{m}_{1}}{{v}_{1}}} $$

$$ =\dfrac{{{m}_{2}}}{{{m}_{1}}}\times \dfrac{{{v}_{2}}}{{{v}_{1}}} $$

$$ =\dfrac{{{m}_{2}}}{{{m}_{1}}}\times \dfrac{{{m}_{1}}}{{{m}_{2}}} $$

$$ =1 $$

So, the ratio is $$1:1$$

The energy of a photon is given by E= hv,where'v' is the frequency of radiation, Use this equation to get the dimensional formula of 'h'.

Given that,

Energy $$E=h\nu $$

Frequency $$=\nu $$

We know that,

$$ E=h\nu $$

$$ h=\dfrac{E}{\nu } $$

The dimension formula of energy

$$E=\left[ {{M}^{1}}{{L}^{2}}{{T}^{-2}} \right]$$

The dimension formula of frequency

$$\nu =\left[ {{T}^{-1}} \right]$$

Now, the dimension formula of h

$$ h=\dfrac{\left[ {{M}^{1}}{{L}^{2}}{{T}^{-2}} \right]}{\left[ {{T}^{-1}} \right]} $$

$$ h=\left[ {{M}^{1}}{{L}^{2}}{{T}^{-1}} \right] $$

Hence, the dimension formula of $$h$$ is $$\left[ {{M}^{1}}{{L}^{2}}{{T}^{-1}} \right]$$

An electron of mass m$$_{e}$$ and a proton of mass m$$_{p}$$ are moving with the same speed . The ratio of their de-Broglie wavelengths$$\lambda _{e}/\lambda _{p}$$ is

1328211_1188053_ans_ee5861f87b5043eab67c0829159d5d99.jpg

Monochromatic light of frequency $$6.0 \times {10^{14}}Hz$$ is produced by a laser$$.$$ What is the energy of a photon in the light beam$$?$$

1167588_1206094_ans_5be657e2f87b475e85f75b671c35c57b.jpg

The work function of a metal is l eV. On making light of wavelength $$3000A$$ incident on this metals, the velocity of photoelectrons emitted from the metal, in m/s will be-

1199426_1216638_ans_634d39d935e04c56a9d724a8f91c2e1e.JPG

Find the frequency of $$1$$ MeV photon. Given wavelength of a $$1$$ kev photon is $$1.24\times { 10 }^{ -9 } m$$.

Given that, Energy of photon, $$E = 1 MeV$$

$$(\lambda)$$ wavelength of 1 kev photon is $$1.24 \times 10^{-9} m$$

$$\lambda = 1.24 \times 10^{-9} m$$

Energy , $$E = \dfrac{hc}{\lambda} = 1 kev = 10^3 eV$$

$$\Rightarrow \dfrac{hc}{1.24 \times 10^{-9}} = 10^3$$

$$\Rightarrow hc = 1.24 \times 10^{-9} \times 10^3 = 1.24 \times 10^{-6} ev.m$$

Now, $$E = 1 MeV = 10^6 ev = \dfrac{hc}{\lambda'}$$

$$\lambda' = \dfrac{hc}{10^6} = \dfrac{1.24 \times 10^{-6} ev.n}{10^6 ev}$$

$$\lambda' = 1.24 \times 10^{-12} m$$

Also, Relation between $$\lambda'$$ (wavelength) and frequency $$(v)$$

$$v = \left(\dfrac{c}{\lambda'} \right) = \dfrac{3 \times 10^8}{1.24 \times 10^{-12}}$$

$$v = 2.42 \times 10^{20} Hz$$

Frequency $$= v = 2.42 \times 10^{20} Hz$$

Proton and alpha particle have same $$K.E$$. Which one has greater de-Broglie wavelength $$?$$

Since De-broglie Wavelength:-

$$\lambda_{pr}=\dfrac{h}{p}=\dfrac{h}{\sqrt{2mE_{pr}}}$$

and

$$\lambda_{\alpha}=\dfrac{h}{p}=\dfrac{h}{\sqrt{2mE_{\alpha}}}$$

Since, $$E_{Proton}=E_{\alpha-particle}$$

Hence $$\lambda\propto \dfrac{1}{\sqrt m}$$

$$\therefore $$ Particle with greater mass will have Lesser De-broglie Wavelength and vice-versa.

We have; $$m_{\alpha}>m_{pr}$$

$$\Rightarrow \lambda_{pr}<\lambda_{\alpha}$$

The velocity of an electron of de-Broglie wavelength $$\lambda $$ increases four times. Find the new wavelength.

1166831_1335036_ans_1ba6109c47904077ab77301dd19368c7.jpg

A proton and electron have same velocity. Which one has greater de Broglie wavelength and why?

The de-Broglie wavelength λ is given for mass m and velocity v of a particle as Now for an electron and proton velocity v is given same.Since $$m_p > m_e$$ We have inverse relations of λ and massSo $$λp < λe$$, Thus electron would have greater wavelength than wavelength of proton accelerated with same velocity.

An $$\alpha$$- particle and a proton are accelerated from rest by the same potential. Find the ratio of their de- Broglie wavelength.

Given that;

$$V_{\alpha}=V_{Pr}$$

Since:- $$\lambda=\dfrac{h}{p}$$

$$\Rightarrow \lambda=\dfrac{h}{\sqrt{2mE}}$$

Where $$E=kinetic\ Energy=eV$$ [V=acceleration potential]

$$\Rightarrow \lambda_{Pr}=\dfrac{h}{\sqrt{2m_p(2e)V_{Pr}}}$$

Whereas; $$\lambda_{\alpha}=\dfrac{h}{\sqrt{m_{\alpha}(2e)V_{\alpha}}}$$

Where $$m_{\alpha}=4m_{Pr}$$

and $$V_{\alpha}=V_{Pr}=V$$

$$\Rightarrow \lambda_{Pr}=\dfrac{h}{\sqrt{2m_p(e)V}}$$...........(1)

and $$\lambda_{\alpha}=\dfrac{h}{\sqrt{2(4mp)(2e)V}}$$...........(2)

From (1) and (2)

$$\dfrac{\lambda_{Pr}}{\lambda_{\alpha}}=\dfrac{h}{\sqrt{2m_p(e)V}}\times \dfrac{\sqrt{2(4m_p)(2e)V}}{h}$$

$$=\dfrac{\sqrt{2m_peV(8)}}{\sqrt{2m_peV}}$$

$$=\sqrt{8}:1$$

A deutron and an alpha particle have speeds in the ratio $$2 : 3$$. What is the ratio of the de Broglie wavelengths associated with the particles ?

mass of deutron $$=2m$$

mass of alpha $$=4m$$

$$\therefore \dfrac{{{\lambda _1}}}{{{\lambda _2}}} = \dfrac{{{m_2}{v_2}}}{{{m_1}{v_1}}}$$

$$ = \dfrac{{4m \times 3}}{{2m \times 2}}$$

$$ = 3:1$$

Hence,

we get,

$$3:1$$

A parallel beam of monochromatic light of wavelength 500 nm is incident normally on a perfectly absorbing surface. The power through any cross section of the beam is 10 W. Find the number of photon absorbed by the surface per second.

$$\lambda_{Inc}=500 nm$$.

Hence;

$$E_{Inc}=\dfrac{1240(ev\ A^0)}{\lambda(nm)}$$ $$\{\because E=nh\nu=\dfrac{nhc}{\lambda}\}$$

$$\Rightarrow E_{Inc}=\dfrac{1240}{500}$$

$$=2.48eV$$

$$=2.48\times 1.6\times 10^{10}Joules$$.........(1)

Hence

$$Power=\dfrac{Energy}{time}$$

$$=\dfrac{nh\nu}{time}$$

$$=\dfrac{nhc}{\lambda\,time}$$

$$Power=\dfrac{n}{time}\boxed{\dfrac{hc}{\lambda}}$$..........(2)

From (1) and (2)

No. of photons absorbed per second

$$N=\dfrac{n}{times }=\dfrac{Power}{Energy}$$

$$=\dfrac{10watt}{2.48\times 10^{-19}\times 1.6}$$

$$=\dfrac{10\times 10^{19}}{4}$$

$$=2.5\times 10^{19}Photons$$

Calculate the de Broglie wavelength of a neutron of kinetic energy $$150eV$$.

1683658_1477653_ans_833dcd8579414ac987fc4d7adf46e800.jpg

Write De-Broglie's relation.

De-broglie Relation :

$$\lambda =\dfrac {h}{p}$$ ; this relation proposes that light has both wave-like and particle-like property. It basically establishes the wave-particle duality.

The ratio of potential applied to accelerate the $$\alpha $$- particle and proton in order to have the same de Broglie wavelength is

$$\lambda = \dfrac{h}{{\sqrt {2{m_1}{q_1}{v_1}} }}$$

$$\lambda = \dfrac{h}{{\sqrt {2{m_2}{q_2}{v_2}} }}$$

$$ \Rightarrow {m_1}{q_1}{v_1} = {m_2}{q_2}{v_2}$$

$$ \Rightarrow \dfrac{{{v_1}}}{{{v_2}}} = \frac{{{m_2}{q_2}}}{{{m_1}{q_1}}}$$

$$ = \dfrac{{1 \times 1}}{{4 \times 2}}$$

$$\dfrac{{{v_1}}}{{{v_2}}} = \frac{1}{8}$$

We get, $$\dfrac{{{v_1}}}{{{v_2}}} = \frac{1}{8}.$$

State the conditions required to achieve laser action.

Conditions to achieve laser action
(i) There must be an inverted population i.e. more atoms in the excited state than in the ground state.
(ii) The excited state must be a metastable state.
(iii) The emitted photons must stimulate further emission

Calculate the Compton wavelength for (a) an electron and(b) a proton. What is the photon energy for an electromagnetic wave with a wavelength equal to the Compton wavelength of(c) the electron and (d) the proton?

(a) since the mass of an electron is $$m=9.109 \times 10^{-31} \mathrm{kg}$$, its Compton wavelength is

$$\lambda_{C}=\dfrac{h}{m c}=\dfrac{6.626 \times 10^{-34} \mathrm{J} \cdot \mathrm{s}}{\left(9.109 \times 10^{-31} \mathrm{kg}\right)\left(2.998 \times 10^{8} \mathrm{m} / \mathrm{s}\right)}=2.426 \times 10^{-12} \mathrm{m}=2.43 \mathrm{pm}\\$$

(b) since the mass of a proton is $$m=1.673 \times 10^{-27} \mathrm{kg}$$, its Compton wavelength is

$$\lambda_{C}=\dfrac{6.626 \times 10^{-34} \mathrm{J} \cdot \mathrm{s}}{\left(1.673 \times 10^{-27} \mathrm{kg}\right)\left(2.998 \times 10^{8} \mathrm{m} / \mathrm{s}\right)}=1.321 \times 10^{-15} \mathrm{m}=1.32 \mathrm{fm}\\$$

(c) We note that $$h c=1240 \mathrm{eV} \cdot \mathrm{nm},$$ which gives $$E=(1240 \mathrm{eV} \cdot \mathrm{nm}) / \lambda,$$ where $$E$$ is the energy and $$\lambda$$ is the wavelength.

Thus for the electron,

$$E=(1240 \mathrm{eV} \cdot \mathrm{nm}) /\left(2.426 \times 10^{-3} \mathrm{nm}\right)=5.11 \times 10^{5} \mathrm{eV}=0.511 \mathrm{MeV}\\$$

(d) For the proton

$$E=(1240 \mathrm{eV} \cdot \mathrm{nm}) /\left(1.321 \times 10^{-6} \mathrm{nm}\right)=9.39 \times 10^{8} \mathrm{eV}=939 \mathrm{MeV}\\$$

(a) $$\mathrm{In} \mathrm{MeV} / \mathrm{c},$$ what is the magnitude of the momentum associated with a photon having an energy equal to the electron rest energy? What are the (b) wavelength and (c) frequency of the corresponding radiation?

(a) The rest energy of an electron is given by $$E=m_{e} c^{2}$$. Thus the momentum of the photon in question is given by

$$\begin{aligned}p &=\dfrac{E}{c}=\dfrac{m_{e} c^{2}}{c}=m_{e} c=\left(9.11 \times 10^{-31} \mathrm{kg}\right)\left(2.998 \times 10^{8} \mathrm{m} / \mathrm{s}\right)=2.73 \times 10^{-22} \mathrm{kg} \cdot \mathrm{m} / \mathrm{s} \\&=0.511 \mathrm{MeV} / \mathrm{c}\end{aligned}\\$$

(b) $$\lambda=\dfrac{h}{p}=\dfrac{6.63 \times 10^{-34} \mathrm{J} \cdot \mathrm{s}}{2.73 \times 10^{-22} \mathrm{kg} \cdot \mathrm{m} / \mathrm{s}}=2.43 \times 10^{-12} \mathrm{m}=2.43 \mathrm{pm}\\$$

(c) $$f=\dfrac{c}{\lambda}=\dfrac{2.998 \times 10^{8} \mathrm{m} / \mathrm{s}}{2.43 \times 10^{-12} \mathrm{m}}=1.24 \times 10^{20} \mathrm{Hz}\\$$

The meter was once defined as 1650763.73 wavelengths of the orange light emitted by a source containing krypton- 86 atoms. What is the photon energy of that light?

The energy of a photon is given by $$E=h f$$, where $$h$$ is the Planck constant and $$f$$ is the frequency. The wavelength $$\lambda$$ is related to the frequency by $$\lambda f=c,$$ so $$E=h c / \lambda .$$

Since,

$$\begin{array}{c} h=6.626 \times 10^{-34} \mathrm{J} \cdot \mathrm{s} \text { and } c=2.998 \times 10^{8} \mathrm{m} / \mathrm{s} \\h c=\dfrac{\left(6.626 \times 10^{-34} \mathrm{J} \cdot \mathrm{s}\right)\left(2.998 \times 10^{8} \mathrm{m} / \mathrm{s}\right)}{\left(1.602 \times 10^{-19} \mathrm{J} / \mathrm{eV}\right)\left(10^{-9} \mathrm{m} / \mathrm{nm}\right)}=1240 \mathrm{eV} \cdot \mathrm{nm}\end{array}\\$$

Thus,

$$E=\dfrac{1240 \mathrm{eV} \cdot \mathrm{nm}}{\lambda}\\$$

With

$$\lambda=(1,650,763.73)^{-1} \mathrm{m}=6.0578021 \times 10^{-7} \mathrm{m}=605.78021 \mathrm{nm}\\$$

we find the energy to be

$$E=\dfrac{h c}{\lambda}=\dfrac{1240 \mathrm{eV} \cdot \mathrm{nm}}{605.78021 \mathrm{nm}}=2.047 \mathrm{eV}\\$$

Under ideal conditions, a visual sensation can occur in the human visual system if the light of wavelength 550 nm is absorbed by the eyes retina at a rate as low as 100 photons per second. What is the corresponding rate at which energy is absorbed by the retina?

Following Sample Problem - "Emission and absorption of light as photons," we have

$$P=\dfrac{R h c}{\lambda}=\dfrac{(100 / \mathrm{s})\left(6.63 \times 10^{-34} \mathrm{J} \cdot \mathrm{s}\right)\left(2.998 \times 10^{8} \mathrm{m} / \mathrm{s}\right)}{550 \times 10^{-9} \mathrm{m}}=3.6 \times 10^{-17} \mathrm{W}\\$$

Calculate the de Broglie wavelength of (a) a 1.00 keV electron,(b) a 1.00 keV photon, and (c) a 1.00 keV neutron.

(a) We need to use the relativistic formula

$$p=\sqrt{(E / c)^{2}-m_{e}^{2} c^{2}} \approx E / c \approx K / c\\$$

$$\left(\text { since } E \gg m_{e} c^{2}\right) .$$ So

$$\lambda=\dfrac{h}{p} \approx \dfrac{h c}{K}=\dfrac{1240 \mathrm{eV} \cdot \mathrm{nm}}{50 \times 10^{9} \mathrm{eV}}=2.5 \times 10^{-8} \mathrm{nm}=0.025 \mathrm{fm}\\$$

(b) With $$R=5.0 \mathrm{fm},$$ we obtain $$R / \lambda=2.0 \times 10^{2}$$

What is the maximum wavelength shift for a Compton collision between a photon and a free proton?

The $$(1-\cos \phi)$$ factor in Eq. $$38-11$$ is largest when $$\phi=180^{\circ} .$$ Thus, We obtain

$$\Delta \lambda_{\max }=\dfrac{h c}{m_{p} c^{2}}\left(1-\cos 180^{\circ}\right)=\dfrac{1240 \mathrm{MeV} \cdot \mathrm{fm}}{938 \mathrm{MeV}}(1-(-1))=2.64 \mathrm{fm}\\$$

where we have used the value $$h c=1240 \mathrm{eV} \cdot \mathrm{nm}=1240 \mathrm{MeV} \cdot \mathrm{fm}$$

What is the photon energy for yellow light from a highway sodium lamp at a wavelength of 589 nm?

Since,

$$h=6.626 \times 10^{-34} \mathrm{J} \cdot \mathrm{s} \text { and } c=2.998 \times 10^{8} \mathrm{m} / \mathrm{s}\\$$

$$h c=\dfrac{\left(6.626 \times 10^{-34} \mathrm{J} \cdot \mathrm{s}\right)\left(2.998 \times 10^{8} \mathrm{m} / \mathrm{s}\right)}{\left(1.602 \times 10^{-19} \mathrm{J} / \mathrm{eV}\right)\left(10^{-9} \mathrm{m} / \mathrm{nm}\right)}=1240 \mathrm{eV} \cdot \mathrm{nm}\\$$

Thus,

$$E=\dfrac{1240 \mathrm{eV} \cdot \mathrm{nm}}{\lambda}\\$$

With $$\lambda=589 \mathrm{nm},$$ we obtain

$$E=\dfrac{h c}{\lambda}=\dfrac{1240 \mathrm{eV} \cdot \mathrm{nm}}{589 \mathrm{nm}}=2.11 \mathrm{eV}\\$$

Calculate the percentage change in photon energy during a collision like that in Fig. $$38-5$$ for $$\phi=90^{\circ}$$ and for radiation in (a) the microwave range, with $$\lambda=3.0 \mathrm{cm} ;$$ (b) the visible range, with $$\lambda=500 \mathrm{nm} ;(\mathrm{c})$$ the x-ray range, with $$\lambda=25 \mathrm{pm} ;$$ and (d) the gamma-ray range, with a gamma photon energy of $$1.0 \mathrm{MeV}$$(e) What are your conclusions about the feasibility of detecting the Compton shift in these various regions of the electromagnetic spectrum, judging solely by the criterion of energy loss in a single photon-electron encounter?

(a) The dfractional change is

$$\begin{aligned}\dfrac{\Delta E}{E} &=\dfrac{\Delta(h c / \lambda)}{h c / \lambda}=\lambda \Delta\left(\dfrac{1}{\lambda}\right)=\lambda\left(\dfrac{1}{\lambda^{\prime}}-\dfrac{1}{\lambda}\right)=\dfrac{\lambda}{\lambda^{\prime}}-1=\dfrac{\lambda}{\lambda+\Delta \lambda}-1 \\&=-\dfrac{1}{\lambda / \Delta \lambda+1}=-\dfrac{1}{\left(\lambda / \lambda_{C}\right)(1-\cos \phi)^{-1}+1}\end{aligned}\\$$

If $$\lambda=3.0 \mathrm{cm}=3.0 \times 10^{10} \mathrm{pm}$$ and $$\phi=90^{\circ},$$ the result is

$$\dfrac{\Delta E}{E}=-\dfrac{1}{\left(3.0 \times 10^{10} \mathrm{pm} / 2.43 \mathrm{pm}\right)\left(1-\cos 90^{\circ}\right)^{-1}+1}=-8.1 \times 10^{-11}=-8.1 \times 10^{-9} \%\\$$

(b) $$\mathrm{Now} \lambda=500 \mathrm{nm}=5.00 \times 10^{5} \mathrm{pm}$$ and $$\phi=90^{\circ},$$ so

$$\dfrac{\Delta E}{E}=-\dfrac{1}{\left(5.00 \times 10^{5} \mathrm{pm} / 2.43 \mathrm{pm}\right)\left(1-\cos 90^{\circ}\right)^{-1}+1}=-4.9 \times 10^{-6}=-4.9 \times 10^{-4} \%\\$$

$$\dfrac{\Delta E}{E}=-\dfrac{1}{(25 \mathrm{pm} / 2.43 \mathrm{pm})\left(1-\cos 90^{\circ}\right)^{-1}+1}=-8.9 \times 10^{-2}=-8.9 \%\\$$

(d) In this case,

$$\begin{array}{l}\lambda=h c / E=1240 \mathrm{nm} \cdot \mathrm{eV} / 1.0 \mathrm{MeV}=1.24 \times 10^{-3} \mathrm{nm}=1.24 \mathrm{pm} \\\dfrac{\Delta E}{E}=-\dfrac{1}{(1.24 \mathrm{pm} / 2.43 \mathrm{pm})\left(1-\cos 90^{\circ}\right)^{-1}+1}=-0.66=-66 \%\end{array}\\$$

(e) From the calculation above, we see that the shorter the wavelength the greater the dfractional energy change for the photon as a result of the Compton scattering. since $$\Delta E / E$$ is virtually zero for microwave and visible light, the Compton effect is significant only in the x-ray to gamma-ray range of the electromagnetic spectrum.

The highest achievable resolving power of a microscope is limited only by the wavelength used; that is, the smallest item that can be distinguished has dimensions about equal to the wavelength. Suppose one wishes to see inside an atom. Assuming the atom to have a diameter of 100 pm, this means that one must be able to resolve a width of, say, 10 pm. (a) If an electron microscope is used, what minimum electron energy is required? (b) If a light microscope is used, what minimum photon energy is required? (c) Which microscope seems more practical? Why?

(a) We solve $$v$$ from $$\lambda=h / p=h /\left(m_{p} v\right)$$

$$V=\dfrac{h}{m_{p} \lambda}=\dfrac{6.626 \times 10^{-34} \mathrm{J} \cdot \mathrm{s}}{\left(1.6705 \times 10^{-27} \mathrm{kg}\right)\left(0.100 \times 10^{-12} \mathrm{m}\right)}=3.96 \times 10^{6} \mathrm{m} / \mathrm{s}\\$$

(b) We set $$e V=K=\dfrac{1}{2} m_{p} v^{2}$$ and solve for the voltage:

$$V=\dfrac{m_{p} v^{2}}{2 e}=\dfrac{\left(1.6705 \times 10^{-27} \mathrm{kg}\right)\left(3.96 \times 10^{6} \mathrm{m} / \mathrm{s}\right)^{2}}{2\left(1.60 \times 10^{-19} \mathrm{C}\right)}=8.18 \times 10^{4} \mathrm{V}=81.8 \mathrm{kV}\\$$

In an old-fashioned television set, electrons are accelerated through a potential difference of $$25.0 \mathrm{kV}$$. What is the de Broglie wavelength of such electrons? (Relativity is not needed.)

If $$K$$ is given in electron volts, then

$$\begin{aligned}\lambda &=\dfrac{h}{p}=\dfrac{h}{\sqrt{2 m K}}=\dfrac{6.626 \times 10^{-34} \mathrm{J} \cdot \mathrm{s}}{\sqrt{2\left(9.109 \times 10^{-31} \mathrm{kg}\right)\left(1.602 \times 10^{-19} \mathrm{J} / \mathrm{eV}\right) K}}=\dfrac{1.226 \times 10^{-9} \mathrm{m} \cdot \mathrm{eV}^{1 / 2}}{\sqrt{K}} \\&=\dfrac{1.226 \mathrm{nm} \cdot \mathrm{eV}^{1 / 2}}{\sqrt{K}}\end{aligned}\\$$

where $$K$$ is the kinetic energy. Thus,

$$K=\left(\dfrac{1.226 \mathrm{nm} \cdot \mathrm{eV}^{1 / 2}}{\lambda}\right)^{2}=\left(\dfrac{1.226 \mathrm{nm} \cdot \mathrm{eV}^{1 / 2}}{590 \mathrm{nm}}\right)^{2}=4.32 \times 10^{-6} \mathrm{eV}\\$$

An electron, an alpha particle and a proton have the same kinetic energy. Which one of these particles has (i) the shortest and (ii) the largest, de Broglie wavelength?

De Broglie wavelength of particle of mass m in terms of kinetic energy $$(E_k)$$ is $$\lambda=\dfrac{h}{\sqrt{2mE_k}} \propto \dfrac{1}{m}$$ for the same kinetic energy.
(i) Out of given particles, the mass of alpha particle is maximum, so de Broglie wavelength associated with alpha particle is the shortest.
(ii) As mass of electron is least, so electron has largest de-Broglie wavelength.

Define intensity of radiation on the basis of photon picture of light. Write its SI unit.

The amount of light energy or photon energy incident per metre square per second is intensity of radiation.
SI unit:$$\dfrac{W}{m^2}$$ or $$J/s-m^2$$

State de-Broglie hypothesis.

According to hypothesis of de Broglie "The atomic particles of matter moving with a given velocity, cam display the wave like properties."
i.e.$$ \lambda=\dfrac{h}{mv}\ \ (mathematically)$$

What is the wavelength of (a) a photon with energy $$1.00 \mathrm{eV}$$(b) an electron with energy $$1.00 \mathrm{eV}$$(c) a photon of energy $$1.00 \mathrm{GeV},$$ and (d) an electron with energy $$1.00 \mathrm{GeV} ?$$

The wavelength associated with the unknown particle is

$$\lambda_{p}=\dfrac{h}{p_{p}}=\dfrac{h}{m_{p} V_{p}}\\$$

where $$p_{p}$$ is its momentum, $$m_{p}$$ is its mass, and $$v_{p}$$ is its speed. The classical relationship $$p_{p}$$ $$=m_{p} V_{p}$$ was used. Similarly, the wavelength associated with the electron is $$\lambda_{e}=h /\left(m_{e} V_{e}\right)$$ where $$m_{e}$$ is its mass and $$V_{e}$$ is its speed. The ratio of the wavelengths is

$$\lambda_{p} / \lambda_{e}=\left(m_{e} V_{e}\right) /\left(m_{p} V_{p}\right)\\$$

$$\mathrm{So}$$

$$m_{p}=\dfrac{V_{e} \lambda_{e}}{V_{p} \lambda_{p}} m_{e}=\dfrac{9.109 \times 10^{-31} \mathrm{kg}}{3\left(1.813 \times 10^{-4}\right)}=1.675 \times 10^{-27} \mathrm{kg}\\$$

According to Appendix B, this is the mass of a neutron.

Using the classical equations for momentum and kinetic energy, show that an electron's de Broglie wavelength in nanometers can be written as $$\lambda=1.226 / \sqrt{K},$$ in which $$K$$ is the electron's kinetic energy in electron-volts.

The uncertainty in the momentum is

$$\Delta p=m \Delta V=(0.50 \mathrm{kg})(1.0 \mathrm{m} / \mathrm{s})=0.50 \mathrm{kg} \cdot \mathrm{m} / \mathrm{s}\\$$

where $$\Delta v$$ is the uncertainty in the velocity. Solving the uncertainty relationship $$\Delta x \Delta p \geq \hbar$$ for the minimum uncertainty in the coordinate $$x$$, we obtain

$$\Delta X=\dfrac{\hbar}{\Delta p}=\dfrac{0.60 \mathrm{J} \cdot \mathrm{s}}{2 \pi(0.50 \mathrm{kg} \cdot \mathrm{m} / \mathrm{s})}=0.19 \mathrm{m}\\$$

A bullet of mass $$40 \mathrm{g }$$ travels at $$1000 \mathrm{m} / \mathrm{s}$$. Although the bullet is clearly too large to be treated as a matter-wave, determine what Eq. $$38-17$$ predicts for the de Broglie wavelength of the bullet at that speed.

The de Broglie wavelength for the bullet is

$$\lambda=\dfrac{h}{p}=\dfrac{h}{m V}=\dfrac{6.63 \times 10^{-34} \mathrm{J} \cdot \mathrm{s}}{\left(40 \times 10^{-3} \mathrm{kg}\right)(1000 \mathrm{m} / \mathrm{s})}=1.7 \times 10^{-35} \mathrm{m}\\$$

What are (a) the energy of a photon corresponding to wavelength $$1.00 \mathrm{nm}$$(b) the kinetic energy of an electron with de Broglie wavelength $$1.00 \mathrm{nm},(\mathrm{c})$$ the energy of a photon corresponding to wavelength $$1.00 \mathrm{fm},$$ and $$(\mathrm{d})$$ the kinetic energy of an electron with de Broglie wavelength $$1.00 \mathrm{fm} ?$$

(a) The wave function is now given by

$$\Psi(x, t)=\psi_{0}\left[e^{i(k x-\omega t)}+e^{-i(k x+\omega t)}\right]=\psi_{0} e^{-i \omega t}\left(e^{i k x}+e^{-i k x}\right)\\$$

Thus,

$$\begin{aligned}\left.\Psi(x, t)\right|^{2} &=\left|\psi_{0} e^{-i \omega t}\left(e^{i k x}+e^{-i k x}\right)\right|^{2}=\left|\psi_{0} e^{-i \omega t}\right|^{2}\left|e^{i k x}+e^{-i k x}\right|^{2}=\psi_{0}^{2}\left|e^{i k x}+e^{-i k x}\right|^{2} \\&=\psi_{0}^{2}|(\cos k X+i \sin k X)+(\cos k X-i \sin k X)|^{2}=4 \psi_{0}^{2}(\cos k X)^{2} \\&=2 \psi_{0}^{2}(1+\cos 2 k X)\end{aligned}\\$$

(b) Consider two plane matter waves, each with the same amplitude $$\psi_{0} / \sqrt{2}$$ and traveling in opposite directions along the $$x$$ axis. The combined wave $$\Psi$$ is a standing Wave:

$$\Psi(x, t)=\psi_{0} e^{i(k x-\omega t)}+\psi_{0} e^{-i(k x+\omega t)}=\psi_{0}\left(e^{i k x}+e^{-i k x}\right) e^{-i \omega t}=\left(2 \psi_{0} \cos k X\right) e^{-i \omega t}\\$$

Thus, the squared amplitude of the matter wave is

$$|\Psi(x, t)|^{2}=\left(2 \psi_{0} \cos k x\right)^{2}\left|e^{-i \omega t}\right|^{2}=2 \psi_{0}^{2}(1+\cos 2 k x)\\$$

which is shown below.

This gives

$$2 k x=2\left(\dfrac{2 \pi}{\lambda}\right)=(2 n+1) \pi, \quad(n=0,1,2,3, \dots)\\$$

We solve for $$x$$

$$X=\dfrac{1}{4}(2 n+1) \lambda\\$$

(d) The most probable positions for finding the particle are where $$|\Psi(x, t)| \propto(1+\cos 2 k x)$$

reaches its maximum. Thus cos $$2 k x=1,$$ or

$$2 k x=2\left(\dfrac{2 \pi}{\lambda}\right)=2 n \pi, \quad(n=0,1,2,3, \dots)\\$$

We solve for $$x$$ and find $$x=\dfrac{1}{2} n \lambda$$

1711122_1777567_ans_e1f45ea1e95c49d8b078fecc3195069e.png

A proton and a deuteron have the same velocity; what is the ratio of thier de-Broglie wavelengths?

De Broglie wavelength $$\lambda=\dfrac{h}{mv}\propto \dfrac{1}{m}$$ for the same velocity V.
$$\dfrac{\lambda_p}{\lambda_d}=\dfrac{m_d}{m_p}=\dfrac{2m_p}{m_p}=\dfrac{2}{1}=2:1$$

Why are de Broglie waves associated with a moving football not visible?
The wavelength $$'\lambda'$$ of a photon and the de Broglie wavelength of an electron have the same value.Show that the energy of photon is $$\dfrac{2\lambda mc}{h}$$ times the kinetic energy of electron, where m,c,h have their usual meanings.

Due to large mass of a football the de Broglie wavelength associated with a moving football is much smaller than its dimensions, so its wave nature is not visible
de Broglie wavelength of electron $$\lambda=\dfrac{h}{mv}\Rightarrow v=\dfrac{h}{m\lambda}...(i)$$
Energy of photon $$E=\dfrac{hc}{\lambda}...(ii)$$
Ratio of energy of photon and kinetic energy of electrons
$$\dfrac{E}{E_k}=\dfrac{hc/ \lambda}{\dfrac{1}{2} mv^2}=\dfrac{2hc}{\lambda mv^2}$$
Substituting value of v from (i), we get
$$\dfrac{E}{E_k}=\dfrac{2hc}{\lambda m(h/m\lambda)^2}=\dfrac{2\lambda mc}{h}$$
$$\therefore $$Energy of photon=$$\dfrac{2\lambda mc}{h}\times$$ kinetic energy of electron

Determine the value of the de Broglie wavelength associated with the electron orbiting in the ground state of hydrogen atom(Given $$E_n= - (13.6/n^2)$$eV and Bohr radius $$ r0=0.53A^\circ$$). How will the de Broglie wavelength change when it is in the first excited state?

In ground state, the kinetic energy of the electron is
$$K=-E=\dfrac{+13.6eV}{1^2}=13.6\times1.6\times10^{-19}J=2.18\times10^{-18}J$$
de Broglie wavelength $$\lambda=\dfrac{h}{p}=\dfrac{h}{\sqrt{2mK}}$$
$$\lambda_1=\dfrac{6..63\times10^{-34}}{\sqrt{2\times9.1\times10^{-31}\times2.18\times10^{-18}}}$$
$$=0.33\times10^{-9}=0.33nm$$
Kinetic energy in the first excited state (n = 2)
$$K=-E=+\dfrac{13.6}{2^2}eV=+3.4eV=3.4\times1.6\times10^{-19}J=0.54\times10^{-18}J$$
de Broglie wavelength, $$\lambda_2=\dfrac{h}{\sqrt{2mK}}$$
$$=\dfrac{6..63\times10^{-34}}{\sqrt{2\times9.1\times10^{-31}\times0.544\times10^{-18}}} $$
$$=2\times0.33nm=0.66nm $$
i.e., de Broglie wavelength will increase(or double).

Which of the two:(i) light and (ii) moving material particle is concerned with de-Broglie hypotheses?

Moving material particle is concerned with de Broglie hypothesis.

Which of the following moving with the same velocity has the longest de Broglie wavelength; electron,proton,deuteron, $$\alpha$$ particle?

De Broglie wavelength $$\lambda=\dfrac{h}{p}=\dfrac{h}{\sqrt{2mE}}\propto\dfrac{1}{\sqrt{m}}$$ for same energy E.
As the mass of electron is least, de Broglie wavelength of electron is the longest.

The de-Broglie wavelength of a neutron of kinetic energy K is $$\lambda.$$ When its kinetic energy is 4 K, what is the de-Broglie wavelength of the neutron ?

Given

Kinetic energy $$k_1 = k$$

Wave length $$\lambda_1 = \lambda$$

We know

$$\lambda = \dfrac{h}{P}$$ $$K.E. = \dfrac{1}{2}mv^2$$

$$K.E. = \dfrac{P^2}{2m}$$

So, $$\lambda = \dfrac{h}{\sqrt{2m(K.E)}}$$ $$P = \sqrt{2m(K.E)}$$

So, $$\lambda \propto \dfrac{1}{\sqrt{K.E}}$$ ($$\because$$ mass is constant)

$$\dfrac{\lambda_1}{\lambda_2} = \sqrt{\dfrac{k_2}{k_1}}$$

$$\lambda_2 = \sqrt{\dfrac{k_1}{k_2}}$$

$$\lambda_2 = \sqrt{\dfrac{k}{4k}} \lambda$$

$$\lambda_2 = \dfrac{\lambda}{2}$$

An electromagnetic wave of wavelength $$\lambda_1$$ is incident on a photosensitive surface of negligible work function. If the photo-electrons emitted from this surface have the de-Broglie wavelength prove that $$\lambda=\left(\dfrac{2mc}{h}\right)\lambda_1^2$$

Kinetic energy of electrons,E_k=energy of photon of e.m. wave $$=\dfrac{hc}{\lambda}...(1)$$

de Broglie wavelength,$$\lambda_1=\dfrac{h}{\sqrt{2mE_k}}$$or $$\lambda_1^2=\dfrac{h^2}{2mE_k}$$

Using (1), we get

$$\lambda_1^2=\dfrac{h^2}{2m\left(\dfrac{hc}{\lambda}\right)} \Rightarrow \lambda=\left(\dfrac{2mc}{h}\right)\lambda_1^2$$

Do all the electrons that absorb a photon come out as photoelectrons?

No, most electrons get scattered into the metal. Only a few come out of the surface of the metal.

An electron and a proton possess equal kinetic energy. Which of these has the greater de Broglie wavelength?

de Broglie wavelength, $$\lambda=\dfrac{h}{\sqrt{2me_K}}$$

For given kinetic energy $$E_K,\lambda\propto \dfrac{1}{\sqrt{m}}$$

If $$\lambda_c,\lambda_p$$are de Broglie wavelengths of electron and proton and $$m_e,m_p$$

the masses of electron and proton respectively, then $$\dfrac{\lambda_e}{\lambda_p}=\sqrt{\dfrac{m_p}{m_e}}$$

As $$m_p>m_e,$$ it follows $$\lambda_e>\lambda_p,$$i.e., de Broglie wavelength of electron is greater.

The terminology of different part of the electromagnetic spectrum is given in the text ,Use the formula E = hv (for energy of a radiation .: photon ) and obtain the photon energy in units of eV for different parts of the electromagnetic spectrum .In what way are the different scales of photon energies that you obtain related to the sources of electromagnetic radiation ?

The frequency of a r- ray photon ,
$$ v = 5 \times 10^{20} Hz$$
Therefore , energy of a r-ray photon ,
$$ E = hv = 6 . 62 \times 10^{-34} \times 5 \times 10^{20}J $$
$$ = \dfrac{6.62 \times 10^{-34}\times 5 \times 10^{20}}{1.6 \times 10^{-19}}$$
$$ = 2 .07 MeV $$
Frequency of an X - ray photon ,
$$ E = hv = \dfrac{6.62 \times 10^{-34} \times 5 \times 18^{18}}{1.6 \times 10^{-19}} = 2.07 \times 10^{4} eV $$
$$ = 20 .7 keV $$
Frequency of an U V light photon ,
$$ E = hv = 6.62 \times 10^{-34} \times 5 \times 10^{15}$$
$$ = \dfrac{6.62\times 10^{34}\times 5 \times 10^{15}}{1.6 \times 10^{-19}}$$
$$ 20 . 7 eV $$

Establish formula to find de-Broglie wavelength of electron , proton and $$ \alpha $$ particle and unchanged particles.

de-Broglie Hypothesis and Wavelength of Matter Wave:

A natural question arises: As radiation has dual (wave particle) nature, the particles of nature (the electrons, protons, etc), also exhibit wave-like character. In $$1924$$, the French Physicist de-Broglie (pronounced as de brog) $$(1892-1987)$$ put forward the bold hypothesis that moving particles of matter should display wave like properties under suitable conditions. He reasoned that nature was symmetrical and that the two basic physical entities-matter and energy, must have symmetrical character. If radiation shows dual aspects, so should matter. de-Broglie proposed that the wavelength $$ \lambda $$ associated with a particle of $$p$$ momentum is given by the relation

$$ \lambda = \dfrac{h}{p} = \dfrac{h}{mv} $$ …………….. (1)

Where $$m$$ is the mass of the particle and $$v$$ its speed. Equation (1) is known as the de-Broglie relation and the wavelength A of the matter wave is called de-Broglie wavelength. The dual aspect of matter is evident in the de-Broglie relation (1), A is the attribute of a wave while on the right hand side the momentum p is a typical attribute of a particle. Planck’s constant h relates the two attributes. Equation (1) for a material particle is basically a hypothesis whose validity can be tested only by experiment. However, it is interesting to see that it is satisfied also by a photon for a photon, as we have seen

$$ p = \dfrac{hv}{c} $$

$$ \therefore $$ $$ \dfrac{h}{p} = \dfrac{c}{v} = \lambda $$

Clearly from equation (1), $$ \lambda $$ is smaller for a heavier particle (large $$m$$) or more energetic particle (large $$v$$). For example, the de-Broglie wavelength of a ball of mass $$10\, gm$$ moving with a speed of $$ 2\,ms^{-1} $$ is easily calculated as

$$ \lambda = \dfrac{h}{p} = \dfrac{h}{mv} = \dfrac{6.63 \times 10^{-34} J-s}{(10^{-2}\,kg)(2\,ms^{-1})} $$

$$ = 3.31 \times 10^{-34}\,m $$

This wavelength is so small that it is beyond any measurement. This is the reason why macroscopic objects in our daily life do not show wave-like properties, on the other hand, in the sub-atomic domain, the wave character of particles is significant and measurable.

Consider an electron [mass $$(m)$$ charge, $$(e)$$] accelerated from rest through a potential $$V$$. The kinetic energy $$K$$ of the electron equal to the work done $$(eV)$$ on it.

By the electric field

$$ K = eV $$

Now $$ K = \dfrac{1}{2} mv^2 = \dfrac{p^2}{2m} $$

So that $$ p = \sqrt{2mK} = \sqrt{2meV} $$

The de-Broglie wavelength $$ \lambda $$ of the electron is

then ,

$$ \lambda = \dfrac{h}{p} = \dfrac{h}{\sqrt{2mK}} = \dfrac{h}{\sqrt{2meV}} $$ ........(2)

The variation of potential with wave length

Wavelength of Matter Waves Associated with Different Types of Particles (Refer Fig.13.12)

Now we will find out the wavelength of matter waves related to difference particles.

(a) If $$m$$ is the mass and $$q$$ is charge on ant particle and it is accelerated by potential $$V$$, then $$ K = qV $$

$$ \therefore $$ $$ \lambda = \dfrac{h}{\sqrt{2mK}} = \dfrac{h}{\sqrt{2mqV}} $$

For electron, $$ m = m_e = 9.1 \times 10^{-31} \,kg $$

$$ q = e = 1.6 \times 10^{-19} C $$

$$ \therefore $$ $$ \lambda_e = \dfrac{6.63 \times 10^{-34} Js}{\sqrt{(2 \times 9.1 \times 10^{-31} kg \times 1.6 \times 10^{-19} C)V}} $$

$$ = \dfrac{12.27}{\sqrt{V}} \times 10^{-10} m = \dfrac{12.27}{\sqrt{V}} \mathring A $$ ..............(1)

For proton , $$ m_p = 1.67 \times 10^{-27} \,kg $$

$$ q = e = 1.6 \times 10^{-19} C $$

$$ \lambda_p = \dfrac{6.63 \times 10^{-34}}{\sqrt{(2 \times 1.67 \times 10^{-27}kg \times 1.6 \times 10^{-19} C)V}} $$

$$ = \dfrac{0.286}{\sqrt{V}} $$ ............(2)

For deutron, $$ m_d = 2m_p $$ and $$ q = e $$

$$ \lambda_d = \dfrac{0.0202}{\sqrt{V}} \mathring A $$ ...........(3)

For alpha particle,

$$ m_{\alpha} = 4m_p $$ and $$ q = 2e $$

$$ \lambda_{\alpha} = \dfrac{0.101}{\sqrt{V}} \mathring A $$ ............(4)

(b) For unchanged particles like neutron and gas atoms

Mean kinetic energy of electrons

$$ K = \dfrac{3}{2} kT $$

where $$ k = 1.38 \times 10^{-23} \, J/K $$ is Boltzmann constant

$$ \because $$ $$ \lambda = \dfrac{h}{\sqrt{2mK}} = \dfrac{h}{\sqrt{3mKT}} $$ .........(5)

For $$1$$ neutron or one proton

$$ m_n = m_p = 1.67 \times 10^{-27} \,kg $$

$$ \lambda = \dfrac{25.2}{\sqrt{T}} \mathring A $$

Sometimes thermal energy is taken as $$kT$$

$$ K = kT $$

$$ \therefore $$ $$ \lambda = \dfrac{h}{\sqrt{2mkT}} $$ ............(6)

In this situation , the wavelength of neutron will be

$$ \lambda = \dfrac{30.8}{\sqrt{T}} \mathring A $$

The graph between $$ \lambda $$ and $$ \sqrt{T} $$ (Refer Fig.13.13)

1758505_1836778_ans_fca6c20f36f24ea2bdc723e6d15244f4.png

Work function for sodium is $$ 2.3\,eV $$. Find out the maximum wavelength of light, which can emit photoelectrons from sodium.

Work function of sodium $$ (\phi) = 2.3\,eV $$

Work function $$ (\phi) = hv_0 = \dfrac{hc}{\lambda_0} $$

$$ \lambda_0 = \dfrac{hc}{\phi} $$

$$ = \dfrac{6.63 \times 10^{-34} \times 3 \times 10^8}{2.3\,eV} $$

$$ = \dfrac{6.63 \times 10^{-34} \times 3 \times 10^8}{2.3 \times 1.6 \times 10^{-19}} $$

$$ = 539 \times 10^{-9} = 539 \,nm $$

A neutron with kinetic energy $$T= 25\ eV$$ strikes a stationary deuteron (heavy hydrogen nucleus). Find the de Broglie wavelengths of both particles in the frame of their centre of inertia.

1881063_1854514_ans_cc7e51caa4464ff6a0191a0da4a280dd.jpg

A photon with energy $$ \hbar \omega=250 \mathrm{keV} $$ is scattered at an angle $$ \theta=120^{\circ} $$ by a stationary free electron. Find the energy of the scattered photon.

Given:

$$ \hbar \omega=250 \mathrm{keV} $$

$$ \theta=120^{\circ} $$

$$E_p=\dfrac{\hbar \omega}{1+2\left(\hbar \omega / m c^{2}\right) \sin (\theta / 2)}=0.144 \mathrm{MeV} $$

Two identical non-relativistic particles move at right angles to each other, possessing de Broglie wavelengths $$ \lambda_{1}$$ and $$\lambda_2 $$. Find the de Broglie wavelength of each particle in the frame of their centre of inertia.

1881065_1854515_ans_8344ddbb210444cc9c99c34d46651473.jpg

Calculate the most probable de Broglie wavelength of hydrogen molecules being in thermodynamic equilibrium at room temperature.

1881068_1854518_ans_e8dafbc804f5437284facffea72bb366.jpg

Find the energy of a photon having a wavelength of $$ 3.00 \times 10^{2} $$ nm. Express your answers in units of electron volts, noting that $$ 1 \mathrm{eV}=1.60 \times 10^{-19} \mathrm{J} $$

We find the energy of the photons from Equation, $$ E=h f $$
$$ \quad E=h f=\dfrac{h c}{\lambda} $$

$$\begin{array}{l}E=\dfrac{\left(6.63 \times 10^{-34} \mathrm{J} \cdot \mathrm{s}\right)\left(3.00 \times 10^{8} \mathrm{m} / \mathrm{s}\right)}{3.00 \times 10^{2} \mathrm{nm}}\left(\dfrac{1 \mathrm{nm}}{10^{-9} \mathrm{m}}\right)\left(\dfrac{1 \mathrm{eV}}{1.60 \times 10^{-19} \mathrm{J}}\right) \\E=4.14 \mathrm{eV}\end{array}$$

Find the energy of a photon having a frequency of $$\quad 5.00 \times 10^{17} \mathrm{Hz} $$

We find the energy of the photons from Equation 35.1, $$ E=h f $$
$$ \quad E=h f=\left(6.63 \times 10^{-34} \mathrm{J} \cdot \mathrm{s}\right)\left(5.00 \times 10^{17} \mathrm{Hz}\right)\left(\dfrac{1 \mathrm{eV}}{1.60 \times 10^{-19} \mathrm{J}}\right) $$
$$=2.07 \times 10^{3} \mathrm{eV}=2.07 \mathrm{keV}$$

Electromagnetic radiation of wavelength $$ \lambda=0.30 \mu \mathrm{m} $$ falls on a photocell operating in the saturation mode. The corresponding spectral sensitivity of the photocell is $$ J=4.8 \mathrm{mA} / \mathrm{W} $$. Find the yield of photoelectrons, i.e. the number of photoelectrons produced by each incident photon.

Suppose $$ N $$ photons fall on the photocell per sec. Then the power incident is $$ N \dfrac{2\pi hc}{\lambda} $$

This will give rise to a photocurrent of $$ N \dfrac{2\pi hc}{\lambda}\cdot J $$

which means that $$ N \dfrac{2\pi hc}{e \lambda} \cdot J $$

Electrons have been emitted. Thus the number of photoelectron produced by each photon is $$ w = \dfrac{2\pi h c J}{e \lambda} = 0 \cdot 0198 \approx 0 \cdot 02 $$

Find the de Broglie wavelength of hydrogen molecules, which corresponds to their most probable velocity at room temperature.

1881067_1854516_ans_28ad77982eb3438a8bef5a58761ec332.jpg

An $$\alpha$$-particle and a proton are accelerated from rest by a potential difference of $$100 V$$. After this, their de Broglie wavelengths are $$\lambda_{\alpha}$$ and $$\lambda_{p}$$ respectively. The ratio $$\dfrac{\lambda_{p}}{\lambda_{\alpha}}$$, to the nearest integer, is:

We have, $$\dfrac{1}{2}mv^{2}=eV$$

De broglie wavelength= $$\lambda=\dfrac{h}{mv}$$

$$\lambda = \dfrac{h}{\sqrt{2meV}}$$

$$\lambda_{p}=\dfrac{h}{\sqrt{2(m)eV}}$$....(1)

$$\lambda_{\alpha}=\dfrac{h}{\sqrt{2(4m)2eV}}$$....(2)

Now, $$\dfrac{\lambda_{p}}{\lambda_{\alpha}}=\sqrt{8} \simeq 3$$

(a) Obtain the de Broglie wavelength of a neutron of kinetic energy 150 eV. As you have seen in Exercise 11.31, an electron beam of this energy is suitable for crystal diffraction experiments. Would a neutron beam of the same energy be equally suitable? Explain.($$m_n = 1.675 \times 10^{27}$$kg)
(b) Obtain the de Broglie wavelength associated with thermal neutrons at room temperature ($$27^o C$$). Hence, explain why a fast neutron beam needs to be thermalised with the environment before it can be used for neutron diffraction experiments.

Exercise 11.31:
Crystal diffraction experiments can be performed using X-rays, or electrons accelerated through appropriate voltage. Which probe has greater energy? (For quantitative comparison, take the wave length of the probe equal to 1 A∘ which is of the order of inter-atomic spacing in the lattice) ($$m_e=9.11 \times 10^{-31} kg$$)

(a)The De Broglie wavelength of the neutron is $$=2.327\times 10^{-12}m$$.

Kinetic energy of the neutron, $$K=150eV$$

$$=150\times 1.6\times 10^{-19}$$

$$=2.4\times 10^{-19}J$$

Mass of a neutron, $$m_e=1.675\times 10^{-27}kg$$

The relation that gives the kinetic energy of neutron is:.

$$K=\dfrac{1}{2}m_ev^2$$

$$m_ev=\sqrt{Km_e}$$

De-Broglie wavelength of the neutron is given as;

$$\lambda=\dfrac{h}{m_ev}$$

$$\lambda=\dfrac{h}{\sqrt{2Km_e}}$$

The wavelength of the neutron is inversely proportional to the square root of its mass. So, there will be a decrease in wavelength with increase in mass and vice versa.

$$\therefore \lambda=\dfrac{6.6\times 10^{-34}}{\sqrt{2\times 2.4\times 10^{-17}\times 1.675\times 10^{-27}}}$$

$$=2.327\times 10^{-12}m$$

So, the neutron beam of the same energy $$(150 eV)$$ will not be suitable.

(b)

Room temperature, $$T=27^0C=27+273=300K$$

The relation for average kinetic energy of the neutron is:

$$E=\dfrac{3}{2}kT$$

The value of $$k=$$ Boltzmann constant $$=1.38\times 10^{-23}\,J\,mol^{-1}K^{-1}$$

The wavelength of the neutron is given as:

$$\lambda=\dfrac{h}{\sqrt{2m_eE}}=\dfrac{h}{\sqrt{3m_ekT}}$$

$$=\dfrac{6.6\times 10^{-34}}{\sqrt{3\times 1.675\times 10^{-27}\times 1.38\times 10^{-23}\times 300}}$$

$$=1.447\times 10^{-10}m$$

The wavelength is comparable to the inter atomic spacing of a crystal, Hence, the high energy neutron beam should first be thermallsed, before using it for diffraction.

An electron in an excited state of $$Li^{2+}$$ ion has angular momentum 3h/2$$\pi$$. The de Broglie wavelength of the electron in this state in $$p \pi \alpha_0$$ (where $$\alpha_0$$ is the Bohr radius). The value of $$p$$ is :

Angular momentum, $$L =\dfrac{nh}{2\pi} = \dfrac{3h}{2\pi}$$

$$ \Rightarrow n =3$$

Also, Wavelength$$ \lambda = \dfrac{h}{p} = \dfrac{hr}{mvr}= \dfrac{hr}{ \dfrac{3h}{2\pi}}=\dfrac{2 \pi r}{3}$$ ...(1)

But, $$r = a_0 \dfrac{n^2}{Z}$$ ....(2)

Substituting (2) in (1), $$ \lambda = \dfrac{2 \pi}{3} a_0 \dfrac{n^2}{Z}= \dfrac{2 \pi}{3}a_0 \dfrac{3^2}{3}=2 \pi a_0$$

On comparing with the given expression $$p \pi a_0$$

$$ \Rightarrow p=2$$

Estimating the following two numbers should be interesting. The first number will tell you why radio engineers do not need to worry much about photons. The second number tells you why our eye can never count photons, even in barely detectable light.
(a) The number of photons emitted per second by a medium wave transmitter of 10 kW power, emitting radio waves of wave length 500 m.

(b) The number of photons entering the pupil of our eye per second corresponding to the minimum intensity of white light that we humans can perceive $$(~\,10^{10}\, W\, m^{2})$$. Take the area of the pupil to be about $$0.4\, cm^2$$, and the average frequency of white light to be about $$6\, \times\, 10^{14}\, Hz$$.

(a). $$P=10^4W$$

$$E_1=\dfrac{hc}{\lambda}$$

$$\Rightarrow\dfrac{6.6\times10^{-34}\times3\times10^{8}}{500}$$

$$=3.96\times10^{-28}$$

$$P=nE$$

$$\Rightarrow n=\dfrac{10^4}{3.96\times10^{-28}}=3\times10^{31}\ photons/s$$

We see that the energy of a radio photon is exceedingly small, and the number of photons emitted per second in a radio beam is enormously large. There is, therefore, the negligible error involved in ignoring the existence of a minimum quantum of energy (photon) and treating the total energy of a radio wave is continuous.

(b). $$I=10^{-10}Wm^{-2}$$

$$A=0.4cm^2$$

$$E=h\nu$$

$$\Rightarrow6.6\times10^{-34}\times6\times10^{14}=3.96\times10^{-19}$$

$$I=nE$$

$$n=\dfrac{10^{10}}{3.96\times10^{-19}}=2.52\times10^{8}m^2/s$$

$$n_A=n\times A$$

$$\Rightarrow2.52\times10^{8}\times0.4\times10^{-4}=10^4s^{-1}$$

Though this number is not as large as in (a) above, it is large enough for us never to sense or count individual photons by our eye.

An electron microscope uses electrons accelerated by a voltage of 50 kV. Determine the de-Broglie wavelength associated with the electrons. Taking other factors, such as numerical aperture etc. to be same, how does the resolving power of an electron microscope compare with that of an optical microscope which uses yellow light? $$\left( {{\lambda _y} = 5.9\; \times {{10}^{ - 7}}\;{\text{m}}} \right)$$

Given:- Accelerating voltage=$$V=50kV$$

$$ =50\times { 10 }^{ 3 }V$$

Solution:-Using de-broglie's equation.

$$ \lambda =\cfrac { h }{ p } \quad \longrightarrow \left( 1 \right)$$

$$\lambda$$=Wavelength of moving particle.

$$\\ P$$=Momentum of moving particle.

$$ h$$=Planck's constant$$=6.63\times { 10 }^{ -3 }{ J }s$$

now from mechanics we know,

$$\\ P=\sqrt { 2mk } =\sqrt { 2mqV } $$

Where,$$P$$=momentum of particle

$$M$$=mass of particle.

$$ K$$=Kinetic energy of particle.

$$V$$= Electric potential of particle( Accelerating voltage).

$$q$$=charge of particle.

In the case of electron,$$q=e=1.6\times { 10 }^{ -19 }C$$

Substitution of $$ \left( 1 \right)$$

$$\therefore \quad \lambda =\cfrac { h }{ \sqrt { 2meV } }$$

$$ \lambda =\cfrac { 6.63\times { 10 }^{ -34 } }{ \sqrt { 2\times 9.1\times { 10 }^{ -31 }\times 1.6\times { 10 }^{ -19 }\times 50\times { 10 }^{ 3 } } } $$

$$ \lambda =\cfrac { 6.63\times { 10 }^{ -34 } }{ 120.66\times { 10 }^{ -24 } } $$

$$\lambda =5.467\times { 10 }^{ -12 }m$$

Whereas wavelength of yellow light, $$\lambda_y=590nm$$

$$ =5.9 \times { 10 }^{ -7 }m$$

The wavelength of the accelerated electron is about $$10^5$$ times less than the yellow light.

Since resolving power of a microscope is inversely proportional to the wavelength of light hence the resolving power of the electron microscope is about $$10^5$$ times more than that of an optical microscope.

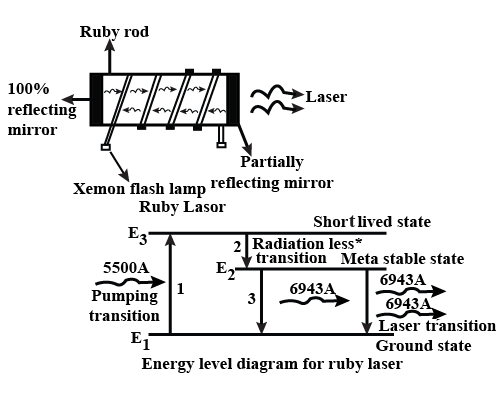
Explain the working of Ruby Laser with the help of energy level diagram.

The Ruby laser was first developed by T. Maiman in 1960. It consists of a single crystal of ruby rod of length $$10 cm$$ and $$0.8 cm$$ in diameter. A ruby is a crystal of aluminium oxide $${ Al }_{ 2 }{ O }_{ 3 }$$, in which some of aluminium ions $$\left( { Al }^{ 3+ } \right)$$ are replaced by the chromium ions $$\left( { Cr }^{ 3+ } \right)$$. The opposite ends of ruby rod are flat and parallel; one end is fully silvered and the other is partially silvered i.e., semi transparent. The ruby rod is surrounded by a helical xenon flash tube which provides the pumping light to raise the chromium ions to upper energy level (Fig.). In the xenon flash tube, each flash lasts several milliseconds and in each flash a few thousand joules of energy is consumed.

Energy diagram:
The simplified energy level diagram of chromium ions in a ruby laser, indicating appropriate excitation an decay is shown in Fig. In normal state, most of the chromium ions are in the ground state $${ E }_{ 1 }$$. When the ruby rod is irradiated by a flash of light, the $$5500\mathring { A }$$ radiation (green colour) photons are absorbed by the chromium ions which are pumped to the excited state $${ E }_{ 3 }$$. The excited ion gives up part of its energy to the crystal lattice and decay without giving any radiation to the meta stable state $${ E }_{ 2 }$$. Since, the state $${ E }_{ 2 }$$ has a much longer lifetime $$\left( { 10 }^{ -3 }s \right)$$, the number of ions in this state goes on increasing. Thus population inversion is achieved between the states $${ E }_{ 2 }$$ and $${ E }_{ 1 }$$. When the excited ion from the metastable state $${ E }_{ 2 }$$ drops down spontaneously to the ground state $${ E }_{ 1 }$$, it emits a photon of wavelength $$6943\mathring { A }$$.
This photon travels through the ruby rod and is reflected back and forth by the silvered ends until it stimulates other excited ion and causes it to emit a fresh photon in phase with stimulating photon. Thus the reflections will amount to the additional stimulated emission - the so called amplification by stimulated emission. This stimulated emission is the laser transition. Finally, a pulse of red light of wave-length $$6943\mathring { A } $$ emerges through the partially silvered end of the crystal.

The work function of iron is $$4.7 eV$$. Calculate the cut-off frequency and the corresponding cut off wavelength for this metal.

Given,

Work function of Iron $$=h{ v }_{ 0 }=4.7eV$$
$$=4.7\times 1.6\times { 10 }^{ -19 }J$$
Planck's constant $$=h=6.626\times { 10 }^{ -34 }Js$$
Velocity of light $$=c=3\times { 10 }^{ 8 }{ ms }^{ -1 }$$
Now,

Work function of Iron $$=h{ v }_{ 0 }=4.7\times 1.6\times { 10 }^{ -19 }$$
$${ v }_{ 0 }=\dfrac { 4.7\times 1.6\times { 10 }^{ -19 } }{ 6.626\times { 10 }^{ -34 } }$$
$${ v }_{ 0 }=1.135\times { 10 }^{ 15 }Hz$$
Since, $$c={ v }_{ 0 }{ \lambda }_{ 0 }$$
$$h{ v }_{ 0 }=\dfrac { hc }{ { \lambda }_{ 0 } }$$
$$\Rightarrow 4.7\times 1.6\times { 10 }^{ -19 }=\dfrac { 6.626\times { 10 }^{ -34 }\times 3\times { 10 }^{ 8 } }{ { \lambda }_{ 0 } }$$
$${ \lambda }_{ 0 }=\dfrac { 6.626\times { 10 }^{ -34 }\times 3\times { 10 }^{ 8 } }{ 4.7\times 1.6\times { 10 }^{ -19 } }$$
$$=2.643\times { 10 }^{ -7 }m$$
$${ \lambda }_{ 0 }=2.643\times { 10 }^{ -7 }m=2643\mathring { A } $$

Draw a neat sketch of Ruby Laser. Explain its working with the help of energy level diagram.

The Ruby Laser consists of a single crystal of ruby rod of length $$10$$cm and $$0.8$$cm in diameter. A ruby is a crystal of aluminium oxide $$Al_2O_3$$, in which some of aluminium ions $$(Al^{3+})$$ are replaced by the chromium ions $$(Cr^{3+})$$. The opposite ends of ruby rod are flat and parallel; one end is fully silvered and the other is partially silvered (i.e.) semi-transparent. The ruby rod is surrounded by a helical xenon flash tube which provides the pumping light to raise the chromium ions to upper energy level(figure). In the xenon flash tube, each flash lasts several milliseconds and in each flash a few thousand joules of energy is consumed.
The simplified energy level diagram of chromium ions in a ruby laser, indicating appropriate excitation and decay is shown in figure.
In normal state, most of the chromium ions are in the ground state $$E_1$$. When the ruby rod is irradiated by a flash of light, the $$5500\overset{o}{A}$$ radiation (green colour) photons are absorbed by the chromium ions which are pumped to the excited state $$E_3$$. The excited ion gives up part of its energy to the crystal lattice and decay without giving any radiation to the meta stable state $$E_2$$. Since, the state $$E_2$$ has a much longer lifetime $$(10^{-3}s)$$, the number of ions in this state goes on increasing. Thus population inversion is achieved between the states $$E_2$$ and $$E_1$$. When the excited ion from the metastable state $$E_2$$ drops down spontaneously to the ground state $$E_1$$, it emits a photon of wavelength $$6943\overset{o}{A}$$. This photon travels through the ruby rod and is reflected back and forth by the silvered ends until it stimulates other excited ion and causes it to emit a fresh photon in phase with stimulating photon. Thus the reflections will amount to the additional stimulated emission-the so called amplification by stimulated emission. This stimulated emission is the laser transition. Finally, a pulse of red light of wavelength $$6943\overset{o}{A}$$ emerges through the partially silvered end of the crystal.

A beam of light has three wavelengths $$4144 A^{o}$$,$$4972\mathring{A}$$ and $$6216\mathring{A} $$ with a total intensity of $$3.6\times 10^{-3} Wm^{-2}$$ equally distributed amongst the three wavelengths. The beam falls normally on an area $$1.0 cm^2$$ of a clean metallic surface of work function $$2.3 $$eV. Assume that the there is no loss of light by reflection and that each energetically capable photon ejects one electron. Calculate a number of photoelectrons liberated in two seconds.

1322237_1046255_ans_9e0bab9b79ba4bb68ad1e47bd5155278.jpg

Violet light $$(\lambda=4000\ \mathring { A } )$$ of intensity $$4\ watt/{m}^{2}$$ falls normally on a surface of area $$10\ cm\times 20\ cm$$. Find
(a) the energy received by the surface per second,
(b) the number of photons hitting the surface per second,
(c) if surface is tilted such that plane of the surface makes an angle $${30}^{o}$$ with light beam, find the number of photons hitting the surface per second.

(a) Energy received per second per unit area
$$E=IA\cos { \theta } =4\times 0.02\ J=0.08\ J$$.
(b) $$n\ h\left( c/\lambda \right) =E$$
$$\Rightarrow n=\dfrac { 0.08\times 4000\times { 10 }^{ -10 } }{ 6.63\times { 10 }^{ -34 }\times 3\times { 10 }^{ 8 } } =\dfrac { 32\times { 10 }^{ 17 } }{ 19.89 } =1.609\times { 10 }^{ 17 }$$
(c) $$n=\dfrac { IA\cos { {60}^{o} } \times \lambda }{ hc } =\dfrac { 1 }{ 2 } \times \dfrac { 32\times { 10 }^{ 17 } }{ 19.89 } =0.805\times { 10 }^{ 17 }$$.

Calculate number of photons passing through a ring of unit area in unit time if light of intensity $$100W{m}^{2}$$ and of wavelength $$400nm$$ is falling normally on the ring.

Given : $$\lambda = 900\ nm = 900\times 10^{-9} \ m$$

Energy of one photon $$E = \dfrac{hc}{\lambda }$$

$$\implies \ E = \dfrac{6.6\times 10^{-34}\times 3\times 10^8}{400\times 10^{-9}} = 4.95\times 10^{-19} \ J$$

Total energy of light falling per second per unit area $$E_{t} = 100 \ J$$

Number of photons $$N = \dfrac{E_t}{E} = \dfrac{100}{4.95\times 10^{-19}} = 2\times 10^{20}$$ photons per second

Atoms of a hydrogen like gas are in a particular excited energy level. When these atoms de-excite they emits photons of different energies. Maximum and minimum energies of emitted photons are $$E_{max}=52.224\ eV$$ and $$E_{min}=1.224\ eV$$ respectively. Calculate the principle quantum number of initially excited level. (lonisation energy of hydrogen atom $$=13.6\ eV$$)

1321445_1022420_ans_cc35209ee8c943629d3551df09647978.jpg

The photoelectric threshold wavelength of a metal is 230nm. Determine the maximum kinetic energy in joule and in eV of the ejected electron for the metal surface when it is exposed to a radiation of wavelength 180 nm. [Plank's constant : h = $$6.63 \times 10^{-34}$$ Js, velocity of light; c = $$3 \times 10^8$$ m/s)

1321760_1072762_ans_69e77247064349d2b69b8c1cce1ee568.jpg

X- rays of wavelength $$\lambda$$ falls on a photosensitive surface emitting electrons.Assuming that the work function of the surface can be neglected, prove that the de Broglie wavelength of electrons emitted will be $$\sqrt{\cfrac{h\lambda}{2mc}}$$

Energy of the X-rays of wavelength$$=h\dfrac{c}{\lambda}$$
As work function is neglected,

$$\dfrac{1}{2}m_ev_e^2=h\dfrac{c}{\lambda}$$

$$v_e^2=\dfrac{2hc}{m_e \lambda}$$

$$v_e=\sqrt{\dfrac{2hc}{m_e \lambda}}$$

De Brogile wavelength $$=\dfrac{h}{m_ev_e}$$

De Brogile wavelength $$=\dfrac{h\sqrt{m\lambda}}{m_e\sqrt{2hc}}$$

$$=\sqrt{\dfrac{h \lambda}{2m_ec}}$$

When an electron in hydrogen atom jumps from the third excited state to the ground state. how would the de broglie wavelength have associated with the electron change?

We know De Broglie wavelength can be related as

$$\lambda=\dfrac{h}{p}$$ where h=planks constant and p= momentum of the electron.

Also momentum $$p=mv$$ and kinetic energy$${E}_{K}=\dfrac{1}{2}m{v}^{2}$$

From above equation we can relate momentum p and kinetic energy as,

$$p=\sqrt{2m{E}_{K}}$$

Now ratio wavelength of hydrogen atom when the atom jumps from third excited state to ground state viz(n=4 to n=1)

$$\dfrac { { \lambda }_{ 1 } }{ { \lambda }_{ 2 } } =\dfrac { \dfrac { h }{ { p }_{ 1 } } }{ \dfrac { h }{ { p }_{ 2 } } } =\dfrac { { p }_{ 2 } }{ { p }_{ 1 } } =\dfrac { \sqrt { 2m{ E }_{ K2 } } }{ \sqrt { 2m{ E }_{ K1 } } } $$ -------(A)

Also we know $${E}_{Kn}=\dfrac{-13.6{Z}^{2}}{{n}^{2}}$$

so, ratio of wavelength of Ground state{n = 1 }nto 3rd excited state { n = 4}
$\bold{\frac{\lambda_{n=1}}{\lambda_{n=4}}}=\frac{1}{4}$

Hence, answer is 1 : 4

The ionisation potential of hydrogen atom is $$13.6V$$.Draw the energy level diagram showing four levels.Calculate (i) the energy of the photon emitted when an electron falls from the third orbit to the second orbit (ii) the wavelength of this photon (value of h and c as above)
what will be the minimum energy of a photon which can be absorbed by hydrogen atom at ordinary temperature ?

$$E=13.6\left(\dfrac{1}{2^2},\dfrac{-1}{3^2}\right)$$
$$=13.6 \left(\dfrac{1}{4}-\dfrac{1}{9}\right)$$
$$13.6\times \dfrac{5}{4\times 9}$$
$$1.89eV$$
$$1.9 eV$$

Calculate the de Broglie wavelength associated with an electron accelerated through a potential difference of 1 kV.

1053433_1176370_ans_8631ca1ed7fb45059e7be9ef4d7d20e8.png

5% energy of a monochromatic light source is converted into light of wavelength 5600 $$A^0 $$. If the power of the source be 100 W, then how many photons of light will be emitted by it per second?

$$\lambda = 5600A$$

Energy of one photon is $$E = h\nu = h\times \cfrac {c}{\lambda}$$$$E = 6.63\times 10^34 \times 3\times 10^8/(5600\times 10^{-10}) = 3.616 \times 10^{-19} J$$

A$$ 100 watt$$ bulb requires $$100 joule$$ of energy per second.

Energy radiated by the bulb as visible light per second =$$ 5$$% of$$ 100 = 5 Joule$$

Number of photons emitted per second=Energy radiated per sec/ energy of one photon

$$= 5/(3.616 \times 10^{-19})$$

$$= 1.38 \times 10^{19}$$

If the ratio of de-Broglle wavelength of a proton and an $$\alpha-particle$$ is $$1:3$$ , then

$${ \lambda }_{ \alpha }=$$ De-Broglle wave length of $$\alpha$$ particle

$$\Rightarrow { \lambda }_{ \rho }=$$ De-Broglle wave length of proton

$$\Rightarrow { \lambda }_{ \alpha }=\dfrac{h}{\sqrt{2m_{\alpha}k_{\varepsilon}}}$$

$$\Rightarrow { \lambda }_{ \rho t }=\dfrac{h}{\sqrt{2m_{\rho}k_{\varepsilon}}}$$ $$k_{\varepsilon}=$$ kinetic energy of proton

$$\Rightarrow \dfrac { \lambda _{ \rho } }{ \lambda _{ \alpha } } =\dfrac { h }{ \sqrt { 2m_{ \rho }{ k }_{ \varepsilon } } } \times \dfrac { \sqrt { 2m_{ \alpha }{ k }_{ \varepsilon } } }{ h } $$

$$=\sqrt { \dfrac { 2m_{ \alpha }{ k }_{ \varepsilon } }{ 2m_{ \rho }{ k }_{ \varepsilon } } } $$

$$=\sqrt { \dfrac { m_{ \alpha } }{ m_{ \rho } } } $$

$$=\sqrt { \dfrac { 4m_{ \rho } }{ m_{ \rho } } } $$

$$=\sqrt { \dfrac { 4 }{ 1 } } $$

$$=\dfrac{2}{1}$$

$$=2:1$$

Hence, the answer is $$2:1.$$

$$1.5mW$$ of $$400nm$$ light is directed at a photoelectric cell. If $$0.1\%$$ of the incident photons produce photo electrons, find the current in the cell.

Power; $$P=1.5\ mw$$

$$=1.5\times 10^{-3}$$ watt

Hence, Energy of each photon = $$hc/\lambda$$

$$=\dfrac {6.62\times 10^{-34}\times 3 \times 10^8}{400\times 10^{-9}} $$

$$=4.96\times 10^{-19}$$ Joule

and Number of photo-electrons emitted per second

$$=\dfrac {P}{Energy\ taken\ by \ each}$$

$$=\dfrac {1.5\times 10^{-3}}{4.96\times 10^{-19}}$$

$$n=3\times 10^{15}$$

No. of photon electrons that produced current

$$=0.1\%$$ of $$n$$

$$=\dfrac {0.1}{100}\times 3\times 10^{15}$$

$$N=3\times 10^{12}$$

Hence, current $$I=Ne$$

$$=N\times 1.6\times 10^{-16}$$

$$=3\times 10^{12}\times 1.6\times 10^{-19}$$

$$=4.8\times 10^{-7}$$

$$=0.48\mu A$$

An electron microscope uses electrons accelerated by a potential difference 50 kV. Calculate the de Broglie wavelength of the electrons. Compare the resolving power of an electron microscope with that of an optical microscope, which uses visible light of wavelength 550 nm. Assume the numerical aperture of the objective lens of the microscopes are the same.

2047287_1393480_ans_96d8f7d024bd43f3907ff242331f6236.jpg

Derived Einstein's Photoelectric equation. Explain photoelectric effect with help of this equation.

Einstein's Photoelectric equation:
By conservation of energy
The energy of incident photon=maximum K.E of $$e^-+$$ work function
$$hv=\dfrac{1}{2}mV^2_{max}+W_0$$
$$(W_0=\dfrac{hv_0}{Thres\,\,hold \,\,frequency})$$
$$K_{max}=hv-hv_0$$
$$K_{max}=h(v-v_0)$$
(1) Explanation of the effect of intensity: The increase of intensity means the increase the number of photons striking the metal surface at a unit time. As each photon ejects only one $$e^-$$ so the number if ejection electron increases.
(2) Explanation of threshold frequency: If $$v\propto v_0$$ That is the frequency of incident radiation is less than the threshold frequency, the kinetic energy of photoelectrons becomes negative. This is no physical meaning.
(3) Explanation of kinetic energy: If $$v>V_0$$ then the maximum kinetic energy of $$e^-$$ increases linearly with frequency v.
(4) Explanation of time lag: Photoelectric is the result of elastic collision b/w photon & $$e^-$$. The transfer of energy of a photon to $$e^-$$ is one lump, not continuous absorption.

Find the maximum kinetic energy of the photo electrons ejected when light of wavelength 350 nm is incident on a cesium surface. Work function of cesium = 1.9eV.

$$\lambda=350nn=350\times10^{-9}m$$
$$\phi =1.9eV$$

Max KE of electrons is given as:

$$E= \dfrac { hc }{ \lambda } -\phi $$

$$=\dfrac { 6.63\times 10^{ -34 }\times 3\times { 10 }^{ 8 } }{ 350\times { 10 }^{ -9 }\times { 1.6 }\times { 10 }^{ -19 } } -1.9$$

$$=1.65ev=1.6ev.$$

The electric-field at a point associated with a light wave is $$E=(100Vm^{ -1 })$$sin$$[(3.0\times10^{ 10 }s^{ -1 })t]$$sin$$[(6.0\times10^{ 10 }s^{ -1 })t]$$ If this light falls on a 2.0 eV, what will be the maximum kinetic energy of the photoelectrons?

E = $$100$$ sin $$[(3\times10^{15}s^{-1})t]$$ sin $$[6\times10^{15}s^{-1})t]$$

= $$100$$ $$\dfrac { 1 }{ 2 } $$ [cos[$$(9times10^{-15}s^{-1})$$t] $$-$$ cos $$[3\times10^{15}s^{-1})$$t]]

The anular velocity $$\omega$$ are $$9\times10^{15}$$ and $$3\times10^{15}$$

for largest K.E.

$$f_{max}$$ $$=$$ $$\dfrac { { W }_{ max } }{ 2\pi } $$ $$=$$ $$\dfrac { 9\times { 10 }^{ 15 } }{ 2\pi } $$

$$E-{ \phi }_{ 0 }=K.E.$$

$$\Rightarrow hf-{ \phi }_{ 0 }=K.E.$$

$$\Rightarrow\dfrac { 6.63\times { 10 }^{ -34 }\times 9\times { 10 }^{ 15 } }{ 2\pi \times 1.6\times { 10 }^{ -19 } } -2=K.E$$

$$\Rightarrow K.E = 3.938$$ $$ev=3.93$$ $$ev.$$

A totally reflecting, small plane mirror placed horizontally faces a parallel beam of light as shown in figure (42-E1). The mass of the mirror is 20 g. Assume that there is no absorption in the lens and that 30% of the light emitted by the source goes through the lens. Find the power of the source needed to support the weight of the mirror. Take $$g=10ms^{-2}$$.

m = 20 g
The weight of the mirror is balanced. Thus force exerted by the photons is equal to weight

$$p=\dfrac { h }{ \lambda } $$

and $$E=\dfrac { hc }{ \lambda } =p\cdot c$$

$$\Rightarrow \dfrac { E }{ t } =\dfrac { p }{ t } c$$

$$\Rightarrow$$ Rate of change of momentum = Power/c
30% of light passes through the lens.
Thus it exerts force.

Remaining is reflected.

$$\therefore$$ Force exerted = 2 (rate of change of momentum)
$$=2\times Power/c$$

$$30$$ % $$\left( \dfrac { 2\times Power }{ c } \right) =mg$$
$$\Rightarrow Power= \dfrac { 20\times { 10 }^{ -3 }\times 10\times 3\times { 10 }^{ 8 }\times 10 }{ 2\times 3 } =10w=100MW$$

A light beam of wavelength 400 nm is incident on a metal plate of work function 2-2e V. (a) A particular electron absorbs a photon and makes two collisions before coming out of the metal. Assuming that 10% of the extra energy is lost to the metal in each collision, find the kinectic energy of this electron as it comes out of the metal. (b) Under the same assumptions, find the maximum number of collisions the electron can suffer before it becomes unable to come out of the metal.

a) When $$\lambda $$ = $$400$$ $$nm$$
Energy of photon = $$\frac {\displaystyle{ hc }}{\displaystyle{ \lambda }} $$ = $$\frac {\displaystyle{ 1240 }}{\displaystyle{ 400 }} $$ = $$3.1$$ $$eV$$
This energy given to electron But for the first collision energy lost

$$= 3.1$$ $$eV$$ $$\times$$ $$10$$% = $$0.31$$ $$eV$$

for second collision energy lost

$$= 3.1$$ $$eV$$ $$\times$$ $$10$$% $$=$$ $$0.31$$ $$eV$$

Total energy lost the two collision

= $$0.31+0.31$$ $$=$$ $$0.62$$ $$eV$$

K.E of photon electron when it comes out of metal
$$=$$ $$hc/\lambda $$ - work function - Energy lost due to collision
$$=$$$$3.1$$ $$eV$$ $$-$$ $$2.2-0.62=0.31$$ $$eV$$

b) For the $$3^{rd}$$ collision the energy lost $$=0.31$$ $$eV$$
Which just equative the KE lost in the $$3^{rd}$$ collision electron. It just comes out of the metal

Hence in the fourth collision electron becomes unable to come out of the metal
Hence maxium number of collision $$=4.$$

Electrons accelerated to an energy of $$50 \mathrm{GeV}$$ have a de Broglie wavelength $$\lambda$$ small enough for them to probe the structure within a target nucleus by scattering from the structure. Assume that the energy is so large that the extreme relativistic relation $$p=$$ $$E / c$$ between momentum magnitude $$p$$ and energy $$E$$ applies. (In this extreme situation, the kinetic energy of an electron is much greater than its rest energy.) (a) What is $$\lambda ?$$ (b) If the target nucleus has radius $$R=5.0 \mathrm{fm},$$ what is the ratio $$R / \lambda ?$$sodium is 590 nm.

(a) The momentum of the electron is

$$p=\dfrac{h}{\lambda}=\dfrac{6.63 \times 10^{-34} \mathrm{J} \cdot \mathrm{s}}{0.20 \times 10^{-9} \mathrm{m}}=3.3 \times 10^{-24} \mathrm{kg} \cdot \mathrm{m} / \mathrm{s}\\$$

(b) The momentum of the photon is the same as that of the electron:

$$p=3.3 \times 10^{-24} \mathrm{kg} \cdot \mathrm{m} / \mathrm{s}\\$$

$$K_{e}=\dfrac{p^{2}}{2 m_{e}}=\dfrac{\left(3.3 \times 10^{-24} \mathrm{kg} \cdot \mathrm{m} / \mathrm{s}\right)^{2}}{2\left(9.11 \times 10^{-31} \mathrm{kg}\right)}=6.0 \times 10^{-18} \mathrm{J}=38 \mathrm{eV}\\$$

(d) The kinetic energy of the photon is

$$K_{\mathrm{ph}}=p c=\left(3.3 \times 10^{-24} \mathrm{kg} \cdot \mathrm{m} / \mathrm{s}\right)\left(2.998 \times 10^{8} \mathrm{m} / \mathrm{s}\right)=9.9 \times 10^{-16} \mathrm{J}=6.2 \mathrm{keV}\\$$

The existence of the atomic nucleus was discovered in 1911 by Ernest Rutherford, who properly interpreted some experiments in which a beam of alpha particles was scattered from a metal foil of atoms such as gold. (a) If the alpha particles had akinetic energy of 7.5 MeV, what was their de Broglie wavelength? (b) Explain whether the wave nature of the incident alpha particles should have been taken into account in interpreting these experiments. The mass of an alpha particle is 4.00 u(atomic mass units), and its distance of closest approach to the nuclear center in these experiments was about 30 fm. (The wave nature of matter was not postulated until more than a decade after these crucial experiments were first performed.)

The wave function is now given by

$$\Psi(x, t)=\psi_{0} e^{-i(k x+\omega t)}\\$$

This function describes a plane matter wave traveling in the negative $$x$$ direction. An example of the actual particles that fit this description is a free electron with linear momentum

$$\vec{p}=-(h k / 2 \pi) \hat{\mathrm{i}}$$ and kinetic energy

$$K=\dfrac{p^{2}}{2 m_{e}}=\dfrac{h^{2} k^{2}}{8 \pi^{2} m_{e}}\\$$

X rays of wavelength 0.0100 nm are directed in the positive direction of an $$x$$ axis onto a target containing loosely bound electrons. For Compton scattering from one of those electrons, at an angle of $$180^{\circ},$$ what are (a) the Compton shift, (b) the corresponding change in photon energy, (c) the kinetic energy of the recoiling electron, and (d) the angle between the positive direction of the $$x$$ axis and the electron's direction of motion?

(a) We know that,

$$\Delta \lambda=\dfrac{h}{m_{e} c}(1-\cos \phi)=(2.43 \mathrm{pm})\left(1-\cos 180^{\circ}\right)=+4.86 \mathrm{pm}\\$$

(b) Using the value $$h c=1240 \mathrm{eV} \cdot \mathrm{nm}$$, the change in photon energy is

$$\Delta E=\dfrac{h c}{\lambda^{\prime}}-\dfrac{h c}{\lambda}=(1240 \mathrm{eV} \cdot \mathrm{nm})\left(\dfrac{1}{0.01 \mathrm{nm}+4.86 \mathrm{pm}}-\dfrac{1}{0.01 \mathrm{nm}}\right)=-40.6 \mathrm{keV}\\$$

(d) The electron will move straight ahead after the collision, since it has acquired some of the forward linear momentum from the photon. Thus, the angle between $$+x$$ and the direction of the electron's motion is zero.

Gamma rays of photon energy $$0.511 \mathrm{MeV}$$ are directed onto an aluminum target and are scattered in various directions by loosely bound electrons there. (a) What is the wavelength of the incident gamma rays?(b) What is the wavelength of gamma rays scattered at $$90.0^{\circ}$$ to the incident beam? (c) What is the photon energy of the rays scattered in this direction?

(a) Using the value $$h c=1240 \mathrm{eV} \cdot \mathrm{nm}$$, we find

$$\lambda=\dfrac{h c}{E}=\dfrac{1240 \mathrm{nm} \cdot \mathrm{eV}}{0.511 \mathrm{MeV}}=2.43 \times 10^{-3} \mathrm{nm}=2.43 \mathrm{pm}\\$$

(b) Now, Eq. 38-11 leads to

$$\begin{aligned}\lambda^{\prime} &=\lambda+\Delta \lambda=\lambda+\dfrac{h}{m_{e} C}(1-\cos \phi)=2.43 \mathrm{pm}+(2.43 \mathrm{pm})\left(1-\cos 90.0^{\circ}\right) \\&=4.86 \mathrm{pm}\end{aligned}\\$$

$$E^{\prime}=E\left(\dfrac{\lambda}{\lambda^{\prime}}\right)=(0.511 \mathrm{MeV})\left(\dfrac{2.43 \mathrm{pm}}{4.86 \mathrm{pm}}\right)=0.255 \mathrm{MeV}\\$$

Consider a balloon filled with helium gas at room temperature and atmospheric pressure. Calculate (a) the average de Broglie wavelength of the helium atoms and (b) the average distance between atoms under these conditions. The average kinetic energy of an atom is equal to $$(3 / 2) k T,$$ where $$k$$ is the Boltzmann constant. (c) Can the atoms be treated as particles under these conditions? Explain.

1711296_1777821_ans_572abd80e5c041c0826e856da0f10b76.png

A $$3.0 \mathrm{MeV}$$ proton is incident on a potential energy barrier of thickness $$10 \mathrm{fm}$$ and height $$10 \mathrm{MeV}$$. What are (a) the transmission coefficient $$T,(\mathrm{b})$$ the kinetic energy $$K_{t}$$ the proton will have on the other side of the barrier if it tunnels through the barrier, and(c) the kinetic energy $$K_{r}$$ it will have if it reflects from the barrier? A $$3.0 \mathrm{MeV}$$ deuteron (the same charge but twice the mass as a proton is incident on the same barrier. What are (d) $$T$$(e) $$K_{t},$$ and(f) $$K_{r} ?$$

(a) The average de Broglie wavelength is

$$\begin{aligned}\lambda_{\mathrm{avg}} &=\dfrac{h}{p_{\mathrm{avg}}}=\dfrac{h}{\sqrt{2 m K_{\mathrm{avg}}}}=\dfrac{h}{\sqrt{2 m(3 k T / 2)}}=\dfrac{h c}{\sqrt{2\left(m c^{2}\right) k T}} \\&=\dfrac{1240 \mathrm{eV} \cdot \mathrm{nm}}{\sqrt{3(4)(938 \mathrm{MeV})\left(8.62 \times 10^{-5} \mathrm{eV} / \mathrm{K}\right)(300 \mathrm{K})}} \\&=7.3 \times 10^{-11} \mathrm{m}=73 \mathrm{pm} .\end{aligned}\\$$

(b) The average separation is

$$d_{\mathrm{avg}}=\dfrac{1}{\sqrt[3]{n}}=\dfrac{1}{\sqrt[3]{p / k T}}=\sqrt[3]{\dfrac{\left(1.38 \times 10^{-23} \mathrm{J} / \mathrm{K}\right)(300 \mathrm{K})}{1.01 \times 10^{5} \mathrm{Pa}}}=3.4 \mathrm{nm}\\$$

Neutrons in thermal equilibrium with matter have an average kinetic energy of $$(3 / 2) k T,$$ where $$k$$ is the Boltzmann constant and$$T,$$ which may be taken to be $$300 \mathrm{K},$$ is the temperature of the environment of the neutrons. (a) What is the average kinetic energy of such a neutron?(b) What is the corresponding de Broglie wavelength?

1711262_1777815_ans_67d8eb3e591a4e2a9a3bf0671356d72d.png

A spectral emission line is an electromagnetic radiation that is emitted in a wavelength range narrow enough to be taken as a single wavelength. One such emission line that is important in astronomy has a wavelength of 21 cm. What is the photon energy in the electromagnetic wave at that wavelength?

(a) Since

$$E_{\mathrm{ph}}=h / \lambda=1240 \mathrm{eV} \cdot \mathrm{nm} / 680 \mathrm{nm}=1.82 \mathrm{eV}<\Phi=2.28 \mathrm{eV}\\$$

there is no photoelectric emission.

(b) The cutoff wavelength is the longest wavelength of photons that will cause photoelectric emission. In sodium, this is given by

$$E_{\mathrm{ph}}=h c / \lambda_{\max }=\Phi\\$$

$$\lambda_{\max }=h c / \Phi=(1240 \mathrm{eV} \cdot \mathrm{nm}) / 2.28 \mathrm{eV}=544 \mathrm{nm}\\$$

(a) The smallest amount of energy needed to eject an electron from metallic sodium is $$2.28 \mathrm{eV}$$. Does sodium show a photoelectric effect for red light, with $$\lambda=680 \mathrm{nm} ?$$ (That is, does the light cause electron emission?) (b) What is the cutoff wavelength for photoelectric emission from sodium? (c) To what color does that wavelength correspond?

1711463_1777845_ans_67ef3e227c5544998739debaffb072af.png

Show that $$\Delta E / E$$, the fractional loss of energy of a photon during a collision with a particle of mass $$m$$, is given by
$$\dfrac{\Delta E}{E}=\dfrac{h f^{\prime}}{m c^{2}}(1-\cos \phi)\\$$
where $$E$$ is the energy of the incident photon, $$f^{\prime}$$ is the frequency of the scattered photon, and $$\phi$$ is defined as in Fig. $$38-5$$

With no loss of generality, we assume the electron is initially at rest (which simply means we are analyzing the collision from its initial rest frame). If the photon gave all its momentum and energy to the (free) electron, then the momentum and the kinetic energy of the electron would become

$$p=\dfrac{h f}{c}, \quad K=h f\\$$

respectively. Plugging these expressions into Eq. (with $$\mathrm{m}$$ referring to the mass of the electron) leads to

$$\begin{array}{l}(p c)^{2}=K^{2}+2 K m c^{2} \\(h f)^{2}=(h f)^{2}+2 h f m c^{2}\end{array}\\$$

which is clearly impossible, since the last term $$\left(2 h f m c^{2}\right)$$ is not zero. We have shown that considering total momentum and energy absorption of a photon by a free electron leads to an inconsistency in the mathematics, and thus cannot be expected to happen in nature.

$$(a)$$ Show that $$ Equation $$ $$N(E)=\frac{8\sqrt{2}\pi m^{3/2}}{h^3}E^{1/2}$$ can be written as $$N(E) = CE^{1/2}$$ $$(B)$$ Evaluate $$C$$ in terms of meters and electron-volts. $$(c)$$ Calculate $$ N(E)$$ for $$E = 5.00 eV.$$

$$(a)$$ Equation
$$N(E)=\frac{8\sqrt{2}\pi m^{3/2}}{h^3}E^{1/2}$$
for the density of states associated with the conduction electrons of a metal. This can be written
$$N/(E)=CE^{1/2}$$
where
$$C=\frac{8\sqrt{2}\pi m^{3/2}}{h^3}$$$$=\frac{8\sqrt{2}\pi (9.109\times 10^{-31}kg)^{3/2}}{(6.626\times 10^{-34}J.s)^3}=1.062\times 10^{56}kg^{3/2}/J^3.s^3$$
$$(b)$$Now, $$1J = 1kg.m^2/s^2$$ (think of the equation for kinetic energy $$K=\frac{1}{2}mv^{2}$$), so $$1 kg = 1 J.s^2.m^{-2}.$$ Thus, the units of $$C$$ can be written as
$$(J.s^2)^{3/2},(m^{-2})^{3/2}.J^{-3}.s^{-3}=J^{-3/2}.m^{-3}$$
This means
$$C=(1.062 \times 10^{56}J^{-3/2}.m^{-3})(1.602\times 10^{-19}J/eV)^{3/2}=6.81\times 10^{27}m^{-3}.eV^{-3/2}$$
$$(c)$$ If $$E=5.00 eV$$,then
$$N(E)=(6.81\times10^{27}m^{-3}.eV^{-3/2})(5.00eV)^{1/2}= 1.52\times10^{28}eV^{-1}.m^{-3}.$$

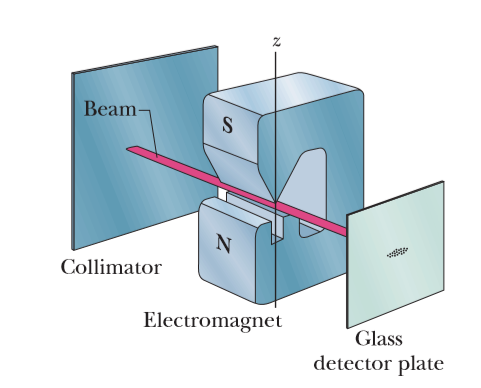
What is the acceleration of a silver atom as it passes through the deflecting magnet in the SternGerlach experiment of the above figure if the magnetic field gradient is $$1.4 \ T/mm$$?

The force on the silver atom is given by
$$F_z = \frac {-dU}{dz} = \frac {d}{dz} {(\times -\mu_z B)} ={\mu_z } \frac {dB}{dz}$$
where $$\mu_z$$ is the z component of the magnetic dipole moment of the silver atom, and B is
the magnetic field. The acceleration is
$$a= \frac{F_z}{M} = \frac{\mu_z (dB/dz)}{M}$$.
where M is the mass of a silver atom. Using the data given in Sample Problem —“Beam
separation in a Stern-Gerlach experiment,” we obtain
$$ a =\frac{ (9.27\times 10^{-24}J/T )(1.4\times 10^3 T/m)}{1.8 \times 10^{-25}kg} = 7.2 \times 10^4 m/s^2 $$.

A $$20 \ keV$$ electron is brought to rest by colliding twice with target nuclei (Assume the nuclei remain stationary.) The wavelength associated with the photon emitted in the second collision is $$130 \ pm$$ greater than that associated with the photon emitted in the first collision. (a) What is the kinetic energy of the electron after the first collision? What are (b) the wavelength $$\lambda_1$$ and (c) the energy $$E_1$$ associated with the first photon? What are (d) $$\lambda_2$$ and (e) $$E_2$$ associated with the second photon?

1754101_1778348_ans_2cb1fdf6ce1a4c05badc9b92044333fc.jpg

A certain heliumneon laser emits red light in a narrow band of wavelengths centered at $$632.8 nm$$ and with a wavelength width (such as on the scale above) of $$0.0100 nm$$. What is the corresponding frequency width for the emission?

Since $$\Delta \lambda <<\lambda $$, we find $$\Delta f$$ is equal to

$$\left | \Delta \left ( \dfrac{c}{\lambda} \right ) \right |\approx \dfrac{c\Delta \lambda}{\lambda ^{2}}=\dfrac{\left ( 3.0*10^{8}m/s \right )\left ( 0.0100*10^{-9}m \right )}{\left ( 632.8*10^{-9}m \right )^{2}}=7.49*10^{9}Hz$$.

A photon with momentum $$ p=1.02 \mathrm{MeV} / \mathrm{c}, $$ where $$ c $$ is the velocity of light, is scattered by a stationary free electron, changing in the process its momentum to the value $$ p^{\prime}=0.255 \mathrm{MeV} / \mathrm{c} $$. At what angle is the photon scattered?

1927567_1854967_ans_08dbea4384d34bd6b34ebb6caaafd58c.PNG

Zinc is a bivalent metal. Calculate $$(a)$$ the number density of conduction electrons, $$(b)$$ the Fermi energy, $$(c)$$ the Fermi speed, and $$(d)$$ the de Broglie wavelength corresponding to this electron speed. See Appendix $$F$$ for the needed data on zinc. $$m_ec^2=511\times10^3eV$$

$$(a)$$ The conduction electrons per cubic meter in zinc:
$$n=\frac{2(7.133g/cm^3)}{(65.37g/mol)/(6.02\times 10^{23}mol)}=1.31\times 10^{23}cm^{-3}=1.31\times 10^{29}m^{-3}$$
$$(b)$$ $$E_F=\frac{0.121h^2}{m_e}n^{2/3}=\frac{0.121(6.63\times 10^{-34}J.s)^2(1.31\times 10^{29}m^{-3})^{2/3}}{(9.11\times 10^{-31}kg)(1.60\times 10^{-19}J/eV)}=9.43eV$$
$$(c)$$ Equating the Fermi energy to$$\frac{1}{2}m_ev_{F}^{2}$$we find
$$v_F=\sqrt{\frac{2E_Fc^2}{m_ec^2}}=\sqrt{\frac{2(9.43eV)(2.998\times 10^8m/s)^2}{511\times 10^3eV}}=1.82\times 10^{6}m/s$$
$$(d)$$ The de Broglie wavelength is
$$\lambda =\frac{h}{m_ev_F}=\frac{6.63\times 10^{-34}J.s}{(9.11\times 10^{-31}kg)(1.82\times 10^6 m/s)}=0.40nm$$

What is the wavelength associated with a photon that will induce a transition of an electron spin from parallel to antiparallel orientation in a magnetic field of magnitude 0.200T? Assume that. $$ l = 0 $$

1758035_1778312_ans_50de750550294dbabf973764abab06af.jpg

Silver is a monovalent metal. Calculate $$(a)$$ thenumber density of conduction electrons, $$(b)$$ the Fermi energy, $$(c)$$ theFermi speed, and $$(d)$$ the de Broglie wavelength corresponding to thiselectron speed. See Appendix $$F$$ for the needed data on silver.

$$(a)$$ According to Appendix $$F$$ the molar mass of silver is $$107.870 g/mol$$ and the density
is $$10.49 g/cm^3$$ . The mass of a silver atom is
$$\frac{107.870 \times 10^{-3}kg/mol}{6.022\times 10^{23}mol^{-1}}=1.791\times 10^{-25}kg$$
We note that silver is monovalent, so there is one valence electron per atom. As,
$$n=\frac{\rho }{M}=\frac{10.49\times 10^{-3}kg/m^{3}}{1.791\times 10^{-25}kg}=5.86\times 10^{28}m^{-3}.$$
$$(b)$$ The Fermi energy is
$$E_F=\frac{0.121h^2}{m}n^{2/3}=\frac{(0.121)(6.626\times 10^{-34}J.s)^2}{9.109\times 10^{-31}kg}=(5.86\times 10^{28}m^{-3})^{2/3}$$
$$=8.80\times10^{-19}J=5.49eV$$
$$(c)$$ Since $$E_F = \frac{1}{2}mv_{F}^{2},$$
$$v_{F}=\sqrt{\frac{2E_F}{m}}=\sqrt{\frac{2(8.80\times 10^{-19}J)}{9.109\times 10^{-31}kg}}=1.39\times 10^6 m/s$$
$$(d)$$ The de Broglie wavelength is
$$\lambda =\frac{h}{mv_F}=\frac{6.626\times 10^{-34}J.s}{(9.109\times 10^{-31}kg)(1.39\times 10^{6}m/s)}=5.22\times 10^{-10}m$$

A photon is scattered at an angle $$ \theta=120^{\circ} $$ by a stationary free electron. As a result, the electron acquires a kinetic energy $$ T=0.45 \mathrm{MeV} . $$ Find the energy that the photon had prior to scattering.

1927571_1854968_ans_39e8c23182b64c9d8c6a8273958dc0b6.png

The wavelength of light from the spectral emission line of sodium is $$589 nm$$. Find the kinetic energy at which (a) electron and (b) neutron would have the same De-Broglie wavelength. Given that mass of neutron $$= 1.66 \times 10^{-27} kg$$.

Here, $$\lambda = 589 nm = 589 \times 10^{-9} m$$
The de Broglie wavelength of a particle having energy E is given by
$$\lambda = \dfrac{h}{\sqrt{2 m E}}$$

or $$E = \dfrac{h^2}{2 m\lambda^2}$$

a. For electron : Here, $$\lambda = 589 nm = 589 \times 10^{-9} m$$ and $$m = 9.1 \times 10^{-27} kg$$

$$\therefore E = \dfrac{h^2}{2 m \lambda^2} = \dfrac{(6.62 \times 10^{-34})^2}{2 \times 9.1 \times 10^{-31} \times (589 \times 10^{-9})^2}$$

$$= 6.94 \times 10^{-25} J$$

b. For neutron : Here, $$\lambda = 589 nm = 589 \times 10^{-9} m$$ and $$m = 1.66 \times 10^{-27} kg$$

$$\therefore E = \dfrac{h^2}{2 m \lambda^2} = \dfrac{(6.62 \times 10^{-34})^2}{2 \times 1.66 \times 10^{-27} \times (589 \times 10^{-9} )^2}$$

$$= 3.81 \times 10^{-28} J$$

A plank of mass 'm' is lying on a rough surface having coefficient of friction $$'\mu'$$ in situation as shown in the figure. Find the acceleration of the plank assuming that it slips and surface of body exposed to radiation is black body.

$$E = $$ Energy received by surface per second is $$IA \cos \theta = I ab \, \cos \theta$$
Number of photons received by the surface per second,
$$N = \dfrac{E}{hc/\lambda} = \dfrac{I ab \cos \theta \lambda}{hc}$$
$$\Delta P_{one \, photon} = \dfrac{h}{\lambda}$$
$$\Rightarrow F_{radian} = \Delta P_{one \, photon} . N = \dfrac{I ab \cos \theta}{c}$$
Let us draw the FBD of the plank
$$F \sin \theta - \mu N = m \alpha$$ ___(i)
$$N = mg + F \cos \theta$$ ___(ii)
From Eqs. (i) and (ii), we get
$$\alpha = \dfrac{F \sin \theta - \mu (mg + F \cos \theta}{m}$$
2042650_1966857_ans_7a40cd47503d4e4fbb2fcb8e36b3098b.png

2042650_1966857_ans_7a40cd47503d4e4fbb2fcb8e36b3098b.png

Determine the De-Broglie wavelength of a proton, whose kinetic energy is equal to the rest mass energy of an electrons. Given that the mass of the electron is $$9.11 \times 10^{-31} kg$$ and mass of proton is $$1837$$ times as that of the electron.

Here, mass of electron, $$m_0 = 9.1 \times 10^{-31} kg$$
mass of proton, $$m = 1837 \times 9.1 \times 10^{-31} = 1.67 \times 10^{-27} kg$$
Let $$v$$ be the velocity of the proton. Then,
$$\dfrac{1}{2} mv^2 = m_0 c^2$$

or $$m^2 v^2 = 2mm_0c^2$$

or $$mv = \sqrt{2 mm_0 c}$$

$$= \sqrt{2 \times 1.67 \times 10^{-27} \times 9.1 \times 10^{-31}} \times 3 \times 10^8$$

$$= 1.654 \times 10^{-20} kg ms^{-1}$$

Therefore, de Broglie wavelength of the proton,

$$\lambda = \dfrac{h}{mv} = \dfrac{6.62 \times 10^{-34}}{1.654 \times 10^{-20}} = 4 \times 10^{-14} m$$

In a photocell the plates P and Q have a separation of $$5 cm$$ which are connected through a galvanometer without any cell. Bichromatic light of wavelengths $$4000 \mathring{A}$$ and $$6000 \mathring{A}$$ are incident on plate Q whose work function is $$2.39 eV$$, If a uniform magnetic field B exists parallel to the plates, find the minimum value for B for which the galvanometer shows zero deflection.

Energy of photons corresponding to light of wavelength $$\lambda_1 = 4000 \mathring{A}$$ is $$E_1 = \dfrac{12375}{4000} = 3.1 eV$$

And that corresponding to $$\lambda_2 = 6000 \mathring{A}$$ is,
$$E_2 = \dfrac{12375}{6000} = 2.06 eV$$

As, $$E_2 < W $$ and $$E_1 > W$$

Photoelectric emission is possible with $$\lambda_1$$ only.
Photoelectrons experience magnetic force and move along a circular path. The galvanometer will indicate zero deflection if the photoelectrons just complete semi-circular path before reaching the plate.
Thus, $$d = r = 5 cm$$

Therefore, $$r = 5 cm = 0.05 m$$

Further, $$r = \dfrac{mv}{qB} = \dfrac{\sqrt{2Km}}{qB}$$

$$B_{min} = \dfrac{\sqrt{2Km}}{rq}$$

$$K = E_1 - W = (3.1 - 2.39) = 0.71 eV$$

Substituting the values, we have,

$$B_{min} = \dfrac{\sqrt{2 \times 0.71 \times 1.6 \times 10^{-19} \times 9.109 \times 10^{-31}}}{0.05 \times 1.6 \times 10^{-19}} = 5.68 \times 10^{-5} T$$

Electron beams are accelerated to potentials $$40 kV$$ and $$150 V$$. Estimate the wavelengths of the electrons in the two beams. Given : $$h = 6.6 \times 10^{-34} Js, m = 9.1 \times 10^{-31} kg$$ and $$1eV = 1.6 \times 10^{-19} J$$.

We have $$\lambda = \dfrac{h}{mv} = \dfrac{h}{\sqrt{2meV}}$$
Substituting the given values, we get,

$$\lambda = \dfrac{6.6 \times 10^{-34}}{\sqrt{2 \times 9.1 \times 10^{-31} \times 1.6 \times 10^{-19} \times 40 \times 10^3}}$$

$$\lambda = 0.613 \times 10^{-11} m = 0.0613 \mathring{A}$$
This is for $$40 kV$$ beam

$$\lambda = \dfrac{6.6 \times 10^{-34}}{\sqrt{2 \times 9.1 \times 10^{-31} \times 1.6 \times 10^{-19} \times 150}}$$

$$\lambda = 10^{-10} m = 1 \mathring{A}$$

This is for $$150 V$$ beam

Sun gives light at the rate of $$1400 $$ W of area perpendicular to the direction of light. Assume wavelength (sunlight) $$= 6000 \mathring{A}$$. Calculate the
(a) Number of photons per second arriving at $$1$$ squared metres at earth.
(b) Number of photons emitted from the sun per second assuming that the average radius of earth's orbit is $$1.49 m$$.

$$I = 1400 Wm^{-2} ; \lambda = 6000 \mathring{A}$$

a. Energy of the photon, $$E = hv = \dfrac{hc}{\lambda} (c = 3 \times 10^8 ms^{-1})$$
Let $$n$$ be the number of photons received per second per unit area.

$$\therefore n = \dfrac{IA}{E} = \dfrac{(1400 \times 1) \times (6000 \times 10^{-10})}{6.63 \times 10^{-34} \times 3 \times 10^8}$$
$$= 4.22 \times 10^{21}$$

b. Total energy emitted per second = power (W)
Number of photons emitted from the sun per second,
$$n = \dfrac{power \, of \, sun (W)}{energy \, of \, a \, photons} = \dfrac{I \times (4 \pi R^2) \times (6000 \times 10^{-10})}{6.63 \times 10^{-34} \times 3 \times 10^8}$$
(R: average radius of Earth's orbit)
$$= 1.178 \times 10^{45}$$

Dual Nature Of Radiation And Matter - Class 12 Medical Physics - Extra Questions

An electron in an atom absorbs radiation of wavelength 392.n.m and later on it emits energy in the from of photons of two different wavelengths. If one of the wavelength is 712 n.m. Calculate the other.

The energy of the photons causing the photoelectrons emission

How many photons are emitted per second by $$a\ 5\ mW$$ laser source operating at $$632.8\ nm$$?

If the kinetic energy of the particle is increased to $$16$$ times previous the percentage change in the deBrogille wavelength of the particle is

The electron with The electron with de Broglie wavelength $$\lambda $$ is bombarded on a metal target. Found that photons are emitted through de Broglie wavelength.

The stopping potential in an experiment of photon is 2eV. What is the maximum kinetic energy of photoelectrons emitted ?

Electrons with de Broglie wavelength $$\lambda$$ are bombarded on a metal target. It is found that photons are emitted from the metal target. The minimum wavelength of emitted photons is [m = mass of eletron]

A nucleus $$X$$ is in the higher energy state where its energy is $$450 \mathrm { keV }$$ . If it comes to ground state (assuming ground state energy to be zero), what is the wavelength of the photon emitted?

Visible light has wavelengths in the range of $$400\, nm$$ to $$780\, nm$$. Calculate the range of energy of the photons of visible light.

Two neutral particles are kept 1 m apart. Suppose by some mechanism some charge is transferred from one particle to the other and the electric potential energy lost is completely converted into a photon. Calculate the longest and the next smaller wavelength of the photon possible.

A 100 W light bulb is placed at the center of a spherical chamber of radius 20 cm. Assume that 60% of the energy supplied to the bulb is converted into light and that the surface of the chamber is perfectly absorbing. Find the pressure exerted by the light on the surface of the chamber.

Find the maximum magnitude of the linear momentum of a photoelectron emitted when light of wavelength 400 nm falls on a metal having work function 2.5eV.

Calculate de Broglie wavelength for an average helium atom in a furnace at $$400\,K$$. Given the mass of helium $$= 4.002\,amu$$.

At what rate does the Sun emit photons? For simplicity, assume that the Sun's entire emission at the rate of $$3.9 \times 10^{26} \mathrm{W}$$ is at the single wavelength of $$550 \mathrm{nm}$$

Light of wavelength $$2.40 \mathrm{pm}$$ is directed onto a target containing free electrons. (a) Find the wavelength of light scattered at $$30.0^{\circ}$$ from the incident direction. (b) Do the same for a scattering angle of $$120^{\circ}$$

What percentage increase in wavelength leads to a $$75 \%$$ loss of photon energy in a photon-free electron collision?

What amount of energy should be added to an electron to reduce its de Broglie wavelength from 100 to 50 pm?

The radius of an $$\alpha$$-particle moving in a circle in a constant magnetic field is half of the radius of an electron moving in circular path in the same field. The de Broglie wavelength of $$\alpha$$-particle is $$x$$ times that of the electrons. Find $$x$$ (an integer).

An $$\alpha$$-particle and a proton are accelerated from rest by a potential difference of $$100\ V$$. After this, their de Broglie wavelengths are $$\lambda_{\alpha}$$ and $$\lambda_p$$, respectively. The ratio $$\lambda_p/\lambda_{\alpha}$$, to the nearest integer, is:

Calculate the (a) smaller and (b) larger value of the semiclassical angle between the electron spin angular momentum vector and the magnetic field in a SternGerlach experiment. Bear inmind that the orbital angular momentum of the valence electron in the silver atom is zero.

An electron and photon have same energy 100 eV. Which has greater associated wavelength?

If an electron has a wavelength does it also have a colour?

What is the momentum of a photon if the wavelength of X-rays is 1 angstrom?

A parallel beam of monochromatic light of wavelength $$500\ nm$$ is incident normally on a perfectly absorbing surface. The power through any cross-section of the beam is $$10 W$$. The number of photons absorbed per second by the surface is $$k\times 10^{19}$$. what is a value of k?

De Broglie wavelength for an average helium atom in a furnace at 400 K is $$k\times 10^{-10} m$$. Find the value of k. Here, Given the mass of helium $$=4.002 amu$$

If the wavelength of electromagnetic radiation is doubled, what happens to the energy of photon?

Give an example where energy is converted into matter

Why we do not observe de Broglie wave in daily life?

An insulated metal plate yields photoelectrons when first illumminated by ultraviolet light but then after some time photoelectron emission stops. Explain

Explain the concept of de Broglie waves (matter wave).

(a) An X-ray tube produces a continuous spectrum of radiation with its short wavelength end at 0.45 . What is the maximum energy of a photon in the radiation?(b) From your answer to (a), guess what order of accelerating voltage(for electrons) is required in such a tube?

Fill in the blanks with suitable answerThe energy of a photon is given by the formula _____________

You might have seen mercury street lamps. The light blue glow given by these lamps has a wavelength of = 436nm. What is its frequency?

State how de-Broglie wavelength $$(\lambda )$$ of moving particles varies with their linear momentum (p).

Derive an expression for de Broglie wavelength of matter waves.

A ball of mass 0.12 kg is moving with a speed 20 m/s. Calculate the de Broglie wavelength. (Planck constant $$h = 6.62 \times 10^{-34} J.s$$)

Show with the help of a labelled graph how their wavelength $$(\lambda)$$ varies with their linear momentum (p).

Find the de Broglie wavelength of electrons moving with a speed of $$7\times 10^6ms^{-1}$$.

Calculate the momentum of a photo of energy $$6\times 10^{-19}$$J.

Assume that a 100 W sodium vapour lamp rediates its energy uniformly in all directions in the form of photons with an associated wavelength of 589 nm.At what rate are photons emitted from the lamp?

S is isotropic monochromatic source of constant power P. r is very large and v is frequency of radiation .The number of photons crossing per unit time the given surface is in $$n=\dfrac{P\Delta S cos \theta}{k \pi vr^2h}$$ .Find k if $$\Delta S$$ is the area of small section.

Assume that a 100 W sodium vapour lamp rediates its energy uniformly in all directions in the form of photons with an associated wavelength of 589 nm.At what distance from the lamp will the average flux of photons be 1.00 photons /$$(cm^2s)$$ ?

An electron, an alpha $$(\alpha)$$ particle and a proton have same kinetic energies. Which one of these particles has largest de Broglie wavelength?

An $$\alpha$$ particle moves in circular path of radius $$0.83cm$$. In the presence of a magnetic field of $$0.25Wb/{m}^{2}$$. Find the De Broglie wavelength associated with the particle

Find the energy of photon in each of the following:A. Microwaves of wavelength $$1.5\ cm$$B. Red light of wavelength $$660\ nm$$C. Radiowaves of frequency $$96\ MHz$$D. $$X-$$rays of wavelength $$0.17\ nm$$

When light of frequency $$2.2\times 10^{15}Hz$$ is incident on a metal surface, photoelectrons emitted can be stopped by a retarding potential of $$6.6\ V$$. For light of frequency $$4.6\times 10^{15}Hz$$, the reverse potential is $$16.5\ V$$. Find $$h$$

In an experiment of photoelectric effect, the slope of the cut-off voltage versus frequency of incident light is found to be $$4.2\times 10^{-15} V s$$. Calculate the value of Plank's constant.

What kinetic energy of a neuron will be associated by the de-broglie wavelength $$1.32 \times 10^{-10}m$$?

An atom absorbs a photon of wavelength $$500 nm $$ emits another photon of wavelength $$700nm$$ find the net energy absorbed by the atom in the process

What is photoelectric effect? State and explain its characteristics.

Find the frequency of 1 MeV photon. Given wavelength of a 1 keV photon is $$1.24 \times {10^{ - 9}}m$$Hint: $$E = h\nu $$

The energy of a photo is equal to the kinetic energy of proton. Let $$ \lambda_1 $$ be the de-Broglie wavelength of the photon and $$ \lambda_2 $$ be the wavelength of the radiation and the de-Broglie wavelength of a photon of that radiation?

A $$1\ MeV$$ positron and a $$1\ MeV$$ electron meet each moving in opposite directions. They annihilate each other by emitting two photons. If the rest mass energy of an electron is $$0.51\ MeV$$, the wavelength of each photon is ?

What is the de-Broglie wavelength of an electron beam accelerated through a potential difference of $$25 \,V$$?

Find the de-Broglie wave length related to an election accelerated by $$10^4$$ volt

Find the typical de-Broglie wavelength of an electron in a metal at $${27}^{o}C$$ and compare it with the mean separation between two electrons in a metal which is given to be about $$2\times{10}^{-10}m$$

The radius of two bohr radius of a hydrogen like atom are $$r_1$$ and $$r_2$$. Find the wave length of photon when electron jumps from $$r_2$$ to $$r_1$$.

An electron and a proton have the same kinetic energy. Which one of the two has the larger de Broglie wavelength and why?

What will be the energy of each photon in monochromatic light of frequency $$5\times10^{14}Hz$$?

Find out the ratio between de-Broglie wavelength of proton and a-particle of equal energy.

Calculate the de Broglie wavelengths of an electron, proton, and uranium atom, all having the same kinetic energy $$100\ eV $$.

At room temperature $$ (T = 300\,K)$$ neutron are in thermal equilibrium. Calculate its de-Broglie wavelength.

According to de-Broglie hypothesis, write formula of wavelength of matter waves.

Derive the expression for a de Broglie wavelength $$ \lambda $$ of a relativistic particle moving with kinetic energy T. At what values of T does the error in determining $$ \lambda $$ using the non-relativistic formula not exceed $$1\% $$ for an electron and a proton ?

Give reasons for the followingLaser is used in cutting metals.

State the factors on which the following dependi) Kinetic energy of photo electrons.ii) Number of photo electrons.

Distinguish between ordinary light and laser light.

Give reasons for the followingOrdinary key chain laser light should not be directly viewed.

The de Broglie wavelength of an electron moving with a velocity of $$1.5\times 10^8 ms^{-1}$$ is equal to that of a photon. Find the ratio of the kinetic energy of the photon to that of the electron.

A monochromatic source of light operating at 200 W emits $$4\times 10^{20}$$ photons per second. Find the wavelength of the light $$(in \times 10^{-7}m)$$

The ratio of energy of photon of $$\lambda$$ = 2000 A$$^{o}$$ to that of $$\lambda$$ = 4000 A$$^{o}$$

The ratio of the energy of a photon of 2000 nm wavelength radiation to that of 4000 nm radiation is :

Find the typical de Broglie wavelength associated with a He atom in helium gas at room temperature ($$27 °C$$) and 1 atm pressure; and compare it with the mean separation between two atoms under these conditions.

(a) Why photoelectric effect cannot be explained on the basis of wave nature of light? Give reasons.(b) Write the basic features of photon picture of electromagnetic radiation on which Einstein's photoelectric equation is based.

Given the ground state energy $$E_0 = - 13.6 \,eV$$ and Bohr radius $$a_0 = 0.53 \, \overset{o}{A}$$ . Find out how the de Broglie wavelength associated with the electron orbiting in the ground state would change when it jumps into the first excited state.

Yellow colours seen in fireworks are due to the emission of light with wavelength around 588 nm when sodium salts are burned. Calculate the frequency of yellow light of wave length 588 nm.

What is photoelectric effect? Give Einsteins explanation of the phenomenon.

List any three applications of laser.

Draw a neat diagram of Helium -Neon gas laser tube.

Calculate the (a) smaller and (b) larger value of the semiclassical angle between the electron spin angular momentum vector and the magnetic field in a SternGerlach experiment. Bear in
mind that the orbital angular momentum of the valence electron in the silver atom is zero.

A parallel beam of monochromatic light of wavelength $$500\ nm$$ is incident normally on a perfectly absorbing surface. The power through any cross-section of the beam is $$10 W$$.
The number of photons absorbed per second by the surface is $$k\times 10^{19}$$. what is a value of k?

(a) An X-ray tube produces a continuous spectrum of radiation with its short wavelength end at 0.45 . What is the maximum energy of a photon in the radiation?
(b) From your answer to (a), guess what order of accelerating voltage(for electrons) is required in such a tube?

Fill in the blanks with suitable answer
The energy of a photon is given by the formula _____________

Assume that a 100 W sodium vapour lamp rediates its energy uniformly in all directions in the form of photons with an associated wavelength of 589 nm.
At what rate are photons emitted from the lamp?

Assume that a 100 W sodium vapour lamp rediates its energy uniformly in all directions in the form of photons with an associated wavelength of 589 nm.
At what distance from the lamp will the average flux of photons be 1.00 photons /$$(cm^2s)$$ ?

Find the energy of photon in each of the following:
A. Microwaves of wavelength $$1.5\ cm$$
B. Red light of wavelength $$660\ nm$$
C. Radiowaves of frequency $$96\ MHz$$
D. $$X-$$rays of wavelength $$0.17\ nm$$

Find the frequency of 1 MeV photon. Given wavelength of a 1 keV photon is $$1.24 \times {10^{ - 9}}m$$

Hint: $$E = h\nu $$

Give reasons for the following
Laser is used in cutting metals.

State the factors on which the following depend
i) Kinetic energy of photo electrons.
ii) Number of photo electrons.

Give reasons for the following
Ordinary key chain laser light should not be directly viewed.

(a) Why photoelectric effect cannot be explained on the basis of wave nature of light? Give reasons.
(b) Write the basic features of photon picture of electromagnetic radiation on which Einstein's photoelectric equation is based.

Monochromatic light of frequency $$6 \times 10^{14}$$ Hz is produced by a laser. The power emitted is $$2 \times 10^{-3}$$ W
(i) What is the energy of the photon in the light beam?
(ii) How many photons per second, on an average are emitted by the source ?