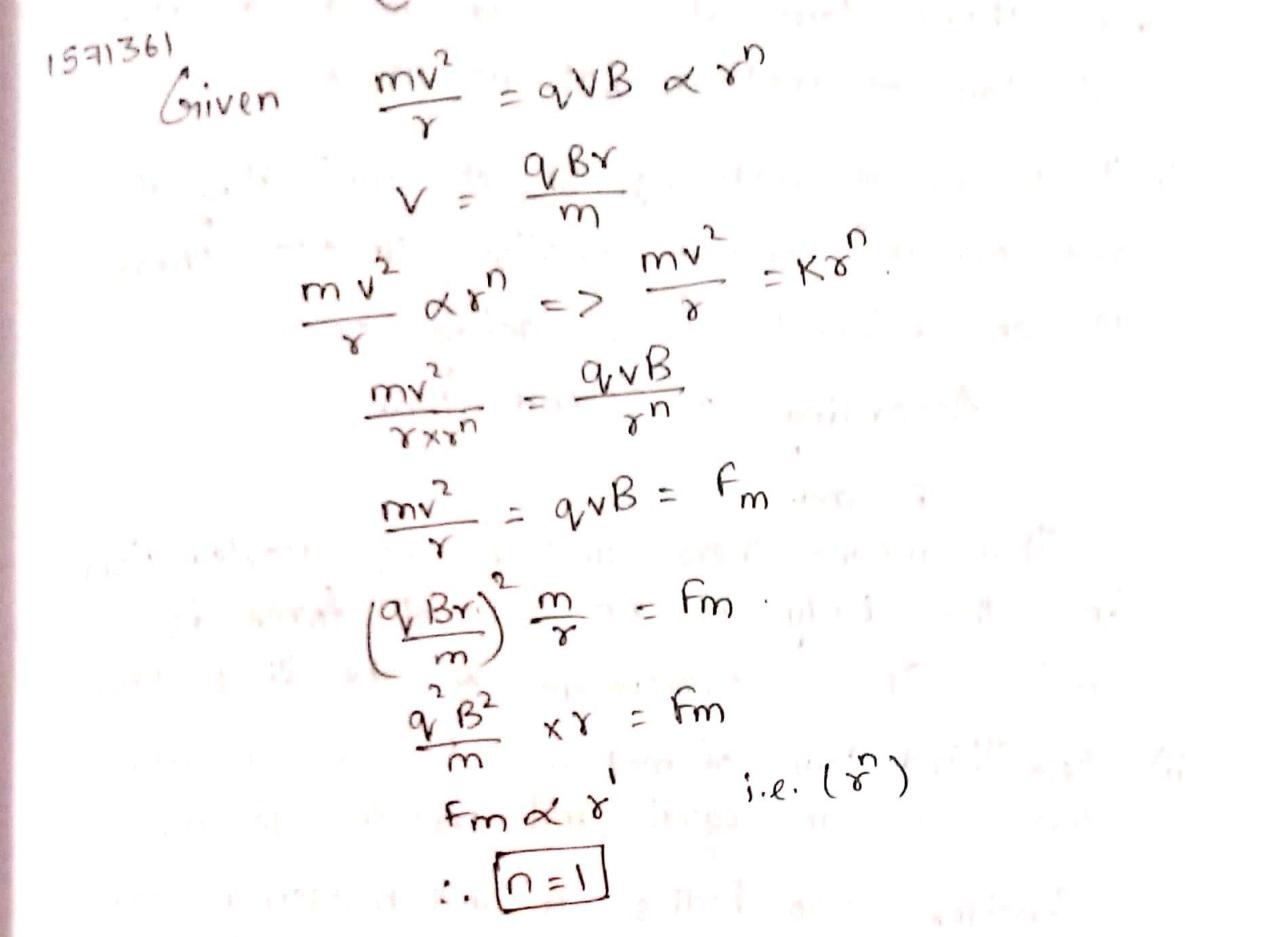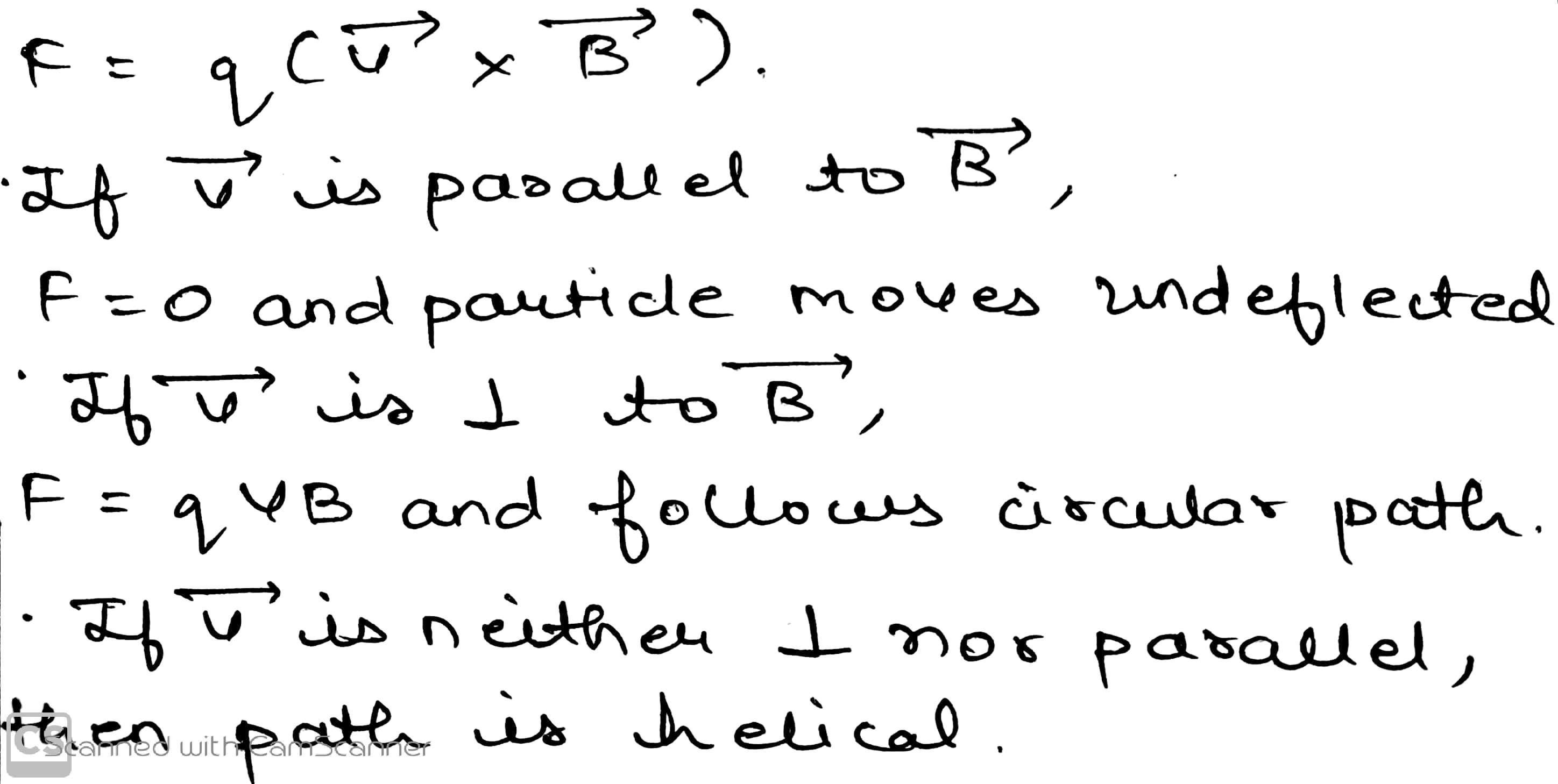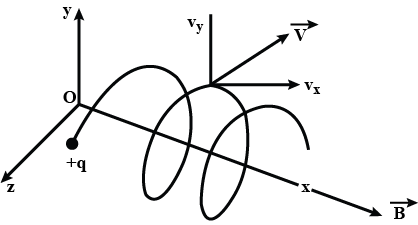Moving Charges And Magnetism - Class 12 Medical Physics - Extra Questions
In a nuclear experiment a proton with kinetic energy $$1.0 MeV$$ moves in a circular path in a uniform magnetic field. What energy must
(a) an alpha particle ($$q=+2e, m = 4.0 u$$) and
(b) a deuteron ($$q=+e, m = 2.0 u$$) have if they are to circulate in the same circular path?
The Biot-Savart Law(14)
In a long, straight, vertical lightning stroke, electrons move downward and positive ions move upward and constitute a current of magnitude $$20.0 \,kA$$. At a location $$50.0 \,m$$ east of the middle of the stroke, a free electron drifts through the air toward the west with a speed of $$300 \,m/s$$.
(a) Make a sketch showing the various vectors involved. Ignore the effect of the Earths magnetic field.
(b) Find the vector force the lightning stroke exerts on the electron.
(c) Find the radius of the electron's path.
(d) Is it a good approximation to model the electron as moving in a uniform field? Explain your answer.
(e) If it does not collide with any obstacles, how many revolutions will the electron complete during the $$60.0-\mu s$$ duration of the lightning stroke?
The Biot-Savart Law(19)
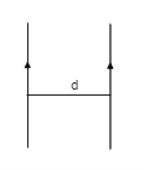
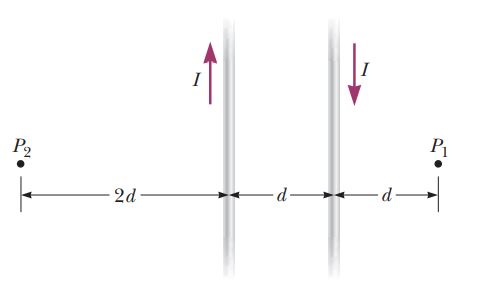
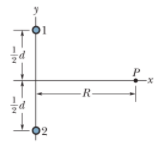
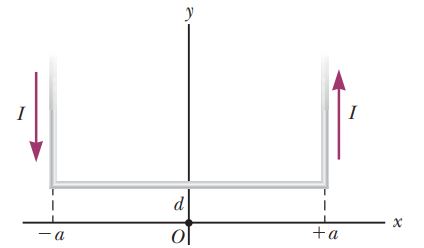
The two wires shown in Figure are separated by $$d = 10.0 \,cm$$ and carry currents of $$I = 5.00 \,A$$ in opposite directions. Find the magnitude and direction of the net magnetic field
(a) at a point midway between the wires;
(b) at point $$P_1, \,10.0 \,cm$$ to the right of the wire on the right; and
(c) at point $$P_2, \,2d = 20.0 \,cm$$ to the left of the wire on the left.
The Biot-Savart Law(20)
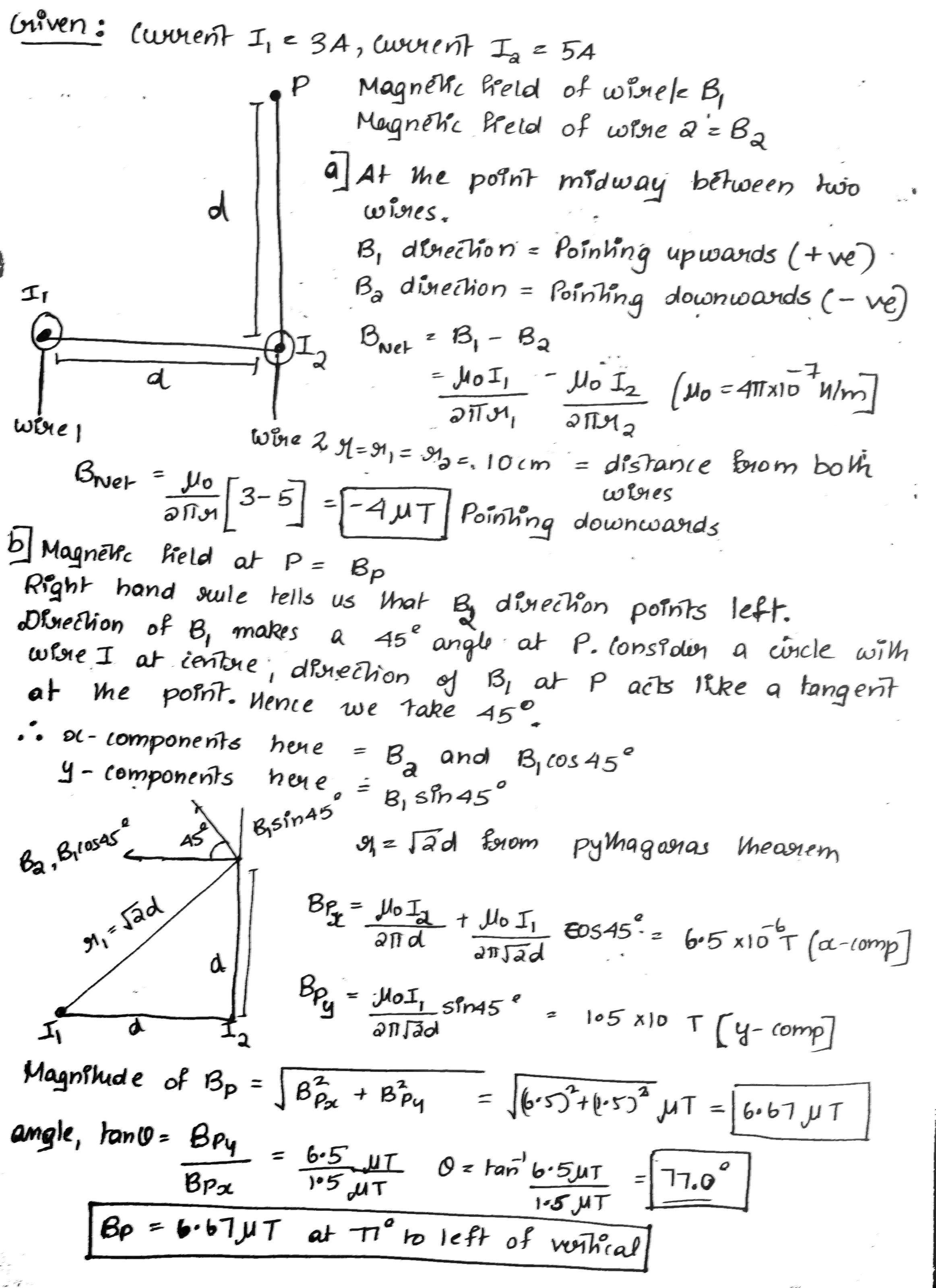
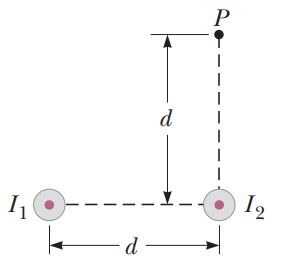
Two long, parallel wires carry currents of $$I_1 = 3.00 \,A$$ and $$I_2 = 5.00 \,A$$ in the directions indicated in Figure.
(a) Find the magnitude and direction of the magnetic field at a point midway between the wires.
(b) Find the magnitude and direction of the magnetic field at point $$P$$, located $$d = 20.0 \,cm$$ above the wire carrying the $$5.00-A$$ current.
The Biot-Savart Law(14)
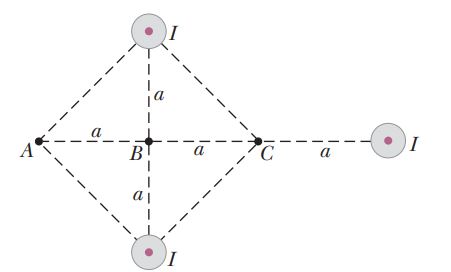
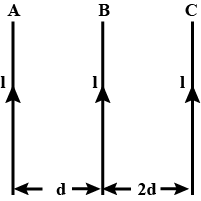
Three long, parallel conductors each carry a current of $$I = 2.00 A$$. Figure is an end view of the conductors, with each current coming out of the page. Taking $$a = 1.00 \,cm$$, determine the magnitude and direction of the magnetic field at
(a) point A,
(b) point B, and
(c) point C.
The Magnetic Force Between Two Parallel Conductors (27)
Two long, parallel wires are attracted to each other by a force per unit length of $$320 \mu \,N/m$$. One wire carries a current of $$20.0 \,A$$ to the right and is located along the line $$y = 0.500 \,m$$. The second wire lies along the x axis. Determine the value of $$y$$ for the line in the plane of the two wires along which the total magnetic field is zero.
The Biot-Savart Law(18)
A wire carrying a current $$I$$ is bent into the shape of an equilateral triangle of side $$L$$.
(a) Find the magnitude of the magnetic field at the center of the triangle.
(b) At a point halfway between the center and any vertex, is the field stronger or weaker than at the center?Give a qualitative argument for your answer.
Ampres Law(30)
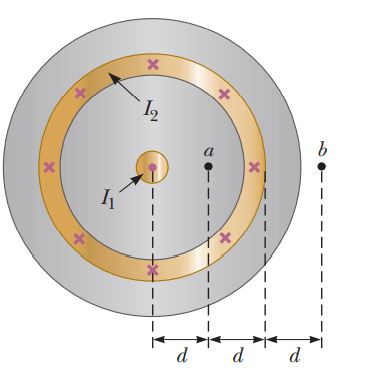
Figure is a cross-sectional view of a coaxial cable. The center conductor is surrounded by a rubber layer, an outer conductor, and another rubber layer. In a particular application, the current in the inner conductor is $$I_1 = 1.00 \,A$$ out of the page and the current in the outer conductor is $$I_2 = 3.00 \,A$$ into the page. Assuming the distance $$d = 1.00 \,mm$$, determine the magnitude and direction of the magnetic field at
(a) point a and
(b) point b.
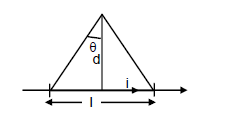
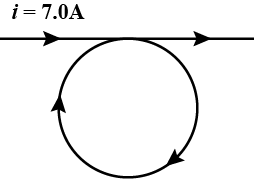
A conductor consists of a circular loop of radius $$R=10\ cm$$ and two straight, long sections as shown in figure.The wire lies in the plane of the paper and carries a current of $$i=7.00\ A$$. Determine the magnitude and direction of the magnetic field at the centre of the loop.
Are there components of the magnetic field that are not determined by the measurement of the force?Explain
An electron moves through a uniform magnetic field given by $$\vec{B}={B}_{x}\hat{i}+(3{B}_{x})\hat{j}$$.At a particular instant,the electron has the velocity $$\vec{v}=(2.0\hat{i}+4.0\hat{j})m/s$$ and the magnetic force acting on it is $$(6.4\times {10}^{-19}N)\hat{k}$$.Find $$x$$ such that $$x=-{B}_{x}$$.
Repeat your calculation for a proton having the same velocity.
Calculate the scalar product $$\vec{B}\cdot \vec{F}$$.What is the angle between $$\vec{B}$$ and $$\vec{F}$$ ?
Through what potential difference would the deuteron have to be accelerated to acquire this speed?
If $$F$$ is the force acting on the electron, find $$x$$ such that $$x=F\times {10}^{16}$$.
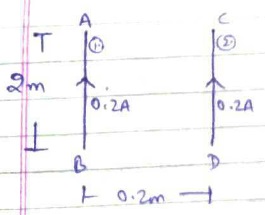
Two 2 m long parallel wires are placed in vacuum at a distance 0.2 m. If current 0.2 A flows in both the wires in the same direction, calculate the force acting per unit length between them.
& $${ B }_{ 2 }=\dfrac { { \mu }_{ 0 } }{ 2\pi } \times \dfrac { { I }_{ 2 } }{ R } $$
$$\Rightarrow { F }_{ 2 }=\dfrac { { \mu }_{ 0 } }{ 2\pi } \times \dfrac { { I }_{ 1 }{ I }_{ 2 }L }{ R } $$
Where, $${ I }_{ 1 }={ I }_{ 2 }=I=0.2A$$
$$L=2m$$, $$R=0.2m$$
So, force, $${ F }_{ b }=\dfrac { 40\times { 10 }^{ -9 } }{ 2\pi } \times \dfrac { 0.2\times 0.2\times 2 }{ 0.2 } =8\times { 10 }^{ -8 }N$$
Write the expression for magnetic potential energy of a magnetic dipole kept in a uniform magnetic field and explain the terms.
An electron is moving along x-axis in x-y plane with velocity of $${10}^{2}m/s$$. A magnetic field of magnitude $$10T$$ is present in the region along z-axis. If the magnitude of force on the particle is $$1.6m\times {10}^{-16}N$$, find $$m$$
What is the magnetic force per unit length experienced by wire C as shown in figure ? (Assume that all wires are parallel and indefinitely long)
A circular coil of $$N$$ turns and diameter $$d$$ carries a current $$I$$. It is unwounded and rewound to make another coil of diameter $$2d$$ $$I$$ remaining the same. Calculate the ratio of the magnetic moments of the new coil and the original coil.
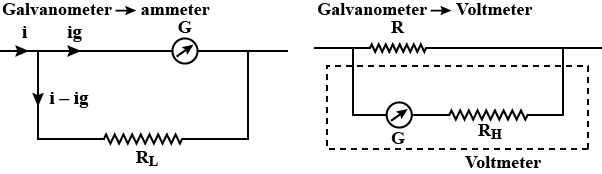
Give the principle of moving coil galvanometer? What is the advantage of radial magnetic field in the galvanometer?
A slightly divergent beam of non-relativistic charged particles accelerated by a potential difference $$V$$ propagates from a point $$A$$ along the axis of a straight solenoid. The beam is brought into focus at a distance $$l$$ from the point $$A$$ at two successive values of magnetic induction $$B_{1}$$ and $$B_{2}$$. Find the specific charge $$q/m$$ of the particles.
An alpha particle is projected vertically upward with a speed of $$3.0\times {10}^{4}km$$ $${s}^{-1}$$ in a region where a magnetic field of magnitude $$1.0T$$ exists in the direction south to north. Find the magnetic force that acts on the $$\alpha$$ particle.
A magnetic field of $$\left( {4.0 \times {{10}^{ - 3}}\vec k} \right)T$$ exerts a force of $$\left( {4.0\vec i + 3.0\vec j} \right) \times {10^{ - 10}}N$$ on a particle having a charge of $$1.0 \times {10^{ - 9}}C$$ and going in the X-Y plane. Find the velocity of the particle.
A cyclotron's oscillator frequency is $$10\ MHz$$. What should be the operating magnetic field for accelerating protons? If the radius $$r$$ its 'dees' is $$60\ cm$$, calculate the kinetic energy (in $$MeV$$) of the proton beem produces by the accelerator.
Answer the following:
What is it necessary to introduce a cylindrical soft iron core inside the coil of a galvanometer?
What should be the orientation of a magnetic dipole in a uniform magnetic field so that its potential energy is maximum?
The magnitude $$F$$ of the force between two straight parallel current carrying conductors kept at a distance $$d$$ apart in air is given by
$$F=\dfrac {\mu_0 I_1 I_2}{2\pi d} $$
Where $$I_1$$ and $$I_2$$ are the currents flowing through the two wires.
Use this expression, and the sign convention that the:
Force of attraction is assigned a negative sign and force of repulsion is assigned a positive sign.'
Draw graphs showing dependence of $$F$$ on
$$d$$ when the product $$I_1 I_2$$ is maintained at a constant positive value.
When product is maintained a positive value, Force will be attractive (-ve)
(a) How would you demonstrate that a momentary current can be obtained by the suitable use of a magnet. a coil of wire and a galvanometer?
(b) What is the source of energy associated with the current obtained in part(a)?
(a) When there is a relative motion between the coil and the magnet. the magnetic flux linked with the coil changes. If the north pole of the magnet is moved towards the coil. the magnetic flux through the coil increases as shown in above figure. Due to change in the magnetic flux linked with the coil. an e.m.f is induced in the coil. This e.m.f. causes a current to flow in the coil if the circuit of the coil is closed.
(b)The source of energy associated with the current obtained in part (a) is mechanical energy.
Why are the polar pieces of stable magnetic used in a galvanometer made of concave shape?
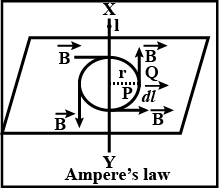
Write the mathematical form of Ampere's circuital law.
A cyclotrons dee radius is $$0.5m$$ and $$1.7T$$ cross-sectional magnetic field is working. Calculate the maximum kinetic energy gained by the proton.
Show how does a small circular carrying loop behave as a magnetic dipole?
When current flows through a current carrying loop, then loop behaves as magnetic dipole or bar magnet. Or we may say one face is like magnetic south pole $$S$$ and second face like north pole $$N$$. Face at which current is anticlockwise is north pole and face at which current is clockwise is called south pole.
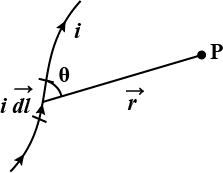
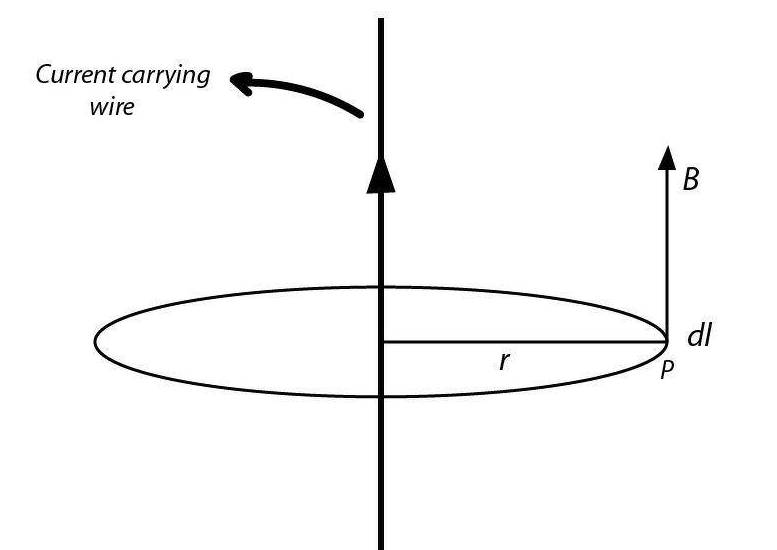
Explain Biot-Savart's law. Derive the magnetic field generated by a straight and finite-length current-carrying conductor with the helo of this law. Show that the magnetic field at a perpendicular distance $$d$$ from an infinite length currently carrying conductor is $$B=\cfrac { { \mu }_{ 0 }I }{ 2\pi d } $$
Biot-Savart's law was given by French Physicist Biot and Savart on the basis of experiments done by them for the calculation of magnitude of magnetic field at any point due to a current carrying conducting wire. Here, we shall study the relation between current and the magnetic field it produces.
Figure shows a conductor wire $$XY$$ carrying $$p$$. current $$I$$. Consider an infinitestimal element $$dl$$ of the conductor. The magnetic field $$dB$$ due to this element is to be determined at a point $$P$$ which is at a distance of $$r$$ from it. Let $$\theta$$ be the angle between $$dl$$ and the position figure. Biot Savart's law vector $$r$$. Direction of vector $$\vec { dl } $$ is in the direction of current
According to Biot-Savart's Law: The magnitude of the magnetic field $$d\vec { B } $$
(i) is directly proportional to the current $$I$$
$$\left| \vec { dB } \right| \propto I...(1)$$
(ii) is directly proportional to the element length
$$\left| \vec { dB } \right| \propto \left| \vec { dl } \right| ....(2)$$
(iii) is directly proportional to the sine of the angle between vector $$\vec { r } $$ and $$\vec { dl } $$ that is $$\sin \theta$$
$$\left| \vec { dB } \right| \propto \sin \theta........(3)$$
(iv) is inversely proportional to the square of the distance $$r$$
$$\left| \vec { dB } \right| \propto \cfrac { 1 }{ { r }^{ 2 } } ....(4)$$
from the equations (1), (2), (3), (4)
$$\left| \vec { dB } \right| \propto \cfrac { I\left| \vec { dl } \right| \sin { \theta } }{ { r }^{ 2 } } ....(5)\quad or\quad \left| \vec { dB } \right| \propto \cfrac { { \mu }_{ 0 } }{ 4\pi } \cfrac { I\left| \vec { dl } \right| \sin { \theta } }{ { r }^{ 2 } } ....(6)$$
Here, $$\cfrac { { \mu }_{ 0 } }{ 4\pi } =$$ proportionality constant whose value in vacuum is $${ 10 }^{ -7 }N/{ A }^{ 2 }$$s and its unit is $$\cfrac { N }{ { A }^{ 2 } } \quad or\quad \cfrac { Wb }{ A\times m } \quad or\quad \cfrac { T\times m }{ A } ;\quad { \mu }_{ 0 }=4\pi \times { 10 }^{ -7 }\cfrac { N }{ { A }^{ 2 } } \quad or\quad \cfrac { Wb }{ A\times m } $$
Here, $$\mu$$ is called the permeability of free space (or vacuum). If there is some other medium around the conducting wire, then the magnitude of the magnetic field will be:
$$\left| \vec { dB } \right| \propto \cfrac { { \mu }_{ m } }{ 4\pi } \cfrac { I\left| \vec { dl } \right| \sin { \theta } }{ { r }^{ 2 } } ....(7)$$
Where $${ \mu }_{ }={ \mu }_{ 0 }{ \mu }_{ r }$$ is the permeability of a specific medium, which is dependent on the medium
$$\quad \therefore { \mu }_{ r }=\cfrac { { \mu }_{ m } }{ { \mu }_{ 0 } } =$$ Relative permeability
vector form: From equation (7)
$$\vec { dB } =\cfrac { { \mu }_{ m } }{ 4\pi } \cfrac { I\vec { dl } \sin { \theta } }{ { r }^{ 2 } } \hat { r } $$
$$\because \hat { r } =\cfrac { \vec { r } }{ \left| \vec { r } \right| } =\cfrac { \vec { r } }{ r } $$
$$\therefore \vec { dB } =\cfrac { { \mu }_{ m } }{ 4\pi } I\cfrac { \vec { dl } \times \hat { r } }{ { r }^{ 2 } } $$
or $$\vec { dB } =\cfrac { { \mu }_{ 0 } }{ 4\pi } \cfrac { I\left( \vec { dl } \times \hat { r } \right) }{ { r }^{ 3 } } ...(8)\left[ \because \hat { r } =\cfrac { \vec { r } }{ r } \right] $$
It is clear from the equation (8) that the direction of $$\vec { dB } $$ will be perpendicular to the surface formed by $$\vec { dl } $$ and $$\vec { r } $$ and would be up and down depending on the Right Handed Cork Screw Rule. In the figure the direction of $$\vec { dB } $$ at point $$P$$ is downwards perpendicular to the surface, and is represented by $$(X)$$ sign whereas at point $$P'$$ the direction of $$\vec { dB } $$ is outwards perpendicular to the surface of the paper and represented by $$(.)$$ sign
Magnetic Field due to a Straight Current Carrying Wire of Infiite Length
Since, the length of the wire is infinite, hence the ends $$x$$ and $$y$$ are at infinite distance. Therefore, the internal angle made by them at point $$P$$ would be
$${ \phi }_{ 1 }={ \phi }_{ 2 }=\cfrac { \pi }{ 2 } $$
Therefre, from equation (7) magnetic field due to a straight current carrying wire of infinite length,
$$B=\cfrac { { \mu }_{ 0 }I }{ 4\pi d } \left[ \sin { \cfrac { \pi }{ 2 } } +\sin { \cfrac { \pi }{ 2 } } \right] =\cfrac { { \mu }_{ 0 }I }{ 4\pi d } (1+1)\left[ \because \sin { \cfrac { \pi }{ 2 } } =1 \right] $$
or $$B=\cfrac { { \mu }_{ 0 }I }{ 2\pi d } $$
Define Biot-Savart's law in vector form.
Two $$2m's$$ long parallel wires are placed in vacuum at a distance $$0.2m$$. If current $$0.2A$$ flows in both the wires in the same direction, calculate the force acting per unit length of the coil.
What is the initial angle in degrees between the dipole moment and the magnetic field?
$$\textbf{Step 1 - Given data}$$
Dipole moment, $$M = 0.020\ J/T$$
Magnetic field, $$B = 52 \times 10^{-3} T$$
Final kinetic energy, $$KE_{f} = 0.80\ mJ = 0.80\times 10^{-3} J$$
Initial kinetic energy, $$KE_{i} = 0$$
$$\textbf{Step 2 - By Energy conservation}$$
$$KE_{i} + PE_{i} = KE_{f} + PE_{f}$$
$$0 - MB\cos \theta = 0.80\times 10^{-3} - MB\cos 0$$
$$-0.020 \times 52 \times 10^{-3} \times \cos \theta = 0.80\times 10^{-3} - 0.020 \times 52 \times 10^{-3}$$
$$\cos \theta = 1 - 0.8 = 0.2$$
$$\theta \sim 77^{\circ}$$
$$x=0,y=-0.500 m,z=0$$
If M is the magnitude of the magnetic field, find $$x$$ such that $$x=100\times M$$.
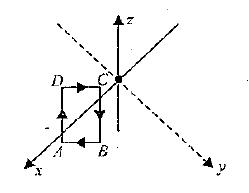
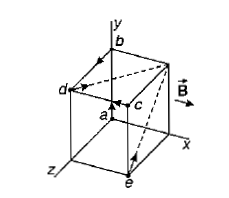
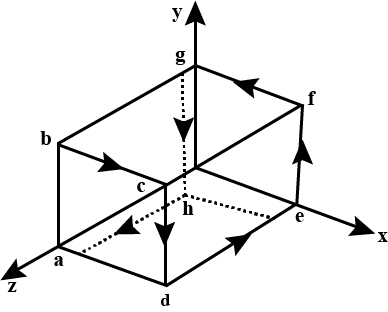
Each of the lettered points at the corners of the cube in figure represents a positive charge q moving with a velocity of magnitude v in the direction indicated.The region in the figure is in a uniform magnetic field $$\vec{B}$$,parallel to the x-axis and directed toward the right .Find the magnitude and direction of the force on each charge.
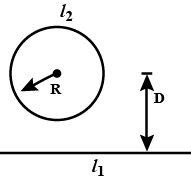
A circular loop of radius R carries current $${I}_{2}$$ in a clockwise direction as shown in figure. The centre of the loop is a distance D above a long,straight wire.What are the magnitude and direction of the current $${I}_{1}$$ in the wire if the magnetic field at the centre of loop is zero?
A $$-4.80\mu C$$ charge is moving at a constant velocity of $$6.80\times {10}^{5}m/s$$ in the +x direction relative to a reference frame.At the instant when the point charge is at the origin,what is the magnetic field vector it produces at the following points x=0,y=0.500 m,z=0?
A particular type of fundamental particle decays by transforming into an electron $$e^{-}$$ and a positron $$e^{+}$$. Suppose the decaying particle is at rest in a uniform magnetic field $$\vec{B}$$ of magnitude $$3.53 mT$$ and the $$e^{-}$$ and $$e^{+}$$ move away from the decay point in paths lying in a plane perpendicular to $$\vec{B}$$. How long after the decay do the $$e^{-}$$ and $$e^{+}$$ collide?
Is the magnetic dipole moment a vector or a scalar quantity? Write its unit.
A moving charged particle q travelling along the positive x-axis enters a uniform magnetic field B. When will the force acting on q be maximum?
The magnetic moment of a thin round loop with current, if the radius of the loop is equal to $$R=100\:mm$$ and the magnetic field at its centre is equal to $$B=6.0\:\mu T$$, is $$30 \times 10^{-x} A-m^2$$. Find the value of $$x$$.
If the expression in vector form, for the magnetic force $$\vec F$$ acting on a charged particle moving with velocity $$\vec V$$ in the presence of a magnetic field $$\vec B$$ is given by $$\overrightarrow { F } =a*q\overrightarrow { v } \times \overrightarrow { r } $$. Find a.
If the magnetic moment of the coil is $$36 \times 10^{-X} Am^2$$. Find $$X$$?
Find out the angle(in degrees) at which an electron moving through a magnetic field experiences the maximum force.
If expressions for the magnetic field at a point due to a current element, in C.G.S.system is given by $$d\overrightarrow { B } =\frac { μ_{ 0 } }{ 4π } \frac { i(d\overrightarrow { l\times \overrightarrow { r } } ) }{ { a*r }^{ 3 } } $$. Find a.
Can a charged particle be accelerated by a magnetic field.Can its speed be increased?
Calculate the components of the magnetic field you can find from this information.
A closed curve encircles several conductors.The line integral $$\int{\vec{B}\cdot d\vec{l}}$$ around this curve is $$3.83\times {10}^{-7} T-m$$. If you were to integrate around the curve in the opposite direction, what could be the value of the line integral?
A circular coil of $$300$$ turns and average area $$5 \times {10}^{-3} {m}^{2}$$ carries a current of $$15 A$$. Calculate the magnitude of magnetic moment associated with the coil.
Draw a neat and labelled diagram of suspended coil type moving coil galvanometer.
The given image show suspended coil type moving coil galvanometer.
A charge q enters perpendicularly with the direction of a magnetic field $$\bar{B}$$ with a velocity $$\bar{V}$$. What would be the force acting on this charge?
You are provided with one low resistance $$R_{L}$$ and one high resistance $$R_{H}$$ and two galvanometers. One galvanometer is to be converted to an ammeter and the other to a voltmeter. Show how you will do this with the help of simple, labelled diagrams
A galvanometer can be converted to an ammeter and an voltmeter as shown in the above diagram/.
The Magnetic Force Between Two Parallel Conductors(22)
Two parallel wires separated by $$4.00 \,cm$$ repel each other with a force per unit length of $$2.00 \times 10^{-4} \,N/m$$. The current in one wire is $$5.00 \,A$$.
(a) Find the current in the other wire.
(b) Are the currents in the same direction or in opposite directions?
(c) What would happen if the direction of one current were reversed and doubled?
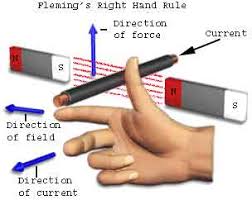
Write the expression for Lorentz magnetic force on a particle of charge $$'q'$$ moving with velocity $$\overset{\rightarrow}{v}$$ in a magnetic field $$\overset{\rightarrow }{B}$$.Show that no work is done by this force on the charged particle
q=charge of the moving particle
$$\bar{B}=$$ magnetic field$$\bar{v}=$$ Velocity
$$\bar{F}=$$ magnetic force $$=q(\bar{V}\times \bar{B})$$
$$\bar{F}=q(\bar{V}\times \bar{B})$$
Here, $$\bar{F}$$ is cross product of $$\bar{V}$$ and $$\bar{B}$$
so,work done $$=W=f,d$$
$$=Fd \cos 90^o$$
$$=0$$
A wire of a length 2 m carrying a current of 1 A is bend to form a circle. The magnetic moment of the coil is $$\left ( in A - m^{2} \right )$$:
(a) $$1/\pi $$
(b) $$\pi /2$$
Define watt. Write down an equation linking watts, volts and amperes.
A proton moving with velocity $$V$$ is acted upon by electric field $$E$$ and magnetic field $$B$$. The proton will move undeflected if
Observe the figure
Identify the device shown in the figure.
$$x=0,y=-0.500 m,z=+0.500 m$$
A solenoid has an inductance of $$1 0$$ henry and a resistance of $$2$$ ohm. It is connected to a $$10$$ volt battery. How long will it take for the magnetic energy to energy to reach $$1/4$$ of its maximum value?
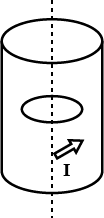
A long circular tube of length $$10$$m and radius $$0.3$$m carries a current I along its curved surface as shown. A wire-loop of resistance $$0.005$$ ohm and of radius $$0.1$$m is placed inside the tube with its axis coinciding with the axis of the tube. The current varies as $$I=I_0\cos(300 t)$$ where $$I_0$$ is constant. If the magnetic moment of the loop is $$N\mu_oI_0\sin(300 t)$$, then 'N' is?
Answer the following question:
An electron moving horizontally with a velocity of $$4\times 10^4\ m/s$$ enters a region of uniform magnetic field of $$10^{-5}\ T$$ acting vertically downward as shown in the figure.
Draw its trajectory and find out the time it takes to come out of the region of magnetic field.
The Magnetic Force Between Two Parallel Conductors(21)
Two long, parallel conductors, separated by $$10.0 \,cm$$, carry currents in the same direction. The first wire carries a current $$I_1 = 5.00 \,A$$, and the second carries $$I_2 =8.00 \,A$$.
(a) What is the magnitude of the magnetic field created by $$I_1$$ at the location of $$I_2$$?
(b) What is the force per unit length exerted by $$I_1$$ on $$I_2$$?
(c) What is the magnitude of the magnetic field created by $$I_2$$ at the location of $$I_1$$?
(d) What is the force per length exerted by $$I_2$$ on $$I_1$$?
State the rule to determine the direction of current induced in a coil due to its rotation in a magnetic field.
The rule to determine the direction of the current induced in a coil is given by Fleming's right-hand rule :
Fleming's Right hand rule - If the forefinger, second (central) finger and thumb of the right hand are stretched at right angles to each other, with the forefinger in the direction of the field, the thumb in the direction of the motion of the wire then the induced current in the wire is in the direction of the second or central finger.
In the relation $$\vec{F}=q(\vec{v}\times \vec{B})$$,which pairs are always perpendicular to each other.
___________ law gives the quantitative relationship between current and magnetic field due to the current carrying conductor.
State Ampere's circuital law.
What are the units of magnetic moments and magnetic induction?
Mention the significance of Lenz's law.
Explain inconsistency of Ampere's circuital law during charging of a capacitor.
Inconsistency of ampere's law Maxwell explain the ampere's law is valid only for steady current or when the electric field does not change the time. To see this inconsistency consider a parallel plate capacitor being charged by a battery.During the charging time varying current flows through connecting wires applying to amperes law for loop $${l_{1\,}}\,and\,{l_2}$$
$$\oint\limits_{{l_1}} {\overrightarrow {B.} \overrightarrow {dl} = {\mu _0}i} $$
$$But,\,\oint\limits_{{l_2}} {\overrightarrow {B.} \overrightarrow {dl} = 0} $$
(since no current flows through the region between the plates). But practical it is observed that there is a magnetic field between the plates.Hence ampere's law fails i.e. $$\oint\limits_{{l_1}} {\overrightarrow {B.} \overrightarrow {dl} \ne {\mu _0}i} $$ .
Modified ampere's circuital law vampires maxwell's circuital law: Maxwell assume that some sort of current must be flowing between the capacitor plates during charging process.He named it the displacement current. hence modified law is as follows:
$$\oint\limits_{{l_1}} {\overrightarrow {B.} \overrightarrow {dl} = } {\mu _o}\left( {{i_c} + {i_d}} \right)$$ or $$\oint\limits_{{l_1}} {\overrightarrow {B.} \overrightarrow {dl} = {\mu _0}\left( {{i_c} + {\varepsilon _0}\frac{{d{\varphi _E}}}{{dt}}} \right)} $$
where $${i_c}$$=to conduction current=current due to flow of charges in a conductor and
$${i_d}$$ = displacement current= $${\varepsilon_o}{\dfrac{d\varphi_E}{dt}}$$ current due to the changing electric field between the plates of the capacitor
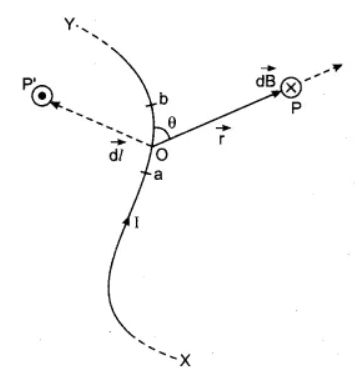
Biot - savarts law
$$ dB^{\rightarrow}= \dfrac{\mu o}{4\pi}$$ $$\dfrac{idl^{\rightarrow }\times r^{\rightarrow }}{ | r |^{3}}$$
Express $$90$$cm as a percent of $$4.5$$m.
A charged particle is moving in a magnetic field, match the different quantities of a particle in entries of column I with the entries of column II.
Equal currents are flowing in four infintely long wires.Distance between two wires is same and directions of currents are shown in figure.Match the following two columns.
$$x=0.500 m, y=0, z=0$$
A short bar magnet of magnetic moment $$m = 0.32\, JT^{-1}$$ is placed in a uniform magnetic field of $$0.15 T$$. If the bar is free to rotate in the plane of the field, which orientation would correspond to its (a) stable, and (b) unstable equilibrium? What is the potential energy of the magnet in each case?
A bar magnet of magnetic moment $$1.5 J T^{-1}$$ lies aligned with the direction of a uniform magnetic field of 0.22 T.
(a) What is the amount of work required by an external torque to turn the magnet so as to align its magnetic moment: (i) normal to the field direction, (ii) opposite to the field direction?
(b) What is the torque on the magnet in cases (i) and (ii)?
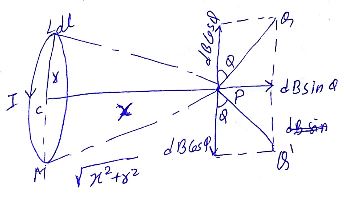
State Biot - Savart law. Deduce the expression for the magnetic field at a point on the axis of a current carrying circular loop of radius 'R' distant 'x' from the center. Hence, write the magnetic field at the center of a loop.
Biot- Savart law states that for charge in rest produce electric field, but when in motion current flow and it induces magnetic fields.
Biot-Savart law helps in calculating force(magnetic) at any point.
Let us consider a circular loop of
Radius r with center C, P be a,
Point at distance x from C
Now considering small section
$$LP\bot dl\text{ and } MP\bot dl$$
$$LP=MP=\sqrt { { x }^{ 2 }+{ r }^{ 2 } } $$ (1)
Using Biot-Savart law
$$dB=\dfrac{\mu_0}{4\pi} \dfrac{Idl\sin 90°}{(r^2+x^2})$$ (2)
$$dB\cos\theta$$ components balance each other and
$$B=\int dB\sin\theta$$
$$\int { \dfrac { { { \mu }_{ 0 } } }{ 4\pi } \left[ \dfrac { Idl }{ \left( { r }^{ 2 }+{ x }^{ 2 } \right) } \right] \dfrac { r }{ \sqrt { { r }^{ 2 }+{ x }^{ 2 } } } } $$
$$\sin\theta=\dfrac { r }{ \sqrt { { r }^{ 2 }+{ x }^{ 2 } } } $$
$$|therefore B=\dfrac { { \mu }_{ 0 } }{ 4\pi } \dfrac { rI }{ \left( { r }^{ 2 }+{ x }^{ 2 } \right) ^{ \dfrac { 3 }{ 2 } } } \int { dl } $$
$$\dfrac { { \mu }_{ 0 } }{ 4\pi } \dfrac { { \mu }_{ 0 }Ir }{ 4\pi \left( { r }^{ 2 }+{ x }^{ 2 } \right) ^{ \dfrac { 3 }{ 2 } } } \times 2\pi r$$
$$\therefore\vec B=\dfrac { { \mu }_{ 0 } }{ 4\pi } \dfrac { { \mu }_{ 0 }Ir }{ 4\pi \left( { r }^{ 2 }+{ x }^{ 2 } \right) ^{ \dfrac { 3 }{ 2 } } } \times 2\pi r$$
$$=\dfrac { { \mu }_{ 0 }Ir }{ 2\pi \left( { r }^{ 2 }+{ x }^{ 2 } \right) ^{ \dfrac { 3 }{ 2 } } } $$
And magnetic field at center of the loop is
$$\vec B=\dfrac { { \mu }_{ 0 }Ir }{ 2\pi \left( { r }^{ 2 }+{ x }^{ 2 } \right) ^{ \dfrac { 3 }{ 2 } } } $$
Putting $$x=0$$
$$\overset { \rightarrow }{ B } =\dfrac { { \mu }_{ 0 }Ir }{ 2{ r }^{ 3 } } $$
A positively charged croquet ball rolls at 4.0 m/s northward through a 2.00 T magnetic field which points westward.
If the charge on the croquet ball is 1.0 C, how much force acts on the croquet ball due to the magnetic field and in what direction?
Write the expression, in a vector form, for the Lorentz magnetic force $$\overrightarrow F $$ due to a charge moving with velocity $$\overrightarrow V $$ in a magnetic field $$\overrightarrow B $$. What is the direction of the magnetic force?
(a) State Ampere's circuital law. Use this law to obtain the expression for the magnetic field inside an air cored toroid of average radius r having 'n' turns per unit length and carrying a steady current I.
(b) An observer to the left of a solenoid of N terms each of cross section area A observes that a steady current I in it flows in the clockwise direction. Depict the magnetic field lines due to the solenoid specifying its polarity and show that it acts as a bar magnet of magnetic momentum $$m = NIA$$
(a)
According to Ampere's circuital law, the line integral of magnetic field induction along a closed curve is equal to the total current passing through the surface enclosed in the closed curve times the permeability of the medium.
$$\oint \vec B . \vec {dl} = \mu_o I_{enclosed}$$
Applying ampere's law for the given toroid,
$$B (2 \pi r) = \mu_o NI$$
But, $$N = 2 \pi r n$$
$$B = \mu_o n I$$
(b)
The observer sees south pole as shown in the attached figure.
Magnetic moment due to a loop is given by:
$$m = iA$$
For N turns, $$i = NI$$
$$m = NIA$$
According to Ampere's swimming rule, if a man swims along a direction opposite to the direction of the current, south pole of the needle deflects towards his __________.
In a field, the force experienced by a charge depends upon its velocity and becomes zero, when it is at rest. What is the nature of the field?
Write the expression for the Lorentz force $$F$$ in vector form.
Explain how electric current with Lorentz-Drude theory of electrons.
A circular coil of $$250$$ turns and diameter $$18 cm$$ carries a current of $$12 A$$. What is the magnitude of magnetic moment associated with the coil ?
State Biot-Savart law.
Bio Savart Law: The magnetic field at any point due to an element of a conductor carrying current is
(1) directly proportional to (a) the strength of the current $$i$$,
(b) length of the element $$dl$$ (c) sine of the angle $$\theta$$ between the element in the direction of current and the line joining the element to the point P.
i.e., $$dB \propto i, dB \propto \delta, dB \propto sin \theta$$
(2) inversely proportional to the square of the distance r of the point P from the centre of the element.
$$dB = \dfrac{\mu_0}{4 \pi} \times \dfrac{I dl sin \theta}{r^2}$$
(1) directly proportional to (a) the strength of the current $$i$$,
(b) length of the element $$dl$$ (c) sine of the angle $$\theta$$ between the element in the direction of current and the line joining the element to the point P.
i.e., $$dB \propto i, dB \propto \delta, dB \propto sin \theta$$
(2) inversely proportional to the square of the distance r of the point P from the centre of the element.
$$dB = \dfrac{\mu_0}{4 \pi} \times \dfrac{I dl sin \theta}{r^2}$$
State and explain Ampere's circuital law.
Amperes circulate law: The line integral of magnetic field of induction $$\vec{B}$$ around any closed path in free space is equal to absolute permeability of free space $$\mu_0$$ times the total current flowing through area bounded by the path.
Mathematically, $$\phi \vec{B}\cdot \vec{dl}=\mu_0I$$
where B-magnetic induction, I-Total current, dl-length element of path, $$\mu_0$$-Permeability of the space.
Explanation:
(a) Ampere's law is generalisation of Biot-Savart's law and is used to determine magnetic field at any point due to distribution of current.
(b) Consider a long straight current carrying conductor XY, placed in vacuum. A steady current 'I' flows through it from the end Y to X as shown in the figure.
(c) Imagine a closed curve(amperian loop) around the conductor having radius 'r'.
(d) The loop is assumed to be made of large number of small elements each of length $$\vec{dl}$$.
(e) Its direction is along the direction of traced loop.
(f) Let $$\vec{B}$$ be the strength of magnetic field around the conductor.
(g) All the scalar product of $$\vec{B}$$ and $$\vec{dl}$$ give the product of $$\mu_0$$ and I.
It is given by $$\phi=\vec{B}\cdot\vec{dl}=$$ $$B dl$$ $$\cos\theta$$
Mathematically, $$\phi \vec{B}\cdot \vec{dl}=\mu_0I$$
where B-magnetic induction, I-Total current, dl-length element of path, $$\mu_0$$-Permeability of the space.
Explanation:
(a) Ampere's law is generalisation of Biot-Savart's law and is used to determine magnetic field at any point due to distribution of current.
(b) Consider a long straight current carrying conductor XY, placed in vacuum. A steady current 'I' flows through it from the end Y to X as shown in the figure.
(c) Imagine a closed curve(amperian loop) around the conductor having radius 'r'.
(d) The loop is assumed to be made of large number of small elements each of length $$\vec{dl}$$.
(e) Its direction is along the direction of traced loop.
(f) Let $$\vec{B}$$ be the strength of magnetic field around the conductor.
(g) All the scalar product of $$\vec{B}$$ and $$\vec{dl}$$ give the product of $$\mu_0$$ and I.
It is given by $$\phi=\vec{B}\cdot\vec{dl}=$$ $$B dl$$ $$\cos\theta$$
where, $$\theta$$ =angle between $$\vec{B}$$ and $$\vec{dl}$$
Write Biot-Savart law.
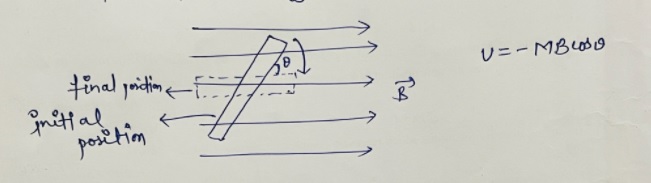
Write the path of motion of an electron when it enters in magnetic field at
(a) perpendicular
(b) an angle $$\theta$$.
The relation between magnetic field and current is given by Biot-Savart law. Illustrate Biot-Savart law with necessary figure.
According to Biot-Savart Law, magnetic field due to an element carrying current $$I$$ in the direction $$\vec {dl}$$ at a point $$\vec r$$ from the element is given by:
$$\vec {dB} = \cfrac{\mu_o I}{4 \pi r^3}(\vec {dl} \times \vec r)$$
Biot-Savart Law can be explained by the attached figure. Consider a wire carrying current $$I$$. To find the net magnetic field due to the wire at point P, a small element of length $$\vec {dl}$$ is chosen and its magnetic field $$\vec {dB}$$ is found using the Biot-savart law as mentioned above. The net magnetic field at the point $$P$$ can be found by integrating the magnetic field at $$P$$ over complete length of wire. It must be noted that direction of the magnetic field can be quickly found using the right hand thumb rule.
State and explain Biot-Savart Law.
Hint: The Biot-Savart law states how the value of the magnetic field at a specific point in space from one short segment of current-carrying conductor depends on each factor that influences the field.
Solution:
Step1: Application of Biot-Savart law
The Biot-Savart Law is used to determine the magnetic field intensity B near a current carrying conductor in terms of magnetic field intensity generated by its source current element. Consider a wire carrying an electric current I and also consider an infinitely small length of a wire dl at a distance r from point A
Step2: Statement of Biot-Savart law
It is clear from above
free body diagram that, Biot-Savart Law states that magnetic
intensity dB at a point A due to current I flowing through
a small element dl is,
a) Directly proportional
to current (I).
b) Directly proportional
to the length of the element (dl).
c) Directly proportional
to the sine of angle θ between the direction of current and the line joining
the element dl from point A.
d) Inversely
proportional to the square of the distance (x) of point A from the
element dl.
$$dB\alpha \dfrac{{Idl\sin \theta }}{{{r^2}}}$$
$$dB = K\dfrac{{Idl\sin \theta }}{{{r^2}}}$$
Where, $$K = \dfrac{{{\mu _0}{\mu _r}}}{{4\pi }}$$
μ0= Absolute
permittivity of air in vacuum
μr= relative
permittivity.
Write the special features of Magnetic Lorentz force.
State Biot-Savart's law? Define the unit of current.
Let $$AB$$ is a conductor carrying current $$i$$. Consider a small element $$dl$$ length of the conductor, due to this the magnetic field $$dB$$ is produced at a point $$P$$ distance $$r$$ from $$dl$$, $$\theta$$ is angle by $$dl$$ to point $$P$$, then the intensity of field $$dB$$ is:
(1) Directly proportional to the current $$i$$ $$dB \propto i$$.
(2) Directly proportional to the length of the conductor $$dB \propto dl$$.
(3) Directly proportional to the sine of the angle between the line joining the point and $$dl$$ $$dB \propto \sin{\theta}$$.
(4) Inversely proportional to the square of the distance of the point $$P$$ from the line $$dB \propto \dfrac{1}{{r}^{2}}$$. Combining all the four
$$dB \propto \dfrac{idl \sin{\theta}}{{r}^{2}}$$
$$dB = k \dfrac{idl \sin{\theta}}{{r}^{2}}$$ $$k$$ is constant
$$k = \dfrac{{\mu}_{0}}{4 \pi} = {10}^{-7} {N}/{{A}^{2}}$$
$$dB = \dfrac{{\mu}_{0}}{4 \pi} \dfrac{idl \sin{\theta}}{{r}^{2}}= {10}^{-7} \dfrac{idl \sin{\theta}}{{r}^{2}} {Wb}/{{m}^{2}}$$
In above formula $$dl = 1 m$$, $$\sin{\theta} = 1$$, $$\theta = 90$$
$$r = 1 m$$; $$dB = {10}^{-7} {Wb}/{m}$$
$$i = 1$$ Ampere
Hence one ampere current is that current which produces a field of $${10}^{-7} {Wb}/{{m}^{2}}$$ at the centre of a conductor of length $$1 m$$ placed in the form of an arc of a circle of radius $$1 m$$.
(1) Directly proportional to the current $$i$$ $$dB \propto i$$.
(2) Directly proportional to the length of the conductor $$dB \propto dl$$.
(3) Directly proportional to the sine of the angle between the line joining the point and $$dl$$ $$dB \propto \sin{\theta}$$.
(4) Inversely proportional to the square of the distance of the point $$P$$ from the line $$dB \propto \dfrac{1}{{r}^{2}}$$. Combining all the four
$$dB \propto \dfrac{idl \sin{\theta}}{{r}^{2}}$$
$$dB = k \dfrac{idl \sin{\theta}}{{r}^{2}}$$ $$k$$ is constant
$$k = \dfrac{{\mu}_{0}}{4 \pi} = {10}^{-7} {N}/{{A}^{2}}$$
$$dB = \dfrac{{\mu}_{0}}{4 \pi} \dfrac{idl \sin{\theta}}{{r}^{2}}= {10}^{-7} \dfrac{idl \sin{\theta}}{{r}^{2}} {Wb}/{{m}^{2}}$$
In above formula $$dl = 1 m$$, $$\sin{\theta} = 1$$, $$\theta = 90$$
$$r = 1 m$$; $$dB = {10}^{-7} {Wb}/{m}$$
$$i = 1$$ Ampere
Hence one ampere current is that current which produces a field of $${10}^{-7} {Wb}/{{m}^{2}}$$ at the centre of a conductor of length $$1 m$$ placed in the form of an arc of a circle of radius $$1 m$$.
A moving charge can produce a magnetic field. How does a current loop behaves like a magnetic dipole?
When an electric current flows in a closed loop of wire, placed in a uniform magnetic field, the magnetic forces produce a torque which tends to rotate the loop so that area of the loop is perpendicular to the direction of the magnetic field.
Consider a rectangular coil $$PQRS$$ placed in an external magnetic field as shown in diagram (a). Let $$'I'$$ be the current flowing through the coil. Each part of the coil experiences one Lorentz. Each part of the forces is$$\vec{F_1}, \ \vec{F_2}, \ \vec{F_3}$$ and $$\vec{F_4}$$ as shown. The forces are equal in magnitude but act in opposite directions along the same straight line. Hence they cancel out
The force $$\vec{F_1}= I (\vec{PQ} \times \vec{B})$$
$$F_1= IlB$$ when $$\theta =90^0$$ $$\vec{F_1} $$ acts in direction perpendicular to the plane of paper.
Similarly, $$\vec{F_3}= I (\vec{RS} \times \vec{B}$$
$$F_3= IB $$ when $$\theta = 90^0$$
The two forces constitute a couple and so rotates the coil in the anticlockwise. The torque is given by
$$\tau= \text{ force x arm of couple }$$
$$\tau= Fb cos \theta$$
$$\tau= IlB \ b cos \theta$$
$$\tau= IAB cos \theta$$
The area vector $$A$$ makes an angle $$\alpha$$ with the $$\vec{B}$$ so $$\theta + \alpha = 90^0$$
$$cos \theta= cos(90- \alpha )= sin \alpha$$
$$\therefore \tau= NIAB \ \ sin\alpha$$
$$\tau= P_m B \ sin \alpha$$
$$\vec{\tau}= \vec{P_m} \times \vec{B}$$ where $$P_m= NIA $$ called the magnetic dipole moment of the loop.
If a circular coil of $$100$$ turns and radius $$10$$cm carries a current of $$1$$A, find the magnetic dipole moment of the coil.
Define magnetization. Write its SI unit and dimensions.
State and explain Ampere's circuital law.
$$\bullet$$$$\textbf{Statement}$$: Ampere's law states that the magnetic field line integral around a closed path is equal to the product of the magnetic permeability of that space and the total current across the area limited by that path.
$$\int\vec B.\vec{dl}=\mu_0I$$
Here, $$B$$ is magnetic field intensity
$$ \mu_0$$ is the permeability of free space
$$I$$ is the total enclosed current
Here, $$B$$ is magnetic field intensity
$$ \mu_0$$ is the permeability of free space
$$I$$ is the total enclosed current
$$\bullet$$$$ \textbf {Application of Ampere's law}$$
Finding the magnetic field due to infinite straight wire by using Ampere circuital law:
We'll find the magnetic field at a point due to a long straight current carrying conductor.
For this we imagine an Ampereian loop which is circular with the centre at the wire and passing through the point P.
$$\int\vec B.\vec{dl}=\mu_0I$$
Since the path is a circle, the magnetic field intensity $$\vec B$$ is uniform throughout because every point is equidistant.
$$\mu_0I=B.\int dl=B \times 2\pi r$$ $${( \int dl= 2 \pi r})$$
$$\therefore B=\cfrac{\mu_0I}{2\pi r}=\cfrac{\mu_0}{4\pi} \cfrac{2I}r$$
State Biot-Savart's law. Define unit of current.
Let AB is a conductor carrying current i. Consider a small element dl length of the conductor, due to this the magnetic field dB is produced at a point P distance r from dl, $$\theta$$ is angle by dl to point P, then the intensity of field dB is:
(1) Directly proportional to the current i dB $$\propto$$ i
(2) Directly proportional to the length of the conductor. dB $$\propto$$ dl
(3) Directly proportional to the sine of the angle between the line joining the point and dl dB $$\propto$$ sin $$\theta$$
(4) Inversely proportional to the square of the distance of the point P from the line $$dB \propto \dfrac{1}{r^2}$$ Combining all the four
$$dB \propto \dfrac{idl sin \theta}{r^2}$$
$$dB = k \dfrac{idl sin \theta}{r^2} k$$ is constant
$$k = \dfrac{\mu_0}{4 \pi} = 10^{-7} N/A^2$$
$$dB = \dfrac{\mu_0 }{4 \pi} \dfrac{idl sin \theta}{r^2} = 10^{-7} \dfrac{idl sin \theta}{r^2} Wb/m^2$$
In above formula $$dl = 1 m, sin \theta = 1, \theta = 90$$
$$r = 1m, dB = 10^{-7} Wb/m$$
i = 1 Ampere.
Hence one ampere current is that current which produces a field of $$10^{-7} Wb/m^2$$ at the centre of a conductor of length 1 m placed in the form of an arc of a circle of radius 1 m.
A long circular tube of length $$10 m$$ and radius 0.3 m carries a current I along its curved surface as shown. A wire-loop of resistance 0.0005 ohm and of radius 0.1 m is placed inside the tube with its axis coinciding with the axis of the tube. The current varies as $$I=I_0 cos (300 t)$$ where $$ I_0$$ is constant. If the magnetic moment of the loop is $$ N\, \mu_0\,I_0 sin (300 t)$$, then 'N' is
A uniform magnetic field of magnitude $$0.20\ T$$ exists in space from east to west. With what speed should a particle of mass $$0.010\ g$$ and having a charge $$1.0\times 10^{-5}C$$ be projected from south to north so that it moves with a uniform velocity?
Write Ampere circuital law in mathematical form. Derive an expression of magnetic field at the axis of a current carrying long solenoid. Draw necessary diagram.
The Ampere's law mathematical formula is,
$$\oint \vec B \cdot \vec {dl} = \mu _0 I$$
Let the magnetic fielld along the path PQ be B and along SR be 0. As the path PS and RQ be perpendicular to the axis of solenoid, The magnetic field component along these path is zero,
Therefore the path PS and QR will not contribute to magnetic field.
Total number of turns in length l=Nl,
The line integral of magnetic field along the path PQRS is,
$$\oint_{PQRS}\vec B \cdot \vec {dl}=\oint _{P}^{Q}\vec B \cdot \vec {dl}+\oint_{Q}^{R} \vec B \cdot \vec {dl}+\oint _{R}^{S}\vec B \cdot \vec {dl}+\oint _{S}^{P}\vec B\cdot \vec{dl}$$
Thus, we have,
$$\oint_{PQRS}\vec B \cdot \vec {dl}=Bl +0+0+0 = Bl\ (1)$$
Now by , Ampere's circuital law,
=$$\mu_0NlI\ (2)$$
From (1) and (2),
$$Bl=\mu_0NlI$$
$$B=\mu_0 NI$$
A particle moves in a circle of diameter $$1.0\ cm$$ under the action of a magnetic field of $$0.40\ tesla$$. An electric field of $$200\ Vm^{-1}$$ makes the path straight. Find the charge/mass ratio of the particle.
(a) What is shunt?
(b) State Ampere's circuital law. Using the law, obtain an expression for the magnetic field well aside the solenoid of finite length.
A small magnetised needle $$P$$ placed at point $$O$$ and the arrow shows the direction of its magnetic moment. The other arrow shows different position and orientation of another identical magnets ($$Q$$). In which configuration the system is not in equilibrium?
(c) Which configuration corresponds to the lowest potential energy among all the configurations shown?
A wire is bent in the form of an equilateral triangle of side 100 cm and carries a current of 2A. It is placed in the magnetic field of induction 2.0 T directed perpendicular to the plane of the paper. The direction and magnitude of the magnetic force acting on each side of the triangle will be.
length $$l = 100 cm = 1m$$
current $$i = 2A$$
$$vec{B} = 2T$$ Ref. image
By the left hand fleming's rule
$$F = B \propto l$$
$$F_1 = 2 \times 2 \times 1 = 4N$$
$$F_2 = 2 \times 2 \times 1 = 4N$$
$$F_3 = 2 \times 2 \times 1 = 4N$$ Ref. image
Resultant force of $$F_1$$ and $$F_2$$ $$\cos 120 = -\dfrac{1}{2}$$
$$F_r = \sqrt{F_1^2 + F_2^2 + 2F_1 F_2 \cos 120} = \sqrt{(4)^2 + (4)^2 - 2 \times (4)^2 \times \dfrac{1}{2}}$$
$$= 4$$
$$F_{net} = F_r - F_3$$
$$= 4 - 4 = 0$$ Ref. image
$$\therefore$$ the magnetic force due to the loop. is zero
$$F_1 = 4N $$ which is acting on $$BC$$ side towards the centre
$$F_2 = 4N$$ which is acting on $$AC$$ side towards the centre
$$F_3 = 4N$$ which is acting on $$AB$$ side towards the centre.
A particle of mass 'm' with charge 'q' moving with a uniform speed 'v' normal to a uniform magnetic field 'B', describe a circular path of radius 'r'. Derive expression for
(i) time period of revolution
(ii) kinetic energy of the particle
A magnetic field of $$8\hat{k}mT$$ exerts a force of $$(4.0\hat{i}+3.0\hat{j})\times 10^{-10}N$$ on a particle having a charging $$5\times 10^{-10}C$$ and going in the $$X-Y$$ plane. Find the velocity of the particles.
A proton moves along horizontal line towards observer.What will be the pattern of concentric circular field lines of magnetic field which produced due to its motion.
Concentric circular field lines will be anti-clockwise as seen by observer.
A bar magnet of magnetic moment $$1.5 J T^{1}$$ lies aligned with the direction of a uniform magnetic field of $$0.22 T$$.
What is the amount of work required by an external torque to turn the magnet so as to align its magnetic moment: (i) normal to the field direction, (ii) opposite to the field direction?
A straight, long wire carries a current of $$20\ A$$. Another wire carrying equal current is placed parallel to it. If the force acting on a length of $$10\ cm$$ of the second wire is $$2.0\times 10^{-5}N$$, what is the separation between them?
Force acting on $$10 cm$$ of wire is $$2 \times 10^{-5} N$$
$$\dfrac{dF}{dI} = \dfrac{\mu_0 i_ 1 i_2}{2 \pi d}$$
$$\Rightarrow \dfrac{2 \times 10^{-5}}{10 \times 10^{-2}} = \dfrac{\mu_0 \times 20 \times 20}{2 \pi d}$$
$$\Rightarrow d = \dfrac{4 \pi \times 10^{-7} \times 20 \times 20 \times 10 \times 10^{-2}}{2 \pi \times 2 \times 10^{-5}} = 400 \times 10^{-3} = 0.4 m = 40 cm$$
A coil of $$N$$ turns and radius $$R$$ carries a current $$I$$. It is unwound and rewound to make a square coil of side $$a$$ having same number of turns $$N$$. Keeping the current $$I$$ same find the ratio of the magnetic moments of the square coil and the circular coil.
A uniform magnetic field $$\bar{B}=B_{0}\bar{k}$$ is acting in the region where a circular current carrying loop is placed in x-y plane. Match the columns.
| column I | Column II | ||
| (A) | Equilibrium of loop | (p) | Along z-axis |
| (B) | torque of the loop | (q) | Zero |
| (C) | Magnetic moment of the loop | (r) | Stable |
| (D) | Potential energy of loop | (s) | None of the above |
A current carrying loop along $$x-y$$ plane where magnitude field exist in $$z-$$ direction $$\vec B=\vec B o \hat k$$
vectors $$\vec B$$ and $$\vec A$$ are along same direction
so,
zarque $$=I(\vec B\times \vec A)=0$$
Magnitude energy $$\vec M=I\vec A$$, along $$z-$$axis
Potential energy $$u=-\vec M.\vec B$$ would be $$(*-ve)$$
and $$z=0$$ & $$u < 0$$ implise atable equilibrium
$$\therefore \ $$ combination: $$(A)\to (r)\quad (B)\to (q)\quad (C)\to (p)\quad (D)\to (s)$$
State Ampere's circuital law. Use it to find magnetic field due to an infinity long thin current carrying wire.
Ampere's circuital law states that the line integral of the magnetic field $$\vec{B}$$ around any closed circuit is equal to $$\mu_0$$ (permeability constant) times the total current $$I$$ passing through this closed circuit.
Mathematically,
$$\oint \vec{B}. \vec{dl}=\mu_0 I$$
Consider the figure given above.
Let the current through the long straight wire is $$I$$ and here from the wire at distance $$r$$ at point $$P$$ we have to find the magnetic field .
Taking the circular path as the Ampere's circle then we get that $$dl$$ is parallel to $$B$$ at every place applying the cork screw rule .
Therefore , here applying the Ampere's circuital law we get ,
$$\oint \vec{B}. \vec{dl}=\oint B \,dl\, cos 0^0=B\oint dl=B\times 2\pi r$$
Now here,
$$B2\pi r=\mu_0 I$$
$$\implies B=\dfrac{\mu_0 I}{2\pi r}=\dfrac{\mu_0}{4\pi} \dfrac{2I}{r}$$
A flat circular coil of 100 turns and radius 10 cm carries a current of 1 A. Then the magnetic dipole moment of the coil is_______ A.
A long wire with a small current element of length $$1cm$$ is placed at the origin and carries a current of $$10$$ A long the X-axis. Find out the magnitude and direction of the magnetic field due to the element on the Y-axis at a distance $$0.5$$m from it.
$$Q_1=Q_2=45^o$$ $$\left(\dfrac{0.5}{0.5}=\tan \theta\right)$$
$$Q_1=45$$
$$B=\dfrac{M_0}{4 \pi}\, \dfrac{l}{r}(\sin \phi_1+ \sin \phi_2)$$
$$=\dfrac{M_0}{4\pi}\times \dfrac{10}(0.5\times 10^{-2})\times (\sin 45+ \sin 45)$$
$$=\dfrac{10^{7}\times 10}{0.5 \times 10^{-2}}\times \sqrt2$$
$$B= 2.8 \times 10^{-4 \pi}$$
Magnetic force acting on the charged particle projected perpendicular to magnetic field is proportional to $$r^n$$, where r is radius of circular path. Find n.
'Biot Savart' law of magnetism is analogous to?
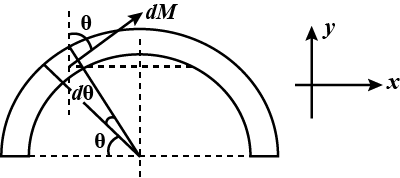
Derive an expression for magnitude of magnetic dipole moment of a revolving electron.
A circular coil of $$300 $$ turns and diameter $$14 cm$$ carries a current of $$15 A$$. Calculate the magnitude of the magnetic dipole moment associated with the coil.
Magnetic moment of a revolving electron let the electron rotate about an axis with angular velocity $$w$$
Angular velcoity $$= w\, rod/s$$
$$w = 2\pi f$$
frequency $$f = \dfrac{w}{2\pi}Hz$$
Rotating charge tends to induced current.
Equivalent current $$=qf = \dfrac{wq}{2\pi}$$
Present case can be thought of as a current-carrying loop
Let the radius be $$a$$
then $$\vec{A} = \pi a^2\hat{n}$$
$$\hat{n}$$- direction perpendicular to rotation
Magnetic moment $$= IA$$
$$= \dfrac{wq}{2\pi} \times \pi a^2$$
$$= \dfrac{wqa^2}{2}$$
for an electron $$q = e = 1.6\times 10^{-19}C$$
$$\therefore $$ Magnetic moment $$= \dfrac{wea^2}{2}$$
Now,
given, $$N = 300, D = 14cm = 14\times 10^{-2}m, i = 15A$$
Magnetic moment $$= NiA$$
$$= Ni\dfrac{\pi}{4}D^2$$
$$= 300\times 10 \times \dfrac{\pi}{4} (14 \times 10^{-2})^2$$
$$M = 69.27Am^2$$
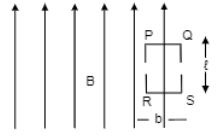
Sometimes we show an idealised magnetic field which is uniform in a given region and falls to zero abruptly. One such field is represented in figure. Using Ampere's law over the path PQRS, show that such a field is not possible.
We know, $$\displaystyle \int B \times dl = \mu_0 i$$. Theoritically $$B = 0$$ at A
If, a current is passed through the loop PQRS, then
$$B = \dfrac{\mu_0 i}{2 (\ell + b)}$$ will exist in its vicinity.
Now, As the $$\vec{B}$$ at A is zero. So there'll be no interaction
However practically this is not true. As a current carrying loop, irrespective of its near about position is always affected by an existing magnetic field.
Two circular coils made of similar wires but of radii 20 and 40 cm are connected in parallel . Find the ratio of the magnetic field at their centers.
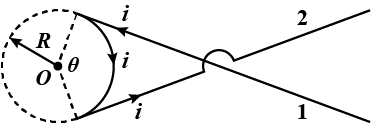
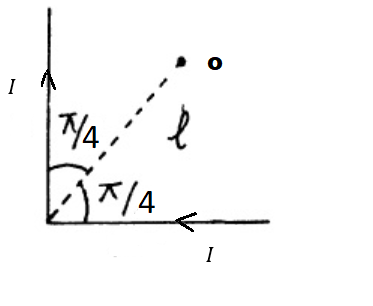
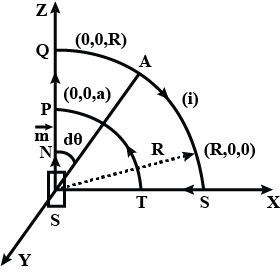
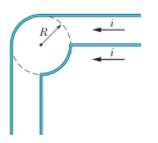
In Figure, two infinitely long wires carry equal currents $$i$$. Each follows a $$90^{\circ}$$ arc on the circumference of the same circle of radius $$R$$. Show that the magnetic field $$\vec{B}$$ at the center of the circle is the same as the field $$\vec{B}$$ a distance $$R$$ below an infinite straight wire carrying a current $$i$$ to the left.
Suppose that $$\pm 4$$ are the limits to the values of $$m_l$$ for an electron in an atom. (a) How many different values of the electrons $$\mu_{orb,z}$$ are possible? (b) What is the greatest magnitude of those possible values? Next, if the atom is in a magnetic field of magnitude $$0.250$$ T, in the positive direction of the z-axis, what are (c) the maximum energy and (d) the minimum energy associated with those
possible values of $$\mu_{orb,z}$$?
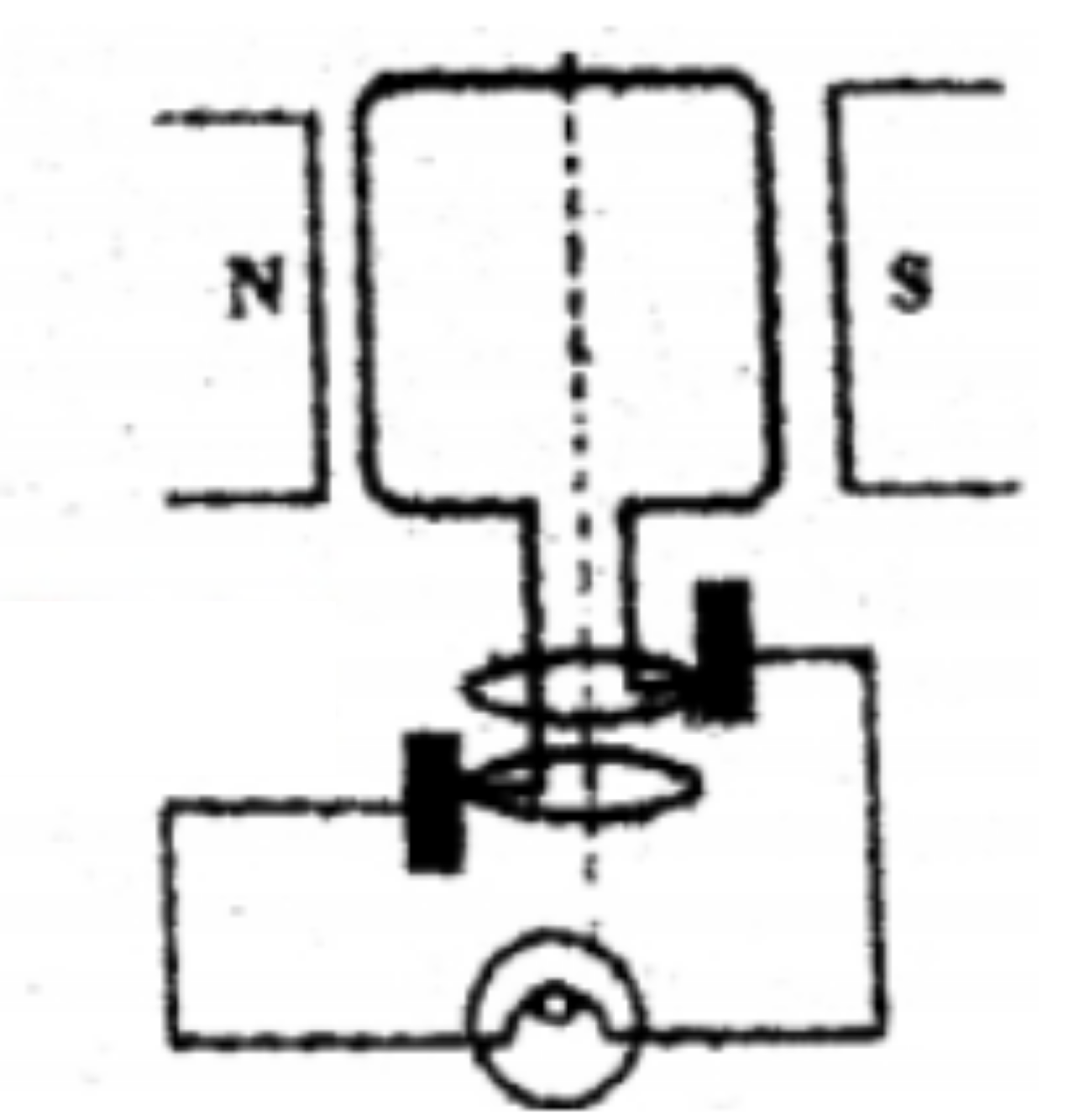
With the help of neat diagram describe how you can generate induced current in the circuit.
The generation of an induced current when a conductor is placed in the region of changing magnetic field is called Electromagnetic Induction. The current only induce in the conductor coil if the magnetic field around and coil changes. This can only happen when:
Magnet moves towards the coil or move away from it.
Coil move toward the magnet or move away from it.
Both move towards each other ( or we can also say loop and magnet move in opposite direction with same speed, magnet moving in $$+x$$ direction and coil moving in $$-x$$ direction.
In the given diagram all these conditions can be shown. And the galvanometer will detect the presence of electric current in the conductor loop. These conditions are the only condition when current will induce in the coil conductor.
Magnet moves towards the coil or move away from it.
Coil move toward the magnet or move away from it.
Both move towards each other ( or we can also say loop and magnet move in opposite direction with same speed, magnet moving in $$+x$$ direction and coil moving in $$-x$$ direction.
In the given diagram all these conditions can be shown. And the galvanometer will detect the presence of electric current in the conductor loop. These conditions are the only condition when current will induce in the coil conductor.
A particle undergoes uniform circular motion of radius $$26.1 mm$$ in a uniform magnetic field. The magnetic force on the particle has a magnitude of $$1.60 \times10^{-17}N$$. What is the kinetic energy of the particle?
Figure shows, in cross section, two long parallel wires that are separated by distance $$d =18.6 cm$$. Each carries $$4.23 A$$, out of the page in wire 1 and into the page in wireIn unit-vector notation, what is the net magnetic field at point $$P$$ at distance $$R =34.2 cm$$, due to the two currents?
Draw the labelled diagram of a moving coil galvanometer. Prove that in a radial magnetic field, the deflection of the coil is directly proportional to the current flowing in the coil.
Moving coil galvanometer: A galvanometer is used to detect current in circuit.
Construction: It consists of a rectanglular coil wound on a non-conducting metallic frame and is suspended by phosphor brone strip between the pole-pieces $$(N$$ and $$S)$$ of a strong permanent magnet.
A soft iron core in cylindrical form is placed between the coil.
One end of coil is attached to suspension wire which also serves as one terminal $$(T_1)$$ of galvanometer. The other end of coil is connected to a loosely coiled strip. Which serves as the other terminal $$(T_2)$$. The other end of the suspension is attached to a torsion head which canbe rotated to set the coil in zero position. A mirror $$(M)$$ is fixed on the phosphor bronze strip by means of which the deflection of the coil is measured by the lamp and scale arrangement. The levelling screws are also provided at the base of the instrument.
The pole pieces of the permanent magnet are cylindrical so that the magnetic field is radial at any position of the coil.
Principle and working: When current $$(I)$$ is passed in the coil, torque $$T$$ acts on the coil, given by
$$T=NIAB\sin \theta$$
Where $$\theta $$ is the angle between the normal to plane of coil and the magnetic field or strength $$B, N$$ is the number of turns in a coil.
A current carrying coil, in the presence of a magnetic field, experience a torque, which
i.e, Deflection, $$\theta \propto T$$ ( Torque)
When the magnetic field is radial, as in the case of cylindrical pole and soft iron core, then in every position of coil in the plane of coil is parallel to the magnetic field lines, so then in every position of coil the plane of the coil, is parallel to the magnetic field lines, so that $$\theta =90^o$$, and $$\sin 90^o=1$$. The coil experiences a uniform coupler.
Deflecting torque, $$T=NIAB$$
If $$C$$ is the torsional rigidity of the wire and is the twist of suspension strip, then resorting torque $$=C\theta$$
For equilibrium, deflecting torque = resorting torque
i.e. $$NIAB=C\theta$$
$$\therefore \theta =\dfrac{NAB}{C}I$$ ....(i)i.e.
$$\theta \propto I$$
Construction: It consists of a rectanglular coil wound on a non-conducting metallic frame and is suspended by phosphor brone strip between the pole-pieces $$(N$$ and $$S)$$ of a strong permanent magnet.
A soft iron core in cylindrical form is placed between the coil.
One end of coil is attached to suspension wire which also serves as one terminal $$(T_1)$$ of galvanometer. The other end of coil is connected to a loosely coiled strip. Which serves as the other terminal $$(T_2)$$. The other end of the suspension is attached to a torsion head which canbe rotated to set the coil in zero position. A mirror $$(M)$$ is fixed on the phosphor bronze strip by means of which the deflection of the coil is measured by the lamp and scale arrangement. The levelling screws are also provided at the base of the instrument.
The pole pieces of the permanent magnet are cylindrical so that the magnetic field is radial at any position of the coil.
Principle and working: When current $$(I)$$ is passed in the coil, torque $$T$$ acts on the coil, given by
$$T=NIAB\sin \theta$$
Where $$\theta $$ is the angle between the normal to plane of coil and the magnetic field or strength $$B, N$$ is the number of turns in a coil.
A current carrying coil, in the presence of a magnetic field, experience a torque, which
i.e, Deflection, $$\theta \propto T$$ ( Torque)
When the magnetic field is radial, as in the case of cylindrical pole and soft iron core, then in every position of coil in the plane of coil is parallel to the magnetic field lines, so then in every position of coil the plane of the coil, is parallel to the magnetic field lines, so that $$\theta =90^o$$, and $$\sin 90^o=1$$. The coil experiences a uniform coupler.
Deflecting torque, $$T=NIAB$$
If $$C$$ is the torsional rigidity of the wire and is the twist of suspension strip, then resorting torque $$=C\theta$$
For equilibrium, deflecting torque = resorting torque
i.e. $$NIAB=C\theta$$
$$\therefore \theta =\dfrac{NAB}{C}I$$ ....(i)i.e.
$$\theta \propto I$$
If an electron in an atom has an orbital angular
momentum with $$m=0$$, what are the components (a) $$L_{orb,z}$$, and
(b) $$\mu_{orb,z}$$? If the atom is in an external magnetic field that has a magnitude $$35\, mT$$, and is directed along the z-axis, what are (c) the
energy $$U_{orb}$$ associated with and (d) the energy $$U_{spin}$$ associated
with $$\vec \mu_s$$? If, instead, the electron has, what are (e) $$L_{orb,z}$$,
(f)$$\mu_{orb,z}$$, (g)$$U_{orb}$$, and (h)$$U_{spin}$$?
Answer the following question:
Write the expression for the force $$\vec F$$ acting on a particle of mass $$m$$ and charge $$q$$ moving with velocity $$\vec V$$ in a magnetic field $$\vec B$$ Under what conditions will it move in a circular path?
Answer the following question:
Draw the magnetic field lines due to two straight, long, parallel conductors carrying currents $$I_1$$ and $$I_2$$ in the same direction. Write an expression for the force acting per unit length on one conductor due to other. Is this force attractive or repulsive?
When a charged particle moving with velocity $$\vec{V}$$ is subjected to magnetic field $$\vec{B}$$ the force acting on it is non-zero. Would the particle gain any energy?
Answer the following question:
Show that the kinetic energy of the particle moving in magnetic field remains constant.
Describe the motion of a charged particle in a cyclotron if the frequency of the radio frequency (rf) field were doubled.
Show that the magnetic field $$B$$ at a point in between the plates of a parallel plate capacitor during charging is $$\cfrac { { \mu }_{ 0 }{ \varepsilon }_{ 0 }r }{ 2 } \cfrac { dE }{ dt } $$
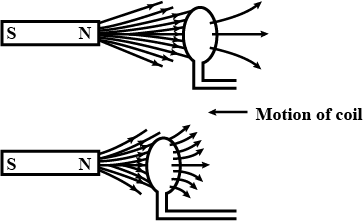
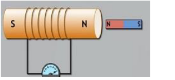
A copper coil is connected to a galvanometer. What would happen if a bar magnet is
(i) pushed into the coil with its north pole entering first
(ii) held at rest inside the coil
(iii) pulled out again?
Name the scientist who discovered the relationship between electric current and magnetic field.
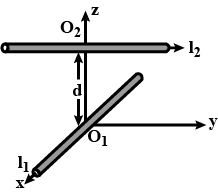
Two long wires carrying current $$I_{1}$$ and $$I_{2}$$ are arranged as shown in Fig. the one carrying current $$I_{1}$$ is along is the X-axis. the other carrying current $$I_{2}$$ is along a line parallel to the force exerted at $$o_{2}$$ because of the wire along the x-axis. Find the force exerted by the wire at $$O_2$$ along the x axis.
Use (i) the Ampere's law for $$H $$ and (ii) continuity of lines of $$ B$$, to conclude that inside a bar magnet, (a) lines of $$ H$$ run from the N-pole to S- pole, while (b) lines of $$ B $$ must run from the S-pole to N-pole.
Consider an Amperian loop C inside and outside the magnet NS on side PQ of magnet then
$$ \int_{P}^{Q}\underset{H}{\rightarrow }.\underset{dl}{\rightarrow }$$
$$ \int_{P}^{Q}\underset{H}{\rightarrow }.\underset{dl}{\rightarrow }$$
$$=\int_{Q}^{P}\dfrac{\underset{B}{\rightarrow }}{u_{0}}\underset{dl}{\rightarrow } $$
(a) What kind of energy change takes place when a magnet is moved towards a coil having a galvanometer at its ends?
(b) Name the phenomenon
A bar magnet is placed in a uniform magnetic field such that its magnetic moment makes angle a with the direction of $$\overset{\rightarrow}{B}$$. Derive a expression for its potential energy.
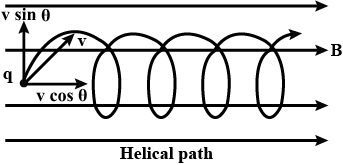
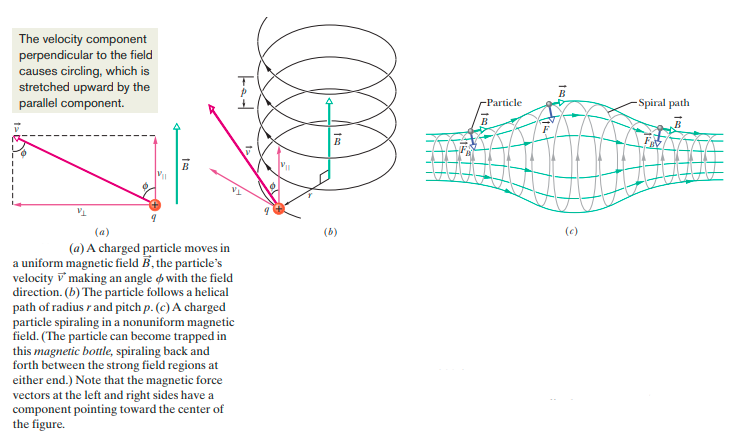
Any charged particle enters in a uniform magnetic field at an angle $$\theta$$ (Where $${0}^{o}< \theta < {90}^{o}$$). How will be the path the particle? Calculate its pitch.
Motion of Charged Particle when $${0}^{o}< \theta < {90}^{o}$$
When a charged particle enters in the magnetic field at an angle $$\theta$$ other than $${0}^{o}$$ and $${90}^{o}$$, then its velocity $$v$$ can be resolved in two perpendicular components as under:
(i) $$v\cos \theta$$- along the magnetic field
(ii) $$v\sin \theta$$- perpendicular to magnetic field
Due to the component $$v\cos \theta$$ the path will be straight line while due to component $$v\sin \theta$$, the path will be circular. Hence the resultant path of the particle will become 'Helical' as shown in the figure. The radius of this helical path,
$$r=\cfrac{mv\sin \theta}{qB}$$
and time period of this circular motion
$$T=\cfrac { 2\pi r }{ v\sin { \theta } } =\cfrac { 2\pi r }{ v\sin { \theta } } \times \cfrac { mv\sin { \theta } }{ qB } $$
or $$T=\cfrac{2\pi m}{qB}$$
and the frequency $$f=\cfrac{1}{T}=\cfrac{qB}{2\pi m}$$
Pitch of the Helical Path: The distance travelled in one time period along the axis of the helical path is called the pitch of the path. Therefore,
Pitch $$=v\cos \theta \times T$$
or pitch $$=v\cos \theta \times \cfrac{2\pi m}{B}$$
or pitch $$=\cfrac{2\pi mv\cos \theta}{qB}$$
When a charged particle enters in the magnetic field at an angle $$\theta$$ other than $${0}^{o}$$ and $${90}^{o}$$, then its velocity $$v$$ can be resolved in two perpendicular components as under:
(i) $$v\cos \theta$$- along the magnetic field
(ii) $$v\sin \theta$$- perpendicular to magnetic field
Due to the component $$v\cos \theta$$ the path will be straight line while due to component $$v\sin \theta$$, the path will be circular. Hence the resultant path of the particle will become 'Helical' as shown in the figure. The radius of this helical path,
$$r=\cfrac{mv\sin \theta}{qB}$$
and time period of this circular motion
$$T=\cfrac { 2\pi r }{ v\sin { \theta } } =\cfrac { 2\pi r }{ v\sin { \theta } } \times \cfrac { mv\sin { \theta } }{ qB } $$
or $$T=\cfrac{2\pi m}{qB}$$
and the frequency $$f=\cfrac{1}{T}=\cfrac{qB}{2\pi m}$$
Pitch of the Helical Path: The distance travelled in one time period along the axis of the helical path is called the pitch of the path. Therefore,
Pitch $$=v\cos \theta \times T$$
or pitch $$=v\cos \theta \times \cfrac{2\pi m}{B}$$
or pitch $$=\cfrac{2\pi mv\cos \theta}{qB}$$
Two long parallel wires are $$4cm$$ apart. In them current $$I$$ and $$3I$$ are flowing in the same direction. Where would be the magnetic field generated by both should be zero?
Let at point $$P$$ magnetic field is zero
$${ \vec { B } }_{ 1 }+{ \vec { B } }_{ 2 }=0$$
$${ \vec { B } }_{ 1 }$$ and $${ \vec { B } }_{ 2 }$$ are in opposite direction,
$${ \vec { B } }_{ 1 }={ \vec { B } }_{ 2 }$$
$$\cfrac { { \mu }_{ 0 }{I}_{1} }{ 2\pi {d}_{1} } =\cfrac { { \mu }_{ 0 }{I}_{2} }{ 2\pi {d}_{2} }$$
$$\cfrac{I}{x}=\cfrac{3I}{(4-x)}$$
$$\cfrac{1}{x}=\cfrac{3}{4-x}$$
$$3x=4-x$$
$$4x=4$$
$$x=1$$
So, at distance of $$1cm$$ from left current carrying wire, the net magnetic is zero.
$${ \vec { B } }_{ 1 }+{ \vec { B } }_{ 2 }=0$$
$${ \vec { B } }_{ 1 }$$ and $${ \vec { B } }_{ 2 }$$ are in opposite direction,
$${ \vec { B } }_{ 1 }={ \vec { B } }_{ 2 }$$
$$\cfrac { { \mu }_{ 0 }{I}_{1} }{ 2\pi {d}_{1} } =\cfrac { { \mu }_{ 0 }{I}_{2} }{ 2\pi {d}_{2} }$$
$$\cfrac{I}{x}=\cfrac{3I}{(4-x)}$$
$$\cfrac{1}{x}=\cfrac{3}{4-x}$$
$$3x=4-x$$
$$4x=4$$
$$x=1$$
So, at distance of $$1cm$$ from left current carrying wire, the net magnetic is zero.
Show that in a cyclotron inside the dee, the time taken to complete half-circular path is not dependent on the radius of the path.
Protons are accelerated in a cyclotron so that the maximum curvature radius of their trajectory is equal to $$r = 50\ cm$$. Find : (a) the kinetic energy of the protons when the acceleration is completed if the magnetic induction in the cyclotron is $$B = 1.0\ T$$;
(b) the minimum frequency of the cyclotron's oscillator at which the kinetic energy of the protons amounts to $$T = 20\ MeV$$ by the end of acceleration.
Find the interaction force of two coils with magnetic moments $$p_{1m} = 4.0\ mA . m^{2}$$ and $$p_{2m} = 6.0\ mA.m^{2}$$ and collinear axes if the separation between the coils is equal to $$l = 20\ cm$$ which exceeds considerably their linear dimensions.
Find the magnetic moment of a thin round loop with current if the radius of the loop is equal to $$R = 100\ mm$$ and the magnetic induction at its centre is equal to $$B = 6.0\ \mu T$$.
Up to what values of kinetic energy does the period of revolution of an electron and a proton in a uniform magnetic field exceed that at non-relativistic velocities by $$\eta = 1.0\%$$?
An electron starts moving in a uniform electric field of strength $$E = 10\ kV/cm$$. How soon after the start will the kinetic energy of the electron become equal to its rest energy?
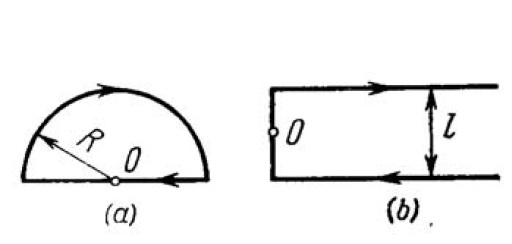
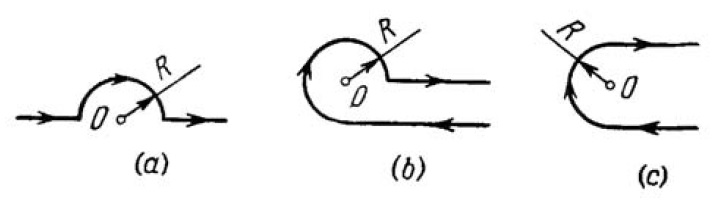
Find the magnitude and direction of a force vector acting on a unit length of a thin wire, carrying a current $$I = 8.0\ A$$, at point $$O$$, if the wire is bent as shown in
(a) Fig. a, with curvature radius $$R = 10\ cm$$;
(b) Fig. b, the distance between the long parallel segments of the wire being equal to $$l = 20\ cm$$.
In a betatron the magnetic induction on an equilibrium orbit with radius $$r = 20\ cm$$ varies during a time interval $$\triangle t = 1.0\ ms$$ at parctically constant rate from zero to $$B = 0.40\ T$$. Find the energy acquired by the electron per revolution.
The Biot-Savart Law(3)
Calculate the magnitude of the magnetic field at a point $$25.0 \,cm$$ from a long, thin conductor carrying a current of $$2.00 \,A$$.
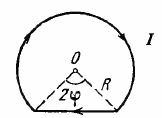
A current $$I = 5.0\ A$$ flows along a thin wire shaped as shown in Fig. The radius of a curved part of the wire is equal to $$R = 120\ mm$$, the angle $$2\varphi = 90^{\circ}$$. Find the magnetic induction of the field at the point $$O$$.
Two protons move parallel to each other with an equal velocity $$v=300\ \text{km/s}$$. The ratio of forces of magnetic and electrical interaction of the protons is given as $$x\times10^{-6}.$$ Find $$x$$
An $$\alpha-\text{particle}$$ is describing a circle of radius $$0.45\ \text{m}$$ in a field of magnetic induction of $$1.2\ \text{T}.$$ If its kinetic energy is $$14.3\times 10^{X} \in eV\}$$. The mass of $$\alpha-\text{particle}$$ is $$6.8\times 10^{-27}\ \text{kg}$$ and its charge is twice the charge of proton, i.e., $$3.2\times 10^{-19}\ \text{C}$$. Find out the value of X?
Calculate the magnetic moment of a thin wire with a current $$I=0.8\ A$$, wound tightly on a half a toroid. The diameter of the cross-section of the toroid is equal to $$d=5.0\ cm$$, the number of turns is $$N=500$$.
The magnetic moment of circular current is given by $$AI$$, $$I$$ being the circulating current and $$A$$ is the area of cross-section; the direction is perpendicular to the plane of current. Now, for an element of toroid of length $$rd \theta$$, its magnetic moment is along the direction of arrow as shown, of magnitude (perpendicular to its cross-section)$$=$$ current $$\times$$ area $$\times $$ number of turns in the length $$rd \theta$$.
$$dM=I\dfrac {\pi d^2}{4} \left(\dfrac {N}{\pi r}rd\theta \right )=\dfrac {N}{4}d^2Id\theta$$
Resolving dM into components along x and y, we get $$d M \sin\theta$$ and $$d M \cos\theta$$, components along y from neighboring elements cancel out to zero, and components along x are added. So
$$\displaystyle M=\int dM sin\theta=\int_0^{\pi}\dfrac {N}{4}\cdot d^2Isin\theta d\theta=\frac {Nd^2I}{2}$$
Putting the given values, we get $$M=5\ Am^2$$.
$$dM=I\dfrac {\pi d^2}{4} \left(\dfrac {N}{\pi r}rd\theta \right )=\dfrac {N}{4}d^2Id\theta$$
Resolving dM into components along x and y, we get $$d M \sin\theta$$ and $$d M \cos\theta$$, components along y from neighboring elements cancel out to zero, and components along x are added. So
$$\displaystyle M=\int dM sin\theta=\int_0^{\pi}\dfrac {N}{4}\cdot d^2Isin\theta d\theta=\frac {Nd^2I}{2}$$
Putting the given values, we get $$M=5\ Am^2$$.
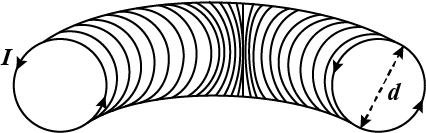
A current I flows in a rectangularly shaped wire whose center lies at $$(x_0, 0, 0)$$ and whose vertices are located at the point $$A(x_0+d, -a, -b), B(x_0-d, a, -b), C(x_0-d, a, +b)$$, and $$D(x_0+d, -a, +b)$$ respectively. Assume that a, b, d $$< < x_0$$. Find the magnitude of magnetic dipole moment vector of the rectangular wire frame in J/T. (Given: $$b=10 m, I=0.01 A, d=4m, a=3m$$.)
Magnetic dipole moment, $$\vec{m}=I\vec{S} $$ where S is the area of rectangular frame.
Here, $$\vec{S}=\vec{BA}\times \vec{AD}=[(A_x-B_x)\hat i+(A_y-B_y)\hat j+(A_z-B_z)\hat k]\times [(D_x-A_x)\hat i+(D_y-A_y)\hat j+(D_z-A_z)\hat k]$$
$$=[(x_0+d-x_0+d)\hat i+(-a-a)\hat j+(-b+b)\hat k]\times [(x_0+d-x_0-d)\hat i+(-a+a)\hat j+(b+b)\hat k]$$
$$=(2d\hat i-2a\hat j)\times (2b)\hat k=-4bd\hat j-4ba\hat i=-4b(a\hat i+d\hat j)$$
Thus, $$ \vec{m}=-4bI(a\hat i+d\hat j)$$
$$|\vec{m}|=4bI\sqrt{a^2+d^2}=4(10)(0.01)\sqrt{3^2+4^2}=2 J/T$$
Here, $$\vec{S}=\vec{BA}\times \vec{AD}=[(A_x-B_x)\hat i+(A_y-B_y)\hat j+(A_z-B_z)\hat k]\times [(D_x-A_x)\hat i+(D_y-A_y)\hat j+(D_z-A_z)\hat k]$$
$$=[(x_0+d-x_0+d)\hat i+(-a-a)\hat j+(-b+b)\hat k]\times [(x_0+d-x_0-d)\hat i+(-a+a)\hat j+(b+b)\hat k]$$
$$=(2d\hat i-2a\hat j)\times (2b)\hat k=-4bd\hat j-4ba\hat i=-4b(a\hat i+d\hat j)$$
Thus, $$ \vec{m}=-4bI(a\hat i+d\hat j)$$
$$|\vec{m}|=4bI\sqrt{a^2+d^2}=4(10)(0.01)\sqrt{3^2+4^2}=2 J/T$$
A charged particle passes through a region that could have electric field only or magnetic field only or both electric and magnetic fields or none of the fields. Match Column I with Column II
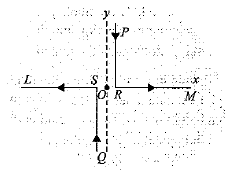
A pair of stationary and infinitely long bent wires is placed in the x-y plane as shown in figure. Each wire carries current of $$10A$$. Segments $$L$$ and $$M$$ are along the x-axis.Segments $$P$$ and $$Q$$ are parallel to the y-axis such that $$OS=OR=0.02m$$. Find the magnitude and direction of the magnetic induction at origin $$O$$ in the form of $$x\times 10^{-4}$$. What is x.
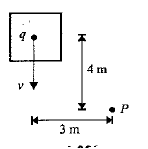
An elevator carrying a charge of $$0.5\ C$$ is moving down with a velocity of $$5\times { 10 }^{ 3 }\ m$$ $${ s }^{ -1 }$$. The elevator is $$4\ m$$ from the bottom and $$3\ m$$ horizontally form $$P$$ as shown in figure. What magnetic field (in $$\mu T$$) does it produce at point $$P$$?
Two protons move parallel to each other with an equal velocity $$v=300km$$ $${s}^{-1}$$. Find the ratio of forces of magnetic and electric interaction of the protons. Give your answer after multiplying by $$10^6$$.
Challenge Problems(80)
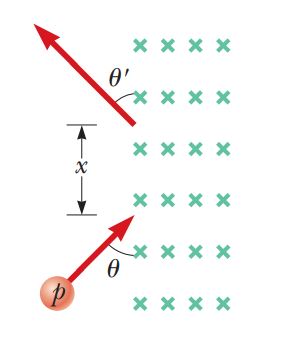
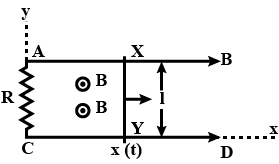
A proton moving in the plane of the page has a kinetic energy of $$6.00 \,MeV$$. A magnetic field of magnitude $$B = 1.00 \,T$$ is directed into the page. The proton enters the magnetic field with its velocity vector at an angle $$\theta = 45.0^{o}$$ to the linear boundary of the field as shown in Figure.
(a) Find $$x$$, the distance from the point of entry to where the proton will leave the field.
(b) Determine $$\theta$$, the angle between the boundary and the proton's velocity vector as it leaves the field.
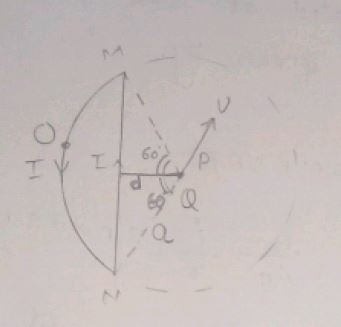
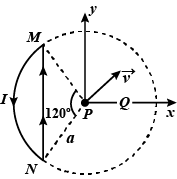
A wire loop carrying current is placed in the x-y plane as shown in figure. If a particle with charge $$+Q$$ and mass $$m$$ is placed at the center $$P$$ and given a velocity $$\vec { v } $$ along $$NP$$, If its instantaneous acceleration is given by $$\vec { a } ={ 10 }^{ -x }\cfrac { 2QvI }{ a } \left[ \sqrt { 3 } -\cfrac { \pi }{ 3 } \right] $$. Find x.
$$\cos { 60 } =\cfrac { d }{ a } $$
$$d=a\cos { 60 } $$
Magnetic field at Point P due to straight wire
$$MN={ B }_{ MN }$$
$${ B }_{ MN }=\cfrac { { \mu }_{ 0 } }{ 4\pi } \cfrac { I }{ d } \left[ \sin { 60 } +\sin { 60 } \right] $$
$$=\cfrac { { \mu }_{ 0 } }{ 4\pi } \cfrac { I }{ a\cos { 60 } } \times \sin { 60 } $$
$$=\cfrac { { \mu }_{ 0 } }{ 4\pi } \cfrac { I }{ a } \times 2\sqrt { 3 } \bigotimes $$
Circular arc$${ B }_{ MON }=\cfrac { \theta }{ 2\pi } \cfrac { { \mu }_{ 0 }I }{ 2a } =\cfrac { 2{ \pi }/{ 3 } }{ 2\pi } \cfrac { { \mu }_{ 0 }I }{ 2a } $$
$$=\cfrac { { \mu }_{ 0 } }{ 4\pi } \cfrac { I }{ a } \times \cfrac { 2\pi }{ 3 } \bigodot $$
Net magnetic field$$={ B }_{ MN }-{ B }_{ MON }$$
$$=\cfrac { { \mu }_{ 0 } }{ 4\pi } \cfrac { I }{ a } \times 2\sqrt { 3 } -\cfrac { { \mu }_{ 0 } }{ 4\pi } \cfrac { I }{ a } \times \cfrac { 2\sqrt { 3 } }{ 3 } \pi $$
$$=\cfrac { { \mu }_{ 0 } }{ 2\pi } \cfrac { I }{ a } \left[ \sqrt { 3 } -\cfrac { \pi }{ 3 } \right] $$
Force on charge$$=Q\vec { } \times \vec { } $$
$$=QVB\sin { } $$
$$=QV\cfrac { { \mu }_{ 0 } }{ 2\pi } \cfrac { I }{ a } \left[ \sqrt { 3 } -\cfrac { \pi }{ 3 } \right] $$
$$m\times a=\cfrac { { \mu }_{ 0 } }{ 4\pi } \cfrac { 2QVI }{ a } \left[ \sqrt { 3 } -\cfrac { \pi }{ 3 } \right] $$
$$a={ 10 }^{ -7 }\times \cfrac { 2QVI }{ am } \left[ \sqrt { 3 } -\cfrac { \pi }{ 3 } \right] $$
But $$a={ 10 }^{ -7 }\times \cfrac { 2QVI }{ am } \left[ \sqrt { 3 } -\cfrac { \pi }{ 3 } \right] $$
So, $$x=7$$
$$d=a\cos { 60 } $$
Magnetic field at Point P due to straight wire
$$MN={ B }_{ MN }$$
$${ B }_{ MN }=\cfrac { { \mu }_{ 0 } }{ 4\pi } \cfrac { I }{ d } \left[ \sin { 60 } +\sin { 60 } \right] $$
$$=\cfrac { { \mu }_{ 0 } }{ 4\pi } \cfrac { I }{ a\cos { 60 } } \times \sin { 60 } $$
$$=\cfrac { { \mu }_{ 0 } }{ 4\pi } \cfrac { I }{ a } \times 2\sqrt { 3 } \bigotimes $$
Circular arc$${ B }_{ MON }=\cfrac { \theta }{ 2\pi } \cfrac { { \mu }_{ 0 }I }{ 2a } =\cfrac { 2{ \pi }/{ 3 } }{ 2\pi } \cfrac { { \mu }_{ 0 }I }{ 2a } $$
$$=\cfrac { { \mu }_{ 0 } }{ 4\pi } \cfrac { I }{ a } \times \cfrac { 2\pi }{ 3 } \bigodot $$
Net magnetic field$$={ B }_{ MN }-{ B }_{ MON }$$
$$=\cfrac { { \mu }_{ 0 } }{ 4\pi } \cfrac { I }{ a } \times 2\sqrt { 3 } -\cfrac { { \mu }_{ 0 } }{ 4\pi } \cfrac { I }{ a } \times \cfrac { 2\sqrt { 3 } }{ 3 } \pi $$
$$=\cfrac { { \mu }_{ 0 } }{ 2\pi } \cfrac { I }{ a } \left[ \sqrt { 3 } -\cfrac { \pi }{ 3 } \right] $$
Force on charge$$=Q\vec { } \times \vec { } $$
$$=QVB\sin { } $$
$$=QV\cfrac { { \mu }_{ 0 } }{ 2\pi } \cfrac { I }{ a } \left[ \sqrt { 3 } -\cfrac { \pi }{ 3 } \right] $$
$$m\times a=\cfrac { { \mu }_{ 0 } }{ 4\pi } \cfrac { 2QVI }{ a } \left[ \sqrt { 3 } -\cfrac { \pi }{ 3 } \right] $$
$$a={ 10 }^{ -7 }\times \cfrac { 2QVI }{ am } \left[ \sqrt { 3 } -\cfrac { \pi }{ 3 } \right] $$
But $$a={ 10 }^{ -7 }\times \cfrac { 2QVI }{ am } \left[ \sqrt { 3 } -\cfrac { \pi }{ 3 } \right] $$
So, $$x=7$$
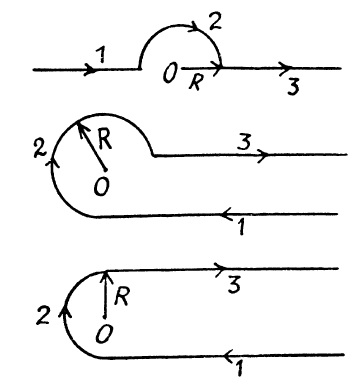
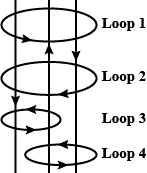
Three wires are carrying same constant current $$i$$ indifferent directions. Four loops enclosing the wires in different manners are shown in figure. The direction of $$d\vec { l } $$ is shown in figure.
A wire carrying current $$i$$ has the configuration shown in the figure. Two semi-infinite straight sections, each tangent to the same circle, are connected by a circular arc, of angle $$\theta$$, along the circumference of the circle, with all sections lying in the same plane. What must $$\theta$$ (in rad) be in order for $$B$$ to be zero at the center of the circle?
Magnetic field at $$O$$ die to wire 1 is
$$\vec { { B }_{ 1 } } =\cfrac { { \mu }_{ 0 } }{ 4\pi R } \bigodot $$
and that due to wire 2 is
$$\vec { { B }_{ 2 } } =\cfrac { { \mu }_{ 0 } }{ 4\pi R } \bigodot $$
$$B=\vec { { B }_{ 1 } } +\vec { { B }_{ 2 } } =\cfrac { { \mu }_{ 0 } }{ 2\pi R } \bigodot $$
Magnetic field at the centre due to circular arc subtending angle $$\theta$$ at the centre is given by
$$\vec { { B }_{ arc } } =\cfrac { { \mu }_{ 0 } }{ 2R } \left( \cfrac { \theta }{ 2\pi } \right) \bigotimes $$
If $$\vec { { B }_{ net } } =0\quad \vec { B } +\vec { { B }_{ arc } } =0\quad $$
$$\Rightarrow \vec { B } =-\vec { { B }_{ arc } } $$
$$\Rightarrow \cfrac { { \mu }_{ 0 } }{ 2\pi R } \bigodot =-\cfrac { { \mu }_{ 0 }i }{ 2R } \left( \cfrac { \theta }{ 2\pi } \right) \bigotimes $$
$$\Rightarrow \cfrac { { \mu }_{ 0 } }{ 2\pi R } =\cfrac { { \mu }_{ 0 }i }{ 2R } \left( \cfrac { \theta }{ 2\pi } \right) \bigotimes \Rightarrow \quad \cfrac { 1 }{ \pi } =\cfrac { \theta }{ 2\pi } \Rightarrow \quad \theta =2rad$$
$$\vec { { B }_{ 1 } } =\cfrac { { \mu }_{ 0 } }{ 4\pi R } \bigodot $$
and that due to wire 2 is
$$\vec { { B }_{ 2 } } =\cfrac { { \mu }_{ 0 } }{ 4\pi R } \bigodot $$
$$B=\vec { { B }_{ 1 } } +\vec { { B }_{ 2 } } =\cfrac { { \mu }_{ 0 } }{ 2\pi R } \bigodot $$
Magnetic field at the centre due to circular arc subtending angle $$\theta$$ at the centre is given by
$$\vec { { B }_{ arc } } =\cfrac { { \mu }_{ 0 } }{ 2R } \left( \cfrac { \theta }{ 2\pi } \right) \bigotimes $$
If $$\vec { { B }_{ net } } =0\quad \vec { B } +\vec { { B }_{ arc } } =0\quad $$
$$\Rightarrow \vec { B } =-\vec { { B }_{ arc } } $$
$$\Rightarrow \cfrac { { \mu }_{ 0 } }{ 2\pi R } \bigodot =-\cfrac { { \mu }_{ 0 }i }{ 2R } \left( \cfrac { \theta }{ 2\pi } \right) \bigotimes $$
$$\Rightarrow \cfrac { { \mu }_{ 0 } }{ 2\pi R } =\cfrac { { \mu }_{ 0 }i }{ 2R } \left( \cfrac { \theta }{ 2\pi } \right) \bigotimes \Rightarrow \quad \cfrac { 1 }{ \pi } =\cfrac { \theta }{ 2\pi } \Rightarrow \quad \theta =2rad$$
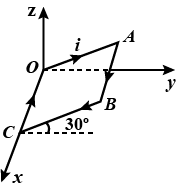
Find the magnetic moment of the current carrying loop OABCO shown in figure.
Given that , i = 4.0 A, OA=20 cm and AB =10 cm.
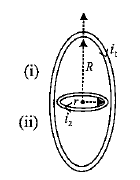
A coil of radius $$R$$ carries current $${i}_{1}$$. Another concentric coil of radius $$r(r<<R)$$ carries current $${i}_{2}$$. Places of two coils are mutually perpendicular and both the coils are free to rotate about common diameter. If the maximum kinetic energy of smaller coil when both are released is $$\cfrac { { \mu }_{ 0 }{ i }_{ 1 }{ i }_{ 2 }\pi { r }^{ 2 }MR }{ X{ \left( { MR }^{ 2 }+{ mr }^{ 2 } \right) } } $$. Find X?Masses of coils are $$M$$ and $$m$$, respectively.
A conductor carries a constant current I along the closed path abcdefgha involving 8 of the 12 edges each of length l.Find the magnetic dipole moment of the closed path. The answer is $$M=xI{l}^{2}\hat{j}$$ then x is
$$Area=l\times l=l^2$$
For make closed loops we assumed that current along wire ad,cf,lh & bg flows in opposite direction which make the net current in that wires zeroWe know that
$$\left| \vec { M } \right| =NIA$$ and its direction is determined by right hand screw rule
So,
$$\vec { { M }_{ abcda } } =I{ l }^{ 2 }\left( \hat { -k } \right) \quad \left( N=1 \right) $$
$$\vec { { M }_{ aefcd } } =I{ l }^{ 2 }\left( \hat { i } \right) $$
$$\vec { { M }_{ efghe } } =I{ l }^{ 2 }\left( \hat { k } \right) $$
$$\vec { { M }_{ habgh } } =I{ l }^{ 2 }\left( \hat { -i } \right) $$
$$\vec { { M }_{ adeha } } =I{ l }^{ 2 }\hat { j } $$
$$\vec { { M }_{ bcfgh } } =I{ l }^{ 2 }\hat { j } $$
$$\vec { { M }_{ circuit } } =\sum { \vec { { M }_{ loops } } } $$
$$=I{ l }^{ 2 }\left( \hat { -k } \right) +I{ l }^{ 2 }\hat { i } $$
$$I{ l }^{ 2 }(\hat { k } )+I{ l }^{ 2 }(\hat { i } )+I{ l }^{ 2 }\hat { j } +I{ l }^{ 2 }\hat { j } $$
$$\vec { { M }_{ circuit } } =2I{ l }^{ 2 }\hat { j } $$
$$x=0,y=0,z=+0.500 m$$
Find $$x$$ such that $$x=100\times{F}_{2}$$
A bar magnet of magnetic moment $$2.0A-{m}^{2}$$ is free to rotate about a vertical axis through its centre. The magnet is released from rest from the east-west position. The kinetic energy of the magnet as it takes the north-south position is found to be $$\alpha\times {10}^{-8}J$$, where $$\alpha$$ and $$\beta$$ are the single digit integers. Then find the value of $$\alpha/ \beta$$. The horizontal component of the earth's magnetic field is $$B=25\mu T$$.Earth's magnetic field is from south to north.
Potential energy of bar magnet is given by
$$U=-\vec{M}*\vec{B}$$
initial angle between $$\vec{M}$$ and $$ \vec{B}=90^{\circ}$$
Final angle between $$\vec{M}$$ and $$ \vec{B}=0^{\circ}$$
$$\therefore U_{i}=-MBcos90^{\circ}=0$$
$$U_{f}=-MBcos0^{\circ}=-MB$$
$$\therefore \Delta U=U_{f}-U_{i}=-MB$$
and hence work done $$=-MB$$
$$=-2*25*10^{-6}$$
$$-5*10^{-5}J$$
$$\therefore $$ KE gained by magnet
$$=5*10^{-5}J$$
in question KE=$$\alpha *10^{-\beta }$$
$$\therefore \alpha =5 , \beta =5$$
$$\therefore \frac{\alpha }{\beta }=1$$
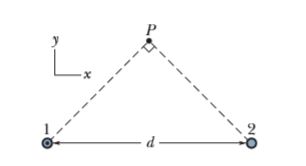
A pair of point charges,$$q=+4.00\mu C$$ and $${q}^{'}=-1.50\mu C$$,are moving in a reference frame as shown in figure.At this instant, the magnitude of the magnetic field produced at the origin is 164$$\times10^{-x}$$. Find the value of x. (Take $$v=2.00\times {10}^{5}m/s$$ and $${v}^{'}=8.00\times {10}^{5}m/s$$.)
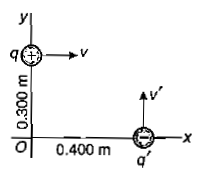
x=0.500 m,y=0.500m,z=0
A straight magnetised wire of magnetic moment '$$M$$' is bent as shown. Find resultant magnetic moment in each case.
An electron enters perpendicularly to a uniform magnetic field $$0.1N/amp-m$$ at a speed of $${ 10 }^{ 5 }m/s$$. Calculate the Lorentz force on the electron.
(a) Write using Biot - Savart Law, the expression for magnetic field $$\vec B$$ due to an element $$\vec {dl}$$ carrying current $$I$$ at a distance $$\vec r$$ from it in a vector form.
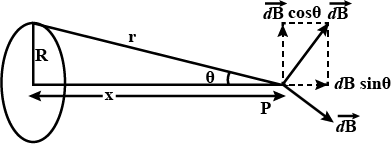
Hence derive the expression for the magnetic field due to a current carrying loop of radius $$R$$ at a point P distant $$x$$ from its centre along the axis of the loop.
(b) Explain how Biot - Savart law enables one to express the Ampere's circuital law in the integral form, viz.,
$$\vec B . \vec {dl} = \mu_o I$$
where $$I$$ is the total current passing through the surface.
(a)
According to Biot-Savart Law, magnetic field due to a current carrying element dl is:
$$\vec {dB} = \dfrac{\mu_o I}{4 \pi r^3} (\vec {dl} \times \vec r)$$
The magnetic field due to a current carrying circular loop is shown in the figure. Vertical components of the magnetic field cancel out by the diametrically opposite end on the wire.
Horizontal component due to an element dl is given by:
$$dB = \dfrac{\mu_o I}{4 \pi r^2}sin \theta dl$$
$$dB = \dfrac{ \mu_o IR}{4 \pi r^3} dl$$
$$\int dB = \dfrac{\mu_o I R}{4 \pi r^3} \int dl$$
$$B = \dfrac{\mu_o I R }{ 4 \pi (R^2+x^2)^{3/2}} 2 \pi R$$
$$B = \dfrac{\mu_o I R^2}{2(R^2+x^2)^{3/2}}$$
(b)
From Biot-Savart Law, it can be concluded that the magnetic field around an infinitely long current carrying conductor is
$$B = \dfrac{\mu_o I}{2 \pi r}$$
or $$B \times 2 \pi r = \mu_o I$$
$$\int B.dl = \mu_o I$$
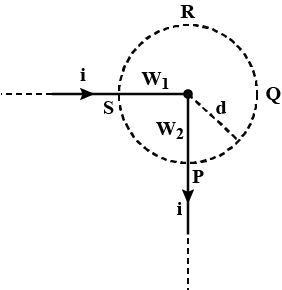
Figure shows a long wire bent at the middle to form a right angle. Show that the magnitudes of the magnetic fields at the points $$Q$$ and $$R$$ are unequal and find these magnitudes. The wire $$w_{1}$$ and the circumference circle are coplanar and $$w_{2}$$ is perpendicular to plane of paper. Also find the ratio of field at $$Q$$ and $$R$$.
An electron is projected horizontally with a kinetic energy of $$10keV$$. A magnetic field of strength $$1.0\times {10}^{-7}T$$ exists in the vertically upward direction. (a) Will the electron deflect towards right or towards left of its motion ? (b) Calculate the sideways deflection of the electron in travelling through $$1m$$. Make appropriate approximations.
$$\begin{array}{l} K.E=10KeV=1.6\times { 10^{ -15 } }J,\, \\ \vec { B } ={ 10^{ -7 } }T \\ By\ right-hand rule, the\, electron\, will\, be\, deflected\, towards\, left. \\ \dfrac { 1 }{ 2 } m{ v^{ 2 } }=K.E \\ v=\sqrt { \dfrac { { KE\times 2 } }{ m } } \\ F=qvB \\ a=\dfrac { { qvB } }{ { { m_{ e } } } } \\ Applying\, s=ut+\dfrac { 1 }{ 2 } a{ t^{ 2 } }=\dfrac { 1 }{ 2 } \dfrac { { qvB } }{ { { m_{ e } } } } \times \dfrac { { { x^{ 2 } } } }{ { { v^{ 2 } } } } =\dfrac { { qB{ x^{ 2 } } } }{ { 2{ m_{ e } }v } } =\dfrac { { qB{ x^{ 2 } } } }{ { 2{ m_{ e } }\sqrt { \dfrac { { KE\times 2 } }{ m } } } } =\dfrac { 1 }{ 2 } \times \dfrac { { 1.6\times { { 10 }^{ -19 } }\times { { 10 }^{ -7 } }\times { 1^{ 2 } } } }{ { 9.1\times { { 10 }^{ -31 } }\sqrt { \dfrac { { 1.6\times { { 10 }^{ -15 } }\times 2 } }{ { 9.1\times { { 10 }^{ -31 } } } } } } } \\ s=0.0148\simeq 1.5\times { 10^{ -2 } }cm \end{array}$$
Two circular loops of radii R and r(R >> r) have same centre and carry currents I and i respectively. Find the maximum torque and maximum angular acceleration of smaller loop, if it is free to rotate about y axis where as the bigger loop is fixed. (Neglect the inductance of the system). The mass of the smaller loop is m.
A long, straight wire carries a current $$i$$. Let $$B_{1}$$ be the magnetic field at a point $$P$$ at a distance $$d$$ from the wire. Consider a section of length $$l$$ of this wire such that the point $$P$$ lies on a perpendicular bisector of the section. Let $$B_{2}$$ be the magnetic field at this point due to this section only. Find the value of $$d/l$$ so that $$B_{2}$$ differs from $$B_{1}$$ by $$1\%$$.
$$B_{1}=\dfrac{\mu_0I}{2\pi d}$$
$$B_2=\dfrac{\mu_0I}{4\pi d}(2\times sin\theta)=\dfrac{\mu_0I}{4\pi d}$$
$$=\dfrac{2\times l}{2\sqrt{d^2+\dfrac{l^2}{4}}}=\dfrac{\mu_0Il}{4\pi d\sqrt{d^2+\dfrac{l^2}{4}}}$$
$$B_1-B_2=\dfrac{1}{100B_2}$$
$$\Rightarrow \dfrac{\mu_0I}{2\pi d}-\dfrac{\mu_0Il}{4\pi d\sqrt{d^2+\dfrac{l^2}{4}}}=\dfrac{\mu_0I}{200\pi d}$$
$$\Rightarrow \dfrac{\mu_0I}{4\pi d\sqrt{d^2+\dfrac{l^2}{4}}}=\dfrac{\mu_0Il}{\pi d}\left(\dfrac{1}{2}-\dfrac{1}{200}\right)$$
$$\Rightarrow \dfrac{l}{d^2+\dfrac{l^2}{4}}=\left(\dfrac{99\times 4}{200}\right)^2=\dfrac{156816}{40000}$$
$$=3.92$$
$$\Rightarrow l^2=3.92d^2+\dfrac{3.92}{4}l^2\left(\dfrac{1-3.92}{4}\right)l^2=3.92d^2$$
$$\Rightarrow 0.02l^2=3.92d^2$$
$$\Rightarrow \dfrac{d^2}{l^2}=\dfrac{0.02}{3.92}=\dfrac{d}{l}=\sqrt{\dfrac{0.02}{3.92}}=0.07$$
A very long wire carrying a current $$I = 5.0\ A$$ is bent a right angles. Find the magnetic induction at a point lying on the perpendicular bisector to the wire, drawn through the point of bending, at a distance $$l = 35\ cm$$ from it.
Hint: Find net magnetic field due to each wire and then find resultant magnetic field.
Step 1: Find the magnetic field at a point 0 due to each wire.
The magnetic field at a point 0 at a distance of $$l=35\text{cm}$$ is given by:
$$B=\dfrac{\mu_0I}{4\pi l}\left[\sin\theta_1 + \sin \theta_2 \right]$$, where $$\theta_1$$ and $$\theta_2$$ are that angle made by the line joining the end points of wire to O with that perpendicular drawn from O on the wire.
We have, $$|\vec{B_1}| = |\vec{B_2}| =\dfrac{\mu_0I}{4\pi l}\left[\sin 45^\circ + \sin 90^\circ \right]$$ $$ = \dfrac{{{\mu _0}I(1+\sqrt 2) }}{{4\pi l\sqrt2}}$$
Step 2: Find net magnetic field.
Magnetic field due to both wires is in same direction
So, $$\left|\vec{B_0}\right|= |\vec{B_1}| + |\vec{B_2}| = \dfrac{\mu_0I\sqrt2(1+\sqrt{2})}{4\pi l} $$
$$= \dfrac{4 \pi \times 5 (2+\sqrt{2})}{4\pi \times 0.35} $$
$$=48.77T$$
What are the applications of Ampere's law ?
In the figure, two long straight wires at separation $$d =16.0\hspace{0.05cm} cm$$ carry currents $$i_{1}= 3.61\hspace{0.05cm} mA$$ and $$i_2 = 3.00i_{1}$$ out of the page. (a) Where on the x-axis is the net magnetic field equal to zero? (b) If the two currents are doubled, isthe zero-field point shifted toward wire 1, shifted toward wire 2 or unchanged?
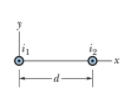
The Biot-Savart Law(14)
One long wire carries current $$30.0 \,A$$ to the left along the x axis. A second long wire carries current $$50.0 \,A$$ to the right along the line $$(y = 0.280 \,m, z = 0)$$.
(a) Where in the plane of the two wires is the total magnetic field equal to zero?
(b) A particle with a charge of $$-2.00 \,\mu C$$ is moving with a velocity of $$150\hat{i} \,Mm/s$$ along the line $$(y = 0.100 \,m, z = 0)$$. Calculate the vector magnetic force acting on the particle.
(c) What If? A uniform electric field is applied to allow this particle to pass through this region undeflected. Calculate the required vector electric field.
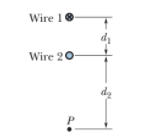
In the figure, two long straight wires are perpendicular to the page and separated by distance $$d_{1}=0.75\hspace{0.05cm} cm$$. Wire $$1$$ carries $$6.5 A$$ into the page. What are the (a) magnitude and (b) direction(into or out of the page) of the current in wire $$2$$ if the net magnetic field due to the two currents is zero at point P located at distance $$d_{2}=1.50\hspace{0.05cm}cm$$ from wire $$2$$?
A 2.50 MeV electron moves perpendicularly to a magnetic field in a path with a $$3.0 \mathrm{cm}$$ radius of curvature. What is the magnetic field $$B ?$$ (See Problem 53 .)
An electron of kinetic energy $$1.20 keV$$ circles in a plane perpendicular to a uniform magnetic field. The orbit radius is $$25.0 cm$$. Find
(a) the electrons speed,
(b) the magnetic field magnitude,
(c) the circling frequency, and
(d) the period of the motion.
In the figure, part of a long insulated wire carrying current $$i=5.78\hspace{0.05cm}mA$$ is bent into a circular section of radius $$R=1.89\hspace{0.05cm}cm$$. In unit-vector notation, what is the magnetic field at the center of curvature $$C$$ if the circular sections (a) lies in the plane of the page as shown and (b) is perpendicular to the plane of the page after being rotated $$90^{\circ}$$ counterclockwise as indicated?
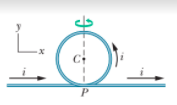
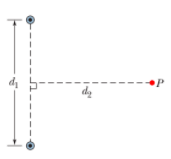
Figure shows two very long straight wires (in cross section) that each carry a current of $$4.00\hspace{0.05cm}A$$ directly out of the page. Distance $$d_{1}=6.00\hspace{0.05cm}m$$ and distance $$d_{2}=4.00\hspace{0.05cm}m$$. What is the magnitude of the net magnetic field at point P, which lies on the a perpendicular bisector to the wires?
An electron is accelerated from rest through potential difference $$V$$ and then enters a region of uniform magnetic field, where it undergoes uniform circular motion. The figure gives the radius $$r$$ of that motion versus $$V^{1/2}$$. The vertical axis scale is set by $$r_{s}=3.0mm$$, and the horizontal axis scale is set by $$V_{s}^{1/2} = 40.0V^{1/2}$$. What is the magnitude of the magnetic field?
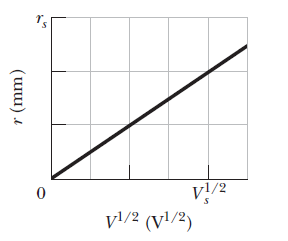
An alpha particle can be produced in certain radioactive decays of nuclei and consists of two protons and two neutrons. The particle has a charge of $$q = +2e$$ and a mass of $$4.00 u$$, where $$u$$ is the atomic mass unit, with $$1 u = 1.661 \times 10^{-27} kg$$. Suppose an alpha particle travels in a circular path of radius $$4.50 cm$$ in a uniform magnetic field with $$B = 1.20 T$$. Calculate
(a) its speed,
(b) its period of revolution,
(c) its kinetic energy, and
(d) the potential difference through which it would have to be accelerated to achieve this energy.
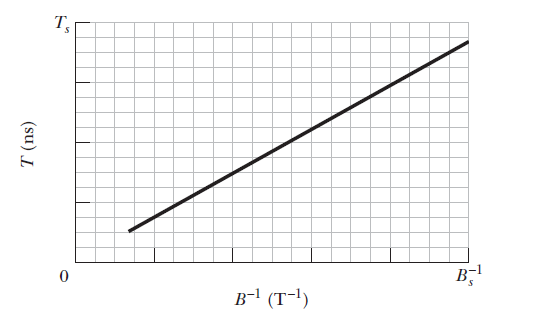
A certain particle is sent into a uniform magnetic field, with the particles velocity vector perpendicular to the direction of the field. The figure gives the period $$T$$ of the particles motion versus the $$inverse$$ of the field magnitude $$B$$. The vertical axis scale is set by $$T_{s}=40.0ns$$, and the horizontal axis scale is set by $$B_{s}^{-1}=5.0T^{-1}$$. What is the ratio $$m/q$$ of the particles mass to the magnitude of its charge?
One long wire lies along an $$x$$ axis and carries a current of $$30 A$$ in the positive $$x$$ direction.A second long wire is perpendicular to the $$xy$$ plane, passes through the point $$(0, 4.0 m, 0)$$, and carries a current of $$40 A$$ in the positive $$z$$ direction.What is the magnitude of the resulting magnetic field at the point $$(0, 2.0\ m, 0)$$?
A proton traveling at $$23.0^{0}$$ with respect to the direction of a magnetic field of strength $$2.60 mT$$ experiences a magnetic force of $$6.50 \times 10^{-17} N$$. Calculate
(a) the protons speed and
(b) its kinetic energy in electron-volts.
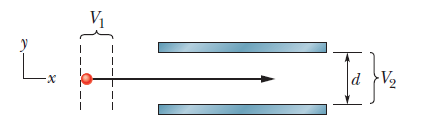
In the figure, an electron accelerated from rest through potential difference $$V_{1}=1.00kV$$ enters the gap between two parallel plates having separation $$d=20.0mm$$ and potential difference $$V_{2}=100V$$. The lower plate is at the lower potential. Neglecting and assuming that the electron's velocity vector is perpendicular to the electric field vector between the plates. In unit-vector notation, what uniform magnetic field allows the electron to travel in a straight line in the gap?
A cyclotron with dee radius $$53.0 cm$$ is operated at an oscillator frequency of $$12.0 MHz$$ to accelerate protons.
(a) What magnitude $$B$$ of magnetic field is required to achieve resonance?
(b) At that field magnitude, what is the kinetic energy of a proton emerging from the cyclotron?
Figure shows, in cross section, two long parallel wires spaced by distance $$d 10.0 cm$$; each carries $$100 A$$, out of the page in wirePoint $$P$$ is on a perpendicular bisector of the line connecting the wires. In unit-vector notation, what is the net magnetic field at $$P$$ if the current in wire 2 is (a) out of the page and (b) into the page?
The Biot-Savart Law(17)
Determine the magnetic field (in terms of $$I, \,a$$, and $$d$$ ) at the origin due to the current loop in Figure. The loop extends to infinity above the figure.
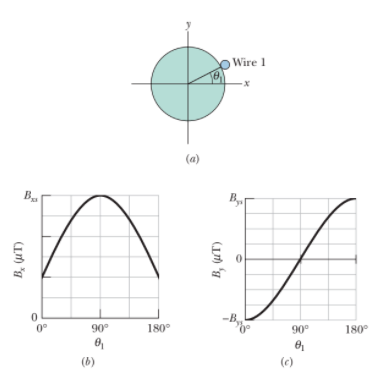
Two long straight thin wires with current lie against an
equally long plastic cylinder, at radius R=20.0 cm from the cylinder’s central axis. Figure (a) shows, in cross section, the cylinder
and wire 1 but not wire 2.With wire 2 fixed in place, wire 1 is moved around the cylinder, from angle $$\theta_{1}=0^{\circ}$$ to angle $$\theta_{1}=180^{\circ}$$, through the first and second quadrants of the $$xy$$ coordinate system. The net magnetic filed $$\vec{B}$$ at the center of the cylinder is measures as the function of $$\theta_{1}$$. Figure(b) gives the $$x$$ component $$B_{x}$$ of that field as a function of $$\theta_{1}$$ (the vertical scale is set by $$B_{xx}=6.0\hspace{0.05cm} \mu T)$$ and figure (c) gives the $$y$$ componenet of $$B_{y}$$ (the vertical scale is set by $$B_{yx}=4.0 \mu T$$ (a)At what angle $$\theta_{2}$$ is wire located? What are the (b) size and (c) direction (into or out of the page) of the current in wire 1 and the (d) size and (e) direction of the current in wire 2?
In a particular region, there is uniform current density of $$15\hspace{0.05cm}A/m^2$$ in positive $$z$$ direction. What is the value of $$\oint {\vec{B}\cdot d\vec{s}}$$ when that line integral is calculated along a closed path consisting of the three straight-line segments from $$(x,y,z)$$ coordinates $$(4d,0,0)$$ to $$(4d,3d,0)$$ to $$(0,0,0)$$ to $$(4d,0,0)$$ where d=20cm?
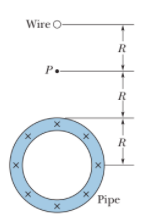
In the figure, a long circular pipe with outside radius R=2.6cm carries a (uniformly distributed) current i=8.00 mA into the page. A wire runs parallel to the pipe at a distance of 3.00R from center to center. Find the (a) magnitude and (b) direction (into or out of the page) of the current in the wire such that the net magnetic field at point P has the same magnitude as the net magnetic field at the center of the pipe but is in the opposite direction.
Two long wires lie in an $$xy$$ plane, and each carries a current in the positive direction of the $$x$$ axis. Wire 1 is at $$y =10.0\ cm$$ and carries $$6.00\ A$$; wire 2 is at $$y =5.00\ cm$$ and carries $$10.0\ A$$. (a) In unit-vector notation, what is the net magnetic field $$\vec{B}$$ at the origin? (b) At what value of $$y$$ does $$\vec{B}=0$$? (c) If the current in wire 1 is reversed, at what value of $$y$$ does $$\vec{B}=0$$?
In the figure, a charged particle moves into a region of uniform
magnetic field $$\vec{B}$$, goes through half a circle, and then exits that region. The particle is either a proton or an electron (you must decide which). It spends $$130 ns$$ in the region.
(a) What is the magnitude of $$\vec{B}$$?
(b) If the particle is sent back through the magnetic field (along the same initial path) but with $$2.00$$ times its previous kinetic energy, how much time does it spend in the field during this trip?
An electron follows a helical path in a uniform magnetic field of magnitude $$0.300 T$$. The pitch of the path is $$6.00 \mu m$$, and the magnitude of the magnetic force on the electron is $$2.00 \times10^{-15} N$$. What is the electrons speed?
Reference to given figure, is very useful for interpreting this problem.
The distance travelled parallel to $$\vec{B}$$ is $$d_{||}=v_{||}\dfrac{2\pi m_{e}}{|q|B}$$
using $$T=\dfrac{2\pi r}{v} = \dfrac{2\pi}{v} = \dfrac{mv}{|q|B} = \dfrac{2\pi m}{|q|B}$$. Thus, using the values given in the problem and
$$v_{||}=\dfrac{d_{||}eB}{2\pi m_{e}}$$
$$v_{||}=50.3km/s$$
Also, since the magnetic force is $$|q|B_{\perp}$$, then we find $$v_{\perp} = 41.7km/s$$.
The speed id therefore $$v=\sqrt{v_{\perp}^{2}+v_{||}^{2}} = 65.3km/s$$.
The distance travelled parallel to $$\vec{B}$$ is $$d_{||}=v_{||}\dfrac{2\pi m_{e}}{|q|B}$$
using $$T=\dfrac{2\pi r}{v} = \dfrac{2\pi}{v} = \dfrac{mv}{|q|B} = \dfrac{2\pi m}{|q|B}$$. Thus, using the values given in the problem and
$$v_{||}=\dfrac{d_{||}eB}{2\pi m_{e}}$$
$$v_{||}=50.3km/s$$
Also, since the magnetic force is $$|q|B_{\perp}$$, then we find $$v_{\perp} = 41.7km/s$$.
The speed id therefore $$v=\sqrt{v_{\perp}^{2}+v_{||}^{2}} = 65.3km/s$$.
A student makes a short electromagnet by winding 300 turns of wire around a wooden cylinder of diameter d=5cm. The coil is connected to a battery producing a current of 4.0 A in the wire. (a) What is the magnitude of the magnetic dipole moment of this device? (b) At what axial distance $$z>>d$$ will the magnetic field have the magnitude $$5.0\hspace{0.05cm} \mu T$$ (approximately one-tenth that ofEarth’s magnetic field)?
Three long wires all lie in an $$xy$$ plane parallel to the $$x$$ axis. They are spaced equally, $$10 cm$$ apart. The two outer wires each carry a current of $$5.0 A$$ in the positive $$x$$ direction. What is the magnitude of the force on a $$3.0 m$$ section of either of the outer wires if the current in the center wire is $$3.2 A$$ (a) in the positive $$x$$ direction and (b) in the negative $$x$$ direction?
Find an expression for the magnetic field at the centre of a circular coil of N- turns, radius $$r$$, carrying current $$I$$.
The figure shows a current loop ABCDEFA carrying a current $$i =
5.00 A$$. The sides of the loop are parallel to the coordinate axes shown, with $$AB = 20.0 cm$$,$$BC = 30.0 cm$$, and $$FA = 10.0 cm$$. In unit-vector notation, what is the magnetic dipole moment of this loop? (Hint: Imagine equal and opposite currents $$i$$ in the line segment $$AD$$; then treat the two rectangular loops ABCDA and ADEFA.)
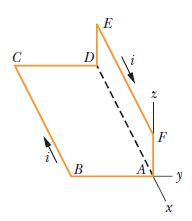
State and explain Biot-Savart law. Use it to derive an expression for the magnetic field produced at a point near long current carrying wire.
Biot Savart law: Suppose the current $$I$$ is flowing in a conductor and there is a small current element $$'ab'$$ of length $$\Delta l$$. According to Biot-Savart's law the magnetic field $$( \Delta B)$$ produced due to this current element at a point $$P$$ distant $$r$$ from the element is given by
$$\Delta B \propto \dfrac{I \Delta l\sin \theta }{r^2}$$ or $$\Delta B=\dfrac{\mu}{4\pi}\dfrac{I\Delta l \sin \theta }{r^2}$$ .....(i)
where $$\dfrac{\mu}{4\pi}$$ is a constant proportionality. It depends on the medium between the current element and point observation $$(P). \mu$$ is called the permeability of medium. Equation (I) is called Blot-Savart law. The product of current $$(I)$$ and length element $$(\Delta l)$$ ( i.e. $$| \Delta I$$) is called the current element. Current element is a vector quantity, its direction is along the direction of current. If the conductor be placed in vacuum ( or air ), then $$\mu$$ is replaced by $$\mu_0$$, where $$\mu_0$$ is called permeability of free space ( or air ). In S.I system $$\mu_0=4\pi \times 10^{-7}$$ weber/ ampere-meter ( or newton/ ampere).
Thus $$\dfrac{\mu_0}{4\pi}=10^{-7}\ weber/ ampere \times metre$$
As in most cases the medium surrounding the conductor is air, therefore, in general Blot-Savart law is written as
$$\Delta B=\dfrac{\mu_0}{4\pi}\dfrac{I\Delta l\sin \theta}{r^2}$$
The direction of magnetic field is perpendicular to the plane containing current element and the line joining point of observation to current element. So in vector form the expression for magnetic field takes the form
$$\Delta \vec B=\dfrac{\mu_0}{4\pi}\dfrac{I\Delta \vec l \times \vec r}{r^3}$$
Derivation of formula for magnetic field due to a current carrying wire using Blot Savart law: Consider a wire $$EF$$ carrying $$l$$ in upward direction. The point of observation is $$P$$ at a finite distance $$R$$ from distance $$R$$ from the wire. If $$PM$$ is perpendicular dropped from $$P$$ on wire: then $$PM=R$$. The wire may be supposed to be formed of a large number of small current elements. Consider a small element $$CD$$ of length $$\delta l$$ at a distance $$I$$ from $$M$$.
Let $$\angle CPM=\varphi$$
And $$\angle CPD =\delta \varphi, \angle PDM =\theta$$
The length $$\delta l$$ is very small, so that $$\angle PCM$$ may also be taken equal to $$\theta$$.
The perpendicular dropped from $$C$$ on $$PD$$ is $$CN$$. The angle formed between elements
$$I \vec{\delta I}$$ and $$\vec r(=\overline {CP})$$ is $$( \pi -\theta )$$. Therefore according to Blot Savart law, the magnetic field due to current element $$I \vec {\delta I}$$ at $$P$$ is
$$\delta B=\dfrac{\mu_0}{4\pi}\dfrac{I\delta \sin ( \pi -\theta)}{r^2}=\dfrac{\mu_0}{4\pi}\dfrac{I\delta l \sin \theta }{r^2}$$ .... (i)
But in $$\Delta CND, \sin \theta =\sin ( \angle CDN)=\dfrac{CN}{CD}=\dfrac{r\delta \varphi}{\delta l}$$
or $$\delta l\sin \theta =r\delta \varphi$$
$$\therefore$$ From equation (i)
$$\delta B=\dfrac{\mu_0}{4\pi}\dfrac{Ir-\delta \varphi}{r^2}=\dfrac{\mu_0}{4\pi}\dfrac{I\delta \varphi}{r}$$ ... (ii)
Again from fig.
$$\cos \varphi =\dfrac{R}{r}\Rightarrow r=\dfrac{R}{\cos \varphi}$$
From equation (ii)
$$\delta B=\dfrac{\mu_0}{4\pi}\dfrac{I\cos \varphi \delta \varphi}{R}$$ ....(iii)
If the wire is of finite length and its ends make angles $$\alpha$$ and $$\beta$$ with line $$MP$$, then net magnetic field $$(B)$$ at $$P$$ is obtained by summing over magnetic fields due to all current elements. i,e
$$B=\displaystyle \int_{-\beta}^{\alpha}{\dfrac{\mu_0}{4\pi}}\dfrac{I\cos \varphi d\varphi}{R}=\dfrac{\mu_0I}{4\mu R}\displaystyle \int_{-\beta}^{\alpha}{\cos \varphi d\varphi}$$
$$\dfrac{\mu_0I}{4\pi R}[\sin \varphi]_{-\beta}^{\alpha}=\dfrac{\mu_0I}{4\pi R}[ \sin \alpha -\sin ( -\beta)]$$
i.e,e $$B=\dfrac{\mu_0I}{4\pi R}(\sin \alpha +\sin \beta )$$
This expression for magnetic field due to current carrying wire of finite length.
If the wire is of infinite length ( or very long ), then $$\alpha =\beta \Rightarrow \pi /2$$
$$\therefore B=\dfrac{\mu_0I}{4\pi R}\left( \sin \dfrac{\pi}{1}+\sin \dfrac{\pi}{2}\right)=\dfrac{\mu_0I}{4\pi R}[1+1]$$ or $$B=\dfrac{\mu_0I}{2\pi R}$$
$$\Delta B \propto \dfrac{I \Delta l\sin \theta }{r^2}$$ or $$\Delta B=\dfrac{\mu}{4\pi}\dfrac{I\Delta l \sin \theta }{r^2}$$ .....(i)
where $$\dfrac{\mu}{4\pi}$$ is a constant proportionality. It depends on the medium between the current element and point observation $$(P). \mu$$ is called the permeability of medium. Equation (I) is called Blot-Savart law. The product of current $$(I)$$ and length element $$(\Delta l)$$ ( i.e. $$| \Delta I$$) is called the current element. Current element is a vector quantity, its direction is along the direction of current. If the conductor be placed in vacuum ( or air ), then $$\mu$$ is replaced by $$\mu_0$$, where $$\mu_0$$ is called permeability of free space ( or air ). In S.I system $$\mu_0=4\pi \times 10^{-7}$$ weber/ ampere-meter ( or newton/ ampere).
Thus $$\dfrac{\mu_0}{4\pi}=10^{-7}\ weber/ ampere \times metre$$
As in most cases the medium surrounding the conductor is air, therefore, in general Blot-Savart law is written as
$$\Delta B=\dfrac{\mu_0}{4\pi}\dfrac{I\Delta l\sin \theta}{r^2}$$
The direction of magnetic field is perpendicular to the plane containing current element and the line joining point of observation to current element. So in vector form the expression for magnetic field takes the form
$$\Delta \vec B=\dfrac{\mu_0}{4\pi}\dfrac{I\Delta \vec l \times \vec r}{r^3}$$
Derivation of formula for magnetic field due to a current carrying wire using Blot Savart law: Consider a wire $$EF$$ carrying $$l$$ in upward direction. The point of observation is $$P$$ at a finite distance $$R$$ from distance $$R$$ from the wire. If $$PM$$ is perpendicular dropped from $$P$$ on wire: then $$PM=R$$. The wire may be supposed to be formed of a large number of small current elements. Consider a small element $$CD$$ of length $$\delta l$$ at a distance $$I$$ from $$M$$.
Let $$\angle CPM=\varphi$$
And $$\angle CPD =\delta \varphi, \angle PDM =\theta$$
The length $$\delta l$$ is very small, so that $$\angle PCM$$ may also be taken equal to $$\theta$$.
The perpendicular dropped from $$C$$ on $$PD$$ is $$CN$$. The angle formed between elements
$$I \vec{\delta I}$$ and $$\vec r(=\overline {CP})$$ is $$( \pi -\theta )$$. Therefore according to Blot Savart law, the magnetic field due to current element $$I \vec {\delta I}$$ at $$P$$ is
$$\delta B=\dfrac{\mu_0}{4\pi}\dfrac{I\delta \sin ( \pi -\theta)}{r^2}=\dfrac{\mu_0}{4\pi}\dfrac{I\delta l \sin \theta }{r^2}$$ .... (i)
But in $$\Delta CND, \sin \theta =\sin ( \angle CDN)=\dfrac{CN}{CD}=\dfrac{r\delta \varphi}{\delta l}$$
or $$\delta l\sin \theta =r\delta \varphi$$
$$\therefore$$ From equation (i)
$$\delta B=\dfrac{\mu_0}{4\pi}\dfrac{Ir-\delta \varphi}{r^2}=\dfrac{\mu_0}{4\pi}\dfrac{I\delta \varphi}{r}$$ ... (ii)
Again from fig.
$$\cos \varphi =\dfrac{R}{r}\Rightarrow r=\dfrac{R}{\cos \varphi}$$
From equation (ii)
$$\delta B=\dfrac{\mu_0}{4\pi}\dfrac{I\cos \varphi \delta \varphi}{R}$$ ....(iii)
If the wire is of finite length and its ends make angles $$\alpha$$ and $$\beta$$ with line $$MP$$, then net magnetic field $$(B)$$ at $$P$$ is obtained by summing over magnetic fields due to all current elements. i,e
$$B=\displaystyle \int_{-\beta}^{\alpha}{\dfrac{\mu_0}{4\pi}}\dfrac{I\cos \varphi d\varphi}{R}=\dfrac{\mu_0I}{4\mu R}\displaystyle \int_{-\beta}^{\alpha}{\cos \varphi d\varphi}$$
$$\dfrac{\mu_0I}{4\pi R}[\sin \varphi]_{-\beta}^{\alpha}=\dfrac{\mu_0I}{4\pi R}[ \sin \alpha -\sin ( -\beta)]$$
i.e,e $$B=\dfrac{\mu_0I}{4\pi R}(\sin \alpha +\sin \beta )$$
This expression for magnetic field due to current carrying wire of finite length.
If the wire is of infinite length ( or very long ), then $$\alpha =\beta \Rightarrow \pi /2$$
$$\therefore B=\dfrac{\mu_0I}{4\pi R}\left( \sin \dfrac{\pi}{1}+\sin \dfrac{\pi}{2}\right)=\dfrac{\mu_0I}{4\pi R}[1+1]$$ or $$B=\dfrac{\mu_0I}{2\pi R}$$
A uniform magnetic field $$\vec B$$ is set up along the positive $$x-$$axis. A particle of charge $$'q'$$ and mass $$'m'$$ moving with a velocity $$\vec V$$ enters the field at the origin in $$x-y$$ plane such that it has velocity components both along perpendicular to the magnetic field $$\vec B$$. Trace, giving reason, the trajectory followed by the particle.
Find out the expression for the distance moved by the particle along the magnetic field in one rotation.
If component $$v_x$$ of the velocity vector is along the magnetic field, and remain constant, the charge particle will follow a helical trajectory; as shown in figure.
If the velocity component $$v_y$$ is perpendicular to the magnetic field $$B$$, the magnetic force acts like a centripetal force $$qv_y\ B$$.
So, $$qv_y B=\dfrac {mv^2_y}{r}\ \Rightarrow \ v_y=\dfrac {qBr}{m}$$
Since tangent velocity $$v_y=r \omega$$
$$\Rightarrow \ r\omega =\dfrac {qBr}{m}\ \Rightarrow \ \omega =\dfrac {qB}{m}$$
Time taken for one revolution, $$T=\dfrac {2\pi}{\omega}=\dfrac {2\pi m}{qB}$$
and the distance moved along the magnetic field in the helical path is
$$x=v_x. T=v_x.\dfrac {2\pi m}{qB}$$.
If the velocity component $$v_y$$ is perpendicular to the magnetic field $$B$$, the magnetic force acts like a centripetal force $$qv_y\ B$$.
So, $$qv_y B=\dfrac {mv^2_y}{r}\ \Rightarrow \ v_y=\dfrac {qBr}{m}$$
Since tangent velocity $$v_y=r \omega$$
$$\Rightarrow \ r\omega =\dfrac {qBr}{m}\ \Rightarrow \ \omega =\dfrac {qB}{m}$$
Time taken for one revolution, $$T=\dfrac {2\pi}{\omega}=\dfrac {2\pi m}{qB}$$
and the distance moved along the magnetic field in the helical path is
$$x=v_x. T=v_x.\dfrac {2\pi m}{qB}$$.
A wire $$AB$$ is carrying a steady current of $$12\ A$$ and is lying on the table. Another wire $$CD$$ carrying $$5A$$ is held directly above $$AB$$ at a height of $$1\ mm$$. Find the mass per unit length of the wire $$CD$$ so that it remains suspended at its position when left free. Give the direction of the current flowing in $$CD$$ with respect to that in $$AB$$.
Current carrying conductors repel each other if current flows in opposite direction.Current carrying conductors attract each other if current flows in the same direction. If wire $$CD$$ remain suspended above $$AB$$ then,
$$F_{repulsion}=$$Weight
$$\dfrac {\mu_0 I_1 I_2 l}{2\pi r}=mg$$
where $$r=$$ Separation between the wire
$$\dfrac {m}{l}=\dfrac {\mu_0 I_1 I_2}{2\pi rg}$$
$$=\dfrac {2\times 10^{-7}\times 12\times 5}{1\times 10^{-3}\times 10}$$
$$1.2\times 10^{-3}kg/m$$
Current in $$CD$$ should be in opposite direction to that in $$AB$$.
$$F_{repulsion}=$$Weight
$$\dfrac {\mu_0 I_1 I_2 l}{2\pi r}=mg$$
where $$r=$$ Separation between the wire
$$\dfrac {m}{l}=\dfrac {\mu_0 I_1 I_2}{2\pi rg}$$
$$=\dfrac {2\times 10^{-7}\times 12\times 5}{1\times 10^{-3}\times 10}$$
$$1.2\times 10^{-3}kg/m$$
Current in $$CD$$ should be in opposite direction to that in $$AB$$.
A beam of protons passes undeflected with a horizontal velocity $$v$$, through a region of electric and magnetic field, mutually perpendicular to each other and normal to the direction of the beam. If the magnitudes of the electric nad magnetic fields are $$50\ kV/m$$ and $$100\ mT$$ respectively; calculate the
Force with which it strikes a target on the screen. if the proton beam current is equal to $$0.80\ mA$$.
Figure shows an arrangement as a Helmholtz coil. It consists of two circular coaxial coils, each of 200 turns and radius R=25 cm, separated by a distance s=R. The two coils carry equal currents i=12.2 mA in the same direction. Find the magnitude of the net magnetic field at P, midway between the coils.
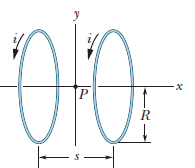
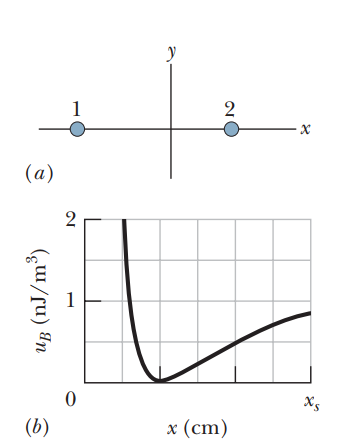
Figure a shows, in cross section, two wires that are straight, parallel, and very long. The ratio $$i_1/i_2$$ of the current carried by wire 1 to that carried by wire 2 is 1/Wire 1 is fixed in place. Wire 2 can be moved along the positive side of the x axis so as to change the magnetic energy
density $$u_B$$ set up by the two currents at the origin. Figure b gives $$u_B$$ as a function of the position x of wireThe curve has an symptote of $$u_b=1.96nJ/m^3$$ as $$x \rightarrow \infty $$, and the horizontal axis scale is set by $$x_s60.0cm$$.What is the value of (a) $$i_1$$ and (b) $$i_2$$?
Write Ampere's Law. Obtain the expression for magnetic at the axis of long solenoid giving the necessary diagram.
Verify the Ampere's law for magnetic field of a point dipole of dipole moment $$ m = m\hat{k} $$. Take C as the closed curve running clockwise along (i) the z-aixs from $$ z=a> 0$$ to $$z= R $$; (ii) along the quarter circle of radius R and center at the origin, in the first quadrant of x-z plane; (iii) along the x-axis from x= R to x=a, and (iv) along the quarter circle of radius a and centre at the origin in the first quadrant of x-z plane.
In figure from P to Q every point on z-axis lies on dipole is in $$ \hat{k} $$ direction
so all points on z-axis lies on axial dipole NS placed at origin.
So magnetic field induction (B) at a point (0,0,z) from magnetic dipole (center at origin) and having magnetic moment
So magnetic field induction (B) at a point (0,0,z) from magnetic dipole (center at origin) and having magnetic moment
$$ \underset{m}{\rightarrow }\hat{k} $$ of magnitude $$ (\underset{m}{\rightarrow }) $$
Find the magnetic induction of the field at the point $$O$$ if a current-carrying wire has the shape shown in Fig. The radius of the curved part of the wire is $$R$$, the linear parts are assumed to be very long.
(a) From symmetry
$$B_{0} = B_{1} + B_{2} + B_{3}$$
$$= 0 + \dfrac {\mu_{0}}{4\pi} \dfrac {i}{R} \pi + 0 = \dfrac {\mu_{0}}{4} \dfrac {i}{R}$$
(b) From symmetry
$$B_{0} = B_{1} + B_{2} + B_{3}$$
$$= \dfrac {\mu_{0}}{4\pi} \dfrac {i}{R} + \dfrac {\mu_{0}}{2\pi} \dfrac {i}{R} \dfrac {3\pi}{2} + 0 = \dfrac {\mu_{0}}{4\pi} \dfrac {i}{R} \left [1 + \dfrac {3\pi}{2}\right ]$$
(c) From symmetry
$$B_{0} = B_{1} + B_{2} + B_{3}$$
$$= \dfrac {\mu_{0}}{4\pi} \dfrac {i}{R} + \dfrac {\mu_{0}}{4\pi} \dfrac {i}{R} \pi + \dfrac {\mu_{0}}{4\pi} \dfrac {i}{R} = \dfrac {\mu_{0}}{4\pi} \dfrac {i}{R} (2 + \pi)$$.
A conducting wire $$XY$$ of mass $$m$$ and negligible resistance slides smoothly on two parallel conducting wires as shown in Fig. The closed circuit has a resistance $$R$$ due to $$AC. AB$$ and $$C$$ are perfect conductors. There is a magnetic field $$B = B(t)\hat {k}$$.
If $$B$$ is independent of time, obtain $$v(t)$$, assuming $$v(0) = u_{0}$$, show that the decrease in kinetic energy of $$XY$$ equals the heat lost in $$R$$.
In a cyclotron, protons are to be accelerated. The radius of its D is $$60 \,cm.$$ and its oscillator frequency is $$10 \,MHz.$$ What will be the kinetic energy of the proton thus accelerated ?
(Proton mass $$= 1.67 \times 10^{-27} kg, e = 1.60 \times 10^{-19}C, eV = 1.6 \times 10^{-19}J$$)
The magnitude $$F$$ of the force between two straight parallel current carrying conductors kept at a distance $$d$$ apart in air is given by
$$F=\dfrac {\mu_0 I_1 I_2}{2\pi d} $$
Where $$I_1$$ and $$I_2$$ are the currents flowing through the two wires.
Use this expression, and the sign convention that the:
Force of attraction is assigned a negative sign and force of repulsion is assigned a positive sign.'
Draw graphs showing dependence of $$F$$ on
$$I_1 I_2$$ when $$d$$ is kept constant.
We know that $$F$$ is an attractive $$(-ve)$$ force when the currents $$I_1$$ and $$I_2$$ are 'like' current i.e. when the product $$I_1 \ I_2$$ is positive.
Similarly $$F$$ is a repulsive $$(+ve)$$ force when the currents $$I_1$$ and $$I_2$$are 'unlike' currents, i.e. when the product $$I_1 \ I_2$$ is negative.
Now $$F \propto (I_1 \ I_2)$$, when $$d$$ is kept constant and $$F \propto 1/d$$ when $$I_1 \ I_2$$ is kept constant.
The required graphs, therefore, have the forms shown below:
Similarly $$F$$ is a repulsive $$(+ve)$$ force when the currents $$I_1$$ and $$I_2$$are 'unlike' currents, i.e. when the product $$I_1 \ I_2$$ is negative.
Now $$F \propto (I_1 \ I_2)$$, when $$d$$ is kept constant and $$F \propto 1/d$$ when $$I_1 \ I_2$$ is kept constant.
The required graphs, therefore, have the forms shown below:
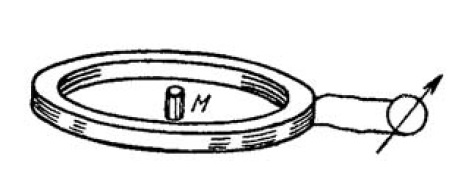
A small cylindrical magnet $$M$$ (Fig.) is placed in the centre of a thin coil of radius $$a$$ consisting of $$N$$ turns. The coil is connected to a ballistic galvanometer. The active resistance of the whole circuit is equal to $$R$$. Find the magnetic moment of the magnet if its removal from the coil results in a charge $$q$$ flowing through the galvanometer.
Let $$\vec {p}_{m}$$ be the magnetic moment of the magnet $$M$$. Then the magnetic field due to this magnet is,
$$\dfrac {\mu_{0}}{4\pi} \left [\dfrac {3(\vec {p}_{m}\cdot \vec {r})\vec {r}}{r^{5}} - \dfrac {\vec {p}_{m}}{r^{3}}\right ]$$.
The flux associated with this, when the magnet is along the axis at a distance $$x$$ from the centre, is
$$\Phi = \dfrac {\mu_{0}}{4\pi} \int \left [\dfrac {3(\vec {p}_{m} \cdot \vec {r})\vec {r}}{r^{5}} - \dfrac {\vec {p}_{m}}{r^{3}}\right ]\cdot d\vec {S} = \Phi_{1} - \Phi_{2}$$.
where, $$\varphi_{2} = \dfrac {\mu_{0}}{4\pi} p_{m} \int_{0}^{a} \dfrac {2\pi \rho d\rho}{(x^{2} + \rho^{2})^{3/2}} = \dfrac {\mu_{0} p_{m}}{3} \left (\dfrac {1}{x} - \dfrac {1}{\sqrt {x^{2} + a^{2}}}\right )$$
and $$\Phi_{1} = \dfrac {3\mu_{0} p_{m} x^{2}}{4\pi} \int_{0}^{a} \dfrac {2\pi \rho d\rho}{(x^{2} + \rho^{2})^{5/2}}$$
$$= \dfrac {\mu_{0}p_{m} x^{2}}{2} \left (\dfrac {1}{x^{3}} - \dfrac {1}{(x^{2} + a^{2})^{3/2}}\right )$$
So, $$\Phi = \dfrac {-\mu_{0} p_{m} a^{2}}{2(x^{2} + a^{2})^{3/2}}$$
When the flux changes, an e.m.f. $$-N \dfrac {d\Phi}{dt}$$ is induced and a current $$-\dfrac {N}{R} \dfrac {d\Phi}{dt}$$ flows. The total charge $$q$$, flowing, as the magnet is removed to infinity from $$x = 0$$ is,
$$q = \dfrac {N}{R}\Phi (x = 0) = \dfrac {N}{R} \cdot \dfrac {\mu_{0} p_{m}}{2a}$$
or, $$p_{m} = \dfrac {2aqR}{N\mu_{0}}$$.
$$\dfrac {\mu_{0}}{4\pi} \left [\dfrac {3(\vec {p}_{m}\cdot \vec {r})\vec {r}}{r^{5}} - \dfrac {\vec {p}_{m}}{r^{3}}\right ]$$.
The flux associated with this, when the magnet is along the axis at a distance $$x$$ from the centre, is
$$\Phi = \dfrac {\mu_{0}}{4\pi} \int \left [\dfrac {3(\vec {p}_{m} \cdot \vec {r})\vec {r}}{r^{5}} - \dfrac {\vec {p}_{m}}{r^{3}}\right ]\cdot d\vec {S} = \Phi_{1} - \Phi_{2}$$.
where, $$\varphi_{2} = \dfrac {\mu_{0}}{4\pi} p_{m} \int_{0}^{a} \dfrac {2\pi \rho d\rho}{(x^{2} + \rho^{2})^{3/2}} = \dfrac {\mu_{0} p_{m}}{3} \left (\dfrac {1}{x} - \dfrac {1}{\sqrt {x^{2} + a^{2}}}\right )$$
and $$\Phi_{1} = \dfrac {3\mu_{0} p_{m} x^{2}}{4\pi} \int_{0}^{a} \dfrac {2\pi \rho d\rho}{(x^{2} + \rho^{2})^{5/2}}$$
$$= \dfrac {\mu_{0}p_{m} x^{2}}{2} \left (\dfrac {1}{x^{3}} - \dfrac {1}{(x^{2} + a^{2})^{3/2}}\right )$$
So, $$\Phi = \dfrac {-\mu_{0} p_{m} a^{2}}{2(x^{2} + a^{2})^{3/2}}$$
When the flux changes, an e.m.f. $$-N \dfrac {d\Phi}{dt}$$ is induced and a current $$-\dfrac {N}{R} \dfrac {d\Phi}{dt}$$ flows. The total charge $$q$$, flowing, as the magnet is removed to infinity from $$x = 0$$ is,
$$q = \dfrac {N}{R}\Phi (x = 0) = \dfrac {N}{R} \cdot \dfrac {\mu_{0} p_{m}}{2a}$$
or, $$p_{m} = \dfrac {2aqR}{N\mu_{0}}$$.
The magnetic induction in a betatron on an equilibrium orbit of radius $$r$$ varies during the acceleration time at practically constant rate from zero to $$B$$. Assuming the initial velocity of the electron to be equal to zero, find:
(a) the energy acquired by the electron during the acceleration time;
(b) the corresponding distance covered by the electron if the acceleration time is equal to $$\triangle t$$.
Analysis Model: Particle in a Field (Magnetic)(1)
At the equator, near the surface of the Earth, the magnetic field is approximately $$50.0 \mu T$$ northward, and the electric field is about $$100 \,N/C$$ downward in fair weather. Find the gravitational, electric, and magnetic forces on an electron in this environment, assuming that the electron has an instantaneous velocity of $$6.00 \times 106 \,m/s$$ directed to the east.
Experiment Deflection of the galvanometer needle increases decreases Number of turns increased Strong magnet is used Magnet/solenoid moves with grater speed
Using magnet of high strength, and increasing the number of turns in the solenoid, the experiment is repeated. On the basis of experiment is repeated. On the basis of the experiments complete the table (3.2).
(i) Why did the galvanometer needle deflect in the experiment ?
(ii) Which were the instances in which there was a flow of current through the solenoid ?
(iii) Which were the instances in which the current increased ?
| Experiment | Deflection of the galvanometer needle | |
| increases | decreases | |
| Number of turns increased | ||
| Strong magnet is used | ||
| Magnet/solenoid moves with grater speed | ||
(i) Whenever there is a change in the magnetic flux linked with a coil, an emf is induced in the coil.
(ii) Whenever there is a relative motion between the magnet and the solenoid, there is flow of electricity.
(iii) Number of turns increased. Strong Magnet used Magnet / Solenoid moves with greater speed.
(ii) Whenever there is a relative motion between the magnet and the solenoid, there is flow of electricity.
(iii) Number of turns increased. Strong Magnet used Magnet / Solenoid moves with greater speed.
Analysis Model: Particle in a Field (Magnetic)(9)
A proton travels with a speed of $$5.02 \times 10^6 \,m/s$$ in a direction that makes an angle of $$60.0^{o}$$ with the direction of a magnetic field of magnitude $$0.180 \,T$$ in the positive x direction. What are the magnitudes of
(a) the magnetic force on the proton and
(b) the protons acceleration?
Challenge Problems(78)
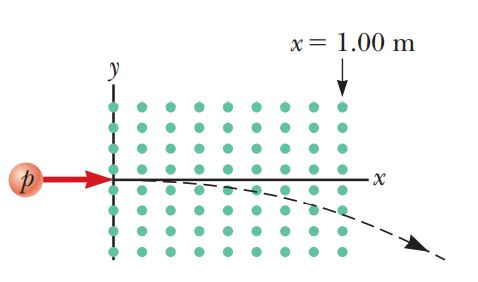
Protons having a kinetic energy of $$5.00 \,MeV (1 \,eV = 1.60 \times 10^{-19} \,J)$$ are moving in the positive x direction and enter a magnetic field $$\overrightarrow{B} = 0.050 0\hat{k} \,T$$ directed out of the plane of the page and extending from $$x = 0$$ to $$x = 1.00 \,m$$ as shown in Figure.
(a) Ignoring relativistic effects, find the angle a between the initial velocity vector of the proton beam and the velocity vector after the beam emerges from the field.
(b) Calculate the y component of the protons' momenta as they leave the magnetic field.
The Biot-Savart Law(10)
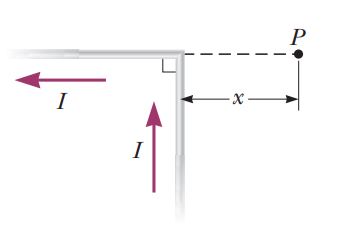
An infinitely long wire carrying a current $$I$$ is bent at a right angle as shown in Figure. Determine the magnetic field at point $$P$$, located a distance $$x$$ from the corner of the wire.
The Biot-Savart Law(13)
A current path shaped as shown in Figure produces a magnetic field at $$P$$, the center of the arc. If the arc subtends an angle of $$\theta = 30.0^{0}$$ and the radius of the arc is $$0.600 \,m$$, what are the magnitude and direction of the field produced at $$P$$ if the current is $$3.00 \,A$$?
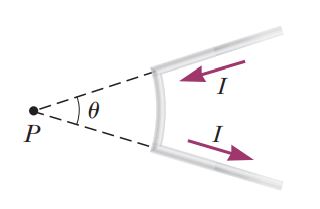
The Biot-Savart Law(8)
A conductor consists of a circular loop of radius $$R$$ and two long, straight sections as shown in Figure. The wire lies in the plane of the paper and carries a current $$I$$.
(a) What is the direction of the magnetic field at the center of the loop?
(b) Find an expression for the magnitude of the magnetic field at the center of the loop.
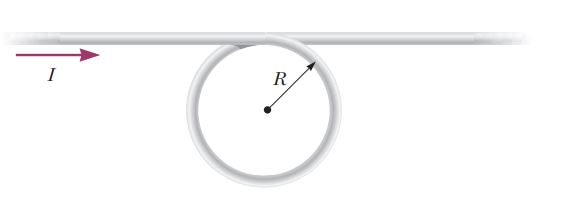
Conceptual Questions
Explain why two parallel wires carrying currents in opposite directions repel each other.
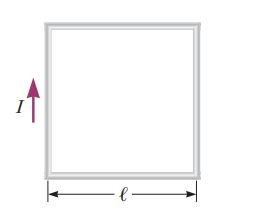
The Biot-Savart Law(5)
(a) A conducting loop in the shape of a square of edge length $$l = 0.400 \,m$$ carries a current $$I = 10.0 \,A$$ as shown on Figure. Calculate the magnitude and direction of the magnetic field at the center of the square.
(b) What If? If this conductor is reshaped to form a circular loop and carries the same current, what is the value of the magnetic field at the center?
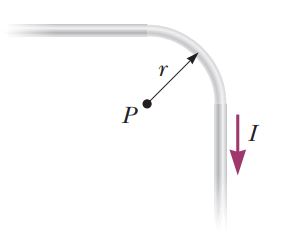
The Biot-Savart Law(8)
A long, straight wire carries a current $$I$$. A right-angle bend is made in the middle of the wire. The bend forms an arc of a circle of radius $$r$$ as shown in Figure. Determine the magnetic field at point $$P$$, the center of the arc.
The Biot-Savart Law(6)
In Niels Bohr's 1913 model of the hydrogen atom, an electron circles the proton at a distance of $$5.29 \times 10^{-11} \,m$$ with a speed of $$2.19 \times 10^6 \,m/s$$. Compute the magnitude of the magnetic field this motion produces at the location of the proton.
Conceptual Questions
Compare Ampres law with the BiotSavart law. Which is more generally useful for calculating $$\overrightarrow{B}$$ for a current carrying conductor?
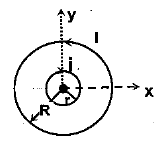
(a) Using Biot-Savarts law, derive an expression for the magnetic field at the centre of a circular coil of radius $$R$$, number of turns $$N$$, carrying current $$i$$.
(b) Two small identical circular coils marked 1, 2 carry equal currents and are placed with their geometric axes perpendicular to each other as shown in the figure. Derive an expression for the resultant magnetic field at $$O$$.
[see image 1]
(a) According to Biot-Savarts law, magnetic field due to current element Idl at the centre $$O$$ of a coil is
$$\overrightarrow{dB} = \dfrac{\mu_0}{4\pi} I \dfrac{(d\vec{I}\times \vec{R})}{R^3}$$
$$dB = \dfrac{\mu_0}{4\pi} \dfrac{Idl}{R^2}$$ $$(\because \sin 90^o = 1)$$
The direction of $$d \vec{l}$$ is along the tangent
so $$d\vec{l} \bot \vec{R}$$
Magnetic field die to whole coil is
$$B = \dfrac{\mu_0 I}{4\pi R^2}\int dl$$ or $$B = \dfrac{\mu_0I}{4\pi R^2} . l$$
$$\Rightarrow B = \dfrac{\mu_0 I}{4\pi R^2} . 2\pi R$$ or $$B = \dfrac{\mu_0 I}{2R}$$
In case of $$N$$ number of turns
$$B = \dfrac{\mu_0 NI}{2R}$$
(b) Field at '$$O$$' due to $$1^{st}$$ loop is
$$B_1 = \dfrac{\mu_0 IR^2}{2(x^2 + R^2)^{3/2}}$$
[see image 2]
$$\vec{B}_1$$ is directed towards the centre of the loop.
Field at '$$O$$' due to $$2^{nd}$$ loop is
$$B_2 = \dfrac{\mu_0 IR^2}{2(x^2 + R^2)^{3/2}}$$
$$\vec{B}_2$$ is directed away from the centre of the loop because current flows in second loop is anticlockwise.
As $$\vec{B}_1 \bot \vec{B}_2$$, so the net field at $$O$$ is
$$B = \sqrt{B_1^2 + B_2^2}$$ or $$B = \dfrac{\mu_0 IR^2 \sqrt{2}}{2(x^2 + R^2)^{3/2}}$$
In case $$x > > R$$
$$\therefore B = \dfrac{\mu_0 IR^2\sqrt{2}}{2x^3}$$
(a) According to Biot-Savarts law, magnetic field due to current element Idl at the centre $$O$$ of a coil is
$$\overrightarrow{dB} = \dfrac{\mu_0}{4\pi} I \dfrac{(d\vec{I}\times \vec{R})}{R^3}$$
$$dB = \dfrac{\mu_0}{4\pi} \dfrac{Idl}{R^2}$$ $$(\because \sin 90^o = 1)$$
The direction of $$d \vec{l}$$ is along the tangent
so $$d\vec{l} \bot \vec{R}$$
Magnetic field die to whole coil is
$$B = \dfrac{\mu_0 I}{4\pi R^2}\int dl$$ or $$B = \dfrac{\mu_0I}{4\pi R^2} . l$$
$$\Rightarrow B = \dfrac{\mu_0 I}{4\pi R^2} . 2\pi R$$ or $$B = \dfrac{\mu_0 I}{2R}$$
In case of $$N$$ number of turns
$$B = \dfrac{\mu_0 NI}{2R}$$
(b) Field at '$$O$$' due to $$1^{st}$$ loop is
$$B_1 = \dfrac{\mu_0 IR^2}{2(x^2 + R^2)^{3/2}}$$
[see image 2]
$$\vec{B}_1$$ is directed towards the centre of the loop.
Field at '$$O$$' due to $$2^{nd}$$ loop is
$$B_2 = \dfrac{\mu_0 IR^2}{2(x^2 + R^2)^{3/2}}$$
$$\vec{B}_2$$ is directed away from the centre of the loop because current flows in second loop is anticlockwise.
As $$\vec{B}_1 \bot \vec{B}_2$$, so the net field at $$O$$ is
$$B = \sqrt{B_1^2 + B_2^2}$$ or $$B = \dfrac{\mu_0 IR^2 \sqrt{2}}{2(x^2 + R^2)^{3/2}}$$
In case $$x > > R$$
$$\therefore B = \dfrac{\mu_0 IR^2\sqrt{2}}{2x^3}$$
Class 12 Medical Physics Extra Questions
- Alternating Current Extra Questions
- Atoms Extra Questions
- Current Electricity Extra Questions
- Dual Nature Of Radiation And Matter Extra Questions
- Electric Charges And Fields Extra Questions
- Electromagnetic Induction Extra Questions
- Electromagnetic Waves Extra Questions
- Electrostatic Potential And Capacitance Extra Questions
- Magnetism And Matter Extra Questions
- Moving Charges And Magnetism Extra Questions
- Nuclei Extra Questions
- Ray Optics And Optical Instruments Extra Questions
- Semiconductor Electronics: Materials, Devices And Simple Circuits Extra Questions
- Wave Optics Extra Questions