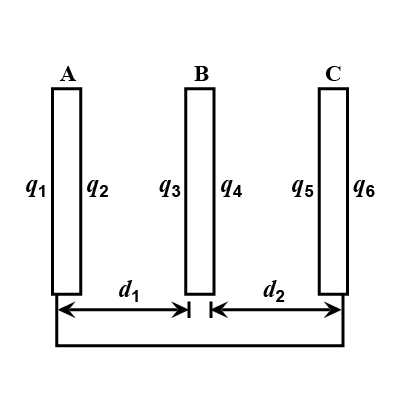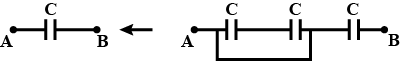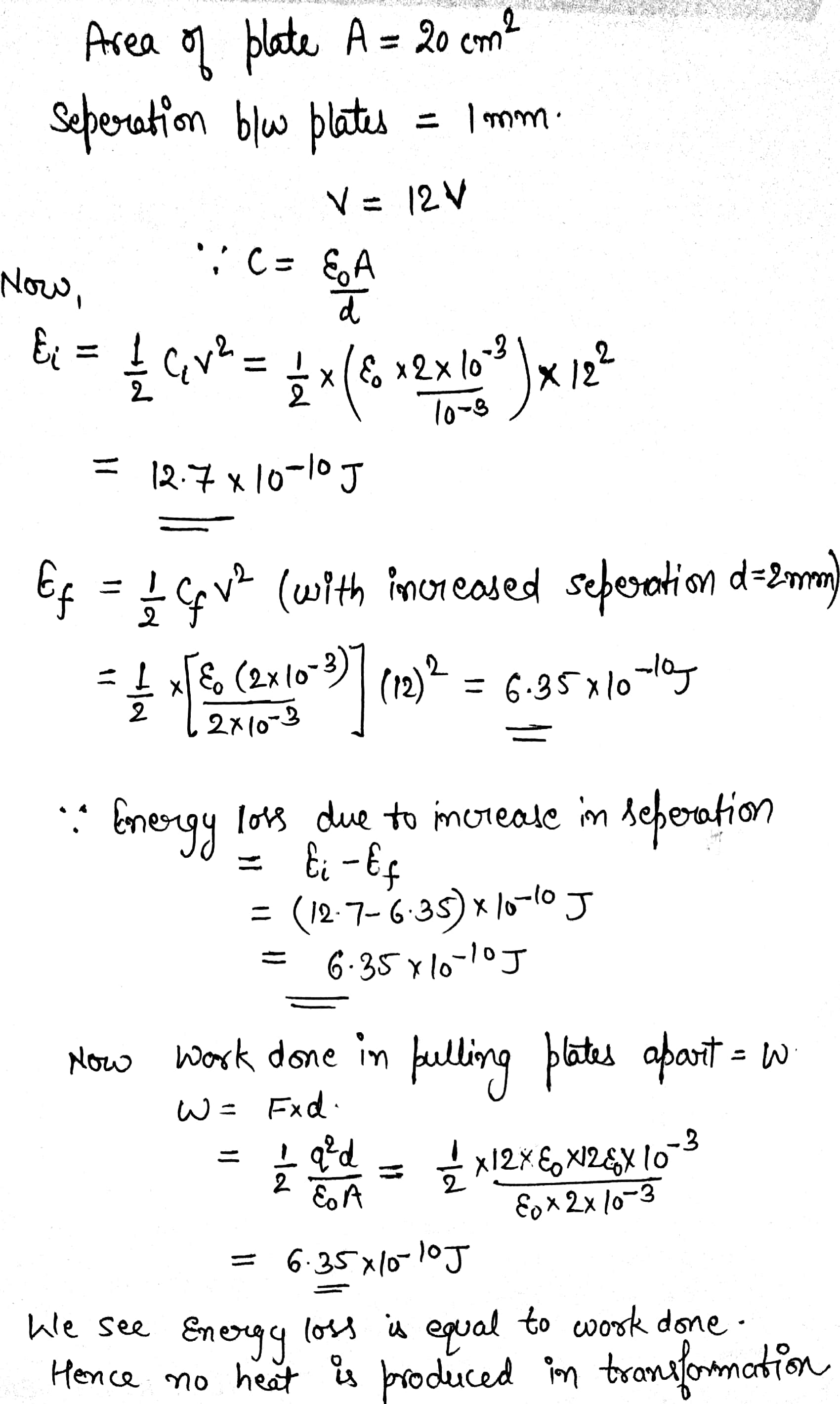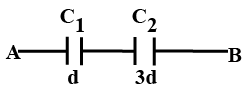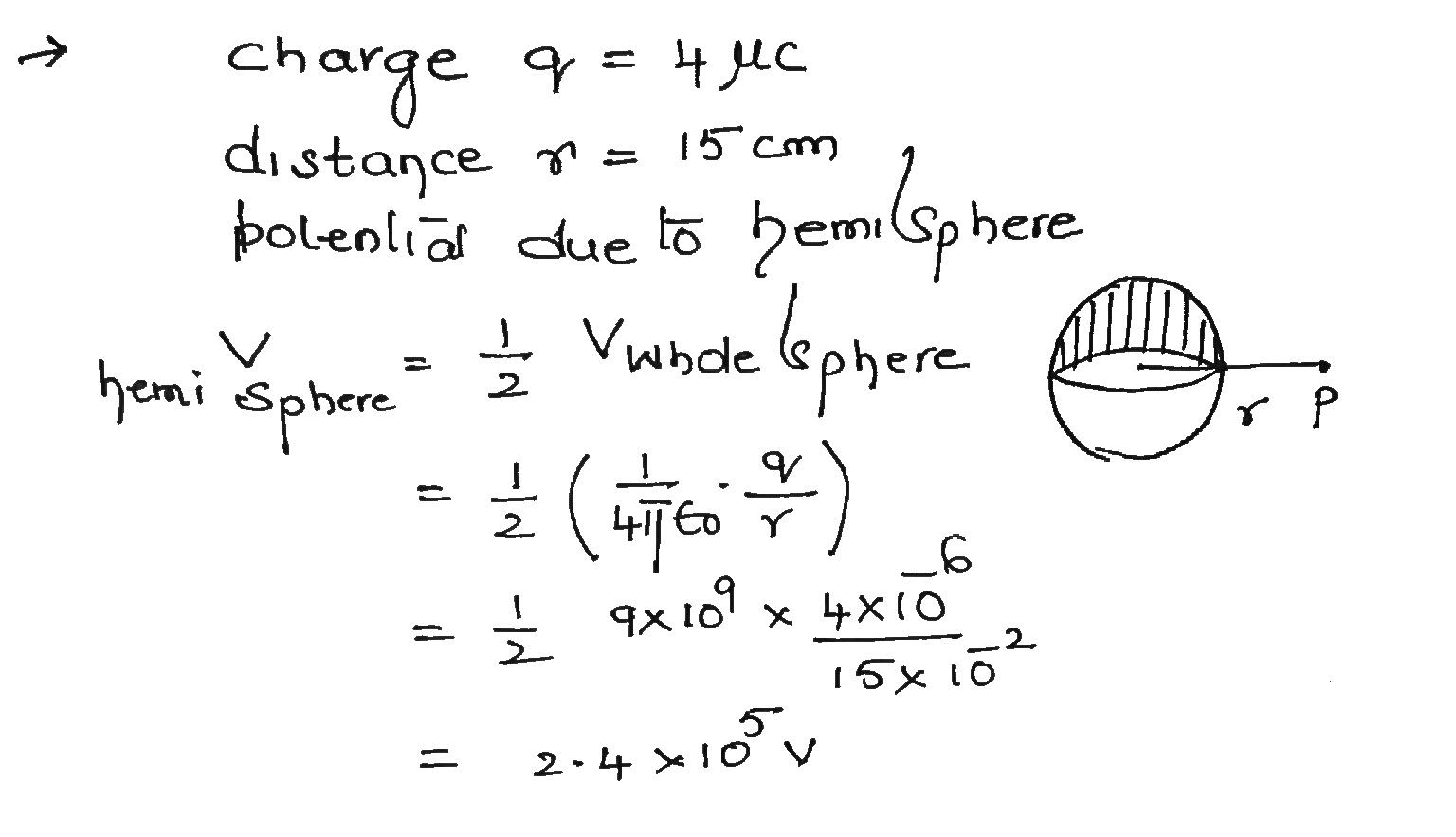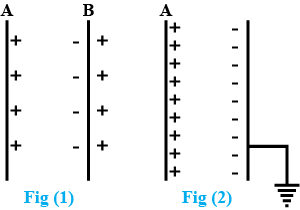Electrostatic Potential And Capacitance - Class 12 Medical Physics - Extra Questions
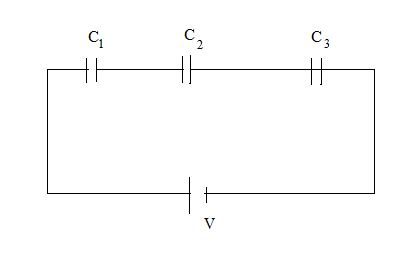
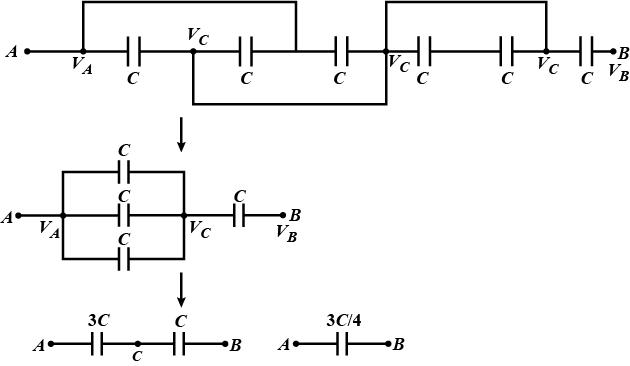
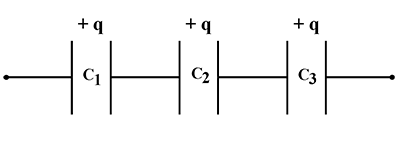
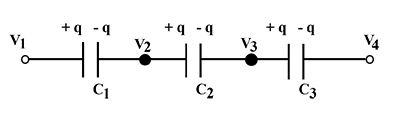
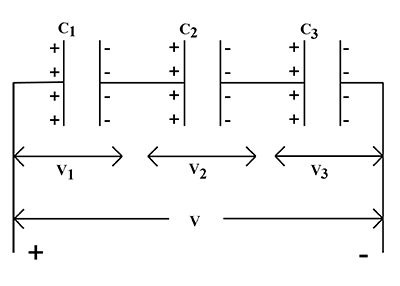
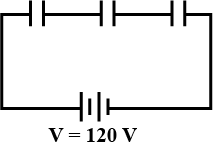
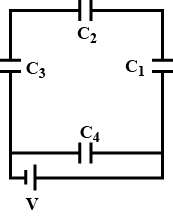
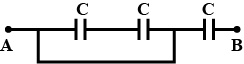
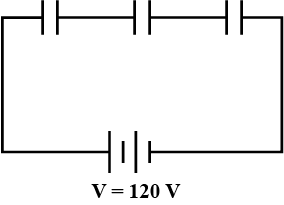
Three capacitors each of capacitance $$9\ pF$$ are connected in series as shown in figure.
(a) What is the total capacitance of the combination?
(b) What is the potential difference across each capacitor, if the combination is connected to a $$120\ volt$$ supply?
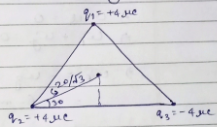
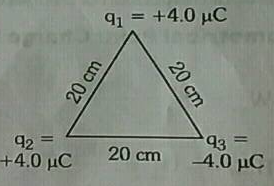
Three point charges $$Q_1=25\mu$$C, $$Q_2=50\mu$$C and $$Q_3=100\mu$$C, are kept at the corners A, B and C respectively of an equilateral triangle ABC having each side equal to $$7.5$$m. Calculate the total electrostatic potential energy of the system.
Explain series combination of Capacitors. Derive the formula for equivalent capacitance.
When one terminal of a capacitor is connected to the terminal of another capacitors , called series combination of capacitors. In series, each capacitor has same charge flow from battery. The three capacitors $$C_1, C_2$$ and $$C_3$$ are in series.
Now, charge on first capacitor is $$Q_1=C_1V_1$$, charge on second capacitor is $$Q_2=C_2V_2$$ and charge on third capacitor is $$Q_3=C_3V_3$$.
In series, $$Q_1=Q_2=Q_2=Q$$ and $$Q=C_{eq}V$$
Also, $$V=V_1+V_2+V_3$$
$$\dfrac{Q}{C_{eq}}=\dfrac{Q}{C_1}+\dfrac{Q}{C_2}+\dfrac{Q}{C_3}$$
$$\dfrac{1}{C_{eq}}=\dfrac{1}{C_1}+\dfrac{1}{C_2}+\dfrac{1}{C_3}$$, this is the formula for equivalent capacitance in series.
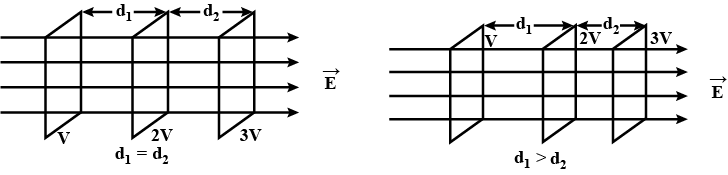
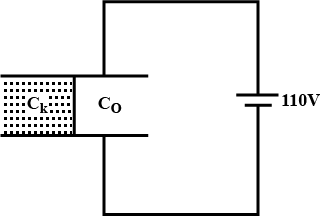
In the arrangement shown in fig. plate B has a charge equal to 60 $$\mu C$$ The ratio $$d_1/d_2$$ isThen
$$q_1=$$____
$$q_2=$$____
$$q_3=$$____
$$q_4=$$____
$$q_5=$$____
$$q_6=$$____
$${ d }_{ 1 }=2{ d }_{ 2 }$$
$${ q }_{ 3 }+{ q }_{ 4 }=60\mu c$$
$${ q }_{ 2 }=-{ q }_{ 3 }$$
$${ q }_{ 5 }=-{ q }_{ 4 }$$
$$\dfrac { { q }_{ 3 }\times { d }_{ 1 } }{ A{ \epsilon}_{ 0 } } =\dfrac { { q }_{ 4 }{ d }_{ 2 } }{ A{ \epsilon }_{ 0 } } $$
$${ q }_{ 3 }{ d }_{ 1 }={ q }_{ 4 }{ d }_{ 2 }$$
$$2{ q }_{ 3 }={ q }_{ 4 }$$
$$3{ q }_{ 3 }=60$$
$$\boxed { { q }_{ 3 }=20 } $$
so,
$${ q }_{ 1 }=20\mu c$$
$${ q }_{ 2 }=-20\mu c$$
$${ q }_{ 3 }=20\mu c$$
$${ q }_{ 4 }=40\mu c$$
$${ q }_{ 5 }=-40\mu c$$
$${ q }_{ 6 }=40\mu c$$
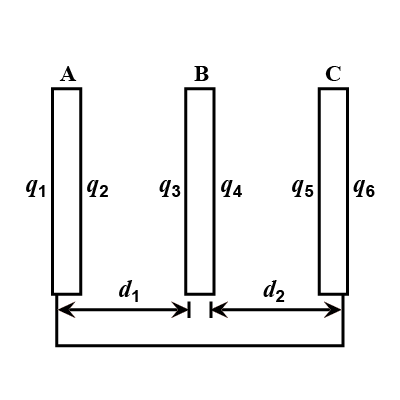
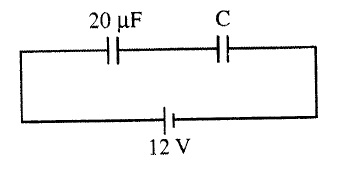
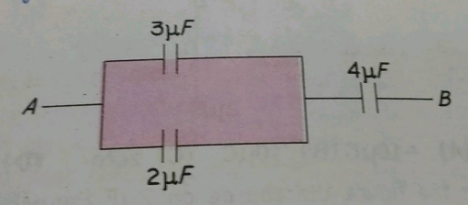
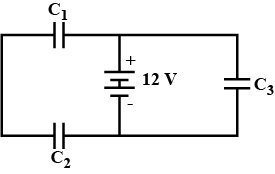
Two capacitors are connected as shown in figure below. If the equivalent capacitance of the combination is $$4 \mu F$$
(i) Calculate the value of $$C$$.
(ii) Calculate the charge on each capacitor.
(iii) What will be the potential drop across each capacitor?
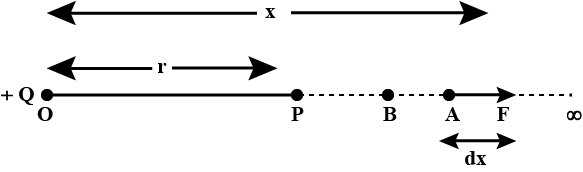
Show that electric potential at a point P, at a distance 'r' from a fixed point charge Q, is given by $$\displaystyle V=\left(\displaystyle\frac{1}{4\pi \epsilon_0}\right)\displaystyle\frac{Q}{r}$$.
A parallel plate capacitor has circular plates of $$10\ cm$$ radius separated by an air gap of $$1\ mm$$. It is charged by connecting the plates to a $$100\ volt$$ battery. Find the change in energy stored in the capacitor when the plates are moved to a distance of $$1\ cm$$ and the plates are maintained in connection with the battery.
A parallel plate capacitor with air has a capacity of $$8\ pF$$. Calculate the capacity of the capacitor if the distance between the plates in halved and the space between them is fully filled with a substance of dielectric constant $$5$$.
Define electric potential and write down its dimension.
(a) A charged rod P attracts rod R whereas P repels another charged rod Q. What type of force is developed between Q and R?
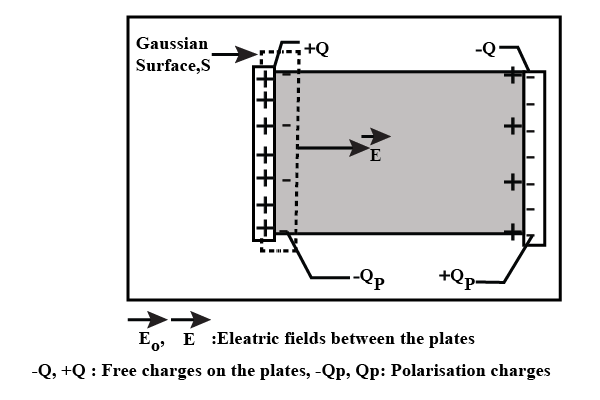
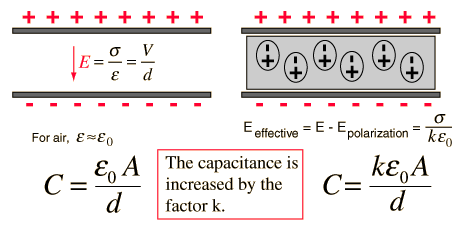
(b) Define the capacitance of capacitor. Derive and expression for the capacity at a parallel plate capacitor with a dielectric slab placed in between the plates of capacitor.
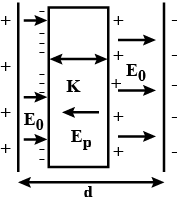
For a capacitor, the distance between two plates is $$5x$$, the electric field between them is $$E_{0}$$, now dielectric slab having dielectric constant $$3$$ and thickness $$3x$$ is placed between them in contact with one plate. In this condition what is the potential difference between its two plates?
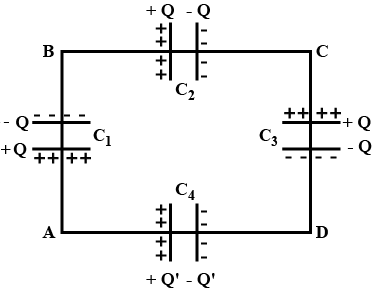
A network of four capacitors of capacity equal to $${C_1} = C,\,\,{C_2} = 2C,\,\,{C_3} = 3C$$ and $${C_4} = 4C$$ are connected to a battery as shown in the figure. The ratio of the charges on $${C_2}$$ and $${C_4}$$ is:
On what factors does the capacitance of a parallel plate capacitors depends?
Define electric potential due to a point charge and arrive at the expression for the electric potential at a point due to a point charge in its vicinity.
The electrostatic potential at any point in an electrostatic field is defined as the work done in carrying a unit positive charge from infinity to that point against the electrostatic force of the field.
Consider a point Charge $$+Q$$ at $$O$$.
Let $$P$$ be a point at a distance $$r$$ from $$O$$.
Consider a point $$A$$ at a distance $$x$$ from $$O$$.
The magnitude of electrostatic force on unit-positive charge at $$A$$, is
$$\quad F=\cfrac { 1 }{ 4\pi { \varepsilon }_{ 0 } } \cfrac { Q\times i }{ { x }^{ 2 } } $$
$$F=\cfrac { Q }{ 4\pi { \varepsilon }_{ 0 }{ x }^{ 2 } } $$ along $$OP$$
Work Done in moving a unit positive charge from $$A$$ to $$B$$ through a small distance $$dx$$ is,
$$\Delta W=\vec { F } .d\vec { x } =Fdx\cos { { 180 }^{ o } } $$
$$\Delta W=-Fdx$$
$$\Delta W=\cfrac { -Q }{ 4\pi { \varepsilon }_{ 0 }{ x }^{ 2 } } dx$$
Total work done in moving a unit positive change from infinity to the point $$P$$ is,
$$W=\displaystyle \int _{ \infty }^{ r }{ \cfrac { -1 }{ 4\pi { \varepsilon }_{ 0 } } \cfrac { Q }{ { x }^{ 2 } } } dx=-\cfrac { Q }{ 4\pi { \varepsilon }_{ 0 }{ x }^{ 2 } } \int _{ \infty }^{ r }{ \cfrac { 1 }{ x^2 } } dx$$
$$W=-\cfrac { Q }{ 4\pi { \varepsilon }_{ 0 } } { \left[ \cfrac { 1 }{ x } \right] }_{ \infty }^{ r }=\cfrac { Q }{ 4\pi { \varepsilon }_{ 0 } } \left[ \cfrac { 1 }{ r } -\cfrac { 1 }{ \infty } \right] $$
$$W=\cfrac { Q }{ 4\pi { \varepsilon }_{ 0 }r }$$
By definition, this work done is equal to the electrostatic potential (V) at that point due to $$Q$$.
$$V=\cfrac { 1 }{ 4\pi { \varepsilon }_{ 0 } } \cfrac { Q }{ r } $$
Consider a point Charge $$+Q$$ at $$O$$.
Let $$P$$ be a point at a distance $$r$$ from $$O$$.
Consider a point $$A$$ at a distance $$x$$ from $$O$$.
The magnitude of electrostatic force on unit-positive charge at $$A$$, is
$$\quad F=\cfrac { 1 }{ 4\pi { \varepsilon }_{ 0 } } \cfrac { Q\times i }{ { x }^{ 2 } } $$
$$F=\cfrac { Q }{ 4\pi { \varepsilon }_{ 0 }{ x }^{ 2 } } $$ along $$OP$$
Work Done in moving a unit positive charge from $$A$$ to $$B$$ through a small distance $$dx$$ is,
$$\Delta W=\vec { F } .d\vec { x } =Fdx\cos { { 180 }^{ o } } $$
$$\Delta W=-Fdx$$
$$\Delta W=\cfrac { -Q }{ 4\pi { \varepsilon }_{ 0 }{ x }^{ 2 } } dx$$
Total work done in moving a unit positive change from infinity to the point $$P$$ is,
$$W=\displaystyle \int _{ \infty }^{ r }{ \cfrac { -1 }{ 4\pi { \varepsilon }_{ 0 } } \cfrac { Q }{ { x }^{ 2 } } } dx=-\cfrac { Q }{ 4\pi { \varepsilon }_{ 0 }{ x }^{ 2 } } \int _{ \infty }^{ r }{ \cfrac { 1 }{ x^2 } } dx$$
$$W=-\cfrac { Q }{ 4\pi { \varepsilon }_{ 0 } } { \left[ \cfrac { 1 }{ x } \right] }_{ \infty }^{ r }=\cfrac { Q }{ 4\pi { \varepsilon }_{ 0 } } \left[ \cfrac { 1 }{ r } -\cfrac { 1 }{ \infty } \right] $$
$$W=\cfrac { Q }{ 4\pi { \varepsilon }_{ 0 }r }$$
By definition, this work done is equal to the electrostatic potential (V) at that point due to $$Q$$.
$$V=\cfrac { 1 }{ 4\pi { \varepsilon }_{ 0 } } \cfrac { Q }{ r } $$
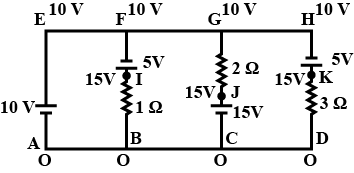
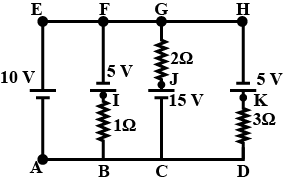
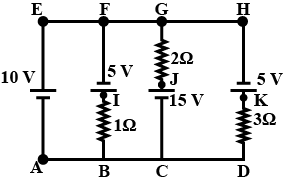
In the following circuit potential at point 'A' is zero then determine Potential at each point.
Three capacitors having capacitances $$20\mu F, 30\mu F$$ and $$40\mu F$$ are connected in series with a $$12\ V$$ battery. Find the charge on each of the capacitors. How much work has been done by the battery in charging the capacitors?
Match the columns.
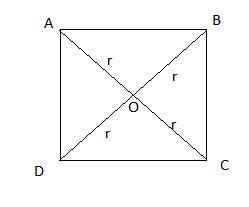
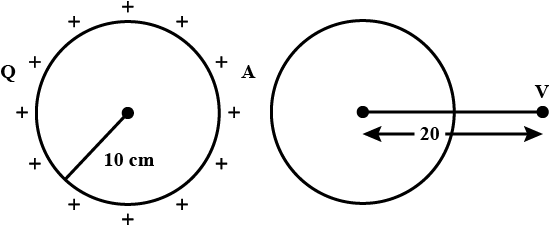
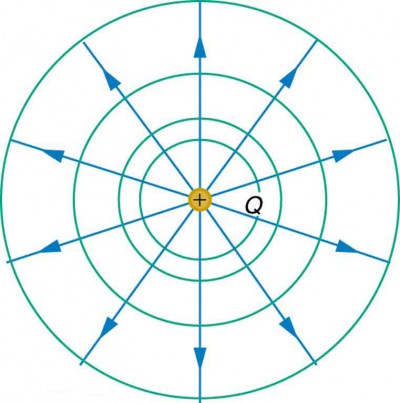
What is the electric potential at the center of the triangle in figure.
$$\because$$ Electric potential is a sealer quantity
$$\therefore$$ It can be added algebraically.
$$\Rightarrow V_{net}=V_{1}+V_{2}+V_{3}$$
$$\Rightarrow V_{net}=\dfrac{kq_{1}}{r}+\dfrac{kq_{2}}{r}+\dfrac{kq_{3}}{r}$$
$$\Rightarrow V_{net}=\dfrac{k}{r}(q_{1}+q_{2}+q_{3})$$
$$\Rightarrow V_{net}=\dfrac{9\times 10^{9}}{\left(\dfrac{20}{\sqrt{3}}\times 100\right)}(+4+4-4)\times 10^{-6}$$
$$=\dfrac{9\times 10^{9}\times 4\times \sqrt{3}\times 100\times 10^{-6}}{20}$$
$$V_{net}=3.078\times 10^{5}V$$
In the following circuit potential at point 'A' is zero then determine Potential difference across each resistance.
$$\quad As\quad given\quad the\quad potential\quad of\quad A\quad is\quad 0V\quad therefore\quad \\ \quad \quad \quad \quad { V }_{ A }={ V }_{ B }={ V }_{ C }={ V }_{ D }=0V\\ And\quad { V }_{ E }={ V }_{ F }={ V }_{ G }={ V }_{ H }=10V\\ Therefore\quad potential\quad across\quad I\quad resistor\quad becomes\quad \\ \quad \quad 10+5=15V\\ And\quad potential\quad across\quad J\quad resistor\\ \quad 15-10=5V\\ And\quad potential\quad across\quad K\quad resistor\quad becomes\\ \quad 10+5=15V\quad $$
The equivalent capacitance between A and B are:
The equivalent capacitance is $$C$$.
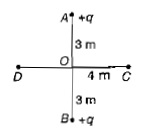
Calculate in the given figure: Charge at $$O$$ is $$10\mu C$$ $$(i)$$ Electric potentials at point $$A$$ and $$B$$, $$(ii)$$ work done in taking the same amount of negative charge from $$A$$ to $$B$$, $$(OA=0.10\ m, OB=0.20\ m$$), assume that the charge at $$O$$ stays fixed
If the difference between the radii of the two sphere of a spherical conductor is increased state whether the capacitance will increase or decrease.
A capacitor of capacitance $$10 \mu F$$ is connected to battery of emf $$20\ V$$. Without disconnecting the source a dielectric $$(K=4)$$ is introduced to fill the space between two plates of the capacitor. Calculate the-
(a) charge before the dielectric was introduced.
(b) charge After the dielectric was introduced.
A nucleus has charged of + $$50$$ e A proton is located at a distance of $$10$$ m The potential at this point in volt will be-
What is meant by saying that the electric potential at a point is $$1\ Volt$$?
What should be the charge on a sphere of radius 2 cm so that when it is brought in contact with another sphere of radius 5 cm carrying a charge of $$10\mu C$$, there is no transfer of charge between the spheres?
A $$ 5.0\mu F$$ capacitor is charged to 12 V. The positive of this capacitor is now connected to the negative terminal of a 12 V battery and vice versa. Calculate the heat developed in the connecting wires.
A parallel plate air capacitor is connected to a battery.If plates of the capacitor are pulled farther apart, then state whether the following statements are true or flase
a. Strength of electric field inside the capacitor remains unchanged, if battery is disconnected before pulling the plates.
b. During the process, work is done by external force applied to pull the plates irrespective of whether the battery is disconnected or not.
c.Strain energy in the capacitor decreases if the battery remains connected
A parallel-plate capacitor of capacitance $$5 \mu F$$ is connected to a battery of emf $$6 V.$$ The separation between the plates is $$2 mm$$. A dielectric slab of thickness $$1 mm$$ and dielectric constant $$5$$ is inserted into the gap to occupy the lower half of it. Find the capacitance of the new combination.
Answer the following questions.
Derive an expression for equivalent capacitance of three capacitors when connected in series.
Derive an expression for equivalent capacitance of three capacitors when connected in parallel.
In a fig (a) Three capacitors of capacitances $$ C_{1} $$ , $$ C_{2} $$ , $$ C_{3} $$ are connected in series between points A and D. In series' first plate of each capacitor has charge +Q and second plate of each capacitor has charge -Q i.e., charge on each capacitor is Q.
Let the potential differences across the capacitors $$ C_{1} $$
$$ C_{2} $$ , $$ C_{3} $$ be $$V_{1} $$ , $$ V_{2} $$ , $$V_{3} $$
respectively. As the second plate of first capacitor $$C_{1} $$ and first plate of second capacitor $$C_{2} $$ are connected together, their potentials are equal.
Let the potential differences across the capacitors $$ C_{1} $$
$$ C_{2} $$ , $$ C_{3} $$ be $$V_{1} $$ , $$ V_{2} $$ , $$V_{3} $$
respectively. As the second plate of first capacitor $$C_{1} $$ and first plate of second capacitor $$C_{2} $$ are connected together, their potentials are equal.
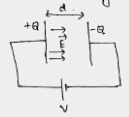
A test charge 'q' is mover without acceleration from A to C along the path from A to B and then from B to C in electric field E as shown in the figure.
At which point (of the two) is the electric potential more and why?
Where is the energy stored due to an electric charge?
What is electric potential? Write its formula and unit.
Electric Potential In fig. 3.1 it is shown that in electric field due to a configuration of charges, the work done in carrying a test charge $$ \left(\mathrm{q}_{0}\right) $$ from point $$ \mathrm{A} $$ to $$ \mathrm{B} $$, depends only upon the distance between $$ \mathrm{A} $$ and $$ \mathrm{B} $$ not on the path adopted.
"Electric potential is the factor which decides the direction of flow of electric charge."It is scalar quantity and it is denoted by V. As liquids flow from higher gravitation level to the lower level; heatflows from higher temperature to the lower temperature, similarly charge (positive) flows from higherelectric potential to the lower potential. Negative charge flows from lower electric potential to the higherpotential.
If $$ \mathrm{V}_{\mathrm{A}} $$ and $$ \mathrm{V}_{\mathrm{B}} $$ be the electric potentials at points $$ \mathrm{A} $$ and $$ \mathrm{B} $$ respectively, then the potential difference betweenpoints A and B is given below,$$\mathrm{V}_{\mathrm{B}}-\mathrm{V}_{\mathrm{A}}=\dfrac{W_{\mathrm{AB}}}{q_0}\ldots(1)$$
Where, $$ W_{A B} $$ is the work done in carrying test charge $$ +q_{0} $$ from $$ A $$ to $$ B $$.
Here we assume that in this process, the test charge does not disturb the source of field, i.e., all the charges remain at their position. If for a displacement, the change in potential energy is $$ \cup_{B}-U_{A} $$, then the potential difference between the points A and B can be given as
$$V_{B}-V_{A}=\dfrac{U_{B}-U_{A}}{q_{0}}=\dfrac{\Delta U}{q_{0}}\ldots (2)$$
Therefore from equations (1) and (2),
$$V_{B}-V_{A}=\dfrac{U_{B}-U_{A}}{q_{0}}=\dfrac{W_{A B}}{q_{0}}\ldots (3)$$
If $$ \mathrm{q}_{0}=+1 \mathrm{C}, $$ then $$ \mathrm{V}_{\mathrm{B}}-\mathrm{V}_{\mathrm{A}}=\mathrm{W}_{\mathrm{AB}} $$
"Electric potential is the factor which decides the direction of flow of electric charge."It is scalar quantity and it is denoted by V. As liquids flow from higher gravitation level to the lower level; heatflows from higher temperature to the lower temperature, similarly charge (positive) flows from higherelectric potential to the lower potential. Negative charge flows from lower electric potential to the higherpotential.
If $$ \mathrm{V}_{\mathrm{A}} $$ and $$ \mathrm{V}_{\mathrm{B}} $$ be the electric potentials at points $$ \mathrm{A} $$ and $$ \mathrm{B} $$ respectively, then the potential difference betweenpoints A and B is given below,$$\mathrm{V}_{\mathrm{B}}-\mathrm{V}_{\mathrm{A}}=\dfrac{W_{\mathrm{AB}}}{q_0}\ldots(1)$$
Where, $$ W_{A B} $$ is the work done in carrying test charge $$ +q_{0} $$ from $$ A $$ to $$ B $$.
Here we assume that in this process, the test charge does not disturb the source of field, i.e., all the charges remain at their position. If for a displacement, the change in potential energy is $$ \cup_{B}-U_{A} $$, then the potential difference between the points A and B can be given as
$$V_{B}-V_{A}=\dfrac{U_{B}-U_{A}}{q_{0}}=\dfrac{\Delta U}{q_{0}}\ldots (2)$$
Therefore from equations (1) and (2),
$$V_{B}-V_{A}=\dfrac{U_{B}-U_{A}}{q_{0}}=\dfrac{W_{A B}}{q_{0}}\ldots (3)$$
If $$ \mathrm{q}_{0}=+1 \mathrm{C}, $$ then $$ \mathrm{V}_{\mathrm{B}}-\mathrm{V}_{\mathrm{A}}=\mathrm{W}_{\mathrm{AB}} $$
Conceptual Questions
If you were asked to design a capacitor in which small size and large capacitance were required, what would be the two most important factors in your design?
A parallel-plate capacitor is formed by two discs with a uniform poorly conducting medium between them. The capacitor was initially charged and then disconnected from a voltage source. Neglecting the edge effects, show that there is no magnetic field between capacitor plates.
A charge $$q$$ is distributed uniformly over the volume of a ball of radius $$R$$. Assuming the permittivity to be equal to unity, find:
(a) the electrostatic self-energy of the ball;
(b) the ratio of the energy $$W_{1}$$ stored in the ball to the energy $$W_{2}$$ pervading the surrounding space.
Distinguish between electric potential and electric potential energy.
Two concentric shells of radii $$d$$ and $$2d$$ respectively are placed far away from a parallel plate capacitor. Each plate of the capacitor is a square of side $$d$$ and separation between the plates is $$d/4\pi$$. The charge on the plates are $$q$$ and $$-q$$. Then the keys $$k_1$$ and $$k_2$$ are closed, find the charges on the shells and electric potential energy left in the parallel plate capacitor in equilibrium.
let the new charge on the parallel plate capacitor be $$+q_1$$ and that on the concentric shells be $$(q - q_1)$$, such that the potential differences across the shell would be same as the potential difference across the plates.
$$\phi_{innershell} = \dfrac{(q - q_1)}{4\pi \varepsilon_0(2d)} + \dfrac{-(q - q_1)}{4\pi \varepsilon_0 d} = \dfrac{-(q - q_1)}{4\pi \varepsilon(2d)}$$
$$\phi_{outershell} = \dfrac{(q - q_1)}{4\pi \varepsilon_0(2d)} + \dfrac{-(q - q_1)}{4\pi \varepsilon_0(2d)} = 0$$
Potential difference, $$V_{shells} = \phi{outer} - \phi{inner} = \dfrac{(q - q_1)}{4\pi \varepsilon_0(2d)}$$
for parallel plate, $$V_{plates} = \dfrac{q_1}{4\pi \varepsilon_0 d}$$
$$V_{shells} = V_{plates}$$
$$\dfrac{(q - q_1)}{4\pi \varepsilon_0(2d)} = \dfrac{q_1}{4\pi \varepsilon_0 d}$$
$$\Longrightarrow (q - q_1) = 2q_1$$
$$q_1 = q/3$$
$$\therefore$$ Charge on the outer shell $$= (q - q_1) = \dfrac{2}{3}q$$
Charge on the inner shell $$= 2q/3$$
Energy left in the parallel plate capacitor $$= \dfrac{1}{2}\dfrac{q^2_1}{C} = \dfrac{q^2}{72\in \varepsilon_0 d}$$
$$\phi_{innershell} = \dfrac{(q - q_1)}{4\pi \varepsilon_0(2d)} + \dfrac{-(q - q_1)}{4\pi \varepsilon_0 d} = \dfrac{-(q - q_1)}{4\pi \varepsilon(2d)}$$
$$\phi_{outershell} = \dfrac{(q - q_1)}{4\pi \varepsilon_0(2d)} + \dfrac{-(q - q_1)}{4\pi \varepsilon_0(2d)} = 0$$
Potential difference, $$V_{shells} = \phi{outer} - \phi{inner} = \dfrac{(q - q_1)}{4\pi \varepsilon_0(2d)}$$
for parallel plate, $$V_{plates} = \dfrac{q_1}{4\pi \varepsilon_0 d}$$
$$V_{shells} = V_{plates}$$
$$\dfrac{(q - q_1)}{4\pi \varepsilon_0(2d)} = \dfrac{q_1}{4\pi \varepsilon_0 d}$$
$$\Longrightarrow (q - q_1) = 2q_1$$
$$q_1 = q/3$$
$$\therefore$$ Charge on the outer shell $$= (q - q_1) = \dfrac{2}{3}q$$
Charge on the inner shell $$= 2q/3$$
Energy left in the parallel plate capacitor $$= \dfrac{1}{2}\dfrac{q^2_1}{C} = \dfrac{q^2}{72\in \varepsilon_0 d}$$
A parallel plate capacitor is charged by a battery and the battery remains connected, a dielectric slab is inserted in the space between the plates. Explain what changes if any, occur in the values of the
(i) potential difference between the plates
(ii) electric field between the plates
(ii) energy stored in the capacitor
$$V\rightarrow constant$$ because battery nemans connected.
$$E = \dfrac {E_{0}}{4} \rightarrow k$$ decreases
$$3.U = \dfrac {1}{2} CV^{2}$$
$$U$$ is same but $$C$$ become $$kC$$
So, $$U = \dfrac {1}{2} CV^{2} \cdot k (k$$ increases)
i.e. Energy store $$\uparrow$$.
A glass plate totally fills up the gap between the electrodes of a parallel-plate capacitor whose capacitance in the absence of that glass plate is equal to $$C = 20\ nF$$. The capacitor is connected to a dc voltage source $$V = 100\ V$$. The plate is slowly, and without friction, extracted from the gap. Find the capacitor energy increment and the mechanical work performed in the process of plate extraction.
A system consists of two thin concentric metal shells of radii $$R_{1}$$ and $$R_{2}$$ with corresponding charges $$q_{1}$$ and $$q_{2}$$. Find the self-energy values $$W_{1}$$ and $$W_{2}$$ of each shell, the interaction energy of the shells $$W_{12}$$, and the total electric energy of the system.
A capacitor of capacitance $$C_{1} = 1.0\mu F$$ carrying initially a voltage $$V = 300\ V$$ is connected in parallel with an uncharged capacitor of capacitance $$C_{2} = 2.0\mu F$$. Find the increment of the electric energy of this system by the moment equilibrium is reached. Explain the result obtained.
Electric Potential and Potential Energy Due to Point Charges(23)
A particle with charge $$+q$$ is at the origin. A particle with charge $$-2q$$ is at $$x=2.00 \,m$$ on the x axis.
(a) For what finite value(s) of x is the electric field zero?
(b) For what finite value(s) of x is the electric potential zero?
Find the mean electrostatic potential produced by an electron in the centre of a hydrogen atom if the electron is in the ground state for which the wave function is $$ \psi (r) = A e^{-r/r_1} $$, where $$A$$ is a certain constant, $$r_1$$ is the first Bohr radius.
A point charge $$q = 3.0\mu C$$ is located at the centre of a spherical layer of uniform isotropic dielectric with permittivity $$\epsilon = 3.0$$. The inside radius of the layer is equal to $$a = 250\ mm$$, the outside radius is $$b = 500\ mm$$. Find the electrostatic energy inside the dielectric layer.
The equivalent capacity between $$A$$ and $$B$$ is.
A uniform electric field of $$10 NC^{-1}$$ exists in the vertically downward direction. Find the increase in the electric potential as one goes up through a height of $$50$$ cm.
A large conducting plane has a surface charge density $$1.0 \times 10^{-4}\ C m^{-2}$$. Find the electrostatic energy stored in a cubical volume of edge $$1.0\ cm$$ in front of the plane.
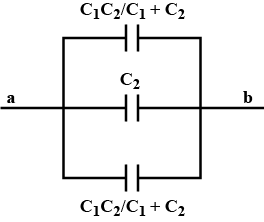
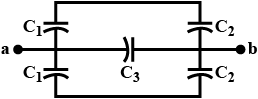
Find the equivalent capacitance of the system shown in figure between the point $$a$$ and $$b$$.
Above combination is in series and parallal.
$$C_{eq}$$ between a & b
$$C_{eq}= \dfrac{C_1 C_2}{C_1 + C_2} + C_3 + \dfrac{C_1C_2}{C_1 + C_2}$$
$$C_{eq}= C_3 + \dfrac{2C_1 C_2}{C_1 + C_2} $$ ($$\therefore$$ The three are parallel)
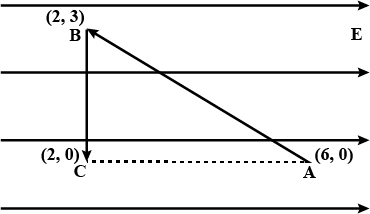
An electric field $$\vec{E}=(\vec{i}20+\vec{j}30)NC^{-1}$$ exists in the space. If the potential at the origin is taken to be zero, find the potential at $$(2m, 2m)$$.
A parallel-plate capacitor having plate area $$20\ cm^2$$ and separation between the plates $$1.00\ mm$$ is connected to a battery of $$12.0\ V$$. The plates are pulled apart to increase the separation to $$2.0\ mm$$. How much energy is absorbed by the battery during the process?
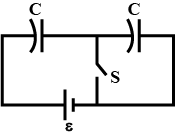
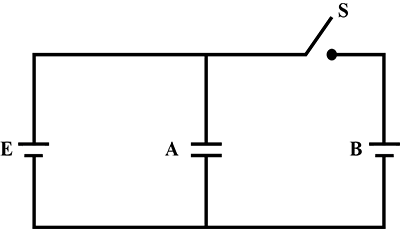
Consider the situation shown in the figure. The switch $$S$$ is open for a long time and then closed. Find the work done by the battery.
A parallel-plate capacitor having plate area $$20 cm^2$$ and separation between the plates 1.00 mm is connected to a battery of $$12.0 V$$. The plates are pulled apart to increase the separation to $$2.0 mm$$. Show and justify that no heat is produced during this transfer of charge as the separation is increased.
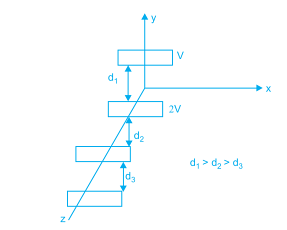
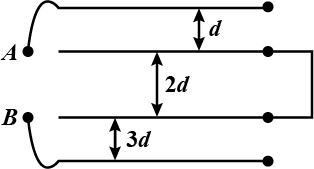
If the area of each plate is $$A$$ (figure) and the successive separations are $$d,2d$$ and $$3d$$, the equivalent capacitance across $$A$$ and $$B$$ is $$\cfrac { { \varepsilon }_{ 0 }A }{ xd } $$. Find $$x$$ :
The equivalent circuit is shown in figure.
Here, $$\displaystyle C_1=\frac{A\epsilon_0}{d}$$ and $$\displaystyle C_2=\frac{A\epsilon_0}{3d}=\frac{C_1}{3}$$
As they are in series so equivalent capacitance is $$\displaystyle C_{AB}=\frac{C_1C_2}{C_1+C_2}=\frac{C_1(C_1/3)}{C_1+(C_1/3)}=\frac{C_1}{4}=\frac{A\epsilon_0}{4d}$$
Here, $$\displaystyle C_1=\frac{A\epsilon_0}{d}$$ and $$\displaystyle C_2=\frac{A\epsilon_0}{3d}=\frac{C_1}{3}$$
As they are in series so equivalent capacitance is $$\displaystyle C_{AB}=\frac{C_1C_2}{C_1+C_2}=\frac{C_1(C_1/3)}{C_1+(C_1/3)}=\frac{C_1}{4}=\frac{A\epsilon_0}{4d}$$
In an hydrogen atom, the electron revolves around the nucleus in an orbit of radius $$0.53 \times {10^{ - 10}}m.$$ Then the electrical potential produced by the nucleus at the position of the electron is
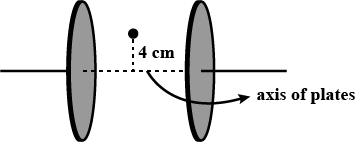
Two circular plates of radius 0.1 m are used to form a parallel plate capacitor. if displacement current between the plates is $$2\pi$$ ampere, then find magnetic field produced by displacement current 4 cm from the axis of the plates.
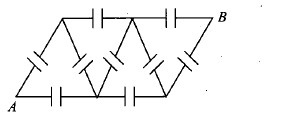
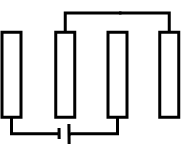
Some capacitors each of capacitance $$30\mu F$$ are connected as shown in Fig. Calculate equivalent capacitance between terminals A and B.
$$Q=\dfrac{11}{15}CV$$
Hence, $$Q=C_{eq}V=\dfrac{11}{15}CV$$
$$C_{eq}=\dfrac{11}{15}C=\dfrac{11}{15}30=22\mu C$$
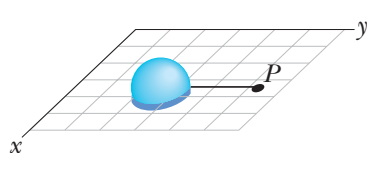
The above figure shows a hemisphere with a charge of $$4.00 \ \mu C$$ distributed uniformly through its volume. The hemisphere lies on an $$xy$$ plane the way half a grapefruit might lie face down on a kitchen table. Point $$P$$ is located on the plane, along a radial line from the hemisphere's center of curvature, at radial distance $$15 \ cm$$. What is the electric potential at point $$P$$ due to the hemisphere?
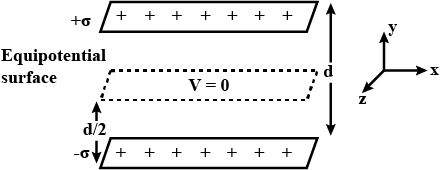
Two uniformly large parallel thin plates having charge densities $$+\sigma $$ and $$-\sigma $$ are kept in the X-Z plane at a distance 'd' apart. Sketch an equipotential surface due to electric field between the plates. If a particle of mass m and charge '-q' remains stationary between the plates, what is the magnitude and direction of this field?
The equipotential surface is at a distance d/2 from either plate in X-Z plane. For a particle of charge (-q) at rest between the plates, then
Weight mg acts vertically downward
Electric force $$qE$$ vertically upward
so $$mg = qE$$
$$E = \dfrac{mg}{q},$$ Vertically downward, i.e., along (-) Y-axis.
Weight mg acts vertically downward
Electric force $$qE$$ vertically upward
so $$mg = qE$$
$$E = \dfrac{mg}{q},$$ Vertically downward, i.e., along (-) Y-axis.
A $$10 V$$ battery is connected to a series of $$n$$ capacitors, each of capacitance $$2.0 µF$$. If the total stored energy is $$25 µJ$$, what is $$n$$?
Define electric potential.
Define the term electric potential. State its S.I. unit.
Write the S.I. unit of capacitance.
What is an equipotential surface?
Find equivalent capacitance between points $$A$$ and $$B$$ as shown in figure.
At what point on the line joining the two charge is the electric potential zero.
Let the potential at point A be 0.
$$\frac{kq_{1}}{x}+\frac{kq_{2}}{d-x}=0$$
$$\frac{kq_{1}}{x}=-\frac{kq_{2}}{d-x}$$
$$\Rightarrow \frac{q_{1}}{x}=\frac{q_{2}}{x-d}$$
$$\Rightarrow x=\frac{q_{1}d}{q_{1}-q_{2}}$$
Name the physical quantity whose $$SI$$ unit is $$J/C$$. is it a scalar or a vector quantity?
A 12pF capacitor is connected to a 50 V battery . How much of electrostatic energy is stored in the capacitor?
What is the equivalent capacitance of the combination ?
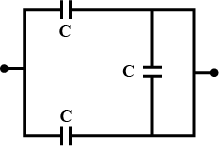
Two condensers A and B each having slabs of dielectric constant $$K = 2$$ are connected in series. When they are connected across 230 V supply, potential across A is 130 V and that across B is 100 V. If the dielectric in the condenser of smaller capacitance is replaced by one for which $$K=5$$ what will be the values of potential difference across them?
What is the charge density on each surface of the dielectric?
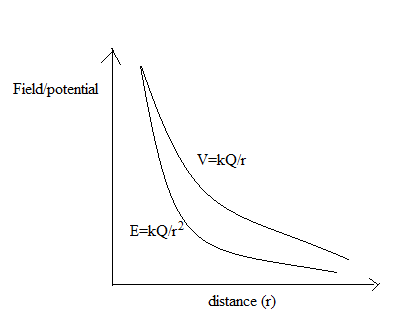
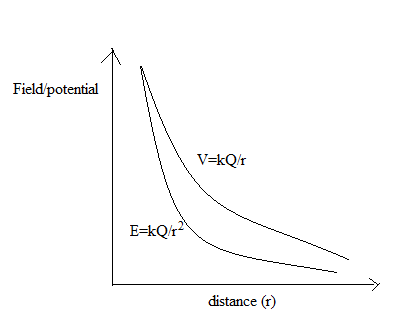
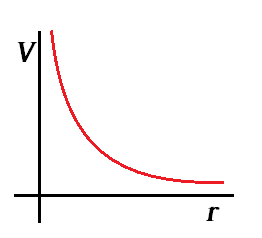
Draw a plot showing the variation of (i) electric field $$\left(E\right)$$ and (ii) electric potential $$\left(V\right)$$ with distance $$r$$ due to a point charge $$Q$$.
The electric field due to point charge Q is $$E=kQ/r^2$$ and the potential is $$ V=kQ/r$$
Thus, the graph E,V vs r will be as shown in figure.
If $$100$$ joule of work must be done to move electric charge equal to $$4\ C$$ from a place, where potential is $$-10$$ volt to another place, where potential is V volt, find the value of V.
State whether true or false : The unit of voltage is $$JC^{-1}$$.
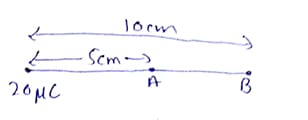
A charge of $$20\mu C$$ produces an electric field. Two points are $$10\ cm$$ and $$5\ cm$$ away from this charge. Find the values of potentials at these points and also find the amount of work done to take an electron from one point to the other.
$$V_A=\cfrac{1}{4\pi {\epsilon}_0} \cfrac{q}{r_A} = \cfrac{9 \times {10}^9 \times 20 \times {10}^{-6}}{0.05}$$
$$V_A=36 \times {10}^{-5} \; V$$
$$V_B=\cfrac{1}{4\pi {\epsilon}_0} \cfrac{q}{r_B} = \cfrac{9 \times {10}^9 \times 20 \times {10}^{-6}}{0.1}$$
$$V_B=18 \times {10}^{-5} \; V$$
$$\text{Work done} = e \triangle{V}$$
$$W = 1.6 \times {10}^{-19} (36 \times {10}^{-5} - 18 \times {10}^{-5})$$
$$W=28.8 \times {10}^{-24} j = 0.18meV$$
$$ABCD$$ is a square of side $$0.2\ m$$. Charges of $$2\times 10^{-9}, 4\times 10^{-9}, 8\times 10^{-9}$$ coulomb are placed at the corners A, B and C respectively. Calculate the work required to transfer a charge of $$2\times 10^{-9}$$ coulomb from corner D to the centre of the square.
$$AC=BD=\sqrt{(0.2)^{2}+(0.2)^{2}}$$
$$=\sqrt{2}\times 0.2=0.28\; m$$
$$\therefore \: AO=BO=CO=\dfrac{0.28\;m}{2}=0.14\; m$$
$$V$$ i.e, Potential at $$O; \: V_{o}=\dfrac{1}{4\pi \varepsilon _{0}}\left [ \dfrac{q_{1}}{AO}+\dfrac{q_{2}}{BO}+\dfrac{q_{3}}{CO} \right ]$$
$$V$$ i.e, Potential at $$D; \: V_{D}=\dfrac{1}{4\pi \varepsilon _{0}}\left [ \dfrac{q_{1}}{AD}+\dfrac{q_{2}}{BD}+\dfrac{q_{3}}{CD} \right ]$$
Work done $$=q[V_{o}-V_{D}]$$
$$=\dfrac{2\times 10^{-9}}{4\pi \varepsilon _{0}}\left [ \dfrac{2\times 10^{-9}}{0.14}+\dfrac{4\times 10^{-9}}{0.14}+\dfrac{8\times 10^{-9}}{0.14}- \dfrac{2\times 10^{-9}}{0.2}-\dfrac{4\times 10^{-9}}{0.28}-\dfrac{8\times 10^{-9}}{0.2}\right ]$$
On solving, we get
$$W=2\times 10^{-9}\times 2\times 10^{9}\left [ \dfrac{14\times 10^{-9}}{0.14}-\dfrac{10\times 10^{-9}}{0.2}-\dfrac{4\times 10^{-9}}{0.28} \right ]$$
$$=4\times \left [ 10^{-7}-0.5\times 10^{-7}-0.14\times 10^{-7} \right ]$$
$$=5.40\times 10^{-7}$$ Joules.
What is the nature of the charge on the plates of capacitor ?
The earth has Volume 'V' and surface area 'A' then its capacitance would be
Calculate the electrostatic potential energy for a system of three point charges placed at the corners of an equilateral triangle of side 'a'.
Find expression for electric potential due to point Q at distance r
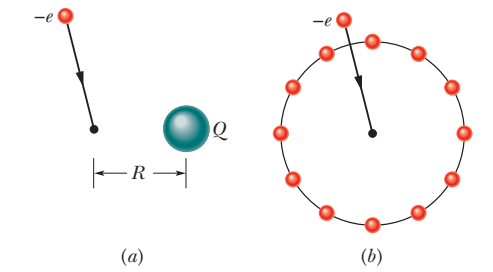
In the above figure (a), we move an electron from an infinite distance to a point at distance $$R=8.00 \ cm$$ from a tiny charged ball. The move requires work $$W=2.16 \times 10^{-13} \ J$$ by us.
(a) What is the charge $$Q$$ on the ball? In figure (b), the ball has been sliced up and the slices spread out so that an equal amount of charge is at the hour positions on a circular clock face of radius $$R=8.00 \ cm$$. Now the electron is brought from an infinite distance to the center of the circle.
(b) With that addition of the electron to the system of $$12$$ charged particles, what is the change in the electric potential energy of the system?
A spherical drop of capacitance $$12\mu F$$ is broken into eight drops of equal radius. Then, what is the capacitance of each small drop in $$\mu F$$?
Draw $$3$$ equipotential surface corresponding to a field that uniformly increases in magnitude but remains constant along Z-direction. How are these surface different from that of a constant electric field along Z-direction?
For constant electric field $$\underset{E}{\rightarrow}$$ For increasing electric field
Difference : For constant electric field, the equipotential surface are equidistant for same potential difference between surfaces; while for increasing electric field, the separation between these surfaces decreases, in the direction of increasing field, for the same potential difference between them.
Difference : For constant electric field, the equipotential surface are equidistant for same potential difference between surfaces; while for increasing electric field, the separation between these surfaces decreases, in the direction of increasing field, for the same potential difference between them.
Three identical capacitors $$C_1, C_2$$ and $$C_3$$ have a capacitance of $$1.0 \mu F$$ each and they are uncharged initially. They are connected in a circuit as shown in the figure and $$C_1$$ is then filled completely with a dielectric material of relative permittivity $$\in_r$$. The cell electromotive force (emf) $$V_o = 8V$$. First, the switch $$S_1$$ is closed while the switch $$S_2$$ is kept open. When the capacitor $$C_3$$ is fully charged, $$S_1$$ is opened and $$S_2$$ is closed simultaneously. When all the capacitors reach equilibrium, the charge on $$C_3$$ is found to be $$5\mu C$$. The value of $$4\times \in_r$$ is:
The capacitor $$C_3$$ charges to $$8 \mu C$$ as the switch $$S_1$$ is closed.
Ref. image 1
But when switch $$S_1$$ is opened and $$S_2$$ is closed, then capacitor $$C_3$$ is charged to $$5 \mu C$$, thus the net charge $$8 \mu C - 5 \mu C = 3 \mu C$$ resides on $$C_1$$ and $$C_2$$, as they are connected in series.
Ref. image 2
So, Apply the Kirchhoff loop,
$$\dfrac{q_1}{C_1} + \dfrac{q_2}{C_1 \varepsilon_r} = \dfrac{q_3}{C_3}$$
$$\dfrac{q}{C} \left(1 + \dfrac{1}{\varepsilon_r} \right) = \dfrac{5}{1}$$
$$3 \left(1 + \dfrac{1}{\varepsilon_r}\right) = 5$$
$$\varepsilon_r = 1.5$$
Show that the effective capacitance, C, of a series combination, of three capacitors, $$C_1, C_2$$ and $$C_3$$ is given by
$$C=\frac {C_1C_2C_3}{(C_1C_2+C_2C_3+C_3C_1)}$$
Three capacitors each of capacitance 9 pF are connected in series as shown in figure.
(a) What is the total capacitance of the combination?
(b) What is the potential difference across each capacitor, if the combination is connected to a 120 volt supply?
A parallel plate capacitor has plates with area $$A$$ & separation $$d$$. A battery charges the plates to a potential difference of $$V_0$$. The battery is then disconnected & a di-electric slab of constant $$K$$ & thickness $$d$$ is introduced. Calculate the positive work done by the system (capacitor + slab) on the man who introduces the slab.
Identical charges q each are placed at the eight corners of a cube of side b. Find the electrostatic potential energy of a charge +q placed at the center of the cube
A charge of 5$$\mu$$ C is placed at the center of a square ABCD of side 10 cm. Find the work done (in $$\mu$$J) in moving a charge of 1$$\mu$$C from A to B.
For a square ABCD, $$OA=OB=OC=OD=r$$
As charge $$5 \mu C$$ is placed on center O so every point A,B,C and D have same potential $$V=5k/r$$.
Thus potential difference $$(dV)$$ between A and B will be zero.
Work done $$W=qdV=1(0)=0$$
As charge $$5 \mu C$$ is placed on center O so every point A,B,C and D have same potential $$V=5k/r$$.
Thus potential difference $$(dV)$$ between A and B will be zero.
Work done $$W=qdV=1(0)=0$$
At a point due to a point charge, the values of electric field intensity and potential are 32 N$$C^{-1}$$ and 16 J $$C^{-1}$$ ,respectively. Calculate the
a. magnitude of the charge,and
b. distance of the charge from the point of observation.
How much energy in kJ will be stored by a capacitor of 470 $$\mu F$$ when charged by a battery of 20 V?
A parallel plate capacitor is charged by a battery.The battery is disconnected and a dielectric slab is inserted to completely fill the space between the plates. How will (i) its capacitance, (ii) electric field between the plates and (iii) energy stored in the capacitor be affected ? Justify your answer giving necessary mathematical expressions for each case.
A parallel-plate capacitor has the air as a medium between its plates and its capacitance is C. A slab of the dielectric constant K is introduced so as to fill the left half of space of the capacitor, as shown. What is the new capacitance of the capacitor?
What is the work done in moving a charge of $$50 nC$$ between two points on an equipotential surface?
An uncharged capacitor C is connected to a battery through a resistance R. Show that by the time the capacitor gets fully charged, the energy dissipated in R is the same as the energy stored in C.
A parallel plate capacitor with air between the plates has a capacitance of 8 pF (1pF =$$ 10^{-12}$$ F). What will be the capacitance if the distance between the plates is reduced by half, and the space between them is filled with a substance of dielectric constant 6?
Two charges $$2\mu C$$ and $$-2\mu C$$ are placed at points A and B 6 cm apart.(a) Identify an equipotential surface of the system.(b) What is the direction of the electric field at every point on this surface?
Three capacitors each of capacitance $$9 pF$$ are connected in series.(a) What is the total capacitance of the combination?(b) What is the potential difference across each capacitor if the combination is connected to a $$120 V$$ supply?
Exercise: In a parallel plate capacitor with air between the plates, each plate has an area of $$6\times 10^{-3} m^{2}$$ and the distance between the plates is 3 mm. Calculate the capacitance of the capacitor. If this capacitor is connected to a 100 V supply, what is the charge on each plate of the capacitor?
Explain what would happen if in the capacitor given in Exercise a $$3 mm$$ thick mica sheet (of dielectric constant = 6) were inserted between the plates,(a) While the voltage supply remained connected.(b) After the supply was disconnected.
(a) While the voltage supply remained connected.
(b) After the supply was disconnected.
A cylindrical capacitor has two co-axial cylinders of length 15 cm and radii 1.5 cm and 1.4 cm. The outer cylinder is earthed and the inner cylinder is given a charge of $$3.5 \mu C$$. Determine the capacitance of the system and the potential of the inner cylinder. Neglect end effects (i.e., bending of field lines at the ends).
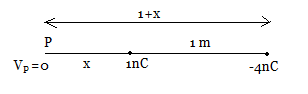
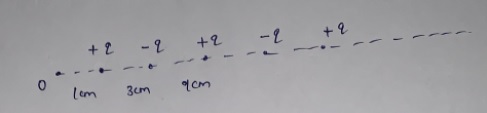
An infinite number of charges, each equal to q, are placed along the x-axis at $$x=1,\,x=2,\,x=4,\,x=8$$ and so on. What is the potential at $$x=0$$ due to this set of charges?
Write a relation for polarisation $$\overrightarrow{P}$$ of a dielectric material in the presence of an external electric field $$\overrightarrow{E}$$.
joule coulomb$$^{-1}$$ is same as ___________.
Draw a plot showing the variation of (i) electric field $$\left(E\right)$$ and (ii) electric potential $$\left(V\right)$$ with distance $$r$$ due to a point charge $$Q$$.
The field at distance r due to point charge Q is $$E=kQ/r^2$$ and the potential is $$V=kQ/r$$
The variation of field E and potential V with distance is as shown in figure.
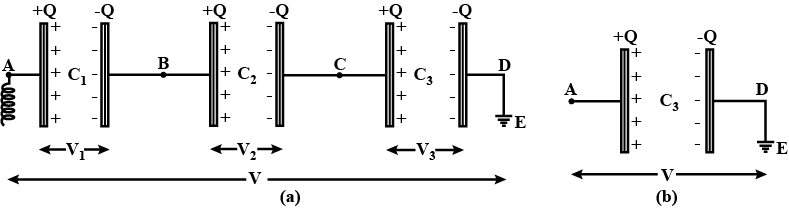
Obtain an expression for equivalent capacitance when three capacitors $$C_1, C_2$$ and $$C_3$$ are connected in series.
Consider that three capacitors having capacitance $$C_1, C_2$$ and $$C_3$$ are connected in series to each other shown in the figure above,
Consider that $$+q$$ charge is given to first plat of first capacitor. By induction a charge $$(-q)$$ will produce at internal surface of second plate of this capacitor and so on.
Consider that potential between the plates of capacitor are $$C_1, C_2$$ and $$C_3$$ respectively so,
$$V_1=\dfrac{q}{C_1}, \ V_2=\dfrac{q}{C_2}$$ and $$V_3=\dfrac{q}{C_3}$$
Now $$V=V_1+V_2+V_3$$
$$\therefore$$ $$V=\dfrac{q}{C_1}+\dfrac{q}{C_2}+\dfrac{q}{C_3}$$ ...(i)
If equivalent capacitance of combination of capacitors is $$C$$ then
$$V=\dfrac{q}{C}$$ ...(ii)
By equations (i) and (ii), we get
$$\dfrac{q}{C}=\dfrac{q}{C_1}+\dfrac{q}{C_2}+\dfrac{q}{C_3}$$
$$\implies $$ $$\dfrac{1}{C}=\dfrac{1}{C_1}+\dfrac{1}{C_2}+\dfrac{1}{C_3}$$
Consider that $$+q$$ charge is given to first plat of first capacitor. By induction a charge $$(-q)$$ will produce at internal surface of second plate of this capacitor and so on.
Consider that potential between the plates of capacitor are $$C_1, C_2$$ and $$C_3$$ respectively so,
$$V_1=\dfrac{q}{C_1}, \ V_2=\dfrac{q}{C_2}$$ and $$V_3=\dfrac{q}{C_3}$$
Now $$V=V_1+V_2+V_3$$
$$\therefore$$ $$V=\dfrac{q}{C_1}+\dfrac{q}{C_2}+\dfrac{q}{C_3}$$ ...(i)
If equivalent capacitance of combination of capacitors is $$C$$ then
$$V=\dfrac{q}{C}$$ ...(ii)
By equations (i) and (ii), we get
$$\dfrac{q}{C}=\dfrac{q}{C_1}+\dfrac{q}{C_2}+\dfrac{q}{C_3}$$
$$\implies $$ $$\dfrac{1}{C}=\dfrac{1}{C_1}+\dfrac{1}{C_2}+\dfrac{1}{C_3}$$
Obtain an expression for equivalent capacitance C, when three capacitors having capacitance $$C_1, C_2$$ and $$C_3$$ are connected m series.
Let three capacitors $$C_1, C_2$$ and $$C_3$$ are connected in series. We know charge remains same in series combination.
$$V_1=\displaystyle\frac{q}{C_1}$$
$$V_2=\displaystyle\frac{q}{C_2}$$
$$V_3=\displaystyle\frac{q}{C_3}$$
$$V=V_1+V_2+V_3=q\left(\displaystyle\frac{1}{C_1}+\frac{1}{C_2}+\frac{1}{C_3}\right)$$
If the $$3$$ capacitors are replaced by a single capacitor such that on giving it charge q is capacitance is C then $$V=\displaystyle\frac{q}{C}$$
$$\therefore \displaystyle\frac{q}{C}=q\left(\displaystyle\frac{1}{C_1}+\frac{1}{C_2}+\frac{1}{C_3}\right)$$
or $$\displaystyle\frac{1}{C}=\frac{1}{C_1}+\frac{1}{C_2}+\frac{1}{C_3}$$
$$V_1=\displaystyle\frac{q}{C_1}$$
$$V_2=\displaystyle\frac{q}{C_2}$$
$$V_3=\displaystyle\frac{q}{C_3}$$
$$V=V_1+V_2+V_3=q\left(\displaystyle\frac{1}{C_1}+\frac{1}{C_2}+\frac{1}{C_3}\right)$$
If the $$3$$ capacitors are replaced by a single capacitor such that on giving it charge q is capacitance is C then $$V=\displaystyle\frac{q}{C}$$
$$\therefore \displaystyle\frac{q}{C}=q\left(\displaystyle\frac{1}{C_1}+\frac{1}{C_2}+\frac{1}{C_3}\right)$$
or $$\displaystyle\frac{1}{C}=\frac{1}{C_1}+\frac{1}{C_2}+\frac{1}{C_3}$$
Calculate the potential at a point due to a charge of $$3\times {10}^{-9}C$$ located $$9\times {10}^{-2}m$$ away from it.
Calculate the potential at a point due to a charge of $$4\times 10^{-7}C$$ located at $$0.09\ m$$ away.
Two point charges $$5 \times 10^{-8} C$$ and $$-3 \times 10^{-8} C$$ are located 16 cm apart. At what point on the line joining these charges the electric potential will be zero?
Draw a neat labelled diagram of a parallel plate capacitor completely filled with dielectric.
Given diagram show parallel plate capacitor completely filled with dielectric.
Define electric capacity. Derive an expression for the capacitance of a parallel plate capacitor in which a dielectric medium of dielectric constant $$K$$ fills the space between the plates. Draw the necessary diagram.
Capacitance or electric capacity indicates the ability of a system to store charge. It is defined as the ratio of charge stored in the conductors to the potential difference across the conductors. Its SI unit is Farad ($$F$$). Hence:
$$C = \cfrac{Q}{V}$$
To derive the expression of capacitance of parallel plate capacitor of conductor area $$A$$ and distance between the conductors as $$d$$ with a dielectric of dielectric constant $$K$$ carrying a charge $$Q$$ and potential difference $$V$$, refer to the attached figure.
Electric field between plates of the capacitor can be found using Gauss Law.
$$E = \cfrac{\sigma}{K\varepsilon_o }$$
$$E = \cfrac{Q}{K\varepsilon_o A }$$ as $$\sigma = \cfrac{Q}{A}$$
Electric field is defined as the gradient of potential.
$$E = \cfrac{V}{d}$$
$$\implies V = \cfrac{Qd}{K\varepsilon_o A }$$
By definition of capacitance,
$$C = \cfrac{Q}{V}$$
$$=\cfrac{K\varepsilon_o A }{d}$$
Write the definition of electric potential. Calculate the electric potential due to a point charge Q at a distance r from it. Draw a graph between electric potential V and distance r for a point charge Q.
Electric potential is the amount of electric potential energy that a unitary point electric charge would have if located at any point in space, and is equal to the work done by an external agent in carrying a unit of positive charge from the arbitrarily chosen reference point (usually infinity) to that point without any acceleration.
Electric potential due to point charge Q at a distance r is
$$V=-\int_{\infty}^{r}Edr$$
$$=\int_{-\infty}^{r}\dfrac{Q}{4\pi \epsilon_0 r^2}dr$$
$$=\dfrac{Q}{4\pi \epsilon_0 r}$$
Deduce an expression for the effective capacitance of capacitors of $$C_{1}, C_{2}$$ and $$C_{3}$$ connected in series
Capacitors in series: Consider three capacitors of capacitance $$C_{1}, C_{2}$$ and $$C_{3}$$ connected in series. Let $$V$$ be the potential difference applied across the series combination. Each capacitor carries the same amount of charge $$q$$. Let $$V_{1}, V_{2}, V_{3}$$ be the potential difference across the capacitors $$C_{1}, C_{2}, C_{3}$$ respectively. Thus $$V = V_{1} + V_{2} + V_{3}$$.
The potential difference across each capacitor is,
$$V_{1} = \dfrac {q}{C_{1}}; V_{2} = \dfrac {q}{C_{2}}; V_{3} = \dfrac {q}{C_{3}}$$;
$$V = \dfrac {q}{C_{1}} + \dfrac {q}{C_{2}} +\dfrac {q}{C_{3}} = q\left [\dfrac {1}{C_{1}} +\dfrac {1}{C_{2}} + \dfrac {1}{C_{3}}\right ]$$
If $$C_S$$ be the effective capacitance of the series combination, it should acquire a charge $$q$$ when a voltage $$V$$ is applied across it.
$$V = \dfrac {q}{C_{S}} = \dfrac {q}{C_{1}} + \dfrac {q}{C_{2}} + \dfrac {q}{C_{3}}$$
$$\therefore \dfrac {1}{C_{S}} = \dfrac {1}{C_{1}} + \dfrac {1}{C_{2}} + \dfrac {1}{C_{3}}$$
The potential difference across each capacitor is,
$$V_{1} = \dfrac {q}{C_{1}}; V_{2} = \dfrac {q}{C_{2}}; V_{3} = \dfrac {q}{C_{3}}$$;
$$V = \dfrac {q}{C_{1}} + \dfrac {q}{C_{2}} +\dfrac {q}{C_{3}} = q\left [\dfrac {1}{C_{1}} +\dfrac {1}{C_{2}} + \dfrac {1}{C_{3}}\right ]$$
If $$C_S$$ be the effective capacitance of the series combination, it should acquire a charge $$q$$ when a voltage $$V$$ is applied across it.
$$V = \dfrac {q}{C_{S}} = \dfrac {q}{C_{1}} + \dfrac {q}{C_{2}} + \dfrac {q}{C_{3}}$$
$$\therefore \dfrac {1}{C_{S}} = \dfrac {1}{C_{1}} + \dfrac {1}{C_{2}} + \dfrac {1}{C_{3}}$$
Derive the formula for equivalent capacitance when the capacitors are connected in series.
Let the capacitance of each capacitor be $$C_1,$$ $$C_2$$ and $$C_3$$ and their equivalent capacitance be $$C_{eq}$$.
As these capacitors are connected in series, thus charge across each capacitor is same as $$Q$$.
When some electrical components, let say 3, are connected in series with each other, the potential difference of the battery $$V$$ gets divided across each component as $$V_1,$$ $$V_2$$ and $$V_3$$ as shown in the figure.$$\therefore$$ $$V = V_1 +V_2 + V_3$$
Using $$V = \dfrac{Q}{C}$$
We get $$\dfrac{Q}{C_{eq}} = \dfrac{Q}{C_1}+\dfrac{Q}{C_2}+\dfrac{Q}{C_3}$$
$$\implies$$ Equivalent capacitance for series combination $$\dfrac{1}{C_{eq}} = \dfrac{1}{C_1}+\dfrac{1}{C_2}+\dfrac{1}{C_3}$$
In general, $$\dfrac{1}{C_{eq}} = \dfrac{1}{C_1}+\dfrac{1}{C_2}+ ..........+\dfrac{1}{C_n}$$
Derive the expression for the capacitance of a parallel plate capacitor.
$$\textbf{Step 1 - Draw figure and find electric field}$$
Let the two plates be parallel to each other, each carrying
a surface charge density $$+\sigma$$ and $$-\sigma$$ respectively.
$$A$$ is the area of plates and $$d$$ is the separation between them
The electric field of a thin charged plate is given by
$$E = \dfrac {\sigma}{2\varepsilon_{0}}$$ and is directed normally outward from the plate.
The total electric field between the two places is given as
$$\vec {E} = \vec {E}_{A} + \vec {E}_{B}$$
$$\vec {E} = \dfrac {\sigma}{2\varepsilon_{0}} \hat {i} + \dfrac {-\sigma}{2\varepsilon_{0}} (-\hat {i}) = \dfrac {\sigma}{\varepsilon_{0}} \hat {i}$$
$$E = |\vec {E}| = \dfrac {\sigma}{\varepsilon_{0}} = \dfrac {\dfrac {Q}{A}}{\varepsilon_{0}} = \dfrac {Q}{A\varepsilon_{0}}$$
$$\textbf{Step 2 - Potential difference between the two plates}$$
Potential difference $$V = E\times d = \dfrac {Qd}{A \varepsilon_{0}}$$
$$\textbf{Step 3 - Capacitance}$$
The capacitance is
$$C = \dfrac {Q}{V} = \dfrac {Q}{\dfrac {Qd}{A\varepsilon_{0}}} = \dfrac {\varepsilon_{0}A}{d}$$
In a parallel plate capacitor with increase in distance between the plates, its capacity ................
Derive an expression for the electric potential due to a point charge :
TWO point charges $$+2nc$$ and $$-4nc$$ are $$1\ m$$ apart in air. Find the positions along the line joining the two charges at which resultant potential is zero.
Let the potential at point P is zero which is situated at a distance $$x$$ to the left of $$1nC$$ charge as shown in the figure.
Potential due a charge $$q$$ is given by $$V = \dfrac{kq}{r}$$ where $$k = \dfrac{1}{4\pi \epsilon_o}$$
Thus potential at point P $$V_p = \dfrac{k(1nC)}{x} - \dfrac{k (4nC)}{1+x}$$
But $$V_p =0$$
$$\therefore$$ $$ \dfrac{k(1nC)}{x} - \dfrac{k (4nC)}{1+x}=0$$
Or $$ \dfrac{1}{x} - \dfrac{4}{1+x}=0$$
Or $$ \dfrac{1}{x} = \dfrac{4}{1+x}$$
Or $$3x = 1$$
$$\implies$$ $$x =0.33 m$$
Two identified parallel plate capacitors $$A$$ and $$B$$ are connected to a battery of $$V$$ volts with the switch $$S$$ closed. The switch is now opened and the free space between the plates of the capacitors is filled with a dielectric of dielectric constant $$K$$. Find the ratio of the total electrostatic energy stored in both capacitors before and after the introduction of the dielectric.
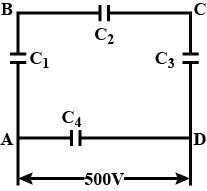
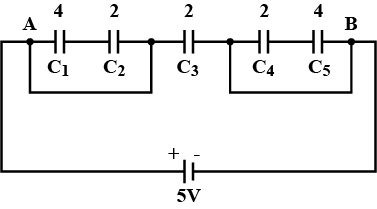
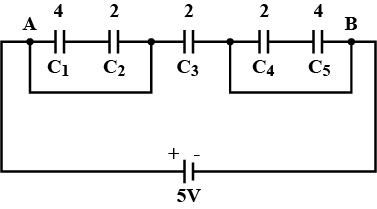
A network of four $$10 \mu F$$ capacitors is connected to a $$500V$$ supply, as shown in fig. Determine (a) the equivalent capacitance of the network and (b) the charge on each capacitor.(Note, the charge on a capacitor is the charge on the place with higher potential, equal and opposite to the charge on the plate with lower potential).
$$C_1 = C_2 = C_3 = C_4 = 10 \mu F$$
$$C_1 , C_2$$ and $$C_3$$ are in series
So
$$\dfrac{1}{C'} = \dfrac{1}{C_1} + \dfrac{1}{C_2} + \dfrac{1}{C_3}$$
$$\Rightarrow C' = \dfrac{10}{3} \mu F$$
$$C_{AD} = C_{eq} = C' + C_4$$ [$$\because$$ They are in parallel]
$$\Rightarrow C_{eq} = \dfrac{10}{3} + 10 = \dfrac{40}{3} \mu F$$
Charge on $$C_4 = 10 \mu F \times 500 v = 5 \times 10^{-3} C$$
Charge of $$C_1 , C_2$$ and $$C_3$$ will be same as they are in series
So charge on $$C_1 , C_2$$ and $$C_3$$
$$= C' \times V = \dfrac{10}{3} \mu F \times 500 = \dfrac{5}{3} \times 10^{-3} C$$
Each of the plates shown in the figure has surface area $$( 96/ \epsilon_0) \times 10^{-12}\ m^2$$ on one side and the separation between the consecutive plates is $$4.0\ mm$$. The emf of the battery connected is $$10\ \text{volts}$$. Find the magnitude of the charge supplied by the battery to each of the plates connected to it.
Here three capacitors are formed
And each of
Surface area of the plates is $$A = \dfrac{96}{\varepsilon_0} \times 10^{-12} f.m$$
The distance between the plates is $$d = 4 mm = 4 \times 10^{-3} m$$
$$\therefore$$ Capacitance of a capacitor
$$C = \dfrac{\varepsilon_0 A}{d} = \dfrac{\varepsilon_0 \dfrac{96 \times 10^{-12}}{\varepsilon_0}}{4 \times 10^{-3}} = 24 \times 10^{-9} F$$
$$\therefore$$ As three capacitor are arranged is series
So, $$C_{eq} = \dfrac{C}{q} = \dfrac{24 \times 10^{-9}}{3} = 8 \times 10^{-9}$$
$$\therefore $$ The total charge to a capacitor
$$q=CV$$
$$= 8 \times 10^{-9} \times 10 =8 \times 10^{-8} C$$
$$\therefore$$ The charge of a single Plate $$ q'= 2 \times 8 \times 10^{-8} = 16 \times 10^{-8} = 0.16 \times 10^{-6} = 0.16 \mu C$$
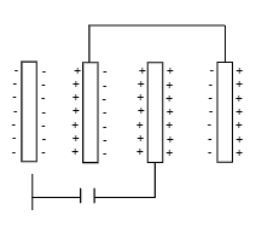
Predict the polarity of the capacitor in the situation described by figure
It is required to construct a $$10 \mu F$$ capacitor which can be connected across a $$200V$$ battery. Capacitors of capacitance $$10\mu F$$ are available but they can withstand only $$50V$$ Design a combination which can yield the desired result
Identify and explain about the diode whose characteristics curve is:
The capacity and the energy stored in a parallel plate condenser with air between its plates are respectively $$C_{0}$$ and $$W_{0}$$. If the air between the plates is replaced by glass (dielectric constant$$=5$$) find the capacitance of the consider and the energy stored in it.
Three identical capacitors $$C1, C2$$ and $$C3$$ of capacitance $$6\ mF$$ each are connected to a $$12\ V$$ battery as shown
Find:
charge on each capacitor
equivalent capacitance of the network
energy stored in the network of capacitors
A slab of material of dielectric constant K has the same area as the plates of a parallel plate capacitor but has a thickness t (t<d). Find the ratio of the capacitance with dielectric inside it to its capacitance without the dielectric.
Where Given
k = Dielectric constant
t = thickness of dielectric
Here; the net electric field experienced by the dielectric is
$$\vec{E} = \vec{E}_0 - \vec{E}_p $$ where $$\vec{E_0}$$. ___(1)
the applied E. Field and $$\vec{E_p}$$ is the electric field that is produced inside the dielectric due to polarization of charges.
Potential ditlerence between the plates :
$$V = E_0 (d - t) + Et.$$ __(2) $$\because E = \dfrac{dv}{dx}$$
But $$E = \dfrac{E_0}{k}$$ __(3)
from (2) and (3)
$$\Rightarrow V = E_0 \left[d - t + \dfrac{t}{k} \right]$$ __(4)
$$E_0 = \dfrac{\varepsilon}{\varepsilon_0} = \dfrac{Q}{A \varepsilon_0}$$ __(5)
$$V = \dfrac{Q}{A \varepsilon_0} \left[d - t + \dfrac{t}{k} \right]$$ __(6)
Since $$Q = CV \Rightarrow C = \dfrac{V}{Q} $$ __(7)
From (6) and (7)
$$C_k = \dfrac{\varepsilon_0 A}{\left(d - t + \dfrac{t}{k} \right)} $$ and $$C = \dfrac{\varepsilon_0 A}{d}$$
Hence,
the ratio of the two:-
$$\dfrac{Ck}{C} = \dfrac{\dfrac{\varepsilon_0 A}{\left(d - t + \dfrac{t}{k}\right)}}{\dfrac{\varepsilon_0 A}{d}}$$
$$= \dfrac{d}{\left(d - t + \dfrac{t}{k} \right)}$$
A proton is moved 15 cm on path parallel to the field lines of a uniform electric field of $$2.0\times 10^{5}$$ V/m
What are the possible change in potential ?consider both cases of a moving the proton .
In a conductor, a point P is at a higher potential than another point Q. In which direction do the electrons move?
Find the potential energy of an electric dipole (length 4 cm) each experiences a torque of $$ 4\sqrt { 3 } $$ Nm placed in a from electric field angle $$ 60^\circ q = 1 + nc. $$
Derive the expression for the capacitance of a parallel plate capacitore having plate area A and plate separation d.
Let a parallel plate capacitor be applied a voltage $$V$$ across its terminals due to which a charge $$Q$$ develops across its ends.
Separation between plates is $$d$$ and area of plates is $$A$$.
From gauss's theorem one can show electric field inside the capaciton plates $$Q$$,
$$E = \dfrac{\sigma}{\epsilon_o}$$, where $$\sigma = \dfrac{Q}{A}$$ (charge / Area)
$$\Rightarrow E = \dfrac{Q}{A \epsilon_o}$$
Now, voltage across the plates is related by :
$$V = Ed$$ [In general , $$dV = - \vec{E}. d \vec{r}$$ but we take as $$\vec{E}$$ is uniform]
$$\Rightarrow V = \dfrac{Qd}{A \epsilon_o} \Rightarrow \dfrac{Q}{V} = \dfrac{A \epsilon_o}{d}$$
Now, capacitance is defined by $$C = \dfrac{Q}{V}$$, thus we get :-
$$C = \dfrac{A \epsilon_o}{d} $$
An infinite number of electric charges each equal to 2 nano coulombs in magnitude are placed along x-axis at x=1 cm, x= 3cm , x= 9 cm , x= 27 cm ...... and so on. In these setup if the consecutive charges have opposite sign, then the electric potential at x = 0 will be?
$$\textbf{Step 1 - Potential due to a charge, Refer Figure}$$
$$V = \dfrac {kq}{r}$$
$$\textbf{Step 2 - At x = 0, potential due to all charges}$$
$$V = \dfrac {kq}{0.01} - \dfrac {kq}{0.03} + \dfrac {kq}{0.09} - \dfrac {kq}{0.27} + .....$$
$$= kq \left [100 - \dfrac {100}{3} + \dfrac {100}{9} + \dfrac {100}{27} + .....\right ]$$
$$= 100 \times 9\times 10^{9} \times 2\times 10^{-9} \left [1 - \dfrac {1}{3} + \dfrac {1}{9} - \dfrac {1}{27} + \dfrac {1}{81} .....\right ]$$
$$= 100 \times 9\times 10^{-9 + 9} \times 2 \left [ \dfrac {1}{1 - \dfrac {1}{3}}\right ]$$
$$= 100 \times 18 \left [\dfrac {3}{3 - 1}\right ]$$
$$= 100 \times 18 \left [\dfrac {3}{2}\right ]$$
$$V = 2700\ volt$$
How many time constants will elapse before the energy stored in the capacitor reaches half of its equilibrium value in a charging $$RC$$ circuit ?
The potential at a point 0.1 m from an isolated point charge is +100 volt.
(i) Find the nature of the charge.
(ii) Calculate magnitude of the point charge.
Find equivalent capacity between A and B if capacity of each cap. is $$2 \mu F$$.
Take point $$'C'$$ and $$'D'$$
Redraw the circuit.
Now, $${C_2}||\,\,{C_3}||\,\,{C_4}$$
Equivalent $${C_6}$$ of $${C_2}||\,\,{C_3}||\,\,{C_4} = 2 + 2 + 2 = 6$$
Now,
$${C_1}||\,\,{C_6}||\,\,{C_5}$$ are in series.
$$\begin{array}{l} \dfrac { 1 }{ { { C_{ eq } }\, \, of\, circuit } } =\dfrac { 1 }{ 2 } +\dfrac { 1 }{ 6 } +\dfrac { 1 }{ 2 } =\dfrac { { 2+1+3 } }{ 6 } =\dfrac { 7 }{ 6 } \\ { C_{ eq } }=\dfrac { 6 }{ 7 } \end{array}$$
Electric Potential on the surface of a charged spherical shell of radius 10 cm is 50 volt. Find the value of electric potential at a distance of 20 cm from the center of spherical shell.
Potential at surface = 50 V
$$V = \dfrac{K.Q}{R}$$
$$50 = \dfrac{K.Q}{0.1}$$
KQ= 5
potential at 200 m from centre
$$V=\dfrac{K.Q}{r}$$
$$V= \dfrac{5}{0.2}$$ = 25 volt
$$V = \dfrac{K.Q}{R}$$
$$50 = \dfrac{K.Q}{0.1}$$
KQ= 5
potential at 200 m from centre
$$V=\dfrac{K.Q}{r}$$
$$V= \dfrac{5}{0.2}$$ = 25 volt
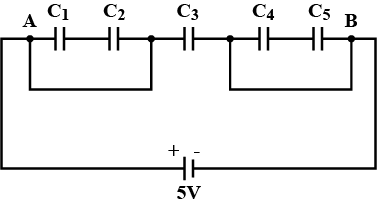
In the figure given below, Find the
maximum charge supplied by the battery, and
Given circuit,
$$(C_1 = C_5 = 4 \mu F , C_2 = C_3 = C_4 = 2 \mu F)$$
Ref. image
From about circuit diagram $$C_1$$ & $$C_2$$ and $$C_4$$ & $$C_5$$ are shorted with wire. So total potential drop to move from $$C_1$$ to $$C_2$$ and $$C_4$$ to $$C_5$$ will be zero.
$$\therefore C_{eq} = C_3 = 2 \mu F$$
charge supply by battery
$$q = C_{eq} \times V$$
$$= 2 \times 10^{-6} \times 5$$
$$q = 10 \times 10^{-6}$$
$$q = 10 \mu C$$
Electric field inside the capacitor is $$100$$ V/m and dielectric constant $$=5.5$$. What is the polarization?
Explain the concept of a parallel plate capacitor. State its any 'two' applications.
The surface of an isolated charge conductor is an equipotential surface with a potential V with respect to some arbitrary zero reference level, usually the ground. $$V > 0$$ if charge on the conductor is positive and $$V < 0$$ for negative charge. If the charge is increased. V increases in the same proportion. i.e.
$$Q \, \propto \, V$$
Removing proportionality
$$Q = CV$$
C is called the capacitance.
Consider a metal plate A whose potential is raised to V by depositing a charge $$+Q$$ on it. Now if an uncharged metal plate B is brought close to A A, then the negative charge will be induced on the surface near A and positive free change on the surface of B away from A as know below.
Ref. image.
Now if plate B is grounded, the free positive charge on B will go into the earth. The bound negative charge $$(-Q)$$ on B will lower the potential of A by say $$V_1$$ due to the presence of plate A in the electric field generated by the negative charge on B.
Now net potential on $$A = V - V_1$$
Capacity $$= \dfrac{Q}{V - V_1}$$
As $$(V - V_1)$$ has decreased from V the capacity or capacitance of plate A has increased.
This system of plates together is called a parallel plate capacitor.
Application of parallel plate capacitors:-
1) Energy storage capacitor banks are used for power factor correction with inductive loads
2) $$DC$$ power supplies sometimes use parallel capacitors in order to better filter the output signal and eliminate the $$AC$$ ripple.
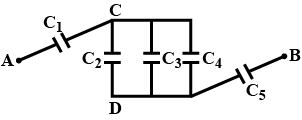
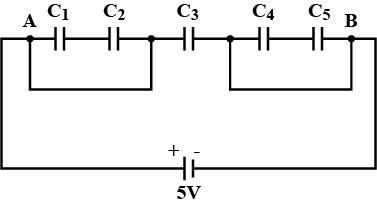
In the figure given below, Find the
equivalent capacitance of the network between points A and B
Given : $$C_1 = C_5 = 4 \mu F , C_2 = C_3 = C_4 = 2 \mu F$$.
Given circuit,
$$(C_1 = C_5 = 4 \mu F , C_2 = C_3 = C_4 = 2 \mu F)$$
Ref. image
from about circuit diagram $$C_1 \, \& \, C_2$$ and $$C_4 \,\& \, C_5$$ are shorted with wire. So total potential drop to move from $$C_1 $$ to $$C_2$$ and $$C_4$$ to $$C_5$$ will be zero
$$\therefore C_{eq} = C_3 = 2 \mu F$$
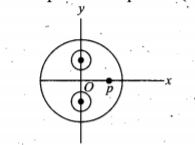
A non-conducting sphere of radius R=5 cm has its center at the origin O of the coordinate system as shown in fig. Its has two spherical cavities of radius r= 1 cm, whose centers are at (0, 3 cm), (0, -3 cm), respectively, and solid material of the sphere has uniform positive charge density $$ p=1/ \pi \mu Cm^{-3} $$ calculate electric potential at point P(4 cm, 0).
Identical charges -q each are placed at eight corners of a cube of each side b, find the electrostatic potential energy of a charge +q which is placed at the centre of the cube.
A parallel-plate capacitor having plate area $$400 cm^2$$ and separation between the plates $$1.0 mm$$ is connected to a power supply of $$100 V.$$ A dielectric slab of thickness 0.5 mm and dielectric constant 5.0 is inserted into the gap. a) Find the increase in electrostatic energy.b) If the power supply is now disconnected and the dielectric slab is taken out, find the further increase in energy. c) Why does the energy increase in inserting the slab as Well as in taking it out ?
An infinite nonconducting sheet has a surface charge density $$\sigma = +5.80 \ pC/m^2$$.
(a) How much work is done by the electric field due to the sheet if a particle of charge $$q=+1.60 \times 10^{-19} \ C$$ is moved from the sheet to a point $$P$$ at distance $$d= 3.56 \ cm$$ from the sheet?
(b) If the electric potential $$V$$ is defined to be zero on the sheet, what is $$V$$ at $$P$$?
Draw an equipotential surface in a uniform electric field.
As Electric Field is uniform, so gap between two consecutive equipotential surfaces will be same.
Properties of equipotential surface:
$$\bullet$$ Electric field lines are always perpendicular to equipotential surface
$$\bullet$$ Equipotential surfaces never intersect
A capacitor of capacitance $$C_1$$ =6.00 µF is connected in series with a capacitor of capacitance $$C_2$$ = 4.00 µF, and a potential difference of 200 V is applied across the pair. (a) Calculate the equivalent capacitance.What are (b) charge $$q_1$$ and (c) potential difference $$V_1$$ on capacitor 1 and (d) $$q_2$$ and (e) $$ V_2 $$ on capacitor 2?
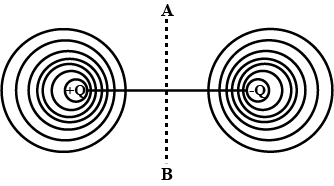
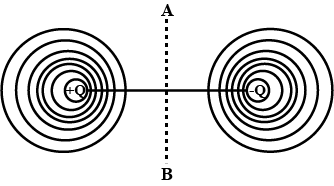
Draw an equipotential surface for a system consisting of two charges Q=Q seperated by a distance r in air. Locate the points where the potential due to the dipole is zero.
The equipotential surface for the system is as shown.
Electric potential is zero at all points in the plane passing through the dipole equator AB.
Figure shows the field lines due to a negative point charge. Give the sign of the potential energy difference of a small negative charge between the points A and B.
A certain capacitor is charged to a potential difference V. If you wish to increase its stored energy by 10%, by what percentage should you increase V?
Three capacitors C$$_1$$, C$$_2$$ and C$$_3$$ are connected in series. Obtain the relation for equivalent capacitance.
Series Combination of Capacitors :
To obtain small capacity from capacitors of large capacity, series combination of capacitors is adopted. In following diagram three capacitors of capacitance C$$_1$$, C$$_2$$ and C$$_3$$ are joined in series. In this combination the charge stored on each capacitor will be the same as that given to combination. Since q is same for all capacitor, then their individual potential differences will be different say V$$_1$$, V$$_2$$, V$$_3$$ respectively. If V be the total potential difference of the combination then :
$$V = V_1 + V_2 + V_3$$ ....(1)
$$\because$$ $$q = C_1 V_1 = C_2 V_2 = C_2 V_3$$
$$\therefore$$ $$V_1 = \frac{q}{C_1}; V_2 = \frac{q}{C_2}; V_3 = \frac{q}{C_3}$$
If $$C$$ be the equivalent capacitance of the combination then :
$$q = CV$$ $$\Rightarrow$$ $$V = \frac{q}{C}$$
Therefore from equation (1), we get :
$$\frac{q}{C} = \frac{q}{C_1} + \frac{q}{C_2} + \frac{q}{C_3}$$
or $$\frac{1}{C} = \frac{1}{C_1} + \frac{1}{C_2} + \frac{1}{C_3}$$ ...(2)
Similarly, $$n$$ capacitors can be joined in series :
$$\frac{1}{C} = \frac{1}{C_1} + \frac{1}{C_2} + \frac{1}{C_3} +.... + \frac{1}{C_n} $$
To obtain small capacity from capacitors of large capacity, series combination of capacitors is adopted. In following diagram three capacitors of capacitance C$$_1$$, C$$_2$$ and C$$_3$$ are joined in series. In this combination the charge stored on each capacitor will be the same as that given to combination. Since q is same for all capacitor, then their individual potential differences will be different say V$$_1$$, V$$_2$$, V$$_3$$ respectively. If V be the total potential difference of the combination then :
$$V = V_1 + V_2 + V_3$$ ....(1)
$$\because$$ $$q = C_1 V_1 = C_2 V_2 = C_2 V_3$$
$$\therefore$$ $$V_1 = \frac{q}{C_1}; V_2 = \frac{q}{C_2}; V_3 = \frac{q}{C_3}$$
If $$C$$ be the equivalent capacitance of the combination then :
$$q = CV$$ $$\Rightarrow$$ $$V = \frac{q}{C}$$
Therefore from equation (1), we get :
$$\frac{q}{C} = \frac{q}{C_1} + \frac{q}{C_2} + \frac{q}{C_3}$$
or $$\frac{1}{C} = \frac{1}{C_1} + \frac{1}{C_2} + \frac{1}{C_3}$$ ...(2)
Similarly, $$n$$ capacitors can be joined in series :
$$\frac{1}{C} = \frac{1}{C_1} + \frac{1}{C_2} + \frac{1}{C_3} +.... + \frac{1}{C_n} $$
A parallel plate capacitor each with plate area A and separation 'd' is charged to a potential difference V. The battery used to charge it is then disconnected. A dielectric slab of thickness d and dielectric constant K is now placed between the plates. What change if any, will take place in
Capacitance of the capacitor
Justify your answer in each case.
Show that the equipotential surfaces are closed together in the regions of strong field and far apart in the regions of weak field. Draw equipotential surface for an electric dipole.
Equipotential surfaces are closer togehter in the regions of strong feild and furthure apart in the regions of weak field.
$$ E= -\dfrac{dV}{dr} $$
E= negative potential gradient
For same change in dv, equipotential surfaces. $$ E= -\dfrac{dV}{dr} $$
where 'dr' represents the distance between
$$ E= -\dfrac{dV}{dr} $$
E= negative potential gradient
For same change in dv, equipotential surfaces. $$ E= -\dfrac{dV}{dr} $$
where 'dr' represents the distance between
A parallel plate is charged by a battery. When battery remains connected, a dielectric slab is inserted in the space between the plates. Explain what charges if any, occur in the values of
Capacitance
Describe schematically the equipotential surface s corresponding to
A field that uniformly increases in magnitude bur remains in a constant (say $$z$$) direction,
The surface where the potential has a constant value are called the equipotential surfaces. The potential in a direction perpendicular to the direction of the field remains constant irrespective of the magnitude of the field. Hence, equipotential surface would correspond to planes parallel to $$x -y$$ plane. The separation between the planes decreases for same potential differences. That's why $$x-y$$ planes getting closer and closer along the $$z-direction.
Three capacitors each of capacitance $$9\ pF$$ are connected in series
What is the total capacitance of the combination?
$$C_1=C_2=C_3=9\ pF=9\times 10^{-12}F, v=120$$ volt,
Total capacitance of the combination
$$\dfrac {1}{C}=\dfrac {1}{C_1}+\dfrac {1}{C_2}+\dfrac {1}{C_3}$$
$$=3\times \dfrac {1}{9\times 10^{-12}}=\dfrac {1}{3\times 10^{-12}}$$
$$\therefore C=3\times 10^{-12}F=3pF$$
Describe schematically the equipotential surface s corresponding to
a uniform grid consisting of long equally spaced parallel charged wired in a plane
A spherically varying shape near the grid which gradually reaches the shape of the planes parallel to the grid at for distances.
What is the equivalent capacitances when the capacitors of capacitance $$2\mu F$$ are connected in series combination ?
What is the effect on capacitance on a parallel plate capacitor when the capacitor is immersed in oil ? (The dielectric constant of oil is 2 )
Describe schematically the equipotential surface s corresponding to
A single positive charge at the origin and a
Concentric spherical surface gradually increasing in spacing
Describe schematically the equipotential surface s corresponding to
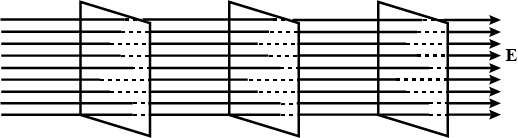
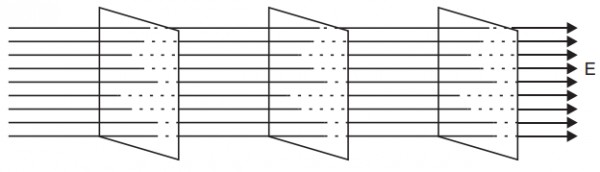
A constant electric field in the $$z$$-direction
Equally spaced $$x-y$$ planes
What is the equivalent capacitance in series combination when $$n$$ capacitors of equal capacitance C?
An isolated parallel plate capacitor is charged upto a certain potential difference.When a 3mm thick slab is introduced between the plates then in order to maintain the same potential difference, the distance between the plates is increased by 2.4mm. Find the dielectric constant of the slab. (assume charge remains constant)
Any given statement in Column-I can have correct matching with ONE OR MORE statement(s) in Column-II.
Column-I gives certain situations in which capacitance of a capacitor is changed by different means.Column-II gives resulting effect under different conditions. Match the statements in column-I with the corresponding statements in column-II
Identical metal plates are located in air at equal distance $$d$$ from one another. The area of each plate is equal to $$A$$. If the capacitance of the system between $$P$$ and $$Q$$ if the plates are interconnected as shown in the figure is given as $$\cfrac { x }{ 3 } { \varepsilon }_{ 0 }\cfrac { A }{ d } $$. Find $$x$$ :
Match the following :Diagonally checked rectangle represents dielectric slab.
Two parallel plate capacitors $$A$$ & $$B$$ have the same separation $$d = 8.85 \times 10^{-4}\space m$$ between the plates. The plate areas of $$A$$ & $$B$$ are $$0.04\space m^2$$ & $$0.02\space m^2$$ respectively. A slab of di-electric constant (relative permitivity) $$K = 9$$ has dimensions such that it can easily fill the space between the plates of capacitor $$B$$.
(i) The di-electric slab is placed inside $$A$$ as shown in the figure $$(a) \space A$$ is then charged to a potential difference of $$110\space volt$$. Calculate the capacitance of $$A$$ and the energy stored in it.
(ii) The battery is disconnected & then the di-electric slab is removed from $$A$$. Find the work done by the external agency in removing the slab from $$A$$.
(iii) The same di-electric slab is now placed inside $$B$$, filling it completely. The two capacitors $$A$$ & $$B$$ are then connected as shown in Figure $$(c)$$. Calculate the energy stored in the system.
$$(i)$$ Capacitor $$A$$
Plate area $$A$$$$=0.04 m^2$$
Plate area $$B$$$$=0.02 m^2$$
As per the given case,
Capacitor $$A$$ is combination of two capacitors $$C_K$$ and $$C_o$$ in parallel.
$$\Rightarrow C_A=C_K+C_o$$
$$=\cfrac{K\varepsilon_oA_1}{d}+\cfrac{K\varepsilon_oA_2}{d}$$
$$=\cfrac{885\times 10^{-12}}{8.85\times 10^{-4}}\left[10\times 0.02\right]$$
$$\Rightarrow C_A=2\times 10^{-9}F$$
Energy stored in capacitor $$=U_A=\cfrac{1}{2}C_AV2$$
$$\cfrac { 1 }{ 2 } \times 2\times { 10 }^{ -9 }\times \left( 110 \right) ^{ 2 }$$
$$=1.21\times 10^{-5}\quad J$$
$$(ii)$$ Work done in removing slab
$$W=U^\prime_A - U_A$$
Where,
$$U^\prime_A$$ Energy of capacitor without slab
Charge $$Q=C_AV=2\times 10^{-9}\times 110=2.2\times 10^{-7}C$$
Capacitor $$C^\prime_A=\cfrac{\varepsilon_o\left(A_1+A_2\right)}{d}$$
$$=\cfrac{8.85\times 10^{-12}\left(0.02+0.02\right)}{8.85\times 10^{-4}}$$
$$=0.4\times 10^{-9}F$$
$$W=6.05\times 10^{-5}-1.21\times 10^{-5}=4.84\times 10^{-5}J$$
$$(iii)$$ Energy store when $$A$$ and $$B$$ are connected $$=U$$
$$C_B=\cfrac{K\varepsilon_oA_1}{d}=\cfrac{9\times 8.85\times10^{-12}\times 0.02}{8.85\times 10^{-4}}=1.8\times10^{-9}F$$
Capacitor $$A$$ and $$B$$ are in parallel.
$$C=C^\prime_A+C^\prime_B$$
$$C=\left(0.4\times 10^{-9}\right)+\left(1.8 \times 10^{-9}\right)=2.2\times 10^{-9}F$$
Energy tored in system $$=U=\cfrac{Q^2}{2C}$$
$$=\cfrac{\left(2.2\times 10^{-7}\right)^2}{2\times 2.2\times 10^{-9}}$$
$$=1.1\times 10^{-5}J$$
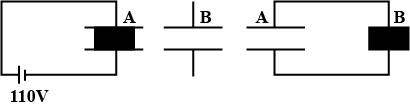
Suppose $$n$$ conducting plates are placed face to face, and the
distance between two successive plates is $$d$$. Each plate is half of
the area of the previous one. If area of first plate is $$A$$. If the area of the first plate is $$A$$, the equivalent capacitance of the system is given as $$\cfrac { { \varepsilon }_{ 0 }A }{ d({ x }^{ n }-2) } $$. Find $$x$$ :
The capacitance of a capacitor becomes $$4/3$$ times its original value if a dielectric slab of thickness $$t=d/2$$ is inserted between the plates ($$d$$ is the separation between the plates). What is the dielectric constant of the slab?
If a cell of emf $$V$$ is connected as shown in figure and a dielectric of dielectric constant $$k$$ is inserted between the first and second plates, the charge on the $$n$$th plate is given as $$\cfrac { { \varepsilon }_{ 0 }A }{ 2d({ x }^{ n-1 }-2+\cfrac { 1 }{ k } ) } V$$. Find $$x$$
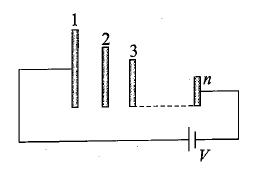
Two identical capacitors are connected in series, and the combination is connected with a battery, as shown. Some changes in capacitor $$1$$ are now made independently after the steady state is achieved as listed in column I. Some effects that may occur in the new steady state due to these changes on capacitor $$2$$ are listed in column II. Match the changes on capacitor I in column I with the corresponding effect on capacitor $$2$$ in column II :
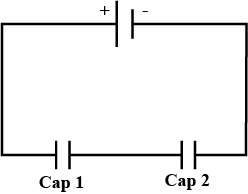
Two parallel plate capacitors of capacitances $$C_1$$ and $$C_2$$ such that $$C_1 = 2C_2$$ are connected across a battery of $$V$$ volts as shown in the figure. Initially the key ($$k$$) is kept closed to fully charge the capacitors. The key is now thrown open and a dielectric slab of dielectric constant '$$K$$' is inserted in the two capacitors to completely fill the gap between the plates. The ratio of the net capacitance before and after inserting the slab is $$\dfrac{x}{K}$$. Find $$x$$.
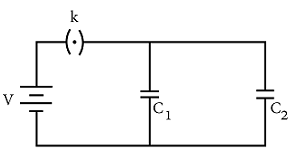
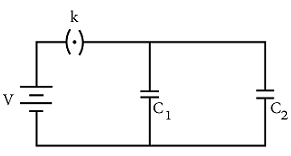
Two parallel plate capacitors of capacitances $$C_1$$ and $$C_2$$ such that $$C_1 = 2C_2$$ are connected across a battery of $$V$$ volts as shown in the figure. Initially the key ($$k$$) is kept closed to fully charge the capacitors. The key is now thrown open and a dielectric slab of dielectric constant '$$K$$' is inserted in the two capacitors to completely fill the gap between the plates. The ratio of the energies stored in the combination, before and after the introduction of the dielectric slab:
Two fixed, equal, positive charges, each of magnitude $$5 \times 10^{-5} C$$ are located at points A and B separated by a distance of 6 m. An equal and opposite charge moves towards them along the line COD, the perpendicular bisector of the line AB. The moving charge when it reaches the point C at a distance of 4 m from O, has a kinetic energy of 4 J. If the distance of the farthest point D which the negative charge will reach before returning towards C is $$x$$, then find the value of $$x^2/12$$.
Two parallel plates have equal and opposite charges. When the space between the plates is evacuated, the electric field is $$E_0=3.20\times 10^5 V/m$$. When space is filled with a dielectric, the electric field is $$E=2.50\times 10^5 V/m$$. The dielectric constant is approximately given as $$\dfrac{x+10}{10}$$. Find $$x$$.(mention answer in decimal)
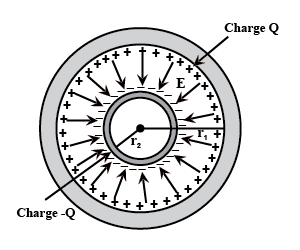
A spherical capacitor consists of two concentric spherical conductors, held in position by suitable insulating supports (Fig.). Show that the capacitance of a spherical capacitor is given by
$$c=\displaystyle\frac{4\pi \epsilon _0\,r_1r_2}{r_1-r_2}$$
where $$r_{1}$$ and $$r_{ 2}$$ are the radii of outer and inner spheres, respectively.
Show that the force on each plate of a parallel plate capacitor has a magnitude equal to $$(\frac{1}{2})$$ QE, where Q is the charge on the capacitor, and E is the magnitude of electric field between the plates. Explain the origin of the factor .
A parallel plate capacitor is to be designed with a voltage rating 1 kV, using a material of dielectric constant 3 and dielectric strength about $$10^{7}\ Vm^{-1}$$. (Dielectric strength is the maximum electric field a material can tolerate without breakdown, i.e., without starting to conduct electricity through partial ionisation.) For safety, we should like the field never to exceed, say 10% of the dielectric strength.What minimum area of the plates is required to have a capacitance of 50 pF ?
A spherical capacitor has an inner sphere of radius 12 cm and an outer sphere of radius 13 cm. The outer sphere is earthed and the inner sphere is given a charge of $$2.5 \mu C$$. The space between the concentric spheres is filled with a liquid of dielectric constant 32.(a) Determine the capacitance of the capacitor.(b) What is the potential of the inner sphere?
(c) Compare
the capacitance of this capacitor with that of an isolated
sphere of radius 12 cm. Explain why the latter is much smaller.
(b) What is the potential of the inner sphere?
A slab of material of dielectric constant K has the same area as that of the plates of a parallel plate capacitor but has the thickness d/2, where d is the separation between the plates. Find out the expression for its capacitance when the slab is inserted between the plates of the capacitor .
Hint:- Write the expression of potential difference between the plates when the slab is inserted and hence find capacitance by using the formula,$$c=\frac{q}{v}$$
Now, the gap between plates is divided in two parts, for distance t=$$\frac d2$$there is electric field E and for the remaining distance
(d-t) the electric field is $${ E }_{ 0 }$$
Step 1: Write the expression of capacitance before the slab is inserted.
Initially, when there is a vacuum between the two plates, the capacitance of the capacitor is
$${ C }_{ 0 }=\dfrac { { \varepsilon }_{ 0 }A }{ d } $$
where A is the area of parallel plates
Suppose that the capacitor is connected to a battery, an electric field $${ E }_{ 0 }$$ is produced
Step 2: Write the expression of potential difference after the slab is inserted between the plates of the capacitor
if we insert the dielectric slab of thickness t=d/2 the electric field is reduced to E
Now, the gap between plates is divided in two parts, for distance t=$$\frac d2$$there is electric field E and for the remaining distance
(d-t) the electric field is $${ E }_{ 0 }$$
If V be the potential difference between the plates of the capacitor, then
$$V={ E }_{ t }+{ E }_{ 0 }(d-t)\\ V=\dfrac { Ed }{ 2 } +\dfrac { { E }_{ 0 }d }{ 2 } =\dfrac { d }{ 2 } (E+{ E }_{ 0 })\quad \quad \quad \quad (t=\dfrac { d }{ 2 } )$$
$$V=\dfrac { d }{ 2 } (\dfrac { { E }_{ 0 } }{ K } +{ E }_{ 0 })=\dfrac { d{ E }_{ 0 } }{ 2K } (K+1)\quad \quad \quad \quad (\quad as\quad \dfrac { { E }_{ 0 } }{ E } =K)$$
$$now\quad { E }_{ 0 }=\dfrac { \sigma }{ { \varepsilon }_{ 0 } } =\dfrac { q }{ { \varepsilon }_{ 0 }A } \\ \Rightarrow V=\dfrac { d }{ 2K } \dfrac { q }{ { \varepsilon }_{ 0 }A } (K+1)$$
Step 3:Calculate capacitance after dielectric slab is inserted.
$$C=\frac {q}{V}$$
$$C= \dfrac {2K\epsilon_o A }{d(k+1)}$$
(a) Deduce the expression for the potential energy of a system of two charges $$q_1$$ and $$q_2$$ located $$\overrightarrow{r_1}$$ and $$\overrightarrow{r_2}$$, respectively, in an external electric field.
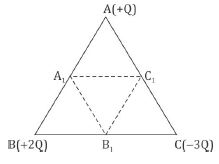
(b) Three point charges, + Q + 2Q and - 3Q are placed at the vertices of an equilateral triangle ABC of side l. If these charges are displaced to the mid-point $$A_1, B_1$$ and $$C_1$$, respectively, find the amount of the work done in shifting the charges to the new locations.
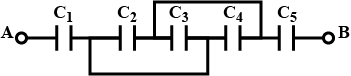
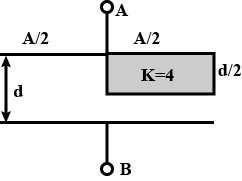
In the figure shown find the equivalent capacitance between terminals 'A' and 'B'. The letters have their usual meaning capacitance is $$\displaystyle\frac{x\varepsilon_0A}{10d}$$ then x is?
This is the case where $$C_1$$ & $$C_3$$ were in parallel and $$C_2$$ is in series.
$${ C }_{ 1 }=\dfrac { { \varepsilon }_{ 0 }A/2 }{ d/2 } ,\quad { C }_{ 3 }=\dfrac { 4{ \varepsilon }_{ 0 }A/2 }{ d/2 } ,\quad { C }_{ 2 }=\dfrac { { \varepsilon }_{ 0 }A }{ d/2 } $$
$$=$$ $${ C }_{ 1 }=\dfrac { { \varepsilon }_{ 0 }A }{ d } $$
$${ C }_{ 2 }=\dfrac { 2{ \varepsilon }_{ 0 }A }{ d } $$
$${ C }_{ 3 }=\dfrac { 4{ \varepsilon }_{ 0 }A }{ d } $$
$$\dfrac { 1 }{ ceff } =\dfrac { 1 }{ { C }_{ 1 }+{ C }_{ 3 } } +\dfrac { 1 }{ { C }_{ 2 } } $$
$$=\dfrac { 1 }{ ceff } =\dfrac { 1 }{ \dfrac { { \varepsilon }_{ 0 }A }{ d } +\dfrac { 4{ \varepsilon }_{ 0 }A }{ d } } +\dfrac { 1 }{ \dfrac { 2{ \varepsilon }_{ 0 }A }{ d } } $$
$$=\dfrac { 1d }{ 5{ \varepsilon }_{ 0 }A } +\dfrac { d }{ 2{ \varepsilon }_{ 0 }A } =\dfrac { d }{ { \varepsilon }_{ 0 }A } \left[ \dfrac { 1 }{ 5 } +\frac { 1 }{ 2 } \right] $$
$$\boxed { \dfrac { 1 }{ ceff } =\dfrac { 7d }{ 10\varepsilon _{ 0 }A } } $$
$$N$$ conducting plares are placed face to face as shown in figure. Distance between any two plates is $$d$$. Area of the plates is $$A,\cfrac { A }{ 2 } ,\cfrac { A }{ 4 } ,\cfrac { A }{ 8 } ...\cfrac { A }{ 2(n-1) } $$. The equivalent capacitance of the system is _____.
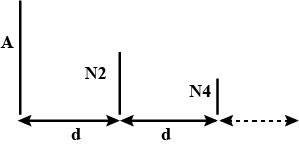
Derive the formula for the electric potential energy of an electric dipole in a uniform electric field.
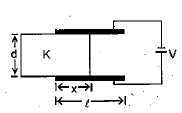
Figure shows a parallel plate capacitor with plates of width $$b$$ and length $$\ell$$. The separation between the plates is $$d$$. The plates are rigidly clamped and connected to a battery of $$emf$$V. A dielectric slab of thickness $$d$$ and dielectric constant $$K$$ is slowly inserted between the plates.
(a) Calculate the energy of the system when a length $$x$$ of the slab is introduced into the capacitor.
(b) What force should be applied on the slab to ensure that goes slowly into the capacitor? Neglect any effect of friction or gravity.
The electric field at a point due to a point charge is $$30N/C$$ and the electric potential at that point is $$15J/C$$ respectively. What is the distance of the point from the charge and the magnitude of the charge?
$$27$$ drops of the same size are charged at $$220\ V$$ each. They combine to form a bigger drop. Calculate the potential of the bigger drop.
A parallel-plate capacitor having plate area $$ 25 cm^2 $$ and separation $$1.00 mm $$ is connected to a battery of $$6.0 V $$. Calculate the charge flown through the battery. How much work has been done by the battery during the process?
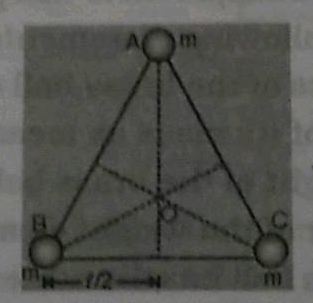
Three mass points each of mass $$m$$ are placed at the vertices of an equilateral triangle of side $$1$$ . What is the gravitational potential at the centroid of the triangle.
A parallel-plate air capacitor has a capacitance of $$4 \mu F $$ what be its new capacitance if a slab of dielectric constant 5 is introduced filling the entire space between the two plates?
Illustrate a condition in which :
Electric field is not zero but potential is zero
From figure we can see that point P is equidistant from the two charges of same magnitude but opposite nature.
Hence, potential at P is $$V=0$$
But as clear from figure again, that the field due to two charges are not opposite to each other and hence there will be a net field at P that is $$E\neq 0$$
Illustrate a condition in which :
Electric field is zero but potential is not zero.
(A) Estimate the speed with which electrons emitted from a heated emitter of an evacuated tube impinge on the collector maintained at a potential difference of 500 V with respect to the emitter. Ignore the small initial speeds of the electrons. The specific charge of the electron, i.e., its e/m is given to be $$1.76 \times {10^{11}}C$$ $$k{g^{ - 1}}$$
(B) Use the same formula you employ in (a) to obtain electron speed for a collector potential of 10 MV. Do you see what is wrong? In what way is the formula to be modified?
Find the equivalent capacitance of three capacitors of capacitance $$3 \mu F$$, $$10 \mu F$$ and $$15 \mu F$$ connected in (1) series (2) parallel.
The capacity of parallel plate condenser is 5uF. When a glass plate is between the plates of the conductor its potential becomes 1/8 th of the original value. The value of the dielectric constant will be :
What is an equipotential surface? Mention any two characteristics of equipotential surfaces.
A parallel plate capacitor is charged by a battery, which is then disconnected. A dielectric slab is then inserted in the space between the plates. Explain what changes, if any, occur in the values of
(i) capacitance.
(ii) potential difference between the plates.
(iii) electric field between the plates.
(iv) the energy stored in the capacitor.
What does mean by energy stored in capacitor?
Prove that-
"The ratio of change in potentials of conductors after connecting two charged conductors is inversely proportional to their capacitances".
Draw a curve between electric field and distance for an uniformly for an uniformly charged non-conducting sphere.
Energy stored in a capacitor : A capacitor is a device to store energy. The process of charging up a capacitor involves the transferring of electric charges from its one plate to another.The work done in charging the capacitor is stored as its electrical potential energy. Consider two insulated conductor A and B of capacitance $$C_1, C_2$$ and carrying charges $$Q_1$$ and $$Q_2$$. Let $$V_1$$ and $$V_2$$ be their respective potentials.
$$Q_1=C_1V_2$$ and $$Q_2=C_2V_2$$
If connect with wire charge flow higher to lower potential
Total charge on system $$Q_1+Q_2$$
Total capacitance $$C_1+C_2$$
$$V=\dfrac{Q}{C}=\dfrac{Q_1+Q_2}{C_1+C_2}=\dfrac{C_1V_1+C_2V_2}{C_1+C_2}$$
$$V\propto \dfrac{1}{C_1+C_2}$$
Electric field distance curve by uniformly charged non- conducting sphere.
E outside $$(r>r_0)$$
$$E=\dfrac{KQ}{r^2}$$
$$E$$ inside $$(r<r_0)$$
$$E=\dfrac{KQ.r}{r_0^3}$$
$$Q_1=C_1V_2$$ and $$Q_2=C_2V_2$$
If connect with wire charge flow higher to lower potential
Total charge on system $$Q_1+Q_2$$
Total capacitance $$C_1+C_2$$
$$V=\dfrac{Q}{C}=\dfrac{Q_1+Q_2}{C_1+C_2}=\dfrac{C_1V_1+C_2V_2}{C_1+C_2}$$
$$V\propto \dfrac{1}{C_1+C_2}$$
Electric field distance curve by uniformly charged non- conducting sphere.
E outside $$(r>r_0)$$
$$E=\dfrac{KQ}{r^2}$$
$$E$$ inside $$(r<r_0)$$
$$E=\dfrac{KQ.r}{r_0^3}$$
Figure shows two identical parallel plate capacitors connected to a battery through a switch S. Initially, the switch is closed so that the capacitors are completely charged. The switch is now opened and the free space between the plates of the capacitors is filled with a dielectric of dielectric constantFind the ratio of the initial total energy stored in the capacitors to the final total energy stored.
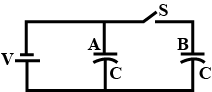
Briefly explain the principle of a capacitor. Derive an expression for the capacitance of a parallel plate capacitor, whose plates are separated by a dielectric medium
$$\large \textbf{(a) Principle of capacitor}$$ -
Whenever two neutral conductors are placed nearby, and a potential difference is applied to them, then equal and opposite charges are induced on them.
Therefore, due to these charges, Energy is stored in the form of Electric Field in the gap between them.
A capacitor is device used to store Energy.
The charge appearing on the conductors is directly proportional to the Potential difference applied to them. i.e.
$$Q\propto V$$
$$\Rightarrow\ \ Q = CV$$
Where C is the constant of proportionality, called capacitance of the system, it depends on physical dimensions of the conductors.
$$\large \textbf{(b) Derivation of Capacitance}$$
$$\textbf{Step 1: Electric field inside capacitor}$$
Let, $$\sigma = \cfrac QA$$ be the charge per unit area of both the plates.
The gap($$d$$) between plates is generally very small as compared to the Area($$A$$) of the plates.
So for calculating Electric Field inside, the plates can be assumed to be infinite.
So,
$$E_1=\dfrac{\sigma}{2\epsilon_0}$$ (Rightwards)
$$E_2=\dfrac{\sigma}{2\epsilon_0}$$ (Rightwards)
Therefore, Net Electric field in the air gap $$E_0=E_1+E_2=\dfrac{\sigma}{\epsilon_0}$$
Now, when a dielectric of dielectric constant $$K$$ is present between the plates.
So, Net electric field $$E_{net}=\cfrac {E_0}{K}=\dfrac{\sigma}{K\epsilon_0}$$
$$\textbf{Step 2: Potential diffrence between plates}$$
P.D. between plates (1) and (2)
$$V_{12}=E_{net}\times d=\dfrac{\sigma}{K\epsilon_0}\times d$$
However, $$\sigma =\dfrac{Q}{A}$$
So, $$V_{12}=\dfrac{Qd}{KA\epsilon_0}$$ $$....(1)$$
$$\textbf{Step 3: Capacitance of capacitor}$$
$$C=\dfrac{Q}{V}=\dfrac{Q}{Qd/KA\epsilon_0}=\dfrac{KA\epsilon_0}{d}$$ (from equation $$1$$)
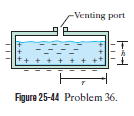
As a safety engineer,you must evaluate the practice of storing flammable conducting liquids in nonconducting containers.The company supplying a certain liquid has been using a squat, cylindrical plastic container of radius r = 0.20 m and filling it to height h = 10 cm, which is not the containers full interior height (Fig. 25-44).Your investigation reveals that during handling at the company, the exterior surface of the container commonly acquires a negative charge density of magnitude 2.0 C/m$$^2$$ (approximately uniform). Because the liquid is a conducting material, the charge on the container induces charge separation within the liquid. (a) How much negative charge is induced in the center of the liquids bulk? (b) Assume the capacitance of the central portion of the liquid relative to ground is 35 pF. What is the potential energy associated with the negative charge in that effective capacitor? (c) If a spark occurs between the ground and the central portion of the liquid (through the venting port), the potential energy can be fed into the spark.The minimum spark energy needed to ignite the liquid is 10 mJ. In this situation, can a spark ignite the liquid?
There are 27 drops of a conducting fluid. each drop has radius r and each of them is charged to same potential $$ V_1$$ they are then combined to form a bigger drop. the potential of the bigger drop is $$ V_2 $$ find the ratio $$ V_2 /V_1 $$ ignore the change in density of fluid on combining the drops.
Between the plates of a parallel-plate capacitor there is a metallic plate whose thickness takes up $$\eta = 0.60$$ of the capacitor gap. When that plate is absent the capacitor has a capacity $$C = 20\ nF$$. The capacitor is connected to a dc voltage source $$V = 100\ V$$. The metallic plate is slowly extracted from the gap. Find:
(a) the energy increment of the capacitor;
(b) the mechanical work performed in the process of plate extraction.
Electric Potential and Potential Energy
Due to Point Charges (12)
(a) Calculate the electric potential $$0.250 \,cm$$ from an
electron.
(b) What is the electric potential difference
between two points that are $$0.250 \,cm$$ and $$0.750 \,cm$$ from an electron?
(c) How would the answers change if
the electron were replaced with a proton?
Determine (a) the capacitance and (b) the maximum potential difference that can be applied to a Teflonfilled parallel-plate capacitor having a plate area of $$1.75 cm^2$$ and a plate separation of $$0.040 0 mm$$.
A parallel-plate capacitor of plate separation $$d$$ is charged to a potential difference $$\Delta V_0$$. A dielectric slabof thickness $$d$$ and dielectric constant $$k$$ is introduced between the plates while the battery remains connected to the plates.
(a) Show that the ratio of energy stored after the dielectric is introduced to the energy stored in the empty capacitor is $$U/U_0 = k$$.
(b) Give a physical explanation for this increase in stored energy.
(c) What happens to the charge on the capacitor? Note:This situation is not the same as in Example 26.5, in which the battery was removed from the circuit before the dielectric was introduced.
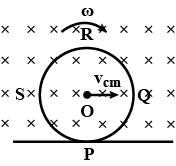
A conducting disc of radius 'r' is rotating as well as translating on a smooth horizontal surface, where a uniform magnetic field B acting into the plane of paper is present as shown in the figure. Velocity of centre of mass is given as $$v_{cm} = 2r\omega,$$ where $$\omega$$ is the angular velocity of the ring. Match the following cases. [O is the centre of ring PQRS).
First list gives the segment of ring and second list gives the Emf induced.
| List-I | List-II | ||
| P | PR | 1. | 5Brv/4 |
| Q | PS | 2. | Brv |
| R | PO | 3. | 2Brv |
| S | RO | 4. | 3Brv/4 |
For OP
$$v = v_{cm} - wx$$
$$d\varepsilon = \int_0^r dxv$$
$$= \int_0^r B(2\omega r - \omega x)dx$$
$$= \left.\begin{matrix}B \left(2\omega r x - \dfrac{\omega x^2}{2}\right)\end{matrix}\right|_0^r$$
$$=B\left(2\omega r^2 - \dfrac{\omega r^2}{2}\right)$$
$$v_0 - v_p = \dfrac{3B\omega r^2}{2}$$ ---- (1)
for OR
$$d\varepsilon = B \left(2\omega r x+\dfrac{\omega x^2}{2}\right)_0^r$$
$$v_R - v_0 = \dfrac{5B\omega r^2}{2} $$ ...(2)
Then $$v_R - v_P = 4 B\omega r^2$$
$$=\dfrac{4 B v r}{2}$$
$$\varepsilon PR= 2B r v$$
for OS
$$d \varepsilon = \left.\begin{matrix}B \dfrac{\omega x^2}{2} \end{matrix}\right|_0^R$$
$$= \dfrac{B\omega r^2}{2}$$
$$v_s - v_0 = \dfrac{B \omega r^2}{2} = \dfrac{B vr}{4}$$ ...(3)
for OR
$$v_0 - v_R = \dfrac{B vr}{4}$$ ...(4)
$$\varepsilon_{PS} = \dfrac{3B\omega r^2}{2} + \dfrac{B \omega r^2}{2}$$
$$= 2B \omega r^2$$
$$\varepsilon_{PS} = B vr$$ ...from (1) & (3)
$$\varepsilon_{PD} = \dfrac{3B vr}{4}$$ ..from (1)
$$\varepsilon_{RD} = \dfrac{5 B vr}{4}$$ ...from (2)
$$P - 3$$
$$Q-2$$
$$ R-4$$
$$S-1$$
Class 12 Medical Physics Extra Questions
- Alternating Current Extra Questions
- Atoms Extra Questions
- Current Electricity Extra Questions
- Dual Nature Of Radiation And Matter Extra Questions
- Electric Charges And Fields Extra Questions
- Electromagnetic Induction Extra Questions
- Electromagnetic Waves Extra Questions
- Electrostatic Potential And Capacitance Extra Questions
- Magnetism And Matter Extra Questions
- Moving Charges And Magnetism Extra Questions
- Nuclei Extra Questions
- Ray Optics And Optical Instruments Extra Questions
- Semiconductor Electronics: Materials, Devices And Simple Circuits Extra Questions
- Wave Optics Extra Questions