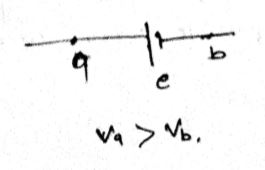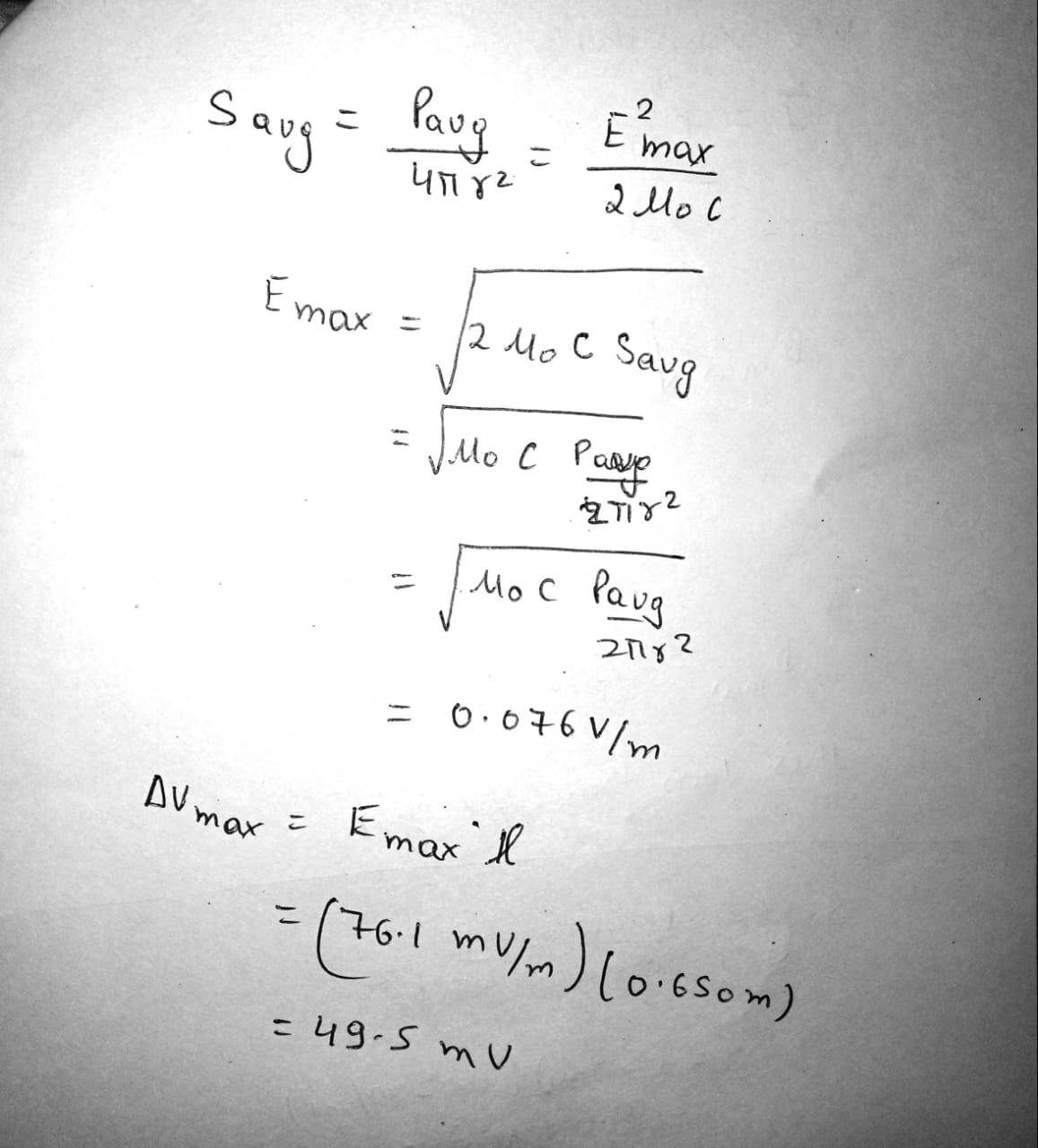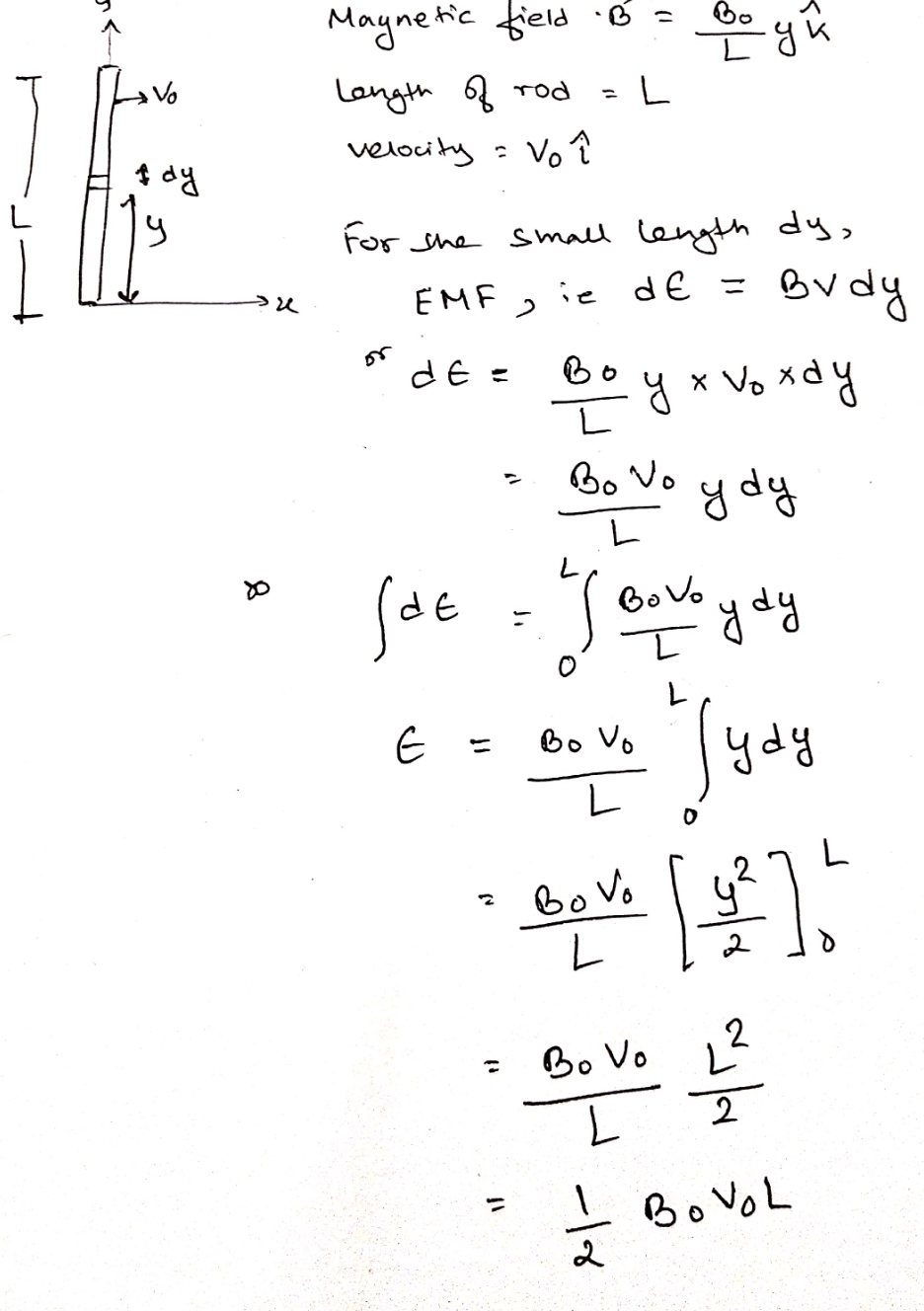Electromagnetic Induction - Class 12 Medical Physics - Extra Questions
Define coefficient of mutual induction. If in the primary coil of a transformer, the current decreases from $$0.8A$$ to $$0.2A$$ in $$4$$ milliseconds, calculate the induced e.m.f in the secondary coil. Mutual inductance is $$1.76H$$.
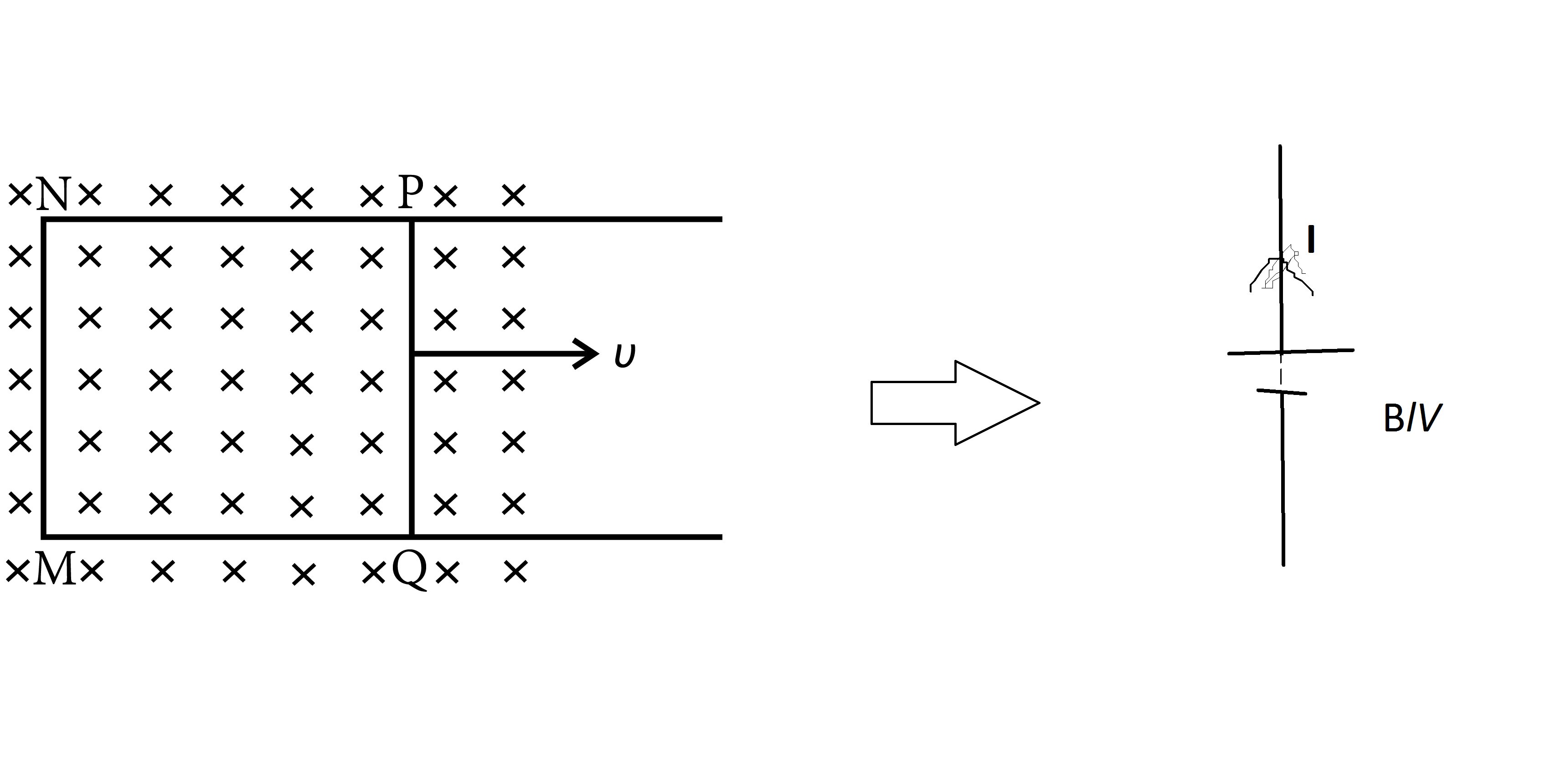
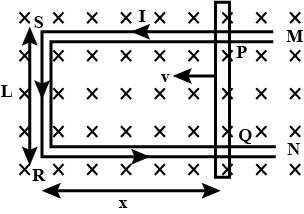
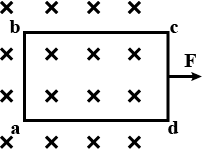
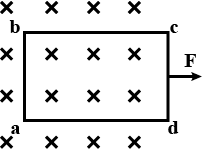
A rectangular frame of wire $$abcd$$ has dimensions $$32\ cm\times 8.0\ cm$$ and a total resistance of $$2.0\Omega$$. It is pulled out of a magnetic field $$B = 0.020\ T$$ by applying a force of $$3.2\times 10^{-5}N$$ (figure). It is found that the frame moves with constant speed. Find the emf induced in the loop.
Answer the following :
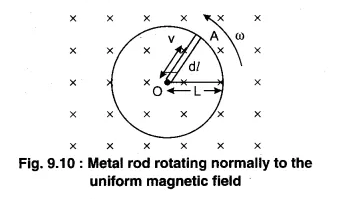
A metallic rod $$PQ$$ of length $$l$$ is rotated with an angular velocity $$\omega$$ about an axis passing through its mid-point (O) and perpendicular to the plane of the paper, in uniform magnetic field $$\vec{B}$$, as shown in the figure. What is thee potential difference developed between the two ends of the rod, P and Q ?

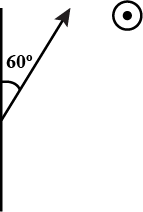
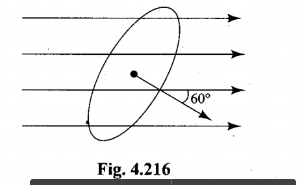
A wire length $$10cm$$ translates in a direction making an angle of $${60}^{o}$$ with its length. The plane of motion is perpendicular to a uniform magnetic field of $$1.0T$$ that exists in the space. Find the emf induced between the ends of the rod if the speed of translation is $$20cm$$ $${s}^{-1}$$
Figure shows a metallic wire of resistance $$0.20\Omega$$ sliding on a horizontal, U-shaped metallic rail. The separation between the parallel arms is $$20cm$$. An electric current of $$2.0\mu A$$ passes through the wire when it is slid at a rate of $$20cm$$ $${s}^{-1}$$. If the horizontal component of the earth's magnetic field is $$3.0\times { 10 }^{ -5 }T$$. Calculate the dip at the place.
A current of $$1.0A$$ is established in a tightly wound solenoid of radius $$2cm$$ having $$1000$$ turns/metre. Find the magnetic energy stored in each metre of the solenoid.
An average emf of $$20V$$ is induced in an inductor when the current in it is changed from $$2.5A$$ in one direction to the same value in the opposite direction in $$0.1s$$. Find the self-inductance of the inductor.
How many times, the current produced by $$AC$$ Generator reverses its direction in one complete revolution of its coil?
How many times $$AC$$ supply in India reversed its direction in one second.
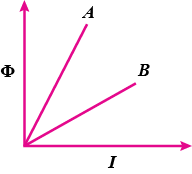
A plot of magnetic flux $$(\varphi )$$ versus current $$(I)$$ is shown in the figure for two inductors $$A$$ and $$B$$. Which of the two has larger value of self inductance?
Solve a problem differing from the foregoing one by a magnetic field with induction $$B = 0.8\ T$$ replacing the electric field.
An inductor with an inductance of $$3.00H$$ and a resistance of $$7.00\Omega$$ is connected to the terminals of a battery with an emf of $$12.0V$$ and negligible internal resistance. Find the initial rate of increase of current in the circuit.
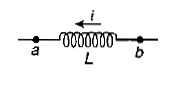
Which end of the inductor, $$a$$ or $$b$$, is at a higher potential?
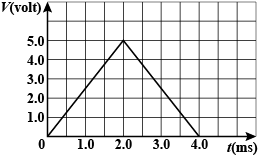
The potential difference across a $$150mH$$ inductor as a function of time is shown in figure. Assume that the initial value of the current in the inductor is zero. What is the current when $$t=2.0ms$$?
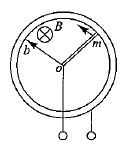
According to which law current $$I$$ flowing in the rod must vary for the rod to rotate at a constant angular speed. Begin to measure the time from the instant when the rod is in its right-hand horizontal position. Consider the current to be positive when it flows from the axis of rotation toward the ring.
Interpret K' - K.
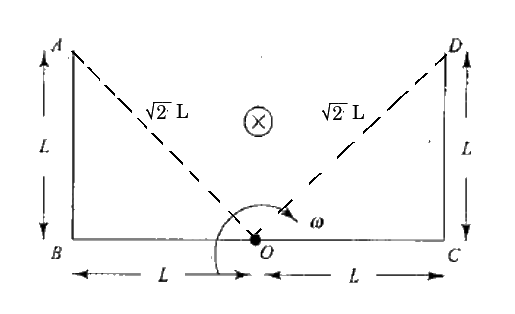
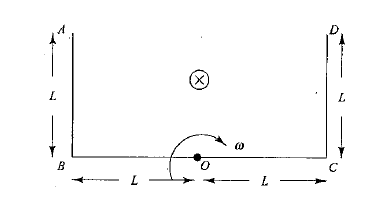
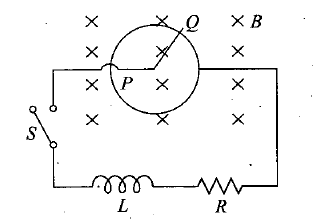
A frame $$ABCD$$ is rotating with an angular velocity $$\omega$$ about an axis passing through point $$O$$ perpendicular to the plane of paper as shown in the figure. A uniform magnetic field $$\vec { B } $$ is applied into the plane of the paper in the region as in the figure. Match the following.
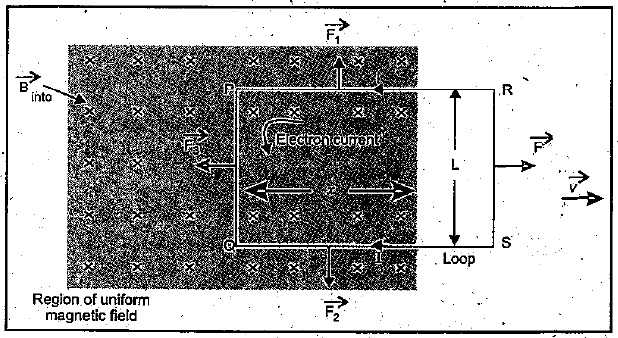
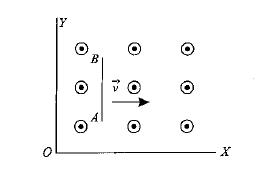
A conducting rod $$AB$$ moves parallel to the x-axis in a uniform magnetic field pointing in the positive z direction. The end $$A$$ of the rod gets positively charged. explain.
The magnetic flux linked with the armature coil changed in a generator =$$\Phi (t) = xNBA\cos (\omega t)$$ then x=
A solenoid has a cross sectional area of $$6.0 \times 10^{-4} m^{2}$$, consists of 400 turns per meter, and carries a current 0.4 A and are connected to a circumference of the solenoid. The ends of the coil are connected to a 1.5$$\Omega$$ resistor. Suddenly, a switch is opened, and the current in the solenoid dies to zero in a time 0.050 s. Find the average current passing through the coil during this time.
The voltage applied to a purely inductive coil of self inductance $$15.9mH$$ is given by the equation $$V=100sin 314t$$ + $$75sin942t$$ + $$450sin1570t.$$
Find the equation of current wave.
Additional Problems(67)
(a) A flat, circular coil does not actually produce a uniform magnetic field in the area it encloses. Nevertheless, estimate the inductance of a flat, compact, circular coil with radius $$R$$ and $$N$$ turns by assuming the field at its center is uniform over its area. (b) A circuit on a laboratory table consists of a $$1.50-volt$$ battery, a $$270-\Omega$$ resistor, a switch, and three $$30.0-cm$$-long patch cords connecting them. Suppose the circuit is arranged to be circular. Think of it as a flat coil with one turn. Compute the order of magnitude of its inductance and (c) of the time constant describing how fast the current increases when you close the switch.
Energy Carried by Electromagnetic Waves(31)
Review. An AM radio station broadcasts isotropically (equally in all directions) with an average power of $$4.00 \,kW$$. A receiving antenna $$65.0 \,cm$$ long is at a location $$4.00 \,mi$$ from the transmitter. Compute the amplitude of the emf that is induced by this signal between the ends of the receiving antenna.
A solenoid of length $$1 m$$ and $$0.05 m$$ diameter has $$500$$ turns. If a current of $$2 A$$ passes through the coil, calculate the co-efficient of self induction of the coil.
On what factors does the induced electromotive force depend?
Give two definitions of mutual inductance and write its unit.
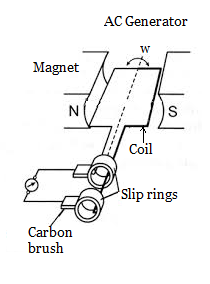
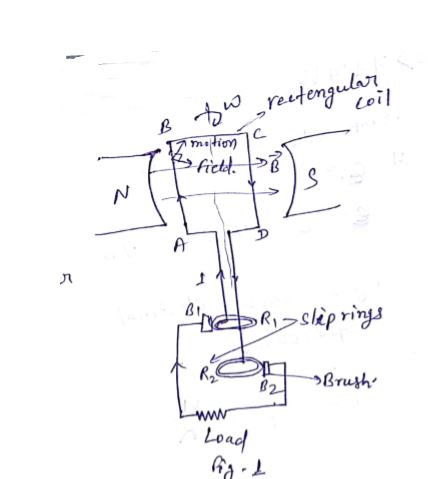
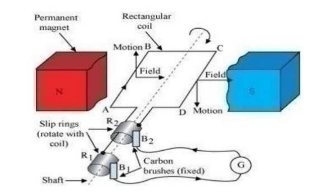
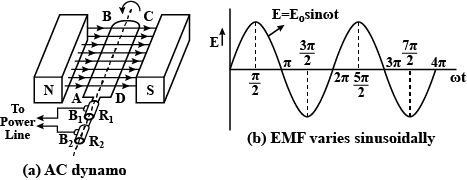
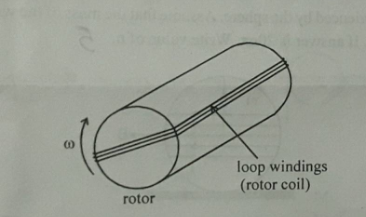
What is an AC generator? Obtain an expression for the sinusoidal emf induced in the coil of ac generator, rotating with a uniform angular speed in a uniform magnetic field.
When the number of turn in a coil is doubled without, any change in the length of the coil , its self inductance becomes
A conducting circular loop having a radius of $$5.0 $$ cm, is placed perpendicular to a magnetic field of $$0.50 T$$. It is removed from the field in $$0.50 s$$. Find the average emf produced in the loop during this time.
A circular coil of $$200$$ turns and of radius $$20 cm$$ carries a current of $$5A$$. Calculate the magnetic induction at a point along its axis, at a distance three times the radius of the coil from its centre.
A stiff semi-circular wire of radius $$R$$ is rotated in a uniform magnetic field $$B$$ about an axis passing through its ends. If the frequency of rotation of wire is $$f$$, calculate the amplitude of alternating emf induced in the wire.
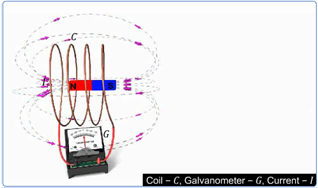
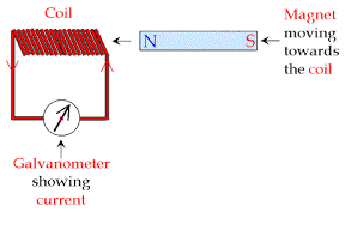
A coil of insulated copper wire is connected to a galvanometer. What will happen if a bar magnet is pushed into the coil?
A pair of adjacent coils has a mutual inductance of $$1.5 H$$. If the current in one coil changes from $$0$$ to $$10 A$$ in $$0.2 s$$, what is the change of flux linkage with the other coil?
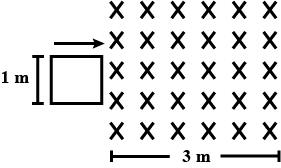
Figure shows a square loop of resistance 1 $$\Omega $$ of side 1 m being moved towards right at a constant speed of 1 m/s. The front edge enters the 3 m wide magnetic field (B = 1T) at t = 0 Draw the graph of current induced in the loop as time passes ( Take anticlockwise direction of current as positive)
In a fluorescent lamp choke (a small transformer) $$100$$V of reverse voltage is produced when the choke current changes uniformly from $$0.25$$A to $$0$$ in a duration of $$0.025$$ms. The self-inductance of the choke (in mH) is estimated to be _______.
What is a solenoid? Draw a diagram with a solenoid connected in a circuit. How can you increase the strength of a solenoid?
A circular coil of wire consist of exactly 100 turns with a total resistance 0.20 $$\omega$$. The area of the coil is $$100 cm^2$$. The coil is kept in a uniform magnetic field B as shown in fig 4.The magnetic field is increased at a constant rate of 2 T/s. Find the induced current in the coil in A
Two discharge tubes have identical material structure and the same gas is filled in them. The length of one tube is $$10 cm$$ and that of the other tube is $$20 cm$$. Sparking starts in both the tubes when the potential difference between the cathode and the anode is $$100 V$$. If the pressure in the shorter tube is $$1.0 mm$$ of mercury, what is the pressure in the longer tube ?
The current in a long solenoid of radius $$R$$ and having $$n$$ turns per unit length is given by $$i={i}_{0}\sin \omega t$$. A coil having $$N$$ turns is wound around it near the centre. Find (a) the induced emf in the coil and (b) the mutual inductance between the solenoid and the coil.
Name one device which converts electrical energy into mechanical energy.
Name the phenomenon which is made use of in an electric generator.
If you hold a coil of wire next to a magnet, no current will flow in the coil. What else in needed to induce a current?
The inductance of a closely wound coil is such that an emf of 3.00 mV is induced when the current changes at the rate of 5.00 A/s. A steady current of 8.00 A produces a magnetic flux of $$40.0\mu Wb$$ through each turn. (a) Calculate the inductance of the coil. (b) How many turns does the coil have?
How can the magnitude of the induced current be increased?
Suggest two ways in an a.c. generator to produce a higher e.m.f.
A magnetic substance of volume $$30 cm^{3}$$ is placed in a magnetising field of $$5$$ oersted. It produces a magnetic moment of $$6 A/m^{2}$$ . Calculate the magnetic induction.
Two identical loops, one of copper and another of aluminium are rotated with the same speed in the same magnetic field. In which case, the
(a) The induced emf and
(b) induced current will be more and why?
A series RLC circuit is driven by a generator at a frequency of $$2000Hz$$ and an emf amplitude of $$170 V$$. The inductance is $$60.0 mH$$, the capacitance is $$0.400\mu F$$, and the resistance is $$200\Omega$$. (a) What is the phase constant in radians? (b) What is the current amplitude?
A horizontal wire $$20 m$$ long extending from east to west is falling with a velocity of $$10 m/s$$ normal to the Earths magnetic field of $$0.5*10^{-4} T$$. What is the value of induced emf in the wire?
A horizontal straight wire $$10m$$ long extending from east to west is falling with a speed of $$5.0ms^{-1}$$, at right angles to the horizontal component of the earth's magnetic filed, $$0.30*10^{4}Wbm^{2}$$.
(a) What is the instantaneous value of the emf induced in the wire?
(b) What is the direction of the emf?
(c) Which end of the wire is at the higher electrical potential?
Maximum voltage produced in an AC generator completing $$60$$ cycles in $$30$$ seconds is $$250\,V.$$
What is the maximum emf produced when the armature completes $$1800$$ rotation ?
Conceptual Questions
Consider this thesis: "Joseph Henry, America's first professional physicist, caused a basic change in the human view of the Universe when he discovered self-induction during a school vacation at the Albany Academy aboutBefore that time, one could think of the Universe as composed of only one thing: matter. The energy that temporarily maintains the current after a battery is removed from a coil, on the other hand, is not energy that belongs to any chunk of matter. It is energy in the massless magnetic field surrounding the coil. With Henry's discovery, Nature forced us to admit that the Universe consists of fields as well as matter."
(a) Argue for or against the statement.
(b) In your view, what makes up the Universe?
A 1.0 m long metallic rod is rotated with an angular frequency of 400 rad $$s^{-1}$$ about an axis normal to the rod passing through its one end. The other end of the rod is in contact with a circular metallic ring. A constant and uniform magnetic field of 0.5 T parallel to the axis exists everywhere. Calculate the emf developed between the centre and the ring.
A pair of adjacent coil has a mutual inductance of $$1.5 \,H$$. If the current in one coil changes from $$0$$ to $$20 \,A$$ in $$0.5$$ sec, what is the change of flux linkage with the other coil?
A spectral line caused by the transition $$^{3} D1 \rightarrow ^{3}P_{0} $$ experiences the Zeeman splitting in a weak magnetic field. When observed at right angles to the magnetic field direction, the interval between the neighbouring components of the split line is $$ \Delta \omega = 1.32 \times 10^{10}\,s^{-1}$$. Find the magnetic field induction B at the point where the source is located.
Derive the expression for the self inductance of a long solenoid of cross sectional area $$A$$ and length $$l$$, having $$n$$ turns per unit length.
Define self-inductance of a coil. Show that magnetic energy required to build up the current I in coil of coil of self inductance L is given by $$\displaystyle \frac{1}{2}LI^{2}$$
Two concentric circular coils of radii r and R are placed coaxially with centres coiciding. If R >> r then calculate the mutual inductance between the coils.
An aircraft having a wingspan of $$20.48 m$$ flies due north at a speed of $$40{ ms }^{ -1 }$$. If the vertical component of earth's magnetic field at the place is $$2\times { 10 }^{ -5 }T$$, calculate the emf induced between the ends of the wings.
The unit of self-inductance in SI system is ________ .
Name and state the principle of a simple a.c. generator. What is its use?
State one factor that determines the magnitude of induced e.m.f.
What is the source of energy associated with the current obtained in part when a magnet is moved towards a coil having a galvanometer at its ends?
$$Match \: the \: statements \: in \: Column \: A, \: with \: those \: in \: Column \: B.$$
Define the term 'self-inductance' of a coil. Write its S.I. unit.
Fill in the blanks.
The type of electric current that changes its direction twice during one cycle of the dynamo is called _____________ .
State Faraday's laws of electromagnetic induction.
What is motional emf? State any two factors on which it depends.
Two coils A and B have mutual inductance $$2\times { 10 }^{ -2 }$$ henry. If the current in the primary is $$i=5sin(10\pi t)$$, then the maximum value of e.m.f. induced in coil B is :
What is a generator state the principle on which generators work
Describe the activity that shows that a current-carrying conductor experiences a force perpendicular to its length and the external magnetic field. How does Flemings' left-hand rule help us to find the direction of the force acting on the current-carrying conductor?
The current through an indicator of $$1H$$ is given by $$i=3t\sin { t } $$. Find the voltage across the inductor.
the self inductance of the primary coil.
At the instant when the current in an inductor is increasing at a rate of $$0.0640A/s$$, the magnitude of the self-induced emf is $$0.0160V$$. If the inductor is a solenoid with $$400$$ turns, what is the average magnetic flux through each turn when the current is $$0.720A$$?
When a current of $$4A$$ between two coils changes to $$12A$$ in $$0.5s$$ in primary and induces an emf of $$50mV$$ in the secondary. Calculate the mutual inductance between the two coils.
At the instant when the current in an inductor is increasing at a rate of $$0.0640A/s$$, the magnitude of the self-induced emf is $$0.0160V$$. What is the inductance of the inductor?
The current (in Ampere) in an inductor is given by $$I=5+16t$$, where $$t$$ is in seconds. The self-induced emf in it is $$10mV$$. Find the self-inductance.
Two bar magnets are placed side by side by side that the north pole of one magnet is next to the south pole of the other magnet. If these magnets are then pushed toward a coil of wire, would you expect an emf to be induced in the coil. Explain your answer.
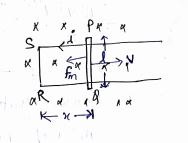
emf induced in the arm PQ
Current in a circuit falls from $$5.0 A$$ to $$0.0 A$$ in $$0.1\ s$$. If an average emf of $$200\ V$$ induced, find an estimate of the self-inductance of the circuit.
A rectangular wire loop of sides 8 cm and 2 cm with a small cut is moving out of a region of uniform magnetic field of magnitude 0.3 T directed normal to the loop. What is the emf developed across the cut if the velocity of the loop is 1 cm $$s^{-1}$$ in a direction normal to the (a) longer side, (b) shorter side of the loop? For how long does the induced voltage last in each case?
(a) A rod of length l is moved horizontally with a uniform velocity 'v' in a direction perpendicular to its length through a region in which a uniform magnetic field is acting vertically downward. Derive the expression for the emf induced across the ends of the rod.
(b) How does one understand this motional emf by invoking the Lorentz force acting on the free charge carriers of the conductor? Explain.
The property of a conductor which enables to induce an EMF due to change of current in the same coil is ____________.
Derive Faradays law of induction from law of conservation of energy.
An emf of 2V is induced in a coil when current in it is changed from 0A to 10A in 0.40 sec. Find the coefficient of self-inductance of the coil.
A metal rod $$\cfrac { 1 }{ \sqrt { \pi } } m$$ long rotates about one of its ends perpendicular to a plane whose magnetic induction is $$4\times { 10 }^{ -3 }T$$. Calculate the number of revolutions made by the rod per second if the e.m.f induced between the ends of the rod is $$16mV$$.
A coil of self inductance $$2\cdot 5 H$$ and resistance $$20\Omega$$ is connected to a battery of emf 120V having internal resistance of $$5 \Omega$$. Find the current in the circuit in steady state.
Write Faraday's law of electromagnetic induction.
Write the Faraday's law of electromagnetic induction.
Current in a circuit fall from $$5.0$$A to zero in $$0.1$$S. If an average emf of $$100$$ Volt is induced then calculate self-inductance of a inductor in the circuit.
State Faraday's laws of electromagnetic induction and Lenz's law.
Explain self-induction of a coil. Arrive at an expression for the induced emf in a coil and the rate of change of current in it.
Current in a circuit falls from $$5.0 A$$ to $$0.0 A$$ in $$0.1 sec$$. If an average emf of $$200 V$$ is induced, give an estimate of the self-inductance of the circuit.
What are the methods of producing induced emf?
What is the self inductance of a straight conductor?
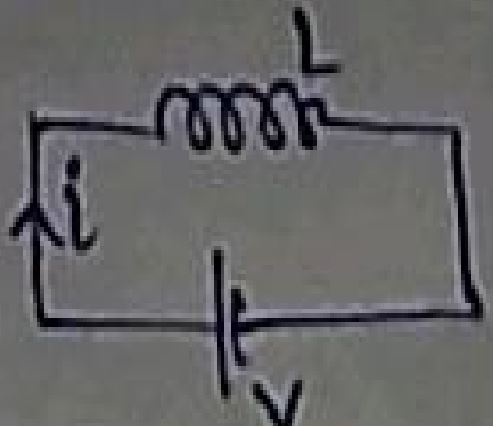
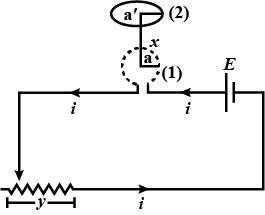
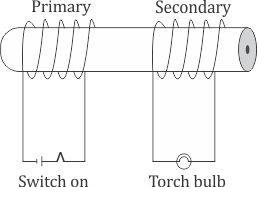
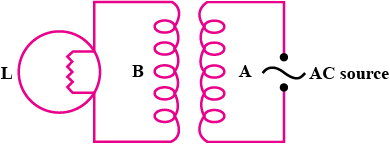
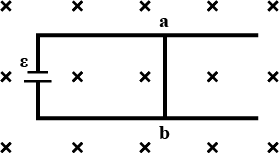
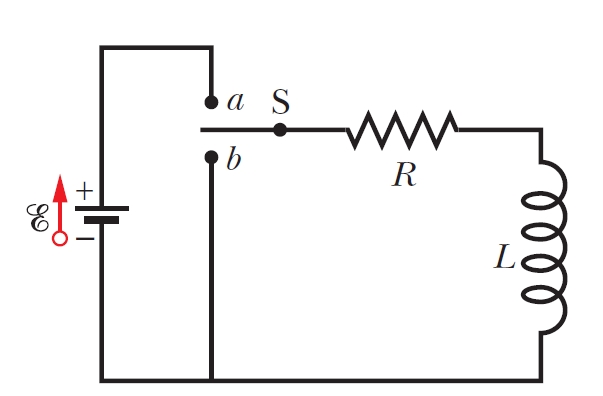
a) Switch in the primary is kept in the ON position. Will the bulb in the secondary glow? Justify your answer.
b) When the current in the primary is switched OFF. What happens to the magnetic field in the secondary coil? How will this change influence the current in the secondary and the glow in the electric bulb?
Explain seld induction and mutual induction.
Draw a labelled diagram of an ac generator. Obtain the expression for the emf induced in the rotating coil of N turns each of cross-sectional area A, in the presence of a magnetic field $$\overrightarrow{B}$$.
Current in a circuit falls from 5.0 A to 0.0 A in 0.1 s. If an average emf of 200V induced, calculate the self-inductance of the circuit.
What is the effect on self inductance of a solenoid, if a core of soft iron is placed in it?
Derive expression for the self-induction of solenoid. What factors affect its value and how?
A rectangular coil has $$60$$ turns and its length and width is $$20\ cm$$. and $$10\ cm$$ respectively. The coil rotates at a speed of $$1800$$ rotation per minute in a uniform magnetic field of $$0.5\ T$$ about its one of the diameter. Calculate maximum induced emf will be
A charged particle oscillates about its equilibrium position with an frequency of $$100\ MHz$$. What is the frequency of electromagnetic waves produced by the oscillator?
A circular coil of cross-sectional area $$200cm^2$$ and 20 turns is rotated about the vertical diameter with angular speed of $$50 rad {s}^{-1}$$ in a uniform magnetic field of magnetic $$3.0 \times10^{-2}T$$ . Calculate the maximum value of the current in the coil.
A circular coil of cross-sectional area $$ 20 cm^2$$ and $$20$$ turns is rotated about the diameter with angular speed of 50 rad $$s^{-1}$$ in a uniform magnetic field of magnetic $$3.0 \times 10^{-2}T$$. Calculate the maximum value of the current in the coil.
Draw a labeled diagram of AC generator.Derive the expression for the instantaneous value of the emf induced in the coil.
Why self induction is called inertia of electricity?
A solenoid of $$500$$ turns, diameter 2$$0 cm$$ and resistance $$2$$ $$\Omega$$ is rotated about its vertical diameter through $$\pi$$ radian in 1/4 s, when a horizontal field of $$3 \times 10^{-5} T$$ acts normal to its plane. Find the emf induced and current thereof.
A rectangular frame of wire $$abcd$$ has dimensions $$32\ cm\times 8.0\ cm$$ and a total resistance of $$2.0\Omega$$. It is pulled out of a magnetic field $$B = 0.020\ T$$ by applying a force of $$3.2\times 10^{-5}N$$ (figure). It is found that the frame moves with constant speed. What is constant speed of the frame?
Define coefficient of self inductance and write its unit.
Derive the expression for the motional emf induced in a conductor moving in a uniform magnetic field.
Match the followings.
What is self inductance? Name the factors on which self inductance depends.
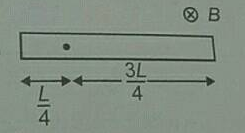
What will be the magnitude and polarity of induced emf across the rod, if it is rotating about an axis at a distance $$\cfrac{L}{4}$$ from one of its ends?
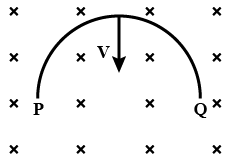
A semicircle loop $$PQ$$ of radius $$'R'$$ is moved with velocity $$'v'$$ in transverse magnetic field as shown in figure. The value of induced emf. at the end of loop is :-
What is eddy current? Mention two applications of eddy current.
A $$200km$$ long telegraph wire has a capacitance of $$0.014\mu F/km$$. If it carries an ac of $$5kHz$$, what should be the inductance required to be connected in series, so that the impedance is minimum?
Take $$\pi=\sqrt {10}$$
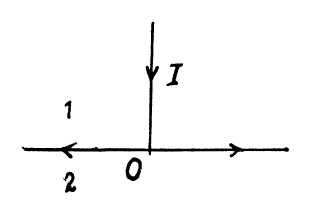
A direct current $$I$$ flows along a lengthy straight wire. From the point $$O$$ (Fig.) the current spreads radially all over an infinite conducting plane perpendicular to the wire. Find the magnetic induction at all points of space.
A rectangular coil of area $$A$$, having the number of turns $$N$$ is rotated at $$f$$ revolutions per second in a uniform magnetic field $$B$$ the field is perpendicular to the coil. Prove that the maximum emf induced in the coil is $$2 \pi fNBA$$.
A coil having resistance $$20\Omega$$ and inductance $$2H$$ is connected to a battery of emf $$4.0V$$. Find (a) the current at $$0.20s$$ after the connection is made and (b) the magnetic field energy in the coil at the instant
A conducting circular loop of area $$1$$ nm is placed compulsary with a long, straight wire at a distance of current which changes from $$10$$ A to zero in $$0.1$$ s. Find the average emf induced in the loop in $$0.1$$ s.
A coil draws a current of 1ampere and a power of 100 watt from an AC.Source of 100 volt and $$\frac { 5\sqrt { 22 } }{ \pi } $$ Hertz.Find the inductance and resistance of the coil
A copper disc of radius $$0.1$$m is rotated about its center with $$20$$ revolution per second in a uniform magnetic field of $$0.1$$T with its plane perpendicular to the field. The emf induced across the radius of the disc is?
On what principle $$AC$$ generator works?
A conducting disc of radius r rotates with a small constant angular velocity $$\omega$$ about its axis. A uniform magnetic field B exists parallel to the axis of rotations. Find the motional emf between the center and the periphery of the disc.
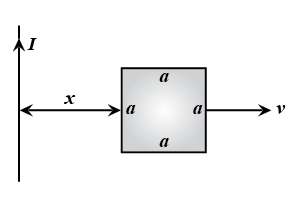
Figure shows a straight, long wire carrying a current $$i$$ and a rod of length $$l$$ coplanar with the wire and perpendicular to it. The rod moves with a constant velocity $$v$$ in direction parallel to the wire. The distance of the wire from the centre of the rod is $$x$$. Find the motional emf induced in the rod.

A constant current exists in a inductor-coil connected to a battery. The coil is short-circuited and the battery is removed. Show that the charge flown through the coil after the short-circuiting is the same as that which flows in one time constant before the short-circuiting.
An LR circuit has $$L=1.0H$$ and $$R=20\Omega$$. It is connected across an emf of $$2.0V$$ at $$t=0$$ What are the values of the self-induced emf in the circuit at the times indicated there in?
Consider a small cube of volume $$1{mm}^{2}$$ at the centre of a circular loop of radius $$10cm$$ carrying a current of $$4A$$. Find the magnetic energy stored inside the cube.
The magnetic field at a point inside a $$2.0mH$$ inductor-coil becomes $$0.80$$ of its maximum value in $$20\mu s$$ when the inductor is joined to a battery. Find the resistance of the circuit.
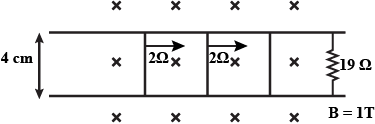
Consider the situation shown in figure. The wires $${ P }_{ 1 }{ Q }_{ 1 }$$ and $${ P }_{ 2 }{ Q }_{ 2 }$$ are made to slide on the rails with the same speed $$5cm$$ $${s}^{-1}$$. Find the electric current in the $$19\Omega$$ resistor if (a) both the wires move towards right and (b) if $${ P }_{ 1 }{ Q }_{ 1 }$$ moves towards left but $${ P }_{ 2 }{ Q }_{ 2 }$$ moves towards right

A long wire carries a current of $$4.00A$$. Find the energy stored in the magnetic field inside a volume of $$1.00{mm}^{2}$$ at a distance of $$10.0cm$$ from the wire.
An inductor of inductance $$2.00H$$ is joined in series with a resistor of resistance $$200\Omega$$ and a battery of emf $$2.00V$$. At $$t=10ms$$, find (a) the current in the circuit, (b) the power delivered by the battery, (c) the power dissipated in heating the resistor and (d) the rate at which energy is being stored in magnetic field.
An ac generator with emf $$\xi=\xi _{m}\sin \omega _{d}t$$, where $$\xi _{m}=25.0V$$ and $$\omega _{d}=377rad/s$$, is connected to a $$4.15\mu F$$ capacitor. (a) What is the maximum value of the current? (b) When the current is a maximum, what is the emf of the generator? (c) When the emf of the generator is $$-12.5 V$$ and increasing in magnitude, what is the current?
Explain the various part of $$AC$$ generator.
On what factors does the magnitude of the emf induced in the circuit due to magnetic flux depend?
How does one understand this motional emf by invoking the Lorentz force acting on the free charge carriers of the conductor? Explain.
State the rule to determine the direction of a current induced in coil due to its rotation in a magnetic field.
At a certain location in the Philippines Earth's magnetic field of $$39\hspace{0.05cm} \mu T$$ is horizontal and directed due north. Suppose the net filed is zero exactly $$8.0\hspace{0.05cm} cm$$ above a long, straight, horizontal wire that carries a constant current. What are the (a) magnitude and (b) direction of the current?
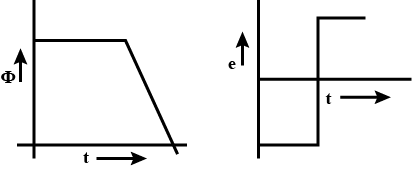
A bar magnet $$M$$ is dropped so that it falls vertically through the coil $$C$$. The graph obtained for voltage produced across the coil versus time is showing in figure(b)
Explain the shape of the graph.
Answer the following questions
Define mutual inductance.
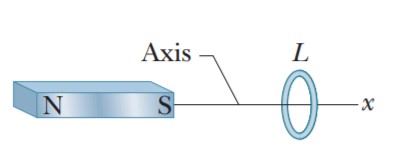
The figure shows a loop model (loop L) for a paramagnetic
material. (a) Sketch the field lines through and about the material
due to the magnet. What is the direction of (b) the loops net magnetic dipole moment $$\vec \mu$$, (c) the conventional current i in the loop
(clockwise or counterclockwise in the figure), and (d) the magnetic
force acting on the loop?
In Figure , a wire forms a closed circular loop, of radius $$R=2.0m$$ and resistance $$4.0\Omega $$. The circle is centered on a long straight wire; at time $$t=0$$, the current in the long straight wire is 5.0 A rightward.
Thereafter, the current changes according to $$i=5.0A-(2.0A/s^2)t^2$$. (The straight wire is insulated; so there is no electrical contact between it and the wire of the loop.) What is the magnitude of the current induced in the loop
at times $$t>0$$?
A 12 H inductor carries a current of 2.0 A. At what rate must the current be changed to produce a 60 V emf in the inductor?
A cylindrical bar magnet is kept along the axis of a circular coil and neat it as shown in figure. Will there be any induced emf at the terminals of the coil, when the magnet is rotated About its own axis.
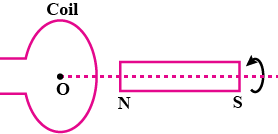
In the given diagram, a coil $$B$$ is connected to low voltage bulb $$L$$ and placed parallel to another coil $$A$$ as shown. Explain bulb gets dimmer if the coil $$B$$ moves upwards.

Define $$1$$ henry.
The magnetic field of a cylindrical magnet that has a pole-face diameter of 3.3 cm can be varied sinusoidally between 29.6 T and 30.0 T at a frequency of 15 Hz. (The current in a wire wrapped around a permanent magnet is varied to give this variation in the net field.)
At a radial distance of 1.6 cm, what is the amplitude of the electric field induced by the variation?
A long cylindrical solenoid with 100 turns/cm has a radius of 1.6 cm. Assume that the magnetic field it produces is parallel to its axis and is uniform in its interior. (a) What is its inductance per meter of length? (b) If the current changes at the rate of 13 A/s, what emf is induced per meter?
In the given diagram, a coil $$B$$ is connected to low voltage bulb $$L$$ and placed parallel to another coil $$A$$ as shown. Explain bulb lights if the coil $$B$$ moves upwards.
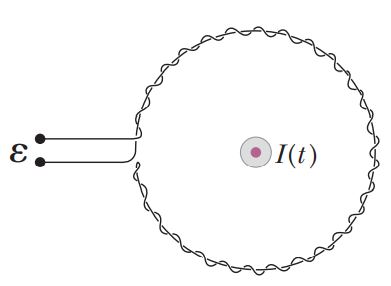
Consider an infinitely long wire carrying a current $$I(t)$$, with $$\dfrac {dI}{dt} = \lambda = constant$$.
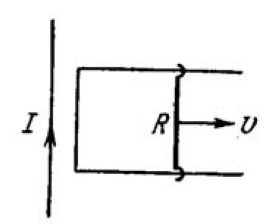
Find the current produced in the rectangular loop of wire $$ABCD$$ if its resistance is $$R$$ (Fig.).

State two factors on which the magnitude of induced e.m.f. depend.
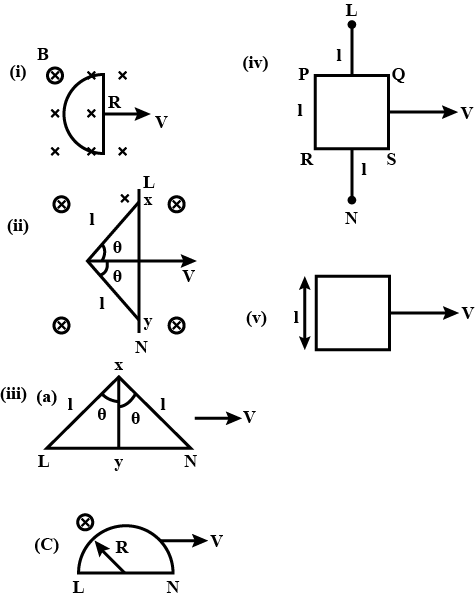
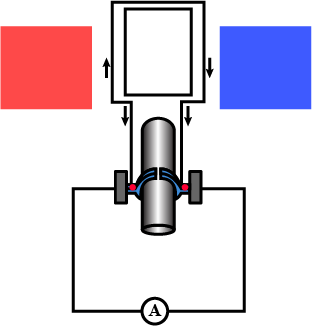
Identify the figures and explain their use.
On what factor do induced emf of a rotating coil (rectangular loop) in a magnetic field depend?
How would we wrap two coils so that maximum value of induced emf is obtained?
Define the coefficient of mutual inductance. Give its unit and dimensional formula.
A conducting wire is in North-South direction. It is freely dropped towards Earth. Is an emf induced between its ends? Why?
What is the value of self inductance, keeping the number of turns in the coil same and doubling the cross-sectional area?
A coil in a magnetic field is removed with:
(i) fast seed,
(ii) slow speed.
In which case, is the induced emf and work done more?
The self inductance of a coil is $$ 1 H $$. What do you understand?
A conducting wire of length $$ 20 cm $$ is moving normally in a magnetic field of $$ 5 \times 10^4 Wb/m. $$ If the conducting wire covers $$ 1m $$ distance in $$ 4s $$, then determine induced emf at the ends of the conducting wire.
A metallic rod of length $$ 2m $$ is moved (i) vertically ,(ii) horizontally with a speed of $$ 15 km/h $$ from West to East. If the horizontal component of Earth's magnetic field is $$ 0.5 \times 10^{-5} Wb/m^2 $$, calculate induced emf between the ends of the rod in each case.
A conducting rod of length $$ L $$ is rotated in a magnetic field $$ B $$ with an angular velocity $$ \omega $$, so that the rotational plane of rod is perpendicular to the magnetic field Determine the induced emf between the ends of the rod.
A coil is made from soft iron of length $$ 0.1 m $$and radius $$ 0.01m. $$ If the relative magnetisation of soft iron is $$ 1200 $$, then calculate the number of turns in the coil.
[Self inductance of coil is $$ 0.25 H $$].
The magnetic flux linked with the coil of $$ 50 turns $$ is $$ \phi_B=0.02 $$ cos $$ 100 \pi t $$ Wb. Determine:
(a)Mximum induced volatage.
(b)Induced emf at $$ t=0.01s. $$
(c) Induced electric current at $$ t=0.005 s. $$
(if external resistance is $$100 \Omega $$)
If a current of $$ 5 A $$ flowing in a primary coil nullifies in $$ 2 $$ min, then induced emf is $$ 25 kV $$. Calculate the coefficient of mutual inductance.
What is self induction? Explain the experiments of self induction and calculate self inductance for a solenoid.
A conducting rod of length $$ 1m $$ rotates with an angular velocity at the rate $$ 50 $$ revolutions per second normally to a magnetic field of $$ 0.001 T $$ from one end. Calculate the induced emf between the ends of the rod.
A solenoid of radius $$ 2 cm $$ and $$ 100 $$ turns has a length of $$ 50 cm $$. If vacuum is inside the solenoid, then calculate the self inductance of solenoid.
What do you mean by electromagnetic induction? State Faradays law of induction.
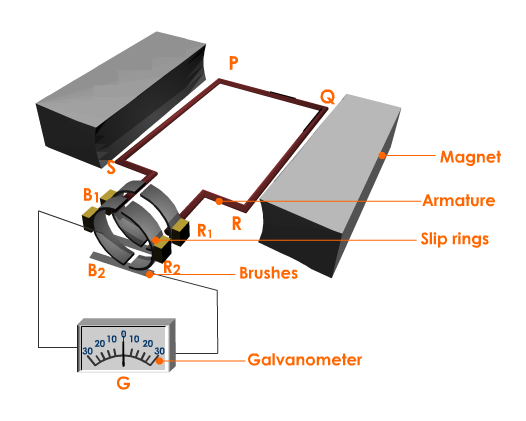
Current is induced when the armature of a generator rotates. Slip rings and brushes are the ways and means by which this current is brought to the outer circuit. Is the arrangement necessary if the magnet in generator is made to rotate ?
There is only one type of generator AC generator. Write down your responses about this statement.
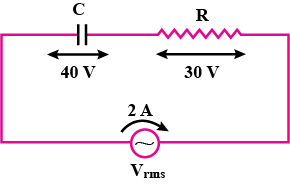
The diagram shown above is an arrangement for producing $$10\,V$$ AC using electromagnetic induction. Observe the diagram carefully and answer the question.
Find out the frequency by drawing a time emf graph if the armature completes $$10$$ cycles in $$5$$ seconds.
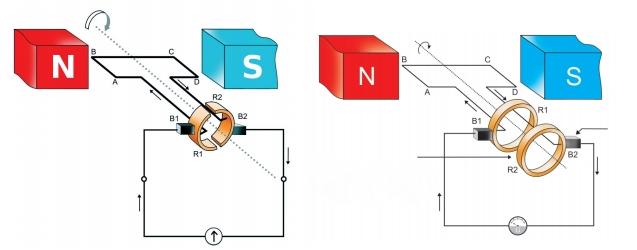
Write down the similarities and differences in the structure of an AC generator and a DC generator.
Parts of an AC generator are given below.
Field magnet, Armature, Slip rings, Brush.
a. Explain the position of these parts in an AC generator.
b. Write down the functions of any two.
When $$50 \,Hz$$ AC is used, how many times will the direction of current change in the circuit ?
Line diagrams of a generator are given.
What is the specialty of the electricity reaching the galvanometer if the armatures of both the generators are made to rotate ?
Maximum voltage produced in an AC generator completing $$60$$ cycles in $$30$$ seconds is $$250\,V.$$
What is the period of the armature.
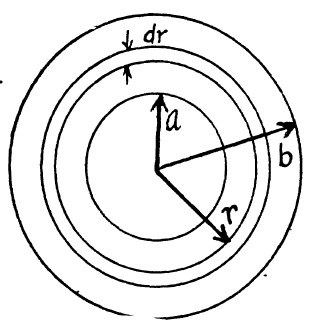
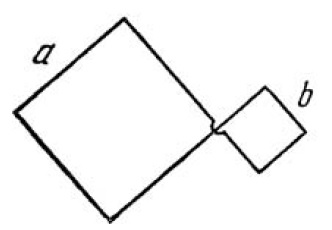
A plane loop shown in Fig. is shaped as two squares with sides $$a = 20\ cm$$ and $$b = 10\ cm$$ and is introduced into a uniform magnetic field at right angles to the loop's plane. The magnetic induction varies with time as $$B = B_{0}\sin \omega t$$, where $$B_{0} = 10\ mT$$ the current induced in the loop if its resistance per unit length is equal to $$\rho = 50\ m\Omega/ m$$. The inductance of the loop is to be neglected.
Lenz's Law (26)
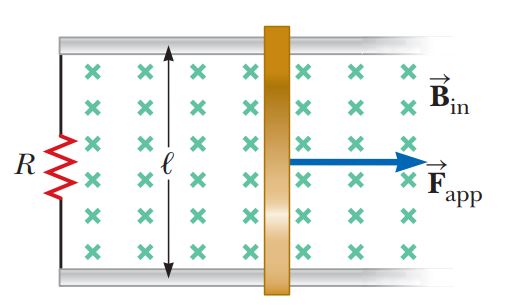
Consider the arrangement shown in Figure. Assume that $$R = 6.00 \,\Omega, \,$$, and a uniform $$2.50-T$$ magnetic field is directed into the page. At what speed should the bar be moved to produce a current of $$0.500 \,A$$ in the resistor?
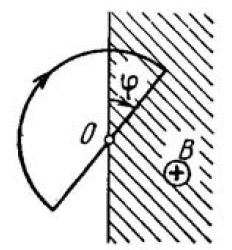
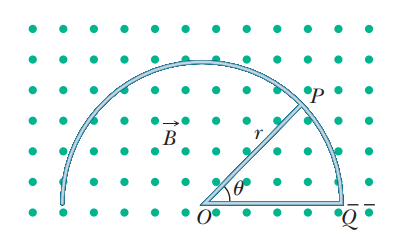
A wire loop enclosing a semi-circle of radius $$a$$ is located on the boundary of a uniform magnetic field of induction $$B$$ (Fig.). At the moment $$t = 0$$ the loop is set into rotation with a constant angular acceleration $$\beta$$ about an axis $$O$$ coinciding with a line of vector $$B$$ on the boundary. Find the emf induced in the loop as a function of time $$t$$. Draw the approximate plot of this function. The arrow in the figure shows the emf direction taken to be positive.
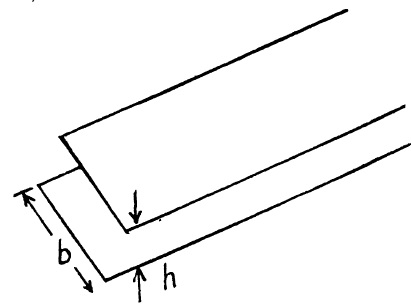
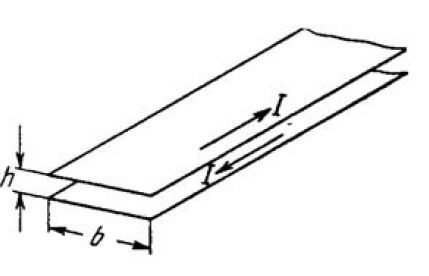
Calculate the inductance of a unit length of a double taped line (Fig.) if the tapes are separated by a distance $$h$$ which is considerably less than their width $$b$$, namely, $$b/h = 50$$.
A current $$I_{0} = 1.9\ A$$ flows in a long closed solenoid. The wire it is wound of is in a superconducting state. Find the current flowing in the solenoid when the length of the solenoid is increased by $$\eta = 5\%$$.
In a certain region of the inertial reference frame there is magnetic field with induction $$B$$ rotating with angular velocity $$\omega$$. Find $$\bigtriangledown \times E$$ in this region as a function of vectors $$\omega$$ and $$B$$.
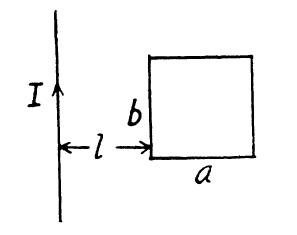
Calculate the mutual inductance of a long straight wire and a rectangular frame with sides $$a$$ and $$b$$. The frame and the wire lie in the same plane, with the side $$L$$ being closest to the wire, separated by a distance $$l$$ from it and oriented parallel to it.
If a rotor in a power generator completes $$3000$$ rotations in a minute.
Which type of AC is produced here, single-phase or three-phase ?
A non-relativistic point charge $$q$$ moves with a constant velocity $$v$$. Using the field transformation formulas, find the magnetic induction $$B$$ produced by this charge at the point whose position relative to the charge is determined by the radius vector $$r$$.
Maximum voltage produced in an AC generator completing $$60$$ cycles in $$30$$ seconds is $$250\,V.$$
How many cycles are completed in $$T / 2$$ seconds ?
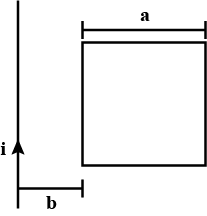
(a) Obtain an expression for the mutual inductance between a long straight wire and a square loop of side a as shown in Fig.
(b) Now assume that the straight wire carries a current of 50 A and the loop is moved to the right with a constant velocity, v = 10 m/s. Calculate the induced emf in the loop at the instant when x = 0.2 m. Take a = 0.1 m and assume that the loop has a large resistance.
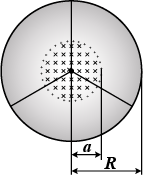
A line charge $$\lambda $$ per unit length is lodged uniformly onto the rim of a wheel of mass $$M$$ and radius $$R$$. The wheel has light non-conducting spokes and is free to rotate without friction about its axis as shown in above figure. A uniform magnetic field extends over a circular region within the rim. It is given by,
$$B\, =\, -B_0\, k\, \quad\, (r\, \leq \, a;\, a\, <\, R)$$, or $$ B\,=\,0$$ (otherwise).
What is the angular velocity of the wheel after the field is suddenly switched off?
It is desired to measure the magnitude of field between the poles of a powerful loud speaker magnet. A small flat search coil of area $$2\, cm^2$$ with 25 closely wound turns, is positioned normal to the field direction, and then quickly snatched out of the field region. Equivalently, one can give it a quick $$90^{\circ}$$ turn to bring its plane parallel to the field direction). The total charge flown in the coil (measured by a ballistic galvanometer connected to coil) is 7.5 mC. The combined resistance of the coil and the galvanometer is 0.50 $$\Omega$$. Estimate the field strength of magnet.
Explain in detail the principle, construction and working of a single phase AC generator.
What is self inductance? Establish expression for self inductance of a long solenoid.
Figure shows a square frame of wire having a total resistance r placed coplaner with a long, straight wire. The wire carries a current i given by $$i = {i_0}\sin \omega t.$$ . Find (a) the flux of the magnetic field through the square frame; (b) the emf induced in the frame and (c) the heat developed in the frame in the time interval 0 to $${{20\pi } \over \omega }$$ .
Prove theoretically, the relation between e.m.f. induced and rate of change of magnetic flux in a coil moving in a uniform magnetic field.
Define self-inductance of a coil. (a) Obtain an expression for the energy stored in a solenoid of self-inductance $$'L'$$ when the current though it grows from zero to $$'I'$$.
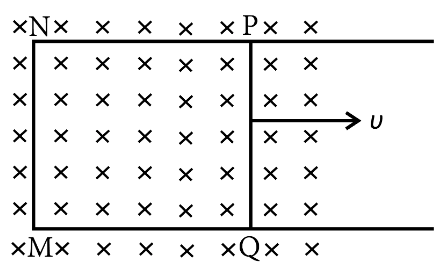
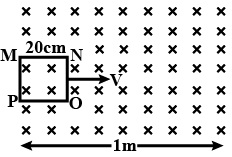
(b) A square loop MNOP of side 20 cm is placed horizontally in a uniform magnetic field acting vertically downwards as shown in the figure. The loop is pulled with a constant velocity of 20 cm $$s^{-1}$$ till it goes out of the field.
(i) Depict the direction of the induced current in the loop as it goes out of the field. For how long would the current in the loop persist?
(ii) Plot a graph showing the variation of magnetic flux and induced emf as a function of time.
(b) A square loop MNOP of side 20 cm is placed horizontally in a uniform magnetic field acting vertically downwards as shown in the figure. The loop is pulled with a constant velocity of 20 cm $$s^{-1}$$ till it goes out of the field.
(i) Depict the direction of the induced current in the loop as it goes out of the field. For how long would the current in the loop persist?
(ii) Plot a graph showing the variation of magnetic flux and induced emf as a function of time.
A closed coil having 100 turns is rotated in a uniform magnetic field $$B=4.0\ \times { 10 }^{ -4 }T$$ about a diameter which is perpendicular to the field. The angular velocity of rotation is 300 revolution per minute. The area of the coil is $$25\ { cm }^{ 2 }$$ and its resistance is $$4.0\ \Omega$$. Find (a) the average emf developed in half a turn from a position where the coil is perpendicular to the magnetic field, (b)the average emf in full turn and (c) the net charge displaced in part (a).
In a motor, a rotor is fitted with the armature that has current of 10 A. The rotor rotates with angular speed of 3 rad/s.Magnetic field of magnitude 2 T varies in direction is such a way that it is always perpendicular to the loop area. If the rotor coil has N number of turns and area of each loop is $$0.45 m^2$$ then find the value N. Given that motor consumes 2106 W power and there are no losses.
Deduce an equation $$U=\cfrac { 1 }{ 2 } L{ I }^{ 2 }$$ for an inductor.
An infinitesimally small bat magnet $$\bar M$$ is pointing and moving with the speed $$v$$ in the $$\bar x-$$direction. A small closed circular conducting loop of radius $$a$$ and negligible self inductance lies in the $$y-z$$ plane with its centre at $$x=0$$ and its axes coinciding with the $$x-$$axis. Find the force opposing the motion of the magnet, if the resistance of the loop is $$R$$. Assume that the distance $$x$$ of the magnet from the centre of the loop is much greater than $$a$$.
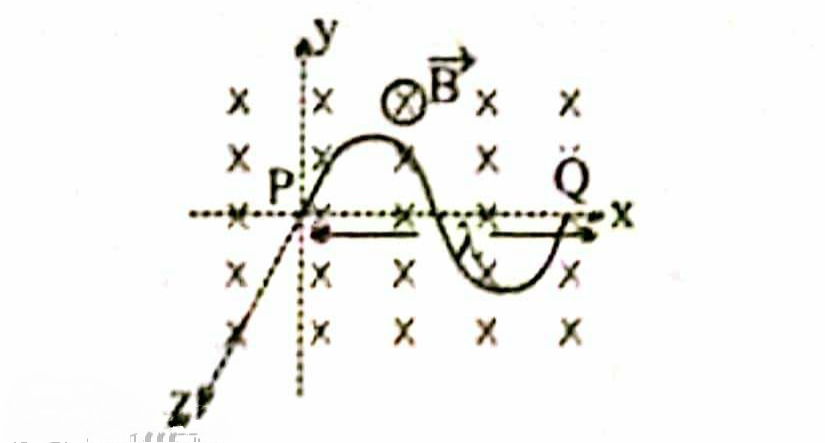
A wire forming one cycle of sine curve is moved in $$x-y$$ plane with velocity $$\vec V={V}_{x}\hat i+{V}_{y}\hat j$$. There exist a magnetic field $$\vec B=-{B}_{0}\hat k$$. Find the motional emf developed across the ends $$PQ$$ of wire.
The magnetic field in a region is given by $$\overrightarrow { B } =\cfrac { { B }_{ 0 } }{ L } xk$$, where $$L$$ is a fixed length. A conducting rod of length $$L$$ lies along the X-axis between the origin and the point $$(L,0,0)$$. If the rod moves with a velocity $$\overrightarrow { v } ={ v }_{ 0 }\hat { j } $$, find the emf induced between the ends of the rod
Crosses represent uniform magnetic field directed into the paper. A conductor XY moves in the field towards right side. Find the direction of induced current in the conductor. Name the rule you applied. What will be the direction of current if the direction of field and the direction of motion of the conductor both are reversed?

The figure shows a small circular coil of area A suspended from a point O by a string of length l in a uniform magnetic induction B in the horizontal direction. If the coil is set into oscillations likes simple pendulum by displacing it a small angle $${\theta _0}$$ as shown, find emf induced in the coil as a function of time. Assume the plane of the coil is always in the plane of string.

A conducting circular loop is placed in a uniform magnetic field $$B=0.020T$$ with its plane perpendicular to the field. Somehow, the radius of the loop starts shrinking at a constant rate of $$1 mm/s.$$ Find the induced current in the loop at an instant when the radius is $$2 cm.$$
Find the induced emf about ends of the rod in each case.

Consider the situation shown in the figure. The wire PQ has mass m, resistance r and can slide on the smooth horizontal parallel rails of separated by a distance $$l$$. The resistance of the rails is negligible . A uniform magnetic field B exist in the rectangular region and a resistance R connects the rails outside the field region. At t=0, the wire PQ is pushed towards right with a speed of $$v_{0}$$. Find
(a) the current in the loop in an instant when the speed of the wire PQ is v.
(b) the acceleration of the wire at this instant
(c) Velocity v as a function
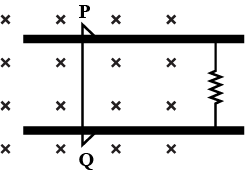
A coil has an inductance of 5H and resistance $$20\Omega$$ . An emf of $$100$$v is applied to it. What is the energy stored in the magnetic field, when the current has reached its final value .
A coil of resistance $$40\Omega$$ is connected across a $$4.0$$V battery. $$0.10$$s after the battery is connected, the current in the coil is $$63$$mA. Find the inductance of the coil.
Two protons are projected simultaneously from a fixed point with the same velocity v into a region, where there exists a uniform magnetic field. The magnetic field strength at B and it is prependicular to the initial direction of v. One proton starts at time t=o and another proton at t=$$\frac { \pi m }{ 2qB } $$. The separation between then at time $$\frac { \pi m }{ 2qB } $$ (where, m and q are the mass and charge of proton), will be approximately.
The closed loop $$(P Q R S)$$ of wire is moved out of a uniform magnetic field at right angles to the plane of the paper as shown. Predict the direction of induced current in the loop.
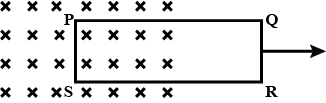
Figure shows a smooth pair of thick metallic rails connected across a battery of emf $$\varepsilon $$ having a negligible internal resistance. A wire $$ab$$ of length $$l$$ and resistance $$r$$ can slide smoothly on the rails. The entire system lies in a horizontal plane and is immersed in a uniform vertical magnetic field $$B$$. At an instant $$t$$, the wire is given a small velocity $$v$$ towards right. (A) Find the current in it at this instant. What is the direction of the current? (b) What is the force acting on the wire at this instant? (c) Show that after some time the wire $$ab$$ will slide with a constant velocity. Find this velocity.
Find the mutual inductance between the circular coil of radius $$a^{'}$$ and the loop of radius $$ a $$ as shown in figure when the slider on the rheostat is moved. The total resistance of rheostat is R and the distance between the center of two coils is x.
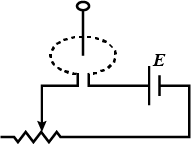
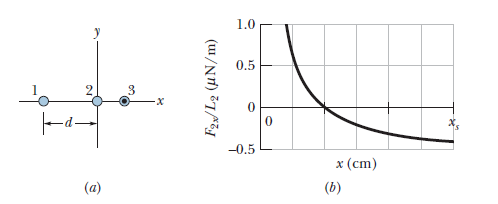
Figure (a) shows, in cross section, three current-carrying wires that are long, straight, and parallel to one another. Wires 1 and 2 are fixed in place on an $$x$$ axis, with separation d.Wire 1 has a current of 0.750 A, but the direction of the current is not given. Wire 3, with a current of 0.250 A out of the page, can be moved along the $$x$$ axis to the right of wireAs wire 3 is moved, the magnitude of the net magnetic force $$\vec{F_{2}}$$ on wire 2 due to the currents in wires 1 and 3 changes. The $$x$$ component of that force is $$F_{2x}$$ and the value per unit length of wire 2 is $$F_{2x}/L_{2}$$. Figure (b) gives $$F_{2x}/L_{2}$$ versus the position $$x$$ of wireThe plot has an asymptote $$F_{2x}/L_{2}=-0.627\hspace{0.05cm} \mu N/m$$ as $$x \rightarrow \infty$$. The horizontal scale is set by $$x_{s}=12\hspace{0.05cm}cm$$. cm. What are the (a) size and (b) direction (into or out of the page) of the current in wire 2?
An ac generator has emf $$\xi=\xi _{m}\sin\left ( \omega _{d}t-\pi/4 \right )$$, where $$\xi _{m}=30.0V$$ and $$\omega _{d}=350rad/s$$. The current produced in a connected circuit is $$i\left ( t \right )=I\sin \left ( \omega _{d}t-3\pi /4 \right )$$, where $$I=620 mA$$. At what time after $$t=0$$ does (a) the generator emf first reach a maximum and (b) the current first reach a maximum? (c) The circuit contains a single element other than the generator. Is it a capacitor, an inductor, or a resistor? Justify your answer. (d) What is the value of the capacitance, inductance, or resistance, as the case may be?
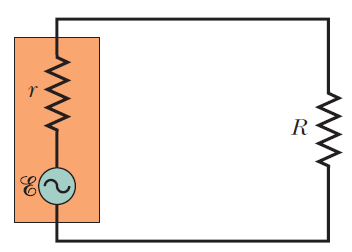
For above figure, show that the average rate at which energy is dissipated in resistance $$R$$ is a maximum when $$R$$ is equal to the internal resistance $$r$$ of the $$ac$$ generator. (we tacitly assumed that $$r=0$$.)
An ac generator with emf amplitude $$\xi _{m}=220V$$ and operating at frequency $$400Hz$$ causes oscillations in a series RLC circuit having $$R=200\Omega$$, $$L=150 mH$$ and $$C=24.0\mu F$$. Find (a) the capacitive reactance $$X_{C}$$, (b) the impedance $$Z$$ and (c) the current amplitude $$I$$. A second capacitor of the same capacitance is then connected in series with the other components. Determine whether the values of (d) $$X_{C}$$, (e) $$Z$$ and (f) $$I$$ increase, decrease or remain the same.
A long vertical wire carries an unknown current. Coaxial with the wire is a long, thin, cylindrical conducting surface that carries a current of $$30 mA$$ upward. The cylindrical surface has a radius of $$3.0 mm$$. If the magnitude of the magnetic field at a point $$5.0 mm$$ from the wire is $$1.0\mu T$$, what are the (a) size and (b) direction of the current in the wire?
Figure shows a circuit having a coil of resistance $$R=2.5 \Omega$$ and inductance 'L' connected to a conducting rod PQ which can slide on a perfectly conducting circular ring of radius 10 cm with its centre at 'P'.
Assume that friction and gravity are absent and a constant uniform magnetic field of 5 T exists as shown in figure. At t =0,the circuit is switched on and simultaneously a time varying external torque is applied on the rod so that it rotates about 'P' with a constant angular velocity 40 rad/s.Find the magnitude of this torque ( in 'P') when current reaches half of its maximum value.Neglect the self inductance of the loop formed by the circuit.
(a) In an $$RLC$$ circuit, can the amplitude of the voltage across an inductor be greater than the amplitude of the generator emf? (b) Consider an $$RLC$$ circuit with emf amplitude $$\xi _{m}=10V$$, resistance $$R=10\Omega$$, inductance $$L=1.0 H$$ and capacitance $$C=1.0\mu F$$. Find the amplitude of the voltage across the inductor at resonance.
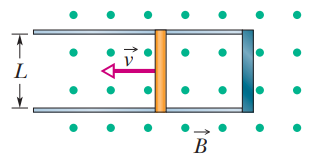
In Figure , a metal rod is forced to move with constant velocity $$\overrightarrow {v}$$ along two parallel metal rails, connected with a strip of metal at one end. A magnetic field of magnitude B = 0.350 T points out of the page.
(a) If the rails are separated by L = 25.0 cm and the speed of the rod is 55.0 cm/s, what emf is generated?
(b) If the rod has a resistance of $$18.0\Omega $$ and the rails and connector have negligible resistance, what is the current in the rod?
(c) At what rate is energy being transferred to thermal energy?
Faraday's Law of Induction (10)
Scientific work is currently under way to determine whether weak oscillating magnetic fields can affect human health. For example, one study found that drivers of trains had a higher incidence of blood cancer than other railway workers, possibly due to long exposure to mechanical devices in the train engine cab. Consider a magnetic field of magnitude $$1.00 \times 10^{-3} \,T$$, oscillating sinusoidally at $$60.0 \,Hz$$. If the diameter of a red blood cell is $$8.00 \,mm$$, determine the maximum emf that can be generated around the perimeter of a cell in this field.
An $$ac$$ generator produces emf $$\xi =\xi _{m}\sin \left ( \omega _{d}t-\pi /4 \right )$$, where $$\xi _{m}=30.0V$$ and $$\omega _{d}=350rad/s$$. The current in the circuit attached to the generator is $$i\left ( t \right )=I\sin \left ( \omega _{d}t+\pi /4 \right )$$, where $$I=620 mA$$. (a) At what time after $$t=0$$ does the generator emf first reach a maximum? (b) At what time after $$t=0$$ does the current first reach a maximum? (c) The circuit contains a single element other than the generator. Is it a capacitor, an inductor, or a resistor? Justify your answer. (d) What is the value of the capacitance, inductance or resistance as the case may be?
The figure shows a loop
model (loop L) for a diamagnetic
material. (a) Sketch the magnetic
field lines within and about the material due to the bar magnet. What is the direction of (b) the loops net magnetic dipole moment $$\vec \mu$$,
(c) the conventional current i in the loop (clockwise or counterclockwise in the figure), and (d) the magnetic force on the loop?
A rectangular loop and a circular loop are moving out of a uniform magnetic field region to a field free region with a constant velocity. In which loop do you the induced emf to be a constant during the passage out of the field region? The field to the loop.

Answer the following question
A conduction rod of length $$'I'$$ with one end pivoted, is rotated with a uniform angular speed $$'\omega '$$ in a vertical plane, normal to a uniform magnetic field $$'B'$$. Deduce an expression for the emf induced in this rod.
If resistance of rod is $$R$$, what is the current induced in it?
A wheel with $$8$$ metallic spokes each $$50\ cm$$ long is rotated with a speed of $$12\ rev/min$$ in a plane normal to the horizontal component of the Earth's magnetic field. The Earth's magnetic field at the plane is $$0.4\ G$$ and the angle of dip is $$60^{o}$$. Calculate the emf induced between the axle and the rim of the wheel.
How will the value of emf be affected if the number of spokes were increasde?
In Figure , a 120- turn coil of radius 1.8 cm and resistance $$5.3\Omega $$ is coaxial with a solenoid of 220 turns/cm and diameter 3.2 cm. The
solenoid current drops from 1.5 A to zero in time interval $$\Delta t=25ms$$. What current is induced in the coil during $$\Delta
$$?
In above figure, a three-phase generator G produces electrical power that is transmitted by means of three wires. The electric potentials (each relative to a common reference level) are $$V_{1}=A\sin \omega _{d}t$$ for wire $$1$$, $$V_{2}=A\sin \left ( \omega _{d}t-120^{0}\right )$$ for wire $$2$$, and $$V_{3}=A\sin \left ( \omega _{d}t-240^{0}\right )$$ for wire $$3$$. Some types of industrial equipment (for example, motors) have three terminals and are designed to be connected directly to these three wires. To use a more conventional two-terminal device (for example, a lightbulb), one connects it to any two of the three wires. Show that the potential difference between any two of the wires (a) oscillates sinusoidally with angular frequency $$\omega _{d}$$ and (b) has an amplitude of $$A\sqrt{3}$$ .

Answer the following questions
A rod of length $$I$$ is moved horizontally with a uniform velocity $$'v'$$ in a direction perpendicular to its length through a region in which a uniform magnetic field is acting vertically downward. Derive the expression for the emf induced across the ends of the rod.

The switch in Figure is closed on a at time t = 0.
What is the ratio $$\mathscr{E}_L/\mathscr{E}$$ of the inductor’s self-induced emf to the battery’s emf (a) just after t = 0 and
(b) at $$t = 2.00\tau
_L$$? (c) At what multiple of $$\tau
_L$$ will $$\mathscr{E}_L/\mathscr{E}=0.500$$?
Five long wires A,B,C,D and E each carrying current I are arranged to form edges of a pentagonal prism as shown in Fig.4.6 Each carries out of the plane of paper.
(a) what will be magnetic induction at a point on the axis O Axis is at a distance R from each wire.
(b) What will be the field if current in one of the wires (say A) is switched off
(c) What if current in one of the wire (say) A is reversed
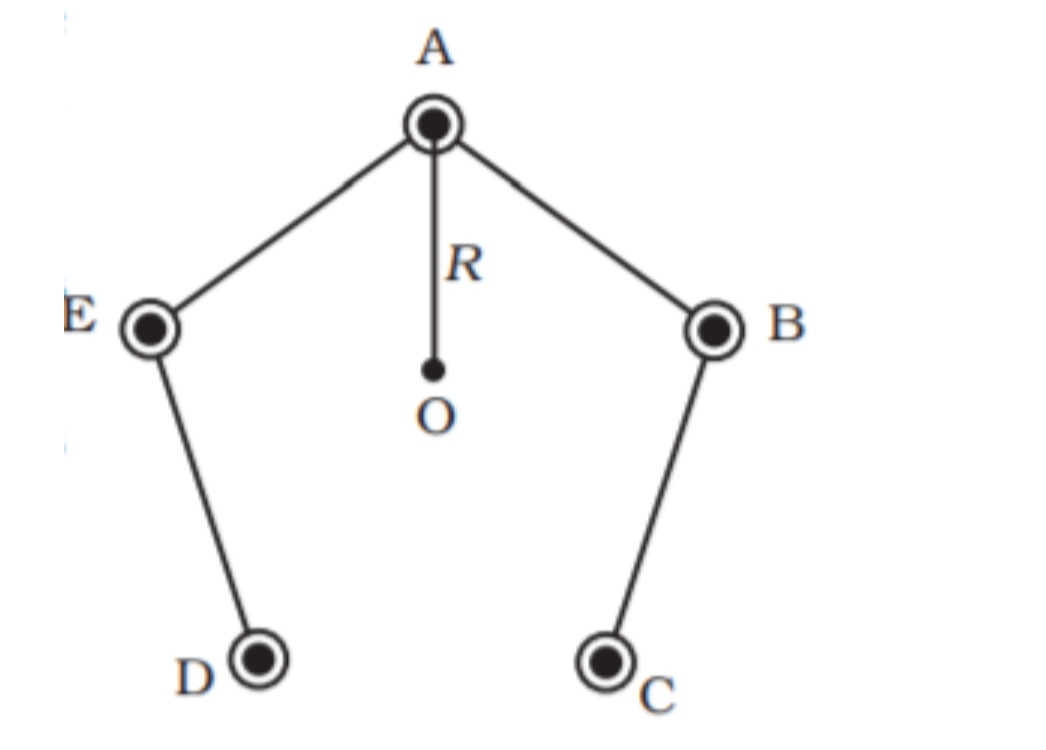
Figure shows a wire that has been bent into a circular arc of radius r = 24.0 cm, centered at O. A straight wire OP can be rotated about O and makes sliding contact with the arc at P. Another straight wire OQ completes the conducting loop. The three wires have cross-sectional area $$1.20mm^2$$ and resistivity $$1.70 \times 10^{-8} \Omega \cdot m$$, and the apparatus lies in a uniform magnetic field of magnitude B = 0.150 T directed out of the figure.Wire OP begins from rest at angle $$\theta =0$$ and has constant angular acceleration of $$12rad/s^2$$. As functions of $$\theta $$ (in rad), find (a) the loops resistance and (b) the magnetic flux through the loop. (c) For what $$\theta $$ is the induced current maximum and (d) what is that maximum?
A uniform magnetic field $$\overrightarrow {B}$$ is perpendicular to the plane of a circular wire loop of radius r. The magnitude of the field varies with time according to $$B=B_0e^{-t/\tau }$$, where $$B_0$$ and $$\tau$$ are constants. Find an expression for the emf in the loop as a function of time.
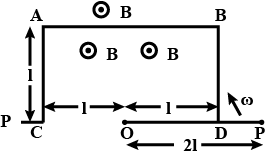
$$ODBAC$$ is a fixed rectangular conductor of negligible resistance $$(CO$$ is not connected) and $$OP$$ is a conductor which rotates clockwise with an angular velocity $$\omega$$ (Fig.). The entire system is in a uniform magnetic field $$B$$ whose direction is along the normal to the surface of the rectangular conductor $$ABDC$$. The conductor $$OP$$ is in electric contact with $$ABDC$$. The rotating conductor has a resistance of $$\lambda$$ per unit length. Find the current in the rotating conductor, as it rotates by $$180^{\circ}$$.
A long solenoid $$'S'$$ has $$n$$ turns per meter, with diameter $$'a'$$. At the centre of this coil we place a smaller coil of $$'N'$$ turns and diameter $$'b'$$ (where $$b < a$$). If the current in the solenoid increases linearly, with time, what is the induced emf appearing in the smaller coil. Plot graph showing nature of variation in emf, if current varies as a function of $$mt^{2} + c$$.
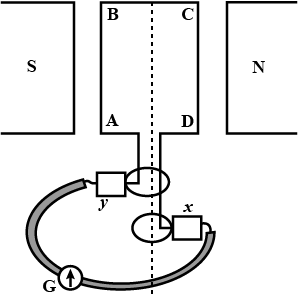
(i)Two circular coils P and Q are kept close to each other, of which coil P carries a current. If coil P is moved towards Q, will some current be induced in coil Q? Give reason for your answer and name the phenomenon involved.
(ii) What happens if coil P is moved away from Q?
(iii) State any two methods of inducing current in a coil.
Two solenoids are part of the spark coil of an automobile. When the current in one solenoid falls from 6.0 A to zero in 2.5 ms, an emf of 30 kV is induced in the other solenoid. What is the mutual inductance M of the solenoids?
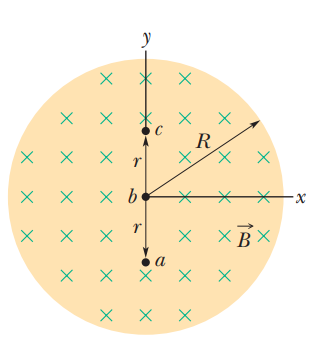
Figure shows a uniform magnetic field $$\overrightarrow {B}$$ confined to a cylindrical volume of radius R. The magnitude of $$\overrightarrow {B}$$ is decreasing at a constant rate of 10 mT/s. In
unit-vector notation, what is the initial acceleration of an electron released at (a) point a (radial distance r = 5.0 cm), (b) point b (r = 0), and (c) point c (r = 5.0 cm)?
In Figure a, a circular loop of wire is concentric with a solenoid and lies in a plane perpendicular to the solenoid’s central axis. The loop has radius 6.00 cm. The solenoid has radius 2.00 cm, consists of 8000 turns/m, and has a current $$i_{sol}$$ varying with time t as given in Figure b, where the vertical axis scale is set by $$i_s=1.00A$$ and the horizontal axis scale is set by $$t_s=2.0s$$. Figure c shows, as a function of time, the energy $$E_{th}$$ that is transferred to thermal energy of the loop; the vertical axis scale is set by $$E_s=100.0nJ$$.What is the loop’s resistance?
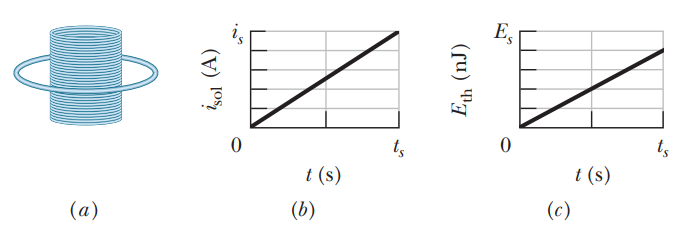
Describe the principle , construction and working of a single phase A.C. generator.
A $$\Pi-shaped$$ conductor is located in a uniform magnetic field perpendicular to the plane of the conductor and varying with time at the rate $$\overset {\cdot}{B} = 0.10\ T/s$$. A conducting connector starts moving with an acceleration $$w = 10\ cm/s^{2}$$ along the parallel bars of the conductor. The length of the connector is equal to $$l = 20\ cm$$. Find the emf induced in the loop $$t = 2.0\ s$$ after the beginning of the motion, if at the moment $$t = 0$$ the loop area and the magnetic induction are equal to zero. The inductance of the loop is to be neglected.
In a Faraday disc dynamo, a metal disc of radius $$R$$ rotates with an angular velocity $$\omega$$ about an axis perpendicular to the plane of the disc and passing through its center. The disc is placed in a magnetic field $$B$$ acting perpendicular to the plane of the disc. Determine the induced emf between the rim and the axis of the disc.
A long straight wire carrying a current $$I$$ and a $$\Pi-shaped$$ conductor with sliding connector are located in the same plane as shown in Fig. The connection of length $$l$$ and resistance $$R$$ slides to the right with a constant velocity $$v$$. Find the current induced in the loop as a function of separation $$r$$ between the connector and the straight wire. The resistance of the $$\Pi-shaped$$ conductor and the self-inductance of the loop are assumed to be negligible.
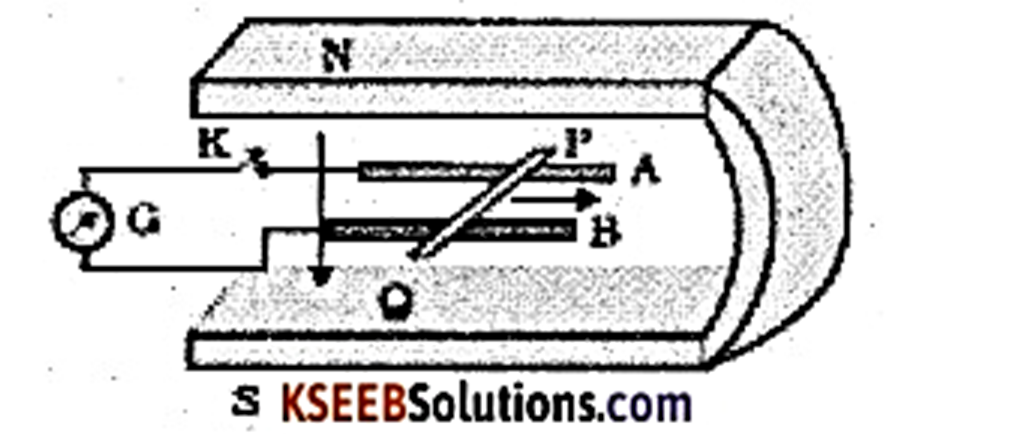
Above figure shows a metal rod $$PQ$$ resting on the smooth rails $$AB$$ and positioned between the poles of a permenent magnet. The rails, the rod, and the magnetic filed are in three mutual perpendicular directions. A galvanometer $$G$$ connects the rail through a switch $$K$$. Length of the rod is $$15cm$$, $$B=0.50T$$, resistanbce of the closed-loop containing the rod is $$9.0$$. Assume the filed to be uniform.
(a) Suppose $$K$$ is open and the rod is moved with a speed of $$12cm$$ $$s^{-1}$$ in the direction shown. Give the polarity and magnitude of the induced emf.
(b) Is there an excess charge build up at the ends of the rods when $$K$$ is open? What is $$K$$ is closed?
(c) With $$K$$ open and the rod moving uniformly, there is no net force on the electrons in the rod $$PQ$$ even through they do experience magnetic force due to the motion of the rod. Explain.
(d) What is the retarding force on the rod when $$K$$ is closed?
(e) How much power is required (by an external agent) to keep the rod moving at the same speed ($$=12cm$$ $$s^{-1}$$) when $$K$$ is closed? How much power is required when $$K$$ is open?
(f) How much power is dissipated as heat in the closed-circuit? What is the source of this power?
(g) What is the induced emf in the moving rod if the magnetic field is parallel to the rails instead of being perpendicular?
A long straight solenoid of cross-sectional diameter $$d = 5\ cm$$ and with $$n = 20$$ turns per one cm of its length has a round turn of copper wire of cross-sectional area $$S = 1.0\ mm^{2}$$ tightly put on its winding. Find the current flowing in the turn if the current in the solenoid winding is increased with a constant velocity $$I = 100\ A/s$$. The inductance of the turn is to be neglected.
A current $$I$$ flows along a thin wire shaped as a regular polygon with $$n$$ sides which can be inscribed into a circle of radius $$R$$. Find the magnetic induction at the centre of the polygon. Analyse the obtained expression at $$n\rightarrow \infty$$.
In the middle of a long solenoid there is a coaxial ring of square cross-section, made of conducting material with resistivity $$\rho$$. The thickness of the ring is equal to $$h$$, its inside and outside radii are equal to $$a$$ and $$b$$ respectively. Find the current induced in the ring if the magnetic induction produced by the solenoid varies with time as $$B = \beta t$$ where $$\beta$$ is a constant. The inductance of the ring is to be neglected.
Faraday's Law of Induction (7)
To monitor the breathing of a hospital patient, a thin belt is girded around the patient's chest. The belt is a $$200$$-turn coil. When the patient inhales, the area encircled by the coil increases by $$39.0 \,cm^2$$. The magnitude of the Earth's magnetic field is $$50.0 \mu T$$ and makes an angle of $$28.0^{o}$$ with the plane of the coil. Assuming a patient takes $$1.80 \,s$$ to inhale, find the average inducede mf in the coil during this time interval.
Conceptual Questions(5)
A circular loop of wire is located in a uniform and constant magnetic field. Describe how an emf can be induced in the loop in this situation.
Faraday's Law of Induction (8)
A strong electromagnet produces a uniform magnetic field of $$1.60 \,T$$ over a cross-sectional area of $$0.200 m^2$$. A coil having $$200$$ turns and a total resistance of $$20.0 \Omega$$ is placed around the electromagnet. The current in the electromagnet is then smoothly reduced until it reaches zero in $$20.0 \,ms$$. What is the current induced in the coil?
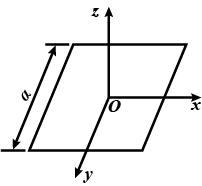
A quadratic undeformabe superconducting loop of mass $$m$$ and side $$a$$ lies in a horizontal plane in a nonuniform magnetic field whose induction varies in space according to the law $${B}_{x}=-\alpha x$$, $${B}_{y}=0$$, $${B}_{z}=\alpha z+{B}_{0}$$ (Figure). The inductance of the loop is $$L$$. At the initial moment, the centre of the loop coincides with the origin $$O$$, and its sides are parallel to the $$x-$$ and $$y-$$ axes. The current in the loop is zero, and it is released.
How will it move and where will it be in time $$t$$ after the beginning of motion?
Faraday's Law of Induction (1)
A flat loop of wire consisting of a single turn of cross sectional area $$8.00 \,cm^2$$ is perpendicular to a magnetic field that increases uniformly in magnitude from $$0.500 \,T$$ to $$2.50 \,T$$ in $$1.00 \,s$$. What is the resulting induced current if the loop has a resistance of $$2.00 \,\Omega$$?
A direct current flowing through the winding of a long cylindrical solenoid of radius $$R$$ produces in it a uniform magnetic field of induction $$B$$. An electron flies into the solenoid along the radius between its turns (at right angles to the solenoid axis) at a velocity $$v$$ (figure). After a certain time, the electron deflected by the magnetic field leaves the solenoid.
Determine the time $$t$$ during which the electron moves in the solenoid.
Magnetron is a device consisting of a filament of radius $$a$$ and a coaxial cylindrical anode of radius $$b$$ which are located in a uniform magnetic field parallel to the filament. An accelerating potential difference $$V$$ is applied between the filament and the anode. Find the value of magnetic induction at which the electrons leaving the filament with zero velocity reach the anode.
Faraday's Law of Induction (18)
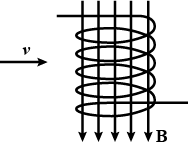
When a wire carries an AC current with a known frequency, you can use a Rogowski coil to determine the amplitude $$I_{max}$$ of the current without disconnecting the wire to shunt the current through a meter. The Rogowski coil, shown in Figure, simply clips around the wire. It consists of a toroidal conductor wrapped around a circular return cord. Let $$n$$ represent the number of turns in the toroid per unit distance along it. Let A represent the cross-sectional area of the toroid. Let $$I(t) = I_{max} \sin \omega t$$ represent the current to be measured.
(a) Show that the amplitude of the emf induced in the Rogowski coil is $$\varepsilon_{max}= \mu_0 n A\omega I_{max}$$.
(b) Explain why the wire carrying the unknown current need not be at the center of the Rogowski coil and why the coil will not respond to nearby currents that it does not enclose.
Lenz's Law (31)
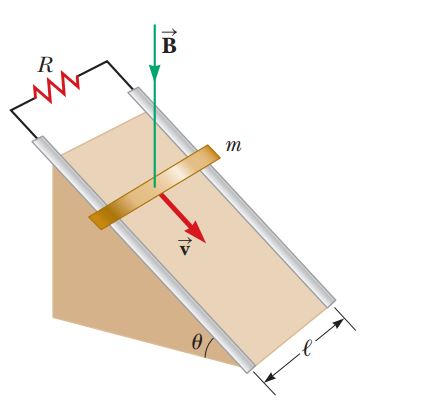
Review. Figure shows a bar of mass $$m =0.200 \,kg$$ that can slide without friction on a pair of rails separated by a distance $$l= 1.20 \,m$$ and located on an inclined plane that makes an angle $$\theta = 25.0^{o}$$ with respect to the ground. The resistance of the resistor is $$R = 1.00 \Omega$$ and a uniform magnetic field of magnitude $$B = 0.500 \,T$$ is directed downward, perpendicular to the ground, over the entire region through which the bar moves. With what constant speed $$v$$ does the bar slide along the rails?
Lenz's Law (21)
A helicopter (Figure) has blades of length $$3.00 \,m$$, extending out from a central hub and rotating at $$2.00 \,rev/s$$. If the vertical component of the Earths magnetic field is $$50.0 \mu T$$, what is the emf induced between the blade tip and the center hub?

Class 12 Medical Physics Extra Questions
- Alternating Current Extra Questions
- Atoms Extra Questions
- Current Electricity Extra Questions
- Dual Nature Of Radiation And Matter Extra Questions
- Electric Charges And Fields Extra Questions
- Electromagnetic Induction Extra Questions
- Electromagnetic Waves Extra Questions
- Electrostatic Potential And Capacitance Extra Questions
- Magnetism And Matter Extra Questions
- Moving Charges And Magnetism Extra Questions
- Nuclei Extra Questions
- Ray Optics And Optical Instruments Extra Questions
- Semiconductor Electronics: Materials, Devices And Simple Circuits Extra Questions
- Wave Optics Extra Questions