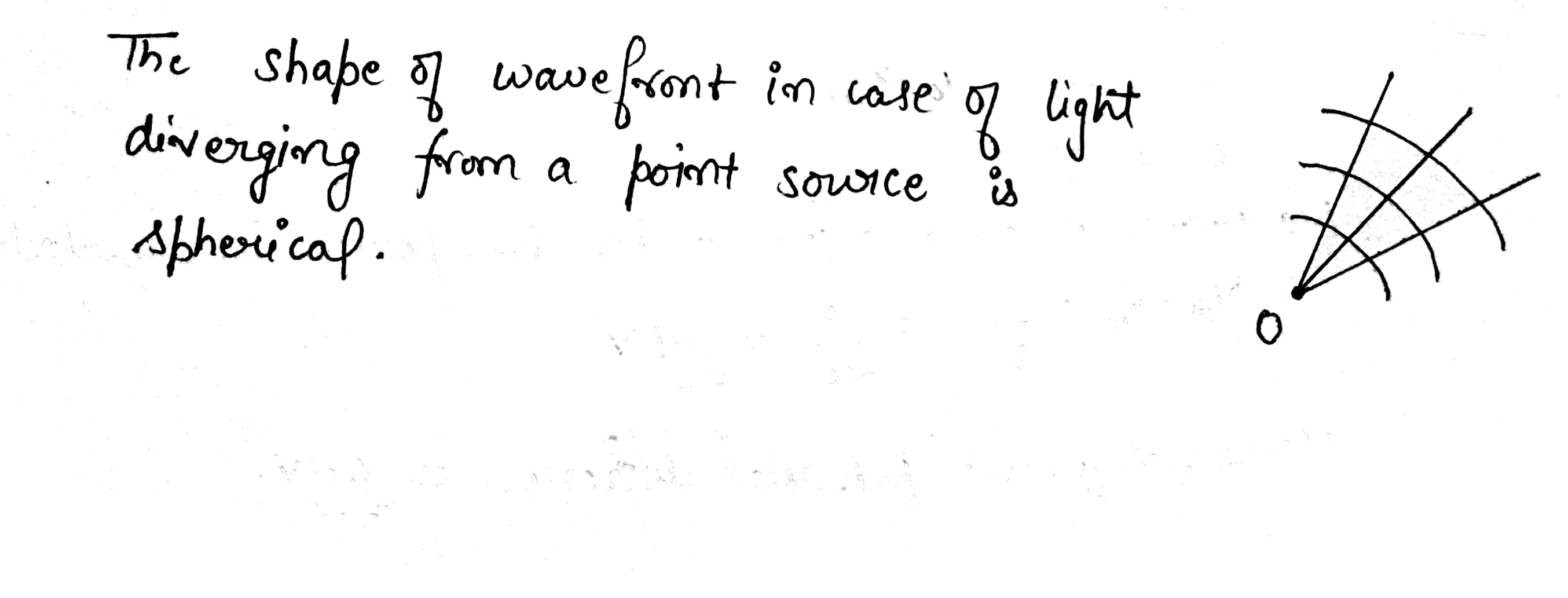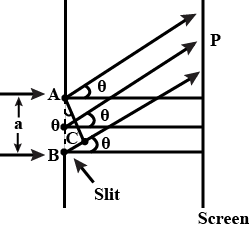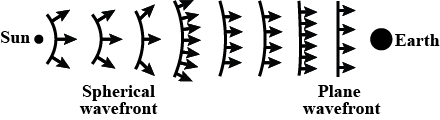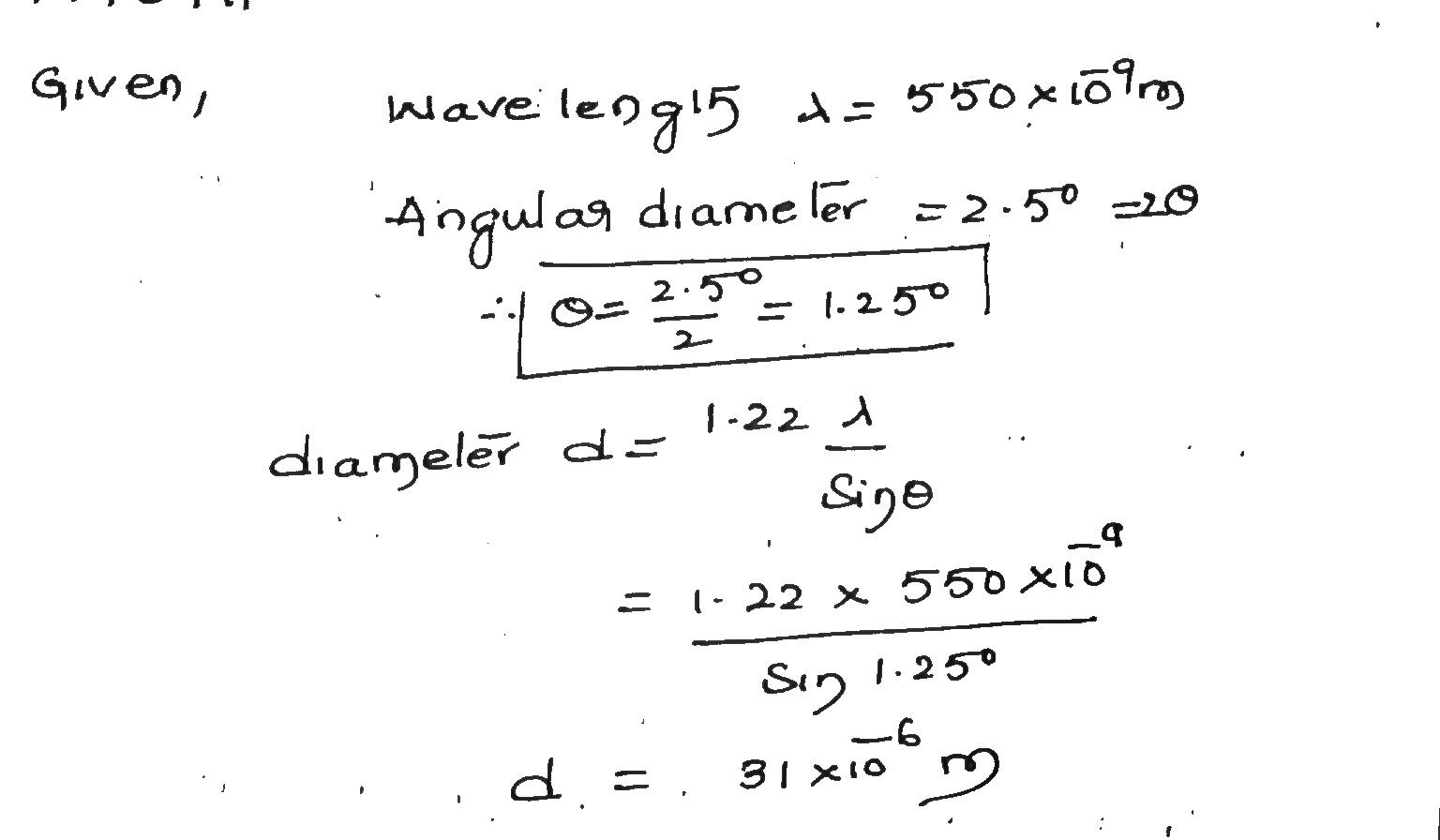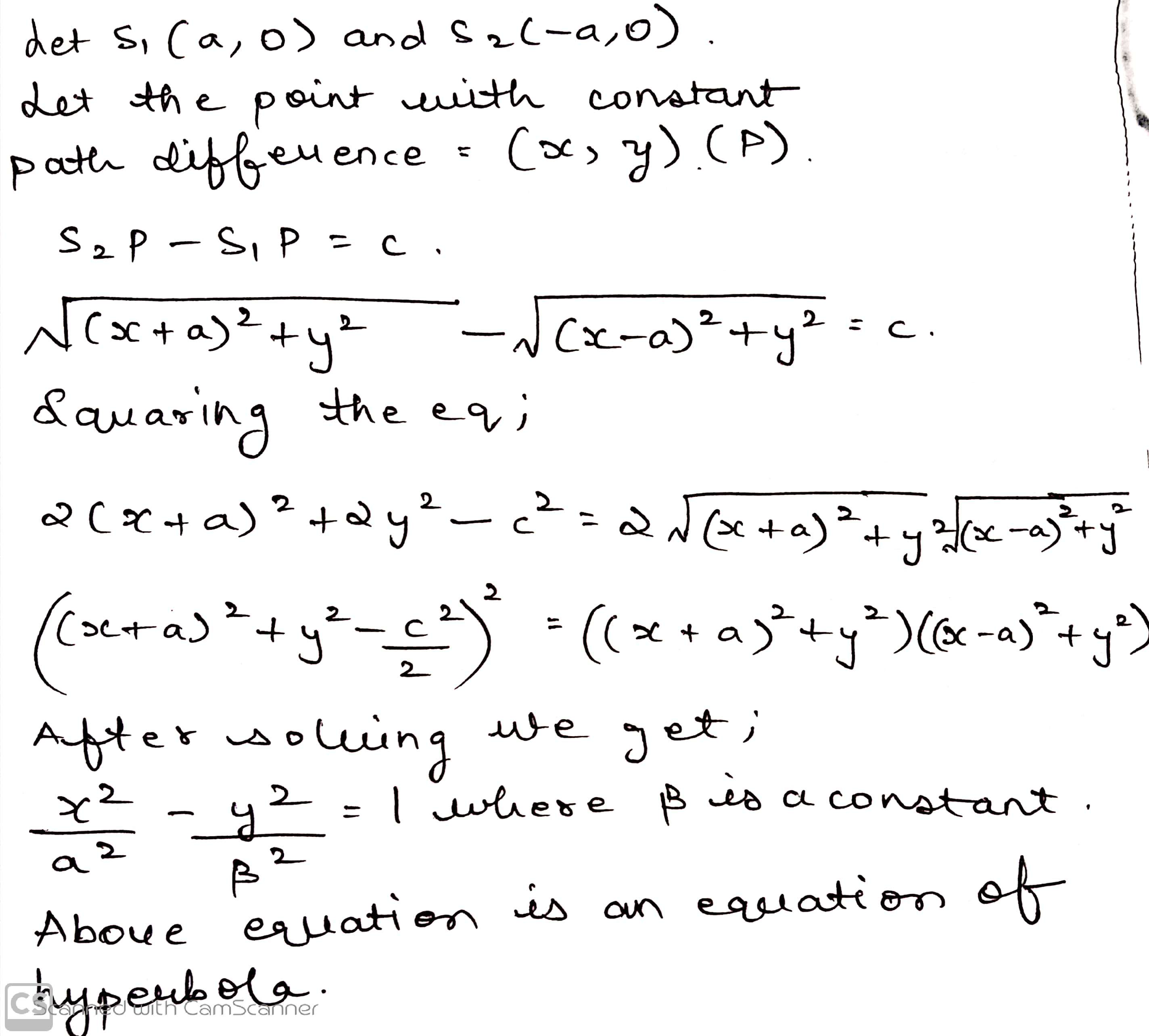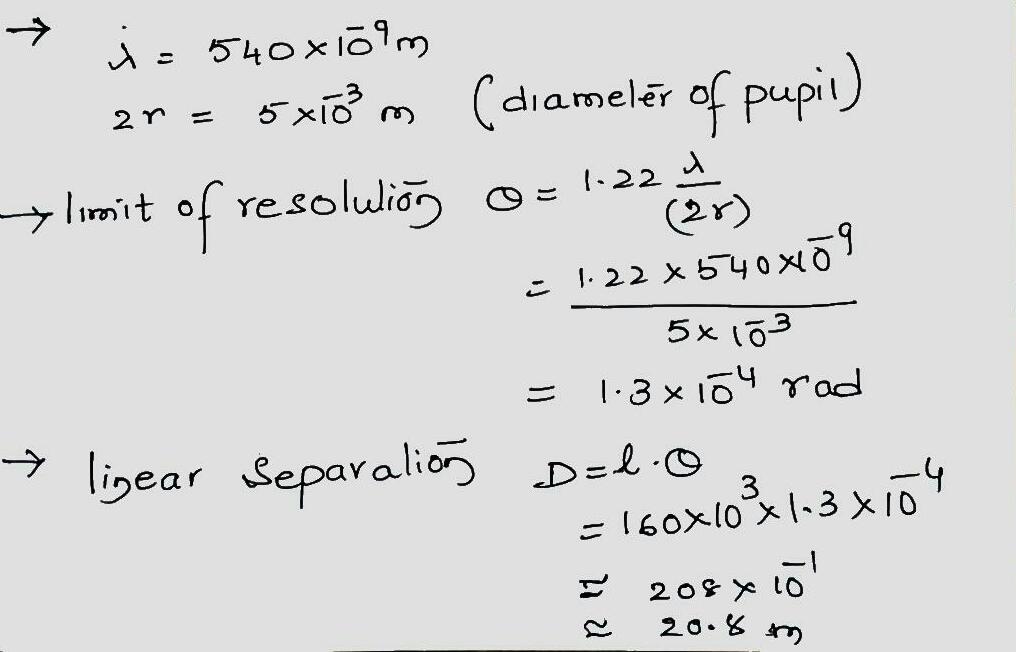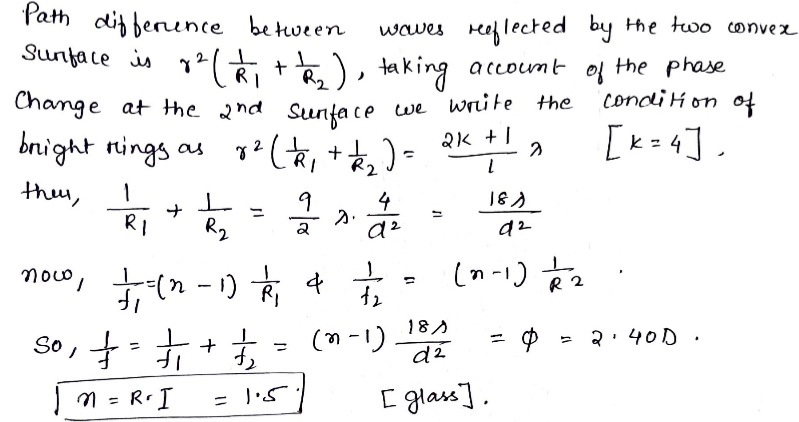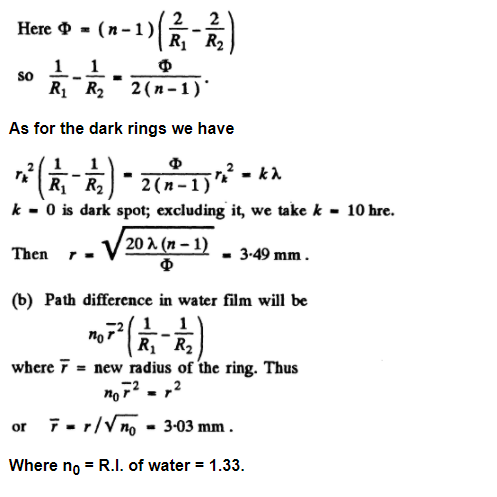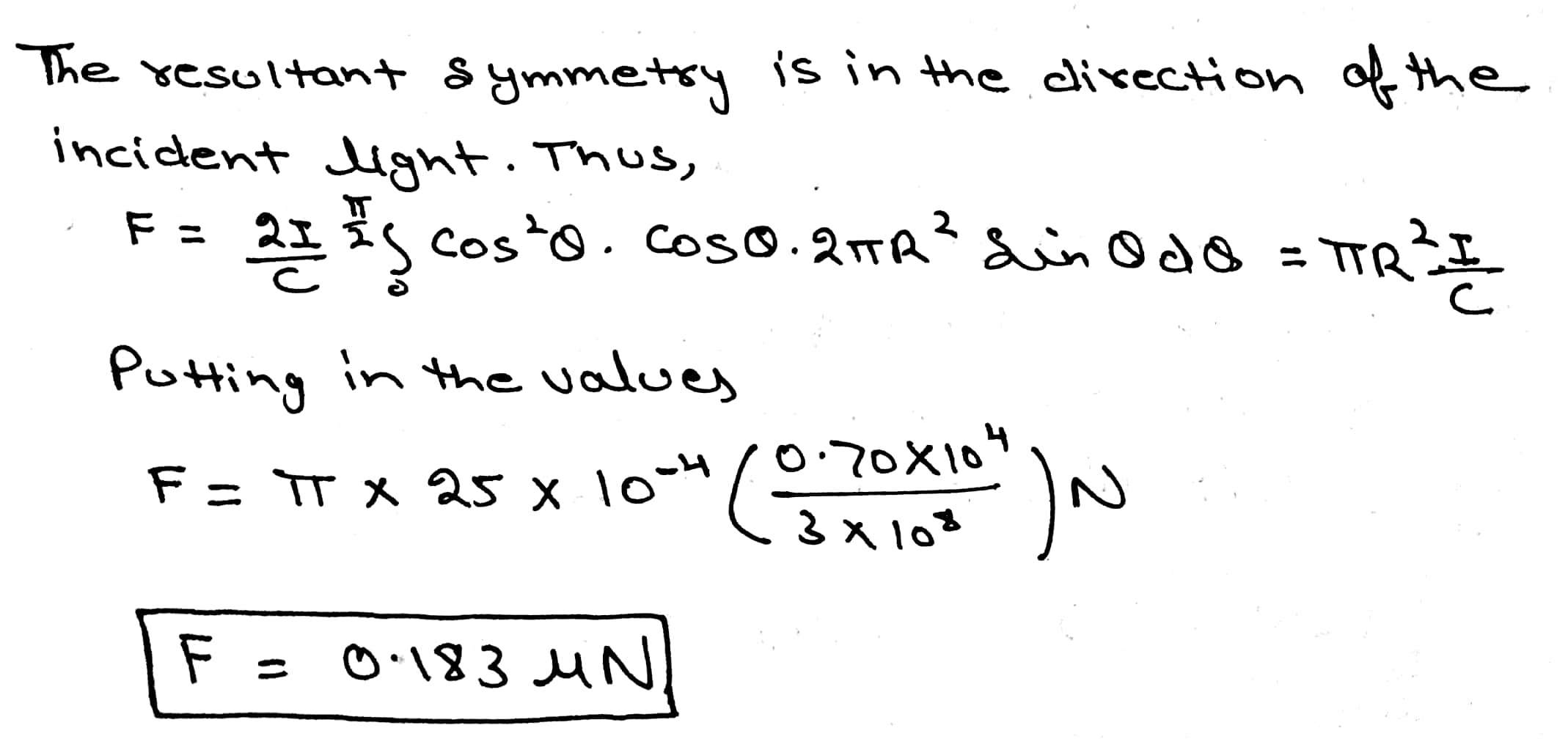Wave Optics - Class 12 Medical Physics - Extra Questions
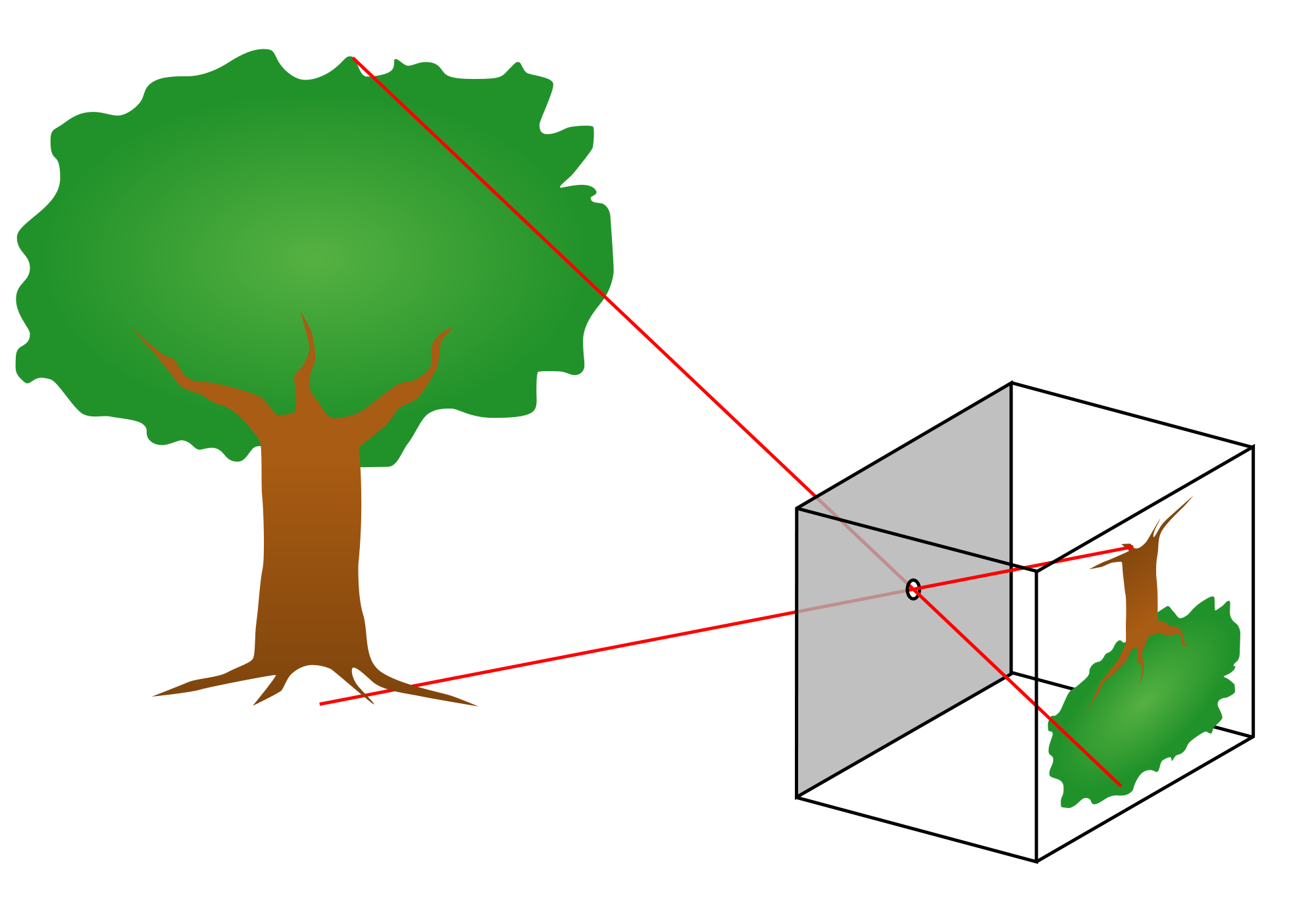
Draw and explain the process of formation of image with a pinhole camera?
1. The light ray which is coming from top of the tree goes towards the bottom of the pinhole camera screen through the pinhole.
2. The light ray which is coming from bottom of the tree goes towards the top of the pinhole camera screen through the pinhole.
3. In this way the light coming in a particular direction from each point of the tree, will be able to enter into the pinhole and the light going in other directions is blocked.
4. This leads the formation of an inverted images.
5. If we increase the size of the hole of pinhole camera, we get blurred image on the screen.
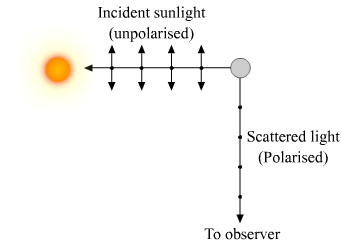
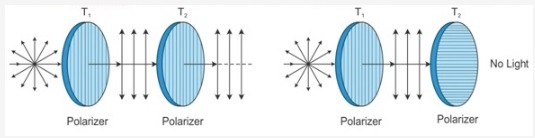
What is the difference between polarised light and unpolarised light?
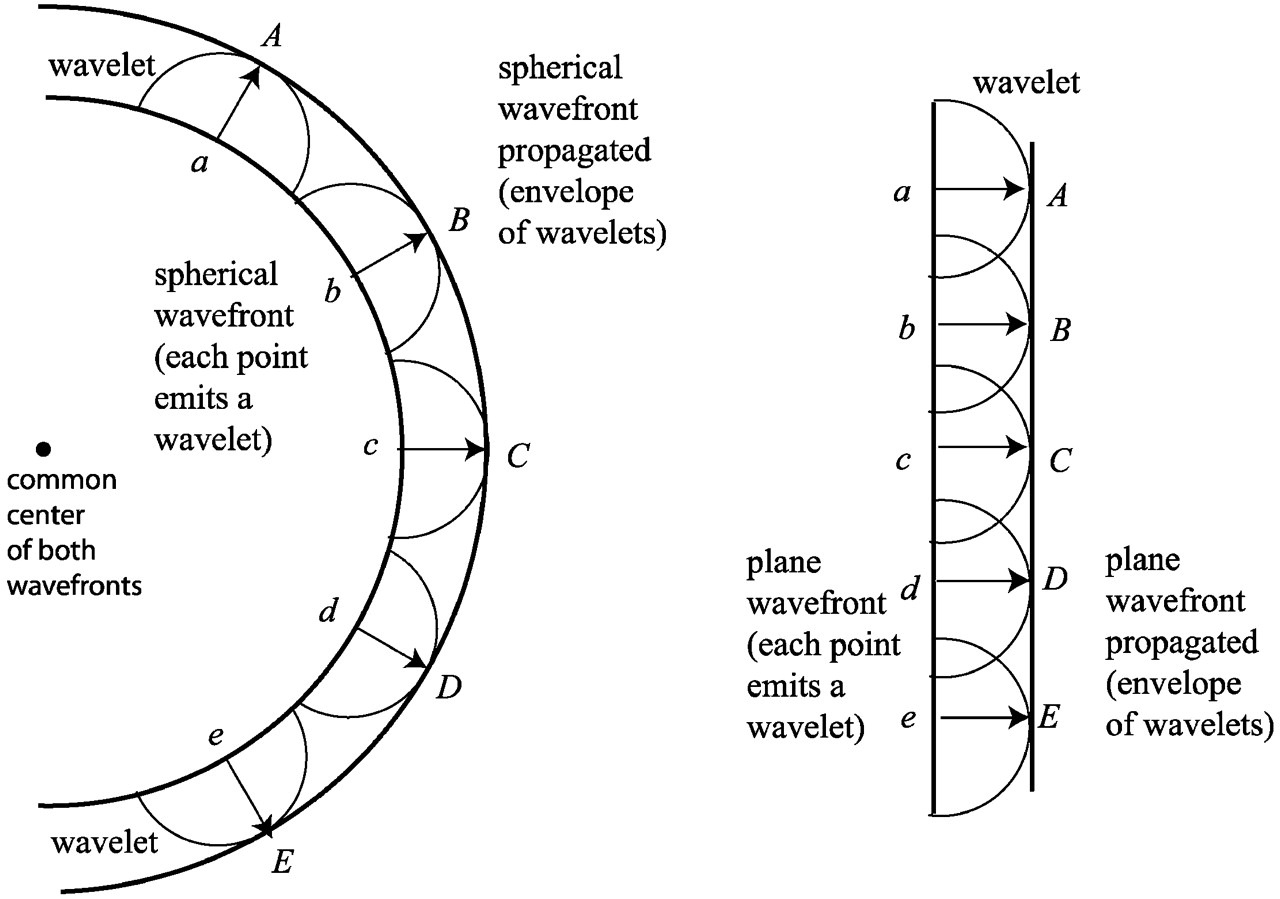
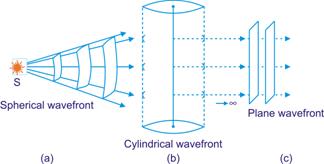
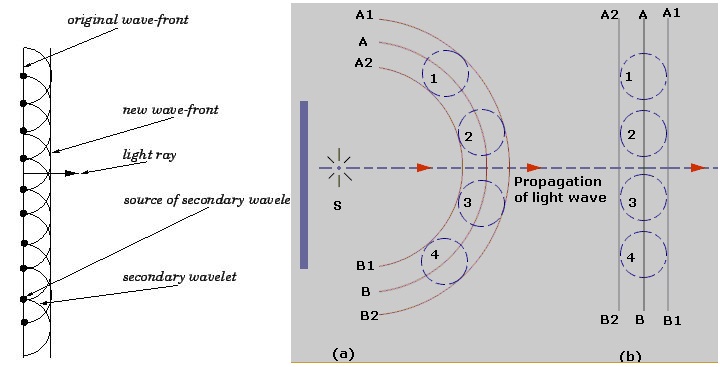
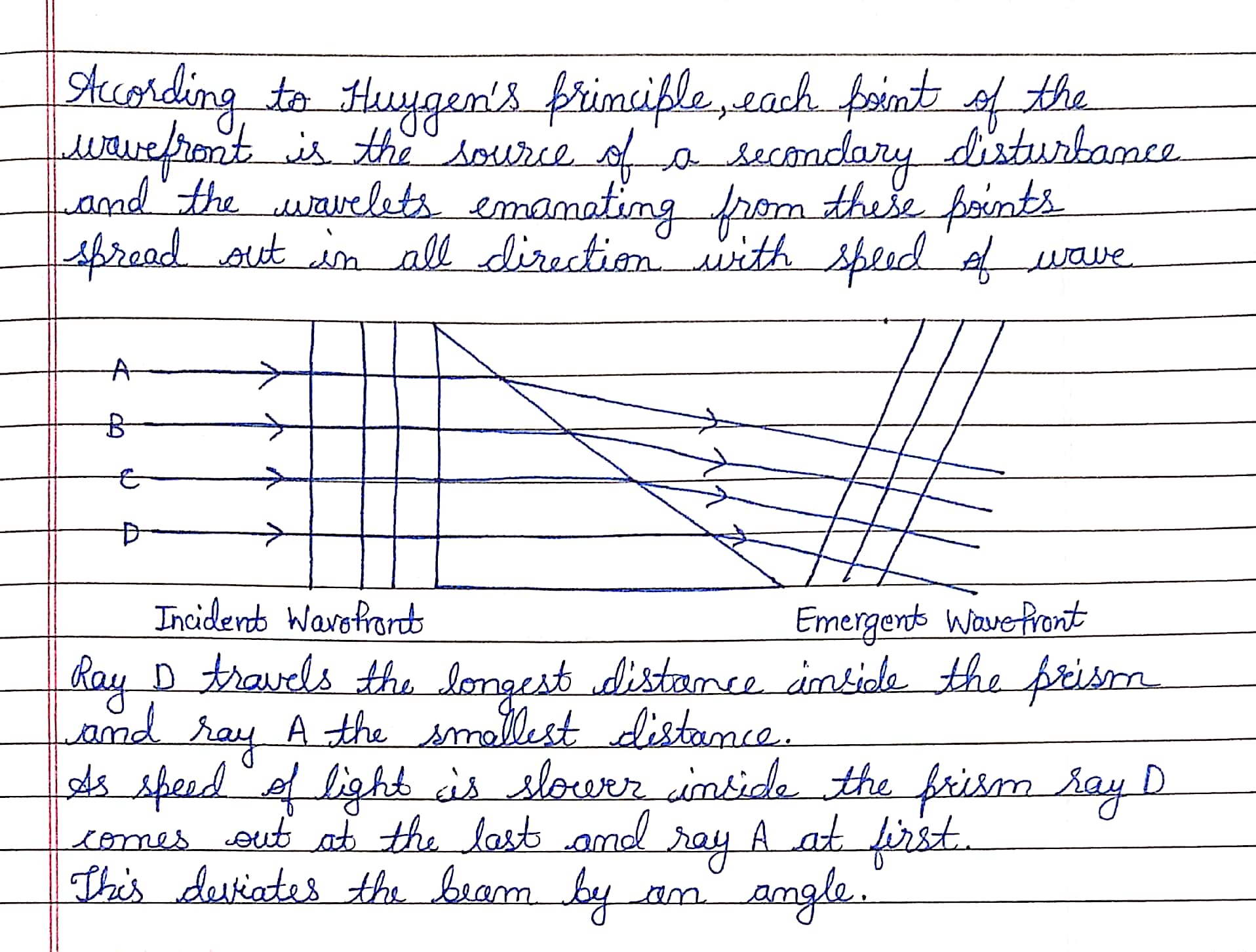
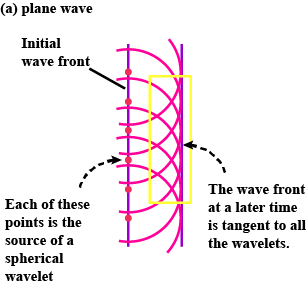
Explain Huygen's construction of spherical wavefront.
Consider a point source of monochromatic light S in a homogeneous medium. The light waves travel with the same speed($$v$$) in all the directions. After the time $$'t'$$, the waves will reach all the points which are at a distance $$vt$$ from S. This is the spherical wavefront XY. Let A, B, C be points on the wavefront. To find the new wavefront after a time $$\Delta t$$, we draw spheres of radius $$v\Delta t$$ with A, B and C as centres. The tangents drawn to these spheres is the new spherical wavefront.
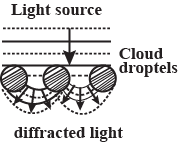
What is 'diffraction of light'? Explain its two types.
(i) Define Resolving Power of a simple astronomical telescope.
(ii) State one advantage of a reflecting telescope over refracting telescope.
You are provided with a narrow and parallel beam of light. State how you will determine experimentally, whether it is a beam of ordinary(unpolarised) light, partially polarised light or completely polarised light.
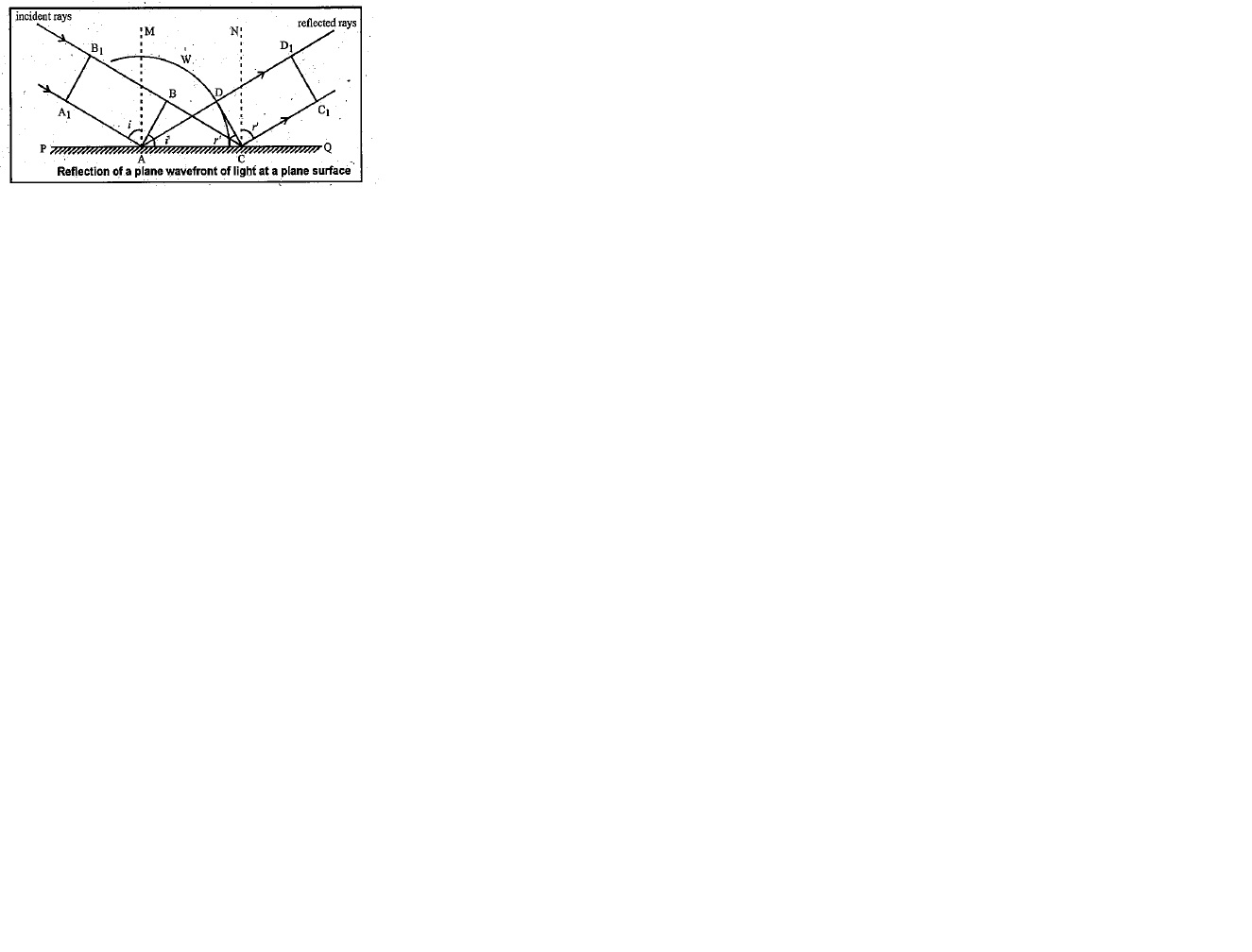
Draw a neat labelled diagram of reflection of light from a plane reflecting surface on the basis of wave theory.
In the given diagram:
PQ-Plane mirror, AM and CN-Normal to PQ
AB- Incident wavefront
$$i$$-Angle of incidence
CD-Reflected wavefront
$$r$$-Angle of reflection
W-Wavelet originating at A and radius AD$$=$$BC
$$i$$-Angle of incidence
CD-Reflected wavefront
$$r$$-Angle of reflection
W-Wavelet originating at A and radius AD$$=$$BC
A point is situated at $$7 cm$$ and $$7.2 cm$$ from two coherent sources. Find the nature of illumination at the point if wavelength of light is $$4000\mathring { A } $$.
What do you mean by diffraction of light? The light of wavelength $$5000\mathring { A } $$ is falling normally a slit of width $$2\times {10}^{-5}$$ metre. Find the angular width of central maxima in the diffraction pattern.
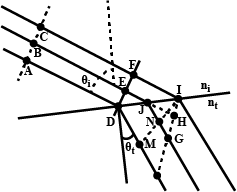
Figure shows plane waves refracted from air to water using Huygen's principle a,b,c,d,e are lengths on the diagram. Find the ratio of refractive index of water w.r.t. air.
$$\sin i = \dfrac{b}{c}$$
$$\sin r = \dfrac{d}{c}$$
$$(1) \sin i = \mu \sin r$$
$$\dfrac{b}{c} = \mu \dfrac{d}{c}$$
$$\mu = \dfrac{b}{d}$$
$$\sin r = \dfrac{d}{c}$$
$$(1) \sin i = \mu \sin r$$
$$\dfrac{b}{c} = \mu \dfrac{d}{c}$$
$$\mu = \dfrac{b}{d}$$
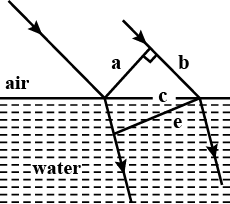
When a pin is moved along the principal axis of a small concave mirror, the image position coincides with the object at a point 0.5 m the mirror. If the mirror is placed at a depth of 0.2 m in a transparent liquid, the same phenomenon occurs when the pin is placed 0.4 m from the mirror. Find the refractive index of the liquid shown in fig 31.87
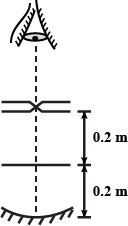
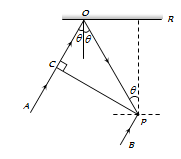
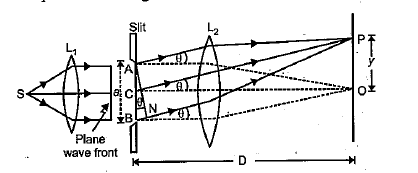
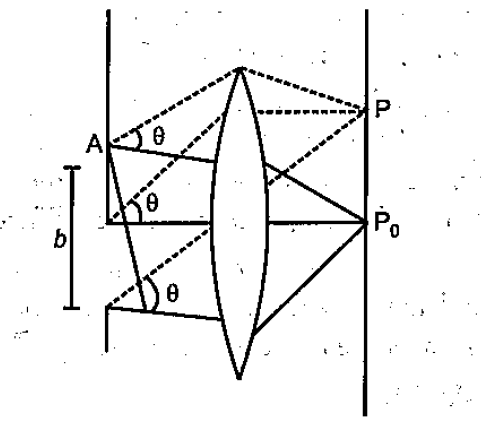
In the adjacent diagram, $$CP$$ represents a wavefront and $$AO$$ and $$BP$$, the corresponding two ray. Find the condition on $$\theta$$ for constructive interference at $$P$$ between the ray $$BP$$ and reflected ray $$OP$$.
Given that,
Wave front = CP
Reflect ray = OP
AO and BP the corresponding two rays
Now, according to diagram
$$ PR=d $$
$$ PO=d\sec \theta $$
$$ CO=PO\cos 2\theta $$
Now, put the value of PO
$$CO=d\sec \theta \cos 2\theta $$
Now, path difference between the two rays
$$ \Delta =CO+PO $$
$$ \Delta =d\sec \theta +d\sec \theta \cos 2\theta $$
Now, phase difference between the two rays
$$\phi =\pi $$
Now, for constructive interference should be
$$ \Delta =\dfrac{\lambda }{2},\dfrac{3\lambda }{2}.... $$
$$ dsec\theta +dsec\theta cos2\theta =\dfrac{\lambda }{2} $$
$$ d\sec \theta \left( 1+\cos 2\theta \right)=\dfrac{\lambda }{2} $$
$$ \dfrac{d}{\cos \theta }\left( 2{{\cos }^{2}}\theta \right)=\dfrac{\lambda }{2} $$
$$ \cos \theta =\dfrac{\lambda }{4d} $$
$$ \theta ={{\cos }^{-1}}\left( \dfrac{\lambda }{4d} \right) $$
Hence, the condition on $$\theta $$ is $${{\cos }^{-1}}\left( \dfrac{\lambda }{4d} \right)$$
Unpolarised and Polarised Light.
What will happen to two soap bubbles of different radii which are in contact with each other?
Find the intensity at a point on a screen in Young's double slit experiment where the interfering waves of equal intensity have a path difference of (i) $$\frac{\lambda}{4}$$, and (ii) $$\frac{\lambda}{3}$$.
Why is the interference pattern not detected, when two coherent sources are far apart?
State the essential condition for diffraction of light to take place.
State the importance of coherent sources in the phenomenon of interference.
What are coherent sources of light?
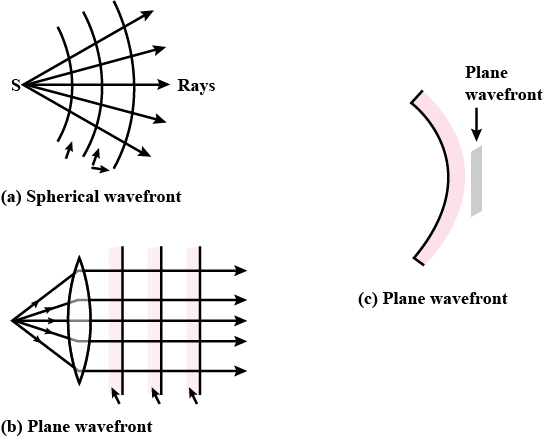
What is the shape of the wave front in each of the following cases:
(i) Light diverging from a point source.
(ii) Light emerging out of a convex lens when a point source is placed at its focus.
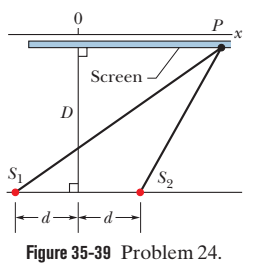
(iii) The portion of a wave front of light from a distant star intercepted by the earth.
(i) The wave front will be spherical of increasing radius, [see fig (a)]
(ii) The rays coming out of the convex lend, when point source is at focus, are parallel, to wave front is plane, [see fig (b)].
(iii) The wave front starting from star is spherical. As star is very far from the earth, so the wave front intercepted by earth is a very small portion of a sphere of large radius; which is plane (i.e. wave front intercepted by earth is plane) [see fig (c)].
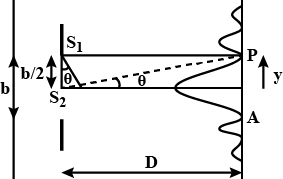
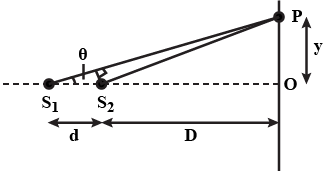
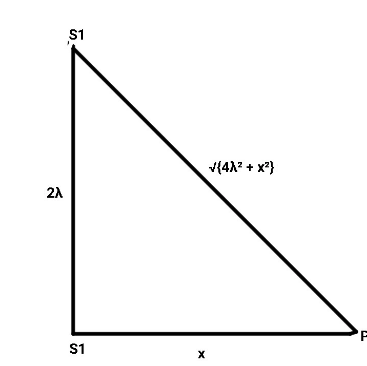
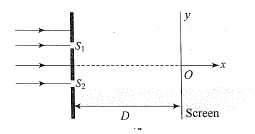
Fig. $$29.17$$(a) shows two coherent sources $$S_1$$ and $$S_2$$ which emit light of wavelength $$\lambda$$ in phase. The phase separation between the sources is $$3\lambda$$. A circular wire of radius $$R>>I$$ is placed symmetrically to $$S_1$$ and $$S_2$$ as illustrated. Find the angular positions $$\theta$$ on the wire for which constructive interference occurs.
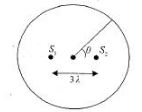
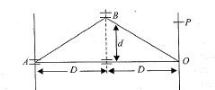
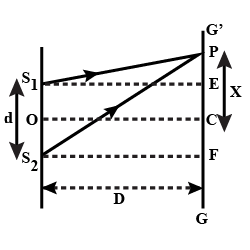
Consider the arrangement shown in Fig $$29.15$$(a). The distance $$D$$ is large, compared to $$d$$. Find minimum value of $$d$$ so that there is a dark fringe at $$O$$. For, the same value of $$d$$ find $$x$$ at which next bright fringes is formed.
Path difference$$=AB+BO-2D$$
$$\displaystyle 2\sqrt{(D^2+d^2)}-2D=\displaystyle \frac{\lambda}{2} $$
or $$\displaystyle 2\sqrt{(D^2+d^2)}=\displaystyle\frac{\lambda}{2}+2D$$
or $$4(D^2+d^2)=\displaystyle\frac{\lambda^2}{4}+4D^2+2\lambda D$$
Eliminate $$\displaystyle\frac{\lambda^2}{4}$$ as $$\lambda<<D.$$ or $$d=\displaystyle\sqrt\frac{\lambda D}{2}$$
$$\displaystyle 2\sqrt{(D^2+d^2)}-2D=\displaystyle \frac{\lambda}{2} $$
or $$\displaystyle 2\sqrt{(D^2+d^2)}=\displaystyle\frac{\lambda}{2}+2D$$
or $$4(D^2+d^2)=\displaystyle\frac{\lambda^2}{4}+4D^2+2\lambda D$$
Eliminate $$\displaystyle\frac{\lambda^2}{4}$$ as $$\lambda<<D.$$ or $$d=\displaystyle\sqrt\frac{\lambda D}{2}$$
In a single slit diffraction pattern, (a) the intensity $$I$$, at a point where the total phase difference between the wavelets from top to bottom of the slit is 66 rad. (b) If this point is $$7^0$$ away from the central maxima. Find the width of the slit. Given: $$\lambda = 600 nm.$$
In young's double-slit experiment using mono chromatic light of wavelength A the intensity of light at a point on the screen where path difference is $$\lambda$$ is K units. What is the intensity if light at a point where path difference is $$\lambda /3$$?
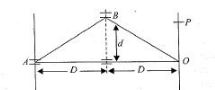
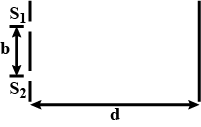
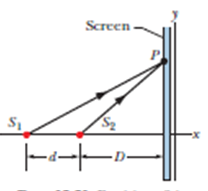
In Fig. $$ 35-39, $$ two isotropic point sources $$ S_{1} $$ and $$ S_{2} $$ emit light in phase at wavelength $$ \lambda $$ and at the same amplitude. The sources are separated by distance $$ 2 d=6.00 \lambda . $$ They lie on an axis that is parallel to an $$ x $$ axis, which runs along a viewing screen at distance $$ D= 20.0 \lambda . $$ The origin lies on the perpendicular bisector between the sources. The figure shows two rays reaching point $$ P $$ on the screen, at position $$ x_{P} $$.
At what value of $$ x_{P} $$ do the rays have the maximum possible phase difference?
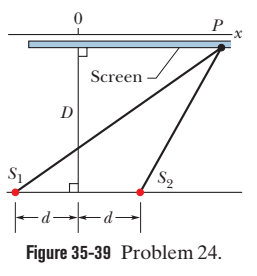
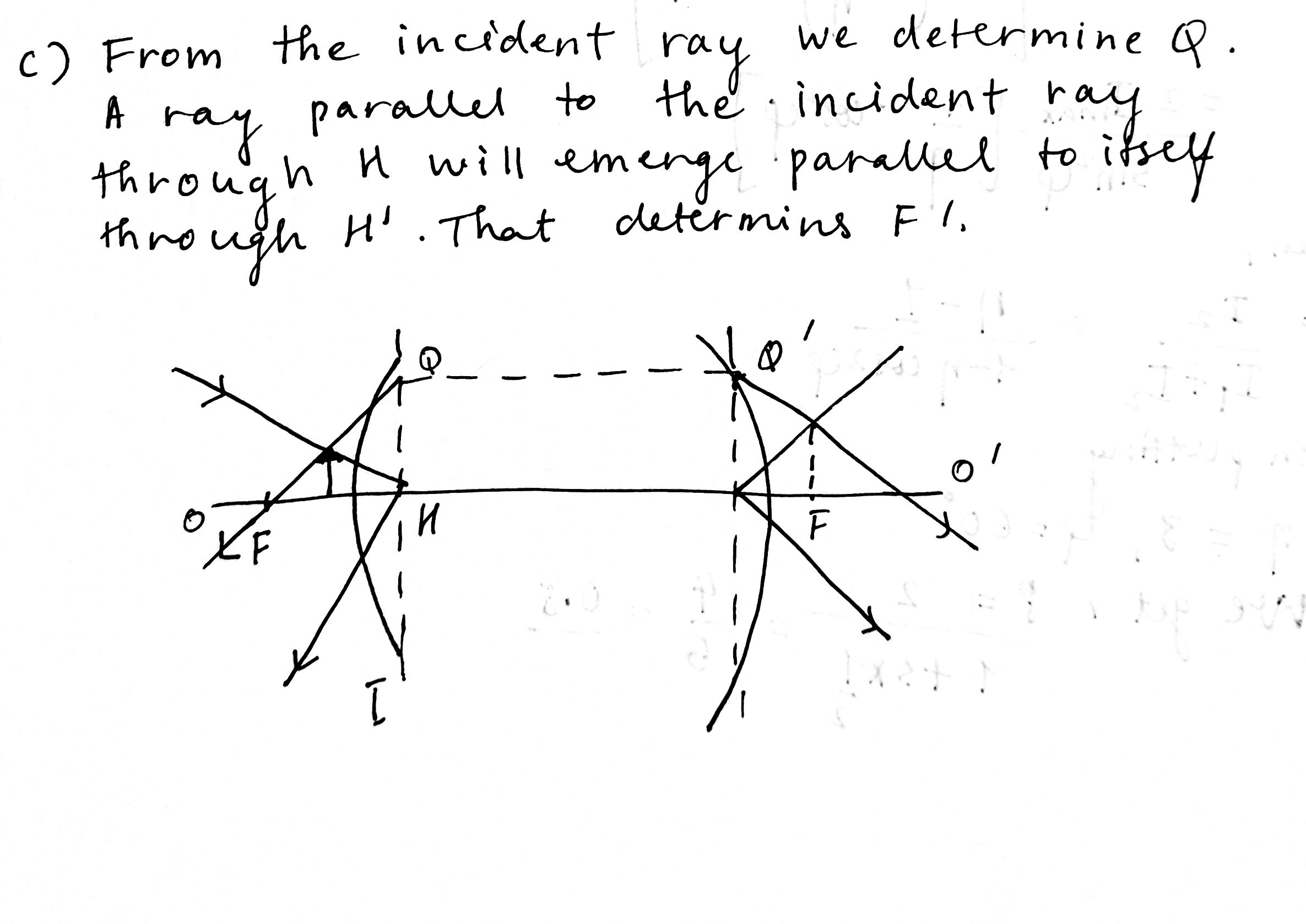
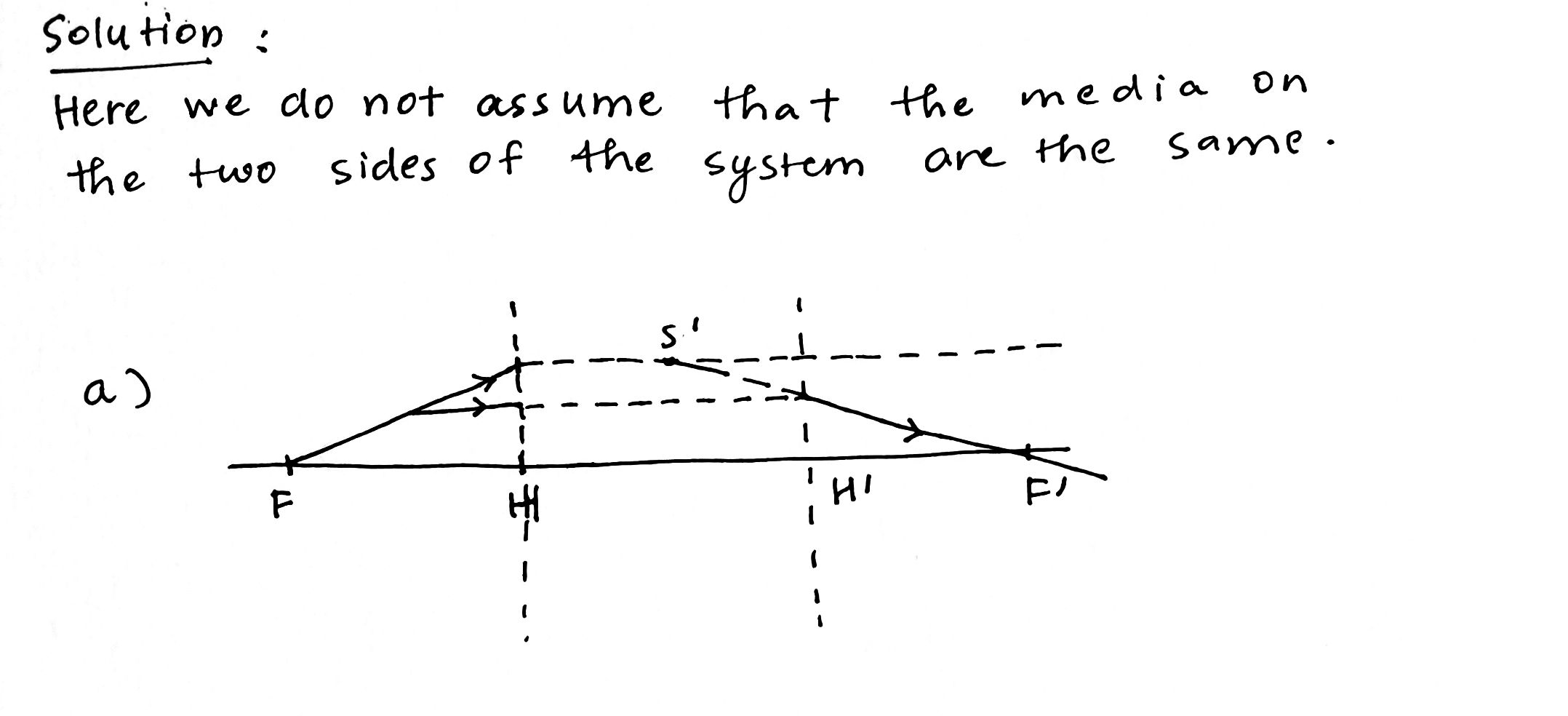
An optical system is located in air. Let $$ O O^{\prime} $$ be its optical axis, $$ F $$ and $$ F^{\prime} $$ are the front and rear focal points, $$ H $$ and $$ H^{\prime} $$ are the front and rear principal planes, $$ P $$ and $$ P^{\prime} $$ are the conjugate points. By means of plotting find:
The positions $$ F, F^{\prime}, $$ and $$ H^{\prime} $$ (Fig. $$ c, $$ where the path of the ray of light is shown before and after passing through the system).
How much diffraction spreading does a light beam undergo? One quantitative answer is the full width at half maximum of the central maximum of the single-slit Fraunhofer diffraction pattern. You can evaluate this angle of spreading in this problem.(a) In Equation $$ 38.2, $$ define $$ \phi=\pi a \sin \theta / \lambda $$ and show that at the point where $$ I=0.5 I_{\text {max }} $$ we must have $$ \phi=\sqrt{2} \sin \phi . $$ (b) Let $$ y_{1}=\sin \phi $$ and $$ y_{2}=\phi / \sqrt{2} . $$ Plot $$ y_{1} $$ and $$ y_{2} $$ on the same set of axes over a range from $$ \phi=1 $$ rad to $$ \phi=\pi / 2 $$ rad. Determine $$ \phi $$ from the point of intersection of the two curves.(c) Then show that if the fraction $$ \lambda / a $$ is not large, the angular full width at half maximum of the central diffraction maximum is $$ \theta=0.885 \lambda / a $$ (d) What If? Another method to solve the transcendental equation $$ \phi=\sqrt{2} \sin \phi $$ in part $$ (a) $$ is to guess a first value of $$ \phi $$, use a computer or calculator to see how nearly it fits, and continue to update your estimate until the equation balances. How many steps (iterations) does this process take?
(a) From Equation $$ 38.2, \dfrac{I}{I_{\max }}=\left[\dfrac{\sin (\phi)}{\phi}\right]^{2} $$ where we define
$$ \phi \equiv \dfrac{\pi a \sin \theta}{\lambda} $$
Therefore, when $$ \dfrac{I}{I_{\max }}=\dfrac{1}{2} $$ we must have
$$ \dfrac{\sin \phi}{\phi}=\dfrac{1}{\sqrt{2}}, \quad $$ or $$ \quad\left[\sin \phi=\dfrac{\phi}{\sqrt{2}}\right] $$
(b) Let $$ y_{1}=\sin \phi $$ and $$ y_{2}=\dfrac{\phi}{\sqrt{2}} $$
A plot of $$ y_{1} $$ and $$ y_{2} $$ in the range $$ 1.00 \leq \phi \leq \dfrac{\pi}{2} $$ is shown in ANS. FIG. $$ \mathrm{P} 38.72(\mathrm{b}) $$
The solution to the transcendental equation is found to be $$ \phi=1.39 \mathrm{rad} $$
(c) $$ \dfrac{\pi a \sin \theta}{\lambda}=\phi \quad $$ gives $$ \sin \theta=\left(\dfrac{\phi}{\pi}\right) \dfrac{\lambda}{a} . $$ If $$ \dfrac{\lambda}{a} $$ is small, then $$ \theta \approx\left(\dfrac{\phi}{\pi}\right) \dfrac{\lambda}{a} $$
This gives the half-width, measured away from the maximum at $$ \theta=0 . $$ The pattern is symmetric, so the full width is given by
$$\begin{aligned}\Delta \theta &=\left(\dfrac{\phi}{\pi}\right) \dfrac{\lambda}{a}-\left(-\left(\dfrac{\phi}{\pi}\right) \dfrac{\lambda}{a}\right)=2\left(\dfrac{\phi}{\pi}\right) \dfrac{\lambda}{a}=2\left(\dfrac{1.39 \mathrm{rad}}{\pi}\right) \dfrac{\lambda}{a} \\&=\dfrac{0.885 \lambda}{a}\end{aligned}$$
(d) $$ \begin{array}{|l|l|l} \phi & & \sqrt{2} \sin \phi & \\\hline 1 & 1.19 & \text{bigger than} \ \phi \\2 & 1.29 & \text{smaller than} \phi \\1.5 & 1.41 & smaller \\1.4 & 1.394 & \\1.39 & 1.391 & bigger \\1.395 & 1.392 & \\1.392 & 1.3917 & smaller \\1.3915 & 1.39154 & bigger \\1.39152 & 1.39155 & bigger \\1.3916 & 1.391568 & smaller \\1.39158 & 1.391563 & \\1.39157 & 1.391561 & \\1.39156 & 1.391558 & \\1.391559 & 1.3915578 & \\1.391558 & 1.3915575 & \\1.391557 & 1.3915573 & \\1.3915574 & 1.3915574 &\end{array}$$
We get the answer as 1.3915574 to seven digits after 17 steps.
Clever guessing, like using the value of $$ \sqrt{2} \sin \phi $$ as the next guess for $$ \phi $$, could reduce this to around 13 steps.
Answer in brief:
What is a wavefront ? How is it related to rays of light ? What is the shape of the wavefront at a point far away from the source of light ?
In as interference experiment , two sources of light are used of intensities $$I$$ and $$4I$$. Find out the intensities at those points where the phase difference of two waves superimposing are
$$ \pi $$
The phase difference between light waves from two slits in Young's double slit experiment is $$\pi$$. Will the central fringe be bright or dark?
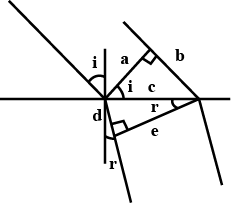
State the two laws of reflection of light.
A convex lens of diameter $$8cm$$ is used to focus a parallel beam of light of wavelength $$620nm$$. Light is focused at a distance $$20cm$$, from the lens. What would be the radius of central bright fringe?
The two slits in Young's double-slit experiment are illuminated by two different sodium lamps emitting light of the same wavelength. No interference pattern will be observed on the screen. Mark 0 for False and 1 for True.
What will be the effect on the width of the central bright fringe in the diffraction pattern of a single slit if:
$$(1)$$ Monochromatic light of smaller wavelength is used.
$$(2)$$ Slit is made narrower
What is the difference between polarised light and unpolarished light based on the direction of electric vector $$(\vec {E})$$?
What is meant by diffraction of light?
Diffraction is slight bending of light as it pass around the edge of an object. The amount of bending depends upon the wavelength of the light to the size of the opening.If the opening is much larger than light wavelength's, the bending will be almost unnoticeable.
In a single slit diffraction experiment first minimum for $$\lambda _{1}=660nm$$ coincides with first maxima for wavelength $$\lambda _{2}$$, calculate $$\lambda _{2}$$.
Why are coherent sources required to create interference of light?
In a Young's double slit experiment, two narrow vertical slits placed $$0.800\ mm$$ apart are illuminated by the same source of yellow light of wavelength $$589\ nm$$. How far are the adjacent bright bands in the interference pattern observed on a screen $$2.00\ m$$ away?
No interference pattern is detected when two coherent sources are infinitely close to each other. Why?
What should be the aperture or obstacle to observe diffraction with it?
What type of wavefront will emerge:
From a far light source?
Write statement of Huygen's principle of direction
What is the shape of the wavefront in each of the following cases:
Light diverging from a point source.
A laser produces a beam a few millimeters wide, with uniform intensity across its width. A hair is stretched vertically across the front of the laser to cross the beam.
How is the diffraction pattern it produces on a distant screen related to that of a vertical slit equal in width to the hair?
Find the positions of the principal planes, the focal length and the sign of the optical power of a thick convex-concave glass lens
(a) whose thickness is equal to $$ d $$ and curvature radii of the surfaces are the same and equal to $$ R $$;
In a single-slit diffraction pattern, assuming each side maximum is halfway between the adjacent minima, find the ratio of the intensity of (a) the first-order side maximum to the intensity of the central maximum.
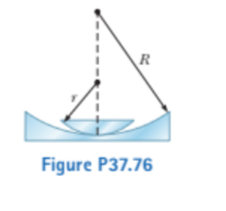
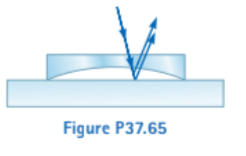
A plano-convex lens having a radius of curvature of r = 4.00 m is placed on a concave glass surface whose radius of curvature is R 5 12.0 m as shown in Figure P37.Assuming 500-nm light is incident normal to the flat surface of the lens, determine the radius of the 100th bright ring.
For bright rings the gap t between surfaces is given by $$2t = (m + \frac{1}{2}) \lambda$$.
The first bright ring has m = 0 and the hundredth has m = 99.
The first bright ring has m = 0 and the hundredth has m = 99.
A ....... of light consists of a bundle of light rays.
Light is a form of ........
.......... happens when two or more waves overlap.
___________ are drawn on light rays to show the direction in which light travels.
Name the physical quantity which remains same for microwaves 1 mm and UV radiation of $$6000^{\circ}_{A}$$ in a vacuum
Write the definition of wavefront.
Which theory of light proposed the presence of ether medium for propogation of light?
What are Fraunhofer lines? What is their impotance?
How did Fresnel construct a biprism in order to study interference of light?
What is the shape of the wavefront diverging from a point source of light?
If the incidence is at polarising angle, the angle between Reflected ray and the Refracted ray from a surface is _________.
Write any four the necessary conditions for interference of light.
What is wavefront of light waves?
Define coherent sources of light.
Name the phenomenon which is responsible for bending of light around sharp corners of an obstacle. Under what conditions does this phenomenon take place?
What should be the order of the size of obstacle or aperture for diffraction of light?
What change, if any, is observed in frequency and wavelength when light travels fro air to glass?
Light consists of _____ colours
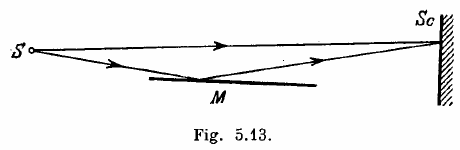
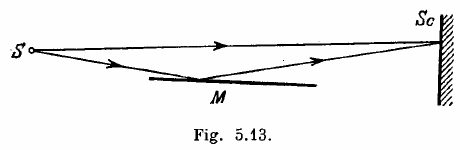
In Lloyd's mirror experiment (Fig.) a light wave emitted directly be the source S (narrow slit) interferes with the wave reflected form a mirror M. As s result, an interference fringe pattern is formed on the screen Sc. the source and the mirror are separated by a distance l=100 cm. At a certain position of the source, the fringe width on the screen was equal to Δx=0.25 mm, and after source was moved away from the mirror plane by Δh=0.60mm, the fringe width decreased η=1.5 times. Find the wavelength of light.
From the general formula
$$\displaystyle \Delta x\ =\ \frac{l\lambda }{d}$$
we find that
$$\dfrac{\Delta x}{\eta } \ =\ \dfrac{l\lambda }{d\ +\ 2\Delta h}$$
since $$ d $$ increases to $$\displaystyle +2\Delta h$$ when the source is moved away from the plane mirror by $$\displaystyle \Delta h$$.
Thus
$$ \displaystyle \begin{array}{{>{\displaystyle}l}}\eta d\ =\ d\ +\ 2\Delta h\ \\\end{array} $$
or $$\displaystyle d=\displaystyle 2\Delta h\displaystyle /( \eta -1)$$
Finally
$$\displaystyle \lambda \ =\ \frac{2\Delta h\Delta x}{( \eta -1) l} =0.6\ Micro\ m$$
the central bright maxima is twice as wide as the other maxima.
Consider a monochromatic beam of light incident on a slit of width a. Interference occurs between the light that passes through different parts of the slit, resulting in what is called a diffraction pattern. Viewed on a distant screen, the diffraction pattern consists of alternating bright and dark interference fringes. The central bright fringe is twice as wide, and much brighter, than the other bright fringes. Central bright fringe can be explained by wave theory of light, using the principle of constructive interference.
According to Huygen's principle, each portion of the slit acts as a source of light waves. Hence, light from one portion of slit can interfere with lights of other portion, and the resultant intensity depends on the direction, $$\theta $$. Centres of first dark fringes will be found at angle of $$sin{ \theta }_{ dark }=\pm \frac { \lambda }{ a } $$
Between these two, the central maxima is found with a width of $$\frac { 2\lambda }{ a } $$. Others will lie between $$\frac { n\lambda }{ a } $$ and $$\frac { (n+1)\lambda }{ a } $$, thus having a width of only $$\frac { \lambda }{ a } $$.
Hence central maxima is twice in width.
According to Huygen's principle, each portion of the slit acts as a source of light waves. Hence, light from one portion of slit can interfere with lights of other portion, and the resultant intensity depends on the direction, $$\theta $$. Centres of first dark fringes will be found at angle of $$sin{ \theta }_{ dark }=\pm \frac { \lambda }{ a } $$
Between these two, the central maxima is found with a width of $$\frac { 2\lambda }{ a } $$. Others will lie between $$\frac { n\lambda }{ a } $$ and $$\frac { (n+1)\lambda }{ a } $$, thus having a width of only $$\frac { \lambda }{ a } $$.
Hence central maxima is twice in width.
Define the term 'coherent sources' which are required to produce interference pattern in Young's double slit experiment.
Distinguish between linearly polarised and unpolarised light.
Show that the light waves are transverse in nature.
The bending of a wave around a barrier is called .......... .
Answer the following questions:(a) In a single slit diffraction experiment, the width of the slit is made double the original width. How does this affect the size and intensity of the central diffraction band?
(b) In what way is diffraction from each slit related to the interference pattern in a double-slit experiment?
(c) When a tiny circular obstacle is placed in the path of light from a distant source, a bright spot is seen at the centre of the shadow of the obstacle. Explain why?
(d) Two students are separated by a 7 m partition wall in a room 10 m high. If both light and sound waves can bend around obstacles, how is it that the students are unable to see each other even though they can converse easily.
(e) Ray optics is based on the assumption that light travels in a straight line. Diffraction effects (observed when light propagates through small apertures/slits or around small obstacles) disprove this assumption. Yet the ray optics assumption is so commonly used in understanding location and several other properties of images in optical instruments. What is the justification?
(b) In what way is diffraction from each slit related to the interference pattern in a double-slit experiment?
(c) When a tiny circular obstacle is placed in the path of light from a distant source, a bright spot is seen at the centre of the shadow of the obstacle. Explain why?
(d) Two students are separated by a 7 m partition wall in a room 10 m high. If both light and sound waves can bend around obstacles, how is it that the students are unable to see each other even though they can converse easily.
(e) Ray optics is based on the assumption that light travels in a straight line. Diffraction effects (observed when light propagates through small apertures/slits or around small obstacles) disprove this assumption. Yet the ray optics assumption is so commonly used in understanding location and several other properties of images in optical instruments. What is the justification?
A parallel beam of light of wavelength 500 nm falls on a narrow slit and the resulting diffraction pattern is observed on a screen 1 m away. It is observed that the first minimum is at a distance of 2.5 mm from the centre of the screen. Find the width of the slit.
Answer the following questions:(a) When a low flying aircraft passes overhead, we sometimes notice a slight shaking of the picture on our TV screen. Suggest a possible explanation.
(b) As you have learnt in the text, the principle of linear superposition of wave displacement is basic to understanding intensity distributions in diffraction and interference patterns. What is the justification of this principle?
In deriving the single slit diffraction pattern, it was stated that the intensity is zero at angles of n$$\lambda$$/a. Justify this by suitably dividing the slit to bring out the cancellation.
Write two characteristic features distinguishing the diffraction pattern from the interference fringes obtained in Young's double slit experiment.
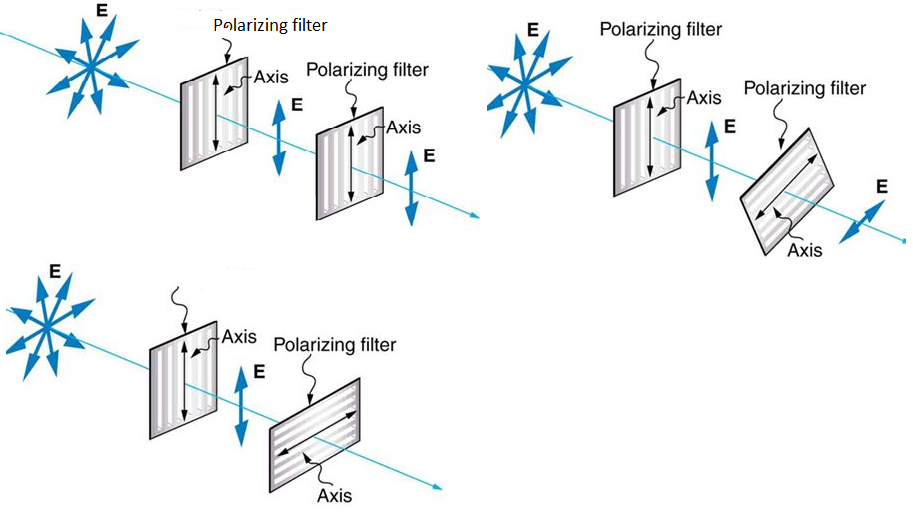
(a) What is linearly polarized light. Describe briefly using a diagram how sunlight is polarised.
(b) Unpolarised light is incident on a Polaroid. How would the intensity of transmitted light change when the Polaroid is rotated?
(a) Natural light is unpolarised i.e, the electric vector takes all possible directions in the transverse plane, rapidly and randomly, during a measurement. A polarizer transits only one components. This resulting light is called linear or plane polarized
The incident sunlight is unpolarised. The dot and double arrows show the polarization in the perpendicular and in the plane of the figure. Under the influence of the electric field of the incident wave,the electrons in the molecules of the atmosphere acquire components of motion in both these directions. An observer looking at $$90^{\circ}$$9to the directions of the sun, the charge accelerating parallel to the double arrows do not radiate energy towards this observer since their acceleration has no transverse component. The radiations scattered by the molecule is therefore represented by dots. It is linearly polarized perpendicular to the plane of the figure
(b) If the unpolarised light is incident on a Polaroid, the intensity is reduced by half. Even if the polaroid is rotated by angle $$\theta$$ the average over $$cos^2\theta=\dfrac{1}{2}$$. From Malus' law:$$I=I_0cos^2\theta$$
The incident sunlight is unpolarised. The dot and double arrows show the polarization in the perpendicular and in the plane of the figure. Under the influence of the electric field of the incident wave,the electrons in the molecules of the atmosphere acquire components of motion in both these directions. An observer looking at $$90^{\circ}$$9to the directions of the sun, the charge accelerating parallel to the double arrows do not radiate energy towards this observer since their acceleration has no transverse component. The radiations scattered by the molecule is therefore represented by dots. It is linearly polarized perpendicular to the plane of the figure
$$\implies \left|I\right|=I_0\left|cos^2\theta\right|$$
$$=\dfrac{I_0}{2}$$
Hence intensity remains unchanged when polaroid is rotated.
How does the angular separation between fringes in single slit diffraction experiment change when the distance of separation between the slit and screen is doubled?
Why was corpuscular theory of light discarded?
Due to diffraction, light encroaches into the ....................... shadow of an obstacle.
Name any two characteristics of light explained by Huygens wave theory?
What is shape of wavefront originating from
i) a point source and ii) a line source?
i) The wave front originating from a point source is spherical in shape. It is because, the locus of all such points, which are equidistant from the point source, is a sphere.
ii) The wave front originating from a line source is cylindrical in shape. It is because, all the points, which are equidistant from the linear source, lie on the surface of a cylinder.
ii) The wave front originating from a line source is cylindrical in shape. It is because, all the points, which are equidistant from the linear source, lie on the surface of a cylinder.
State any two methods by which ordinary light can be polarised.
State any one difference between interference of light and diffraction of light.
What is meant by coherent sources of light?
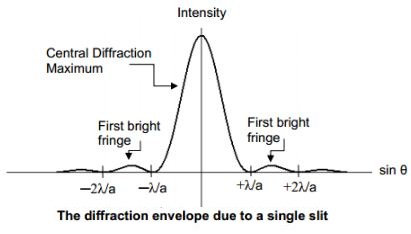
Draw a graph to show the relative intensity distribution for a single slit diffraction pattern. Obtain the expression for the width of central maxima. If slit width is doubled then what is the effect on width of central maxima?
Let the width of the slit be through which diffraction pattern is obtained be $$b$$ and $$\lambda$$ be the wavelength of light used.
The first minima of diffraction pattern is formed at point P on one side and at A of other side.
Path difference between the light rays reaching at point P $$\Delta x = S_2 P - S_1P$$
$$\therefore $$ $$\Delta x = \dfrac{b}{2}\sin\theta$$
For first minima, path difference must be equal to $$\dfrac{\lambda}{2}$$
$$\therefore$$ $$\dfrac{b}{2}\sin\theta = \dfrac{\lambda}{2}$$
OR $$b \sin\theta = \lambda$$
As $$\theta$$ is very small, thus $$\sin\theta \approx \tan\theta = \dfrac{y}{D}$$
OR $$b\times \dfrac{y}{D} = \lambda$$ $$\implies y = \dfrac{\lambda D}{b}$$
Width of central maxima $$PA = 2y = \dfrac{2\lambda D}{b}$$
$$\implies$$ $$PA \propto \dfrac{1}{b}$$
Hence the width of central maxima formed becomes half of its initial value as the slit width is doubled.
How will you identify with the help of an experiment whether a given beam of light is of polarized light or of unplolarised light?
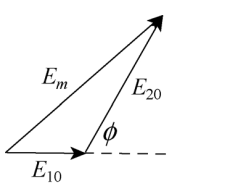
Unpolarised light is passed through a polarised $$P_1$$. When this polarised beam passes through another polarised $$P_2$$ and if the pass axis of $$P_2$$ makes angle $$\theta$$ with the pass axis of $$P_1$$, then write the expression for the polarised beam passing through $$P_2$$. Draw a plot showing the variation of intensity when $$\theta$$ varies from $$0$$ to $$2\pi$$.
Here,
- $$E$$ is unpolarized light passes through a polarizer $$P_1$$ and again this polarized light pass through a polarizer $$P_2$$, the pass axis of $$P_2$$ makes angle $$\theta$$ with the pass axis of $$P_1$$,
- Expression for the polarised beam passing through the $$P_2$$ is $$I=I_ocos^2\theta ,$$Here $$I=$$Intensity of unpolarised light, $$I_o=$$Intensity of polarised light, and $$\theta$$ is the angle between Polarizer $$P_1$$ and $$P_2$$. This is known as malus' law.
State Huygens' principle.
Write any two applications of interference.
We obtained alternate dark and bright regions if we look at the shadow by an obstacle closed to geometrical shadow.
a) Mention the phenomenon behind it.
b) Differentiate the interference pattern with a coherently illuminated single slit diffraction pattern.
The word PHYSICS is written in red ink and the work CHEMISTRY is written in blue ink on a white piece of paper. They are viewed in red light. Which word will you be able to read? Why?
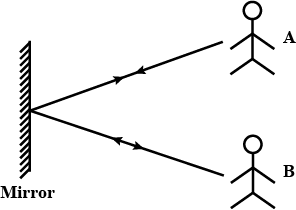
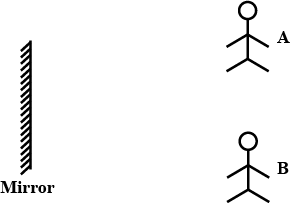
A and B are facing the mirror and standing in such a way that A can see B and B can see A. Explain this phenomenon.
The light rays from A falls on the mirror and gets reflected and reaches
B, the light from B falls on the mirror and reflects to reach A. The
path of light is just reversed as shown.
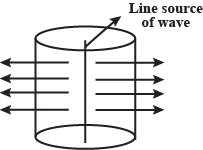
With what type of source of light are cylindrical wave fronts associated?
Line source of light are associated with cylindrical wave fronts.
What is diffraction?
What is wavefront? Explain laws of refraction of light on the bases of Huygens wave theory.
The locus of point on which all particle oscillate in same phase is called as wavefront.
Here we must take into account a different speed of light in the upper and lower media. If the speed of light in vacuum is c, we express the speed in the upper medium by the ratio $$c/n_i$$, where $$n_i$$ is the refractive index. Similarly, the speed of light in the lower medium is $$c/n_t$$. The points D, E and F on the incident wavefront arrive at points D, J and I of the plane interface at different times. In the absence of the refracting surface, the wavefront GI is formed at the instant ray DF reaches I. During the progress of ray CF from F to I in time t, however, the ray AD has entered the lower medium, where the speed is different. Thus if the distance DG is $$v_it$$, a wavelet of radius $$v_tt$$ is constructed with center at D. The radius DM can also be expressed as
$$DM = v_t t$$
$$DM = v_t\Big (\dfrac{DG}{v_i}\Big)$$
Similarly, a wavelet of radius $$(ni/nt)JH$$ is drawn centered at J. The new wavefront KI includes point I on the interface and is tangent to the two wavelets at points M and N. The geometric relationship between the angles $$\theta_i$$ and $$\theta_t$$, formed by the representative incident ray AD and refracted ray DL, is Snell's law, which may be expressed as
$$n_i sin \theta_i = n_tsin \theta_t$$
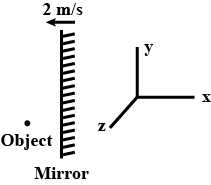
A plane mirror in y-z plane is moving with -2i m/s as shown. The object shown has velocity $$(3i+j-4k) m/s$$ . What is the velocity of the image ?
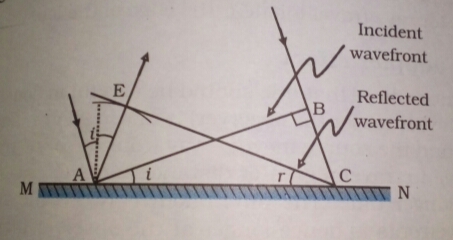
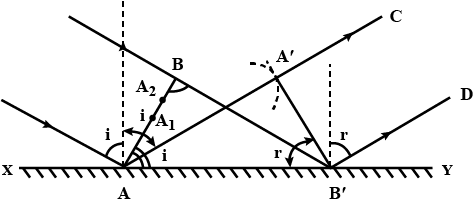
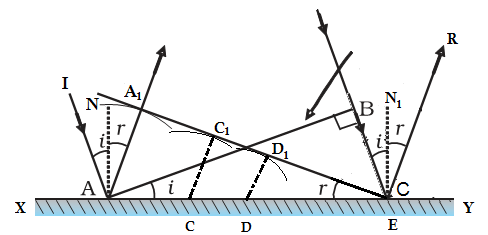
State Huygen's principle. Using Huygen's wave theory, prove the laws of reflection.
According to Huygen's principle ,each point of the wavefront is the source of a secondary disturbance and the wavelets emanating from these points spread out in all directions with the speed of the wave.
These wavelets emanating from the wavefront are usually referred to as Secondary wavelets and if we draw a common tangent to all these spheres, we obtain the new position of the wavefront at a later time.
Referring to the figure,
If we consider a plane wave AB incident at an angle i on the surface MN.
If,
$$v$$ : speed of the wave in the medium
$$\tau$$: time taken by the wavefront to advance from point B to C
Then,
$$BC= v \tau$$
Let CE be the tangent plane drawn from C to the sphere ,
$$AE = BC= v \tau$$
Now, on considering triangles EAC and BAC. We can see that they are congruent and therefore,
the angles i and r would be equal. This proves the law of reflection
These wavelets emanating from the wavefront are usually referred to as Secondary wavelets and if we draw a common tangent to all these spheres, we obtain the new position of the wavefront at a later time.
Referring to the figure,
If we consider a plane wave AB incident at an angle i on the surface MN.
If,
$$v$$ : speed of the wave in the medium
$$\tau$$: time taken by the wavefront to advance from point B to C
Then,
$$BC= v \tau$$
Let CE be the tangent plane drawn from C to the sphere ,
$$AE = BC= v \tau$$
Now, on considering triangles EAC and BAC. We can see that they are congruent and therefore,
the angles i and r would be equal. This proves the law of reflection
What is wavefront? Describe Huygen's theory of secondary wavelets.
A wavefront is a surface over which an optical wave has a constant phase. For example, a wavefront could be the surface over which the wave has a maximum (the crest of a water wave, for example) or a minimum (the trough of the same wave) value.
Huygens wave theory describes about the wave nature of nature of wave propagation. When applied to the propagation of light waves, this principle states that:
"Every point on a wave-front may be considered a source of secondary spherical wavelets which spread out in the forward direction at the speed of light. The new wave-front is the tangential surface to all of these secondary wavelets."
What is meant by diffraction? Light of wavelength $$5000\overset{o}{A}$$ is falling normally on a slit of width $$2\times 10^{-5}$$m. Find the angular width of the central maxima in the diffraction pattern.
State the conditions to get constructive and destructive interference of light.
In Young's experiment, the wavelength of monochromatic light used is 6000 $$\mathop {\text{A}}\limits^{\text{o}} $$. the optical path difference between the rays from the two coherent sources at point P on the screen is 0.0075 mm and at a point Q on the screen is 0.0015 mm. How many bright and dark bands are observed between the two points P and Q?
Tow monochromatic coherent source of wavelength $$5000\ \mathring { A }$$ are placed along the line normal to the screen as shown in the figure.
(a) Determine the condition for maxima at the point $$P$$.
(b) Find the order of the centre bright fringe if $$d=0.5\ mm, D=1\ m$$
(a) The optical path difference at $$P$$ is
$$p=S_{1}P-S_{2}P=d\cos \theta$$
Since. $$\cos \theta=1\dfrac {\theta^{2}}{2}$$, where is small,
Therefore, $$p=d\left( 1-\dfrac {\theta^{2}}{2}\right)$$
$$=d\left[ 1-\dfrac {y^{2}}{2D^{2}}\right] \quad \quad$$ where $$D+d \approx D$$ and $$\theta=y/D$$
For $$nth$$ maxima, $$p=n \lambda$$
$$\therefore \quad y=D\sqrt { 2\left( 1-\dfrac { n\lambda }{ d } \right) } $$
(b) At the central maxima, $$\theta =0$$
$$\therefore \quad p=d=n \lambda$$
or $$n=\dfrac {d}{\lambda}=\dfrac {0.5}{0.5\ \times 10^{-3}}=1000$$
$$p=S_{1}P-S_{2}P=d\cos \theta$$
Since. $$\cos \theta=1\dfrac {\theta^{2}}{2}$$, where is small,
Therefore, $$p=d\left( 1-\dfrac {\theta^{2}}{2}\right)$$
$$=d\left[ 1-\dfrac {y^{2}}{2D^{2}}\right] \quad \quad$$ where $$D+d \approx D$$ and $$\theta=y/D$$
For $$nth$$ maxima, $$p=n \lambda$$
$$\therefore \quad y=D\sqrt { 2\left( 1-\dfrac { n\lambda }{ d } \right) } $$
(b) At the central maxima, $$\theta =0$$
$$\therefore \quad p=d=n \lambda$$
or $$n=\dfrac {d}{\lambda}=\dfrac {0.5}{0.5\ \times 10^{-3}}=1000$$
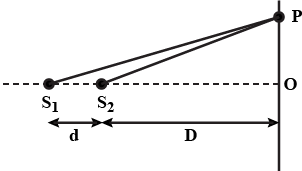
State Huygen's principle.
Whether the diffraction effects from a slit will be more clearly visible or less clearly, if the slit-width is increased?
The Young's double slit experiment is done in a medium of refractive index 4/A light of 600 nm wavelength is falling on the slits have 0.45 mm separation. The lower slit $$S_{2} $$ is covered by a thin glass sheet of thickness 10.4 mm and refractive index 1.The interference pattern is observed on a screen placed at 1.5 m from the slits as shown in the fig.
(All wavelength in this problem are for the given medium of refractive index 4/Ignore dispersion.) Find the location of central maxima (bring fringe with zero path difference ) on the y-axis.
$$d=0.45\times { 10 }^{ -3 }m\\ D=1.5m\\ t=10.4\times { 10 }^{ -3 }m\\ { \mu }_{ med }=\cfrac { 4 }{ 3 } \\ { \mu }_{ glass }=1.5\\ \Delta { x }_{ 1 }={ S }_{ 1 }P-{ S }_{ 2 }P\quad =\cfrac { yd }{ D } $$
Path difference due to glass sheet
$$\Delta { x }_{ 2 }=\left( \cfrac { { \mu }_{ glass } }{ { \mu }_{ med } } -1 \right) t$$
For central maximum $$\Delta { x }_{ 1 }=\Delta { x }_{ 2 }$$
$$\cfrac { yd }{ D } =\left( \cfrac { { \mu }_{ glass } }{ { \mu }_{ med } } -1 \right) t\\ \Rightarrow y=4.33m$$
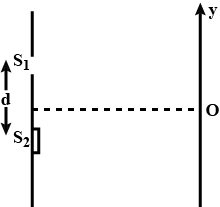
Can we perform Young's double slit experiment with sound waves? To get a reasonable "fringe pattern", what should be the order of separation between the slits? How can the bright fringes and the dark fringes be detected in this case?
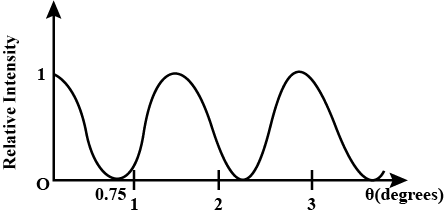
Light of wavelength $$520\ mm$$ passing through a double slit, produces interference pattern of relative intensity versus angular position $$\theta$$ as shown in the figure. Find the separation d between the slits.
Sketch the emergent wavefront
R.E.F image
According to Huygen's principle, each point of the
wavefront is the source of a secondary distance
and the wavelets emanating from these prints
speed out in all direction with speed of wave
Ray D travels the longest distance inside the prism
and ray A the smallest distance.
As speed of light is slower inside the prism ray D
comes at the last and ray A at first
This deviates the from by an angle.
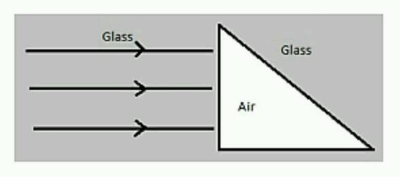
In a single slit diffraction experiment, the width of the slit is made double the original width. How does this affect the size and intensity of the central diffraction band?
In Young's double slit experiment the slits are $$0.5\ mm$$ apart and the interference is observed on a screen at a distance of $$100\ cm$$ from the slit. It is found that the $$9th$$ bright fringe is at a distance of $$7.5mm$$ from the second dark fringe from the centre of the fringe pattern on same side. Find the wavelength of the light used.
Draw the type of wave front that corresponds to a beam of monochromatic light
i) Coming from a very far off source and
ii) Diverging radially from a point source
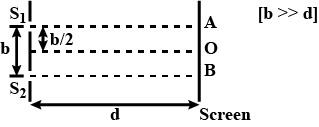
White light is used to illuminate the two slits b distance apart and the screen is placed at a distance directly in front of one of the slits on the screen. It is found that certain wavelength are missing then find the wavelength if $$( b < < d )$$
White light contains all wavelengths from visible spectrum.
Setup diagram :-
We know, path difference $$(\Delta x)$$ at a certain vertical distance $$(y)$$ from $$O$$ on the screen as :-
$$\Delta x=\dfrac{by}{d}$$.
On taking point which is directly in front of one of the slits, $$(A$$ or $$B)$$
we have,
$$y=b/2$$
so, $$\Delta x=\dfrac{b^2}{2d}\rightarrow (i)$$
certain wavelengths would be missing when it destructively inteferes at $$A$$ ( or $$B$$).
condition for destructive Interference,
$$\Delta x=(2x+1)\dfrac{\lambda }{2}\rightarrow (iii)(n\in Z)$$
so from $$(i)$$ & $$(ii)$$,
$$\Delta x=\dfrac{b^2}{2d}=(2x+1)\dfrac{\lambda}{2}\Rightarrow \lambda=\dfrac{b^2}{(2x+1)d}, n\in Z$$
For a single slit of width $$"a"$$, the first minimum of the interference pattern of a monochromatic light of wavelength $$e$$ occurs at an angle of $$\lambda / a$$. At the same angle of $$\lambda/a$$ we get a maximum for two narrow slits separated by a distance $$"a"$$. Explain.
Who proposed the wave theory of light?
The number of images formed depends on the angle between the __________ the light.
State two drawbacks of newton's corpuscular theory.
Explain the construction of plane wavefront using Huygen's principle.
State two conditions for sustained interference of light. Also write the expression for the fringe width
Light waves from coherent sources arrive at two points on a screen with path differences of $$0$$ and $$\dfrac{\lambda}{2}$$ . Find the ratio of intensities of light at these twp points.
What is the essential condition for diffraction of light to occur?
Conditions for diffraction were :-
The condition is the width of obstacle must be less than or comparable with wavelength of light used.
REF.Image
State with reason, how the linear width of central maximum will be affected if (i) monochromatic yellow light is replaced with red light , and (ii) distance between the slit and the screen is increased.
For the single slit diffraction,
For maxima (central):
Angular width = $$\theta$$
$$\theta$$ is very small
$$\theta\, \simeq \, \sin \, \theta \, \simeq \, \tan \, \theta =\dfrac{y}{D}$$
$$y= D \, \theta$$
$$y= \left(\dfrac{D \, \lambda}{a}\right)$$
So, Linear width of central maxima$$=2y= \dfrac{2\, D\, \lambda}{a}$$
(i) As we know that wave length $$(\lambda)$$ of red light is more than yellow light .
$$ \lambda_{red} > \lambda_{yellow}$$
So, $$ \beta_{red} > \beta_{yellow}$$
So, linear width of central maximum will increase if monochromatic yellow light is replaced with red light.
(ii) If distance between slit and screen (D) is increased then also the linear width of central maximum will increase.
Derive the relation a $$\sin \theta = \lambda$$ for first minimum of the diffraction pattern produced due to a single slit of width 'a' using light of wavelength $$\lambda$$.
A point 'P' is on the screen.
At point p:
The path difference =$$\triangle \,x\longrightarrow A$$
$$\longrightarrow x=(BP=AP)=BC$$
In $$\Delta $$ABC$$
$$sin\theta=\frac{BC}{AB}=\frac{\Delta x}{a}$$
$$\Delta x=asin\theta$$------(1)
From experimental observations, we know that intensity at central maxima at $$\theta=0$$ and
secondary maxim at $$\theta=(n+\frac{1}{2})$$$$\frac{\lambda}{a}$$
and has minima at $$\theta=\frac{h\lambda}{a}$$
So, $$sin$$$$\theta=\frac{h\lambda}{a}$$ (for minima)
For 1st minima, $$n=1$$
$$sin\theta=\frac{\lambda}{a}$$ $$\Rightarrow$$ $$\boxed{\lambda sin\theta}$$
Hence, proved
Ray optics is based on the assumption that light travels in a straight line. Diffraction effects (observed when light propagates through small apertures/slits or around small obstacles) disprove this assumption. Yet the ray optics assumption is so commonly used in understanding location and several other properties of images in optical instruments. What is the justification ?
State Huygen's principle.
Huygen's principle: Every point on the wavefront act as a source and produce secondary spherical wavelets. Tangent on the secondary wavelets at any time t represent wave front at that time.
Using the monochromatic light of same wavelength in the experimental set-up of the diffraction pattern as well as in the interference pattern where the slit separation is $$1$$mm.$$10$$ interference fringes are found to be within the central maximum of the diffraction pattern. Determine the width of the single slit, if the screen is kept at the distance from the slit in the two cases.
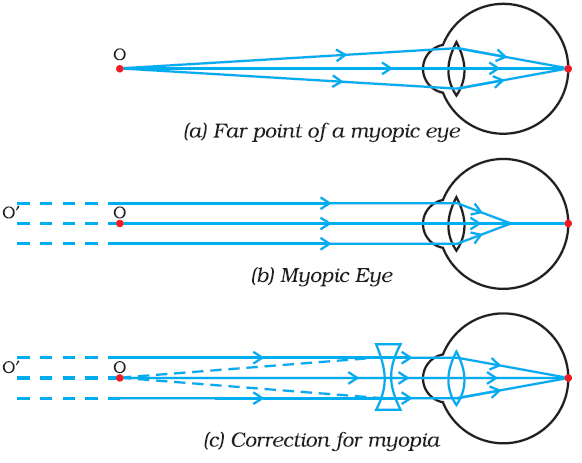
A nearsighted person cannot see objects clearly beyond $$ 25.0 \,cm $$ (her far point). If she has no astigmatism and contact lenses are prescribed for her, -'what power and type of lens are required to correct her vision ?
Nearsighted person has myopia.
Given far point =25.0 cm, to correct vision we need to shift far point at infinity.
See diagram, using lens formula
$$\frac{1}{f}=\frac{1}{v}-\frac{1}{u}$$ in this question $$u= -25$$ $$cm$$ and $$v=\infty$$
$$\frac{1}{f}=\frac{1}{-\infty}-\frac{1}{-25}$$
$$\frac{1}{f}=-\frac{1}{25} \implies f=-25 cm = -0.25 m$$
power of a lens $$P=\frac{1}{f}$$ where f is in meter and $$P$$ is in Diopter.
so $$P=\frac{1}{-0.25}=-4 D$$
power of lens $$4$$ $$D$$, and $$-$$sign signifies lens is diverging i.e concave lens
Why does swimmer see only hazy contours of objects when he opens his eyes under water , while they are distinctly visible if he is using a mask ?
When illuminated, four equally spaced parallel slits act as multiple coherent sources, each differing in phase from the adjacent one by an angle $$\phi$$. Use a phasor diagram to determine the smallest value of $$\phi$$ for which the resultant of the four waves (assumed to be of equal amplitude) is zero.
In a $$YDSE$$, let $$D = 120\ cm$$ and $$d = 0.250\ cm$$. The slits are illuminated with coherent $$600\ nm$$ light. Calculate the distance y above the central maximum for which the average intensity on the screen is $$75.0\%$$ of the maximum.
Differentiate between a ray and a wave front.
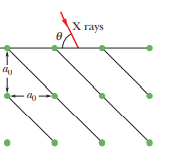
In figure, first order reflection from the reflection planes shown occurs when an x-ray beam of wavelength 0.260 nm makes an angle $$\theta = 63.8^o$$ with the top face of the crystal. What is the unit cell size $$a_a$$?
If you double the width of a single slit, the intensity of the central maximum of the diffraction pattern increases by a factor of $$ 4, $$ even though the energy passing through the slit only doubles. Explain this quantitatively.
A camera lens with index of refraction greater than 1.30 is coated with a thin transparent film of index of refraction 1.25 to eliminate by interference the reflection of light at wavelength $$\lambda$$ that is incident perpendicularly on the lens. What multiple of $$\lambda$$ gives the minimum film thickness needed?
How does the ordinary light differ from the plane polarised light?
In Fig. $$ 35-39, $$ two isotropic point sources $$ S_{1} $$ and $$ S_{2} $$ emit light in phase at wavelength $$ \lambda $$ and at the same amplitude. The sources are separated by distance $$ 2 d=6.00 \lambda . $$ They lie on an axis that is parallel to an $$ x $$ axis, which runs along a viewing screen at distance $$ D= 20.0 \lambda . $$ The origin lies on the perpendicular bisector between the sources. The figure shows two rays reaching point $$ P $$ on the screen, at position $$ x_{P} $$.
At what value of $$ x_{P} $$ do the rays have the minimum possible phase difference?
A Polaroid (I) is placed in front of a monochromatic source. Another Polaroid (II) is placed in front of this Polaroid (I) and rotated till no light passes. A third Polaroid (III) is now placed in between (I) and (II). In this case, will light emerge from (II)? Explain.
In a single-slit diffraction experiment, the width of the slit is made double the original width. How does this affect the size and intensity of the central diffraction band?
Can two identical and independent sodium lamps act as coherent sources? Give reason for your answer.
What is the shape of the wavefront on earth for sunlight?
Answer the following questions
(i) Distinguish between unpolarised light and inearly polarised light. How does one get linearly light with the help of a Polaroid?
(ii) A narrow beam of unpolarised of light of intensity $$I_0$$ is incident on a Polaroid $$P_1$$. The light transmitted by it is then incident on a second Polaroid $$P_2$$ with its pass axis making angle of $$60^0$$ relative to the pass axis of $$P_1$$. FInd the intensity of the light transmitted by $$P_2$$.
Find the ratio of intensities at two points on a screen in Young's double slit experiment when waves from the two slits have a path difference of (i) 0 and (ii) $$\frac{\lambda}{4}$$.
What are coherent source of light? Why are coherent sources required to produce interference of light? Give an example of interference in everyday life.
In June $$ 1985, $$ a laser beam was sent out from the Air Force Optical Station on Maui, Hawaii, and reflected back from the shuttle Discovery as it sped by $$ 354 \mathrm{km} $$ overhead. The diameter of the central maximum of the beam at the shuttle position was said to be $$ 9.1 \mathrm{m} $$ and the beam wavelength was $$ 500 \mathrm{nm} . $$ What is the effective diameter of the laser aperture at the Maui ground station? (Hint: A laser beam spreads only because of diffraction; assume a circular exit aperture.)
How is a wave front defined? Using Huygen's construction draw a figure showing the propagation of a plane wave reflecting at the interface of the two media. Show that the angle of incidence is equal to angle of reflection.
Wave front: A
wave front is a locus of particles of medium all vibrating in the same
phase.
Law of Reflection: Let XY be a reflecting surface at which a wave front is being incident obliquely. Let v be the speed of the wave front and at time t = 0, the wave front touches the surface XY at A.
After time t, the point B of
wave front reaches the point B' of the surface.
According to Huygen's principle each point of wavefront acts as a source of
secondary waves.
When the point A of wavefront strikes the reflecting surface, then due to presence of reflecting surface, it cannot advance further; but the secondary wavelet originating from point A begins to spread in all directions in the first medium with speed v.
As the wavefront AB advances
further, its points $$A_1, A_2, A_3 ...$$ etc. strike the reflecting surface
successively and send spherical secondary wavelets in the first medium.
First of all the secondary wavelet starts from point A and traverses distance AA' (= vt) in first medium in time t. In the same time t, the point B of wavefront, after travelling a distance BB', reaches point B' (of the surface), from where the secondary wavelet now starts.
Now taking A as centre we draw a spherical arc of radius AA' (= vt) and draw tangent A'B' on this arc from point B'. As the incident wavefront AB advances, the secondary wavelets starting from points between A and B', one after the other and will touch A'B' simultaneously.
According to Huygen's
principle wavefront A'B' represents the new position of AB, i.e., A'B' is the
reflected wavefront corresponding to incident wavefront AB.
Now in right-angled triangles
ABB' and AA'B'
$$\angle ABB' = \angle AA'B'$$
(both are equal to $$90^0$$)
side BB' = side M' (both are
equal to vt)
and side AB' is common. i.e.,
both triangles are congruent.
$$\therefore \ \ \angle
BAB' = \angle AB'A'$$
i.e., incident wavefront AB and
reflected wavefront A'B' make equal angles with the reflecting surface XY. As
the rays are always normal to the wavefront, therefore the incident and the
reflected rays make equal angles with the normal drawn on the surface XY,
i.e.,
Angle of incidence i = Angle of
reflection r
This is the second law of reflection.
Since AB, A'B' and XY are all in the plane of paper, therefore the perpendiculars dropped on them will also be in the same plane.
Therefore we conclude that the incident ray, reflected ray and the normal at the point of incidence, all lie in the same plane.
This is the first law of
reflection.
Thus Huygen's principle explains both the laws of reflection.
Answer the following questions.
(i) What is linearly polarized light? Describe briefly using a diagram how sunlight is polarised.
(ii) Unpolarised light is incident on a polaroid. How would the intensity of transmitted light change when the polaroid is rotated?
i) Molecules in air behave like a dipole radiator. When the sunlight falls on a molecule, dipole molecule does not scatter energy along the dipole axis, however the electric field vector of light wave vibrates just in one direction perpendicular to the direction of the propagation. The light wave having direction of electric field vector in a plane is said to be linearly polarised.
In figure. a dipole molecule is lying along x-axis. Molecules behave like dipole radiators and scatter no energy along the dipole axis.
The unpolarised light travelling along x-axis strikes on the dipole molecule get scattered along y and z directions. Light traversing along y and z directions is plane polarised light.
(ii) In figure unpolarised light falls on the polaroid, and transmitted light has electric vibrations in the plane consisting of polaroid axis and direction of wave propagation as shown in Fig.
If polaroid is rotated the plane of polarisation will change. however the intensity of transmitted light remain unchanged.
In figure. a dipole molecule is lying along x-axis. Molecules behave like dipole radiators and scatter no energy along the dipole axis.
The unpolarised light travelling along x-axis strikes on the dipole molecule get scattered along y and z directions. Light traversing along y and z directions is plane polarised light.
(ii) In figure unpolarised light falls on the polaroid, and transmitted light has electric vibrations in the plane consisting of polaroid axis and direction of wave propagation as shown in Fig.
If polaroid is rotated the plane of polarisation will change. however the intensity of transmitted light remain unchanged.
A partially plane polarised beam of light is passed through a Polaroid. Show graphically the variation of the transmitted light intensity with angle of rotation of the polaroid.
Distinguish between polarised and unpolarised light. Does the intensity of polarised light emitted by a Polarised depend on its orientation? Explain briefly.
The vibrations in a beam of polarised light make an angle of $$60^0$$ with the axis of the polaroid sheet. What percentage of light is transmitted through the sheet?
The intensity at the central maxima (O) in a Young's double slit experiment is IIf the distance OP equals one-third of the fringe width of the pattern, show that the intensity at point P would be $$\frac{I_0}{4}$$.
Why is the diffraction of sound waves more evident in daily experience than that of light wave?
What is the shape of the wavefront on earth for sunlight?
As the sun is very-very far from the earth so can be considered at infinity and sun can be considered as a point source which gives spherical wavefront. The size of the earth is very small as compared to distance of sun from earth and size of the sun so the plane wavefront reaches on earth as shown in figure here.
Whose direction is given by the line perpendicular to wavefront?
What type of wavefront will emerge:
From a point of source?
Light with wavelength $$\lambda = 0.50 \mu m$$ falls on a slit of width $$b = 10 \mu m $$ at an angle $${\theta}_{0} = {30}^{o}$$ to its normal. Find the angular position of the minima located on both the sides of the central Fraunhofer maximum.
The relation $$b \sin \theta = k \lambda$$ for minima (when light is incident normally on the slit) has a simple interpretation : $$b \sin \theta$$ is the path difference between extreme wave normals emitted at angle $$\theta$$
When light is incident at an angle $$\theta_0$$ the path difference is $$b (\sin \theta - \sin \theta_0)$$ and the condition of minima is $$b (\sin \theta - \sin \theta_0) = k \lambda$$
For the first minima $$b (\sin \theta - \sin \theta_0) = \pm \lambda $$ or $$\sin \theta = \sin \theta_0 \pm \dfrac{\lambda}{b}$$
Putting in numbers $$\theta_0 = 30^{\circ} , \lambda = 0.50 \mu m \ b = 10 \mu m$$
$$\sin \theta = \dfrac{1}{2} \pm \dfrac{1}{20} = 0.55 $$ or $$ 0.45$$
$$\theta_{+1} = 33^{\circ} - 20'$$ and $$\theta_{-1} = 26^{\circ} 44'$$
What is the shape of the wavefront in each of the following cases:
The portion of the wavefront of light from a distant star intercepted by the Earth.
In as interference experiment , two sources of light are used of intensities $$I$$ and $$4I$$. Find out the intensities at those points where the phase difference of two waves superimposing are $$ \dfrac{\pi }{2} $$.
A beam of plane-polarized light falls on the surface of water at the Brewster angle. The polarization plane of the electric vector of the electromagnetic waves makes an angle $$\varphi = 45^o$$ with the incidence place. Find the reflection coefficient.
What is the shape of the wavefront in each of the following cases:
Light emerging out of a convex lens when a point source is placed at its focus.
What are coherent source ?
Write a definition of interference of light .
Many cells are transparent and colourless. Structures of great interest in biology and medicine can be practically invisible to ordinary microscopy. To indicate the size and shape of cell structures, an interference microscope scope reveals a difference in index of refraction as a shift in interference fringes. The idea is exemplified in the following problem. An air wedge is formed between two glass plates in contact along one edge and slightly separated at the opposite edge as in Figure. When the plates are illuminated with monochromatic light from above, the reflected light has 85 dark fringes. Calculate the number of dark fringes that appear if water (n = 1.33) replaces the air between the plates.
A narrow slit $$S$$ transmitting light of wavelength $$\lambda$$ is placed a distance $$d$$ above a large plane mirror as shown in fig $$29.16$$ (a). The light coming directly from the slit and that after reflection interference coverage at $$P$$ on the screen placed at a distance $$D$$ from the slit. What will be the intensity at a point just above $$O$$? What will be $$x$$ for which first maxima occurs?
a) Since there is a phase difference of $$\pi$$ between direct light and reflecting light, the intensity just above the mirror will be zero.
b) Here, $$2d=$$ equivalent slit separation
$$D=$$ Distance between slit and screen.
We know for bright fringe,
$$\Delta x=\dfrac {y\times 2d}{D}=n \lambda$$
But as there is a phase reversal of $$\lambda /2$$
$$\Rightarrow \dfrac {y \times 2d}{D}+\dfrac {\lambda}{2}=n \lambda$$
$$ \Rightarrow \dfrac {y \times 2d}{D}=n\lambda -\dfrac {\lambda}{2}$$
$$\Rightarrow y=\dfrac {\lambda D}{4d}$$
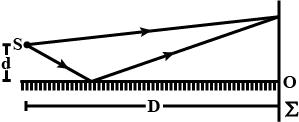
A monochromatic parallel beam of light of wavelength $$\lambda$$ is incident normally on the plane containing slits $${S}_{1}$$ and $${S}_{2}$$. The slits are of unequal width such that intensity only due to one slit on screen is four times that only due to the other slit. The screen is placed along y-axis as shown in figure. The distance between slits is $$d$$ and that between the screen and slits is $$D$$. Match the statements in column I with results in Column II
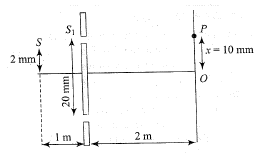
In YDSE, if the thickness of a glass slab $$(\mu =1.5)$$ which should be placed before the upper slit $$S1$$ so that the central maximum now lies at a point where 5th bright fringe was lying earlier (before inserting the slab) is $$Y*10,000 \mathring{A}$$. (Wavelength of light used is $$5000\mathring{A}$$.) Find Y?
In Young's double-slit experiment, the point source $$S$$ is placed slighttly off the central axis as shown in figure. If $$\lambda=500nm$$, then match the following.
Explain Huygen's principle of secondary wavelets.
Huygen's principle of secondary wavelets: In order to explain the propagation of waves in medium Huygen propounded a principle known as Huygens principle of secondary wavelets. It made the three following assumptions:
(i) When a disturbance is caused in a medium, the particles of the medium start vibrating. The surface in the medium, on which each particle vibrates in same phase, is called the wave front. In a homogeneous medium, the wave front is normal to the direction of propagation of the wave. If the source is like a point at a finite distance, the wave front is always spherical. If the source is very far (i.e. at infinite distance) the wave front is plane. If the source is in form of a slit at a finite distance, the wave front is cylindrical.
(ii) Every point of the medium on a given wave front is a centre of originating new disturbance. This new disturbance is called the secondary wavelet. If the medium is homogeneous, the secondary wavelets travel with the same speed as the speed with which the original wave front travels.
(iii) The common tangential surface (or envelope) drawn on these secondary wavelets at any instant, represents the position of new wave front at that instant.
For example in Fig. (a) let $$AB$$ be the position of spherical wave front at any instant originated from a point source $$S$$. According to Huygen's principle, secondary wavelets are given out from each particle of medium on this wave front $$AB$$, which travel forward with the speed $$v$$ of the original wave front. Hence to obtain the position of new wave front after time $$t$$, draw spheres of radius $$vt$$ with such point $$a$$, $$b$$, $$c$$, $$d$$..... of the wave front $$AB$$ as centre. The common envelope of all these spheres is $${A}_{1}{B}_{1}$$ which represents the position of new wave front after a time $$t$$. It may be mentioned here that the wave front $$AB$$, not only produces the wave front $${A}_{1}{B}_{1}$$ forward moving, but it will also produce a wave front $${A}^{'}{B}^{'}$$ moving backwards. Huygen could not successfully explain the absence of the backward wave front $${A}^{'}{B}^{'}$$.
In the same manner, the forward movement of plane wave front is explained in Fig.
(i) When a disturbance is caused in a medium, the particles of the medium start vibrating. The surface in the medium, on which each particle vibrates in same phase, is called the wave front. In a homogeneous medium, the wave front is normal to the direction of propagation of the wave. If the source is like a point at a finite distance, the wave front is always spherical. If the source is very far (i.e. at infinite distance) the wave front is plane. If the source is in form of a slit at a finite distance, the wave front is cylindrical.
(ii) Every point of the medium on a given wave front is a centre of originating new disturbance. This new disturbance is called the secondary wavelet. If the medium is homogeneous, the secondary wavelets travel with the same speed as the speed with which the original wave front travels.
(iii) The common tangential surface (or envelope) drawn on these secondary wavelets at any instant, represents the position of new wave front at that instant.
For example in Fig. (a) let $$AB$$ be the position of spherical wave front at any instant originated from a point source $$S$$. According to Huygen's principle, secondary wavelets are given out from each particle of medium on this wave front $$AB$$, which travel forward with the speed $$v$$ of the original wave front. Hence to obtain the position of new wave front after time $$t$$, draw spheres of radius $$vt$$ with such point $$a$$, $$b$$, $$c$$, $$d$$..... of the wave front $$AB$$ as centre. The common envelope of all these spheres is $${A}_{1}{B}_{1}$$ which represents the position of new wave front after a time $$t$$. It may be mentioned here that the wave front $$AB$$, not only produces the wave front $${A}_{1}{B}_{1}$$ forward moving, but it will also produce a wave front $${A}^{'}{B}^{'}$$ moving backwards. Huygen could not successfully explain the absence of the backward wave front $${A}^{'}{B}^{'}$$.
In the same manner, the forward movement of plane wave front is explained in Fig.
(a) Describe briefly how a diffraction pattern is obtained on a screen due to a single narrow slit illuminated by a monochromatic source of light. Hence obtain the conditions for the angular width of secondary maxima and secondary minima.
(b) Two wavelengths of sodium light 590 nm and 596 nm are used in turn to study the diffraction taking place at a single slit of aperture $$2 \times 10^{-6} m$$. The distance between the slit and the screen is 1.5 m. Calculate the separation between the positions of first maxima of the diffraction pattern obtained in the two cases.
(a)
The phenomenon of diffraction of light around the sharp corners of an obstacle and spreading into the regions of geometrical shadow is called diffraction.
From the diagram, approximate path difference is given by:
$$BN = AB sin (\theta) = a sin(\theta)$$
For $$BN = n\lambda$$, constructive interference occurs
Hence, $$\dfrac{n\lambda}{a} = sin (\theta_n)$$
This is the nth bright fringe.
$$tan \theta_n = \dfrac{y_n}{D}$$
For small $$\theta_n$$,
$$sin \theta_n \approx tan \theta_n$$
$$y_n = \dfrac{n\lambda D}{a}$$
Width of the secondary maximum,
$$\beta = y_n - y_{n-1} = \dfrac{\lambda D}{a}$$
Following same lines, width of secondary minimum comes out to be the same.
(b)
For first maximum,
$$y_1 = \dfrac{\lambda D}{a}$$
For 590 nm,
$$y_{1,590} = \dfrac{590 \times 10^{-9} \times 1.5}{2 \times 10^{-6}}$$
$$y_{1,590} = 0.4425 m$$
For 596 nm,
$$y_{1,596} = \dfrac{596 \times 10^{-9} \times 1.5}{2 \times 10^{-6}}$$
$$y_{1,596} = 0.447 m$$
Separation is
$$y_{1,596} - y_{1,590} = 0.0045 m$$
(a) In Young's double slit experiment, describe briefly how bright and dark fringes are obtained on the screen kept in front of a double slit. Hence obtain the expression for the fringe width.
(b) The ratio of the intensities at minima to the maxima in the Young's double slit experiment is 9:Find the ratio of the widths of the two slits.
(a)
When light waves from two illuminated slits is incident on the screen, the path traveled by each light wave is different. This path difference leads to a phase difference in the two light waves. The path difference is different for each point on the screen and hence, intensity is different for all the points. This leads to the formation and bright and dark fringes on the screen.
Consider point P on the screen as shown in the figure.
$$S_2P^2 = S_2F^2 + PF^2$$
$$S_2 P = \sqrt { D^2 + (x+\dfrac{d}{2})^2 }$$
Similarly,
$$S_1P = \sqrt { D^2 + (x-\dfrac{d}{2})^2 }$$
Path difference is given by:
$$S_2P - S_1P = \sqrt {D^2 + (x+\dfrac{d}{2})^2} - \sqrt { D^2 + (x-\dfrac{d}{2})^2 } $$
Using binomial expansion,
$$S_2P - S_1P = D (1 + \dfrac{1}{2}(\dfrac{x}{D} + \dfrac{d}{2D})^2 + ... ) - D(1+\dfrac{1}{2} (\dfrac{x}{D} - \dfrac{d}{2D})^2+....)$$
Ignoring higher order terms,
$$\Delta x = S_2P-S_1P \approx \dfrac{xd}{D}$$
For constructive interference i.e. bright fringes,
$$n \lambda = \dfrac{xd}{D}$$
$$x_n = \dfrac{n \lambda D}{d}$$
Fringe width is equal to the distance between two consecutive maxima.
$$\beta = x_n - x_{n-1} = \dfrac{n\lambda D}{d} - \dfrac{(n-1) \lambda D}{d}$$
$$\beta = \dfrac{\lambda D}{d}$$
(b)
$$\dfrac{ I_{max} }{I_{min} } = \dfrac{(a_1+a_2)^2}{(a_1-a_2)^2} = \dfrac{9}{25}$$
Solving, $$\dfrac{a_1}{a_2} = \dfrac{4}{1}$$
Ratio of slit widths, $$\dfrac{w_1}{w_2} = \dfrac{a_1^2}{a_2^2} = 16$$
Use Huygen's principle to explain the formation of diffraction pattern due to a single slit illuminated by a monochromatic source of light.
When the width of the slit is made double the original width, how would this affect the size and intensity of the central diffraction band?
Consider a parallel beam of monochromatic light is incident normally in a slit of width b as shown in the figure. Consider a particular point P on the screen receives waves from all the secondary sources. All these aves start from different places and give the resultant intensity at the point $$P$$. At $$P_0$$ all waves are travelling same optical path. As the all waves are in phase thus the interference of maximum intensity is observed.
The intensity at the point P is given by $$I=I_0 \dfrac{sin^{2} \alpha}{\alpha}$$, where $$\alpha= \dfrac{\pi b sin\theta}{\lambda}$$
For central maxima $$\alpha =0$$ thus $$I=I_0$$
Width of central maxima is given by $$\beta= \dfrac{2D \lambda}{b}$$
D= Distance between the screen and slit; $$\lambda=$$ wavelength of the light and $$b=$$ size of the slit.
So with the increase in size of the slit the width of the central maxima decrease. Hence double the size of the slits would results in half the width of the central maxima.
(a) Define a wavefront. Using Huygen's principle, verify the laws of reflection at a plane surface.
(b) In a single slit diffraction experiment, the width of the slit is made double the original width. How does this affect the size and intensity of the central diffraction bond? Explain.
(c) When a tiny circular obstacle is placed in the path of light from a distant source, a bright spot is seen at the centre of the obstacle. Explain why.
(a) Wavefront :
A wavefront is defined as the continuous locus of all the particles which are vibrating in the same phase.
The perpendicular line drawn at any point on the wavefront represents the direction of propagation of the wave at that point.
Verification of Laws of Reflection using Huygen's Principle
In the given figure, AB is the wavefront incident on a reflecting surface XY with an angle of incidence i as shown in figure. According to Huygen’s principle, every point on AB acts as a source of secondary wavelets. At first, wave incidents at point A and then to points C, D and E. They form a sphere of radii AA1, CC1 and DD1 as shown in figure.
A1E represents the tangential envelope of the secondary wavelet in forward direction.
In ΔABE and ΔAA1E,
∠ABE = ∠AA1E = 90°
Side AE = Side AE
AA1 = BE = distance travelled by wave in same time
So, these triangles are congruent.
So, ∠BAE = i and ∠BEA =r
Thus, i = r
Hence, angle of incidence is equal to the angle of reflection. This is the first law of reflection.
Since, the incident wavefront AB, normal and reflected wavefront A1E lies in same plane, it verifies the second law of reflection.
In this way, laws of reflection is verified by Huygens’s principle.
(b) The width of the central maximum is given by $$\dfrac{2D \lambda}{d}$$ where d is the slit width.
On doubling the width of the slit, the size of diffraction band reduces to half value.
When the width of central maxima is reduced to half, area of central diffraction band will become one fourth. And hence the intensity will become four times.
(c) It is so because wave diffracted from the edge of the circular obstacle interfere to form constructive interference at the centre of the obstacle.
In a double slit experiment, the distance between the slits is 3 mm and the slits are 2 m away from the screen. Two interference patterns can be seen on the screen one due to light with wavelength 480 nm, and the other due to light with wavelength 600 nm. What is the separation on the screen between the fifth order bright fringes of the two interference patterns?
Two coherent point sources $${S}_{1}$$ and $${S}_{2}$$ vibrating in phase emit light of wavelength $$\lambda$$. The separation between the sources is $$2\lambda$$. Consider a line passing through $${S}_{2}$$ and perpendicular to the line $${S}_{1}{S}_{2}$$. What is the smallest distance from $${S}_{2}$$ where a minimum of intensity occurs?
Two point source $$S_1$$ and $$S_2$$ are shown in figure. Here $$P$$ is the point where we have to find path difference of source $$S_1$$ and $$S_2$$. For minimum intensity of light, path difference must be equal to path difference for dark e.g $$\Delta x=\lambda/2, 3\lambda/2, 5\lambda/2.........$$
Consider $$\Delta x=(2\lambda-\lambda/2)=3\lambda/2$$
Now, path difference$$=S_1P-S_2P$$
$$\Delta x=\sqrt{(4\lambda ^2+x^2)}-x$$
$$3\lambda/2 +x=\sqrt{4\lambda^2+x^2}$$
Taking square on both sides,
$$9\lambda ^2/4+x^2+3\lambda x=4\lambda^2+x^2$$
$$3\lambda x=4\lambda ^2-9\lambda^2/4$$
$$x=7\lambda/12$$
The smallest distance from $$S_2$$ where a minimum of intensity occurs is $$7\lambda/12$$
The intensity at the maximum in a Young's double slit experiment is $$I_{0}$$. Distance between two slits is d = $$5\lambda $$,where $$\lambda $$ is the wavelength of light used in the experiment . What will be the intensity in front of one the slits on the screen place at a distance D = 2 m
Given that,
maximum intensity $$= I_{0}$$ silt width (d) = $$ 5\lambda $$ .
at front of a slid, $$ y = \dfrac{d}{2} = \dfrac{5\lambda }{2}$$ at A
then path difference, $$ \triangle x = \dfrac{dy}{D} = \dfrac{5\lambda }{2}(\dfrac{5\lambda }{2})$$
$$ \triangle x = \dfrac{25\lambda ^{2}}{4}$$
thus, total phare difference, $$8= \dfrac{2\pi }{\lambda }\triangle x = \dfrac{2\pi }{x} . \dfrac{25\lambda ^{2}}{4} = \dfrac{25\lambda }{2}\pi $$
so intensity at point A,
$$ I = I_{0}cos^{2}8/2 = I_{0}cos^{2}(\dfrac{25\lambda }{2}\pi )$$
If $$ \lambda $$ is even, then $$ cos^{2}(\dfrac{25\lambda \pi }{2}) = 1, I=I_{0}\Rightarrow $$ maximum
but $$ \lambda $$ is odd means $$ cos^{2}(\dfrac{25\lambda \pi }{2}) = 0\, I = 0 \Rightarrow $$ maximum
A beam of light consisting of two wavelengths $$500\ nm$$ and $$400\ nm$$ is used to obtain interference fringes in Young's double slit experiment. The distance between the slits is $$0.3\ mm$$ and the distance between the slits and the screen is $$1.5\ m$$. Compute the least distance of the point from the central maximum, where the bright fringes due to both the wavelengths coincide.
Explain why the intensity of light coming out of a polaroid does not change irrespective of the orientation of the pass axis of the polaroid.
A polaroid consists of long-chain molecules aligned in a particular direction.
To show light waves are transverse in nature:
Take two polaroids $$T_1$$ and $$T_2$$ cut with their faces parallel
to the axis of the crystal
When polaroid $$T_1$$ is rotated about the direction of the propagation of light as axis,
the intensity of the transmitted light remains the same.
When $$T_2$$ is rotated gradually,
the intensity goes on decreasing and the transmitted light disappears completely
when $$T_2$$ is perpendicular to $$T_1$$.
This happens because the polaroid allows only those vibrations of light which
are parallel to its axis.
This is true only if a light has vibrations in all possible directions and hence is a transverse wave.
Light waves are transverse waves.
So, they have electric vectors in all possible directions.
When a Polaroid is placed in between the path of the light,
the electric vectors which are parallel to the pass-axis of the polaroid pass through it.
Even if the polaroid is rotated, there would be other electric vectors which pass through it. So,
the intensity of light does not change irrespective of the orientation of pass-axis of the polaroid.
Light waves are transverse waves. So, they have electric vectors in all possible directions.
When a Polaroid is placed in between the path of the light,
the electric vectors which are parallel to the pass-axis of the polaroid pass through it.
Even if the polaroid is rotated, there would be other electric vectors which pass through it.
So, the intensity of light does not change irrespective of the orientation of pass-axis of the polaroid.
Unpolarised light is passed through a polaroid $$P_1$$. When this polarized beam passes through another polaroid $$P_2$$ and if the pass axis.of $$P_2$$' makes.angle 0 with the pass axis of $$P_1$$, then write the expression for the polarised bearn.passing through $$P_2$$. Draw a plot showing the variation of intensity When $$\theta$$ varies from 0 to $$2\pi$$.
Light of wavelength $$550\ nm$$ falls on a slit that is $$3.50 \times 10^{-3} mm$$ wide. Estimate how far from the central maximum is the first diffraction maximum fringe if the screen is $$10.0\ m$$ away?
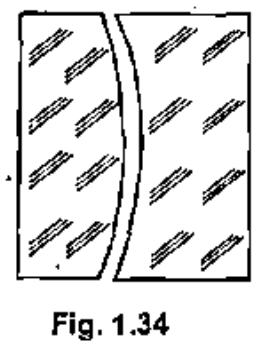
A plano-parallel plate is cut as shown in Fig. 1.34 and the lenses thus obtained are slightly drawn apart. How will a beam of parallel rays change after passing through this system if the beam is incident (a) from the side of the convex lens ? (b) How will the behaviour of the beam depend on the distance between the lenses ?
Light of wavelength $$560\ nm$$ goes through a pinhole of diameter $$0.20\ mm$$ and falls on a wall at a distance of $$2.00\ m$$. What will be the radius of the central bright spot formed on the wall?
A convex lens of diameter $$8.0\ cm$$ is used to focus a parallel beam of light of wavelength $$620\ nm$$. If the light be focused at a distance of $$20\ cm$$ from the lens, what would be the radius of the central bright spot formed?
Figure $$ 35-40 $$ shows two isotropic point sources of light $$ \left(S_{1} \text { and } S_{2}\right) $$ that emit in phase at wavelength $$ 400 \mathrm{nm} $$ and at the same amplitude. A detection point $$ P $$ is shown on an $$x $$ axis that extends through source $$ S_{1} $$. The phase difference $$ \phi $$ between the light arriving at point $$ P $$ from the two sources is to be measured as $$ P $$ is moved along the $$ x $$ axis from $$ x=0 $$ out to $$ x=+\infty $$. The results out to $$ x_{s}=10 \times 10^{-7} \mathrm{m} $$ are given in Fig. $$ 35-41 . $$ On the way out to $$ +\infty, $$ what is the greatest value of $$ x $$ at which the light arriving at $$ P $$ from $$ S_{1} $$ is exactly out of phase with the light arriving at $$ P $$ from $$ S_{2} ? $$
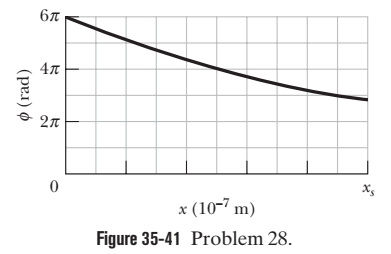
Two waves of the same frequency have amplitudes $$ 1.00 $$ and $$ 2.00 . $$ They interfere at a point where their phase difference is $$ 60.0^{\circ} . $$ What is the resultant amplitude?
The intensity is proportional to the square of the resultant field amplitude.
Let the electric field components of the two waves be written as
$$E_{1}=E_{10} \sin \omega t $$
$$E_{2}=E_{20} \sin (\omega t+\phi)$$
where $$ E_{10}=1.00, E_{20}=2.00, $$ and $$ \phi=60^{\circ} . $$
The resultant field is $$ E=E_{1}+E_{2} . $$
We use the phasor diagram to calculate the amplitude of $$ E $$
The phasor diagram is shown on the right.
The resultant amplitude $$ E_{m} $$ is given by the trigonometric law of cosines:
$$E_{m}^{2}=E_{10}^{2}+E_{20}^{2}-2 E_{10} E_{20} \cos \left(180^{\circ}-\phi\right)$$
Thus $$E_{m}=\sqrt{(1.00)^{2}+(2.00)^{2}-2(1.00)(2.00) \cos 120^{\circ}}=2.65$$
Note: Summing over the horizontal components of the two fields gives
$$\sum E_{h}=E_{10} \cos 0+E_{20} \cos 60^{\circ}=1.00+(2.00) \cos 60^{\circ}=2.00$$
Similarly, the sum over the vertical components is
$$\sum E_{v}=E_{10} \sin 0+E_{20} \sin 60^{\circ}=1.00 \sin 0^{\circ}+(2.00) \sin 60^{\circ}=1.732$$
The resultant amplitude is
$$E_{m}=\sqrt{(2.00)^{2}+(1.732)^{2}}=2.65$$
which agrees with what we found above.
The phase angle relative to the phasor representing $$ E_{1} $$ is
$$\beta=\tan ^{-1}\left(\dfrac{1.732}{2.00}\right)=40.9^{\circ}$$
Thus, the resultant field can be written as $$ E=(2.65) \sin \left(\omega t+40.9^{\circ}\right) $$
Let the electric field components of the two waves be written as
$$E_{1}=E_{10} \sin \omega t $$
$$E_{2}=E_{20} \sin (\omega t+\phi)$$
where $$ E_{10}=1.00, E_{20}=2.00, $$ and $$ \phi=60^{\circ} . $$
The resultant field is $$ E=E_{1}+E_{2} . $$
We use the phasor diagram to calculate the amplitude of $$ E $$
The phasor diagram is shown on the right.
The resultant amplitude $$ E_{m} $$ is given by the trigonometric law of cosines:
$$E_{m}^{2}=E_{10}^{2}+E_{20}^{2}-2 E_{10} E_{20} \cos \left(180^{\circ}-\phi\right)$$
Thus $$E_{m}=\sqrt{(1.00)^{2}+(2.00)^{2}-2(1.00)(2.00) \cos 120^{\circ}}=2.65$$
Note: Summing over the horizontal components of the two fields gives
$$\sum E_{h}=E_{10} \cos 0+E_{20} \cos 60^{\circ}=1.00+(2.00) \cos 60^{\circ}=2.00$$
Similarly, the sum over the vertical components is
$$\sum E_{v}=E_{10} \sin 0+E_{20} \sin 60^{\circ}=1.00 \sin 0^{\circ}+(2.00) \sin 60^{\circ}=1.732$$
The resultant amplitude is
$$E_{m}=\sqrt{(2.00)^{2}+(1.732)^{2}}=2.65$$
which agrees with what we found above.
The phase angle relative to the phasor representing $$ E_{1} $$ is
$$\beta=\tan ^{-1}\left(\dfrac{1.732}{2.00}\right)=40.9^{\circ}$$
Thus, the resultant field can be written as $$ E=(2.65) \sin \left(\omega t+40.9^{\circ}\right) $$
In Fig. $$ 35-39, $$ two isotropic point sources $$ S_{1} $$ and $$ S_{2} $$ emit light in phase at wavelength $$ \lambda $$ and at the same amplitude. The sources are separated by distance $$ 2 d=6.00 \lambda . $$ They lie on an axis that is parallel to an $$ x $$ axis, which runs along a viewing screen at distance $$ D= 20.0 \lambda . $$ The origin lies on the perpendicular bisector between the sources. The figure shows two rays reaching point $$ P $$ on the screen, at position $$ x_{P} $$.
What multiple of $$ \lambda $$ gives the phase difference when $$ x_{P}=6.00 \lambda ?$$
Entoptic halos. If someone looks at a bright outdoor lamp in otherwise dark surroundings, the lamp appears to be surrounded by bright and dark rings (hence halos) that are actually a circular diffraction pattern as in Fig. $$ 36-10, $$ with the central maximum overlapping the direct light from the lamp. The diffraction is produced by structures within the cornea or lens of the eye (hence entoptic ). If the lamp is monochromatic at wavelength $$ 550 \mathrm{nm} $$ and the first dark ring subtends angular diameter $$ 2.5^{\circ} $$ in the observer's view, what is the (linear) diameter of the structure producing the diffraction?
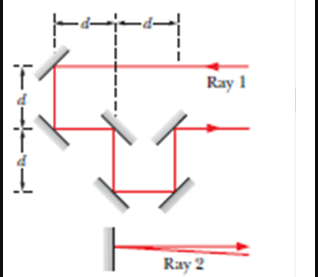
Two light rays, initially in phase and with a wavelength of 500 nm, go through different paths by reflecting from the various mirrors shown in Fig. (Such a reflection dos not itself produce a phase shift.) (a) What least value of distance $$d$$ will put the rays exactly out of phase when they emerge from the region? (Ignore the slight tilt of the path for ray 2.) (b) Repeat the question assuming that the entire apparatus is immersed in a protein solution with an index of refraction of 1.38.
In Figure 35-50, two isotropic point sources $$S_1$$ and $$S_2$$ emit light i phase at wavelength $$\lambda$$ and at the same amplitude. The sources are separated by distance $$d = 6.00 \lambda$$ on an x-axis. A viewing screen is at distance $$D = 20.0 \lambda$$ from $$S_2$$ and parallel to the y axis. The figure shows two rays reaching point $$P$$ on the screen, at heiht $$y_p$$ (a) At what value of $$y_p$$ do the rays have the minimum possible phase difference? (b) What multiple of $$\lambda$$ gives that minimum phase difference? (c) At what value of $$y_p$$ do the rays have the maximum possible phase difference? What multiple of $$\lambda$$ gives (d) that maximum phase difference and (e) the phase difference when $$y_p = d$$? (f) When $$y_p = d$$, is the resulting intensity at point $$P$$ maximum, minimum, intermediate but closer to maximum, or intermediate but closer minimum?
In conventional television, signals are broadcast from towers to home receivers. Even when a receiver is not in direct view of a tower because of a hill or building, it can still intercept a signal if the signal diffracts enough around the obstacle, into the obstacle's "shadow region." Previously, television signals had a wavelength of about $$ 50 \mathrm{cm}, $$ but digital television signals that are transmitted from towers have a wavelength of about $$ 10 \mathrm{mm} $$
Did this change in wavelength increase or decrease the diffraction of the signals into the shadow regions of obstacles?
(a) What are coherent sources of light? State two conditions for two light sources to be coherent.
(b) Derive a mathematical expression for the width of interference fringes obtained in Young's double slit experiment with the help of a suitable diagram.
(c) If s is the size of the source and b its distance from the plane of the two slits, what should be the criterion for the interference fringes to be seen?
OR
(a) In Young's double slit experiment, describe briefty how bright and dark fringes are obtained on the screen kept in front of a double slit. Hence obtain the expression for the fringe width.
(b) The ratio of the intensities at minima to the maxima in the Young's double slit experiment is 9 :Find the ratio of the widths of the two slits.
Assume that Rayleigh's criterion gives the limit of resolution of an astronaut's eye looking down on Earth's surface from a typical space shuttle altitude of $$ 400 \mathrm{km} $$.
(a) Under that idealized assumption, estimate the smallest linear width on Earth's surface that the astronaut can resolve. Take the astronaut's pupil diameter to be $$ 5 \mathrm{mm} $$ and the wavelength of visible light to be $$ 550 \mathrm{nm} $$.
(b) Can the astronaut resolve the Great Wall of China (Fig. $$ 36-40 $$ ), which is more than $$ 3000 \mathrm{km} $$ long, $$5$$ to $$ 10 \mathrm{m} $$ thick at its base, $$ 4 \mathrm{m} $$ thick at its top, and $$ 8 \mathrm{m} $$ in height?
(c) Would the astronaut be able to resolve any unmistakable sign of intelligent life on Earth's surface?
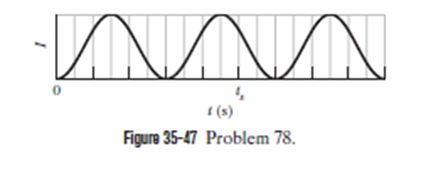
A thin film of liquid is held in a horizontal circular ring, with air on both sides of the film. A beam of light at wavelength 550 nm is directed perpendicularly onto the film, and the intensity I of its reflection is monitored. Figure 35-47 gives intensity I as a function of time t: the horizontal scale is set by t = 20.0 s. The intensity changes because of evaporation from the two sides of the film. Assumed that the film is flat and has parallel sides, a radius of 1.80 cm, and an index of refraction of 1.Also assume that the film's volume decreases at a constant rate. Find that rate
Two rectangular glass plates (n = 1.60) are in contact along one edge and are separated along the opposite edge (Fig. 35-45). Light with a wavelength of 600 nm is incident perpendicularly onto the top plate. The air between the plates acts as a thin film. Nice dark fringes and eight bright fringes are observed from above the top plate. If the distance between the two plates along the separated edges is increased by 600 nm, how many dark fringes will there then be across the top plate?
A $$ 0.10 -mm- $$ wide slit is illuminated by light of wavelength $$ 589 \mathrm{nm} . $$ Consider a point $$ P $$ on a viewing screen on which the diffraction pattern of the slit is viewed; the point is at $$ 30^{\circ} $$ from the central axis of the slit. What is the phase difference between the Huygens wavelets arriving at point $$ P $$ from the top and midpoint of the slit?
If mirror $$M_2$$ in a Michelson interferometer (Fig. ) is moved through 0.233 mm, a shift of 792 bright fringes occurs. What is the wavelength of the light producing the fringe pattern?
Nuclear-pumped x-ray lasers are seen as a possible weapon to destroy ICBM booster rockets at ranges up to $$ 2000 \mathrm{km} $$
One limitation on such a device is the spreading of the beam due to diffraction, with resulting dilution of beam intensity. Consider such a laser operating at a wavelength of $$ 1.40 \mathrm{nm} $$. The element that emits light is the end of a wire with diameter $$ 0.200 \mathrm{mm} $$
(a) Calculate the diameter of the central beam at a target $$ 2000 \mathrm{km} $$ away from the beam source.
(b) What is the ratio of the beam intensity at the target to that at the end of the wire? (The laser is fired from space, so neglect any atmospheric absorption.)
A beam of x rays with wavelengths ranging from $$ 0.120 \mathrm{nm} $$ to $$ 0.0700 \mathrm{nm} $$ scatters from a family of reflecting planes in a crystal. The plane separation is $$ 0.250 \mathrm{nm} $$. It is observed that scattered beams are produced for $$ 0.100 \mathrm{nm} $$ and $$ 0.0750 \mathrm{nm} . $$ What is the angle between the incident and scattered beams?
In Fig. $$ 36-48, $$ let a beam of x rays of wavelength $$ 0.125 \mathrm{nm} $$ be incident on an $$ \mathrm{NaCl} $$ crystal at angle $$ \theta=45.0^{\circ} $$ to the top face of the crystal and a family of reflecting planes.
Let the reflecting planes have separation $$ d=0.252 \mathrm{nm} . $$
The crystal is turned through angle $$ \phi $$ around an axis perpendicular to the plane of the page until these reflecting planes give diffraction maxima.
What are the
(a) smaller and
(b) larger value of $$ \phi $$ if the crystal is turned clockwise and the
(c) smaller and
(d) larger value of $$ \phi $$ if it is turned counterclockwise?
In an experiment to monitor the Moon's surface with a light beam, pulsed radiation from a ruby laser $$ (\lambda=0.69 \mu \mathrm{m}) $$ was directed to the Moon through a reflecting telescope with a mirror radius of $$ 1.3 \mathrm{m} $$. A reflector on the Moon behaved like a circular flat mirror with radius $$ 10 \mathrm{cm}, $$ reflecting the light directly back toward the telescope on Earth. The reflected light was then detected after being brought to a focus by this telescope. Approximately what fraction of the original light energy was picked up by the detector? Assume that for each direction of travel all the energy is in the central diffraction peak.
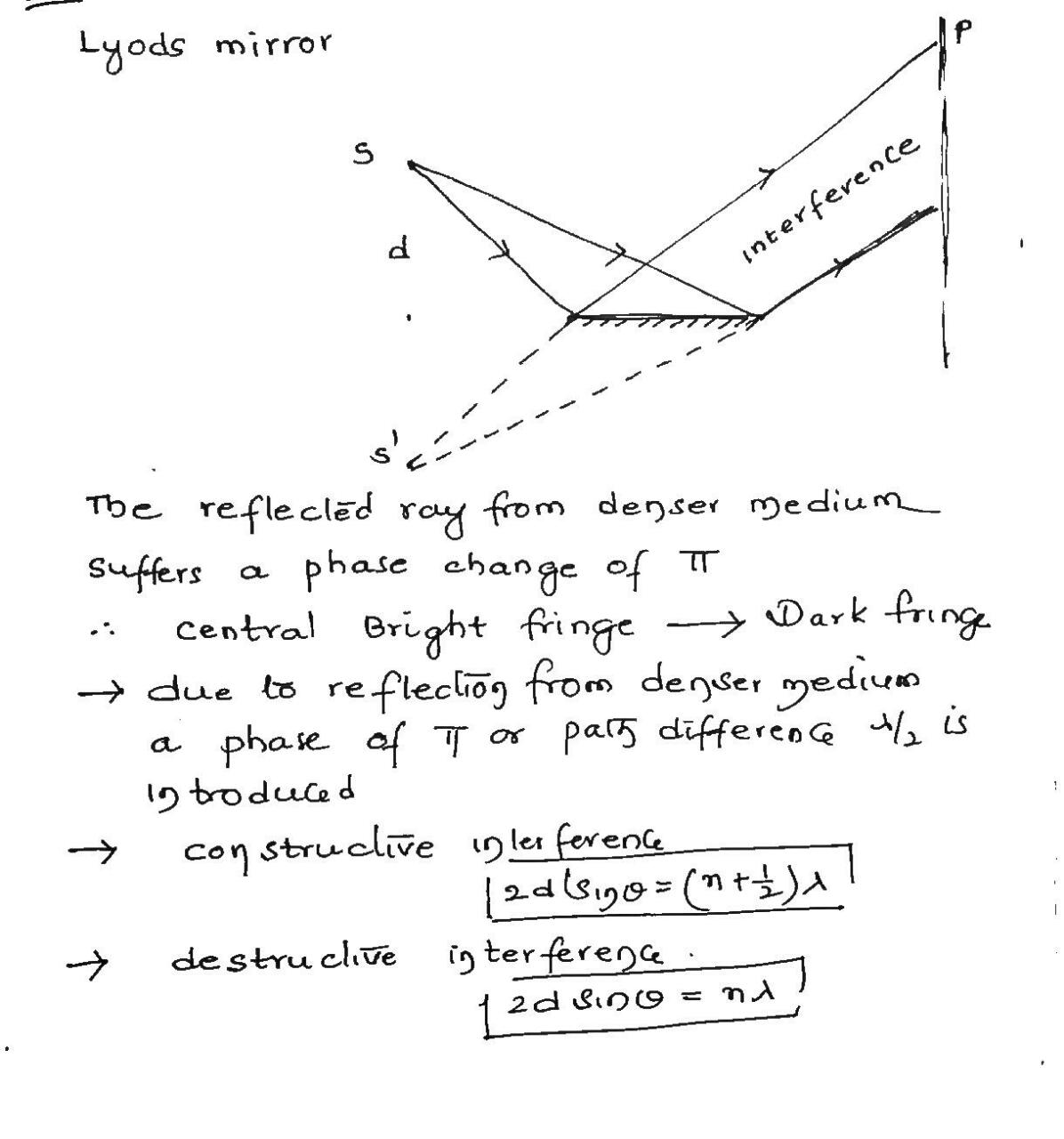
Lloyd's Mirror. In Fig. , monochromatic light of wavelength $$\lambda$$ diffracts through a narrow slit S in an otherwise opaque screen. On the other side, a plane mirror is perpendicular to the screen and a distance h from the slit. A viewing screen A is a distance much greater than h. (Because it sits in a plane through the focal point of the lens, screen A is effectively very distant. The lens plays no other role in the experiment and can otherwise be neglected.) Light that travels from the slit directly to A interferes with light from the slit that reflected from the mirror to A. The reflection causes a half wavelength phase shift. (a) Is the fringe that corresponds to a zero path length difference bright or dark? Find expressions (like Eqs. 35-14 and 35-16) that locate (b) the bright fringes and (c) the dark fringes in the interference pattern. (Hint : Consider the image of S produced by the mirror as seen from a point on the viewing screen, and then consider Young's two-slit interference.)
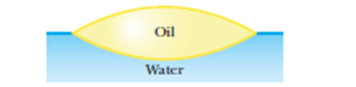
In Fig. , an oil drop $$(n = 1.20)$$ floats on the surface of water $$(n = 1.33)$$ and is viewed from overhead when illuminated by sunlight shining vertically downward and reflected vertically upward. (a) Are the outer (thinnest) regions of the drop bright or dark? The oil film displays several spectra of colors.(b) Move from the rim inward to the third blue band and using a wavelength of 475 nm for blue light, determine the film thickness there. (c) If the oil thickness increases, why do the colors gradually fade and then disappear?
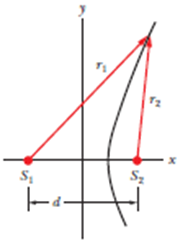
The two point sources in Fig. emit coherent waves. Show that all curves (such as the one shown), over which the phase difference for rays $$r_1$$ and $$r_2$$ is a constant, are hyperbolas (Hint: A constant phase difference implies a constant difference in length between $$r_1$$ and $$r_2$$.)
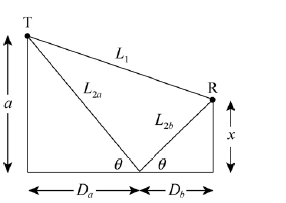
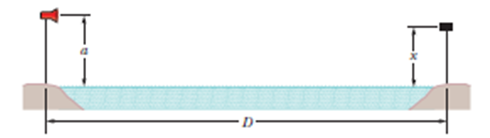
In Fig. , a microwave transmitter at height a above the water level of a wide lake transmits microwaves of wavelength $$\lambda$$ toward a receiver on the opposite shore, a distance x above the water level. The microwaves reflecting from the water interfere with the microwaves arriving directly from the transmitter.
Assuming that the lake width D is much greater than a and x, and that $$\lambda \geq a$$, find an expression that gives the values of x for which the signal at the receiver is maximum. (Hint : Does the reflection cause a phase change?)
The wave that goes directly to the receiver travels a distance $$L_1$$ and the reflected wave travels a distance $$L_2$$. Since the index of refraction of water is greater than that of air this last wave suffers a phase change on reflection of half a wavelength. To obtain constructive interference at the receiver, the difference $$L_2 - L_1$$ must be an odd multiple of a half wavelength. Consider the diagram on the right. The right triangle on the left,,formed by the vertical line from the water to transmitter T, the ray incident on the water, and the water line, gives $$D_a = a/ \tan \theta$$. The right triangle on the right, formed by the vertical line from the water to the receiver R, the reflected ray, and the water line leads to $$D_b = x/ \tan \theta$$. Since $$D_a + D_b = D$$.
$$\tan \theta = \frac{a + x} {D}$$.
We use the identty $$\sin^{2} \theta = \tan^{2} \theta/\left (1 + \tan^{2} \theta \right )$$ to show that
$$ \sin \theta = \left ( a + x \right )/ sqrt{D^{2} + \left (a + x \right )^{2}}$$
This means
$$L_{2a} = \frac{a} {\sin \theta} = \frac{a \sqrt{D^{2} + \left (a + x \right )^{2}}} {a + x}$$
and
$$L_{2b} = \frac{a} {\sin \theta} = \frac{a \sqrt{D^{2} + \left (a + x \right )^{2}}} {a + x}$$
$$ L_2 = L_{2a} + L_{2b} = \frac{\left (a + x \right ) \sqrt{D^{2} + \left (a + x \right )^{2}}} {a + x} = \sqrt{D^{2} + \left (a + x \right )^{2}}$$
Using the binomial theorem, with $$D^{2}$$ large and $$a^{2} + x^{2} $$ small, we approximate this expression $$L_2 \approx D + \left (a + x \right )^{2} /2D$$. The distance traveled by the direct wave is $$L_1 = D + sqrt{D^{2} + \left (a - x \right )^{2}}$$. Using the binomial theorem, we approximate this expression : $$L_1 \approx D + \left (a - x \right )^{2} /2D$$. Thus,
$$L_2 - L_1 \approx D + \frac{a^{2} + 2ax + x^{2}} {2D} - D - \frac{a^{2} - 2ax + x^{2}} {2D} = \frac{2ax} {D}$$.
Setting this equal to $$\left (m + \frac{1} {2} \right ) \lambda$$, where m is zero or a positive integer, we find $$x = \left (m + \frac{1} {2} \right ) \left (D/2a \right )\lambda$$.
$$\tan \theta = \frac{a + x} {D}$$.
We use the identty $$\sin^{2} \theta = \tan^{2} \theta/\left (1 + \tan^{2} \theta \right )$$ to show that
$$ \sin \theta = \left ( a + x \right )/ sqrt{D^{2} + \left (a + x \right )^{2}}$$
This means
$$L_{2a} = \frac{a} {\sin \theta} = \frac{a \sqrt{D^{2} + \left (a + x \right )^{2}}} {a + x}$$
and
$$L_{2b} = \frac{a} {\sin \theta} = \frac{a \sqrt{D^{2} + \left (a + x \right )^{2}}} {a + x}$$
$$ L_2 = L_{2a} + L_{2b} = \frac{\left (a + x \right ) \sqrt{D^{2} + \left (a + x \right )^{2}}} {a + x} = \sqrt{D^{2} + \left (a + x \right )^{2}}$$
Using the binomial theorem, with $$D^{2}$$ large and $$a^{2} + x^{2} $$ small, we approximate this expression $$L_2 \approx D + \left (a + x \right )^{2} /2D$$. The distance traveled by the direct wave is $$L_1 = D + sqrt{D^{2} + \left (a - x \right )^{2}}$$. Using the binomial theorem, we approximate this expression : $$L_1 \approx D + \left (a - x \right )^{2} /2D$$. Thus,
$$L_2 - L_1 \approx D + \frac{a^{2} + 2ax + x^{2}} {2D} - D - \frac{a^{2} - 2ax + x^{2}} {2D} = \frac{2ax} {D}$$.
Setting this equal to $$\left (m + \frac{1} {2} \right ) \lambda$$, where m is zero or a positive integer, we find $$x = \left (m + \frac{1} {2} \right ) \left (D/2a \right )\lambda$$.
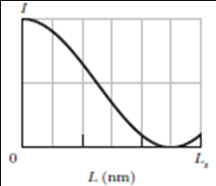
In Fig. a the waves along rays 1 and 2 are initially in phase, with the same wavelength $$\lambda$$ in air. Ray 2 goes through a material with length L and index of refraction n.The rays are then reflected by mirrors to a common point P on a screen. Suppose that we can vary L from 0 to 2400 nm. Suppose also that, from $$L = 0$$ to $$L_s = 900 \space nm$$ the intensity I of the light at point P varies with L as given in Fig. 35-At what values of L greater than $$L_x$$ is intensity I (a) maximum and (b) zero? (c) What multiple of $$\lambda$$ gives the phase difference between ray 1 and ray 2 at common point P when $$L = 1200 \space nm$$?
An astronaut in a space shuttle claims she can just barely resolve two point sources on Earth's surface, $$ 160 \mathrm{km} $$ below.
Calculate their
(a) angular and
(b) linear separation, assuming ideal conditions. Take $$ \lambda=540 \mathrm{nm} $$ and the pupil diameter of the astronaut's eye to be $$ 5.0 \mathrm{mm} $$
The D line in the spectrum of sodium is a doublet with wavelengths 589.0 and 589.6 nm. Calculate the minimum number of lines needed in a grating that will resolve this doublet in the second-order spectrum.
Consider a point at the focal point of a convergent lens. Another convergent lens of short focal length is placed on the other side. What is the nature of the wavefronts emerging from the final image?
Consider a point $$F$$ on focus of converging lens $$L_1$$. The light rays from $$F$$, becomes parallel after refraction through $$L_1$$. When these parallel rays falls on converging lens $$L_2$$ placed co-axial on the other side of $$F$$ of $$L_1$$. $$L_2$$ converges the rays at it’s focus at $$I$$. It now behave like a point source of rays and form a spherical wave front.
What is the diffraction o light? Draw a graph showing the variation intensity with angle in a single slit diffraction experiment. Write one feature which distinguishes the observed pattern from the double slit interference pattern.
How would the diffraction pattern of a single slit be affected when:
(i) The width of the slit is decreased?
(ii) The monochromatic source of light is replaced by a source of white light?
White light (consisting of wavelengths from $$ 400 \mathrm{nm} $$ to $$ 700 \mathrm{nm} $$ ) is normally incident on a grating. Show that, no matter what the value of the grating spacing $$ d, $$ the second order and third order overlap.
The human eye has an approximate angular resolution of $$\phi = 5.8 \times 10^{-4} rad$$ and a typical photo printer prints a minimum of $$300 dpi$$ (dots per inch, $$1 inch = 2.54 cm$$). At what minimal distance $$z$$ should a printed page be held so that one does not see the individual dots.
Answer the following questions
(i) Why are coherent sources necessary to produce a sustained interference pattern?
(ii) In Young's double slit experiment using monochromatic light of wavelength, the intensity of light at a point on the screen where path difference is, is K units. Find out the intensity of light at a point where path difference is.
A plane light wave with wavelength $$\lambda = 0.60 \mu m$$ falls normally on the face of a glass wedge with refracting angle $$\theta = {15}^{o}$$. The opposite face of the wedge is opaque and has a slit of width $$b = 10 \mu m$$ parallel to edge, Find:
(a) the angle $$\Delta \theta$$ between the direction to the Fraunhofer maximum of zeroth order and that of inceident light;
(b) angular width of the Fraunhofer maximum zeroth order.
(a) This case is analogous to the previous one except that the incident wave moves in glass of $$RI \ n$$. Thus the expression for the path difference for light diffracted at angle $$\theta$$ from the normal to the hypotenuse of the wedge is $$b (\sin \theta - n \sin \Theta)$$
we write $$\theta = \Theta + \Delta \theta$$
Then for the direction of principal Fraunhofer maximum $$b (\sin (\Theta + \Delta \theta) - n \sin \Theta) = 0$$ or $$\Delta \theta = \sin^{-1} (n \sin \Theta) - \Theta$$
Using $$\Theta = 15^{\circ} , n = 1.5 $$ we get $$\Delta \theta = 7.84^{\circ}$$
(b) The width of the central maximum is obtained from $$(\lambda = 0.60 \mu \ m, b = 10 \mu m$)$$
$$b (\sin \theta_1 - n \sin \Theta) = \pm \lambda$$
Thus $$\theta_{+1} = \sin^{-1} \left(n \sin \Theta + \dfrac{\lambda}{b} \right) = 26.63^{\circ}$$
$$\theta_{-1} = \sin^{-1} \left(n \sin \Theta \dfrac{\lambda}{b} \right) = 19.16^{\circ}$$
$$\therefore \delta \theta = \theta_{+1} - \theta_{-1} = 7.47^{\circ}$$
An opaque ball of diameter $$D = 40 mm$$ is placed between a source of light with wavelength $$\lambda = 0.55 \mu m$$ and photographic plate. the distance between the source and the ball is $$ a = 12 m$$ and that between the ball and photographic plate is $$b = 18 m$$ Find:
(a) the image dimension $$y'$$ on the plate if the transverse dimension of the source is $$y = 6.0 mm$$ .
(b) the minimum height of irregularities, covering the surface of the ball at random, at which the ball obstructs light.
Answer in brief:
What is meant by coherent sources ? What are the two methods for obtaining coherent sources in the laboratory ?
Two sources are said to be coherent when the waves emitted from them have the same frequency and constant phase difference.
(1) Division of wavefront where wave front is divided into two or more parts with the help of mirrors, lenses, and prisms. The common methods are Young's double-slit arrangement, Fresnel's biprism method, Lloyd's mirror method, etc.
(2) Division of amplitude where the amplitude of the incoming beam is divided into two or more parts by partial reflection or refraction. These divided parts travel different paths and reunited later to produce interference. Eg: Newton's rings, Michelson's interferometer etc.
(1) Division of wavefront where wave front is divided into two or more parts with the help of mirrors, lenses, and prisms. The common methods are Young's double-slit arrangement, Fresnel's biprism method, Lloyd's mirror method, etc.
(2) Division of amplitude where the amplitude of the incoming beam is divided into two or more parts by partial reflection or refraction. These divided parts travel different paths and reunited later to produce interference. Eg: Newton's rings, Michelson's interferometer etc.
What do you understand by diffraction of light ? Compare between diffraction of sound and diffraction of light .
A plane light wave with wavelength $$0.60 \mu m$$ falls normally on a long opaque strip $$0.70 mm$$ wide. Behind it a screen is placed at a distance $$100 cm$$. Using Fig 5.19, find the ratio of intensities of light in the middle of the diffraction pattern and at the edge of the geometrical shadow.
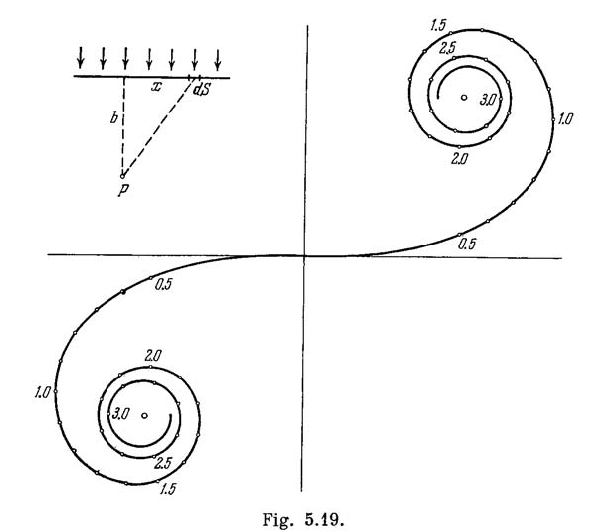
Describe Huygen's principle for light waves
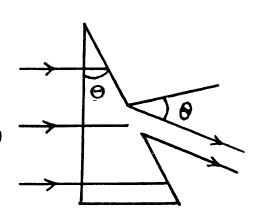
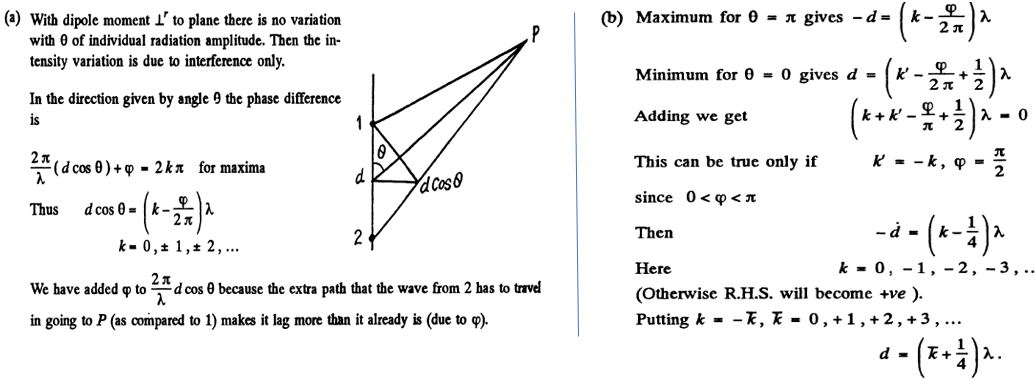
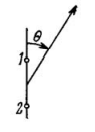
The system given in the figure is consists of two coherent point source 1 and 2 located in a certain plane so that their dipole moments are oriented at right angles to that plane. The sources are separated by a distance d, the radiation wavelength is equal to $$\lambda$$. Taking into account that the oscillations of source 2 lag in phase behind the oscillations of source 1 by $$\varphi ( \varphi < \pi)$$, find:
(a) the angles $$\theta$$ at which the radiation intensity is maximum;
(b) the conditions under which the radiation intensity in the direction $$\theta = \pi$$ is maximum and in the opposite direction, minimum.
(a) $$ cos \theta = (k - \varphi /2 \pi) \lambda /d $$, k = 0, $$\pm 1, \pm2$$, .... ;
(b) $$\varphi = \pi/2, d/\lambda$$ = k + 1/4, k = 0, 1, 2...
(b) $$\varphi = \pi/2, d/\lambda$$ = k + 1/4, k = 0, 1, 2...
Calculate the position of the principal planes points of a thick convex-concave glass lens if the curvature radius of the convex surface is equal to $$ R_{1}=10.0 \mathrm{cm} $$ and of the concave surface to $$ R_{2}=5.0 \mathrm{cm} $$ and the lens thickness is $$ d=3.0 \mathrm{cm} . $$
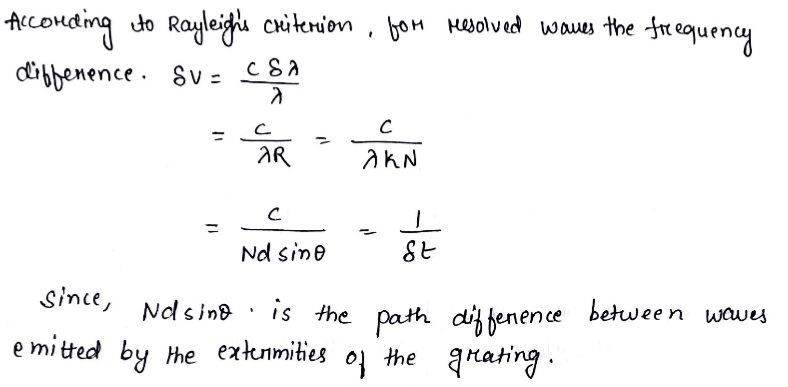
Using diffraction grating as an example, demonstrate that the frequency difference of two maxima resolved according to the Rayleigh's criterion is equal to the reciprocal of the difference of propagation times of extreme interfering oscillations ,i.e, $$\delta\nu = 1/\delta t$$
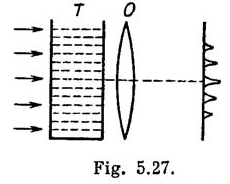
Figure 5.27, illustrates an arrangement employed in observation of diffraction of light by ultrasound. A plane light wave with wavelength $$\lambda = 0.55 \mu m$$ passes through the water-filled tank T in which a standing ultrasonic wave is sustained at a frequency $$\nu = 4.7 MHz$$ . As a result of diffraction of light by the optically inhomogeneous periodic structure of diffraction spectrum can be observed in a focal plane of objective O wth the focal length $$ f = 35 cm $$. The separation between neighboring maxima is $$\Delta x = 0.60 mm$$. Find the propagation velocity of ultrasonic oscillations in water.
a) By each polarizer separately.
Light falls normally on a transparent diffraction grating of width $$l = 6.5 cm$$ with 200 lines per milimeter. The spectrum under investigation includes a spectral line with $$\lambda = 670.8 nm $$ consisting of two components differing by $$\delta\lambda = 0.015 nm$$ Find:
(a) in what order of spectrum these components will be resolved.
(b) the least difference of wavelengths that can be resolved by this grating in a wavelength region $$\lambda \approx 670 nm$$.
At what thickness will a thick convex-concave glass lens in the air
(a) serve as a telescope provided the curvature radius of its convex surface is $$ \Delta R=1.5 \mathrm{cm} $$ greater than that of its concave surface?
A transparent diffraction grating of a quartz spectrograph is 25 mm wide and has 250 lines per mm. the focal length of an objective in whose focal plane a photographic plate is located is equal to 80 cm. Light falls on grating at right angles. The spectrum under investigation includes a doublet with components of wavelengths 310.154 and 310.184 nm Determine:
(a) the distance on the photographic plate between the components of this doublet in the spectra of the first and second order;
(b) whether these components will be resolved in these orders of the spectrum.
Suppose $$ F $$ and $$ F^{\prime} $$ are the front and rear focal points of an optical system, and $$ H $$ and $$ H^{\prime} $$ are its front and rear principal points. By means of plotting find the position of the image $$ S^{\prime} $$ of the point $$ S $$ for the following relative positions of the points $$ S, F, F^{\prime}, H $$ and $$ \boldsymbol{H}^{\prime}: $$$$\bullet F S H H^{\prime} F^{\prime} $$
A telescope system consists of two glass balls with radii $$ R_{1}=5.0 \mathrm{cm} $$ and $$ R_{2}=1.0 \mathrm{cm} . $$ What are the distance between the centres of the balls and the magnification of the system if the bigger ball serves as an objective?
Two plane brought into contact with their spherical surfaces. Find the optical power of such a system if in reflected light with wavelength $$\lambda = 0.60 \mu m$$ the diameter of fifth brigth ring is d= 150.mm.
A plano-convex glass lens with curvature radius of spherical surface R = 12.5 cm is pressed against a glass plate. The diameters of the tenth and fifteenth dark Newton's rings in reflected light are equal to $$d_1$$ = 1.00 mm and $$d_2$$ = 1.50 mm. Find the wavelength of light.
The convex surface of a plano-convex glass lens with curvature radius R = 40 cm comes into contact with a glass plate. A certain ring observed in reflected light has a radius r = 2.5 mm. Watching the given ring, the lens was gradually removed from the plate by a distance $$\Delta h = 5.0 \mu m$$. What has the radius of that ring become equal to ?
Find the positions of the principal planes, the focal length and the sign of the optical power of a thick convex-concave glass lens
(b) whose refractive surfaces are concentric and have the curvature radii $$ R_{1} $$ and $$ R_{2}\left(R_{2}>R_{1}\right) $$
Two identical thick symmetrical biconvex lenses are put close together. The thickness of each lens equals the curvature radius of its surfaces, i.e. $$ d=R=3.0 \mathrm{cm}. $$ Find the optical power of this system in the air.
A ray of light propagating in an isotropic medium with refractive index $$ n $$ varying gradually from point to point has a curvature radius $$ \rho $$ determined by the formula
$$\dfrac{1}{\rho}=\dfrac{\partial}{\partial N}(\ln n)$$
where the derivative is taken with respect to the principal normal to the ray. Derive this formula, assuming that in such a medium the law of refraction $$ n \sin \theta= $$ const holds. Here $$ \theta $$ is the angle between the ray and the direction of the vector $$ \nabla n $$ at a given point.
At what thickness will a thick convex-concave glass lens in the air
(b) have the optical power equal to -1.0 D if the curvature radii of its convex and concave surfaces are equal to 10.0 and $$ 7.5 \mathrm{cm} $$ respectively?
Two thin symmetric glass lenses, one biconvex and the other biconcave, are brought into contact to make a system with other biconcave, are brought into contact to make a system with optical power $$\phi$$ = 0.50 D. Newton's rings are observed in reflected light with wavelength $$\lambda = 0.61 \mu m$$. Determine:
(a) the radius of the tenth dark ring;
(b) how the radius of that ring will change when the space between the lenses is filled up with water.
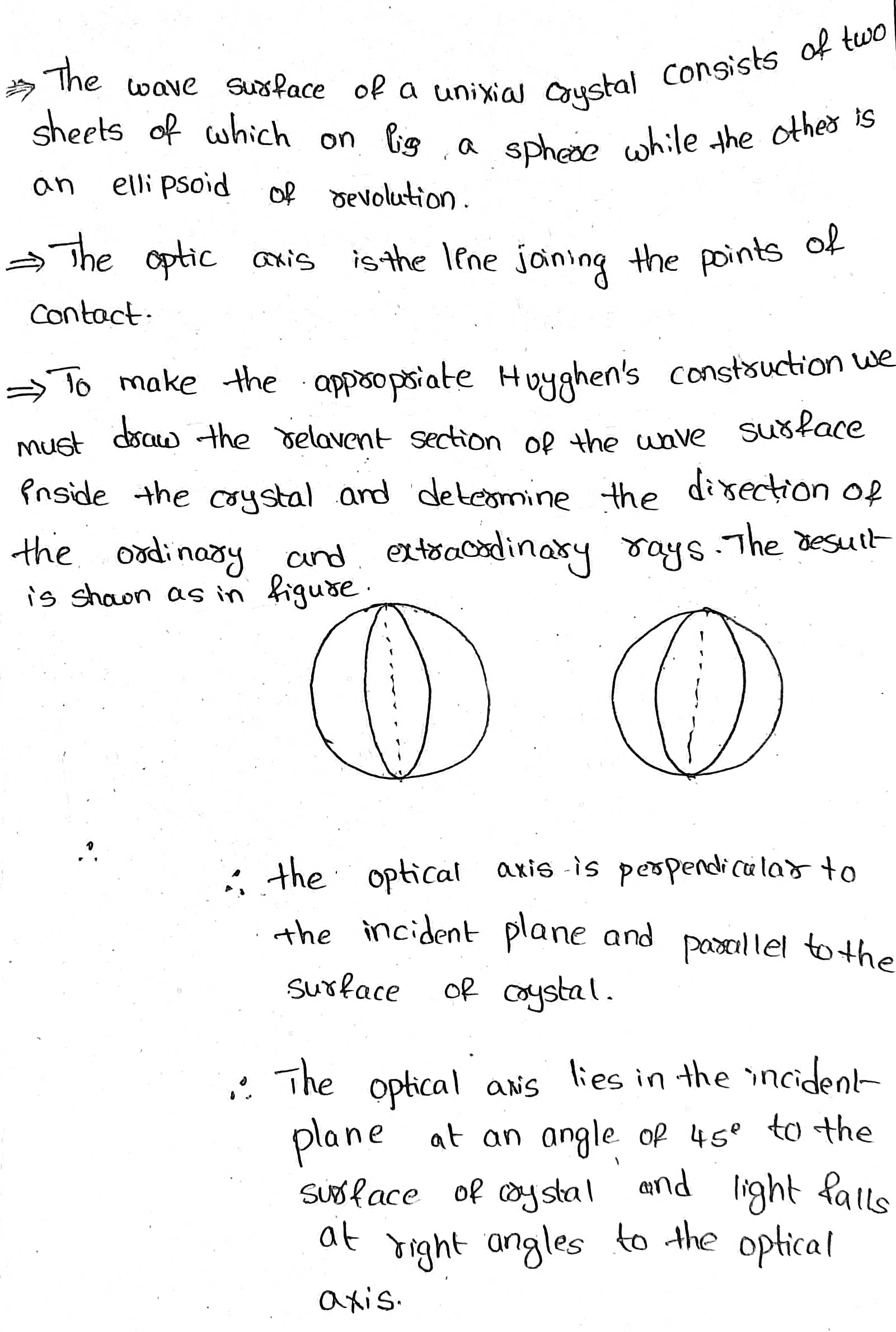
Is perpendicular to the incidence plane and parallel to the surface of the crystal?
From the standpoint of the corpuscular theory demonstrate that the momentum transferred by a beam of parallel light rays per unit time does not depend on its spectral composition but depends only on the energy flux $$ \Phi_{e} $$
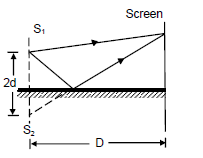
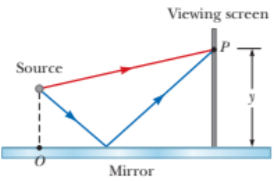
Interference effects are produced at point P on a screen as a result of direct rays from a 500-nm source and reflected rays from the mirror as shown in Figure. Assume the source is 100 m to the left of the screen and 1.00 cm above the mirror. Find the distance y to the first dark band above the mirror.
A screen is placed a distance $$ L $$ from a single slit of width $$ a, $$ which is illuminated with light of wavelength$$ \lambda . $$ Assume $$ L>>a . $$ If the distance between the minima for $$ m=m_{1} $$ and $$ m=m_{2} $$ in the diffraction pattern is $$ \Delta y $$, what is the width of the slit?
To acquire circular polarization after passing through that plate.
An isotropic point source of radiation power $$ P $$ is located on the axis of an ideal mirror plate. The distance between the source and the plate exceeds the radius of the plate $$ \eta $$ -fold. In terms of the corpuscular theory find the force that light exerts on the plate.
A laser emits a light pulse of duration $$ \tau=0.13 $$ ms and energy $$ E=10 \mathrm{J} $$. Find the mean pressure exerted by such a light pulse when it is focussed into a spot of diameter $$ d=10 \mu \mathrm{m} $$ on a surface perpendicular to the beam and possessing a reflection coefficient $$ \rho=0.50 $$
A plane light wave of intensity $$ I=0.20 \mathrm{W} / \mathrm{cm}^{2} $$ falls on a plane mirror surface with reflection coefficient $$ \rho=0.8 $$. The angle of incidence is $$ 45^{\circ} . $$ In terms of the corpuscular theory find the magnitude of the normal pressure exerted by light on that surface.
Holding your hand at arm's length, you can readily block sunlight from reaching your eyes. Why can you not block sound from reaching your ears this way?
To experience only rotation of polarization plane
A plane light wave of intensity $$ I=0.70 $$ W/cm $$ ^{2} $$ illuminates a sphere with ideal mirror surface. The radius of the sphere is $$ R=5.0 \mathrm{cm} . $$ From the standpoint of the corpuscular theory find the force that light exerts on the sphere.
Why is the following situation impossible? A technician is sending laser light of wavelength $$ 632.8 \mathrm{nm} $$ through a pair of slits separated by $$ 30.0 \mu \mathrm{m}. $$ Each slit is of width $$ 2.00 \mu \mathrm{m} . $$ The screen on which he projects the pattern is not wide enough, so light from the $$ m=15 $$ interference maximum misses the edge of the screen and passes into the next lab station, startling a coworker.
A plano-concave lens having index of refraction 1.50 is placed on a flat glass plate as shown in Figure P37.Its curved surface, with radius of curvature 8.00 m, is on the bottom. The lens is illuminated from above with yellow sodium light of wavelength 589 nm, and a series of concentric bright and dark rings is observed by reflection. The interference pattern has a dark spot at the center that is surrounded by 50 dark rings, the largest of which is at the outer edge of the lens. (a) What is the thickness of the air layer at the center of the interference pattern? (b) Calculate the radius of the outermost dark ring. (c) Find the focal length of the lens.
Light reflecting from the upper interface of the air layer suffers no phase change, while light reflecting from the lower interface is reversed $$180^o$$. Then there is indeed a dark fringe at the outer circumference of the lens, and a dark fringe wherever the air thickness t satisfies
$$2t = m \lambda$$ $$m = 0, 1, 2, ...$$
In the water of uniform depth, a wide pier is supported on pilings in several parallel rows $$ 2.80 \mathrm{m} $$ apart. Ocean waves of uniform wavelength roll in, moving in a direction that makes an angle of $$ 80.0^{\circ} $$ with the rows of pilings. Find the three longest wavelengths of waves that are strongly reflected by the pilings.
Both sides of a uniform film that has index of refraction n and thickness d are in contact with air. For normal incidence of light, an intensity minimum is observed in the reflected light at $$\lambda_2$$ and an intensity maximum is observed at $$\lambda_1$$, where $$\lambda_1 > \lambda_2$$. (a) Assuming no intensity minima are observed between $$\lambda_1$$ and $$\lambda_2$$, find an expression for the integer m in Equations 37.17 and 37.18 in terms of the wavelengths $$\lambda_1$$ and $$\lambda_2$$. (b) Assuming n = 1.40, $$\lambda_1 = 500$$ nm, and $$\lambda_2 = 370$$ nm, determine the best estimate for the thickness of the film.
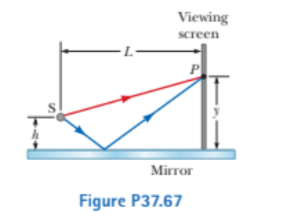
Interference fringes are produced using Lloyds mirror and a source S of wavelength $$\lambda = 606$$ nm as shown in Figure P37.Fringes separated by $$\Delta y = 1.20$$ mm are formed on a screen a distance L = 2.00 m from the source. Find the vertical distance h of the source above the reflecting surface.
The scale of a map is a number of kilometers per centimeter specifying the distance on the ground that any distance on the map represents. The scale of a spectrum is its dispersion, a number of nanometers per centimeter, specifying the change in wavelength that a distance across the spectrum represents. You must know the dispersion if you want to compare one spectrum with another or make a measurement of, for example, a Doppler shift. Let $$ y $$ represent the position relative to the center of a diffraction pattern projected onto a flat-screen at distance $$ L $$ by a diffraction grating with slit spacing $$ d . $$ The dispersion is $$ d \lambda / d y . $$
Prove that the dispersion is given by
$$\dfrac{d \lambda}{d y}=\dfrac{L^{2} d}{m\left(L^{2}+y^{2}\right)^{3 / 2}}$$
Why is the following situation impossible? A piece of transparent material having an index of refraction n 5 1.50 is cut into the shape of a wedge as shown in Figure. Both the top and bottom surfaces of the wedge are in contact with air. Monochromatic light of wavelength $$\lambda$$ = 632.8 nm is normally incident from above, and the wedge is viewed from above. Let h = 1.00 mm represent the height of the wedge and , $$l =$$ 0.500 m its length. A thin-film interference pattern appears in the wedge due to reflection from the top and bottom surfaces. You have been given the task of counting the number of bright fringes that appear in the entire length , of the wedge. You find this task tedious, and your concentration is broken by a noisy distraction after accurately counting 5 000 bright fringes.
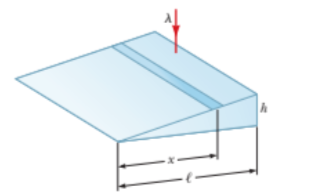
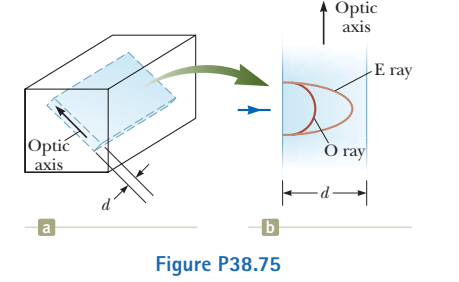
Figure $$ \mathrm{P} 38.75 \mathrm{a} $$ is a three-dimensional sketch of a birefringent crystal. The dotted lines illustrate how a thin, parallel-faced slab of material could be cut from the larger specimen with the crystal's optic axis parallel to the faces of the plate. A section cut from the crystal in this manner is known as a retardation plate. When a beam of light is incident on the plate perpendicular to the direction of the optic axis as shown given Fig(b), the O ray and the E ray travel along a single straight line, but with different speeds. The figure shows the wavefronts for the two rays.
(a) Let the thickness of the plate be $$ d . $$ Show that the phase difference between the $$ \mathrm{O} $$ ray and the $$ \mathrm{E} $$ ray after traveling the thickness of the plate is
$$\theta=\dfrac{2 \pi d}{\lambda}\left|n_{O}-n_{E}\right|$$
where $$ \lambda $$ is the wavelength in air.
(b) In a particular case, the incident light has a wavelength of 550 nm. Find the minimum value of $$ d $$ for a quartz plate for which $$ \theta=\pi / 2 . $$ Such a plate is called a quarter-wave plate. Use values of $$ n_{O} $$ and $$ n_{E} $$ from Table 38.1 .
Class 12 Medical Physics Extra Questions
- Alternating Current Extra Questions
- Atoms Extra Questions
- Current Electricity Extra Questions
- Dual Nature Of Radiation And Matter Extra Questions
- Electric Charges And Fields Extra Questions
- Electromagnetic Induction Extra Questions
- Electromagnetic Waves Extra Questions
- Electrostatic Potential And Capacitance Extra Questions
- Magnetism And Matter Extra Questions
- Moving Charges And Magnetism Extra Questions
- Nuclei Extra Questions
- Ray Optics And Optical Instruments Extra Questions
- Semiconductor Electronics: Materials, Devices And Simple Circuits Extra Questions
- Wave Optics Extra Questions